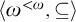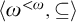1 Introduction
Computably enumerable equivalence relations appear quite often in mathematical logic and effective mathematics. For instance they appear as relations of provable equivalence of formal systems, and as word problems or isomorphism problems of effectively presented structures. A useful and natural way to compare the relative complexity of ceers is by computable reducibility (or, simply, reducibility) of equivalence relations on the set
of natural numbers: If
$A, B$
are equivalence relations on
, then A is computably reducible (or, simply, reducible) to B (notation:
$A\leq B$
) if there is a computable function f such that
$x\mathrel {A} y$
if and only if
$f(x) \mathrel {B} f(y)$
, for all
. Most of the initial investigations of ceers under the reducibility
$\leq $
were oriented towards identifying universal ceers in logic and algebra. A ceer A is called universal if
$B \leq A$
for every ceer B. For instance, provable equivalence in Peano Arithmetic, or in other related systems, gives a universal ceer [Reference Bernardi and Sorbi7]. Miller III [Reference Miller15] proved that there exists a finitely presented group G such that its equality is a universal ceer; he also proved that the isomorphism relation between finite presentations of groups is a universal ceer. A comprehensive survey on universal ceers can be found in [Reference Andrews, Badaev, Sorbi, Day, Fellows, Greenberg, Khoussainov, Melnikov and Rosamond2]. There has also been study of the relationship between ceers and the c.e. algebraic structures which have the ceer as its domain, see, e.g., [Reference Fokina, Khoussainov, Semukhin and Turetsky8, Reference Gavruskin, Jain, Khoussainov and Stephan10–Reference Khoussainov, Manea, Miller and Nowotka12].
When restricted to ceers, the reducibility
$\leq $
gives rise to a degree structure called
of which the degree of the universal ceers is the greatest element. We say that two equivalence relations A and B on
are equivalent (denoted by
$A\equiv B$
) if
$A\leq B$
and
$B\leq A$
. The degree of A is the set of the equivalence relations that are equivalent to A. The degrees are partially ordered by the partial orderingrelation induced by computable reducibility. If P is a property of equivalence relations, thenwe say that a degree has property P if some member of the degree has property P. In the other direction, we will often transfer to ceers properties that should be more appropriately understood on degrees such as order-theoretic properties like the property of being a strong minimal cover, etc. In particular, given ceers
$A,B$
, we say that A is a strong minimal cover of B, if
$B<A$
and for every
$C\leq A$
, either
$C\equiv A$
, or
$C\leq B$
.
The first paper explicitly directed to a systematic investigation of the above defined degree structure
was [Reference Gao and Gerdes9]. Andrews and Sorbi provide in [Reference Andrews and Sorbi5] a thorough investigation of this structure, with an emphasis on existence and non-existence of meets and joins, minimal and strong minimal covers, definable classes of degrees, and automorphisms. They propose a partition of the ceers into three classes: the finite ceers (i.e., the ceers with finitely many equivalence classes), the light ceers (i.e., those ceers A such that
, where
is the identity ceer), and the remaining ceers (called dark ceers). They show that no pair of incomparable dark ceers has join or meet. The same authors show in [Reference Andrews, Schweber and Sorbi4] that the first-order theory of the poset
as well as the theories of the sub-posets
and
, comprised of the degrees of light and dark ceers, respectively, are computably isomorphic to true first-order arithmetic.
For the convenience of the reader here we collect some definitions about ceers.
Definition 1.1.
-
• The uniform join operation
is the operation on equivalence relations defined by
. -
• A ceer A is self-full if whenever f is a reduction of A to A then
intersects all A-equivalence classes; otherwise A is non-self-full. -
• Equivalently [Reference Andrews and Sorbi5, Observation 4.2], a ceer A is self-full if and only if
, where
is the ceer with only one equivalence class. -
• The ceer
is defined by equality, i.e.,
if and only if
$x=y$
. -
• A ceer A is finite if it has only finitely many classes.
-
• A ceer A is light if
. -
• A ceer A is dark if it is neither finite nor light.
-
• The posets
,
, and
are the degree structures of the finite, light, and dark ceers. We write
${\textbf {Ceers} \smallsetminus \textbf {Fin}}$
for the degree structure of ceers which have infinitely many classes.
1.1 Non-self-full strong minimal covers: towards a theory of initial segments for the structure of ceers
What is still missing is a satisfying theory of initial segments of
, which leaves our understanding of the structure far behind our understanding of other familiar degree structures, possessing already well-established theories of initial segments. Very little is indeed known in this regard about
, besides the observations on minimal covers and strong minimal covers in [Reference Andrews and Sorbi5], or the observation [Reference Andrews, Lempp, Miller, Ng, San Mauro and Sorbi3] that there is an initial segment I of the light degrees (namely those between the degree of
, and the degree of
$R_{K}$
, where
$x \mathrel {R_{K}} y$
if and only if
$x=y$
, or
$x,y$
both belong to the halting set K) such that one can embed every finite distributive lattice as an initial segment
$I'$
of I. Note that I is not an initial segment in
, but only in the light degrees, so this does not imply results about initial segments in
. This follows from the fact that the
$1$
-degrees of the non-simple c.e. sets can be isomorphically embedded onto I [Reference Andrews, Lempp, Miller, Ng, San Mauro and Sorbi3, Theorem 2.4] and that every finite distributive lattice can be embedded as an initial segment of these c.e.
$1$
-degrees [Reference Lachlan13].
This paper aims at giving a first contribution to fill in this gap. For this it is very important to develop new techniques for building strong minimal covers. In the structure
we know that every non-universal degree has a strong minimal cover. In particular, this splits into two cases, based on whether the non-universal degree is self-full.
If a degree
$\mathbf {d}$
is self-full, then it has a strong minimal cover
$\mathbf {e}$
such that, for any other degree
$\mathbf {x}$
, if
$\mathbf {x}> \mathbf {d}$
, then
$\mathbf {x}\geq \mathbf {e}$
[Reference Andrews and Sorbi5, Lemma 4.5]. Thus every self-full degree has exactly one strong minimal cover. On the other hand, we know [Reference Andrews and Sorbi5, Corollary 7.11] that every non-universal non-self-full degree
$\mathbf {d}$
has infinitely many incomparable self-full strong minimal covers
$\mathbf {e}_1, \mathbf {e}_1, \ldots $
. Since these strongly minimal covers are self-full, they each have exactly one strong minimal cover. With an eye towards understanding the initial segments of
, unfortunately this does not help us embed wide posets as initial segments of the structure. In particular, while we have infinitely many strong minimal covers of the degree of
(which, we recall, is the ceer defined by equality), each of these only has one strong minimal cover, which allows an embedding of the tree
, but not of
, where
(where
$|\alpha |$
denotes the length of
$\alpha $
).
We will show however (Theorem 2.1) that non-self-full ceers C with the extra property that
each have infinitely many incomparable strong minimal covers A which are also non-self-full and
.
Thus, we get an embedding of the poset
of the finite strings of numbers (where
$\tau \subseteq \sigma $
if
$\tau $
is an initial segment of
$\sigma $
) as an initial segment of
${\textbf {Ceers} \smallsetminus \textbf {Fin}}$
. Note that since
$\mathbf {Fin}$
has order type
and is bounded by every other ceer, classifying the initial segments in
is equivalent to classifying the initial segments of
${\textbf {Ceers} \smallsetminus \textbf {Fin}}$
.
Further, in Corollary 3.11 we extend this embedding to an embedding of the free distributive lattice generated by
viewed as a lower semilattice as an initial segment J of
${\textbf {Ceers} \smallsetminus \textbf {Fin}}$
(see Definition 3.3). We note in Observation 3.12 that the embedding we find is not a lattice-embedding (i.e., the degrees in question do not have joins in the ceers, though they do in J).
We leave the following questions open:
Question 1.2. Does every non-self-full ceer have a non-self-full strong minimal cover?
Note that it follows from [Reference Andrews and Badaev1, Corollary 3.3.4] that the assumption used in this paper that
is strictly stronger than non-self-fullness.
Question 1.3. If C is non-self-full and
, then does C have incomparable strong minimal covers
$A_1$
and
$A_2$
so that
and
$A_0, A_1$
have supremum in the structure of ceers?
1.2 Notations and terminology
Our notations and terminology from computability theory are standard and can be found in [Reference Rogers16] or [Reference Soare17]. If A is an equivalence relation on
and
, then the A-closure of V is
$[V]_A=\{x: \exists {y\in V}\,( x \mathrel {A} y)\}$
. The A-equivalence class of a number x is denoted by [x]A.
We recall the notion of restriction of a ceer to a c.e. set, see [Reference Andrews and Sorbi5, Section 2.3]. If A is a ceer and W is a nonempty c.e. set then fix a computable surjection
, and define
$A{\restriction} W$
to be the ceer
$$ \begin{align*} x \mathrel{A{\restriction} W} y \Leftrightarrow \pi(x) \mathrel{A} \pi(y). \end{align*} $$
It is immediate to see that up to
$\equiv $
,
$A{\restriction} W$
does not depend on the chosen computable surjection.
Lemma 1.4. Let
$A,B$
be ceers:
-
(1) For every nonempty c.e. set W,
$A{\restriction} W \leq A$
. -
(2)
$A \leq B$
if and only if there exists a nonempty c.e. set W such that
$A \equiv B{\restriction} W$
. -
(3) If
$U,V$
are c.e. sets and for every
$u\in U$
, there is some
$v\in V$
so that
$u \mathrel {A} v$
, then
$A{\restriction} U \leq A{\restriction} V$
.
Proof The second follows from the fact that if f is a reduction of A to B then
$A \equiv B{\restriction} W$
, where
. For the last claim, define a map from
$A{\restriction} U$
to
$A{\restriction} V$
as follows. Fix
and
. Then for every V-class X, if the range of
$\pi $
intersects X then so does the range of
$\varphi $
. So, for every n, define
$g(n)$
to be the first m seen so that
$\pi (n)\mathrel {A}\varphi (m)$
. It is straightforward to check that this is a reduction of
$A{\restriction} U$
(as defined using
$\pi $
) to
$A{\restriction} V$
(as defined using
$\varphi $
). The first condition follows from the third with
.
Definition 1.5. We generalize the uniform join operation to finitely many summands. Let
$(X_{i})_{i <n}$
be equivalence relations, with
$n\ge 1$
. For each
$i<n$
, let
, and for
let
$(x)_{i,n}$
be
$\frac {x-i}{n}$
. Then let
If
$f_0,\ldots f_{n-1}$
are computable functions from
to
, then define
to be the function given by
if
.
For A any ceer and
$\sim $
any c.e. subset of
, define
$A_{/\sim }$
to be the equivalence relation generated by A and
$\sim $
. Note that if
$X ($
here,
$X=A\cup {\sim })$
is a c.e. set of pairs, then the equivalence relation E generated by X is defined by
$x \mathrel {E} y$
if and only if
$$ \begin{align*} \exists n \exists z_1,\ldots z_n \left( z_1=x\wedge z_n=y \wedge \bigwedge_{i=1}^{n-1} (z_i,z_{i+1})\in X\right), \end{align*} $$
so E is a ceer.
If A is any ceer and
$\sim $
any c.e. subset of
, we say that
$\sim $
is A-closed if whenever
$x\sim y$
and
$x\mathrel {A} x'$
and
$y\mathrel {A} y'$
, then also
$x'\sim y'$
. That is,
$\sim $
collapses whole A-classes together.
If f is a computable function from
to
, and
$\sim $
is a c.e. subset of
, define
$\sim _{f}=\{(a,b):(f(a),f(b))\in \sim \}$
.
Lemma 1.6. If f is a reduction of A to B and
$\sim $
is a transitive c.e. subset of
which is B-closed, then
$A_{/\sim _f}\leq B_{/\sim }$
.
Proof We will see that f is a reduction of
$A_{/\sim _f}$
to
$B_{/\sim }$
.
Suppose
$a \mathrel {A_{/\sim _f}} b$
. Then there are
$z_1,\ldots z_n$
so that
$z_1=x\wedge z_n=y\wedge \bigwedge _{i=1}^{n-1} (z_i,z_{i+1})\in A\cup {\sim _f}$
. Then
$f(z_1)=f(x)\wedge f(z_n)=f(y) \wedge \bigwedge _{i=1}^{n-1} (f(z_i), f(z_{i+1}))\in B\cup {\sim }$
. So,
$f(a) B_{/\sim } f(b)$
.
Since
$\sim $
is transitive and B-closed,
$B\cup {\sim }$
is an equivalence relation, so
$B_{/\sim }= B\cup {\sim }$
. So, if
$f(a)\mathrel {B_{/\sim }} f(b)$
, then either
$f(a) \mathrel {B} f(b)$
or
$f(a)\sim f(b)$
. In either case, we have
$a\mathrel {A_{/\sim _f} }b$
.
Applying the above to the case of a uniform join, we get:
Lemma 1.7. If
$f_0,\ldots , f_{n-1}$
are reductions witnessing
$A_i\leq B_i$
for
$i<n$
and
$\sim $
is a transitive c.e. subset of
which is
-closed, then
2 Non-self-full strong minimal covers
Since a ceer A is self-full if and only
, a ceer A satisfying
, such as the one we construct in the next theorem, is non-self-full.
Theorem 2.1. Given a ceer C so that
and a non-universal ceer
$B\geq C$
, there exists a ceer A which is a strong minimal cover of C so that
.
Proof Let
$C,B$
be as in the statement of the theorem. We want to build A so as to satisfy the following requirements:
As already observed,
$\mathrm {NSF}$
is a strictly stronger requirement than ensuring that A is non-self-full. Satisfaction of the
$\mathrm {D}$
-requirements guarantees that
$A \nleq B$
. The
$\mathrm {R}$
requirement in conjunction with the
$\mathrm {D}$
-requirements ensure that
$C < A$
. In particular, we cannot have
$A\leq C$
since
$C\leq B$
and the
$\mathrm {D}$
-requirements ensure
$A\nleq B$
. Finally if
$X\leq A$
, and by Lemma 1.4 (2)
$X\equiv A{\restriction} W_{i}$
for some i, then requirement
$\mathrm {SMC}_{i}$
guarantees that either
$A \leq X$
and thus
$A \equiv X$
, or
$X \leq C$
. Hence satisfaction of all
$\mathrm {SMC}$
-requirements yields that A is a strong minimal cover of C.
As we construct the ceer A, we begin with
and as stages go by, we say we A-collapse, or often just say collapse, elements n and m. This means that at stage
$s+1$
, we let
$A_{s+1}$
be the equivalence relation generated by
$A_s$
along with the pairs that we collapse during stage s.
2.1 Informal description of the strategies to satisfy requirements
The
$\mathrm {NSF}$
strategy
Wewill fix a computable infinite and coinfinite set
$I_\lambda $
and we will ensure that if
$x\in I_\lambda $
, then
$[x]_A=\{x\}$
. This ensures that
, so
. Here the symbol
denotes the complement of
${I_\lambda}$
.
The
$\mathrm {D}_i$
-strategies
We will have a c.e. set which we will call
$D_\alpha $
for some node
$\alpha $
, and we will cause collapse on this set only for the purpose of ensuring that
$\varphi _i$
is not a reduction of A to B. We will play a diagonalizing strategy which in a finitary way guarantees that
$\varphi _{i}$
is not a reduction witnessing
$A \leq B$
. To do this we carry out a finite amount of A-collapsing on the elements of
$D_{\alpha }$
.
We now describe the strategy that
$\alpha $
runs on the set
$D_\alpha $
. We call this strategy the finitary-diagonalization strategy. We fix ahead of time a universal ceer U, with computable approximations
(namely,
,
$U_{s} \subseteq U_{s+1}$
, and
is a finite set of pairs of which we can compute the canonical index uniformly in s). Let also
be a computable approximation (defined in the same way) for the ceer B. We fix the enumeration
of
$D_\alpha $
. The strategy has a parameter
$n_{\alpha }$
, which begins as
$n_{\alpha }=0$
and acts at each stage s + 1 when
$\alpha $
is visited and
$\varphi _{i}(a_j)\mathrel {B_s} \varphi _{i}(a_k)$
if and only if
$a_j \mathrel {A_s} a_k$
for each
$a_j,a_k\in D_\alpha $
with
$j,k<n_{\alpha }$
. In this case, we increment
$n_{\alpha } =n_{\alpha }+1$
and for each
$a_j,a_k\in D_\alpha $
with
$j,k<n_{\alpha }$
, we collapse
$a_j \mathrel {A_{s+1}} a_k$
if and only if
$j \mathrel {U_s} k$
. This is the only cause for collapse inside
$D_\alpha $
. A priori, there are two possible outcomes of this strategy: In the first case,
$\lim _s n_{\alpha }$
is finite, and thus we will never again see that
$\varphi _{i}(a_j) \mathrel {B_s} \varphi _{i}(a_k)$
if and only if
$a_j \mathrel {A_s} a_k$
for each
$a_j,a_k\in D_\alpha $
with
$j,k<n_{\alpha }$
. Thus
$\varphi _{i}$
is not a reduction of A to B. In the second case,
$\lim _s n_{\alpha }=\infty $
. But then
$a_j \mathrel {A} a_k$
if and only if
$j \mathrel {U} k$
. Thus
$j\mapsto \varphi _{i}(a_j)$
is a reduction of U to B. Since B is non-universal by hypothesis of the theorem, this infinitary outcome is simply impossible. It is to emphasize this fact that we call this strategy the finitary-diagonalization strategy.
The
$\mathrm {R}$
-strategy
We will fix a computable set
$K_\lambda =\{x: x\equiv 0\ \mod 3\}$
and we will directly encode C onto
$A{\restriction} K_\lambda $
. Then the map
$f(x)=3x$
will give a reduction of C to A. We note that, as opposed to the NSF-strategy, it will not be the case that
. In fact, many nodes
$\alpha $
on the true path will be building their own sets
$K_\alpha $
which will necessarily have representatives of the same A-classes as
$K_\lambda $
. We will need to build these sets
$K_\alpha $
in order to put a copy of C into
$A{\restriction} W_i$
for
$\mathrm {SMC}_i$
-strategies. Further, these must represent the same A-classes as
$K_\lambda $
, because we cannot afford to encode
, which might be strictly above C.
The
$\mathrm {SMC}_i$
-strategies
Here we use the Chinese boxes technique employed by Lachlan in the proof of [Reference Lachlan14, Theorem 2]. A node
$\alpha $
on the true path will put numbers s into either
$S_{\alpha\,\widehat {\;}f}$
or
$S_{\alpha\,\widehat {\;}\infty }$
. When we see a member of
$S_{\alpha\,\widehat {\;}f}$
be A-equivalent to a number in
$W_i$
,
$\alpha $
will collapse together every number (aside from those A-equivalent to a member of
$K_\lambda $
) in
$S_{\alpha\,\widehat {\;}f}$
to a single class with s (the current stage) and put s into
$S_{\alpha\,\widehat {\;}\infty }$
. In this case, we then make
$S_{\alpha\,\widehat {\;}f}$
empty.
Under the outcome that only finitely often puts numbers into
$S_{\alpha\,\widehat {\;}\infty }$
, the effect of this procedure is that almost every A-class (aside from some copies of
held by higher-priority strategies, e.g., the NSF-strategy, or sets
$D_\beta $
being used for
$D_i$
-strategies, or sets
$I_\beta $
as described in the next paragraph) will be represented by members of
$S_{\alpha\,\widehat {\;}f}\cup K_\lambda $
, and
$S_{\alpha\,\widehat {\;}f}$
has no member equivalent to a number in
$W_i$
. Then
$A{\restriction} W_i$
will have to reduce to
, coming from the elements A-equivalent to
$K_\lambda $
along with the finitely many copies of
, and
.
Under the outcome that infinitely often puts numbers into
$S_{\alpha\,\widehat {\;}\infty }$
, we have that the entire set
$S_{\alpha\,\widehat {\;}\infty }$
is comprised of members which are A-equivalent to numbers in
$W_i$
. Thus
$A{\restriction} S_{{\alpha}\,\widehat {\;}{\infty}} \leq A{\restriction} W_i$
. In this case, the goal is to ensure that
$A\leq A{\restriction} S_{{\alpha}\,\widehat {\;}{\infty}} $
. We do this by having a copy
$K_\alpha $
of
$K_\lambda $
inside
$S_{{\alpha}\,\widehat {\;}{\infty}} $
and having a copy
$I_\alpha $
of
inside
$S_{{\alpha}\,\widehat {\;}{\infty}} $
. This suffices to give us a reduction of A to
$A{\restriction} S_{{\alpha}\,\widehat {\;}{\infty}} $
. We send each copy of
$K_\lambda $
into
$K_{{\alpha}\,\widehat {\;}{\infty}}$
(i.e., we send an x in some copy of
$K_\lambda $
to a representative of its own A-class which is in
$K_{{\alpha}\,\widehat {\;}{\infty}}$
), and each of the (finitely many) copies of
being used by higher-priority strategies and
$I_{{\alpha}\,\widehat {\;}{\infty}}$
itself into
$I_{{\alpha}\,\widehat {\;}{\infty}}$
. This uses the immediate fact that
.
We now move onto a description of how these strategies fit together into the construction.
2.2 Informal description of the construction
We employ an infinite-injury priority construction on the priority tree
. We use standard notations and terminology about strings. In particular if
then we write
$\alpha <_{L} \beta $
to mean that
$\alpha $
is to the left of
$\beta $
and
$\alpha \leq \beta $
to denote that either
$\alpha <_{L} \beta $
or
$\alpha \subseteq \beta $
, the latter meaning that
$\alpha $
is an initial segment of
$\beta $
. We write
$\alpha \subset \beta $
if
$\alpha \subseteq \beta $
and
$\alpha \ne \beta $
. The empty string is denoted by the symbol
$\lambda $
. If
$\alpha \ne \lambda $
then
$\alpha ^{-}$
denotes the immediate predecessor of
$\alpha $
along
$\alpha $
. The symbol
$|\alpha |$
denotes the length of
$\alpha $
. As usual in computability constructions that use tree arguments, the construction will identify the true path
through
, that is the unique infinite path through
such that for every n, its restriction
is the leftmost string of length n which is visited in the construction infinitely many times.
2.2.1 The parameters of
$\alpha $
Each node
has parameters
$S_{\alpha }$
,
$K_{\alpha }$
,
$I_{\alpha }$
,
$D_{\alpha }$
,
$M_{\alpha }$
. The values of these sets depend of course on the stage, and should therefore be denoted by
$S_{\alpha ,s}$
,
$K_{\alpha ,s}$
,
$I_{\alpha ,s}$
,
$D_{\alpha ,s}$
,
$M_{\alpha ,s}$
, although we will omit specifying the approximating stage unless strictly necessary. If
$\alpha $
is on the true path of the construction then the limit value
$S_{\alpha }$
will be an infinite computable set consisting of the numbers which have been enumerated in
$S_{\alpha }$
after the last stage
$s_{\alpha }$
at which
$\alpha $
has been initialized if there is any such stage, otherwise
$s_{\alpha }=0$
. There is yet another parameter, a number
$n_{\alpha }$
which pertains only to nodes
$\alpha \ne \lambda $
such that
$\alpha = (\alpha ^{-})\,\widehat {\;}f$
, and is used in the finitary-diagonalization strategy.
A node
$\alpha =(\alpha ^-)\,\widehat {\;}\infty $
will be working towards satisfying
$\mathrm {SMC}_{|\alpha |-1}$
and will have to ensure that
$A\leq A{\restriction} W_{|\alpha |-1}$
. Such an
$\alpha $
will be on the true path only if every element of
$S_\alpha $
is A-equivalent to a member of
$W_{|\alpha |-1}$
. By injuring all strategies to the right,
$\alpha $
will ensure that
. For the equivalence
, it will be essential that each equivalence class of the copy of C which is encoded in A has representatives in
$S_\alpha $
. This is precisely the role of the set
$K_\alpha $
. Similarly, it is needed that
. This is the role of
$I_\alpha $
. On
$I_\alpha $
, we will encode a copy of
which will be unrelated to the rest of
$S_\alpha $
precisely to ensure
. For
$\alpha =(\alpha ^-)\,\widehat {\;}\infty $
,
$D_\alpha $
will be empty. Finally,
$M_\alpha $
is the stream of numbers given for
$\alpha\,\widehat {\;}\infty $
and
$\alpha\,\widehat {\;}f$
to work with.
A node
$\alpha =(\alpha ^-)\,\widehat {\;}f$
will automatically have
$\mathrm {SMC}_{|\alpha |-1}$
satisfied (if this
$\alpha $
is on the true path) and will instead work towards satisfying a D-requirement. This will be done by the finitary-diagonalization strategy on the set
$D_\alpha $
. The parameter
$n_\alpha $
will describe the progress of the finitary-diagonalization strategy. The sets
$K_\alpha $
and
$I_\alpha $
are empty, and once again
$M_\alpha $
is the stream of numbers for
$\alpha\,\widehat {\;}\infty $
and
$\alpha\,\widehat {\;}f$
to work with.
Partitioning
$S_{\alpha }$
At any stage s, we will have
$S_{\lambda }= \{i: i\leq s\}\cup \{x: x\equiv 0\ \mod 3\}$
, and partition
$S_{\lambda }$
into
$K_{\lambda }=\{x: x\equiv 0\ \mod 3\}$
,
$I_{\lambda }=\{x\leq s: x\equiv 1\ \mod 3\}$
,
$M_{\lambda }=\{x \leq s: x\equiv 2\ \mod 3\}$
, and
$D_\lambda =\emptyset $
. If
$\alpha \ne \lambda $
then at stage s, if
$s\in M_{\alpha ^-}$
then s may enter
$S_{\alpha }$
(in particular,
$S_\alpha \subseteq \{x:x\leq s\}$
). In fact,
$S_\alpha $
will be the set of stages at which the node
$\alpha $
is visited since its last initialization. At each stage, if
$\alpha =(\alpha ^-)\,\widehat {\;}\infty $
then
and
$S_\alpha $
is partitioned by
$K_\alpha $
,
$I_\alpha $
,
$M_\alpha $
. One out of every three elements which enter
$S_\alpha $
will be put into
$K_\alpha $
, one out of every three will be put into
$I_\alpha $
, and one out of every three will be put into
$M_\alpha $
. If
$\alpha = (\alpha ^-)\,\widehat {\;}f$
, we define
$K_\alpha =I_\alpha =\emptyset $
, and
$S_\alpha $
is partitioned by
$D_\alpha , M_\alpha $
. One out of every two elements which enter
$S_\alpha $
will be put into
$D_\alpha $
, and one out of every two elements which enter
$S_\alpha $
will be put into
$M_\alpha $
. The limit value
$S_{\alpha }$
will then turn out to be partitioned by the (limit values of the) sets
$K_\alpha $
,
$I_\alpha $
,
$M_\alpha $
if
$\alpha = \lambda $
or
$\alpha =(\alpha ^{-})\,\widehat {\;}\infty $
, or
$D_\alpha , M_\alpha $
if
$\alpha =(\alpha ^{-})\,\widehat {\;}f$
. Moreover, every
$S_{\alpha }$
with
$\alpha \ne \lambda $
will be contained in
$M_{\alpha ^{-}}$
.
We will also have a single global set K (approximated by
$K_{s}$
at stage s), which is the set of elements which are A-equivalent to a member of
$K_\lambda $
. That is,
$K=[K_\lambda ]_{A}$
. This will include
$K_\alpha $
for every node
$\alpha $
. This will even include numbers which enter a set
$K_\alpha $
before
$\alpha $
is injured. Moreover, K may contain numbers which themselves are never enumerated into any set
$K_\alpha $
. This is a consequence of the fact that when we witness injury to
$\alpha $
, we will collapse all of the numbers in
$S_\alpha \smallsetminus K$
to a single class, and a representative of this class may enter
$K_\beta $
for some
$\beta $
. In this case, we will place the single representative of the class into
$K_\beta $
, but the remainder of the class will be in K, despite never having been enumerated into any set
$K_\gamma $
.
2.2.2 More formal description of the strategy of a node
$\alpha $
in isolation
We now look at the strategies employed by the nodes on
(in fact, to describe the effects of the strategy employed by
$\alpha $
, we assume that
and
$\alpha $
works in isolation), describing some procedures which will be used in the formal construction.
Each node
$\alpha $
on the tree will be working with the c.e. set
$W_{\lvert \alpha \rvert }$
to choose its outcome. Also,
$\alpha $
builds
$S_{\alpha }$
,
$K_{\alpha }$
,
$I_{\alpha }$
,
$D_{\alpha }$
,
$M_{\alpha }$
, and constructs particular ceers on
$K_{\alpha }$
,
$I_{\alpha }$
,
$D_{\alpha }$
. We distinguish the three cases
$\alpha =\lambda $
,
$\alpha =(\alpha ^{-})\,\widehat {\;}\infty $
, and
$\alpha =(\alpha ^{-})\,\widehat {\;}f$
.
$\alpha =\lambda $
: Winning
$\mathrm {R}$
and
$\mathrm {NSF}$
We reserve
$K_{\lambda }$
and
$I_{\lambda }$
to meet the overall requirements
$\mathrm {R}$
and
$\mathrm {NSF}$
. Specifically, on
$K_\lambda $
(which will be exactly
$\{x: x\equiv 0\ \mod 3\}$
) we place a copy of C. Thus
$x\mapsto 3x$
will give a reduction witnessing
$C \leq A$
, and we let
$I_{\lambda }$
(which will limit to exactly
$\{x: x\equiv 1\ \mod 3\}$
) be a copy of
:
-
• (Coding C in
$K_{\lambda }$
) Towards making the reduction
$C \leq A$
, for every
let
$x^\lambda _n = 3n$
be the nth element of
$K_\lambda $
. At every stage s, we will A-collapse
$x^\lambda _n \mathrel {A} x^\lambda _m$
if and only if
$x^\lambda _n, x^\lambda _m\leq s$
and
$n \mathrel {C_s} m$
. The construction will guarantee that we cause no additional A-collapses on
$K_\lambda $
. The notation
$x^\lambda _n$
here refers to the nth element of
$K_\lambda $
. For nodes
$\alpha =\alpha ^-\,\widehat {\;}\infty $
, we will have
$x^\alpha _n$
similarly refer to the nth element of
$K_\alpha $
. -
• We let
$I_{\lambda }$
be a copy of
, by never A-collapsing throughout the construction any pair of distinct elements of
$I_{\lambda }$
. We will not collapse these elements with any other elements, so Lemma 2.14 will guarantee that
.
$\alpha =(\alpha ^{-})\,\widehat {\;}\infty $
If we visit
$\alpha ^-$
at stage s and do not end the stage, it is because s enters
$M_{\alpha ^-}$
. Suppose that at infinitely many stages,
$\alpha ^{-}$
takes outcome
$\infty $
. At stage s,
$\alpha ^{-}$
takes outcome
$\infty $
if and only if at that stage
$W_{|\alpha ^{-}|}$
contains an element
$x \in [S_{\alpha ^{-}\,\widehat {\;}f}]_A$
which is not in K. We will call such stages
$\alpha ^-$
-expansionary. In this case all elements of
$S_{\alpha ^-\,\widehat {\;}f}$
which are not in K will collapse together into the class of s, and we enumerate s into
$S_{\alpha }$
. In this case, we will make
$S_{\alpha ^-\,\widehat {\;}f}=\emptyset $
as we injure
$\alpha ^-\,\widehat {\;}f$
. This means that the x we found in
$W_{|\alpha ^-|}\cap [S_{\alpha ^-\,\widehat {\;}f}]_A$
must be A-equivalent to a number which entered
$S_{\alpha ^-\,\widehat {\;}f}$
since the last time
$\alpha $
was visited. This s then enters one of
$K_\alpha $
,
$I_\alpha $
, or
$M_\alpha $
. If we take this outcome infinitely often, then
$S_\alpha $
will be an infinite computable set.
-
• K-procedure at
$\alpha $
. If s becomes the nth element of
$K_{\alpha }$
(we express this by writing
$s=x^{\alpha }_{n}$
) then we A-collapse
$s \mathrel {A} x^\lambda _n$
. Moreover we will cause no additional A-collapse on the elements of
$K_{\alpha }$
apart from the ones inherited from C through
$K_{\lambda }$
. -
• The equivalence
. We will cause no additional A-collapse on the elements of
$I_{\alpha }$
, so they will be pairwise non-A-equivalent as they were when first enumerated in
$I_{\alpha }$
, and thus
. -
• The reduction
$A \leq A{\restriction} S_{\alpha }$
. Since every element of
$S_{\alpha }$
is in a class which intersects
$W_{|\alpha ^{-}|}$
, a reduction
$A \leq A{\restriction} S_{\alpha }$
yields
$A\leq A {\restriction} W_{|\alpha ^{-}|}$
by Lemma 1.4(3), thus satisfying the requirement
$\mathrm {SMC}_{\lvert \alpha ^-\rvert }$
. Assuming
$\alpha $
is on the true path,
will be partitioned into
$[S_{\beta }]_A\smallsetminus K$
for
$\beta <_{L} \alpha $
,
$[I_\gamma ]_A, [D_\gamma ]_A$
for
$\gamma \subset \alpha $
, and
$[S_\alpha ]_A$
(note that all of K, and thus
$[K_\gamma ]_A$
for all
$\gamma $
is contained in
$[S_{\alpha }]_A$
as every element of
$K_\gamma $
is collapsed with an element of
$K_\lambda $
, and
$K_\alpha $
, being infinite, contains an element
$x^\alpha _n A$
-equivalent to
$x^\lambda _n$
for each n). We will show in the Disjointness Lemma below that these blocks are pairwise A-disjoint. Further, this is a computable partition (note that
$[S_{\beta }]_A\smallsetminus K$
for
$\beta <_L\alpha $
is a c.e. set since it contains only finitely many classes, since we are assuming that
). So, to reduce A to
$A{\restriction} S_{\alpha }$
comes down to reducing each of
$[S_{\beta }]_A\smallsetminus K$
for
$\beta <_{L}\alpha $
,
$[I_\gamma ]_A, [D_\gamma ]_A$
for
$\gamma \subset \alpha $
, and
$[S_\alpha ]_A A$
-disjointly into
$S_\alpha $
. Each of
$[S_{\beta }]_A\smallsetminus K$
for
$\beta <_{L}\alpha $
will be finite ceers. Each of
$[I_\gamma ]_A, [D_\gamma ]_A$
for
$\gamma \subset \alpha $
will be either empty or equivalent to
. Since
$I_\alpha $
is a copy of
, we build a reduction by reducing
$[I_\alpha ]_A$
along with each of
$[S_{\beta }]_A\smallsetminus K$
for
$\beta <_{L}\alpha $
,
$[I_\gamma ]_A, [D_\gamma ]_A$
for
$\gamma \subset \alpha $
to
$I_\alpha $
. The rest of
$[S_\alpha ]_A$
gets sent to a member of
$S_\alpha $
in its own equivalence class.
$\alpha =(\alpha ^{-})\,\widehat {\;}f$
Suppose now that
$\alpha =\alpha ^-\,\widehat {\;}f$
is on the true path.
-
• The finitary-diagonalization strategy at
$\alpha $
. Strategy
$\alpha $
works towards satisfying
$\mathrm {D}_{i}$
where i equals the number of bits f occurring in the string
$\alpha ^{-}$
(we let
$\#(\alpha )$
be this number). That is,
$\#(\alpha )=\lvert \{\beta :\beta\, \widehat {\;}f\subset \alpha ^-\}\rvert $
. Strategy
$\alpha $
carries out the finitary-diagonalization strategy described in Section 2.1.1, which we know will cause only finitely many collapses. Therefore,
$A{\restriction} D_\alpha $
will be equivalent to
. -
• The reduction
$A {\restriction} W_{|\alpha ^{-}|} \leq C$
. We see in this case that
, meeting
$\mathrm {SMC}_{\lvert \alpha ^-\rvert }$
. If
then
$W_{|\alpha ^{-}|} \cap [S_\alpha ]_A\smallsetminus K$
is empty. Once again,
is partitioned into
$[S_{\beta }]_A\smallsetminus K$
for
$\beta <_{L}\alpha $
,
$[I_\gamma ]_A, [D_\gamma ]_A$
for
$\gamma \subset \alpha $
, and
$[S_\alpha ]_A$
. So,
$A{\restriction} W_{|\alpha ^{-}|}$
can be written as a uniform join of
$A{\restriction} W_{|\alpha ^{-}|}\cap [S_{\beta }]_A\smallsetminus K$
for
$\beta <_L\alpha $
,
$A{\restriction} W_{|\alpha ^{-}|}\cap [I_\gamma ]_A$
,
$A{\restriction} W_{|\alpha ^{-}|}\cap [D_\gamma ]_A$
, for
$\gamma \subset \alpha $
, and
$A{\restriction} W_{|\alpha ^{-}|}\cap K$
, since
$W_{|\alpha ^{-}|}\cap [S_\alpha ]_A\smallsetminus K$
is empty. The first of these is a finite ceer, the second reduces to
, the third reduces to
, and
$A{\restriction} W_{|\alpha ^-|}\cap K\leq A{\restriction} K_\lambda \equiv C$
. Thus,
$A{\restriction} W_{|\alpha ^{-}|}$
reduces to a uniform join of finitely many copies of
, some finite ceers, and C, which reduces to
.
2.3 Formal construction
Let s be a stage. We proceed by substeps t at stage s. At substep t of s we define: (1) a string
$\alpha _{s,t} \supset \alpha _{s,t-1}$
, such that
$\lvert \alpha _{s,t}\rvert =t$
; (2) the values of the parameters relative to this string; and (3) a new value
$A_{s,t}$
of the ceer A. To do this we may need to know the current values of the parameters relative to other strings
$\beta $
, and of A as well. We assume that these values are the ones assigned to them at the end of substep
$t-1$
if
$t>0$
, or at the end of the previous stage if
$t=0$
. After completing substep t, we may end stage s and go on to stage
$s+1$
, or we may move on to substep
$t+1$
.
Remark 2.2 (Saving on notations)
When describing the actions and the parameters at any substep t of any stage s, for simplicity we will omit specifying the subscript
$s,t$
. Thus for instance, we refer to
$S_\alpha $
instead of
$S_{\alpha ,s,t} ($
being clear from the context whether we mean the value at the beginning of the substep, or the value which we define at the end of the substep
$)$
, and for any set X,
$[X]_{A}$
will stand for
$[X]_{A_{s,t}}$
, etc.
A stage
$s+1$
is
$\alpha $
-expansionary if
$\alpha $
is visited at that stage, does not end the stage, and
$W_{|\alpha |}$
contains an element
$x \in [S_{\alpha\,\widehat {\;}f}]_A\smallsetminus K$
. Note that in this case, we will injure
$\alpha\,\widehat {\;}f$
, in particular setting
$S_{\alpha\,\widehat {\;}f}=\emptyset $
. Thus, x must be A-equivalent to an element which entered
$S_{\alpha\,\widehat {\;}f}$
since the last
$\alpha $
-expansionary stage.
Stage
$0$
Let
$\alpha _{0}=\lambda $
. Let
$S_{\lambda } = K_\lambda = \{x: x\equiv 0\ \mod 3\}$
. Define
$x^\lambda _n=3n$
for every n. All other sets are empty. Let
.
Initialize all
$\beta \ne \lambda $
by setting
$S_\beta = K_{\beta }= I_{\beta } =D_{\beta }=M_{\beta } =\emptyset $
, and
$n_{\beta }=0$
.
Stage
$s+1$
Substep
$0$
: Let
$\alpha _{s+1,0}=\lambda $
. If
$s+1\equiv 0\ \mod 3$
, then we update
$K_\lambda $
by A-collapsing
$3x$
with
$3y$
if and only if
$3x,3y\leq s+1$
and
$x\mathrel {C_{s+1}}y$
. We then end the stage. If
$s+1\equiv 1\ \mod 3$
, then put
$s+1$
into
$S_\lambda $
and
$I_\lambda $
. We then end the stage. Finally, if
$s+1 \equiv 2\ \mod 3$
, we put
$s+1$
into
$S_\lambda $
and
$M_\lambda $
. We then proceed to the next substep.
Substep
$t+1$
: After completing stage
$s+1$
substep t, having defined
$\alpha =\alpha _{s+1,t}$
and the relevant parameters for
$\alpha $
without having stopped the stage at t, we distinguish the following two cases:
-
• If
$s+1$
is
$\alpha $
-expansionary, then: Let
$\alpha _{s+1, t+1}=\alpha\,\widehat {\;}\infty $
. Carry out the following procedures:-
– Perform the dumping procedure. A-collapse
$S_{\alpha\,\widehat {\;}f} \smallsetminus K$
into the equivalence class of
$s+1$
. Enumerate
$s+1$
into
$S_{\alpha\,\widehat {\;}\infty }$
. We initialize all requirements
$>_L \alpha\,\widehat {\;}\infty $
, and in particular we set
$S_{\beta }=K_\beta =I_\beta =D_\beta =M_\beta =\emptyset $
and
$n_\beta =0$
for all
$\beta \supseteq \alpha\,\widehat {\;}f$
. -
– Perform the partition procedure. If the cardinality
$\left |S_{\alpha\,\widehat {\;}\infty }\right | \equiv 1\ \mod 3$
then we enumerate
$s+1$
into
$K_{\alpha\,\widehat {\;}\infty }$
. If
$|S_{\alpha\,\widehat {\;}\infty }| \equiv 2\ \mod 3$
then we enumerate
$s{\,+\,}1$
into
$I_{\alpha\,\widehat {\;}\infty }$
. If
$|S_{\alpha\,\widehat {\;}\infty }| \equiv 0\ \mod 3$
then we enumerate
$s+1$
into
$M_{\alpha\,\widehat {\;}\infty }$
. -
– Perform the K-procedure. If
$s+1$
was enumerated into
$K_{\alpha\,\widehat {\;}\infty }$
and it is the nth element of
$K_{\alpha\,\widehat {\;}\infty }$
, then we write
$s+1= x_n^{\alpha\,\widehat {\;}\infty }$
and we collapse
$s+1 \mathrel {A} x^{\lambda }_{n}$
. -
– If we put
$s+1$
into
$K_{\alpha\,\widehat {\;}\infty }$
or
$I_{\alpha\,\widehat {\;}\infty }$
, end the stage. If we put
$s+1$
into
$M_{\alpha\,\widehat {\;}\infty }$
, then proceed to the next substep.
-
-
• If
$s+1$
is not
$\alpha $
-expansionary then let
$\alpha _{s+1,t+1} = \alpha\,\widehat {\;}f$
and enumerate
$s+1$
into
$S_{\alpha\,\widehat {\;}f}$
.-
– Perform the partition procedure. If
$|S_{\alpha\,\widehat {\;}f}|$
is odd, then we put
$s+1$
into
$D_{\alpha\,\widehat {\;}f}$
. Otherwise, we place
$s+1$
into
$M_{\alpha\,\widehat {\;}f}$
. -
– Perform the finitary-diagonalization-procedure. For this, we refer to the informal description of the strategy given earlier as regards notations and terminology. In particular,
$a_j$
refers to the jth element in
$D_\alpha $
. The finitary-diagonalization strategy at
$\alpha\,\widehat {\;}f$
requires attention if
$|D_\alpha |\geq n_\alpha $
and for each
$$ \begin{align*} \varphi_{\#\alpha,s}(a_j)\mathrel{B_s} \varphi_{\#\alpha,s}(a_k) \Leftrightarrow a_j \mathrel{A} a_k, \end{align*} $$
$a_j,a_k\in D_\alpha $
with
$j,k<n_{\alpha }$
. If this happens then we act by incrementing
$n_{\alpha }=n_{\alpha }+1$
and by A-collapsing
$a_j \mathrel {A} a_k$
if and only if
$j \mathrel {U_s} k$
, for each
$a_j,a_k\in D_\alpha $
with
$j,k<n_{\alpha }$
.
-
– If we put
$s+1$
into
$D_{\alpha\,\widehat {\;}f}$
, end the stage. If we put
$s+1$
into
$M_{\alpha\,\widehat {\;}f}$
, then proceed to the next substep.
-
Finally let
$\alpha _{s+1}= \alpha _{s+1,\widehat {t}}$
and
$A_{s+1}= A_{s+1,\widehat {t}}$
, where
$\widehat {t}$
is the last substep of stage
$s+1$
(which we show exists in Lemma 2.3).
2.4 Verification
We first observe that every stage terminates. This is because every node ends the stage when it is visited for the first time.
Lemma 2.3. Every stage has a last substep.
Proof By induction, we may assume that all previous stages have terminated, thus there are only finitely many
$\alpha $
so that
$S_\alpha $
is non-empty. Suppose towards a contradiction that stage s does not terminate. Then there is some t so that
$S_{\alpha _{s,t}}$
is empty at the beginning of the substep of the stage. Then we make
$|S_{\alpha _{s,t}}|=1$
, and therefore s is placed into
$K_\alpha $
or
$D_\alpha $
and the stage terminates.
We say that
$\alpha $
is on the true path at stage s, or s is an
$\alpha $
-true stage if
$\alpha \subseteq \alpha _{s}$
.
Next we verify that we do not accidentally cause more collapse than intended. This will be necessary for instance to show that
$A{\restriction} K_\lambda \equiv C$
.
Lemma 2.4.
-
(1) At every substep t of every stage s and nodes
$\gamma \neq \beta $
, if
$x\mathrel {A} y$
for
$x\in S_\gamma $
,
$y\in S_\beta $
then either
$\gamma \subseteq \beta $
and
$x\in M_\gamma $
,
$\beta \subseteq \gamma $
and
$y\in M_\beta $
, or
$x,y\in K$
. -
(2) At the beginning of stage
$s+1$
substep t, if
$s+1\in M_{\alpha _{s+1,t}}$
, and
$y\in S_\beta $
for any
$\beta $
and
$s+1\mathrel {A} y$
, then
$\beta \subseteq \alpha _{s+1,t}$
and
$y\in M_\beta $
. -
(3) For each
$\alpha $
,
$[I_\alpha ]_A$
,
$[D_{\alpha }]_A$
,
$[M_{\alpha }]_A\smallsetminus K $
, K are always disjoint sets.
Proof We prove all three claims by simultaneous induction on substeps of stages. They are clearly true at stage
$0$
since the only
$\alpha $
with
$S_\alpha \neq \emptyset $
is
$\lambda $
and no collapse has happened at stage
$0$
.
We consider each of the actions taken during the construction and see that they maintain these conditions. At each step, the substep 0 only introduces a fresh number to the construction and can only cause collapse if both numbers are in
$K_\lambda $
. Thus it maintains all three conditions. We consider
$\alpha =\alpha _{s+1,t}$
as we take the (
$t+1$
)th substep and look at each case. First suppose that
$s+1$
is an
$\alpha $
-expansionary stage.
During the dumping procedure, we put
$s+1$
into
$S_{\alpha\,\widehat {\;}\infty }$
and collapse all elements of
$S_{\alpha\,\widehat {\;}f}\smallsetminus K$
to be A-equivalent with
$s+1$
. We also make
$S_\delta = \emptyset $
for every
$\delta \supseteq \alpha\,\widehat {\;}f$
. By inductive hypothesis, each element of
$S_{\alpha\,\widehat {\;}f}\smallsetminus K$
could only be A-equivalent to a
$y\in S_\delta $
if
$\delta \supseteq \alpha\,\widehat {\;}f$
or
$\delta \subset \alpha\,\widehat {\;}f$
and
$y\in M_\delta $
. Also, by the inductive hypothesis on the second condition,
$s+1$
itself is only A-equivalent to
$y\in S_\delta $
if
$\delta \subseteq \alpha $
and
$y\in M_\delta $
. Thus the first condition is maintained by the dumping procedure. The third condition is also preserved since no set
$I_\alpha $
,
$D_\alpha $
,
$M_\alpha $
, or K has been increased, and the collapse we caused did not cause collapse between any of these sets by the inductive hypothesis on the first condition. The second condition is changed slightly. Since now
$s+1$
itself has entered
$S_{\alpha\,\widehat {\;}\infty }$
, but is the only representative of its class in
$S_{\alpha\,\widehat {\;}\infty }$
, we have the additional possibility that
$y=s+1$
itself and
$\delta =\alpha\,\widehat {\;}\infty $
. The condition only talks about the beginning of the substep, so this is not a direct violation of the second condition, but this affects the possibilities we must consider if
$s+1$
enters
$M_{\alpha\,\widehat {\;}\infty }$
during the partition procedure.
Next, during the partition procedure, no collapse is caused and no
$S_\beta $
is changed, so the first condition is preserved. If
$s+1$
is not placed into
$M_{\alpha\,\widehat {\;}\infty }$
, then the second condition holds vacuously. If it is placed in
$M_{\alpha\,\widehat {\;}\infty }$
, then we had
$s+1$
only A-equivalent to
$y\in S_\delta $
if
$\delta \subseteq \alpha $
and
$y\in M_\delta $
or if
$y=s+1$
and
$\delta =\alpha\,\widehat {\;}\infty $
. In the latter case, since
$s+1$
entered
$M_{\alpha\,\widehat {\;}\infty }$
, the condition still holds. Finally, the only new class in
$[I_\beta ]_A$
,
$[D_{\beta }]_A$
,
$[M_{\beta }]_A\smallsetminus K $
is the class of
$s+1$
itself, by the second condition,
$s+1$
is not A-equivalent to any other member of
$S_{\alpha\,\widehat {\;}\infty }$
, so the third condition is preserved.
The K-procedure only occurs if
$s+1$
entered
$K_{\alpha\,\widehat {\;}\infty }$
. In this case, the second condition holds vacuously after this as
$s+1\notin M_{\alpha\,\widehat {\;}\infty }$
. In this case,
$s+1$
collapses with an element of
$K_\lambda $
. Thus the first statement is preserved because this only collapses a class into K and the statement allows for two elements of K. The third statement is preserved as well, since the inductive hypotheses imply that both
$s+1$
and each member of
$K_\lambda $
are A-non-equivalent to any member of
$[I_\gamma ]_A$
,
$[D_{\gamma }]_A$
,
$[M_\gamma ]_A\smallsetminus K $
for any
$\gamma $
.
Now we suppose that
$s+1$
is not an
$\alpha $
-expansionary stage. All three statements are clearly preserved by adding
$s+1$
to
$S_{\alpha\,\widehat {\;}f}$
. During the partition procedure no collapse or entry into any
$S_\beta $
happens, so the first statement is preserved. Since
$s+1$
is not A-equivalent to any member of
$S_{\alpha\,\widehat {\;}f}$
except
$s+1$
itself by the inductive hypothesis on the second condition, the third condition is also preserved. Again the second condition has the new possibility that
$y=s+1$
itself and
$\delta =\alpha\,\widehat {\;}f$
, which maintains the second condition if
$s+1$
enters
$M_{\alpha\,\widehat {\;}f}$
. If
$s+1$
enters
$D_{\alpha\,\widehat {\;}f}$
, the condition holds vacuously.
During the finitary-diagonalization-procedure, collapse can happen only between members of
$D_{\alpha\,\widehat {\;}f}$
. Since the inductive hypothesis shows that each of these numbers can only be A-equivalent to
$x\in S_\delta $
for
$\delta \neq \alpha\,\widehat {\;}f$
if
$\delta \subset \alpha\,\widehat {\;}f$
and
$x\in M_\delta $
, the first statement is preserved. This collapse can only involve
$s+1$
if
$s+1$
has entered
$D_{\alpha\,\widehat {\;}f}$
, in which case the second statement holds vacuously. Similarly, since each of these elements of
$D_{\alpha\,\widehat {\;}f}$
is not A-equivalent to any member of
$I_{\alpha\,\widehat {\;}f}$
or K or
$M_{\alpha\,\widehat {\;}f}$
by inductive hypothesis, the third condition is maintained as well.
We introduce some convenient notation:
Definition 2.5. For every
$\alpha $
such that there is a biggest stage
$s_{\alpha }$
at which
$\alpha $
is initialized
$($
taking
$s_{\alpha }=0$
if
$\alpha = \lambda )$
, if
$P_{\alpha }\in \{S_{\alpha }, K_{\alpha }, I_{\alpha }, D_{\alpha }, M_{\alpha }\}$
then let
$$ \begin{align*} P_{\alpha}= \bigcup_{t \ge s_{\alpha}} P_{\alpha,t}. \end{align*} $$
For every string
$\alpha $
, at any stage and substep, let
$$ \begin{align*} R_{\alpha} &= \begin{cases} I_\alpha, &\textrm{if}\ \alpha=\lambda\ \text{or}\ \alpha= (\alpha^{-})\,\widehat{\;}\infty,\\ D_\alpha, &\textrm{if}\ \alpha=\alpha^{-}\,\widehat{\;}f, \end{cases}\\ S^{-}_{<_{L} \alpha} &=\bigcup \{S_{\beta}\smallsetminus K: \beta<_{L}\alpha\}.\\ \end{align*} $$
Lemma 2.6 (Disjointness Lemma)
For any
, the
$($
limiting values of the
$)$
following sets are pairwise disjoint:
$[R_\alpha ]_A$
,
$[S^-_{<_L\alpha }]_A$
, K,
$[M_\alpha ]_A \smallsetminus K$
. Further, for any
$\beta \subset \alpha $
, these sets are all disjoint from
$[R_\beta ]_A$
.
Proof This follows immediately from Lemma 2.4 since each of these sets are disjoint at each stage.
Lemma 2.7. For every
$\alpha $
on the true path, and for every x,
$$ \begin{align*} x \in K \cup [S^{-}_{<_{L}\alpha}]_{A} \cup \left[\bigcup_{\beta \subseteq \alpha} R_{\beta}\right]_{A} \cup \left([M_{\alpha}]_{A} \smallsetminus K\right). \end{align*} $$
Proof For
$\alpha =\lambda $
, the claim is trivial because every x lies in
$K_{\lambda } \cup I_{\lambda } \cup M_{\lambda }$
.
Suppose by induction that the claim is true of
$\alpha $
on the true path. We distinguish as usual the two possible cases
or
.
Assume first that
$\alpha\,\widehat {\;}\infty $
is on the true path, and let x be any number. If
$x \in K \cup [S^{-}_{<_{L}\alpha }]_{A} \cup [\bigcup _{\beta \subseteq \alpha } R_{\beta }]_{A}$
then the claim is trivial. Note that
$S^{-}_{<_{L}\alpha }= S^{-}_{<_{L}(\alpha )\,\widehat {\;}\infty }$
. So suppose that
$x \in [M_{\alpha }]_{A}\smallsetminus K$
. Then by the dumping procedure,
$x \in [S_{\alpha\,\widehat {\;}\infty }]_{A}$
, which gives
$x\in [R_{\alpha\,\widehat {\;}\infty }]_{A} \cup [M_{\alpha\,\widehat {\;}\infty }]_{A}$
.
Assume now that
$\alpha\,\widehat {\;}f$
is on the true path, and let x be any number. Again, the case which deserves some attention is when
$x \in [M_{\alpha }]_{A}\smallsetminus K$
. Then either
$x\in [S_{\alpha\,\widehat {\;}\infty }]_A$
or
$x\in [S_{\alpha\,\widehat {\;}f}]_A$
. In the former case,
$x\in [S^-_{<_L \alpha\,\widehat {\;}f}]_A$
. In the latter,
$x\in [R_{\alpha\,\widehat {\;}f}]_A$
or
$x\in [M_{\alpha\,\widehat {\;}f}]_A$
. In any case, the statement is true for
$\alpha\,\widehat {\;}f$
.
Lemma 2.8. For every
$m,n, \beta , \gamma $
, if
$x^{\beta }_{m}[s]$
and
$x^{\gamma }_{n}[t]$
are defined, then
$x^{\beta }_{m}[s]\mathrel {A} x^{\gamma }_{n}[t]$
if and only if
$m \mathrel {C} n$
.
Proof We A-collapse
$x^{\beta }_{m}[s] \mathrel {A} x^{\lambda }_{m}$
and
$x^{\beta }_{n}[t] \mathrel {A} x^{\lambda }_{n}$
. Thus we cause the collapse
$x^{\beta }_{m}[s]\mathrel {A} x^{\gamma }_{n}[t]$
when we update
$K_\lambda $
during substep
$0$
of some stage if and only if we cause the collapse
$x^{\lambda }_{m} \mathrel {A} x^{\lambda }_{n}$
if and only if
$m \mathrel {C} n$
. Note that we only ever cause A-collapse during the construction either during a dumping procedure, where we do not collapse elements in K, or during a finitary-diagonalization strategy, where we collapse elements of
$D_\gamma $
for some
$\gamma $
, which are not in K by Lemma 2.4, or during the K-procedure where we collapse an element which is not yet in K, by the second claim in Lemma 2.4, to an element of
$K_\lambda $
. Thus we never unintentionally collapse together distinct members of K.
Lemma 2.9. If
then each of the sets
$S_\alpha $
,
$K_{\alpha }$
,
$R_\alpha $
, and
$M_\alpha $
is computable
$($
not uniformly
$)$
. If
then each of these sets is finite. If
then each of these sets is infinite.
Proof We check the claim that refers to strings
, as the part that refers to strings
is obvious.
If
then let
$s_0$
be the last stage at which
$S_\alpha $
is initialized. Then
$s>s_0$
enters
$S_{\alpha }$
if and only if it enters at stage s. Thus
$S_\alpha $
is computable. It is infinite since s enters
$S_\alpha $
at every stage s where
$\alpha $
is visited.Footnote
1
The rest of the claim is obvious by the way
$S_{\alpha }$
is partitioned into the other relevant sets.
Lemma 2.10.
$C\leq A$
.
Proof For each pair
$n,m$
, we have ensured that
$n \mathrel {C} m \Leftrightarrow x^\lambda _n \mathrel {A} x^\lambda _m$
byLemma 2.8.
Lemma 2.11. For every k, there is an
$\alpha $
on the true path with
$\#(\alpha ) = k$
.
Proof For every
$\alpha \ne \lambda $
on the true path such that
$W_{\lvert \alpha ^{-}\rvert } =\emptyset $
we have
$\alpha = \alpha ^{-}\,\widehat {\;}f$
. Thus there are infinitely many fs along the true path, so there is an
$\alpha $
on the true path with
$\#(\alpha ) = k$
.
Lemma 2.12.
$A\not \leq B$
. Thus
$A\not \leq C$
.
Proof Given any k, we want to show that
$\varphi _k$
is not a reduction of A to B. Let
$\alpha $
be on the true path with
$\alpha =(\alpha ^{-})\,\widehat {\;}f$
and
$\#(\alpha ) = k$
. Then
$D_\alpha $
is infinite. On the set
$D_\alpha $
,
$\alpha $
runs the finitary-diagonalization strategy. As we have argued in the description of the finitary-diagonalization strategy, the only possible outcome is the finite diagonalization outcome which ensures that
$\varphi _k$
is not a reduction of A to B.
Lemma 2.13. If
then
and
.
Proof First of all we show that if
then
. Note that we only ever cause A-collapse either during substep 0, where we collapse elements in
$K_\lambda $
thus we do not collapse elements in
$R_\alpha $
; during a dumping procedure, where we do not collapse elements in
$R_\alpha $
; or during a finitary-diagonalization strategy, where we collapse elements of
$D_\gamma $
for some
$\gamma $
, which are not A-equivalent to elements of
$R_\alpha $
unless
$R_\alpha =D_\gamma $
, in which case this is a collapse for the sake of
$\alpha $
’s finitary-diagonalization strategy; or during a K-procedure where we collapse an element of
$K_\alpha $
to an element of
$K_\lambda $
, neither of which can be equivalent to a member of
$R_\alpha $
. Thus we never unintentionally collapse together members of
$R_\alpha $
. So, we can focus on the strategy itself. If
$R_\alpha =I_\alpha $
, then we never collapse any elements, so
$I_\alpha $
is comprised of distinct elements, so
. In the case of
$R_\alpha =D_\alpha $
, note that we cause a total of finitely many collapses via the finitary-diagonalization strategy since
$\lim _{s\rightarrow \infty } n_{\alpha ,s}<\infty $
. So
.
For any
$\alpha $
,
$A {\restriction} (S^{-}_{<_{L}\alpha } \cup \bigcup _{\beta \subseteq \alpha } R_{\beta })$
is equivalent to
by the Disjointness Lemma and the fact that
$S^{-}_{<_{L}\alpha }$
is finite (the latter being needed to see that the partition is computable). Each direct summand is finite or equivalent to
, and one of them (
$A {\restriction} R_\alpha $
) is equivalent to
, so
.
Lemma 2.14.
. In particular, A is non-self-full.
Proof It is immediate from the previous lemma that
. Further, since
$I_\lambda $
is computable, the Disjointness Lemma implies that
. Thus,
Lemma 2.15. If
$\alpha\,\widehat {\;}\infty $
is on the true path then
$A \leq A{\restriction} S_{\alpha\,\widehat {\;}\infty }\leq A{\restriction} W_{\lvert \alpha \rvert }$
and the requirement
$\mathrm {SMC}_{|\alpha |}$
is satisfied.
Proof In view of Lemma 2.13, there exist a computable function providing a reduction from
$A{\restriction} (S^{-}_{<_{L}\alpha\,\widehat {\;}\infty }\cup \bigcup _{\beta \subseteq \alpha\,\widehat {\;}\infty } R_{\beta })$
to
, and a computable reduction of
to
$A{\restriction} I_{\alpha\,\widehat {\;}\infty }$
. This lets us build a partial computable function f which has domain
$S^{-}_{<_{L}\alpha\,\widehat {\;}\infty }\cup \bigcup _{\beta \subseteq \alpha\,\widehat {\;}\infty } R_{\beta }$
and range
$I_{\alpha\,\widehat {\;}\infty }$
and for
$x,y$
in the domain,
$x \mathrel {A} y$
if and only if
$f(x) \mathrel {A} f(y)$
.
To define a reduction g witnessing
$A \leq A {\restriction} S_{\alpha\,\widehat {\;}\infty }$
, consider any number x. We use Lemma 2.7, and we search for a y in
$K_\lambda \cup S^{-}_{<_{L}\alpha\,\widehat {\;}\infty } \cup \bigcup _{\beta \subseteq \alpha\,\widehat {\;}\infty } R_{\beta } \cup M_{\alpha\,\widehat {\;}\infty }$
so that
$x \mathrel {A} y$
using simultaneous effective listings of these four sets:
-
(1) If we first find
$y=x^\lambda _n \in K_\lambda $
then let
$g(x)=x^{\alpha\,\widehat {\;}\infty }_n$
. -
(2) If we first find
$y \in S^{-}_{<_{L} \alpha\,\widehat {\;}\infty } \cup \bigcup _{\beta \subseteq \alpha\,\widehat {\;}\infty } R_{\beta }$
then let
$g(x)=f(y)$
. -
(3) If we first find
$y \in M_{\alpha\,\widehat {\;}\infty }$
, then we let
$g (x)=y$
.
We will show that g is a function with domain
and range
$S_{\alpha\,\widehat {\;}\infty }$
so that
$x\mathrel {A}y$
if and only if
$g(x)\mathrel {A} g(y)$
, showing that
$A\leq A{\restriction} S_{\alpha\,\widehat {\;}\infty }$
. By the Disjointness Lemma, the only thing to check is
$ x_{0} \mathrel {A} x_{1} \Leftrightarrow g(x_{0}) \mathrel {A} g(x_{1}), $
for a pair
$x_{0}, x_{1} \in K$
such that we use (1) to define
$g(x_{0})$
, but we use (3) to define
$g(x_{1})$
. Note that in both cases (1) and (3), we define
$g(x)$
to be A-equivalent to x. So we have
$g (x_0) \mathrel {A} g (x_1)$
if and only if
$x_0 \mathrel {A} x_1$
.
But if
$A \leq A{\restriction} S_{\alpha\,\widehat {\;}\infty }$
then by Lemma 1.4(3)
$A \leq A{\restriction} W_{|\alpha |}$
since every member of
$S_{\alpha\,\widehat {\;}\infty }$
is A-equivalent to a member of
$W_{|\alpha |}$
, as
$s+1$
enters
$S_{\alpha\,\widehat {\;}\infty }$
only at
$\alpha $
-expansionary stages, where we see
$s+1 \mathrel {A} x$
for some
$x\in W_{\lvert \alpha \rvert }$
. Thus the requirement
$\mathrm {SMC}_{|\alpha |}$
is satisfied.
Lemma 2.16. If
$\alpha\,\widehat {\;}f$
is on the true path, then
and requirement
$\mathrm {SMC}_{|\alpha |}$
is satisfied.
Proof Suppose now that
$\alpha\,\widehat {\;}f$
is on the true path. Since
$\alpha\,\widehat {\;}f$
is on
, we have that
$W_{|\alpha |} \cap [S_{\alpha\,\widehat {\;}f}]_A \smallsetminus K$
is empty.
Thus Lemmas 2.6 and 2.7 show that
$A{\restriction} W_{|\alpha |}$
is partitioned by:
But the first summand reduces to
$A{\restriction} K$
, which is equivalent to C, the second is a finite ceer, and the third reduces to
$A{\restriction} \bigcup _{\beta \subseteq \alpha\,\widehat {\;}f}R_\beta $
, which is equivalent to
by Lemma 2.13. So, the uniform join of all of these reduces to
.
Lemma 2.17. If
$X< A$
, then
$X\leq C$
.
Proof Let i be so
$X\equiv A{\restriction} W_i$
by Lemma 1.4 and let
$\alpha $
be so
$\lvert \alpha \rvert =i$
and
$\alpha $
is on the true path. We consider two cases:
Case 1: If
$\alpha\,\widehat {\;}\infty $
is on the true path, then Lemma 2.15 shows that
$A\leq A{\restriction} S_{\alpha\,\widehat {\;}\infty }\leq A {\restriction} W_i\equiv X$
.
Case 2: If
$\alpha\,\widehat {\;}f$
is on the true path, then Lemma 2.16 shows that
.
This ends the proof of the theorem.
$\dashv $
3 Initial segments in the structure
Let
bethe poset with universe the set of finite strings of natural numbers partially ordered by the relation
$\sigma \subseteq \tau $
if
$\sigma $
is an initial substring of
$\tau $
. In the following we use notations and terminology about finite strings of numbers, similar to those introduced at the beginning of Section 2.2 for strings in the tree of strategies
. The following corollary is an application of Theorem 2.1:
Corollary 3.1. There is an initial segment of
${\textbf {Ceers} \smallsetminus \textbf {Fin}}$
isomorphic to
.
Proof We begin with
, and note that
. Theorem 2.1 allows us to build infinitely many incomparable strong minimal covers each of which satisfies
. Repeating as such lets us embed
as an initial segment of
${\textbf {Ceers} \smallsetminus \textbf {Fin}}$
.
In more details, we can refer to a linear ordering
$\preceq $
of
of order type
, so that if
$\sigma \subseteq \tau $
then
$\sigma \preceq \tau $
. For instance define
, and let
$h(\sigma )$
be the least n so that
$\sigma \in \Gamma _n$
. Define
$\sigma \preceq \tau $
if
$h(\sigma )<h(\tau )$
or
$h(\sigma )=h(\tau )$
and
$\sigma $
is quasi-lexicographically less than
$\tau $
.
We start at “step
$\lambda $
” by setting
. When time comes to build
$A_{\sigma }$
, with
$\sigma \ne \lambda $
(this happens at “step
$\sigma $
”, i.e., at step n, with
$\sigma $
the nth string in
$\preceq $
), then we use Theorem 2.1 to make
$A_{\sigma }$
a strong minimal cover of
$A_{\sigma ^{-}}$
, and
$A_{\sigma }$
not reducible to
$\bigoplus \{A_{\tau }: \tau \prec \sigma \}$
(the universal degree is join-irreducible, i.e., there is no pair of incomparable degrees
$b,c$
so that the universal degree is the least upper bound of b and c (see [Reference Andrews, Lempp, Miller, Ng, San Mauro and Sorbi3, Proposition 2.6]), so this uniform join is not universal). Remember that all these
$A_{\sigma }$
s satisfy
. In particular, all these
$A_{\sigma }$
s are non-self-full.
Let us check that the mapping
$\sigma \mapsto A_{\sigma }$
provides in fact an embedding of
. If
$\sigma \subseteq \tau $
then either
$A_{\sigma }= A_{\tau }$
or
$A_{\tau }$
is built after
$A_{\sigma }$
so there is a computable function
$f_{\sigma ,\tau }$
which reduces
$A_{\sigma }\leq A_{\tau }$
. More precisely, in the construction of
$A_\tau $
using Theorem 2.1 we encode
$C=A_{\tau ^-}$
directly onto
$K_\lambda =\{x: x\equiv 0\ \mod 3\}$
, so
$f_{\sigma ,\tau }(x) =3^{|\tau |-|\sigma |} \cdot x$
.
Suppose towards a contradiction that there are
$\sigma $
and
$\tau $
with
$\sigma \nsubseteq \tau $
and
$A_{\sigma } \leq A_{\tau }$
. Take such a pair with
$\tau $
of minimal length. If the length of
$\tau $
is
$0$
, then
$A_\sigma $
is above
$A_{\langle \sigma (0)\rangle }$
, which is strictly above
by Theorem 2.1. So, we must have the length of
$\tau $
is
$>0$
. But then
$A_\sigma \leq A_\tau $
implies that either
$A_\sigma \equiv A_\tau $
or
$A_\sigma \leq A_{\tau ^-}$
. The latter case contradicts the minimality of the length of
$\tau $
. In the former case, let
$\rho $
be the
$\preceq $
-greater of
$\tau $
and
$\sigma $
. Then
$A_\rho $
is constructed so that
, contradicting
$A_\sigma \equiv A_\tau $
.
Thus, we have an embedding of
as an initial segment of
${\textbf {Ceers} \smallsetminus \textbf {Fin}}$
.
Corollary 3.2. The partial order
obtained by placing
on top of
is embeddable as an initial segment of
.
Proof The finite ceers have order type
and are initial in
. Corollary 3.1 shows that
is an initial segment on top of that.
Notice that
is in fact a lower semilattice with least element. We now turn towards extending the embedding given by Corollary 3.1 to an embedding of the free distributive lattice generated by the lower semilattice
into
${\textbf {Ceers} \smallsetminus \textbf {Fin}}$
. To do this, we identify for each nonempty tuple
$\sigma _0,\ldots , \sigma _{n-1}$
a ceer
$B_{\sigma _0,\ldots ,\sigma _{n-1}}$
to act as the join of the ceers
$A_{\sigma _0},\ldots , A_{\sigma _{n-1}}$
. We begin by recalling the definition:
Definition 3.3. The free distributive lattice generated by the lower semilattice
$\langle Q,\wedge \rangle $
is a distributive lattice D which has a function
$i: Q\rightarrow D$
which preserves meets, so that
$D,i$
satisfy the universal property: If L is any distributive lattice and
$f:Q\rightarrow L$
preserves meets, then there is a unique lattice-homomorphism
$h: D\rightarrow L$
so that
$f=h\circ i$
.
We will recall a constructive lattice-theoretic characterization of the free distributive lattice generated by the lower semilattice
below in Definition 3.8 and Lemma 3.9.
Fix a sequence of ceers
as built in Corollary 3.1. We define a map which assigns, to any nonempty finite subset
$\sigma _{0},\ldots \sigma _{n-1}$
of
a ceer
$B_{\sigma _0,\ldots , \sigma _{n-1}}$
as follows:
Definition 3.4. For each nonempty tuple
$\sigma _0,\ldots ,\sigma _{n-1}$
, we assign the ceer
$B_{\sigma _0, \ldots , \sigma _{n-1}}$
which is the ceer generated by
plus the set
$\sim $
of pairs defined by:
where
$f_{\tau ,\sigma }$
for
$\tau \subseteq \sigma $
is the reduction from
$A_\tau $
into
$A_\sigma $
as defined in the proof Corollary 3.1.
$($
In other words, we mod out
so that for each
$i,j< n$
, we identify the copy of
$A_{\sigma _i\wedge \sigma _j}$
in
$A_{\sigma _i}$
with the copy of
$A_{\sigma _i\wedge \sigma _j}$
in
$A_{\sigma _j}$
.
$)$
Remark 3.5. We will also denote
$B_{\sigma _0,\ldots , \sigma _{n-1}}$
by the expression
.
Remark 3.6. If we did not mod out to identify the copies of
$A_{\sigma _i\wedge \sigma _j}$
in
$A_{\sigma _i}$
and in
$A_{\sigma _j}$
in Definition 3.4, then we would be putting
below
$B_{\sigma _i,\sigma _j}$
, which we are constructing to be the join of
$A_{\sigma _i}$
and
$A_{\sigma _j}$
. But it is possible that
. This would mean that we would not be constructing an embedding to an initial segment in
${\textbf {Ceers} \smallsetminus \textbf {Fin}}$
.
Obviously,
$B_{\sigma _0,\ldots , \sigma _{n-1}}\equiv B_{\sigma _{p(0)},\ldots , \sigma _{p(n-1)}}$
for every permutation p of the set
$\{0, \ldots , n-1\}$
.
Theorem 3.7. The following hold for
$m, n>0{:}$
-
(1) If
$\sigma _i\supseteq \sigma _{j}$
with
$i,j<n$
and
$i \ne j$
, then
$B_{\sigma _0,\ldots ,\sigma _{n-1}} \equiv B_{\sigma _0, \ldots ,\sigma _{j-1}, \sigma _{j+1}, \ldots , \sigma _{n-1}}$
. Hence, where
$$ \begin{align*} B_{\sigma_0,\ldots,\sigma_{n-1}}\equiv B_{\sigma_{i_{0}},\ldots, \sigma_{i_{k-1}}}, \end{align*} $$
$\{\sigma _{i_{0}},\ldots ,\sigma _{i_{k-1}}\}$
is the
$\subseteq $
-antichain comprised of the
$\subseteq $
-maximal elements in
$\{\sigma _0,\ldots ,\sigma _{n-1}\}$
.
-
(2) If
$\{ \sigma _{0}, \ldots , \sigma _{n-1}\}$
is a
$\subseteq $
-antichain and
$X<B_{\sigma _0,\ldots \sigma _{n-1}}$
, then there exists
$i < n$
so that
$X\leq B_{\sigma _0,\ldots , \sigma _i^-, \ldots , \sigma _{n-1}}$
. Further, the only degrees of infinite ceers below
$B_{\sigma _0,\ldots , \sigma _{n-1}}$
are degrees of the form
$B_{\tau _0,\ldots ,\tau _{m-1}}$
where
$(\forall {j<m}\,)(\exists {i< n}\,)[\tau _{j} \subseteq \sigma _i]$
. -
(3) If
$\{ \sigma _{0}, \ldots , \sigma _{n-1}\}$
and
$\{\tau _{0}, \ldots , \tau _{m-1}\}$
are
$\subseteq $
-antichains, then
$$ \begin{align*} B_{\tau_0,\ldots,\tau_{m-1}}\leq B_{\sigma_0,\ldots, \sigma_{n-1}} \Leftrightarrow (\forall{j<m}\,)(\exists{i< n}\,)[\tau_{j}\subseteq \sigma_{i}]. \end{align*} $$
Proof
-
(1) We have
$\sigma _i \supseteq \sigma _{j}$
, with
$i,j<n$
and
$i \ne j$
. In the definition of
$\sim $
, we mod out the entirety of the copy of
$A_{\sigma _j}$
with a part of
$A_{\sigma _i}$
. It follows from Lemma 1.4(2) that -
(2) Suppose that
$X < B_{\sigma _0,\dots , \sigma _{n-1}}$
, and f is a reduction from X to
$B_{\sigma _0,\dots , \sigma _{n-1}}$
. Let
. Hence
by Lemma 1.4(2).Let
$W_{e_i}=\{x\in W_e: x\equiv i\ \mod n\}$
, and
$\alpha _i$
be the node of length
$e_i$
on the true path of the construction of
$A_{\sigma _i}$
in Theorem 2.1.Case 1: For each
$i< n$
,
$\alpha _{i}\,\widehat {\;}\infty $
is on the true path. Then (use the argument in the proof that
$A_{\sigma _i}$
is a strong minimal cover of
$A_{\sigma _i^-}$
to give the reduction on each component individually) we get reductions
$f_i$
witnessing
$A_{\sigma _{i}}\leq A_{\sigma _{i}} {\restriction} W_{e_{i}}$
. Thus
by Lemma 1.7 as
$\sim $
is transitive and
-closed. Finally, note that
$\sim $
includes relations on the set
$K_\lambda $
in each
$A_{\sigma _i}$
. But in the reductions
$f_i$
, each element in
$K_\lambda $
is sent to an image in its own equivalence class. Thus
. Thus That is,
$B_{\sigma _0,\ldots ,\sigma _{n-1}}\leq X$
.
Case 2: There is some
$i<n$
so that
$\alpha _{i}\,\widehat {\;}f$
is on the true path. So
. Let f be the reduction as such and note that
$f(x^\lambda _n)=2n$
. It follows that We note that in the latter reduction, we are collapsing the copy of
with the copy of
in any one of the
$A_{\sigma _i}$
, and that
$\sim $
does not touch the sets
$I_\lambda $
in any of the
$A_{\sigma _j}$
. Since f sends
$K_\lambda $
in
$A_{\sigma }$
(which is a copy of
$A_{\sigma ^-}$
) exactly to
$A_{\sigma ^-}$
, Lemma 1.7 yields where
$\sim '$
is as in the definition of
$B_{\sigma _0,\ldots , \sigma _i^-,\dots ,\sigma _{n-1}}$
. That is,
$ X\leq B_{\sigma _0,\ldots , \sigma _i^-,\dots ,\sigma _{n-1}} $
.
Now, suppose X is an infinite ceer and
$X\leq B_{\sigma _0,\ldots ,\sigma _{n-1}}$
. We can repeatedly apply the above condition until either we represent X as
$B_{\tau _0,\ldots ,\tau _{n-1 }}$
or until we get to tuple of
$\tau $
s which is no longer an anti-chain. In this case, we can use the result of (1) and then repeat. This process is monotonically decreasing in the sum of the lengths of the strings, so it must either terminate with
$X\equiv B_{\tau _0,\ldots ,\tau _{m-1 }}$
and every
$\tau _j$
being an initial substring of some
$\sigma _i$
for
$i<n$
, or the sum of the lengths of the strings must go to 0, in which case we have
. But since X is infinite, this latter case gives
and of course
$\lambda $
is an initial segment of
$\sigma _0$
. -
(3) Let
$\{ \sigma _{0}, \ldots , \sigma _{n-1}\}$
and
$\{\tau _{0}, \ldots , \tau _{m-1}\}$
be two
$\subseteq $
-antichains. It is immediate by definition that
$$ \begin{align*} (\forall{j<m}\,)(\exists{i<n}\,)[ \tau_{j}\subseteq \sigma_{i}] \Rightarrow B_{\tau_0,\ldots,\tau_{m-1}}\leq B_{\sigma_0,\ldots, \sigma_{n-1}}. \end{align*} $$
Next, we suppose that
$B_{\tau _0,\ldots ,\tau _{m-1}}\leq B_{\sigma _0,\ldots , \sigma _{n-1}}$
and show
$\tau _j$
is an initial segment of some
$\sigma _i$
. In particular, we have that
$A_{\tau _j} \leq B_{\sigma _0,\ldots , \sigma _{n-1}}$
. We use the previous result to see that
$A_{\tau _j} \equiv B_{\rho _0,\ldots , \rho _k}$
for some antichain of
$\rho $
s which are initial segments of the sequence of
$\sigma $
s. But then
$A_{\tau _j}\geq A_{\rho _i}$
for each i, which implies that
$\rho _i\subseteq \tau _j$
for each
$i<k$
. Since the sequence of
$\rho $
s forms an antichain, we conclude that
$k=0$
and
$\rho _0=\tau _j$
. Then
$\tau _j$
is an initial substring of some
$\sigma $
.
We now recall some lattice-theoretic facts that will help us show that we indeed have an embedding of the free distributive lattice generated by the lower semilattice
.
Definition 3.8. Given a poset
$Q=\langle Q, \leq \rangle $
, and a subset
$X \subseteq Q$
, let
$(X]=\{y\in Q: \exists {x \in X}\, (y\leq x)\}$
.
Let also
$P_{<\infty }(Q)$
be the set of nonempty finite subsets of Q.
Let
$\mathcal {L}(Q)=\langle \{(X]: X \in P_{<\infty }(Q)\}, \subseteq \rangle $
, and let us use the symbol
$(P_{<\infty }(Q)]$
to denote the universe of this poset.
Lemma 3.9. If Q is a lower semilattice then
$\mathcal {L}(Q)$
is the free distributive lattice generated by the lower semilattice Q. If Q is a lower semilattice with least element then
$\mathcal {L}(Q)$
has least element.
Proof Suppose that
$Q=\langle Q, \wedge \rangle $
is a lower semilattice. Clearly
$\mathcal {L}(Q)$
is an upper semilattice, with join operation
$\lor $
given by
$(X]\lor (Y]=(X \cup Y]$
, and having inclusion as the partial ordering relation. To show that
$\mathcal {L}(Q)$
is also a lower semilattice, it is enough to observe that it is closed under
$\cap $
, as if
$X,Y \in P_{<\infty }(Q)$
then
$(X] \cap (Y]=(\{x\wedge y: x \in X, y \in Y\}]$
. A straightforward calculation shows that the lattice is distributive.
Next we show that
$\mathcal {L}(Q)$
enjoys the universal property of free objects, making it the free distributive lattice on the lower semilattice Q. Let
$i: Q \rightarrow (P_{<\infty }(Q)]$
be given by
$i(x)=(\{x\}]$
. Then i preserves meets. If now
$L=\langle L, \lor , \wedge\rangle $
is a distributive lattice, and
$f: Q\rightarrow L$
preserves meets, then the mapping
$h: (P_{<\infty }(Q)] \rightarrow L$
, given by
$h((X])=\bigvee _{x\in X} f(x)$
is easily seen to be the unique lattice-theoretic homomorphism so that
$f=h\circ i$
. To see that h preserves meets, notice that by distributivity and properties of f,
$$ \begin{align*} h((X])\wedge h((Y])&=\left(\bigvee_{x\in X} f(x)\right) \wedge \left(\bigvee_{y\in Y} f(y)\right)\\ &=\bigvee_{x\in X, y \in Y} \left(f(x) \wedge f(y) \right)\\ &=\bigvee_{x\in X, y \in Y} f(x\wedge y)=h((X]\cap (Y]). \end{align*} $$
If
$Q=\langle Q, \wedge , 0\rangle $
is a lower semilattice with least element
$0$
, then the least element of
$\mathcal {L}(Q)$
is
$(\{0\}]$
.
Remark 3.10. Notice that if
$Q=\langle Q, \wedge , 0\rangle $
is a lower semilattice with least element then
$\mathcal {L}(Q)$
can be alternatively viewed as the free distributive lattice with least element generated by the lower semilattice Q with least element. The definition of the free distributive lattice with least element is defined as in Definition 3.3, but requiring all maps to preserve least element. That is, the free distributive lattice with least element generated by the lower semilattice with least element
$\langle Q,\wedge ,0\rangle $
is a distributive lattice D with least element which has a function
$i: Q\rightarrow D$
which preserves meets and least element, so that
$D,i$
satisfy the universal property: If L is any distributive lattice with least element and
$f:Q\rightarrow L$
preserves meets and least element, then there is a unique lattice-homomorphism preserving least element
$h: D\rightarrow L$
so that
$f=h\circ i$
.
Corollary 3.11. The free distributive lattice
on the lower semilattice
embeds as an initial segment of the degrees
${\textbf {Ceers} \smallsetminus \textbf {Fin}}$
.
Proof If
$Q=\langle Q, \leq \rangle $
is a poset, and
$X \in P_{<\infty }(Q)$
then there exists a finite
$\leq $
-antichain
$X'$
such that
$(X]=(X']$
: This
$X'$
is unique, and we denote it by
$X^{M}$
, since it is the set of the
$\leq $
-maximal elements in X. It is not difficult to see that if
$X,Y \in P_{<\infty }(Q)$
then
$$ \begin{align*} (X] \subseteq (Y] \Leftrightarrow (\forall{x\in X^{M}}\,)(\exists{y \in Y^{M}}\,)[x \leq y]. \end{align*} $$
Therefore we can use items (1) and (3) of Theorem 3.7 to show that the mapping
$$ \begin{align*} (X] \mapsto B_{\sigma_{0}, \ldots, \sigma_{n-1}} \end{align*} $$
(where X is a nonempty finite subset of
and
$X^{M}=\{\sigma _{0}, \ldots , \sigma _{n-1}\}$
) order-theoretically embeds
to the degrees of ceers. Item (2) of Theorem 3.7 shows that, up to equivalence, the range of this embedding is an initial segment of
${\textbf {Ceers} \smallsetminus \textbf {Fin}}$
. The least element in the embedding is the degree of
.
Notice that the embedding of the previous corollary maps meets of
to meets of
(since the image is an initial segment), but maps joins to joins of the image, which need not be joins of
. We now show that in fact the embedding distinctly does not map joins to joins. In fact, even in the simplest case where
$\sigma \wedge \tau \neq \lambda $
,
$A_\sigma $
and
$A_\tau $
do not have a join. In the following, if
$u,v$
are numbers, then
$\langle u,v\rangle $
denotes the string of length
$2$
comprised of
$u,v$
.
Observation 3.12. For any
with
$j\neq k$
,
$A_{\langle i,j\rangle }$
and
$A_{\langle i, k\rangle }$
do not have a join in the ceers. In particular,
$B_{\langle i,j\rangle ,\langle i,k\rangle }$
is not a join since
.
Proof From Theorem 3.7,
$B_{\langle i,j\rangle ,\langle i,k\rangle }$
bounds no other degree which is above both
$A_{\langle i,j\rangle }$
and
$A_{\langle i, k\rangle }$
; thus if there is a join of
$A_{\langle i,j\rangle }$
with
$A_{\langle i, k\rangle }$
, the join must be
$B_{\langle i,j\rangle ,\langle i,k\rangle }$
. So, it suffices to show
.
We will show this by taking a supposed reduction g of
$B_{\langle i,j\rangle ,\langle i,k\rangle }$
to
and showing that in this case some
$S_\alpha $
for
$\alpha $
of the form
$\alpha =(\alpha ^{-})\,\widehat {\;}\infty $
on the true path in the construction of
$A_{\langle i,j\rangle }$
must be sent entirely to the evens or entirely to the odds, but it can’t be the odds as
$A_{\langle i,j\rangle } \leq A_{\langle i,j\rangle }{\restriction} S_\alpha $
and
$A_{\langle i,j\rangle } \not \leq A_{\langle i,k\rangle }$
. The symmetric argument shows that some
$S_{\alpha '}$
for
$\alpha '$
on the true path in the construction of
$A_{\langle i,k\rangle }$
must be sent entirely to the odds. But then the two copies of
$A_{i}$
which are equivalent in
$B_{\langle i,j\rangle ,\langle i,k\rangle }$
via
$\sim $
are not equivalent in their g-images, yielding a contradiction.
Thus suppose that
$B_{\langle i,j\rangle ,\langle i,k\rangle }$
reduces to
via the function g. Let X be the set of x so that
$g(2x)$
is odd. That is, X is the pre-image of
$A_{\langle i, k\rangle }$
on the copy of
$A_{\langle i,j\rangle }$
inside
$B_{\langle i,j\rangle ,\langle i,k\rangle }$
. Similarly, let Y be the set of x so that
$g(2x)$
is even. That is, Y is the preimage of
$A_{\langle i,j\rangle }$
on the copy of
$A_{\langle i,j\rangle }$
inside
$B_{\langle i,j\rangle ,\langle i,k\rangle }$
. Since
$X=W_a$
and
$Y=W_b$
for some
give a partition of
, either the true path in the construction of
$A_{\langle i,j\rangle }$
has
$\infty $
as the ath bit or the bth bit. To see this, suppose both the ath bit and the bth bit of the true path is an f. Then for any
$\beta $
along the true path of length greater than a or b,
$S_\beta \smallsetminus K$
(referencing the sets with these names in the construction of
$A_{\langle i,j\rangle }$
) would be disjoint from both X and Y. But X and Y partition
, so this is impossible.
If the former is the case (i.e., the ath bit is
$\infty $
), then by Lemma 2.15 we have
$A_{\langle i,j\rangle } \leq A_{\langle i,j\rangle }{\restriction} S_{\alpha } \leq A_{\langle i,j\rangle }{\restriction} X\leq A_{\langle i, k\rangle }$
which contradicts Corollary 3.1, and thus the latter must be the case. But then an entire
$S_\alpha $
is contained in Y for some
. Thus every class in K intersects Y. So, the entire copy of
$A_i$
inside
$A_{\langle i,j\rangle }$
must be sent to even numbers. The symmetric argument (taking X to be the set of x so that
$g(2x+1)$
is even, and Y to be the set of x so that
$g(2x+1)$
is odd) shows that the entire copy of
$A_i$
inside
$A_{\langle i, k\rangle }$
must be sent to odd numbers. But then g is not a reduction after all, because the two copies of
$A_i$
(the one inside
$A_{\langle i,j\rangle }$
and the one inside
$A_{\langle i, k\rangle }$
) are equivalent in
$B_{\langle i,j\rangle ,\langle i,k\rangle }$
, but their images are not equivalent in
.
We now characterize the initial segments of
, giving a characterization of the countable distributive lattices that we know how to embed as an initial segment of
${\textbf {Ceers} \smallsetminus \textbf {Fin}}$
.
Corollary 3.13. A countable distributive lattice L is isomorphic to an initial segment of
if and only if
-
(1) L satisfies the descending chain condition
$($
i.e., there is no infinite descending chain
$);$
-
(2) the poset of its join-irreducible elements is order-theoretic isomorphic to a subtree of
.
Therefore, any countable distributive lattice satisfying these conditions can be embedded as an initial segment of
${\textbf {Ceers} \smallsetminus \textbf {Fin}}$
.
Proof Let L satisfy the descending chain condition, and let J be the partially ordered set of its join-irreducible elements. Then every element a of L can be identified with the finite antichain of J comprised of the maximal elements of J which are below a [Reference Balbes and Dwinger6, Section III.2]. Therefore (looking at the proof of Lemma 3.9), it is easy to see that if J is a lower semilattice then L is isomorphic with
$\mathcal {L}(J)$
. Suppose in addition that J is (up to isomorphism) a subtree of
. Then clearly this isomorphism extends to an isomorphism of
$\mathcal {L}(J)$
with an initial segment of
. It follows that if L satisfies the two conditions of the corollary then L is isomorphic to an initial segment of
${\textbf {Ceers} \smallsetminus \textbf {Fin}}$
.
In the other direction, suppose that L is isomorphic to an initial segment of
. Then trivially L satisfies the descending chain condition. Moreover the isomorphism must send the join-irreducible elements of L to an initial segment of join-irreducible elements of
which are ceers of the form
$A_{\sigma }$
, so after all J is isomorphic to a subtree of
.
Acknowledgments
Andrewswas partially supported by NSF Grant 1600228. Sorbi is a member of INDAM-GNSAGA, and he was partially supported by PRIN 2017 Grant “Mathematical Logic: models, sets, computability.”
