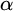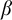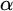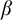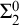1 Introduction
1.1 Motivation and basic definitions
The goal of this paper is to shed light on our understanding of large scale properties and patterns of infinite strings. Our hope is to answer the questions of the following types. How does one define large scale properties of infinite strings? What does it mean for two strings to possess the same large scale invariants? How can we compare large scale properties of one string with those of the other string? What are the large scale characteristics of (algorithmically) random strings? To answer these and similar types of questions we employ concepts and ideas from coarse geometry and geometric group theory.
In coarse geometry and geometric group theory, a foundational concept is that of quasi-isometry between metric spaces. Suppose that we are given two metric spaces
![]() $\mathcal M_1=(M_1, d_1)$
and
$\mathcal M_1=(M_1, d_1)$
and
![]() $\mathcal M_2=(M_2, d_2)$
. A map
$\mathcal M_2=(M_2, d_2)$
. A map
![]() $\,f:M_1\rightarrow M_2$
is called an
$\,f:M_1\rightarrow M_2$
is called an
![]() $(A,B,C)$
-quasi-isometry, where
$(A,B,C)$
-quasi-isometry, where
![]() $A\geqslant 1$
,
$A\geqslant 1$
,
![]() $B\geqslant 0$
, and
$B\geqslant 0$
, and
![]() $C\geqslant 0$
, if the following two properties are satisfied:
$C\geqslant 0$
, if the following two properties are satisfied:
-
1. For all
 $x,y\in M_1$
we have
$x,y\in M_1$
we have  $$ \begin{align*}(1/A) \cdot d_1(x,y) -B \leqslant d_2(f(x), f(y))\leqslant A \cdot d_1(x,y) +B. \end{align*} $$
$$ \begin{align*}(1/A) \cdot d_1(x,y) -B \leqslant d_2(f(x), f(y))\leqslant A \cdot d_1(x,y) +B. \end{align*} $$
-
2. For every element
 $y\in M_2$
there is an
$y\in M_2$
there is an
 $x\in M_1$
such that
$x\in M_1$
such that
 $d_2(y, f(x))\leqslant C$
.
$d_2(y, f(x))\leqslant C$
.
We call the first property quasi-isometric inequality, the second one density property, and the constants
![]() $A, B, C$
will be called quasi-isometry constants (of the mapping f).
$A, B, C$
will be called quasi-isometry constants (of the mapping f).
Let
![]() $\,f:\mathcal M_1\rightarrow \mathcal M_2$
be an
$\,f:\mathcal M_1\rightarrow \mathcal M_2$
be an
![]() $(A,B,C)$
-quasi-isometry. If
$(A,B,C)$
-quasi-isometry. If
![]() $B=0$
, the mapping becomes bi-Lipschitz (and hence continuous) and injective. Therefore the quasi-isometry f can be viewed as a bi-Lipschitz map with distortion B between the metric spaces (in case
$B=0$
, the mapping becomes bi-Lipschitz (and hence continuous) and injective. Therefore the quasi-isometry f can be viewed as a bi-Lipschitz map with distortion B between the metric spaces (in case
![]() $B>0$
). If
$B>0$
). If
![]() $C=0$
, the quasi-isometry f becomes onto.
$C=0$
, the quasi-isometry f becomes onto.
The quasi-isometry relation between metric spaces is an equivalence relation. Transitivity and reflexivity of this relation is evident. To see that this relation is symmetric, consider an
![]() $(A,B,C)$
-quasi-isometry
$(A,B,C)$
-quasi-isometry
![]() $\,f:\mathcal M_1\rightarrow \mathcal M_2$
. Define
$\,f:\mathcal M_1\rightarrow \mathcal M_2$
. Define
![]() $\,\bar {f}$
which “reverses” f from
$\,\bar {f}$
which “reverses” f from
![]() $\mathcal M_2$
into
$\mathcal M_2$
into
![]() $\mathcal M_1$
as follows. For all
$\mathcal M_1$
as follows. For all
![]() $y\in M_2$
, if
$y\in M_2$
, if
![]() $y\in Range(f)$
, then select an x from
$y\in Range(f)$
, then select an x from
![]() $\,f^{-1}(y)$
and set
$\,f^{-1}(y)$
and set
![]() $\,\bar {f}(y)=x$
. Otherwise, select an
$\,\bar {f}(y)=x$
. Otherwise, select an
![]() $x^{\prime }\in M_1$
such that
$x^{\prime }\in M_1$
such that
![]() $d_2(y, f(x^{\prime }))\leqslant C$
and set
$d_2(y, f(x^{\prime }))\leqslant C$
and set
![]() $\,\bar {f}(y)=x^{\prime }$
. It is easy to see that
$\,\bar {f}(y)=x^{\prime }$
. It is easy to see that
![]() $\,\bar {f}$
determines a quasi-isometry from metric space
$\,\bar {f}$
determines a quasi-isometry from metric space
![]() $\mathcal M_2$
into
$\mathcal M_2$
into
![]() $\mathcal M_1$
.
$\mathcal M_1$
.
We give two examples. For the first example, consider the spaces
![]() $\mathbb Z^n$
(the n-dimensional grid of integers) and
$\mathbb Z^n$
(the n-dimensional grid of integers) and
![]() $\mathbb R^n$
with their natural metrics. These are quasi-isometric via the identity map from
$\mathbb R^n$
with their natural metrics. These are quasi-isometric via the identity map from
![]() $\mathbb Z^n$
into
$\mathbb Z^n$
into
![]() $\mathbb R^n$
. Informally, two metric spaces
$\mathbb R^n$
. Informally, two metric spaces
![]() $\mathcal M_1$
and
$\mathcal M_1$
and
![]() $\mathcal M_2$
are quasi-isometric if these spaces look the same from far away. We will make this comment precise in the section on asymptotic cones.
$\mathcal M_2$
are quasi-isometric if these spaces look the same from far away. We will make this comment precise in the section on asymptotic cones.
The second example is from group theory. Let G be a finitely generated group, say with a generator set S. Consider the Cayley graph
![]() $\Gamma (G,S)$
of G based on S. The metric in
$\Gamma (G,S)$
of G based on S. The metric in
![]() $\Gamma (G,S)$
is given by the shortest-path distance in the graph
$\Gamma (G,S)$
is given by the shortest-path distance in the graph
![]() $\Gamma (G,S)$
. By varying the set S of generators of the group, we vary the Cayley graphs, and hence corresponding metric spaces. It turns out that all these metric spaces are quasi-isometric to each other. In other words, the quasi-isometry class of the Cayley graphs
$\Gamma (G,S)$
. By varying the set S of generators of the group, we vary the Cayley graphs, and hence corresponding metric spaces. It turns out that all these metric spaces are quasi-isometric to each other. In other words, the quasi-isometry class of the Cayley graphs
![]() $\Gamma (G,S)$
is invariant of the group G even if we change the generators of the group. It turns out that some important properties of groups are quasi-isometry invariants. Examples include being virtually nilpotent, virtually free, hyperbolic, having polynomial growth rate, being finitely presentable, having decidable word problem, having the same asymptotic cones [Reference Van Den Dries and Wilkie13, Reference Drutu and Kapovich4, Reference Gromov, Niblo and Roller7]. Studying quasi-isometry invariants of groups proved to be crucial in solving many problems in group theory [Reference Gromov5
–
Reference Gromov, Niblo and Roller7]. Nowadays finding quasi-isometry invariants of groups is an important theme in geometric group theory.
$\Gamma (G,S)$
is invariant of the group G even if we change the generators of the group. It turns out that some important properties of groups are quasi-isometry invariants. Examples include being virtually nilpotent, virtually free, hyperbolic, having polynomial growth rate, being finitely presentable, having decidable word problem, having the same asymptotic cones [Reference Van Den Dries and Wilkie13, Reference Drutu and Kapovich4, Reference Gromov, Niblo and Roller7]. Studying quasi-isometry invariants of groups proved to be crucial in solving many problems in group theory [Reference Gromov5
–
Reference Gromov, Niblo and Roller7]. Nowadays finding quasi-isometry invariants of groups is an important theme in geometric group theory.
Recall that by infinite string we mean a mapping
![]() $\alpha $
from
$\alpha $
from
![]() $\omega $
(the set of natural numbers) into a finite alphabet
$\omega $
(the set of natural numbers) into a finite alphabet
![]() $\Sigma $
. So,
$\Sigma $
. So,
![]() $\alpha $
is viewed as the infinite sequence
$\alpha $
is viewed as the infinite sequence
![]() $\alpha (0) \alpha (1) \alpha (2) \ldots $
. Natural numbers
$\alpha (0) \alpha (1) \alpha (2) \ldots $
. Natural numbers
![]() $i\in \omega $
are called positions of the string
$i\in \omega $
are called positions of the string
![]() $\alpha $
. In formal language theory, logic and applications, infinite strings
$\alpha $
. In formal language theory, logic and applications, infinite strings
![]() $\alpha $
are one of the main objects of investigation. These objects are discrete and somewhat boring from a geometry point of view. How are the coarse geometry concepts (e.g., quasi-isometry) relevant to the study of large scale properties of infinite strings? How does one introduce the concepts of coarse geometry into understanding large scale properties of the infinite strings? One possible answer comes from a simple observation that each string
$\alpha $
are one of the main objects of investigation. These objects are discrete and somewhat boring from a geometry point of view. How are the coarse geometry concepts (e.g., quasi-isometry) relevant to the study of large scale properties of infinite strings? How does one introduce the concepts of coarse geometry into understanding large scale properties of the infinite strings? One possible answer comes from a simple observation that each string
![]() $\alpha $
has the natural metric inherited from the set
$\alpha $
has the natural metric inherited from the set
![]() $\omega $
of natural numbers. The elements of
$\omega $
of natural numbers. The elements of
![]() $\alpha $
are positions
$\alpha $
are positions
![]() $i,j$
in
$i,j$
in
![]() $\alpha $
and the distance
$\alpha $
and the distance
![]() $d_{\alpha }(i,j)$
between the positions is the natural distance
$d_{\alpha }(i,j)$
between the positions is the natural distance
![]() $|i-j|$
. So,
$|i-j|$
. So,
![]() $\alpha $
as a metric space is simply
$\alpha $
as a metric space is simply
![]() $(\omega ; d_{\alpha })$
; the quasi-isometry type of
$(\omega ; d_{\alpha })$
; the quasi-isometry type of
![]() $(\omega ; d_{\alpha })$
is the metric space
$(\omega ; d_{\alpha })$
is the metric space
![]() $\mathbb R_{\geqslant 0}$
of all positive reals. So, from a quasi-isometry view point,
$\mathbb R_{\geqslant 0}$
of all positive reals. So, from a quasi-isometry view point,
![]() $\alpha $
viewed as a metric space
$\alpha $
viewed as a metric space
![]() $(\omega ; d)$
is still somewhat uneventful. However, one crucial difference between the metric spaces
$(\omega ; d)$
is still somewhat uneventful. However, one crucial difference between the metric spaces
![]() $(\omega ; d_{\alpha })$
and
$(\omega ; d_{\alpha })$
and
![]() $\alpha $
from the setting of large scale/coarse geometry is that the metric space
$\alpha $
from the setting of large scale/coarse geometry is that the metric space
![]() $\alpha $
possesses the natural coloring associated with it. Namely, for every position
$\alpha $
possesses the natural coloring associated with it. Namely, for every position
![]() $i\in \omega $
in
$i\in \omega $
in
![]() $\alpha $
, the color of the position i is
$\alpha $
, the color of the position i is
![]() $\sigma $
exactly when
$\sigma $
exactly when
![]() $\alpha (i)=\sigma $
.
$\alpha (i)=\sigma $
.
The observation above suggests the idea of applying the notions of coarse geometry (such as the concept of quasi-isometry) to colored metric spaces. Precisely this is what we propose in this paper. We investigate quasi-isometries of colored metric spaces with strings
![]() $\alpha $
as our primary objects (as colored metric spaces), thus initiating the study of large scale properties of strings.
$\alpha $
as our primary objects (as colored metric spaces), thus initiating the study of large scale properties of strings.
A colored metric space
![]() $\mathcal M$
is a tuple
$\mathcal M$
is a tuple
![]() $(M; d, Cl)$
, where
$(M; d, Cl)$
, where
![]() $(M;d)$
is the underlying metric space with metric d, and
$(M;d)$
is the underlying metric space with metric d, and
![]() $Cl: M \rightarrow 2^{\Sigma }$
is a color function; the set
$Cl: M \rightarrow 2^{\Sigma }$
is a color function; the set
![]() $\Sigma $
is a finite set of colors called an alphabet. If
$\Sigma $
is a finite set of colors called an alphabet. If
![]() $\sigma \in Cl(m) $
then we say that the element
$\sigma \in Cl(m) $
then we say that the element
![]() $m\in M$
has color
$m\in M$
has color
![]() $\sigma $
. We allow elements to have several (including none) colors.
$\sigma $
. We allow elements to have several (including none) colors.
Example 1.1. As mentioned above, infinite strings
![]() $\alpha $
over
$\alpha $
over
![]() $\Sigma $
are colored metric spaces of the form
$\Sigma $
are colored metric spaces of the form
![]() $(\omega ; d, \alpha )$
, where d is the natural metric (so, for all
$(\omega ; d, \alpha )$
, where d is the natural metric (so, for all
![]() $i, j \in \omega $
we have
$i, j \in \omega $
we have
![]() $d(i,j)=|i-j|$
) and
$d(i,j)=|i-j|$
) and
![]() $\alpha : \omega \rightarrow \Sigma $
is the color function. Every element in
$\alpha : \omega \rightarrow \Sigma $
is the color function. Every element in
![]() $\alpha $
has a unique color. We always assume that the cardinality
$\alpha $
has a unique color. We always assume that the cardinality
![]() $|\Sigma |$
of
$|\Sigma |$
of
![]() $\Sigma $
is at least
$\Sigma $
is at least
![]() $2$
. So, we identify the colored metric space
$2$
. So, we identify the colored metric space
![]() $(\omega ; d,\alpha )$
with
$(\omega ; d,\alpha )$
with
![]() $\alpha $
.
$\alpha $
.
Denote the set of all infinite strings over
![]() $\Sigma $
, considered as colored metric spaces, by
$\Sigma $
, considered as colored metric spaces, by
![]() $\Sigma ^{\omega }$
. These metric spaces will be our main objects of study. The set of all finite words over
$\Sigma ^{\omega }$
. These metric spaces will be our main objects of study. The set of all finite words over
![]() $\Sigma $
is denoted by
$\Sigma $
is denoted by
![]() $\Sigma ^{\star }$
.
$\Sigma ^{\star }$
.
Example 1.2. Let
![]() $G=(V; E, Cl)$
be a colored graph. The graph G has its natural distance d inherited from the path-distance metric on G. Here we assume that the graph
$G=(V; E, Cl)$
be a colored graph. The graph G has its natural distance d inherited from the path-distance metric on G. Here we assume that the graph
![]() $(V,E)$
is symmetric (that is, E is subset of the set of 2-element subsets of V), and
$(V,E)$
is symmetric (that is, E is subset of the set of 2-element subsets of V), and
![]() $Cl:V\rightarrow \Sigma $
is the given coloring function. For d to be the proper metric we need to assume that G is connected.
$Cl:V\rightarrow \Sigma $
is the given coloring function. For d to be the proper metric we need to assume that G is connected.
We now adapt the definition of quasi-isometry on metric spaces (given at the beginning of this section) for colored metric spaces.
Definition 1.3. Let
![]() $\mathcal M_1=(M_1; d_1, Cl_1)$
and
$\mathcal M_1=(M_1; d_1, Cl_1)$
and
![]() $\mathcal M_2=(M_2; d_2, Cl_2)$
be two colored metric spaces. A color preserving quasi-isometry
$\mathcal M_2=(M_2; d_2, Cl_2)$
be two colored metric spaces. A color preserving quasi-isometry
![]() $\,f: M_1\rightarrow M_2$
will be called a quasi-isometry from
$\,f: M_1\rightarrow M_2$
will be called a quasi-isometry from
![]() $\mathcal M_1$
into
$\mathcal M_1$
into
![]() $\mathcal M_2$
.
$\mathcal M_2$
.
From now on we write
![]() $\mathcal M_1\leqslant _{QI} \mathcal M_2$
if there is a quasi-isometry from
$\mathcal M_1\leqslant _{QI} \mathcal M_2$
if there is a quasi-isometry from
![]() $\mathcal M_1$
into
$\mathcal M_1$
into
![]() $\mathcal M_2$
. As mentioned above, for metric spaces (with no colors) the relation
$\mathcal M_2$
. As mentioned above, for metric spaces (with no colors) the relation
![]() $\leqslant _{QI}$
is an equivalence relation, and hence the relation is symmetric. In contrast, for colored metric spaces, however, the symmetry property does not hold. For instance, the mapping
$\leqslant _{QI}$
is an equivalence relation, and hence the relation is symmetric. In contrast, for colored metric spaces, however, the symmetry property does not hold. For instance, the mapping
![]() $\,f: \omega \rightarrow \omega $
(on the metric space
$\,f: \omega \rightarrow \omega $
(on the metric space
![]() $(\omega ; d))$
defined as
$(\omega ; d))$
defined as
![]() $\,f(i)=2i$
is a quasi-isometry from the infinite string
$\,f(i)=2i$
is a quasi-isometry from the infinite string
![]() $0^{\omega }=00000\ldots $
into the string
$0^{\omega }=00000\ldots $
into the string
![]() $(01)^{\omega }=010101\ldots $
. There is no quasi-isometric mapping in the opposite direction.
$(01)^{\omega }=010101\ldots $
. There is no quasi-isometric mapping in the opposite direction.
If
![]() $\mathcal M_1 \leqslant _{QI} \mathcal M_2$
and
$\mathcal M_1 \leqslant _{QI} \mathcal M_2$
and
![]() $\mathcal M_2 \leqslant _{QI} \mathcal M_1$
then we write this by
$\mathcal M_2 \leqslant _{QI} \mathcal M_1$
then we write this by
![]() $\mathcal M_1\sim _{QI} \mathcal M_2$
. The relation
$\mathcal M_1\sim _{QI} \mathcal M_2$
. The relation
![]() $\sim _{QI}$
is an equivalence relation in the class of all colored metric spaces, in particular on the set
$\sim _{QI}$
is an equivalence relation in the class of all colored metric spaces, in particular on the set
![]() $\Sigma ^{\omega }$
. Formally, we give the following definition:
$\Sigma ^{\omega }$
. Formally, we give the following definition:
Definition 1.4. The equivalence classes of
![]() $\sim _{QI}$
on
$\sim _{QI}$
on
![]() $\Sigma ^{\omega }$
are called quasi-isometry types or, equivalently, large scale geometries. From now on we set
$\Sigma ^{\omega }$
are called quasi-isometry types or, equivalently, large scale geometries. From now on we set
![]() $\Sigma _{QI}^{\omega }=\Sigma ^{\omega }/{\sim}_{QI}$
. Denote the large scale geometry of string
$\Sigma _{QI}^{\omega }=\Sigma ^{\omega }/{\sim}_{QI}$
. Denote the large scale geometry of string
![]() $\alpha $
by
$\alpha $
by
![]() $[\alpha ]$
. Thus,
$[\alpha ]$
. Thus,
Remark 1.5. A simple yet important note is the following. If f is a color preserving quasi-isometry from
![]() $\mathcal M_1$
into
$\mathcal M_1$
into
![]() $\mathcal M_2$
and there is a constant D such that for all
$\mathcal M_2$
and there is a constant D such that for all
![]() $y\in M_2$
there exists an
$y\in M_2$
there exists an
![]() $x\in M_1$
with
$x\in M_1$
with
![]() $d_2(y, f(x))\leqslant D$
and
$d_2(y, f(x))\leqslant D$
and
![]() $Cl_1(x)=Cl_2(y)$
, then one can construct a quasi-isometry from
$Cl_1(x)=Cl_2(y)$
, then one can construct a quasi-isometry from
![]() $\mathcal M_2$
to
$\mathcal M_2$
to
![]() $\mathcal M_1$
by “reversing” the mapping f as we described earlier.
$\mathcal M_1$
by “reversing” the mapping f as we described earlier.
The fact that
![]() $\leqslant _{QI}$
on colored metric spaces is not symmetric implies that we can compare large scale geometries of these spaces, and consider the partial order
$\leqslant _{QI}$
on colored metric spaces is not symmetric implies that we can compare large scale geometries of these spaces, and consider the partial order
![]() $\leqslant _{QI}$
on the quasi-isometry types. In particular, the partial order
$\leqslant _{QI}$
on the quasi-isometry types. In particular, the partial order
![]() $\leqslant _{QI}$
can be restricted to the large scale geometries of colored metric spaces over a fixed underlying metric space such that
$\leqslant _{QI}$
can be restricted to the large scale geometries of colored metric spaces over a fixed underlying metric space such that
![]() $\omega $
or
$\omega $
or
![]() $\mathbb Z$
or
$\mathbb Z$
or
![]() $\mathbb Z^2$
with their natural metrics. From this viewpoint the quasi-isometry on colored metric spaces is a much refined version of the usual quasi-isometry relation on uncolored metric space. This is because the quasi-isometry type of every uncolored metric space trivializes to a singleton.
$\mathbb Z^2$
with their natural metrics. From this viewpoint the quasi-isometry on colored metric spaces is a much refined version of the usual quasi-isometry relation on uncolored metric space. This is because the quasi-isometry type of every uncolored metric space trivializes to a singleton.
1.2 Informal description of results
Introduction of large scale geometries on colored metric spaces of the type
![]() $\alpha $
and the quasi-isometry relation
$\alpha $
and the quasi-isometry relation
![]() $\leqslant _{QI}$
poses many natural questions. Most of these are mathematical translations of the questions that we posed at the beginning of this paper.
$\leqslant _{QI}$
poses many natural questions. Most of these are mathematical translations of the questions that we posed at the beginning of this paper.
The first question is concerned with understanding the partial order
![]() $\leqslant _{QI}$
on the set
$\leqslant _{QI}$
on the set
![]() $\Sigma _{QI}^{\omega }$
of all large scale geometries. The order presents an algebraic tool aimed at classification of global patterns that occur on strings. Among many results, we prove that the order has the greatest large scale geometry, and in Section 3 we show that the partial order has infinite chains and infinite antichains. We also study density property of the partial
$\Sigma _{QI}^{\omega }$
of all large scale geometries. The order presents an algebraic tool aimed at classification of global patterns that occur on strings. Among many results, we prove that the order has the greatest large scale geometry, and in Section 3 we show that the partial order has infinite chains and infinite antichains. We also study density property of the partial
![]() $\leqslant _{QI}$
. Recall that a partial order is dense if for any two distinct comparable elements x and y of the partial order there exists an element z strictly between x and y. We show that the density property is prevalent for the quasi-isometry order
$\leqslant _{QI}$
. Recall that a partial order is dense if for any two distinct comparable elements x and y of the partial order there exists an element z strictly between x and y. We show that the density property is prevalent for the quasi-isometry order
![]() $\leqslant _{QI}$
. We also prove that there are infinitely many minimal large scale geometries.
$\leqslant _{QI}$
. We also prove that there are infinitely many minimal large scale geometries.
The second question is related to understanding the quasi-isometry relation
![]() $\sim _{QI}$
on
$\sim _{QI}$
on
![]() $\Sigma ^{\omega }$
. One way to do it is to restrict the relation
$\Sigma ^{\omega }$
. One way to do it is to restrict the relation
![]() $\sim _{QI}$
to various subsets of infinite words and, given such a subset X, understand the partial order
$\sim _{QI}$
to various subsets of infinite words and, given such a subset X, understand the partial order
![]() $\leqslant _{QI}$
on the set of equivalence classes under
$\leqslant _{QI}$
on the set of equivalence classes under
![]() $\sim _{QI}$
in X. For instance, in Section 3.4 we restrict the relation
$\sim _{QI}$
in X. For instance, in Section 3.4 we restrict the relation
![]() $\sim _{QI}$
to eventually periodic strings, and give a full description of quasi-isometry types and the order
$\sim _{QI}$
to eventually periodic strings, and give a full description of quasi-isometry types and the order
![]() $\leqslant _{QI}$
on this class of strings. The other way is to simplify or refine the definition of quasi-isometry. Section 4.2 gives an intuitively syntactically easier yet equivalent definition of the relation
$\leqslant _{QI}$
on this class of strings. The other way is to simplify or refine the definition of quasi-isometry. Section 4.2 gives an intuitively syntactically easier yet equivalent definition of the relation
![]() $\leqslant _{QI}$
that we call component-wise reducibility. We also give a more refined version of
$\leqslant _{QI}$
that we call component-wise reducibility. We also give a more refined version of
![]() $\sim _{QI}$
, called color-equivalence. We show that color-equivalence is strictly stronger than
$\sim _{QI}$
, called color-equivalence. We show that color-equivalence is strictly stronger than
![]() $\sim _{QI}$
equivalence relation. Finally, it is natural to ask if quasi-isometric maps between strings can be replaced with order preserving quasi-isometric embeddings. We give a negative answer to this question; however, we prove that the answer is positive modulo
$\sim _{QI}$
equivalence relation. Finally, it is natural to ask if quasi-isometric maps between strings can be replaced with order preserving quasi-isometric embeddings. We give a negative answer to this question; however, we prove that the answer is positive modulo
![]() $\sim _{QI}$
equivalence relation.
$\sim _{QI}$
equivalence relation.
The third question is related to describing various sets of large scale geometries. So, let L be a set (usually called a language) of infinite strings over an alphabet
![]() $\Sigma $
. One naturally considers the set
$\Sigma $
. One naturally considers the set
![]() $[L]$
consisting of all large scale geometries of strings in L. Thus we have:
$[L]$
consisting of all large scale geometries of strings in L. Thus we have:
![]() $[L]=\{[\alpha ]\mid \alpha \in L\}$
. We call the set
$[L]=\{[\alpha ]\mid \alpha \in L\}$
. We call the set
![]() $[L]$
the atlas of L. The question we ask is related to understanding the atlas
$[L]$
the atlas of L. The question we ask is related to understanding the atlas
![]() $[L]$
given a description of L. In particular, a natural algorithmic question is if there exists an algorithm that, given descriptions of languages
$[L]$
given a description of L. In particular, a natural algorithmic question is if there exists an algorithm that, given descriptions of languages
![]() $L_1$
and
$L_1$
and
![]() $L_2$
, decides whether the atlases
$L_2$
, decides whether the atlases
![]() $[L_1]$
and
$[L_1]$
and
![]() $[L_2]$
coincide. In Section 5, we use Büchi automata as our description tools and provide a full characterization of the atlases defined by Büchi automata. Our characterization theorem implies that there are only finitely many atlases
$[L_2]$
coincide. In Section 5, we use Büchi automata as our description tools and provide a full characterization of the atlases defined by Büchi automata. Our characterization theorem implies that there are only finitely many atlases
![]() $[L]$
described by Büchi automata. As a consequence of our characterization, we show that for Büchi automata recognizable languages
$[L]$
described by Büchi automata. As a consequence of our characterization, we show that for Büchi automata recognizable languages
![]() $L_1$
and
$L_1$
and
![]() $L_2$
there is a linear time algorithm (in the size of automata) for deciding the equality of the atlases
$L_2$
there is a linear time algorithm (in the size of automata) for deciding the equality of the atlases
![]() $[L_1]$
and
$[L_1]$
and
![]() $[L_2]$
. This contrasts with the PSPACE completeness of the equality problem for Büchi languages. This part of the work links large scale geometries with automata theory and complexity theory.
$[L_2]$
. This contrasts with the PSPACE completeness of the equality problem for Büchi languages. This part of the work links large scale geometries with automata theory and complexity theory.
The fourth question addresses the complexity of quasi-isometry relation on infinite strings in terms of arithmetical hierarchy, thus connecting the topic with computability theory. Recall that isometry is color preserving and distance preserving map. So, quasi-isometry relation is weaker than isometry relation since each isometry is a quasi-isometry. Hence, one might expect that quasi-isometry is easier to detect than the isometry. We prove that the quasi-isometry relation on computable infinite strings is
![]() $\Sigma _2^0$
-complete. This is in contrast to
$\Sigma _2^0$
-complete. This is in contrast to
![]() $\Pi _1^0$
-completeness of the isometry relation on computable strings. These are explained in Section 6.
$\Pi _1^0$
-completeness of the isometry relation on computable strings. These are explained in Section 6.
The fifth question asks how one encodes large scale geometries of colored metric spaces
![]() $\alpha $
into “limit” structures. For this, we define structures obtained from “looking at
$\alpha $
into “limit” structures. For this, we define structures obtained from “looking at
![]() $\alpha $
from far away”. Dries and Wilkie [Reference Van Den Dries and Wilkie13], using ultrafilters, formalized this intuitive notion for metric spaces through the concept of asymptotic cone. Their work gave a logical context to Gromov’s work in [Reference Gromov5, Reference Gromov, Niblo and Roller7], where it is proved that groups of polynomial growth are virtually nilpotent. We invoke the concept of asymptotic cone and study the relationship between large scale geometries of infinite strings and their asymptotic cones. In Section 7 we prove theorems akin to results on asymptotic cones in geometric group theory. For instance, we show that asymptotic cones of Martin-Löf random strings coincide when scaling factors are computable. These results bridge the topic of this paper with algorithmic randomness and model theory.
$\alpha $
from far away”. Dries and Wilkie [Reference Van Den Dries and Wilkie13], using ultrafilters, formalized this intuitive notion for metric spaces through the concept of asymptotic cone. Their work gave a logical context to Gromov’s work in [Reference Gromov5, Reference Gromov, Niblo and Roller7], where it is proved that groups of polynomial growth are virtually nilpotent. We invoke the concept of asymptotic cone and study the relationship between large scale geometries of infinite strings and their asymptotic cones. In Section 7 we prove theorems akin to results on asymptotic cones in geometric group theory. For instance, we show that asymptotic cones of Martin-Löf random strings coincide when scaling factors are computable. These results bridge the topic of this paper with algorithmic randomness and model theory.
1.3 Basic properties of the order
 $(\Sigma _{QI}^{\omega }, \leqslant _{QI})$
$(\Sigma _{QI}^{\omega }, \leqslant _{QI})$
The quasi-isometry relation
![]() $\leqslant _{QI}$
on the strings set
$\leqslant _{QI}$
on the strings set
![]() $\Sigma ^{\omega }$
naturally defines the partially ordered set
$\Sigma ^{\omega }$
naturally defines the partially ordered set
![]() $ (\Sigma _{QI}^{\omega }, \leqslant _{QI})$
on the set of all large scale geometries
$ (\Sigma _{QI}^{\omega }, \leqslant _{QI})$
on the set of all large scale geometries
![]() $[\alpha ]$
. We denote this partially ordered set by
$[\alpha ]$
. We denote this partially ordered set by
![]() $\Sigma _{QI}^{\omega }$
, thus identifying it with its domain. We now need simple definitions related to partially ordered sets. Say that
$\Sigma _{QI}^{\omega }$
, thus identifying it with its domain. We now need simple definitions related to partially ordered sets. Say that
![]() $[\beta ]$
covers
$[\beta ]$
covers
![]() $[\alpha ]$
if
$[\alpha ]$
if
![]() $[\alpha ]\neq [\beta ]$
,
$[\alpha ]\neq [\beta ]$
,
![]() $[\alpha ]\leqslant _{QI} [\beta ]$
, and for all
$[\alpha ]\leqslant _{QI} [\beta ]$
, and for all
![]() $[\gamma ]$
such that
$[\gamma ]$
such that
![]() $[\alpha ]\leqslant _{QI} [\gamma ] \leqslant _{QI} [\beta ]$
we have
$[\alpha ]\leqslant _{QI} [\gamma ] \leqslant _{QI} [\beta ]$
we have
![]() $[\gamma ]=[\alpha ]$
or
$[\gamma ]=[\alpha ]$
or
![]() $[\gamma ]=[\beta ]$
. An element is an atom if it covers a minimal element in the partial order.
$[\gamma ]=[\beta ]$
. An element is an atom if it covers a minimal element in the partial order.
Here is an easy proposition. In this proposition
![]() $\sigma \in \Sigma $
; also for any finite word
$\sigma \in \Sigma $
; also for any finite word
![]() $v\in \Sigma ^{\star }$
,
$v\in \Sigma ^{\star }$
,
![]() $v^{\omega }$
denotes the infinite string
$v^{\omega }$
denotes the infinite string
![]() $vvvv\ldots $
. Part (2) of the proposition will be strengthened later.
$vvvv\ldots $
. Part (2) of the proposition will be strengthened later.
Proposition 1.6. The partial order
![]() $\Sigma _{QI}^{\omega }$
has the following properties:
$\Sigma _{QI}^{\omega }$
has the following properties:
-
1. There exists a greatest element.
-
2. There exist at least
 $|\Sigma |$
minimal elements.
$|\Sigma |$
minimal elements. -
3. There exist at least
 $|\Sigma |\cdot (|\Sigma |-1)/2$
atoms.
$|\Sigma |\cdot (|\Sigma |-1)/2$
atoms.
Proof Let
![]() $\Sigma = \{\sigma _1, ... , \sigma _k\}$
. For Part (1), we claim that
$\Sigma = \{\sigma _1, ... , \sigma _k\}$
. For Part (1), we claim that
![]() $\alpha = (\sigma _1...\sigma _k)^\omega $
is the greatest element in
$\alpha = (\sigma _1...\sigma _k)^\omega $
is the greatest element in
![]() $\Sigma _{QI}$
. Indeed, take any
$\Sigma _{QI}$
. Indeed, take any
![]() $\beta \in \Sigma ^{\omega }$
. We write
$\beta \in \Sigma ^{\omega }$
. We write
![]() $\alpha $
as
$\alpha $
as
![]() $v_0 v_1 \ldots $
where each
$v_0 v_1 \ldots $
where each
![]() $v_i$
is
$v_i$
is
![]() $\sigma _1\ldots \sigma _k$
. Define
$\sigma _1\ldots \sigma _k$
. Define
![]() $\,f:\beta \rightarrow \alpha $
so that f maps any position n (in
$\,f:\beta \rightarrow \alpha $
so that f maps any position n (in
![]() $\beta $
) to the position
$\beta $
) to the position
![]() $k_n$
in the portion
$k_n$
in the portion
![]() $v_n$
of the string
$v_n$
of the string
![]() $\alpha $
such that
$\alpha $
such that
![]() $\beta (n)=\alpha (k_n)$
. The mapping f is a witness of
$\beta (n)=\alpha (k_n)$
. The mapping f is a witness of
![]() $\beta \leqslant _{QI} \alpha $
. For Part (2), consider the quasi-isometry types
$\beta \leqslant _{QI} \alpha $
. For Part (2), consider the quasi-isometry types
![]() $[\sigma _{i}^{\omega }]$
. These form minimal elements in
$[\sigma _{i}^{\omega }]$
. These form minimal elements in
![]() $\Sigma _{QI}^{\omega }$
. Indeed, if
$\Sigma _{QI}^{\omega }$
. Indeed, if
![]() $\alpha \leqslant _{QI} \sigma ^{\omega }_i$
, then each element of
$\alpha \leqslant _{QI} \sigma ^{\omega }_i$
, then each element of
![]() $\alpha $
has color
$\alpha $
has color
![]() $\sigma _i$
. For Part (3), consider
$\sigma _i$
. For Part (3), consider
![]() $\sigma _i (\sigma _j)^{\omega }$
, where
$\sigma _i (\sigma _j)^{\omega }$
, where
![]() $i\neq j$
. Clearly,
$i\neq j$
. Clearly,
![]() $\sigma _j^{\omega }\leqslant _{QI} \sigma _i (\sigma _j)^{\omega }$
. Now assume that
$\sigma _j^{\omega }\leqslant _{QI} \sigma _i (\sigma _j)^{\omega }$
. Now assume that
![]() $\beta \neq \sigma _j^{\omega }$
and
$\beta \neq \sigma _j^{\omega }$
and
![]() $\beta \leqslant _{QI} \sigma _i (\sigma _j)^{\omega }$
. Then finitely many positions of
$\beta \leqslant _{QI} \sigma _i (\sigma _j)^{\omega }$
. Then finitely many positions of
![]() $\beta $
are colored with
$\beta $
are colored with
![]() $\sigma _i$
, and all other positions are colored with
$\sigma _i$
, and all other positions are colored with
![]() $\sigma _j$
. Hence,
$\sigma _j$
. Hence,
![]() $\beta \sim _{QI} \sigma _i (\sigma _j)^{\omega }$
. Therefore, each
$\beta \sim _{QI} \sigma _i (\sigma _j)^{\omega }$
. Therefore, each
![]() $\sigma _i (\sigma _j)^{\omega }$
is an atom in the partial order
$\sigma _i (\sigma _j)^{\omega }$
is an atom in the partial order
![]() $\Sigma _{QI}^{\omega }$
. Thus, we have found at least
$\Sigma _{QI}^{\omega }$
. Thus, we have found at least
![]() $k\cdot (k-1)/2$
of the atoms.⊣
$k\cdot (k-1)/2$
of the atoms.⊣
2 Small cross over lemma
A quasi-isometry
![]() $g:\alpha \rightarrow \beta $
can produce cross-overs, for example, pairs n and m of integers such that
$g:\alpha \rightarrow \beta $
can produce cross-overs, for example, pairs n and m of integers such that
![]() $n<m$
and
$n<m$
and
![]() $g(m)< g(n)$
. Note that this definition of cross-over uses the natural linear order present on
$g(m)< g(n)$
. Note that this definition of cross-over uses the natural linear order present on
![]() $\omega $
. The definition of quasi-isometry does not obviously prohibit large cross-overs; in other words, for n and m with
$\omega $
. The definition of quasi-isometry does not obviously prohibit large cross-overs; in other words, for n and m with
![]() $n<m$
the distances
$n<m$
the distances
![]() $g(m)-g(n)$
might potentially be unbounded. For instance, the following two colored metric spaces
$g(m)-g(n)$
might potentially be unbounded. For instance, the following two colored metric spaces
![]() $\ldots 00000001111111\ldots $
and
$\ldots 00000001111111\ldots $
and
![]() $\ldots 11111110000000\ldots $
with underlining domain
$\ldots 11111110000000\ldots $
with underlining domain
![]() $\mathbb Z$
are quasi-isometric and have arbitrary large cross-overs. Nevertheless, the next lemma, that we call Small Cross Over Lemma, shows that there is a uniform bound on cross-overs on colored metric space
$\mathbb Z$
are quasi-isometric and have arbitrary large cross-overs. Nevertheless, the next lemma, that we call Small Cross Over Lemma, shows that there is a uniform bound on cross-overs on colored metric space
![]() $\alpha \in \Sigma ^{\omega }$
. Namely, for the quasi-isometric map
$\alpha \in \Sigma ^{\omega }$
. Namely, for the quasi-isometric map
![]() $g:\alpha \rightarrow \beta $
there exists a positive constant D such that for all
$g:\alpha \rightarrow \beta $
there exists a positive constant D such that for all
![]() $n<m$
such that
$n<m$
such that
![]() $g(m)<g(n)$
we have
$g(m)<g(n)$
we have
![]() $g(n)-g(m)\leqslant D$
. We note that the proof of the lemma does not use the fact that the spaces are colored. In this sense, the lemma is a quasi-isometric property of the metric space
$g(n)-g(m)\leqslant D$
. We note that the proof of the lemma does not use the fact that the spaces are colored. In this sense, the lemma is a quasi-isometric property of the metric space
![]() $\omega $
with its natural distance. Later we will use this lemma sometimes without an explicit reference to it.
$\omega $
with its natural distance. Later we will use this lemma sometimes without an explicit reference to it.
Lemma 2.1 (Small Cross Over Lemma)
For any quasi-isometry constants
![]() $(A,B,C)$
there are constants
$(A,B,C)$
there are constants
![]() $D\leqslant 0$
and
$D\leqslant 0$
and
![]() $D^{\prime }\leqslant 0$
such that for all
$D^{\prime }\leqslant 0$
such that for all
![]() $(A,B,C)$
-quasi-isometry maps
$(A,B,C)$
-quasi-isometry maps
![]() $g:\alpha \rightarrow \beta $
we have the following:
$g:\alpha \rightarrow \beta $
we have the following:
-
1. For all
 $n,m \in \omega $
if
$n,m \in \omega $
if
 $n<m$
and
$n<m$
and
 $g(m)< g(n)$
we have
$g(m)< g(n)$
we have
 $g(m)-g(n)\geqslant D$
.
$g(m)-g(n)\geqslant D$
. -
2. For all
 $n,m \in \omega $
if
$n,m \in \omega $
if
 $n<m$
and
$n<m$
and
 $g(m)< g(n)$
then
$g(m)< g(n)$
then
 $n-m\geqslant D^{\prime }$
.
$n-m\geqslant D^{\prime }$
.
Proof For the first part of the lemma, suppose that for some integers
![]() $n< m$
we have
$n< m$
we have
![]() $g(m)-g(n)=D$
that provides a cross-over for a constant
$g(m)-g(n)=D$
that provides a cross-over for a constant
![]() $D \leqslant 0$
. Our goal is to find a lower bound for the constant D. We refer the reader to Figure 1 in order to follow the arguments below.
$D \leqslant 0$
. Our goal is to find a lower bound for the constant D. We refer the reader to Figure 1 in order to follow the arguments below.

Figure 1 Small Cross Over Lemma.
In the list
![]() $g(m+1), g(m+2), \ldots $
, select the minimal integer p such that
$g(m+1), g(m+2), \ldots $
, select the minimal integer p such that
![]() $p\geqslant g(n)+1$
, that is
$p\geqslant g(n)+1$
, that is
![]() $p=\min (g([m+1,\infty )) \cap [g(n)+1, \infty ))$
. Define
$p=\min (g([m+1,\infty )) \cap [g(n)+1, \infty ))$
. Define
![]() $q = \min (g^{-1}(p) \cap [m+1, \infty ))$
. So, we have
$q = \min (g^{-1}(p) \cap [m+1, \infty ))$
. So, we have
![]() $q\geqslant m+1$
and
$q\geqslant m+1$
and
![]() $p=g(q)$
. Then, since g is an
$p=g(q)$
. Then, since g is an
![]() $(A,B,C)$
-quasi-isometry we obtain
$(A,B,C)$
-quasi-isometry we obtain
 $$ \begin{align*} d_{\beta}(g(n), p) & \geqslant \frac{1}{A} \cdot d_{\alpha}(n,q)-B \geqslant \frac{1}{A} d_{\alpha}(n,m)-B\\ & \geqslant \frac{1}{A} \cdot \frac{1}{A} (d_{\beta}(g(n), g(m))-B)-B\\ & = -\frac{D}{A^2} -\frac{(A^2+1)}{A^2} B. \end{align*} $$
$$ \begin{align*} d_{\beta}(g(n), p) & \geqslant \frac{1}{A} \cdot d_{\alpha}(n,q)-B \geqslant \frac{1}{A} d_{\alpha}(n,m)-B\\ & \geqslant \frac{1}{A} \cdot \frac{1}{A} (d_{\beta}(g(n), g(m))-B)-B\\ & = -\frac{D}{A^2} -\frac{(A^2+1)}{A^2} B. \end{align*} $$
We have
![]() $g([m,q]) \subset [0,g(n)] \cup [p,\infty )$
by our definition of p and q. Note
$g([m,q]) \subset [0,g(n)] \cup [p,\infty )$
by our definition of p and q. Note
![]() $g(m)\in [0,g(n)]$
and
$g(m)\in [0,g(n)]$
and
![]() $g(q)\in [p,\infty )$
. Hence, there exists
$g(q)\in [p,\infty )$
. Hence, there exists
![]() $r \in [m, q-1]$
such that
$r \in [m, q-1]$
such that
![]() $g(r)\in [0,g(n)]$
and
$g(r)\in [0,g(n)]$
and
![]() $g(r+1)\in [g(p),\infty )$
, which means
$g(r+1)\in [g(p),\infty )$
, which means
From these two systems of inequalities we have the inequality:
So we have
that was desired to be proved.
Note that the lemma states that the distance
![]() $g(m)-g(n)$
is uniformly bounded from below when n and m form a cross-over pair. Since g is a quasi-isometry, for all pairs
$g(m)-g(n)$
is uniformly bounded from below when n and m form a cross-over pair. Since g is a quasi-isometry, for all pairs
![]() $n<m$
that form a cross-over, the distance between
$n<m$
that form a cross-over, the distance between
![]() $n-m$
is also universally bounded from below. This proves the second part of the lemma.
$n-m$
is also universally bounded from below. This proves the second part of the lemma.
We note that the claimed constants D and
![]() $D^{\prime }$
are independent on any particular
$D^{\prime }$
are independent on any particular
![]() $(A,B,C)$
-quasi-isometry f; namely, D and
$(A,B,C)$
-quasi-isometry f; namely, D and
![]() $D^{\prime }$
depend on
$D^{\prime }$
depend on
![]() $(A, B, C)$
only.⊣
$(A, B, C)$
only.⊣
Corollary 2.2. There exists a computable function that, given quasi-isometry constants
![]() $A, B$
, C, computes constants D and
$A, B$
, C, computes constants D and
![]() $D^{\prime }$
stated in the lemma.
$D^{\prime }$
stated in the lemma.
Consider an
![]() $(A,B,C)$
-quasi-isometry
$(A,B,C)$
-quasi-isometry
![]() $\,f:\alpha \rightarrow \beta $
. Let
$\,f:\alpha \rightarrow \beta $
. Let
![]() $[x,y]$
be an interval in
$[x,y]$
be an interval in
![]() $\beta $
, where
$\beta $
, where
![]() $x\leqslant y$
, and consider two values
$x\leqslant y$
, and consider two values
![]() $M_{xy}= \max\, f^{-1}([x,y])$
and
$M_{xy}= \max\, f^{-1}([x,y])$
and
![]() $m_{xy}= \min\, f^{-1}([x,y])$
. We would like to measure the size of the interval between
$m_{xy}= \min\, f^{-1}([x,y])$
. We would like to measure the size of the interval between
![]() $m_{xy}$
and
$m_{xy}$
and
![]() $M_{xy}$
in terms of the length of the interval
$M_{xy}$
in terms of the length of the interval
![]() $[x,y]$
.
$[x,y]$
.
Lemma 2.3. For the
![]() $(A,B,C)$
-quasi-isometry
$(A,B,C)$
-quasi-isometry
![]() $\,f:\alpha \rightarrow \beta $
there exist constants
$\,f:\alpha \rightarrow \beta $
there exist constants
![]() $A^{\prime }$
and
$A^{\prime }$
and
![]() $B^{\prime }$
such that for all positions
$B^{\prime }$
such that for all positions
![]() $x, y\in \beta $
with
$x, y\in \beta $
with
![]() $x\leqslant y$
we have
$x\leqslant y$
we have
Proof The inequality in the definition of
![]() $(A,B,C)$
-quasi-isometry for function f implies:
$(A,B,C)$
-quasi-isometry for function f implies:
 $$ \begin{align*} (1/A)\cdot &d_{\beta}(f(n),f(m))-(B/A)\leqslant d_{\alpha}(n,m)\\ &\leqslant A\cdot d_{\beta}(f(n),f(m))+AB. \end{align*} $$
$$ \begin{align*} (1/A)\cdot &d_{\beta}(f(n),f(m))-(B/A)\leqslant d_{\alpha}(n,m)\\ &\leqslant A\cdot d_{\beta}(f(n),f(m))+AB. \end{align*} $$
Therefore, we have
 $$ \begin{align*} d_{\alpha}(m_{xy},M_{xy}) &\leqslant A \cdot d_{\beta}(f(m_{xy}),f(M_{xy})) +AB\\ &\leqslant A \cdot d_{\beta}(x,y) +AB. \end{align*} $$
$$ \begin{align*} d_{\alpha}(m_{xy},M_{xy}) &\leqslant A \cdot d_{\beta}(f(m_{xy}),f(M_{xy})) +AB\\ &\leqslant A \cdot d_{\beta}(x,y) +AB. \end{align*} $$
For the lower bound we have:
So, we need to rewrite the lower bound in terms of the length of the interval x and y. For this we use the quasi-isometry inequality twice:
 $$ \begin{align*} &d_{\beta}(f(m_{xy}),f(M_{xy}))\geqslant (1/A) d_{\alpha}(m_{xy}, M_{xy})-B\\ &\quad\geqslant(1/A) d_{\alpha}(\min\, f^{-1}(x), \max\, f^{-1}(y))-B \\ &\quad\geqslant(1/A)((1/A)d_{\beta}(x,y)-B)-B\\ &\quad=(1/A^2)d_{\beta}(x,y)-((A+1)/A)B. \end{align*} $$
$$ \begin{align*} &d_{\beta}(f(m_{xy}),f(M_{xy}))\geqslant (1/A) d_{\alpha}(m_{xy}, M_{xy})-B\\ &\quad\geqslant(1/A) d_{\alpha}(\min\, f^{-1}(x), \max\, f^{-1}(y))-B \\ &\quad\geqslant(1/A)((1/A)d_{\beta}(x,y)-B)-B\\ &\quad=(1/A^2)d_{\beta}(x,y)-((A+1)/A)B. \end{align*} $$
All these give us the desired constants
![]() $A^{\prime }$
and
$A^{\prime }$
and
![]() $B^{\prime }$
.⊣
$B^{\prime }$
.⊣
In terms of the last lemma, we note that we can tune our constants
![]() $A^{\prime }$
and
$A^{\prime }$
and
![]() $B^{\prime }$
using the Small Cross-Over Lemma. Indeed, consider the values
$B^{\prime }$
using the Small Cross-Over Lemma. Indeed, consider the values
![]() $M^{\prime }_{xy}= \max ([x,y] \cap f(\alpha ))$
and
$M^{\prime }_{xy}= \max ([x,y] \cap f(\alpha ))$
and
![]() $m^{\prime }_{xy}= \min ([x,y] \cap f(\alpha ))$
. Then due to the density condition of quasi-isometricity it holds that
$m^{\prime }_{xy}= \min ([x,y] \cap f(\alpha ))$
. Then due to the density condition of quasi-isometricity it holds that
![]() $d_{\beta }(y,M^{\prime }_{xy}) \leqslant 2C$
and
$d_{\beta }(y,M^{\prime }_{xy}) \leqslant 2C$
and
![]() $d_{\beta }(x,m^{\prime }_{xy}) \leqslant 2C$
. Also from Lemma 2.1 we have
$d_{\beta }(x,m^{\prime }_{xy}) \leqslant 2C$
. Also from Lemma 2.1 we have
Hence, by the triangular inequality,
![]() $ d_{\beta }(f(m_{xy}),f(M_{xy})) \geqslant d_{\beta }(x,y) -4C+2D$
.
$ d_{\beta }(f(m_{xy}),f(M_{xy})) \geqslant d_{\beta }(x,y) -4C+2D$
.
In summary, we have the following:
Set
![]() $A^{\prime } = A$
and
$A^{\prime } = A$
and
![]() $B^{\prime } = \max \{(4C+B-2D)/A, AB\} $
.
$B^{\prime } = \max \{(4C+B-2D)/A, AB\} $
.
We have the next immediate corollary (that can also be proved easily without the use of the lemmas above):
Corollary 2.4. Let
![]() $\,f:\alpha \rightarrow \beta $
be a quasi-isometry. There is a
$\,f:\alpha \rightarrow \beta $
be a quasi-isometry. There is a
![]() $C>0$
such that
$C>0$
such that
![]() $|f^{-1}(y)|<C$
for all
$|f^{-1}(y)|<C$
for all
![]() $y\in \beta $
.⊣
$y\in \beta $
.⊣
3 Algebraic properties of the order
 $(\Sigma _{QI}^{\omega }, \leqslant _{QI})$
$(\Sigma _{QI}^{\omega }, \leqslant _{QI})$
The partially ordered set
![]() $(\Sigma _{QI}^{\omega }, \leqslant _{QI})$
is an algebraic tool that allows us to study large scale properties of infinite strings and compare them. Proposition 1.6 already describes some of the elementary properties of this partial order. In this section we further embrace this partial order and derive some nontrivial properties of it.
$(\Sigma _{QI}^{\omega }, \leqslant _{QI})$
is an algebraic tool that allows us to study large scale properties of infinite strings and compare them. Proposition 1.6 already describes some of the elementary properties of this partial order. In this section we further embrace this partial order and derive some nontrivial properties of it.
3.1 Infinite chains and antichains
A natural question is if the partially ordered set
![]() $(\Sigma _{QI}^{\omega }; \leqslant _{QI})$
is infinite. We positively answer this question in two ways. On the one hand we show that the partial order has infinite chains, and on the other hand we show that the order has infinite antichains.
$(\Sigma _{QI}^{\omega }; \leqslant _{QI})$
is infinite. We positively answer this question in two ways. On the one hand we show that the partial order has infinite chains, and on the other hand we show that the order has infinite antichains.
Theorem 3.1 (Infinite Chain Theorem)
The order
![]() $\Sigma _{QI}^{\omega }$
has a chain of the type of integers, that is, a collection
$\Sigma _{QI}^{\omega }$
has a chain of the type of integers, that is, a collection
![]() $\{\alpha _n\}_{n \in \mathbb {Z}}$
of strings such that
$\{\alpha _n\}_{n \in \mathbb {Z}}$
of strings such that
![]() $[\alpha _n <_{QI} \alpha _{n+1}]$
for all
$[\alpha _n <_{QI} \alpha _{n+1}]$
for all
![]() $n\in \mathbb {Z}$
.
$n\in \mathbb {Z}$
.
Proof Take two distinct elements in
![]() $\Sigma $
, say
$\Sigma $
, say
![]() $0$
and
$0$
and
![]() $1$
, respectively. Define the following sequence
$1$
, respectively. Define the following sequence
![]() $\{\alpha _n\}_{n\in \mathbb Z}$
of infinite strings from
$\{\alpha _n\}_{n\in \mathbb Z}$
of infinite strings from
![]() $\Sigma ^{\omega }$
:
$\Sigma ^{\omega }$
:
 $$ \begin{align*} \alpha_n = \begin{cases} (01)^{2^n}(011)^{2^n}...(01^{2^k})^{2^n}... & (n\geqslant0), \\ (01)(01^{2^{2^{-n}}})...(01^{(2^k)^{2^{-n}}})... & (n<0). \end{cases} \end{align*} $$
$$ \begin{align*} \alpha_n = \begin{cases} (01)^{2^n}(011)^{2^n}...(01^{2^k})^{2^n}... & (n\geqslant0), \\ (01)(01^{2^{2^{-n}}})...(01^{(2^k)^{2^{-n}}})... & (n<0). \end{cases} \end{align*} $$
The idea behind this definition is the following. The string
![]() $\alpha _0$
is of the form:
$\alpha _0$
is of the form:
Let us call the substrings
![]() $(01^{2^k})$
blocks of
$(01^{2^k})$
blocks of
![]() $\alpha _0$
. The above definition tells us that
$\alpha _0$
. The above definition tells us that
![]() $\alpha _1$
is obtained from
$\alpha _1$
is obtained from
![]() $\alpha _0$
by doubling each block of
$\alpha _0$
by doubling each block of
![]() $\alpha _0$
. Similarly,
$\alpha _0$
. Similarly,
![]() $\alpha _{-1}$
is obtained from
$\alpha _{-1}$
is obtained from
![]() $\alpha _0$
by removing every other block. This process is propagated to all
$\alpha _0$
by removing every other block. This process is propagated to all
![]() $\alpha _n$
's.
$\alpha _n$
's.
We show that
![]() $\alpha _n \leqslant _{QI} \alpha _{n+1}$
for all
$\alpha _n \leqslant _{QI} \alpha _{n+1}$
for all
![]() $n\geqslant 0$
. For negative n, the proof is similar. In
$n\geqslant 0$
. For negative n, the proof is similar. In
![]() $\alpha _n$
consider the segment of the form
$\alpha _n$
consider the segment of the form
 $$ \begin{align*}\underbrace{(01^{2^{k+1}})(01^{2^{k+1}})\ldots (01^{2^{k+1}})}_{2^n \text{ times}}. \end{align*} $$
$$ \begin{align*}\underbrace{(01^{2^{k+1}})(01^{2^{k+1}})\ldots (01^{2^{k+1}})}_{2^n \text{ times}}. \end{align*} $$
We map this segment of
![]() $\alpha _n$
into the following segment of the string
$\alpha _n$
into the following segment of the string
![]() $\alpha _{n+1}$
:
$\alpha _{n+1}$
:
 $$ \begin{align*}\underbrace{(01^{2^{k}})(01^{2^{k}})(01^{2^{k}})(01^{2^{k}})\ldots (01^{2^{k}})(01^{2^{k}})}_{2^{n+1} \text{ times}}. \end{align*} $$
$$ \begin{align*}\underbrace{(01^{2^{k}})(01^{2^{k}})(01^{2^{k}})(01^{2^{k}})\ldots (01^{2^{k}})(01^{2^{k}})}_{2^{n+1} \text{ times}}. \end{align*} $$
The mapping sends the block
![]() $(01^{2^{k+1}})$
in
$(01^{2^{k+1}})$
in
![]() $\alpha _n$
into
$\alpha _n$
into
![]() $(01^{2^{k}})^2$
in
$(01^{2^{k}})^2$
in
![]() $\alpha _{n+1}$
in an obvious injective way. This mapping can easily be seen to be a quasi-isometry from
$\alpha _{n+1}$
in an obvious injective way. This mapping can easily be seen to be a quasi-isometry from
![]() $\alpha _n$
into
$\alpha _n$
into
![]() $\alpha _{n+1}$
. We refer the reader to Figure 2.
$\alpha _{n+1}$
. We refer the reader to Figure 2.

Figure 2 The mapping from
![]() $(01^{2^{k+1}})$
-block in
$(01^{2^{k+1}})$
-block in
![]() $\alpha _n$
into
$\alpha _n$
into
![]() $(01^{2^{k}})(01^{2^{k}})$
-block in
$(01^{2^{k}})(01^{2^{k}})$
-block in
![]() $\alpha _{n+1}$
.
$\alpha _{n+1}$
.
Now we need to prove that there is no quasi-isometric mapping from
![]() $\alpha _{n+1}$
into
$\alpha _{n+1}$
into
![]() $\alpha _n$
. For the sake of contradiction assume that g is an
$\alpha _n$
. For the sake of contradiction assume that g is an
![]() $(A,B,C)$
-quasi-isometry from
$(A,B,C)$
-quasi-isometry from
![]() $\alpha _{n+1}$
into
$\alpha _{n+1}$
into
![]() $\alpha _n$
. Then using Lemma 2.3 and Lemma 2.1, one sees that g needs to be strictly monotone on all but finitely many positions of
$\alpha _n$
. Then using Lemma 2.3 and Lemma 2.1, one sees that g needs to be strictly monotone on all but finitely many positions of
![]() $\alpha _{n+1}$
with color
$\alpha _{n+1}$
with color
![]() $0$
; that is, we need to have
$0$
; that is, we need to have
![]() $M \in \omega $
such that for all
$M \in \omega $
such that for all
![]() $m,m^{\prime }>M$
and
$m,m^{\prime }>M$
and
![]() $m>m^{\prime }$
we have if
$m>m^{\prime }$
we have if
![]() $\alpha _{n+1}(m) = \alpha _{n+1}(m^{\prime }) = 0$
then
$\alpha _{n+1}(m) = \alpha _{n+1}(m^{\prime }) = 0$
then
![]() $g(m)> g(m^{\prime })$
.
$g(m)> g(m^{\prime })$
.
We now show that we have a contradiction. Let
![]() $m_{i,n}$
and
$m_{i,n}$
and
![]() $m_{j, n+1}$
be the positions of the ith
$m_{j, n+1}$
be the positions of the ith
![]() $0$
in
$0$
in
![]() $\alpha _n$
and jth
$\alpha _n$
and jth
![]() $0$
in
$0$
in
![]() $\alpha _{n+1}$
, respectively. Now assume that
$\alpha _{n+1}$
, respectively. Now assume that
![]() $m_{i,n+1}> M$
and
$m_{i,n+1}> M$
and
![]() $g(m_{i,n+1}) = m_{j,n}$
. Then from monotonicity and injectivity of g on all positions colored
$g(m_{i,n+1}) = m_{j,n}$
. Then from monotonicity and injectivity of g on all positions colored
![]() $0$
in
$0$
in
![]() $\alpha _{n+1}$
, we should have
$\alpha _{n+1}$
, we should have
Together with the
![]() $(A,B,C)$
-quasi-isometry condition, this implies
$(A,B,C)$
-quasi-isometry condition, this implies
![]() $m_{j+k,n} - m_{j,n} \leqslant A(m_{i+k,n+1} - m_{i,n+1}) + B$
and hence
$m_{j+k,n} - m_{j,n} \leqslant A(m_{i+k,n+1} - m_{i,n+1}) + B$
and hence
which in particular says the value
![]() $r(k)$
is uniformly bounded with respect to k. On the other hand, from the construction of
$r(k)$
is uniformly bounded with respect to k. On the other hand, from the construction of
![]() $\alpha _n$
and
$\alpha _n$
and
![]() $\alpha _{n+1}$
one can observe that the growth rate of
$\alpha _{n+1}$
one can observe that the growth rate of
![]() $m_{k,n}$
with respect to k is much faster than that of
$m_{k,n}$
with respect to k is much faster than that of
![]() $m_{k,n+1}$
; more precisely, one can verify that
$m_{k,n+1}$
; more precisely, one can verify that
![]() $m_{2^n \cdot k , n} = \mathcal O(2^k)$
holds for each
$m_{2^n \cdot k , n} = \mathcal O(2^k)$
holds for each
![]() $n \in \omega $
, and thus
$n \in \omega $
, and thus
![]() $m_{2^n \cdot k , n+1} = m_{2^{n+1} \cdot \frac {k}{2} , n+1} = \mathcal O(2^{\frac {k}{2}})$
holds when k is even. This implies
$m_{2^n \cdot k , n+1} = m_{2^{n+1} \cdot \frac {k}{2} , n+1} = \mathcal O(2^{\frac {k}{2}})$
holds when k is even. This implies
![]() $r(k)$
is unbounded, which is a contradiction.⊣
$r(k)$
is unbounded, which is a contradiction.⊣
Theorem 3.2 (Infinite Antichain Theorem)
The partial order
![]() $\Sigma _{QI}^{\omega }$
has a countable antichain
$\Sigma _{QI}^{\omega }$
has a countable antichain
![]() $\{\beta _n\}_{n \in \omega }$
.
$\{\beta _n\}_{n \in \omega }$
.
Proof As above we assume that
![]() $0,1\in \Sigma $
. Consider the following sequence of strings
$0,1\in \Sigma $
. Consider the following sequence of strings
![]() $\beta _n$
,
$\beta _n$
,
![]() $n\in \omega $
:
$n\in \omega $
:
We claim that this sequence forms an antichain in
![]() $\Sigma _{QI}^{\omega }$
. Take any
$\Sigma _{QI}^{\omega }$
. Take any
![]() $n,m \in \omega $
and suppose
$n,m \in \omega $
and suppose
![]() $\beta _n \leqslant _{QI} \beta _m$
via an
$\beta _n \leqslant _{QI} \beta _m$
via an
![]() $(A,B,C)$
-quasi-isometry f. We will show that
$(A,B,C)$
-quasi-isometry f. We will show that
![]() $n=m$
.
$n=m$
.
Let
![]() $A_{s,t}$
be the “tth block” of zeros in
$A_{s,t}$
be the “tth block” of zeros in
![]() $\beta _{s}$
. We can represent
$\beta _{s}$
. We can represent
![]() $A_{s,t}$
as the interval
$A_{s,t}$
as the interval
 $$ \begin{align*} A_{s,t} = [2\sum_{i=0}^{t-1}i^{s},2\sum_{i=0}^{t-1}i^{s}+(t)^{s}-1]. \end{align*} $$
$$ \begin{align*} A_{s,t} = [2\sum_{i=0}^{t-1}i^{s},2\sum_{i=0}^{t-1}i^{s}+(t)^{s}-1]. \end{align*} $$
Since f is a quasi-isometry, an easy argument shows that there exists
![]() $k,l \in \omega $
such that (1)
$k,l \in \omega $
such that (1)
![]() $\,f(A_{n,k}) \subseteq A_{m,l}$
, and (2) for every
$\,f(A_{n,k}) \subseteq A_{m,l}$
, and (2) for every
![]() $k^{\prime } \in \omega $
, we have
$k^{\prime } \in \omega $
, we have
![]() $\,f(A_{n,k^{\prime }+k}) \subseteq A_{m,k^{\prime }+l}$
. Intuitively, these say that from some point the quasi-isometry f maps
$\,f(A_{n,k^{\prime }+k}) \subseteq A_{m,k^{\prime }+l}$
. Intuitively, these say that from some point the quasi-isometry f maps
![]() $\beta _n$
in the “block by block” manner without vacancy—one can easily verify that, without this property f generates unbounded distortions (and thus is not a quasi-isometry). Now note that we have:
$\beta _n$
in the “block by block” manner without vacancy—one can easily verify that, without this property f generates unbounded distortions (and thus is not a quasi-isometry). Now note that we have:
Therefore, we should have a positive upper and lower bounds on the ratio
 $$ \begin{align*} \frac{|A_{n,k^{\prime}+k}|}{|A_{m,k^{\prime}+l}|} = \frac{(k^{\prime}+k)^n}{(k^{\prime}+l)^m} \end{align*} $$
$$ \begin{align*} \frac{|A_{n,k^{\prime}+k}|}{|A_{m,k^{\prime}+l}|} = \frac{(k^{\prime}+k)^n}{(k^{\prime}+l)^m} \end{align*} $$
with respect to
![]() $k^{\prime }$
. The only case that satisfies this condition is
$k^{\prime }$
. The only case that satisfies this condition is
![]() $n=m$
.⊣
$n=m$
.⊣
The trivial large scale geometries
![]() $[0^{\omega }]$
and
$[0^{\omega }]$
and
![]() $[1^{\omega }]$
, as we noted, are minimal elements of
$[1^{\omega }]$
, as we noted, are minimal elements of
![]() $\Sigma _{QI}^{\omega }$
. The next theorem shows one way to build nontrivial minimal large scale geometries.
$\Sigma _{QI}^{\omega }$
. The next theorem shows one way to build nontrivial minimal large scale geometries.
Theorem 3.3 (Minimal Elements Theorem)
Let
![]() $\{a_n\}_{n \in \omega }$
be a sequence such that
$\{a_n\}_{n \in \omega }$
be a sequence such that
![]() $\lim _{n \to \infty } a_n = \infty $
. Then the large scale geometry of the string
$\lim _{n \to \infty } a_n = \infty $
. Then the large scale geometry of the string
![]() $\alpha = 0^{a_0}1^{a_1}0^{a_2}1^{a_3}...0^{a_{2k}}1^{a_{2k+1}}\ldots $
is a minimal element in any partial order
$\alpha = 0^{a_0}1^{a_1}0^{a_2}1^{a_3}...0^{a_{2k}}1^{a_{2k+1}}\ldots $
is a minimal element in any partial order
![]() $\Sigma _{QI}^{\omega }$
with
$\Sigma _{QI}^{\omega }$
with
![]() $0,1 \in \Sigma $
.
$0,1 \in \Sigma $
.
Proof Suppose that
![]() $\beta \leqslant _{QI} \alpha $
via an
$\beta \leqslant _{QI} \alpha $
via an
![]() $(A,B,C)$
-quasi-isometry f. Our goal is to show that
$(A,B,C)$
-quasi-isometry f. Our goal is to show that
![]() $\alpha \sim _{QI} \beta $
. It suffices to show that there exists a constant D such that for every sufficiently large
$\alpha \sim _{QI} \beta $
. It suffices to show that there exists a constant D such that for every sufficiently large
![]() $y \in \alpha $
(i.e., for every
$y \in \alpha $
(i.e., for every
![]() $y \geqslant Y$
with some fixed constant Y) there exists an
$y \geqslant Y$
with some fixed constant Y) there exists an
![]() $x \in \beta $
with
$x \in \beta $
with
![]() $|y-f(x)| \leqslant D$
and
$|y-f(x)| \leqslant D$
and
![]() $Cl(x) = Cl(y)$
. Indeed, assuming such a condition we can construct a quasi-isometry
$Cl(x) = Cl(y)$
. Indeed, assuming such a condition we can construct a quasi-isometry
![]() $g:\alpha \to \beta $
as follows; for each
$g:\alpha \to \beta $
as follows; for each
![]() $y \in \alpha $
,
$y \in \alpha $
,
-
1. if there exists
 $y'\in \alpha $
such that
$y'\in \alpha $
such that
 $|y'-y|\leqslant D$
for which there is
$|y'-y|\leqslant D$
for which there is
 $x'\in \beta $
with
$x'\in \beta $
with
 $\,f(x')=y'$
, then let
$\,f(x')=y'$
, then let
 $g(y)=x'$
;
$g(y)=x'$
; -
2. otherwise, let
 $x\in \beta $
be any position such that
$x\in \beta $
be any position such that
 $Cl(x) = Cl(y)$
, and let
$Cl(x) = Cl(y)$
, and let
 $g(y) = x$
.
$g(y) = x$
.
Here
![]() $g(y)$
is well-defined in case 2, as
$g(y)$
is well-defined in case 2, as
![]() $\beta $
clearly contains both of
$\beta $
clearly contains both of
![]() $0$
and
$0$
and
![]() $1$
as its color. It is easy to verify that g is a quasi-isometry—recall the argument in Remark 1.5, and observe that the case 2 happens only for finitely many y’s.
$1$
as its color. It is easy to verify that g is a quasi-isometry—recall the argument in Remark 1.5, and observe that the case 2 happens only for finitely many y’s.
Now we prove existence of the constant D. Enumerate all elements of the image of f as
![]() $\{y_n\}_{n\in \omega }$
, where
$\{y_n\}_{n\in \omega }$
, where
![]() $y_n < y_{n+1}$
for all n. Then by definition of
$y_n < y_{n+1}$
for all n. Then by definition of
![]() $(A,B,C)$
-quasi-isometry, we have
$(A,B,C)$
-quasi-isometry, we have
![]() $y_{n+1} - y_n \leqslant 2C+1$
(as otherwise there is y between
$y_{n+1} - y_n \leqslant 2C+1$
(as otherwise there is y between
![]() $y_n$
and
$y_n$
and
![]() $y_{n+1}$
that violates the density property). On the other hand, it is clear from the construction of
$y_{n+1}$
that violates the density property). On the other hand, it is clear from the construction of
![]() $\alpha $
that every sufficiently large
$\alpha $
that every sufficiently large
![]() $y \in \alpha $
is a member of a single-colored interval I in
$y \in \alpha $
is a member of a single-colored interval I in
![]() $\alpha $
with the size greater than
$\alpha $
with the size greater than
![]() $2C+1$
. Thus for such a y, one can find
$2C+1$
. Thus for such a y, one can find
![]() $x \in \beta $
such that
$x \in \beta $
such that
![]() $|y-f(x)| \leqslant 2C+1$
and
$|y-f(x)| \leqslant 2C+1$
and
![]() $Cl(x) = Cl(y)$
.⊣
$Cl(x) = Cl(y)$
.⊣
By this result, the strings
![]() $\beta _n$
constructed in the Infinite Antichain Theorem are all minimal. Hence, we have the following corollary:
$\beta _n$
constructed in the Infinite Antichain Theorem are all minimal. Hence, we have the following corollary:
Corollary 3.4. The partially ordered set
![]() $\Sigma _{QI}^{\omega }$
possesses infinitely many minimal elements.⊣
$\Sigma _{QI}^{\omega }$
possesses infinitely many minimal elements.⊣
3.2 Density theorem
Recall that a partial order
![]() $\leqslant $
is dense if for all
$\leqslant $
is dense if for all
![]() $x, y$
the condition
$x, y$
the condition
![]() $x\leqslant y$
and
$x\leqslant y$
and
![]() $x\neq y$
implies existence of z such that
$x\neq y$
implies existence of z such that
![]() $x\leqslant z\leqslant y$
and
$x\leqslant z\leqslant y$
and
![]() $z\not \in \{x,y\}$
. Since
$z\not \in \{x,y\}$
. Since
![]() $\Sigma _{QI}^{\omega }$
has atoms, this order is not dense. However, the goal of this section is to show the density property for
$\Sigma _{QI}^{\omega }$
has atoms, this order is not dense. However, the goal of this section is to show the density property for
![]() $\leqslant _{QI}$
is prevalent.
$\leqslant _{QI}$
is prevalent.
We start with the lemma showing that all
![]() $(A,B,C)$
-quasi-isometries between strings are bounded by one linear function; the function depends on the constants
$(A,B,C)$
-quasi-isometries between strings are bounded by one linear function; the function depends on the constants
![]() $A, B, C$
only and not the quasi-isometries.
$A, B, C$
only and not the quasi-isometries.
Lemma 3.5. For given
![]() $A, B, C \in \omega $
, there is a constant
$A, B, C \in \omega $
, there is a constant
![]() $D^{\prime } \in \omega $
such that for all
$D^{\prime } \in \omega $
such that for all
![]() $(A,B, C)$
-quasi isometries
$(A,B, C)$
-quasi isometries
![]() $\,f: \alpha \to \beta $
and
$\,f: \alpha \to \beta $
and
![]() $n \in \omega $
we have
$n \in \omega $
we have
![]() $\,f(n) \leqslant An + D'$
.
$\,f(n) \leqslant An + D'$
.
Proof Let
![]() $\,f:\alpha \to \beta $
be an
$\,f:\alpha \to \beta $
be an
![]() $(A,B, C)$
-quasi-isometry. The constant C tells us that there is
$(A,B, C)$
-quasi-isometry. The constant C tells us that there is
![]() $n_0 \in \omega $
such that
$n_0 \in \omega $
such that
![]() $\,f(n_0) \in [0,C]$
. Thus, by the Small Cross Over Lemma there is a bound D (which is independent of the choice of f) such that
$\,f(n_0) \in [0,C]$
. Thus, by the Small Cross Over Lemma there is a bound D (which is independent of the choice of f) such that
![]() $\,f(0) \leqslant D$
. Since f is an
$\,f(0) \leqslant D$
. Since f is an
![]() $(A,B, C)$
-quasi-isometry, we have
$(A,B, C)$
-quasi-isometry, we have
So, we let
![]() $D'=B+D$
.⊣
$D'=B+D$
.⊣
For the density theorem we use the following standard notation. For string
![]() $\alpha $
, let
$\alpha $
, let
![]() $\alpha \hspace {-.4em}\upharpoonright _k$
be the string
$\alpha \hspace {-.4em}\upharpoonright _k$
be the string
![]() $\alpha (0)\ldots \alpha (k)$
, where
$\alpha (0)\ldots \alpha (k)$
, where
![]() $k \in \omega $
. Since we will be handling finite approximations to quasi-isometric mappings, we need the following definition.
$k \in \omega $
. Since we will be handling finite approximations to quasi-isometric mappings, we need the following definition.
Definition 3.6. Let
![]() $A, B, C \in \omega $
be quasi-isometry constants, and let
$A, B, C \in \omega $
be quasi-isometry constants, and let
![]() $D \leqslant 0$
be the largest cross over bound for
$D \leqslant 0$
be the largest cross over bound for
![]() $(A,B,C)$
-quasi-isometries that is given by Lemma 2.1. A function
$(A,B,C)$
-quasi-isometries that is given by Lemma 2.1. A function
![]() $\,f: \alpha \hspace {-.4em}\upharpoonright _n \to \beta $
is possibly extendable to
$\,f: \alpha \hspace {-.4em}\upharpoonright _n \to \beta $
is possibly extendable to
![]() $(A,B,C)$
-quasi-isometry if it satisfies the following conditions:
$(A,B,C)$
-quasi-isometry if it satisfies the following conditions:
-
1. f is color preserving.
-
2. For all
 $k,m \in \mathrm {dom}(f)$
, we have
$k,m \in \mathrm {dom}(f)$
, we have  $$ \begin{align*}(1/A)\cdot d(k,m)-B < d(f(k),f(m))< A\cdot d(k,m)+B. \end{align*} $$
$$ \begin{align*}(1/A)\cdot d(k,m)-B < d(f(k),f(m))< A\cdot d(k,m)+B. \end{align*} $$
-
3. Let
 $M_n = \max \{f(x) \mid x \in \mathrm {dom}(f)\}$
. If
$M_n = \max \{f(x) \mid x \in \mathrm {dom}(f)\}$
. If
 $M_n> C-D$
, then for any
$M_n> C-D$
, then for any
 $y < M_n-{(C-D)}$
there exists an
$y < M_n-{(C-D)}$
there exists an
 $x < n$
such that
$x < n$
such that
 $d(y,f(x))\leqslant C$
.
$d(y,f(x))\leqslant C$
.
Let
![]() $\alpha , \beta \in \Sigma ^{\omega }$
and
$\alpha , \beta \in \Sigma ^{\omega }$
and
![]() $A, B, C \in \omega $
be quasi-isometry constants. Our goal is to construct a rooted tree
$A, B, C \in \omega $
be quasi-isometry constants. Our goal is to construct a rooted tree
![]() $T(\alpha , \beta , A,B, C)$
with the following properties:
$T(\alpha , \beta , A,B, C)$
with the following properties:
-
1. The tree
 $T(\alpha , \beta , A,B, C)$
is finitely branching and computable in
$T(\alpha , \beta , A,B, C)$
is finitely branching and computable in
 $\alpha $
and
$\alpha $
and
 $\beta $
. In particular, if
$\beta $
. In particular, if
 $\alpha $
and
$\alpha $
and
 $\beta $
are computable then so is
$\beta $
are computable then so is
 $T(\alpha , \beta , A,B, C)$
.
$T(\alpha , \beta , A,B, C)$
. -
2. For any n one can effectively compute, with an oracle for
 $\alpha $
and
$\alpha $
and
 $\beta $
, the number of nodes in the tree at distance n from the root. Note that Part (1) does not always imply Part (2).
$\beta $
, the number of nodes in the tree at distance n from the root. Note that Part (1) does not always imply Part (2). -
3. The tree
 $T(\alpha , \beta , A,B, C)$
is infinite if and only if there exists an
$T(\alpha , \beta , A,B, C)$
is infinite if and only if there exists an
 $(A,B, C)$
-quasi-isometric map from
$(A,B, C)$
-quasi-isometric map from
 $\alpha $
into
$\alpha $
into
 $\beta $
.
$\beta $
. -
4. There is a bijection between
 $(A,B, C)$
-quasi-isometric maps from
$(A,B, C)$
-quasi-isometric maps from
 $\alpha $
to
$\alpha $
to
 $\beta $
and the set
$\beta $
and the set
 $[T(\alpha , \beta , A,B, C)]$
of all infinite paths of the tree
$[T(\alpha , \beta , A,B, C)]$
of all infinite paths of the tree
 $T(\alpha , \beta , A,B, C)$
.
$T(\alpha , \beta , A,B, C)$
.
The nodes of
![]() $T(\alpha , \beta , A,B, C)$
are finite partial functions that can possibly be extended to
$T(\alpha , \beta , A,B, C)$
are finite partial functions that can possibly be extended to
![]() $(A,B, C)$
-quasi-isometric maps from
$(A,B, C)$
-quasi-isometric maps from
![]() $\alpha $
to
$\alpha $
to
![]() $\beta $
. Here is a formal construction of the tree
$\beta $
. Here is a formal construction of the tree
![]() $T(\alpha , \beta , A,B, C)$
:
$T(\alpha , \beta , A,B, C)$
:
-
1. The root of the tree
 $T(\alpha , \beta , A,B, C)$
is the empty set
$T(\alpha , \beta , A,B, C)$
is the empty set
 $\emptyset $
, that is, nowhere defined partial function.
$\emptyset $
, that is, nowhere defined partial function. -
2. Let x be a leaf of the tree
 $T(\alpha , \beta , A,B, C)$
constructed so far, and
$T(\alpha , \beta , A,B, C)$
constructed so far, and
 $\,f_x$
be the partial function associated with x. We identify x and
$\,f_x$
be the partial function associated with x. We identify x and
 $\,f_x$
. We assume that
$\,f_x$
. We assume that-
(a) x is at distance n from the root, and
 $\,f_x=\{(0,i_0), \ldots , (n, i_{n})\}$
.
$\,f_x=\{(0,i_0), \ldots , (n, i_{n})\}$
. -
(b) The function
 $\,f_x$
is possibly extendable to
$\,f_x$
is possibly extendable to
 $(A,B,C)$
-quasi-isometry.
$(A,B,C)$
-quasi-isometry. -
(c)
 $i_n\leqslant An+D'$
, where
$i_n\leqslant An+D'$
, where
 $D'$
is from Lemma 3.5.
$D'$
is from Lemma 3.5.
-
-
3. List all possibly extendable extensions
 $\phi $
of
$\phi $
of
 $\,f_x$
such that the domain of
$\,f_x$
such that the domain of
 $\phi $
is
$\phi $
is
 $\{0,1,\ldots , n, n+1\}$
. The children of
$\{0,1,\ldots , n, n+1\}$
. The children of
 $\,f_x$
are all these functions
$\,f_x$
are all these functions
 $\phi $
.
$\phi $
.
In Part 2 of the construction the number of extensions
![]() $\phi $
of
$\phi $
of
![]() $\,f_x$
is finite since these extensions must satisfy the quasi-isometry condition. If such extensions
$\,f_x$
is finite since these extensions must satisfy the quasi-isometry condition. If such extensions
![]() $\phi $
of
$\phi $
of
![]() $\,f_x$
do not exist, then the node x becomes a leaf. Finally, Lemma 3.5 guarantees that the root of the tree has finitely many children. Hence, the tree is finitely branching.
$\,f_x$
do not exist, then the node x becomes a leaf. Finally, Lemma 3.5 guarantees that the root of the tree has finitely many children. Hence, the tree is finitely branching.
Lemma 3.7. The following are true:
-
1. There is a bijection between the set of all infinite paths of
 $T(\alpha , \beta , A,B, C)$
and the set of all
$T(\alpha , \beta , A,B, C)$
and the set of all
 $(A,B,C)$
-quasi-isometric maps from
$(A,B,C)$
-quasi-isometric maps from
 $\alpha $
to
$\alpha $
to
 $\beta $
.
$\beta $
. -
2. The tree
 $T(\alpha , \beta , A,B, C)$
is infinite if and only if there is an
$T(\alpha , \beta , A,B, C)$
is infinite if and only if there is an
 $(A,B, C)$
-quasi-isometric map from
$(A,B, C)$
-quasi-isometric map from
 $\alpha $
into
$\alpha $
into
 $\beta $
.
$\beta $
.
Proof Let
![]() $\,f:\alpha \to \beta $
be an
$\,f:\alpha \to \beta $
be an
![]() $(A,B,C)$
-quasi-isometry and let
$(A,B,C)$
-quasi-isometry and let
![]() $\,f_n = f\hspace {-.4em}\upharpoonright _n$
. We show that
$\,f_n = f\hspace {-.4em}\upharpoonright _n$
. We show that
![]() $\,f_n$
satisfies the last condition of possibly-extendable function (i.e., the condition 3 in Definition 3.6); Conditions 1 and 2 of Definition 3.6 clearly hold. Assume the contrary, letting
$\,f_n$
satisfies the last condition of possibly-extendable function (i.e., the condition 3 in Definition 3.6); Conditions 1 and 2 of Definition 3.6 clearly hold. Assume the contrary, letting
![]() $y < M_n - (C-D)$
be an element such that no
$y < M_n - (C-D)$
be an element such that no
![]() $x \in \{0,\ldots , n\}$
satisfies
$x \in \{0,\ldots , n\}$
satisfies
![]() $\,f_n(x) \in \{y-C,\ldots , y+C\}$
. As f is an
$\,f_n(x) \in \{y-C,\ldots , y+C\}$
. As f is an
![]() $(A,B,C)$
-quasi-isometry, there should be an
$(A,B,C)$
-quasi-isometry, there should be an
![]() $x'> n $
that satisfies
$x'> n $
that satisfies
![]() $\,f(x') \in \{y-C,\ldots , y+C\}$
. But then, for
$\,f(x') \in \{y-C,\ldots , y+C\}$
. But then, for
![]() $x'' \in f_n^{-1}(M_n)$
, we have
$x'' \in f_n^{-1}(M_n)$
, we have
![]() $\,f(x') - f(x'') \leqslant (y+C) - M_n < D$
. This contradicts the Small Cross Over Lemma.
$\,f(x') - f(x'') \leqslant (y+C) - M_n < D$
. This contradicts the Small Cross Over Lemma.
If
![]() $x_1, x_2, \ldots $
is an infinite path through the tree
$x_1, x_2, \ldots $
is an infinite path through the tree
![]() $T(\alpha , \beta , A,B)$
then the mapping f defined as the limit of the sequence
$T(\alpha , \beta , A,B)$
then the mapping f defined as the limit of the sequence
![]() $\,f_{x_1}, f_{x_2}, \ldots $
is an
$\,f_{x_1}, f_{x_2}, \ldots $
is an
![]() $(A,B, C)$
-quasi-isometry from
$(A,B, C)$
-quasi-isometry from
![]() $\alpha $
to
$\alpha $
to
![]() $\beta $
.⊣
$\beta $
.⊣
From Lemma 3.7 above we immediately have the following.
Corollary 3.8. Let
![]() $\alpha , \beta \in \Sigma ^\omega $
be given. If for each
$\alpha , \beta \in \Sigma ^\omega $
be given. If for each
![]() $k \in \omega $
there is a function
$k \in \omega $
there is a function
![]() $\,f:\alpha \hspace {-.4em}\upharpoonright _k \to \beta $
that is possibly extendable to
$\,f:\alpha \hspace {-.4em}\upharpoonright _k \to \beta $
that is possibly extendable to
![]() $(A,B,C)$
-quasi-isometry, then there is an
$(A,B,C)$
-quasi-isometry, then there is an
![]() $(A,B, C)$
-quasi-isometry from
$(A,B, C)$
-quasi-isometry from
![]() $\alpha $
to
$\alpha $
to
![]() $\beta $
.
$\beta $
.
Let
![]() $\alpha , \beta \in \Sigma ^\omega $
, and let
$\alpha , \beta \in \Sigma ^\omega $
, and let
![]() $Cl(\beta )$
be the set of all colors of the string
$Cl(\beta )$
be the set of all colors of the string
![]() $\beta $
. Also let
$\beta $
. Also let
![]() $w, v$
be finite strings over
$w, v$
be finite strings over
![]() $Cl(\beta )$
respectively of lengths
$Cl(\beta )$
respectively of lengths
![]() $n,m\in \omega $
. Define the following two strings obtained by changing the initial segments of
$n,m\in \omega $
. Define the following two strings obtained by changing the initial segments of
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
:
$\beta $
:
Also, assume that every letter present in one of these two strings occurs in both strings infinitely often. With these conditions, we have the following simple lemma that informally states that in quasi-isometries initial segments of strings do not matter.
Lemma 3.9. Under assumptions above
![]() $\alpha \leqslant _{QI} \beta $
if and only if
$\alpha \leqslant _{QI} \beta $
if and only if
![]() $\alpha ' \leqslant _{QI} \beta '$
.
$\alpha ' \leqslant _{QI} \beta '$
.
Proof If
![]() $\alpha \leqslant _{QI}\beta $
via
$\alpha \leqslant _{QI}\beta $
via
![]() $\,f:\alpha \to \beta $
, then take
$\,f:\alpha \to \beta $
, then take
![]() $n'\geqslant n$
such that for any
$n'\geqslant n$
such that for any
![]() $i\geqslant n'$
we have
$i\geqslant n'$
we have
![]() $\,f(i) \geqslant m$
. Define
$\,f(i) \geqslant m$
. Define
![]() $\,f':\alpha '\to \beta '$
as follows. For all
$\,f':\alpha '\to \beta '$
as follows. For all
![]() $j\leqslant n'$
, make
$j\leqslant n'$
, make
![]() $\,f'$
color preserving. For all
$\,f'$
color preserving. For all
![]() $i> n$
set
$i> n$
set
![]() $\,f'(i)=f(i)$
. This is a quasi-isometry. The converse can be shown in a similar way.⊣
$\,f'(i)=f(i)$
. This is a quasi-isometry. The converse can be shown in a similar way.⊣
Theorem 3.10 (Density Theorem)
Let
![]() $\alpha , \beta \in \Sigma ^\omega $
be given. Assume
$\alpha , \beta \in \Sigma ^\omega $
be given. Assume
![]() $\alpha <_{QI} \beta $
, and every letter in
$\alpha <_{QI} \beta $
, and every letter in
![]() $\alpha $
or
$\alpha $
or
![]() $\beta $
occurs in both
$\beta $
occurs in both
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
infinitely often. Then there exists
$\beta $
infinitely often. Then there exists
![]() $\gamma \in \Sigma ^\omega $
such that
$\gamma \in \Sigma ^\omega $
such that
![]() $\alpha <_{QI} \gamma <_{QI} \beta $
.
$\alpha <_{QI} \gamma <_{QI} \beta $
.
Proof Note that the assumption of the theorem (that letters that occur in
![]() $\alpha $
or
$\alpha $
or
![]() $\beta $
must occur in both of these strings infinitely often) is important. For instance, no
$\beta $
must occur in both of these strings infinitely often) is important. For instance, no
![]() $\gamma $
exists such that
$\gamma $
exists such that
![]() $0^\omega <_{QI} \gamma <_{QI} 10^\omega $
.
$0^\omega <_{QI} \gamma <_{QI} 10^\omega $
.
Let
![]() $\alpha <_{QI} \beta $
via f. We can assume (if necessary, by taking
$\alpha <_{QI} \beta $
via f. We can assume (if necessary, by taking
![]() $QI$
-equivalent strings
$QI$
-equivalent strings
![]() $\alpha '\sim _{QI} \alpha $
and
$\alpha '\sim _{QI} \alpha $
and
![]() $\beta '\sim _{QI} \beta $
) that f is injective and monotonic. The reader can verify this (or the reader can refer to Theorem 4.11). So,
$\beta '\sim _{QI} \beta $
) that f is injective and monotonic. The reader can verify this (or the reader can refer to Theorem 4.11). So,
![]() $\beta $
is of the form
$\beta $
is of the form
where the length of finite strings
![]() $w_k$
are all uniformly bounded by a constant. By
$w_k$
are all uniformly bounded by a constant. By
![]() $p(n)$
we denote the position of
$p(n)$
we denote the position of
![]() $\alpha (n)$
in
$\alpha (n)$
in
![]() $\beta $
, that is,
$\beta $
, that is,
![]() $p(n) = n+\sum _{i=0}^{n-1} |w_i|$
.
$p(n) = n+\sum _{i=0}^{n-1} |w_i|$
.
An informal idea of constructing
![]() $\gamma $
is the following. Initially
$\gamma $
is the following. Initially
![]() $\gamma $
starts copying
$\gamma $
starts copying
![]() $\alpha $
until an initial segment of
$\alpha $
until an initial segment of
![]() $\alpha $
such that no mapping from
$\alpha $
such that no mapping from
![]() $\beta $
can possibly be extended to a
$\beta $
can possibly be extended to a
![]() $(1,1,1)$
-quasi-isometry into
$(1,1,1)$
-quasi-isometry into
![]() $\gamma $
built. From that point on,
$\gamma $
built. From that point on,
![]() $\gamma $
switches to
$\gamma $
switches to
![]() $\beta $
and copies
$\beta $
and copies
![]() $\beta $
until an initial segment of
$\beta $
until an initial segment of
![]() $\gamma $
is built such that no mapping from
$\gamma $
is built such that no mapping from
![]() $\gamma $
can possibly be extended to a
$\gamma $
can possibly be extended to a
![]() $(2,2,2)$
-quasi-isometry into
$(2,2,2)$
-quasi-isometry into
![]() $\alpha $
built. Then
$\alpha $
built. Then
![]() $\gamma $
switches to
$\gamma $
switches to
![]() $\alpha $
and continues on copying
$\alpha $
and continues on copying
![]() $\alpha $
. Below is a formal description.
$\alpha $
. Below is a formal description.
In what follows we inductively define the sequence
![]() $\gamma _k$
of infinite strings, where
$\gamma _k$
of infinite strings, where
![]() $k\in \omega $
. The strings
$k\in \omega $
. The strings
![]() $\gamma _k$
will always be of the form
$\gamma _k$
will always be of the form
![]() $\gamma _k = \alpha (0) u_0^{(k)} \alpha (1) u_1^{(k)} \ldots $
, where for each i and k, the string
$\gamma _k = \alpha (0) u_0^{(k)} \alpha (1) u_1^{(k)} \ldots $
, where for each i and k, the string
![]() $u_i^{(k)}$
is either
$u_i^{(k)}$
is either
![]() $w_i$
or an empty string.
$w_i$
or an empty string.
Let
![]() $p_k(n)$
be the position of
$p_k(n)$
be the position of
![]() $\alpha (n)$
in the string
$\alpha (n)$
in the string
![]() $\gamma _k$
, that is,
$\gamma _k$
, that is,
![]() $p_k(n) = n+\sum _{i=0}^{n-1} |w_i^{(k)}|$
. Call a string
$p_k(n) = n+\sum _{i=0}^{n-1} |w_i^{(k)}|$
. Call a string
![]() $\delta $
an extension of a finite string w if it has w as its prefix (i.e.,
$\delta $
an extension of a finite string w if it has w as its prefix (i.e.,
![]() $\delta = w\delta '$
for some
$\delta = w\delta '$
for some
![]() $\delta '$
). Now we define the sequence
$\delta '$
). Now we define the sequence
![]() $\{\gamma _k\}_{k\in \omega }$
as follows:
$\{\gamma _k\}_{k\in \omega }$
as follows:
-
• Set
 $\gamma _0 :=\alpha $
.
$\gamma _0 :=\alpha $
. -
• For given
 $k \geqslant 1$
we proceed as follows.
$k \geqslant 1$
we proceed as follows.-
– Assume
 $k-1$
is even. Find
$k-1$
is even. Find
 $n_k \in \omega $
such that no mapping
$n_k \in \omega $
such that no mapping
 $\,f: \beta \hspace {-.4em}\upharpoonright _{n_k} \to \gamma _{k-1}$
exists that can possibly be extendable to
$\,f: \beta \hspace {-.4em}\upharpoonright _{n_k} \to \gamma _{k-1}$
exists that can possibly be extendable to
 $(k,k,k)$
-quasi-isometry. Such
$(k,k,k)$
-quasi-isometry. Such
 $n_k$
exists because
$n_k$
exists because
 $\beta \not \leqslant _{QI}\gamma _{k-1}$
(by inductive hypothesis). Take a sufficiently large s, say
$\beta \not \leqslant _{QI}\gamma _{k-1}$
(by inductive hypothesis). Take a sufficiently large s, say
 $s = kn_k + D_k$
, where
$s = kn_k + D_k$
, where
 $D_k$
is a constant in Lemma 3.5 for
$D_k$
is a constant in Lemma 3.5 for
 $(k,k,k)$
-quasi-isometry constant, and set Note that any map from
$(k,k,k)$
-quasi-isometry constant, and set Note that any map from $$ \begin{align*}\gamma_k = \gamma_{k-1}\hspace{-.4em}\upharpoonright_s\beta(s+1)\beta(s+2)\ldots. \end{align*} $$
$$ \begin{align*}\gamma_k = \gamma_{k-1}\hspace{-.4em}\upharpoonright_s\beta(s+1)\beta(s+2)\ldots. \end{align*} $$
 $\beta \hspace {-.4em}\upharpoonright _{n_k}$
to any extension of
$\beta \hspace {-.4em}\upharpoonright _{n_k}$
to any extension of
 $\gamma _{k-1}\hspace {-.4em}\upharpoonright _s$
is not possibly extendable to a
$\gamma _{k-1}\hspace {-.4em}\upharpoonright _s$
is not possibly extendable to a
 $(k,k,k)$
-quasi-isometry. Note that, by Lemma 3.9, we also have
$(k,k,k)$
-quasi-isometry. Note that, by Lemma 3.9, we also have
 $\gamma _k \not \leqslant _{QI}\alpha $
.
$\gamma _k \not \leqslant _{QI}\alpha $
.
-
– Assume that
 $k-1$
is odd. Find
$k-1$
is odd. Find
 $n_k \in \text {range} (p_{k-1})$
such that no map
$n_k \in \text {range} (p_{k-1})$
such that no map
 $\,f: \gamma _{k-1} \hspace {-.4em}\upharpoonright _{n_k} \to \alpha $
is possibly extendable to
$\,f: \gamma _{k-1} \hspace {-.4em}\upharpoonright _{n_k} \to \alpha $
is possibly extendable to
 $(k,k,k)$
-quasi-isometry; this is possible because
$(k,k,k)$
-quasi-isometry; this is possible because
 $\gamma _{k-1} \not \leqslant _{QI}\alpha $
. Let
$\gamma _{k-1} \not \leqslant _{QI}\alpha $
. Let
 $s = p_{k-1}^{-1}(n_k)$
(thus we have
$s = p_{k-1}^{-1}(n_k)$
(thus we have
 $\gamma _{k-1} \hspace {-.4em}\upharpoonright _{n_k} = \alpha (0) u_0^{(k-1)} \alpha (1) u_1^{(k-1)} \ldots \alpha (s)$
), and just as above, set Note that, by Lemma 3.9, we have
$\gamma _{k-1} \hspace {-.4em}\upharpoonright _{n_k} = \alpha (0) u_0^{(k-1)} \alpha (1) u_1^{(k-1)} \ldots \alpha (s)$
), and just as above, set Note that, by Lemma 3.9, we have $$ \begin{align*} \gamma_k = \gamma_{k-1} \hspace{-.4em}\upharpoonright_{n_k} \alpha (s+1)\alpha (s+2) \ldots. \end{align*} $$
$$ \begin{align*} \gamma_k = \gamma_{k-1} \hspace{-.4em}\upharpoonright_{n_k} \alpha (s+1)\alpha (s+2) \ldots. \end{align*} $$
 $\beta \not \leqslant _{QI}\gamma _k$
.
$\beta \not \leqslant _{QI}\gamma _k$
.
-
Let
![]() $\gamma = \lim _{k\to \infty } \gamma _k$
. Now we show that
$\gamma = \lim _{k\to \infty } \gamma _k$
. Now we show that
![]() $\gamma \not \leqslant _{QI} \alpha $
. Assume that
$\gamma \not \leqslant _{QI} \alpha $
. Assume that
![]() $\gamma \leqslant _{QI} \alpha $
via a quasi-isometry. Select the smallest even k such that
$\gamma \leqslant _{QI} \alpha $
via a quasi-isometry. Select the smallest even k such that
![]() $\gamma \leqslant _{QI} \alpha $
via a
$\gamma \leqslant _{QI} \alpha $
via a
![]() $(k,k,k)$
-quasi-isometry g. Consider the construction of
$(k,k,k)$
-quasi-isometry g. Consider the construction of
![]() $\gamma _k$
. The string
$\gamma _k$
. The string
![]() $\gamma _k$
has the prefix
$\gamma _k$
has the prefix
![]() $\gamma _{k-1} \hspace {-.4em}\upharpoonright _{n_k}$
such that no map
$\gamma _{k-1} \hspace {-.4em}\upharpoonright _{n_k}$
such that no map
![]() $\,f: \gamma _{k-1} \hspace {-.4em}\upharpoonright _{n_k} \to \alpha $
is possibly extendable to
$\,f: \gamma _{k-1} \hspace {-.4em}\upharpoonright _{n_k} \to \alpha $
is possibly extendable to
![]() $(k,k,k)$
-quasi-isometry. By construction,
$(k,k,k)$
-quasi-isometry. By construction,
![]() $\gamma _{k-1} \hspace {-.4em}\upharpoonright _{n_k}$
is a prefix of
$\gamma _{k-1} \hspace {-.4em}\upharpoonright _{n_k}$
is a prefix of
![]() $\gamma $
, that is,
$\gamma $
, that is,
![]() $\gamma \hspace {-.4em}\upharpoonright _{n_k}= \gamma _{k-1} \hspace {-.4em}\upharpoonright _{n_k}$
. Hence, g restricted to
$\gamma \hspace {-.4em}\upharpoonright _{n_k}= \gamma _{k-1} \hspace {-.4em}\upharpoonright _{n_k}$
. Hence, g restricted to
![]() $ \gamma _{k-1} \hspace {-.4em}\upharpoonright _{n_k}$
is possibly extendable to a
$ \gamma _{k-1} \hspace {-.4em}\upharpoonright _{n_k}$
is possibly extendable to a
![]() $(k,k,k)$
-quasi-isometry. Contradiction. Similarly, one can show that
$(k,k,k)$
-quasi-isometry. Contradiction. Similarly, one can show that
![]() $\gamma \not \geqslant _{QI} \beta $
. Finally note that
$\gamma \not \geqslant _{QI} \beta $
. Finally note that
![]() $\gamma $
is of the form
$\gamma $
is of the form
![]() $\alpha (0) u_0 \alpha (1) u_1 \ldots $
, where
$\alpha (0) u_0 \alpha (1) u_1 \ldots $
, where
![]() $u_i$
is either
$u_i$
is either
![]() $w_i$
or an empty string for each i. This implies that
$w_i$
or an empty string for each i. This implies that
![]() $\alpha \leqslant _{QI} \gamma \leqslant _{QI} \beta $
.⊣
$\alpha \leqslant _{QI} \gamma \leqslant _{QI} \beta $
.⊣
Corollary 3.11. Let
![]() $\alpha , \beta \in \Sigma ^\omega $
be given. Assume
$\alpha , \beta \in \Sigma ^\omega $
be given. Assume
![]() $\alpha <_{QI} \beta $
, and every letter in
$\alpha <_{QI} \beta $
, and every letter in
![]() $\alpha $
or
$\alpha $
or
![]() $\beta $
occurs in both
$\beta $
occurs in both
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
infinitely many often. Then there is a countable antichain
$\beta $
infinitely many often. Then there is a countable antichain
![]() $\{\gamma ^{(n)}\}$
such that
$\{\gamma ^{(n)}\}$
such that
![]() $\alpha <_{QI} \gamma ^{(n)} <_{QI} \beta $
for each
$\alpha <_{QI} \gamma ^{(n)} <_{QI} \beta $
for each
![]() $n\in \omega $
.
$n\in \omega $
.
Proof Assume we have constructed
![]() $\gamma ^{(0)},\ldots ,\gamma ^{(n)}$
such that
$\gamma ^{(0)},\ldots ,\gamma ^{(n)}$
such that
![]() $\alpha <_{QI} \gamma ^{(i)} <_{QI} \beta $
for each
$\alpha <_{QI} \gamma ^{(i)} <_{QI} \beta $
for each
![]() $i\leqslant n$
. Then construct
$i\leqslant n$
. Then construct
![]() $\gamma ^{(n+1)}$
via the same construction of
$\gamma ^{(n+1)}$
via the same construction of
![]() $\gamma $
in the proof of Theorem 3.10, but
$\gamma $
in the proof of Theorem 3.10, but
![]() $n_k$
is a number such that
$n_k$
is a number such that
-
1. no map
 $\,f: \beta \hspace {-.4em}\upharpoonright _{n_k} \to \gamma _{k-1}$
or
$\,f: \beta \hspace {-.4em}\upharpoonright _{n_k} \to \gamma _{k-1}$
or
 $\,f: \gamma ^{(i)} \hspace {-.4em}\upharpoonright _{n_k} \to \gamma _{k-1} (i\leqslant n)$
is possibly extendable to
$\,f: \gamma ^{(i)} \hspace {-.4em}\upharpoonright _{n_k} \to \gamma _{k-1} (i\leqslant n)$
is possibly extendable to
 $(k,k,k)$
-quasi-isometry; and
$(k,k,k)$
-quasi-isometry; and -
2. if
 $k-1$
is odd, then the finite string
$k-1$
is odd, then the finite string
 $\beta (n_{k-1}+1)\ldots \beta (n_k)$
contains every color in
$\beta (n_{k-1}+1)\ldots \beta (n_k)$
contains every color in
 $Cl(\beta )$
.
$Cl(\beta )$
.
Notice that the condition 2 is imposed to assure that any color in
![]() $\gamma ^{(n)}$
occurs in it infinitely often. This property of
$\gamma ^{(n)}$
occurs in it infinitely often. This property of
![]() $\gamma ^{(n)}$
is required to apply Lemma 3.9 when we compare
$\gamma ^{(n)}$
is required to apply Lemma 3.9 when we compare
![]() $\gamma _k$
and
$\gamma _k$
and
![]() $\gamma ^{(n)}$
in the construction of
$\gamma ^{(n)}$
in the construction of
![]() $\gamma ^{(m)}$
,
$\gamma ^{(m)}$
,
![]() $m>n$
.⊣
$m>n$
.⊣
The reader can easily notice that the proof of the Density Theorem can be carried out effectively. We state this as the next corollary.
Corollary 3.12. Let
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
be computable strings such that
$\beta $
be computable strings such that
![]() $\alpha <_{QI} \beta $
via a computable quasi-isometry. Then there exists a computable string
$\alpha <_{QI} \beta $
via a computable quasi-isometry. Then there exists a computable string
![]() $\gamma $
such that
$\gamma $
such that
![]() $\alpha <_{QI} \gamma <_{QI} \beta $
.⊣
$\alpha <_{QI} \gamma <_{QI} \beta $
.⊣
3.3 Ideals and filters in
 $\Sigma ^{\omega }_{QI}$
$\Sigma ^{\omega }_{QI}$
Recall that a filter in the partially ordered set
![]() $\Sigma ^{\omega }_{QI}$
is any set X such that for all
$\Sigma ^{\omega }_{QI}$
is any set X such that for all
![]() $x\in X$
and
$x\in X$
and
![]() $x\leqslant y$
we have
$x\leqslant y$
we have
![]() $y\in X$
. A filter X is principal if X has the least element. Similarly, a set Y is called an ideal if for all
$y\in X$
. A filter X is principal if X has the least element. Similarly, a set Y is called an ideal if for all
![]() $x\in Y $
and
$x\in Y $
and
![]() $y\leqslant x$
we have
$y\leqslant x$
we have
![]() $y\in Y$
. Our goal is to give several natural examples of filters and ideals in the partial order
$y\in Y$
. Our goal is to give several natural examples of filters and ideals in the partial order
![]() $\Sigma ^{\omega }_{QI}$
that give some insight into algebraic properties of the partial order
$\Sigma ^{\omega }_{QI}$
that give some insight into algebraic properties of the partial order
![]() $\leqslant _{QI}$
.
$\leqslant _{QI}$
.
In this section the alphabet
![]() $\Sigma $
is
$\Sigma $
is
![]() $\{0,1\}$
. For alphabets of larger sizes the concepts and results of this section can easily be extended. Consider the string
$\{0,1\}$
. For alphabets of larger sizes the concepts and results of this section can easily be extended. Consider the string
from
![]() $\{0,1\}^{\omega }$
, where
$\{0,1\}^{\omega }$
, where
![]() $n_i, m_i\geqslant 1$
. Call the substrings
$n_i, m_i\geqslant 1$
. Call the substrings
![]() $0^{n_i}$
and
$0^{n_i}$
and
![]() $1^{m_i}$
the
$1^{m_i}$
the
![]() $0$
-blocks and
$0$
-blocks and
![]() $1$
-blocks, respectively. Define:
$1$
-blocks, respectively. Define:
-
•
 $\mathcal F(0)=\{[\alpha ]\mid $
there exists a constant B such that the lengths of
$\mathcal F(0)=\{[\alpha ]\mid $
there exists a constant B such that the lengths of
 $0$
-blocks in
$0$
-blocks in
 $\alpha $
are bounded by
$\alpha $
are bounded by
 $B\}$
,
$B\}$
, -
•
 $\mathcal F(1)=\{[\alpha ]\mid $
there exists a constant B such that the lengths of
$\mathcal F(1)=\{[\alpha ]\mid $
there exists a constant B such that the lengths of
 $1$
-blocks in
$1$
-blocks in
 $\alpha $
are bounded by
$\alpha $
are bounded by
 $B\}.$
$B\}.$
Theorem 3.13. The sets
![]() $\mathcal F(0)$
,
$\mathcal F(0)$
,
![]() $\mathcal F(1)$
are principal filters.
$\mathcal F(1)$
are principal filters.
Proof We prove that
![]() $\mathcal F(0)$
is a filter. Let
$\mathcal F(0)$
is a filter. Let
![]() $\alpha \in \mathcal F(0)$
and
$\alpha \in \mathcal F(0)$
and
![]() $\alpha \leqslant _{QI} \beta $
through an
$\alpha \leqslant _{QI} \beta $
through an
![]() $(A, B, C)$
-quasi-isometry f. We need to show that
$(A, B, C)$
-quasi-isometry f. We need to show that
![]() $\beta \in \mathcal F(0)$
. Assume, for the sake of contradiction, that the lengths of
$\beta \in \mathcal F(0)$
. Assume, for the sake of contradiction, that the lengths of
![]() $0$
-blocks in
$0$
-blocks in
![]() $\beta $
are unbounded. Let B be the length of the largest
$\beta $
are unbounded. Let B be the length of the largest
![]() $0$
-block in
$0$
-block in
![]() $\alpha $
. Now, take a
$\alpha $
. Now, take a
![]() $0$
-block
$0$
-block
![]() $\beta (i)\ldots \beta (i+n_0)$
in
$\beta (i)\ldots \beta (i+n_0)$
in
![]() $\beta $
, where
$\beta $
, where
![]() $n_0$
is sufficiently large. We give bound on the value of
$n_0$
is sufficiently large. We give bound on the value of
![]() $n_0$
below. Since f is a quasi-isometry, there exists a
$n_0$
below. Since f is a quasi-isometry, there exists a
![]() $\beta (i_0)$
that belongs to the block
$\beta (i_0)$
that belongs to the block
![]() $\beta (i)\ldots \beta (i+n_0)$
such that
$\beta (i)\ldots \beta (i+n_0)$
such that
![]() $\beta (i_0)$
has a preimage
$\beta (i_0)$
has a preimage
![]() $\alpha (j_0)$
and
$\alpha (j_0)$
and
![]() $\beta (i_0)$
is within distance C from the center of the
$\beta (i_0)$
is within distance C from the center of the
![]() $0$
-block
$0$
-block
![]() $\beta (i)\ldots \beta (i+n_0)$
. The length of the block in
$\beta (i)\ldots \beta (i+n_0)$
. The length of the block in
![]() $\alpha $
that contains
$\alpha $
that contains
![]() $\alpha (j_0)$
is bounded by B. We conclude that the string
$\alpha (j_0)$
is bounded by B. We conclude that the string
must contain
![]() $1$
. The length of this string is
$1$
. The length of this string is
![]() $2B+2$
. There exists a constant D such that f-image of all intervals of length
$2B+2$
. There exists a constant D such that f-image of all intervals of length
![]() $2B+2$
is contained in the intervals in
$2B+2$
is contained in the intervals in
![]() $\beta $
of length at most D. So, if
$\beta $
of length at most D. So, if
![]() $n_0=2D$
then the f-image of the interval
$n_0=2D$
then the f-image of the interval
must be inside of
![]() $\beta (i)\ldots \beta (i+n_0)$
. This implies that the original
$\beta (i)\ldots \beta (i+n_0)$
. This implies that the original
![]() $0$
-block
$0$
-block
![]() $\beta (i)\ldots \beta {(i+n_0)}$
contains
$\beta (i)\ldots \beta {(i+n_0)}$
contains
![]() $1$
since f preserves colors. It must be the case that
$1$
since f preserves colors. It must be the case that
![]() $n_0\leqslant 2D$
. Hence,
$n_0\leqslant 2D$
. Hence,
![]() $\beta \in \mathcal F(0)$
. Finally, it is clear that
$\beta \in \mathcal F(0)$
. Finally, it is clear that
![]() $[1^{\omega }]$
is the least element in
$[1^{\omega }]$
is the least element in
![]() $\mathcal F(0)$
. Hence,
$\mathcal F(0)$
. Hence,
![]() $\mathcal F(0)$
is a principal filter. The same proof shows that the set
$\mathcal F(0)$
is a principal filter. The same proof shows that the set
![]() $\mathcal F(1)$
is a principal filter.⊣
$\mathcal F(1)$
is a principal filter.⊣
Now we define the following two sets:
-
•
 $\mathcal I(u)=\{[\alpha ]\mid $
there is no universal bound on the lengths of both
$\mathcal I(u)=\{[\alpha ]\mid $
there is no universal bound on the lengths of both
 $0$
-blocks and
$0$
-blocks and
 $1$
-blocks in
$1$
-blocks in
 $\alpha \}$
.
$\alpha \}$
. -
•
 $\mathcal F(b)=\{[\alpha ]\mid $
there is a constant B such that the lengths of both
$\mathcal F(b)=\{[\alpha ]\mid $
there is a constant B such that the lengths of both
 $0$
-blocks and
$0$
-blocks and
 $1$
-blocks in
$1$
-blocks in
 $\alpha $
are bounded by
$\alpha $
are bounded by
 $ B\}$
.
$ B\}$
.
Corollary 3.14. The set
![]() $\mathcal I(u)$
is an ideal.
$\mathcal I(u)$
is an ideal.
Proof Let
![]() $\alpha \in \mathcal I(u)$
and
$\alpha \in \mathcal I(u)$
and
![]() $\beta \leqslant _{QI} \alpha $
. If there is a universal bound on the lengths of all
$\beta \leqslant _{QI} \alpha $
. If there is a universal bound on the lengths of all
![]() $0$
-blocks in
$0$
-blocks in
![]() $\beta $
then from the theorem above we would have a universal bound on the lengths of
$\beta $
then from the theorem above we would have a universal bound on the lengths of
![]() $0$
-blocks in
$0$
-blocks in
![]() $\alpha $
. This is a contradiction. Similarly, there could not be a universal bound on the lengths of
$\alpha $
. This is a contradiction. Similarly, there could not be a universal bound on the lengths of
![]() $1$
-blocks in
$1$
-blocks in
![]() $\beta $
.⊣
$\beta $
.⊣
Corollary 3.15. The set
![]() $\mathcal F(b)$
is the singleton
$\mathcal F(b)$
is the singleton
![]() $\{[(01)^{\omega }]\}$
.
$\{[(01)^{\omega }]\}$
.
Proof Assume that
![]() $\alpha =0^{n_0}1^{m_0} 0^{n_1}1^{m_1}\ldots $
and there is a constant B such that
$\alpha =0^{n_0}1^{m_0} 0^{n_1}1^{m_1}\ldots $
and there is a constant B such that
![]() $1\leqslant n_i, m_i\leqslant B$
for all i. Consider a mapping
$1\leqslant n_i, m_i\leqslant B$
for all i. Consider a mapping
![]() $\,f: (01)^\omega \to \alpha $
that maps the ith occurrence of
$\,f: (01)^\omega \to \alpha $
that maps the ith occurrence of
![]() $0$
and
$0$
and
![]() $1$
in
$1$
in
![]() $(01)^\omega $
to any position of the blocks
$(01)^\omega $
to any position of the blocks
![]() $0^{n_i}$
and
$0^{n_i}$
and
![]() $1^{m_i}$
in
$1^{m_i}$
in
![]() $\alpha $
, respectively. Then f witnesses
$\alpha $
, respectively. Then f witnesses
![]() $(01)^\omega \leqslant _{QI} \alpha $
. Also the string
$(01)^\omega \leqslant _{QI} \alpha $
. Also the string
![]() $(01)^\omega $
is the greatest element of
$(01)^\omega $
is the greatest element of
![]() $\{0,1\}_{QI}^{\omega }$
, as shown in the proof of Proposition 1.6. Thus we have
$\{0,1\}_{QI}^{\omega }$
, as shown in the proof of Proposition 1.6. Thus we have
![]() $\alpha \leqslant _{QI} (01)^\omega $
.⊣
$\alpha \leqslant _{QI} (01)^\omega $
.⊣
The results above imply that the element
![]() $(01)^{\omega }$
is the least upper bound of any two elements
$(01)^{\omega }$
is the least upper bound of any two elements
![]() $\alpha \in \mathcal F(0)$
and
$\alpha \in \mathcal F(0)$
and
![]() $\beta \in \mathcal F(1)$
.
$\beta \in \mathcal F(1)$
.
Corollary 3.16. For all
![]() $\alpha \in \mathcal F(0)$
,
$\alpha \in \mathcal F(0)$
,
![]() $\beta \in \mathcal F(1)$
,
$\beta \in \mathcal F(1)$
,
![]() $\gamma \in \Sigma ^{\omega }$
, if
$\gamma \in \Sigma ^{\omega }$
, if
![]() $\alpha \leqslant _{QI} \gamma $
and
$\alpha \leqslant _{QI} \gamma $
and
![]() $\beta \leqslant _{QI} \gamma $
then
$\beta \leqslant _{QI} \gamma $
then
![]() $\gamma \sim _{QI} (01)^{\omega }$
.
$\gamma \sim _{QI} (01)^{\omega }$
.
One of the natural algebraic operations on strings is the join operation
![]() $\oplus $
. The join operation
$\oplus $
. The join operation
![]() $\oplus $
, given
$\oplus $
, given
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
, produces the string
$\beta $
, produces the string
![]() $\alpha \oplus \beta $
defined as
$\alpha \oplus \beta $
defined as
![]() $\alpha (0)\beta (0)\alpha (1)\beta (1)\ldots $
. This operation is used in computability theory and complexity theory to produce the least upper bounds for various computability and complexity theoretic reducibilities on sets.
$\alpha (0)\beta (0)\alpha (1)\beta (1)\ldots $
. This operation is used in computability theory and complexity theory to produce the least upper bounds for various computability and complexity theoretic reducibilities on sets.
Note that
![]() $\alpha \leqslant _{QI} \alpha \oplus \beta $
and
$\alpha \leqslant _{QI} \alpha \oplus \beta $
and
![]() $\beta \leqslant _{QI} \alpha \oplus \beta $
. So
$\beta \leqslant _{QI} \alpha \oplus \beta $
. So
![]() $[\alpha \oplus \beta ]$
is an upper bound for all
$[\alpha \oplus \beta ]$
is an upper bound for all
![]() $[\alpha ]$
and
$[\alpha ]$
and
![]() $[\beta ]$
. However, the operation
$[\beta ]$
. However, the operation
![]() $\oplus $
does not always produce the least upper bound. Indeed, consider the strings
$\oplus $
does not always produce the least upper bound. Indeed, consider the strings
We can construct a quasi-isometry from
![]() $\alpha $
to
$\alpha $
to
![]() $\beta $
by mapping the
$\beta $
by mapping the
![]() $(0)^{2^n}(1)^{2^n}$
-block in
$(0)^{2^n}(1)^{2^n}$
-block in
![]() $\alpha $
to the
$\alpha $
to the
![]() $(0)^{2^{n+1}}(1)^{2^{n+1}}$
-block in
$(0)^{2^{n+1}}(1)^{2^{n+1}}$
-block in
![]() $\beta $
; a quasi-isometry from
$\beta $
; a quasi-isometry from
![]() $\beta $
to
$\beta $
to
![]() $\alpha $
can be also constructed in a similar way. So we have
$\alpha $
can be also constructed in a similar way. So we have
![]() $\alpha \sim _{QI} \beta $
, and hence the least upper bound for
$\alpha \sim _{QI} \beta $
, and hence the least upper bound for
![]() $[\alpha ]$
and
$[\alpha ]$
and
![]() $[\beta ]$
is
$[\beta ]$
is
![]() $[\alpha ]$
. However,
$[\alpha ]$
. However,
![]() $[\alpha \oplus \beta ] =[(01)^\omega ]$
, and
$[\alpha \oplus \beta ] =[(01)^\omega ]$
, and
![]() $[(01)^{\omega }] \neq [\alpha ]$
,
$[(01)^{\omega }] \neq [\alpha ]$
,
![]() $[(01)^{\omega })] \neq \ [\beta ]$
, and
$[(01)^{\omega })] \neq \ [\beta ]$
, and
![]() $[\alpha ]=[\beta ]$
.
$[\alpha ]=[\beta ]$
.
Even though the operation
![]() $\oplus $
is not well-behaved on the
$\oplus $
is not well-behaved on the
![]() $\sim _{QI}$
-equivalence classes, the operation can still be useful in constructing counter-examples as shown in the next corollary.
$\sim _{QI}$
-equivalence classes, the operation can still be useful in constructing counter-examples as shown in the next corollary.
Corollary 3.17. The filters
![]() $\mathcal F(0)$
and
$\mathcal F(0)$
and
![]() $\mathcal F(1)$
have infinite chains and infinite antichains.
$\mathcal F(1)$
have infinite chains and infinite antichains.
Proof The chain constructed in Theorem 3.1 is in
![]() $\mathcal F(0)$
. Hence, both
$\mathcal F(0)$
. Hence, both
![]() $\mathcal F(0)$
and
$\mathcal F(0)$
and
![]() $\mathcal F(1)$
have countable chains. Let
$\mathcal F(1)$
have countable chains. Let
![]() $\beta _n$
,
$\beta _n$
,
![]() $n \in \omega $
, be the sequence from the proof of Theorem 3.2:
$n \in \omega $
, be the sequence from the proof of Theorem 3.2:
Using this sequence, construct the following new sequence
![]() $\{\beta _n \oplus 1^\omega \}_{n \in \omega }$
. Each string
$\{\beta _n \oplus 1^\omega \}_{n \in \omega }$
. Each string
![]() $\beta _n \oplus 1^\omega $
belongs to the filter
$\beta _n \oplus 1^\omega $
belongs to the filter
![]() $\mathcal F(0)$
. In the same manner as in the proof of Theorem 3.2 one can show that
$\mathcal F(0)$
. In the same manner as in the proof of Theorem 3.2 one can show that
![]() $\{\beta _n \oplus 1^\omega \}_{n \in \omega } \subset \mathcal {F}(1)$
is an antichain. Similarly
$\{\beta _n \oplus 1^\omega \}_{n \in \omega } \subset \mathcal {F}(1)$
is an antichain. Similarly
![]() $\{\beta _n \oplus 0^\omega \}_{n \in \omega } \subset \mathcal {F}(0)$
is an antichain.⊣
$\{\beta _n \oplus 0^\omega \}_{n \in \omega } \subset \mathcal {F}(0)$
is an antichain.⊣
Corollary 3.18. The ideal
![]() $\mathcal I(u)$
has an infinite antichain consisting of minimal elements. Moreover, the ideal does not have maximal elements.
$\mathcal I(u)$
has an infinite antichain consisting of minimal elements. Moreover, the ideal does not have maximal elements.
Proof The minimal elements constructed in Theorem 3.3 are clearly in the ideal
![]() $\mathcal I(u)$
. For the second part we adapt the proof of the Density Theorem. Assume that
$\mathcal I(u)$
. For the second part we adapt the proof of the Density Theorem. Assume that
![]() $\alpha $
is a maximal element. We can represent
$\alpha $
is a maximal element. We can represent
![]() $\alpha $
as follows:
$\alpha $
as follows:
where
![]() $n_0< n_1< n_2< \dotsb $
. Note that
$n_0< n_1< n_2< \dotsb $
. Note that
![]() $\alpha <_{QI} (01)^{\omega }$
. If we apply the proof of the Density Theorem directly, then we might produce
$\alpha <_{QI} (01)^{\omega }$
. If we apply the proof of the Density Theorem directly, then we might produce
![]() $\gamma $
such that
$\gamma $
such that
![]() $\alpha <_{QI} \gamma <_{QI} (01)^{\omega }$
with
$\alpha <_{QI} \gamma <_{QI} (01)^{\omega }$
with
![]() $\gamma \not \in \mathcal I(u)$
. To guarantee that
$\gamma \not \in \mathcal I(u)$
. To guarantee that
![]() $\gamma \in \mathcal I(u)$
we need to slightly change the proof of the Density Theorem. Namely, every time when
$\gamma \in \mathcal I(u)$
we need to slightly change the proof of the Density Theorem. Namely, every time when
![]() $\gamma $
copies a part of
$\gamma $
copies a part of
![]() $\alpha $
, it should include a
$\alpha $
, it should include a
![]() $0$
-block and also a
$0$
-block and also a
![]() $1$
-block whose lengths are greater that the lengths of all
$1$
-block whose lengths are greater that the lengths of all
![]() $0$
-blocks and
$0$
-blocks and
![]() $1$
-blocks in
$1$
-blocks in
![]() $\gamma $
that has been built so far. It is clear that this condition can be satisfied. This puts
$\gamma $
that has been built so far. It is clear that this condition can be satisfied. This puts
![]() $\gamma $
into the ideal
$\gamma $
into the ideal
![]() $\mathcal I (u)$
.⊣
$\mathcal I (u)$
.⊣
3.4 Quasi-isometry on eventually periodic strings
In this section we describe the isomorphism type of the partial order
![]() $\leqslant _{QI}$
restricted to the set of all eventually periodic strings of
$\leqslant _{QI}$
restricted to the set of all eventually periodic strings of
![]() $\Sigma ^{\omega }$
. These are the strings that have a particularly simple structure:
$\Sigma ^{\omega }$
. These are the strings that have a particularly simple structure:
Definition 3.19. A string
![]() $\alpha \in \Sigma ^{\omega }$
is eventually periodic if there are finite words
$\alpha \in \Sigma ^{\omega }$
is eventually periodic if there are finite words
![]() $x, u\in \Sigma ^\star $
such that
$x, u\in \Sigma ^\star $
such that
![]() $\alpha =xuuu \ldots $
. We write such
$\alpha =xuuu \ldots $
. We write such
![]() $\alpha $
as
$\alpha $
as
![]() $xu^{\omega }$
. Call u the period of
$xu^{\omega }$
. Call u the period of
![]() $\alpha $
. If x is the empty string then
$\alpha $
. If x is the empty string then
![]() $\alpha $
is periodic.
$\alpha $
is periodic.
Let
![]() $\alpha $
be a string (that can possibly be finite). Recall that
$\alpha $
be a string (that can possibly be finite). Recall that
![]() $Cl(\alpha )$
denotes the set of all colors that appear in
$Cl(\alpha )$
denotes the set of all colors that appear in
![]() $\alpha $
, that is,
$\alpha $
, that is,
One obvious quasi-isometry invariant of the string
![]() $\alpha \in \Sigma ^{\omega }$
is the set of all colors that appear in
$\alpha \in \Sigma ^{\omega }$
is the set of all colors that appear in
![]() $\alpha $
. Namely, if
$\alpha $
. Namely, if
![]() $\,f: \alpha \rightarrow \beta $
is a quasi-isometry then
$\,f: \alpha \rightarrow \beta $
is a quasi-isometry then
![]() $Cl(\alpha )\subseteq Cl(\beta )$
. This implies that if
$Cl(\alpha )\subseteq Cl(\beta )$
. This implies that if
![]() $\alpha \sim _{QI} \beta $
then
$\alpha \sim _{QI} \beta $
then
![]() $Cl(\alpha )=Cl(\beta )$
.
$Cl(\alpha )=Cl(\beta )$
.
Theorem 3.20. For eventually periodic words
![]() $\alpha $
,
$\alpha $
,
![]() $\beta $
we have
$\beta $
we have
![]() $\alpha \leqslant _{QI} \beta $
iff there are
$\alpha \leqslant _{QI} \beta $
iff there are
![]() $x,y, u, v \in \Sigma ^{\star }$
such that
$x,y, u, v \in \Sigma ^{\star }$
such that
![]() $\alpha =xu^{\omega }$
,
$\alpha =xu^{\omega }$
,
![]() $\beta =yv^{\omega }$
,
$\beta =yv^{\omega }$
,
![]() $Cl(x)\subseteq Cl(y)$
, and
$Cl(x)\subseteq Cl(y)$
, and
![]() $Cl(u) \subseteq Cl(v)$
.
$Cl(u) \subseteq Cl(v)$
.
Proof If
![]() $\alpha \leqslant _{QI} \beta $
then it is easy to select finite strings
$\alpha \leqslant _{QI} \beta $
then it is easy to select finite strings
![]() $x,y, u, v$
that satisfy the statement of the theorem.
$x,y, u, v$
that satisfy the statement of the theorem.
Assume that there are
![]() $x,y, u, v \in \Sigma ^{\star }$
such that
$x,y, u, v \in \Sigma ^{\star }$
such that
![]() $\alpha =xu^{\omega }$
,
$\alpha =xu^{\omega }$
,
![]() $\beta =yv^{\omega }$
,
$\beta =yv^{\omega }$
,
![]() $Cl(x)\subseteq Cl(y)$
and
$Cl(x)\subseteq Cl(y)$
and
![]() $Cl(u) \subseteq Cl(v)$
. Construct a quasi-isometry f from
$Cl(u) \subseteq Cl(v)$
. Construct a quasi-isometry f from
![]() $\alpha $
to
$\alpha $
to
![]() $\beta $
as follows. First, map the prefix x into the prefix y so that colors are preserved. Secondly, we consider the set
$\beta $
as follows. First, map the prefix x into the prefix y so that colors are preserved. Secondly, we consider the set
![]() $X=\{x_1,\ldots , x_k\}$
of all distinct colors that appear in u. Now map every
$X=\{x_1,\ldots , x_k\}$
of all distinct colors that appear in u. Now map every
![]() $x_i$
-colored position in the kth copy of u in the string
$x_i$
-colored position in the kth copy of u in the string
![]() $\alpha $
into an
$\alpha $
into an
![]() $x_i$
colored position in the kth copy of v in the string
$x_i$
colored position in the kth copy of v in the string
![]() $\beta $
. Set
$\beta $
. Set
![]() $A=\max \{|x|, |y|, |u|, |v|\}$
and
$A=\max \{|x|, |y|, |u|, |v|\}$
and
![]() $A=B=C$
. It is clear that f preserves colors and the quasi-isometry inequality between the distances
$A=B=C$
. It is clear that f preserves colors and the quasi-isometry inequality between the distances
![]() $d(x,y)$
and
$d(x,y)$
and
![]() $d(f(x), f(y))$
with quasi-isometry constants
$d(f(x), f(y))$
with quasi-isometry constants
![]() $A, B, C$
as required.⊣
$A, B, C$
as required.⊣
Consider the following two sets:
 $$ \begin{align*} E_P=&\{[\alpha] \mid \alpha \text{ is eventually periodic string over } \Sigma\}, \text{ and }\\ &\quad P=\{[\alpha] \mid \alpha \text{ is periodic string over }\Sigma\}. \end{align*} $$
$$ \begin{align*} E_P=&\{[\alpha] \mid \alpha \text{ is eventually periodic string over } \Sigma\}, \text{ and }\\ &\quad P=\{[\alpha] \mid \alpha \text{ is periodic string over }\Sigma\}. \end{align*} $$
So, we have two partially ordered sets
![]() $\mathcal E_P$
and
$\mathcal E_P$
and
![]() $\mathcal P$
obtained by restricting the order
$\mathcal P$
obtained by restricting the order
![]() $\leqslant _{QI}$
on the sets
$\leqslant _{QI}$
on the sets
![]() $E_P$
and P, respectively.
$E_P$
and P, respectively.
Let
![]() $\mathcal X$
be the partially ordered set of all nonempty subsets of
$\mathcal X$
be the partially ordered set of all nonempty subsets of
![]() $\Sigma $
with respect to set-theoretic inclusion. Let
$\Sigma $
with respect to set-theoretic inclusion. Let
![]() $\mathcal Y$
be the partially ordered set
$\mathcal Y$
be the partially ordered set
![]() $\mathcal X \times \mathcal X$
, where the order is component-wise order. We have the following corollary that fully characterize the isomorphism types of
$\mathcal X \times \mathcal X$
, where the order is component-wise order. We have the following corollary that fully characterize the isomorphism types of
![]() $\mathcal E_P$
and
$\mathcal E_P$
and
![]() $\mathcal P$
.
$\mathcal P$
.
Corollary 3.21. The following is true:
-
1. The partially ordered set
 $\mathcal E_P$
is isomorphic to
$\mathcal E_P$
is isomorphic to
 $\mathcal X \times \mathcal X$
.
$\mathcal X \times \mathcal X$
. -
2. The partially ordered set
 $\mathcal P$
is isomorphic to
$\mathcal P$
is isomorphic to
 $\mathcal X$
.
$\mathcal X$
.
Proof Let
![]() $A=\{a_1,\ldots , a_k\}$
and
$A=\{a_1,\ldots , a_k\}$
and
![]() $B=\{b_1, \ldots , b_n\}$
be elements of
$B=\{b_1, \ldots , b_n\}$
be elements of
![]() $\mathcal X(\Sigma )$
. Associate with the pair
$\mathcal X(\Sigma )$
. Associate with the pair
![]() $(A,B)$
the infinite string
$(A,B)$
the infinite string
![]() $a_1\ldots a_k (b_1\ldots b_n)^{\omega }$
. This establishes the mapping from
$a_1\ldots a_k (b_1\ldots b_n)^{\omega }$
. This establishes the mapping from
![]() $\mathcal X \times \mathcal X$
into
$\mathcal X \times \mathcal X$
into
![]() $\mathcal E_P$
. By Theorem 3.20 this is an isomorphism from
$\mathcal E_P$
. By Theorem 3.20 this is an isomorphism from
![]() $\mathcal X \times \mathcal X$
onto
$\mathcal X \times \mathcal X$
onto
![]() $\mathcal E_P$
. The second part is proved similarly.⊣
$\mathcal E_P$
. The second part is proved similarly.⊣
Let
![]() $\,f:\alpha \rightarrow \beta $
be a quasi-isometric map., and let
$\,f:\alpha \rightarrow \beta $
be a quasi-isometric map., and let
![]() $\Phi $
be a property. Say that f is eventually
$\Phi $
be a property. Say that f is eventually
![]() $\Phi $
if there is an index i such that f restricted to the suffix
$\Phi $
if there is an index i such that f restricted to the suffix
![]() $\alpha _i=\alpha (i) \alpha (i+1) \alpha (i+2)\ldots $
satisfies
$\alpha _i=\alpha (i) \alpha (i+1) \alpha (i+2)\ldots $
satisfies
![]() $\Phi $
. A quasi-isometry f does not need to be eventually order preserving map; neither f needs to be eventual embedding (that is, eventually injective map). Now we show that if
$\Phi $
. A quasi-isometry f does not need to be eventually order preserving map; neither f needs to be eventual embedding (that is, eventually injective map). Now we show that if
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are eventually periodic words, then f can be computable eventually order preserving injective map.
$\beta $
are eventually periodic words, then f can be computable eventually order preserving injective map.
Theorem 3.22. For eventually periodic strings
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
such that
$\beta $
such that
![]() $\alpha \leqslant _{QI} \beta $
there exists a computable quasi-isometric map
$\alpha \leqslant _{QI} \beta $
there exists a computable quasi-isometric map
![]() $\,f_{\alpha }:\alpha \rightarrow \beta $
which is eventually order preserving and eventually injective.
$\,f_{\alpha }:\alpha \rightarrow \beta $
which is eventually order preserving and eventually injective.
Proof Let
![]() $\alpha =xuuu\ldots $
and
$\alpha =xuuu\ldots $
and
![]() $ \beta =yvvv\ldots $
. Assume that
$ \beta =yvvv\ldots $
. Assume that
![]() $Cl(x)\subseteq Cl(y)$
and
$Cl(x)\subseteq Cl(y)$
and
![]() $Cl(u) \subseteq Cl(v)$
. Our desired mapping
$Cl(u) \subseteq Cl(v)$
. Our desired mapping
![]() $\,f_{\alpha }$
maps x into y by preserving colors. This is where
$\,f_{\alpha }$
maps x into y by preserving colors. This is where
![]() $\,f_{\alpha }$
need not be order preserving embedding. So, it suffices to construct a computable quasi-isometric embedding from
$\,f_{\alpha }$
need not be order preserving embedding. So, it suffices to construct a computable quasi-isometric embedding from
![]() $\alpha _1=u^{\omega }$
to
$\alpha _1=u^{\omega }$
to
![]() $\beta _1=v^{\omega }$
. Let
$\beta _1=v^{\omega }$
. Let
![]() $X=\{x_1,\ldots , x_k\}$
be the set of all colors that appear in u, and hence in v. Let
$X=\{x_1,\ldots , x_k\}$
be the set of all colors that appear in u, and hence in v. Let
![]() $a_i$
be the number of times that color
$a_i$
be the number of times that color
![]() $x_i$
appears in u. Clearly
$x_i$
appears in u. Clearly
![]() $a_i\geqslant 1$
. Consider the new string
$a_i\geqslant 1$
. Consider the new string
![]() $v_1$
obtained by writing v exactly
$v_1$
obtained by writing v exactly
![]() $a_1+\ldots +a_n$
times, that is,
$a_1+\ldots +a_n$
times, that is,
![]() $v_1=(v)^{a_1+a_2+\ldots + a_n}$
. now it is easy to see that there exists an embedding
$v_1=(v)^{a_1+a_2+\ldots + a_n}$
. now it is easy to see that there exists an embedding
![]() $\,f'$
from u into
$\,f'$
from u into
![]() $v_1$
that preserves colors and the order. We now easily propagate this mapping
$v_1$
that preserves colors and the order. We now easily propagate this mapping
![]() $\,f'$
to a color preserving embedding
$\,f'$
to a color preserving embedding
![]() $\,f_{\alpha }$
from
$\,f_{\alpha }$
from
![]() $\alpha _1$
into
$\alpha _1$
into
![]() $\beta _1$
. The map
$\beta _1$
. The map
![]() $\,f_{\alpha }:\alpha \rightarrow \beta $
thus built is a desired quasi-isometry.⊣
$\,f_{\alpha }:\alpha \rightarrow \beta $
thus built is a desired quasi-isometry.⊣
4 Component-wise reducibility
In this section we recast the definition of quasi-isometry, and give an equivalent but intuitively clearer description of the
![]() $\leqslant _{QI}$
-reducibility. Our intuitively clearer description is called component-wise reducibility. A string
$\leqslant _{QI}$
-reducibility. Our intuitively clearer description is called component-wise reducibility. A string
![]() $\alpha $
is component-wise reducible to string
$\alpha $
is component-wise reducible to string
![]() $\beta $
if we can partition
$\beta $
if we can partition
![]() $\alpha =u_1u_2\ldots $
and
$\alpha =u_1u_2\ldots $
and
![]() $\beta =v_1 v_2\ldots $
so that the sizes of the segments
$\beta =v_1 v_2\ldots $
so that the sizes of the segments
![]() $u_i$
,
$u_i$
,
![]() $v_j$
are uniformly bounded, and for each i all colors present in
$v_j$
are uniformly bounded, and for each i all colors present in
![]() $u_i$
are also present in
$u_i$
are also present in
![]() $v_i$
. It is easy to see that if
$v_i$
. It is easy to see that if
![]() $\alpha $
is component-wise reducible to
$\alpha $
is component-wise reducible to
![]() $\beta $
then there is a quasi-isometry from
$\beta $
then there is a quasi-isometry from
![]() $\alpha $
to
$\alpha $
to
![]() $\beta $
. We will show that the converse is also true. Our tool will be the decomposition theorem (which is interesting in its own right) that decomposes any quasi-isometric function
$\beta $
. We will show that the converse is also true. Our tool will be the decomposition theorem (which is interesting in its own right) that decomposes any quasi-isometric function
![]() $\,f:\alpha \rightarrow \beta $
into a finite sequence consisting of (1) more elementary quasi-isometric functions and (2) monotonic quasi-isometric embeddings.
$\,f:\alpha \rightarrow \beta $
into a finite sequence consisting of (1) more elementary quasi-isometric functions and (2) monotonic quasi-isometric embeddings.
4.1 Decomposing quasi-isometries
In this section we want to understand the quasi-isometric mappings syntactically. For instance, we want to know to what extend quasi-isometric mapping can be replaced by monotonic and/or injective quasi-isometries.
Lemma 4.1. Let
![]() $\,f:\alpha \rightarrow \beta $
be a quasi-isometry. We can decompose this map into a sequence
$\,f:\alpha \rightarrow \beta $
be a quasi-isometry. We can decompose this map into a sequence
![]() $\alpha \xrightarrow {f_1} \gamma \xrightarrow {f_2} \beta $
of quasi-isometries such that
$\alpha \xrightarrow {f_1} \gamma \xrightarrow {f_2} \beta $
of quasi-isometries such that
![]() $\,f_1$
is an injection and
$\,f_1$
is an injection and
![]() $\,f_2$
is a monotonic surjection. Moreover,
$\,f_2$
is a monotonic surjection. Moreover,
![]() $\gamma $
is quasi-isometric to
$\gamma $
is quasi-isometric to
![]() $\beta $
.
$\beta $
.
Proof We define
![]() $\gamma $
using
$\gamma $
using
![]() $\beta $
and the quasi-isometry f. For each position i in string
$\beta $
and the quasi-isometry f. For each position i in string
![]() $\beta $
consider
$\beta $
consider
![]() $\,f^{-1}(i)$
. If
$\,f^{-1}(i)$
. If
![]() $\,f^{-1}(i)=\emptyset $
then replace i with the position
$\,f^{-1}(i)=\emptyset $
then replace i with the position
![]() $(i, \emptyset )$
and color this position with
$(i, \emptyset )$
and color this position with
![]() $\beta (i)$
. Otherwise, let
$\beta (i)$
. Otherwise, let
![]() $j_{i,1}< \cdots < j_{i,k}$
be all f-preimages of i in the string
$j_{i,1}< \cdots < j_{i,k}$
be all f-preimages of i in the string
![]() $\alpha $
listed in their natural order. Replace the position i in
$\alpha $
listed in their natural order. Replace the position i in
![]() $\beta $
with positions
$\beta $
with positions
and color positions in this interval by color
![]() $\beta (i)$
. Thus, we have defined the new string
$\beta (i)$
. Thus, we have defined the new string
![]() $\gamma $
. Let us map elements
$\gamma $
. Let us map elements
![]() $(i,1)$
,
$(i,1)$
,
![]() $(i,2)$
,
$(i,2)$
,
![]() $\ldots $
,
$\ldots $
,
![]() $(i,k)$
in
$(i,k)$
in
![]() $\gamma $
into the position i of
$\gamma $
into the position i of
![]() $\beta $
. If i has no f-preimage then map
$\beta $
. If i has no f-preimage then map
![]() $(i,\emptyset )$
on i. This determines the function
$(i,\emptyset )$
on i. This determines the function
![]() $\,f_2$
stated in the lemma. Clearly,
$\,f_2$
stated in the lemma. Clearly,
![]() $\,f_2$
is a surjective quasi-isometry. The function
$\,f_2$
is a surjective quasi-isometry. The function
![]() $\,f_1$
is obtained from f as follows. For every
$\,f_1$
is obtained from f as follows. For every
![]() $i\in \beta $
if
$i\in \beta $
if
![]() $\,f^{-1}(i)\neq \emptyset $
, then map elements
$\,f^{-1}(i)\neq \emptyset $
, then map elements
![]() $j_{i,1}, \ldots , j_{i, k}$
on the elements
$j_{i,1}, \ldots , j_{i, k}$
on the elements
![]() $(i,1)$
,
$(i,1)$
,
![]() $(i,2)$
,
$(i,2)$
,
![]() $\ldots $
,
$\ldots $
,
![]() $(i,k)$
, respectively. The mapping is an injective quasi-isometry from
$(i,k)$
, respectively. The mapping is an injective quasi-isometry from
![]() $\alpha $
into
$\alpha $
into
![]() $\gamma $
. Finally, it is also easy to see that
$\gamma $
. Finally, it is also easy to see that
![]() $\beta \leqslant _{QI} \gamma $
through the map
$\beta \leqslant _{QI} \gamma $
through the map
![]() $i\rightarrow (i, \emptyset )$
if
$i\rightarrow (i, \emptyset )$
if
![]() $\,f^{-1}(i)=\emptyset $
, and
$\,f^{-1}(i)=\emptyset $
, and
![]() $i\rightarrow (i,1)$
if
$i\rightarrow (i,1)$
if
![]() $\,f^{-1}(i)\neq \emptyset $
.⊣
$\,f^{-1}(i)\neq \emptyset $
.⊣
It is not too hard to see that the process described in the proof can be carried out uniformly on
![]() $\alpha $
,
$\alpha $
,
![]() $\beta $
and f.
$\beta $
and f.
Corollary 4.2. There exists a procedure that given strings
![]() $\alpha $
,
$\alpha $
,
![]() $\beta $
and a quasi-isometry
$\beta $
and a quasi-isometry
![]() $\,f: \alpha \rightarrow \beta $
produces the decomposition
$\,f: \alpha \rightarrow \beta $
produces the decomposition
![]() $\alpha \xrightarrow {f_1} \gamma \xrightarrow {f_2} \beta $
as in Lemma 4.1. In particular, if
$\alpha \xrightarrow {f_1} \gamma \xrightarrow {f_2} \beta $
as in Lemma 4.1. In particular, if
![]() $\alpha $
,
$\alpha $
,
![]() $\beta $
and f are computable then so is the decomposition.⊣
$\beta $
and f are computable then so is the decomposition.⊣
Lemma 4.3. Let
![]() $\,f:\alpha \rightarrow \beta $
be a quasi-isometry. We can decompose this map into a sequence
$\,f:\alpha \rightarrow \beta $
be a quasi-isometry. We can decompose this map into a sequence
![]() $\alpha \xrightarrow {f_1} \gamma \xrightarrow {f_2} \beta $
of quasi-isometries such that
$\alpha \xrightarrow {f_1} \gamma \xrightarrow {f_2} \beta $
of quasi-isometries such that
![]() $\,f_1$
is a surjection and
$\,f_1$
is a surjection and
![]() $\,f_2$
is a monotonic injection. Moreover,
$\,f_2$
is a monotonic injection. Moreover,
![]() $\gamma $
is quasi-isometric to
$\gamma $
is quasi-isometric to
![]() $\beta $
.
$\beta $
.
Proof Let
![]() $\gamma $
be a string that is obtained by eliminating each position of
$\gamma $
be a string that is obtained by eliminating each position of
![]() $\beta $
that is not in the image of f, and construct
$\beta $
that is not in the image of f, and construct
![]() $\,f_1$
and
$\,f_1$
and
![]() $\,f_2$
in an obvious way. It is clear that
$\,f_2$
in an obvious way. It is clear that
![]() $\beta \leqslant _{QI} \gamma $
.⊣
$\beta \leqslant _{QI} \gamma $
.⊣
We note that just as the corollary above, the uniform version of this lemma is also true.
Definition 4.4. We say that a map
![]() $h:\alpha \to \beta $
is an atomic crossing map if the following holds. We have a sequence (possibly finite)
$h:\alpha \to \beta $
is an atomic crossing map if the following holds. We have a sequence (possibly finite)
![]() $(a_0,b_0), (a_1, b_1), \ldots $
of pairs of positions in
$(a_0,b_0), (a_1, b_1), \ldots $
of pairs of positions in
![]() $\alpha $
such that for some C and all i we have
$\alpha $
such that for some C and all i we have
![]() $(a_{i} < b_{i} < a_{i+1})$
and
$(a_{i} < b_{i} < a_{i+1})$
and
![]() $(b_i - a_i \leqslant C)$
and
$(b_i - a_i \leqslant C)$
and
 $$ \begin{align*} h(a) = \left\{ \begin{array}{lll} b_i & \text{if }a = a_i, \\ a_i & \text{if }a = b_i, \\ a & \text{otherwise.} \end{array} \right. \end{align*} $$
$$ \begin{align*} h(a) = \left\{ \begin{array}{lll} b_i & \text{if }a = a_i, \\ a_i & \text{if }a = b_i, \\ a & \text{otherwise.} \end{array} \right. \end{align*} $$
Clearly, every atomic crossing map is bijective.
Definition 4.5. Let
![]() $\,f:\alpha \rightarrow \gamma $
be a quasi-isometry. The cross-over constant of f is the maximal
$\,f:\alpha \rightarrow \gamma $
be a quasi-isometry. The cross-over constant of f is the maximal
![]() $D_f$
that witnesses a cross-over. In other words, the value of
$D_f$
that witnesses a cross-over. In other words, the value of
![]() $D_f$
equals to
$D_f$
equals to
Note that if the cross-over constant
![]() $D_f$
equals
$D_f$
equals
![]() $0$
then the quasi-isometry f is a monotonic nondecreasing function.
$0$
then the quasi-isometry f is a monotonic nondecreasing function.
Lemma 4.6. Let
![]() $\,f:\alpha \rightarrow \gamma $
be an injective quasi-isometry such that
$\,f:\alpha \rightarrow \gamma $
be an injective quasi-isometry such that
![]() $D_f> 0$
. We can decompose this map into a sequence
$D_f> 0$
. We can decompose this map into a sequence
![]() $\alpha \xrightarrow {f_1} \gamma _1 \xrightarrow {f_2} \gamma $
of quasi-isometries such that
$\alpha \xrightarrow {f_1} \gamma _1 \xrightarrow {f_2} \gamma $
of quasi-isometries such that
![]() $\,f_1$
is an injection,
$\,f_1$
is an injection,
![]() $D_{f_1}< D_{f}$
,
$D_{f_1}< D_{f}$
,
![]() $\,f_2$
is a finite composition of atomic crossing maps, and
$\,f_2$
is a finite composition of atomic crossing maps, and
![]() $\gamma $
is quasi-isometric to
$\gamma $
is quasi-isometric to
![]() $\gamma _1$
.
$\gamma _1$
.
Proof let us list all pairs
![]() $(a_0, b_0), (a_1, b_1), \ldots $
that constitute maximal crossings via f, that is,
$(a_0, b_0), (a_1, b_1), \ldots $
that constitute maximal crossings via f, that is,
![]() $a_i<b_i$
and
$a_i<b_i$
and
![]() $\,f(a_i) -f(b_i) = D_f$
. We list these pairs in the way that
$\,f(a_i) -f(b_i) = D_f$
. We list these pairs in the way that
![]() $b_i < a_{i+1}$
holds for each i, which is possible as we prove below. Without loss of generality let
$b_i < a_{i+1}$
holds for each i, which is possible as we prove below. Without loss of generality let
![]() $a_i \leqslant a_{i+1}$
for each i. First we have
$a_i \leqslant a_{i+1}$
for each i. First we have
![]() $a_i \neq a_j$
for every
$a_i \neq a_j$
for every
![]() $i \neq j$
, as otherwise we have
$i \neq j$
, as otherwise we have
![]() $\,f(b_i) = f(b_j) = f(a_i) - D_f$
, which contradicts injectivity of f; in a similar way we can show
$\,f(b_i) = f(b_j) = f(a_i) - D_f$
, which contradicts injectivity of f; in a similar way we can show
![]() $b_i \neq b_j$
for every
$b_i \neq b_j$
for every
![]() $i \neq j$
. Next we have
$i \neq j$
. Next we have
![]() $\,f(a_i) < f(a_j)$
for each
$\,f(a_i) < f(a_j)$
for each
![]() $i < j$
, as otherwise
$i < j$
, as otherwise
![]() $\,f(a_i) - f(b_j)> f(a_j) - f(b_j) = D_f$
while
$\,f(a_i) - f(b_j)> f(a_j) - f(b_j) = D_f$
while
![]() $a_i < a_j < b_j$
, which contradicts the fact that
$a_i < a_j < b_j$
, which contradicts the fact that
![]() $D_f$
is the cross-over constant of f; in a similar way we can show
$D_f$
is the cross-over constant of f; in a similar way we can show
![]() $\,f(b_i) < f(b_j)$
for each
$\,f(b_i) < f(b_j)$
for each
![]() $i < j$
. Lastly we have
$i < j$
. Lastly we have
![]() $b_i < a_{i+1}$
for every i, as otherwise we have
$b_i < a_{i+1}$
for every i, as otherwise we have
![]() $\,f(a_{i+1})- f(b_i)> f(a_i)- f(b_i) = D_f$
while
$\,f(a_{i+1})- f(b_i)> f(a_i)- f(b_i) = D_f$
while
![]() $a_{i+1} < b_i$
, again which contradicts the fact that
$a_{i+1} < b_i$
, again which contradicts the fact that
![]() $D_f$
is the cross-over constant of f.
$D_f$
is the cross-over constant of f.
Now we construct
![]() $\,f_1$
by “undoing” each maximal crossing in f. It is done by a function g that swaps the positions
$\,f_1$
by “undoing” each maximal crossing in f. It is done by a function g that swaps the positions
![]() $\,f(a_i)$
and
$\,f(a_i)$
and
![]() $\,f(b_i)$
in
$\,f(b_i)$
in
![]() $\gamma $
for each i. Formally, we define g as the following function:
$\gamma $
for each i. Formally, we define g as the following function:
 $$ \begin{align*} g(a) = \left\{ \begin{array}{lll} f(b_i) & \text{if }a = f(a_i), \\ f(a_i) & \text{if }a = f(b_i), \\ a & \text{otherwise.} \end{array} \right. \end{align*} $$
$$ \begin{align*} g(a) = \left\{ \begin{array}{lll} f(b_i) & \text{if }a = f(a_i), \\ f(a_i) & \text{if }a = f(b_i), \\ a & \text{otherwise.} \end{array} \right. \end{align*} $$
Notice that g satisfies all conditions of atomic crossing maps except that the sequence that defines g, namely
![]() $(f(b_0), f(a_0)),(f(b_1), f(a_1)),\ldots \hspace {-.04em},$
may not satisfy
$(f(b_0), f(a_0)),(f(b_1), f(a_1)),\ldots \hspace {-.04em},$
may not satisfy
![]() $\,f(a_i) < f(b_{i+1})$
for some i. In what follows we decompose g into a finite composition of atomic crossing maps.
$\,f(a_i) < f(b_{i+1})$
for some i. In what follows we decompose g into a finite composition of atomic crossing maps.
If the sequence
![]() $(f(a_0), f(b_0)),(f(a_1), f(b_1)),\ldots $
is finite, then an aforementioned decomposition of g is clearly possible. If it is infinite, then for each
$(f(a_0), f(b_0)),(f(a_1), f(b_1)),\ldots $
is finite, then an aforementioned decomposition of g is clearly possible. If it is infinite, then for each
![]() $k = 0,1, \ldots , D_f -1$
define a sequence
$k = 0,1, \ldots , D_f -1$
define a sequence
![]() $(a_0^{(k)}, b_0^{(k)}), (a_1^{(k)}, b_1^{(k)}), \ldots $
by
$(a_0^{(k)}, b_0^{(k)}), (a_1^{(k)}, b_1^{(k)}), \ldots $
by
As we have
![]() $\,f(b_{i+1})> f(b_i)$
for each i, we have
$\,f(b_{i+1})> f(b_i)$
for each i, we have
![]() $a_{i+1}^{(k)} \geqslant a_i^{(k)}+D_f = b_i^{(k)}$
; we also have
$a_{i+1}^{(k)} \geqslant a_i^{(k)}+D_f = b_i^{(k)}$
; we also have
![]() $a_{i+1}^{(k)} \neq b_i^{(k)}$
because f is injective. Thus we have
$a_{i+1}^{(k)} \neq b_i^{(k)}$
because f is injective. Thus we have
![]() $a_{i+1}^{(k)}> b_i^{(k)}$
for each i, and the sequence
$a_{i+1}^{(k)}> b_i^{(k)}$
for each i, and the sequence
![]() $(a_0^{(k)}, b_0^{(k)}), (a_1^{(k)}, b_1^{(k)}), \ldots $
defines an atomic crossing map, say
$(a_0^{(k)}, b_0^{(k)}), (a_1^{(k)}, b_1^{(k)}), \ldots $
defines an atomic crossing map, say
![]() $g_k$
. Clearly, we have
$g_k$
. Clearly, we have
![]() $g = g_{D_f-1} \circ \cdots \circ g_0$
.
$g = g_{D_f-1} \circ \cdots \circ g_0$
.
Now let
![]() $\gamma _1$
be a string that is obtained by swapping each color of
$\gamma _1$
be a string that is obtained by swapping each color of
![]() $\gamma $
at the positions
$\gamma $
at the positions
![]() $\,f(a_i)$
and
$\,f(a_i)$
and
![]() $f(b_i)$
, and let
$f(b_i)$
, and let
![]() $f_1 {{\kern-2.3pt}={\kern-2.3pt}} g {{\kern-2.3pt}\circ{\kern-2.3pt}} f$
and
$f_1 {{\kern-2.3pt}={\kern-2.3pt}} g {{\kern-2.3pt}\circ{\kern-2.3pt}} f$
and
![]() $f_2 {{\kern-2.3pt}={\kern-2.3pt}} g^{-1} {{\kern-2.3pt}={\kern-2.3pt}} g$
. Below we prove
$f_2 {{\kern-2.3pt}={\kern-2.3pt}} g^{-1} {{\kern-2.3pt}={\kern-2.3pt}} g$
. Below we prove
![]() $D_{f_1} {{\kern-2.3pt}<{\kern-2.3pt}} D_f$
holds; all other desired properties of
$D_{f_1} {{\kern-2.3pt}<{\kern-2.3pt}} D_f$
holds; all other desired properties of
![]() $f_1, f_2$
and
$f_1, f_2$
and
![]() $\gamma _1$
are easy to derive from their construction.
$\gamma _1$
are easy to derive from their construction.
Below we prove
![]() $\,f_1(a) -f_1(b) < D_f$
for each pair
$\,f_1(a) -f_1(b) < D_f$
for each pair
![]() $(a,b)$
of positions such that
$(a,b)$
of positions such that
![]() $a<b$
. The inequality holds if
$a<b$
. The inequality holds if
![]() $(a,b) = (a_i,b_i)$
for some i, as every maximal crossing in f is undone by g. Otherwise we have
$(a,b) = (a_i,b_i)$
for some i, as every maximal crossing in f is undone by g. Otherwise we have
![]() $\,f(a) -f(b) < D_f$
, so it suffices to show
$\,f(a) -f(b) < D_f$
, so it suffices to show
![]() $\,f_1(a) -f_1(b) < D_f$
for each
$\,f_1(a) -f_1(b) < D_f$
for each
![]() $(a,b)$
such that
$(a,b)$
such that
![]() $a<b$
and
$a<b$
and
![]() $\,f_1(a) -f_1(b)> f(a) -f(b)$
. Notice that we have
$\,f_1(a) -f_1(b)> f(a) -f(b)$
. Notice that we have
![]() $\,f_1(a) = f(b_i) < f(a)$
if
$\,f_1(a) = f(b_i) < f(a)$
if
![]() $a = a_i$
,
$a = a_i$
,
![]() $\,f_1(a) = f(a_i)> f(a)$
if
$\,f_1(a) = f(a_i)> f(a)$
if
![]() $a = b_i$
, or
$a = b_i$
, or
![]() $\,f_1(a) = f(a)$
otherwise. From this observation, it suffices to verify the cases in which
$\,f_1(a) = f(a)$
otherwise. From this observation, it suffices to verify the cases in which
![]() $b = a_j$
holds for some j, or
$b = a_j$
holds for some j, or
![]() $a = b_i$
holds for some i. We verify the former case as follows; the latter can be checked in a similar way.
$a = b_i$
holds for some i. We verify the former case as follows; the latter can be checked in a similar way.
-
• If
 $a {{\kern-2.3pt}={\kern-2.3pt}} a_i$
for some i, then we have
$a {{\kern-2.3pt}={\kern-2.3pt}} a_i$
for some i, then we have
 $i{{\kern-2.3pt}<{\kern-2.3pt}}j$
and hence
$i{{\kern-2.3pt}<{\kern-2.3pt}}j$
and hence
 $f_1(a) {{\kern-2.3pt}-{\kern-2.3pt}} f_1(b) {{\kern-2.3pt}={\kern-2.3pt}} f(b_i) {{\kern-2.3pt}-{\kern-2.3pt}} f(b_j) {{\kern-2.3pt}<{\kern-2.3pt}}0$
.
$f_1(a) {{\kern-2.3pt}-{\kern-2.3pt}} f_1(b) {{\kern-2.3pt}={\kern-2.3pt}} f(b_i) {{\kern-2.3pt}-{\kern-2.3pt}} f(b_j) {{\kern-2.3pt}<{\kern-2.3pt}}0$
. -
• If
 $a {{\kern-2pt}={\kern-2pt}} b_i$
for some i, then
$a {{\kern-2pt}={\kern-2pt}} b_i$
for some i, then
 $f_1(a) {{\kern-2pt}-{\kern-2pt}} f_1(b) {{\kern-2pt}={\kern-2pt}} f(a_i) {{\kern-2pt}-{\kern-2pt}} f(b_j) {{\kern-2pt}<{\kern-2pt}} f(a_i) {{\kern-2pt}-{\kern-2pt}} f(b_i) {{\kern-2pt}={\kern-2pt}} D_f$
.
$f_1(a) {{\kern-2pt}-{\kern-2pt}} f_1(b) {{\kern-2pt}={\kern-2pt}} f(a_i) {{\kern-2pt}-{\kern-2pt}} f(b_j) {{\kern-2pt}<{\kern-2pt}} f(a_i) {{\kern-2pt}-{\kern-2pt}} f(b_i) {{\kern-2pt}={\kern-2pt}} D_f$
. -
• Otherwise, we have
 $\,f_1(a) -f_1(b) = f(a) - f(b_j)$
. Notice that
$\,f_1(a) -f_1(b) = f(a) - f(b_j)$
. Notice that
 $a<b = a_j<b_j$
, and hence
$a<b = a_j<b_j$
, and hence
 $\,f(a) - f(b_j) \leqslant D_f$
holds; we also have
$\,f(a) - f(b_j) \leqslant D_f$
holds; we also have
 $\,f(a) - f(b_j) \neq D_f$
, as the equality holds only if
$\,f(a) - f(b_j) \neq D_f$
, as the equality holds only if
 $(a,b_j) = (a_i,b_i)$
for some i. Thus we have
$(a,b_j) = (a_i,b_i)$
for some i. Thus we have
 $\,f_1(a) -f_1(b) < D_f$
.⊣
$\,f_1(a) -f_1(b) < D_f$
.⊣
Corollary 4.7. Let
![]() $\,f:\alpha \rightarrow \gamma $
be an injective quasi-isometry such that
$\,f:\alpha \rightarrow \gamma $
be an injective quasi-isometry such that
![]() $D_f> 0$
. We can decompose this map into a sequence
$D_f> 0$
. We can decompose this map into a sequence
![]() $\alpha \xrightarrow {f_1} \alpha _1 \xrightarrow {f_2} \gamma $
of quasi-isometries such that
$\alpha \xrightarrow {f_1} \alpha _1 \xrightarrow {f_2} \gamma $
of quasi-isometries such that
![]() $\,f_1$
is a finite composition of atomic crossing maps,
$\,f_1$
is a finite composition of atomic crossing maps,
![]() $\,f_2$
is an injection,
$\,f_2$
is an injection,
![]() $D_{f_2}< D_{f}$
, and
$D_{f_2}< D_{f}$
, and
![]() $\alpha $
is quasi-isometric to
$\alpha $
is quasi-isometric to
![]() $\alpha _1$
.
$\alpha _1$
.
Proof Use a construction similar to the one from the proof of Lemma 4.6, but swapping colors of
![]() $\alpha $
rather than
$\alpha $
rather than
![]() $\gamma $
.⊣
$\gamma $
.⊣
From the last lemma, we can construct a uniform procedure that decomposes an injective quasi-isometry into monotonic injective and bijective ones. Unlike Corollary 4.2, the procedure also depends on quasi-isometry constants.
Corollary 4.8. There exists a uniform procedure that given strings
![]() $\alpha $
and
$\alpha $
and
![]() $\gamma $
, an injective quasi-isometry
$\gamma $
, an injective quasi-isometry
![]() $\,f: \alpha \rightarrow \gamma $
and the quasi-isometry constants
$\,f: \alpha \rightarrow \gamma $
and the quasi-isometry constants
![]() $(A,B, C)$
of f, produces a decomposition of f into a sequence
$(A,B, C)$
of f, produces a decomposition of f into a sequence
![]() $\alpha \xrightarrow {f_1} \gamma _1 \xrightarrow {f_2} \gamma $
of quasi-isometries such that
$\alpha \xrightarrow {f_1} \gamma _1 \xrightarrow {f_2} \gamma $
of quasi-isometries such that
![]() $\,f_1$
is a monotonic injection,
$\,f_1$
is a monotonic injection,
![]() $\,f_2$
is a finite composition of atomic crossing maps, and
$\,f_2$
is a finite composition of atomic crossing maps, and
![]() $\gamma $
is quasi-isometric to
$\gamma $
is quasi-isometric to
![]() $\gamma _1$
.
$\gamma _1$
.
Proof First, compute an upper bound
![]() $\hat D_f$
of the cross-over constant
$\hat D_f$
of the cross-over constant
![]() $D_f$
. It can be computed from the quasi-isometry constants
$D_f$
. It can be computed from the quasi-isometry constants
![]() $(A,B, C)$
via Lemma 2.1. Then let
$(A,B, C)$
via Lemma 2.1. Then let
![]() $\gamma = \gamma _{\hat D_f}$
,
$\gamma = \gamma _{\hat D_f}$
,
![]() $\,f = f_{\hat D_f}$
, and for each
$\,f = f_{\hat D_f}$
, and for each
![]() $k = \hat D_f, \ldots , 1$
, decompose
$k = \hat D_f, \ldots , 1$
, decompose
![]() $\,f_k$
into a sequence
$\,f_k$
into a sequence
![]() $\alpha \xrightarrow {f_{k-1}} \gamma _{k-1} \xrightarrow {g_{k-1}} \gamma _k$
as in the proof of Lemma 4.6 that is modified in the following way: at the beginning of the procedure, we list all pairs
$\alpha \xrightarrow {f_{k-1}} \gamma _{k-1} \xrightarrow {g_{k-1}} \gamma _k$
as in the proof of Lemma 4.6 that is modified in the following way: at the beginning of the procedure, we list all pairs
![]() $(a_0, b_0), (a_1, b_1), \ldots $
such that
$(a_0, b_0), (a_1, b_1), \ldots $
such that
![]() $a_i < b_i$
and
$a_i < b_i$
and
![]() $\,f(a_i) - f(b_i) = k$
rather than
$\,f(a_i) - f(b_i) = k$
rather than
![]() $\,f(a_i) - f(b_i) = D_f$
. As
$\,f(a_i) - f(b_i) = D_f$
. As
![]() $k \geqslant D_{f_k}$
holds for each k, the resulting list is either empty, or the same as the one via the original procedure. Notice that in the former case the modified procedure returns
$k \geqslant D_{f_k}$
holds for each k, the resulting list is either empty, or the same as the one via the original procedure. Notice that in the former case the modified procedure returns
![]() $\gamma _{k-1} = \gamma _k$
,
$\gamma _{k-1} = \gamma _k$
,
![]() $\,f_{k-1} = f_k$
and
$\,f_{k-1} = f_k$
and
![]() $g_{k-1} = \mathrm {id}$
. Through this we obtain the sequence
$g_{k-1} = \mathrm {id}$
. Through this we obtain the sequence
![]() $\alpha \xrightarrow {f_{0}} \gamma _{0} \xrightarrow {g} \gamma $
, where
$\alpha \xrightarrow {f_{0}} \gamma _{0} \xrightarrow {g} \gamma $
, where
![]() $g = g_{\hat D_f-1} \circ \cdots \circ g_0$
; this is a decomposition with the desired properties.⊣
$g = g_{\hat D_f-1} \circ \cdots \circ g_0$
; this is a decomposition with the desired properties.⊣
From Corollary 4.7, we can obtain a decomposition procedure that corresponds to Corollary 4.8.
Corollary 4.9. There exists a uniform procedure that given strings
![]() $\alpha $
and
$\alpha $
and
![]() $\gamma $
, an injective quasi-isometry
$\gamma $
, an injective quasi-isometry
![]() $\,f: \alpha \rightarrow \gamma $
and the quasi-isometry constants
$\,f: \alpha \rightarrow \gamma $
and the quasi-isometry constants
![]() $(A,B, C)$
of f, produces a decomposition of f into a sequence
$(A,B, C)$
of f, produces a decomposition of f into a sequence
![]() $\alpha \xrightarrow {f_1} \alpha _1 \xrightarrow {f_2} \gamma $
of quasi-isometries such that
$\alpha \xrightarrow {f_1} \alpha _1 \xrightarrow {f_2} \gamma $
of quasi-isometries such that
![]() $\,f_1$
is a finite composition of atomic crossing maps,
$\,f_1$
is a finite composition of atomic crossing maps,
![]() $\,f_2$
is a monotonic injection, and
$\,f_2$
is a monotonic injection, and
![]() $\alpha $
is quasi-isometric to
$\alpha $
is quasi-isometric to
![]() $\alpha _1$
.⊣
$\alpha _1$
.⊣
In Corollary 4.7, we have
![]() $\,f_1 = \mathrm {id}$
if f is bijective. Thus we have the following yet another corollary.
$\,f_1 = \mathrm {id}$
if f is bijective. Thus we have the following yet another corollary.
Corollary 4.10. Any bijective quasi-isometry can be decomposed into a finite sequences of atomic crossing maps.⊣
We combine the results above into the following theorem.
Theorem 4.11 (Decomposition Theorem)
There exists a procedure that given
![]() $(A, B, C)$
-quasi-isometry
$(A, B, C)$
-quasi-isometry
![]() $\,f:\alpha \to \beta $
produces a decomposition of f into quasi-isometries
$\,f:\alpha \to \beta $
produces a decomposition of f into quasi-isometries
![]() $\alpha \xrightarrow {f_1} \gamma _1 \xrightarrow {f_2} \gamma _2 \xrightarrow {f_3} \beta $
with one of the following sets of properties (and each set of properties can be realized):
$\alpha \xrightarrow {f_1} \gamma _1 \xrightarrow {f_2} \gamma _2 \xrightarrow {f_3} \beta $
with one of the following sets of properties (and each set of properties can be realized):
-
1.
 $\,f_1$
is a bijection,
$\,f_1$
is a bijection,
 $\,f_2$
is a monotonic injection, and
$\,f_2$
is a monotonic injection, and
 $\,f_3$
is a monotonic surjection.
$\,f_3$
is a monotonic surjection. -
2.
 $\,f_1$
is a monotonic injection,
$\,f_1$
is a monotonic injection,
 $\,f_2$
is a bijection, and
$\,f_2$
is a bijection, and
 $\,f_3$
is a monotonic surjection.
$\,f_3$
is a monotonic surjection. -
3.
 $\,f_1$
is a bijection,
$\,f_1$
is a bijection,
 $\,f_2$
is a monotonic surjection, and
$\,f_2$
is a monotonic surjection, and
 $\,f_3$
is a monotonic injection.
$\,f_3$
is a monotonic injection.
Proof The case
![]() $1$
and
$1$
and
![]() $2$
are derived from Corollary 4.2, 4.8 and 4.7. To show the case
$2$
are derived from Corollary 4.2, 4.8 and 4.7. To show the case
![]() $3$
, first apply Lemma 4.3 and then Corollary 4.2 to the surjection; notice, from the construction, that Lemma 4.1 decomposes a surjection into a bijection and a monotonic surjection.⊣
$3$
, first apply Lemma 4.3 and then Corollary 4.2 to the surjection; notice, from the construction, that Lemma 4.1 decomposes a surjection into a bijection and a monotonic surjection.⊣
From all of the above, we thus have the following corollary.
Corollary 4.12. If
![]() $\alpha \leqslant _{QI} \beta $
, then there is
$\alpha \leqslant _{QI} \beta $
, then there is
![]() $\beta ' \sim _{QI} \beta $
so that
$\beta ' \sim _{QI} \beta $
so that
![]() $\alpha \leqslant _{QI} \beta '$
via strictly monotonic quasi-isometry.
$\alpha \leqslant _{QI} \beta '$
via strictly monotonic quasi-isometry.
4.2 Component-wise reducibility
In this section we formulate an equivalent more intuitive condition for quasi-isometry between colored metric spaces. Recall that
![]() $Cl(u)$
denotes the set of all colors present in the string u.
$Cl(u)$
denotes the set of all colors present in the string u.
Definition 4.13. Say
![]() $\alpha $
is component-wise reducible to
$\alpha $
is component-wise reducible to
![]() $\beta $
, written
$\beta $
, written
![]() $\alpha \leqslant _{CR} \beta $
, if we can partition
$\alpha \leqslant _{CR} \beta $
, if we can partition
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
as
$\beta $
as
so that
![]() $Cl(u_i)\subseteq Cl(v_i)$
for all i and
$Cl(u_i)\subseteq Cl(v_i)$
for all i and
![]() $|u_j|,|v_j|$
are uniformly bounded by a constant C. Call these representations of
$|u_j|,|v_j|$
are uniformly bounded by a constant C. Call these representations of
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
witnessing partitions and intervals
$\beta $
witnessing partitions and intervals
![]() $u_i$
and
$u_i$
and
![]() $v_i$
partitioning intervals. If the sequence
$v_i$
partitioning intervals. If the sequence
![]() $u_1$
,
$u_1$
,
![]() $u_2$
,
$u_2$
,
![]() $\ldots $
is computable then we call this a computable partitioning of
$\ldots $
is computable then we call this a computable partitioning of
![]() $\alpha $
.
$\alpha $
.
It is clear that
![]() $\alpha \leqslant _{CR} \beta $
implies
$\alpha \leqslant _{CR} \beta $
implies
![]() $\alpha \leqslant _{QI} \beta $
: any color-preserving map that maps each interval
$\alpha \leqslant _{QI} \beta $
: any color-preserving map that maps each interval
![]() $u_i$
in
$u_i$
in
![]() $\alpha $
to
$\alpha $
to
![]() $v_i$
in
$v_i$
in
![]() $\beta $
is a quasi-isometry. Now our goal is to show that
$\beta $
is a quasi-isometry. Now our goal is to show that
![]() $\leqslant _{QI}$
implies
$\leqslant _{QI}$
implies
![]() $\leqslant _{CR}$
. One of the key lemmas is the following.
$\leqslant _{CR}$
. One of the key lemmas is the following.
Lemma 4.14. Suppose
![]() $\alpha \leqslant _{QI} \beta $
via an atomic crossing map
$\alpha \leqslant _{QI} \beta $
via an atomic crossing map
![]() $\,f: \alpha \to \beta $
and
$\,f: \alpha \to \beta $
and
![]() $\beta \leqslant _{CR} \gamma $
. Then
$\beta \leqslant _{CR} \gamma $
. Then
![]() $\alpha \leqslant _{CR} \gamma $
.
$\alpha \leqslant _{CR} \gamma $
.
Proof Let
![]() $\beta = v_1v_2\ldots $
and
$\beta = v_1v_2\ldots $
and
![]() $\gamma = w_1w_2\ldots $
be witnessing partitions for
$\gamma = w_1w_2\ldots $
be witnessing partitions for
![]() $\beta \leqslant _{CR} \gamma $
. We initially partition
$\beta \leqslant _{CR} \gamma $
. We initially partition
![]() $\alpha $
in the following way:
$\alpha $
in the following way:
where
![]() $|u_n| = |v_n|$
for all n. In what follows we show that if we merge some
$|u_n| = |v_n|$
for all n. In what follows we show that if we merge some
![]() $u_n$
’s and
$u_n$
’s and
![]() $v_n$
’s in a careful way, then we obtain witnessing partitions of
$v_n$
’s in a careful way, then we obtain witnessing partitions of
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
. From these partitions we can then derive witnessing partitions of
$\beta $
. From these partitions we can then derive witnessing partitions of
![]() $\alpha $
and
$\alpha $
and
![]() $\gamma $
.
$\gamma $
.
Let
![]() $(a_1, b_1), (a_2, b_2), \ldots $
be the sequence of crossing pairs that define the quasi-isometric atomic crossing map
$(a_1, b_1), (a_2, b_2), \ldots $
be the sequence of crossing pairs that define the quasi-isometric atomic crossing map
![]() $\,f: \alpha \rightarrow \beta $
. We can assume that no interval
$\,f: \alpha \rightarrow \beta $
. We can assume that no interval
![]() $u_i$
contains one of these crossing pairs. Indeed, if
$u_i$
contains one of these crossing pairs. Indeed, if
![]() $u_i$
contains a crossing pair
$u_i$
contains a crossing pair
![]() $(a, b)$
then we can simply change
$(a, b)$
then we can simply change
![]() $\alpha $
by interchanging colors at positions a and b. Similarly, if
$\alpha $
by interchanging colors at positions a and b. Similarly, if
![]() $(a,b)$
is a crossing pair and
$(a,b)$
is a crossing pair and
![]() $\alpha (a)=\alpha (b)$
we can change the map f be sending a to a and b to b. The output of the process described is a new atomic crossing map
$\alpha (a)=\alpha (b)$
we can change the map f be sending a to a and b to b. The output of the process described is a new atomic crossing map
![]() $\,f':\alpha ' \to \beta $
, where
$\,f':\alpha ' \to \beta $
, where
![]() $\alpha ' \sim _{QI} \alpha $
is obtained from
$\alpha ' \sim _{QI} \alpha $
is obtained from
![]() $\alpha $
by switching colors, and
$\alpha $
by switching colors, and
![]() $\,f'$
is obtained from f by switching images in every crossing pair
$\,f'$
is obtained from f by switching images in every crossing pair
![]() $(a,b)$
that belongs to some
$(a,b)$
that belongs to some
![]() $u_i$
.
$u_i$
.
Assume that
![]() $(a,b)$
is a crossing pair such that
$(a,b)$
is a crossing pair such that
![]() $a\in u_i$
and
$a\in u_i$
and
![]() $b\in u_{i+j}$
. In this case we say that
$b\in u_{i+j}$
. In this case we say that
![]() $u_i$
contains the left-end of the crossing pair
$u_i$
contains the left-end of the crossing pair
![]() $(a,b)$
and
$(a,b)$
and
![]() $u_{i+j}$
contains the right-end of the crossing pair. If
$u_{i+j}$
contains the right-end of the crossing pair. If
![]() $j>1$
, we can replace
$j>1$
, we can replace
![]() $u_i$
with the segment
$u_i$
with the segment
![]() $u_i u_{i+1}\ldots u_{i+j-1}$
and
$u_i u_{i+1}\ldots u_{i+j-1}$
and
![]() $v_i$
with
$v_i$
with
![]() $v_iv_{i+1}\ldots v_{i+j-1}$
. This changes the partition of
$v_iv_{i+1}\ldots v_{i+j-1}$
. This changes the partition of
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
but does not change the quasi-isometry map f. Also, the sizes of the new partitioning intervals are uniformly bounded. Thus, we can always assume that the partition
$\beta $
but does not change the quasi-isometry map f. Also, the sizes of the new partitioning intervals are uniformly bounded. Thus, we can always assume that the partition
![]() $\alpha =u_1 u_2u_2\ldots $
is such that
$\alpha =u_1 u_2u_2\ldots $
is such that
![]() $|u_i|=|v_i|$
for all i, all crossing pairs occur between neighboring intervals only, and
$|u_i|=|v_i|$
for all i, all crossing pairs occur between neighboring intervals only, and
![]() $\alpha (a)\neq \alpha (b)$
for all crossing pairs
$\alpha (a)\neq \alpha (b)$
for all crossing pairs
![]() $(a,b)$
.
$(a,b)$
.
Starting from
![]() $n=1$
, we incrementally check if we should merge
$n=1$
, we incrementally check if we should merge
![]() $u_n$
and
$u_n$
and
![]() $u_{n+1}$
(and thus
$u_{n+1}$
(and thus
![]() $v_n$
and
$v_n$
and
![]() $v_{n+1}$
). To assure that they can be kept separated, we need to check the following conditions. Note that the second condition below is indispensable. Figure 3 illustrates a situation in which the lack of the condition causes a problem.
$v_{n+1}$
). To assure that they can be kept separated, we need to check the following conditions. Note that the second condition below is indispensable. Figure 3 illustrates a situation in which the lack of the condition causes a problem.
-
1. Let
 $m<n$
be the largest number that is declared as a separated partition (i.e.,
$m<n$
be the largest number that is declared as a separated partition (i.e.,
 $u_m$
and
$u_m$
and
 $u_{m+1}$
are kept separated and
$u_{m+1}$
are kept separated and
 $u_{m+1}\ldots u_{n}$
are all merged). Then
$u_{m+1}\ldots u_{n}$
are all merged). Then
 $Cl(u_{m+1}\ldots u_{n}) \subseteq Cl(v_{m+1}\ldots v_{n})$
.
$Cl(u_{m+1}\ldots u_{n}) \subseteq Cl(v_{m+1}\ldots v_{n})$
. -
2. If a crossing pair
 $(a_k, b_k)$
belongs to
$(a_k, b_k)$
belongs to
 $u_n u_{n+1}$
, then
$u_n u_{n+1}$
, then
 $Cl(b_k)$
appears in
$Cl(b_k)$
appears in
 $v_{n+1+i}$
for some sufficiently small i.
$v_{n+1+i}$
for some sufficiently small i.

Figure 3 With the condition 1 only, we may have a problem.
This idea is realized as the following procedure which generates a merging policy
![]() $\varphi :\omega \to \{0,1\}$
: here,
$\varphi :\omega \to \{0,1\}$
: here,
![]() $\varphi $
indicates that
$\varphi $
indicates that
![]() $u_n$
and
$u_n$
and
![]() $u_{n+1}$
should be merged for each
$u_{n+1}$
should be merged for each
![]() $n \in \varphi ^{-1}(0)$
, and should be kept separated for each
$n \in \varphi ^{-1}(0)$
, and should be kept separated for each
![]() $n \in \varphi ^{-1}(1)$
. For instance,
$n \in \varphi ^{-1}(1)$
. For instance,
![]() $\varphi (n)=0$
,
$\varphi (n)=0$
,
![]() $\varphi (n+1)=0$
and
$\varphi (n+1)=0$
and
![]() $\varphi (n+2)=1$
means that
$\varphi (n+2)=1$
means that
![]() $u_n, u_{n+1}, u_{n+2}$
are merged and
$u_n, u_{n+1}, u_{n+2}$
are merged and
![]() $u_{n+2}$
is the last interval merged with
$u_{n+2}$
is the last interval merged with
![]() $u_n$
.
$u_n$
.
-
1. Set
 $n=1$
,
$n=1$
,
 $i=0$
, and let
$i=0$
, and let
 $\varphi :\omega \to \{0,1\}$
be a currently undefined function. Here n and i represent the following situation of the procedure: we have declared that
$\varphi :\omega \to \{0,1\}$
be a currently undefined function. Here n and i represent the following situation of the procedure: we have declared that
 $u_{n-1}$
and
$u_{n-1}$
and
 $u_n$
should be kept separated, and
$u_n$
should be kept separated, and
 $u_n,\ldots \hspace {-.04em},u_{n+i}$
should be merged. Formally, through the procedure it always holds that
$u_n,\ldots \hspace {-.04em},u_{n+i}$
should be merged. Formally, through the procedure it always holds that
 $\varphi (n-1) = 1$
and
$\varphi (n-1) = 1$
and
 $\varphi (n) = \ldots = \varphi (n+i-1) = 0$
, and
$\varphi (n) = \ldots = \varphi (n+i-1) = 0$
, and
 $\varphi $
is defined over
$\varphi $
is defined over
 $\{1,\ldots \hspace {-.04em} n+i-1\}$
.
$\{1,\ldots \hspace {-.04em} n+i-1\}$
. -
2. If no crossing pair exists between
 $u_{n+j}$
and
$u_{n+j}$
and
 $u_{n+j+1}$
for some
$u_{n+j+1}$
for some
 $j\in \{i, \ldots \hspace {-.04em}, i+|\Sigma | \}$
, then let
$j\in \{i, \ldots \hspace {-.04em}, i+|\Sigma | \}$
, then let
 $\varphi (k)=0$
for each k such that
$\varphi (k)=0$
for each k such that
 $n+i \leqslant k \leqslant n+j-1$
,
$n+i \leqslant k \leqslant n+j-1$
,
 $\varphi (n+j)=1$
, and
$\varphi (n+j)=1$
, and
 $n=n+j+1$
,
$n=n+j+1$
,
 $i=0$
. In other words, we declare that
$i=0$
. In other words, we declare that
 $u_{n+i},\ldots \hspace {-.04em},u_{n+j}$
should be merged (together with
$u_{n+i},\ldots \hspace {-.04em},u_{n+j}$
should be merged (together with
 $u_{n},\ldots \hspace {-.04em},u_{n+i-1}$
, which have been already declared to be merged) while
$u_{n},\ldots \hspace {-.04em},u_{n+i-1}$
, which have been already declared to be merged) while
 $u_{n+j}$
and
$u_{n+j}$
and
 $u_{n+j+1}$
should be kept separated.
$u_{n+j+1}$
should be kept separated. -
3. Otherwise, we check if
 $$ \begin{align*}Cl(u_n \ldots u_{n+j}) \subseteq Cl(v_n \ldots v_{n+j}) \ \text{for all }j \in \{i, \ldots, i + |\Sigma|\} \ \ (\star). \end{align*} $$
$$ \begin{align*}Cl(u_n \ldots u_{n+j}) \subseteq Cl(v_n \ldots v_{n+j}) \ \text{for all }j \in \{i, \ldots, i + |\Sigma|\} \ \ (\star). \end{align*} $$
-
4. If
 $(\star )$
holds, then find a letter that occurs twice or more in positions
$(\star )$
holds, then find a letter that occurs twice or more in positions
 $b_{k}, \ldots , b_{k+|\Sigma |}$
, where
$b_{k}, \ldots , b_{k+|\Sigma |}$
, where
 $b_k$
belongs to
$b_k$
belongs to
 $u_{n+i+1}$
. Let
$u_{n+i+1}$
. Let
 $b_{k+\ell }$
be the earliest position among them, and set and
$b_{k+\ell }$
be the earliest position among them, and set and $$ \begin{align*}\varphi (n+i)=\ldots =\varphi (n+i+\ell-1)=0, \ \varphi(n+i+\ell)=1,\end{align*} $$
$$ \begin{align*}\varphi (n+i)=\ldots =\varphi (n+i+\ell-1)=0, \ \varphi(n+i+\ell)=1,\end{align*} $$
 $n= n+i+\ell +1$
,
$n= n+i+\ell +1$
,
 $i=0$
.
$i=0$
.
-
5. If
 $(\star )$
does not hold, then take (say, the largest)
$(\star )$
does not hold, then take (say, the largest)
 $j \in \{i, \ldots , i + |\Sigma |\}$
such that
$j \in \{i, \ldots , i + |\Sigma |\}$
such that
 $Cl(u_n \ldots u_{n+j}) \not \subseteq Cl(v_n \ldots v_{n+j})$
, let
$Cl(u_n \ldots u_{n+j}) \not \subseteq Cl(v_n \ldots v_{n+j})$
, let
 $\varphi (n+i)=\ldots =\varphi (n+i+j)=0$
and let
$\varphi (n+i)=\ldots =\varphi (n+i+j)=0$
and let
 $i= j+1$
.
$i= j+1$
. -
6. Go to 2.
Notice that, in step 4 of the procedure, the pigeonhole principle guarantees that it is always possible to find such multiple occurrences. Now collect all positions for which
![]() $\varphi $
in the above procedure eventually assigns
$\varphi $
in the above procedure eventually assigns
![]() $1$
, and let
$1$
, and let
![]() $\{n_k\}$
be its ordered enumeration. The following shows that the merging policy via
$\{n_k\}$
be its ordered enumeration. The following shows that the merging policy via
![]() $\varphi $
indeed gives us witnessing partitions.
$\varphi $
indeed gives us witnessing partitions.
Claim. The sequence
![]() $\{n_k\}$
is an infinite sequence
$\{n_k\}$
is an infinite sequence
![]() $\{n_k\}_{k \in \omega }$
, and there is a bound D such that
$\{n_k\}_{k \in \omega }$
, and there is a bound D such that
![]() $n_{k+1} - n_k \leqslant D$
for all
$n_{k+1} - n_k \leqslant D$
for all
![]() $k \in \omega $
. Furthermore we have
$k \in \omega $
. Furthermore we have
![]() $Cl(u_{n_{k-1}+1} \ldots u_{{n_k}}) \subseteq Cl(v_{n_{k-1}+1} \ldots v_{{n_k}})$
for all
$Cl(u_{n_{k-1}+1} \ldots u_{{n_k}}) \subseteq Cl(v_{n_{k-1}+1} \ldots v_{{n_k}})$
for all
![]() $k \in \omega $
, where we assume
$k \in \omega $
, where we assume
![]() $n_{-1} = 1$
.⊣
$n_{-1} = 1$
.⊣
The color inclusion part of the claim is immediate to show, as it is assured in the step 3 of the procedure. Thus it suffices to show that the condition checked in 3 is always true if
![]() $i \geqslant D'$
for some constant
$i \geqslant D'$
for some constant
![]() $D'$
.
$D'$
.
For its proof, let n and i be given, where
![]() $n = n_k+1$
for some k, a crossing pair
$n = n_k+1$
for some k, a crossing pair
![]() $(a_{l+j},b_{l+j})$
lies between
$(a_{l+j},b_{l+j})$
lies between
![]() $u_{n+j}$
and
$u_{n+j}$
and
![]() $u_{n+j+1}$
for each
$u_{n+j+1}$
for each
![]() $j \in \{i, \ldots , i + |\Sigma |\}$
, and assume
$j \in \{i, \ldots , i + |\Sigma |\}$
, and assume
![]() $Cl(u_n \ldots u_{n+j}) \not \subseteq Cl(v_n \ldots v_{n+j})$
for some
$Cl(u_n \ldots u_{n+j}) \not \subseteq Cl(v_n \ldots v_{n+j})$
for some
![]() $j \in \{i, \ldots , i + |\Sigma |\}$
. This holds only if either of the following is true: (1) there is a crossing pair
$j \in \{i, \ldots , i + |\Sigma |\}$
. This holds only if either of the following is true: (1) there is a crossing pair
![]() $(a_h,b_h)$
that lies between
$(a_h,b_h)$
that lies between
![]() $u_{n-1}$
and
$u_{n-1}$
and
![]() $u_n$
, and
$u_n$
, and
![]() $\alpha (b_h)$
does not occur in
$\alpha (b_h)$
does not occur in
![]() $v_n \ldots v_{n+j}$
; or (2)
$v_n \ldots v_{n+j}$
; or (2)
![]() $\alpha (a_{l+j})$
does not occur in
$\alpha (a_{l+j})$
does not occur in
![]() $v_n \ldots v_{n+j}$
.
$v_n \ldots v_{n+j}$
.
The case (1) occurs only if
![]() $j < |\Sigma |-1$
, as the choice of
$j < |\Sigma |-1$
, as the choice of
![]() $n_k$
in step 4 of the procedure assures that
$n_k$
in step 4 of the procedure assures that
![]() $\alpha (b_h) = \alpha (b_{h+h'})$
for some
$\alpha (b_h) = \alpha (b_{h+h'})$
for some
![]() $h' \leqslant |\Sigma |-1$
. The case (2) occurs only for finitely many j’s (indeed it’s up to
$h' \leqslant |\Sigma |-1$
. The case (2) occurs only for finitely many j’s (indeed it’s up to
![]() $|\Sigma |-1$
times), as in such a case
$|\Sigma |-1$
times), as in such a case
![]() $v_n \ldots v_{n+j+1}$
should contain strictly more colors than
$v_n \ldots v_{n+j+1}$
should contain strictly more colors than
![]() $v_n \ldots v_{n+j}$
. The whole argument shows that the condition
$v_n \ldots v_{n+j}$
. The whole argument shows that the condition
![]() $(\star )$
in step 3 of the procedure above is always true if
$(\star )$
in step 3 of the procedure above is always true if
![]() $i \geqslant |\Sigma |\cdot (|\Sigma |+1)$
holds; the case (1) does not occur if
$i \geqslant |\Sigma |\cdot (|\Sigma |+1)$
holds; the case (1) does not occur if
![]() $i \geqslant |\Sigma | -1$
, and after that the case (2) occurs only up to
$i \geqslant |\Sigma | -1$
, and after that the case (2) occurs only up to
![]() $|\Sigma | -1$
times, where each occurrence increases i to up to
$|\Sigma | -1$
times, where each occurrence increases i to up to
![]() $|\Sigma | + 1$
.
$|\Sigma | + 1$
.
Theorem 4.15.
![]() $\alpha \leqslant _{QI} \beta $
implies
$\alpha \leqslant _{QI} \beta $
implies
![]() $\alpha \leqslant _{CR} \beta $
.
$\alpha \leqslant _{CR} \beta $
.
Proof Let
![]() $\,f:\alpha \to \beta $
be a quasi-isometry. By Theorem 4.11 and Corollary 4.10, it can be decomposed into quasi-isometry maps
$\,f:\alpha \to \beta $
be a quasi-isometry. By Theorem 4.11 and Corollary 4.10, it can be decomposed into quasi-isometry maps
![]() $\alpha \xrightarrow {f_1} \gamma \xrightarrow {f_2} \beta $
, where
$\alpha \xrightarrow {f_1} \gamma \xrightarrow {f_2} \beta $
, where
![]() $\,f_1$
is a finite concatenation of atomic crossing quasi-isometries and
$\,f_1$
is a finite concatenation of atomic crossing quasi-isometries and
![]() $\,f_2$
is monotonic. For any monotonic quasi-isometric map
$\,f_2$
is monotonic. For any monotonic quasi-isometric map
![]() $g:\alpha '\to \beta '$
we easily have
$g:\alpha '\to \beta '$
we easily have
![]() $\alpha '\leqslant _{CR}\beta '$
: Indeed, enumerate all elements of the image of g as
$\alpha '\leqslant _{CR}\beta '$
: Indeed, enumerate all elements of the image of g as
![]() $\{b_n\}_{n\in \omega }$
, where
$\{b_n\}_{n\in \omega }$
, where
![]() $b_n < b_{n+1}$
for all n, let
$b_n < b_{n+1}$
for all n, let
![]() $u_n = g^{-1}(b_n)$
and
$u_n = g^{-1}(b_n)$
and
![]() $v_n = [b_n, b_{n+1}-1]$
. Then
$v_n = [b_n, b_{n+1}-1]$
. Then
![]() $\alpha '= u_1u_2\ldots $
and
$\alpha '= u_1u_2\ldots $
and
![]() $\beta '=v_1v_2\ldots $
are witnessing partitions. Hence we have
$\beta '=v_1v_2\ldots $
are witnessing partitions. Hence we have
![]() $\gamma \leqslant _{CR}\beta $
, and Lemma 4.14 completes the proof.⊣
$\gamma \leqslant _{CR}\beta $
, and Lemma 4.14 completes the proof.⊣
From the proofs of Theorem 4.15 and the Decomposition Theorem 4.11, we obtain the following corollary:
Corollary 4.16. Let
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
be computable strings. Then there exists a computable quasi-isometry
$\beta $
be computable strings. Then there exists a computable quasi-isometry
![]() $\,f: \alpha \rightarrow \beta $
if and only if there exists a computable partition of
$\,f: \alpha \rightarrow \beta $
if and only if there exists a computable partition of
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
witnessing component-wise reducibility of
$\beta $
witnessing component-wise reducibility of
![]() $\alpha $
to
$\alpha $
to
![]() $\beta $
.
$\beta $
.
As an application of Theorem 4.15, we can provide an alternative proof for constructing minimal elements in the partial order
![]() $\Sigma ^{\omega }_{QI}$
:
$\Sigma ^{\omega }_{QI}$
:
Corollary 4.17. Let
![]() $\{a_n\}_{n \in \omega }$
be a sequence such that
$\{a_n\}_{n \in \omega }$
be a sequence such that
![]() $\lim _{n \to \infty } a_n = \infty $
. Then the large scale geometry of the string
$\lim _{n \to \infty } a_n = \infty $
. Then the large scale geometry of the string
![]() $\alpha = 0^{a_0}1^{a_1}0^{a_2}1^{a_3}...0^{a_{2k}}1^{a_{2k+1}}\ldots $
is a minimal element in any partial order
$\alpha = 0^{a_0}1^{a_1}0^{a_2}1^{a_3}...0^{a_{2k}}1^{a_{2k+1}}\ldots $
is a minimal element in any partial order
![]() $\Sigma _{QI}^{\omega }$
with
$\Sigma _{QI}^{\omega }$
with
![]() $0,1 \in \Sigma $
.
$0,1 \in \Sigma $
.
Proof Suppose
![]() $\beta \leqslant _{CR} \alpha $
, and let
$\beta \leqslant _{CR} \alpha $
, and let
![]() $\alpha = u_1u_2\ldots $
and
$\alpha = u_1u_2\ldots $
and
![]() $\beta = v_1v_2\ldots $
be witnessing partitions. Then for sufficiently large
$\beta = v_1v_2\ldots $
be witnessing partitions. Then for sufficiently large
![]() $N \in \omega $
we have the following: for each
$N \in \omega $
we have the following: for each
![]() $i>N$
, if
$i>N$
, if
![]() $Cl(u_i) = \{0,1\}$
then
$Cl(u_i) = \{0,1\}$
then
![]() $Cl(u_{i-1})=\{0\}$
and
$Cl(u_{i-1})=\{0\}$
and
![]() $Cl(u_{i+1})=\{1\}$
, or vice versa. Now modify the witnessing partitions as follows: for each
$Cl(u_{i+1})=\{1\}$
, or vice versa. Now modify the witnessing partitions as follows: for each
![]() $i>N$
such that
$i>N$
such that
![]() $Cl(u_i) = \{0,1\}$
, if
$Cl(u_i) = \{0,1\}$
, if
![]() $Cl(v_i) = \{0\}$
or
$Cl(v_i) = \{0\}$
or
![]() $Cl(v_i) = \{1\}$
, then either move the boundary between
$Cl(v_i) = \{1\}$
, then either move the boundary between
![]() $v_{i-1}$
and
$v_{i-1}$
and
![]() $v_i$
(respectively, between
$v_i$
(respectively, between
![]() $u_{i-1}$
and
$u_{i-1}$
and
![]() $u_i$
) one position to the left, or move the boundary between
$u_i$
) one position to the left, or move the boundary between
![]() $v_i$
and
$v_i$
and
![]() $v_{i+1}$
(respectively between
$v_{i+1}$
(respectively between
![]() $u_i$
and
$u_i$
and
![]() $u_{i+1}$
) one position to the right, depending on whether
$u_{i+1}$
) one position to the right, depending on whether
![]() $v_{i-1}$
or
$v_{i-1}$
or
![]() $v_{i+1}$
contains the color missing in
$v_{i+1}$
contains the color missing in
![]() $v_i$
. Concatenating
$v_i$
. Concatenating
![]() $u_1,\ldots ,u_{N-1}$
and
$u_1,\ldots ,u_{N-1}$
and
![]() $v_1,\ldots ,v_{N-1}$
we have witnessing partitions of
$v_1,\ldots ,v_{N-1}$
we have witnessing partitions of
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
.⊣
$\beta $
.⊣
4.3 Refinement of component-wise reducibility
One could attempt to go further, namely say
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are color-equivalent if they are component-wise reducible to each other via the same witnessing partitions. A formal definition is this:
$\beta $
are color-equivalent if they are component-wise reducible to each other via the same witnessing partitions. A formal definition is this:
Definition 4.18. We say that
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are color-equivalent, written
$\beta $
are color-equivalent, written
![]() $\alpha \sim _{cl} \beta $
, if we can partition
$\alpha \sim _{cl} \beta $
, if we can partition
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
as
$\beta $
as
such that
![]() $Cl(u_i) = Cl(v_i)$
for all i and
$Cl(u_i) = Cl(v_i)$
for all i and
![]() $|u_j|,|v_j|$
are uniformly bounded by a constant C. Call these presentations of
$|u_j|,|v_j|$
are uniformly bounded by a constant C. Call these presentations of
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
witnessing partitions and intervals
$\beta $
witnessing partitions and intervals
![]() $u_i$
and
$u_i$
and
![]() $v_i$
partitioning intervals.
$v_i$
partitioning intervals.
It is clear that
![]() $\alpha \sim _{cl} \beta $
implies that
$\alpha \sim _{cl} \beta $
implies that
![]() $\alpha \sim _{CR} \beta $
(and hence
$\alpha \sim _{CR} \beta $
(and hence
![]() $\alpha \sim _{QI} \beta $
). A natural question arises if
$\alpha \sim _{QI} \beta $
). A natural question arises if
![]() $\alpha \sim _{QI} \beta $
implies their color-equivalence. Below, we give a negative answer to this question.
$\alpha \sim _{QI} \beta $
implies their color-equivalence. Below, we give a negative answer to this question.
Proposition 4.19. Suppose
![]() $|\Sigma | \geqslant 3$
. Then there are sequences
$|\Sigma | \geqslant 3$
. Then there are sequences
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
such that
$\beta $
such that
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are quasi-isometric via monotonic embeddings but
$\beta $
are quasi-isometric via monotonic embeddings but
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are not color-equivalent.
$\beta $
are not color-equivalent.
Proof Consider a 3 letter alphabet
![]() $\{0,1, *\}$
. We define strings
$\{0,1, *\}$
. We define strings
![]() $\alpha ,\beta \in \Sigma ^\omega $
as follows. We first define
$\alpha ,\beta \in \Sigma ^\omega $
as follows. We first define
![]() $\beta $
by:
$\beta $
by:
Thus, the nth-part of
![]() $\beta $
is the string
$\beta $
is the string
![]() $0 (*)^n 1 (*)^n 0(*)^{2n+1}$
. The string
$0 (*)^n 1 (*)^n 0(*)^{2n+1}$
. The string
![]() $\alpha $
is obtained from
$\alpha $
is obtained from
![]() $\beta $
by omitting the second occurrence of
$\beta $
by omitting the second occurrence of
![]() $0$
in the nth-substring of
$0$
in the nth-substring of
![]() $\beta $
. So,
$\beta $
. So,
![]() $\alpha $
can be written as
$\alpha $
can be written as
Thus, the nth-substring of
![]() $\alpha $
is
$\alpha $
is
![]() $0 (*)^n 1 (*)^n(*)^{2n+1}$
.
$0 (*)^n 1 (*)^n(*)^{2n+1}$
.
Building the desired monotonic injective quasi-isometry
![]() $\,f: \alpha \to \beta $
is straightforward. The function f maps the nth-part
$\,f: \alpha \to \beta $
is straightforward. The function f maps the nth-part
![]() $0 (*)^n 1 (*)^n(*)^{2n+1}$
of
$0 (*)^n 1 (*)^n(*)^{2n+1}$
of
![]() $\alpha $
in injective and monotonic manner into the nth-substring
$\alpha $
in injective and monotonic manner into the nth-substring
![]() $0 (*)^n 1 (*)^n 0(*)^{2n+1}$
of
$0 (*)^n 1 (*)^n 0(*)^{2n+1}$
of
![]() $\beta $
by simply omitting the second
$\beta $
by simply omitting the second
![]() $0$
from its range.
$0$
from its range.
Defining monotonic and quasi-isometric embedding
![]() $g: \beta \to \alpha $
needs a little bit more care. The function g maps the nth-part
$g: \beta \to \alpha $
needs a little bit more care. The function g maps the nth-part
![]() $0 (*)^n 1 (*)^n 0(*)^{2n+1}$
of
$0 (*)^n 1 (*)^n 0(*)^{2n+1}$
of
![]() $\beta $
by “stretching” it along
$\beta $
by “stretching” it along
![]() $0 (*)^{2n} 1 (*)^{2n} (*)^{4n+1} \ 0 (*)^{2n+1} 1 (*)^{2n+1} (*)^{4n+2+1}$
, the
$0 (*)^{2n} 1 (*)^{2n} (*)^{4n+1} \ 0 (*)^{2n+1} 1 (*)^{2n+1} (*)^{4n+2+1}$
, the
![]() $(2n)$
th- and
$(2n)$
th- and
![]() $(2n+1)$
th-parts of
$(2n+1)$
th-parts of
![]() $\alpha $
. More formally, g is defined as follows:
$\alpha $
. More formally, g is defined as follows:
-
• g maps the initial segment
 $0 (*)^n 1 (*)^n$
of the nth-part of
$0 (*)^n 1 (*)^n$
of the nth-part of
 $\beta $
into the
$\beta $
into the
 $(2n)$
th-part
$(2n)$
th-part
 $0(*)^{2n}1 (*)^{2n} (*)^{4n+1}$
of
$0(*)^{2n}1 (*)^{2n} (*)^{4n+1}$
of
 $\alpha $
.
$\alpha $
. -
• g maps the rest of the nth-part of
 $\beta $
, that is
$\beta $
, that is
 $0(*)^{2n+1}$
, into the
$0(*)^{2n+1}$
, into the
 $(2n+1)$
th-part
$(2n+1)$
th-part
 $0 (*)^{2n+1} 1 (*)^{2n+1} (*)^{4n+2+1}$
of
$0 (*)^{2n+1} 1 (*)^{2n+1} (*)^{4n+2+1}$
of
 $\alpha $
(by omitting
$\alpha $
(by omitting
 $1$
from the range of the function g).
$1$
from the range of the function g).
Clearly, the function g can be built such that we have
![]() $d(i,j) \leqslant d(g(i),g(j)) \leqslant 6d(i,j)$
for all positions
$d(i,j) \leqslant d(g(i),g(j)) \leqslant 6d(i,j)$
for all positions
![]() $i, j$
in
$i, j$
in
![]() $\beta $
. Thus g is a witness for quasi-isometric monotonic embedding from
$\beta $
. Thus g is a witness for quasi-isometric monotonic embedding from
![]() $\beta $
into
$\beta $
into
![]() $\alpha $
.
$\alpha $
.
Now we show that
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are not color-equivalent. Assuming the contrary, suppose there are partitions
$\beta $
are not color-equivalent. Assuming the contrary, suppose there are partitions
![]() $\alpha =u_1u_2\ldots $
and
$\alpha =u_1u_2\ldots $
and
![]() $\beta =v_1v_2\ldots $
that witness color-equivalence of
$\beta =v_1v_2\ldots $
that witness color-equivalence of
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
. Notice that the occurrence of
$\beta $
. Notice that the occurrence of
![]() $0$
and
$0$
and
![]() $1$
in
$1$
in
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
become more and more sparse as n increases, while
$\beta $
become more and more sparse as n increases, while
![]() $|u_i|$
and
$|u_i|$
and
![]() $|v_i|$
are uniformly bounded. Thus for sufficiently large i, it holds that each of
$|v_i|$
are uniformly bounded. Thus for sufficiently large i, it holds that each of
![]() $u_i$
and
$u_i$
and
![]() $v_i$
contains at most one
$v_i$
contains at most one
![]() $0$
and/or
$0$
and/or
![]() $1$
.
$1$
.
Now suppose
![]() $0 \in Cl(u_i) \cap Cl(u_j)$
for
$0 \in Cl(u_i) \cap Cl(u_j)$
for
![]() $i < j$
with sufficiently large i, which implies
$i < j$
with sufficiently large i, which implies
![]() $0 \in Cl(v_i) \cap Cl(v_j)$
. Then because of the construction of
$0 \in Cl(v_i) \cap Cl(v_j)$
. Then because of the construction of
![]() $\alpha $
and the observation above (i.e., each of
$\alpha $
and the observation above (i.e., each of
![]() $u_i$
and
$u_i$
and
![]() $u_j$
contains at most one
$u_j$
contains at most one
![]() $0$
and/or
$0$
and/or
![]() $1$
), there exists k such that
$1$
), there exists k such that
![]() $i<k<j$
and
$i<k<j$
and
![]() $1 \in Cl(u_k)$
. On the other hand, for such i and j, there can be a case that
$1 \in Cl(u_k)$
. On the other hand, for such i and j, there can be a case that
![]() $1 \not \in Cl(v_l)$
for every
$1 \not \in Cl(v_l)$
for every
![]() $i<l<j$
; this is clear from the construction of
$i<l<j$
; this is clear from the construction of
![]() $\beta $
, as the succession of its nth- and
$\beta $
, as the succession of its nth- and
![]() $(n+1)$
th-substrings looks like
$(n+1)$
th-substrings looks like
Here, again notice that each of
![]() $v_i$
and
$v_i$
and
![]() $v_j$
contains at most one
$v_j$
contains at most one
![]() $0$
and/or
$0$
and/or
![]() $1$
(in particular it does not contain multiple
$1$
(in particular it does not contain multiple
![]() $0$
’s). Thus for the k that satisfies the property above, there can be a case that
$0$
’s). Thus for the k that satisfies the property above, there can be a case that
![]() $Cl(u_k)\neq Cl(v_k)$
. This is a contradiction.⊣
$Cl(u_k)\neq Cl(v_k)$
. This is a contradiction.⊣
We say that a mapping
![]() $\,f:\alpha \rightarrow \beta $
is an eventual embedding if there exists an n such that f restricted to the domain
$\,f:\alpha \rightarrow \beta $
is an eventual embedding if there exists an n such that f restricted to the domain
![]() $\{n+1, n+2, \ldots \}$
is an embedding. One can ask if color-equivalence between
$\{n+1, n+2, \ldots \}$
is an embedding. One can ask if color-equivalence between
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
implies that one can find quasi-isometries
$\beta $
implies that one can find quasi-isometries
![]() $\,f: \alpha \rightarrow \beta $
and
$\,f: \alpha \rightarrow \beta $
and
![]() $g: \beta \rightarrow \alpha $
such that f and g are eventual embedding. The next proposition gives an easy negative answer.
$g: \beta \rightarrow \alpha $
such that f and g are eventual embedding. The next proposition gives an easy negative answer.
Proposition 4.20. There are color-equivalent strings
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
such that no eventual embedding witnesses quasi-isometry from
$\beta $
such that no eventual embedding witnesses quasi-isometry from
![]() $\alpha $
into
$\alpha $
into
![]() $\beta $
.
$\beta $
.
Proof Consider the following colored metric spaces over the alphabet
![]() $\{0,1\}$
:
$\{0,1\}$
:
One can construct witnessing partitions of
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
as follows, for example:
$\beta $
as follows, for example:
 $$\begin{align*} \alpha &= 001|001|1|001|1|1|001|1|1|1\ldots\\ \beta &= 011|011|1|011|1|1|011|1|1|1\ldots \end{align*}$$
$$\begin{align*} \alpha &= 001|001|1|001|1|1|001|1|1|1\ldots\\ \beta &= 011|011|1|011|1|1|011|1|1|1\ldots \end{align*}$$
We now prove that no eventual embeddings exist witnessing quasi-isometry from
![]() $\alpha $
into
$\alpha $
into
![]() $\beta $
. Let
$\beta $
. Let
![]() $\,f:\alpha \rightarrow \beta $
be an eventual embedding with quasi-isometry constants A, B, and C. Let
$\,f:\alpha \rightarrow \beta $
be an eventual embedding with quasi-isometry constants A, B, and C. Let
![]() $i_n$
and
$i_n$
and
![]() $i_n+1$
be the sequence of consecutive positions in
$i_n+1$
be the sequence of consecutive positions in
![]() $\alpha $
with color
$\alpha $
with color
![]() $0$
. Since f is a quasi-isometry we have
$0$
. Since f is a quasi-isometry we have
There must exist a position
![]() $i_n$
such that
$i_n$
such that
![]() $\,f ({i_n})< f(i_n+1)$
and the number of consecutive
$\,f ({i_n})< f(i_n+1)$
and the number of consecutive
![]() $1$
’s between
$1$
’s between
![]() $\,f ({i_n})$
and
$\,f ({i_n})$
and
![]() $ f(i_n+1)$
in
$ f(i_n+1)$
in
![]() $\beta $
is greater than
$\beta $
is greater than
![]() $A+B$
. Hence,
$A+B$
. Hence,
![]() $\,f(i_n+1)-f(i_n)> A+B$
. This is a contradiction.⊣
$\,f(i_n+1)-f(i_n)> A+B$
. This is a contradiction.⊣
5 Büchi automata and large scale geometries
Let
![]() $L \subseteq \Sigma ^{\omega }$
be a language. To simplify our arguments we assume that
$L \subseteq \Sigma ^{\omega }$
be a language. To simplify our arguments we assume that
![]() $\Sigma =\{0,1\}$
. The notion of quasi-isometry leads us to consider the quasi-isometry types of strings from L. Formally, we give the following definition:
$\Sigma =\{0,1\}$
. The notion of quasi-isometry leads us to consider the quasi-isometry types of strings from L. Formally, we give the following definition:
Definition 5.1. An atlas is a set of quasi-isometry types. In particular, the atlas of the language L is the set
![]() $[L]=\{[\alpha ] \mid \alpha \in L\}$
, where
$[L]=\{[\alpha ] \mid \alpha \in L\}$
, where
![]() $[\alpha ]$
is the quasi-isometry type of
$[\alpha ]$
is the quasi-isometry type of
![]() $\alpha $
.
$\alpha $
.
A question of a general character is concerned with understanding the set
![]() $[L]$
given a description of L. In particular, a natural question is if one can decide that
$[L]$
given a description of L. In particular, a natural question is if one can decide that
![]() $[L_1]=[L_2]$
given descriptions of languages
$[L_1]=[L_2]$
given descriptions of languages
![]() $L_1$
and
$L_1$
and
![]() $L_2$
. In this section, we study the atlases defined by Büchi automata recognizable languages. We show that for Büchi automata recognizable languages
$L_2$
. In this section, we study the atlases defined by Büchi automata recognizable languages. We show that for Büchi automata recognizable languages
![]() $L_1$
and
$L_1$
and
![]() $L_2$
there is an efficient algorithm that decides if
$L_2$
there is an efficient algorithm that decides if
![]() $[L_1]=[L_2]$
. We recall basic definitions for Büchi automata.
$[L_1]=[L_2]$
. We recall basic definitions for Büchi automata.
Definition 5.2. A Büchi automaton
![]() $\mathcal M$
is a quadruple
$\mathcal M$
is a quadruple
![]() $(S,\iota ,\Delta ,F)$
, where S is a finite set of states,
$(S,\iota ,\Delta ,F)$
, where S is a finite set of states,
![]() $\iota \in S$
is the initial state,
$\iota \in S$
is the initial state,
![]() $\Delta \subset S \times \Sigma \times S$
is the transition table, and
$\Delta \subset S \times \Sigma \times S$
is the transition table, and
![]() $F \subseteq S$
is the set of accepting states. The triples
$F \subseteq S$
is the set of accepting states. The triples
![]() $(s,\sigma , s')\in \Delta $
are called transitions of
$(s,\sigma , s')\in \Delta $
are called transitions of
![]() $\mathcal M$
.
$\mathcal M$
.
A run of the automaton
![]() $\mathcal M$
on string
$\mathcal M$
on string
![]() $\alpha =\sigma _0 \sigma _1 \dots \in \Sigma ^{\omega }$
is a sequence of states
$\alpha =\sigma _0 \sigma _1 \dots \in \Sigma ^{\omega }$
is a sequence of states
![]() $r=s_0,s_1,\dots $
such that
$r=s_0,s_1,\dots $
such that
![]() $s_0 = \iota $
and
$s_0 = \iota $
and
![]() $(s_i,\sigma _{i},s_{i+1}) \in \Delta $
for all
$(s_i,\sigma _{i},s_{i+1}) \in \Delta $
for all
![]() $i \in \omega $
. Note that
$i \in \omega $
. Note that
![]() $\mathcal M$
can have several (possibly none) runs on
$\mathcal M$
can have several (possibly none) runs on
![]() $\alpha $
. The run is accepting if the set
$\alpha $
. The run is accepting if the set
![]() $Inf(r)=\{s: \exists ^\infty i (s_i=s)\}$
has a state from F. The automaton
$Inf(r)=\{s: \exists ^\infty i (s_i=s)\}$
has a state from F. The automaton
![]() $\mathcal M$
accepts the string
$\mathcal M$
accepts the string
![]() $\alpha $
if the automaton has an accepting run on
$\alpha $
if the automaton has an accepting run on
![]() $\alpha $
.
$\alpha $
.
Definition 5.3. The language accepted by the automaton
![]() $\mathcal M$
, denoted
$\mathcal M$
, denoted
![]() $L(\mathcal M)$
, is the set of all infinite words accepted by
$L(\mathcal M)$
, is the set of all infinite words accepted by
![]() $\mathcal M$
. We call the atlas defined by the language
$\mathcal M$
. We call the atlas defined by the language
![]() $L(\mathcal M)$
Büchi recognizable atlas.
$L(\mathcal M)$
Büchi recognizable atlas.
Example 5.4. Here we provide two examples.
-
1. Let L be the language
 $\{\alpha \mid \alpha \text { has finitely many }1\text {s}\}$
. This is Büchi recognizable language. The atlas defined by L is a two-element set
$\{\alpha \mid \alpha \text { has finitely many }1\text {s}\}$
. This is Büchi recognizable language. The atlas defined by L is a two-element set
 $\{[0^{\omega }], [10^{\omega }]\}$
. The complement
$\{[0^{\omega }], [10^{\omega }]\}$
. The complement
 $\bar {L}$
of L is also Büchi recognizable. The atlas defined by
$\bar {L}$
of L is also Büchi recognizable. The atlas defined by
 $\bar {L}$
is
$\bar {L}$
is
 $[\Sigma ^{\omega }]-\{[0^{\omega }], [10^{\omega }]\}$
.
$[\Sigma ^{\omega }]-\{[0^{\omega }], [10^{\omega }]\}$
. -
2. Let L be the language
This is Büchi recognizable language. The atlas defined by L is $$ \begin{align*} \{\alpha\mid \text{the length of any }0\text{-block in }\alpha \text{ is even}\}. \end{align*} $$
$$ \begin{align*} \{\alpha\mid \text{the length of any }0\text{-block in }\alpha \text{ is even}\}. \end{align*} $$
 $[\Sigma ^{\omega }]$
. The complement
$[\Sigma ^{\omega }]$
. The complement
 $\bar {L}$
of L is Büchi recognizable. The atlas of the complement
$\bar {L}$
of L is Büchi recognizable. The atlas of the complement
 $\bar {L}$
is also
$\bar {L}$
is also
 $[\Sigma ^{\omega }]$
.
$[\Sigma ^{\omega }]$
.
We aim to describe the atlases defined by Büchi recognizable languages. For this we need to do some state space analysis of the automation
![]() $\mathcal M$
.
$\mathcal M$
.
Let
![]() $\mathcal M=(S,\iota ,\Delta ,F)$
be a Büchi automaton. The state space S of the automaton
$\mathcal M=(S,\iota ,\Delta ,F)$
be a Büchi automaton. The state space S of the automaton
![]() $\mathcal M$
can naturally be considered as a directed labeled graph. Namely, we put a directed edge from state s to
$\mathcal M$
can naturally be considered as a directed labeled graph. Namely, we put a directed edge from state s to
![]() $S'$
and label the edge with
$S'$
and label the edge with
![]() $\sigma \in \Sigma $
if and only if
$\sigma \in \Sigma $
if and only if
![]() $(s, \sigma , s')$
is a transition of
$(s, \sigma , s')$
is a transition of
![]() $\mathcal M$
. So, we can apply the concepts of graph theory to the space S. A loop in
$\mathcal M$
. So, we can apply the concepts of graph theory to the space S. A loop in
![]() $\mathcal M$
is a path L of states
$\mathcal M$
is a path L of states
![]() $s_1, \ldots , s_{n+1}$
in the state space S such that
$s_1, \ldots , s_{n+1}$
in the state space S such that
![]() $s_1=s_{n+1}$
. We say that a word
$s_1=s_{n+1}$
. We say that a word
![]() $\sigma _1\ldots \sigma _n$
labels the loop L if
$\sigma _1\ldots \sigma _n$
labels the loop L if
![]() $(s_i, \sigma _i, s_{i+1})\in \Delta $
for
$(s_i, \sigma _i, s_{i+1})\in \Delta $
for
![]() $1\leqslant i \leqslant n$
. If all symbols
$1\leqslant i \leqslant n$
. If all symbols
![]() $\sigma _i$
are
$\sigma _i$
are
![]() $0$
only, then we say that the loop is a 0-loop. Similarly, if all symbols
$0$
only, then we say that the loop is a 0-loop. Similarly, if all symbols
![]() $\sigma _i$
are
$\sigma _i$
are
![]() $1$
only, then we say that the loop is a 1-loop. In the loop L we do not require that the states are pairwise distinct. Any state in a loop is called a loop state.
$1$
only, then we say that the loop is a 1-loop. In the loop L we do not require that the states are pairwise distinct. Any state in a loop is called a loop state.
By removing the labels from the edges in the space of transitions of S, we turn the state space S of the automaton
![]() $\mathcal M$
into a directed graph. Hence, we can write S as a disjoint union of its strongly connected components (sccs). Call a strongly connected component
$\mathcal M$
into a directed graph. Hence, we can write S as a disjoint union of its strongly connected components (sccs). Call a strongly connected component
![]() $X\subseteq S$
nontrivial if the cardinality
$X\subseteq S$
nontrivial if the cardinality
![]() $|X|$
of X is greater than
$|X|$
of X is greater than
![]() $1$
. Thus, we write S as the union
$1$
. Thus, we write S as the union
where T is the union of trivial strongly connected components and each
![]() $S_i$
is a nontrivial strongly connected component. Note that every successful run of the automaton
$S_i$
is a nontrivial strongly connected component. Note that every successful run of the automaton
![]() $\mathcal M$
on every infinite string
$\mathcal M$
on every infinite string
![]() $\alpha $
eventually ends up in one of the strongly connected components
$\alpha $
eventually ends up in one of the strongly connected components
![]() $S_i$
of the automaton
$S_i$
of the automaton
![]() $\mathcal M$
. Consider Büchi automata
$\mathcal M$
. Consider Büchi automata
![]() $\mathcal M_1$
,
$\mathcal M_1$
,
![]() $\ldots $
,
$\ldots $
,
![]() $\mathcal M_k$
such that the initial states and the state diagrams of
$\mathcal M_k$
such that the initial states and the state diagrams of
![]() $\mathcal M_i$
all coincide with that of
$\mathcal M_i$
all coincide with that of
![]() $\mathcal M$
but
$\mathcal M$
but
![]() $F_i=F\cap S_i$
. It is clear that
$F_i=F\cap S_i$
. It is clear that
Hence, describing the atlas
![]() $[L(\mathcal M)]$
boils down to describing the atlases of
$[L(\mathcal M)]$
boils down to describing the atlases of
![]() $[L(\mathcal M_i)]$
,
$[L(\mathcal M_i)]$
,
![]() $i=1, \ldots , k$
.
$i=1, \ldots , k$
.
Assume that a string
![]() $\alpha $
is accepted by
$\alpha $
is accepted by
![]() $\mathcal M_i$
. Then we can write
$\mathcal M_i$
. Then we can write
![]() $\alpha $
as
$\alpha $
as
![]() $v\alpha '$
so that an accepting run of
$v\alpha '$
so that an accepting run of
![]() $\mathcal M_i$
after reading v stays inside
$\mathcal M_i$
after reading v stays inside
![]() $S_i$
. Therefore, the large scale geometry
$S_i$
. Therefore, the large scale geometry
![]() $[\alpha ]$
of
$[\alpha ]$
of
![]() $\alpha $
is quasi-isometric to either
$\alpha $
is quasi-isometric to either
![]() $[0\alpha ']$
or
$[0\alpha ']$
or
![]() $[1\alpha ']$
or both. Based on this observation, we can postulate the following assumption till the end of this section unless otherwise stated.
$[1\alpha ']$
or both. Based on this observation, we can postulate the following assumption till the end of this section unless otherwise stated.
Postulate. The state space S can be written as
![]() $\{q_0\}\cup S'$
so that (1)
$\{q_0\}\cup S'$
so that (1)
![]() $q_0$
is the only initial state and
$q_0$
is the only initial state and
![]() $q_0\not \in S'$
, (2)
$q_0\not \in S'$
, (2)
![]() $S'$
is the only nontrivial strongly connected component of
$S'$
is the only nontrivial strongly connected component of
![]() $\mathcal M$
, and (3) any transition from
$\mathcal M$
, and (3) any transition from
![]() $q_0$
goes into
$q_0$
goes into
![]() $S'$
.
$S'$
.
From now on, our goal is to describe atlases of Büchi recognizable languages accepted by automata that satisfy the postulate above.
Lemma 5.5. If
![]() $\mathcal M$
has a 0-loop and a 1-loop, then the atlas
$\mathcal M$
has a 0-loop and a 1-loop, then the atlas
![]() $[L(\mathcal M)]$
coincides with the atlas
$[L(\mathcal M)]$
coincides with the atlas
![]() $[\Sigma ^{\omega }]\setminus X$
for some
$[\Sigma ^{\omega }]\setminus X$
for some
![]() $X\subseteq \{[0^\omega ], [1^{\omega }], [10^\omega ], [01^{\omega }]\}$
.
$X\subseteq \{[0^\omega ], [1^{\omega }], [10^\omega ], [01^{\omega }]\}$
.
Proof Assume that
![]() $L_0$
is a 0-loop and
$L_0$
is a 0-loop and
![]() $L_1$
is a 1-loop. Let
$L_1$
is a 1-loop. Let
![]() $\alpha $
be a string with infinitely many
$\alpha $
be a string with infinitely many
![]() $0$
s and infinitely many
$0$
s and infinitely many
![]() $1$
s. Say,
$1$
s. Say,
![]() $\alpha =0^{n_0}1^{m_0}0^{n_1}1^{m_1}\ldots $
, where
$\alpha =0^{n_0}1^{m_0}0^{n_1}1^{m_1}\ldots $
, where
![]() $n_i>0$
and
$n_i>0$
and
![]() $m_i>0$
for all i. We can build a string
$m_i>0$
for all i. We can build a string
![]() $\beta $
of the form
$\beta $
of the form
so that the following properties are satisfied:
-
1. The string
 $\beta $
is accepted by
$\beta $
is accepted by
 $\mathcal M$
.
$\mathcal M$
. -
2. For all i we have
 $n_i=n_i^{\prime }+c_i$
and
$n_i=n_i^{\prime }+c_i$
and
 $m_i=m_i^{\prime }+c_i^{\prime }$
, where
$m_i=m_i^{\prime }+c_i^{\prime }$
, where
 $c_i<|S|$
and
$c_i<|S|$
and
 $c_i^{\prime } <|S|$
.
$c_i^{\prime } <|S|$
. -
3. The string v labels a path from a state
 $s_0$
in
$s_0$
in
 $L_0$
to a state
$L_0$
to a state
 $s_1$
in
$s_1$
in
 $L_1$
.
$L_1$
. -
4. The string w labels a path from
 $s_1$
to
$s_1$
to
 $s_0$
.
$s_0$
. -
5. The string u is a string that labels a path from the initial state to
 $s_0$
.
$s_0$
.
This implies that
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are
$\beta $
are
![]() $\leqslant _{CR}$
-reducible to each other. Hence
$\leqslant _{CR}$
-reducible to each other. Hence
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are quasi-isometric.
$\beta $
are quasi-isometric.
Note that none of the strings
![]() $0^\omega $
,
$0^\omega $
,
![]() $1^{\omega }$
,
$1^{\omega }$
,
![]() $10^\omega $
,
$10^\omega $
,
![]() $01^{\omega }$
is quasi-isometric to a string with both infinitely many
$01^{\omega }$
is quasi-isometric to a string with both infinitely many
![]() $0$
s and
$0$
s and
![]() $1$
s. Also, these four strings are pairwise not quasi-isometric. Hence, the choice of X is dependent on whether or not
$1$
s. Also, these four strings are pairwise not quasi-isometric. Hence, the choice of X is dependent on whether or not
![]() $\mathcal M$
accepts some (or all) of these four strings. For instance,
$\mathcal M$
accepts some (or all) of these four strings. For instance,
![]() $0^{\omega }\in X$
iff
$0^{\omega }\in X$
iff
![]() $0^{\omega }$
is not accepted by
$0^{\omega }$
is not accepted by
![]() $\mathcal M$
. We proved the lemma.⊣
$\mathcal M$
. We proved the lemma.⊣
Lemma 5.6. If
![]() $\mathcal M$
has no 0-loop and has no 1-loop, then the atlas
$\mathcal M$
has no 0-loop and has no 1-loop, then the atlas
![]() $[L(\mathcal M)]$
equals the singleton atlas
$[L(\mathcal M)]$
equals the singleton atlas
![]() $[\{(01)^\omega \}]$
.
$[\{(01)^\omega \}]$
.
Proof Let
![]() $\alpha =\sigma _0 \sigma _1\ldots $
be a string accepted by the automaton
$\alpha =\sigma _0 \sigma _1\ldots $
be a string accepted by the automaton
![]() $\mathcal M$
. Let
$\mathcal M$
. Let
![]() $\rho =s_1, s_2, \ldots $
be an accepting run of
$\rho =s_1, s_2, \ldots $
be an accepting run of
![]() $\mathcal M$
on
$\mathcal M$
on
![]() $\alpha $
. Write
$\alpha $
. Write
![]() $\alpha $
as
$\alpha $
as
![]() $w_1 w_2\ldots $
so that
$w_1 w_2\ldots $
so that
-
1. the length of each
 $w_i$
is bounded by
$w_i$
is bounded by
 $|S|$
, and
$|S|$
, and -
2. the run
 $\rho $
along each
$\rho $
along each
 $w_i$
has a loop; that loop within
$w_i$
has a loop; that loop within
 $w_i$
contains both
$w_i$
contains both
 $0$
and
$0$
and
 $1$
.
$1$
.
This implies that
![]() $(01)^{\omega }$
and
$(01)^{\omega }$
and
![]() $\alpha $
are
$\alpha $
are
![]() $\leqslant _{CR}$
-reducible to each other. Hence
$\leqslant _{CR}$
-reducible to each other. Hence
![]() $\alpha $
and
$\alpha $
and
![]() $(01)^{\omega }$
are quasi-isometric.⊣
$(01)^{\omega }$
are quasi-isometric.⊣
Lemma 5.7. Suppose that
![]() $\mathcal M$
contains no 1-loop but has a 0-loop
$\mathcal M$
contains no 1-loop but has a 0-loop
![]() $L_0$
. Then the atlas
$L_0$
. Then the atlas
![]() $[L(\mathcal M)]$
coincides with one of the following atlases:
$[L(\mathcal M)]$
coincides with one of the following atlases:
Proof The assumption of the lemma implies that if
![]() $\alpha $
is accepted by
$\alpha $
is accepted by
![]() $\mathcal M$
then
$\mathcal M$
then
-
1. The string
 $\alpha $
contains infinitely many
$\alpha $
contains infinitely many
 $0$
s, and
$0$
s, and -
2. The length of any sequence of consecutive
 $1$
s occurring in
$1$
s occurring in
 $\alpha $
is bounded by
$\alpha $
is bounded by
 $|S|$
.
$|S|$
.
If
![]() $L(\mathcal M)=V0^{\omega }$
for some regular language
$L(\mathcal M)=V0^{\omega }$
for some regular language
![]() $V\subseteq \Sigma ^\star $
, then the atlas
$V\subseteq \Sigma ^\star $
, then the atlas
![]() $[L(\mathcal M)]$
is either
$[L(\mathcal M)]$
is either
![]() $[\{0^{\omega }\}]$
or
$[\{0^{\omega }\}]$
or
![]() $[\{10^{\omega }\}]$
or
$[\{10^{\omega }\}]$
or
![]() $[\{0^{\omega }, 10^{\omega }\}]$
.
$[\{0^{\omega }, 10^{\omega }\}]$
.
Thus, we assume that
![]() $\mathcal M$
accepts a string with infinitely many
$\mathcal M$
accepts a string with infinitely many
![]() $1$
s’. Let
$1$
s’. Let
![]() $\alpha $
be any string of the form
$\alpha $
be any string of the form
![]() $0^{t_1} 10^{t_2}1\ldots $
, where all
$0^{t_1} 10^{t_2}1\ldots $
, where all
![]() $t_i>0$
for all i. We can build a string
$t_i>0$
for all i. We can build a string
![]() $\beta $
of the form
$\beta $
of the form
so that the following are true:
-
1. The string
 $\beta $
is accepted by
$\beta $
is accepted by
 $\mathcal M$
,
$\mathcal M$
, -
2.
 $t_i=n_i+c_i$
, where
$t_i=n_i+c_i$
, where
 $c_i<|S|$
for all i,
$c_i<|S|$
for all i, -
3. v is a string that labels a path from a state
 $s_0$
in
$s_0$
in
 $L_0$
back to
$L_0$
back to
 $s_0$
, and
$s_0$
, and -
4. The string v contains
 $1$
.
$1$
.
The string
![]() $\beta $
is quasi-isometric to the string
$\beta $
is quasi-isometric to the string
![]() $\beta '$
obtained from
$\beta '$
obtained from
![]() $\beta $
by replacing all occurrences of v with
$\beta $
by replacing all occurrences of v with
![]() $1$
and removing the prefix u. In turn
$1$
and removing the prefix u. In turn
![]() $\beta '$
and
$\beta '$
and
![]() $\alpha $
are
$\alpha $
are
![]() $\leqslant _{CR}$
reducible to each other. Hence,
$\leqslant _{CR}$
reducible to each other. Hence,
![]() $\alpha \sim _{QI} \beta $
.
$\alpha \sim _{QI} \beta $
.
Now suppose that
![]() $\beta $
is accepted by
$\beta $
is accepted by
![]() $\mathcal M$
and
$\mathcal M$
and
![]() $\beta $
has infinitely many
$\beta $
has infinitely many
![]() $1$
’s. Then
$1$
’s. Then
![]() $\beta $
is of the form
$\beta $
is of the form
![]() $u0^{n_1}1^{m_1} 0^{n_2} 1^{m_2}\ldots ,$
where we have
$u0^{n_1}1^{m_1} 0^{n_2} 1^{m_2}\ldots ,$
where we have
![]() $n_i, m_i>0$
for all i. As noted above the numbers
$n_i, m_i>0$
for all i. As noted above the numbers
![]() $m_i$
are uniformly bounded. The string
$m_i$
are uniformly bounded. The string
![]() $\beta $
is quasi-isometric to the string
$\beta $
is quasi-isometric to the string
![]() $\beta '$
obtained from
$\beta '$
obtained from
![]() $\beta $
by replacing every
$\beta $
by replacing every
![]() $1^{m_i}$
with just
$1^{m_i}$
with just
![]() $1$
and removing the prefix u. Clearly
$1$
and removing the prefix u. Clearly
![]() $\beta '$
is of the form desired.
$\beta '$
is of the form desired.
Note that
![]() $\mathcal M$
might also accept some (including none) of the strings quasi-isometric to either
$\mathcal M$
might also accept some (including none) of the strings quasi-isometric to either
![]() $[\{0^{\omega }\}]$
,
$[\{0^{\omega }\}]$
,
![]() $[\{10^{\omega }\}]$
, or both. Hence, the atlas
$[\{10^{\omega }\}]$
, or both. Hence, the atlas
![]() $[L(\mathcal M)]$
coincides with
$[L(\mathcal M)]$
coincides with
where X is a subset of
![]() $\{[0^{\omega }], [10^{\omega }]\}$
.⊣
$\{[0^{\omega }], [10^{\omega }]\}$
.⊣
Obviously the next lemma follows from the above:
Lemma 5.8. Suppose that
![]() $\mathcal M$
contains no 0-loop but has a 1-loop
$\mathcal M$
contains no 0-loop but has a 1-loop
![]() $L_0$
. Then the atlas
$L_0$
. Then the atlas
![]() $[L(\mathcal M)]$
coincides with one of the following atlases:
$[L(\mathcal M)]$
coincides with one of the following atlases:
We now remove our postulate put on the state space of Büchi automata. Using equality
![]() $(\star )$
given above, and the lemmas, we obtain the following characterization result:
$(\star )$
given above, and the lemmas, we obtain the following characterization result:
Theorem 5.9 (Characterization Theorem)
Any Büchi recognizable atlas
![]() $[L]$
is a finite union of atlases from the following list:
$[L]$
is a finite union of atlases from the following list:
-
•
 $[\Sigma ^{\omega }]\setminus X$
, where
$[\Sigma ^{\omega }]\setminus X$
, where
 $X\subseteq \{[0^\omega ], [1^{\omega }], [10^\omega ], [01^{\omega }]\}$
,
$X\subseteq \{[0^\omega ], [1^{\omega }], [10^\omega ], [01^{\omega }]\}$
, -
•
 $[\{0^{n_1} 10^{n_2}\ldots \mid n_i>0\}] \cup X$
, where
$[\{0^{n_1} 10^{n_2}\ldots \mid n_i>0\}] \cup X$
, where
 $X\subseteq \{[0^{\omega }], [10^{\omega }]\}$
.
$X\subseteq \{[0^{\omega }], [10^{\omega }]\}$
. -
•
 $[\{1^{n_1} 01^{n_2} \ldots \mid n_i>0\}] \cup X$
, where
$[\{1^{n_1} 01^{n_2} \ldots \mid n_i>0\}] \cup X$
, where
 $X \subseteq \{[1^{\omega }], [01^{\omega }]\}$
.
$X \subseteq \{[1^{\omega }], [01^{\omega }]\}$
. -
•
 $[\{0^{\omega }\}]$
,
$[\{0^{\omega }\}]$
,
 $[\{10^{\omega }\}]$
,
$[\{10^{\omega }\}]$
,
 $[\{0^{\omega }, 10^{\omega }\}]$
,
$[\{0^{\omega }, 10^{\omega }\}]$
,
 $[\{(01)^\omega \}]$
,
$[\{(01)^\omega \}]$
, -
•
 $[\{1^{\omega }\}]$
,
$[\{1^{\omega }\}]$
,
 $[\{01^{\omega }\}]$
,
$[\{01^{\omega }\}]$
,
 $[\{1^{\omega }, 01^{\omega }\}]$
.⊣
$[\{1^{\omega }, 01^{\omega }\}]$
.⊣
This theorem has a complexity-theoretic implication. Consider the following Atlas Equality Problem. Design an algorithm that given Büchi automata
![]() $\mathcal M_1$
and
$\mathcal M_1$
and
![]() $\mathcal M_2$
decides if
$\mathcal M_2$
decides if
![]() $[L(\mathcal M_1)]$
and
$[L(\mathcal M_1)]$
and
![]() $[L(\mathcal M_2)]$
coincide. Below we prove that the Atlas Equality problem is decidable in linear time. In comparison, the language equality problem for Büchi automata is PSPACE complete.
$[L(\mathcal M_2)]$
coincide. Below we prove that the Atlas Equality problem is decidable in linear time. In comparison, the language equality problem for Büchi automata is PSPACE complete.
Corollary 5.10. There exists a linear time algorithm that, given Büchi automata
![]() $\mathcal A$
and
$\mathcal A$
and
![]() $\mathcal B$
, decides if the atlases
$\mathcal B$
, decides if the atlases
![]() $[L(\mathcal A)]$
and
$[L(\mathcal A)]$
and
![]() $[L(\mathcal B)]$
coincide.
$[L(\mathcal B)]$
coincide.
Proof Note that the running time is measured in terms of the sizes of
![]() $\mathcal A$
and
$\mathcal A$
and
![]() $\mathcal B$
. So, let
$\mathcal B$
. So, let
![]() $\mathcal M$
be a Büchi automaton. We want to find atlases from the list provided in Theorem 5.9 such that the union of these atlases equals
$\mathcal M$
be a Büchi automaton. We want to find atlases from the list provided in Theorem 5.9 such that the union of these atlases equals
![]() $[L(\mathcal M)]$
. For this, we decompose
$[L(\mathcal M)]$
. For this, we decompose
![]() $\mathcal M$
into automata
$\mathcal M$
into automata
![]() $\mathcal M_1$
,
$\mathcal M_1$
,
![]() $\ldots $
,
$\ldots $
,
![]() $\mathcal M_k$
as in the equality
$\mathcal M_k$
as in the equality
![]() $(\star )$
, where each
$(\star )$
, where each
![]() $\mathcal M_i$
satisfies the postulate. This decomposition can be done in linear time (e.g., using Tarjan’s algorithm that finds strongly connected components of directed graphs). Now for each
$\mathcal M_i$
satisfies the postulate. This decomposition can be done in linear time (e.g., using Tarjan’s algorithm that finds strongly connected components of directed graphs). Now for each
![]() $\mathcal M_i$
, we check the assumptions of Lemma 5.5 through Lemma 5.8.
$\mathcal M_i$
, we check the assumptions of Lemma 5.5 through Lemma 5.8.
As an example, the assumptions of Lemma 5.5 can be checked as follows. In order to check if
![]() $\mathcal M_i$
contains a 0-loop, we remove all transitions labeled with
$\mathcal M_i$
contains a 0-loop, we remove all transitions labeled with
![]() $1$
from the state diagram of
$1$
from the state diagram of
![]() $\mathcal M_i$
. This gives us a directed graph whose edges are transitions labelled with
$\mathcal M_i$
. This gives us a directed graph whose edges are transitions labelled with
![]() $0$
. This modified graph has a loop iff
$0$
. This modified graph has a loop iff
![]() $\mathcal M_i$
has a 0-loop. Similarly, to check if
$\mathcal M_i$
has a 0-loop. Similarly, to check if
![]() $\mathcal M_i$
contains a 1-loop, we remove all transitions labeled with
$\mathcal M_i$
contains a 1-loop, we remove all transitions labeled with
![]() $1$
. This new directed graph has a loop iff
$1$
. This new directed graph has a loop iff
![]() $\mathcal M_i$
has a 1-loop. To find the set X from (the statement of) the lemma we just need to check which of the strings
$\mathcal M_i$
has a 1-loop. To find the set X from (the statement of) the lemma we just need to check which of the strings
![]() $0^{\omega }$
,
$0^{\omega }$
,
![]() $1^{\omega }$
,
$1^{\omega }$
,
![]() $10^{\omega }$
,
$10^{\omega }$
,
![]() $01^{\omega }$
is accepted by
$01^{\omega }$
is accepted by
![]() $\mathcal M_i$
. This is based on standard graph algorithms (such as the path problem that given two vertices s and t in a directed graph determines if there exists a path from s to t). All these can be done in linear time on the size of
$\mathcal M_i$
. This is based on standard graph algorithms (such as the path problem that given two vertices s and t in a directed graph determines if there exists a path from s to t). All these can be done in linear time on the size of
![]() $\mathcal M_i$
.
$\mathcal M_i$
.
The argument shows that we can find, in linear time on the size of
![]() $\mathcal M$
, the atlases from the list provided in Theorem 5.9 such that the union of these atlases is the atlas
$\mathcal M$
, the atlases from the list provided in Theorem 5.9 such that the union of these atlases is the atlas
![]() $[L(\mathcal M)]$
. Thus, given Büchi automata
$[L(\mathcal M)]$
. Thus, given Büchi automata
![]() $\mathcal A$
and
$\mathcal A$
and
![]() $\mathcal B$
we can decide in linear time if
$\mathcal B$
we can decide in linear time if
![]() $[L(\mathcal A)]=[L(\mathcal B)]$
.⊣
$[L(\mathcal A)]=[L(\mathcal B)]$
.⊣
6 The quasi-isometry problem
In this section our goal is two fold. The first goal is to give a computability-theoretic treatment of the quasi-isometry problem. The second goal is to study the complexity of quasi-isometric mappings from
![]() $\alpha $
into
$\alpha $
into
![]() $\beta $
given that
$\beta $
given that
![]() $\alpha \leqslant _{QI} \beta $
. We study both questions using the language of the arithmetical hierarchy. In particular we assume that the reader is familiar with basics of computability theory: the halting set,
$\alpha \leqslant _{QI} \beta $
. We study both questions using the language of the arithmetical hierarchy. In particular we assume that the reader is familiar with basics of computability theory: the halting set,
![]() $\Sigma _n^0$
-sets,
$\Sigma _n^0$
-sets,
![]() $\Sigma _n^0$
-complete sets, oracle computation, and the low basis theorem [Reference Jockusch and Soare8]. A standard enumeration of all computably enumerable (c.e.) sets is denoted by
$\Sigma _n^0$
-complete sets, oracle computation, and the low basis theorem [Reference Jockusch and Soare8]. A standard enumeration of all computably enumerable (c.e.) sets is denoted by
![]() $W_0, W_1, W_2, \ldots $
. We also use a typical example of a
$W_0, W_1, W_2, \ldots $
. We also use a typical example of a
![]() $\Sigma _2^0$
-complete set, the set of indices of all finite sets; that is
$\Sigma _2^0$
-complete set, the set of indices of all finite sets; that is
![]() $FIN=\{i\mid W_i$
is a finite set
$FIN=\{i\mid W_i$
is a finite set
![]() $\}$
[Reference Rogers12].
$\}$
[Reference Rogers12].
Formally, the quasi-isometry problem (over the alphabet
![]() $\Sigma $
) is the set:
$\Sigma $
) is the set:
By restricting this set to computable sequences
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
we have:
$\beta $
we have:
To achieve the first goal let us give an upper bound (in terms of the arithmetical hierarchy) for the set
![]() $QIP_c$
. Consider computable strings
$QIP_c$
. Consider computable strings
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
. Let
$\beta $
. Let
![]() $(A, B, C)$
be quasi-isometry constants. Consider the tree
$(A, B, C)$
be quasi-isometry constants. Consider the tree
![]() $T(\alpha , \beta , A,B, C)$
constructed in Section 3.2. By the Lemma 3.7 the tree is infinite if and only if
$T(\alpha , \beta , A,B, C)$
constructed in Section 3.2. By the Lemma 3.7 the tree is infinite if and only if
![]() $\alpha \leqslant _{QI} \beta $
. Thus,
$\alpha \leqslant _{QI} \beta $
. Thus,
![]() $\alpha \leqslant _{QI} \beta $
if and only if there exist
$\alpha \leqslant _{QI} \beta $
if and only if there exist
![]() $(A, B,C)$
such that the tree
$(A, B,C)$
such that the tree
![]() $T(\alpha , \beta , A,B, C)$
is infinite. Note that if
$T(\alpha , \beta , A,B, C)$
is infinite. Note that if
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are computable then the tree is also computable. Checking if the tree
$\beta $
are computable then the tree is also computable. Checking if the tree
![]() $T(\alpha , \beta , A,B, C)$
is infinite is a
$T(\alpha , \beta , A,B, C)$
is infinite is a
![]() $\Pi _2^0$
-conditions. This implies that
$\Pi _2^0$
-conditions. This implies that
![]() $QIP_c$
is a
$QIP_c$
is a
![]() $\Sigma _3^0$
-set. At first glance, this bound seems to be a sharp bound. The theorem below, however, shows that
$\Sigma _3^0$
-set. At first glance, this bound seems to be a sharp bound. The theorem below, however, shows that
![]() $QIP_c$
is a
$QIP_c$
is a
![]() $\Sigma _2^0$
-complete set. The theorem also (partially) answers our second question posed at the beginning of this section.
$\Sigma _2^0$
-complete set. The theorem also (partially) answers our second question posed at the beginning of this section.
Theorem 6.1. The following statements are true:
-
1. The quasi-isometry problem for the pairs
 $(\alpha ,\beta )$
of all computable strings is a
$(\alpha ,\beta )$
of all computable strings is a
 $\Sigma _2^0$
-complete set.
$\Sigma _2^0$
-complete set. -
2. If
 $\alpha \leqslant _{QI}\beta $
, then there exists a quasi-isometry between
$\alpha \leqslant _{QI}\beta $
, then there exists a quasi-isometry between
 $\alpha $
and
$\alpha $
and
 $\beta $
computable in the halting set relative to
$\beta $
computable in the halting set relative to
 $\alpha $
and
$\alpha $
and
 $\beta $
. Furthermore, if
$\beta $
. Furthermore, if
 $\alpha $
and
$\alpha $
and
 $\beta $
are computable then there exists a low quasi-isometry from
$\beta $
are computable then there exists a low quasi-isometry from
 $\alpha $
into
$\alpha $
into
 $\beta $
.
$\beta $
.
Proof For the first part of the theorem, let us start showing that
![]() $QIP_c$
is a
$QIP_c$
is a
![]() $\Sigma _2^0$
-set. For arbitrary computable strings
$\Sigma _2^0$
-set. For arbitrary computable strings
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
(given by c.e. indices i and j, respectively), and
$\beta $
(given by c.e. indices i and j, respectively), and
![]() $(A, B, C)$
quasi-isometry constants, consider the tree
$(A, B, C)$
quasi-isometry constants, consider the tree
![]() $T(\alpha , \beta , A,B, C)$
and a node x at level n of the tree. The node x determines a partial mapping
$T(\alpha , \beta , A,B, C)$
and a node x at level n of the tree. The node x determines a partial mapping
![]() $\,f_x=\{(0,i_0), \ldots , (n, i_n)\}$
that can possibly be extended to an
$\,f_x=\{(0,i_0), \ldots , (n, i_n)\}$
that can possibly be extended to an
![]() $(A, B,C)$
-quasi-isometry. The crucial point is that we can put a bound on
$(A, B,C)$
-quasi-isometry. The crucial point is that we can put a bound on
![]() $i_n$
that depends on
$i_n$
that depends on
![]() $(A, B, C)$
. The bound is computable from
$(A, B, C)$
. The bound is computable from
![]() $(A, B, C)$
only. Hence, the tree
$(A, B, C)$
only. Hence, the tree
![]() $T(\alpha , \beta , A,B, C)$
is such that given n we can compute the number of all nodes at level n of the tree. Therefore, the set
$T(\alpha , \beta , A,B, C)$
is such that given n we can compute the number of all nodes at level n of the tree. Therefore, the set
![]() $L=\{n \mid $
the tree
$L=\{n \mid $
the tree
![]() $T(\alpha , \beta , A,B, C)$
has a node at level
$T(\alpha , \beta , A,B, C)$
has a node at level
![]() $n\}$
is computable. Hence, the set
$n\}$
is computable. Hence, the set
is a
![]() $\Pi _1^0$
set. Thus,
$\Pi _1^0$
set. Thus,
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are quasi-isometric if and only if there are constants
$\beta $
are quasi-isometric if and only if there are constants
![]() $(A,B,C)$
such that the tree
$(A,B,C)$
such that the tree
![]() $T(\alpha , \beta , A,B, C)$
is infinite. This implies that the quasi-isometry problem for computable strings is a
$T(\alpha , \beta , A,B, C)$
is infinite. This implies that the quasi-isometry problem for computable strings is a
![]() $\Sigma _2^0$
-set.
$\Sigma _2^0$
-set.
Consider the following
![]() $\Sigma _2^0$
-complete set
$\Sigma _2^0$
-complete set
![]() $FIN=\{i\mid W_i$
is finite
$FIN=\{i\mid W_i$
is finite
![]() $\}$
. We will reduce
$\}$
. We will reduce
![]() $FIN$
to
$FIN$
to
![]() $QIP_c$
. For each i we construct two infinite strings
$QIP_c$
. For each i we construct two infinite strings
![]() $\alpha _i$
and
$\alpha _i$
and
![]() $\beta _i$
such that
$\beta _i$
such that
![]() $W_i$
is finite if and only if
$W_i$
is finite if and only if
![]() $\alpha _i$
and
$\alpha _i$
and
![]() $\beta _i$
are quasi-isometric. For this we start enumerating
$\beta _i$
are quasi-isometric. For this we start enumerating
![]() $W_i$
by stages
$W_i$
by stages
![]() $1$
,
$1$
,
![]() $2$
,
$2$
,
![]() $\ldots $
. At stage
$\ldots $
. At stage
![]() $0$
, we construct
$0$
, we construct
![]() $\alpha _{i,0}$
and
$\alpha _{i,0}$
and
![]() $\beta _{i,0}$
finite prefixes that can be extended to
$\beta _{i,0}$
finite prefixes that can be extended to
![]() $(1,1,1 )$
-quasi-isometries and set
$(1,1,1 )$
-quasi-isometries and set
![]() $A_0=B_0=C_0=1$
. Assume that by stage
$A_0=B_0=C_0=1$
. Assume that by stage
![]() $s>0$
we have built finite prefixes
$s>0$
we have built finite prefixes
![]() $\alpha _{i,s-1}$
(of
$\alpha _{i,s-1}$
(of
![]() $\alpha _i$
) and
$\alpha _i$
) and
![]() $\beta _{i,s-1}$
(of
$\beta _{i,s-1}$
(of
![]() $\beta _i$
). At this stage we also assume that the strings
$\beta _i$
). At this stage we also assume that the strings
![]() $\alpha _{i,s-1}$
and
$\alpha _{i,s-1}$
and
![]() $\beta _{i,s-1}$
have extensions that are
$\beta _{i,s-1}$
have extensions that are
![]() $(A_{s-1}, B_{s-1}, C_{s-1})$
-quasi-isometric. If at stage s the enumeration of
$(A_{s-1}, B_{s-1}, C_{s-1})$
-quasi-isometric. If at stage s the enumeration of
![]() $W_i$
outputs a new element, then we extend
$W_i$
outputs a new element, then we extend
![]() $\alpha _{i,s-1}$
to
$\alpha _{i,s-1}$
to
![]() $\alpha _{i,s}$
and
$\alpha _{i,s}$
and
![]() $\beta _{i,s-1}$
to
$\beta _{i,s-1}$
to
![]() $\beta _{i,s}$
so there is no
$\beta _{i,s}$
so there is no
![]() $(A_{s-1}, B_{s-1}, C_{s-1})$
-quasi-isometry between
$(A_{s-1}, B_{s-1}, C_{s-1})$
-quasi-isometry between
![]() $\alpha _{i,s}$
and
$\alpha _{i,s}$
and
![]() $\beta _{i,s}$
. This can easily be achieved by appending a long finite string of one color at the end of
$\beta _{i,s}$
. This can easily be achieved by appending a long finite string of one color at the end of
![]() $\alpha _{i,s-1}$
and a long finite string of another color at the end of the string
$\alpha _{i,s-1}$
and a long finite string of another color at the end of the string
![]() $\beta _{i,s-1}$
. Then we select constants
$\beta _{i,s-1}$
. Then we select constants
![]() $(A_s, B_s, C_s)$
such that the finite strings
$(A_s, B_s, C_s)$
such that the finite strings
![]() $\alpha _{i,s}$
and
$\alpha _{i,s}$
and
![]() $\beta _{i,s}$
can be extended to an
$\beta _{i,s}$
can be extended to an
![]() $(A_s, B_s, C_s)$
-quasi-isometry and
$(A_s, B_s, C_s)$
-quasi-isometry and
![]() $A_{s}>A_{s-1}$
,
$A_{s}>A_{s-1}$
,
![]() $B_s>B_{s-1}$
, and
$B_s>B_{s-1}$
, and
![]() $C_s> C_{s-1}$
. If
$C_s> C_{s-1}$
. If
![]() $W_i$
at stage s does not enumerate a new element then we extend
$W_i$
at stage s does not enumerate a new element then we extend
![]() $\alpha _{i,s-1}$
to
$\alpha _{i,s-1}$
to
![]() $\alpha _{i,s}$
and
$\alpha _{i,s}$
and
![]() $\beta _{i,s-1}$
to
$\beta _{i,s-1}$
to
![]() $\beta _{i,s}$
such that the new extended finite strings
$\beta _{i,s}$
such that the new extended finite strings
![]() $\alpha _{i,s}$
and
$\alpha _{i,s}$
and
![]() $\beta _{i,s}$
have
$\beta _{i,s}$
have
![]() $(A_{s-1}, B_{s-1}, C_{s-1})$
-quasi-isometric extensions and we set
$(A_{s-1}, B_{s-1}, C_{s-1})$
-quasi-isometric extensions and we set
![]() $A_s=A_{s-1}$
,
$A_s=A_{s-1}$
,
![]() $B_s=B_{s-1}$
,
$B_s=B_{s-1}$
,
![]() $C_s=C_{s-1}$
.
$C_s=C_{s-1}$
.
Thus, if
![]() $W_i$
is infinite then there is an infinite sequence
$W_i$
is infinite then there is an infinite sequence
![]() $s_1$
,
$s_1$
,
![]() $s_2$
,
$s_2$
,
![]() $\ldots $
of increasing stages at which the enumeration of
$\ldots $
of increasing stages at which the enumeration of
![]() $W_i$
increases the size of
$W_i$
increases the size of
![]() $W_i$
. Hence, from stage
$W_i$
. Hence, from stage
![]() $s_{i+1}$
on
$s_{i+1}$
on
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are not
$\beta $
are not
![]() $(A_{s_i}, B_{s_i}, C_{s_i})$
-quasi-isometric. This implies that
$(A_{s_i}, B_{s_i}, C_{s_i})$
-quasi-isometric. This implies that
![]() $W_i$
is infinite then
$W_i$
is infinite then
![]() $\alpha _i$
and
$\alpha _i$
and
![]() $\beta _i$
are not quasi-isometric. If
$\beta _i$
are not quasi-isometric. If
![]() $W_i$
is finite then the sequences
$W_i$
is finite then the sequences
![]() $\{(A_s, B_s, C_s)\}_{s\in \omega }$
stabilizes and
$\{(A_s, B_s, C_s)\}_{s\in \omega }$
stabilizes and
![]() $\alpha _i$
and
$\alpha _i$
and
![]() $\beta _i$
built are quasi-isometric.
$\beta _i$
built are quasi-isometric.
To prove the second part of the theorem, consider strings
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
such that
$\beta $
such that
![]() $\alpha \leqslant _{QI} \beta $
. The tree
$\alpha \leqslant _{QI} \beta $
. The tree
![]() $T(\alpha , \beta , A,B, C)$
is computable with oracle for
$T(\alpha , \beta , A,B, C)$
is computable with oracle for
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
. Hence, there exists a quasi-isometry
$\beta $
. Hence, there exists a quasi-isometry
![]() $\,f: \alpha \rightarrow \beta $
such that f is computable with an oracle for the halting sets for
$\,f: \alpha \rightarrow \beta $
such that f is computable with an oracle for the halting sets for
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
. Moreover, by the Low Basis theorem, if
$\beta $
. Moreover, by the Low Basis theorem, if
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are computable then f can be chosen to be low. This proves the second part of the theorem.⊣
$\beta $
are computable then f can be chosen to be low. This proves the second part of the theorem.⊣
The isometry problem for colored computable metric spaces is a refined version of the quasi-isometry problem. In this sense, somewhat intuitively, one might expect that quasi-isometry is easier to detect than the isometry. However, the opposite is true. The isometry problem for computable colored metric spaces
![]() $\alpha \in \Sigma ^{\omega }$
is a
$\alpha \in \Sigma ^{\omega }$
is a
![]() $\Pi _1^0$
-complete set (which is not too hard to see) as opposed to
$\Pi _1^0$
-complete set (which is not too hard to see) as opposed to
![]() $\Sigma _2^0$
-completeness of the quasi-isometry problem.
$\Sigma _2^0$
-completeness of the quasi-isometry problem.
We conclude this section by referring an interesting related fact found by [Reference Lou10]. From Theorem 6.1 we know if
![]() $\alpha \leqslant _{QI} \beta $
and both
$\alpha \leqslant _{QI} \beta $
and both
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are computable then there exists a quasi-isometry from
$\beta $
are computable then there exists a quasi-isometry from
![]() $\alpha $
to
$\alpha $
to
![]() $\beta $
which is computable in the halting set. Is this bound sharp, that is, are there computable
$\beta $
which is computable in the halting set. Is this bound sharp, that is, are there computable
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
such that
$\beta $
such that
![]() $\alpha \leqslant _{QI} \beta $
but no computable function can witness the inequality? It is shown in [Reference Lou10] that the answer is positive.
$\alpha \leqslant _{QI} \beta $
but no computable function can witness the inequality? It is shown in [Reference Lou10] that the answer is positive.
Theorem 6.2 [Reference Lou10]
There exists a pair of strings
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
that satisfies the following properties:
$\beta $
that satisfies the following properties:
-
1.
 $\alpha $
and
$\alpha $
and
 $\beta $
are computable.
$\beta $
are computable. -
2.
 $\alpha \leqslant _{QI} \beta $
holds.
$\alpha \leqslant _{QI} \beta $
holds. -
3. There is no computable quasi-isometry from
 $\alpha $
to
$\alpha $
to
 $\beta $
.⊣
$\beta $
.⊣
7 Asymptotic cones
Consider a colored metric space
![]() $\alpha \in \Sigma ^{\omega }$
. Let us zoom out this metric space further and further away. Formally, consider the following sequence of colored metric spaces:
$\alpha \in \Sigma ^{\omega }$
. Let us zoom out this metric space further and further away. Formally, consider the following sequence of colored metric spaces:
![]() $X_{0,\alpha }=(\alpha , d_0)$
,
$X_{0,\alpha }=(\alpha , d_0)$
,
![]() $X_{1,\alpha }=(\alpha ,d_1)$
,
$X_{1,\alpha }=(\alpha ,d_1)$
,
![]() $X_{2,\alpha }=(\alpha ,d_2)$
,
$X_{2,\alpha }=(\alpha ,d_2)$
,
![]() $\ldots $
, where
$\ldots $
, where
![]() $d_n(i,j)=|i-j|/n$
. Intuitively, when n approaches infinity, the sequence produces a limit structure. This limit structure presents large scale properties of
$d_n(i,j)=|i-j|/n$
. Intuitively, when n approaches infinity, the sequence produces a limit structure. This limit structure presents large scale properties of
![]() $\alpha $
. How do we formally define this limit structure? The notion of asymptotic cone gives one possible formalization of the limit structure.
$\alpha $
. How do we formally define this limit structure? The notion of asymptotic cone gives one possible formalization of the limit structure.
7.1 Basic facts about asymptotic cones
Let
![]() $\mathcal F$
be a nonprincipal ultrafilter on
$\mathcal F$
be a nonprincipal ultrafilter on
![]() $\omega $
. Recall that a nonprincipal ultrafilter on
$\omega $
. Recall that a nonprincipal ultrafilter on
![]() $\omega $
is a nonempty maximal (with respect to the set-theoretic inclusion) subset of
$\omega $
is a nonempty maximal (with respect to the set-theoretic inclusion) subset of
![]() $P(\omega )$
that satisfies the following properties:
$P(\omega )$
that satisfies the following properties:
-
1. No finite set belongs to
 $\mathcal F$
. So,
$\mathcal F$
. So,
 $\mathcal F$
does not contain the empty set.
$\mathcal F$
does not contain the empty set. -
2. For all
 $A, B\in \mathcal F$
we have
$A, B\in \mathcal F$
we have
 $A\cap B\in \mathcal F$
.
$A\cap B\in \mathcal F$
. -
3. For all
 $A, B\subseteq \omega $
if
$A, B\subseteq \omega $
if
 $A\in \mathcal F$
and
$A\in \mathcal F$
and
 $A\subseteq B$
then
$A\subseteq B$
then
 $B \in \mathcal F$
.
$B \in \mathcal F$
.
Every ultrafilter
![]() $\mathcal F$
has the following two properties: (1) For every set
$\mathcal F$
has the following two properties: (1) For every set
![]() $A\subseteq \omega $
, either
$A\subseteq \omega $
, either
![]() $A\in \mathcal F$
or
$A\in \mathcal F$
or
![]() $\omega \setminus A\in \mathcal F$
. (2) For all pairwise disjoint sets
$\omega \setminus A\in \mathcal F$
. (2) For all pairwise disjoint sets
![]() $A, B\subseteq \omega $
if
$A, B\subseteq \omega $
if
![]() $A\cup B\in \mathcal F$
then either
$A\cup B\in \mathcal F$
then either
![]() $A\in \mathcal F$
or
$A\in \mathcal F$
or
![]() $B\in \mathcal F$
.
$B\in \mathcal F$
.
Definition 7.1. A scaling factor is any strictly increasing monotonic function
![]() $s: \omega \rightarrow \omega $
such that
$s: \omega \rightarrow \omega $
such that
![]() $s(0)=1$
.
$s(0)=1$
.
Let
![]() $\alpha \in \Sigma ^{\omega }$
. Define the following sequence of metric spaces:
$\alpha \in \Sigma ^{\omega }$
. Define the following sequence of metric spaces:
where
![]() $d_n(i,j)=|i-j|/s(n)$
. Informally, with the scaling factor
$d_n(i,j)=|i-j|/s(n)$
. Informally, with the scaling factor
![]() $s(n)$
, this sequence presents the zooming out process of the string
$s(n)$
, this sequence presents the zooming out process of the string
![]() $\alpha $
. For instance, in the metric space
$\alpha $
. For instance, in the metric space
![]() $X_{0,\alpha , s}$
the distance from
$X_{0,\alpha , s}$
the distance from
![]() $0$
to
$0$
to
![]() $s(n)$
equals
$s(n)$
equals
![]() $s(n)$
, while in
$s(n)$
, while in
![]() $X_{n, \alpha ,s}$
the distance from
$X_{n, \alpha ,s}$
the distance from
![]() $0$
to
$0$
to
![]() $s(n)$
is scaled down to
$s(n)$
is scaled down to
![]() $1$
. We assume that the domains of these metric spaces are pairwise disjoint:
$1$
. We assume that the domains of these metric spaces are pairwise disjoint:
![]() $X_{i,\alpha ,s}\cap X_{j,\alpha , s}=\emptyset $
for all
$X_{i,\alpha ,s}\cap X_{j,\alpha , s}=\emptyset $
for all
![]() $i\neq j$
.
$i\neq j$
.
Let
![]() $\mathbf {a}=(a_n)_{n\geqslant 0}$
be a sequence, where
$\mathbf {a}=(a_n)_{n\geqslant 0}$
be a sequence, where
![]() $a_n\in X_{n, \alpha , s}$
for each n. Call the sequence
$a_n\in X_{n, \alpha , s}$
for each n. Call the sequence
![]() $\mathcal F$
-bounded, or bounded for short, if there is a constant L (that depends on a) such that the set
$\mathcal F$
-bounded, or bounded for short, if there is a constant L (that depends on a) such that the set
![]() $\{n \mid d_n(0, a_n) < L \}$
belong to the ultrafilter
$\{n \mid d_n(0, a_n) < L \}$
belong to the ultrafilter
![]() $\mathcal F$
.
$\mathcal F$
.
We now define
![]() $\mathbf {B}(\mathcal F, s)$
to be the set of all bounded sequences
$\mathbf {B}(\mathcal F, s)$
to be the set of all bounded sequences
![]() $\mathbf {a}=(a_n)_{n\geqslant 0}$
. Say that two bounded sequences a and b are
$\mathbf {a}=(a_n)_{n\geqslant 0}$
. Say that two bounded sequences a and b are
![]() $\mathcal F$
-equivalent, written
$\mathcal F$
-equivalent, written
![]() $\mathbf {a}\sim _{\mathcal F} \mathbf {b}$
, if for any
$\mathbf {a}\sim _{\mathcal F} \mathbf {b}$
, if for any
![]() $\varepsilon>0$
the set
$\varepsilon>0$
the set
![]() $\{n \mid d_n(a_n,b_n)\leqslant \varepsilon \}$
belongs to the filter
$\{n \mid d_n(a_n,b_n)\leqslant \varepsilon \}$
belongs to the filter
![]() $\mathcal F$
. This is an equivalence relation on the set
$\mathcal F$
. This is an equivalence relation on the set
![]() $\mathbf {B}(\mathcal F, s)$
since
$\mathbf {B}(\mathcal F, s)$
since
![]() $\mathcal F$
is an ultrafilter.
$\mathcal F$
is an ultrafilter.
Definition 7.2. Define the asymptotic cone of
![]() $\alpha $
, written
$\alpha $
, written
![]() $Cone(\alpha , \mathcal F, s)$
, with respect to the function
$Cone(\alpha , \mathcal F, s)$
, with respect to the function
![]() $s(n)$
and the ultrafilter
$s(n)$
and the ultrafilter
![]() $\mathcal F$
as the quotient set
$\mathcal F$
as the quotient set
equipped with the following metric D and color
![]() $Cl$
:
$Cl$
:
-
1.
 $D(\mathbf {a}, \mathbf {b} )=r$
iff
$D(\mathbf {a}, \mathbf {b} )=r$
iff
 $\{n \mid r-\varepsilon \leqslant d_n(a_n,b_n)\leqslant r+\varepsilon \}\in \mathcal F$
for all
$\{n \mid r-\varepsilon \leqslant d_n(a_n,b_n)\leqslant r+\varepsilon \}\in \mathcal F$
for all
 $\varepsilon>0$
.
$\varepsilon>0$
. -
2.
 $Cl(\mathbf {a})=\sigma $
iff
$Cl(\mathbf {a})=\sigma $
iff
 $\{n\mid a_n$
has color
$\{n\mid a_n$
has color
 $\sigma \}\in \mathcal F$
.
$\sigma \}\in \mathcal F$
.
The definition implies the following. The metric space
![]() $Cone(\alpha , \mathcal F, s)$
with the metric D is isometric to the metric space
$Cone(\alpha , \mathcal F, s)$
with the metric D is isometric to the metric space
![]() $\mathbb R_{\geqslant 0}$
of all positive reals. So, we can simply refer to the elements a of the asymptotic cone as reals. In addition, since
$\mathbb R_{\geqslant 0}$
of all positive reals. So, we can simply refer to the elements a of the asymptotic cone as reals. In addition, since
![]() $\mathcal F$
is ultrafilter, the color function
$\mathcal F$
is ultrafilter, the color function
![]() $Cl$
assigns to every real
$Cl$
assigns to every real
![]() $\mathbf {a} \in Cone(\alpha , \mathcal F, s)$
at least one color. In particular, some elements of the asymptotic cone might have several colors. Also, note that asymptotic cones are dependent on ultrafilters
$\mathbf {a} \in Cone(\alpha , \mathcal F, s)$
at least one color. In particular, some elements of the asymptotic cone might have several colors. Also, note that asymptotic cones are dependent on ultrafilters
![]() $\mathcal F$
and the scaling factors s.
$\mathcal F$
and the scaling factors s.
A key property of asymptotic cones construction is that quasi-isometry between
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
implies bi-Lipschitz equivalence between the asymptotic cones
$\beta $
implies bi-Lipschitz equivalence between the asymptotic cones
![]() $Cone(\alpha , \mathcal F, s)$
and
$Cone(\alpha , \mathcal F, s)$
and
![]() $Cone(\beta , \mathcal F, s)$
. In other words, asymptotic cones are quasi-isometry invariants. The proof is standard with the difference that our metric spaces are colored. However, since our base metric space is a linear order
$Cone(\beta , \mathcal F, s)$
. In other words, asymptotic cones are quasi-isometry invariants. The proof is standard with the difference that our metric spaces are colored. However, since our base metric space is a linear order
![]() $\mathbb \omega $
, the conclusion of our theorem is a little stronger as it implies order perseverance.
$\mathbb \omega $
, the conclusion of our theorem is a little stronger as it implies order perseverance.
Theorem 7.3. If strings
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
have the same large scale geometry then there are color-preserving and order preserving homeomorphisms
$\beta $
have the same large scale geometry then there are color-preserving and order preserving homeomorphisms
 $$ \begin{align*} &H:Cone(\alpha, \mathcal F, s)\rightarrow Cone(\beta, \mathcal F, s) \text{ and}\\ &\ \ G:Cone(\beta, \mathcal F, s) \rightarrow Cone(\alpha, \mathcal F, s), \end{align*} $$
$$ \begin{align*} &H:Cone(\alpha, \mathcal F, s)\rightarrow Cone(\beta, \mathcal F, s) \text{ and}\\ &\ \ G:Cone(\beta, \mathcal F, s) \rightarrow Cone(\alpha, \mathcal F, s), \end{align*} $$
constants
![]() $C_H$
and
$C_H$
and
![]() $C_G$
such that for all elements
$C_G$
such that for all elements
![]() $\mathbf {a}, \mathbf {b} \in Cone(\alpha , \mathcal F, s)$
and
$\mathbf {a}, \mathbf {b} \in Cone(\alpha , \mathcal F, s)$
and
![]() $\mathbf {c}, \mathbf {d} \in Cone(\beta , \mathcal F, s)$
we have:
$\mathbf {c}, \mathbf {d} \in Cone(\beta , \mathcal F, s)$
we have:
 $$ \begin{align*} &(1/C_{H} )\cdot D(\mathbf{a}, \mathbf{b})\leqslant D(H(\mathbf{a}), H(\mathbf{b}))\leqslant C_{H}\cdot D(\mathbf{a}, \mathbf{b}), \\ &\qquad\qquad\qquad\text{ and }\\ &(1/C_{G}) \cdot D(\mathbf{c}, \mathbf{d})\leqslant D(G(\mathbf{c}), G(\mathbf{d}))\leqslant C_{G}\cdot D(\mathbf{c}, \mathbf{d}). \end{align*} $$
$$ \begin{align*} &(1/C_{H} )\cdot D(\mathbf{a}, \mathbf{b})\leqslant D(H(\mathbf{a}), H(\mathbf{b}))\leqslant C_{H}\cdot D(\mathbf{a}, \mathbf{b}), \\ &\qquad\qquad\qquad\text{ and }\\ &(1/C_{G}) \cdot D(\mathbf{c}, \mathbf{d})\leqslant D(G(\mathbf{c}), G(\mathbf{d}))\leqslant C_{G}\cdot D(\mathbf{c}, \mathbf{d}). \end{align*} $$
Proof Let
![]() $h:\alpha \rightarrow \beta $
and
$h:\alpha \rightarrow \beta $
and
![]() $g:\beta \rightarrow \alpha $
be
$g:\beta \rightarrow \alpha $
be
![]() $(A_1,B_1, C_1)$
and
$(A_1,B_1, C_1)$
and
![]() $(A_2, B_2, C_2)$
quasi-isometries, respectively. These functions induce quasi-isometries between the colored metric spaces
$(A_2, B_2, C_2)$
quasi-isometries, respectively. These functions induce quasi-isometries between the colored metric spaces
![]() $X_{n, \alpha , s}$
and
$X_{n, \alpha , s}$
and
![]() $X_{n, \beta , s}$
. In particular, for the function h and each
$X_{n, \beta , s}$
. In particular, for the function h and each
![]() $X_{n,\alpha , s}$
and
$X_{n,\alpha , s}$
and
![]() $X_{n,\beta , s}$
we have:
$X_{n,\beta , s}$
we have:
where
![]() $i,j$
and
$i,j$
and
![]() $h(i), h(j)$
are elements of the spaces
$h(i), h(j)$
are elements of the spaces
![]() $X_{n,\alpha , s}$
and
$X_{n,\alpha , s}$
and
![]() $X_{n, \beta , s}$
, respectively. Hence, for
$X_{n, \beta , s}$
, respectively. Hence, for
![]() $\mathbf { a}=(a_n)_{n\geqslant 0}$
and
$\mathbf { a}=(a_n)_{n\geqslant 0}$
and
![]() $\mathbf {b}=(b_n)_{n\geqslant 0}$
we have
$\mathbf {b}=(b_n)_{n\geqslant 0}$
we have
Taking the limits and setting
![]() $H(\mathbf {a})=(h(a_n))_{n\geqslant 0}$
, we see that
$H(\mathbf {a})=(h(a_n))_{n\geqslant 0}$
, we see that
So, the desired
![]() $C_{H}$
is just
$C_{H}$
is just
![]() $A_1$
. The function G is constructed the same way. Note that both H and G preserve colors. One thing that needs to be observed is that H is onto. This follows from the condition put on the quasi-isometry h: for every
$A_1$
. The function G is constructed the same way. Note that both H and G preserve colors. One thing that needs to be observed is that H is onto. This follows from the condition put on the quasi-isometry h: for every
![]() $a^{\prime }\in \beta $
there exists an
$a^{\prime }\in \beta $
there exists an
![]() $a\in \alpha $
such that
$a\in \alpha $
such that
![]() $|a^{\prime }-h(a)|\leqslant C_1$
. Hence for any element
$|a^{\prime }-h(a)|\leqslant C_1$
. Hence for any element
![]() $\mathbf { a}^{\prime }=(a_n^{\prime })_{n\geqslant 0}$
in
$\mathbf { a}^{\prime }=(a_n^{\prime })_{n\geqslant 0}$
in
![]() $Cone(\beta , \mathcal F, s)$
there exists an element
$Cone(\beta , \mathcal F, s)$
there exists an element
![]() $\mathbf {a}=(a_n)_{n\geqslant 0}$
in
$\mathbf {a}=(a_n)_{n\geqslant 0}$
in
![]() $Cone(\alpha , \mathcal F, s)$
such that
$Cone(\alpha , \mathcal F, s)$
such that
![]() $D(H({a}), \mathbf {a}^{\prime })=0$
, that is,
$D(H({a}), \mathbf {a}^{\prime })=0$
, that is,
![]() $H(\mathbf {a})=\mathbf {a}^{\prime }$
. Finally, Small Cross Over Lemma 2.1 guarantees that if
$H(\mathbf {a})=\mathbf {a}^{\prime }$
. Finally, Small Cross Over Lemma 2.1 guarantees that if
![]() $\mathbf {a}\leqslant \mathbf {b}$
then it must be the case that
$\mathbf {a}\leqslant \mathbf {b}$
then it must be the case that
![]() $H(\mathbf {a})\leqslant H(\mathbf {b})$
.⊣
$H(\mathbf {a})\leqslant H(\mathbf {b})$
.⊣
The theorem naturally poses several questions. Do there exist nonquasi-isometric strings that have the same asymptotic cones? Do there exist quasi-isometric strings that can produce nonisometric asymptotic cones? Can asymptotic cones determine quasi-isometry types of strings from a specified class (of strings)? The rest of this section will answer all these questions.
Lemma 7.4. The set
![]() $\{ \mathbf {b} {{\kern-2pt}\in{\kern-2pt}} Cone(\alpha , \mathcal {F},s) \ | \ \sigma {{\kern-2pt}\in{\kern-2pt}} Cl(\mathbf {b}) \}$
is closed for every color
$\{ \mathbf {b} {{\kern-2pt}\in{\kern-2pt}} Cone(\alpha , \mathcal {F},s) \ | \ \sigma {{\kern-2pt}\in{\kern-2pt}} Cl(\mathbf {b}) \}$
is closed for every color
![]() $\sigma {{\kern-2pt}\in{\kern-2pt}} \Sigma $
.
$\sigma {{\kern-2pt}\in{\kern-2pt}} \Sigma $
.
Proof For
![]() $\sigma \in \Sigma $
, consider the set
$\sigma \in \Sigma $
, consider the set
![]() $\{ \mathbf {b} \in Cone(\alpha , \mathcal {F},s) \ | \ \sigma \in Cl(\mathbf {b}) \}$
. Let
$\{ \mathbf {b} \in Cone(\alpha , \mathcal {F},s) \ | \ \sigma \in Cl(\mathbf {b}) \}$
. Let
![]() $\mathbf {a} = (a_{n})_{n \geqslant 0}$
be a limit point of this set, and let
$\mathbf {a} = (a_{n})_{n \geqslant 0}$
be a limit point of this set, and let
![]() $\mathbf {a_m}= (a_{m,n})_{n \geqslant 0}$
be a point in
$\mathbf {a_m}= (a_{m,n})_{n \geqslant 0}$
be a point in
![]() $Cone(\alpha , \mathcal {F},s)$
of color
$Cone(\alpha , \mathcal {F},s)$
of color
![]() $\sigma $
such that
$\sigma $
such that
![]() $D(\mathbf {a},\mathbf {a_m}) \leqslant 2^{-m}$
. Without loss of generality we can assume that every point in
$D(\mathbf {a},\mathbf {a_m}) \leqslant 2^{-m}$
. Without loss of generality we can assume that every point in
![]() $\mathbf {a_m}$
has the color
$\mathbf {a_m}$
has the color
![]() $\sigma $
; if not, the smallest position of
$\sigma $
; if not, the smallest position of
![]() $X_{n,\alpha ,s}$
with the color
$X_{n,\alpha ,s}$
with the color
![]() $\sigma $
can be substituted for each differently colored
$\sigma $
can be substituted for each differently colored
![]() $a_{m,n}$
.
$a_{m,n}$
.
For each
![]() $n \in \omega $
, let
$n \in \omega $
, let
![]() $i_n$
be a number that satisfies
$i_n$
be a number that satisfies
Now let us set
![]() $\mathbf {b} = (b_n)_{n\geqslant 0}$
, where
$\mathbf {b} = (b_n)_{n\geqslant 0}$
, where
![]() $b_n = a_{i_n,n}$
. Each
$b_n = a_{i_n,n}$
. Each
![]() $b_n$
has the color
$b_n$
has the color
![]() $\sigma $
. We also have
$\sigma $
. We also have
![]() $\mathbf {a} \sim \mathbf {b}$
. Indeed, for each m we have
$\mathbf {a} \sim \mathbf {b}$
. Indeed, for each m we have
Here, the inclusion part is straightforward from the definition of
![]() $\mathbf {b}$
; and the membership part is true because
$\mathbf {b}$
; and the membership part is true because
![]() $D(\mathbf { a},\mathbf {a_m}) \leqslant 2^{-m}$
holds, and thus for any
$D(\mathbf { a},\mathbf {a_m}) \leqslant 2^{-m}$
holds, and thus for any
![]() $\varepsilon>0$
we have
$\varepsilon>0$
we have
Now because
![]() $\mathcal F$
is upward closed, we have
$\mathcal F$
is upward closed, we have
![]() $\{n \mid d_n(a_n, b_n) \leqslant 2^{-m}\} \in \mathcal F$
, which proves
$\{n \mid d_n(a_n, b_n) \leqslant 2^{-m}\} \in \mathcal F$
, which proves
![]() $\mathbf { a} \sim \mathbf {b}$
. Thus
$\mathbf { a} \sim \mathbf {b}$
. Thus
![]() $\sigma \in Cl(\mathbf {a})$
.⊣
$\sigma \in Cl(\mathbf {a})$
.⊣
7.2 Asymptotic cones and quasi-isometry types
The next theorem states that all asymptotic cones of quasi-isometric eventually periodic strings are isometric. In particular, these asymptotic cones fully characterize quasi-isometry types of eventually periodic strings.
Theorem 7.5. For an eventually periodic string
![]() $\alpha =uv^{\omega }$
, all asymptotic cones
$\alpha =uv^{\omega }$
, all asymptotic cones
![]() $Cone(\alpha , \mathcal F, s)$
equal the colored metric space
$Cone(\alpha , \mathcal F, s)$
equal the colored metric space
![]() $(\mathbb R_{\geqslant 0}; d, Cl)$
such that every real
$(\mathbb R_{\geqslant 0}; d, Cl)$
such that every real
![]() $r>0$
has colors of v and the real
$r>0$
has colors of v and the real
![]() $0$
has colors of both u and v.
$0$
has colors of both u and v.
Proof Let
![]() $\mathcal F$
be any ultrafilter and
$\mathcal F$
be any ultrafilter and
![]() $s:\omega \rightarrow \omega $
be a scaling factor. It is easy to see that
$s:\omega \rightarrow \omega $
be a scaling factor. It is easy to see that
![]() $0$
has all colors of both u and v. Let r be a positive real number. We want to show that r has all colors present in v. So, let
$0$
has all colors of both u and v. Let r be a positive real number. We want to show that r has all colors present in v. So, let
![]() $\sigma $
be a color present in v. There is a sequence
$\sigma $
be a color present in v. There is a sequence
![]() $(a_n)_{n\geqslant 0}$
such that
$(a_n)_{n\geqslant 0}$
such that
![]() $a_n$
is an element of
$a_n$
is an element of
![]() $X_{n, \alpha }$
with the color
$X_{n, \alpha }$
with the color
![]() $\sigma $
, and for every
$\sigma $
, and for every
![]() $\varepsilon>0$
there is an
$\varepsilon>0$
there is an
![]() $N_{\varepsilon }$
such that for all
$N_{\varepsilon }$
such that for all
![]() $n>N_{\varepsilon }$
we have
$n>N_{\varepsilon }$
we have
![]() $|d_n(a_n,0)-r|\leqslant \varepsilon $
. Indeed, for each
$|d_n(a_n,0)-r|\leqslant \varepsilon $
. Indeed, for each
![]() $n \in \omega $
such that
$n \in \omega $
such that
![]() $|u|/s(n) < r$
let
$|u|/s(n) < r$
let
![]() $a_n$
be any element which has the color
$a_n$
be any element which has the color
![]() $\sigma $
and satisfies
$\sigma $
and satisfies
![]() $(|u|+i|v|)/s(n)\leqslant d_n(0,a_n) < (|u|+(i+1)|v|)/s(n)$
, where i is the unique integer which satisfies
$(|u|+i|v|)/s(n)\leqslant d_n(0,a_n) < (|u|+(i+1)|v|)/s(n)$
, where i is the unique integer which satisfies
![]() $(|u|+i|v|)/s(n)\leqslant r < (|u|+(i+1)|v|)/s(n)$
. So, we have
$(|u|+i|v|)/s(n)\leqslant r < (|u|+(i+1)|v|)/s(n)$
. So, we have
![]() $|d_n(a_n,0)-r| \leqslant |v|/s(n)$
. This inequality implies the claim since every ultrafiler contains all co-finite sets.⊣
$|d_n(a_n,0)-r| \leqslant |v|/s(n)$
. This inequality implies the claim since every ultrafiler contains all co-finite sets.⊣
We now prove a theorem akin to a known result in geometric group theory stating that there are nonquasi-isometric groups that realize the same cones. For instance, in [Reference Dioubina and Polterovich1, Reference Dioubina and Polterovich2] it is proved that all asymptotic cones of nonelementary hyperbolic group are isometric.
Theorem 7.6. There are nonquasi-isometric strings
![]() $\alpha , \beta \in \{0,1\}^{\omega }$
, a scale factor
$\alpha , \beta \in \{0,1\}^{\omega }$
, a scale factor
![]() $s(n)$
, and an ultrafilter
$s(n)$
, and an ultrafilter
![]() $\mathcal F$
such that
$\mathcal F$
such that
![]() $Cone (\alpha , \mathcal F, s)=Cone(\beta , \mathcal F, s)$
. Moreover,
$Cone (\alpha , \mathcal F, s)=Cone(\beta , \mathcal F, s)$
. Moreover,
![]() $\alpha, {\beta \in \mathcal F(1)}$
.
$\alpha, {\beta \in \mathcal F(1)}$
.
Proof We consider the exponential function as the scaling factor:
![]() $s(n)=2^n$
. We need to construct strings
$s(n)=2^n$
. We need to construct strings
![]() $\alpha $
,
$\alpha $
,
![]() $\beta $
and an ultrafilter
$\beta $
and an ultrafilter
![]() $\mathcal F$
that satisfy the theorem. Let the string
$\mathcal F$
that satisfy the theorem. Let the string
![]() $\alpha $
be the characteristic function of the set of powers of
$\alpha $
be the characteristic function of the set of powers of
![]() $2$
, that is,
$2$
, that is,
![]() $\alpha (i)=1$
if and only if
$\alpha (i)=1$
if and only if
![]() $i=2^k$
for some
$i=2^k$
for some
![]() $k\geqslant 0$
.
$k\geqslant 0$
.
Let
![]() $\mathcal F$
be any ultrafilter. Consider the asymptotic cone
$\mathcal F$
be any ultrafilter. Consider the asymptotic cone
![]() $Cone(\alpha , \mathcal F, s)$
. Note that every co-finite set belongs to
$Cone(\alpha , \mathcal F, s)$
. Note that every co-finite set belongs to
![]() $\mathcal F$
. This implies that the asymptotic cone coincides with the colored metric space
$\mathcal F$
. This implies that the asymptotic cone coincides with the colored metric space
![]() $(\mathbb R_{\geqslant 0}; d, Cl)$
, where d is the usual metric on reals, all reals have color
$(\mathbb R_{\geqslant 0}; d, Cl)$
, where d is the usual metric on reals, all reals have color
![]() $0$
, and real r has also color
$0$
, and real r has also color
![]() $1$
if and only if r is an integer power of
$1$
if and only if r is an integer power of
![]() $2$
or
$2$
or
![]() $r=0$
.
$r=0$
.
We need to construct a string
![]() $\beta \in \{0,1\}^{\omega }$
and an ultrafilter
$\beta \in \{0,1\}^{\omega }$
and an ultrafilter
![]() $\mathcal F$
such that
$\mathcal F$
such that
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are not quasi-isometric but the asymptotic cone
$\beta $
are not quasi-isometric but the asymptotic cone
![]() $Cone(\beta , \mathcal F, s)$
coincides with the above colored metric space
$Cone(\beta , \mathcal F, s)$
coincides with the above colored metric space
![]() $(\mathbb R_{\geqslant 0}; d, Cl)$
.
$(\mathbb R_{\geqslant 0}; d, Cl)$
.
Let
![]() $n_0, n_1, n_2, \ldots $
be an increasing sequence of positive integers. Assume that these integers satisfy the following order:
$n_0, n_1, n_2, \ldots $
be an increasing sequence of positive integers. Assume that these integers satisfy the following order:
Let B be the set consisting of all the members of this sequence, that is,
We define
![]() $\beta \in \{0,1\}^{\omega }$
as follows. The string
$\beta \in \{0,1\}^{\omega }$
as follows. The string
![]() $\beta $
has one at position i if and only if for some member
$\beta $
has one at position i if and only if for some member
![]() $s\in B$
we have
$s\in B$
we have
![]() $i=2^s$
.
$i=2^s$
.
Let
![]() $\mathcal F$
be an ultrafilter that contains the set B. Consider the asymptotic cone
$\mathcal F$
be an ultrafilter that contains the set B. Consider the asymptotic cone
![]() $Cone(\beta , \mathcal F, s)$
. We can view the domain of this cone as the set
$Cone(\beta , \mathcal F, s)$
. We can view the domain of this cone as the set
![]() $\mathbb R_{\geqslant 0}$
. Since
$\mathbb R_{\geqslant 0}$
. Since
![]() $s(n)=2^n$
is the exponential scaling factor, in the cone
$s(n)=2^n$
is the exponential scaling factor, in the cone
![]() $Cone(\beta , \mathcal F, s)$
every dyadic number of the form
$Cone(\beta , \mathcal F, s)$
every dyadic number of the form
![]() $q/2^i$
gets color
$q/2^i$
gets color
![]() $0$
. Since dyadic numbers are dense in
$0$
. Since dyadic numbers are dense in
![]() $R_{\geqslant 0}$
, by Lemma 7.4, every real r gets color
$R_{\geqslant 0}$
, by Lemma 7.4, every real r gets color
![]() $0$
in the cone
$0$
in the cone
![]() $Cone(\beta , \mathcal F, s)$
. Now we need to show that r gets color
$Cone(\beta , \mathcal F, s)$
. Now we need to show that r gets color
![]() $1$
if and only if r is an integer power of
$1$
if and only if r is an integer power of
![]() $2$
. In what follows we prove the “if” part. The “only if” part is clear from the construction of
$2$
. In what follows we prove the “if” part. The “only if” part is clear from the construction of
![]() $\beta $
; notice that
$\beta $
; notice that
![]() $\beta $
is obtained by replacing some
$\beta $
is obtained by replacing some
![]() $1$
’s in
$1$
’s in
![]() $\alpha $
with
$\alpha $
with
![]() $0$
’s.
$0$
’s.
So assume that
![]() $r=2^i$
for some integer i. Consider the colored metric spaces
$r=2^i$
for some integer i. Consider the colored metric spaces
![]() $X_{n_j+k, \beta , s}$
where
$X_{n_j+k, \beta , s}$
where
![]() $i\leqslant j$
and
$i\leqslant j$
and
![]() $0\leqslant k \leqslant j$
. Due to the definition of
$0\leqslant k \leqslant j$
. Due to the definition of
![]() $\beta $
, the color of the point in
$\beta $
, the color of the point in
![]() $X_{n_j+k, \beta , s}$
at distance
$X_{n_j+k, \beta , s}$
at distance
![]() $2^i$
from
$2^i$
from
![]() $0$
with respect to
$0$
with respect to
![]() $d_{n_j+k}$
is
$d_{n_j+k}$
is
![]() $1$
. The set
$1$
. The set
is obtained by eliminating finite number of elements in B, and hence it belongs to the ultrafilter. Hence, the real
![]() $2^i$
has color
$2^i$
has color
![]() $1$
in the asymptotic cone
$1$
in the asymptotic cone
![]() $Cone(\beta , \mathcal F, s)$
.
$Cone(\beta , \mathcal F, s)$
.
To finish the proof, we just need to show that we can select the set B so that
![]() $\alpha \not \leqslant _{QI} \beta $
. This can be done, for instance, by letting
$\alpha \not \leqslant _{QI} \beta $
. This can be done, for instance, by letting
![]() $n_{k+1} = 2^{n_k}$
. Then one can show that
$n_{k+1} = 2^{n_k}$
. Then one can show that
![]() $\alpha \not \leqslant _{QI} \beta $
by comparing frequency of occurrences of
$\alpha \not \leqslant _{QI} \beta $
by comparing frequency of occurrences of
![]() $1$
’s in
$1$
’s in
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
(cf. the proof of Theorem 3.1). As a side note observe that
$\beta $
(cf. the proof of Theorem 3.1). As a side note observe that
![]() $\beta \leqslant _{QI} \alpha $
.⊣
$\beta \leqslant _{QI} \alpha $
.⊣
In contrast to the theorem above, we show that the same colored metric space can produce two asymptotic cones that are not (even) quasi-isometric. This is similar to the result in geometric group theory where one group can realize two non homeomorphic asymptotic cones [Reference Velickovic and Simon14].
Theorem 7.7. There exists a string
![]() $\alpha $
and scaling factors
$\alpha $
and scaling factors
![]() $s_0$
,
$s_0$
,
![]() $s_1$
such that for any ultrafilter
$s_1$
such that for any ultrafilter
![]() $\mathcal {F}$
the asymptotic cones
$\mathcal {F}$
the asymptotic cones
![]() $Cone(\alpha , \mathcal F, s_0)$
and
$Cone(\alpha , \mathcal F, s_0)$
and
![]() $Cone(\alpha , \mathcal F, s_1)$
are not quasi-isometric.
$Cone(\alpha , \mathcal F, s_1)$
are not quasi-isometric.
Proof We construct
![]() $\alpha $
and two scaling factors
$\alpha $
and two scaling factors
![]() $s_0$
and
$s_0$
and
![]() $s_1$
such that in the asymptotic cone
$s_1$
such that in the asymptotic cone
![]() $Cone(\alpha , \mathcal F, s_0)$
all reals
$Cone(\alpha , \mathcal F, s_0)$
all reals
![]() $r>1$
have color
$r>1$
have color
![]() $0$
, and in the asymptotic cone
$0$
, and in the asymptotic cone
![]() $Cone(\alpha , \mathcal F, s_1)$
all reals
$Cone(\alpha , \mathcal F, s_1)$
all reals
![]() $r>1$
have color
$r>1$
have color
![]() $1$
only. These two metric spaces are clearly not quasi-isometric. The idea is to design
$1$
only. These two metric spaces are clearly not quasi-isometric. The idea is to design
![]() $s_0$
and
$s_0$
and
![]() $s_1$
so that the filter
$s_1$
so that the filter
![]() $\mathcal F$
sees more and more
$\mathcal F$
sees more and more
![]() $0$
colors as
$0$
colors as
![]() $s_0$
scales
$s_0$
scales
![]() $\alpha $
down, and more and more
$\alpha $
down, and more and more
![]() $1$
colors as
$1$
colors as
![]() $s_1$
scales
$s_1$
scales
![]() $\alpha $
down.
$\alpha $
down.
Define the natural numbers
![]() $p_n$
and
$p_n$
and
![]() $q_n$
inductively;
$q_n$
inductively;
![]() $p_n$
will indicate the lengths of
$p_n$
will indicate the lengths of
![]() $1$
-blocks in
$1$
-blocks in
![]() $\alpha $
and
$\alpha $
and
![]() $q_n$
will indicate the lengths of
$q_n$
will indicate the lengths of
![]() $0$
-blocks in
$0$
-blocks in
![]() $\alpha $
. We start by setting
$\alpha $
. We start by setting
![]() $p_1=q_1=1$
.
$p_1=q_1=1$
.
 $$ \begin{align*} p_{n+1} = n \sum_{i=1}^n (p_i + q_i) \ \text{ and } \ q_{n+1} = n \biggl( \sum_{i=1}^n (p_i + q_i) + p_{n+1} \biggr). \end{align*} $$
$$ \begin{align*} p_{n+1} = n \sum_{i=1}^n (p_i + q_i) \ \text{ and } \ q_{n+1} = n \biggl( \sum_{i=1}^n (p_i + q_i) + p_{n+1} \biggr). \end{align*} $$
Now consider the string
![]() $\alpha = 0^{p_1} 1^{q_1} 0^{p_2} 1^{q_2} \ldots $
, and define the following two scale functions:
$\alpha = 0^{p_1} 1^{q_1} 0^{p_2} 1^{q_2} \ldots $
, and define the following two scale functions:
-
•
 $s_0(n) = \sum _{i=1}^n (p_i + q_i)$
, and
$s_0(n) = \sum _{i=1}^n (p_i + q_i)$
, and -
•
 $s_1(n) = \bigl ( \sum _{i=1}^n (p_i + q_i) + p_{n+1} \bigr )$
.
$s_1(n) = \bigl ( \sum _{i=1}^n (p_i + q_i) + p_{n+1} \bigr )$
.
Consider the sequence
![]() $\{X_{n, \alpha , s_j}\}_{n\in \omega }$
of metric spaces. Recall that the metric
$\{X_{n, \alpha , s_j}\}_{n\in \omega }$
of metric spaces. Recall that the metric
![]() $d_{j,n}$
in the space
$d_{j,n}$
in the space
![]() $X_{n, \alpha , s_j}$
is defined as
$X_{n, \alpha , s_j}$
is defined as
![]() $d_{j,n}(x,y)= |y-x|/s_j(n) \ (j=0,1)$
. Then all points a in the metric space
$d_{j,n}(x,y)= |y-x|/s_j(n) \ (j=0,1)$
. Then all points a in the metric space
![]() $X_{n, \alpha , s_j}$
such that
$X_{n, \alpha , s_j}$
such that
![]() $1 < d_{j,n}(0,a) < n $
have the color j. Hence for all
$1 < d_{j,n}(0,a) < n $
have the color j. Hence for all
![]() $r>1$
and all ultrafilters
$r>1$
and all ultrafilters
![]() $\mathcal F$
the color of r is
$\mathcal F$
the color of r is
![]() $0$
in
$0$
in
![]() $Cone(\alpha , \mathcal F, s_0)$
and
$Cone(\alpha , \mathcal F, s_0)$
and
![]() $1$
in
$1$
in
![]() $Cone(\alpha , \mathcal F, s_1)$
.⊣
$Cone(\alpha , \mathcal F, s_1)$
.⊣
7.3 Asymptotic cones of algorithmically random strings
In the last two decades the theory of algorithmic randomness has attracted the attention of many experts in computability, logic, complexity, and reverse mathematics. Many variants of algorithmic randomness and related notions for strings have been introduced and investigated. These include Martin-Löf tests, Schnorr tests, prefix-free complexity,
![]() $1$
-generic sets, K-triviality, martingales, connections to differentiability, Solovay and related reducibilities. The monographs by Downey and Hirschfeldt [Reference Downey and Hirschfeldt3] and by Nies [Reference Nies11] expose recent advances in the area.
$1$
-generic sets, K-triviality, martingales, connections to differentiability, Solovay and related reducibilities. The monographs by Downey and Hirschfeldt [Reference Downey and Hirschfeldt3] and by Nies [Reference Nies11] expose recent advances in the area.
Martin-Löf tests, that we write ML-tests for short, play a central role in the theory of algorithmic randomness for infinite strings. For completeness, here we define Martin-Löf randomness in the case of infinite binary strings. We view the set
![]() $\{0,1\}^{\omega }$
as an infinite binary tree. This is a Cantor space with the canonical topology generated by the cones
$\{0,1\}^{\omega }$
as an infinite binary tree. This is a Cantor space with the canonical topology generated by the cones
![]() $C( w)$
consisting of all infinite binary strings extending the finite string w. We can equip this space with Lebesgue measure induced by the following function
$C( w)$
consisting of all infinite binary strings extending the finite string w. We can equip this space with Lebesgue measure induced by the following function
![]() $\lambda (C(w))=2^{-|w|}$
.
$\lambda (C(w))=2^{-|w|}$
.
Let
![]() $V\subseteq \omega \times \{0,1\}^\star $
be a computably enumerable set. Given such V, consider its nth slice
$V\subseteq \omega \times \{0,1\}^\star $
be a computably enumerable set. Given such V, consider its nth slice
![]() $V_n=\{v\in \{0,1\}^{\star } \mid (n,v)\in V\}$
, where
$V_n=\{v\in \{0,1\}^{\star } \mid (n,v)\in V\}$
, where
![]() $n \in \omega $
. Each
$n \in \omega $
. Each
![]() $V_n$
describes the open set
$V_n$
describes the open set
![]() $\mathcal O_V(n)=\bigcup _{v\in V_n} C(v)$
.
$\mathcal O_V(n)=\bigcup _{v\in V_n} C(v)$
.
Definition 7.8. The set V is a Martin-Löf test, or ML-test for short, if the measure of the open set
![]() $\mathcal O_V(n)$
is bounded by
$\mathcal O_V(n)$
is bounded by
![]() $2^{-n}$
for all n.
$2^{-n}$
for all n.
For the ML-test
![]() $V,$
the intersection
$V,$
the intersection
![]() $ \bigcap _{n} \mathcal O_V(n)$
is a set of measure zero. We call this intersection set the effective null-set generated by V.
$ \bigcap _{n} \mathcal O_V(n)$
is a set of measure zero. We call this intersection set the effective null-set generated by V.
Definition 7.9. Let V be an ML-test. An infinite binary sequence
![]() $\alpha \in \{0,1\}^{\omega }$
passes the
$\alpha \in \{0,1\}^{\omega }$
passes the
![]() $ML$
-test V if
$ML$
-test V if
![]() $\alpha $
does not belong to the effective null-set generated by V, that is
$\alpha $
does not belong to the effective null-set generated by V, that is
![]() $\alpha \not \in \bigcap _{n} \mathcal O_V(n)$
. The string
$\alpha \not \in \bigcap _{n} \mathcal O_V(n)$
. The string
![]() $\alpha $
is Martin-Löf random, or ML-random for short, if it passes all Martin-Löf tests.
$\alpha $
is Martin-Löf random, or ML-random for short, if it passes all Martin-Löf tests.
There are only countably many
![]() $ML$
-tests, hence the union of all null-sets given by tests is a set of measure zero. Therefore, the set of all
$ML$
-tests, hence the union of all null-sets given by tests is a set of measure zero. Therefore, the set of all
![]() $ML$
-random sequences has Lebesgue measure one.
$ML$
-random sequences has Lebesgue measure one.
For our theorem below, we need one more concept. Let
![]() $V\subseteq \omega \times \{0,1\}^{\star }$
be a computably enumerable set. We call V Solovay test if the sum of all measures of the open sets
$V\subseteq \omega \times \{0,1\}^{\star }$
be a computably enumerable set. We call V Solovay test if the sum of all measures of the open sets
![]() $\mathcal O_V(n)$
is bounded. String
$\mathcal O_V(n)$
is bounded. String
![]() $\alpha $
passes the Solovay test V, if
$\alpha $
passes the Solovay test V, if
![]() $\alpha \not \in \mathcal O_V(n)$
except for finitely many n’s. It turns out passing all Solovay tests is equivalent to passing all ML-tests. In other words, a string
$\alpha \not \in \mathcal O_V(n)$
except for finitely many n’s. It turns out passing all Solovay tests is equivalent to passing all ML-tests. In other words, a string
![]() $\alpha $
is ML-random if and only if
$\alpha $
is ML-random if and only if
![]() $\alpha $
is Solovay random (cf. Proposition 3.2.19 in [Reference Nies11]). We will use this fact in our next theorem. The theorem shows that all asymptotic cones of ML-random strings are isometric to each other, and thus they are independent on ultrafilters and scaling factors as long as the scaling functions are computable.
$\alpha $
is Solovay random (cf. Proposition 3.2.19 in [Reference Nies11]). We will use this fact in our next theorem. The theorem shows that all asymptotic cones of ML-random strings are isometric to each other, and thus they are independent on ultrafilters and scaling factors as long as the scaling functions are computable.
Theorem 7.10. If
![]() $\alpha $
is Martin-Löf random, then for all computable scaling factors s and ultrafilters
$\alpha $
is Martin-Löf random, then for all computable scaling factors s and ultrafilters
![]() $\mathcal F$
, the asymptotic cone
$\mathcal F$
, the asymptotic cone
![]() $Cone(\alpha , \mathcal F, s)$
coincides with the space
$Cone(\alpha , \mathcal F, s)$
coincides with the space
![]() $(\mathcal R_{\geqslant 0}; d, C)$
, where all reals have all colors from alphabet
$(\mathcal R_{\geqslant 0}; d, C)$
, where all reals have all colors from alphabet
![]() $\Sigma $
.
$\Sigma $
.
Proof Suppose
![]() $Cone(\alpha , \mathcal {F}, s)$
does not have some color, say
$Cone(\alpha , \mathcal {F}, s)$
does not have some color, say
![]() $0$
, at r. Below we prove that
$0$
, at r. Below we prove that
![]() $\alpha $
is not Solovay random. First, we show that there exists
$\alpha $
is not Solovay random. First, we show that there exists
![]() $\varepsilon>0$
for which the following formula is valid:
$\varepsilon>0$
for which the following formula is valid:
Here,
![]() $\exists ^\infty n \in \omega [\varphi (n)]$
means that
$\exists ^\infty n \in \omega [\varphi (n)]$
means that
![]() $\varphi (n)$
is true for infinitely many n’s. For its proof, assume the contrary and suppose for every
$\varphi (n)$
is true for infinitely many n’s. For its proof, assume the contrary and suppose for every
![]() $\varepsilon>0$
we have
$\varepsilon>0$
we have
Here,
![]() $\forall ^\infty n \in \omega [\varphi (n)]$
means that
$\forall ^\infty n \in \omega [\varphi (n)]$
means that
![]() $\varphi (n)$
is true except for finitely many n’s. Then we can construct an element
$\varphi (n)$
is true except for finitely many n’s. Then we can construct an element
![]() $(a_n)$
of
$(a_n)$
of
![]() $Cone(\alpha , \mathcal {F}, s)$
such that
$Cone(\alpha , \mathcal {F}, s)$
such that
![]() $\frac {a_n}{s(n)} \xrightarrow {n \to \infty } r$
and
$\frac {a_n}{s(n)} \xrightarrow {n \to \infty } r$
and
![]() $\alpha (a_n) = 0$
for each sufficiently large n. Hence
$\alpha (a_n) = 0$
for each sufficiently large n. Hence
![]() $Cone(\alpha , \mathcal {F}, s)$
has the color
$Cone(\alpha , \mathcal {F}, s)$
has the color
![]() $0$
at r (recall that any ultrafilter
$0$
at r (recall that any ultrafilter
![]() $\mathcal {F}$
contains every co-finite set), which is a contradiction.
$\mathcal {F}$
contains every co-finite set), which is a contradiction.
Now let
![]() $\varepsilon $
be a positive real for which the formula above is valid, and consider the set
$\varepsilon $
be a positive real for which the formula above is valid, and consider the set
Without loss of generality we assume that r and
![]() $\varepsilon $
are rational numbers. The set
$\varepsilon $
are rational numbers. The set
![]() $G_n$
can be described by the set
$G_n$
can be described by the set
![]() $V_n \subseteq \{0,1\}^\star $
that consists of all finite strings in
$V_n \subseteq \{0,1\}^\star $
that consists of all finite strings in
![]() $\Sigma $
of length
$\Sigma $
of length
![]() $s(n)(r+\varepsilon )$
whose terminal segments of length
$s(n)(r+\varepsilon )$
whose terminal segments of length
![]() $2s(n)\varepsilon $
do not contain
$2s(n)\varepsilon $
do not contain
![]() $0$
. Let V be a test of which nth slice is
$0$
. Let V be a test of which nth slice is
![]() $V_n$
. Then V is computably enumerable, and the sum of the measures of
$V_n$
. Then V is computably enumerable, and the sum of the measures of
![]() $G_n$
is bounded, as the size of the interval
$G_n$
is bounded, as the size of the interval
![]() $[{s(n)(r-\varepsilon)},{s(n)(r+\varepsilon )]}$
increases at least linearly with respect to n because s is a strictly increasing function that takes values in natural numbers. So, we produced a Solovay test V that the string
$[{s(n)(r-\varepsilon)},{s(n)(r+\varepsilon )]}$
increases at least linearly with respect to n because s is a strictly increasing function that takes values in natural numbers. So, we produced a Solovay test V that the string
![]() $\alpha $
fails, that is,
$\alpha $
fails, that is,
![]() $\alpha \in G_n$
for infinitely many n. Hence
$\alpha \in G_n$
for infinitely many n. Hence
![]() $\alpha $
is not Solovay random.⊣
$\alpha $
is not Solovay random.⊣
8 Open questions
There are several natural open questions and directions of research related to understanding quasi-isometries between infinite strings. One would, for instance, like to understand algebraic properties of the partial order
![]() $\Sigma _{QI}^{\omega }$
. For example, one might ask if this partial order is a semi-lattice. Another example is related to automorphisms of this partial order. In the case when
$\Sigma _{QI}^{\omega }$
. For example, one might ask if this partial order is a semi-lattice. Another example is related to automorphisms of this partial order. In the case when
![]() $\Sigma =\{0,1\}$
, the structure
$\Sigma =\{0,1\}$
, the structure
![]() $\Sigma _{QI}^{\omega }$
has an obvious automorphism that given
$\Sigma _{QI}^{\omega }$
has an obvious automorphism that given
![]() $\alpha \in \Sigma ^{\omega }$
produces
$\alpha \in \Sigma ^{\omega }$
produces
![]() $\beta $
that is obtained by replacing
$\beta $
that is obtained by replacing
![]() $0$
with
$0$
with
![]() $1$
and
$1$
and
![]() $1$
with
$1$
with
![]() $0$
in
$0$
in
![]() $\alpha $
. Does the partial order posses any other nontrivial automorphism?
$\alpha $
. Does the partial order posses any other nontrivial automorphism?
One can also study model-theoretic properties of the partial order
![]() $\Sigma _{QI}^{\omega }$
. For instance, one might want to describe relations of this structure definable in the first-order logic. One possible step towards this would be to investigate if the first-order theory of
$\Sigma _{QI}^{\omega }$
. For instance, one might want to describe relations of this structure definable in the first-order logic. One possible step towards this would be to investigate if the first-order theory of
![]() $\Sigma _{QI}^{\omega }$
decidable.
$\Sigma _{QI}^{\omega }$
decidable.
From perspective of computability theory, it is also interesting to investigate the properties of
![]() $\leqslant _{QI}$
either by restraining the class of infinite strings (e.g., by considering computable strings only) or by refining the relation
$\leqslant _{QI}$
either by restraining the class of infinite strings (e.g., by considering computable strings only) or by refining the relation
![]() $\leqslant _{QI}$
to computable quasi-isometries only. This direction is pursued by [Reference Lou10], where both of strings and quasi-isometries between strings are restricted to computable ones.
$\leqslant _{QI}$
to computable quasi-isometries only. This direction is pursued by [Reference Lou10], where both of strings and quasi-isometries between strings are restricted to computable ones.
Acknowledgments
The authors thank Kazushige Terui for discussions. The first author thanks JSPS and RIMS of Kyoto University for support. The second author is supported by ERATO HASUO Metamathematics for Systems Design Project (No. JPMJER1603), JST.
This paper is an extended and corrected version of [Reference Khoussainov and Takisaka9] presented at proceeding of Thirty-Second Annual ACM/IEEE Symposium on Logic in Computer Science (LICS 2017).