Published online by Cambridge University Press: 20 July 2020
In a recent paper by M. Rathjen and the present author it has been shown that the statement “every normal function has a derivative” is equivalent to 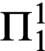 $\Pi ^1_1$
-bar induction. The equivalence was proved over
$\Pi ^1_1$
-bar induction. The equivalence was proved over  $\mathbf {ACA_0}$
, for a suitable representation of normal functions in terms of dilators. In the present paper, we show that the statement “every normal function has at least one fixed point” is equivalent to
$\mathbf {ACA_0}$
, for a suitable representation of normal functions in terms of dilators. In the present paper, we show that the statement “every normal function has at least one fixed point” is equivalent to  $\Pi ^1_1$
-induction along the natural numbers.
$\Pi ^1_1$
-induction along the natural numbers.
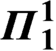 ${\boldsymbol{\varPi}}_{\mathbf{1}}^{\mathbf{1}}$
-Comprehension, PhD thesis, University of Leeds, 2018. Available at http://etheses.whiterose.ac.uk/20929/ (accessed 10 May, 2019).Google Scholar
${\boldsymbol{\varPi}}_{\mathbf{1}}^{\mathbf{1}}$
-Comprehension, PhD thesis, University of Leeds, 2018. Available at http://etheses.whiterose.ac.uk/20929/ (accessed 10 May, 2019).Google Scholar ${\varPi}_{1}^{1}$
-comprehension as a well-ordering principle
. Advances in Mathematics, vol. 355 (2019), Article no. 106767.CrossRefGoogle Scholar
${\varPi}_{1}^{1}$
-comprehension as a well-ordering principle
. Advances in Mathematics, vol. 355 (2019), Article no. 106767.CrossRefGoogle Scholar ${\varPi}_2^1$
-logic, part 1: Dilators
. Annals of Pure and Applied Logic, vol. 21 (1981), pp. 75–219.Google Scholar
${\varPi}_2^1$
-logic, part 1: Dilators
. Annals of Pure and Applied Logic, vol. 21 (1981), pp. 75–219.Google Scholar