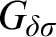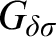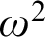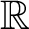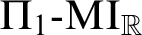1 Introduction
The purpose of this article is to compute the reverse-mathematical strength of the assertion that all
![]() $\boldsymbol \Sigma ^0_3$
Gale-Stewart games on
$\boldsymbol \Sigma ^0_3$
Gale-Stewart games on
![]() $\mathbb {N}$
of length
$\mathbb {N}$
of length
![]() $\omega ^2$
are determined (Theorem 1.1).
$\omega ^2$
are determined (Theorem 1.1).
That
![]() $\boldsymbol \Sigma ^0_{3}$
games on
$\boldsymbol \Sigma ^0_{3}$
games on
![]() $\mathbb {N}$
of length
$\mathbb {N}$
of length
![]() $\omega $
are determined is a theorem of Davis [Reference Davis7] from 1964. This was also the last natural pointclass within the arithmetical hierarchy of such sets the determinacy of which could be proved in analysis, that is, second order number theory, for Martin (improving a result of Friedman [Reference Friedman8]) showed that the determinacy of
$\omega $
are determined is a theorem of Davis [Reference Davis7] from 1964. This was also the last natural pointclass within the arithmetical hierarchy of such sets the determinacy of which could be proved in analysis, that is, second order number theory, for Martin (improving a result of Friedman [Reference Friedman8]) showed that the determinacy of
![]() $\omega $
-length games with payoff sets in the class
$\omega $
-length games with payoff sets in the class
![]() $\boldsymbol \Sigma ^{0}_{4}$
could not be proven in analysis. Games of length
$\boldsymbol \Sigma ^{0}_{4}$
could not be proven in analysis. Games of length
![]() $\omega $
played with real moves are a different matter, where we identify a real with an element of Baire space
$\omega $
played with real moves are a different matter, where we identify a real with an element of Baire space
![]() $\mathbb {N}^{\mathbb {N}}$
. Essentially then these games are equivalent to a particular kind of games of
$\mathbb {N}^{\mathbb {N}}$
. Essentially then these games are equivalent to a particular kind of games of
![]() $\omega ^2$
-many moves on
$\omega ^2$
-many moves on
![]() $\mathbb {N}$
. By the proof of Martin’s Borel determinacy theorem [Reference Martin14],
$\mathbb {N}$
. By the proof of Martin’s Borel determinacy theorem [Reference Martin14],
![]() $\boldsymbol \Sigma ^0_3$
-determinacy for games on
$\boldsymbol \Sigma ^0_3$
-determinacy for games on
![]() $\mathbb {R}$
is provable in third-order arithmetic, and similarly by adapting the arguments for games on
$\mathbb {R}$
is provable in third-order arithmetic, and similarly by adapting the arguments for games on
![]() $\mathbb {N}$
one can show that
$\mathbb {N}$
one can show that
![]() $\boldsymbol \Sigma ^0_4$
-determinacy for games on
$\boldsymbol \Sigma ^0_4$
-determinacy for games on
![]() $\mathbb {R}$
is not. Determinacy for all games of length
$\mathbb {R}$
is not. Determinacy for all games of length
![]() $\omega ^2$
with moves in
$\omega ^2$
with moves in
![]() $\mathbb {N}$
and payoffs in these pointclasses is stronger, however. The first author has established equivalences for open (or
$\mathbb {N}$
and payoffs in these pointclasses is stronger, however. The first author has established equivalences for open (or
![]() $\boldsymbol \Sigma ^0_1$
),
$\boldsymbol \Sigma ^0_1$
),
![]() $F_{\sigma }$
(or
$F_{\sigma }$
(or
![]() $\boldsymbol \Sigma ^{0}_{2}$
; see [Reference Aguilera3]), and Borel (or
$\boldsymbol \Sigma ^{0}_{2}$
; see [Reference Aguilera3]), and Borel (or
![]() $\boldsymbol \Delta ^1_1$
; see [Reference Aguilera1]) games of length
$\boldsymbol \Delta ^1_1$
; see [Reference Aguilera1]) games of length
![]() $\omega ^{2}$
, and this article provides the analogue for
$\omega ^{2}$
, and this article provides the analogue for
![]() $G_{\delta \sigma }$
(or
$G_{\delta \sigma }$
(or
![]() $\boldsymbol \Sigma ^0_3$
) games.
$\boldsymbol \Sigma ^0_3$
) games.
Winning strategies (for either player) for the effective (so lightface) versions of the
![]() $\Sigma ^{0}_{1}$
and
$\Sigma ^{0}_{1}$
and
![]() $\Sigma ^{0}_{2}$
classes were shown to be definable over
$\Sigma ^{0}_{2}$
classes were shown to be definable over
 $L_{\omega _{1}^{ck}}$
(Kleene and Moschovakis), and to belong to the next admissible set after the closure ordinal of monotone-
$L_{\omega _{1}^{ck}}$
(Kleene and Moschovakis), and to belong to the next admissible set after the closure ordinal of monotone-
![]() $\Sigma ^{1}_{1}$
inductive definitions (Solovay) respectively, in the 1970s. The second author located [Reference Welch19] the strategies for
$\Sigma ^{1}_{1}$
inductive definitions (Solovay) respectively, in the 1970s. The second author located [Reference Welch19] the strategies for
![]() $\Sigma ^{0}_{3}$
-games as being definable over the least level
$\Sigma ^{0}_{3}$
-games as being definable over the least level
![]() $L_{\beta } $
which supported a nesting (Definition 3.1). Hachtman, [Reference Hachtman9], then took this nesting concept and showed that the
$L_{\beta } $
which supported a nesting (Definition 3.1). Hachtman, [Reference Hachtman9], then took this nesting concept and showed that the
![]() $L_{\beta }$
that supported nestings were models of
$L_{\beta }$
that supported nestings were models of
![]() $\boldsymbol \Pi ^{1}_{2}$
-monotone induction. It is a feature of the argument below for the longer games, that we use in addition Hachtman’s characterisation. A fourth and final equivalence to the least such nesting ordinal can be given in terms of the definability of the complete semi-decidable set for a notion of higher type recursion in
$\boldsymbol \Pi ^{1}_{2}$
-monotone induction. It is a feature of the argument below for the longer games, that we use in addition Hachtman’s characterisation. A fourth and final equivalence to the least such nesting ordinal can be given in terms of the definability of the complete semi-decidable set for a notion of higher type recursion in
![]() $^2\mathsf {E}$
. This is due to the second author and shall appear elsewhere.
$^2\mathsf {E}$
. This is due to the second author and shall appear elsewhere.
The main theorem we prove is:
Theorem 1.1. The following are equivalent over
![]() ${\mathsf {ZFC}}$
:
${\mathsf {ZFC}}$
:
-
(1)
 $\boldsymbol \Sigma ^0_3$
games of length
$\boldsymbol \Sigma ^0_3$
games of length
 $\omega ^2$
with moves in
$\omega ^2$
with moves in
 $\mathbb {N}$
are determined.
$\mathbb {N}$
are determined. -
(2) There is a transitive model of
 ${\mathsf {KP}} + {\mathsf {AD}} + \Pi _1\text{\rm -MI}_{\mathbb {R}}$
which contains
${\mathsf {KP}} + {\mathsf {AD}} + \Pi _1\text{\rm -MI}_{\mathbb {R}}$
which contains
 $\mathbb {R}$
.
$\mathbb {R}$
.
Below, we adopt the convention that
![]() ${\mathsf {AD}}$
includes a clause asserting the existence of
${\mathsf {AD}}$
includes a clause asserting the existence of
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
Here,
![]() $\Pi _1\textrm {-MI}_{\mathbb {R}}$
is the axiom stating that every monotone
$\Pi _1\textrm {-MI}_{\mathbb {R}}$
is the axiom stating that every monotone
![]() $\Pi _1$
operator on
$\Pi _1$
operator on
![]() $\mathbb {R}$
has a least fixed point. Let us be more precise: a
$\mathbb {R}$
has a least fixed point. Let us be more precise: a
![]() $\Pi _1$
operator on
$\Pi _1$
operator on
![]() $\mathbb {R}$
is a function
$\mathbb {R}$
is a function
which is given by
for some
![]() $\Pi _1$
formula
$\Pi _1$
formula
![]() $\phi $
in the language of set theory and some set a. We say
$\phi $
in the language of set theory and some set a. We say
![]() $\Phi $
is monotone if
$\Phi $
is monotone if
For such a
![]() $\Phi $
, we may inductively define
$\Phi $
, we may inductively define
 $$ \begin{align*} \Phi^0 &= \Phi(\varnothing),\\ \Phi^{\alpha} &= \Phi\left(\bigcup_{\beta<\alpha} \Phi^{\beta}\right). \end{align*} $$
$$ \begin{align*} \Phi^0 &= \Phi(\varnothing),\\ \Phi^{\alpha} &= \Phi\left(\bigcup_{\beta<\alpha} \Phi^{\beta}\right). \end{align*} $$
Let
![]() $\Phi ^\infty $
be the least fixed point of the operator
$\Phi ^\infty $
be the least fixed point of the operator
![]() $\Phi $
and let
$\Phi $
and let
![]() $|\Phi |$
denote the least ordinal
$|\Phi |$
denote the least ordinal
![]() $\alpha $
such that
$\alpha $
such that
![]() $\Phi ^\infty = \Phi ^\alpha $
. The axiom of
$\Phi ^\infty = \Phi ^\alpha $
. The axiom of
![]() $\Pi _1\textrm {-MI}_{\mathbb {R}}$
says that for every monotone
$\Pi _1\textrm {-MI}_{\mathbb {R}}$
says that for every monotone
![]() $\Pi _1$
operator on
$\Pi _1$
operator on
![]() $\mathbb {R}$
, the sequence
$\mathbb {R}$
, the sequence
![]() $\{\Phi ^\alpha :\alpha \leq |\Phi |\}$
exists. The axiom
$\{\Phi ^\alpha :\alpha \leq |\Phi |\}$
exists. The axiom
![]() $\Pi _1\textrm {-MI}_{\mathbb {N}}$
is defined analogously, but in terms of operators on
$\Pi _1\textrm {-MI}_{\mathbb {N}}$
is defined analogously, but in terms of operators on
![]() $\mathbb {N}$
; over
$\mathbb {N}$
; over
![]() ${\mathsf {KP}}$
+ V = L, it is equivalent to
${\mathsf {KP}}$
+ V = L, it is equivalent to
 $\boldsymbol \Pi ^1_2\textrm {-MI}$
, as long as
$\boldsymbol \Pi ^1_2\textrm {-MI}$
, as long as
![]() $\mathcal {P}(\mathbb {N})$
does not exist (this is because
$\mathcal {P}(\mathbb {N})$
does not exist (this is because
![]() $\boldsymbol \Pi ^1_2$
-MI admits only real parameters and we allowed arbitrary parameters in the definition of
$\boldsymbol \Pi ^1_2$
-MI admits only real parameters and we allowed arbitrary parameters in the definition of
![]() $\Pi _1$
-MI
$\Pi _1$
-MI
![]() $_{\mathbb {N}}$
– this simplifies some arguments but does not increase the consistency strength).
$_{\mathbb {N}}$
– this simplifies some arguments but does not increase the consistency strength).
From Theorem 1.1, we can deduce that the theory
![]() ${\mathsf {ZFC}} +$
“
${\mathsf {ZFC}} +$
“
![]() $\boldsymbol \Sigma ^0_3$
-determinacy for games of length
$\boldsymbol \Sigma ^0_3$
-determinacy for games of length
![]() $\omega ^2$
” lies in consistency strength between the theories
$\omega ^2$
” lies in consistency strength between the theories
and
Theorem 1.1 should be regarded as an analogue of the corresponding result for games of length
![]() $\omega $
:
$\omega $
:
Theorem 1.2 (Hachtman [Reference Hachtman9])
The following are equivalent over
 $\boldsymbol \Pi ^1_1\text {-}\mathsf {CA}_0$
:
$\boldsymbol \Pi ^1_1\text {-}\mathsf {CA}_0$
:
-
(1)
 $\Sigma ^0_3$
games of length
$\Sigma ^0_3$
games of length
 $\omega $
with moves in
$\omega $
with moves in
 $\mathbb {N}$
are determined.
$\mathbb {N}$
are determined. -
(2) There is a
 $\beta $
-model of
$\beta $
-model of
 ${\mathsf {KP}} + \Pi ^1_2\text {-}\mathsf {MI}$
.
${\mathsf {KP}} + \Pi ^1_2\text {-}\mathsf {MI}$
.
Hachtman’s theorem plays an important role in the proof of Theorem 1.1. As in previous proofs of determinacy for definable games of length
![]() $\omega ^2$
(see e.g., [Reference Aguilera1, Reference Aguilera3, Reference Aguilera and Müller4]), part of the argument consists in “lifting” the reversals for determinacy of games of length
$\omega ^2$
(see e.g., [Reference Aguilera1, Reference Aguilera3, Reference Aguilera and Müller4]), part of the argument consists in “lifting” the reversals for determinacy of games of length
![]() $\omega $
to locate the winning strategies for games on
$\omega $
to locate the winning strategies for games on
![]() $\mathbb {R}$
in the
$\mathbb {R}$
in the
![]() $L(\mathbb {R})$
-hierarchy. The main novelty here is that the stage by which these strategies appear is characterized in terms of a certain non-standard model of
$L(\mathbb {R})$
-hierarchy. The main novelty here is that the stage by which these strategies appear is characterized in terms of a certain non-standard model of
![]() ${\mathsf {KP}}$
which cannot exist in V, but only in a generic extension of it. As part of the proof of the main theorem, we shall state a general upper bound for the complexity of these strategies, as well as for winning strategies for games of length
${\mathsf {KP}}$
which cannot exist in V, but only in a generic extension of it. As part of the proof of the main theorem, we shall state a general upper bound for the complexity of these strategies, as well as for winning strategies for games of length
![]() $\omega ^2$
in some sufficiently closed subclass of the Borel sets (see Claim 4.5 within the proof of Theorem 4.1, as well as Remark 4.7).
$\omega ^2$
in some sufficiently closed subclass of the Borel sets (see Claim 4.5 within the proof of Theorem 4.1, as well as Remark 4.7).
2 Monotone Induction in
 $L(\mathbb {R})$
$L(\mathbb {R})$
We refer the reader to Barwise [Reference Barwise5] for general background in admissible sets, to Moschovakis [Reference Moschovakis17] for general background in descriptive set theory, and to Jech [Reference Jech10] for general background in forcing and constructibility.
The first step towards proving Theorem 1.1 is reducing the assertion that there is a transitive model of
![]() ${\mathsf {KP}} + {\mathsf {AD}} + \Pi _1\textrm {-MI}_{\mathbb {R}}$
to this theory holding in a specific model:
${\mathsf {KP}} + {\mathsf {AD}} + \Pi _1\textrm {-MI}_{\mathbb {R}}$
to this theory holding in a specific model:
Lemma 2.1 (
 ${\mathsf {KP}}$
)
${\mathsf {KP}}$
)
Suppose
![]() $\Pi _1\textrm {-MI}_{\mathbb {R}}$
holds. Then,
$\Pi _1\textrm {-MI}_{\mathbb {R}}$
holds. Then,
![]() ${\mathsf {KP}} + \Pi _1\textrm {-MI}_{\mathbb {R}}$
holds in
${\mathsf {KP}} + \Pi _1\textrm {-MI}_{\mathbb {R}}$
holds in
![]() $L(\mathbb {R})$
.
$L(\mathbb {R})$
.
Proof That
![]() $L(\mathbb {R})\models {\mathsf {KP}}$
is a theorem of
$L(\mathbb {R})\models {\mathsf {KP}}$
is a theorem of
![]() ${\mathsf {KP}}$
. Let
${\mathsf {KP}}$
. Let
![]() $\Phi $
be a
$\Phi $
be a
![]() $\Pi _1$
monotone operator in
$\Pi _1$
monotone operator in
![]() $L(\mathbb {R})$
, say, given by a
$L(\mathbb {R})$
, say, given by a
![]() $\Pi _1$
formula
$\Pi _1$
formula
![]() $\phi $
and a set a. Consider the operator
$\phi $
and a set a. Consider the operator
![]() $\Phi '$
given by
$\Phi '$
given by
i.e., by
This is an operator of the form
for some
![]() $\Pi _1$
formula
$\Pi _1$
formula
![]() $\phi '$
and is monotone, so the sequence
$\phi '$
and is monotone, so the sequence
![]() $\{(\Phi ')^\alpha :\alpha \leq |\Phi '|\}$
exists. Moreover, the operator
$\{(\Phi ')^\alpha :\alpha \leq |\Phi '|\}$
exists. Moreover, the operator
![]() $\Phi '$
belongs to
$\Phi '$
belongs to
![]() $L(\mathbb {R})$
and has the same least fixed point as
$L(\mathbb {R})$
and has the same least fixed point as
![]() $\Phi $
. Since all ordinals belong to
$\Phi $
. Since all ordinals belong to
![]() $L(\mathbb {R})$
and
$L(\mathbb {R})$
and
![]() $L(\mathbb {R})\models {\mathsf {KP}}$
,
$L(\mathbb {R})\models {\mathsf {KP}}$
,
![]() $\{(\Phi ')^\alpha :\alpha \leq |\Phi '|\}$
belongs to
$\{(\Phi ')^\alpha :\alpha \leq |\Phi '|\}$
belongs to
![]() $L(\mathbb {R})$
, so
$L(\mathbb {R})$
, so
![]() $\Phi ^\infty \in L(\mathbb {R})$
, as desired.⊣
$\Phi ^\infty \in L(\mathbb {R})$
, as desired.⊣
Below, recall that
![]() ${\mathsf {DC}}$
denotes the Principle of Dependent Choices, stating that every tree with no terminal nodes has a branch. For a set X,
${\mathsf {DC}}$
denotes the Principle of Dependent Choices, stating that every tree with no terminal nodes has a branch. For a set X,
![]() ${\mathsf {DC}}_X$
denotes the restriction of
${\mathsf {DC}}_X$
denotes the restriction of
![]() ${\mathsf {DC}}$
to trees whose nodes are indexed by finite sequences of elements of X. In the case that
${\mathsf {DC}}$
to trees whose nodes are indexed by finite sequences of elements of X. In the case that
![]() $X = \mathbb {R}$
and
$X = \mathbb {R}$
and
![]() ${\mathsf {DC}}_{\mathbb {R}}$
holds, branches through such trees can themselves be coded by reals, so
${\mathsf {DC}}_{\mathbb {R}}$
holds, branches through such trees can themselves be coded by reals, so
![]() ${\mathsf {DC}}_{\mathbb {R}}$
relativizes downwards to transitive inner models that contain
${\mathsf {DC}}_{\mathbb {R}}$
relativizes downwards to transitive inner models that contain
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
Corollary 2.2. The following are equivalent over
![]() ${\mathsf {ZFC}}$
:
${\mathsf {ZFC}}$
:
-
(1) There is a transitive model of
 ${\mathsf {KP}} + {\mathsf {AD}} + \Pi _1\text {-}\mathsf {MI}_{\mathbb {R}}$
which contains all reals.
${\mathsf {KP}} + {\mathsf {AD}} + \Pi _1\text {-}\mathsf {MI}_{\mathbb {R}}$
which contains all reals. -
(2) Let
 $\beta $
be least such that
$\beta $
be least such that
 $L_\beta (\mathbb {R}) \models \Pi _1\text {-}\mathsf {MI}_{\mathbb {R}}$
. Then
$L_\beta (\mathbb {R}) \models \Pi _1\text {-}\mathsf {MI}_{\mathbb {R}}$
. Then
 $L_\beta (\mathbb {R})\models {\mathsf {AD}} + {\mathsf {DC}}$
.
$L_\beta (\mathbb {R})\models {\mathsf {AD}} + {\mathsf {DC}}$
.
Proof To see that (2) implies (1), it suffices to show that
![]() $L_\beta (\mathbb {R})$
satisfies
$L_\beta (\mathbb {R})$
satisfies
![]() ${\mathsf {KP}}$
. First, by a reflection argument, we see that
${\mathsf {KP}}$
. First, by a reflection argument, we see that
![]() $L_\beta (\mathbb {R})$
satisfies “
$L_\beta (\mathbb {R})$
satisfies “
![]() $\mathcal {P}(\mathbb {R})$
does not exist,” so in
$\mathcal {P}(\mathbb {R})$
does not exist,” so in
![]() $L_\beta (\mathbb {R})$
every set is a surjective image of
$L_\beta (\mathbb {R})$
every set is a surjective image of
![]() $\mathbb {R}$
. Then, we see that
$\mathbb {R}$
. Then, we see that
![]() $L_\beta (\mathbb {R})$
satisfies (boldface)
$L_\beta (\mathbb {R})$
satisfies (boldface)
![]() $\Sigma _1$
-Separation for sets of reals and thus for arbitrary sets.
$\Sigma _1$
-Separation for sets of reals and thus for arbitrary sets.
![]() $\Sigma _1$
-Separation is true because it is equivalent to
$\Sigma _1$
-Separation is true because it is equivalent to
![]() $\Pi _1$
-Separation, and this follows from
$\Pi _1$
-Separation, and this follows from
![]() $\Pi _1{-}\mathsf {MI}_{\mathbb {R}}$
(instances of separation are inductions of length
$\Pi _1{-}\mathsf {MI}_{\mathbb {R}}$
(instances of separation are inductions of length
![]() $1$
). To prove
$1$
). To prove
![]() $\Delta _0$
-Collection, suppose that
$\Delta _0$
-Collection, suppose that
for some
![]() $\Delta _0$
formula
$\Delta _0$
formula
![]() $\phi $
. By
$\phi $
. By
![]() $\Sigma _1$
-Separation, there is a transitive set
$\Sigma _1$
-Separation, there is a transitive set
![]() $B \in L_\beta (\mathbb {R})$
such that
$B \in L_\beta (\mathbb {R})$
such that
![]() $A,p \in B$
and
$A,p \in B$
and
(This follows e.g., from the argument of Steel [Reference Steel, Kechris, Löwe and Steel18, Lemma 1.11].) It follows that
so
![]() $L_\beta (\mathbb {R})$
satisfies
$L_\beta (\mathbb {R})$
satisfies
![]() $\Delta _0$
-Collection.
$\Delta _0$
-Collection.
Conversely, suppose there is a transitive model M of
![]() ${\mathsf {KP}} + {\mathsf {AD}} + \Pi _1\textrm {-MI}_{\mathbb {R}}$
which contains all reals. By Lemma 2.1,
${\mathsf {KP}} + {\mathsf {AD}} + \Pi _1\textrm {-MI}_{\mathbb {R}}$
which contains all reals. By Lemma 2.1,
Since M contains all reals (hence all strategies for Gale-Stewart games on
![]() $\mathbb {N}$
), it follows that
$\mathbb {N}$
), it follows that
![]() $L(\mathbb {R})^M = L_{{\mathsf {Ord}}\cap M}(\mathbb {R})$
and that
$L(\mathbb {R})^M = L_{{\mathsf {Ord}}\cap M}(\mathbb {R})$
and that
Letting
![]() $\beta $
be least such that
$\beta $
be least such that
![]() $L_\beta (\mathbb {R}) \models \Pi _1$
-
$L_\beta (\mathbb {R}) \models \Pi _1$
-
![]() $\mathsf {MI}_{\mathbb {R}}$
, we have
$\mathsf {MI}_{\mathbb {R}}$
, we have
![]() $\beta \leq {\mathsf {Ord}}\cap M$
, so
$\beta \leq {\mathsf {Ord}}\cap M$
, so
Since
![]() $L_\beta (\mathbb {R})$
contains all reals, it satisfies
$L_\beta (\mathbb {R})$
contains all reals, it satisfies
![]() ${\mathsf {DC}}_{\mathbb {R}}$
. By minimality, no
${\mathsf {DC}}_{\mathbb {R}}$
. By minimality, no
![]() $L_\gamma (\mathbb {R})$
is a model of separation, for
$L_\gamma (\mathbb {R})$
is a model of separation, for
![]() $\gamma <\beta $
, and, in fact, for all such
$\gamma <\beta $
, and, in fact, for all such
![]() $\gamma $
, there is a subset of
$\gamma $
, there is a subset of
![]() $\mathbb {R}$
not in
$\mathbb {R}$
not in
![]() $L_\gamma (\mathbb {R})$
which is definable over
$L_\gamma (\mathbb {R})$
which is definable over
![]() $L_\gamma (\mathbb {R})$
. Thus, for every
$L_\gamma (\mathbb {R})$
. Thus, for every
![]() $\gamma <\beta $
, there is a surjection
$\gamma <\beta $
, there is a surjection
which is definable over
![]() $L_\gamma (\mathbb {R})$
(see e.g., Steel [Reference Steel, Kechris, Löwe and Steel18]). Hence, every set in
$L_\gamma (\mathbb {R})$
(see e.g., Steel [Reference Steel, Kechris, Löwe and Steel18]). Hence, every set in
![]() $L_\beta (\mathbb {R})$
is coded by a set of reals in
$L_\beta (\mathbb {R})$
is coded by a set of reals in
![]() $L_\beta (\mathbb {R})$
, so, by
$L_\beta (\mathbb {R})$
, so, by
![]() ${\mathsf {DC}}_{\mathbb {R}}$
,
${\mathsf {DC}}_{\mathbb {R}}$
,
as desired.⊣
3 Generic
 $\Sigma_2$
-Extendibility
$\Sigma_2$
-Extendibility
The next step for proving Theorem 1.1 is locating the simplest winning strategies for
![]() $\boldsymbol \Sigma ^0_3$
games on reals. The result requires some definitions:
$\boldsymbol \Sigma ^0_3$
games on reals. The result requires some definitions:
Definition 3.1. Let
![]() $x\in \mathbb {R}$
and M be a model of
$x\in \mathbb {R}$
and M be a model of
![]() ${\mathsf {KP}} + V = L[x]$
. An x-nesting on an ordinal
${\mathsf {KP}} + V = L[x]$
. An x-nesting on an ordinal
![]() $\beta $
and M is a sequence of pairs
$\beta $
and M is a sequence of pairs
![]() $(\zeta _n, s_n)$
for
$(\zeta _n, s_n)$
for
![]() $n\in \mathbb {N}$
such that
$n\in \mathbb {N}$
such that
-
(1)
 $\zeta _n < \zeta _{n+1} < \beta $
for all n,
$\zeta _n < \zeta _{n+1} < \beta $
for all n, -
(2)
 $L_\beta [x]$
is the wellfounded part of M,
$L_\beta [x]$
is the wellfounded part of M, -
(3)
 $M \models s_{n+1} < s_n$
for all n and each
$M \models s_{n+1} < s_n$
for all n and each
 $s_n$
belongs to the illfounded part of M, and
$s_n$
belongs to the illfounded part of M, and -
(4)
 $M\models L_{\zeta _n}[x]\prec _{\Sigma _2} (L_{s_n}[x])^M$
for all n.
$M\models L_{\zeta _n}[x]\prec _{\Sigma _2} (L_{s_n}[x])^M$
for all n.
Given an ordinal
![]() $\beta $
and a real x, if such a sequence exists for some model M, we say that
$\beta $
and a real x, if such a sequence exists for some model M, we say that
![]() $\beta $
admits an x-nesting. Observe that if
$\beta $
admits an x-nesting. Observe that if
is an x-nesting on
![]() $\beta $
and M, then
$\beta $
and M, then
 $$ \begin{align*}\beta \geq \mathop{\mathrm{sup}}\limits_{n\in\mathbb{N}} \zeta_n.\end{align*} $$
$$ \begin{align*}\beta \geq \mathop{\mathrm{sup}}\limits_{n\in\mathbb{N}} \zeta_n.\end{align*} $$
Here we shall have that taking a least such
![]() $\beta $
results in the supremum of the lower ends of the
$\beta $
results in the supremum of the lower ends of the
![]() $\Sigma _2$
-end-extensions being
$\Sigma _2$
-end-extensions being
![]() $\beta $
itself.
$\beta $
itself.
Lemma 3.2. Suppose that
![]() $\beta $
is least that supports an infinite x-nesting
$\beta $
is least that supports an infinite x-nesting
![]() $\{(\zeta _n, s_n):n\in \mathbb {N}\}$
. Then
$\{(\zeta _n, s_n):n\in \mathbb {N}\}$
. Then
 $\beta = \mathop {\mathrm {sup}}\limits _{n\in \mathbb {N}}\zeta _n$
.
$\beta = \mathop {\mathrm {sup}}\limits _{n\in \mathbb {N}}\zeta _n$
.
Proof Suppose otherwise for a contradiction and that
 $\zeta \ := \mathop {\mathrm {sup}}\limits _{n\in \mathbb {N}}\zeta _n < \beta $
. (We shall drop mention of the uniform parameter x.) Note first that for such
$\zeta \ := \mathop {\mathrm {sup}}\limits _{n\in \mathbb {N}}\zeta _n < \beta $
. (We shall drop mention of the uniform parameter x.) Note first that for such
![]() $\zeta _n$
.
$\zeta _n$
.
![]() $L_{ \zeta _n}\prec _{\Sigma _1} L_{\zeta }$
.
$L_{ \zeta _n}\prec _{\Sigma _1} L_{\zeta }$
.
Then, in M, for arbitrarily large
![]() $\tilde \zeta < \zeta $
, also with
$\tilde \zeta < \zeta $
, also with
![]() $L_{\tilde \zeta }\prec _{\Sigma _1} L_{\zeta }$
, there are
$L_{\tilde \zeta }\prec _{\Sigma _1} L_{\zeta }$
, there are
![]() $\tilde s> \zeta $
with
$\tilde s> \zeta $
with
![]() $L_{\tilde \zeta }\prec _{\Sigma _2} L_{\tilde s}$
. We note that any such
$L_{\tilde \zeta }\prec _{\Sigma _2} L_{\tilde s}$
. We note that any such
![]() $\tilde s$
must be in the illfounded part of M. Suppose not. By definition of
$\tilde s$
must be in the illfounded part of M. Suppose not. By definition of
![]() $\zeta $
there will be some
$\zeta $
there will be some
![]() $\bar \zeta> \tilde \zeta $
with a
$\bar \zeta> \tilde \zeta $
with a
![]() $\Sigma _2$
-end-extension to some
$\Sigma _2$
-end-extension to some
![]() $\bar s$
where
$\bar s$
where
![]() $L_{\bar \zeta }\prec _{\Sigma _2} L_{\bar s}$
and
$L_{\bar \zeta }\prec _{\Sigma _2} L_{\bar s}$
and
![]() $\bar s$
certainly in the illfounded part of M (just take some sufficiently large
$\bar s$
certainly in the illfounded part of M (just take some sufficiently large
![]() $\zeta _m$
). However now we have two overlapping
$\zeta _m$
). However now we have two overlapping
![]() $\Sigma _2$
-extendible pairs with
$\Sigma _2$
-extendible pairs with
![]() $\tilde \zeta < \bar \zeta < \tilde s< \bar s$
.
$\tilde \zeta < \bar \zeta < \tilde s< \bar s$
.
Claim:
![]() $L_{\tilde \zeta }\prec _{\Sigma _2} L_{\bar \zeta }\prec _{\Sigma _2} L_{\bar s}$
.
$L_{\tilde \zeta }\prec _{\Sigma _2} L_{\bar \zeta }\prec _{\Sigma _2} L_{\bar s}$
.
Proof We only need to justify the first substructure relation. This is an exercise. (Any
![]() $\Sigma _2$
statement about
$\Sigma _2$
statement about
![]() $\vec x$
from
$\vec x$
from
![]() $L_{\tilde \zeta }$
true in
$L_{\tilde \zeta }$
true in
![]() $L_{\bar \zeta }$
upwardly persists in being true in
$L_{\bar \zeta }$
upwardly persists in being true in
![]() $L_\tau $
for any
$L_\tau $
for any
![]() $\tau \in [\bar \zeta, \bar s]$
and so in particular is true in
$\tau \in [\bar \zeta, \bar s]$
and so in particular is true in
![]() $L_{\tilde s}$
. By downward
$L_{\tilde s}$
. By downward
![]() $\Sigma _2$
-reflection it is true in
$\Sigma _2$
-reflection it is true in
![]() $L_{\tilde \zeta }$
.)⊣
$L_{\tilde \zeta }$
.)⊣
Claim:
![]() $\bar \zeta $
admits an infinite nesting.
$\bar \zeta $
admits an infinite nesting.
Proof By a Barwise Compactness argument, let M be any illfounded model with wellfounded part equal to
![]() $L_{\bar \zeta }$
. By the double
$L_{\bar \zeta }$
. By the double
![]() $\Sigma _2$
-end-extension configuration in the last claim we can repeatedly use
$\Sigma _2$
-end-extension configuration in the last claim we can repeatedly use
![]() $\Sigma _2$
-reflection and have that
$\Sigma _2$
-reflection and have that
![]() $L_{\tilde \zeta }$
has arbitrarily large
$L_{\tilde \zeta }$
has arbitrarily large
![]() $\Sigma _2$
-end-extensions
$\Sigma _2$
-end-extensions
![]() $L_\tau $
with
$L_\tau $
with
![]() $\tau <\bar \zeta $
. By overspill it has such end-extensions
$\tau <\bar \zeta $
. By overspill it has such end-extensions
![]() $L_t$
for
$L_t$
for
![]() $t\in On^M$
with t in the illfounded part of M. However then it is easy to see that
$t\in On^M$
with t in the illfounded part of M. However then it is easy to see that
![]() $\bar \zeta $
has an infinite nesting supported in M.⊣
$\bar \zeta $
has an infinite nesting supported in M.⊣
But the last Claim contradicts the choice of
![]() $\beta $
. Hence we can recursively define an infinite sequence of nested pairs
$\beta $
. Hence we can recursively define an infinite sequence of nested pairs
![]() $(\zeta _n,s_n)$
in M confident that the upper end
$(\zeta _n,s_n)$
in M confident that the upper end
![]() $s_n$
is in the illfounded part of M, and hence the recursion is successful.⊣
$s_n$
is in the illfounded part of M, and hence the recursion is successful.⊣
Definition 3.3. Let
![]() $x\in \mathbb {R}$
. We denote by
$x\in \mathbb {R}$
. We denote by
![]() $\beta _x$
the least ordinal
$\beta _x$
the least ordinal
![]() $\beta $
such that all
$\beta $
such that all
 $\Sigma ^0_3(x)$
games on
$\Sigma ^0_3(x)$
games on
![]() $\mathbb {N}$
have a winning strategy definable over
$\mathbb {N}$
have a winning strategy definable over
![]() $L_\beta [x]$
; we denote by
$L_\beta [x]$
; we denote by
![]() $\alpha _x$
the least ordinal such that
$\alpha _x$
the least ordinal such that
Theorem 3.4 [Reference Welch20]
For every
![]() $x\in \mathbb {R}$
,
$x\in \mathbb {R}$
,
![]() $\beta _x$
is the least ordinal that admits an x-nesting.
$\beta _x$
is the least ordinal that admits an x-nesting.
If
![]() $\{(\zeta _n, s_n):n\in \mathbb {N}\}$
is an x-nesting on
$\{(\zeta _n, s_n):n\in \mathbb {N}\}$
is an x-nesting on
![]() $\beta $
and M, then
$\beta $
and M, then
![]() $M\models L_{\zeta _n}[x] \prec _{\Sigma _2} (L_{s_n}[x])^M$
and hence
$M\models L_{\zeta _n}[x] \prec _{\Sigma _2} (L_{s_n}[x])^M$
and hence
![]() $M\models L_{\zeta _n}[x] \prec _{\Sigma _1} (L_{s_n}[x])^M$
. It follows that
$M\models L_{\zeta _n}[x] \prec _{\Sigma _1} (L_{s_n}[x])^M$
. It follows that
From this and Theorem 3.4, we see that
![]() $\alpha _x < \beta _x$
for all x.
$\alpha _x < \beta _x$
for all x.
We would like to generalise Theorem 3.4 to games on
![]() $\mathbb {R}$
and
$\mathbb {R}$
and
![]() $L(\mathbb {R})$
. For this, a natural candidate is the least ordinal
$L(\mathbb {R})$
. For this, a natural candidate is the least ordinal
![]() $\beta $
that satisfies Definition 3.1, but with M a model of
$\beta $
that satisfies Definition 3.1, but with M a model of
![]() $V = L(\mathbb {R})$
with
$V = L(\mathbb {R})$
with
![]() $\mathbb {R}^M = \mathbb {R}$
, and with condition (4) replaced by
$\mathbb {R}^M = \mathbb {R}$
, and with condition (4) replaced by
 $$ \begin{align*}L_{\zeta_n}(\mathbb{R}) \prec_{\Sigma_2} L_{s_n}(\mathbb{R})^M.\end{align*} $$
$$ \begin{align*}L_{\zeta_n}(\mathbb{R}) \prec_{\Sigma_2} L_{s_n}(\mathbb{R})^M.\end{align*} $$
The problem with this approach is that such an ordinal cannot exist, because of a very general fact. Here, recall that
![]() $\Theta $
denotes the least ordinal such that there is no surjection from
$\Theta $
denotes the least ordinal such that there is no surjection from
![]() $\mathbb {R}$
onto
$\mathbb {R}$
onto
![]() $\Theta $
.
$\Theta $
.
Lemma 3.5. Let M be an illfounded model of
![]() ${\mathsf {KP}} + V = L(\mathbb {R})$
with
${\mathsf {KP}} + V = L(\mathbb {R})$
with
![]() $\mathbb {R}^M = \mathbb {R}$
and let
$\mathbb {R}^M = \mathbb {R}$
and let
![]() $L_\alpha (\mathbb {R})$
be the wellfounded part of M. If
$L_\alpha (\mathbb {R})$
be the wellfounded part of M. If
![]() $\alpha <\Theta ^M$
, then
$\alpha <\Theta ^M$
, then
![]() $\omega < {\text {cof}}\,(\alpha )$
.
$\omega < {\text {cof}}\,(\alpha )$
.
Proof Assume towards a contradiction that
![]() ${\text {cof}}\,(\alpha ) = \omega $
. Since
${\text {cof}}\,(\alpha ) = \omega $
. Since
![]() $\alpha <\Theta ^M$
, for every M-ordinal
$\alpha <\Theta ^M$
, for every M-ordinal
![]() $\beta $
with
$\beta $
with
![]() $\alpha <\beta <\Theta ^M$
, there is a surjection
$\alpha <\beta <\Theta ^M$
, there is a surjection
 $$ \begin{align*}f:\mathbb{R}\twoheadrightarrow (L_\beta(\mathbb{R}))^M\end{align*} $$
$$ \begin{align*}f:\mathbb{R}\twoheadrightarrow (L_\beta(\mathbb{R}))^M\end{align*} $$
in M. Choose such a
![]() $\beta $
and such an f. Letting
$\beta $
and such an f. Letting
be cofinal in
![]() $\alpha $
and
$\alpha $
and
![]() $n\in \mathbb {N}$
, there is
$n\in \mathbb {N}$
, there is
![]() $x_n\in \mathbb {R}$
such that
$x_n\in \mathbb {R}$
such that
![]() $f(x_n) = \alpha _n$
. Because
$f(x_n) = \alpha _n$
. Because
![]() $\mathbb {R}^M = \mathbb {R}$
, and the Axiom of Dependent Choices holds in V, there is some
$\mathbb {R}^M = \mathbb {R}$
, and the Axiom of Dependent Choices holds in V, there is some
![]() $x\in \mathbb {R}$
coding each
$x\in \mathbb {R}$
coding each
![]() $x_n$
. By
$x_n$
. By
![]() $\Delta _0$
-collection, the image of
$\Delta _0$
-collection, the image of
![]() $\{x_n:n\in \mathbb {N}\}$
under f, i.e., the sequence
$\{x_n:n\in \mathbb {N}\}$
under f, i.e., the sequence
belongs to M, which is a contradiction.⊣
The solution is to look for nestings in generic extensions of V. Below, we denote by
 $\Sigma _1^{L_{\alpha }(\mathbb {R})}$
the pointclass of all sets which are
$\Sigma _1^{L_{\alpha }(\mathbb {R})}$
the pointclass of all sets which are
![]() $\Sigma _1$
-definable over
$\Sigma _1$
-definable over
![]() $L_\alpha (\mathbb {R})$
, with parameters in
$L_\alpha (\mathbb {R})$
, with parameters in
![]() $\mathbb {R} \cup \{\mathbb {R}\}$
. Given a pointclass
$\mathbb {R} \cup \{\mathbb {R}\}$
. Given a pointclass
![]() $\Gamma $
, we denote by
$\Gamma $
, we denote by
![]() $\Game ^{\mathbb {R}}\Gamma $
the pointclass of all sets of the form
$\Game ^{\mathbb {R}}\Gamma $
the pointclass of all sets of the form
with
![]() $A \in \Gamma $
. In the following lemma, we speak of filters
$A \in \Gamma $
. In the following lemma, we speak of filters
![]() $g\subset \text {Coll}(\omega,\mathbb {R})$
which are
$g\subset \text {Coll}(\omega,\mathbb {R})$
which are
![]() $L(\mathbb {R})$
-generic. Such a g may be identified with a real number which codes
$L(\mathbb {R})$
-generic. Such a g may be identified with a real number which codes
![]() $\mathbb {R}$
and belongs to
$\mathbb {R}$
and belongs to
![]() $L[g]$
and thus one may define the ordinals
$L[g]$
and thus one may define the ordinals
![]() $\alpha _g$
and
$\alpha _g$
and
![]() $\beta _g$
.
$\beta _g$
.
Lemma 3.6. Let
![]() $g\subset \text {Coll}(\omega,\mathbb {R})$
be
$g\subset \text {Coll}(\omega,\mathbb {R})$
be
![]() $L(\mathbb {R})$
-generic. Then,
$L(\mathbb {R})$
-generic. Then,
 $$ \begin{align*}\Sigma_1^{L_{\alpha_g}(\mathbb{R})}\subset \Game^{\mathbb{R}}\boldsymbol\Sigma^0_3,\end{align*} $$
$$ \begin{align*}\Sigma_1^{L_{\alpha_g}(\mathbb{R})}\subset \Game^{\mathbb{R}}\boldsymbol\Sigma^0_3,\end{align*} $$
where
![]() $\alpha _g$
is computed in
$\alpha _g$
is computed in
![]() $L[g]$
and
$L[g]$
and
![]() $\mathbb {R} = \mathbb {R}^V$
.
$\mathbb {R} = \mathbb {R}^V$
.
Proof Let
![]() $\gamma \leq \alpha _g$
be admissible, but
$\gamma \leq \alpha _g$
be admissible, but
![]() $\Sigma _1$
-projectible to
$\Sigma _1$
-projectible to
![]() $\mathbb {R}$
Footnote
1
and let
$\mathbb {R}$
Footnote
1
and let
![]() $A\subset \mathbb {R}$
be
$A\subset \mathbb {R}$
be
![]() $\Pi _1$
-definable over
$\Pi _1$
-definable over
![]() $L_\gamma (\mathbb {R})$
. Given
$L_\gamma (\mathbb {R})$
. Given
![]() $a \in \mathbb {R}$
, we define a
$a \in \mathbb {R}$
, we define a
![]() $\boldsymbol \Sigma ^0_3$
game
$\boldsymbol \Sigma ^0_3$
game
![]() $G(a,A)$
(uniformly in a) on
$G(a,A)$
(uniformly in a) on
![]() $\mathbb {R}$
with the property that Player II has a winning strategy in it if, and only if,
$\mathbb {R}$
with the property that Player II has a winning strategy in it if, and only if,
![]() $a \in A$
. Since the winning condition for Player II is
$a \in A$
. Since the winning condition for Player II is
![]() $\boldsymbol \Pi ^0_3$
, this implies that all
$\boldsymbol \Pi ^0_3$
, this implies that all
 $\Pi _1^{L_{\alpha _g}(\mathbb {R})}$
subsets of
$\Pi _1^{L_{\alpha _g}(\mathbb {R})}$
subsets of
![]() $\mathbb {R}$
are
$\mathbb {R}$
are
 $\Game ^{\mathbb {R}}\boldsymbol \Pi ^0_3$
. Since
$\Game ^{\mathbb {R}}\boldsymbol \Pi ^0_3$
. Since
![]() $\boldsymbol \Sigma ^0_3$
games on reals are determined, the dual class of
$\boldsymbol \Sigma ^0_3$
games on reals are determined, the dual class of
 $\Game ^{\mathbb {R}}\boldsymbol \Pi ^0_3$
is
$\Game ^{\mathbb {R}}\boldsymbol \Pi ^0_3$
is
 $\Game ^{\mathbb {R}}\boldsymbol \Sigma ^0_3$
, so this in turn implies that all
$\Game ^{\mathbb {R}}\boldsymbol \Sigma ^0_3$
, so this in turn implies that all
 $\Sigma _1^{L_{\alpha _g}(\mathbb {R})}$
subsets of
$\Sigma _1^{L_{\alpha _g}(\mathbb {R})}$
subsets of
![]() $\mathbb {R}$
are
$\mathbb {R}$
are
 $\Game ^{\mathbb {R}}\boldsymbol \Sigma ^0_3$
, which yields the result. This game we define combines the
$\Game ^{\mathbb {R}}\boldsymbol \Sigma ^0_3$
, which yields the result. This game we define combines the
![]() $\Sigma ^0_3$
games from [Reference Welch19] with the games on reals of Martin-Steel [Reference Martin, Steel, Kechris, Löwe and Steel15]. The new feature in this game is the appearance of the generic g––this seems unavoidable, by Lemma 3.5.
$\Sigma ^0_3$
games from [Reference Welch19] with the games on reals of Martin-Steel [Reference Martin, Steel, Kechris, Löwe and Steel15]. The new feature in this game is the appearance of the generic g––this seems unavoidable, by Lemma 3.5.
Let
![]() $\varphi $
be the formula defining A over
$\varphi $
be the formula defining A over
![]() $L_\gamma (\mathbb {R})$
from a parameter
$L_\gamma (\mathbb {R})$
from a parameter
![]() $x_A \in \mathbb {R}$
and let
$x_A \in \mathbb {R}$
and let
![]() $\varphi _\gamma $
be a
$\varphi _\gamma $
be a
![]() $\Sigma _1$
formula with one free variable such that for some real
$\Sigma _1$
formula with one free variable such that for some real
![]() $x_\gamma $
,
$x_\gamma $
,
![]() $\varphi _\gamma (x_\gamma )$
holds in
$\varphi _\gamma (x_\gamma )$
holds in
![]() $L_\gamma (\mathbb {R})$
but in no proper initial segment of
$L_\gamma (\mathbb {R})$
but in no proper initial segment of
![]() $L_\gamma (\mathbb {R})$
.
$L_\gamma (\mathbb {R})$
.
Let
![]() $\mathcal {L}$
be the language of set theory with an additional collection of constants
$\mathcal {L}$
be the language of set theory with an additional collection of constants
![]() $\{\dot x_i:i\in \mathbb {N}\}$
and let
$\{\dot x_i:i\in \mathbb {N}\}$
and let
![]() $\{\psi _i:i\in \mathbb {N}\}$
enumerate all formulae in this language in such a way that
$\{\psi _i:i\in \mathbb {N}\}$
enumerate all formulae in this language in such a way that
![]() $\psi _i$
contains only constants among
$\psi _i$
contains only constants among
![]() $\dot x_0, \dot x_1, \ldots, \dot x_i$
. We also fix a ternary formula
$\dot x_0, \dot x_1, \ldots, \dot x_i$
. We also fix a ternary formula
![]() $\theta (\cdot,\cdot,\cdot )$
such that in any model of
$\theta (\cdot,\cdot,\cdot )$
such that in any model of
![]() ${\mathsf {KP}} + V = L(\mathbb {R})$
,
${\mathsf {KP}} + V = L(\mathbb {R})$
,
![]() $\theta $
defines the graph of an
$\theta $
defines the graph of an
![]() $\mathbb {R}$
-parametrized family of wellorders the union of whose fields include all of V. More precisely, we assume that, provably in
$\mathbb {R}$
-parametrized family of wellorders the union of whose fields include all of V. More precisely, we assume that, provably in
![]() ${\mathsf {KP}} + V = L(\mathbb {R})$
,
${\mathsf {KP}} + V = L(\mathbb {R})$
,
-
•
 $\theta $
holds of a triple
$\theta $
holds of a triple
 $(x,\alpha, a)$
only if
$(x,\alpha, a)$
only if
 $x\in \mathbb {R}$
and
$x\in \mathbb {R}$
and
 $\alpha $
is an ordinal and
$\alpha $
is an ordinal and -
• for every set a there is a real x and an ordinal
 $\alpha $
such that
$\alpha $
such that
 $\theta (x,\alpha,a)$
.
$\theta (x,\alpha,a)$
.
Such a formula is found easily e.g., by appealing to Steel [Reference Steel, Kechris, Löwe and Steel18, Section 1]. Finally, we fix two recursive injections
![]() $n(\cdot )$
and
$n(\cdot )$
and
![]() $m(\cdot )$
from
$m(\cdot )$
from
![]() $\{\psi _i:i\in \mathbb {N}\}$
into the set of odd integers and whose ranges are disjoint.
$\{\psi _i:i\in \mathbb {N}\}$
into the set of odd integers and whose ranges are disjoint.
In the game
![]() $G(A,x)$
, Players I and II together build a structure in the language of set theory containing certain real numbers and a partial function
$G(A,x)$
, Players I and II together build a structure in the language of set theory containing certain real numbers and a partial function
More specifically,
-
(1) During turn
 $2i+1$
, Player II plays a real number
$2i+1$
, Player II plays a real number
 $x_{2i+1}$
and either “accepts” or “rejects” the formula
$x_{2i+1}$
and either “accepts” or “rejects” the formula
 $\psi _i$
.
$\psi _i$
. -
(2) During turn
 $2i$
, Player I plays a real number
$2i$
, Player I plays a real number
 $x_{2i}$
. In addition, Player I may play a pair
$x_{2i}$
. In addition, Player I may play a pair
 $(j,k)$
and select a formula
$(j,k)$
and select a formula
 $\psi $
as the value of
$\psi $
as the value of
 $f(j,k)$
, but only if the following conditions are met:
$f(j,k)$
, but only if the following conditions are met:-
(a) Player II has previously accepted the formula “the unique x satisfying
 $\psi $
is an ordinal” and
$\psi $
is an ordinal” and -
(b) either
 $k = 0$
, or
$k = 0$
, or
 $f(j,k-1)$
has been defined previously, and, moreover, Player II has previously accepted the formula “the unique x satisfying
$f(j,k-1)$
has been defined previously, and, moreover, Player II has previously accepted the formula “the unique x satisfying
 $\psi $
is smaller than the unique x satisfying
$\psi $
is smaller than the unique x satisfying
 $f(j,k-1)$
.”
$f(j,k-1)$
.”
-
Let T be the collection of all formulae accepted by Player II. The rules of the game are:
-
(3) During the course of the game, Player II must play a,
 $x_\gamma $
, and
$x_\gamma $
, and
 $x_A$
. If so, let
$x_A$
. If so, let
 $i_a$
,
$i_a$
,
 $i_\gamma $
, and
$i_\gamma $
, and
 $i_A$
be such that
$i_A$
be such that
 $x_{i_a} = a$
,
$x_{i_a} = a$
,
 $x_{i_\gamma } = x_\gamma $
, and
$x_{i_\gamma } = x_\gamma $
, and
 $x_{i_A} = x_A$
.
$x_{i_A} = x_A$
. -
(4) T must be a complete, consistent theory containing the axioms:
-
(a)
 ${\mathsf {KP}} + V = L(\mathbb {R})$
;
${\mathsf {KP}} + V = L(\mathbb {R})$
; -
(b)
 $\dot x_i \in \mathbb {R}$
, for each
$\dot x_i \in \mathbb {R}$
, for each
 $i\in \mathbb {R}$
;
$i\in \mathbb {R}$
; -
(c)
 $\dot x_i(m) = k$
, but only if
$\dot x_i(m) = k$
, but only if
 $x_i(m) = k$
;
$x_i(m) = k$
; -
(d)
 $\varphi _\gamma (\dot x_{i_\gamma })$
+ “no proper initial segment of me satisfies
$\varphi _\gamma (\dot x_{i_\gamma })$
+ “no proper initial segment of me satisfies
 $\varphi _\gamma (\dot x_{i_\gamma })$
”; and
$\varphi _\gamma (\dot x_{i_\gamma })$
”; and -
(e) the Skolem axioms
as well as $$ \begin{align*}\exists x\in\mathbb{R}\, \chi(x) \to \chi(\dot x_{n(\chi)}),\end{align*} $$
for every formula
$$ \begin{align*}\exists x\in\mathbb{R}\, \chi(x) \to \chi(\dot x_{n(\chi)}),\end{align*} $$
for every formula $$ \begin{align*}\exists x\, \chi(x) \to \exists x\, \exists \alpha\in{\mathsf{Ord}}\, \Big(\theta(\dot x_{m(\chi)},\alpha, x) \wedge \chi(x)\Big), \end{align*} $$
$$ \begin{align*}\exists x\, \chi(x) \to \exists x\, \exists \alpha\in{\mathsf{Ord}}\, \Big(\theta(\dot x_{m(\chi)},\alpha, x) \wedge \chi(x)\Big), \end{align*} $$
 $\chi $
;
$\chi $
;
-
(f)
 $\varphi (\dot x_{i_a}, \dot x_{i_A})$
.
$\varphi (\dot x_{i_a}, \dot x_{i_A})$
.
Otherwise, Player II loses the game.
-
-
(5) If there is
 $j\in \mathbb {N}$
such that for every
$j\in \mathbb {N}$
such that for every
 $k\in \mathbb {N}$
, the value of
$k\in \mathbb {N}$
, the value of
 $f(j,k)$
is specified by Player I at some point in the game, then she wins; otherwise, Player II wins.
$f(j,k)$
is specified by Player I at some point in the game, then she wins; otherwise, Player II wins.
This is a game in which Player II attempts to construct a model that looks like
![]() $L_\gamma (\mathbb {R})$
and incorporates the reals specified by Player I. Because we demand that the theory contain the Skolem axioms, it will have a minimal model containing all reals played during the course of the game (and none other). We shall denote by
$L_\gamma (\mathbb {R})$
and incorporates the reals specified by Player I. Because we demand that the theory contain the Skolem axioms, it will have a minimal model containing all reals played during the course of the game (and none other). We shall denote by
![]() $M_p$
the model associated to a run p of the game. Condition (3) states that, during this game, Player I simultaneously carries out infinitely many attempts to find an infinite descending sequence in Player II’s model, and wins if one of those attempts is successful.
$M_p$
the model associated to a run p of the game. Condition (3) states that, during this game, Player I simultaneously carries out infinitely many attempts to find an infinite descending sequence in Player II’s model, and wins if one of those attempts is successful.
Clearly this is a
![]() $\boldsymbol \Sigma ^0_3$
game on
$\boldsymbol \Sigma ^0_3$
game on
![]() $\mathbb {R}$
for Player I (so a
$\mathbb {R}$
for Player I (so a
![]() $\boldsymbol \Pi ^0_3$
game for Player II). We need to show that Player II has a winning strategy in the game if, and only if,
$\boldsymbol \Pi ^0_3$
game for Player II). We need to show that Player II has a winning strategy in the game if, and only if,
![]() $a \in A$
i.e., if, and only if,
$a \in A$
i.e., if, and only if,
If (3.1) in fact holds, then Player II has a simple winning strategy obtained by playing the theory of
![]() $L_\gamma (\mathbb {R})$
and making sure that if x is a real played during the course of the game, then every real definable from x in
$L_\gamma (\mathbb {R})$
and making sure that if x is a real played during the course of the game, then every real definable from x in
![]() $L_\gamma (\mathbb {R})$
is also played at some point in the game. The point is that any winning strategy for Player II requires that she actually play the theory of
$L_\gamma (\mathbb {R})$
is also played at some point in the game. The point is that any winning strategy for Player II requires that she actually play the theory of
![]() $L_\gamma (\mathbb {R})$
; we verify this now.
$L_\gamma (\mathbb {R})$
; we verify this now.
To see this, let
![]() $\sigma $
be a winning strategy for Player II. Suppose that there is a run of the game consistent with
$\sigma $
be a winning strategy for Player II. Suppose that there is a run of the game consistent with
![]() $\sigma $
in which Player II accepts a formula not satisfied by
$\sigma $
in which Player II accepts a formula not satisfied by
![]() $L_\gamma (\mathbb {R})$
. Let X be a countable elementary substructure of some sufficiently large
$L_\gamma (\mathbb {R})$
. Let X be a countable elementary substructure of some sufficiently large
![]() $V_\kappa $
such that
$V_\kappa $
such that
![]() $\sigma \in X$
and let
$\sigma \in X$
and let
be the collapse embedding. Write
![]() $\bar \sigma = \pi ^{-1}(\sigma )$
and
$\bar \sigma = \pi ^{-1}(\sigma )$
and
![]() $\bar \gamma = \pi ^{-1}(\gamma )$
. Let
$\bar \gamma = \pi ^{-1}(\gamma )$
. Let
![]() $p_0$
be a partial play in W which is consistent with
$p_0$
be a partial play in W which is consistent with
![]() $\bar \sigma $
and in which Player II has accepted a formula not satisfied by
$\bar \sigma $
and in which Player II has accepted a formula not satisfied by
![]() $L_{\bar \gamma }(\mathbb {R}^W)$
. Observe that
$L_{\bar \gamma }(\mathbb {R}^W)$
. Observe that
![]() $\bar \sigma $
is simply the restriction of
$\bar \sigma $
is simply the restriction of
![]() $\sigma $
to partial plays belonging to W. Let
$\sigma $
to partial plays belonging to W. Let
![]() $h\subset \text {Coll}(\omega,\mathbb {R}^W)$
be W-generic, with
$h\subset \text {Coll}(\omega,\mathbb {R}^W)$
be W-generic, with
![]() $h \in V$
. Thus,
$h \in V$
. Thus,
![]() $\bar \gamma $
admits no h-nesting in
$\bar \gamma $
admits no h-nesting in
![]() $L[h]$
. (This is because of the elementarity between V and W:
$L[h]$
. (This is because of the elementarity between V and W:
![]() $\gamma $
admits no g-nesting in
$\gamma $
admits no g-nesting in
![]() $V[g]$
and this is forced over V by a condition
$V[g]$
and this is forced over V by a condition
![]() $g_0$
. Without loss of generality,
$g_0$
. Without loss of generality,
![]() $g_0$
belongs to X and thus to W, and h extends
$g_0$
belongs to X and thus to W, and h extends
![]() $g_0$
. The existence of a g-nesting over
$g_0$
. The existence of a g-nesting over
![]() $\gamma $
is easily seen to be
$\gamma $
is easily seen to be
![]() $\Sigma ^1_1(g, x_\gamma )$
where
$\Sigma ^1_1(g, x_\gamma )$
where
![]() $x_\gamma $
is a real coding
$x_\gamma $
is a real coding
![]() $\gamma $
, and thus first-order expressible over the next
$\gamma $
, and thus first-order expressible over the next
![]() $(g,x_\gamma )$
-admissible.) Working in
$(g,x_\gamma )$
-admissible.) Working in
![]() $L[h]$
, extend
$L[h]$
, extend
![]() $p_0$
by having Player II play according to
$p_0$
by having Player II play according to
![]() $\bar \sigma $
and having Player I play recursive reals, and selecting values for f as in the proof of [Reference Welch19, Theorem 4] (see the proof of (4) on pp. 426–428). The values of f are natural numbers, so every move by Player I results in an extension of
$\bar \sigma $
and having Player I play recursive reals, and selecting values for f as in the proof of [Reference Welch19, Theorem 4] (see the proof of (4) on pp. 426–428). The values of f are natural numbers, so every move by Player I results in an extension of
![]() $p_0$
which belongs to W and, hence, to the domain of
$p_0$
which belongs to W and, hence, to the domain of
![]() $\bar \sigma $
, so that this procedure is well defined. Although it is not immediately clear whether the full play p belongs to W, it certainly belongs to
$\bar \sigma $
, so that this procedure is well defined. Although it is not immediately clear whether the full play p belongs to W, it certainly belongs to
![]() $L[h]$
and thus to V. In addition, all initial segments of p are consistent with
$L[h]$
and thus to V. In addition, all initial segments of p are consistent with
![]() $\bar \sigma $
and hence with
$\bar \sigma $
and hence with
![]() $\sigma $
, so that p is a play won by Player II. However, the proof of [Reference Welch20, Theorem 2] (appealing to that of [Reference Welch19, Theorem 4]) shows that p is a winning play for Player I unless
$\sigma $
, so that p is a play won by Player II. However, the proof of [Reference Welch20, Theorem 2] (appealing to that of [Reference Welch19, Theorem 4]) shows that p is a winning play for Player I unless
![]() $\bar \gamma $
admits an h-nesting in
$\bar \gamma $
admits an h-nesting in
![]() $L[h]$
, so we have reached a contradiction, thus proving the claim.
$L[h]$
, so we have reached a contradiction, thus proving the claim.
Suppose that
![]() $\sigma $
is a winning strategy for Player II in the game. To each
$\sigma $
is a winning strategy for Player II in the game. To each
![]() $b \in \mathcal {P}_{\omega _1}(\mathbb {R})$
, we shall associate the play
$b \in \mathcal {P}_{\omega _1}(\mathbb {R})$
, we shall associate the play
![]() $p_b$
of the game that results from Player II playing according to
$p_b$
of the game that results from Player II playing according to
![]() $\sigma $
, and Player I enumerating the reals of b (in any fixed order) and not specifying any values of f. Denote by
$\sigma $
, and Player I enumerating the reals of b (in any fixed order) and not specifying any values of f. Denote by
![]() $M_b$
the minimal model of the theory whose reals are precisely the reals played in the course of
$M_b$
the minimal model of the theory whose reals are precisely the reals played in the course of
![]() $p_b$
(so in particular
$p_b$
(so in particular
![]() $b \subset \mathbb {R}^{M_b}$
). Because
$b \subset \mathbb {R}^{M_b}$
). Because
![]() $\sigma $
demands that Player II play the theory of
$\sigma $
demands that Player II play the theory of
![]() $L_\gamma (\mathbb {R})$
, M is wellfounded and thus of the form
$L_\gamma (\mathbb {R})$
, M is wellfounded and thus of the form
 $L_{\gamma _b}(\mathbb {R}^{M_b})$
. The proof of the subclaim on p. 116 of Martin–Steel [Reference Martin, Steel, Kechris, Löwe and Steel15] shows that if
$L_{\gamma _b}(\mathbb {R}^{M_b})$
. The proof of the subclaim on p. 116 of Martin–Steel [Reference Martin, Steel, Kechris, Löwe and Steel15] shows that if
![]() $c\in \mathcal {P}_{\omega _1}(\mathbb {R})$
and
$c\in \mathcal {P}_{\omega _1}(\mathbb {R})$
and
![]() $b\subset c$
, then
$b\subset c$
, then
![]() $\mathbb {R}^{M_b} \subset \mathbb {R}^{M_c}$
and there is a (unique) elementary embedding from
$\mathbb {R}^{M_b} \subset \mathbb {R}^{M_c}$
and there is a (unique) elementary embedding from
 $L_{\gamma _b}(\mathbb {R}^{M_b})$
into
$L_{\gamma _b}(\mathbb {R}^{M_b})$
into
![]() $L_{\gamma _c}(\mathbb {R}^{M_c})$
obtained by mapping each real to itself and each element of
$L_{\gamma _c}(\mathbb {R}^{M_c})$
obtained by mapping each real to itself and each element of
 $L_{\gamma _b}(\mathbb {R}^{M_b})$
(which is definable from some real
$L_{\gamma _b}(\mathbb {R}^{M_b})$
(which is definable from some real
![]() $x \in \mathbb {R}^{M_b}$
) to the element of
$x \in \mathbb {R}^{M_b}$
) to the element of
![]() $L_{\gamma _c}(\mathbb {R}^{M_c})$
that has the same definition. The directed system
$L_{\gamma _c}(\mathbb {R}^{M_c})$
that has the same definition. The directed system
 $$ \begin{align*}\mathcal{D} = \{L_{\gamma_b}(\mathbb{R}^{M_b}):b\in\mathcal{P}_{\omega_1}(\mathbb{R})\}\end{align*} $$
$$ \begin{align*}\mathcal{D} = \{L_{\gamma_b}(\mathbb{R}^{M_b}):b\in\mathcal{P}_{\omega_1}(\mathbb{R})\}\end{align*} $$
is countably closed, so its direct limit is wellfounded and hence of the form
![]() $L_{\gamma ^*}(\mathbb {R})$
. Because of rule (4d) of the game,
$L_{\gamma ^*}(\mathbb {R})$
. Because of rule (4d) of the game,
so
![]() $\gamma ^* = \gamma $
. By rule (4f),
$\gamma ^* = \gamma $
. By rule (4f),
![]() $L_\gamma (\mathbb {R})\models \varphi (a)$
. This completes the proof of the lemma.⊣
$L_\gamma (\mathbb {R})\models \varphi (a)$
. This completes the proof of the lemma.⊣
4 Integrating Borel Games
In this section, we prove Theorem 4.1, a general result on games of length
![]() $\omega ^2$
and the complexity of winning strategies of games on reals. It is obtained by “integrating” winning strategies for games on
$\omega ^2$
and the complexity of winning strategies of games on reals. It is obtained by “integrating” winning strategies for games on
![]() $\mathbb {N}$
, provided they are obtained in a sufficiently uniform way. All the various parts of the proof of Theorem 4.1 are already present in the literature, but the abstraction might not be immediately obvious, so we lay out all the main points for the reader’s convenience. We mention that, although we state the theorem for Borel pointclasses, it can be extended to larger classes under large-cardinal assumptions. We leave these generalizations to the reader. Below,
$\mathbb {N}$
, provided they are obtained in a sufficiently uniform way. All the various parts of the proof of Theorem 4.1 are already present in the literature, but the abstraction might not be immediately obvious, so we lay out all the main points for the reader’s convenience. We mention that, although we state the theorem for Borel pointclasses, it can be extended to larger classes under large-cardinal assumptions. We leave these generalizations to the reader. Below,
![]() ${\mathsf {KPi}}$
denotes the extension of
${\mathsf {KPi}}$
denotes the extension of
![]() ${\mathsf {KP}}$
by the axiom asserting that every set is contained in an admissible set. Admissible ordinals which are limits of admissibles are called recursively inaccessible ordinals; x-recursively inaccessible ordinals and
${\mathsf {KP}}$
by the axiom asserting that every set is contained in an admissible set. Admissible ordinals which are limits of admissibles are called recursively inaccessible ordinals; x-recursively inaccessible ordinals and
![]() $\mathbb {R}$
-recursively inaccessible ordinals are defined similarly. For other undefined notions below, we refer the reader to Moschovakis [Reference Moschovakis17].
$\mathbb {R}$
-recursively inaccessible ordinals are defined similarly. For other undefined notions below, we refer the reader to Moschovakis [Reference Moschovakis17].
Theorem 4.1 (
 ${\mathsf {ZFC}}$
)
${\mathsf {ZFC}}$
)
Let
![]() $\Delta ^0_1\subset \Gamma \subset \Delta ^1_1$
be an
$\Delta ^0_1\subset \Gamma \subset \Delta ^1_1$
be an
![]() $\omega $
-parametrized pointclass and let
$\omega $
-parametrized pointclass and let
![]() $\boldsymbol \Gamma $
be the associated boldface pointclass. Suppose that
$\boldsymbol \Gamma $
be the associated boldface pointclass. Suppose that
![]() $\Gamma $
is closed under recursive substitutions, finite unions, and finite intersections. Let
$\Gamma $
is closed under recursive substitutions, finite unions, and finite intersections. Let
![]() $\phi $
be some fixed formula in the language of set theory and let
$\phi $
be some fixed formula in the language of set theory and let
if such exists.
Suppose that for a Turing cone of x, every
![]() $\Gamma (x)$
game for which Player I has a winning strategy has a winning strategy in
$\Gamma (x)$
game for which Player I has a winning strategy has a winning strategy in
![]() $L_{\gamma _x}[x]$
, and let
$L_{\gamma _x}[x]$
, and let
![]() $\gamma _{\mathbb {R}}$
be the least
$\gamma _{\mathbb {R}}$
be the least
![]() $\mathbb {R}$
-recursively inaccessible ordinal such that
$\mathbb {R}$
-recursively inaccessible ordinal such that
 $$ \begin{align*}\Vdash^{L(\mathbb{R})}_{\text{Coll}(\omega,\mathbb{R})}L_{\gamma_{\mathbb{R}}}[g]\models \phi(g).\end{align*} $$
$$ \begin{align*}\Vdash^{L(\mathbb{R})}_{\text{Coll}(\omega,\mathbb{R})}L_{\gamma_{\mathbb{R}}}[g]\models \phi(g).\end{align*} $$
Then,
-
(1)
 $\Game ^{\mathbb {R}}\boldsymbol \Gamma \subset \Sigma _1^{L_{\gamma _{\mathbb {R}}}(\mathbb {R})}$
and
$\Game ^{\mathbb {R}}\boldsymbol \Gamma \subset \Sigma _1^{L_{\gamma _{\mathbb {R}}}(\mathbb {R})}$
and -
(2) Suppose
 $\boldsymbol \Gamma $
has the scale property and that
$\boldsymbol \Gamma $
has the scale property and that
 $L_{\gamma _{\mathbb {R}}}(\mathbb {R})\models {\mathsf {AD}}$
. Then, all games of length
$L_{\gamma _{\mathbb {R}}}(\mathbb {R})\models {\mathsf {AD}}$
. Then, all games of length
 $\omega ^2$
with payoff in
$\omega ^2$
with payoff in
 $\boldsymbol \Gamma $
and moves in
$\boldsymbol \Gamma $
and moves in
 $\mathbb {N}$
are determined.
$\mathbb {N}$
are determined.
Proof Before proving the theorem, let us mention the following lemma which will be used repeatedly without mention:
Lemma 4.2. Let
![]() $\alpha $
be an ordinal. Then, the following are equivalent:
$\alpha $
be an ordinal. Then, the following are equivalent:
-
(1)
 $L_\alpha (\mathbb {R})\models {\mathsf {KP}}$
.
$L_\alpha (\mathbb {R})\models {\mathsf {KP}}$
. -
(2)
 $L_\alpha (\mathbb {R})\models $
“
$L_\alpha (\mathbb {R})\models $
“
 $\Vdash _{\text {Coll}(\omega,\mathbb {R})}{\mathsf {KP}}$
.”
$\Vdash _{\text {Coll}(\omega,\mathbb {R})}{\mathsf {KP}}$
.” -
(3) If
 $g\subset \text {Coll}(\omega,\mathbb {R})$
is
$g\subset \text {Coll}(\omega,\mathbb {R})$
is
 $L(\mathbb {R})$
-generic, then
$L(\mathbb {R})$
-generic, then
 $L_\alpha [g]\models {\mathsf {KP}}$
.
$L_\alpha [g]\models {\mathsf {KP}}$
.
And similarly for
![]() ${\mathsf {KPi}}$
.
${\mathsf {KPi}}$
.
Proof We prove the part of the lemma which concerns
![]() ${\mathsf {KP}}$
. Suppose
${\mathsf {KP}}$
. Suppose
![]() $g\subset \text {Coll}(\omega,\mathbb {R})$
is
$g\subset \text {Coll}(\omega,\mathbb {R})$
is
![]() $L(\mathbb {R})$
-generic and
$L(\mathbb {R})$
-generic and
![]() $L_\alpha [g]\models {\mathsf {KP}}$
. Since
$L_\alpha [g]\models {\mathsf {KP}}$
. Since
![]() $\mathbb {R} \in L_\alpha [g]$
,
$\mathbb {R} \in L_\alpha [g]$
,
![]() $L_\alpha (\mathbb {R})\models {\mathsf {KP}}$
. It is verified in the course of the proof of Mathias [Reference Mathias16, Theorem 10.17] that this implies
$L_\alpha (\mathbb {R})\models {\mathsf {KP}}$
. It is verified in the course of the proof of Mathias [Reference Mathias16, Theorem 10.17] that this implies
Now, suppose that g is
![]() $L(\mathbb {R})$
-generic and
$L(\mathbb {R})$
-generic and
Since g is
![]() $L(\mathbb {R})$
-generic, it decides every formula in the forcing language, in the sense that for every
$L(\mathbb {R})$
-generic, it decides every formula in the forcing language, in the sense that for every
![]() $\varphi $
, there is a condition in g forcing
$\varphi $
, there is a condition in g forcing
![]() $\varphi $
or
$\varphi $
or
![]() $\lnot \varphi $
. By combining Mathias [Reference Mathias16, Theorem 10.11] and Mathias [Reference Mathias16, Proposition 10.12], we see that
$\lnot \varphi $
. By combining Mathias [Reference Mathias16, Theorem 10.11] and Mathias [Reference Mathias16, Proposition 10.12], we see that
![]() $L_\alpha [g]\models {\mathsf {KP}}$
.
$L_\alpha [g]\models {\mathsf {KP}}$
.
To obtain the part of the lemma which concerns
![]() ${\mathsf {KPi}}$
, we simply apply the first part to every
${\mathsf {KPi}}$
, we simply apply the first part to every
![]() $\mathbb {R}$
-admissible ordinal
$\mathbb {R}$
-admissible ordinal
![]() ${\leq }\ \alpha $
.⊣
${\leq }\ \alpha $
.⊣
We begin with the proof of (1). It is based on the argument from [Reference Aguilera and Müller4] for showing that the
 $\Game ^{\mathbb {R}}\Pi ^1_{n+1}$
subsets of
$\Game ^{\mathbb {R}}\Pi ^1_{n+1}$
subsets of
![]() $\mathbb {R}$
are all
$\mathbb {R}$
are all
![]() $\Sigma _1$
-definable over the least inner model of
$\Sigma _1$
-definable over the least inner model of
![]() ${\mathsf {ZF}}$
with n Woodin cardinals containing the reals. The details are made simpler by the fact that
${\mathsf {ZF}}$
with n Woodin cardinals containing the reals. The details are made simpler by the fact that
![]() $\Gamma \subset \Delta ^1_1$
, but harder by the fact that we work with fragments of
$\Gamma \subset \Delta ^1_1$
, but harder by the fact that we work with fragments of
![]() ${\mathsf {ZFC}}$
. We shall use the notation from [Reference Aguilera and Müller4].
${\mathsf {ZFC}}$
. We shall use the notation from [Reference Aguilera and Müller4].
Let G be a game of length
![]() $\omega $
on
$\omega $
on
![]() $\mathbb {R}$
with payoff in
$\mathbb {R}$
with payoff in
![]() $\boldsymbol \Gamma $
. For simplicity, let us assume the payoff is in
$\boldsymbol \Gamma $
. For simplicity, let us assume the payoff is in
![]() $\Gamma $
. Given
$\Gamma $
. Given
![]() $A\subset \mathbb {R}$
, denote by
$A\subset \mathbb {R}$
, denote by
![]() $G_A$
the variant of the game G in which each player is required to choose each individual move from the elements of A. If A is countable and
$G_A$
the variant of the game G in which each player is required to choose each individual move from the elements of A. If A is countable and
![]() $x_A$
is a real coding A, then
$x_A$
is a real coding A, then
![]() $G_A$
can be simulated by a game on natural numbers, which we denote by
$G_A$
can be simulated by a game on natural numbers, which we denote by
![]() $G(x_A)$
. We first show:
$G(x_A)$
. We first show:
Claim 4.3. The following are equivalent:
-
(1) Player I has a winning strategy in G and
-
(2) There is a closed, cofinal
 $C\subset \mathcal {P}_{\omega _1}(\mathbb {R})$
such that Player I has a winning strategy in
$C\subset \mathcal {P}_{\omega _1}(\mathbb {R})$
such that Player I has a winning strategy in
 $G_A$
for all
$G_A$
for all
 $A \in C$
.
$A \in C$
.
Proof Suppose Player I has a winning strategy
![]() $\sigma $
in G and let C be the set of all countable sets of reals closed under
$\sigma $
in G and let C be the set of all countable sets of reals closed under
![]() $\sigma $
. Then C is closed and cofinal and Player I has a winning strategy in
$\sigma $
. Then C is closed and cofinal and Player I has a winning strategy in
![]() $G_A$
for all
$G_A$
for all
![]() $A\in C$
. The argument is symmetric for Player I and II and G is a Borel game, so it is determined, by Martin’s theorem [Reference Martin14]. Therefore, the claim follows.
$A\in C$
. The argument is symmetric for Player I and II and G is a Borel game, so it is determined, by Martin’s theorem [Reference Martin14]. Therefore, the claim follows.
Thus if Player I has a winning strategy in G, then she has one in
![]() $G_A$
for almost every A. It follows that if
$G_A$
for almost every A. It follows that if
![]() $x_A$
codes A, then Player I has a winning strategy in
$x_A$
codes A, then Player I has a winning strategy in
![]() $G(x_A)$
. By hypothesis, there is one such strategy in
$G(x_A)$
. By hypothesis, there is one such strategy in
![]() $L_{\gamma _{x_A}}[x_A]$
. Let
$L_{\gamma _{x_A}}[x_A]$
. Let
![]() $\psi (x_A)$
be the
$\psi (x_A)$
be the
![]() $\Sigma _1$
formula expressing in
$\Sigma _1$
formula expressing in
![]() ${\mathsf {KPi}}$
that there is a winning strategy for Player I for the game
${\mathsf {KPi}}$
that there is a winning strategy for Player I for the game
![]() $G(x_A)$
.
$G(x_A)$
.
Claim 4.4. The following are equivalent:
-
(1) Player I has a winning strategy in G and
-
(2)
 $\Vdash ^{L_{\gamma _{\mathbb {R}}}(\mathbb {R})}_{\text {Coll}(\omega,\mathbb {R})}\psi (g)$
.
$\Vdash ^{L_{\gamma _{\mathbb {R}}}(\mathbb {R})}_{\text {Coll}(\omega,\mathbb {R})}\psi (g)$
.
Proof Suppose Player I has a winning strategy in G and let W be the transitive collapse of a countable elementary substructure of some large
![]() $V_\kappa $
. Let
$V_\kappa $
. Let
![]() $A = \mathbb {R}^W$
. By the previous claim, Player I has a winning strategy in
$A = \mathbb {R}^W$
. By the previous claim, Player I has a winning strategy in
![]() $G_A$
. Let
$G_A$
. Let
![]() $h\subset \text {Coll}(\omega,A)$
be W-generic. Thus, h codes A, so
$h\subset \text {Coll}(\omega,A)$
be W-generic. Thus, h codes A, so
Now,
![]() $\psi $
is a
$\psi $
is a
![]() $\Sigma _1$
formula. By a theorem of Mathias [Reference Mathias16], every formula true in
$\Sigma _1$
formula. By a theorem of Mathias [Reference Mathias16], every formula true in
![]() $L_{\gamma _h}[h]$
is forced; it follows that
$L_{\gamma _h}[h]$
is forced; it follows that
The elementarity between W and V yields that
as desired. Suppose now that Player I does not have a winning strategy in G. Then, by Borel determinacy, Player II has a winning strategy in G. Repeating the above argument, we see that

It follows that we cannot possibly have
 $$ \begin{align*}\Vdash^{L_{\gamma_{\mathbb{R}}}(\mathbb{R})}_{\text{Coll}(\omega,\mathbb{R})}\psi(g),\end{align*} $$
$$ \begin{align*}\Vdash^{L_{\gamma_{\mathbb{R}}}(\mathbb{R})}_{\text{Coll}(\omega,\mathbb{R})}\psi(g),\end{align*} $$
for
![]() $\psi $
is a
$\psi $
is a
![]() $\Sigma _1$
formula, so otherwise by forcing over
$\Sigma _1$
formula, so otherwise by forcing over
![]() $L(\mathbb {R})$
we should be able to construct winning strategies for both players in
$L(\mathbb {R})$
we should be able to construct winning strategies for both players in
![]() $G(g)$
, which is absurd.
$G(g)$
, which is absurd.
Since
![]() $\psi $
is
$\psi $
is
![]() $\Sigma _1$
, this last claim completes the proof of (1).
$\Sigma _1$
, this last claim completes the proof of (1).
Let us proceed now to the proof of (2); we sketch it. Let
![]() $\gamma = \gamma _{\mathbb {R}}$
. The argument is similar to the one used in [Reference Aguilera and Müller4] to prove Projective Determinacy for games of length
$\gamma = \gamma _{\mathbb {R}}$
. The argument is similar to the one used in [Reference Aguilera and Müller4] to prove Projective Determinacy for games of length
![]() $\omega ^2$
. The difference is that we have not shown in general that
$\omega ^2$
. The difference is that we have not shown in general that
 $$ \begin{align*}\Sigma_1^{L_{\gamma}(\mathbb{R})}\subset\Game^{\mathbb{R}}\boldsymbol\Gamma,\end{align*} $$
$$ \begin{align*}\Sigma_1^{L_{\gamma}(\mathbb{R})}\subset\Game^{\mathbb{R}}\boldsymbol\Gamma,\end{align*} $$
although we conjecture that it is true, under the hypotheses of the theorem.
Suppose that
![]() $L_{\gamma }(\mathbb {R})\models {\mathsf {AD}}$
. By the Kechris–Woodin determinacy transfer theorem [Reference Kechris and Woodin13], all subsets of
$L_{\gamma }(\mathbb {R})\models {\mathsf {AD}}$
. By the Kechris–Woodin determinacy transfer theorem [Reference Kechris and Woodin13], all subsets of
![]() $\mathbb {R}$
which are
$\mathbb {R}$
which are
![]() $\Sigma _1$
-definable over
$\Sigma _1$
-definable over
![]() $L_{\gamma }(\mathbb {R})$
are determined.Footnote
2
By (1), all sets in
$L_{\gamma }(\mathbb {R})$
are determined.Footnote
2
By (1), all sets in
![]() $\Game ^{\mathbb {R}}\boldsymbol \Gamma $
are determined. Applying Steel [Reference Steel, Kechris, Löwe and Steel18, Theorem 2.1] to
$\Game ^{\mathbb {R}}\boldsymbol \Gamma $
are determined. Applying Steel [Reference Steel, Kechris, Löwe and Steel18, Theorem 2.1] to
![]() $L_{\gamma }(\mathbb {R})$
, we see that
$L_{\gamma }(\mathbb {R})$
, we see that
 $\Sigma _1^{L_{\gamma }(\mathbb {R})}$
has the scale property. Because
$\Sigma _1^{L_{\gamma }(\mathbb {R})}$
has the scale property. Because
![]() $L_{\gamma }(\mathbb {R})$
is admissible by hypothesis,
$L_{\gamma }(\mathbb {R})$
is admissible by hypothesis,
 $\Sigma _1^{L_\gamma (\mathbb {R})}$
is closed under real universal quantification, so, by a well-known theorem of Moschovakis (see [Reference Moschovakis17, 4E.7]), every relation in
$\Sigma _1^{L_\gamma (\mathbb {R})}$
is closed under real universal quantification, so, by a well-known theorem of Moschovakis (see [Reference Moschovakis17, 4E.7]), every relation in
 $\Sigma _1^{L_\gamma (\mathbb {R})}$
(hence every relation in
$\Sigma _1^{L_\gamma (\mathbb {R})}$
(hence every relation in
![]() $\Game ^{\mathbb {R}}\boldsymbol \Gamma $
) can be uniformized by a function in
$\Game ^{\mathbb {R}}\boldsymbol \Gamma $
) can be uniformized by a function in
 $\Sigma _1^{L_\gamma (\mathbb {R})} $
.
$\Sigma _1^{L_\gamma (\mathbb {R})} $
.
Claim 4.5. Every
![]() $\boldsymbol \Gamma $
game on reals has a winning strategy which is
$\boldsymbol \Gamma $
game on reals has a winning strategy which is
![]() $\Sigma _1$
-definable over
$\Sigma _1$
-definable over
![]() $L_{\gamma }(\mathbb {R})$
.
$L_{\gamma }(\mathbb {R})$
.
Proof Sketch This follows from adapting the proof of Moschovakis’ third periodicity theorem [Reference Moschovakis17, Theorem 6E.1] to games on
![]() $\mathbb {R}$
using the assumption that
$\mathbb {R}$
using the assumption that
![]() $\boldsymbol \Gamma $
has the scale property. The strategy is built from a scale on a
$\boldsymbol \Gamma $
has the scale property. The strategy is built from a scale on a
![]() $\Game ^{\mathbb {R}}\boldsymbol \Gamma $
set and a uniformizing function, both of which can be taken to belong to
$\Game ^{\mathbb {R}}\boldsymbol \Gamma $
set and a uniformizing function, both of which can be taken to belong to
 $\Sigma _1^{L_{\gamma }(\mathbb {R})}$
. We refer the reader to [Reference Aguilera2, Lemma 3] for a few more details.⊣
$\Sigma _1^{L_{\gamma }(\mathbb {R})}$
. We refer the reader to [Reference Aguilera2, Lemma 3] for a few more details.⊣
Now, the determinacy of
![]() $\boldsymbol \Gamma $
games of length
$\boldsymbol \Gamma $
games of length
![]() $\omega ^2$
follows by the following general fact:
$\omega ^2$
follows by the following general fact:
Lemma 4.6. Let
![]() $\Lambda $
and
$\Lambda $
and
![]() $\Pi $
be pointclasses closed under continuous preimages and finite unions and intersections. Suppose that
$\Pi $
be pointclasses closed under continuous preimages and finite unions and intersections. Suppose that
![]() $\Lambda \subset \Pi $
and every game on reals in
$\Lambda \subset \Pi $
and every game on reals in
![]() $\Lambda $
has a winning strategy in
$\Lambda $
has a winning strategy in
![]() $\Pi $
. Suppose moreover that
$\Pi $
. Suppose moreover that
![]() $\Pi $
is closed under real quantifiers and countable unions and has the uniformization property, and every game on
$\Pi $
is closed under real quantifiers and countable unions and has the uniformization property, and every game on
![]() $\mathbb {N}$
in
$\mathbb {N}$
in
![]() $\Pi $
is determined. Then, every game of length
$\Pi $
is determined. Then, every game of length
![]() $\omega ^2$
with moves in
$\omega ^2$
with moves in
![]() $\mathbb {N}$
and payoff in
$\mathbb {N}$
and payoff in
![]() $\Lambda $
is determined.
$\Lambda $
is determined.
Proof Sketch This can be proved by localising the argument of Blass [Reference Blass6] that
![]() ${\mathsf {AD}}_{\mathbb {R}}$
implies that every game of length
${\mathsf {AD}}_{\mathbb {R}}$
implies that every game of length
![]() $\omega ^2$
is determined. We refer the reader to [Reference Aguilera1, Lemma 3.11] for a few more details.⊣
$\omega ^2$
is determined. We refer the reader to [Reference Aguilera1, Lemma 3.11] for a few more details.⊣
Let
![]() $\Lambda = \boldsymbol \Gamma $
and
$\Lambda = \boldsymbol \Gamma $
and
 $\Pi = \Sigma _1^{L_\gamma (\mathbb {R})}$
. Since
$\Pi = \Sigma _1^{L_\gamma (\mathbb {R})}$
. Since
![]() $\gamma $
is
$\gamma $
is
![]() $\mathbb {R}$
-admissible,
$\mathbb {R}$
-admissible,
 $\Sigma _1^{L_\gamma (\mathbb {R})}$
is closed under real quantifiers and countable unions. Thus, the hypotheses of the lemma are satisfied, so every game of length
$\Sigma _1^{L_\gamma (\mathbb {R})}$
is closed under real quantifiers and countable unions. Thus, the hypotheses of the lemma are satisfied, so every game of length
![]() $\omega ^2$
on
$\omega ^2$
on
![]() $\mathbb {N}$
with payoff in
$\mathbb {N}$
with payoff in
![]() $\boldsymbol \Gamma $
is determined. This completes the proof of the theorem.⊣
$\boldsymbol \Gamma $
is determined. This completes the proof of the theorem.⊣
Remark 4.7. Although we did not need this fact, we point out that the proof of Lemma 4.6 gives a bound on the complexity of winning strategies for
![]() $\Lambda $
games of length
$\Lambda $
games of length
![]() $\omega ^2$
with moves in
$\omega ^2$
with moves in
![]() $\mathbb {N}$
. These games are obtained from the strategies for games on
$\mathbb {N}$
. These games are obtained from the strategies for games on
![]() $\mathbb {R}$
with payoff
$\mathbb {R}$
with payoff
![]() $\Lambda $
, together with appropriate uniformizing functions. The hypotheses of the lemma imply that these strategies and functions belong to
$\Lambda $
, together with appropriate uniformizing functions. The hypotheses of the lemma imply that these strategies and functions belong to
![]() $\Pi $
, and the closure properties on
$\Pi $
, and the closure properties on
![]() $\Pi $
will imply that the strategies for
$\Pi $
will imply that the strategies for
![]() $\Lambda $
games of length
$\Lambda $
games of length
![]() $\omega ^2$
with moves in
$\omega ^2$
with moves in
![]() $\mathbb {N}$
also belong to
$\mathbb {N}$
also belong to
![]() $\Pi $
.
$\Pi $
.
5 Putting Everything Together
Before proving the main theorem, we need a lemma that characterizes
![]() $\beta _g$
without referring to generic extensions:
$\beta _g$
without referring to generic extensions:
Lemma 5.1. Let
![]() $g\subset \text {Coll}(\omega,\mathbb {R})$
be
$g\subset \text {Coll}(\omega,\mathbb {R})$
be
![]() $L(\mathbb {R})$
-generic. Let
$L(\mathbb {R})$
-generic. Let
![]() $\beta = \beta _g$
, as computed in
$\beta = \beta _g$
, as computed in
![]() $L[g]$
. Then,
$L[g]$
. Then,
![]() $\beta $
is the least ordinal such that
$\beta $
is the least ordinal such that
Proof Putting together Theorems 2.1, 3.11, and 4.2 of Hachtman [Reference Hachtman9], we see that
![]() $\beta $
is least such that
$\beta $
is least such that
 $$ \begin{align*}L_\beta[g]\models\boldsymbol\Pi^1_2\text{-}\mathsf{MI}_{\mathbb{N}}.\end{align*} $$
$$ \begin{align*}L_\beta[g]\models\boldsymbol\Pi^1_2\text{-}\mathsf{MI}_{\mathbb{N}}.\end{align*} $$
Since
![]() $\boldsymbol \Pi ^1_2$
is the same as
$\boldsymbol \Pi ^1_2$
is the same as
![]() $\Pi _1$
over
$\Pi _1$
over
![]() $H(\omega _1)$
(with parameters), provably in
$H(\omega _1)$
(with parameters), provably in
![]() ${\mathsf {KPi}}$
,
${\mathsf {KPi}}$
,
![]() $\beta $
is least such that
$\beta $
is least such that
Using the fact that in
![]() $L_\beta [g]$
there is a bijection between
$L_\beta [g]$
there is a bijection between
![]() $\mathbb {N}$
and
$\mathbb {N}$
and
![]() $\mathbb {R}^V$
, it is easy to show, by an argument like the one of Lemma 2.1, that
$\mathbb {R}^V$
, it is easy to show, by an argument like the one of Lemma 2.1, that
To prove the converse, let
![]() $\eta $
be least such that
$\eta $
be least such that
We show that
Thus, let
![]() $\Phi $
be a
$\Phi $
be a
![]() $\Pi _1$
operator in
$\Pi _1$
operator in
![]() $L_\eta [g]$
, say, given by
$L_\eta [g]$
, say, given by
for some set
![]() $a\in L_\eta [g]$
. Working in
$a\in L_\eta [g]$
. Working in
![]() $L_\eta (\mathbb {R})$
, let
$L_\eta (\mathbb {R})$
, let
![]() $\tau $
be a
$\tau $
be a
![]() $\text {Coll}(\omega,\mathbb {R})$
-name for a and let
$\text {Coll}(\omega,\mathbb {R})$
-name for a and let
![]() $p_0$
be a condition forcing that
$p_0$
be a condition forcing that
![]() $\Phi $
is monotone. We consider the following operator
$\Phi $
is monotone. We consider the following operator
![]() $\Psi $
that inductively constructs a name for a set of natural numbers:
$\Psi $
that inductively constructs a name for a set of natural numbers:
Since
![]() $\phi $
is
$\phi $
is
![]() $\Pi _1$
,
$\Pi _1$
,
![]() $\Psi $
is a
$\Psi $
is a
![]() $\Pi _1$
operator using
$\Pi _1$
operator using
![]() $\tau $
,
$\tau $
,
![]() $p_0$
and
$p_0$
and
![]() $\text {Coll}(\omega,\mathbb {R})$
as parameters. It is monotone, for if
$\text {Coll}(\omega,\mathbb {R})$
as parameters. It is monotone, for if
![]() $X\subset Y$
, and
$X\subset Y$
, and
![]() $(p,n)\in \Psi (X)$
, then
$(p,n)\in \Psi (X)$
, then
![]() $p \leq p_0$
and
$p \leq p_0$
and
![]() $p\Vdash \phi (n,X[g],\tau [g])$
. But then p forces that
$p\Vdash \phi (n,X[g],\tau [g])$
. But then p forces that
![]() $\phi $
is monotone, so that
$\phi $
is monotone, so that
![]() $p\Vdash \phi (n,Y[g],\tau [g])$
; thus,
$p\Vdash \phi (n,Y[g],\tau [g])$
; thus,
![]() $(p,n) \in Y$
. It follows that
$(p,n) \in Y$
. It follows that
![]() $\Psi $
has a least fixed point,
$\Psi $
has a least fixed point,
![]() $\Psi ^\infty $
. Since
$\Psi ^\infty $
. Since
![]() $\Psi ^\infty \in L_\eta [g]$
,
$\Psi ^\infty \in L_\eta [g]$
,
![]() $L_\eta [g]$
can compute
$L_\eta [g]$
can compute
![]() $\Psi ^\infty [g]$
and it is easy to see that
$\Psi ^\infty [g]$
and it is easy to see that
so
![]() $L_\eta [g]$
satisfies
$L_\eta [g]$
satisfies
![]() $\Pi _1$
-
$\Pi _1$
-
![]() $\mathsf {MI}_{\mathbb {N}}$
, as claimed.⊣
$\mathsf {MI}_{\mathbb {N}}$
, as claimed.⊣
We are now ready to prove the main theorem:
Theorem 5.2. The following are equivalent over
![]() ${\mathsf {ZFC}}$
:
${\mathsf {ZFC}}$
:
-
(1)
 $\boldsymbol \Sigma ^0_3$
games of length
$\boldsymbol \Sigma ^0_3$
games of length
 $\omega ^2$
with moves in
$\omega ^2$
with moves in
 $\mathbb {N}$
are determined.
$\mathbb {N}$
are determined. -
(2) There is a transitive model of
 ${\mathsf {KP}} + {\mathsf {AD}} + \Pi _1\textrm {-MI}_{\mathbb {R}}$
containing
${\mathsf {KP}} + {\mathsf {AD}} + \Pi _1\textrm {-MI}_{\mathbb {R}}$
containing
 $\mathbb {R}$
.
$\mathbb {R}$
.
Proof Let
![]() $g\subset \text {Coll}(\omega,\mathbb {R})$
be
$g\subset \text {Coll}(\omega,\mathbb {R})$
be
![]() $L(\mathbb {R})$
-generic. By Corollary 2.2 and Lemma 5.1, it suffices to prove that the following are equivalent:
$L(\mathbb {R})$
-generic. By Corollary 2.2 and Lemma 5.1, it suffices to prove that the following are equivalent:
-
(1)
 $\boldsymbol \Sigma ^0_3$
games of length
$\boldsymbol \Sigma ^0_3$
games of length
 $\omega ^2$
with moves in
$\omega ^2$
with moves in
 $\mathbb {N}$
are determined and
$\mathbb {N}$
are determined and -
(2)
 $L_{\beta _g}(\mathbb {R})\models {\mathsf {AD}}$
, where
$L_{\beta _g}(\mathbb {R})\models {\mathsf {AD}}$
, where
 $\beta _g$
is computed in
$\beta _g$
is computed in
 $L[g]$
.
$L[g]$
.
Since
it follows that
and thus
 $L_{\beta _g}(\mathbb {R}) \models {\mathsf {AD}}$
if, and only if,
$L_{\beta _g}(\mathbb {R}) \models {\mathsf {AD}}$
if, and only if,
 $L_{\alpha _g}(\mathbb {R}) \models {\mathsf {AD}}$
. If
$L_{\alpha _g}(\mathbb {R}) \models {\mathsf {AD}}$
. If
![]() $\boldsymbol \Sigma ^0_3$
games of length
$\boldsymbol \Sigma ^0_3$
games of length
![]() $\omega ^2$
are determined, then
$\omega ^2$
are determined, then
 $\Game ^{\mathbb {R}}\boldsymbol \Sigma ^0_3$
games of length
$\Game ^{\mathbb {R}}\boldsymbol \Sigma ^0_3$
games of length
![]() $\omega $
are determined, so
$\omega $
are determined, so
 $L_{\beta _g}(\mathbb {R})\models {\mathsf {AD}}$
by Lemma 3.6.
$L_{\beta _g}(\mathbb {R})\models {\mathsf {AD}}$
by Lemma 3.6.
Conversely, suppose
 $L_{\beta _g}(\mathbb {R})\models {\mathsf {AD}}$
. We apply Theorem 4.1 with
$L_{\beta _g}(\mathbb {R})\models {\mathsf {AD}}$
. We apply Theorem 4.1 with
 $\Gamma = \Sigma ^0_3$
.
$\Gamma = \Sigma ^0_3$
.
![]() $\boldsymbol \Sigma ^0_3$
has the scale property by a theorem of Kechris [Reference Kechris12]. Using a universal
$\boldsymbol \Sigma ^0_3$
has the scale property by a theorem of Kechris [Reference Kechris12]. Using a universal
![]() $\Pi ^1_2$
formula, there is a first-order formula expressing
$\Pi ^1_2$
formula, there is a first-order formula expressing
![]() $\boldsymbol \Pi ^1_2$
-MI over every model of
$\boldsymbol \Pi ^1_2$
-MI over every model of
![]() ${\mathsf {KP}}$
, and we choose this as the formula
${\mathsf {KP}}$
, and we choose this as the formula
![]() $\phi $
in the statement of Theorem 4.1. All
$\phi $
in the statement of Theorem 4.1. All
 $ \Sigma ^0_3(x)$
games for which Player I has a winning strategy have winning strategies in
$ \Sigma ^0_3(x)$
games for which Player I has a winning strategy have winning strategies in
![]() $L_{\alpha _x+1}[x]$
by [Reference Welch19], and in particular in
$L_{\alpha _x+1}[x]$
by [Reference Welch19], and in particular in
![]() $L_{\gamma _x}[x]$
, since
$L_{\gamma _x}[x]$
, since
![]() $\gamma _x = \beta _x$
by Hachtman [Reference Hachtman9].
$\gamma _x = \beta _x$
by Hachtman [Reference Hachtman9].
By Lemma 5.1,
![]() $\beta _g$
does not depend on g, so it is least such that
$\beta _g$
does not depend on g, so it is least such that
 $$ \begin{align*} \Vdash^{L(\mathbb{R} )}_{\text{Coll}(\omega,\mathbb{R})} L_{\beta_g}[g]\models \boldsymbol\Pi^1_2\text{-MI}.\end{align*} $$
$$ \begin{align*} \Vdash^{L(\mathbb{R} )}_{\text{Coll}(\omega,\mathbb{R})} L_{\beta_g}[g]\models \boldsymbol\Pi^1_2\text{-MI}.\end{align*} $$
We have verified all hypotheses, so all
![]() $\boldsymbol \Sigma ^0_3$
games of length
$\boldsymbol \Sigma ^0_3$
games of length
![]() $\omega ^2$
on
$\omega ^2$
on
![]() $\mathbb {N}$
are determined by Theorem 4.1.⊣
$\mathbb {N}$
are determined by Theorem 4.1.⊣
Acknowledgements
The first author was partially supported by FWF grant I4513-N and FWO grant 3E017319.