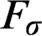 $F_\sigma $ GAMES AND REFLECTION IN
$F_\sigma $ GAMES AND REFLECTION IN 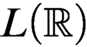 $L(\mathbb {R})$
$L(\mathbb {R})$Published online by Cambridge University Press: 21 July 2020
We characterize the determinacy of 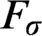 $F_\sigma $
games of length
$F_\sigma $
games of length 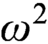 $\omega ^2$
in terms of determinacy assertions for short games. Specifically, we show that
$\omega ^2$
in terms of determinacy assertions for short games. Specifically, we show that 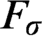 $F_\sigma $
games of length
$F_\sigma $
games of length 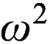 $\omega ^2$
are determined if, and only if, there is a transitive model of
$\omega ^2$
are determined if, and only if, there is a transitive model of  ${\mathsf {KP}}+{\mathsf {AD}}$
containing
${\mathsf {KP}}+{\mathsf {AD}}$
containing 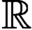 $\mathbb {R}$
and reflecting
$\mathbb {R}$
and reflecting 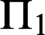 $\Pi _1$
facts about the next admissible set.
$\Pi _1$
facts about the next admissible set.
As a consequence, one obtains that, over the base theory 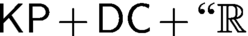 ${\mathsf {KP}} + {\mathsf {DC}} + ``\mathbb {R}$
exists,” determinacy for
${\mathsf {KP}} + {\mathsf {DC}} + ``\mathbb {R}$
exists,” determinacy for 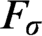 $F_\sigma $
games of length
$F_\sigma $
games of length 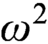 $\omega ^2$
is stronger than
$\omega ^2$
is stronger than  ${\mathsf {AD}}$
, but weaker than
${\mathsf {AD}}$
, but weaker than 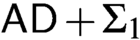 ${\mathsf {AD}} + \Sigma _1$
-separation.
${\mathsf {AD}} + \Sigma _1$
-separation.