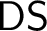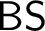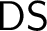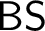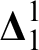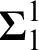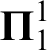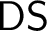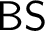1. Introduction
We study the difficulty of the following two (Weihrauch equivalent) computational problems:
-
• Given an ill-founded countable linear order, find an infinite Decreasing Sequence in it (
 $\mathsf {DS}$
).
$\mathsf {DS}$
). -
• Given a countable quasi-order which is not well, find a Bad Sequence in it (
 $\mathsf {BS}$
).
$\mathsf {BS}$
).
Motivation for the first stems from the treatment of ordinals in reverse mathematics. When working within models of subsystems of second order arithmetic, the notion of well-order depends on the fixed model. This leads to the so-called pseudo-well-orders, i.e., ill-founded linear orders s.t. no descending sequence exists within the model itself. Such a linear order would appear to be well-founded from the point of view of the model. As a classic example of a pseudo-well-order, consider Kleene’s computable linear order with no hyperarithmetic descending sequence [Reference Sacks38, Lemma III.2.1]. Such a linear order is a well-order when seen within the
![]() $\omega $
-model
$\omega $
-model
![]() $\mathrm {HYP}$
consisting exactly of the hyperarithmetic sets. Pseudo-well-orders were first studied in [Reference Harrison23] and proved to be a powerful tool in reverse mathematics, especially when working at the level of
$\mathrm {HYP}$
consisting exactly of the hyperarithmetic sets. Pseudo-well-orders were first studied in [Reference Harrison23] and proved to be a powerful tool in reverse mathematics, especially when working at the level of
![]() $\mathrm {ATR}_0$
(see [Reference Simpson41, Section V.4]). Our first task can essentially be rephrased as being concerned with the difficulty of revealing a pseudo-ordinal as not actually being an ordinal.
$\mathrm {ATR}_0$
(see [Reference Simpson41, Section V.4]). Our first task can essentially be rephrased as being concerned with the difficulty of revealing a pseudo-ordinal as not actually being an ordinal.
Our second task can be seen as a abstraction of the computational content of theorems in well-quasi-order (wqo) theory. There are many famous theorems asserting that wqo’s are closed under certain operations. Examples such as Kruskal’s tree theorem, as well as Extended Kruskal’s theorem and Higman’s theorem, have been well-studied in proof theory via their proof-theoretic ordinals (see [Reference Simpson, Harrington, Morley, Šcedrov and Simpson39]). However, in their usual form these results lack computational content. Indeed, these theorems state that a certain quasi-order
![]() $(Q,\preceq _Q)$
is a wqo. Phrasing a result of this kind in the classical
$(Q,\preceq _Q)$
is a wqo. Phrasing a result of this kind in the classical
![]() $\Pi ^1_2$
-form would yield a statement of the type “given an infinite sequence
$\Pi ^1_2$
-form would yield a statement of the type “given an infinite sequence
![]() $(q_n)_{n\in \mathbb {N}}$
in Q, find a pair of indexes
$(q_n)_{n\in \mathbb {N}}$
in Q, find a pair of indexes
![]() $i<j$
s.t.
$i<j$
s.t.
![]() $q_i \preceq _Q q_j$
.” Such a pair
$q_i \preceq _Q q_j$
.” Such a pair
![]() $(i,j)$
would be a witness of the fact that the sequence
$(i,j)$
would be a witness of the fact that the sequence
![]() $(q_n)_{n\in \mathbb {N}}$
is not bad. However, while proving that
$(q_n)_{n\in \mathbb {N}}$
is not bad. However, while proving that
![]() $(Q,\preceq _Q)$
is a wqo can be “hard” (in particular Extended Kruskal’s theorem is not provable in
$(Q,\preceq _Q)$
is a wqo can be “hard” (in particular Extended Kruskal’s theorem is not provable in
 $\boldsymbol {\Pi }^1_1\mathrm {-CA}_0$
[Reference Simpson, Harrington, Morley, Šcedrov and Simpson39]), producing a pair of witnesses for each infinite sequence is a
$\boldsymbol {\Pi }^1_1\mathrm {-CA}_0$
[Reference Simpson, Harrington, Morley, Šcedrov and Simpson39]), producing a pair of witnesses for each infinite sequence is a
![]() $\preceq _Q$
-computable problem (as it can be solved by an extensive search)!
$\preceq _Q$
-computable problem (as it can be solved by an extensive search)!
These theorems are very extreme examples of a well-known difference between reverse mathematics and computable analysis: quoting [Reference Gherardi and Marcone19] “the computable analyst is allowed to conduct an unbounded search for an object that is guaranteed to exist by (nonconstructive) mathematical knowledge, whereas the reverse mathematician has the burden of an existence proof with limited means.”
On the other hand, considering the contrapositives of the above theorems can reveal some (otherwise hidden) computational content. For example, to show that a given quasi-order is not a wqo it suffices to produce a bad sequence in it. Extended Kruskal’s theorem or Higman’s theorem can be stated in the form “given a bad sequence for the derived quasi-order, find a bad sequence for the original quasi-order.” Our second problem trivially is an upper bound for all these statements, as we disregard any particular reason for why the given quasi-order is not a wqo, and just start with the promise that it is not. Our results thus lay the groundwork for a future exploration of the computational content of individual theorems from wqo theory.
We use the framework of Weihrauch reducibility for our investigation. This means that we compare the problems under investigation to a scaffolding of benchmark problems by asking whether there is an otherwise computable uniform procedure that solves one problem while invoking a single oracle call to the other problem. We are not constrained to particular weak systems in proving that these procedures are actually correct, but rather use whatever proof techniques of ordinary mathematics are suitable. In particular, we can take aspects like the ill-foundedness of the given linear order as external promises not represented in the coding of the input. We can use the fact freely in reasoning about the correctness of our procedure, but there is no evidence provided as input of the procedure.
1.1. Summary of our results
There are a number of problems whose degrees are milestones in the Weihrauch lattice and are often used as benchmarks to calibrate the uniform strength of the multi-valued function under analysis. Some of them roughly correspond to the so-called big five subsystems of second order arithmetic: computable problems correspond to
![]() $\mathrm {RCA}_0$
,
$\mathrm {RCA}_0$
,
![]() $\mathsf {C}_{{2^{\mathbb {N}}}}$
(closed choice on the Cantor space) corresponds to
$\mathsf {C}_{{2^{\mathbb {N}}}}$
(closed choice on the Cantor space) corresponds to
![]() $\mathrm {WKL}_0$
,
$\mathrm {WKL}_0$
,
![]() $\mathsf {lim}$
(limit in the Baire space) and its iterations correspond to
$\mathsf {lim}$
(limit in the Baire space) and its iterations correspond to
![]() $\mathrm {ACA}_0$
,
$\mathrm {ACA}_0$
,
![]() $\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
(closed choice on the Baire space) and its variants
$\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
(closed choice on the Baire space) and its variants
![]() $\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
and
$\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
and
![]() $\mathsf {TC}_{{\mathbb {N}^{\mathbb {N}}}}$
correspond to
$\mathsf {TC}_{{\mathbb {N}^{\mathbb {N}}}}$
correspond to
![]() $\mathrm {ATR}_0$
,
$\mathrm {ATR}_0$
,
 ${\boldsymbol {\Pi }^1_1}\text {-}\mathsf {CA}$
corresponds to
${\boldsymbol {\Pi }^1_1}\text {-}\mathsf {CA}$
corresponds to
 $\boldsymbol {\Pi }^1_1\mathrm {-CA}_0$
.
$\boldsymbol {\Pi }^1_1\mathrm {-CA}_0$
.

Figure 1 An overview of some parts of the Weihrauch lattice. The solid frame collects the degrees belonging to the lower cone of
![]() $\mathsf {DS}$
, while the dashed frame collects principles that are not Weihrauch reducible to
$\mathsf {DS}$
, while the dashed frame collects principles that are not Weihrauch reducible to
![]() $\mathsf {DS}$
. The only principle shown which is above
$\mathsf {DS}$
. The only principle shown which is above
![]() $\mathsf {DS}$
is
$\mathsf {DS}$
is
![]() $\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
. We do not know whether
$\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
. We do not know whether
![]() $ \mathsf {KL} $
is reducible to
$ \mathsf {KL} $
is reducible to
![]() $\mathsf {DS}$
.
$\mathsf {DS}$
.
We show that
![]() $\mathsf {DS}$
does not belong to this “explored” part of the lattice. To put it in a nutshell, our results show that it is difficult to solve
$\mathsf {DS}$
does not belong to this “explored” part of the lattice. To put it in a nutshell, our results show that it is difficult to solve
![]() $\mathsf {DS}$
, but that
$\mathsf {DS}$
, but that
![]() $\mathsf {DS}$
is rather weak in solving other problems. For example,
$\mathsf {DS}$
is rather weak in solving other problems. For example,
![]() $\mathsf {DS}$
has computable inputs without any hyperarithmetic solutions. On the other hand,
$\mathsf {DS}$
has computable inputs without any hyperarithmetic solutions. On the other hand,
![]() $\mathsf {DS}$
uniformly computes only the limit computable functions. We provide a few characterizations that tell us what the greatest Weihrauch degree with representatives of particular types below
$\mathsf {DS}$
uniformly computes only the limit computable functions. We provide a few characterizations that tell us what the greatest Weihrauch degree with representatives of particular types below
![]() $\mathsf {DS}$
is, and include some general observations on this approach. The diagram in Figure 1 shows the relations between
$\mathsf {DS}$
is, and include some general observations on this approach. The diagram in Figure 1 shows the relations between
![]() $\mathsf {DS}$
and several other Weihrauch degrees. Dashed arrows represent Weihrauch reducibility in the direction of the arrow, solid arrows represent strict Weihrauch reducibility.Next, we generalize our results by exploring how different presentations of the same order can affect the uniform strength of the same computational task (finding descending sequences in it). We study the problems
$\mathsf {DS}$
and several other Weihrauch degrees. Dashed arrows represent Weihrauch reducibility in the direction of the arrow, solid arrows represent strict Weihrauch reducibility.Next, we generalize our results by exploring how different presentations of the same order can affect the uniform strength of the same computational task (finding descending sequences in it). We study the problems
![]() ${\boldsymbol {\Gamma }}\text {-}\mathsf {DS}$
and
${\boldsymbol {\Gamma }}\text {-}\mathsf {DS}$
and
![]() ${\boldsymbol {\Gamma }}\text {-}\mathsf {BS}$
, where the name of the input order carries “less accessible information” on the order itself (namely
${\boldsymbol {\Gamma }}\text {-}\mathsf {BS}$
, where the name of the input order carries “less accessible information” on the order itself (namely
![]() $a \le _L b$
is assumed to be a
$a \le _L b$
is assumed to be a
![]() $\Gamma $
-condition relative to the name of the order). We summarize the results in Figure 2.
$\Gamma $
-condition relative to the name of the order). We summarize the results in Figure 2.

Figure 2 Diagram presenting the relations between the various generalizations of
![]() $\mathsf {DS}$
.
$\mathsf {DS}$
.
1.2. Structure of the paper
After a short introduction on the preliminary notions on represented spaces and Weihrauch reducibility (§2), we define the deterministic part of a multi-valued function and explore the algebraic properties of the operator
![]() $\mathrm {Det}_{ \mathbf {X} }(\cdot )$
(§3). These results will be very useful in the study of the problems
$\mathrm {Det}_{ \mathbf {X} }(\cdot )$
(§3). These results will be very useful in the study of the problems
![]() $\mathsf {DS}$
and
$\mathsf {DS}$
and
![]() $\mathsf {BS}$
(§4) and their generalizations
$\mathsf {BS}$
(§4) and their generalizations
![]() ${\boldsymbol {\Gamma }}\text {-}\mathsf {DS}$
and
${\boldsymbol {\Gamma }}\text {-}\mathsf {DS}$
and
![]() ${\boldsymbol {\Gamma }}\text {-}\mathsf {BS}$
(§5).
${\boldsymbol {\Gamma }}\text {-}\mathsf {BS}$
(§5).
2. Background
For an introduction to Weihrauch reducibility, we point the reader to [Reference Brattka, Hölzl, Kuyper, Vollmer and Vallée10]; for represented spaces to [Reference Pauly36]. Below we briefly introduce the notions we will need, as well as state useful results. Those familiar with Weihrauch reducibility should read Definition 2.2 where we define the first-order part of a problem, recently studied by Dzhafarov et al. [Reference Dzhafarov, Solomon and Yokoyama17].
A represented space
![]() $\textbf {X}$
is a set X together with a (possibly partial) surjection
$\textbf {X}$
is a set X together with a (possibly partial) surjection
![]() $\delta _{\textbf {X}} :\subseteq {\mathbb {N}^{\mathbb {N}}} \to X$
. We can transfer notions of computability from
$\delta _{\textbf {X}} :\subseteq {\mathbb {N}^{\mathbb {N}}} \to X$
. We can transfer notions of computability from
![]() ${\mathbb {N}^{\mathbb {N}}}$
to
${\mathbb {N}^{\mathbb {N}}}$
to
![]() $\textbf {X}$
as follows. For each
$\textbf {X}$
as follows. For each
![]() $x \in X$
, we say that p is a (
$x \in X$
, we say that p is a (
![]() $\delta _{\textbf {X}}$
-)name of x if
$\delta _{\textbf {X}}$
-)name of x if
![]() $\delta _{\textbf {X}}(p) = x$
. We say that
$\delta _{\textbf {X}}(p) = x$
. We say that
![]() $x \in X$
is (
$x \in X$
is (
![]() $\delta _{\mathbf {X}}$
-)computable if it has a computable (
$\delta _{\mathbf {X}}$
-)computable if it has a computable (
![]() $\delta _{\textbf {X}}$
-)name.
$\delta _{\textbf {X}}$
-)name.
We list some relevant examples. Let
![]() $\mathbf {LO} = (\mathrm {LO},\ \delta _{\mathbf {LO}})$
be the represented space of linear orders with domain contained in
$\mathbf {LO} = (\mathrm {LO},\ \delta _{\mathbf {LO}})$
be the represented space of linear orders with domain contained in
![]() $\mathbb {N}$
, where each linear order
$\mathbb {N}$
, where each linear order
![]() $(L, \le _L)$
is represented by the characteristic function of the set
$(L, \le _L)$
is represented by the characteristic function of the set
![]() $\{\langle a,b \rangle \in \mathbb {N} : a\le _L b\}$
. Let
$\{\langle a,b \rangle \in \mathbb {N} : a\le _L b\}$
. Let
![]() $\textbf {WO} = (\mathrm {WO},\delta _{\mathbf {WO}})$
be the represented space of well-orders with domain contained in
$\textbf {WO} = (\mathrm {WO},\delta _{\mathbf {WO}})$
be the represented space of well-orders with domain contained in
![]() $\mathbb {N}$
, where
$\mathbb {N}$
, where
![]() $\delta _{\mathrm {WO}}$
is the restriction of
$\delta _{\mathrm {WO}}$
is the restriction of
![]() $\delta _{\mathrm {LO}}$
to codes of well-orders. Similarly, let
$\delta _{\mathrm {LO}}$
to codes of well-orders. Similarly, let
![]() $\mathbf {QO} = (\mathrm {QO},\ \delta _{\mathbf {QO}})$
be the represented space of quasi-orders (represented via the characteristic function of the relation). Let also
$\mathbf {QO} = (\mathrm {QO},\ \delta _{\mathbf {QO}})$
be the represented space of quasi-orders (represented via the characteristic function of the relation). Let also
![]() $\mathbf {Tr}$
be the space of subtrees of
$\mathbf {Tr}$
be the space of subtrees of
![]() ${\mathbb {N}^{<\mathbb {N}}}$
, represented by characteristic functions. For every string
${\mathbb {N}^{<\mathbb {N}}}$
, represented by characteristic functions. For every string
![]() $\sigma \in {\mathbb {N}^{<\mathbb {N}}}$
we denote with
$\sigma \in {\mathbb {N}^{<\mathbb {N}}}$
we denote with
![]() $\sigma [n]$
the prefix of length n of
$\sigma [n]$
the prefix of length n of
![]() $\sigma $
.
$\sigma $
.
We will formalize the problems under investigation as partial multi-valued functions between represented spaces
![]() $f :\subseteq \textbf {X} \rightrightarrows \textbf {Y}$
. For each
$f :\subseteq \textbf {X} \rightrightarrows \textbf {Y}$
. For each
![]() $x \in X$
,
$x \in X$
,
![]() $f(x)$
denotes the set of possible outputs corresponding to the input x. The domain
$f(x)$
denotes the set of possible outputs corresponding to the input x. The domain
![]() $\operatorname {dom}(f)$
is the set of all
$\operatorname {dom}(f)$
is the set of all
![]() $x \in X$
such that
$x \in X$
such that
![]() $f(x)$
is nonempty. We often refer to each
$f(x)$
is nonempty. We often refer to each
![]() $x \in \operatorname {dom}(f)$
as an f-instance and each
$x \in \operatorname {dom}(f)$
as an f-instance and each
![]() $y \in f(x)$
as an f-solution to x. When we define a problem, we will often not specify its domain explicitly, in which case its domain should be taken to be as large as possible. The codomain of
$y \in f(x)$
as an f-solution to x. When we define a problem, we will often not specify its domain explicitly, in which case its domain should be taken to be as large as possible. The codomain of
![]() $f :\subseteq \textbf {X} \rightrightarrows \textbf {Y}$
is
$f :\subseteq \textbf {X} \rightrightarrows \textbf {Y}$
is
![]() $\textbf {Y}$
. If
$\textbf {Y}$
. If
![]() $f :\subseteq \textbf {X} \rightrightarrows \textbf {Y}$
is such that
$f :\subseteq \textbf {X} \rightrightarrows \textbf {Y}$
is such that
![]() $f(x)$
is a singleton for each
$f(x)$
is a singleton for each
![]() $x \in \operatorname {dom}(f)$
, then we say that f is single-valued. We indicate that by writing
$x \in \operatorname {dom}(f)$
, then we say that f is single-valued. We indicate that by writing
![]() $f :\subseteq \textbf {X} \to \textbf {Y}$
. In this case we will write
$f :\subseteq \textbf {X} \to \textbf {Y}$
. In this case we will write
![]() $f(x) = y$
instead of (the formally correct)
$f(x) = y$
instead of (the formally correct)
![]() $f(x) = \{y\}$
. An example of a single-valued problem is the identity function
$f(x) = \{y\}$
. An example of a single-valued problem is the identity function
![]() $\operatorname {id}: {\mathbb {N}^{\mathbb {N}}} \to {\mathbb {N}^{\mathbb {N}}}$
.
$\operatorname {id}: {\mathbb {N}^{\mathbb {N}}} \to {\mathbb {N}^{\mathbb {N}}}$
.
We can define the computability or continuity of problems via realizers: we say that a function
![]() $F :\subseteq {\mathbb {N}^{\mathbb {N}}} \to {\mathbb {N}^{\mathbb {N}}}$
is a realizer of a problem
$F :\subseteq {\mathbb {N}^{\mathbb {N}}} \to {\mathbb {N}^{\mathbb {N}}}$
is a realizer of a problem
![]() $f :\subseteq \textbf {X} \rightrightarrows \textbf {Y}$
if whenever p is a name for some
$f :\subseteq \textbf {X} \rightrightarrows \textbf {Y}$
if whenever p is a name for some
![]() $x \in \operatorname {dom}(f)$
,
$x \in \operatorname {dom}(f)$
,
![]() $F(p)$
is a name for some
$F(p)$
is a name for some
![]() $y \in f(x)$
. A problem is computable (respectively continuous) if it has a computable (respectively continuous) realizer.
$y \in f(x)$
. A problem is computable (respectively continuous) if it has a computable (respectively continuous) realizer.
In order to measure the relative uniform computational strength of problems, we use Weihrauch reducibility. A problem f is Weihrauch reducible to a problem g, written
![]() $f \le _{\mathrm {W}} g$
, if there are computable maps
$f \le _{\mathrm {W}} g$
, if there are computable maps
![]() $\Phi , \Psi :\subseteq {\mathbb {N}^{\mathbb {N}}} \to {\mathbb {N}^{\mathbb {N}}}$
such that if p is a name for some
$\Phi , \Psi :\subseteq {\mathbb {N}^{\mathbb {N}}} \to {\mathbb {N}^{\mathbb {N}}}$
such that if p is a name for some
![]() $x \in \operatorname {dom}(f)$
, then
$x \in \operatorname {dom}(f)$
, then
-
1.
 $\Phi (p)$
is a name for some
$\Phi (p)$
is a name for some
 $y \in \operatorname {dom}(g)$
and
$y \in \operatorname {dom}(g)$
and -
2. if q is a name for some element of
 $g(y)$
, then
$g(y)$
, then
 $\Psi (p,q)$
is a name for some element of
$\Psi (p,q)$
is a name for some element of
 $f(x)$
.
$f(x)$
.
This means that there is a procedure for solving f which is computable except for a single invocation to an oracle for g. Equivalently, there is a computable procedure which transforms realizers for g into realizers for f. A problem f is strongly Weihrauch reducible to a problem g, written
![]() $f \le _{\mathrm {sW}} g$
, if there are computable maps
$f \le _{\mathrm {sW}} g$
, if there are computable maps
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
as above, except that
$\Psi $
as above, except that
![]() $\Psi $
is not allowed access to p in its computation.
$\Psi $
is not allowed access to p in its computation.
Weihrauch reducibility and strong Weihrauch reducibility are quasi-orders, so they define a degree structure on problems:
![]() $f \equiv _{\mathrm {W}} g$
if
$f \equiv _{\mathrm {W}} g$
if
![]() $f \le _{\mathrm {W}} g$
and
$f \le _{\mathrm {W}} g$
and
![]() $g \le _{\mathrm {W}} f$
(likewise for
$g \le _{\mathrm {W}} f$
(likewise for
![]() $\le _{\mathrm {sW}}$
). Both the Weihrauch degrees and the strong Weihrauch degrees form lattices (see [Reference Brattka, Hölzl, Kuyper, Vollmer and Vallée11, Theorems 3.9 and 3.10]). There are several natural operations on problems which also lift to the
$\le _{\mathrm {sW}}$
). Both the Weihrauch degrees and the strong Weihrauch degrees form lattices (see [Reference Brattka, Hölzl, Kuyper, Vollmer and Vallée11, Theorems 3.9 and 3.10]). There are several natural operations on problems which also lift to the
![]() $\equiv _{\mathrm {W}}$
-degrees and the
$\equiv _{\mathrm {W}}$
-degrees and the
![]() $\equiv _{\mathrm {sW}}$
-degrees. Below we present the operations that we need in this paper.
$\equiv _{\mathrm {sW}}$
-degrees. Below we present the operations that we need in this paper.
The parallel product
![]() $f \times g$
is defined by
$f \times g$
is defined by
![]() $(f \times g)(x,y) = f(x) \times g(y)$
. We call f a cylinder if
$(f \times g)(x,y) = f(x) \times g(y)$
. We call f a cylinder if
![]() $f \equiv _{\mathrm {sW}} f \times \operatorname {id}$
. If f is a cylinder, then
$f \equiv _{\mathrm {sW}} f \times \operatorname {id}$
. If f is a cylinder, then
![]() $g \le _{\mathrm {W}} f$
if and only if
$g \le _{\mathrm {W}} f$
if and only if
![]() $g \le _{\mathrm {sW}} f$
[Reference Brattka and Gherardi6, Corollary 3.6]. This is useful for establishing nonreductions because if f is a cylinder, then it suffices to diagonalize against all strong Weihrauch reductions from g to f in order to show that
$g \le _{\mathrm {sW}} f$
[Reference Brattka and Gherardi6, Corollary 3.6]. This is useful for establishing nonreductions because if f is a cylinder, then it suffices to diagonalize against all strong Weihrauch reductions from g to f in order to show that
![]() $g \not \le _{\mathrm {W}} f$
. Cylinders will also be useful when working with compositional products (discussed below). Observe that for every problem f,
$g \not \le _{\mathrm {W}} f$
. Cylinders will also be useful when working with compositional products (discussed below). Observe that for every problem f,
![]() $f \times \operatorname {id}$
is a cylinder which is Weihrauch equivalent to f.
$f \times \operatorname {id}$
is a cylinder which is Weihrauch equivalent to f.
The parallelization
![]() $\widehat {f}$
is defined by
$\widehat {f}$
is defined by
 $\widehat {f}((x_n)_{n \in \mathbb {N}}) = \prod _{n \in \mathbb {N}} f(x_n)$
. In other words, given a countable sequence of f-instances,
$\widehat {f}((x_n)_{n \in \mathbb {N}}) = \prod _{n \in \mathbb {N}} f(x_n)$
. In other words, given a countable sequence of f-instances,
![]() $\widehat {f}$
asks for an f-solution for each given f-instance.
$\widehat {f}$
asks for an f-solution for each given f-instance.
The composition of
![]() $f :\subseteq \textbf {Y} \rightrightarrows \textbf {Z}$
and
$f :\subseteq \textbf {Y} \rightrightarrows \textbf {Z}$
and
![]() $g :\subseteq \textbf {X} \rightrightarrows \textbf {Y}$
is defined by
$g :\subseteq \textbf {X} \rightrightarrows \textbf {Y}$
is defined by
![]() $\operatorname {dom}(f \circ g) = \{x \in \operatorname {dom}(g) : g(x) \subseteq \operatorname {dom}(f)\}$
and
$\operatorname {dom}(f \circ g) = \{x \in \operatorname {dom}(g) : g(x) \subseteq \operatorname {dom}(f)\}$
and
 $(f \circ g)(x) = \bigcup _{y \in g(x)} f(y)$
for
$(f \circ g)(x) = \bigcup _{y \in g(x)} f(y)$
for
![]() $x \in \operatorname {dom}(f \circ g)$
. The composition does not respect
$x \in \operatorname {dom}(f \circ g)$
. The composition does not respect
![]() $\le _{\mathrm {W}}$
or
$\le _{\mathrm {W}}$
or
![]() $\le _{\mathrm {sW}}$
. Instead, for any problems f and g (regardless of domain and codomain), we can consider the compositional product
$\le _{\mathrm {sW}}$
. Instead, for any problems f and g (regardless of domain and codomain), we can consider the compositional product
![]() $f * g$
, which satisfies the following property:
$f * g$
, which satisfies the following property:
 $$ \begin{align*} f * g \equiv_{\mathrm{W}} \max_{\le_{\mathrm{W}}} \{f_1 \circ g_1 : f_1 \le_{\mathrm{W}} f \land g_1 \le_{\mathrm{W}} g\}. \end{align*} $$
$$ \begin{align*} f * g \equiv_{\mathrm{W}} \max_{\le_{\mathrm{W}}} \{f_1 \circ g_1 : f_1 \le_{\mathrm{W}} f \land g_1 \le_{\mathrm{W}} g\}. \end{align*} $$
This captures what can be achieved by first applying g, possibly followed by some computation, and then applying f. The compositional product was first introduced in [Reference Brattka, Gherardi and Pauly10], and proven to be well-defined in [Reference Brattka and Rakotoniaina13]. A useful tool is the cylindrical decomposition lemma [Reference Brattka and Rakotoniaina13, Lemma 3.10]: for all problems f and g, if
![]() $F \equiv _{\mathrm {W}} f$
and
$F \equiv _{\mathrm {W}} f$
and
![]() $G \equiv _{\mathrm {W}} g$
are both cylinders, then there is some computable map
$G \equiv _{\mathrm {W}} g$
are both cylinders, then there is some computable map
![]() $\Phi $
such that
$\Phi $
such that
![]() $f * g \equiv _{\mathrm {W}} F \circ \Phi \circ G$
. For each problem f, let
$f * g \equiv _{\mathrm {W}} F \circ \Phi \circ G$
. For each problem f, let
![]() $f^{[n]}$
denote the n-fold iteration of the compositional product of f with itself, i.e.,
$f^{[n]}$
denote the n-fold iteration of the compositional product of f with itself, i.e.,
![]() $f^{[1]} = f$
,
$f^{[1]} = f$
,
![]() $f^{[2]} = f * f$
, and so on.
$f^{[2]} = f * f$
, and so on.
The jump of
![]() $f :\subseteq \textbf {X} \rightrightarrows \textbf {Y}$
is the problem
$f :\subseteq \textbf {X} \rightrightarrows \textbf {Y}$
is the problem
![]() $f' :\subseteq \textbf {X}' \rightrightarrows \textbf {Y}$
defined by
$f' :\subseteq \textbf {X}' \rightrightarrows \textbf {Y}$
defined by
![]() $f'(x) := f(x)$
, where
$f'(x) := f(x)$
, where
![]() $\textbf {X}'$
is the represented space
$\textbf {X}'$
is the represented space
![]() $(X,\delta _{\mathbf {X}'})$
and
$(X,\delta _{\mathbf {X}'})$
and
![]() $\delta _{\mathbf {X}'}$
takes in input a convergent sequence
$\delta _{\mathbf {X}'}$
takes in input a convergent sequence
![]() $(p_n)_{n\in \mathbb {N}}$
in
$(p_n)_{n\in \mathbb {N}}$
in
![]() ${\mathbb {N}^{\mathbb {N}}}$
and returns
${\mathbb {N}^{\mathbb {N}}}$
and returns
![]() $\delta _{\mathbf {X}}(\lim _{n\to \infty } p_n)$
. In other words,
$\delta _{\mathbf {X}}(\lim _{n\to \infty } p_n)$
. In other words,
![]() $f'$
is the following task: given a sequence which converges to a name of an f-instance, produce an f-solution to that instance. The jump respects
$f'$
is the following task: given a sequence which converges to a name of an f-instance, produce an f-solution to that instance. The jump respects
![]() $\le _{\mathrm {sW}}$
but does not lift to the
$\le _{\mathrm {sW}}$
but does not lift to the
![]() $\equiv _{\mathrm {W}}$
-degrees. We use
$\equiv _{\mathrm {W}}$
-degrees. We use
![]() $f^{(n)}$
to denote the n-th jump of a problem. If we define
$f^{(n)}$
to denote the n-th jump of a problem. If we define
![]() $\mathsf {lim} :\subseteq ({\mathbb {N}^{\mathbb {N}}})^{\mathbb {N}} \to {\mathbb {N}^{\mathbb {N}}}$
by
$\mathsf {lim} :\subseteq ({\mathbb {N}^{\mathbb {N}}})^{\mathbb {N}} \to {\mathbb {N}^{\mathbb {N}}}$
by
![]() $\mathsf {lim}((p_n)_{n \in \mathbb {N}}) := \lim _{n \to \infty } p_n$
then it is straightforward from the definition that
$\mathsf {lim}((p_n)_{n \in \mathbb {N}}) := \lim _{n \to \infty } p_n$
then it is straightforward from the definition that
![]() $f^{(n)}\le _{\mathrm {W}} f* \mathsf {lim}^{[n]}$
. The converse reduction does not hold in general. However if f is a cylinder, then for each n,
$f^{(n)}\le _{\mathrm {W}} f* \mathsf {lim}^{[n]}$
. The converse reduction does not hold in general. However if f is a cylinder, then for each n,
![]() $f^{(n)}$
is a cylinder and
$f^{(n)}$
is a cylinder and
![]() $f^{(n)} \equiv _{\mathrm {W}} f * \mathsf {lim}^{[n]}$
(see [Reference Brattka, Hölzl, Kuyper, Vollmer and Vallée11, Proposition 6.14]). In particular, since
$f^{(n)} \equiv _{\mathrm {W}} f * \mathsf {lim}^{[n]}$
(see [Reference Brattka, Hölzl, Kuyper, Vollmer and Vallée11, Proposition 6.14]). In particular, since
![]() $\mathsf {lim}$
is a cylinder,
$\mathsf {lim}$
is a cylinder,
 $\mathsf {lim}^{(n)} \equiv _{\mathrm {W}} \mathsf {lim}^{[n+1]}$
for each n. We say that a problem is arithmetic if it is Weihrauch reducible to
$\mathsf {lim}^{(n)} \equiv _{\mathrm {W}} \mathsf {lim}^{[n+1]}$
for each n. We say that a problem is arithmetic if it is Weihrauch reducible to
![]() $\mathsf {lim}^{(n)}$
for some n.
$\mathsf {lim}^{(n)}$
for some n.
Next we introduce some problems which are milestones in the Weihrauch lattice. Apart from
![]() $\mathsf {lim}$
and its jumps, most prominent is the family of problems of (closed) choice
$\mathsf {lim}$
and its jumps, most prominent is the family of problems of (closed) choice
![]() $\mathsf {C}_{\textbf {X}}$
defined below. For a represented space
$\mathsf {C}_{\textbf {X}}$
defined below. For a represented space
![]() $\mathbf {X}$
, let
$\mathbf {X}$
, let
![]() $\mathcal {A}(X)$
denote the space of closed subsets of
$\mathcal {A}(X)$
denote the space of closed subsets of
![]() $\mathbf {X}$
. These are given by the ability to recognize membership in the complement. We define
$\mathbf {X}$
. These are given by the ability to recognize membership in the complement. We define
![]() $\mathsf {C}_{\textbf {X}} :\subseteq \mathcal {A}(X) \rightrightarrows X$
by
$\mathsf {C}_{\textbf {X}} :\subseteq \mathcal {A}(X) \rightrightarrows X$
by
![]() $\mathsf {C}_{\textbf {X}}(A) := A$
. In other words,
$\mathsf {C}_{\textbf {X}}(A) := A$
. In other words,
![]() $\mathsf {C}_{\textbf {X}}$
is the task of producing an element of
$\mathsf {C}_{\textbf {X}}$
is the task of producing an element of
![]() $\mathbf {X}$
given a way to recognize wrong answers. Define unique choice
$\mathbf {X}$
given a way to recognize wrong answers. Define unique choice
![]() $\mathsf {UC}_{\textbf {X}}$
to be the restriction of
$\mathsf {UC}_{\textbf {X}}$
to be the restriction of
![]() $\mathsf {C}_{\textbf {X}}$
to closed sets which are singletons. By definition,
$\mathsf {C}_{\textbf {X}}$
to closed sets which are singletons. By definition,
![]() $\mathsf {UC}_{\textbf {X}}$
is single-valued.
$\mathsf {UC}_{\textbf {X}}$
is single-valued.
Of particular interest to us are
![]() $\mathsf {C}_{\mathbb {N}}$
,
$\mathsf {C}_{\mathbb {N}}$
,
![]() $\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
, and
$\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
, and
![]() $\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
. We can view elements of
$\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
. We can view elements of
![]() $\mathcal {A}(\mathbb {N})$
to be given as an enumeration of its complement. Thus,
$\mathcal {A}(\mathbb {N})$
to be given as an enumeration of its complement. Thus,
![]() $\mathsf {C}_{\mathbb {N}}$
is the task of finding a natural number not occurring in a given list. Given a name for a closed set
$\mathsf {C}_{\mathbb {N}}$
is the task of finding a natural number not occurring in a given list. Given a name for a closed set
![]() $A \subseteq {\mathbb {N}^{\mathbb {N}}}$
, we can compute a tree
$A \subseteq {\mathbb {N}^{\mathbb {N}}}$
, we can compute a tree
![]() $T \subseteq {\mathbb {N}^{<\mathbb {N}}}$
such that the set
$T \subseteq {\mathbb {N}^{<\mathbb {N}}}$
such that the set
![]() $[T]$
of (infinite) paths on T is A. Conversely, given a tree
$[T]$
of (infinite) paths on T is A. Conversely, given a tree
![]() $T \subseteq {\mathbb {N}^{<\mathbb {N}}}$
, we can compute a name for the closed set
$T \subseteq {\mathbb {N}^{<\mathbb {N}}}$
, we can compute a name for the closed set
![]() $[T]$
. Therefore we can view
$[T]$
. Therefore we can view
![]() $\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
as the problem of computing a path on a given ill-founded subtree of
$\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
as the problem of computing a path on a given ill-founded subtree of
![]() ${\mathbb {N}^{<\mathbb {N}}}$
. Similarly, we can view
${\mathbb {N}^{<\mathbb {N}}}$
. Similarly, we can view
![]() $\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
as the problem of computing the unique path on a given subtree of
$\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
as the problem of computing the unique path on a given subtree of
![]() ${\mathbb {N}^{<\mathbb {N}}}$
. Both
${\mathbb {N}^{<\mathbb {N}}}$
. Both
![]() $\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
and
$\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
and
![]() $\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
are closed under compositional product [Reference Brattka and Gherardi5, Theorem 7.3]. We have:
$\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
are closed under compositional product [Reference Brattka and Gherardi5, Theorem 7.3]. We have:
Theorem 2.1 [Reference Kihara, Marcone and Pauly26, Corollary 3.4]
If
![]() $f:\subseteq {\mathbb {N}^{\mathbb {N}}} \rightrightarrows \mathbf {X}$
is Weihrauch reducible to
$f:\subseteq {\mathbb {N}^{\mathbb {N}}} \rightrightarrows \mathbf {X}$
is Weihrauch reducible to
![]() $\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
, then for every
$\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
, then for every
![]() $x\in \operatorname {dom}(\,f)$
,
$x\in \operatorname {dom}(\,f)$
,
![]() $f(x)$
contains some y hyperarithmetical relative to x.
$f(x)$
contains some y hyperarithmetical relative to x.
Another prominent problem is
![]() $ \mathsf {LPO} : {\mathbb {N}^{\mathbb {N}}} \to \{0,1\}$
, defined by
$ \mathsf {LPO} : {\mathbb {N}^{\mathbb {N}}} \to \{0,1\}$
, defined by
![]() $ \mathsf {LPO} (p) := 0$
if
$ \mathsf {LPO} (p) := 0$
if
![]() $p = 0^{\mathbb {N}}$
and
$p = 0^{\mathbb {N}}$
and
![]() $ \mathsf {LPO} (p) := 1$
otherwise. Its jump
$ \mathsf {LPO} (p) := 1$
otherwise. Its jump
![]() $ \mathsf {LPO} '$
(and its iterated jumps
$ \mathsf {LPO} '$
(and its iterated jumps
![]() $ \mathsf {LPO} ^{(k)}$
) will play an important technical role. We notice that
$ \mathsf {LPO} ^{(k)}$
) will play an important technical role. We notice that
 $\mathsf {lim}^{(n)}\equiv _{\mathrm {W}}\widehat { \mathsf {LPO} ^{(n)}}$
(see e.g., [Reference Brattka, Hölzl, Kuyper, Vollmer and Vallée11, Theorem 6.7 and Proposition 6.10]).
$\mathsf {lim}^{(n)}\equiv _{\mathrm {W}}\widehat { \mathsf {LPO} ^{(n)}}$
(see e.g., [Reference Brattka, Hölzl, Kuyper, Vollmer and Vallée11, Theorem 6.7 and Proposition 6.10]).
Next we define the represented space
![]() $\boldsymbol {\Gamma }(\textbf {X})$
of all
$\boldsymbol {\Gamma }(\textbf {X})$
of all
![]() $\boldsymbol {\Gamma }$
-definable subsets of a computable metric space X, where
$\boldsymbol {\Gamma }$
-definable subsets of a computable metric space X, where
 $\boldsymbol {\Gamma } \in \{ \boldsymbol {\Sigma }^0_k, \boldsymbol {\Pi }^0_k, \boldsymbol {\Delta }^0_k, \boldsymbol {\Sigma }^1_1, \boldsymbol {\Pi }^1_1, \boldsymbol {\Delta }^1_1 \}$
. This is based on the well-known concept of Borel codes [Reference Moschovakis33]. For a more detailed development in the context of computable analysis we refer to [Reference Goh20]. A more abstract and general treatment is provided in [Reference Pauly and de Brecht37]. A
$\boldsymbol {\Gamma } \in \{ \boldsymbol {\Sigma }^0_k, \boldsymbol {\Pi }^0_k, \boldsymbol {\Delta }^0_k, \boldsymbol {\Sigma }^1_1, \boldsymbol {\Pi }^1_1, \boldsymbol {\Delta }^1_1 \}$
. This is based on the well-known concept of Borel codes [Reference Moschovakis33]. For a more detailed development in the context of computable analysis we refer to [Reference Goh20]. A more abstract and general treatment is provided in [Reference Pauly and de Brecht37]. A
 $\delta _{\boldsymbol {\Sigma }^0_1}$
-name for a set
$\delta _{\boldsymbol {\Sigma }^0_1}$
-name for a set
![]() $B \subseteq X$
is a sequence of indices of rational open balls whose union is B. A
$B \subseteq X$
is a sequence of indices of rational open balls whose union is B. A
 $\delta _{\boldsymbol {\Pi }^0_k}$
-name for a set is a
$\delta _{\boldsymbol {\Pi }^0_k}$
-name for a set is a
 $\delta _{\boldsymbol {\Sigma }^0_k}$
-name for its complement. (Note that
$\delta _{\boldsymbol {\Sigma }^0_k}$
-name for its complement. (Note that
 $\delta _{\boldsymbol {\Pi }^0_1}$
agrees with how we represented closed sets previously.) A
$\delta _{\boldsymbol {\Pi }^0_1}$
agrees with how we represented closed sets previously.) A
 $\delta _{\boldsymbol {\Delta }^0_k}$
-name for a set is a pair of
$\delta _{\boldsymbol {\Delta }^0_k}$
-name for a set is a pair of
 $\delta _{\boldsymbol {\Sigma }^0_k}$
-names, one for the set itself and one for its complement. A
$\delta _{\boldsymbol {\Sigma }^0_k}$
-names, one for the set itself and one for its complement. A
 $\delta _{\boldsymbol {\Sigma }^0_{k+1}}$
-name for a set
$\delta _{\boldsymbol {\Sigma }^0_{k+1}}$
-name for a set
![]() $B \subseteq X$
is a sequence of names for
$B \subseteq X$
is a sequence of names for
 $\boldsymbol {\Pi }^0_k$
sets whose union is B.
$\boldsymbol {\Pi }^0_k$
sets whose union is B.
A
 $\delta _{\boldsymbol {\Sigma }^1_1}$
-name for a set
$\delta _{\boldsymbol {\Sigma }^1_1}$
-name for a set
![]() $S \subseteq X$
is a
$S \subseteq X$
is a
 $\delta _{\boldsymbol {\Pi }^0_1}$
-name for a set
$\delta _{\boldsymbol {\Pi }^0_1}$
-name for a set
![]() $P \subseteq {\mathbb {N}^{\mathbb {N}}} \times X$
such that
$P \subseteq {\mathbb {N}^{\mathbb {N}}} \times X$
such that
![]() $S = \{x \in X: (\exists g)((g,x) \in P)\}$
. We define
$S = \{x \in X: (\exists g)((g,x) \in P)\}$
. We define
 $\delta _{\boldsymbol {\Pi }^1_1}$
and
$\delta _{\boldsymbol {\Pi }^1_1}$
and
 $\delta _{\boldsymbol {\Delta }^1_1}$
similarly to
$\delta _{\boldsymbol {\Delta }^1_1}$
similarly to
 $\delta _{\boldsymbol {\Pi }^0_k}$
and
$\delta _{\boldsymbol {\Pi }^0_k}$
and
 $\delta _{\boldsymbol {\Delta }^0_k}$
. If X is
$\delta _{\boldsymbol {\Delta }^0_k}$
. If X is
![]() $\mathbb {N}$
, we can think of a
$\mathbb {N}$
, we can think of a
 $\delta _{\boldsymbol {\Sigma }^1_1}$
-name for
$\delta _{\boldsymbol {\Sigma }^1_1}$
-name for
![]() $S \subseteq \mathbb {N}$
as a sequence
$S \subseteq \mathbb {N}$
as a sequence
![]() $(T_n)_{n \in \mathbb {N}}$
of subtrees of
$(T_n)_{n \in \mathbb {N}}$
of subtrees of
![]() ${\mathbb {N}^{<\mathbb {N}}}$
such that
${\mathbb {N}^{<\mathbb {N}}}$
such that
![]() $n \in S$
if and only if
$n \in S$
if and only if
![]() $T_n$
is ill-founded.
$T_n$
is ill-founded.
In practice, we rarely construct
![]() $\delta _{\boldsymbol {\Gamma }}$
-names explicitly. If we want to construct a
$\delta _{\boldsymbol {\Gamma }}$
-names explicitly. If we want to construct a
![]() $\delta _{\boldsymbol {\Gamma }}$
-name for a set
$\delta _{\boldsymbol {\Gamma }}$
-name for a set
![]() $A \subseteq X$
, we typically only check that there is a
$A \subseteq X$
, we typically only check that there is a
![]() $\boldsymbol {\Gamma }$
-formula which defines A. By invoking computable closure properties, one can construct a computable map which takes a
$\boldsymbol {\Gamma }$
-formula which defines A. By invoking computable closure properties, one can construct a computable map which takes a
![]() $\boldsymbol {\Gamma }$
-formula
$\boldsymbol {\Gamma }$
-formula
![]() $\phi $
and its parameter p to a
$\phi $
and its parameter p to a
![]() $\delta _{\boldsymbol {\Gamma }}$
-name for the set defined by
$\delta _{\boldsymbol {\Gamma }}$
-name for the set defined by
![]() $\phi $
. Conversely, one can construct a computable map which takes a
$\phi $
. Conversely, one can construct a computable map which takes a
![]() $\delta _{\boldsymbol {\Gamma }}$
-name p for a set A to a
$\delta _{\boldsymbol {\Gamma }}$
-name p for a set A to a
![]() $\boldsymbol {\Gamma }$
-formula
$\boldsymbol {\Gamma }$
-formula
![]() $\phi $
with parameter p which defines A.
$\phi $
with parameter p which defines A.
We define the (single-valued) functions
![]() ${\boldsymbol {\Gamma }}\text {-}\mathsf {CA}:\subseteq \boldsymbol {\Gamma }(\mathbb {N})\to {2^{\mathbb {N}}}$
corresponding to comprehension principles: given a
${\boldsymbol {\Gamma }}\text {-}\mathsf {CA}:\subseteq \boldsymbol {\Gamma }(\mathbb {N})\to {2^{\mathbb {N}}}$
corresponding to comprehension principles: given a
![]() $\delta _{\boldsymbol {\Gamma }}$
-name p for a subset A of
$\delta _{\boldsymbol {\Gamma }}$
-name p for a subset A of
![]() $\mathbb {N}$
, produce its characteristic function. Notice that, for each k and each
$\mathbb {N}$
, produce its characteristic function. Notice that, for each k and each
 $A\in \boldsymbol {\Sigma }^0_{k+1}$
, we can use
$A\in \boldsymbol {\Sigma }^0_{k+1}$
, we can use
![]() $ \mathsf {LPO} ^{(k)}$
to check whether
$ \mathsf {LPO} ^{(k)}$
to check whether
![]() $n\in A$
(intuitively, for every p we can use
$n\in A$
(intuitively, for every p we can use
![]() $ \mathsf {LPO} ^{(k)}$
to answer a
$ \mathsf {LPO} ^{(k)}$
to answer a
 $\Sigma ^{0,p}_{k+1}$
question). This shows that, for each k,
$\Sigma ^{0,p}_{k+1}$
question). This shows that, for each k,
 $$ \begin{align*} \mathsf{lim}^{(k)} \equiv_{\mathrm{W}} \widehat{ \mathsf{LPO} ^{(k)}} \equiv_{\mathrm{W}} {\boldsymbol{\Sigma}^0_{k+1}}\text{-}\mathsf{CA}, \end{align*} $$
$$ \begin{align*} \mathsf{lim}^{(k)} \equiv_{\mathrm{W}} \widehat{ \mathsf{LPO} ^{(k)}} \equiv_{\mathrm{W}} {\boldsymbol{\Sigma}^0_{k+1}}\text{-}\mathsf{CA}, \end{align*} $$
somewhat implicitly written in [Reference Brattka, de Brecht and Pauly4]. The problem
 ${\boldsymbol {\Pi }^1_1}\text {-}\mathsf {CA}$
can be seen as the analogue of
${\boldsymbol {\Pi }^1_1}\text {-}\mathsf {CA}$
can be seen as the analogue of
 $\boldsymbol {\Pi }^1_1\mathrm {-CA}_0$
. It is Weihrauch equivalent to the parallelization of
$\boldsymbol {\Pi }^1_1\mathrm {-CA}_0$
. It is Weihrauch equivalent to the parallelization of
![]() $\chi _{\Pi ^1_1} $
, which is the characteristic function of a
$\chi _{\Pi ^1_1} $
, which is the characteristic function of a
![]() $\Pi ^1_1$
-complete set. It is convenient to think of
$\Pi ^1_1$
-complete set. It is convenient to think of
![]() $\chi _{\Pi ^1_1} $
as the function that takes in input a subtree of
$\chi _{\Pi ^1_1} $
as the function that takes in input a subtree of
![]() ${\mathbb {N}^{<\mathbb {N}}}$
and checks whether it is well-founded.
${\mathbb {N}^{<\mathbb {N}}}$
and checks whether it is well-founded.
We can also define
![]() $\boldsymbol {\Gamma }$
-choice
$\boldsymbol {\Gamma }$
-choice
![]() ${\boldsymbol {\Gamma }}\text {-}\mathsf {C}_{\textbf {X}} :\subseteq \boldsymbol {\Gamma }(\textbf {X}) \rightrightarrows \textbf {X}$
by
${\boldsymbol {\Gamma }}\text {-}\mathsf {C}_{\textbf {X}} :\subseteq \boldsymbol {\Gamma }(\textbf {X}) \rightrightarrows \textbf {X}$
by
![]() ${\boldsymbol {\Gamma }}\text {-}\mathsf {C}_{\textbf {X}}(A) := A$
. In other words,
${\boldsymbol {\Gamma }}\text {-}\mathsf {C}_{\textbf {X}}(A) := A$
. In other words,
![]() ${\boldsymbol {\Gamma }}\text {-}\mathsf {C}_{\textbf {X}}$
is the task of producing an element of a nonempty
${\boldsymbol {\Gamma }}\text {-}\mathsf {C}_{\textbf {X}}$
is the task of producing an element of a nonempty
![]() $\boldsymbol {\Gamma }$
-set A, given a
$\boldsymbol {\Gamma }$
-set A, given a
![]() $\delta _{\boldsymbol {\Gamma }}$
-name of A. We can define
$\delta _{\boldsymbol {\Gamma }}$
-name of A. We can define
![]() $\boldsymbol {\Gamma }\text {-}\mathsf {UC}_{\textbf {X}} :\subseteq \boldsymbol {\Gamma }(\textbf {X}) \to \textbf {X}$
analogously. When reducing problems to
$\boldsymbol {\Gamma }\text {-}\mathsf {UC}_{\textbf {X}} :\subseteq \boldsymbol {\Gamma }(\textbf {X}) \to \textbf {X}$
analogously. When reducing problems to
![]() $\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
and
$\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
and
![]() $\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
, the following facts are helpful:
$\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
, the following facts are helpful:
 ${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}} \equiv _{\mathrm {W}} \mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
and
${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}} \equiv _{\mathrm {W}} \mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
and
 $\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}} \equiv _{\mathrm {W}} \boldsymbol {\Sigma }^1_1\text {-}\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
(see [Reference Kihara, Marcone and Pauly26]).
$\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}} \equiv _{\mathrm {W}} \boldsymbol {\Sigma }^1_1\text {-}\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
(see [Reference Kihara, Marcone and Pauly26]).
We define the represented spaces
![]() $\boldsymbol {\Gamma }(\textbf {LO})$
and
$\boldsymbol {\Gamma }(\textbf {LO})$
and
![]() $\boldsymbol {\Gamma }(\textbf {QO})$
by restricting the codomain of
$\boldsymbol {\Gamma }(\textbf {QO})$
by restricting the codomain of
![]() $\delta _{\boldsymbol {\Gamma }}$
to the set of subsets of
$\delta _{\boldsymbol {\Gamma }}$
to the set of subsets of
![]() $\mathbb {N}$
which are characteristic functions of linear orders and quasiorders respectively. This will be used in §5.
$\mathbb {N}$
which are characteristic functions of linear orders and quasiorders respectively. This will be used in §5.
We will often construct linear orders using the following method. For every tree
![]() $T\subseteq {\mathbb {N}^{<\mathbb {N}}}$
, we define the Kleene–Brouwer order
$T\subseteq {\mathbb {N}^{<\mathbb {N}}}$
, we define the Kleene–Brouwer order
![]() $\mathrm {KB}(T)$
on T as follows:
$\mathrm {KB}(T)$
on T as follows:
![]() $\sigma \le _{\mathrm {KB}} \tau $
if and only if
$\sigma \le _{\mathrm {KB}} \tau $
if and only if
![]() $\tau \sqsubseteq \sigma $
or
$\tau \sqsubseteq \sigma $
or
![]() $\sigma \le _{lex} \tau $
. The map
$\sigma \le _{lex} \tau $
. The map
![]() $T\mapsto \mathrm {KB}(T)$
from
$T\mapsto \mathrm {KB}(T)$
from
![]() $\mathbf {Tr}$
to
$\mathbf {Tr}$
to
![]() $\textbf {LO}$
is computable. It is known that
$\textbf {LO}$
is computable. It is known that
![]() $\mathrm {KB}(T)$
is a well-order if and only if T is well-founded (see e.g., [Reference Simpson41, Lemma V.1.3]).
$\mathrm {KB}(T)$
is a well-order if and only if T is well-founded (see e.g., [Reference Simpson41, Lemma V.1.3]).
Finally we present a notion recently studied by Dzhafarov et al. [Reference Dzhafarov, Solomon and Yokoyama17]:
Definition 2.2. Let
![]() $\mathcal {F}$
be the set of first-order problems, i.e., the set of problems with codomain
$\mathcal {F}$
be the set of first-order problems, i.e., the set of problems with codomain
![]() $\mathbb {N}$
. For every problem
$\mathbb {N}$
. For every problem
![]() $f:\subseteq \mathbf {Y} \rightrightarrows \mathbf {Z}$
, the first-order part of f is the multi-valued function
$f:\subseteq \mathbf {Y} \rightrightarrows \mathbf {Z}$
, the first-order part of f is the multi-valued function
![]() ${}^1{f}:\subseteq {\mathbb {N}^{\mathbb {N}}}\times \mathbf {Y} \rightrightarrows \mathbb {N}$
defined as follows:
${}^1{f}:\subseteq {\mathbb {N}^{\mathbb {N}}}\times \mathbf {Y} \rightrightarrows \mathbb {N}$
defined as follows:
-
• instances are pairs
 $(p,y)$
s.t.
$(p,y)$
s.t.
 $y\in \operatorname {dom}(\,f)$
and for every
$y\in \operatorname {dom}(\,f)$
and for every
 $z\in f(y)$
and every name t for z,
$z\in f(y)$
and every name t for z,
 $\Phi _p(t)(0)\downarrow $
, where
$\Phi _p(t)(0)\downarrow $
, where
 $\Phi _{(\cdot )}$
is a fixed universal Turing functional and
$\Phi _{(\cdot )}$
is a fixed universal Turing functional and -
• a solution for
 $(p,y)$
is any n s.t. there is a name t for a solution
$(p,y)$
is any n s.t. there is a name t for a solution
 $z\in f(y)$
s.t.
$z\in f(y)$
s.t.
 $\Phi _p(t)(0)\downarrow =n$
.
$\Phi _p(t)(0)\downarrow =n$
.
The motivation for this notion comes from the following fact:
Proposition 2.3 [Reference Dzhafarov, Solomon and Yokoyama17]
For every problem f,
 $$ \begin{align*} {}^1{f} \equiv_{\mathrm{W}} \max_{\le_{\mathrm{W}}}\{ g\in \mathcal{F} : g \le_{\mathrm{W}} f\}. \end{align*} $$
$$ \begin{align*} {}^1{f} \equiv_{\mathrm{W}} \max_{\le_{\mathrm{W}}}\{ g\in \mathcal{F} : g \le_{\mathrm{W}} f\}. \end{align*} $$
We conclude this section with the following proposition:
Proposition 2.4.
 ${}^1{\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}}\equiv _{\mathrm {W}} {\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}_{\mathbb {N}}$
.
${}^1{\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}}\equiv _{\mathrm {W}} {\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}_{\mathbb {N}}$
.
Proof It is known that
 ${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}_{\mathbb {N}}<_{\mathrm {W}} \widehat {{\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}_{\mathbb {N}}}<_{\mathrm {W}} \mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
[Reference Astor, Dzhafarov, Solomon and Suggs1, Theorem 3.34]. On the other hand, if
${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}_{\mathbb {N}}<_{\mathrm {W}} \widehat {{\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}_{\mathbb {N}}}<_{\mathrm {W}} \mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
[Reference Astor, Dzhafarov, Solomon and Suggs1, Theorem 3.34]. On the other hand, if
![]() $f:\subseteq \mathbf {X} \rightrightarrows \mathbb {N}$
is s.t.
$f:\subseteq \mathbf {X} \rightrightarrows \mathbb {N}$
is s.t.
![]() $f\le _{\mathrm {W}} \mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
via
$f\le _{\mathrm {W}} \mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
via
![]() $\Phi ,\Psi $
then, for every name p of some
$\Phi ,\Psi $
then, for every name p of some
![]() $x\in \operatorname {dom}(\,f)$
,
$x\in \operatorname {dom}(\,f)$
,
![]() $\Phi (p)$
is the name of an ill-founded tree
$\Phi (p)$
is the name of an ill-founded tree
![]() $T_p$
and, for every
$T_p$
and, for every
![]() $t\in [T_p]$
we have
$t\in [T_p]$
we have
![]() $\Psi (t)(0)\in f(x)$
. This means that we can compute a solution choosing an element from
$\Psi (t)(0)\in f(x)$
. This means that we can compute a solution choosing an element from
 $$ \begin{align*} \{ n \in\mathbb{N} : (\exists t \in {\mathbb{N}^{\mathbb{N}}})(t\in [T_p] \land \Psi(t)(0)=n) \}, \end{align*} $$
$$ \begin{align*} \{ n \in\mathbb{N} : (\exists t \in {\mathbb{N}^{\mathbb{N}}})(t\in [T_p] \land \Psi(t)(0)=n) \}, \end{align*} $$
which is a
 $\Sigma ^{1,p}_1$
subset of
$\Sigma ^{1,p}_1$
subset of
![]() $\mathbb {N}$
.⊣
$\mathbb {N}$
.⊣
We will characterize the first-order part of
![]() $\mathsf {DS}$
in Theorem 4.10.
$\mathsf {DS}$
in Theorem 4.10.
3. The deterministic part of a problem
Definition 3.1. Let
![]() $\mathbf {X}$
be a represented space and
$\mathbf {X}$
be a represented space and
![]() $f:\subseteq \mathbf {Y} \rightrightarrows \mathbf {Z}$
be a multi-valued function. We define
$f:\subseteq \mathbf {Y} \rightrightarrows \mathbf {Z}$
be a multi-valued function. We define
![]() $\mathrm {Det}_{ \mathbf {X} }(\,f):\subseteq {\mathbb {N}^{\mathbb {N}}} \times \mathbf {Y} \to \mathbf {X}$
by
$\mathrm {Det}_{ \mathbf {X} }(\,f):\subseteq {\mathbb {N}^{\mathbb {N}}} \times \mathbf {Y} \to \mathbf {X}$
by
 $$ \begin{align*} \mathrm{Det}_{ \mathbf{X} }(\,f)(p,y) = x :\hspace{-1mm}\iff (\forall z \in \delta_{\mathbf{Z}}^{-1}(\,f(y)))(\delta_{\mathbf{X}}(\Phi_p(z)) = x),\end{align*} $$
$$ \begin{align*} \mathrm{Det}_{ \mathbf{X} }(\,f)(p,y) = x :\hspace{-1mm}\iff (\forall z \in \delta_{\mathbf{Z}}^{-1}(\,f(y)))(\delta_{\mathbf{X}}(\Phi_p(z)) = x),\end{align*} $$
where
![]() $\Phi _{(\cdot )}$
is a universal Turing functional. The domain of
$\Phi _{(\cdot )}$
is a universal Turing functional. The domain of
![]() $\mathrm {Det}_{ \mathbf {X} }(\,f)$
is maximal for this to be well-defined. We just write
$\mathrm {Det}_{ \mathbf {X} }(\,f)$
is maximal for this to be well-defined. We just write
![]() $\mathrm {Det}_{ }(\,f)$
for
$\mathrm {Det}_{ }(\,f)$
for
![]() $\mathrm {Det}_{ {\mathbb {N}^{\mathbb {N}}} }(\,f)$
.
$\mathrm {Det}_{ {\mathbb {N}^{\mathbb {N}}} }(\,f)$
.
Notice that
![]() $\mathrm {Det}_{ }(\,f)$
is always a cylinder. This is not true for all
$\mathrm {Det}_{ }(\,f)$
is always a cylinder. This is not true for all
![]() $\textbf {X}$
(if
$\textbf {X}$
(if
![]() $\mathbf {X}=\mathbb {N}$
then
$\mathbf {X}=\mathbb {N}$
then
![]() $\mathrm {Det}_{ \mathbf {X} }(\,f)$
always has computable solutions, and therefore
$\mathrm {Det}_{ \mathbf {X} }(\,f)$
always has computable solutions, and therefore
![]() $\operatorname {id}\not \le _{\mathrm {sW}} \mathrm {Det}_{ \mathbf {X} }(\,f)$
).
$\operatorname {id}\not \le _{\mathrm {sW}} \mathrm {Det}_{ \mathbf {X} }(\,f)$
).
Our interest in the principle
![]() $\mathrm {Det}_{ \mathbf {X} }(f)$
lies in the fact that it has the maximal Weihrauch degree of all (single-valued!) functions with codomain
$\mathrm {Det}_{ \mathbf {X} }(f)$
lies in the fact that it has the maximal Weihrauch degree of all (single-valued!) functions with codomain
![]() $\mathbf {X}$
that are Weihrauch below f:
$\mathbf {X}$
that are Weihrauch below f:
Theorem 3.2.
![]() $\mathrm {Det}_{ \mathbf {X} }(f) \equiv _{\mathrm {W}} \max _{\le _{\mathrm {W}}} \{g : \subseteq \mathbf {W} \to \mathbf {X} : g \le _{\mathrm {W}} f\}$
.
$\mathrm {Det}_{ \mathbf {X} }(f) \equiv _{\mathrm {W}} \max _{\le _{\mathrm {W}}} \{g : \subseteq \mathbf {W} \to \mathbf {X} : g \le _{\mathrm {W}} f\}$
.
Proof Clearly,
![]() $\mathrm {Det}_{ \mathbf {X} }(f)$
is itself present in the set on the right hand side. Assume
$\mathrm {Det}_{ \mathbf {X} }(f)$
is itself present in the set on the right hand side. Assume
![]() $g:\subseteq \mathbf {W} \to \mathbf {X}$
satisfies
$g:\subseteq \mathbf {W} \to \mathbf {X}$
satisfies
![]() $g \le _{\mathrm {W}} f$
with reduction witnesses
$g \le _{\mathrm {W}} f$
with reduction witnesses
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
. Given a name q for an input to g, let
$\Psi $
. Given a name q for an input to g, let
![]() $y = \delta _{\mathbf {Y}}(\Phi (q))$
be the value f is called on, and let p be a name for the function
$y = \delta _{\mathbf {Y}}(\Phi (q))$
be the value f is called on, and let p be a name for the function
![]() $\Psi (q,\cdot )$
. Then
$\Psi (q,\cdot )$
. Then
![]() $\mathrm {Det}_{ \mathbf {X} }(f)(p,y) = g(\delta _{\mathbf {W}}(q))$
. ⊣
$\mathrm {Det}_{ \mathbf {X} }(f)(p,y) = g(\delta _{\mathbf {W}}(q))$
. ⊣
In the same spirit, we can identify several other operators
![]() $\Lambda _{\mathcal {Y}}$
of the type
$\Lambda _{\mathcal {Y}}$
of the type
![]() $\Lambda _{\mathcal {Y}}(f):= \max _{\le _{\mathrm {W}}} \{ g \in \mathcal {Y} : g\le _{\mathrm {W}} f \}$
. In particular the proof strategy used in Theorem 3.2 can be used to prove that
$\Lambda _{\mathcal {Y}}(f):= \max _{\le _{\mathrm {W}}} \{ g \in \mathcal {Y} : g\le _{\mathrm {W}} f \}$
. In particular the proof strategy used in Theorem 3.2 can be used to prove that
![]() $\Lambda _{\mathcal {U}_N}$
and
$\Lambda _{\mathcal {U}_N}$
and
![]() $\Lambda _{\mathcal {V}_N}$
are total, where
$\Lambda _{\mathcal {V}_N}$
are total, where
![]() $\mathcal {U}_N$
is the set of first-order problems with codomain N, and
$\mathcal {U}_N$
is the set of first-order problems with codomain N, and
![]() $\mathcal {V}_N$
is the set of problems in
$\mathcal {V}_N$
is the set of problems in
![]() $\mathcal {U}_N$
which are also single-valued. This will come into play in Theorem 4.31 and in Theorem 4.33.
$\mathcal {U}_N$
which are also single-valued. This will come into play in Theorem 4.31 and in Theorem 4.33.
Corollary 3.3.
![]() $\mathrm {Det}_{ \mathbf {X} }(\cdot )$
is an interior degree-theoretic operator on Weihrauch degrees, i.e.,
$\mathrm {Det}_{ \mathbf {X} }(\cdot )$
is an interior degree-theoretic operator on Weihrauch degrees, i.e.,
 $$ \begin{align*} &\mathrm{Det}_{ \mathbf{X} }(\mathrm{Det}_{ \mathbf{X} }(f)) \equiv_{\mathrm{W}} \mathrm{Det}_{ \mathbf{X} }(f) \le_{\mathrm{W}} f; \\ &\quad f \le_{\mathrm{W}} g \Rightarrow \mathrm{Det}_{ \mathbf{X} }(f) \le_{\mathrm{W}} \mathrm{Det}_{ \mathbf{X} }(g). \end{align*} $$
$$ \begin{align*} &\mathrm{Det}_{ \mathbf{X} }(\mathrm{Det}_{ \mathbf{X} }(f)) \equiv_{\mathrm{W}} \mathrm{Det}_{ \mathbf{X} }(f) \le_{\mathrm{W}} f; \\ &\quad f \le_{\mathrm{W}} g \Rightarrow \mathrm{Det}_{ \mathbf{X} }(f) \le_{\mathrm{W}} \mathrm{Det}_{ \mathbf{X} }(g). \end{align*} $$
3.1. Impact of the codomain space
We make some basic observations on how the space
![]() $\mathbf {X}$
impacts the degrees
$\mathbf {X}$
impacts the degrees
![]() $\mathrm {Det}_{ \mathbf {X} }(f)$
for arbitrary f. Clearly, whenever
$\mathrm {Det}_{ \mathbf {X} }(f)$
for arbitrary f. Clearly, whenever
![]() $\mathbf {Y}$
computably embeds into
$\mathbf {Y}$
computably embeds into
![]() $\mathbf {X}$
(i.e., there is a computable injection
$\mathbf {X}$
(i.e., there is a computable injection
![]() $\mathbf {Y}\to \mathbf {X}$
with computable inverse), then
$\mathbf {Y}\to \mathbf {X}$
with computable inverse), then
![]() $\mathrm {Det}_{ \mathbf {Y} }(f) \le _{\mathrm {W}} \mathrm {Det}_{ \mathbf {X} }(f)$
. In general, we obtain many different operations. To see this, we consider the point degree spectrum of a represented space as introduced by Kihara and Pauly [Reference Kihara and Pauly28]. The point degree spectrum of
$\mathrm {Det}_{ \mathbf {Y} }(f) \le _{\mathrm {W}} \mathrm {Det}_{ \mathbf {X} }(f)$
. In general, we obtain many different operations. To see this, we consider the point degree spectrum of a represented space as introduced by Kihara and Pauly [Reference Kihara and Pauly28]. The point degree spectrum of
![]() $(X,\,\delta _{\mathbf {X}})$
is the set of Medvedev degrees of the form
$(X,\,\delta _{\mathbf {X}})$
is the set of Medvedev degrees of the form
![]() $\delta ^{-1}_{\mathbf {X}}(x)$
for
$\delta ^{-1}_{\mathbf {X}}(x)$
for
![]() $x \in X$
.
$x \in X$
.
The spectrum of
![]() $\mathbf {Y}$
is included in that of
$\mathbf {Y}$
is included in that of
![]() $\mathbf {X}$
iff
$\mathbf {X}$
iff
![]() $\mathbf {Y}$
can be decomposed into countably many parts each of which embeds into
$\mathbf {Y}$
can be decomposed into countably many parts each of which embeds into
![]() $\mathbf {X}$
[Reference Kihara and Pauly28, Lemma 3.6]. If the spectrum of
$\mathbf {X}$
[Reference Kihara and Pauly28, Lemma 3.6]. If the spectrum of
![]() $\mathbf {Y}$
is not included in that of
$\mathbf {Y}$
is not included in that of
![]() $\mathbf {X}$
, we can consider a constant function y witnessing this. Then
$\mathbf {X}$
, we can consider a constant function y witnessing this. Then
![]() $\mathrm {Det}_{ \mathbf {X} }(y) <_{\mathrm {W}} \mathrm {Det}_{ \mathbf {Y} }(y) \equiv _{\mathrm {W}} y$
. We have thus seen that if
$\mathrm {Det}_{ \mathbf {X} }(y) <_{\mathrm {W}} \mathrm {Det}_{ \mathbf {Y} }(y) \equiv _{\mathrm {W}} y$
. We have thus seen that if
![]() $\mathrm {Det}_{ \mathbf {X} }(f) \equiv _{\mathrm {W}} \mathrm {Det}_{ \mathbf {Y} }(f)$
for all f, then
$\mathrm {Det}_{ \mathbf {X} }(f) \equiv _{\mathrm {W}} \mathrm {Det}_{ \mathbf {Y} }(f)$
for all f, then
![]() $\mathbf {X}$
and
$\mathbf {X}$
and
![]() $\mathbf {Y}$
must have the same point degree spectrum. Miller [Reference Miller32] has shown that the spectrum of
$\mathbf {Y}$
must have the same point degree spectrum. Miller [Reference Miller32] has shown that the spectrum of
![]() $[0,1]^\omega $
is not contained in the Turing degrees (i.e., the spectrum of
$[0,1]^\omega $
is not contained in the Turing degrees (i.e., the spectrum of
![]() ${2^{\mathbb {N}}}$
), which was extended in [Reference Kihara and Pauly28] to the result that the spectrum of a computable Polish space is contained in the Turing degrees relative to some oracle iff that space is countably dimensional. The spectra of further spaces have been explored in [Reference Kihara, Ng and Pauly27].
${2^{\mathbb {N}}}$
), which was extended in [Reference Kihara and Pauly28] to the result that the spectrum of a computable Polish space is contained in the Turing degrees relative to some oracle iff that space is countably dimensional. The spectra of further spaces have been explored in [Reference Kihara, Ng and Pauly27].
We can extend the separation arguments based on the spectrum by considering sequences rather than just constant functions.Footnote
1
Whenever we have a sequence
![]() $f_0 : \mathbb {N} \to \mathbf {X}_0$
and a function
$f_0 : \mathbb {N} \to \mathbf {X}_0$
and a function
![]() $g_0 : \subseteq {\mathbb {N}^{\mathbb {N}}} \to \mathbf {X}_1$
with
$g_0 : \subseteq {\mathbb {N}^{\mathbb {N}}} \to \mathbf {X}_1$
with
![]() $f_0 \equiv _{\mathrm {W}} g_0$
, then there is a sequence
$f_0 \equiv _{\mathrm {W}} g_0$
, then there is a sequence
![]() $h: \mathbb {N} \to \mathbf {X}_1$
with
$h: \mathbb {N} \to \mathbf {X}_1$
with
![]() $f_0 \equiv _{\mathrm {W}} h$
. A Weihrauch reduction
$f_0 \equiv _{\mathrm {W}} h$
. A Weihrauch reduction
![]() $f \le _{\mathrm {W}} g$
for
$f \le _{\mathrm {W}} g$
for
![]() $f : \mathbb {N} \to \mathbf {X}$
and
$f : \mathbb {N} \to \mathbf {X}$
and
![]() $g : \mathbb {N} \to \mathbf {Y}$
gives rise to a computable partial function
$g : \mathbb {N} \to \mathbf {Y}$
gives rise to a computable partial function
![]() $F : \subseteq \mathbf {Y}^{\mathbb {N}} \to \mathbf {X}^{\mathbb {N}}$
with
$F : \subseteq \mathbf {Y}^{\mathbb {N}} \to \mathbf {X}^{\mathbb {N}}$
with
![]() $F(g) = f$
. It follows that it suffices to separate
$F(g) = f$
. It follows that it suffices to separate
![]() $\mathbf {Y}^{\mathbb {N}}$
and
$\mathbf {Y}^{\mathbb {N}}$
and
![]() $\mathbf {X}^{\mathbb {N}}$
via their spectrum to conclude that
$\mathbf {X}^{\mathbb {N}}$
via their spectrum to conclude that
![]() $\mathrm {Det}_{ \mathbf {X} }(\cdot )$
and
$\mathrm {Det}_{ \mathbf {X} }(\cdot )$
and
![]() $\mathrm {Det}_{ \mathbf {Y} }(\cdot )$
are distinct operators. In particular, Miller’s result implies that there is a function with codomain
$\mathrm {Det}_{ \mathbf {Y} }(\cdot )$
are distinct operators. In particular, Miller’s result implies that there is a function with codomain
![]() $\mathbb {R}$
that is not equivalent to any function with codomain
$\mathbb {R}$
that is not equivalent to any function with codomain
![]() ${\mathbb {N}^{\mathbb {N}}}$
.
${\mathbb {N}^{\mathbb {N}}}$
.
3.2. The deterministic part and the first-order part
Let us now explore the interplay between the deterministic part and the first-order part.
Proposition 3.4.
![]() ${}^1{\mathrm {Det}_{ }(f)} \equiv _{\mathrm {W}} \mathrm {Det}_{ \mathbb {N} }(f) \le _{\mathrm {W}} \mathrm {Det}_{ }({}^1{f})$
.
${}^1{\mathrm {Det}_{ }(f)} \equiv _{\mathrm {W}} \mathrm {Det}_{ \mathbb {N} }(f) \le _{\mathrm {W}} \mathrm {Det}_{ }({}^1{f})$
.
Proof By considering what the relevant maxima in the characterizations are taken about, it is clear that
![]() $\mathrm {Det}_{ \mathbb {N} }(f) \le _{\mathrm {W}} {}^1{\mathrm {Det}_{ }(f)}$
and
$\mathrm {Det}_{ \mathbb {N} }(f) \le _{\mathrm {W}} {}^1{\mathrm {Det}_{ }(f)}$
and
![]() $\mathrm {Det}_{ \mathbb {N} }(f) \le _{\mathrm {W}} \mathrm {Det}_{ }({}^1{f})$
. To see that
$\mathrm {Det}_{ \mathbb {N} }(f) \le _{\mathrm {W}} \mathrm {Det}_{ }({}^1{f})$
. To see that
![]() ${}^1{\mathrm {Det}_{ }(f)} \le _{\mathrm {W}} \mathrm {Det}_{ \mathbb {N} }(f)$
, we consider a function
${}^1{\mathrm {Det}_{ }(f)} \le _{\mathrm {W}} \mathrm {Det}_{ \mathbb {N} }(f)$
, we consider a function
![]() $f : \subseteq {\mathbb {N}^{\mathbb {N}}} \to {\mathbb {N}^{\mathbb {N}}}$
and a multi-valued function
$f : \subseteq {\mathbb {N}^{\mathbb {N}}} \to {\mathbb {N}^{\mathbb {N}}}$
and a multi-valued function
![]() $g:\subseteq {\mathbb {N}^{\mathbb {N}}} \rightrightarrows \mathbb {N}$
with
$g:\subseteq {\mathbb {N}^{\mathbb {N}}} \rightrightarrows \mathbb {N}$
with
![]() $g \le _{\mathrm {W}} f$
. But this reduction actually yields some choice function of g, showing that
$g \le _{\mathrm {W}} f$
. But this reduction actually yields some choice function of g, showing that
![]() $g \le _{\mathrm {W}} \mathrm {Det}_{ \mathbb {N} }(f)$
. ⊣
$g \le _{\mathrm {W}} \mathrm {Det}_{ \mathbb {N} }(f)$
. ⊣
Open Question 3.5. Is there some f with
![]() $\mathrm {Det}_{ \mathbb {N} }(f) <_{\mathrm {W}} \mathrm {Det}_{ }({}^1{f})$
?
$\mathrm {Det}_{ \mathbb {N} }(f) <_{\mathrm {W}} \mathrm {Det}_{ }({}^1{f})$
?
The question above asks whether whenever there is a countable cover making a partial function on Baire space piecewise computable, there also is a partition of the same or lower complexity that renders the function piecewise computable. The complexity here is not merely the complexity of the individual pieces, but the Weihrauch degree of the map that assigns the piece to any Baire space element.
Proposition 3.6.
 $\mathrm {Det}_{ }(f) \le _{\mathrm {W}} \widehat {\mathrm {Det}_{ \mathbb {N} }(f)}$
.
$\mathrm {Det}_{ }(f) \le _{\mathrm {W}} \widehat {\mathrm {Det}_{ \mathbb {N} }(f)}$
.
Proof A function
![]() $f : \subseteq {\mathbb {N}^{\mathbb {N}}} \to {\mathbb {N}^{\mathbb {N}}}$
is reducible to the parallelization of its uncurried form
$f : \subseteq {\mathbb {N}^{\mathbb {N}}} \to {\mathbb {N}^{\mathbb {N}}}$
is reducible to the parallelization of its uncurried form
![]() $F : \subseteq \mathbb {N} \times {\mathbb {N}^{\mathbb {N}}} \to \mathbb {N}$
where
$F : \subseteq \mathbb {N} \times {\mathbb {N}^{\mathbb {N}}} \to \mathbb {N}$
where
![]() $F(n,p) = f(p)(n)$
. ⊣
$F(n,p) = f(p)(n)$
. ⊣
Corollary 3.7.
 $\mathrm {Det}_{ }(f) \le _{\mathrm {W}} \widehat {{}^1{f}}$
.
$\mathrm {Det}_{ }(f) \le _{\mathrm {W}} \widehat {{}^1{f}}$
.
3.3. Interaction with other operations on Weihrauch degrees
A first straightforward observation is that
![]() $\mathrm {Det}_{ }(f)\,\square \, \mathrm {Det}_{ }(g) \le _{\mathrm {W}} \mathrm {Det}_{ }(f\,\square \, g)$
whenever
$\mathrm {Det}_{ }(f)\,\square \, \mathrm {Det}_{ }(g) \le _{\mathrm {W}} \mathrm {Det}_{ }(f\,\square \, g)$
whenever
![]() $\square $
is a degree-theoretic operator that preserves single-valuedness. We will look at the interaction with the usual well-studied operations on Weihrauch degrees. Besides those introduced in §2, we consider
$\square $
is a degree-theoretic operator that preserves single-valuedness. We will look at the interaction with the usual well-studied operations on Weihrauch degrees. Besides those introduced in §2, we consider
![]() $\sqcup $
and
$\sqcup $
and
![]() $\sqcap $
, the join and meet in the Weihrauch lattice, and the finite parallelization
$\sqcap $
, the join and meet in the Weihrauch lattice, and the finite parallelization
![]() $^*$
(which essentially is closure under
$^*$
(which essentially is closure under
![]() $\times $
). See [Reference Brattka, Hölzl, Kuyper, Vollmer and Vallée11, Section 3] for definitions. The diamond operator
$\times $
). See [Reference Brattka, Hölzl, Kuyper, Vollmer and Vallée11, Section 3] for definitions. The diamond operator
![]() ${}^\diamond $
was introduced in [Reference Neumann and Pauly34], and corresponds to the possibility of using the oracle an arbitrary (but finite) number of times (essentially closure under compositional product).
${}^\diamond $
was introduced in [Reference Neumann and Pauly34], and corresponds to the possibility of using the oracle an arbitrary (but finite) number of times (essentially closure under compositional product).
It is imminent from the definition that
![]() $\mathrm {Det}_{ }(f)\sqcup \mathrm {Det}_{ }(g) \equiv _{\mathrm {W}} \mathrm {Det}_{ }(f \sqcup g)$
.
$\mathrm {Det}_{ }(f)\sqcup \mathrm {Det}_{ }(g) \equiv _{\mathrm {W}} \mathrm {Det}_{ }(f \sqcup g)$
.
Moreover
![]() $\mathrm {Det}_{ }(f \sqcap g) \le _{\mathrm {W}} \mathrm {Det}_{ }(f)$
and
$\mathrm {Det}_{ }(f \sqcap g) \le _{\mathrm {W}} \mathrm {Det}_{ }(f)$
and
![]() $\mathrm {Det}_{ }(f \sqcap g) \le _{\mathrm {W}} \mathrm {Det}_{ }(g)$
by monotonicity, hence
$\mathrm {Det}_{ }(f \sqcap g) \le _{\mathrm {W}} \mathrm {Det}_{ }(g)$
by monotonicity, hence
![]() $\mathrm {Det}_{ }(f \sqcap g) \le _{\mathrm {W}} \mathrm {Det}_{ }(f)\sqcap \mathrm {Det}_{ }(g)$
, as
$\mathrm {Det}_{ }(f \sqcap g) \le _{\mathrm {W}} \mathrm {Det}_{ }(f)\sqcap \mathrm {Det}_{ }(g)$
, as
![]() $\sqcap $
is the meet on Weihrauch degrees [Reference Brattka and Gherardi6, Proposition 3.11]. To see that the inequality can be strict, let
$\sqcap $
is the meet on Weihrauch degrees [Reference Brattka and Gherardi6, Proposition 3.11]. To see that the inequality can be strict, let
![]() $p,q \in {2^{\mathbb {N}}}$
be a minimal pair of Turing degrees (which we identify with the constant functions returning these values). Then
$p,q \in {2^{\mathbb {N}}}$
be a minimal pair of Turing degrees (which we identify with the constant functions returning these values). Then
![]() $\mathrm {Det}_{ }(p \sqcap q) \equiv _{\mathrm {W}} \operatorname {id}_{\mathbb {N}^{\mathbb {N}}} <_{\mathrm {W}} \mathrm {Det}_{ }(p) \sqcap \mathrm {Det}_{ }(q) \equiv _{\mathrm {W}} p \sqcap q$
.
$\mathrm {Det}_{ }(p \sqcap q) \equiv _{\mathrm {W}} \operatorname {id}_{\mathbb {N}^{\mathbb {N}}} <_{\mathrm {W}} \mathrm {Det}_{ }(p) \sqcap \mathrm {Det}_{ }(q) \equiv _{\mathrm {W}} p \sqcap q$
.
Our principle
![]() $\mathsf {DS}$
(to be defined) already witnesses that the deterministic part does not distribute over
$\mathsf {DS}$
(to be defined) already witnesses that the deterministic part does not distribute over
![]() $\times $
and
$\times $
and
![]() $*$
, and does not commute with
$*$
, and does not commute with
![]() $^*$
,
$^*$
,
![]() $^\diamond $
and
$^\diamond $
and
![]() $\widehat {\phantom {f}}$
: we will prove that
$\widehat {\phantom {f}}$
: we will prove that
![]() $\mathrm {Det}_{ }(\mathsf {DS})\equiv _{\mathrm {W}} \mathsf {lim}$
(Theorem 4.16), while
$\mathrm {Det}_{ }(\mathsf {DS})\equiv _{\mathrm {W}} \mathsf {lim}$
(Theorem 4.16), while
![]() $ \mathsf {LPO} '\le _{\mathrm {W}} \mathsf {DS} \times \mathsf {DS}$
(Theorem 4.18). Here we also give another example with a more computability-theoretic flavor:
$ \mathsf {LPO} '\le _{\mathrm {W}} \mathsf {DS} \times \mathsf {DS}$
(Theorem 4.18). Here we also give another example with a more computability-theoretic flavor:
Example 3.8. There is a Weihrauch degree f such that:
 $$ \begin{align*}\mathrm{Det}_{ }(f) \equiv_{\mathrm{W}} \operatorname{id} <_{\mathrm{W}} f <_{\mathrm{W}} f \times f \equiv_{\mathrm{W}} f^\diamond \equiv_{\mathrm{W}} \widehat{f} \equiv_{\mathrm{W}} \mathrm{Det}_{ }(f \times f). \end{align*} $$
$$ \begin{align*}\mathrm{Det}_{ }(f) \equiv_{\mathrm{W}} \operatorname{id} <_{\mathrm{W}} f <_{\mathrm{W}} f \times f \equiv_{\mathrm{W}} f^\diamond \equiv_{\mathrm{W}} \widehat{f} \equiv_{\mathrm{W}} \mathrm{Det}_{ }(f \times f). \end{align*} $$
Indeed, consider the degrees of points in the spaces
![]() $\mathbb {R}_<$
,
$\mathbb {R}_<$
,
![]() $\mathbb {R}_>$
and
$\mathbb {R}_>$
and
![]() $\mathbb {R}$
(see [Reference Kihara, Ng and Pauly27] for details). Let
$\mathbb {R}$
(see [Reference Kihara, Ng and Pauly27] for details). Let
![]() $x \in \mathbb {R}$
be neither left-c.e. nor right-c.e.; i.e., it lacks computable names in both
$x \in \mathbb {R}$
be neither left-c.e. nor right-c.e.; i.e., it lacks computable names in both
![]() $\mathbb {R}_<$
and
$\mathbb {R}_<$
and
![]() $\mathbb {R}_>$
. Then
$\mathbb {R}_>$
. Then
![]() $x \in \mathbb {R}_<$
and
$x \in \mathbb {R}_<$
and
![]() $x \in \mathbb {R}_>$
have quasi-minimal degrees, that is do not compute any non-computable elements of Cantor space. We define
$x \in \mathbb {R}_>$
have quasi-minimal degrees, that is do not compute any non-computable elements of Cantor space. We define
![]() $f\colon \mathbf {2} \to \mathbb {R}_< + \mathbb {R}_>$
by
$f\colon \mathbf {2} \to \mathbb {R}_< + \mathbb {R}_>$
by
![]() $f(0) = x \in \mathbb {R}_<$
and
$f(0) = x \in \mathbb {R}_<$
and
![]() $f(1) = x \in \mathbb {R}_>$
. The quasi-minimality implies that
$f(1) = x \in \mathbb {R}_>$
. The quasi-minimality implies that
![]() $\mathrm {Det}_{ }(f) \equiv _{\mathrm {W}} \operatorname {id}$
. However,
$\mathrm {Det}_{ }(f) \equiv _{\mathrm {W}} \operatorname {id}$
. However,
![]() $f \times f$
is equivalent to the constant function returning
$f \times f$
is equivalent to the constant function returning
![]() $x \in \mathbb {R}$
, which is also equivalent to the constant function returning the decimal expansion of x. Thus,
$x \in \mathbb {R}$
, which is also equivalent to the constant function returning the decimal expansion of x. Thus,
![]() $f \times f \equiv _{\mathrm {W}} \mathrm {Det}_{ }(f \times f)$
. Any of
$f \times f \equiv _{\mathrm {W}} \mathrm {Det}_{ }(f \times f)$
. Any of
![]() $f^*$
,
$f^*$
,
![]() $f * f$
,
$f * f$
,
![]() $f^\diamond $
and
$f^\diamond $
and
![]() $\widehat {f}$
clearly share the same degree.
$\widehat {f}$
clearly share the same degree.
Theorem 3.9. For every represented space
![]() $\mathbf {X}$
and every problems
$\mathbf {X}$
and every problems
![]() $f,g$
,
$f,g$
,
Proof Fix a single-valued h with codomain
![]() $\mathbf {X}$
and assume, without loss of generality, that
$\mathbf {X}$
and assume, without loss of generality, that
![]() $\operatorname {dom}(h)\subset {\mathbb {N}^{\mathbb {N}}}$
(if h is single-valued then the map
$\operatorname {dom}(h)\subset {\mathbb {N}^{\mathbb {N}}}$
(if h is single-valued then the map
![]() $p\mapsto h\circ \delta _{}(p)$
is single-valued as well, where
$p\mapsto h\circ \delta _{}(p)$
is single-valued as well, where
![]() $\delta _{}$
is the representation map for the domain of h). Assume also, for the sake of readability, that f and g are cylinders (if not we can just replace f with
$\delta _{}$
is the representation map for the domain of h). Assume also, for the sake of readability, that f and g are cylinders (if not we can just replace f with
![]() $f \times \operatorname {id}{}$
, as
$f \times \operatorname {id}{}$
, as
![]() $\mathrm {Det}_{ \mathbf {X} }(\cdot )$
is a degree-theoretic operation).
$\mathrm {Det}_{ \mathbf {X} }(\cdot )$
is a degree-theoretic operation).
By the cylindrical decomposition lemma, there is a computable function
![]() $\Phi _e$
s.t.
$\Phi _e$
s.t.
Let
![]() $\Phi ,\Psi $
be two maps witnessing this strong reduction. Define
$\Phi ,\Psi $
be two maps witnessing this strong reduction. Define
![]() $\phi $
as the restriction of
$\phi $
as the restriction of
![]() $\delta _{\mathbf {X}}\circ \Psi \circ f \circ \Phi _e$
to
$\delta _{\mathbf {X}}\circ \Psi \circ f \circ \Phi _e$
to
![]() $\operatorname {dom}(g \circ \Phi \circ h)$
. The choice of the domain of
$\operatorname {dom}(g \circ \Phi \circ h)$
. The choice of the domain of
![]() $\phi $
guarantees that
$\phi $
guarantees that
![]() $\phi $
is single-valued: intuitively
$\phi $
is single-valued: intuitively
![]() $\phi $
witnesses the “second part” of the reduction
$\phi $
witnesses the “second part” of the reduction
![]() $h\le _{\mathrm {sW}} f \circ \Phi _e\circ g$
, and the fact that h is single-valued implies that so is
$h\le _{\mathrm {sW}} f \circ \Phi _e\circ g$
, and the fact that h is single-valued implies that so is
![]() $\phi $
. In particular,
$\phi $
. In particular,
![]() $\phi \le _{\mathrm {W}} \mathrm {Det}_{ \mathbf {X} }(f)$
(as
$\phi \le _{\mathrm {W}} \mathrm {Det}_{ \mathbf {X} }(f)$
(as
![]() $\phi \le _{\mathrm {W}} f$
trivially). Since
$\phi \le _{\mathrm {W}} f$
trivially). Since
![]() $h\le _{\mathrm {W}} \phi * g$
we have that
$h\le _{\mathrm {W}} \phi * g$
we have that
![]() $h\le _{\mathrm {W}} \mathrm {Det}_{ \mathbf {X} } (f)* g$
.⊣
$h\le _{\mathrm {W}} \mathrm {Det}_{ \mathbf {X} } (f)* g$
.⊣
Notice that this implies the choice elimination theorem [Reference Brattka, Hölzl, Kuyper, Vollmer and Vallée11, Theorem 7.25], as
![]() $\mathrm {Det}_{ }(\mathsf {C}_{{2^{\mathbb {N}}}})\equiv _{\mathrm {W}}\operatorname {id}{}$
[Reference Brattka and Gherardi6, Corollary 8.8].
$\mathrm {Det}_{ }(\mathsf {C}_{{2^{\mathbb {N}}}})\equiv _{\mathrm {W}}\operatorname {id}{}$
[Reference Brattka and Gherardi6, Corollary 8.8].
Corollary 3.10. If g is single-valued with codomain ![]() ${\mathbb{N}^{\mathbb{N}}}$
then
${\mathbb{N}^{\mathbb{N}}}$
then ![]() $\mathrm {Det}(f* g)\equiv_{\mathrm {W}} \mathrm {Det}(f) * g$
.
$\mathrm {Det}(f* g)\equiv_{\mathrm {W}} \mathrm {Det}(f) * g$
.
Proof This follows from Theorem 3.9, as ![]() $\mathrm {Det} (f) * \mathrm {Det}(g)\le _{\mathrm {W}}\mathrm {Det}(f* g)$
always holds and
$\mathrm {Det} (f) * \mathrm {Det}(g)\le _{\mathrm {W}}\mathrm {Det}(f* g)$
always holds and ![]() $\mathrm {Det}(g)\equiv _{\mathrm {W}} g$
as g is single-valued with codomain
$\mathrm {Det}(g)\equiv _{\mathrm {W}} g$
as g is single-valued with codomain ![]() ${\mathbb{N}^{\mathbb{N}}}$
.⊣
${\mathbb{N}^{\mathbb{N}}}$
.⊣
Corollary 3.11. For every cylinder f and every
![]() $k\in \mathbb {N}$
$k\in \mathbb {N}$
 $$ \begin{align*} \mathrm{Det}_{ }(f)^{(k)} \equiv_{\mathrm{W}}\mathrm{Det}_{ }(f^{(k)}). \end{align*} $$
$$ \begin{align*} \mathrm{Det}_{ }(f)^{(k)} \equiv_{\mathrm{W}}\mathrm{Det}_{ }(f^{(k)}). \end{align*} $$
Proof The left-to-right reduction is straightforward as
 $$ \begin{align*} \mathrm{Det}_{ }(f)^{(k)} \le_{\mathrm{W}} \mathrm{Det}_{ }(f)*\mathsf{lim}^{[k]} \le_{\mathrm{W}} f *\mathsf{lim}^{[k]} \equiv_{\mathrm{W}} f^{(k)},\end{align*} $$
$$ \begin{align*} \mathrm{Det}_{ }(f)^{(k)} \le_{\mathrm{W}} \mathrm{Det}_{ }(f)*\mathsf{lim}^{[k]} \le_{\mathrm{W}} f *\mathsf{lim}^{[k]} \equiv_{\mathrm{W}} f^{(k)},\end{align*} $$
where the last equality follows from the fact that f is a cylinder. Since
![]() $\mathrm {Det}_{ }(f)^{(k)}$
is single-valued, this implies
$\mathrm {Det}_{ }(f)^{(k)}$
is single-valued, this implies
![]() $\mathrm {Det}_{ }(f)^{(k)}\le _{\mathrm {W}} \mathrm {Det}_{ }(f^{(k)})$
.
$\mathrm {Det}_{ }(f)^{(k)}\le _{\mathrm {W}} \mathrm {Det}_{ }(f^{(k)})$
.
The right-to-left reduction follows from Theorem 3.9 as
 $$ \begin{align*} \mathrm{Det}_{ }(f^{(k)}) \equiv_{\mathrm{W}} \mathrm{Det}_{ }(f*\mathsf{lim}^{[k]})\le_{\mathrm{W}}\mathrm{Det}_{ }(f) *\mathsf{lim}^{[k]} \equiv_{\mathrm{W}}\mathrm{Det}_{ }(f)^{(k)},\end{align*} $$
$$ \begin{align*} \mathrm{Det}_{ }(f^{(k)}) \equiv_{\mathrm{W}} \mathrm{Det}_{ }(f*\mathsf{lim}^{[k]})\le_{\mathrm{W}}\mathrm{Det}_{ }(f) *\mathsf{lim}^{[k]} \equiv_{\mathrm{W}}\mathrm{Det}_{ }(f)^{(k)},\end{align*} $$
where the last equality follows from the fact that
![]() $\mathrm {Det}_{ }(f)$
is a cylinder. ⊣
$\mathrm {Det}_{ }(f)$
is a cylinder. ⊣
The previous corollary can be generalized in a straightforward way to any represented space
![]() $\mathbf {X}$
s.t.
$\mathbf {X}$
s.t.
![]() $\mathrm {Det}_{ \mathbf {X} }(f)$
is a cylinder. Notice that it is false (in general) if f is not a cylinder: take
$\mathrm {Det}_{ \mathbf {X} }(f)$
is a cylinder. Notice that it is false (in general) if f is not a cylinder: take
![]() $f= {\mathsf {C}}_{2}$
and
$f= {\mathsf {C}}_{2}$
and
![]() $k=1$
. Since
$k=1$
. Since
 $\mathsf {C}_2'\equiv _{\mathrm {W}} \mathsf {RT}^{{1}}_{{2}} $
(see e.g., [Reference Anglès D'Auriac and Kihara1, Fact 2.3 and Proposition 3.4]) we have
$\mathsf {C}_2'\equiv _{\mathrm {W}} \mathsf {RT}^{{1}}_{{2}} $
(see e.g., [Reference Anglès D'Auriac and Kihara1, Fact 2.3 and Proposition 3.4]) we have
 $\mathrm {Det}(\mathsf {C}_2') \le _{\mathrm {W}} \mathsf {RT}^{{1}}_{{2}} $
, hence in particular
$\mathrm {Det}(\mathsf {C}_2') \le _{\mathrm {W}} \mathsf {RT}^{{1}}_{{2}} $
, hence in particular
![]() $\mathsf {lim} \not \le _{\mathrm {W}} \mathrm {Det}_{ }(\mathsf {C}_2')$
. On the other hand
$\mathsf {lim} \not \le _{\mathrm {W}} \mathrm {Det}_{ }(\mathsf {C}_2')$
. On the other hand
![]() $\mathsf {lim} \le _{\mathrm {W}} \mathrm {Det}_{ }(\mathsf {C}_2)'$
(as
$\mathsf {lim} \le _{\mathrm {W}} \mathrm {Det}_{ }(\mathsf {C}_2)'$
(as
![]() $\mathrm {Det}({\mathsf {C}_2 })$
is a cylinder).
$\mathrm {Det}({\mathsf {C}_2 })$
is a cylinder).
Definition 3.12. Given some
![]() $f:\subseteq {\mathbb {N}^{\mathbb {N}}} \rightrightarrows {\mathbb {N}^{\mathbb {N}}}$
let
$f:\subseteq {\mathbb {N}^{\mathbb {N}}} \rightrightarrows {\mathbb {N}^{\mathbb {N}}}$
let
![]() $?f:\subseteq {\mathbb {N}^{\mathbb {N}}} \rightrightarrows {\mathbb {N}^{\mathbb {N}}}$
be defined by
$?f:\subseteq {\mathbb {N}^{\mathbb {N}}} \rightrightarrows {\mathbb {N}^{\mathbb {N}}}$
be defined by
![]() $0^\omega \in ?f(0^\omega )$
and
$0^\omega \in ?f(0^\omega )$
and
![]() $0^n1p \in ?f(0^n1q)$
iff
$0^n1p \in ?f(0^n1q)$
iff
![]() $p \in f(q)$
.
$p \in f(q)$
.
It is easy to see that
![]() $?$
defines an operation on Weihrauch degrees, and represents the idea of being able to maybe ask a question to f – but never having to decide to forgo this (which would be the case for
$?$
defines an operation on Weihrauch degrees, and represents the idea of being able to maybe ask a question to f – but never having to decide to forgo this (which would be the case for
![]() $1 \sqcup f$
). Many well-studied principles are equivalent to their maybe-variants, this in particular holds for all pointed fractals. We introduce the operation here to be able to express how the deterministic part interacts with the notion of completion
$1 \sqcup f$
). Many well-studied principles are equivalent to their maybe-variants, this in particular holds for all pointed fractals. We introduce the operation here to be able to express how the deterministic part interacts with the notion of completion
![]() $\overline {(\cdot )}$
introduced by Brattka and Gherardi [Reference Brattka and Gherardi7, Reference Brattka, Gherardi and Hölzl8].
$\overline {(\cdot )}$
introduced by Brattka and Gherardi [Reference Brattka and Gherardi7, Reference Brattka, Gherardi and Hölzl8].
Proposition 3.13.
![]() $\mathrm {Det}_{ }(\overline {f}) \equiv _{\mathrm {W}} \mathrm {Det}_{ }(?f)\equiv _{\mathrm {W}} ?\mathrm {Det}_{ }(f)$
.
$\mathrm {Det}_{ }(\overline {f}) \equiv _{\mathrm {W}} \mathrm {Det}_{ }(?f)\equiv _{\mathrm {W}} ?\mathrm {Det}_{ }(f)$
.
Proof To show that
![]() $\mathrm {Det}_{ }(\overline {f}) \le _{\mathrm {W}} \mathrm {Det}_{ }(?f)$
, without loss of generality assume that
$\mathrm {Det}_{ }(\overline {f}) \le _{\mathrm {W}} \mathrm {Det}_{ }(?f)$
, without loss of generality assume that
![]() $f:\subseteq {\mathbb {N}^{\mathbb {N}}} \rightrightarrows {\mathbb {N}^{\mathbb {N}}}$
and consider a function
$f:\subseteq {\mathbb {N}^{\mathbb {N}}} \rightrightarrows {\mathbb {N}^{\mathbb {N}}}$
and consider a function
![]() $g : \subseteq {\mathbb {N}^{\mathbb {N}}} \to {\mathbb {N}^{\mathbb {N}}}$
with
$g : \subseteq {\mathbb {N}^{\mathbb {N}}} \to {\mathbb {N}^{\mathbb {N}}}$
with
![]() $g \le _{\mathrm {W}} \overline {f}$
witnessed by
$g \le _{\mathrm {W}} \overline {f}$
witnessed by
![]() $\Phi ,\Psi $
. Now if for some prefix w the computation of
$\Phi ,\Psi $
. Now if for some prefix w the computation of
![]() $\Psi (w,\cdot )$
outputs two different things depending on the second part of the input, then in order for g to be a function, we have the guarantee that all extensions of w in the domain of g will be mapped to inputs in the domain of f, i.e., we are actually calling f rather than making use of
$\Psi (w,\cdot )$
outputs two different things depending on the second part of the input, then in order for g to be a function, we have the guarantee that all extensions of w in the domain of g will be mapped to inputs in the domain of f, i.e., we are actually calling f rather than making use of
![]() $\overline {f}$
. On the other hand, if
$\overline {f}$
. On the other hand, if
![]() $\Psi (w,\cdot )$
would output the same thing regardless of the second argument, we can postpone actually calling f (which
$\Psi (w,\cdot )$
would output the same thing regardless of the second argument, we can postpone actually calling f (which
![]() $?f$
lets us do) and go with that output for the time being. This reasoning establishes that
$?f$
lets us do) and go with that output for the time being. This reasoning establishes that
![]() $g \le _{\mathrm {W}} ?f$
.
$g \le _{\mathrm {W}} ?f$
.
To see that
![]() $\mathrm {Det}_{ }(?f) \le _{\mathrm {W}} ?\mathrm {Det}_{ }(f)$
, we just inspect the technical definition of
$\mathrm {Det}_{ }(?f) \le _{\mathrm {W}} ?\mathrm {Det}_{ }(f)$
, we just inspect the technical definition of
![]() $\mathrm {Det}_{ }(\cdot )$
.
$\mathrm {Det}_{ }(\cdot )$
.
Finally, for
![]() $?\mathrm {Det}_{ }(f) \le _{\mathrm {W}} \mathrm {Det}_{ }(\overline {f})$
we observe that
$?\mathrm {Det}_{ }(f) \le _{\mathrm {W}} \mathrm {Det}_{ }(\overline {f})$
we observe that
![]() $?\mathrm {Det}_{ }(f)$
is single-valued with codomain
$?\mathrm {Det}_{ }(f)$
is single-valued with codomain
![]() ${\mathbb {N}^{\mathbb {N}}}$
, thus it suffices to show
${\mathbb {N}^{\mathbb {N}}}$
, thus it suffices to show
![]() $?\mathrm {Det}_{ }(f) \le _{\mathrm {W}} \overline {f}$
. But already
$?\mathrm {Det}_{ }(f) \le _{\mathrm {W}} \overline {f}$
. But already
![]() $?f \le _{\mathrm {W}} \overline {f}$
holds:
$?f \le _{\mathrm {W}} \overline {f}$
holds:
![]() $\overline {f}$
accepts an input that is completely void of information. We provide this as long as our
$\overline {f}$
accepts an input that is completely void of information. We provide this as long as our
![]() $?f$
instance does not want to use f; if it ever does, we have the relevant f-instance which we can then feed into
$?f$
instance does not want to use f; if it ever does, we have the relevant f-instance which we can then feed into
![]() $\overline {f}$
. Note that we do not get a strong reduction here, in general. ⊣
$\overline {f}$
. Note that we do not get a strong reduction here, in general. ⊣
3.4. Previous appearances in the literature
While the deterministic part as such has not been introduced before, and in particular the observation that it is always well-defined is new, there are several results in the literature on Weihrauch degrees that implicitly use it. Already in the first paper introducing the modern definition of Weihrauch reducibility [Reference Gherardi and Marcone19], it was shown that
![]() $\mathrm {Det}_{ }(\mathsf {C}_{{2^{\mathbb {N}}}}) \equiv _{\mathrm {W}} \operatorname {id}$
. It was observed in [Reference Le Roux and Pauly29] that the argument actually even establishes that
$\mathrm {Det}_{ }(\mathsf {C}_{{2^{\mathbb {N}}}}) \equiv _{\mathrm {W}} \operatorname {id}$
. It was observed in [Reference Le Roux and Pauly29] that the argument actually even establishes that
![]() $\mathrm {Det}_{ \mathbf {X} }(\mathsf {C}_{{2^{\mathbb {N}}}}) \equiv _{\mathrm {W}} \operatorname {id}$
for any computably admissible space
$\mathrm {Det}_{ \mathbf {X} }(\mathsf {C}_{{2^{\mathbb {N}}}}) \equiv _{\mathrm {W}} \operatorname {id}$
for any computably admissible space
![]() $\mathbf {X}$
.
$\mathbf {X}$
.
In [Reference Kihara, Marcone and Pauly26] the principle
![]() ${\mathsf {wList}}_{{2^{\mathbb {N}}},\leq \omega }$
which produces an enumeration of the elements of a countable closed subset of Cantor space was introduced, and [Reference Kihara, Marcone and Pauly26, Proposition 6.14] states that
${\mathsf {wList}}_{{2^{\mathbb {N}}},\leq \omega }$
which produces an enumeration of the elements of a countable closed subset of Cantor space was introduced, and [Reference Kihara, Marcone and Pauly26, Proposition 6.14] states that
 $\mathrm {Det}_{ }({\mathsf {wList}}_{{2^{\mathbb {N}}},\leq \omega }) \equiv _{\mathrm {W}} \mathsf {lim}$
. The authors also proved the following result, which will be useful in Proposition 5.18:
$\mathrm {Det}_{ }({\mathsf {wList}}_{{2^{\mathbb {N}}},\leq \omega }) \equiv _{\mathrm {W}} \mathsf {lim}$
. The authors also proved the following result, which will be useful in Proposition 5.18:
Theorem 3.14 [Reference Kihara, Marcone and Pauly26, Theorem 8.5]
 $\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}} \equiv _{\mathrm {W}} \mathrm {Det}_{ }(\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}})\equiv _{\mathrm {W}}\mathrm {Det}_{ }(\widehat {\mathsf {TC}_{{\mathbb {N}^{\mathbb {N}}}}})$
.
$\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}} \equiv _{\mathrm {W}} \mathrm {Det}_{ }(\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}})\equiv _{\mathrm {W}}\mathrm {Det}_{ }(\widehat {\mathsf {TC}_{{\mathbb {N}^{\mathbb {N}}}}})$
.
This, in particular, shows that
![]() $\mathrm {Det}_{ }(\cdot )$
is not useful to separate principles that are between
$\mathrm {Det}_{ }(\cdot )$
is not useful to separate principles that are between
![]() $\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
and
$\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
and
![]() $\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
.
$\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
.
In the context of probabilistic computation [Reference Brattka, Gherardi and Marcone9, Reference Brattka and Pauly12], the fact that the upper cones of non-trivial enumeration degrees are measure zero is equivalent to the statement that if
![]() $f:\subseteq {\mathbb {N}^{\mathbb {N}}} \rightrightarrows {\mathbb {N}^{\mathbb {N}}}$
has the property that
$f:\subseteq {\mathbb {N}^{\mathbb {N}}} \rightrightarrows {\mathbb {N}^{\mathbb {N}}}$
has the property that
![]() $f(p)$
has positive measure for every
$f(p)$
has positive measure for every
![]() $p \in \operatorname {dom}(f)$
and
$p \in \operatorname {dom}(f)$
and
![]() $\mathbf {X}$
is an effectively countably based space, then there is some g with
$\mathbf {X}$
is an effectively countably based space, then there is some g with
![]() $\mathrm {Det}_{ \mathbf {X} }(f) \le _{\mathrm {W}} {}^1{g}$
.
$\mathrm {Det}_{ \mathbf {X} }(f) \le _{\mathrm {W}} {}^1{g}$
.
4. Finding descending sequences
Let us formally define the problem of finding descending sequences in an ill-founded linear order as a multi-valued function.
Definition 4.1. Let
![]() $\mathsf {DS}:\subseteq \mathbf {LO} \rightrightarrows {\mathbb {N}^{\mathbb {N}}}$
be the multi-valued function defined as
$\mathsf {DS}:\subseteq \mathbf {LO} \rightrightarrows {\mathbb {N}^{\mathbb {N}}}$
be the multi-valued function defined as
with
![]() $\operatorname {dom}(\mathsf {DS}):= \mathrm {LO} \backslash \mathrm {WO}$
.
$\operatorname {dom}(\mathsf {DS}):= \mathrm {LO} \backslash \mathrm {WO}$
.
4.1. The uniform strength of
 $\mathsf {DS}$
$\mathsf {DS}$
We can immediately notice the following:
Proposition 4.2.
![]() $\mathsf {DS}\le _{\mathrm {W}} \mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
but
$\mathsf {DS}\le _{\mathrm {W}} \mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
but
![]() $\mathsf {DS}\not \le _{\mathrm {W}} \mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
.
$\mathsf {DS}\not \le _{\mathrm {W}} \mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
.
Proof To show that
![]() $\mathsf {DS}\le _{\mathrm {W}}\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
it is enough to notice that being a descending sequence in a linear order L is a
$\mathsf {DS}\le _{\mathrm {W}}\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
it is enough to notice that being a descending sequence in a linear order L is a
 $\Pi ^{0,L}_1$
property. In other words, we can obtain a descending sequence through L by choosing a path through the tree
$\Pi ^{0,L}_1$
property. In other words, we can obtain a descending sequence through L by choosing a path through the tree
To show that
![]() $\mathsf {DS}\not \le _{\mathrm {W}}\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
, recall that there is a computable linear order with no hyperarithmetic descending sequence (see e.g., [Reference Sacks38, Lemma III.2.1]). A reduction
$\mathsf {DS}\not \le _{\mathrm {W}}\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
, recall that there is a computable linear order with no hyperarithmetic descending sequence (see e.g., [Reference Sacks38, Lemma III.2.1]). A reduction
![]() $\mathsf {DS}\le _{\mathrm {W}}\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
would therefore contradict Theorem 2.1.⊣
$\mathsf {DS}\le _{\mathrm {W}}\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
would therefore contradict Theorem 2.1.⊣
In particular, this shows that
![]() $\mathsf {DS}$
is not an arithmetic problem (i.e.,
$\mathsf {DS}$
is not an arithmetic problem (i.e.,
 $\mathsf {DS}\not \le _{\mathrm {W}}\mathsf {lim}^{(n)}$
, for any n).
$\mathsf {DS}\not \le _{\mathrm {W}}\mathsf {lim}^{(n)}$
, for any n).
Proposition 4.3.
![]() $\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}} \equiv _{\mathrm {W}} \mathsf {lim}* \mathsf {DS}$
.
$\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}} \equiv _{\mathrm {W}} \mathsf {lim}* \mathsf {DS}$
.
Proof The reduction
![]() $\mathsf {lim}* \mathsf {DS}\le _{\mathrm {W}} \mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
follows from the fact that both
$\mathsf {lim}* \mathsf {DS}\le _{\mathrm {W}} \mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
follows from the fact that both
![]() $\mathsf {lim}$
and
$\mathsf {lim}$
and
![]() $\mathsf {DS}$
are reducible to
$\mathsf {DS}$
are reducible to
![]() $\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
and that
$\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
and that
![]() $\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
is closed under compositional product.
$\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
is closed under compositional product.
To prove the left-to-right reduction notice that, given a tree T, we can computably build the linear order
![]() $\mathrm {KB}(T)$
. It is known that
$\mathrm {KB}(T)$
. It is known that
![]() $[T]\neq \emptyset $
iff
$[T]\neq \emptyset $
iff
![]() $\mathrm {KB}(T)$
is ill-founded (see e.g., [Reference Simpson41, Lemma V.1.3]). Moreover, given a infinite descending sequence
$\mathrm {KB}(T)$
is ill-founded (see e.g., [Reference Simpson41, Lemma V.1.3]). Moreover, given a infinite descending sequence
![]() $(\sigma _n)_{n\in \mathbb {N}}$
in
$(\sigma _n)_{n\in \mathbb {N}}$
in
![]() $\mathrm {KB}(T)$
, the sequence
$\mathrm {KB}(T)$
, the sequence
![]() $(\sigma _n^{\smallfrown } 0^\omega )_{n\in \mathbb {N}}$
converges to some
$(\sigma _n^{\smallfrown } 0^\omega )_{n\in \mathbb {N}}$
converges to some
![]() $x\in [T]$
, and therefore the claim follows. ⊣
$x\in [T]$
, and therefore the claim follows. ⊣
We can generalize the problem
![]() $\mathsf {DS}$
to the context of quasi-orders. It is easy to see that the problem of finding descending sequences in a quasi-order is Weihrauch equivalent to
$\mathsf {DS}$
to the context of quasi-orders. It is easy to see that the problem of finding descending sequences in a quasi-order is Weihrauch equivalent to
![]() $\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
. Indeed, on the one hand, being a descending sequence in a quasi-order P is a
$\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
. Indeed, on the one hand, being a descending sequence in a quasi-order P is a
 $\Pi ^{0,P}_1$
property. On the other hand, every tree, ordered by the prefix relation, is a partial order where the descending sequences provide arbitrarily long prefixes of a path.
$\Pi ^{0,P}_1$
property. On the other hand, every tree, ordered by the prefix relation, is a partial order where the descending sequences provide arbitrarily long prefixes of a path.
When working with non-well quasi-orders, it is more natural to ask for bad sequences instead.
Definition 4.4. We define the multi-valued function
![]() $\mathsf {BS}:\subseteq \mathbf {QO} \rightrightarrows {\mathbb {N}^{\mathbb {N}}}$
as
$\mathsf {BS}:\subseteq \mathbf {QO} \rightrightarrows {\mathbb {N}^{\mathbb {N}}}$
as
where
![]() $\operatorname {dom}(\mathsf {BS})$
is the set of quasi-orders that are not well-quasi-orders.
$\operatorname {dom}(\mathsf {BS})$
is the set of quasi-orders that are not well-quasi-orders.
It follows from the definition that every ill-founded linear order is a non-well quasi-order and that every bad sequence through an ill-founded linear order is indeed a descending sequence.
By expanding a bit on a classical argument we can prove that the two problems are uniformly equivalent.
Proposition 4.5.
![]() $\mathsf {DS}\equiv _{\mathrm {W}} \mathsf {BS}$
.
$\mathsf {DS}\equiv _{\mathrm {W}} \mathsf {BS}$
.
Proof The left-to-right reduction is trivial, so we only need to show that
![]() $\mathsf {BS}\le _{\mathrm {W}}\mathsf {DS}$
. Let P be a non-well quasi-order. We will first compute an extension R of P s.t. every two elements of P are R-comparable, then we will computably pick an element from each R-equivalence class, so as to obtain a linear order.
$\mathsf {BS}\le _{\mathrm {W}}\mathsf {DS}$
. Let P be a non-well quasi-order. We will first compute an extension R of P s.t. every two elements of P are R-comparable, then we will computably pick an element from each R-equivalence class, so as to obtain a linear order.
We define R iteratively as follows: at every stage s s.t.
![]() $s\in P$
, we define the R-relation between s and t, for every
$s\in P$
, we define the R-relation between s and t, for every
![]() $t\in P$
s.t.
$t\in P$
s.t.
![]() $t<s$
. If
$t<s$
. If
![]() $t \,|_{P}\, s$
then we define
$t \,|_{P}\, s$
then we define
![]() $s \prec _R t$
. Otherwise we define the R-relation between s and t so as to extend P.
$s \prec _R t$
. Otherwise we define the R-relation between s and t so as to extend P.
It is easy to see that if
![]() $(p_i)_{i\in \mathbb {N}}$
is an
$(p_i)_{i\in \mathbb {N}}$
is an
![]() $\prec _R$
-descending sequence then it is a P-bad sequence. Indeed, for every
$\prec _R$
-descending sequence then it is a P-bad sequence. Indeed, for every
![]() $i,j$
s.t.
$i,j$
s.t.
![]() $i<j$
, if
$i<j$
, if
![]() $p_i \preceq _P p_j$
then
$p_i \preceq _P p_j$
then
![]() $p_i \preceq _R p_j$
(as R extends P), contradicting the fact that
$p_i \preceq _R p_j$
(as R extends P), contradicting the fact that
![]() $(p_i)_{i\in \mathbb {N}}$
is an
$(p_i)_{i\in \mathbb {N}}$
is an
![]() $\prec _R$
-descending sequence. Moreover R is ill-founded: indeed every
$\prec _R$
-descending sequence. Moreover R is ill-founded: indeed every
![]() $\prec _P$
-descending sequence is also an
$\prec _P$
-descending sequence is also an
![]() $\prec _R$
-descending sequence. On the other hand, every P-antichain
$\prec _R$
-descending sequence. On the other hand, every P-antichain
![]() $(q_i)_{i\in \mathbb {N}}$
has a subsequence
$(q_i)_{i\in \mathbb {N}}$
has a subsequence
![]() $(q_{i_k})_{k\in \mathbb {N}}$
that is an
$(q_{i_k})_{k\in \mathbb {N}}$
that is an
![]() $\prec _R$
-descending sequence (define
$\prec _R$
-descending sequence (define
![]() $q_{i_k}$
inductively by letting
$q_{i_k}$
inductively by letting
![]() $i_k$
be the smallest integer s.t.
$i_k$
be the smallest integer s.t.
![]() $q_{i_k}>q_j$
, for every
$q_{i_k}>q_j$
, for every
![]() $j<k$
).
$j<k$
).
To conclude the proof it is enough to show that we can uniformly compute a linear order L by choosing an element from each R-equivalence class. We define L as the restriction of R to the set
Clearly L is isomorphic to the quotient order induced by R on the set of R-equivalence classes, hence it is ill-founded. Moreover, every
![]() $<_L$
-descending sequence is an
$<_L$
-descending sequence is an
![]() $\prec _R$
-descending sequence, and therefore
$\prec _R$
-descending sequence, and therefore
![]() $\mathsf {DS}(L)\subset \mathsf {BS}(P)$
.⊣
$\mathsf {DS}(L)\subset \mathsf {BS}(P)$
.⊣
We will show that
![]() $\mathsf {DS}$
(and hence
$\mathsf {DS}$
(and hence
![]() $\mathsf {BS}$
) is quite weak in terms of uniform computational strength (a fortiori
$\mathsf {BS}$
) is quite weak in terms of uniform computational strength (a fortiori
![]() $\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}\not \le _{\mathrm {W}}\mathsf {DS}$
). Let us first underline the following useful proposition.
$\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}\not \le _{\mathrm {W}}\mathsf {DS}$
). Let us first underline the following useful proposition.
Proposition 4.6.
![]() $\mathsf {DS}$
is a cylinder.
$\mathsf {DS}$
is a cylinder.
Proof Let
![]() $p\in {\mathbb {N}^{\mathbb {N}}}$
and L be an ill-founded linear order. Define
$p\in {\mathbb {N}^{\mathbb {N}}}$
and L be an ill-founded linear order. Define
 $$ \begin{align*} M:&=\{ (p[n],n): n\in L \},\\ (p[n],n) &\le_M (p[m],m) :\hspace{-1mm}\iff n \le_L m. \end{align*} $$
$$ \begin{align*} M:&=\{ (p[n],n): n\in L \},\\ (p[n],n) &\le_M (p[m],m) :\hspace{-1mm}\iff n \le_L m. \end{align*} $$
It is easy to see that M is computably isomorphic to L, and hence it is a valid input for
![]() $\mathsf {DS}$
. In particular, letting
$\mathsf {DS}$
. In particular, letting
![]() $((p[n_i],n_i))_{i\in \mathbb {N}}\in \mathsf {DS}(M)$
, we have that
$((p[n_i],n_i))_{i\in \mathbb {N}}\in \mathsf {DS}(M)$
, we have that
![]() $(n_i)_{i\in \mathbb {N}}$
is a descending sequence in L and
$(n_i)_{i\in \mathbb {N}}$
is a descending sequence in L and
![]() $p = \bigcup _{i\in \mathbb {N}} p[n_i]$
.⊣
$p = \bigcup _{i\in \mathbb {N}} p[n_i]$
.⊣
Definition 4.7. Let
![]() ${\boldsymbol {\Gamma }}\mathsf {-Bound}:\subseteq \boldsymbol {\Gamma }(\mathbb {N}) \rightrightarrows \mathbb {N}$
be the first-order problem that takes as input a finite
${\boldsymbol {\Gamma }}\mathsf {-Bound}:\subseteq \boldsymbol {\Gamma }(\mathbb {N}) \rightrightarrows \mathbb {N}$
be the first-order problem that takes as input a finite
![]() $\boldsymbol {\Gamma }$
subset of the natural numbers and returns a bound for it. Formally
$\boldsymbol {\Gamma }$
subset of the natural numbers and returns a bound for it. Formally
 $$ \begin{align*} \operatorname{dom}({\boldsymbol{\Gamma}}\mathsf{-Bound})&:=\{ A\in \boldsymbol{\Gamma}(\mathbb{N}) : (\forall^\infty n)(A(n)=0) \},\\ {\boldsymbol{\Gamma}}\mathsf{-Bound}(A)&:=\{ n\in\mathbb{N} : (\forall m\ge n)(A(m)=0) \}, \end{align*} $$
$$ \begin{align*} \operatorname{dom}({\boldsymbol{\Gamma}}\mathsf{-Bound})&:=\{ A\in \boldsymbol{\Gamma}(\mathbb{N}) : (\forall^\infty n)(A(n)=0) \},\\ {\boldsymbol{\Gamma}}\mathsf{-Bound}(A)&:=\{ n\in\mathbb{N} : (\forall m\ge n)(A(m)=0) \}, \end{align*} $$
where
![]() $\forall ^\infty $
is a shorthand for “for all but finitely many.”
$\forall ^\infty $
is a shorthand for “for all but finitely many.”
The principle
 ${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
has been studied in [Reference Astor, Dzhafarov, Solomon and Suggs1] under the name
${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
has been studied in [Reference Astor, Dzhafarov, Solomon and Suggs1] under the name
 ${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}^{\vphantom {g}\mathsf {cof}}_{\mathbb {N}}$
: notice indeed that the reduction
${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}^{\vphantom {g}\mathsf {cof}}_{\mathbb {N}}$
: notice indeed that the reduction
 ${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}^{\vphantom {g}\mathsf {cof}}_{\mathbb {N}}\le _{\mathrm {sW}}{\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
is trivial. On the other hand, given a finite
${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}^{\vphantom {g}\mathsf {cof}}_{\mathbb {N}}\le _{\mathrm {sW}}{\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
is trivial. On the other hand, given a finite
![]() $\boldsymbol {\Pi }^1_1$
subset X of
$\boldsymbol {\Pi }^1_1$
subset X of
![]() $\mathbb {N}$
we can consider the set
$\mathbb {N}$
we can consider the set
Clearly Y is a
![]() $\boldsymbol {\Pi }^1_1$
initial segment of
$\boldsymbol {\Pi }^1_1$
initial segment of
![]() $\mathbb {N}$
, and therefore
$\mathbb {N}$
, and therefore
![]() $\mathbb {N}\backslash {Y}$
is a valid input for
$\mathbb {N}\backslash {Y}$
is a valid input for
 ${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}^{\vphantom {g}\mathsf {cof}}_{\mathbb {N}}$
. Moreover a name for Y can be uniformly computed from a name of X and
${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}^{\vphantom {g}\mathsf {cof}}_{\mathbb {N}}$
. Moreover a name for Y can be uniformly computed from a name of X and
 ${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}^{\vphantom {g}\mathsf {cof}}_{\mathbb {N}}(\mathbb {N}\backslash {Y})\subset {\boldsymbol {\Pi }^1_1}\mathsf {-Bound}(X)$
. This shows that
${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}^{\vphantom {g}\mathsf {cof}}_{\mathbb {N}}(\mathbb {N}\backslash {Y})\subset {\boldsymbol {\Pi }^1_1}\mathsf {-Bound}(X)$
. This shows that
 ${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}\le _{\mathrm {sW}}{\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}^{\vphantom {g}\mathsf {cof}}_{\mathbb {N}}$
and hence the two problems are (strongly) Weihrauch equivalent.
${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}\le _{\mathrm {sW}}{\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}^{\vphantom {g}\mathsf {cof}}_{\mathbb {N}}$
and hence the two problems are (strongly) Weihrauch equivalent.
In other words, given an instance X of
 ${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
we can, without loss of generality, assume that X is an initial segment of
${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
we can, without loss of generality, assume that X is an initial segment of
![]() $\mathbb {N}$
.
$\mathbb {N}$
.
Proposition 4.8.
 ${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}<_{\mathrm {W}}\mathsf {DS}$
.
${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}<_{\mathrm {W}}\mathsf {DS}$
.
Proof Let X be a
![]() $\boldsymbol {\Pi }^1_1$
initial segment of
$\boldsymbol {\Pi }^1_1$
initial segment of
![]() $\mathbb {N}$
. By considering the Kleene-Brouwer ordering, we can think of a name for X as a sequence
$\mathbb {N}$
. By considering the Kleene-Brouwer ordering, we can think of a name for X as a sequence
![]() $(L_n)_{n\in \mathbb {N}}$
of linear orders s.t.
$(L_n)_{n\in \mathbb {N}}$
of linear orders s.t.
![]() $n\in X$
iff
$n\in X$
iff
![]() $L_n$
is well-founded.
$L_n$
is well-founded.
Define the linear order
![]() $L:=\bigcup _n \{n\}\times L_n$
, ordered lexicographically. Notice that L is ill-founded as X is not all of
$L:=\bigcup _n \{n\}\times L_n$
, ordered lexicographically. Notice that L is ill-founded as X is not all of
![]() $\mathbb {N}$
. Moreover, for every
$\mathbb {N}$
. Moreover, for every
![]() $<_L$
-descending sequence
$<_L$
-descending sequence
![]() $((n_i,a_i))_{i\in \mathbb {N}}$
, we have that
$((n_i,a_i))_{i\in \mathbb {N}}$
, we have that
 $n_0\in {\boldsymbol {\Pi }^1_1}\mathsf {-Bound}(X)$
. Indeed, for every
$n_0\in {\boldsymbol {\Pi }^1_1}\mathsf {-Bound}(X)$
. Indeed, for every
![]() $n\in X$
and every
$n\in X$
and every
![]() $a\in L_n$
, the pair
$a\in L_n$
, the pair
![]() $(n,a)$
lies in the well-founded part of L.
$(n,a)$
lies in the well-founded part of L.
The fact that the reduction is strict follows from the fact that every solution to
 ${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
is computable, whereas there is a computable input for
${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
is computable, whereas there is a computable input for
![]() $\mathsf {DS}$
with no hyperarithmetic solution. ⊣
$\mathsf {DS}$
with no hyperarithmetic solution. ⊣
We now show that
 ${}^1{\mathsf {DS}}\equiv _{\mathrm {W}} {\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
. Let us first prove the following lemma, which will also be useful to prove Theorem 4.16.
${}^1{\mathsf {DS}}\equiv _{\mathrm {W}} {\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
. Let us first prove the following lemma, which will also be useful to prove Theorem 4.16.
Lemma 4.9. Suppose that f is a problem which is Weihrauch reducible to
![]() $\mathsf {DS}$
via the computable maps
$\mathsf {DS}$
via the computable maps
![]() $\Phi ,\Psi $
. For every f-instance X, let
$\Phi ,\Psi $
. For every f-instance X, let
![]() $\le ^X$
be the linear order defined by
$\le ^X$
be the linear order defined by
![]() $\Phi ^X$
. We can uniformly compute a sequence
$\Phi ^X$
. We can uniformly compute a sequence
![]() $(\,F_s)_{s\in \mathbb {N}}$
of finite
$(\,F_s)_{s\in \mathbb {N}}$
of finite
![]() $<^X$
-descending sequences s.t. (1) for every s,
$<^X$
-descending sequences s.t. (1) for every s,
![]() $\Psi ^{X\oplus F_s}$
outputs some
$\Psi ^{X\oplus F_s}$
outputs some
![]() $j\in \mathbb {N}$
; (2) for cofinitely many s,
$j\in \mathbb {N}$
; (2) for cofinitely many s,
![]() $F_s$
extends to an infinite
$F_s$
extends to an infinite
![]() $<^X$
-descending sequence.
$<^X$
-descending sequence.
Proof Fix an f-instance X and run
![]() $\Phi ^X$
for s steps. This produces a finite linear order
$\Phi ^X$
for s steps. This produces a finite linear order
![]() $\le ^X_s$
. Define
$\le ^X_s$
. Define
 $$ \begin{align*} D_s := \{F \subseteq\, \le^X_s : {}&{} F \text{ is a} <^X_s\text{-descending sequence and } |F|\ge 1 \text{ and } \\ & \Psi^{X \oplus F} \text{ outputs some } j \in \mathbb{N} \text{ in }s \text{ steps}\}. \end{align*} $$
$$ \begin{align*} D_s := \{F \subseteq\, \le^X_s : {}&{} F \text{ is a} <^X_s\text{-descending sequence and } |F|\ge 1 \text{ and } \\ & \Psi^{X \oplus F} \text{ outputs some } j \in \mathbb{N} \text{ in }s \text{ steps}\}. \end{align*} $$
Note that
![]() $D_s$
is finite and
$D_s$
is finite and
![]() $t<s$
implies
$t<s$
implies
![]() $D_t\subset D_s$
. If
$D_t\subset D_s$
. If
![]() $D_s\neq \emptyset $
we define
$D_s\neq \emptyset $
we define
![]() $F_s$
to be the
$F_s$
to be the
![]() $<_{\mathbb {N}}$
-least element of
$<_{\mathbb {N}}$
-least element of
![]() $D_s$
such that
$D_s$
such that
 $$ \begin{align*} \textstyle (\forall F \in D_s)\left(\min_{<^X}(\,F) \le^X_s \min_{<^X}(\,F_s)\right). \end{align*} $$
$$ \begin{align*} \textstyle (\forall F \in D_s)\left(\min_{<^X}(\,F) \le^X_s \min_{<^X}(\,F_s)\right). \end{align*} $$
This ensures that if any
![]() $F \in D_s$
extends to an infinite
$F \in D_s$
extends to an infinite
![]() $<^X$
-descending sequence, then so does
$<^X$
-descending sequence, then so does
![]() $F_s$
. Observe that
$F_s$
. Observe that
![]() $(\,F_s)_{s}$
is uniformly computable from X. If
$(\,F_s)_{s}$
is uniformly computable from X. If
![]() $D_s=\emptyset $
we define
$D_s=\emptyset $
we define
![]() $F_s:=F_t$
where t is the first index greater than s s.t.
$F_s:=F_t$
where t is the first index greater than s s.t.
![]() $D_t\neq \emptyset $
. (We will show below that such t exists, so we can computably search for it.)
$D_t\neq \emptyset $
. (We will show below that such t exists, so we can computably search for it.)
Notice that for cofinitely many s,
![]() $D_s\neq \emptyset $
. Indeed, let S be an infinite
$D_s\neq \emptyset $
. Indeed, let S be an infinite
![]() $<^X$
-descending sequence (there must exist one because
$<^X$
-descending sequence (there must exist one because
![]() $<^X$
is a
$<^X$
is a
![]() $\mathsf {DS}$
-instance). Since
$\mathsf {DS}$
-instance). Since
![]() $\Psi ^{X \oplus S}$
outputs some f-solution j of X, there is some finite nonempty initial segment F of S and some
$\Psi ^{X \oplus S}$
outputs some f-solution j of X, there is some finite nonempty initial segment F of S and some
![]() $t \in \mathbb {N}$
such that
$t \in \mathbb {N}$
such that
![]() $\Psi ^{X \oplus F}$
outputs j in t steps. Hence for all sufficiently large s, we have that
$\Psi ^{X \oplus F}$
outputs j in t steps. Hence for all sufficiently large s, we have that
![]() $F \in D_s$
. This shows that the sequence
$F \in D_s$
. This shows that the sequence
![]() $(\,F_s)_{s\in \mathbb {N}}$
is well-defined. Moreover, as already observed, for every
$(\,F_s)_{s\in \mathbb {N}}$
is well-defined. Moreover, as already observed, for every
![]() $t\ge s$
,
$t\ge s$
,
![]() $F_t$
extends to an infinite
$F_t$
extends to an infinite
![]() $<^X$
-descending sequence.
$<^X$
-descending sequence.
The fact that, for every s,
![]() $\Psi ^{X\oplus F_s}$
outputs some
$\Psi ^{X\oplus F_s}$
outputs some
![]() $j\in \mathbb {N}$
follows from the definition of
$j\in \mathbb {N}$
follows from the definition of
![]() $D_s$
.⊣
$D_s$
.⊣
In particular, if f has codomain
![]() $\mathbb {N}$
the above lemma implies that, for cofinitely many s,
$\mathbb {N}$
the above lemma implies that, for cofinitely many s,
![]() $\Psi ^{X\oplus F_s}$
outputs some f-solution for X.
$\Psi ^{X\oplus F_s}$
outputs some f-solution for X.
Theorem 4.10.
 ${}^1{\mathsf {DS}} \equiv _{\mathrm {W}} {\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
.
${}^1{\mathsf {DS}} \equiv _{\mathrm {W}} {\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
.
Proof If
 $f \le _{\mathrm {W}} {\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
, then
$f \le _{\mathrm {W}} {\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
, then
![]() $f \le _{\mathrm {W}} \mathsf {DS}$
by Proposition 4.8. Since
$f \le _{\mathrm {W}} \mathsf {DS}$
by Proposition 4.8. Since
 ${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
is first order,
${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
is first order,
![]() $f \le _{\mathrm {W}} {}^1{\mathsf {DS}}$
.
$f \le _{\mathrm {W}} {}^1{\mathsf {DS}}$
.
To prove the converse reduction, suppose that
![]() $f \le _{\mathrm {W}} \mathsf {DS}$
as witnessed by the maps
$f \le _{\mathrm {W}} \mathsf {DS}$
as witnessed by the maps
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
. Given an f-instance X, let
$\Psi $
. Given an f-instance X, let
![]() $(\,F_s)_{s\in \mathbb {N}}$
be as in Lemma 4.9. Let
$(\,F_s)_{s\in \mathbb {N}}$
be as in Lemma 4.9. Let
![]() $\le ^X$
denote the linear order represented by
$\le ^X$
denote the linear order represented by
![]() $\Phi ^X$
. Define the following
$\Phi ^X$
. Define the following
 $\Pi ^{1,X}_1$
set:
$\Pi ^{1,X}_1$
set:
where
![]() $\mathrm {Ext}$
denotes the set of finite sequences that extend to an infinite
$\mathrm {Ext}$
denotes the set of finite sequences that extend to an infinite
![]() $<^X$
-descending sequence.
$<^X$
-descending sequence.
Notice that A is finite as, for cofinitely many s,
![]() $F_s$
is extendible. In particular A is a valid instance of
$F_s$
is extendible. In particular A is a valid instance of
 ${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
and, for every
${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
and, for every
 $b\in {\boldsymbol {\Pi }^1_1}\mathsf {-Bound}(A)$
,
$b\in {\boldsymbol {\Pi }^1_1}\mathsf {-Bound}(A)$
,
![]() $F_b$
is extendible to an infinite
$F_b$
is extendible to an infinite
![]() $<^X$
-descending sequence. By construction,
$<^X$
-descending sequence. By construction,
![]() $\Psi ^{X\oplus F_b}$
commits to some
$\Psi ^{X\oplus F_b}$
commits to some
![]() $j\in \mathbb {N}$
. The fact that
$j\in \mathbb {N}$
. The fact that
![]() $F_b$
is extendible guarantees that j is a valid f-solution of X.⊣
$F_b$
is extendible guarantees that j is a valid f-solution of X.⊣
Corollary 4.11.
![]() $\mathsf {DS} <_{\mathrm {W}} \mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
.
$\mathsf {DS} <_{\mathrm {W}} \mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
.
Proof If
![]() $\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}\le _{\mathrm {W}}\mathsf {DS}$
then, by Proposition 2.4,
$\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}\le _{\mathrm {W}}\mathsf {DS}$
then, by Proposition 2.4,
 ${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}_{\mathbb {N}}\le _{\mathrm {W}} {\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
. However, this would imply that
${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}_{\mathbb {N}}\le _{\mathrm {W}} {\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
. However, this would imply that
 $\widehat {{\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}_{\mathbb {N}}}\le _{\mathrm {W}} \widehat {{\boldsymbol {\Pi }^1_1}\mathsf {-Bound}}$
, contradicting [Reference Astor, Dzhafarov, Solomon and Suggs1, Corollary 3.23]. ⊣
$\widehat {{\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}_{\mathbb {N}}}\le _{\mathrm {W}} \widehat {{\boldsymbol {\Pi }^1_1}\mathsf {-Bound}}$
, contradicting [Reference Astor, Dzhafarov, Solomon and Suggs1, Corollary 3.23]. ⊣
Definition 4.12. Let
![]() $f:\subseteq \mathbf {X} \rightrightarrows \mathbb {N}$
be a multi-valued function. We say that f is upwards-closed if whenever
$f:\subseteq \mathbf {X} \rightrightarrows \mathbb {N}$
be a multi-valued function. We say that f is upwards-closed if whenever
![]() $n \in f(x)$
, then
$n \in f(x)$
, then
![]() $m \in f(x)$
for all
$m \in f(x)$
for all
![]() $m> n$
.
$m> n$
.
It is straightforward from the definition that
 ${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
is upwards-closed.
${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
is upwards-closed.
Lemma 4.13. If f is upwards-closed then
![]() $\mathrm {Det}_{ \mathbb {N} }(f)\le _{\mathrm {W}} \mathsf {C}_{\mathbb {N}}$
.
$\mathrm {Det}_{ \mathbb {N} }(f)\le _{\mathrm {W}} \mathsf {C}_{\mathbb {N}}$
.
Proof Let g be a single-valued function with codomain
![]() $\mathbb {N}$
and suppose that
$\mathbb {N}$
and suppose that
![]() $g \le _{\mathrm {W}} f$
as witnessed by
$g \le _{\mathrm {W}} f$
as witnessed by
![]() $\Phi , \Psi $
. Given a name p for a g-instance x, we use
$\Phi , \Psi $
. Given a name p for a g-instance x, we use
![]() $\mathsf {C}_{\mathbb {N}}$
to guess some
$\mathsf {C}_{\mathbb {N}}$
to guess some
![]() $n, t$
such that
$n, t$
such that
![]() $\Psi (p,n)$
converges to some k in at most t steps, and such that for no
$\Psi (p,n)$
converges to some k in at most t steps, and such that for no
![]() $m> n$
it ever happens that
$m> n$
it ever happens that
![]() $\Psi (p,m)$
converges to anything but k. Since f is upwards-closed and g is single-valued, such
$\Psi (p,m)$
converges to anything but k. Since f is upwards-closed and g is single-valued, such
![]() $n,t$
must exist. Moreover, the associated k is equal to
$n,t$
must exist. Moreover, the associated k is equal to
![]() $g(x)$
. ⊣
$g(x)$
. ⊣
Proposition 4.14.
 $\mathrm {Det}_{ \mathbb {N} }({\boldsymbol {\Pi }^1_1}\mathsf {-Bound})\equiv _{\mathrm {W}} \mathrm {Det}_{ \mathbb {N} }(\mathsf {C}_{\mathbb {N}}) \equiv _{\mathrm {W}} \mathsf {C}_{\mathbb {N}}$
, and therefore
$\mathrm {Det}_{ \mathbb {N} }({\boldsymbol {\Pi }^1_1}\mathsf {-Bound})\equiv _{\mathrm {W}} \mathrm {Det}_{ \mathbb {N} }(\mathsf {C}_{\mathbb {N}}) \equiv _{\mathrm {W}} \mathsf {C}_{\mathbb {N}}$
, and therefore
![]() $\mathrm {Det}_{ \mathbb {N} }(\mathsf {DS})\equiv _{\mathrm {W}} \mathsf {C}_{\mathbb {N}}$
.
$\mathrm {Det}_{ \mathbb {N} }(\mathsf {DS})\equiv _{\mathrm {W}} \mathsf {C}_{\mathbb {N}}$
.
Proof Let us first notice that
![]() $\mathsf {C}_{\mathbb {N}}\equiv _{\mathrm {W}}\mathsf {UC}_{\mathbb {N}}$
[Reference Brattka and Gherardi5, Proposition 6.2] and therefore
$\mathsf {C}_{\mathbb {N}}\equiv _{\mathrm {W}}\mathsf {UC}_{\mathbb {N}}$
[Reference Brattka and Gherardi5, Proposition 6.2] and therefore
![]() $\mathrm {Det}_{ \mathbb {N} }(\mathsf {C}_{\mathbb {N}}) \equiv _{\mathrm {W}} \mathsf {C}_{\mathbb {N}}$
. The fact that
$\mathrm {Det}_{ \mathbb {N} }(\mathsf {C}_{\mathbb {N}}) \equiv _{\mathrm {W}} \mathsf {C}_{\mathbb {N}}$
. The fact that
 $\mathrm {Det}_{ \mathbb {N} }({\boldsymbol {\Pi }^1_1}\mathsf {-Bound})\le _{\mathrm {W}} \mathsf {C}_{\mathbb {N}}$
follows from Lemma 4.13. To prove the converse reduction it is enough to show that
$\mathrm {Det}_{ \mathbb {N} }({\boldsymbol {\Pi }^1_1}\mathsf {-Bound})\le _{\mathrm {W}} \mathsf {C}_{\mathbb {N}}$
follows from Lemma 4.13. To prove the converse reduction it is enough to show that
 $\mathsf {UC}_{\mathbb {N}}\le _{\mathrm {W}} {\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
.
$\mathsf {UC}_{\mathbb {N}}\le _{\mathrm {W}} {\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
.
Let
![]() $(n_i)_{i\in \mathbb {N}}$
be an enumeration of the complement of
$(n_i)_{i\in \mathbb {N}}$
be an enumeration of the complement of
![]() $\{x\}\subset \mathbb {N}$
. Define
$\{x\}\subset \mathbb {N}$
. Define
 $$ \begin{align*} m(s)&:=\min\{j\in\mathbb{N} : (\forall i<s)(n_i \neq j) \},\\ A&:=\{ s \in\mathbb{N} : (\exists t>s )(m(t)\neq m(s)) \}. \end{align*} $$
$$ \begin{align*} m(s)&:=\min\{j\in\mathbb{N} : (\forall i<s)(n_i \neq j) \},\\ A&:=\{ s \in\mathbb{N} : (\exists t>s )(m(t)\neq m(s)) \}. \end{align*} $$
Clearly
![]() $\lim _{s\to \infty } m(s) =x$
, which implies that A is finite. Since m is computable (relative to
$\lim _{s\to \infty } m(s) =x$
, which implies that A is finite. Since m is computable (relative to
![]() $(n_i)_{i\in \mathbb {N}}$
), A is a valid input for
$(n_i)_{i\in \mathbb {N}}$
), A is a valid input for
 ${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
. Moreover, for every
${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
. Moreover, for every
 $b\in {\boldsymbol {\Pi }^1_1}\mathsf {-Bound}(A)$
we have
$b\in {\boldsymbol {\Pi }^1_1}\mathsf {-Bound}(A)$
we have
![]() $m(b)=x$
.
$m(b)=x$
.
This implies that
![]() $\mathsf {C}_{\mathbb {N}}\le _{\mathrm {W}} \mathrm {Det}_{ \mathbb {N} }(\mathsf {DS})$
. To conclude the proof we notice that, for every single-valued g with codomain
$\mathsf {C}_{\mathbb {N}}\le _{\mathrm {W}} \mathrm {Det}_{ \mathbb {N} }(\mathsf {DS})$
. To conclude the proof we notice that, for every single-valued g with codomain
![]() $\mathbb {N}$
we have
$\mathbb {N}$
we have
 $$ \begin{align*} g\le_{\mathrm{W}} \mathsf{DS} \Rightarrow g \le_{\mathrm{W}} {\boldsymbol{\Pi}^1_1}\mathsf{-Bound} \Rightarrow g\le_{\mathrm{W}} \mathrm{Det}_{ \mathbb{N} }({\boldsymbol{\Pi}^1_1}\mathsf{-Bound})\equiv_{\mathrm{W}} \mathsf{C}_{\mathbb{N}}. \end{align*} $$
$$ \begin{align*} g\le_{\mathrm{W}} \mathsf{DS} \Rightarrow g \le_{\mathrm{W}} {\boldsymbol{\Pi}^1_1}\mathsf{-Bound} \Rightarrow g\le_{\mathrm{W}} \mathrm{Det}_{ \mathbb{N} }({\boldsymbol{\Pi}^1_1}\mathsf{-Bound})\equiv_{\mathrm{W}} \mathsf{C}_{\mathbb{N}}. \end{align*} $$
⊣
Notice that
 ${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}\not \le _{\mathrm {W}} \mathsf {C}_{\mathbb {N}}$
: indeed
${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}\not \le _{\mathrm {W}} \mathsf {C}_{\mathbb {N}}$
: indeed
![]() $\widehat {\mathsf {C}_{\mathbb {N}}}\equiv _{\mathrm {W}} \mathsf {lim}$
, while
$\widehat {\mathsf {C}_{\mathbb {N}}}\equiv _{\mathrm {W}} \mathsf {lim}$
, while
 $\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}<_{\mathrm {W}}\widehat {{\boldsymbol {\Pi }^1_1}\mathsf {-Bound}}$
(see Proposition 5.21). This implies that
$\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}<_{\mathrm {W}}\widehat {{\boldsymbol {\Pi }^1_1}\mathsf {-Bound}}$
(see Proposition 5.21). This implies that
 $\mathrm {Det}_{ \mathbb {N} }({\boldsymbol {\Pi }^1_1}\mathsf {-Bound})<_{\mathrm {W}} {\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
. In this regard, we observe the following:
$\mathrm {Det}_{ \mathbb {N} }({\boldsymbol {\Pi }^1_1}\mathsf {-Bound})<_{\mathrm {W}} {\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
. In this regard, we observe the following:
Proposition 4.15. The Weihrauch degree of
![]() $\mathsf {C}_{\mathbb {N}}$
is the highest Weihrauch degree containing both of the following:
$\mathsf {C}_{\mathbb {N}}$
is the highest Weihrauch degree containing both of the following:
-
1. a representative which is single-valued and has codomain
 $\mathbb {N}$
and
$\mathbb {N}$
and -
2. a representative which is upwards-closed.
Proof To prove that
![]() $\mathsf {C}_{\mathbb {N}}$
satisfies point 1, consider
$\mathsf {C}_{\mathbb {N}}$
satisfies point 1, consider
![]() $\mathsf {UC}_{\mathbb {N}}$
, which is Weihrauch equivalent to
$\mathsf {UC}_{\mathbb {N}}$
, which is Weihrauch equivalent to
![]() $\mathsf {C}_{\mathbb {N}}$
[Reference Brattka and Gherardi5, Proposition 6.2]. To prove that
$\mathsf {C}_{\mathbb {N}}$
[Reference Brattka and Gherardi5, Proposition 6.2]. To prove that
![]() $\mathsf {C}_{\mathbb {N}}$
satisfies point
$\mathsf {C}_{\mathbb {N}}$
satisfies point
![]() $2$
, consider the problem
$2$
, consider the problem
 ${\boldsymbol {\Sigma }^0_1}\mathsf {-Bound}$
that produces a bound for a finite
${\boldsymbol {\Sigma }^0_1}\mathsf {-Bound}$
that produces a bound for a finite
![]() $\boldsymbol {\Sigma }^0_1$
subset of
$\boldsymbol {\Sigma }^0_1$
subset of
![]() $\mathbb {N}$
. Clearly
$\mathbb {N}$
. Clearly
 ${\boldsymbol {\Sigma }^0_1}\mathsf {-Bound}$
is upwards closed. The reduction
${\boldsymbol {\Sigma }^0_1}\mathsf {-Bound}$
is upwards closed. The reduction
 ${\boldsymbol {\Sigma }^0_1}\mathsf {-Bound}\le _{\mathrm {W}}\mathsf {C}_{\mathbb {N}}$
follows from the fact that, for every
${\boldsymbol {\Sigma }^0_1}\mathsf {-Bound}\le _{\mathrm {W}}\mathsf {C}_{\mathbb {N}}$
follows from the fact that, for every
 $A\in \operatorname {dom}({\boldsymbol {\Sigma }^0_1}\mathsf {-Bound})$
, the set
$A\in \operatorname {dom}({\boldsymbol {\Sigma }^0_1}\mathsf {-Bound})$
, the set
is a
 $\Pi ^{0,A}_1$
subset of
$\Pi ^{0,A}_1$
subset of
 ${\boldsymbol {\Sigma }^0_1}\mathsf {-Bound}(A)$
. To prove the converse reduction, let p be a name for some
${\boldsymbol {\Sigma }^0_1}\mathsf {-Bound}(A)$
. To prove the converse reduction, let p be a name for some
![]() $B\in \operatorname {dom}(\mathsf {C}_{\mathbb {N}})$
. Define
$B\in \operatorname {dom}(\mathsf {C}_{\mathbb {N}})$
. Define
![]() $m(s)$
to be the least number not enumerated in p by stage s. Clearly
$m(s)$
to be the least number not enumerated in p by stage s. Clearly
![]() $\lim _{s\to \infty } m(s) = \min B$
. In particular this implies that there are only finitely many stages s s.t.
$\lim _{s\to \infty } m(s) = \min B$
. In particular this implies that there are only finitely many stages s s.t.
![]() $m(s)\neq \min B$
. Using
$m(s)\neq \min B$
. Using
 ${\boldsymbol {\Sigma }^0_1}\mathsf {-Bound}$
we can obtain a stage b s.t.
${\boldsymbol {\Sigma }^0_1}\mathsf {-Bound}$
we can obtain a stage b s.t.
![]() $m(b)=\min B$
, hence solving
$m(b)=\min B$
, hence solving
![]() $\mathsf {C}_{\mathbb {N}}$
.
$\mathsf {C}_{\mathbb {N}}$
.
Finally the maximality of
![]() $\mathsf {C}_{\mathbb {N}}$
follows from Lemma 4.13: indeed suppose
$\mathsf {C}_{\mathbb {N}}$
follows from Lemma 4.13: indeed suppose
![]() $f: \textbf {X} \to \mathbb {N}$
is Weihrauch equivalent to some g which is upwards-closed. By Lemma 4.13, we have
$f: \textbf {X} \to \mathbb {N}$
is Weihrauch equivalent to some g which is upwards-closed. By Lemma 4.13, we have
![]() $\mathrm {Det}_{ \mathbb {N} }(g)\le _{\mathrm {W}} \mathsf {C}_{\mathbb {N}}$
. By definition of
$\mathrm {Det}_{ \mathbb {N} }(g)\le _{\mathrm {W}} \mathsf {C}_{\mathbb {N}}$
. By definition of
![]() $\mathrm {Det}_{ }(\cdot )$
, we have
$\mathrm {Det}_{ }(\cdot )$
, we have
![]() $f \le _{\mathrm {W}} \mathrm {Det}_{ \mathbb {N} }(g)$
, hence
$f \le _{\mathrm {W}} \mathrm {Det}_{ \mathbb {N} }(g)$
, hence
![]() $f \le _{\mathrm {W}} \mathsf {C}_{\mathbb {N}}$
.⊣
$f \le _{\mathrm {W}} \mathsf {C}_{\mathbb {N}}$
.⊣
Let us now characterize the deterministic part of
![]() $\mathsf {DS}$
.
$\mathsf {DS}$
.
Theorem 4.16.
![]() $\mathrm {Det}_{ }(\mathsf {DS})\equiv _{\mathrm {W}}\mathsf {lim}$
.
$\mathrm {Det}_{ }(\mathsf {DS})\equiv _{\mathrm {W}}\mathsf {lim}$
.
Proof Let us first prove that
![]() $\mathsf {lim}\le _{\mathrm {W}}\mathsf {DS}$
. Let
$\mathsf {lim}\le _{\mathrm {W}}\mathsf {DS}$
. Let
![]() $\mathsf {J}$
be the Turing jump operator, i.e.,
$\mathsf {J}$
be the Turing jump operator, i.e.,
![]() $\mathsf {J}(p)(e)=1$
iff
$\mathsf {J}(p)(e)=1$
iff
![]() $\varphi _e^p(e)$
halts. It is known that
$\varphi _e^p(e)$
halts. It is known that
![]() $\mathsf {J}\equiv _{\mathrm {sW}} \mathsf {lim}$
(see [Reference Brattka, Hölzl, Kuyper, Vollmer and Vallée11, Theorem 6.7]). By relativizing the construction in [Reference Marcone and Shore31, Lemma 4.2] we have that, for every p, we can p-computably build a linear order L of type
$\mathsf {J}\equiv _{\mathrm {sW}} \mathsf {lim}$
(see [Reference Brattka, Hölzl, Kuyper, Vollmer and Vallée11, Theorem 6.7]). By relativizing the construction in [Reference Marcone and Shore31, Lemma 4.2] we have that, for every p, we can p-computably build a linear order L of type
![]() $\omega +\omega ^*$
s.t. every descending sequence through L computes
$\omega +\omega ^*$
s.t. every descending sequence through L computes
![]() $\mathsf {J}(p)$
. This shows that
$\mathsf {J}(p)$
. This shows that
![]() $\mathsf {lim}\equiv _{\mathrm {W}}\mathsf {J}\le _{\mathrm {W}} \mathsf {DS}$
.
$\mathsf {lim}\equiv _{\mathrm {W}}\mathsf {J}\le _{\mathrm {W}} \mathsf {DS}$
.
To prove that
![]() $\mathrm {Det}_{ }(\mathsf {DS}) \le _{\mathrm {W}} \mathsf {lim}$
, suppose that
$\mathrm {Det}_{ }(\mathsf {DS}) \le _{\mathrm {W}} \mathsf {lim}$
, suppose that
![]() $f :\subseteq \textbf {X} \to {\mathbb {N}^{\mathbb {N}}}$
is single-valued and
$f :\subseteq \textbf {X} \to {\mathbb {N}^{\mathbb {N}}}$
is single-valued and
![]() $f\le _{\mathrm {W}}\mathsf {DS}$
as witnessed by the maps
$f\le _{\mathrm {W}}\mathsf {DS}$
as witnessed by the maps
![]() $\Phi $
,
$\Phi $
,
![]() $\Psi $
. For every n, define
$\Psi $
. For every n, define
![]() $f_n$
by
$f_n$
by
![]() $f_n(X):=f(X)(n)$
. The maps
$f_n(X):=f(X)(n)$
. The maps
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
witness that
$\Psi $
witness that
![]() $f_n\le _{\mathrm {W}}\mathsf {DS}$
as well (modulo a trivial coding). Given an f-instance X, consider the sequences
$f_n\le _{\mathrm {W}}\mathsf {DS}$
as well (modulo a trivial coding). Given an f-instance X, consider the sequences
![]() $(F_{s,n}\!)_{s\in \mathbb {N}}$
obtained by applying Lemma 4.9 to each
$(F_{s,n}\!)_{s\in \mathbb {N}}$
obtained by applying Lemma 4.9 to each
![]() $f_n$
. Define the sequence
$f_n$
. Define the sequence
![]() $(p_s\!)_{s\in \mathbb {N}}$
in
$(p_s\!)_{s\in \mathbb {N}}$
in
![]() ${\mathbb {N}^{\mathbb {N}}}$
as
${\mathbb {N}^{\mathbb {N}}}$
as
![]() $p_s(n):= \Psi ^{X\oplus F_{s,n}}(0)$
. Notice that, by Lemma 4.9, for every n,
$p_s(n):= \Psi ^{X\oplus F_{s,n}}(0)$
. Notice that, by Lemma 4.9, for every n,
![]() $\Psi ^{X\oplus F_{s,n}}$
outputs some number, therefore
$\Psi ^{X\oplus F_{s,n}}$
outputs some number, therefore
![]() $p_s(n)$
is well-defined and is uniformly computable from X. Moreover, since
$p_s(n)$
is well-defined and is uniformly computable from X. Moreover, since
![]() $f_n$
is single-valued and, for cofinitely many s,
$f_n$
is single-valued and, for cofinitely many s,
![]() $F_{s,n}$
is extendible, the sequence
$F_{s,n}$
is extendible, the sequence
![]() $(\Psi ^{X\oplus F_{s,n}}(0))_{s\in \mathbb {N}}$
is eventually constant and equal to
$(\Psi ^{X\oplus F_{s,n}}(0))_{s\in \mathbb {N}}$
is eventually constant and equal to
![]() $f_n(X)$
. In particular this shows that, letting
$f_n(X)$
. In particular this shows that, letting
![]() $p:=\lim _{s\to \infty } p_s$
, for each n we have
$p:=\lim _{s\to \infty } p_s$
, for each n we have
![]() $p(n)=f_n(X)$
, i.e.,
$p(n)=f_n(X)$
, i.e.,
![]() $p=f(X)$
. ⊣
$p=f(X)$
. ⊣
This result shows that, despite the fact that
![]() $\mathsf {DS}$
can have very complicated solutions, it is rather weak from the uniform point of view. In fact, its lower Weihrauch cone misses many arithmetic problems. In particular we have:
$\mathsf {DS}$
can have very complicated solutions, it is rather weak from the uniform point of view. In fact, its lower Weihrauch cone misses many arithmetic problems. In particular we have:
Corollary 4.17.
![]() $\mathsf {DS}~|_{\mathrm {W}~} \mathsf {LPO} '$
.
$\mathsf {DS}~|_{\mathrm {W}~} \mathsf {LPO} '$
.
Proof Since
![]() $ \mathsf {LPO} $
is single-valued, so is
$ \mathsf {LPO} $
is single-valued, so is
![]() $ \mathsf {LPO} '$
. Since
$ \mathsf {LPO} '$
. Since
![]() $ \mathsf {LPO} '\not \le _{\mathrm {W}} \mathsf {lim}$
(see [Reference Brattka, Gherardi and Pauly10, Corollary 12.3 and Theorem 12.7]), it follows from Theorem 4.16 that
$ \mathsf {LPO} '\not \le _{\mathrm {W}} \mathsf {lim}$
(see [Reference Brattka, Gherardi and Pauly10, Corollary 12.3 and Theorem 12.7]), it follows from Theorem 4.16 that
![]() $ \mathsf {LPO} '\not \le _{\mathrm {W}} \mathsf {DS}$
. On the other hand,
$ \mathsf {LPO} '\not \le _{\mathrm {W}} \mathsf {DS}$
. On the other hand,
![]() $\mathsf {DS}\not \le _{\mathrm {W}} \mathsf {LPO} '$
, as
$\mathsf {DS}\not \le _{\mathrm {W}} \mathsf {LPO} '$
, as
![]() $ \mathsf {LPO} '$
always has computable solutions.⊣
$ \mathsf {LPO} '$
always has computable solutions.⊣
Notice that Theorem 4.16 implies also that
![]() $\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}} \not \le _{\mathrm {W}} \mathsf {C}_{{2^{\mathbb {N}}}} * \mathsf {DS}$
. Indeed, on the one hand
$\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}} \not \le _{\mathrm {W}} \mathsf {C}_{{2^{\mathbb {N}}}} * \mathsf {DS}$
. Indeed, on the one hand
![]() $\mathrm {Det}_{ }(\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}})\equiv _{\mathrm {W}} \mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
(Theorem 3.14), while, on the other hand, by Theorem 3.9, if f is single-valued and
$\mathrm {Det}_{ }(\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}})\equiv _{\mathrm {W}} \mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
(Theorem 3.14), while, on the other hand, by Theorem 3.9, if f is single-valued and
![]() $f\le _{\mathrm {W}} \mathsf {C}_{{2^{\mathbb {N}}}}* \mathsf {DS}$
then
$f\le _{\mathrm {W}} \mathsf {C}_{{2^{\mathbb {N}}}}* \mathsf {DS}$
then
![]() $f\le _{\mathrm {W}} \mathsf {DS}$
(as
$f\le _{\mathrm {W}} \mathsf {DS}$
(as
![]() $\mathrm {Det}_{ }(\mathsf {C}_{{2^{\mathbb {N}}}})\equiv _{\mathrm {W}}\operatorname {id}$
) and hence
$\mathrm {Det}_{ }(\mathsf {C}_{{2^{\mathbb {N}}}})\equiv _{\mathrm {W}}\operatorname {id}$
) and hence
![]() $\mathrm {Det}_{ }(\mathsf {C}_{{2^{\mathbb {N}}}}*\mathsf {DS})\equiv _{\mathrm {W}}\mathrm {Det}_{ }(\mathsf {DS})\equiv _{\mathrm {W}}\mathsf {lim}$
.
$\mathrm {Det}_{ }(\mathsf {C}_{{2^{\mathbb {N}}}}*\mathsf {DS})\equiv _{\mathrm {W}}\mathrm {Det}_{ }(\mathsf {DS})\equiv _{\mathrm {W}}\mathsf {lim}$
.
Using Corollary 4.17 we can prove that
![]() $\mathsf {DS}$
is not closed under (parallel) product:
$\mathsf {DS}$
is not closed under (parallel) product:
Theorem 4.18.
![]() $ \mathsf {LPO} '\le _{\mathrm {W}} \mathsf {DS}\times \mathsf {lim}$
and therefore
$ \mathsf {LPO} '\le _{\mathrm {W}} \mathsf {DS}\times \mathsf {lim}$
and therefore
![]() $\mathsf {DS}$
is not closed under product.
$\mathsf {DS}$
is not closed under product.
Proof Let
![]() $(p_n)_{n\in \mathbb {N}}$
be a sequence in
$(p_n)_{n\in \mathbb {N}}$
be a sequence in
![]() ${\mathbb {N}^{\mathbb {N}}}$
converging to an instance p of
${\mathbb {N}^{\mathbb {N}}}$
converging to an instance p of
![]() $ \mathsf {LPO} $
. For each s define
$ \mathsf {LPO} $
. For each s define
 $$ \begin{align*} g(s):= \begin{cases} i+1 & \text{if } i\le s \land p_s(i)\neq 0 \land (\forall j<i)(p_s(j)=0),\\ 0 & \text{otherwise.} \end{cases}\end{align*} $$
$$ \begin{align*} g(s):= \begin{cases} i+1 & \text{if } i\le s \land p_s(i)\neq 0 \land (\forall j<i)(p_s(j)=0),\\ 0 & \text{otherwise.} \end{cases}\end{align*} $$
Let us define a linear order L inductively: at stage
![]() $s=0$
we put
$s=0$
we put
![]() $0$
into L. At stage
$0$
into L. At stage
![]() $s+1$
we do the following:
$s+1$
we do the following:
-
1. if
 $g(s)=g(s+1)$
we put
$g(s)=g(s+1)$
we put
 $2(s+1)$
immediately below
$2(s+1)$
immediately below
 $2s$
;
$2s$
; -
2. if
 $g(s)\neq g(s+1)$
and
$g(s)\neq g(s+1)$
and
 $g(s+1)=0$
we put
$g(s+1)=0$
we put
 $2(s+1)$
at the bottom; and
$2(s+1)$
at the bottom; and -
3. if
 $g(s)\neq g(s+1)$
and
$g(s)\neq g(s+1)$
and
 $g(s+1)>0$
we put
$g(s+1)>0$
we put
 $2(s+1)$
at the top and we put
$2(s+1)$
at the top and we put
 $2s+1$
immediately above
$2s+1$
immediately above
 $0$
.
$0$
.
This construction produces a linear order on a computable subset of
![]() $\mathbb {N}$
. It is clear that g and L are uniformly computable in
$\mathbb {N}$
. It is clear that g and L are uniformly computable in
![]() $(p_n)_{n\in \mathbb {N}}$
. Notice that if
$(p_n)_{n\in \mathbb {N}}$
. Notice that if
![]() $ \mathsf {LPO} (p)=1$
then there is an s s.t. for every
$ \mathsf {LPO} (p)=1$
then there is an s s.t. for every
![]() $t\ge s$
,
$t\ge s$
,
![]() $g(t)=g(s)$
(this follows by definition of limit in the Baire space). In particular, L has order type
$g(t)=g(s)$
(this follows by definition of limit in the Baire space). In particular, L has order type
![]() $n+\omega ^*$
. On the other hand, if
$n+\omega ^*$
. On the other hand, if
![]() $ \mathsf {LPO} (p)=0$
we distinguish three cases: if
$ \mathsf {LPO} (p)=0$
we distinguish three cases: if
![]() $g(s)$
is eventually constantly
$g(s)$
is eventually constantly
![]() $0$
then L has order type
$0$
then L has order type
![]() $\omega ^*$
. If there are infinitely many s s.t.
$\omega ^*$
. If there are infinitely many s s.t.
![]() $g(s)>0$
then g is unbounded (because for each i,
$g(s)>0$
then g is unbounded (because for each i,
![]() $\lim _s p_s(i) = p(i) = 0$
so g eventually stays above i). In particular, if there are infinitely many s and infinitely many t s.t.
$\lim _s p_s(i) = p(i) = 0$
so g eventually stays above i). In particular, if there are infinitely many s and infinitely many t s.t.
![]() $g(s)=0$
and
$g(s)=0$
and
![]() $g(t)>0$
then L has order type
$g(t)>0$
then L has order type
![]() $\omega ^*+\zeta $
, where
$\omega ^*+\zeta $
, where
![]() $\zeta :=\omega ^*+\omega $
is the order type of the integers. If instead
$\zeta :=\omega ^*+\omega $
is the order type of the integers. If instead
![]() $g(s)> 0$
for all sufficiently large s, then L has order type
$g(s)> 0$
for all sufficiently large s, then L has order type
![]() $n+\zeta $
. In all cases, L is ill-founded.
$n+\zeta $
. In all cases, L is ill-founded.
We consider the input
![]() $(L,(p_n)_{n\in \mathbb {N}})$
for
$(L,(p_n)_{n\in \mathbb {N}})$
for
![]() $\mathsf {DS}\times \mathsf {lim}$
. Given an
$\mathsf {DS}\times \mathsf {lim}$
. Given an
![]() $<_L$
-descending sequence
$<_L$
-descending sequence
![]() $(q_n)_{n\in \mathbb {N}}$
, we compute a solution for
$(q_n)_{n\in \mathbb {N}}$
, we compute a solution for
![]() $ \mathsf {LPO} '((p_n)_{n\in \mathbb {N}})= \mathsf {LPO} (p)$
as follows: if
$ \mathsf {LPO} '((p_n)_{n\in \mathbb {N}})= \mathsf {LPO} (p)$
as follows: if
![]() $q_0$
is odd or
$q_0$
is odd or
![]() $g(q_0/2)=0$
then we return
$g(q_0/2)=0$
then we return
![]() $0$
, otherwise we return
$0$
, otherwise we return
![]() $p(i)$
where i is s.t.
$p(i)$
where i is s.t.
![]() $g(q_0/2)=i+1$
.
$g(q_0/2)=i+1$
.
Notice that if
![]() $ \mathsf {LPO} (p)=1$
then the
$ \mathsf {LPO} (p)=1$
then the
![]() $\omega ^*$
part of
$\omega ^*$
part of
![]() $\leq _L$
is the final segment of the even numbers that starts with the first index
$\leq _L$
is the final segment of the even numbers that starts with the first index
![]() $2s$
s.t. for every
$2s$
s.t. for every
![]() $t\ge s$
,
$t\ge s$
,
![]() $g(t)=i+1$
and
$g(t)=i+1$
and
![]() $p(i)=1$
. In particular every
$p(i)=1$
. In particular every
![]() $<_L$
-descending sequence starts with some even
$<_L$
-descending sequence starts with some even
![]() $q_0$
s.t.
$q_0$
s.t.
![]() $g(q_0/2)>0$
. On the other hand, if
$g(q_0/2)>0$
. On the other hand, if
![]() $ \mathsf {LPO} (p)=0$
then, by definition of
$ \mathsf {LPO} (p)=0$
then, by definition of
![]() $ \mathsf {LPO} $
, we have that
$ \mathsf {LPO} $
, we have that
![]() $p=0^{\mathbb {N}}$
. In this case, the above procedure must return
$p=0^{\mathbb {N}}$
. In this case, the above procedure must return
![]() $0$
so it produces the correct solution. This proves that
$0$
so it produces the correct solution. This proves that
![]() $ \mathsf {LPO} ' \le _{\mathrm {W}} \mathsf {DS} \times \mathsf {lim}$
.
$ \mathsf {LPO} ' \le _{\mathrm {W}} \mathsf {DS} \times \mathsf {lim}$
.
The fact that
![]() $\mathsf {DS}$
is not closed under product follows from the fact that
$\mathsf {DS}$
is not closed under product follows from the fact that
![]() $\mathsf {lim} \le _{\mathrm {W}} \mathsf {DS}$
(Theorem 4.16) and Corollary 4.17. ⊣
$\mathsf {lim} \le _{\mathrm {W}} \mathsf {DS}$
(Theorem 4.16) and Corollary 4.17. ⊣
4.2. Combinatorial principles on linear orders
We introduce the following notation to phrase many combinatorial principles from reverse mathematics as multi-valued functions.
Definition 4.19. Let
![]() $\mathsf {FindC}^{{X}}_{{Y}}:\subseteq \mathbf {LO} \rightrightarrows \mathbf {LO}$
be the partial multi-valued function defined as
$\mathsf {FindC}^{{X}}_{{Y}}:\subseteq \mathbf {LO} \rightrightarrows \mathbf {LO}$
be the partial multi-valued function defined as
 $$ \begin{align*} \mathsf{FindC}^{{X}}_{{Y}}(L):=\{ M\in \mathrm{LO}: M\subset L \text{ and } \operatorname{ordtype}(M)\in Y \}, \end{align*} $$
$$ \begin{align*} \mathsf{FindC}^{{X}}_{{Y}}(L):=\{ M\in \mathrm{LO}: M\subset L \text{ and } \operatorname{ordtype}(M)\in Y \}, \end{align*} $$
with domain being the set of
![]() $L\in \mathrm {LO}$
s.t.
$L\in \mathrm {LO}$
s.t.
![]() $\operatorname {ordtype}(L)\in X$
and there is some
$\operatorname {ordtype}(L)\in X$
and there is some
![]() $M\subset L$
s.t.
$M\subset L$
s.t.
![]() $\operatorname {ordtype}(M)\in Y$
.
$\operatorname {ordtype}(M)\in Y$
.
Similarly we define
![]() $\mathsf {FindS}^{X}:\subseteq \mathbf {LO} \rightrightarrows {\mathbb {N}^{\mathbb {N}}}$
to be the partial multi-valued function that takes as input a countable linear order L s.t.
$\mathsf {FindS}^{X}:\subseteq \mathbf {LO} \rightrightarrows {\mathbb {N}^{\mathbb {N}}}$
to be the partial multi-valued function that takes as input a countable linear order L s.t.
![]() $\operatorname {ordtype}(L)\in X$
and produces a string
$\operatorname {ordtype}(L)\in X$
and produces a string
![]() $\langle b,x_0,x_1,\ldots \rangle $
s.t.
$\langle b,x_0,x_1,\ldots \rangle $
s.t.
![]() $b\in \{0,1\}$
and, for all i, if
$b\in \{0,1\}$
and, for all i, if
![]() $b=0$
then
$b=0$
then
![]() $x_i <_L x_{i+1}$
while if
$x_i <_L x_{i+1}$
while if
![]() $b=1$
then
$b=1$
then
![]() $x_{i+1}<_L x_i$
.
$x_{i+1}<_L x_i$
.
If X or Y is not specified, we assume that it contains every countable order type.
There is an extensive literature that studies the “ascending/descending sequence principle” (
![]() $\mathrm {ADS}$
) and the “chain/antichain principle” (
$\mathrm {ADS}$
) and the “chain/antichain principle” (
![]() $\mathrm {CAC}$
) (see e.g. [Reference Hirschfeldt and Shore24, Reference Jockusch, Kastermans, Lempp, Lerman and Solomon25]). These principles and, several of their variations, have been studied from the point of view of Weihrauch reducibility in [Reference Brattka3].
$\mathrm {CAC}$
) (see e.g. [Reference Hirschfeldt and Shore24, Reference Jockusch, Kastermans, Lempp, Lerman and Solomon25]). These principles and, several of their variations, have been studied from the point of view of Weihrauch reducibility in [Reference Brattka3].
Notice that, in particular, the problem
![]() $\mathsf {ADS}$
(given a linear order, produce an infinite ascending sequence or infinite descending sequence) corresponds to
$\mathsf {ADS}$
(given a linear order, produce an infinite ascending sequence or infinite descending sequence) corresponds to
![]() $\mathsf {FindS}^{}$
. Similarly the problem
$\mathsf {FindS}^{}$
. Similarly the problem
![]() $\mathsf {General}\text {-}\mathsf {SADS}$
(given a stable—i.e., of order type
$\mathsf {General}\text {-}\mathsf {SADS}$
(given a stable—i.e., of order type
![]() $\omega +n,n+\omega ^*$
or
$\omega +n,n+\omega ^*$
or
![]() $\omega +\omega ^*$
—linear order, produce an infinite ascending or descending sequence), corresponds to
$\omega +\omega ^*$
—linear order, produce an infinite ascending or descending sequence), corresponds to
![]() $\mathsf {FindS}^{X}$
, where
$\mathsf {FindS}^{X}$
, where
![]() $X =\{\omega +n,n+\omega ^*,\omega +\omega ^*\!\}$
.
$X =\{\omega +n,n+\omega ^*,\omega +\omega ^*\!\}$
.
Proposition 4.20.
 $ \mathsf {LPO} '\le _{\mathrm {W}} \mathsf {FindS}^{\{\omega ,n+\omega ^*\}}$
.
$ \mathsf {LPO} '\le _{\mathrm {W}} \mathsf {FindS}^{\{\omega ,n+\omega ^*\}}$
.
Proof Let
![]() $(p_i)_{i\in \mathbb {N}}$
be a sequence in
$(p_i)_{i\in \mathbb {N}}$
be a sequence in
![]() ${\mathbb {N}^{\mathbb {N}}}$
converging to an instance p of
${\mathbb {N}^{\mathbb {N}}}$
converging to an instance p of
![]() $ \mathsf {LPO} $
. For every
$ \mathsf {LPO} $
. For every
![]() $s\in \mathbb {N}$
we define (as we did in the proof of Theorem 4.18)
$s\in \mathbb {N}$
we define (as we did in the proof of Theorem 4.18)
 $$ \begin{align*} g(s):= \begin{cases} i+1 & \text{if } i\le s \land p_s(i)\neq 0 \land (\forall j<i)(p_s(j)=0),\\ 0 & \text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} g(s):= \begin{cases} i+1 & \text{if } i\le s \land p_s(i)\neq 0 \land (\forall j<i)(p_s(j)=0),\\ 0 & \text{otherwise.} \end{cases} \end{align*} $$
Let us define a linear order
![]() $\le _L$
on
$\le _L$
on
![]() $\mathbb {N}$
inductively: for each stage s we define a linear order on
$\mathbb {N}$
inductively: for each stage s we define a linear order on
![]() $\{0,\ldots ,s\}$
. At stage
$\{0,\ldots ,s\}$
. At stage
![]() $s=0$
there are no decisions to make. At stage
$s=0$
there are no decisions to make. At stage
![]() $s+1$
we do the following:
$s+1$
we do the following:
-
1. if
 $0=g(s)=g(s+1)$
we put
$0=g(s)=g(s+1)$
we put
 $s+1$
immediately above s;
$s+1$
immediately above s; -
2. if
 $0<g(s)=g(s+1)$
we put
$0<g(s)=g(s+1)$
we put
 $s+1$
immediately below s; and
$s+1$
immediately below s; and -
3. if
 $g(s)\neq g(s+1)$
we put
$g(s)\neq g(s+1)$
we put
 $s+1$
at the top.
$s+1$
at the top.
It is clear that g and
![]() $\leq _L$
are uniformly computable in
$\leq _L$
are uniformly computable in
![]() $(p_n)_{n\in \mathbb {N}}$
. Notice that if
$(p_n)_{n\in \mathbb {N}}$
. Notice that if
![]() $ \mathsf {LPO} (p)=1$
then there is an s s.t. for every
$ \mathsf {LPO} (p)=1$
then there is an s s.t. for every
![]() $t\ge s$
,
$t\ge s$
,
![]() $g(t)=i+1$
, where i is the smallest integer s.t.
$g(t)=i+1$
, where i is the smallest integer s.t.
![]() $p(i)=1$
(this follows by definition of limit in the Baire space). In particular,
$p(i)=1$
(this follows by definition of limit in the Baire space). In particular,
![]() $\le _L$
has order type
$\le _L$
has order type
![]() $n+\omega ^*$
. On the other hand, if
$n+\omega ^*$
. On the other hand, if
![]() $ \mathsf {LPO} (p)=0$
then g is either eventually constantly
$ \mathsf {LPO} (p)=0$
then g is either eventually constantly
![]() $0$
or unbounded. In both cases the linear order
$0$
or unbounded. In both cases the linear order
![]() $\le _L$
has order type
$\le _L$
has order type
![]() $\omega $
.
$\omega $
.
In other words
![]() $(\mathbb {N},\le _L)$
has order type
$(\mathbb {N},\le _L)$
has order type
![]() $\omega $
iff
$\omega $
iff
![]() $ \mathsf {LPO} '((p_i)_{i\in \mathbb {N}})=0$
. Since the output of
$ \mathsf {LPO} '((p_i)_{i\in \mathbb {N}})=0$
. Since the output of
 $\mathsf {FindS}^{\{\omega ,n+\omega ^*\}}((\mathbb {N},\le _L))$
comes with an indication of the order type of the solution, this defines a reduction from
$\mathsf {FindS}^{\{\omega ,n+\omega ^*\}}((\mathbb {N},\le _L))$
comes with an indication of the order type of the solution, this defines a reduction from
![]() $ \mathsf {LPO} '$
to
$ \mathsf {LPO} '$
to
![]() $\mathsf {FindS}^{\{\omega ,n+\omega ^\ast \}}.$
⊣
$\mathsf {FindS}^{\{\omega ,n+\omega ^\ast \}}.$
⊣
Corollary 4.21.
 $\mathsf {FindS}^{\{\omega , n+\omega ^*\}} ~|_{\mathrm {W}~} \mathsf {DS}$
, and hence
$\mathsf {FindS}^{\{\omega , n+\omega ^*\}} ~|_{\mathrm {W}~} \mathsf {DS}$
, and hence
![]() $\mathsf {General}\text {-}\mathsf {SADS} ~|_{\mathrm {W}~} \mathsf {DS}$
.
$\mathsf {General}\text {-}\mathsf {SADS} ~|_{\mathrm {W}~} \mathsf {DS}$
.
Proof The fact that
 $\mathsf {FindS}^{\{\omega , n+\omega ^*\}} \not \le _{\mathrm {W}} \mathsf {DS}$
follows from Proposition 4.20 and the fact that
$\mathsf {FindS}^{\{\omega , n+\omega ^*\}} \not \le _{\mathrm {W}} \mathsf {DS}$
follows from Proposition 4.20 and the fact that
![]() $ \mathsf {LPO} '\not \le _{\mathrm {W}}\mathsf {DS}$
(Corollary 4.17). Moreover, since
$ \mathsf {LPO} '\not \le _{\mathrm {W}}\mathsf {DS}$
(Corollary 4.17). Moreover, since
![]() $\mathsf {FindS}^{\{\omega , n+\omega ^*\}}$
is a restriction of
$\mathsf {FindS}^{\{\omega , n+\omega ^*\}}$
is a restriction of
![]() $\mathsf {General}\text {-}\mathsf {SADS}$
, we have
$\mathsf {General}\text {-}\mathsf {SADS}$
, we have
![]() $\mathsf {General}\text {-}\mathsf {SADS}\not \le _{\mathrm {W}}\mathsf {DS}$
.
$\mathsf {General}\text {-}\mathsf {SADS}\not \le _{\mathrm {W}}\mathsf {DS}$
.
To show that the converse reduction cannot hold it is enough to notice that
![]() $\mathsf {General}\text {-}\mathsf {SADS}$
is an arithmetic problem, while
$\mathsf {General}\text {-}\mathsf {SADS}$
is an arithmetic problem, while
![]() $\mathsf {DS}\not \le _{\mathrm {W}}\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
(Proposition 4.2). ⊣
$\mathsf {DS}\not \le _{\mathrm {W}}\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
(Proposition 4.2). ⊣
In particular this implies that
![]() $\mathsf {ADS}$
, as well as the stable chain/antichain principle
$\mathsf {ADS}$
, as well as the stable chain/antichain principle
![]() $\mathsf {SCAC}$
, and the weakly stable chain/antichain principle
$\mathsf {SCAC}$
, and the weakly stable chain/antichain principle
![]() $\mathsf {WSCAC}$
are Weihrauch incomparable with
$\mathsf {WSCAC}$
are Weihrauch incomparable with
![]() $\mathsf {DS}$
(as they are all arithmetic problems, and
$\mathsf {DS}$
(as they are all arithmetic problems, and
![]() $\mathsf {General}\text {-}\mathsf {SADS}$
is reducible to all of them, see [Reference Brattka3]).
$\mathsf {General}\text {-}\mathsf {SADS}$
is reducible to all of them, see [Reference Brattka3]).
Proposition 4.22.
![]() $\mathsf {FindC}^{{}}_{{\{ \omega ,n+\omega ^*\}}} \le _{\mathrm {W}} \mathsf {DS}$
.
$\mathsf {FindC}^{{}}_{{\{ \omega ,n+\omega ^*\}}} \le _{\mathrm {W}} \mathsf {DS}$
.
Proof Given a linear order
![]() $(L,\le _L)$
we can computably build the linear order
$(L,\le _L)$
we can computably build the linear order
![]() $Q:=L+L^*$
. Formally we define
$Q:=L+L^*$
. Formally we define
![]() $(Q,\le _Q)$
as
$(Q,\le _Q)$
as
![]() $Q:=\{0\}\times L \cup \{1\}\times L$
and
$Q:=\{0\}\times L \cup \{1\}\times L$
and
Notice that Q is always ill-founded, hence it is a valid input for
![]() $\mathsf {DS}$
. Given
$\mathsf {DS}$
. Given
![]() $(q_i)_{i\in \mathbb {N}}\in \mathsf {DS}(Q)$
, we computably build the sequence
$(q_i)_{i\in \mathbb {N}}\in \mathsf {DS}(Q)$
, we computably build the sequence
![]() $(x_i)_{i\in \mathbb {N}}$
defined by
$(x_i)_{i\in \mathbb {N}}$
defined by
![]() $x_i:=\pi _1 q_i$
where
$x_i:=\pi _1 q_i$
where
![]() $\pi _i:= (a_0,a_1)\mapsto a_i$
.
$\pi _i:= (a_0,a_1)\mapsto a_i$
.
We distinguish three cases:
-
1. if
 $\pi _0 q_i =0$
for every i then
$\pi _0 q_i =0$
for every i then
 $(x_i)_{i\in \mathbb {N}}$
is an
$(x_i)_{i\in \mathbb {N}}$
is an
 $\omega ^*$
-sequence in L;
$\omega ^*$
-sequence in L; -
2. if
 $\pi _0 q_i =1$
for every i then
$\pi _0 q_i =1$
for every i then
 $(x_i)_{i\in \mathbb {N}}$
is an
$(x_i)_{i\in \mathbb {N}}$
is an
 $\omega $
-sequence in L; and
$\omega $
-sequence in L; and -
3. if there is a k s.t. for all
 $i<k$
we have
$i<k$
we have
 $\pi _0 q_i = 1$
and for all
$\pi _0 q_i = 1$
and for all
 $j\ge k$
we have
$j\ge k$
we have
 $\pi _0 q_j = 0$
then, by point
$\pi _0 q_j = 0$
then, by point
 $1$
,
$1$
,
 $(x_j)_{j\ge k}$
is an
$(x_j)_{j\ge k}$
is an
 $\omega ^*$
-sequence in L, hence
$\omega ^*$
-sequence in L, hence
 $(x_i)_{i\in \mathbb {N}}$
is of type
$(x_i)_{i\in \mathbb {N}}$
is of type
 $n+\omega ^*$
, with
$n+\omega ^*$
, with
 $n\le k$
.
$n\le k$
.
In any case the sequence
![]() $(x_i)_{i\in \mathbb {N}}$
is a valid solution for
$(x_i)_{i\in \mathbb {N}}$
is a valid solution for
![]() $\mathsf {FindC}^{{}}_{{\{ \omega ,n+\omega ^*\}}}$
.⊣
$\mathsf {FindC}^{{}}_{{\{ \omega ,n+\omega ^*\}}}$
.⊣
4.3. Relations with Ramsey theorems
We now explore the relations between
![]() $\mathsf {DS}$
and Ramsey’s theorem for n-tuples and k colors. Let us recall the basic definitions.
$\mathsf {DS}$
and Ramsey’s theorem for n-tuples and k colors. Let us recall the basic definitions.
Definition 4.23. For every
![]() $A\subset \mathbb {N}$
, let
$A\subset \mathbb {N}$
, let
![]() $[A]^n:=\{ B\subset A: |B|=n\}$
be the set of subsets of A with cardinality n. A map
$[A]^n:=\{ B\subset A: |B|=n\}$
be the set of subsets of A with cardinality n. A map
![]() $c\colon [\mathbb {N}]^n\to k$
is called a k-coloring of
$c\colon [\mathbb {N}]^n\to k$
is called a k-coloring of
![]() $[\mathbb {N}]^n$
, where
$[\mathbb {N}]^n$
, where
![]() $k\ge 2$
. An infinite set H s.t.
$k\ge 2$
. An infinite set H s.t.
![]() $c([H]^n)=\{i\}$
for some
$c([H]^n)=\{i\}$
for some
![]() $i<k$
is called a homogeneous solution for c, or simply homogeneous.
$i<k$
is called a homogeneous solution for c, or simply homogeneous.
The set
![]() $\mathcal {C}_{n,k}$
of k-colorings of
$\mathcal {C}_{n,k}$
of k-colorings of
![]() $[\mathbb {N}]^n$
can be seen as a represented space, where a name for a coloring c is the string
$[\mathbb {N}]^n$
can be seen as a represented space, where a name for a coloring c is the string
![]() $p\in {\mathbb {N}^{\mathbb {N}}}$
s.t. for each
$p\in {\mathbb {N}^{\mathbb {N}}}$
s.t. for each
![]() $(i_0,\ldots ,i_{n-1})\in [\mathbb {N}]^n$
,
$(i_0,\ldots ,i_{n-1})\in [\mathbb {N}]^n$
,
![]() $p(\langle i_0,\ldots ,i_{n-1} \rangle )=c(i_0,\ldots ,i_{n-1})$
.
$p(\langle i_0,\ldots ,i_{n-1} \rangle )=c(i_0,\ldots ,i_{n-1})$
.
We define
![]() $\mathsf {RT}^{{n}}_{{k}} :\mathcal {C}_{n,k} \rightrightarrows {2^{\mathbb {N}}}$
as the total multi-valued function that maps a coloring c to the set of all homogeneous sets for c. Similarly we define
$\mathsf {RT}^{{n}}_{{k}} :\mathcal {C}_{n,k} \rightrightarrows {2^{\mathbb {N}}}$
as the total multi-valued function that maps a coloring c to the set of all homogeneous sets for c. Similarly we define
 $\mathsf {RT}^{{n}}_{{\mathbb {N}}} :\bigcup _{k\ge 1}\mathcal {C}_{n,k} \rightrightarrows {2^{\mathbb {N}}}$
as
$\mathsf {RT}^{{n}}_{{\mathbb {N}}} :\bigcup _{k\ge 1}\mathcal {C}_{n,k} \rightrightarrows {2^{\mathbb {N}}}$
as
![]() $\mathsf {RT}^{{n}}_{{\mathbb {N}}} (c):=\mathsf {RT}^{{n}}_{{k}} (c)$
, where
$\mathsf {RT}^{{n}}_{{\mathbb {N}}} (c):=\mathsf {RT}^{{n}}_{{k}} (c)$
, where
![]() $k-1$
is the maximum of the range of c. Note that the input for
$k-1$
is the maximum of the range of c. Note that the input for
![]() $\mathsf {RT}^{{n}}_{{\mathbb {N}}} $
does not include information on which colors appear in the range of the coloring.
$\mathsf {RT}^{{n}}_{{\mathbb {N}}} $
does not include information on which colors appear in the range of the coloring.
We also define
![]() $\mathsf {cRT}^{{n}}_{{k}} :\mathcal {C}_{n,k} \rightrightarrows k$
as the multi-valued function that produces only the color of a homogeneous solution. We define
$\mathsf {cRT}^{{n}}_{{k}} :\mathcal {C}_{n,k} \rightrightarrows k$
as the multi-valued function that produces only the color of a homogeneous solution. We define
![]() $\mathsf {cRT}^{{n}}_{{\mathbb {N}}} $
analogously.
$\mathsf {cRT}^{{n}}_{{\mathbb {N}}} $
analogously.
Notice that
![]() $\mathsf {cRT}^{{n}}_{{k}} \equiv _{\mathrm {W}} \mathsf {RT}^{{n}}_{{k}} $
iff
$\mathsf {cRT}^{{n}}_{{k}} \equiv _{\mathrm {W}} \mathsf {RT}^{{n}}_{{k}} $
iff
![]() $n=1$
. Indeed the output of
$n=1$
. Indeed the output of
![]() $\mathsf {cRT}^{{n}}_{{k}} $
is always computable, while for
$\mathsf {cRT}^{{n}}_{{k}} $
is always computable, while for
![]() $n>1$
there are computable k-colorings with no computable homogeneous solutions. Similarly
$n>1$
there are computable k-colorings with no computable homogeneous solutions. Similarly
![]() $\mathsf {cRT}^{{n}}_{{\mathbb {N}}} \equiv _{\mathrm {W}} \mathsf {RT}^{{n}}_{{\mathbb {N}}} $
iff
$\mathsf {cRT}^{{n}}_{{\mathbb {N}}} \equiv _{\mathrm {W}} \mathsf {RT}^{{n}}_{{\mathbb {N}}} $
iff
![]() $n=1$
. Moreover the equivalence cannot be lifted to a strong Weihrauch equivalence. Indeed
$n=1$
. Moreover the equivalence cannot be lifted to a strong Weihrauch equivalence. Indeed
 $\mathsf {RT}^{{1}}_{{k}} $
and
$\mathsf {RT}^{{1}}_{{k}} $
and
 $\mathsf {cRT}^{{1}}_{{k}} $
are incomparable from the point of view of strong Weihrauch reducibility. The uniform computational content of Ramsey’s theorems is well-studied (see e.g., [Reference Anglès D'Auriac and Kihara1, Reference Dorais, Dzhafarov, Hirst, Mileti and Shafer14, Reference Dzhafarov, Goh, Hirschfeldt, Patey and Pauly16, Reference Patey35]).
$\mathsf {cRT}^{{1}}_{{k}} $
are incomparable from the point of view of strong Weihrauch reducibility. The uniform computational content of Ramsey’s theorems is well-studied (see e.g., [Reference Anglès D'Auriac and Kihara1, Reference Dorais, Dzhafarov, Hirst, Mileti and Shafer14, Reference Dzhafarov, Goh, Hirschfeldt, Patey and Pauly16, Reference Patey35]).
In comparing
![]() $\mathsf {RT}^{{n}}_{{k}} $
with
$\mathsf {RT}^{{n}}_{{k}} $
with
![]() $\mathsf {DS}$
, we immediately notice that
$\mathsf {DS}$
, we immediately notice that
 $\mathsf {RT}^{{2}}_{{2}} \not \le _{\mathrm {W}} \mathsf {DS}$
. This follows from the fact that
$\mathsf {RT}^{{2}}_{{2}} \not \le _{\mathrm {W}} \mathsf {DS}$
. This follows from the fact that
 $\mathsf {ADS}\le _{\mathrm {W}} \mathsf {RT}^{{2}}_{{2}} $
(see e.g., [Reference Hirschfeldt and Shore24]), while
$\mathsf {ADS}\le _{\mathrm {W}} \mathsf {RT}^{{2}}_{{2}} $
(see e.g., [Reference Hirschfeldt and Shore24]), while
![]() $\mathsf {ADS}\not \le _{\mathrm {W}}\mathsf {DS}$
(see the remarks after Corollary 4.21). Hence
$\mathsf {ADS}\not \le _{\mathrm {W}}\mathsf {DS}$
(see the remarks after Corollary 4.21). Hence
![]() $\mathsf {RT}^{{n}}_{{k}} \not \le _{\mathrm {W}} \mathsf {DS}$
for all
$\mathsf {RT}^{{n}}_{{k}} \not \le _{\mathrm {W}} \mathsf {DS}$
for all
![]() $n,k \geq 2$
.
$n,k \geq 2$
.
Proposition 4.24.
 $\mathsf {RT}^{{1}}_{{\mathbb {N}}} <_{\mathrm {W}}{\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
, and hence
$\mathsf {RT}^{{1}}_{{\mathbb {N}}} <_{\mathrm {W}}{\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
, and hence
 $\mathsf {RT}^{{1}}_{{\mathbb {N}}} <_{\mathrm {W}}\mathsf {DS}$
.
$\mathsf {RT}^{{1}}_{{\mathbb {N}}} <_{\mathrm {W}}\mathsf {DS}$
.
Proof Given a coloring
![]() $c\colon \mathbb {N}\to k$
, consider the
$c\colon \mathbb {N}\to k$
, consider the
 $\Sigma ^{0,c}_2$
set
$\Sigma ^{0,c}_2$
set
It is easy to see that X is finite, as
![]() $\operatorname {ran}(c)\subset k$
and if there is no c-homogeneous set with color i then there are finitely many
$\operatorname {ran}(c)\subset k$
and if there is no c-homogeneous set with color i then there are finitely many
![]() $j\in \mathbb {N}$
s.t.
$j\in \mathbb {N}$
s.t.
![]() $c(j)=i$
. In particular, given a bound b for X there is a homogeneous solution with color
$c(j)=i$
. In particular, given a bound b for X there is a homogeneous solution with color
![]() $c(b)$
.
$c(b)$
.
The separation follows from the fact that
 ${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}\not \le _{\mathrm {W}}\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
(as
${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}\not \le _{\mathrm {W}}\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
(as
 $\widehat {{\boldsymbol {\Pi }^1_1}\mathsf {-Bound}}\not \le _{\mathrm {W}}\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
, see [Reference Astor, Dzhafarov, Solomon and Suggs1, Fact 3.25]), while
$\widehat {{\boldsymbol {\Pi }^1_1}\mathsf {-Bound}}\not \le _{\mathrm {W}}\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
, see [Reference Astor, Dzhafarov, Solomon and Suggs1, Fact 3.25]), while
 $\mathsf {RT}^{{1}}_{{\mathbb {N}}} <_{\mathrm {W}}\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
(in particular
$\mathsf {RT}^{{1}}_{{\mathbb {N}}} <_{\mathrm {W}}\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
(in particular
 $\mathsf {RT}^{{1}}_{{\mathbb {N}}} <_{\mathrm {W}} \mathsf {C}_{\mathbb {N}}'$
, see [Reference Anglès D'Auriac and Kihara1, Proposition 7.2 and Corollary 7.6]). The fact that
$\mathsf {RT}^{{1}}_{{\mathbb {N}}} <_{\mathrm {W}} \mathsf {C}_{\mathbb {N}}'$
, see [Reference Anglès D'Auriac and Kihara1, Proposition 7.2 and Corollary 7.6]). The fact that
 $\mathsf {RT}^{{1}}_{{\mathbb {N}}} <_{\mathrm {W}}\mathsf {DS}$
follows from
$\mathsf {RT}^{{1}}_{{\mathbb {N}}} <_{\mathrm {W}}\mathsf {DS}$
follows from
 ${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}<_{\mathrm {W}}\mathsf {DS}$
(Proposition 4.8). ⊣
${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}<_{\mathrm {W}}\mathsf {DS}$
(Proposition 4.8). ⊣
We now show that
 $\mathsf {RT}^{{1}}_{{\mathbb {N}}} $
is the strongest problem among those that are reducible to
$\mathsf {RT}^{{1}}_{{\mathbb {N}}} $
is the strongest problem among those that are reducible to
![]() $\mathsf {DS}$
and whose instances always have finitely many solutions.
$\mathsf {DS}$
and whose instances always have finitely many solutions.
Definition 4.25. Let
![]() $f:\subseteq \mathbf {X} \rightrightarrows \mathbb {N}$
. We say that f is pointwise finite if, for each
$f:\subseteq \mathbf {X} \rightrightarrows \mathbb {N}$
. We say that f is pointwise finite if, for each
![]() $x\in \operatorname {dom}(f)$
,
$x\in \operatorname {dom}(f)$
,
![]() $|f(x)|$
is finite.
$|f(x)|$
is finite.
Notice that
 $\mathsf {cRT}^{{1}}_{{k}} $
and
$\mathsf {cRT}^{{1}}_{{k}} $
and
 $\mathsf {cRT}^{{1}}_{{\mathbb {N}}} $
are pointwise finite, as for each k-coloring c we have
$\mathsf {cRT}^{{1}}_{{\mathbb {N}}} $
are pointwise finite, as for each k-coloring c we have
 $|\mathsf {cRT}^{{1}}_{{k}} (c)|=|\mathsf {cRT}^{{1}}_{{\mathbb {N}}} (c)|\le k$
.
$|\mathsf {cRT}^{{1}}_{{k}} (c)|=|\mathsf {cRT}^{{1}}_{{\mathbb {N}}} (c)|\le k$
.
Lemma 4.26. Let g be upwards-closed and let f be pointwise finite. If
![]() $f\le _{\mathrm {W}} g$
then
$f\le _{\mathrm {W}} g$
then
 $f\le _{\mathrm {W}} \mathsf {RT}^{{1}}_{{\mathbb {N}}} $
.
$f\le _{\mathrm {W}} \mathsf {RT}^{{1}}_{{\mathbb {N}}} $
.
Proof Suppose that
![]() $f \le _{\mathrm {W}} g$
as witnessed by
$f \le _{\mathrm {W}} g$
as witnessed by
![]() $\Phi , \Psi $
. Let p be the name for the f-instance x we are given.
$\Phi , \Psi $
. Let p be the name for the f-instance x we are given.
We define a coloring c as follows: we dove-tail all computations
![]() $\Psi (p,n)$
for
$\Psi (p,n)$
for
![]() $n \in \mathbb {N}$
. Whenever some computation converges to some
$n \in \mathbb {N}$
. Whenever some computation converges to some
![]() $j \in \mathbb {N}$
, we define
$j \in \mathbb {N}$
, we define
![]() $c(i):=j$
where i is the first element on which c is not defined yet. Since g is upwards-closed, we know that for all but finitely many n,
$c(i):=j$
where i is the first element on which c is not defined yet. Since g is upwards-closed, we know that for all but finitely many n,
![]() $\Psi (p,n)$
has to converge to some
$\Psi (p,n)$
has to converge to some
![]() $j_n \in f(x)$
. This implies that
$j_n \in f(x)$
. This implies that
![]() $\operatorname {ran}(c)$
contains only finitely many distinct elements. Moreover, any element repeating infinitely often is a correct solution to
$\operatorname {ran}(c)$
contains only finitely many distinct elements. Moreover, any element repeating infinitely often is a correct solution to
![]() $f(x)$
, therefore we can find a
$f(x)$
, therefore we can find a
![]() $y\in f(x)$
by applying
$y\in f(x)$
by applying
 $\mathsf {RT}^{{1}}_{{\mathbb {N}}} $
to c and returning the color of the solution.⊣
$\mathsf {RT}^{{1}}_{{\mathbb {N}}} $
to c and returning the color of the solution.⊣
Theorem 4.27. If f is pointwise finite then
![]() $f\le _{\mathrm {W}} \mathsf {DS}$
iff
$f\le _{\mathrm {W}} \mathsf {DS}$
iff
 $f\le _{\mathrm {W}} \mathsf {RT}^{{1}}_{{\mathbb {N}}} $
.
$f\le _{\mathrm {W}} \mathsf {RT}^{{1}}_{{\mathbb {N}}} $
.
Proof The right-to-left implication always holds as
 $\mathsf {RT}^{{1}}_{{\mathbb {N}}} <_{\mathrm {W}}\mathsf {DS}$
(Proposition 4.24). On the other hand, if f is pointwise finite and
$\mathsf {RT}^{{1}}_{{\mathbb {N}}} <_{\mathrm {W}}\mathsf {DS}$
(Proposition 4.24). On the other hand, if f is pointwise finite and
![]() $f\le _{\mathrm {W}}\mathsf {DS}$
then, by Theorem 4.10 we have
$f\le _{\mathrm {W}}\mathsf {DS}$
then, by Theorem 4.10 we have
 $f\le _{\mathrm {W}}{\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
. Since
$f\le _{\mathrm {W}}{\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
. Since
 ${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
is upwards-closed, by Lemma 4.26 we have
${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
is upwards-closed, by Lemma 4.26 we have
 $f\le _{\mathrm {W}}\mathsf {RT}^{{1}}_{{\mathbb {N}}} $
.⊣
$f\le _{\mathrm {W}}\mathsf {RT}^{{1}}_{{\mathbb {N}}} $
.⊣
By Lemma 4.26 we also have the following:
Proposition 4.28. The Weihrauch degree of
 $\mathsf {RT}^{{1}}_{{\mathbb {N}}} $
is the highest Weihrauch degree such that:
$\mathsf {RT}^{{1}}_{{\mathbb {N}}} $
is the highest Weihrauch degree such that:
-
1. it contains a representative which is pointwise finite and
-
2. it is Weihrauch reducible to some problem which is upwards-closed.
Proof Point 1 holds because
 $\mathsf {cRT}^{{1}}_{{\mathbb {N}}} $
is pointwise finite and
$\mathsf {cRT}^{{1}}_{{\mathbb {N}}} $
is pointwise finite and
 $\mathsf {cRT}^{{1}}_{{\mathbb {N}}} \equiv _{\mathrm {W}} \mathsf {RT}^{{1}}_{{\mathbb {N}}} $
. Point 2 holds because
$\mathsf {cRT}^{{1}}_{{\mathbb {N}}} \equiv _{\mathrm {W}} \mathsf {RT}^{{1}}_{{\mathbb {N}}} $
. Point 2 holds because
 $\mathsf {RT}^{{1}}_{{\mathbb {N}}} <_{\mathrm {W}}{\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
(Proposition 4.24) and
$\mathsf {RT}^{{1}}_{{\mathbb {N}}} <_{\mathrm {W}}{\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
(Proposition 4.24) and
 ${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
is upwards-closed. Finally, the maximality follows from Lemma 4.26.⊣
${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
is upwards-closed. Finally, the maximality follows from Lemma 4.26.⊣
Lemma 4.29. If f is upwards-closed and
 $f\le _{\mathrm {W}} \mathsf {RT}^{{1}}_{{\mathbb {N}}} $
then
$f\le _{\mathrm {W}} \mathsf {RT}^{{1}}_{{\mathbb {N}}} $
then
![]() $f\le _{\mathrm {W}}\mathsf {C}_{\mathbb {N}}$
.
$f\le _{\mathrm {W}}\mathsf {C}_{\mathbb {N}}$
.
Proof Recall that
 $\mathsf {RT}^{{1}}_{{\mathbb {N}}} \equiv _{\mathrm {W}}\mathsf {cRT}^{{1}}_{{\mathbb {N}}} $
and let
$\mathsf {RT}^{{1}}_{{\mathbb {N}}} \equiv _{\mathrm {W}}\mathsf {cRT}^{{1}}_{{\mathbb {N}}} $
and let
![]() $\Phi ,\Psi $
be two computable maps witnessing
$\Phi ,\Psi $
be two computable maps witnessing
 $f\le _{\mathrm {W}}\mathsf {cRT}^{{1}}_{{\mathbb {N}}} $
. Let p be a name for some
$f\le _{\mathrm {W}}\mathsf {cRT}^{{1}}_{{\mathbb {N}}} $
. Let p be a name for some
![]() $x\in \operatorname {dom}(f)$
and let c be the coloring represented by
$x\in \operatorname {dom}(f)$
and let c be the coloring represented by
![]() $\Phi (p)$
. We define the following
$\Phi (p)$
. We define the following
 $\Pi ^{0,p}_1$
set
$\Pi ^{0,p}_1$
set
 $$ \begin{align*} A:= \{\langle n,c_0,\ldots,c_k,s \rangle: {}&{} (\forall i)(\exists j\le k)(c(i)=c_j) \text{ and }\\ & (\forall j\le k)(\exists i<s)(c(i)=c_j) \text{ and }\\ & (\forall j\le k)(\Psi(p,c_j)\downarrow \rightarrow \Psi(p,c_j)\le n) \}. \end{align*} $$
$$ \begin{align*} A:= \{\langle n,c_0,\ldots,c_k,s \rangle: {}&{} (\forall i)(\exists j\le k)(c(i)=c_j) \text{ and }\\ & (\forall j\le k)(\exists i<s)(c(i)=c_j) \text{ and }\\ & (\forall j\le k)(\Psi(p,c_j)\downarrow \rightarrow \Psi(p,c_j)\le n) \}. \end{align*} $$
Notice that, if
![]() $\langle n,c_0,\ldots ,c_k,s \rangle \in A$
then, by the first two conditions, there is a
$\langle n,c_0,\ldots ,c_k,s \rangle \in A$
then, by the first two conditions, there is a
![]() $j\le k$
s.t.
$j\le k$
s.t.
![]() $c_j$
is a valid solution for
$c_j$
is a valid solution for
 $\mathsf {cRT}^{{1}}_{{\mathbb {N}}} (c)$
. In particular
$\mathsf {cRT}^{{1}}_{{\mathbb {N}}} (c)$
. In particular
![]() $\Psi (p,c_j)\downarrow $
and is a correct solution for
$\Psi (p,c_j)\downarrow $
and is a correct solution for
![]() $f(x)$
(as
$f(x)$
(as
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
witness that
$\Psi $
witness that
 $f \le _{\mathrm {W}} \mathsf {cRT}^{{1}}_{{\mathbb {N}}} $
). Since f is upwards-closed, every number greater than
$f \le _{\mathrm {W}} \mathsf {cRT}^{{1}}_{{\mathbb {N}}} $
). Since f is upwards-closed, every number greater than
![]() $\Psi (p,c_j)$
is a valid solution. In particular, the third condition implies that
$\Psi (p,c_j)$
is a valid solution. In particular, the third condition implies that
![]() $n\ge \Psi (p,c_j)$
and therefore
$n\ge \Psi (p,c_j)$
and therefore
![]() $n\in f(x)$
.⊣
$n\in f(x)$
.⊣
Notice that the previous lemma provides an alternative proof for the fact that
 ${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}\not \le _{\mathrm {W}} \mathsf {RT}^{{1}}_{{\mathbb {N}}} $
, as
${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}\not \le _{\mathrm {W}} \mathsf {RT}^{{1}}_{{\mathbb {N}}} $
, as
 ${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}\not \le _{\mathrm {W}}\mathsf {C}_{\mathbb {N}}$
.
${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}\not \le _{\mathrm {W}}\mathsf {C}_{\mathbb {N}}$
.
If we consider only bounded pointwise finite functions, we can improve Theorem 4.27 by replacing
 $\mathsf {RT}^{{1}}_{{\mathbb {N}}} $
with
$\mathsf {RT}^{{1}}_{{\mathbb {N}}} $
with
 $\mathsf {RT}^{{1}}_{{k}} $
.
$\mathsf {RT}^{{1}}_{{k}} $
.
Lemma 4.30. If f has codomain k, then
 $f \le _{\mathrm {W}} \mathsf {RT}^{{1}}_{{\mathbb {N}}} $
iff
$f \le _{\mathrm {W}} \mathsf {RT}^{{1}}_{{\mathbb {N}}} $
iff
 $f \le _{\mathrm {W}} \mathsf {RT}^{{1}}_{{k}} $
.
$f \le _{\mathrm {W}} \mathsf {RT}^{{1}}_{{k}} $
.
Proof The right-to-left implication is trivial, so let us prove the left-to-right one. Since
 $\mathsf {RT}^{{1}}_{{\mathbb {N}}} \le _{\mathrm {W}} {\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
and
$\mathsf {RT}^{{1}}_{{\mathbb {N}}} \le _{\mathrm {W}} {\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
and
 ${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
is upwards-closed, it suffices to show that if g is upwards-closed and
${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
is upwards-closed, it suffices to show that if g is upwards-closed and
![]() $f \le _{\mathrm {W}} g$
, then
$f \le _{\mathrm {W}} g$
, then
 $f \le _{\mathrm {W}} \mathsf {RT}^{{1}}_{{k}} $
. The proof closely follows the one of Lemma 4.26. Suppose that
$f \le _{\mathrm {W}} \mathsf {RT}^{{1}}_{{k}} $
. The proof closely follows the one of Lemma 4.26. Suppose that
![]() $f \le _{\mathrm {W}} g$
as witnessed by
$f \le _{\mathrm {W}} g$
as witnessed by
![]() $\Phi , \Psi $
. Let p be the name for the f-instance x we are given. We define a k-coloring c as follows: we dove-tail all computations
$\Phi , \Psi $
. Let p be the name for the f-instance x we are given. We define a k-coloring c as follows: we dove-tail all computations
![]() $\Psi (p,n)$
for
$\Psi (p,n)$
for
![]() $n \in \mathbb {N}$
. Whenever some computation converges to some
$n \in \mathbb {N}$
. Whenever some computation converges to some
![]() $j < k$
, we define
$j < k$
, we define
![]() $c(i):=j$
where i is the first element on which c is not defined yet. Since g is upwards-closed, we know that for all but finitely many n,
$c(i):=j$
where i is the first element on which c is not defined yet. Since g is upwards-closed, we know that for all but finitely many n,
![]() $\Psi (p,n)$
has to converge to some
$\Psi (p,n)$
has to converge to some
![]() $j_n < k$
which lies in
$j_n < k$
which lies in
![]() $f(x)$
. Moreover, any element repeating infinitely often is a correct solution to
$f(x)$
. Moreover, any element repeating infinitely often is a correct solution to
![]() $f(x)$
, therefore we can find a
$f(x)$
, therefore we can find a
![]() $y\in f(x)$
by applying
$y\in f(x)$
by applying
 $\mathsf {RT}^{{1}}_{{k}} $
to c and returning the color of the solution. ⊣
$\mathsf {RT}^{{1}}_{{k}} $
to c and returning the color of the solution. ⊣
Theorem 4.31. If f has codomain k, then
![]() $f \le _{\mathrm {W}} \mathsf {DS}$
iff
$f \le _{\mathrm {W}} \mathsf {DS}$
iff
 $f \le _{\mathrm {W}} \mathsf {RT}^{{1}}_{{k}} $
.
$f \le _{\mathrm {W}} \mathsf {RT}^{{1}}_{{k}} $
.
Proof The right-to-left implication always holds as
 $\mathsf {RT}^{{1}}_{{k}} \le _{\mathrm {W}}\mathsf {RT}^{{1}}_{{\mathbb {N}}} $
trivially and
$\mathsf {RT}^{{1}}_{{k}} \le _{\mathrm {W}}\mathsf {RT}^{{1}}_{{\mathbb {N}}} $
trivially and
 $\mathsf {RT}^{{1}}_{{\mathbb {N}}} <_{\mathrm {W}}\mathsf {DS}$
(Proposition 4.24). The left-to-right implication follows from Theorem 4.27 and Lemma 4.30.⊣
$\mathsf {RT}^{{1}}_{{\mathbb {N}}} <_{\mathrm {W}}\mathsf {DS}$
(Proposition 4.24). The left-to-right implication follows from Theorem 4.27 and Lemma 4.30.⊣
To conclude the section we notice how we can improve the results if we restrict our attention to single-valued functions. Define the problem
![]() $\mathsf {lim}_k :\subseteq k^{\mathbb {N}} \to k$
as the limit in the discrete space k.
$\mathsf {lim}_k :\subseteq k^{\mathbb {N}} \to k$
as the limit in the discrete space k.
Lemma 4.32. If f has codomain k and is single-valued, then
![]() $f \le _{\mathrm {W}} \mathsf {lim}_k$
iff
$f \le _{\mathrm {W}} \mathsf {lim}_k$
iff
 $f \le _{\mathrm {W}} \mathsf {RT}^{{1}}_{{k}} $
.
$f \le _{\mathrm {W}} \mathsf {RT}^{{1}}_{{k}} $
.
Proof The left-to-right implication is trivial as
 $\mathsf {lim}_k\le _{\mathrm {W}}\mathsf {RT}^{{1}}_{{k}} $
. To prove the converse direction recall that
$\mathsf {lim}_k\le _{\mathrm {W}}\mathsf {RT}^{{1}}_{{k}} $
. To prove the converse direction recall that
 $\mathsf {RT}^{{1}}_{{k}} \equiv _{\mathrm {W}}\mathsf {cRT}^{{1}}_{{k}} $
and let the reduction
$\mathsf {RT}^{{1}}_{{k}} \equiv _{\mathrm {W}}\mathsf {cRT}^{{1}}_{{k}} $
and let the reduction
 $f\le _{\mathrm {W}}\mathsf {cRT}^{{1}}_{{k}} $
be witnessed by the maps
$f\le _{\mathrm {W}}\mathsf {cRT}^{{1}}_{{k}} $
be witnessed by the maps
![]() $\Phi ,\Psi $
. Let p be a name for some
$\Phi ,\Psi $
. Let p be a name for some
![]() $x\in \operatorname {dom}(f)$
and let c be the coloring represented by
$x\in \operatorname {dom}(f)$
and let c be the coloring represented by
![]() $\Phi (p)$
. Notice that, since f is single-valued, for every solution
$\Phi (p)$
. Notice that, since f is single-valued, for every solution
 $j\in \mathsf {cRT}^{{1}}_{{k}} (c)$
we have
$j\in \mathsf {cRT}^{{1}}_{{k}} (c)$
we have
![]() $\Psi (p,j)=f(x)$
. Furthermore, since the range of c is finite, there are only finitely many i such that
$\Psi (p,j)=f(x)$
. Furthermore, since the range of c is finite, there are only finitely many i such that
![]() $c(i)$
is not a solution. If we then define
$c(i)$
is not a solution. If we then define
 $$ \begin{align*} n_i:= \begin{cases} \Psi(p,c(i)) & \text{if } \Psi(p,c(i)) \text{ converges in }i\text{ steps and } \Psi(p,c(i))<k, \\ 0 & \text{otherwise,} \end{cases}\end{align*} $$
$$ \begin{align*} n_i:= \begin{cases} \Psi(p,c(i)) & \text{if } \Psi(p,c(i)) \text{ converges in }i\text{ steps and } \Psi(p,c(i))<k, \\ 0 & \text{otherwise,} \end{cases}\end{align*} $$
we have that the sequence
![]() $(n_i)_{i\in \mathbb {N}} \in k^{\mathbb {N}}$
converges to
$(n_i)_{i\in \mathbb {N}} \in k^{\mathbb {N}}$
converges to
![]() $f(x)$
. Therefore we can use
$f(x)$
. Therefore we can use
![]() $\mathsf {lim}_k$
to obtain
$\mathsf {lim}_k$
to obtain
![]() $f(x)$
.⊣
$f(x)$
.⊣
Theorem 4.33. If f has codomain k and is single-valued, then
![]() $f \le _{\mathrm {W}} \mathsf {lim}_k$
iff
$f \le _{\mathrm {W}} \mathsf {lim}_k$
iff
![]() $f \le _{\mathrm {W}} \mathsf {DS}$
.
$f \le _{\mathrm {W}} \mathsf {DS}$
.
5. Presentation of orders
In this section we study how the presentation of a linear/quasi order can influence the uniform computational strength of the problems
![]() $\mathsf {DS}$
and
$\mathsf {DS}$
and
![]() $\mathsf {BS}$
.
$\mathsf {BS}$
.
Definition 5.1. For every
 $\boldsymbol {\Gamma } \in \{ \boldsymbol {\Sigma }^0_k,\, \boldsymbol {\Pi }^0_k,\, \boldsymbol {\Delta }^0_k,\, \boldsymbol {\Sigma }^1_1,\, \boldsymbol {\Pi }^1_1,\, \boldsymbol {\Delta }^1_1 \}$
we define the problem
$\boldsymbol {\Gamma } \in \{ \boldsymbol {\Sigma }^0_k,\, \boldsymbol {\Pi }^0_k,\, \boldsymbol {\Delta }^0_k,\, \boldsymbol {\Sigma }^1_1,\, \boldsymbol {\Pi }^1_1,\, \boldsymbol {\Delta }^1_1 \}$
we define the problem
![]() ${\boldsymbol {\Gamma }}\text {-}\mathsf {DS} :\subseteq \boldsymbol {\Gamma }(\mathbf {LO}) \rightrightarrows {\mathbb {N}^{\mathbb {N}}}$
as
${\boldsymbol {\Gamma }}\text {-}\mathsf {DS} :\subseteq \boldsymbol {\Gamma }(\mathbf {LO}) \rightrightarrows {\mathbb {N}^{\mathbb {N}}}$
as
![]() ${\boldsymbol {\Gamma }}\text {-}\mathsf {DS}(L) := \mathsf {DS}(L)$
. Similarly we define
${\boldsymbol {\Gamma }}\text {-}\mathsf {DS}(L) := \mathsf {DS}(L)$
. Similarly we define
![]() ${\boldsymbol {\Gamma }}\text {-}\mathsf {BS}:\subseteq \boldsymbol {\Gamma }(\mathbf {QO}) \rightrightarrows {\mathbb {N}^{\mathbb {N}}}$
as
${\boldsymbol {\Gamma }}\text {-}\mathsf {BS}:\subseteq \boldsymbol {\Gamma }(\mathbf {QO}) \rightrightarrows {\mathbb {N}^{\mathbb {N}}}$
as
![]() ${\boldsymbol {\Gamma }}\text {-}\mathsf {BS}(P) := \mathsf {BS}(P)$
.
${\boldsymbol {\Gamma }}\text {-}\mathsf {BS}(P) := \mathsf {BS}(P)$
.
Despite the fact that
![]() $\mathsf {DS} \equiv _{\mathrm {W}} \mathsf {BS}$
(Proposition 4.5), it is not the case that
$\mathsf {DS} \equiv _{\mathrm {W}} \mathsf {BS}$
(Proposition 4.5), it is not the case that
![]() ${\boldsymbol {\Gamma }}\text {-}\mathsf {DS} \equiv _{\mathrm {W}} {\boldsymbol {\Gamma }}\text {-}\mathsf {BS}$
in general. In particular, we will show that
${\boldsymbol {\Gamma }}\text {-}\mathsf {DS} \equiv _{\mathrm {W}} {\boldsymbol {\Gamma }}\text {-}\mathsf {BS}$
in general. In particular, we will show that
 ${\boldsymbol {\Sigma }^0_k}\text {-}\mathsf {BS} \not \le _{\mathrm {W}} {\boldsymbol {\Sigma }^0_k}\text {-}\mathsf {DS}$
(Theorem 5.14) and
${\boldsymbol {\Sigma }^0_k}\text {-}\mathsf {BS} \not \le _{\mathrm {W}} {\boldsymbol {\Sigma }^0_k}\text {-}\mathsf {DS}$
(Theorem 5.14) and
 ${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {BS} \not \le _{\mathrm {W}} {\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS}$
(Corollary 5.24).
${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {BS} \not \le _{\mathrm {W}} {\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS}$
(Corollary 5.24).
Furthermore, we strengthen Corollary 4.11 by showing that
 ${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS} <_{\mathrm {W}} \mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
(Theorem 5.22). In other words, even if we are allowed to feed
${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS} <_{\mathrm {W}} \mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
(Theorem 5.22). In other words, even if we are allowed to feed
![]() $\mathsf {DS}$
a code for a
$\mathsf {DS}$
a code for a
![]() $\boldsymbol {\Sigma }^1_1$
linear ordering, we still cannot compute
$\boldsymbol {\Sigma }^1_1$
linear ordering, we still cannot compute
![]() $\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
. On the other hand, we already showed that if we are allowed to perform a relatively small amount of post-processing (namely
$\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
. On the other hand, we already showed that if we are allowed to perform a relatively small amount of post-processing (namely
![]() $\mathsf {lim}$
) on the output of
$\mathsf {lim}$
) on the output of
![]() $\mathsf {DS}$
, then we can compute
$\mathsf {DS}$
, then we can compute
![]() $\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
(Proposition 4.3). In particular, the use of
$\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
(Proposition 4.3). In particular, the use of
![]() $\mathsf {lim}$
absorbs any difference in uniform strength between
$\mathsf {lim}$
absorbs any difference in uniform strength between
![]() $\mathsf {DS}$
and
$\mathsf {DS}$
and
 ${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS}$
and collapses the whole hierarchy (up to
${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS}$
and collapses the whole hierarchy (up to
 ${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS}$
) to
${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS}$
) to
![]() $\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
.
$\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
.
Many of our separations are derived by analyzing the first-order part of the problems in question, or more generally by characterizing the problems satisfying certain properties (such as single-valuedness or having restricted codomain) which lie below the problems in question. On the contrary, we prove Theorem 5.22 using very different techniques due to Anglès d’Auriac and Kihara [Reference Astor, Dzhafarov, Solomon and Suggs2].
Before beginning our analysis, we record some preliminary observations. Note that
 $\mathsf {DS}={\boldsymbol {\Delta }^0_1}\text {-}\mathsf {DS}$
and
$\mathsf {DS}={\boldsymbol {\Delta }^0_1}\text {-}\mathsf {DS}$
and
 $\mathsf {BS}={\boldsymbol {\Delta }^0_1}\text {-}\mathsf {BS}$
. It is straightforward to see that, for every
$\mathsf {BS}={\boldsymbol {\Delta }^0_1}\text {-}\mathsf {BS}$
. It is straightforward to see that, for every
![]() $\boldsymbol {\Gamma }$
,
$\boldsymbol {\Gamma }$
,
![]() ${\boldsymbol {\Gamma }}\text {-}\mathsf {DS} \le _{\mathrm {W}}{\boldsymbol {\Gamma }}\text {-}\mathsf {BS}$
. Moreover, for every
${\boldsymbol {\Gamma }}\text {-}\mathsf {DS} \le _{\mathrm {W}}{\boldsymbol {\Gamma }}\text {-}\mathsf {BS}$
. Moreover, for every
![]() $\boldsymbol {\Gamma },\boldsymbol {\Gamma }'$
s.t.
$\boldsymbol {\Gamma },\boldsymbol {\Gamma }'$
s.t.
![]() $\boldsymbol {\Gamma }(X)\subset \boldsymbol {\Gamma }'(X)$
we have
$\boldsymbol {\Gamma }(X)\subset \boldsymbol {\Gamma }'(X)$
we have
![]() ${\boldsymbol {\Gamma }}\text {-}\mathsf {DS} \le _{\mathrm {W}} {\boldsymbol {\Gamma }'}\text {-}\mathsf {DS}$
and
${\boldsymbol {\Gamma }}\text {-}\mathsf {DS} \le _{\mathrm {W}} {\boldsymbol {\Gamma }'}\text {-}\mathsf {DS}$
and
![]() ${\boldsymbol {\Gamma }}\text {-}\mathsf {BS} \le _{\mathrm {W}} {\boldsymbol {\Gamma }'}\text {-}\mathsf {BS}$
.
${\boldsymbol {\Gamma }}\text {-}\mathsf {BS} \le _{\mathrm {W}} {\boldsymbol {\Gamma }'}\text {-}\mathsf {BS}$
.
Notice also that the set of bad sequences through a
![]() $\boldsymbol {\Delta }^1_1$
-quasi-order is
$\boldsymbol {\Delta }^1_1$
-quasi-order is
![]() $\boldsymbol {\Delta }^1_1$
, hence it is straightforward to see that
$\boldsymbol {\Delta }^1_1$
, hence it is straightforward to see that
 ${\boldsymbol {\Delta }^1_1}\text {-}\mathsf {BS}\le _{\mathrm {W}}{\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}\equiv _{\mathrm {W}}\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
. This shows also that
${\boldsymbol {\Delta }^1_1}\text {-}\mathsf {BS}\le _{\mathrm {W}}{\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}\equiv _{\mathrm {W}}\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
. This shows also that
![]() ${\boldsymbol {\Gamma }}\text {-}\mathsf {BS}\le _{\mathrm {W}} \mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
for every arithmetic
${\boldsymbol {\Gamma }}\text {-}\mathsf {BS}\le _{\mathrm {W}} \mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
for every arithmetic
![]() $\boldsymbol {\Gamma }$
.
$\boldsymbol {\Gamma }$
.
Proposition 5.2. For every
 $\boldsymbol {\Gamma } \in \{ \boldsymbol {\Sigma }^0_k,\, \boldsymbol {\Pi }^0_k,\, \boldsymbol {\Delta }^0_k,\, \boldsymbol {\Sigma }^1_1,\, \boldsymbol {\Pi }^1_1,\, \boldsymbol {\Delta }^1_1 \}$
the problems
$\boldsymbol {\Gamma } \in \{ \boldsymbol {\Sigma }^0_k,\, \boldsymbol {\Pi }^0_k,\, \boldsymbol {\Delta }^0_k,\, \boldsymbol {\Sigma }^1_1,\, \boldsymbol {\Pi }^1_1,\, \boldsymbol {\Delta }^1_1 \}$
the problems
![]() ${\boldsymbol {\Gamma }}\text {-}\mathsf {DS}$
and
${\boldsymbol {\Gamma }}\text {-}\mathsf {DS}$
and
![]() ${\boldsymbol {\Gamma }}\text {-}\mathsf {BS}$
are cylinders.
${\boldsymbol {\Gamma }}\text {-}\mathsf {BS}$
are cylinders.
Proof The proof is a straightforward generalization of the proof of Proposition 4.6. ⊣
Theorem 5.3. For every
![]() $k\in \mathbb {N}$
and every
$k\in \mathbb {N}$
and every
![]() $\boldsymbol {\Gamma }\in \{ \boldsymbol {\Sigma }, \boldsymbol {\Pi }, \boldsymbol {\Delta }\}$
$\boldsymbol {\Gamma }\in \{ \boldsymbol {\Sigma }, \boldsymbol {\Pi }, \boldsymbol {\Delta }\}$
 $$ \begin{align*} {\boldsymbol{\Gamma}^0_{k+1}}\text{-}\mathsf{DS} &\equiv_{\mathrm{W}} {\boldsymbol{\Gamma}^0_1}\text{-}\mathsf{DS} * \mathsf{lim}^{[k]}\equiv_{\mathrm{W}} {\boldsymbol{\Gamma}^0_1}\text{-}\mathsf{DS}^{(k)},\\[-3pt] {\boldsymbol{\Gamma}^0_{k+1}}\text{-}\mathsf{BS} &\equiv_{\mathrm{W}} {\boldsymbol{\Gamma}^0_1}\text{-}\mathsf{BS} * \mathsf{lim}^{[k]}\equiv_{\mathrm{W}} {\boldsymbol{\Gamma}^0_1}\text{-}\mathsf{BS}^{(k)}. \end{align*} $$
$$ \begin{align*} {\boldsymbol{\Gamma}^0_{k+1}}\text{-}\mathsf{DS} &\equiv_{\mathrm{W}} {\boldsymbol{\Gamma}^0_1}\text{-}\mathsf{DS} * \mathsf{lim}^{[k]}\equiv_{\mathrm{W}} {\boldsymbol{\Gamma}^0_1}\text{-}\mathsf{DS}^{(k)},\\[-3pt] {\boldsymbol{\Gamma}^0_{k+1}}\text{-}\mathsf{BS} &\equiv_{\mathrm{W}} {\boldsymbol{\Gamma}^0_1}\text{-}\mathsf{BS} * \mathsf{lim}^{[k]}\equiv_{\mathrm{W}} {\boldsymbol{\Gamma}^0_1}\text{-}\mathsf{BS}^{(k)}. \end{align*} $$
Proof Fix k and
![]() $\boldsymbol {\Gamma }$
as above. The reduction
$\boldsymbol {\Gamma }$
as above. The reduction
 ${\boldsymbol {\Gamma }^0_{k+1}}\text {-}\mathsf {DS} \le _{\mathrm {W}} {\boldsymbol {\Gamma }^0_1}\text {-}\mathsf {DS} * \mathsf {lim}^{[k]}$
follows from the fact that
${\boldsymbol {\Gamma }^0_{k+1}}\text {-}\mathsf {DS} \le _{\mathrm {W}} {\boldsymbol {\Gamma }^0_1}\text {-}\mathsf {DS} * \mathsf {lim}^{[k]}$
follows from the fact that
 $$ \begin{align*} \mathsf{lim}^{[k]}\equiv_{\mathrm{W}} {\boldsymbol{\Sigma}^0_k}\text{-}\mathsf{CA}\equiv_{\mathrm{W}} {\boldsymbol{\Pi}^0_k}\text{-}\mathsf{CA}\equiv_{\mathrm{W}} {\boldsymbol{\Delta}^0_{k+1}}\text{-}\mathsf{CA},\end{align*} $$
$$ \begin{align*} \mathsf{lim}^{[k]}\equiv_{\mathrm{W}} {\boldsymbol{\Sigma}^0_k}\text{-}\mathsf{CA}\equiv_{\mathrm{W}} {\boldsymbol{\Pi}^0_k}\text{-}\mathsf{CA}\equiv_{\mathrm{W}} {\boldsymbol{\Delta}^0_{k+1}}\text{-}\mathsf{CA},\end{align*} $$
hence we can use
![]() $\mathsf {lim}^{[k]}$
to compute a
$\mathsf {lim}^{[k]}$
to compute a
![]() $\boldsymbol {\Gamma }^0_1$
-name for the input linear order, and then apply
$\boldsymbol {\Gamma }^0_1$
-name for the input linear order, and then apply
 ${\boldsymbol {\Gamma }^0_1}\text {-}\mathsf {DS}$
to get a descending sequence.
${\boldsymbol {\Gamma }^0_1}\text {-}\mathsf {DS}$
to get a descending sequence.
Let us now prove the converse reduction. Since both
![]() $\mathsf {lim}^{[k]}$
and
$\mathsf {lim}^{[k]}$
and
 ${\boldsymbol {\Gamma }^0_1}\text {-}\mathsf {DS}$
are cylinders, by the cylindrical decomposition there is an e s.t.
${\boldsymbol {\Gamma }^0_1}\text {-}\mathsf {DS}$
are cylinders, by the cylindrical decomposition there is an e s.t.
 $$ \begin{align*} {\boldsymbol{\Gamma}^0_1}\text{-}\mathsf{DS} * \mathsf{lim}^{[k]}\equiv_{\mathrm{W}} {\boldsymbol{\Gamma}^0_1}\text{-}\mathsf{DS} \circ \Phi_e\circ \mathsf{lim}^{[k]}.\end{align*} $$
$$ \begin{align*} {\boldsymbol{\Gamma}^0_1}\text{-}\mathsf{DS} * \mathsf{lim}^{[k]}\equiv_{\mathrm{W}} {\boldsymbol{\Gamma}^0_1}\text{-}\mathsf{DS} \circ \Phi_e\circ \mathsf{lim}^{[k]}.\end{align*} $$
Given any
 $p \in \operatorname {dom}({\boldsymbol {\Gamma }^0_1}\text {-}\mathsf {DS} \circ \Phi _e\circ \mathsf {lim}^{[k]})$
, the string
$p \in \operatorname {dom}({\boldsymbol {\Gamma }^0_1}\text {-}\mathsf {DS} \circ \Phi _e\circ \mathsf {lim}^{[k]})$
, the string
![]() $q:=\Phi _e(\mathsf {lim}^{[k]}(p))$
is a
$q:=\Phi _e(\mathsf {lim}^{[k]}(p))$
is a
![]() $\boldsymbol {\Gamma }^0_1$
-name for a linear order
$\boldsymbol {\Gamma }^0_1$
-name for a linear order
![]() $L_p$
. Since q is
$L_p$
. Since q is
 $\Delta ^{0,p}_{k+1}$
, the condition
$\Delta ^{0,p}_{k+1}$
, the condition
![]() $a\le _{L_p} b$
is
$a\le _{L_p} b$
is
 $\Gamma ^{0,p}_{k+1}$
for every
$\Gamma ^{0,p}_{k+1}$
for every
![]() $a,b$
. This shows that, given an input p we can uniformly compute a
$a,b$
. This shows that, given an input p we can uniformly compute a
 $\boldsymbol {\Gamma }^0_{k+1}$
-name for the linear order
$\boldsymbol {\Gamma }^0_{k+1}$
-name for the linear order
![]() $L_p$
, and hence use
$L_p$
, and hence use
 ${\boldsymbol {\Gamma }^0_{k+1}}\text {-}\mathsf {DS}$
to compute an
${\boldsymbol {\Gamma }^0_{k+1}}\text {-}\mathsf {DS}$
to compute an
![]() $<_{L_p}$
-descending sequence.
$<_{L_p}$
-descending sequence.
The equivalence
 ${\boldsymbol {\Gamma }^0_1}\text {-}\mathsf {DS} * \mathsf {lim}^{[k]}\equiv _{\mathrm {W}} {\boldsymbol {\Gamma }^0_1}\text {-}\mathsf {DS}^{(k)}$
follows from the fact that
${\boldsymbol {\Gamma }^0_1}\text {-}\mathsf {DS} * \mathsf {lim}^{[k]}\equiv _{\mathrm {W}} {\boldsymbol {\Gamma }^0_1}\text {-}\mathsf {DS}^{(k)}$
follows from the fact that
 ${\boldsymbol {\Gamma }^0_1}\text {-}\mathsf {DS}$
is a cylinder.
${\boldsymbol {\Gamma }^0_1}\text {-}\mathsf {DS}$
is a cylinder.
The same reasoning works, mutatis mutandis, to show that
 $$ \begin{align*} {\boldsymbol{\Gamma}^0_{k+1}}\text{-}\mathsf{BS} \equiv_{\mathrm{W}} {\boldsymbol{\Gamma}^0_1}\text{-}\mathsf{BS} * \mathsf{lim}^{[k]}\equiv_{\mathrm{W}} {\boldsymbol{\Gamma}^0_1}\text{-}\mathsf{BS}^{(k)}. \end{align*} $$
$$ \begin{align*} {\boldsymbol{\Gamma}^0_{k+1}}\text{-}\mathsf{BS} \equiv_{\mathrm{W}} {\boldsymbol{\Gamma}^0_1}\text{-}\mathsf{BS} * \mathsf{lim}^{[k]}\equiv_{\mathrm{W}} {\boldsymbol{\Gamma}^0_1}\text{-}\mathsf{BS}^{(k)}. \end{align*} $$
⊣
Using this theorem, the relativized version of Proposition 4.5 can be proved explicitly as follows:
Corollary 5.4. For every
![]() $k\ge 1$
,
$k\ge 1$
,
 ${\boldsymbol {\Delta }^0_k}\text {-}\mathsf {DS} \equiv _{\mathrm {W}} {\boldsymbol {\Delta }^0_k}\text {-}\mathsf {BS}.$
${\boldsymbol {\Delta }^0_k}\text {-}\mathsf {DS} \equiv _{\mathrm {W}} {\boldsymbol {\Delta }^0_k}\text {-}\mathsf {BS}.$
Proof Using Proposition 4.5 and Theorem 5.3 we immediately have
 $$ \begin{align*} {\boldsymbol{\Delta}^0_{k+1}}\text{-}\mathsf{BS} \equiv_{\mathrm{W}} \mathsf{BS}* \mathsf{lim}^{[k]}\equiv_{\mathrm{W}} \mathsf{DS} * \mathsf{lim}^{[k]}\equiv_{\mathrm{W}} {\boldsymbol{\Delta}^0_{k+1}}\text{-}\mathsf{DS},\end{align*} $$
$$ \begin{align*} {\boldsymbol{\Delta}^0_{k+1}}\text{-}\mathsf{BS} \equiv_{\mathrm{W}} \mathsf{BS}* \mathsf{lim}^{[k]}\equiv_{\mathrm{W}} \mathsf{DS} * \mathsf{lim}^{[k]}\equiv_{\mathrm{W}} {\boldsymbol{\Delta}^0_{k+1}}\text{-}\mathsf{DS},\end{align*} $$
as
 $\mathsf {DS}={\boldsymbol {\Delta }^0_1}\text {-}\mathsf {DS}$
and
$\mathsf {DS}={\boldsymbol {\Delta }^0_1}\text {-}\mathsf {DS}$
and
 $\mathsf {BS}={\boldsymbol {\Delta }^0_1}\text {-}\mathsf {BS}$
.⊣
$\mathsf {BS}={\boldsymbol {\Delta }^0_1}\text {-}\mathsf {BS}$
.⊣
This implies also that, for every k,
 ${\boldsymbol {\Sigma }^0_k}\text {-}\mathsf {BS} \le _{\mathrm {W}} {\boldsymbol {\Delta }^0_{k+1}}\text {-}\mathsf {DS}$
and
${\boldsymbol {\Sigma }^0_k}\text {-}\mathsf {BS} \le _{\mathrm {W}} {\boldsymbol {\Delta }^0_{k+1}}\text {-}\mathsf {DS}$
and
 ${\boldsymbol {\Pi }^0_k}\text {-}\mathsf {BS}\le _{\mathrm {W}} {\boldsymbol {\Delta }^0_{k+1}}\text {-}\mathsf {DS}$
.
${\boldsymbol {\Pi }^0_k}\text {-}\mathsf {BS}\le _{\mathrm {W}} {\boldsymbol {\Delta }^0_{k+1}}\text {-}\mathsf {DS}$
.
5.1.
 $\Gamma $
$\Gamma $
 $^0_k$
-
$^0_k$
-
 $\mathsf {DS}$
and
$\mathsf {DS}$
and
 $\Gamma $
$\Gamma $
 $^0_k$
-
$^0_k$
-
 $\mathsf {BS}$
$\mathsf {BS}$
We will now show that the hierarchy of
![]() $\boldsymbol {\Gamma }$
-
$\boldsymbol {\Gamma }$
-
![]() $\mathsf {DS}$
problems does not collapse at any finite level. First we study the hierarchy of
$\mathsf {DS}$
problems does not collapse at any finite level. First we study the hierarchy of
 ${\boldsymbol {\Delta }^0_k}\text {-}\mathsf {DS}$
problems by characterizing their first-order parts (Theorem 5.5). Then we prove the analogues of Theorem 4.31 and Theorem 4.33 for
${\boldsymbol {\Delta }^0_k}\text {-}\mathsf {DS}$
problems by characterizing their first-order parts (Theorem 5.5). Then we prove the analogues of Theorem 4.31 and Theorem 4.33 for
 ${\boldsymbol {\Delta }^0_k}\text {-}\mathsf {DS}$
(Proposition 5.8).
${\boldsymbol {\Delta }^0_k}\text {-}\mathsf {DS}$
(Proposition 5.8).
For any sequence of problems
![]() $f_s :\subseteq \textbf {X}_s \rightrightarrows \textbf {Y}_s$
,
$f_s :\subseteq \textbf {X}_s \rightrightarrows \textbf {Y}_s$
,
![]() $s \in \mathbb {N}$
, the countable coproduct of the sequence is the problem
$s \in \mathbb {N}$
, the countable coproduct of the sequence is the problem
![]() $\bigsqcup _{s \in \mathbb {N}} f_s :\subseteq \bigsqcup _s \textbf {X}_i \rightrightarrows \bigsqcup _s \textbf {Y}_i$
defined by
$\bigsqcup _{s \in \mathbb {N}} f_s :\subseteq \bigsqcup _s \textbf {X}_i \rightrightarrows \bigsqcup _s \textbf {Y}_i$
defined by
 $\left (\bigsqcup _{s \in \mathbb {N}} f_s\right )(s,x) := \{s\} \times f_s(x)$
. The problem
$\left (\bigsqcup _{s \in \mathbb {N}} f_s\right )(s,x) := \{s\} \times f_s(x)$
. The problem
![]() $\bigsqcup _{s \in \mathbb {N}} f_s$
allows us access to exactly one
$\bigsqcup _{s \in \mathbb {N}} f_s$
allows us access to exactly one
![]() $f_s$
of our choice.
$f_s$
of our choice.
Theorem 5.5. For every
![]() $k \ge 1$
,
$k \ge 1$
,
 $$ \begin{align*}{}^1{{\boldsymbol{\Delta}^0_k}\text{-}\mathsf{DS} } \equiv_{\mathrm{W}} \left(\bigsqcup_{s \in \mathbb{N}} {\boldsymbol{\Delta}^0_k}\text{-}\mathsf{C}_{s}\right) * {\boldsymbol{\Pi}^1_1}\mathsf{-Bound}.\end{align*} $$
$$ \begin{align*}{}^1{{\boldsymbol{\Delta}^0_k}\text{-}\mathsf{DS} } \equiv_{\mathrm{W}} \left(\bigsqcup_{s \in \mathbb{N}} {\boldsymbol{\Delta}^0_k}\text{-}\mathsf{C}_{s}\right) * {\boldsymbol{\Pi}^1_1}\mathsf{-Bound}.\end{align*} $$
We split the proof into two lemmas.
Lemma 5.6. For every
![]() $k\ge 1$
, if
$k\ge 1$
, if
![]() $f:\subseteq \mathbf {X} \rightrightarrows \mathbb {N}$
and
$f:\subseteq \mathbf {X} \rightrightarrows \mathbb {N}$
and
 $f \le _{\mathrm {W}} {\boldsymbol {\Delta }^0_k}\text {-}\mathsf {DS}$
then
$f \le _{\mathrm {W}} {\boldsymbol {\Delta }^0_k}\text {-}\mathsf {DS}$
then
 $$ \begin{align*} f \le_{\mathrm{W}} \left(\bigsqcup_{s \in \mathbb{N}} {\boldsymbol{\Delta}^0_k}\text{-}\mathsf{C}_{s}\right) * {\boldsymbol{\Pi}^1_1}\mathsf{-Bound}.\end{align*} $$
$$ \begin{align*} f \le_{\mathrm{W}} \left(\bigsqcup_{s \in \mathbb{N}} {\boldsymbol{\Delta}^0_k}\text{-}\mathsf{C}_{s}\right) * {\boldsymbol{\Pi}^1_1}\mathsf{-Bound}.\end{align*} $$
Proof Fix Turing functionals
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
which witness that
$\Psi $
which witness that
 $f \le _{\mathrm {W}} {\boldsymbol {\Delta }^0_k}\text {-}\mathsf {DS}$
. Given an f-instance with name x,
$f \le _{\mathrm {W}} {\boldsymbol {\Delta }^0_k}\text {-}\mathsf {DS}$
. Given an f-instance with name x,
![]() $\Phi ^x$
is a
$\Phi ^x$
is a
 $\Delta ^{0,x}_k$
-code for the linear order
$\Delta ^{0,x}_k$
-code for the linear order
![]() $\le ^x$
. Consider the
$\le ^x$
. Consider the
 $\Sigma ^{0,x}_k$
set
$\Sigma ^{0,x}_k$
set
 $$ \begin{align*} D := \{F \in \mathbb{N} : {}&{} F \text{ codes a non-empty finite} <^x\!\!\text{-descending sequence and } \\ & \Psi^{x \oplus F} \text{ outputs some } j \in \mathbb{N}\}. \end{align*} $$
$$ \begin{align*} D := \{F \in \mathbb{N} : {}&{} F \text{ codes a non-empty finite} <^x\!\!\text{-descending sequence and } \\ & \Psi^{x \oplus F} \text{ outputs some } j \in \mathbb{N}\}. \end{align*} $$
We can uniformly express D as the increasing union over
![]() $s \in \mathbb {N}$
of finite sets
$s \in \mathbb {N}$
of finite sets
![]() $D_s \subseteq \{0,\ldots ,s\}$
, which are uniformly
$D_s \subseteq \{0,\ldots ,s\}$
, which are uniformly
 $\Pi ^{0,x}_{k-1}$
.
$\Pi ^{0,x}_{k-1}$
.
We now define the set
where
![]() $\mathrm {Ext}_x$
is the set of finite sequences that extend to an infinite
$\mathrm {Ext}_x$
is the set of finite sequences that extend to an infinite
![]() $<^x$
-descending sequence. It is easy to see that A is
$<^x$
-descending sequence. It is easy to see that A is
 $\Pi ^{1,x}_1,$
as being extendible in a
$\Pi ^{1,x}_1,$
as being extendible in a
![]() $\Delta ^0_k$
-linear order is a
$\Delta ^0_k$
-linear order is a
![]() $\Sigma ^1_1$
property.
$\Sigma ^1_1$
property.
We show that A is finite. Since
![]() $\le ^x$
is a
$\le ^x$
is a
 ${\boldsymbol {\Delta }^0_k}\text {-}\mathsf {DS}$
-instance, we can fix an infinite
${\boldsymbol {\Delta }^0_k}\text {-}\mathsf {DS}$
-instance, we can fix an infinite
![]() $<^x$
-descending sequence S. By definition of Weihrauch reducibility,
$<^x$
-descending sequence S. By definition of Weihrauch reducibility,
![]() $\Psi ^{x \oplus S}$
outputs some f-solution
$\Psi ^{x \oplus S}$
outputs some f-solution
![]() $j \in \mathbb {N}$
. By the continuity of
$j \in \mathbb {N}$
. By the continuity of
![]() $\Psi $
, there is some finite non-empty initial segment F of S such that
$\Psi $
, there is some finite non-empty initial segment F of S such that
![]() $\Psi ^{x \oplus F}$
outputs j. Hence for all sufficiently large s, we have
$\Psi ^{x \oplus F}$
outputs j. Hence for all sufficiently large s, we have
![]() $F \in D_s$
.
$F \in D_s$
.
This shows that we can apply
 ${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
to A to obtain some
${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
to A to obtain some
![]() $b \in \mathbb {N}$
which bounds A. Note that
$b \in \mathbb {N}$
which bounds A. Note that
![]() $D_b$
must be nonempty. We now define the following non-empty subset of
$D_b$
must be nonempty. We now define the following non-empty subset of
![]() $D_b$
:
$D_b$
:
 $$ \begin{align*} B:=\left\{ F \in D_b : (\forall G\in D_b)\left(\min_{<^x}(G) \le^x \min_{<^x}(\,F)\right) \right\}.\end{align*} $$
$$ \begin{align*} B:=\left\{ F \in D_b : (\forall G\in D_b)\left(\min_{<^x}(G) \le^x \min_{<^x}(\,F)\right) \right\}.\end{align*} $$
Notice that all the quantifications are bounded. In particular, B is a (non-empty)
 $\Delta ^{0,x}_k$
subset of
$\Delta ^{0,x}_k$
subset of
![]() $D_b$
because
$D_b$
because
![]() $D_b$
is
$D_b$
is
 $\Pi ^{0,x}_{k-1}$
and
$\Pi ^{0,x}_{k-1}$
and
![]() $\le ^x$
is
$\le ^x$
is
 $\Delta ^{0,x}_k$
. Notice also that the definition of B ensures that each of its elements is extendible (as we know that there is some extendible element in
$\Delta ^{0,x}_k$
. Notice also that the definition of B ensures that each of its elements is extendible (as we know that there is some extendible element in
![]() $D_b$
). In particular, this shows that, for every
$D_b$
). In particular, this shows that, for every
![]() $F\in B$
, it is enough to run
$F\in B$
, it is enough to run
![]() $\Psi ^{x \oplus F}$
to compute an f-solution for the original instance. We can find such
$\Psi ^{x \oplus F}$
to compute an f-solution for the original instance. We can find such
![]() $F \in B$
by applying
$F \in B$
by applying
 $\left (\bigsqcup _s {\boldsymbol {\Delta }^0_k}\text {-}\mathsf {C}_{s}\right )(b,B)$
.⊣
$\left (\bigsqcup _s {\boldsymbol {\Delta }^0_k}\text {-}\mathsf {C}_{s}\right )(b,B)$
.⊣
Notice that
 $(\bigsqcup _s {\boldsymbol {\Delta }^0_1}\text {-}\mathsf {C}_{s})$
is computable, hence in case
$(\bigsqcup _s {\boldsymbol {\Delta }^0_1}\text {-}\mathsf {C}_{s})$
is computable, hence in case
![]() $k=1$
we obtain Proposition 4.5.
$k=1$
we obtain Proposition 4.5.
Lemma 5.7. For every
![]() $k\ge 1$
,
$k\ge 1$
,
 $$ \begin{align*}\left(\bigsqcup_{s \in \mathbb{N}} {\boldsymbol{\Delta}^0_k}\text{-}\mathsf{C}_{s}\right) * {\boldsymbol{\Pi}^1_1}\mathsf{-Bound}\le_{\mathrm{W}} {\boldsymbol{\Delta}^0_k}\text{-}\mathsf{DS}. \end{align*} $$
$$ \begin{align*}\left(\bigsqcup_{s \in \mathbb{N}} {\boldsymbol{\Delta}^0_k}\text{-}\mathsf{C}_{s}\right) * {\boldsymbol{\Pi}^1_1}\mathsf{-Bound}\le_{\mathrm{W}} {\boldsymbol{\Delta}^0_k}\text{-}\mathsf{DS}. \end{align*} $$
Proof Using the cylindrical decomposition we can write
 $$ \begin{align*} \left(\bigsqcup_{s \in \mathbb{N}} {\boldsymbol{\Delta}^0_k}\text{-}\mathsf{C}_{s}\right) * {\boldsymbol{\Pi}^1_1}\mathsf{-Bound} \equiv_{\mathrm{W}} \left(\left(\bigsqcup_{s \in \mathbb{N}} {\boldsymbol{\Delta}^0_k}\text{-}\mathsf{C}_{s}\right) \times \operatorname{id}\right) \circ \Phi_e \circ ({\boldsymbol{\Pi}^1_1}\mathsf{-Bound}\times \operatorname{id}{}) \end{align*} $$
$$ \begin{align*} \left(\bigsqcup_{s \in \mathbb{N}} {\boldsymbol{\Delta}^0_k}\text{-}\mathsf{C}_{s}\right) * {\boldsymbol{\Pi}^1_1}\mathsf{-Bound} \equiv_{\mathrm{W}} \left(\left(\bigsqcup_{s \in \mathbb{N}} {\boldsymbol{\Delta}^0_k}\text{-}\mathsf{C}_{s}\right) \times \operatorname{id}\right) \circ \Phi_e \circ ({\boldsymbol{\Pi}^1_1}\mathsf{-Bound}\times \operatorname{id}{}) \end{align*} $$
for some computable map
![]() $\Phi _e$
. Let
$\Phi _e$
. Let
![]() $\Phi _1,\Phi _2$
be computable maps s.t.
$\Phi _1,\Phi _2$
be computable maps s.t.
![]() $\Phi _e(p) = \langle \Phi _1(p),\Phi _2(p) \rangle $
. Then we have
$\Phi _e(p) = \langle \Phi _1(p),\Phi _2(p) \rangle $
. Then we have
 $$ \begin{align*} \left(\left(\bigsqcup_{s \in \mathbb{N}} {\boldsymbol{\Delta}^0_k}\text{-}\mathsf{C}_{s}\right) \times \operatorname{id}{}\right) \circ \Phi_e \circ ({\boldsymbol{\Pi}^1_1}\mathsf{-Bound}\times \operatorname{id}{})(\langle p_1,p_2 \rangle) \\ = \left\langle \left(\bigsqcup_{s \in \mathbb{N}} {\boldsymbol{\Delta}^0_k}\text{-}\mathsf{C}_{s}\right)\Phi_1({\boldsymbol{\Pi}^1_1}\mathsf{-Bound}(p_1),p_2), \Phi_2({\boldsymbol{\Pi}^1_1}\mathsf{-Bound}(p_1),p_2) \right\rangle. \end{align*} $$
$$ \begin{align*} \left(\left(\bigsqcup_{s \in \mathbb{N}} {\boldsymbol{\Delta}^0_k}\text{-}\mathsf{C}_{s}\right) \times \operatorname{id}{}\right) \circ \Phi_e \circ ({\boldsymbol{\Pi}^1_1}\mathsf{-Bound}\times \operatorname{id}{})(\langle p_1,p_2 \rangle) \\ = \left\langle \left(\bigsqcup_{s \in \mathbb{N}} {\boldsymbol{\Delta}^0_k}\text{-}\mathsf{C}_{s}\right)\Phi_1({\boldsymbol{\Pi}^1_1}\mathsf{-Bound}(p_1),p_2), \Phi_2({\boldsymbol{\Pi}^1_1}\mathsf{-Bound}(p_1),p_2) \right\rangle. \end{align*} $$
Given an instance
![]() $\langle p_1,p_2 \rangle $
of the above composition, we can think of
$\langle p_1,p_2 \rangle $
of the above composition, we can think of
![]() $p_1$
as coding an input A to
$p_1$
as coding an input A to
 ${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
via a tree T s.t. for each i,
${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
via a tree T s.t. for each i,
![]() $i\in A$
iff the subtree
$i\in A$
iff the subtree
![]() $T_i:=\{ \sigma \in T : \sigma (0)=i \}$
of T is well-founded. For any
$T_i:=\{ \sigma \in T : \sigma (0)=i \}$
of T is well-founded. For any
 $b \in {\boldsymbol {\Pi }^1_1}\mathsf {-Bound}(p_1)$
,
$b \in {\boldsymbol {\Pi }^1_1}\mathsf {-Bound}(p_1)$
,
![]() $\Phi _1(b,p_2)$
must be a name for an instance of
$\Phi _1(b,p_2)$
must be a name for an instance of
 $\bigsqcup _{s \in \mathbb {N}} {\boldsymbol {\Delta }^0_k}\text {-}\mathsf {C}_{s}$
. Then
$\bigsqcup _{s \in \mathbb {N}} {\boldsymbol {\Delta }^0_k}\text {-}\mathsf {C}_{s}$
. Then
![]() $\pi _1\Phi _1(b,p_2)$
is a number s and
$\pi _1\Phi _1(b,p_2)$
is a number s and
![]() $\pi _2\Phi _1(b,p_2)$
is a
$\pi _2\Phi _1(b,p_2)$
is a
![]() $\boldsymbol {\Delta }^0_k$
-name for a non-empty subset
$\boldsymbol {\Delta }^0_k$
-name for a non-empty subset
![]() $A_s$
of
$A_s$
of
![]() $\{0,\ldots , s-1\}$
, where
$\{0,\ldots , s-1\}$
, where
![]() $\pi _i(\langle p_1,p_2 \rangle )=p_i$
denotes the projection on the i-th component. Regardless of whether
$\pi _i(\langle p_1,p_2 \rangle )=p_i$
denotes the projection on the i-th component. Regardless of whether
 $b \in {\boldsymbol {\Pi }^1_1}\mathsf {-Bound}(p_1)$
, we will interpret
$b \in {\boldsymbol {\Pi }^1_1}\mathsf {-Bound}(p_1)$
, we will interpret
![]() $\pi _1\Phi _1(b,p_2)$
and
$\pi _1\Phi _1(b,p_2)$
and
![]() $\pi _2\Phi _1(b,p_2)$
as above.
$\pi _2\Phi _1(b,p_2)$
as above.
We define a
 $\Delta ^{0,\langle p_1,p_2 \rangle }_k$
linear order as follows. First define
$\Delta ^{0,\langle p_1,p_2 \rangle }_k$
linear order as follows. First define
 $$ \begin{align*} L:=\{ (\sigma, n) : {}&{} \sigma\in p_1 \text{ and } \\ & \pi_1 \Phi_1(\sigma(0), p_2) \text{ outputs a number in less than } |\sigma| \text{ steps and} \\ & n \text{ lies in the set named by } \pi_2 \Phi_1(\sigma(0), p_2) \}. \end{align*} $$
$$ \begin{align*} L:=\{ (\sigma, n) : {}&{} \sigma\in p_1 \text{ and } \\ & \pi_1 \Phi_1(\sigma(0), p_2) \text{ outputs a number in less than } |\sigma| \text{ steps and} \\ & n \text{ lies in the set named by } \pi_2 \Phi_1(\sigma(0), p_2) \}. \end{align*} $$
We order the elements of L by
It is easy to see that
![]() $(L,\le _L)$
is
$(L,\le _L)$
is
 $\Delta ^{0,\langle p_1,p_2 \rangle }_k$
. Notice that it is a linear order, as the pairs are ordered lexicographically where the first components are ordered according to the Kleene–Brouwer order on
$\Delta ^{0,\langle p_1,p_2 \rangle }_k$
. Notice that it is a linear order, as the pairs are ordered lexicographically where the first components are ordered according to the Kleene–Brouwer order on
![]() ${\mathbb {N}^{<\mathbb {N}}}$
and the second components are ordered according to the order on
${\mathbb {N}^{<\mathbb {N}}}$
and the second components are ordered according to the order on
![]() $\mathbb {N}$
.
$\mathbb {N}$
.
Let
![]() $(q_i)_{i\in \mathbb {N}}$
be an
$(q_i)_{i\in \mathbb {N}}$
be an
![]() $<_L$
-descending sequence, with
$<_L$
-descending sequence, with
![]() $q_i=(\sigma _i,n_i)$
. Notice that for each i there is a
$q_i=(\sigma _i,n_i)$
. Notice that for each i there is a
![]() $j>i$
s.t.
$j>i$
s.t.
![]() $\sigma _j <_{\mathrm {KB}} \sigma _i$
. Indeed, if there is an i s.t. for all
$\sigma _j <_{\mathrm {KB}} \sigma _i$
. Indeed, if there is an i s.t. for all
![]() $j>i$
we have
$j>i$
we have
![]() $\sigma _j = \sigma _i$
then, by definition of
$\sigma _j = \sigma _i$
then, by definition of
![]() $\le _L$
, the sequence
$\le _L$
, the sequence
![]() $(n_j)_{j>i}$
would be a descending sequence in the natural numbers, which is impossible.
$(n_j)_{j>i}$
would be a descending sequence in the natural numbers, which is impossible.
This implies that there is a subsequence
![]() $(q_{i_k})_{k\in \mathbb {N}}$
s.t.
$(q_{i_k})_{k\in \mathbb {N}}$
s.t.
![]() $(\sigma _{i_k})_{k\in \mathbb {N}}$
is a
$(\sigma _{i_k})_{k\in \mathbb {N}}$
is a
![]() $<_{\mathrm {KB}}$
-descending sequence. In particular, this implies that
$<_{\mathrm {KB}}$
-descending sequence. In particular, this implies that
![]() $T_{\sigma _0(0)}$
is ill-founded, i.e.,
$T_{\sigma _0(0)}$
is ill-founded, i.e.,
 $\sigma _0(0)\in {\boldsymbol {\Pi }^1_1}\mathsf {-Bound}(p_1)$
. Moreover, by definition of L, this implies that
$\sigma _0(0)\in {\boldsymbol {\Pi }^1_1}\mathsf {-Bound}(p_1)$
. Moreover, by definition of L, this implies that
![]() $n_0$
lies in the set named by
$n_0$
lies in the set named by
![]() $\pi _2 \Phi _1(\sigma _0(0), p_2)$
.
$\pi _2 \Phi _1(\sigma _0(0), p_2)$
.
In other words, given an
![]() $<_L$
-descending sequence
$<_L$
-descending sequence
![]() $(q_i)_{i\in \mathbb {N}}$
we have that
$(q_i)_{i\in \mathbb {N}}$
we have that
 $(\pi _1 q_0) (0) \in {\boldsymbol {\Pi }^1_1}\mathsf {-Bound}(p_1)$
and
$(\pi _1 q_0) (0) \in {\boldsymbol {\Pi }^1_1}\mathsf {-Bound}(p_1)$
and
 $\pi _2 q_0 \in \left (\bigsqcup _{s \in \mathbb {N}} {\boldsymbol {\Delta }^0_k}\text {-}\mathsf {C})_{s}\right )\Phi _1({\boldsymbol {\Pi }^1_1}\mathsf {-Bound}(p_1),p_2)$
. From this we can compute
$\pi _2 q_0 \in \left (\bigsqcup _{s \in \mathbb {N}} {\boldsymbol {\Delta }^0_k}\text {-}\mathsf {C})_{s}\right )\Phi _1({\boldsymbol {\Pi }^1_1}\mathsf {-Bound}(p_1),p_2)$
. From this we can compute
![]() $\Phi _2(\pi _1 q_0, p_2)$
as well. This establishes the desired reduction.⊣
$\Phi _2(\pi _1 q_0, p_2)$
as well. This establishes the desired reduction.⊣
This completes the proof of Theorem 5.5.
With a small modification of the argument in the proof of Lemma 5.6 we can prove the following:
Proposition 5.8. Fix
![]() $k\ge 1$
. For every
$k\ge 1$
. For every
![]() $f:\subseteq \mathbf {X} \rightrightarrows \mathbb {N}$
,
$f:\subseteq \mathbf {X} \rightrightarrows \mathbb {N}$
,
 $$ \begin{align*} f \le_{\mathrm{W}} {\boldsymbol{\Delta}^0_k}\text{-}\mathsf{DS} \iff f \le_{\mathrm{W}} {\boldsymbol{\Pi}^1_1}\mathsf{-Bound} \times \mathsf{lim}^{[k-1]}.\end{align*} $$
$$ \begin{align*} f \le_{\mathrm{W}} {\boldsymbol{\Delta}^0_k}\text{-}\mathsf{DS} \iff f \le_{\mathrm{W}} {\boldsymbol{\Pi}^1_1}\mathsf{-Bound} \times \mathsf{lim}^{[k-1]}.\end{align*} $$
If, in particular, f has codomain N for some
![]() $N\ge 1$
then
$N\ge 1$
then
 $$ \begin{align*}f \le_{\mathrm{W}} {\boldsymbol{\Delta}^0_k}\text{-}\mathsf{DS} \iff f \le_{\mathrm{W}} \mathsf{RT}^{{1}}_{{N}} * \mathsf{lim}^{[k-1]}.\end{align*} $$
$$ \begin{align*}f \le_{\mathrm{W}} {\boldsymbol{\Delta}^0_k}\text{-}\mathsf{DS} \iff f \le_{\mathrm{W}} \mathsf{RT}^{{1}}_{{N}} * \mathsf{lim}^{[k-1]}.\end{align*} $$
If, additionally, f is single-valued, then
 $$ \begin{align*}f \le_{\mathrm{W}} {\boldsymbol{\Delta}^0_k}\text{-}\mathsf{DS} \iff f \le_{\mathrm{W}} \mathsf{lim}_N*\mathsf{lim}^{[k-1]}. \end{align*} $$
$$ \begin{align*}f \le_{\mathrm{W}} {\boldsymbol{\Delta}^0_k}\text{-}\mathsf{DS} \iff f \le_{\mathrm{W}} \mathsf{lim}_N*\mathsf{lim}^{[k-1]}. \end{align*} $$
Proof The right-to-left implication follows from Proposition 4.8 and Theorem 5.3:
 $$ \begin{align*} {\boldsymbol{\Pi}^1_1}\mathsf{-Bound} \times \mathsf{lim}^{[k-1]} & \le_{\mathrm{W}} {\boldsymbol{\Pi}^1_1}\mathsf{-Bound}*\mathsf{lim}^{[k-1]} \\ & \le_{\mathrm{W}} \mathsf{DS}*\mathsf{lim}^{[k-1]}\equiv_{\mathrm{W}}{\boldsymbol{\Delta}^0_k}\text{-}\mathsf{DS}. \end{align*} $$
$$ \begin{align*} {\boldsymbol{\Pi}^1_1}\mathsf{-Bound} \times \mathsf{lim}^{[k-1]} & \le_{\mathrm{W}} {\boldsymbol{\Pi}^1_1}\mathsf{-Bound}*\mathsf{lim}^{[k-1]} \\ & \le_{\mathrm{W}} \mathsf{DS}*\mathsf{lim}^{[k-1]}\equiv_{\mathrm{W}}{\boldsymbol{\Delta}^0_k}\text{-}\mathsf{DS}. \end{align*} $$
To prove the left-to-right implication, fix a pair of Turing functionals
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
witnessing the reduction
$\Psi $
witnessing the reduction
 $f \le _{\mathrm {W}} {\boldsymbol {\Delta }^0_k}\text {-}\mathsf {DS}$
. Fix an f-instance with name x and let
$f \le _{\mathrm {W}} {\boldsymbol {\Delta }^0_k}\text {-}\mathsf {DS}$
. Fix an f-instance with name x and let
![]() $\le ^x$
be the
$\le ^x$
be the
 $\Delta ^{0,x}_k$
linear order defined by
$\Delta ^{0,x}_k$
linear order defined by
![]() $\Phi ^x$
.
$\Phi ^x$
.
Define D,
![]() $D_s$
and A as in the proof of Lemma 5.6. In that proof, we applied
$D_s$
and A as in the proof of Lemma 5.6. In that proof, we applied
 ${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
to A to obtain
${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
to A to obtain
![]() $b \in \mathbb {N}$
. Then we restricted our attention to
$b \in \mathbb {N}$
. Then we restricted our attention to
![]() $B \subseteq D_b$
. Here we will still apply
$B \subseteq D_b$
. Here we will still apply
 ${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
to A, but we will concurrently consider a subset
${\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
to A, but we will concurrently consider a subset
![]() $B_s$
of each
$B_s$
of each
![]() $D_s$
. For each s, define
$D_s$
. For each s, define
 $$ \begin{align*} B_s&:=\left\{ F \in D_s : (\forall G\in D_s)\left(\min_{<^x}(G) \le^x \min_{<^x}(\,F)\right) \right\},\\ F_s&:= \min B_s, \end{align*} $$
$$ \begin{align*} B_s&:=\left\{ F \in D_s : (\forall G\in D_s)\left(\min_{<^x}(G) \le^x \min_{<^x}(\,F)\right) \right\},\\ F_s&:= \min B_s, \end{align*} $$
where
![]() $F_s$
is intended to be the empty sequence if
$F_s$
is intended to be the empty sequence if
![]() $B_s$
(and hence
$B_s$
(and hence
![]() $D_s$
) is empty.
$D_s$
) is empty.
Notice that
![]() $B_s \subset \{0,\ldots ,s-1\}$
is
$B_s \subset \{0,\ldots ,s-1\}$
is
![]() $\boldsymbol {\Delta }^0_k$
(as each
$\boldsymbol {\Delta }^0_k$
(as each
![]() $D_s$
is
$D_s$
is
 $\boldsymbol {\Pi }^0_{k-1}$
) and therefore
$\boldsymbol {\Pi }^0_{k-1}$
) and therefore
![]() $F_s$
is
$F_s$
is
![]() $\boldsymbol {\Delta }^0_k$
. Since
$\boldsymbol {\Delta }^0_k$
. Since
 $\mathsf {lim}^{[k-1]}\equiv _{\mathrm {W}} {\boldsymbol {\Delta }^0_k}\text {-}\mathsf {CA}$
, it can determine which
$\mathsf {lim}^{[k-1]}\equiv _{\mathrm {W}} {\boldsymbol {\Delta }^0_k}\text {-}\mathsf {CA}$
, it can determine which
![]() $B_s$
is nonempty, and compute
$B_s$
is nonempty, and compute
![]() $F_s$
if
$F_s$
if
![]() $B_s$
is nonempty. Therefore the sequence
$B_s$
is nonempty. Therefore the sequence
![]() $(\,F_s)_{s\in \mathbb {N}}$
can be computed using
$(\,F_s)_{s\in \mathbb {N}}$
can be computed using
![]() $\mathsf {lim}^{[k-1]}$
. For every
$\mathsf {lim}^{[k-1]}$
. For every
 $b\in {\boldsymbol {\Pi }^1_1}\mathsf {-Bound}(A)$
we have that
$b\in {\boldsymbol {\Pi }^1_1}\mathsf {-Bound}(A)$
we have that
![]() $F_b$
is extendible to an infinite
$F_b$
is extendible to an infinite
![]() $<^x$
-descending sequence and that
$<^x$
-descending sequence and that
![]() $\Psi ^{x \oplus F_s}$
converges to some f-solution j (see also the proof of Lemma 5.6).
$\Psi ^{x \oplus F_s}$
converges to some f-solution j (see also the proof of Lemma 5.6).
Assume now that f has codomain N for some
![]() $N\ge 1$
. We can modify the above argument as follows: after computing the sequence
$N\ge 1$
. We can modify the above argument as follows: after computing the sequence
![]() $(\,F_s)_{s\in \mathbb {N}}$
, we consider the
$(\,F_s)_{s\in \mathbb {N}}$
, we consider the
 $\mathsf {RT}^{{1}}_{{N}} $
-instance c defined as
$\mathsf {RT}^{{1}}_{{N}} $
-instance c defined as
 $$ \begin{align*} c(s):= \begin{cases} 0 & \text{if } F_s=\langle \rangle,\\ \Psi^{x \oplus F_s}(0) &\text{otherwise}. \end{cases}\end{align*} $$
$$ \begin{align*} c(s):= \begin{cases} 0 & \text{if } F_s=\langle \rangle,\\ \Psi^{x \oplus F_s}(0) &\text{otherwise}. \end{cases}\end{align*} $$
Since
![]() $F_s$
is nonempty and extendible for cofinitely many s, if
$F_s$
is nonempty and extendible for cofinitely many s, if
![]() $c(s) = i$
for infinitely many s (i.e., c has an
$c(s) = i$
for infinitely many s (i.e., c has an
 $\mathsf {RT}^{{1}}_{{N}} $
-solution of color i), then there is an extendible
$\mathsf {RT}^{{1}}_{{N}} $
-solution of color i), then there is an extendible
![]() $F_s$
s.t.
$F_s$
s.t.
![]() $\Psi ^{x \oplus F_s}(0)=i$
, hence i is an f-solution.
$\Psi ^{x \oplus F_s}(0)=i$
, hence i is an f-solution.
If, additionally, f is single-valued, then there is only one possible i s.t. c has a homogeneous solution with color i. This shows that the sequence
![]() $(c(s))_{s\in \mathbb {N}}$
has a limit, and therefore it suffices to use
$(c(s))_{s\in \mathbb {N}}$
has a limit, and therefore it suffices to use
![]() $\mathsf {lim}_N$
to get the solution.
$\mathsf {lim}_N$
to get the solution.
The fact that
 $\mathsf {RT}^{{1}}_{{N}} * \mathsf {lim}^{[k-1]}$
and
$\mathsf {RT}^{{1}}_{{N}} * \mathsf {lim}^{[k-1]}$
and
![]() $\mathsf {lim}_N * \mathsf {lim}^{[k-1]}$
are reducible to
$\mathsf {lim}_N * \mathsf {lim}^{[k-1]}$
are reducible to
 ${\boldsymbol {\Delta }^0_k}\text {-}\mathsf {DS}$
follows from the fact that the compositional product is a degree theoretic operation, as
${\boldsymbol {\Delta }^0_k}\text {-}\mathsf {DS}$
follows from the fact that the compositional product is a degree theoretic operation, as
 $\mathsf {RT}^{{1}}_{{N}} \le _{\mathrm {W}} \mathsf {DS}$
(Theorem 4.31),
$\mathsf {RT}^{{1}}_{{N}} \le _{\mathrm {W}} \mathsf {DS}$
(Theorem 4.31),
![]() $\mathsf {lim}_N\le _{\mathrm {W}} \mathsf {DS}$
(Theorem 4.16), and
$\mathsf {lim}_N\le _{\mathrm {W}} \mathsf {DS}$
(Theorem 4.16), and
 ${\boldsymbol {\Delta }^0_k}\text {-}\mathsf {DS} \equiv _{\mathrm {W}} \mathsf {DS}*\mathsf {lim}^{[k-1]}$
(Theorem 5.3).⊣
${\boldsymbol {\Delta }^0_k}\text {-}\mathsf {DS} \equiv _{\mathrm {W}} \mathsf {DS}*\mathsf {lim}^{[k-1]}$
(Theorem 5.3).⊣
Notice that
 ${\boldsymbol {\Pi }^1_1}\mathsf {-Bound} \times \mathsf {lim}^{[k-1]}$
is not a first-order problem, so the first statement in Proposition 5.8 is not an alternative characterization of
${\boldsymbol {\Pi }^1_1}\mathsf {-Bound} \times \mathsf {lim}^{[k-1]}$
is not a first-order problem, so the first statement in Proposition 5.8 is not an alternative characterization of
 ${}^1{{\boldsymbol {\Delta }^0_k}\text {-}\mathsf {DS}}$
. It can be rephrased as
${}^1{{\boldsymbol {\Delta }^0_k}\text {-}\mathsf {DS}}$
. It can be rephrased as
 $$ \begin{align*} {}^1{{\boldsymbol{\Delta}^0_k}\text{-}\mathsf{DS}} \equiv_{\mathrm{W}} {}^1{({\boldsymbol{\Pi}^1_1}\mathsf{-Bound} \times \mathsf{lim}^{[k-1]})}.\end{align*} $$
$$ \begin{align*} {}^1{{\boldsymbol{\Delta}^0_k}\text{-}\mathsf{DS}} \equiv_{\mathrm{W}} {}^1{({\boldsymbol{\Pi}^1_1}\mathsf{-Bound} \times \mathsf{lim}^{[k-1]})}.\end{align*} $$
This concludes our discussion of the first-order problems that are Weihrauch reducible to
 ${\boldsymbol {\Delta }^0_k}\text {-}\mathsf {DS}$
. As for the deterministic part of
${\boldsymbol {\Delta }^0_k}\text {-}\mathsf {DS}$
. As for the deterministic part of
 ${\boldsymbol {\Delta }^0_k}\text {-}\mathsf {DS}$
:
${\boldsymbol {\Delta }^0_k}\text {-}\mathsf {DS}$
:
Corollary 5.9. For every
![]() $k\ge 1$
,
$k\ge 1$
,
 $\mathrm {Det}_{ }({\boldsymbol {\Delta }^0_k}\text {-}\mathsf {DS}) \equiv _{\mathrm {W}} \mathsf {lim}^{[k]}$
.
$\mathrm {Det}_{ }({\boldsymbol {\Delta }^0_k}\text {-}\mathsf {DS}) \equiv _{\mathrm {W}} \mathsf {lim}^{[k]}$
.
Proof This follows from
![]() $\mathrm {Det}_{ }(\mathsf {DS})\equiv _{\mathrm {W}}\mathsf {lim}$
(Theorem 4.16) and the fact that, for cylinders, the jump commutes with the deterministic part (Corollary 3.11).⊣
$\mathrm {Det}_{ }(\mathsf {DS})\equiv _{\mathrm {W}}\mathsf {lim}$
(Theorem 4.16) and the fact that, for cylinders, the jump commutes with the deterministic part (Corollary 3.11).⊣
Theorem 5.10. For every
![]() $k\ge 1$
,
$k\ge 1$
,
 $$ \begin{align*} {\boldsymbol{\Delta}^0_k}\text{-}\mathsf{DS} <_{\mathrm{W}} {\boldsymbol{\Delta}^0_{k+1}}\text{-}\mathsf{DS}. \end{align*} $$
$$ \begin{align*} {\boldsymbol{\Delta}^0_k}\text{-}\mathsf{DS} <_{\mathrm{W}} {\boldsymbol{\Delta}^0_{k+1}}\text{-}\mathsf{DS}. \end{align*} $$
In particular this shows that the
![]() $\boldsymbol {\Gamma }$
-
$\boldsymbol {\Gamma }$
-
![]() $\mathsf {DS}$
-hierarchy does not collapse at any finite level.
$\mathsf {DS}$
-hierarchy does not collapse at any finite level.
Proof This follows directly from Proposition 5.8 or, alternatively, from Corollary 5.9. Indeed it suffices to notice that, for every
![]() $k\ge 1$
,
$k\ge 1$
,
 $ \mathsf {LPO} ^{(k)}\le _{\mathrm {W}} \mathsf {lim}^{[k+1]}$
but
$ \mathsf {LPO} ^{(k)}\le _{\mathrm {W}} \mathsf {lim}^{[k+1]}$
but
 $ \mathsf {LPO} ^{(k)}\not \le _{\mathrm {W}} \mathsf {lim}^{[k]}$
, as
$ \mathsf {LPO} ^{(k)}\not \le _{\mathrm {W}} \mathsf {lim}^{[k]}$
, as
![]() $ \mathsf {LPO} ^{(k)}$
is the characteristic function of a
$ \mathsf {LPO} ^{(k)}$
is the characteristic function of a
 $\Sigma ^0_{k+1}$
-complete set while
$\Sigma ^0_{k+1}$
-complete set while
![]() $\mathsf {lim}^{[k]}$
is
$\mathsf {lim}^{[k]}$
is
 $\Sigma ^0_{k+1}$
-measurable.⊣
$\Sigma ^0_{k+1}$
-measurable.⊣
Theorem 5.11. For every
![]() $k\ge 1$
,
$k\ge 1$
,
 ${\boldsymbol {\Delta }^0_{k+1}}\text {-}\mathsf {DS} \equiv _{\mathrm {W}} {\boldsymbol {\Pi }^0_k}\text {-}\mathsf {DS}$
.
${\boldsymbol {\Delta }^0_{k+1}}\text {-}\mathsf {DS} \equiv _{\mathrm {W}} {\boldsymbol {\Pi }^0_k}\text {-}\mathsf {DS}$
.
Proof The right-to-left reduction is trivial. To prove the left-to-right one it suffices to show that
 ${\boldsymbol {\Delta }^0_1}\text {-}\mathsf {DS}' \equiv _{\mathrm {W}} {\boldsymbol {\Pi }^0_1}\text {-}\mathsf {DS}$
and the proof will follow from Theorem 5.3 as
${\boldsymbol {\Delta }^0_1}\text {-}\mathsf {DS}' \equiv _{\mathrm {W}} {\boldsymbol {\Pi }^0_1}\text {-}\mathsf {DS}$
and the proof will follow from Theorem 5.3 as
 $$ \begin{align*} {\boldsymbol{\Delta}^0_{k+1}}\text{-}\mathsf{DS} \equiv_{\mathrm{W}} {\boldsymbol{\Delta}^0_1}\text{-}\mathsf{DS}' * \mathsf{lim}^{[k-1]} \equiv_{\mathrm{W}} {\boldsymbol{\Pi}^0_1}\text{-}\mathsf{DS} * \mathsf{lim}^{[k-1]} \equiv_{\mathrm{W}}{\boldsymbol{\Pi}^0_k}\text{-}\mathsf{DS}.\end{align*} $$
$$ \begin{align*} {\boldsymbol{\Delta}^0_{k+1}}\text{-}\mathsf{DS} \equiv_{\mathrm{W}} {\boldsymbol{\Delta}^0_1}\text{-}\mathsf{DS}' * \mathsf{lim}^{[k-1]} \equiv_{\mathrm{W}} {\boldsymbol{\Pi}^0_1}\text{-}\mathsf{DS} * \mathsf{lim}^{[k-1]} \equiv_{\mathrm{W}}{\boldsymbol{\Pi}^0_k}\text{-}\mathsf{DS}.\end{align*} $$
Let
![]() $p=(p_n)_{n\in \mathbb {N}}$
be a sequence in
$p=(p_n)_{n\in \mathbb {N}}$
be a sequence in
![]() ${\mathbb {N}^{\mathbb {N}}}$
converging to the characteristic function of an ill-founded linear order L. In the following it is convenient to consider also the sequence
${\mathbb {N}^{\mathbb {N}}}$
converging to the characteristic function of an ill-founded linear order L. In the following it is convenient to consider also the sequence
![]() $q=(q_n)_{n\in \mathbb {N}}$
, where
$q=(q_n)_{n\in \mathbb {N}}$
, where
![]() $q_n(i):=p_n(\langle i,i \rangle )$
. Clearly q converges to the characteristic function of
$q_n(i):=p_n(\langle i,i \rangle )$
. Clearly q converges to the characteristic function of
![]() $\operatorname {dom}(L)$
and is uniformly computable from p.
$\operatorname {dom}(L)$
and is uniformly computable from p.
For sake of readability, define the formula
Intuitively
![]() $\varphi $
says that, for each
$\varphi $
says that, for each
![]() $i<|\sigma |$
,
$i<|\sigma |$
,
![]() $\sigma (i)$
codes the positions in which the sequence
$\sigma (i)$
codes the positions in which the sequence
![]() $(x_n)_{n\in \mathbb {N}}$
changes for the last time in the i-th row. Let us also write
$(x_n)_{n\in \mathbb {N}}$
changes for the last time in the i-th row. Let us also write
![]() $x_\sigma := |\sigma |-1$
. We define
$x_\sigma := |\sigma |-1$
. We define
 $$ \begin{align*} M:=\{ (\sigma,\tau)\in{\mathbb{N}^{<\mathbb{N}}}\times {\mathbb{N}^{<\mathbb{N}}} : {}& \varphi(q,\sigma) \land{} \\ & q_{\sigma(x_\sigma)+1}(x_\sigma)=1 \land{} \\ & \varphi(p,\tau) \land |\tau|= \langle x_\sigma,x_\sigma \rangle+1\}. \end{align*} $$
$$ \begin{align*} M:=\{ (\sigma,\tau)\in{\mathbb{N}^{<\mathbb{N}}}\times {\mathbb{N}^{<\mathbb{N}}} : {}& \varphi(q,\sigma) \land{} \\ & q_{\sigma(x_\sigma)+1}(x_\sigma)=1 \land{} \\ & \varphi(p,\tau) \land |\tau|= \langle x_\sigma,x_\sigma \rangle+1\}. \end{align*} $$
Notice that the first two conditions imply that
![]() $x_\sigma \in L$
. Intuitively
$x_\sigma \in L$
. Intuitively
![]() $x_{\sigma }$
is the
$x_{\sigma }$
is the
![]() $\le _{\mathbb {N}}$
-largest element that is witnessed by
$\le _{\mathbb {N}}$
-largest element that is witnessed by
![]() $\sigma $
to enter in L. The last line says that
$\sigma $
to enter in L. The last line says that
![]() $\tau $
is exactly as long as needed to witness all the relations between the elements of L that are
$\tau $
is exactly as long as needed to witness all the relations between the elements of L that are
![]() $\le _{\mathbb {N}} x_\sigma $
.
$\le _{\mathbb {N}} x_\sigma $
.
We order the set M as follows:
Notice that M is a
 $\Pi ^{0,p}_1$
linear order as M is
$\Pi ^{0,p}_1$
linear order as M is
 $\Pi ^{0,p}_1$
and the order
$\Pi ^{0,p}_1$
and the order
![]() $\le _M$
is p-computable: indeed, given two pairs
$\le _M$
is p-computable: indeed, given two pairs
![]() $(\sigma _0,\tau _0),(\sigma _1,\tau _1)\in M$
, we can use the longer string between
$(\sigma _0,\tau _0),(\sigma _1,\tau _1)\in M$
, we can use the longer string between
![]() $\tau _0$
and
$\tau _0$
and
![]() $\tau _1$
to p-compute whether
$\tau _1$
to p-compute whether
![]() $x_{\sigma _0} \le _L x_{\sigma _1}$
. Notice also that, for each l, there is exactly one string
$x_{\sigma _0} \le _L x_{\sigma _1}$
. Notice also that, for each l, there is exactly one string
![]() $\sigma $
of length l witnessing
$\sigma $
of length l witnessing
![]() $\varphi (q,\sigma )$
(by minimality). The third line in the definition of M implies that if
$\varphi (q,\sigma )$
(by minimality). The third line in the definition of M implies that if
![]() $\sigma $
satisfies the first two conditions then there is a unique
$\sigma $
satisfies the first two conditions then there is a unique
![]() $\tau $
s.t.
$\tau $
s.t.
![]() $(\sigma ,\tau )\in M$
. The linearity of M follows by the linearity of L.
$(\sigma ,\tau )\in M$
. The linearity of M follows by the linearity of L.
To conclude the proof it is enough to notice that if
![]() $((\sigma _i,\tau _i))_{i\in \mathbb {N}}$
is an
$((\sigma _i,\tau _i))_{i\in \mathbb {N}}$
is an
![]() $<_M$
-descending sequence then
$<_M$
-descending sequence then
![]() $(x_{\sigma _i})_{i\in \mathbb {N}}$
is an
$(x_{\sigma _i})_{i\in \mathbb {N}}$
is an
![]() $<_L$
-descending sequence.⊣
$<_L$
-descending sequence.⊣
The following is essentially a classical result (see e.g., [Reference Downey, Ershov, Goncharov, Nerode, Remmel and Marek15, Theorem 2.4]). The proof is simple enough that we can briefly sketch it.
Theorem 5.12. For every
![]() $k\ge 1$
,
$k\ge 1$
,
 ${\boldsymbol {\Sigma }^0_k}\text {-}\mathsf {DS} \equiv _{\mathrm {W}} {\boldsymbol {\Delta }^0_k}\text {-}\mathsf {DS}$
.
${\boldsymbol {\Sigma }^0_k}\text {-}\mathsf {DS} \equiv _{\mathrm {W}} {\boldsymbol {\Delta }^0_k}\text {-}\mathsf {DS}$
.
Proof Given a
![]() $\boldsymbol {\Sigma }^0_k$
linear order L, we can uniformly consider a sequence
$\boldsymbol {\Sigma }^0_k$
linear order L, we can uniformly consider a sequence
![]() $((L_s, \le _s))_{s\in \mathbb {N}}$
of
$((L_s, \le _s))_{s\in \mathbb {N}}$
of
![]() $\boldsymbol {\Delta }^0_k$
linear orders approximating L. We then define
$\boldsymbol {\Delta }^0_k$
linear orders approximating L. We then define
 $$ \begin{align*} M:=\{ (q,s) &: q\in L_s \text{ and } (\forall t<s)(q\notin L_t) \}, \\ (p,s)\le_M (q,t) &:\hspace{-1mm}\iff p\le_L q. \end{align*} $$
$$ \begin{align*} M:=\{ (q,s) &: q\in L_s \text{ and } (\forall t<s)(q\notin L_t) \}, \\ (p,s)\le_M (q,t) &:\hspace{-1mm}\iff p\le_L q. \end{align*} $$
Notice that
![]() $(p,s)\le _M (q,t)$
can be written also as
$(p,s)\le _M (q,t)$
can be written also as
![]() $p=q \lor (\forall i)(q\not \le _i p)$
, hence M is
$p=q \lor (\forall i)(q\not \le _i p)$
, hence M is
 $\Delta ^{0,L}_k$
. Moreover, since for every
$\Delta ^{0,L}_k$
. Moreover, since for every
![]() $q\in L$
there is a unique s s.t.
$q\in L$
there is a unique s s.t.
![]() $(q,s)\in M$
, it is easy to see that M is computably isomorphic to L. In particular, given an
$(q,s)\in M$
, it is easy to see that M is computably isomorphic to L. In particular, given an
![]() $<_M$
-descending sequence we can obtain an
$<_M$
-descending sequence we can obtain an
![]() $<_L$
-descending sequence by projection.⊣
$<_L$
-descending sequence by projection.⊣
Corollary 5.13. For every
![]() $k \geq 1$
, we have
$k \geq 1$
, we have
 $$ \begin{align*}{\boldsymbol{\Pi}^0_k}\text{-}\mathsf{DS} \equiv_{\mathrm{W}} {\boldsymbol{\Pi}^0_k}\text{-}\mathsf{BS} \equiv_{\mathrm{W}} {\boldsymbol{\Delta}^0_{k+1}}\text{-}\mathsf{BS} \equiv_{\mathrm{W}} {\boldsymbol{\Delta}^0_{k+1}}\text{-}\mathsf{DS} \equiv_{\mathrm{W}} {\boldsymbol{\Sigma}^0_{k+1}}\text{-}\mathsf{DS}. \end{align*} $$
$$ \begin{align*}{\boldsymbol{\Pi}^0_k}\text{-}\mathsf{DS} \equiv_{\mathrm{W}} {\boldsymbol{\Pi}^0_k}\text{-}\mathsf{BS} \equiv_{\mathrm{W}} {\boldsymbol{\Delta}^0_{k+1}}\text{-}\mathsf{BS} \equiv_{\mathrm{W}} {\boldsymbol{\Delta}^0_{k+1}}\text{-}\mathsf{DS} \equiv_{\mathrm{W}} {\boldsymbol{\Sigma}^0_{k+1}}\text{-}\mathsf{DS}. \end{align*} $$
Proof It is straightforward to see that
 ${\boldsymbol {\Pi }^0_k}\text {-}\mathsf {DS} \le _{\mathrm {W}} {\boldsymbol {\Pi }^0_k}\text {-}\mathsf {BS} \le _{\mathrm {W}} {\boldsymbol {\Delta }^0_{k+1}}\text {-}\mathsf {BS}$
. By Corollary 5.4,
${\boldsymbol {\Pi }^0_k}\text {-}\mathsf {DS} \le _{\mathrm {W}} {\boldsymbol {\Pi }^0_k}\text {-}\mathsf {BS} \le _{\mathrm {W}} {\boldsymbol {\Delta }^0_{k+1}}\text {-}\mathsf {BS}$
. By Corollary 5.4,
 ${\boldsymbol {\Delta }^0_{k+1}}\text {-}\mathsf {BS} \equiv _{\mathrm {W}} {\boldsymbol {\Delta }^0_{k+1}}\text {-}\mathsf {DS}$
. It follows from Theorem 5.11 that the first four problems are equivalent. Finally,
${\boldsymbol {\Delta }^0_{k+1}}\text {-}\mathsf {BS} \equiv _{\mathrm {W}} {\boldsymbol {\Delta }^0_{k+1}}\text {-}\mathsf {DS}$
. It follows from Theorem 5.11 that the first four problems are equivalent. Finally,
 ${\boldsymbol {\Delta }^0_{k+1}}\text {-}\mathsf {DS} \equiv _{\mathrm {W}} {\boldsymbol {\Sigma }^0_{k+1}}\text {-}\mathsf {DS}$
by Theorem 5.12.⊣
${\boldsymbol {\Delta }^0_{k+1}}\text {-}\mathsf {DS} \equiv _{\mathrm {W}} {\boldsymbol {\Sigma }^0_{k+1}}\text {-}\mathsf {DS}$
by Theorem 5.12.⊣
Theorem 5.14. For every
![]() $k\ge 1$
,
$k\ge 1$
,
 $ \mathsf {LPO} ^{(k)}\le _{\mathrm {W}} {\boldsymbol {\Sigma }^0_k}\text {-}\mathsf {BS}$
and therefore
$ \mathsf {LPO} ^{(k)}\le _{\mathrm {W}} {\boldsymbol {\Sigma }^0_k}\text {-}\mathsf {BS}$
and therefore
 ${\boldsymbol {\Sigma }^0_k}\text {-}\mathsf {BS}\not \le _{\mathrm {W}} {\boldsymbol {\Sigma }^0_k}\text {-}\mathsf {DS}$
.
${\boldsymbol {\Sigma }^0_k}\text {-}\mathsf {BS}\not \le _{\mathrm {W}} {\boldsymbol {\Sigma }^0_k}\text {-}\mathsf {DS}$
.
Proof The second statement follows from the first because
 $ \mathsf {LPO} ^{(k)} \not \le _{\mathrm {W}} {\boldsymbol {\Delta }^0_k}\text {-}\mathsf {DS}$
(proof of Theorem 5.10) and
$ \mathsf {LPO} ^{(k)} \not \le _{\mathrm {W}} {\boldsymbol {\Delta }^0_k}\text {-}\mathsf {DS}$
(proof of Theorem 5.10) and
 ${\boldsymbol {\Delta }^0_k}\text {-}\mathsf {DS} \equiv _{\mathrm {W}} {\boldsymbol {\Sigma }^0_k}\text {-}\mathsf {DS}$
(Theorem 5.12).
${\boldsymbol {\Delta }^0_k}\text {-}\mathsf {DS} \equiv _{\mathrm {W}} {\boldsymbol {\Sigma }^0_k}\text {-}\mathsf {DS}$
(Theorem 5.12).
To prove the first statement, it is enough to show that
 $ \mathsf {LPO} '\le _{\mathrm {W}}{\boldsymbol {\Sigma }^0_1}\text {-}\mathsf {BS}$
, and the claim will follow by Theorem 5.3 as
$ \mathsf {LPO} '\le _{\mathrm {W}}{\boldsymbol {\Sigma }^0_1}\text {-}\mathsf {BS}$
, and the claim will follow by Theorem 5.3 as
 $$ \begin{align*} \mathsf{LPO} ^{(k)} \le_{\mathrm{W}} \mathsf{LPO} '*\mathsf{lim}^{[k-1]} \le_{\mathrm{W}} {\boldsymbol{\Sigma}^0_1}\text{-}\mathsf{BS} * \mathsf{lim}^{[k-1]}\equiv_{\mathrm{W}}{\boldsymbol{\Sigma}^0_k}\text{-}\mathsf{BS}.\end{align*} $$
$$ \begin{align*} \mathsf{LPO} ^{(k)} \le_{\mathrm{W}} \mathsf{LPO} '*\mathsf{lim}^{[k-1]} \le_{\mathrm{W}} {\boldsymbol{\Sigma}^0_1}\text{-}\mathsf{BS} * \mathsf{lim}^{[k-1]}\equiv_{\mathrm{W}}{\boldsymbol{\Sigma}^0_k}\text{-}\mathsf{BS}.\end{align*} $$
Let
![]() $(p_s)_{s\in \mathbb {N}}$
be a sequence in
$(p_s)_{s\in \mathbb {N}}$
be a sequence in
![]() ${\mathbb {N}^{\mathbb {N}}}$
converging to an instance p of
${\mathbb {N}^{\mathbb {N}}}$
converging to an instance p of
![]() $ \mathsf {LPO} $
. For every
$ \mathsf {LPO} $
. For every
![]() $s\in \mathbb {N}$
we define (as we did in the proofs of Theorem 4.18 and Proposition 4.20)
$s\in \mathbb {N}$
we define (as we did in the proofs of Theorem 4.18 and Proposition 4.20)
 $$ \begin{align*} g(s):= \begin{cases} i+1 & \text{if } i\le s \land p_s(i)\neq 0 \land (\forall j<i)(p_s(j)=0),\\ 0 & \text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} g(s):= \begin{cases} i+1 & \text{if } i\le s \land p_s(i)\neq 0 \land (\forall j<i)(p_s(j)=0),\\ 0 & \text{otherwise.} \end{cases} \end{align*} $$
Let us define a quasi-order Q inductively: at stage
![]() $s=0$
we add
$s=0$
we add
![]() $\langle g(0),0 \rangle $
. At stage
$\langle g(0),0 \rangle $
. At stage
![]() $s+1$
we do the following:
$s+1$
we do the following:
-
1. if
 $g(s)=g(s+1)$
we put
$g(s)=g(s+1)$
we put
 $\langle g(s),s+1 \rangle $
immediately below
$\langle g(s),s+1 \rangle $
immediately below
 $\langle g(s),s \rangle $
and
$\langle g(s),s \rangle $
and -
2. if
 $g(s)\neq g(s+1)$
we put
$g(s)\neq g(s+1)$
we put
 $\langle g(s+1),s+1 \rangle $
at the top and we put
$\langle g(s+1),s+1 \rangle $
at the top and we put
 $\langle -1,s+1 \rangle $
at the bottom. Moreover we collapse to a single equivalence class all the elements
$\langle -1,s+1 \rangle $
at the bottom. Moreover we collapse to a single equivalence class all the elements
 $\langle g,t \rangle $
with
$\langle g,t \rangle $
with
 $t\le s$
and
$t\le s$
and
 $g\neq -1$
.
$g\neq -1$
.
This construction produces a quasi-order
![]() $(Q,\preceq _Q)$
which is computable in
$(Q,\preceq _Q)$
which is computable in
![]() $(p_s)_{s\in \mathbb {N}}$
.
$(p_s)_{s\in \mathbb {N}}$
.
Notice that if there is an s s.t. for every
![]() $t\ge s$
,
$t\ge s$
,
![]() $g(t)=g(s)$
(in particular, this is the case if
$g(t)=g(s)$
(in particular, this is the case if
![]() $ \mathsf {LPO} (p)=1$
) then the equivalence classes of
$ \mathsf {LPO} (p)=1$
) then the equivalence classes of
![]() $\preceq _Q$
form a linear order of type
$\preceq _Q$
form a linear order of type
![]() $n+\omega ^*$
and every
$n+\omega ^*$
and every
![]() $\preceq _Q$
-bad sequence is a descending sequence of the form
$\preceq _Q$
-bad sequence is a descending sequence of the form
![]() $(\langle g(s),s_n \rangle )_{n\in \mathbb {N}}$
for some strictly increasing sequence
$(\langle g(s),s_n \rangle )_{n\in \mathbb {N}}$
for some strictly increasing sequence
![]() $(s_n)_{n\in \mathbb {N}}$
. On the other hand, if the sequence
$(s_n)_{n\in \mathbb {N}}$
. On the other hand, if the sequence
![]() $(g(s))_{s\in \mathbb {N}}$
does not stabilize then the equivalence classes of
$(g(s))_{s\in \mathbb {N}}$
does not stabilize then the equivalence classes of
![]() $\preceq _Q$
are linearly ordered as
$\preceq _Q$
are linearly ordered as
![]() $\omega ^*,$
where all the elements
$\omega ^*,$
where all the elements
![]() $\langle g,s \rangle $
with
$\langle g,s \rangle $
with
![]() $g\neq -1$
are equivalent and lie in the top equivalence class. This shows that the construction produces a non-well quasi-order.
$g\neq -1$
are equivalent and lie in the top equivalence class. This shows that the construction produces a non-well quasi-order.
For every
![]() $\preceq _Q$
-bad sequence
$\preceq _Q$
-bad sequence
![]() $(\langle g_n,s_n \rangle )_{n\in \mathbb {N}}$
produced by
$(\langle g_n,s_n \rangle )_{n\in \mathbb {N}}$
produced by
 ${\boldsymbol {\Sigma }^0_1}\text {-}\mathsf {BS}(Q)$
, we compute the solution for
${\boldsymbol {\Sigma }^0_1}\text {-}\mathsf {BS}(Q)$
, we compute the solution for
![]() $ \mathsf {LPO} '((p_s)_{s\in \mathbb {N}})= \mathsf {LPO} (p)$
by returning
$ \mathsf {LPO} '((p_s)_{s\in \mathbb {N}})= \mathsf {LPO} (p)$
by returning
![]() $0$
if
$0$
if
![]() $g_1 \le 0$
and
$g_1 \le 0$
and
![]() $1$
otherwise. We consider two cases. If the sequence
$1$
otherwise. We consider two cases. If the sequence
![]() $(g(s))_{s\in \mathbb {N}}$
stabilizes, then the sequence
$(g(s))_{s\in \mathbb {N}}$
stabilizes, then the sequence
![]() $(g_n)_{n\in \mathbb {N}}$
is constant. Furthermore, its value is
$(g_n)_{n\in \mathbb {N}}$
is constant. Furthermore, its value is
![]() $0$
if
$0$
if
![]() $ \mathsf {LPO} (p)=0$
, otherwise its value is positive. On the other hand, if the sequence
$ \mathsf {LPO} (p)=0$
, otherwise its value is positive. On the other hand, if the sequence
![]() $(g(s))_{s\in \mathbb {N}}$
does not stabilize, then
$(g(s))_{s\in \mathbb {N}}$
does not stabilize, then
![]() $ \mathsf {LPO} (p) = 0$
. Furthermore, for every
$ \mathsf {LPO} (p) = 0$
. Furthermore, for every
![]() $n>0$
, we have
$n>0$
, we have
![]() $g_n=-1 \leq 0$
. (The first element
$g_n=-1 \leq 0$
. (The first element
![]() $\langle g_0,s_0 \rangle $
may lie in the top equivalence class, in which case
$\langle g_0,s_0 \rangle $
may lie in the top equivalence class, in which case
![]() $g_0$
may be positive. Hence we check
$g_0$
may be positive. Hence we check
![]() $g_1$
instead of
$g_1$
instead of
![]() $g_0$
).⊣
$g_0$
).⊣
5.2.
 $\Gamma $
$\Gamma $
 $^1_1$
-
$^1_1$
-
 $\mathsf {DS}$
and
$\mathsf {DS}$
and
 $\Gamma $
$\Gamma $
 $^1_1$
-
$^1_1$
-
 $\mathsf {BS}$
$\mathsf {BS}$
We now turn our attention to the analytic classes. Notice first of all that being a descending sequence through a
![]() $\boldsymbol {\Sigma }^1_1$
linear order is a
$\boldsymbol {\Sigma }^1_1$
linear order is a
![]() $\boldsymbol {\Sigma }^1_1$
-property, hence
$\boldsymbol {\Sigma }^1_1$
-property, hence
 ${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS} \le _{\mathrm {W}}{\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}\equiv _{\mathrm {W}} \mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
. We will show that
${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS} \le _{\mathrm {W}}{\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}\equiv _{\mathrm {W}} \mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
. We will show that
 ${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS}$
is the strongest
${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS}$
is the strongest
![]() $\mathsf {DS}$
-principle that is still reducible to
$\mathsf {DS}$
-principle that is still reducible to
![]() $\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
(Theorem 5.25).
$\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
(Theorem 5.25).
Proposition 5.15.
 ${\boldsymbol {\Delta }^1_1}\text {-}\mathsf {DS}\equiv _{\mathrm {W}} \mathsf {DS} * \mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
and
${\boldsymbol {\Delta }^1_1}\text {-}\mathsf {DS}\equiv _{\mathrm {W}} \mathsf {DS} * \mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
and
 ${\boldsymbol {\Delta }^1_1}\text {-}\mathsf {BS}\equiv _{\mathrm {W}} \mathsf {BS} * \mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
.
${\boldsymbol {\Delta }^1_1}\text {-}\mathsf {BS}\equiv _{\mathrm {W}} \mathsf {BS} * \mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
.
Proof We will only prove the first statement. The proof of the second statement is similar.
To prove the left-to-right reduction, given a
![]() $\boldsymbol {\Delta }^1_1$
name for L we use
$\boldsymbol {\Delta }^1_1$
name for L we use
 ${\boldsymbol {\Delta }^1_1}\text {-}\mathsf {CA}$
(which is known to be equivalent to
${\boldsymbol {\Delta }^1_1}\text {-}\mathsf {CA}$
(which is known to be equivalent to
![]() $\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
, see [Reference Kihara, Marcone and Pauly26, Theorem 3.11]) to compute a
$\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
, see [Reference Kihara, Marcone and Pauly26, Theorem 3.11]) to compute a
![]() $\boldsymbol {\Delta }^0_1$
name for L. We can then apply
$\boldsymbol {\Delta }^0_1$
name for L. We can then apply
![]() $\mathsf {DS}$
to find a descending sequence through L.
$\mathsf {DS}$
to find a descending sequence through L.
To prove the converse reduction, using the cylindrical decomposition we can write
for some computable function
![]() $\Phi _e$
. In particular, given
$\Phi _e$
. In particular, given
![]() $T\subset {\mathbb {N}^{<\mathbb {N}}}$
with a unique path x,
$T\subset {\mathbb {N}^{<\mathbb {N}}}$
with a unique path x,
![]() $\Phi _e(x)$
is the characteristic function of a linear order L. Notice that x is
$\Phi _e(x)$
is the characteristic function of a linear order L. Notice that x is
 $\Delta ^{1,T}_1$
-computable. Indeed,
$\Delta ^{1,T}_1$
-computable. Indeed,
 $$ \begin{align*} x(n)=k & \iff (\exists \sigma \in T)(\sigma\in \mathrm{Ext} \land \sigma(n)=k) \\ & \iff (\forall \tau \in T)(\tau\in \mathrm{Ext} \rightarrow \tau(n)=k), \end{align*} $$
$$ \begin{align*} x(n)=k & \iff (\exists \sigma \in T)(\sigma\in \mathrm{Ext} \land \sigma(n)=k) \\ & \iff (\forall \tau \in T)(\tau\in \mathrm{Ext} \rightarrow \tau(n)=k), \end{align*} $$
where
![]() $\mathrm {Ext}$
is the set of finite strings that extend to a path through T (
$\mathrm {Ext}$
is the set of finite strings that extend to a path through T (
![]() $\sigma \in \mathrm {Ext}$
is a
$\sigma \in \mathrm {Ext}$
is a
 $\Sigma ^{1,T}_1$
property). We can therefore obtain a
$\Sigma ^{1,T}_1$
property). We can therefore obtain a
 $\Delta ^{1,T}_1$
name for L as
$\Delta ^{1,T}_1$
name for L as
and hence we use
 ${\boldsymbol {\Delta }^1_1}\text {-}\mathsf {DS}$
to find a descending sequence through L.⊣
${\boldsymbol {\Delta }^1_1}\text {-}\mathsf {DS}$
to find a descending sequence through L.⊣
In particular, this implies that
![]() $\boldsymbol {\Delta }^1_1$
is the first level at which we can compute
$\boldsymbol {\Delta }^1_1$
is the first level at which we can compute
![]() $\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
. Indeed, for every k, we showed in the proof of Theorem 5.10 that
$\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
. Indeed, for every k, we showed in the proof of Theorem 5.10 that
 $ \mathsf {LPO} ^{(k)}\not \le _{\mathrm {W}}{\boldsymbol {\Delta }^0_k}\text {-}\mathsf {DS}$
, while
$ \mathsf {LPO} ^{(k)}\not \le _{\mathrm {W}}{\boldsymbol {\Delta }^0_k}\text {-}\mathsf {DS}$
, while
 $\mathsf {lim}^{[k]}\le _{\mathrm {W}} \mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
(see [Reference Brattka and Gherardi5, Section 6]).
$\mathsf {lim}^{[k]}\le _{\mathrm {W}} \mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
(see [Reference Brattka and Gherardi5, Section 6]).
By adapting the proof of Corollary 5.4, we can relativize Proposition 4.5 and obtain the following:
Corollary 5.16.
 ${\boldsymbol {\Delta }^1_1}\text {-}\mathsf {DS} \equiv _{\mathrm {W}} {\boldsymbol {\Delta }^1_1}\text {-}\mathsf {BS}.$
${\boldsymbol {\Delta }^1_1}\text {-}\mathsf {DS} \equiv _{\mathrm {W}} {\boldsymbol {\Delta }^1_1}\text {-}\mathsf {BS}.$
Similarly, the proofs of Theorem 5.5 and of Proposition 5.8 lead to the following equivalences:
Theorem 5.17.
 $$ \begin{align*} {}^1{{\boldsymbol{\Delta}^1_1}\text{-}\mathsf{DS}} \equiv_{\mathrm{W}} {}^1{({\boldsymbol{\Pi}^1_1}\mathsf{-Bound} \times \mathsf{UC}_{{\mathbb{N}^{\mathbb{N}}}})} \equiv_{\mathrm{W}} \left(\bigsqcup_{s \in \mathbb{N}} {\boldsymbol{\Delta}^1_1}\text{-}\mathsf{C}_{s}\right) * {\boldsymbol{\Pi}^1_1}\mathsf{-Bound}. \end{align*} $$
$$ \begin{align*} {}^1{{\boldsymbol{\Delta}^1_1}\text{-}\mathsf{DS}} \equiv_{\mathrm{W}} {}^1{({\boldsymbol{\Pi}^1_1}\mathsf{-Bound} \times \mathsf{UC}_{{\mathbb{N}^{\mathbb{N}}}})} \equiv_{\mathrm{W}} \left(\bigsqcup_{s \in \mathbb{N}} {\boldsymbol{\Delta}^1_1}\text{-}\mathsf{C}_{s}\right) * {\boldsymbol{\Pi}^1_1}\mathsf{-Bound}. \end{align*} $$
The deterministic part of
 ${\boldsymbol {\Delta }^1_1}\text {-}\mathsf {DS}$
and
${\boldsymbol {\Delta }^1_1}\text {-}\mathsf {DS}$
and
 ${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS}$
can be easily characterized using Proposition 5.15, as the following proposition shows.
${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS}$
can be easily characterized using Proposition 5.15, as the following proposition shows.
Proposition 5.18.
 $\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}\equiv _{\mathrm {W}} \mathrm {Det}_{ }({\boldsymbol {\Delta }^1_1}\text {-}\mathsf {DS})\equiv _{\mathrm {W}}\mathrm {Det}_{ }({\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS}) $
.
$\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}\equiv _{\mathrm {W}} \mathrm {Det}_{ }({\boldsymbol {\Delta }^1_1}\text {-}\mathsf {DS})\equiv _{\mathrm {W}}\mathrm {Det}_{ }({\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS}) $
.
Proof The reductions
 $\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}\le _{\mathrm {W}} \mathrm {Det}_{ }({\boldsymbol {\Delta }^1_1}\text {-}\mathsf {DS})\le _{\mathrm {W}}\mathrm {Det}_{ }({\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS})$
are straightforward from
$\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}\le _{\mathrm {W}} \mathrm {Det}_{ }({\boldsymbol {\Delta }^1_1}\text {-}\mathsf {DS})\le _{\mathrm {W}}\mathrm {Det}_{ }({\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS})$
are straightforward from
 $\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}\le _{\mathrm {W}} {\boldsymbol {\Delta }^1_1}\text {-}\mathsf {DS}$
(Proposition 5.15),
$\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}\le _{\mathrm {W}} {\boldsymbol {\Delta }^1_1}\text {-}\mathsf {DS}$
(Proposition 5.15),
 ${\boldsymbol {\Delta }^1_1}\text {-}\mathsf {DS} \le _{\mathrm {W}}{\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS}$
(trivial) and the fact that
${\boldsymbol {\Delta }^1_1}\text {-}\mathsf {DS} \le _{\mathrm {W}}{\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS}$
(trivial) and the fact that
![]() $\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
is single-valued. To prove that
$\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
is single-valued. To prove that
 $\mathrm {Det}_{ }({\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS})\le _{\mathrm {W}}\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
it is enough to notice that
$\mathrm {Det}_{ }({\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS})\le _{\mathrm {W}}\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
it is enough to notice that
 ${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS} \le _{\mathrm {W}} \mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
, and therefore
${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS} \le _{\mathrm {W}} \mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
, and therefore
 $\mathrm {Det}_{ }({\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS})\le _{\mathrm {W}}\mathrm {Det}_{ }(\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}})\equiv _{\mathrm {W}} \mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
(Theorem 3.14).⊣
$\mathrm {Det}_{ }({\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS})\le _{\mathrm {W}}\mathrm {Det}_{ }(\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}})\equiv _{\mathrm {W}} \mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
(Theorem 3.14).⊣
In particular, the deterministic part does not help us separate
 ${\boldsymbol {\Delta }^1_1}\text {-}\mathsf {DS}$
and
${\boldsymbol {\Delta }^1_1}\text {-}\mathsf {DS}$
and
 ${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS}$
. Instead, we separate them by considering their first-order parts. We characterized
${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS}$
. Instead, we separate them by considering their first-order parts. We characterized
 ${}^1{{\boldsymbol {\Delta }^1_1}}\text {-}\mathsf {DS}$
in Theorem 5.17. Notice that our proof (see the proof of Proposition 5.8) cannot be extended to establish the same result for
${}^1{{\boldsymbol {\Delta }^1_1}}\text {-}\mathsf {DS}$
in Theorem 5.17. Notice that our proof (see the proof of Proposition 5.8) cannot be extended to establish the same result for
 ${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS}$
, because the definition of the corresponding
${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS}$
, because the definition of the corresponding
![]() $(\,F_s)_{s\in \mathbb {N}}$
would not be
$(\,F_s)_{s\in \mathbb {N}}$
would not be
![]() $\boldsymbol {\Sigma }^1_1$
.
$\boldsymbol {\Sigma }^1_1$
.
Proposition 5.19.
 $\widehat {{\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}_{\mathbb {N}}} \le _{\mathrm {W}} {\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS}$
.
$\widehat {{\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}_{\mathbb {N}}} \le _{\mathrm {W}} {\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS}$
.
Proof Let
![]() $(A_i)_{i\in \mathbb {N}}$
be a sequence of non-empty
$(A_i)_{i\in \mathbb {N}}$
be a sequence of non-empty
![]() $\boldsymbol {\Sigma }^1_1$
subsets of
$\boldsymbol {\Sigma }^1_1$
subsets of
![]() $\mathbb {N}$
. We define
$\mathbb {N}$
. We define
 $$ \begin{align*} L&:=\{ (n, \sigma)\in \mathbb{N}\times {\mathbb{N}^{<\mathbb{N}}} : |\sigma|=n \land (\forall i<n)(\sigma(i)\in A_i) \},\\ &\quad (n,\sigma) \le_L (m,\tau) \iff n>m \lor (n=m \land \sigma \le_{lex} \tau). \end{align*} $$
$$ \begin{align*} L&:=\{ (n, \sigma)\in \mathbb{N}\times {\mathbb{N}^{<\mathbb{N}}} : |\sigma|=n \land (\forall i<n)(\sigma(i)\in A_i) \},\\ &\quad (n,\sigma) \le_L (m,\tau) \iff n>m \lor (n=m \land \sigma \le_{lex} \tau). \end{align*} $$
It is easy to see that L is a
![]() $\boldsymbol {\Sigma }^1_1$
linear order (the linearity follows from the linearity of
$\boldsymbol {\Sigma }^1_1$
linear order (the linearity follows from the linearity of
![]() $\le $
and of
$\le $
and of
![]() $\le _{lex}$
).
$\le _{lex}$
).
Let
![]() $((n_i,\sigma _i))_{i\in \mathbb {N}}$
be an
$((n_i,\sigma _i))_{i\in \mathbb {N}}$
be an
![]() $<_L$
-descending sequence. Notice that, since each
$<_L$
-descending sequence. Notice that, since each
![]() $A_i\subset \mathbb {N}$
, for each n the set
$A_i\subset \mathbb {N}$
, for each n the set
![]() $\{ \sigma \in {\mathbb {N}^{<\mathbb {N}}} : (n,\sigma )\in L\}$
is
$\{ \sigma \in {\mathbb {N}^{<\mathbb {N}}} : (n,\sigma )\in L\}$
is
![]() $\le _{lex}$
-well-founded. Therefore there must be a subsequence
$\le _{lex}$
-well-founded. Therefore there must be a subsequence
![]() $((n_{i_k},\sigma _{i_k}))_{k\in \mathbb {N}}$
s.t. the sequence
$((n_{i_k},\sigma _{i_k}))_{k\in \mathbb {N}}$
s.t. the sequence
![]() $(n_{i_k})_{k\in \mathbb {N}}$
is strictly increasing.
$(n_{i_k})_{k\in \mathbb {N}}$
is strictly increasing.
This implies that, for each n, there is some m s.t.
![]() $|\sigma _m|\ge n$
. In particular, by definition of L,
$|\sigma _m|\ge n$
. In particular, by definition of L,
![]() $(\forall i<n )(\sigma _m(i)\in A_i)$
and the claim follows.⊣
$(\forall i<n )(\sigma _m(i)\in A_i)$
and the claim follows.⊣
Proposition 5.19 implies that
 ${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}_{\mathbb {N}}\le _{\mathrm {W}} {}^1{{\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS}}$
. This, together with
${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}_{\mathbb {N}}\le _{\mathrm {W}} {}^1{{\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS}}$
. This, together with
 ${}^1{\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}}\equiv _{\mathrm {W}} {\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}_{\mathbb {N}}$
(Proposition 2.4) and the observation that
${}^1{\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}}\equiv _{\mathrm {W}} {\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}_{\mathbb {N}}$
(Proposition 2.4) and the observation that
 ${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS} \le _{\mathrm {W}} \mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
, immediately yields the following:
${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS} \le _{\mathrm {W}} \mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
, immediately yields the following:
Corollary 5.20.
 ${}^1{\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}}\equiv _{\mathrm {W}}{}^1{{\boldsymbol {\Sigma }^1_1}}\text {-}\mathsf {DS} \equiv _{\mathrm {W}} {\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}_{\mathbb {N}}.$
${}^1{\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}}\equiv _{\mathrm {W}}{}^1{{\boldsymbol {\Sigma }^1_1}}\text {-}\mathsf {DS} \equiv _{\mathrm {W}} {\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}_{\mathbb {N}}.$
As a consequence,
![]() $\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
and
$\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
and
 ${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS}$
cannot be separated by means of their first-order part. But
${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS}$
cannot be separated by means of their first-order part. But
 ${\boldsymbol {\Delta }^1_1}\text {-}\mathsf {DS}$
and
${\boldsymbol {\Delta }^1_1}\text {-}\mathsf {DS}$
and
 ${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS}$
can, albeit somewhat indirectly:
${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS}$
can, albeit somewhat indirectly:
Proposition 5.21.
 ${\boldsymbol {\Delta }^1_1}\text {-}\mathsf {DS} <_{\mathrm {W}} {\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS}$
.
${\boldsymbol {\Delta }^1_1}\text {-}\mathsf {DS} <_{\mathrm {W}} {\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS}$
.
Proof Notice first of all that
 $\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}\le _{\mathrm {W}} \widehat {{\boldsymbol {\Pi }^1_1}\mathsf {-Bound}}$
. Indeed, given a tree
$\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}\le _{\mathrm {W}} \widehat {{\boldsymbol {\Pi }^1_1}\mathsf {-Bound}}$
. Indeed, given a tree
![]() $T\subset {\mathbb {N}^{<\mathbb {N}}}$
with a unique path, we can consider the following sequence of
$T\subset {\mathbb {N}^{<\mathbb {N}}}$
with a unique path, we can consider the following sequence of
 $\Pi ^{1,T}_1$
sets:
$\Pi ^{1,T}_1$
sets:
Clearly each
![]() $A_n$
is bounded by
$A_n$
is bounded by
![]() $x(n)$
, where x is the unique path through T. Given
$x(n)$
, where x is the unique path through T. Given
 $f\in \widehat {{\boldsymbol {\Pi }^1_1}\mathsf {-Bound}}((A_n)_{n\in \mathbb {N}})$
, consider the space
$f\in \widehat {{\boldsymbol {\Pi }^1_1}\mathsf {-Bound}}((A_n)_{n\in \mathbb {N}})$
, consider the space
![]() $X:=\{ \sigma \in {\mathbb {N}^{<\mathbb {N}}} : (\forall i<|\sigma |)(\sigma (i)\le f(i)) \}$
and define
$X:=\{ \sigma \in {\mathbb {N}^{<\mathbb {N}}} : (\forall i<|\sigma |)(\sigma (i)\le f(i)) \}$
and define
![]() $T_f:= T \cap X$
. Notice that
$T_f:= T \cap X$
. Notice that
![]() $[T_f]=[T]$
. In particular, since
$[T_f]=[T]$
. In particular, since
![]() $[X]$
is f-computably compact, we can uniformly (in f) compute the unique path through
$[X]$
is f-computably compact, we can uniformly (in f) compute the unique path through
![]() $[T_f]$
(see [Reference Brattka, Hölzl, Kuyper, Vollmer and Vallée11, Theorem 7.23 and Corollary 7.26]).
$[T_f]$
(see [Reference Brattka, Hölzl, Kuyper, Vollmer and Vallée11, Theorem 7.23 and Corollary 7.26]).
If
 $\widehat {{\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}_{\mathbb {N}}} \le _{\mathrm {W}} {\boldsymbol {\Delta }^1_1}\text {-}\mathsf {DS}$
then, by Theorem 5.17,
$\widehat {{\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}_{\mathbb {N}}} \le _{\mathrm {W}} {\boldsymbol {\Delta }^1_1}\text {-}\mathsf {DS}$
then, by Theorem 5.17,
 ${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}_{\mathbb {N}} \le _{\mathrm {W}}\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}} \times {\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
and therefore
${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}_{\mathbb {N}} \le _{\mathrm {W}}\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}} \times {\boldsymbol {\Pi }^1_1}\mathsf {-Bound}$
and therefore
 $$ \begin{align*} \widehat{{\boldsymbol{\Sigma}^1_1}\text{-}\mathsf{C}_{\mathbb{N}}} \le_{\mathrm{W}}\widehat{(\mathsf{UC}_{{\mathbb{N}^{\mathbb{N}}}} \times {\boldsymbol{\Pi}^1_1}\mathsf{-Bound})} \equiv_{\mathrm{W}} \widehat{{\boldsymbol{\Pi}^1_1}\mathsf{-Bound}}, \end{align*} $$
$$ \begin{align*} \widehat{{\boldsymbol{\Sigma}^1_1}\text{-}\mathsf{C}_{\mathbb{N}}} \le_{\mathrm{W}}\widehat{(\mathsf{UC}_{{\mathbb{N}^{\mathbb{N}}}} \times {\boldsymbol{\Pi}^1_1}\mathsf{-Bound})} \equiv_{\mathrm{W}} \widehat{{\boldsymbol{\Pi}^1_1}\mathsf{-Bound}}, \end{align*} $$
contradicting
 $\widehat {{\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}_{\mathbb {N}}} \not \le _{\mathrm {W}} \widehat {{\boldsymbol {\Pi }^1_1}\mathsf {-Bound}}$
[Reference Astor, Dzhafarov, Solomon and Suggs2, Corollary 3.23].⊣
$\widehat {{\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}_{\mathbb {N}}} \not \le _{\mathrm {W}} \widehat {{\boldsymbol {\Pi }^1_1}\mathsf {-Bound}}$
[Reference Astor, Dzhafarov, Solomon and Suggs2, Corollary 3.23].⊣
To separate
 ${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS}$
from
${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS}$
from
![]() $\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
we generalize a technique based on inseparable
$\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
we generalize a technique based on inseparable
![]() $\Pi ^1_1$
sets, first used in [Reference Astor, Dzhafarov, Solomon and Suggs2] to separate
$\Pi ^1_1$
sets, first used in [Reference Astor, Dzhafarov, Solomon and Suggs2] to separate
 $\widehat {{\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}_{\mathbb {N}}}$
from
$\widehat {{\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {C}_{\mathbb {N}}}$
from
![]() $\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
. Consider the problem
$\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
. Consider the problem
![]() $\mathsf {ATR}_2:\mathrm {LO}\times {2^{\mathbb {N}}} \rightrightarrows \{0,1\}\times {\mathbb {N}^{\mathbb {N}}}$
defined in [Reference Goh21, Definition 8.2]. It can be seen as a two-sided version of
$\mathsf {ATR}_2:\mathrm {LO}\times {2^{\mathbb {N}}} \rightrightarrows \{0,1\}\times {\mathbb {N}^{\mathbb {N}}}$
defined in [Reference Goh21, Definition 8.2]. It can be seen as a two-sided version of
![]() $\mathsf {ATR}$
: it takes in input a pair
$\mathsf {ATR}$
: it takes in input a pair
![]() $(L,A)$
and produces a pair
$(L,A)$
and produces a pair
![]() $(i,Y)$
s.t. either
$(i,Y)$
s.t. either
![]() $i=0$
and Y is a
$i=0$
and Y is a
![]() $<_L$
-infinite descending sequence or
$<_L$
-infinite descending sequence or
![]() $i=1$
and Y is a jump (pseudo)hierarchy starting from A. Jun Le Goh proved that
$i=1$
and Y is a jump (pseudo)hierarchy starting from A. Jun Le Goh proved that
![]() $\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}<_{\mathrm {W}} \mathsf {ATR}_2 <_{\mathrm {W}} \mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
[Reference Goh21, Corollaries 8.5 and 8.7].
$\mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}<_{\mathrm {W}} \mathsf {ATR}_2 <_{\mathrm {W}} \mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
[Reference Goh21, Corollaries 8.5 and 8.7].
Before proving the next theorem, we introduce the following notion of reducibility: for every
![]() $A,B \subset {\mathbb {N}^{\mathbb {N}}}$
, we say that A is Muchnik reducible to B, and write
$A,B \subset {\mathbb {N}^{\mathbb {N}}}$
, we say that A is Muchnik reducible to B, and write
![]() $A\le _w B$
if, for every
$A\le _w B$
if, for every
![]() $b\in B$
there is a Turing functional
$b\in B$
there is a Turing functional
![]() $\Phi _e$
s.t.
$\Phi _e$
s.t.
![]() $\Phi _e(b)\in A$
. Muchnik reducibility is the non-uniform version of Medvedev reducibility. For an extended presentation on these notions of reducibility see e.g., [Reference Simpson40].
$\Phi _e(b)\in A$
. Muchnik reducibility is the non-uniform version of Medvedev reducibility. For an extended presentation on these notions of reducibility see e.g., [Reference Simpson40].
Theorem 5.22.
 $\mathsf {ATR}_2 ~|_{\mathrm {W}~} {\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS}$
, and therefore
$\mathsf {ATR}_2 ~|_{\mathrm {W}~} {\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS}$
, and therefore
 ${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS} <_{\mathrm {W}}\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
.
${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS} <_{\mathrm {W}}\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
.
Proof The fact that
 ${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS} \not \le _{\mathrm {W}} \mathsf {ATR}_2$
follows from the fact that
${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS} \not \le _{\mathrm {W}} \mathsf {ATR}_2$
follows from the fact that
 $\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}} \equiv _{\mathrm {W}} \mathsf {lim} *{\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS}$
while
$\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}} \equiv _{\mathrm {W}} \mathsf {lim} *{\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS}$
while
![]() $\mathsf {lim}*\mathsf {ATR}_2 <_{\mathrm {W}} \mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
[Reference Goh21, Corollary 8.5].
$\mathsf {lim}*\mathsf {ATR}_2 <_{\mathrm {W}} \mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
[Reference Goh21, Corollary 8.5].
Let us now prove that
 $\mathsf {ATR}_2 \not \le _{\mathrm {W}} {\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS}$
. Assume toward a contradiction that there is a reduction witnessed by the maps
$\mathsf {ATR}_2 \not \le _{\mathrm {W}} {\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS}$
. Assume toward a contradiction that there is a reduction witnessed by the maps
![]() $\Phi ,\Psi $
. Let
$\Phi ,\Psi $
. Let
![]() $(L_e)_{e\in \mathbb {N}}$
be an enumeration of the computable linear orders. Define the sets
$(L_e)_{e\in \mathbb {N}}$
be an enumeration of the computable linear orders. Define the sets
 $$ \begin{align*} S_e &:= {\boldsymbol{\Sigma}^1_1}\text{-}\mathsf{DS} (\Phi(L_e)),\\ DS_e &:= \{ (x_n)_{n} \in {\mathbb{N}^{\mathbb{N}}}: (x_n)_{n} \text{ is an }<_{L_e}\text{-descending sequence} \},\\ JH_e &:= \{ (y_n)_{n} \in {\mathbb{N}^{\mathbb{N}}}: (y_n)_{n} \text{ is a jump hierarchy on } L_e \}. \end{align*} $$
$$ \begin{align*} S_e &:= {\boldsymbol{\Sigma}^1_1}\text{-}\mathsf{DS} (\Phi(L_e)),\\ DS_e &:= \{ (x_n)_{n} \in {\mathbb{N}^{\mathbb{N}}}: (x_n)_{n} \text{ is an }<_{L_e}\text{-descending sequence} \},\\ JH_e &:= \{ (y_n)_{n} \in {\mathbb{N}^{\mathbb{N}}}: (y_n)_{n} \text{ is a jump hierarchy on } L_e \}. \end{align*} $$
Notice that, for each e,
![]() $S_e$
is
$S_e$
is
![]() $\Sigma ^1_1$
(being a descending sequence through a
$\Sigma ^1_1$
(being a descending sequence through a
![]() $\Sigma ^1_1$
linear order is a
$\Sigma ^1_1$
linear order is a
![]() $\Sigma ^1_1$
condition) while
$\Sigma ^1_1$
condition) while
![]() $DS_e$
and
$DS_e$
and
![]() $JH_e$
are arithmetic.
$JH_e$
are arithmetic.
Define now the sets
 $$ \begin{align*} B&:=\{ e\in\mathbb{N} : DS_e \not\le_w S_e \},\\ C&:=\{ e\in\mathbb{N} : JH_e \not\le_w S_e \}, \end{align*} $$
$$ \begin{align*} B&:=\{ e\in\mathbb{N} : DS_e \not\le_w S_e \},\\ C&:=\{ e\in\mathbb{N} : JH_e \not\le_w S_e \}, \end{align*} $$
where
![]() $\le _w$
represents Muchnik reducibility. In particular, if X is (hyper)arithmetic and Y is
$\le _w$
represents Muchnik reducibility. In particular, if X is (hyper)arithmetic and Y is
![]() $\Sigma ^1_1$
then
$\Sigma ^1_1$
then
![]() $X\not \le _w Y$
is a
$X\not \le _w Y$
is a
![]() $\Sigma ^1_1$
condition, and therefore
$\Sigma ^1_1$
condition, and therefore
![]() $B,C\in \Sigma ^1_1(\mathbb {N})$
.
$B,C\in \Sigma ^1_1(\mathbb {N})$
.
We now claim that
![]() $B\cap C=\emptyset $
. Indeed, assume by contradiction that this is not the case and let
$B\cap C=\emptyset $
. Indeed, assume by contradiction that this is not the case and let
![]() $e\in B\cap C$
. By definition of B and C this means that there are two descending sequences
$e\in B\cap C$
. By definition of B and C this means that there are two descending sequences
![]() $(q_n)_{n\in \mathbb {N}}$
and
$(q_n)_{n\in \mathbb {N}}$
and
![]() $(p_n)_{n\in \mathbb {N}}$
in
$(p_n)_{n\in \mathbb {N}}$
in
![]() $\Phi (L_e)$
s.t.
$\Phi (L_e)$
s.t.
![]() $(q_n)_{n\in \mathbb {N}}$
does not compute any
$(q_n)_{n\in \mathbb {N}}$
does not compute any
![]() $< _{L_e}$
-descending sequence and
$< _{L_e}$
-descending sequence and
![]() $(p_n)_{n\in \mathbb {N}}$
does not compute any jump hierarchy on
$(p_n)_{n\in \mathbb {N}}$
does not compute any jump hierarchy on
![]() $L_e$
.
$L_e$
.
In particular, if we run the backward functional
![]() $\Psi $
on
$\Psi $
on
![]() $(q_n)_{n\in \mathbb {N}}$
and
$(q_n)_{n\in \mathbb {N}}$
and
![]() $(p_n)_{n\in \mathbb {N}}$
then, by continuity, there is an n s.t.
$(p_n)_{n\in \mathbb {N}}$
then, by continuity, there is an n s.t.
![]() $\Psi ((q_i)_{i<n})$
commits to producing a jump hierarchy on
$\Psi ((q_i)_{i<n})$
commits to producing a jump hierarchy on
![]() $L_e$
and
$L_e$
and
![]() $\Psi ((p_i)_{i<n})$
commits to producing an
$\Psi ((p_i)_{i<n})$
commits to producing an
![]() $<_{L_e}$
-descending sequence. Without loss of generality, assume that
$<_{L_e}$
-descending sequence. Without loss of generality, assume that
![]() $q_n \le _{\Phi (L_e)} p_n$
(in the opposite case we just swap the roles of
$q_n \le _{\Phi (L_e)} p_n$
(in the opposite case we just swap the roles of
![]() $(q_n)_{n\in \mathbb {N}}$
and
$(q_n)_{n\in \mathbb {N}}$
and
![]() $(p_n)_{n\in \mathbb {N}}$
) and consider the sequence
$(p_n)_{n\in \mathbb {N}}$
) and consider the sequence
Notice that
![]() $\Psi (r)$
must produce an
$\Psi (r)$
must produce an
![]() $<_{L_e}$
-descending sequence, contradicting the fact that
$<_{L_e}$
-descending sequence, contradicting the fact that
![]() $(q_n)_{n\in \mathbb {N}}$
does not compute any
$(q_n)_{n\in \mathbb {N}}$
does not compute any
![]() $<_{L_e}$
-descending sequence.
$<_{L_e}$
-descending sequence.
Let
![]() $\mathbf {wf_{LO}}$
be the set of indexes for the computable well-orderings and let
$\mathbf {wf_{LO}}$
be the set of indexes for the computable well-orderings and let
![]() $\mathbf {hds}$
be the set of indexes for computable linear orderings with a hyperarithmetic descending sequence. Notice that
$\mathbf {hds}$
be the set of indexes for computable linear orderings with a hyperarithmetic descending sequence. Notice that
![]() $\mathbf {wf_{LO}}\subset B$
, because for each e in
$\mathbf {wf_{LO}}\subset B$
, because for each e in
![]() $\mathbf {wf_{LO}}$
,
$\mathbf {wf_{LO}}$
,
![]() $DS_e = \emptyset \not \le _w A$
for every non-empty set A. Likewise,
$DS_e = \emptyset \not \le _w A$
for every non-empty set A. Likewise,
![]() $\mathbf {hds}\subset C$
, as any ill-founded linear order which has a hyperarithmetic descending sequence cannot support a jump hierarchy (seeFootnote
2
[Reference Friedman18, Theorem 4]).
$\mathbf {hds}\subset C$
, as any ill-founded linear order which has a hyperarithmetic descending sequence cannot support a jump hierarchy (seeFootnote
2
[Reference Friedman18, Theorem 4]).
Since
![]() $B,C$
are disjoint and
$B,C$
are disjoint and
![]() $\Sigma ^1_1$
, by
$\Sigma ^1_1$
, by
![]() $\Sigma ^1_1$
-separation there must be a
$\Sigma ^1_1$
-separation there must be a
![]() $\Delta ^1_1$
set separating them. Such a set would separate
$\Delta ^1_1$
set separating them. Such a set would separate
![]() $\mathbf {wf_{LO}}$
and
$\mathbf {wf_{LO}}$
and
![]() $\mathbf {hds}$
as well. This contradicts the fact that every
$\mathbf {hds}$
as well. This contradicts the fact that every
![]() $\Sigma ^1_1$
set which separates
$\Sigma ^1_1$
set which separates
![]() $\mathbf {wf_{LO}}$
and
$\mathbf {wf_{LO}}$
and
![]() $\mathbf {hds}$
must be
$\mathbf {hds}$
must be
![]() $\Sigma ^1_1$
-complete [Reference Gregoriades, Kispéter and Pauly22].⊣
$\Sigma ^1_1$
-complete [Reference Gregoriades, Kispéter and Pauly22].⊣
Finally we turn our attention to
 ${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {BS}$
and
${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {BS}$
and
 ${\boldsymbol {\Pi }^1_1}\text {-}\mathsf {DS}$
. We show below that these problems are much stronger in uniform computational strength than the problems considered so far. Indeed all the
${\boldsymbol {\Pi }^1_1}\text {-}\mathsf {DS}$
. We show below that these problems are much stronger in uniform computational strength than the problems considered so far. Indeed all the
![]() ${\boldsymbol {\Gamma }}\text {-}\mathsf {DS}$
problems, where
${\boldsymbol {\Gamma }}\text {-}\mathsf {DS}$
problems, where
 $\boldsymbol {\Gamma } = \boldsymbol {\Sigma }^1_1$
or below, are s.t.
$\boldsymbol {\Gamma } = \boldsymbol {\Sigma }^1_1$
or below, are s.t.
In other words,
![]() ${\boldsymbol {\Gamma }}\text {-}\mathsf {DS}$
is arithmetically Weihrauch equivalent to
${\boldsymbol {\Gamma }}\text {-}\mathsf {DS}$
is arithmetically Weihrauch equivalent to
![]() $\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
, which is prominent among the problems that are considered to be “
$\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
, which is prominent among the problems that are considered to be “
![]() $\mathrm {ATR}_0$
analogues in the Weihrauch lattice” [Reference Kihara, Marcone and Pauly26].
$\mathrm {ATR}_0$
analogues in the Weihrauch lattice” [Reference Kihara, Marcone and Pauly26].
On the other hand, a natural analogue of
 $\boldsymbol {\Pi }^1_1\mathrm {-CA}_0$
in the Weihrauch lattice is
$\boldsymbol {\Pi }^1_1\mathrm {-CA}_0$
in the Weihrauch lattice is
 ${\boldsymbol {\Pi }^1_1}\text {-}\mathsf {CA}$
, which can be phrased as “given a sequence
${\boldsymbol {\Pi }^1_1}\text {-}\mathsf {CA}$
, which can be phrased as “given a sequence
![]() $(T_n)_{n\in \mathbb {N}}$
of trees in
$(T_n)_{n\in \mathbb {N}}$
of trees in
![]() ${\mathbb {N}^{<\mathbb {N}}}$
, produce
${\mathbb {N}^{<\mathbb {N}}}$
, produce
![]() $x\in {2^{\mathbb {N}}}$
s.t., for every n,
$x\in {2^{\mathbb {N}}}$
s.t., for every n,
![]() $x(n)=1$
iff
$x(n)=1$
iff
![]() $[T_n]=\emptyset $
.”
$[T_n]=\emptyset $
.”
We can notice that, using [Reference Marcone, Hodges, Hyland, Steinhorn and Truss30, Theorem 6.5],
 ${\boldsymbol {\Pi }^1_1}\text {-}\mathsf {CA}$
is equivalent to the problem of finding the leftmost path through an ill-founded tree. Using this fact we show that
${\boldsymbol {\Pi }^1_1}\text {-}\mathsf {CA}$
is equivalent to the problem of finding the leftmost path through an ill-founded tree. Using this fact we show that
 ${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {BS}$
and
${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {BS}$
and
 ${\boldsymbol {\Pi }^1_1}\text {-}\mathsf {DS}$
are in the realm of
${\boldsymbol {\Pi }^1_1}\text {-}\mathsf {DS}$
are in the realm of
 $\boldsymbol {\Pi }^1_1\mathrm {-CA}_0$
.
$\boldsymbol {\Pi }^1_1\mathrm {-CA}_0$
.
Theorem 5.23.
 ${\boldsymbol {\Pi }^1_1}\text {-}\mathsf {CA}\le _{\mathrm {W}}{\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {BS}$
.
${\boldsymbol {\Pi }^1_1}\text {-}\mathsf {CA}\le _{\mathrm {W}}{\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {BS}$
.
Proof Let
![]() $T\subset {\mathbb {N}^{<\mathbb {N}}}$
be an ill-founded tree. For each
$T\subset {\mathbb {N}^{<\mathbb {N}}}$
be an ill-founded tree. For each
![]() $\sigma \in T$
, let
$\sigma \in T$
, let
![]() $T_\sigma :=\{\tau \in T : \tau \sqsubseteq \sigma \lor \sigma \sqsubseteq \tau \}$
. We define a quasi-order on the extendible strings in T:
$T_\sigma :=\{\tau \in T : \tau \sqsubseteq \sigma \lor \sigma \sqsubseteq \tau \}$
. We define a quasi-order on the extendible strings in T:
 $$ \begin{align*} Q&:=\{ \sigma \in T: [T_\sigma]\neq \emptyset\},\\ \sigma\preceq_Q \tau &:\hspace{-1mm}\iff (\exists \rho \in Q)(\rho <_{lex} \sigma) \lor \tau \sqsubseteq \sigma. \end{align*} $$
$$ \begin{align*} Q&:=\{ \sigma \in T: [T_\sigma]\neq \emptyset\},\\ \sigma\preceq_Q \tau &:\hspace{-1mm}\iff (\exists \rho \in Q)(\rho <_{lex} \sigma) \lor \tau \sqsubseteq \sigma. \end{align*} $$
It is easy to see that
![]() $(Q,\preceq _Q)$
is
$(Q,\preceq _Q)$
is
 $\Sigma ^{1,T}_1$
. Moreover, all the
$\Sigma ^{1,T}_1$
. Moreover, all the
![]() $\sigma $
which are not prefixes of the leftmost path collapse in a bottom equivalence class. This shows that the equivalence classes of Q are linearly ordered as
$\sigma $
which are not prefixes of the leftmost path collapse in a bottom equivalence class. This shows that the equivalence classes of Q are linearly ordered as
![]() $1+\omega ^*$
. To conclude the proof it is enough to notice that any
$1+\omega ^*$
. To conclude the proof it is enough to notice that any
![]() $<_Q$
-descending sequence gives longer and longer prefixes of the leftmost path, hence it computes
$<_Q$
-descending sequence gives longer and longer prefixes of the leftmost path, hence it computes
 ${\boldsymbol {\Pi }^1_1}\text {-}\mathsf {CA}$
. ⊣
${\boldsymbol {\Pi }^1_1}\text {-}\mathsf {CA}$
. ⊣
Corollary 5.24.
 ${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS} <_{\mathrm {W}} {\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {BS}$
.
${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS} <_{\mathrm {W}} {\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {BS}$
.
Proof We have
 ${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS} \le _{\mathrm {W}} \mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}} <_{\mathrm {W}} {\boldsymbol {\Pi }^1_1}\text {-}\mathsf {CA} \le _{\mathrm {W}} {\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {BS}$
.⊣
${\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {DS} \le _{\mathrm {W}} \mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}} <_{\mathrm {W}} {\boldsymbol {\Pi }^1_1}\text {-}\mathsf {CA} \le _{\mathrm {W}} {\boldsymbol {\Sigma }^1_1}\text {-}\mathsf {BS}$
.⊣
Theorem 5.25.
 ${\boldsymbol {\Pi }^1_1}\text {-}\mathsf {CA}\le _{\mathrm {W}} {\boldsymbol {\Pi }^1_1}\text {-}\mathsf {DS}$
.
${\boldsymbol {\Pi }^1_1}\text {-}\mathsf {CA}\le _{\mathrm {W}} {\boldsymbol {\Pi }^1_1}\text {-}\mathsf {DS}$
.
Proof Let
![]() $T\subset {\mathbb {N}^{<\mathbb {N}}}$
be an ill-founded tree. For each
$T\subset {\mathbb {N}^{<\mathbb {N}}}$
be an ill-founded tree. For each
![]() $\sigma \in T$
, let
$\sigma \in T$
, let
![]() $T_\sigma :=\{\tau \in T : \tau \sqsubseteq \sigma \lor \sigma \sqsubseteq \tau \}$
. We define a linear order
$T_\sigma :=\{\tau \in T : \tau \sqsubseteq \sigma \lor \sigma \sqsubseteq \tau \}$
. We define a linear order
 $$ \begin{align*} L&:= \{ \sigma\in T : (\forall \tau \le_{lex} \sigma)([T_{\tau}]=\emptyset \lor \tau \sqsubseteq \sigma) \},\\ \le_L &:= \le_{\mathrm{KB}(T)}. \end{align*} $$
$$ \begin{align*} L&:= \{ \sigma\in T : (\forall \tau \le_{lex} \sigma)([T_{\tau}]=\emptyset \lor \tau \sqsubseteq \sigma) \},\\ \le_L &:= \le_{\mathrm{KB}(T)}. \end{align*} $$
Clearly
![]() $(L,\le _L)$
is a
$(L,\le _L)$
is a
 $\Pi ^{1,T}_1$
linear order. Notice that if
$\Pi ^{1,T}_1$
linear order. Notice that if
![]() $\sigma \in L$
and
$\sigma \in L$
and
![]() $[T_\sigma ]\neq \emptyset $
then
$[T_\sigma ]\neq \emptyset $
then
![]() $\sigma $
must be a prefix of the leftmost path. Moreover if
$\sigma $
must be a prefix of the leftmost path. Moreover if
![]() $\rho $
is strictly lexicographically above the leftmost path then
$\rho $
is strictly lexicographically above the leftmost path then
![]() $\rho \notin L$
. In other words, L is the subset of T that is lexicographically below the leftmost path.
$\rho \notin L$
. In other words, L is the subset of T that is lexicographically below the leftmost path.
Moreover, every string that is not a prefix of the leftmost path lies in the well-founded part of L (by definition of
![]() $\mathrm {KB}$
). In particular every
$\mathrm {KB}$
). In particular every
![]() $<_L$
-descending sequence computes arbitrarily long prefixes of the leftmost path.⊣
$<_L$
-descending sequence computes arbitrarily long prefixes of the leftmost path.⊣
6. Conclusions
In this paper we explored the uniform computational content of the problem
![]() $\mathsf {DS}$
, and showed how it lies “on the side” w.r.t. the part of the Weihrauch lattice explored so far. We now draw the attention to some of the questions that did not receive an answer.
$\mathsf {DS}$
, and showed how it lies “on the side” w.r.t. the part of the Weihrauch lattice explored so far. We now draw the attention to some of the questions that did not receive an answer.
The problem
![]() $ \mathsf {KL} $
is the multi-valued function corresponding to König’s lemma, and it can be phrased as “find a path through an infinite finitely-branching tree.” It is known that
$ \mathsf {KL} $
is the multi-valued function corresponding to König’s lemma, and it can be phrased as “find a path through an infinite finitely-branching tree.” It is known that
 $ \mathsf {KL} \equiv _{\mathrm {W}} \mathsf {C}_{{2^{\mathbb {N}}}}' \equiv _{\mathrm {W}} \widehat {\mathsf {RT}^{{1}}_{{2}} }$
.
$ \mathsf {KL} \equiv _{\mathrm {W}} \mathsf {C}_{{2^{\mathbb {N}}}}' \equiv _{\mathrm {W}} \widehat {\mathsf {RT}^{{1}}_{{2}} }$
.
Open Question 6.1.
![]() $ \mathsf {KL} \le _{\mathrm {W}} \mathsf {DS}$
?
$ \mathsf {KL} \le _{\mathrm {W}} \mathsf {DS}$
?
We know that, if such a reduction exists, it must be strict (as
![]() $ \mathsf {KL} $
is an arithmetic problem). On the other hand, none of the characterizations we used in §4 to describe the lower cone of
$ \mathsf {KL} $
is an arithmetic problem). On the other hand, none of the characterizations we used in §4 to describe the lower cone of
![]() $\mathsf {DS}$
can be used to prove a separation.
$\mathsf {DS}$
can be used to prove a separation.
In §3.4 we introduced the problem
![]() ${\mathsf {wList}}_{{2^{\mathbb {N}}},\leq \omega }$
. Similarly to
${\mathsf {wList}}_{{2^{\mathbb {N}}},\leq \omega }$
. Similarly to
![]() $\mathsf {DS}$
, this problem does not fit well within the effective Baire hierarchy:
$\mathsf {DS}$
, this problem does not fit well within the effective Baire hierarchy:
 $\mathrm {Det}_{ }({\mathsf {wList}}_{{2^{\mathbb {N}}},\leq \omega })\equiv _{\mathrm {W}} \mathsf {lim}$
, but
$\mathrm {Det}_{ }({\mathsf {wList}}_{{2^{\mathbb {N}}},\leq \omega })\equiv _{\mathrm {W}} \mathsf {lim}$
, but
 ${\mathsf {wList}}_{{2^{\mathbb {N}}},\leq \omega }^{[3]} \equiv _{\mathrm {W}} \mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
[Reference Kihara, Marcone and Pauly26, Proposition 6.14 and Corollary 6.16], hence in particular
${\mathsf {wList}}_{{2^{\mathbb {N}}},\leq \omega }^{[3]} \equiv _{\mathrm {W}} \mathsf {UC}_{{\mathbb {N}^{\mathbb {N}}}}$
[Reference Kihara, Marcone and Pauly26, Proposition 6.14 and Corollary 6.16], hence in particular
![]() ${\mathsf {wList}}_{{2^{\mathbb {N}}},\leq \omega }$
is not arithmetic.
${\mathsf {wList}}_{{2^{\mathbb {N}}},\leq \omega }$
is not arithmetic.
Open Question 6.2.
![]() ${\mathsf {wList}}_{{2^{\mathbb {N}}},\leq \omega } \le _{\mathrm {W}} \mathsf {DS}$
?
${\mathsf {wList}}_{{2^{\mathbb {N}}},\leq \omega } \le _{\mathrm {W}} \mathsf {DS}$
?
Our results imply that
![]() $\mathsf {DS} \not \le _{\mathrm {W}} {\mathsf {wList}}_{{2^{\mathbb {N}}},\leq \omega }$
(as
$\mathsf {DS} \not \le _{\mathrm {W}} {\mathsf {wList}}_{{2^{\mathbb {N}}},\leq \omega }$
(as
![]() $\mathsf {DS}*\mathsf {DS} \equiv _{\mathrm {W}} \mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
), and hence a reduction would be strict.
$\mathsf {DS}*\mathsf {DS} \equiv _{\mathrm {W}} \mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
), and hence a reduction would be strict.
In the context of
![]() ${\boldsymbol {\Gamma }}\text {-}\mathsf {DS}$
, there are a few problems that resisted full characterization. In particular:
${\boldsymbol {\Gamma }}\text {-}\mathsf {DS}$
, there are a few problems that resisted full characterization. In particular:
Open Question 6.3.
 ${\boldsymbol {\Delta }^0_2}\text {-}\mathsf {DS} \le _{\mathrm {W}} {\boldsymbol {\Sigma }^0_1}\text {-}\mathsf {BS}$
?
${\boldsymbol {\Delta }^0_2}\text {-}\mathsf {DS} \le _{\mathrm {W}} {\boldsymbol {\Sigma }^0_1}\text {-}\mathsf {BS}$
?
We expect that an answer to this question will yield a solution for every k (by relativization).
We notice that, in the statements involving
![]() ${\boldsymbol {\Gamma }}\text {-}\mathsf {BS}$
we proved slightly more than what claimed: indeed, in all the reductions, the quasi-order built is a linear quasi-order, i.e., a quasi-order whose equivalence classes are linearly ordered. Notice that every bad sequence through a non-well linear quasi-order is actually a descending sequence. If we introduce the problem
${\boldsymbol {\Gamma }}\text {-}\mathsf {BS}$
we proved slightly more than what claimed: indeed, in all the reductions, the quasi-order built is a linear quasi-order, i.e., a quasi-order whose equivalence classes are linearly ordered. Notice that every bad sequence through a non-well linear quasi-order is actually a descending sequence. If we introduce the problem
![]() ${\boldsymbol {\Gamma }}\text {-}\mathsf {DS}_{LQO}$
by restricting
${\boldsymbol {\Gamma }}\text {-}\mathsf {DS}_{LQO}$
by restricting
![]() ${\boldsymbol {\Gamma }}\text {-}\mathsf {BS}$
to linear quasi-orders, our results imply that
${\boldsymbol {\Gamma }}\text {-}\mathsf {BS}$
to linear quasi-orders, our results imply that
 $$ \begin{align*} {\boldsymbol{\Delta}^0_k}\text{-}\mathsf{DS} <_{\mathrm{W}} {\boldsymbol{\Sigma}^0_{k+1}}\text{-}\mathsf{DS}_{LQO} \le_{\mathrm{W}} {\boldsymbol{\Sigma}^0_{k+1}}\text{-}\mathsf{BS}. \end{align*} $$
$$ \begin{align*} {\boldsymbol{\Delta}^0_k}\text{-}\mathsf{DS} <_{\mathrm{W}} {\boldsymbol{\Sigma}^0_{k+1}}\text{-}\mathsf{DS}_{LQO} \le_{\mathrm{W}} {\boldsymbol{\Sigma}^0_{k+1}}\text{-}\mathsf{BS}. \end{align*} $$
A natural question is therefore
Open Question 6.4.
 ${\boldsymbol {\Sigma }^0_{k+1}}\text {-}\mathsf {BS} \le _{\mathrm {W}} {\boldsymbol {\Sigma }^0_{k+1}}\text {-}\mathsf {DS}_{LQO}$
?
${\boldsymbol {\Sigma }^0_{k+1}}\text {-}\mathsf {BS} \le _{\mathrm {W}} {\boldsymbol {\Sigma }^0_{k+1}}\text {-}\mathsf {DS}_{LQO}$
?
A negative answer would imply that the possibility of having infinite antichains provides extra uniform strength.
A very important structure that is left out of the picture is the one of partial orders. In the same spirit of the paper we can consider the problems
![]() ${\boldsymbol {\Gamma }}\text {-}\mathsf {DS}_{PO}$
and
${\boldsymbol {\Gamma }}\text {-}\mathsf {DS}_{PO}$
and
![]() ${\boldsymbol {\Gamma }}\text {-}\mathsf {BS}_{PO}$
. The former is readily seen to be equivalent to
${\boldsymbol {\Gamma }}\text {-}\mathsf {BS}_{PO}$
. The former is readily seen to be equivalent to
![]() $\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
(see also the comment before Definition 4.4). Our results implicitly characterize
$\mathsf {C}_{{\mathbb {N}^{\mathbb {N}}}}$
(see also the comment before Definition 4.4). Our results implicitly characterize
![]() ${\boldsymbol {\Gamma }}\text {-}\mathsf {BS}_{PO}$
for
${\boldsymbol {\Gamma }}\text {-}\mathsf {BS}_{PO}$
for
 $\boldsymbol {\Gamma }\in \{ \boldsymbol {\Delta }^0_k, \boldsymbol {\Pi }^0_k \}$
(by transitivity, as
$\boldsymbol {\Gamma }\in \{ \boldsymbol {\Delta }^0_k, \boldsymbol {\Pi }^0_k \}$
(by transitivity, as
![]() ${\boldsymbol {\Gamma }}\text {-}\mathsf {DS} \le _{\mathrm {W}} {\boldsymbol {\Gamma }}\text {-}\mathsf {BS}_{PO}\le _{\mathrm {W}} {\boldsymbol {\Gamma }}\text {-}\mathsf {BS}$
).
${\boldsymbol {\Gamma }}\text {-}\mathsf {DS} \le _{\mathrm {W}} {\boldsymbol {\Gamma }}\text {-}\mathsf {BS}_{PO}\le _{\mathrm {W}} {\boldsymbol {\Gamma }}\text {-}\mathsf {BS}$
).
Open Question 6.5. What is the relation between
 ${\boldsymbol {\Sigma }^0_1}\text {-}\mathsf {BS}_{PO}$
and the problems
${\boldsymbol {\Sigma }^0_1}\text {-}\mathsf {BS}_{PO}$
and the problems
 $\mathsf {DS}\equiv _{\mathrm {W}} {\boldsymbol {\Sigma }^0_1}\text {-}\mathsf {DS}$
,
$\mathsf {DS}\equiv _{\mathrm {W}} {\boldsymbol {\Sigma }^0_1}\text {-}\mathsf {DS}$
,
 ${\boldsymbol {\Sigma }^0_1}\text {-}\mathsf {DS}_{LQO}$
and
${\boldsymbol {\Sigma }^0_1}\text {-}\mathsf {DS}_{LQO}$
and
 ${\boldsymbol {\Sigma }^0_1}\text {-}\mathsf {BS}$
?
${\boldsymbol {\Sigma }^0_1}\text {-}\mathsf {BS}$
?
Answering these questions would yield very interesting insights on how the possibility of equivalent non-equal elements can enhance the uniform computational strength.
Acknowledgments
The second author is grateful to Mathieu Hoyrup for answering a question on the impact of the codomain on the deterministic part, and to Linda Westrick for several helpful discussions. The third author thanks Alberto Marcone for many valuable suggestions during the preparation of the draft. He also thanks Damir Dzhafarov, Giovanni Soldà and Vittorio Cipriani for useful discussions on the topics of the paper. His research was partially supported by the Italian PRIN 2017 Grant “Mathematical Logic: models, sets, computability.” The authors made significant progress while all attending the BIRS-CMO workshop “Reverse Mathematics of Combinatorial Principles (19w5111).”