Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-02-11T09:43:37.507Z Has data issue: false hasContentIssue false
  • English
  • Français

THE FIELD OF p-ADIC NUMBERS WITH A PREDICATE FOR THE POWERS OF AN INTEGER

Published online by Cambridge University Press:  21 March 2017

NATHANAËL MARIAULE
NATHANAËL MARIAULE*
Affiliation:
INSTITUT DE MATHÉMATIQUES DE JUSSIEU - PARIS RIVE GAUCHE UNIVERSITÉ PARIS DIDEROT 75205 PARIS CEDEX 13, FRANCEE-mail: nathanael.mariaule@imj-prg.fr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we prove the decidability of the theory of ℚp in the language (+, −,⋅, 0, 1, Pn(n ∈ ℕ)) expanded by a predicate for the multiplicative subgroup nℤ (where n is a fixed integer). There are two cases: if 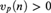$v_p \left( n \right) > 0$ then the group determines a cross-section and we get an axiomatization of the theory and a result of quantifier elimination. If 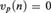$v_p \left( n \right) = 0$, then we use the Mann property of the group to get an axiomatization of the theory.

Keywords

p-adically closed fieldsexpansion of valued fields
Type
Articles
Information
The Journal of Symbolic Logic , Volume 82 , Issue 1 , March 2017 , pp. 166 - 182
Copyright
Copyright © The Association for Symbolic Logic 2017 

References

REFERENCES

Belegradek, O. and Zilber, B., The model theory of the field of reals with a subgroup of the unit circle . Journal of the London Mathematical Society, vol. 78 (2008), no. 3, pp. 563–579.Google Scholar
Evertse, J. H., On sums of S-units and linear recurrences . Composition Mathematica, vol. 53 (1984), no. 2, pp. 225–244.Google Scholar
Guignot, F., Théorie des modèles du groupe valué (ℤ, +, vp ), Séminaires de structures algébriques ordonnées, no. 89 (2014), preprint.Google Scholar
Günaydin, A. and van den Dries, L., The fields of real and complex numbers with a small multiplicative group . Proceedings of the London Mathematical Society, vol. 93 (2006), no. 1, pp. 43–81.Google Scholar
Lang, S., Algebra, third ed., Springer, Berlin, 2002.CrossRefGoogle Scholar
Laurent, M., Équations diophantiennes exponentielles . Inventiones Mathematicae, vol. 78 (1984), pp. 299–327.Google Scholar
Mann, H., On linear relations between roots of unity . Mathematika, vol. 12 (1965), pp. 101–117.Google Scholar
Prestel, A. and Roquette, P., Formally P-adic fields, Springer, Berlin, 1984.CrossRefGoogle Scholar
Robinson, A. and Zakon, E., Elementary properties of ordered abelian groups . Transactions of the American Mathematical Society, vol. 96 (1960), pp. 222–236.Google Scholar
van den Dries, L., The field of reals with a predicate for the powers of two . Manuscripta mathematica, vol. 54 (1985), pp. 187–195.Google Scholar
van der Poorten, A. J. and Schlickewei, H.P., Additive relations in fields . Journal of the Australian Mathematical Society, vol. 51 (1991), pp. 154–170.Google Scholar
Zakon, E., Generalized archimedean groups . Transactions of the American Mathematical Society, vol. 99 (1961), pp. 21–40.CrossRefGoogle Scholar
Zilber, B., A note on the model theory of the complex field with roots of unity, available at www.maths.ox.ac.uk/∼zilber, 1990.Google Scholar
Zilber, B., Complex roots of unity on the real plane, available at www.maths.ox.ac.uk/∼zilber, 2003.Google Scholar