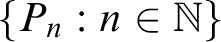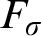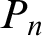1 Introduction
Let us recall that a subset A of a perfect Polish space X is universally meager (
$A\in \mathbf {UM}$
; see [Reference Bartoszyński1, Reference Bartoszyński2, Reference Zakrzewski24, Reference Zakrzewski25]), if for every Borel isomorphism f between X and any perfect Polish space Y the image of A under f is meager in Y (this class of sets was earlier introduced and studied by Grzegorek [Reference Grzegorek8–Reference Grzegorek10] under the name of absolutely of the first category sets).
Let us also recall that A is perfectly meager (
$A\in \mathbf {PM}$
), if for all perfect subsets P of X, the set
$A\cap P$
is meager in P. Clearly,
$A\in \mathbf {PM}$
if and only if for every perfect subset P of X, there exists an
$F_\sigma $
-set F in X such that
$A \subseteq F$
and
$F\cap P$
is meager in P (cf. [Reference Bartoszyński2, Theorem 6]).
We shall say that A is countably perfectly meager (
$A\in \mathbf {PM}_\sigma $
), if for every sequence of perfect subsets
$\{P_n: n \in \mathbb N\}$
of X, there exists an
$F_\sigma $
-set F in X such that
$A \subseteq F$
and
$F\cap P_n$
is meager in
$P_n$
for each n.
It follows directly from the definition that the class
$\mathbf {PM}_\sigma $
is, exactly as the other two classes, a
$\sigma $
-ideal of subsets of the underlying space X (shortly: a
$\sigma $
-ideal on X), i.e., it is hereditary, closed under taking countable unions and contains all singletons.
One readily checks that
$\mathbf {UM}\subseteq \mathbf {PM}$
and it is consistent that
$\mathbf {UM}\subsetneq \mathbf {PM}$
but also that
$\mathbf {UM}= \mathbf {PM}$
(see [Reference Bartoszyński1]).
Bartoszyński [Reference Bartoszyński2, Theorem 7,
$(3)\Rightarrow (2)\Rightarrow (1)$
] proved that
$\mathbf {PM}_\sigma \subseteq \mathbf {UM}$
. Actually, it is in that paper where the property used by us to define the class
$\mathbf {PM}_\sigma $
first appeared (without any specific name) and where it was claimed that this property characterizes universally meager sets in the Cantor space
$2^{\mathbb N}$
. Unfortunately, there is a flaw in the part of the argument showing the inclusion
$\mathbf {UM}\subseteq \mathbf {PM}_\sigma $
(cf. [Reference Bartoszyński2, Theorem 7,
$(1)\Rightarrow (3)$
]).
In fact, the following theorem immediately implies that it is consistent (in particular, true under CH) that there exists a universally meager subset of
$2^{\mathbb N}$
which is not countably perfectly meager in
$2^{\mathbb N}$
.
Theorem 1.1. Let T be a subset of
$2^{\mathbb N}$
of cardinality
$2^{\aleph _0}$
. There exist a set
$H\subseteq T\times 2^{\mathbb N}$
intersecting each vertical section
$\{t\}\times 2^{\mathbb N}$
,
$t\in T$
, in a singleton and a homeomorphic copy E of H in
$2^{\mathbb N}$
which is not a
$\mathbf {PM}_\sigma $
-set in
$2^{\mathbb N}$
. In particular, T is a continuous injective image of E.
Under the notation from Theorem 1.1 it follows that if T is universally meager then H is universally meager as well (
$\mathbf {UM}$
being closed with respect to preimages under continuous injections, see [Reference Zakrzewski24]) and so is its homeomorphic copy E. A refinement of this argument also shows that, at least consistently, in contrast to both
$\mathbf {PM}$
and
$\mathbf {UM}$
the class
$\mathbf {PM}_\sigma $
is not closed with respect to homeomorphic images (see Theorem 3.1(3)). Consequently, unlike in the case of
$\mathbf {PM}$
and
$\mathbf {UM}$
, the statement that a subspace A of a Polish space is countably perfectly meager makes sense only if we specify a Polish space X in which it is embedded. We shall therefore speak of countably perfectly meager sets in X unless X is clear from the context.
In Section 2 we present various characterizations and some examples of countably perfectly meager sets in
$2^{\mathbb N}$
. These include (for the definitions see Section 2.2):
-
• sets perfectly meager in the transitive sense, in particular:
-
–
$\gamma $
-sets, -
– strongly meager sets.
-
-
• sets with the Hurewicz property and no perfect subsets,
-
•
$\lambda '$
-sets.
Section 3 is largely devoted to a proof of Theorem 1.1. We derive from it various examples of subsets of
$2^{\mathbb N}$
which are universally meager but not countably perfectly meager in
$2^{\mathbb N}$
.
In particular, if there is a
$\lambda $
-set in
$2^{\mathbb N}$
of cardinality of the continuum, then there is also one which is not countably perfectly meager in
$2^{\mathbb N}$
(see Theorem 3.1(2)).
Moreover, if there exists a
$\lambda '$
-set in
$2^{\mathbb N}$
of cardinality of the continuum, then there is also one whose homeomorphic copy is not countably perfectly meager in
$2^{\mathbb N}$
(see Theorem 3.1(3)). This strengthens the result of Sierpiński [Reference Sierpiński21] that
$\lambda '$
-property is not invariant under homeomorphisms.
We end Section 3 with a proof based on one of the characterizations of Section 2 that the class
$\mathbf {PM}_\sigma $
is closed under products in the sense that if A and B are
$\mathbf {PM}_\sigma $
-sets in perfect Polish spaces X and Y, respectively, then
$A\times B$
is a
$\mathbf {PM}_\sigma $
-set in
$X\times Y$
(see Theorem 3.2).
In Section 4 we gather some additional comments.
In Section 4.1 we present an example of a countably perfectly meager set in
$2^{\mathbb N}$
which has neither the Hurewicz property nor
$\lambda '$
-property (see Example 4.1). We also give an example of a countably perfectly meager set in
$2^{\mathbb N}$
which is not perfectly meager in the transitive sense (see Example 4.4).
Section 4.2 contains remarks on some
$\sigma $
-ideals related to the classes
$\mathbf {PM}$
and
$\mathbf {PM}_\sigma $
.
2 Characterizations and examples of countably perfectly meager sets
2.1 Characterizations of countably perfectly meager sets
In this subsection A is always a subset of a perfect (i.e., with no isolated points) Polish (i.e., a separable completely metrizable) topological space X and
$\mathbf {PM}_\sigma $
is the family of all subsets of X which are countably perfectly meager in X.
Let us recall that A is an
$s_0$
-set if for every perfect (i.e., non-empty, closed, and with no isolated points) set P there is a copy of the Cantor set
$K\subseteq P$
with
$K\cap A=\emptyset $
. Clearly, every perfectly meager set has property
$s_0$
.
Theorem 2.1. The following are equivalent:
-
(1)
$A\in \mathbf {PM}_\sigma $
. -
(2) For every sequence
$\{K_n: n \in \mathbb N\}$
of copies of the Cantor set in X there is an
$F_{\sigma }$
-set F in X such that
$A\subseteq F$
and
$K_m\not \subseteq F$
for each
$m\in \mathbb N$
. -
(3) For every sequence
$\{K_n: n \in \mathbb N\}$
of copies of the Cantor set in X there are closed sets
$F_n$
in X such that
$A\subseteq \bigcup _n F_n$
and
$K_m\not \subseteq F_n$
for each
$m, n\in \mathbb N$
. -
(4) For every sequence
$\{K_n: n \in \mathbb N\}$
of pairwise disjoint copies of the Cantor set in X there are closed sets
$F_n$
in X such that
$A\subseteq \bigcup _n F_n$
and
$K_m\not \subseteq F_n$
for each
$m, n\in \mathbb N$
. -
(5) A is an
$s_0$
-set and for every sequence
$\{K_n: n \in \mathbb N\}$
of pairwise disjoint and disjoint from A copies of the Cantor set in X there are closed sets
$F_n$
in X such that
$A\subseteq \bigcup _n F_n$
and
$K_m\not \subseteq F_n$
for each
$m, n\in \mathbb N$
.
Proof The implications
$(1)\Rightarrow (2)\Rightarrow (3) \Rightarrow (4)$
are obvious.
To prove that
$(4) \Rightarrow (5) $
, it only suffices to show that if
$(4)$
holds, then A is an
$s_0$
-set. To see this, let us fix a perfect set P and let
$K_0, K_1,\ldots $
be pairwise disjoint copies of the Cantor set in P such that each non-empty relatively open set in P contains some
$K_n$
. Now, by (4),
$A \subseteq \bigcup _n F_n$
for some closed sets
$F_n$
in X such that no
$F_n$
covers any
$K_m$
. It follows that
$F_n \cap P$
is nowhere dense in P for each n and so there exists a perfect set
$K \subseteq P$
disjoint from
$\bigcup _n F_n$
. Then
$K\cap A=\emptyset $
as well.
To prove that
$(5)\Rightarrow (1)$
, we shall need the following simple observation.
Claim 2.2. For every sequence of perfect sets
$\{P_n: n \in \mathbb N\}$
in X, there is a sequence of pairwise disjoint Cantor sets
$\{K_n: n \in \mathbb N\}$
with
$K_n\subseteq P_n$
for each n.
Indeed, first pick points
$x_i\in P_i$
with
$x_i\neq x_j$
for
$i\neq j$
, and then choose successively the Cantor sets
$K_n$
in
$P_n$
disjoint from
$K_i$
, for
$i < n$
, and
$\{x_j: j>n\}$
.
Now let us assume (5) and let
$\{P_n: n \in \mathbb N\}$
be a sequence of perfect subsets of X.
For each n let
$\{U^n_m: m \in \mathbb N\}$
be a basis of non-empty relatively open subsets of
$P_n$
and for each m let us pick a Cantor set
$K^n_m\subseteq U^n_m$
. By the claim and the fact that A is an
$s_0$
-set we may assume that the sets
$K^n_m$
,
$n,m\in \mathbb N$
, are pairwise disjoint and disjoint from A.
By (5), there are closed sets
$F_i$
in X such that
$A\subseteq \bigcup _i F_i$
and
$K^n_m\not \subseteq F_i$
for each
$m, n, i\in \mathbb N$
. Letting
$F=\bigcup _i F_i$
we easily conclude that
$F\cap P_n$
is meager in
$P_n$
for each n.⊣
As a corollary let us formulate a characterization of countably perfectly meager sets stated and partially proved by Bartoszyński in [Reference Bartoszyński1].
Theorem 2.3. The following are equivalent:
-
(1)
$A\in \mathbf {PM}_\sigma $
. -
(2) For every sequence of countable dense-in-itself sets
$\{A_n: n \in ~\mathbb N~\}$
there are sets
$B_n \subseteq A_n$
such that
$\overline {A_n}=\overline {B_n}$
for each
$n\in \mathbb N$
and
$\bigcup _n B_n$
is a
$G_\delta $
-set relative to
$A \cup \bigcup _n A_n$
.
Proof
$(1)\Rightarrow (2)$
was proved by Bartoszyński [Reference Bartoszyński1, Theorem 7,
$(3)\Rightarrow (2)$
].
$(2)\Rightarrow (1)$
. To prove that
$A\in \mathbf {PM}_\sigma $
, we shall check that A satisfies condition
$(5)$
of Theorem 2.1.
First note that
$A \in \mathbf {PM}$
(for a proof see [Reference Bartoszyński1, Theorem 6,
$(2)\Rightarrow (1)$
]; in fact, Bartoszyński [Reference Bartoszyński1, Theorem 7,
$(2)\Rightarrow (1)$
] proved that
$A\in \mathbf {UM}$
) which implies that A is an
$s_0$
-set.
Let
$\{K_n: n \in \mathbb N\}$
be a sequence of (pairwise disjoint but this assumption is superfluous) copies of the Cantor set disjoint from A. We shall show that there is an
$F_\sigma $
-set F such that
$A\subseteq F$
and
$K_n \backslash F\neq \emptyset $
for each n. To this end, for each n let us choose a countable dense subset
$A_n$
of
$K_n$
. By
$(2)$
, there are sets
$B_n \subseteq A_n$
such that
$\overline {B_n}=K_n$
for each
$n\in \mathbb N$
and a
$G_\delta $
-subset G of X such that
$(A \cup \bigcup _n A_n)\cap G=\bigcup _n B_n$
. Let
$F=X\backslash G$
. Then
$A\subseteq F$
and for each n we have
$B_n\subseteq K_n\backslash F$
, so F is as required.⊣
Remark 2.4. The characterization of
$\mathbf {PM}_\sigma $
-sets from Theorem 2.3 should be compared with the following characterization of
$\mathbf {PM}$
-sets by Bennett, Hosobuchi, and Lutzer [Reference Bennett, Hosobuchi and Lutzer4] (for a short proof see [Reference Bartoszyński1, Theorem 6]):
The following are equivalent:
-
(1)
$A\in \mathbf {PM}$
. -
(2) For every countable dense-in-itself set
$A_0$
there exists a set
$B_0 \subseteq A$
such that
$\overline {A_0}=\overline {B_0}$
and
$B_0$
is a
$G_\delta $
-set relative to
$A \cup A_0$
.
Our last characterization of
$\mathbf {PM}_\sigma $
-sets is closely related to a characterization of
$\mathbf {UM}$
sets (cf. Remark 2.7).
Theorem 2.5. The following are equivalent:
-
(1)
$A\in \mathbf {PM}_\sigma $
. -
(2) For every continuous bijection
$f:\mathbb N^{\mathbb N}\thinspace {\rightarrow}\thinspace X$
there are closed sets
$F_n$
in X such that
$A\subseteq \bigcup _n F_n$
and
$f^{-1}(F_n)$
is nowhere dense in
$\mathbb N^{\mathbb N}$
for each
$n\in \mathbb N$
.
Proof
$(1)\Rightarrow (2)$
. Since open sets in
$\mathbb N^{\mathbb N}$
are mapped by f onto Borel sets, one can choose a sequence
$\{B_n: n \in \mathbb N\}$
of Borel subsets of X such that
$\{f^{-1}(B_n): n \in \mathbb N\}$
is a basis of the topology of
$\mathbb N^{\mathbb N}$
. For each n let us pick a Cantor set
$K_n\subseteq B_n$
. Since
$A\in \mathbf {PM}_\sigma $
, there are closed sets
$F_n$
in X such that
$A\subseteq \bigcup _n F_n$
and
$K_m\not \subseteq F_n$
for each
$m, n\in \mathbb N$
. It readily follows that
$f^{-1}(F_n)$
is nowhere dense in
$\mathbb N^{\mathbb N}$
for each
$n\in \mathbb N$
.
$(2)\Rightarrow (1)$
. To prove that
$A\in \mathbf {PM}_\sigma $
, we shall check condition
$(4)$
of Theorem 2.1.
Let
$\{K_n: n \in \mathbb N\}$
be a sequence of pairwise disjoint Cantor sets in X.
A key observation is the following fact.
Claim 2.6. There is a continuous bijection
$f:\mathbb N^{\mathbb N}\thinspace {\rightarrow}\thinspace X$
such that
$f^{-1}(K_n)$
is open in
$\mathbb N^{\mathbb N}$
for each
$n\in \mathbb N$
.
To prove the claim, let
$\tau $
be the (perfect Polish) topology of X and let us first extend
$\tau $
to the topology
$\tau '$
whose basic open sets are elements of
$\tau $
and relatively open subsets of
$K_n$
’s. More precisely, let
$\tau _n$
be the topology generated by
$\tau \cup \{K_n\}$
and then let
$\tau '$
be the topology generated by
$\bigcup _n\tau _n$
. This topology is Polish (cf. [Reference Kechris12, 13.A, Exercise 7.15]) and it is easy to check that it is also perfect. It follows (cf. [Reference Kechris12, 7.15]) that there is a bijection
$f:\mathbb N^{\mathbb N}\thinspace {\rightarrow}\thinspace X$
which is continuous in the sense of
$\tau '$
hence also in the sense of
$\tau $
.
Having proved the claim we may now apply the assumption about A to find closed sets
$F_n$
in X such that
$A\subseteq \bigcup _n F_n$
and
$f^{-1}(F_n)$
is nowhere dense in
$\mathbb N^{\mathbb N}$
for each
$n\in \mathbb N$
. But
$f^{-1}(K_m)$
being open in
$\mathbb N^{\mathbb N}$
we conclude that
$K_m\not \subseteq F_n$
for each
$m, n\in \mathbb N$
. This shows that A satisfies condition
$(4)$
of Theorem 2.1 completing the proof.⊣
Remark 2.7. The characterization of
$\mathbf {PM}_\sigma $
-sets from Theorem 2.5 should be compared with the following characterization of
$\mathbf {UM}$
-sets (cf. [Reference Zakrzewski25, Theorem 2.4]):
The following are equivalent:
-
(1)
$A\in \mathbf {UM}$
. -
(2) For every continuous bijection
$f:\mathbb N^{\mathbb N}\thinspace {\rightarrow}\thinspace X$
there are sets
$F_n$
in X such that
$A\subseteq \bigcup _n F_n$
and
$f^{-1}(F_n)$
is closed and nowhere dense in
$\mathbb N^{\mathbb N}$
for each
$n\in \mathbb N$
.
In particular, in view of Theorem 2.5, this gives another proof of the inclusion
$\mathbf {PM}_\sigma \subseteq \mathbf {UM}$
.
2.2 Examples of countably perfectly meager sets
Let us recall that a subset A of
$2^{\mathbb N}$
is perfectly meager in the transitive sense (
$A\in \mathbf {AFC'}$
; cf. [Reference Nowik, Scheepers and Weiss15, Reference Nowik and Weiss16, Reference Weiss23]) if for every perfect subset P of
$2^{\mathbb N}$
, there exists an
$F_\sigma $
-set F in X such that
$A \subseteq F$
and
$F\cap (P+t)$
is meager in
$P+t$
for each
$t\in 2^{\mathbb N}$
or, equivalently (cf. [Reference Nowik and Weiss16, Lemma 6]), if for every sequence
$\{K_n: n \in \mathbb N\}$
of copies of the Cantor set in
$2^{\mathbb N}$
there are closed sets
$F_n$
in
$2^{\mathbb N}$
such that
$A\subseteq \bigcup _n F_n$
and
$K_m+t\not \subseteq F_n$
for each
$m, n\in \mathbb N$
and
$t\in 2^{\mathbb N}$
. Combining this with Theorem 2.1 we get the following result which somewhat strengthens the fact that
$\mathbf {AFC'}\subseteq \mathbf {UM}$
established by Nowik and Weiss [Reference Nowik and Weiss16, Theorem 2] by a similar argument.
Theorem 2.8. Every subset of
$2^{\mathbb N}$
which is perfectly meager in the transitive sense is countably perfectly meager in
$2^{\mathbb N}$
.
As a corollary we obtain a list of some classical classes of sets which being perfectly meager in the transitive sense are countably perfectly meager as well.
Corollary 2.9. The following collections of subsets of
$2^{\mathbb N}$
are countably perfectly meager in
$2^{\mathbb N}$
:
-
(1) meager-additive sets,
-
(2)
$\gamma $
-sets, -
(3) strongly meager sets,
-
(4) Sierpiński sets.
Proof (1). See [Reference Zindulka26, Proposition 6.6].
(2). See [Reference Nowik, Scheepers and Weiss15]. This also follows from (1), since by [Reference Nowik and Weiss17, Proposition 3.7], every
$\gamma $
-set is meager-additive.
(3). See [Reference Nowik, Scheepers and Weiss15, Theorem 9].
(4). This follows from (3), since Pawlikowski [Reference Pawlikowski18] proved that every Sierpiński set is strongly meager.⊣
The following result gives more examples of universally meager sets which are countably perfectly meager as well.
Let us recall that given a perfect Polish space X a set
$A\subseteq X$
-
• has the Hurewicz property, if every continuous image of A in
$\mathbb N^{\mathbb N}$
is bounded in the ordering
$\leq ^*$
of eventual domination, -
• is a
$\lambda '$
-set in X if every countable set
$D\subseteq X$
is relatively
$G_{\delta }$
in
$A \cup D$
.
The cardinal number
$\mathfrak {b}$
is the minimal cardinality of a subset of
$\mathbb N^{\mathbb N}$
which is unbounded in the ordering
$\leq ^*$
.
Proposition 2.10. The following collections of sets are countably perfectly meager in the respective spaces:
-
(1) subsets of a perfect Polish space X with the Hurewicz property and no perfect subsets; in particular, subsets of X of cardinality less than
$\mathfrak {b}$
, -
(2)
$\lambda '$
-subsets in a perfect Polish space X, in particular:-
(a) sets in
$\mathbb N^{\mathbb N}$
of the form
$\{f_\alpha :\alpha < \mathfrak {b}\}$
where-
•
$\alpha <\beta <\mathfrak {b}$
implies
$f_\alpha <^*f_\beta $
, -
• for every
$f\in \mathbb N^{\mathbb N}$
there is
$\alpha < \mathfrak {b}$
with
$f_\alpha \nleq ^*f$
.
-
-
(b) Hausdorff
$(\omega _1,\omega _1^{*})$
-gaps in
${\mathcal P}(\mathbb N)$
.
-
Proof (1). This was actually shown in Proposition 2.3 of Zakrzewski [Reference Zakrzewski24].
(2). Let A be a
$\lambda '$
-set in X. To prove that
$A\in \mathbf {PM}_\sigma $
, we shall check condition
$(5)$
of Theorem 2.1. Clearly, A is an
$s_0$
-set. For a sequence
$\{K_n: n \in \mathbb N\}$
of pairwise disjoint and disjoint from A copies of the Cantor set in X for each n let us pick a point
$d_n\in K_n$
and let
$D=\{d_n: n\in \mathbb N\}$
. Then, A being a
$\lambda '$
-set, there is an
$F_\sigma $
set F in X such that
$A\subseteq F$
and
$F\cap D=\emptyset $
, so
$d_n$
witnesses that
$K_n\not \subseteq F$
for any
$n\in \mathbb N$
.
Sets described in (a) and (b) are classical examples of
$\lambda '$
sets due to Rothberger and Hausdorff (see [Reference Miller, Kunen and Vaughan14]).⊣
Remark 2.11. An easier way of proving that every Sierpiński set in
$2^{\mathbb N}$
is in
$\mathbf {PM}_\sigma$
(cf. Corollary 2.9) is to combine Proposition 2.10(1) with Theorem 7 of Fremlin and Miller [Reference Fremlin and Miller6] which states that every Sierpiński set has the Hurewicz property.
Likewise, another way of proving that every
$\gamma $
-set in
$2^{\mathbb N}$
is in
$\mathbf {PM}_\sigma$
(cf. Corollary 2.9) is to combine Proposition 2.10(1) with Theorem 2 of Galvin and Miller [Reference Galvin and Miller7] which states that every
$\gamma $
-set has the Hurewicz property.
On the other hand, the set described in Proposition 2.10(2)(a) is
$\lambda '$
in
$\mathbb N^{\mathbb N}$
but does not have the Hurewicz property as an unbounded subset of
$\mathbb N^{\mathbb N}$
. Likewise, not every subset of
$2^{\mathbb N}$
with the Hurewicz property and no perfect subsets (cf. Proposition 2.10(1)) is a
$\lambda '$
-set in
$2^{\mathbb N};$
see Example 4.1 in the comment section below.
3
$\mathbf {PM}_\sigma $
versus
$\mathbf {UM}$
Theorem 1.1, which we are now going to prove, reveals an essential difference between the classes
$\mathbf {UM}$
and
$\mathbf {PM}_\sigma $
.
Proof of Theorem 1.1 Let
$C_0, C_1,\ldots $
be pairwise disjoint meager Cantor sets in
$2^{\mathbb N}$
such that:
-
(1) each non-empty open set in
$2^{\mathbb N}$
contains some
$C_n$
.
Let
$P = 2^{\mathbb N}\backslash \bigcup _n C_n$
.
We shall justify the theorem in three steps (A), (B), and (C).
(A) We claim that there exists a set
$H\subseteq T\times P$
intersecting each vertical section
$\{t\}\times P$
,
$t\in T$
, in a singleton, such that each
$F_\sigma $
-set in
$2^{\mathbb N}\times 2^{\mathbb N}$
containing H contains also
$\{t\}\times V$
for some
$t\in T$
and a non-empty open set V in
$2^{\mathbb N}$
.
Indeed, let
$\{F_t: \ t\in T\}$
be a parametrization on T of all
$F_\sigma $
-sets in
$2^{\mathbb N}\times 2^{\mathbb N}$
. For each
$t\in T$
, we pick
$(t,\varphi (t))\in (\{t\}\times P)\backslash F_t$
, whenever this is possible, and we let
$\varphi (t)$
be an arbitrary fixed element of P, otherwise.
Let us check that the graph
$H=\{(t,\varphi (t)): t\in T \}$
has the required property.
Let F be an
$F_\sigma $
-set in
$2^{\mathbb N}\times 2^{\mathbb N}$
containing H, and let
$t\in T$
be such that
$F=F_t$
. Then
$(t,\varphi (t))\in F_t$
, hence
$F_t$
contains
$\{t \}\times P$
. Consequently, P being a dense
$G_\delta $
-set in
$2^{\mathbb N}$
, the Baire category theorem provides a non-empty open set V in
$2^{\mathbb N}$
with
$\{t \}\times V\subseteq F_t$
, completing the proof of the claim.
(B) For any
$s\in 2^{<\mathbb N} $
let
$N_s=\{x\in 2^{\mathbb N}: s\subseteq x \}$
be the standard basic open set in
$2^{\mathbb N}$
determined by s.
Let
$\sim $
be the equivalence relation on
$2^{\mathbb N}\times 2^{\mathbb N}$
, whose equivalence classes are given by:
$$ \begin{align*}[(x,y)]_{\sim}=\left\{ \begin{array}{@{}ll} N_{x|n}\times \{y\}, & \text{if}\ y\in C_n, \\ \{(x,y) \}, & \text{if}\ y\in P. \end{array}\right.\end{align*} $$
Let
$\pi (x,y)=[(x,y)]_{\sim }$
be the quotient map onto the quotient space
$K=({2^{\mathbb N}\times 2^{\mathbb N}})/\sim $
(whose topology consists of sets
$U\subseteq K$
such that
$\pi ^{-1}(U)$
is open in
$2^{\mathbb N}\times 2^{\mathbb N}$
).
Claim. The space K is homeomorphic to
$2^{\mathbb N}$
.
The equivalence classes of
$\sim $
form an upper-semicontinuous decomposition of
$2^{\mathbb N}\times 2^{\mathbb N}$
(i.e., the saturation of every closed set in
$2^{\mathbb N}\times 2^{\mathbb N}$
is closed). It follows that the decomposition space
$K={2^{\mathbb N}\times 2^{\mathbb N}}/\sim $
is metrizable (cf. [Reference Engelking5, Theorem 4.2.13]). Moreover, K is compact, zero-dimensional, and has no isolated points, and hence the claim follows. However, for reader’s convenience, we shall provide a direct argument to that effect, avoiding the metrization theorem.
Let
$\mathscr {B}$
consist of clopen subsets of
$2^{\mathbb N}\times 2^{\mathbb N}$
of the form
$N_s\times N_t$
, where
$s,t\in 2^{<\mathbb N}$
and
$N_t\cap C_k =\emptyset $
for each
$k<{\textrm {length}}(s)$
. We shall show that
$\{\pi (B):B\in \mathscr {B}\}$
is a countable basis for K consisting of clopen sets.
First, let us note that each set from
$\mathscr {B}$
is saturated, i.e., is the union of equivalence classes. Indeed, if
$(x, y) \in N_s \times N_t$
,
$N_t\cap \bigcup _{k<n}C_k=\emptyset $
and
$n={\textrm {length}}(s)$
, then either
$y\in P$
and then
$[(x,y)]_{\sim }=\{(x,y)\}$
or
$y\in C_m$
for some
$m\geq n$
which implies that
$[(x,y)]_{\sim }= N_{x|m}\times \{y\}\subseteq N_s \times N_t$
.
It follows that for each
$B\in \mathscr {B}$
,
$\pi (B)$
and
$\pi ((2^{\mathbb N}\times 2^{\mathbb N})\backslash B)$
are disjoint open sets in K, hence
$\pi (B)$
is clopen in K.
Next, let us fix an open set W in K and let
$c=\pi (x,y)\in W$
. Then, since
$\pi ^{-1}(W)$
is open in
$2^{\mathbb N}\times 2^{\mathbb N}$
and
$(x,y)\in \pi ^{-1}(W)$
, we have
$N_{x|n}\times N_{y|m}\subseteq \pi ^{-1}(W)$
for some n and m. Moreover, if
$y\in \bigcup _k C_k$
, then we additionally assume that n is the unique k for which
$y\in C_k$
(let us note that in this case
$(x,y)\in N_{x|n}\times \{y\}\subseteq \pi ^{-1}(W)$
). In any case,
$y\notin \bigcup _{k<n} C_k$
and
$\bigcup _{k<n} C_k$
being closed, there is large enough
$m'\geq m$
for which
$N_{y|m'}\cap \bigcup _{k<n} C_k=\emptyset $
. Then
$B=N_{x|n}\times N_{y|m'}\in \mathscr {B}$
and
$\pi (B)$
is a neighbourhood of c contained in W.
We have checked that
$\{\pi (B):B\in \mathscr {B}\}$
is a countable basis for K consisting of clopen sets. Clearly, no
$\pi (B)$
is a singleton, hence K has no isolated points.
Finally, the equivalence classes of
$\sim $
are closed in
$2^{\mathbb N}\times 2^{\mathbb N}$
, hence the singletons of K are closed.
It follows that the space K, being
$T_1$
and having a basis consisting of clopen sets, is also Hausdorff and it is compact as a continuous image of
$2^{\mathbb N}\times 2^{\mathbb N}$
. Consequently, being a compact, Hausdorff, second countable, zero-dimensional topological space without isolated points, K is homeomorphic to
$2^{\mathbb N}$
, which completes the proof of the claim.
Let us also note that the sets
-
(2)
$P_s=\pi (N_s\times C_n)$
,
where
$s\in 2^{<\mathbb N}$
and
$n={\textrm {length}}(s)$
are perfect subsets of K.
(C) Finally, let
$E=\pi (H)$
(cf. (A)). Clearly, E is a homeomorphic copy of H in K and T is the injective image of E under the continuous function
$\text {proj}_1\circ \pi ^{-1}|E$
, where
$\text {proj}_1$
is the projection of
$2^{\mathbb N}\times 2^{\mathbb N}$
onto the first axis.
We shall show that
-
(3) E is not a
$\mathbf {PM}_\sigma $
-set in K.
To that end, let us consider an
$F_\sigma $
-set
$F^*$
in K such that
$E\subseteq F^*$
. Then
-
(4)
$F=\pi ^{-1}(F^*)$
is an
$F_{\sigma }$
-set in
$2^{\mathbb N}\times 2^{\mathbb N}$
containing H, so there are
$t\in T$
and a non-empty open set V in
$2^{\mathbb N}$
such
$\{t\}\times V\subseteq F$
(cf. (A)).
Let us fix
$C_n\subseteq V$
(cf. (1)) and let
$s=t|n$
be the unique sequence in
$2^n$
such that
$t\in N_s$
. We have
$\{t\}\times C_n\subseteq F$
and let us notice that
$\pi (\{t\}\times C_n)=P_s$
(cf. (2)).
Consequently,
$P_s\subseteq F^*$
(cf. (4)).
It follows that any
$F_\sigma $
-set in K containing E also contains some
$P_s$
, which confirms (3), completing the proof of the theorem.⊣
As a corollary we have the following result which shows that, at least consistency-wise, the classes
$\mathbf {UM}$
and
$\mathbf {PM}_\sigma $
are different (part (1)).
Its part (2) strengthens the result of Nowik, Scheepers, and Weiss [Reference Nowik, Scheepers and Weiss15] that assuming the Continuum Hypothesis there is a
$\lambda $
-set in
$2^{\mathbb N}$
which is not perfectly meager in the transitive sense (A is a
$\lambda $
-set if every countable set
$D\subseteq A$
is relatively
$G_{\delta }$
in A).
Part (3) strengthens the result of Sierpiński [Reference Sierpiński21] that (assuming the continuum hypothesis)
$\lambda '$
-property is not invariant under homeomorphisms.
Theorem 3.1.
-
(1) If there exists a universally meager set in
$2^{\mathbb N}$
of cardinality of the continuum, then there is also one which is not countably perfectly meager. -
(2) If there exists a
$\lambda $
-set in
$2^{\mathbb N}$
of cardinality of the continuum, then there is also one which is not countably perfectly meager. -
(3) If there exists a
$\lambda '$
-set in
$2^{\mathbb N}$
of cardinality of the continuum, then there is also one whose homeomorphic copy in
$2^{\mathbb N}$
is not countably perfectly meager. In particular, the class
$\mathbf {PM}_\sigma $
is not closed with respect to homeomorphic images.
In particular, assuming the continuum hypothesis there is a
$\lambda '$
-set in
$2^{\mathbb N}$
whose homeomorphic copy in
$2^{\mathbb N}$
is not countably perfectly meager.
Proof We keep the notation from the proof of Theorem 1.1. For a set
$T\subseteq 2^{\mathbb N}$
of cardinality
$2^{\aleph _0}$
let
$H\subseteq T\times P$
and
$E\subseteq 2^{\mathbb N}$
satisfy the assertions of Theorem 1.1.
(1) and (2). It suffices to notice that if T is either universally meager or a
$\lambda $
-set, then so is E, respectively (cf. [Reference Zakrzewski24]). But
$E\not \in \mathbf {PM}_\sigma $
.
(3). It can be readily checked that if T is a
$\lambda '$
-set in
$2^{\mathbb N}$
, then H is
$\lambda '$
-set in
$2^{\mathbb N}\times P$
. Since P can be homeomorphically embedded as a
$G_\delta $
-set in
$2^{\mathbb N}$
, we may identify H with a
$\lambda '$
-set in
$2^{\mathbb N}$
. But then E is a homeomorphic copy of H in
$2^{\mathbb N}$
which is not
$\mathbf {PM}_\sigma $
in
$2^{\mathbb N}$
.⊣
We close this section by showing that like
$\mathbf {UM}$
(see [Reference Zakrzewski24]) (but, at least consistency-wise, unlike
$\mathbf {PM}$
; see [Reference RecŁaw19]), the class
$\mathbf {PM}_\sigma $
is closed under products.
Theorem 3.2. The product of two countably perfectly meager sets is countably perfectly meager in the sense that if A and B are
$\mathbf {PM}_\sigma $
-sets in perfect Polish spaces X and Y, respectively, then
$A\times B$
is a
$\mathbf {PM}_\sigma $
-set in
$X\times Y$
.
Proof Let A and B be
$\mathbf {PM}_\sigma $
-sets in perfect Polish spaces X and Y, respectively.
To prove that
$A\times B$
is a
$\mathbf {PM}_\sigma $
-set in
$X\times Y$
, we shall check condition (3) of Theorem 2.1.
Let
$\{K_n: n \in \mathbb N\}$
be a sequence of Cantor sets in
$Z=X\times Y$
and for each n let
$L_n$
and
$M_n$
be the images of
$K_n$
under projections of Z onto X and Y, respectively.
Let
$S=\{n\in \mathbb N: L_n \text { is uncountable} \}$
and for each
$n\in S$
let us pick a Cantor set
$L_n'\subseteq L_n$
. Likewise, let
$T=\{n\in \mathbb N: M_n \text { is uncountable} \}$
and for each
$n\in T$
let us pick a Cantor set
$M_n'\subseteq M_n$
.
The sets A and B being countably perfectly meager, there are sequences
$\{F^A_i:i\in \mathbb N\}$
and
$\{F^B_j:j\in \mathbb N\}$
of closed sets in X and Y, respectively, such that
$A\subseteq \bigcup _i F^A_i$
,
$B\subseteq \bigcup _j F^B_j$
,
$L_m'\not \subseteq F^A_i$
, and
$M_n'\not \subseteq F^B_j$
whenever
$m\in S,\ n\in T$
, and
$n,m,j,i\in \mathbb N$
.
Let
$F_{i,j}= F^A_i \times F^B_j$
for
$i,j \in \mathbb N$
.
Clearly,
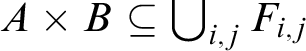$A\times B \subseteq \bigcup _{i,j} F_{i,j}$
and we claim that for any
$n, i, j$
we have
$K_n\not \subseteq F_{i,j}$
.
Indeed, let us notice that
$S\cup T =\mathbb N$
since for each n we have
$K_n\subseteq L_n\times M_n$
. It follows that either
$L_n'\not \subseteq F^A_i$
(if
$n\in S$
) or
$M_n'\not \subseteq F^B_j$
(if
$n\in T$
), so in either case
$K_n\not \subseteq F_{i,j}$
. This completes the proof.⊣
4 Comments
4.1
$\mathbf {PM}_\sigma $
versus
$\mathbf {\lambda '}$
, Hurewicz property, and
$\mathbf {AFC'}$
The relationship of classes of subsets of
$2^{\mathbb N}$
with the Hurewicz property (and no perfect subsets; cf. Proposition 2.10(1)), or of
$\lambda '$
-sets (cf. Proposition 2.10(2)), or of
$\mathbf {AFC'}$
-sets (cf. Theorem 2.9) to an apparently larger class of
$\mathbf {PM}_\sigma $
-sets seems particularly close.
For example, the characterizations of
$\mathbf {PM}_\sigma $
-sets given in Theorem 2.1 somewhat resemble the following characterization of sets with the Hurewicz property, obtained by Just, Miller, Scheepers, and Szeptycki [Reference Just, Miller, Scheepers and Szeptycki11, Theorem 5.7]:
$A\subseteq 2^{\mathbb N}$
has the Hurewicz property if and only if for every sequence
$\{K_n: n \in \mathbb N\}$
of copies of the Cantor set in
$2^{\mathbb N}$
disjoint from A there are closed sets
$F_n$
in
$2^{\mathbb N}$
such that
$A\subseteq \bigcup _n F_n$
and
$K_m\cap F_n=\emptyset $
for each
$m, n\in \mathbb N$
. In particular, if
$A\subseteq 2^{\mathbb N}$
has either the Hurewicz property or
$\lambda '$
-property, then for every countable set
$D\subseteq 2^{\mathbb N}$
disjoint from A there is an
$F_{\sigma }$
-set F in
$2^{\mathbb N}$
such that
$A\subseteq F$
and
$F\cap D=\emptyset $
.
The following example, based on a result of Bartoszyński and Shelah [Reference Bartoszyński and Shelah3] and classical ideas of Rothberger (cf. [Reference Miller, Kunen and Vaughan14]), shows that there exists (in ZFC) a countably perfectly meager set in
$2^{\mathbb N}$
of cardinality
$\mathfrak {b}$
which lacks the latter property and thus has neither the Hurewicz nor
$\lambda '$
property. It also shows that the Hurewicz and
$\lambda '$
properties are not the same.
Example 4.1. Inductively, one easily constructs a subset
$\{f_\alpha :\alpha < \mathfrak {b}\}$
of
$\mathbb N^{\mathbb N}$
with the following properties (cf. Proposition 2.10(2(a))):
-
•
$f_\alpha $
is strictly increasing, -
•
$\alpha <\beta <\mathfrak {b}$
implies
$f_\alpha <^*f_\beta $
, -
• for every
$f\in \mathbb N^{\mathbb N}$
there is
$\alpha <\mathfrak {b}$
with
$f_\alpha \nleq ^*f$
.
By identifying each
$f_\alpha $
with the characteristic function of its range, we obtain a homeomorphic copy A of
$\{f_\alpha :\alpha < \mathfrak {b}\}$
in
$2^{\mathbb N}$
.
Let
$B=A\cup \mathbb Q$
, where
$\mathbb Q$
consists of all eventually zero binary sequences. Then:
-
•
$\{f_\alpha :\alpha < \mathfrak {b}\}$
, being unbounded in
$\mathbb N^{\mathbb N}$
, does not have the Hurewicz property, -
•
$\{f_\alpha :\alpha < \mathfrak {b}\}$
is a
$\lambda '$
-set in
$\mathbb N^{\mathbb N}$
(cf. Proposition 2.10(2)(a)), -
• B has the Hurewicz property and has no perfect subsets (cf. [Reference Bartoszyński and Shelah3, Theorem 1], [Reference Tsaban22, Theorem 2.12], and Remark 4.2 below) so, by Proposition 2.10(1), B is countably perfectly meager in
$2^{\mathbb N}$
, -
• A is countably perfectly meager in
$2^{\mathbb N}$
as a subset of B, -
• A does not the Hurewicz property as the homeomorphic image of
$\{f_\alpha :\alpha < \mathfrak {b}\}$
, -
• if F is any
$F_{\sigma }$
-set in
$2^{\mathbb N}$
such that
$A\subseteq F$
, then
$F\cap \mathbb Q\neq \emptyset$
(since otherwise F viewed as a subset of
$\mathbb N^{\mathbb N}$
is bounded, whereas A is unbounded). In particular, neither A nor B are
$\lambda '$
-sets in
$2^{\mathbb N}$
.
Remark 4.2. It seems useful to indicate another proof of the fact that the set B described in Example 4.1 has the Hurewicz property. In fact, in the argument below it is enough to assume that
$\{f_\alpha :\alpha < \mathfrak {b}\}$
is any well-ordered by eventual domination and unbounded subset of
$\mathbb N^{\mathbb N}$
,
$h:\mathbb N^{\mathbb N}\thinspace {\rightarrow}\thinspace P$
is a homeomorphism onto the set P of irrationals in
$I=[0,1]$
,
$\mathbb Q=I\backslash P$
,
$A=\{h(f_\alpha ):\alpha < \mathfrak {b}\}$
, and
$B=A\cup \mathbb Q$
.
Let us recall that the Hurewicz property of
$H\subseteq I$
is equivalent to the following covering property (this is the original Hurewicz’s definition; cf. [Reference Tsaban22]):
for each sequence
$\mathscr {U}_1, \mathscr {U}_2,\ldots $
of open in I covers of H, there are finite subfamilies
${\mathcal F}_n\subseteq \mathscr {U}_n$
such that
$H\subseteq \bigcup _n \bigcap _{m\geq n}(\bigcup {\mathcal F}_m)$
.
Proof Let
$\mathscr {U}_1, \mathscr {U}_2,\ldots $
be open in I covers of B and let
$G=\bigcap _n(\bigcup \mathscr {U}_n)$
. Since
$I\backslash G=P\backslash G$
is
$\sigma $
-compact and so is
$S=h^{-1}(P\backslash G)$
, there is
$f\in \mathbb N^{\mathbb N}$
such that
$g \leq ^*f$
for any
$g\in S$
. Let us pick
$\alpha < \mathfrak {b}$
so that
$f_\alpha \nleq ^* f$
. Then
$T=\{g\in \mathbb N^{\mathbb N}: f_\alpha \leq ^* g \}$
is an
$F_\sigma $
-set in
$\mathbb N^{\mathbb N}$
disjoint from S and
$f_\beta \in T$
, whenever
$\beta \geq \alpha $
.
Let
$L=h(T)\cup \mathbb Q$
. Then
$|B\backslash L|< \mathfrak {b}$
, as
$B\backslash L\subseteq \{h(f_\xi ): \xi <\alpha \}$
. Consequently,
$B\backslash L$
has the Hurewicz property and since
$B\backslash L\subseteq G$
, there are finite collections
${\mathcal F}^{\prime }_n\subseteq \mathscr {U}_n$
such that
$B\backslash L\subseteq \bigcup _n \bigcap _{m\geq n}(\bigcup {\mathcal F}^{\prime }_m)$
.
Let us notice that the set L is
$\sigma $
-compact in I so it also has the Hurewicz property and since
$L\subseteq G$
, we can pick finite
${\mathcal F}^{\prime \prime }_n\subseteq \mathscr {U}_n$
such that
$L\subseteq \bigcup _n \bigcap _{m\geq n}(\bigcup {\mathcal F}^{\prime }_m)$
.
Then, letting
${\mathcal F}_n={\mathcal F}^{\prime }_n\cup {\mathcal F}^{\prime \prime }_n$
, we get finite collections
${\mathcal F}_n\subseteq \mathscr {U}_n$
such that
$B\subseteq \bigcup _n \bigcap _{m\geq n}(\bigcup {\mathcal F}_m)$
. This shows that B has the Hurewicz property.⊣
The fact that
$\mathbf {AFC'}$
-subsets of
$2^{\mathbb N}$
are closely related to
$\mathbf {PM}_\sigma $
-sets in
$2^{\mathbb N}$
is revealed by the following characterization of Bartoszyński (private communication). We are grateful to Tomek Bartoszyński for allowing us to include his result in our paper.
Proposition 4.3 (T. Bartoszyński)
For a set
$A\subseteq 2^{\mathbb N}$
the following are equivalent:
-
(1)
$A\in \mathbf {PM}_\sigma $
. -
(2) For every perfect subset P of
$2^{\mathbb N}$
, there exists an
$F_\sigma $
-set F in
$2^{\mathbb N}$
such that
$A \subseteq F$
and
$F\cap (P+q)$
is meager in
$P+q$
for every
$q\in \mathbb Q$
, where
$\mathbb Q$
consists of all eventually zero binary sequences.
Proof Implication
$(1)\Rightarrow (2)$
follows directly from the definition of countably perfectly meager sets.
To prove that
$(2)\Rightarrow (1)$
, we shall appeal to condition (2) of Theorem 2.1. So let
$\{K_n: n \in \mathbb N\}$
be a sequence of Cantor sets in
$2^{\mathbb N}$
. For each n one can pick a non-empty relatively open compact set
$L_n$
in
$K_n$
(an intersection of
$K_n$
with a basic neighborhood in
$2^{\mathbb N}$
) and
$q_n \in \mathbb Q$
such that all points in
$T_n = L_n + q_n$
have n first coordinates zero, and the sets
$T_n$
are pairwise disjoint. Then the union P of
$\{0\}$
and the sets
$T_n$
is perfect and
$(K_n+q_n) \cap P$
has relatively non-empty interior in P for each
$n\in \mathbb N$
.
Using (2), we fix an
$F_\sigma $
-set F in
$2^{\mathbb N}$
such that
$A \subseteq F$
and
$(F+q)\cap P$
is meager in P for every
$q\in \mathbb Q$
.
But now it is clear that
$K_n\subseteq F$
for no
$n\in \mathbb N$
, since otherwise we would have
$(K_n+q_n)\cap P\subseteq (F+q_n)\cap P$
, contradicting the choice of F.⊣
The following example is a slight modification of a remarkable construction of Recław [Reference RecŁaw20] and shows that, at least consistently, there exists a countably perfectly meager in
$2^{\mathbb N}$
, in fact a
$\lambda '$
-set in
$2^{\mathbb N}$
, which is not perfectly meager in the transitive sense (a similar construction was also used by Weiss [Reference Weiss23, Theorem 3] in his proof that the existence of a universally meager set in
$2^{\mathbb N}$
of cardinality of the continuum implies that there is also one which is not perfectly meager in the transitive sense). This is also yet another (cf. Theorem 3.1) strengthening of the result of Nowik, Scheepers, and Weiss [Reference Nowik, Scheepers and Weiss15] that under the Continuum Hypothesis there is a
$\lambda $
-set in
$2^{\mathbb N}$
which is not perfectly meager in the transitive sense.
Example 4.4. Let us assume that there exists a
$\lambda '$
-set in
$2^{\mathbb N}$
of cardinality of the continuum.
Let
$C,\ D$
be disjoint copies of the Cantor set in
$2^{\mathbb N}$
such that
-
(1) the operation
$+$
of addition is a homeomorphism between
$C\times D$
and
$C+D$
(cf. [Reference RecŁaw20]).
Let
$T\subseteq C$
be a
$\lambda '$
-set in C of cardinality of the continuum.
Arguing as in part (A) of the proof of Theorem 1.1, we obtain a set
$H\subseteq T\times D$
intersecting each vertical section
$\{t\}\times D$
,
$t\in T$
, in a singleton, such that
-
(2) each
$F_\sigma $
-set in
$C\times D$
containing H contains also
$\{t\}\times D$
for some
$t\in T$
.
Now, T being a
$\lambda '$
-set in C, one readily checks that H is a
$\lambda '$
-set in
$C\times D$
(cf. the proof of Theorem 3.1(3)). It follows that (cf. (1)), if we let
$Y=+(H)$
, then Y is a
$\lambda '$
-set in
$C+ D$
and hence also in
$2^{\mathbb N}$
.
On the other hand, Y is not perfectly meager in the transitive sense. Indeed, if F is an arbitrary
$F_\sigma $
-set in
$2^{\mathbb N}$
with
$Y\subseteq F$
and we let
$E= (+)^{-1}(F\cap (C+ D))$
, then E is an
$F_\sigma $
-set in
$C\times D$
containing H so it also contains (cf. (2))
$\{t\}\times D$
for some
$t\in T$
. Consequently,
$t+D\subseteq F,$
completing the proof.
4.2 Remarks on related
$\sigma $
-ideals
In this section
${\mathcal F}$
always denotes a countable (possibly finite but non-empty) collection of perfect sets in a perfect Polish space X.
If I is a
$\sigma $
-ideal of subsets of X, then by
$I^*$
we denote the
$\sigma $
-ideal generated by the closed subsets of X which belong to I.
4.2.1 The
$\sigma $
-ideals
$MGR({\mathcal F})$
Following Kechris and Solecki [Reference Kechris and Solecki13] let us put
$$ \begin{align*}MGR({\mathcal F})=\{A\subseteq X: A\cap P \text{ is meager in}\ P\ \text{for every } P\in{\mathcal F} \}. \end{align*} $$
Let us note that
$MGR({\mathcal F})$
is a
$\sigma $
-ideal on X generated by Borel, in fact
$F_{\sigma \delta }$
-sets, and fulfills the c.c.c. Moreover, the quotient Boolean algebra
$Bor(X)/(MGR({\mathcal F})\cap Bor(X))$
is isomorphic to the Cohen algebra (cf. [Reference Bartoszyński2]). Clearly, the intersection of all
$\sigma $
-ideals of the form
$MGR({\mathcal F})$
is precisely the
$\sigma $
-ideal
$\mathbf {PM}$
.
On the other hand, by [Reference Zakrzewski24, Theorem 2.1], the
$\sigma $
-ideal
$\mathbf {UM}$
is the intersection of all
$\sigma $
-ideals I on X such that the quotient Boolean algebra
$Bor(X)/(I\cap Bor(X))$
is isomorphic to the Cohen algebra. Any such I is precisely of the form
$\mathscr {M}(X,\tau )$
, by which we denote the
$\sigma $
-ideal consisting of meager sets with respect to a perfect Polish topology
$\tau $
on X giving the original Borel structure of X.
4.2.2 The
$\sigma $
-ideals
$MGR^*({\mathcal F})$
By the definition (see the beginning of Section 4), the
$\sigma $
-ideal
$MGR^*({\mathcal F})$
consists of such sets
$A\subseteq X$
that there exists an
$F_\sigma $
-set F in X with
$A\subseteq F$
and such that
$F\cap P$
is meager in P for every
$P\in {\mathcal F}$
. It is the
$\sigma $
-ideal
$MGR^*({\mathcal F})$
(not the
$\sigma $
-ideal
$MGR({\mathcal F})$
erroneously employed in [Reference Bartoszyński2, Theorem 7,
$(1)\Rightarrow (3)$
]) that is relevant to the definition of countably perfectly meager sets. Indeed, the intersection of all
$\sigma $
-ideals of the form
$MGR^*({\mathcal F})$
is precisely the
$\sigma $
-ideal
$\mathbf {PM}_\sigma $
.
It turns out that not all of the
$\sigma $
-ideals of the form
$MGR^*({\mathcal F})$
fulfill the c.c.c. Let us elaborate on this a little further with the help of a theory developed by Kechris and Solecki [Reference Kechris and Solecki13].
Proposition 4.5.
-
(1) If every non-empty open set U in X contains a nowhere dense set
$P\in {\mathcal F}$
, then the
$\sigma $
-ideal
$MGR^*({\mathcal F})$
does not fulfill the c.c.c. -
(2) The intersection of all
$\sigma $
-ideals in X generated by closed sets which fulfill the c.c.c. is precisely the
$\sigma $
-ideal
$\mathbf {PM}$
. -
(3) The intersection of all
$\sigma $
-ideals of the form
$MGR^*({\mathcal F})$
which fulfill the c.c.c. is precisely the
$\sigma $
-ideal
$\mathbf {PM}$
. -
(4) The intersection of all
$\sigma $
-ideals of the form
$MGR^*({\mathcal F})$
which do not fulfill the c.c.c. is precisely the
$\sigma $
-ideal
$\mathbf {PM}_\sigma $
.
Proof (1). This immediately follows from [Reference Kechris and Solecki13, Lemma 9].
(2) and (3). First, let
$A\in \mathbf {PM}$
and let I be a
$\sigma $
-ideal in X which is generated by closed sets and fulfills the c.c.c. Then, by [Reference Kechris and Solecki13, Theorem 3], I is of the form
$MGR({\mathcal F})$
for a countable family of perfect subsets of X. Consequently,
$A\in I$
.
For the other direction, assume that
$A\in MGR^*({\mathcal F})$
for every
${\mathcal F}$
such that the
$\sigma $
-ideal
$MGR^*({\mathcal F})$
fulfills the c.c.c. Suppose that P is an arbitrary perfect subset of X and let
${\mathcal F}=\{P\}$
. Then we have
$MGR^*({\mathcal F})=MGR({\mathcal F})$
, so the
$\sigma $
-ideal
$MGR^*({\mathcal F})$
fulfills the c.c.c. Consequently,
$A\in MGR^*({\mathcal F})$
which just means that
$A\cap P$
is meager in P, completing the proof that
$A\in \mathbf {PM}$
.
(4). Let us assume that
$A\in MGR^*({\mathcal F})$
for every
${\mathcal F}$
such that the
$\sigma $
-ideal
$MGR^*({\mathcal F})$
does not fulfill the c.c.c. To prove that
$A\in \mathbf {PM}_\sigma $
, let
${\mathcal F}$
be an arbitrary countable family of perfect subsets of X. By extending
${\mathcal F}$
, if necessary, we may assume that every non-empty open set U in X contains a nowhere dense set
$P\in {\mathcal F}$
. By part (1), the
$\sigma $
-ideal
$MGR^*({\mathcal F})$
does not fulfill the c.c.c. Consequently,
$A\in MGR^*({\mathcal F})$
and we are done.⊣
4.2.3 The
$\sigma $
-ideals
$\mathscr {M}^*(X,\tau )$
In this subsection
$\tau $
always denotes a perfect Polish topology on X giving the original Borel structure of X. Recall that
$\mathscr {M}(X,\tau )$
is the
$\sigma $
-ideal of meager sets with respect to
$\tau $
and
$\mathscr {M}^*(X,\tau )$
consists of such
$A\subseteq X$
that there exists an
$F_\sigma $
-set F in X (with the original Polish topology) with
$A\subseteq F$
and
$F\in \mathscr {M}(X,\tau )$
.
It turns out that we can characterize perfectly meager and countably perfectly meager sets with the help of the
$\sigma $
-ideals
$\mathscr {M}^*(X,\tau )$
in an analogous way to their characterizations in terms of the
$\sigma $
-ideals
$MGR^*({\mathcal F})$
(cf. Proposition 4.5).
Proposition 4.6.
-
(1) The intersection of all
$\sigma $
-ideals of the form
$\mathscr {M}^*(X,\tau )$
which fulfill the c.c.c. is precisely the
$\sigma $
-ideal
$\mathbf {PM}$
. -
(2) The intersection of all
$\sigma $
-ideals of the form
$\mathscr {M}^*(X,\tau )$
is precisely the
$\sigma $
-ideal
$\mathbf {PM}_\sigma $
. Moreover, for a set A to be countably perfectly meager it is enough to belong to all
$\sigma $
-ideals of the form
$\mathscr {M}^*(X,\tau )$
which do not fulfill the c.c.c.
Proof (1). This follows directly from points (2) and (3) of Proposition 4.5, since every
$\sigma $
-ideal of the form
$MGR^*({\mathcal F})$
is also of the form
$\mathscr {M}^*(X,\tau )$
which in turn is generated by closed sets.
(2). Let us assume that
$A\in \mathbf {PM}_\sigma $
and let
$\{U_n:n\in \mathbb N\}$
be a basis of a perfect Polish topology
$\tau $
on X such that every
$U_n$
is an (uncountable) Borel set in X. For each n let us pick a Cantor set
$K_n\subseteq U_n$
. We complete the argument exactly as in the proof of implication
$(1)\Rightarrow (2)$
in Theorem 2.5.
For the other direction we again use the fact that every
$\sigma $
-ideal of the form
$MGR^*({\mathcal F})$
is also of the form
$\mathscr {M}^*(X,\tau )$
and apply point (4) of Proposition 4.5.⊣
Acknowledgment
We thank the referee for the comments which improved the exposition of this paper.
