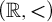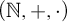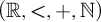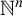1 Introduction
We are interested in structures on the set of real numbers, especially expansions of the real field
![]() $(\mathbb R,+,\cdot )$
by locally path connected sets, having the property that each path component of each definable set (allowing parameters, and of any arity) is definable. Variations on the theme arise by considering connected components and quasicomponents. Our original motivation lies in real-analytic geometry, but we have come to believe that a more foundational investigation is in order. Thus, in this paper, we provide some fundamental logical results and some examples.
$(\mathbb R,+,\cdot )$
by locally path connected sets, having the property that each path component of each definable set (allowing parameters, and of any arity) is definable. Variations on the theme arise by considering connected components and quasicomponents. Our original motivation lies in real-analytic geometry, but we have come to believe that a more foundational investigation is in order. Thus, in this paper, we provide some fundamental logical results and some examples.
Some global conventions
The reader is assumed to be familiar with basic topology (e.g., [Reference Munkres18]) and mathematical logic (especially o-minimality, e.g., [Reference van den Dries5]). Our default is that definability (in any given structure) allows parameters (from the underlying set of the structure) and we identify interdefinable structures. Whenever syntactic dependence on the language is relevant, we shall make it clear. We always regard each
![]() $\mathbb R^n$
as equipped with its usual topology, and subsets of
$\mathbb R^n$
as equipped with its usual topology, and subsets of
![]() $\mathbb R^n$
with the induced topology. We abbreviate “connected component” by “component.” The set of all nonnegative integers is denoted by
$\mathbb R^n$
with the induced topology. We abbreviate “connected component” by “component.” The set of all nonnegative integers is denoted by
![]() $\mathbb N$
.
$\mathbb N$
.
Proofs of results stated in this introduction are postponed to later in the paper.
Definitions. A structure with underlying set
![]() $\mathbb R$
is:
$\mathbb R$
is:
-
(1) path-component closed, or PCC for short, if for every definable set E, each path component of E is definable;
-
(2) component closed, or CC for short, if (1) holds with “component” in place of “path component”;
-
(3) quasicomponent closed, or QCC for short, if (1) holds with “quasicomponent” in place of “path component.”
Note that every structure on
![]() $\mathbb R$
satisfying any of these conditions defines the usual order
$\mathbb R$
satisfying any of these conditions defines the usual order
![]() $<$
on
$<$
on
![]() $\mathbb R$
. (Consider
$\mathbb R$
. (Consider
![]() $\{\, (x,y)\in \mathbb R^2: x\neq y\,\}$
.) Thus, the definitions are really about expansions of
$\{\, (x,y)\in \mathbb R^2: x\neq y\,\}$
.) Thus, the definitions are really about expansions of
![]() $(\mathbb R,<)$
.
$(\mathbb R,<)$
.
We suspect that, in this generality, none of these conditions imply any of the others, but our candidates for counterexamples are ad hoc and unverified as yet. Currently we are most interested in PCC structures, but simultaneous consideration of the other two conditions is natural.
Trivially, the expansion of
![]() $\mathbb R$
by each subset of
$\mathbb R$
by each subset of
![]() $\mathbb R^n$
as n ranges over the positive integers is PCC, CC and QCC. Thus, abstractly, every structure on
$\mathbb R^n$
as n ranges over the positive integers is PCC, CC and QCC. Thus, abstractly, every structure on
![]() $\mathbb R$
has a least expansion that is PCC, CC and QCC; of course, this holds also for each of the conditions individually and pairwise. Relative to known results, it is easy to see that there exist two concrete classes of nontrivial examples.
$\mathbb R$
has a least expansion that is PCC, CC and QCC; of course, this holds also for each of the conditions individually and pairwise. Relative to known results, it is easy to see that there exist two concrete classes of nontrivial examples.
Proposition 1.1. Every o-minimal expansion of
![]() $(\mathbb R,<)$
is PCC, CC and QCC. Every expansion of
$(\mathbb R,<)$
is PCC, CC and QCC. Every expansion of
![]() $(\mathbb R,+,\cdot ,\mathbb N)$
is PCC, CC and QCC.
$(\mathbb R,+,\cdot ,\mathbb N)$
is PCC, CC and QCC.
O-minimal expansions of
![]() $(\mathbb R,<)$
have been studied extensively. Expansions of
$(\mathbb R,<)$
have been studied extensively. Expansions of
![]() $(\mathbb R,+,\cdot ,\mathbb N)$
are too complicated for us to study as definability theory (every real projective set is definable). The main underlying reason for starting this investigation was to see if certain properties of o-minimal expansions of
$(\mathbb R,+,\cdot ,\mathbb N)$
are too complicated for us to study as definability theory (every real projective set is definable). The main underlying reason for starting this investigation was to see if certain properties of o-minimal expansions of
![]() $(\mathbb R,+,\cdot )$
extend to some other settings. Thus, we are interested in PCC structures on the real field that are generated by locally path connected sets, but neither are o-minimal nor define
$(\mathbb R,+,\cdot )$
extend to some other settings. Thus, we are interested in PCC structures on the real field that are generated by locally path connected sets, but neither are o-minimal nor define
![]() $\mathbb N$
. Recent work of the third author [Reference Savatovsky21] provides some examples, but by construction, they are easily seen to interpret
$\mathbb N$
. Recent work of the third author [Reference Savatovsky21] provides some examples, but by construction, they are easily seen to interpret
![]() $(\mathbb N,+,\cdot )$
(and thus to have undecidable theories). We show here that the interpretability of
$(\mathbb N,+,\cdot )$
(and thus to have undecidable theories). We show here that the interpretability of
![]() $(\mathbb N,+,\cdot )$
is unavoidable, even in much leaner structures.
$(\mathbb N,+,\cdot )$
is unavoidable, even in much leaner structures.
Notation
Throughout,
![]() $\mid $
indicates the usual divisibility relation on
$\mid $
indicates the usual divisibility relation on
![]() $\mathbb N$
, regarded as the set
$\mathbb N$
, regarded as the set
![]() $\{\, (n,dn): n,d\in \mathbb N\,\}$
.
$\{\, (n,dn): n,d\in \mathbb N\,\}$
.
By Robinson [Reference Robinson20],
![]() $(\mathbb N,<,\mid )$
is interdefinable with
$(\mathbb N,<,\mid )$
is interdefinable with
![]() $(\mathbb N,+,\cdot )$
, hence also with the expansion of
$(\mathbb N,+,\cdot )$
, hence also with the expansion of
![]() $\mathbb N$
by all arithmetic sets (of any arity); we tend to use this fact without further mention.
$\mathbb N$
by all arithmetic sets (of any arity); we tend to use this fact without further mention.
Theorem 1.2. If
![]() $\mathfrak R$
is an expansion of
$\mathfrak R$
is an expansion of
![]() $(\mathbb R,<,+)$
by Boolean combinations of open subsets of various
$(\mathbb R,<,+)$
by Boolean combinations of open subsets of various
![]() $\mathbb R^n$
, and is PCC, CC or QCC, then exactly one of the following holds.
$\mathbb R^n$
, and is PCC, CC or QCC, then exactly one of the following holds.
-
(1)
 $\mathfrak R$
is o-minimal.
$\mathfrak R$
is o-minimal. -
(2) There is a strictly increasing
 $\sigma \colon \mathbb N\to \mathbb R$
such that
$\sigma \colon \mathbb N\to \mathbb R$
such that
 $\{\, (\sigma (m),\sigma (n)): m \mid n\,\}$
is definable.
$\{\, (\sigma (m),\sigma (n)): m \mid n\,\}$
is definable.
As we shall see later, every expansion of
![]() $(\mathbb R,<,+,\mid )$
by subsets of various
$(\mathbb R,<,+,\mid )$
by subsets of various
![]() $\mathbb N^n$
is PCC, CC and QCC. Trivially, there are plenty of examples of expansions of
$\mathbb N^n$
is PCC, CC and QCC. Trivially, there are plenty of examples of expansions of
![]() $(\mathbb R,+,\cdot )$
for which it is known that condition (2) holds without the assumption of PCC, CC or QCC, but there are also such examples for which every definable set is a finite union of locally path connected definable sets: see [Reference Friedman and Miller8, Reference Friedman and Miller9, Reference Miller13, Reference Miller and Tyne17, Reference Thamrongthanyalak23].
$(\mathbb R,+,\cdot )$
for which it is known that condition (2) holds without the assumption of PCC, CC or QCC, but there are also such examples for which every definable set is a finite union of locally path connected definable sets: see [Reference Friedman and Miller8, Reference Friedman and Miller9, Reference Miller13, Reference Miller and Tyne17, Reference Thamrongthanyalak23].
Corollary 1.3. If
![]() $\mathfrak R$
is a PCC expansion of
$\mathfrak R$
is a PCC expansion of
![]() $(\mathbb R,<,+)$
generated by topological submanifolds, and
$(\mathbb R,<,+)$
generated by topological submanifolds, and
![]() $\mathfrak R$
is not o-minimal, then no expansion of
$\mathfrak R$
is not o-minimal, then no expansion of
![]() $\mathfrak R$
has a decidable theory.
$\mathfrak R$
has a decidable theory.
This is perhaps not so surprising, but also not as discouraging as it might seem. Definability is generally more important than abstract interpretability in the analytic geometry of expansions of
![]() $(\mathbb R,<)$
.
$(\mathbb R,<)$
.
Theorem 1.2 relies on the following technical result.
Proposition 1.4. If
![]() $\emptyset \neq A\subseteq \mathbb R$
has empty interior and
$\emptyset \neq A\subseteq \mathbb R$
has empty interior and
![]() $f\colon A\to A$
is strictly increasing and strictly dominates the identity, then there is a strictly increasing
$f\colon A\to A$
is strictly increasing and strictly dominates the identity, then there is a strictly increasing
![]() $\sigma \colon \mathbb N\to \mathbb R$
such that every expansion of
$\sigma \colon \mathbb N\to \mathbb R$
such that every expansion of
![]() $(\mathbb R,<,f)$
that is PCC, CC or QCC defines
$(\mathbb R,<,f)$
that is PCC, CC or QCC defines
![]() $\{\, (\sigma (m),\sigma (n)): m \mid n\,\}$
.
$\{\, (\sigma (m),\sigma (n)): m \mid n\,\}$
.
(By “strictly dominates the identity” we mean that
![]() $x<f(x)$
for all x in the domain of f. For logicians: The function f is regarded as a subset of
$x<f(x)$
for all x in the domain of f. For logicians: The function f is regarded as a subset of
![]() $\mathbb R^2$
, not the interpretation of a unary function symbol.) A key step in the proof is the special case that
$\mathbb R^2$
, not the interpretation of a unary function symbol.) A key step in the proof is the special case that
![]() $A=\mathbb N$
and f is the usual successor function on
$A=\mathbb N$
and f is the usual successor function on
![]() $\mathbb N$
.
$\mathbb N$
.
Proposition 1.5. Every expansion of
![]() $(\mathbb R,<,\mathbb N)$
that is PCC, CC or QCC defines
$(\mathbb R,<,\mathbb N)$
that is PCC, CC or QCC defines
![]() $\mid $
.
$\mid $
.
Via quantifier elimination in an appropriate language, it is easy to see that
![]() $(\mathbb R,<, \mathbb N)$
does not define
$(\mathbb R,<, \mathbb N)$
does not define
![]() $\{\, 2n: n\in \mathbb N\,\}$
; then it does not define
$\{\, 2n: n\in \mathbb N\,\}$
; then it does not define
![]() $\mid $
, and so is neither PCC, CC nor QCC.
$\mid $
, and so is neither PCC, CC nor QCC.
It appears to us at this time that dealing with arbitrary expansions of
![]() $(\mathbb R,<,+)$
is daunting, especially those that define a bijection between a bounded interval and an unbounded interval. Thus, we first attempt to understand some less complicated structures.
$(\mathbb R,<,+)$
is daunting, especially those that define a bijection between a bounded interval and an unbounded interval. Thus, we first attempt to understand some less complicated structures.
From now on:
![]() $\mathfrak R$
denotes a fixed, but arbitrary, expansion of
$\mathfrak R$
denotes a fixed, but arbitrary, expansion of
![]() $(\mathbb R,<)$
.
$(\mathbb R,<)$
.
We say that
![]() $\mathfrak R$
is locally o-minimal if for each definable
$\mathfrak R$
is locally o-minimal if for each definable
![]() $E\subseteq \mathbb R$
and
$E\subseteq \mathbb R$
and
![]() $x\in \mathbb R$
there is an open interval U containing x such that
$x\in \mathbb R$
there is an open interval U containing x such that
![]() $E\cap U$
is a finite union of points and open intervals. (One might find different definitions in the literature, but as far as we know, all are equivalent over
$E\cap U$
is a finite union of points and open intervals. (One might find different definitions in the literature, but as far as we know, all are equivalent over
![]() $(\mathbb R,<)$
.) Evidently, every o-minimal expansion of
$(\mathbb R,<)$
.) Evidently, every o-minimal expansion of
![]() $(\mathbb R,<)$
is locally o-minimal, but there are locally o-minimal expansions of
$(\mathbb R,<)$
is locally o-minimal, but there are locally o-minimal expansions of
![]() $(\mathbb R,<)$
that are not o-minimal. Of particular importance in this paper is that the expansion of
$(\mathbb R,<)$
that are not o-minimal. Of particular importance in this paper is that the expansion of
![]() $(\mathbb R,<,+)$
by all subsets of each
$(\mathbb R,<,+)$
by all subsets of each
![]() $\mathbb N^n$
(as n ranges over positive integers), is locally o-minimal (see, e.g., [Reference Friedman and Miller8]), and so the same is true of all of its reducts. Thus,
$\mathbb N^n$
(as n ranges over positive integers), is locally o-minimal (see, e.g., [Reference Friedman and Miller8]), and so the same is true of all of its reducts. Thus,
![]() $(\mathbb R,<,\mathbb N)$
is locally o-minimal, but neither PCC, CC nor QCC.
$(\mathbb R,<,\mathbb N)$
is locally o-minimal, but neither PCC, CC nor QCC.
Proposition 1.6. The following are equivalent:
-
(1)
 $\mathfrak R$
is locally o-minimal.
$\mathfrak R$
is locally o-minimal. -
(2) If
 $E\subseteq \mathbb R^n$
is bounded and definable, then the expansion of
$E\subseteq \mathbb R^n$
is bounded and definable, then the expansion of
 $(\mathbb R,<)$
by all definable subsets of E is o-minimal.
$(\mathbb R,<)$
by all definable subsets of E is o-minimal. -
(3) Every definable set is locally path connected.
-
(4) For every definable set, its components are the same as its path components and its quasicomponents.
-
(5) Components of bounded definable subsets of
 $\mathbb R^2$
are path connected.
$\mathbb R^2$
are path connected. -
(6) Quasicomponents of bounded definable subsets of
 $\mathbb R^2$
are connected.
$\mathbb R^2$
are connected. -
(7) If
 $A\subseteq \mathbb R$
is definable and has empty interior, then A is closed and discrete.
$A\subseteq \mathbb R$
is definable and has empty interior, then A is closed and discrete.
(Most of the implications are either trivial or easy exercises in topology that can be done on their own, but (2)
![]() $\Rightarrow $
(3) will require some explanation.)
$\Rightarrow $
(3) will require some explanation.)
Corollary 1.7. If
![]() $\mathfrak R$
is locally o-minimal, then it is PCC if and only if it is CC, if and only if it is QCC.
$\mathfrak R$
is locally o-minimal, then it is PCC if and only if it is CC, if and only if it is QCC.
Thus, when dealing with locally o-minimal expansions of
![]() $(\mathbb R,<)$
, we may work with any of the conditions (PCC, CC or QCC) as convenient. We present a class of examples.
$(\mathbb R,<)$
, we may work with any of the conditions (PCC, CC or QCC) as convenient. We present a class of examples.
Proposition 1.8. Let
![]() $\mathfrak R$
be an expansion of
$\mathfrak R$
be an expansion of
![]() $(\mathbb R,<,+,\mid )$
by subsets of various
$(\mathbb R,<,+,\mid )$
by subsets of various
![]() $\mathbb N^n$
.
$\mathbb N^n$
.
-
(1) Every bounded definable set is definable in
 $(\mathbb R,<,+)$
.
$(\mathbb R,<,+)$
. -
(2) If E is definable and connected, then for all
 $x,y\in E$
there is a path in E definable in
$x,y\in E$
there is a path in E definable in
 $(\mathbb R,<,+)$
joining x to y.
$(\mathbb R,<,+)$
joining x to y. -
(3)
 $\mathfrak R$
is PCC.
$\mathfrak R$
is PCC.
Remarks. (a) Thus,
![]() $\mathfrak R$
is not just locally o-minimal, but “locally o-minimal with respect to
$\mathfrak R$
is not just locally o-minimal, but “locally o-minimal with respect to
![]() $(\mathbb R,<,+)$
.” This is neither surprising nor necessarily original, nor it is difficult to then derive (2). The point is that
$(\mathbb R,<,+)$
.” This is neither surprising nor necessarily original, nor it is difficult to then derive (2). The point is that
![]() $\mathfrak R$
is PCC; our proof of this requires (2) and our proof of (1). (b) Trivially, the theory of the expansion of
$\mathfrak R$
is PCC; our proof of this requires (2) and our proof of (1). (b) Trivially, the theory of the expansion of
![]() $\mathbb R$
by all subsets of each
$\mathbb R$
by all subsets of each
![]() $\mathbb N^n$
interprets every countable theory. Thus, in contrast to its local geometry, the model theory of
$\mathbb N^n$
interprets every countable theory. Thus, in contrast to its local geometry, the model theory of
![]() $\mathfrak R$
can be quite wild. (c) The group structure is not necessary for either (1) or (3) to hold, but (2) can fail. To illustrate, it is not hard to check (or see [Reference Miller and Thamrongthanyalak15]) that the expansion of
$\mathfrak R$
can be quite wild. (c) The group structure is not necessary for either (1) or (3) to hold, but (2) can fail. To illustrate, it is not hard to check (or see [Reference Miller and Thamrongthanyalak15]) that the expansion of
![]() $(\mathbb R,<)$
by all subsets of each
$(\mathbb R,<)$
by all subsets of each
![]() $\mathbb N^n$
is PCC, and every definable subset of any
$\mathbb N^n$
is PCC, and every definable subset of any
![]() $(-\infty ,b)^n$
with
$(-\infty ,b)^n$
with
![]() $b\in \mathbb R$
is definable in
$b\in \mathbb R$
is definable in
![]() $(\mathbb R,<)$
. But there is no definable path joining any point in the definable set
$(\mathbb R,<)$
. But there is no definable path joining any point in the definable set
![]() $(-\infty ,1)\times (-\infty ,2)$
to the point
$(-\infty ,1)\times (-\infty ,2)$
to the point
![]() $(1,2)$
.
$(1,2)$
.
Observe that
![]() $\mathbb N$
is
$\mathbb N$
is
![]() $\emptyset $
-interdefinable with
$\emptyset $
-interdefinable with
![]() $\mathbb Z$
over
$\mathbb Z$
over
![]() $(\mathbb R,<,+)$
. By combining results 1.5, 1.7 and 1.8, we obtain the following characterization.
$(\mathbb R,<,+)$
. By combining results 1.5, 1.7 and 1.8, we obtain the following characterization.
Theorem 1.9. If
![]() $\mathfrak R$
is an expansion of
$\mathfrak R$
is an expansion of
![]() $(\mathbb R,<,+,\mathbb Z)$
by subsets of various
$(\mathbb R,<,+,\mathbb Z)$
by subsets of various
![]() $\mathbb Z^n$
, then
$\mathbb Z^n$
, then
![]() $\mathfrak R$
is PCC, CC or QCC if and only if it defines all arithmetic sets.
$\mathfrak R$
is PCC, CC or QCC if and only if it defines all arithmetic sets.
We now say more about the original motivation for this work. One might be interested in understanding “reachability” properties of given
![]() $E\subseteq \mathbb R^n$
. This can be made more precise by considering what is known if
$E\subseteq \mathbb R^n$
. This can be made more precise by considering what is known if
![]() $(\mathbb R,+,\cdot ,E)$
is o-minimal. Since path components of E are definable, it suffices to consider the case that E is path connected; then it is path connected in a strong sense: (a) there is a definable map
$(\mathbb R,+,\cdot ,E)$
is o-minimal. Since path components of E are definable, it suffices to consider the case that E is path connected; then it is path connected in a strong sense: (a) there is a definable map
![]() $\gamma \colon E^2\times [0,1]\to E$
such that, for all
$\gamma \colon E^2\times [0,1]\to E$
such that, for all
![]() $x,y\in E$
, the path
$x,y\in E$
, the path
![]() $t\mapsto \gamma (x,y,t)\colon [0,1]\to E$
is rectifiable and joins x to y; (b) if moreover E is compact, then there is a definable function
$t\mapsto \gamma (x,y,t)\colon [0,1]\to E$
is rectifiable and joins x to y; (b) if moreover E is compact, then there is a definable function
![]() $f\colon [0,\infty )\to [0,\infty )$
such that, for all
$f\colon [0,\infty )\to [0,\infty )$
such that, for all
![]() $x,y\in E$
, the length of
$x,y\in E$
, the length of
![]() $t\mapsto \gamma (x,y,t)$
is bounded by
$t\mapsto \gamma (x,y,t)$
is bounded by
![]() $f(\| x-y\|)$
. (See [Reference van den Dries and Miller6, 4.21] for details.) These are desirable properties in real-analytic geometry and control theory, and we hope that at least something similar will hold for certain cases that
$f(\| x-y\|)$
. (See [Reference van den Dries and Miller6, 4.21] for details.) These are desirable properties in real-analytic geometry and control theory, and we hope that at least something similar will hold for certain cases that
![]() $(\mathbb R,+,\cdot ,E)$
is not o-minimal. Here is a case of particular interest. Let
$(\mathbb R,+,\cdot ,E)$
is not o-minimal. Here is a case of particular interest. Let
![]() $\omega $
be a nonzero real number, S be the logarithmic spiral
$\omega $
be a nonzero real number, S be the logarithmic spiral
![]() $ \{\, e^t\cos (\omega t),e^t\sin (\omega t): t \in \mathbb R\,\} $
, and E be definable in
$ \{\, e^t\cos (\omega t),e^t\sin (\omega t): t \in \mathbb R\,\} $
, and E be definable in
![]() $(\mathbb R,+,\cdot ,S)$
. Evidently,
$(\mathbb R,+,\cdot ,S)$
. Evidently,
![]() $(\mathbb R,+,\cdot ,S)$
is not locally o-minimal, but it is known to have a number of desirable analytic-geometric properties; see, e.g., [Reference Miller14, 4.4], [Reference Miller and Thamrongthanyalak16], and [Reference Tychonievich25, Theorem 4.1.1]. Some of these properties, in combination with Theorem 1.2, reveal that
$(\mathbb R,+,\cdot ,S)$
is not locally o-minimal, but it is known to have a number of desirable analytic-geometric properties; see, e.g., [Reference Miller14, 4.4], [Reference Miller and Thamrongthanyalak16], and [Reference Tychonievich25, Theorem 4.1.1]. Some of these properties, in combination with Theorem 1.2, reveal that
![]() $(\mathbb R,+,\cdot ,S)$
is not PCC, but perhaps there might be PCC expansions of
$(\mathbb R,+,\cdot ,S)$
is not PCC, but perhaps there might be PCC expansions of
![]() $(\mathbb R,+,\cdot ,S)$
in which most of these good properties, or variants thereof, are preserved. At present, all we know is that there exist PCC expansions
$(\mathbb R,+,\cdot ,S)$
in which most of these good properties, or variants thereof, are preserved. At present, all we know is that there exist PCC expansions
![]() $(\mathbb R,+,\cdot ,S)$
that preserve some of its good properties but fail to preserve some others. It remains to be seen if enough of the properties useful for reachability analysis can be preserved in a PCC expansion of
$(\mathbb R,+,\cdot ,S)$
that preserve some of its good properties but fail to preserve some others. It remains to be seen if enough of the properties useful for reachability analysis can be preserved in a PCC expansion of
![]() $(\mathbb R,+,\cdot ,S)$
. See also [Reference Aschenbrenner and Thamrongthanyalak1, Reference Lafferriere and Miller11, Reference Sokantika and Thamrongthanyalak22, Reference Thamrongthanyalak24] for some related material on reachability properties of sets definable in certain expansions of
$(\mathbb R,+,\cdot ,S)$
. See also [Reference Aschenbrenner and Thamrongthanyalak1, Reference Lafferriere and Miller11, Reference Sokantika and Thamrongthanyalak22, Reference Thamrongthanyalak24] for some related material on reachability properties of sets definable in certain expansions of
![]() $(\mathbb R,<)$
.
$(\mathbb R,<)$
.
The previous paragraph explains somewhat why we have so far mentioned only working over the real line. But the question does arise: What about expansions of other dense linear orders, or even more generally, first-order topological structures as defined in [Reference Pillay19]? We defer discussion of these more general settings to the end of the paper.
Some history and attributions
The original questions underlying this research were raised by Thamrongthanyalak in conversations with Miller. Some early results, including some first steps toward Theorem 1.9, were documented in [Reference Miller and Thamrongthanyalak15]. (See also [Reference Fornasiero7].) Savatovsky became interested in the project after attending a presentation by Miller at Universität Konstanz in May 2017, subsequently leading to the establishment of Proposition 1.5 and the motivating case (namely,
![]() $\mathfrak R=(\mathbb R,<,+,\mid )$
) for Proposition 1.8. The proof of Proposition 1.8.3 presented here is due essentially to Dolich. Some earlier work of Kawakami et al. [Reference Kawakami, Takeuchi, Tanaka and Tsuboi10, Section 4] is related to Proposition 1.8.1, but the different setting makes comparisons cumbersome.
$\mathfrak R=(\mathbb R,<,+,\mid )$
) for Proposition 1.8. The proof of Proposition 1.8.3 presented here is due essentially to Dolich. Some earlier work of Kawakami et al. [Reference Kawakami, Takeuchi, Tanaka and Tsuboi10, Section 4] is related to Proposition 1.8.1, but the different setting makes comparisons cumbersome.
2 Proofs
We now provide proofs of the results stated in the introduction (but not in the same order as they were stated). As before,
![]() $\mathfrak R$
denotes an arbitrary expansion of
$\mathfrak R$
denotes an arbitrary expansion of
![]() $(\mathbb R,<)$
.
$(\mathbb R,<)$
.
We begin with some conventions and routine facts from topology. Let Y be a topological space and
![]() $X\subseteq Y$
. The closure of X is denoted by
$X\subseteq Y$
. The closure of X is denoted by
![]() $\overline X$
. We say that X is locally connected if, in the subspace topology, X has a basis consisting of connected sets. If
$\overline X$
. We say that X is locally connected if, in the subspace topology, X has a basis consisting of connected sets. If
![]() $u,v\in X$
, then a path in X from u to v is a continuous map
$u,v\in X$
, then a path in X from u to v is a continuous map
![]() $\gamma $
from a nonempty compact interval
$\gamma $
from a nonempty compact interval
![]() $[a,b]\subseteq \mathbb R$
into Y such that
$[a,b]\subseteq \mathbb R$
into Y such that
![]() $\gamma (a)=u$
,
$\gamma (a)=u$
,
![]() $\gamma (b)=v$
, and
$\gamma (b)=v$
, and
![]() $\gamma ([a,b])\subseteq X$
. The set X is path connected if for every
$\gamma ([a,b])\subseteq X$
. The set X is path connected if for every
![]() $u,v\in X$
there is a path in X from u to v, and is locally path connected if, in the subspace topology, X has a basis consisting of path-connected sets.
$u,v\in X$
there is a path in X from u to v, and is locally path connected if, in the subspace topology, X has a basis consisting of path-connected sets.
2.1
Here are some facts to keep in mind.
-
• The component of
 $y\in Y$
is the union of all connected sets containing y (and similarly for path components).
$y\in Y$
is the union of all connected sets containing y (and similarly for path components). -
• The quasicomponent of
 $y\in Y$
is the intersection of all clopen sets containing y.
$y\in Y$
is the intersection of all clopen sets containing y. -
• If X is a component or a quasicomponent of Y, then X is closed.
-
• If Y is locally connected, then its quasicomponents and its components are the same.
-
• If Y is locally path connected, then its path components and its components are the same (which in turn are the same as its quasicomponents).
-
• If Y has a countable basis at
 $y\in Y$
consisting of connected sets and
$y\in Y$
consisting of connected sets and
 $Y\setminus \{y\}$
is locally path connected, then Y is locally path connected.
$Y\setminus \{y\}$
is locally path connected, then Y is locally path connected.
Remark. There are closed subsets of
![]() $\mathbb R^2$
having quasicomponents that are not components, e.g.,
$\mathbb R^2$
having quasicomponents that are not components, e.g.,
![]() $\{-1,1\}\times \mathbb R$
is a quasicomponent of the closure of the union of the boundaries of the boxes
$\{-1,1\}\times \mathbb R$
is a quasicomponent of the closure of the union of the boundaries of the boxes
![]() $ (-1+2^{-n}, 1-2^{-n})\times (-2^n,2^n)$
,
$ (-1+2^{-n}, 1-2^{-n})\times (-2^n,2^n)$
,
![]() $n\in \mathbb N$
.
$n\in \mathbb N$
.
Proof of Proposition 1.1 Suppose that
![]() $\mathfrak R$
expands
$\mathfrak R$
expands
![]() $(\mathbb R,+,\cdot ,\mathbb N)$
. We show that
$(\mathbb R,+,\cdot ,\mathbb N)$
. We show that
![]() $\mathfrak R$
is PCC, CC and QCC. Let
$\mathfrak R$
is PCC, CC and QCC. Let
![]() $n\in \mathbb N$
. Recall (see, e.g., [Reference van den Dries5, p. 16]) that there exist
$n\in \mathbb N$
. Recall (see, e.g., [Reference van den Dries5, p. 16]) that there exist
![]() $m\in \mathbb N$
and
$m\in \mathbb N$
and
![]() $Z\subseteq \mathbb R^m\times \mathbb R^n$
such that Z is
$Z\subseteq \mathbb R^m\times \mathbb R^n$
such that Z is
![]() $\emptyset $
- definable in
$\emptyset $
- definable in
![]() $(\mathbb R,+,\cdot ,\mathbb N)$
and
$(\mathbb R,+,\cdot ,\mathbb N)$
and
![]() $ \bigl \{\, \{\, y\in \mathbb R^n: (a,y)\in Z\,\}: a\in \mathbb R^m\,\bigr \} $
is exactly the collection of the closed subsets of
$ \bigl \{\, \{\, y\in \mathbb R^n: (a,y)\in Z\,\}: a\in \mathbb R^m\,\bigr \} $
is exactly the collection of the closed subsets of
![]() $\mathbb R^n$
. Let
$\mathbb R^n$
. Let
![]() $E\subseteq \mathbb R^n$
. If X is either a component or a quasicomponent of E, then X is closed in E, and so
$E\subseteq \mathbb R^n$
. If X is either a component or a quasicomponent of E, then X is closed in E, and so
![]() $(\mathbb R,+,\cdot ,\mathbb N,E)$
defines X. Let X be a path component of E; we show that
$(\mathbb R,+,\cdot ,\mathbb N,E)$
defines X. Let X be a path component of E; we show that
![]() $(\mathbb R,+,\cdot ,\mathbb N,E)$
defines X. It suffices to fix
$(\mathbb R,+,\cdot ,\mathbb N,E)$
defines X. It suffices to fix
![]() $x\in X$
and show that the set of all
$x\in X$
and show that the set of all
![]() $v\in \mathbb R^n$
for which there is a path in E from x to v is definable in
$v\in \mathbb R^n$
for which there is a path in E from x to v is definable in
![]() $(\mathbb R,Z,E)$
. Now,
$(\mathbb R,Z,E)$
. Now,
![]() $v\in X$
if and only if there is a continuous
$v\in X$
if and only if there is a continuous
![]() $\gamma \colon [0,1]\to \mathbb R^n$
such that
$\gamma \colon [0,1]\to \mathbb R^n$
such that
![]() $\gamma (0)=x$
,
$\gamma (0)=x$
,
![]() $\gamma (1)=v$
, and the image of
$\gamma (1)=v$
, and the image of
![]() $[0,1]$
under
$[0,1]$
under
![]() $\gamma $
is contained in E. To put this another way,
$\gamma $
is contained in E. To put this another way,
![]() $v\in X$
if and only if there exists
$v\in X$
if and only if there exists
![]() $a\in \mathbb R^m$
such that: the fiber
$a\in \mathbb R^m$
such that: the fiber
![]() $Z_a:=\{\, y\in \mathbb R^n: (a,y)\in Z\,\}$
is a bounded subset of E; for all
$Z_a:=\{\, y\in \mathbb R^n: (a,y)\in Z\,\}$
is a bounded subset of E; for all
![]() $t\in [0,1]$
there exists a unique
$t\in [0,1]$
there exists a unique
![]() $y\in \mathbb R^n$
such that
$y\in \mathbb R^n$
such that
![]() $(t,y)\in [0,1]\times Z_a$
; and, the points
$(t,y)\in [0,1]\times Z_a$
; and, the points
![]() $(0,x)$
and
$(0,x)$
and
![]() $(1,v)$
belong to
$(1,v)$
belong to
![]() $[0,1]\times Z_a$
. (The resulting function is continuous because its graph is closed.) As the set of all such v is definable in
$[0,1]\times Z_a$
. (The resulting function is continuous because its graph is closed.) As the set of all such v is definable in
![]() $(\mathbb R,+,\cdot ,\mathbb N,E)$
, so is X.
$(\mathbb R,+,\cdot ,\mathbb N,E)$
, so is X.
Suppose that
![]() $\mathfrak R$
is o-minimal. We show that
$\mathfrak R$
is o-minimal. We show that
![]() $\mathfrak R$
is PCC, CC and QCC. Each definable set has only finitely many components, each of which is definable [Reference van den Dries5, Chapter 3, (2.18) and (2.19).7]. Hence,
$\mathfrak R$
is PCC, CC and QCC. Each definable set has only finitely many components, each of which is definable [Reference van den Dries5, Chapter 3, (2.18) and (2.19).7]. Hence,
![]() $\mathfrak R$
is CC. For PCC and QCC, it suffices by the basic topological facts to show that every definable set is locally path connected. By cell decomposition and a routine induction on dimension, it suffices to let
$\mathfrak R$
is CC. For PCC and QCC, it suffices by the basic topological facts to show that every definable set is locally path connected. By cell decomposition and a routine induction on dimension, it suffices to let
![]() $C\subseteq \mathbb R^n$
be a cell of
$C\subseteq \mathbb R^n$
be a cell of
![]() $\mathfrak R$
and
$\mathfrak R$
and
![]() $y\in \overline {C}\setminus C$
, and show that
$y\in \overline {C}\setminus C$
, and show that
![]() $\{y\}\cup C$
is locally path connected. It is an exercise to see that
$\{y\}\cup C$
is locally path connected. It is an exercise to see that
![]() $\{y\}\cup C$
is locally connected at y (indeed, see [Reference van den Dries5, Chapter 3, (2.19).8]), that is, in the subspace topology,
$\{y\}\cup C$
is locally connected at y (indeed, see [Reference van den Dries5, Chapter 3, (2.19).8]), that is, in the subspace topology,
![]() $\{y\}\cup C$
has a basis at y consisting of connected sets; as we are working over
$\{y\}\cup C$
has a basis at y consisting of connected sets; as we are working over
![]() $\mathbb R$
, we may take this basis to be countable. Now,
$\mathbb R$
, we may take this basis to be countable. Now,
![]() $(\{y\}\cup C)\setminus \{y\}=C$
, and cells are locally path connected. By the last item of 2.1,
$(\{y\}\cup C)\setminus \{y\}=C$
, and cells are locally path connected. By the last item of 2.1,
![]() $\{y\}\cup C$
is locally path connected at y (as was to be shown).
$\{y\}\cup C$
is locally path connected at y (as was to be shown).
Proof of Proposition 1.6 This is mostly just an exercise, so we give only an outline.
(1)
![]() $\Rightarrow $
(2). Let
$\Rightarrow $
(2). Let
![]() $\mathfrak R$
be locally o-minimal. Let
$\mathfrak R$
be locally o-minimal. Let
![]() $E\subseteq \mathbb R^n$
be bounded and definable. We contend that the expansion of
$E\subseteq \mathbb R^n$
be bounded and definable. We contend that the expansion of
![]() $(\mathbb R,<)$
by all definable subsets of E is o-minimal. By the Bolzano–Weierstrass Theorem, every bounded subset of
$(\mathbb R,<)$
by all definable subsets of E is o-minimal. By the Bolzano–Weierstrass Theorem, every bounded subset of
![]() $\mathbb R$
definable in
$\mathbb R$
definable in
![]() $\mathfrak R$
is a finite union of points and open intervals. Thus, there is an open interval
$\mathfrak R$
is a finite union of points and open intervals. Thus, there is an open interval
![]() $I\subseteq \mathbb R$
such that the expansion of
$I\subseteq \mathbb R$
such that the expansion of
![]() $(I,<)$
by all subsets of E definable in
$(I,<)$
by all subsets of E definable in
![]() $\mathfrak R$
is o-minimal. It is now routine to see that the expansion of
$\mathfrak R$
is o-minimal. It is now routine to see that the expansion of
![]() $(\mathbb R,<)$
by all definable subsets of E is also o-minimal.
$(\mathbb R,<)$
by all definable subsets of E is also o-minimal.
(2)
![]() $\Rightarrow $
(3). Recall the proof of Proposition 1.1.
$\Rightarrow $
(3). Recall the proof of Proposition 1.1.
(3)
![]() $\Rightarrow $
(4) is just topology, and (4)
$\Rightarrow $
(4) is just topology, and (4)
![]() $\Rightarrow $
((5) & (6)) is trivial.
$\Rightarrow $
((5) & (6)) is trivial.
(5)
![]() $\Rightarrow $
(7). If
$\Rightarrow $
(7). If
![]() $E\subseteq \mathbb R$
has empty interior and a limit point c, then
$E\subseteq \mathbb R$
has empty interior and a limit point c, then
is connected, but not path connected.
(6)
![]() $\Rightarrow $
(7). If
$\Rightarrow $
(7). If
![]() $E\subseteq \mathbb R$
has empty interior and a limit point c, then
$E\subseteq \mathbb R$
has empty interior and a limit point c, then
![]() $\{(c,0),(c,1)\}$
is a quasicomponent of its union with
$\{(c,0),(c,1)\}$
is a quasicomponent of its union with
![]() $(E\setminus \{c\})\times [0,1]$
.
$(E\setminus \{c\})\times [0,1]$
.
(7)
![]() $\Rightarrow $
(1). The boundary of every definable subset of
$\Rightarrow $
(1). The boundary of every definable subset of
![]() $\mathbb R$
is closed and discrete.
$\mathbb R$
is closed and discrete.
Proof of Proposition 1.5 Suppose that
![]() $\mathfrak R$
defines
$\mathfrak R$
defines
![]() $\mathbb N$
and is PCC, CC or QCC. We show that
$\mathbb N$
and is PCC, CC or QCC. We show that
![]() $\mathfrak R$
defines
$\mathfrak R$
defines
![]() $\mid $
. For
$\mid $
. For
![]() $d\in \mathbb N$
, put
$d\in \mathbb N$
, put
![]() $d\mathbb N:=\{\, dn: n\in \mathbb N\,\}$
. As
$d\mathbb N:=\{\, dn: n\in \mathbb N\,\}$
. As
![]() $a\mid b$
if and only if
$a\mid b$
if and only if
![]() $b\mathbb N\subseteq a\mathbb N$
, it suffices to show that
$b\mathbb N\subseteq a\mathbb N$
, it suffices to show that
![]() $\bigcup _{d\in \mathbb N}( \{d\}\times d\mathbb N)$
is definable.
$\bigcup _{d\in \mathbb N}( \{d\}\times d\mathbb N)$
is definable.
First we show that each
![]() $d\mathbb N$
is definable. Let
$d\mathbb N$
is definable. Let
![]() $\mathbb S_0$
be the intersection of the boundary of
$\mathbb S_0$
be the intersection of the boundary of
![]() $(0,\infty )^3$
with the union of the boundaries of the boxes
$(0,\infty )^3$
with the union of the boundaries of the boxes
![]() $(-n,n)^3$
,
$(-n,n)^3$
,
![]() $0<n\in \mathbb N$
. Put
$0<n\in \mathbb N$
. Put
![]() $P=\{\, (x,0,z)\in \mathbb R^3: x,z>0\,\}$
. For
$P=\{\, (x,0,z)\in \mathbb R^3: x,z>0\,\}$
. For
![]() $d\in \mathbb N$
, put
$d\in \mathbb N$
, put
In words,
![]() $\mathbb {S}_d$
is the result of replacing
$\mathbb {S}_d$
is the result of replacing
![]() $\mathbb S_0\cap P$
by shifting it d units in the positive x direction and then filling in the resulting gaps with the line segments
$\mathbb S_0\cap P$
by shifting it d units in the positive x direction and then filling in the resulting gaps with the line segments
![]() $[0,d]\times \{0\}\times \{n\}$
,
$[0,d]\times \{0\}\times \{n\}$
,
![]() $n>0$
. (See Figure 1 for
$n>0$
. (See Figure 1 for
![]() $d=2$
.) Observe that
$d=2$
.) Observe that
![]() $\mathbb S_d$
is locally path connected, definable in
$\mathbb S_d$
is locally path connected, definable in
![]() $(\mathbb R,<,\mathbb N)$
and
$(\mathbb R,<,\mathbb N)$
and
![]() $(d,0,0)\in \mathbb S_d$
. Let
$(d,0,0)\in \mathbb S_d$
. Let
![]() $C_d$
be the component of
$C_d$
be the component of
![]() $\mathbb S_d$
that contains
$\mathbb S_d$
that contains
![]() $(d,0,0)$
; then
$(d,0,0)$
; then
![]() $C_d$
is also the path component and the quasicomponent that contains
$C_d$
is also the path component and the quasicomponent that contains
![]() $(d,0,0)$
, and thus is definable. The intersection of
$(d,0,0)$
, and thus is definable. The intersection of
![]() $C_d$
with the positive x-axis is the set
$C_d$
with the positive x-axis is the set
![]() $\{\, (d(n+1),0,0):n\in \mathbb N\,\}$
. (See Figure 2 for
$\{\, (d(n+1),0,0):n\in \mathbb N\,\}$
. (See Figure 2 for
![]() $d=2$
.) As
$d=2$
.) As
![]() $C_d$
is definable, so is
$C_d$
is definable, so is
![]() $d\mathbb N$
. Note that we could have obtained
$d\mathbb N$
. Note that we could have obtained
![]() $d\mathbb N$
instead by first obtaining the set
$d\mathbb N$
instead by first obtaining the set
![]() $\{\, dn+1: n\in \mathbb N\,\}$
, which is the intersection of the positive x-axis with the component of
$\{\, dn+1: n\in \mathbb N\,\}$
, which is the intersection of the positive x-axis with the component of
![]() $\mathbb S_d$
that contains
$\mathbb S_d$
that contains
![]() $(1,0,0)$
.
$(1,0,0)$
.

Figure 1
![]() $\mathbb S_2$
near the origin.
$\mathbb S_2$
near the origin.

Figure 2
![]() $C_2$
near the origin.
$C_2$
near the origin.
Let
![]() $+{\restriction } \mathbb N^2$
denote addition on
$+{\restriction } \mathbb N^2$
denote addition on
![]() $\mathbb N$
, regarded as a subset of
$\mathbb N$
, regarded as a subset of
![]() $\mathbb R^3$
. Examination of the construction of the sets
$\mathbb R^3$
. Examination of the construction of the sets
![]() $\mathbb S_d$
yields that
$\mathbb S_d$
yields that
![]() $\bigcup _{d\in \mathbb N}( \{d\}\times \mathbb S_d)$
is locally path connected and definable in
$\bigcup _{d\in \mathbb N}( \{d\}\times \mathbb S_d)$
is locally path connected and definable in
![]() $(\mathbb R,<,+{\restriction }\mathbb N^2)$
(because shifting by d units along the positive x-axis is uniformly definable). Let C be the component of
$(\mathbb R,<,+{\restriction }\mathbb N^2)$
(because shifting by d units along the positive x-axis is uniformly definable). Let C be the component of
![]() $ \{\, (t,1,0,0): t\in \mathbb R\,\}\cup \bigcup _{d\in \mathbb N}( \{d\}\times \mathbb S_d) $
that contains
$ \{\, (t,1,0,0): t\in \mathbb R\,\}\cup \bigcup _{d\in \mathbb N}( \{d\}\times \mathbb S_d) $
that contains
![]() $(1,1,0,0)$
. Again, C is also the path component and the quasicomponent that contains
$(1,1,0,0)$
. Again, C is also the path component and the quasicomponent that contains
![]() $(1,1,0,0)$
, and thus is definable. Observe that
$(1,1,0,0)$
, and thus is definable. Observe that
![]() $ C\cap \{\, (j,k,0,0): j,k\in \mathbb N\,\}=\bigcup _{d\in \mathbb N}\{\, (d,dn+1,0,0): n\in \mathbb N\,\}. $
Thus,
$ C\cap \{\, (j,k,0,0): j,k\in \mathbb N\,\}=\bigcup _{d\in \mathbb N}\{\, (d,dn+1,0,0): n\in \mathbb N\,\}. $
Thus,
![]() $\bigcup _{d\in \mathbb N}(\{d\}\times \{\, dn+1: n\in \mathbb N\,\})$
is definable, yielding that
$\bigcup _{d\in \mathbb N}(\{d\}\times \{\, dn+1: n\in \mathbb N\,\})$
is definable, yielding that
![]() $\bigcup _{d\in \mathbb N}( \{d\}\times d\mathbb N)$
is definable (as was to be shown). Hence, in order to finish the proof, it suffices to show that
$\bigcup _{d\in \mathbb N}( \{d\}\times d\mathbb N)$
is definable (as was to be shown). Hence, in order to finish the proof, it suffices to show that
![]() $\{\, (a,b,c)\in \mathbb N^3: a\leq b\And a+b=c\,\}$
is definable (as then
$\{\, (a,b,c)\in \mathbb N^3: a\leq b\And a+b=c\,\}$
is definable (as then
![]() $+{\restriction }\mathbb N^2$
is also definable).
$+{\restriction }\mathbb N^2$
is also definable).
Let
![]() $\chi $
denote the characteristic function of the set of odd natural numbers as a subset of
$\chi $
denote the characteristic function of the set of odd natural numbers as a subset of
![]() $\mathbb R$
. For each
$\mathbb R$
. For each
![]() $m,n\in \mathbb N$
with
$m,n\in \mathbb N$
with
![]() $m\leq n$
, let
$m\leq n$
, let
![]() $\varGamma _{m,n}$
be the union of the images of the paths
$\varGamma _{m,n}$
be the union of the images of the paths
 $$ \begin{align*} t\mapsto (m,n,t,\chi(m)t,\chi(n)t)\colon& [0,1]\to\mathbb R^5, \\ t\mapsto (t,n,1,\chi(m),\chi(n))\colon& [m,m+1]\to \mathbb R^5, \\ t\mapsto (m+1,t,1,\chi(m),\chi(n))\colon& [n,n+1]\to\mathbb R^5, \\ t\mapsto (m+1,n+1,t,\chi(m)t,\chi(n)t)\colon& [0,1]\to\mathbb R^5. \end{align*} $$
$$ \begin{align*} t\mapsto (m,n,t,\chi(m)t,\chi(n)t)\colon& [0,1]\to\mathbb R^5, \\ t\mapsto (t,n,1,\chi(m),\chi(n))\colon& [m,m+1]\to \mathbb R^5, \\ t\mapsto (m+1,t,1,\chi(m),\chi(n))\colon& [n,n+1]\to\mathbb R^5, \\ t\mapsto (m+1,n+1,t,\chi(m)t,\chi(n)t)\colon& [0,1]\to\mathbb R^5. \end{align*} $$
Each path is definable in
![]() $(\mathbb R,<)$
, and
$(\mathbb R,<)$
, and
![]() $\varGamma _{m,n}$
is definable in
$\varGamma _{m,n}$
is definable in
![]() $(\mathbb R,<)$
, connected and compact. If
$(\mathbb R,<)$
, connected and compact. If
![]() $j,k\in \mathbb N$
and
$j,k\in \mathbb N$
and
![]() $j\leq k$
, then
$j\leq k$
, then
![]() $\varGamma _{j,k}\cap \varGamma _{m,n}$
is equal to one of the following:
$\varGamma _{j,k}\cap \varGamma _{m,n}$
is equal to one of the following:
It is perhaps helpful to regard the pair
![]() $(\chi (m),\chi (n))\in \{0,1\}^2$
as a color assigned to the projection of
$(\chi (m),\chi (n))\in \{0,1\}^2$
as a color assigned to the projection of
![]() $\varGamma _{m,n}$
on the first three coordinates, and then to regard projections having different colors as being disjoint except possibly at the endpoints in the
$\varGamma _{m,n}$
on the first three coordinates, and then to regard projections having different colors as being disjoint except possibly at the endpoints in the
![]() $xy$
-plane (see Figure 3). Hence, for each
$xy$
-plane (see Figure 3). Hence, for each
![]() $d\in \mathbb N$
,
$d\in \mathbb N$
,
![]() $ \{d\}\times \bigcup _{k\in \mathbb N}\varGamma _{k,d+k} $
is the component of
$ \{d\}\times \bigcup _{k\in \mathbb N}\varGamma _{k,d+k} $
is the component of
![]() $ \{d\}\times \bigcup _{m,n\in \mathbb N}\varGamma _{m,n} $
that contains
$ \{d\}\times \bigcup _{m,n\in \mathbb N}\varGamma _{m,n} $
that contains
![]() $(d,0,d,0,0,0)$
. Let L be the line in
$(d,0,d,0,0,0)$
. Let L be the line in
![]() $\mathbb R^6$
containing both the origin and
$\mathbb R^6$
containing both the origin and
![]() $(1,0,1,0,0,0)$
. Put
$(1,0,1,0,0,0)$
. Put
![]() $ E=L\cup \bigl (\mathbb N\times \bigcup _{m\leq n\in \mathbb N}\varGamma _{m,n}\bigr ) $
and note that E is definable in
$ E=L\cup \bigl (\mathbb N\times \bigcup _{m\leq n\in \mathbb N}\varGamma _{m,n}\bigr ) $
and note that E is definable in
![]() $(\mathbb R,<,\mathbb N,2\mathbb N)$
. Let D be the component of E that contains the origin. As before, D is definable. It is routine to see that
$(\mathbb R,<,\mathbb N,2\mathbb N)$
. Let D be the component of E that contains the origin. As before, D is definable. It is routine to see that
![]() $ L\cup \bigcup _{d,k\in \mathbb N} \bigl (\{d\}\times \varGamma _{k,d+k}\bigr ) $
is closed, contained in D, and open in D; thus,
$ L\cup \bigcup _{d,k\in \mathbb N} \bigl (\{d\}\times \varGamma _{k,d+k}\bigr ) $
is closed, contained in D, and open in D; thus,
![]() $ D=L\cup \bigcup _{d,k\in \mathbb N} \bigl (\{d\}\times \varGamma _{k,d+k}\bigr ) $
. If
$ D=L\cup \bigcup _{d,k\in \mathbb N} \bigl (\{d\}\times \varGamma _{k,d+k}\bigr ) $
. If
![]() $(a,b,c)\in \mathbb N^3$
, then
$(a,b,c)\in \mathbb N^3$
, then
![]() $(a,b,c,0,0,0)\in D$
if and only if
$(a,b,c,0,0,0)\in D$
if and only if
![]() $a\leq b$
and
$a\leq b$
and
![]() $c=a+b$
. Hence,
$c=a+b$
. Hence,
![]() $\{\, (a,b,c)\in \mathbb N^3: a\leq b\And a+b=c\,\}$
is definable, as was to be shown.
$\{\, (a,b,c)\in \mathbb N^3: a\leq b\And a+b=c\,\}$
is definable, as was to be shown.
Note
We did not need PCC, CC or QCC per se, only that certain rather special kinds of path-connected subsets of certain rather special definable sets are definable. We discuss this further at the end of the paper.

Figure 3 The projection of
![]() $\varGamma _{m,n}$
on the first three coordinates.
$\varGamma _{m,n}$
on the first three coordinates.
Proof of Theorem 1.4 Let
![]() $\emptyset \neq A\subseteq \mathbb R$
have empty interior and
$\emptyset \neq A\subseteq \mathbb R$
have empty interior and
![]() $f\colon A\to A$
be strictly increasing and strictly dominating the identity. We find a strictly increasing
$f\colon A\to A$
be strictly increasing and strictly dominating the identity. We find a strictly increasing
![]() $\sigma \colon \mathbb N\to \mathbb R$
such that every expansion of
$\sigma \colon \mathbb N\to \mathbb R$
such that every expansion of
![]() $(\mathbb R,<,f)$
that is PCC, CC or QCC also defines
$(\mathbb R,<,f)$
that is PCC, CC or QCC also defines
![]() $\{\, (\sigma (m),\sigma (n)): m \mid n\,\}$
. Note that A cannot have a maximal element and there exists
$\{\, (\sigma (m),\sigma (n)): m \mid n\,\}$
. Note that A cannot have a maximal element and there exists
![]() $a_0\in A$
such that
$a_0\in A$
such that
![]() $A\cap [a_0,\infty )$
is infinite. By replacing A with
$A\cap [a_0,\infty )$
is infinite. By replacing A with
![]() $A\cap [a_0,\infty )$
and f with its restriction to
$A\cap [a_0,\infty )$
and f with its restriction to
![]() $A\cap [a_0,\infty )$
we reduce to the case that
$A\cap [a_0,\infty )$
we reduce to the case that
![]() $\min A$
exists; for ease of notation, say
$\min A$
exists; for ease of notation, say
![]() $\min A=0$
. We obtain a subset S of
$\min A=0$
. We obtain a subset S of
![]() $\mathbb R^3$
by repeating the construction of
$\mathbb R^3$
by repeating the construction of
![]() $\mathbb S_1$
(as in the proof of 1.5), but with A instead of
$\mathbb S_1$
(as in the proof of 1.5), but with A instead of
![]() $\mathbb N$
, and f instead of the successor function on
$\mathbb N$
, and f instead of the successor function on
![]() $\mathbb N$
. Note that S is definable in
$\mathbb N$
. Note that S is definable in
![]() $(\mathbb R,<,f)$
. Let P be the path component of S that contains
$(\mathbb R,<,f)$
. Let P be the path component of S that contains
![]() $f(0)$
. Note that P is a component and a quasicomponent of S, and the intersection of P with
$f(0)$
. Note that P is a component and a quasicomponent of S, and the intersection of P with
![]() $[0,\infty )\times \{0\}\times \{0\}$
is the orbit of f on
$[0,\infty )\times \{0\}\times \{0\}$
is the orbit of f on
![]() $f(0)$
. Thus, it suffices to assume that A is the image of a strictly increasing function
$f(0)$
. Thus, it suffices to assume that A is the image of a strictly increasing function
![]() $\mathbb N\to \mathbb R$
and f is the successor function on A; then
$\mathbb N\to \mathbb R$
and f is the successor function on A; then
![]() $\bigl ((-\infty ,\sup A),<,A\bigr )$
is isomorphic to
$\bigl ((-\infty ,\sup A),<,A\bigr )$
is isomorphic to
![]() $(\mathbb R,<,\mathbb N)$
and we apply Proposition 1.5 to finish.
$(\mathbb R,<,\mathbb N)$
and we apply Proposition 1.5 to finish.
Proof of Theorem 1.2 Let
![]() $\mathfrak R$
be an expansion of
$\mathfrak R$
be an expansion of
![]() $(\mathbb R,<,+)$
by Boolean combinations of open sets. Suppose that
$(\mathbb R,<,+)$
by Boolean combinations of open sets. Suppose that
![]() $\mathfrak R$
is PCC, CC or QCC, but is not o-minimal. We find a strictly increasing
$\mathfrak R$
is PCC, CC or QCC, but is not o-minimal. We find a strictly increasing
![]() $\sigma \colon \mathbb N\to \mathbb R$
such that
$\sigma \colon \mathbb N\to \mathbb R$
such that
![]() $\{\, (\sigma (m),\sigma (n)): m \mid n\,\}$
is definable. It suffices by the proof of Theorem 1.4 to show that
$\{\, (\sigma (m),\sigma (n)): m \mid n\,\}$
is definable. It suffices by the proof of Theorem 1.4 to show that
![]() $\mathfrak R$
defines the range of a strictly increasing sequence in
$\mathfrak R$
defines the range of a strictly increasing sequence in
![]() $\mathbb R$
. By Dougherty and Miller [Reference Dougherty and Miller4] and Dolich et al. [Reference Dolich, Miller and Steinhorn3],
$\mathbb R$
. By Dougherty and Miller [Reference Dougherty and Miller4] and Dolich et al. [Reference Dolich, Miller and Steinhorn3],
![]() $\mathfrak R$
defines an infinite discrete
$\mathfrak R$
defines an infinite discrete
![]() $A\subseteq \mathbb R$
. If A is closed, then at least one of
$A\subseteq \mathbb R$
. If A is closed, then at least one of
![]() $A\cap [0,\infty )$
or
$A\cap [0,\infty )$
or
![]() $-A\cap [0,\infty )$
is the range of a strictly increasing sequence. Suppose now that A is not closed. Put
$-A\cap [0,\infty )$
is the range of a strictly increasing sequence. Suppose now that A is not closed. Put
![]() $F=\overline {A}\setminus A$
; then F is nonempty, has no interior, and is closed (because A is locally closed).
$F=\overline {A}\setminus A$
; then F is nonempty, has no interior, and is closed (because A is locally closed).
Suppose that F has no isolated points; then there exists
![]() $N\in \mathbb N $
such that
$N\in \mathbb N $
such that
![]() $F\cap [-N,N]$
is a Cantor set. The set of negatives of lengths of the maximal open intervals of
$F\cap [-N,N]$
is a Cantor set. The set of negatives of lengths of the maximal open intervals of
![]() $[-N,N]\setminus F$
is definable and the range of a strictly increasing sequence of real numbers.
$[-N,N]\setminus F$
is definable and the range of a strictly increasing sequence of real numbers.
Suppose that F has an isolated point c. Let
![]() $x,y\in \mathbb R$
be such that
$x,y\in \mathbb R$
be such that
![]() $F\cap (x,y)=\{c\}$
. As c is a limit point of A, at least one of
$F\cap (x,y)=\{c\}$
. As c is a limit point of A, at least one of
![]() $A\cap (x,c)$
or
$A\cap (x,c)$
or
![]() $A\cap (c,y)$
is infinite and discrete; assume the former (the latter is similar). By increasing x, we have that
$A\cap (c,y)$
is infinite and discrete; assume the former (the latter is similar). By increasing x, we have that
![]() $A\cap (x,c)$
is the range of a strictly increasing sequence (because
$A\cap (x,c)$
is the range of a strictly increasing sequence (because
![]() $A\cap (x,c)$
has no limit points in
$A\cap (x,c)$
has no limit points in
![]() $(x,c)$
).
$(x,c)$
).
Remark. The last paragraph of the proof does not require the group structure.
We now begin to work toward the proof of Proposition 1.8.
2.2
Let
![]() $\mathfrak R_0$
be an o-minimal expansion of
$\mathfrak R_0$
be an o-minimal expansion of
![]() $(\mathbb R,<,+)$
such that every bounded set definable in
$(\mathbb R,<,+)$
such that every bounded set definable in
![]() $\mathfrak R$
is definable in
$\mathfrak R$
is definable in
![]() $\mathfrak R_0$
. Let
$\mathfrak R_0$
. Let
![]() $E\subseteq \mathbb R^n$
be connected and definable in
$E\subseteq \mathbb R^n$
be connected and definable in
![]() $\mathfrak R$
. Let
$\mathfrak R$
. Let
![]() $x,y\in E$
. Then there is a path in E definable in
$x,y\in E$
. Then there is a path in E definable in
![]() $\mathfrak R_0$
joining x to y.
$\mathfrak R_0$
joining x to y.
Proof As
![]() $\mathfrak R$
is locally o-minimal, E is path connected. As images of paths are compact, there exist
$\mathfrak R$
is locally o-minimal, E is path connected. As images of paths are compact, there exist
![]() $N\in \mathbb N$
and a path in
$N\in \mathbb N$
and a path in
![]() $E\cap [-N,N]^n$
joining x to y. By assumption,
$E\cap [-N,N]^n$
joining x to y. By assumption,
![]() $E\cap [-N,N]^n$
is definable in
$E\cap [-N,N]^n$
is definable in
![]() $\mathfrak R_0$
. By o-minimality, the path components of
$\mathfrak R_0$
. By o-minimality, the path components of
![]() $E\cap [-N,N]^n$
are definable in
$E\cap [-N,N]^n$
are definable in
![]() $\mathfrak R_0$
. Thus, we may reduce to the case that
$\mathfrak R_0$
. Thus, we may reduce to the case that
![]() $E\cap [-N,N]^n$
is path connected. By Cell Decomposition and Curve Selection, there is a path in
$E\cap [-N,N]^n$
is path connected. By Cell Decomposition and Curve Selection, there is a path in
![]() $E\cap [-N,N]^n$
joining x to y that is definable in
$E\cap [-N,N]^n$
joining x to y that is definable in
![]() $\mathfrak R_0$
.
$\mathfrak R_0$
.
For the remainder of this section, our approach will be more model theoretic than our earlier material. In particular, we use both “expansion” and “reduct” in the traditional first-order syntactic sense, “quantifier-free definable” means “defined by a quantifier-free formula of the language under consideration,” and “QE” abbreviates “quantifier elimination.”
Let
![]() $T_{\mathbb Q}$
be the theory of ordered
$T_{\mathbb Q}$
be the theory of ordered
![]() $\mathbb Q$
-vector spaces with a distinguished positive element, in the language
$\mathbb Q$
-vector spaces with a distinguished positive element, in the language
![]() $L_{\mathbb Q}:=\{\, <,+,0,1\,\}\cup \{\, \lambda _q: q\in \mathbb Q\,\}$
, where
$L_{\mathbb Q}:=\{\, <,+,0,1\,\}\cup \{\, \lambda _q: q\in \mathbb Q\,\}$
, where
![]() $0<1$
and
$0<1$
and
![]() $\lambda _q$
is intended to indicate left scalar multiplication by q. Let
$\lambda _q$
is intended to indicate left scalar multiplication by q. Let
![]() $\left \lfloor \phantom {x}\right \rfloor $
be a new unary function symbol and put
$\left \lfloor \phantom {x}\right \rfloor $
be a new unary function symbol and put
![]() $L_{\mathbb Q}'=L_{\mathbb Q}\cup \{\left \lfloor \phantom {x}\right \rfloor \}$
. Let
$L_{\mathbb Q}'=L_{\mathbb Q}\cup \{\left \lfloor \phantom {x}\right \rfloor \}$
. Let
![]() $T_{\mathbb Q}'$
be the union of
$T_{\mathbb Q}'$
be the union of
![]() $T_{\mathbb Q}$
and the universal closures of the following:
$T_{\mathbb Q}$
and the universal closures of the following:
-
•
 $\left \lfloor \left \lfloor x\right \rfloor +y\right \rfloor =\left \lfloor x\right \rfloor +\left \lfloor y\right \rfloor $
,
$\left \lfloor \left \lfloor x\right \rfloor +y\right \rfloor =\left \lfloor x\right \rfloor +\left \lfloor y\right \rfloor $
, -
•
 $0\leq x<1\rightarrow \left \lfloor x\right \rfloor =0$
,
$0\leq x<1\rightarrow \left \lfloor x\right \rfloor =0$
, -
•
 $\left \lfloor 1\right \rfloor =1$
,
$\left \lfloor 1\right \rfloor =1$
, -
•
 $\left \lfloor x\right \rfloor \leq x<\left \lfloor x\right \rfloor +1$
.
$\left \lfloor x\right \rfloor \leq x<\left \lfloor x\right \rfloor +1$
.
Observe that as
![]() $T_{\mathbb Q}$
is universally axiomatizable, so is
$T_{\mathbb Q}$
is universally axiomatizable, so is
![]() $T_{\mathbb Q}'$
. By [Reference Miller12, Appendix],
$T_{\mathbb Q}'$
. By [Reference Miller12, Appendix],
![]() $T_{\mathbb Q}'$
has QE and is complete.Footnote
1
It is easy to see that
$T_{\mathbb Q}'$
has QE and is complete.Footnote
1
It is easy to see that
![]() $(\mathbb R,<,+,\mathbb N)$
is
$(\mathbb R,<,+,\mathbb N)$
is
![]() $\emptyset $
-interdefinable with
$\emptyset $
-interdefinable with
![]() $ (\mathbb R,<,+,0,1, (q.x)_{q\in \mathbb Q},\left \lfloor \phantom {x}\right \rfloor ) $
, where
$ (\mathbb R,<,+,0,1, (q.x)_{q\in \mathbb Q},\left \lfloor \phantom {x}\right \rfloor ) $
, where
![]() $\left \lfloor \phantom {x}\right \rfloor $
denotes the usual “floor” function
$\left \lfloor \phantom {x}\right \rfloor $
denotes the usual “floor” function
![]() $t\mapsto \max (\mathbb Z\cap (-\infty ,t])$
for
$t\mapsto \max (\mathbb Z\cap (-\infty ,t])$
for
![]() $t\in \mathbb R$
. Thus,
$t\in \mathbb R$
. Thus,
![]() $\operatorname {\mathrm {Th}}(\mathbb R,<,+,\mathbb N)$
is bi-interpretable with
$\operatorname {\mathrm {Th}}(\mathbb R,<,+,\mathbb N)$
is bi-interpretable with
![]() $T_{\mathbb Q}'$
. It is more convenient to prove Proposition 1.8 by working over
$T_{\mathbb Q}'$
. It is more convenient to prove Proposition 1.8 by working over
![]() $(\mathbb R,<,+,\mathbb Z)$
instead of
$(\mathbb R,<,+,\mathbb Z)$
instead of
![]() $(\mathbb R,<,+,\mathbb N)$
.
$(\mathbb R,<,+,\mathbb N)$
.
Let
![]() $\mathfrak Z$
be a structure on
$\mathfrak Z$
be a structure on
![]() $\mathbb Z$
in a language
$\mathbb Z$
in a language
![]() $L_{\mathfrak {Z}}$
such that:
$L_{\mathfrak {Z}}$
such that:
-
•
 $L_{\mathfrak {Z}}$
has no function or constant symbols;
$L_{\mathfrak {Z}}$
has no function or constant symbols; -
• there is a symbol
 $Z\in L_{\mathfrak Z}$
that is interpreted as
$Z\in L_{\mathfrak Z}$
that is interpreted as
 $\mathbb Z$
in
$\mathbb Z$
in
 $\mathfrak Z$
;
$\mathfrak Z$
; -
•
 $\operatorname {\mathrm {Th}}(\mathfrak Z)$
has QE;
$\operatorname {\mathrm {Th}}(\mathfrak Z)$
has QE; -
•
 $\mathfrak Z$
defines
$\mathfrak Z$
defines
 $<$
and
$<$
and
 $\mid $
(hence also all arithmetic sets).
$\mid $
(hence also all arithmetic sets).
Put
![]() $L=L_{\mathbb Q}'\cup L_{\mathfrak Z}$
and
$L=L_{\mathbb Q}'\cup L_{\mathfrak Z}$
and
![]() $ T=T_{\mathbb Q}'\cup \{\forall x\,(Zx \leftrightarrow \left \lfloor x\right \rfloor =x)\}\cup \{\, \sigma ^Z: \sigma \in \operatorname {\mathrm {Th}}(\mathfrak Z)\,\} $
, where
$ T=T_{\mathbb Q}'\cup \{\forall x\,(Zx \leftrightarrow \left \lfloor x\right \rfloor =x)\}\cup \{\, \sigma ^Z: \sigma \in \operatorname {\mathrm {Th}}(\mathfrak Z)\,\} $
, where
![]() $\sigma ^Z$
denotes the relativization of
$\sigma ^Z$
denotes the relativization of
![]() $\sigma $
to Z (see, e.g., [Reference Chang and Keisler2] for a definition). We will show that T has QE. The proof is an extension of that of the corresponding result for
$\sigma $
to Z (see, e.g., [Reference Chang and Keisler2] for a definition). We will show that T has QE. The proof is an extension of that of the corresponding result for
![]() $T_{\mathbb Q}'$
, but the added complication justifies outlining some details. We begin by disposing of a number of routine technical observations and lemmas (the proofs of which we leave mostly to the reader). Unless indicated otherwise, “term” means “L- term.”
$T_{\mathbb Q}'$
, but the added complication justifies outlining some details. We begin by disposing of a number of routine technical observations and lemmas (the proofs of which we leave mostly to the reader). Unless indicated otherwise, “term” means “L- term.”
Every term is a finite composition of
![]() $\left \lfloor \phantom {x}\right \rfloor $
and
$\left \lfloor \phantom {x}\right \rfloor $
and
![]() $L_{\mathbb Q}$
-terms. Every finite composition of
$L_{\mathbb Q}$
-terms. Every finite composition of
![]() $\lfloor \phantom {x}\rfloor $
is T- equivalent to
$\lfloor \phantom {x}\rfloor $
is T- equivalent to
![]() $\left \lfloor \phantom {x}\right \rfloor $
. Every
$\left \lfloor \phantom {x}\right \rfloor $
. Every
![]() $L_{\mathbb Q}$
-term in variables
$L_{\mathbb Q}$
-term in variables
![]() $x_1,\dots ,x_n$
is
$x_1,\dots ,x_n$
is
![]() $T_{\mathbb Q}$
-equivalent to one of the form
$T_{\mathbb Q}$
-equivalent to one of the form
![]() $\sum _{i=1}^n\lambda _{q_i}x_i+\lambda _{q_0}1$
for some
$\sum _{i=1}^n\lambda _{q_i}x_i+\lambda _{q_0}1$
for some
![]() $n\in \mathbb N$
and
$n\in \mathbb N$
and
![]() $q_1,\dots ,q_n\in \mathbb Q$
; we tend to write
$q_1,\dots ,q_n\in \mathbb Q$
; we tend to write
![]() $ \sum _{i=1}^nq_ix_i+q_0 $
instead of
$ \sum _{i=1}^nq_ix_i+q_0 $
instead of
![]() $ \sum _{i=1}^n\lambda _{q_i}x_i+\lambda _{q_0}1 $
. If
$ \sum _{i=1}^n\lambda _{q_i}x_i+\lambda _{q_0}1 $
. If
![]() $\tau _1$
and
$\tau _1$
and
![]() $\tau _2$
are
$\tau _2$
are
![]() $L_{\mathbb Q}$
-terms in variables
$L_{\mathbb Q}$
-terms in variables
![]() $x_1,\dots ,x_n$
, then there is an
$x_1,\dots ,x_n$
, then there is an
![]() $L_{\mathbb Q}$
-term
$L_{\mathbb Q}$
-term
![]() $\sigma $
in the same variables such that
$\sigma $
in the same variables such that
 $$ \begin{gather*} T_{\mathbb Q}\vdash \tau_1x_1\cdots x_n=\tau_2x_1\cdots x_n \leftrightarrow \sigma x_1\cdots x_n=0,\\ T_{\mathbb Q}\vdash \tau_1x_1\cdots x_n<\tau_2x_1\cdots x_n \leftrightarrow \sigma x_1\cdots x_n<0. \end{gather*} $$
$$ \begin{gather*} T_{\mathbb Q}\vdash \tau_1x_1\cdots x_n=\tau_2x_1\cdots x_n \leftrightarrow \sigma x_1\cdots x_n=0,\\ T_{\mathbb Q}\vdash \tau_1x_1\cdots x_n<\tau_2x_1\cdots x_n \leftrightarrow \sigma x_1\cdots x_n<0. \end{gather*} $$
In what follows, we tend to let
![]() $\mathfrak B$
(allowing subscripts) denote an arbitrary model of T, with underlying set B (allowing corresponding subscripts). Let
$\mathfrak B$
(allowing subscripts) denote an arbitrary model of T, with underlying set B (allowing corresponding subscripts). Let
![]() $Z(\mathfrak B)$
denote the interpretation of the symbol Z in
$Z(\mathfrak B)$
denote the interpretation of the symbol Z in
![]() $\mathfrak B$
. Note that
$\mathfrak B$
. Note that
![]() $Z(\mathfrak B)=\{\, b\in B: \left \lfloor b\right \rfloor =b\,\}$
. We recall a lemma used in the proof of QE of
$Z(\mathfrak B)=\{\, b\in B: \left \lfloor b\right \rfloor =b\,\}$
. We recall a lemma used in the proof of QE of
![]() $T_{\mathbb Q}'$
, restated for our current purposes, followed by some routine consequences.
$T_{\mathbb Q}'$
, restated for our current purposes, followed by some routine consequences.
2.3
For all
![]() $b\in Z(\mathfrak {B})$
and positive integers m there exists a unique
$b\in Z(\mathfrak {B})$
and positive integers m there exists a unique
![]() ${i\in \{0,\dots , m-1\}}$
such that
${i\in \{0,\dots , m-1\}}$
such that
![]() $ \frac 1m(b+i) \in Z(\mathfrak {B}) $
.
$ \frac 1m(b+i) \in Z(\mathfrak {B}) $
.
2.4
Let
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $\tau (x_1,\dots ,x_n)$
be a term.
$\tau (x_1,\dots ,x_n)$
be a term.
-
1. There is a finite partition
 $\mathcal C$
of
$\mathcal C$
of
 $Z(\mathfrak B)$
into sets
$Z(\mathfrak B)$
into sets
 $\emptyset $
-definable in the reduct of
$\emptyset $
-definable in the reduct of
 $\mathfrak B$
to
$\mathfrak B$
to
 $L_{\mathfrak {Z}}$
such that, for each
$L_{\mathfrak {Z}}$
such that, for each
 $C\in \mathcal C$
, there exist
$C\in \mathcal C$
, there exist
 $q\in \mathbb Q$
and a term
$q\in \mathbb Q$
and a term
 $\sigma (x_1,\dots ,x_{n-1})$
with
$\sigma (x_1,\dots ,x_{n-1})$
with
 $\tau =\sigma +qx_n$
on
$\tau =\sigma +qx_n$
on
 $B^{n-1}\times C$
. (More precisely: The restriction to
$B^{n-1}\times C$
. (More precisely: The restriction to
 $B^{n-1}\times C$
of the interpretation of
$B^{n-1}\times C$
of the interpretation of
 $\tau $
in
$\tau $
in
 $\mathfrak B$
is equal to the restriction to
$\mathfrak B$
is equal to the restriction to
 $B^{n-1}\times C$
of the interpretation of
$B^{n-1}\times C$
of the interpretation of
 $\sigma +qx_n$
in
$\sigma +qx_n$
in
 $\mathfrak B$
.)
$\mathfrak B$
.) -
2. There is a finite partition
 $\mathcal C$
of
$\mathcal C$
of
 $Z(\mathfrak B)$
into sets
$Z(\mathfrak B)$
into sets
 $\emptyset $
-definable in the reduct of
$\emptyset $
-definable in the reduct of
 $\mathfrak B$
to
$\mathfrak B$
to
 $L_{\mathfrak Z}$
such that, for each
$L_{\mathfrak Z}$
such that, for each
 $C\in \mathcal C$
, there exist
$C\in \mathcal C$
, there exist
 $q,r\in \mathbb Q$
and a term
$q,r\in \mathbb Q$
and a term
 $\sigma (x_1,\dots ,x_{n-1})$
such that for all
$\sigma (x_1,\dots ,x_{n-1})$
such that for all
 $(b,c)\in B^{n-1}\times C$
, if
$(b,c)\in B^{n-1}\times C$
, if
 $\tau (b,c)\in Z(\mathfrak B)$
, then
$\tau (b,c)\in Z(\mathfrak B)$
, then
 $\tau (b,c)=\sigma (b)+qc+r$
and both
$\tau (b,c)=\sigma (b)+qc+r$
and both
 $\sigma (b)$
and
$\sigma (b)$
and
 $qc+r$
lie in
$qc+r$
lie in
 $Z(\mathfrak B)$
.
$Z(\mathfrak B)$
. -
3. Let
 $m\leq n$
,
$m\leq n$
,
 $b\in B^m$
and D be the definable closure of b in the reduct of
$b\in B^m$
and D be the definable closure of b in the reduct of
 $\mathfrak B$
to
$\mathfrak B$
to
 $L_{\mathbb Q}'$
. There is a finite partition
$L_{\mathbb Q}'$
. There is a finite partition
 $\mathcal C$
of
$\mathcal C$
of
 $[0,1)^{n-m}$
into sets that are D-definable in the reduct of
$[0,1)^{n-m}$
into sets that are D-definable in the reduct of
 $\mathfrak B$
to
$\mathfrak B$
to
 $L_{\mathbb Q}$
such that, for each
$L_{\mathbb Q}$
such that, for each
 $C\in \mathcal C$
, there exist
$C\in \mathcal C$
, there exist
 $q_1,\dots ,q_{n-m}\in \mathbb Q$
and
$q_1,\dots ,q_{n-m}\in \mathbb Q$
and
 $d,e\in D$
with
$d,e\in D$
with
 $\tau {\restriction } (\{b\}\times C)=\sum _{i=m+1}^{n}q_ix_i+d$
and
$\tau {\restriction } (\{b\}\times C)=\sum _{i=m+1}^{n}q_ix_i+d$
and
 $\left \lfloor \tau \right \rfloor {\restriction } (\{b\}\times C)=e$
.
$\left \lfloor \tau \right \rfloor {\restriction } (\{b\}\times C)=e$
.
We omit proofs. (Generally, proceed via 2.3 and induction on terms, noting that the interesting cases tend to be when
![]() $\tau $
is of the form
$\tau $
is of the form
![]() $\left \lfloor \phi \right \rfloor $
.)
$\left \lfloor \phi \right \rfloor $
.)
2.5
Every subset of
![]() $Z(\mathfrak B)^n$
that is quantifier-free definable in
$Z(\mathfrak B)^n$
that is quantifier-free definable in
![]() $(\mathfrak B, (b)_{b\in B})$
is definable in
$(\mathfrak B, (b)_{b\in B})$
is definable in
![]() $(Z(\mathfrak B), (R(\mathfrak B))_{R\in L_{\mathfrak Z}})$
, where
$(Z(\mathfrak B), (R(\mathfrak B))_{R\in L_{\mathfrak Z}})$
, where
![]() $R(\mathfrak B)$
is the interpretation of R in
$R(\mathfrak B)$
is the interpretation of R in
![]() $\mathfrak B$
.
$\mathfrak B$
.
Sketch of proof.
As every arithmetic set is
![]() $\emptyset $
-definable in
$\emptyset $
-definable in
![]() $\mathfrak Z$
, there is a bijection from
$\mathfrak Z$
, there is a bijection from
![]() $Z(\mathfrak B)^n$
to
$Z(\mathfrak B)^n$
to
![]() $Z(\mathfrak B)$
that is quantifier-free definable in
$Z(\mathfrak B)$
that is quantifier-free definable in
![]() $\mathfrak B$
. Thus, it suffices to consider subsets of
$\mathfrak B$
. Thus, it suffices to consider subsets of
![]() $Z(\mathfrak B)$
that are atomically defined in
$Z(\mathfrak B)$
that are atomically defined in
![]() $(\mathfrak B, (b)_{b\in B})$
. Functions given by unary terms of
$(\mathfrak B, (b)_{b\in B})$
. Functions given by unary terms of
![]() $(\mathfrak B, (b)_{b\in B})$
are given by compositions of
$(\mathfrak B, (b)_{b\in B})$
are given by compositions of
![]() $\left \lfloor \phantom {x}\right \rfloor $
and functions of the form
$\left \lfloor \phantom {x}\right \rfloor $
and functions of the form
![]() $qx+b$
with
$qx+b$
with
![]() $b\in B$
. Employ 2.4.1 and 2.4.2 as needed.⊣
$b\in B$
. Employ 2.4.1 and 2.4.2 as needed.⊣
2.6
Let
![]() $Y\subseteq B^{m+n}$
be quantifier-free definable in
$Y\subseteq B^{m+n}$
be quantifier-free definable in
![]() $\mathfrak B$
and
$\mathfrak B$
and
![]() $(u,z)\in B^m\times Z(\mathfrak B)^n$
. Let D be the definable closure of
$(u,z)\in B^m\times Z(\mathfrak B)^n$
. Let D be the definable closure of
![]() $(u,z)$
in the reduct of
$(u,z)$
in the reduct of
![]() $\mathfrak B$
to
$\mathfrak B$
to
![]() $L_{\mathbb Q}'$
. Then
$L_{\mathbb Q}'$
. Then
 $$ \begin{align*} \{\, x\in B^n: (u,x)\in Y\,\}\cap \prod_{i=1}^n[z_i,z_i+1) \end{align*} $$
$$ \begin{align*} \{\, x\in B^n: (u,x)\in Y\,\}\cap \prod_{i=1}^n[z_i,z_i+1) \end{align*} $$
is D-definable in the reduct of
![]() $\mathfrak B$
to
$\mathfrak B$
to
![]() $L_{\mathbb Q}$
.
$L_{\mathbb Q}$
.
Sketch of proof.
It suffices to show the result for atomically defined sets. Employ 2.4.3.⊣
2.7 T is complete and has QE
Proof As the L-structure
![]() $ (\mathbb Q,<,+,0,1,(\lambda _q)_{q\in \mathbb Q}, \lfloor \phantom {x}\rfloor ,\mathfrak Z) $
embeds into every model of T, it is enough to show that T has QE. We employ one of the standard “embedding tests.” Let
$ (\mathbb Q,<,+,0,1,(\lambda _q)_{q\in \mathbb Q}, \lfloor \phantom {x}\rfloor ,\mathfrak Z) $
embeds into every model of T, it is enough to show that T has QE. We employ one of the standard “embedding tests.” Let
![]() $\mathfrak {B}_1,\mathfrak {B}_2\vDash T$
and
$\mathfrak {B}_1,\mathfrak {B}_2\vDash T$
and
![]() $\mathfrak {A}$
(with underlying set A) be a substructure of
$\mathfrak {A}$
(with underlying set A) be a substructure of
![]() $\mathfrak {B}_1$
that is also embedded into
$\mathfrak {B}_1$
that is also embedded into
![]() $\mathfrak {B}_2$
. Assume that
$\mathfrak {B}_2$
. Assume that
![]() $\mathfrak {B}_2$
is
$\mathfrak {B}_2$
is
![]() $\operatorname {card}(B_1)^+$
- saturated. We show that the embedding extends to an embedding of
$\operatorname {card}(B_1)^+$
- saturated. We show that the embedding extends to an embedding of
![]() $\mathfrak {B}_1$
into
$\mathfrak {B}_1$
into
![]() $\mathfrak {B}_2$
.
$\mathfrak {B}_2$
.
We first reduce to the case that
![]() $Z(\mathfrak B_1)=Z(\mathfrak A)$
as follows. Suppose there exists
$Z(\mathfrak B_1)=Z(\mathfrak A)$
as follows. Suppose there exists
![]() $c_1\in Z(\mathfrak B_1)\setminus Z(\mathfrak A)$
; we show that we may replace
$c_1\in Z(\mathfrak B_1)\setminus Z(\mathfrak A)$
; we show that we may replace
![]() $\mathfrak A$
with the substructure of
$\mathfrak A$
with the substructure of
![]() $\mathfrak B_1$
generated over
$\mathfrak B_1$
generated over
![]() $\mathfrak A$
by
$\mathfrak A$
by
![]() $c_1$
. (Then iterate as needed.) In order to reduce clerical clutter, let us assume that the embedding of
$c_1$
. (Then iterate as needed.) In order to reduce clerical clutter, let us assume that the embedding of
![]() $\mathfrak A$
into
$\mathfrak A$
into
![]() $\mathfrak B_2$
is just the identity on A. As
$\mathfrak B_2$
is just the identity on A. As
![]() $\operatorname {\mathrm {Th}}(\mathfrak Z)$
has QE, there exists
$\operatorname {\mathrm {Th}}(\mathfrak Z)$
has QE, there exists
![]() $c_2\in B_2$
such that the
$c_2\in B_2$
such that the
![]() $L_{\mathfrak Z}$
-type of
$L_{\mathfrak Z}$
-type of
![]() $c_2$
over
$c_2$
over
![]() $A\cap Z(\mathfrak {B}_2)$
is equal to the
$A\cap Z(\mathfrak {B}_2)$
is equal to the
![]() $L_{\mathfrak Z}$
-type of
$L_{\mathfrak Z}$
-type of
![]() $c_1$
over
$c_1$
over
![]() $A\cap Z(\mathfrak {B}_1)$
. It suffices now to show that the quantifier-free L-type of
$A\cap Z(\mathfrak {B}_1)$
. It suffices now to show that the quantifier-free L-type of
![]() $c_2$
over A is equal to the quantifier-free L-type of
$c_2$
over A is equal to the quantifier-free L-type of
![]() $c_1$
over A. We illustrate by dealing with a special case. Let: m and n be positive integers;
$c_1$
over A. We illustrate by dealing with a special case. Let: m and n be positive integers;
![]() $\tau $
be an n-ary term;
$\tau $
be an n-ary term;
![]() $a\in A^{n-1}$
; R be an m-ary relation symbol of
$a\in A^{n-1}$
; R be an m-ary relation symbol of
![]() $L_{\mathfrak Z}$
; and
$L_{\mathfrak Z}$
; and
![]() $a'\in A^{m-1}$
. If follows from 2.4.3. applied to each of
$a'\in A^{m-1}$
. If follows from 2.4.3. applied to each of
![]() $\mathfrak B_1$
and
$\mathfrak B_1$
and
![]() $\mathfrak B_2$
that if
$\mathfrak B_2$
that if
![]() $\mathfrak B_1\vDash R(\tau (a,c_1),a')$
, then
$\mathfrak B_1\vDash R(\tau (a,c_1),a')$
, then
![]() $\mathfrak B_2\vDash R(\tau (a,c_2),a')$
. (Other cases are handled similarly using 2.4.1 or 2.4.2.)
$\mathfrak B_2\vDash R(\tau (a,c_2),a')$
. (Other cases are handled similarly using 2.4.1 or 2.4.2.)
Now assume that
![]() $Z(\mathfrak B_1)=Z(\mathfrak A)$
and let
$Z(\mathfrak B_1)=Z(\mathfrak A)$
and let
![]() $c_1\in B\setminus A$
. As
$c_1\in B\setminus A$
. As
![]() $T_{\mathbb Q}'$
has QE, there exists
$T_{\mathbb Q}'$
has QE, there exists
![]() $c_2\in B_2$
such that the
$c_2\in B_2$
such that the
![]() $L_{\mathbb Q}'$
- type of
$L_{\mathbb Q}'$
- type of
![]() $c_2$
over the image of A (under the embedding) is equal to the
$c_2$
over the image of A (under the embedding) is equal to the
![]() $L_{\mathbb Q}'$
-type of
$L_{\mathbb Q}'$
-type of
![]() $c_1$
over A. The rest of the proof is similar to (but easier than) the previous case. We omit details.
$c_1$
over A. The rest of the proof is similar to (but easier than) the previous case. We omit details.
Proof of Proposition 1.8 Suppose that
![]() $\mathfrak R$
is an expansion of
$\mathfrak R$
is an expansion of
![]() $(\mathbb R,<,+,\mid )$
by subsets of various
$(\mathbb R,<,+,\mid )$
by subsets of various
![]() $\mathbb N^n$
. By passing to an extension by definitions, we assume that
$\mathbb N^n$
. By passing to an extension by definitions, we assume that
![]() $ \mathfrak R=(\mathbb R,<,+,0,1,(qx)_{q\in \mathbb Q},\left \lfloor \phantom {x}\right \rfloor ,\mathfrak Z) $
where
$ \mathfrak R=(\mathbb R,<,+,0,1,(qx)_{q\in \mathbb Q},\left \lfloor \phantom {x}\right \rfloor ,\mathfrak Z) $
where
![]() $\mathfrak Z$
is the expansion of
$\mathfrak Z$
is the expansion of
![]() $\mathbb Z$
by all subsets of each
$\mathbb Z$
by all subsets of each
![]() $\mathbb Z^n$
that are
$\mathbb Z^n$
that are
![]() $\emptyset $
-definable in
$\emptyset $
-definable in
![]() $\mathfrak R$
. (Remark: By 2.5, every definable subset of any
$\mathfrak R$
. (Remark: By 2.5, every definable subset of any
![]() $\mathbb Z^n$
is
$\mathbb Z^n$
is
![]() $\emptyset $
-definable, and so
$\emptyset $
-definable, and so
![]() $\mathfrak Z$
is equal to the structure induced on
$\mathfrak Z$
is equal to the structure induced on
![]() $\mathbb Z$
in
$\mathbb Z$
in
![]() $\mathfrak R$
.) By 2.7,
$\mathfrak R$
.) By 2.7,
![]() $\operatorname {\mathrm {Th}}(\mathfrak R)$
has QE and is axiomatized by T. By QE and 2.6, every bounded set definable in
$\operatorname {\mathrm {Th}}(\mathfrak R)$
has QE and is axiomatized by T. By QE and 2.6, every bounded set definable in
![]() $\mathfrak R$
is definable in
$\mathfrak R$
is definable in
![]() $(\mathbb R,<,+)$
, i.e., Proposition 1.8.1 holds; then Proposition 1.8.2 is immediate via 2.2. It remains to show that
$(\mathbb R,<,+)$
, i.e., Proposition 1.8.1 holds; then Proposition 1.8.2 is immediate via 2.2. It remains to show that
![]() $\mathfrak R$
is CC.
$\mathfrak R$
is CC.
Let
![]() $E\subseteq \mathbb R^n$
be definable in
$E\subseteq \mathbb R^n$
be definable in
![]() $\mathfrak R$
. We must show that each component of E is definable. Let
$\mathfrak R$
. We must show that each component of E is definable. Let
![]() $m\in \mathbb N$
,
$m\in \mathbb N$
,
![]() $c\in \mathbb R^m$
and
$c\in \mathbb R^m$
and
![]() $X\subseteq \mathbb R^{m+n}$
be
$X\subseteq \mathbb R^{m+n}$
be
![]() $\emptyset $
- definable in
$\emptyset $
- definable in
![]() $\mathfrak R$
such that
$\mathfrak R$
such that
![]() $E=\{\, e\in \mathbb R^n: (c,e)\in X\,\}$
. Via QE, 2.5, 2.1 and model-theoretic compactness, there exist
$E=\{\, e\in \mathbb R^n: (c,e)\in X\,\}$
. Via QE, 2.5, 2.1 and model-theoretic compactness, there exist
-
•
 $N\in \mathbb N$
,
$N\in \mathbb N$
, -
• sets
 $Y_1,\dots ,Y_N\subseteq \mathbb R^{m+n}$
that are
$Y_1,\dots ,Y_N\subseteq \mathbb R^{m+n}$
that are
 $\emptyset $
- definable in
$\emptyset $
- definable in
 $(\mathbb R,<,+,1)$
,
$(\mathbb R,<,+,1)$
, -
• maps
 $F_1,\dots ,F_N\colon \mathbb R^{m+n}\to \mathbb R^m$
that are
$F_1,\dots ,F_N\colon \mathbb R^{m+n}\to \mathbb R^m$
that are
 $\emptyset $
- definable in
$\emptyset $
- definable in
 $\mathfrak R$
.
$\mathfrak R$
.
such that, for each
![]() $z\in \mathbb Z^n$
, there exists
$z\in \mathbb Z^n$
, there exists
![]() $J\subseteq \{1,\dots ,N\}$
such that the sets
$J\subseteq \{1,\dots ,N\}$
such that the sets
partition
![]() $ E\cap \prod _{k=1}^n[z_k, z_k+1) $
into cells of
$ E\cap \prod _{k=1}^n[z_k, z_k+1) $
into cells of
![]() $(\mathbb R,<,+)$
. The set of all
$(\mathbb R,<,+)$
. The set of all
![]() $z\in \mathbb Z^n$
such that
$z\in \mathbb Z^n$
such that
![]() $\prod _{k=1}^n[z_k, z_k+1)$
intersects E is definable in
$\prod _{k=1}^n[z_k, z_k+1)$
intersects E is definable in
![]() $\mathfrak R$
, and the possible descriptions of the cells in
$\mathfrak R$
, and the possible descriptions of the cells in
![]() $E\cap \prod _{k=1}^n[z_k, z_k+1)$
can be coded uniformly in z by subsets of
$E\cap \prod _{k=1}^n[z_k, z_k+1)$
can be coded uniformly in z by subsets of
![]() $\{0,1\}^d$
for some
$\{0,1\}^d$
for some
![]() $d\in \mathbb N$
. Thus, there exist
$d\in \mathbb N$
. Thus, there exist
![]() $m\in \mathbb N$
and definable
$m\in \mathbb N$
and definable
![]() $S\subseteq \mathbb Z^m\times \mathbb R^n$
such that, letting A be the projection of S on the first m coordinates, the fibers
$S\subseteq \mathbb Z^m\times \mathbb R^n$
such that, letting A be the projection of S on the first m coordinates, the fibers
![]() $S_a$
(
$S_a$
(
![]() $=\{\, e\in \mathbb R^n: (a,e)\in S\,\}$
) of S over A partition E into connected sets that are each definable in
$=\{\, e\in \mathbb R^n: (a,e)\in S\,\}$
) of S over A partition E into connected sets that are each definable in
![]() $(\mathbb R,<,+)$
. As any expansion of
$(\mathbb R,<,+)$
. As any expansion of
![]() $(\mathbb Z,<,\{0\})$
has Definable Choice, we reduce to the case that
$(\mathbb Z,<,\{0\})$
has Definable Choice, we reduce to the case that
![]() $a\mapsto S_a$
is injective. Let G be the set of all pairs
$a\mapsto S_a$
is injective. Let G be the set of all pairs
![]() $(a,b)\in A^2$
such that
$(a,b)\in A^2$
such that
![]() $ (S_a\cap \overline {S_b})\cup (S_b\cap \overline {S_a})\neq \emptyset $
; then G is definable in
$ (S_a\cap \overline {S_b})\cup (S_b\cap \overline {S_a})\neq \emptyset $
; then G is definable in
![]() $\mathfrak R$
, hence also in
$\mathfrak R$
, hence also in
![]() $\mathfrak Z$
. As
$\mathfrak Z$
. As
![]() $\mathfrak Z$
defines all arithmetic sets, each graph component of
$\mathfrak Z$
defines all arithmetic sets, each graph component of
![]() $(A,G)$
is definable in
$(A,G)$
is definable in
![]() $\mathfrak Z$
. (To put this another way: Since G is computable from A, each graph component of
$\mathfrak Z$
. (To put this another way: Since G is computable from A, each graph component of
![]() $(A,G)$
is computably enumerable from A, hence definable in
$(A,G)$
is computably enumerable from A, hence definable in
![]() $(\mathbb Z,+,\cdot , A)$
.) It is an exercise (cf. [Reference van den Dries5, Chapter 3, (2.19).5]) to see that C is a graph component of
$(\mathbb Z,+,\cdot , A)$
.) It is an exercise (cf. [Reference van den Dries5, Chapter 3, (2.19).5]) to see that C is a graph component of
![]() $(A,G)$
if and only if
$(A,G)$
if and only if
![]() $\bigcup _{a\in C}S_a$
is a component of E.
$\bigcup _{a\in C}S_a$
is a component of E.
3 Concluding remarks
Examination of the proof of Proposition 1.8 yields a number of other results; below are three illustrative examples.
3.1
Let
![]() $\mathfrak R$
be an expansion of
$\mathfrak R$
be an expansion of
![]() $(\mathbb R,<,+,1,\mathbb Z)$
by subsets of various
$(\mathbb R,<,+,1,\mathbb Z)$
by subsets of various
![]() $\mathbb Z^n$
. Then
$\mathbb Z^n$
. Then
![]() $\operatorname {\mathrm {Th}}(\mathfrak R)$
is axiomatized over the union of
$\operatorname {\mathrm {Th}}(\mathfrak R)$
is axiomatized over the union of
![]() $\operatorname {\mathrm {Th}}(\mathbb R,<,+,1)$
and the relativization to
$\operatorname {\mathrm {Th}}(\mathbb R,<,+,1)$
and the relativization to
![]() $\mathbb Z$
of the theory of the structure induced on
$\mathbb Z$
of the theory of the structure induced on
![]() $\mathbb Z$
in
$\mathbb Z$
in
![]() $\mathfrak R$
by expressing that
$\mathfrak R$
by expressing that
![]() $(\mathbb Z,+,1)$
is a substructure of
$(\mathbb Z,+,1)$
is a substructure of
![]() $(\mathbb R,+,1)$
and, for every
$(\mathbb R,+,1)$
and, for every
![]() $r\in \mathbb R$
, there is a unique
$r\in \mathbb R$
, there is a unique
![]() $k\in \mathbb Z$
such that
$k\in \mathbb Z$
such that
![]() $k\leq r<k+1$
.
$k\leq r<k+1$
.
3.2
If
![]() $\mathfrak R_0$
is a reduct in the sense of definability of
$\mathfrak R_0$
is a reduct in the sense of definability of
![]() $(\mathbb R,<,+)$
over
$(\mathbb R,<,+)$
over
![]() $(\mathbb R,<)$
, and
$(\mathbb R,<)$
, and
![]() $\mathfrak R$
is an expansion of
$\mathfrak R$
is an expansion of
![]() $(\mathfrak R_0,\mathbb N)$
by subsets of various
$(\mathfrak R_0,\mathbb N)$
by subsets of various
![]() $\mathbb N^n$
, then
$\mathbb N^n$
, then
![]() $\mathfrak R$
is PCC, CC or QCC if and only if it defines
$\mathfrak R$
is PCC, CC or QCC if and only if it defines
![]() $\mid $
.
$\mid $
.
(For the QE, replace
![]() $\mathfrak R_0$
with the expansion in the syntactic sense of
$\mathfrak R_0$
with the expansion in the syntactic sense of
![]() $(\mathbb R,<,0,1)$
by all
$(\mathbb R,<,0,1)$
by all
![]() $\{0,1\}$
-definable functions of
$\{0,1\}$
-definable functions of
![]() $\mathfrak R_0$
. Every such function is
$\mathfrak R_0$
. Every such function is
![]() $\emptyset $
-definable in
$\emptyset $
-definable in
![]() $({\mathbb R,<,} +,1)$
.)
$({\mathbb R,<,} +,1)$
.)
3.3
Let G be a divisible additive subgroup of
![]() $\mathbb R$
containing
$\mathbb R$
containing
![]() $1$
and
$1$
and
![]() $\mathfrak G$
be an expansion of
$\mathfrak G$
be an expansion of
![]() $(G,<,+,\mathbb Z)$
by subsets of various
$(G,<,+,\mathbb Z)$
by subsets of various
![]() $\mathbb Z^n$
. If
$\mathbb Z^n$
. If
![]() $\mathfrak G$
defines
$\mathfrak G$
defines
![]() $\mid $
, then for all
$\mid $
, then for all
![]() $E\subseteq G^n$
definable in
$E\subseteq G^n$
definable in
![]() $\mathfrak G$
and
$\mathfrak G$
and
![]() $x\in E$
,
$x\in E$
,
![]() $\mathfrak G$
defines the set of
$\mathfrak G$
defines the set of
![]() $y\in E$
for which there is a definable-in-
$y\in E$
for which there is a definable-in-
![]() $(G,<,+)$
continuous map
$(G,<,+)$
continuous map
![]() $\gamma \colon [a,b]\to E$
such that
$\gamma \colon [a,b]\to E$
such that
![]() $\gamma (a)=x$
and
$\gamma (a)=x$
and
![]() $\gamma (b)=y$
.
$\gamma (b)=y$
.
(The appropriate analogue of 2.2 follows from [Reference van den Dries5, p. 100].)
We now return to a question hinted at in the introduction: To what extent does Proposition 1.5 depend on working over
![]() $\mathbb R$
?
$\mathbb R$
?
The notion of PCC is problematic in more general settings. The usual definition of “path” includes the requirement that the domain of a path be a compact subinterval of
![]() $\mathbb R$
, and in practice, one typically uses that
$\mathbb R$
, and in practice, one typically uses that
![]() $-x$
is an order-reversing bijection of
$-x$
is an order-reversing bijection of
![]() $\mathbb R$
and all infinite compact intervals are definably isomorphic in the vector space
$\mathbb R$
and all infinite compact intervals are definably isomorphic in the vector space
![]() $(\mathbb R,+,(rx)_{r\in \mathbb R})$
. We can get around this in some special settings. Let
$(\mathbb R,+,(rx)_{r\in \mathbb R})$
. We can get around this in some special settings. Let
![]() $(M,<)$
be a linear order. If
$(M,<)$
be a linear order. If
![]() $X\subseteq M^n$
, then we say that a path in X, relative to
$X\subseteq M^n$
, then we say that a path in X, relative to
![]() $(M,<)$
, is a continuous map f from an interval
$(M,<)$
, is a continuous map f from an interval
![]() $[a,b]$
into
$[a,b]$
into
![]() $M^n$
such that
$M^n$
such that
![]() $f([a,b])\subseteq X$
, and declare a piecewise path in X (relative to
$f([a,b])\subseteq X$
, and declare a piecewise path in X (relative to
![]() $(M,<)$
) to be a finite sequence
$(M,<)$
) to be a finite sequence
of paths in X (for some
![]() $p\in \mathbb N$
) such that
$p\in \mathbb N$
) such that
![]() $\gamma _k(b_k)=\gamma _{k+1}(a_{k+1})$
for
$\gamma _k(b_k)=\gamma _{k+1}(a_{k+1})$
for
![]() $k=1,\dots ,p$
. We say that
$k=1,\dots ,p$
. We say that
![]() $\gamma $
is injective if each
$\gamma $
is injective if each
![]() $\gamma _j$
is injective and the images
$\gamma _j$
is injective and the images
![]() $\gamma ([a_1,b_1))$
, …,
$\gamma ([a_1,b_1))$
, …,
![]() $\gamma ([a_{p},b_{p}))$
,
$\gamma ([a_{p},b_{p}))$
,
![]() $\gamma ([a_{p+1},b_{p+1}])$
are pairwise disjoint. The image of
$\gamma ([a_{p+1},b_{p+1}])$
are pairwise disjoint. The image of
![]() $\gamma $
is the union of the images of the
$\gamma $
is the union of the images of the
![]() $\gamma _k$
. We abuse terminology somewhat and say that X is path connected relative to
$\gamma _k$
. We abuse terminology somewhat and say that X is path connected relative to
![]() $(M,<)$
if for all
$(M,<)$
if for all
![]() $u,v\in X$
there is a piecewise path
$u,v\in X$
there is a piecewise path
![]() $\gamma $
in X such that u and v are contained in the image of
$\gamma $
in X such that u and v are contained in the image of
![]() $\gamma $
. If the piecewise paths can be taken to be injective, then we say that X is injectively path connected relative to
$\gamma $
. If the piecewise paths can be taken to be injective, then we say that X is injectively path connected relative to
![]() $(M,<)$
. Now fix an expansion
$(M,<)$
. Now fix an expansion
![]() $\mathfrak {M}$
of
$\mathfrak {M}$
of
![]() $(M,<)$
and
$(M,<)$
and
![]() $A\subseteq M$
. We can specialize these definitions to the notion “A-definable in
$A\subseteq M$
. We can specialize these definitions to the notion “A-definable in
![]() $\mathfrak {M}$
” in a mostly obvious fashion. (Some authors might require that X be A-definable in order to call it A- definably path connected relative to
$\mathfrak {M}$
” in a mostly obvious fashion. (Some authors might require that X be A-definable in order to call it A- definably path connected relative to
![]() $\mathfrak {M}$
, but we do not.) If
$\mathfrak {M}$
, but we do not.) If
![]() $A=M$
, then we omit mention of A. (Thus, definably path connected relative to
$A=M$
, then we omit mention of A. (Thus, definably path connected relative to
![]() $(\mathbb R,<,+,\cdot ,\mathbb N)$
is the same as path connected in the usual sense.) An examination of the proof of Proposition 1.5 yields the following technical result, thus establishing that working over
$(\mathbb R,<,+,\cdot ,\mathbb N)$
is the same as path connected in the usual sense.) An examination of the proof of Proposition 1.5 yields the following technical result, thus establishing that working over
![]() $\mathbb R$
is not necessary if one is willing to modify a few definitions.
$\mathbb R$
is not necessary if one is willing to modify a few definitions.
3.4
Let D be a dense subset of
![]() $\mathbb R$
that contains
$\mathbb R$
that contains
![]() $\mathbb N$
. Let
$\mathbb N$
. Let
![]() $A\subseteq D$
and
$A\subseteq D$
and
![]() $\mathfrak {D}$
be an expansion of
$\mathfrak {D}$
be an expansion of
![]() $(D,<,\mathbb N)$
such that for all
$(D,<,\mathbb N)$
such that for all
![]() $E\subseteq F\subseteq D^7$
, if F is
$E\subseteq F\subseteq D^7$
, if F is
![]() $\emptyset $
-definable in
$\emptyset $
-definable in
![]() $(D,<,\mathbb N)$
and E is maximally
$(D,<,\mathbb N)$
and E is maximally
![]() $\emptyset $
-definably injectively path connected relative to
$\emptyset $
-definably injectively path connected relative to
![]() $(D,<,(n)_{n\in \mathbb N})$
, then E is A-definable in
$(D,<,(n)_{n\in \mathbb N})$
, then E is A-definable in
![]() $\mathfrak {D}$
. Then
$\mathfrak {D}$
. Then
![]() $\mid $
is A-definable in
$\mid $
is A-definable in
![]() $\mathfrak {D}$
.
$\mathfrak {D}$
.
(A priori, the hypothesis is weaker than PCC for expansions of
![]() $(\mathbb R,<)$
. We leave nonarchimedean settings to the interested reader.)
$(\mathbb R,<)$
. We leave nonarchimedean settings to the interested reader.)
As an application, we obtain the converse of 3.3, hence also the following extension of Theorem 1.9.
3.5
Let G be a divisible subgroup of
![]() $\mathbb R$
containing
$\mathbb R$
containing
![]() $1$
and
$1$
and
![]() $\mathfrak G$
be an expansion of
$\mathfrak G$
be an expansion of
![]() $(G,<,+,\mathbb Z)$
by subsets of various
$(G,<,+,\mathbb Z)$
by subsets of various
![]() $\mathbb Z^n$
. Then
$\mathbb Z^n$
. Then
![]() $\mathfrak G$
defines
$\mathfrak G$
defines
![]() $\mid $
if and only if for all E definable in
$\mid $
if and only if for all E definable in
![]() $\mathfrak G$
and
$\mathfrak G$
and
![]() $x\in E$
,
$x\in E$
,
![]() $\mathfrak G$
defines the set of all
$\mathfrak G$
defines the set of all
![]() $y\in E$
for which there is a definable-in-
$y\in E$
for which there is a definable-in-
![]() $(G,<,+)$
continuous map
$(G,<,+)$
continuous map
![]() $\gamma \colon [a,b]\to E$
such that
$\gamma \colon [a,b]\to E$
such that
![]() $\gamma (a)=x$
and
$\gamma (a)=x$
and
![]() $\gamma (b)=y$
.
$\gamma (b)=y$
.
As we have defined it, the notion of CC is of little use in more general settings, even for o-minimal expansions of dense linear orders. To illustrate, every expansion of a totally disconnected linear order is trivially CC. However, there is a natural generalization of the notion of CC to first-order topological structures (as defined in [Reference Pillay19]): Every definable set A should be a union of definable sets C that are maximal with respect to the property of not being disconnected by any pair of definable open sets. In [Reference van den Dries5], such sets C are called definably connected components of A (and are definable by definition).
In o-minimal structures, all definable sets are unions of finitely many definably connected components [Reference van den Dries5, p. 57]. But by QE of
![]() $\operatorname {\mathrm {Th}}(\mathbb R,<)$
, there is no piecewise path definable in
$\operatorname {\mathrm {Th}}(\mathbb R,<)$
, there is no piecewise path definable in
![]() $(\mathbb R,<)$
joining any point in
$(\mathbb R,<)$
joining any point in
![]() $(-\infty ,1)\times (-\infty ,2)$
to the point
$(-\infty ,1)\times (-\infty ,2)$
to the point
![]() $(1,2)$
. Thus, in
$(1,2)$
. Thus, in
![]() $(\mathbb R,<)$
, the set
$(\mathbb R,<)$
, the set
![]() $(-\infty ,1)\times (-\infty ,2)\cup \{(1,2)\}$
is path connected and definably connected, but not definably path connected relative to
$(-\infty ,1)\times (-\infty ,2)\cup \{(1,2)\}$
is path connected and definably connected, but not definably path connected relative to
![]() $(\mathbb R,<)$
.
$(\mathbb R,<)$
.
Let
![]() $\mathfrak {M}$
be as before. Under any reasonable definition, M should be regarded as
$\mathfrak {M}$
be as before. Under any reasonable definition, M should be regarded as
![]() $\emptyset $
-definably injectively path connected in
$\emptyset $
-definably injectively path connected in
![]() $\mathfrak {M}$
—but M need not be definably connected in
$\mathfrak {M}$
—but M need not be definably connected in
![]() $\mathfrak {M}$
, even if
$\mathfrak {M}$
, even if
![]() $(M,<)$
is densely ordered (say, if
$(M,<)$
is densely ordered (say, if
![]() $\mathfrak {M}$
is weakly o-minimal, but not o-minimal). This failure of the fundamental topological fact that path connectedness implies connectedness invalidates many of the techniques used in our arguments over
$\mathfrak {M}$
is weakly o-minimal, but not o-minimal). This failure of the fundamental topological fact that path connectedness implies connectedness invalidates many of the techniques used in our arguments over
![]() $(\mathbb R,<)$
. However, it is known that if
$(\mathbb R,<)$
. However, it is known that if
![]() $(M,<)$
is densely ordered and M is definably connected in
$(M,<)$
is densely ordered and M is definably connected in
![]() $\mathfrak {M}$
, then the implication is essentially restored for definable data. Hence, we have the following corollary of 3.4, the proof of which we leave as an exercise (familiarity with some results in [Reference Miller12] will be needed).
$\mathfrak {M}$
, then the implication is essentially restored for definable data. Hence, we have the following corollary of 3.4, the proof of which we leave as an exercise (familiarity with some results in [Reference Miller12] will be needed).
3.6
Let D be a dense subset of
![]() $\mathbb R$
that contains
$\mathbb R$
that contains
![]() $\mathbb N$
. Let
$\mathbb N$
. Let
![]() $\mathfrak {D}$
be an expansion of
$\mathfrak {D}$
be an expansion of
![]() $(D,<,\mathbb N)$
such that D is definably connected in
$(D,<,\mathbb N)$
such that D is definably connected in
![]() $\mathfrak {D}$
and every definable set is a union of definably connected components. Then
$\mathfrak {D}$
and every definable set is a union of definably connected components. Then
![]() $\mid $
is definable in
$\mid $
is definable in
![]() $\mathfrak {D}$
.
$\mathfrak {D}$
.
In particular, if
![]() $\mathfrak R$
is an expansion of
$\mathfrak R$
is an expansion of
![]() $(\mathbb R,<,\mathbb N)$
such that every definable set is a union of definably connected components (an a priori weaker condition than CC), then
$(\mathbb R,<,\mathbb N)$
such that every definable set is a union of definably connected components (an a priori weaker condition than CC), then
![]() $\mid $
is definable.
$\mid $
is definable.
We leave any potential generalizations of QCC to the interested reader.
Acknowledgments
Research of Dolich was funded in part by PSC-CUNY Grant 61234-00 49. Research of Miller was funded in part by a Simons Visiting Professorship, hosted by Mathematisches Forschungsinstitut Oberwolfach, Universität Konstanz, and Université Savoie Mont Blanc (Bourget-du-Lac). Research of Thamrongthanyalak was conducted in part while a Zassenhaus Assistant Professor at Ohio State University. We thank David Marker, Russell Miller, Serge Randriambololona, Charles Steinhorn and Erik Walsberg for helpful observations.