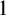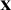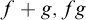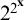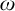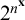1 Skolem problem
Let
$Sk$
be the smallest set of functions
$f:{\mathbb {R}}^{>0}\to {\mathbb {R}}^{>0}$
containing the constant function
$1$
and the identity function
${\mathbf {x}}$
, and such that if
$f,g\in Sk$
, then also
$f+g,fg$
and
$f^g$
are in
$Sk$
. A Skolem function is a function belonging to
$Sk$
. Each Skolem function restricts to a function
$f:{\mathbb {N}}^{>0}\to {\mathbb {N}}^{>0}$
from positive integers to positive integers and it is determined by its restriction.
We order
$Sk$
by
$f< g$
if
$f(x)<g(x)$
for all large enough x in
${\mathbb {R}}$
(or equivalently in
${\mathbb {N}}$
). This defines a total order. Indeed Hardy [Reference Hardy17] established the corresponding result for a larger class of functions. The totality of the order also follows from the fact that the structure
${\mathbb {R}}_{\exp } = ({\mathbb {R}},<,+,\cdot ,\exp )$
is o-minimal [Reference Wilkie26] and the Skolem functions are definable in
${\mathbb {R}}_{\exp }$
.
In this paper we study the order type of
$Sk$
and its fragments. Skolem [Reference Skolem25] conjectured that
$(Sk,<)$
is a well order and its order type is
$\varepsilon _{0} = \mathop {\mathrm {sup}}\limits \{\omega , \omega ^\omega , \omega ^{\omega ^\omega },\ldots \}$
(the least ordinal
$\varepsilon $
such that
$\varepsilon = \omega ^\varepsilon $
). He also exhibited a well ordered subset of order type
$\varepsilon _{0}$
, namely the subset generated from
$1$
and
${\mathbf {x}}$
using the operations
$+,\cdot $
and exponentiation
$g\mapsto {\mathbf {x}}^g$
with base
${\mathbf {x}}$
. Ehrenfeucht [Reference Ehrenfeucht13], using the tree theorem of Kruskal [Reference Kruskal18], proved that
$Sk$
is indeed well ordered. Levitz [Reference Levitz19] showed that its order type is at most equal to the smallest critical epsilon-number (the least ordinal
$\alpha $
such that
$\alpha = \varepsilon _{\alpha }$
). This improves the earlier bound
$\Gamma _0$
established by Schmidt [Reference Schmidt23], where
$\Gamma _0$
is the Feferman–Schütte ordinal.
Given a well ordered set X, we write
$|X|$
for the order type of X. If
$f\in Sk$
, we let
$|f|$
be the order type of the set of Skolem functions less than f. The Skolem functions
$<2^{\mathbf {x}}$
coincide with the nonzero polynomial functions with coefficients in
${\mathbb {N}}$
, so
$|2^{\mathbf {x}}| = |\omega ^\omega |$
.
In [Reference Levitz19] Levitz introduced the following definition: a regular function is a Skolem function g such that for every Skolem function
$f<g$
, one has
$f^{\mathbf {x}} < g$
. The first regular functions are
$g_0= 2$
and
$g_1= 2^{2^{\mathbf {x}}}$
and it is not difficult to show that the regular functions
$<2^{{\mathbf {x}}^{\mathbf {x}}}$
are exactly the functions of the form
$2^{n^{\mathbf {x}}}$
with
$2\leq n \in {\mathbb {N}}$
. Levitz proved that
$|g_{1+\alpha }| \leq \varepsilon _{\alpha }$
, where
$(g_{\alpha })_\alpha $
is a transfinite enumeration of the regular functions, and
$ (\varepsilon _\alpha )_\alpha $
is an enumeration of the epsilon numbers (i.e. the ordinals
$\varepsilon $
satisfying
$\varepsilon = \omega ^\varepsilon $
). Levitz’s result then yields
$|2^{2^{\mathbf {x}}}| \leq \varepsilon _0$
,
$2^{3^{\mathbf {x}}} \leq \varepsilon _1$
and
$|2^{{\mathbf {x}}^{\mathbf {x}}}| \leq \varepsilon _\omega $
(since
$g_{1+\omega }= g_\omega = 2^{{\mathbf {x}}^{\mathbf {x}}}$
).
In [Reference van den Dries and Levitz10] van den Dries and Levitz made a dramatic improvement on Levitz’s bound on
$g_1$
by showing that
$|2^{2^{x}}| = \omega ^{\omega ^{\omega }}$
. Here we prove the following bound on the fragments determined by the first
$\omega $
regular functions. Let
$\omega _0 = 1$
and
$\omega _{n+1} = \omega ^{\omega _n}$
for
$n\in {\mathbb {N}}$
. We have:
Theorem 14.1.
$|2^{n^{\mathbf {x}}}| \leq \omega _{n+1}$
for
$n\geq 1$
. In particular
$|2^{3^{\mathbf {x}}}| \leq \omega _4 = \omega ^{\omega ^{\omega ^\omega }}$
.
Theorem 14.1 should be compared with Levit’z bound
$|2^{3^{\mathbf {x}}}| \leq \varepsilon _1$
. As a consequence we obtain the following upper bound on
$2^{{\mathbf {x}}^{\mathbf {x}}}$
, which improves Levitz’s
$\varepsilon _\omega $
bound.
Theorem 14.2.
$|2^{{\mathbf {x}}^{\mathbf {x}}}| \leq \varepsilon _0$
.
A novel feature of our approach is the use of Conway’s surreal numbers [Reference Conway7] for asymptotic calculations, justified by the fact that the Skolem functions can be embedded in the exponential field of surreal numbers, that is, one can associate a surreal number to each Skolem function preserving the field operations, exponentiation, and ordering. Our main result is as follows.
Theorem 11.1. Let
$c\geq 1$
be a surreal number and let Q be a Skolem function. The set of real numbers
$r\in {\mathbb {R}}$
such that there is a Skolem function h satisfying
$(h/Q)^c = r + o(1)$
has no accumulation points in
${\mathbb {R}}$
.
The case
$c=1$
of the theorem says that, if we fix a Skolem function
$Q(x)$
, the set of real numbers r such that there is a Skolem function
$h(x)$
with
$\lim _{x\to \infty }h(x)/Q(x) = r$
, has no accumulation points in
${\mathbb {R}}$
. This special case is sufficient to obtain the bounds above, and also yields a different proof of the upper bound in [Reference van den Dries and Levitz10]. It turns out that, for technical reasons, we need to consider the general case
$c\geq 1$
in order to prove the special case
$c=1$
.
In the preliminary part of the paper, we prove a result concerning the order type of the set of finite sums
$\sum A$
of a well ordered set A of positive elements of an ordered group (Theorem 4.5). Unlike the known bounds by Carruth [Reference Carruth6] and other authors, our bound takes into account the set of archimedean classes of A.
The equality of two Skolem functions (given the defining expressions) is decidable [Reference Richardson22], but it is an open problem whether the order
$<$
is decidable. Gurevič [Reference Gurevič15] established the decidability of
$<$
below
$2^{{\mathbf {x}}^2}$
and showed that the decidability of
$<$
below
$2^{2^{\mathbf {x}}}$
is Turing equivalent to the decidability of the equality of two “exponential constants,” where the exponential constants are the elements in the smallest subset
$\mathbb {E}^+ \subset {\mathbb {R}}$
containing
$1$
and closed under addition, multiplication, division, and the real exponential function. In [Reference van den Dries and Levitz10] van den Dries and Levitz proved that if the quotient
$f/g$
of two Skolem functions smaller than
$2^{2^{\mathbf {x}}}$
tends to a limit in
${\mathbb {R}}$
, then the limit is in
$\mathbb {E}^+$
. They announced that the result could be extended to the whole class of Skolem functions using the work of [Reference Dahn8], where a version of the field of transseries made its first appearance. In the last part of the paper we give a proof of these facts using surreal numbers.
2 Asymptotic relations
Given
$f,g$
in an ordered abelian group, we write
$f\preceq g$
if
$|f|\leq n|g|$
for some
$n\in {\mathbb {N}}$
. We say in this case that f is dominated by g. If both
$f\preceq g$
and
$g\preceq f$
hold, we say that f and g belong to the same archimedean class, and we write
$f\asymp g$
. We say that f is strictly dominated by g if we have both
$f\preceq g$
and
$f\not \asymp g$
; we write
$f\prec g$
to express this relation. We define
$f\sim g$
as
$f-g \prec f$
and we say in this case that f is asymptotic to g. Notice that
$\sim $
is a symmetric relation. Indeed assume
$f-g \prec f$
and let us prove that
$f-g\prec g$
. This is clear if
$f\preceq g$
. On the other hand if
$g \prec f$
, then clearly
$f-g \asymp f$
, contradicting the assumption.
We write
$f = o(g)$
if
$f\prec g$
and
$f= O(g)$
if
$f\preceq g$
.
The set of germs at
$+\infty $
of the Skolem functions generates an ordered field by the results of [Reference Hardy17] or [Reference Wilkie26] cited in the introduction, so we can use the above notations for the Skolem functions. By the cited results, the quotient
$f(x)/g(x)$
of two Skolem functions tends to a limit in
${\mathbb {R}}\cup \{+ \infty \}$
for
$x\to +\infty $
. We then have
$f\prec g$
if
$f/g$
tends to
$0$
;
$f\sim g$
if
$f(x)/g(x)$
tends to
$1$
; and
$f\asymp g$
if
$f/g$
tends to a nonzero limit in
${\mathbb {R}}$
. Note that
$f\asymp g$
if and only if there is a nonzero real number r such that
$f \sim rg$
. We will prove as a special case of Theorem 11.1 that, if we fix g and let f vary in
$Sk$
, then the corresponding real r ranges in a subset of
${\mathbb {R}}$
without accumulation points.
3 Ordinal arithmetic
Let
${\mathbf {On}}$
be the class of all ordinal numbers. Given
$\alpha \in {\mathbf {On}}$
and
$\beta \in {\mathbf {On}}$
, we write
$\alpha + \beta $
and
$\alpha \beta $
(or sometimes
$\alpha \cdot \beta $
) for the ordinal sum and product of the given ordinals, and
$\alpha ^\beta $
for the ordinal exponentiation. We identify each ordinal with the set of its predecessor and we denote by
$\omega $
the first infinite ordinal, which can also be thought as the set of all finite ordinals, that is, the set of natural numbers
${\mathbb {N}}$
.
Definition 3.1. Given a sequence
$(\alpha _i)_i$
of ordinals, we define inductively:
-
(1)
$\sum _{i<0} \alpha _i = 0$
; -
(2)
$\sum _{i<\beta +1}\alpha _i = \sum _{i<\beta }\alpha _i + \alpha _\beta $
; -
(3)
$\sum _{i<\lambda } \alpha _i = {\mathrm {sup}}_{\beta <\lambda } \sum _{i<\beta } \alpha _i$
for
$\lambda $
a limit ordinal.
We recall that every ordinal
$\alpha $
can be written in a unique way in the form
$\alpha = \sum _{i<n}\omega ^{\gamma _i} n_i$
where
$n\in {\mathbb {N}}$
,
$(\gamma _i)_{i<n}$
is a decreasing sequence of ordinals, and
$n_i\in {\mathbb {N}}^{>0}$
for each
$i<n$
. This is called the Cantor normal form of
$\alpha $
.
We write
$\alpha \oplus \beta $
and
$\alpha \odot \beta $
for the Hessenberg sum and product [Reference Sierpiński24]. We recall the definitions below.
Definition 3.2. Given
$\alpha \in {\mathbf {On}}$
and
$\beta \in {\mathbf {On}}$
, we can find
$k\in {\mathbb {N}}$
and a decreasing finite sequence of ordinals
$(\gamma _i)_{i<k}$
such that
$\alpha = \sum _{i<k}\omega ^{\gamma _i}m_i$
and
$\beta =\sum _{i<k}\omega ^{\gamma _i}n_i$
with
$m_i,n_i < \omega $
(possibly zero). We define
$$ \begin{align*}\alpha \oplus \beta= \sum\limits_{i<k} \omega^{\gamma_i} (m_i+n_i).\end{align*} $$
Definition 3.3. If
$\alpha = \sum _{i<k}\omega ^{\alpha _i}m_i$
and
$\beta = \sum _{i<l}\omega ^{\beta _j}n_j$
are two ordinals in Cantor normal form, their Hessenberg product is defined as
$$ \begin{align*}\alpha \odot \beta = \bigoplus\limits_{i<k,j<l}\omega^{\alpha_i \oplus \beta_j} m_i n_j.\end{align*} $$
We shall need transfinite iterations of the Hessenberg sum and product.
Definition 3.4. Given a sequence of ordinals
$(\alpha _i)_{i}$
we define inductively:
-
(1)
$\bigoplus _{i<0} \alpha _i = 0$
, -
(2)
$\bigoplus _{i<\beta +1} \alpha _i = (\bigoplus _{i<\beta } \alpha _i) \oplus \alpha _{\beta ,}$
-
(3)
$\bigoplus _{i<\lambda } \alpha _i = {\mathrm {sup}}_{\beta < \lambda } \bigoplus _{i<\beta } \alpha _i$
for
$\lambda $
limit.
The paper [Reference Lipparini20] contains some comparison results between
$\sum _{i<\beta }$
and
$\bigoplus _{i<\beta }$
. Similarly we define the transfinite iteration of the Hessenberg product.
Definition 3.5. Given a sequence of ordinals
$(\alpha _i)_{i}$
we define inductively:
-
(1)
$\bigodot _{i<0} \alpha _i = 1$
, -
(2)
$\bigodot _{i<\beta +1} \alpha _i = (\bigodot _{i<\beta } \alpha _i) \odot \alpha _{\beta ,}$
-
(3)
$\bigodot _{i<\lambda } \alpha _i = \limsup _{\beta < \lambda } \bigodot _{i<\beta } \alpha _i$
for
$\lambda $
limit.
Definition 3.6. Given two ordinals
$\alpha $
and
$\beta $
we define
${{\alpha }^{\odot \beta }} = \bigodot _{i<\beta } \alpha $
.
Proposition 3.7. If
$n<\omega $
, then
${{n}^{\odot \gamma }} = n^{\gamma }$
for every
$\gamma \in {\mathbf {On}}$
.
Proof. We can assume
$n > 1 $
. Write
$\gamma = \omega \beta + k$
with
$\beta \in {\mathbf {On}}$
and
$k<\omega $
. Since
$n<\omega $
,
$n^\omega = \omega $
, and therefore
$n^{\omega \beta + k} = \omega ^\beta n^k$
. On the other hand by [Reference Altman1, Lemma 3.6] we have
${{n}^{\odot \omega \beta + k}} =\omega ^\beta n^k =n^{\omega \beta + k}$
, thus concluding the proof. ⊣
Lemma 3.8. If
$\alpha \geq \beta $
, then
$\alpha \oplus \beta \leq \alpha +\beta 2$
.
Proof. We can assume
$\beta>0$
. Let
$\alpha =\sum _{i<k}\omega ^{\alpha _{i}}m_{i}$
and
$\beta =\sum _{j<l}\omega ^{\beta _{j}}n_{j}$
be Cantor normal forms. For some
$i_0 \leq k$
,
$\alpha \oplus \beta $
has the form
$\sum _{i< i_{0}}\omega ^{\alpha _{i}}m_{i}+\omega ^{\beta _{0}}n_{0}+\rho $
with
$\rho <\omega ^{\beta _{0}}\leq \beta $
. Since
$\omega ^{\beta _0} n_0 \leq \beta $
, we obtain
$\alpha \oplus \beta \leq \alpha + \beta + \beta = \alpha + \beta 2$
. ⊣
Lemma 3.9.
$\alpha \beta \; \leq \; \bigoplus _{i<\beta }\alpha \; \leq \; \alpha 2\beta $
.
Proof. By induction on
$\beta $
based on Lemma 3.8. The case when
$\beta $
is zero or a limit ordinal follows at once from the induction hypothesis. If
$\beta = \gamma +1$
, then
$\alpha (\gamma +1) \leq \bigoplus _{i<\gamma +1} \alpha = (\bigoplus _{i<\gamma } \alpha ) \oplus \alpha \leq \alpha 2 \gamma \oplus \alpha \leq \alpha 2 \gamma + \alpha 2 = \alpha 2 (\gamma +1)$
, where we used Lemma 3.8 and the induction hypothesis. ⊣
Corollary 3.10. If
$\lambda $
is limit, then
$\bigoplus _{i<\lambda }\alpha = \alpha \lambda $
.
Proof. If
$\beta $
is limit, then
$2\beta = \beta $
, so we can conclude by Lemma 3.9. ⊣
Let
$\alpha $
be an ordinal. We say that
$\alpha $
is additively closed if the sum of two ordinals less than
$\alpha $
is less than
$\alpha $
. Similarly,
$\alpha $
is multiplicatively closed if the product of two ordinals less than
$\alpha $
is less than
$\alpha $
. We obtain an equivalent definition using the Hessenberg sum and product. The additively closed ordinals
$>0$
are the ordinals of the form
$\omega ^\delta $
for some
$\delta $
; the multiplicatively closed ordinals
$>1$
are the ordinals of the form
$\omega ^{\omega ^\delta }$
for some
$\delta $
[Reference Sierpiński24].
Proposition 3.11. If
$\alpha \in {\mathbf {On}}$
and
$\lambda $
is a limit ordinal, then
${{\alpha }^{\odot \lambda }} = \alpha ^\lambda $
. Moreover
$\alpha ^\lambda $
is additively closed.
Proof. The case
$\alpha <\omega $
follows from Proposition 3.7. Assume
$\alpha \geq \omega $
and consider first the special case
$\alpha = \omega ^\gamma $
. For every
$\beta $
it is easy to verify by induction that
${{({\omega ^\gamma })}^{\odot \beta }} = \bigodot _{i<\beta } \omega ^{\gamma } = \omega ^{\bigoplus _{i<\beta } \gamma }$
. Now take
$\beta = \lambda $
. Since
$\lambda $
is limit, by Corollary 3.10,
$\bigoplus _{i<\lambda } \gamma = \gamma \lambda $
, so
${{({\omega ^\gamma })}^{\odot \lambda }} = \omega ^{\gamma \lambda }$
.
For a general
$\alpha \geq \omega $
, let
$\delta>0$
be such that
$\omega ^\delta \leq \alpha < \omega ^{\delta +1}$
. Since
$\lambda $
is limit,
$(\delta +1)\lambda = \delta \lambda $
. The result now follows from the inequalities
${{\alpha }^{\odot \lambda }} \leq {(\omega ^{\delta +1})^{\odot \lambda }} = \omega ^{(\delta +1)\lambda } = \omega ^{\delta \lambda } \leq \alpha ^\lambda \leq {\alpha ^{\odot \lambda }}$
. ⊣
Corollary 3.12. For
$\beta \in {\mathbf {On}}$
, let
$\beta =\lambda + k$
with
$\lambda $
a limit ordinal or zero and
$k<\omega $
. Then
${\alpha ^{\odot \beta }} = {\alpha ^{\lambda }} \odot {\alpha ^{\odot k}}$
.
4 Well ordered subsets of ordered groups
The Hessenberg sum and product can be characterized as follows. Consider disjoint well ordered sets A and B of order type
$\alpha $
and
$\beta $
respectively. By [Reference Carruth6] or [Reference de Jongh and Parikh12] the Hessenberg sum
$\alpha \oplus \beta $
is the sup of all ordinals
$\gamma $
such that one can extend the given partial order on
$A\cup B$
to a total order of order type
$\gamma $
; the Hessenberg product
$\alpha \odot \beta $
is the sup of all ordinals
$\gamma $
such that one can extend the componentwise partial order on
$A\times B$
to a total order of order type
$\gamma $
. By the cited papers, the sups are achieved. An immediate consequence of the above characterization is the following:
Fact 4.1. Let
$X = (X,<)$
be a totally ordered set and let
$A, B\subseteq X$
be well ordered subsets. We have:
-
(1)
$A\cup B$
is well ordered and
$|A\cup B|\leq |A|\oplus |B|.$
-
(2) Let
$f:X\times X \to X$
be a binary function which is weakly increasing in both arguments and let
$f(A,B) := \{f(a,b):a\in A, b\in B\}$
. Then
$f(A,B)$
is well ordered and
$|f(A,B)|\leq |A| \odot |B|$
.
Given two sets A and B of Skolem functions we write:
$A+B$
for the set of all sums
$f+g$
with
$f\in A$
and
$g\in B$
;
$AB$
for the set of all products
$fg$
with
$f\in A$
and
$g\in B$
;
$A^B$
for the set of all functions of the form
$f^g$
with
$f\in A$
and
$g\in B$
. We write
$A/\!\asymp $
for the ordered set of all
$\asymp $
classes of elements of A, and similarly for
$A/\!\sim $
.
Corollary 4.2. Let A and B be sets of Skolem functions. Then:
-
(1)
$A\cup B$
has of order type
$\leq |A| \oplus |B|$
. -
(2)
$A+B,\; AB$
and
$A^B$
have order type
$\leq |A|\odot |B|$
. -
(3)
$AB/\!\asymp $
has order type
$\leq |A/\! \asymp | \odot |B/\! \asymp |$
.
Proof. The first two points are immediate from Fact 4.1. To prove point (3) we use again Fact 4.1 together with the observation that the
$\asymp $
-class of
$fg$
depends only on the respective
$\asymp $
-classes of f and g, and this dependence is weakly increasing in both arguments. ⊣
Given a subset
$A \subset Sk$
, we write
$\sum A$
for the set of finite nonempty sums of elements from A. We want to give an upper bound on
$|\sum A|$
. The definition of
$\sum A$
can be given more generally for a subset A of an ordered abelian group G, so it is convenient to work in this context. If A is a well ordered subset of
$G^{> 0}$
,
$\sum A$
is well ordered and Carruth [Reference Carruth6] gave an upper bound on its order type in terms of the order type of A. In Theorem 4.5 we obtain a different bound which takes into account the set of archimedean classes of A.
Lemma 4.3. Let
$(G,+,<)$
be an ordered abelian group and let
$A\subseteq G^{>0}$
be a well ordered subset of order type
$\alpha $
. Suppose all the elements of A belong to distinct archimedean classes. Then the order type of
$\sum A$
is
$\leq \omega ^{\alpha }$
.
Proof. Let
$(a_{i}:i<\alpha )$
be an increasing enumeration of A. Let
$x\in \sum A$
. Then x can be written uniquely in the form
$x=\sum _{i<\alpha }a_{i}n_{i}$
where
$n_{i}\in {\mathbb {N}}$
and
$n_{i}=0$
for all but finitely many i. We associate to x the ordinal
$\bigoplus _{i<\alpha }\omega ^{i}n_{i}$
. This defines an increasing map from
$\sum A$
to
$\omega ^{\alpha }$
yielding the desired result. ⊣
Lemma 4.4. Let
$(G,+,<)$
be an ordered abelian group and let
$A\subseteq G^{>0}$
be a well ordered subset of order type
$\alpha \geq 2$
. Suppose all the elements of A belong to the same archimedean class. Then
$$ \begin{align*} |\sum A| \leq \alpha^{\omega}.\end{align*} $$
(If
$|A| \leq 1$
, clearly
$|\sum A| \leq \omega $
.)
Proof. Let
$b\in \sum A$
, let
$(\sum A)^{<b}$
be the set of elements less than b in
$\sum A$
. Since all elements of A belong to the archimedean class of its least element, there exists
$m\in {\mathbb {N}}$
, depending on b, such that every element of
$(\sum A)^{<b}$
is the sum of at most m elements of A. By induction on
$i\leq m$
using Corollary 4.2, the set of sums of i elements of A has order type
$\leq {\alpha ^{\odot i}}$
. By the same corollary it then follows by induction on m that
$|(\sum A)^{<b}| \leq \bigoplus _{i=1}^m {\alpha ^{\odot i}}$
. Now for each
$i\leq m$
,
${\alpha ^{\odot i}} < {\alpha ^{\odot \omega }}$
and
${\alpha ^{\odot \omega }} = \alpha ^\omega $
is additively closed (Proposition 3.11). It follows that
$|(\sum A)^{<b}| < \alpha ^\omega $
. Since this holds for every
$b\in \sum A$
, we can conclude that
$|\sum A| \leq \alpha ^\omega $
. ⊣
Theorem 4.5. Let
$(G,+,<)$
be an ordered abelian group, let
$A\subseteq G^{>0}$
be a well ordered set of order type
$\alpha \geq 2$
and let
$\beta = |A/\! \asymp\! |$
be the order type of the set of archimedean classes of A. Then the order type of
$\sum A$
is
$\leq {(\alpha ^\omega )^{\odot \beta }}$
.
Proof. Let
$B\subseteq A$
be a set of representatives for the archimedean classes of A and let
$(b_{i} \operatorname {\mbox { : }} i<\beta )$
be an increasing enumeration of B. We reason by induction on
$\beta $
. The case
$\beta =1$
is Lemma 4.4.
Case
$\beta $
limit. For
$b\in G^{>0}$
, let
$A^{\preceq b}$
be the subset of A consisting of the elements
$\preceq b$
and let
$A^{\asymp b}$
be the set of elements of A which are
$\asymp b$
. Then
$\sum A = \bigcup _{\gamma < \beta } \sum (A^{\preceq b_\gamma })$
. The sets in the union are pairwise initial segments of one another. It follows that the order type of the union is the sup of the respective order types. By induction
$|\sum A| \leq {\mathrm {sup}}_{\gamma <\beta } {(\alpha ^\omega )^{\odot \gamma }} = {(\alpha ^\omega )^{\odot \beta }}$
.
Case
$\beta = \gamma + 1$
. We have
$\sum A = \sum (A^{\prec b_\gamma }) + \sum (A^{\asymp b_\gamma })$
. By the induction hypothesis
$|\sum (A^{\prec b_\gamma })| \leq {(\alpha ^\omega )^{\odot \gamma }}$
. The elements of
$A^{\asymp b_\gamma }$
live in a single archimedean class, so
$|\sum (A^{\asymp b_\gamma })| \leq \alpha ^\omega $
. It follows that
$|\sum A| \leq {(\alpha ^\omega )^{\odot \gamma }} \odot \alpha ^\omega = {({\alpha ^{\omega }})^{\odot (\gamma +1)}} $
. ⊣
We define a sequence of countable ordinals as follows.
Definition 4.6. Let
$\omega _0 = 1$
and, inductively,
$\omega _{n+1} = \omega ^{\omega _n}$
.
Remark 4.7. For all
$n\in {\mathbb {N}}$
,
$\omega _n$
is multiplicatively closed.
Proof. Clearly the product of two ordinals
$<1$
is
$<1$
, so the property holds for
$n=0$
. For
$n\geq 1$
,
$\omega _n$
has the form
$\omega ^{\omega ^\delta }$
(e.g.
$\omega _1 = \omega = \omega ^{\omega ^0}$
and
$\omega _2 = \omega ^\omega = \omega ^{\omega ^1}$
), so it is multiplicatively closed. ⊣
For our applications we need the following lemma.
Lemma 4.8. Let
$2 \leq n < \omega $
. If
$\alpha <\omega _{n+1}$
and
$\beta < \omega _{n}$
, then
${(\alpha ^\omega )^{\odot \beta }} < \omega _{n+1}$
.
Proof. We can write
$\beta = \lambda + k$
where
$\lambda $
is a limit ordinal or zero and
$k<\omega $
. By Corollary 3.12 we have
${({\alpha ^{\omega }})^{\odot \beta }} = \alpha ^{\omega \lambda } \odot {({\alpha ^{\omega }})^{\odot k}}$
. Since
$\alpha < \omega _{n+1}= \omega ^{\omega _n}$
and
$\omega _n$
is a limit ordinal, there is some
$\gamma <\omega _n$
such that
$\alpha \leq \omega ^{\gamma }$
. Since
$\omega $
and
$\lambda $
are
$<\omega _n$
and
$\omega _n$
is multiplicatively closed, we have
$\omega \lambda <\omega _n$
, hence
$\alpha ^{\omega \lambda } < \omega _{n+1}$
. Similarly,
${({\alpha ^{\omega }})^{\odot k}}= {{\alpha ^{\omega }}^{\odot k}}< \omega _{n+1}$
. Now since
$\omega _{n+1}$
is multiplicatively closed,
$\alpha ^{\omega \lambda } \odot ({{\alpha ^{\omega }}^{\odot k}})<\omega _{n+1}$
, as desired. ⊣
Corollary 4.9. Let
$(G,+,<)$
be an ordered abelian group, let
$A\subseteq G^{>0}$
be a well ordered set of order type
$<\omega _{n+1}$
whose set of archimedean classes has order type
$<\omega _n$
. Then the order type of
$\sum A$
is
$<\omega _{n+1}$
and its set of archimedean classes has order type
$<\omega _n$
.
Proof. By Lemma 4.8 and Theorem 4.5, together with the observation that the set of archimedean classes does not changes under taking finite sums. ⊣
Another interesting bound on
$|\sum A|$
is contained in [Reference van den Dries and Ehrlich9]: if
$|A| \leq \alpha $
, then
$|\sum A| \leq \omega ^{\omega \alpha }$
. For our purposes we need the bound in Corollary 4.9 which takes into account also the order type of the archimedean classes of A. Note that both bounds imply that if
$|A|<\varepsilon _{0}$
, then
$|\sum A| < \varepsilon _{0}$
.
5 Generalized power series
Given an ordered field K, a multiplicative subgroup
$\mathfrak {M}$
of
$K^{>0}$
is called a group of monomials if for each nonzero element x of K there is one and only one
${\mathfrak {m}}\in \mathfrak {M}$
such that
$x\asymp {\mathfrak {m}}$
. We assume some familiarity with Hahn’s field
${\mathbb {R}}((\mathfrak {M}))$
of generalized power series [Reference Hahn16], but we recall a few definitions. An element of
${\mathbb {R}}((\mathfrak {M}))$
is a formal sum
$f= \sum _{i<\alpha } {\mathfrak {m}}_i r_i$
where
$\alpha $
is an ordinal,
$({\mathfrak {m}}_i)_{i<\alpha }$
is a decreasing sequence in
$\mathfrak {M}$
, and
$0\neq r_i\in {\mathbb {R}}$
for each
$i<\alpha $
. We say that
$\{{\mathfrak {m}}_i \mid i<\alpha \}$
is the support of the series
$\sum _{i<\alpha } {\mathfrak {m}}_i r_i$
. The sum and product of generalized series is defined in the obvious way. We order
${\mathbb {R}}((\mathfrak {M}))$
by
$f = \sum _{i<\alpha } {\mathfrak {m}}_i r_i> 0 \iff r_0 > 0$
. This makes
${\mathbb {R}}((\mathfrak {M}))$
into an ordered field with
$\mathfrak {M}$
as a group of monomials (where we identify
${\mathfrak {m}}\in \mathfrak {M}$
with
${\mathfrak {m}}1\in {\mathbb {R}}((\mathfrak {M}))$
).
A family
$(f_i)_{i\in I}$
of elements of
${\mathbb {R}}((\mathfrak {M}))$
is summable if each monomial
${\mathfrak {m}}\in \mathfrak {M}$
is contained in the support of finitely many
$f_i$
and there is no strictly increasing sequence
$({\mathfrak {m}}_n)_{n\in {\mathbb {N}}}$
of monomials such that each
${\mathfrak {m}}_n$
belongs to the support of some
$f_i$
. In this case
$\sum _{i\in I}f_i\in {\mathbf{No}}$
is defined adding the coefficients of the corresponding monomials.
To prove that
${\mathbb {R}}((\mathfrak {M}))$
is a field, we write a nonzero element x of
${\mathbb {R}}((\mathfrak {M}))$
in the form
$r{\mathfrak {m}}(1+\varepsilon )$
with
$r\in {\mathbb {R}}^*, {\mathfrak {m}}\in \mathfrak {M}$
and
$\varepsilon \prec 1$
and observe that
$x^{-1} = r^{-1}{\mathfrak {m}}^{-1}\left (\sum _{n\in {\mathbb {N}}} (-1)^n \varepsilon ^n \right )$
where the summability of
$(-1)^n \varepsilon ^n$
is ensured by Neumann’s Lemma [Reference Neumann21]. More generally Neumann’s Lemma says that if
$\varepsilon $
is an infinitesimal element of
${\mathbb {R}}((\mathfrak {M}))$
and
$(r_n)_{n\in {\mathbb {N}}}$
is any sequence of real numbers, then
$(r_n \varepsilon ^n)_{n\in {\mathbb {N}}}$
is summable, so we can evaluate the formal power series
$P(X) = \sum _{n\in {\mathbb {N}}} r_n X^n$
at any infinitesimal element of
${\mathbb {R}}((\mathfrak {M}))$
.
Given f and g in
${\mathbb {R}}((\mathfrak {M}))$
we say that g is a truncation of f if
$f = \sum _{i<\alpha } {\mathfrak {m}}_i r_i$
and
$g = \sum _{i<\beta } {\mathfrak {m}}_i r_i\in {\mathbb {R}}((\mathfrak {M}))$
for some
$\beta <\alpha $
. If
$\mathfrak {G}\subseteq \mathfrak {M}$
is a subset, we write
${\mathbb {R}}((\mathfrak {G}))$
for the set of all
$f\in {\mathbb {R}}((\mathfrak {M}))$
whose support is contained in
$\mathfrak {G}$
.
6 Surreal numbers
Conway’s field
${\mathbf{No}}$
of surreal numbers [Reference Conway7, Reference Gonshor14] is an ordered real closed field extending the field
${\mathbb {R}}$
of real numbers and containing a copy of the ordinal numbers. In particular
${\mathbf{No}}$
is a proper class, and admits a group of monomials
$\mathfrak {M}\subset {\mathbf{No}}^{>0}$
which is itself a proper class. We can define generalized power series with monomials in
$\mathfrak {M}$
exactly as above, but we denote the resulting field as
${\mathbb {R}}((\mathfrak {M} ))_{\mathbf{On}}$
, where the subscript is meant to emphasize that, although
$\mathfrak {M}$
is a proper class, the support of a generic element
$\sum _{i<\alpha } {\mathfrak {m}}_i r_i$
of
${\mathbf{No}}$
is a set (because
$\alpha $
is still assumed to be an ordinal). Conway [Reference Conway7] showed that we can identity
${\mathbf{No}}$
with
${\mathbb {R}}((\mathfrak {M}))_{\mathbf {On}}$
, where the class
$\mathfrak {M} \subset {\mathbf{No}}$
of monomials is defined explicitly (it coincides with the image of Conway’s omega-map).
A surreal
$x = \sum _{i<\alpha } {\mathfrak {m}}_i r_i \in {\mathbb {R}}((\mathfrak {M}))_{\mathbf {On}}$
is purely infinite if all monomials
${\mathfrak {m}}_i$
in its support are
$>1$
(hence infinite). We write
${\mathbf{No}}^\uparrow $
for the (nonunitary) ring of purely infinite surreals. We observe that every
$x\in {\mathbf{No}}$
can be written in a unique way in the form
$x = x^\uparrow + x^\circ + x^\downarrow $
where
$x^\uparrow \in {\mathbf{No}}^\uparrow $
,
$x^\circ \in {\mathbb {R}}$
and
$x^\downarrow \prec 1$
. This yields a direct sum decomposition of
${\mathbb {R}}$
-vector spaces
$$ \begin{align*}{\mathbf{No}} = {\mathbf{No}}^\uparrow +{\mathbb {R}} + o(1),\end{align*} $$
where
$o(1)$
is the set of elements
$\prec 1$
. Gonshor [Reference Gonshor14] defined an isomorphism of ordered groups
$\exp :({\mathbf{No}},+,<)\to ({\mathbf{No}}^{>0},\cdot ,<)$
extending the real exponential function and satisfying
$\exp (x) \geq 1+x$
for all
$x\in {\mathbf{No}}$
and
$\exp (x) = \sum _{n\in {\mathbb {N}}}\frac {x^n}{n!}$
for
$x\prec 1$
(we need
$x\prec 1$
to ensure the summability of the series). Gonshor’s
$\exp $
is defined in such a way that
$\exp ({\mathbf{No}}^\uparrow ) = \mathfrak {M}$
, namely the monomials are the images of the purely infinite numbers. The stated properties are already sufficient to ensure that
${\mathbf{No}}$
, with Gonshor’s
$\exp $
, is a model of the elementary theory
$T_{\exp }$
of the real exponential field
${\mathbb {R}}_{\exp }=({\mathbb {R}},<,+,\cdot ,\exp )$
; in other words
$({\mathbf{No}},\exp )$
satisfies all the property which are true in
${\mathbb {R}}_{\exp }$
and are expressible by a first-order formula in the ring language and a symbol for the exponential function [Reference van den Dries and Ehrlich9]. A discussion of these issues can also be found in [Reference Berarducci and Mantova5], where other fields of generalized power series admitting an exponential map resembling the surreal
$\exp $
have been considered.
As long as we are only interested in the elementary theory of
${\mathbf{No}}$
as an exponential field, both the choice of the monomials
$\mathfrak {M}\subset {\mathbf{No}}$
and the details of the definition of
$\exp $
on
${\mathbf{No}}^\uparrow $
are not important. However they become important for summability issues and the properties of infinite sums, so we need to state a few more facts that are needed in this paper (all of them can be found in [Reference Berarducci and Mantova4]). We denote by
$\log :{\mathbf{No}}^{>0}\to {\mathbf{No}}$
the compositional inverse of
$\exp $
and we also write
$e^x$
for
$\exp (x)$
. It can be shown that if
$x \prec 1$
, then
$\log (1+x) = \sum _{n=1}^\infty \frac {(-1)^{n+1}}{n}x^n$
. An important fact, that depends on the choice of
$\mathfrak {M}\subset {\mathbf{No}}^{>0}$
, is that
$\omega $
is a monomial (where
$\omega $
is the least infinite ordinal seen as a surreal). More generally, for each
$n\in {\mathbb {N}}$
,
$\log _n(\omega )$
is an infinite monomial [Reference Gonshor14], where
$\log _0(\omega ) = \omega $
and
$\log _{n+1}(\omega ) = \log (\log _n(\omega ))$
. This fact is used in [Reference Berarducci and Mantova4] to show that
${\mathbf{No}}$
contains an isomorphic copy of the field
$\mathbb {T}$
of transseries as an exponential field (the notation
$\mathbb {T}$
is used in [Reference Aschenbrenner, van den Dries and van der Hoeven2] and refers to the version of the transseries defined [Reference van den Dries, Macintyre and Marker11] under the name “logarithmic exponential series).” Moreover
${\mathbf{No}}$
admits a differential operator
$\partial :{\mathbf{No}}\to {\mathbf{No}}$
extending the one on
$\mathbb {T}$
[Reference Berarducci, Kuhlmann, Mantova and Matusinski3, Reference Berarducci and Mantova4]. Since
${\mathbf{No}}^\uparrow $
is closed under multiplication by a real number, any real power
${\mathfrak {m}}^r= e^{r \log ({\mathfrak {m}})}$
of a monomial is again a monomial. Moreover, if
${\mathfrak {m}}$
is an infinite monomial,
$e^{\mathfrak {m}}$
is again a monomial (because
$\exp ({\mathbf{No}}^\uparrow ) = \mathfrak{M}$
).
From the equations
${\mathbf{No}}={\mathbb {R}}((\mathfrak {M}))_{\mathbf{On}}$
and
$\mathfrak {M}= e^{{\mathbf{No}}^\uparrow }$
it follows that every surreal can be written in a unique way in the form
$\sum _{i<\alpha } e^{\gamma _i} a_i$
where
$\alpha $
is an ordinal,
$(\gamma _i)_{i<\alpha }$
is a decreasing sequence in
${\mathbf{No}}^\uparrow $
and
$a_i \in {\mathbb {R}}^*$
(the empty sum is
$0$
). Following [Reference Berarducci, Kuhlmann, Mantova and Matusinski3], we call this representation Ressayre form.
7 Surreal expansions of Skolem functions
Since the surreal numbers are a model of
$T_{\exp }$
there is a unique map from
$Sk$
to
${\mathbf{No}}$
sending the identity function
${\mathbf {x}}$
into
$\omega $
and preserving
$1,+,\cdot $
and the function
$(a,b)\mapsto a^b$
where
$a^b = e^{b\log (a)}$
. Since
$\omega $
is greater than any natural number, this map preserves the order, so it is an embedding of ordered semirings endowed with an exponential
$(a,b)\mapsto a^b$
. We identify a Skolem function
$f= f({\mathbf {x}})\in Sk$
with its image
$f(\omega )\in {\mathbf{No}}$
under this embedding, and we define the Ressayre form of
$f\in Sk$
as the Ressayre form of the surreal number
$f(\omega )$
.
If we identify the transseries
$\mathbb {T}$
with a subfield of
${\mathbf{No}}$
(as in [Reference Berarducci and Mantova4]), it is easy to see that the image of the embedding of
$Sk$
in
${\mathbf{No}}$
is contained in
$\mathbb {T}$
, but we shall not need this fact.
We can consider the Ressayre form of a Skolem function
$f(x)$
as an asymptotic development for
$x\to +\infty $
. For example consider the Skolem function
$({\mathbf {x}}+1)^{\mathbf {x}}$
and identify
${\mathbf {x}}$
with
$\omega \in {\mathbf{No}}$
. To find its Ressayre form we write
$({\mathbf {x}}+1)^{\mathbf {x}} = e^{{\mathbf {x}} \log (1+{\mathbf {x}})}$
and we expand
$\log (1+{\mathbf {x}})$
as follows
$$ \begin{align*} \log(1+{\mathbf{x}}) &= \log({\mathbf{x}}(1+{\mathbf{x}}^{-1})) \\ & = \log({\mathbf{x}}) + \sum\limits_{n=1}^{\infty} \frac{(-1)^{n+1}}{n}{\mathbf{x}}^{-n}\\ &= \log({\mathbf{x}}) + {\mathbf{x}}^{-1} - {\mathbf{x}}^{-2}/2 + \cdots \end{align*} $$
Now, using
${\mathbf {x}}^{\mathbf {x}} = e^{{\mathbf {x}} \log ({\mathbf {x}})}$
and
$\exp (\varepsilon ) = \sum _{n\in {\mathbb {N}}} \varepsilon ^n/n! = 1 + \varepsilon + \cdots $
for
$\varepsilon \prec 1$
, we obtain
$$ \begin{align*} ({\mathbf{x}}+1)^{\mathbf{x}} &= \exp({\mathbf{x}} \log({\mathbf{x}}) +1 - {\mathbf{x}}^{-1}/2 + \cdots) \\ & = e {\mathbf{x}}^{\mathbf{x}} (1 -{\mathbf{x}}^{-1}/2 + \cdots) \\ & = e {\mathbf{x}}^{\mathbf{x}} - e2^{-1} {\mathbf{x}}^{{\mathbf{x}}-1} + \cdots \end{align*} $$
Replacing
${\mathbf {x}}$
with
$\omega $
we find the Ressayre form of the surreal
$(\omega +1)^\omega $
.
8 Finer asymptotic relations
The results in this section are stated for
${\mathbf{No}}$
but they hold more generally in every model of
$T_{\exp }$
. We identify
$Sk$
as a subset of
${\mathbf{No}}$
as discussed in the previous section. In particular
${\mathbf {x}} = \omega \in {\mathbf{No}}$
.
Definition 8.1. Let
$1 \leq c \in {\mathbb {K}}$
. Given two positive surreals f and g we define
$f\sim _c g$
if
$f^c \sim g^c$
and
$f\asymp _c g$
if
$f^c \asymp g^c$
.
When
$c=1$
, the relations
$\sim _c$
and
$\asymp _c$
become the usual
$\sim $
and
$\asymp $
relations. When
$c>1$
we obtain finer equivalence relations. One of the main ideas of this paper is to try to understand how many classes modulo
$\sim _c$
there are inside a class modulo
$\asymp _c$
. We are primarily interested in the case
$c=1$
, but we need to consider the general case to carry out the induction. In our terminology, the paper of [Reference van den Dries and Levitz10] deals with the case when c is equal
${\mathbf {x}}^n$
for some
$n\in {\mathbb {N}}$
, but we need to follow a different approach to be able to generalize it. A consequence of our main result (Theorem 11.1) is that the set of
$\sim _c$
-classes within any class modulo
$\asymp _c$
has order type
$\leq \omega $
.
In this section we establish some basic properties of
$\sim _c$
and
$\asymp _c$
. In particular we show that
$f \asymp _c g \iff c(f-g) \preceq g$
and
$f \sim _c g \iff c(f-g) \prec g$
, yielding a characterization of these relations which does not depend on the exponential function.
Lemma 8.2. For any
$t\in {\mathbb {K}}$
we have
$t\preceq 1$
if and only if
$e^t \asymp 1$
.
Proof. We have
$t\preceq 1$
if and only if there is
$k\in {\mathbb {N}}$
such that
$-k \leq t\leq k$
. This happens if and only if
$e^{-k} \leq e^{t} \leq e^k$
for some
$k\in {\mathbb {N}}$
, or equivalently
$e^t \asymp 1$
(because
$e^{-k}\asymp 1 \asymp e^k$
). ⊣
Lemma 8.3. For
$t\in {\mathbb {K}}$
we have
$t\prec 1$
if and only if
$e^t \sim 1$
.
Proof. We have
$t\prec 1$
if and only if
$-1/k\leq t \leq 1/k$
for all positive
$k\in {\mathbb {N}}$
. This happens if and only if
$e^{-1/k} \leq e^{t} \leq e^{1/k}$
for all positive
$k\in {\mathbb {N}}$
, or equivalently
$e^t \sim 1$
(because
$|e^t -1|\leq |e^{1/k} - e^{-1/k}|$
and
$|e^{1/k} - e^{-1/k}|$
becomes smaller than any positive real for k sufficiently large). ⊣
Proposition 8.4. Let
$c\geq c' \geq 1$
and let
$f,g>0$
.
-
(1) If
$f\asymp _c g$
, then
$f\asymp _{c'} g$
. -
(2) If
$f\sim _c g$
, then
$f\sim _{c'} g$
.
In particular, if
$f\asymp _c g$
, then
$f\asymp g$
.
Proof. We first observe that, for
$z\in {\mathbb {K}}^{>0}$
and
$d\in {\mathbb {K}}^{\geq 1}$
, we have
$z<1 \implies z^d < z$
and
$z>1 \implies z^d > z$
, so in any case
$|z-1| \leq |z^d-1|$
. Taking
$z = f/g$
and
$d=c/c'$
, we deduce that
$|(f/g)^{c'}-1| \leq |(f/g)^c - 1|$
. Thus if
$f\sim _c g$
, then
$f\sim _{c'} g$
. This proves (2).
To prove (1) assume that
$f\asymp _c g$
and let
$r\in {\mathbb {R}}^{>0}$
be such that
$(f/g)^c \sim r$
. Now observe that
$(f/g)^{c'}$
is between
$1$
and
$(f/g)^c \sim r>0$
, hence it is asymptotic to a positive real. ⊣
Lemma 8.5. For
$c\ge 1$
and
$z>0$
, we have
-
(1)
$z^c \asymp 1 \iff z = 1 + O(1/c)$
; -
(2)
$z^c\sim 1 \iff z = 1 + o(1/c)$
.
Proof. The case
$c \preceq 1$
can be reduced the case
$c=1$
using Proposition 8.4. If
$c\succ 1$
, we can assume
$z\sim 1$
, as otherwise both sides of either equivalence are false. We can thus write
$z = 1+\varepsilon $
for some
$\varepsilon \prec 1$
. The results follow from the following chains of equivalences.
$$ \begin{align*} \begin{array}{ll} \begin{array}{ll} & z^c \asymp 1\\ \iff &e^{c\log(1+\varepsilon)} \asymp 1 \\ \iff & c\log(1+\varepsilon) \preceq 1 \\ \iff & \log(1+\varepsilon)\preceq 1/c \\ \iff & \varepsilon \preceq 1/c \end{array}& \begin{array}{ll} & z^c \sim 1\\ \iff &e^{c\log(1+\varepsilon)} \sim 1 \\ \iff & c\log(1+\varepsilon) \prec 1 \\ \iff & \log(1+\varepsilon)\prec 1/c \\ \iff & \varepsilon \prec 1/c \end{array} \end{array} \end{align*} $$
where in the last step of both columns we used
$\log (1+\varepsilon )\sim \varepsilon $
(which follows from
$\varepsilon \prec 1$
).⊣
Proposition 8.6. For
$c\ge 1$
and
$f,g>0$
, we have:
-
(1)
$f \asymp _c g \iff c(f-g) \preceq g$
; -
(2)
$f \sim _c g \iff c(f-g) \prec g$
.
Proof. By Lemma 8.5 with
$z=f/g$
. ⊣
Proposition 8.7. Let
$c>{\mathbb {N}}$
,
$z> 0$
and
$r\in {\mathbb {R}}$
. Then
$$ \begin{align*}z^c \sim e^r \iff z = 1 + r/c + o(1/c).\end{align*} $$
Proof. Let
$z = 1 + r/c + o(1/c)$
. Then
$z^c=(1+r/c+o(1/c))^c \sim e^r$
. Conversely, assume
$z^c \sim e^r$
. Then in particular
$z^c \asymp 1$
. By Lemma 8.5,
$z = 1 + O(1/c)$
so we can write
$z = 1 + s/c + o(1/c)$
for some
$s\in {\mathbb {R}}$
. By the previous part
$e^s \sim e^r$
, hence
$s= r$
. ⊣
Proposition 8.8. Let
$c\ge 1$
and
$f,g,a,b>0$
.
-
(1) if
$f\asymp _c a$
and
$g\asymp _c b$
, then
$fg\asymp _c ab$
and
$f+g \asymp _c a+b$
; -
(2) If
$f\sim _c a$
and
$g\sim _c b$
, then
$fg \sim _c ab$
and
$f+g\sim _c a+b$
.
Proof. Assume
$f\asymp _c a$
and
$g\asymp _c b$
. By Proposition 8.6,
$c(f-a) \preceq a$
and
$c(g-b) \preceq b$
. Since
$a,b$
are positive,
$c(f-a) \preceq a+b$
and
$c(g-b) \preceq a+b$
. It follows that
$c(f+g - (a+b)) \preceq a+b$
, hence
$f+g\asymp _c a+b$
.
In order to prove
$fg\asymp _c ab$
we recall that
$f\asymp _c a$
means
$f^c \asymp a^c$
and
$g\asymp _c b$
means
$g^c \asymp b^c$
. Multiplying we obtain
$(fg)^c \asymp (ab)^c$
.
The proof of second part is essentially the same: it suffices to replace
$\preceq $
with
$\prec $
and
$\asymp _c$
with
$\sim _c$
. ⊣
9 The support of a Skolem function
We consider
$Sk$
as a substructure of
${\mathbf{No}}={\mathbb {R}}((\mathfrak {M}))_{\mathbf {On}}$
through the embedding induced by the identification
${\mathbf {x}} = \omega $
. Given
$f\in Sk$
, we can then write
$f=\sum _{i<\alpha } {\mathfrak {m}}_i r_i$
with
$\alpha \in {\mathbf {On}}$
,
${\mathfrak {m}}_i\in \mathfrak {M}$
and
$r_i\in {\mathbb {R}}^*$
. It thus makes sense to consider the support of a Skolem function, that is, the set of monomials
${\mathfrak {m}}_i$
which can appear in the above representation. We recall that a surreal number is an omnific integer if it belongs to the subring
${\mathbf{No}}^\uparrow + {\mathbb {Z}} \subset {\mathbf{No}}$
. We show that every Skolem function is an omnific integer, so it does not have infinitesimal monomials in its support. More generally we prove that a monomial in the support of a Skolem function is either
$1$
or
$\geq {\mathbf {x}}$
(so it cannot be
$\log ({\mathbf {x}})$
or
$\sqrt {{\mathbf {x}}}$
, say). To this aim we first show that every Skolem function belongs to a subfield
${\mathbb {K}} \subset {\mathbf{No}}$
which is similar to the field of transseries defined in [Reference van den Dries, Macintyre and Marker11], but unlike the transseries it is not closed under
$\log $
, although it is closed under
$\exp $
.
Definition 9.1. Let
${\mathbf {x}} = \omega \in {\mathbf{No}}$
. Working inside
${\mathbf{No}}$
we define
-
(1)
$\mathfrak {G}_0 = {\mathbf {x}}^{\mathbb {Z}}$
and
${\mathbb {K}}_0 = {\mathbb {R}}((\mathfrak {G}_0))$
; -
(2)
$\mathfrak {G}_{n+1} = e^{{\mathbb {K}}_n^\uparrow } {\mathbf {x}}^{{\mathbb {K}}_n^\uparrow +{\mathbb {Z}}} = e^{{\mathbb {K}}_n^\uparrow + \log ({\mathbf {x}})({\mathbb {K}}^\uparrow +{\mathbb {Z}})}$
and
${\mathbb {K}}_{n+1} = {\mathbb {R}}((\mathfrak {G}_{n+1}))$
.
Let
$\mathfrak {G} = \bigcup _n \mathfrak {G}_n$
and let
${\mathbb {K}} = \bigcup _n {\mathbb {K}}_n \subseteq {\mathbb {R}}((\mathfrak {G}))$
. Finally, let
${\mathbb {K}}^\uparrow = {\mathbb {K}}\cap {\mathbf{No}}^\uparrow $
.
We recall that a subfield of
${\mathbf{No}}$
is truncation closed if whenever it contains
$\sum _{i<\alpha } {\mathfrak {m}}_i r_i$
, it also contains its truncations
$\sum _{i<\beta }{\mathfrak {m}}_i r_i$
for all
$\beta < \alpha $
. Since
${\mathbb {K}}$
is an increasing union of the fields
${\mathbb {R}}((\mathfrak {G}_n))$
, it is obviously a subfield of
${\mathbf{No}}$
closed under truncations.
Theorem 9.2.
${\mathbb {K}}$
is a truncation closed subfield of
${\mathbf{No}}$
closed under
$\exp $
. If f and g are positive elements of the semiring
${\mathbb {K}}^\uparrow + {\mathbb {N}} \subset {\mathbb {K}}$
, then
$f^g = e^{g\log (f)} \in {\mathbb {K}}^\uparrow + {\mathbb {N}}$
. It follows that
$Sk \subseteq {\mathbb {K}}^\uparrow + {\mathbb {N}}$
. In particular every Skolem function is an omnific integer.
Proof. For each
$n\in {\mathbb {N}}$
,
$\mathfrak {G}_n$
is a multiplicative group and therefore
${\mathbb {K}}_n$
is a field. Moreover
$\mathfrak {G}_0\subseteq \mathfrak {G}_1$
and inductively
$\mathfrak {G}_n \subseteq \mathfrak {G}_{n+1}$
and
${\mathbb {K}}_n \subseteq {\mathbb {K}}_{n+1}$
. The fact that
${\mathbb {K}}$
is a truncation closed subfield of
${\mathbb {R}}((\mathfrak {G}))$
is clear. To show that
${\mathbb {K}}$
is closed under
$\exp $
, let
$x\in {\mathbb {K}}$
and write
$e^x = e^{x^\uparrow } e^{x^\circ } e^{x^\downarrow }$
. Now it suffices to observe that
$e^{{\mathbf {x}}^\uparrow }\in \mathfrak {G}$
,
$e^{{\mathbf {x}}^\circ }\in {\mathbb {R}}$
and
$e^{{\mathbf {x}}^\downarrow } = \sum _{n\in {\mathbb {N}}} ({\mathbf {x}}^\downarrow )^n/n!\in {\mathbb {K}}$
. More generally
${\mathbb {K}}$
is closed under the evaluation of a power series at an infinitesimal element. It remains to show that if
$a,b$
are positive elements of
${\mathbb {K}}^\uparrow + {\mathbb {N}}$
, then
$a^b\in {\mathbb {K}}^\uparrow +{\mathbb {N}}$
. ⊣
Claim 1. If
${\mathfrak {m}}\in \mathfrak {G}$
and
$0<t\in {\mathbb {K}}^\uparrow $
, then
${\mathfrak {m}}^t\in \mathfrak {G}$
.
To prove the claim, write
${\mathfrak {m}} = e^\gamma {\mathbf {x}}^{\theta + n}$
with
$\gamma ,\theta \in {\mathbb {K}}^\uparrow $
and
$n\in {\mathbb {Z}}$
. Then
${\mathfrak {m}}^t = e^{t \gamma } {\mathbf {x}}^{t(\theta + n)}\in \mathfrak {G}$
, as desired.
Claim 2. Let a and b be positive elements of
${\mathbb {K}}^\uparrow + {\mathbb {N}}$
. Then
$a^b \in {\mathbb {K}}^\uparrow + {\mathbb {N}}$
. Moreover if
$a\geq 2$
(i.e.
$a\neq 1$
) and
$b>{\mathbb {N}}$
, then
$a^b\in {\mathbb {K}}^\uparrow $
.
We can write
$b=b^\uparrow + n$
for some
$n\in {\mathbb {N}}$
and
$0< b^\uparrow \in {\mathbb {K}}^\uparrow $
. Since
${\mathbb {K}}^\uparrow + {\mathbb {N}}$
is closed under finite products,
$a^n\in {\mathbb {K}}^\uparrow + {\mathbb {N}}$
. It remains to show that
$a^{b^\uparrow }\in {\mathbb {K}}^\uparrow $
. This is clear if
$a\in {\mathbb {N}}$
. If
$a{\not \in } {\mathbb {N}}$
, we can write
$$ \begin{align*}a = r{\mathfrak {m}} (1+\varepsilon),\end{align*} $$
where
$1<{\mathfrak {m}} \in \mathfrak {G}$
is the leading monomial of a,
$r\in {\mathbb {R}}^{>0}$
and
$\varepsilon \prec 1$
. Then
$$ \begin{align*}a^{b^\uparrow} = r^{b^\uparrow}{\mathfrak {m}}^{b^\uparrow} (1+\varepsilon)^{b^\uparrow}.\end{align*} $$
By Claim 1
${\mathfrak {m}}^{b^\uparrow }\in \mathfrak {G}$
. By definition of
$\mathfrak {G}$
we also have
$r^{b^\uparrow } = e^{{b^\uparrow }\log (r)} \in \mathfrak {G}$
. The third factor
$(1+\varepsilon )^{b^\uparrow }$
can be written in the form
$$ \begin{align*} (1+\varepsilon)^{b^\uparrow} &= e^{{b^\uparrow}\log(1+\varepsilon)}\\ &={e^{({b^\uparrow}\log(1+\varepsilon))}}^\uparrow {e^{(b^{\uparrow} \log(1+\varepsilon))}}^\circ {e^{(b^{\uparrow} \log(1+\varepsilon))}}^\downarrow. \end{align*} $$
Since
$\log (1+\varepsilon ) = \sum _{n=1}^\infty \frac {(-1)^{n+1}}{n}\varepsilon ^n \in {\mathbb {K}}$
and
$b^\uparrow \in {\mathbb {K}}$
, we have
${b^\uparrow }\log (1+\varepsilon )\in {\mathbb {K}}$
, so
$e^{({b^\uparrow }\log (1+\varepsilon ))^\uparrow }\in \mathfrak {G}$
. Moreover
${e^{(b^\uparrow \log (1+\varepsilon ))}}^\circ \in {\mathbb {R}}$
. The element
$\delta = ({b^\uparrow }\log (1+\varepsilon ))^\downarrow $
is an infinitesimal element of
${\mathbb {K}}$
and
$e^{\delta }=\sum _{n\in {\mathbb {N}}}\frac {\delta ^n}{n!}$
is a power series in
$\delta $
, so it belongs to
${\mathbb {K}}$
. We have thus proved that
$(1+\varepsilon )^{b^\uparrow }\in {\mathbb {K}}$
and therefore
$a^{b^\uparrow }\in {\mathbb {K}}$
.
It remains to show that if
$a\geq 2$
, then
$a^{b^\uparrow }$
is purely infinite. Since
$a = r{\mathfrak {m}}(1+\varepsilon )$
is an omnific integer, each monomial in the support of
$\varepsilon $
is
$\geq {\mathfrak {m}}^{-1}$
. It follows that each monomial in the support of
$(1+\varepsilon )^{b^\uparrow }$
is
${\mathfrak {m}}^{-n}$
for some
$n\in {\mathbb {N}}$
. Since
$a^{b^\uparrow }=r^{b^\uparrow }{\mathfrak {m}}^{b^\uparrow } (1+\varepsilon )^{b^\uparrow }$
, it follows that every monomial in the support of
$a^{b^\uparrow }$
is
$\geq r^{b^\uparrow }{\mathfrak {m}}^{b^\uparrow }{\mathfrak {m}}^{- n} = r^n(r{\mathfrak {m}})^{b^\uparrow -n}$
, which is infinite. We conclude that
$a^{b^\uparrow } \in {\mathbb {K}}^\uparrow $
, as desired.
It follows from the claim that the set of positive elements of the semiring
${\mathbb {K}}^\uparrow + {\mathbb {N}}$
is closed under the operation
$a,b\mapsto a^b$
and therefore it contains
$Sk$
.
Proposition 9.3. For every Skolem function f there is a purely infinite surreal number g and some
$n\in {\mathbb {N}}$
such that
$f = g+n$
. Moreover g is a Skolem function.
Proof. By Theorem 9.2,
$f=g+n$
with
$g\in {\mathbb {K}}^\uparrow $
and
$n\in {\mathbb {N}}$
, so we only need to show that
$g\in Sk$
. We proceed by induction on the formation of the Skolem terms. The case when f is the sum or product of shorter terms is immediate. It remains to consider the case when
$f = a^b$
with
$a\geq 2$
and
$b>{\mathbb {N}}$
. In this case by Theorem 9.2,
$a^b\in {\mathbb {K}}^\uparrow $
, so it is purely infinite. ⊣
Theorem 9.4. The monomial
${\mathbf {x}}$
is the smallest infinite monomial in
${\mathbb {K}}$
.
Proof. We prove by induction on
$n\in {\mathbb {N}}$
that if
$1<{\mathfrak {m}} \in \mathfrak {M}_n$
, then
${\mathfrak {m}} \geq {\mathbf {x}}$
. This is clear for
$n=0$
since
$\mathfrak {M}_0 = {\mathbf {x}}^{\mathbb {Z}}$
. Let
$1<{\mathfrak {m}} \in \mathfrak {M}_{n+1}$
and assume the result holds for the monomials in
$\mathfrak {M}_n$
. By definition
${\mathfrak {m}}= e^\gamma {\mathbf {x}}^{\theta +k}=e^{\gamma + \log ({\mathbf {x}})(\theta +k)}$
with
$\gamma ,\theta \in {\mathbb {K}}_n^\uparrow $
and
$k\in {\mathbb {Z}}$
. By the induction hypothesis,
${\mathbf {x}}$
is the smallest infinite monomial in
${\mathbb {K}}_n$
. If for a contradiction
$1<{\mathfrak {m}}<{\mathbf {x}} = e^{\log ({\mathbf {x}})}$
, then
$$ \begin{align*}0<\gamma + \log({\mathbf{x}})(\theta + k) < \log({\mathbf{x}}).\end{align*} $$
Case 1. If
$\gamma \asymp \log ({\mathbf {x}})(\theta + k)$
, then
$\log ({\mathbf {x}}) \asymp \frac {\gamma }{\theta +k}\in {\mathbb {K}}_n$
, contradicting the induction hypothesis.
Case 2. If
$\gamma \succ \log ({\mathbf {x}})(\theta + k)$
, then
$0<\gamma <2 \log ({\mathbf {x}})$
, against the induction hypothesis.
Case 3. If
$\gamma \prec \log ({\mathbf {x}})(\theta + k)$
, we obtain
$0 < \log ({\mathbf {x}})(\theta + k) < 2\log ({\mathbf {x}})$
, whence
$0 < \theta + k < 2$
. Since
$\theta $
is purely infinite and
$k\in {\mathbb {Z}}$
, we obtain
$\theta =0$
, hence
$\gamma \prec \log (x)$
, contradicting the induction hypothesis. ⊣
Corollary 9.5. If
${\mathfrak {m}}$
is a monomial in the support of a Skolem function, then either
${\mathfrak {m}}=1$
or
${\mathfrak {m}}\geq {\mathbf {x}}$
.
Proof. Immediate from Theorem 9.4 and the inclusion
$Sk\subset {\mathbb {K}}^\uparrow + {\mathbb {N}}$
(Theorem 9.2). ⊣
Corollary 9.6. For
$f,g\in Sk$
we have:
-
(1)
$f\sim g \iff f = g + O(g/{\mathbf {x}})$
. -
(2)
$f^{\mathbf {x}} \asymp g^{\mathbf {x}} \iff f \sim g$
.
Proof. The first part follows from Theorem 9.4 and Theorem 9.2, observing that
$f-g\in {\mathbb {K}}$
. For (2) we take
$z=f/g$
and
$c={\mathbf {x}}$
in Lemma 8.5 to obtain
$f^{\mathbf {x}} \asymp g^{\mathbf {x}}$
if and only if
$f = g + O(g/{\mathbf {x}})$
. By the first part this happens if and only if
$f\sim g$
. ⊣
Corollary 9.7. For any
$A\subseteq Sk$
, we have
$|A^{\mathbf {x}}/\! \asymp | = |A/\! \sim |$
.
Proof. By part (2) of Corollary 9.6. ⊣
10 Components
Let f be a Skolem function. We say that f is additively irreducible if it cannot be written as a sum of two smaller Skolem functions; f is multiplicatively irreducible if it cannot be written as a product of two smaller Skolem functions; Following [Reference Levitz19] we say that f is a component if it is both additively and multiplicatively irreducible.
Remark 10.1. We can write every Skolem function as a finite sum of finite products of components (not necessarily in a unique way).
Proposition 10.2. Every component has the form
$1$
,
${\mathbf {x}}$
or
$f^g$
. If
$f^g$
is a component, then f is multiplicatively irreducible and g is additively irreducible. Every component
$> {\mathbf {x}}$
can be written in the form
$f^g$
where
$f\geq 2$
,
$g\geq {\mathbf {x}}$
, and g is a component.
Proof. A Skolem functions
$<{\mathbf {x}}$
is a positive integers, so it is either
$1$
or additively reducible. It follows that a component is either
$1$
, or
${\mathbf {x}}$
, or
$>{\mathbf {x}}$
. In the latter case it must have the form
$f^g$
(because it cannot be of the form
$f+g$
or
$fg$
). The rest follows at once from the following identities:
-
• if
$f=f_1 f_2$
, then
$f^g = f_1^g f_2^g$
; -
• if
$g=g_1 + g_2$
, then
$f^g = f^{g_1}f^{g_2}$
; -
• if
$g=g_1g_2$
, then
$f^g = (f^{g_1})^{g_2}$
.
⊣
Corollary 10.3. For every Skolem function h one of the following cases holds:
-
(1)
$h = f \cdot g$
where
$f \geq {\mathbf {x}}$
and
$g\geq {\mathbf {x}}$
; -
(2)
$h = f^{g}$
where
$f \geq 2$
and g is a component
$\geq {\mathbf {x}}$
; -
(3)
$h = f + g$
, where
$f \asymp h$
and f is a component; -
(4)
$h=1$
or
$h={\mathbf {x}}$
.
11 Main theorem
We work inside the surreal numbers
${\mathbf{No}}$
and identify
$Sk$
as a subset of
${\mathbf{No}}$
, with
${\mathbf {x}}=\omega \in {\mathbf{No}}$
. Our main result is the following.
Theorem 11.1. Let
$c\geq 1$
be a surreal number and let
$Q\in Sk$
. The set of real numbers
$r\in {\mathbb {R}}^{>0}$
such that there is
$h\in Sk$
satisfying
$(h/Q)^c \sim r$
, is well ordered and has no accumulation points in
${\mathbb {R}}$
(hence it has order type
$\leq \omega $
).
Proof. Given Q and c, the set of reals
$r\in {\mathbb {R}}^{>0}$
such that there is
$h\in Sk$
with
$(h/Q)^c \sim r$
is in order preserving bijection with the set of Skolem functions
$\asymp _c Q$
, so it is well ordered (as
$Sk$
is well ordered). A well ordered subset of
${\mathbb {R}}^{>0}$
has an accumulation point if and only if it contains a strictly increasing and bounded sequence. Assuming for the sake of a contradiction that the theorem fails, let Q be minimal in the well order of
$Sk$
such that there exist a surreal number
$c\geq 1$
, a strictly increasing and bounded sequence of positive real numbers
$(r_n)_{n\in {\mathbb {N}}}$
, and a sequence
$(h_n)_{n\in {\mathbb {N}}}$
of Skolem functions, such that
$$ \begin{align*}(h_n/Q)^c \sim r_n.\end{align*} $$
By the assumptions, for all
$n\in {\mathbb {N}}$
, we have
$$ \begin{align*} h_n \asymp_c Q \end{align*} $$
which in turn implies
$h_n \asymp Q$
(by Proposition 8.4). In other words, all the functions
$h_n$
belong to the archimedean class of Q. Let us also notice that, given
$c\geq 1$
as above, the minimality property of Q implies that Q is minimal in its
$\asymp _c$
-class in
$Sk$
(using the fact that if
$Q'\asymp _c Q$
, there is
$s\in {\mathbb {R}}^{>0}$
with
$(h_n/Q')^c \sim sr_n$
for all
$n\in {\mathbb {N}}$
).
Now let h be the least Skolem function
$\asymp Q$
, and note that its multiples
$nh$
(
$n\in {\mathbb {N}}$
) are cofinal in the archimedean class of Q. There is
$N\in {\mathbb {N}}$
such that
$h_n \leq Nh$
for all
$n\in {\mathbb {N}}$
, for otherwise the sequence
$(r_n)_{n\in {\mathbb {N}}}$
is unbounded. We call the least such N the characteristic bound of the sequence
$(h_n)_{n\in {\mathbb {N}}}$
.
We now choose
$(h_n)_n$
with the additional property that
$(h_n)_n$
has minimal characteristic bound
$N\in {\mathbb {N}}$
. Note that the characteristic bound N is only defined for those sequences
$(h_n)_n$
such that there is
$c\geq 1$
and a strictly increasing bounded sequence
$r_n\sim (h_n/Q)^c$
as above, but it does not depend on the choice of c, so we can minimize N before choosing c. Finally we fix the exponent
$c\geq 1$
and we get a strictly increasing bounded sequence
$(r_n)_n$
of positive real numbers such that
$(h_n/Q)^c \sim r_n$
.
Along the sequence
$(h_n)_n$
there is one of the cases of Corollary 10.3 which holds infinitely often. By taking a subsequence we can thus assume to be in one of the following cases:
-
(1) for all
$n\in {\mathbb {N}}$
,
$h_n = f_n \cdot g_n$
where
$f_n \geq {\mathbf {x}}$
and
$g_n\geq {\mathbf {x}}$
; -
(2) for all
$n\in {\mathbb {N}}$
,
$h_n = f_n^{g_n}$
where
$f_n \geq 2$
and
$g_n \geq {\mathbf {x}}$
; -
(3) for all
$n\in {\mathbb {N}}$
,
$h_n = f_n + g_n$
, where
$f_n \asymp Q$
and
$f_n$
is a component;
with
$(f_n)_n$
and
$(g_n)_n$
weakly increasing (taking advantage of the fact that
$Sk$
is well ordered).
We will need the following observation. Define
$r\in {\mathbb {R}}^{>0}$
by
$(Q/h_0)^c\sim r$
and let
$r^{\prime }_n = r_nr$
. Notice that
$$ \begin{align*}(h_n/h_0)^c \sim r^{\prime}_n\end{align*} $$
for all
$n\in {\mathbb {N}}$
and observe that
$(r^{\prime }_n)_n$
is again increasing and bounded.
Case 1. Suppose
$h_n = f_n \cdot g_n$
where
$f_n\geq {\mathbf {x}}$
and
$g_n\geq {\mathbf {x}}$
for all
$n\in {\mathbb {N}}$
. By our assumptions
$r^{\prime }_n \sim (h_n/h_0)^c = (f_n/f_0)^c (g_n/g_0)^c $
. Both factors in the last expression are
$\geq 1$
because the sequences
$(f_n)_n$
and
$(g_n)_n$
are weakly increasing. It then follows that there are real numbers
$s_n\geq 1$
and
$t_n\geq 1$
such that
$$ \begin{align*} (f_n/f_0)^c \sim s_n, \quad \quad \quad (g_n /g_0)^c \sim t_n \end{align*} $$
and
$r^{\prime }_n = s_n t_n$
. Since
$(r^{\prime }_n)_n$
is bounded, the sequences
$(s_n)_{n\in {\mathbb {N}}}$
and
$(t_n)_{n\in {\mathbb {N}}}$
must also be bounded. Since both
$f_n$
and
$g_n$
are
$\geq {\mathbf {x}}$
and their product is
$h_n$
, they are both
$\prec h_n \asymp Q$
. In particular
$f_0$
and
$g_0$
are
$\prec Q$
. By the minimality of Q, the sequences
$(s_n)_n$
and
$(t_n)_n$
are eventually constant, hence
$(r^{\prime }_n)_n$
is eventually constant, a contradiction.
In the next case we use the full strength of the fact that we work with all the equivalence relations
$\sim _c$
and not only with
$\sim $
.
Case 2. Suppose
$h_n=f_n^{g_n}$
where
$f_n\geq 2$
and
$g_n\geq {\mathbf {x}}$
for all
$n\in {\mathbb {N}}$
. Note that
$r^{\prime }_n \sim (h_n/h_0)^c \geq h_n/h_0 = f_n^{g_n}/f_0^{g_0} \geq f_0^{g_n-g_0} \geq 2^{g_n-g_0}$
for
$n\in {\mathbb {N}}$
. Since
$(r^{\prime }_n)_n$
is bounded in
${\mathbb {R}}$
, there is
$M \in {\mathbb {N}}$
such that
$g_n-g_0 < M$
for all
$n\in {\mathbb {N}}$
. If the difference between two Skolem functions is bounded by a natural number, then it is equal to a natural number (Proposition 9.3). Since
$(g_n)_{n\in {\mathbb {N}}}$
is weakly increasing, there must be some
$k\in {\mathbb {N}}$
such that
$g_n = g_k$
for all
$n\ge k$
. For
$n\geq k$
we have
$(h_n/h_k)^c \sim s r^{\prime }_n$
where
$s\in {\mathbb {R}}^{>0}$
is defined by
$s \sim (h_0/h_k)^c$
. Taking a subsequence we can assume
$k=0$
. Thus
$s=1$
and
$$ \begin{align*}r^{\prime}_n \sim (h_n/h_0)^c = (f_n/f_0)^{g_0 c}\end{align*} $$
for all
$n\in {\mathbb {N}}$
. Since
$f_n\geq 2$
and
$g_n\geq {\mathbf {x}}$
, we have
$f_n \prec f_n^{g_n} = h_n \asymp Q$
for all
$n\in {\mathbb {N}}$
. Since
$(f_n/f_0)^{g_0 c} \sim r^{\prime }_n$
and
$f_0 \prec Q$
, by the minimality of Q we deduce that
$(r^{\prime }_n)_{n\in {\mathbb {N}}}$
is eventually constant, a contradiction.
We have shown that a sequence
$(h_n)_n$
with minimal characteristic bound falls necessarily under case 3, so it cannot consist entirely of components. It remains to deal with case 3.
Case 3. Suppose that
$h_n = f_n + g_n$
where
$f_n \asymp Q$
and
$f_n$
is a component for all
$n\in {\mathbb {N}}$
. It suffices to consider the cases
$c=1$
and
$c>{\mathbb {N}}$
, for if
$c\asymp c'$
and
$(h_n/Q)^c \sim r_n$
, then
$(h_n/Q)^{c'} \sim r_n^t$
, where
$t\in {\mathbb {R}}^{>0}$
is such that
$t \sim c'/c$
. Taking a subsequence we can further assume that either
$g_n \asymp Q$
for all
$n\in {\mathbb {N}}$
, or
$g_n \prec Q$
for all
$n\in {\mathbb {N}}$
.
Case
$c=1$
. The assumption
$(h_n/Q)^c \sim r_n$
becomes
$h_n/Q \sim r_n$
. Recall that
$h_n = f_n+g_n$
. Consider first the subcase with
$g_n \asymp Q$
for all
$n\in {\mathbb {N}}$
. Then all the functions
$h_n,f_n,g_n$
are in the archimedean class of Q, so there are positive real numbers
$a_n\in {\mathbb {R}}^{>0}$
and
$b_n\in {\mathbb {R}}^{>0}$
such that
$$ \begin{align*}a_n \sim f_n/Q \quad \text{ and } \quad b_n \sim g_n/Q\end{align*} $$
for all
$n\in {\mathbb {N}}$
. It follows that
$a_n+b_n = r_n$
for all
$n\in {\mathbb {N}}$
. Since
$(r_n)_n$
is bounded, it follows that
$(a_n)_n$
and
$(b_n)_n$
are also bounded. Recall that Q is minimal in its
$\asymp _c$
-class. Since
$c=1$
, this means that Q is minimal in its archimedean class, so the functions
$h_n,f_n,g_n$
are all
$\geq Q$
. If N is the characteristic bound of
$(h_n)_n$
, we have
$f_n \geq Q$
and
$g_n \geq Q$
and
$f_n+g_n = h_n \leq NQ$
, so both
$(h_n)_n$
and
$(g_n)_n$
have characteristic bound
$\leq N-1$
. By the minimality of N, we deduce that the sequences
$(a_n)_n$
and
$(b_n)_n$
are eventually constant, hence their sum
$(r_n)_n$
is also eventually constant, a contradiction.
Now consider the subcase with
$g_n \prec Q$
for all
$n\in {\mathbb {N}}$
. Then the functions
$h_n$
and
$f_n$
are in the archimedean class of Q, but
$g_n$
is in a lower archimedean class. It follows that
$$ \begin{align*}r_n \sim h_n/Q = (f_n+g_n)/Q \sim f_n/Q\end{align*} $$
for all
$n\in {\mathbb {N}}$
. The sequence
$(f_n)_n$
is then a counterexample to the theorem with the same characteristic bound than
$(h_n)_n$
but consisting entirely of components. We have already shown that this cannot happen, so we have a contradiction.
Case
$c>{\mathbb {N}}$
. We are still inside the case
$h_n = f_n+g_n$
with
$h_n$
a component. By Proposition 8.7 the condition
$(h_n/h_0)^c \sim r^{\prime }_n$
can be rewritten in the form
$$ \begin{align} h_n/h_0 - 1 = s_n/c + o(1/c) \end{align} $$
where
$s_n = \log (r^{\prime }_n)$
for
$n\in {\mathbb {N}}$
. Note that since
$(h_n)_n$
is increasing, we have
$r^{\prime }_n \geq 1$
, so
$\log (r^{\prime }_n)$
is well defined and
$\geq 0$
. Moreover
$(s_n)_n$
is strictly increasing. Using
$h_n = f_n+g_n$
, Equation 11.1 becomes
$$ \begin{align*}(f_n-f_0) + (g_n-g_0) = s_n(f_0+g_0)(1/c +o(1/c)).\end{align*} $$
Dividing by
$f_0$
and multiplying by c, it can be rewritten as
$$ \begin{align*} c\left(\frac{f_n}{f_0}-1\right) + \left(\frac{c}{f_0} \right) \left( g_n - g_0\right) = s_n \left( 1 + \frac{g_0}{f_0} \right) + o(1) \end{align*} $$
Since
$g_0 \preceq Q \asymp f_0$
the right-hand-side is finite. The two summands on the left are
$\geq 0$
and their sum is finite, so they are both finite, that is, they can be written as a real number plus an infinitesimal. This means that we can define
$a_n\in {\mathbb {R}}$
and
$b_n\in {\mathbb {R}}$
by the equations
$$ \begin{align*} a_n = c\left(\frac{f_n}{f_0}-1\right) + o(1) \quad \text{and} \quad b_n = \left(\frac{c}{f_0} \right) \left( g_n - g_0\right) + o(1). \end{align*} $$
We can then write
$$ \begin{align} a_n + b_n = s_n \left( 1 + \frac{g_0}{f_0}\right) + o(1). \end{align} $$
Since
$(f_n)_n$
and
$(g_n)_n$
are weakly increasing, the sequences of real numbers
$(a_n)_n$
and
$(b_n)_n$
are weakly increasing. Moreover, since
$(s_n)_{n\in {\mathbb {N}}}$
is bounded and
$g_0/f_0$
does not depend on n,
$(a_n)_{n\in {\mathbb {N}}}$
and
$(b_n)_{n\in {\mathbb {N}}}$
are also bounded.
By Proposition 8.7 (and the assumption
$c>{\mathbb {N}}$
) the definition of
$a_n$
can be rewritten in the form
$$ \begin{align*}(f_n/f_0)^c \sim e^{a_n}.\end{align*} $$
We claim that
$(a_n)_n$
is eventually constant. If
$f_0<Q$
this follows from the minimality property of Q, so we can assume
$Q\leq f_0$
. We also have
$f_0 \leq h_0 \leq h_n \asymp _c Q$
, so all the functions
$f_n$
are in the
$\asymp _c$
-class of Q and therefore there is a real number
$s\in {\mathbb {R}}^{>0}$
such that
$$ \begin{align*}(f_n/Q)^c \sim se^{a_n}\end{align*} $$
for all
$n\in {\mathbb {N}}$
. Assuming for a contradiction that
$(a_n)_n$
is not eventually constant,
$(f_n)_n$
would be a counterexample to the theorem with a characteristic bound at most equal to that of
$(h_n)_n$
(because
$f_n \leq h_n$
). However
$(f_n)_n$
has the additional property that it consists entirely of components and we have already shown that this cannot happen. This contradiction shows that
$(a_n)_n$
is indeed eventually constant.
We now claim that
$(b_n)_{n\in {\mathbb {N}}}$
is eventually constant. By our definitions we have
$b_n = (c/f_0)(g_n - g_0)+o(1)$
so we can write
$$ \begin{align} g_n - g_0 = b_n P + o(P) \end{align} $$
where
$P= f_0/c$
.
We distinguish three subcases.
Subcase 1. If
$g_0 \prec P$
, then for all n we have
$g_n = b_n P+o(1)$
, or equivalently
$g_n/P = b_n+o(1)$
. Since
$P=f_0/c \prec f_0 \asymp Q$
, by the minimality of Q we conclude that
$(b_n)_{n\in {\mathbb {N}}}$
is eventually constant (possibly
$0$
), as desired.
Subcase 2. If
$g_0 \asymp P$
, then there is
$r\in {\mathbb {R}}^{>0}$
such that
$g_0 \sim r P$
, so
$g_n = (b_n+r) P+o(1)$
for all
$n\in {\mathbb {N}}$
. Reasoning as above,
$(b_n+r)_{n\in {\mathbb {N}}}$
is eventually constant, hence so is
$(b_n)_{n\in {\mathbb {N}}}$
.
Subcase 3. If
$g_0 \succ P$
, we divide Equation 11.3 by
$g_0$
obtaining
$(g_n/g_0 - 1) = b_n (P/g_0) + o(P/g_0)$
. Now we multiply by
$c'= g_0/P$
to get
$c' (g_n/g_0-1) = b_n + o(1)$
. Since
$c'>{\mathbb {N}}$
, by Proposition 8.7 we obtain
$\left (\frac {g_n}{g_0}\right )^{c'}\sim e^{b_n}$
. If
$g_0<Q$
, then by the minimality of Q we conclude that
$(b_n)_{n\in {\mathbb {N}}}$
is eventually constant, as desired. In the opposite case we have
$g_0 \asymp _c Q$
(since
$Q\le g_0 \le h_0 \asymp _c Q$
). The new exponent
$c'$
is in the same archimedean class of c, because
$c'=(g_0/f_0)c$
and
$g_0\asymp f_0$
, thus
$c/c' = \gamma + o(1)$
for some real
$\gamma>0$
. Raising to the power
$\gamma $
both sides of the relation
$\left (\frac {g_n}{g_0}\right )^{c'}\sim e^{b_n}$
we then obtain
$\left (\frac {g_n}{g_0}\right )^{c} \sim e^{b_n\gamma }$
. Since
$g_0 \asymp _c Q$
, there is a real
$r>0$
such that
$\left (\frac {g_n}{Q}\right )^{c} \sim r e^{b_n\gamma }$
. All the functions
$h_n$
,
$f_n$
,
$g_n$
are in the same archimedean class, namely that of Q. Since
$h_n = f_n + g_n$
, it follows that the characteristic bound of
$(g_n)_n$
is lower than the characteristic bound N of
$(h_n)_n$
. By the minimality of N, we deduce that
$(re^{b_n\gamma })_n$
is eventually constant, hence also
$(b_n)_n$
is eventually constant, as desired.
From Equation (11.2) we can now conclude that
$(s_n)_{n\in {\mathbb {N}}}$
is also eventually constant, against the assumptions. This contradiction concludes the proof. ⊣
Corollary 11.2. Let
$1\leq c \in {\mathbf{No}}$
. The set of
$\sim _c$
-classes of Skolem functions within any class modulo
$\asymp _c$
has order type
$\leq \omega $
. In particular, the set of asymptotic classes of Skolem functions within any archimedean class has order type
$\leq \omega $
.
Proof. Fix
$Q\in Sk$
. For every
$h\asymp _c Q$
, the
$\sim _c$
-class of h is determined by the real number
$r\in {\mathbb {R}}^{>0}$
defined by
$r\sim (h/Q)^c$
, so we can apply Theorem 11.1. ⊣
We need the following corollary to obtain an upper bound on the order type of the set of Skolem functions
$<2^{{\mathbf {x}}^{\mathbf {x}}}$
.
Corollary 11.3. For any
$A\subseteq Sk$
,
$|A^{\mathbf {x}} /\! \asymp | \;= \; |A/\! \sim \! | \;\leq \;\omega |A/\! \asymp \!| $
.
Proof. The first equality is Corollary 9.7. The inequality
$ |A/\! \sim \!| \;\leq \;\omega |A/\! \asymp \!| $
follows from Corollary 11.2. ⊣
We give below other consequences of the main theorem.
Corollary 11.4. Let
$Q= \sum _{i<\alpha } {\mathfrak {m}}_i r_i \in {\mathbf{No}}$
and let
${\mathfrak {m}}$
a monomial smaller than all monomials
${\mathfrak {m}}_i$
in the support of Q. Then there is a well ordered subset
$D\subseteq {\mathbb {R}}$
without accumulation points such that for every Skolem function f, if f (seen as an element of
${\mathbf{No}}$
) has a truncation of the form
$Q+r{\mathfrak {m}}$
, then
$r\in D$
.
Proof. If
$Q = 0$
the desired result is an immediate consequence of Theorem 11.1. Assume
$Q \neq 0$
. We can write
$f = Q + r{\mathfrak {m}} + o({\mathfrak {m}})$
. Thus
$f/Q = 1 + r {\mathfrak {m}}/Q + o({\mathfrak {m}}/Q)$
. Let
$c = Q/{\mathfrak {m}}$
. Then
$c>{\mathbb {N}}$
and
$f/Q = 1 + r/c + o(1/c)$
. By Proposition 8.7,
$(f/Q)^c \sim e^r$
. Let D be the set of possible values of
$e^r$
as f varies. Since
$Sk$
is well ordered, D is well ordered. Suppose for a contradiction that there is an increasing sequence
$e^{r_n}\in D$
with an accumulation point
$e^r\in {\mathbb {R}}$
. We can then find
$f_n\in Sk$
with
$(f_n/Q)^c \sim e^{r_n}$
, contradicting Theorem 11.1. ⊣
By Theorem 9.4, given two Skolem functions
$f,g$
, the smallest infinite monomial in the support of
$f/g$
(seen as a surreal number) is
${\mathbf {x}}= \omega $
. We thus obtain the following result, which extends to the whole class
$Sk$
the corresponding result of van den Dries and Levitz [Reference van den Dries and Levitz10] for the fragment below
$2^{2^{\mathbf {x}}}$
.
Corollary 11.5. Let
$g\in Sk$
. For every finite sequence
$r_0,\ldots , r_k$
of real numbers (empty if
$k= {-1}$
), there is a well ordered subset
$R = R(g,r_0,\ldots , r_k) \subseteq {\mathbb {R}}$
without accumulation points such that for every
$f\asymp g$
in
$Sk$
satisfying
$$ \begin{align*}f/g = r_0 + r_1/{\mathbf{x}} + \ldots + r_k/{\mathbf{x}}^k + r_{k+1}/{\mathbf{x}}^{k+1}+ O(1/{\mathbf{x}}^{k+2})\end{align*} $$
we have
$r_{k+1}\in R$
.
12 Levitz’s regular functions
We say that
$f\in Sk$
is an additive scale if the sum of two Skolem functions less than f is less than f. We define f to be a multiplicative scale if the product of two Skolem functions less than f is less than f. Clearly every additive scale is additively irreducible and every multiplicative scale is multiplicatively irreducible. It is also easy to see that a multiplicative scale
$f\neq 2$
is an additive scale. Indeed if f is not an additive scale, there is
$g<f$
with
$g+g \geq f$
. Since
$f\neq 2$
, we have
$g\neq 1$
, so
$gg \geq g+g \geq f$
, contradicting the fact that f is a multiplicative scale. We have thus proved that a multiplicative scale
$\neq 2$
is a component (recall that f is a component if it is both additively and multiplicatively irreducible).
We say that
$h\in Sk$
is regular if
$h\neq 1$
and for all Skolem functions
$f<h$
we have
$f^{\mathbf {x}} < h$
. Regular functions play a crucial role in the work of Levitz [Reference Levitz19]. Every regular function is a multiplicative scale, so it is either equal to
$2$
or a component. In the rest of the sections we characterize the regular functions
$\leq 2^{{\mathbf {x}}^{\mathbf {x}}}$
.
Proposition 12.1. The components
$<{\mathbf {x}}^{\mathbf {x}}$
are
$1,{\mathbf {x}}$
and
$p^{\mathbf {x}}$
with
$p\in {\mathbb {N}}$
prime.
Proof. If h is a component
$>{\mathbf {x}}$
, we can write
$h = f^g$
where
$f\geq 2$
is multiplicatively irreducible and g is a component
$\geq {\mathbf {x}}$
(Proposition 10.2). Since
$h <{\mathbf {x}}^{\mathbf {x}}$
, we must have
$g\leq {\mathbf {x}}$
and
$f<{\mathbf {x}}$
, so
$h = p^{\mathbf {x}}$
with p a prime in
${\mathbb {N}}$
. ⊣
Lemma 12.2. Let
$n>0$
. If f is a Skolem function
$<2^{(n+1)^{\mathbf {x}}}$
, then there is
$k\in {\mathbb {N}}$
such that
$f<2^{n^{\mathbf {x}} {\mathbf {x}}^k}$
. It follows that
$f^{\mathbf {x}} < 2^{(n+1)^{\mathbf {x}}}$
, hence
$2^{(n+1)^{\mathbf {x}}}$
is a regular function.
Proof. For a contradiction let
$n>0$
be minimal such that the statement fails. Let
$H_n\subset Sk$
be the set of Skolem functions bounded by one of the functions
$2^{n^{\mathbf {x}} {\mathbf {x}}^k}$
as k ranges in
${\mathbb {N}}$
. Let
$f< 2^{(n+1)^{\mathbf {x}}}$
be the minimal Skolem function such that
$f{\not \in } H_n$
. We need to consider the following cases.
-
(1) f is not a component;
-
(2) f is either
$1$
or
${\mathbf {x}}$
; -
(3) f is a component of the form
$a^{\mathbf {x}}$
; -
(4) f is a component of the form
$a^b$
with
$b>{\mathbf {x}}$
.
Case (2) is clearly impossible. Cases (1) and (3) are also impossible by the minimality of f and the fact that
$H_n$
is closed under sums, products and exponentiation to the power
${\mathbf {x}}$
. Finally, in case (4), by Proposition 12.1, we can write
$b= p^{\mathbf {x}}$
with p prime
$<n+1$
. Let
$q\in {\mathbb {N}}$
be minimal such that
$qp \geq n+1$
and notice that
$2 \leq q\leq n$
. We must have
$a < (2^{q^{\mathbf {x}}})$
, so by the minimality of n we have
$a<2^{(q-1)^{\mathbf {x}} {\mathbf {x}}^k}$
for some
$k\in {\mathbb {N}}$
. It follows that
$f=a^b < 2^{((q-1)p)^{\mathbf {x}} {\mathbf {x}}^k}\leq 2^{n^{\mathbf {x}} {\mathbf {x}}^k}$
. ⊣
Proposition 12.3. Let
$f<2^{{\mathbf {x}}^{\mathbf {x}}}$
be a Skolem function. Then there is
$n\in {\mathbb {N}}$
such that
$f<2^{n^{\mathbf {x}}}$
. It follows that
$2^{{\mathbf {x}}^{\mathbf {x}}}$
is the smallest regular function bigger than
$2^{n^{\mathbf {x}}}$
for all positive
$n\in {\mathbb {N}}$
.
Proof. Let
$f<2^{{\mathbf {x}}^{\mathbf {x}}}$
and assume by induction that the proposition holds for all Skolem functions
$<f$
. If f is not a component, then it is a sum of products of smaller functions, and we conclude observing the the Skolem functions less that
$2^{n^{\mathbf {x}}}$
for some
$n\in {\mathbb {N}}$
form an initial segment closed under sums and products. The cases
$f=1$
or
$f={\mathbf {x}}$
are trivial. It remains to consider the case when f is a component of the form
$a^b$
where
$b>1$
is a component and
$a\geq 2$
. Since
$f=a^b <2^{{\mathbf {x}}^{\mathbf {x}}}$
, we have
$b<{\mathbf {x}}^{\mathbf {x}}$
. By Proposition 12.1, either
$b={\mathbf {x}}$
or
$b = p^{\mathbf {x}}$
for some prime
$p\in {\mathbb {N}}$
. By the induction hypothesis
$a<2^{m^{\mathbf {x}}}$
for some
$m\in {\mathbb {N}}$
, hence in the first case
$f=a^b < 2^{{(m+1)}^{\mathbf {x}}}$
and in the second case
$f=a^b < 2^{m^{\mathbf {x}} p^{\mathbf {x}}}= 2^{(mp)^{\mathbf {x}}}$
. In either case
$f\leq 2^{n^{\mathbf {x}}}$
for a suitable n. ⊣
13 The fragment of van den Dries and Levitz
Van den Dries and Levitz [Reference van den Dries and Levitz10] proved that
$|2^{2^{\mathbf {x}}}| = \omega _3 = \omega ^{\omega ^\omega }$
. As a preparation for the results in the next section we give a proof of the inequality
$|2^{2^{\mathbf {x}}}| \leq \omega _3$
based on Corollary 11.3. Thanks to the fact that Corollary 11.3 holds for the whole class
$Sk$
, we shall then be able to extend the result to bigger fragments with a similar technique.
We recall that given a set
$X\subseteq Sk$
,
$\sum X$
is the set of finite non empty sums of elements of X (we exclude the empty sum because
$0$
is not a Skolem function). Similarly, we write
$\prod X$
for the set of finite products of elements of X, with the convention that the empty product is
$1$
.
Theorem 13.1 ([Reference van den Dries and Levitz10])
$|2^{2^{\mathbf {x}}}|\leq \omega ^{\omega ^\omega }$
. Moreover the set of archimedean classes of the set of Skolem functions
$<2^{2^{\mathbf {x}}}$
has order type
$\leq \omega ^\omega $
.
Proof. Let A be the set of Skolem functions
$< 2^{2^{\mathbf {x}}}$
. We need to prove that
$|A|\leq \omega _3$
and
${\left | A/ \! \asymp \right |} \leq \omega _2$
, where
$A/\! \asymp $
is the set of
$\asymp $
-classes of elements of A.
By Lemma 12.2 for
$n=1$
we can write
$$ \begin{align*}A = \bigcup\limits_{d\in {\mathbb {N}}} S_{d}\end{align*} $$
where
$S_d$
is set of Skolem functions
$<2^{{\mathbf {x}}^d}$
.
By induction on d we show that
$$ \begin{align*}|S_{d}|<\omega_{3} \quad \quad \text{and} \quad \quad {\left| {S_{d}}/ \! \asymp \right|}<\omega_{2}.\end{align*} $$
Granted this, the supremum over d of these ordinals is
$\leq \omega _{3}$
and
$\leq \omega _{2}$
respectively, yielding the desired bounds
$|A|\leq \omega _3$
and
${\left | {A}/ \! \asymp \right |} \leq \omega _2$
.
The case
$d=0$
of the inductive proof is obvious, so assume
$d>0$
. Writing a Skolem function as a finite sum of finite products of components, and observing that
$g^{\mathbf {x}} \leq 2^{{\mathbf {x}}^d} \implies g < 2^{{\mathbf {x}}^{d-1}}$
, we obtain
$$ \begin{align*}S_{d} \subseteq \sum \prod ({\mathbf{x}}^{\mathbb {N}} \cup S_{d-1}^{\mathbf{x}} )\end{align*} $$
By the induction hypothesis
$|S_{d-1}| < \omega _{3}$
and
${\left | {S_{d-1}}/ \! \asymp \right |}<\omega _{2}$
. Now observe that
$|S_{d-1}^{\mathbf {x}}| = |S_{d-1}| < \omega _3$
. Moreover by Corollary 11.3 we have
$$ \begin{align*}{\left| {S_{d-1}^{\mathbf{x}}}/ \! \asymp \right|} \;\leq \; \omega{\left| {S_{d-1}}/ \! \asymp \right|} \;<\;\omega_{2}\end{align*} $$
(because the set of ordinals
$<\omega _2$
is closed under multiplication by
$\omega $
). Letting
$X = {\mathbf {x}}^{\mathbb {N}}\cup S_{d-1}^{\mathbf {x}}$
, it follows that
$|X|<\omega _3$
and
${\left | {X}/ \! \asymp \right |}<\omega _2$
. Now observe that each element of
$\prod X$
is a product of at most
$2$
elements of X (because
${\mathbf {x}}^{\mathbb {N}}$
and
$S_{d-1}^{\mathbf {x}}$
are closed under finite products). By Corollary 4.2 we then obtain
$|\prod X|< \omega _{3}$
and
${\left | {\prod X}/ \! \asymp \right |}<\omega _2$
. By Corollary 4.9 we conclude that
$|\sum \prod X| < \omega _{3}$
and
${\left | {\sum \prod X}/ \! \asymp \right |} < \omega _{2}$
. Since
$S_{d}$
is included in
$\sum \prod X$
we get the desired bounds. ⊣
14 Fragments bounded by larger regular functions
We have seen that
$|2^{2^{\mathbf {x}}}| \leq \omega _3$
. The following result gives bounds on
$|2^{n^{\mathbf {x}}}|$
. In particular
$|2^{3^{\mathbf {x}}}| \leq \omega _4$
,
$|2^{4^{\mathbf {x}}}| \leq \omega _5$
, and so on.
Theorem 14.1. Let
$1\leq n\in {\mathbb {N}}$
. Then
$|2^{(n+1)^{\mathbf {x}}}| < \omega _{n+2}$
. Moreover the set of archimedean classes of the set of Skolem functions
$<2^{(n+1)^{\mathbf {x}}}$
has order type
$\leq \omega _{n+1}$
.
Proof. Let
$A_n$
be the set of all Skolem functions
$<2^{(n+1)^{\mathbf {x}}}$
. We prove by induction on n that
$|A_n| \leq \omega _{n+2}$
and
${\left | {A_n}/ \! \asymp \right |}\leq \omega _{n+1}$
.
For
$n=1$
,
$A_n$
is the set of Skolem functions
$<2^{2^{\mathbf {x}}}$
so we can apply Theorem 13.1.
Assume
$n>1$
. For
$d\in {\mathbb {N}}$
, let
$S_{n,d}$
be the set of Skolem functions
$<2^{n^{\mathbf {x}} {\mathbf {x}}^d}$
. By Lemma 12.2
$$ \begin{align*}A_n = \bigcup\limits_{d\in {\mathbb {N}}} S_{n,d}.\end{align*} $$
By a secondary induction on d we show that
$$ \begin{align*}|S_{n,d}|<\omega_{n+2} \quad \quad \text{and} \quad \quad {\left| {S_{n,d}}/ \! \asymp \right|}<\omega_{n+1}.\end{align*} $$
Granted this, the sup over d of these ordinals is
$\leq \omega _{n+2}$
and
$\leq \omega _{n+1}$
respectively, yielding the desired bounds
$$ \begin{align*}|A_n|\leq \omega_{n+2} \quad \quad \text{and} \quad \quad {\left| {A_n}/ \! \asymp \right|} \leq \omega_{n+1}.\end{align*} $$
The case
$d=0$
of the secondary induction follows from
$$ \begin{align*}S_{n,0} = A_{n-1}\end{align*} $$
applying the primary induction on n.
Assume
$d>0$
. We claim that
$$ \begin{align*}S_{n,d} \subseteq \sum \prod ({\mathbf{x}}^{\mathbb {N}} \cup S_{n,d-1}^{\mathbf{x}} \cup A_{n-2}^{2^{\mathbf{x}}} \cup \cdots \cup A_{n-2}^{n^{\mathbf{x}}}).\end{align*} $$
To prove the claim, it suffices to show that if
$h\in S_{n,d}$
is a component, then it belongs to
${\mathbf {x}}^{\mathbb {N}} \cup S_{n,d-1}^{\mathbf {x}} \cup A_{n-2}^{2^{\mathbf {x}}} \cup \cdots \cup A_{n-2}^{n^{\mathbf {x}}}$
. We can assume that
$h>{\mathbf {x}}$
, so we can write h in the form
$h=f^g$
where
$f\geq 2$
and g is a component
$\geq {\mathbf {x}}$
(Proposition 10.2). Since
$h<2^{{\mathbf {x}}^{\mathbf {x}}}$
, we have
$g<{\mathbf {x}}^{\mathbf {x}}$
, so either
$g= {\mathbf {x}}$
or
$g = p^{\mathbf {x}}$
for some prime
$p\in {\mathbb {N}}$
(Proposition 12.1). Since
$h\in S_{n,d}$
, we have
$h= f^g<2^{n^{\mathbf {x}} {\mathbf {x}}^d}$
. So if
$g={\mathbf {x}}$
we get
$f < 2^{n^{\mathbf {x}} {\mathbf {x}}^{d-1}}$
and therefore
$h \in S_{n,d-1}^{\mathbf {x}}$
. On the other hand if
$g = p^{\mathbf {x}}$
, then from
$f^g<2^{n^{\mathbf {x}} {\mathbf {x}}^d}< 2^{(n+1)^{\mathbf {x}}}$
we obtain
$f< 2^{(n-1)^{\mathbf {x}}}$
and
$p\leq n$
, so
$h\in A_{n-2}^{2^{\mathbf {x}}} \cup \ldots \cup A_{n-2}^{n^{\mathbf {x}}}$
and the claim is proved.
By the primary induction
$|A_{n-2}| \leq \omega _{n}$
. By the secondary induction
$|S_{n,d-1}| < \omega _{n+2}$
and
${\left | {S_{n,d-1}}/ \! \asymp \right |}<\omega _{n+1}$
. It follows that
$|S_{n,d-1}^{\mathbf {x}}| = |S_{n,d-1}| < \omega _{n+2}$
. Moreover by Corollary 11.3 we have
$$ \begin{align*}{\left| {S_{n,d-1}^{\mathbf{x}}}/ \! \asymp \right|} \; \leq \; \omega {\left| {S_{n,d-1}}/ \! \asymp \right|} <\omega_{n+1}.\end{align*} $$
We also have
$|A_{n-2}^{k^{\mathbf {x}}}| = |A_{n-2}|$
and
${\left | {A_{n-2}^{k^{\mathbf {x}}}}/ \! \asymp \right |} \leq |A_{n-2}^{k^{\mathbf {x}}}|$
. Taking the union of these sets it follows that the set
$X={\mathbf {x}}^{\mathbb {N}} \cup S_{n,d-1}^{\mathbf {x}} \cup A_{n-2}^{2^{\mathbf {x}}} \cup \ldots \cup A_{n-2}^{n^{\mathbf {x}}}$
satisfies
$|X|<\omega _{n+2}$
and
${\left | {X}/ \! \asymp \right |}< \omega _{n+1}$
. The same bounds hold for
$\prod X$
because each element of X is a product of at most
$n+1$
elements of X (as X is the union of
$n+1$
sets closed under products). By Corollary 4.9 we conclude that
$|\sum \prod X| < \omega _{n+2}$
and
${\left | {\sum \prod X}/ \! \asymp \right |} < \omega _{n+1}$
. Since
$S_{n,d}$
is included in
$\sum \prod X$
we get the desired bounds. ⊣
Theorem 14.2. The set of Skolem functions
$<2^{{\mathbf {x}}^{\mathbf {x}}}$
has order type
$\leq \varepsilon _{0}$
.
Proof. Immediate from Theorem 14.1 and Proposition 12.3. ⊣
15 Exponential constants
Let
$\mathbb {E}^+\subseteq {\mathbb {R}}^{>0}$
be the smallest set of real numbers containing
$1$
and closed under
$+,\cdot , ^{-1}$
and
$\exp $
. Let
$\mathbb {E} = \mathbb {E}^+ - \mathbb {E}^+$
. Note that
$\mathbb {E}$
is a subring of
${\mathbb {R}}$
,
$\exp (\mathbb {E})\subseteq \mathbb {E}^+$
and
$\mathbb {E}^+\subseteq \mathbb {E}$
(because
$1\in \mathbb {E}$
and
$\mathbb {E}^+\cdot \mathbb {E} \subseteq \mathbb {E}$
). The following result is inspired by the final remarks of [Reference van den Dries and Levitz10]. The authors gave a detailed proof for the fragment below
$2^{2^{\mathbf {x}}}$
, working with Laurent expansions rather than Ressayre forms, and announced a proof for the whole class
$Sk$
using the embryonic form of the transseries in [Reference Dahn8].
Proposition 15.1. Let
$f = \sum _{i<\gamma }e^{\gamma _i} c_i\in {\mathbf{No}}$
be the Ressayre form of a Skolem function f. Then
$c_0\in \mathbb {E}^+$
and
$c_i \in \mathbb {E}$
for every
$i<\alpha $
.
Proof. By induction on the formation of f. The cases
$f=a+b$
or
$f=a\cdot b$
are straightforward, so it suffices to consider the case
$f = a^b$
with
$a\geq 2$
and
$b>{\mathbb {N}}$
(note that in this case b is purely infinite). By definition
$$ \begin{align*}a^b = {e^{(b\log(a))}}^\uparrow {e^{(b \log(a))}}^\circ {e^{(b \log(a))}}^\downarrow.\end{align*} $$
We must study the coefficients of the Ressayre form of
$a^b$
. Note that
${e^{(b\log (a))}}^\uparrow $
is a monomial, so it does not contribute to the coefficients. Let us consider the other two factors.
Write
$a = \sum _{i<\alpha } e^{\gamma _i} a_i = e^{\gamma _0} a_0 (1 + \varepsilon )$
where
$\varepsilon = \sum _{1\leq i <\alpha } \frac {a_i}{a_0} e^{\gamma _i - \gamma _0}$
. Then
$$ \begin{align*}\log(a) = \gamma_0 + \log(a_0) + \log(1+\varepsilon).\end{align*} $$
Since b is purely infinite,
${(b \log (a))}^\circ = (b \log (1+\varepsilon ))^\circ $
. Since
$\log (1+\varepsilon )$
is a power series in
$\varepsilon $
with rational coefficients, and the coefficients
$\frac {a_i}{a_0}$
of
$\varepsilon $
belong to
$\mathbb {E}$
, it follows that
${(b \log (a))}^\circ \in \mathbb {E}$
and therefore
${e^{(b \log (a))}}^\circ \in \mathbb {E}^+$
. This is the leading coefficient of
$a^b$
.
The other coefficients of
$a^b$
come from the power series expansion of
${e^{(b \log (a))}}^\downarrow $
, so they belong to the ring generated by the coefficients of b and those of
$\varepsilon $
, which is included in
$\mathbb {E}$
. ⊣
Acknowledgements
The first author gave a plenary talk at the XXI congress of the Unione Matematica Italiana, Pavia, September 2–7, 2019 where some of the results of this paper were also mentioned. We thank Vincenzo Mantova and an anonymous referee for their comments on a preliminary version which helped to improve the exposition.
Both authors were supported by the Italian research project PRIN 2017, “Mathematical logic: models, sets, computability,” Prot. 2017NWTM8RPRIN.
