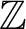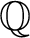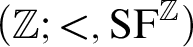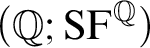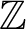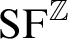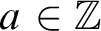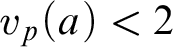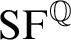1 Introduction
In [Reference Kaplan and Shelah9], Kaplan and Shelah showed under the assumption of Dickson’s conjecture that if
![]() $\mathbb {Z}$
is the additive group of integers implicitly assumed to contain
$\mathbb {Z}$
is the additive group of integers implicitly assumed to contain
![]() $1$
as a distinguished constant and
$1$
as a distinguished constant and
![]() $a \mapsto \,-a$
as a distinguished function, and if
$a \mapsto \,-a$
as a distinguished function, and if
![]() $\text {Pr}$
is the set of
$\text {Pr}$
is the set of
![]() $ a \in \mathbb {Z}$
such that either
$ a \in \mathbb {Z}$
such that either
![]() $ a$
or
$ a$
or
![]() $-a$
is prime, then the theory of
$-a$
is prime, then the theory of
![]() $(\mathbb {Z}; \text {Pr})$
is model complete, decidable, and super-simple of U-rank
$(\mathbb {Z}; \text {Pr})$
is model complete, decidable, and super-simple of U-rank
![]() $1$
. From our current point of view, the above result can be seen as an example of a more general phenomenon where we can often capture aspects of randomness inside a structure using first-order logic and deduce in consequence several model-theoretic properties of that structure. In
$1$
. From our current point of view, the above result can be seen as an example of a more general phenomenon where we can often capture aspects of randomness inside a structure using first-order logic and deduce in consequence several model-theoretic properties of that structure. In
![]() $(\mathbb {Z}; \text {Pr})$
, the conjectural randomness is that of the set of primes with respect to addition. Dickson’s conjecture is useful here as it reflects this randomness in a fashion which can be made first-order. The second author’s work in [Reference Tran14] provides another example with similar themes.
$(\mathbb {Z}; \text {Pr})$
, the conjectural randomness is that of the set of primes with respect to addition. Dickson’s conjecture is useful here as it reflects this randomness in a fashion which can be made first-order. The second author’s work in [Reference Tran14] provides another example with similar themes.
Our viewpoint in particular predicts that there are analogues of Kaplan and Shelah’s results with
![]() $\textrm {Pr}$
replaced by other random subsets of
$\textrm {Pr}$
replaced by other random subsets of
![]() $\mathbb {Z}$
. We confirm the above prediction in this paper without the assumption of any conjecture when
$\mathbb {Z}$
. We confirm the above prediction in this paper without the assumption of any conjecture when
![]() $\textrm {Pr}$
is replaced with the set
$\textrm {Pr}$
is replaced with the set
 $$ \begin{align*}\mathrm{SF}^{\mathbb{Z}} = \{ a \in \mathbb{Z} : \text{ for all } p \text{ primes, } v_p(a) < 2 \},\end{align*} $$
$$ \begin{align*}\mathrm{SF}^{\mathbb{Z}} = \{ a \in \mathbb{Z} : \text{ for all } p \text{ primes, } v_p(a) < 2 \},\end{align*} $$
where
![]() $v_p$
is the p-adic valuation associated with the prime p. We have that
$v_p$
is the p-adic valuation associated with the prime p. We have that
![]() $\mathbb {Z}$
is a structure in the language L of additive groups augmented by a constant symbol for
$\mathbb {Z}$
is a structure in the language L of additive groups augmented by a constant symbol for
![]() $1$
and a function symbol for
$1$
and a function symbol for
![]() $a \mapsto \,-a$
. Then
$a \mapsto \,-a$
. Then
![]() $(\mathbb {Z};\mathrm {SF}^{\mathbb {Z}})$
is a structure in the language
$(\mathbb {Z};\mathrm {SF}^{\mathbb {Z}})$
is a structure in the language
![]() $L_{\mathrm {u}}$
extending L by a unary predicate symbol for
$L_{\mathrm {u}}$
extending L by a unary predicate symbol for
![]() $\mathrm {SF}^{\mathbb {Z}}$
(as indicated by the additional subscript “u”). We will introduce a first-order notion of genericity which captures the partial randomness in the interaction between
$\mathrm {SF}^{\mathbb {Z}}$
(as indicated by the additional subscript “u”). We will introduce a first-order notion of genericity which captures the partial randomness in the interaction between
![]() $\mathrm {SF}^{\mathbb {Z}}$
and the additive structure on
$\mathrm {SF}^{\mathbb {Z}}$
and the additive structure on
![]() $\mathbb {Z}$
. Using a similar idea as in [Reference Kaplan and Shelah9], we obtain:
$\mathbb {Z}$
. Using a similar idea as in [Reference Kaplan and Shelah9], we obtain:
Theorem 1.1. The theory of
![]() $(\mathbb {Z}; \mathrm {SF}^{\mathbb {Z}})$
is model complete, decidable, supersimple of U-rank
$(\mathbb {Z}; \mathrm {SF}^{\mathbb {Z}})$
is model complete, decidable, supersimple of U-rank
![]() $1$
, and is k-independent for all
$1$
, and is k-independent for all
![]() $k \in \mathbb {N}^{\geq 1}$
.
$k \in \mathbb {N}^{\geq 1}$
.
The above theorem gives us without assuming any conjecture the first natural example of a simple unstable expansion of
![]() $\mathbb {Z}$
. From the same notion of genericity, we deduce entirely different consequences for the structure
$\mathbb {Z}$
. From the same notion of genericity, we deduce entirely different consequences for the structure
![]() $(\mathbb {Z}; <, \mathrm {SF}^{\mathbb {Z}})$
in the language
$(\mathbb {Z}; <, \mathrm {SF}^{\mathbb {Z}})$
in the language
![]() $L_{\mathrm {ou}}$
extending
$L_{\mathrm {ou}}$
extending
![]() $L_{\mathrm {u}}$
by a binary predicate symbol for the natural ordering
$L_{\mathrm {u}}$
by a binary predicate symbol for the natural ordering
![]() $<$
(as indicated by the additional subscript “o”):
$<$
(as indicated by the additional subscript “o”):
Theorem 1.2. The theory of
![]() $(\mathbb {Z}; <, \mathrm {SF}^{\mathbb {Z}})$
interprets arithmetic.
$(\mathbb {Z}; <, \mathrm {SF}^{\mathbb {Z}})$
interprets arithmetic.
The proof here is an adaption of the strategy used in [Reference Bateman, Jockusch and Woods2] to show that the theory of
![]() $(\mathbb {N}; +, <, \Pr )$
with
$(\mathbb {N}; +, <, \Pr )$
with
![]() $\Pr $
the set of primes interprets arithmetic. The above two theorems are in stark contrast with one another in view of the fact that
$\Pr $
the set of primes interprets arithmetic. The above two theorems are in stark contrast with one another in view of the fact that
![]() $(\mathbb {Z};<)$
is a minimal proper expansion of
$(\mathbb {Z};<)$
is a minimal proper expansion of
![]() $\mathbb {Z}$
; indeed, it is proven in [Reference Conant6] that adding any new definable set from
$\mathbb {Z}$
; indeed, it is proven in [Reference Conant6] that adding any new definable set from
![]() $(\mathbb {Z};<)$
to
$(\mathbb {Z};<)$
to
![]() $\mathbb {Z}$
results in defining
$\mathbb {Z}$
results in defining
![]() $<$
. On the other hand, it is shown in [Reference Dolich and Goodrick7] that there is no strong expansion of the theory of Presburger arithmetic, so Theorem 1.2 is perhaps not entirely unexpected.
$<$
. On the other hand, it is shown in [Reference Dolich and Goodrick7] that there is no strong expansion of the theory of Presburger arithmetic, so Theorem 1.2 is perhaps not entirely unexpected.
It is also natural to consider the structures
![]() $(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
and
$(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
and
![]() $(\mathbb {Q};<, \mathrm {SF}^{\mathbb {Q}})$
where
$(\mathbb {Q};<, \mathrm {SF}^{\mathbb {Q}})$
where
![]() $\mathbb {Q}$
is the additive group of rational numbers, also implicitly assumed to contain
$\mathbb {Q}$
is the additive group of rational numbers, also implicitly assumed to contain
![]() $1$
as a distinguished constant and
$1$
as a distinguished constant and
![]() $a\mapsto \,-a$
as a distinguished function,
$a\mapsto \,-a$
as a distinguished function,
 $$ \begin{align*}\mathrm{SF}^{\mathbb{Q}} =\{ a \in \mathbb{Q} : v_p(a) < 2 \text{ for all } \text{ primes } p \},\end{align*} $$
$$ \begin{align*}\mathrm{SF}^{\mathbb{Q}} =\{ a \in \mathbb{Q} : v_p(a) < 2 \text{ for all } \text{ primes } p \},\end{align*} $$
and the relation
![]() $<$
on
$<$
on
![]() $\mathbb {Q}$
is the natural ordering. The reader might wonder why chose
$\mathbb {Q}$
is the natural ordering. The reader might wonder why chose
![]() $\mathrm {SF}^{\mathbb {Q}}$
instead of
$\mathrm {SF}^{\mathbb {Q}}$
instead of
![]() $\mathrm {SF}^{\mathbb {Z}}$
or
$\mathrm {SF}^{\mathbb {Z}}$
or
 $\text {ASF}^{\mathbb {Q}} =\{ a \in \mathbb {Q} : |v_p(a)| < 2 \text { for all } \text { primes } p \}.$
From Lemma 2.2 in the next section, we get
$\text {ASF}^{\mathbb {Q}} =\{ a \in \mathbb {Q} : |v_p(a)| < 2 \text { for all } \text { primes } p \}.$
From Lemma 2.2 in the next section, we get
![]() $\mathrm {SF}^{\mathbb {Q}}+\mathrm {SF}^{\mathbb {Q}}= \mathbb {Q}$
,
$\mathrm {SF}^{\mathbb {Q}}+\mathrm {SF}^{\mathbb {Q}}= \mathbb {Q}$
,
![]() $\mathrm {SF}^{\mathbb {Z}}+\mathrm {SF}^{\mathbb {Z}} = \mathbb {Z}$
, and
$\mathrm {SF}^{\mathbb {Z}}+\mathrm {SF}^{\mathbb {Z}} = \mathbb {Z}$
, and
 $\text {ASF}^{\mathbb {Q}} + \text {ASF}^{\mathbb {Q}}=\{ a : v_p(a)>\,-2 \text { for all } \text { primes } p\}$
. Hence, equipping
$\text {ASF}^{\mathbb {Q}} + \text {ASF}^{\mathbb {Q}}=\{ a : v_p(a)>\,-2 \text { for all } \text { primes } p\}$
. Hence, equipping
![]() $\mathbb {Q}$
and
$\mathbb {Q}$
and
![]() $(\mathbb {Q};<)$
with either
$(\mathbb {Q};<)$
with either
![]() $\mathrm {SF}^{\mathbb {Z}}$
or
$\mathrm {SF}^{\mathbb {Z}}$
or
![]() $\text {ASF}^{\mathbb {Q}}$
will result in structures expanding an infinite-index pair of infinite abelian groups with a unary predicate on the smaller group, and therefore, having rather different flavors from
$\text {ASF}^{\mathbb {Q}}$
will result in structures expanding an infinite-index pair of infinite abelian groups with a unary predicate on the smaller group, and therefore, having rather different flavors from
![]() $(\mathbb {Z};\mathrm {SF}^{\mathbb {Z}})$
and
$(\mathbb {Z};\mathrm {SF}^{\mathbb {Z}})$
and
![]() $(\mathbb {Z};<, \mathrm {SF}^{\mathbb {Z}})$
.
$(\mathbb {Z};<, \mathrm {SF}^{\mathbb {Z}})$
.
Viewing
![]() $(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
and
$(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
and
![]() $(\mathbb {Q};<, \mathrm {SF}^{\mathbb {Q}})$
in the obvious way as an
$(\mathbb {Q};<, \mathrm {SF}^{\mathbb {Q}})$
in the obvious way as an
![]() $L_{\mathrm {u}}$
-structure and an
$L_{\mathrm {u}}$
-structure and an
![]() $L_{\mathrm {ou}}$
-structure, the main new technical aspect is in showing that these two structures satisfy suitable notions of genericity and leveraging on them to prove:
$L_{\mathrm {ou}}$
-structure, the main new technical aspect is in showing that these two structures satisfy suitable notions of genericity and leveraging on them to prove:
Theorem 1.3. The theory of
![]() $(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
is model complete, decidable, simple but not supersimple, and is k-independent for all
$(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
is model complete, decidable, simple but not supersimple, and is k-independent for all
![]() $k \in \mathbb {N}^{\geq 1}$
.
$k \in \mathbb {N}^{\geq 1}$
.
From above,
![]() $(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
is “less tame” than
$(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
is “less tame” than
![]() $(\mathbb {Z}; \mathrm {SF}^{\mathbb {Z}})$
. The reader might therefore expect that
$(\mathbb {Z}; \mathrm {SF}^{\mathbb {Z}})$
. The reader might therefore expect that
![]() $(\mathbb {Q};<, \mathrm {SF}^{\mathbb {Q}})$
is wild. However, this is not the case:
$(\mathbb {Q};<, \mathrm {SF}^{\mathbb {Q}})$
is wild. However, this is not the case:
Theorem 1.4. The theory
![]() $(\mathbb {Q}; <, \mathrm {SF}^{\mathbb {Q}})$
is model complete, decidable, is
$(\mathbb {Q}; <, \mathrm {SF}^{\mathbb {Q}})$
is model complete, decidable, is
![]() $\mathrm {NTP}_2$
but is not strong, and is k-independent for all
$\mathrm {NTP}_2$
but is not strong, and is k-independent for all
![]() $k \in \mathbb {N}^{\geq 1}$
.
$k \in \mathbb {N}^{\geq 1}$
.
The paper is arranged as follows. In Section 2, we define the appropriate notions of genericity for the structures under consideration. The model completeness and decidability results are proven in Section 3 and the combinatorial tameness results are proven in Section 4.
1.1 Notation and conventions
Let
![]() $h, k$
, and l range over the set of integers and let m, n, and
$h, k$
, and l range over the set of integers and let m, n, and
![]() $n'$
range over the set of natural numbers (which include zero). We let p range over the set of prime numbers, and denote by
$n'$
range over the set of natural numbers (which include zero). We let p range over the set of prime numbers, and denote by
![]() $v_p$
the p-adic valuation on
$v_p$
the p-adic valuation on
![]() $\mathbb {Q}$
. Let x be a single variable, y a tuple of variables of unspecified length, z the tuple
$\mathbb {Q}$
. Let x be a single variable, y a tuple of variables of unspecified length, z the tuple
![]() $(z_1, \ldots , z_n)$
of variables, and
$(z_1, \ldots , z_n)$
of variables, and
![]() $z'$
the tuple
$z'$
the tuple
 $(z^{\prime }_1, \ldots , z^{\prime }_{n'})$
of variables. For an n-tuple a of elements from a certain set, we let
$(z^{\prime }_1, \ldots , z^{\prime }_{n'})$
of variables. For an n-tuple a of elements from a certain set, we let
![]() $a_i$
denote the i-th component of a for
$a_i$
denote the i-th component of a for
![]() $i \in \{1, \ldots , n\}$
. Suppose G is an additive abelian group. We equip
$i \in \{1, \ldots , n\}$
. Suppose G is an additive abelian group. We equip
![]() $G^m$
with a group structure by structure by setting
$G^m$
with a group structure by structure by setting
![]() $+$
on
$+$
on
![]() $G^m$
to be the coordinate-wise addition. Viewing G and
$G^m$
to be the coordinate-wise addition. Viewing G and
![]() $G^m$
as
$G^m$
as
![]() $\mathbb {Z}$
-module, we define
$\mathbb {Z}$
-module, we define
![]() $ka$
with
$ka$
with
![]() $a \in G$
and
$a \in G$
and
![]() $kb$
with
$kb$
with
![]() $b\in G^m$
accordingly. Suppose, G is moreover an L-structure with
$b\in G^m$
accordingly. Suppose, G is moreover an L-structure with
![]() $1_G$
the distinguished constant. We write k for
$1_G$
the distinguished constant. We write k for
![]() $k1_G$
. For
$k1_G$
. For
![]() $A \subseteq G$
, we let
$A \subseteq G$
, we let
![]() $L(A)$
denote the language extending L by adding constant symbols for elements of A and view G as an
$L(A)$
denote the language extending L by adding constant symbols for elements of A and view G as an
![]() $L(A)$
structure in the obvious way.
$L(A)$
structure in the obvious way.
2 Genericity of the examples
We study the structure
![]() $(\mathbb {Z}; \mathrm {SF}^{\mathbb {Z}})$
indirectly by looking at its definable expansion to a richer language. For given p and l, set
$(\mathbb {Z}; \mathrm {SF}^{\mathbb {Z}})$
indirectly by looking at its definable expansion to a richer language. For given p and l, set
 $$ \begin{align*}U^{\mathbb{Z}}_{p, l} = \{ a \in \mathbb{Z} : v_p(a) \geq l\}.\end{align*} $$
$$ \begin{align*}U^{\mathbb{Z}}_{p, l} = \{ a \in \mathbb{Z} : v_p(a) \geq l\}.\end{align*} $$
Let
 $\mathscr {U}^{\mathbb {Z}} = ( U^{\mathbb {Z}}_{p, l})$
. The definition for
$\mathscr {U}^{\mathbb {Z}} = ( U^{\mathbb {Z}}_{p, l})$
. The definition for
![]() $l \leq 0$
is not too useful as
$l \leq 0$
is not too useful as
 $U^{\mathbb {Z}}_{p, l} =\mathbb {Z}$
in this case. However, we still keep this for the sake of uniformity as we treat
$U^{\mathbb {Z}}_{p, l} =\mathbb {Z}$
in this case. However, we still keep this for the sake of uniformity as we treat
![]() $(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
later. For
$(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
later. For
![]() $m>0$
, set
$m>0$
, set
 $$ \begin{align*}P^{\mathbb{Z}}_m = \{ a \in \mathbb{Z} : v_p(a) < 2 + v_p(m) \text{ for all } p\}.\end{align*} $$
$$ \begin{align*}P^{\mathbb{Z}}_m = \{ a \in \mathbb{Z} : v_p(a) < 2 + v_p(m) \text{ for all } p\}.\end{align*} $$
In particular,
 $ P^{\mathbb {Z}}_1 = \mathrm {SF}^{\mathbb {Z}}$
. Let
$ P^{\mathbb {Z}}_1 = \mathrm {SF}^{\mathbb {Z}}$
. Let
![]() $\mathscr {P}^{\mathbb {Z}} = (P^{\mathbb {Z}}_m)_{m>0}$
. We have that
$\mathscr {P}^{\mathbb {Z}} = (P^{\mathbb {Z}}_m)_{m>0}$
. We have that
![]() $(\mathbb {Z}, \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
is a structure in the language
$(\mathbb {Z}, \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
is a structure in the language
![]() $L_{\mathrm {u}}^*$
extending
$L_{\mathrm {u}}^*$
extending
![]() $L_{\mathrm {u}}$
by families of unary predicate symbols for
$L_{\mathrm {u}}$
by families of unary predicate symbols for
![]() $\mathscr {U}^{\mathbb {Z}}$
and
$\mathscr {U}^{\mathbb {Z}}$
and
![]() $( P^{\mathbb {Z}}_m)_{m>1}$
. Note that
$( P^{\mathbb {Z}}_m)_{m>1}$
. Note that
 $$ \begin{align*}U^{\mathbb{Z}}_{p,l}= \mathbb{Z} \text{ for } l\leq 0,\quad U^{\mathbb{Z}}_{p,l}= p^l\mathbb{Z} \text{ for } l>0, \text{ and} \quad P^{\mathbb{Z}}_m =\bigcup_{d \mid m} d\mathrm{SF}^{\mathbb{Z}} \text{ for } m>0.\end{align*} $$
$$ \begin{align*}U^{\mathbb{Z}}_{p,l}= \mathbb{Z} \text{ for } l\leq 0,\quad U^{\mathbb{Z}}_{p,l}= p^l\mathbb{Z} \text{ for } l>0, \text{ and} \quad P^{\mathbb{Z}}_m =\bigcup_{d \mid m} d\mathrm{SF}^{\mathbb{Z}} \text{ for } m>0.\end{align*} $$
Hence,
 $U^{\mathbb {Z}}_{p, l}$
and
$U^{\mathbb {Z}}_{p, l}$
and
![]() $P^{\mathbb {Z}}_m$
are definable in
$P^{\mathbb {Z}}_m$
are definable in
![]() $( \mathbb {Z}, \mathrm {SF}^{\mathbb {Z}})$
, and so a subset of
$( \mathbb {Z}, \mathrm {SF}^{\mathbb {Z}})$
, and so a subset of
![]() $\mathbb {Z}$
is definable in
$\mathbb {Z}$
is definable in
![]() $(\mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
if and only if it is definable in
$(\mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
if and only if it is definable in
![]() $( \mathbb {Z}, \mathrm {SF}^{\mathbb {Z}})$
.
$( \mathbb {Z}, \mathrm {SF}^{\mathbb {Z}})$
.
Let
![]() $(G; \mathscr {P}^G, \mathscr {U}^G)$
be an
$(G; \mathscr {P}^G, \mathscr {U}^G)$
be an
![]() $L_{\mathrm {u}}^*$
-structure. Then
$L_{\mathrm {u}}^*$
-structure. Then
![]() $\mathscr {U}^G$
is a family indexed by pairs
$\mathscr {U}^G$
is a family indexed by pairs
![]() $(p, l)$
, and
$(p, l)$
, and
![]() $\mathscr {P}^{G}$
is a family indexed by m. For p, l, and m, define
$\mathscr {P}^{G}$
is a family indexed by m. For p, l, and m, define
 $U^G_{p, l} \subseteq G$
to be the member of
$U^G_{p, l} \subseteq G$
to be the member of
![]() $\mathscr {U}^G$
with index
$\mathscr {U}^G$
with index
![]() $(p, l)$
and
$(p, l)$
and
![]() $P^G_m \subseteq G$
to be the member of the family
$P^G_m \subseteq G$
to be the member of the family
![]() $\mathscr {P}^G$
with index m. In particular, we have
$\mathscr {P}^G$
with index m. In particular, we have
 $\mathscr {U}^G = (U^G_{p, l})$
and
$\mathscr {U}^G = (U^G_{p, l})$
and
![]() $P^G = (P^G_m)_{m>0}$
. Clearly, this generalizes the previous definition for
$P^G = (P^G_m)_{m>0}$
. Clearly, this generalizes the previous definition for
![]() $\mathbb {Z}$
.
$\mathbb {Z}$
.
We isolate the basic first-order properties of
![]() $(\mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
. Let
$(\mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
. Let
![]() $\mathrm {Sf}^*_{\mathbb {Z}}$
be a recursive set of
$\mathrm {Sf}^*_{\mathbb {Z}}$
be a recursive set of
![]() $L_{\mathrm {u}}^*$
-sentences such that an
$L_{\mathrm {u}}^*$
-sentences such that an
![]() $L_{\mathrm {u}}^*$
-structure
$L_{\mathrm {u}}^*$
-structure
![]() $(G; \mathscr {U}^G, \mathscr {P}^G)$
is a model of
$(G; \mathscr {U}^G, \mathscr {P}^G)$
is a model of
![]() $\mathrm {Sf}^*_{\mathbb {Z}}$
if and only if
$\mathrm {Sf}^*_{\mathbb {Z}}$
if and only if
![]() $(G; \mathscr {U}^G, \mathscr {P}^G)$
satisfies the following properties:
$(G; \mathscr {U}^G, \mathscr {P}^G)$
satisfies the following properties:
-
(Z1)
 $(G;+,-,0,1)$
is elementarily equivalent to
$(G;+,-,0,1)$
is elementarily equivalent to
 $(\mathbb {Z};+,-,0,1)$
;
$(\mathbb {Z};+,-,0,1)$
; -
(Z2)
 $U^G_{p,l}= G$
for
$U^G_{p,l}= G$
for
 $l\leq 0$
, and
$l\leq 0$
, and
 $U^G_{p,l}= p^lG$
for
$U^G_{p,l}= p^lG$
for
 $l>0$
;
$l>0$
; -
(Z3)
 $1$
is in
$1$
is in
 $P^G_1$
;
$P^G_1$
; -
(Z4) for any given p, we have that
 $pa \in P^G_1$
if and only if
$pa \in P^G_1$
if and only if
 $a\in P^G_1$
and
$a\in P^G_1$
and
 $a \notin U^G_{p,1}$
;
$a \notin U^G_{p,1}$
; -
(Z5)
 $P^G_m =\bigcup _{d \mid m} dP^G_1 $
for all
$P^G_m =\bigcup _{d \mid m} dP^G_1 $
for all
 $m>0$
.
$m>0$
.
The fact that we could choose
![]() $\mathrm {Sf}^*_{\mathbb {Z}}$
to be recursive follows from the well-known decidability of
$\mathrm {Sf}^*_{\mathbb {Z}}$
to be recursive follows from the well-known decidability of
![]() $\mathbb {Z}$
. Clearly,
$\mathbb {Z}$
. Clearly,
![]() $(\mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
is a model of
$(\mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
is a model of
![]() $\mathrm {Sf}^*_{\mathbb {Z}}$
. Several properties which hold in
$\mathrm {Sf}^*_{\mathbb {Z}}$
. Several properties which hold in
![]() $(\mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
also hold in an arbitrary model of
$(\mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
also hold in an arbitrary model of
![]() $\mathrm {Sf}^*_{\mathbb {Z}}$
:
$\mathrm {Sf}^*_{\mathbb {Z}}$
:
Lemma 2.1. Let
![]() $(G; \mathscr {U}^G, \mathscr {P}^G)$
be a model of
$(G; \mathscr {U}^G, \mathscr {P}^G)$
be a model of
![]() $\mathrm {Sf}^*_{\mathbb {Z}}$
. Then we have the following:
$\mathrm {Sf}^*_{\mathbb {Z}}$
. Then we have the following:
-
(i)
 $(G; \mathscr {U}^G)$
is elementarily equivalent to
$(G; \mathscr {U}^G)$
is elementarily equivalent to
 $(\mathbb {Z}; \mathscr {U}^{\mathbb {Z}});$
$(\mathbb {Z}; \mathscr {U}^{\mathbb {Z}});$
-
(ii) for all k, p, l, and
 $m>0$
, we have that
$m>0$
, we have that  $$ \begin{align*}k \in U^G_{p,l} \text{ if and only if } k \in U^{\mathbb{Z}}_{p,l} \ \text{ and }\ k \in P^G_m \text{ if and only if } k \in P^{\mathbb{Z}}_m;\end{align*} $$
$$ \begin{align*}k \in U^G_{p,l} \text{ if and only if } k \in U^{\mathbb{Z}}_{p,l} \ \text{ and }\ k \in P^G_m \text{ if and only if } k \in P^{\mathbb{Z}}_m;\end{align*} $$
-
(iii) for all
 $h\neq 0 $
, p, and l, we have that
$h\neq 0 $
, p, and l, we have that
 $ha \in U^G_{p,l}$
if and only if
$ha \in U^G_{p,l}$
if and only if
 $ a \in U^G_{p,l-v_p(h)}; $
$ a \in U^G_{p,l-v_p(h)}; $
-
(iv) if
 $a\in G$
is in
$a\in G$
is in
 $U^G_{p, 2+v_p(m)}$
for some p, then
$U^G_{p, 2+v_p(m)}$
for some p, then
 $a \notin P^G_m;$
$a \notin P^G_m;$
-
(v) for all
 $h\neq 0$
and
$h\neq 0$
and
 $m>0$
,
$m>0$
,
 $ha \in P^G_{m}$
if and only if we have
$ha \in P^G_{m}$
if and only if we have  $$ \begin{align*}a \in P^G_{m} \ \text{ and } \ a \notin U^G_{p,2+ v_p(m) -v_p(h)} \text{ for all } p \text{ which divides } h;\end{align*} $$
$$ \begin{align*}a \in P^G_{m} \ \text{ and } \ a \notin U^G_{p,2+ v_p(m) -v_p(h)} \text{ for all } p \text{ which divides } h;\end{align*} $$
-
(vi) for all
 $h>0$
and
$h>0$
and
 $m>0$
,
$m>0$
,
 $a \in P^G_{m}$
if and only if
$a \in P^G_{m}$
if and only if
 $ha \in P^G_{mh}$
.
$ha \in P^G_{mh}$
.
Proof Fix a model
![]() $(G; \mathscr {U}^G, \mathscr {P}^G)$
of
$(G; \mathscr {U}^G, \mathscr {P}^G)$
of
![]() $\mathrm {Sf}^*_{\mathbb {Z}}$
. It follows from (Z2) that the same first-order formula defines both
$\mathrm {Sf}^*_{\mathbb {Z}}$
. It follows from (Z2) that the same first-order formula defines both
 $U^G_{p,l}$
in G and
$U^G_{p,l}$
in G and
 $U^{\mathbb {Z}}_{p,l}$
in
$U^{\mathbb {Z}}_{p,l}$
in
![]() $\mathbb {Z}$
. Then using (Z1), we get
$\mathbb {Z}$
. Then using (Z1), we get
![]() $\mathrm {(i)}$
. The first assertion of
$\mathrm {(i)}$
. The first assertion of
![]() $\mathrm {(ii)}$
is immediate from
$\mathrm {(ii)}$
is immediate from
![]() $\mathrm {(i)}$
. Using this, (Z3), and (Z4), we get the second assertion of
$\mathrm {(i)}$
. Using this, (Z3), and (Z4), we get the second assertion of
![]() $\mathrm {(ii)}$
for the case
$\mathrm {(ii)}$
for the case
![]() $m=1$
. For
$m=1$
. For
![]() $m \neq 1$
, we reduce to the case
$m \neq 1$
, we reduce to the case
![]() $m=1$
using property (Z5). Statement
$m=1$
using property (Z5). Statement
![]() $\mathrm {(iii)}$
is an immediate consequence of
$\mathrm {(iii)}$
is an immediate consequence of
![]() $\mathrm {(i)}$
. We only prove below the cases
$\mathrm {(i)}$
. We only prove below the cases
![]() $m = 1$
of
$m = 1$
of
![]() $\textrm{(iv--vi)}$
as the remaining cases of the corresponding statements can be reduced to these using (Z5). Statement
$\textrm{(iv--vi)}$
as the remaining cases of the corresponding statements can be reduced to these using (Z5). Statement
![]() $\mathrm {(iv)}$
is immediate for the case
$\mathrm {(iv)}$
is immediate for the case
![]() $m=1$
using (Z2) and (Z4). The case
$m=1$
using (Z2) and (Z4). The case
![]() $m=1$
of
$m=1$
of
![]() $\mathrm {(v)}$
is precisely the statement of (Z4) when h is prime, and then the proof proceeds by induction. For the case
$\mathrm {(v)}$
is precisely the statement of (Z4) when h is prime, and then the proof proceeds by induction. For the case
![]() $m=1$
of
$m=1$
of
![]() $\mathrm {(vi)}$
, (
$\mathrm {(vi)}$
, (
![]() $\rightarrow $
) follows from (Z5), and (
$\rightarrow $
) follows from (Z5), and (
![]() $\leftarrow $
) follows through a combination of Z5,
$\leftarrow $
) follows through a combination of Z5,
![]() $\mathrm {(v)}$
, and induction on the number of prime divisors of h.⊣
$\mathrm {(v)}$
, and induction on the number of prime divisors of h.⊣
We next consider the structures
![]() $(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
and
$(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
and
![]() $(\mathbb {Q}; <, \mathrm {SF}^{\mathbb {Q}})$
. For given p, l, and
$(\mathbb {Q}; <, \mathrm {SF}^{\mathbb {Q}})$
. For given p, l, and
![]() $m>0$
, in the same fashion as above, we set
$m>0$
, in the same fashion as above, we set
 $$ \begin{align*}U^{\mathbb{Q}}_{p, l} = \{ a \in \mathbb{Q} : v_p(a) \geq l\}\quad \text{ and } \quad \ P^{\mathbb{Q}}_m = \{ a \in \mathbb{Q} : v_p(a) < 2 + v_p(m) \text{ for all } p\},\end{align*} $$
$$ \begin{align*}U^{\mathbb{Q}}_{p, l} = \{ a \in \mathbb{Q} : v_p(a) \geq l\}\quad \text{ and } \quad \ P^{\mathbb{Q}}_m = \{ a \in \mathbb{Q} : v_p(a) < 2 + v_p(m) \text{ for all } p\},\end{align*} $$
and let
 $$ \begin{align*}\mathscr{U}^{\mathbb{Q}} = ( U^{\mathbb{Q}}_{p, l})\quad \text{ and } \quad \mathscr{P}^{\mathbb{Q}} = (P^{\mathbb{Q}}_m)_{m>0}.\end{align*} $$
$$ \begin{align*}\mathscr{U}^{\mathbb{Q}} = ( U^{\mathbb{Q}}_{p, l})\quad \text{ and } \quad \mathscr{P}^{\mathbb{Q}} = (P^{\mathbb{Q}}_m)_{m>0}.\end{align*} $$
Then
![]() $(\mathbb {Q}; \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
is a structure in the language
$(\mathbb {Q}; \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
is a structure in the language
![]() $L_{\mathrm {u}}^*$
. Clearly, every subset of
$L_{\mathrm {u}}^*$
. Clearly, every subset of
![]() $\mathbb {Q}^n$
definable in
$\mathbb {Q}^n$
definable in
![]() $(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
is also definable in
$(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
is also definable in
![]() $(\mathbb {Q}; \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
. A similar statement holds for
$(\mathbb {Q}; \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
. A similar statement holds for
![]() $(\mathbb {Q}; <, \mathrm {SF}^{\mathbb {Q}})$
and
$(\mathbb {Q}; <, \mathrm {SF}^{\mathbb {Q}})$
and
![]() $(\mathbb {Q}; <, \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
. We will show that the reverse implications are also true.
$(\mathbb {Q}; <, \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
. We will show that the reverse implications are also true.
The next lemma backs up the discussion on
![]() $\mathrm {SF}^{\mathbb {Q}}$
and
$\mathrm {SF}^{\mathbb {Q}}$
and
![]() $\mathrm {ASF}^{\mathbb {Q}}$
preceding Theorem 1.3 in the introduction.
$\mathrm {ASF}^{\mathbb {Q}}$
preceding Theorem 1.3 in the introduction.
Lemma 2.2.
![]() $\mathrm {SF}^{\mathbb {Z}}+\mathrm {SF}^{\mathbb {Z}} = \mathbb {Z}$
,
$\mathrm {SF}^{\mathbb {Z}}+\mathrm {SF}^{\mathbb {Z}} = \mathbb {Z}$
,
![]() $\mathrm {SF}^{\mathbb {Q}}+\mathrm {SF}^{\mathbb {Q}}= \mathbb {Q}$
, and
$\mathrm {SF}^{\mathbb {Q}}+\mathrm {SF}^{\mathbb {Q}}= \mathbb {Q}$
, and
 $\mathrm {ASF}^{\mathbb {Q}} + \mathrm {ASF}^{\mathbb {Q}}=\{ a : v_p(a)>\kern3pt {-}2 \text { for all } p\}$
.
$\mathrm {ASF}^{\mathbb {Q}} + \mathrm {ASF}^{\mathbb {Q}}=\{ a : v_p(a)>\kern3pt {-}2 \text { for all } p\}$
.
Proof We first prove that any integer k is a sum of two elements from
![]() $\mathrm {SF}^{\mathbb {Z}}$
. As
$\mathrm {SF}^{\mathbb {Z}}$
. As
![]() $\mathrm {SF}^{\mathbb {Z}} =\kern3pt {-}\mathrm {SF}^{\mathbb {Z}}$
and the cases where
$\mathrm {SF}^{\mathbb {Z}} =\kern3pt {-}\mathrm {SF}^{\mathbb {Z}}$
and the cases where
![]() $k=0$
or
$k=0$
or
![]() $k=1$
are immediate, we assume that
$k=1$
are immediate, we assume that
![]() $k>1$
. It follows from [Reference Rogers13] that the number of square-free positive integers less than k is at least
$k>1$
. It follows from [Reference Rogers13] that the number of square-free positive integers less than k is at least
![]() $\frac {53k}{88}$
. Since
$\frac {53k}{88}$
. Since
 $\frac {53}{88}> \frac {1}{2}$
, this implies k can be written as a sum of two positive square-free integers which gives us
$\frac {53}{88}> \frac {1}{2}$
, this implies k can be written as a sum of two positive square-free integers which gives us
![]() $\mathrm {SF}^{\mathbb {Z}}+\mathrm {SF}^{\mathbb {Z}} = \mathbb {Z}$
. Using this, the other two equalities follow immediately.⊣
$\mathrm {SF}^{\mathbb {Z}}+\mathrm {SF}^{\mathbb {Z}} = \mathbb {Z}$
. Using this, the other two equalities follow immediately.⊣
Lemma 2.3. For all p and l,
 $U^{\mathbb {Q}}_{p,l}$
is existentially
$U^{\mathbb {Q}}_{p,l}$
is existentially
![]() $0$
-definable in
$0$
-definable in
![]() $( \mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
.
$( \mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
.
Proof As
 $U^{\mathbb {Q}}_{p, l+n} = p^nU^{\mathbb {Q}}_{p, l}$
for all l and n, it suffices to show the statement for
$U^{\mathbb {Q}}_{p, l+n} = p^nU^{\mathbb {Q}}_{p, l}$
for all l and n, it suffices to show the statement for
![]() $l=0$
. Fix a prime p. We have for all
$l=0$
. Fix a prime p. We have for all
![]() $a \in \mathrm {SF}^{\mathbb {Q}}$
that
$a \in \mathrm {SF}^{\mathbb {Q}}$
that
 $$ \begin{align*}v_p(a) \geq 0 \ \text { if and only if } p^2 a \notin \mathrm{SF}^{\mathbb{Q}}.\end{align*} $$
$$ \begin{align*}v_p(a) \geq 0 \ \text { if and only if } p^2 a \notin \mathrm{SF}^{\mathbb{Q}}.\end{align*} $$
Using Lemma 2.2, for all
![]() $a \in \mathbb {Q}$
, we have that
$a \in \mathbb {Q}$
, we have that
![]() $v_p(a) \geq 0$
if and only if there are
$v_p(a) \geq 0$
if and only if there are
![]() $a_1, a_2 \in \mathbb {Q}$
such that
$a_1, a_2 \in \mathbb {Q}$
such that
 $$ \begin{align*}\big(a_1\in \mathrm{SF}^{\mathbb{Q}} \wedge v_p(a_1) \geq 0\big) \wedge \big(a_2\in \mathrm{SF}^{\mathbb{Q}} \wedge v_p(a_2) \geq 0\big) \ \text{ and } \ a =a_1+a_2.\end{align*} $$
$$ \begin{align*}\big(a_1\in \mathrm{SF}^{\mathbb{Q}} \wedge v_p(a_1) \geq 0\big) \wedge \big(a_2\in \mathrm{SF}^{\mathbb{Q}} \wedge v_p(a_2) \geq 0\big) \ \text{ and } \ a =a_1+a_2.\end{align*} $$
Hence, the set
 $U^{\mathbb {Q}}_{p, 0} = \{a \in \mathbb {Q} : v_p(a) \geq 0 \} $
is existentially definable in
$U^{\mathbb {Q}}_{p, 0} = \{a \in \mathbb {Q} : v_p(a) \geq 0 \} $
is existentially definable in
![]() $(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
. The desired conclusion follows.⊣
$(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
. The desired conclusion follows.⊣
It is also easy to see that for all m,
![]() $P_m^{\mathbb {Q}} = m \mathrm {SF}^{\mathbb {Q}}$
for all
$P_m^{\mathbb {Q}} = m \mathrm {SF}^{\mathbb {Q}}$
for all
![]() $m>0$
, and so
$m>0$
, and so
![]() $P_m^{\mathbb {Q}}$
is existentially
$P_m^{\mathbb {Q}}$
is existentially
![]() $0$
-definable in
$0$
-definable in
![]() $(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
. Combining with Lemma 2.3, we get:
$(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
. Combining with Lemma 2.3, we get:
Proposition 2.4. Every subset of
![]() $\mathbb {Q}^n$
definable in
$\mathbb {Q}^n$
definable in
![]() $(\mathbb {Q}; \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
is also definable in
$(\mathbb {Q}; \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
is also definable in
![]() $( \mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
. The corresponding statement for the structures
$( \mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
. The corresponding statement for the structures
![]() $(\mathbb {Q}; <, \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
and
$(\mathbb {Q}; <, \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
and
![]() $(\mathbb {Q}; <, \mathrm {SF}^{\mathbb {Q}})$
holds.
$(\mathbb {Q}; <, \mathrm {SF}^{\mathbb {Q}})$
holds.
In view of the first part of Proposition 2.4, we can analyze
![]() $(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
via
$(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
via
![]() $(\mathbb {Q}; \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
in the same way we analyze
$(\mathbb {Q}; \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
in the same way we analyze
![]() $(\mathbb {Z}; \mathrm {SF}^{\mathbb {Z}})$
via
$(\mathbb {Z}; \mathrm {SF}^{\mathbb {Z}})$
via
![]() $(\mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
. Let
$(\mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
. Let
 $\mathrm {Sf}^*_{\mathbb {Q}}$
be a recursive set of
$\mathrm {Sf}^*_{\mathbb {Q}}$
be a recursive set of
![]() $L_{\mathrm {u}}^*$
-sentences such that an
$L_{\mathrm {u}}^*$
-sentences such that an
![]() $L_{\mathrm {u}}^*$
-structure
$L_{\mathrm {u}}^*$
-structure
![]() $(G; \mathscr {U}^G, \mathscr {P}^G)$
is a model of
$(G; \mathscr {U}^G, \mathscr {P}^G)$
is a model of
 $\mathrm {Sf}^*_{\mathbb {Q}}$
if and only if
$\mathrm {Sf}^*_{\mathbb {Q}}$
if and only if
![]() $(G; \mathscr {U}^G, \mathscr {P}^G)$
satisfies the following properties:
$(G; \mathscr {U}^G, \mathscr {P}^G)$
satisfies the following properties:
-
(Q1)
 $(G;+,-,0,1)$
is elementarily equivalent to
$(G;+,-,0,1)$
is elementarily equivalent to
 $(\mathbb {Q};+,-,0,1)$
;
$(\mathbb {Q};+,-,0,1)$
; -
(Q2) for any given p,
 $U_{p,0}^G$
is an n-divisible subgroup of G for all n coprime with p;
$U_{p,0}^G$
is an n-divisible subgroup of G for all n coprime with p; -
(Q3)
 $1\in U_{p,0}^G$
and
$1\in U_{p,0}^G$
and
 $1 \notin U_{p,1}^G$
;
$1 \notin U_{p,1}^G$
; -
(Q4) for any given p,
 $p^{-l}U_{p,l}^G = U_{p, 0}^G$
if
$p^{-l}U_{p,l}^G = U_{p, 0}^G$
if
 $l<0$
and
$l<0$
and
 $U_{p,l} = p^l U_{p, 0}$
if
$U_{p,l} = p^l U_{p, 0}$
if
 $l>0$
;
$l>0$
; -
(Q5)
 $ U_{p, 0}^G / U_{p, 1}^G$
is isomorphic as a group to
$ U_{p, 0}^G / U_{p, 1}^G$
is isomorphic as a group to
 $\mathbb {Z} / p\mathbb {Z}$
;
$\mathbb {Z} / p\mathbb {Z}$
; -
(Q6)
 $1 \in P_1^G$
;
$1 \in P_1^G$
; -
(Q7) for any given p, we have that
 $pa \in P_1^G$
if and only if
$pa \in P_1^G$
if and only if
 $a\in P_1^G$
and
$a\in P_1^G$
and
 $a \notin U_{p,1}^G$
;
$a \notin U_{p,1}^G$
; -
(Q8)
 $P_m^G = m P_1^G$
for
$P_m^G = m P_1^G$
for
 $m>0$
;
$m>0$
;
The fact that we could choose
 $\mathrm {Sf}^*_{\mathbb {Q}}$
to be recursive follows from the well-known decidability of
$\mathrm {Sf}^*_{\mathbb {Q}}$
to be recursive follows from the well-known decidability of
![]() $\mathbb {Q}$
. Obviously,
$\mathbb {Q}$
. Obviously,
![]() $(\mathbb {Q}; \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
is a model of
$(\mathbb {Q}; \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
is a model of
 $\mathrm {Sf}^*_{\mathbb {Q}}$
. Several properties which hold in
$\mathrm {Sf}^*_{\mathbb {Q}}$
. Several properties which hold in
![]() $(\mathbb {Q}; \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
also hold in an arbitrary model of
$(\mathbb {Q}; \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
also hold in an arbitrary model of
 $\mathrm {Sf}^*_{\mathbb {Q}}$
:
$\mathrm {Sf}^*_{\mathbb {Q}}$
:
Lemma 2.5. Let
![]() $(G; \mathscr {U}^G, \mathscr {P}^G)$
be a model of
$(G; \mathscr {U}^G, \mathscr {P}^G)$
be a model of
 $\mathrm {Sf}^*_{\mathbb {Q}}$
. Then we have the following:
$\mathrm {Sf}^*_{\mathbb {Q}}$
. Then we have the following:
-
(i) For all p and all
 $l, l' \in \mathbb {Z}$
with
$l, l' \in \mathbb {Z}$
with
 $l\leq l'$
, we have
$l\leq l'$
, we have
 $U_{p,l}^G$
is a subgroup of G,
$U_{p,l}^G$
is a subgroup of G,
 $U_{p,l'}^G \subseteq U^G_{p,l}$
. Further, we can interpret
$U_{p,l'}^G \subseteq U^G_{p,l}$
. Further, we can interpret
 $U^G_{p, l} / U^G_{p, l'}$
as an L-structure with 1 being
$U^G_{p, l} / U^G_{p, l'}$
as an L-structure with 1 being
 $p^l+U^G_{p, l'}$
, and
$p^l+U^G_{p, l'}$
, and  $$ \begin{align*}U^G_{p, l} / U^G_{p, l'} \cong_{L} \mathbb{Z}/ (p^{l'-l}\mathbb{Z});\end{align*} $$
$$ \begin{align*}U^G_{p, l} / U^G_{p, l'} \cong_{L} \mathbb{Z}/ (p^{l'-l}\mathbb{Z});\end{align*} $$
-
(ii) for all h,
 $k\neq 0$
, p, l, and
$k\neq 0$
, p, l, and
 $m>0$
, we have that where
$m>0$
, we have that where $$ \begin{align*}\frac{h}{k} \in U^G_{p,l} \text{ if and only if } \frac{h}{k} \in U^{\mathbb{Q}}_{p,l} \ \text{ and }\ \frac{h}{k} \in P^G_m \text{ if and only if } \frac{h}{k} \in P^{\mathbb{Q}}_m, \end{align*} $$
$$ \begin{align*}\frac{h}{k} \in U^G_{p,l} \text{ if and only if } \frac{h}{k} \in U^{\mathbb{Q}}_{p,l} \ \text{ and }\ \frac{h}{k} \in P^G_m \text{ if and only if } \frac{h}{k} \in P^{\mathbb{Q}}_m, \end{align*} $$
 $hk^{-1}$
is the obvious element in
$hk^{-1}$
is the obvious element in
 $\mathbb {Q}$
and in
$\mathbb {Q}$
and in
 $G;$
$G;$
-
(iii) the replica of (
 $\mathrm{iii}$
–
$\mathrm{iii}$
–
 $\mathrm{vi}$
) of Lemma 2.1 holds.
$\mathrm{vi}$
) of Lemma 2.1 holds.
Proof Fix a model
![]() $(G; \mathscr {U}^G, \mathscr {P}^G)$
of
$(G; \mathscr {U}^G, \mathscr {P}^G)$
of
 $\mathrm {Sf}^*_{\mathbb {Q}}$
. From (Q2) we have that
$\mathrm {Sf}^*_{\mathbb {Q}}$
. From (Q2) we have that
 $U_{p,0}^G$
is a subgroup of G for all p. It follows from (Q4) that
$U_{p,0}^G$
is a subgroup of G for all p. It follows from (Q4) that
 $U^G_{p,l'} \subseteq U^G_{p,l} $
are subgroups of G for all p and
$U^G_{p,l'} \subseteq U^G_{p,l} $
are subgroups of G for all p and
![]() $l\leq l'$
. With
$l\leq l'$
. With
 $U^G_{p, l} / U^G_{p, l'}$
being interpreted as an L-structure with 1 being
$U^G_{p, l} / U^G_{p, l'}$
being interpreted as an L-structure with 1 being
 $p^l+U^G_{p, l'}$
, we get an L-embedding of
$p^l+U^G_{p, l'}$
, we get an L-embedding of
 $ \mathbb {Z}/ (p^{l'-l}\mathbb {Z})$
into
$ \mathbb {Z}/ (p^{l'-l}\mathbb {Z})$
into
 $U^G_{p, l} / U^G_{p, l'}$
using (Q3) and (Q4). Further, we see that
$U^G_{p, l} / U^G_{p, l'}$
using (Q3) and (Q4). Further, we see that
 $|U^G_{p, l} / U^G_{p, l'}|=p^{(l'-l)}$
using (Q2)–(Q5) and induction on
$|U^G_{p, l} / U^G_{p, l'}|=p^{(l'-l)}$
using (Q2)–(Q5) and induction on
![]() $l'-l$
together with the third isomorphism theorem; and so the aforementioned embedding must be an isomorphism, finishing the proof for
$l'-l$
together with the third isomorphism theorem; and so the aforementioned embedding must be an isomorphism, finishing the proof for
![]() $\mathrm {(i)}$
. The first assertion of
$\mathrm {(i)}$
. The first assertion of
![]() $\mathrm {(ii)}$
follows easily from (Q2)–Q(4). The second assertion for the case
$\mathrm {(ii)}$
follows easily from (Q2)–Q(4). The second assertion for the case
![]() $m=1$
follows from the first assertion, (Q6), and (Q7). Finally, the case with
$m=1$
follows from the first assertion, (Q6), and (Q7). Finally, the case with
![]() $m\not =1$
follows from the case
$m\not =1$
follows from the case
![]() $m=1$
using (Q8). The proof for the replica of
$m=1$
using (Q8). The proof for the replica of
![]() $\mathrm {(iii)}$
from Lemma 2.1 is a consequence of
$\mathrm {(iii)}$
from Lemma 2.1 is a consequence of
![]() $\mathrm {(i)}$
and (Q4). The proofs for replicas of
$\mathrm {(i)}$
and (Q4). The proofs for replicas of
![]() $\textrm{(iv--vi)}$
from Lemma 2.1 are similar to the proofs for
$\textrm{(iv--vi)}$
from Lemma 2.1 are similar to the proofs for
![]() $\textrm{(iv--vi)}$
of Lemma 2.1.⊣
$\textrm{(iv--vi)}$
of Lemma 2.1.⊣
As the reader may expect by now, we will study
![]() $(\mathbb {Q}; <, \mathrm {SF}^{\mathbb {Q}})$
via
$(\mathbb {Q}; <, \mathrm {SF}^{\mathbb {Q}})$
via
![]() $(\mathbb {Q}; <, \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
. Let
$(\mathbb {Q}; <, \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
. Let
![]() $L_{\mathrm {ou}}^*$
be
$L_{\mathrm {ou}}^*$
be
![]() $L_{\mathrm {ou}} \cup L_{\mathrm {u}}^*$
. Then
$L_{\mathrm {ou}} \cup L_{\mathrm {u}}^*$
. Then
![]() $(\mathbb {Q}; <, \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
can be construed as an
$(\mathbb {Q}; <, \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
can be construed as an
![]() $L_{\mathrm {ou}}^*$
-structure in the obvious way. Let
$L_{\mathrm {ou}}^*$
-structure in the obvious way. Let
 $\mathrm {OSf}^*_{\mathbb {Q}}$
be a recursive set of
$\mathrm {OSf}^*_{\mathbb {Q}}$
be a recursive set of
![]() $L_{\mathrm {ou}}^*$
-sentences such that an
$L_{\mathrm {ou}}^*$
-sentences such that an
![]() $L_{\mathrm {ou}}^*$
-structure
$L_{\mathrm {ou}}^*$
-structure
![]() $(G; \mathscr {U}^G, \mathscr {P}^G)$
is a model of
$(G; \mathscr {U}^G, \mathscr {P}^G)$
is a model of
 $\mathrm {OSf}^*_{\mathbb {Q}}$
if and only if
$\mathrm {OSf}^*_{\mathbb {Q}}$
if and only if
![]() $(G; \mathscr {U}^G, \mathscr {P}^G)$
satisfies the following properties:
$(G; \mathscr {U}^G, \mathscr {P}^G)$
satisfies the following properties:
-
(1)
 $(G; <)$
is elementarily equivalent to
$(G; <)$
is elementarily equivalent to
 $(\mathbb {Q};<)$
;
$(\mathbb {Q};<)$
; -
(2)
 $(G; \mathscr {U}^G, \mathscr {P}^G)$
is a model of
$(G; \mathscr {U}^G, \mathscr {P}^G)$
is a model of
 $\mathrm {Sf}^*_{\mathbb {Q}}$
.
$\mathrm {Sf}^*_{\mathbb {Q}}$
.
As
![]() $\text {Th}(\mathbb {Q};<)$
is decidable, we could choose
$\text {Th}(\mathbb {Q};<)$
is decidable, we could choose
 $\mathrm {OSf}^*_{\mathbb {Q}}$
to be recursive.
$\mathrm {OSf}^*_{\mathbb {Q}}$
to be recursive.
Returning to the theory
![]() $\mathrm {Sf}^*_{\mathbb {Z}}$
, we see that it does not fully capture all the first-order properties of
$\mathrm {Sf}^*_{\mathbb {Z}}$
, we see that it does not fully capture all the first-order properties of
![]() $(\mathbb {Z}, \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
. For instance, we will show later in Corollary 2.12 that for all
$(\mathbb {Z}, \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
. For instance, we will show later in Corollary 2.12 that for all
![]() $c \in \mathbb {Z}$
, there is
$c \in \mathbb {Z}$
, there is
![]() $a \in \mathbb {Z}$
such that
$a \in \mathbb {Z}$
such that
while the interested reader can construct models of
![]() $\mathrm {Sf}^*_{\mathbb {Z}}$
where the corresponding statement is not true. Likewise, the theories
$\mathrm {Sf}^*_{\mathbb {Z}}$
where the corresponding statement is not true. Likewise, the theories
 $\mathrm {Sf}^*_{\mathbb {Q}}$
and
$\mathrm {Sf}^*_{\mathbb {Q}}$
and
 $\mathrm {OSf}^*_{\mathbb {Q}}$
do not fully capture all the first-order properties of
$\mathrm {OSf}^*_{\mathbb {Q}}$
do not fully capture all the first-order properties of
![]() $(\mathbb {Q}; \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
and
$(\mathbb {Q}; \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
and
![]() $(\mathbb {Q}; <, \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
.
$(\mathbb {Q}; <, \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
.
To give a precise formulation of the missing first-order properties of
![]() $(\mathbb {Z}, \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
,
$(\mathbb {Z}, \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
,
![]() $(\mathbb {Q}; \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
, and
$(\mathbb {Q}; \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
, and
![]() $(\mathbb {Q}; < \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
, we need more terminologies. Let
$(\mathbb {Q}; < \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
, we need more terminologies. Let
![]() $t(z)$
be an
$t(z)$
be an
![]() $L_{\mathrm {u}}^*$
-term (or equivalently an
$L_{\mathrm {u}}^*$
-term (or equivalently an
![]() $L_{\mathrm {ou}}^*$
-term) with variables in z. An
$L_{\mathrm {ou}}^*$
-term) with variables in z. An
![]() $L_{\mathrm {u}}^*$
-formula (or an
$L_{\mathrm {u}}^*$
-formula (or an
![]() $L_{\mathrm {ou}}^*$
-formula) which is a Boolean combination of formulas having the form
$L_{\mathrm {ou}}^*$
-formula) which is a Boolean combination of formulas having the form
![]() $t(z) =0$
where we allow t to vary is called an equational condition. Similarly, an
$t(z) =0$
where we allow t to vary is called an equational condition. Similarly, an
![]() $L_{\mathrm {ou}}^*$
-formula which is a Boolean combination of formulas having the form
$L_{\mathrm {ou}}^*$
-formula which is a Boolean combination of formulas having the form
![]() $t(z) < 0$
where t is allowed to vary is called an order-condition. For any given p, l define
$t(z) < 0$
where t is allowed to vary is called an order-condition. For any given p, l define
![]() $t(z) \in U_{p,l}$
to be the obvious formula in
$t(z) \in U_{p,l}$
to be the obvious formula in
![]() $L_{\mathrm {u}}^*(z)$
which defines in an arbitrary
$L_{\mathrm {u}}^*(z)$
which defines in an arbitrary
![]() $L_{\mathrm {u}}^*$
-structure
$L_{\mathrm {u}}^*$
-structure
![]() $(G; \mathscr {U}^G, \mathscr {P}^G)$
the set
$(G; \mathscr {U}^G, \mathscr {P}^G)$
the set
 $$ \begin{align*}\{ c \in G^n : t^G(c) \in U^G_{p,l} \}.\end{align*} $$
$$ \begin{align*}\{ c \in G^n : t^G(c) \in U^G_{p,l} \}.\end{align*} $$
Define the quantifier-free formulas
![]() $t(z) \notin U_{p,l}$
,
$t(z) \notin U_{p,l}$
,
![]() $t(z) \in P_m$
, and
$t(z) \in P_m$
, and
![]() $t(z) \notin P_m$
in
$t(z) \notin P_m$
in
![]() $L_{\mathrm {u}}^*(z)$
for p, l, and for
$L_{\mathrm {u}}^*(z)$
for p, l, and for
![]() $m>0$
likewise. For each prime p, an
$m>0$
likewise. For each prime p, an
![]() $L_{\mathrm {u}}^*$
-formula (or an
$L_{\mathrm {u}}^*$
-formula (or an
![]() $L_{\mathrm {ou}}^*$
-formula) which is a Boolean combination of formulas of the form
$L_{\mathrm {ou}}^*$
-formula) which is a Boolean combination of formulas of the form
![]() $t(z) \notin U_{p,l}$
where t and l are allowed to vary is called a p-condition. We call a p-condition as in the previous statement trivial if the Boolean combination is the empty conjunction.
$t(z) \notin U_{p,l}$
where t and l are allowed to vary is called a p-condition. We call a p-condition as in the previous statement trivial if the Boolean combination is the empty conjunction.
A parameter choice of variable type
![]() $(x, z, z')$
is a triple
$(x, z, z')$
is a triple
![]() $(k,m,\Theta )$
such that k is in
$(k,m,\Theta )$
such that k is in
![]() $\mathbb {Z}\setminus \{0 \}$
, m is in
$\mathbb {Z}\setminus \{0 \}$
, m is in
![]() $\mathbb {N}^{\geq 1}$
, and
$\mathbb {N}^{\geq 1}$
, and
 $\Theta = \big ( \theta _p(x,z,z')\big )$
where
$\Theta = \big ( \theta _p(x,z,z')\big )$
where
![]() $\theta _p(x, z, z')$
is a p-condition for each prime p and is trivial for all but finitely many p. We say that an
$\theta _p(x, z, z')$
is a p-condition for each prime p and is trivial for all but finitely many p. We say that an
![]() $L_{\mathrm {u}}^*$
-formula
$L_{\mathrm {u}}^*$
-formula
![]() $\psi (x, z, z')$
is special if it has the form
$\psi (x, z, z')$
is special if it has the form
 $$ \begin{align*}\bigwedge_{p} \theta_p(x, z, z') \wedge \bigwedge_{i=1}^n (kx+z_i\in P_{m}) \wedge \bigwedge_{i'=1}^{n'} (kx+z^{\prime}_i \notin P_{m}),\end{align*} $$
$$ \begin{align*}\bigwedge_{p} \theta_p(x, z, z') \wedge \bigwedge_{i=1}^n (kx+z_i\in P_{m}) \wedge \bigwedge_{i'=1}^{n'} (kx+z^{\prime}_i \notin P_{m}),\end{align*} $$
where
![]() $k, m$
, and
$k, m$
, and
![]() $\theta _p(x, z, z')$
are taken from a parameter choice of variable type
$\theta _p(x, z, z')$
are taken from a parameter choice of variable type
![]() $(x, z, z')$
. Every special formula corresponds to a unique parameter choice and vice versa. Special formulas are special enough that we have a “local to global” phenomenon in the structures of interest but general enough to represent quantifier free formulas. We will explain the former point in the remaining part of the section and make the latter point precise with Theorem 3.1.
$(x, z, z')$
. Every special formula corresponds to a unique parameter choice and vice versa. Special formulas are special enough that we have a “local to global” phenomenon in the structures of interest but general enough to represent quantifier free formulas. We will explain the former point in the remaining part of the section and make the latter point precise with Theorem 3.1.
Let
![]() $\psi (x, z, z')$
be a special formula with parameter choice
$\psi (x, z, z')$
be a special formula with parameter choice
![]() $(k,m,\Theta )$
and
$(k,m,\Theta )$
and
![]() $\theta _p(x, z, z')$
is the p-condition in
$\theta _p(x, z, z')$
is the p-condition in
![]() $\Theta $
for each p. We define the associated equational condition of
$\Theta $
for each p. We define the associated equational condition of
![]() $\varphi (x, z, z' )$
to be the formula
$\varphi (x, z, z' )$
to be the formula
 $$ \begin{align*}\bigwedge_{i =1}^n \bigwedge_{i'=1}^{n'} (z_i\neq z^{\prime}_{i'})\end{align*} $$
$$ \begin{align*}\bigwedge_{i =1}^n \bigwedge_{i'=1}^{n'} (z_i\neq z^{\prime}_{i'})\end{align*} $$
and the associated p-condition of
![]() $\varphi (x, z, z' )$
to be the formula
$\varphi (x, z, z' )$
to be the formula
 $$ \begin{align*}\theta_p(x, z , z') \wedge \bigwedge_{i=1}^n (kx+z_i\notin U_{p, 2+v_p(m)}).\end{align*} $$
$$ \begin{align*}\theta_p(x, z , z') \wedge \bigwedge_{i=1}^n (kx+z_i\notin U_{p, 2+v_p(m)}).\end{align*} $$
It is easy to see that modulo
![]() $\mathrm {Sf}^*_{\mathbb {Z}}$
or
$\mathrm {Sf}^*_{\mathbb {Z}}$
or
 $\mathrm {Sf}^*_{\mathbb {Q}}$
, an arbitrary special formula implies its associated equational condition and its associated p-condition for any prime p.
$\mathrm {Sf}^*_{\mathbb {Q}}$
, an arbitrary special formula implies its associated equational condition and its associated p-condition for any prime p.
Suppose
![]() $(G; \mathscr {U}^G, \mathscr {P}^G)$
and
$(G; \mathscr {U}^G, \mathscr {P}^G)$
and
![]() $(H; \mathscr {U}^H, \mathscr {P}^H)$
are
$(H; \mathscr {U}^H, \mathscr {P}^H)$
are
![]() $L_{\mathrm {u}}^*$
-structures such that the former is an
$L_{\mathrm {u}}^*$
-structures such that the former is an
![]() $L_{\mathrm {u}}^*$
-substructure of the latter. Let
$L_{\mathrm {u}}^*$
-substructure of the latter. Let
![]() $\psi (x, z, z')$
be a special formula,
$\psi (x, z, z')$
be a special formula,
![]() $\psi _{=}(z,z')$
the associated equational condition, and
$\psi _{=}(z,z')$
the associated equational condition, and
![]() $\psi _{p}(x,z,z')$
the associated p-condition for any given prime p. For
$\psi _{p}(x,z,z')$
the associated p-condition for any given prime p. For
![]() $c \in G^n$
and
$c \in G^n$
and
![]() $c' \in G^{n'}$
, we call the quantifier-free
$c' \in G^{n'}$
, we call the quantifier-free
![]() $L_{\mathrm {u}}^*(G)$
-formula
$L_{\mathrm {u}}^*(G)$
-formula
![]() $\psi (x, c, c')$
a G-system. An element
$\psi (x, c, c')$
a G-system. An element
![]() $a\in H$
such that
$a\in H$
such that
![]() $\psi (a, c, c')$
holds is called a solution of
$\psi (a, c, c')$
holds is called a solution of
![]() $\psi (x, c, c')$
in H. We say that
$\psi (x, c, c')$
in H. We say that
![]() $\psi (x, c, c')$
is satisfiable in H if it has a solution in H and infinitely satisfiable in H if it has infinitely many solutions in H. We say that
$\psi (x, c, c')$
is satisfiable in H if it has a solution in H and infinitely satisfiable in H if it has infinitely many solutions in H. We say that
![]() $\psi (x, c, c')$
is nontrivial if
$\psi (x, c, c')$
is nontrivial if
![]() $ \psi _=(c, c')$
holds or more explicitly if c and
$ \psi _=(c, c')$
holds or more explicitly if c and
![]() $c'$
have no common components. For a given p, we say that
$c'$
have no common components. For a given p, we say that
![]() $\psi (x, c, c')$
is p-satisfiable in H if there is
$\psi (x, c, c')$
is p-satisfiable in H if there is
![]() $a_p\in H$
such that
$a_p\in H$
such that
![]() $\psi _p(a_p, c, c')$
holds. A G-system is locally satisfiable in H if it is p-satisfiable in H for all p.
$\psi _p(a_p, c, c')$
holds. A G-system is locally satisfiable in H if it is p-satisfiable in H for all p.
Suppose
![]() $(G; <, \mathscr {U}^G, \mathscr {P}^G)$
and
$(G; <, \mathscr {U}^G, \mathscr {P}^G)$
and
![]() $(H; <, \mathscr {U}^H, \mathscr {P}^H)$
are
$(H; <, \mathscr {U}^H, \mathscr {P}^H)$
are
![]() $L_{\mathrm {ou}}^*$
-structures such that the former is an
$L_{\mathrm {ou}}^*$
-structures such that the former is an
![]() $L_{\mathrm {ou}}^*$
-substructure of the latter. All the definitions in the previous paragraph have obvious adaptations to this new setting as
$L_{\mathrm {ou}}^*$
-substructure of the latter. All the definitions in the previous paragraph have obvious adaptations to this new setting as
![]() $(G; \mathscr {U}^G, \mathscr {P}^G)$
and
$(G; \mathscr {U}^G, \mathscr {P}^G)$
and
![]() $(H;\mathscr {U}^H, \mathscr {P}^H)$
are
$(H;\mathscr {U}^H, \mathscr {P}^H)$
are
![]() $L_{\mathrm {u}}^*$
-structures. For b and
$L_{\mathrm {u}}^*$
-structures. For b and
![]() $b'$
in H such that
$b'$
in H such that
![]() $b<b'$
, define
$b<b'$
, define
A G-system
![]() $\psi (x, c, c')$
is satisfiable in every H-interval if it has a solution in the interval
$\psi (x, c, c')$
is satisfiable in every H-interval if it has a solution in the interval
![]() $(b, b')^H$
for all b and
$(b, b')^H$
for all b and
![]() $b'$
in H such that
$b'$
in H such that
![]() $b<b'$
. The following observation is immediate:
$b<b'$
. The following observation is immediate:
Lemma 2.6. Suppose
![]() $(G; \mathscr {U}^G, \mathscr {P}^G)$
is a model of either
$(G; \mathscr {U}^G, \mathscr {P}^G)$
is a model of either
![]() $\mathrm {Sf}^*_{\mathbb {Z}}$
or
$\mathrm {Sf}^*_{\mathbb {Z}}$
or
 $\mathrm {Sf}^*_{\mathbb {Q}}$
. Then every G-system which is satisfiable in G is nontrivial and locally satisfiable in G.
$\mathrm {Sf}^*_{\mathbb {Q}}$
. Then every G-system which is satisfiable in G is nontrivial and locally satisfiable in G.
It turns out that the converse and more are also true for the structures of interest. We say that a model
![]() $(G; \mathscr {U}^G, \mathscr {P}^G)$
of either
$(G; \mathscr {U}^G, \mathscr {P}^G)$
of either
![]() $\mathrm {Sf}^*_{\mathbb {Z}}$
or
$\mathrm {Sf}^*_{\mathbb {Z}}$
or
 $\mathrm {Sf}^*_{\mathbb {Q}}$
is generic if every nontrivial locally satisfiable G-system is infinitely satisfiable in G. An
$\mathrm {Sf}^*_{\mathbb {Q}}$
is generic if every nontrivial locally satisfiable G-system is infinitely satisfiable in G. An
 $\mathrm {OSf}^*_{\mathbb {Q}}$
model
$\mathrm {OSf}^*_{\mathbb {Q}}$
model
![]() $(G;<, \mathscr {U}^G, \mathscr {P}^G)$
is generic if every nontrivial locally satisfiable G-system is satisfiable in every G-interval. We will later show that
$(G;<, \mathscr {U}^G, \mathscr {P}^G)$
is generic if every nontrivial locally satisfiable G-system is satisfiable in every G-interval. We will later show that
![]() $( \mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
,
$( \mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
,
![]() $(\mathbb {Q}; \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
, and
$(\mathbb {Q}; \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
, and
![]() $(\mathbb {Q}; <, \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
are generic.
$(\mathbb {Q}; <, \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
are generic.
Before that we will show that the above notions of genericity are first-order. Let
![]() $\psi (x, z, z')$
be the special formula corresponding to a parameter choice
$\psi (x, z, z')$
be the special formula corresponding to a parameter choice
![]() $(k,m,\Theta )$
with
$(k,m,\Theta )$
with
 $\Theta = \big ( \theta _p(x,z,z')\big )$
. A boundary of
$\Theta = \big ( \theta _p(x,z,z')\big )$
. A boundary of
![]() $\psi (x,z,z')$
is a number
$\psi (x,z,z')$
is a number
![]() $B \in \mathbb {N}^{>0}$
such that
$B \in \mathbb {N}^{>0}$
such that
![]() $B>\max \{|k|,n\}$
and
$B>\max \{|k|,n\}$
and
![]() $\theta _p(x,z,z')$
is trivial for all
$\theta _p(x,z,z')$
is trivial for all
![]() $p>B$
.
$p>B$
.
Lemma 2.7. Let
![]() $\psi (x, z, z')$
be a special formula, B a boundary of
$\psi (x, z, z')$
be a special formula, B a boundary of
![]() $\psi (x,z,z')$
, and
$\psi (x,z,z')$
, and
![]() $(G; \mathscr {U}^G, \mathscr {P}^G)$
a model of either
$(G; \mathscr {U}^G, \mathscr {P}^G)$
a model of either
![]() $\mathrm {Sf}^*_{\mathbb {Z}}$
or
$\mathrm {Sf}^*_{\mathbb {Z}}$
or
 $\mathrm {Sf}^*_{\mathbb {Q}}$
. Then every G-system
$\mathrm {Sf}^*_{\mathbb {Q}}$
. Then every G-system
![]() $\psi (x, c, c')$
is p-satisfiable for
$\psi (x, c, c')$
is p-satisfiable for
![]() $p>B$
.
$p>B$
.
Proof Let
![]() $\psi (x, z, z')$
be the special formula corresponding to a parameter choice
$\psi (x, z, z')$
be the special formula corresponding to a parameter choice
![]() $(k,m,\Theta )$
, and B,
$(k,m,\Theta )$
, and B,
![]() $(G; \mathscr {U}^G, \mathscr {P}^G)$
as in the statement of the lemma. Suppose
$(G; \mathscr {U}^G, \mathscr {P}^G)$
as in the statement of the lemma. Suppose
![]() $\psi (x, c, c')$
is a G-system,
$\psi (x, c, c')$
is a G-system,
![]() $p>B$
, and
$p>B$
, and
![]() $\psi _p(x,z,z')$
is the associated p-condition of
$\psi _p(x,z,z')$
is the associated p-condition of
![]() $\psi (x,z,z')$
. Then
$\psi (x,z,z')$
. Then
![]() $\psi _p(x, c, c')$
is equivalent to
$\psi _p(x, c, c')$
is equivalent to
 $$ \begin{align*}\bigwedge_{i=1}^n (kx+c_i \notin U_{p, 2+v_p(m)})\ \text{ in } (G; \mathscr{U}^G, \mathscr{P}^G).\end{align*} $$
$$ \begin{align*}\bigwedge_{i=1}^n (kx+c_i \notin U_{p, 2+v_p(m)})\ \text{ in } (G; \mathscr{U}^G, \mathscr{P}^G).\end{align*} $$
We will show a stronger statement that there is a
![]() $a_p\in \mathbb {Z}$
satisfying the latter. Note that for all
$a_p\in \mathbb {Z}$
satisfying the latter. Note that for all
 $d\notin U_{p,0}^G$
, we have that
$d\notin U_{p,0}^G$
, we have that
![]() $(ka+d \notin U_{p, 0})$
for all
$(ka+d \notin U_{p, 0})$
for all
![]() $a\in \mathbb {Z}$
. From Lemma 2.5, we have that
$a\in \mathbb {Z}$
. From Lemma 2.5, we have that
 $U_{p,l}^G \subseteq U_{p,k}^G$
whenever
$U_{p,l}^G \subseteq U_{p,k}^G$
whenever
![]() $k<l$
, so we can assume that
$k<l$
, so we can assume that
 $c_i \in U_{p,0}^G$
for
$c_i \in U_{p,0}^G$
for
![]() $i \in \{1, \ldots , n\}$
. In light of Lemmas 2.1
$i \in \{1, \ldots , n\}$
. In light of Lemmas 2.1
![]() $\mathrm {(i)}$
and 2.5
$\mathrm {(i)}$
and 2.5
![]() $\mathrm {(i)}$
, we have that
$\mathrm {(i)}$
, we have that
 $$ \begin{align*}U^G_{p, 0}/ U^G_{p, 2+v_p(m)} \cong_{L} \mathbb{Z} / (p^{2+v_p(m)}\mathbb{Z}).\end{align*} $$
$$ \begin{align*}U^G_{p, 0}/ U^G_{p, 2+v_p(m)} \cong_{L} \mathbb{Z} / (p^{2+v_p(m)}\mathbb{Z}).\end{align*} $$
It is easy to see that k is invertible
![]() $\mathrm {mod}\ p^{2+v_p(m)}$
and that
$\mathrm {mod}\ p^{2+v_p(m)}$
and that
![]() $p^{2+v_p(m)}>n$
. Choose
$p^{2+v_p(m)}>n$
. Choose
![]() $a_p$
in
$a_p$
in
 $\{0, \ldots , p^{2+v_{p}(m)}-1\}$
such that the images of
$\{0, \ldots , p^{2+v_{p}(m)}-1\}$
such that the images of
![]() $ka_p+c_1, \ldots , ka_p+c_n$
in
$ka_p+c_1, \ldots , ka_p+c_n$
in
 $\mathbb {Z} / (p^{2+v_p(m)}\mathbb {Z})$
are not
$\mathbb {Z} / (p^{2+v_p(m)}\mathbb {Z})$
are not
![]() $0$
. We check that
$0$
. We check that
![]() $a_p$
is as desired.⊣
$a_p$
is as desired.⊣
Corollary 2.8. There is an
![]() $L_{\mathrm {u}}^*$
-theory
$L_{\mathrm {u}}^*$
-theory
![]() $\mathrm {SF}^*_{\mathbb {Z}}$
such that the models of
$\mathrm {SF}^*_{\mathbb {Z}}$
such that the models of
![]() $\mathrm {SF}^*_{\mathbb {Z}}$
are the generic models of
$\mathrm {SF}^*_{\mathbb {Z}}$
are the generic models of
![]() $\mathrm {Sf}^*_{\mathbb {Z}}$
. Similarly, there is an
$\mathrm {Sf}^*_{\mathbb {Z}}$
. Similarly, there is an
![]() $L_{\mathrm {u}}^*$
-theory
$L_{\mathrm {u}}^*$
-theory
![]() $\mathrm {SF}^*_{\mathbb {Q}}$
and an
$\mathrm {SF}^*_{\mathbb {Q}}$
and an
![]() $L_{\mathrm {ou}}^*$
-theory
$L_{\mathrm {ou}}^*$
-theory
![]() $\mathrm {OSF}^*_{\mathbb {Q}}$
satisfying the corresponding condition for
$\mathrm {OSF}^*_{\mathbb {Q}}$
satisfying the corresponding condition for
 $\mathrm {Sf}^*_{\mathbb {Q}}$
and
$\mathrm {Sf}^*_{\mathbb {Q}}$
and
 $\mathrm {OSf}^*_{\mathbb {Q}}$
.
$\mathrm {OSf}^*_{\mathbb {Q}}$
.
In the rest of the paper, we fix
![]() $\mathrm {SF}^*_{\mathbb {Z}}$
,
$\mathrm {SF}^*_{\mathbb {Z}}$
,
![]() $\mathrm {SF}^*_{\mathbb {Q}}$
, and
$\mathrm {SF}^*_{\mathbb {Q}}$
, and
![]() $\mathrm {OSF}^*_{\mathbb {Q}}$
to be as in the previous lemma. We can moreover arrange them to be recursive. In the remaining part of this section, we will show that
$\mathrm {OSF}^*_{\mathbb {Q}}$
to be as in the previous lemma. We can moreover arrange them to be recursive. In the remaining part of this section, we will show that
![]() $(\mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
,
$(\mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
,
![]() $(\mathbb {Q}; \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
, and
$(\mathbb {Q}; \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
, and
![]() $(\mathbb {Q}; <, \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Z}})$
are models of
$(\mathbb {Q}; <, \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Z}})$
are models of
![]() $\mathrm {SF}^*_{\mathbb {Z}}$
,
$\mathrm {SF}^*_{\mathbb {Z}}$
,
![]() $\mathrm {SF}^*_{\mathbb {Q}}$
, and
$\mathrm {SF}^*_{\mathbb {Q}}$
, and
![]() $\mathrm {OSF}^*_{\mathbb {Q}}$
respectively. The proof that the latter are in fact the full axiomatizations of the theories of the former needs to wait until next section. Further we fix
$\mathrm {OSF}^*_{\mathbb {Q}}$
respectively. The proof that the latter are in fact the full axiomatizations of the theories of the former needs to wait until next section. Further we fix
![]() $\mathrm {SF}_{\mathbb {Z}}$
and
$\mathrm {SF}_{\mathbb {Z}}$
and
![]() $\mathrm {SF}_{\mathbb {Q}}$
to be the theories whose models are precisely the
$\mathrm {SF}_{\mathbb {Q}}$
to be the theories whose models are precisely the
![]() $L_{\mathrm {u}}$
-reducts of models of
$L_{\mathrm {u}}$
-reducts of models of
![]() $\mathrm {SF}^*_{\mathbb {Z}}$
and
$\mathrm {SF}^*_{\mathbb {Z}}$
and
![]() $\mathrm {SF}^*_{\mathbb {Q}}$
respectively, and
$\mathrm {SF}^*_{\mathbb {Q}}$
respectively, and
![]() $\mathrm {OSF}_{\mathbb {Q}}$
to be the theory whose models are precisely
$\mathrm {OSF}_{\mathbb {Q}}$
to be the theory whose models are precisely
![]() $L_{\mathrm {ou}}$
reducts of models of
$L_{\mathrm {ou}}$
reducts of models of
![]() $\mathrm {OSF}^*_{\mathbb {Q}}$
. For the reader’s reference, the following table lists all the languages, the corresponding theories, and primary structures under consideration:
$\mathrm {OSF}^*_{\mathbb {Q}}$
. For the reader’s reference, the following table lists all the languages, the corresponding theories, and primary structures under consideration:

Suppose
![]() $h\neq 0$
. For a term
$h\neq 0$
. For a term
![]() $t(z) = k_1 z_1+ \cdots +k_n z_n +e$
, let
$t(z) = k_1 z_1+ \cdots +k_n z_n +e$
, let
![]() $t^h(z)$
be the term
$t^h(z)$
be the term
![]() $k_1z_1+ \cdots +k_nz_n+ he$
. If
$k_1z_1+ \cdots +k_nz_n+ he$
. If
![]() $\varphi (z)$
is a Boolean combination of atomic formulas of the form
$\varphi (z)$
is a Boolean combination of atomic formulas of the form
![]() $t(z) \in U_{p,l}$
or
$t(z) \in U_{p,l}$
or
![]() $t(z) \in P_{m}$
where
$t(z) \in P_{m}$
where
![]() $t(z)$
is an
$t(z)$
is an
![]() $L_{\mathrm {u}}^*$
-term, define
$L_{\mathrm {u}}^*$
-term, define
![]() $\varphi ^h(z)$
to be the formula obtained by replacing
$\varphi ^h(z)$
to be the formula obtained by replacing
![]() $t(z) \in U_{p,l}$
and
$t(z) \in U_{p,l}$
and
![]() $t(z) \in P_{m}$
in
$t(z) \in P_{m}$
in
![]() $\varphi (z)$
with
$\varphi (z)$
with
 $t^h(z) \in U_{p,l+v_p(h)}$
and
$t^h(z) \in U_{p,l+v_p(h)}$
and
![]() $t^h(z) \in P_{mh}$
for every choice of p, l, m, and
$t^h(z) \in P_{mh}$
for every choice of p, l, m, and
![]() $L_{\mathrm {u}}^*$
-term t. It follows from Lemmas 2.1
$L_{\mathrm {u}}^*$
-term t. It follows from Lemmas 2.1
![]() $\mathrm {(iii,vi)}$
and 2.5
$\mathrm {(iii,vi)}$
and 2.5
![]() $\mathrm {(iii)}$
that across models of
$\mathrm {(iii)}$
that across models of
![]() $\mathrm {Sf}^*_{\mathbb {Z}}$
and
$\mathrm {Sf}^*_{\mathbb {Z}}$
and
 $\mathrm {Sf}^*_{\mathbb {Q}}$
,
$\mathrm {Sf}^*_{\mathbb {Q}}$
,
Moreover, if
![]() $\theta (z)$
is a p-condition, then
$\theta (z)$
is a p-condition, then
![]() $\theta ^h(z)$
is also p-condition. If
$\theta ^h(z)$
is also p-condition. If
![]() $\psi (x,z, z')$
is the special formula corresponding to a parameter choice
$\psi (x,z, z')$
is the special formula corresponding to a parameter choice
![]() $(k, m, \Theta )$
with
$(k, m, \Theta )$
with
 $\Theta = \big (\theta _p(x,z,z')\big )$
, then
$\Theta = \big (\theta _p(x,z,z')\big )$
, then
![]() $\psi ^h(x,z, z')$
is the special formula corresponding to the parameter choice
$\psi ^h(x,z, z')$
is the special formula corresponding to the parameter choice
![]() $(k, hm, \Theta ^h)$
with
$(k, hm, \Theta ^h)$
with
 $\Theta ^h = \big (\theta _p^h(x,z,z')\big )$
. It is easy to see from here that:
$\Theta ^h = \big (\theta _p^h(x,z,z')\big )$
. It is easy to see from here that:
Lemma 2.9. For
![]() $h \neq 0$
, any boundary of a special formula
$h \neq 0$
, any boundary of a special formula
![]() $\psi (x,z,z')$
is also a boundary of
$\psi (x,z,z')$
is also a boundary of
![]() $\psi ^h(x,z,z')$
and vice versa.
$\psi ^h(x,z,z')$
and vice versa.
Let
![]() $\psi (x, z, z')$
be a special formula,
$\psi (x, z, z')$
be a special formula,
![]() $(G; \mathscr {U}^G,\mathscr {P}^G)$
a model of either
$(G; \mathscr {U}^G,\mathscr {P}^G)$
a model of either
![]() $\mathrm {Sf}^*_{\mathbb {Z}}$
or
$\mathrm {Sf}^*_{\mathbb {Z}}$
or
 $\mathrm {Sf}^*_{\mathbb {Q}}$
, and
$\mathrm {Sf}^*_{\mathbb {Q}}$
, and
![]() $\psi (x, c, c')$
a G-system. Then
$\psi (x, c, c')$
a G-system. Then
![]() $\psi ^h(x, hc, hc')$
is also a G-system which we refer to as the h-conjugate of
$\psi ^h(x, hc, hc')$
is also a G-system which we refer to as the h-conjugate of
![]() $\psi (x, c, c')$
. This has the property that
$\psi (x, c, c')$
. This has the property that
![]() $\psi ^h(ha,hc,hc')$
if and only if
$\psi ^h(ha,hc,hc')$
if and only if
![]() $\psi (a,c,c')$
for all
$\psi (a,c,c')$
for all
![]() $a \in G$
.
$a \in G$
.
For a and b in
![]() $\mathbb {Z}$
, we write
$\mathbb {Z}$
, we write
![]() $a\equiv _{n}b$
if a and b have the same remainder when divided by n. We need the following version of Chinese remainder theorem:
$a\equiv _{n}b$
if a and b have the same remainder when divided by n. We need the following version of Chinese remainder theorem:
Lemma 2.10. Suppose B is in
![]() $\mathbb {N}^{>0}$
,
$\mathbb {N}^{>0}$
,
![]() $\Theta $
is a family
$\Theta $
is a family
 $\big (\theta _p(x,z)\big )_{p \leq B}$
of
$\big (\theta _p(x,z)\big )_{p \leq B}$
of
![]() $L^*_{\mathrm {u}}$
-formulas with
$L^*_{\mathrm {u}}$
-formulas with
![]() $\theta _p (x,z)$
being a p-condition for each
$\theta _p (x,z)$
being a p-condition for each
![]() $p\leq B$
, and
$p\leq B$
, and
![]() $c \in \mathbb {Z}^n$
is such that
$c \in \mathbb {Z}^n$
is such that
![]() $\theta _p(x,c)$
defines a nonempty set in
$\theta _p(x,c)$
defines a nonempty set in
![]() $(\mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
for all
$(\mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
for all
![]() $p \leq B$
. Then we can find
$p \leq B$
. Then we can find
![]() $D \in \mathbb {N}^{>0}$
and
$D \in \mathbb {N}^{>0}$
and
![]() $r \in \{0, \ldots , D-1\} $
such that for all
$r \in \{0, \ldots , D-1\} $
such that for all
![]() $h\neq 0$
with
$h\neq 0$
with
![]() $\mathrm {gcd}(h,B!)=1$
, we have
$\mathrm {gcd}(h,B!)=1$
, we have
 $$ \begin{align*}a\equiv_{D} hr \text{ implies } \bigwedge_{p \leq B} \theta^h_p(a,hc)\ \ \text{ for all } a \in \mathbb{Z}.\end{align*} $$
$$ \begin{align*}a\equiv_{D} hr \text{ implies } \bigwedge_{p \leq B} \theta^h_p(a,hc)\ \ \text{ for all } a \in \mathbb{Z}.\end{align*} $$
Proof Let B,
![]() $\Theta $
, and c be as stated. Fix
$\Theta $
, and c be as stated. Fix
![]() $h\neq 0$
such that
$h\neq 0$
such that
![]() $\mathrm {gcd}(h,B!)=1$
. Hence,
$\mathrm {gcd}(h,B!)=1$
. Hence,
![]() $v_p(h)=0$
for
$v_p(h)=0$
for
![]() $p\leq B$
, and so the p-condition
$p\leq B$
, and so the p-condition
 $\theta _p^h(x,z)$
is obtained from the p-condition
$\theta _p^h(x,z)$
is obtained from the p-condition
![]() $\theta _p(x,z)$
by replacing any atomic formula
$\theta _p(x,z)$
by replacing any atomic formula
![]() $kx +t(z) \in U_{p, l}$
appearing in
$kx +t(z) \in U_{p, l}$
appearing in
![]() $\theta _p(x,z)$
with
$\theta _p(x,z)$
with
 $kx +t^h(z) \in U_{p, l}$
. Now for
$kx +t^h(z) \in U_{p, l}$
. Now for
![]() $p\leq B$
, let
$p\leq B$
, let
![]() $l_p$
be the largest value of l occurring in an atomic formula in
$l_p$
be the largest value of l occurring in an atomic formula in
![]() $\theta _p(x,z)$
. Set
$\theta _p(x,z)$
. Set
 $$ \begin{align*}D = \prod_{p \leq B} p^{l_p}.\end{align*} $$
$$ \begin{align*}D = \prod_{p \leq B} p^{l_p}.\end{align*} $$
Obtain
![]() $a_p \in \mathbb {Z}$
such that
$a_p \in \mathbb {Z}$
such that
![]() $\theta _p(a_p, c)$
holds in
$\theta _p(a_p, c)$
holds in
![]() $(\mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
. Equivalently, we have
$(\mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
. Equivalently, we have
 $\theta ^h_p(ha_p, hc)$
holds in
$\theta ^h_p(ha_p, hc)$
holds in
![]() $(\mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
. By the Chinese remainder theorem, we get r in
$(\mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
. By the Chinese remainder theorem, we get r in
![]() $\{0, \ldots , D-1\}$
such that
$\{0, \ldots , D-1\}$
such that
 $$ \begin{align*}r\equiv_{p^{l_p}} a_p\quad \text{ for all } p \leq B.\end{align*} $$
$$ \begin{align*}r\equiv_{p^{l_p}} a_p\quad \text{ for all } p \leq B.\end{align*} $$
We check that r is as desired. Suppose
![]() $a \in \mathbb {Z}$
is such that
$a \in \mathbb {Z}$
is such that
![]() $a \equiv _D hr$
. By construction, if
$a \equiv _D hr$
. By construction, if
![]() $p\leq B$
,
$p\leq B$
,
![]() $l \leq l_p$
, and
$l \leq l_p$
, and
![]() $kx+t(z) \in U_{p,l }$
is any atomic formula, then
$kx+t(z) \in U_{p,l }$
is any atomic formula, then
 $ka +t^h(hc) \in U^{\mathbb {Z}}_{p, l}$
if and only if
$ka +t^h(hc) \in U^{\mathbb {Z}}_{p, l}$
if and only if
 $k(ha_p) +t^h(hc) \in U^{\mathbb {Z}}_{p, l}$
. It follows that
$k(ha_p) +t^h(hc) \in U^{\mathbb {Z}}_{p, l}$
. It follows that
 $\theta ^h_p( a, hc)$
is equivalent to
$\theta ^h_p( a, hc)$
is equivalent to
 $\theta ^h_p( ha_p, hc)$
in
$\theta ^h_p( ha_p, hc)$
in
![]() $(\mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
. Thus
$(\mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
. Thus
 $\theta ^h_p( a, hc)$
holds for all
$\theta ^h_p( a, hc)$
holds for all
![]() $p \leq B$
.⊣
$p \leq B$
.⊣
Towards showing that the structures of interest are generic, the key number-theoretic ingredient we need is the following result:
Lemma 2.11. Let
![]() $\psi (x, z, z')$
be a special formula and
$\psi (x, z, z')$
be a special formula and
![]() $\psi (x,c,c')$
a nontrivial
$\psi (x,c,c')$
a nontrivial
![]() $\mathbb {Z}$
-system which is locally satisfiable in
$\mathbb {Z}$
-system which is locally satisfiable in
![]() $\mathbb {Z}$
. For
$\mathbb {Z}$
. For
![]() $h> 0$
, and
$h> 0$
, and
![]() $s, t \in \mathbb {Q}$
with
$s, t \in \mathbb {Q}$
with
![]() $s< t$
, set
$s< t$
, set
 $$ \begin{align*}\Psi^h(hs,ht) = \{ a \in \mathbb{Z}: \psi^h(a,hc,hc') \text{ holds and } hs<a<ht\}.\end{align*} $$
$$ \begin{align*}\Psi^h(hs,ht) = \{ a \in \mathbb{Z}: \psi^h(a,hc,hc') \text{ holds and } hs<a<ht\}.\end{align*} $$
Then there exist
![]() $N \in \mathbb {N}^{>0}$
,
$N \in \mathbb {N}^{>0}$
,
![]() $\varepsilon \in (0,1)$
, and
$\varepsilon \in (0,1)$
, and
![]() $C\in \mathbb {R}$
such that for all
$C\in \mathbb {R}$
such that for all
![]() $h> 0$
with
$h> 0$
with
![]() $\mathrm {gcd}(h,N!)=1$
and
$\mathrm {gcd}(h,N!)=1$
and
![]() $s, t \in \mathbb {Q}$
with
$s, t \in \mathbb {Q}$
with
![]() $s<t$
, we have that
$s<t$
, we have that
 $$ \begin{align*}|\Psi^h(hs,ht)| \geq \varepsilon h(t-s) - \Bigg(\sum_{i=1}^{n}\sqrt{|hks+hc_i|} + \sqrt{|hkt+hc_i|}\Bigg) + C.\end{align*} $$
$$ \begin{align*}|\Psi^h(hs,ht)| \geq \varepsilon h(t-s) - \Bigg(\sum_{i=1}^{n}\sqrt{|hks+hc_i|} + \sqrt{|hkt+hc_i|}\Bigg) + C.\end{align*} $$
Proof Throughout this proof, let
![]() $\psi (x,z,z')$
,
$\psi (x,z,z')$
,
![]() $\psi (x,c,c')$
, and
$\psi (x,c,c')$
, and
![]() $\Psi ^h(hs,ht)$
be as stated. We first make a number of observations. Suppose
$\Psi ^h(hs,ht)$
be as stated. We first make a number of observations. Suppose
![]() $\psi (x,z,z')$
corresponds to the parameter choice
$\psi (x,z,z')$
corresponds to the parameter choice
![]() $(k,m,\Theta )$
and has a boundary B, and
$(k,m,\Theta )$
and has a boundary B, and
![]() $\psi _p(x,z,z')$
is the associated p-condition of
$\psi _p(x,z,z')$
is the associated p-condition of
![]() $\psi (x,z,z')$
. Then
$\psi (x,z,z')$
. Then
![]() $\psi ^h(x,z,z')$
corresponds to the parameter choice
$\psi ^h(x,z,z')$
corresponds to the parameter choice
![]() $(k,hm,\Theta ^h)$
, and B is also a boundary of
$(k,hm,\Theta ^h)$
, and B is also a boundary of
![]() $\psi ^h(x,z,z')$
by Lemma 2.9. Moreover
$\psi ^h(x,z,z')$
by Lemma 2.9. Moreover
 $\psi ^h_p(x,z,z')$
is the associated p-condition of
$\psi ^h_p(x,z,z')$
is the associated p-condition of
![]() $\psi ^h(x,z,z')$
. Since
$\psi ^h(x,z,z')$
. Since
![]() $\psi (x,c,c')$
is locally satisfiable in
$\psi (x,c,c')$
is locally satisfiable in
![]() $\mathbb {Z}$
, we can use Lemma 2.10 to fix
$\mathbb {Z}$
, we can use Lemma 2.10 to fix
![]() $D\in \mathbb {N}^{>0}$
and
$D\in \mathbb {N}^{>0}$
and
![]() $r\in \{0,\ldots , D-1\}$
such that for each
$r\in \{0,\ldots , D-1\}$
such that for each
![]() $h> 0$
with
$h> 0$
with
![]() $\mathrm {gcd}(h,B!)=1$
, we have
$\mathrm {gcd}(h,B!)=1$
, we have
 $$ \begin{align*}a\equiv_{D} hr \text{ implies } \bigwedge_{p \leq B} \psi^h_p(a,hc, hc')\ \ \text{ for all } a \in \mathbb{Z}.\end{align*} $$
$$ \begin{align*}a\equiv_{D} hr \text{ implies } \bigwedge_{p \leq B} \psi^h_p(a,hc, hc')\ \ \text{ for all } a \in \mathbb{Z}.\end{align*} $$
We note that D here is independent of the choice of h for all h with
![]() $\mathrm {gcd}(h,B!)=1$
.
$\mathrm {gcd}(h,B!)=1$
.
We introduce a variant of
![]() $\Psi ^h(hs,ht)$
which is needed in our estimation of
$\Psi ^h(hs,ht)$
which is needed in our estimation of
![]() $|\Psi ^h(hs,ht)|$
. Until the end of the proof, set
$|\Psi ^h(hs,ht)|$
. Until the end of the proof, set
![]() $l_p =2 + v_p(m)$
. Fix primes
$l_p =2 + v_p(m)$
. Fix primes
![]() $p_1, \ldots , p_{n'}$
such that
$p_1, \ldots , p_{n'}$
such that
![]() $p_1> c_i$
for all
$p_1> c_i$
for all
![]() $i \in \{1, \ldots , n\}$
,
$i \in \{1, \ldots , n\}$
,
![]() $p_1> c^{\prime }_{i'}$
for all
$p_1> c^{\prime }_{i'}$
for all
![]() $i' \in \{1, \ldots , n'\}$
, and
$i' \in \{1, \ldots , n'\}$
, and
For
![]() $M>p_{n'}$
,
$M>p_{n'}$
,
![]() $h> 0$
with
$h> 0$
with
![]() $\mathrm {gcd}(h,B!)=1$
, define
$\mathrm {gcd}(h,B!)=1$
, define
![]() $\Psi ^h_{M}(hs,ht)$
to be the set of
$\Psi ^h_{M}(hs,ht)$
to be the set of
![]() $a \in \mathbb {Z}$
such that
$a \in \mathbb {Z}$
such that
![]() $hs<a<ht$
and
$hs<a<ht$
and
 $$ \begin{align*}(a\equiv_{D} hr) \wedge\bigwedge_{B< p \leq M}\left( \bigwedge_{i=1}^{n}(ka+hc_i \not \equiv_{p^{l_{p}+v_p(h)}} 0)\right)\wedge\bigwedge_{i'=1}^{n'}(ka+hc^{\prime}_{i'} \notin P_{hm}^{\mathbb{Z}}).\end{align*} $$
$$ \begin{align*}(a\equiv_{D} hr) \wedge\bigwedge_{B< p \leq M}\left( \bigwedge_{i=1}^{n}(ka+hc_i \not \equiv_{p^{l_{p}+v_p(h)}} 0)\right)\wedge\bigwedge_{i'=1}^{n'}(ka+hc^{\prime}_{i'} \notin P_{hm}^{\mathbb{Z}}).\end{align*} $$
It is not hard to see that
![]() $\Psi ^h(hs,ht)\cap \{a\in \mathbb {Z}: a\equiv _D hr\}\subseteq \Psi ^h_{M}(hs,ht)$
, and the latter is intended to be an upper approximation of the former. The desired lower bound for
$\Psi ^h(hs,ht)\cap \{a\in \mathbb {Z}: a\equiv _D hr\}\subseteq \Psi ^h_{M}(hs,ht)$
, and the latter is intended to be an upper approximation of the former. The desired lower bound for
![]() $|\Psi ^h(hs,ht)|$
will be obtained via a lower bound for
$|\Psi ^h(hs,ht)|$
will be obtained via a lower bound for
![]() $|\Psi ^h_{M}(hs,ht)|$
and an upper bound for
$|\Psi ^h_{M}(hs,ht)|$
and an upper bound for
![]() $|\Psi ^h_{M}(hs,ht)\setminus \Psi ^h(hs,ht)| $
.
$|\Psi ^h_{M}(hs,ht)\setminus \Psi ^h(hs,ht)| $
.
Now we work towards establishing a lower bound on
![]() $|\Psi ^h_{M}(hs,ht))|$
in the case where
$|\Psi ^h_{M}(hs,ht))|$
in the case where
![]() $M> p_{n'} $
,
$M> p_{n'} $
,
![]() $h> 0$
, and
$h> 0$
, and
![]() $\text {gcd}(h, M!)=1$
. The latter assumption implies in particular that
$\text {gcd}(h, M!)=1$
. The latter assumption implies in particular that
![]() $p^{l_p + v_p(h)} = p^{l_p}$
for all
$p^{l_p + v_p(h)} = p^{l_p}$
for all
![]() $p \leq M$
. For
$p \leq M$
. For
![]() $p>B $
, we have that
$p>B $
, we have that
![]() $p>|k|$
and so k is invertible
$p>|k|$
and so k is invertible
![]() $\mathrm {mod}\ p^{l_p}$
. Set
$\mathrm {mod}\ p^{l_p}$
. Set
For
![]() $p\in \Delta $
, as k is invertible
$p\in \Delta $
, as k is invertible
![]() $\mathrm {mod}\ p^{l_p}$
, there are at least
$\mathrm {mod}\ p^{l_p}$
, there are at least
![]() $p^{l_{p}}- n$
(note we have
$p^{l_{p}}- n$
(note we have
![]() $p>B>n$
) choices of
$p>B>n$
) choices of
![]() $r_p$
in
$r_p$
in
![]() $\{0, \ldots , p^{l_{p}}-1 \}$
such that if
$\{0, \ldots , p^{l_{p}}-1 \}$
such that if
![]() $ a \equiv _{p^{l_p}} r_{p}$
, then
$ a \equiv _{p^{l_p}} r_{p}$
, then
 $$ \begin{align*}\bigwedge_{i=1}^n (ka+hc_i \not \equiv_{p^{l_p}} 0).\end{align*} $$
$$ \begin{align*}\bigwedge_{i=1}^n (ka+hc_i \not \equiv_{p^{l_p}} 0).\end{align*} $$
Suppose
![]() $p = p_{i'}$
for some
$p = p_{i'}$
for some
![]() $i' \in \{1, \ldots , n'\}$
. By the assumption that
$i' \in \{1, \ldots , n'\}$
. By the assumption that
![]() $\psi (x,c,c')$
is nontrivial, c has no common components with
$\psi (x,c,c')$
is nontrivial, c has no common components with
![]() $c'$
. Since
$c'$
. Since
![]() $\text {gcd}(h, M!)=1$
, h and p are coprime, and so the components of
$\text {gcd}(h, M!)=1$
, h and p are coprime, and so the components of
![]() $hc$
and
$hc$
and
![]() $hc'$
are pairwise distinct
$hc'$
are pairwise distinct
![]() $\mathrm {mod}\ p^{l_p}$
. As k is invertible
$\mathrm {mod}\ p^{l_p}$
. As k is invertible
![]() $\mathrm {mod}\ p^{l_p}$
, there is exactly one
$\mathrm {mod}\ p^{l_p}$
, there is exactly one
![]() $r_p$
in
$r_p$
in
![]() $\{ 0, \ldots , p^{l_{p}}-1 \}$
such that if
$\{ 0, \ldots , p^{l_{p}}-1 \}$
such that if
![]() $a \equiv _{p^{l_p}} r_p$
, then
$a \equiv _{p^{l_p}} r_p$
, then
 $$ \begin{align*}\bigwedge_{i=1}^n (ka+hc_i \not \equiv_{p^{l_p}} 0) \wedge (ka+hc^{\prime}_{i'} \equiv_{p^{l_p}} 0) \ \text{ and consequently }\ ka+hc^{\prime}_{i'} \notin P_{hm}^{\mathbb{Z}} .\end{align*} $$
$$ \begin{align*}\bigwedge_{i=1}^n (ka+hc_i \not \equiv_{p^{l_p}} 0) \wedge (ka+hc^{\prime}_{i'} \equiv_{p^{l_p}} 0) \ \text{ and consequently }\ ka+hc^{\prime}_{i'} \notin P_{hm}^{\mathbb{Z}} .\end{align*} $$
Now it follows by the Chinese remainder theorem that,
 $$ \begin{align*}|\Psi^h_{M}(hs,ht)|\geq \left\lfloor \frac{ht-hs}{D\prod_{B<p\leq M} p^{l_p}} \right\rfloor \prod_{p \in \Delta}\left(p^{l_p}-n\right).\end{align*} $$
$$ \begin{align*}|\Psi^h_{M}(hs,ht)|\geq \left\lfloor \frac{ht-hs}{D\prod_{B<p\leq M} p^{l_p}} \right\rfloor \prod_{p \in \Delta}\left(p^{l_p}-n\right).\end{align*} $$
Then it follows that,
 $$ \begin{align*}|\Psi^h_{M}(hs,ht)|\geq \frac{ht-hs}{D}\prod_{p \leq p_{n'}}\frac{1}{p^{l_p}}\prod_{p> p_{n'}}^{\leq M} \left(1-\frac{n}{p^{l_p}}\right) - \prod_{p\leq M} p^{l_p}.\end{align*} $$
$$ \begin{align*}|\Psi^h_{M}(hs,ht)|\geq \frac{ht-hs}{D}\prod_{p \leq p_{n'}}\frac{1}{p^{l_p}}\prod_{p> p_{n'}}^{\leq M} \left(1-\frac{n}{p^{l_p}}\right) - \prod_{p\leq M} p^{l_p}.\end{align*} $$
Set
 $$ \begin{align*}\varepsilon = \frac{1}{2D}\prod_{p \leq p_{n'}}\frac{1}{p^{l_p}}\prod_{p> p_{n'}} \left(1-\frac{n}{p^{l_p}}\right).\end{align*} $$
$$ \begin{align*}\varepsilon = \frac{1}{2D}\prod_{p \leq p_{n'}}\frac{1}{p^{l_p}}\prod_{p> p_{n'}} \left(1-\frac{n}{p^{l_p}}\right).\end{align*} $$
Now as
![]() $l_p \geq 2$
, for
$l_p \geq 2$
, for
![]() $U \in \mathbb {N}^{>0}$
with
$U \in \mathbb {N}^{>0}$
with
![]() $U>\max \{p_{n}',n^2\}$
we have that
$U>\max \{p_{n}',n^2\}$
we have that
 $$ \begin{align*}\prod_{p> U} \left(1-\frac{n}{p^{l_p}}\right)>\prod_{p>U}\left(1-\frac{1}{p^{\frac{3}{2}}}\right).\end{align*} $$
$$ \begin{align*}\prod_{p> U} \left(1-\frac{n}{p^{l_p}}\right)>\prod_{p>U}\left(1-\frac{1}{p^{\frac{3}{2}}}\right).\end{align*} $$
Hence, it follows from Euler’s product formula that
![]() $\varepsilon>0$
. We now have
$\varepsilon>0$
. We now have
 $$ \begin{align*}|\Psi^h_{M}(hs,ht)| \geq 2\varepsilon(ht-hs) - \prod_{p\leq M} p^{l_p}.\end{align*} $$
$$ \begin{align*}|\Psi^h_{M}(hs,ht)| \geq 2\varepsilon(ht-hs) - \prod_{p\leq M} p^{l_p}.\end{align*} $$
We note that
![]() $\varepsilon $
is independent of the choice of M and h, and will serve as the promised
$\varepsilon $
is independent of the choice of M and h, and will serve as the promised
![]() $\varepsilon $
in the statement of the lemma.
$\varepsilon $
in the statement of the lemma.
Next we obtain an upper bound on
![]() $|\Psi ^h_{M}(s,t)\setminus \Psi ^h(s,t)|$
for
$|\Psi ^h_{M}(s,t)\setminus \Psi ^h(s,t)|$
for
![]() $M> p_{n'} $
,
$M> p_{n'} $
,
![]() $h> 0$
, and
$h> 0$
, and
![]() $\text {gcd}(h, M!)=1$
. We arrange that
$\text {gcd}(h, M!)=1$
. We arrange that
![]() $k>0$
by replacing c by
$k>0$
by replacing c by
![]() $-c$
and
$-c$
and
![]() $c'$
by
$c'$
by
![]() $-c'$
if necessary. Note that an element
$-c'$
if necessary. Note that an element
![]() $a \in \Psi ^h_{M}(s,t) \setminus \Psi ^h(s,t)$
must be such that
$a \in \Psi ^h_{M}(s,t) \setminus \Psi ^h(s,t)$
must be such that
and
![]() $ka+hc_i$
is a multiple of
$ka+hc_i$
is a multiple of
![]() $p^{l_p}$
for some
$p^{l_p}$
for some
![]() $p>M$
and
$p>M$
and
![]() $i \in \{1, \ldots , n\}$
. For each p and
$i \in \{1, \ldots , n\}$
. For each p and
![]() $i \in \{1, \ldots , n\}$
, the number of non-zero multiples of
$i \in \{1, \ldots , n\}$
, the number of non-zero multiples of
![]() $p^{l_p}$
in
$p^{l_p}$
in
![]() $(hks+hc_i, hkt+hc_i)$
is
$(hks+hc_i, hkt+hc_i)$
is
 $$ \begin{align*}\lfloor hk(t \kern1pt{-}\kern1pt s) p^{-l_p}\rfloor \kern1pt{-}\kern1pt 2, \ \text{or}\ \lfloor hk(t \kern1pt{-}\kern1pt s) p^{-l_p}\rfloor \kern1pt{-}\kern1pt 1, \ \text{or}\ \lfloor hk(t -s) p^{-l_p}\rfloor, \ \text{or}\ \lfloor hk(t -s) p^{-l_p} \rfloor \kern1.2pt{+}\kern1.2pt 1.\end{align*} $$
$$ \begin{align*}\lfloor hk(t \kern1pt{-}\kern1pt s) p^{-l_p}\rfloor \kern1pt{-}\kern1pt 2, \ \text{or}\ \lfloor hk(t \kern1pt{-}\kern1pt s) p^{-l_p}\rfloor \kern1pt{-}\kern1pt 1, \ \text{or}\ \lfloor hk(t -s) p^{-l_p}\rfloor, \ \text{or}\ \lfloor hk(t -s) p^{-l_p} \rfloor \kern1.2pt{+}\kern1.2pt 1.\end{align*} $$
In the last case, as
![]() $l_p \geq 2$
we moreover have
$l_p \geq 2$
we moreover have
 $$ \begin{align*}p^2\leq |hks+hc_i| \quad \text{ or }\quad p^2\leq |hkt+hc_i|,\end{align*} $$
$$ \begin{align*}p^2\leq |hks+hc_i| \quad \text{ or }\quad p^2\leq |hkt+hc_i|,\end{align*} $$
and so
 $$ \begin{align*}p\leq \sqrt{|hks+hc_i|} + \sqrt{|hkt+hc_i|}.\end{align*} $$
$$ \begin{align*}p\leq \sqrt{|hks+hc_i|} + \sqrt{|hkt+hc_i|}.\end{align*} $$
As
![]() $l_p \geq 2$
, we have
$l_p \geq 2$
, we have
![]() $ \lfloor hk(t -s) p^{-l_p}\rfloor \leq hk(t-s)p^{-2}$
. Therefore we have that
$ \lfloor hk(t -s) p^{-l_p}\rfloor \leq hk(t-s)p^{-2}$
. Therefore we have that
 $$ \begin{align*}|\Psi^h_{M}(s,t)\setminus \Psi^h(s,t)|\leq h(t-s)\sum_{p>M}\frac{nk}{p^2} + \left(\sum_{i=1}^{n}\sqrt{|hks+hc_i|} + \sqrt{|hkt+hc_i|}\right) +1 .\end{align*} $$
$$ \begin{align*}|\Psi^h_{M}(s,t)\setminus \Psi^h(s,t)|\leq h(t-s)\sum_{p>M}\frac{nk}{p^2} + \left(\sum_{i=1}^{n}\sqrt{|hks+hc_i|} + \sqrt{|hkt+hc_i|}\right) +1 .\end{align*} $$
We now obtain N and C as in the statement of the lemma. Note that
 $$ \begin{align*}\sum_{p>T}p^{-2} \leq \sum_{n>T}n^{-2} = O( T^{-1}).\end{align*} $$
$$ \begin{align*}\sum_{p>T}p^{-2} \leq \sum_{n>T}n^{-2} = O( T^{-1}).\end{align*} $$
Using this, we obtain
![]() $N \in \mathbb {N}^{>0}$
such that
$N \in \mathbb {N}^{>0}$
such that
![]() $N>p_{n'}$
and
$N>p_{n'}$
and
 $ \sum _{p>N}knp^{-2}< \varepsilon $
where
$ \sum _{p>N}knp^{-2}< \varepsilon $
where
![]() $\varepsilon $
is from the preceding paragraph. Set
$\varepsilon $
is from the preceding paragraph. Set
 $C = - \prod _{p\leq N} p^{l_p} -1 $
. Combining the estimations from the preceding two paragraphs for
$C = - \prod _{p\leq N} p^{l_p} -1 $
. Combining the estimations from the preceding two paragraphs for
![]() $M=N$
it is easy to see that
$M=N$
it is easy to see that
![]() $\varepsilon , N, C$
are as desired.⊣
$\varepsilon , N, C$
are as desired.⊣
Remark 2.12. The above weak lower bound is all we need for our purpose. We expect that a stronger estimate can be obtained using modifications of available techniques in the literature; see for example [Reference Mirsky12].
Corollary 2.13. For all
![]() $c\in \mathbb {Z}$
, there is
$c\in \mathbb {Z}$
, there is
![]() $a\in \mathbb {Z}$
such that
$a\in \mathbb {Z}$
such that
Proof We have that for all
![]() $c\in \mathbb {Z}$
,
$c\in \mathbb {Z}$
,
![]() $\psi (x,c)=(x+c\in \mathrm {SF}^{\mathbb {Z}})\wedge (x+c+1\in \mathrm {SF}^{\mathbb {Z}})$
is a locally satisfiable
$\psi (x,c)=(x+c\in \mathrm {SF}^{\mathbb {Z}})\wedge (x+c+1\in \mathrm {SF}^{\mathbb {Z}})$
is a locally satisfiable
![]() $\mathbb {Z}$
-system. Applying Lemma 2.11 for
$\mathbb {Z}$
-system. Applying Lemma 2.11 for
![]() $h=1$
,
$h=1$
,
![]() $s=0$
, and t sufficiently large we see there is a solution
$s=0$
, and t sufficiently large we see there is a solution
![]() $a\in \mathbb {Z}$
for
$a\in \mathbb {Z}$
for
![]() $\psi (x,c)$
.⊣
$\psi (x,c)$
.⊣
We next prove the main theorem of the section:
Theorem 2.14. The
![]() $\mathrm {Sf}^*_{\mathbb {Z}}$
-model
$\mathrm {Sf}^*_{\mathbb {Z}}$
-model
![]() $( \mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
, the
$( \mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
, the
 $\mathrm {Sf}^*_{\mathbb {Q}}$
-model
$\mathrm {Sf}^*_{\mathbb {Q}}$
-model
![]() $(\mathbb {Q}; \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
, and the
$(\mathbb {Q}; \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
, and the
 $\mathrm {OSf}^*_{\mathbb {Q}}$
-model
$\mathrm {OSf}^*_{\mathbb {Q}}$
-model
![]() $(\mathbb {Q}; <, \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
are generic.
$(\mathbb {Q}; <, \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
are generic.
Proof We get the first part of the theorem by applying Lemma 2.11 for
![]() $h =1$
,
$h =1$
,
![]() $s =0$
, and t sufficiently large. As the second part of the theorem follows easily from the third part, it will be enough to show that the
$s =0$
, and t sufficiently large. As the second part of the theorem follows easily from the third part, it will be enough to show that the
 $\mathrm {OSf}^*_{\mathbb {Q}}$
-model
$\mathrm {OSf}^*_{\mathbb {Q}}$
-model
![]() $(\mathbb {Q}; <, \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
is generic. Throughout this proof, suppose
$(\mathbb {Q}; <, \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
is generic. Throughout this proof, suppose
![]() $\psi (x,z,z)$
is a special formula and
$\psi (x,z,z)$
is a special formula and
![]() $\psi (x, c, c')$
is a
$\psi (x, c, c')$
is a
![]() $\mathbb {Q}$
-system which is nontrivial and locally satisfiable in
$\mathbb {Q}$
-system which is nontrivial and locally satisfiable in
![]() $\mathbb {Q}$
. Our job is to show that the
$\mathbb {Q}$
. Our job is to show that the
![]() $\mathbb {Q}$
-system
$\mathbb {Q}$
-system
![]() $\psi (x, c, c')$
has a solution in the
$\psi (x, c, c')$
has a solution in the
![]() $\mathbb {Q}$
-interval
$\mathbb {Q}$
-interval
![]() $(b, b')^{\mathbb {Q}}$
for an arbitrary choice of
$(b, b')^{\mathbb {Q}}$
for an arbitrary choice of
![]() $b, b' \in \mathbb {Q}$
such that
$b, b' \in \mathbb {Q}$
such that
![]() $b<b'$
.
$b<b'$
.
We first reduce to the special case where
![]() $\psi (x, c, c')$
is also a
$\psi (x, c, c')$
is also a
![]() $\mathbb {Z}$
-system which is nontrivial and locally satisfiable in
$\mathbb {Z}$
-system which is nontrivial and locally satisfiable in
![]() $\mathbb {Z}$
. Let B be the boundary of
$\mathbb {Z}$
. Let B be the boundary of
![]() $\psi (x,z,z')$
and for each p, let
$\psi (x,z,z')$
and for each p, let
![]() $\psi _p(x,z,z')$
be the associated p-condition of
$\psi _p(x,z,z')$
be the associated p-condition of
![]() $\psi (x,z,z')$
. Using the assumption that
$\psi (x,z,z')$
. Using the assumption that
![]() $\psi (x, c, c')$
is locally satisfiable
$\psi (x, c, c')$
is locally satisfiable
![]() $\mathbb {Q}$
-system, for each
$\mathbb {Q}$
-system, for each
![]() $p<B$
we obtain
$p<B$
we obtain
![]() $a_p \in \mathbb {Q}$
such that
$a_p \in \mathbb {Q}$
such that
![]() $\psi _p(a_p,c,c')$
holds. Let
$\psi _p(a_p,c,c')$
holds. Let
![]() $h>0$
be such that
$h>0$
be such that
 $$ \begin{align*}hc \in \mathbb{Z}^n, hc' \in \mathbb{Z}^{n'}, \text{ and } ha_p \in \mathbb{Z} \text{ for all } p<B.\end{align*} $$
$$ \begin{align*}hc \in \mathbb{Z}^n, hc' \in \mathbb{Z}^{n'}, \text{ and } ha_p \in \mathbb{Z} \text{ for all } p<B.\end{align*} $$
Then by the choice of h, and Lemmas 2.7 and 2.9, the h-conjugate
![]() $\psi ^h(x,hc,hc')$
of
$\psi ^h(x,hc,hc')$
of
![]() $\psi (x, c, c')$
is a
$\psi (x, c, c')$
is a
![]() $\mathbb {Z}$
-system which is nontrivial and locally satisfiable in
$\mathbb {Z}$
-system which is nontrivial and locally satisfiable in
![]() $\mathbb {Z}$
. On the other hand,
$\mathbb {Z}$
. On the other hand,
![]() $\psi (x,c,c')$
has a solution in an interval
$\psi (x,c,c')$
has a solution in an interval
![]() $(b,b')^{\mathbb {Q}}$
if and only if
$(b,b')^{\mathbb {Q}}$
if and only if
Hence, by replacing
![]() $\psi (x,z,z')$
with
$\psi (x,z,z')$
with
![]() $\psi ^h(x,z,z')$
,
$\psi ^h(x,z,z')$
,
![]() $\psi (x, c, c')$
with
$\psi (x, c, c')$
with
![]() $\psi ^h(x,hc,hc')$
, and
$\psi ^h(x,hc,hc')$
, and
![]() $(b, b')^{\mathbb {Q}}$
with
$(b, b')^{\mathbb {Q}}$
with
![]() $(hb, hb')^{\mathbb {Q}}$
if necessary we get the desired reduction.
$(hb, hb')^{\mathbb {Q}}$
if necessary we get the desired reduction.
We show
![]() $\psi (x, c, c')$
has a solution in the
$\psi (x, c, c')$
has a solution in the
![]() $\mathbb {Q}$
-interval
$\mathbb {Q}$
-interval
![]() $(b, b')^{\mathbb {Q}}$
for the special case in the preceding paragraph. By an argument similar to the preceding paragraph, it suffices to show that for some
$(b, b')^{\mathbb {Q}}$
for the special case in the preceding paragraph. By an argument similar to the preceding paragraph, it suffices to show that for some
![]() $h\neq 0$
,
$h\neq 0$
,
![]() $\psi ^h(x, hc, hc')$
has a solution in
$\psi ^h(x, hc, hc')$
has a solution in
![]() $(hb, hb')^{\mathbb {Q}}$
. Applying Lemma 2.11 for
$(hb, hb')^{\mathbb {Q}}$
. Applying Lemma 2.11 for
![]() $s =b$
,
$s =b$
,
![]() $t=b'$
, and h sufficiently large satisfying the condition of the lemma, we get the desired conclusion.⊣
$t=b'$
, and h sufficiently large satisfying the condition of the lemma, we get the desired conclusion.⊣
3 Logical tameness
We will next prove that
![]() $\mathrm {SF}^*_{\mathbb {Z}}$
,
$\mathrm {SF}^*_{\mathbb {Z}}$
,
![]() $\mathrm {SF}^*_{\mathbb {Q}}$
, and
$\mathrm {SF}^*_{\mathbb {Q}}$
, and
![]() $\mathrm {OSF}^*_{\mathbb {Q}}$
admit quantifier elimination. We first need a technical lemma saying that modulo
$\mathrm {OSF}^*_{\mathbb {Q}}$
admit quantifier elimination. We first need a technical lemma saying that modulo
![]() $\mathrm {Sf}^*_{\mathbb {Z}}$
or
$\mathrm {Sf}^*_{\mathbb {Z}}$
or
 $\mathrm {Sf}^*_{\mathbb {Q}}$
, an arbitrary quantifier free formula
$\mathrm {Sf}^*_{\mathbb {Q}}$
, an arbitrary quantifier free formula
![]() $\phi (x,y)$
is not much more complicated than a special formula; recall that x always denotes a single variable.
$\phi (x,y)$
is not much more complicated than a special formula; recall that x always denotes a single variable.
Lemma 3.1. Suppose
![]() $\varphi (x,y)$
is a quantifier-free
$\varphi (x,y)$
is a quantifier-free
![]() $L^*_{\mathrm {u}}$
-formula. Then
$L^*_{\mathrm {u}}$
-formula. Then
![]() $\varphi (x,y)$
is equivalent modulo
$\varphi (x,y)$
is equivalent modulo
![]() $\mathrm {Sf}^*_{\mathbb {Z}}$
to a disjunction of quantifier-free formulas of the form
$\mathrm {Sf}^*_{\mathbb {Z}}$
to a disjunction of quantifier-free formulas of the form
where
-
(i)
 $t(y)$
and
$t(y)$
and
 $t'(y)$
are tuples of
$t'(y)$
are tuples of
 $L^*_{\mathrm {u}}$
-terms with length n and
$L^*_{\mathrm {u}}$
-terms with length n and
 $n'$
respectively;
$n'$
respectively; -
(ii)
 $\rho (y)$
is a quantifier-free
$\rho (y)$
is a quantifier-free
 $L^*_{\mathrm {u}}$
-formula,
$L^*_{\mathrm {u}}$
-formula,
 $ \varepsilon (x, y)$
an equational condition, and
$ \varepsilon (x, y)$
an equational condition, and
 $\psi (x, z, z')$
a special formula.
$\psi (x, z, z')$
a special formula.
The corresponding statement with
![]() $\mathrm {Sf}^*_{\mathbb {Z}}$
replaced by
$\mathrm {Sf}^*_{\mathbb {Z}}$
replaced by
 $\mathrm {Sf}^*_{\mathbb {Q}}$
also holds.
$\mathrm {Sf}^*_{\mathbb {Q}}$
also holds.
Proof Let
![]() $\varphi (x, y)$
be a quantifier-free
$\varphi (x, y)$
be a quantifier-free
![]() $L^*_{\mathrm {u}}$
-formula. We will use the following disjunction observation several times in our proof: If
$L^*_{\mathrm {u}}$
-formula. We will use the following disjunction observation several times in our proof: If
![]() $\varphi (x,y)$
is a finite disjunction of quantifier-free
$\varphi (x,y)$
is a finite disjunction of quantifier-free
![]() $L^*_{\mathrm {u}}$
-formulas and we have proven the desired statement for each of those, then the desired statement for
$L^*_{\mathrm {u}}$
-formulas and we have proven the desired statement for each of those, then the desired statement for
![]() $\varphi (x,y)$
follows. In particular, it allows us to assume that
$\varphi (x,y)$
follows. In particular, it allows us to assume that
![]() $\varphi (x, y)$
is the conjunction
$\varphi (x, y)$
is the conjunction
 $$ \begin{align*}\rho(y) \wedge \varepsilon(x, y) \wedge \bigwedge_p \eta_p(x, y) \wedge \bigwedge_{i=1}^n (k_ix+t_i(y) \in P_{m_i}) \wedge \bigwedge_{i=1}^{n'} (k^{\prime}_ix+t^{\prime}_{i}(y) \notin P_{m^{\prime}_i}),\end{align*} $$
$$ \begin{align*}\rho(y) \wedge \varepsilon(x, y) \wedge \bigwedge_p \eta_p(x, y) \wedge \bigwedge_{i=1}^n (k_ix+t_i(y) \in P_{m_i}) \wedge \bigwedge_{i=1}^{n'} (k^{\prime}_ix+t^{\prime}_{i}(y) \notin P_{m^{\prime}_i}),\end{align*} $$
where
![]() $\rho (y)$
is a quantifier-free
$\rho (y)$
is a quantifier-free
![]() $L^*_{\mathrm {u}}$
-formula,
$L^*_{\mathrm {u}}$
-formula,
![]() $\varepsilon (x, y)$
is an equational condition,
$\varepsilon (x, y)$
is an equational condition,
![]() $k_1, \ldots , k_n$
and
$k_1, \ldots , k_n$
and
![]() $k_1', \ldots , k^{\prime }_{n'}$
are in
$k_1', \ldots , k^{\prime }_{n'}$
are in
![]() $\mathbb {Z}\setminus \{0\}$
,
$\mathbb {Z}\setminus \{0\}$
,
![]() $m_1, \ldots , m_n$
and
$m_1, \ldots , m_n$
and
![]() $m^{\prime }_1, \ldots , m^{\prime }_{n'}$
are in
$m^{\prime }_1, \ldots , m^{\prime }_{n'}$
are in
![]() $\mathbb {N}^{\geq 1}$
,
$\mathbb {N}^{\geq 1}$
,
![]() $t_1(y), \ldots , t_n(y)$
and
$t_1(y), \ldots , t_n(y)$
and
![]() $t^{\prime }_1(y), \ldots , t^{\prime }_n(y)$
are
$t^{\prime }_1(y), \ldots , t^{\prime }_n(y)$
are
![]() $L^*_{\mathrm {u}}$
-terms with variables in y,
$L^*_{\mathrm {u}}$
-terms with variables in y,
![]() $\eta _p(x,y)$
is a p-condition for each p, and
$\eta _p(x,y)$
is a p-condition for each p, and
![]() $\eta _p(x,y)$
is trivial for all but finitely many p.
$\eta _p(x,y)$
is trivial for all but finitely many p.
We make further reductions to the form of
![]() $\varphi (x,y)$
. Set
$\varphi (x,y)$
. Set
![]() $t(y) =(t_1(y), \ldots , t_n(y))$
and
$t(y) =(t_1(y), \ldots , t_n(y))$
and
 $t'(y)=(t^{\prime }_1(y), \ldots , t^{\prime }_{n'}(y))$
. Using the disjunction observation and the fact that
$t'(y)=(t^{\prime }_1(y), \ldots , t^{\prime }_{n'}(y))$
. Using the disjunction observation and the fact that
is a tautology for every component
![]() $y_j$
of y, we can assume that either
$y_j$
of y, we can assume that either
![]() $x+ y_j \in P_1$
or
$x+ y_j \in P_1$
or
![]() $x + y_j \notin P_1$
are among the conjuncts of
$x + y_j \notin P_1$
are among the conjuncts of
![]() $\varphi (x, y)$
, and so
$\varphi (x, y)$
, and so
![]() $y_j$
is among the components of
$y_j$
is among the components of
![]() $t(y)$
or
$t(y)$
or
![]() $t'(y)$
. Then we obtain for each prime p a p-condition
$t'(y)$
. Then we obtain for each prime p a p-condition
![]() $\theta _p(x, z, z')$
such that
$\theta _p(x, z, z')$
such that
![]() $\theta _p(x, t(y), t'(y))$
is logically equivalent to
$\theta _p(x, t(y), t'(y))$
is logically equivalent to
![]() $\eta _p( x, y)$
. Let
$\eta _p( x, y)$
. Let
![]() $\xi (x, z, z')$
be the formula
$\xi (x, z, z')$
be the formula
 $$ \begin{align*}\bigwedge_p \theta_p(x, z, z') \wedge \bigwedge_{i=1}^n (k_ix+z_i\in P_{m_i}) \wedge \bigwedge_{i=1}^{n'} (k^{\prime}_ix+z^{\prime}_i \notin P_{m^{\prime}_i}).\end{align*} $$
$$ \begin{align*}\bigwedge_p \theta_p(x, z, z') \wedge \bigwedge_{i=1}^n (k_ix+z_i\in P_{m_i}) \wedge \bigwedge_{i=1}^{n'} (k^{\prime}_ix+z^{\prime}_i \notin P_{m^{\prime}_i}).\end{align*} $$
Clearly,
![]() $\varphi (x,y)$
is equivalent to the formula
$\varphi (x,y)$
is equivalent to the formula
![]() $\rho (y) \wedge \varepsilon (x, y) \wedge \xi (x, t(y), t'(y))$
, so we can assume that
$\rho (y) \wedge \varepsilon (x, y) \wedge \xi (x, t(y), t'(y))$
, so we can assume that
![]() $\varphi (x,y)$
is the latter.
$\varphi (x,y)$
is the latter.
We need a small observation. For a p-condition
![]() $\theta _p(z)$
and
$\theta _p(z)$
and
![]() $h \neq 0$
, we will show that there is another p-condition
$h \neq 0$
, we will show that there is another p-condition
![]() $\eta _p(z)$
such that modulo
$\eta _p(z)$
such that modulo
![]() $\mathrm {Sf}^*_{\mathbb {Z}}$
and
$\mathrm {Sf}^*_{\mathbb {Z}}$
and
 $\mathrm {Sf}^*_{\mathbb {Q}}$
,
$\mathrm {Sf}^*_{\mathbb {Q}}$
,
For the special case where
![]() $\theta _p(z)$
is
$\theta _p(z)$
is
![]() $t(z) \in U_{p, l}$
, the conclusion follows from Lemmas 2.1(iii) and 2.5(iii) and the fact that there is an
$t(z) \in U_{p, l}$
, the conclusion follows from Lemmas 2.1(iii) and 2.5(iii) and the fact that there is an
![]() $L^*_{\mathrm {u}}$
-term
$L^*_{\mathrm {u}}$
-term
![]() $t'(z)$
such that
$t'(z)$
such that
![]() $t'(z, \ldots , z_{i-1}, hz_i, z_{i+1}, \ldots , z_n) = ht(z).$
The statement of the paragraph follows easily from this special case.
$t'(z, \ldots , z_{i-1}, hz_i, z_{i+1}, \ldots , z_n) = ht(z).$
The statement of the paragraph follows easily from this special case.
With
![]() $\varphi (x,y)$
as in the end of the second paragraph, we further reduce the main statement to the special case where there is
$\varphi (x,y)$
as in the end of the second paragraph, we further reduce the main statement to the special case where there is
![]() $k\neq 0$
such that
$k\neq 0$
such that
![]() $k_i = k^{\prime }_{i'} =k$
for all
$k_i = k^{\prime }_{i'} =k$
for all
![]() $i\in \{1, \ldots , n\}$
and
$i\in \{1, \ldots , n\}$
and
![]() $i' \in \{ 1, \ldots , n'\}$
. Choose
$i' \in \{ 1, \ldots , n'\}$
. Choose
![]() $k\neq 0 $
to be a common multiple of
$k\neq 0 $
to be a common multiple of
![]() $k_1, \ldots , k_n$
and
$k_1, \ldots , k_n$
and
![]() $k^{\prime }_1, \ldots k^{\prime }_{n'}$
. Then by Lemmas 2.1(vi) and 2.5(iii), we have for each
$k^{\prime }_1, \ldots k^{\prime }_{n'}$
. Then by Lemmas 2.1(vi) and 2.5(iii), we have for each
![]() $i \in \{1, \ldots , n\} $
that
$i \in \{1, \ldots , n\} $
that
 $$ \begin{align*}k_ix+z_i \in P_{m_i}\ \text{ is equivalent to }\ (kx+kk^{-1}_iz_i \in P_{kk^{-1}_im_i}) \text{ modulo either } \mathrm{Sf}^*_{\mathbb{Z}} \text{ or }\mathrm{Sf}^*_{\mathbb{Q}}.\end{align*} $$
$$ \begin{align*}k_ix+z_i \in P_{m_i}\ \text{ is equivalent to }\ (kx+kk^{-1}_iz_i \in P_{kk^{-1}_im_i}) \text{ modulo either } \mathrm{Sf}^*_{\mathbb{Z}} \text{ or }\mathrm{Sf}^*_{\mathbb{Q}}.\end{align*} $$
We have a similar observation for k and
![]() $k^{\prime }_{i'}$
with
$k^{\prime }_{i'}$
with
![]() $i' \in \{1, \ldots , n'\}$
. The desired reduction easily follows from these observations and the preceding paragraph.
$i' \in \{1, \ldots , n'\}$
. The desired reduction easily follows from these observations and the preceding paragraph.
Continuing with the reduction in the preceding paragraph, we next arrange that there is
![]() $m> 0$
such that
$m> 0$
such that
![]() $m_i = m^{\prime }_{i'} =m$
for all
$m_i = m^{\prime }_{i'} =m$
for all
![]() $i\in \{1, \ldots , n\}$
and
$i\in \{1, \ldots , n\}$
and
![]() $i' \in \{ 1, \ldots , n'\}$
. Let m be a common multiple of
$i' \in \{ 1, \ldots , n'\}$
. Let m be a common multiple of
![]() $m_1, \ldots , m_n$
and
$m_1, \ldots , m_n$
and
![]() $m^{\prime }_1, \ldots m^{\prime }_{n'}$
. By Lemmas 2.1(v,vi) and 2.5(iii), we have for
$m^{\prime }_1, \ldots m^{\prime }_{n'}$
. By Lemmas 2.1(v,vi) and 2.5(iii), we have for
![]() $i \in \{ 1, \ldots , n\}$
that modulo either
$i \in \{ 1, \ldots , n\}$
that modulo either
![]() $\mathrm {Sf}^*_{\mathbb {Z}}$
or
$\mathrm {Sf}^*_{\mathbb {Z}}$
or
![]() $\mathrm {Sf}^*_{\mathbb {Z}}$
or
$\mathrm {Sf}^*_{\mathbb {Z}}$
or
 $\mathrm {Sf}^*_{\mathbb {Q}}$
$\mathrm {Sf}^*_{\mathbb {Q}}$
 $$ \begin{align*}kx+z_i \in P_{m_i} \ \text{ is equivalent to }\ kx+z_i \in P_{m} \wedge \bigwedge_{p \mid \frac{m}{m_i}} kx+z_i \notin U_{p, 2+ v_p(m_i)}\end{align*} $$
$$ \begin{align*}kx+z_i \in P_{m_i} \ \text{ is equivalent to }\ kx+z_i \in P_{m} \wedge \bigwedge_{p \mid \frac{m}{m_i}} kx+z_i \notin U_{p, 2+ v_p(m_i)}\end{align*} $$
and for
![]() $i' \in \{ 1, \ldots , n'\}$
that modulo either
$i' \in \{ 1, \ldots , n'\}$
that modulo either
![]() $\mathrm {Sf}^*_{\mathbb {Z}}$
or
$\mathrm {Sf}^*_{\mathbb {Z}}$
or
 $\mathrm {Sf}^*_{\mathbb {Q}}$
$\mathrm {Sf}^*_{\mathbb {Q}}$
 $$ \begin{align*}kx+z^{\prime}_{i'} \notin P_{m^{\prime}_{i'}} \ \text{ is equivalent to }\ kx+z^{\prime}_{i'} \notin P_{m} \vee \bigvee_{p \mid \frac{m}{m^{\prime}_{i'}}} kx+z^{\prime}_{i'} \in U_{p,2+ v_p(m^{\prime}_{i'})} .\end{align*} $$
$$ \begin{align*}kx+z^{\prime}_{i'} \notin P_{m^{\prime}_{i'}} \ \text{ is equivalent to }\ kx+z^{\prime}_{i'} \notin P_{m} \vee \bigvee_{p \mid \frac{m}{m^{\prime}_{i'}}} kx+z^{\prime}_{i'} \in U_{p,2+ v_p(m^{\prime}_{i'})} .\end{align*} $$
It follows that
![]() $\varphi (x, y)$
is equivalent to a disjunction of formulas of the form we are aiming for. The desired conclusion of the lemma follows from the disjunction observation.⊣
$\varphi (x, y)$
is equivalent to a disjunction of formulas of the form we are aiming for. The desired conclusion of the lemma follows from the disjunction observation.⊣
Corollary 3.2. Suppose
![]() $\varphi (x,y)$
is a quantifier-free
$\varphi (x,y)$
is a quantifier-free
![]() $L^*_{\mathrm {ou}}$
formula. Then
$L^*_{\mathrm {ou}}$
formula. Then
![]() $\varphi (x,y)$
is equivalent modulo
$\varphi (x,y)$
is equivalent modulo
 $\mathrm {OSf}^*_{\mathbb {Q}}$
to a disjunction of quantifier-free formulas of the form
$\mathrm {OSf}^*_{\mathbb {Q}}$
to a disjunction of quantifier-free formulas of the form
where
-
(i)
 $t(y)$
and
$t(y)$
and
 $t'(y)$
are tuples of
$t'(y)$
are tuples of
 $L^*_{\mathrm {ou}}$
-terms with length n and
$L^*_{\mathrm {ou}}$
-terms with length n and
 $n'$
respectively;
$n'$
respectively; -
(ii)
 $\rho (y)$
is a quantifier-free
$\rho (y)$
is a quantifier-free
 $L^*_{\mathrm {ou}}$
-formula,
$L^*_{\mathrm {ou}}$
-formula,
 $ \lambda (x, y)$
an order condition, and
$ \lambda (x, y)$
an order condition, and
 $\psi (x, z, z')$
a special formula.
$\psi (x, z, z')$
a special formula.
In the next lemma, we show a “local quantifier elimination” result.
Lemma 3.3. If
![]() $\varphi (x,z)$
is a p-condition, then modulo either
$\varphi (x,z)$
is a p-condition, then modulo either
![]() $\mathrm {Sf}^*_{\mathbb {Z}}$
or
$\mathrm {Sf}^*_{\mathbb {Z}}$
or
 $\mathrm {Sf}^*_{\mathbb {Q}}$
, the formula
$\mathrm {Sf}^*_{\mathbb {Q}}$
, the formula
![]() $\exists x \varphi (x,z)$
is equivalent to a p-condition
$\exists x \varphi (x,z)$
is equivalent to a p-condition
![]() $\psi (z)$
.
$\psi (z)$
.
Proof If
![]() $\varphi (x,z)$
is a p-condition, then by Lemma 2.1
$\varphi (x,z)$
is a p-condition, then by Lemma 2.1
![]() $(\mathrm {i})$
, modulo
$(\mathrm {i})$
, modulo
![]() $\mathrm {Sf}^*_{\mathbb {Z}}$
, it is a Boolean combination of atomic formulas of the form
$\mathrm {Sf}^*_{\mathbb {Z}}$
, it is a Boolean combination of atomic formulas of the form
![]() $kx +t(z) \in U_{p, l}$
where
$kx +t(z) \in U_{p, l}$
where
![]() $t(z)$
is an
$t(z)$
is an
![]() $L^*_{\mathrm {u}}$
-term, and
$L^*_{\mathrm {u}}$
-term, and
![]() $l>0$
. Let
$l>0$
. Let
![]() $l_p$
be the largest value of l occurring in such atomic formulas, and set
$l_p$
be the largest value of l occurring in such atomic formulas, and set
 $$ \begin{align*}S=\{(m_1,\ldots,m_n): 0 \leq m_i < p^{l_p} \text{ for each }i, \text{ and } (\mathbb{Z}; \mathscr{U}^{\mathbb{Z}}) \models \exists x \varphi(x,m_1,\ldots,m_n)\}.\end{align*} $$
$$ \begin{align*}S=\{(m_1,\ldots,m_n): 0 \leq m_i < p^{l_p} \text{ for each }i, \text{ and } (\mathbb{Z}; \mathscr{U}^{\mathbb{Z}}) \models \exists x \varphi(x,m_1,\ldots,m_n)\}.\end{align*} $$
Then by Lemma 2.1
![]() $(\mathrm {i})$
, modulo
$(\mathrm {i})$
, modulo
![]() $\mathrm {Sf}^*_{\mathbb {Z}}$
,
$\mathrm {Sf}^*_{\mathbb {Z}}$
,
![]() $\exists x \varphi (x,z)$
is equivalent to the p-condition
$\exists x \varphi (x,z)$
is equivalent to the p-condition
 $\bigvee _{(m_1,\ldots ,m_n)\in S} (\bigwedge _{i=1}^{n} (z_i\equiv _{p^{l_p}} m_i))$
.
$\bigvee _{(m_1,\ldots ,m_n)\in S} (\bigwedge _{i=1}^{n} (z_i\equiv _{p^{l_p}} m_i))$
.
Now, we proceed to prove the statement for models of
 $\mathrm {Sf}^*_{\mathbb {Q}}$
. Throughout the rest of the proof, suppose
$\mathrm {Sf}^*_{\mathbb {Q}}$
. Throughout the rest of the proof, suppose
![]() $\varphi (x,z)$
is a p-condition, k,
$\varphi (x,z)$
is a p-condition, k,
![]() $k'$
, l,
$k'$
, l,
![]() $l'$
are in
$l'$
are in
![]() $\mathbb {Z}$
, and
$\mathbb {Z}$
, and
![]() $t(z), t'(z)$
are
$t(z), t'(z)$
are
![]() $L_{\mathrm {u}}^*$
-terms. First, we consider the case where
$L_{\mathrm {u}}^*$
-terms. First, we consider the case where
![]() $\varphi (x,z)$
is a p-condition of the form
$\varphi (x,z)$
is a p-condition of the form
![]() $kx+t(z) \in U_{p,l}$
. The case
$kx+t(z) \in U_{p,l}$
. The case
![]() $k=0$
is trivial. If
$k=0$
is trivial. If
![]() $k \neq 0$
, then
$k \neq 0$
, then
![]() $\exists x (kx+t(z) \in U_{p,l})$
is tautological modulo
$\exists x (kx+t(z) \in U_{p,l})$
is tautological modulo
 $\mathrm {Sf}^*_{\mathbb {Q}}$
following from (Q1) in the definition of
$\mathrm {Sf}^*_{\mathbb {Q}}$
following from (Q1) in the definition of
 $\mathrm {Sf}^*_{\mathbb {Q}}$
and Lemma 2.5(i).
$\mathrm {Sf}^*_{\mathbb {Q}}$
and Lemma 2.5(i).
We next consider the case where
![]() $\varphi (x,z)$
is a finite conjunction of p-conditions in
$\varphi (x,z)$
is a finite conjunction of p-conditions in
![]() $L^*_{\mathrm {u}}(x, z)$
such that one of the conjuncts is
$L^*_{\mathrm {u}}(x, z)$
such that one of the conjuncts is
![]() $kx+t(z) \in U_{p,l}$
with
$kx+t(z) \in U_{p,l}$
with
![]() $k \neq 0$
and the other conjuncts are either of the form
$k \neq 0$
and the other conjuncts are either of the form
![]() $k'x+t'(z) \in U_{p,l'}$
or of the form
$k'x+t'(z) \in U_{p,l'}$
or of the form
![]() $k'x+t'(z) \notin U_{p,l'}$
where we do allow
$k'x+t'(z) \notin U_{p,l'}$
where we do allow
![]() $l'$
to vary. It follows from Lemma 2.5(i) that if
$l'$
to vary. It follows from Lemma 2.5(i) that if
![]() $k = k'$
,
$k = k'$
,
![]() $l\geq l'$
, then
$l\geq l'$
, then
So we have means to replace conjuncts of
![]() $\varphi (x,z)$
by terms independent of the variable x. However, the above will not work if
$\varphi (x,z)$
by terms independent of the variable x. However, the above will not work if
![]() $k \neq k'$
or
$k \neq k'$
or
![]() $l<l'$
. By Lemma 2.5(iii), across models of
$l<l'$
. By Lemma 2.5(iii), across models of
 $\mathrm {Sf}^*_{\mathbb {Q}}$
, we have that
$\mathrm {Sf}^*_{\mathbb {Q}}$
, we have that
 $$ \begin{align*}kx+ t(z) \in U_{p, l} \text{ if and only if } hkx + ht(z) \in U_{p, l+ v_p(h)} \ \ \text{ for all } h \neq 0.\end{align*} $$
$$ \begin{align*}kx+ t(z) \in U_{p, l} \text{ if and only if } hkx + ht(z) \in U_{p, l+ v_p(h)} \ \ \text{ for all } h \neq 0.\end{align*} $$
From this observation, it is easy to see that we can resolve the issue of having
![]() $k \neq k'$
, and moreover arrange that
$k \neq k'$
, and moreover arrange that
![]() $l\geq 0$
which will be used in the next observation. By Lemma 2.5(i,ii), across models of
$l\geq 0$
which will be used in the next observation. By Lemma 2.5(i,ii), across models of
 $\mathrm {Sf}^*_{\mathbb {Q}}$
, we have that
$\mathrm {Sf}^*_{\mathbb {Q}}$
, we have that
 $$ \begin{align*}kx + t(z) \in U_{p, l} \ \text{ if and only if } \ \bigvee_{i=1}^{p^m} kz + t(z) + ip^{l} \in U_{p, l+m} \text{ for all } l\geq 0 \text{ and all } m.\end{align*} $$
$$ \begin{align*}kx + t(z) \in U_{p, l} \ \text{ if and only if } \ \bigvee_{i=1}^{p^m} kz + t(z) + ip^{l} \in U_{p, l+m} \text{ for all } l\geq 0 \text{ and all } m.\end{align*} $$
Using the preceding two observations we resolve the issue of having
![]() $l<l'$
. The statement of the lemma for this case then follows from the second paragraph.
$l<l'$
. The statement of the lemma for this case then follows from the second paragraph.
We now prove the full lemma. It suffices to consider the case where
![]() $\varphi (x,z)$
is a conjunction of atomic formulas. In view of the preceding paragraph, we reduce further to the case where
$\varphi (x,z)$
is a conjunction of atomic formulas. In view of the preceding paragraph, we reduce further to the case where
![]() $\varphi (x,z)$
is of the form
$\varphi (x,z)$
is of the form
 $$ \begin{align*}\bigwedge_{i=1}^m kx+t_i(z) \notin U_{p,l_i}.\end{align*} $$
$$ \begin{align*}\bigwedge_{i=1}^m kx+t_i(z) \notin U_{p,l_i}.\end{align*} $$
We now show that
![]() $\exists x\varphi (x,z)$
is a tautology over
$\exists x\varphi (x,z)$
is a tautology over
 $\mathrm {Sf}^*_{\mathbb {Q}}$
and thus complete the proof. Suppose
$\mathrm {Sf}^*_{\mathbb {Q}}$
and thus complete the proof. Suppose
 $(G; \mathscr {U}^G, \mathscr {P}^G) \models \mathrm {Sf}^*_{\mathbb {Q}} $
and
$(G; \mathscr {U}^G, \mathscr {P}^G) \models \mathrm {Sf}^*_{\mathbb {Q}} $
and
![]() $c \in G^n$
. It suffices to find
$c \in G^n$
. It suffices to find
![]() $a \in G$
such that the p-condition
$a \in G$
such that the p-condition
 $ka+t_i(c) \notin U^G_{p,l_i}$
holds for all
$ka+t_i(c) \notin U^G_{p,l_i}$
holds for all
![]() $i \in \{1, \ldots , m\}$
. Without loss of generality, we assume that
$i \in \{1, \ldots , m\}$
. Without loss of generality, we assume that
![]() $t_1(c), \ldots , t_{m'}(c)$
are not in
$t_1(c), \ldots , t_{m'}(c)$
are not in
 $U^G_{p,l}$
for all l and that
$U^G_{p,l}$
for all l and that
![]() $t_{m'+1}(c), \ldots , t_{m}(c)$
are in
$t_{m'+1}(c), \ldots , t_{m}(c)$
are in
 $U^G_{p,l_0}$
for some
$U^G_{p,l_0}$
for some
![]() $l_0 $
such that
$l_0 $
such that
![]() $l_0 < l_i$
for all
$l_0 < l_i$
for all
![]() $i \in \{1, \ldots , m\}$
. Using Lemma 2.5(ii), choose a such that
$i \in \{1, \ldots , m\}$
. Using Lemma 2.5(ii), choose a such that
 $ka \in U^G_{p,l_0-1} \setminus U^G_{p,l_0}$
. It follows from Lemma 2.5(i) that a is as desired.⊣
$ka \in U^G_{p,l_0-1} \setminus U^G_{p,l_0}$
. It follows from Lemma 2.5(i) that a is as desired.⊣
Theorem 3.4. The theories
![]() $\mathrm {SF}^*_{\mathbb {Z}}$
,
$\mathrm {SF}^*_{\mathbb {Z}}$
,
![]() $\mathrm {SF}^*_{\mathbb {Q}}$
, and
$\mathrm {SF}^*_{\mathbb {Q}}$
, and
![]() $\mathrm {OSF}^*_{\mathbb {Q}}$
admit quantifier elimination.
$\mathrm {OSF}^*_{\mathbb {Q}}$
admit quantifier elimination.
Proof As the three situations are very similar, we will only present here the proof that
![]() $\mathrm {OSF}^*_{\mathbb {Q}}$
admits quantifier elimination. The proof for
$\mathrm {OSF}^*_{\mathbb {Q}}$
admits quantifier elimination. The proof for
![]() $\mathrm {SF}^*_{\mathbb {Z}}$
and
$\mathrm {SF}^*_{\mathbb {Z}}$
and
![]() $\mathrm {SF}^*_{\mathbb {Q}}$
are simpler as there is no ordering involved. Along the way we point out the necessary modifications needed to get the proof for
$\mathrm {SF}^*_{\mathbb {Q}}$
are simpler as there is no ordering involved. Along the way we point out the necessary modifications needed to get the proof for
![]() $\mathrm {SF}^*_{\mathbb {Z}}$
and
$\mathrm {SF}^*_{\mathbb {Z}}$
and
![]() $\mathrm {SF}^*_{\mathbb {Q}}$
. Fix
$\mathrm {SF}^*_{\mathbb {Q}}$
. Fix
![]() $\mathrm {OSF}^*_{\mathbb {Q}}$
-models
$\mathrm {OSF}^*_{\mathbb {Q}}$
-models
![]() $(G; <, \mathscr {U}^G, \mathscr {P}^G)$
and
$(G; <, \mathscr {U}^G, \mathscr {P}^G)$
and
![]() $(H; <, \mathscr {U}^H, \mathscr {P}^H)$
such that the latter is
$(H; <, \mathscr {U}^H, \mathscr {P}^H)$
such that the latter is
![]() $|G|^+$
-saturated. Suppose
$|G|^+$
-saturated. Suppose
 $$ \begin{align*}f \text{ is a partial } L_{\mathrm{ou}}^*\text{-embedding from } (G; <, \mathscr{U}^G, \mathscr{P}^G) \text{ to } (H; <, \mathscr{U}^H , \mathscr{P}^H ),\end{align*} $$
$$ \begin{align*}f \text{ is a partial } L_{\mathrm{ou}}^*\text{-embedding from } (G; <, \mathscr{U}^G, \mathscr{P}^G) \text{ to } (H; <, \mathscr{U}^H , \mathscr{P}^H ),\end{align*} $$
in other words, f is an
![]() $L_{\mathrm {ou}}^*$
-embedding of an
$L_{\mathrm {ou}}^*$
-embedding of an
![]() $L_{\mathrm {ou}}^*$
-substructure of
$L_{\mathrm {ou}}^*$
-substructure of
![]() $(G; <, \mathscr {U}^G, \mathscr {P}^G)$
into
$(G; <, \mathscr {U}^G, \mathscr {P}^G)$
into
![]() $(H; <, \mathscr {U}^H , \mathscr {P}^H)$
. By a standard test, it suffices to show that if
$(H; <, \mathscr {U}^H , \mathscr {P}^H)$
. By a standard test, it suffices to show that if
![]() $\text {Domain}(f) \neq G$
, then there is a partial
$\text {Domain}(f) \neq G$
, then there is a partial
![]() $L_{\mathrm {ou}}^*$
-embedding from
$L_{\mathrm {ou}}^*$
-embedding from
![]() $(G; <, \mathscr {U}^G, \mathscr {P}^G)$
to
$(G; <, \mathscr {U}^G, \mathscr {P}^G)$
to
![]() $(H; <, \mathscr {U}^H, \mathscr {P}^H)$
which properly extends f. For the corresponding statements with
$(H; <, \mathscr {U}^H, \mathscr {P}^H)$
which properly extends f. For the corresponding statements with
![]() $\mathrm {SF}^*_{\mathbb {Z}}$
or
$\mathrm {SF}^*_{\mathbb {Z}}$
or
![]() $\mathrm {SF}^*_{\mathbb {Q}}$
, we need to consider instead
$\mathrm {SF}^*_{\mathbb {Q}}$
, we need to consider instead
![]() $(G; \mathscr {U}^G, \mathscr {P}^G)$
and
$(G; \mathscr {U}^G, \mathscr {P}^G)$
and
![]() $(H; \mathscr {U}^H, \mathscr {P}^H)$
depending on the situation.
$(H; \mathscr {U}^H, \mathscr {P}^H)$
depending on the situation.
We remind the reader that our choice of language includes a symbol for additive inverse, and so
![]() $\text {Domain}(f)$
is automatically a subgroup of G. Suppose
$\text {Domain}(f)$
is automatically a subgroup of G. Suppose
![]() $\text {Domain}(f)$
is not a pure subgroup of G, that is, there is an element
$\text {Domain}(f)$
is not a pure subgroup of G, that is, there is an element
![]() $\text {Domain}(f)$
which is n-divisible in G but not n-divisible in
$\text {Domain}(f)$
which is n-divisible in G but not n-divisible in
![]() $\text {Domain}(f)$
for some
$\text {Domain}(f)$
for some
![]() $n>0$
. Then there is prime p and a in
$n>0$
. Then there is prime p and a in
![]() $G \setminus \text {Domain}(f)$
such that
$G \setminus \text {Domain}(f)$
such that
![]() $pa \in \text {Domain}(f) $
. Using divisibility of H, we get
$pa \in \text {Domain}(f) $
. Using divisibility of H, we get
![]() $b \in H$
such that
$b \in H$
such that
![]() $pb = f(pa)$
. Let g be the extension of f given by
$pb = f(pa)$
. Let g be the extension of f given by
It is routine to check that g is an ordered group isomorphism from
![]() $\langle \text {Domain}(f), a\rangle $
to
$\langle \text {Domain}(f), a\rangle $
to
![]() $\langle \text {Image}(f), b\rangle $
. It is also easy to check using Lemma 2.5(iii) that
$\langle \text {Image}(f), b\rangle $
. It is also easy to check using Lemma 2.5(iii) that
 $ka + a' \in U^G_{p',l}$
if and only if
$ka + a' \in U^G_{p',l}$
if and only if
 $kb + f(a') \in U^G_{p',l}$
and
$kb + f(a') \in U^G_{p',l}$
and
![]() $ka + a' \in P^G_{m}$
if and only if
$ka + a' \in P^G_{m}$
if and only if
![]() $kb + f(a') \in U^G_{m}$
for all k, l, m, primes
$kb + f(a') \in U^G_{m}$
for all k, l, m, primes
![]() $p'$
, and
$p'$
, and
![]() $a' \in \text {Domain}(f)$
. Hence,
$a' \in \text {Domain}(f)$
. Hence,
 $$ \begin{align*}g \text{ is a partial } L_{\mathrm{ou}}^*\text{-embedding } \text{ from } (G; <, \mathscr{U}^G, \mathscr{P}^G) \text{ to } (H; <, \mathscr{U}^H , \mathscr{P}^H ).\end{align*} $$
$$ \begin{align*}g \text{ is a partial } L_{\mathrm{ou}}^*\text{-embedding } \text{ from } (G; <, \mathscr{U}^G, \mathscr{P}^G) \text{ to } (H; <, \mathscr{U}^H , \mathscr{P}^H ).\end{align*} $$
Clearly, g properly extends f, so the desired conclusion follows. The proof for
![]() $\mathrm {SF}^*_{\mathbb {Q}}$
is the same but without the verification that the ordering is preserved. The situation for
$\mathrm {SF}^*_{\mathbb {Q}}$
is the same but without the verification that the ordering is preserved. The situation for
![]() $\mathrm {SF}^*_{\mathbb {Z}}$
is slightly different as H is not divisible. However, for all primes
$\mathrm {SF}^*_{\mathbb {Z}}$
is slightly different as H is not divisible. However, for all primes
![]() $p'$
,
$p'$
,
![]() $p'a$
is in
$p'a$
is in
 $p'G = U^G_{p', 1}$
, and so
$p'G = U^G_{p', 1}$
, and so
![]() $f(p'a)$
is in
$f(p'a)$
is in
 $ U^H_{p', 1} = p'H$
. The proof proceeds similarly using Lemma 2.1(iv–vi).
$ U^H_{p', 1} = p'H$
. The proof proceeds similarly using Lemma 2.1(iv–vi).
The remaining case is when
![]() $\text {Domain}(f) \neq G$
is a pure subgroup of G. Let a be in
$\text {Domain}(f) \neq G$
is a pure subgroup of G. Let a be in
![]() $G \setminus \text {Domain}(f)$
. We need to find b in
$G \setminus \text {Domain}(f)$
. We need to find b in
![]() $H \setminus \text {Image}(f)$
such that
$H \setminus \text {Image}(f)$
such that
 $$ \begin{align*}\text{qftp}_{L_{\mathrm{ou}}^*}(a / \text{Domain}(f)) = \text{qftp}_{L_{\mathrm{ou}}^*}(b / \text{Image}(f)).\end{align*} $$
$$ \begin{align*}\text{qftp}_{L_{\mathrm{ou}}^*}(a / \text{Domain}(f)) = \text{qftp}_{L_{\mathrm{ou}}^*}(b / \text{Image}(f)).\end{align*} $$
By the fact that
![]() $\text {Domain}(f)$
is pure in G, and Corollary 3.2,
$\text {Domain}(f)$
is pure in G, and Corollary 3.2,
 $\text {qftp}_{L_{\mathrm {ou}}^*}(a \mid \text {Domain}(f))$
is isolated by formulas of the form
$\text {qftp}_{L_{\mathrm {ou}}^*}(a \mid \text {Domain}(f))$
is isolated by formulas of the form
where
![]() $\rho (y)$
is a quantifier-free
$\rho (y)$
is a quantifier-free
![]() $L^*_{\mathrm {ou}}$
-formula,
$L^*_{\mathrm {ou}}$
-formula,
![]() $\lambda (x,y)$
is an order condition,
$\lambda (x,y)$
is an order condition,
![]() $\psi (x, z, z')$
is a special formula,
$\psi (x, z, z')$
is a special formula,
![]() $t(y)$
and
$t(y)$
and
![]() $t'(y)$
are tuples of
$t'(y)$
are tuples of
![]() $L_{\mathrm {ou}}^*$
-terms of suitable length, b is a tuple of elements of
$L_{\mathrm {ou}}^*$
-terms of suitable length, b is a tuple of elements of
![]() $\text {Domain}(f)$
of suitable length, and
$\text {Domain}(f)$
of suitable length, and
![]() $\psi (x, t(b), t'(b))$
is a nontrivial
$\psi (x, t(b), t'(b))$
is a nontrivial
![]() $\text {Domain}(f)$
-system. As
$\text {Domain}(f)$
-system. As
![]() $\text {Domain}(f)$
is a pure subgroup of G, we can moreover arrange that
$\text {Domain}(f)$
is a pure subgroup of G, we can moreover arrange that
![]() $\lambda (x,b)$
is simply the formula
$\lambda (x,b)$
is simply the formula
![]() $b_1 < x <b_2$
. Since f is an
$b_1 < x <b_2$
. Since f is an
![]() $L_{\mathrm {ou}}^*$
-embedding,
$L_{\mathrm {ou}}^*$
-embedding,
![]() $\rho (f(b))$
holds,
$\rho (f(b))$
holds,
![]() $f(b_1) < f(b_2)$
, and
$f(b_1) < f(b_2)$
, and
 $\psi \big (x, t(f(b)), t'(f(b))\big ) $
is a nontrivial
$\psi \big (x, t(f(b)), t'(f(b))\big ) $
is a nontrivial
![]() $\text {Image}(f)$
-system. Using the fact that
$\text {Image}(f)$
-system. Using the fact that
![]() $(H; <, \mathscr {U}^H , \mathscr {P}^H )$
is
$(H; <, \mathscr {U}^H , \mathscr {P}^H )$
is
![]() $|G|^+$
-saturated, the problem reduces to showing that
$|G|^+$
-saturated, the problem reduces to showing that
 $$ \begin{align*}\psi\Big(x, f\big(t(b)\big), f\big(t'(b)\big)\Big) \ \text{ has a solution in the interval } (f(b_1), f(b_2))^H.\end{align*} $$
$$ \begin{align*}\psi\Big(x, f\big(t(b)\big), f\big(t'(b)\big)\Big) \ \text{ has a solution in the interval } (f(b_1), f(b_2))^H.\end{align*} $$
As
![]() $\psi (x, t(b), t'(b))$
is satisfiable in G, it is locally satisfiable in G by Lemma 2.6. For each p, let
$\psi (x, t(b), t'(b))$
is satisfiable in G, it is locally satisfiable in G by Lemma 2.6. For each p, let
![]() $\psi _p(x, z, z')$
be the associated p-condition of
$\psi _p(x, z, z')$
be the associated p-condition of
![]() $\psi (x, z, z')$
. By Lemma 3.3, for all p, the formula
$\psi (x, z, z')$
. By Lemma 3.3, for all p, the formula
![]() $\exists x \psi _p(x, z, z')$
is equivalent modulo
$\exists x \psi _p(x, z, z')$
is equivalent modulo
 $\mathrm {Sf}^*_{\mathbb {Q}}$
to a quantifier free formula in
$\mathrm {Sf}^*_{\mathbb {Q}}$
to a quantifier free formula in
![]() $L^*_{\mathrm {u}}(z, z')$
. Hence,
$L^*_{\mathrm {u}}(z, z')$
. Hence,
 $\exists x \psi _p\Big (x, f\big (t(b)\big ), f\big (t'(b)\big )\Big )$
holds in
$\exists x \psi _p\Big (x, f\big (t(b)\big ), f\big (t'(b)\big )\Big )$
holds in
![]() $(H;<, \mathscr {U}^H, \mathscr {P}^H)$
for all p. Thus,
$(H;<, \mathscr {U}^H, \mathscr {P}^H)$
for all p. Thus,
 $$ \begin{align*}\text{the } \text{Image}(f)\text{-system }\psi\Big(x, f\big(t(b)\big), f\big(t'(b)\big)\Big) \text{ is locally satisfiable in } H.\end{align*} $$
$$ \begin{align*}\text{the } \text{Image}(f)\text{-system }\psi\Big(x, f\big(t(b)\big), f\big(t'(b)\big)\Big) \text{ is locally satisfiable in } H.\end{align*} $$
The desired conclusion follows from the genericity of
![]() $(H; <, \mathscr {U}^H, \mathscr {P}^H)$
. The proofs for
$(H; <, \mathscr {U}^H, \mathscr {P}^H)$
. The proofs for
![]() $\mathrm {SF}^*_{\mathbb {Z}}$
and
$\mathrm {SF}^*_{\mathbb {Z}}$
and
![]() $\mathrm {SF}^*_{\mathbb {Q}}$
are similar. However, we have there the formula
$\mathrm {SF}^*_{\mathbb {Q}}$
are similar. However, we have there the formula
 $\bigwedge _{i =1}^k x \neq b_i$
with
$\bigwedge _{i =1}^k x \neq b_i$
with
![]() $k \leq |b|$
instead of the formula
$k \leq |b|$
instead of the formula
![]() $b_1< x< b_2$
, Lemma 3.1 instead of Corollary 3.2, and the corresponding notion of genericity instead of the current one.⊣
$b_1< x< b_2$
, Lemma 3.1 instead of Corollary 3.2, and the corresponding notion of genericity instead of the current one.⊣
Corollary 3.5. The theory
![]() $\mathrm {SF}^*_{\mathbb {Z}}$
is a recursive axiomatization of
$\mathrm {SF}^*_{\mathbb {Z}}$
is a recursive axiomatization of
![]() $\mathrm {Th}(\mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
, and is therefore decidable. Similar statements hold for
$\mathrm {Th}(\mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
, and is therefore decidable. Similar statements hold for
![]() $\mathrm {SF}^*_{\mathbb {Q}}$
in relation to
$\mathrm {SF}^*_{\mathbb {Q}}$
in relation to
![]() $\mathrm {Th}(\mathbb {Q}; \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
and
$\mathrm {Th}(\mathbb {Q}; \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
and
![]() $\mathrm {OSF}^*_{\mathbb {Q}}$
in relation to
$\mathrm {OSF}^*_{\mathbb {Q}}$
in relation to
![]() $\mathrm {Th}(\mathbb {Q}; < \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
.
$\mathrm {Th}(\mathbb {Q}; < \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
.
Proof By Lemma 2.1(ii), the subgroup generated by
![]() $1$
in an arbitrary model
$1$
in an arbitrary model
![]() $(G; \mathscr {U}^G, \mathscr {P}^G)$
of
$(G; \mathscr {U}^G, \mathscr {P}^G)$
of
![]() $\mathrm {SF}^*_{\mathbb {Z}}$
is an isomorphic copy of
$\mathrm {SF}^*_{\mathbb {Z}}$
is an isomorphic copy of
![]() $(\mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
. Hence by Theorem 3.4,
$(\mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
. Hence by Theorem 3.4,
![]() $\mathrm {SF}^*_{\mathbb {Z}}$
is complete, and on the other hand
$\mathrm {SF}^*_{\mathbb {Z}}$
is complete, and on the other hand
![]() $(\mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}}) \models \mathrm {SF}^*_{\mathbb {Z}} $
by Theorem 2.14. The first statement of the corollary follows. The justification of the second statement is obtained in a similar fashion.⊣
$(\mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}}) \models \mathrm {SF}^*_{\mathbb {Z}} $
by Theorem 2.14. The first statement of the corollary follows. The justification of the second statement is obtained in a similar fashion.⊣
Proof of Theorem 1.1, part 1 We show that the
![]() $L_{\mathrm {u}}$
-theory of
$L_{\mathrm {u}}$
-theory of
![]() $(\mathbb {Z}; \mathrm {SF}^{\mathbb {Z}})$
is model complete and decidable. For all p,
$(\mathbb {Z}; \mathrm {SF}^{\mathbb {Z}})$
is model complete and decidable. For all p,
![]() $l\geq 0$
,
$l\geq 0$
,
![]() $m>0$
, and all
$m>0$
, and all
![]() $a \in \mathbb {Z}$
, we have the following:
$a \in \mathbb {Z}$
, we have the following:
-
(1)
 $a \in U^{\mathbb {Z}}_{p, l}$
if and only there is
$a \in U^{\mathbb {Z}}_{p, l}$
if and only there is
 $b\in \mathbb {Z}$
such that
$b\in \mathbb {Z}$
such that
 $p^lb =a$
;
$p^lb =a$
; -
(2)
 $a \notin U^{\mathbb {Z}}_{p, l}$
if and only if for some
$a \notin U^{\mathbb {Z}}_{p, l}$
if and only if for some
 $i \in \{1, \ldots , p^l-1\}$
, there is
$i \in \{1, \ldots , p^l-1\}$
, there is
 $b\in \mathbb {Z}$
such that
$b\in \mathbb {Z}$
such that
 $p^lb =a+i$
;
$p^lb =a+i$
; -
(3)
 $a \in P^{\mathbb {Z}}_m$
if and only if for some
$a \in P^{\mathbb {Z}}_m$
if and only if for some
 $d \mid m$
, there is
$d \mid m$
, there is
 $b\in \mathbb {Z}$
such that
$b\in \mathbb {Z}$
such that
 $a =bd$
and
$a =bd$
and
 $b\in \mathrm {SF}^{\mathbb {Z}}$
;
$b\in \mathrm {SF}^{\mathbb {Z}}$
; -
(4)
 $a \notin P^{\mathbb {Z}}_m$
if and only if for all
$a \notin P^{\mathbb {Z}}_m$
if and only if for all
 $d \mid m$
, either for some
$d \mid m$
, either for some
 $i \in \{1, \ldots , d-1\}$
, there is
$i \in \{1, \ldots , d-1\}$
, there is
 $b\in \mathbb {Z}$
such that
$b\in \mathbb {Z}$
such that
 $db =a+i$
or there is
$db =a+i$
or there is
 $b \in \mathbb {Z}$
such that
$b \in \mathbb {Z}$
such that
 $a =bd$
and
$a =bd$
and
 $b \notin \mathrm {SF}^{\mathbb {Z}}$
.
$b \notin \mathrm {SF}^{\mathbb {Z}}$
.
As
![]() $(\mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}}) \models \mathrm {SF}^*_{\mathbb {Z}}$
, it then follows from Theorem 3.4 and the above observation that every
$(\mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}}) \models \mathrm {SF}^*_{\mathbb {Z}}$
, it then follows from Theorem 3.4 and the above observation that every
![]() $0$
-definable set in
$0$
-definable set in
![]() $(\mathbb {Z}, \mathrm {SF}^{\mathbb {Z}})$
is existentially
$(\mathbb {Z}, \mathrm {SF}^{\mathbb {Z}})$
is existentially
![]() $0$
-definable. Hence, the theory of
$0$
-definable. Hence, the theory of
![]() $(\mathbb {Z}; \mathrm {SF}^{\mathbb {Z}})$
is model complete. The decidability of
$(\mathbb {Z}; \mathrm {SF}^{\mathbb {Z}})$
is model complete. The decidability of
![]() $\text {Th}(\mathbb {Z}; \mathrm {SF}^{\mathbb {Z}})$
is immediate from the preceding corollary.⊣
$\text {Th}(\mathbb {Z}; \mathrm {SF}^{\mathbb {Z}})$
is immediate from the preceding corollary.⊣
Lemma 3.6. Suppose
![]() $a\in \mathbb {Q}$
has
$a\in \mathbb {Q}$
has
![]() $v_p(a)<0$
. Then there is
$v_p(a)<0$
. Then there is
![]() $\varepsilon \in \mathbb {Q}$
such that
$\varepsilon \in \mathbb {Q}$
such that
![]() $v_p(\varepsilon ) \geq 0$
and
$v_p(\varepsilon ) \geq 0$
and
![]() $a+\varepsilon \in \mathrm {SF}^{\mathbb {Q}}$
.
$a+\varepsilon \in \mathrm {SF}^{\mathbb {Q}}$
.
Proof Suppose a is as stated. If
![]() $a \in \mathrm {SF}^{\mathbb {Q}}$
we can choose
$a \in \mathrm {SF}^{\mathbb {Q}}$
we can choose
![]() $\varepsilon =0$
, so suppose a is in
$\varepsilon =0$
, so suppose a is in
 $\mathbb {Q} \setminus \mathrm {SF}^{\mathbb {Q}}$
. We can also arrange that
$\mathbb {Q} \setminus \mathrm {SF}^{\mathbb {Q}}$
. We can also arrange that
![]() $a>0$
. Then there are
$a>0$
. Then there are
![]() $m, n, k \in \mathbb {N}^{\geq 1}$
such that
$m, n, k \in \mathbb {N}^{\geq 1}$
such that
 $$ \begin{align*}a = \frac{m}{np^k},\ (m, n)=1,\ (m, p)=1, \text{ and } (n, p)=1.\end{align*} $$
$$ \begin{align*}a = \frac{m}{np^k},\ (m, n)=1,\ (m, p)=1, \text{ and } (n, p)=1.\end{align*} $$
It suffices to show there is
![]() $b \in \mathbb {Z}$
such that
$b \in \mathbb {Z}$
such that
![]() $m+ p^kb$
is a square-free integer as then
$m+ p^kb$
is a square-free integer as then
 $$ \begin{align*}a+ \frac{b}{n} = \frac{m+ p^kb}{np^k} \in \mathrm{SF}^{\mathbb{Q}}.\end{align*} $$
$$ \begin{align*}a+ \frac{b}{n} = \frac{m+ p^kb}{np^k} \in \mathrm{SF}^{\mathbb{Q}}.\end{align*} $$
For all prime l,
 $p^kb_l+m \notin U^{\mathbb {Q}}_{l,2}$
for
$p^kb_l+m \notin U^{\mathbb {Q}}_{l,2}$
for
![]() $b_l=0$
or
$b_l=0$
or
![]() $1$
. The conclusion then follows from the genericity of
$1$
. The conclusion then follows from the genericity of
![]() $( \mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
as established in Theorem 2.14.⊣
$( \mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
as established in Theorem 2.14.⊣
Corollary 3.7. For all p and l,
 $U^{\mathbb {Q}}_{p, l}$
is universally
$U^{\mathbb {Q}}_{p, l}$
is universally
![]() $0$
-definable in
$0$
-definable in
![]() $(\mathbb {Q}, \mathrm {SF}^{\mathbb {Q}})$
.
$(\mathbb {Q}, \mathrm {SF}^{\mathbb {Q}})$
.
Proof We will instead show that
 $\mathbb {Q}\setminus U^{\mathbb {Q}}_{p, l} = \{ a : v_p(a) < l \}$
is existentially
$\mathbb {Q}\setminus U^{\mathbb {Q}}_{p, l} = \{ a : v_p(a) < l \}$
is existentially
![]() $0$
-definable for all p and l. As
$0$
-definable for all p and l. As
 $\mathbb {Q} \setminus U^{\mathbb {Q}}_{p, l+n} = p^n( \mathbb {Q} \setminus U^{\mathbb {Q}}_{p, l})$
for all p, l, and n, it suffices to show the statement for
$\mathbb {Q} \setminus U^{\mathbb {Q}}_{p, l+n} = p^n( \mathbb {Q} \setminus U^{\mathbb {Q}}_{p, l})$
for all p, l, and n, it suffices to show the statement for
![]() $l=0$
. Fix a prime p. By the preceding lemma we have that for all
$l=0$
. Fix a prime p. By the preceding lemma we have that for all
![]() $ a$
,
$ a$
,
![]() $v_p(a)<0$
if and only if
$v_p(a)<0$
if and only if
 $$ \begin{align*}\text{ there is } \varepsilon \text{ such that } v_p(\varepsilon) \geq 0, a+\varepsilon \in \mathrm{SF}^{\mathbb{Q}} \text{ and } v_p(a+\varepsilon) <0.\end{align*} $$
$$ \begin{align*}\text{ there is } \varepsilon \text{ such that } v_p(\varepsilon) \geq 0, a+\varepsilon \in \mathrm{SF}^{\mathbb{Q}} \text{ and } v_p(a+\varepsilon) <0.\end{align*} $$
We recall that
![]() $\{\varepsilon : v_p(\varepsilon ) \geq 0 \}$
is existentially
$\{\varepsilon : v_p(\varepsilon ) \geq 0 \}$
is existentially
![]() $0$
-definable by Lemma 2.3. Also, for all
$0$
-definable by Lemma 2.3. Also, for all
![]() $a' \in \mathrm {SF}^{\mathbb {Q}}$
, we have that
$a' \in \mathrm {SF}^{\mathbb {Q}}$
, we have that
![]() $v_p(a')< 0$
is equivalent to
$v_p(a')< 0$
is equivalent to
![]() $p^2a' \in \mathrm {SF}^{\mathbb {Q}}$
. The conclusion hence follows.⊣
$p^2a' \in \mathrm {SF}^{\mathbb {Q}}$
. The conclusion hence follows.⊣
Proof of Theorems 1.3 and 1.4, part 1 We show that the
![]() $L_{\mathrm {u}}$
-theory of
$L_{\mathrm {u}}$
-theory of
![]() $(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
and the
$(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
and the
![]() $L_{\mathrm {ou}}$
-theory of
$L_{\mathrm {ou}}$
-theory of
![]() $(\mathbb {Q}; <, \mathrm {SF}^{\mathbb {Q}} )$
are model complete and decidable. The proof is almost exactly the same as that of part 1 of Theorem 1.1. It follows from Lemma 2.3 and Corollary 3.7 that for all p and l, the sets
$(\mathbb {Q}; <, \mathrm {SF}^{\mathbb {Q}} )$
are model complete and decidable. The proof is almost exactly the same as that of part 1 of Theorem 1.1. It follows from Lemma 2.3 and Corollary 3.7 that for all p and l, the sets
 $U^{\mathbb {Q}}_{p, l}$
are existentially and universally
$U^{\mathbb {Q}}_{p, l}$
are existentially and universally
![]() $0$
-definable in
$0$
-definable in
![]() $(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
. For all m,
$(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
. For all m,
![]() $P^{\mathbb {Q}}_m = m\mathrm {SF}^{\mathbb {Q}}$
and
$P^{\mathbb {Q}}_m = m\mathrm {SF}^{\mathbb {Q}}$
and
 $\mathbb {Q} \setminus P^{\mathbb {Q}}_m = m( \mathbb {Q} \setminus \mathrm {SF}^{\mathbb {Q}})$
are clearly existentially
$\mathbb {Q} \setminus P^{\mathbb {Q}}_m = m( \mathbb {Q} \setminus \mathrm {SF}^{\mathbb {Q}})$
are clearly existentially
![]() $0$
-definable. The conclusion follows.⊣
$0$
-definable. The conclusion follows.⊣
Next, we will show that the
![]() $L_{\mathrm {ou}}$
-theory of
$L_{\mathrm {ou}}$
-theory of
![]() $(\mathbb {Z}; <, \mathrm {SF}^{\mathbb {Z}})$
is bi-interpretable with arithmetic. The proof follows closely the arguments from [Reference Bateman, Jockusch and Woods2]. In fact, we can slightly modify Corollary 3.9 to use essentially the same proof at the cost of replacing
$(\mathbb {Z}; <, \mathrm {SF}^{\mathbb {Z}})$
is bi-interpretable with arithmetic. The proof follows closely the arguments from [Reference Bateman, Jockusch and Woods2]. In fact, we can slightly modify Corollary 3.9 to use essentially the same proof at the cost of replacing
![]() $n^2$
with
$n^2$
with
![]() $n^2+n$
.
$n^2+n$
.
Lemma 3.8. Let
![]() $c_1, \ldots , c_n$
be an increasing sequence of natural numbers, and assume that for all primes p, there is a solution to the system of congruence inequations
$c_1, \ldots , c_n$
be an increasing sequence of natural numbers, and assume that for all primes p, there is a solution to the system of congruence inequations
 $$ \begin{align*}x + c_i \notin U^{\mathbb{Z}}_{p, 2} \text{ for all } i \in \{1, \ldots, n\}.\end{align*} $$
$$ \begin{align*}x + c_i \notin U^{\mathbb{Z}}_{p, 2} \text{ for all } i \in \{1, \ldots, n\}.\end{align*} $$
Then there is
![]() $a \in \mathbb {N}$
such that
$a \in \mathbb {N}$
such that
![]() $a+c_1, \ldots , a+c_n$
are consecutive square-free integers.
$a+c_1, \ldots , a+c_n$
are consecutive square-free integers.
Proof Suppose
![]() $c_1, \ldots , c_n$
are as given. Let
$c_1, \ldots , c_n$
are as given. Let
![]() $c^{\prime }_1, \ldots , c^{\prime }_{n'}$
be the listing in increasing order of elements in the set of
$c^{\prime }_1, \ldots , c^{\prime }_{n'}$
be the listing in increasing order of elements in the set of
![]() $c \in \mathbb {N}$
such that
$c \in \mathbb {N}$
such that
![]() $c_1 \leq c \leq c_n$
and
$c_1 \leq c \leq c_n$
and
![]() $c \neq c_i$
for
$c \neq c_i$
for
![]() $i \in \{1, \ldots , n\}$
. The conclusion that there are infinitely many a such that
$i \in \{1, \ldots , n\}$
. The conclusion that there are infinitely many a such that
 $$ \begin{align*}\bigwedge_{i=1}^n (a+c_i \in \mathrm{SF}^{\mathbb{Z}}) \wedge \bigwedge_{i=1}^{n'} (a+c^{\prime}_i \notin \mathrm{SF}^{\mathbb{Z}})\end{align*} $$
$$ \begin{align*}\bigwedge_{i=1}^n (a+c_i \in \mathrm{SF}^{\mathbb{Z}}) \wedge \bigwedge_{i=1}^{n'} (a+c^{\prime}_i \notin \mathrm{SF}^{\mathbb{Z}})\end{align*} $$
follows from the assumptions about
![]() $c_1, \ldots , c_n$
and the genericity of
$c_1, \ldots , c_n$
and the genericity of
![]() $( \mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
as established in Theorem 2.14.⊣
$( \mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
as established in Theorem 2.14.⊣
Corollary 3.9. For all
![]() $n\in \mathbb {N}^{>0}$
, there is
$n\in \mathbb {N}^{>0}$
, there is
![]() $a \in \mathbb {N}$
such that
$a \in \mathbb {N}$
such that
![]() $a+1, a+4, \ldots , a+n^2$
are consecutive square-free integers.
$a+1, a+4, \ldots , a+n^2$
are consecutive square-free integers.
Proof For each p, we can obtain
![]() $a\in \{1,2,\ldots ,p^2-1\} $
such that
$a\in \{1,2,\ldots ,p^2-1\} $
such that
 $$ \begin{align*}a\not\equiv_{p^2}-m^2 \text{ for all } m.\end{align*} $$
$$ \begin{align*}a\not\equiv_{p^2}-m^2 \text{ for all } m.\end{align*} $$
Hence, for any given
![]() $n>0$
and p, the p-condition
$n>0$
and p, the p-condition
 $\bigwedge _{i=1}^{n}(x+i^2\notin U^{\mathbb {Z}}_{p,2})$
has a solution. The result now follows immediately from the preceding lemma.⊣
$\bigwedge _{i=1}^{n}(x+i^2\notin U^{\mathbb {Z}}_{p,2})$
has a solution. The result now follows immediately from the preceding lemma.⊣
Proof of Theorem 1.2 It suffices to show that
![]() $(\mathbb {Z}; <, \mathrm {SF}^{\mathbb {Z}})$
interprets multiplication on
$(\mathbb {Z}; <, \mathrm {SF}^{\mathbb {Z}})$
interprets multiplication on
![]() $\mathbb {N}$
. Let T be the set of
$\mathbb {N}$
. Let T be the set of
![]() $(a, b) \in \mathbb {N}^2$
such that for some
$(a, b) \in \mathbb {N}^2$
such that for some
![]() $n \in \mathbb {N}^{\geq 1},$
$n \in \mathbb {N}^{\geq 1},$
The set T is definable in
![]() $(\mathbb {Z}; <, \mathrm {SF}^{\mathbb {Z}})$
as
$(\mathbb {Z}; <, \mathrm {SF}^{\mathbb {Z}})$
as
![]() $(a, b) \in T$
and
$(a, b) \in T$
and
![]() $b\neq a+1$
if and only if
$b\neq a+1$
if and only if
![]() $a+4\leq b$
,
$a+4\leq b$
,
![]() $a+1$
, and
$a+1$
, and
![]() $a+4$
are consecutive square-free integers, b is square-free, and whenever c, d, and e are consecutive square-free integers with
$a+4$
are consecutive square-free integers, b is square-free, and whenever c, d, and e are consecutive square-free integers with
![]() $a< c <d< e \leq b$
, we have that
$a< c <d< e \leq b$
, we have that
Let S be the set
![]() $\{ n^2 : n \in \mathbb {N}\}$
. If
$\{ n^2 : n \in \mathbb {N}\}$
. If
![]() $c=0$
or there are
$c=0$
or there are
![]() $a, b$
such that
$a, b$
such that
![]() $(a, b) \in T$
and
$(a, b) \in T$
and
![]() $b-a =c$
, then
$b-a =c$
, then
![]() $c=n^2$
for some n. Conversely, if
$c=n^2$
for some n. Conversely, if
![]() $c =n^2$
, then either
$c =n^2$
, then either
![]() $c=0$
or by Corollary 3.9,
$c=0$
or by Corollary 3.9,
Therefore, S is definable in
![]() $(\mathbb {Z}; <, \mathrm {SF}^{\mathbb {Z}})$
. The map
$(\mathbb {Z}; <, \mathrm {SF}^{\mathbb {Z}})$
. The map
![]() $n \mapsto n^2$
in
$n \mapsto n^2$
in
![]() $\mathbb {N}$
is definable in
$\mathbb {N}$
is definable in
![]() $(\mathbb {Z}; <, \mathrm {SF}^{\mathbb {Z}})$
as
$(\mathbb {Z}; <, \mathrm {SF}^{\mathbb {Z}})$
as
![]() $b =a^2$
if and only if
$b =a^2$
if and only if
![]() $b\in S$
and whenever
$b\in S$
and whenever
![]() $c\in S$
is such that
$c\in S$
is such that
![]() $c>b$
and
$c>b$
and
![]() $b, c$
are consecutive in S, we have that
$b, c$
are consecutive in S, we have that
![]() $c-b = 2a+1$
. Finally,
$c-b = 2a+1$
. Finally,
![]() $c =ba$
if and only if
$c =ba$
if and only if
![]() $2c= (b+a)^2-b^2-a^2$
. Thus, multiplication on
$2c= (b+a)^2-b^2-a^2$
. Thus, multiplication on
![]() $\mathbb {N}$
is definable in
$\mathbb {N}$
is definable in
![]() $(\mathbb {Z}; <, \mathrm {SF}^{\mathbb {Z}})$
.⊣
$(\mathbb {Z}; <, \mathrm {SF}^{\mathbb {Z}})$
.⊣
4 Combinatorial tameness
As the theories
![]() $\mathrm {SF}^*_{\mathbb {Z}}$
,
$\mathrm {SF}^*_{\mathbb {Z}}$
,
![]() $\mathrm {SF}^*_{\mathbb {Q}}$
, and
$\mathrm {SF}^*_{\mathbb {Q}}$
, and
![]() $\mathrm {OSF}^*_{\mathbb {Q}}$
are complete, it is convenient to work in the so-called monster models, that is, models which are very saturated and homogeneous. Until the end of the paper, let
$\mathrm {OSF}^*_{\mathbb {Q}}$
are complete, it is convenient to work in the so-called monster models, that is, models which are very saturated and homogeneous. Until the end of the paper, let
![]() $(\mathbb {G}; \mathscr {U}^{\mathbb {G}}, \mathscr {P}^{\mathbb {G}})$
be a monster model of either
$(\mathbb {G}; \mathscr {U}^{\mathbb {G}}, \mathscr {P}^{\mathbb {G}})$
be a monster model of either
![]() $\mathrm {SF}^*_{\mathbb {Z}}$
or
$\mathrm {SF}^*_{\mathbb {Z}}$
or
![]() $\mathrm {SF}^*_{\mathbb {Q}}$
depending on the situation. In the latter case, we suppose
$\mathrm {SF}^*_{\mathbb {Q}}$
depending on the situation. In the latter case, we suppose
![]() $(\mathbb {G}; <, \mathscr {U}^{\mathbb {G}}, \mathscr {P}^{\mathbb {G}})$
is a monster model of
$(\mathbb {G}; <, \mathscr {U}^{\mathbb {G}}, \mathscr {P}^{\mathbb {G}})$
is a monster model of
![]() $\mathrm {OSF}^*_{\mathbb {Q}}$
. We assume that
$\mathrm {OSF}^*_{\mathbb {Q}}$
. We assume that
![]() $\kappa , A$
, and I have small cardinalities compared to
$\kappa , A$
, and I have small cardinalities compared to
![]() $\mathbb {G}$
.
$\mathbb {G}$
.
Our general strategy to prove the tameness of
![]() $\mathrm {SF}^*_{\mathbb {Z}}$
,
$\mathrm {SF}^*_{\mathbb {Z}}$
,
![]() $\mathrm {SF}^*_{\mathbb {Q}}$
, and
$\mathrm {SF}^*_{\mathbb {Q}}$
, and
![]() $\mathrm {OSF}^*_{\mathbb {Q}}$
is to link them to the corresponding “local” facts. The next lemma says that
$\mathrm {OSF}^*_{\mathbb {Q}}$
is to link them to the corresponding “local” facts. The next lemma says that
![]() $\mathrm {SF}^*_{\mathbb {Z}}$
is “locally” supersimple of U-rank
$\mathrm {SF}^*_{\mathbb {Z}}$
is “locally” supersimple of U-rank
![]() $1$
.
$1$
.
Lemma 4.1. Suppose
![]() $(\mathbb {G}; \mathscr {U}^{\mathbb {G}}, \mathscr {P}^{\mathbb {G}}) \models \mathrm {SF}^*_{\mathbb {Z}}$
,
$(\mathbb {G}; \mathscr {U}^{\mathbb {G}}, \mathscr {P}^{\mathbb {G}}) \models \mathrm {SF}^*_{\mathbb {Z}}$
,
![]() $\theta _p(x, y)$
is a consistent p-condition, and b is in
$\theta _p(x, y)$
is a consistent p-condition, and b is in
![]() $\mathbb {G}^{|y|}$
. Then
$\mathbb {G}^{|y|}$
. Then
![]() $\theta _p(x, b)$
does not divide over any base set
$\theta _p(x, b)$
does not divide over any base set
![]() $A\subseteq \mathbb {G}$
.
$A\subseteq \mathbb {G}$
.
Proof Recall that every p-condition is equivalent modulo
![]() $\mathrm {SF}^*_{\mathbb {Z}}$
to a formula in the language L of groups, and the reduct of
$\mathrm {SF}^*_{\mathbb {Z}}$
to a formula in the language L of groups, and the reduct of
![]() $\mathrm {SF}^*_{\mathbb {Z}}$
to L is simply
$\mathrm {SF}^*_{\mathbb {Z}}$
to L is simply
![]() $\text {Th}(\mathbb {Z})$
. Hence, the desired conclusion is an immediate consequence of the well-known fact that
$\text {Th}(\mathbb {Z})$
. Hence, the desired conclusion is an immediate consequence of the well-known fact that
![]() $\text {Th}(\mathbb {Z})$
is superstable of U-rank
$\text {Th}(\mathbb {Z})$
is superstable of U-rank
![]() $1$
; see for example [Reference Belegradek, Peterzil and Wagner3].⊣
$1$
; see for example [Reference Belegradek, Peterzil and Wagner3].⊣
Proof of Theorem 1.1, part 2 We first show that
![]() $\text {Th}(\mathbb {Z}; \mathrm {SF}^{\mathbb {Z}})$
is supersimple of U-rank
$\text {Th}(\mathbb {Z}; \mathrm {SF}^{\mathbb {Z}})$
is supersimple of U-rank
![]() $1$
; see [Reference Kim10, p. 36] for a definition of U-rank or SU-rank. By the fact that
$1$
; see [Reference Kim10, p. 36] for a definition of U-rank or SU-rank. By the fact that
![]() $(\mathbb {Z}; \mathrm {SF}^{\mathbb {Z}})$
has the same definable sets as
$(\mathbb {Z}; \mathrm {SF}^{\mathbb {Z}})$
has the same definable sets as
![]() $(\mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
and Corollary 3.5, we can replace
$(\mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
and Corollary 3.5, we can replace
![]() $\text {Th}(\mathbb {Z}; \mathrm {SF}^{\mathbb {Z}})$
with
$\text {Th}(\mathbb {Z}; \mathrm {SF}^{\mathbb {Z}})$
with
![]() $\mathrm {SF}^*_{\mathbb {Z}}$
. Suppose
$\mathrm {SF}^*_{\mathbb {Z}}$
. Suppose
![]() $(\mathbb {G}; \mathscr {U}^{\mathbb {G}}, \mathscr {P}^{\mathbb {G}}) \models \mathrm {SF}^*_{\mathbb {Z}}$
. Our job is to show that every
$(\mathbb {G}; \mathscr {U}^{\mathbb {G}}, \mathscr {P}^{\mathbb {G}}) \models \mathrm {SF}^*_{\mathbb {Z}}$
. Our job is to show that every
![]() $L^*_{\mathrm {u}}(\mathbb {G})$
-formula
$L^*_{\mathrm {u}}(\mathbb {G})$
-formula
![]() $\varphi (x,b)$
which forks over a small subset A of
$\varphi (x,b)$
which forks over a small subset A of
![]() $\mathbb {G} $
must define a finite set in
$\mathbb {G} $
must define a finite set in
![]() $\mathbb {G}$
. We can easily reduce to the case that
$\mathbb {G}$
. We can easily reduce to the case that
![]() $\varphi (x,b)$
divides over A. Moreover, we can assume that
$\varphi (x,b)$
divides over A. Moreover, we can assume that
![]() $\varphi (x,b)$
is quantifier free by Theorem 3.4 which states that
$\varphi (x,b)$
is quantifier free by Theorem 3.4 which states that
![]() $(\mathbb {G}; \mathscr {U}^{\mathbb {G}}, \mathscr {P}^{\mathbb {G}})$
admits quantifier elimination. Using Lemma 3.1, we can also arrange that
$(\mathbb {G}; \mathscr {U}^{\mathbb {G}}, \mathscr {P}^{\mathbb {G}})$
admits quantifier elimination. Using Lemma 3.1, we can also arrange that
![]() $\varphi (x, b)$
has the form
$\varphi (x, b)$
has the form
where
![]() $\rho (y)$
is a quantifier-free formula,
$\rho (y)$
is a quantifier-free formula,
![]() $\varepsilon (x,y)$
is an equational condition,
$\varepsilon (x,y)$
is an equational condition,
![]() $t(y)$
and
$t(y)$
and
![]() $t'(y)$
are tuples of
$t'(y)$
are tuples of
![]() $L^*_{\mathrm {u}}$
-terms with length n and
$L^*_{\mathrm {u}}$
-terms with length n and
![]() $n'$
respectively, and
$n'$
respectively, and
![]() $\psi (x, z, z')$
is a special formula.
$\psi (x, z, z')$
is a special formula.
Suppose to the contrary that
![]() $\varphi (x,b)$
divides over A but
$\varphi (x,b)$
divides over A but
![]() $\varphi (x,b)$
defines an infinite set in
$\varphi (x,b)$
defines an infinite set in
![]() $\mathbb {G}$
. From the first assumption, we get an infinite ordering I and a family
$\mathbb {G}$
. From the first assumption, we get an infinite ordering I and a family
![]() $(\sigma _i)_{i \in I}$
of
$(\sigma _i)_{i \in I}$
of
![]() $L^*_{\mathrm {u}}$
-automorphisms of
$L^*_{\mathrm {u}}$
-automorphisms of
![]() $(\mathbb {G}; \mathscr {U}^{\mathbb {G}}, \mathscr {P}^{\mathbb {G}})$
such that
$(\mathbb {G}; \mathscr {U}^{\mathbb {G}}, \mathscr {P}^{\mathbb {G}})$
such that
![]() $(\sigma _i (b))_{i \in I}$
is indiscernible over A and
$(\sigma _i (b))_{i \in I}$
is indiscernible over A and
 $\bigwedge _{i \in I} \varphi (x, \sigma _i (b))$
is inconsistent. As
$\bigwedge _{i \in I} \varphi (x, \sigma _i (b))$
is inconsistent. As
![]() $\varphi (x,b)$
defines an infinite set in
$\varphi (x,b)$
defines an infinite set in
![]() $\mathbb {G}$
, we get from the second assumption that
$\mathbb {G}$
, we get from the second assumption that
![]() $\rho (b)$
holds in
$\rho (b)$
holds in
![]() $\mathbb {G}$
,
$\mathbb {G}$
,
![]() $\varepsilon (x, b)$
defines a cofinite set in
$\varepsilon (x, b)$
defines a cofinite set in
![]() $\mathbb {G}$
, and
$\mathbb {G}$
, and
![]() $\psi (x,t(b), t'(b))$
defines an infinite hence non-empty set in
$\psi (x,t(b), t'(b))$
defines an infinite hence non-empty set in
![]() $\mathbb {G}$
. As
$\mathbb {G}$
. As
![]() $(\sigma _i (b))_{i \in I}$
is indiscernible, we have that
$(\sigma _i (b))_{i \in I}$
is indiscernible, we have that
![]() $\rho (\sigma _i (b))$
holds in
$\rho (\sigma _i (b))$
holds in
![]() $\mathbb {G}$
and
$\mathbb {G}$
and
![]() $\varepsilon (x, \sigma _i (b))$
defines a cofinite set in
$\varepsilon (x, \sigma _i (b))$
defines a cofinite set in
![]() $\mathbb {G}$
for all
$\mathbb {G}$
for all
![]() $i \in I$
. Using the saturation of
$i \in I$
. Using the saturation of
![]() $\mathbb {G}$
, we get a finite set
$\mathbb {G}$
, we get a finite set
![]() $\Delta \subseteq I$
such that
$\Delta \subseteq I$
such that
 $$ \begin{align*}\theta_{\Delta}(x):= \bigwedge_{i \in \Delta} \psi\big(x, t(\sigma_i (b)), t'(\sigma_i (b))\big) \text{ defines a finite set in } \mathbb{G}.\end{align*} $$
$$ \begin{align*}\theta_{\Delta}(x):= \bigwedge_{i \in \Delta} \psi\big(x, t(\sigma_i (b)), t'(\sigma_i (b))\big) \text{ defines a finite set in } \mathbb{G}.\end{align*} $$
As
![]() $\theta _{\Delta }(x)$
is a conjunction of
$\theta _{\Delta }(x)$
is a conjunction of
![]() $\mathbb {G}$
-systems given by the same special formula, it is easy to see that
$\mathbb {G}$
-systems given by the same special formula, it is easy to see that
![]() $\theta _{\Delta }(x)$
is also a
$\theta _{\Delta }(x)$
is also a
![]() $\mathbb {G}$
-system.
$\mathbb {G}$
-system.
We will show that
![]() $\theta _{\Delta }(x)$
defines an infinite set and thus obtain the desired contradiction. As
$\theta _{\Delta }(x)$
defines an infinite set and thus obtain the desired contradiction. As
![]() $(\mathbb {G}; \mathscr {U}^{\mathbb {G}}, \mathscr {P}^{\mathbb {G}})$
is a model of
$(\mathbb {G}; \mathscr {U}^{\mathbb {G}}, \mathscr {P}^{\mathbb {G}})$
is a model of
![]() $ \mathrm {SF}^*_{\mathbb {Z}}$
and hence generic, it suffices to show that
$ \mathrm {SF}^*_{\mathbb {Z}}$
and hence generic, it suffices to show that
![]() $\theta _{\Delta }(x)$
is non-trivial and locally satisfiable. As
$\theta _{\Delta }(x)$
is non-trivial and locally satisfiable. As
![]() $\varphi (x,b)$
is consistent,
$\varphi (x,b)$
is consistent,
![]() $t(b)$
has no common components with
$t(b)$
has no common components with
![]() $t'(b)$
. The assumption that
$t'(b)$
. The assumption that
![]() $(\sigma _i(b))_{i \in I}$
is indiscernible gives us that
$(\sigma _i(b))_{i \in I}$
is indiscernible gives us that
![]() $t(\sigma _i(b))$
has no common components with
$t(\sigma _i(b))$
has no common components with
![]() $t'(\sigma _j (b))$
for all i and j in I. It follows that
$t'(\sigma _j (b))$
for all i and j in I. It follows that
![]() $\theta _{\Delta }(x)$
is non-trivial. For each p, let
$\theta _{\Delta }(x)$
is non-trivial. For each p, let
![]() $\psi _p(x, z, z')$
be the associated p-condition of
$\psi _p(x, z, z')$
be the associated p-condition of
![]() $\psi (x,z, z')$
. For all p, we have that
$\psi (x,z, z')$
. For all p, we have that
![]() $\psi _p(x, t(b), t(b'))$
defines a nonempty set and consequently by Lemma 4.1,
$\psi _p(x, t(b), t(b'))$
defines a nonempty set and consequently by Lemma 4.1,
 $$ \begin{align*}\bigwedge_{i \in \Delta}\psi_p\big(x, t(\sigma_i(b)), t'(\sigma_i(b))\big) \text{ defines a nonempty set in } \mathbb{G}.\end{align*} $$
$$ \begin{align*}\bigwedge_{i \in \Delta}\psi_p\big(x, t(\sigma_i(b)), t'(\sigma_i(b))\big) \text{ defines a nonempty set in } \mathbb{G}.\end{align*} $$
We easily check that the above means
![]() $\theta _\Delta (x)$
is p-satisfiable for all p. Thus
$\theta _\Delta (x)$
is p-satisfiable for all p. Thus
![]() $\theta _{\Delta }(x)$
is locally satisfiable which completes our proof that
$\theta _{\Delta }(x)$
is locally satisfiable which completes our proof that
![]() $\text {Th}(\mathbb {Z}, \mathrm {SF}^{\mathbb {Z}})$
has U-rank
$\text {Th}(\mathbb {Z}, \mathrm {SF}^{\mathbb {Z}})$
has U-rank
![]() $1$
.
$1$
.
We will next prove that
![]() $\text {Th}(\mathbb {Z}, \mathrm {SF}^{\mathbb {Z}})$
is k-independent for all
$\text {Th}(\mathbb {Z}, \mathrm {SF}^{\mathbb {Z}})$
is k-independent for all
![]() $k>0$
; see [Reference Chernikov, Palacin and Takeuchi5] for a definition of k-independence. The proof is almost the exact replica of the proof in [Reference Kaplan and Shelah9] except the necessary modifications taken in the current paragraph. Suppose
$k>0$
; see [Reference Chernikov, Palacin and Takeuchi5] for a definition of k-independence. The proof is almost the exact replica of the proof in [Reference Kaplan and Shelah9] except the necessary modifications taken in the current paragraph. Suppose
![]() $l>0$
, and S is an arbitrary subset of
$l>0$
, and S is an arbitrary subset of
![]() $\{ 0, \ldots , l-1\}$
. Our first step is to show that there are
$\{ 0, \ldots , l-1\}$
. Our first step is to show that there are
![]() $a, d \in \mathbb {N}$
such that for
$a, d \in \mathbb {N}$
such that for
![]() $t \in \{0, \ldots , l-1\}$
,
$t \in \{0, \ldots , l-1\}$
,
Let
![]() $n= |S|$
and
$n= |S|$
and
![]() $n' = l -n$
, and let
$n' = l -n$
, and let
![]() $c \in \mathbb {Z}^n$
be the increasing listing of elements in S and
$c \in \mathbb {Z}^n$
be the increasing listing of elements in S and
![]() $c' \in \mathbb {Z}^{n'}$
the increasing listing of elements in
$c' \in \mathbb {Z}^{n'}$
the increasing listing of elements in
![]() $\{0, \ldots , l-1\}\setminus S$
. Choose
$\{0, \ldots , l-1\}\setminus S$
. Choose
![]() $d = (l!)^2$
. We need to find a such that
$d = (l!)^2$
. We need to find a such that
 $$ \begin{align*}\bigwedge_{i=1}^n (a+ c_id \in \mathrm{SF}^{\mathbb{Z}}) \wedge \bigwedge_{i=1}^{n'} (a+ c^{\prime}_id \notin \mathrm{SF}^{\mathbb{Z}}).\end{align*} $$
$$ \begin{align*}\bigwedge_{i=1}^n (a+ c_id \in \mathrm{SF}^{\mathbb{Z}}) \wedge \bigwedge_{i=1}^{n'} (a+ c^{\prime}_id \notin \mathrm{SF}^{\mathbb{Z}}).\end{align*} $$
For
![]() $p\leq l$
, if
$p\leq l$
, if
 $a_p \notin p^2\mathbb {Z} = U_{p,2}^{\mathbb {Z}}$
, then
$a_p \notin p^2\mathbb {Z} = U_{p,2}^{\mathbb {Z}}$
, then
![]() $a_p + c_id \notin p^2\mathbb {Z}$
for all
$a_p + c_id \notin p^2\mathbb {Z}$
for all
![]() $i \in \{1, \ldots , n\}$
. For
$i \in \{1, \ldots , n\}$
. For
![]() $p>l$
, it is easy to see that
$p>l$
, it is easy to see that
![]() $ 0+ c_id \notin p^2\mathbb {Z}$
for all
$ 0+ c_id \notin p^2\mathbb {Z}$
for all
![]() $i \in \{1, \ldots , n\}$
. The desired conclusion follows from the genericity of
$i \in \{1, \ldots , n\}$
. The desired conclusion follows from the genericity of
![]() $(\mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
.
$(\mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
.
Fix
![]() $k>0$
. We construct an explicit
$k>0$
. We construct an explicit
![]() $L_{\mathrm {u}}$
-formula which witnesses the k-independence of
$L_{\mathrm {u}}$
-formula which witnesses the k-independence of
![]() $\text {Th}(\mathbb {Z}, \mathrm {SF}^{\mathbb {Z}})$
. Let
$\text {Th}(\mathbb {Z}, \mathrm {SF}^{\mathbb {Z}})$
. Let
![]() $y =(y_0, \ldots , y_{k-1})$
and let
$y =(y_0, \ldots , y_{k-1})$
and let
![]() $\varphi (x, y)$
be a quantifier-free
$\varphi (x, y)$
be a quantifier-free
![]() $L^*_{\mathrm {u}}$
-formula such that for all
$L^*_{\mathrm {u}}$
-formula such that for all
![]() $a \in \mathbb {Z}$
and
$a \in \mathbb {Z}$
and
![]() $b \in \mathbb {Z}^k$
,
$b \in \mathbb {Z}^k$
,
We will show that for any given
![]() $n>0$
, there are families
$n>0$
, there are families
 $(a_\Delta )_{ \Delta \subseteq \{ 0, \ldots , n-1\}^k}$
and
$(a_\Delta )_{ \Delta \subseteq \{ 0, \ldots , n-1\}^k}$
and
![]() $(b_{ij})_{0\leq i < k, 0 \leq j < n }$
of integers such that
$(b_{ij})_{0\leq i < k, 0 \leq j < n }$
of integers such that
Let
 $f: \mathscr {P}(\{0,\ldots , n-1\}^k) \to \{0,\ldots , 2^{(n^k)}-1\}$
be an arbitrary bijection. Let g be the bijection from
$f: \mathscr {P}(\{0,\ldots , n-1\}^k) \to \{0,\ldots , 2^{(n^k)}-1\}$
be an arbitrary bijection. Let g be the bijection from
![]() $\{ 0, \ldots , n-1\}^k$
to
$\{ 0, \ldots , n-1\}^k$
to
![]() $\{ 0, \ldots , n^k-1\}$
such that if b and
$\{ 0, \ldots , n^k-1\}$
such that if b and
![]() $b'$
are in
$b'$
are in
![]() $\{ 0, \ldots , n-1\}^k $
and
$\{ 0, \ldots , n-1\}^k $
and
![]() $b<_{\text {lex}}b'$
, then
$b<_{\text {lex}}b'$
, then
![]() $g(b)<g(b')$
. More explicitly, we have
$g(b)<g(b')$
. More explicitly, we have
 $$ \begin{align*}g(j_0, \ldots, j_{k-1}) =j_0n^{k-1} + j_1n^{k-2} + \cdots + j_{k-1} \text{ for } (j_0, \ldots, j_{k-1}) \in \{ 0, \ldots, n-1\}^k.\end{align*} $$
$$ \begin{align*}g(j_0, \ldots, j_{k-1}) =j_0n^{k-1} + j_1n^{k-2} + \cdots + j_{k-1} \text{ for } (j_0, \ldots, j_{k-1}) \in \{ 0, \ldots, n-1\}^k.\end{align*} $$
It follows from the preceding paragraph that we can find an arithmetic progression
 $(c_i)_{ i \in \{0, \ldots , n^k 2^{(n^k)} -1 \} }$
such that for all
$(c_i)_{ i \in \{0, \ldots , n^k 2^{(n^k)} -1 \} }$
such that for all
![]() $\Delta \subseteq \{0, \ldots , n-1\}^k$
and
$\Delta \subseteq \{0, \ldots , n-1\}^k$
and
![]() $(j_0, \ldots , j_{k-1})$
in
$(j_0, \ldots , j_{k-1})$
in
![]() $\{ 0, \ldots , n-1\}^k$
, we have that
$\{ 0, \ldots , n-1\}^k$
, we have that
 $$ \begin{align*}c_{f(\Delta)n^k+ g(j_0, \ldots, j_{k-1})} \in \mathrm{SF}^{\mathbb{Z}}\ \text{ if and only if } \ (j_0, \ldots, j_{k-1}) \in \Delta.\end{align*} $$
$$ \begin{align*}c_{f(\Delta)n^k+ g(j_0, \ldots, j_{k-1})} \in \mathrm{SF}^{\mathbb{Z}}\ \text{ if and only if } \ (j_0, \ldots, j_{k-1}) \in \Delta.\end{align*} $$
Suppose
![]() $d = c_1-c_0$
. Set
$d = c_1-c_0$
. Set
![]() $b_{ij} = djn^{k-i-1} $
for
$b_{ij} = djn^{k-i-1} $
for
![]() $i \in \{0, \ldots , k-1\}$
and
$i \in \{0, \ldots , k-1\}$
and
![]() $j \in \{0, \ldots , n-1\}$
, and set
$j \in \{0, \ldots , n-1\}$
, and set
![]() $a_{\Delta } = c_{f(\Delta )n^k}$
for
$a_{\Delta } = c_{f(\Delta )n^k}$
for
![]() $\Delta \subseteq \{ 0, \ldots , n-1\}^k$
. We have
$\Delta \subseteq \{ 0, \ldots , n-1\}^k$
. We have
 $$ \begin{align*}c_{f(\Delta)n^k+ g(j_0, \ldots, j_{k-1})} = c_{f(\Delta)n^k} + d g(j_0, \ldots, j_{k-1}) = a_\Delta + b_{0,j_0}+ \cdots+ b_{k-1,j_{k-1}}.\end{align*} $$
$$ \begin{align*}c_{f(\Delta)n^k+ g(j_0, \ldots, j_{k-1})} = c_{f(\Delta)n^k} + d g(j_0, \ldots, j_{k-1}) = a_\Delta + b_{0,j_0}+ \cdots+ b_{k-1,j_{k-1}}.\end{align*} $$
The conclusion thus follows.⊣
Lemma 4.2. Every p-condition
![]() $\theta _p(x,y)$
is stable in
$\theta _p(x,y)$
is stable in
![]() $\mathrm {SF}^*_{\mathbb {Q}}$
.
$\mathrm {SF}^*_{\mathbb {Q}}$
.
Proof Suppose
![]() $\theta _p(x,y)$
is as in the statement of the lemma. It is clear that if
$\theta _p(x,y)$
is as in the statement of the lemma. It is clear that if
![]() $\theta _p(x,y)$
does not contain the variable x, then it is stable. As stability is preserved under taking Boolean combinations, we can reduce to the case where
$\theta _p(x,y)$
does not contain the variable x, then it is stable. As stability is preserved under taking Boolean combinations, we can reduce to the case where
![]() $\theta _p(x,y)$
is
$\theta _p(x,y)$
is
![]() $kx+t(y) \in U_{p,l}$
with
$kx+t(y) \in U_{p,l}$
with
![]() $k\neq 0$
. We note that for any b and
$k\neq 0$
. We note that for any b and
![]() $b'$
in
$b'$
in
![]() $\mathbb {G}^{|y|}$
, the sets defined by
$\mathbb {G}^{|y|}$
, the sets defined by
![]() $\theta _p(x, b)$
and
$\theta _p(x, b)$
and
![]() $\theta _p(x, b')$
are either the same or disjoint. It follows easily that
$\theta _p(x, b')$
are either the same or disjoint. It follows easily that
![]() $\theta _p(x, y)$
does not have the order property; in other words,
$\theta _p(x, y)$
does not have the order property; in other words,
![]() $\theta _p(x,y)$
is stable. Alternatively, the desired conclusion also follows from the fact that
$\theta _p(x,y)$
is stable. Alternatively, the desired conclusion also follows from the fact that
![]() $( \mathbb {Q}; \mathscr {U}^{\mathbb {Q}})$
is an abelian structure and hence stable; see [Reference Wagner15, p. 49] for the relevant definition and result.⊣
$( \mathbb {Q}; \mathscr {U}^{\mathbb {Q}})$
is an abelian structure and hence stable; see [Reference Wagner15, p. 49] for the relevant definition and result.⊣
Proof of Theorem 1.3, part 2 We first show that
![]() $\text {Th}(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
is simple. By the fact that
$\text {Th}(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
is simple. By the fact that
![]() $(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
has the same definable sets as
$(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
has the same definable sets as
![]() $(\mathbb {Q}; \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
and Corollary 3.5, we can replace
$(\mathbb {Q}; \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
and Corollary 3.5, we can replace
![]() $\text {Th}(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
with
$\text {Th}(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
with
![]() $\mathrm {SF}^*_{\mathbb {Q}}$
. Towards a contradiction, suppose that the latter is not simple. We obtain a formula
$\mathrm {SF}^*_{\mathbb {Q}}$
. Towards a contradiction, suppose that the latter is not simple. We obtain a formula
![]() $\varphi (x,y)$
witnessing the tree property of
$\varphi (x,y)$
witnessing the tree property of
![]() $\mathrm {SF}^*_{\mathbb {Q}}$
; see [Reference Kim10, pp. 24–25] for the definition and proof that this is one of the equivalent characterizations of simplicity. We can arrange that
$\mathrm {SF}^*_{\mathbb {Q}}$
; see [Reference Kim10, pp. 24–25] for the definition and proof that this is one of the equivalent characterizations of simplicity. We can arrange that
![]() $\varphi (x,y)$
is quantifier-free by Theorem 3.4. Recall that disjunction preserves simplicity of formulas; this can be shown directly as an exercise or can be seen immediately from the equivalence between (1) and (3) in [Reference Kim10, Lemma 2.4.1]. Hence using Lemma 3.1, we can arrange that
$\varphi (x,y)$
is quantifier-free by Theorem 3.4. Recall that disjunction preserves simplicity of formulas; this can be shown directly as an exercise or can be seen immediately from the equivalence between (1) and (3) in [Reference Kim10, Lemma 2.4.1]. Hence using Lemma 3.1, we can arrange that
![]() $\varphi (x,y)$
is of the form
$\varphi (x,y)$
is of the form
where
![]() $\rho (y)$
is a quantifier-free
$\rho (y)$
is a quantifier-free
![]() $L^*_{\mathrm {u}}$
-formula,
$L^*_{\mathrm {u}}$
-formula,
![]() $\varepsilon (x, y)$
is an equational condition,
$\varepsilon (x, y)$
is an equational condition,
![]() $t(y)$
and
$t(y)$
and
![]() $t'(y)$
are tuples of
$t'(y)$
are tuples of
![]() $L^*_{\mathrm {u}}$
-terms with lengths n and
$L^*_{\mathrm {u}}$
-terms with lengths n and
![]() $n'$
respectively, and
$n'$
respectively, and
![]() $\psi (x, z, z')$
is a special formula. Let
$\psi (x, z, z')$
is a special formula. Let
 $(\mathbb {G}; \mathscr {U}^{\mathbb {G}}, \mathscr {P}^{\mathbb {G}}) \models \mathrm {SF}^*_{\mathbb {Q}}$
. Then there is
$(\mathbb {G}; \mathscr {U}^{\mathbb {G}}, \mathscr {P}^{\mathbb {G}}) \models \mathrm {SF}^*_{\mathbb {Q}}$
. Then there is
![]() $b \in \mathbb {G}^k$
with
$b \in \mathbb {G}^k$
with
![]() $k=|y|$
, an uncountable cardinal
$k=|y|$
, an uncountable cardinal
![]() $\kappa $
, and a tree
$\kappa $
, and a tree
![]() $(\sigma _s)_{ s \in \omega ^{<\kappa } }$
of
$(\sigma _s)_{ s \in \omega ^{<\kappa } }$
of
![]() $L^*_{\mathrm {u}}$
-automorphisms of
$L^*_{\mathrm {u}}$
-automorphisms of
![]() $(\mathbb {G}; \mathscr {U}^{\mathbb {G}}, \mathscr {P}^{\mathbb {G}})$
with the following properties:
$(\mathbb {G}; \mathscr {U}^{\mathbb {G}}, \mathscr {P}^{\mathbb {G}})$
with the following properties:
-
(1) for all
 $s \in \omega ^{< \kappa }$
,
$s \in \omega ^{< \kappa }$
,
 $\{ \varphi (x, \sigma _{s\frown (i)}(b)) : i \in \omega \}$
is inconsistent;
$\{ \varphi (x, \sigma _{s\frown (i)}(b)) : i \in \omega \}$
is inconsistent; -
(2) for all
 $\hat {s} \in \omega ^\kappa $
,
$\hat {s} \in \omega ^\kappa $
,
 $\{ \varphi (x, \sigma _{\hat {s} \mathord {\upharpoonright } \alpha }(b)): \alpha <\kappa \}$
is consistent;
$\{ \varphi (x, \sigma _{\hat {s} \mathord {\upharpoonright } \alpha }(b)): \alpha <\kappa \}$
is consistent; -
(3) for every
 $\alpha <\kappa $
and
$\alpha <\kappa $
and
 $s, s' \in \omega ^\alpha $
,
$s, s' \in \omega ^\alpha $
,
 $ \text {tp}\big ( (\sigma _{s\frown (i)}(b))_i\big )=\text {tp}\big ( (\sigma _{s'\frown (i)}(b))_i\big )$
.
$ \text {tp}\big ( (\sigma _{s\frown (i)}(b))_i\big )=\text {tp}\big ( (\sigma _{s'\frown (i)}(b))_i\big )$
.
More precisely, we can get b,
![]() $\kappa $
, and
$\kappa $
, and
![]() $(\sigma _t)_{ t \in \omega ^{<\kappa } }$
satisfying (1) and (2) from the fact that
$(\sigma _t)_{ t \in \omega ^{<\kappa } }$
satisfying (1) and (2) from the fact that
![]() $\varphi (x,y)$
witnesses the tree property of
$\varphi (x,y)$
witnesses the tree property of
![]() $\mathrm {SF}^*_{\mathbb {Q}}$
, a standard Ramsey arguments, and the monstrosity of
$\mathrm {SF}^*_{\mathbb {Q}}$
, a standard Ramsey arguments, and the monstrosity of
![]() $(\mathbb {G}; \mathscr {U}^{\mathbb {G}}, \mathscr {P}^{\mathbb {G}})$
. We can then arrange that (3) also holds using the results in [Reference Kim, Kim and Scow11]; a direct argument is also straightforward.
$(\mathbb {G}; \mathscr {U}^{\mathbb {G}}, \mathscr {P}^{\mathbb {G}})$
. We can then arrange that (3) also holds using the results in [Reference Kim, Kim and Scow11]; a direct argument is also straightforward.
We deduce the desired contradiction by showing that there is
![]() $ s \in \omega ^{<\kappa }$
such that
$ s \in \omega ^{<\kappa }$
such that
![]() $\{ \varphi (x, \sigma _{s\frown (i)}(b)) : i \in \omega \}$
is consistent. From (1–3), we get for all
$\{ \varphi (x, \sigma _{s\frown (i)}(b)) : i \in \omega \}$
is consistent. From (1–3), we get for all
![]() $s \in \omega ^{< \kappa }$
that
$s \in \omega ^{< \kappa }$
that
![]() $\rho (\sigma _{s}(b) )$
holds and
$\rho (\sigma _{s}(b) )$
holds and
![]() $\varepsilon (x, \sigma _{s}(b))$
defines a cofinite set. By monstrosity of
$\varepsilon (x, \sigma _{s}(b))$
defines a cofinite set. By monstrosity of
![]() $\mathbb {G}$
, it suffices to find
$\mathbb {G}$
, it suffices to find
![]() $s \in \omega ^{<\kappa }$
such that any finite conjunction of
$s \in \omega ^{<\kappa }$
such that any finite conjunction of
 $\{ \psi \big (x, t(\sigma _{s\frown (i)}(b)),t'(\sigma _{s\frown (i)}(b))\big ) : i \in \omega \}$
defines an infinite set in
$\{ \psi \big (x, t(\sigma _{s\frown (i)}(b)),t'(\sigma _{s\frown (i)}(b))\big ) : i \in \omega \}$
defines an infinite set in
![]() $\mathbb {G}$
. For
$\mathbb {G}$
. For
![]() $s \in \omega ^{<\kappa }$
and a finite
$s \in \omega ^{<\kappa }$
and a finite
![]() $\Delta \subseteq \omega $
, set
$\Delta \subseteq \omega $
, set
 $$ \begin{align*}\theta_{s, \Delta}(x) := \bigwedge_{i \in \Delta} \psi\big(x, t(\sigma_{s\frown (i)}(b)),t'(\sigma_{s\frown (i)}(b))\big).\end{align*} $$
$$ \begin{align*}\theta_{s, \Delta}(x) := \bigwedge_{i \in \Delta} \psi\big(x, t(\sigma_{s\frown (i)}(b)),t'(\sigma_{s\frown (i)}(b))\big).\end{align*} $$
As
![]() $\kappa $
is uncountable, to ensure the desired
$\kappa $
is uncountable, to ensure the desired
![]() $s\in \omega ^{<\kappa }$
exists, it suffices to show for fixed
$s\in \omega ^{<\kappa }$
exists, it suffices to show for fixed
![]() $\Delta $
that for all but countably many
$\Delta $
that for all but countably many
![]() $\alpha < \kappa $
and all
$\alpha < \kappa $
and all
![]() $s \in \omega ^\alpha $
, the formula
$s \in \omega ^\alpha $
, the formula
![]() $\theta _{s, \Delta }(x)$
defines an infinite set in
$\theta _{s, \Delta }(x)$
defines an infinite set in
![]() $\mathbb {G}$
.
$\mathbb {G}$
.
Note that
![]() $\theta _{s, \Delta }(x)$
is a conjunction of
$\theta _{s, \Delta }(x)$
is a conjunction of
![]() $\mathbb {G}$
-systems given by the same special formula, so
$\mathbb {G}$
-systems given by the same special formula, so
![]() $\theta _{s, \Delta }(x)$
is also a
$\theta _{s, \Delta }(x)$
is also a
![]() $\mathbb {G}$
-system. By the genericity of
$\mathbb {G}$
-system. By the genericity of
![]() $\mathrm {SF}^*_{\mathbb {Q}}$
established in Theorem 2.14, we need to check that for all but countably many
$\mathrm {SF}^*_{\mathbb {Q}}$
established in Theorem 2.14, we need to check that for all but countably many
![]() $\alpha < \kappa $
and all
$\alpha < \kappa $
and all
![]() $s \in \omega ^\alpha $
, the
$s \in \omega ^\alpha $
, the
![]() $\mathbb {G}$
-system
$\mathbb {G}$
-system
![]() $\theta _{s, \Delta }(x)$
is nontrivial and locally satisfiable. Indeed, this implies that by (2),
$\theta _{s, \Delta }(x)$
is nontrivial and locally satisfiable. Indeed, this implies that by (2),
![]() $\varphi (x, b)$
is consistent, and so is
$\varphi (x, b)$
is consistent, and so is
![]() $\psi (x, t(b),t'(b))$
. This implies in particular that
$\psi (x, t(b),t'(b))$
. This implies in particular that
![]() $t(b)$
and
$t(b)$
and
![]() $t'(b)$
have no common components. It then follows from (3) that for
$t'(b)$
have no common components. It then follows from (3) that for
![]() $s \in \omega ^{< \kappa }$
and
$s \in \omega ^{< \kappa }$
and
![]() $i, j \in \omega $
,
$i, j \in \omega $
,
 $$ \begin{align*}t(\sigma_{s\frown (i)}(b)) \text{ and } t'(\sigma_{s\frown (j)} (b)) \text{ have no common elements }.\end{align*} $$
$$ \begin{align*}t(\sigma_{s\frown (i)}(b)) \text{ and } t'(\sigma_{s\frown (j)} (b)) \text{ have no common elements }.\end{align*} $$
Hence,
![]() $\theta _{s, \Delta }(x)$
is nontrivial for all
$\theta _{s, \Delta }(x)$
is nontrivial for all
![]() $s \in \omega ^{< \kappa }$
. Let
$s \in \omega ^{< \kappa }$
. Let
![]() $\psi _p(x,z,z')$
be the associated p-condition of
$\psi _p(x,z,z')$
be the associated p-condition of
![]() $\psi (x,z,z')$
. We then get from (2) that
$\psi (x,z,z')$
. We then get from (2) that
![]() $\{ \psi _p(x, t(\sigma _{\hat {s} \mathord {\upharpoonright } \alpha }(b)), t'(\sigma _{\hat {s} \mathord {\upharpoonright } \alpha }(b))): \alpha <\kappa \}$
is consistent for all
$\{ \psi _p(x, t(\sigma _{\hat {s} \mathord {\upharpoonright } \alpha }(b)), t'(\sigma _{\hat {s} \mathord {\upharpoonright } \alpha }(b))): \alpha <\kappa \}$
is consistent for all
![]() $\hat {s} \in \omega ^\kappa $
. By Lemma 4.2, the formula
$\hat {s} \in \omega ^\kappa $
. By Lemma 4.2, the formula
![]() $\psi _p(x, t(y),t'(y) )$
is stable and hence does not witness the tree property. It follows that for all but finitely many
$\psi _p(x, t(y),t'(y) )$
is stable and hence does not witness the tree property. It follows that for all but finitely many
![]() $\alpha < \kappa $
and all
$\alpha < \kappa $
and all
![]() $s \in \omega ^\alpha $
, the set
$s \in \omega ^\alpha $
, the set
 $$ \begin{align*}\{ \psi_p\big(x, t(\sigma_{s\frown (i)} (b)), t'(\sigma_{s\frown (i)} (b))\big) : i \in \omega\} \text{ is consistent}.\end{align*} $$
$$ \begin{align*}\{ \psi_p\big(x, t(\sigma_{s\frown (i)} (b)), t'(\sigma_{s\frown (i)} (b))\big) : i \in \omega\} \text{ is consistent}.\end{align*} $$
For such s, we have that
![]() $\theta _{s, \Delta }(x)$
is p-satisfiable. So for all but countably many
$\theta _{s, \Delta }(x)$
is p-satisfiable. So for all but countably many
![]() $\alpha < \kappa $
and all
$\alpha < \kappa $
and all
![]() $s \in \omega ^\alpha $
,
$s \in \omega ^\alpha $
,
![]() $\theta _{s, \Delta }(x)$
is locally satisfiable which completes the proof that
$\theta _{s, \Delta }(x)$
is locally satisfiable which completes the proof that
![]() $\text {Th}(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
is simple.
$\text {Th}(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
is simple.
We next prove that
![]() $\text {Th}( \mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
is not strong which implies that it is not supersimple; for the definition of strength and the relation to supersimplicity see [Reference Adler1]. Again, we can replace
$\text {Th}( \mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
is not strong which implies that it is not supersimple; for the definition of strength and the relation to supersimplicity see [Reference Adler1]. Again, we can replace
![]() $\text {Th}( \mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
by
$\text {Th}( \mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
by
![]() $\mathrm {SF}^*_{\mathbb {Q}}$
using Proposition 2.4 and Corollary 3.5. For each p, let
$\mathrm {SF}^*_{\mathbb {Q}}$
using Proposition 2.4 and Corollary 3.5. For each p, let
![]() $\varphi _p(x,y)$
with
$\varphi _p(x,y)$
with
![]() $|y|=1$
be the formula
$|y|=1$
be the formula
![]() $x-y \in U_{p,0}$
. For all p and i, set
$x-y \in U_{p,0}$
. For all p and i, set
![]() $b_{p,i} = p^{-i}$
. We will show that
$b_{p,i} = p^{-i}$
. We will show that
 $\big ( \varphi _p(x,y), ( b_{p,i})_{i \in \mathbb {N}} ) \big )$
forms an inp-pattern of infinite depth in
$\big ( \varphi _p(x,y), ( b_{p,i})_{i \in \mathbb {N}} ) \big )$
forms an inp-pattern of infinite depth in
![]() $(\mathbb {Q}; \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
. For distinct i and j in
$(\mathbb {Q}; \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
. For distinct i and j in
![]() $\mathbb {N}$
, we have that
$\mathbb {N}$
, we have that
 $p^{-i} - p^{-j} \notin U^{\mathbb {Q}}_{p,0}$
which implies that
$p^{-i} - p^{-j} \notin U^{\mathbb {Q}}_{p,0}$
which implies that
![]() $\varphi _p(x, b_{p,i}) \wedge \varphi _p(x, b_{p,j}) $
is inconsistent. On the other hand, if S is a finite set of primes, and
$\varphi _p(x, b_{p,i}) \wedge \varphi _p(x, b_{p,j}) $
is inconsistent. On the other hand, if S is a finite set of primes, and
![]() $f: S \to \mathbb {N}$
is an arbitrary function, then for
$f: S \to \mathbb {N}$
is an arbitrary function, then for
![]() $a=\Sigma _{p\in S}b_{p,f(p)}$
we have that
$a=\Sigma _{p\in S}b_{p,f(p)}$
we have that
 $(\mathbb {Q}; \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})\models \bigwedge _{p \in S} \varphi _p(a, b_{p,f(p)})$
. The desired conclusion follows.
$(\mathbb {Q}; \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})\models \bigwedge _{p \in S} \varphi _p(a, b_{p,f(p)})$
. The desired conclusion follows.
Finally, we note that
![]() $(\mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
is a substructure of
$(\mathbb {Z}; \mathscr {U}^{\mathbb {Z}}, \mathscr {P}^{\mathbb {Z}})$
is a substructure of
![]() $(\mathbb {Q}; \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
, and the former theory admits quantifier elimination and has
$(\mathbb {Q}; \mathscr {U}^{\mathbb {Q}}, \mathscr {P}^{\mathbb {Q}})$
, and the former theory admits quantifier elimination and has
![]() $\text {IP}_k$
for all
$\text {IP}_k$
for all
![]() $k>0$
. Therefore, the latter also has
$k>0$
. Therefore, the latter also has
![]() $\text {IP}_k$
for all
$\text {IP}_k$
for all
![]() $k>0$
. In fact, the construction in part 2 of the proof of Theorem 1.1 carries through.⊣
$k>0$
. In fact, the construction in part 2 of the proof of Theorem 1.1 carries through.⊣
Lemma 4.3. Any order-condition has
![]() $\mathrm {NIP}$
in
$\mathrm {NIP}$
in
![]() $\mathrm {OSF}^*_{\mathbb {Q}}$
.
$\mathrm {OSF}^*_{\mathbb {Q}}$
.
Proof The statement immediately follows from the fact that every order condition is a formula in the language of ordered groups and the fact that the reduct of any model of
![]() $\mathrm {OSF}^*_{\mathbb {Q}}$
to this language is an ordered abelian group, which has
$\mathrm {OSF}^*_{\mathbb {Q}}$
to this language is an ordered abelian group, which has
![]() $\text {NIP}$
; see for example [Reference Gurevich and Schmitt8].⊣
$\text {NIP}$
; see for example [Reference Gurevich and Schmitt8].⊣
Proof of Theorem 1.4, part 2 In the proof of part 2 of Theorem 1.3, we have shown that
![]() $\text {Th}(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
is not strong and is k-independent for all
$\text {Th}(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
is not strong and is k-independent for all
![]() $k>0$
, so the corresponding conclusions for
$k>0$
, so the corresponding conclusions for
![]() $\text {Th}(\mathbb {Q}; <, \mathrm {SF}^{\mathbb {Q}})$
also follow. It remains to show that
$\text {Th}(\mathbb {Q}; <, \mathrm {SF}^{\mathbb {Q}})$
also follow. It remains to show that
![]() $\text {Th}(\mathbb {Q};<, \mathrm {SF}^{\mathbb {Q}})$
has
$\text {Th}(\mathbb {Q};<, \mathrm {SF}^{\mathbb {Q}})$
has
![]() $\text {NTP}_2$
. The proof is essentially the same as the proof that
$\text {NTP}_2$
. The proof is essentially the same as the proof that
![]() $\text {Th}(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
is simple, but with extra complications coming from the ordering. By Proposition 2.4 and Corollary 3.5, we can replace
$\text {Th}(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
is simple, but with extra complications coming from the ordering. By Proposition 2.4 and Corollary 3.5, we can replace
![]() $\text {Th}(\mathbb {Q};<, \mathrm {SF}^{\mathbb {Q}})$
with
$\text {Th}(\mathbb {Q};<, \mathrm {SF}^{\mathbb {Q}})$
with
![]() $\mathrm {OSF}_{\mathbb {Q}}^*$
. Towards a contradiction, assume that there is a formula
$\mathrm {OSF}_{\mathbb {Q}}^*$
. Towards a contradiction, assume that there is a formula
![]() $\varphi (x,y)$
witnessing
$\varphi (x,y)$
witnessing
![]() $\text {TP}_2$
(see [Reference Chernikov4, pp. 700–701]). We can arrange that
$\text {TP}_2$
(see [Reference Chernikov4, pp. 700–701]). We can arrange that
![]() $\varphi (x,y)$
is quantifier-free by Theorem 3.4. Disjunctions of formulas with
$\varphi (x,y)$
is quantifier-free by Theorem 3.4. Disjunctions of formulas with
![]() $\text {NTP}_2$
again have
$\text {NTP}_2$
again have
![]() $\text {NTP}_2$
[Reference Chernikov4, p. 701], so using Lemma 3.2 we can arrange that
$\text {NTP}_2$
[Reference Chernikov4, p. 701], so using Lemma 3.2 we can arrange that
![]() $\varphi (x,y)$
is of the form
$\varphi (x,y)$
is of the form
where
![]() $\rho (y)$
is a quantifier-free
$\rho (y)$
is a quantifier-free
![]() $L^*_{\mathrm {ou}}$
-formula
$L^*_{\mathrm {ou}}$
-formula
![]() $, \lambda (x, y)$
is an order condition,
$, \lambda (x, y)$
is an order condition,
![]() $\psi (x, z, z')$
is a special formula, and
$\psi (x, z, z')$
is a special formula, and
![]() $t(y)$
and
$t(y)$
and
![]() $t'(y)$
are tuples of
$t'(y)$
are tuples of
![]() $L^*_{\mathrm {ou}}$
-terms with lengths n and
$L^*_{\mathrm {ou}}$
-terms with lengths n and
![]() $n'$
respectively. Then there is
$n'$
respectively. Then there is
![]() $b \in \mathbb {G}^{k}$
with
$b \in \mathbb {G}^{k}$
with
![]() $k=|y|$
and an array
$k=|y|$
and an array
![]() $(\sigma _{ij})_{ i \in \omega , j \in \omega }$
of
$(\sigma _{ij})_{ i \in \omega , j \in \omega }$
of
![]() $L_{\mathrm {ou}}^*$
-automorphisms of
$L_{\mathrm {ou}}^*$
-automorphisms of
![]() $(\mathbb {G}; <, \mathscr {U}^{\mathbb {G}}, \mathscr {P}^{\mathbb {G}})$
with the following properties:
$(\mathbb {G}; <, \mathscr {U}^{\mathbb {G}}, \mathscr {P}^{\mathbb {G}})$
with the following properties:
-
(1) for all
 $i \in \omega $
,
$i \in \omega $
,
 $\{ \varphi (x, \sigma _{ij}(b)) : j \in \omega \}$
is inconsistent;
$\{ \varphi (x, \sigma _{ij}(b)) : j \in \omega \}$
is inconsistent; -
(2) for all
 $f: \omega \to \omega $
,
$f: \omega \to \omega $
,
 $\{ \varphi (x, \sigma _{if(i)}(b)): i \in \omega \}$
is consistent;
$\{ \varphi (x, \sigma _{if(i)}(b)): i \in \omega \}$
is consistent; -
(3) for all
 $i \in \omega $
,
$i \in \omega $
,
 $(\sigma _{ij}(b))_{j \in \omega }$
is indiscernible over
$(\sigma _{ij}(b))_{j \in \omega }$
is indiscernible over
 $\{ \sigma _{i'j}(b) : i' \in \omega , i'\neq i, j \in \omega \}$
;
$\{ \sigma _{i'j}(b) : i' \in \omega , i'\neq i, j \in \omega \}$
; -
(4) the sequence of “rows”
 $( (\sigma _{ij}(b))_{j \in \omega })_{i \in \omega }$
is indiscernible.
$( (\sigma _{ij}(b))_{j \in \omega })_{i \in \omega }$
is indiscernible.
We could get b,
![]() $\omega $
, and
$\omega $
, and
![]() $(\sigma _{ij})_{ i \in \omega , j \in \omega }$
as above from the definition of
$(\sigma _{ij})_{ i \in \omega , j \in \omega }$
as above from the definition of
![]() $\text {NTP}_2$
, Ramsey arguments, and the monstrosity of
$\text {NTP}_2$
, Ramsey arguments, and the monstrosity of
![]() $(\mathbb {G}; \mathscr {U}^{\mathbb {G}}, \mathscr {P}^{\mathbb {G}})$
; see also [Reference Chernikov4, p. 697] for the type of argument we need to get (3).
$(\mathbb {G}; \mathscr {U}^{\mathbb {G}}, \mathscr {P}^{\mathbb {G}})$
; see also [Reference Chernikov4, p. 697] for the type of argument we need to get (3).
We deduce that the set
![]() $\{ \varphi (x, \sigma _{ij}b) : j \in \omega \}$
is consistent for all
$\{ \varphi (x, \sigma _{ij}b) : j \in \omega \}$
is consistent for all
![]() $i \in \omega $
, which is the desired contradiction. We get from (2) that
$i \in \omega $
, which is the desired contradiction. We get from (2) that
![]() $\rho (\sigma _{ij}b)$
holds for all
$\rho (\sigma _{ij}b)$
holds for all
![]() $i \in \omega $
and
$i \in \omega $
and
![]() $j \in \omega $
. Hence, it suffices to show for all
$j \in \omega $
. Hence, it suffices to show for all
![]() $i \in \omega $
that
$i \in \omega $
that
The order condition
![]() $\lambda (x, y)$
has
$\lambda (x, y)$
has
![]() $\text {NIP}$
by Lemma 4.3, and so it has
$\text {NIP}$
by Lemma 4.3, and so it has
![]() $\text {NTP}_2$
. Using conditions (2–4), we get that
$\text {NTP}_2$
. Using conditions (2–4), we get that
Hence, any finite conjunction from
![]() $\{\lambda (x, \sigma _{ij}(b)): j \in \omega \}$
contains an open interval for all
$\{\lambda (x, \sigma _{ij}(b)): j \in \omega \}$
contains an open interval for all
![]() $i \in \omega $
. For
$i \in \omega $
. For
![]() $i \in \omega $
and a finite
$i \in \omega $
and a finite
![]() $\Delta \subseteq \omega $
, set
$\Delta \subseteq \omega $
, set
 $$ \begin{align*}\theta_{i, \Delta}(x) := \bigwedge_{j \in \Delta} \psi\big(x, t(\sigma_{ij}(b)),t'(\sigma_{ij}(b))\big).\end{align*} $$
$$ \begin{align*}\theta_{i, \Delta}(x) := \bigwedge_{j \in \Delta} \psi\big(x, t(\sigma_{ij}(b)),t'(\sigma_{ij}(b))\big).\end{align*} $$
It suffices to show that
![]() $\theta _{i, \Delta }(x)$
defines a non-empty set in every non-empty
$\theta _{i, \Delta }(x)$
defines a non-empty set in every non-empty
![]() $\mathbb {G}$
-interval.
$\mathbb {G}$
-interval.
We have that
![]() $\theta _{i, \Delta }(x)$
is a conjunction of
$\theta _{i, \Delta }(x)$
is a conjunction of
![]() $\mathbb {G}$
-system given by the same special formula, and so is again a
$\mathbb {G}$
-system given by the same special formula, and so is again a
![]() $\mathbb {G}$
-system. By the genericity of
$\mathbb {G}$
-system. By the genericity of
![]() $\mathrm {OSF}^*_{\mathbb {Q}}$
, the problem reduces to showing
$\mathrm {OSF}^*_{\mathbb {Q}}$
, the problem reduces to showing
![]() $\theta _{i, \Delta }(x)$
is nontrivial and locally satisfiable. By (2),
$\theta _{i, \Delta }(x)$
is nontrivial and locally satisfiable. By (2),
![]() $\varphi (x, b)$
is consistent, and so is
$\varphi (x, b)$
is consistent, and so is
![]() $\psi (x, t(b),t'(b))$
. This implies in particular that
$\psi (x, t(b),t'(b))$
. This implies in particular that
![]() $t(b)$
and
$t(b)$
and
![]() $t'(b)$
have no common components. It then follows from (3) that for
$t'(b)$
have no common components. It then follows from (3) that for
![]() $i \in \omega $
and distinct
$i \in \omega $
and distinct
![]() $j, j' \in \omega $
,
$j, j' \in \omega $
,
Hence,
![]() $\theta _{i, \Delta }(x)$
is nontrivial for all
$\theta _{i, \Delta }(x)$
is nontrivial for all
![]() $i \in \omega $
. Let
$i \in \omega $
. Let
![]() $\psi _p(x,z,z')$
be the associated p-condition of
$\psi _p(x,z,z')$
be the associated p-condition of
![]() $\psi (x,z,z')$
. We then get from (2) that
$\psi (x,z,z')$
. We then get from (2) that
 $\{ \psi _p(x, \sigma _{if(i)}(b)): i \in \omega \}$
is consistent for all
$\{ \psi _p(x, \sigma _{if(i)}(b)): i \in \omega \}$
is consistent for all
![]() $f: \omega \to \omega $
. By Lemma 4.2, the formula
$f: \omega \to \omega $
. By Lemma 4.2, the formula
![]() $\psi _p(x, t(y),t'(y) )$
is stable and hence has
$\psi _p(x, t(y),t'(y) )$
is stable and hence has
![]() $\text {NTP}_2$
. It follows that for all but finitely many
$\text {NTP}_2$
. It follows that for all but finitely many
![]() $i \in \omega $
the set
$i \in \omega $
the set
 $$ \begin{align*}\{ \psi_p\big(x, t(\sigma_{ij} (b)), t'(\sigma_{ij} (b))\big) : j \in \omega\} \text{ is consistent}.\end{align*} $$
$$ \begin{align*}\{ \psi_p\big(x, t(\sigma_{ij} (b)), t'(\sigma_{ij} (b))\big) : j \in \omega\} \text{ is consistent}.\end{align*} $$
Combining with (4), we get that
![]() $\theta _{i, \Delta }(x)$
is p-satisfiable for all p which completes the proof.⊣
$\theta _{i, \Delta }(x)$
is p-satisfiable for all p which completes the proof.⊣
Corollary 4.4. The set
![]() $\mathbb {Z}$
is not definable in
$\mathbb {Z}$
is not definable in
![]() $(\mathbb {Q}; <, \mathrm {SF}^{\mathbb {Q}})$
.
$(\mathbb {Q}; <, \mathrm {SF}^{\mathbb {Q}})$
.
Proof Towards a contradiction, suppose
![]() $\mathbb {Z}$
is definable in
$\mathbb {Z}$
is definable in
![]() $(\mathbb {Q}; <, \mathrm {SF}^{\mathbb {Q}})$
. Then by Theorem 1.2,
$(\mathbb {Q}; <, \mathrm {SF}^{\mathbb {Q}})$
. Then by Theorem 1.2,
![]() $(\mathbb {N}; +, \times , <, 0, 1)$
is interpretable in
$(\mathbb {N}; +, \times , <, 0, 1)$
is interpretable in
![]() $(\mathbb {Q}; <, \mathrm {SF}^{\mathbb {Q}})$
. It then follows from Theorem 1.4 that
$(\mathbb {Q}; <, \mathrm {SF}^{\mathbb {Q}})$
. It then follows from Theorem 1.4 that
![]() $(\mathbb {N}; +, \times , <, 0, 1)$
has
$(\mathbb {N}; +, \times , <, 0, 1)$
has
![]() $\text {NTP}_2$
, but this is well-known to be false.⊣
$\text {NTP}_2$
, but this is well-known to be false.⊣
5 Further questions
There are several further questions we can ask about
![]() $(\mathbb {Z}; \mathrm {SF}^{\mathbb {Z}})$
,
$(\mathbb {Z}; \mathrm {SF}^{\mathbb {Z}})$
,
![]() $(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
, and
$(\mathbb {Q}; \mathrm {SF}^{\mathbb {Q}})$
, and
![]() $(\mathbb {Q}; <, \mathrm {SF}^{\mathbb {Q}})$
. We would like to better understand dividing and forking inside these structures. Ideally, they coincide and have appropriate “local to global” behaviors. It would also be nice to understand imaginaries and definable groups in these structures.
$(\mathbb {Q}; <, \mathrm {SF}^{\mathbb {Q}})$
. We would like to better understand dividing and forking inside these structures. Ideally, they coincide and have appropriate “local to global” behaviors. It would also be nice to understand imaginaries and definable groups in these structures.
One would like to have similar results for “sufficiently random” subsets of
![]() $\mathbb {Z}$
other than
$\mathbb {Z}$
other than
![]() $\text {Pr}$
and
$\text {Pr}$
and
![]() $\mathrm {SF}^{\mathbb {Z}}$
. Another interesting candidate of such a subset is
$\mathrm {SF}^{\mathbb {Z}}$
. Another interesting candidate of such a subset is
![]() $\{\pm pq : p, q \text { are primes}\}$
. Most likely, it is not possible to prove the analogous results without assuming any number-theoretic conjecture. In a rather different direction, is there any sense in which we can say that most subsets of
$\{\pm pq : p, q \text { are primes}\}$
. Most likely, it is not possible to prove the analogous results without assuming any number-theoretic conjecture. In a rather different direction, is there any sense in which we can say that most subsets of
![]() $\mathbb {Z}$
are “sufficiently random” and yield results similar to ours?
$\mathbb {Z}$
are “sufficiently random” and yield results similar to ours?
In [Reference Bateman, Jockusch and Woods2], it is shown under the assumption of Dickson’s Conjecture that the monadic second order theory of
![]() $(\mathbb {N}; S, \text {Pr})$
is decidable where S is the successor function. We hope the analogous result for
$(\mathbb {N}; S, \text {Pr})$
is decidable where S is the successor function. We hope the analogous result for
![]() $( \mathbb {N}; S, \mathrm {SF}^{\mathbb {Z}})$
can be shown without assuming any conjecture. On another note, suppose the field
$( \mathbb {N}; S, \mathrm {SF}^{\mathbb {Z}})$
can be shown without assuming any conjecture. On another note, suppose the field
![]() $\bar {\mathbb {Q}}$
is an algebraic closure of the field
$\bar {\mathbb {Q}}$
is an algebraic closure of the field
![]() $\mathbb {Q}$
, v range over the non-archimedean valuations of
$\mathbb {Q}$
, v range over the non-archimedean valuations of
![]() $\bar {\mathbb {Q}}$
, and
$\bar {\mathbb {Q}}$
, and
 $$ \begin{align*}\text{Sqf}^{ \bar{\mathbb{Q}} } = \{ a \in \bar{\mathbb{Q}} : v(a) <2 \text{ for all } v \}.\end{align*} $$
$$ \begin{align*}\text{Sqf}^{ \bar{\mathbb{Q}} } = \{ a \in \bar{\mathbb{Q}} : v(a) <2 \text{ for all } v \}.\end{align*} $$
Does
 $( \bar {\mathbb {Q}}; \text {Sqf}^{ \bar {\mathbb {Q}} })$
have
$( \bar {\mathbb {Q}}; \text {Sqf}^{ \bar {\mathbb {Q}} })$
have
![]() $\text {NTP}_2$
? Finally, if
$\text {NTP}_2$
? Finally, if
![]() $\mathbb {Z}^\times $
is the multiplicative monoid of integers, can anything be said about
$\mathbb {Z}^\times $
is the multiplicative monoid of integers, can anything be said about
![]() $(\mathbb {Z}^\times; \mathrm {SF}^{\mathbb {Z}})$
?
$(\mathbb {Z}^\times; \mathrm {SF}^{\mathbb {Z}})$
?
Acknowledgments
We would like to thank Utkarsh Agrawal, William Balderrama, Alexander Dunn, Lou van den Dries, Allen Gehret, Itay Kaplan, and Erik Walsberg for discussions and comments at various stages of the project. We would also like to thank the referee for the detailed and insightful reading which allowed us to simplify several arguments. Of course, any remaining errors are our responsibility.