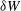1 Introduction
As an early proponent of applying thermodynamics to plasmas, I have been invited by the editors of the Journal of Plasma Physics to submit a brief paper in which I would look today for new ways to apply my methods in a modern context.
This is not intended to be a review, either of my own early work or the many excellent papers on free energy since then. Rather, I would like to recall how I became involved with free energy, and ask whether this might stimulate new ideas today. The basic idea is to relate free energy to the Hermicity of Vlasov operators. In § 3.2, I also report a recent use of free energy to address a problem in astrophysics.
2 Searching for stability
I became interested in free energy as a by-product of searching for methods to determine plasma stability different from case by case mode analysis. Trained otherwise, I learned plasma theory on the job when I joined the fusion energy program at the Oak Ridge National Laboratory, in 1957. I soon learned that instability was the issue, and began looking for the most general ways to recognize a stable state.
Alston Householder, then head of mathematics at Oak Ridge, suggested that I look at the work of the Russian mathematician A. M. Lyapunov, who in the late 1800s had found exact criteria for the stability of mechanical systems (LaSalle & Lefschetz Reference LaSalle and Lefschetz1961). In effect, a Lyapunov stability function is a ‘potential well’. The depth of this potential well is the ‘free energy’, giving the maximum energy in fluctuations from which one could estimate limits on turbulent diffusion coefficients. Lyapunov’s theory concerns finite matrices. By 1962, I had submitted a paper extending his theory to plasma fluids (Fowler Reference Fowler1963).
3 Free energy estimates of transport
My first result applying Lyapunov’s theory to the plasma Vlasov equation soon led me to the Gibbs free energy. Lyapunov’s criterion states that, writing the linearized Vlasov equation as
$\unicode[STIX]{x2202}f_{1}/\unicode[STIX]{x2202}t=Vf_{1}$
, stability requires that the operator V must be transformable to an Hermitian positive-definite operator. In Fowler (Reference Fowler1961), I was able to formulate the known stability of a Maxwellian equilibrium
$g=C_{1}\exp (-E/T)$
as a Lyapunov Hermitian operator, giving, for electrostatic perturbations, in centimeter-gram-second (cgs) units:
$$\begin{eqnarray}H=\unicode[STIX]{x1D6F4}_{j}\int \text{d}\boldsymbol{x}\,\text{d}\boldsymbol{v}[1/2T_{j}(f_{1j}^{2}/g_{j})]+\int \text{d}\boldsymbol{x}(\unicode[STIX]{x1D700}_{o}(-\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D6F7}_{1})^{2}/8\unicode[STIX]{x03C0}),\end{eqnarray}$$
where
$\unicode[STIX]{x1D6F4}$
sums over charge species and
$\unicode[STIX]{x1D700}_{o}$
is a dielectric constant.
I will defer my Lyapunov-based derivation of (3.1) to § 5.1. Here I note that, as was first shown by Newcomb (see appendix, Bernstein Reference Bernstein1958), the first term in (3.1) can be interpreted as an expansion of the Gibb’s free energy
$G(f)$
in powers of
$f_{1}=f-g$
, giving, to second order in
$f_{1}$
:
$$\begin{eqnarray}\displaystyle G(f) & = & \displaystyle fE+Tf\ln (f/C_{1})-T(f-g)\nonumber\\ \displaystyle & = & \displaystyle fE+Tf[(-E/T)+f_{1}/g-1/2(f_{1}/g)^{2}+\cdots \,]-Tf_{1}\nonumber\\ \displaystyle & = & \displaystyle 1/2T(f_{1}^{2}/g)+\cdots\end{eqnarray}$$
Here
$(f\ln f)$
is negative entropy, and
$f$
and
$g$
are normalized to conserve particles so that the added term
$T(f-g)$
integrates to zero.
In Fowler (Reference Fowler, Simon and Thompson1968), I used the Gibb’s free energy to obtain exact nonlinear bounds on kinetic free energy, the free energy being the excess energy in any equilibrium
$f_{o}$
relative to a neighbouring Maxwellian equilibrium. But because
$g$
is stable, the excess energy of nearby equilibria will be small so that the linearized theory in (3.1) gives a good estimate. The idea is to interpret
$f=\unicode[STIX]{x1D6FF}f+f_{o}\approx f_{o}$
if the actual fluctuation
$\unicode[STIX]{x1D6FF}f\ll f_{o}$
. The same idea applies to the linearized MHD free energy
$\unicode[STIX]{x1D6FF}W$
(Bernstein et al.
Reference Bernstein, Frieman, Kruskal and Kulsrud1958).
Two weaknesses in the theory were uncertainty in the dielectric constant representing a coupling of electrostatic energy to non-resonant kinetic effects; and the necessity, for magnetically confined plasmas, to limit the spatial integration volume to a loosely specified local volume of interest with a thickness that could be interpreted as an unknown correlation length (Fowler Reference Fowler, Simon and Thompson1968). Brizard et al. (Reference Brizard, Fowler, Hua and Morrison1991) showed that gyrokinetic theory automatically introduces a dielectric constant which, when extremized, gives the tokamak hierarchy of unstable modes from MHD to drift waves.
3.1 Transport by two-stream instability
An obvious test case concerns the free energy due to two-stream instability between streaming electrons and stationary ions, represented by an electron distribution with
$f_{oe}=N\exp [-(E-up_{z})/T_{e}]$
, to be compared with a Maxwellian
$g=C_{1}\exp (-E/T)$
where
$T$
is a free parameter. Adjusting
$T=T_{e}$
to minimize the free energy gives a free energy per electron approximately equal to the total electron energy
$1/2m_{e}u^{2}$
(Fowler Reference Fowler, Simon and Thompson1968, Krall & Trivelpiece Reference Krall and Trivelpiece1973). Then the diffusion coefficient spreading momentum of the electron stream is bounded by
$D<p_{e}^{2}/\unicode[STIX]{x1D70F}$
where
$p_{e}=m_{e}u$
and
$\unicode[STIX]{x1D70F}$
is the appropriate correlation time. If ions stream through stationary electrons, the result is the same as seen in the reference frame of the ions.
That
$(1/\unicode[STIX]{x1D70F})$
can also be bounded, as the rate of change of the free energy, was shown in Fowler (Reference Fowler1964), giving
$(1/\unicode[STIX]{x1D70F})<1/2d(\ln H)/\text{d}t\approx \unicode[STIX]{x1D714}_{pe}(H^{\ast }/m_{e}v_{e}^{2})^{1/2}$
where
$H^{\ast }$
is the free energy per electron. Thus, not surprisingly, the two-stream momentum diffusion coefficient is bounded by
$D<p_{e}^{2}\unicode[STIX]{x1D6FE}$
for growth constant
$\unicode[STIX]{x1D6FE}<\unicode[STIX]{x1D714}_{pe}$
, similar to results from quasi-linear theory (Kadomtsev Reference Kadomtsev1965).
3.2 Free energy estimates of synchrotron radiation in astrophysical jets
I used my free energy method to estimate transport in a recent paper on properties of an astrophysical jet modelled as a magnetically collimated ‘screw-pinch’ carrying current (Colgate et al.
Reference Colgate, Fowler, Li, Hooper, McClenaghan and Lin2015). These jets are observed by the synchrotron radiation they emit as a consequence of electron acceleration, taken here to be due to MHD kink modes in the pinch. The energy source is fluctuations in the magnetic field. It is observed in laboratory experiments that these fluctuations correlate to give (in cgs units) an electric acceleration
$\boldsymbol{E}=c^{-1}\langle \boldsymbol{v}_{1}\boldsymbol{x}\boldsymbol{B}_{1}\rangle$
where
$\langle \cdots \,\rangle$
indicates a symmetric ‘mean-field’ average (Rusbridge, Gee & Browning Reference Rusbridge, Gee and Browning1997).
For this purpose I took the free energy to be the magnetic energy with constant magnetic helicity
$K=\int \text{d}\boldsymbol{x}(\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B})$
serving as the entropy (similar to Taylor’s theory of magnetic relaxation in reversed field pinches (Taylor Reference Taylor1986)). Here
$\boldsymbol{A}$
is the vector potential giving a magnetic field
$\boldsymbol{B}=\unicode[STIX]{x1D735}\times \boldsymbol{A}$
. Consider a cylindrical jet in the
$z$
direction, giving as the free energy
$\unicode[STIX]{x0394}E$
for a jet of length
$L$
:
$$\begin{eqnarray}\unicode[STIX]{x0394}E=E-\unicode[STIX]{x1D706}_{o}K/(8\unicode[STIX]{x03C0})=(1/4)L\int _{0}^{R1}r\,\text{d}r\,\boldsymbol{B}\boldsymbol{\cdot }(\boldsymbol{B}-\unicode[STIX]{x1D706}_{o}\boldsymbol{A}),\end{eqnarray}$$
where
$\unicode[STIX]{x1D706}_{o}$
is a constant value of
$\unicode[STIX]{x1D706}=(4\unicode[STIX]{x03C0}j_{z}/cB_{z})$
for current density
$j_{z}$
. Variation on
$R_{1}$
was used to show that
$\unicode[STIX]{x0394}E$
is positive only for perturbations localized to the main current channel of the jet.
Taylor’s prescription says that
$\unicode[STIX]{x0394}E=0$
if
$j_{z}(r)$
relaxes so that
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}_{o}$
all across the channel. However, for a jet growing in length, relaxation is not abrupt. Rather, relaxation proceeds more and more slowly as
$\unicode[STIX]{x1D706}(r)$
flattens but never stops for the duration of the jet. Thus one can approximate the coefficient
$D_{r}$
that spreads the current radially across a channel of radius
$R$
simply as
$D_{r}=R^{2}/t$
for a duration
$t$
. By Ohm’s law
$E_{z}=-c^{-1}v_{r}B_{\unicode[STIX]{x1D719}}$
with
$v_{r}=D/R=R/t$
. Then the voltage drop along a jet of length
$L$
is given by
$\unicode[STIX]{x0394}V=t(\text{d}L/\text{d}t)E_{z}=t(0.01c)(R/ct)B_{\unicode[STIX]{x1D719}}=0.01V$
using the total voltage
$V\approx RB_{\unicode[STIX]{x1D719}}$
and
$\text{d}L/\text{d}t=0.01c$
derived in Colgate et al. (Reference Colgate, Fowler, Li, Hooper, McClenaghan and Lin2015). Thus only 1 % of the jet power is utilized in accelerating both ions and electrons, or 0.5 % into the electrons. Then the synchrotron power should be only 0.5 % of the total jet power (‘luminosity’), in reasonable agreement with observations (Krolik Reference Krolik1999).
4 Existence theorem for Lyapunov functions
It was the nonlinear thermodynamic approach in § 3 that caused me and others to characterize the free energy problem as a search for better entropy functions conserved by the nonlinear Vlasov equation – for example, one displaying Landau damping (which is actually reversible, as in plasma echoes). In this paper I suggest sticking with linear theory and search instead for new ways to transform the Vlasov operator
$V$
to Hermitian form.
That linearized plasma dynamics can always be put in Hermitian form can be seen as follows (Fowler Reference Fowler1963, Reference Fowler, Simon and Thompson1968). Let a fluid be represented by a vector
$\unicode[STIX]{x1D6F9}$
that changes in time via a Markovian operator
$T$
, giving:
$$\begin{eqnarray}\displaystyle T(t+\unicode[STIX]{x1D6E5})=T(\unicode[STIX]{x1D6E5})T(t) & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F9}(t+\unicode[STIX]{x1D6E5})=T(\unicode[STIX]{x1D6E5})\unicode[STIX]{x1D6F9}(t). & & \displaystyle\end{eqnarray}$$
$L$
of the form (Fowler Reference Fowler, Simon and Thompson1968): 
$$\begin{eqnarray}\displaystyle & \displaystyle L=\int _{t}^{\infty }\text{d}t^{\prime }[\unicode[STIX]{x1D6F9}(t^{\prime }),C^{\ast }\unicode[STIX]{x1D6F9}(t^{\prime })]=\left(\unicode[STIX]{x1D6F9}(t),\left[\int _{0}^{\infty }\,\text{d}sH\right]\unicode[STIX]{x1D6F9}(t)\right) & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle H=[T^{+}(s)C^{\ast }T(s)]. & \displaystyle\end{eqnarray}$$
$C^{\ast }$
is any positive-definite Hermitian normalization and
$T^{+}$
is the Hermitian conjugate, giving an Hermitian form for
$H$
.
The operator
$H$
can yield a Lyapunov stability function
$L$
if also the time integration yields a finite result, true if
$H$
itself is an Hermitian positive-definite operator. The formal solution of the Vlasov equation is
$T=\exp Vt$
, from which:
$$\begin{eqnarray}L=\left(\unicode[STIX]{x1D6F9}(t),\left[\int _{0}^{\infty }\,\text{d}s(\exp V^{+}sC^{\ast }\exp Vs)\right]\unicode[STIX]{x1D6F9}(t)\right).\end{eqnarray}$$
5 Factoring the Vlasov operator: two examples
Lyapunov theory says that
$V$
must be transformable to Hermitian form if solutions of
$\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}t=Vf$
are stable. In Fowler (Reference Fowler1961, Reference Fowler1963), I used known matrix properties stating that
$V$
can be transformed to an Hermitian operator if
$V$
itself is factorable, giving a product
$V=AH$
where
$H$
is Hermitian and
$A$
is anti-Hermitian.
5.1 Factoring in classical theory
Factorability can be illustrated for Maxwellian distributions with constant density, giving (3.1) as follows. Write
$V$
for electrostatic perturbations as:
$$\begin{eqnarray}\displaystyle & \displaystyle Vf_{1}=v\unicode[STIX]{x2202}f_{1}/\unicode[STIX]{x2202}x+(e/m)(-\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}_{1}/\unicode[STIX]{x2202}x)\unicode[STIX]{x2202}f_{o}/\unicode[STIX]{x2202}v & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F7}f_{1}=\text{e}\int \text{d}x^{\prime }\,\text{d}v^{\prime }[(f_{1}(x^{\prime },v^{\prime })/|x-x^{\prime }|] & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle V=[-(2v\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x)(\unicode[STIX]{x2202}f_{o}/\unicode[STIX]{x2202}E)][(-1/2(\unicode[STIX]{x2202}f_{o}/\unicode[STIX]{x2202}E)^{-1}+1/2e\unicode[STIX]{x1D6F7}]=AH & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}A=[-(2v\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x)(\unicode[STIX]{x2202}f_{o}/\unicode[STIX]{x2202}E)];\quad H=[-1/2(\unicode[STIX]{x2202}f_{o}/\unicode[STIX]{x2202}E)^{-1}+1/2e\unicode[STIX]{x1D6F7}],\end{eqnarray}$$
where
$E=1/2mv^{2}$
. The operator
$V$
is a combination of differential and integral operators, the potential in (5.1b
) being an integral operator. In (5.1c
), we have used
$\unicode[STIX]{x2202}f_{o}/\unicode[STIX]{x2202}x=0$
to factor out, first,
$v\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x$
, then (
$\unicode[STIX]{x2202}f_{o}/\unicode[STIX]{x2202}E$
), giving an anti-Hermitian factor
$A$
and Hermitian
$H$
,
$(\unicode[STIX]{x2202}f_{o}/\unicode[STIX]{x2202}E)^{-1}$
being a scalar Hermitian operator, and
$\unicode[STIX]{x1D6F7}$
being an Hermitian integral operator. It is straightforward to add magnetic interactions using the vector potential (Fowler Reference Fowler1962). Potentials rather than fields are to be preferred, in anticipation of always casting dynamics as the motion of interacting particles, in § 6.
For a stable Maxwellian
$f_{o}=C_{1}\exp (-E/T)$
, the matrix element
$(f_{1},Hf_{1})=\int \text{d}x\,\text{d}v(f_{1}^{\ast }Hf_{1})$
gives the free energy in (3.1). To see this, note that the kinetic term
$\propto T/2$
is correct for one dimension, while integrating the electric field energy by parts gives
$\int \text{d}x\,\text{d}vef_{1}(1/2\unicode[STIX]{x1D719}_{1})=1/2\int \text{d}x\,en_{1}\unicode[STIX]{x1D719}_{1}=\int \text{d}x(1/8\unicode[STIX]{x03C0})(-\unicode[STIX]{x2202}E_{1}/\unicode[STIX]{x2202}x)\unicode[STIX]{x1D719}_{1}=\int \text{d}x(1/8\unicode[STIX]{x03C0})(-\unicode[STIX]{x2202}\unicode[STIX]{x1D719}_{1}/\unicode[STIX]{x2202}x)^{2}$
. In addition to Maxwellians, stability follows also for any
$f_{o}$
that is a monotonic-decreasing function of the energy
$E$
, again corresponding to a nonlinear entropy of the form
$G(f)$
, any such
$G$
being a constant of the motion for the Liouville equation (Kruskal & Oberman Reference Kruskal and Oberman1958).
While the linearized Vlasov equation can be sufficient to calculate the finite free energy of equilibria close to a stable state, to my knowledge there is still no systematic analytic procedure to factor the linearized classical Vlasov operator into Hermitian and anti-Hermitian parts, even though Lyapunov theory in § 4 says that this is always possible.
5.2 Quantum plasmas
The difficulty in factoring the classical Vlasov operator concerns the addition of Hermitian electromagnetic interactions with anti-Hermitian kinetics. By contrast, quantum kinetics, written as
$v\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x\rightarrow h\unicode[STIX]{x2202}^{2}/\unicode[STIX]{x2202}x^{2}$
, with Planck constant
$h$
, is already Hermitian. Indeed, if one had applied Lyapunov theory to derive a wave equation, an equation with a Hermitian Hamiltonian operator would have been the natural outcome, trivially factorable as
$H$
times unity. And the formal Lyapunov solution would yield Feynman path integrals, analogous to (4.4).
An important difference between the classical and quantum versions of Lyapunov theory is that, despite appearances, the quantum version is already ‘nonlinear’. In classical Vlasov theory, nonlinear has meant that one writes the ‘state’
$f$
(the distribution function) as
$f=f_{o}+f_{1}$
for a given
$f_{o}$
and then discards
$f_{1}^{2}$
in the dynamics. In quantum theory, dynamics always looks ‘linear’ in the state
$\unicode[STIX]{x1D713}$
(wave function), with
$\unicode[STIX]{x2202}\unicode[STIX]{x1D713}/\unicode[STIX]{x2202}t=H\unicode[STIX]{x1D713}$
. But, since nothing is discarded, the ‘nonlinearity’ has been hidden in
$H$
. An example is multiple-scattering theory, in which
$H$
describing multiple interactions among particles is expanded in powers of a scattering operator for each particle with kinetic ‘propagators’ between scattering events (Goldberger & Watson Reference Goldberger and Watson1964).
6 Semi-classical quantum free energy
My first thoughts about Lyapunov theory as quantum mechanics came from my observation many years ago that a classical Lyapunov function could be obtained from classical path integrals resembling Feynman’s quantum path integrals, as in (4.4). More recently, I learned that John Dawson had similar ideas. Inspired by Dawson’s suggestion, in his PhD thesis Dean E. Dauger developed a quantum version of a Particle-In-Cell (PIC) simulation code that showed by several examples that this was an expeditious way to calculate classical dynamics, as Feynman path integrals converging on semi-classical paths in the appropriate limits.
I was especially prepared to appreciate what Dauger had accomplished, from my own PhD thesis applying quantum multiple-scattering theory, also in semi-classical limits. But on thinking about it, I realized that, like multiple-scattering expansions, path integrals are beside the point if the goal is to find a better way to calculate free energy, free energy being the ultimate way to avoid having to know anything about detailed dynamical solutions.
6.1 Advantages and disadvantages of a quantum PIC theory
Four important differences between a classical-mechanical and a quantum-mechanical PIC representation of plasmas are:
-
(i) The Vlasov equation is six-dimensional
$(\boldsymbol{x},\boldsymbol{v})$
while the Schrödinger equation is three-dimensional
$(\boldsymbol{x})$
. -
(ii) Quantum mechanics is three-dimensional because it represents classical momentum as a spatial derivative (
$-ih\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x$
) (the square being Hermitian). -
(iii) The fact that the Schrödinger Hamiltonian
$H$
is already Hermitian means that dynamics is determined by the eigenstates of
$H$
. -
(iv) Planck’s constant determines spatial scales where dynamics becomes non-classical.
6.2 Adjusting the Planck constant
Like a quantum wave function, a PIC state is not a fluid: it is a collection of individual particles probing kinetic effects at the deepest levels. In quantum mechanics, the classical fluid representation of a single ion as a delta function
$\unicode[STIX]{x1D6FF}(v-v_{o})$
becomes a ‘wave packet’ in quantum mechanics (Schiff Reference Schiff1949). Quantum PIC cells are wave packets. At temperatures of interest in fusion research and many other plasma applications, binding energy to form atoms is irrelevant, so that all dynamics becomes the dynamics of wave packets, Planck’s constant
$h$
serving only to determine spatial wavelengths inside the PIC wave packet, giving a wavelength
$\unicode[STIX]{x1D706}=h/p$
for momentum
$p$
. Then nothing is lost at classical scales if we increase
$h$
for numerical convenience. For our purposes,
$h$
should be regarded as an adjustable parameter, chosen to be the largest value that does not change the answer.
The quantum mechanical
$H$
is still Hermitian for any fixed value of
$h$
. Thus, as noted in item (iii) above, all dynamics (and the free energy) reduces to a calculation of eigenstates. Determining the eigenstates determines the dynamics.
6.3 PIC eigenstates states
Constructing eigenstates requires a large sampling of states from which a Hamiltonian matrix can be constructed and diagonalized to obtain the eigenstates. Since the Hamiltonian is known, the job of constructing quantum eigenstates can be done once and for all, given a desired geometry such as a tokamak.
From the point of view of plasma theory, calculating eigenstates in any detail probably requires a computer effort comparable to dynamical calculations. But from the point of view of a machine designer, the information in eigenstates separates out system responses that the designer cannot control from those that can be designed. Empirical scaling laws are an example.
How to use computers to construct quantum plasma states was a large part of Dauger’s thesis. What I am suggesting is that this part of Dauger’s work is all we need to determine the free energy of any system, or any other measure of performance. Dauger developed a precise way to construct plasma quantum states, efficient enough to allow him to reconstruct these states after each dynamical time step. I refer the interested reader to his thesis, available online (Dauger Reference Dauger2001).
To summarize: I propose only to adapt Dauger’s technique to construct quantum PIC eigenstates. Given the eigenstates, Dauger’s dynamical PIC code integrating Feynman paths would not be needed. Because the dynamics is Hermitian, the eigenstates are all we need to know.
6.4 Scaling laws
Given the eigenstates, any measurable quantity expressible as a quantum mechanical operator can be calculated. An example is to add to the Hamiltonian an operator
$P$
representing neutral beam injection (or other power sources) and from this construct steady states giving –
$(\unicode[STIX]{x1D713},H\unicode[STIX]{x1D713})=(\unicode[STIX]{x1D713},P\unicode[STIX]{x1D713})$
. The power required is a direct measurement of energy confinement. Similarly, one can add thermonuclear reactions giving then conditions for ignition.
My expectation would be that enough calculations of this sort could be done to develop scaling laws that could be benchmarked against experimental data and PIC or other simulations, all correct methods giving the same results. If so, physics-based scaling laws could replace the empirical scaling that has thus far been the only guide to design machines like the International Thermonuclear Experimental Reactor (ITER).
7 Summary
The conservation of entropy as a constraint in nonlinear Vlasov plasma dynamics has provided useful guidance in estimating plasma free energy governing plasma transport processes in various applications, including a new result in astrophysics discussed in § 3.2.
In this paper, I have traced the deeper reason to be the hidden Hermitian nature of the classical Vlasov operator linearized around a stable state, while the quantum counterpart is the exact Schrödinger Hamiltonian operator that is already Hermitian. From this, I have speculated that it might be profitable to formulate plasma dynamics as quantum transitions among calculable eigenstates, with Planck’s constant adjusted to classical scales, as suggested in § 6.2.
The necessary task is the construction of eigenstates as PIC plasma waves, a method already pioneered in Dean E. Dauger’s PhD thesis cited in § 6. As an example application, I noted that adding enough neutral beam power to the Hamiltonian to achieve steady state would be a direct way to calculate energy leakage, in a form most useful to machine designers.
Thinking quantum mechanically may require less work in the long run, but a new intuition. One might begin by benchmarking quantum PIC calculations of the energy to known results from the ‘linear tokamak’ previously used both for MHD studies (Freidberg Reference Freidberg2015) and for drift waves yielding kinetic transport in tokamaks (Rosenbluth & Rutherford Reference Rosenbluth, Rutherford and Teller1981). The possibility of developing scaling laws, as discussed in § 6.4, might also be tested on linear tokamaks, for which equilibria are one-dimensional. The free energy would just be the difference in energy between neighbouring equilibria found to be accessible through eigenstates containing three-dimensional turbulence; or equivalently, the power required to give steady state, as in § 6.4. Test cases at zero pressure compared to the field (low
$\unicode[STIX]{x1D6FD}$
) could represent external magnetic fields by a scalar potential. Boundary conditions representing machine walls or a magnetic divertor are likely to be very important, since joining the hot plasma to its environment is known to play a large role in heat loss (the tokamak ‘pedestal’, etc.).
Exploring what I am suggesting would take work. But if past experience is a guide, a more exact method to calculate free energy would be worth the effort – both for new applications and for magnetic fusion at a time when ever larger experiments require more and more time to construct and operate.
Or so I have claimed.
In Fowler (Reference Fowler1997), I wrote, with reference to PIC simulations as a new way to conduct ‘pseudo-experiments’ on the computer: ‘It is here that the free energy principle will come into its own …[by] helping …to pose the right questions in the familiar language of thermodynamics’.
Acknowledgements
I thank G. Morales for making me aware of Dauger’s thesis, and I thank the reviewers for suggestions helping me to improve the paper.
