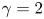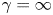1. Introduction
In Part 1 of this two-part series, an analytic solution was derived for tokamak equilibria satisfying the Grad–Shafranov equation. The solutions describe equilibria with arbitrary 
$\beta ,\varepsilon ,\kappa ,\delta ,{q_\ast }$. Also, a wide variety of plasma surface shapes are allowed including D-shapes, inverse D-shapes, smooth surfaces, double-null divertor surfaces and single-null divertor surfaces. The profiles are smooth with the pressure, pressure gradient and current density vanishing at the plasma edge. The solutions are obtained for a special class of the two free functions for which the pressure gradient 
$\textrm{d}p(\psi )/\textrm{d}\psi $ and toroidal field diamagnetic gradient 
$\textrm{d}{F^2}(\psi )/\textrm{d}\psi $ are linear in the flux 
$\psi $. Solutions are derived by separation of variables. Importantly, an underutilized mathematical insight provides us with a good prescription for choosing the separation constants. It is this insight that makes the analytic procedure so robust.
In this paper, the analytic solutions obtained in Part 1 are generalized to include the effects of (i) edge pedestals, (ii) an edge-localized contribution to the bootstrap current and (iii) toroidal flow. Here, a pedestal is defined as a step function jump in a physical quantity of interest at the plasma edge. The structure within the pedestal is not resolved in our analytic model. Such jumps affect the values of certain physical parameters of interest as well as the shape and shift of the core flux surfaces.
Consider first an edge pedestal in the pressure and an edge-localized contribution to the bootstrap current. These effects, using our step function pedestal approximation, result in surface currents. Specifically, these are a perpendicular contribution from the pressure jump and a parallel contribution from the bootstrap current. They are characterized by two additional input parameters, 
${f_P}$ representing the fractional height of the pressure pedestal and 
${f_B}$ representing the fraction of the total bootstrap current localized to the edge region. The analysis shows that these two effects leave the solutions obtained in Part 1 unchanged. The main results are a determination of the jump conditions describing the toroidal and poloidal edge magnetic fields. The fields just outside the surface currents are needed for the post-processing evaluation of several of the plasma parameters of interest, but as stated, do not affect the interior solutions.
The next topics of interest are edge pedestals in the pressure gradient and toroidal current density. Mathematically, the inclusion of such pedestals requires a modification of the free functions 
$p^{\prime}$ and 
$FF^{\prime}$, both initially linear in 
$\psi $. A constant in 
$\psi $ Solov'ev contribution must be added to each function. The solutions remain analytic, although there is a modification to the solution procedure which is described in the main text. In principle, both pedestals are independent. In practice, we focus on the current density pedestal. There is a corresponding non-zero pressure gradient pedestal, but its value, while turning out to be realistic, is not allowed to be a free choice. Instead, it is chosen to have a specific value that greatly simplifies the mathematical analysis allowing for an analytic solution. Also, we recognize that while actual plasmas often distinguish between density and temperature pedestals, the magnetohydrodynamic (MHD) model can only include the combined effects appearing in the pressure. A new parameter 
${f_J}$ is introduced which must be specified as an input. It represents the fractional height of the edge toroidal current density pedestal.
The last new effect of interest is toroidal flow. The modified Grad–Shafranov equation including both toroidal and poloidal flow is well known (Zehrfeld & Green Reference Zehrfeld and Green1972; Maschke & Perrin Reference Maschke and Perrin1980; Morozov & Solov'ev Reference Morozov and Solov'ev1980; Hameiri Reference Hameiri1983; Semenzato, Gruber & Zehrfeld Reference Semenzato, Gruber and Zehrfeld1984; Iacono et al. Reference Iacono, Bondeson, Troyon and Gruber1990). We focus on the limit of zero poloidal flow. In this limit one new free function appears on the right-hand side of the Grad–Shafranov equation: 
$M(\psi )$, the toroidal Mach number. By choosing 
$M = \textrm{const}\textrm{.}$, the effects of flow are still present and non-trivial. This choice allows analytic solutions for two values of the ratio of specific heats 
$\gamma $: 
$\gamma = 2$ corresponding to a two-degree-of-freedom adiabatic energy conservation relation and 
$\gamma = \infty $ corresponding to incompressible flow.
The final result is a generalized analytic solution to the Grad–Shafranov equation. As in Part 1, the solutions describe smooth symmetric limiter surfaces, double-null divertor surfaces and single-null divertor surfaces. The aspect ratio is arbitrary. The plasma 
$\beta $ and kink safety factor 
${q_\ast }$ both have arbitrary amplitudes. The plasma profiles, however, no longer need to vanish on the plasma surface. Pedestals in the pressure, pressure gradient and current density are now allowed to be non-zero. An edge bootstrap current and finite toroidal flow are also allowed. All of these effects are included simultaneously in our analytic solutions and represent the main contribution of Part 2.
For context, we can ask how the additional effects included in Part 2 compare with others already existing in the literature. The effects of surface currents have been treated in specialized sharp boundary tokamak models (see e.g. Freidberg & Grossmann Reference Freidberg and Grossmann1975; D'Ippolito et al. Reference D'Ippolito, Freidberg, Goedbloed and Rem1978) but not to our knowledge in smooth profile models such as considered here. The effects of edge pedestals have been treated by several authors (Solov'ev Reference Solov'ev1968; Freidberg Reference Freidberg1985; Zheng, Wootton & Solano Reference Zheng, Wootton and Solano1996; Weening Reference Weening2000; Shi Reference Shi2005; Cerfon & Freidberg Reference Cerfon and Freidberg2010). Our contribution here is a simpler, more robust procedure for calculating equilibria for general shaped plasma surfaces. Flow has also been treated previously (Clemente & Farengo Reference Clemente and Farengo1984; Throumoulopoulos & Pantis Reference Throumoulopoulos and Pantis1989; Del Zanna & Chiuderi Reference Del Zanna and Chiuderi1996; Tsui et al. Reference Tsui, Navia, Serbeto and Shigueoka2011; Haverkort, de Blank & Koren Reference Haverkort, de Blank and Koren2012; Kuiroukidis & Throumoulopoulos Reference Kuiroukidis and Throumoulopoulos2014) but only for the simpler Solov'ev profiles for 
$p^{\prime}$ and 
$FF^{\prime}$. An exception is the more general solution introduced by Kaltsas, Kuiroukidis & Throumoulopoulos (Reference Kaltsas, Kuiroukidis and Throumoulopoulos2019), which, however, only considers incompressible flows and regular D-shaped tokamaks (even though one can easily see ways for it to be extended).
In summary, we believe our solutions represent a useful next step towards the goal of obtaining analytic solutions to the Grad–Shafranov equation including increasingly more realistic plasma phenomena. As with Part 1, readers wanting a copy of our code should contact the first author (L.G. at lzg0022@auburn.edu).
2. Current status of the analysis
The normalized Grad–Shafranov equation from which we have derived analytic solutions is repeated here for convenience:
\begin{equation}\left. \begin{gathered} {(1 + \hat{\varepsilon }x)\dfrac{{{\partial^2}\psi }}{{\partial {x^2}}} + \dfrac{1}{{1 + {\varepsilon^2}}}\dfrac{{{\partial^2}\psi }}{{\partial {y^2}}} ={-} {\alpha^2}(1 + \hat{\varepsilon }\nu x)\psi \quad \psi (\textrm{surf)} = 0\quad \psi (\textrm{axis)} = 1,}\\ {\hat{\varepsilon } = \dfrac{{2\varepsilon }}{{1 + {\varepsilon^2}}} < 1,}\\ {{\alpha^2} = \dfrac{{2R_0^2{a^2}}}{{\varPsi _0^2}}\left( {{\mu_0}{p_0} + \dfrac{{{B_0}\delta B}}{{1 + {\varepsilon^2}}}} \right) \ge 0,}\\ {\nu = \dfrac{{{\mu_0}{p_0}}}{{{\mu_0}{p_0} + {B_0}\delta B/(1 + {\varepsilon^2})}} \ge 0,}\\ {p(\varPsi ) = {p_0}{{\left( {\dfrac{\varPsi }{{{\varPsi _0}}}} \right)}^2},}\\ {{F^2}(\varPsi ) = R_0^2B_0^2\left[ {1 + \dfrac{{2\delta B}}{{{B_0}}}{{\left( {\dfrac{\varPsi }{{{\varPsi _0}}}} \right)}^2}} \right],}\\ {\varPsi = {\varPsi _0}\psi ,}\\ {R = {R_0}{r^{1/2}} = {R_0}{{(1 + {\varepsilon^2} + 2\varepsilon x)}^{1/2}},}\\ {Z = ay.} \end{gathered} \right\}\end{equation}Solutions have been obtained by separation of variables:
\begin{equation}\left. \begin{gathered} {\textbf{Up}\textrm{ - }\textbf{down}\;\textbf{symmetric}}\\ {\psi (x,y) = {c_1}\cos ({h_1}y){C_1}(x) + \sum\limits_2^4 {\cos ({h_n}y)[{c_n}{C_n}(x) + {s_n}{S_n}(x)]} .}\\ {\textbf{Up}\textrm{ - }\textbf{down}\;\textbf{asymmetric}}\\ \begin{array}{l} \psi (x,y) = {c_1}\cos ({h_1}y){C_1}(x) + \sum\limits_2^4 {\cos ({h_n}y)[{c_n}{C_n}(x) + {s_n}{S_n}(x)]} \\ \quad + {c_5}\sin ({h_1}y){C_5}(x) + \sum\limits_2^3 {\sin ({h_n}y)[{c_{n + 4}}{C_n}(x) + {s_{n + 4}}{S_n}(x)]} . \end{array} \end{gathered}\right\}\end{equation}
The functions 
${C_n}(x),{S_n}(x)$ are cosine-like and sine-like. They are a particularly convenient power-series expansion of Whittaker functions, which are given in Appendix A of Part 1 and in Appendix B of this paper by setting the as yet undefined Mach number parameter 
${M_0} = 0$. The expansion coefficients 
${c_n},{s_n}$ and eigenvalue 
$\alpha $ are determined by satisfying a set of constraints which require the analytic solution to match the function, slope and curvature of a desired model surface at three (for symmetric) and four (for asymmetric) points. The constraints are summarized in table 1. In this table the values of 
${x_\delta },\kappa $ are to be evaluated at the smooth maxima or X-point as appropriate. The coefficients 
${\varLambda _j}$ depend on the shape of the desired model surface and are given in Part 1. All quantities will again be defined in this paper, Part 2, as required.
Table 1. Constraints determining the expansion coefficients 
${c_n},\;{s_n}$.
3. Surface current effects
The analytic solutions obtained in Part 1 assume smooth edge conditions – the pressure, pressure gradient and toroidal current density all vanish on the plasma surface. However, in many tokamak experiments there are boundary phenomena that produce highly localized edge currents. In the context of our analytic solutions, these localized currents can be approximated by ideal surface currents.
The surface currents have no direct impact on the flux surfaces calculated in Part 1. The analytic solutions remain unchanged. What do change are the values of some of the post-processing plasma physics parameters. The reason is that certain parameters are defined in terms of magnetic fields external to the surface current rather than the internal fields, which are the ones corresponding to our analytic solutions. The net result is that many of the previously derived results are still valid but must be renormalized. The goal in this section is to derive the appropriate jump conditions for the fields across the surface currents to allow a quantitative determination of the renormalized plasma parameters.
3.1. Sources of surface current
As stated in § 1, there are two sources of surface currents. First, even if the pressure gradient and toroidal current density vanish smoothly at the plasma edge, there can still be a finite edge pressure, creating a pressure pedestal. From MHD pressure balance across the surface, it follows that this pressure jump must be balanced by a perpendicular surface current; that is, the current direction is perpendicular to both the surface normal and the average magnetic field across the current sheet. Its magnitude is proportional to the difference in fields across the current sheet. Mathematically, the pressure pedestal can be modelled by leaving the free function 
${F^2}(\varPsi /{\varPsi _0})$ unchanged but modifying 
$p(\varPsi /{\varPsi _0})$ in the plasma core as follows:
\begin{equation}p(\varPsi /{\varPsi _0}) = {p_0}{\left( {\frac{\varPsi }{{{\varPsi _0}}}} \right)^2} \to p(\varPsi /{\varPsi _0}) = {p_0}\left[ {{f_P} + (1 - {f_P}){{\left( {\frac{\varPsi }{{{\varPsi _0}}}} \right)}^2}} \right].\end{equation}
Note that 
$p(\textrm{axis}) = p(1) = {p_0}$ and 
$p(\textrm{surf}) = p(0) = {f_P}{p_0}$. We see that 
${f_P} = p(\textrm{surf})/p(\textrm{axis)}$ is the fractional height of the pressure pedestal, and is an additional input quantity. A pressure jump leaves the normalized Grad–Shafranov equation unchanged, but with modified definitions of 
$\alpha $ and 
$\nu $:
\begin{equation}\left. \begin{gathered} {(1 + \hat{\varepsilon }x)\dfrac{{{\partial^2}\psi }}{{\partial {x^2}}} + \dfrac{1}{{1 + {\varepsilon^2}}}\dfrac{{{\partial^2}\psi }}{{\partial {y^2}}} ={-} {\alpha^2}(1 + \hat{\varepsilon }\nu x)\psi ,}\\ {{\alpha^2} = \dfrac{{2R_0^2{a^2}}}{{\varPsi_0^2}}\left[ {{\mu_0}{p_0}(1 - {f_P}) + \dfrac{{{B_0}\delta B}}{{1 + {\varepsilon^2}}}} \right],}\\ {\nu = \dfrac{{{\mu_0}{p_0}(1 - {f_P})}}{{{\mu_0}{p_0}(1 - {f_P}) + {B_0}\delta B/(1 + {\varepsilon^2})}}.} \end{gathered} \right\}\end{equation}The second component of surface current flows perpendicular to the surface but parallel to the average field across the surface. It is assumed to be generated by the portion of the total bootstrap current localized near the edge. This can be seen from the large-aspect-ratio approximation for the flux surface averaged bootstrap current given by (Helander & Sigmar Reference Helander and Sigmar2002)
\begin{equation}{J_B}(\psi ) \equiv \left\langle {\frac{{{\boldsymbol{J}_B}\boldsymbol{\cdot }\boldsymbol{B}}}{B}} \right\rangle \approx{-} 2.42{\varepsilon ^{1/2}}{R_0}p\left[ {\frac{1}{n}\frac{{\textrm{d}n}}{{\textrm{d}\psi }} + 0.054\frac{1}{T}\frac{{\textrm{d}T}}{{\textrm{d}\psi }}} \right].\end{equation}Near the edge, the density and temperature pedestals produce a large localized contribution to the bootstrap current, which corresponds to the parallel component of the surface current.
A convenient definition of the bootstrap fraction is described below. This definition focuses on the 
${\boldsymbol{e}_\phi }$ component of bootstrap current, which is simpler to measure experimentally as compared to the actual bootstrap current which flows parallel to the magnetic field. We denote the parallel surface current by 
${\boldsymbol{K}_\parallel } = {K_{{\parallel} \phi }}{\boldsymbol{e}_\phi } + {K_{{\parallel} P}}{\boldsymbol{e}_P}$, where 
${\boldsymbol{e}_P} = {\boldsymbol{B}_P}/{B_P}$ and 
${K_{{\parallel} \phi }}$ is the component of interest. The corresponding toroidal current generated by 
${K_{{\parallel} \phi }}$ is given by
\begin{equation}{I_{{\parallel} \phi }} = \oint {{K_{{\parallel} \phi }}\,\textrm{d}{l_P},}\end{equation}
with 
$\textrm{d}{l_P}$ the differential poloidal arc length. Next, note that the total toroidal current flowing in the plasma is 
$\hat{I} = I + {I_{{\parallel} \phi }}$, where I is the contribution from the plasma core calculated in Part 1. The definition of the edge-localized portion of bootstrap current 
${f_B}$ is taken as
\begin{equation}{f_B} \equiv \frac{{{I_{{\parallel} \phi }}}}{{\hat{I}}} = \frac{{\hat{I} - I}}{{\hat{I}}} = 1 - \frac{I}{{\hat{I}}}.\end{equation} The quantity 
${f_B}$ is an additional input parameter.
3.2. Surface current analysis
The surface current analysis can now be carried out as follows. Assume we have obtained a smooth edge solution based on the analysis in Part 1. Specifically, we assume that just inside the surface current we know 
${B_\phi }(\theta )$ and 
${B_P}(\theta )$. Next, we give values for the two new surface current fractions 
${f_P}$ and 
${f_B}$. Using this information we calculate the fields just outside the surface current layer 
${\hat{B}_\phi }(\theta )$ and 
${\hat{B}_P}(\theta )$, leading to a self-consistent surface current constraint.
To begin, we make use of Ampere's law and pressure balance across the surface to derive expressions for 
${\hat{B}_\phi }(\theta )$ and 
${\hat{B}_P}(\theta )$. Consider first the toroidal magnetic field. The profiles just inside and outside the surface current are given by
\begin{align}\left. \begin{aligned} {B_\phi }(\theta ) &= {B_0}\dfrac{{{R_0}}}{{R(\theta )}}{\textrm{Inside}\;\textrm{field,}}\\ {{\hat{B}}_\phi }(\theta ) &= {{\hat{B}}_0}\dfrac{{{R_0}}}{{R(\theta )}}{\textrm{Outside}\;\textrm{field,}} \end{aligned} \right\}\end{align}
where the only new quantity is the as yet undetermined exterior central field amplitude 
${\hat{B}_0}$. Observe that 
${\hat{B}_0}$ is the actual vacuum toroidal field on axis, although for mathematical convenience we formulate the analysis in terms of 
${B_0}$, the vacuum field on axis in the absence of surface currents. The relationship between the outside and inside toroidal fields thus defines the poloidal surface current:
\begin{equation}{\mu _0}\frac{{{K_P}}}{{{B_0}}} = \frac{{{{\hat{B}}_\phi }}}{{{B_0}}} - \frac{{{B_\phi }}}{{{B_0}}} = ({\varDelta _B} - 1)\frac{{{R_0}}}{R}\quad {\varDelta _B} = \frac{{{{\hat{B}}_0}}}{{{B_0}}}.\end{equation} Hereafter, the unknown 
${\varDelta _B}$ replaces 
${\hat{B}_0}$ as the constant relating the two toroidal magnetic field profiles.
The relationship between the inside and outside poloidal magnetic fields is determined from the pressure balance jump condition:
\begin{equation}{\left[\kern-0.15em\left[ {p + \frac{{{B^2}}}{{2{\mu_0}}}} \right]\kern-0.15em\right]_{\textrm{Surf}}} = 0 \to 2{\mu _0}{f_P}{p_0} + B_p^2 + B_\phi ^2 = \hat{B}_p^2 + \hat{B}_\phi ^2,\end{equation}which can be rewritten as
\begin{equation}{\mu _0}\frac{{{K_\phi }}}{{{B_0}}} = \frac{{{{\hat{B}}_P}}}{{{B_0}}} - \frac{{{B_P}}}{{{B_0}}} = {\left[ {\frac{{B_P^2}}{{B_0^2}} + {\beta_0}{f_P} - (\Delta_B^2 - 1)\frac{{R_0^2}}{{{R^2}}}} \right]^{1/2}} - \frac{{{B_P}}}{{{B_0}}},\end{equation}
where again 
${\beta _0} = 2{\mu _0}{p_0}/B_0^2$. If for the moment we assume that 
${\varDelta _B}$ is known, then (3.9) expresses the outside poloidal field in terms of known quantities.
3.3. Evaluation of the jump conditions
We are now in a position to complete the evaluation of the surface current constraint. The practical procedure is as follows.
a. Calculate a smooth edge equilibrium as described in Part 1 assuming the geometry and
$\nu $ have been specified. Evaluate ${B_P}(\theta )/{B_0},\;{\beta _0},\;I/{B_0}$.b. Specify the additional pressure pedestal and bootstrap fractions
${f_P}$ and ${f_B}$.c. ‘Guess’ a value for
${\varDelta _B}$.d. Evaluate
${\hat{B}_P}(\theta )/{B_0}$ from (3.9).e. From (3.5) calculate
(3.10)\begin{equation}{f_B} = 1 - \frac{I}{{\hat{I}}} = 1 - \frac{{\oint {\dfrac{{{B_P}}}{{{B_0}}}\,\textrm{d}{l_P}} }}{{\oint {\dfrac{{{{\hat{B}}_P}}}{{{B_0}}}\,\textrm{d}{l_P}} }}.\end{equation}f. Iterate
${\varDelta _B}$ until ${f_B}$ is equal to the desired input value.g. Evaluate
${\hat{B}_\phi }(\theta )/{B_0}$ from (3.7).
Assuming this procedure is successfully carried out, we then have the required expressions for the field jumps across the surface currents. We emphasize that no modifications have been made to the solution procedure in Part 1 that calculates the core profiles. The same expansions and constraints still apply. Once the solution for 
$\psi (x,y)$ is obtained, we can then make use of the jump conditions to define and evaluate modified plasma parameters consistent with standard usage in the fusion community. Several plasma parameters are calculated and compared with the corresponding no-pedestal cases obtained in Part 1. However, we delay presenting these results until the end of the analysis, after a pressure gradient pedestal, current density pedestal and toroidal flow are included.
4. Pressure gradient and current density pedestals
The analysis can be further generalized to include additional edge pedestals. In principle, there are two such pedestals to consider in the MHD model: a pressure gradient pedestal and a toroidal current density pedestal. In practice, we focus on the current density pedestal. There is a corresponding non-zero pressure gradient pedestal, but its value, while turning out to be realistic, is not allowed to be a free choice. Instead, it is chosen to have a specific value that greatly simplifies the mathematical analysis, allowing for simple analytic solutions. In the end a single new free parameter 
${f_J}$ is introduced that must be specified as an input. Its value represents the fractional height of the edge current density pedestal.
4.1. Mathematical modifications to account for pedestals
Mathematically, the procedure to include pressure gradient and current density pedestals requires modifications to the two free functions 
$p(\psi )$ and 
${F^2}(\psi )$. Solov'ev-like terms, linear in 
$\psi $, must be added. The modified free functions can be written as
\begin{equation}\left. \begin{gathered} {p(\varPsi /{\varPsi _0}) = {p_0}\left\{ {{f_P} + (1 - {f_P}){{\left( {\dfrac{\varPsi }{{{\varPsi _0}}}} \right)}^2} + {A_1}\left[ {\left( {\dfrac{\varPsi }{{{\varPsi _0}}}} \right) - {{\left( {\dfrac{\varPsi }{{{\varPsi _0}}}} \right)}^2}} \right]} \right\},}\\ {{F^2}(\varPsi /{\varPsi _0}) = R_0^2B_0^2\left\{ {1 + \dfrac{{2\delta B}}{{{B_0}}}{{\left( {\dfrac{\varPsi }{{{\varPsi _0}}}} \right)}^2} + 2{A_2}\left[ {\left( {\dfrac{\varPsi }{{{\varPsi _0}}}} \right) - {{\left( {\dfrac{\varPsi }{{{\varPsi _0}}}} \right)}^2}} \right]} \right\}.} \end{gathered} \right\}\end{equation}
As before 
$\varPsi = 0$ is the flux on the plasma surface and 
$\varPsi = {\varPsi _0}$ is the flux on the magnetic axis. Thus, 
$1 \ge \varPsi /{\varPsi _0} \ge 0$. As in § 3, 
${f_P} = p(\textrm{surf})/p(\textrm{axis)}$ is the fractional height of the pressure profiles. The ratio 
${F^2}(\textrm{axis})/{F^2}(\textrm{surf}) = 1 + 2\delta B/{B_0}$ again represents the toroidal field paramagnetism/diamagnetism. The remaining two parameters, 
${A_1},{A_2}$, can for the moment be considered free. They will ultimately be related to the as yet undefined current pedestal parameter 
${f_J}$.
4.2. Modified Grad–Shafranov equation
The pedestal analysis begins by introducing the same normalized quantities as previously defined: 
$\psi = \varPsi /{\varPsi _0}$, 
$R = {R_0}{r^{1/2}}$ and 
$Z = ay$. The Grad–Shafranov equation can now be written as
\begin{gather}\left. \begin{gathered} {(1 + \hat{\varepsilon }x)\dfrac{{{\partial^2}\psi }}{{\partial {x^2}}} + \dfrac{1}{{1 + {\varepsilon^2}}}\dfrac{{{\partial^2}\psi }}{{\partial {y^2}}} ={-} {j_\phi }(x,\psi ),}\\ {{j_\phi }(x,\psi ) = \dfrac{{2R_0^2{a^2}}}{{\varPsi _0^2}}\left\{ {\left[ {{\mu_0}{p_0}(1 - {f_P} - {A_1})r + B_0^2\left( {\dfrac{{\delta B}}{{{B_0}}} - {A_2}} \right)} \right]\psi + \left[ {\dfrac{{{\mu_0}{p_0}}}{2}{A_1}r + \dfrac{{B_0^2}}{2}{A_2}} \right]} \right\},}\\ {r = 1 + {\varepsilon^2} + 2\varepsilon x.} \end{gathered} \right\}\end{gather}
A key step in the analysis is to recognize that by choosing 
${A_2}/{A_1}$ to make the ratio of the r term to the constant term in the 
$\psi $ square bracket identical to the same ratio as in the constant square bracket, the result will lead to a simple particular solution for 
$\psi $. This pedestal constraint can be written as
\begin{equation}\frac{{(1 - {f_P} - {A_1})}}{{(\delta B/{B_0} - {A_2})}} = \frac{{{A_1}}}{{{A_2}}} \to {A_2} = \frac{{\delta B}}{{{B_0}}}\frac{{{A_1}}}{{1 - {f_P}}}.\end{equation} The quantity 
${j_\phi }$ then reduces to
\begin{equation}{j_\phi }(x,\psi ) = \frac{{R_0^2}}{{\varPsi _0^2}}\left( {{\mu_0}{p_0}r + \frac{{{B_0}\delta B}}{{1 - {f_P}}}} \right)[2(1 - {f_P} - {A_1})\psi + {A_1}].\end{equation}
We are now in a position to introduce the current pedestal parameter 
${f_J}$. Since the current density is not a pure flux function, its pedestal height varies around the plasma surface. A simple but convenient definition that represents an average of this variation is given by
\begin{equation}{f_J} = \frac{{{J_\phi }(R,\textrm{surf})}}{{{J_\phi }(R,\textrm{axis})}} = \frac{{{j_\phi }(x,0)/{r^{1/2}}}}{{{j_\phi }(x,1)/{r^{1/2}}}} = \frac{{{A_1}}}{{2(1 - {f_P} - {A_1}) + {A_1}}} \to {A_1} = \frac{{2(1 - {f_P}){f_J}}}{{1 + {f_J}}},\end{equation}which leads to
\begin{equation}{j_\phi }(x,\psi ) = \frac{{2R_0^2{a^2}}}{{\varPsi _0^2(1 + {f_J})}}[{\mu _0}{p_0}(1 - {f_P})r + {B_0}\delta B][(1 - {f_J})\psi + {f_J}].\end{equation}
Observe that the pedestal constraint introduced in (4.3) has led to a form of 
${j_\phi }$ that implies that 
$\psi ={-} {f_J}/(1 - {f_J}) = \textrm{const}\textrm{.}$ is a particular solution to the Grad–Shafranov equation.
The final form of the Grad–Shafranov equation is obtained by substituting (4.6) into (4.2), defining modified constants 
$\alpha ,\nu $ plus a shifted flux function 
${\psi _J}(x,y)$:
\begin{equation}\left. \begin{gathered} {(1 + \hat{\varepsilon }x)\dfrac{{{\partial^2}{\psi_J}}}{{\partial {x^2}}} + \dfrac{1}{{1 + {\varepsilon^2}}}\dfrac{{{\partial^2}{\psi_J}}}{{\partial {y^2}}} ={-} {\alpha^2}(1 + \hat{\varepsilon }\nu x){\psi_J},}\\ {{\alpha^2} = \dfrac{{2R_0^2{a^2}}}{{\varPsi_0^2}}\left( {\dfrac{{1 - {f_J}}}{{1 + {f_J}}}} \right)\left[ {{\mu_0}{p_0}(1 - {f_P}) + \dfrac{{{B_0}\delta B}}{{1 + {\varepsilon^2}}}} \right],}\\ {\nu = \dfrac{{{\mu_0}{p_0}(1 - {f_P})}}{{{\mu_0}{p_0}(1 - {f_P}) + {B_0}\delta B/(1 + {\varepsilon^2})}},}\\ {{\psi_J} = \psi + \dfrac{{{f_J}}}{{1 - {f_J}}}.} \end{gathered} \right\}\end{equation}This equation is formally identical to the no-pedestal equation given by (2.1). The only difference is in the flux function boundary constraint. We now require
\begin{equation}\psi (\textrm{surf}) = 0 \to {\psi _J}(\textrm{surf}) = \frac{{{f_J}}}{{1 - {f_J}}}.\end{equation}4.3. Boundary constraints
Consider next the boundary constraints at the matching points. Since 
$\psi $ and 
${\psi _J}$ only differ by a constant, the slope constraints and curvature constraints are the same with or without an edge current pedestal, assuming that the model surfaces (i.e. the Miller model (Miller et al. Reference Miller, Chu, Greene, Lin-Liu and Waltz1998; Todd et al. Reference Todd, Manickam, Okabayashi, Chance, Grimm, Greene and Johnson1979) or the intersecting ellipse model) also remain unchanged.
However, there is one subtlety with the curvature constraints at the inner and outer midplane points with a separatrix. Recall that without a pedestal the midplane surface shapes make use of the fact that at the X-point the two intersecting ellipses must be perpendicular to each other. With a finite edge current the angle is no longer 
$\mathrm{\pi }/2$ and in fact cannot be determined until the whole problem is solved. If the current pedestal is not too large, it is not important to modify the midplane curvature constraints from their no-edge-current values. The only result is that the analytic solution will not match the intersecting ellipse model very accurately at the X-point because of the differing angles. Nevertheless, the solution still satisfies the exact Grad–Shafranov equation, and there is nothing fundamental about the intersecting ellipse shape. Most importantly, the analytic solution will automatically produce the correct angle at the X-point, while the intersecting ellipse model will always have the wrong angle if the edge current is non-zero.
4.4. Solution procedure
Since the boundary condition on 
${\psi _J}(\textrm{surf)}$ is now inhomogeneous, we might at first think that solutions can be found for arbitrary values of 
${\alpha ^2}$. This is not the case, as there is a second normalization condition on the flux that is now non-trivial and must be satisfied, namely that
\begin{equation}{\psi _J}(\textrm{axis}) = \frac{1}{{1 - {f_J}}}.\end{equation}
A useful way to understand the system is as follows. Assume that the geometry and a value of 
$\nu $ are specified. ‘Guess’ a value for 
${\alpha ^2}$ and temporarily ignore the normalization condition on the axis. Because the boundary condition on the surface is inhomogeneous, it is indeed true that we can always find a non-trivial solution, subject to (4.8), that satisfies the 7 or 12 constraint relations at the required surface points. For example, for symmetric plasmas, the constraint relations are now given by
\begin{equation}\left. \begin{gathered} {\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftrightarrow$}} \over A} }(\alpha )\boldsymbol{\cdot }\boldsymbol{u} = \boldsymbol{v},}\\ {\boldsymbol{u} = [{c_1},{c_2},{s_2},{c_3},{s_3},{c_4},{s_4}],}\\ {\boldsymbol{v} = [{\psi_J}(\textrm{surf}),{\psi_J}(\textrm{surf}),{\psi_J}(\textrm{surf}),0,0,0,0]\quad {\psi_J}(\textrm{surf}) = \dfrac{{{f_J}}}{{1 - {f_J}}}.} \end{gathered} \right\}\end{equation}A similar relation holds for the asymmetric case.
However, the normalization condition given by (4.9) will not in general be satisfied. Furthermore, even though the equation is linear we cannot simply scale the solution to satisfy (4.9). If we do, then the inhomogeneous boundary condition at the surface will no longer be satisfied. In other words, one must carefully choose the value of 
$\alpha $ so that (4.9) just happens to be satisfied when the constraint relations are solved subject to (4.8). The parameter 
$\alpha $ is an output of the analysis, not an input.
The value of 
$\alpha $ can be determined in a manner similar to that for the no pedestal case. The 7 × 7 or 12 × 12 set of inhomogeneous constraint relations are solved for a given ‘guess’ for 
$\alpha $ which is then iterated until the error
\begin{equation}E(\alpha ) = {\left[ {\frac{{{\psi _J}(\textrm{axis}) - 1/(1 - {f_J})}}{{\left| {{\psi _J}(\textrm{axis})} \right| + \left| {1/(1 - {f_J})} \right|}}} \right]^2}\end{equation}
has a minimum value at 
$E(\alpha ) = 0$.
4.5. Examples
To demonstrate the effects of pedestals we illustrate two examples with geometric parameters identical to the pedestal-free spherical tokamak equilibrium discussed in Part 1: 
$\varepsilon = 0.75,\;{\kappa _X} = 2.4,\;{\delta _X} = 0.8,\;\nu = 1.04$. The results are shown in figure 1. The first example (top profile curves) has a pedestal only in current density 
$({f_P} = {f_B} = 0,{f_J} = 0.25)$. The second example (bottom profile curves) has pedestals in the pressure 
$({f_P} = 0.2)$ and current density 
$({f_J} = 0.25)$. There is also a bootstrap surface current 
$({f_B} = 0.35)$. As stated, the flux surface plots for both examples are the same since they are not affected by the pressure pedestal or bootstrap current.
Figure 1. Flux surface and midplane profile plots for a spherical tokamak including pedestals. Black curves correspond to the pedestal-free solution while the white curves contain pedestals. In the midplane plots each curve is normalized to unity. The upper plot has only a 
${J_\phi }$ pedestal while the lower plot also has a pressure pedestal and bootstrap current. The labels I and II refer to Part 1 (no pedestals) and Part 2 (with pedestals).
In the flux surface plot, the red boundary curve shows the intersecting ellipse model surface. The thinner black curves are the flux surfaces for the pedestal-free case discussed in Part 1. They are illustrated just for purposes of comparison. The white flux surfaces represent the new solutions including the effects of a current density pedestal. The same colours (black for no-pedestal, no-flow solution, white for the new solution in this paper) are used in the remainder of the paper.
Observe that this pedestal produces a slight inward shift of the flux surfaces. A current density with the same 
${q_0} = 1$ but containing a 
${J_\phi }$ pedestal, has a flatter radial profile with approximately the same 
${J_\phi }$ on axis. The total current has increased implying that 
${J_\phi }$ is larger near the outer boundary, which pushes the pressure inwards so the shift is a little smaller. Also, recall that the slightly larger mismatch at the X-point is due to setting the X-point angle in the intersecting ellipse model surface to 
$\mathrm{\pi }/2$ for convenience, although this is not the correct, self-consistent value. The analytic shaded boundary edge has the correct X-point angle which therefore represents an output of the analysis.
Although the flux surfaces are the same, the two examples have different midplane pressure and current density profiles. This is clearly seen in figure 1. In both plots the edge pedestal in the current density on the outboard side has a similar height. The pedestal on both inboard sides is zero as the parameter 
$\nu $ has been chosen to be at its maximum value, corresponding to zero current density at 
$R = {R_0} - a$. The upper curves show the edge pressure smoothly going to zero while the lower curves show the finite pressure pedestal. These pedestals will have an impact on the plasma parameters of interest as shown shortly.
5. Toroidal flow
5.1. The starting equation
The final case of interest adds toroidal flow to the analysis. A general form of the Grad–Shafranov equation including both toroidal and poloidal flow has been known for many years (Zehrfeld & Green Reference Zehrfeld and Green1972; Maschke & Perrin Reference Maschke and Perrin1980; Morozov & Solov'ev Reference Morozov and Solov'ev1980; Hameiri Reference Hameiri1983; Semenzato et al. Reference Semenzato, Gruber and Zehrfeld1984; Iacono et al. Reference Iacono, Bondeson, Troyon and Gruber1990) and nonlinear numerical codes have been developed to solve this equation (Semenzato et al. Reference Semenzato, Gruber and Zehrfeld1984; Belien et al. Reference Belien, Botchev, Goedbloed, Van der Holst and Keppens2002; Guazzotto et al. Reference Guazzotto, Betti, Manickam and Kaye2004). For readers unfamiliar with the generalized Grad–Shafranov equation in the limit of purely toroidal flow, we present a derivation in Appendix A that leads to a form allowing analytic solutions. This somewhat complicated form is given by
\begin{gather}\left. \begin{gathered} {{\Delta ^*}{\varPsi } = - FF' - {\mu _0}{R^2}{{\left[ {1 + {M^2}\left( {\frac{{{R^2}}}{{R_0^2}} - 1} \right)} \right]}^{1/(\gamma - 1)}}\left\{ {\bar{p}' + \left[ {{M^2}\bar{p}' + \frac{\gamma }{{\gamma - 1}}\bar{p}({M^2})'} \right]\left( {\frac{{{R^2}}}{{R_0^2}} - 1} \right)} \right\},}\\ {{B_\phi } = \frac{{F({\varPsi })}}{R},}\\ {\frac{p}{{\bar{p}({\varPsi })}} = {{\left[ {1 + {M^2}\left( {\frac{{{R^2}}}{{R_0^2}} - 1} \right)} \right]}^{\gamma /(\gamma - 1)}},}\\ {\frac{\rho }{{\bar{\rho }({\varPsi })}} = {{\left[ {1 + {M^2}\left( {\frac{{{R^2}}}{{R_0^2}} - 1} \right)} \right]}^{1/(\gamma - 1)}},}\\ {{\Omega ^2}({\varPsi })R_0^2 = \frac{{2\gamma }}{{\gamma - 1}}\frac{{\bar{p}({\varPsi })}}{{\bar{\rho }({\varPsi })}}{M^2}({\varPsi }).} \end{gathered} \right\}\end{gather}
Observe that three free functions must be specified: the familiar toroidal field and pressure functions 
$F(\varPsi ),\bar{p}(\varPsi )$ as well as a new function representing the square of the effective thermal Mach number 
${M^2}(\varPsi ) = [2\gamma /(\gamma - 1)]M_T^2$ with 
${M_T}(\varPsi ) = {(\bar{\rho }{\varOmega ^2}R_0^2/\bar{p})^{1/2}}$ the standard thermal Mach number. The density function 
$\bar{\rho }(\varPsi )$ and toroidal angular velocity function 
$\varOmega (\varPsi ){R_0}$ are separate free functions but only the combination 
$\bar{\rho }{\varOmega ^2}R_0^2$ appears in the Grad–Shafranov equation. Also, note that 
$\gamma $ is the ratio of specific heats.
We obtain analytic solutions by special choices of 
$F(\varPsi ),\bar{p}(\varPsi ),M(\varPsi )$ that again lead to a linear partial differential equation in 
$\varPsi $. The coefficient of the 
$\varPsi $ term can be reduced to a simple power series in 
${R^2}$ which is convenient for our method of solution. To make this reduction we must restrict 
$\gamma $ to two values: 
$\gamma = 2$ corresponding to adiabatic behaviour and 
$\gamma = \infty $ corresponding to incompressible flow. Recall that the adiabatic index 
$\gamma = (N + 2)/N$, where N is the number of degrees of freedom for fluid motion. Thus, 
$\gamma = 2$ corresponds to two degrees of freedom, parallel and perpendicular to the magnet field. Two other interesting cases,
$\gamma = 5/3,\gamma = 1$, do not lead to simple forms amenable to an analytic solution, similar to the ones presented in this paper. However, different approaches may in the future also provide analytic solutions.
The analysis proceeds in two steps. First, we treat the case of flow with smooth edge conditions in which the pressure, pressure gradient and current density all vanish smoothly at the plasma edge. Second, we add the effects of pedestals and surface currents. The solution proceeds as follows.
5.2. General reduction leading to a linear equation in $\varPsi $
We can reduce (5.1) to a linear equation in 
$\varPsi $ for smooth plasma edge conditions and arbitrary 
$\gamma $, by choosing the three free functions as follows:
\begin{equation}\left. \begin{gathered} {{F^2} = R_0^2B_0^2\left[ {1 + \dfrac{{2\delta B}}{{{B_0}}}{{\left( {\dfrac{\varPsi }{{{\varPsi_0}}}} \right)}^2}} \right],}\\ {\bar{p} = {p_0}{{\left( {\dfrac{\varPsi }{{{\varPsi_0}}}} \right)}^2},}\\ {{M^2} = M_0^2 = \textrm{const}\textrm{.}} \end{gathered} \right\}\end{equation}
Besides the familiar 
${R_0},{B_0}$, two new parameters are introduced: 
${p_0},{M_0}$. These parameters have the following qualitative interpretations. If we approximate the magnetic axis by setting 
$R = {R_0}$, then a short calculation shows that
\begin{equation}\left. \begin{gathered} {{p_0} \approx p{|_{\textrm{axis}}}\quad \textrm{Pressure}\;\textrm{on}\;\textrm{axis,}}\\ {M_0^2 \approx \dfrac{{\gamma - 1}}{{2\gamma }}{{\left. {\dfrac{{\bar{\rho }{\varOmega^2}R_0^2}}{{\bar{p}}}} \right|}_{\textrm{axis}}}\quad \textrm{Mach}\;\textrm{number}\;\textrm{squared}\;\textrm{on}\;\textrm{axis}\textrm{.}} \end{gathered} \right\}\end{equation} Observe that 
${p_0}$ is defined the same way in terms of the flux function as in Part 1. Nevertheless, since the actual pressure is not an exact flux function with non-zero flow, the quantity 
${p_0}$ is only approximately equal to the pressure on axis. The approximations in (5.3) are accurate for large aspect ratio. They are less accurate but still qualitatively correct for tight-aspect-ratio configurations such as the spherical tokamak where the shift between the magnetic and geometric axes can be finite.
We now substitute the free functions into (5.1). A straightforward calculation leads to the desired form of the Grad–Shafranov equation for arbitrary 
$\gamma $:
\begin{equation}{\varDelta ^\ast }\varPsi ={-} \frac{{2R_0^2B_0^2}}{{\varPsi _0^2}}\left[ {\frac{{\delta B}}{{{B_0}}} + \frac{{{\mu_0}{p_0}}}{{B_0^2}}\frac{{{R^2}}}{{R_0^2}}{{\left( {1 - M_0^2 + M_0^2\frac{{{R^2}}}{{R_0^2}}} \right)}^{\gamma /(\gamma - 1)}}} \right]\varPsi = 0.\end{equation}
Observe that the term in parentheses reduces to a simple polynomial in 
${R^2}$ for 
$\gamma = 2$ (adiabatic) or 
$\gamma = \infty $ (incompressible) or more generally 
$\gamma = n/(n - 1)$ with n an integer.
5.3. Normalized equations
As for the case of zero flow, we again introduce normalized variables:
\begin{equation}\left. \begin{gathered} {\varPsi = {\varPsi_0}\psi \quad 1 \ge \psi \ge 0,}\\ {Z = ay\quad - \kappa \le y \le \kappa ,}\\ {R = {R_0}{r^{1/2}} = {R_0}{{(1 + {\varepsilon^2} + 2\varepsilon x)}^{1/2}}\quad - 1 \le x \le 1.} \end{gathered} \right\}\end{equation}The modified Grad–Shafranov equation reduces to
\begin{equation}\left. \begin{gathered} {(1 + \hat{\varepsilon }x)\dfrac{{{\partial^2}\psi }}{{\partial {x^2}}} + \dfrac{1}{{1 + {\varepsilon^2}}}\dfrac{{{\partial^2}\psi }}{{\partial {y^2}}} ={-} {\alpha^2}[1 + \nu G(x)]\psi \quad \psi (\textrm{surf)} = 0,}\\ {\hat{\varepsilon } = \dfrac{{2\varepsilon }}{{1 + {\varepsilon^2}}} < 1,}\\ {{\alpha^2} = \dfrac{{2R_0^2{a^2}}}{{\varPsi_0^2}}\left[ {\dfrac{{{B_0}\delta B}}{{1 + {\varepsilon^2}}} + {\mu_0}{p_0}{{(1 + M_0^2{\varepsilon^2})}^{\gamma /(\gamma - 1)}}} \right] \ge 0,}\\ {\nu = \dfrac{{{\mu_0}{p_0}{{(1 + M_0^2{\varepsilon^2})}^{\gamma /(\gamma - 1)}}}}{{{\mu_0}{p_0}{{(1 + M_0^2{\varepsilon^2})}^{\gamma /(\gamma - 1)}} + {B_0}\delta B/(1 + {\varepsilon^2})}} \ge 0,}\\ {G(x) = (1 + \hat{\varepsilon }x){{\left( {1 + \dfrac{{2M_0^2\varepsilon }}{{1 + M_0^2{\varepsilon^2}}}x} \right)}^{\gamma /(\gamma - 1)}} - 1.} \end{gathered} \right\}\end{equation} Observe that for small 
$\varepsilon $, 
$G(x) \propto \varepsilon x$. The magnetic axis is defined by the condition 
$\psi (\textrm{axis}) = 1$. Also, the range of 
$\nu $ to prevent current reversal on the inboard midplane is given by
\begin{equation}\left. \begin{gathered} {0 \le \nu \le {\nu _{\max }},}\\ {{\nu _{\max }}(\varepsilon ,M_0^2) = - \frac{1}{{G( - 1)}} = \frac{1}{{1 - (1 - \hat{\varepsilon }){{(1 - \hat{\varepsilon }\zeta )}^{\gamma /(\gamma - 1)}}}},}\\ {\zeta (\varepsilon ,M_0^2) = \frac{{M_0^2(1 + {\varepsilon ^2})}}{{1 + M_0^2{\varepsilon ^2}}}.} \end{gathered} \right\}\end{equation}5.4. Two special cases of interest
The two special cases of interest that lead to simple analytic solutions correspond to 
$\gamma = \infty $ (incompressible) and 
$\gamma = 2$ (adiabatic). In both cases (5.6) reduces to an equation that has the form
\begin{equation}\left. \begin{gathered} {(1 + \hat{\varepsilon }x)\frac{{{\partial ^2}\psi }}{{\partial {x^2}}} + \frac{1}{{1 + {\varepsilon ^2}}}\frac{{{\partial ^2}\psi }}{{\partial {y^2}}} = - {\alpha ^2}\left[ {1 + \hat{\varepsilon }{\nu _1}x + {{\hat{\varepsilon }}^2}{\nu _2}{x^2} + {{\hat{\varepsilon }}^3}{\nu _3}{x^3}} \right]\psi \quad \psi (\textrm{surf)} = 0,}\\ {\gamma = \infty :\quad {\nu _1}\textrm{ = (1 + }\zeta )\nu \quad {\nu _2}\textrm{ = }\zeta \nu \quad {\nu _3}\textrm{ = 0, }}\\ {\gamma = 2:\quad {\nu _1}\textrm{ = (1 + 2}\zeta )\nu \quad {\nu _2}\textrm{ = }\zeta (2 + \zeta )\nu \quad {\nu _3}\textrm{ = }{\zeta ^2}\nu .} \end{gathered} \right\}\end{equation}5.5. The solution
Following the procedure described in Part 1 we again find a solution by separation of variables:
\begin{equation}\psi (x,y) = \sum {{X_n}(x){Y_n}(y)} ,\end{equation}
where 
${Y_n},{X_n}$ satisfy
\begin{equation}\left. \begin{gathered} {\dfrac{{{\textrm{d}^2}{Y_n}}}{{\textrm{d}{y^2}}} + h_n^2{Y_n} = 0,}\\ {(1 + \hat{\varepsilon }x)\dfrac{{{\textrm{d}^2}{X_n}}}{{\textrm{d}{x^2}}} + (k_n^2 + \lambda_1^2x + \lambda_2^2{x^2} + \lambda_3^2{x^3}){X_n} = 0,}\\ {k_n^2 = {\alpha^2} - \dfrac{{h_n^2}}{{1 + {\varepsilon^2}}},}\\ {\lambda_1^2 = \hat{\varepsilon }{\alpha^2}{\nu_1},}\\ {\lambda_2^2 = {{\hat{\varepsilon }}^2}{\alpha^2}{\nu_2},}\\ {\lambda_3^2 = {{\hat{\varepsilon }}^3}{\alpha^2}{\nu_3},} \end{gathered} \right\}\end{equation}
and 
$h_n^2$ are the separation constants.
The solutions for 
${Y_n}$ are given by
\begin{equation}{Y_n}(y) = \left\{ \begin{array}{@{}l} \cos ({h_n}y)\\ \sin ({h_n}y)\,. \end{array} \right.\end{equation}
The equation for 
${X_n}$ is slightly more complicated than in Part 1. Recall that the solutions in Part 1 could be written in terms of Whittaker functions although this was of no great help. Instead, a straightforward analytic power series was used to obtain solutions for 
${X_n}$ which was much faster and equally accurate to numerically evaluate, as compared to standard Whittaker function packages. Equally important, analytic forms for the first and second derivatives were derived.
Following the same reasoning as in Part 1, we can again obtain solutions for 
${X_n}$ in terms of power series. These series have a similar but slightly more complicated recursion relation for the expansion coefficients. The main difference is that the solutions no longer have a well-known name (e.g. Whittaker functions) but this is of little consequence. The solutions for 
${X_n}$ are thus written as
\begin{equation}{X_n}(x) = \left\{ \begin{array}{@{}l} {C_n}(x) = \sum {[{{\hat{a}}_m}{x^m}\cos ({k_n}x) + {{\hat{b}}_m}{x^m}\sin ({k_n}x)]} \\ {S_n}(x) = \sum {[{{\tilde{a}}_m}{x^m}\cos ({k_n}x) + {{\tilde{b}}_m}{x^m}\sin ({k_n}x)]} \,. \end{array} \right.\end{equation}
We calculate the recursion relations for the coefficients 
${\hat{a}_m},{\hat{b}_m},{\tilde{a}_m},{\tilde{b}_m}$ as well as analytic first and second derivatives in Appendix B. Hereafter, we can assume that 
${C_n},{S_n}$ are known solutions.
The conclusion from this analysis is that the flux function solution procedures described in Part 1 for smooth, double-null and single-null systems without pedestals apply directly to systems with toroidal flow. The only difference is the generalized form of the expansion functions 
${C_n},{S_n}$.
5.6. Flow with pedestals
Adding edge pedestals to the calculation of flux surfaces with flow is straightforward. The results are nearly identical and only slightly more complicated than the case without flow. The starting point is (5.4), the generalized Grad–Shafranov equation including toroidal flow. To include pedestals we require modified forms of the free functions that contain Solov'ev-type additions. Specifically, for systems with toroidal flow and pedestals we choose the same free functions as without flow (see (4.1)). After introducing normalized coordinates, we see that the Grad–Shafranov equation reduces to
\begin{equation}\left. \begin{gathered} {(1 + \hat{\varepsilon }x)\dfrac{{{\partial^2}\psi }}{{\partial {x^2}}} + \dfrac{1}{{1 + {\varepsilon^2}}}\dfrac{{{\partial^2}\psi }}{{\partial {y^2}}} ={-} {j_\phi }(\rho ,\psi ),}\\ {j_\phi }(x,\psi ) = \dfrac{{2R_0^2{a^2}}}{{(1 + {\varepsilon^2})\varPsi_0^2}}\left\{ {\left[ {{\mu_0}{p_0}(1 - {f_P} - {A_1})g(x) + B_0^2\left( {\dfrac{{\delta B}}{{{B_0}}} - {A_2}} \right)} \right]\psi } \right.\\ \hspace{-7.5pc}\left. + \left[ {\dfrac{{{\mu_0}{p_0}}}{2}{A_1}g(x) + \dfrac{{B_0^2}}{2}{A_2}} \right] \right\},\\ {g(x) = r\frac{\rho }{{\bar{\rho }}}(1 - M_0^2 + M_0^2r) = r{{(1 - M_0^2 + M_0^2r)}^{\gamma /(\gamma - 1)}},}\\ {r = 1 + {\varepsilon^2} + 2\varepsilon x.} \end{gathered} \right\}\end{equation}
We again choose the constants 
${A_1},{A_2}$ to (i) produce a simple particular solution for 
$\psi $ and (ii) introduce the height of the current density pedestal. The required relations are given by (4.3) and (4.5). These values are substituted into (5.13). The result is the desired form of the Grad–Shafranov equation with flow and pedestals:
\begin{equation}\left. \begin{gathered} {(1 + \hat{\varepsilon }x)\dfrac{{{\partial^2}{\psi_J}}}{{\partial {x^2}}} + \dfrac{1}{{1 + {\varepsilon^2}}}\dfrac{{{\partial^2}{\psi_J}}}{{\partial {y^2}}} ={-} {\alpha^2}(1 + \nu G){\psi_J},}\\ {{\alpha^2} = \dfrac{{2R_0^2{a^2}}}{{\varPsi_0^2}}\left( {\dfrac{{1 - {f_J}}}{{1 + {f_J}}}} \right)\left[ {{\mu_0}{p_0}(1 - {f_P}){{(1 + M_0^2{\varepsilon^2})}^{\gamma /(\gamma - 1)}} + \dfrac{{{B_0}\delta B}}{{1 + {\varepsilon^2}}}} \right],}\\ {\nu = \dfrac{{{\mu_0}{p_0}(1 - {f_P}){{(1 + M_0^2{\varepsilon^2})}^{\gamma /(\gamma - 1)}}}}{{{\mu_0}{p_0}(1 - {f_P}){{(1 + M_0^2{\varepsilon^2})}^{\gamma /(\gamma - 1)}} + {B_0}\delta B/(1 + {\varepsilon^2})}},}\\ {{\psi_J}(x,y) = \psi + \dfrac{{{f_J}}}{{1 - {f_J}}}\quad {\psi_J}(\textrm{surf}) = \dfrac{{{f_J}}}{{1 - {f_J}}}\quad {\psi_J}(\textrm{axis}) = \dfrac{1}{{1 - {f_J}}},}\\ {G(x) = (1 + \hat{\varepsilon }x){{\left( {1 + \dfrac{{2M_0^2\varepsilon }}{{1 + M_0^2{\varepsilon^2}}}x} \right)}^{\gamma /(\gamma - 1)}} - 1.} \end{gathered} \right\}\end{equation} Note that this equation is identical in form to the one with pedestals but no flow. The only differences in the equation are slightly modified definitions of 
$\alpha ,\nu $ and the more general form for 
$G(x)$ which corresponds to the generalized 
${C_n}(x),{S_n}(x)$. The conclusion is that with these minor modifications we can use the same solution procedure as for the system without flow.
5.7. Examples
We have run a large number of cases with flow to convince ourselves that the solution procedure works and is robust. For due diligence wherever possible, we also compared our results with the established FLOW code to verify the numerical implementation of our code. A specific example is presented in Appendix C where it is shown that all tests proved highly satisfactory. To demonstrate this statement, we present two examples which simultaneously include all the effects of our generalized analysis in the most complicated geometry. The configurations include pedestals in pressure and current density, an edge bootstrap current, substantial flow, in a single-null diverted tokamak. The two cases have nearly identical parameters: 
$\varepsilon = 0.33,\;\kappa = 1.6,\;\delta = 0.4,\;{\kappa _X} = 2,\;{\delta _X}$ 
$= 0.5,\;\nu = 1,\,{f_B} = 0.35,\;{f_P} = 0.2,\;{f_J} = 0.25,\;{M_0} = 0.6$. The difference is that the case in figure 2 is adiabatic 
$(\gamma = 2)$ while the one in figure 3 is incompressible 
$(\gamma = \infty )$.
Figure 2. Flux surface plot and midplane profiles for the adiabatic case 
$(\gamma = 2)$. Black curves correspond to the reference pedestal-free, flow-free solution while the white curves contain both effects. In the midplane plots each curve is normalized to unity. The blue and red curves represent the solutions with pedestals and flow while the black curves are the reference case with neither effect. The labels I and II refer to Part 1 (no pedestals, no flow) and Part 2 (with pedestals and flow).
Figure 3. Flux surface plot and midplane profiles for the incompressible case 
$(\gamma = \infty )$. Black curves correspond to the reference pedestal-free, flow-free solution while the white curves contain both effects. In the midplane plots each curve is normalized to unity. The blue and red curves represent the solutions with pedestals and flow while the black curves are the reference case with neither effect. The labels I and II refer to Part 1 (no pedestals, no flow) and Part 2 (with pedestals and flow).
We see that the solution procedure works well when flow is included. The most pronounced effect is the not unexpected large outward shift of the flux surfaces due to the flow-generated centrifugal force. A comparison of the two examples indicates that the adiabatic case has a slightly larger shift than the incompressible case.
6. Summary of solution procedure and plasma parameters
We complete the analysis by summarizing the solution procedure for the most general case which then enables the evaluation of the plasma parameters of interest. Assume the following parameters are prescribed as inputs: 
$\varepsilon ,\kappa \;\textrm{or}\;{\kappa _X},\delta \;\textrm{or}\;{\delta _X},\nu ,{f_P},{f_J},{f_B},{q_0},{M_0}$. Solve the normalized Grad–Shafranov equation given by (5.14) yielding 
${\psi _J}(x,y)$ and 
${\alpha ^2}$. From this solution evaluate
\begin{align}\left. \begin{gathered} {{\beta _0} \equiv \frac{{2{\mu _0}{p_0}}}{{B_0^2}} = \frac{{\left( {\dfrac{{1 + {f_J}}}{{1 - {f_J}}}} \right)\dfrac{{{\varepsilon ^2}{\alpha ^2}\nu }}{{(1 - {f_P}){{(1 + M_0^2{\varepsilon ^2})}^{\gamma /(\gamma - 1)}}}}}}{{q_0^2{{[{r^2}{{({\psi _J})}_{xx}}{{({\psi _J})}_{yy}}]}_{\textrm{axis}}} - \left( {\dfrac{{1 + {f_J}}}{{1 - {f_J}}}} \right)(1 + {\varepsilon ^2}){\varepsilon ^2}{\alpha ^2}(1 - \nu )}},}\\ {\frac{{\varPsi _0^2}}{{{a^2}R_0^2B_0^2}} = \varPsi _a^2 = (1 - {f_P}){{(1 + M_0^2{\varepsilon ^2})}^{\gamma /(\gamma - 1)}}\left( {\frac{{1 - {f_J}}}{{1 + {f_J}}}} \right)\frac{{{\beta _0}}}{{{\alpha ^2}\nu }},}\\ {\frac{{2{\mu _0}p(x,y)}}{{B_0^2}} = P(x,y) = {\beta _0}{{\left( {1 + M_0^2{\varepsilon ^2} + 2M_0^2\varepsilon x} \right)}^{\gamma /(\gamma - 1)}}\left[ {(1 - {f_P})\frac{{1 - {f_J}}}{{1 + {f_J}}}\psi _J^2 + \frac{{{f_P} - f_J^2}}{{1 - f_J^2}}} \right],}\\ {\frac{{B_P^2(x,y)}}{{B_0^2}} = b_P^2(x,y) = \frac{{\varPsi _a^2}}{r}\left[ {r{{\left( {\frac{{\partial {\psi _J}}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial {\psi _J}}}{{\partial y}}} \right)}^2}} \right],}\\ {\frac{{{\mu _0}a{J_\phi }(x,y)}}{{{B_0}}} = \frac{{(1 + {\varepsilon ^2})}}{{{r^{1/2}}}}{j_\phi } = {\varPsi _a}(1 + {\varepsilon ^2}){\alpha ^2}\frac{{(1 + \nu G)}}{{{r^{1/2}}}}{\psi _J},}\\ {\frac{{{\mu _0}I}}{{a{B_0}}} = {i_C} = \frac{1}{a}\oint {{b_P}\,\textrm{d}{l_P}} .} \end{gathered} \right\}\end{align}
Note that the first equation determines 
${\beta _0}$, given a value for 
${q_0}$. It can be easily inverted to determine 
${q_0}$ for a specified value of 
${\beta _0}$.
The next step is to take into account the jump conditions due to surface currents. Guess and then iterate a value for the diamagnetic parameter 
${\varDelta _B}$ using the relations
\begin{equation}\left. \begin{gathered} {\frac{{{{\hat{B}}_\phi }(x,y)}}{{{B_0}}} = {\Delta _B}\frac{{{R_0}}}{R},}\\ {\frac{{\hat{B}_P^2(x,y)}}{{B_0^2}} = \frac{{B_P^2(x,y)}}{{B_0^2}} + {\beta _0}{f_P} + 1 - \Delta _B^2.} \end{gathered} \right\}\end{equation}
The iteration constraint determining 
${\varDelta _B}$ is given by
\begin{equation}{f_B} = 1 - \frac{I}{{\hat{I}}} = 1 - \frac{{\displaystyle\oint {\dfrac{{{B_P}}}{{{B_0}}}\,\textrm{d}{l_P}} }}{{\displaystyle\oint {\dfrac{{{{\hat{B}}_P}}}{{{B_0}}}\,\textrm{d}{l_P}} }},\end{equation}
with 
${\hat{B}_P}/{B_0}$ evaluated from (3.9).
With the information just obtained we can now evaluate the plasma parameters of interest. These can be written as follows.
Plasma 
$\beta $ on axis 
${\hat{\beta }_0}$:
\begin{equation}{\hat{\beta }_0} = \frac{{2{\mu _0}p{|_{\textrm{axis}}}}}{{\hat{B}_0^2}} = {\beta _0}\left( {\frac{{B_0^2}}{{\hat{B}_0^2}}} \right){[{(1 + M_0^2{\varepsilon ^2} + 2M_0^2\varepsilon x)^{\gamma /(\gamma - 1)}}]_{\textrm{axis}}}.\end{equation}
Plasma diamagnetism 
$\delta B/{B_0}$:
\begin{equation}\frac{{2\delta B}}{{{B_0}}} = (1 + {\varepsilon ^2})(1 - {f_P}){(1 + M_0^2{\varepsilon ^2})^{\gamma /(\gamma - 1)}}\left( {\frac{{1 - \nu }}{\nu }} \right){\beta _0}.\end{equation}
Magnetic flux on axis 
${\varPsi _0}$:
\begin{equation}{\varPsi _0} = \frac{{\varepsilon {B_0}R_0^2}}{\alpha }{\left( {\frac{{{\beta_0}}}{\nu }} \right)^{1/2}}{\left[ {\left( {\frac{{1 - {f_J}}}{{1 + {f_J}}}} \right)(1 - {f_P}){{(1 + M_0^2{\varepsilon^2})}^{\gamma /(\gamma - 1)}}} \right]^{1/2}}.\end{equation}
Volume-averaged toroidal beta 
${\beta _T}$:
\begin{equation}{\beta _T} = \frac{{2{\mu _0}}}{{B_0^2}}{\langle p\rangle _V} = \frac{{\hat{B}_0^2}}{{B_0^2}}\frac{{\displaystyle\int {P\,\textrm{d}x\,\textrm{d}y} }}{{\displaystyle\int {\textrm{d}x\,\textrm{d}y} }}.\end{equation}
Volume-averaged poloidal beta 
${\beta _P}$:
\begin{equation}{\beta _P} = \frac{{2{\mu _0}{{\langle p\rangle }_V}}}{{{{\langle B_P^2\rangle }_V}}} = \frac{{{{\langle P\rangle }_V}}}{{{{\langle b_P^2\rangle }_V}}} = \frac{{\displaystyle\nu \int {\textrm{d}x\,\textrm{d}y\left( {\dfrac{{1 + G}}{{1 + \hat{\varepsilon }x}}} \right)\left[ {(1 - {f_P})\psi_J^2 + \dfrac{{{f_P} - f_J^2}}{{{{(1 - {f_J})}^2}}}} \right]} }}{{\displaystyle\int {\textrm{d}x\,\textrm{d}y\left( {\dfrac{{1 + \nu G}}{{1 + \hat{\varepsilon }x}}} \right)(1 - {f_P})\psi _J^2} }}.\end{equation}
Total toroidal plasma current 
$\hat{I}$:
\begin{equation}\frac{{\hat{I}}}{I} = \frac{{I + {I_{{\parallel} \phi }}}}{I} = \frac{1}{{1 - {f_B}}}.\end{equation}
Normalized internal inductance per unit length 
${l_i}$:
\begin{equation}{l_i} = \frac{{2{L_i}}}{{{\mu _0}{R_0}}} = \frac{2}{{\mu _0^2{{\hat{I}}^2}{R_0}}}\int {B_P^2\,\textrm{d}\boldsymbol{r}} = \frac{{4\mathrm{\pi }}}{{{\alpha ^2}}}{\left( {\frac{I}{{\hat{I}}}} \right)^2}\frac{{\displaystyle\int {\left({\dfrac{{1 + \nu G}}{{1 + \hat{\varepsilon }x}}} \right)\psi _J^2\,\textrm{d}x\,\textrm{d}y} }}{{{{\left[\displaystyle\int \left( \dfrac{{1 + \nu \hat{\varepsilon }x}}{{1 + \hat{\varepsilon }x}}\right){\psi_J}\,\textrm{d}x\,\textrm{d}y \right]}^2}}}.\end{equation}
Kink safety factor 
${q_\ast }$ (
$\kappa = {\kappa _{95}}$ for divertor surfaces):
\begin{equation}{q_\ast } = \frac{{2\mathrm{\pi }{a^2}{{\hat{B}}_0}}}{{{\mu _0}{R_0}\hat{I}}}\left( {\frac{{1 + {\kappa^2}}}{2}} \right) = \frac{{2\mathrm{\pi }{a^2}{B_0}}}{{{\mu _0}{R_0}I}}\left( {\frac{{1 + {\kappa^2}}}{2}} \right)\left( {\frac{{{{\hat{B}}_0}}}{{{B_0}}}} \right)\left( {\frac{I}{{\hat{I}}}} \right).\end{equation}
Local safety factor 
$q(\psi )$:
\begin{equation}q(\psi ) = \frac{{F(\psi )}}{{2\pi }}\oint_\psi {\frac{{\textrm{d}{l_P}}}{{{R^2}{B_P}}}} = \frac{{F(\psi )}}{{{R_0}{B_0}}}\left[ {\frac{\alpha }{{2\mathrm{\pi }{R_0}}}\oint_\psi {\frac{{\textrm{d}{l_P}}}{{r{b_P}}}} } \right].\end{equation}
To see the effects of pedestals, bootstrap current and flow on the plasma parameters of interest we focus on two critical parameters that constrain experimental operation, 
${\beta _P}$ and 
${q_\ast }$. Using the expressions derived above we evaluate these quantities for four cases of increasing complexity, with the double-null, spherical tokomak configuration described in Part 1 as the starting reference point for each. Recall that this configuration has 
$\varepsilon = 0.75,\;{\kappa _X} = 2.4,\;{\delta _X} = 0.8,\;\nu = 1.04$. Case A adds a current density pedestal. Case B adds current density and pressure pedestals plus a bootstrap current. Cases C and D further add flow for the adiabatic and incompressible cases, respectively. All cases have 
${q_0} = 1$. The results are shown in table 2 including the corresponding reference values from Part 1.
Table 2. Effect of pedestals, bootstrap current and flow on 
${\beta _P}$ and 
${q_\ast }$. The reference values are those obtained in Part 1 for the same geometric cases but with zero pedestals and flow.
An examination of table 2 leads to several anticipated results. Consider Case A corresponding to a current density pedestal, but with no flow, no pressure pedestal and no bootstrap current. A current density pedestal at fixed 
${q_0} = 1$ tends to flatten the current density profile keeping the central value fixed, thus adding to the pedestal free total current. The higher current tends to decrease both 
${q_\ast }$ and 
${\beta _P}$.
In Case B, a pressure pedestal and bootstrap current are added, still keeping zero flow. The additional increase in total current over that in Case A causes a further decrease in 
${q_\ast }$. Adding an edge pressure pedestal while holding the central pressure approximately constant raises the average pressure. This effect tends to increase 
${\beta _P}$ which competes with the 
${\beta _P}$ lowering effects of a current density pedestal and bootstrap current. For the values of parameters chosen, the pressure pedestal dominates and there is a net increase in 
${\beta _P}$.
Case C is the same as Case B except that an adiabatic flow is now added. Since we have kept 
$\nu = 1.04$ at the same value as for the reference case, the implication is that 
${\beta _P}$, as defined in (6.8), will also remain approximately unchanged. Consequently both p and I must either increase or decrease. Qualitatively, at fixed 
${\beta _P}$, an increased pressure gradient near the outer midplane requires additional current for confinement than would be required to balance a weakly varying additional centrifugal force holding the pressure constant. In other words, the current must work harder to confine pressure than rotation. The implication is that holding 
$\nu $ (and correspondingly 
${\beta _P}$) constant while increasing the flow results in an equilibrium with less pressure, less current and an increase in 
${q_\ast }$. This explains the trends in 
${\beta _P}$ and 
${q_\ast }$ in table 2 when flow is added. Observe also that there is very little change in the parameters between the adiabatic (C) and incompressible (D) cases if 
${M_0}$ is held fixed.
Lastly, note that in general, the values of 
${q_\ast }$ with an added current gradient pedestal and bootstrap current are substantially lowered. Depending on parameters, this could put the plasma at risk of a major disruption. To increase 
${q_\ast }$ to a safer value would require decreasing the total current implying that 
${q_0}$ would likely have to be raised above its standard value of unity.
7. Conclusions
The analysis in Part 1 provides analytic solutions to the Grad–Shafranov equation applicable to a wide range of configurations: smooth surface limiter, double-null divertor, single-null divertor, arbitrary 
$\varepsilon ,\kappa ,\delta ,{\beta _T},{\beta _P},{q_0}$. These solutions are all characterized by smooth edge behaviour; that is, the pressure, pressure gradient and toroidal current density all smoothly approach zero at the plasma boundary. Part 2 generalizes the results. Pedestals in pressure, pressure gradient and current density gradient are now included in the analysis. An edge-localized fraction of the bootstrap current is also allowed. Lastly, toroidal flow corresponding to either a 
$\gamma = 2$ adiabatic energy conservation relation or a 
$\gamma = \infty $ incompressible plasma further extends the Part 1 results.
A corresponding set of generalized plasma parameters has also been derived. The new features in Part 2 provide analytic solutions that more closely model actual tokamak plasma behaviour, and this is an important contribution of our analysis. Similar to what we found in Part 1, most of the computational effort is in the post-processing calculation. The solution of the equilibrium problem itself is not computationally intense. Computational times are similar to the ones for the no-pedestal, no-flow case. A Grad–Shafranov solution, flux surface plot and plasma parameter evaluation again require of the order of 2–3 s per tokamak equilibrium.
Editor William Dorland thanks the referees for their advice in evaluating this article.
Funding
This work was supported by the Department of Energy – Fusion Energy Science (L.G., grant no. DE-SC0014196; J.P.F., grant no. DE-FG02-91ER54109).
Declaration of interests
The authors report no conflict of interest.
Appendix A. The generalized Grad–Shafranov equation with toroidal flow
The usual derivation of the Grad–Shafranov equation is generalized to include a toroidal flow velocity. We obtain the modified Grad–Shafranov equation by including poloidal flow and taking the limit as this flow approaches zero. If we set the poloidal flow velocity to zero at the outset, we lose information from several of the key equations. In the end, we obtain a two-dimensional partial differential equation for the poloidal flux with three free functions. The derivation proceeds as follows.
• The 
$\boldsymbol{\nabla }\boldsymbol{\cdot }\textbf{B} = 0$ equation
As in the static case, axisymmetry allows us to introduce a flux function 
$\varPsi$ that automatically guarantees that the 
$\boldsymbol{\nabla }\boldsymbol{\cdot }\textbf{B} = 0$ equation is satisfied. This leads to the following representation for the magnetic field:
\begin{equation}\boldsymbol{B} = \frac{1}{R}\boldsymbol{\nabla }\varPsi \times {\boldsymbol{e}_\phi } + {B_\phi }{\boldsymbol{e}_\phi }.\end{equation}
The three components of the magnetic field are now expressed in terms of the two quantities 
$\varPsi (R,Z)$ and 
${B_\phi }(R,Z)$. The basic unknown in the generalized Grad–Shafranov equation is 
$\varPsi (R,Z)$. As expected, 
$\varPsi (R,Z)$ satisfies the basic definition of a ‘flux function’:
\begin{equation}\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{\nabla }\varPsi = 0.\end{equation}All quantities are eventually expressed in terms of 
$\varPsi (R,Z)$.
• Ampere's law
Ampere's law leads to an expression for the current density in terms of 
$\varPsi$ and 
${B_\phi }$. A simple calculation leads to
\begin{equation}{\mu _0}\boldsymbol{J} = \boldsymbol{\nabla } \times \boldsymbol{B} = \frac{1}{R}\boldsymbol{\nabla }(R{B_\phi }) \times {\boldsymbol{e}_\phi } - {\boldsymbol{e}_\phi }R\boldsymbol{\nabla }\boldsymbol{\cdot }\left( {\frac{{\boldsymbol{\nabla }\varPsi }}{{{R^2}}}} \right).\end{equation}So far, the analysis is identical to the static case.
• Faraday's law
Faraday's law leads to a well-known, simple representation for the electric field. In steady state 
$\partial /\partial t = 0$ implying that
\begin{equation}\boldsymbol{\nabla } \times \boldsymbol{E} = 0 \to \boldsymbol{E} ={-} \boldsymbol{\nabla }\varPhi .\end{equation}The electric field is purely electrostatic.
• The parallel Ohm's law
The parallel component of the ideal MHD Ohm's law reduces to 
$\boldsymbol{E}\boldsymbol{\cdot }\boldsymbol{B} = 0$ which can be written in terms of 
$\Phi (R,Z)$ as
\begin{equation}\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{\nabla }\varPhi = \frac{1}{R}(\boldsymbol{\nabla }\varPsi \times {\boldsymbol{e}_\phi }) \cdot \boldsymbol{\nabla }\varPhi = 0.\end{equation}The general solution to this equation is
\begin{equation}\varPhi (R,Z) = \varPhi (\varPsi ).\end{equation}
The two-dimensional electric potential is actually a function only of the single variable 
$\varPsi$. The functional dependence of 
$\varPhi (\varPsi )$ is a free choice that cannot be determined by the ideal MHD model.
• The velocity 
$\boldsymbol{v}$ from the full Ohm's law
The full Ohm's law, 
$\boldsymbol{E} + \boldsymbol{v} \times \boldsymbol{B} = 0$, can be easily inverted yielding an expression for the velocity:
\begin{equation}\boldsymbol{v} = \frac{{\boldsymbol{E} \times \boldsymbol{B}}}{{{B^2}}} + \frac{{{V_\parallel }}}{B}\boldsymbol{B} ={-} \frac{{\textrm{d}\varPhi }}{{\textrm{d}\varPsi }}\frac{{\boldsymbol{\nabla }\varPsi \times \boldsymbol{B}}}{{{B^2}}} + \frac{{{V_\parallel }}}{B}\boldsymbol{B} = \varOmega \frac{{\boldsymbol{\nabla }\varPsi \times \boldsymbol{B}}}{{{B^2}}} + \frac{{{V_\parallel }}}{B}\boldsymbol{B}.\end{equation}
Here the perpendicular rotational velocity 
$\varOmega (\varPsi ) ={-} \textrm{d}\varPhi /\textrm{d}\varPsi $ has been introduced for convenience and replaces 
$\varPhi (\varPsi )$ as a free function. Observe that 
$\boldsymbol{v}$ is a function of the two quantities 
$\varOmega (\varPsi )$ and 
${V_\parallel }(R,Z)$ with 
${V_\parallel }(R,Z)$ a new, and as yet undetermined unknown.
One immediate consequence of (A 7) is that
\begin{equation}\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{\nabla }\varPsi = 0.\end{equation}There is no flow normal to the flux surfaces.
Since 
$\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{\nabla }\varPsi = 0$ it becomes convenient in the analysis to introduce the poloidal and toroidal components of the velocity, 
${V_p}$ and 
${V_\phi }$, as alternatives to the perpendicular and parallel components 
$\varOmega R$ and 
${V_\parallel }$. Thus, writing 
$\boldsymbol{v} = {V_p}({\boldsymbol{B}_p}/{B_p}) + {V_\phi }{\boldsymbol{e}_\phi }$ with 
${B_p} = {[{(\boldsymbol{\nabla }\varPsi )^2}/{R^2}]^{1/2}}$, equating this expression to (A 7) and taking the limit 
${V_p} \to 0$ leads to
\begin{equation}\left. {\begin{array}{cc@{}}{{V_\parallel } = \dfrac{{{B_\phi }}}{B}{V_\phi } + \dfrac{{{B_p}}}{B}{V_p} \to \dfrac{{{B_\phi }}}{B}{V_\phi },}&{{V_\phi } = \dfrac{{{B_\phi }}}{B}{V_\parallel } - \dfrac{{B_p^2}}{{{B^2}}}\varOmega R,}\\ {\varOmega R ={-} {V_\phi } + \dfrac{{{B_\phi }}}{{{B_p}}}{V_p} \to - {V_\phi },}&{{V_p} = \dfrac{{{B_p}}}{B}\left( {{V_\parallel } + \dfrac{{{B_\phi }}}{B}\varOmega R} \right) \to 0.} \end{array}} \right\}\end{equation}These relations allow us to use either set of velocities interchangeably.
• Conservation of mass
The conservation of mass equation simplifies to
\begin{equation}\boldsymbol{\nabla }\boldsymbol{\cdot }(\rho \boldsymbol{v}) = \boldsymbol{\nabla }\boldsymbol{\cdot }\left( {\frac{{\rho {V_p}}}{{{B_p}}}{\boldsymbol{B}_p}} \right) = {\boldsymbol{B}_p}\boldsymbol{\cdot }\boldsymbol{\nabla }\left( {\frac{{\rho {V_p}}}{{{B_p}}}} \right) = 0.\end{equation}The general solution to this equation is
\begin{equation}\frac{{\rho {V_p}}}{{{B_p}}} = \varGamma (\varPsi ) \to 0,\end{equation}
where 
$\varGamma (\varPsi )$ is a new free function proportional to the poloidal momentum. The case of current interest is pure toroidal flow, corresponding to the limit 
$\varGamma (\varPsi ) \to 0$.
• Conservation of energy
The conservation of energy equation simplifies in a similar way:
\begin{equation}\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{\nabla }\left( {\frac{p}{{{\rho^\gamma }}}} \right) = \frac{{{V_p}}}{{{B_p}}}{\boldsymbol{B}_p}\boldsymbol{\cdot }\boldsymbol{\nabla }\left( {\frac{p}{{{\rho^\gamma }}}} \right) = 0.\end{equation}The general solution is
\begin{equation}\frac{p}{{{\rho ^\gamma }}} = S(\varPsi ) \equiv \frac{{\bar{p}(\varPsi )}}{{\bar{\rho }{{(\varPsi )}^\gamma }}},\end{equation}
with 
$S(\varPsi )$ another free function equivalent to the entropy. It is convenient to replace 
$S(\varPsi )$ with the ratio of two flux functions 
$\bar{p}(\varPsi )/\bar{\rho }{(\varPsi )^\gamma }$. This will make it easy to take the incompressible limit. Although 
$\bar{p}(\varPsi )$ and 
$\bar{\rho }{(\varPsi )^\gamma }$ should be viewed as two independent free functions, only their ratio is needed at this point in the analysis, corresponding to the single function 
$S(\varPsi )$.
• The 
${\boldsymbol{e}_\phi }$ component of the momentum equation
The last equation to analyse is the momentum equation which is decomposed into three independent components along the directions 
${\boldsymbol{e}_\phi },\boldsymbol{B}\;\textrm{and}\;\boldsymbol{\nabla }\varPsi $. A set of short calculations shows that the terms appearing in the 
${\boldsymbol{e}_\phi }$ component reduce to
\begin{equation}\left. \begin{gathered} {{\boldsymbol{e}_\phi }\boldsymbol{\cdot }\boldsymbol{\nabla }p = 0,}\\ {{\boldsymbol{e}_\phi }\boldsymbol{\cdot }\boldsymbol{J} \times \boldsymbol{B} = \dfrac{1}{{{\mu_0}R}}{\boldsymbol{B}_p}\boldsymbol{\cdot }\boldsymbol{\nabla }(R{B_\phi }),}\\ {{\boldsymbol{e}_\phi }\boldsymbol{\cdot }(\rho \boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{\nabla }\boldsymbol{v}) = \dfrac{1}{R}{\boldsymbol{B}_p}\boldsymbol{\cdot }\boldsymbol{\nabla }(\varGamma R{V_\phi }).} \end{gathered} \right\}\end{equation}Combining terms leads to
\begin{equation}\frac{1}{R}{\boldsymbol{B}_p}\boldsymbol{\cdot }\boldsymbol{\nabla }({\mu _0}\varGamma R{V_\phi } - R{B_\phi }) \to - \frac{1}{R}{\boldsymbol{B}_p}\boldsymbol{\cdot }\boldsymbol{\nabla }(R{B_\phi }) = 0,\end{equation}which has as its general solution
\begin{equation}R{B_\phi } = F(\varPsi ).\end{equation}
Here, 
$F(\varPsi )$ is another free function of flux related to the toroidal field.
A summary of the expressions for the 
$\phi $ components of velocity and magnetic field is given by
\begin{equation}\left. \begin{gathered} {{V_\phi } ={-} \varOmega R,}\\ {{B_\phi } = \dfrac{F}{R}.} \end{gathered} \right\}\end{equation}
• The 
$\boldsymbol{B}$ component of the momentum equation
The next step in the analysis is to multiply the momentum equation by 
$1/\rho $ and then take its 
$\boldsymbol{B}$ component. A set of short calculations shows that the resulting terms can be written as
\begin{equation}\left. \begin{gathered} {\dfrac{1}{\rho }\boldsymbol{B}\boldsymbol{\cdot }(\boldsymbol{J} \times \boldsymbol{B}) = 0,}\\ {\dfrac{1}{\rho }\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{\nabla }p = {\boldsymbol{B}_p}\boldsymbol{\cdot }\boldsymbol{\nabla }\left( {\dfrac{\gamma }{{\gamma - 1}}\dfrac{p}{\rho }} \right),}\\ {\boldsymbol{B}\boldsymbol{\cdot }(\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{\nabla }\boldsymbol{v}) ={-} \dfrac{1}{2}{\boldsymbol{B}_p}\boldsymbol{\cdot }\boldsymbol{\nabla }({\varOmega^2}{R^2}).} \end{gathered} \right\}\end{equation}We now combine terms yielding
\begin{equation}{\boldsymbol{B}_p}\boldsymbol{\cdot }\boldsymbol{\nabla }\left( {\frac{\gamma }{{\gamma - 1}}\frac{p}{\rho } - \frac{1}{2}{\varOmega^2}{R^2}} \right) = 0.\end{equation}The general solution is given by
\begin{equation}\frac{\gamma }{{\gamma - 1}}\frac{p}{\rho } - \frac{1}{2}{\varOmega ^2}{R^2} = U(\varPsi ) \equiv \frac{\gamma }{{\gamma - 1}}\frac{{\bar{p}(\varPsi )}}{{\bar{\rho }(\varPsi )}} - \frac{1}{2}{\varOmega ^2}(\varPsi )R_0^2,\end{equation}
where 
$U(\varPsi )$ is another free function. Since 
$U(\varPsi )$ has a different ratio of 
$\bar{p}(\varPsi )/\bar{\rho }(\varPsi )$ from 
$S(\varPsi )$, then 
$\bar{p},\bar{\rho }$ can be considered to be two free functions of 
$\varPsi$ replacing 
$S,U$.
Note that (A 13) and (A 20) can be viewed as two simultaneous equations for 
$p(R,Z)$ and 
$\rho (R,Z)$. Solving yields
\begin{equation}\left. \begin{gathered} {\dfrac{\rho }{{\bar{\rho }}} = {{(1 + {M^2}{\Delta_R})}^{1/(\gamma - 1)}},}\\ {\dfrac{p}{{\bar{p}}} = {{\left( {\dfrac{\rho }{{\bar{\rho }}}} \right)}^\gamma } = {{(1 + {M^2}{\Delta_R})}^{\gamma /(\gamma - 1)}},}\\ {{M^2}(\varPsi ) = \dfrac{{\gamma - 1}}{{2\gamma }}\dfrac{{\bar{\rho }{\varOmega^2}R_0^2}}{{\bar{p}}},}\\ {{\Delta_R}(R) = \dfrac{{{R^2}}}{{R_0^2}} - 1.} \end{gathered} \right\}\end{equation}
Here, 
${M^2}(\varPsi )$ is the square of the effective thermal Mach number. Hereafter, we consider 
$\bar{p},{M^2}$ rather than 
$\bar{p},\bar{\rho }$ as two free functions.
• The 
$\boldsymbol{\nabla }\varPsi $ component of the momentum equation
The last relation of interest is obtained by again multiplying the momentum equation by 
$1/\rho $ and then evaluating its 
$\boldsymbol{\nabla }\varPsi $ component. Some algebra is required. The basic equation can be written as
\begin{equation}\boldsymbol{\nabla }\varPsi \cdot \left( { - \boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{\nabla }\boldsymbol{v} + \frac{1}{\rho }\boldsymbol{J} \times \boldsymbol{B} - \frac{1}{\rho }\boldsymbol{\nabla }p} \right) = 0.\end{equation}The various terms are given by
\begin{gather}\left. \begin{gathered} {\boldsymbol{\nabla }\varPsi \boldsymbol{\cdot }(\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{\nabla }\boldsymbol{v}) ={-} \dfrac{1}{2}{\varOmega^2}\boldsymbol{\nabla }\varPsi \boldsymbol{\cdot }\boldsymbol{\nabla }{R^2},}\\ {\dfrac{1}{\rho }\boldsymbol{\nabla }\varPsi \boldsymbol{\cdot }(\boldsymbol{J} \times \boldsymbol{B}) ={-} \dfrac{{{{(\boldsymbol{\nabla }\varPsi )}^2}}}{{{\mu_0}\rho {R^2}}}({\varDelta^\ast }\varPsi + FF^{\prime}),}\\ \begin{array}{ccccc} & \dfrac{1}{\rho }\boldsymbol{\nabla }\varPsi \boldsymbol{\cdot }\boldsymbol{\nabla }p = \dfrac{1}{\rho }\boldsymbol{\nabla }\varPsi \boldsymbol{\cdot }\boldsymbol{\nabla }[\bar{p}{(1 + {M^2}{\Delta_R})^{\gamma /(\gamma - 1)}}]\\ & \quad = \dfrac{1}{\rho }{(1 + {M^2}{\Delta_R})^{1/(\gamma - 1)}}\left\{ {{{(\boldsymbol{\nabla }\varPsi )}^2}\left[ {\bar{p}^{\prime}(1 + {M^2}{\Delta_R}) + \dfrac{\gamma }{{\gamma - 1}}\bar{p}({M^2})^{\prime}{\Delta_R}} \right]} \right\}\\ & \quad \quad + \dfrac{1}{\rho }{(1 + {M^2}{\Delta_R})^{1/(\gamma - 1)}}(\boldsymbol{\nabla }\varPsi \boldsymbol{\cdot }\boldsymbol{\nabla }{\Delta_R})\dfrac{\gamma }{{\gamma - 1}}\bar{p}{M^2}\\ & \quad = \dfrac{{{{(\boldsymbol{\nabla }\varPsi )}^2}}}{{\bar{\rho }}}\left[ {\bar{p}^{\prime}(1 + {M^2}{\Delta_R}) + \dfrac{\gamma }{{\gamma - 1}}\bar{p}({M^2})^{\prime}{\Delta_R}} \right] + \dfrac{1}{2}{\varOmega^2}\boldsymbol{\nabla }\varPsi \boldsymbol{\cdot }\boldsymbol{\nabla }{R^2}. \end{array} \end{gathered} \right\}\end{gather} Combining terms leads to an expression of the form 
${(\boldsymbol{\nabla }\varPsi )^2}[ \cdots ] = 0$. Thus, setting 
$[ \cdots ] = 0$ leads to the desired form of the modified Grad–Shafranov equation including toroidal flow:
\begin{equation}\left. \begin{gathered} {{\varDelta^\ast }\varPsi ={-} FF^{\prime} - {\mu_0}{R^2}\left( {\dfrac{\rho }{{\bar{\rho }}}} \right)\left\{ {\bar{p}^{\prime} + \left[ {{M^2}\bar{p}^{\prime} + \dfrac{\gamma }{{\gamma - 1}}\bar{p}({M^2})^{\prime}} \right]\left( {\dfrac{{{R^2}}}{{R_0^2}} - 1} \right)} \right\},}\\ {\dfrac{\rho }{{\bar{\rho }}} = {{\left[ {1 + {M^2}\left( {\dfrac{{{R^2}}}{{R_0^2}} - 1} \right)} \right]}^{1/(\gamma - 1)}}.} \end{gathered} \right\}\end{equation}
Observe that, as expected, if 
$\varOmega = 0$ corresponding to zero flow, then 
$\rho = \bar{\rho }$ and (A 24) reduces to the standard Grad–Shafranov equation. Also, note that for arbitrary 
$\gamma $, three free functions need to be specified: 
$F,\bar{p},{M^2}$.
Appendix B. Solution of the ${X_n}$ equation with flow
The task here is to generalize the power-series solution for 
${X_n}$ taking into account the modifications to the basic equation due to flow. The analysis is quite similar to that in Appendix A of Part 1 and ultimately requires only simple additions to the recursion relation. The starting point is the equation for 
${X_n}$ repeated here for convenience:
\begin{equation}\left. \begin{gathered} {\dfrac{{{\textrm{d}^2}{Y_n}}}{{\textrm{d}{y^2}}} + h_n^2{Y_n} = 0,}\\ {(1 + \hat{\varepsilon }x)\dfrac{{{\textrm{d}^2}{X_n}}}{{\textrm{d}{x^2}}} + (k_n^2 + \lambda_1^2x + \lambda_2^2{x^2} + \lambda_3^2{x^3}){X_n} = 0,}\\ {k_n^2 = {\alpha^2} - \dfrac{{h_n^2}}{{1 + {\varepsilon^2}}},}\\ {\lambda_1^2 = \hat{\varepsilon }{\alpha^2}{\nu_1},}\\ {\lambda_2^2 = {{\hat{\varepsilon }}^2}{\alpha^2}{\nu_2},}\\ {\lambda_3^2 = {{\hat{\varepsilon }}^3}{\alpha^2}{\nu_3}.} \end{gathered} \right\}\end{equation}
We again expand the two solutions for 
${X_n}$ (
${C_n}$ and 
${S_n}$) as cosine-like and sine-like series:
\begin{equation}\left. \begin{array}{cc@{}} \begin{aligned} {C_n}(x) &= \sum\limits_{m = 0}^\infty {[{{\hat{a}}_m}{x^m}\cos ({k_n}x) + {{\hat{b}}_m}{x^m}\sin ({k_n}x)]} \\ {{\hat{a}}_0} &= 1\quad {{\hat{b}}_0} = 0 \end{aligned}&{\textrm{Cosine - like}\;\textrm{expansion,}}\\ \begin{aligned} {S_n}(x) &= \sum\limits_{m = 0}^\infty {[{{\tilde{a}}_m}{x^m}\cos ({k_n}x) + {{\tilde{b}}_m}{x^m}\sin ({k_n}x)]} \\ {{\tilde{a}}_0} &= 0\quad {{\tilde{b}}_0} = 1 \end{aligned}&{\textrm{Sine - like}\;\textrm{expansion}\textrm{.}} \end{array} \right\}\end{equation} Each expansion is substituted into (B 1). The result contains two types of terms for both the cosine-like and sine-like expansions, one proportional to 
$\cos ({k_n}x)$, the other to 
$\sin ({k_n}x)$. Each coefficient is set to zero which yields a pair of coupled recursion relations, which are identical for both expansions. Only the non-zero starting coefficients are different. The results are summarized below:
\begin{align}\left. \begin{array}{cc@{}} \begin{aligned} {a_m} & ={-} \dfrac{1}{{m(m - 1)}}[\hat{\varepsilon }(m - 1)(m - 2){a_{m - 1}} + (\lambda_1^2 - \hat{\varepsilon }k_n^2){a_{m - 3}} + \lambda_2^2{a_{m - 4}} \\ & \quad + \lambda_3^2{a_{m - 5}} + 2(m - 1){k_n}{b_{m - 1}} + 2\hat{\varepsilon }(m - 2){k_n}{b_{m - 2}}], \end{aligned}\\ \begin{aligned} {b_m} & ={-} \dfrac{1}{{m(m - 1)}}[\hat{\varepsilon }(m - 1)(m - 2){b_{m - 1}} + (\lambda_1^2 - \hat{\varepsilon }k_n^2){b_{m - 3}} + \lambda_2^2{b_{m - 4}} \\ & \quad + \lambda_3^2{b_{m - 5}}- 2(m - 1){k_n}{a_{m - 1}} - 2\hat{\varepsilon }(m - 2){k_n}{a_{m - 2}}]. \end{aligned} \end{array} \right\}\end{align}
As usual, when using these relations we set 
${a_m} = {b_m} = 0$ for all 
$m \le - 1$. The analysis also requires the first and second derivatives of 
${C_n},{S_n}$. These are easily evaluated and can be written as
\begin{equation}\left.\begin{gathered} {{C^{\prime}}_n}(x) = \sum\limits_{m = 0}^\infty {[( - {k_n}{{\hat{a}}_m}{x^m} + m{{\hat{b}}_m}{x^{m - 1}})\sin ({k_n}x) + ({k_n}{{\hat{b}}_m}{x^m} + m{{\hat{a}}_m}{x^{m - 1}})\cos ({k_n}x)]} ,\\ {{S^{\prime}}_n}(x) = \sum\limits_{m = 0}^\infty {[( - {k_n}{{\tilde{a}}_m}{x^m} + m{{\tilde{b}}_m}{x^{m - 1}})\sin ({k_n}x) + ({k_n}{{\tilde{b}}_m}{x^m} + m{{\tilde{a}}_m}{x^{m - 1}})\cos ({k_n}x)]},\\ {{C^{\prime\prime}}_n}(x) ={-} \dfrac{{k_n^2 + \lambda_1^2x + \lambda_2^2{x^2} + \lambda_3^2{x^3}}}{{1 + \hat{\varepsilon }x}}{C_n}(x),\\ {{S^{\prime\prime}}_n}(x) ={-} \dfrac{{k_n^2 + \lambda_1^2x + \lambda_2^2{x^2} + \lambda_3^2{x^3}}}{{1 + \hat{\varepsilon }x}}{S_n}(x).\end{gathered} \right\}\end{equation}Appendix C. Comparison between the analytic solution and FLOW
As explained in the main part of the text, we have benchmarked the analytic code for the solution of the modified Grad–Shafranov equation against the numerical code FLOW (Guazzotto et al. Reference Guazzotto, Betti, Manickam and Kaye2004), with highly satisfactory results. We demonstrate this good agreement by presenting one typical example. For our benchmark, we use the standard tokamak equilibrium presented in Part 1, with a rotation of 
${M_0} = 0.5$. The other input parameters are: 
$\varepsilon = 1/3$, 
$\delta = 0.6$, 
$\kappa = 1.8$, 
$\nu = 0.3$, 
${q_0} = 1$ and 
$\gamma = 2$. Since FLOW is not designed to allow edge pedestals, we set 
${f_B} = {f_P} = {f_J} = 0$ in this calculation. Thus, we are specifically testing the implementation of the flow part of the core analytic solution. We used 1025 points in each direction for the FLOW grid.
The analytic equilibrium and the one calculated with FLOW are compared in figure 4. In figure 4(a), we show constant 
$\varPsi $ (left) and constant p (right) surfaces. FLOW results are in green and analytic results in black. A one-dimensional plot of the same quantities along the midplane is shown in figure 4(b). There, FLOW results are in blue and analytic results are in red. A reference black curve is also added, showing the result for a static equilibrium with the same input free functions 
$F(\varPsi )$ and 
$p(\varPsi )$, but zero flow. For both 
$\varPsi $ and p the FLOW and analytic results are in excellent agreement. The overlap is so close that it is a difficult to see that there are actually two sets of curves. The solutions with flow differ substantially from the static result.
Figure 4. (a) The 
$\varPsi $ (left) and p (right) contours for the benchmark case. The FLOW results are in green and analytic results in black although they are so close that they appear to overlap. (b) One-dimensional plots of the same quantities in red and blue which appear as a single red curve because of the close overlap. A zero flow curve in black is added for comparison.
