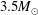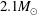1 Introduction
In dense astrophysical plasma, electron species are found in a degenerate state and when the de Broglie wavelength associated with the electron species becomes comparable to or greater than the inter-particle separation, the quantum Bohm force is produced in the plasma. Such dense quantum plasma situations are ubiquitous in many astrophysical objects like supernovas, magnetars, white dwarfs and neutron stars (Jung Reference Jung2001; Opher et al. Reference Opher, Silva, Danger, Decyk and Dawson2001). The field of quantum plasma has widely attracted the attention of several researchers (Pines Reference Pines1961; Haas Reference Haas2005; Manfredi Reference Manfredi2005) and investigations have been motivated by a number of possible applications in microelectronics, nanotechnology, laser fusion and ultracold plasma (Markovich, Ringhofer & Schmeiser Reference Markovich, Ringhofer and Schmeiser1990; Craighead Reference Craighead2000; Glentzer et al. Reference Glentzer, Landen, Neumayer, Lee, Wldmann, Pollaine, Wallance, Gregori, Holl and Bomath2007). Furthermore, whenever the balance between internal pressure and self-gravitational pressure gets disturbed, gravitational collapse in the plasma system occurs. This process is termed as self-gravitational instability and is responsible for fragmentation and structure formation. The concept of self-gravitational instability was first noticed by Jeans (Reference Jeans1929) and then followed by several investigators (Kato & Kumar Reference Kato and Kumar1960; Kumar Reference Kumar1960). The self-gravitational instability in quantum plasma has been also studied considering various parameters. Lundin, Marklund & Brodin (Reference Lundin, Marklund and Brodin2008) have studied the self-gravitational instability including the effect of intrinsic magnetization in a magnetized plasma. The influence of resistivity on Jeans instability in quantum plasma has been investigated by Ren et al. (Reference Ren, Wu, Cao and Chu2009). The work of Ren et al. (Reference Ren, Wu, Cao and Chu2009) has been extended by Wu et al. (Reference Wu, Ren, Cao and Chu2010) incorporating the Hall parameter to study self-gravitational instability with resistivity in a quantum plasma.
Moreover, a lot of studies have been done by considering the zero Larmor radius of ions which is applicable in various astrophysical situations. However, it is found that in many astrophysical regions, this assumption is not valid. The dynamics of the ions is supposed to be classical as the de Broglie wavelength associated with the ions is much smaller than that of the electrons. The gyro-radius of the electrons is negligibly small because of their lighter mass as compared to the ions so the finite Larmor radius (FLR) corrections of the electrons is ignored and considered only for ions, therefore the concept of finite Larmor radius of the ions has been considered by many researchers in their work. In this connection, the stabilizing influence of the FLR corrections on plasma instability has been investigated by Roberts & Taylor (Reference Roberts and Taylor1962). The influence of FLR on Jeans instability of a quantum magneto plasma has been studied by Sharma & Chhajlani (Reference Sharma and Chhajlani2013). One of the interesting features of the strongly magnetized plasma is that it is anisotropic. The presence of a strong magnetic field splits up the plasma pressure into parallel and perpendicular components with respect to the direction of the magnetic field and makes the plasma anisotropic (Mahmood et al.
Reference Mahmood, Hussain, Masood and Saleem2009; Dzhalilov, Kuznetsov & Staude Reference Dzhalilov, Kuznetsov and Staude2011). The Chew–Goldberger–Low (CGL) fluid model has been given by Chew, Goldberger & Low (Reference Chew, Goldberger and Low1956) to study such anisotropic pressure in a strongly magnetized plasma. Several studies have been done in the context of self-gravitational instability in the anisotropic plasma system (Gliddon Reference Gliddon1966; Singh & Kalra Reference Singh and Kalra1986). The self-gravitational instability of an anisotropic plasma with FLR corrections has been studied by Bhatiya (Reference Bhatiya1968a
,Reference Bhatiya
b
). The propagation of magnetoacoustic waves has been studied by Yajima (Reference Yajima1966) using the modified CGL equations with FLR corrections. It is well known that the quantum effects play a significant role at larger number density and such a condition is easily met in highly dense astrophysical bodies. The regime of the quantum plasma as to whether it is collisional or collisionless can be decided on the basis of the quantum coupling parameter (
$G_{q}$
) that can be defined as
$$\begin{eqnarray}\displaystyle G_{q}=\frac{E_{\text{int}}}{E_{F}}=\frac{2me^{2}}{3^{2/3}\unicode[STIX]{x1D700}_{0}\hslash ^{2}\unicode[STIX]{x03C0}^{4/3}}\left(\frac{1}{n^{1/3}}\right), & & \displaystyle\end{eqnarray}$$
where
$E_{\text{int}}$
and
$E_{F}$
represents the interaction energy and Fermi energy respectively. The symbol
$m$
and
$n$
is mass and number density of fluid particle respectively and
$e$
represents electronic charge.
The quantum plasma is collisionless for
$G_{q}<1$
and collisional otherwise. It is clear from the above expression that the quantum coupling parameter is found to be much smaller than unity at higher density. Thus, the dense degenerate bodies are collisionless and the presence of a strong magnetic field in it modifies the characteristics of the system. In this direction, Shukla & Stenflo (Reference Shukla and Stenflo2008) have derived the nonlinear quantum Hall-magnetohydrodynamic (MHD) equations in a dense magnetoplasma including anisotropic pressure of degenerate electrons. The self-gravitational instability in an anisotropic plasma with degenerate electrons has been studied by Prajapati (Reference Prajapati2014). Paret, Martinez & Horvath (Reference Paret, Martinez and Horvath2015) have investigated the role of anisotropic pressure in the structure formation of a white dwarf.
However, for anisotropic plasma systems the viscosity of the plasma is also divided into parallel and perpendicular components (Campos & Mendes Reference Campos and Mendes2000; Pandey & Dwivedi Reference Pandey and Dwivedi2007; Tessema & Torkelsson Reference Tessema and Torkelsson2010). The magnetohydrodynamic waves in an incompressible plasma with tensor viscosity have been investigated by Hollweg (Reference Hollweg1987). The effect of anisotropic viscosity on magnetohydrodynamic wave propagation has been studied by Cherkos & Tessema (Reference Cherkos and Tessema2013). The self-gravitational instability in anisotropic plasma incorporating tensor viscosity has been investigated by Cherkos & Tessema (Reference Cherkos and Tessema2013). Recently, Sharma (Reference Sharma2017) has presented the role of tensor viscosity in a self-gravitational anisotropic plasma with FLR corrections. Furthermore, the role of rotation in a plasma system becomes of great interest due to its wide applications in neutral beam injection (Strait et al.
Reference Strait, Garofalo, Jackson, Okabayashi, Reimerdes, Chu, Fitzpatrick, Groebner, In and Lahaye2007), fusion research (i.e. tokamaks and helical systems) (Ida & Rice Reference Ida and Rice2014), special technical arrangements (i.e. condensers, plasma gun propulsion etc.) and in cosmical physics etc. It also plays a prominent role in fragmentation and star formation. In this regard, the effect of rotation on Jeans instability has been studied by many researchers. Chandrasekhar (Reference Chandrasekhar1961) investigated the effect of a magnetic field and rotation on the Jeans instability in a homogeneous plasma system. The effect of rotation on the self-gravitational instability of an anisotropic plasma with FLR has been studied by Bhatiya (Reference Bhatiya1968a
,Reference Bhatiya
b
). Prajapati, Parihar & Chhajlani (Reference Prajapati, Parihar and Chhajlani2008) have investigated the role of rotation and heat flux on the self-gravitational instability of an anisotropic plasma. Sharma et al. (Reference Sharma, Argal, Tiwari and Prajapati2015) have presented the modified self-gravitational instability of a rotating visco-elastic magnetized plasma. They found that the growth rate of the instability stabilizes due to the presence of rotation. Jain, Sharma & Chhajlani (Reference Jain, Sharma and Chhajlani2015) have investigated the effect of FLR and rotation on self-gravitational instability of a viscous quantum plasma. Moreover, rotation also plays a crucial role in stabilizing the white dwarf stars. Several researchers have mentioned that the stability of a white dwarf is only up to the Chandrashekhar mass limit (
${\approx}1.4M_{\odot }$
) while in some studies, it has been observed that the strong magnetic field and rapid rotation in a white dwarf maintained its stability even above the mass limit
$1.4M_{\odot }$
(Subramanian & Mukhopadhyay Reference Subramanian and Mukhopadhyay2015). This type of star is named a super Chandrashekhar white dwarf and produces luminous supernovae such as SN 2007if, SN 2009dc, SNLS-03 D3bb, SN 2003 fg (Howell et al.
Reference Howell, Sullivan, Nugent, Ellis, Conley, Borgne, Carlberg, Guy, Balam and Basa2006). Franzon & Schramm (Reference Franzon and Schramm2015) have studied the effect of rotation and magnetic field on the white dwarf stars and observed that for a
$10^{15}$
Guass magnetic field strength, the mass of the star can be
$2.9M_{\odot }$
. The roles of rotation and magnetic field in a white dwarf star have been also studied by Subramanian & Mukhopadhyay (Reference Subramanian and Mukhopadhyay2015). Das & Mukhopadhyay (Reference Das and Mukhopadhyay2015) have found that the mass of a strongly magnetized white dwarf can be of the order of
$3.4M_{\odot }$
.
Thus, the strong magnetic field allows us to consider the FLR corrections and tensor viscosity to study the gravitational instability in a degenerate anisotropic plasma. The strong magnetic field is particularly significant when coupled with other features of dense degenerate plasma systems i.e. rotation. The present study is motivated by the observations of Shukla & Stenflo (Reference Shukla and Stenflo2008) and Prajapati (Reference Prajapati2014) in a dense degenerate plasma. The nonlinear quantum Hall-MHD equations are obtained by Shukla & Stenflo (Reference Shukla and Stenflo2008) in a dense magnetoplasma including anisotropic pressure. The effect of the quantum parameter on self-gravitational instability in an anisotropic plasma has been observed by Prajapati (Reference Prajapati2014). Both of the above mentioned works have not considered the effect of FLR corrections, rotation and tensor viscosity in an anisotropic quantum plasma. Hence the formulation of the present work is done using the quantum magnetohydrodynamic and CGL fluid equations to study the self-gravitational instability of an anisotropic quantum plasma incorporating tensor viscosity, rotation and FLR corrections. To present a systematic analysis of the work, we have assumed the direction of rotation in the parallel and perpendicular directions of the magnetic field. However, in the present study our aim is to study how the rotation affects the gravitational instability. Therefore, the effect of rotation in a magnetized system is analysed in following ways
-
(i) with the propagation wave vector is perpendicular to the magnetic field (i.e.
$k\bot H_{0}$
); -
(ii) with the propagation wave vector is parallel to the magnetic field (i.e.
$k\Vert H_{0}$
).
Further, to observe the effect of rotation on the above cases, we have taken the rotational frequency parallel and perpendicular to the direction of magnetic field in each case so that when
$k\bot H_{0}$
, we have taken
$\unicode[STIX]{x1D6FA}\Vert H_{0}$
and
$\unicode[STIX]{x1D6FA}\bot H_{0}$
. Similarly for
$k\Vert H_{0}$
, we have taken
$\unicode[STIX]{x1D6FA}\Vert H_{0}$
and
$\unicode[STIX]{x1D6FA}\bot H_{0}$
.
The paper is organized in the following way; in § 2 the basic set of equations for a self-gravitational anisotropic quantum plasma incorporating tensor viscosity, rotation and FLR corrections is given. The perturbed set of equations and dispersion relation are presented in § 3. The analytical and graphical discussions are shown in § 4. The conclusion is given in the last section.
2 Basic equations
We consider an infinite homogeneous viscous quantum magnetoplasma with uniform rotational frequency
$\unicode[STIX]{x1D734}(\unicode[STIX]{x1D6FA}_{\bot },0,\unicode[STIX]{x1D6FA}_{\Vert })$
and FLR corrections. The basic governing momentum, magnetic induction, Poisson and continuity equations for the considered viscous magneto quantum plasma system are as follows
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \frac{\text{d}\boldsymbol{u}}{\text{d}t}+\frac{\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D72B}}{\unicode[STIX]{x1D70C}}+\frac{\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{p}}{\unicode[STIX]{x1D70C}}-\frac{1}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}}\left(\unicode[STIX]{x1D735}\times \boldsymbol{H}\right)\times \boldsymbol{H}\nonumber\\ \displaystyle & & \displaystyle \quad \displaystyle +\,\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D713}-2\left(\boldsymbol{u}\times \unicode[STIX]{x1D734}\right)-\frac{\hslash ^{2}}{2m_{e}m_{i}}\unicode[STIX]{x1D6FB}\left(\frac{\unicode[STIX]{x1D6FB}^{2}\sqrt{\unicode[STIX]{x1D70C}}}{\sqrt{\unicode[STIX]{x1D70C}}}\right)=0.\end{eqnarray}$$
The symbols
$\boldsymbol{u},\boldsymbol{p},\unicode[STIX]{x1D713},\unicode[STIX]{x1D72B}$
and
$\unicode[STIX]{x1D70C}$
represent the velocity, pressure, gravitational potential, tensor viscosity and density of the fluid respectively. The ion and electron mass are symbolized by
$m_{i}$
and
$m_{e}$
respectively. The uniform magnetic field
$\boldsymbol{H}$
(
$0,0,\boldsymbol{H}_{\mathbf{0}}$
) is assumed to be in the
$z$
-direction.
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{H}}{\unicode[STIX]{x2202}t}=\unicode[STIX]{x1D735}\times \left(\boldsymbol{u}\times \boldsymbol{H}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D713}=4\unicode[STIX]{x03C0}G\unicode[STIX]{x1D70C}, & \displaystyle\end{eqnarray}$$
where
$G$
is the gravitational constant
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(\unicode[STIX]{x1D70C}\boldsymbol{u}\right)=0. & \displaystyle\end{eqnarray}$$
The tensor viscosity
$\unicode[STIX]{x1D72B}$
represented by the second term in (2.1) can be defined in terms of the coefficient of compressive viscosity (
$\unicode[STIX]{x1D702}_{0}$
), shear viscosity (
$\unicode[STIX]{x1D702}_{1}$
and
$\unicode[STIX]{x1D702}_{2}$
) and perpendicular viscosity (
$\unicode[STIX]{x1D702}_{3}$
and
$\unicode[STIX]{x1D702}_{4}$
) such that
$\unicode[STIX]{x1D6F1}_{ij}=-\unicode[STIX]{x1D702}_{0}\unicode[STIX]{x1D70F}_{0ij}-\unicode[STIX]{x1D702}_{1}\unicode[STIX]{x1D70F}_{1ij}-\unicode[STIX]{x1D702}_{2}\unicode[STIX]{x1D70F}_{2ij}-\unicode[STIX]{x1D702}_{3}\unicode[STIX]{x1D70F}_{3ij}-\unicode[STIX]{x1D702}_{4}\unicode[STIX]{x1D70F}_{4ij}$
, where
$\unicode[STIX]{x1D70F}_{ij}=(\unicode[STIX]{x2202}u_{i}/\unicode[STIX]{x2202}x_{j})+(\unicode[STIX]{x2202}u_{j}/\unicode[STIX]{x2202}x_{i})-(2/3)\unicode[STIX]{x1D6FF}_{ij}(\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u})$
. The components of the viscous stress tensor
$\unicode[STIX]{x1D6F1}_{ij}$
are as follows
$$\begin{eqnarray}\displaystyle & \displaystyle \left.\begin{array}{@{}l@{}}\displaystyle \unicode[STIX]{x1D6F1}_{xx}=-\frac{\unicode[STIX]{x1D702}_{0}}{2}\left(\unicode[STIX]{x1D70F}_{xx}+\unicode[STIX]{x1D70F}_{yy}\right)-\frac{\unicode[STIX]{x1D702}_{1}}{2}\left(\unicode[STIX]{x1D70F}_{xx}+\unicode[STIX]{x1D70F}_{yy}\right)-\unicode[STIX]{x1D702}_{3}\unicode[STIX]{x1D70F}_{xy},\\ \displaystyle \unicode[STIX]{x1D6F1}_{yy}=-\frac{\unicode[STIX]{x1D702}_{0}}{2}\left(\unicode[STIX]{x1D70F}_{xx}+\unicode[STIX]{x1D70F}_{yy}\right)-\frac{\unicode[STIX]{x1D702}_{1}}{2}\left(\unicode[STIX]{x1D70F}_{xx}+\unicode[STIX]{x1D70F}_{yy}\right)+\unicode[STIX]{x1D702}_{3}\unicode[STIX]{x1D70F}_{xy},\\ \displaystyle \unicode[STIX]{x1D6F1}_{xy}=\unicode[STIX]{x1D6F1}_{yx}=\frac{\unicode[STIX]{x1D702}_{3}}{2}\left(\unicode[STIX]{x1D70F}_{xx}-\unicode[STIX]{x1D70F}_{yy}\right)+\unicode[STIX]{x1D702}_{1}\unicode[STIX]{x1D70F}_{xy},\\ \displaystyle \unicode[STIX]{x1D6F1}_{xz}=\unicode[STIX]{x1D6F1}_{zx}=\unicode[STIX]{x1D702}_{2}\unicode[STIX]{x1D70F}_{xz}-\unicode[STIX]{x1D702}_{4}\unicode[STIX]{x1D70F}_{yz},\\ \displaystyle \unicode[STIX]{x1D6F1}_{yz}=\unicode[STIX]{x1D6F1}_{zy}=\unicode[STIX]{x1D702}_{2}\unicode[STIX]{x1D70F}_{yz}+\unicode[STIX]{x1D702}_{4}\unicode[STIX]{x1D70F}_{xz},\displaystyle \unicode[STIX]{x1D6F1}_{zz}=-\unicode[STIX]{x1D702}_{0}\unicode[STIX]{x1D70F}_{zz}.\end{array}\right\} & \displaystyle\end{eqnarray}$$
Now, considering the condition
$\unicode[STIX]{x1D702}_{0}\gg \unicode[STIX]{x1D702}_{1}$
,
$\unicode[STIX]{x1D702}_{2}$
,
$\unicode[STIX]{x1D702}_{3}$
and
$\unicode[STIX]{x1D702}_{4}$
in (2.5) and using the value of
$\unicode[STIX]{x1D70F}_{xx}$
,
$\unicode[STIX]{x1D70F}_{yy}$
and
$\unicode[STIX]{x1D70F}_{zz}$
in the form of fluid velocity, the components of the tensor viscosity
$\unicode[STIX]{x1D6F1}_{ij}$
can be given as
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F1}_{xx}=-\frac{\unicode[STIX]{x1D702}_{0}}{3}\left(\frac{\unicode[STIX]{x2202}u_{x}}{\unicode[STIX]{x2202}x}-2\frac{\unicode[STIX]{x2202}u_{z}}{\unicode[STIX]{x2202}z}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F1}_{yy}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F1}_{zz}=-\frac{\unicode[STIX]{x1D702}_{0}}{3}\left(-2\frac{\unicode[STIX]{x2202}u_{x}}{\unicode[STIX]{x2202}x}+4\frac{\unicode[STIX]{x2202}u_{z}}{\unicode[STIX]{x2202}z}\right). & \displaystyle\end{eqnarray}$$
The system of equations is closed with an equation of state for pressure. Theoretically, the pressure
$\boldsymbol{p}$
of the system contains both the ion and electron pressure. Hence the pressure of the system is written in the form
$\unicode[STIX]{x1D735}\boldsymbol{p}=c_{s}^{2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}$
, where
$c_{s}$
is speed of sound. Further, in the white dwarf stars and inside of neutron stars the gravitational force is accountable for new structure formations at quantum scales. The quantum effects manage the dynamics of the particles in dense degenerate systems when the de Broglie wavelength of the plasma particles becomes similar to or greater than the average inter-particle separation. Therefore the wave functions correspond to the particles overlaps with each other. Equivalently, for the temperature (
$T$
) less than the Fermi temperature
$T_{F}$
(where
$T_{F}=m_{e}V_{F}^{2}/K_{B}$
is the Fermi temperature and
$V_{F}=\hslash (\unicode[STIX]{x03C0}^{2}n_{e})^{1/3}/m_{e}$
is the Fermi velocity, here
$n_{e}$
stands for number density of electrons), the plasma particles which obey Maxwell–Boltzmann distribution in the classical regime becomes invalid and new statistics, Fermi–Dirac statistics, describes the plasma dynamics (Haas Reference Haas2005; Lundin et al.
Reference Lundin, Marklund and Brodin2008; Ren et al.
Reference Ren, Wu, Cao and Chu2009; Shukla & Eliasson Reference Shukla and Eliasson2009; Prajapati Reference Prajapati2014; Irfan, Ali & Mirza Reference Irfan, Ali and Mirza2017). The effective speed of sound on the quantum scale is
$c_{s}^{2}=V_{t}^{2}+V_{F}^{2}/3$
, where
$V_{t}$
is the thermal velocity of the fluid particle. Thus, following Haas (Reference Haas2005), the modified pressure term containing the Bohm potential can be represented as
$\unicode[STIX]{x1D735}\boldsymbol{p}+(\hslash ^{2}\unicode[STIX]{x1D70C}/2m_{e}m_{i})\unicode[STIX]{x1D735}(\unicode[STIX]{x1D6FB}^{2}\sqrt{\unicode[STIX]{x1D70C}}/\sqrt{\unicode[STIX]{x1D70C}})$
where
$\unicode[STIX]{x1D735}\boldsymbol{p}=(V_{t}^{2}+V_{F}^{2}/3)\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}$
. Moreover, the strong magnetic field in the plasma system is associated with anisotropic and FLR pressure. Hence the total pressure (
$\boldsymbol{p}$
) in the momentum transfer (2.1) is incorporated by the anisotropic and FLR pressure as mentioned in Bhatiya (Reference Bhatiya1968a
,Reference Bhatiya
b
)
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{p}=p_{\text{aniso}}+P_{\text{flr}}, & \displaystyle\end{eqnarray}$$
where
$p_{\text{aniso}}=(p_{\Vert }-p_{\bot })\boldsymbol{b}\boldsymbol{b}+p_{\bot }\boldsymbol{I}$
in which
$p_{\bot }$
is pressure perpendicular to the magnetic field and
$p_{\Vert }$
is the pressure along the magnetic field,
$\boldsymbol{b}$
is a unit vector directed along the magnetic field and
$\boldsymbol{I}$
is a unit dyadic. The parallel and perpendicular components of pressure can be written as
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}\left(\frac{p_{\Vert }H^{2}}{\unicode[STIX]{x1D70C}^{3}}\right)=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}\left(\frac{p_{\bot }}{\unicode[STIX]{x1D70C}H}\right)=0. & \displaystyle\end{eqnarray}$$
The corrected FLR pressure is represented by
$P_{\text{flr}}$
and its components are given as (Roberts & Taylor Reference Roberts and Taylor1962)
$$\begin{eqnarray}\displaystyle & \displaystyle \left.\begin{array}{@{}c@{}}\displaystyle P_{xx}=-\unicode[STIX]{x1D70C}\unicode[STIX]{x1D708}_{0}\left(\frac{\unicode[STIX]{x2202}u_{x}}{\unicode[STIX]{x2202}y}+\frac{\unicode[STIX]{x2202}u_{y}}{\unicode[STIX]{x2202}x}\right),\quad P_{xy}=P_{yx}=\unicode[STIX]{x1D70C}\unicode[STIX]{x1D708}_{0}\left(\frac{\unicode[STIX]{x2202}u_{x}}{\unicode[STIX]{x2202}x}-\frac{\unicode[STIX]{x2202}u_{y}}{\unicode[STIX]{x2202}y}\right),\\[4.0pt] \displaystyle P_{xz}=P_{zx}=-2\unicode[STIX]{x1D70C}\unicode[STIX]{x1D708}_{0}\left(\frac{\unicode[STIX]{x2202}u_{z}}{\unicode[STIX]{x2202}y}+\frac{\unicode[STIX]{x2202}u_{y}}{\unicode[STIX]{x2202}z}\right),\quad P_{yy}=\unicode[STIX]{x1D70C}\unicode[STIX]{x1D708}_{0}\left(\frac{\unicode[STIX]{x2202}u_{y}}{\unicode[STIX]{x2202}x}+\frac{\unicode[STIX]{x2202}u_{x}}{\unicode[STIX]{x2202}y}\right),\\[4.0pt] \displaystyle P_{yz}=P_{zy}=2\unicode[STIX]{x1D70C}\unicode[STIX]{x1D708}_{0}\left(\frac{\unicode[STIX]{x2202}u_{z}}{\unicode[STIX]{x2202}x}+\frac{\unicode[STIX]{x2202}u_{x}}{\unicode[STIX]{x2202}z}\right),\quad P_{zz}=0,\end{array}\right\} & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D708}_{0}$
is the kinematic viscosity.
3 Linearized perturbed equations and dispersion relation
The governing basic equations are first converted into linearized and perturbed form to derive the general dispersion relation for a viscous quantum magneto plasma system using the following linearized form of the physical quantities
$$\begin{eqnarray}\displaystyle & \displaystyle \left.\begin{array}{@{}c@{}}\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{0}+\unicode[STIX]{x1D70C}_{1},\quad \boldsymbol{u}=\boldsymbol{u}_{0}+\boldsymbol{u}_{1},\quad \unicode[STIX]{x1D713}=\unicode[STIX]{x1D713}_{o}+\unicode[STIX]{x1D713}_{1},\\[5.0pt] \boldsymbol{H}=\boldsymbol{H}_{0}+\boldsymbol{H}_{1},\quad \unicode[STIX]{x1D72B}=\unicode[STIX]{x1D72B}_{\mathbf{0}}+\unicode[STIX]{x1D72B}_{1},\quad p=p_{0}+p_{1}.\end{array}\right\} & \displaystyle\end{eqnarray}$$
Moreover, we shall assume the perturbations in space and time dependent physical quantities to vary in the form
$\text{e}^{\text{i}(k_{\bot }x+k_{\Vert }z-\unicode[STIX]{x1D70E}t)}$
, where
$k_{\bot }$
and
$k_{\Vert }$
are the wavenumbers perpendicular and parallel to the direction of the magnetic field and
$\unicode[STIX]{x1D70E}$
represents the frequency of wave perturbations. Now using the linearized and perturbation form in (2.1)–(2.12) one can write the linearized perturbed set of equations as follows
$$\begin{eqnarray}\displaystyle & \hspace{-60.0pt}\displaystyle -\text{i}\unicode[STIX]{x1D70E}\boldsymbol{ u}_{\mathbf{1}}+\frac{\text{i}\boldsymbol{ k}\boldsymbol{\cdot }\boldsymbol{ p}_{\mathbf{1}}}{\unicode[STIX]{x1D70C}_{0}}-\frac{1}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}\left(\text{i}\boldsymbol{k}\times \boldsymbol{H}_{1}\right)\times \boldsymbol{H}_{\mathbf{0}} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \qquad +\,\text{i}\boldsymbol{k}\unicode[STIX]{x1D713}_{1}-2\left(\boldsymbol{u}_{\mathbf{1}}\times \unicode[STIX]{x1D734}\right)+\frac{\text{i}\boldsymbol{k}\boldsymbol{\cdot }\unicode[STIX]{x1D72B}_{\mathbf{1}}}{\unicode[STIX]{x1D70C}_{0}}+\frac{\hslash ^{2}}{4m_{e}m_{i}}\text{i}\boldsymbol{k}k^{2}\unicode[STIX]{x1D70C}_{1}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle -k^{2}\unicode[STIX]{x1D713}_{1}=4\unicode[STIX]{x03C0}G\unicode[STIX]{x1D70C}_{1}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle -\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70C}_{1}+\unicode[STIX]{x1D70C}_{0}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{u}_{\mathbf{1}}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle -\unicode[STIX]{x1D70E}\boldsymbol{H}_{\mathbf{1}}=\boldsymbol{k}\times \left(\boldsymbol{u}_{\mathbf{1}}\times \boldsymbol{H}_{\mathbf{0}}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F1}_{xx}=-\frac{\text{i}\unicode[STIX]{x1D702}_{0}}{3}\left(k_{\bot }u_{x1}-2k_{\Vert }u_{z1}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F1}_{zz}=-\frac{\text{i}\unicode[STIX]{x1D702}_{0}}{3}\left(-2k_{\bot }u_{x1}+4k_{\Vert }u_{z1}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{p}_{\mathbf{1}}=\left(p_{\Vert 1}-p_{\bot 1}\right)\boldsymbol{b}\boldsymbol{b}+p_{\bot 1}\boldsymbol{I}+\left(p_{\Vert 0}-p_{\bot 0}\right)\left(\boldsymbol{b}_{\mathbf{1}}\boldsymbol{b}+\boldsymbol{b}\boldsymbol{b}_{\mathbf{1}}\right)+P_{flr1}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{p_{\Vert 1}}{p_{\Vert 0}}=\frac{3\unicode[STIX]{x1D70C}_{1}}{\unicode[STIX]{x1D70C}_{0}}-\frac{2H_{1}}{H_{0}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{p_{\bot 1}}{p_{\bot 0}}=\frac{\unicode[STIX]{x1D70C}_{1}}{\unicode[STIX]{x1D70C}_{0}}+\frac{H_{1}}{H_{0}}. & \displaystyle\end{eqnarray}$$
The solution of (3.2)–(3.10) gives the components of the momentum transfer equation which can be represented in matrix form as
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \left[\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D70E}^{2}+\displaystyle \frac{\text{i}\unicode[STIX]{x1D702}_{0}}{3\unicode[STIX]{x1D70C}_{0}}k_{\bot }^{2}\unicode[STIX]{x1D70E}-\unicode[STIX]{x0394}sk_{\Vert }^{2}-\frac{T_{_{2\bot }}^{2}}{\unicode[STIX]{x1D70C}_{0}}k_{\bot }^{2}-\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}k^{2} & \displaystyle \left(-2\unicode[STIX]{x1D6FA}_{\Vert }+\frac{p_{i\,\bot 0}\unicode[STIX]{x1D714}_{L}^{-1}}{2\unicode[STIX]{x1D70C}_{0}}\,\left(k^{2}+k_{\Vert }^{2}\right)\right)\text{i}\unicode[STIX]{x1D70E} & \displaystyle -\left(\frac{2\text{i}\unicode[STIX]{x1D702}_{0}}{3\unicode[STIX]{x1D70C}_{0}}\unicode[STIX]{x1D70E}+\frac{T_{_{\bot }}^{2}}{\unicode[STIX]{x1D70C}_{0}}\right)k_{\bot }k_{\Vert }\\[8.0pt] \displaystyle \left(2\unicode[STIX]{x1D6FA}_{\Vert }-\frac{p_{i\,\bot 0}\unicode[STIX]{x1D714}_{L}^{-1}}{2\unicode[STIX]{x1D70C}_{0}}\,\left(k^{2}+k_{\Vert }^{2}\right)\right)\text{i}\unicode[STIX]{x1D70E} & \displaystyle \unicode[STIX]{x1D70E}^{2}-\unicode[STIX]{x0394}sk_{\Vert }^{2}-\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}k_{\Vert }^{2} & \displaystyle -\left(2\unicode[STIX]{x1D6FA}_{\bot }+\frac{p_{i\,\bot 0}\unicode[STIX]{x1D714}_{L}^{-1}}{\unicode[STIX]{x1D70C}_{0}}k_{\bot }k_{\Vert }\,\right)\text{i}\unicode[STIX]{x1D70E}\\[8.0pt] \displaystyle -\left(\frac{2\text{i}\unicode[STIX]{x1D702}_{0}}{3\unicode[STIX]{x1D70C}_{0}}\unicode[STIX]{x1D70E}+\frac{T_{_{\bot }}^{2}}{\unicode[STIX]{x1D70C}_{0}}\right)k_{\bot }k_{\Vert } & \displaystyle \left(2\unicode[STIX]{x1D6FA}_{\bot }+\frac{p_{i\,\bot 0}\unicode[STIX]{x1D714}_{L}^{-1}}{\unicode[STIX]{x1D70C}_{0}}\,k_{\bot }k_{\Vert }\right)\text{i}\unicode[STIX]{x1D70E} & \displaystyle \left(\unicode[STIX]{x1D70E}^{2}+\frac{4\text{i}\unicode[STIX]{x1D702}_{0}}{3\unicode[STIX]{x1D70C}_{0}}\unicode[STIX]{x1D70E}k_{\Vert }^{2}-\frac{T_{_{3\Vert }}^{2}}{\unicode[STIX]{x1D70C}_{0}}k_{\Vert }^{2}\right)\end{array}\right]\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad \times \left[\begin{array}{@{}c@{}}u_{x}\\ u_{y}\\ u_{z}\end{array}\right]=0,\end{eqnarray}$$
where
$T_{2\bot }^{2}=2p_{\bot 0}-(4\unicode[STIX]{x03C0}G\unicode[STIX]{x1D70C}_{0}^{2}/k^{2})+Q^{2}k^{2}\unicode[STIX]{x1D70C}_{0},T_{\bot }^{2}=p_{\bot 0}-(4\unicode[STIX]{x03C0}G\unicode[STIX]{x1D70C}_{0}^{2}/k^{2})+Q^{2}k^{2}\unicode[STIX]{x1D70C}_{0},$
$$\begin{eqnarray}\displaystyle & \displaystyle T_{3\Vert }^{2}=3p_{\Vert 0}-(4\unicode[STIX]{x03C0}G\unicode[STIX]{x1D70C}_{0}^{2}/k^{2})+Q^{2}k^{2}\unicode[STIX]{x1D70C}_{0},\quad \unicode[STIX]{x0394}s=(p_{\bot 0}-p_{\Vert 0})/\unicode[STIX]{x1D70C}_{0}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle Q^{2}=(\hslash ^{2}k^{2}/4m_{e}m_{i}). & \displaystyle\end{eqnarray}$$
The solution of the above third order matrix yields the following expression which is the general dispersion relation for an anisotropic viscous quantum plasma.
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \left[2\left(\frac{2\text{i}\unicode[STIX]{x1D70E}\unicode[STIX]{x1D702}_{0}}{3}+T_{_{\bot }}^{2}\right)\frac{k_{\Vert }k_{\bot }}{\unicode[STIX]{x1D70C}_{0}}\left(2\unicode[STIX]{x1D6FA}_{\Vert }-\unicode[STIX]{x1D708}_{0}(k^{2}+k_{\Vert }^{2})\right)\left(2\unicode[STIX]{x1D6FA}_{\bot }+2\unicode[STIX]{x1D708}_{0}k_{\bot }k_{\Vert }\right)\right.\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad -\,\left.\left(2\unicode[STIX]{x1D6FA}_{\Vert }-\unicode[STIX]{x1D708}_{0}(k^{2}+k_{\Vert }^{2})\right)^{2}\left(\unicode[STIX]{x1D70E}^{2}+\frac{4\text{i}\unicode[STIX]{x1D702}_{0}}{3\unicode[STIX]{x1D70C}_{0}}k_{\Vert }^{2}\unicode[STIX]{x1D70E}-\frac{T_{_{3\Vert }}^{2}}{\unicode[STIX]{x1D70C}_{0}}k_{\Vert }^{2}\right)-\left(\frac{2\text{i}\unicode[STIX]{x1D70E}\unicode[STIX]{x1D702}_{0}}{3\unicode[STIX]{x1D70C}_{0}}+\frac{T_{\bot }^{2}}{\unicode[STIX]{x1D70C}_{0}}\right)^{2}\left(k_{\bot }k_{\Vert }\right)^{2}\right]\unicode[STIX]{x1D70E}^{2}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad +\,\left(\unicode[STIX]{x1D70E}^{2}+\frac{\text{i}\unicode[STIX]{x1D702}_{0}}{3\unicode[STIX]{x1D70C}_{0}}k_{\bot }^{2}\unicode[STIX]{x1D70E}-\unicode[STIX]{x0394}sk_{\Vert }^{2}-\frac{T_{_{2\bot }}^{2}}{\unicode[STIX]{x1D70C}_{0}}k_{\bot }^{2}-\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}k^{2}\right)\left[\left(\unicode[STIX]{x1D70E}^{2}-\left.\unicode[STIX]{x0394}sk_{\Vert }^{2}-\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}k_{\Vert }^{2}\right)\right.\right.\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad \left.\times \,\left(\unicode[STIX]{x1D70E}^{2}+\frac{4\text{i}\unicode[STIX]{x1D702}_{0}}{3\unicode[STIX]{x1D70C}_{0}}k_{\Vert }^{2}\unicode[STIX]{x1D70E}-\frac{T_{_{3\Vert }}^{2}}{\unicode[STIX]{x1D70C}_{0}}k_{\Vert }^{2}\right)-4\unicode[STIX]{x1D70E}^{2}\left(\unicode[STIX]{x1D6FA}_{\bot }+\unicode[STIX]{x1D708}_{0}k_{\bot }k_{\Vert }\right)^{2}\right]+\left(\frac{2\text{i}\unicode[STIX]{x1D70E}\unicode[STIX]{x1D702}_{0}}{3}+T_{_{\bot }}^{2}\right)^{2}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad \times \left(\frac{k_{\bot }k_{\Vert }^{2}}{\unicode[STIX]{x1D70C}_{0}}\right)^{2}\left(\left.\unicode[STIX]{x0394}s+\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}\right)\right.=0.\end{eqnarray}$$
The above general dispersion relation is obtained for an anisotropic plasma incorporating quantum, FLR, tensor viscosity and rotation. In the absence of rotation, FLR and tensor viscosity, (3.13) resembles the result of Gliddon (Reference Gliddon1966). If we ignore the effect of the quantum parameter, FLR, rotation and self-gravitation in (3.13) then the general dispersion relation takes the same form as the result obtained by Cherkos & Tessema (Reference Cherkos and Tessema2013). Equation (3.13) reduces to the dispersion relation given by Prajapati (Reference Prajapati2014) in the absence of rotation, FLR and tensor viscosity. Thus the tensor viscosity, FLR and rotation significantly modify the dispersion relation of a quantum anisotropic plasma.
4 Discussion of the dispersion relation
Further, we discuss the general dispersion relation (3.13) for transverse and longitudinal modes of propagation to see the importance of rotation with tensor viscosity.
4.1 Transverse mode of propagation (i.e.
$k\bot H_{0}$
)
The dispersion relation (3.13) reduces, for the propagation perpendicular to the direction of the magnetic field, as
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D70E}^{4}+\frac{\text{i}\unicode[STIX]{x1D702}_{0}}{3\unicode[STIX]{x1D70C}_{0}}k^{2}\unicode[STIX]{x1D70E}^{3}-\left\{\left(2\unicode[STIX]{x1D6FA}_{\Vert }-\unicode[STIX]{x1D708}_{0}k^{2}\right)^{2}+4\unicode[STIX]{x1D6FA}_{\bot }^{2}+\left(\frac{T_{_{2\bot }}^{2}}{\unicode[STIX]{x1D70C}_{0}}+\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}\right)k^{2}\right\}\unicode[STIX]{x1D70E}^{2}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad -\,4\unicode[STIX]{x1D6FA}_{\bot }^{2}\frac{\text{i}\unicode[STIX]{x1D702}_{0}}{3\unicode[STIX]{x1D70C}_{0}}k^{2}\unicode[STIX]{x1D70E}+4\unicode[STIX]{x1D6FA}_{\bot }^{2}\left(\frac{T_{_{2\bot }}^{2}}{\unicode[STIX]{x1D70C}_{0}}+\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}\right)k^{2}=0.\end{eqnarray}$$
The obtained dispersion relation (4.1) clearly shows that it is affected due to the quantum, tensor viscosity, FLR corrections and rotation. The constant term of (4.1) is free from the FLR, tensor viscosity and rotation parameter which shows that these parameters do not contribute in the condition of gravitational instability.
To discuss the effect of tensor viscosity with rotation and FLR corrections on self-gravitational instability conveniently we consider the following two cases: rotational axis parallel to the direction of the magnetic field and rotational axis perpendicular to the direction of the magnetic field.
4.1.1 Rotating axis parallel to the magnetic field (i.e.
$\unicode[STIX]{x1D6FA}\Vert H_{0}$
)
When the rotation of system is along the direction of the magnetic field, the dispersion relation (4.1) reduces to the following form
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70E}^{2}+\frac{\text{i}\unicode[STIX]{x1D702}_{0}}{3\unicode[STIX]{x1D70C}_{0}}k^{2}\unicode[STIX]{x1D70E}-\left(2\unicode[STIX]{x1D6FA}-\unicode[STIX]{x1D708}_{0}k^{2}\right)^{2}-\left(\frac{T_{_{2\bot }}^{2}}{\unicode[STIX]{x1D70C}_{0}}+\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}\right)k^{2}=0. & \displaystyle\end{eqnarray}$$
Equation (4.2) is a quadratic equation and has two roots which satisfy the above expression.
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D70E}_{1,2}=\displaystyle \frac{\displaystyle -\frac{\text{i}\unicode[STIX]{x1D702}_{0}k^{2}}{3\unicode[STIX]{x1D70C}_{0}}\pm \sqrt{-\left(\,\frac{\unicode[STIX]{x1D702}_{0}k^{2}}{3\unicode[STIX]{x1D70C}_{0}}\right)^{2}-4\left(-\frac{2p_{\bot 0}^{2}}{\unicode[STIX]{x1D70C}_{0}}k^{2}-\frac{H_{0}^{2}k^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}-Q^{2}k^{4}+\unicode[STIX]{x1D714}_{J}^{2}-\unicode[STIX]{x1D708}_{0}^{2}k^{4}-4\unicode[STIX]{x1D6FA}^{2}+4\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D708}_{0}k^{2}\right)}}{2}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
The obtained roots of (4.2) are purely imaginary and reduce to the roots obtained by Sharma (Reference Sharma2017) excluding rotation of the system. The quantum parameter, tensor viscosity, rotation and FLR decreases the growth rate of viscous self-gravitating mode and thus oppose the gravitational instability of the system while the coupling of FLR and rotation supports the gravitational pressure in enhancing the growth rate of mode. Further if the tensor viscosity of the system is ignored then the obtained expression can be written as
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70E}^{2}-\frac{2p_{\bot 0}^{2}}{\unicode[STIX]{x1D70C}_{0}}k^{2}-\frac{H_{0}^{2}k^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}-Q^{2}k^{4}+\unicode[STIX]{x1D714}_{J}^{2}-\unicode[STIX]{x1D708}_{0}^{2}k^{4}-4\unicode[STIX]{x1D6FA}^{2}+4\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D708}_{0}k^{2}=0. & \displaystyle\end{eqnarray}$$
The above dispersion relation describes the role of rotation, quantum parameter and FLR corrections on the self-gravitational instability. The obtained expression (4.4) becomes identical to the result given by Sharma (Reference Sharma2017) in the absence of rotation and the quantum parameter. Thus, the rotation, FLR and its coupling effect modifies the dispersion relation of anisotropic quantum plasma. The instability of the system can be expressed as
$$\begin{eqnarray}\displaystyle & \displaystyle \left(\unicode[STIX]{x1D708}_{0}^{2}+Q^{2}\right)k^{4}+\left(\frac{2p_{\bot 0}}{\unicode[STIX]{x1D70C}_{0}}+\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}-4\unicode[STIX]{x1D6FA}_{\Vert }\unicode[STIX]{x1D708}_{0}\right)k^{2}+4\unicode[STIX]{x1D6FA}_{\Vert }^{2}<\unicode[STIX]{x1D714}_{J}^{2}. & \displaystyle\end{eqnarray}$$
The inequality (4.5) shows the condition of a self-gravitational instability which is strongly influenced by rotation, FLR and quantum parameter.
The system is unstable for all values of wavenumbers
$k<k_{J1}$
where the critical wavenumber is given as
$$\begin{eqnarray}\displaystyle & \displaystyle k_{J1}^{2}=\frac{\left(4\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D708}_{0}-D_{\bot a}^{2}\right)\pm \sqrt{\left\{\left(4\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D708}_{0}-D_{\bot a}^{2}\right)^{2}-4(Q^{2}+\unicode[STIX]{x1D708}_{0}^{2})(4\unicode[STIX]{x1D6FA}^{2}-\unicode[STIX]{x1D714}_{J}^{2})\right\}}}{2(Q^{2}+\unicode[STIX]{x1D708}_{0}^{2})}, & \displaystyle\end{eqnarray}$$
where
$D_{\bot a}^{2}=2p_{\bot 0}/\unicode[STIX]{x1D70C}_{0}+H_{0}^{2}/4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}$
.
Equation (4.6) shows the modified Jeans critical wavenumber for self-gravitational instability in terms of FLR, quantum and rotation. The modification in wave number due to presence of FLR, rotation and quantum parameter can be seen if one ignores these terms from (4.6), the obtained critical wave number takes the same form as given by Gliddon (Reference Gliddon1966).
Furthermore, the critical Jeans mass
$M_{J1}~(=1.33\unicode[STIX]{x03C0}\unicode[STIX]{x1D706}_{J1}^{3}\unicode[STIX]{x1D70C}_{0})$
of the rotating anisotropic quantum plasma can be expressed by using the critical Jeans wavenumber in
$\unicode[STIX]{x1D706}_{J}~(=2\unicode[STIX]{x03C0}/k_{J})$
and after that substituting it’s expression in
$(4/3)\unicode[STIX]{x03C0}\unicode[STIX]{x1D706}_{J1}^{3}\unicode[STIX]{x1D70C}_{0}$
. Thus the obtained critical Jeans mass can be written as
$$\begin{eqnarray}\displaystyle \hspace{-24.0pt} & & \displaystyle \displaystyle M_{J1}=\frac{64\sqrt{2}\unicode[STIX]{x03C0}^{4}\unicode[STIX]{x1D70C}_{0}}{3}\nonumber\\ \displaystyle \hspace{-24.0pt} & & \displaystyle \displaystyle \quad \times \,\left(\frac{Q^{2}+\unicode[STIX]{x1D708}_{0}^{2}}{-(D_{\bot a}^{2}-4\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D708}_{0})\pm \sqrt{\left\{(D_{\bot a}^{2}-4\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D708}_{0})^{2}-(Q^{2}+\unicode[STIX]{x1D708}_{0}^{2})(16\unicode[STIX]{x1D6FA}^{2}-4\unicode[STIX]{x1D714}_{J}^{2})\right\}}}\right)^{\!3/2}.\end{eqnarray}$$
Using the physical value of the magnetic field strength 10
$^{6}$
–10
$^{16}$
G, temperature
$T\approx 10^{5}{-}10^{7}~\text{K}$
and number density
$n_{0}\approx 10^{29}{-}10^{34}~\text{m}^{-3}$
(Haas Reference Haas2005; Mushtaq & Vladimirov Reference Mushtaq and Vladimirov2011; Franzon & Schramm Reference Franzon and Schramm2015) in the expression of the critical wavenumber (
$k_{J1}$
) and critical Jeans mass (
$M_{J1}$
) for a non-rotating white dwarf, the obtained numerical values of the critical wavenumber and Jeans mass are
$1.34\times 10^{-7}~\text{m}^{-1}$
and
$2.1M_{\odot }$
. Similarly, including the effect of rotation, the obtained numerical values are
$1.2\times 10^{-7}~\text{m}^{-1}$
and
$3.5M_{\odot }$
respectively. Usually it is observed that the white dwarf mass is comparable to the solar mass and it’s stability against gravitational collapse is maintained by the degeneracy pressure of the electrons. Chandrashekhar (Reference Chandrashekhar1931) found a limit for the existence of white dwarfs beyond which the degeneracy pressure becomes weak in stabilizing a white dwarf star. As a result, gravitational collapse and evolution into, for example, black holes, neutron stars etc. occurs. Howell et al. (Reference Howell, Sullivan, Nugent, Ellis, Conley, Borgne, Carlberg, Guy, Balam and Basa2006) and Yamanaka et al. (Reference Yamanaka, Kawabata, Kinugasa, Tanaka, Imada, Maeda, Nomoto, Arai, Chiyonobu and Fukazawa2009) and Scalzo et al. (Reference Scalzo, Aldering, Antilogus, Aragon, Bailey, Baltay, Bongard, Buton, Childress and Chotard2010) have mentioned that the progenitor of more luminous supernovae could be white dwarfs of mass greater than the Chandrashekhar mass limit (
$1.4M_{\odot }$
). Such special types of progenitors are named super Chandrashekhar white dwarf stars. The fast rotation and strong magnetic field strength occupy a vital position in the existence of super Chandrashekhar white dwarfs (Roxburgh Reference Roxburgh1965; Yoon & Langer Reference Yoon and Langer2005; Franzon & Schramm Reference Franzon and Schramm2015).
The comparison of critical wavenumber and Jeans mass of non-rotating with rotating white dwarfs reveals that the presence of rotation works against the self-gravitational collapse and thus makes it more stable.
4.1.2 Rotating axis perpendicular to the magnetic field (i.e.
$\unicode[STIX]{x1D6FA}\bot H_{0}$
)
In this case the influence of rotation, FLR and tensor viscosity in an anisotropic quantum plasma are studied considering the axis of rotation perpendicular to the direction of magnetic field. Therefore,
$\unicode[STIX]{x1D6FA}_{\Vert }$
is ignored from the dispersion relation (4.1) and the reduced form is represented as
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70E}^{4}+\frac{\text{i}\unicode[STIX]{x1D702}_{0}}{3\unicode[STIX]{x1D70C}_{0}}k^{2}\unicode[STIX]{x1D70E}^{3}-\left(\unicode[STIX]{x1D708}_{0}^{2}k^{4}+4\unicode[STIX]{x1D6FA}^{2}+\frac{T_{_{2\bot }}^{2}}{\unicode[STIX]{x1D70C}_{0}}k^{2}+\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}k^{2}\right)\unicode[STIX]{x1D70E}^{2} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \quad -\,4\frac{\text{i}\unicode[STIX]{x1D702}_{0}}{3\unicode[STIX]{x1D70C}_{0}}\unicode[STIX]{x1D6FA}^{2}k^{2}\unicode[STIX]{x1D70E}+4\unicode[STIX]{x1D6FA}^{2}\left(\frac{T_{_{2\bot }}^{2}}{\unicode[STIX]{x1D70C}_{0}}+\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}\right)k^{2}=0. & \displaystyle\end{eqnarray}$$
The fourth degree algebraic polynomial (4.8) shows the dispersion relation for an anisotropic plasma. It contains the combined effect of FLR, tensor viscosity, quantum, rotation and Alfvén velocity in an anisotropic plasma system. In a rotating anisotropic quantum plasma, the presence of FLR coupled the rotating and viscous gravitating mode. This equation reduces to the dispersion relation obtained by Gliddon (Reference Gliddon1966) for the classical non-rotational anisotropic plasma with the consideration of zero FLR corrections. We can recover the result obtained by Cherkos & Tessema (Reference Cherkos and Tessema2013) if we neglect the effect of quantum, self-gravitation, FLR and rotation parameter in the present work. In the absence of quantum, rotation and FLR effect in (4.8), the obtained relation agrees with the dispersion relation given by Cherkos & Tessema (Reference Cherkos and Tessema2013).
To analyse the influence of rotation and tensor viscosity on self-gravitational instability, the FLR corrections is ignored in the dispersion relation (4.8). The obtained form can be written as
$$\begin{eqnarray}\displaystyle & \displaystyle \left(\unicode[STIX]{x1D70E}^{2}+\frac{\text{i}\unicode[STIX]{x1D702}_{0}}{3\unicode[STIX]{x1D70C}_{0}}k^{2}\unicode[STIX]{x1D70E}-\frac{T_{_{2\bot }}^{2}}{\unicode[STIX]{x1D70C}_{0}}k^{2}-\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}k^{2}\right)\left(\unicode[STIX]{x1D70E}^{2}-4\unicode[STIX]{x1D6FA}^{2}\right)=0. & \displaystyle\end{eqnarray}$$
The presence of FLR coupled the pure rotational and viscous gravitating modes with each other and in its absence both the modes in expression (4.9) shows their individual behavior.
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70E}^{2}+\frac{\text{i}\unicode[STIX]{x1D702}_{0}}{3\unicode[STIX]{x1D70C}_{0}}k^{2}\unicode[STIX]{x1D70E}-\frac{2p_{\bot 0}}{\unicode[STIX]{x1D70C}_{0}}k^{2}+\unicode[STIX]{x1D714}_{J}^{2}-Q^{2}k^{4}-\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}k^{2}=0. & \displaystyle\end{eqnarray}$$
The dispersion relation (4.10) describes the role of tensor viscosity with FLR corrections, quantum and anisotropic pressure on the self-gravitating mode in magnetized plasma. Equation (4.10) is a quadratic equation and its roots (
$\unicode[STIX]{x1D70E}_{1}$
and
$\unicode[STIX]{x1D70E}_{2}$
) satisfy the above equation.
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70E}_{1,2}=-\frac{\text{i}\unicode[STIX]{x1D702}_{0}}{6\unicode[STIX]{x1D70C}_{0}}k^{2}\pm \frac{1}{2}\sqrt{4\left(\frac{2p_{\bot 0}}{\unicode[STIX]{x1D70C}_{0}}k^{2}-\unicode[STIX]{x1D714}_{J}^{2}+Q^{2}k^{4}+\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}k^{2}\right)-\left(\frac{\unicode[STIX]{x1D702}_{0}}{3\unicode[STIX]{x1D70C}_{0}}\right)^{2}k^{4}}. & \displaystyle\end{eqnarray}$$
Now the sum and product of the roots are
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70E}_{1}\unicode[STIX]{x1D70E}_{2}=\frac{-2p_{\bot 0}}{\unicode[STIX]{x1D70C}_{0}}k^{2}+\unicode[STIX]{x1D714}_{J}^{2}-Q^{2}k^{4}-\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}k^{2} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70E}_{1}+\unicode[STIX]{x1D70E}_{2}=\frac{-\text{i}\unicode[STIX]{x1D702}_{0}}{3\unicode[STIX]{x1D70C}_{0}}k^{2}. & \displaystyle\end{eqnarray}$$
Hence it is clear from (4.12) and (4.13) that the presence of tensor viscosity has no significant role in self-gravitational instability of a rotating anisotropic quantum plasma.
The second factor of (4.9) shows the pure rotating mode which remains unaffected by the quantum, anisotropic pressure and tensor viscosity.
The effect of tensor viscosity and rotation on the growth rate of a self-gravitational instability is examined numerically. The dispersion relations (4.2) and (4.8) are written in dimensionless form using
$\unicode[STIX]{x1D70E}=\text{i}\unicode[STIX]{x1D6FE}$
and the following dimensionless quantities
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D702}_{\bot }^{\ast }=\frac{\unicode[STIX]{x1D702}_{0}\unicode[STIX]{x1D714}_{J}}{p_{\bot 0}},\quad \unicode[STIX]{x1D6FE}^{\ast }=\frac{\unicode[STIX]{x1D6FE}}{\unicode[STIX]{x1D714}_{J}},\quad k_{\bot }^{\ast }=\frac{k}{\unicode[STIX]{x1D714}_{J}}\sqrt{\frac{p_{\bot 0}}{\unicode[STIX]{x1D70C}_{0}}},\quad \unicode[STIX]{x1D708}_{\bot }^{\ast }=\frac{\unicode[STIX]{x1D708}_{0}\,\unicode[STIX]{x1D70C}_{0}\unicode[STIX]{x1D714}_{J}}{p_{\bot 0}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle V_{a\bot }^{\ast }=\frac{H_{0}}{\sqrt{4\unicode[STIX]{x03C0}p_{\bot 0}}},\quad \unicode[STIX]{x1D6FA}^{\ast }=\frac{\unicode[STIX]{x1D6FA}}{\unicode[STIX]{x1D714}_{J}},\quad Q_{\bot }^{\ast }=\frac{\hslash \unicode[STIX]{x1D70C}_{0}\unicode[STIX]{x1D714}_{J}}{\sqrt{4m_{e}m_{i}}p_{\bot 0}}. & \displaystyle\end{eqnarray}$$
Thus,
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FE}^{\ast 2}+\frac{\unicode[STIX]{x1D702}_{\bot }^{\ast }}{3}k_{\bot }^{\ast 2}\unicode[STIX]{x1D6FE}^{\ast }+4\unicode[STIX]{x1D6FA}^{\ast 2}+\unicode[STIX]{x1D708}_{\bot }^{\ast 2}k_{\bot }^{\ast 4}-4\unicode[STIX]{x1D6FA}^{\ast }\unicode[STIX]{x1D708}_{\bot }^{\ast }k_{\bot }^{\ast 2}+2k_{\bot }^{\ast 2}-1+Q_{\bot }^{\ast 2}k_{\bot }^{\ast 4}+V_{a\bot }^{\ast 2}k_{\bot }^{\ast 2}=0 & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D6FE}^{\ast 4}+\frac{\unicode[STIX]{x1D702}_{\bot }^{\ast }}{3}k_{\bot }^{\ast 2}\unicode[STIX]{x1D6FE}^{\ast 3}+\left(\unicode[STIX]{x1D708}_{\bot }^{\ast 2}k_{\bot }^{\ast 4}+4\unicode[STIX]{x1D6FA}^{\ast 2}+2k_{\bot }^{\ast 2}-1+Q_{\bot }^{\ast 2}k_{\bot }^{\ast 4}+V_{a\bot }^{\ast 2}k_{\bot }^{\ast 2}\right)\unicode[STIX]{x1D6FE}^{\ast 2}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad +\,\frac{4\unicode[STIX]{x1D702}_{\bot }^{\ast }}{3}\unicode[STIX]{x1D6FA}^{\ast 2}k_{\bot }^{\ast 2}\unicode[STIX]{x1D6FE}^{\ast }+4\unicode[STIX]{x1D6FA}^{\ast 2}\left(2k_{\bot }^{\ast 2}-1+Q_{\bot }^{\ast 2}k_{\bot }^{\ast 4}+V_{a\bot }^{\ast 2}k_{\bot }^{\ast 2}\right)=0.\end{eqnarray}$$
Equation (4.16) is plotted in figures 1 and 2 to see the variation of growth rate of a self-gravitational instability against the wavenumber for different values of tensor viscosity
$\unicode[STIX]{x1D702}_{\bot }^{\ast }$
and rotation
$\unicode[STIX]{x1D6FA}^{\ast }$
respectively. The value of quantum (
$Q_{\bot }^{\ast }$
), FLR (
$\unicode[STIX]{x1D708}_{\bot }^{\ast }$
) and Alfvén velocity (
$V_{a\bot }^{\ast }$
) are taken as 2.0, 1.4 and 0.9 respectively. In figures 1 and 2, the growth rate is higher for the lower values of tensor viscosity and rotation and thus one can says that both the parameters (tensor viscosity and rotation) have a stabilizing effect on the growth rate of an anisotropic self-gravitating quantum plasma system.
Figure 1. Normalized wave frequency versus normalized wavenumber plotted for various values of tensor viscosity when the rotational axis is parallel to the perpendicular mode of propagation.
Figure 2. Normalized wave frequency versus normalized wavenumber is plotted for different values of rotation when rotational axis is parallel and wave propagation is perpendicular to the magnetic field.
Figure 3. Normalized wave frequency versus normalized wavenumber is plotted to see the effect of FLR corrections when rotational axis and wave propagation are transverse to the magnetic field.
Figure 4. Normalized wave frequency versus normalized wavenumber is plotted to see the effect of quantum when rotational axis and wave propagation are transverse to the magnetic field.
We have solved (4.17) numerically and plotted in figures 3–5 the variation of growth rate of a self-gravitational instability for several values of FLR, quantum and Alfvén velocity respectively. The solid curve is for the FLR corrections
$\unicode[STIX]{x1D708}_{\bot }^{\ast }=0.0$
, the dashed curve is for
$\unicode[STIX]{x1D708}_{\bot }^{\ast }=1.4$
and the dotted curve is for
$\unicode[STIX]{x1D708}_{\bot }^{\ast }=2.0$
. It is observed that the growth rates corresponding to the solid curve are higher as compared to the dashed and dotted curves which reveals that the FLR corrections maintains a crucial role in stabilizing the self-gravitational collapse of the viscous anisotropic quantum plasma system. Similarly, observing the behaviour of the curves in figures 4 and 5 one can conclude that the quantum and Alfvén velocity both work against the self-gravitational collapsing pressure and thus try to move the considered plasma system towards stability.
Figure 5. Normalized wave frequency versus normalized wavenumber is plotted to see the effect of magnetic strength when rotational axis and wave propagation are transverse to the magnetic field.
4.2 Longitudinal mode of propagation (i.e.
$k\Vert H_{0}$
)
In this section the perturbations of the considered system are assumed to be move along the direction of the magnetic field. Therefore, the perpendicular wave vector (
$k_{\bot }$
) is ignored from the dispersion relation (3.13) and the obtained form is
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \left\{-4\left(\unicode[STIX]{x1D6FA}_{\Vert }-\unicode[STIX]{x1D708}_{0}k^{2}\right)^{2}\unicode[STIX]{x1D70E}^{2}+\left(\unicode[STIX]{x1D70E}^{2}-\unicode[STIX]{x0394}sk^{2}-\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}k^{2}\right)^{2}\right\}\left(\unicode[STIX]{x1D70E}^{2}+\frac{4\text{i}\unicode[STIX]{x1D702}_{0}}{3\unicode[STIX]{x1D70C}_{0}}k^{2}\unicode[STIX]{x1D70E}-\frac{T_{_{3\Vert }}^{2}}{\unicode[STIX]{x1D70C}_{0}}k^{2}\right)\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad -\,4\unicode[STIX]{x1D70E}^{2}\unicode[STIX]{x1D6FA}_{\bot }^{2}\left(\unicode[STIX]{x1D70E}^{2}-\unicode[STIX]{x0394}sk^{2}-\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}k^{2}\right)=0.\end{eqnarray}$$
Expression (4.18) clearly represents that the dispersion relation for anisotropic quantum plasma in the longitudinal mode of propagation is affected by rotation, FLR corrections and tensor viscosity. Further, we discuss the effect of rotation with tensor viscosity on the Jeans instability of an anisotropic quantum plasma considering similar cases to those mentioned in § 4.1
4.2.1 Rotating axis parallel to the magnetic field (i.e.
$\unicode[STIX]{x1D6FA}\Vert H_{0}$
)
The dispersion relation is obtained by substituting the rotation longitudinal to the magnetic field and ignoring transvers rotational axis i.e.
$\unicode[STIX]{x1D6FA}_{\bot }=0$
in (4.18). Thus the reduced form is
$$\begin{eqnarray}\displaystyle & \displaystyle \left\{\left(\unicode[STIX]{x1D70E}^{2}-\unicode[STIX]{x0394}sk^{2}-\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}k^{2}\right)^{2}-4\unicode[STIX]{x1D70E}^{2}\left(\unicode[STIX]{x1D6FA}-\unicode[STIX]{x1D708}_{0}k^{2}\right)^{2}\right\}\left(\unicode[STIX]{x1D70E}^{2}+\frac{4\text{i}\unicode[STIX]{x1D702}_{0}}{3\unicode[STIX]{x1D70C}_{0}}k^{2}\unicode[STIX]{x1D70E}-\frac{T_{_{3\Vert }}^{2}}{\unicode[STIX]{x1D70C}_{0}}k^{2}\right)=0. & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
The absence of rotational axis perpendicular to the direction of the magnetic field splits the dispersion relation of the longitudinal mode of propagation into two separate modes. Thus, the coupled modes (Alfvén and viscous self-gravitating) in the absence of a perpendicular rotational axis are separated out from each other.
The obtained Alfvén mode can be written in expanded form as
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D70E}^{4}-2\left\{\left(\frac{p_{\bot 0}}{\unicode[STIX]{x1D70C}_{0}}-\frac{p_{\Vert 0}}{\unicode[STIX]{x1D70C}_{0}}+\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}\,-\,4\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D708}_{0}\right)k^{2}+2\left(\unicode[STIX]{x1D6FA}^{2}+\unicode[STIX]{x1D708}_{0}^{2}k^{4}\right)\right\}\unicode[STIX]{x1D70E}^{2}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad +\,\left(\frac{p_{\bot 0}}{\unicode[STIX]{x1D70C}_{0}}-\frac{p_{\Vert 0}}{\unicode[STIX]{x1D70C}_{0}}+\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}\right)^{2}k^{4}.\end{eqnarray}$$
The presence of the tensor viscosity and quantum parameter have no influence on the Alfvén mode. In the absence of rotation, the mode (4.20) resembles (31) of Sharma (Reference Sharma2017). The expression (4.20) recovers the Alfvén mode obtained by Gliddon (Reference Gliddon1966), Cherkos & Tessema (Reference Cherkos and Tessema2013), Prajapati (Reference Prajapati2014) if we ignore rotation and the FLR corrections in the present work. Thus, the rotation of the system and FLR corrections modify the Alfvén mode given by Gliddon (Reference Gliddon1966), Cherkos & Tessema (Reference Cherkos and Tessema2013), Prajapati (Reference Prajapati2014) and Sharma (Reference Sharma2017). Expression (4.20) is a quadratic equation in
$\unicode[STIX]{x1D70E}^{2}$
, where
$\unicode[STIX]{x1D70E}$
is the growth rate of the Alfvén mode and can be given as
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70E}_{1,2}^{2} & = & \displaystyle \displaystyle \left(\unicode[STIX]{x0394}s+\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}-4\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D708}_{0}\right)k^{2}+2\unicode[STIX]{x1D71B}^{2}\pm 2\left\{\unicode[STIX]{x1D71B}^{4}+\unicode[STIX]{x1D71B}^{2}\left(\unicode[STIX]{x0394}s+\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}-4\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D710}_{0}\right)k^{2}\right.\nonumber\\ \displaystyle & & \displaystyle \displaystyle \left.-\,2\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D710}_{0}\left(\unicode[STIX]{x0394}s+\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}-2\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D708}_{0}\right)k^{4}\right\}^{1/2},\end{eqnarray}$$
where
$\unicode[STIX]{x1D71B}^{2}=(\unicode[STIX]{x1D6FA}^{2}+\unicode[STIX]{x1D708}_{0}^{2}k^{4})$
.
It is clear that the growth rate of the Alfvén mode is modified by the rotation and FLR corrections. The modified Alfvé modes propagate with two different velocities due to the influence of the FLR corrections and the rotation of the system. Now, to discuss the instability of the mode we write the sum and product of the roots as
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70E}_{1}^{2}+\unicode[STIX]{x1D70E}_{2}^{2}=2\left\{\left(\frac{p_{\bot 0}}{\unicode[STIX]{x1D70C}_{0}}-\frac{p_{\Vert 0}}{\unicode[STIX]{x1D70C}_{0}}+\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}-4\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D708}_{0}\right)k^{2}+2\left(\unicode[STIX]{x1D6FA}^{2}+\unicode[STIX]{x1D708}_{0}^{2}k^{4}\right)\right\} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70E}_{1}^{2}\unicode[STIX]{x1D70E}_{2}^{2}=\left(\frac{p_{\bot 0}}{\unicode[STIX]{x1D70C}_{0}}-\frac{p_{\Vert 0}}{\unicode[STIX]{x1D70C}_{0}}+\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}\right)^{2}. & \displaystyle\end{eqnarray}$$
Hence, for
$(p_{\bot 0}/\unicode[STIX]{x1D70C}_{0})+(H_{0}^{2}/4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0})<(p_{\Vert 0}/\unicode[STIX]{x1D70C}_{0})$
there exist imaginary roots which make the Alfvén mode unstable and it results in the firehose instability in the anisotropic plasma system due to the dominance of the parallel anisotropic pressure over the sum of the magnetic pressure and perpendicular anisotropic pressure.
If we ignore the FLR corrections to see the influence of rotation on the Alfvén mode, (4.20) reduces as
$$\begin{eqnarray}\displaystyle \hspace{-12.0pt} & \displaystyle \unicode[STIX]{x1D70E}^{4}-2\left\{\!\left(\frac{p_{\bot 0}}{\unicode[STIX]{x1D70C}_{0}}-\frac{p_{\Vert 0}}{\unicode[STIX]{x1D70C}_{0}}+\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}\right)k^{2}+2\unicode[STIX]{x1D6FA}^{2}\right\}\unicode[STIX]{x1D70E}^{2}+\left(\frac{p_{\bot 0}}{\unicode[STIX]{x1D70C}_{0}}-\frac{p_{\Vert 0}}{\unicode[STIX]{x1D70C}_{0}}+\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}\right)^{2}k^{4}. & \displaystyle\end{eqnarray}$$
Equation (4.24) shows the role of rotation on the propagation of the Alfvén mode. The solution of (4.24) can be written as
$$\begin{eqnarray}\displaystyle & \displaystyle \hspace{-24.0pt}\unicode[STIX]{x1D70E}_{1,2}^{2}=\left(\frac{p_{\bot 0}}{\unicode[STIX]{x1D70C}_{0}}-\frac{p_{\Vert 0}}{\unicode[STIX]{x1D70C}_{0}}+\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}\right)\!k^{2}+2\unicode[STIX]{x1D6FA}^{2}\pm 2\unicode[STIX]{x1D6FA}\sqrt{\!\unicode[STIX]{x1D6FA}^{2}+\left(\frac{p_{\bot 0}}{\unicode[STIX]{x1D70C}_{0}}-\frac{p_{\Vert 0}}{\unicode[STIX]{x1D70C}_{0}}+\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}\right)k^{2}}. & \displaystyle\end{eqnarray}$$
It is clear from the above solution that the rotation of the system has a reducing effect on the parallel anisotropic pressure and thus opposes the firehose instability.
Now, the obtained gravitating mode is
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70E}^{2}+\frac{4\text{i}\unicode[STIX]{x1D702}_{0}}{3\unicode[STIX]{x1D70C}_{0}}k_{\Vert }^{2}\unicode[STIX]{x1D70E}-\frac{3p_{\Vert 0}}{\unicode[STIX]{x1D70C}_{0}}k_{\Vert }^{2}+\unicode[STIX]{x1D714}_{J}^{2}-Q^{2}k^{4}. & \displaystyle\end{eqnarray}$$
The presence of tensor viscosity plays a significant role in the self-gravitating mode while the FLR corrections and rotation have no influence. In the absence of tensor viscosity, the gravitating mode recovers the mode given by Prajapati (Reference Prajapati2014). For a classical anisotropic plasma, the expression (4.26) takes the same form as the result obtained by Sharma (Reference Sharma2017). Thus, the obtained gravitating mode is improved by the presence of tensor viscosity and quantum in an anisotropic self-gravitating plasma.
The growth rate of gravitating mode (4.26) is found to be
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70E}=-\frac{2\text{i}\unicode[STIX]{x1D702}_{0}}{3\unicode[STIX]{x1D70C}_{0}}k^{2}\pm \sqrt{\frac{3p_{\Vert 0}}{\unicode[STIX]{x1D70C}_{0}}k^{2}-\unicode[STIX]{x1D714}_{J}^{2}+Q^{2}k^{4}-\left(\frac{2\unicode[STIX]{x1D702}_{0}}{3\unicode[STIX]{x1D70C}_{0}}\right)^{2}k^{4}}. & \displaystyle\end{eqnarray}$$
In the absence of tensor viscosity, (4.27) reduces to
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70E}=\pm \sqrt{\frac{3p_{\Vert 0}}{\unicode[STIX]{x1D70C}_{0}}k^{2}-\unicode[STIX]{x1D714}_{J}^{2}+Q^{2}k^{4}}. & \displaystyle\end{eqnarray}$$
Clearly the parallel anisotropic and degeneracy pressure opposes the growth rate of gravitational collapse.
4.2.2 Rotating axis perpendicular to the magnetic field (i.e.
$\unicode[STIX]{x1D6FA}\bot H_{0}$
)
In this subsection the rotation of the system is considered to be across the direction of the magnetic field in the longitudinal mode of propagation. Therefore the parallel rotational frequency
$\unicode[STIX]{x1D6FA}_{\Vert }$
is ignored from the dispersion relation (36) and the reduced form is
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \left(\unicode[STIX]{x1D70E}^{2}+\frac{4\text{i}\unicode[STIX]{x1D702}_{0}}{3\unicode[STIX]{x1D70C}_{0}}k^{2}\unicode[STIX]{x1D70E}-\frac{3p_{\Vert 0}}{\unicode[STIX]{x1D70C}_{0}}k^{2}+\unicode[STIX]{x1D714}_{J}^{2}-Q^{2}k^{4}\right)\left\{-4\unicode[STIX]{x1D710}_{0}^{2}k^{4}\unicode[STIX]{x1D70E}^{2}+\left(\unicode[STIX]{x1D70E}^{2}-\unicode[STIX]{x0394}sk_{\Vert }^{2}-\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}k^{2}\right)^{2}\right\}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad -\,4\unicode[STIX]{x1D6FA}^{2}\unicode[STIX]{x1D70E}^{2}\left(\unicode[STIX]{x1D70E}^{2}-\unicode[STIX]{x0394}sk^{2}-\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}k^{2}\right)=0.\end{eqnarray}$$
The presence of rotation couples the viscous gravitating mode with the modified Alfvén mode. In the absence of quantum and rotation, (4.29) recovers the result of Sharma (Reference Sharma2017). The dispersion relation (4.29) reduces to the result given by Prajapati (Reference Prajapati2014) in the absence of tensor viscosity, rotation and FLR corrections. Thus the presence of rotation, tensor viscosity, quantum and FLR corrections modified the dispersion relation of anisotropic plasma.
In the absence of rotation, the dispersion relation (4.29) separates out into viscous gravitating and Alfvén modes. The obtained viscous gravitating mode is similar to the gravitating mode (4.26) and the Alfvén mode is similar to (31) of Sharma (Reference Sharma2017).
Now, to see the influence of rotation we have ignored the FLR corrections, equation (4.29) takes the form
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \left(\unicode[STIX]{x1D70E}^{2}-\unicode[STIX]{x0394}sk^{2}-\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}k^{2}\right)\left\{\unicode[STIX]{x1D70E}^{4}+\text{i}\unicode[STIX]{x1D70E}^{3}\left(\frac{4\unicode[STIX]{x1D702}_{0}}{3\unicode[STIX]{x1D70C}_{0}}k^{2}\right)+\unicode[STIX]{x1D70E}^{2}\left(-\unicode[STIX]{x0394}sk^{2}-\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}k^{2}-\frac{3p_{\Vert 0}}{\unicode[STIX]{x1D70C}}k^{2}\right.\right.\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad +\left.\unicode[STIX]{x1D714}_{J}^{2}-Q^{2}k^{4}-4\unicode[STIX]{x1D6FA}^{2}\right)+\text{i}\unicode[STIX]{x1D70E}\frac{4\unicode[STIX]{x1D702}_{0}}{3\unicode[STIX]{x1D70C}_{0}}k^{2}\left(-\unicode[STIX]{x0394}sk^{2}-\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}k^{2}\right)\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad +\left.\left(-\frac{3p_{\Vert 0}}{\unicode[STIX]{x1D70C}_{0}}k^{2}+\unicode[STIX]{x1D714}_{J}^{2}-Q^{2}k^{4}\right)\left(-\unicode[STIX]{x0394}sk^{2}-\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}k^{2}\right)\right\}=0.\end{eqnarray}$$
The first factor of (4.30) represents the Alfvén mode which is identical to the result of Gliddon (Reference Gliddon1966), Cherkos & Tessema (Reference Cherkos and Tessema2013), Prajapati (Reference Prajapati2014) and Sharma (Reference Sharma2017). Now, if we put the constant term of the second factor of (4.23) to be less than zero then it gives imaginary roots which are responsible for the instability of the system. Hence from the second factor of (4.30)
$$\begin{eqnarray}\displaystyle & \displaystyle \left(-\frac{3p_{\Vert 0}}{\unicode[STIX]{x1D70C}_{0}}k^{2}+\unicode[STIX]{x1D714}_{J}^{2}-Q^{2}k^{4}\right)\left(-\unicode[STIX]{x0394}sk^{2}-\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}k^{2}\right)<0. & \displaystyle\end{eqnarray}$$
It gives the gravitational instability criterion
$(3p_{\Vert 0}/\unicode[STIX]{x1D70C}_{0})k^{2}+Q^{2}k^{4}<\unicode[STIX]{x1D714}_{J}^{2}$
and firehose instability condition
$(p_{\bot 0}+H_{0}^{2}/4\unicode[STIX]{x03C0})<p_{\Vert 0}$
. The presence of rotation has no influence on both the instability criteria in the longitudinal mode of propagation when rotation is perpendicular to the direction of the magnetic field.
To study the effect of rotation and FLR corrections on the Alfvén mode numerically, the dispersion relation (4.24) is plotted. Figure 6 depicts the variation of growth rate of Alfvén mode as a function of wavenumber for the presence and absence of rotation and FLR corrections. Curves A
$_{1}$
and A
$_{2}$
are for stable (
$p_{\bot 0}+H_{0}^{2}/4\unicode[STIX]{x03C0}=2.5\unicode[STIX]{x1D70C}_{0}$
,
$p_{\Vert 0}=0.5\unicode[STIX]{x1D70C}_{0}$
) and unstable
$(p_{\bot 0}+H_{0}^{2}/4\unicode[STIX]{x03C0}=0.5\unicode[STIX]{x1D70C}_{0},p_{\Vert 0}=2.5\unicode[STIX]{x1D70C}_{0})$
firehose modes respectively. The curves B
$_{1}$
and B
$_{2}$
are for stable and unstable firehose modes with rotation respectively, and C
$_{1}$
and C
$_{2}$
are for stable and unstable firehose mode with rotation and FLR corrections respectively. The presence of rotation and FLR corrections reduces the unstable region and thus has a stabilizing effect on the firehose mode by reducing the effect of parallel anisotropic pressure.
Figure 6. Growth rate of Alfvén mode versus wavenumber is plotted to see the effect of rotation and FLR corrections.
Moreover, to analyse the influence of tensor viscosity on the growth rate of the Jeans instability in the longitudinal mode of propagation for the rotational axis perpendicular to the magnetic field the second factor of the dispersion relation (4.30) is normalized as
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D6FE}^{\ast 4}+\frac{4\unicode[STIX]{x1D702}_{\Vert }^{\ast }}{3}k_{\Vert }^{\ast 2}\unicode[STIX]{x1D6FE}^{\ast 3}+\left(-\unicode[STIX]{x1D712}k_{\Vert }^{2}+V_{a\Vert }^{\ast 2}k_{\Vert }^{\ast 2}+3k_{\Vert }^{2}-1+Q^{\ast 2}k_{\Vert }^{\ast 4}+4\unicode[STIX]{x1D6FA}^{\ast 2}\right)\unicode[STIX]{x1D6FE}^{\ast 2}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad +\,\frac{4\unicode[STIX]{x1D702}_{\Vert }^{\ast }}{3}k_{\Vert }^{\ast 2}\left(-\unicode[STIX]{x1D712}k_{\Vert }^{2}+V_{a\Vert }^{\ast 2}k_{\Vert }^{\ast 2}\right)\unicode[STIX]{x1D6FE}^{\ast }+\left(3k_{\Vert }^{2}-1+Q^{\ast 2}k_{\Vert }^{\ast 4}\right)\left(-\unicode[STIX]{x1D712}k_{\Vert }^{2}+V_{a\Vert }^{\ast 2}k_{\Vert }^{\ast 2}\right)=0,\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle & \displaystyle \left.\begin{array}{@{}c@{}}\displaystyle k_{\Vert }^{\ast }=\frac{k\,}{\unicode[STIX]{x1D714}_{J}}\sqrt{\frac{p_{\Vert 0}}{\unicode[STIX]{x1D70C}_{0}}},\quad \unicode[STIX]{x1D712}=\frac{p_{\Vert 0}-p_{\bot 0}}{p_{\Vert 0}},\quad \unicode[STIX]{x1D702}_{\Vert }^{\ast }=\,\frac{\unicode[STIX]{x1D702}_{0}\unicode[STIX]{x1D714}_{J}}{3p_{\Vert 0}},\\[15.0pt] \displaystyle Q_{\Vert }^{\ast }=\frac{\hslash \unicode[STIX]{x1D70C}_{0}\unicode[STIX]{x1D714}_{J}}{\sqrt{4m_{e}m_{i}}p_{\Vert 0}},\quad \unicode[STIX]{x1D708}_{\Vert }^{\ast }=\frac{\unicode[STIX]{x1D708}_{0}\,\unicode[STIX]{x1D70C}_{0}\unicode[STIX]{x1D714}_{J}}{p_{\Vert }},\quad V_{a\Vert }^{\ast }=\frac{H_{0}}{\sqrt{4\unicode[STIX]{x03C0}p_{\Vert 0}}}.\end{array}\right\} & \displaystyle\end{eqnarray}$$
The normalized growth rate versus normalized wavenumber has been plotted in figure 7 to compare the growth rate of the self-gravitational instability in both transverse and longitudinal modes of propagation by solving (4.17) and (4.32). The solid and dashed curves represent the variation of growth rate in the transverse and longitudinal modes of propagation respectively. The nature of the curves shows that the growth rate stabilizes faster in the longitudinal mode.
Figure 7. Normalized wave frequency versus normalized wavenumber is plotted to compare the effect of tensor viscosity in transverse and longitudinal modes of propagation when the rotational axis is perpendicular to magnetic field
5 Conclusion
We have focused on investigating the influence of rotation, FLR corrections and tensor viscosity on the self-gravitational instability of an anisotropic quantum plasma. It is found that in the transverse mode of propagation with a parallel rotational axis, the obtained critical Jeans mass is affected by the rotation, quantum and FLR corrections while it remains unaffected by tensor viscosity. The estimated Jeans mass for rotating and non-rotating white dwarf stars is
$3.5M_{\odot }$
and
$2.1M_{\odot }$
respectively. The difference in these masses reveals that the rotational frequency has a significant role in stabilizing the white dwarf star. The FLR corrections, rotational frequency and quantum parameter has a stabilizing influence on the growth rate of self-gravitational collapse. In the case of a longitudinal mode of propagation for a rotational axis parallel to the magnetic field, the analytical as well as numerical results show that the growth rate of the self-gravitating instability stabilizes due to the tensor viscosity and quantum parameter while the growth rate of the firehose instability is stabilized by the FLR corrections and rotational frequency due to suppression of the parallel anisotropic pressure. The presence of a perpendicular rotational frequency in the longitudinal mode coupled the viscous gravitating mode with the modified Alfvén mode. The growth rate of self-gravitational instability of the viscous anisotropic degenerate plasma stabilizes faster in the longitudinal mode than the transverse mode of propagation.
Acknowledgements
The authors greatly acknowledge the financial support of SERB-DST, New Delhi (SB/FTP/PS-075/2014).
