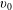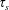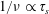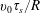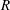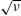1 Introduction
Tokamak fusion reactors desire to operate such that the alpha particles born at high energy slow down by electron and then ion drag and thereby deposit nearly all their energy in the background plasma before being lost. However, near the edge of a tokamak, magnetic field ripple,
![]() $\unicode[STIX]{x1D6FF}\ll 1$
, due to the finite number,
$\unicode[STIX]{x1D6FF}\ll 1$
, due to the finite number,
![]() $N\gg 1$
, of toroidal field coils can result in trapping in small localized ripple wells that can lead to collisional ripple losses (larger than the axisymmetric collisional losses) by mechanisms considered by Galeev et al. (Reference Galeev, Sagdeev, Furth and Rosenbluth1969), Stringer (Reference Stringer1972), Connor & Hastie (Reference Connor and Hastie1973), and Ho & Kulsrud (Reference Ho and Kulsrud1987). These collisional ripple loss calculations did not consider alpha particles which have a slowing down tail background distribution function rather than a Maxwellian background distribution. In the following sections we formulate and solve for collisional transport in a ripple tokamak by considering both the
$N\gg 1$
, of toroidal field coils can result in trapping in small localized ripple wells that can lead to collisional ripple losses (larger than the axisymmetric collisional losses) by mechanisms considered by Galeev et al. (Reference Galeev, Sagdeev, Furth and Rosenbluth1969), Stringer (Reference Stringer1972), Connor & Hastie (Reference Connor and Hastie1973), and Ho & Kulsrud (Reference Ho and Kulsrud1987). These collisional ripple loss calculations did not consider alpha particles which have a slowing down tail background distribution function rather than a Maxwellian background distribution. In the following sections we formulate and solve for collisional transport in a ripple tokamak by considering both the
![]() $1/\unicode[STIX]{x1D708}$
and
$1/\unicode[STIX]{x1D708}$
and
![]() $\sqrt{\unicode[STIX]{x1D708}}$
regimes, where
$\sqrt{\unicode[STIX]{x1D708}}$
regimes, where
![]() $\unicode[STIX]{x1D708}$
refers to the relevant collision frequency and the regime is characterized by the
$\unicode[STIX]{x1D708}$
refers to the relevant collision frequency and the regime is characterized by the
![]() $\unicode[STIX]{x1D708}$
dependence of its diffusivity.
$\unicode[STIX]{x1D708}$
dependence of its diffusivity.
In the
![]() $1/\unicode[STIX]{x1D708}$
regime the radial magnetic drift departure or step, primarly due to the gradient of the magnetic field (that is, the
$1/\unicode[STIX]{x1D708}$
regime the radial magnetic drift departure or step, primarly due to the gradient of the magnetic field (that is, the
![]() $\unicode[STIX]{x1D735}B$
magnetic drift), is determined by collisions. The evaluation of ripple transport of alphas in the
$\unicode[STIX]{x1D735}B$
magnetic drift), is determined by collisions. The evaluation of ripple transport of alphas in the
![]() $1/\unicode[STIX]{x1D708}$
regime when pitch angle scattering by the ions dominates is a re-application of the method of Stringer (Reference Stringer1972) as substantially improved by Connor & Hastie (Reference Connor and Hastie1973). When electron drag dominates a similar, but approximate, calculation is performed. Ripple transport of alphas in the
$1/\unicode[STIX]{x1D708}$
regime when pitch angle scattering by the ions dominates is a re-application of the method of Stringer (Reference Stringer1972) as substantially improved by Connor & Hastie (Reference Connor and Hastie1973). When electron drag dominates a similar, but approximate, calculation is performed. Ripple transport of alphas in the
![]() $\sqrt{\unicode[STIX]{x1D708}}$
regime is based on a careful collisional boundary layer analysis as recently put forth by Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017), rather than the approximate treatments of Galeev et al. (Reference Galeev, Sagdeev, Furth and Rosenbluth1969) and Ho & Kulsrud (Reference Ho and Kulsrud1987). In the
$\sqrt{\unicode[STIX]{x1D708}}$
regime is based on a careful collisional boundary layer analysis as recently put forth by Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017), rather than the approximate treatments of Galeev et al. (Reference Galeev, Sagdeev, Furth and Rosenbluth1969) and Ho & Kulsrud (Reference Ho and Kulsrud1987). In the
![]() $\sqrt{\unicode[STIX]{x1D708}}$
regime the
$\sqrt{\unicode[STIX]{x1D708}}$
regime the
![]() $\boldsymbol{E}\times \boldsymbol{B}$
drift in a flux surface reduces the radial step so it is no longer determined by collisions where
$\boldsymbol{E}\times \boldsymbol{B}$
drift in a flux surface reduces the radial step so it is no longer determined by collisions where
![]() $\boldsymbol{E}$
and
$\boldsymbol{E}$
and
![]() $\boldsymbol{B}$
are the electric and magnetic fields. In this regime the
$\boldsymbol{B}$
are the electric and magnetic fields. In this regime the
![]() $\boldsymbol{E}\times \boldsymbol{B}$
drift is large enough that a narrow velocity space boundary layer arises so that only pitch angle scattering collisions need be considered. Our evaluation in the
$\boldsymbol{E}\times \boldsymbol{B}$
drift is large enough that a narrow velocity space boundary layer arises so that only pitch angle scattering collisions need be considered. Our evaluation in the
![]() $1/\unicode[STIX]{x1D708}$
regime allows general ripple,
$1/\unicode[STIX]{x1D708}$
regime allows general ripple,
![]() $qN\unicode[STIX]{x1D6FF}\sim \unicode[STIX]{x1D700}\gg \unicode[STIX]{x1D6FF}$
; while that in the
$qN\unicode[STIX]{x1D6FF}\sim \unicode[STIX]{x1D700}\gg \unicode[STIX]{x1D6FF}$
; while that in the
![]() $\sqrt{\unicode[STIX]{x1D708}}$
regime assumes strong ripple,
$\sqrt{\unicode[STIX]{x1D708}}$
regime assumes strong ripple,
![]() $qN\unicode[STIX]{x1D6FF}\gg \unicode[STIX]{x1D700}\gg \unicode[STIX]{x1D6FF}$
, where
$qN\unicode[STIX]{x1D6FF}\gg \unicode[STIX]{x1D700}\gg \unicode[STIX]{x1D6FF}$
, where
![]() $\unicode[STIX]{x1D700}\simeq a/R$
is the inverse aspect ratio with a the minor radius near the separatrix,
$\unicode[STIX]{x1D700}\simeq a/R$
is the inverse aspect ratio with a the minor radius near the separatrix,
![]() $R$
the major radius, and
$R$
the major radius, and
![]() $q$
the safety factor. We do not consider the weak ripple limit (
$q$
the safety factor. We do not consider the weak ripple limit (
![]() $qN\unicode[STIX]{x1D6FF}\ll \unicode[STIX]{x1D700}$
) of Linsker & Boozer (Reference Linsker and Boozer1982) that evaluates
$qN\unicode[STIX]{x1D6FF}\ll \unicode[STIX]{x1D700}$
) of Linsker & Boozer (Reference Linsker and Boozer1982) that evaluates
![]() $1/\unicode[STIX]{x1D708}$
ripple transport due to small radial magnetic drift steps causing small poloidal angle phase shifts in banana turning point locations after many bounces. The transport associated with this effect differs from the weak ripple (
$1/\unicode[STIX]{x1D708}$
ripple transport due to small radial magnetic drift steps causing small poloidal angle phase shifts in banana turning point locations after many bounces. The transport associated with this effect differs from the weak ripple (
![]() $qN\unicode[STIX]{x1D6FF}\ll \unicode[STIX]{x1D700}$
) limit of our general
$qN\unicode[STIX]{x1D6FF}\ll \unicode[STIX]{x1D700}$
) limit of our general
![]() $1/\unicode[STIX]{x1D708}$
regime evaluation because we do not consider ripple effects on the turning points of alphas with banana trapped orbits in the nearly axisymmetric tokamak magnetic field. Indeed, based on the Linsker & Boozer (Reference Linsker and Boozer1982) estimate of their equation (5) or (26) such effects are expected to be rather small. In the pedestal, if
$1/\unicode[STIX]{x1D708}$
regime evaluation because we do not consider ripple effects on the turning points of alphas with banana trapped orbits in the nearly axisymmetric tokamak magnetic field. Indeed, based on the Linsker & Boozer (Reference Linsker and Boozer1982) estimate of their equation (5) or (26) such effects are expected to be rather small. In the pedestal, if
![]() $q\sim 5$
–7,
$q\sim 5$
–7,
![]() $\unicode[STIX]{x1D700}\sim 1/3$
, and
$\unicode[STIX]{x1D700}\sim 1/3$
, and
![]() $\unicode[STIX]{x1D6FF}\sim 1/100$
, with
$\unicode[STIX]{x1D6FF}\sim 1/100$
, with
![]() $N\sim 16$
–20 (see Paul et al. (Reference Paul, Landreman, Poli, Spong, Smith and Dorland2017) for more specific numbers), then
$N\sim 16$
–20 (see Paul et al. (Reference Paul, Landreman, Poli, Spong, Smith and Dorland2017) for more specific numbers), then
![]() $\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF}\sim 1/3-1/4$
. Toroidal field coil ripple can be somewhat smaller (by adding coils, for example) so we will order
$\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF}\sim 1/3-1/4$
. Toroidal field coil ripple can be somewhat smaller (by adding coils, for example) so we will order
![]() $\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF}\sim 1$
when it is possible to do so and still obtain simple analytic results that are useful for insight and numerical checks.
$\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF}\sim 1$
when it is possible to do so and still obtain simple analytic results that are useful for insight and numerical checks.
Sections 2 and 3 present some background on alpha particle behaviour and the drift kinetic formalism we use to consistently retain the various collisional transport processes. These sections also serve to introduce most of the notation. In § 4 we give phenomenological estimates for all the transport processes we evaluate in the latter sections. In § 5 we briefly review axisymmetric tokamak collisional transport as evaluated in greater detail by Hsu, Catto & Sigmar (Reference Hsu, Catto and Sigmar1990). We then go on to § 6 to consider
![]() $1/\unicode[STIX]{x1D708}$
transport in the pitch angle scattering and electron drag dominated limits, and give a brief explanation of the difficulty of treating both at the same time, even with a boundary layer analysis about the ripple trapped–passing boundary. Section 7 presents the evaluation of transport in the
$1/\unicode[STIX]{x1D708}$
transport in the pitch angle scattering and electron drag dominated limits, and give a brief explanation of the difficulty of treating both at the same time, even with a boundary layer analysis about the ripple trapped–passing boundary. Section 7 presents the evaluation of transport in the
![]() $\sqrt{\unicode[STIX]{x1D708}}$
regime for
$\sqrt{\unicode[STIX]{x1D708}}$
regime for
![]() $qN\unicode[STIX]{x1D6FF}\gg \unicode[STIX]{x1D700}\gg \unicode[STIX]{x1D6FF}$
. The analysis is performed by assuming the
$qN\unicode[STIX]{x1D6FF}\gg \unicode[STIX]{x1D700}\gg \unicode[STIX]{x1D6FF}$
. The analysis is performed by assuming the
![]() $\boldsymbol{E}\times \boldsymbol{B}$
drift in a flux surface is strong enough to create a boundary layer narrower than that due to ripple,
$\boldsymbol{E}\times \boldsymbol{B}$
drift in a flux surface is strong enough to create a boundary layer narrower than that due to ripple,
![]() $\unicode[STIX]{x1D6FF}^{1/2}$
. Due to the careful boundary layer analysis the
$\unicode[STIX]{x1D6FF}^{1/2}$
. Due to the careful boundary layer analysis the
![]() $\sqrt{\unicode[STIX]{x1D708}}$
regime picks up a logarithmic correction that depends on ripple, collisions, and
$\sqrt{\unicode[STIX]{x1D708}}$
regime picks up a logarithmic correction that depends on ripple, collisions, and
![]() $\boldsymbol{E}\times \boldsymbol{B}$
drift as first pointed out by Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017). Our results are summarized in § 8, where we indicate that the two ripple transport mechanisms considered are a serious concern for tokamak reactors. Appendix A gives more details on the procedure of Stringer (Reference Stringer1972) and Connor & Hastie (Reference Connor and Hastie1973) as needed to extend their analysis to handle particle transport.
$\boldsymbol{E}\times \boldsymbol{B}$
drift as first pointed out by Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017). Our results are summarized in § 8, where we indicate that the two ripple transport mechanisms considered are a serious concern for tokamak reactors. Appendix A gives more details on the procedure of Stringer (Reference Stringer1972) and Connor & Hastie (Reference Connor and Hastie1973) as needed to extend their analysis to handle particle transport.
2 Alpha background
The isotropic slowing down tail solution
![]() $f_{s}=f_{s}(\boldsymbol{r},v)$
satisfies
$f_{s}=f_{s}(\boldsymbol{r},v)$
satisfies
where the coefficient of the
![]() $\unicode[STIX]{x1D6FF}(v-v_{0})$
function is the fusion birth rate for alphas:
$\unicode[STIX]{x1D6FF}(v-v_{0})$
function is the fusion birth rate for alphas:
The alphas of mass
![]() $M$
and charge number
$M$
and charge number
![]() $Z$
are born with birth speed
$Z$
are born with birth speed
![]() $v_{0}$
. The alpha collision operator is
$v_{0}$
. The alpha collision operator is
![]() $C$
, with
$C$
, with
![]() $c$
the speed of light,
$c$
the speed of light,
![]() $e$
the charge on a proton and
$e$
the charge on a proton and
![]() $\boldsymbol{B}$
the magnetic field.
$\boldsymbol{B}$
the magnetic field.
We expect alphas to be born on surfaces of constant pressure so that they have the usual slowing down distribution function on a flux surface to lowest order for small poloidal gyroradius and ripple (
![]() $\unicode[STIX]{x1D6FF}\sim \unicode[STIX]{x1D700}/qN$
):
$\unicode[STIX]{x1D6FF}\sim \unicode[STIX]{x1D700}/qN$
):
with
![]() $\unicode[STIX]{x1D713}$
the poloidal flux function,
$\unicode[STIX]{x1D713}$
the poloidal flux function,
![]() $H(v_{0}-v)$
the Heaviside step function,
$H(v_{0}-v)$
the Heaviside step function,
![]() $\unicode[STIX]{x1D70F}_{s}$
the alpha slowing down time
$\unicode[STIX]{x1D70F}_{s}$
the alpha slowing down time
and
![]() $v_{c}$
the critical speed defined by summing over background ions
$v_{c}$
the critical speed defined by summing over background ions
Electron and bulk ion densities and temperatures are denoted by
![]() $n_{j}$
and
$n_{j}$
and
![]() $T_{j}$
, with
$T_{j}$
, with
![]() $m$
the electron mass and
$m$
the electron mass and
![]() $M_{i}$
the mass of a bulk ion of charge
$M_{i}$
the mass of a bulk ion of charge
![]() $Z_{i}$
. The density of slowing down alphas is
$Z_{i}$
. The density of slowing down alphas is
where we assume
![]() $v_{0}^{3}\gg v_{c}^{3}$
as is the case for the deuterium–tritium (D–T) fusion reaction. Self-collisions are unimportant for the alphas. They are effectively a trace population since
$v_{0}^{3}\gg v_{c}^{3}$
as is the case for the deuterium–tritium (D–T) fusion reaction. Self-collisions are unimportant for the alphas. They are effectively a trace population since
![]() $n_{s}/n_{e}\sim T_{i}/Mv_{0}^{2}\ll 1$
, based on the alpha heating estimate
$n_{s}/n_{e}\sim T_{i}/Mv_{0}^{2}\ll 1$
, based on the alpha heating estimate
![]() $n_{s}Mv_{0}^{2}\sim n_{e}T_{i}$
.
$n_{s}Mv_{0}^{2}\sim n_{e}T_{i}$
.
To obtain the slowing down distribution function the usual collision operator for alphas is employed (see Cordey Reference Cordey1976), namely,
where
To obtain this form and generalizations of it expansions of the collision operator are employed for
![]() $v_{e}\gg v\gg v_{i}$
, where
$v_{e}\gg v\gg v_{i}$
, where
![]() $v_{e}=\sqrt{2T_{e}/m}$
and
$v_{e}=\sqrt{2T_{e}/m}$
and
![]() $v_{i}=\sqrt{2T_{i}/M_{i}}$
are the electron and typical bulk ion thermal speeds. Typically,
$v_{i}=\sqrt{2T_{i}/M_{i}}$
are the electron and typical bulk ion thermal speeds. Typically,
![]() $v_{0}\gtrsim v_{c}\sim v_{\unicode[STIX]{x1D706}}$
, with
$v_{0}\gtrsim v_{c}\sim v_{\unicode[STIX]{x1D706}}$
, with
![]() $v_{0}/v_{c}\sim 3$
for D–T fusion. Equation (2.3) is the solution of (2.1) with (2.7) inserted since a delta function sink resides in
$v_{0}/v_{c}\sim 3$
for D–T fusion. Equation (2.3) is the solution of (2.1) with (2.7) inserted since a delta function sink resides in
![]() $\unicode[STIX]{x1D70F}_{s}^{-1}v_{c}^{3}\unicode[STIX]{x1D735}_{v}\boldsymbol{\cdot }(v^{-3}\boldsymbol{v}f)\rightarrow -4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70F}_{s}^{-1}v_{c}^{3}f(\unicode[STIX]{x1D713},v=0)\unicode[STIX]{x1D6FF}(\boldsymbol{v})$
as
$\unicode[STIX]{x1D70F}_{s}^{-1}v_{c}^{3}\unicode[STIX]{x1D735}_{v}\boldsymbol{\cdot }(v^{-3}\boldsymbol{v}f)\rightarrow -4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70F}_{s}^{-1}v_{c}^{3}f(\unicode[STIX]{x1D713},v=0)\unicode[STIX]{x1D6FF}(\boldsymbol{v})$
as
![]() $v\rightarrow 0$
.
$v\rightarrow 0$
.
3 Drift kinetic formulation
For the Vlasov operator we use the drift kinetic equation of Hazeltine (Reference Hazeltine1973) in
![]() $\boldsymbol{r}$
,
$\boldsymbol{r}$
,
![]() $v$
or
$v$
or
and gyrophase
![]() $\unicode[STIX]{x1D711}$
variables, with an electrostatic electric field
$\unicode[STIX]{x1D711}$
variables, with an electrostatic electric field
where the total electrostatic potential is
![]() $\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D713})+\unicode[STIX]{x1D719}(\boldsymbol{r})$
with
$\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D713})+\unicode[STIX]{x1D719}(\boldsymbol{r})$
with
![]() $\unicode[STIX]{x1D719}(\boldsymbol{r})$
a periodic function of the poloidal,
$\unicode[STIX]{x1D719}(\boldsymbol{r})$
a periodic function of the poloidal,
![]() $\unicode[STIX]{x1D717}$
, and toroidal,
$\unicode[STIX]{x1D717}$
, and toroidal,
![]() $\unicode[STIX]{x1D701}$
, angles that also depends on the poloidal flux function
$\unicode[STIX]{x1D701}$
, angles that also depends on the poloidal flux function
![]() $\unicode[STIX]{x1D713}$
. Then
$\unicode[STIX]{x1D713}$
. Then
 $$\begin{eqnarray}\displaystyle (v_{\Vert }\boldsymbol{b}+\boldsymbol{v}_{d})\boldsymbol{\cdot }\left(\unicode[STIX]{x1D735}f-{\displaystyle \frac{Ze}{Mv}}{\displaystyle \frac{\unicode[STIX]{x2202}f}{\unicode[STIX]{x2202}v}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}\right) & = & \displaystyle {\displaystyle \frac{v_{\Vert }}{B}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\{f\left[\boldsymbol{B}+{\displaystyle \frac{Mc}{Ze}}\unicode[STIX]{x1D735}\times (v_{\Vert }\boldsymbol{b})\right]\right\}\nonumber\\ \displaystyle & & \displaystyle -\,{\displaystyle \frac{Ze}{Mv}}v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}{\displaystyle \frac{\unicode[STIX]{x2202}f}{\unicode[STIX]{x2202}v}}=C\{f\}+{\displaystyle \frac{S\unicode[STIX]{x1D6FF}(v-v_{0})}{4\unicode[STIX]{x03C0}v^{2}}},\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (v_{\Vert }\boldsymbol{b}+\boldsymbol{v}_{d})\boldsymbol{\cdot }\left(\unicode[STIX]{x1D735}f-{\displaystyle \frac{Ze}{Mv}}{\displaystyle \frac{\unicode[STIX]{x2202}f}{\unicode[STIX]{x2202}v}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}\right) & = & \displaystyle {\displaystyle \frac{v_{\Vert }}{B}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\{f\left[\boldsymbol{B}+{\displaystyle \frac{Mc}{Ze}}\unicode[STIX]{x1D735}\times (v_{\Vert }\boldsymbol{b})\right]\right\}\nonumber\\ \displaystyle & & \displaystyle -\,{\displaystyle \frac{Ze}{Mv}}v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}{\displaystyle \frac{\unicode[STIX]{x2202}f}{\unicode[STIX]{x2202}v}}=C\{f\}+{\displaystyle \frac{S\unicode[STIX]{x1D6FF}(v-v_{0})}{4\unicode[STIX]{x03C0}v^{2}}},\qquad\end{eqnarray}$$
where
![]() $f$
is the alpha distribution function,
$f$
is the alpha distribution function,
![]() $C\{f\}$
is the linear collision operator (2.7) for alphas, and
$C\{f\}$
is the linear collision operator (2.7) for alphas, and
The preceding form of the drift kinetic equation is adequate for our purposes as it gives the correct electric and magnetic drifts. It does not give the proper small parallel velocity correction
![]() $(v_{\bot }^{2}/2\unicode[STIX]{x1D6FA})\boldsymbol{b}\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\times \boldsymbol{b}$
, to the parallel streaming term, as discussed in Boozer (Reference Boozer1980), Parra & Catto (Reference Parra and Catto2008), and Landreman & Catto (Reference Landreman and Catto2013). We neglect this small parallel streaming correction from here on as it is of no importance, and we assume
$(v_{\bot }^{2}/2\unicode[STIX]{x1D6FA})\boldsymbol{b}\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\times \boldsymbol{b}$
, to the parallel streaming term, as discussed in Boozer (Reference Boozer1980), Parra & Catto (Reference Parra and Catto2008), and Landreman & Catto (Reference Landreman and Catto2013). We neglect this small parallel streaming correction from here on as it is of no importance, and we assume
![]() $Ze\unicode[STIX]{x1D719}\ll Ze\unicode[STIX]{x1D6F7}\sim T_{i}\sim T_{e}$
. In addition, we may view
$Ze\unicode[STIX]{x1D719}\ll Ze\unicode[STIX]{x1D6F7}\sim T_{i}\sim T_{e}$
. In addition, we may view
![]() $v=v(E,\unicode[STIX]{x1D713})$
by using
$v=v(E,\unicode[STIX]{x1D713})$
by using
whenever we need to keep non-radial components of the
![]() $(c/B)\boldsymbol{b}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}$
drift. Moreover, we use
$(c/B)\boldsymbol{b}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}$
drift. Moreover, we use
The turning points of a trapped particle are always at the same value of
![]() $B$
as it moves on a flux surface even in the presence of precession.
$B$
as it moves on a flux surface even in the presence of precession.
In the preceding, the magnetic field is
and the alpha gyrofrequency is
Using
![]() $\unicode[STIX]{x1D713}$
,
$\unicode[STIX]{x1D713}$
,
![]() $\unicode[STIX]{x1D717}$
, and
$\unicode[STIX]{x1D717}$
, and
![]() $\unicode[STIX]{x1D701}$
as the variables, with
$\unicode[STIX]{x1D701}$
as the variables, with
and
![]() $q=q(\unicode[STIX]{x1D713})$
the safety factor, the Clebsch and Boozer (Reference Boozer1981) representations for the magnetic field are
$q=q(\unicode[STIX]{x1D713})$
the safety factor, the Clebsch and Boozer (Reference Boozer1981) representations for the magnetic field are
with
![]() $K(\unicode[STIX]{x1D713},\unicode[STIX]{x1D717},\unicode[STIX]{x1D701})$
periodic in
$K(\unicode[STIX]{x1D713},\unicode[STIX]{x1D717},\unicode[STIX]{x1D701})$
periodic in
![]() $\unicode[STIX]{x1D717}$
and
$\unicode[STIX]{x1D717}$
and
![]() $\unicode[STIX]{x1D701}$
. The preceding give
$\unicode[STIX]{x1D701}$
. The preceding give
and
as well as
![]() $\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC}=0=\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}$
. In addition,
$\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC}=0=\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}$
. In addition,
with
![]() $G/qI\sim rB_{p}/qRB_{t}\sim \unicode[STIX]{x1D700}^{2}/q^{2}\ll 1$
,
$G/qI\sim rB_{p}/qRB_{t}\sim \unicode[STIX]{x1D700}^{2}/q^{2}\ll 1$
,
![]() $\unicode[STIX]{x1D700}$
the inverse aspect ratio, and
$\unicode[STIX]{x1D700}$
the inverse aspect ratio, and
![]() $B_{p}$
and
$B_{p}$
and
![]() $B_{t}$
the poloidal and toroidal magnetic fields. In addition, we are ignoring finite gyroradius corrections, but will retain finite poloidal gyroradius effects by assuming
$B_{t}$
the poloidal and toroidal magnetic fields. In addition, we are ignoring finite gyroradius corrections, but will retain finite poloidal gyroradius effects by assuming
![]() $q/\unicode[STIX]{x1D700}\gg 1$
.
$q/\unicode[STIX]{x1D700}\gg 1$
.
The ripple
![]() $\unicode[STIX]{x1D6FF}$
due to
$\unicode[STIX]{x1D6FF}$
due to
![]() $N$
toroidal field coils is defined as
$N$
toroidal field coils is defined as
with
![]() $\unicode[STIX]{x1D6FF}\ll \unicode[STIX]{x1D700}$
. We consider the ripple trapping wells as being due to the toroidal magnetic field that is produced by the
$\unicode[STIX]{x1D6FF}\ll \unicode[STIX]{x1D700}$
. We consider the ripple trapping wells as being due to the toroidal magnetic field that is produced by the
![]() $N$
toroidal field coils. We will often make use of the simple form
$N$
toroidal field coils. We will often make use of the simple form
to obtain explicit results. This simple form allows magnetic field minima away from
![]() $\unicode[STIX]{x1D717}=0$
. For ripple extending to the magnetic axis a form such as
$\unicode[STIX]{x1D717}=0$
. For ripple extending to the magnetic axis a form such as
![]() $\unicode[STIX]{x1D6FF}\simeq \unicode[STIX]{x1D6FF}_{0}+(\unicode[STIX]{x1D6FF}_{a}-\unicode[STIX]{x1D6FF}_{0})(r/a)^{p}$
can be used with
$\unicode[STIX]{x1D6FF}\simeq \unicode[STIX]{x1D6FF}_{0}+(\unicode[STIX]{x1D6FF}_{a}-\unicode[STIX]{x1D6FF}_{0})(r/a)^{p}$
can be used with
![]() $p$
an integer and poloidal variation of the ripple ignored. Forms with poloidally dependent ripple are not considered in order to obtain carefully evaluated analytic results. However, the evaluations in the
$p$
an integer and poloidal variation of the ripple ignored. Forms with poloidally dependent ripple are not considered in order to obtain carefully evaluated analytic results. However, the evaluations in the
![]() $1/\unicode[STIX]{x1D708}$
are performed quite generally, with the simple form of (3.16) only being used to get explicit results in the final steps. Following Stringer (Reference Stringer1972) and Connor & Hastie (Reference Connor and Hastie1973), the extrema in the magnetic field are found from
$1/\unicode[STIX]{x1D708}$
are performed quite generally, with the simple form of (3.16) only being used to get explicit results in the final steps. Following Stringer (Reference Stringer1972) and Connor & Hastie (Reference Connor and Hastie1973), the extrema in the magnetic field are found from
![]() $\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}B=0$
at fixed
$\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}B=0$
at fixed
![]() $\unicode[STIX]{x1D6FC}$
to be given by
$\unicode[STIX]{x1D6FC}$
to be given by
![]() $\unicode[STIX]{x1D700}\sin \unicode[STIX]{x1D717}\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}+N\unicode[STIX]{x1D6FF}\sin (N\unicode[STIX]{x1D701})\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}=0$
or
$\unicode[STIX]{x1D700}\sin \unicode[STIX]{x1D717}\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}+N\unicode[STIX]{x1D6FF}\sin (N\unicode[STIX]{x1D701})\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}=0$
or
If
![]() $qN\unicode[STIX]{x1D6FF}\,\ll \unicode[STIX]{x1D700}$
then the ripple wells are only near
$qN\unicode[STIX]{x1D6FF}\,\ll \unicode[STIX]{x1D700}$
then the ripple wells are only near
![]() $\unicode[STIX]{x1D717}=0$
and
$\unicode[STIX]{x1D717}=0$
and
![]() $\unicode[STIX]{x1D717}=\pm \unicode[STIX]{x03C0}$
. However, for
$\unicode[STIX]{x1D717}=\pm \unicode[STIX]{x03C0}$
. However, for
![]() $qN\unicode[STIX]{x1D6FF}\,>\unicode[STIX]{x1D700}$
ripple wells exist for all
$qN\unicode[STIX]{x1D6FF}\,>\unicode[STIX]{x1D700}$
ripple wells exist for all
![]() $\unicode[STIX]{x1D717}$
. To see this more clearly we note that because
$\unicode[STIX]{x1D717}$
. To see this more clearly we note that because
![]() $N\gg 1$
the ripples have a short toroidal extent compared to the tokamak circumference so the variation
$N\gg 1$
the ripples have a short toroidal extent compared to the tokamak circumference so the variation
![]() $\unicode[STIX]{x1D717}$
of a trapped alpha during its bounce motion in a ripple is small while
$\unicode[STIX]{x1D717}$
of a trapped alpha during its bounce motion in a ripple is small while
![]() $N\unicode[STIX]{x1D701}$
varies by a full bounce period. To introduce magnetic field minima containing ripple trapped particles at all
$N\unicode[STIX]{x1D701}$
varies by a full bounce period. To introduce magnetic field minima containing ripple trapped particles at all
![]() $\unicode[STIX]{x1D717}$
requires
$\unicode[STIX]{x1D717}$
requires
![]() $qN\unicode[STIX]{x1D6FF}>\unicode[STIX]{x1D700}|\!\sin \unicode[STIX]{x1D717}|>\unicode[STIX]{x1D700}$
. Consequently, we will assume the ordering
$qN\unicode[STIX]{x1D6FF}>\unicode[STIX]{x1D700}|\!\sin \unicode[STIX]{x1D717}|>\unicode[STIX]{x1D700}$
. Consequently, we will assume the ordering
![]() $qN\unicode[STIX]{x1D6FF}\sim \unicode[STIX]{x1D700}$
when possible, and use
$qN\unicode[STIX]{x1D6FF}\sim \unicode[STIX]{x1D700}$
when possible, and use
![]() $qN\unicode[STIX]{x1D6FF}\,\gg \unicode[STIX]{x1D700}$
to further simplify expressions. Retaining a slow poloidally varying ripple introduces a small order
$qN\unicode[STIX]{x1D6FF}\,\gg \unicode[STIX]{x1D700}$
to further simplify expressions. Retaining a slow poloidally varying ripple introduces a small order
![]() $\unicode[STIX]{x1D6FF}$
correction to (3.17). We do not expect it to result in a qualitative change in our results.
$\unicode[STIX]{x1D6FF}$
correction to (3.17). We do not expect it to result in a qualitative change in our results.
In an axisymmetric tokamak of inverse aspect ratio
![]() $\unicode[STIX]{x1D700}$
there is a single well and the fraction of particles that are trapped is
$\unicode[STIX]{x1D700}$
there is a single well and the fraction of particles that are trapped is
![]() $\unicode[STIX]{x1D700}^{1/2}$
. In a tokamak with
$\unicode[STIX]{x1D700}^{1/2}$
. In a tokamak with
![]() $N$
field ripples the trapped fraction in each ripple well is
$N$
field ripples the trapped fraction in each ripple well is
![]() $\unicode[STIX]{x1D6FF}^{1/2}$
. Consequently, transit averages in simple ripple wells such as
$\unicode[STIX]{x1D6FF}^{1/2}$
. Consequently, transit averages in simple ripple wells such as
![]() $B\simeq B_{0}[1-\unicode[STIX]{x1D6FF}\cos (N\unicode[STIX]{x1D701})]$
are very similar to those in standard axisymmetric tokamak wells
$B\simeq B_{0}[1-\unicode[STIX]{x1D6FF}\cos (N\unicode[STIX]{x1D701})]$
are very similar to those in standard axisymmetric tokamak wells
![]() $B\simeq B_{0}(1-\unicode[STIX]{x1D700}\cos \unicode[STIX]{x1D717})$
.
$B\simeq B_{0}(1-\unicode[STIX]{x1D700}\cos \unicode[STIX]{x1D717})$
.
To retain axisymmetric and ripple transport systematically it is convenient to separate
![]() $f$
into two terms by introducing one function
$f$
into two terms by introducing one function
![]() $f_{\ast }$
that only depends on what would be the constants of motion if we were in the axisymmetric limit and a remainder function
$f_{\ast }$
that only depends on what would be the constants of motion if we were in the axisymmetric limit and a remainder function
![]() $h$
. Therefore, we let
$h$
. Therefore, we let
where
![]() $f_{\ast }\simeq f_{s}\gg h$
,
$f_{\ast }\simeq f_{s}\gg h$
,
and a variable that is not the drift kinetic constant of the motion in the presence of ripple,
Because our tokamak is rippled
![]() $(v_{\Vert }\boldsymbol{b}+\boldsymbol{v}_{d})\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{\ast }\neq 0$
. Then we may write
$(v_{\Vert }\boldsymbol{b}+\boldsymbol{v}_{d})\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{\ast }\neq 0$
. Then we may write
 $$\begin{eqnarray}\displaystyle & & \displaystyle (v_{\Vert }\boldsymbol{b}+\boldsymbol{v}_{d})\boldsymbol{\cdot }\unicode[STIX]{x1D735}f_{\ast }+{\displaystyle \frac{v_{\Vert }}{B}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\{h\left[\boldsymbol{B}+{\displaystyle \frac{Mc}{Ze}}\unicode[STIX]{x1D735}\times (v_{\Vert }\boldsymbol{b})\right]\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,{\displaystyle \frac{Ze}{Mv}}v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}{\displaystyle \frac{\unicode[STIX]{x2202}f}{\unicode[STIX]{x2202}v}}=C\{f\}+{\displaystyle \frac{S\unicode[STIX]{x1D6FF}(v-v_{0})}{4\unicode[STIX]{x03C0}v^{2}}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (v_{\Vert }\boldsymbol{b}+\boldsymbol{v}_{d})\boldsymbol{\cdot }\unicode[STIX]{x1D735}f_{\ast }+{\displaystyle \frac{v_{\Vert }}{B}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\{h\left[\boldsymbol{B}+{\displaystyle \frac{Mc}{Ze}}\unicode[STIX]{x1D735}\times (v_{\Vert }\boldsymbol{b})\right]\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,{\displaystyle \frac{Ze}{Mv}}v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}{\displaystyle \frac{\unicode[STIX]{x2202}f}{\unicode[STIX]{x2202}v}}=C\{f\}+{\displaystyle \frac{S\unicode[STIX]{x1D6FF}(v-v_{0})}{4\unicode[STIX]{x03C0}v^{2}}},\end{eqnarray}$$
where in going from (3.4) to (3.21) only a small term proportional
![]() $\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}$
to is neglected.
$\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}$
to is neglected.
Recall that in an axisymmetric tokamak
and the alphas try to move on a surface of constant canonical angular momentum
where we used
![]() $R^{2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}\rightarrow B^{-1}(I\,\boldsymbol{b}-\boldsymbol{b}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D713})$
and neglect gyromotion in the last form on the right.
$R^{2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}\rightarrow B^{-1}(I\,\boldsymbol{b}-\boldsymbol{b}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D713})$
and neglect gyromotion in the last form on the right.
To rewrite the kinetic equation we use
In an axisymmetric tokamak
![]() $\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}\rightarrow v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(Iv_{\Vert }/\unicode[STIX]{x1D6FA})$
and
$\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}\rightarrow v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(Iv_{\Vert }/\unicode[STIX]{x1D6FA})$
and
![]() $\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(Iv_{||}/\unicode[STIX]{x1D6FA})\rightarrow 0$
(see appendix B of Parra & Catto (Reference Parra and Catto2010)). Due to ripple we must keep the difference
$\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(Iv_{||}/\unicode[STIX]{x1D6FA})\rightarrow 0$
(see appendix B of Parra & Catto (Reference Parra and Catto2010)). Due to ripple we must keep the difference
![]() $\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}-v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(Iv_{\Vert }/\unicode[STIX]{x1D6FA})$
. However, we can neglect
$\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}-v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(Iv_{\Vert }/\unicode[STIX]{x1D6FA})$
. However, we can neglect
![]() $\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(Iv_{\Vert }/\unicode[STIX]{x1D6FA})$
as small since it can only depend on the departure from axisymmetry and it is also small in the drift. As a result, we find
$\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(Iv_{\Vert }/\unicode[STIX]{x1D6FA})$
as small since it can only depend on the departure from axisymmetry and it is also small in the drift. As a result, we find
 $$\begin{eqnarray}\displaystyle & & \displaystyle v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}h+\left[\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}-v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left({\displaystyle \frac{Iv_{\Vert }}{\unicode[STIX]{x1D6FA}}}\right)\right]{\displaystyle \frac{\unicode[STIX]{x2202}f_{\ast }}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{\ast }}}+{\displaystyle \frac{v_{\Vert }}{\unicode[STIX]{x1D6FA}}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }[h\unicode[STIX]{x1D735}\times (v_{\Vert }\boldsymbol{b})]\nonumber\\ \displaystyle & & \displaystyle \qquad -\,{\displaystyle \frac{Ze}{Mv}}v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}{\displaystyle \frac{\unicode[STIX]{x2202}f_{\ast }}{\unicode[STIX]{x2202}v}}=C\{f\}+{\displaystyle \frac{S\unicode[STIX]{x1D6FF}(v-v_{0})}{4\unicode[STIX]{x03C0}v^{2}}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}h+\left[\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}-v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left({\displaystyle \frac{Iv_{\Vert }}{\unicode[STIX]{x1D6FA}}}\right)\right]{\displaystyle \frac{\unicode[STIX]{x2202}f_{\ast }}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{\ast }}}+{\displaystyle \frac{v_{\Vert }}{\unicode[STIX]{x1D6FA}}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }[h\unicode[STIX]{x1D735}\times (v_{\Vert }\boldsymbol{b})]\nonumber\\ \displaystyle & & \displaystyle \qquad -\,{\displaystyle \frac{Ze}{Mv}}v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}{\displaystyle \frac{\unicode[STIX]{x2202}f_{\ast }}{\unicode[STIX]{x2202}v}}=C\{f\}+{\displaystyle \frac{S\unicode[STIX]{x1D6FF}(v-v_{0})}{4\unicode[STIX]{x03C0}v^{2}}},\end{eqnarray}$$
where we have also neglected
![]() $v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}\unicode[STIX]{x2202}h/\unicode[STIX]{x2202}v$
as small since we assume both
$v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}\unicode[STIX]{x2202}h/\unicode[STIX]{x2202}v$
as small since we assume both
![]() $h$
and
$h$
and
![]() $\unicode[STIX]{x1D719}$
are small.
$\unicode[STIX]{x1D719}$
are small.
It is convenient to be able to relate
![]() $f_{s}$
and
$f_{s}$
and
![]() $f_{\ast }$
by Taylor expansion by defining
$f_{\ast }$
by Taylor expansion by defining
from which it follows that our kinetic equation becomes
 $$\begin{eqnarray}\displaystyle & & \displaystyle v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}h+\left[\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}-v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left({\displaystyle \frac{Iv_{\Vert }}{\unicode[STIX]{x1D6FA}}}\right)\right]{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}+{\displaystyle \frac{v_{\Vert }}{\unicode[STIX]{x1D6FA}}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }[h\unicode[STIX]{x1D735}\times (v_{\Vert }\boldsymbol{b})]\nonumber\\ \displaystyle & & \displaystyle \qquad -\,{\displaystyle \frac{Ze}{Mv}}v_{||}\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}v}}=C\{f_{\ast }-f_{s}+h\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}h+\left[\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}-v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left({\displaystyle \frac{Iv_{\Vert }}{\unicode[STIX]{x1D6FA}}}\right)\right]{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}+{\displaystyle \frac{v_{\Vert }}{\unicode[STIX]{x1D6FA}}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }[h\unicode[STIX]{x1D735}\times (v_{\Vert }\boldsymbol{b})]\nonumber\\ \displaystyle & & \displaystyle \qquad -\,{\displaystyle \frac{Ze}{Mv}}v_{||}\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}v}}=C\{f_{\ast }-f_{s}+h\},\end{eqnarray}$$
where we use the approximations
and
that are consistent with assuming
![]() $(Iv_{\Vert }/\unicode[STIX]{x1D6FA})f_{s}^{-1}\unicode[STIX]{x2202}f_{s}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}\ll 1$
. In an axisymmetric tokamak the left side of (3.27) reduces to
$(Iv_{\Vert }/\unicode[STIX]{x1D6FA})f_{s}^{-1}\unicode[STIX]{x2202}f_{s}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}\ll 1$
. In an axisymmetric tokamak the left side of (3.27) reduces to
as the streaming term is larger than the drift term and the
![]() $\unicode[STIX]{x1D719}$
term is unimportant. We always assume that to lowest order the slowing distribution function
$\unicode[STIX]{x1D719}$
term is unimportant. We always assume that to lowest order the slowing distribution function
![]() $f_{s}$
holds. In the next section and in the summary we will discuss that the consistency of this assumption requires that the radial diffusion is weak compared to slowing down and results in an important constraint.
$f_{s}$
holds. In the next section and in the summary we will discuss that the consistency of this assumption requires that the radial diffusion is weak compared to slowing down and results in an important constraint.
We will often make use of
![]() $\unicode[STIX]{x1D713}$
,
$\unicode[STIX]{x1D713}$
,
![]() $\unicode[STIX]{x1D717}$
, and
$\unicode[STIX]{x1D717}$
, and
![]() $\unicode[STIX]{x1D701}$
independent variables. In these variables, the divergence of an arbitrary vector
$\unicode[STIX]{x1D701}$
independent variables. In these variables, the divergence of an arbitrary vector
![]() $\boldsymbol{A}$
can be written as
$\boldsymbol{A}$
can be written as
Then, for example,
Using these variables and assuming streaming dominates for the alphas gives the lowest order equation to be
For the passing alphas,
![]() $h\rightarrow h_{p}$
and it must be a periodic flux function to lowest order as the passing trace out a flux surface. Therefore, we write
$h\rightarrow h_{p}$
and it must be a periodic flux function to lowest order as the passing trace out a flux surface. Therefore, we write
The lowest order trapped alpha distribution function,
![]() $h\rightarrow \bar{h}_{t}$
, must be even in
$h\rightarrow \bar{h}_{t}$
, must be even in
![]() $v_{\Vert }$
and need not be periodic in
$v_{\Vert }$
and need not be periodic in
![]() $\unicode[STIX]{x1D717}$
and
$\unicode[STIX]{x1D717}$
and
![]() $\unicode[STIX]{x1D701}$
. For it we must allow
$\unicode[STIX]{x1D701}$
. For it we must allow
To annihilate the streaming term to next order we introduce the transit average along the exact
![]() $\boldsymbol{B}$
:
$\boldsymbol{B}$
:
 $$\begin{eqnarray}\bar{A}={\displaystyle \frac{\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\ell \,A/v_{\Vert }}{\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\ell /v_{\Vert }}}={\displaystyle \frac{\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D70F}\,A}{\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D70F}\,}}={\displaystyle \frac{\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D717}\,A/v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}}{\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D717}\,/v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}}}={\displaystyle \frac{\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,A/v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}}{\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,/v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}}},\end{eqnarray}$$
$$\begin{eqnarray}\bar{A}={\displaystyle \frac{\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\ell \,A/v_{\Vert }}{\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\ell /v_{\Vert }}}={\displaystyle \frac{\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D70F}\,A}{\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D70F}\,}}={\displaystyle \frac{\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D717}\,A/v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}}{\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D717}\,/v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}}}={\displaystyle \frac{\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,A/v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}}{\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,/v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}}},\end{eqnarray}$$
with
![]() $A$
arbitrary,
$A$
arbitrary,
![]() $\text{d}\unicode[STIX]{x1D70F}=\text{d}\ell /v_{||}=\text{d}\unicode[STIX]{x1D717}/v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}=\text{d}\unicode[STIX]{x1D701}/v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}$
, and
$\text{d}\unicode[STIX]{x1D70F}=\text{d}\ell /v_{||}=\text{d}\unicode[STIX]{x1D717}/v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}=\text{d}\unicode[STIX]{x1D701}/v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}$
, and
![]() $q\,\text{d}\unicode[STIX]{x1D717}=\text{d}\unicode[STIX]{x1D701}$
for
$q\,\text{d}\unicode[STIX]{x1D717}=\text{d}\unicode[STIX]{x1D701}$
for
![]() $\unicode[STIX]{x1D6FC}$
fixed (as denoted by the subscript on the loop integral) for the trapped. Here the integrals are over a full bounce for trapped particles and over all
$\unicode[STIX]{x1D6FC}$
fixed (as denoted by the subscript on the loop integral) for the trapped. Here the integrals are over a full bounce for trapped particles and over all
![]() $\unicode[STIX]{x1D717}$
or
$\unicode[STIX]{x1D717}$
or
![]() $\unicode[STIX]{x1D701}$
for passing particles as they trace out a flux surface. We transit average by allowing
$\unicode[STIX]{x1D701}$
for passing particles as they trace out a flux surface. We transit average by allowing
![]() $B=B(\unicode[STIX]{x1D713},\unicode[STIX]{x1D717},\unicode[STIX]{x1D701})$
and
$B=B(\unicode[STIX]{x1D713},\unicode[STIX]{x1D717},\unicode[STIX]{x1D701})$
and
![]() $v_{||}=v_{\Vert }(\unicode[STIX]{x1D713},\unicode[STIX]{x1D717},\unicode[STIX]{x1D701})$
with
$v_{||}=v_{\Vert }(\unicode[STIX]{x1D713},\unicode[STIX]{x1D717},\unicode[STIX]{x1D701})$
with
![]() $\unicode[STIX]{x1D717}$
and
$\unicode[STIX]{x1D717}$
and
![]() $\unicode[STIX]{x1D701}$
at fixed
$\unicode[STIX]{x1D701}$
at fixed
![]() $\unicode[STIX]{x1D6FC}$
related by
$\unicode[STIX]{x1D6FC}$
related by
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D701}-q\unicode[STIX]{x1D717}$
.
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D701}-q\unicode[STIX]{x1D717}$
.
Then, using
and
the transit averaged equation to the requisite order becomes
for the trapped and the passing. Our transit averaged equation retains all the ripple neoclassical transport effects we are interested in as well as the standard axisymmetric neoclassical banana regime transport. In the axisymmetric limit
![]() $\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}\rightarrow 0$
and
$\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}\rightarrow 0$
and
![]() $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}\rightarrow 0$
giving
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}\rightarrow 0$
giving
![]() $\bar{h}_{t}\rightarrow 0$
. The linearity of the collision operator allows (3.40) to be split into the axisymmetric/passing and non-axisymmetric/trapped equations:
$\bar{h}_{t}\rightarrow 0$
. The linearity of the collision operator allows (3.40) to be split into the axisymmetric/passing and non-axisymmetric/trapped equations:
and
The axisymmetric equation for the passing contains only a drive
![]() $f_{\ast }-f_{s}$
and response
$f_{\ast }-f_{s}$
and response
![]() $\bar{h}_{p}$
odd in
$\bar{h}_{p}$
odd in
![]() $v_{||}$
, while the non-axisymmetric equation has a drive
$v_{||}$
, while the non-axisymmetric equation has a drive
![]() $\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}$
and response
$\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}$
and response
![]() $\bar{h}_{t}$
even in
$\bar{h}_{t}$
even in
![]() $v_{\Vert }$
. When non-axisymmetric effects are present
$v_{\Vert }$
. When non-axisymmetric effects are present
![]() $\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}=0$
for the passing along with
$\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}=0$
for the passing along with
![]() $\unicode[STIX]{x2202}\bar{h}_{p}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}=0$
. Consequently, there is no drive term for the passing and we are left with the homogeneous equation
$\unicode[STIX]{x2202}\bar{h}_{p}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}=0$
. Consequently, there is no drive term for the passing and we are left with the homogeneous equation
![]() $\overline{C\{\bar{h}_{p}\}}=0$
with ripple response
$\overline{C\{\bar{h}_{p}\}}=0$
with ripple response
![]() $\bar{h}_{p}=0$
. For the trapped, however,
$\bar{h}_{p}=0$
. For the trapped, however,
![]() $\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}\neq 0$
, so there is a drive term to make
$\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}\neq 0$
, so there is a drive term to make
![]() $\bar{h}_{t}\neq 0$
. For the trapped it is convenient to use
$\bar{h}_{t}\neq 0$
. For the trapped it is convenient to use
![]() $\unicode[STIX]{x1D713}$
,
$\unicode[STIX]{x1D713}$
,
![]() $\unicode[STIX]{x1D6FC}$
, and
$\unicode[STIX]{x1D6FC}$
, and
![]() $\unicode[STIX]{x1D701}$
variables for
$\unicode[STIX]{x1D701}$
variables for
![]() $\bar{h}_{t}$
. As a result, we employ
$\bar{h}_{t}$
. As a result, we employ
We have also assumed
![]() $\unicode[STIX]{x2202}f_{s}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}\gg \unicode[STIX]{x2202}\bar{h}_{t}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}$
.
$\unicode[STIX]{x2202}f_{s}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}\gg \unicode[STIX]{x2202}\bar{h}_{t}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}$
.
For the passing it is useful to introduce the flux surface average
 $$\begin{eqnarray}\langle A\rangle ={\displaystyle \frac{\displaystyle \oint \text{d}\unicode[STIX]{x1D717}\,\text{d}\unicode[STIX]{x1D701}\,A/\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}}{\displaystyle \oint \text{d}\unicode[STIX]{x1D717}\,\text{d}\unicode[STIX]{x1D701}/\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}}}={\displaystyle \frac{\displaystyle \oint \text{d}\unicode[STIX]{x1D717}\,\text{d}\unicode[STIX]{x1D701}\,A/B^{2}}{\displaystyle \oint \text{d}\unicode[STIX]{x1D717}\,\text{d}\unicode[STIX]{x1D701}/\,B^{2}}}\end{eqnarray}$$
$$\begin{eqnarray}\langle A\rangle ={\displaystyle \frac{\displaystyle \oint \text{d}\unicode[STIX]{x1D717}\,\text{d}\unicode[STIX]{x1D701}\,A/\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}}{\displaystyle \oint \text{d}\unicode[STIX]{x1D717}\,\text{d}\unicode[STIX]{x1D701}/\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}}}={\displaystyle \frac{\displaystyle \oint \text{d}\unicode[STIX]{x1D717}\,\text{d}\unicode[STIX]{x1D701}\,A/B^{2}}{\displaystyle \oint \text{d}\unicode[STIX]{x1D717}\,\text{d}\unicode[STIX]{x1D701}/\,B^{2}}}\end{eqnarray}$$
to rewrite the passing kinetic equation as
The passing collisional constraint determines the velocity space dependence required of the transit averaged
![]() $\bar{h}_{p}$
in response to the poloidal as well as velocity space variation of the radial drift drive term
$\bar{h}_{p}$
in response to the poloidal as well as velocity space variation of the radial drift drive term
In this regime the radial magnetic drift of the passing across flux surfaces is disrupted by collisions, but the collisional fluxes in velocity space across the trapped–passing boundary must balance to maintain a vanishing perturbed axisymmetric trapped distribution function
![]() $\bar{h}_{t}\,=0$
. The trapped response vanishes because
$\bar{h}_{t}\,=0$
. The trapped response vanishes because
![]() $\overline{v_{\Vert }/B\,}=0$
, thereby removing the drive term
$\overline{v_{\Vert }/B\,}=0$
, thereby removing the drive term
In (3.42) collisions cause radial steps that prevent the ripple trapped from returning to their starting point making
![]() $\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}\neq 0$
(unless the departure from axisymmetry is omnigeneous – see Landreman & Catto (Reference Landreman and Catto2012), Calvo et al. (Reference Calvo, Parra, Alonso and Velasco2014) and Helander (Reference Helander2014), for example). The radial steps randomized by collisions generate the trapped response
$\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}\neq 0$
(unless the departure from axisymmetry is omnigeneous – see Landreman & Catto (Reference Landreman and Catto2012), Calvo et al. (Reference Calvo, Parra, Alonso and Velasco2014) and Helander (Reference Helander2014), for example). The radial steps randomized by collisions generate the trapped response
![]() $\bar{h}_{t}$
. When drifts within a flux surface are negligible (
$\bar{h}_{t}$
. When drifts within a flux surface are negligible (
![]() $\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC}}\rightarrow 0$
) the
$\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC}}\rightarrow 0$
) the
![]() $1/\unicode[STIX]{x1D708}$
radial diffusivity regime is recovered. When the drifts within a flux surface become significant the radial drift decreases and the radial diffusivity is reduced to roughly a
$1/\unicode[STIX]{x1D708}$
radial diffusivity regime is recovered. When the drifts within a flux surface become significant the radial drift decreases and the radial diffusivity is reduced to roughly a
![]() $\sqrt{\unicode[STIX]{x1D708}}$
dependence. Normally only the
$\sqrt{\unicode[STIX]{x1D708}}$
dependence. Normally only the
![]() $\boldsymbol{E}\times \boldsymbol{B}$
is retained in the
$\boldsymbol{E}\times \boldsymbol{B}$
is retained in the
![]() $\sqrt{\unicode[STIX]{x1D708}}$
regime.
$\sqrt{\unicode[STIX]{x1D708}}$
regime.
An alternate form of (3.42) can be found by introducing the second adiabatic invariant
![]() $J$
,
$J$
,
with the last form using Boozer coordinates. Then for
![]() $\bar{f}=\bar{f}(\unicode[STIX]{x1D713},\unicode[STIX]{x1D6FC},v,\unicode[STIX]{x1D707})$
$\bar{f}=\bar{f}(\unicode[STIX]{x1D713},\unicode[STIX]{x1D6FC},v,\unicode[STIX]{x1D707})$
 $$\begin{eqnarray}\displaystyle & & \displaystyle \overline{{\displaystyle \frac{v_{\Vert }}{\unicode[STIX]{x1D6FA}}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\,[\bar{f}\,\unicode[STIX]{x1D735}\,\times \,(v_{||}\boldsymbol{b})]}={\displaystyle \frac{Mc}{Ze\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D70F}}}\!\left[\left.{\displaystyle \frac{\unicode[STIX]{x2202}\bar{f}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}\right|_{\unicode[STIX]{x1D6FC}}\!\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}{\displaystyle \frac{\text{d}\unicode[STIX]{x1D701}v_{\Vert }}{\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}}}\right)-{\displaystyle \frac{\unicode[STIX]{x2202}\bar{f}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}\left.{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}}\right|_{\unicode[STIX]{x1D713}}\!\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}{\displaystyle \frac{\text{d}\unicode[STIX]{x1D701}v_{\Vert }}{\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}}}\!\right)\!\right]\nonumber\\ \displaystyle & & \displaystyle \qquad ={\displaystyle \frac{1}{\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D70F}}}\left(\left.{\displaystyle \frac{\unicode[STIX]{x2202}\bar{f}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}}{\displaystyle \frac{\unicode[STIX]{x2202}J}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}\right|_{\unicode[STIX]{x1D6FC}}-{\displaystyle \frac{\unicode[STIX]{x2202}\bar{f}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}\left.{\displaystyle \frac{\unicode[STIX]{x2202}J}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}}\right|_{\unicode[STIX]{x1D713}}\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \overline{{\displaystyle \frac{v_{\Vert }}{\unicode[STIX]{x1D6FA}}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\,[\bar{f}\,\unicode[STIX]{x1D735}\,\times \,(v_{||}\boldsymbol{b})]}={\displaystyle \frac{Mc}{Ze\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D70F}}}\!\left[\left.{\displaystyle \frac{\unicode[STIX]{x2202}\bar{f}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}\right|_{\unicode[STIX]{x1D6FC}}\!\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}{\displaystyle \frac{\text{d}\unicode[STIX]{x1D701}v_{\Vert }}{\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}}}\right)-{\displaystyle \frac{\unicode[STIX]{x2202}\bar{f}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}\left.{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}}\right|_{\unicode[STIX]{x1D713}}\!\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}{\displaystyle \frac{\text{d}\unicode[STIX]{x1D701}v_{\Vert }}{\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}}}\!\right)\!\right]\nonumber\\ \displaystyle & & \displaystyle \qquad ={\displaystyle \frac{1}{\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D70F}}}\left(\left.{\displaystyle \frac{\unicode[STIX]{x2202}\bar{f}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}}{\displaystyle \frac{\unicode[STIX]{x2202}J}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}\right|_{\unicode[STIX]{x1D6FC}}-{\displaystyle \frac{\unicode[STIX]{x2202}\bar{f}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}\left.{\displaystyle \frac{\unicode[STIX]{x2202}J}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}}\right|_{\unicode[STIX]{x1D713}}\right).\end{eqnarray}$$
The
![]() $J$
integral is to be performed at fixed
$J$
integral is to be performed at fixed
![]() $\unicode[STIX]{x1D6FC}$
such that
$\unicode[STIX]{x1D6FC}$
such that
![]() $J=J(\unicode[STIX]{x1D713},\unicode[STIX]{x1D6FC},v,\unicode[STIX]{x1D707})$
. Neglecting the
$J=J(\unicode[STIX]{x1D713},\unicode[STIX]{x1D6FC},v,\unicode[STIX]{x1D707})$
. Neglecting the
![]() $\unicode[STIX]{x2202}\bar{h}_{t}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}$
term as small compared to the
$\unicode[STIX]{x2202}\bar{h}_{t}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}$
term as small compared to the
![]() $\unicode[STIX]{x2202}f_{s}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}$
term leads to our trapped kinetic equation with
$\unicode[STIX]{x2202}f_{s}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}$
term leads to our trapped kinetic equation with
 $$\begin{eqnarray}\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}=-{\displaystyle \frac{1}{\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D70F}}}\left.{\displaystyle \frac{\unicode[STIX]{x2202}J}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}}\right|_{\unicode[STIX]{x1D713}}\end{eqnarray}$$
$$\begin{eqnarray}\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}=-{\displaystyle \frac{1}{\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D70F}}}\left.{\displaystyle \frac{\unicode[STIX]{x2202}J}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}}\right|_{\unicode[STIX]{x1D713}}\end{eqnarray}$$
and
 $$\begin{eqnarray}\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC}}={\displaystyle \frac{1}{\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D70F}}}\left.{\displaystyle \frac{\unicode[STIX]{x2202}J}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}\right|_{\unicode[STIX]{x1D6FC}}.\end{eqnarray}$$
$$\begin{eqnarray}\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC}}={\displaystyle \frac{1}{\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D70F}}}\left.{\displaystyle \frac{\unicode[STIX]{x2202}J}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}\right|_{\unicode[STIX]{x1D6FC}}.\end{eqnarray}$$
The
![]() $\unicode[STIX]{x1D6FC}$
dependence of
$\unicode[STIX]{x1D6FC}$
dependence of
![]() $J$
acts as the drive for the ripple transport, or said another way, it is responsible for the departure from omnigenity.
$J$
acts as the drive for the ripple transport, or said another way, it is responsible for the departure from omnigenity.
In the next section we will use the preceding expressions to make estimates of the neoclassical and ripple transport levels.
4 Phenomenological transport estimates
In the following subsections we modify the standard diffusivity estimates to make them appropriate for alphas in the axisymmetric and ripple transport regimes. In making these estimates we treat
![]() $\ell n(v_{0}/v_{c})\sim 1$
for simplicity.
$\ell n(v_{0}/v_{c})\sim 1$
for simplicity.
4.1 Axisymmetric regime
For an axisymmetric tokamak, collisional alpha transport is evaluated by solving the passing equation
![]() $\overline{C\{f_{\ast }-f_{s}+\bar{h}_{p}\}}=0$
with
$\overline{C\{f_{\ast }-f_{s}+\bar{h}_{p}\}}=0$
with
![]() $\bar{h}_{t}\,=0$
for the trapped. For the passing
$\bar{h}_{t}\,=0$
for the trapped. For the passing
![]() $f_{\ast }-f_{s}\sim (\unicode[STIX]{x1D70C}_{p0}/a_{\unicode[STIX]{x1D6FC}})f_{s}$
, with
$f_{\ast }-f_{s}\sim (\unicode[STIX]{x1D70C}_{p0}/a_{\unicode[STIX]{x1D6FC}})f_{s}$
, with
![]() $\unicode[STIX]{x1D70C}_{p0}\simeq q\unicode[STIX]{x1D70C}_{0}/\unicode[STIX]{x1D700}$
the poloidal gyroradius at birth,
$\unicode[STIX]{x1D70C}_{p0}\simeq q\unicode[STIX]{x1D70C}_{0}/\unicode[STIX]{x1D700}$
the poloidal gyroradius at birth,
![]() $\unicode[STIX]{x1D70C}_{0}=v_{0}/\unicode[STIX]{x1D6FA}$
the gyroradius at birth,
$\unicode[STIX]{x1D70C}_{0}=v_{0}/\unicode[STIX]{x1D6FA}$
the gyroradius at birth,
![]() $\unicode[STIX]{x1D700}\sim a/R$
in the ripple region of minor radius
$\unicode[STIX]{x1D700}\sim a/R$
in the ripple region of minor radius
![]() $a$
, and
$a$
, and
![]() $\unicode[STIX]{x2202}f_{s}/\unicode[STIX]{x2202}r\sim f_{s}/a_{\unicode[STIX]{x1D6FC}}$
, where the radial scale of the alpha density
$\unicode[STIX]{x2202}f_{s}/\unicode[STIX]{x2202}r\sim f_{s}/a_{\unicode[STIX]{x1D6FC}}$
, where the radial scale of the alpha density
![]() $a_{\unicode[STIX]{x1D6FC}}$
is allowed to be less than the minor radius a for near axis burn or within the pedestal. Assuming pitch angle scattering dominates gives the trapped fraction as
$a_{\unicode[STIX]{x1D6FC}}$
is allowed to be less than the minor radius a for near axis burn or within the pedestal. Assuming pitch angle scattering dominates gives the trapped fraction as
![]() $\unicode[STIX]{x1D700}^{1/2}$
, the step size as a banana width
$\unicode[STIX]{x1D700}^{1/2}$
, the step size as a banana width
![]() $q\unicode[STIX]{x1D70C}_{0}/\unicode[STIX]{x1D700}^{1/2}$
, so that
$q\unicode[STIX]{x1D70C}_{0}/\unicode[STIX]{x1D700}^{1/2}$
, so that
![]() $\bar{h}_{p}\sim f_{s}q\unicode[STIX]{x1D70C}_{0}/\unicode[STIX]{x1D700}^{1/2}a_{\unicode[STIX]{x1D6FC}}$
, and an effective collision time of
$\bar{h}_{p}\sim f_{s}q\unicode[STIX]{x1D70C}_{0}/\unicode[STIX]{x1D700}^{1/2}a_{\unicode[STIX]{x1D6FC}}$
, and an effective collision time of
![]() $\unicode[STIX]{x1D700}\unicode[STIX]{x1D70F}_{s}$
. The diffusivity (
$\unicode[STIX]{x1D700}\unicode[STIX]{x1D70F}_{s}$
. The diffusivity (
![]() $D\sim \mathscr{F}\unicode[STIX]{x1D6E5}^{2}/\unicode[STIX]{x1D70F}$
with
$D\sim \mathscr{F}\unicode[STIX]{x1D6E5}^{2}/\unicode[STIX]{x1D70F}$
with
![]() $\mathscr{F}$
the trapped fraction,
$\mathscr{F}$
the trapped fraction,
![]() $\unicode[STIX]{x1D6E5}$
the step,
$\unicode[STIX]{x1D6E5}$
the step,
![]() $\unicode[STIX]{x1D70F}$
the correlation time) is then
$\unicode[STIX]{x1D70F}$
the correlation time) is then
as in Catto (Reference Catto1988). The pitch angle scattering pre-factor
![]() $(v_{\unicode[STIX]{x1D706}}/v)^{3}$
plays no role because in this limit it only enters as a multiplier in the solubility constraint.
$(v_{\unicode[STIX]{x1D706}}/v)^{3}$
plays no role because in this limit it only enters as a multiplier in the solubility constraint.
However, if electron drag dominates then this estimate must be modified in accordance with the Nocentini, Tessarotto & Engelmann (Reference Nocentini, Tessarotto and Engelmann1975) evaluation. In this case the trapped fraction and banana width step remain unchanged, but the effective collision time is just the slowing down time, giving the
![]() $\unicode[STIX]{x1D700}$
smaller result
$\unicode[STIX]{x1D700}$
smaller result
The
![]() $v_{\Vert }>0$
passing alphas are moving to larger
$v_{\Vert }>0$
passing alphas are moving to larger
![]() $\unicode[STIX]{x1D713}$
surfaces to keep
$\unicode[STIX]{x1D713}$
surfaces to keep
![]() $\unicode[STIX]{x1D713}_{\ast }$
constant as
$\unicode[STIX]{x1D713}_{\ast }$
constant as
![]() $v$
is reduced by drag, while the
$v$
is reduced by drag, while the
![]() $v_{\Vert }<0$
passing alphas move to smaller
$v_{\Vert }<0$
passing alphas move to smaller
![]() $\unicode[STIX]{x1D713}$
surfaces. More alphas move out then in, resulting in transport due to electron drag.
$\unicode[STIX]{x1D713}$
surfaces. More alphas move out then in, resulting in transport due to electron drag.
Although the ratio
is small, in practice the neoclassical diffusivity is between
![]() $D_{\text{axi}}^{\text{pas}}$
and
$D_{\text{axi}}^{\text{pas}}$
and
![]() $D_{\text{axi}}^{\text{drag}}$
as shown by Hsu et al. (Reference Hsu, Catto and Sigmar1990). Their plots compare their exact results with the Nocentini et al. (Reference Nocentini, Tessarotto and Engelmann1975) and Catto (Reference Catto1988) results, given by their equations (33a) and (33b), and in rough agreement with the preceding estimates.
$D_{\text{axi}}^{\text{drag}}$
as shown by Hsu et al. (Reference Hsu, Catto and Sigmar1990). Their plots compare their exact results with the Nocentini et al. (Reference Nocentini, Tessarotto and Engelmann1975) and Catto (Reference Catto1988) results, given by their equations (33a) and (33b), and in rough agreement with the preceding estimates.
To maintain a slowing down distribution function we need the slowing down time to be short compared to the time for diffusive losses to takes to place, that is, we need
![]() $\unicode[STIX]{x1D70F}_{s}D_{\text{axi}}^{\text{pas}}/a_{\unicode[STIX]{x1D6FC}}^{2}\ll 1$
or
$\unicode[STIX]{x1D70F}_{s}D_{\text{axi}}^{\text{pas}}/a_{\unicode[STIX]{x1D6FC}}^{2}\ll 1$
or
Consequently, we need to keep the alpha poloidal gyroradius at birth comparable or less than the radial scale length of the alpha density.
4.2 The
 $1/\unicode[STIX]{x1D708}$
regime
$1/\unicode[STIX]{x1D708}$
regime
To evaluate transport in the
![]() $1/\unicode[STIX]{x1D708}$
regime we solve the trapped equation with no toroidal rotation
$1/\unicode[STIX]{x1D708}$
regime we solve the trapped equation with no toroidal rotation
when the passing response is zero,
![]() $\bar{h}_{p}=0$
. Pitch angle scattering dominates when
$\bar{h}_{p}=0$
. Pitch angle scattering dominates when
![]() $\unicode[STIX]{x1D6FF}(v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3})\ll 1$
, where the boundary layer width due to ripple is of order
$\unicode[STIX]{x1D6FF}(v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3})\ll 1$
, where the boundary layer width due to ripple is of order
![]() $\unicode[STIX]{x1D6FF}^{1/2}$
. Using
$\unicode[STIX]{x1D6FF}^{1/2}$
. Using
![]() $\overline{C\{\bar{h}_{t}\}}\sim \bar{h}_{t}v_{\unicode[STIX]{x1D706}}^{3}/v_{0}^{3}\unicode[STIX]{x1D70F}_{s}\unicode[STIX]{x1D6FF}$
this equation gives the estimate
$\overline{C\{\bar{h}_{t}\}}\sim \bar{h}_{t}v_{\unicode[STIX]{x1D706}}^{3}/v_{0}^{3}\unicode[STIX]{x1D70F}_{s}\unicode[STIX]{x1D6FF}$
this equation gives the estimate
with
![]() $\unicode[STIX]{x1D70C}_{\ast }=\unicode[STIX]{x1D70C}_{0}/a_{\unicode[STIX]{x1D6FC}}\ll 1$
,
$\unicode[STIX]{x1D70C}_{\ast }=\unicode[STIX]{x1D70C}_{0}/a_{\unicode[STIX]{x1D6FC}}\ll 1$
,
![]() $\boldsymbol{v}_{d}\sim v_{0}\unicode[STIX]{x1D70C}_{0}/R$
, and a normalized pitch angle scattering frequency
$\boldsymbol{v}_{d}\sim v_{0}\unicode[STIX]{x1D70C}_{0}/R$
, and a normalized pitch angle scattering frequency
![]() $\unicode[STIX]{x1D708}_{\ast p}$
of
$\unicode[STIX]{x1D708}_{\ast p}$
of
The
![]() $N$
toroidal field coils result in ripple wells of depth
$N$
toroidal field coils result in ripple wells of depth
![]() $\unicode[STIX]{x1D6FF}$
resulting in a trapped fraction of
$\unicode[STIX]{x1D6FF}$
resulting in a trapped fraction of
![]() $\mathscr{F}\sim \unicode[STIX]{x1D6FF}^{1/2}$
. The pitch angle scattering time is
$\mathscr{F}\sim \unicode[STIX]{x1D6FF}^{1/2}$
. The pitch angle scattering time is
![]() $(v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3})\unicode[STIX]{x1D70F}_{s}$
is larger than the slowing down time, but the effective ripple trapped collision time
$(v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3})\unicode[STIX]{x1D70F}_{s}$
is larger than the slowing down time, but the effective ripple trapped collision time
![]() $\unicode[STIX]{x1D70F}\sim (v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3})\unicode[STIX]{x1D70F}_{s}\unicode[STIX]{x1D6FF}$
is smaller. The radial magnetic drift estimate for the alphas,
$\unicode[STIX]{x1D70F}\sim (v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3})\unicode[STIX]{x1D70F}_{s}\unicode[STIX]{x1D6FF}$
is smaller. The radial magnetic drift estimate for the alphas,
![]() $v_{0}\unicode[STIX]{x1D70C}_{0}/R$
, is insensitive to the number of coils since it is due to the nearly axisymmetric toroidal field. It gives the radial
$v_{0}\unicode[STIX]{x1D70C}_{0}/R$
, is insensitive to the number of coils since it is due to the nearly axisymmetric toroidal field. It gives the radial
![]() $\unicode[STIX]{x1D735}B$
drift as
$\unicode[STIX]{x1D735}B$
drift as
![]() $V\sim \;v_{0}\unicode[STIX]{x1D70C}_{0}/R$
(the poloidal gyroradius does not enter in the absence of axisymmetric banana motion). Then a smaller step
$V\sim \;v_{0}\unicode[STIX]{x1D70C}_{0}/R$
(the poloidal gyroradius does not enter in the absence of axisymmetric banana motion). Then a smaller step
![]() $\unicode[STIX]{x1D6E5}\sim V\unicode[STIX]{x1D70F}\sim \,\unicode[STIX]{x1D6FF}\,(v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3})\,\unicode[STIX]{x1D70C}_{0}v_{0}\unicode[STIX]{x1D70F}_{s}/R$
occurs because
$\unicode[STIX]{x1D6E5}\sim V\unicode[STIX]{x1D70F}\sim \,\unicode[STIX]{x1D6FF}\,(v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3})\,\unicode[STIX]{x1D70C}_{0}v_{0}\unicode[STIX]{x1D70F}_{s}/R$
occurs because
![]() $\unicode[STIX]{x1D6FF}\,(v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3})\ll 1$
. As a result, we expect an alpha diffusivity
$\unicode[STIX]{x1D6FF}\,(v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3})\ll 1$
. As a result, we expect an alpha diffusivity
![]() $D\sim \mathscr{F}\unicode[STIX]{x1D6E5}^{2}/\unicode[STIX]{x1D70F}$
of
$D\sim \mathscr{F}\unicode[STIX]{x1D6E5}^{2}/\unicode[STIX]{x1D70F}$
of
due to pitch angle scattering.
Our estimate assumes large ripple
![]() $\unicode[STIX]{x1D6FF}\gg \unicode[STIX]{x1D700}/qN$
and is the same as Galeev et al. (Reference Galeev, Sagdeev, Furth and Rosenbluth1969), and also the same as the Ho & Kulsrud (Reference Ho and Kulsrud1987) estimate for electrons when their power of
$\unicode[STIX]{x1D6FF}\gg \unicode[STIX]{x1D700}/qN$
and is the same as Galeev et al. (Reference Galeev, Sagdeev, Furth and Rosenbluth1969), and also the same as the Ho & Kulsrud (Reference Ho and Kulsrud1987) estimate for electrons when their power of
![]() $\unicode[STIX]{x1D700}_{h}=\unicode[STIX]{x1D6FF}$
in (3) is corrected to read
$\unicode[STIX]{x1D700}_{h}=\unicode[STIX]{x1D6FF}$
in (3) is corrected to read
![]() $\unicode[STIX]{x1D700}_{h}^{1/2}$
as would be expected by their argument. This estimate is consistent with the large ripple tokamak limit of Stringer (Reference Stringer1972) and the more general treatment of Connor & Hastie (Reference Connor and Hastie1973). Interestingly, it is smaller than the very near quasisymmetry stellarator estimate from equation (7) of Calvo et al. (Reference Calvo, Parra, Alonso and Velasco2014) that implies
$\unicode[STIX]{x1D700}_{h}^{1/2}$
as would be expected by their argument. This estimate is consistent with the large ripple tokamak limit of Stringer (Reference Stringer1972) and the more general treatment of Connor & Hastie (Reference Connor and Hastie1973). Interestingly, it is smaller than the very near quasisymmetry stellarator estimate from equation (7) of Calvo et al. (Reference Calvo, Parra, Alonso and Velasco2014) that implies
![]() $D_{1/\unicode[STIX]{x1D708}}^{\text{CPAV}}\sim \unicode[STIX]{x1D6FF}(v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3})\unicode[STIX]{x1D70F}_{s}\unicode[STIX]{x1D70C}_{0}^{2}v_{0}^{2}/R^{2}$
, but larger than the Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2013) less quasisymmetric stellarator estimate that suggests
$D_{1/\unicode[STIX]{x1D708}}^{\text{CPAV}}\sim \unicode[STIX]{x1D6FF}(v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3})\unicode[STIX]{x1D70F}_{s}\unicode[STIX]{x1D70C}_{0}^{2}v_{0}^{2}/R^{2}$
, but larger than the Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2013) less quasisymmetric stellarator estimate that suggests
![]() $D_{1/\unicode[STIX]{x1D708}}^{CPVA}\sim \,\,\unicode[STIX]{x1D6FF}^{2}(v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3})\unicode[STIX]{x1D70F}_{s}\unicode[STIX]{x1D70C}_{0}^{2}v_{0}^{2}/R^{2}$
.
$D_{1/\unicode[STIX]{x1D708}}^{CPVA}\sim \,\,\unicode[STIX]{x1D6FF}^{2}(v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3})\unicode[STIX]{x1D70F}_{s}\unicode[STIX]{x1D70C}_{0}^{2}v_{0}^{2}/R^{2}$
.
To keep
![]() $1/\unicode[STIX]{x1D708}$
ripple losses due to pitch angle scattering from depleting the lowest order slowing down distribution during a slowing down time we need the ripple to be small enough to keep
$1/\unicode[STIX]{x1D708}$
ripple losses due to pitch angle scattering from depleting the lowest order slowing down distribution during a slowing down time we need the ripple to be small enough to keep
![]() $\unicode[STIX]{x1D70F}_{s}D_{1/\unicode[STIX]{x1D708}}^{\text{pas}}/a_{\unicode[STIX]{x1D6FC}}^{2}\ll 1$
. Needing
$\unicode[STIX]{x1D70F}_{s}D_{1/\unicode[STIX]{x1D708}}^{\text{pas}}/a_{\unicode[STIX]{x1D6FC}}^{2}\ll 1$
. Needing
![]() $\bar{h}_{t}\ll f_{s}$
with
$\bar{h}_{t}\ll f_{s}$
with
![]() $\unicode[STIX]{x1D6FF}(v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3})\ll 1$
this gives a condition that is difficult to satisfy,
$\unicode[STIX]{x1D6FF}(v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3})\ll 1$
this gives a condition that is difficult to satisfy,
The ratio of pitch angle scattering
![]() $1/\unicode[STIX]{x1D708}$
ripple transport to neoclassical,
$1/\unicode[STIX]{x1D708}$
ripple transport to neoclassical,
implies that
![]() $1/\unicode[STIX]{x1D708}$
regime ripple transport dominates at small collisionalities when
$1/\unicode[STIX]{x1D708}$
regime ripple transport dominates at small collisionalities when
![]() $D_{1/\unicode[STIX]{x1D708}}^{\text{pas}}\;>\;D_{\text{axi}}^{\text{pas}}$
or
$D_{1/\unicode[STIX]{x1D708}}^{\text{pas}}\;>\;D_{\text{axi}}^{\text{pas}}$
or
Our estimate does not account for electron drag, which does not trap and de-trap alphas, but does change their radial step size as they slow. Electron drag dominates when
![]() $\unicode[STIX]{x1D6FF}\,(v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3})\gg 1$
. Using
$\unicode[STIX]{x1D6FF}\,(v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3})\gg 1$
. Using
![]() $\unicode[STIX]{x1D70F}\sim \unicode[STIX]{x1D70F}_{s}$
,
$\unicode[STIX]{x1D70F}\sim \unicode[STIX]{x1D70F}_{s}$
,
![]() $V\sim v_{0}\unicode[STIX]{x1D70C}_{0}/R$
,
$V\sim v_{0}\unicode[STIX]{x1D70C}_{0}/R$
,
![]() $\unicode[STIX]{x1D6E5}\sim V\unicode[STIX]{x1D70F}\sim \,\,\unicode[STIX]{x1D70C}_{0}v_{0}\unicode[STIX]{x1D70F}_{s}/R$
, and
$\unicode[STIX]{x1D6E5}\sim V\unicode[STIX]{x1D70F}\sim \,\,\unicode[STIX]{x1D70C}_{0}v_{0}\unicode[STIX]{x1D70F}_{s}/R$
, and
![]() $\mathscr{F}\sim \unicode[STIX]{x1D6FF}^{1/2}$
gives the estimate
$\mathscr{F}\sim \unicode[STIX]{x1D6FF}^{1/2}$
gives the estimate
Electron drag ripple loss and pitch angle scattering of ripple trapped are comparable when
For D–T fusion
![]() $v_{0}/v_{c}\sim 3$
with
$v_{0}/v_{c}\sim 3$
with
![]() $v_{\unicode[STIX]{x1D706}}\sim v_{c}$
, indicating that for a ripple
$v_{\unicode[STIX]{x1D706}}\sim v_{c}$
, indicating that for a ripple
![]() $\unicode[STIX]{x1D6FF}>1/30$
, electron drag could dominate.
$\unicode[STIX]{x1D6FF}>1/30$
, electron drag could dominate.
Keeping
![]() $1/\unicode[STIX]{x1D708}$
ripple losses due to electron drag from depleting the lowest order slowing down distribution during a slowing down time requires
$1/\unicode[STIX]{x1D708}$
ripple losses due to electron drag from depleting the lowest order slowing down distribution during a slowing down time requires
![]() $\unicode[STIX]{x1D70F}_{s}D_{1/\unicode[STIX]{x1D708}}^{\text{drag}}/a_{\unicode[STIX]{x1D6FC}}^{2}\ll 1$
or
$\unicode[STIX]{x1D70F}_{s}D_{1/\unicode[STIX]{x1D708}}^{\text{drag}}/a_{\unicode[STIX]{x1D6FC}}^{2}\ll 1$
or
This inequality is difficult to satisfy in this electron drag dominated limit since it requires
to find a self-consistent solution.
Electron drag ripple loss compares and axisymmetric neoclassical compare as
Consequently,
![]() $D_{1/\unicode[STIX]{x1D708}}^{\text{drag}}\;>\;D_{\text{axi}}^{\text{drag}}$
when
$D_{1/\unicode[STIX]{x1D708}}^{\text{drag}}\;>\;D_{\text{axi}}^{\text{drag}}$
when
which differs by
![]() $\unicode[STIX]{x1D6FF}^{1/2}\unicode[STIX]{x1D700}^{1/2}v_{0}^{3/2}/v_{\unicode[STIX]{x1D706}}^{3/2}$
from the pitch angle scattering inequality.
$\unicode[STIX]{x1D6FF}^{1/2}\unicode[STIX]{x1D700}^{1/2}v_{0}^{3/2}/v_{\unicode[STIX]{x1D706}}^{3/2}$
from the pitch angle scattering inequality.
Once the ripple is large enough to satisfy
![]() $q\unicode[STIX]{x1D708}_{\ast d}<\unicode[STIX]{x1D6FF}^{1/4}\unicode[STIX]{x1D700}^{1/4}$
electron drag transport enters the
$q\unicode[STIX]{x1D708}_{\ast d}<\unicode[STIX]{x1D6FF}^{1/4}\unicode[STIX]{x1D700}^{1/4}$
electron drag transport enters the
![]() $1/\unicode[STIX]{x1D708}$
ripple loss regime only if (4.15) is satisfied. Similarly, when
$1/\unicode[STIX]{x1D708}$
ripple loss regime only if (4.15) is satisfied. Similarly, when
![]() $q\unicode[STIX]{x1D708}_{\ast }<\unicode[STIX]{x1D700}^{3/4}\unicode[STIX]{x1D6FF}^{3/4}(v_{\unicode[STIX]{x1D706}}^{3}/v_{0}^{3})^{1/2}$
the ripple is large enough for pitch angle scattering to be in the
$q\unicode[STIX]{x1D708}_{\ast }<\unicode[STIX]{x1D700}^{3/4}\unicode[STIX]{x1D6FF}^{3/4}(v_{\unicode[STIX]{x1D706}}^{3}/v_{0}^{3})^{1/2}$
the ripple is large enough for pitch angle scattering to be in the
![]() $1/\unicode[STIX]{x1D708}$
ripple loss regime provided (4.6) is satisfied.
$1/\unicode[STIX]{x1D708}$
ripple loss regime provided (4.6) is satisfied.
4.3 The
 $\surd \unicode[STIX]{x1D708}$
regime
$\surd \unicode[STIX]{x1D708}$
regime
As the toroidal rotation increases we enter the
![]() $\sqrt{\unicode[STIX]{x1D708}}$
regime. Once again only the trapped matter since
$\sqrt{\unicode[STIX]{x1D708}}$
regime. Once again only the trapped matter since
![]() $\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}=0$
provides no drive for the passing. For the trapped we must solve
$\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}=0$
provides no drive for the passing. For the trapped we must solve
where we expect
with
![]() $\unicode[STIX]{x1D714}=\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC}}$
the toroidal
$\unicode[STIX]{x1D714}=\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC}}$
the toroidal
![]() $\boldsymbol{E}\times \boldsymbol{B}$
drift frequency in a flux surface. In the
$\boldsymbol{E}\times \boldsymbol{B}$
drift frequency in a flux surface. In the
![]() $\sqrt{\unicode[STIX]{x1D708}}$
regime
$\sqrt{\unicode[STIX]{x1D708}}$
regime
![]() $\overline{C\{\bar{h}\}}\ll \overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC}}\unicode[STIX]{x2202}\bar{h}_{t}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}$
except in a narrow boundary layer requiring the toroidal drift frequency to be fast compared to the effective pitch angle scattering frequency,
$\overline{C\{\bar{h}\}}\ll \overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC}}\unicode[STIX]{x2202}\bar{h}_{t}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}$
except in a narrow boundary layer requiring the toroidal drift frequency to be fast compared to the effective pitch angle scattering frequency,
Moreover, away from the boundary layer
gives
A boundary layer narrower than
![]() $\unicode[STIX]{x1D6FF}^{1/2}$
is only possible if pitch angle scattering is the dominant collisional process. Therefore, in the boundary layer we must balance
$\unicode[STIX]{x1D6FF}^{1/2}$
is only possible if pitch angle scattering is the dominant collisional process. Therefore, in the boundary layer we must balance
This balance between the strong
![]() $\boldsymbol{E}\times \boldsymbol{B}$
drift within the flux surface and collisions, further reduces the width
$\boldsymbol{E}\times \boldsymbol{B}$
drift within the flux surface and collisions, further reduces the width
![]() $w$
in pitch angle
$w$
in pitch angle
![]() $\unicode[STIX]{x1D706}$
of the boundary layer by enhancing the pitch angle scattering time
$\unicode[STIX]{x1D706}$
of the boundary layer by enhancing the pitch angle scattering time
![]() $\unicode[STIX]{x1D70F}_{s}v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3}$
:
$\unicode[STIX]{x1D70F}_{s}v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3}$
:
The balance between collisions and
![]() $\boldsymbol{E}\times \boldsymbol{B}$
drift then gives the normalized width of the boundary layer
$\boldsymbol{E}\times \boldsymbol{B}$
drift then gives the normalized width of the boundary layer
![]() $w$
to be
$w$
to be
indicating that the alphas must
![]() $\boldsymbol{E}\times \boldsymbol{B}$
drift on a flux surface faster than they pitch angle scatter off the ions. The effective trapped fraction is estimated from this boundary layer width to be
$\boldsymbol{E}\times \boldsymbol{B}$
drift on a flux surface faster than they pitch angle scatter off the ions. The effective trapped fraction is estimated from this boundary layer width to be
with
![]() $w\ll \unicode[STIX]{x1D6FF}^{1/2}$
giving (4.20). Then the effective correlation time to move the alphas out of the ripple traps is then the pitch angle scattering time multiplied by the fraction squared,
$w\ll \unicode[STIX]{x1D6FF}^{1/2}$
giving (4.20). Then the effective correlation time to move the alphas out of the ripple traps is then the pitch angle scattering time multiplied by the fraction squared,
The effective step size in the presence of
![]() $\boldsymbol{E}\times \boldsymbol{B}$
drift is
$\boldsymbol{E}\times \boldsymbol{B}$
drift is
as the toroidal
![]() $\boldsymbol{E}\times \boldsymbol{B}$
drift now limits the radial step. The narrower boundary layer results in
$\boldsymbol{E}\times \boldsymbol{B}$
drift now limits the radial step. The narrower boundary layer results in
![]() $\mathscr{F}$
,
$\mathscr{F}$
,
![]() $\unicode[STIX]{x1D70F}$
, and
$\unicode[STIX]{x1D70F}$
, and
![]() $\unicode[STIX]{x1D6E5}$
being independent of
$\unicode[STIX]{x1D6E5}$
being independent of
![]() $\unicode[STIX]{x1D6FF}$
. Therefore, the pitch angle scattering diffusivity in the
$\unicode[STIX]{x1D6FF}$
. Therefore, the pitch angle scattering diffusivity in the
![]() $\sqrt{\unicode[STIX]{x1D708}}$
regime is
$\sqrt{\unicode[STIX]{x1D708}}$
regime is
These estimates are consistent with the Galeev et al. (Reference Galeev, Sagdeev, Furth and Rosenbluth1969) and Ho & Kulsrud (Reference Ho and Kulsrud1987) estimates for ions except they did not keep
![]() $q$
. Like them, we assume large ripple,
$q$
. Like them, we assume large ripple,
![]() $\unicode[STIX]{x1D6FF}\gg \unicode[STIX]{x1D700}/qN$
. A more detailed boundary layer analysis presented later modifies this estimate slightly because of boundary layer subtleties found by Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017) that introduce a
$\unicode[STIX]{x1D6FF}\gg \unicode[STIX]{x1D700}/qN$
. A more detailed boundary layer analysis presented later modifies this estimate slightly because of boundary layer subtleties found by Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017) that introduce a
![]() $[\ell n(\unicode[STIX]{x1D6FF}^{1/2}/w)]^{1/2}$
factor in the denominator of
$[\ell n(\unicode[STIX]{x1D6FF}^{1/2}/w)]^{1/2}$
factor in the denominator of
![]() $D_{\sqrt{\unicode[STIX]{x1D708}}}^{\text{pas}}$
.
$D_{\sqrt{\unicode[STIX]{x1D708}}}^{\text{pas}}$
.
To avoid depleting the slowing down distribution function during
![]() $\sqrt{\unicode[STIX]{x1D708}}$
regime ripple transport requires
$\sqrt{\unicode[STIX]{x1D708}}$
regime ripple transport requires
![]() $\unicode[STIX]{x1D70F}_{s}D_{\sqrt{\unicode[STIX]{x1D708}}}^{\text{pas}}/a_{\unicode[STIX]{x1D6FC}}^{2}\ll 1$
or very strong toroidal rotation satisfying
$\unicode[STIX]{x1D70F}_{s}D_{\sqrt{\unicode[STIX]{x1D708}}}^{\text{pas}}/a_{\unicode[STIX]{x1D6FC}}^{2}\ll 1$
or very strong toroidal rotation satisfying
As
![]() $v_{\unicode[STIX]{x1D706}}\sim v_{c}\gg v_{i}$
, sonic rotation seems required even though
$v_{\unicode[STIX]{x1D706}}\sim v_{c}\gg v_{i}$
, sonic rotation seems required even though
![]() $\unicode[STIX]{x1D70C}_{0}/a_{\unicode[STIX]{x1D6FC}}\ll 1$
since
$\unicode[STIX]{x1D70C}_{0}/a_{\unicode[STIX]{x1D6FC}}\ll 1$
since
![]() $v_{0}\unicode[STIX]{x1D70F}_{s}/R\gg 1$
.
$v_{0}\unicode[STIX]{x1D70F}_{s}/R\gg 1$
.
Comparing
![]() $\sqrt{\unicode[STIX]{x1D708}}$
to axisymmetric banana regime neoclassical transport yields
$\sqrt{\unicode[STIX]{x1D708}}$
to axisymmetric banana regime neoclassical transport yields
which will be larger than unity as we expect
Normally the toroidal rotation frequency will be strong enough that the weaker
![]() $\sqrt{\unicode[STIX]{x1D708}}$
regime transport replaces the stronger
$\sqrt{\unicode[STIX]{x1D708}}$
regime transport replaces the stronger
![]() $1/\unicode[STIX]{x1D708}$
regime transport. Even when
$1/\unicode[STIX]{x1D708}$
regime transport. Even when
![]() $\unicode[STIX]{x1D6FF}(v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3})\ll 1$
, the transition occurs at about
$\unicode[STIX]{x1D6FF}(v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3})\ll 1$
, the transition occurs at about
![]() $D_{\sqrt{\unicode[STIX]{x1D708}}}^{\text{pas}}\sim D_{1/\unicode[STIX]{x1D708}}^{\text{pas}}$
or
$D_{\sqrt{\unicode[STIX]{x1D708}}}^{\text{pas}}\sim D_{1/\unicode[STIX]{x1D708}}^{\text{pas}}$
or
as might be expected from (4.20). As
![]() $\unicode[STIX]{x1D70F}_{s}\sim 1~\text{s}$
, we expect there will normally be enough toroidal rotation to make
$\unicode[STIX]{x1D70F}_{s}\sim 1~\text{s}$
, we expect there will normally be enough toroidal rotation to make
![]() $\unicode[STIX]{x1D714}\,\unicode[STIX]{x1D70F}_{s}\unicode[STIX]{x1D6FF}v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3}\gg q$
unless
$\unicode[STIX]{x1D714}\,\unicode[STIX]{x1D70F}_{s}\unicode[STIX]{x1D6FF}v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3}\gg q$
unless
![]() $\unicode[STIX]{x1D6FF}$
is tiny.
$\unicode[STIX]{x1D6FF}$
is tiny.
If
![]() $\unicode[STIX]{x1D6FF}(v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3})\gg 1$
, then drag dominates in the
$\unicode[STIX]{x1D6FF}(v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3})\gg 1$
, then drag dominates in the
![]() $1/\unicode[STIX]{x1D708}$
regime and the transition condition becomes
$1/\unicode[STIX]{x1D708}$
regime and the transition condition becomes
![]() $D_{\sqrt{\unicode[STIX]{x1D708}}}^{\text{pas}}\sim D_{1/\unicode[STIX]{x1D708}}^{\text{drag}}$
, giving a lower toroidal rotation for the transition to the pitch angle scattering dominated
$D_{\sqrt{\unicode[STIX]{x1D708}}}^{\text{pas}}\sim D_{1/\unicode[STIX]{x1D708}}^{\text{drag}}$
, giving a lower toroidal rotation for the transition to the pitch angle scattering dominated
![]() $\sqrt{\unicode[STIX]{x1D708}}$
regime of
$\sqrt{\unicode[STIX]{x1D708}}$
regime of
In the
![]() $\sqrt{\unicode[STIX]{x1D708}}$
regime we assume the
$\sqrt{\unicode[STIX]{x1D708}}$
regime we assume the
![]() $\boldsymbol{E}\times \boldsymbol{B}$
dominates over the
$\boldsymbol{E}\times \boldsymbol{B}$
dominates over the
![]() $\unicode[STIX]{x1D735}B$
by taking
$\unicode[STIX]{x1D735}B$
by taking
![]() $Ze\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}>M\unicode[STIX]{x1D707}\unicode[STIX]{x2202}B/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}$
or
$Ze\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}>M\unicode[STIX]{x1D707}\unicode[STIX]{x2202}B/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}$
or
where
![]() $\unicode[STIX]{x1D714}\;\sim c\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}\sim c|\boldsymbol{E}|/RB_{p}$
. Consequently, to enter the
$\unicode[STIX]{x1D714}\;\sim c\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}\sim c|\boldsymbol{E}|/RB_{p}$
. Consequently, to enter the
![]() $\sqrt{\unicode[STIX]{x1D708}}$
regime with
$\sqrt{\unicode[STIX]{x1D708}}$
regime with
![]() $\boldsymbol{E}\times \boldsymbol{B}$
the dominant drift requires a large electric field and/or the birth alpha gyroradius to be small compared to the minor radius. In
$\boldsymbol{E}\times \boldsymbol{B}$
the dominant drift requires a large electric field and/or the birth alpha gyroradius to be small compared to the minor radius. In
![]() $H$
mode pedestals (Kagan & Catto Reference Kagan and Catto2008)
$H$
mode pedestals (Kagan & Catto Reference Kagan and Catto2008)
so that using
![]() $v_{0}/v_{\unicode[STIX]{x1D706}}\sim 3$
and
$v_{0}/v_{\unicode[STIX]{x1D706}}\sim 3$
and
![]() $v_{i}/v_{\unicode[STIX]{x1D706}}\sim (m/M)^{1/6}\sim 1/4$
, with
$v_{i}/v_{\unicode[STIX]{x1D706}}\sim (m/M)^{1/6}\sim 1/4$
, with
![]() $v_{i}=(2T_{i}/M_{i})^{1/2}$
, we expect
$v_{i}=(2T_{i}/M_{i})^{1/2}$
, we expect
![]() $q\unicode[STIX]{x1D70C}_{0}/a<1/10$
or less to be required. If the
$q\unicode[STIX]{x1D70C}_{0}/a<1/10$
or less to be required. If the
![]() $\boldsymbol{E}\times \boldsymbol{B}$
and
$\boldsymbol{E}\times \boldsymbol{B}$
and
![]() $\unicode[STIX]{x1D735}B$
drifts compete such that
$\unicode[STIX]{x1D735}B$
drifts compete such that
![]() $\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC}}$
vanishes at isolated flux surfaces for
$\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC}}$
vanishes at isolated flux surfaces for
![]() $\unicode[STIX]{x1D707}\simeq \unicode[STIX]{x1D706}v_{0}^{2}/2B_{0}$
with
$\unicode[STIX]{x1D707}\simeq \unicode[STIX]{x1D706}v_{0}^{2}/2B_{0}$
with
![]() $\unicode[STIX]{x1D706}\simeq 1$
to be in the narrow boundary layer, then superbanana-plateau transport can occur in small regions of phase space as discussed in detail in Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017). We ignore such effects. Also, we do not consider direct orbit losses or collisionless stochastic diffusion in the vicinity of the separatrix since the difficult issue of the collisional filling of the unconfined loss regions would need to be evaluated. Instead, we simply assume the birth flux surface departure is small compared to the alpha radial scale. This assumption also avoids the issue of stochastic diffusion in the vicinity of the separatrix.
$\unicode[STIX]{x1D706}\simeq 1$
to be in the narrow boundary layer, then superbanana-plateau transport can occur in small regions of phase space as discussed in detail in Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017). We ignore such effects. Also, we do not consider direct orbit losses or collisionless stochastic diffusion in the vicinity of the separatrix since the difficult issue of the collisional filling of the unconfined loss regions would need to be evaluated. Instead, we simply assume the birth flux surface departure is small compared to the alpha radial scale. This assumption also avoids the issue of stochastic diffusion in the vicinity of the separatrix.
5 Neoclassical alpha transport simplifications and notation
For
![]() $H$
mode operation the plasma density and ion temperature profiles are rather flat until they approach the pedestal, where a rapid drop in the density occurs with an often weaker drop in the ion temperature. Moreover, the radial variation of
$H$
mode operation the plasma density and ion temperature profiles are rather flat until they approach the pedestal, where a rapid drop in the density occurs with an often weaker drop in the ion temperature. Moreover, the radial variation of
![]() $v_{c}^{3}$
is unimportant since
$v_{c}^{3}$
is unimportant since
![]() $v_{c}^{3}\ll v_{0}^{3}$
for D–T (
$v_{c}^{3}\ll v_{0}^{3}$
for D–T (
![]() $v_{c}^{3}\sim v_{0}^{3}$
for D–
$v_{c}^{3}\sim v_{0}^{3}$
for D–
![]() $\text{He}^{\text{3}}$
). The ion and electron densities enter as ratios in
$\text{He}^{\text{3}}$
). The ion and electron densities enter as ratios in
![]() $v_{c}^{3}$
, with the electron and ion temperatures equilibrated. As a result, for D–T we can assume the strongest radial variation of the alphas is due to
$v_{c}^{3}$
, with the electron and ion temperatures equilibrated. As a result, for D–T we can assume the strongest radial variation of the alphas is due to
![]() $S\unicode[STIX]{x1D70F}_{s}$
and we may approximate
$S\unicode[STIX]{x1D70F}_{s}$
and we may approximate
![]() $f_{s\ast }$
by
$f_{s\ast }$
by
If we write the
![]() $\unicode[STIX]{x1D713}$
dependence of the slowing down density as an exponential
$\unicode[STIX]{x1D713}$
dependence of the slowing down density as an exponential
then for
![]() $\unicode[STIX]{x1D705}$
a slowly varying function we may use
$\unicode[STIX]{x1D705}$
a slowly varying function we may use
to write
to retain finite orbit effects, by defining
with
![]() $RB_{p}\unicode[STIX]{x2202}n_{s}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}\sim n_{s}/a_{\unicode[STIX]{x1D6FC}}$
and
$RB_{p}\unicode[STIX]{x2202}n_{s}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}\sim n_{s}/a_{\unicode[STIX]{x1D6FC}}$
and
![]() $a_{\unicode[STIX]{x1D6FC}}$
the radial scale length of the alpha density profile. Based on the preceding, for D–T we can use
$a_{\unicode[STIX]{x1D6FC}}$
the radial scale length of the alpha density profile. Based on the preceding, for D–T we can use
We assume
![]() $Q\ll 1$
so we may use
$Q\ll 1$
so we may use
We are, of course, assuming that gyroradius corrections from the full expression for the canonical angular momentum will be small, that is, we assume that at birth
The drag and pitch angle scattering collision operators are
and
where
![]() $\unicode[STIX]{x1D706}=B_{0}v_{\bot }^{2}/v^{2}B$
and
$\unicode[STIX]{x1D706}=B_{0}v_{\bot }^{2}/v^{2}B$
and
![]() $\unicode[STIX]{x1D709}=v_{||}/v$
, with
$\unicode[STIX]{x1D709}=v_{||}/v$
, with
![]() $B_{0}$
any convenient normalization constant or flux function such as the on axis value or
$B_{0}$
any convenient normalization constant or flux function such as the on axis value or
![]() $\sqrt{\langle B^{2}\rangle }$
. Transit averaging gives
$\sqrt{\langle B^{2}\rangle }$
. Transit averaging gives
and
 $$\begin{eqnarray}\overline{C_{\text{pas}}\{g\}}={\displaystyle \frac{2v_{\unicode[STIX]{x1D706}}^{3}B_{0}}{\unicode[STIX]{x1D70F}_{s}v^{3}\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}/\unicode[STIX]{x1D709}B}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\left[\unicode[STIX]{x1D706}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}{\displaystyle \frac{\text{d}\unicode[STIX]{x1D701}\unicode[STIX]{x1D709}}{B^{2}}}{\displaystyle \frac{\unicode[STIX]{x2202}g}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\right)\right],\end{eqnarray}$$
$$\begin{eqnarray}\overline{C_{\text{pas}}\{g\}}={\displaystyle \frac{2v_{\unicode[STIX]{x1D706}}^{3}B_{0}}{\unicode[STIX]{x1D70F}_{s}v^{3}\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}/\unicode[STIX]{x1D709}B}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\left[\unicode[STIX]{x1D706}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}{\displaystyle \frac{\text{d}\unicode[STIX]{x1D701}\unicode[STIX]{x1D709}}{B^{2}}}{\displaystyle \frac{\unicode[STIX]{x2202}g}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\right)\right],\end{eqnarray}$$
with the subscribe a reminder that
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D713}$
are to be held fixed when transit averaging.
$\unicode[STIX]{x1D713}$
are to be held fixed when transit averaging.
6 Axisymmetric neoclassical alpha transport: a brief summary
The
![]() $v_{0}^{3}\gg v_{c}^{3}\sim v_{\unicode[STIX]{x1D706}}^{3}$
limit of axisymmetric neoclassical alpha transport is briefly summarized to indicate how it relates to the neoclassical ripple transport of alphas.
$v_{0}^{3}\gg v_{c}^{3}\sim v_{\unicode[STIX]{x1D706}}^{3}$
limit of axisymmetric neoclassical alpha transport is briefly summarized to indicate how it relates to the neoclassical ripple transport of alphas.
Keeping pitch angle scatter as well as drag, and expanding for
![]() $Q\ll 1$
, we must solve
$Q\ll 1$
, we must solve
However,
![]() $\bar{h}_{t}=0$
for the axisymmetric trapped response so we may employ flux surface averages to obtain the passing equation
$\bar{h}_{t}=0$
for the axisymmetric trapped response so we may employ flux surface averages to obtain the passing equation
For this axisymmetric portion of the solution the ripples may be assumed small since
![]() $\unicode[STIX]{x1D6FF}\ll \unicode[STIX]{x1D700}\ll 1$
and the flux surface average simplifies to
$\unicode[STIX]{x1D6FF}\ll \unicode[STIX]{x1D700}\ll 1$
and the flux surface average simplifies to
 $$\begin{eqnarray}\langle A\rangle \rightarrow {\displaystyle \frac{\displaystyle \oint \,\text{d}\unicode[STIX]{x1D717}\,A/\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}}{\displaystyle \oint \,\text{d}\unicode[STIX]{x1D717}/\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}}}={\displaystyle \frac{\displaystyle \oint \,\text{d}\unicode[STIX]{x1D717}\,A/B^{2}}{\displaystyle \oint \,\text{d}\unicode[STIX]{x1D717}/B^{2}}}.\end{eqnarray}$$
$$\begin{eqnarray}\langle A\rangle \rightarrow {\displaystyle \frac{\displaystyle \oint \,\text{d}\unicode[STIX]{x1D717}\,A/\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}}{\displaystyle \oint \,\text{d}\unicode[STIX]{x1D717}/\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}}}={\displaystyle \frac{\displaystyle \oint \,\text{d}\unicode[STIX]{x1D717}\,A/B^{2}}{\displaystyle \oint \,\text{d}\unicode[STIX]{x1D717}/B^{2}}}.\end{eqnarray}$$
To relate this equation to that of Hsu et al. (Reference Hsu, Catto and Sigmar1990) we continue to use the odd function
and define the poloidal angle independent dimensionless function
![]() $P$
via
$P$
via
with
then
and our axisymmetric passing equation becomes
 $$\begin{eqnarray}\displaystyle & & \displaystyle {\displaystyle \frac{(v^{3}+v_{c}^{3})}{2v_{\unicode[STIX]{x1D706}}^{3}}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}v}}[v(P+2B_{0}\overline{\unicode[STIX]{x1D709}/B})H(v_{0}-v)]\nonumber\\ \displaystyle & & \displaystyle \qquad +\,{\displaystyle \frac{B_{0}H(v_{0}-v)}{\langle B/\unicode[STIX]{x1D709}\rangle }}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\left[\unicode[STIX]{x1D706}\left\langle \unicode[STIX]{x1D709}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}(P+2\unicode[STIX]{x1D709}B_{0}/B)\right\rangle \right]=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\displaystyle \frac{(v^{3}+v_{c}^{3})}{2v_{\unicode[STIX]{x1D706}}^{3}}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}v}}[v(P+2B_{0}\overline{\unicode[STIX]{x1D709}/B})H(v_{0}-v)]\nonumber\\ \displaystyle & & \displaystyle \qquad +\,{\displaystyle \frac{B_{0}H(v_{0}-v)}{\langle B/\unicode[STIX]{x1D709}\rangle }}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\left[\unicode[STIX]{x1D706}\left\langle \unicode[STIX]{x1D709}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}(P+2\unicode[STIX]{x1D709}B_{0}/B)\right\rangle \right]=0,\end{eqnarray}$$
where
![]() $\overline{\unicode[STIX]{x1D709}/B}\,\langle B/\unicode[STIX]{x1D709}\rangle =1$
. Using
$\overline{\unicode[STIX]{x1D709}/B}\,\langle B/\unicode[STIX]{x1D709}\rangle =1$
. Using
![]() $\unicode[STIX]{x1D709}^{2}=1-\unicode[STIX]{x1D706}B/B_{0}$
gives
$\unicode[STIX]{x1D709}^{2}=1-\unicode[STIX]{x1D706}B/B_{0}$
gives
![]() $2\unicode[STIX]{x1D709}\unicode[STIX]{x2202}\unicode[STIX]{x1D709}/\unicode[STIX]{x2202}\unicode[STIX]{x1D706}=-B/B_{0}$
so this becomes
$2\unicode[STIX]{x1D709}\unicode[STIX]{x2202}\unicode[STIX]{x1D709}/\unicode[STIX]{x2202}\unicode[STIX]{x1D706}=-B/B_{0}$
so this becomes
since
The preceding equation for
![]() $P$
is in agreement with equation (7) of Hsu et al. (Reference Hsu, Catto and Sigmar1990) in the large drag limit. For the passing in the large aspect limit
$P$
is in agreement with equation (7) of Hsu et al. (Reference Hsu, Catto and Sigmar1990) in the large drag limit. For the passing in the large aspect limit
 $$\begin{eqnarray}\langle \unicode[STIX]{x1D709}\rangle ={\displaystyle \frac{\displaystyle \oint \,\text{d}\unicode[STIX]{x1D703}\,\unicode[STIX]{x1D709}/B^{2}}{\displaystyle \oint \,\text{d}\unicode[STIX]{x1D703}/B^{2}}}\simeq {\displaystyle \frac{\displaystyle \oint \,\text{d}\unicode[STIX]{x1D703}\,\unicode[STIX]{x1D709}}{2\unicode[STIX]{x03C0}}}={\displaystyle \frac{4\sqrt{2\unicode[STIX]{x1D700}}E(k)}{2\unicode[STIX]{x03C0}\sqrt{(1-\unicode[STIX]{x1D700})k^{2}+2\unicode[STIX]{x1D700}}}},\end{eqnarray}$$
$$\begin{eqnarray}\langle \unicode[STIX]{x1D709}\rangle ={\displaystyle \frac{\displaystyle \oint \,\text{d}\unicode[STIX]{x1D703}\,\unicode[STIX]{x1D709}/B^{2}}{\displaystyle \oint \,\text{d}\unicode[STIX]{x1D703}/B^{2}}}\simeq {\displaystyle \frac{\displaystyle \oint \,\text{d}\unicode[STIX]{x1D703}\,\unicode[STIX]{x1D709}}{2\unicode[STIX]{x03C0}}}={\displaystyle \frac{4\sqrt{2\unicode[STIX]{x1D700}}E(k)}{2\unicode[STIX]{x03C0}\sqrt{(1-\unicode[STIX]{x1D700})k^{2}+2\unicode[STIX]{x1D700}}}},\end{eqnarray}$$
with
![]() $\unicode[STIX]{x1D700}=r/R$
and
$\unicode[STIX]{x1D700}=r/R$
and
![]() $k^{2}=2\unicode[STIX]{x1D700}\unicode[STIX]{x1D706}/[1-(1-\unicode[STIX]{x1D700})\unicode[STIX]{x1D706}]$
.
$k^{2}=2\unicode[STIX]{x1D700}\unicode[STIX]{x1D706}/[1-(1-\unicode[STIX]{x1D700})\unicode[STIX]{x1D706}]$
.
The drag only result of Nocentini et al. (Reference Nocentini, Tessarotto and Engelmann1975) is
while the pitch angle scattering only solution of Catto (Reference Catto1988) is
with
![]() $P=0$
for the trapped. Hsu et al. (Reference Hsu, Catto and Sigmar1990) point out that the drag solution fails at the trapped–passing separatrix, and the pitch angle scattering solution does not satisfy the jump condition obtained by integrating (6.8) across the delta function alpha birth source.
$P=0$
for the trapped. Hsu et al. (Reference Hsu, Catto and Sigmar1990) point out that the drag solution fails at the trapped–passing separatrix, and the pitch angle scattering solution does not satisfy the jump condition obtained by integrating (6.8) across the delta function alpha birth source.
Hsu et al. (Reference Hsu, Catto and Sigmar1990) solve the general problem for arbitrary aspect ratio concentric circular flux surfaces by separation of variables and a Sturm–Liouville eigenvalue procedure similar to that of Cordey (Reference Cordey1976) by writing
The eigenfunctions
![]() $\unicode[STIX]{x1D6EC}_{k}$
satisfy the eigenvalue equation (Cordey Reference Cordey1976; Hsu et al.
Reference Hsu, Catto and Sigmar1990)
$\unicode[STIX]{x1D6EC}_{k}$
satisfy the eigenvalue equation (Cordey Reference Cordey1976; Hsu et al.
Reference Hsu, Catto and Sigmar1990)
with
![]() $\unicode[STIX]{x1D705}_{n}$
the
$\unicode[STIX]{x1D705}_{n}$
the
![]() $n\text{th}$
eigenvalue associated with the normalization
$n\text{th}$
eigenvalue associated with the normalization
and the trapped–passing separatrix
![]() $(\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}_{c})$
boundary condition
$(\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}_{c})$
boundary condition
The associated orthogonality condition is
for
![]() $j\neq k$
. Continuing to follow Hsu et al. (Reference Hsu, Catto and Sigmar1990) gives for our simplified version of their (12a),
$j\neq k$
. Continuing to follow Hsu et al. (Reference Hsu, Catto and Sigmar1990) gives for our simplified version of their (12a),
where integrating across
![]() $v_{0}$
using
$v_{0}$
using
yields the jump condition
 $$\begin{eqnarray}V_{k}(\unicode[STIX]{x1D713},v_{0})=\unicode[STIX]{x1D70E}_{k}\equiv {\displaystyle \frac{\displaystyle \int _{0}^{\unicode[STIX]{x1D706}_{c}}\,\text{d}\unicode[STIX]{x1D706}\,\unicode[STIX]{x1D6EC}_{k}}{\displaystyle \int _{0}^{\unicode[STIX]{x1D706}_{c}}\text{d}\unicode[STIX]{x1D706}\,\unicode[STIX]{x1D6EC}_{k}^{2}\unicode[STIX]{x2202}\langle \unicode[STIX]{x1D709}\rangle /\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}.\end{eqnarray}$$
$$\begin{eqnarray}V_{k}(\unicode[STIX]{x1D713},v_{0})=\unicode[STIX]{x1D70E}_{k}\equiv {\displaystyle \frac{\displaystyle \int _{0}^{\unicode[STIX]{x1D706}_{c}}\,\text{d}\unicode[STIX]{x1D706}\,\unicode[STIX]{x1D6EC}_{k}}{\displaystyle \int _{0}^{\unicode[STIX]{x1D706}_{c}}\text{d}\unicode[STIX]{x1D706}\,\unicode[STIX]{x1D6EC}_{k}^{2}\unicode[STIX]{x2202}\langle \unicode[STIX]{x1D709}\rangle /\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}.\end{eqnarray}$$
For the D–T case considered here the limiting solution for
![]() $v_{0}^{3}\gg v_{c}^{3}\sim v_{\unicode[STIX]{x1D706}}^{3}$
is simply
$v_{0}^{3}\gg v_{c}^{3}\sim v_{\unicode[STIX]{x1D706}}^{3}$
is simply
with the more general solution given in Hsu et al. (Reference Hsu, Catto and Sigmar1990). The first eigenvalue
![]() $\unicode[STIX]{x1D705}_{1}$
is typically order unity and the other
$\unicode[STIX]{x1D705}_{1}$
is typically order unity and the other
![]() $\unicode[STIX]{x1D705}_{n}$
are typically large.
$\unicode[STIX]{x1D705}_{n}$
are typically large.
The axisymmetric neoclassical alpha radial particle (
![]() $d=0$
) and radial heat (
$d=0$
) and radial heat (
![]() $d=1$
) fluxes are evaluated as in Hsu et al. (Reference Hsu, Catto and Sigmar1990) from
$d=1$
) fluxes are evaluated as in Hsu et al. (Reference Hsu, Catto and Sigmar1990) from
The results are typically above the Nocentini et al. (Reference Nocentini, Tessarotto and Engelmann1975) and below the Catto (Reference Catto1988) results.
Notice that for the axisymmetric neoclassical particle fluxes ambipolarity is automatically satisfied because if we sum over all species momentum conservation gives
As a result,
where here
![]() $\unicode[STIX]{x1D6E4}_{0}^{\text{neo}}$
,
$\unicode[STIX]{x1D6E4}_{0}^{\text{neo}}$
,
![]() $Z$
, and
$Z$
, and
![]() $M$
are the species particle flux, charge number and mass.
$M$
are the species particle flux, charge number and mass.
7
 $1/\unicode[STIX]{x1D708}$
ripple transport of alphas
$1/\unicode[STIX]{x1D708}$
ripple transport of alphas
In the
![]() $1/\unicode[STIX]{x1D708}$
regime
$1/\unicode[STIX]{x1D708}$
regime
![]() $\bar{h}_{p}=0$
for the passing, while for the trapped we must solve
$\bar{h}_{p}=0$
for the passing, while for the trapped we must solve
for
![]() $\bar{h}_{t}=\bar{h}_{t}(\unicode[STIX]{x1D713},\unicode[STIX]{x1D6FC},v,\unicode[STIX]{x1D707})$
. We consider the two limits of pitch angle scattering and electron drag dominating. In all situations considered for
$\bar{h}_{t}=\bar{h}_{t}(\unicode[STIX]{x1D713},\unicode[STIX]{x1D6FC},v,\unicode[STIX]{x1D707})$
. We consider the two limits of pitch angle scattering and electron drag dominating. In all situations considered for
![]() $1/\unicode[STIX]{x1D708}$
transport both sets of turning points (
$1/\unicode[STIX]{x1D708}$
transport both sets of turning points (
![]() $v_{\Vert }=0$
) for a charge of fixed
$v_{\Vert }=0$
) for a charge of fixed
![]() $\unicode[STIX]{x1D707}$
are at the same value of
$\unicode[STIX]{x1D707}$
are at the same value of
![]() $B$
as the motion is on a fixed field line of constant
$B$
as the motion is on a fixed field line of constant
![]() $\unicode[STIX]{x1D713}$
and
$\unicode[STIX]{x1D713}$
and
![]() $\unicode[STIX]{x1D6FC}$
. For the simple form of (3.16) this means the poloidal angle of the two turning points must be at the same value of
$\unicode[STIX]{x1D6FC}$
. For the simple form of (3.16) this means the poloidal angle of the two turning points must be at the same value of
![]() $\unicode[STIX]{x1D700}\cos \unicode[STIX]{x1D717}+\unicode[STIX]{x1D6FF}\cos [N(\unicode[STIX]{x1D6FC}-q\unicode[STIX]{x1D717})]$
. In the
$\unicode[STIX]{x1D700}\cos \unicode[STIX]{x1D717}+\unicode[STIX]{x1D6FF}\cos [N(\unicode[STIX]{x1D6FC}-q\unicode[STIX]{x1D717})]$
. In the
![]() $1/\unicode[STIX]{x1D708}$
regime trapped alphas in local wells cannot be detrapped or trapped without collisions.
$1/\unicode[STIX]{x1D708}$
regime trapped alphas in local wells cannot be detrapped or trapped without collisions.
7.1 Pitch angle scattering dominates:
 $\unicode[STIX]{x1D6FF}(v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3})\ll 1$
$\unicode[STIX]{x1D6FF}(v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3})\ll 1$
Our pitch angle scattering evaluation ignores drag in the alpha collision operator so that
 $$\begin{eqnarray}\overline{C\{\bar{h}_{t}\}}={\displaystyle \frac{2v_{\unicode[STIX]{x1D706}}^{3}B_{0}}{\unicode[STIX]{x1D70F}_{s}v^{3}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}/\unicode[STIX]{x1D709}\,B\right)}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\left[\unicode[STIX]{x1D706}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\;\unicode[STIX]{x1D709}/B^{2}\right){\displaystyle \frac{\unicode[STIX]{x2202}\bar{h}_{t}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\right]\end{eqnarray}$$
$$\begin{eqnarray}\overline{C\{\bar{h}_{t}\}}={\displaystyle \frac{2v_{\unicode[STIX]{x1D706}}^{3}B_{0}}{\unicode[STIX]{x1D70F}_{s}v^{3}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}/\unicode[STIX]{x1D709}\,B\right)}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\left[\unicode[STIX]{x1D706}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\;\unicode[STIX]{x1D709}/B^{2}\right){\displaystyle \frac{\unicode[STIX]{x2202}\bar{h}_{t}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\right]\end{eqnarray}$$
and uses
 $$\begin{eqnarray}\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}=-{\displaystyle \frac{B_{0}v^{2}(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC})\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}/B\right)}{\unicode[STIX]{x1D6FA}_{0}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}/\unicode[STIX]{x1D709}\,B\right)}}.\end{eqnarray}$$
$$\begin{eqnarray}\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}=-{\displaystyle \frac{B_{0}v^{2}(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC})\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}/B\right)}{\unicode[STIX]{x1D6FA}_{0}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}/\unicode[STIX]{x1D709}\,B\right)}}.\end{eqnarray}$$
This limit is valid when
![]() $\unicode[STIX]{x1D6FF}(v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3})\ll 1$
.
$\unicode[STIX]{x1D6FF}(v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3})\ll 1$
.
As a result of the preceding, we must solve
where we use
To keep
![]() $\unicode[STIX]{x2202}\bar{h}_{t}/\unicode[STIX]{x2202}\unicode[STIX]{x1D706}$
well behaved in the deeply trapped limit, the constant of integration must vanish. This also avoids a jump at the trapped–passing boundary where we make
$\unicode[STIX]{x2202}\bar{h}_{t}/\unicode[STIX]{x2202}\unicode[STIX]{x1D706}$
well behaved in the deeply trapped limit, the constant of integration must vanish. This also avoids a jump at the trapped–passing boundary where we make
![]() $\bar{h}_{t}=0$
to match
$\bar{h}_{t}=0$
to match
![]() $\bar{h}_{p}=0$
for the passing that must satisfy
$\bar{h}_{p}=0$
for the passing that must satisfy
![]() $\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}=0$
. Integrating once gives
$\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}=0$
. Integrating once gives
Integrating again from the trapped–passing boundary associated with the maximum ripple magnetic field ![]() (where
(where ![]() ) to
) to
![]() $\unicode[STIX]{x1D706}$
we obtain the pitch angle scattering solution
$\unicode[STIX]{x1D706}$
we obtain the pitch angle scattering solution
 $$\begin{eqnarray}\bar{h}_{t}={\displaystyle \frac{B_{0}\unicode[STIX]{x1D70F}_{s}v^{5}}{3\unicode[STIX]{x1D6FA}_{0}v_{\unicode[STIX]{x1D706}}^{3}}}{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}\int _{B_{0}/\underset{B}{\frown }}^{\unicode[STIX]{x1D706}}\,\text{d}\unicode[STIX]{x1D706}{\displaystyle \frac{(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC})\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}^{3}/B^{2}\right)}{\unicode[STIX]{x1D706}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}/B^{2}\right)}}.\end{eqnarray}$$
$$\begin{eqnarray}\bar{h}_{t}={\displaystyle \frac{B_{0}\unicode[STIX]{x1D70F}_{s}v^{5}}{3\unicode[STIX]{x1D6FA}_{0}v_{\unicode[STIX]{x1D706}}^{3}}}{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}\int _{B_{0}/\underset{B}{\frown }}^{\unicode[STIX]{x1D706}}\,\text{d}\unicode[STIX]{x1D706}{\displaystyle \frac{(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC})\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}^{3}/B^{2}\right)}{\unicode[STIX]{x1D706}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}/B^{2}\right)}}.\end{eqnarray}$$
We will continue to work with this general expression for now, rather than ignoring curvature drift and using (3.16) to find the approximate results
and
These approximate results if used here give a slight difference with a final result smaller by a factor 3/4. The approximate results of (7.8) and (7.9) follow the procedure of Stringer (Reference Stringer1972) and Connor & Hastie (Reference Connor and Hastie1973) that take advantage of the slow variation of
![]() $\unicode[STIX]{x1D717}$
while
$\unicode[STIX]{x1D717}$
while
![]() $\unicode[STIX]{x1D701}$
varies between its two values at the lower of the magnetic field maximums
$\unicode[STIX]{x1D701}$
varies between its two values at the lower of the magnetic field maximums ![]() for fixed
for fixed
![]() $\unicode[STIX]{x1D6FC}$
. Their procedure notes that
$\unicode[STIX]{x1D6FC}$
. Their procedure notes that
![]() $-\unicode[STIX]{x03C0}<N\unicode[STIX]{x1D701}<\unicode[STIX]{x03C0}$
implies
$-\unicode[STIX]{x03C0}<N\unicode[STIX]{x1D701}<\unicode[STIX]{x03C0}$
implies
![]() $-\unicode[STIX]{x03C0}/Nq<\unicode[STIX]{x1D717}+(\unicode[STIX]{x1D6FC}/q)<\unicode[STIX]{x03C0}/Nq$
so that
$-\unicode[STIX]{x03C0}/Nq<\unicode[STIX]{x1D717}+(\unicode[STIX]{x1D6FC}/q)<\unicode[STIX]{x03C0}/Nq$
so that
![]() $\unicode[STIX]{x1D717}$
varies very little along a ripple trapped orbit at fixed
$\unicode[STIX]{x1D717}$
varies very little along a ripple trapped orbit at fixed
![]() $\unicode[STIX]{x1D6FC}$
for
$\unicode[STIX]{x1D6FC}$
for
![]() $N\gg 1$
. It will be used shortly to simplify (7.20).
$N\gg 1$
. It will be used shortly to simplify (7.20).
The alpha particle (
![]() $d=0$
) and heat (
$d=0$
) and heat (
![]() $d=1$
) ripple fluxes are calculated from
$d=1$
) ripple fluxes are calculated from
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{d}^{\text{rip}} & = & \displaystyle \left\langle \int \,\text{d}^{3}v(Mv^{2}/2)^{d}\bar{h}_{t}\boldsymbol{v}_{m}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}\right\rangle \nonumber\\ \displaystyle & \simeq & \displaystyle (1/2\unicode[STIX]{x1D6FA}_{0})\left\langle \int \,\text{d}^{3}v(Mv^{2}/2)^{d}v^{2}\unicode[STIX]{x1D706}\bar{h}_{t}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}\times \boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\ell nB\right\rangle ,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{d}^{\text{rip}} & = & \displaystyle \left\langle \int \,\text{d}^{3}v(Mv^{2}/2)^{d}\bar{h}_{t}\boldsymbol{v}_{m}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}\right\rangle \nonumber\\ \displaystyle & \simeq & \displaystyle (1/2\unicode[STIX]{x1D6FA}_{0})\left\langle \int \,\text{d}^{3}v(Mv^{2}/2)^{d}v^{2}\unicode[STIX]{x1D706}\bar{h}_{t}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}\times \boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\ell nB\right\rangle ,\end{eqnarray}$$
where
![]() $\boldsymbol{v}_{m}$
is the magnetic drift and we use
$\boldsymbol{v}_{m}$
is the magnetic drift and we use
![]() $\langle \int \!\text{d}^{3}v\,f_{s}\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}\rangle =\langle \unicode[STIX]{x1D735}\boldsymbol{\cdot }[\unicode[STIX]{x1D6FA}^{-1}\boldsymbol{b}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D713}\int \text{d}^{3}v\,f_{s}v_{\Vert }^{2}]\rangle =0$
. The last form of the ripple flux is obtained by using
$\langle \int \!\text{d}^{3}v\,f_{s}\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}\rangle =\langle \unicode[STIX]{x1D735}\boldsymbol{\cdot }[\unicode[STIX]{x1D6FA}^{-1}\boldsymbol{b}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D713}\int \text{d}^{3}v\,f_{s}v_{\Vert }^{2}]\rangle =0$
. The last form of the ripple flux is obtained by using
![]() $v_{\Vert }$
small to ignore the curvature drift compared to the
$v_{\Vert }$
small to ignore the curvature drift compared to the
![]() $\unicode[STIX]{x1D735}B$
drift. The
$\unicode[STIX]{x1D735}B$
drift. The
![]() $\,\boldsymbol{E}\times \boldsymbol{B}$
drift does not enter even though it has been implicitly retained.
$\,\boldsymbol{E}\times \boldsymbol{B}$
drift does not enter even though it has been implicitly retained.
Using the Boozer representation for the field
and
where we sum over both signs of
![]() $\unicode[STIX]{x1D70E}$
, yields
$\unicode[STIX]{x1D70E}$
, yields
To evaluate the fluxes we use
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D709}/\unicode[STIX]{x2202}\unicode[STIX]{x1D706}=-B/2\unicode[STIX]{x1D709}B_{0}$
to integrate by parts to find
$\unicode[STIX]{x2202}\unicode[STIX]{x1D709}/\unicode[STIX]{x2202}\unicode[STIX]{x1D706}=-B/2\unicode[STIX]{x1D709}B_{0}$
to integrate by parts to find
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{B_{0}/\underset{B}{\frown }}^{B_{0}/B}\text{d}\unicode[STIX]{x1D706}{\displaystyle \frac{\unicode[STIX]{x1D706}}{\unicode[STIX]{x1D709}}}\left[\int _{B_{0}/\underset{B}{\frown }}^{\unicode[STIX]{x1D706}}\,\text{d}\unicode[STIX]{x1D706}{\displaystyle \frac{(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC})\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}^{3}/B^{2}\right)}{\unicode[STIX]{x1D706}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}/B^{2}\right)}}\right]\nonumber\\ \displaystyle & & \displaystyle \quad ={\displaystyle \frac{2B_{0}}{B}}\int _{B_{0}/\underset{B}{\frown }}^{B_{0}/B}\,\text{d}\unicode[STIX]{x1D706}\,\unicode[STIX]{x1D709}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\left[\unicode[STIX]{x1D706}\int _{B_{0}/\underset{B}{\frown }}^{\unicode[STIX]{x1D706}}\,\text{d}\unicode[STIX]{x1D706}{\displaystyle \frac{(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC})\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}^{3}/B^{2}\right)}{\unicode[STIX]{x1D706}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}/B^{2}\right)}}\right]\nonumber\\ \displaystyle & & \displaystyle \quad ={\displaystyle \frac{2B_{0}}{B}}\int _{B_{0}/\underset{B}{\frown }}^{B_{0}/B}\text{d}\unicode[STIX]{x1D706}\,\unicode[STIX]{x1D709}\left[\int _{B_{0}/\underset{B}{\frown }}^{\unicode[STIX]{x1D706}}\,\text{d}\unicode[STIX]{x1D706}{\displaystyle \frac{(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC})\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}^{3}/B^{2}\right)}{\unicode[STIX]{x1D706}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}/B^{2}\right)}}\right]\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\left[{\displaystyle \frac{(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC})\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}^{3}/B^{2}\right)}{\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}/B^{2}\right)}}\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{B_{0}/\underset{B}{\frown }}^{B_{0}/B}\text{d}\unicode[STIX]{x1D706}{\displaystyle \frac{\unicode[STIX]{x1D706}}{\unicode[STIX]{x1D709}}}\left[\int _{B_{0}/\underset{B}{\frown }}^{\unicode[STIX]{x1D706}}\,\text{d}\unicode[STIX]{x1D706}{\displaystyle \frac{(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC})\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}^{3}/B^{2}\right)}{\unicode[STIX]{x1D706}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}/B^{2}\right)}}\right]\nonumber\\ \displaystyle & & \displaystyle \quad ={\displaystyle \frac{2B_{0}}{B}}\int _{B_{0}/\underset{B}{\frown }}^{B_{0}/B}\,\text{d}\unicode[STIX]{x1D706}\,\unicode[STIX]{x1D709}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\left[\unicode[STIX]{x1D706}\int _{B_{0}/\underset{B}{\frown }}^{\unicode[STIX]{x1D706}}\,\text{d}\unicode[STIX]{x1D706}{\displaystyle \frac{(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC})\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}^{3}/B^{2}\right)}{\unicode[STIX]{x1D706}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}/B^{2}\right)}}\right]\nonumber\\ \displaystyle & & \displaystyle \quad ={\displaystyle \frac{2B_{0}}{B}}\int _{B_{0}/\underset{B}{\frown }}^{B_{0}/B}\text{d}\unicode[STIX]{x1D706}\,\unicode[STIX]{x1D709}\left[\int _{B_{0}/\underset{B}{\frown }}^{\unicode[STIX]{x1D706}}\,\text{d}\unicode[STIX]{x1D706}{\displaystyle \frac{(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC})\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}^{3}/B^{2}\right)}{\unicode[STIX]{x1D706}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}/B^{2}\right)}}\right]\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\left[{\displaystyle \frac{(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC})\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}^{3}/B^{2}\right)}{\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}/B^{2}\right)}}\right].\end{eqnarray}$$
Integrating the first term on the right side by parts again using
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D709}^{3}/\unicode[STIX]{x2202}\unicode[STIX]{x1D706}=-3B\unicode[STIX]{x1D709}/2B_{0}$
yields
$\unicode[STIX]{x2202}\unicode[STIX]{x1D709}^{3}/\unicode[STIX]{x2202}\unicode[STIX]{x1D706}=-3B\unicode[STIX]{x1D709}/2B_{0}$
yields
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{B_{0}/\underset{B}{\frown }}^{B_{0}/B}\,\text{d}\unicode[STIX]{x1D706}{\displaystyle \frac{\unicode[STIX]{x1D706}}{\unicode[STIX]{x1D709}}}\left[\int _{B_{0}/\underset{B}{\frown }}^{\unicode[STIX]{x1D706}}\,\text{d}\unicode[STIX]{x1D706}{\displaystyle \frac{(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC})\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}^{3}/B^{2}\right)}{\unicode[STIX]{x1D706}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}/B^{2}\right)}}\right]\nonumber\\ \displaystyle & & \displaystyle \quad ={\displaystyle \frac{2B_{0}}{B}}\int _{B_{0}/\underset{B}{\frown }}^{B_{0}/B}\,\text{d}\unicode[STIX]{x1D706}\,\unicode[STIX]{x1D709}\,\left(1+{\displaystyle \frac{2B_{0}\unicode[STIX]{x1D709}^{2}}{3\unicode[STIX]{x1D706}B}}\right){\displaystyle \frac{(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC})\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}^{3}/B^{2}\right)}{\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}/B^{2}\right)}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{B_{0}/\underset{B}{\frown }}^{B_{0}/B}\,\text{d}\unicode[STIX]{x1D706}{\displaystyle \frac{\unicode[STIX]{x1D706}}{\unicode[STIX]{x1D709}}}\left[\int _{B_{0}/\underset{B}{\frown }}^{\unicode[STIX]{x1D706}}\,\text{d}\unicode[STIX]{x1D706}{\displaystyle \frac{(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC})\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}^{3}/B^{2}\right)}{\unicode[STIX]{x1D706}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}/B^{2}\right)}}\right]\nonumber\\ \displaystyle & & \displaystyle \quad ={\displaystyle \frac{2B_{0}}{B}}\int _{B_{0}/\underset{B}{\frown }}^{B_{0}/B}\,\text{d}\unicode[STIX]{x1D706}\,\unicode[STIX]{x1D709}\,\left(1+{\displaystyle \frac{2B_{0}\unicode[STIX]{x1D709}^{2}}{3\unicode[STIX]{x1D706}B}}\right){\displaystyle \frac{(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC})\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}^{3}/B^{2}\right)}{\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}/B^{2}\right)}}.\end{eqnarray}$$
Neglecting curvature drift and other
![]() $\unicode[STIX]{x1D709}^{2}$
terms compared to order unity terms and assuming
$\unicode[STIX]{x1D709}^{2}$
terms compared to order unity terms and assuming
![]() $(\oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}\unicode[STIX]{x2202}B/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC})/(\oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709})$
is a slow function of
$(\oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}\unicode[STIX]{x2202}B/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC})/(\oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709})$
is a slow function of
![]() $\unicode[STIX]{x1D706}$
, we integrate by parts one final time to obtain
$\unicode[STIX]{x1D706}$
, we integrate by parts one final time to obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{B_{0}/\underset{B}{\frown }}^{B_{0}/B}\,\text{d}\unicode[STIX]{x1D706}{\displaystyle \frac{\unicode[STIX]{x1D706}}{\unicode[STIX]{x1D709}}}\left[\int _{B_{0}/\underset{B}{\frown }}^{\unicode[STIX]{x1D706}}\,\text{d}\unicode[STIX]{x1D706}{\displaystyle \frac{(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC})\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}^{3}/B^{2}\right)}{\unicode[STIX]{x1D706}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}/B^{2}\right)}}\right]\simeq {\displaystyle \frac{4B_{0}^{2}}{3B^{2}}}\underset{\unicode[STIX]{x1D709}}{\frown }^{3}{\displaystyle \frac{(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC})\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\underset{\unicode[STIX]{x1D709}}{\frown }^{3}\right)}{\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\underset{\unicode[STIX]{x1D709}}{\frown }\right)}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\cdots \simeq -2\underset{\unicode[STIX]{x1D709}}{\frown }^{3}{\displaystyle \frac{\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\underset{\unicode[STIX]{x1D709}}{\frown }\unicode[STIX]{x2202}B/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}|_{\unicode[STIX]{x1D701}}\right)}{\underset{B}{\frown }\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\underset{\unicode[STIX]{x1D709}}{\frown }\right)}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{B_{0}/\underset{B}{\frown }}^{B_{0}/B}\,\text{d}\unicode[STIX]{x1D706}{\displaystyle \frac{\unicode[STIX]{x1D706}}{\unicode[STIX]{x1D709}}}\left[\int _{B_{0}/\underset{B}{\frown }}^{\unicode[STIX]{x1D706}}\,\text{d}\unicode[STIX]{x1D706}{\displaystyle \frac{(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC})\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}^{3}/B^{2}\right)}{\unicode[STIX]{x1D706}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}/B^{2}\right)}}\right]\simeq {\displaystyle \frac{4B_{0}^{2}}{3B^{2}}}\underset{\unicode[STIX]{x1D709}}{\frown }^{3}{\displaystyle \frac{(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC})\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\underset{\unicode[STIX]{x1D709}}{\frown }^{3}\right)}{\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\underset{\unicode[STIX]{x1D709}}{\frown }\right)}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\cdots \simeq -2\underset{\unicode[STIX]{x1D709}}{\frown }^{3}{\displaystyle \frac{\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\underset{\unicode[STIX]{x1D709}}{\frown }\unicode[STIX]{x2202}B/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}|_{\unicode[STIX]{x1D701}}\right)}{\underset{B}{\frown }\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\underset{\unicode[STIX]{x1D709}}{\frown }\right)}},\end{eqnarray}$$
with ![]() . Inserting the preceding, noticing
. Inserting the preceding, noticing
![]() $G/I\simeq rB_{p}/RB_{t}\simeq \unicode[STIX]{x1D700}^{2}/q$
, and using
$G/I\simeq rB_{p}/RB_{t}\simeq \unicode[STIX]{x1D700}^{2}/q$
, and using
![]() $\unicode[STIX]{x2202}(B/B_{0})/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}\simeq \unicode[STIX]{x1D700}\sin \unicode[STIX]{x1D703}$
and
$\unicode[STIX]{x2202}(B/B_{0})/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}\simeq \unicode[STIX]{x1D700}\sin \unicode[STIX]{x1D703}$
and
![]() $\unicode[STIX]{x2202}(B/B_{0})/\unicode[STIX]{x2202}\unicode[STIX]{x1D701}\simeq N\unicode[STIX]{x1D6FF}\sin (N\unicode[STIX]{x1D701})$
, gives the ripple driven radial particle (
$\unicode[STIX]{x2202}(B/B_{0})/\unicode[STIX]{x2202}\unicode[STIX]{x1D701}\simeq N\unicode[STIX]{x1D6FF}\sin (N\unicode[STIX]{x1D701})$
, gives the ripple driven radial particle (
![]() $d=0$
) and heat (
$d=0$
) and heat (
![]() $d=1$
) fluxes associated with pitch angle scattering to be
$d=1$
) fluxes associated with pitch angle scattering to be
 $$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{d}^{\text{pas}}\simeq -{\displaystyle \frac{2\unicode[STIX]{x03C0}B_{0}^{2}\unicode[STIX]{x1D700}\unicode[STIX]{x1D70F}_{s}}{3\unicode[STIX]{x1D6FA}_{0}^{2}qv_{\unicode[STIX]{x1D706}}^{3}}}\left(\int _{0}^{v_{0}}\text{d}v\,v^{9}\left({\displaystyle \frac{Mv^{2}}{2}}\right)^{d}{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}\right)\left\langle \sin \unicode[STIX]{x1D717}\underset{\unicode[STIX]{x1D709}}{\frown }^{3}{\displaystyle \frac{\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\underset{\unicode[STIX]{x1D709}}{\frown }\unicode[STIX]{x2202}B/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}|_{\unicode[STIX]{x1D701}}\right)}{\underset{B}{\frown }\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\underset{\unicode[STIX]{x1D709}}{\frown }\right)}}\right\rangle .\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{d}^{\text{pas}}\simeq -{\displaystyle \frac{2\unicode[STIX]{x03C0}B_{0}^{2}\unicode[STIX]{x1D700}\unicode[STIX]{x1D70F}_{s}}{3\unicode[STIX]{x1D6FA}_{0}^{2}qv_{\unicode[STIX]{x1D706}}^{3}}}\left(\int _{0}^{v_{0}}\text{d}v\,v^{9}\left({\displaystyle \frac{Mv^{2}}{2}}\right)^{d}{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}\right)\left\langle \sin \unicode[STIX]{x1D717}\underset{\unicode[STIX]{x1D709}}{\frown }^{3}{\displaystyle \frac{\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\underset{\unicode[STIX]{x1D709}}{\frown }\unicode[STIX]{x2202}B/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}|_{\unicode[STIX]{x1D701}}\right)}{\underset{B}{\frown }\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\underset{\unicode[STIX]{x1D709}}{\frown }\right)}}\right\rangle .\end{eqnarray}$$
Using
![]() $v_{0}\gg v_{c}$
to integrate we find
$v_{0}\gg v_{c}$
to integrate we find
 $$\begin{eqnarray}\displaystyle \int _{0}^{v_{0}}\text{d}v\,v^{9}\left({\displaystyle \frac{Mv^{2}}{2}}\right)^{d}{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}} & \simeq & \displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}\left({\displaystyle \frac{S\unicode[STIX]{x1D70F}_{s}}{4\unicode[STIX]{x03C0}}}\right)\int _{0}^{v_{0}}\text{d}v\,v^{6}\left({\displaystyle \frac{Mv^{2}}{2}}\right)^{d}\nonumber\\ \displaystyle & = & \displaystyle {\displaystyle \frac{(Mv_{0}^{2}/2)^{d}v_{o}^{7}}{4\unicode[STIX]{x03C0}(7+2d)}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}\left[{\displaystyle \frac{n_{s}}{\ell n(v_{0}/v_{c})}}\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{0}^{v_{0}}\text{d}v\,v^{9}\left({\displaystyle \frac{Mv^{2}}{2}}\right)^{d}{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}} & \simeq & \displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}\left({\displaystyle \frac{S\unicode[STIX]{x1D70F}_{s}}{4\unicode[STIX]{x03C0}}}\right)\int _{0}^{v_{0}}\text{d}v\,v^{6}\left({\displaystyle \frac{Mv^{2}}{2}}\right)^{d}\nonumber\\ \displaystyle & = & \displaystyle {\displaystyle \frac{(Mv_{0}^{2}/2)^{d}v_{o}^{7}}{4\unicode[STIX]{x03C0}(7+2d)}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}\left[{\displaystyle \frac{n_{s}}{\ell n(v_{0}/v_{c})}}\right].\end{eqnarray}$$
Assuming
we obtain our most general form for the
![]() $1/\unicode[STIX]{x1D708}$
fluxes due to pitch angle scattering to be
$1/\unicode[STIX]{x1D708}$
fluxes due to pitch angle scattering to be
 $$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{d}^{\text{pas}}\simeq -{\displaystyle \frac{(Mv_{0}^{2}/2)^{d}\unicode[STIX]{x1D700}^{2}B_{0}^{2}\unicode[STIX]{x1D70F}_{s}v_{0}^{7}(\unicode[STIX]{x2202}n_{s}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713})}{6(7+2d)q^{2}\unicode[STIX]{x1D6FA}_{0}^{2}v_{\unicode[STIX]{x1D706}}^{3}\ell n(v_{0}/v_{c})}}\left\langle \sin \unicode[STIX]{x1D717}\,\underset{\unicode[STIX]{x1D709}}{\frown }^{3}{\displaystyle \frac{\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\underset{\unicode[STIX]{x1D709}}{\frown }\unicode[STIX]{x2202}B/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}|_{\unicode[STIX]{x1D701}}\right)}{(\unicode[STIX]{x1D700}B_{0}/q)\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\underset{\unicode[STIX]{x1D709}}{\frown }\right)}}\right\rangle .\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{d}^{\text{pas}}\simeq -{\displaystyle \frac{(Mv_{0}^{2}/2)^{d}\unicode[STIX]{x1D700}^{2}B_{0}^{2}\unicode[STIX]{x1D70F}_{s}v_{0}^{7}(\unicode[STIX]{x2202}n_{s}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713})}{6(7+2d)q^{2}\unicode[STIX]{x1D6FA}_{0}^{2}v_{\unicode[STIX]{x1D706}}^{3}\ell n(v_{0}/v_{c})}}\left\langle \sin \unicode[STIX]{x1D717}\,\underset{\unicode[STIX]{x1D709}}{\frown }^{3}{\displaystyle \frac{\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\underset{\unicode[STIX]{x1D709}}{\frown }\unicode[STIX]{x2202}B/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}|_{\unicode[STIX]{x1D701}}\right)}{(\unicode[STIX]{x1D700}B_{0}/q)\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\underset{\unicode[STIX]{x1D709}}{\frown }\right)}}\right\rangle .\end{eqnarray}$$
To simplify we now use approximation (7.8) and assume the poloidal variation of
![]() $\unicode[STIX]{x2202}B/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}$
is slow so we can use
$\unicode[STIX]{x2202}B/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}$
is slow so we can use
![]() $\sin (\unicode[STIX]{x1D717}-q^{-1}\unicode[STIX]{x1D701})\simeq \sin \unicode[STIX]{x1D717}$
. The details are presented in the appendix A and yield
$\sin (\unicode[STIX]{x1D717}-q^{-1}\unicode[STIX]{x1D701})\simeq \sin \unicode[STIX]{x1D717}$
. The details are presented in the appendix A and yield
 $$\begin{eqnarray}\displaystyle \left\langle \sin ^{2}\unicode[STIX]{x1D717}\sqrt{[1-(B/\underset{B}{\frown })]^{3}}\right\rangle & = & \displaystyle {\displaystyle \frac{1}{4\unicode[STIX]{x03C0}^{2}}}\int _{\text{all}}\,\text{d}\unicode[STIX]{x1D717}\sin ^{2}\unicode[STIX]{x1D703}\int _{\text{all}}\text{d}(N\unicode[STIX]{x1D701})\sqrt{[1-(B/\underset{B}{\frown })]^{3}}\qquad \nonumber\\ \displaystyle & \equiv & \displaystyle {\displaystyle \frac{4\sqrt{2}}{3\unicode[STIX]{x03C0}}}\unicode[STIX]{x1D6FF}^{3/2}W(\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left\langle \sin ^{2}\unicode[STIX]{x1D717}\sqrt{[1-(B/\underset{B}{\frown })]^{3}}\right\rangle & = & \displaystyle {\displaystyle \frac{1}{4\unicode[STIX]{x03C0}^{2}}}\int _{\text{all}}\,\text{d}\unicode[STIX]{x1D717}\sin ^{2}\unicode[STIX]{x1D703}\int _{\text{all}}\text{d}(N\unicode[STIX]{x1D701})\sqrt{[1-(B/\underset{B}{\frown })]^{3}}\qquad \nonumber\\ \displaystyle & \equiv & \displaystyle {\displaystyle \frac{4\sqrt{2}}{3\unicode[STIX]{x03C0}}}\unicode[STIX]{x1D6FF}^{3/2}W(\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF}),\end{eqnarray}$$
with the ripple scattering coefficient defined as a function of a single parameter by
 $$\begin{eqnarray}\displaystyle & & \displaystyle W(\unicode[STIX]{x1D6FE})={\displaystyle \frac{3}{16\unicode[STIX]{x03C0}\sqrt{2}\,\unicode[STIX]{x1D6FE}^{2}}}\int _{0}^{U}{\displaystyle \frac{\text{d}X\cos X\sin ^{2}X}{\sqrt{\unicode[STIX]{x1D6FE}^{2}-\sin ^{2}X}}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\int _{X}^{Y_{1}(X)}\text{d}Y[\cos X-\cos Y+(X-Y)\sin X]^{3/2}\rightarrow \;\;\left\{\begin{array}{@{}ll@{}}1-3\unicode[STIX]{x1D6FE} & \unicode[STIX]{x1D6FE}\ll 1\\ 0.02/\unicode[STIX]{x1D6FE}^{3} & \unicode[STIX]{x1D6FE}\gg 1.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle W(\unicode[STIX]{x1D6FE})={\displaystyle \frac{3}{16\unicode[STIX]{x03C0}\sqrt{2}\,\unicode[STIX]{x1D6FE}^{2}}}\int _{0}^{U}{\displaystyle \frac{\text{d}X\cos X\sin ^{2}X}{\sqrt{\unicode[STIX]{x1D6FE}^{2}-\sin ^{2}X}}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\int _{X}^{Y_{1}(X)}\text{d}Y[\cos X-\cos Y+(X-Y)\sin X]^{3/2}\rightarrow \;\;\left\{\begin{array}{@{}ll@{}}1-3\unicode[STIX]{x1D6FE} & \unicode[STIX]{x1D6FE}\ll 1\\ 0.02/\unicode[STIX]{x1D6FE}^{3} & \unicode[STIX]{x1D6FE}\gg 1.\end{array}\right.\end{eqnarray}$$
The upper limit
![]() $U$
of the
$U$
of the
![]() $X$
integral is
$X$
integral is
![]() $\unicode[STIX]{x03C0}/2$
when
$\unicode[STIX]{x03C0}/2$
when
![]() $\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF}>1$
, while for
$\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF}>1$
, while for
![]() $\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF}<1$
it is
$\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF}<1$
it is
![]() $\sin ^{-1}(\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF})$
. The upper limit of the
$\sin ^{-1}(\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF})$
. The upper limit of the
![]() $Y$
integral is the zero of
$Y$
integral is the zero of
![]() $\cos X-\cos Y_{1}+(X-Y_{1})\sin X=0$
adjacent to
$\cos X-\cos Y_{1}+(X-Y_{1})\sin X=0$
adjacent to
![]() $Y=X$
. This monotonically decreasing function is plotted as
$Y=X$
. This monotonically decreasing function is plotted as
![]() $G$
in figure 1 in Connor & Hastie (Reference Connor and Hastie1973), where it is compared to the similar, but somewhat less accurate result of Stringer (Reference Stringer1972). Only accessible values of
$G$
in figure 1 in Connor & Hastie (Reference Connor and Hastie1973), where it is compared to the similar, but somewhat less accurate result of Stringer (Reference Stringer1972). Only accessible values of
![]() $\unicode[STIX]{x1D717}$
and
$\unicode[STIX]{x1D717}$
and
![]() $\unicode[STIX]{x1D701}$
are to be integrated over in the flux surface average. In particular,
$\unicode[STIX]{x1D701}$
are to be integrated over in the flux surface average. In particular, ![]() are not accessible bythe ripple trapped so
are not accessible bythe ripple trapped so ![]() is the value of
is the value of
![]() $\unicode[STIX]{x1D701}$
for which
$\unicode[STIX]{x1D701}$
for which ![]() . For weak ripple,
. For weak ripple,
![]() $\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF}>1$
, some values of
$\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF}>1$
, some values of
![]() $\unicode[STIX]{x1D717}$
will not be accessible by the ripple trapped. The relevant details of the Stringer (Reference Stringer1972) and Connor & Hastie (Reference Connor and Hastie1973) treatments are given in appendix A.
$\unicode[STIX]{x1D717}$
will not be accessible by the ripple trapped. The relevant details of the Stringer (Reference Stringer1972) and Connor & Hastie (Reference Connor and Hastie1973) treatments are given in appendix A.
Using the preceding we obtain
yielding an alpha particle diffusivity due to pitch angle scattering of
with
![]() $W(\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF})\leqslant 1$
. The preceding is in agreement with our phenomenological estimate when
$W(\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF})\leqslant 1$
. The preceding is in agreement with our phenomenological estimate when
![]() $W/\ell n(v_{0}/v_{c})\sim 1$
, but with a rather small coefficient that seems to be due to the slowing down distribution based on (7.18).
$W/\ell n(v_{0}/v_{c})\sim 1$
, but with a rather small coefficient that seems to be due to the slowing down distribution based on (7.18).
The weak ripple limit reduces
![]() $D_{0}^{\text{pas}}$
by order
$D_{0}^{\text{pas}}$
by order
![]() $(qN\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D700})^{3}\ll 1$
. In this limit, when
$(qN\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D700})^{3}\ll 1$
. In this limit, when
![]() $(\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D700})^{5/8}\sim 1/qN$
,
$(\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D700})^{5/8}\sim 1/qN$
,
![]() $D_{0}^{\text{pas}}$
becomes comparable to the result of Linsker & Boozer (Reference Linsker and Boozer1982) who find a diffusivity of roughly
$D_{0}^{\text{pas}}$
becomes comparable to the result of Linsker & Boozer (Reference Linsker and Boozer1982) who find a diffusivity of roughly
![]() $(\unicode[STIX]{x1D6FF}^{2}/\unicode[STIX]{x1D700}^{1/2}qN)(\unicode[STIX]{x1D70F}_{s}v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3})(\unicode[STIX]{x1D70C}_{0}v_{0}/R)^{2}$
due to the effect of very weak ripple on the turning points (at
$(\unicode[STIX]{x1D6FF}^{2}/\unicode[STIX]{x1D700}^{1/2}qN)(\unicode[STIX]{x1D70F}_{s}v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3})(\unicode[STIX]{x1D70C}_{0}v_{0}/R)^{2}$
due to the effect of very weak ripple on the turning points (at
![]() $\unicode[STIX]{x1D717}\simeq \pm \unicode[STIX]{x03C0}$
) of the non-ripple trapped banana regime alphas in the nearly axisymmetric limit (also see Davidson (Reference Davidson1976) and Tsang (Reference Tsang1977)). By assuming
$\unicode[STIX]{x1D717}\simeq \pm \unicode[STIX]{x03C0}$
) of the non-ripple trapped banana regime alphas in the nearly axisymmetric limit (also see Davidson (Reference Davidson1976) and Tsang (Reference Tsang1977)). By assuming
![]() $\unicode[STIX]{x1D700}N\unicode[STIX]{x1D6FF}/q\ll 1$
, that is,
$\unicode[STIX]{x1D700}N\unicode[STIX]{x1D6FF}/q\ll 1$
, that is,
![]() $I\unicode[STIX]{x2202}B/\unicode[STIX]{x2202}\unicode[STIX]{x1D717}\gg G\unicode[STIX]{x2202}B/\unicode[STIX]{x2202}\unicode[STIX]{x1D701}$
, we are ignoring the radial drift effect evaluated by Davidson (Reference Davidson1976), Tsang (Reference Tsang1977), and Linsker & Boozer (Reference Linsker and Boozer1982). This radial drift is of order
$I\unicode[STIX]{x2202}B/\unicode[STIX]{x2202}\unicode[STIX]{x1D717}\gg G\unicode[STIX]{x2202}B/\unicode[STIX]{x2202}\unicode[STIX]{x1D701}$
, we are ignoring the radial drift effect evaluated by Davidson (Reference Davidson1976), Tsang (Reference Tsang1977), and Linsker & Boozer (Reference Linsker and Boozer1982). This radial drift is of order
![]() $\unicode[STIX]{x1D6FF}Na\unicode[STIX]{x1D70C}_{0}v_{0}/qR^{2}$
and appears to be negligible unless
$\unicode[STIX]{x1D6FF}Na\unicode[STIX]{x1D70C}_{0}v_{0}/qR^{2}$
and appears to be negligible unless
![]() $(\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D700})^{5/8}<1/qN$
. Stochastic effects due to ripple may play a role at low collisionalities and were considered by Goldston, White & Boozer (Reference Goldston, White and Boozer1981).
$(\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D700})^{5/8}<1/qN$
. Stochastic effects due to ripple may play a role at low collisionalities and were considered by Goldston, White & Boozer (Reference Goldston, White and Boozer1981).
The ripple departure from axisymmetry means that ambipolarity,
is no longer intrinsic. However, the alpha density
![]() $n_{s}$
is so small they may be treated as a trace population. Consequently, the radial electric field adjusts the ion and electron particle transport to maintain ambipolarity as discussed for a plasma without alphas by Galeev et al. (Reference Galeev, Sagdeev, Furth and Rosenbluth1969).
$n_{s}$
is so small they may be treated as a trace population. Consequently, the radial electric field adjusts the ion and electron particle transport to maintain ambipolarity as discussed for a plasma without alphas by Galeev et al. (Reference Galeev, Sagdeev, Furth and Rosenbluth1969).
7.2 Electron drag dominates:
 $\unicode[STIX]{x1D6FF}(v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3})\gg 1$
$\unicode[STIX]{x1D6FF}(v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3})\gg 1$
To make the electron drag estimate we ignore pitch angle scatter and ion drag by keeping only
In this limit
![]() $\unicode[STIX]{x1D6FF}(v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3})\gg 1$
and we must solve
$\unicode[STIX]{x1D6FF}(v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3})\gg 1$
and we must solve
 $$\begin{eqnarray}{\displaystyle \frac{1}{\unicode[STIX]{x1D70F}_{s}v^{2}}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}v}}(v^{3}\bar{h}_{t})=\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}=-{\displaystyle \frac{B_{0}v^{2}(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC})\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}/B\right)}{\unicode[STIX]{x1D6FA}_{0}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}/\unicode[STIX]{x1D709}\,B\right)}}{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}.\end{eqnarray}$$
$$\begin{eqnarray}{\displaystyle \frac{1}{\unicode[STIX]{x1D70F}_{s}v^{2}}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}v}}(v^{3}\bar{h}_{t})=\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}=-{\displaystyle \frac{B_{0}v^{2}(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC})\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}/B\right)}{\unicode[STIX]{x1D6FA}_{0}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}/\unicode[STIX]{x1D709}\,B\right)}}{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}.\end{eqnarray}$$
By performing the bounce averages in
![]() $\unicode[STIX]{x1D701}$
at fixed
$\unicode[STIX]{x1D701}$
at fixed
![]() $\unicode[STIX]{x1D6FC}$
we will again be able to take advantage of the slow variation
$\unicode[STIX]{x1D6FC}$
we will again be able to take advantage of the slow variation
![]() $\unicode[STIX]{x1D703}$
of while
$\unicode[STIX]{x1D703}$
of while
![]() $\unicode[STIX]{x1D701}$
varies between its two values at the lower of the magnetic field maxima. Again, the
$\unicode[STIX]{x1D701}$
varies between its two values at the lower of the magnetic field maxima. Again, the
![]() $\,\boldsymbol{E}\times \boldsymbol{B}$
does not enter even though it is implicitly retained.
$\,\boldsymbol{E}\times \boldsymbol{B}$
does not enter even though it is implicitly retained.
When solving for
![]() $\bar{h}_{t}$
we must avoid a step at
$\bar{h}_{t}$
we must avoid a step at
![]() $v_{0}$
. Consequently, we integrate from
$v_{0}$
. Consequently, we integrate from
![]() $v$
to
$v$
to
![]() $v_{0}$
, where
$v_{0}$
, where
![]() $\bar{h}_{t}(v>v_{0})=0$
, to find the piecewise continuous electron drag solution
$\bar{h}_{t}(v>v_{0})=0$
, to find the piecewise continuous electron drag solution
 $$\begin{eqnarray}\bar{h}_{t}={\displaystyle \frac{B_{0}\unicode[STIX]{x1D70F}_{s}(v_{0}^{2}-v^{2})}{2\unicode[STIX]{x1D6FA}_{0}\;\;}}{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}{\displaystyle \frac{(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC})\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}/B\right)}{\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}/\unicode[STIX]{x1D709}\,B\right)}}\{H[\unicode[STIX]{x1D706}-(B_{0}/\underset{B}{\frown })]-H[\unicode[STIX]{x1D706}-(B_{0}/B)]\},\end{eqnarray}$$
$$\begin{eqnarray}\bar{h}_{t}={\displaystyle \frac{B_{0}\unicode[STIX]{x1D70F}_{s}(v_{0}^{2}-v^{2})}{2\unicode[STIX]{x1D6FA}_{0}\;\;}}{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}{\displaystyle \frac{(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC})\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}/B\right)}{\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}/\unicode[STIX]{x1D709}\,B\right)}}\{H[\unicode[STIX]{x1D706}-(B_{0}/\underset{B}{\frown })]-H[\unicode[STIX]{x1D706}-(B_{0}/B)]\},\end{eqnarray}$$
where we insert Heaviside step functions as a reminder that the trapped must satisfy ![]() . In this case the radial alpha flux occurs because electron drag acts to reduce flux surface departure of the larger (smaller) number of alphas inside (outside) the flux surface. The result is outward particle and heat fluxes. The boundary layer about
. In this case the radial alpha flux occurs because electron drag acts to reduce flux surface departure of the larger (smaller) number of alphas inside (outside) the flux surface. The result is outward particle and heat fluxes. The boundary layer about ![]() is not expected to appreciably change this result. A non-trivial boundary layer analysis is required to make
is not expected to appreciably change this result. A non-trivial boundary layer analysis is required to make ![]() and will be discussed in the next subsection. The procedure is more involved than one used in a later section since a separable solution of the homogeneous equation that vanishes above the birth speed does not exist.
and will be discussed in the next subsection. The procedure is more involved than one used in a later section since a separable solution of the homogeneous equation that vanishes above the birth speed does not exist.
Neglecting curvature drift corrections by taking
![]() $\,\unicode[STIX]{x1D709}^{2}\ll 1$
, and assuming slow poloidal variation of
$\,\unicode[STIX]{x1D709}^{2}\ll 1$
, and assuming slow poloidal variation of
![]() $\unicode[STIX]{x2202}B/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}$
so we can use (7.9), gives
$\unicode[STIX]{x2202}B/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}$
so we can use (7.9), gives
Using
![]() $\sin \unicode[STIX]{x1D717}\sin (\unicode[STIX]{x1D717}-q^{-1}\unicode[STIX]{x1D701})\simeq \sin ^{2}\unicode[STIX]{x1D717}$
in the flux expression (7.13) gives the electron drag result
$\sin \unicode[STIX]{x1D717}\sin (\unicode[STIX]{x1D717}-q^{-1}\unicode[STIX]{x1D701})\simeq \sin ^{2}\unicode[STIX]{x1D717}$
in the flux expression (7.13) gives the electron drag result
Then
and
 $$\begin{eqnarray}\displaystyle & & \displaystyle {\displaystyle \frac{B}{B_{0}}}\int _{B_{0}/\underset{B}{\frown }}^{B_{0}/B}\,\text{d}\unicode[STIX]{x1D706}{\displaystyle \frac{\unicode[STIX]{x1D706}^{2}}{\unicode[STIX]{x1D709}}}=-2\int _{B_{0}/\underset{B}{\frown }}^{B_{0}/B}\text{d}\unicode[STIX]{x1D706}\,\unicode[STIX]{x1D706}^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\nonumber\\ \displaystyle & & \displaystyle \quad =2{\displaystyle \frac{B_{0}^{2}}{\underset{B}{\frown }^{2}}}\left\{\sqrt{1-B/\underset{B}{\frown }}+{\displaystyle \frac{2+3B/\underset{B}{\frown }}{15}}\sqrt{(1-B/\underset{B}{\frown }^{3})}\right\}\simeq 2\sqrt{1-B/\underset{B}{\frown }}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\displaystyle \frac{B}{B_{0}}}\int _{B_{0}/\underset{B}{\frown }}^{B_{0}/B}\,\text{d}\unicode[STIX]{x1D706}{\displaystyle \frac{\unicode[STIX]{x1D706}^{2}}{\unicode[STIX]{x1D709}}}=-2\int _{B_{0}/\underset{B}{\frown }}^{B_{0}/B}\text{d}\unicode[STIX]{x1D706}\,\unicode[STIX]{x1D706}^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\nonumber\\ \displaystyle & & \displaystyle \quad =2{\displaystyle \frac{B_{0}^{2}}{\underset{B}{\frown }^{2}}}\left\{\sqrt{1-B/\underset{B}{\frown }}+{\displaystyle \frac{2+3B/\underset{B}{\frown }}{15}}\sqrt{(1-B/\underset{B}{\frown }^{3})}\right\}\simeq 2\sqrt{1-B/\underset{B}{\frown }}\end{eqnarray}$$
give
where
 $$\begin{eqnarray}\displaystyle \left\langle \sin ^{2}\unicode[STIX]{x1D717}\sqrt{[1-(B/\underset{B}{\frown })]}\right\rangle & = & \displaystyle {\displaystyle \frac{1}{4\unicode[STIX]{x03C0}^{2}}}\int _{\text{all}}\,\text{d}\unicode[STIX]{x1D717}\sin ^{2}\unicode[STIX]{x1D703}\int _{\text{all}}\text{d}(N\unicode[STIX]{x1D701})\sqrt{[1-(B/\underset{B}{\frown })]}\nonumber\\ \displaystyle & \equiv & \displaystyle {\displaystyle \frac{4\sqrt{2}}{3\unicode[STIX]{x03C0}}}\unicode[STIX]{x1D6FF}^{1/2}D(\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF})\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left\langle \sin ^{2}\unicode[STIX]{x1D717}\sqrt{[1-(B/\underset{B}{\frown })]}\right\rangle & = & \displaystyle {\displaystyle \frac{1}{4\unicode[STIX]{x03C0}^{2}}}\int _{\text{all}}\,\text{d}\unicode[STIX]{x1D717}\sin ^{2}\unicode[STIX]{x1D703}\int _{\text{all}}\text{d}(N\unicode[STIX]{x1D701})\sqrt{[1-(B/\underset{B}{\frown })]}\nonumber\\ \displaystyle & \equiv & \displaystyle {\displaystyle \frac{4\sqrt{2}}{3\unicode[STIX]{x03C0}}}\unicode[STIX]{x1D6FF}^{1/2}D(\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF})\end{eqnarray}$$
is the drag coefficient derived in appendix A to be
 $$\begin{eqnarray}\displaystyle D\,(\unicode[STIX]{x1D6FE}) & = & \displaystyle {\displaystyle \frac{\sqrt{2}}{\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FE}^{2}}}\int _{0}^{U}{\displaystyle \frac{\text{d}X\cos X\sin ^{2}X}{\sqrt{\unicode[STIX]{x1D6FE}^{2}-\sin ^{2}X}}}\int _{X}^{Y_{0}}\,\text{d}Y[\cos X-\cos Y+(X-Y)\sin X]^{1/2}\nonumber\\ \displaystyle & \rightarrow & \displaystyle \left\{\begin{array}{@{}ll@{}}1-{\displaystyle \frac{\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FE}}{3}}\left[\ell n\left({\displaystyle \frac{2}{\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FE}}}\right)+{\displaystyle \frac{17}{6}}\right] & \unicode[STIX]{x1D6FE}\ll 1\\ O(1/\unicode[STIX]{x1D6FE}^{3}) & \unicode[STIX]{x1D6FE}\gg 1.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle D\,(\unicode[STIX]{x1D6FE}) & = & \displaystyle {\displaystyle \frac{\sqrt{2}}{\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FE}^{2}}}\int _{0}^{U}{\displaystyle \frac{\text{d}X\cos X\sin ^{2}X}{\sqrt{\unicode[STIX]{x1D6FE}^{2}-\sin ^{2}X}}}\int _{X}^{Y_{0}}\,\text{d}Y[\cos X-\cos Y+(X-Y)\sin X]^{1/2}\nonumber\\ \displaystyle & \rightarrow & \displaystyle \left\{\begin{array}{@{}ll@{}}1-{\displaystyle \frac{\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FE}}{3}}\left[\ell n\left({\displaystyle \frac{2}{\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FE}}}\right)+{\displaystyle \frac{17}{6}}\right] & \unicode[STIX]{x1D6FE}\ll 1\\ O(1/\unicode[STIX]{x1D6FE}^{3}) & \unicode[STIX]{x1D6FE}\gg 1.\end{array}\right.\end{eqnarray}$$
Using this result we obtain the flux due to drag to be
giving the alpha particle diffusivity due to drag of
with
![]() $D\,(\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF})\leqslant 1$
. The diffusivity due to drag is consistent with our earlier phenomenological estimate when
$D\,(\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF})\leqslant 1$
. The diffusivity due to drag is consistent with our earlier phenomenological estimate when
![]() $D/\ell n(v_{0}/v_{c})\sim 1$
and again has a small coefficient due to (7.31).
$D/\ell n(v_{0}/v_{c})\sim 1$
and again has a small coefficient due to (7.31).
As expected, the ratio of the pitch angle scattering to electron drag results is
which is larger (smaller) than unity when electron drag (pitch angle scatter) ripple loss dominates.
The pitch angle scattering and electron drag solutions in the
![]() $1/\unicode[STIX]{x1D708}$
regime are not exact since in reality both effects will enter in combination while we have calculated them separately. However, these results are a useful indication of when ripple starts to become a problem.
$1/\unicode[STIX]{x1D708}$
regime are not exact since in reality both effects will enter in combination while we have calculated them separately. However, these results are a useful indication of when ripple starts to become a problem.
7.3 Pitch angle scattering and drag
With both pitch angle scattering and drag the full equation must be solved:
 $$\begin{eqnarray}\displaystyle & & \displaystyle {\displaystyle \frac{2v_{\unicode[STIX]{x1D706}}^{3}B_{0}}{\unicode[STIX]{x1D70F}_{s}v^{3}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}/\unicode[STIX]{x1D709}\,B\right)}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\left[\unicode[STIX]{x1D706}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\;\unicode[STIX]{x1D709}/B^{2}\right){\displaystyle \frac{\unicode[STIX]{x2202}\bar{h}_{t}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\right]+{\displaystyle \frac{1}{\unicode[STIX]{x1D70F}_{s}v^{2}}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}v}}[(v^{3}+v_{c}^{3})\bar{h}_{t}]\nonumber\\ \displaystyle & & \displaystyle \quad ={\displaystyle \frac{2B_{0}^{2}v^{2}}{3\unicode[STIX]{x1D6FA}_{0}}}{\displaystyle \frac{(\unicode[STIX]{x2202}^{2}/\unicode[STIX]{x2202}\unicode[STIX]{x1D706}\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC})\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}^{3}/B^{2}\right)}{\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}/\unicode[STIX]{x1D709}B\,\right)}}\simeq -{\displaystyle \frac{B_{0}\unicode[STIX]{x1D700}v^{2}}{q\unicode[STIX]{x1D6FA}_{0}}}{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}\sin \left({\displaystyle \frac{\unicode[STIX]{x1D6FC}}{q}}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,{\displaystyle \frac{(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D706})\left(\unicode[STIX]{x1D706}\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}\right)}{\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}/\unicode[STIX]{x1D709}\,\right)}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\displaystyle \frac{2v_{\unicode[STIX]{x1D706}}^{3}B_{0}}{\unicode[STIX]{x1D70F}_{s}v^{3}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}/\unicode[STIX]{x1D709}\,B\right)}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\left[\unicode[STIX]{x1D706}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\;\unicode[STIX]{x1D709}/B^{2}\right){\displaystyle \frac{\unicode[STIX]{x2202}\bar{h}_{t}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\right]+{\displaystyle \frac{1}{\unicode[STIX]{x1D70F}_{s}v^{2}}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}v}}[(v^{3}+v_{c}^{3})\bar{h}_{t}]\nonumber\\ \displaystyle & & \displaystyle \quad ={\displaystyle \frac{2B_{0}^{2}v^{2}}{3\unicode[STIX]{x1D6FA}_{0}}}{\displaystyle \frac{(\unicode[STIX]{x2202}^{2}/\unicode[STIX]{x2202}\unicode[STIX]{x1D706}\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC})\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}^{3}/B^{2}\right)}{\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}/\unicode[STIX]{x1D709}B\,\right)}}\simeq -{\displaystyle \frac{B_{0}\unicode[STIX]{x1D700}v^{2}}{q\unicode[STIX]{x1D6FA}_{0}}}{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}\sin \left({\displaystyle \frac{\unicode[STIX]{x1D6FC}}{q}}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,{\displaystyle \frac{(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D706})\left(\unicode[STIX]{x1D706}\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}\right)}{\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}/\unicode[STIX]{x1D709}\,\right)}}.\end{eqnarray}$$
However, this general
![]() $1/\unicode[STIX]{x1D708}$
does not seem to be an analytically tractable problem. To see the reason we seek a separable solution to the homogeneous equation
$1/\unicode[STIX]{x1D708}$
does not seem to be an analytically tractable problem. To see the reason we seek a separable solution to the homogeneous equation
 $$\begin{eqnarray}{\displaystyle \frac{2B_{0}}{\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}/\unicode[STIX]{x1D709}\,B\right)}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\left[\unicode[STIX]{x1D706}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\;\unicode[STIX]{x1D709}/B^{2}\right){\displaystyle \frac{\unicode[STIX]{x2202}H}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\right]+{\displaystyle \frac{v}{v_{\unicode[STIX]{x1D706}}^{3}}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}v}}[(v^{3}+v_{c}^{3})H]=0,\end{eqnarray}$$
$$\begin{eqnarray}{\displaystyle \frac{2B_{0}}{\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}/\unicode[STIX]{x1D709}\,B\right)}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\left[\unicode[STIX]{x1D706}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\;\unicode[STIX]{x1D709}/B^{2}\right){\displaystyle \frac{\unicode[STIX]{x2202}H}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\right]+{\displaystyle \frac{v}{v_{\unicode[STIX]{x1D706}}^{3}}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}v}}[(v^{3}+v_{c}^{3})H]=0,\end{eqnarray}$$
by taking
then for the separation constant
![]() $\unicode[STIX]{x1D70E}$
we would find
$\unicode[STIX]{x1D70E}$
we would find
 $$\begin{eqnarray}{\displaystyle \frac{v}{v_{\unicode[STIX]{x1D706}}^{3}V}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}v}}[(v^{3}+v_{c}^{3})V]=\unicode[STIX]{x1D70E}=-{\displaystyle \frac{2B_{0}}{\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}/\unicode[STIX]{x1D709}\,B\right)\unicode[STIX]{x1D6EC}}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\left[\unicode[STIX]{x1D706}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\;\unicode[STIX]{x1D709}/B^{2}\right){\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6EC}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\right].\end{eqnarray}$$
$$\begin{eqnarray}{\displaystyle \frac{v}{v_{\unicode[STIX]{x1D706}}^{3}V}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}v}}[(v^{3}+v_{c}^{3})V]=\unicode[STIX]{x1D70E}=-{\displaystyle \frac{2B_{0}}{\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}/\unicode[STIX]{x1D709}\,B\right)\unicode[STIX]{x1D6EC}}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\left[\unicode[STIX]{x1D706}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\;\unicode[STIX]{x1D709}/B^{2}\right){\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6EC}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\right].\end{eqnarray}$$
But demanding
![]() $V(v>v_{0})=0$
means there is only the trivial solution
$V(v>v_{0})=0$
means there is only the trivial solution
![]() $V=0$
.
$V=0$
.
8
 $\surd \unicode[STIX]{x1D708}$
ripple transport of alphas
$\surd \unicode[STIX]{x1D708}$
ripple transport of alphas
In the
![]() $\surd \unicode[STIX]{x1D708}$
regime
$\surd \unicode[STIX]{x1D708}$
regime
![]() $\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}=0$
and
$\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}=0$
and
![]() $\unicode[STIX]{x2202}\bar{h}_{p}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}=0$
for the passing, giving
$\unicode[STIX]{x2202}\bar{h}_{p}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}=0$
for the passing, giving
![]() $\overline{C\{\bar{h}_{p}\}}=0$
and therefore
$\overline{C\{\bar{h}_{p}\}}=0$
and therefore
![]() $\bar{h}_{p}=0.$
Here we must be careful to keep the
$\bar{h}_{p}=0.$
Here we must be careful to keep the
![]() $v\unicode[STIX]{x2202}v/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}$
term to retain the
$v\unicode[STIX]{x2202}v/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}$
term to retain the
![]() $\boldsymbol{E}\times \boldsymbol{B}$
drift within a flux surface. This toroidal drift results in a very narrow collisional boundary layer in which alphas detrap and retrap.
$\boldsymbol{E}\times \boldsymbol{B}$
drift within a flux surface. This toroidal drift results in a very narrow collisional boundary layer in which alphas detrap and retrap.
For the ripple trapped we must solve
for the transit average trapped response
![]() $\bar{h}_{t}=\bar{h}_{t}(\unicode[STIX]{x1D713},\unicode[STIX]{x1D6FC},v,\unicode[STIX]{x1D707})$
. For simplicity we consider only the case when the
$\bar{h}_{t}=\bar{h}_{t}(\unicode[STIX]{x1D713},\unicode[STIX]{x1D6FC},v,\unicode[STIX]{x1D707})$
. For simplicity we consider only the case when the
![]() $\boldsymbol{E}\times \boldsymbol{B}$
drift dominates and define its associated toroidal rotation frequency
$\boldsymbol{E}\times \boldsymbol{B}$
drift dominates and define its associated toroidal rotation frequency
![]() $\unicode[STIX]{x1D714}$
via
$\unicode[STIX]{x1D714}$
via
 $$\begin{eqnarray}\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC}}={\displaystyle \frac{Mc}{Ze}}{\displaystyle \frac{(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713})\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,v_{\Vert }\right)}{\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}/v_{\Vert }\right)}}\simeq -c{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}\equiv -\unicode[STIX]{x1D714}.\end{eqnarray}$$
$$\begin{eqnarray}\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC}}={\displaystyle \frac{Mc}{Ze}}{\displaystyle \frac{(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713})\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,v_{\Vert }\right)}{\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}/v_{\Vert }\right)}}\simeq -c{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}\equiv -\unicode[STIX]{x1D714}.\end{eqnarray}$$
In a rippled tokamak the
![]() $\boldsymbol{E}\times \boldsymbol{B}$
drift in a flux surface is mostly toroidal. If
$\boldsymbol{E}\times \boldsymbol{B}$
drift in a flux surface is mostly toroidal. If
![]() $\unicode[STIX]{x1D735}B$
drifts dominate then
$\unicode[STIX]{x1D735}B$
drifts dominate then
![]() $\unicode[STIX]{x1D714}\rightarrow -(Mc\unicode[STIX]{x1D707}/Ze)\unicode[STIX]{x2202}B/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}\simeq (q\unicode[STIX]{x1D706}v^{2}/2\unicode[STIX]{x1D6FA}aR)\cos (\unicode[STIX]{x1D6FC}/q)$
and a similar procedure can be employed. If
$\unicode[STIX]{x1D714}\rightarrow -(Mc\unicode[STIX]{x1D707}/Ze)\unicode[STIX]{x2202}B/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}\simeq (q\unicode[STIX]{x1D706}v^{2}/2\unicode[STIX]{x1D6FA}aR)\cos (\unicode[STIX]{x1D6FC}/q)$
and a similar procedure can be employed. If
![]() $\boldsymbol{E}\times \boldsymbol{B}$
and
$\boldsymbol{E}\times \boldsymbol{B}$
and
![]() $\unicode[STIX]{x1D735}B$
drifts cancel superbanana-plateau transport must retained (Calvo et al.
Reference Calvo, Parra, Velasco and Alonso2017).
$\unicode[STIX]{x1D735}B$
drifts cancel superbanana-plateau transport must retained (Calvo et al.
Reference Calvo, Parra, Velasco and Alonso2017).
We also use the more complete expressions for
 $$\begin{eqnarray}\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}\,\,={\displaystyle \frac{2B_{0}^{2}v^{2}}{3\unicode[STIX]{x1D6FA}_{0}}}{\displaystyle \frac{(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D706})(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC})\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}^{3}/B^{2}\right)}{\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}/\unicode[STIX]{x1D709}\,B\right)}},\end{eqnarray}$$
$$\begin{eqnarray}\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}\,\,={\displaystyle \frac{2B_{0}^{2}v^{2}}{3\unicode[STIX]{x1D6FA}_{0}}}{\displaystyle \frac{(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D706})(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC})\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}^{3}/B^{2}\right)}{\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}/\unicode[STIX]{x1D709}\,B\right)}},\end{eqnarray}$$
and
 $$\begin{eqnarray}\overline{C\{\bar{h}_{t}\}}={\displaystyle \frac{2v_{\unicode[STIX]{x1D706}}^{3}B_{0}}{\unicode[STIX]{x1D70F}_{s}v^{3}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}/\unicode[STIX]{x1D709}\,B\right)}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\left[\unicode[STIX]{x1D706}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\;\unicode[STIX]{x1D709}/B^{2}\right){\displaystyle \frac{\unicode[STIX]{x2202}\bar{h}_{t}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\right].\end{eqnarray}$$
$$\begin{eqnarray}\overline{C\{\bar{h}_{t}\}}={\displaystyle \frac{2v_{\unicode[STIX]{x1D706}}^{3}B_{0}}{\unicode[STIX]{x1D70F}_{s}v^{3}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}/\unicode[STIX]{x1D709}\,B\right)}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\left[\unicode[STIX]{x1D706}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\;\unicode[STIX]{x1D709}/B^{2}\right){\displaystyle \frac{\unicode[STIX]{x2202}\bar{h}_{t}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\right].\end{eqnarray}$$
As a result, we are led to consider
 $$\begin{eqnarray}\displaystyle -\unicode[STIX]{x1D714}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{h}_{t}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}} & = & \displaystyle {\displaystyle \frac{2v_{\unicode[STIX]{x1D706}}^{3}B_{0}}{\unicode[STIX]{x1D70F}_{s}v^{3}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}/\unicode[STIX]{x1D709}B\right)}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\nonumber\\ \displaystyle & & \displaystyle \times \,\left\{\unicode[STIX]{x1D706}\left[\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}/B^{2}\right){\displaystyle \frac{\unicode[STIX]{x2202}\bar{h}_{t}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}-{\displaystyle \frac{B_{0}\unicode[STIX]{x1D70F}_{s}v^{5}}{3\unicode[STIX]{x1D6FA}_{0}v_{\unicode[STIX]{x1D706}}^{3}}}{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}\left({\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}}\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,{\displaystyle \frac{\unicode[STIX]{x1D709}^{3}}{B^{2}}}\right)\right]\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -\unicode[STIX]{x1D714}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{h}_{t}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}} & = & \displaystyle {\displaystyle \frac{2v_{\unicode[STIX]{x1D706}}^{3}B_{0}}{\unicode[STIX]{x1D70F}_{s}v^{3}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}/\unicode[STIX]{x1D709}B\right)}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\nonumber\\ \displaystyle & & \displaystyle \times \,\left\{\unicode[STIX]{x1D706}\left[\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}/B^{2}\right){\displaystyle \frac{\unicode[STIX]{x2202}\bar{h}_{t}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}-{\displaystyle \frac{B_{0}\unicode[STIX]{x1D70F}_{s}v^{5}}{3\unicode[STIX]{x1D6FA}_{0}v_{\unicode[STIX]{x1D706}}^{3}}}{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}\left({\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}}\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,{\displaystyle \frac{\unicode[STIX]{x1D709}^{3}}{B^{2}}}\right)\right]\right\}.\end{eqnarray}$$
Notice that this form reduces to the solution in the
![]() $1/\unicode[STIX]{x1D708}$
regime when
$1/\unicode[STIX]{x1D708}$
regime when
![]() $\boldsymbol{E}\times \boldsymbol{B}$
drift is unimportant. We begin with this form to insure that the
$\boldsymbol{E}\times \boldsymbol{B}$
drift is unimportant. We begin with this form to insure that the
![]() $1/\unicode[STIX]{x1D708}$
regime is being properly retained.
$1/\unicode[STIX]{x1D708}$
regime is being properly retained.
Neglecting curvature drift and assuming weak
![]() $\unicode[STIX]{x1D717}$
variation during a ripple trapped bounce leads to the simplified form
$\unicode[STIX]{x1D717}$
variation during a ripple trapped bounce leads to the simplified form
 $$\begin{eqnarray}-\unicode[STIX]{x1D714}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{h}_{t}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}}={\displaystyle \frac{2v_{\unicode[STIX]{x1D706}}^{3}}{\unicode[STIX]{x1D70F}_{s}v^{3}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}/\unicode[STIX]{x1D709}\right)}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\left\{\left(\unicode[STIX]{x1D706}\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}\right)\left[{\displaystyle \frac{\unicode[STIX]{x2202}\bar{h}_{t}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}+{\displaystyle \frac{B_{0}\unicode[STIX]{x1D700}\unicode[STIX]{x1D70F}_{s}v^{5}}{2q\unicode[STIX]{x1D6FA}_{0}v_{\unicode[STIX]{x1D706}}^{3}}}{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}\sin \left({\displaystyle \frac{\unicode[STIX]{x1D6FC}}{q}}\right)\right]\right\}.\end{eqnarray}$$
$$\begin{eqnarray}-\unicode[STIX]{x1D714}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{h}_{t}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}}={\displaystyle \frac{2v_{\unicode[STIX]{x1D706}}^{3}}{\unicode[STIX]{x1D70F}_{s}v^{3}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}/\unicode[STIX]{x1D709}\right)}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\left\{\left(\unicode[STIX]{x1D706}\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709}\right)\left[{\displaystyle \frac{\unicode[STIX]{x2202}\bar{h}_{t}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}+{\displaystyle \frac{B_{0}\unicode[STIX]{x1D700}\unicode[STIX]{x1D70F}_{s}v^{5}}{2q\unicode[STIX]{x1D6FA}_{0}v_{\unicode[STIX]{x1D706}}^{3}}}{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}\sin \left({\displaystyle \frac{\unicode[STIX]{x1D6FC}}{q}}\right)\right]\right\}.\end{eqnarray}$$
Ho & Kulsrud (Reference Ho and Kulsrud1987) assume any field line between two mirror points is at fixed poloidal angle (see their comments below equation (13)). Consequently, they are assuming large ripple with
![]() $\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF}\ll 1$
based on the Stringer (Reference Stringer1972) and Connor & Hastie (Reference Connor and Hastie1973) treatments. Using this same assumption we can replace (3.16) by
$\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF}\ll 1$
based on the Stringer (Reference Stringer1972) and Connor & Hastie (Reference Connor and Hastie1973) treatments. Using this same assumption we can replace (3.16) by
with
and then let
![]() $\unicode[STIX]{x1D700}\rightarrow \;\,\unicode[STIX]{x1D6FF}$
and
$\unicode[STIX]{x1D700}\rightarrow \;\,\unicode[STIX]{x1D6FF}$
and
![]() $\unicode[STIX]{x1D717}\rightarrow N\unicode[STIX]{x1D701}$
in the usual tokamak bounce averages (see, for example, the Appendix of Catto, Parra & Pusztai (Reference Catto, Parra and Pusztai2017)). Introducing the new independent variable
$\unicode[STIX]{x1D717}\rightarrow N\unicode[STIX]{x1D701}$
in the usual tokamak bounce averages (see, for example, the Appendix of Catto, Parra & Pusztai (Reference Catto, Parra and Pusztai2017)). Introducing the new independent variable
![]() $\unicode[STIX]{x1D705}$
by
$\unicode[STIX]{x1D705}$
by
with
![]() $\unicode[STIX]{x1D705}=1$
the ripple trapped–passing boundary and
$\unicode[STIX]{x1D705}=1$
the ripple trapped–passing boundary and
![]() $\unicode[STIX]{x1D705}=0$
the deeply ripple trapped, we use
$\unicode[STIX]{x1D705}=0$
the deeply ripple trapped, we use
to obtain
 $$\begin{eqnarray}{\displaystyle \frac{(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D706})(\unicode[STIX]{x1D706}\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709})}{\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}/\unicode[STIX]{x1D709}\right)}}\simeq -{\displaystyle \frac{1}{2\unicode[STIX]{x1D705}K(\unicode[STIX]{x1D705})}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D705}}}[E(\unicode[STIX]{x1D705})-(1-\unicode[STIX]{x1D705}^{2})K(\unicode[STIX]{x1D705})]\,\substack{ \longrightarrow \\ \unicode[STIX]{x1D705}\rightarrow 1}\,-{\displaystyle \frac{1}{2}},\end{eqnarray}$$
$$\begin{eqnarray}{\displaystyle \frac{(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D706})(\unicode[STIX]{x1D706}\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D709})}{\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}/\unicode[STIX]{x1D709}\right)}}\simeq -{\displaystyle \frac{1}{2\unicode[STIX]{x1D705}K(\unicode[STIX]{x1D705})}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D705}}}[E(\unicode[STIX]{x1D705})-(1-\unicode[STIX]{x1D705}^{2})K(\unicode[STIX]{x1D705})]\,\substack{ \longrightarrow \\ \unicode[STIX]{x1D705}\rightarrow 1}\,-{\displaystyle \frac{1}{2}},\end{eqnarray}$$
where we use the full bounce results
and
with
![]() $E(\unicode[STIX]{x1D705})\rightarrow 1+(1-\unicode[STIX]{x1D705}^{2})[\ell n(4/\sqrt{1-\unicode[STIX]{x1D705}^{2}})-(1/2)]/2+\cdots \,$
and
$E(\unicode[STIX]{x1D705})\rightarrow 1+(1-\unicode[STIX]{x1D705}^{2})[\ell n(4/\sqrt{1-\unicode[STIX]{x1D705}^{2}})-(1/2)]/2+\cdots \,$
and
![]() $K(\unicode[STIX]{x1D705})\rightarrow \ell n(4/\sqrt{1-\unicode[STIX]{x1D705}^{2}})+\cdots$
. As a result, using
$K(\unicode[STIX]{x1D705})\rightarrow \ell n(4/\sqrt{1-\unicode[STIX]{x1D705}^{2}})+\cdots$
. As a result, using
 $$\begin{eqnarray}\displaystyle & & \displaystyle {\displaystyle \frac{1}{\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}/\unicode[STIX]{x1D709}\right)}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\left[\unicode[STIX]{x1D706}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\;\unicode[STIX]{x1D709}\right){\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\right]\simeq {\displaystyle \frac{1}{8\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D705}K(\unicode[STIX]{x1D705})}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D705}}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left\{{\displaystyle \frac{[E(\unicode[STIX]{x1D705})-(1-\unicode[STIX]{x1D705}^{2})K(\unicode[STIX]{x1D705})]}{\unicode[STIX]{x1D705}}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D705}}}\right\}\,\substack{ \longrightarrow \\ \unicode[STIX]{x1D705}\rightarrow 1}\,{\displaystyle \frac{1}{4\unicode[STIX]{x1D6FF}\ell n\left({\displaystyle \frac{16}{1-\unicode[STIX]{x1D705}^{2}}}\right)}}{\displaystyle \frac{\unicode[STIX]{x2202}^{2}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D705}^{2}}}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\displaystyle \frac{1}{\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}/\unicode[STIX]{x1D709}\right)}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\left[\unicode[STIX]{x1D706}\left(\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\,\text{d}\unicode[STIX]{x1D701}\;\unicode[STIX]{x1D709}\right){\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}}\right]\simeq {\displaystyle \frac{1}{8\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D705}K(\unicode[STIX]{x1D705})}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D705}}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left\{{\displaystyle \frac{[E(\unicode[STIX]{x1D705})-(1-\unicode[STIX]{x1D705}^{2})K(\unicode[STIX]{x1D705})]}{\unicode[STIX]{x1D705}}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D705}}}\right\}\,\substack{ \longrightarrow \\ \unicode[STIX]{x1D705}\rightarrow 1}\,{\displaystyle \frac{1}{4\unicode[STIX]{x1D6FF}\ell n\left({\displaystyle \frac{16}{1-\unicode[STIX]{x1D705}^{2}}}\right)}}{\displaystyle \frac{\unicode[STIX]{x2202}^{2}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D705}^{2}}}\end{eqnarray}$$
the equation for
![]() $\bar{h}_{t}$
becomes
$\bar{h}_{t}$
becomes
Continuing to take
![]() $\unicode[STIX]{x1D705}\rightarrow 1$
and defining
$\unicode[STIX]{x1D705}\rightarrow 1$
and defining
and
gives the boundary layer form of the equation to be
which is valid when
![]() $k\gg 1$
. Here Im denotes the imaginary part.
$k\gg 1$
. Here Im denotes the imaginary part.
To solve the preceding equation in the boundary layer we take
to obtain
which has the particular solution
As this solution does not vanish at
![]() $\unicode[STIX]{x1D702}=0$
we must use the homogeneous solutions to satisfy this boundary condition.
$\unicode[STIX]{x1D702}=0$
we must use the homogeneous solutions to satisfy this boundary condition.
For
![]() $1\ll \ell n(1/\unicode[STIX]{x1D702})\ll 1/k\unicode[STIX]{x1D702}^{2}$
one homogeneous solution starts off as
$1\ll \ell n(1/\unicode[STIX]{x1D702})\ll 1/k\unicode[STIX]{x1D702}^{2}$
one homogeneous solution starts off as
where the coefficient is chosen to cancel the particular solution at
![]() $\unicode[STIX]{x1D702}=0$
. The other begins as
$\unicode[STIX]{x1D702}=0$
. The other begins as
with
![]() $C$
an unknown constant (see appendix D of Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017)). These represent possible inner solutions. Defining a new variable
$C$
an unknown constant (see appendix D of Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017)). These represent possible inner solutions. Defining a new variable
the homogeneous equation becomes
which slightly away from
![]() $\unicode[STIX]{x1D702}=0$
can be approximated by
$\unicode[STIX]{x1D702}=0$
can be approximated by
since
![]() $k\gg 1$
. The decaying solution to this equation is
$k\gg 1$
. The decaying solution to this equation is
where the coefficient is chosen to cancel the particular solution as
![]() $\unicode[STIX]{x1D702}\rightarrow 0$
to satisfy the boundary condition. Taking the inner limit of this outer solution gives
$\unicode[STIX]{x1D702}\rightarrow 0$
to satisfy the boundary condition. Taking the inner limit of this outer solution gives
which allows us to match the terms linear in
![]() $\unicode[STIX]{x1D702}$
to determine the constant
$\unicode[STIX]{x1D702}$
to determine the constant
![]() $C$
to be
$C$
to be
Consequently, a adequate matched asymptotic solution for the trapped alphas up to the trapped–passing boundary and away from it is
where both
![]() $k$
and
$k$
and
![]() $L$
are proportional to
$L$
are proportional to
![]() $\unicode[STIX]{x1D70F}_{s}$
. Forming
$\unicode[STIX]{x1D70F}_{s}$
. Forming
![]() $\bar{h}_{t}$
gives
$\bar{h}_{t}$
gives
with Re denoting the real part is to be taken.
Next we evaluate the particle and heat fluxes
To perform the pitch angle integral we let
so that
and
Recalling that
![]() $\unicode[STIX]{x1D6FC}/q\simeq -\unicode[STIX]{x1D717}$
and noting that only
$\unicode[STIX]{x1D6FC}/q\simeq -\unicode[STIX]{x1D717}$
and noting that only
![]() $\sin (\unicode[STIX]{x1D6FC}/q)\simeq -\sin \unicode[STIX]{x1D717}$
terms contribute when evaluating flux surface averages, we find
$\sin (\unicode[STIX]{x1D6FC}/q)\simeq -\sin \unicode[STIX]{x1D717}$
terms contribute when evaluating flux surface averages, we find
 $$\begin{eqnarray}\displaystyle & & \displaystyle \text{Re}\left\langle \sin \unicode[STIX]{x1D717}\,\text{e}^{-\text{i}\unicode[STIX]{x1D717}}\int _{B_{0}/\underset{B}{\frown }}^{B_{0}/B}\,\text{d}\unicode[STIX]{x1D706}{\displaystyle \frac{\unicode[STIX]{x1D706}}{\unicode[STIX]{x1D709}}}[\text{e}^{-(1-\text{i})\unicode[STIX]{x1D702}\sqrt{2k\ell n(\sqrt{2k})}\,}-1]\right\rangle \nonumber\\ \displaystyle & & \displaystyle \qquad \simeq -{\displaystyle \frac{1}{2}}\text{Re}\left\langle \text{i}\int _{B_{0}/\underset{B}{\frown }}^{B_{0}/B}\,\text{d}\unicode[STIX]{x1D706}{\displaystyle \frac{\unicode[STIX]{x1D706}}{\unicode[STIX]{x1D709}}}[\text{e}^{-8(1-\text{i})(1-\unicode[STIX]{x1D705})\sqrt{2k\ell n(\sqrt{2k})}}-1]\right\rangle .\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \text{Re}\left\langle \sin \unicode[STIX]{x1D717}\,\text{e}^{-\text{i}\unicode[STIX]{x1D717}}\int _{B_{0}/\underset{B}{\frown }}^{B_{0}/B}\,\text{d}\unicode[STIX]{x1D706}{\displaystyle \frac{\unicode[STIX]{x1D706}}{\unicode[STIX]{x1D709}}}[\text{e}^{-(1-\text{i})\unicode[STIX]{x1D702}\sqrt{2k\ell n(\sqrt{2k})}\,}-1]\right\rangle \nonumber\\ \displaystyle & & \displaystyle \qquad \simeq -{\displaystyle \frac{1}{2}}\text{Re}\left\langle \text{i}\int _{B_{0}/\underset{B}{\frown }}^{B_{0}/B}\,\text{d}\unicode[STIX]{x1D706}{\displaystyle \frac{\unicode[STIX]{x1D706}}{\unicode[STIX]{x1D709}}}[\text{e}^{-8(1-\text{i})(1-\unicode[STIX]{x1D705})\sqrt{2k\ell n(\sqrt{2k})}}-1]\right\rangle .\end{eqnarray}$$
Then using
 $$\begin{eqnarray}\displaystyle \langle \unicode[STIX]{x1D709}^{-1}\rangle & = & \displaystyle {\displaystyle \frac{\displaystyle \int _{0}^{\sin ^{-1}\unicode[STIX]{x1D705}}\unicode[STIX]{x1D709}^{-1}\text{d}(N\unicode[STIX]{x1D701}/2)}{\displaystyle \int _{0}^{\unicode[STIX]{x03C0}/2}\text{d}(N\unicode[STIX]{x1D701}/2)}}={\displaystyle \frac{\sqrt{2}}{\unicode[STIX]{x03C0}\sqrt{\unicode[STIX]{x1D6FF}}}}\int _{0}^{\unicode[STIX]{x03C0}/2}{\displaystyle \frac{\text{d}\unicode[STIX]{x1D711}}{\sqrt{1-\unicode[STIX]{x1D705}^{2}\sin ^{2}\unicode[STIX]{x1D711}}}}\nonumber\\ \displaystyle & = & \displaystyle {\displaystyle \frac{\sqrt{2}\,K(\unicode[STIX]{x1D705})}{\unicode[STIX]{x03C0}\sqrt{\unicode[STIX]{x1D6FF}}}}\simeq {\displaystyle \frac{\ell n[16/(1-\,\unicode[STIX]{x1D705}^{2})]}{\unicode[STIX]{x03C0}\sqrt{2\unicode[STIX]{x1D6FF}}}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \langle \unicode[STIX]{x1D709}^{-1}\rangle & = & \displaystyle {\displaystyle \frac{\displaystyle \int _{0}^{\sin ^{-1}\unicode[STIX]{x1D705}}\unicode[STIX]{x1D709}^{-1}\text{d}(N\unicode[STIX]{x1D701}/2)}{\displaystyle \int _{0}^{\unicode[STIX]{x03C0}/2}\text{d}(N\unicode[STIX]{x1D701}/2)}}={\displaystyle \frac{\sqrt{2}}{\unicode[STIX]{x03C0}\sqrt{\unicode[STIX]{x1D6FF}}}}\int _{0}^{\unicode[STIX]{x03C0}/2}{\displaystyle \frac{\text{d}\unicode[STIX]{x1D711}}{\sqrt{1-\unicode[STIX]{x1D705}^{2}\sin ^{2}\unicode[STIX]{x1D711}}}}\nonumber\\ \displaystyle & = & \displaystyle {\displaystyle \frac{\sqrt{2}\,K(\unicode[STIX]{x1D705})}{\unicode[STIX]{x03C0}\sqrt{\unicode[STIX]{x1D6FF}}}}\simeq {\displaystyle \frac{\ell n[16/(1-\,\unicode[STIX]{x1D705}^{2})]}{\unicode[STIX]{x03C0}\sqrt{2\unicode[STIX]{x1D6FF}}}},\end{eqnarray}$$
we obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \text{Re}\left\langle \sin \unicode[STIX]{x1D717}\,\text{e}^{-\text{i}\unicode[STIX]{x1D717}}\int _{B_{0}/\underset{B}{\frown }}^{B_{0}/B}\,\text{d}\unicode[STIX]{x1D706}{\displaystyle \frac{\unicode[STIX]{x1D706}}{\unicode[STIX]{x1D709}}}[\text{e}^{-(1-\text{i})\unicode[STIX]{x1D702}\sqrt{2k\ell n(\sqrt{2k})}\,}-1]\right\rangle \nonumber\\ \displaystyle & & \displaystyle \quad \simeq -{\displaystyle \frac{\sqrt{2\unicode[STIX]{x1D6FF}}}{\unicode[STIX]{x03C0}}}\text{Re}\left\{\text{i}\int _{0}^{1}\,\text{d}\unicode[STIX]{x1D705}\,\unicode[STIX]{x1D705}[\text{e}^{-8(1-\text{i})(1-\unicode[STIX]{x1D705})\sqrt{2k\ell n(\sqrt{2k})}\,}-1]\ln \left({\displaystyle \frac{8}{1-\unicode[STIX]{x1D705}}}\right)\right\}\nonumber\\ \displaystyle & & \displaystyle \quad \simeq -{\displaystyle \frac{\sqrt{\unicode[STIX]{x1D6FF}}\ell n[64\sqrt{2k\ell n(\sqrt{2k})}]}{8\unicode[STIX]{x03C0}\sqrt{k\ell n(\sqrt{2k})}}}\text{Re}\left[\text{i}\int _{0}^{8\sqrt{2k\ell n(\sqrt{2k})}}\,\text{d}\unicode[STIX]{x1D712}\text{e}^{-(l-\text{i})\unicode[STIX]{x1D712}}\right]\nonumber\\ \displaystyle & & \displaystyle =\sqrt{\unicode[STIX]{x1D6FF}}{\displaystyle \frac{\ell n[64\sqrt{2k\ell n(\sqrt{2k})}]}{16\unicode[STIX]{x03C0}\sqrt{k\ell n(\sqrt{2k})}}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \text{Re}\left\langle \sin \unicode[STIX]{x1D717}\,\text{e}^{-\text{i}\unicode[STIX]{x1D717}}\int _{B_{0}/\underset{B}{\frown }}^{B_{0}/B}\,\text{d}\unicode[STIX]{x1D706}{\displaystyle \frac{\unicode[STIX]{x1D706}}{\unicode[STIX]{x1D709}}}[\text{e}^{-(1-\text{i})\unicode[STIX]{x1D702}\sqrt{2k\ell n(\sqrt{2k})}\,}-1]\right\rangle \nonumber\\ \displaystyle & & \displaystyle \quad \simeq -{\displaystyle \frac{\sqrt{2\unicode[STIX]{x1D6FF}}}{\unicode[STIX]{x03C0}}}\text{Re}\left\{\text{i}\int _{0}^{1}\,\text{d}\unicode[STIX]{x1D705}\,\unicode[STIX]{x1D705}[\text{e}^{-8(1-\text{i})(1-\unicode[STIX]{x1D705})\sqrt{2k\ell n(\sqrt{2k})}\,}-1]\ln \left({\displaystyle \frac{8}{1-\unicode[STIX]{x1D705}}}\right)\right\}\nonumber\\ \displaystyle & & \displaystyle \quad \simeq -{\displaystyle \frac{\sqrt{\unicode[STIX]{x1D6FF}}\ell n[64\sqrt{2k\ell n(\sqrt{2k})}]}{8\unicode[STIX]{x03C0}\sqrt{k\ell n(\sqrt{2k})}}}\text{Re}\left[\text{i}\int _{0}^{8\sqrt{2k\ell n(\sqrt{2k})}}\,\text{d}\unicode[STIX]{x1D712}\text{e}^{-(l-\text{i})\unicode[STIX]{x1D712}}\right]\nonumber\\ \displaystyle & & \displaystyle =\sqrt{\unicode[STIX]{x1D6FF}}{\displaystyle \frac{\ell n[64\sqrt{2k\ell n(\sqrt{2k})}]}{16\unicode[STIX]{x03C0}\sqrt{k\ell n(\sqrt{2k})}}},\end{eqnarray}$$
where the imaginary integral does not contribute and
![]() $\unicode[STIX]{x1D712}=8(1-\unicode[STIX]{x1D705})\sqrt{2k\ell n(\sqrt{2k})}$
.
$\unicode[STIX]{x1D712}=8(1-\unicode[STIX]{x1D705})\sqrt{2k\ell n(\sqrt{2k})}$
.
We also make use of
where
From the preceding we obtain
which is valid in the limit of
![]() $\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF}\ll 1$
. Notice that the diffusivity is of order
$\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF}\ll 1$
. Notice that the diffusivity is of order
Within logarithmic factors as in Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017) this result agrees with our phenomenological estimate, but notice that the coefficient is small due to the collisional boundary layer analysis. Interestingly,
![]() $D_{0}^{\sqrt{\unicode[STIX]{x1D708}}}$
only depends logarithmically on the ripple
$D_{0}^{\sqrt{\unicode[STIX]{x1D708}}}$
only depends logarithmically on the ripple
![]() $\unicode[STIX]{x1D6FF}$
because (8.17) or (8.41) require a very narrow boundary layer of width
$\unicode[STIX]{x1D6FF}$
because (8.17) or (8.41) require a very narrow boundary layer of width
![]() $(qv_{\unicode[STIX]{x1D706}}^{3}/\unicode[STIX]{x1D714}\,\unicode[STIX]{x1D70F}_{s}v_{0}^{3})^{1/2}\ll \unicode[STIX]{x1D6FF}^{1/2}$
. These boundary layers become comparable,
$(qv_{\unicode[STIX]{x1D706}}^{3}/\unicode[STIX]{x1D714}\,\unicode[STIX]{x1D70F}_{s}v_{0}^{3})^{1/2}\ll \unicode[STIX]{x1D6FF}^{1/2}$
. These boundary layers become comparable,
![]() $(qv_{\unicode[STIX]{x1D706}}^{3}/\unicode[STIX]{x1D714}\,\unicode[STIX]{x1D70F}_{s}v_{0}^{3})^{1/2}\sim \unicode[STIX]{x1D6FF}^{1/2}$
, at the transition between the
$(qv_{\unicode[STIX]{x1D706}}^{3}/\unicode[STIX]{x1D714}\,\unicode[STIX]{x1D70F}_{s}v_{0}^{3})^{1/2}\sim \unicode[STIX]{x1D6FF}^{1/2}$
, at the transition between the
![]() $\sqrt{\unicode[STIX]{x1D708}}$
and
$\sqrt{\unicode[STIX]{x1D708}}$
and
![]() $1/\unicode[STIX]{x1D708}$
regimes.
$1/\unicode[STIX]{x1D708}$
regimes.
9 Summary
We formulate and solve for the neoclassical transport of alphas in a rippled tokamak by evaluating the
![]() $1/\unicode[STIX]{x1D708}$
and
$1/\unicode[STIX]{x1D708}$
and
![]() $\sqrt{\unicode[STIX]{x1D708}}$
regime modifications of Galeev et al. (Reference Galeev, Sagdeev, Furth and Rosenbluth1969), Stringer (Reference Stringer1972), Connor & Hastie (Reference Connor and Hastie1973), and Ho & Kulsrud (Reference Ho and Kulsrud1987) associated with alpha birth and slowing. The formulation also retains the standard axisymmetric neoclassical effects of Nocentini et al. (Reference Nocentini, Tessarotto and Engelmann1975), Catto (Reference Catto1988), and Hsu et al. (Reference Hsu, Catto and Sigmar1990). The ripple transport of alphas differs from that of the bulk ions and electrons because of its slowing down tail distribution function and the need to consider electron drag as well as pitch angle scatter. Moreover, the approximate variational treatment of Galeev et al. (Reference Galeev, Sagdeev, Furth and Rosenbluth1969) and boundary layer analysis of Ho & Kulsrud (Reference Ho and Kulsrud1987) in the
$\sqrt{\unicode[STIX]{x1D708}}$
regime modifications of Galeev et al. (Reference Galeev, Sagdeev, Furth and Rosenbluth1969), Stringer (Reference Stringer1972), Connor & Hastie (Reference Connor and Hastie1973), and Ho & Kulsrud (Reference Ho and Kulsrud1987) associated with alpha birth and slowing. The formulation also retains the standard axisymmetric neoclassical effects of Nocentini et al. (Reference Nocentini, Tessarotto and Engelmann1975), Catto (Reference Catto1988), and Hsu et al. (Reference Hsu, Catto and Sigmar1990). The ripple transport of alphas differs from that of the bulk ions and electrons because of its slowing down tail distribution function and the need to consider electron drag as well as pitch angle scatter. Moreover, the approximate variational treatment of Galeev et al. (Reference Galeev, Sagdeev, Furth and Rosenbluth1969) and boundary layer analysis of Ho & Kulsrud (Reference Ho and Kulsrud1987) in the
![]() $\sqrt{\unicode[STIX]{x1D708}}$
regime is avoided by a more complete and rigorous boundary layer analysis similar to that of Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017). Our
$\sqrt{\unicode[STIX]{x1D708}}$
regime is avoided by a more complete and rigorous boundary layer analysis similar to that of Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017). Our
![]() $\sqrt{\unicode[STIX]{x1D708}}$
regime evaluation assumes large ripple (
$\sqrt{\unicode[STIX]{x1D708}}$
regime evaluation assumes large ripple (
![]() $\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF}\gg 1$
) and the results are given by (8.42) and (8.43). In this
$\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF}\gg 1$
) and the results are given by (8.42) and (8.43). In this
![]() $\sqrt{\unicode[STIX]{x1D708}}$
regime drag is unimportant. The
$\sqrt{\unicode[STIX]{x1D708}}$
regime drag is unimportant. The
![]() $1/\unicode[STIX]{x1D708}$
regime evaluations presented here allow general ripple (
$1/\unicode[STIX]{x1D708}$
regime evaluations presented here allow general ripple (
![]() $\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF}\sim 1$
) and the results with only pitch angle scattering (
$\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF}\sim 1$
) and the results with only pitch angle scattering (
![]() $\unicode[STIX]{x1D6FF}v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3}\ll 1$
) are given by equations (7.23) and (7.24), while those keeping only electron drag (
$\unicode[STIX]{x1D6FF}v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3}\ll 1$
) are given by equations (7.23) and (7.24), while those keeping only electron drag (
![]() $\unicode[STIX]{x1D6FF}v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3}\gg 1$
) are given by equations (7.36) and (7.37). When pitch angle scatter and electron drag compete in the
$\unicode[STIX]{x1D6FF}v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3}\gg 1$
) are given by equations (7.36) and (7.37). When pitch angle scatter and electron drag compete in the
![]() $1/\unicode[STIX]{x1D708}$
regime (
$1/\unicode[STIX]{x1D708}$
regime (
![]() $\unicode[STIX]{x1D6FF}v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3}\sim 1$
) and the ripple is strong (
$\unicode[STIX]{x1D6FF}v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3}\sim 1$
) and the ripple is strong (
![]() $\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF}\ll 1$
), the transition from the axisymmetric banana regime to the
$\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF}\ll 1$
), the transition from the axisymmetric banana regime to the
![]() $1/\unicode[STIX]{x1D708}$
occurs when the time for an birth alpha to travel a connection length is substantially smaller than the slowing down time, roughly
$1/\unicode[STIX]{x1D708}$
occurs when the time for an birth alpha to travel a connection length is substantially smaller than the slowing down time, roughly
![]() $qR/\unicode[STIX]{x1D70F}_{s}v_{0}\sim \unicode[STIX]{x1D6FF}^{1/4}\unicode[STIX]{x1D700}^{1/2}$
, or more precisely
$qR/\unicode[STIX]{x1D70F}_{s}v_{0}\sim \unicode[STIX]{x1D6FF}^{1/4}\unicode[STIX]{x1D700}^{1/2}$
, or more precisely
For the axisymmetric banana regime we simplify by using
![]() $\unicode[STIX]{x1D6FF}v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3}\sim 1$
and taking
$\unicode[STIX]{x1D6FF}v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3}\sim 1$
and taking
to obtain an estimate between the Nocentini et al. (Reference Nocentini, Tessarotto and Engelmann1975) and Catto (Reference Catto1988) limits to be in better agreement with the precise results of Hsu et al. (Reference Hsu, Catto and Sigmar1990). Our
![]() $1/\unicode[STIX]{x1D708}$
calculation assumes small alpha birth gyroradius,
$1/\unicode[STIX]{x1D708}$
calculation assumes small alpha birth gyroradius,
to keep the alpha distribution function near the slowing down distribution that is assumed to have a radial scale length of
![]() $a_{\unicode[STIX]{x1D6FC}}$
. To keep
$a_{\unicode[STIX]{x1D6FC}}$
. To keep
![]() $\unicode[STIX]{x1D70F}_{s}D_{\text{axi}}^{\text{ban}}/a_{\unicode[STIX]{x1D6FC}}^{2}\ll 1$
we need
$\unicode[STIX]{x1D70F}_{s}D_{\text{axi}}^{\text{ban}}/a_{\unicode[STIX]{x1D6FC}}^{2}\ll 1$
we need
![]() $\unicode[STIX]{x1D70C}_{0}/a_{\unicode[STIX]{x1D6FC}}\ll \unicode[STIX]{x1D700}^{1/2}/q\ll 1$
, which is typically less restrictive than (9.3).
$\unicode[STIX]{x1D70C}_{0}/a_{\unicode[STIX]{x1D6FC}}\ll \unicode[STIX]{x1D700}^{1/2}/q\ll 1$
, which is typically less restrictive than (9.3).
It is unlikely that (9.3) can be satisfied for any feasible
![]() $\unicode[STIX]{x1D6FF}$
. However, the inability to satisfy (9.3) is good news! It means that for all practical purposes there is no significant
$\unicode[STIX]{x1D6FF}$
. However, the inability to satisfy (9.3) is good news! It means that for all practical purposes there is no significant
![]() $1/\unicode[STIX]{x1D708}$
regime so that axisymmetric neoclassical banana regime transport transitions almost directly into less dangerous
$1/\unicode[STIX]{x1D708}$
regime so that axisymmetric neoclassical banana regime transport transitions almost directly into less dangerous
![]() $\sqrt{\unicode[STIX]{x1D708}}$
regime for alpha ripple transport!
$\sqrt{\unicode[STIX]{x1D708}}$
regime for alpha ripple transport!
Moreover, for
![]() $\unicode[STIX]{x1D6FF}v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3}\sim 1$
and
$\unicode[STIX]{x1D6FF}v_{0}^{3}/v_{\unicode[STIX]{x1D706}}^{3}\sim 1$
and
![]() $\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF}\ll 1$
, the transition from the
$\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF}\ll 1$
, the transition from the
![]() $1/\unicode[STIX]{x1D708}$
to
$1/\unicode[STIX]{x1D708}$
to
![]() $\sqrt{\unicode[STIX]{x1D708}}$
regime happens when a significant fraction of a full toroidal rotation happens in a slowing down time, roughly
$\sqrt{\unicode[STIX]{x1D708}}$
regime happens when a significant fraction of a full toroidal rotation happens in a slowing down time, roughly
![]() $\unicode[STIX]{x1D714}\unicode[STIX]{x1D70F}_{s}\sim q$
, or more carefully
$\unicode[STIX]{x1D714}\unicode[STIX]{x1D70F}_{s}\sim q$
, or more carefully
where
![]() $2k_{0}\simeq 128\,\unicode[STIX]{x1D714}\,\unicode[STIX]{x1D70F}_{s}\unicode[STIX]{x1D6FF}v_{0}^{3}/qv_{\unicode[STIX]{x1D706}}^{3}\sim 128\unicode[STIX]{x1D714}\,\unicode[STIX]{x1D70F}_{s}/q\gg 1$
is required for our boundary layer analysis to be valid. Normally,
$2k_{0}\simeq 128\,\unicode[STIX]{x1D714}\,\unicode[STIX]{x1D70F}_{s}\unicode[STIX]{x1D6FF}v_{0}^{3}/qv_{\unicode[STIX]{x1D706}}^{3}\sim 128\unicode[STIX]{x1D714}\,\unicode[STIX]{x1D70F}_{s}/q\gg 1$
is required for our boundary layer analysis to be valid. Normally,
![]() $\unicode[STIX]{x1D714}\,\unicode[STIX]{x1D70F}_{s}\gg \,q$
.
$\unicode[STIX]{x1D714}\,\unicode[STIX]{x1D70F}_{s}\gg \,q$
.
To remain near a slowing down distribution the
![]() $\sqrt{\unicode[STIX]{x1D708}}$
regime requires the alpha birth gyroradius to satisfy the much stricter condition of
$\sqrt{\unicode[STIX]{x1D708}}$
regime requires the alpha birth gyroradius to satisfy the much stricter condition of
Even with the small coefficient, rotation larger than the
![]() $\unicode[STIX]{x1D735}B$
drift level
$\unicode[STIX]{x1D735}B$
drift level
![]() $(\unicode[STIX]{x1D714}R>\unicode[STIX]{x1D70C}_{0}v_{0}/R)$
and small
$(\unicode[STIX]{x1D714}R>\unicode[STIX]{x1D70C}_{0}v_{0}/R)$
and small
![]() $\unicode[STIX]{x1D70C}_{0}/a_{\unicode[STIX]{x1D6FC}}$
may be required to avoid depletion of the alpha slowing down tail distribution function.
$\unicode[STIX]{x1D70C}_{0}/a_{\unicode[STIX]{x1D6FC}}$
may be required to avoid depletion of the alpha slowing down tail distribution function.
To estimate the size of quantities for D–T fusion we use
![]() $v_{0}\simeq 1.3\times 10^{9}~\text{cm}~\text{s}^{-1}$
for a 3.5 MeV alpha, and
$v_{0}\simeq 1.3\times 10^{9}~\text{cm}~\text{s}^{-1}$
for a 3.5 MeV alpha, and
![]() $\unicode[STIX]{x1D70F}_{s}=\unicode[STIX]{x1D70F}_{ee}M/Z^{2}m\simeq 0.63~\text{s}$
for
$\unicode[STIX]{x1D70F}_{s}=\unicode[STIX]{x1D70F}_{ee}M/Z^{2}m\simeq 0.63~\text{s}$
for
![]() $T_{e}\simeq 10~\text{keV}$
and
$T_{e}\simeq 10~\text{keV}$
and
![]() $n_{e}\simeq 10^{14}~\text{cm}^{-3}$
, with
$n_{e}\simeq 10^{14}~\text{cm}^{-3}$
, with
![]() $\unicode[STIX]{x1D70F}_{ee}$
the electron collision time. We note that even if the alpha pressure was comparable to the plasma pressure that the slowing down alpha density
$\unicode[STIX]{x1D70F}_{ee}$
the electron collision time. We note that even if the alpha pressure was comparable to the plasma pressure that the slowing down alpha density
![]() $n_{s}$
would be small compared to the plasma density
$n_{s}$
would be small compared to the plasma density
![]() $n_{s}/n_{e}\sim 1/300$
. Consequently, the alphas are not expected to play a role in ambipolarity so any radial electric field due to ripple is due to the balance of
$n_{s}/n_{e}\sim 1/300$
. Consequently, the alphas are not expected to play a role in ambipolarity so any radial electric field due to ripple is due to the balance of
![]() $1/\unicode[STIX]{x1D708}$
regime electron transport and
$1/\unicode[STIX]{x1D708}$
regime electron transport and
![]() $\sqrt{v}$
regime ion transport or the radial electric field associated with an axisymmetric tokamak and determined by convservation of toroidal angular momentum (see Parra & Catto Reference Parra and Catto2008, Reference Parra and Catto2009, Reference Parra and Catto2010, must be smaller in this situation), giving an inadequate rotation level of
$\sqrt{v}$
regime ion transport or the radial electric field associated with an axisymmetric tokamak and determined by convservation of toroidal angular momentum (see Parra & Catto Reference Parra and Catto2008, Reference Parra and Catto2009, Reference Parra and Catto2010, must be smaller in this situation), giving an inadequate rotation level of
![]() $\unicode[STIX]{x1D714}R\sim q\unicode[STIX]{x1D70C}_{i}v_{i}/\unicode[STIX]{x1D700}a$
. Then the
$\unicode[STIX]{x1D714}R\sim q\unicode[STIX]{x1D70C}_{i}v_{i}/\unicode[STIX]{x1D700}a$
. Then the
![]() $\unicode[STIX]{x1D735}B$
drift will dominant and is expected to play a role similar to the
$\unicode[STIX]{x1D735}B$
drift will dominant and is expected to play a role similar to the
![]() $\boldsymbol{E}\times \boldsymbol{B}$
. The assumptions used to derive the alpha collision operator are satisfied since
$\boldsymbol{E}\times \boldsymbol{B}$
. The assumptions used to derive the alpha collision operator are satisfied since
![]() $v_{0}\ll v_{e}=(2T_{e}/m)^{1/2}\simeq 6\times 10^{9}~\text{cm}~\text{s}^{-1}$
and
$v_{0}\ll v_{e}=(2T_{e}/m)^{1/2}\simeq 6\times 10^{9}~\text{cm}~\text{s}^{-1}$
and
![]() $v_{0}\gg v_{i}=(2T_{i}/M_{i})^{1/2}\simeq 10^{8}~\text{cm}~\text{s}^{-1}$
. Moreover, for equal amounts of D and
$v_{0}\gg v_{i}=(2T_{i}/M_{i})^{1/2}\simeq 10^{8}~\text{cm}~\text{s}^{-1}$
. Moreover, for equal amounts of D and
![]() $T$
,
$T$
,
![]() $v_{0}/v_{c}\simeq 3.25$
and
$v_{0}/v_{c}\simeq 3.25$
and
![]() $v_{\unicode[STIX]{x1D706}}^{3}/v_{c}^{3}\simeq 3/5$
, so our assumptions that
$v_{\unicode[STIX]{x1D706}}^{3}/v_{c}^{3}\simeq 3/5$
, so our assumptions that
![]() $v_{0}^{3}\gg v_{c}^{3}\sim v_{\unicode[STIX]{x1D706}}^{3}$
are satisfied. In addition, we note that for
$v_{0}^{3}\gg v_{c}^{3}\sim v_{\unicode[STIX]{x1D706}}^{3}$
are satisfied. In addition, we note that for
![]() $B_{0}=5~\text{T}$
,
$B_{0}=5~\text{T}$
,
![]() $\unicode[STIX]{x1D6FA}_{0}\simeq 2.4\times 10^{8}~\text{rad}~\text{s}^{-1}$
, giving
$\unicode[STIX]{x1D6FA}_{0}\simeq 2.4\times 10^{8}~\text{rad}~\text{s}^{-1}$
, giving
![]() $\unicode[STIX]{x1D70C}_{0}\simeq 5.4~\text{cm}$
, which must be small compared to the radial scale length
$\unicode[STIX]{x1D70C}_{0}\simeq 5.4~\text{cm}$
, which must be small compared to the radial scale length
![]() $a_{\unicode[STIX]{x1D6FC}}$
of the alphas.
$a_{\unicode[STIX]{x1D6FC}}$
of the alphas.
From the preceding numbers and
![]() $R\simeq 10~\text{m}$
, we obtain
$R\simeq 10~\text{m}$
, we obtain
![]() $R/\unicode[STIX]{x1D70F}_{s}v_{0}\simeq 1.2\times 10^{-6}$
. Consequently, based on (9.3), we expect that tokamaks will operate with the alphas well into the
$R/\unicode[STIX]{x1D70F}_{s}v_{0}\simeq 1.2\times 10^{-6}$
. Consequently, based on (9.3), we expect that tokamaks will operate with the alphas well into the
![]() $\sqrt{\unicode[STIX]{x1D708}}$
ripple transport regime with
$\sqrt{\unicode[STIX]{x1D708}}$
ripple transport regime with
![]() $\unicode[STIX]{x1D714}\unicode[STIX]{x1D70F}_{s}\gg q$
. Indeed, if we assume
$\unicode[STIX]{x1D714}\unicode[STIX]{x1D70F}_{s}\gg q$
. Indeed, if we assume
![]() $\unicode[STIX]{x1D714}R\simeq v_{i}$
, then we find
$\unicode[STIX]{x1D714}R\simeq v_{i}$
, then we find
![]() $\unicode[STIX]{x1D714}\unicode[STIX]{x1D70F}_{s}\simeq 6.3\times 10^{4}$
, giving
$\unicode[STIX]{x1D714}\unicode[STIX]{x1D70F}_{s}\simeq 6.3\times 10^{4}$
, giving
![]() $\sqrt{\unicode[STIX]{x1D708}}$
regime ripple transport. Then the key issue becomes avoiding the depletion of the alpha slowing down distribution by satisfying (9.5).
$\sqrt{\unicode[STIX]{x1D708}}$
regime ripple transport. Then the key issue becomes avoiding the depletion of the alpha slowing down distribution by satisfying (9.5).
In summary, ripple transport of alphas will be in the
![]() $\sqrt{\unicode[STIX]{x1D708}}$
regime, rather than the
$\sqrt{\unicode[STIX]{x1D708}}$
regime, rather than the
![]() $1/\unicode[STIX]{x1D708}$
regime, thereby suppressing ripple transport well below the
$1/\unicode[STIX]{x1D708}$
regime, thereby suppressing ripple transport well below the
![]() $1/\unicode[STIX]{x1D708}$
level. However, alpha ripple transport in the
$1/\unicode[STIX]{x1D708}$
level. However, alpha ripple transport in the
![]() $\sqrt{\unicode[STIX]{x1D708}}$
regime will be a serious issue for tokamak reactors as it will be well above the axisymmetric neoclassical level and can deplete the alpha slowing down distribution function unless toroidal rotation is strong.
$\sqrt{\unicode[STIX]{x1D708}}$
regime will be a serious issue for tokamak reactors as it will be well above the axisymmetric neoclassical level and can deplete the alpha slowing down distribution function unless toroidal rotation is strong.
Acknowledgements
I would like to thank E. Paul (U. Maryland) for bringing the Stringer and Connor & Hastie publications to my attention, and Professor F. Parra (Oxford U.) for discussions on the material in § 7.3 and bringing an error to my attention, Professor A. Schekochihin (Oxford U.) for arranging yet another visit to Oxford and the use of his Merton College office during the early writing stages of this manuscript, and Merton College for its unequalled hospitality. I also thank Ryan White (MIT) and Professor N. Loureiro (MIT) for suggesting the problem. I am grateful to the referees for a careful reading of the manuscript and helpful suggestions. The work was supported the US Department of Energy grant DE-FG02-91ER-54109.
Appendix A. Stringer (Reference Stringer1972) and Connor & Hastie (Reference Connor and Hastie1973)
The extremal along the magnetic field
are found for fixed
![]() $\unicode[STIX]{x1D6FC}$
from
$\unicode[STIX]{x1D6FC}$
from
If
![]() $qN\unicode[STIX]{x1D6FF}\ll \unicode[STIX]{x1D700}$
, then even if
$qN\unicode[STIX]{x1D6FF}\ll \unicode[STIX]{x1D700}$
, then even if
![]() $\sin (N\unicode[STIX]{x1D701})\rightarrow \pm 1$
, the minima must be near
$\sin (N\unicode[STIX]{x1D701})\rightarrow \pm 1$
, the minima must be near
![]() $\unicode[STIX]{x1D717}=0$
. In this weak ripple limit the well centres are near the equatorial plane and
$\unicode[STIX]{x1D717}=0$
. In this weak ripple limit the well centres are near the equatorial plane and
![]() $N\unicode[STIX]{x1D701}$
varies over less than
$N\unicode[STIX]{x1D701}$
varies over less than
![]() $2\unicode[STIX]{x03C0}$
. In the
$2\unicode[STIX]{x03C0}$
. In the
![]() $qN\unicode[STIX]{x1D6FF}\gg \unicode[STIX]{x1D700}$
the strong ripple can localize the ripple well minima away from the equatorial plane.
$qN\unicode[STIX]{x1D6FF}\gg \unicode[STIX]{x1D700}$
the strong ripple can localize the ripple well minima away from the equatorial plane.
More precisely, the minima occur at
where
![]() $m$
is an integer or zero satisfying
$m$
is an integer or zero satisfying
![]() $0\leqslant m\leqslant N$
to keep
$0\leqslant m\leqslant N$
to keep
![]() $2\unicode[STIX]{x03C0}\geqslant \breve{\unicode[STIX]{x1D701}}\geqslant 0$
and we will soon see that
$2\unicode[STIX]{x03C0}\geqslant \breve{\unicode[STIX]{x1D701}}\geqslant 0$
and we will soon see that
![]() $\unicode[STIX]{x1D717}$
variation is weak for
$\unicode[STIX]{x1D717}$
variation is weak for
![]() $N\gg 1$
. The adjacent maxima occur at
$N\gg 1$
. The adjacent maxima occur at
The minima, maxima, and lower maxima are found by assuming that
![]() $\unicode[STIX]{x1D717}$
varies only slightly during a bounce when
$\unicode[STIX]{x1D717}$
varies only slightly during a bounce when
![]() $N\gg 1$
. The minima and lower maxima must satisfy
$N\gg 1$
. The minima and lower maxima must satisfy
giving
Even for large ripple,
![]() $qN\unicode[STIX]{x1D6FF}\gg \unicode[STIX]{x1D700}$
, the variation in
$qN\unicode[STIX]{x1D6FF}\gg \unicode[STIX]{x1D700}$
, the variation in ![]() is small, even though
is small, even though ![]() varies over almost a full
varies over almost a full
![]() $2\unicode[STIX]{x03C0}$
.
$2\unicode[STIX]{x03C0}$
.
Only the lower maximum of the magnetic field,
enters in our integrals, where we must choose the smaller of the two possible values of ![]() . Using the minimum field
. Using the minimum field
and expanding
![]() $\cos \breve{\unicode[STIX]{x1D717}}$
about
$\cos \breve{\unicode[STIX]{x1D717}}$
about ![]() at fixed
at fixed
![]() $\unicode[STIX]{x1D6FC}$
gives the lower maximato be
$\unicode[STIX]{x1D6FC}$
gives the lower maximato be
 $$\begin{eqnarray}\displaystyle & & \displaystyle \underset{B}{\frown }\simeq B_{0}\left\{\vphantom{\frac{1}{2}}1-\unicode[STIX]{x1D700}\cos \breve{\unicode[STIX]{x1D717}}-(\unicode[STIX]{x1D700}/qN)(\unicode[STIX]{x03C0}-2\sin ^{-1}[(\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF})|\!\sin \unicode[STIX]{x1D717}|])|\!\sin \unicode[STIX]{x1D717}|\right.\nonumber\\ \displaystyle & & \displaystyle \left.\qquad +\,\unicode[STIX]{x1D6FF}\sqrt{1-(\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF})^{2}\sin ^{2}\unicode[STIX]{x1D717}}\vphantom{\frac{1}{2}}\right\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \underset{B}{\frown }\simeq B_{0}\left\{\vphantom{\frac{1}{2}}1-\unicode[STIX]{x1D700}\cos \breve{\unicode[STIX]{x1D717}}-(\unicode[STIX]{x1D700}/qN)(\unicode[STIX]{x03C0}-2\sin ^{-1}[(\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF})|\!\sin \unicode[STIX]{x1D717}|])|\!\sin \unicode[STIX]{x1D717}|\right.\nonumber\\ \displaystyle & & \displaystyle \left.\qquad +\,\unicode[STIX]{x1D6FF}\sqrt{1-(\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF})^{2}\sin ^{2}\unicode[STIX]{x1D717}}\vphantom{\frac{1}{2}}\right\},\end{eqnarray}$$
where
![]() $\breve{\unicode[STIX]{x1D717}}\simeq \unicode[STIX]{x1D717}$
except in
$\breve{\unicode[STIX]{x1D717}}\simeq \unicode[STIX]{x1D717}$
except in
![]() $\cos \breve{\unicode[STIX]{x1D717}}$
,
$\cos \breve{\unicode[STIX]{x1D717}}$
,
In addition, we can form
 $$\begin{eqnarray}\displaystyle \underset{B}{\frown }-\breve{B} & = & \displaystyle B_{0}\{\unicode[STIX]{x1D700}(\cos \breve{\unicode[STIX]{x1D717}}-\cos \underset{\unicode[STIX]{x1D717}}{\frown })+\unicode[STIX]{x1D6FF}[\cos (N\breve{\unicode[STIX]{x1D701}})-\cos (N\underset{\unicode[STIX]{x1D701}}{\frown })]\}\nonumber\\ \displaystyle & \simeq & \displaystyle 2B_{0}\unicode[STIX]{x1D6FF}\left\{\vphantom{\frac{1}{2}}\sqrt{1-(\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF})^{2}\sin ^{2}\unicode[STIX]{x1D717}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,(\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF})[(\unicode[STIX]{x03C0}/2)-\sin ^{-1}[(\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF})|\!\sin \unicode[STIX]{x1D717}|]]|\!\sin \unicode[STIX]{x1D717}|\vphantom{\frac{1}{2}}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \underset{B}{\frown }-\breve{B} & = & \displaystyle B_{0}\{\unicode[STIX]{x1D700}(\cos \breve{\unicode[STIX]{x1D717}}-\cos \underset{\unicode[STIX]{x1D717}}{\frown })+\unicode[STIX]{x1D6FF}[\cos (N\breve{\unicode[STIX]{x1D701}})-\cos (N\underset{\unicode[STIX]{x1D701}}{\frown })]\}\nonumber\\ \displaystyle & \simeq & \displaystyle 2B_{0}\unicode[STIX]{x1D6FF}\left\{\vphantom{\frac{1}{2}}\sqrt{1-(\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF})^{2}\sin ^{2}\unicode[STIX]{x1D717}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,(\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF})[(\unicode[STIX]{x03C0}/2)-\sin ^{-1}[(\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF})|\!\sin \unicode[STIX]{x1D717}|]]|\!\sin \unicode[STIX]{x1D717}|\vphantom{\frac{1}{2}}\right\}\end{eqnarray}$$
as in Stringer (Reference Stringer1972) and Connor & Hastie (Reference Connor and Hastie1973), where here the distinction between ![]() ,
,
![]() $\breve{\unicode[STIX]{x1D717}}$
, and
$\breve{\unicode[STIX]{x1D717}}$
, and
![]() $\unicode[STIX]{x1D717}$
no longer matters on the right side.
$\unicode[STIX]{x1D717}$
no longer matters on the right side.
Similarly, we can also form ![]()
Expanding using ![]() gives
gives
and
where
Along the magnetic field ![]() giving for
giving for
![]() $p=1$
and 3,
$p=1$
and 3,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\text{all}}\text{d}(N\unicode[STIX]{x1D701})\sqrt{[1-(B/\underset{B}{\frown })]^{p}}\simeq \unicode[STIX]{x1D6FF}^{p/2}\int _{\text{all}}\text{d}(N\unicode[STIX]{x1D701})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\left\{(\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF})(N\underset{\unicode[STIX]{x1D701}}{\frown }-N\unicode[STIX]{x1D701})\sin \unicode[STIX]{x1D717}+[\cos (N\unicode[STIX]{x1D701})-\!\cos (N\underset{\unicode[STIX]{x1D701}}{\frown })]\right\}^{p/2},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\text{all}}\text{d}(N\unicode[STIX]{x1D701})\sqrt{[1-(B/\underset{B}{\frown })]^{p}}\simeq \unicode[STIX]{x1D6FF}^{p/2}\int _{\text{all}}\text{d}(N\unicode[STIX]{x1D701})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\left\{(\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF})(N\underset{\unicode[STIX]{x1D701}}{\frown }-N\unicode[STIX]{x1D701})\sin \unicode[STIX]{x1D717}+[\cos (N\unicode[STIX]{x1D701})-\!\cos (N\underset{\unicode[STIX]{x1D701}}{\frown })]\right\}^{p/2},\end{eqnarray}$$
where we can view ![]() . To get the same signs and form as Connor & Hastie (Reference Connor and Hastie1973) and conveniently keep track of signs, we let
. To get the same signs and form as Connor & Hastie (Reference Connor and Hastie1973) and conveniently keep track of signs, we let
![]() $Y=N\unicode[STIX]{x1D701}+\unicode[STIX]{x03C0}$
so that
$Y=N\unicode[STIX]{x1D701}+\unicode[STIX]{x03C0}$
so that
![]() $\cos (N\unicode[STIX]{x1D701})=-\!\cos Y$
and
$\cos (N\unicode[STIX]{x1D701})=-\!\cos Y$
and
![]() $\unicode[STIX]{x1D701}=0$
is at
$\unicode[STIX]{x1D701}=0$
is at
![]() $\unicode[STIX]{x03C0}$
, and
$\unicode[STIX]{x03C0}$
, and ![]() so that
so that ![]() and we may take
and we may take
Then
Continuing, using
and the up–down symmetry of the
![]() $\unicode[STIX]{x1D717}$
integral, and then noting that the 0 to
$\unicode[STIX]{x1D717}$
integral, and then noting that the 0 to
![]() $\unicode[STIX]{x03C0}/2$
and
$\unicode[STIX]{x03C0}/2$
and
![]() $\unicode[STIX]{x03C0}/2$
to
$\unicode[STIX]{x03C0}/2$
to
![]() $\unicode[STIX]{x03C0}$
contributions to the
$\unicode[STIX]{x03C0}$
contributions to the
![]() $\unicode[STIX]{x1D717}$
integral are equal, gives
$\unicode[STIX]{x1D717}$
integral are equal, gives
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\text{all}}\,\text{d}\unicode[STIX]{x1D717}\sin ^{2}\unicode[STIX]{x1D703}\int _{\text{all}}\text{d}(N\unicode[STIX]{x1D701})\sqrt{[1-(B/\underset{B}{\frown })]^{p}}\nonumber\\ \displaystyle & & \displaystyle \quad ={\displaystyle \frac{4\unicode[STIX]{x1D6FF}^{p/2}}{(\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF})^{2}}}\int _{0}^{U}{\displaystyle \frac{\text{d}X\cos X\sin ^{2}X}{\sqrt{(\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF})^{2}-\sin ^{2}X}}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{X}^{Y_{1}(X)}\,\text{d}Y[\cos X-\!\cos Y+(X-Y)\sin X]^{p/2}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\text{all}}\,\text{d}\unicode[STIX]{x1D717}\sin ^{2}\unicode[STIX]{x1D703}\int _{\text{all}}\text{d}(N\unicode[STIX]{x1D701})\sqrt{[1-(B/\underset{B}{\frown })]^{p}}\nonumber\\ \displaystyle & & \displaystyle \quad ={\displaystyle \frac{4\unicode[STIX]{x1D6FF}^{p/2}}{(\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF})^{2}}}\int _{0}^{U}{\displaystyle \frac{\text{d}X\cos X\sin ^{2}X}{\sqrt{(\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF})^{2}-\sin ^{2}X}}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{X}^{Y_{1}(X)}\,\text{d}Y[\cos X-\!\cos Y+(X-Y)\sin X]^{p/2}.\end{eqnarray}$$
The lower limit
![]() $Y=X$
corresponds to
$Y=X$
corresponds to ![]() (the lower maximum), while the upper limit
(the lower maximum), while the upper limit
![]() $U$
also corresponds to
$U$
also corresponds to ![]() but not at a maximum, instead it satisfies
but not at a maximum, instead it satisfies
![]() $\cos X-\!\cos Y_{1}+(X-Y_{1})\sin X=0$
(note for
$\cos X-\!\cos Y_{1}+(X-Y_{1})\sin X=0$
(note for
![]() $X\rightarrow -X$
,
$X\rightarrow -X$
,
![]() $Y_{1}\rightarrow -Y_{1}$
). Consequently, like Connor & Hastie (Reference Connor and Hastie1973) we integrate between two maxima. The upper limit
$Y_{1}\rightarrow -Y_{1}$
). Consequently, like Connor & Hastie (Reference Connor and Hastie1973) we integrate between two maxima. The upper limit
![]() $U$
of the
$U$
of the
![]() $X$
integral is
$X$
integral is
![]() $\unicode[STIX]{x03C0}/2$
when
$\unicode[STIX]{x03C0}/2$
when
![]() $\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF}>1$
, while for
$\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF}>1$
, while for
![]() $\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF}<1$
it is
$\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF}<1$
it is
![]() $\sin ^{-1}(\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF})$
.
$\sin ^{-1}(\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF})$
.
To get the maximum value for normalization we consider
![]() $\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF}\ll 1$
$\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF}\ll 1$
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\text{all}}\,\text{d}\unicode[STIX]{x1D717}\sin ^{2}\unicode[STIX]{x1D703}\int _{\text{all}}\text{d}(N\unicode[STIX]{x1D701})\sqrt{[1-(B/\underset{B}{\frown })]^{p}}\simeq {\displaystyle \frac{4\unicode[STIX]{x1D6FF}^{p/2}}{(\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF})^{2}}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{0}^{\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF}}{\displaystyle \frac{\text{d}X\,X^{2}}{\sqrt{(\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF})^{2}-X^{2}}}}\int _{X}^{Y_{1}}\,\text{d}Y(1-\!\cos Y-XY)^{p/2},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\text{all}}\,\text{d}\unicode[STIX]{x1D717}\sin ^{2}\unicode[STIX]{x1D703}\int _{\text{all}}\text{d}(N\unicode[STIX]{x1D701})\sqrt{[1-(B/\underset{B}{\frown })]^{p}}\simeq {\displaystyle \frac{4\unicode[STIX]{x1D6FF}^{p/2}}{(\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF})^{2}}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{0}^{\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF}}{\displaystyle \frac{\text{d}X\,X^{2}}{\sqrt{(\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF})^{2}-X^{2}}}}\int _{X}^{Y_{1}}\,\text{d}Y(1-\!\cos Y-XY)^{p/2},\end{eqnarray}$$
where for
![]() $X\ll 1$
,
$X\ll 1$
,
![]() $Y_{1}$
satisfies
$Y_{1}$
satisfies
![]() $1-\!\cos Y_{1}\simeq Y_{1}X$
giving
$1-\!\cos Y_{1}\simeq Y_{1}X$
giving
![]() $Y_{1}\simeq 2\unicode[STIX]{x03C0}-2\sqrt{\unicode[STIX]{x03C0}X}$
. Letting
$Y_{1}\simeq 2\unicode[STIX]{x03C0}-2\sqrt{\unicode[STIX]{x03C0}X}$
. Letting
![]() $Y=2y$
and making use of
$Y=2y$
and making use of
![]() $X\ll 1$
to neglect order
$X\ll 1$
to neglect order
![]() $X^{2}$
corrections gives
$X^{2}$
corrections gives
For the
![]() $p=3$
case
$p=3$
case
 $$\begin{eqnarray}\displaystyle \int _{X}^{Y_{1}}\,\text{d}Y(1-\!\cos Y-XY)^{3/2} & \simeq & \displaystyle 4\sqrt{2}\left(\int _{X/2}^{Y_{1}/2}\,\text{d}y\sin ^{3}y-{\displaystyle \frac{3X}{2}}\int _{0}^{\unicode[STIX]{x03C0}}\,\text{d}y\,y\sin y\right)\nonumber\\ \displaystyle & \simeq & \displaystyle {\displaystyle \frac{16}{3}}\sqrt{2\,}\left(1-{\displaystyle \frac{9\unicode[STIX]{x03C0}}{8}}X+\cdots \,\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{X}^{Y_{1}}\,\text{d}Y(1-\!\cos Y-XY)^{3/2} & \simeq & \displaystyle 4\sqrt{2}\left(\int _{X/2}^{Y_{1}/2}\,\text{d}y\sin ^{3}y-{\displaystyle \frac{3X}{2}}\int _{0}^{\unicode[STIX]{x03C0}}\,\text{d}y\,y\sin y\right)\nonumber\\ \displaystyle & \simeq & \displaystyle {\displaystyle \frac{16}{3}}\sqrt{2\,}\left(1-{\displaystyle \frac{9\unicode[STIX]{x03C0}}{8}}X+\cdots \,\right).\end{eqnarray}$$
Then letting
![]() $X=(\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF})x$
and
$X=(\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF})x$
and
![]() $\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF}$
gives
$\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF}$
gives
which for
![]() $p=3$
agrees with Connor & Hastie (Reference Connor and Hastie1973) and gives
$p=3$
agrees with Connor & Hastie (Reference Connor and Hastie1973) and gives
![]() $16\unicode[STIX]{x03C0}\sqrt{2}\,\unicode[STIX]{x1D6FF}^{3/2}/3$
as the normalization coefficient.
$16\unicode[STIX]{x03C0}\sqrt{2}\,\unicode[STIX]{x1D6FF}^{3/2}/3$
as the normalization coefficient.
The case
![]() $p=1$
is more involved. We split the integral
$p=1$
is more involved. We split the integral
For the first term we use
with
![]() $C=0.916$
Catalan’s constant. For the second integral we let
$C=0.916$
Catalan’s constant. For the second integral we let
![]() $z=\unicode[STIX]{x03C0}-y$
to obtain
$z=\unicode[STIX]{x03C0}-y$
to obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\unicode[STIX]{x03C0}/2}^{Y_{1}/2}\,\text{d}y\sqrt{\sin ^{2}y-Xy}=\int _{\sqrt{\unicode[STIX]{x03C0}X}}^{\unicode[STIX]{x03C0}/2}\text{d}z\sqrt{\sin ^{2}z+X(z-\unicode[STIX]{x03C0})}\nonumber\\ \displaystyle & & \displaystyle \quad \simeq \int _{\sqrt{\unicode[STIX]{x03C0}X}}^{\unicode[STIX]{x03C0}/2}\text{d}z\sin z+{\displaystyle \frac{X}{2}}\int _{\sqrt{\unicode[STIX]{x03C0}X}}^{\unicode[STIX]{x03C0}/2}\text{d}z{\displaystyle \frac{z-\unicode[STIX]{x03C0}}{\sin z}}\simeq 1+X\left\{C+{\displaystyle \frac{\unicode[STIX]{x03C0}}{4}}\left[\ell n\left({\displaystyle \frac{\unicode[STIX]{x03C0}X}{4}}\right)-2\right]\right\}.\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\unicode[STIX]{x03C0}/2}^{Y_{1}/2}\,\text{d}y\sqrt{\sin ^{2}y-Xy}=\int _{\sqrt{\unicode[STIX]{x03C0}X}}^{\unicode[STIX]{x03C0}/2}\text{d}z\sqrt{\sin ^{2}z+X(z-\unicode[STIX]{x03C0})}\nonumber\\ \displaystyle & & \displaystyle \quad \simeq \int _{\sqrt{\unicode[STIX]{x03C0}X}}^{\unicode[STIX]{x03C0}/2}\text{d}z\sin z+{\displaystyle \frac{X}{2}}\int _{\sqrt{\unicode[STIX]{x03C0}X}}^{\unicode[STIX]{x03C0}/2}\text{d}z{\displaystyle \frac{z-\unicode[STIX]{x03C0}}{\sin z}}\simeq 1+X\left\{C+{\displaystyle \frac{\unicode[STIX]{x03C0}}{4}}\left[\ell n\left({\displaystyle \frac{\unicode[STIX]{x03C0}X}{4}}\right)-2\right]\right\}.\qquad\end{eqnarray}$$
Consequently,
Then again letting
![]() $X=(\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF})x$
we obtain
$X=(\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF})x$
we obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\text{all}}\,\text{d}\unicode[STIX]{x1D717}\sin ^{2}\unicode[STIX]{x1D703}\int _{\text{all}}\text{d}(N\unicode[STIX]{x1D701})\sqrt{[1-(B/\underset{B}{\frown })]\,}\simeq 16\sqrt{2}\,\unicode[STIX]{x1D6FF}^{1/2}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{0}^{1}{\displaystyle \frac{\text{d}x\,x^{2}}{\sqrt{1-x^{2}}}}\left\{1+{\displaystyle \frac{\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FE}x}{8}}\left[\ell n\left({\displaystyle \frac{\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FE}x}{4}}\right)-2\right]\right\}\nonumber\\ \displaystyle & & \displaystyle \quad \simeq 4\unicode[STIX]{x03C0}\sqrt{2}\,\unicode[STIX]{x1D6FF}^{1/2}\left\{1+{\displaystyle \frac{\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FE}}{3}}\left[\ell n\left({\displaystyle \frac{\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FE}}{2}}\right)-{\displaystyle \frac{17}{6}}\right]\right\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\text{all}}\,\text{d}\unicode[STIX]{x1D717}\sin ^{2}\unicode[STIX]{x1D703}\int _{\text{all}}\text{d}(N\unicode[STIX]{x1D701})\sqrt{[1-(B/\underset{B}{\frown })]\,}\simeq 16\sqrt{2}\,\unicode[STIX]{x1D6FF}^{1/2}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{0}^{1}{\displaystyle \frac{\text{d}x\,x^{2}}{\sqrt{1-x^{2}}}}\left\{1+{\displaystyle \frac{\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FE}x}{8}}\left[\ell n\left({\displaystyle \frac{\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FE}x}{4}}\right)-2\right]\right\}\nonumber\\ \displaystyle & & \displaystyle \quad \simeq 4\unicode[STIX]{x03C0}\sqrt{2}\,\unicode[STIX]{x1D6FF}^{1/2}\left\{1+{\displaystyle \frac{\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FE}}{3}}\left[\ell n\left({\displaystyle \frac{\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FE}}{2}}\right)-{\displaystyle \frac{17}{6}}\right]\right\},\end{eqnarray}$$
where we use 4.241.2 of Gradshteyn & Ryzhik (Reference Gradshteyn and Ryzhik2007),
As a result, the normalization coefficient for
![]() $p=1$
is
$p=1$
is
![]() $2\unicode[STIX]{x03C0}\sqrt{2}\,\unicode[STIX]{x1D6FF}^{1/2}$
.
$2\unicode[STIX]{x03C0}\sqrt{2}\,\unicode[STIX]{x1D6FF}^{1/2}$
.
When
![]() $\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF}\gg 1$
then
$\unicode[STIX]{x1D700}/qN\unicode[STIX]{x1D6FF}\gg 1$
then
![]() $U=\unicode[STIX]{x03C0}/2$
and we must evaluate
$U=\unicode[STIX]{x03C0}/2$
and we must evaluate
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\text{all}}\,\text{d}\unicode[STIX]{x1D717}\sin ^{2}\unicode[STIX]{x1D703}\int _{\text{all}}\text{d}(N\unicode[STIX]{x1D701})\sqrt{[1-(B/\underset{B}{\frown })]^{p}}\nonumber\\ \displaystyle & & \displaystyle \quad \simeq {\displaystyle \frac{4\unicode[STIX]{x1D6FF}^{1/2}}{\unicode[STIX]{x1D6FE}^{3}}}\int _{0}^{\unicode[STIX]{x03C0}/2}\text{d}X\cos X\sin ^{2}X\left[1+{\displaystyle \frac{\sin ^{2}X}{2\unicode[STIX]{x1D6FE}^{2}}}+\cdots \,\right]\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{X}^{Y_{1}}\,\text{d}Y[\cos X-\!\cos Y+(X-Y)\sin X]^{p/2},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\text{all}}\,\text{d}\unicode[STIX]{x1D717}\sin ^{2}\unicode[STIX]{x1D703}\int _{\text{all}}\text{d}(N\unicode[STIX]{x1D701})\sqrt{[1-(B/\underset{B}{\frown })]^{p}}\nonumber\\ \displaystyle & & \displaystyle \quad \simeq {\displaystyle \frac{4\unicode[STIX]{x1D6FF}^{1/2}}{\unicode[STIX]{x1D6FE}^{3}}}\int _{0}^{\unicode[STIX]{x03C0}/2}\text{d}X\cos X\sin ^{2}X\left[1+{\displaystyle \frac{\sin ^{2}X}{2\unicode[STIX]{x1D6FE}^{2}}}+\cdots \,\right]\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{X}^{Y_{1}}\,\text{d}Y[\cos X-\!\cos Y+(X-Y)\sin X]^{p/2},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D717}\simeq 0$
implies
$\unicode[STIX]{x1D717}\simeq 0$
implies
![]() $\sin X\simeq \unicode[STIX]{x1D6FE}\unicode[STIX]{x1D717}\leqslant 1$
. Notice that for
$\sin X\simeq \unicode[STIX]{x1D6FE}\unicode[STIX]{x1D717}\leqslant 1$
. Notice that for
![]() $X=0$
,
$X=0$
,
![]() $Y_{1}=2\unicode[STIX]{x03C0}$
(or
$Y_{1}=2\unicode[STIX]{x03C0}$
(or
![]() $N\unicode[STIX]{x1D701}=\unicode[STIX]{x03C0}$
), and for
$N\unicode[STIX]{x1D701}=\unicode[STIX]{x03C0}$
), and for
![]() $X=\unicode[STIX]{x03C0}/2$
,
$X=\unicode[STIX]{x03C0}/2$
,
![]() $Y_{1}=\unicode[STIX]{x03C0}/2$
(or
$Y_{1}=\unicode[STIX]{x03C0}/2$
(or
![]() $N\unicode[STIX]{x1D701}=-\unicode[STIX]{x03C0}/2$
); while for
$N\unicode[STIX]{x1D701}=-\unicode[STIX]{x03C0}/2$
); while for
![]() $X=0=Y$
,
$X=0=Y$
,
![]() $N\unicode[STIX]{x1D701}=-\unicode[STIX]{x03C0}$
.
$N\unicode[STIX]{x1D701}=-\unicode[STIX]{x03C0}$
.