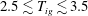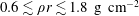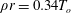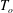1 Introduction
Operation of inertial fusion targets generally involve the implosion of a shell around deuterium–tritium (DT) gas. The imploding shell, usually composed of compressed cold DT or a high-Z material, compresses and heats the DT gas inside it to fusion ignition conditions (Atzeni & Meyer-Ter-Vehn Reference Atzeni and Meyer-Ter-Vehn2004). Much work has concerned stability of the imploding shell (Haan Reference Haan1991; Lindl Reference Lindl1995; Amendt et al. Reference Amendt, Colvin, Tipton, Hinkel, Edwards, Landen, Ramshaw, Suter, Varnum and Watt2002, Reference Amendt, Colvin, Ramshaw, Robey and Landen2003). Drive non-uniformity and surface finish can both seed hydrodynamic instability growth in the shell material. This can either disrupt the shell during implosion or generate shell–fuel mix. In the case of a high-Z shell, a perturbed shell can also result in higher radiation losses from the DT gas due to the larger exposed shell surface area. All these effects can inhibit fusion ignition.
In this paper, we investigate the stability of the igniting DT gas itself in targets with a high-Z shell surrounding a DT fuel region, also referred to here as ‘high-Z shell targets’. During implosion, the shell will launch shocks and/or acoustic waves into the DT gas, which will bounce on the origin and return to the shell. In many high-Z shell targets, the first shock sent into the DT is very strong and sets the adiabat of the DT gas, while the first rebound shock is relatively weak with a pressure jump of a factor of two to four. Subsequent waves sent through the DT gas are typically acoustic in nature and the gas is quasi-adiabatically compressed. If these waves are perturbed due to perturbations on the shell when they are launched, they can potentially re-imprint the shell. Furthermore, perturbations in the DT gas may affect the total fusion reactivity in the gas. These effects are typically not considered in one-dimensional (1-D) codes, and can be hard to fully compute in 2-D or 3-D codes due to the large material convergences of most conventional inertial confinement fusion (ICF) target designs.
Fortunately, perturbations in the DT gas are damped both by electron thermal conduction and radiation coupling when a high-Z shell is present. The damping lengths and rates depend on the density and temperature of the DT gas and perturbation wavelength. If the damping rates in a given target are large enough, non-spherical perturbations transmitted through the DT gas can be ignored when calculating shell instability. In general, strong damping in the DT gas implies that a given target is more robust to implosion asymmetry, and drives the gas to an isobaric and isothermal equilibrium ignition (Lackner et al. Reference Lackner, Colgate, Johnson, Kirkpatrick, Menikoff and Petschek1993) configuration.
To model this damping, we derive a dispersion relation for the combined process of electron thermal conduction and radiation coupling in DT gas for high-Z shell targets by implementing a perturbation analysis about a uniform background. We find radiation coupling is effective at damping low-order perturbations near ignition conditions in typical targets with high-Z shells undergoing equilibrium ignition that achieve areal densities (
$\unicode[STIX]{x1D70C}r$
) in the range
$0.6\lesssim \unicode[STIX]{x1D70C}r\lesssim 1.8~\text{g}~\text{cm}^{-2}$
at ignition. We find electron thermal conduction is very effective at damping short-wavelength perturbations. We also derive a simple constraint between temperature and areal density of DT gas that maximizes radiation damping of perturbations for the longest wavelengths that can affect implosion stability, which maximizes the robustness of the ignition process against non-uniformity. We find that for an ignition temperature of 3 keV, it is optimum for the areal density to be
$1.0~\text{g}~\text{cm}^{-2}$
.
2 Derivation of dispersion relation
The hydrodynamic equations governing DT gas are
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\boldsymbol{u}\unicode[STIX]{x1D70C})=0 & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70C}\left(\frac{\unicode[STIX]{x2202}\boldsymbol{u}}{\unicode[STIX]{x2202}t}+\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}\right)=-f\unicode[STIX]{x1D735}P & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}\unicode[STIX]{x1D700}}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\boldsymbol{u}\unicode[STIX]{x1D70C}\unicode[STIX]{x1D700})=-P\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D705}_{e}\unicode[STIX]{x1D735}T-P_{B}, & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D700}$
is the energy per unit mass of the DT gas (
$\text{keV}~\text{g}^{-1}$
),
$P_{B}$
is the bremsstrahlung power rate per unit volume (
$\text{keV}~\text{cm}^{-3}~\text{s}^{-1}$
) and
$\unicode[STIX]{x1D705}_{e}$
is the electron thermal conduction coefficient (
$1/(\text{s}~\text{cm})$
). The density
$\unicode[STIX]{x1D70C}$
is in (
$\text{g}~\text{cm}^{-3}$
) and velocity
$\boldsymbol{u}$
in (
$\text{cm}~\text{s}^{-1}$
). We assume that the DT gas is equi-molar, and that the electron and ion temperatures are uniform and equal to
$T$
(keV). We allow for the radiation temperature
$T_{p}$
, which is determined by the high-Z shell acting as a hohlraum, to be different from
$T$
. We assume that the radiation energy density and pressure are negligible at and before ignition, therefore the pressure
$P$
is equal to the sum of the ion and electron pressures,
$P=2nT$
where
$n$
is the ion number density. The factor
$f$
appearing in the momentum equation is present for unit conversion: as we have defined it
$P$
has units of (
$\text{keV}~\text{cm}^{-3}$
) and
$f=1.6022\times 10^{-9}$
converts those units to (
$\text{dynes}~\text{cm}^{-2}=\text{ergs}~\text{cm}^{-3}$
) as needed in the momentum equation. We also ignore viscosity.
The bremsstrahlung power term is written as
$$\begin{eqnarray}\displaystyle & \displaystyle P_{B}=n_{e}\unicode[STIX]{x1D708}_{B}\sqrt{\frac{m_{e}c^{2}T}{2}}I_{B}(T_{p},T) & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D708}_{B}=\frac{4}{\unicode[STIX]{x03C0}^{3/2}}\unicode[STIX]{x1D6FC}Zc\unicode[STIX]{x1D70E}_{T}n_{e} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle I_{B}(T_{p},T)=I_{B}(\unicode[STIX]{x1D6FE})=\int _{0}^{\infty }\,\text{d}\unicode[STIX]{x1D700}\text{e}^{-\unicode[STIX]{x1D700}/2}K_{o}(\unicode[STIX]{x1D700}/2)\frac{\text{e}^{\unicode[STIX]{x1D700}/\unicode[STIX]{x1D6FE}}-\text{e}^{\unicode[STIX]{x1D700}}}{\text{e}^{\unicode[STIX]{x1D700}/\unicode[STIX]{x1D6FE}}-1} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D6FE}=T_{p}/T, & \displaystyle\end{eqnarray}$$
where
$I_{B}(\unicode[STIX]{x1D6FE})$
is a dimensionless integral,
$K_{o}$
the Bessel function of the second kind order zero,
$T_{p}$
is the temperature characterizing the blackbody radiation field inside the DT gas (this temperature is set by the high-Z shell),
$\unicode[STIX]{x1D708}_{B}$
is a bremsstrahlung rate,
$\unicode[STIX]{x1D70E}_{T}$
the Thomson cross-section,
$\unicode[STIX]{x1D6FC}$
the fine structure constant and
$n_{e}=n$
the electron density. The bremsstrahlung power term assumes the DT gas is optically thin (there is no radiation conduction term here, only coupling to a hohlraum blackbody radiation field), which is generally the case in high-Z shell ICF targets at ignition conditions. The electron thermal conduction coefficient is
$$\begin{eqnarray}\unicode[STIX]{x1D705}_{e}=1.185\sqrt{\frac{2}{\unicode[STIX]{x03C0}}}\frac{c}{r_{e}^{2}Z\ln \unicode[STIX]{x1D6EC}_{ei}}\left(\frac{T}{m_{e}c^{2}}\right)^{5/2},\end{eqnarray}$$
where
$r_{e}$
is the classical electron radius and
$\ln \unicode[STIX]{x1D6EC}_{ei}$
is the Coulomb logarithm.
In linearizing the hydrodynamic equations, we take as the zero-order solution a uniform medium at temperature
$T_{o}=T_{p}$
, density
$\unicode[STIX]{x1D70C}_{o}$
(number density
$n_{o}$
), specific energy
$\unicode[STIX]{x1D700}_{o}$
and zero mean velocity
$\boldsymbol{u}_{o}=0$
. This assumption of a uniform medium is valid for high-Z shell targets igniting in equilibrium ignition near stagnation, where the mean velocity of the gas is zero. We also assume planar symmetry in calculating the dispersion relation. The first-order energy, momentum and continuity equations are
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70C}_{o}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D700}_{1}}{\unicode[STIX]{x2202}t}+P_{o}\frac{\unicode[STIX]{x2202}u_{1}}{\unicode[STIX]{x2202}x}=\unicode[STIX]{x1D705}_{\text{eo}}\frac{\unicode[STIX]{x2202}^{2}T_{1}}{\unicode[STIX]{x2202}x^{2}}-\frac{\unicode[STIX]{x2202}P_{B}}{\unicode[STIX]{x2202}T}T_{1} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70C}_{o}\frac{\unicode[STIX]{x2202}u_{1}}{\unicode[STIX]{x2202}t}=-f\frac{\unicode[STIX]{x2202}P_{1}}{\unicode[STIX]{x2202}x} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}_{1}}{\unicode[STIX]{x2202}t}=-\unicode[STIX]{x1D70C}_{o}\frac{\unicode[STIX]{x2202}u_{1}}{\unicode[STIX]{x2202}x}, & \displaystyle\end{eqnarray}$$
where we note that
$I_{B}(\unicode[STIX]{x1D6FE}=1)=0$
and
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}P_{B}}{\unicode[STIX]{x2202}T}=2.83n_{o}\unicode[STIX]{x1D708}_{B}\sqrt{\frac{m_{e}c^{2}}{2T_{o}}}\equiv n_{o}\bar{\unicode[STIX]{x1D708}}_{B} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D705}_{\text{eo}}=1.185\sqrt{\frac{2}{\unicode[STIX]{x03C0}}}\frac{c}{r_{e}^{2}Z\ln \unicode[STIX]{x1D6EC}_{ei}}\left(\frac{T_{o}}{m_{e}c^{2}}\right)^{5/2}. & \displaystyle\end{eqnarray}$$
We eliminate
$\unicode[STIX]{x1D700}_{1}$
and
$T_{1}$
in favour of
$P_{1}$
using the ideal gas equation of state
$P=R\unicode[STIX]{x1D70C}T=2nT$
,
$R=2N_{A}/2.5$
where
$N_{A}$
is Avogadro’s number,
$$\begin{eqnarray}\displaystyle & \displaystyle T_{1}=\left(P_{1}-P_{o}\frac{\unicode[STIX]{x1D70C}_{1}}{\unicode[STIX]{x1D70C}_{o}}\right)\frac{1}{R\unicode[STIX]{x1D70C}_{o}} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D700}_{1}=\frac{3}{2}\frac{P_{1}-P_{o}(\unicode[STIX]{x1D70C}_{1}/\unicode[STIX]{x1D70C}_{o})}{\unicode[STIX]{x1D70C}_{o}} & \displaystyle\end{eqnarray}$$
resulting in the first-order energy equation
$$\begin{eqnarray}n_{o}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}(3P_{1}-5P_{o}\unicode[STIX]{x1D70C}_{1}/\unicode[STIX]{x1D70C}_{o})=\left(\unicode[STIX]{x1D705}_{\text{eo}}\frac{\unicode[STIX]{x2202}^{2}}{\unicode[STIX]{x2202}x^{2}}-n_{o}\bar{\unicode[STIX]{x1D708}}_{B}\right)\left(P_{1}-P_{o}\frac{\unicode[STIX]{x1D70C}_{1}}{\unicode[STIX]{x1D70C}_{o}}\right).\end{eqnarray}$$
Assuming Fourier mode form of the first-order variables, e.g.
$\unicode[STIX]{x1D70C}_{1}=\bar{\unicode[STIX]{x1D70C}}\text{e}^{\text{i}(\unicode[STIX]{x1D714}t-kx)}$
, results in the matrix equation
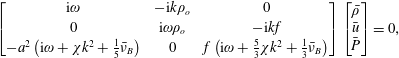$$\begin{eqnarray}\left[\begin{array}{@{}ccc@{}}\text{i}\unicode[STIX]{x1D714} & -\text{i}k\unicode[STIX]{x1D70C}_{o} & 0\\ 0 & \text{i}\unicode[STIX]{x1D714}\unicode[STIX]{x1D70C}_{o} & -\text{i}kf\\ -a^{2}\left(\text{i}\unicode[STIX]{x1D714}+\unicode[STIX]{x1D712}k^{2}+{\textstyle \frac{1}{5}}\bar{\unicode[STIX]{x1D708}}_{B}\right) & 0 & f\left(\text{i}\unicode[STIX]{x1D714}+{\textstyle \frac{5}{3}}\unicode[STIX]{x1D712}k^{2}+{\textstyle \frac{1}{3}}\bar{\unicode[STIX]{x1D708}}_{B}\right)\end{array}\right]\left[\begin{array}{@{}c@{}}\bar{\unicode[STIX]{x1D70C}}\\ \bar{u}\\ \bar{P}\end{array}\right]=0,\end{eqnarray}$$
where
$a=\sqrt{(5/3)(P_{o}\,f/\unicode[STIX]{x1D70C}_{o})}$
(
$\text{cm}~\text{s}^{-1}$
) is the adiabatic sound speed (recall
$f$
is for unit conversion from
$\text{keV}~\text{cm}^{-3}$
to
$\text{dynes}~\text{cm}^{-2}$
) and
$\unicode[STIX]{x1D712}=\unicode[STIX]{x1D705}_{\text{eo}}/5n$
is an electron conduction diffusivity. Setting the determinant to zero results in the following dispersion relation
$$\begin{eqnarray}\frac{3}{5}a^{2}\frac{k^{2}}{\unicode[STIX]{x1D714}^{2}}\left(\unicode[STIX]{x1D6FC}_{b}+5a^{2}\frac{k^{2}}{\unicode[STIX]{x1D714}^{2}}\unicode[STIX]{x1D6FC}_{e}+5\text{i}\right)-\left(\unicode[STIX]{x1D6FC}_{b}+5a^{2}\frac{k^{2}}{\unicode[STIX]{x1D714}^{2}}\unicode[STIX]{x1D6FC}_{e}+3\text{i}\right)=0,\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FC}_{e}=\unicode[STIX]{x1D714}\unicode[STIX]{x1D712}/a^{2}$
and
$\unicode[STIX]{x1D6FC}_{b}=\bar{\unicode[STIX]{x1D708}}_{B}/\unicode[STIX]{x1D714}$
are dimensionless rates for electron thermal conduction and bremsstrahlung, respectively. Solving for
$k^{2}$
and taking the positive root corresponding to damped acoustic waves (Mihalas & Weibel-Mihalas Reference Mihalas and Weibel-Mihalas1984) gives
$$\begin{eqnarray}k^{2}=\frac{\unicode[STIX]{x1D714}^{2}}{a^{2}}\frac{25\unicode[STIX]{x1D6FC}_{e}-3(5\text{i}+\unicode[STIX]{x1D6FC}_{b})+\sqrt{9(5\text{i}+\unicode[STIX]{x1D6FC}_{b})^{2}+150(\text{i}+\unicode[STIX]{x1D6FC}_{b})\unicode[STIX]{x1D6FC}_{e}+625\unicode[STIX]{x1D6FC}_{e}^{2}}}{30\unicode[STIX]{x1D6FC}_{e}}.\end{eqnarray}$$
3 Results
For dispersion relation (2.19), we assume the frequency
$\unicode[STIX]{x1D714}$
is real and wavenumber
$k=k_{r}+\text{i}k_{i}$
has real and imaginary components. The wavelength
$\unicode[STIX]{x1D706}$
of a perturbation is related to the real wavenumber component,
$\unicode[STIX]{x1D706}=2\unicode[STIX]{x03C0}/k_{r}$
. The distance over which a perturbation damps by one e-folding, also known as the attenuation length, is given by
$|1/k_{i}|$
. A dimensionless measure of the attenuation length for a given perturbation is given by the ratio of the attenuation length to wavelength of the perturbation, which is defined as
$\unicode[STIX]{x1D6EC}=|1/(\unicode[STIX]{x1D706}k_{i})|=|k_{r}/(2\unicode[STIX]{x03C0}k_{i})|$
. For a given temperature,
$\unicode[STIX]{x1D6EC}$
only depends on the combination
$\unicode[STIX]{x1D70C}\unicode[STIX]{x1D706}$
which has units of areal density, where
$\unicode[STIX]{x1D70C}$
is the density of the DT gas.
Shown in figure 1 is the dimensionless attenuation length
$\unicode[STIX]{x1D6EC}$
as a function of
$\unicode[STIX]{x1D70C}\unicode[STIX]{x1D706}$
for a temperature
$T_{o}=3$
keV in DT gas. The blue curve takes into account both electron thermal conduction and radiation coupling. The minimum at higher
$\unicode[STIX]{x1D70C}\unicode[STIX]{x1D706}$
is due to radiation coupling, and the minimum at lower
$\unicode[STIX]{x1D70C}\unicode[STIX]{x1D706}$
is due to electron thermal conduction. The black and red curves take into account only electron thermal conduction and only radiation coupling, respectively: for the black curve the limit
$\unicode[STIX]{x1D6FC}_{b}\rightarrow 0$
is taken and for the red curve the limit
$\unicode[STIX]{x1D6FC}_{e}\rightarrow 0$
is taken. The minima of
$\unicode[STIX]{x1D6EC}$
are of order unity, implying a perturbation damps significantly upon travelling one wavelength. Shown in figure 2 is the corresponding dimensionless propagation speed
$(\unicode[STIX]{x1D714}/k_{r})/a_{\text{adiabatic}}$
, where
$a_{\text{adiabatic}}=\sqrt{(5/3)(P_{o}f/\unicode[STIX]{x1D70C}_{o})}$
is the adiabatic propagation speed for
$T_{o}=3$
keV.
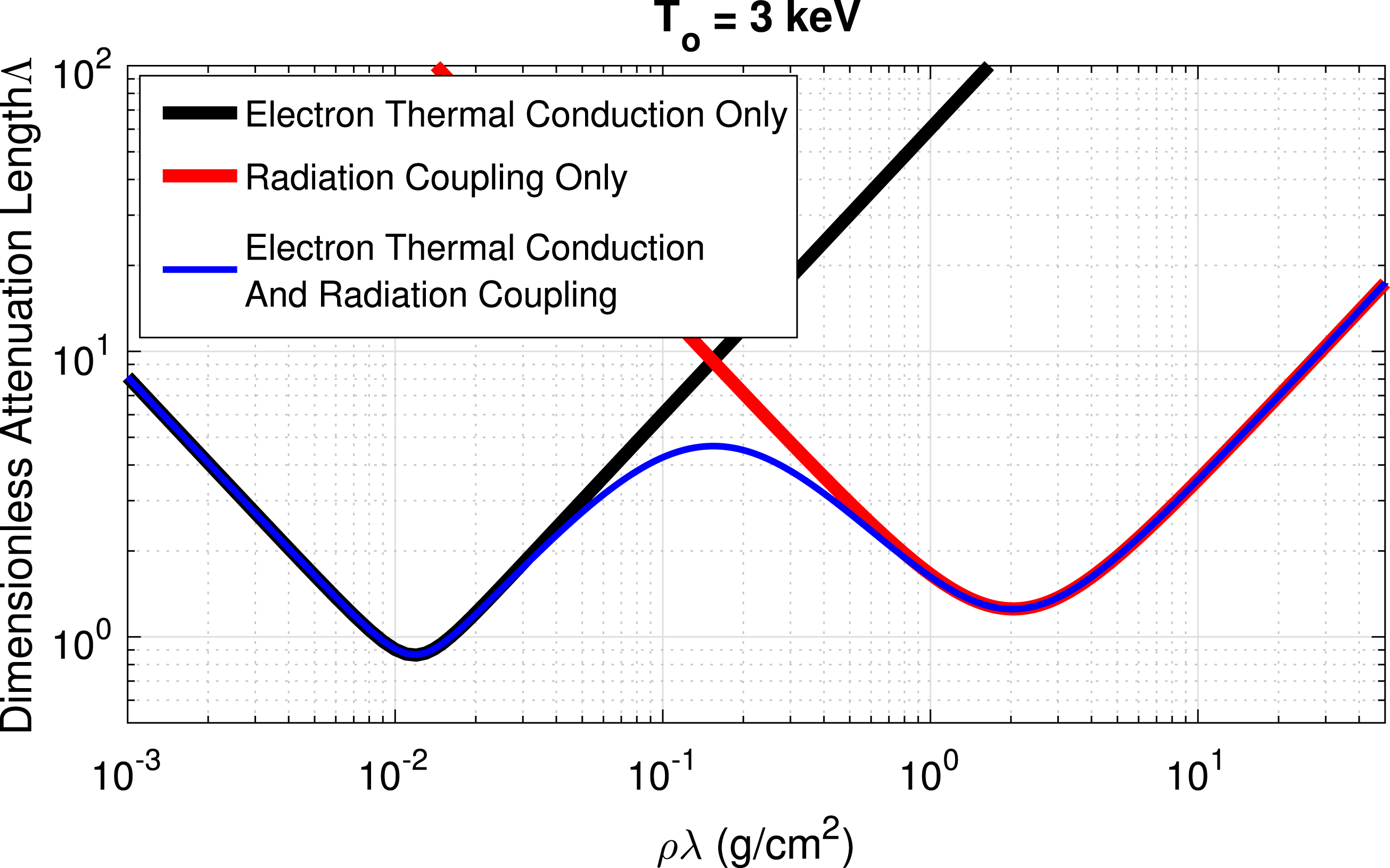
Figure 1. Shown is the dimensionless damping length
$\unicode[STIX]{x1D6EC}$
in DT gas as a function of
$\unicode[STIX]{x1D70C}\unicode[STIX]{x1D706}$
for a temperature of
$T_{o}=3$
keV, considering radiation coupling only (red curve), electron thermal conduction only (black curve) and both combined (blue curve). The minimum at higher
$\unicode[STIX]{x1D70C}\unicode[STIX]{x1D706}$
is due to radiation damping, and the minimum at lower
$\unicode[STIX]{x1D70C}\unicode[STIX]{x1D706}$
is due to electron thermal conduction. For wavelengths near the minimum perturbations are strongly damped, decaying by roughly one e-folding upon travelling the distance of one wavelength.
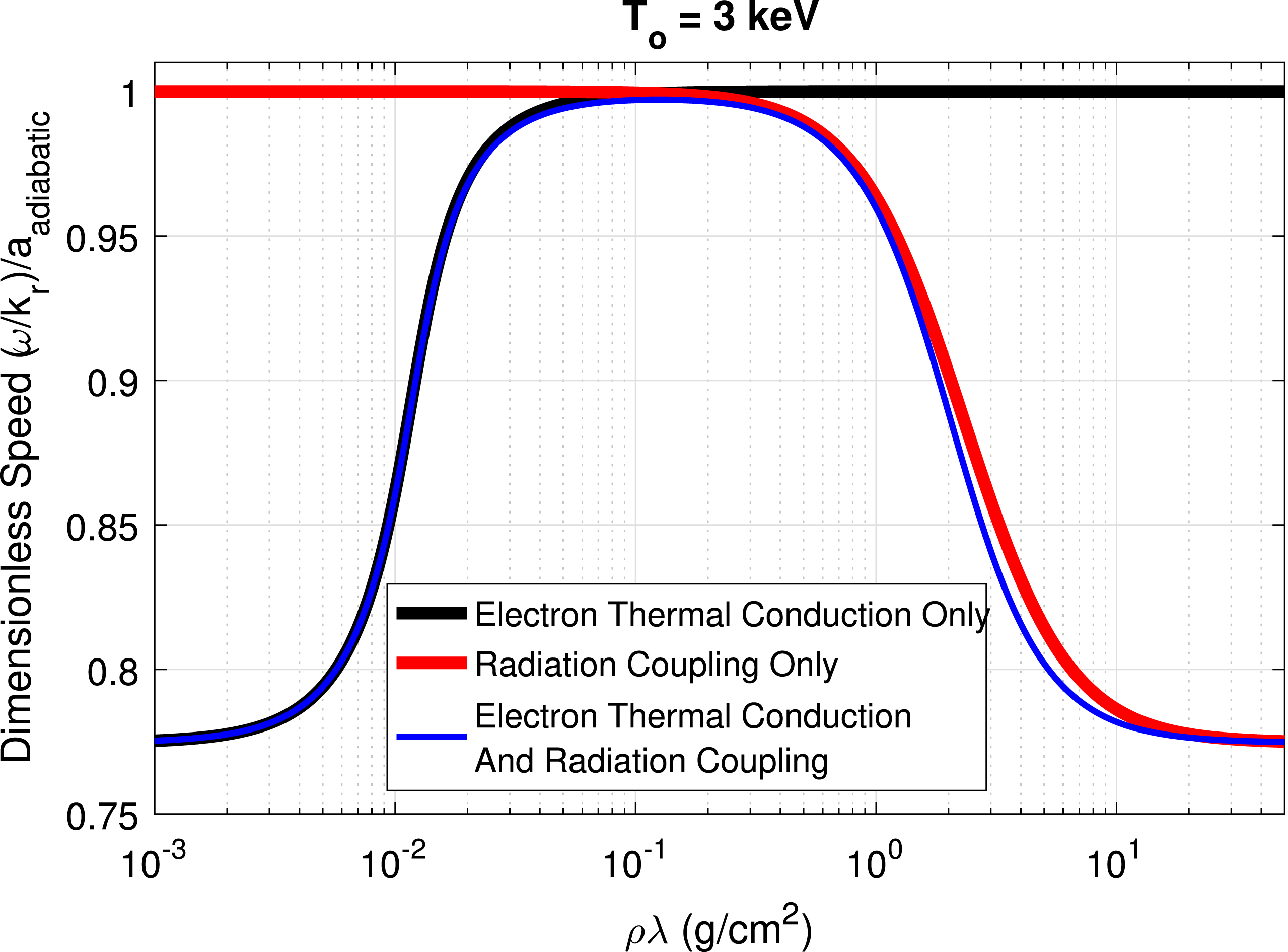
Figure 2. Shown is the dimensionless wave propagation speed as a function of
$\unicode[STIX]{x1D70C}\unicode[STIX]{x1D706}$
. For very short wavelength, electron thermal conduction is dominant and makes the fluid isothermal. For very long wavelengths, radiation coupling is dominant and also makes the fluid isothermal. Thus for very long and short wavelengths, perturbations propagate isothermally with negligible damping (
$(\unicode[STIX]{x1D714}/k_{r})/a_{\text{adiabatic}}\approx \sqrt{3/5}$
and
$k_{i}\approx 0$
). In between these two regimes are transition regions for both radiation and electron thermal conduction where the imaginary component of the wavenumber
$k_{i}$
is large, and strong damping occurs (small
$\unicode[STIX]{x1D6EC}$
).
For radiation alone (
$\unicode[STIX]{x1D6FC}_{e}\rightarrow 0$
), at very short wavelength (small
$\unicode[STIX]{x1D70C}\unicode[STIX]{x1D706}$
) the radiation coupling time is long compared to the oscillation period (
$\unicode[STIX]{x1D6FC}_{b}$
is very small). Radiation coupling has little effect and acoustic waves propagate adiabatically (
$(\unicode[STIX]{x1D714}/k_{r})/a_{\text{adiabatic}}=1$
). At very long wavelength the radiation coupling time is short compared to the oscillation period (
$\unicode[STIX]{x1D6FC}_{b}$
is very large), and radiation coupling effectively makes the gas isothermal, resulting in isothermal wave propagation (
$(\unicode[STIX]{x1D714}/k_{r})/a_{\text{adiabatic}}=\sqrt{3/5}$
). Only in between these two limits is the imaginary component of the wavenumber
$k_{i}$
significant (small
$\unicode[STIX]{x1D6EC}$
), resulting in damping.
For electron thermal conduction alone (
$\unicode[STIX]{x1D6FC}_{b}\rightarrow 0$
), at very short wavelength (small
$\unicode[STIX]{x1D70C}\unicode[STIX]{x1D706}$
) the wavenumber
$k_{r}$
is large. Since electron thermal conduction flux is proportional to
$k_{r}^{2}$
, this results in strong smoothing of temperature fluctuations, effectively making the gas isothermal. For long wavelengths,
$k_{r}^{2}$
is small, and electron thermal conduction has little effect, resulting in adiabatic wave propagation. Again, only between these two limiting cases is the imaginary component of the wavenumber
$k_{i}$
significant, resulting in damping. Maximum wave damping (small
$\unicode[STIX]{x1D6EC}$
) in general occurs at different
$\unicode[STIX]{x1D70C}\unicode[STIX]{x1D706}$
for radiation and electron thermal conduction, as can be seen in figure 1, and thus when both effects are considered simultaneously two separate minima are observed.
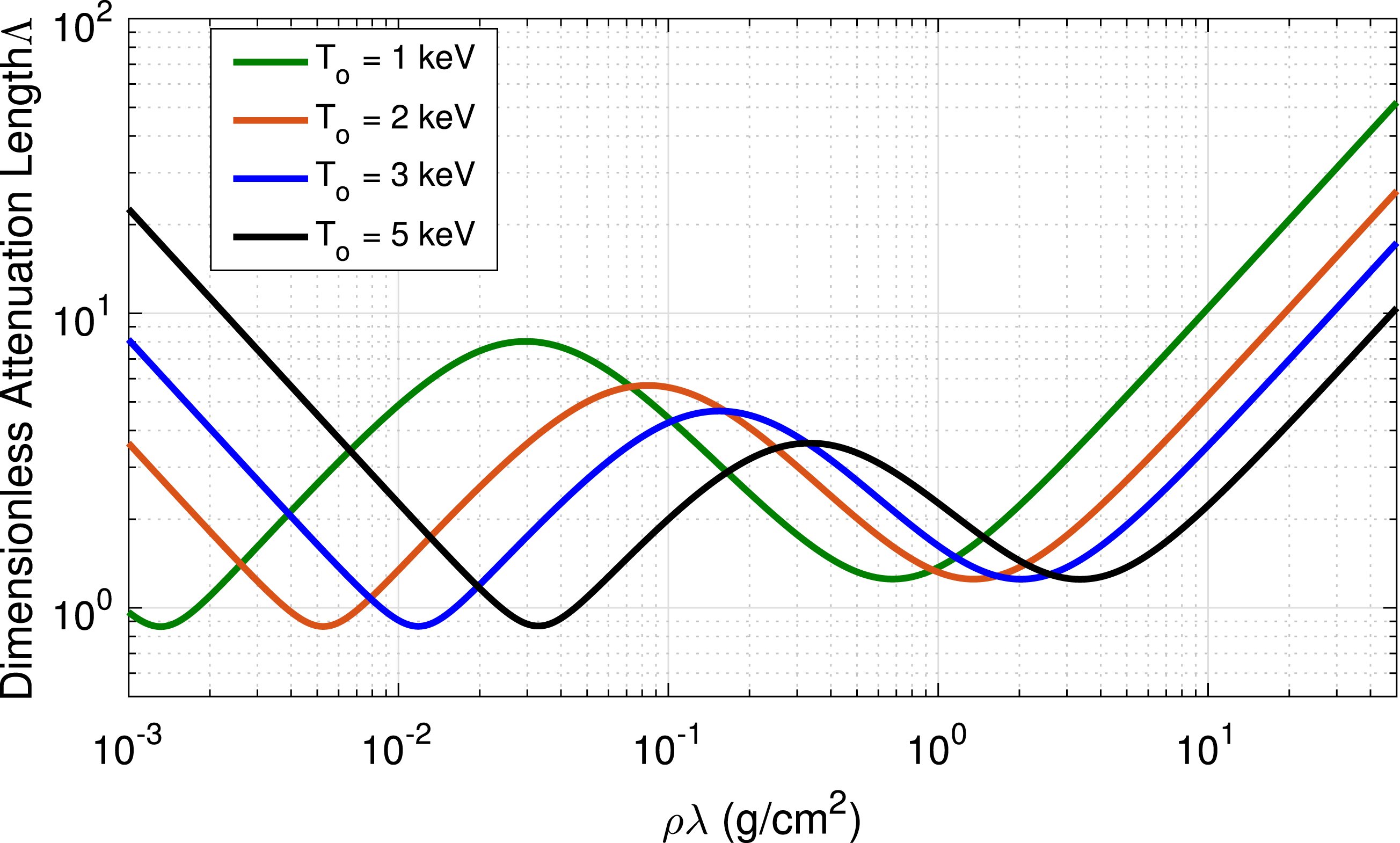
Figure 3. Shown is the dimensionless damping length
$\unicode[STIX]{x1D6EC}$
for three different temperatures in DT gas. As the temperature is increased, the minima for both electron thermal conduction and radiation coupling move to larger
$\unicode[STIX]{x1D70C}\unicode[STIX]{x1D706}$
, with temperature having a larger effect on the location of the minimum associated with electron thermal conduction. The optimum areal density range for a typical high-Z shell target with ignition temperature ranging from 2.5 to 3.5 keV is 0.6 to
$1.8~\text{g}~\text{cm}^{-2}$
. In this range, all perturbation modes in the DT gas, including long-wavelength low-order modes with
$\unicode[STIX]{x1D706}\approx 2r$
will be strongly stabilized. One can also define a path through
$T-\unicode[STIX]{x1D70C}r$
space during implosion and ignition which optimizes overall robustness against non-uniformity, given by
$\unicode[STIX]{x1D70C}r=0.34T_{o}$
, by assuming the DT areal density
$\unicode[STIX]{x1D70C}r$
is matched to the location of the minima of
$\unicode[STIX]{x1D6EC}$
associated with radiation coupling within a factor of two,
$\unicode[STIX]{x1D70C}r=\unicode[STIX]{x1D70C}\unicode[STIX]{x1D706}^{\text{min}}/2$
.
Shown in figure 3 is
$\unicode[STIX]{x1D6EC}$
as a function of
$\unicode[STIX]{x1D70C}\unicode[STIX]{x1D706}$
for four different DT gas temperatures:
$T_{o}=1$
, 2, 3 and 5 keV. One can see that increasing the temperature shifts the minima of the curve (locations of maximum damping) to larger
$\unicode[STIX]{x1D70C}\unicode[STIX]{x1D706}$
. We can analytically derive an expression for the minimum of
$\unicode[STIX]{x1D6EC}$
and associated
$\unicode[STIX]{x1D70C}\unicode[STIX]{x1D706}$
value for radiation coupling. Taking the limit
$\unicode[STIX]{x1D6FC}_{e}\rightarrow 0$
results in the dispersion relation
$$\begin{eqnarray}k^{2}=\frac{5}{3}\frac{\unicode[STIX]{x1D714}^{2}}{a^{2}}\frac{\unicode[STIX]{x1D6FC}_{b}+3\text{i}}{\unicode[STIX]{x1D6FC}_{b}+5\text{i}}.\end{eqnarray}$$
The real and imaginary wavenumber components are readily found to be
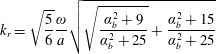$$\begin{eqnarray}\displaystyle & \displaystyle k_{r}=\sqrt{\frac{5}{6}}\frac{\unicode[STIX]{x1D714}}{a}\sqrt{\sqrt{\frac{\unicode[STIX]{x1D6FC}_{b}^{2}+9}{\unicode[STIX]{x1D6FC}_{b}^{2}+25}}+\frac{\unicode[STIX]{x1D6FC}_{b}^{2}+15}{\unicode[STIX]{x1D6FC}_{b}^{2}+25}} & \displaystyle\end{eqnarray}$$
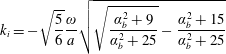$$\begin{eqnarray}\displaystyle & \displaystyle k_{i}=-\sqrt{\frac{5}{6}}\frac{\unicode[STIX]{x1D714}}{a}\sqrt{\sqrt{\frac{\unicode[STIX]{x1D6FC}_{b}^{2}+9}{\unicode[STIX]{x1D6FC}_{b}^{2}+25}}-\frac{\unicode[STIX]{x1D6FC}_{b}^{2}+15}{\unicode[STIX]{x1D6FC}_{b}^{2}+25}} & \displaystyle\end{eqnarray}$$
and the dimensionless attenuation coefficient is found to be
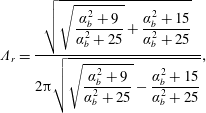$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{r}=\frac{\sqrt{\sqrt{{\displaystyle \frac{\unicode[STIX]{x1D6FC}_{b}^{2}+9}{\unicode[STIX]{x1D6FC}_{b}^{2}+25}}}+{\displaystyle \frac{\unicode[STIX]{x1D6FC}_{b}^{2}+15}{\unicode[STIX]{x1D6FC}_{b}^{2}+25}}}}{2\unicode[STIX]{x03C0}\sqrt{\sqrt{{\displaystyle \frac{\unicode[STIX]{x1D6FC}_{b}^{2}+9}{\unicode[STIX]{x1D6FC}_{b}^{2}+25}}}-{\displaystyle \frac{\unicode[STIX]{x1D6FC}_{b}^{2}+15}{\unicode[STIX]{x1D6FC}_{b}^{2}+25}}}},\end{eqnarray}$$
where the subscript
$r$
indicates the result is assuming radiation coupling only. By taking the derivative with respect to
$\unicode[STIX]{x1D6FC}_{b}$
we find
$\unicode[STIX]{x1D6EC}_{r}$
is a minimum at
$\unicode[STIX]{x1D6FC}_{b}^{\text{min}}=\sqrt{15}$
with
$\unicode[STIX]{x1D6EC}_{r}^{\text{min}}=1.253$
and
$k_{r}^{\text{min}}=1.235\sqrt{(5/6)}(\unicode[STIX]{x1D714}/a)$
. Using
$\unicode[STIX]{x1D706}^{\text{min}}=2\unicode[STIX]{x03C0}/k_{r}^{\text{min}}$
and
$\unicode[STIX]{x1D714}=\bar{\unicode[STIX]{x1D708}}_{B}/\sqrt{15}$
we find
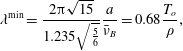$$\begin{eqnarray}\unicode[STIX]{x1D706}^{\text{min}}=\frac{2\unicode[STIX]{x03C0}\sqrt{15}}{1.235\sqrt{\frac{5}{6}}}\frac{a}{\bar{\unicode[STIX]{x1D708}}_{B}}=0.68\frac{T_{o}}{\unicode[STIX]{x1D70C}},\end{eqnarray}$$
where we have plugged in expressions for
$a$
and
$\bar{\unicode[STIX]{x1D708}}_{B}$
. Therefore, we find damping due to radiation coupling is strongest when
$$\begin{eqnarray}\unicode[STIX]{x1D70C}\unicode[STIX]{x1D706}=0.68T_{o}.\end{eqnarray}$$
4 Significance for ICF
Consider central DT gas undergoing equilibrium ignition in a high-Z shell inertial fusion target. We expect the DT gas to be most stable when low-order perturbations with wavelength equal to the diameter of the gas are as strongly damped as possible. We express this constraint by setting
$\unicode[STIX]{x1D706}=2r$
where
$r$
is the radius of the DT gas, which can also be written as
$\unicode[STIX]{x1D70C}r=\unicode[STIX]{x1D70C}\unicode[STIX]{x1D706}/2$
where we have expressed the constraint in terms of the areal density
$\unicode[STIX]{x1D70C}r$
of the DT. We then require
$\unicode[STIX]{x1D70C}\unicode[STIX]{x1D706}$
to be near
$\unicode[STIX]{x1D70C}\unicode[STIX]{x1D706}^{\text{min}}$
. When this is the case, low-order perturbations with wavelength of order the DT gas size, as well as all perturbations with shorter wavelengths, will be damped significantly (almost an e-folding) upon travelling across the DT gas.
The minimum of
$\unicode[STIX]{x1D6EC}_{r}$
is fairly broad, which means that for a broad range of
$\unicode[STIX]{x1D70C}\unicode[STIX]{x1D706}$
near
$\unicode[STIX]{x1D70C}\unicode[STIX]{x1D706}^{\text{min}}$
damping is significant. If we define
$\unicode[STIX]{x1D6EC}_{r}<1.5$
as ‘strong damping’ and assume an ignition temperature of
$T_{o}=3$
keV, then damping is strong in the range
$1.17\lesssim \unicode[STIX]{x1D70C}\unicode[STIX]{x1D706}\lesssim 3.55~\text{g}~\text{cm}^{-2}$
, which taking
$\unicode[STIX]{x1D706}=2r$
corresponds to an areal density range
$0.58\lesssim \unicode[STIX]{x1D70C}r\lesssim 1.78~\text{g}~\text{cm}^{-2}$
. It is desirable for a high-Z shell target with an ignition temperature near 3 keV to ignite with an areal density in this range.
When
$\unicode[STIX]{x1D70C}\unicode[STIX]{x1D706}=\unicode[STIX]{x1D70C}\unicode[STIX]{x1D706}^{\text{min}}$
, damping will be strongest. Utilizing (3.6) along with
$\unicode[STIX]{x1D70C}r=\unicode[STIX]{x1D70C}\unicode[STIX]{x1D706}^{\text{min}}/2$
, we arrive at the very simple formula
$$\begin{eqnarray}\unicode[STIX]{x1D70C}r=0.34T_{o},\end{eqnarray}$$
which gives the optimum value of the areal density as a function of DT gas temperature. This suggests that it is optimal to design a high-Z shell target such that (4.1) holds during the implosion and ignition of the DT gas. Many high-Z shell targets have ignition temperatures in the range of 2.5 to 3.5 keV due to radiation trapping by the high-Z shell. If we take an ignition temperature of
$T_{o}=3$
keV, this would result in an areal density at ignition of
$1.0~\text{g}~\text{cm}^{-2}$
. Achieving this areal density provides maximum robustness against implosion non-uniformity.
We also note that electron thermal conduction only contributes to stabilization of very short-wavelength modes corresponding to
$\unicode[STIX]{x1D70C}\unicode[STIX]{x1D706}\ll 0.6~\text{g}~\text{cm}^{-2}$
. One cannot match the areal density achieved in a target to the minima corresponding to electron thermal conduction (
$\unicode[STIX]{x1D70C}r$
of order
$10^{-2}~\text{g}~\text{cm}^{-2}$
), as the areal density would then be too small to effectively stop alpha particles, inhibiting bootstrap heating (Atzeni & Meyer-Ter-Vehn Reference Atzeni and Meyer-Ter-Vehn2004).
Our results can also be visualized in terms of a dimensionless damping time versus a dimensionless wavelength for specific example targets. Shown in figure 4 is the e-folding damping time of perturbations
$\unicode[STIX]{x1D70F}$
for two different high-Z shell targets normalized to the characteristic implosion time scale
$\unicode[STIX]{x1D70F}_{c}=r_{s}/v_{\text{imp}}$
, where
$r_{s}$
is the compressed fuel radius at stagnation,
$v_{\text{imp}}$
is the peak shell implosion velocity and
$T_{o}=3$
keV. The
$x$
-axis is a dimensionless perturbation wavelength
$\unicode[STIX]{x1D706}/r_{s}$
. One can see that for
$\unicode[STIX]{x1D706}=2r_{s}$
, perturbations damp by approximately one e-folding in one characteristic implosion time
$\unicode[STIX]{x1D70F}_{c}$
, with
$\unicode[STIX]{x1D70F}/\unicode[STIX]{x1D70F}_{c}$
smaller in target 1 than in target 2. All shorter wavelengths are damped more quickly. For
$\unicode[STIX]{x1D706}/r_{s}\gtrsim 0.4$
radiation is the dominant damping mechanism and electron thermal conduction has little effect. For
$\unicode[STIX]{x1D706}/r_{s}\lesssim 0.4$
electron thermal conduction begins to have an effect and further decreases the damping time for shorter wavelength. Note that damping is stronger for the target with
$\unicode[STIX]{x1D70C}r=1~\text{g}~\text{cm}^{-2}$
as compared to the target with
$\unicode[STIX]{x1D70C}r=0.75~\text{g}~\text{cm}^{-2}$
.
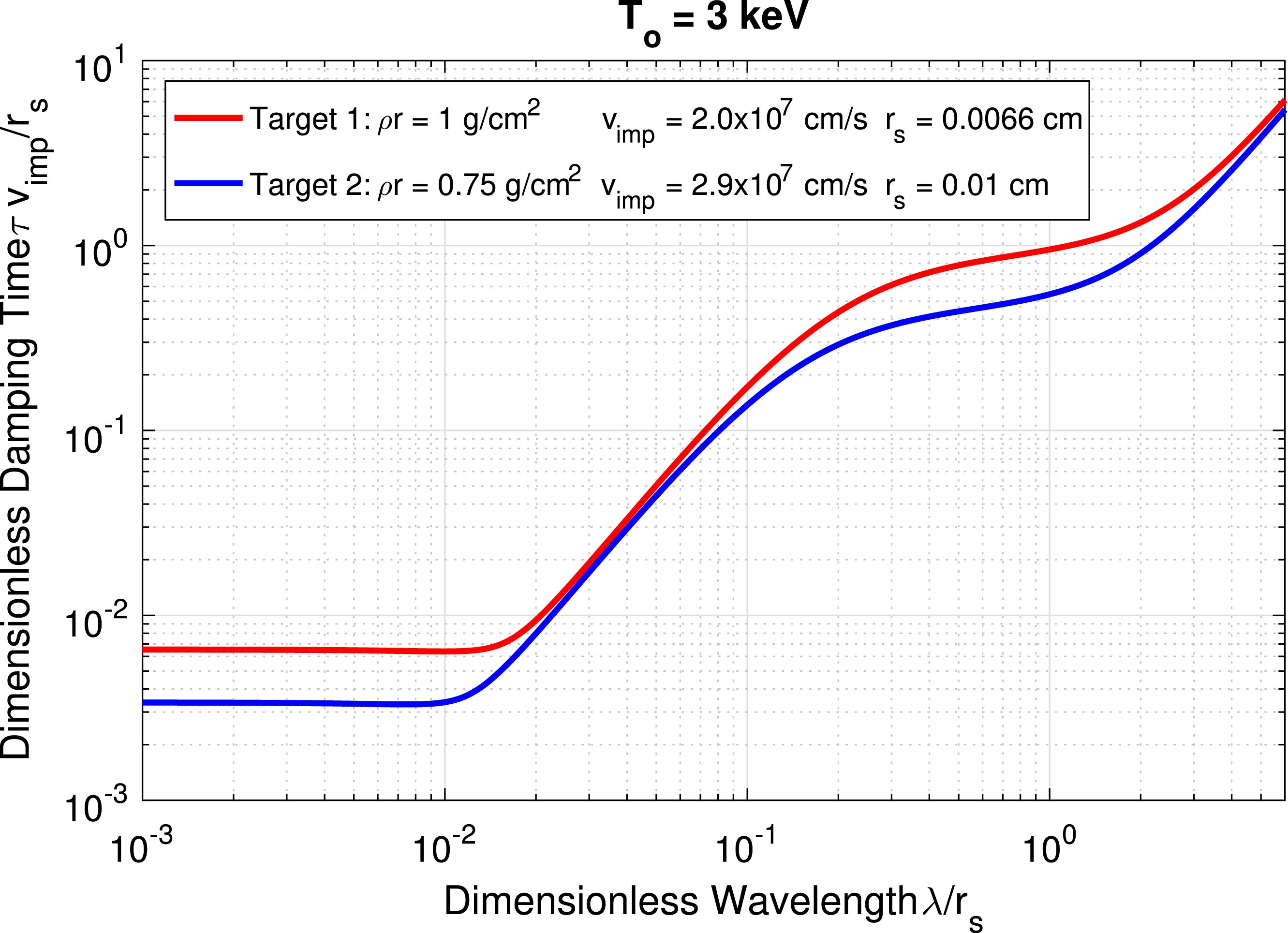
Figure 4. Shown is the dimensionless damping time
$\unicode[STIX]{x1D70F}v_{\text{imp}}/r_{s}$
versus the dimensionless perturbation wavelength
$\unicode[STIX]{x1D706}/r_{s}$
for two different example targets, where
$\unicode[STIX]{x1D70F}=k_{r}/(k_{i}\unicode[STIX]{x1D714})$
,
$v_{\text{imp}}$
is the shell peak implosion velocity,
$r_{s}$
is the shell stagnation radius and
$\unicode[STIX]{x1D70F}_{c}=r_{s}/v_{\text{imp}}$
is a characteristic shell stagnation time scale. For
$\unicode[STIX]{x1D706}=2r_{s}$
, perturbations damp by approximately one e-folding in time
$t_{c}$
, with damping stronger for target 1, which achieves larger areal density. The damping time
$\unicode[STIX]{x1D70F}$
decreases as perturbation wavelength decreases. For
$\unicode[STIX]{x1D706}/r_{s}\gtrsim 0.4$
radiation coupling is the dominant damping mechanism and electron thermal conduction has little effect. For
$\unicode[STIX]{x1D706}/r_{s}\lesssim 0.4$
electron thermal conduction begins to have an effect and further decreases the damping time for shorter wavelength. Note that both targets are within the desired areal density range of
$0.6\lesssim \unicode[STIX]{x1D70C}r\lesssim 1.8~\text{g}~\text{cm}^{-2}$
.
5 Conclusion
We have shown both radiation coupling and electron thermal conduction damp acoustic perturbations in igniting DT gas of typical high-Z shell ICF targets, and that radiation coupling is responsible for damping of low-order (long-wavelength) modes. Furthermore, we have shown that damping is significant for a broad range of areal density at typical ignition temperatures for high-Z shell targets, and models of shell stability that do not include feedback from shocks and waves launched through the DT gas are more accurate in this range.
Of note is the lower bound of
${\sim}0.6~\text{g}~\text{cm}^{-2}$
for the desired areal density of DT gas at ignition, and the optimum areal density for most high-Z shell targets of
${\sim}1~\text{g}~\text{cm}^{-2}$
. Most conventional high-Z shell targets are designed to achieve an areal density of only
${\sim}0.3~\text{g}~\text{cm}^{-2}$
in order to meet the alpha bootstrap heating requirement (Lindl Reference Lindl1995). These results suggest it may be highly advantageous to go to larger areal densities to improve target robustness to drive and implosion non-uniformity and to achieve stronger and more uniform equilibrium ignition.
In our analysis, we linearized about a uniform background solution. Thus we assumed that any acoustic waves of concern traversing the DT gas and their non-spherical perturbations are weak. Furthermore, we assumed that the background solution consisted of a uniform DT plasma with zero velocity undergoing equilibrium ignition. This assumption is only valid near stagnation when the DT is neither compressing nor expanding. Future work will consider the effect of an adiabatic compression/expansion background solution as well as the effect of radiation coupling on strong shocks with perturbations.
