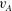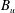1 Introduction with overview of the problem

Magnetic reconnection is a fundamental plasma process that occurs in a wide variety of laboratory, space and astrophysical plasmas. Its definition is meaningful in plasmas that are almost ideal, i.e. in those cases where magnetic field lines ‘move’ with the plasma in the vast majority of the domain, while the breaking of the magnetic field line connectivity occurs only in very localized diffusion regions. This reconnection process can enable a rapid conversion of magnetic energy into thermal, supra-thermal and bulk kinetic energy. As such, magnetic reconnection is believed to play a key role in many of the most striking and energetic phenomena such as sawtooth crashes, magnetospheric substorms, coronal mass ejections, stellar and gamma-ray flares (Tajima & Shibata Reference Tajima and Shibata1997; Kulsrud Reference Kulsrud2005; Yamada, Kulsrud & Ji Reference Yamada, Kulsrud and Ji2010).

In order to explain the magnetic energy conversion rates associated with these phenomena, it is essential to know the rate at which magnetic reconnection occurs. The reconnection rate quantifies the temporal rate of change of magnetic flux that undergoes the reconnection process. When the system under consideration is translationally invariant in one direction, the reconnection rate can be expressed as

(1.1) $$\begin{eqnarray}\frac{\text{d}\unicode[STIX]{x1D6F7}}{\text{d}t}=\frac{\text{d}}{\text{d}t}\int _{S}\boldsymbol{B}\boldsymbol{\cdot }\text{d}\boldsymbol{S}=\oint _{\unicode[STIX]{x2202}S}\boldsymbol{E}\boldsymbol{\cdot }\text{d}\boldsymbol{l}=\int _{X\text{-}line}E_{z}\,\text{d}l.\end{eqnarray}$$

Here, $\unicode[STIX]{x1D6F7}$ is the magnetic flux through the surface $S$ bounded by the contour $\unicode[STIX]{x2202}S$ encompassing the $X$ -line. An $X$ -line is the projection of an hyperbolic point for the magnetic field along the ignorable direction. Therefore, the reconnection rate is a measure of the rate at which magnetic flux is transported across the $X$ -line. In a more general three-dimensional case, the evaluation of the reconnection rate is more subtle. A general approach (Hesse, Forbes & Birn Reference Hesse, Forbes and Birn2005) would be to quantify the reconnection rate as

(1.2) $$\begin{eqnarray}\frac{\text{d}\unicode[STIX]{x1D6F7}}{\text{d}t}=\max \left(\int E_{\Vert }\,\text{d}s\right),\end{eqnarray}$$

where $s$ represents the parametrization of the magnetic field lines, and the integral has to be performed over all field lines passing through the non-ideal region (where $E_{\Vert }=\boldsymbol{E}\boldsymbol{\cdot }\boldsymbol{B}/|\boldsymbol{B}|\neq 0$ ). The measure (1.2) is an attractive choice for quantifying the reconnection rate, but there are some caveats associated with it. Indeed, there could be some ambiguity related to the field line integration of $E_{\Vert }$ , as in regions where magnetic field lines are stochastic (Borgogno et al. Reference Borgogno, Grasso, Porcelli, Califano, Pegoraro and Farina2005), or it may be not possible to distinguish between reconnection and simple diffusion (Huang, Bhattacharjee & Boozer Reference Huang, Bhattacharjee and Boozer2014). In addition, this measure can be applied only in the presence of a non-vanishing magnetic field. If this is not the case, the reconnection rate may be calculated by combining the line integrals of $E_{\Vert }$ along magnetic separators (Lau & Finn Reference Lau and Finn1990; Greene Reference Greene1998; Wilmot-Smith & Hornig Reference Wilmot-Smith and Hornig2011), which are magnetic field lines connecting two null points (i.e. points at which $|\boldsymbol{B}|=0$ ). As this brief discussion may suggest, a completely general and practical measure of the reconnection rate is still lacking, and indeed, it constitutes an important ongoing area of research (see, for example, the discussion given by Dorelli & Bhattacharjee (Reference Dorelli and Bhattacharjee2008) in the context of the Earth’s magnetosphere).

The problem of determining the reconnection rate of a magnetic reconnection process dates back to the 1950s. At that time, the astrophysical community was trying to understand if magnetic reconnection could have served as the mechanism underlying solar flares, which are bursts of high-energy radiation from the Sun’s atmosphere that strongly affect the space weather surrounding the Earth. A simple resistive magnetohydrodynamic (MHD) model of magnetic field line merging was proposed by Sweet (Reference Sweet and Lehnert1958), and then, with the contribution of Parker (Reference Parker1957), the reconnection rate was evaluated. They considered a quasi-stationary reconnection process occurring within a two-dimensional current sheet. Then, assuming an incompressible flow, the normalized reconnection rate (per unit length) can be shown to be

(1.3) $$\begin{eqnarray}\frac{1}{v_{A}B_{u}}\frac{\text{d}\unicode[STIX]{x1D6F7}}{\text{d}t}\sim S^{-1/2}(1+P_{m})^{1/4}.\end{eqnarray}$$

In this formula, $S:=v_{A}L/\unicode[STIX]{x1D702}$ and $P_{m}:=\unicode[STIX]{x1D708}/\unicode[STIX]{x1D702}$ are the Lundquist number and the magnetic Prandtl number, respectively. As usual, $\unicode[STIX]{x1D702}$ indicates the magnetic diffusivity and $\unicode[STIX]{x1D708}$ the kinematic viscosity. The Lundquist number is evaluated using the current sheet half-length $L$ and the Alfvén speed $v_{A}=B_{u}(\unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D70C})^{-1/2}$ , where $B_{u}$ is the reversing magnetic field upstream of the current sheet. In reality, equation (1.3) is not exactly the Sweet–Parker formula for the reconnection rate, but represents its generalization to account for plasma viscosity (Park, Monticello & White Reference Park, Monticello and White1984).

The Sweet–Parker model of reconnection is faster than simple diffusion, but for very large $S$ systems, such as those found in most space and astrophysical environments, it is far too slow to explain the observed fast energy release rates. In order to bypass this limitation, Petschek (Reference Petschek and Hess1964) proposed a different model in which a relatively short reconnection layer acts as a source for two pairs of slow mode shocks, allowing for much faster reconnection rates. This model was subsequently generalized by Priest & Forbes (Reference Priest and Forbes1986), who put forward a wider family of ‘almost-uniform models’ that include Petschek’s model as a special case. However, these models have not been supported by numerical simulations (Biskamp Reference Biskamp1986), which have shown that Petschek-like configurations cannot be sustained in the context of MHD with constant resistivity. Petschek’s mechanism can occur within the resistive-MHD framework if the plasma resistivity increases sharply in the reconnection layer (Kulsrud Reference Kulsrud2001, Reference Kulsrud2011), but the difficulties in firmly establishing the nature and details of such anomalous resistivity have led the scientific community to look for alternatives.

An important advance occurred when Bhattacharjee et al. (Reference Bhattacharjee, Huang, Yang and Rogers2009), and later Cassak, Shay & Drake (Reference Cassak, Shay and Drake2009), showed that the predictions of the Sweet–Parker model break down for large $S$ values because of the occurrence of the plasmoid instability (Biskamp Reference Biskamp1986; Tajima & Shibata Reference Tajima and Shibata1997; Loureiro, Schekochihin & Cowley Reference Loureiro, Schekochihin and Cowley2007; Comisso & Grasso Reference Comisso and Grasso2016; Comisso et al. Reference Comisso, Lingam, Huang and Bhattacharjee2016). In the high Lundquist number regime, the reconnection process in the nonlinear regime becomes strongly time dependent due to the continuous formation, merging and ejection of plasmoids. An estimation of the time-averaged reconnection rate in this regime was proposed by Huang & Bhattacharjee (Reference Huang and Bhattacharjee2010), as well as by Uzdensky, Loureiro & Schekochihin (Reference Uzdensky, Loureiro and Schekochihin2010), and it has been generalized to account for plasma viscosity as (Comisso, Grasso & Waelbroeck Reference Comisso, Grasso and Waelbroeck2015; Comisso & Grasso Reference Comisso and Grasso2016)

(1.4) $$\begin{eqnarray}\frac{1}{v_{A}B_{u}}\left\langle \frac{\text{d}\unicode[STIX]{x1D6F7}}{\text{d}t}\right\rangle \sim 10^{-2}(1+P_{m})^{-1/2},\end{eqnarray}$$

where $\langle \cdots \rangle$ denotes a time average. This formula shows that, for high Lundquist numbers, the (time-averaged) reconnection rate becomes independent of the Lundquist number (but not the magnetic Prandtl number) and much higher than the Sweet–Parker rate for very large $S$ -values.

Other MHD models of reconnection have also been investigated. In particular, since the pioneering work by Matthaeus & Lamkin (Reference Matthaeus and Lamkin1986), turbulence effects have been shown to produce a distribution of reconnection sites that is capable of increasing the global reconnection rate (Servidio et al. Reference Servidio, Matthaeus, Shay, Cassak and Dmitruk2009). The impact of turbulence and the plasmoid instability on the reconnection rate has caused a rethinking of magnetic reconnection in MHD plasmas. However, in many situations, the current layers that form reach scales at which two fluid/kinetic effects become important. In all these cases, an MHD description fails to reproduce accurately the physics of the reconnection process, and two-fluid and kinetic effects must be considered.

For the aforementioned reasons, a complementary path in investigating fast magnetic reconnection has been pursued at least since the 1990s by means of numerical simulations of Hall-MHD, two-fluid and kinetic models. Several research groups have shown that collisionless effects were able to strongly speed up the reconnection process (Aydemir Reference Aydemir1992; Ottaviani & Porcelli Reference Ottaviani and Porcelli1993; Wang & Bhattacharjee Reference Wang and Bhattacharjee1993; Mandt, Denton & Drake Reference Mandt, Denton and Drake1994; Biskamp, Schwarz & Drake Reference Biskamp, Schwarz and Drake1995; Kleva, Drake & Waelbroeck Reference Kleva, Drake and Waelbroeck1995; Ma & Bhattacharjee Reference Ma and Bhattacharjee1996; Grasso et al. Reference Grasso, Pegoraro, Porcelli and Califano1999; Shay et al. Reference Shay, Drake, Rogers and Denton1999; Birn et al. Reference Birn, Drake, Shay, Rogers, Denton, Hesse, Kuznetsova, Ma, Bhattacharjee and Otto2001; Porcelli et al. Reference Porcelli, Borgogno, Califano, Grasso, Ottaviani and Pegoraro2002). In particular, numerical simulations consistently demonstrated that the reconnection rate in certain collisionless regimes becomes

(1.5) $$\begin{eqnarray}\frac{1}{v_{A}B_{u}}\frac{\text{d}\unicode[STIX]{x1D6F7}}{\text{d}t}\sim 0.1,\end{eqnarray}$$

a value that is compatible with many observations and experiments (Yamada et al. Reference Yamada, Kulsrud and Ji2010), meaning that collisionless effects may be crucial to explain many magnetic reconnection phenomena. Note that even here (and in the following) we have considered the reconnection rate per unit length in the out-of-plane direction, whereas $v_{A}$ and $B_{u}$ are evaluated upstream of the ion diffusion region, which can be seen as the region where $E_{z}+(\boldsymbol{v}_{i}\times \boldsymbol{B})_{z}\neq 0$ . Although the relation (1.5) was found to be valid only in the steady-state limit, or in the vicinity of the peak reconnection rate, it was nevertheless surprising to discover that $(v_{A}B_{u})^{-1}\text{d}\unicode[STIX]{x1D6F7}/\text{d}t$ seemed to be unaffected by the microphysics and macrophysics of specific models. This intriguing result led Shay et al. (Reference Shay, Drake, Rogers and Denton1999) to speculate that the aforementioned value could be universal. Such a conjecture stimulated a long debate in the plasma physics and astrophysics communities – one that continues to this day. Is the reconnection rate value of $0.1$ truly universal? What are the physical reasons of this particular value?

In order to explain the fast reconnection rates observed in numerical simulations, Shay et al. (Reference Shay, Drake, Rogers and Denton1999) brought forward an argument by Mandt et al. (Reference Mandt, Denton and Drake1994), who proposed that fast magnetic reconnection is enabled by the presence of fast dispersive waves. These waves would speed up the reconnection process by giving rise to the development of a Petschek-type outflow configuration. In contrast, the absence of dispersive waves would lead to an extended Sweet–Parker-type layer, forcing collisionless reconnection to be slow in large systems (Rogers et al. Reference Rogers, Denton, Drake and Shay2001). This argument, however, was found not to be true. Indeed, numerical simulations have shown that fast magnetic reconnection also occurs in electron–positron plasmas, which do not support fast dispersive waves (Bessho & Bhattacharjee Reference Bessho and Bhattacharjee2005; Daughton & Karimabadi Reference Daughton and Karimabadi2007; Chacón et al. Reference Chacón, Simakov, Lukin and Zocco2008; Zenitani & Hesse Reference Zenitani and Hesse2008). More recently, Liu et al. (Reference Liu, Daughton, Karimabadi, Li and Gary2014) and Stanier et al. (Reference Stanier, Simakov, Chacón and Daughton2015) have reconsidered this argument and have shown that, in an electron–ion plasma, fast reconnection is also manifested in the strongly magnetized limit (where fast dispersive waves are suppressed) defined by $\unicode[STIX]{x1D6FD}:=2\unicode[STIX]{x1D707}_{0}n_{0}k_{B}(T_{e}+T_{i})/B^{2}\ll m_{e}/m_{i}$ and $B_{u}^{2}\ll (m_{e}/m_{i})B^{2}$ .

While several works have shown that fast dispersive waves are not required for fast magnetic reconnection, they have also confirmed that the maximum/steady-state reconnection rate satisfies (1.5) (e.g. Daughton & Karimabadi Reference Daughton and Karimabadi2007; Liu et al. Reference Liu, Daughton, Karimabadi, Li and Gary2014; Stanier et al. Reference Stanier, Simakov, Chacón and Daughton2015). There are also some works that have argued against the ${\sim}0.1$ value of the maximum/steady-state reconnection rate (e.g. Porcelli et al. Reference Porcelli, Borgogno, Califano, Grasso, Ottaviani and Pegoraro2002; Fitzpatrick Reference Fitzpatrick2004; Bhattacharjee, Germaschewski & Ng Reference Bhattacharjee, Germaschewski and Ng2005; Andrés, Dmitruk & Gómez Reference Andrés, Dmitruk and Gómez2016). In light of the subtlety of the problem, we shall elucidate the conditions under which one should expect a maximum/steady-state reconnection rate ${\sim}0.1$ . We will also present some thoughts on this apparent commonality of the reconnection rate, which still remain a mystery, and constitutes an important unsolved problem in magnetic reconnection theory. We refer to this problem as the ‘ $0.1$ problem’.

2 Thoughts on the interpretation of this problem

Hitherto, we have focused on summarizing some important discoveries and ideas that underlie the reconnection rate and the $0.1$ problem. In this section, we will present some thoughts as to how to interpret this problem.

The first important point that cannot be overlooked is that not all of the collisionless reconnection processes give rise to a peak/steady-state reconnection rate ${\sim}0.1$ . Indeed, this value is attained only if the system under consideration is strongly unstable (e.g. the tearing stability parameter $\unicode[STIX]{x1D6E5}^{\prime }$ is greater than a certain threshold) and/or forced (e.g. the externally imposed flow or magnetic perturbation exceeds a certain threshold). In the following, we will assume that this is the case. Otherwise, the reconnection rate can be arbitrarily low (e.g. Rutherford-like evolution).

In principle, there are no fundamental reasons to believe that different physical models – e.g. Hall-MHD, extended-MHD, multi-fluid, gyrofluid, hybrid, gyrokinetic, kinetic – which are characterized by different physics at the $X$ -line, should yield the same peak/steady-state reconnection rate. Indeed, one may think that the commonality of the ${\sim}0.1$ value is just a coincidence. However, if the same motif is repeated many times, that cannot be coincidence (Christie Reference Christie1936), especially when one considers all the differences inherent in the many numerical simulations that have reported this reconnection rate. In particular, it appears that:

1. (1) The steady-state reconnection rate is not linked to the microphysics of the electron diffusion region (e.g. Shay & Drake Reference Shay and Drake1998; Stanier et al. Reference Stanier, Simakov, Chacón and Daughton2015).

2. (2) The ${\sim}0.1$ value of the reconnection rate is independent of the system size (e.g. Shay et al. Reference Shay, Drake, Swisdak and Rogers2004; Comisso et al. Reference Comisso, Grasso, Waelbroeck and Borgogno2013).

3. (3) The ${\sim}0.1$ value occurs even when the field structures (e.g. current density) are very different (e.g. Liu et al. Reference Liu, Daughton, Karimabadi, Li and Gary2014; Stanier et al. Reference Stanier, Simakov, Chacón and Daughton2015).

4. (4) Three-dimensional simulations, despite exhibiting great differences in the structure of the reconnection layer, give reconnection rates similar to those of two-dimensional simulations (e.g. Daughton et al. Reference Daughton, Nakamura, Karimabadi, Roytershteyn and Loring2014; Guo et al. Reference Guo, Liu, Daughton and Li2015).

5. (5) Simulations in turbulent scenarios lead to current sheets characterized by the same reconnection rate as in the standard laminar picture (e.g. Wendel et al. Reference Wendel, Olson, Hesse, Aunai, Kuznetsova, Karimabadi, Daughton and Adrian2013; Daughton et al. Reference Daughton, Nakamura, Karimabadi, Roytershteyn and Loring2014).

To correctly interpret the aforementioned results, we argue that is necessary to shift the focus from the reconnection rate itself, and we conjecture that the reconnection rate is actually not the real ‘universal quantity’, but it is derived from a more fundamental one, the aspect ratio of the ion diffusion region $\unicode[STIX]{x1D6E5}/L$ . It is not the former that is ${\sim}0.1$ , but it is the latter which takes on this value. Then, from mass conservation in steady state, $\unicode[STIX]{x1D735}\boldsymbol{\cdot }(n\boldsymbol{v})=0$ , one obtains

(2.1) $$\begin{eqnarray}\frac{v_{in}}{v_{out}}\frac{n_{in}}{n_{out}}\sim \frac{\unicode[STIX]{x1D6E5}}{L}\sim 0.1.\end{eqnarray}$$

It is only when the flow is incompressible, $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{v}=0$ , and the outflow velocity is $v_{out}\sim v_{A}$ , that the reconnection rate turns out to be ${\sim}0.1$ . The discrepancy between the aspect ratio and the reconnection rate can become particularly evident when considering magnetic reconnection in the relativistic regime. Indeed, the inflow velocity may increase due to Lorentz contraction as per the relation $v_{in}/v_{out}\sim (\unicode[STIX]{x1D6FE}_{out}n_{out}/\unicode[STIX]{x1D6FE}_{in}n_{in})\unicode[STIX]{x1D6E5}/L$ , where $n$ is the proper particle number density and $\unicode[STIX]{x1D6FE}:=(1-v^{2}/c^{2})^{-1/2}$ . This reconnection rate enhancement has been clearly found in electron–positron plasmas, which are characterized by $\unicode[STIX]{x1D6E5}\sim L[S^{-1}(1+P_{m})^{1/2}+H^{-1}]^{1/2}$ , where $H:=f^{-1}(2L/\unicode[STIX]{x1D706}_{e})^{2}$ is the thermal–inertial number (Comisso & Asenjo Reference Comisso and Asenjo2014) and $f=K_{3}(\unicode[STIX]{x1D701})/K_{2}(\unicode[STIX]{x1D701})$ is the relativistic thermal factor ( $K_{n}$ indicates the modified Bessel function of the second kind of order $n$ and $\unicode[STIX]{x1D701}$ defines the ratio of rest-mass energy to thermal energy). Indeed, in the strictly collisionless regime, Liu et al. (Reference Liu, Guo, Daughton, Li and Hesse2015) have performed kinetic simulations that have shown an enhancement of $v_{in}/v_{out}$ consistent with the increase of $\unicode[STIX]{x1D6FE}_{in}/\unicode[STIX]{x1D6FE}_{out}$ .

There is another important point that needs to be considered. This involves an essential difference between collisional and collisionless reconnection. In collisional-MHD models, the thickness of the diffusion region depends on its length $L$ , precisely

(2.2) $$\begin{eqnarray}\frac{\unicode[STIX]{x1D6E5}}{L^{1/2}}\sim \left(\frac{\unicode[STIX]{x1D702}}{v_{A}}\right)^{1/2}(1+P_{m})^{1/4}.\end{eqnarray}$$

On the other hand, in two-fluid/kinetic collisionless models, the width of the ion diffusion region depends only on the details of the microphysics of the reconnection process:

(2.3a-d ) $$\begin{eqnarray}\unicode[STIX]{x1D6E5}\sim \unicode[STIX]{x1D70C}_{se}=\frac{c_{se}}{\unicode[STIX]{x1D714}_{ci}},\quad \unicode[STIX]{x1D70C}_{s}=\frac{c_{s}}{\unicode[STIX]{x1D714}_{ci}},\quad \unicode[STIX]{x1D706}_{i}=\frac{c}{\unicode[STIX]{x1D714}_{pi}},\quad \unicode[STIX]{x1D706}_{e}=\frac{c}{\unicode[STIX]{x1D714}_{pe}},\ldots .\end{eqnarray}$$

This width is associated with very different length scales, such as the cold ion sound Larmor radius $\unicode[STIX]{x1D70C}_{se}$ , the ion sound Larmor radius $\unicode[STIX]{x1D70C}_{s}$ , the ion skin depth $\unicode[STIX]{x1D706}_{i}$ , the positron/electron skin depth $\unicode[STIX]{x1D706}_{e}$ , etc. Therefore, if $\unicode[STIX]{x1D6E5}/L\sim 0.1$ holds true for all the different two-fluid/kinetic models, it means that $L$ self-adjusts in such a way to match the observed aspect ratio.

Given the above refocusing observations, the key question of the $0.1$ problem shifts to: why does the ion diffusion region self-adjust in such a way that the length obeys $L\sim 10\unicode[STIX]{x1D6E5}$ ?

Here, without intending to furnish a solution to this problem, we provide qualitative arguments to illustrate why $L$ cannot be significantly different from $10\unicode[STIX]{x1D6E5}$ . This can be shown heuristically in the following manner. Let us start by assuming $L=\unicode[STIX]{x1D6E5}$ and examine its validity. This limit has been studied extensively in the past (e.g. Priest Reference Priest, Kundu and Holman1985; Priest & Forbes Reference Priest and Forbes2000) and is relevant to the solution of the $0.1$ problem (e.g. P. A. Cassak and M. A. Shay, private communication, 2016). In this instance, it is possible to demonstrate that the reconnection rate vanishes in a plasma. To this purpose, one can exploit the symmetries of the problem, which dictate that

(2.4a,b ) $$\begin{eqnarray}v_{x}(\pm x,\mp y)=\pm v_{x}(x,y),\quad v_{y}(\pm x,\mp y)=\mp v_{y}(x,y),\end{eqnarray}$$

(2.5a,b ) $$\begin{eqnarray}B_{x}(\pm x,\mp y)=\mp B_{x}(x,y),\quad B_{y}(\pm x,\mp y)=\pm B_{y}(x,y),\end{eqnarray}$$

if the reconnection occurs at a symmetric $X$ -point configuration, with the $X$ -point situated at the origin. Combining the above properties with the fact that the reconnection rate for $L=\unicode[STIX]{x1D6E5}$ must be invariant under a point reflection of the velocity field

(2.6) $$\begin{eqnarray}(v_{x},v_{y},B_{x},B_{y})\mapsto (-v_{x},-v_{y},B_{x},B_{y}),\end{eqnarray}$$

it follows that the only possible solution is $v_{in}=v_{out}=0$ . This implies that the reconnection process chokes itself off if $L=\unicode[STIX]{x1D6E5}$ . It is straightforward to check that a steady reconnection process is also not possible for $L<\unicode[STIX]{x1D6E5}$ . Indeed, in this case, the current density at the $X$ -point would act to decrease the inflow velocity.

Next, we consider the case $L>\unicode[STIX]{x1D709}\unicode[STIX]{x1D6E5}$ , where $\unicode[STIX]{x1D709}\gg 1$ represents a coefficient that will be discussed soon. If a current sheet remains stable over time for arbitrarily large $\unicode[STIX]{x1D709}$ , the possibility of obtaining a fast reconnection rate ${\sim}0.1$ would be precluded. However, extended current sheets are subject to a tearing-like (plasmoid) instability (Comisso et al. Reference Comisso, Lingam, Huang and Bhattacharjee2016). This implies that for $\unicode[STIX]{x1D709}>\unicode[STIX]{x1D709}_{c}$ , with $\unicode[STIX]{x1D709}_{c}$ indicating a critical threshold value, the global current sheet breaks up and is replaced by a chain of plasmoids/flux ropes of different sizes separated by smaller current sheets (Shibata & Tanuma Reference Shibata and Tanuma2001).

In a reconnection layer dominated by the presence of plasmoids, the complexity of the dynamics gives rise to a strongly time-dependent process (e.g. Daughton et al. Reference Daughton, Roytershteyn, Albright, Karimabadi, Yin and Bowers2009). Nevertheless, if this process can reach a statistical steady state, we may expect that the current sheet located at the main $X$ -point, which is the one that determines the global reconnection rate, should not be longer than the marginally stable sheet (Huang & Bhattacharjee Reference Huang and Bhattacharjee2010; Uzdensky et al. Reference Uzdensky, Loureiro and Schekochihin2010; Comisso et al. Reference Comisso, Grasso and Waelbroeck2015; Comisso & Grasso Reference Comisso and Grasso2016). Indeed, the fractal cascade arising from the plasmoid instability terminates when the length of the innermost local current layer is shorter than the critical length $L_{c}=\unicode[STIX]{x1D709}_{c}\unicode[STIX]{x1D6E5}$ . The local current sheet situated at the primary $X$ -point could be subjected to continual stretching by plasmoids moving in the outflow direction, but the plasmoid instability occurs if its length exceeds $L_{c}$ . Thus, it is reasonable to assume that the length of the local current sheet at the main $X$ -point should not exceed $L_{c}$ . As a consequence, the length of the main diffusion region remains bounded from above, but a clear-cut value of $\unicode[STIX]{x1D709}_{c}$ remains unknown. Although at present there are no analytical estimates of the aspect ratio of the main diffusion region, numerical simulations have found $\unicode[STIX]{x1D709}_{c}\sim 50$ in the collisionless regime (Daughton, Scudder & Karimabadi Reference Daughton, Scudder and Karimabadi2006; Ji & Daughton Reference Ji and Daughton2011).

According to the above arguments, it is clear that the length of the ion diffusion region that determines the reconnection rate is bounded from above and below as $\unicode[STIX]{x1D6E5}<L\lesssim 50\unicode[STIX]{x1D6E5}$ in a quasi-steady (or statistical steady state) strongly driven/unstable collisionless reconnection process.

3 Final remarks

We have seen that the maximum/steady-state reconnection rate is regulated by the length of the ion diffusion region. However, so far we have not stressed the importance of the boundary conditions on the diffusion region length. Boundary condition may indeed have a strong impact on the length of the current sheets if the computational domain is not sufficiently large. Therefore, the choice of the boundary conditions require extra caution. For example, periodic boundary conditions in computational domains that are not sufficiently large may force the length of a current sheet to remain small, limiting the duration in which the results are physically meaningful (Daughton et al. Reference Daughton, Scudder and Karimabadi2006).

The knowledge of the maximum/steady-state reconnection rate is crucial when trying to understand whether magnetic reconnection can be fast enough to account for the energy release time scales observed in a specific system. This is because most of the magnetic flux reconnection takes place during this stage of the process. It is therefore not surprising that much of the magnetic reconnection research done to date has focused on this issue. However, we wish to end our discussion by noting that there are other important questions that lie beyond the paradigm of the maximum/steady-state reconnection rate. While this observable could be insensitive to many features of the specific model, the reconnection rate evolution is not. Indeed, it can be extremely different in diverse systems, since the initial evolution of any reconnection process depends on the details of the microphysics as well as the large-scale ideal-MHD conditions. This initial (typically linear) stage could be completely negligible in terms of magnetic flux reconnection, but it is crucial for determining whether a particular system has enough time to accumulate the magnetic energy that is mostly liberated during the faster stage of the reconnection process. This issue, which is commonly referred to as the onset problem, is also an important and active area of research.