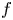1. Introduction
Charged particles in a plasma interact with each other through the long-range Coulomb collisions and, in a particle-in-cell simulation, these interactions can be modelled with the so-called binary-collision methods. The two widely used schemes are by Takizuka & Abe (Reference Takizuka and Abe1977) and by Nanbu (Reference Nanbu1997). If equal particle weights are used, both these methods preserve kinetic momentum and energy in local homogeneous simulations, which explains the popularity of these two schemes. Also, the convergence properties of the methods are well established. In Wang et al. (Reference Wang, Lin, Caflisch, Cohen and Dimits2008), collisional relaxation rates from these models are evaluated in a spatially homogeneous plasma with no electric field or magnetic fields and the accuracy of the methods is compared as a function of time step and number of test particles per cell showing an $O(\sqrt {\varDelta t})$![]() dependency for the accuracy of electron–electron collisions while including electron–ion collisions was independent of $\varDelta t$
dependency for the accuracy of electron–electron collisions while including electron–ion collisions was independent of $\varDelta t$![]() . Nanbu's method was further tested by Dimits et al. (Reference Dimits, Wang, Caflisch, Cohen and Huang2009), but again excluding fields. In global simulations, including configuration-space effects, the conservation properties generally depend on time step, number of test particles, particle sampling method, interpolation schemes and implementation of electromagnetic fields as well. The account of these effects is less established.
. Nanbu's method was further tested by Dimits et al. (Reference Dimits, Wang, Caflisch, Cohen and Huang2009), but again excluding fields. In global simulations, including configuration-space effects, the conservation properties generally depend on time step, number of test particles, particle sampling method, interpolation schemes and implementation of electromagnetic fields as well. The account of these effects is less established.
The importance of momentum and energy conservation itself depends on what quantity one is interested in, the time scale of the simulations (compared with collision time) and, also, the relative importance of the collisions compared with, for example, turbulent effects and particle noise. In Kiviniemi, Heikkinen & Peeters (Reference Kiviniemi, Heikkinen and Peeters2000), a momentum-conserving binary-collision model and a test-particle collision model were compared in the case of an externally induced radial field. Starting from zero parallel flow, it was shown that both methods give initially the same radial particle flux. After that the parallel velocity starts to develop in the momentum-conserving case and the flux decays. Since the development of parallel flow is a slower process than the changes in the mean radial electric field $\left \langle E_r\right \rangle$![]() , it is also possible to simulate a quasi-steady state of $E_r$
, it is also possible to simulate a quasi-steady state of $E_r$![]() in order to investigate the accuracy of neoclassical analytic estimates as a function of gradient scale lengths, as done in Kiviniemi, Heikkinen & Peeters (Reference Kiviniemi, Heikkinen and Peeters2002). Violation of momentum conservation in numerical realizations can be mitigated, for example, by forcing the curl of electric field $\boldsymbol{E}$
in order to investigate the accuracy of neoclassical analytic estimates as a function of gradient scale lengths, as done in Kiviniemi, Heikkinen & Peeters (Reference Kiviniemi, Heikkinen and Peeters2002). Violation of momentum conservation in numerical realizations can be mitigated, for example, by forcing the curl of electric field $\boldsymbol{E}$![]() to zero with small adjustments in the radial component $E_r$
to zero with small adjustments in the radial component $E_r$![]() (Heikkinen et al. Reference Heikkinen, Korpilo, Janhunen, Kiviniemi, Leerink and Ogando2012). Finally, if also magnetic fluctuations are included in the simulation model, they contribute to both the conserved toroidal angular momentum and the energy (see, e.g. Hirvijoki et al. Reference Hirvijoki, Burby, Pfefferlé and Brizard2020). Consequently, the binary-collision models should be considered in conjunction with the invariants of the collisionless dynamics.
(Heikkinen et al. Reference Heikkinen, Korpilo, Janhunen, Kiviniemi, Leerink and Ogando2012). Finally, if also magnetic fluctuations are included in the simulation model, they contribute to both the conserved toroidal angular momentum and the energy (see, e.g. Hirvijoki et al. Reference Hirvijoki, Burby, Pfefferlé and Brizard2020). Consequently, the binary-collision models should be considered in conjunction with the invariants of the collisionless dynamics.
In this work, we first take a look at the conventional conserved quantities and, as an example, demonstrate how even these can be inaccurate if the collision cell is too wide compared with the gradient scale length. After that we briefly discuss the conserved quantities in a drift-kinetic electromagnetic model, and propose how the accuracy of the conservation properties could potentially be improved while still using the standard binary-collision model.
2. Classic binary-collisions model
In performing particle-in-cell simulations and using the widely used binary-collision models (Takizuka & Abe Reference Takizuka and Abe1977; Nanbu Reference Nanbu1997), collisional effects are naturally implemented so that they only change those parts of momentum and energy that directly depend on the particle distribution function. For example, in the 6-D Vlasov–Maxwell model, the fields $\boldsymbol{E}$![]() and $\boldsymbol{B}$
and $\boldsymbol{B}$![]() are kept fixed during the collisional step. Correspondingly, the global functionals
are kept fixed during the collisional step. Correspondingly, the global functionals
should remain constant during the collisional step. Here, $m_s$![]() and $F_s$
and $F_s$![]() are the mass and distribution function of species $s$
are the mass and distribution function of species $s$![]() , and $\boldsymbol{x}$
, and $\boldsymbol{x}$![]() and $\boldsymbol{v}$
and $\boldsymbol{v}$![]() are the location of particle in configuration and velocity space, respectively.
are the location of particle in configuration and velocity space, respectively.
In a binary-collision algorithm with equal particle weights, implementing this strategy amounts to requiring that the kinetic energy and momentum are conserved in a pairwise collision between the particles $p_1$![]() and $p_2$
and $p_2$![]() . Effectively, one requires that the following conditions are met:
. Effectively, one requires that the following conditions are met:
where $t_{n+1} = t_n + \varDelta t$![]() and $\varDelta t$
and $\varDelta t$![]() is the time step. While convergence of these methods as a function of time step and number of test particles per cell has been demonstrated in homogeneous backgrounds (Wang et al. Reference Wang, Lin, Caflisch, Cohen and Dimits2008), we will next show that, even in the absence of fluctuating fields, these methods can be inaccurate if the background profiles change significantly within one collision cell.
is the time step. While convergence of these methods as a function of time step and number of test particles per cell has been demonstrated in homogeneous backgrounds (Wang et al. Reference Wang, Lin, Caflisch, Cohen and Dimits2008), we will next show that, even in the absence of fluctuating fields, these methods can be inaccurate if the background profiles change significantly within one collision cell.
2.1. Effect of collision-cell width on the accuracy of binary-collision models
In axisymmetric tokamak geometry, the conservation of toroidal angular momentum is important to properly describe neoclassical and turbulent transport of particles and heat. In Kiviniemi et al. (Reference Kiviniemi, Heikkinen and Peeters2002), the effect of steep gradients on the accuracy of neoclassical analytic estimates was tested but not the effect of the size of the collision cell with respect to the gradient length scale of the background. Here, this effect is tested using the full-$f$![]() particle-in-cell code ELMFIRE (Korpilo et al. Reference Korpilo, Gurchenko, Gusakov, Heikkinen, Janhunen, Kiviniemi, Leerink, Niskala and Perevalov2016), running it in neoclassical mode and computing the bootstrap current similarly as in Kiviniemi et al. (Reference Kiviniemi, Leerink, Niskala, Heikkinen, Korpilo and Janhunen2014). To investigate the effect of the number of collision cells on the simulation accuracy and the numerical precision of the results, the number of cells, $N_{cells} = N \times N$
particle-in-cell code ELMFIRE (Korpilo et al. Reference Korpilo, Gurchenko, Gusakov, Heikkinen, Janhunen, Kiviniemi, Leerink, Niskala and Perevalov2016), running it in neoclassical mode and computing the bootstrap current similarly as in Kiviniemi et al. (Reference Kiviniemi, Leerink, Niskala, Heikkinen, Korpilo and Janhunen2014). To investigate the effect of the number of collision cells on the simulation accuracy and the numerical precision of the results, the number of cells, $N_{cells} = N \times N$![]() , was varied in a scan as $N = 30$
, was varied in a scan as $N = 30$![]() , 100, 200, 300, 450 (see figure 1). The important relation in such study is the relation between the cell width and the gradient scale lengths but since the bootstrap current itself heavily depends on the profiles we keep gradient scale lengths fixed as $L_n = L_T = 0.06$
, 100, 200, 300, 450 (see figure 1). The important relation in such study is the relation between the cell width and the gradient scale lengths but since the bootstrap current itself heavily depends on the profiles we keep gradient scale lengths fixed as $L_n = L_T = 0.06$![]() m. The simulation domain was thus partitioned in $N$
m. The simulation domain was thus partitioned in $N$![]() uniformly distributed collision cells in both radial and poloidal directions. The total number of particles was kept fixed between the simulations. For the case $N = 450$
uniformly distributed collision cells in both radial and poloidal directions. The total number of particles was kept fixed between the simulations. For the case $N = 450$![]() the number of particles per cell is approximately 300 on average, which is sufficiently high for convergence of the collisional rates (Wang et al. Reference Wang, Lin, Caflisch, Cohen and Dimits2008).
the number of particles per cell is approximately 300 on average, which is sufficiently high for convergence of the collisional rates (Wang et al. Reference Wang, Lin, Caflisch, Cohen and Dimits2008).

Figure 1. Scan of bootstrap current $j_{bs}$![]() as a function of normalized binary-collision cell size, $\varDelta r/L_T$
as a function of normalized binary-collision cell size, $\varDelta r/L_T$![]() . The $j_{bs}$
. The $j_{bs}$![]() values are collected from the maximum current density location, and the error bars represent one standard deviation around the mean value and compared with analytic estimates of Sauter and Hager. The ion part of the total current is shown with stars. Here $\varDelta r$
values are collected from the maximum current density location, and the error bars represent one standard deviation around the mean value and compared with analytic estimates of Sauter and Hager. The ion part of the total current is shown with stars. Here $\varDelta r$![]() is the collision cell width in the radial direction and $L_T = 0.06$
is the collision cell width in the radial direction and $L_T = 0.06$![]() m is the temperature gradient scale length in the middle of the pedestal.
m is the temperature gradient scale length in the middle of the pedestal.
The formation of bootstrap current is a two-step process where, at first, the ion current results from orbit topologies. As a second step, this ion current is transferred to electrons via collisions. Both of these steps can be affected by the cell width but, as seen in figure 1, the ion current is small compared with total current and is not significantly affected by the number of cells. Thus, collisions are mostly responsible for the cell-width effect. For the total current, increasing the number of binary-collision cells improved the quantitative agreement between the converged ELMFIRE simulation result and the analytical estimates of Sauter, Angioni & Lin-Liu (Reference Sauter, Angioni and Lin-Liu1999) and Hager & Chang (Reference Hager and Chang2016). With $300 \times 300$![]() collision cells, the simulated mean bootstrap current density is within 3 % from both theoretical predictions. Adding more collision cells did not notably change the result, but with fewer cells, ELMFIRE predicts distinctly lower $j_{bs}$
collision cells, the simulated mean bootstrap current density is within 3 % from both theoretical predictions. Adding more collision cells did not notably change the result, but with fewer cells, ELMFIRE predicts distinctly lower $j_{bs}$![]() values. The two cases with the sparsest grids remain well below their corresponding analytical estimates, the relative difference for both is around 20 %. The simulated $j_{bs}$
values. The two cases with the sparsest grids remain well below their corresponding analytical estimates, the relative difference for both is around 20 %. The simulated $j_{bs}$![]() experiences strong temporal fluctuations which produce significant uncertainties. The error bars in figure 1 illustrate one standard deviation from the mean and their size does not change when the number of collision cells is altered.
experiences strong temporal fluctuations which produce significant uncertainties. The error bars in figure 1 illustrate one standard deviation from the mean and their size does not change when the number of collision cells is altered.
Part of this puzzle is that the particles are paired for collisions from finite sized neighbourhoods, the extent of which is determined by the number of collision cells used. The denser the grid is, the smaller the volume one cell covers. The binary-collision operator used in ELMFIRE assumes that the plasma background properties stay similar within each of these collision cells. Most importantly the background density and temperature should not vary substantially over one collision cell as the collision frequency which determines the scattering angle in the binary-collision model depends directly on background temperature through the Coulomb logarithm but also implicitly through the statistical increase in relative velocity as the average velocities of particles are significantly different in the inner and outer side of the collision cell. In addition, it is also directly proportional to density. During a simulation, the particle density is sampled to the simulation grid, and thus, the density considered in the collisions is fixed in each of the spatial grid cells. The smallest studied collision grid had size $30 \times 30$![]() which is sparser than the $50 \times 50$
which is sparser than the $50 \times 50$![]() grid describing the density background in the radial and poloidal directions, violating the assumption for the collision operator. For the larger collision grids tested in the scan, the resolution for the density is no longer a limiting factor, but accurate enough temperature resolution is also required.
grid describing the density background in the radial and poloidal directions, violating the assumption for the collision operator. For the larger collision grids tested in the scan, the resolution for the density is no longer a limiting factor, but accurate enough temperature resolution is also required.
The plasma temperature profile determines the speeds of individual particles. In particular, across a steep pedestal, the temperature changes abruptly and so do the velocities of the particles in that region. When particles collide, their relative velocity is scattered and new velocities for both particles are calculated from the result. The collision process inevitably introduces non-locality in the updated particle velocities because the colliding particles are paired at random within a collision cell. The random pairing is an approximation compared with true collisions but is often considered sufficient in simulation. However, depending on the used grid size, the particles can have significant distance between each other. Even if at the continuous level the Landau operator is local and describes Coulomb collisions at a resolution comparable to that of the Debye length – the effective distance beyond which the interaction is screened – practical implementations in kinetic simulations of fusion plasmas rarely are able to resolve this distance.
The differences observed between the studied simulation cases could result, for example, from the introduced finite spatial sampling of the background temperature. The thermal speed of the particles relate to temperature through the equation for $v_{th} = \sqrt {2T /m}$![]() , and the change of average temperature within a collision cell with radial width $\varDelta r$
, and the change of average temperature within a collision cell with radial width $\varDelta r$![]() can be approximated by $\varDelta r \partial _r T = (\varDelta r/L_T)T$
can be approximated by $\varDelta r \partial _r T = (\varDelta r/L_T)T$![]() with $L_T$
with $L_T$![]() the temperature gradient length scale. Inside a cell of the sparsest studied collision grid, the difference in temperature $\varDelta r/L_T$
the temperature gradient length scale. Inside a cell of the sparsest studied collision grid, the difference in temperature $\varDelta r/L_T$![]() can be around 10 % when $L_T = 0.06$
can be around 10 % when $L_T = 0.06$![]() m, which at the very high temperatures involved becomes significant. In contrast, with a grid size $300 \times 300$
m, which at the very high temperatures involved becomes significant. In contrast, with a grid size $300 \times 300$![]() , the difference is less than 1 %. Since the collision frequency is a function of the plasma temperature, one can expect a direct effect from not resolving the temperature accurately enough. Finally, numerical estimation of the bootstrap current requires accurate modelling of parallel flow velocity and, in the ELMFIRE simulations, the average parallel velocity of a particle species is sampled from the individual particle velocities which allows small inaccuracies to accumulate. Therefore, more accurate description of the velocity distribution obtained with denser collision grids is likely to improve the simulated bootstrap current $j_{bs}$
, the difference is less than 1 %. Since the collision frequency is a function of the plasma temperature, one can expect a direct effect from not resolving the temperature accurately enough. Finally, numerical estimation of the bootstrap current requires accurate modelling of parallel flow velocity and, in the ELMFIRE simulations, the average parallel velocity of a particle species is sampled from the individual particle velocities which allows small inaccuracies to accumulate. Therefore, more accurate description of the velocity distribution obtained with denser collision grids is likely to improve the simulated bootstrap current $j_{bs}$![]() .
.
3. Conserved quantities in an electromagnetic drift-kinetic model
If electromagnetic fluctuations are included in the simulations, they affect the quantities that are conserved by the collisionless dynamics. Considering then also the collisional dynamics, the binary-collision model should retain the invariants of the collision-free model. For fusion plasmas, an electromagnetic drift-kinetic model that results as the $k_\perp \rho \ll 1$![]() limiting case of the electromagnetic gyrokinetic model (Burby & Brizard Reference Burby and Brizard2019) is of particular interest. The analysis of the conserved quantities for such a model can be found, for example in Hirvijoki et al. (Reference Hirvijoki, Burby, Pfefferlé and Brizard2020).
limiting case of the electromagnetic gyrokinetic model (Burby & Brizard Reference Burby and Brizard2019) is of particular interest. The analysis of the conserved quantities for such a model can be found, for example in Hirvijoki et al. (Reference Hirvijoki, Burby, Pfefferlé and Brizard2020).
For this case, the ‘kinetic-momentum’- and the ‘kinetic energy’-like functionals, that the binary-collision algorithm should leave invariant for fixed values of the fields $\boldsymbol{E}_1$![]() and $\boldsymbol{B}_1$
and $\boldsymbol{B}_1$![]() , are given by
, are given by
where the summation over $s$![]() again refers to particle species. Here, $\boldsymbol{B}_0=\boldsymbol {\nabla }\times \boldsymbol{A}_0$
again refers to particle species. Here, $\boldsymbol{B}_0=\boldsymbol {\nabla }\times \boldsymbol{A}_0$![]() is the background magnetic field, with $\boldsymbol{b}_0=\boldsymbol{B}_0/|\boldsymbol{B}_0|$
is the background magnetic field, with $\boldsymbol{b}_0=\boldsymbol{B}_0/|\boldsymbol{B}_0|$![]() the corresponding unit vector. The dynamical fields in the system are the distributional densities $F_s$
the corresponding unit vector. The dynamical fields in the system are the distributional densities $F_s$![]() , which include the phase-space Jacobian, and the electric and magnetic field perturbations $\boldsymbol{E}_1$
, which include the phase-space Jacobian, and the electric and magnetic field perturbations $\boldsymbol{E}_1$![]() and $\boldsymbol{B}_1$
and $\boldsymbol{B}_1$![]() . The single drift-centre kinetic energy function in the model (Hirvijoki et al. Reference Hirvijoki, Burby, Pfefferlé and Brizard2020) is given by
. The single drift-centre kinetic energy function in the model (Hirvijoki et al. Reference Hirvijoki, Burby, Pfefferlé and Brizard2020) is given by
From the global functionals, we identify the individual particle contributions, namely
Regardless of what exactly a conservative binary-collision algorithm does, it should satisfy the pairwise conservation of toroidal angular momentum and total energy
with the notation $P_{1,n}\equiv P(\boldsymbol{x}_{1,t_n},u_{1,t_n})$![]() , etc. and $(x_{t_n},u_{t_n},\mu _{t_n})$
, etc. and $(x_{t_n},u_{t_n},\mu _{t_n})$![]() and $(x_{t_{n+1}},u_{t_{n+1}},\mu _{t_{n+1}})$
and $(x_{t_{n+1}},u_{t_{n+1}},\mu _{t_{n+1}})$![]() referring to the particle coordinates before and after the collisional time step $\varDelta t$
referring to the particle coordinates before and after the collisional time step $\varDelta t$![]() .
.
The standard binary-collision algorithms, however, are not designed to preserve these particular invariants in the presence of the perturbations $\boldsymbol{E}_1$![]() and $\boldsymbol{B}_1$
and $\boldsymbol{B}_1$![]() , resulting in deviations $\varDelta P$
, resulting in deviations $\varDelta P$![]() and $\varDelta E$
and $\varDelta E$![]() such that
such that
Since the field fluctuations by definition are supposed to be small, the new values for velocities from a standard binary-collision step nevertheless are expected to approximately retain the invariants, and significant errors to accumulate only over time. Consequently, a small perturbation, for example a shift in the location or velocity of particle one, $\boldsymbol{x}_1$![]() , at every time step, could potentially be used to make the deviations $\varDelta E$
, at every time step, could potentially be used to make the deviations $\varDelta E$![]() and $\varDelta P$
and $\varDelta P$![]() to vanish.
to vanish.
3.1. Potential corrections to conserving $P$ and $E$
and $E$
Using $(x_1,x_2,x_3)$![]() for the configuration space coordinates of particle 1 after the standard binary-collision step has been taken and the errors $\varDelta P$
for the configuration space coordinates of particle 1 after the standard binary-collision step has been taken and the errors $\varDelta P$![]() and $\varDelta E$
and $\varDelta E$![]() are known, we could adjust, say, two of the coordinates according to
are known, we could adjust, say, two of the coordinates according to
to reduce the error. Furthermore, this corrective step can be iterated to suppress the error significantly. In the three-dimensional case, there is freedom to choose any two out of the three available components for tuning the quantities $P$![]() and $E$
and $E$![]() . In toroidal coordinates, the relative errors in momentum appear to be quite small. The correction terms depend much on the numerical parameters and mainly on radial coordinate, $P \approx P(r)$
. In toroidal coordinates, the relative errors in momentum appear to be quite small. The correction terms depend much on the numerical parameters and mainly on radial coordinate, $P \approx P(r)$![]() . Other corrections are very small.
. Other corrections are very small.
In figure 2, the correction method is tested with a simple test case for sinusoidal $|\boldsymbol{B}_1|/|\boldsymbol{B}_0| = O(10^{-3})$![]() fluctuations. Repeated binary collisions of two particles are carried out and, after each binary collision, $P$
fluctuations. Repeated binary collisions of two particles are carried out and, after each binary collision, $P$![]() and $E$
and $E$![]() are corrected using (3.10) (‘0’ refers to the error just after binary collision). The standard deviation of the error compared with $P$
are corrected using (3.10) (‘0’ refers to the error just after binary collision). The standard deviation of the error compared with $P$![]() ($E$
($E$![]() ) before the binary collision is shown. It can be seen that the correction in $P$
) before the binary collision is shown. It can be seen that the correction in $P$![]() is small, $O(10^{-10})$
is small, $O(10^{-10})$![]() , while the relative error in $E$
, while the relative error in $E$![]() is of the order of $10^{-4}$
is of the order of $10^{-4}$![]() . Tuning with $\varDelta r$
. Tuning with $\varDelta r$![]() together with poloidal ($\varDelta \theta$
together with poloidal ($\varDelta \theta$![]() ) or toroidal ($\varDelta \phi$
) or toroidal ($\varDelta \phi$![]() ) correction shows the best performance confirming that in practise the radial coordinate $r$
) correction shows the best performance confirming that in practise the radial coordinate $r$![]() tunes $P\approx P(r)$
tunes $P\approx P(r)$![]() after which the fine tuning of E is done with either $\theta$
after which the fine tuning of E is done with either $\theta$![]() or $\phi$
or $\phi$![]() .
.

Figure 2. Relative change of $E$![]() and $P$
and $P$![]() just after binary collisions (index ‘0’ in the $x$
just after binary collisions (index ‘0’ in the $x$![]() label) and after iterative corrections.
label) and after iterative corrections.
If a scheme, such as the one described above, is adopted to enforce the conservation properties, one can expect at least some level of artificial transport. We can try to estimate the level of such induced transport in the following manner. Say the bare binary-collision algorithm, without fluctuating fields, provides a change in the parallel velocity $\varDelta u$![]() . In the presence of fluctuations, this induces an additional change in the toroidal canonical momentum which we can approximate from
. In the presence of fluctuations, this induces an additional change in the toroidal canonical momentum which we can approximate from
If we shift the particle position in the radial direction, the dominant change in the canonical toroidal momentum becomes
where $B_{0,p}$![]() is the poloidal component of the unperturbed magnetic field. In trying to counter the change in the toroidal momentum credited for the fluctuating fields during a Coulomb collision, the particle's radial position then needs to be shifted by the amount
is the poloidal component of the unperturbed magnetic field. In trying to counter the change in the toroidal momentum credited for the fluctuating fields during a Coulomb collision, the particle's radial position then needs to be shifted by the amount
The associated diffusion coefficient can be estimated from $D\sim (\varDelta r)^{2}/\varDelta t$![]() , which together with $(\varDelta u)^{2}/\varDelta t\sim \nu u^{2}$
, which together with $(\varDelta u)^{2}/\varDelta t\sim \nu u^{2}$![]() and $\nu$
and $\nu$![]() denoting the collision frequency, leads to the estimate
denoting the collision frequency, leads to the estimate
Even if the magnetic fluctuations were comparable with the poloidal magnetic field, the term $(B_0/B_{0,p})^{2}(B_1/B_0)^{4}$![]() would remain considerably less than one. Consequently, we expect that the transport from the corrective algorithm would remain at most at the level of classical diffusion and likely be significantly less than that.
would remain considerably less than one. Consequently, we expect that the transport from the corrective algorithm would remain at most at the level of classical diffusion and likely be significantly less than that.
4. Conclusions
In this work, we have demonstrated that the accuracy of the widely used binary-collision algorithm decreases when the collision grid cell size reaches a significant fraction of the gradient scale length of the plasma background. This indicates that, while the standard binary-collision algorithm works well in homogeneous backgrounds, either very small collision cell sizes should be used in the steep gradient regions at the tokamak edge or the collision algorithm modified. We then suggested one possibility to modify the existing binary-collision algorithms to regain the conservation of the quantities important in transport simulations when electromagnetic fluctuations are present. We expect such minor modifications to be also practical enough for implementations.
Acknowledgements
The work has been supported by the Academy of Finland (T.K., grant number 316088), (E.H., grant number 315278) and is part (T.K.) of Eurofusion enabling research projects ‘Model for reactor relevant pedestals’ (CCFE-04) and ‘MAGYK: Mathematics and Algorithms for GYrokinetic and Kinetic models’ (MPG-04). This work has been carried out within the framework of the EUROfusion Consortium and has received funding from the Euratom research and training programme 2014–2018 and 2019–2020 under grant agreement no. 633053. The views and opinions expressed herein do not necessarily reflect those of the European Commission. The CSC – IT Center for Science is acknowledged for generous allocation of computational resources for this work.
Editor Luίs O. Silva thanks the referees for their advice in evaluating this article.
Declaration of interests
The authors report no conflict of interest.