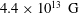1 Introduction
Neutron stars (NS) have been an attractive research area (Baade & Zwicky Reference Baade and Zwicky1934) due to their exotic environments and being one of the important ingredients in stellar evolution. NS comprising of iron/oxygen/carbon and helium nuclei (Massey Reference Massey1976; Shukla, Mamun & Mendis Reference Shukla, Mamun and Mendis2011) are dense enough 
$(n_{s}\gtrsim 10^{30}~\text{cm}^{-3})$ to be treated as a degenerate plasma system (Lai Reference Lai2001; Chabrier, Saumon & Potekhin Reference Chabrier, Saumon and Potekhin2006), thus quantum corrections become quite important for such stars (Abdikian & Mahmood Reference Abdikian and Mahmood2016). The physics of the highly degenerate NS crust involves several applications, ranging (Chamel & Haensel Reference Chamel and Haensel2008) from nuclear and condensed matter physics to general relativity. The initial signals detected from neutron stars emerging from radio pulsars were found to spin many times in one second. Then, strongly magnetized NS, known as pulsars, were observed to spin down and their periods were found to increase continuously. In this context, (Hewish et al. Reference Hewish, Bell, Pilkington, Scott and Collins1968) the rotating dipole model was applied to find the spin-down rate of the pulsars, prescribing that the required surface magnetic fields should be in the range 
$(10^{11}{-}10^{13})~\text{G}$ for the first detected pulsars. It was depicted in Chabrier, Douchin & Potekhin (Reference Chabrier, Douchin and Potekhin2002), Harding & Lai (Reference Harding and Lai2006) that the magnetic field for radio pulsars is 
$B_{o}$ 
$=(10^{11}{-}10^{14})~\text{G}$, whereas for anomalous X-ray pulsars the superstrong magnetic field may be higher i.e. 
$B_{o}\sim (10^{14}{-}10^{15})~\text{G}$ (Lewin & Van Der Klis Reference Lewin and Van Der Klis2005). At such a high magnetic field the cyclotron energy 
$\hbar \unicode[STIX]{x1D714}_{ce}(=eB/\unicode[STIX]{x1D714}_{ce})$ may be of the order of or much larger than the electron Fermi energy (Tsintsadze & Tsintsadze Reference Tsintsadze and Tsintsadze2012), 
$E_{F}(=({(3\unicode[STIX]{x03C0}^{2})^{2/3}\hbar }^{2}/2m_{e})n_{e}^{2/3})$ i.e. 
$\hbar \unicode[STIX]{x1D714}_{ce}\gg E_{F}$.
Moreover, due to the fact that bound state species such as hydrogen and molecules are present in the photosphere of neutron stars, pulsars etc., the degenerate thermodynamic properties of protons, free electrons and bound species in these environments are significantly modified by the magnetic field. These modified thermodynamic properties of the plasma and the propagation of proper waves is an important research area (Tsintsadze Reference Tsintsadze2010) in supernovae, pulsars, the convective zone of the Sun, white dwarfs, brown dwarfs, the early prestellar period of the evolution of the universe as well as in laboratory situations such as laser–matter interaction experiments. On the theoretical front, a lot of effort has been devoted in the direction (Abrahams & Shapiro Reference Abrahams and Shapiro1991; Kouveliotou, Ventura & Van Den Heuvel Reference Kouveliotou, Ventura and Van Den Heuvel2001; Lai Reference Lai2001; Tsintsadze & Tsintsadze Reference Tsintsadze and Tsintsadze2009a,Reference Tsintsadze and Tsintsadzeb, Reference Tsintsadze and Tsintsadze2010) of describing the thermodynamic properties of strongly magnetized matter under NS conditions. However, the impact of this modified thermodynamics, particularly magnetic field quantization, has not received much attention in the literature (Shah et al. Reference Shah, Iqbal, Tsintsadze, Masood and Qureshi2012), although it may be of great interest to formulate both linear and the nonlinear modes in quantum astrophysical environments. On the other hand, it is well known that the nonlinear effects appearing due to large amplitude oscillations in the plasma system may introduce a shock wave, whereas in the presence of dispersive effects, being balanced by the nonlinearity of the system, one may have a soliton structure. In this context, the Korteweg–de Vries (KdV) equation is well known for classical ion acoustic waves (Sagdeev Reference Sagdeev1966; Chen Reference Chen1984), and solitary waves in a weakly ionized classical gas have been reported in Stenflo, Tsintsadze & Buadze (Reference Stenflo, Tsintsadze and Buadze1989). Low frequency magnetosonic solitons are investigated in a magnetized spin-1/2 degenerate plasma, while opting for the Sagdeev potential approach (Marklund, Eliasson & Shukla Reference Marklund, Eliasson and Shukla2007), where the authors found that rarefractive magnetosonic solitons may exist due to a balance between nonlinearities and the quantum diffraction term. Nonlinear magnetosonic waves in quantum dissipative magnetized plasmas are investigated in Masood et al. (Reference Masood, Jhangir, Eliasson and Siddiq2014). Linear and weak nonlinear propagation of magnetosonic waves in a degenerate plasma using perturbation theory was formulated in Haas & Mahmood (Reference Haas and Mahmood2018), modified KdV was derived having coefficients which are a strong function of quantum effects. Various linear and nonlinear aspects of magnetoacoustic waves are investigated (Masood et al. Reference Masood, Shah, Mushtaq and Salimullah2009; Masood, Jehan & Mirza Reference Masood, Jehan and Mirza2010; Lui et al. Reference Lui, Wang, Wang, Li, Yao and Yang2011; Lui, Wang & Yang Reference Lui, Wang and Yang2013; Iqbal et al. Reference Iqbal, Younas, Khan and Murtaza2019). However, in all of the above mentioned literature regarding magnetosonic waves, magnetized plasmas are considered without taking into account the quantized magnetic pressure, which is the subject matter of the present study.
In this work, we aim to investigate the impact of quantized magnetic pressure on the linear and nonlinear properties of low frequency fast magnetosonic waves in a weakly ionized, dispersive degenerate neutron, electron–ion plasma in the atmosphere of a pulsar. The paper is organized as follows: in § 2, we derive the linear dispersion relation of fast magnetosonic waves using new set of quantum hydrodynamic equations. Section 3 presents the nonlinear behaviour of fast magnetosonic waves, and a brief summary is presented in § 4.
2 Basic formalism
Here, we consider a weakly ionized, quantum neutron–electron ion plasma in the presence of a super strong magnetic field 
$\hat{z}\,H_{0}$, in the atmosphere of a pulsar, where 
$H_{0}$ is the strength of the magnetic field and 
$\hat{z}$ is the unit vector along the 
$z$-axis in a Cartesian coordinate system. We shall formulate here a new quantum magnetohydrodynamic set of equations for the weakly ionized pulsars under study, where all components of the neutron star are in a degenerate state. For our theoretical description, the neutron dynamics is governed by the neutron momentum equation
$$\begin{eqnarray}n_{N}\frac{\text{d}\boldsymbol{p}_{N}}{\text{d}t}=-\unicode[STIX]{x1D735}P_{FN}+\frac{\hbar ^{2}n_{N}}{2m_{N}}\unicode[STIX]{x1D735}\frac{1}{\sqrt{n_{N}}}\unicode[STIX]{x0394}\sqrt{n_{N}}+\boldsymbol{f}_{N},\end{eqnarray}$$and the neutron continuity equation
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}n_{N}}{\unicode[STIX]{x2202}t}+\text{div}\,n_{N}\boldsymbol{u}_{N}=0,\end{eqnarray}$$ where 
$p_{N}$ is the neutron momentum, 
$f_{N}=m_{N}n_{N}\sum _{i}v_{Ni}(\boldsymbol{u}_{i}-\boldsymbol{u}_{N})$ is the neutron collisional frequency, 
$P_{FN}={(3\unicode[STIX]{x03C0}^{2})^{2/3}\hbar }^{2}/5m_{N}(n_{N})^{5/3}$ is the neutron Fermi pressure 
$\hbar$ is Planck’s constant divided by 
$2\unicode[STIX]{x03C0}$, 
$m_{N}$, 
$n_{N},u_{N}$ are the mass, number density and velocity of the neutrons respectively, 
$v_{Ni}$ is the neutron–ion collisional frequency and 
$u_{i}$ is the velocity of ions. Here, we suppose that the neutron–electron collision frequency 
$\unicode[STIX]{x1D708}_{Ne}$ is comparatively small. It was shown in Tsintsadze et al. (Reference Tsintsadze, Rozina, Ruby and Tsintsadze2018) that in the presence of a quantized magnetic pressure, the plasma becomes anisotropic, and the associated momentum equations in the directions perpendicular and parallel to the applied superstrong magnetic field are respectively
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}\boldsymbol{p}_{xj}}{\text{d}t}=e_{j}\left(\boldsymbol{E}+\frac{1}{c}(\boldsymbol{u}_{j}\times \boldsymbol{H})\right)_{x}-\frac{1}{n_{j}}\unicode[STIX]{x1D735}_{x}P_{xj}+\frac{\hslash ^{2}}{2m_{j}}\unicode[STIX]{x1D735}_{x}\frac{1}{\sqrt{n_{j}}}(\unicode[STIX]{x1D6FB}^{2}\sqrt{n_{j}})+\frac{1}{n_{j}}\boldsymbol{f}_{xj}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}\boldsymbol{p}_{zj}}{\text{d}t}=e_{j}\left(\boldsymbol{E}+\frac{1}{c}(\boldsymbol{u}_{j}\times \boldsymbol{H})\right)_{z}-\frac{1}{n_{j}}\unicode[STIX]{x1D735}_{z}P_{zj}+\frac{\hslash ^{2}}{2m_{j}}\unicode[STIX]{x1D735}_{z}\frac{1}{\sqrt{n_{j}}}(\unicode[STIX]{x1D6FB}^{2}\sqrt{n_{j}})+\frac{1}{n_{j}}\boldsymbol{f}_{zj}, & \displaystyle\end{eqnarray}$$with the continuity equation
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}n_{j}}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }(n_{j}\boldsymbol{u}_{j})=0. & & \displaystyle\end{eqnarray}$$We shall also make use of the quasineutral condition
$$\begin{eqnarray}\underset{j}{\sum }e_{j}n_{j}=0\end{eqnarray}$$and Maxwell’s equation
$$\begin{eqnarray}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{H}=0,\end{eqnarray}$$ where 
$j$ represents plasma species, 
$j=(e,i)$, 
$x$ and 
$z$ are the directions perpendicular and parallel to the external field respectively, 
$e$ is the magnitude of electron charge, 
$c$ is the speed of light in a vacuum, 
$n_{j}$, 
$m_{j}$ and 
$u_{j}$ are the number density, mass and velocity of plasma species 
$j$ respectively, 
$E$ is the electrostatic field. The collisional force of each plasma particle 
$f_{j}$ in (2.3) and (2.4) in the presence of magnetic pressure inhomogeneity is defined as
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \boldsymbol{f}_{xj}=m_{j}n_{j}\displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D710}_{j\unicode[STIX]{x1D6FC}}(\boldsymbol{u}_{\unicode[STIX]{x1D6FC}}-\boldsymbol{u}_{j})_{x}\\ \displaystyle \boldsymbol{f}_{zj}=m_{j}n_{j}\displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D710}_{j\unicode[STIX]{x1D6FC}}(\boldsymbol{u}_{\unicode[STIX]{x1D6FC}}-\boldsymbol{u}_{j})_{z}\end{array}\right\}. & & \displaystyle\end{eqnarray}$$ Here, 
$\unicode[STIX]{x1D710}_{j\unicode[STIX]{x1D6FC}}$ is the collisional frequency of particle 
$\unicode[STIX]{x1D6FC}$ with 
$j$ and 
$u_{\unicode[STIX]{x1D6FC}},u_{j}$ are their relative velocities respectively. We note here that when collisions between particles are very frequent (Tsintsadze et al. Reference Tsintsadze, Rozina, Ruby and Tsintsadze2018) the velocities of different plasma species must in fact be almost equal. It is quite evident from (2.1)–(2.8) that, if 
$\unicode[STIX]{x1D710}_{ei}$, 
$\unicode[STIX]{x1D710}_{eN}$ and 
$\unicode[STIX]{x1D710}_{iN}$ are significantly large, the frictional forces can be balanced by other terms only if the relative velocities of different species, 
$u_{i}-u_{e}$, 
$u_{N}-u_{e}$ and 
$u_{N}-u_{i}$ are small i.e. 
$u_{i}\simeq u_{e}$, 
$u_{N}\simeq u_{e}$ and 
$u_{N}\simeq u_{i}$, which in turn leads to the relation (Tsintsadze et al. Reference Tsintsadze, Rozina, Shah and Murtaza2008).
$$\begin{eqnarray}\frac{n_{e}}{n_{0e}}\simeq \frac{n_{N}}{n_{N0}}\simeq \frac{n_{i}}{n_{0i}}.\end{eqnarray}$$ The influence of a super strong magnetic field on the thermodynamic properties of a Fermi gas was presented in Tsintsadze (Reference Tsintsadze2010), Tsintsadze & Tsintsadze (Reference Tsintsadze and Tsintsadze2015) to emphasize that strongly magnetized systems hold the inequality 
$E_{F}\ll \hbar \unicode[STIX]{x1D714}_{ce}$, hence the consequent perpendicular, 
$P_{xe}$, and parallel, 
$P_{ze}$, components of the magnetic pressure are
$$\begin{eqnarray}\displaystyle & \displaystyle P_{xe}=\frac{\hbar \unicode[STIX]{x1D714}_{ce}}{3}n_{e}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle P_{ze}=\unicode[STIX]{x1D6FE}\left(\frac{n_{e}}{H}\right)^{2}n_{e}, & \displaystyle\end{eqnarray}$$ where 
$n_{e}=\hbar \unicode[STIX]{x1D714}_{ce}m_{e}P_{Fe}/{\unicode[STIX]{x03C0}^{2}\hbar }^{3}$ with 
$P_{Fe}=(3\unicode[STIX]{x03C0}^{2})^{1/3}\hbar n_{e}^{1/3}$ as the Fermi momentum at the Fermi level and 
$\unicode[STIX]{x1D6FE}={\unicode[STIX]{x03C0}^{4}\hslash }^{4}c^{2}/3m_{e}e^{2}$. It is clear from the above expressions that for strongly magnetized NS the dependence of magnetic pressure on magnetic field intensity is quite different in the perpendicular and parallel directions. It may be noted here that the proton motion is also quantized into Landau levels due to the high magnetic field, but their corresponding cyclotron energy is much smaller than the electron cyclotron energy, i.e. 
$\hbar \unicode[STIX]{x1D714}_{cp}=\hbar \unicode[STIX]{x1D714}_{ce}(m_{e}/m_{p})$ (here 
$\unicode[STIX]{x1D714}_{cp}$, 
$\unicode[STIX]{x1D714}_{ce},m_{p},m_{e}$ are the cyclotron frequencies and masses of protons and electrons respectively.)
3 Linear dispersion equation
We shall follow Riemann’s solution, to formulate the linear dispersive properties of one-dimensional fast magnetosonic waves propagating across the magnetic field, while assuming that 
$m_{e}\ll m_{i}\simeq m_{N}$ and 
$n_{e}\simeq n_{i}\ll n_{N}$. In this context, by adding (2.1)–(2.6), we may obtain
$$\begin{eqnarray}\displaystyle n_{N}\frac{\text{d}p_{xN}}{\text{d}t} & = & \displaystyle \frac{1}{c}(\boldsymbol{J}\times \boldsymbol{H})_{x}-\unicode[STIX]{x1D735}_{x}\left(P_{FN}+\mathop{\sum }_{j=e,i}P_{xj}\right)+\frac{\hbar ^{2}n_{N}}{2m_{N}}\unicode[STIX]{x1D735}_{x}\frac{1}{\sqrt{n_{N}}}\unicode[STIX]{x0394}\sqrt{n_{N}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\hbar ^{2}n_{e}}{2m_{e}}\unicode[STIX]{x1D735}_{x}\frac{1}{\sqrt{n_{e}}}\unicode[STIX]{x0394}\sqrt{n_{e}}+\frac{\hbar ^{2}n_{i}}{2m_{i}}\unicode[STIX]{x1D735}_{x}\frac{1}{\sqrt{n_{i}}}\unicode[STIX]{x0394}\sqrt{n_{i}}.\end{eqnarray}$$We shall also make use of Magneto-hydrodynamic (MHD) equations
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{H}}{\unicode[STIX]{x2202}t}=\unicode[STIX]{x1D735}\times (\boldsymbol{u}\times \boldsymbol{H}) & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{J}=\frac{c}{4\unicode[STIX]{x03C0}}(\unicode[STIX]{x1D735}\times \boldsymbol{H}), & \displaystyle\end{eqnarray}$$ where 
$J=-en_{e}u_{e}+Z_{i}en_{i}u_{i}$ is the plasma current density defined in the MHD approximation, 
$P_{xj}$ is the quantized pressure of species 
$j$ in a direction perpendicular to the external field. Let us rewrite (3.1) by making use of (3.3)
$$\begin{eqnarray}\frac{\text{d}p_{xN}}{\text{d}t}=-\frac{1}{n_{N}}\unicode[STIX]{x1D735}_{x}\left(P_{FN}+P_{xe}+\frac{H^{2}}{8\unicode[STIX]{x03C0}}\right)+\frac{1}{4\unicode[STIX]{x03C0}n_{N}}(H\boldsymbol{\cdot }\unicode[STIX]{x1D735})H_{x}+\frac{\hbar ^{2}}{2m_{e}}\frac{n_{e}}{n_{N}}\unicode[STIX]{x1D735}_{x}\frac{1}{\sqrt{n_{e}}}\unicode[STIX]{x0394}\sqrt{n_{e}}.\end{eqnarray}$$ It may be noticed here that the diffraction term of neutrons and ions can be ignored as compared to the electron diffraction term due to different possible inequalities 
$n_{e}/n_{N}\ll m_{e}/m_{N}$ or 
$n_{e}/n_{N}\gg m_{e}/m_{N}=m_{e}/m_{i}$, consequently, the electrons may play an important role in exciting fast, degenerate magnetosonic waves. Using (2.9), we may re-write (3.4) as
$$\begin{eqnarray}\frac{\text{d}p_{xN}}{\text{d}t}=-\frac{1}{n_{N}}\unicode[STIX]{x1D735}_{x}\left(P_{FN}+P_{xe}+\frac{H^{2}}{8\unicode[STIX]{x03C0}}\right)+\frac{1}{4\unicode[STIX]{x03C0}n_{N}}(H\boldsymbol{\cdot }\unicode[STIX]{x1D735})H_{x}+\frac{\hbar ^{2}}{2m_{e}}\frac{n_{e}}{n_{N}}\unicode[STIX]{x1D735}_{x}\frac{1}{\sqrt{n_{N}}}\unicode[STIX]{x0394}\sqrt{n_{N}},\end{eqnarray}$$or in linearized form we may write
$$\begin{eqnarray}\frac{\text{d}\unicode[STIX]{x1D6FF}p_{xN}}{\text{d}t}=-\frac{1}{n_{0N}}\unicode[STIX]{x1D735}_{x}\left(\unicode[STIX]{x1D6FF}P_{FN}+\unicode[STIX]{x1D6FF}P_{xe}+\frac{H_{0}^{2}}{4\unicode[STIX]{x03C0}}\frac{\unicode[STIX]{x1D6FF}H_{z}}{H_{0}}\right)+\frac{H_{0}}{4\unicode[STIX]{x03C0}n_{0N}}\unicode[STIX]{x1D735}_{z}H_{x}+\frac{\hslash ^{2}}{4m_{e}}\frac{n_{0e}}{n_{N0}}\unicode[STIX]{x1D735}_{x}\unicode[STIX]{x1D6FB}^{2}\frac{\unicode[STIX]{x1D6FF}n_{N}}{n_{0N}},\end{eqnarray}$$ where 
$H_{z},H_{x}$, are the components of the magnetic field along and perpendicular to the external magnetic field respectively. Similarly, we can write the oscillations of the pressure expressions form (2.10), while taking into account equation (2.9)
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}P_{xe}=P_{0ex}\left(\frac{\unicode[STIX]{x1D6FF}H_{z}}{H_{0}}+\frac{\unicode[STIX]{x1D6FF}n_{N}}{n_{0N}}\right),\end{eqnarray}$$ where 
$P_{0ex}=(\hbar \unicode[STIX]{x1D714}_{ce0}/3)n_{0e}$. Further, let us now write down the components of the magnetic field from (3.2) as
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}H_{x}}{\unicode[STIX]{x2202}t}=H_{0}\unicode[STIX]{x1D735}_{z}u_{x}.\end{eqnarray}$$Then, by making use of (3.6)–(3.8), (2.2), we may obtain the dispersion relation of fast, degenerate, neutron magnetosonic waves that are propagating perpendicular to the applied superstrong magnetic field
$$\begin{eqnarray}\unicode[STIX]{x1D714}^{2}=k_{x}^{2}(V_{FN}^{2}+C_{x}^{2}+V_{A}^{2})^{1/2}+\frac{\hslash ^{2}k_{x}^{4}}{4m_{e}m_{N}}\frac{n_{0e}}{n_{0N}},\end{eqnarray}$$ where 
$V_{FN}=(3\unicode[STIX]{x03C0}^{2})^{1/3}\hbar /m_{N}(n_{0N})^{1/3}$ is the neutron Fermi speed, 
$C_{x}=\sqrt{2P_{x0e}/m_{N}n_{0N}}=\sqrt{2/3(\hbar \unicode[STIX]{x1D714}_{ce0}/m_{N})(n_{0e}/n_{0N})}$ is the magnetic neutron acoustic speed and 
$V_{A}=H_{0}/\sqrt{4\unicode[STIX]{x03C0}m_{N}n_{0N}}$ is the neutron Alfvén speed. For a weakly dispersive medium, equation (3.9) may be written as
$$\begin{eqnarray}\unicode[STIX]{x1D714}=k_{x}(V_{FN}^{2}+C_{x}^{2}+V_{A}^{2})^{1/2}+\unicode[STIX]{x1D706}k_{x}^{3},\end{eqnarray}$$ where 
$\unicode[STIX]{x1D706}=(\hslash ^{2}/8m_{e}m_{N})(n_{0e}/n_{0N})(1/\sqrt{V_{FN}^{2}+C_{x}^{2}+V_{A}^{2}})$ is the dispersive parameter. The above equation describes that sufficiently long waves may exist in a weakly dispersive pulsar having a finite limit on the phase velocity at 
$k=0$. In the following section, we shall show that the dispersive properties of nonlinear fast magnetosonic waves, in the presence of a quantized magnetic pressure, are governed by a modified KDV equation.
4 Solitary fast magnetosonic waves in a weakly dispersive pulsar
To show that nonlinear stationary waves can be formed in the dispersive pulsar atmosphere, we shall follow the method presented in Whitham (Reference Whitham1974), Landau & Lifshitz (Reference Landau and Lifshitz1987), Tsintsadze, Hussain & Murtaza (Reference Tsintsadze, Hussain and Murtaza2011) and Tsintsadze et al. (Reference Tsintsadze, Rozina, Ruby and Tsintsadze2018). For this purpose, in order to consider the 
$x$-dimensional propagation of fast magnetosonic waves travelling across the quantized magnetic field, let us re-write equations (2.2), (3.2), (3.5) respectively as
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}n_{N}}{\unicode[STIX]{x2202}t}=-n_{N}\frac{\unicode[STIX]{x2202}u_{xN}}{\unicode[STIX]{x2202}x} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}H_{z}}{\text{d}t}=-H_{z}\frac{\unicode[STIX]{x2202}u_{x}}{\unicode[STIX]{x2202}x} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}u_{xN}}{\unicode[STIX]{x2202}t}+u_{xN}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}u_{xN}=-\frac{1}{m_{N}n_{N}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(P_{FN}+P_{xe}+\frac{H_{z}^{2}}{8\unicode[STIX]{x03C0}}\right)+\frac{\hbar ^{2}}{2m_{e}m_{N}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\frac{1}{\sqrt{n_{N}}}\frac{\unicode[STIX]{x2202}^{2}}{\unicode[STIX]{x2202}x^{2}}\sqrt{n_{N}}\qquad . & \displaystyle\end{eqnarray}$$ Here, 
$P_{FN}$ is the neutron Fermi pressure and 
$P_{xe}$ is the electron magnetic pressure defined in (2.11). Since the magnetic field is favoured by conduction currents frozen in the interior part of NS (Chabrier et al. Reference Chabrier, Douchin and Potekhin2002), we shall apply here the frozen-in condition to reflect that the lines of magnetic force are frozen with the magnetic field lines to move with them i.e. 
$H_{z}/n_{N}=\text{constant}$, then we may have
$$\begin{eqnarray}P_{xe}=P_{0e}\left(\frac{n_{N}}{n_{0N}}\right)^{2}\quad \text{and}\quad H_{z}^{2}=H_{0}^{2}\left(\frac{n_{N}}{n_{0N}}\right)^{2},\end{eqnarray}$$ where 
$P_{0e}=(\hbar \unicode[STIX]{x1D714}_{ce}(n_{0N})/3)n_{0e}$. For a weakly dispersive medium, let us linearize the last term of (4.3), to obtain from (4.1)–(4.3)
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}n_{N}}{\unicode[STIX]{x2202}t}+n_{N}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}u_{xN}=0 & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}u_{xN}}{\unicode[STIX]{x2202}t}+u_{xN}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}u_{xN}=-\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}(\unicode[STIX]{x1D6FC}n_{N}^{2/3}+\unicode[STIX]{x1D6FD}n_{N})+\frac{\hbar ^{2}}{2m_{e}m_{N}}\frac{\unicode[STIX]{x2202}^{3}}{\unicode[STIX]{x2202}x^{3}}\frac{n_{N}}{n_{0N}} & \displaystyle\end{eqnarray}$$ where here 
$\unicode[STIX]{x1D6FC}=(3\unicode[STIX]{x03C0}^{2})^{2/3}\hbar ^{2}/2m_{N}^{2}$, and 
$\unicode[STIX]{x1D6FD}=((2\hbar \unicode[STIX]{x1D714}_{ce}/3)n_{0e}+H_{0}^{2}/4\unicode[STIX]{x03C0})1/n_{0N}^{2}m_{N}$. Now, if we ignore the last term in the above equation and look for Riemann’s solution of (4.5) and (4.6) for a simple plane wave propagating in the positive 
$x$-direction, we have
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}u_{xN}}{\unicode[STIX]{x2202}n_{N}}=\sqrt{\frac{2}{3}\unicode[STIX]{x1D6FC}\frac{1}{n_{N}^{4/3}}+\frac{\unicode[STIX]{x1D6FD}}{n_{N}}},\end{eqnarray}$$or
$$\begin{eqnarray}n_{N}=\frac{1}{\unicode[STIX]{x1D6FD}^{3}}\left\{-\frac{\unicode[STIX]{x1D6FC}}{3}+\left(\frac{\unicode[STIX]{x1D6FC}}{3}+\unicode[STIX]{x1D6FD}n_{0N}^{1/3}\right)\left(1+\frac{\unicode[STIX]{x1D6FD}u_{N}}{2\left(\displaystyle \frac{\unicode[STIX]{x1D6FC}}{3}+\unicode[STIX]{x1D6FD}n_{0N}^{1/3}\right)^{3/2}}\right)^{2/3}\right\}^{3}.\end{eqnarray}$$ Substitution of (4.8) into (4.6) may lead to a modified KdV equation with complex nonlinearity. To get a simplified KdV equation, let us simplify (4.8) for two particular cases: (i) if the neutron degenerate pressure is much more than the electron magnetic pressure i.e. 
$\unicode[STIX]{x1D6FC}\gg 3\unicode[STIX]{x1D6FD}n_{0N}^{1/3}$, equation (4.8) reduces to
$$\begin{eqnarray}n_{N}=\frac{m_{N}^{3}u_{N}^{3}}{3^{5/2}\unicode[STIX]{x03C0}^{2}\hbar ^{3}},\end{eqnarray}$$ and (ii) conversely, if 
$\unicode[STIX]{x1D6FC}\ll 3\unicode[STIX]{x1D6FD}n_{0N}^{1/3}$, we may obtain from (4.8)
$$\begin{eqnarray}n_{N}=n_{0N}\left(1+\frac{u_{N}}{\sqrt{\unicode[STIX]{x1D6FD}n_{0N}}}\right)^{2}.\end{eqnarray}$$To show that both cases will lead to a soliton solution, let us substitute the density expression (4.10) into (4.6) to obtain the KdV equation
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}u_{xN}}{\unicode[STIX]{x2202}t}+(u_{xN}+\unicode[STIX]{x1D702})\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}u_{xN}=\unicode[STIX]{x1D70E}\frac{\unicode[STIX]{x2202}^{3}u_{xN}}{\unicode[STIX]{x2202}x^{3}}\end{eqnarray}$$having the solitary wave solution
$$\begin{eqnarray}u_{xN}=u_{x0N}\left\{\cosh \left[\left(\frac{u_{x0N}}{12\unicode[STIX]{x1D70E}}\right)^{1/2}(x-\unicode[STIX]{x1D702}t-\frac{1}{3}u_{x0N}t)\right]\right\}^{-2}.\end{eqnarray}$$ Here, 
$\unicode[STIX]{x1D702}=\frac{3}{4}\unicode[STIX]{x1D6FC}n_{0N}^{1/6}\sqrt{1/\unicode[STIX]{x1D6FD}}+\sqrt{\unicode[STIX]{x1D6FD}n_{0N}}/2$ and 
$\unicode[STIX]{x1D70E}=\hbar ^{2}/4m_{e}m_{N}\sqrt{\unicode[STIX]{x1D6FD}n_{0N}}$. We want to emphasize here that, since the sign of the last term of (4.11) is positive, the obtained solitary waves will be rarefractive.
5 Summary
We have presented a graphical analysis of (3.9), (4.10) and (4.12) to study the magnetic field quantization effects on the dispersive properties of fast, degenerate, magnetosonic neutron waves that are propagating perpendicular to an applied superstrong magnetic field. For the graphical analysis the typical parameters of an astrophysical degenerate plasma, present in the magnetosphere of a highly magnetized star such as a radio pulsar or magnetar, are chosen (Bailes Reference Bailes1989; Zhang & Harding Reference Zhang and Harding2000; Chabrier et al. Reference Chabrier, Douchin and Potekhin2002; Harding & Lai Reference Harding and Lai2006), which in the cgs system of units are: 
$n_{0e}=(10^{22}{-}10^{23})~\text{cm}^{-3}$, 
$n_{0N}=(10^{30}{-}10^{34})~\text{cm}^{-3}$, 
$u_{x0N}=(1{-}2)\times 10^{7}~\text{cm}~\text{s}^{-1}$, 
$H_{0}=(10^{10}{-}10^{14})~\text{G}$ with the physical constants 
$c=3\times 10^{10}$, 
$m_{e}=9.1\times 10^{-28}$, 
$m_{N}=1.6749286\times 10^{-24}$, 
$e=4.8\times 10^{-10}$, 
$h=1.05\times 10^{-27}$. We have displayed equation (3.9) in figure 1 to show that the angular frequency 
$(\unicode[STIX]{x1D714})$ of a fast magnetosonic wave increases by increasing the strength of the magnetic field 
$H_{0}$. Figure 2 depicts that the neutron number density 
$(n_{N})$ decreases with the increase of magnetic field strength, as shown in (4.10). The impact of the quantized magnetic field and neutron density on the dispersive properties of solitons, given in (4.12), are displayed in figure 3(a,b), respectively, to show that the width of the soliton decreases by increasing the magnetic field intensity, while it increases by increasing the neutron density concentration.
Figure 1. Normalized angular frequency 
$(\unicode[STIX]{x1D714})$ of fast, degenerate, neutron magnetosonic waves is plotted against the wavenumber 
$(k_{x})$ (as given by (3.9)) for different values of the magnetic field, 
$H_{0}=6\times 10^{10}~\text{G}$ (green curve), 
$H_{0}=3\times 10^{10}~\text{G}$ (blue curve) and 
$H_{0}=8\times 10^{10}~\text{G}$ (red curve), while assuming 
$n_{0e}=10^{22}~\text{cm}^{-3}$ and 
$n_{0N}=10^{30}~\text{cm}^{-3}$.
Figure 2. The neutrons number density 
$(n_{N})$ is plotted against the neutron velocity 
$(u_{N})$ (as given by (4.10)), for different magnetic field strengths 
$H_{0}=1\times 10^{11}~\text{G}$ (green curve), 
$H_{0}=2\times 10^{11}~\text{G}$ (blue curve) and 
$H_{0}=3\times 10^{11}~\text{G}$ (red curve), other parameters are the same as in figure 1.
Figure 3. (a) The 
$x$-dimensional neutron velocity 
$(u_{xN})$ of fast magnetosonic neutron waves is plotted against the 
$x$-coordinate for different magnetic field values (as given by (4.12)), 
$H_{0}=1\times 10^{11}~\text{G}$ (red curve), 
$H_{0}=2\times 10^{11}~\text{G}$ (blue curve) and 
$H_{0}=3\times 10^{11}~\text{G}$ (green curve). Here we consider 
$n_{0e}=10^{22}~\text{cm}^{-3}$, 
$n_{0N}=10^{33}~\text{cm}^{-3}$, the neutron velocity 
$u_{x0N}=1\times 10^{7}~\text{cm}~\text{s}^{-1}$ and time 
$t=(10^{-15}~\text{s})$. (b) The 
$x$-dimensional neutron velocity 
$(u_{xN})$ of fast magnetosonic neutron waves is plotted against the 
$x$-coordinate (as given by (4.12)), for different neutron density concentrations; 
$n_{0N}=10^{33}~\text{cm}^{-3}$, (red curve) 
$n_{0N}=3\times 10^{33}~\text{cm}^{-3}$ (blue curve), 
$n_{0N}=5\times 10^{33}~\text{cm}^{-3}$ (green curve), with the neutron velocity 
$u_{x0N}=1\times 10^{7}~\text{cm}~\text{s}^{-1}$, 
$n_{0e}=10^{22}~\text{cm}^{-3}$, 
$H_{0}=1\times 10^{11}~\text{G}$ and time 
$t=(10^{-15}~\text{s})$.
To conclude, in this paper we have investigated both linear and weakly nonlinear propagation of fast magnetosonic waves in a strongly magnetized, degenerate weakly ionized dispersive neutron, electron–ion plasma in the atmosphere of a pulsar. It is shown that the linear propagation frequency of a fast magnetosonic wave increases as a function of both the neutron degenerate pressure and electron magnetic pressure via the neutron acoustic speed. It is depicted that sufficiently long linear waves may exist in a weakly dispersive neutron star (pulsar), having a finite limit on the phase velocity at cutoff. Next, the weak nonlinear features of one-dimensional fast, degenerate magnetosonic waves are formulated with the aid of Riemann’s solution for simple plane waves, to obtain a general expression for the neutron density as a function of both neutron degenerate pressure and electron magnetic pressure, which further was discussed for two special cases by comparing the neutron degenerate pressure with the electron magnetic pressures. The obtained neutron density expressions correspond to two different types of KdV equation, having coefficients which are a strong function of both quantized magnetic pressures and neutron density concentration, the consequent solitary wave solutions are found to be rarefractive.
