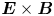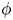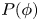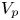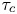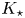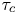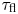1. Introduction
Turbulence plays a major role in the dynamics and confinement of fusion plasmas, both in current and future experimental devices (i.e. ITER Claessens Reference Claessens2020). Low-frequency instabilities evolve and saturate into a turbulent electric field $\boldsymbol {E}$![]() which, mainly via the $\boldsymbol {E}\times \boldsymbol {B}$
which, mainly via the $\boldsymbol {E}\times \boldsymbol {B}$![]() drift ($\boldsymbol {B}$
drift ($\boldsymbol {B}$![]() , the magnetic field), tends to transport plasma across magnetic surfaces, toward the walls. Such radial fluxes are particularly dangerous in the scrape-off layer (SOL) region (Krasheninnikov Reference Krasheninnikov2001; Lipschultz et al. Reference Lipschultz, Bonnin, Counsell, Kallenbach, Kukushkin, Krieger, Leonard, Loarte, Neu and Pitts2007) which absorbs most of the plasma exhaust and transfers it to the divertor. Understanding and controlling this type of transport in tokamak devices has been one of the major challenges for fusion science in the past decades (Bourdelle et al. Reference Bourdelle, Garbet, Imbeaux, Casati, Dubuit, Guirlet and Parisot2007; Angioni et al. Reference Angioni, Fable, Greenwald, Maslov, Peeters, Takenaga and Weisen2009; Fülöp & Nordman Reference Fülöp and Nordman2009).
, the magnetic field), tends to transport plasma across magnetic surfaces, toward the walls. Such radial fluxes are particularly dangerous in the scrape-off layer (SOL) region (Krasheninnikov Reference Krasheninnikov2001; Lipschultz et al. Reference Lipschultz, Bonnin, Counsell, Kallenbach, Kukushkin, Krieger, Leonard, Loarte, Neu and Pitts2007) which absorbs most of the plasma exhaust and transfers it to the divertor. Understanding and controlling this type of transport in tokamak devices has been one of the major challenges for fusion science in the past decades (Bourdelle et al. Reference Bourdelle, Garbet, Imbeaux, Casati, Dubuit, Guirlet and Parisot2007; Angioni et al. Reference Angioni, Fable, Greenwald, Maslov, Peeters, Takenaga and Weisen2009; Fülöp & Nordman Reference Fülöp and Nordman2009).
Both the edge and the SOL plasma (Zweben et al. Reference Zweben, Boedo, Grulke, Hidalgo, LaBombard, Maqueda, Scarin and Terry2007) are characterized by the presence of intermittent phenomena comparable in magnitude to the amplitude of turbulence. Intermittency (Antar et al. Reference Antar, Krasheninnikov, Devynck, Doerner, Hollmann, Boedo, Luckhardt and Conn2001b) is represented by transient, coherent structures with high density gradients such as blobs (Antar et al. Reference Antar, Devynck, Garbet and Luckhardt2001a; Pereira et al. Reference Pereira, Sokolov, Toufen, Guimarães-Filho, Caldas and Gentle2019; Cheng et al. Reference Cheng, Yan, Hong, Zhao, Lan, Qian, Liu, Zhao, Liu and Yang2010), Alfvén modes or edge-localized modes (Leonard Reference Leonard2014; Zohm Reference Zohm1996). The emergence of such rare, high-amplitude, fluctuations is captured at a statistical level, through the distribution $P(\phi )$![]() of electric field values $\phi (\boldsymbol {x},t)$
of electric field values $\phi (\boldsymbol {x},t)$![]() , which is non-Gaussian. Implicitly, the departure from Gaussianity is characteristic also for field derivatives $\partial _i\phi, \partial _{ii}\phi$
, which is non-Gaussian. Implicitly, the departure from Gaussianity is characteristic also for field derivatives $\partial _i\phi, \partial _{ii}\phi$![]() (Gonçalves et al. Reference Gonçalves, Henriques, Hidalgo, Silva, Figueiredo, Naulin, Nielsen and Mendonça2018). The latter are directly related to particle drift and vorticity, and thus to transport.
(Gonçalves et al. Reference Gonçalves, Henriques, Hidalgo, Silva, Figueiredo, Naulin, Nielsen and Mendonça2018). The latter are directly related to particle drift and vorticity, and thus to transport.
In the present work we are concerned with understanding and describing how the non-Gaussian features of a turbulent stochastic potential $\phi (\boldsymbol {x},t)$![]() affect the transport in the case of a biased, incompressible, two-dimensional velocity field $\boldsymbol {v}(\boldsymbol {x},t) = \hat {e}_z\times \boldsymbol {\nabla }\phi (\boldsymbol {x},t)+\boldsymbol {V}_p$
affect the transport in the case of a biased, incompressible, two-dimensional velocity field $\boldsymbol {v}(\boldsymbol {x},t) = \hat {e}_z\times \boldsymbol {\nabla }\phi (\boldsymbol {x},t)+\boldsymbol {V}_p$![]() . We work in the cartesian coordinate system $\boldsymbol{x}\equiv (x,y,z)$
. We work in the cartesian coordinate system $\boldsymbol{x}\equiv (x,y,z)$![]() and $\hat{e}_z$
and $\hat{e}_z$![]() is the unit vector along the Oz direction. This type of dynamics is relevant not only for the $\boldsymbol {E}\times \boldsymbol {B}$
is the unit vector along the Oz direction. This type of dynamics is relevant not only for the $\boldsymbol {E}\times \boldsymbol {B}$![]() drift in tokamak plasmas (with $\boldsymbol {B}$
drift in tokamak plasmas (with $\boldsymbol {B}$![]() along the $Oz$
along the $Oz$![]() direction) in the presence of a poloidal velocity $\boldsymbol {V}_p$
direction) in the presence of a poloidal velocity $\boldsymbol {V}_p$![]() , but also for other systems: incompressible fluids, astrophysical plasmas (Zank et al. Reference Zank, Dosch, Hunana, Florinski, Matthaeus and Webb2011), magnetic field lines wandering (Ghilea et al. Reference Ghilea, Ruffolo, Chuychai, Sonsrettee, Seripienlert and Matthaeus2011; Negrea, Petrisor & Shalchi Reference Negrea, Petrisor and Shalchi2017), etc.
, but also for other systems: incompressible fluids, astrophysical plasmas (Zank et al. Reference Zank, Dosch, Hunana, Florinski, Matthaeus and Webb2011), magnetic field lines wandering (Ghilea et al. Reference Ghilea, Ruffolo, Chuychai, Sonsrettee, Seripienlert and Matthaeus2011; Negrea, Petrisor & Shalchi Reference Negrea, Petrisor and Shalchi2017), etc.
Despite the amount of work done within this topic (Corrsin Reference Corrsin1951; Kraichnan Reference Kraichnan1968; Kraichnan & Montgomery Reference Kraichnan and Montgomery1980; Isichenko Reference Isichenko1992; Ottaviani Reference Ottaviani1992; Reuss & Misguich Reference Reuss and Misguich1996; Pommois, Veltri & Zimbardo Reference Pommois, Veltri and Zimbardo2001; Vlad et al. Reference Vlad, Spineanu, Misguich and Balescu1998a, Reference Vlad, Spineanu, Misguich and Balescu2001), the problem of turbulent transport is, in general, poorly understood due to its complex features. The essence of the problem can be stated as follows: we do not have simple ways to evaluate the diffusion coefficients from the Eulerian properties of the velocity field. Moreover, non-Gaussianity is rarely taken into account, by accident, when simulating realistic flows, thus little it is known about its effects. A solid understanding of such processes might enable possibilities of controlling the turbulent transport in fusion devices and its damaging consequences.
The present theoretical analysis requires a priori knowledge of the statistical properties of the potential $\phi$![]() : the turbulence spectrum $S(\boldsymbol {k},\omega )$
: the turbulence spectrum $S(\boldsymbol {k},\omega )$![]() and the distribution $P(\phi )$
and the distribution $P(\phi )$![]() . To acquire such information, one needs to use high-quality gyro-kinetic simulations (Jenko & Dorland Reference Jenko and Dorland2001; Wang et al. Reference Wang, Lin, Tang, Lee, Ethier, Lewandowski, Rewoldt, Hahm and Manickam2006) complemented by diagnostic techniques (Casati et al. Reference Casati, Gerbaud, Hennequin, Bourdelle, Candy, Clairet, Garbet, Grandgirard, Gürcan and Heuraux2009; Gao et al. Reference Gao, Zhang, Han, Zhang, Kong, Qu, Wang, Wen, Liu and Huang2015; Gonçalves et al. Reference Gonçalves, Henriques, Hidalgo, Silva, Figueiredo, Naulin, Nielsen and Mendonça2018). In tokamak devices, the spectrum shows a fast decay in frequency and along the radial direction with a peaked profile (at some specific wavenumber $k_0$
. To acquire such information, one needs to use high-quality gyro-kinetic simulations (Jenko & Dorland Reference Jenko and Dorland2001; Wang et al. Reference Wang, Lin, Tang, Lee, Ethier, Lewandowski, Rewoldt, Hahm and Manickam2006) complemented by diagnostic techniques (Casati et al. Reference Casati, Gerbaud, Hennequin, Bourdelle, Candy, Clairet, Garbet, Grandgirard, Gürcan and Heuraux2009; Gao et al. Reference Gao, Zhang, Han, Zhang, Kong, Qu, Wang, Wen, Liu and Huang2015; Gonçalves et al. Reference Gonçalves, Henriques, Hidalgo, Silva, Figueiredo, Naulin, Nielsen and Mendonça2018). In tokamak devices, the spectrum shows a fast decay in frequency and along the radial direction with a peaked profile (at some specific wavenumber $k_0$![]() ) along the poloidal direction (Fonck et al. Reference Fonck, Cosby, Durst, Paul, Bretz, Scott, Synakowski and Taylor1993; Jenko & Dorland Reference Jenko and Dorland2002; Casati et al. Reference Casati, Gerbaud, Hennequin, Bourdelle, Candy, Clairet, Garbet, Grandgirard, Gürcan and Heuraux2009; Holland et al. Reference Holland, White, McKee, Shafer, Candy, Waltz, Schmitz and Tynan2009; Shafer et al. Reference Shafer, Fonck, McKee, Holland, White and Schlossberg2012; Qi et al. Reference Qi, Kwon, Hahm, Yi and Choi2019). One can use the spectrum $S(\boldsymbol {k},\omega ) = \langle |\tilde {\phi }(\boldsymbol {k},\omega )|^2\rangle$
) along the poloidal direction (Fonck et al. Reference Fonck, Cosby, Durst, Paul, Bretz, Scott, Synakowski and Taylor1993; Jenko & Dorland Reference Jenko and Dorland2002; Casati et al. Reference Casati, Gerbaud, Hennequin, Bourdelle, Candy, Clairet, Garbet, Grandgirard, Gürcan and Heuraux2009; Holland et al. Reference Holland, White, McKee, Shafer, Candy, Waltz, Schmitz and Tynan2009; Shafer et al. Reference Shafer, Fonck, McKee, Holland, White and Schlossberg2012; Qi et al. Reference Qi, Kwon, Hahm, Yi and Choi2019). One can use the spectrum $S(\boldsymbol {k},\omega ) = \langle |\tilde {\phi }(\boldsymbol {k},\omega )|^2\rangle$![]() with ${\boldsymbol{k}}$
with ${\boldsymbol{k}}$![]() the wavevector and $\omega$
the wavevector and $\omega$![]() the frequency, to derive, as a Fourier transform, under the assumption of homogeneity, the auto-correlation function $\mathcal{E}(\boldsymbol {x},\boldsymbol {x}^\prime ;t,t^\prime ) =\langle \phi (\boldsymbol {x},t)\phi (\boldsymbol {x}^\prime,t^\prime )\rangle \equiv \mathcal {E}(\boldsymbol {x}-\boldsymbol {x}^\prime ;t-t^\prime )$
the frequency, to derive, as a Fourier transform, under the assumption of homogeneity, the auto-correlation function $\mathcal{E}(\boldsymbol {x},\boldsymbol {x}^\prime ;t,t^\prime ) =\langle \phi (\boldsymbol {x},t)\phi (\boldsymbol {x}^\prime,t^\prime )\rangle \equiv \mathcal {E}(\boldsymbol {x}-\boldsymbol {x}^\prime ;t-t^\prime )$![]() .
.
Regarding the probability distribution function (PDF) $P(\phi )$![]() , the experimental evidence (van Milligen et al. Reference van Milligen, Sánchez, Carreras, Lynch, LaBombard, Pedrosa, Hidalgo, Gonçalves and Balbín2005; Gonçalves et al. Reference Gonçalves, Henriques, Hidalgo, Silva, Figueiredo, Naulin, Nielsen and Mendonça2018; Riva et al. Reference Riva, Militello, Elmore, Omotani, Dudson and Walkden2019; Wang et al. Reference Wang, Tynan, Hong, Nie, Chen, Ke, Wu, Long, Zheng and Xu2019; Beadle & Ricci Reference Beadle and Ricci2020) indicates that, in the edge and SOL regions, the potential is approximately Gaussian $P(\phi )\sim \exp {(-\phi ^2)}$
, the experimental evidence (van Milligen et al. Reference van Milligen, Sánchez, Carreras, Lynch, LaBombard, Pedrosa, Hidalgo, Gonçalves and Balbín2005; Gonçalves et al. Reference Gonçalves, Henriques, Hidalgo, Silva, Figueiredo, Naulin, Nielsen and Mendonça2018; Riva et al. Reference Riva, Militello, Elmore, Omotani, Dudson and Walkden2019; Wang et al. Reference Wang, Tynan, Hong, Nie, Chen, Ke, Wu, Long, Zheng and Xu2019; Beadle & Ricci Reference Beadle and Ricci2020) indicates that, in the edge and SOL regions, the potential is approximately Gaussian $P(\phi )\sim \exp {(-\phi ^2)}$![]() at negative values $\phi <0$
at negative values $\phi <0$![]() and has an exponential-like distribution $P(\phi )\sim \exp {(-\lambda |\phi |)}$
and has an exponential-like distribution $P(\phi )\sim \exp {(-\lambda |\phi |)}$![]() in the positive range $\phi >0$
in the positive range $\phi >0$![]() . This is equivalent with a change both of the skewness and kurtosis of the distribution. Note that the departure from Gaussianity is rather the rule than the exception: all turbulence models (Navier–Stokes, Hasegawa–Mima, Vlasov–Maxwell, etc.) include convective nonlinearities which lead, implicitly, to non-Gaussian solutions (Anderson & Botha Reference Anderson and Botha2015; Anderson & Hnat Reference Anderson and Hnat2017).
. This is equivalent with a change both of the skewness and kurtosis of the distribution. Note that the departure from Gaussianity is rather the rule than the exception: all turbulence models (Navier–Stokes, Hasegawa–Mima, Vlasov–Maxwell, etc.) include convective nonlinearities which lead, implicitly, to non-Gaussian solutions (Anderson & Botha Reference Anderson and Botha2015; Anderson & Hnat Reference Anderson and Hnat2017).
The paper is structured as follows. Section 2 is dedicated to a description of the model used to simulate non-Gaussian plasma turbulence. Two methods, the decorrelation trajectory method (DTM), 2.2, and direct numerical simulation (DNS), 2.3, used to investigate the diffusive transport are also briefly presented. Section 3 is devoted to a three step analysis: semi-analytical estimations of the diffusive transport are provided in 3.1, which are further confirmed and refined by a two-level numerical analysis in 3.2, which is finally explained from a microscopic point of view in 3.3. Finally, § 4 is dedicated to conclusions and perspectives.
2. Theory
We describe the motion of ions in a magnetically confined plasma using a simple geometric set-up: the strong magnetic field is considered constant $\boldsymbol {B}=B_0\hat {e}_z$![]() while the ions are subject to a drift-type motion in the perpendicular plane $\boldsymbol {x}\equiv (x,y)$
while the ions are subject to a drift-type motion in the perpendicular plane $\boldsymbol {x}\equiv (x,y)$![]() in the presence of an effective poloidal velocity (originating from magnetic drifts or plasma rotation) $\boldsymbol {V}_p \equiv V_p \hat {e}_y$
in the presence of an effective poloidal velocity (originating from magnetic drifts or plasma rotation) $\boldsymbol {V}_p \equiv V_p \hat {e}_y$![]()
The statistical description of transport in this context is as follows (Palade Reference Palade2021; Vlad, Palade & Spineanu Reference Vlad, Palade and Spineanu2021): an ensemble of stochastic fields $\{\phi (\boldsymbol {x},t)\}$![]() with known Eulerian properties is considered to drive an associated ensemble of trajectories via equation (2.1). The diffusion coefficient is computed as the Lagrangian correlation $D(t) = 1/2d_t\langle \boldsymbol {x}^2(t)\rangle \equiv \langle \boldsymbol {v}(0)\boldsymbol {x}(t)\rangle$
with known Eulerian properties is considered to drive an associated ensemble of trajectories via equation (2.1). The diffusion coefficient is computed as the Lagrangian correlation $D(t) = 1/2d_t\langle \boldsymbol {x}^2(t)\rangle \equiv \langle \boldsymbol {v}(0)\boldsymbol {x}(t)\rangle$![]() with the initial conditions $\boldsymbol {x}(0)=0$
with the initial conditions $\boldsymbol {x}(0)=0$![]() . Using the characteristic correlation length $\lambda _c$
. Using the characteristic correlation length $\lambda _c$![]() , correlation time $\tau _c$
, correlation time $\tau _c$![]() and velocity amplitude $V=\varPhi /\lambda _c$
and velocity amplitude $V=\varPhi /\lambda _c$![]() , $\varPhi = \sqrt {\langle \phi ^2(\boldsymbol {0},0)\rangle }$
, $\varPhi = \sqrt {\langle \phi ^2(\boldsymbol {0},0)\rangle }$![]() , one can define the Kubo number (Vlad et al. Reference Vlad, Spineanu, Misguich and Balescu1998a) $K_\star$
, one can define the Kubo number (Vlad et al. Reference Vlad, Spineanu, Misguich and Balescu1998a) $K_\star$![]()
as a measure of the correlation time relative to the specific time of flight $\tau _{{\rm fl}}=\lambda _c/V$![]() . Another interpretation of $K_\star$
. Another interpretation of $K_\star$![]() is that of turbulence strength. Consequently, one can distinguish two regimes of transport: the quasilinear (weak/high-frequency turbulence, $K_\star \ll 1$
is that of turbulence strength. Consequently, one can distinguish two regimes of transport: the quasilinear (weak/high-frequency turbulence, $K_\star \ll 1$![]() ) and the strong/low-frequency ($K_\star \gg 1$
) and the strong/low-frequency ($K_\star \gg 1$![]() ) regimes. The quasilinear asymptotic diffusion coefficient can be exactly evaluated as $D^\infty \sim K_\star ^2\lambda _c^2/\tau _c$
) regimes. The quasilinear asymptotic diffusion coefficient can be exactly evaluated as $D^\infty \sim K_\star ^2\lambda _c^2/\tau _c$![]() while in the strong limit the transport is anomalous $D^\infty \sim K_\star ^{1-\gamma }$
while in the strong limit the transport is anomalous $D^\infty \sim K_\star ^{1-\gamma }$![]() with $\gamma \in (0,1)$
with $\gamma \in (0,1)$![]() . Although still under debate, it has been proposed (Isichenko Reference Isichenko1992) and confirmed within some degree of numerical error (Ottaviani Reference Ottaviani1992; Reuss & Misguich Reference Reuss and Misguich1996; Hauff & Jenko Reference Hauff and Jenko2006) that the anomalous exponent is roughly $\gamma \approx 3/10$
. Although still under debate, it has been proposed (Isichenko Reference Isichenko1992) and confirmed within some degree of numerical error (Ottaviani Reference Ottaviani1992; Reuss & Misguich Reference Reuss and Misguich1996; Hauff & Jenko Reference Hauff and Jenko2006) that the anomalous exponent is roughly $\gamma \approx 3/10$![]() .
.
2.1. Turbulence description
The statistical approach to turbulent transport requires the modelling of the potential $\phi$![]() as a non-Gaussian, zero-averaged, homogeneous random field. In order to do that, we assume (as a technical commodity Vio, Andreani & Wamsteker Reference Vio, Andreani and Wamsteker2001; Liu et al. Reference Liu, Li, Sun and Yu2019; Palade & Vlad Reference Palade and Vlad2021) that the non-Gaussian field $\phi (\boldsymbol {x},t)$
as a non-Gaussian, zero-averaged, homogeneous random field. In order to do that, we assume (as a technical commodity Vio, Andreani & Wamsteker Reference Vio, Andreani and Wamsteker2001; Liu et al. Reference Liu, Li, Sun and Yu2019; Palade & Vlad Reference Palade and Vlad2021) that the non-Gaussian field $\phi (\boldsymbol {x},t)$![]() can be related to another, fictitious, Gaussian field $\varphi (\boldsymbol {x},t)$
can be related to another, fictitious, Gaussian field $\varphi (\boldsymbol {x},t)$![]() with known correlation function $\mathcal {E}(\boldsymbol {x}-\boldsymbol {x}^\prime,t-t^\prime ) = \langle \varphi (\boldsymbol {x},t)\varphi (\boldsymbol {x}^\prime,t^\prime )\rangle$
with known correlation function $\mathcal {E}(\boldsymbol {x}-\boldsymbol {x}^\prime,t-t^\prime ) = \langle \varphi (\boldsymbol {x},t)\varphi (\boldsymbol {x}^\prime,t^\prime )\rangle$![]() via a nonlinear transformation $\phi (\boldsymbol {x},t) = f(\varphi (\boldsymbol {x},t))$
via a nonlinear transformation $\phi (\boldsymbol {x},t) = f(\varphi (\boldsymbol {x},t))$![]() . The function $f$
. The function $f$![]() must be chosen such that both fields are zero averaged $\langle \phi (\boldsymbol {x},t)\rangle = \langle \varphi (\boldsymbol {x},t)\rangle = 0$
must be chosen such that both fields are zero averaged $\langle \phi (\boldsymbol {x},t)\rangle = \langle \varphi (\boldsymbol {x},t)\rangle = 0$![]() and have the same amplitude of fluctuations $\langle \phi ^2(\boldsymbol {x},t)\rangle = \langle \varphi ^2(\boldsymbol {x},t)\rangle = \mathcal {E}(\boldsymbol {0},0)=V_0$
and have the same amplitude of fluctuations $\langle \phi ^2(\boldsymbol {x},t)\rangle = \langle \varphi ^2(\boldsymbol {x},t)\rangle = \mathcal {E}(\boldsymbol {0},0)=V_0$![]() .
.
It can be easily proven that a local nonlinear transformation preserves the homogeneity property. This means that the field $\phi (\boldsymbol {x},t)$![]() is also homogeneous, i.e. its correlation function is only distance dependent $\langle \phi (\boldsymbol {x},t)\phi (\boldsymbol {x}^\prime,t^\prime )\rangle =\langle f(\varphi (\boldsymbol {x},t))f(\varphi (\boldsymbol {x}^\prime,t^\prime ))\rangle = \mathcal {E}^\prime (\boldsymbol {x}-\boldsymbol {x}^\prime,t-t^\prime )$
is also homogeneous, i.e. its correlation function is only distance dependent $\langle \phi (\boldsymbol {x},t)\phi (\boldsymbol {x}^\prime,t^\prime )\rangle =\langle f(\varphi (\boldsymbol {x},t))f(\varphi (\boldsymbol {x}^\prime,t^\prime ))\rangle = \mathcal {E}^\prime (\boldsymbol {x}-\boldsymbol {x}^\prime,t-t^\prime )$![]() .
.
Straightforwardly, we can generically compute the correlation of the derivatives as well as the skewness $s$![]() and the excess kurtosis $\delta \kappa$
and the excess kurtosis $\delta \kappa$![]() of the non-Gaussian field $\phi$
of the non-Gaussian field $\phi$![]()
Experimental measurements in the SOL of various tokamak devices (Filippas et al. Reference Filippas, Bengston, Li, Meier, Ritz and Powers1995; Antar et al. Reference Antar, Devynck, Garbet and Luckhardt2001a,Reference Antar, Krasheninnikov, Devynck, Doerner, Hollmann, Boedo, Luckhardt and Connb; van Milligen et al. Reference van Milligen, Sánchez, Carreras, Lynch, LaBombard, Pedrosa, Hidalgo, Gonçalves and Balbín2005; Casati et al. Reference Casati, Gerbaud, Hennequin, Bourdelle, Candy, Clairet, Garbet, Grandgirard, Gürcan and Heuraux2009; Riva et al. Reference Riva, Militello, Elmore, Omotani, Dudson and Walkden2019) have shown PDFs of electrostatic fluctuations which exhibit longer tails as well as skewness, especially in the positive part of the distribution. For these reasons, we choose a particularly simple nonlinear transformation to construct the non-Gaussian fields: $f(\varphi ) \sim \varphi +\alpha \varphi ^2+\beta \varphi ^3-\alpha V_0$![]()
Note that, up to first order, the skewness is controlled by the $\alpha$![]() parameter and the kurtosis by $\beta$
parameter and the kurtosis by $\beta$![]() . Also, the correlation is virtually unchanged due to its second-order parametric dependence $\mathcal {E}^\prime \approx \mathcal {E} +2\alpha ^2 \mathcal {E} (\mathcal {E} -V_0)+6\beta ^2 \mathcal {E} (\mathcal {E} ^2-V_0^2)$
. Also, the correlation is virtually unchanged due to its second-order parametric dependence $\mathcal {E}^\prime \approx \mathcal {E} +2\alpha ^2 \mathcal {E} (\mathcal {E} -V_0)+6\beta ^2 \mathcal {E} (\mathcal {E} ^2-V_0^2)$![]() . This enables us to approximate $\mathcal {E}^\prime \approx \mathcal {E}$
. This enables us to approximate $\mathcal {E}^\prime \approx \mathcal {E}$![]() since $\alpha,\beta \sim 10^{-2,-1}$
since $\alpha,\beta \sim 10^{-2,-1}$![]() for a good agreement with experimental distributions (Filippas et al. Reference Filippas, Bengston, Li, Meier, Ritz and Powers1995; Riva et al. Reference Riva, Militello, Elmore, Omotani, Dudson and Walkden2019).
for a good agreement with experimental distributions (Filippas et al. Reference Filippas, Bengston, Li, Meier, Ritz and Powers1995; Riva et al. Reference Riva, Militello, Elmore, Omotani, Dudson and Walkden2019).
We note that the presence of a poloidal velocity field $V_p$![]() implies that the turbulent field $\phi$
implies that the turbulent field $\phi$![]() moves with this velocity, which should modify the turbulence statistics. However, since we consider a homogeneous turbulence and the experimental measurements of field statistics are usually performed in the laboratory system, such modifications are not present.
moves with this velocity, which should modify the turbulence statistics. However, since we consider a homogeneous turbulence and the experimental measurements of field statistics are usually performed in the laboratory system, such modifications are not present.
Our model of intermittency (2.6) captures the stochastic features of turbulence ($\phi$![]() being a random field) and also the departure from a Gaussian distribution (through the $f(\cdot )$
being a random field) and also the departure from a Gaussian distribution (through the $f(\cdot )$![]() transformation). Yet, we acknowledge that true intermittency exhibits other features such as scale symmetry breaking and deviation from homogeneity. Such elements are beyond the scope of the present work.
transformation). Yet, we acknowledge that true intermittency exhibits other features such as scale symmetry breaking and deviation from homogeneity. Such elements are beyond the scope of the present work.
2.2. Decorrelation trajectory method
The DTM has been used in the past decades to investigate various types of turbulent transport in tokamak plasmas (Vlad et al. Reference Vlad, Spineanu, Misguich and Balescu1998a, Reference Vlad, Spineanu, Misguich, Reuss, Balescu, Itoh and Itoh2004; Vlad & Spineanu Reference Vlad and Spineanu2016; Croitoru et al. Reference Croitoru, Palade, Vlad and Spineanu2017) as well as in some astrophysical systems (Negrea Reference Negrea2019). The method is semi-analytical, since it describes the transport via a set of deterministic objects called decorrelation trajectories (DTs) (Vlad et al. Reference Vlad, Spineanu, Misguich and Balescu1998a) which are used to compute the diffusion (2.12)
The main assumption of DTM is that trajectories with similar initial conditions should remain similar at all times. If this is true, one can replace the ensemble of real stochastic potentials $\{\phi (\boldsymbol {x},t)\}$![]() with a set of deterministic conditional potentials $\{\varPhi ^S(\boldsymbol {x},t)\}$
with a set of deterministic conditional potentials $\{\varPhi ^S(\boldsymbol {x},t)\}$![]() which are defined as conditional averages over real potentials in sub-ensembles $(S)$
which are defined as conditional averages over real potentials in sub-ensembles $(S)$![]() , i.e. $\varPhi ^S(\boldsymbol {x},t)=\langle \phi (\boldsymbol {x},t)\rangle ^S$
, i.e. $\varPhi ^S(\boldsymbol {x},t)=\langle \phi (\boldsymbol {x},t)\rangle ^S$![]() . The DTs $\boldsymbol {X}^S(t)$
. The DTs $\boldsymbol {X}^S(t)$![]() are solutions for the equation (2.11).
are solutions for the equation (2.11).
For our non-Gaussian case, we define the sub-ensembles via the initial values (at $\boldsymbol {x} = 0$![]() and $t=0$
and $t=0$![]() ) of the auxiliary field $\varphi$
) of the auxiliary field $\varphi$![]() as
as
where each $S$![]() has a probabilistic weight $P(S)=\prod _{i\in \{0,x,y\}}\exp (-(\varphi _i^S)^2/V_{ii}/2)$
has a probabilistic weight $P(S)=\prod _{i\in \{0,x,y\}}\exp (-(\varphi _i^S)^2/V_{ii}/2)$![]() with $V_{ii}=\langle [\partial _i\varphi (0)]^2\rangle = -\partial _{ii}\mathcal {E}(0,0)$
with $V_{ii}=\langle [\partial _i\varphi (0)]^2\rangle = -\partial _{ii}\mathcal {E}(0,0)$![]() . From a straightforward calculus of $\varPhi ^S = \langle \phi \rangle ^S=\langle f(\varphi )\rangle ^S$
. From a straightforward calculus of $\varPhi ^S = \langle \phi \rangle ^S=\langle f(\varphi )\rangle ^S$![]() we complete the DTM model
we complete the DTM model

The function $\sigma$![]() is, in fact, a measure of field fluctuations within a sub-ensemble $S$
is, in fact, a measure of field fluctuations within a sub-ensemble $S$![]() which turns out to be independent of $S$
which turns out to be independent of $S$![]() : $\sigma (\boldsymbol {x},t) = \langle \delta \varphi ^2(\boldsymbol {x},t)\rangle ^S$
: $\sigma (\boldsymbol {x},t) = \langle \delta \varphi ^2(\boldsymbol {x},t)\rangle ^S$![]() . Note that, in the Gaussian limit $\alpha =\beta = 0$
. Note that, in the Gaussian limit $\alpha =\beta = 0$![]() , the model simplifies to $\varPhi ^S\to \varPsi ^S$
, the model simplifies to $\varPhi ^S\to \varPsi ^S$![]() , as has been used in previous studies (Vlad et al. Reference Vlad, Spineanu, Misguich and Balescu1998a; Vlad & Spineanu Reference Vlad and Spineanu2016; Croitoru et al. Reference Croitoru, Palade, Vlad and Spineanu2017; Negrea Reference Negrea2019). The DTM method is equivalent to neglecting trajectory fluctuations (Vlad et al. Reference Vlad, Spineanu, Misguich and Balescu1998b) within a sub-ensemble. For more details on the method see Vlad et al. (Reference Vlad, Spineanu, Misguich and Balescu1998a, Reference Vlad, Spineanu, Misguich and Balescu2001, Reference Vlad, Spineanu, Misguich, Reuss, Balescu, Itoh and Itoh2004) and Croitoru et al. (Reference Croitoru, Palade, Vlad and Spineanu2017).
, as has been used in previous studies (Vlad et al. Reference Vlad, Spineanu, Misguich and Balescu1998a; Vlad & Spineanu Reference Vlad and Spineanu2016; Croitoru et al. Reference Croitoru, Palade, Vlad and Spineanu2017; Negrea Reference Negrea2019). The DTM method is equivalent to neglecting trajectory fluctuations (Vlad et al. Reference Vlad, Spineanu, Misguich and Balescu1998b) within a sub-ensemble. For more details on the method see Vlad et al. (Reference Vlad, Spineanu, Misguich and Balescu1998a, Reference Vlad, Spineanu, Misguich and Balescu2001, Reference Vlad, Spineanu, Misguich, Reuss, Balescu, Itoh and Itoh2004) and Croitoru et al. (Reference Croitoru, Palade, Vlad and Spineanu2017).
2.3. DNS method
The purpose of DNS is to investigate turbulent transport as it is, without resorting to any approximations, closures or supplementary models.
In our case, this is achieved by constructing a statistical ensemble of Gaussian random fields (GRFs) $\varphi (\boldsymbol {x},t)$![]() with the correct correlation function which will be used to derive the ensemble of non-Gaussian fields $\phi$
with the correct correlation function which will be used to derive the ensemble of non-Gaussian fields $\phi$![]() via the prescribed transformation $\phi =f(\varphi )$
via the prescribed transformation $\phi =f(\varphi )$![]() . For each realization, (2.1) is solved and a trajectory is obtained. The transport coefficients, diffusion and average velocity, are computed as simple statistical averages over the ensemble. DNS tries to mimic the whole (real) statistical problem resorting to numerical tools (Palade Reference Palade2021; Palade & Vlad Reference Palade and Vlad2021; Vlad et al. Reference Vlad, Palade and Spineanu2021).
. For each realization, (2.1) is solved and a trajectory is obtained. The transport coefficients, diffusion and average velocity, are computed as simple statistical averages over the ensemble. DNS tries to mimic the whole (real) statistical problem resorting to numerical tools (Palade Reference Palade2021; Palade & Vlad Reference Palade and Vlad2021; Vlad et al. Reference Vlad, Palade and Spineanu2021).
We underline that the turbulent character of the potential is captured both by the chaotic nature of the random fields and by the statistical approach, which considers an ensemble of such stochastic objects.
The main source of errors in DNS is an insufficient numerical representation of the ensemble. In practice, we use a spectral representation of GRFs as discussed in Palade & Vlad (Reference Palade and Vlad2021) with improved Eulerian and Lagrangian convergences

where $\boldsymbol {k}_j$![]() are randomly distributed within the compact support of the spectrum $S(\boldsymbol {k})$
are randomly distributed within the compact support of the spectrum $S(\boldsymbol {k})$![]() and $\zeta _j = \pm 1$
and $\zeta _j = \pm 1$![]() is randomly chosen. In practice, we use $N_c\sim 10^d$
is randomly chosen. In practice, we use $N_c\sim 10^d$![]() as this was found to ensure both the Gaussianity of the field as well as the details of the correlation function. Good statistical convergence is found, both at the Eulerian and Lagrangian levels, to be satisfied by ensembles with dimension $M\sim 10^5$
as this was found to ensure both the Gaussianity of the field as well as the details of the correlation function. Good statistical convergence is found, both at the Eulerian and Lagrangian levels, to be satisfied by ensembles with dimension $M\sim 10^5$![]() .
.
This is the standard approach of DNS to transport. It is suitable for GRFs since the field $\varphi$![]() is naturally Gaussian via the central limit theorem. In order to tackle the problem of non-Gaussian $\phi$
is naturally Gaussian via the central limit theorem. In order to tackle the problem of non-Gaussian $\phi$![]() , we compute as such (2.17) the fields $\varphi$
, we compute as such (2.17) the fields $\varphi$![]() and solve the following equation of motion:
and solve the following equation of motion:
Note that the above equation (2.18) is equivalent to (2.1) given the fact that $\phi = f(\varphi )$![]() . The rest of the method remains unchanged. For more details see Palade, Vlad & Spineanu (Reference Palade, Vlad and Spineanu2021), Hauff & Jenko (Reference Hauff and Jenko2006), Palade & Vlad (Reference Palade and Vlad2021), Vlad et al. (Reference Vlad, Palade and Spineanu2021) and Palade (Reference Palade2021).
. The rest of the method remains unchanged. For more details see Palade, Vlad & Spineanu (Reference Palade, Vlad and Spineanu2021), Hauff & Jenko (Reference Hauff and Jenko2006), Palade & Vlad (Reference Palade and Vlad2021), Vlad et al. (Reference Vlad, Palade and Spineanu2021) and Palade (Reference Palade2021).
3. Results
In order to capture the basic physical processes related to non-Gaussianity, we use two simple model correlation functions $\mathcal {E}_1$![]() and $\mathcal {E}_2$
and $\mathcal {E}_2$![]() for the $\varphi$
for the $\varphi$![]() field
field

with $\lambda _x=\lambda _y=1$![]() and $\tau _c = 10$
and $\tau _c = 10$![]() . Thus, $V_0 = 1$
. Thus, $V_0 = 1$![]() . These choices are in agreement with the gross features of turbulence spectra from incompressible plasmas and fluids (Levinson et al. Reference Levinson, Beall, Powers and Bengtson1984; Boldyrev Reference Boldyrev2005; Casati et al. Reference Casati, Gerbaud, Hennequin, Bourdelle, Candy, Clairet, Garbet, Grandgirard, Gürcan and Heuraux2009; Gao et al. Reference Gao, Zhang, Han, Zhang, Kong, Qu, Wang, Wen, Liu and Huang2015).
. These choices are in agreement with the gross features of turbulence spectra from incompressible plasmas and fluids (Levinson et al. Reference Levinson, Beall, Powers and Bengtson1984; Boldyrev Reference Boldyrev2005; Casati et al. Reference Casati, Gerbaud, Hennequin, Bourdelle, Candy, Clairet, Garbet, Grandgirard, Gürcan and Heuraux2009; Gao et al. Reference Gao, Zhang, Han, Zhang, Kong, Qu, Wang, Wen, Liu and Huang2015).
In figure 1(a,b) we show how the proposed transformation $f(\varphi ) \sim \varphi +\alpha \varphi ^2+\beta \varphi ^3-\alpha$![]() distorts the Gaussian distribution both for the potential and its derivatives. Note how, through appropriate combinations of $\alpha$
distorts the Gaussian distribution both for the potential and its derivatives. Note how, through appropriate combinations of $\alpha$![]() and $\beta$
and $\beta$![]() (the brown line), the resulting PDF is closer to Gaussianity in the negative domain $\phi <0$
(the brown line), the resulting PDF is closer to Gaussianity in the negative domain $\phi <0$![]() and similar to an exponential distribution in the positive part $\phi >0$
and similar to an exponential distribution in the positive part $\phi >0$![]() (as observed in measurements). Also, due to the relation between $\partial _i\phi$
(as observed in measurements). Also, due to the relation between $\partial _i\phi$![]() and $\varphi$
and $\varphi$![]() , the distribution of derivatives $P(\partial _i\phi )$
, the distribution of derivatives $P(\partial _i\phi )$![]() is free of any skewness.
is free of any skewness.

Figure 1. PDF of potential values (a) and potential derivatives (b) generated randomly in accordance with the nonlinear transformation from (2.6).
In figure 2(a,b) we plot the change in correlation $\delta \mathcal {E} = \mathcal {E}^\prime -\mathcal {E}$![]() under the effects of non-Gaussianity for the first model, $\mathcal {E}_1$
under the effects of non-Gaussianity for the first model, $\mathcal {E}_1$![]() . The results are in agreement with the analytical estimation (2.6) in that the departure is $\delta \mathcal {E}\sim \mathcal {O}(\alpha ^2,\beta ^2)\sim 1\,\%\mathcal {E}$
. The results are in agreement with the analytical estimation (2.6) in that the departure is $\delta \mathcal {E}\sim \mathcal {O}(\alpha ^2,\beta ^2)\sim 1\,\%\mathcal {E}$![]() and virtually negligible, especially in the strongly correlated area $|\boldsymbol {x}|\sim 0$
and virtually negligible, especially in the strongly correlated area $|\boldsymbol {x}|\sim 0$![]() . For $\mathcal {E}_2$
. For $\mathcal {E}_2$![]() the profiles are extremely similar.
the profiles are extremely similar.

Figure 2. Relative changes $\delta \mathcal {E}_1 = \mathcal {E}_1^\prime - \mathcal {E}_1$![]() of the correlation function in the spatial domain at different small $\alpha, \beta$
of the correlation function in the spatial domain at different small $\alpha, \beta$![]() values.
values.
3.1. Analytical estimations
Our first level of analysis is the analytical one. We intend to estimate the change of the diffusion coefficient induced by non-Gaussian features of turbulence. In order to do that, we start by considering a simplified case of frozen turbulence, when the potential is time independent $\varphi (\boldsymbol {x},t) \equiv \varphi (\boldsymbol {x})$![]() . This case can be obtained setting $\tau _c\to \infty$
. This case can be obtained setting $\tau _c\to \infty$![]() . Due to the Hamiltonian structure of the equations (2.1), the trajectories are closed and both the fictitious and the real potentials are conserved $\varphi (\boldsymbol {x}(t)) = \varphi (\boldsymbol {x}(0)) = \varphi (\boldsymbol {0})\implies \phi (\boldsymbol {x}(t)) = \phi (\boldsymbol {x}(0)) = \phi (\boldsymbol {0})$
. Due to the Hamiltonian structure of the equations (2.1), the trajectories are closed and both the fictitious and the real potentials are conserved $\varphi (\boldsymbol {x}(t)) = \varphi (\boldsymbol {x}(0)) = \varphi (\boldsymbol {0})\implies \phi (\boldsymbol {x}(t)) = \phi (\boldsymbol {x}(0)) = \phi (\boldsymbol {0})$![]() . For further purposes, let us denote the following function:
. For further purposes, let us denote the following function:
With this notation, it turns out that the equations of motion in the Gaussian and non-Gaussian ($0$![]() index) cases become
index) cases become
It can be easily shown, via a variable transformation, that $\boldsymbol {x}(t) = \boldsymbol {x}_0(A[\varphi (\boldsymbol {0})]t)$![]() . This exact relation allows us to relate the running diffusion coefficients between these two cases, non-Gaussian $D(t)$
. This exact relation allows us to relate the running diffusion coefficients between these two cases, non-Gaussian $D(t)$![]() and the Gaussian limit $D_0(t)$
and the Gaussian limit $D_0(t)$![]() . In order to do that, let us denote the ‘conditional diffusion’ for trajectories starting at equal potential values as
. In order to do that, let us denote the ‘conditional diffusion’ for trajectories starting at equal potential values as
for which it holds true that $d(t;\varphi (\boldsymbol {0}))= A[\varphi (\boldsymbol {0})]d_0(A[\varphi (\boldsymbol {0})]t;\varphi (\boldsymbol {0}))$![]() . Finally, we write
. Finally, we write
Without any proof, we assume that some sort of generalized mean value theorem is valid and these two integrals can be related through an effective potential
On the other hand, the anomalous feature of transport is reflected in the asymptotic behaviour of running Lagrangian averages $L(t)$![]() which algebraically decay $L_0(t)\sim t^{-\gamma }$
which algebraically decay $L_0(t)\sim t^{-\gamma }$![]() (Isichenko Reference Isichenko1992; Ottaviani Reference Ottaviani1992; Reuss & Misguich Reference Reuss and Misguich1996; Reuss, Vlad & Misguich Reference Reuss, Vlad and Misguich1998; Vlad et al. Reference Vlad, Spineanu, Misguich and Balescu1998a, Reference Vlad, Spineanu, Misguich, Reuss, Balescu, Itoh and Itoh2004). At small times $t\ll \tau _{{\rm fl}}$
(Isichenko Reference Isichenko1992; Ottaviani Reference Ottaviani1992; Reuss & Misguich Reference Reuss and Misguich1996; Reuss, Vlad & Misguich Reference Reuss, Vlad and Misguich1998; Vlad et al. Reference Vlad, Spineanu, Misguich and Balescu1998a, Reference Vlad, Spineanu, Misguich, Reuss, Balescu, Itoh and Itoh2004). At small times $t\ll \tau _{{\rm fl}}$![]() the dependence of $L(t)$
the dependence of $L(t)$![]() can usually be analytically computed. The presence of a decorrelation mechanism (finite $\tau _c$
can usually be analytically computed. The presence of a decorrelation mechanism (finite $\tau _c$![]() in our case) tends to saturate asymptotically all Lagrangian quantities at values which can be estimated (Vlad et al. Reference Vlad, Spineanu, Misguich and Balescu1998a, Reference Vlad, Spineanu, Misguich, Reuss, Balescu, Itoh and Itoh2004) as $\lim _{t\to \infty } L(t) =L^\infty \approx L(\tau _c)$
in our case) tends to saturate asymptotically all Lagrangian quantities at values which can be estimated (Vlad et al. Reference Vlad, Spineanu, Misguich and Balescu1998a, Reference Vlad, Spineanu, Misguich, Reuss, Balescu, Itoh and Itoh2004) as $\lim _{t\to \infty } L(t) =L^\infty \approx L(\tau _c)$![]() . We assume this to be true both for diffusion $D(t)$
. We assume this to be true both for diffusion $D(t)$![]() and $\varphi _{{\rm eff}}(t)$
and $\varphi _{{\rm eff}}(t)$![]() .
.
Combining all these behaviours, the algebraic decay $D(t)\sim t^{-\gamma }, \varphi _{{\rm eff}}(t)\sim t^{-\zeta }$![]() , the approximate saturation at the decorrelation time $D^\infty \approx D(\tau _c), \varphi ^\infty _{{\rm eff}} \approx \varphi _{{\rm eff}}(\tau _c)$
, the approximate saturation at the decorrelation time $D^\infty \approx D(\tau _c), \varphi ^\infty _{{\rm eff}} \approx \varphi _{{\rm eff}}(\tau _c)$![]() and the assumed relation between Gaussian and non-Gaussian diffusion (3.9), one can show that
and the assumed relation between Gaussian and non-Gaussian diffusion (3.9), one can show that

These estimations suggest that $\alpha$![]() has only a quadratic effect on the diffusion coefficient. This aspect can be understood from another perspective, analysing how the Lagrangian correlation of velocities $L_v(t) = \langle v_x(0)v_x(t)\rangle$
has only a quadratic effect on the diffusion coefficient. This aspect can be understood from another perspective, analysing how the Lagrangian correlation of velocities $L_v(t) = \langle v_x(0)v_x(t)\rangle$![]() (the time derivative of $D(t)$
(the time derivative of $D(t)$![]() ) varies with $\alpha$
) varies with $\alpha$![]() up to the first order
up to the first order
Note that $\varphi (0)$![]() and $\partial _i\varphi (0)$
and $\partial _i\varphi (0)$![]() are uncorrelated Gaussian quantities. Moreover, Lumley's theorem (Monin & Yaglom Reference Monin and Yaglom1973) assures us that the space derivatives $\partial _i\varphi (t)$
are uncorrelated Gaussian quantities. Moreover, Lumley's theorem (Monin & Yaglom Reference Monin and Yaglom1973) assures us that the space derivatives $\partial _i\varphi (t)$![]() remain Gaussian quantities at all times. Only the distribution of Lagrangian potentials $\varphi (t)$
remain Gaussian quantities at all times. Only the distribution of Lagrangian potentials $\varphi (t)$![]() might depart from Gaussianity in the case of finite $\tau _c$
might depart from Gaussianity in the case of finite $\tau _c$![]() , but only slightly. Thus, the derivative $\partial _\alpha L_v(t)$
, but only slightly. Thus, the derivative $\partial _\alpha L_v(t)$![]() is roughly made up of averages of products of three Gaussian quantities and, therefore, is zero. This means that $L_v(t)$
is roughly made up of averages of products of three Gaussian quantities and, therefore, is zero. This means that $L_v(t)$![]() is roughly independent of $\alpha$
is roughly independent of $\alpha$![]() up to first order. The same goes for the diffusion.
up to first order. The same goes for the diffusion.
Following the above reasoning and estimations (3.10), we expect that the non-Gaussian diffusion will vary roughly as $\mathcal {O}(\beta ), \mathcal {O}(\alpha ^2)$![]() . For this reason, we define a response function (susceptibility $\chi$
. For this reason, we define a response function (susceptibility $\chi$![]() ) to quantify the possible linear dependency between diffusion variation and turbulence excess kurtosis (as a measurable quantity)
) to quantify the possible linear dependency between diffusion variation and turbulence excess kurtosis (as a measurable quantity)
3.2. Numerical results
We intend to test further if the analytical estimations found above bear any meaning in real situations. For that, we use the statistical methods described previously: DNS and DTM. We underline that DNS is an exact-in-principle method which is hindered in practice only by the numerical resolution, thus, it requires a large amount of CPU resources. DTM is an approximation which provides only qualitative results and it is easy to implement numerically. The purpose of DTM in this work is to serve as a supplementary test for the results of DNS which might be plagued with a small, but uncertain, degree of numerical inaccuracy.
We perform numerical simulations of the running diffusion coefficients $D(t)$![]() for the incompressible motion (2.1) where the potential $\phi (\boldsymbol {x},t)$
for the incompressible motion (2.1) where the potential $\phi (\boldsymbol {x},t)$![]() is described via a fictitious field $\varphi (\boldsymbol {x},t)$
is described via a fictitious field $\varphi (\boldsymbol {x},t)$![]() ( 2.6) with known Eulerian correlation ( 3.1). The numerical method for trajectory propagation both in ( 2.18) (DNS) and ( 2.11) (DTM) is a fourth-order Runge–Kutta method with a fixed time step $\Delta t\sim 10^{-1}\min (\tau _c,\lambda _c^2)$
( 2.6) with known Eulerian correlation ( 3.1). The numerical method for trajectory propagation both in ( 2.18) (DNS) and ( 2.11) (DTM) is a fourth-order Runge–Kutta method with a fixed time step $\Delta t\sim 10^{-1}\min (\tau _c,\lambda _c^2)$![]() . The simulation time is $t_{\max }\sim 5\tau _c$
. The simulation time is $t_{\max }\sim 5\tau _c$![]() . The number of trajectories simulated with DNS is routinely $N_p \sim 10^5$
. The number of trajectories simulated with DNS is routinely $N_p \sim 10^5$![]() while the number of sub-ensembles used in DTM $N_s\sim 10^5$
while the number of sub-ensembles used in DTM $N_s\sim 10^5$![]() . These resolutions are chosen for numerical accuracy and statistical precision. Using dedicated programming procedures, typical simulations on personal computers require in terms of CPU time $t_{{\rm CPU}}^{{\rm DTM}}\sim 1\,\min$
. These resolutions are chosen for numerical accuracy and statistical precision. Using dedicated programming procedures, typical simulations on personal computers require in terms of CPU time $t_{{\rm CPU}}^{{\rm DTM}}\sim 1\,\min$![]() and $t_{{\rm CPU}}^{{\rm DNS}}\sim 10\,\min$
and $t_{{\rm CPU}}^{{\rm DNS}}\sim 10\,\min$![]() .
.
Beyond diving into the matter of non-Gaussianity, let us have a look at a typical running diffusion coefficient $D(t)$![]() obtained in the case $\alpha = \beta = 0$
obtained in the case $\alpha = \beta = 0$![]() . The results of both methods are shown in figure 3 at $\tau _c = 10$
. The results of both methods are shown in figure 3 at $\tau _c = 10$![]() and $\tau _c\to \infty$
and $\tau _c\to \infty$![]() . In the case of frozen turbulence one can see the algebraic decay of diffusion $D(t)\sim t^{-\gamma }$
. In the case of frozen turbulence one can see the algebraic decay of diffusion $D(t)\sim t^{-\gamma }$![]() . The effect of finite $\tau _c$
. The effect of finite $\tau _c$![]() is the saturation of diffusion to a constant value $D^\infty = D(t\to \infty )$
is the saturation of diffusion to a constant value $D^\infty = D(t\to \infty )$![]() . Note that DTM reproduces the qualitative behaviour of trapping and decorrelation at all times. Yet, the results are quantitatively different in the asymptotic region $t\gg \tau _{{\rm fl}}$
. Note that DTM reproduces the qualitative behaviour of trapping and decorrelation at all times. Yet, the results are quantitatively different in the asymptotic region $t\gg \tau _{{\rm fl}}$![]() . This is a due to the overestimation of trapping in the DTM approximation. Consequently, DTM overestimates the $\gamma$
. This is a due to the overestimation of trapping in the DTM approximation. Consequently, DTM overestimates the $\gamma$![]() exponent too and we expect it will overestimate the effect of intermittency in the strong/low-frequency turbulence regime.
exponent too and we expect it will overestimate the effect of intermittency in the strong/low-frequency turbulence regime.

Figure 3. Running diffusion coefficient $D(t)$![]() obtained for the correlation $\mathcal {E}_1, V_p = 0$
obtained for the correlation $\mathcal {E}_1, V_p = 0$![]() in the case $\tau _c\to \infty$
in the case $\tau _c\to \infty$![]() (blue) and $\tau _c = 10$
(blue) and $\tau _c = 10$![]() (red) with the use of DNS (full line) and DTM (dashed line).
(red) with the use of DNS (full line) and DTM (dashed line).
We investigate further the dependence of the diffusion on $\alpha$![]() and find that both methods, DTM and DNS, predict a negligible variation (figure 4). The results are in line with our analytical estimation that $\alpha$
and find that both methods, DTM and DNS, predict a negligible variation (figure 4). The results are in line with our analytical estimation that $\alpha$![]() affects the transport only at second order. A very weak linear dependence supplemented by a weak quadratic one can be observed.
affects the transport only at second order. A very weak linear dependence supplemented by a weak quadratic one can be observed.

Figure 4. Asymptotic values of diffusion at $\beta = 0, \tau _c = 10, V_p = 0$![]() vs the skewness $s$
vs the skewness $s$![]() obtained with the use of DTM (blue line) and DNS (red line).
obtained with the use of DTM (blue line) and DNS (red line).
Given this fact, let us set $\alpha = 0$![]() and look further at how $\beta$
and look further at how $\beta$![]() affects the diffusion. The mechanism can be seen at work in figure 5, where several running diffusion profiles $D(t)$
affects the diffusion. The mechanism can be seen at work in figure 5, where several running diffusion profiles $D(t)$![]() are shown for different $\beta$
are shown for different $\beta$![]() values. As expected, the effect is visible only at larger times, at least at the order of $\tau _{{\rm fl}}$
values. As expected, the effect is visible only at larger times, at least at the order of $\tau _{{\rm fl}}$![]() , and it results in a decrease of the diffusion coefficient. This behaviour can be quantified further by inspecting the variation of the asymptotic diffusion $D^\infty$
, and it results in a decrease of the diffusion coefficient. This behaviour can be quantified further by inspecting the variation of the asymptotic diffusion $D^\infty$![]() with $\beta$
with $\beta$![]() .
.

Figure 5. Running diffusion profiles $D(t)$![]() obtained with DNS for the correlation $\mathcal {E}_1$
obtained with DNS for the correlation $\mathcal {E}_1$![]() with $\tau _c =10$
with $\tau _c =10$![]() and $V_p = 0$
and $V_p = 0$![]() at different $\beta$
at different $\beta$![]() values and $\alpha = 0$
values and $\alpha = 0$![]() .
.
We plot in figure 6 asymptotic diffusion coefficients computed for different values of $\beta$![]() with DNS (blue) for the correlation function $\mathcal {E}_1$
with DNS (blue) for the correlation function $\mathcal {E}_1$![]() and with DTM (red) for $\mathcal {E}_2$
and with DTM (red) for $\mathcal {E}_2$![]() . Our expectation that the $\beta$
. Our expectation that the $\beta$![]() parameter drives a linear change in the diffusion is confirmed. Also, it must be emphasized how close the results of DTM to those of DNS are, given the fact that they use two distinct correlations.
parameter drives a linear change in the diffusion is confirmed. Also, it must be emphasized how close the results of DTM to those of DNS are, given the fact that they use two distinct correlations.

Figure 6. The relative asymptotic diffusion dependence on the excess kurtosis obtained with DTM for $\mathcal {E}_2$![]() (blue line) and with DNS for $\mathcal {E}_1$
(blue line) and with DNS for $\mathcal {E}_1$![]() (red line).
(red line).
Going further into understanding the effects of intermittency, we plot in figure 7 profiles of asymptotic diffusion coefficients vs the Kubo number at different values of the $\beta$![]() parameter. As expected from the results of figure 6 the effect of $\beta$
parameter. As expected from the results of figure 6 the effect of $\beta$![]() is to inhibit the overall values of diffusion. However, something supplementary must be underlined: in the high $K_\star$
is to inhibit the overall values of diffusion. However, something supplementary must be underlined: in the high $K_\star$![]() region, that of trajectory trapping, the profiles are approximately parallel to each other and to the $\sim K_\star ^{-0.3}$
region, that of trajectory trapping, the profiles are approximately parallel to each other and to the $\sim K_\star ^{-0.3}$![]() line. This tells us that the Kubo number scaling is universal $\gamma = 0.3$
line. This tells us that the Kubo number scaling is universal $\gamma = 0.3$![]() and it is unaffected by non-Gaussianity.
and it is unaffected by non-Gaussianity.

Figure 7. Asymptotic diffusion coefficient vs the Kubo number at different $\beta$![]() values. The results are obtained with DNS for $\mathcal {E}_1$
values. The results are obtained with DNS for $\mathcal {E}_1$![]() and $V_p = 0$
and $V_p = 0$![]() .
.
After confirming the linear behaviour in $\beta$![]() , we look into the dependence of the susceptibility $\chi$
, we look into the dependence of the susceptibility $\chi$![]() on the Kubo number $K_\star$
on the Kubo number $K_\star$![]() . We have performed extensive numerical simulations both with DTM and DNS varying both the Kubo number (through $\tau _c$
. We have performed extensive numerical simulations both with DTM and DNS varying both the Kubo number (through $\tau _c$![]() ) and the $\beta$
) and the $\beta$![]() parameter. Final results are shown in figure 8, where we plot $\chi (K_\star )$
parameter. Final results are shown in figure 8, where we plot $\chi (K_\star )$![]() obtained with DNS at several distinct $V_p$
obtained with DNS at several distinct $V_p$![]() values. As one can see, at small correlation times, this quantity is null. It increases only quadratically with $K_\star$
values. As one can see, at small correlation times, this quantity is null. It increases only quadratically with $K_\star$![]() , until around $\tau _c$
, until around $\tau _c$![]() of the order of the time of flight and saturates for $V_d=0$
of the order of the time of flight and saturates for $V_d=0$![]() . An interesting effect of the average velocity can be seen in figure 8, which consists in the strong attenuation of the effect of the kurtosis. The susceptibility has a strong algebraic decay in these conditions.
. An interesting effect of the average velocity can be seen in figure 8, which consists in the strong attenuation of the effect of the kurtosis. The susceptibility has a strong algebraic decay in these conditions.

Figure 8. Susceptibility $\chi$![]() as a function of Kubo number $K_\star$
as a function of Kubo number $K_\star$![]() obtained with DNS for $\mathcal {E}_1$
obtained with DNS for $\mathcal {E}_1$![]() at distinct $V_p$
at distinct $V_p$![]() values.
values.
In figure 9 we show the profile of $\chi$![]() obtained with DTM in the case of $V_p = 0$
obtained with DTM in the case of $V_p = 0$![]() . The method is able to confirm what was found with DNS: the susceptibility grows to a maximum around the time of flight and decays at larger values of $K_\star$
. The method is able to confirm what was found with DNS: the susceptibility grows to a maximum around the time of flight and decays at larger values of $K_\star$![]() . As expected, since DTM overestimates the trapping, it also overestimates the decay of $\chi$
. As expected, since DTM overestimates the trapping, it also overestimates the decay of $\chi$![]() .
.

Figure 9. Susceptibility $\chi$![]() as a function of Kubo number $K_\star$
as a function of Kubo number $K_\star$![]() obtained with DTM for $\mathcal {E}_2$
obtained with DTM for $\mathcal {E}_2$![]() at $V_p = 0$
at $V_p = 0$![]() .
.
We underline that high Kubo number regimes $K_\star \gg 1$![]() are less relevant for a realistic tokamak plasma. Yet, we have considered in our simulations a wide parametric region $K_\star \in (0,100)$
are less relevant for a realistic tokamak plasma. Yet, we have considered in our simulations a wide parametric region $K_\star \in (0,100)$![]() in order to offer a complete, quantitative, representation of the effects found.
in order to offer a complete, quantitative, representation of the effects found.
3.3. Microscopic analysis
The effect of non-Gaussianity on transport can be understood from a microscopic perspective, following how individual trajectories change, or how their statistics is modified.
One can start the analysis from the limiting case of frozen turbulence $\tau _c\to \infty$![]() . While the trajectories remain unchanged (see § 3.1) the velocity is changed by a factor $A[\varphi (\boldsymbol {0})]$
. While the trajectories remain unchanged (see § 3.1) the velocity is changed by a factor $A[\varphi (\boldsymbol {0})]$![]() . The consequence is that the diffusion across that particular equipotential line becomes $d(t;\varphi (\boldsymbol {0})) = A[\varphi (\boldsymbol {0})]d_0(A[\varphi (\boldsymbol {0})]t;\varphi (\boldsymbol {0}))$
. The consequence is that the diffusion across that particular equipotential line becomes $d(t;\varphi (\boldsymbol {0})) = A[\varphi (\boldsymbol {0})]d_0(A[\varphi (\boldsymbol {0})]t;\varphi (\boldsymbol {0}))$![]() . This is equivalent to a change of the trajectory's period by a factor $A^{-1}[\varphi (\boldsymbol {0})]$
. This is equivalent to a change of the trajectory's period by a factor $A^{-1}[\varphi (\boldsymbol {0})]$![]() . The statistical effects can be seen in figure 10 where the PDF of the periods $P(T)$
. The statistical effects can be seen in figure 10 where the PDF of the periods $P(T)$![]() is plotted at different $\beta$
is plotted at different $\beta$![]() values with $\alpha = 0$
values with $\alpha = 0$![]() .
.

Figure 10. PDF $P(T)$![]() of the trajectory periods at different $\beta$
of the trajectory periods at different $\beta$![]() values in frozen turbulence $\tau _c\to \infty$
values in frozen turbulence $\tau _c\to \infty$![]() and no poloidal velocity $V_p = 0$
and no poloidal velocity $V_p = 0$![]() .
.
One can notice that the intermittency lowers the general values of the periods. This is a natural consequence of the fact that $A[\varphi (0)]>1$![]() . The effect is more pronounced at small and intermediate values $T\sim \tau _{{\rm fl}}$
. The effect is more pronounced at small and intermediate values $T\sim \tau _{{\rm fl}}$![]() since the low-frequency trajectories, i.e. $T\gg \tau _{{\rm fl}}$
since the low-frequency trajectories, i.e. $T\gg \tau _{{\rm fl}}$![]() , are those with low values of the potential $\varphi (\boldsymbol {0})\sim 0$
, are those with low values of the potential $\varphi (\boldsymbol {0})\sim 0$![]() . For the latter, the factor $A[\varphi (\boldsymbol {0})]\sim 1$
. For the latter, the factor $A[\varphi (\boldsymbol {0})]\sim 1$![]() .
.
Although at small times $t\ll \tau _{{\rm fl}}$![]() all trajectories contribute to the diffusion, their average is only slightly dependent on $\beta$
all trajectories contribute to the diffusion, their average is only slightly dependent on $\beta$![]() . The effect becomes more pronounced at times of the order of the time of flight. The fact that the distributions of slow trajectories $T\gg \tau _{{\rm fl}}$
. The effect becomes more pronounced at times of the order of the time of flight. The fact that the distributions of slow trajectories $T\gg \tau _{{\rm fl}}$![]() are almost unchanged explains why the asymptotic behaviour of diffusion in the nonlinear regime $K_\star \gg 1$
are almost unchanged explains why the asymptotic behaviour of diffusion in the nonlinear regime $K_\star \gg 1$![]() is universal: the scaling law $D\sim K^{1-\gamma }$
is universal: the scaling law $D\sim K^{1-\gamma }$![]() is invariant to non-Gaussianity at $K_\star \gg 1$
is invariant to non-Gaussianity at $K_\star \gg 1$![]() .
.
On the other hand, the distribution of potentials is changed. Thus, the effect of non-Gaussianity on diffusion results both from a change in the weight of each equipotential line and from the distortion of time periods.
Furthermore, we underline that, if the turbulence is frozen, both the distribution of Lagrangian potentials and that of Lagrangian velocities (Lumley's theorem, due to the divergenceless property of the Eulerian velocity field) are invariant in time. Under these two strong constrains, it is clear that the only microscopic effect of non-Gaussianity is the redistribution of trajectory frequencies. Other dynamical phenomena which might affect the transport are not present.
Finally, we note how the distribution of small-valued potentials $\phi \ll \varPhi$![]() is virtually unchanged due to the shape of $f$
is virtually unchanged due to the shape of $f$![]() (the nonlinear mapping between $\varphi$
(the nonlinear mapping between $\varphi$![]() and $\phi$
and $\phi$![]() ). These small values are linked to long low-frequency trajectories, thus, to the behaviour of diffusion in the nonlinear regime $K_\star \gg 1, \tau _c\gg \tau _{{\rm fl}}$
). These small values are linked to long low-frequency trajectories, thus, to the behaviour of diffusion in the nonlinear regime $K_\star \gg 1, \tau _c\gg \tau _{{\rm fl}}$![]() . This explains why the scaling behaviour ($\gamma$
. This explains why the scaling behaviour ($\gamma$![]() ) is unchanged by intermittency.
) is unchanged by intermittency.
4. Conclusions
In the present work we have analysed the effects of non-Gaussian turbulent electric fields on the turbulent transport in magnetized fusion plasmas. The non-Gaussianity of $\phi (\boldsymbol {x},t)$![]() is considered a sign of intermittency and it is designed to be in agreement with experimental data on field statistics. We consider the simple case of $\boldsymbol {E}\times \boldsymbol {B}$
is considered a sign of intermittency and it is designed to be in agreement with experimental data on field statistics. We consider the simple case of $\boldsymbol {E}\times \boldsymbol {B}$![]() drift-type dynamics in a constant magnetic field in a slab geometry. The transport is characterized by the resulting diffusion coefficient.
drift-type dynamics in a constant magnetic field in a slab geometry. The transport is characterized by the resulting diffusion coefficient.
In order to mimic the experimental data, the non-Gaussian field $\phi$![]() is modelled using a nonlinear transformation $f$
is modelled using a nonlinear transformation $f$![]() from a fictitious Gaussian turbulent field $\varphi$
from a fictitious Gaussian turbulent field $\varphi$![]() . The transport and the turbulence model are analysed on three distinct levels: analytical, numerical and physical.
. The transport and the turbulence model are analysed on three distinct levels: analytical, numerical and physical.
The analytical analysis suggests that, for small values of skewness and kurtosis, the diffusion decreases linearly with the excess kurtosis $\delta \kappa$![]() while the dependency on skewness can be neglected. The numerical analysis, which is performed using two distinct statistical methods (DTM and DNS), confirms the analytical estimations: indeed, only the kurtosis of the non-Gaussian field affects the diffusion in a linear manner. Moreover, exploring numerically the main dependence of the response coefficient $\chi (K_\star )$
while the dependency on skewness can be neglected. The numerical analysis, which is performed using two distinct statistical methods (DTM and DNS), confirms the analytical estimations: indeed, only the kurtosis of the non-Gaussian field affects the diffusion in a linear manner. Moreover, exploring numerically the main dependence of the response coefficient $\chi (K_\star )$![]() on correlation time, an interesting behaviour was found. In the quasilinear regime, the effects of intermittency are small $\chi \to 0$
on correlation time, an interesting behaviour was found. In the quasilinear regime, the effects of intermittency are small $\chi \to 0$![]() . At the other end of the spectrum, $K_\star \gg 1$
. At the other end of the spectrum, $K_\star \gg 1$![]() , $\chi$
, $\chi$![]() saturates to a maximum, which is reached after the time of flight $\tau _{{\rm fl}}$
saturates to a maximum, which is reached after the time of flight $\tau _{{\rm fl}}$![]() , i.e. $K_\star = 1-2$
, i.e. $K_\star = 1-2$![]() . The presence of a poloidal velocity induces an algebraic decay of the susceptibility $\chi \sim K_\star ^{-\zeta }\to 0$
. The presence of a poloidal velocity induces an algebraic decay of the susceptibility $\chi \sim K_\star ^{-\zeta }\to 0$![]() in the nonlinear regime. To summarize our findings:
in the nonlinear regime. To summarize our findings:

Our results suggest that the specific correlation time of turbulence $\tau _c$![]() as well as the departure from Gaussianity might serve as control parameters for the anomalous transport of plasma.
as well as the departure from Gaussianity might serve as control parameters for the anomalous transport of plasma.
Declaration of interests
The authors report no conflict of interest.
Acknowledgements
This work has been carried out within the framework of the EUROfusion Consortium and has received funding from the Euratom research and training programme 2014–2018 and 2019–2020 under grant agreement No. 633053. The views and opinions expressed herein do not necessarily reflect those of the European Commission.
Editor Per Helander thanks the referees for their advice in evaluating this article.