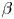1. Introduction
Tokamaks and reversed-field pinches (RFPs) are toroidal fusion plasma devices with a similar magnetic geometry. In both types of reactors, the combination of an imposed toroidal magnetic field combined with a poloidal magnetic field, associated with an induced toroidal current, result in helical magnetic field lines around the toroidal axis. The difference between tokamaks and RFPs is the strength of the toroidal magnetic field, which needs to be much larger than the poloidal field in tokamaks but is of the same order of magnitude in RFPs. This requirement arises from the threatening magnetohydrodynamic (MHD) instabilities, or disruptions, in tokamaks (Biskamp Reference Biskamp1993), which lead to loss of confinement and possibly damage the reactor.
RFPs work in this unstable regime, but take advantage of the nonlinear saturation of the instability, thereby bypassing the risk of disruptions and avoiding the need of a very strong (and costly) toroidal magnetic field. Whereas in early research on the RFP the unstable character was seen as a drawback for fusion, it has become increasingly clear that the self-organization of the RFP is actually an asset to reach self-sustained fusion. Indeed in the 2000s, quasi-single-helicity (QSH) states were detected within turbulent flows in the reversed-field experiment (RFX) (Escande et al. Reference Escande, Martin, Ortolani, Buffa, Franz, Marrelli, Martines, Spizzo, Cappello and Murari2000; Martin et al. Reference Martin, Buffa, Cappello, D'Angelo, Escande, Franz, Marrelli, Martines, Ortolani and Spizzo2000, Reference Martin, Marrelli, Spizzo, Franz, Piovesan, Predebon, Bolzonella, Cappello, Cravotta and Escande2003). These states are characterized by the appearance of a quiescent helical structure in the plasma core, which improves the plasma confinement (Frassinetti et al. Reference Frassinetti, Predebon, Koguchi, Yagi, Hirano, Sakakita, Spizzo and White2006; Terranova et al. Reference Terranova, Alfier, Bonomo, Franz, Innocente and Pasqualotto2007; Wyman et al. Reference Wyman, Chapman, Ahn, Almagri, Anderson, Bonomo, Brower, Combs, Craig and Den Hartog2008). Later studies showed that the persistence of these QSH states and the appearance of a single-helical axis at high-current regimes (Piovesan et al. Reference Piovesan, Zuin, Alfier, Bonfiglio, Bonomo, Canton, Cappello, Carraro, Cavazzana and Escande2009) can be increased by applying helical magnetic perturbations (Piovesan et al. Reference Piovesan, Bonfiglio, Bonomo, Cappello, Carraro, Cavazzana, Gobbin, Marrelli, Martin and Martines2011, Reference Piovesan, Bonfiglio, Auriemma, Bonomo, Carraro, Cavazzana, De Masi, Fassina, Franz and Gobbin2013).
These results motivated part of the fusion community to reconsider the RFP as a serious candidate for nuclear fusion (Lorenzini et al. Reference Lorenzini, Martines, Piovesan, Terranova, Zanca, Zuin, Alfier, Bonfiglio, Bonomo and Canton2009). Even though the road to ignition, i.e. self-sustained fusion, is still long for RFPs and they might not be the most promising geometry to attain the eventual goal of fusion research, they constitute an interesting example of plasma self-organization and their investigation can help to develop ideas which might be useful for other reactor geometries. Recently, the RFP has therefore received renewed attention, focusing on various aspects, such as fast ion transport (Bonofiglo et al. Reference Bonofiglo, Anderson, Gobbin, Spong, Boguski, Parke, Kim and Egedal2019), ion-temperature-gradient modes (Li et al. Reference Li, Liu, Kong, Guo and Dong2019), sophisticated three-dimensional equilibria (Qu et al. Reference Qu, Dewar, Ebrahimi, Anderson, Hudson and Hole2020) and reconnection (Momo et al. Reference Momo, Isliker, Cavazzana, Zuin, Cordaro, Lopez-Bruna, Martines, Predebon, Rea and Spolaore2020). A recent review, centred on the Madison Symmetric Torus experiment, can be found in the paper by Sarff (Reference Sarff2020).
Acting on the RFP magnetic field to improve its confinement properties is evidently an important path to investigate. For instance, applying helical magnetic perturbations seem to be a promising way to affect the self-organized state in an RFP (Bonfiglio et al. Reference Bonfiglio, Veranda, Cappello, Escande and Chacón2013). Such perturbations were shown to be able to influence the shape of the plasma by imposing their helical pitch to the plasma (Veranda et al. Reference Veranda, Bonfiglio, Cappello, Escande, Auriemma, Borgogno, Chacón, Fassina, Franz and Gobbin2017). Another obvious way to affect the dynamics would be to directly change the global shape of the plasma. The optimization of the confinement quality for toroidal fusion plasmas by changing the plasma shape has been the subject of many studies, in particular for tokamaks. For instance, it has been shown that shaping has a beneficial effect on the $\beta$![]() limits of tokamaks (Troyon et al. Reference Troyon, Gruber, Saurenmann, Semenzato and Succi1984), and increases the total plasma current $I$
limits of tokamaks (Troyon et al. Reference Troyon, Gruber, Saurenmann, Semenzato and Succi1984), and increases the total plasma current $I$![]() in the case of elliptic cross-sections, which thus yields a better confinement. Furthermore, shaping of a tokamak cross-section can lead to qualitative differences in the plasma flow patterns (Morales et al. Reference Morales, Bos, Schneider and Montgomery2012; Oueslati & Firpo Reference Oueslati and Firpo2020). Investigations on the influence of shaping on the confinement properties of RFPs are, however, relatively scarce. The literature on RFPs contains some rare examples of experimental observations (Almagri et al. Reference Almagri, Assadi, Dexter, Prager, Sarff and Sprott1987; Oomens, Lassing & Meer Reference Oomens, Lassing and Meer1990) and numerical investigations where two-dimensional equilibrium studies were carried out to investigate the shaping effect on RFP plasmas (Paccagnella, Bondeson & Lütjens Reference Paccagnella, Bondeson and Lütjens1991; Guo et al. Reference Guo, Xu, Wang and Liu2013). Their work led to the conclusion that shaping does not bring an advantage to the plasma dynamics in RFPs and is even destabilizing in the case in which the poloidal cross-section is elongated. These studies focused on the linear stability properties of RFPs, but did not consider the fully developed nonlinear dynamics.
in the case of elliptic cross-sections, which thus yields a better confinement. Furthermore, shaping of a tokamak cross-section can lead to qualitative differences in the plasma flow patterns (Morales et al. Reference Morales, Bos, Schneider and Montgomery2012; Oueslati & Firpo Reference Oueslati and Firpo2020). Investigations on the influence of shaping on the confinement properties of RFPs are, however, relatively scarce. The literature on RFPs contains some rare examples of experimental observations (Almagri et al. Reference Almagri, Assadi, Dexter, Prager, Sarff and Sprott1987; Oomens, Lassing & Meer Reference Oomens, Lassing and Meer1990) and numerical investigations where two-dimensional equilibrium studies were carried out to investigate the shaping effect on RFP plasmas (Paccagnella, Bondeson & Lütjens Reference Paccagnella, Bondeson and Lütjens1991; Guo et al. Reference Guo, Xu, Wang and Liu2013). Their work led to the conclusion that shaping does not bring an advantage to the plasma dynamics in RFPs and is even destabilizing in the case in which the poloidal cross-section is elongated. These studies focused on the linear stability properties of RFPs, but did not consider the fully developed nonlinear dynamics.
Here we proceed one step further in the investigation of the effect of changing the shape of the cross-section of RFPs by considering the fully nonlinear dynamics within a resistive fluid description. More precisely, we investigate the effect of elongation of the poloidal cross-section on plasmas in driven incompressible MHD flow in cylindrical geometry. We thereto perform direct numerical simulations using a three-dimensional pseudo-spectral solver (Morales et al. Reference Morales, Leroy, Bos and Schneider2014b). We consider the simplified case where the torus is modelled by a straight periodic cylinder. The choice of this simplification is justified as follows. In Morales et al. (Reference Morales, Bos, Schneider and Montgomery2014a), we compared the straight-cylinder approach to fully toroidal simulations. We showed that most of the qualitative features remained unchanged. The most significant change was the appearance of a toroidally invariant mode, the influence of which we do therefore necessarily neglect in the present work. It is true that considering the effect of curvature on the dynamics of RFPs could be interesting, but we aim at understanding the two effects (curvature and shape of the cross-section) independently to pinpoint the most important physical effects, before considering their possible interplay. Furthermore, in Paccagnella et al. (Reference Paccagnella, Bondeson and Lütjens1991), the influence of curvature was considered with respect to the stability properties of RFPs and its effect was shown to be minor.
In the present work, it is shown that elongation of the cross-section has a significant effect on the pressure statistics in the plasma and on the turbulence properties in general. In particular, assessing the value of the $\beta$![]() -parameter, and its recent generalization to take into account the turbulent pressure gradients, illustrates how the dynamics are influenced by the shaping of the geometry. We also reveal the presence of non-negligible local poloidal angular momentum, when the cross-section is circular.
-parameter, and its recent generalization to take into account the turbulent pressure gradients, illustrates how the dynamics are influenced by the shaping of the geometry. We also reveal the presence of non-negligible local poloidal angular momentum, when the cross-section is circular.
The remainder of this article is organized as follows. Section 2 presents the governing equations, recalling briefly the numerics and the relevant physical parameters. Numerical results on the influence of shaping on the reversal properties, pressure statistics, spectral characteristics and local angular momentum are investigated in § 3. Section 4 concludes the investigation.
2. Equations, numerical methods and parameters
2.1. Viscoresistive MHD equations and geometry
In the present work, we consider a plasma characterized by constant and uniform permeability $\mu$![]() , permittivity $\epsilon$
, permittivity $\epsilon$![]() and conductivity $\sigma$
and conductivity $\sigma$![]() . The more complicated case of non-uniform conductivity was considered by Futatani, Morales & Bos (Reference Futatani, Morales and Bos2015). In the MHD description that we consider, the governing equations are the incompressible Navier–Stokes equations including the Lorentz force and the induction equation. Normalizing these equations by the Alfvén velocity $C_A=B_0/\sqrt {\rho \mu }$
. The more complicated case of non-uniform conductivity was considered by Futatani, Morales & Bos (Reference Futatani, Morales and Bos2015). In the MHD description that we consider, the governing equations are the incompressible Navier–Stokes equations including the Lorentz force and the induction equation. Normalizing these equations by the Alfvén velocity $C_A=B_0/\sqrt {\rho \mu }$![]() , a reference magnetic field $B_0$
, a reference magnetic field $B_0$![]() and a conveniently chosen lengthscale $\mathcal {L}$
and a conveniently chosen lengthscale $\mathcal {L}$![]() leads to the following expressions for the evolution of the velocity $\boldsymbol {u}$
leads to the following expressions for the evolution of the velocity $\boldsymbol {u}$![]() and magnetic field $\boldsymbol {B}$
and magnetic field $\boldsymbol {B}$![]() :
:
and
where $P_m$![]() is the magnetic Prandtl number $P_m=\nu \mu \sigma$
is the magnetic Prandtl number $P_m=\nu \mu \sigma$![]() , $\nu$
, $\nu$![]() the viscosity, $S$
the viscosity, $S$![]() the Lundquist number (defined below) and $\rho =1$
the Lundquist number (defined below) and $\rho =1$![]() the density. The current density is given by
the density. The current density is given by
The velocity field $\boldsymbol {u}$![]() and the magnetic field $\boldsymbol {B}$
and the magnetic field $\boldsymbol {B}$![]() are both divergence free,
are both divergence free,
The incompressibility condition (2.4) allows obtaining the pressure $P$![]() from the velocity field by taking the divergence of (2.1) and solving the resulting Poisson equation. The pressure thereby plays, in this system, the role of a Lagrange multiplier, which enforces incompressibility of the velocity field. We think it is important to retain this feature (incompressibility) in the dynamics unlike in a number of previous investigations of RFPs (e.g. Cappello & Biskamp Reference Cappello and Biskamp1996; Cappello & Escande Reference Cappello and Escande2000; Richardson, Finn & Delzanno Reference Richardson, Finn and Delzanno2010; Veranda et al. Reference Veranda, Bonfiglio, Cappello, Escande, Auriemma, Borgogno, Chacón, Fassina, Franz and Gobbin2017; Futch et al. Reference Futch, Craig, Hesse and Jacobson2018), where the pressure was entirely neglected invoking low-$\beta$
from the velocity field by taking the divergence of (2.1) and solving the resulting Poisson equation. The pressure thereby plays, in this system, the role of a Lagrange multiplier, which enforces incompressibility of the velocity field. We think it is important to retain this feature (incompressibility) in the dynamics unlike in a number of previous investigations of RFPs (e.g. Cappello & Biskamp Reference Cappello and Biskamp1996; Cappello & Escande Reference Cappello and Escande2000; Richardson, Finn & Delzanno Reference Richardson, Finn and Delzanno2010; Veranda et al. Reference Veranda, Bonfiglio, Cappello, Escande, Auriemma, Borgogno, Chacón, Fassina, Franz and Gobbin2017; Futch et al. Reference Futch, Craig, Hesse and Jacobson2018), where the pressure was entirely neglected invoking low-$\beta$![]() dynamics. Indeed, in some recent RFP investigations, the pressure is retained (Mizuguchi et al. Reference Mizuguchi, Sanpei, Fujita, Oki, Himura, Masamune and Ichiguchi2012) and recently we focused on the importance of the pressure dynamics (Chahine & Bos Reference Chahine and Bos2018). In particular, we illustrated in MHD simulations in cylindrical geometry that, to understand the dynamics of the plasma, the important quantity to monitor is not the pressure but its gradient. We therefore introduced a quantity $\beta _{\boldsymbol {\nabla }}$
dynamics. Indeed, in some recent RFP investigations, the pressure is retained (Mizuguchi et al. Reference Mizuguchi, Sanpei, Fujita, Oki, Himura, Masamune and Ichiguchi2012) and recently we focused on the importance of the pressure dynamics (Chahine & Bos Reference Chahine and Bos2018). In particular, we illustrated in MHD simulations in cylindrical geometry that, to understand the dynamics of the plasma, the important quantity to monitor is not the pressure but its gradient. We therefore introduced a quantity $\beta _{\boldsymbol {\nabla }}$![]() , which compares the influence of the pressure gradient to the magnetic effects ($\boldsymbol {j}\times \boldsymbol {B}$
, which compares the influence of the pressure gradient to the magnetic effects ($\boldsymbol {j}\times \boldsymbol {B}$![]() ) acting on the momentum balance. The definition of this quantity and its interpretation will be given in § 3.2.
) acting on the momentum balance. The definition of this quantity and its interpretation will be given in § 3.2.
In the present work, we thus take into account the influence of pressure on the dynamics but we neglect all compressibility effects. Note that imposing incompressibility was shown to diminish the reversal of the magnetic field (Finn, Nebel & Bathke Reference Finn, Nebel and Bathke1992) and this will thus necessarily be the case in the present investigation. We note here that the resistivity profile can also influence the reversal (Bonfiglio, Cappello & Escande Reference Bonfiglio, Cappello and Escande2016). The combined influence of shaping, compressibility and non-uniform resistivity would constitute an interesting perspective but would complicate disentangling the different effects.
In figure 1, we illustrate the considered geometry and we indicate the direction of the imposed current density and magnetic field. Initially, in the plasma, a uniform current density $j_0$![]() in the $z$
in the $z$![]() -direction and an axial magnetic field $B_{z0}$
-direction and an axial magnetic field $B_{z0}$![]() are imposed, which results in a helically shaped magnetic field. The current density $j_0$
are imposed, which results in a helically shaped magnetic field. The current density $j_0$![]() will induce an elliptical poloidal magnetic field $B_{p0}$
will induce an elliptical poloidal magnetic field $B_{p0}$![]() parallel to the elliptic boundaries. At later times, the magnetic field will reorganize through an interplay with the velocity field and the total magnetic field will then consist of $B_{z0}$
parallel to the elliptic boundaries. At later times, the magnetic field will reorganize through an interplay with the velocity field and the total magnetic field will then consist of $B_{z0}$![]() and $B_{p0}$
and $B_{p0}$![]() plus the self-induced contributions. At the boundaries, the velocity is imposed to be zero and the magnetic field is parallel to the boundaries. The value of the poloidal parallel magnetic field at the boundary is fixed and its value is determined by $j_0$
plus the self-induced contributions. At the boundaries, the velocity is imposed to be zero and the magnetic field is parallel to the boundaries. The value of the poloidal parallel magnetic field at the boundary is fixed and its value is determined by $j_0$![]() . The expression of $B_{p0}$
. The expression of $B_{p0}$![]() in cylindrical coordinates reads,
in cylindrical coordinates reads,
with $c$![]() the ellipticity which can be expressed as a function of the ellipse's major semi-axis $a$
the ellipticity which can be expressed as a function of the ellipse's major semi-axis $a$![]() and minor semi-axis $b$
and minor semi-axis $b$![]() , i.e.,
, i.e.,
Note that the coordinates we use are cylindrical and not elliptical coordinates so that only in the case of the circle, the radial vector $\boldsymbol {e}_r$![]() is everywhere perpendicular to the boundary.
is everywhere perpendicular to the boundary.

Figure 1. Sketch of the cylindrical geometry and imposed magnetic field and current density.
2.2. Numerical methods
Equations (2.1) and (2.2) are solved using a pseudo-spectral method in a periodic domain of size ${\rm \pi} \times {\rm \pi}\times 8{\rm \pi}$![]() with $64\times 64\times 512$
with $64\times 64\times 512$![]() grid points. The aspect ratio of the physical domain containing the plasma is $L_z/2{\rm \pi} b =4$
grid points. The aspect ratio of the physical domain containing the plasma is $L_z/2{\rm \pi} b =4$![]() . Spatial derivatives are evaluated in Fourier space and multiplications are computed in physical space. To avoid aliasing errors, i.e. the production of small scales owing to nonlinear terms which are not resolved on the grid, the velocity and magnetic fields are dealiased at each time step by truncating its Fourier coefficients using the 2/3 rule (Canuto et al. Reference Canuto, Hussaini, Quarteroni and Zang1987). Using the incompressibility condition of the fluid, the pressure term can be eliminated by solving a Poisson equation. A semi-implicit time-advancing scheme of Adams–Bashforth type is used to solve the equations with exact integration of the dissipative and magnetic diffusion terms. Boundary conditions are imposed using a volume penalization method to build the cylindrical domain. Detailed description and validation of the method can be found in the paper by Morales et al. (Reference Morales, Leroy, Bos and Schneider2014b), and an application of the method to investigate RFPs in toroidal domains is reported in previous work (Morales et al. Reference Morales, Bos, Schneider and Montgomery2014a; Futatani et al. Reference Futatani, Morales and Bos2015). We have verified by assessing the high-wavenumber range of the kinetic and magnetic energy spectra that the resolution for all simulations was sufficient to resolve all down to the smallest dynamical flow scales.
. Spatial derivatives are evaluated in Fourier space and multiplications are computed in physical space. To avoid aliasing errors, i.e. the production of small scales owing to nonlinear terms which are not resolved on the grid, the velocity and magnetic fields are dealiased at each time step by truncating its Fourier coefficients using the 2/3 rule (Canuto et al. Reference Canuto, Hussaini, Quarteroni and Zang1987). Using the incompressibility condition of the fluid, the pressure term can be eliminated by solving a Poisson equation. A semi-implicit time-advancing scheme of Adams–Bashforth type is used to solve the equations with exact integration of the dissipative and magnetic diffusion terms. Boundary conditions are imposed using a volume penalization method to build the cylindrical domain. Detailed description and validation of the method can be found in the paper by Morales et al. (Reference Morales, Leroy, Bos and Schneider2014b), and an application of the method to investigate RFPs in toroidal domains is reported in previous work (Morales et al. Reference Morales, Bos, Schneider and Montgomery2014a; Futatani et al. Reference Futatani, Morales and Bos2015). We have verified by assessing the high-wavenumber range of the kinetic and magnetic energy spectra that the resolution for all simulations was sufficient to resolve all down to the smallest dynamical flow scales.
Simulations are started from random initial conditions and the dynamics are observed to evolve towards an initial-condition independent statistically stationary state. To obtain the results presented in § 3, the equations are integrated for $10^4 \tau _A$![]() Alfvén times, with $\tau _A = \mathcal {L}/C_A$
Alfvén times, with $\tau _A = \mathcal {L}/C_A$![]() . The results presented in the following are all obtained during the statistically stationary state.
. The results presented in the following are all obtained during the statistically stationary state.
2.3. Shaping parameters
In the present investigation, we focus on the influence of the shape of the cross-section on the confinement properties of the plasma. The parameters should be carefully chosen to disentangle the effect of changing the geometry from the effect of changing other control parameters. Considering a periodic cylinder instead of a torus is motivated by this attempt to reduce the number of control parameters to a strict minimum. Even in this simplified geometry, the way in which the parameters are varied is not unique. For instance, if the same toroidal current-density $J_z$![]() is chosen for two geometries, the mean current $I_z$
is chosen for two geometries, the mean current $I_z$![]() will be the same, only if the surface $A$
will be the same, only if the surface $A$![]() of the cross-section is kept constant, a condition which we will impose. This will also lead to equal values of the toroidal magnetic flux $\psi =B_z A$
of the cross-section is kept constant, a condition which we will impose. This will also lead to equal values of the toroidal magnetic flux $\psi =B_z A$![]() for a given imposed toroidal magnetic field $B_z$
for a given imposed toroidal magnetic field $B_z$![]() .
.
The poloidal magnetic $B_p$![]() field is computed from the current density. Its reference value is evaluated as an average over the circular or elliptic boundary. Necessarily, keeping the surface $A$
field is computed from the current density. Its reference value is evaluated as an average over the circular or elliptic boundary. Necessarily, keeping the surface $A$![]() , $J_z$
, $J_z$![]() and $B_z$
and $B_z$![]() fixed, the average value $\overline B_p$
fixed, the average value $\overline B_p$![]() varies when changing the shape of the cross-section (the bar indicates a boundary average). Therefore, the pinch ratio, defined as
varies when changing the shape of the cross-section (the bar indicates a boundary average). Therefore, the pinch ratio, defined as
where the brackets denote a volume average, depends on the value of the ellipticity $c$![]() .
.
An important parameter in non-ideal MHD is the Lundquist number, which is defined as
where the Alfvén velocity is based on the poloidal field strength, $C_A = B_p/\sqrt {\rho \mu }$![]() with the magnetic diffusivity $\lambda =(\mu \sigma )^{-1}$
with the magnetic diffusivity $\lambda =(\mu \sigma )^{-1}$![]() and the (minor) diameter $2b$
and the (minor) diameter $2b$![]() as reference quantities. We have chosen $b$
as reference quantities. We have chosen $b$![]() , rather than $a$
, rather than $a$![]() , as the smallest minor radius which will probably determine the confinement quality. Imposing the same value of $S$
, as the smallest minor radius which will probably determine the confinement quality. Imposing the same value of $S$![]() for different values of the ellipticity allows determining the value of $\lambda$
for different values of the ellipticity allows determining the value of $\lambda$![]() . In all our simulations, the value of the magnetic Prandtl number is chosen to be unity.
. In all our simulations, the value of the magnetic Prandtl number is chosen to be unity.
3. Results
3.1. F-$\varTheta$ dependence
dependence
The imposed magnetic field in RFPs is unstable for large values of $\varTheta$![]() and $S$
and $S$![]() , and it will form a dynamic helical structure with a certain amount of chaotic or turbulent motion superimposed.
, and it will form a dynamic helical structure with a certain amount of chaotic or turbulent motion superimposed.
The modification of the magnetic field can be quantified by the field reversal parameter $F$![]() , which represents the normalized toroidal field at the boundary,
, which represents the normalized toroidal field at the boundary,
As the current increases, the kink instability increases, which leads to the decrease of the toroidal magnetic field at the boundary, so that $F$![]() decreases as a function of $\varTheta$
decreases as a function of $\varTheta$![]() . This behaviour can be qualitatively predicted by Taylor's theory (Taylor Reference Taylor1974) and more sophisticated theories allow to improve this agreement (Reiman Reference Reiman1980, Reference Reiman1981; Taylor Reference Taylor1986). In studies by Paccagnella et al. (Reference Paccagnella, Bondeson and Lütjens1991) and Guo et al. (Reference Guo, Xu, Wang and Liu2013) based on two-dimensional equilibrium equations, it was shown that shaping does not alter the $F$
. This behaviour can be qualitatively predicted by Taylor's theory (Taylor Reference Taylor1974) and more sophisticated theories allow to improve this agreement (Reiman Reference Reiman1980, Reference Reiman1981; Taylor Reference Taylor1986). In studies by Paccagnella et al. (Reference Paccagnella, Bondeson and Lütjens1991) and Guo et al. (Reference Guo, Xu, Wang and Liu2013) based on two-dimensional equilibrium equations, it was shown that shaping does not alter the $F$![]() -$\varTheta$
-$\varTheta$![]() curve.
curve.
To be able to systematically assess the $F-\varTheta$![]() dependence, we carry out preliminary simulations for cylinders of small aspect ratio ${L_z}/{2{\rm \pi} b}\sim 2$
dependence, we carry out preliminary simulations for cylinders of small aspect ratio ${L_z}/{2{\rm \pi} b}\sim 2$![]() , an ellipticity $a=1.6$
, an ellipticity $a=1.6$![]() and moderate Lundquist number $S\sim 4200$
and moderate Lundquist number $S\sim 4200$![]() . We compare with Taylor's prediction (Taylor Reference Taylor1974) and simulations with circular cross-section. Figure 2 shows the results of the field-reversal parameter $F$
. We compare with Taylor's prediction (Taylor Reference Taylor1974) and simulations with circular cross-section. Figure 2 shows the results of the field-reversal parameter $F$![]() versus $\varTheta$
versus $\varTheta$![]() , which are in reasonable agreement with the two previous studies (Paccagnella et al. Reference Paccagnella, Bondeson and Lütjens1991; Guo et al. Reference Guo, Xu, Wang and Liu2013). In these references it was shown that shaping had a small destabilizing effect for large curvature, but the $F-\varTheta$
, which are in reasonable agreement with the two previous studies (Paccagnella et al. Reference Paccagnella, Bondeson and Lütjens1991; Guo et al. Reference Guo, Xu, Wang and Liu2013). In these references it was shown that shaping had a small destabilizing effect for large curvature, but the $F-\varTheta$![]() curve was unaffected. Indeed, the two geometries yield roughly the same behaviour.
curve was unaffected. Indeed, the two geometries yield roughly the same behaviour.

Figure 2. Field-reversal parameter $F$![]() as a function of the pinch parameter $\varTheta$
as a function of the pinch parameter $\varTheta$![]() for cylinders with circular and elliptic cross-section. Also shown is Taylor's prediction (Taylor Reference Taylor1974) for reference.
for cylinders with circular and elliptic cross-section. Also shown is Taylor's prediction (Taylor Reference Taylor1974) for reference.
These moderate-Lundquist simulations allow a parametric investigation of the $F-\varTheta$![]() dependence for two different ellipticities. Carrying this out for higher values of $S$
dependence for two different ellipticities. Carrying this out for higher values of $S$![]() would require substantially more computational resources. In the remainder of this investigation, we will consider, at a higher value of the Lundquist number, three different ellipticities but focus on only one $F-\varTheta$
would require substantially more computational resources. In the remainder of this investigation, we will consider, at a higher value of the Lundquist number, three different ellipticities but focus on only one $F-\varTheta$![]() value for each geometry. We have thereto performed simulations for values of the Lundquist number ranging up to $S \approx 2\times 10^4$
value for each geometry. We have thereto performed simulations for values of the Lundquist number ranging up to $S \approx 2\times 10^4$![]() and a larger aspect ratio $L_z/2{\rm \pi} b = 4$
and a larger aspect ratio $L_z/2{\rm \pi} b = 4$![]() . These higher values of the Lundquist number are still several orders of magnitude smaller than those in experimental RFPs, which are currently out of reach using precise numerical schemes. We consider three shapes, i.e. cylindrical devices with different cross-sections: a circle with radius $a=1$
. These higher values of the Lundquist number are still several orders of magnitude smaller than those in experimental RFPs, which are currently out of reach using precise numerical schemes. We consider three shapes, i.e. cylindrical devices with different cross-sections: a circle with radius $a=1$![]() , an ellipse with $a=1.2$
, an ellipse with $a=1.2$![]() and $b=0.83$
and $b=0.83$![]() and an ellipse with $a=1.4$
and an ellipse with $a=1.4$![]() and $b=0.714$
and $b=0.714$![]() . In the statistically steady states considered at this higher Lundquist number, both the $F$
. In the statistically steady states considered at this higher Lundquist number, both the $F$![]() and $\varTheta$
and $\varTheta$![]() parameter fluctuate around their steady value, which is also plotted in figure 2. It is observed that these results are in the $F$
parameter fluctuate around their steady value, which is also plotted in figure 2. It is observed that these results are in the $F$![]() –$\varTheta$
–$\varTheta$![]() plane situated closer to Taylor's prediction, which is obtained using statistical mechanics of ideal MHD (Taylor Reference Taylor1974). We do not know whether higher values of $S$
plane situated closer to Taylor's prediction, which is obtained using statistical mechanics of ideal MHD (Taylor Reference Taylor1974). We do not know whether higher values of $S$![]() will allow to approach this theoretical prediction even closer. The fluctuations are for $\varTheta$
will allow to approach this theoretical prediction even closer. The fluctuations are for $\varTheta$![]() inferior to $0.5\,\%$
inferior to $0.5\,\%$![]() . The absolute value of the fluctuations of the $F$
. The absolute value of the fluctuations of the $F$![]() -parameter are of the order of $0.01$
-parameter are of the order of $0.01$![]() (for instance, fluctuating between $F=-0.07$
(for instance, fluctuating between $F=-0.07$![]() and $F=-0.082$
and $F=-0.082$![]() for the circular geometry).
for the circular geometry).
We observe thus that the effect of shaping is small on the global behaviour of the magnetic field, as characterized by $F$![]() and $\varTheta$
and $\varTheta$![]() . The present results indicate that the influence of the Lundquist number is significantly larger than that of shaping in the considered range of parameters. The reversal parameter is a global parameter and does not give insight into the fine structure of the dynamics. It is this fine structure, constituted by the nonlinear interplay of a large number of modes, which will determine the confinement quality of a reactor. The modification of the fine structure is in the following assessed by evaluating pressure gradients and the modal behaviour of the flow.
. The present results indicate that the influence of the Lundquist number is significantly larger than that of shaping in the considered range of parameters. The reversal parameter is a global parameter and does not give insight into the fine structure of the dynamics. It is this fine structure, constituted by the nonlinear interplay of a large number of modes, which will determine the confinement quality of a reactor. The modification of the fine structure is in the following assessed by evaluating pressure gradients and the modal behaviour of the flow.
3.2. The role of the pressure: $\beta$ and gradient-$\beta$
and gradient-$\beta$
Clearly, in fusion research, the plasma pressure plays a major role. In the present investigation, we do not focus on the confinement quality of the system, but rather on the dynamics and the velocity field. Therefore, we will assess the influence of shaping on the pressure and its influence on the dynamics. In figure 3, we show visualizations of the pressure fluctuations in cross-sections of the domains at the highest considered Lundquist number. Spatial fluctuations of the pressure are observed in all geometries. In particular, in the elliptic cases, the strongest values of the absolute pressure are situated in the centre of the domain and lower pressure values are observed close to the wall. In the circular case, the value of the pressure is smaller than for the elliptic cases. We will now focus on different measures of the influence of pressure on the dynamics.

Figure 3. Instantaneous visualizations of the pressure field for $S \approx 2 \times 10^4$![]() in cross-sections through the cylinders for the three different ellipticities. From (a–c), $a=1$
in cross-sections through the cylinders for the three different ellipticities. From (a–c), $a=1$![]() , $a=1.2$
, $a=1.2$![]() , $a=1.4$
, $a=1.4$![]() .
.
Classically, to assess the influence of the pressure on the plasma dynamics, the quantity $\beta$![]() is evaluated, which measures the importance of the plasma pressure compared with the magnetic pressure,
is evaluated, which measures the importance of the plasma pressure compared with the magnetic pressure,
where the brackets indicate a volume average over the plasma volume of interest. Other definitions are also used (Wesson & Campbell Reference Wesson and Campbell2011) based on the value of $\boldsymbol {B}$![]() at the wall of the plasma, for instance. Clearly, ${\beta }$
at the wall of the plasma, for instance. Clearly, ${\beta }$![]() is an important parameter because the plasma pressure is a key parameter in the analysis of the confinement quality. However, if we are interested in the turbulence properties and the velocity field in general, it is the pressure gradients that are important. It is known from turbulence research that estimating simply the order of magnitude of pressure gradients by ${O}(\boldsymbol {\nabla } P) \sim P/L$
is an important parameter because the plasma pressure is a key parameter in the analysis of the confinement quality. However, if we are interested in the turbulence properties and the velocity field in general, it is the pressure gradients that are important. It is known from turbulence research that estimating simply the order of magnitude of pressure gradients by ${O}(\boldsymbol {\nabla } P) \sim P/L$![]() , with $L$
, with $L$![]() a macroscopic lengthscale, can seriously underestimate their magnitude because the pressure gradients are, in general, dominated by small-scale contributions $l\ll L$
a macroscopic lengthscale, can seriously underestimate their magnitude because the pressure gradients are, in general, dominated by small-scale contributions $l\ll L$![]() . Therefore, we recently introduced the alternative, gradient-based $\beta$
. Therefore, we recently introduced the alternative, gradient-based $\beta$![]() s (Chahine & Bos Reference Chahine and Bos2018),
s (Chahine & Bos Reference Chahine and Bos2018),
It is only when ${\beta '_{\boldsymbol {\nabla }}}$![]() is small compared to unity that the influence of the pressure term might be negligible in the dynamics, compared with the influence of the other terms in the velocity equation. This is not necessarily the case when $\beta$
is small compared to unity that the influence of the pressure term might be negligible in the dynamics, compared with the influence of the other terms in the velocity equation. This is not necessarily the case when $\beta$![]() is small.
is small.
In figure 4, we show the behaviour of the different versions of $\beta$![]() . The size of the temporal fluctuations of the different quantities around the time-averaged value are indicated by error bars. In agreement with the results of Chahine & Bos (Reference Chahine and Bos2018), the value of $\beta$
. The size of the temporal fluctuations of the different quantities around the time-averaged value are indicated by error bars. In agreement with the results of Chahine & Bos (Reference Chahine and Bos2018), the value of $\beta$![]() is decreasing for increasing values of the Lundquist number. We see that for the highest values of $S$
is decreasing for increasing values of the Lundquist number. We see that for the highest values of $S$![]() , $\beta$
, $\beta$![]() has dropped most importantly in the circular geometry. This is not inconsistent with figure 3, which shows that the normalized pressure is weaker in this geometry than in the other two. Indeed, focusing only on this observation, one might be tempted to extrapolate and assume that the pressure plays no dominant role in the dynamics at high values of $S$
has dropped most importantly in the circular geometry. This is not inconsistent with figure 3, which shows that the normalized pressure is weaker in this geometry than in the other two. Indeed, focusing only on this observation, one might be tempted to extrapolate and assume that the pressure plays no dominant role in the dynamics at high values of $S$![]() . However, the gradient based $\beta '_{\boldsymbol {\nabla }}$
. However, the gradient based $\beta '_{\boldsymbol {\nabla }}$![]() remains approximately constant when the Lundquist number is increased. This shows that the influence of the pressure gradients does not become less important for larger $S$
remains approximately constant when the Lundquist number is increased. This shows that the influence of the pressure gradients does not become less important for larger $S$![]() .
.

Figure 4. Lundquist-number dependence of three alternative definitions of $\beta$![]() in cylinders with ellipticity (a) $a=1$
in cylinders with ellipticity (a) $a=1$![]() , (b) $a=1.2$
, (b) $a=1.2$![]() , (c) $a=1.4$
, (c) $a=1.4$![]() . Whereas the pressure based $\beta$
. Whereas the pressure based $\beta$![]() is strongly decreasing with $S$
is strongly decreasing with $S$![]() , the gradient-based value $\beta '_{\boldsymbol {\nabla }}$
, the gradient-based value $\beta '_{\boldsymbol {\nabla }}$![]() is roughly constant.
is roughly constant.
These observations are quite robust and qualitatively independent on the shape of the cylinder. What changes however, is the $S$![]() -dependence of ${\beta }_{\boldsymbol {\nabla }}$
-dependence of ${\beta }_{\boldsymbol {\nabla }}$![]() . This indicates that $\langle \|\boldsymbol {\nabla } B^2 \|\rangle / \langle \| \boldsymbol {J}\times \boldsymbol {B}\|\rangle$
. This indicates that $\langle \|\boldsymbol {\nabla } B^2 \|\rangle / \langle \| \boldsymbol {J}\times \boldsymbol {B}\|\rangle$![]() is influenced by the ellipticity of the cylinder cross-section. From the vector identity $\boldsymbol {J}\times \boldsymbol {B}=-\boldsymbol {\nabla } B^2/2+\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla } \boldsymbol {B}$
is influenced by the ellipticity of the cylinder cross-section. From the vector identity $\boldsymbol {J}\times \boldsymbol {B}=-\boldsymbol {\nabla } B^2/2+\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla } \boldsymbol {B}$![]() , this shows that the different behaviour is associated with the curvature term $\boldsymbol {B}\boldsymbol {\cdot } \boldsymbol {\nabla } \boldsymbol {B}$
, this shows that the different behaviour is associated with the curvature term $\boldsymbol {B}\boldsymbol {\cdot } \boldsymbol {\nabla } \boldsymbol {B}$![]() , which seems to be affected by the shaping. Shaping does therefore change the magnetic structure of the flow. We will further investigate this in the following, considering spectral considerations. Before that, we will visualize the magnetic structure of the simulated plasmas.
, which seems to be affected by the shaping. Shaping does therefore change the magnetic structure of the flow. We will further investigate this in the following, considering spectral considerations. Before that, we will visualize the magnetic structure of the simulated plasmas.
3.3. Characterization of the velocity and magnetic field
In figure 5, we show magnetic flux lines in cross-sections through the three cylindrical geometries. The lines correspond to iso-values of the axial component of the magnetic vector potential. This potential is computed from the induced field, i.e. the imposed field is subtracted from the total magnetic field.

Figure 5. Flux lines in a cross-section through the differently shaped geometries. From left to right, the cross-sections are a circle with radius $a=1$![]() , an ellipse with major semi-axis $a=1.2$
, an ellipse with major semi-axis $a=1.2$![]() and one with $a=1.4$
and one with $a=1.4$![]() , for $S \approx 2\times 10^4$
, for $S \approx 2\times 10^4$![]() . Visualized is the induced field, i.e. the magnetic field without the imposed contribution.
. Visualized is the induced field, i.e. the magnetic field without the imposed contribution.
The most dramatic difference is observed for the $a=1.4$![]() geometry. Indeed, for the circular cross-section, the iso-lines are mostly concentric. Changing the shape, for $a=1.2$
geometry. Indeed, for the circular cross-section, the iso-lines are mostly concentric. Changing the shape, for $a=1.2$![]() , a separatrix appears at the edges of the ellipse and for $a=1.4$
, a separatrix appears at the edges of the ellipse and for $a=1.4$![]() , the central flux surfaces are destroyed and magnetic islands appear. Clearly, the shape of the magnetic field is dramatically altered by the shaping in this latter geometry, compared with the circular cross-section.
, the central flux surfaces are destroyed and magnetic islands appear. Clearly, the shape of the magnetic field is dramatically altered by the shaping in this latter geometry, compared with the circular cross-section.
In figure 6, axial magnetic fluctuations are shown in various poloidal cross-sections. The fluctuations of the axial magnetic field are obtained by showing the magnetic field without the axially invariant ($k_z=0$![]() ) magnetic contribution. Only in a few sections is a clear poloidal mode structure observed. From these observations, it seems relatively clear that no single-helicity state is present in our simulations. A large number of modes seems to be evolving simultaneously and instantaneous local visualizations are not the best tool to illustrate this.
) magnetic contribution. Only in a few sections is a clear poloidal mode structure observed. From these observations, it seems relatively clear that no single-helicity state is present in our simulations. A large number of modes seems to be evolving simultaneously and instantaneous local visualizations are not the best tool to illustrate this.

Figure 6. Poloidal cross-sections of the cylinder, illustrating the axial magnetic fluctuations at $t=9.8\times 10^3 \tau _A$![]() for $S \approx 2\times 10^4$
for $S \approx 2\times 10^4$![]() . The geometries are a circle with radius $a=1$
. The geometries are a circle with radius $a=1$![]() , an ellipse with major semi-axis $a=1.2$
, an ellipse with major semi-axis $a=1.2$![]() and one with $a=1.4$
and one with $a=1.4$![]() .
.
To analyse the presence of different modes, we visualize now the effect of shaping on these helical modes by evaluating the axially Fourier-transformed magnetic field. In figure 7, we observe that all considered cases show strong fluctuations, which illustrates that we are in a highly nonlinear regime, far away from quasi-static equilibria.

Figure 7. Axial spectra of kinetic (a) and magnetic (b) energy, normalized respectively by the total kinetic and magnetic energy. Three shapes are considered, respectively from top to bottom, a circle with radius $a=1$![]() , an ellipse with major semi-axis $a=1.2$
, an ellipse with major semi-axis $a=1.2$![]() and one with $a=1.4$
and one with $a=1.4$![]() , for $S \approx 2\times 10^4$
, for $S \approx 2\times 10^4$![]() .
.
Figure 7 shows the predominance of a magnetic mode with toroidal mode number $n=7$![]() in the circular case, which is consistent with what has been observed in the RFX-mod device (Lorenzini et al. Reference Lorenzini, Martines, Piovesan, Terranova, Zanca, Zuin, Alfier, Bonfiglio, Bonomo and Canton2009; Martin et al. Reference Martin, Apolloni, Puiatti, Adamek, Agostini, Alfier, Annibaldi, Antoni, Auriemma and Barana2009). In the elliptical case ($a=1.2$
in the circular case, which is consistent with what has been observed in the RFX-mod device (Lorenzini et al. Reference Lorenzini, Martines, Piovesan, Terranova, Zanca, Zuin, Alfier, Bonfiglio, Bonomo and Canton2009; Martin et al. Reference Martin, Apolloni, Puiatti, Adamek, Agostini, Alfier, Annibaldi, Antoni, Auriemma and Barana2009). In the elliptical case ($a=1.2$![]() ), a tendency for mode $n=14$
), a tendency for mode $n=14$![]() to dominate is observed, while the magnetic modes $n=3$
to dominate is observed, while the magnetic modes $n=3$![]() and $n=4$
and $n=4$![]() contain most of the magnetic energy for $a=1.4$
contain most of the magnetic energy for $a=1.4$![]() . This last case seems to be closer to a multiple-helicity state, where it is not a single mode which contains most of the energy. Similar spectral differences are observed in the kinetic spectra, where $n=0$
. This last case seems to be closer to a multiple-helicity state, where it is not a single mode which contains most of the energy. Similar spectral differences are observed in the kinetic spectra, where $n=0$![]() and $n=1$
and $n=1$![]() are the dominating kinetic modes in the circular case, $n=14$
are the dominating kinetic modes in the circular case, $n=14$![]() in the $a=1.2$
in the $a=1.2$![]() elliptical case and $n=8$
elliptical case and $n=8$![]() in the $a=1.4$
in the $a=1.4$![]() elliptical case. A different representation of the modal dynamics is shown in the appendix, where the modal spectra are plotted using the double-logarithmic scale for the different cases.
elliptical case. A different representation of the modal dynamics is shown in the appendix, where the modal spectra are plotted using the double-logarithmic scale for the different cases.
We have not carried out a detailed poloidal mode composition, which is in particular less convenient in the elliptical geometries, and we have therefore no further interpretation of the possible underlying instabilities, which could be external tearing modes or other MHD instabilities. We think that a linear instability analysis of the present system would allow further insights in the origin of the magnetic structures. However, because the modal spectra indicate the large range of active modes, the outcome of such an analysis is of limited use in the here considered fully turbulent state.
It is clear from these observations that shaping significantly influences the topology of the velocity and magnetic fields, both qualitatively and quantitatively. All three geometries do however show the presence of a large range of active scales.
3.4. Poloidal angular momentum
The presented results show a clear influence of the shape of the cross-section on the dynamics. It would be beneficial if we could understand these differences in the light of a clear, large-scale dynamical feature which changes through the shaping. We have identified one such feature which behaves quite differently in the differently shaped geometries. This quantity is the poloidal angular momentum, a quantity which has received considerable attention in two-dimensional flows.
In fact, an interesting difference between two-dimensional flows in circular or elliptical domains is the change in dynamics associated with a form of symmetry breaking of the large-scale flow patterns. Indeed in 2-D turbulence, changing the flow geometry from circular to elliptical leads to the generation of angular momentum (Keetels, Clercx & van Heijst Reference Keetels, Clercx and van Heijst2008). This effect was shown to persist in 2-D MHD turbulence (Bos, Neffaa & Schneider Reference Bos, Neffaa and Schneider2008, Reference Bos, Neffaa and Schneider2010) and its investigation is considered to be interesting in the context of confinement studies, because large-scale poloidal motion could enhance radial transport barriers and stabilize MHD instabilities (Shan & Montgomery Reference Shan and Montgomery1994).
An analysis of a similar possibility in the present geometry is shown in figure 8, where for a given time instant, the angular momentum associated with the poloidal flow is computed for each cross-section. Its definition is
where $\boldsymbol {r}$![]() is the radial vector, pointing from the centreline of the geometry outwards and $A$
is the radial vector, pointing from the centreline of the geometry outwards and $A$![]() is the surface of the poloidal cross-section. In a periodic cylinder with circular cross-section, global angular momentum can only be created by viscous effects. However, locally, at a given axial position, the angular momentum can be strong. This is exactly what is observed for the case of a circular geometry, where locally large values of the poloidal angular momentum exist. Through the associated rotating motion, confinement could be improved, because rotation suppresses instabilities (Shan & Montgomery Reference Shan and Montgomery1994). Note that this is one particular time instant, but qualitatively the same effect is observed at different time instants, with local fluctuations of $L_u$
is the surface of the poloidal cross-section. In a periodic cylinder with circular cross-section, global angular momentum can only be created by viscous effects. However, locally, at a given axial position, the angular momentum can be strong. This is exactly what is observed for the case of a circular geometry, where locally large values of the poloidal angular momentum exist. Through the associated rotating motion, confinement could be improved, because rotation suppresses instabilities (Shan & Montgomery Reference Shan and Montgomery1994). Note that this is one particular time instant, but qualitatively the same effect is observed at different time instants, with local fluctuations of $L_u$![]() , which are largest in amplitude in the circular geometry. Possibly, this structure is associated with the $n=1$
, which are largest in amplitude in the circular geometry. Possibly, this structure is associated with the $n=1$![]() velocity mode observed in the temporal spectrum of the kinetic energy in figure 7(a).
velocity mode observed in the temporal spectrum of the kinetic energy in figure 7(a).

Figure 8. The $z$![]() -dependence of the instantaneous poloidal angular momentum for the three geometries at $t=11\times 10^3\tau _A$
-dependence of the instantaneous poloidal angular momentum for the three geometries at $t=11\times 10^3\tau _A$![]() .
.
This observation is somewhat the opposite of what is observed in investigations of spontaneous spin-up in 2-D systems. There, it is seen that the generation of angular moment is absent in circular 2-D domains and becomes more important in elliptical domains (Keetels et al. Reference Keetels, Clercx and van Heijst2008).
The important amount of circular movement characterized here by the poloidal angular momentum is perhaps simply owing to the fact that a circular shape is more compatible with circular movement, compared with non-circular-shaped cross-sections. However, such a poloidal flow could be beneficial for confinement, which shows here that with respect to that effect, circular domains might be favourable for good confinement. This is also what was concluded, for different reasons, by Guo et al. (Reference Guo, Xu, Wang and Liu2013). This observation is clearly of speculative nature and further research is required to investigate the link between poloidal angular momentum, shaping and the turbulent dynamics of the RFP.
4. Conclusion
Direct numerical simulations of viscoresistive MHD show that in periodic cylindrical geometry in the RFP regime, the shape of the cross-section significantly changes the nonlinear dynamics. Moreover, different helical states can be observed and different toroidal modes are excited in different geometries. Modifying the elliptical elongation leads to different modal behaviours.
We quantified first the influence of shaping on the $F-\varTheta$![]() characteristics and showed that the influence of shaping on these global quantities is less important than a change in the Lundquist number. For other quantities, which do not concern the global properties, the picture is different. Indeed, shaping in our simulations significantly modified the magnetic flux-lines in a cross-section. It was observed that for circular and moderately elliptical cross-section, the contours of the magnetic flux surfaces were roughly concentric. However, when the domain became elliptical enough ($a=1.4$
characteristics and showed that the influence of shaping on these global quantities is less important than a change in the Lundquist number. For other quantities, which do not concern the global properties, the picture is different. Indeed, shaping in our simulations significantly modified the magnetic flux-lines in a cross-section. It was observed that for circular and moderately elliptical cross-section, the contours of the magnetic flux surfaces were roughly concentric. However, when the domain became elliptical enough ($a=1.4$![]() in our simulations), the contours started to show two magnetic islands.
in our simulations), the contours started to show two magnetic islands.
Perhaps most obvious in our simulations was the generation of local poloidal angular momentum in the circular geometry, which is absent in the more elliptical shapes. The presence of such local but large-scale poloidal structures could possibly stabilize the plasma dynamics. It seems with respect to this feature that circular cross-sections are better candidates to improve confinement. However, the addition of toroidal curvature to the system might alter this feature. As a matter of fact, in toroidal geometry, a quasi-single helicity state was observed to be more persistent than in a cylindrical geometry (Morales et al. Reference Morales, Bos, Schneider and Montgomery2014a). How poloidal flow structures containing angular momentum and helical modes are related and how they interact deserves further attention.
The most important outcome of this work is therefore not the determination of a certain value of the elongation most efficient to obtain an optimal confinement, but the mere fact that elongation radically changes the dynamics of RFPs. We would therefore encourage experimentalists to consider the poloidal shape of the confining magnetic field as an important control parameter for RFP design and operation, because different modes are triggered when the shape of the cross-section is modified. If an experiment allows for a simple modification of the plasma shape, it might give more freedom to obtain a competitive fusion plasma.
Acknowledgements
The authors acknowledge the help and comments of J.A. Morales and discussion with D. Bonfiglio, D.F. Escande and M. Veranda. We acknowledge PMCS2I and P2CHPD for the use of their facilities.
Editor Steve Tobias thanks the referees for their advice in evaluating this article.
Funding
We acknowledge support by the French Federation for Magnetic Fusion Studies (FR-FCM) and of the Eurofusion consortium from the Euratom research and training programme 2014–2018 and 2019–2020 under grant agreement No633053. The views and opinions expressed herein do not necessarily reflect those of the European Commission. We further acknowledge IDRIS (Project No. 22206)
Declaration of interests
The authors report no conflict of interest.
Data availability statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Appendix A
A.1. Temporal evolution of modal spectra
To complete the modal analysis carried out in § 3.3, we show in figure 9 the modal spectra in double-logarithmic representation. For each spectrum, four time instants are shown during the statistically steady state. The most striking observation is the large number of active modes. In this representation, we cannot clearly identify a dominant mode in the system. Quasi-single helicity states might be attainable, but this is certainly not observed in the present results.

Figure 9. Axial mode spectra of kinetic energy fluctuations (a,b) and magnetic fluctuations (e,f) in cylinders with ellipticity (a,d) $a=1$![]() , (b,e) $a=1.2$
, (b,e) $a=1.2$![]() , (c,f) $a=1.4$
, (c,f) $a=1.4$![]() . Spectra are shown at four different time instants during the statistically steady state. The Lundquist number is $S\approx 2\times 10^4$
. Spectra are shown at four different time instants during the statistically steady state. The Lundquist number is $S\approx 2\times 10^4$![]() .
.