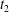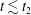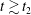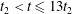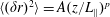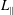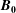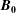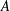1 Introduction
Turbulence in space and terrestrial laboratory plasmas remains one of the most active research areas in plasma physics. Space and fusion plasmas are turbulent, weakly collisional and magnetized. Plasma turbulence governs particle and energy transport and describing such transport is a key goal of the plasma physics community. Turbulence in space plasmas likely plays an important role in several observed phenomena, such as solar coronal heating, solar wind heating and the acceleration of solar particles in the heliosphere. Furthermore, the turbulence also affects how solar energetic particles and cosmic rays propagate through space. In terrestrial laboratories, turbulence may reduce the confinement for plasma fusion by enhancing transport across the confining magnetic field.
Iroshnikov (Reference Iroshnikov1963) and Kraichnan (Reference Kraichnan1965) independently developed an isotropic theory for incompressible magnetohydrodynamics (MHD) turbulence suggesting that the nonlinear interactions of the large-scale Alfvén waves lead to a turbulent energy cascade down to smaller scales. Years after, it was demonstrated that anisotropy is an important characteristic in incompressible MHD turbulence, i.e. the anisotropic turbulent cascade transfers energy to smaller scales in the perpendicular direction with respect to the background magnetic field (Sridhar & Goldreich Reference Sridhar and Goldreich1994; Goldreich & Sridhar Reference Goldreich and Sridhar1995; Montgomery & Matthaeus Reference Montgomery and Matthaeus1995; Ghosh & Goldstein Reference Ghosh and Goldstein1997; Matthaeus et al. Reference Matthaeus, Oughton, Ghosh and Hossain1998; Cho & Vishniac Reference Cho and Vishniac2000; Maron & Goldreich Reference Maron and Goldreich2001). The phenomenon of turbulent cascade due to the nonlinear interactions between counterpropagating Alfvén waves, which is the fundamental building block of plasma turbulence, has been experimentally tested (Howes et al. Reference Howes, Drake, Nielson, Carter, Kletzing and Skiff2012; Drake et al. Reference Drake, Schroeder, Howes, Kletzing, Skiff, Carter and Auerbach2013; Howes & Nielson Reference Howes and Nielson2013; Howes et al. Reference Howes, Nielson, Drake, Schroeder, Skiff, Kletzing and Carter2013; Nielson, Howes & Dorland Reference Nielson, Howes and Dorland2013).
One significant effect of the turbulence is the tangling of the magnetic field lines, or magnetic field wander. Due to plasma turbulence, the magnetic field lines may become stochastic and get separated from each other leading to the spreading of particles that travel along the field lines. The magnetic field wander in turbulent plasmas impacts the propagation of the energetic particles in astrophysical space as well as the heat and particle transport in fusion plasmas. The problem of field line wandering and its impacts on other physical processes is one of the unresolved problems of plasma physics. For instance, understanding the wandering of magnetic field lines in solar wind turbulence will enable the prediction of the scattering of the solar energetic particles – arising from coronal mass ejections and flares that may occur on the Sun’s surface – determining the energetic particle fluxes near the Earth, where they can potentially damage communication satellites or harm astronauts in orbit.
Models of the propagation of the cosmic rays and the solar energetic particles through a stochastic magnetic field were first proposed by Jokipii (Reference Jokipii1966) and Jokipii & Parker (Reference Jokipii and Parker1968). The authors describe the transport of the energetic particles in the context of the field line random walk (FLRW) theory using a quasilinear statistical calculation of the motion of charged particles in a spatially random magnetic field. Advanced models implementing nonlinear calculations of FLRW theory were developed later to estimate the diffusion of the field line wandering (Matthaeus et al.
Reference Matthaeus, Gray, Pontius and Bieber1995). Recently, several models were developed to study the separation of the magnetic field lines, implementing various models of turbulence, including slab turbulence (Schlickeiser Reference Schlickeiser1989; Shalchi & Kourakis Reference Shalchi and Kourakis2007a
,Reference Shalchi and Kourakis
b
; Shalchi Reference Shalchi2010b
), two-dimensional turbulence (Shalchi & Kourakis Reference Shalchi and Kourakis2007a
,Reference Shalchi and Kourakis
b
; Guest & Shalchi Reference Guest and Shalchi2012), composite models including slab plus two-dimensional components (Bieber, Wanner & Matthaeus Reference Bieber, Wanner and Matthaeus1996; Shalchi & Kourakis Reference Shalchi and Kourakis2007a
,Reference Shalchi and Kourakis
b
; Qin & Shalchi Reference Qin and Shalchi2013) and other three-dimensional models including MHD turbulence (Zimbardo et al.
Reference Zimbardo, Veltri, Basile and Principato1995; Zimbardo, Veltri & Pommois Reference Zimbardo, Veltri and Pommois2000; Maron, Chandran & Blackman Reference Maron, Chandran and Blackman2004; Zimbardo, Pommois & Veltri Reference Zimbardo, Pommois and Veltri2006; Shalchi Reference Shalchi2010a
; Ragot Reference Ragot2011; Beresnyak Reference Beresnyak2013; Ruffolo & Matthaeus Reference Ruffolo and Matthaeus2013; Shalchi & Kolly Reference Shalchi and Kolly2013). In the latter works, the superdiffusive behaviour of the magnetic field lines has been confirmed in three-dimensional MHD simulations for scales comparable to or less than the injection scale
![]() $l_{0}$
, but for scales much larger than
$l_{0}$
, but for scales much larger than
![]() $l_{0}$
the field lines follow a diffusive law.
$l_{0}$
the field lines follow a diffusive law.
The magnetic field line wander may also impact the process of magnetic reconnection. For instance, it has been shown that the rate of magnetic reconnection can be enhanced due to magnetic field line wandering (see e.g. Lazarian & Vishniac Reference Lazarian and Vishniac1999; Lazarian, Vishniac & Cho Reference Lazarian, Vishniac and Cho2004).
In fusion plasmas, it has been suggested that the destruction of the magnetic flux surfaces in a tokamak can be caused by magnetic field wander arising due to the turbulent fluctuations in the confining magnetic field (Rechester & Rosenbluth Reference Rechester and Rosenbluth1978). Many subsequent works investigated the role of the magnetic field line wander in enhancing heat transport in fusion plasmas (Krommes, Oberman & Kleva Reference Krommes, Oberman and Kleva1983; Haas & Thyagaraja Reference Haas and Thyagaraja1986; Laval Reference Laval1993; Spatschek Reference Spatschek2008). Advanced direct numerical simulations of weakly collisional plasma turbulence using nonlinear gyrokinetic simulations were used to explore the role of the wandering of the magnetic field lines in fusion plasmas (Nevins, Wang & Candy Reference Nevins, Wang and Candy2011; Wang et al.
Reference Wang, Nevins, Candy, Hatch, Terry and Guttenfelder2011; Hatch et al.
Reference Hatch, Pueschel, Jenko, Nevins, Terry and Doerk2012, Reference Hatch, Pueschel, Jenko, Nevins, Terry and Doerk2013). For example, it is found that the wandering of the magnetic field lines does occur in fusion plasmas, but that it does not significantly enhance the heat transport in the plasma (Nevins et al.
Reference Nevins, Wang and Candy2011; Wang et al.
Reference Wang, Nevins, Candy, Hatch, Terry and Guttenfelder2011). Additionally, it has been shown that the stochasticity of the magnetic field lines in gyrokinetic turbulence may induce the non-zonal transition – proposed as an explanation of the high-
![]() $\unicode[STIX]{x1D6FD}$
runaway – in CYCLONE base case plasmas once a certain threshold of electron normalized plasma pressure is exceeded (Pueschel, Terry & Hatch Reference Pueschel, Terry and Hatch2014).
$\unicode[STIX]{x1D6FD}$
runaway – in CYCLONE base case plasmas once a certain threshold of electron normalized plasma pressure is exceeded (Pueschel, Terry & Hatch Reference Pueschel, Terry and Hatch2014).
Previous studies of magnetic field wander estimated what is called the mean square displacement,
![]() $\langle (\unicode[STIX]{x1D6FF}r)^{2}\rangle$
, to describe the spread of the stochastic magnetic field lines. It is found that the quantity
$\langle (\unicode[STIX]{x1D6FF}r)^{2}\rangle$
, to describe the spread of the stochastic magnetic field lines. It is found that the quantity
![]() $\langle (\unicode[STIX]{x1D6FF}r)^{2}\rangle$
is fit to a power-law function,
$\langle (\unicode[STIX]{x1D6FF}r)^{2}\rangle$
is fit to a power-law function,
![]() $\propto l_{B}^{p}$
, (
$\propto l_{B}^{p}$
, (
![]() $l_{B}$
is the distance along the magnetic field line), however, the value of
$l_{B}$
is the distance along the magnetic field line), however, the value of
![]() $p$
was found to vary from a model to another. For example, analytic modelling of anisotropic three-dimensional turbulence (Shalchi & Kolly Reference Shalchi and Kolly2013) shows that the wandering of the magnetic field lines is diffusive, i.e.
$p$
was found to vary from a model to another. For example, analytic modelling of anisotropic three-dimensional turbulence (Shalchi & Kolly Reference Shalchi and Kolly2013) shows that the wandering of the magnetic field lines is diffusive, i.e.
![]() $p=1$
. Non-diffusive transport (
$p=1$
. Non-diffusive transport (
![]() $p\neq 1$
) of the field line wandering has also been found in other analytical as well as numerical works (see e.g. Lazarian & Vishniac Reference Lazarian and Vishniac1999; Shalchi & Kourakis Reference Shalchi and Kourakis2007a
,Reference Shalchi and Kourakis
b
; Beresnyak Reference Beresnyak2013; Lazarian & Yan Reference Lazarian and Yan2014).
$p\neq 1$
) of the field line wandering has also been found in other analytical as well as numerical works (see e.g. Lazarian & Vishniac Reference Lazarian and Vishniac1999; Shalchi & Kourakis Reference Shalchi and Kourakis2007a
,Reference Shalchi and Kourakis
b
; Beresnyak Reference Beresnyak2013; Lazarian & Yan Reference Lazarian and Yan2014).
In this present work, we focus on the development of magnetic field wander using nonlinear gyrokinetic simulations of weakly collisional plasma turbulence. We will study how small-scale turbulence (turbulent fluctuations having scales ranging between ion and electron scales) affects the stochasticity and the separation of the magnetic field lines. In figure 1 we sketch the magnetic power spectrum of solar wind turbulence (Sahraoui et al.
Reference Sahraoui, Goldstein, Robert and Khotyaintsev2009; Alexandrova et al.
Reference Alexandrova, Lacombe, Mangeney, Grappin and Maksimovic2012). The cascade of the energy starts to occur near the outer scale
![]() $l\approx 10^{6}$
km down to the electron scale. The gyrokinetic simulation considered in our study describes turbulence between ion and electron scales (see red box in figure 1). Within these scales it has been shown that the turbulent energy cascade is controlled by kinetic Alfvén wave turbulence (Howes et al.
Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006). It is worth noting that a steeper magnetic power spectrum
$l\approx 10^{6}$
km down to the electron scale. The gyrokinetic simulation considered in our study describes turbulence between ion and electron scales (see red box in figure 1). Within these scales it has been shown that the turbulent energy cascade is controlled by kinetic Alfvén wave turbulence (Howes et al.
Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006). It is worth noting that a steeper magnetic power spectrum
![]() ${\sim}k^{-7/3}$
below the proton gyroscale was first obtained within electron MHD turbulence (see, e.g. Biskamp, Schwarz & Drake Reference Biskamp, Schwarz and Drake1996; Biskamp et al.
Reference Biskamp, Schwarz, Zeiler, Celani and Drake1999; Cho & Lazarian Reference Cho and Lazarian2004). As a consequence of applying critical balance conditions at subproton scales the anisotropy
${\sim}k^{-7/3}$
below the proton gyroscale was first obtained within electron MHD turbulence (see, e.g. Biskamp, Schwarz & Drake Reference Biskamp, Schwarz and Drake1996; Biskamp et al.
Reference Biskamp, Schwarz, Zeiler, Celani and Drake1999; Cho & Lazarian Reference Cho and Lazarian2004). As a consequence of applying critical balance conditions at subproton scales the anisotropy
![]() $k_{\Vert }\sim k_{\bot }^{1/3}$
(
$k_{\Vert }\sim k_{\bot }^{1/3}$
(
![]() $k_{\Vert }$
and
$k_{\Vert }$
and
![]() $k_{\bot }$
are the parallel and perpendicular wavenumber components with respect to the local magnetic field) was obtained in electron MHD turbulence (Cho & Lazarian Reference Cho and Lazarian2004, Reference Cho and Lazarian2009). Furthermore, Cho & Vishniac (Reference Cho and Vishniac2000) argued that this scale-dependent anisotropy can be measured only with respect to the local magnetic field direction rather than the global mean field.
$k_{\bot }$
are the parallel and perpendicular wavenumber components with respect to the local magnetic field) was obtained in electron MHD turbulence (Cho & Lazarian Reference Cho and Lazarian2004, Reference Cho and Lazarian2009). Furthermore, Cho & Vishniac (Reference Cho and Vishniac2000) argued that this scale-dependent anisotropy can be measured only with respect to the local magnetic field direction rather than the global mean field.

Figure 1. Schematic of the magnetic energy wavenumber spectrum in the solar wind showing the form of the spectrum in the energy containing inertial and dissipation ranges. Ranges for the typical Larmor radius scales for protons
![]() $\unicode[STIX]{x1D70C}EP_{,p}$
and electrons
$\unicode[STIX]{x1D70C}EP_{,p}$
and electrons
![]() $\unicode[STIX]{x1D70C}EP_{,e}$
from solar energetic particle events are depicted. The area of the spectrum indicated by red line is the range of gyrokinetic (GK) turbulence scale considered in this study.
$\unicode[STIX]{x1D70C}EP_{,e}$
from solar energetic particle events are depicted. The area of the spectrum indicated by red line is the range of gyrokinetic (GK) turbulence scale considered in this study.
We investigate two features that characterize the wandering of the magnetic field lines as a function of the amplitude of the turbulence: (i) the stochasticity of the field lines and (ii) the spreading of the magnetic field lines. Developing a simple model of the spreading of magnetic field lines as a function of the amplitude of the turbulence is a critical step in constructing a reliable predictive model for the propagation of solar energetic particles in the heliosphere. The amplitude of the turbulence is characterized in our study by computing the nonlinearity parameter
![]() $\unicode[STIX]{x1D712}$
, a dimensionless measure of the ratio of the magnitude of the nonlinear to the linear terms in the equations of motion. Alternatively, the nonlinear parameter may be interpreted as
$\unicode[STIX]{x1D712}$
, a dimensionless measure of the ratio of the magnitude of the nonlinear to the linear terms in the equations of motion. Alternatively, the nonlinear parameter may be interpreted as
![]() $\unicode[STIX]{x1D712}\simeq t_{l}/t_{n}$
, the ratio of the linear wave period
$\unicode[STIX]{x1D712}\simeq t_{l}/t_{n}$
, the ratio of the linear wave period
![]() $t_{l}$
to the nonlinear time scale
$t_{l}$
to the nonlinear time scale
![]() $t_{n}$
. A unique aspect of this study is the use of nonlinear gyrokinetic simulations of turbulence – in which the microphysics of collisionless turbulent cascade and small-scale magnetic reconnection near the electron scales is resolved – to quantify the separation of the stochastic magnetic field lines.
$t_{n}$
. A unique aspect of this study is the use of nonlinear gyrokinetic simulations of turbulence – in which the microphysics of collisionless turbulent cascade and small-scale magnetic reconnection near the electron scales is resolved – to quantify the separation of the stochastic magnetic field lines.
2 Simulations and results
We use the astrophysical gyrokinetics code AstroGK to study the magnetic field line wander in gyrokinetic turbulence. The AstroGK code, which is described in detail in Numata et al. (Reference Numata, Howes, Tatsuno, Barnes and Dorland2010), solves the gyrokinetic equation coupled to the gyro-averaged Maxwell equations (Frieman & Chen Reference Frieman and Chen1982; Howes et al.
Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006). AstroGK computes the time evolution of the perturbed gyro-averaged distribution function
![]() $h_{s}$
for each species
$h_{s}$
for each species
![]() $s$
and the fluctuating electromagnetic fields, defined by the scalar potential
$s$
and the fluctuating electromagnetic fields, defined by the scalar potential
![]() $\unicode[STIX]{x1D719}$
, parallel vector potential
$\unicode[STIX]{x1D719}$
, parallel vector potential
![]() $A_{\Vert }$
and the parallel magnetic field perturbation
$A_{\Vert }$
and the parallel magnetic field perturbation
![]() $\unicode[STIX]{x1D6FF}B_{\Vert }$
. Here,
$\unicode[STIX]{x1D6FF}B_{\Vert }$
. Here,
![]() $\Vert$
refers to the parallel direction with respect to the background magnetic field
$\Vert$
refers to the parallel direction with respect to the background magnetic field
![]() $\boldsymbol{B}_{\mathbf{0}}=B_{0}\hat{\boldsymbol{z}}$
. The simulation domain is assumed to be a periodic box elongated along the equilibrium magnetic field with size
$\boldsymbol{B}_{\mathbf{0}}=B_{0}\hat{\boldsymbol{z}}$
. The simulation domain is assumed to be a periodic box elongated along the equilibrium magnetic field with size
![]() $L_{\Vert }\times L_{\bot }^{2}$
, where
$L_{\Vert }\times L_{\bot }^{2}$
, where
![]() $L_{\bot }$
(
$L_{\bot }$
(
![]() $L_{\Vert }$
) is the size of the simulation box along
$L_{\Vert }$
) is the size of the simulation box along
![]() $x$
and
$x$
and
![]() $y$
(along
$y$
(along
![]() $z$
direction) directions perpendicular to
$z$
direction) directions perpendicular to
![]() $\boldsymbol{B}_{\mathbf{0}}$
, and
$\boldsymbol{B}_{\mathbf{0}}$
, and
![]() $L_{\bot }\ll L_{\Vert }$
. We assume two plasma species, protons and electrons with a real mass ratio
$L_{\bot }\ll L_{\Vert }$
. We assume two plasma species, protons and electrons with a real mass ratio
![]() $m_{i}/m_{e}=1836$
.
$m_{i}/m_{e}=1836$
.
The numerical code AstroGK has been used in early studies to investigate solar wind turbulence (Howes et al.
Reference Howes, Dorland, Cowley, Hammett, Quataert, Schekochihin and Tatsuno2008b
, Reference Howes, TenBarge, Dorland, Quataert, Schekochihin, Numata and Tatsuno2011b
). Nonlinear gyrokinetic simulations (TenBarge & Howes Reference TenBarge and Howes2013; TenBarge, Howes & Dorland Reference TenBarge, Howes and Dorland2013) have been found to reproduce the scaling of the turbulence magnetic energy spectrum waves down to the scales of the electron Larmor radius
![]() $\unicode[STIX]{x1D70C}_{e}$
, (Alexandrova et al.
Reference Alexandrova, Lacombe, Mangeney, Grappin and Maksimovic2012). For our study, we choose fixed plasma parameters for the proton-to-electron temperature ratio
$\unicode[STIX]{x1D70C}_{e}$
, (Alexandrova et al.
Reference Alexandrova, Lacombe, Mangeney, Grappin and Maksimovic2012). For our study, we choose fixed plasma parameters for the proton-to-electron temperature ratio
![]() $T_{i}/T_{e}=1$
and the proton plasma
$T_{i}/T_{e}=1$
and the proton plasma
![]() $\unicode[STIX]{x1D6FD}_{i}=1$
, where
$\unicode[STIX]{x1D6FD}_{i}=1$
, where
![]() $\unicode[STIX]{x1D6FD}_{i}=v_{th_{i}}^{2}/v_{A}^{2}$
,
$\unicode[STIX]{x1D6FD}_{i}=v_{th_{i}}^{2}/v_{A}^{2}$
,
![]() $v_{th_{i}}=(2T_{i}/m_{i})^{1/2}$
is the ion thermal speed and
$v_{th_{i}}=(2T_{i}/m_{i})^{1/2}$
is the ion thermal speed and
![]() $v_{A}$
is the Alfvén speed. The spatial resolution of the simulation domain is
$v_{A}$
is the Alfvén speed. The spatial resolution of the simulation domain is
![]() $n_{x}\times n_{y}\times n_{z}=64\times 64\times 32$
, representing the number of points along
$n_{x}\times n_{y}\times n_{z}=64\times 64\times 32$
, representing the number of points along
![]() $x$
,
$x$
,
![]() $y$
and
$y$
and
![]() $z$
directions, and velocity space resolution is a polar grid of 32 pitch angles by 16 energy levels. Also, we choose
$z$
directions, and velocity space resolution is a polar grid of 32 pitch angles by 16 energy levels. Also, we choose
![]() $\unicode[STIX]{x1D716}=L_{\bot }/L_{\Vert }=0.0163$
. We use an oscillating Langevin antenna (TenBarge, Howes, Dorland & Hammett Reference TenBarge, Howes, Dorland and Hammett2014) to drive four counterpropagating wave modes at the domain perpendicular scale
$\unicode[STIX]{x1D716}=L_{\bot }/L_{\Vert }=0.0163$
. We use an oscillating Langevin antenna (TenBarge, Howes, Dorland & Hammett Reference TenBarge, Howes, Dorland and Hammett2014) to drive four counterpropagating wave modes at the domain perpendicular scale
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{i}=5$
, where
$k_{\bot }\unicode[STIX]{x1D70C}_{i}=5$
, where
![]() $k_{\bot }$
is the perpendicular wavenumber component and
$k_{\bot }$
is the perpendicular wavenumber component and
![]() $\unicode[STIX]{x1D70C}_{i}$
is the proton Larmor radius. To investigate how the tangling of the magnetic field lines is affected by the amplitude of the turbulence we consider seven simulation runs differing only by the amplitude of the driving. The average value of the nonlinearity parameter for each of these runs is presented in table 1.
$\unicode[STIX]{x1D70C}_{i}$
is the proton Larmor radius. To investigate how the tangling of the magnetic field lines is affected by the amplitude of the turbulence we consider seven simulation runs differing only by the amplitude of the driving. The average value of the nonlinearity parameter for each of these runs is presented in table 1.
Table 1. For simulation Runs 1–7, time-averaged nonlinearity parameter
![]() $\overline{\unicode[STIX]{x1D712}}$
with its standard deviation
$\overline{\unicode[STIX]{x1D712}}$
with its standard deviation
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D712}$
. Interaction time
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D712}$
. Interaction time
![]() $t_{1}$
, saturation time
$t_{1}$
, saturation time
![]() $t_{2}$
and final simulation time
$t_{2}$
and final simulation time
![]() $t_{f}$
normalized to the linear kinetic Alfvén wave period
$t_{f}$
normalized to the linear kinetic Alfvén wave period
![]() $t_{l}=1.74\unicode[STIX]{x1D714}_{A0}^{-1}$
for the domain-scale waves at
$t_{l}=1.74\unicode[STIX]{x1D714}_{A0}^{-1}$
for the domain-scale waves at
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{i}=5$
.
$k_{\bot }\unicode[STIX]{x1D70C}_{i}=5$
.

The specific definition used for the nonlinearity parameter in this paper is
where
![]() $b$
is an order-unity dimensionless parameter,
$b$
is an order-unity dimensionless parameter,
![]() $B_{0}$
is the equilibrium magnetic field amplitude,
$B_{0}$
is the equilibrium magnetic field amplitude,
![]() $\unicode[STIX]{x1D6FF}B_{\bot }(k_{\bot })$
is the amplitude of fluctuations at a particular perpendicular Fourier wavenumber,
$\unicode[STIX]{x1D6FF}B_{\bot }(k_{\bot })$
is the amplitude of fluctuations at a particular perpendicular Fourier wavenumber,
![]() $k_{\bot }=\sqrt{k_{x}^{2}+k_{y}^{2}}$
and
$k_{\bot }=\sqrt{k_{x}^{2}+k_{y}^{2}}$
and
![]() $k_{\Vert }$
is the average parallel wavenumber associated with magnetic field fluctuations having that particular perpendicular wavenumber. The strength of the nonlinearity in kinetic Alfvén wave turbulence is characterized by the nonlinearity parameter
$k_{\Vert }$
is the average parallel wavenumber associated with magnetic field fluctuations having that particular perpendicular wavenumber. The strength of the nonlinearity in kinetic Alfvén wave turbulence is characterized by the nonlinearity parameter
![]() $\unicode[STIX]{x1D712}$
given in (2.1) and it is estimated in analogy to the one considered in incompressible MHD, i.e. the ratio of the magnitude of the nonlinear to the linear terms,
$\unicode[STIX]{x1D712}$
given in (2.1) and it is estimated in analogy to the one considered in incompressible MHD, i.e. the ratio of the magnitude of the nonlinear to the linear terms,
![]() $\unicode[STIX]{x1D712}\sim (k_{\bot }\unicode[STIX]{x1D6FF}v_{\bot })/(k_{\Vert }v_{ph})$
, where
$\unicode[STIX]{x1D712}\sim (k_{\bot }\unicode[STIX]{x1D6FF}v_{\bot })/(k_{\Vert }v_{ph})$
, where
![]() $\unicode[STIX]{x1D6FF}v_{\bot }$
is the fluctuating bulk velocity and
$\unicode[STIX]{x1D6FF}v_{\bot }$
is the fluctuating bulk velocity and
![]() $v_{ph}$
is the phase speed of kinetic Alfvén waves (or Alfvén waves in case of incompressible MHD). First, we choose a value
$v_{ph}$
is the phase speed of kinetic Alfvén waves (or Alfvén waves in case of incompressible MHD). First, we choose a value
![]() $b=1$
for the order-unity parameter in our calculation of
$b=1$
for the order-unity parameter in our calculation of
![]() $\unicode[STIX]{x1D712}$
. Because the oscillating Langevin antenna (TenBarge et al.
Reference TenBarge, Howes, Dorland and Hammett2014) yields a finite-time correlated driving, the power input into the plasma varies with time, meaning that the amplitude of the turbulence, which determines the nonlinearity parameter, varies in time. Therefore, we specify here how to determine the nonlinearity parameter based on turbulent magnetic field at a single point in time. To avoid any direct influence of the driving at
$\unicode[STIX]{x1D712}$
. Because the oscillating Langevin antenna (TenBarge et al.
Reference TenBarge, Howes, Dorland and Hammett2014) yields a finite-time correlated driving, the power input into the plasma varies with time, meaning that the amplitude of the turbulence, which determines the nonlinearity parameter, varies in time. Therefore, we specify here how to determine the nonlinearity parameter based on turbulent magnetic field at a single point in time. To avoid any direct influence of the driving at
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{i}=5$
in our computation of the nonlinearity parameter for each run, we compute the nonlinearity parameter using the average amplitude of the seven perpendicular Fourier modes with
$k_{\bot }\unicode[STIX]{x1D70C}_{i}=5$
in our computation of the nonlinearity parameter for each run, we compute the nonlinearity parameter using the average amplitude of the seven perpendicular Fourier modes with
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{i}=10$
and
$k_{\bot }\unicode[STIX]{x1D70C}_{i}=10$
and
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{i}=25/\sqrt{5}$
to obtain a value
$k_{\bot }\unicode[STIX]{x1D70C}_{i}=25/\sqrt{5}$
to obtain a value
![]() $\unicode[STIX]{x1D6FF}B_{\bot }(k_{\bot })$
at a mode-weighted average
$\unicode[STIX]{x1D6FF}B_{\bot }(k_{\bot })$
at a mode-weighted average
![]() $\langle k_{\bot }\unicode[STIX]{x1D70C}_{i}\rangle \simeq 10.67$
. Here, three modes correspond to
$\langle k_{\bot }\unicode[STIX]{x1D70C}_{i}\rangle \simeq 10.67$
. Here, three modes correspond to
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{i}=10$
and four modes correspond to
$k_{\bot }\unicode[STIX]{x1D70C}_{i}=10$
and four modes correspond to
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{i}=25/\sqrt{5}$
. We also estimate the weighted-average value of
$k_{\bot }\unicode[STIX]{x1D70C}_{i}=25/\sqrt{5}$
. We also estimate the weighted-average value of
![]() $\unicode[STIX]{x1D6FF}B_{\bot }$
in the expression (2.1) as
$\unicode[STIX]{x1D6FF}B_{\bot }$
in the expression (2.1) as
![]() $(3\unicode[STIX]{x1D6FF}B_{\bot }(k_{\bot }=10)+4\unicode[STIX]{x1D6FF}B_{\bot }(k_{\bot }=25/\sqrt{5}))/7$
. It is widely acknowledged that the turbulent cascade in magnetized plasma turbulence is anisotropic (Zweben, Menyuk & Taylor Reference Zweben, Menyuk and Taylor1979; Montgomery & Turner Reference Montgomery and Turner1981; Shebalin, Matthaeus & Montgomery Reference Shebalin, Matthaeus and Montgomery1983; Oughton, Priest & Matthaeus Reference Oughton, Priest and Matthaeus1994; Sridhar & Goldreich Reference Sridhar and Goldreich1994; Goldreich & Sridhar Reference Goldreich and Sridhar1995; Cho & Vishniac Reference Cho and Vishniac2000; Galtier et al.
Reference Galtier, Nazarenko, Newell and Pouquet2000; Boldyrev Reference Boldyrev2006), with energy transferred to smaller perpendicular scales more rapidly than to smaller parallel scales, leading to fluctuations with the characteristic anisotropy
$(3\unicode[STIX]{x1D6FF}B_{\bot }(k_{\bot }=10)+4\unicode[STIX]{x1D6FF}B_{\bot }(k_{\bot }=25/\sqrt{5}))/7$
. It is widely acknowledged that the turbulent cascade in magnetized plasma turbulence is anisotropic (Zweben, Menyuk & Taylor Reference Zweben, Menyuk and Taylor1979; Montgomery & Turner Reference Montgomery and Turner1981; Shebalin, Matthaeus & Montgomery Reference Shebalin, Matthaeus and Montgomery1983; Oughton, Priest & Matthaeus Reference Oughton, Priest and Matthaeus1994; Sridhar & Goldreich Reference Sridhar and Goldreich1994; Goldreich & Sridhar Reference Goldreich and Sridhar1995; Cho & Vishniac Reference Cho and Vishniac2000; Galtier et al.
Reference Galtier, Nazarenko, Newell and Pouquet2000; Boldyrev Reference Boldyrev2006), with energy transferred to smaller perpendicular scales more rapidly than to smaller parallel scales, leading to fluctuations with the characteristic anisotropy
![]() $k_{\bot }\gg k_{\Vert }$
at small scales. The estimation of the wavenumber parallel to the local total magnetic field (as opposed to the equilibrium magnetic field) is numerically challenging (TenBarge & Howes Reference TenBarge and Howes2012), so we use the scaling expected for a kinetic Alfvén wave cascade
$k_{\bot }\gg k_{\Vert }$
at small scales. The estimation of the wavenumber parallel to the local total magnetic field (as opposed to the equilibrium magnetic field) is numerically challenging (TenBarge & Howes Reference TenBarge and Howes2012), so we use the scaling expected for a kinetic Alfvén wave cascade
![]() $k_{\Vert }\propto k_{\bot }^{1/3}$
, giving a value
$k_{\Vert }\propto k_{\bot }^{1/3}$
, giving a value
![]() $k_{\Vert }(k_{\bot }\unicode[STIX]{x1D70C}_{i}=10.67)\simeq 1.29k_{\Vert 0}$
with
$k_{\Vert }(k_{\bot }\unicode[STIX]{x1D70C}_{i}=10.67)\simeq 1.29k_{\Vert 0}$
with
![]() $k_{\Vert 0}=2\unicode[STIX]{x03C0}/L_{\Vert }$
. With these specific choices, the nonlinearity parameter for each simulation can be computed as a function of time,
$k_{\Vert 0}=2\unicode[STIX]{x03C0}/L_{\Vert }$
. With these specific choices, the nonlinearity parameter for each simulation can be computed as a function of time,
![]() $\unicode[STIX]{x1D712}(t)$
. Table 1 lists the average value of the nonlinearity parameter
$\unicode[STIX]{x1D712}(t)$
. Table 1 lists the average value of the nonlinearity parameter
![]() $\overline{\unicode[STIX]{x1D712}}$
and its standard deviation
$\overline{\unicode[STIX]{x1D712}}$
and its standard deviation
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D712}$
for Runs 1–7, taken over the period over which each simulation is saturated,
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D712}$
for Runs 1–7, taken over the period over which each simulation is saturated,
![]() $t_{2}<t<t_{f}$
, as discussed in § 2.1.
$t_{2}<t<t_{f}$
, as discussed in § 2.1.
The characteristic linear time scale
![]() $t_{l}$
is estimated from the linear frequency of a kinetic Alfvén wave at the domain scale,
$t_{l}$
is estimated from the linear frequency of a kinetic Alfvén wave at the domain scale,
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{i}=5$
. A numerical solution of the collisionless linear gyrokinetic dispersion relation (Howes et al.
Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006) for the kinetic Alfvén wave frequency of these domain-scale waves gives
$k_{\bot }\unicode[STIX]{x1D70C}_{i}=5$
. A numerical solution of the collisionless linear gyrokinetic dispersion relation (Howes et al.
Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006) for the kinetic Alfvén wave frequency of these domain-scale waves gives
![]() $\unicode[STIX]{x1D714}_{0}=3.6\unicode[STIX]{x1D714}_{A0}$
where
$\unicode[STIX]{x1D714}_{0}=3.6\unicode[STIX]{x1D714}_{A0}$
where
![]() $\unicode[STIX]{x1D714}_{A0}=k_{\Vert 0}V_{A}$
, or a linear kinetic Alfvén wave period
$\unicode[STIX]{x1D714}_{A0}=k_{\Vert 0}V_{A}$
, or a linear kinetic Alfvén wave period
![]() $t_{l}=1.74\unicode[STIX]{x1D714}_{A0}^{-1}$
.
$t_{l}=1.74\unicode[STIX]{x1D714}_{A0}^{-1}$
.
The turbulence is initially driven by four counterpropagating kinetic Alfvén wave modes with
![]() $(k_{\bot 0}\unicode[STIX]{x1D70C}_{i},k_{\bot 0}\unicode[STIX]{x1D70C}_{i},k_{\Vert 0}\unicode[STIX]{x1D70C}_{i}/\unicode[STIX]{x1D716})=(5,0,\pm 1)$
and
$(k_{\bot 0}\unicode[STIX]{x1D70C}_{i},k_{\bot 0}\unicode[STIX]{x1D70C}_{i},k_{\Vert 0}\unicode[STIX]{x1D70C}_{i}/\unicode[STIX]{x1D716})=(5,0,\pm 1)$
and
![]() $(0,5,\pm 1)$
, where
$(0,5,\pm 1)$
, where
![]() $k_{\bot 0}=2\unicode[STIX]{x03C0}/L_{\bot }$
and
$k_{\bot 0}=2\unicode[STIX]{x03C0}/L_{\bot }$
and
![]() $\unicode[STIX]{x1D716}=\unicode[STIX]{x1D70C}_{i}/(2\unicode[STIX]{x03C0}L_{\Vert })$
.
$\unicode[STIX]{x1D716}=\unicode[STIX]{x1D70C}_{i}/(2\unicode[STIX]{x03C0}L_{\Vert })$
.
Coulomb collisions in the gyrokinetic simulations are included (Abel et al.
Reference Abel, Barnes, Cowley, Dorland and Schekochihin2008; Barnes et al.
Reference Barnes, Abel, Dorland, Ernst, Hammett, Ricci, Rogers, Schekochihin and Tatsuno2009) to smooth out the small-scale structures that develop in velocity space, enabling irreversibility of the plasma heating process (Howes et al.
Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006). We specify ion and electron collision frequencies
![]() $\unicode[STIX]{x1D708}_{i}=0.2\unicode[STIX]{x1D714}_{A0}$
and
$\unicode[STIX]{x1D708}_{i}=0.2\unicode[STIX]{x1D714}_{A0}$
and
![]() $\unicode[STIX]{x1D708}_{e}=0.5\unicode[STIX]{x1D714}_{A0}$
, leading to weakly collisional dynamics with
$\unicode[STIX]{x1D708}_{e}=0.5\unicode[STIX]{x1D714}_{A0}$
, leading to weakly collisional dynamics with
![]() $\unicode[STIX]{x1D708}_{s}/\unicode[STIX]{x1D714}_{0}\ll 1$
. The numerical convergence of the power spectrum was already tested for simulation run 3 by doubling the spatial resolution of the simulation and verifying that the saturated magnetic energy spectrum was unchanged, and it is reported in TenBarge & Howes (Reference TenBarge and Howes2013) (see figure 1).
$\unicode[STIX]{x1D708}_{s}/\unicode[STIX]{x1D714}_{0}\ll 1$
. The numerical convergence of the power spectrum was already tested for simulation run 3 by doubling the spatial resolution of the simulation and verifying that the saturated magnetic energy spectrum was unchanged, and it is reported in TenBarge & Howes (Reference TenBarge and Howes2013) (see figure 1).
2.1 Development and saturation of the turbulent magnetic power spectrum
As modes driven at the scale of the simulation domain rise in amplitude, they begin to interact nonlinearly, leading to a cascade of their energy to smaller scales. After sufficient time has passed, the turbulent energy dissipated by kinetic mechanisms rises to match the energy input into the turbulence by the driving, causing the turbulent energy spectrum to reach a statistically steady state. In figure 2, we display the one-dimensional perpendicular magnetic power spectrum,
![]() $E_{\bot }(k_{\bot })=\int \text{d}k_{z}\int \text{d}\unicode[STIX]{x1D703}k_{\bot }|\unicode[STIX]{x1D6FF}\boldsymbol{B}_{\bot }(\boldsymbol{k})|^{2}/8\unicode[STIX]{x03C0}$
, where the wavevector components are expressed in cylindrical coordinates
$E_{\bot }(k_{\bot })=\int \text{d}k_{z}\int \text{d}\unicode[STIX]{x1D703}k_{\bot }|\unicode[STIX]{x1D6FF}\boldsymbol{B}_{\bot }(\boldsymbol{k})|^{2}/8\unicode[STIX]{x03C0}$
, where the wavevector components are expressed in cylindrical coordinates
![]() $(k_{\bot },\unicode[STIX]{x1D703},k_{z})$
. The spectra shown in figure 2 range from over-strong turbulence with
$(k_{\bot },\unicode[STIX]{x1D703},k_{z})$
. The spectra shown in figure 2 range from over-strong turbulence with
![]() $\unicode[STIX]{x1D712}>1$
(Run 1, blue), critically balanced, strong turbulence with
$\unicode[STIX]{x1D712}>1$
(Run 1, blue), critically balanced, strong turbulence with
![]() $\unicode[STIX]{x1D712}\simeq 1$
(Run 4, red) to weak turbulence with
$\unicode[STIX]{x1D712}\simeq 1$
(Run 4, red) to weak turbulence with
![]() $\unicode[STIX]{x1D712}<1$
(Run 6, yellow). The
$\unicode[STIX]{x1D712}<1$
(Run 6, yellow). The
![]() $E_{\bot }(k_{\bot })$
spectra plotted here are obtained through averaging over the full time interval from the saturation of the turbulent cascade (at time
$E_{\bot }(k_{\bot })$
spectra plotted here are obtained through averaging over the full time interval from the saturation of the turbulent cascade (at time
![]() $t_{2}$
, as defined below) until the end of the simulation at
$t_{2}$
, as defined below) until the end of the simulation at
![]() $t_{f}$
. These time averaged
$t_{f}$
. These time averaged
![]() $E_{\bot }(k_{\bot })$
spectra are fit to the function
$E_{\bot }(k_{\bot })$
spectra are fit to the function
![]() $C(k_{\bot }\unicode[STIX]{x1D70C}_{i})^{\unicode[STIX]{x1D6FC}}\exp (-k_{\bot }\unicode[STIX]{x1D70C}_{e})$
(Alexandrova et al.
Reference Alexandrova, Lacombe, Mangeney, Grappin and Maksimovic2012; TenBarge et al.
Reference TenBarge, Howes and Dorland2013), where
$C(k_{\bot }\unicode[STIX]{x1D70C}_{i})^{\unicode[STIX]{x1D6FC}}\exp (-k_{\bot }\unicode[STIX]{x1D70C}_{e})$
(Alexandrova et al.
Reference Alexandrova, Lacombe, Mangeney, Grappin and Maksimovic2012; TenBarge et al.
Reference TenBarge, Howes and Dorland2013), where
![]() $C$
and
$C$
and
![]() $\unicode[STIX]{x1D6FC}$
are fitting parameters and
$\unicode[STIX]{x1D6FC}$
are fitting parameters and
![]() $\unicode[STIX]{x1D70C}_{e}=v_{th_{e}}/\unicode[STIX]{x1D6FA}_{e}$
is the electron Larmor gyroradius.
$\unicode[STIX]{x1D70C}_{e}=v_{th_{e}}/\unicode[STIX]{x1D6FA}_{e}$
is the electron Larmor gyroradius.

Figure 2. The time-averaged one-dimensional perpendicular magnetic energy spectrum
![]() $E_{\bot }(k_{\bot })$
computed for three kinetic Alfvén wave turbulence simulations: Run 1 (blue) with
$E_{\bot }(k_{\bot })$
computed for three kinetic Alfvén wave turbulence simulations: Run 1 (blue) with
![]() $\overline{\unicode[STIX]{x1D712}}=4.9$
, Run 4 (red) with
$\overline{\unicode[STIX]{x1D712}}=4.9$
, Run 4 (red) with
![]() $\overline{\unicode[STIX]{x1D712}}=1.3$
and Run 6 (yellow) with
$\overline{\unicode[STIX]{x1D712}}=1.3$
and Run 6 (yellow) with
![]() $\overline{\unicode[STIX]{x1D712}}=0.44$
. Fits to
$\overline{\unicode[STIX]{x1D712}}=0.44$
. Fits to
![]() $C(k_{\bot }\unicode[STIX]{x1D70C}_{i})^{\unicode[STIX]{x1D6FC}}\exp (-k_{\bot }\unicode[STIX]{x1D70C}_{e})$
are overplotted.
$C(k_{\bot }\unicode[STIX]{x1D70C}_{i})^{\unicode[STIX]{x1D6FC}}\exp (-k_{\bot }\unicode[STIX]{x1D70C}_{e})$
are overplotted.

Figure 3. The time evolution of (a) the perpendicular magnetic energy spectrum
![]() $E_{\bot }(k_{\bot }\unicode[STIX]{x1D70C}_{i}=20.6)$
, (b) the spectral index
$E_{\bot }(k_{\bot }\unicode[STIX]{x1D70C}_{i}=20.6)$
, (b) the spectral index
![]() $\unicode[STIX]{x1D6FC}$
from the fit to the function
$\unicode[STIX]{x1D6FC}$
from the fit to the function
![]() $A(k_{\bot }\unicode[STIX]{x1D70C}_{i})^{\unicode[STIX]{x1D6FC}}\exp (-k_{\bot }\unicode[STIX]{x1D70C}_{e})$
, (c) the normalized total heating rate,
$A(k_{\bot }\unicode[STIX]{x1D70C}_{i})^{\unicode[STIX]{x1D6FC}}\exp (-k_{\bot }\unicode[STIX]{x1D70C}_{e})$
, (c) the normalized total heating rate,
![]() ${\hat{H}}=H/P_{in}$
, the normalized rate of change of energy of turbulent fluctuations
${\hat{H}}=H/P_{in}$
, the normalized rate of change of energy of turbulent fluctuations
![]() ${\hat{W}}={\dot{W}}/P_{in}$
(
${\hat{W}}={\dot{W}}/P_{in}$
(
![]() ${\dot{W}}=-\text{d}W/\text{d}t$
) and the sum
${\dot{W}}=-\text{d}W/\text{d}t$
) and the sum
![]() ${\hat{H}}+{\hat{W}}$
, where
${\hat{H}}+{\hat{W}}$
, where
![]() $P_{in}$
is the power input into the plasma by the Langevin antenna driving. Columns from left to right are for Run 1 (
$P_{in}$
is the power input into the plasma by the Langevin antenna driving. Columns from left to right are for Run 1 (
![]() $\overline{\unicode[STIX]{x1D712}}=4.9$
), Run 2 (
$\overline{\unicode[STIX]{x1D712}}=4.9$
), Run 2 (
![]() $\overline{\unicode[STIX]{x1D712}}=3.4$
) and Run 3 (
$\overline{\unicode[STIX]{x1D712}}=3.4$
) and Run 3 (
![]() $\overline{\unicode[STIX]{x1D712}}=1.6$
).
$\overline{\unicode[STIX]{x1D712}}=1.6$
).
We evaluate the time scale of the saturation of the turbulent magnetic energy spectrum by following the evolution of the amplitude of the spectrum at
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{i}=20.6$
, a position in the middle of the dynamic range of the simulation, as a function of the normalized time
$k_{\bot }\unicode[STIX]{x1D70C}_{i}=20.6$
, a position in the middle of the dynamic range of the simulation, as a function of the normalized time
![]() $t/t_{l}$
. Figure 3(a) displays the time evolution of the one-dimensional perpendicular magnetic spectrum
$t/t_{l}$
. Figure 3(a) displays the time evolution of the one-dimensional perpendicular magnetic spectrum
![]() $E_{\bot }(k_{\bot }\unicode[STIX]{x1D70C}_{i}=20.6)$
for Run 1 (
$E_{\bot }(k_{\bot }\unicode[STIX]{x1D70C}_{i}=20.6)$
for Run 1 (
![]() $\overline{\unicode[STIX]{x1D712}}=4.9$
), Run 2 (
$\overline{\unicode[STIX]{x1D712}}=4.9$
), Run 2 (
![]() $\overline{\unicode[STIX]{x1D712}}=3.4$
) and Run 3 (
$\overline{\unicode[STIX]{x1D712}}=3.4$
) and Run 3 (
![]() $\overline{\unicode[STIX]{x1D712}}=1.6$
), left to right. These runs correspond to a range of turbulent amplitudes, from over-strong turbulence (above critical balance) with
$\overline{\unicode[STIX]{x1D712}}=1.6$
), left to right. These runs correspond to a range of turbulent amplitudes, from over-strong turbulence (above critical balance) with
![]() $\unicode[STIX]{x1D712}>1$
to approximately critically balanced, strong turbulence with
$\unicode[STIX]{x1D712}>1$
to approximately critically balanced, strong turbulence with
![]() $\unicode[STIX]{x1D712}\simeq 1$
. These plots demonstrate the existence of two time scales that characterize the evolution of the turbulent magnetic field when driving by counterpropagating kinetic Alfvén waves from uniform magnetic field conditions. First, the energy in Fourier modes with
$\unicode[STIX]{x1D712}\simeq 1$
. These plots demonstrate the existence of two time scales that characterize the evolution of the turbulent magnetic field when driving by counterpropagating kinetic Alfvén waves from uniform magnetic field conditions. First, the energy in Fourier modes with
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{i}=20.6$
rises as a steep power law in time
$k_{\bot }\unicode[STIX]{x1D70C}_{i}=20.6$
rises as a steep power law in time
![]() $\propto t^{b_{1}}$
for times
$\propto t^{b_{1}}$
for times
![]() $t<t_{1}$
, denoted by the first vertical blue line in figure 3. Next, the rate of increase of energy in mode
$t<t_{1}$
, denoted by the first vertical blue line in figure 3. Next, the rate of increase of energy in mode
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{i}=20.6$
decreases to less steep approximate power law
$k_{\bot }\unicode[STIX]{x1D70C}_{i}=20.6$
decreases to less steep approximate power law
![]() $\propto t^{b_{2}}$
, with
$\propto t^{b_{2}}$
, with
![]() $b_{2}<b_{1}$
, over the time interval
$b_{2}<b_{1}$
, over the time interval
![]() $t_{1}<t<t_{2}$
. For times
$t_{1}<t<t_{2}$
. For times
![]() $t>t_{2}$
, the energy in modes with
$t>t_{2}$
, the energy in modes with
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{i}=20.6$
remains approximately constant, indicating that the region of the turbulent cascade has reached a statistically steady state.
$k_{\bot }\unicode[STIX]{x1D70C}_{i}=20.6$
remains approximately constant, indicating that the region of the turbulent cascade has reached a statistically steady state.
We interpret these two time scales in the following way. At times
![]() $t<t_{1}$
, the energy of the modes with
$t<t_{1}$
, the energy of the modes with
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{i}=20.6$
is dominated by the energy input from nonlinear interactions among lower wavenumber modes, leading to simple power-law increase in amplitude. At
$k_{\bot }\unicode[STIX]{x1D70C}_{i}=20.6$
is dominated by the energy input from nonlinear interactions among lower wavenumber modes, leading to simple power-law increase in amplitude. At
![]() $t=t_{1}$
, the amplitude of the modes with
$t=t_{1}$
, the amplitude of the modes with
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{i}=20.6$
has risen to a sufficient level that these modes are able to interact nonlinearly with counterpropagating fluctuations to transfer their energy to yet higher wavenumber modes; therefore, the rate of energy increase for the
$k_{\bot }\unicode[STIX]{x1D70C}_{i}=20.6$
has risen to a sufficient level that these modes are able to interact nonlinearly with counterpropagating fluctuations to transfer their energy to yet higher wavenumber modes; therefore, the rate of energy increase for the
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{i}=20.6$
modes diminishes for
$k_{\bot }\unicode[STIX]{x1D70C}_{i}=20.6$
modes diminishes for
![]() $t_{1}<t<t_{2}$
. The second time scale
$t_{1}<t<t_{2}$
. The second time scale
![]() $t_{2}$
signifies the time when this nonlinear energy loss to higher wavenumber modes increases sufficiently to balance the nonlinear energy input from lower wavenumber modes, effectively marking the saturation of a fully developed turbulent cascade.
$t_{2}$
signifies the time when this nonlinear energy loss to higher wavenumber modes increases sufficiently to balance the nonlinear energy input from lower wavenumber modes, effectively marking the saturation of a fully developed turbulent cascade.
To further illuminate the physical significance of these two time scales, we present two more measure of the turbulent cascade as a function of time. First, in figure 3(b), we present the time evolution of spectral index
![]() $\unicode[STIX]{x1D6FC}$
of the one-dimensional perpendicular magnetic spectrum when fit to the functional form
$\unicode[STIX]{x1D6FC}$
of the one-dimensional perpendicular magnetic spectrum when fit to the functional form
![]() $C(k_{\bot }\unicode[STIX]{x1D70C}_{i})^{\unicode[STIX]{x1D6FC}}\exp (-k_{\bot }\unicode[STIX]{x1D70C}_{e})$
with free adjustable parameters
$C(k_{\bot }\unicode[STIX]{x1D70C}_{i})^{\unicode[STIX]{x1D6FC}}\exp (-k_{\bot }\unicode[STIX]{x1D70C}_{e})$
with free adjustable parameters
![]() $\unicode[STIX]{x1D6FC}$
for the spectral exponent and
$\unicode[STIX]{x1D6FC}$
for the spectral exponent and
![]() $C$
as an arbitrary amplitude.
$C$
as an arbitrary amplitude.
Figure 3(c), we plot diagnostics of the global power balance in each of the simulations. Further details of the power balance diagnostics in AstroGK are described in the Appendix of TenBarge et al. (Reference TenBarge, Howes and Dorland2013), so here we present only a brief description. Energy conservation dictates that the rate of change total fluctuating power (Howes et al.
Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006; Schekochihin et al.
Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009) in the turbulent plasma in AstroGK,
![]() ${\dot{W}}=-\text{d}W/\text{d}t$
, is given by
${\dot{W}}=-\text{d}W/\text{d}t$
, is given by
![]() ${\dot{W}}=P_{in}-H$
, where
${\dot{W}}=P_{in}-H$
, where
![]() $P_{in}$
is the power input into the plasma by the Langevin antenna driving and
$P_{in}$
is the power input into the plasma by the Langevin antenna driving and
![]() $H$
is the energy lost from the fluctuations due to collisional (and numerical) dissipation. Note that the heating
$H$
is the energy lost from the fluctuations due to collisional (and numerical) dissipation. Note that the heating
![]() $H\geqslant 0$
because collisional dissipation can only heat the plasma, removing energy irreversibly from turbulent field and plasma fluctuations and leading to thermal heating of the plasma species (which is not contained in
$H\geqslant 0$
because collisional dissipation can only heat the plasma, removing energy irreversibly from turbulent field and plasma fluctuations and leading to thermal heating of the plasma species (which is not contained in
![]() $W$
). In a statistically steady state, one has a time averaged
$W$
). In a statistically steady state, one has a time averaged
![]() $\langle {\dot{W}}\rangle \simeq 0$
, so therefore the time-averaged antenna power input into the plasma is
$\langle {\dot{W}}\rangle \simeq 0$
, so therefore the time-averaged antenna power input into the plasma is
![]() $\langle P_{in}\rangle \simeq \langle H\rangle \geqslant 0$
, meaning that, on average, all of the input power is collisionally dissipated by the plasma. For plotting convenience, we choose to normalize the power balance by dividing by
$\langle P_{in}\rangle \simeq \langle H\rangle \geqslant 0$
, meaning that, on average, all of the input power is collisionally dissipated by the plasma. For plotting convenience, we choose to normalize the power balance by dividing by
![]() $P_{in}$
, leading to a normalized expression for instantaneous energy conservation,
$P_{in}$
, leading to a normalized expression for instantaneous energy conservation,
![]() ${\hat{W}}+{\hat{H}}$
, where
${\hat{W}}+{\hat{H}}$
, where
![]() ${\hat{W}}={\dot{W}}/P_{in}$
and
${\hat{W}}={\dot{W}}/P_{in}$
and
![]() ${\hat{H}}=H/P_{in}$
. Energy is not conserved exactly by the AstroGK code due to a small amount of numerical dissipation, but the energy is typically conserved within a few per cent (TenBarge et al.
Reference TenBarge, Howes and Dorland2013), as seen by the small departures of this sum from 1 in figure 3(c). Note that although the slope of the magnetic energy spectrum (figure 3
b) has reached a steady value at
${\hat{H}}=H/P_{in}$
. Energy is not conserved exactly by the AstroGK code due to a small amount of numerical dissipation, but the energy is typically conserved within a few per cent (TenBarge et al.
Reference TenBarge, Howes and Dorland2013), as seen by the small departures of this sum from 1 in figure 3(c). Note that although the slope of the magnetic energy spectrum (figure 3
b) has reached a steady value at
![]() $t_{2}$
, the normalized heating rate
$t_{2}$
, the normalized heating rate
![]() ${\hat{H}}$
(figure 3
c) does continue to increase after this time. Although the definition of
${\hat{H}}$
(figure 3
c) does continue to increase after this time. Although the definition of
![]() $t_{2}$
as the saturation time of the turbulent cascade agrees qualitatively with the expected scaling with turbulent amplitude, the slight increase of energy (manifesting an increasing heating rate) after
$t_{2}$
as the saturation time of the turbulent cascade agrees qualitatively with the expected scaling with turbulent amplitude, the slight increase of energy (manifesting an increasing heating rate) after
![]() $t_{2}$
suggests that the turbulence does experience a slow evolution beyond
$t_{2}$
suggests that the turbulence does experience a slow evolution beyond
![]() $t_{2}$
. Investigating how this slow evolution alters the properties of the turbulence will be explored in future works.
$t_{2}$
. Investigating how this slow evolution alters the properties of the turbulence will be explored in future works.
Figure 3(b), it is clear that second time scale
![]() $t_{2}$
is the saturation time for the development of the turbulent energy spectrum. This is the time required for the turbulent energy input at large scales to be transferred nonlinearly down to sufficiently scales that the turbulent energy is dissipated by kinetic mechanisms, irreversibly converted into plasma heat. It is interesting to note that, when normalized to the linear period
$t_{2}$
is the saturation time for the development of the turbulent energy spectrum. This is the time required for the turbulent energy input at large scales to be transferred nonlinearly down to sufficiently scales that the turbulent energy is dissipated by kinetic mechanisms, irreversibly converted into plasma heat. It is interesting to note that, when normalized to the linear period
![]() $t_{l}$
of the kinetic Alfvén waves that are driven at the domain scale, we generally find
$t_{l}$
of the kinetic Alfvén waves that are driven at the domain scale, we generally find
![]() $t_{2}/t_{l}<1$
, in contrast to the typical time scale assumed for strong turbulence that the saturation time
$t_{2}/t_{l}<1$
, in contrast to the typical time scale assumed for strong turbulence that the saturation time
![]() $t_{2}\sim t_{l}$
. The likely explanation is the dispersive nature of kinetic Alfvén waves is that in the limit
$t_{2}\sim t_{l}$
. The likely explanation is the dispersive nature of kinetic Alfvén waves is that in the limit
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{i}\gg 1$
, the kinetic Alfvén wave frequency scales as
$k_{\bot }\unicode[STIX]{x1D70C}_{i}\gg 1$
, the kinetic Alfvén wave frequency scales as
![]() $\unicode[STIX]{x1D714}\propto k_{\bot }\unicode[STIX]{x1D70C}_{i}k_{\Vert }v_{A}$
, meaning that smaller-scale kinetic Alfvén waves have increasingly short period when normalized to the parallel wavenumber. Therefore, the full turbulent cascade develops more rapidly than the usual expectation from the non-dispersive inertial range. This result also demonstrates that driving turbulence simulations by counterpropagating kinetic Alfvén waves is a very efficient means of generating a turbulent spectrum.
$\unicode[STIX]{x1D714}\propto k_{\bot }\unicode[STIX]{x1D70C}_{i}k_{\Vert }v_{A}$
, meaning that smaller-scale kinetic Alfvén waves have increasingly short period when normalized to the parallel wavenumber. Therefore, the full turbulent cascade develops more rapidly than the usual expectation from the non-dispersive inertial range. This result also demonstrates that driving turbulence simulations by counterpropagating kinetic Alfvén waves is a very efficient means of generating a turbulent spectrum.
Looking at the third row of figure 3, we see that the point at which the normalized rate of energy increase in the plasma due to driving
![]() ${\dot{W}}/P_{in}$
is overtaken by the rate of heating due to dissipation
${\dot{W}}/P_{in}$
is overtaken by the rate of heating due to dissipation
![]() $H/P_{in}$
falls within the time interval
$H/P_{in}$
falls within the time interval
![]() $t_{1}<t<t_{2}$
. By the time
$t_{1}<t<t_{2}$
. By the time
![]() $t_{2}$
is reached, the rate of heating
$t_{2}$
is reached, the rate of heating
![]() $H/P_{in}$
dominates over the rate of energy increase in the turbulent plasma. At
$H/P_{in}$
dominates over the rate of energy increase in the turbulent plasma. At
![]() $t>t_{2}$
, eventually the time-averaged change of the turbulent plasma energy
$t>t_{2}$
, eventually the time-averaged change of the turbulent plasma energy
![]() $\langle {\dot{W}}/P_{in}\rangle \rightarrow 0$
, leaving
$\langle {\dot{W}}/P_{in}\rangle \rightarrow 0$
, leaving
![]() $H/P_{in}\simeq 1$
, indicating that all of the input power is collisionally dissipated, heating the plasma irreversibly.
$H/P_{in}\simeq 1$
, indicating that all of the input power is collisionally dissipated, heating the plasma irreversibly.
The same qualitative behaviour of the development and saturation of the turbulent cascade is also found for cases of weak turbulence,
![]() $\unicode[STIX]{x1D712}<1$
, as shown in figure 4. Here, we plot the same rows of information as in figure 3 for Run 5 (
$\unicode[STIX]{x1D712}<1$
, as shown in figure 4. Here, we plot the same rows of information as in figure 3 for Run 5 (
![]() $\overline{\unicode[STIX]{x1D712}}=0.83$
) and Run 6 (
$\overline{\unicode[STIX]{x1D712}}=0.83$
) and Run 6 (
![]() $\overline{\unicode[STIX]{x1D712}}=0.44$
). Again, two time scales are observed, a first time scale
$\overline{\unicode[STIX]{x1D712}}=0.44$
). Again, two time scales are observed, a first time scale
![]() $t_{1}$
where the power-law increase of the
$t_{1}$
where the power-law increase of the
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{i}=20.6$
decreases to a slower rate and the saturation time scale
$k_{\bot }\unicode[STIX]{x1D70C}_{i}=20.6$
decreases to a slower rate and the saturation time scale
![]() $t_{2}$
where spectral index of the perpendicular magnetic energy spectrum reaches a statistically steady value and the rate of heating
$t_{2}$
where spectral index of the perpendicular magnetic energy spectrum reaches a statistically steady value and the rate of heating
![]() $H/P_{in}$
dominates over the rate of energy increase in the turbulent plasma
$H/P_{in}$
dominates over the rate of energy increase in the turbulent plasma
![]() ${\dot{W}}/P_{in}$
.
${\dot{W}}/P_{in}$
.
For all of the Runs 1–7, the times
![]() $t_{1}$
and
$t_{1}$
and
![]() $t_{2}$
, normalized to the linear kinetic Alfvén wave period at the domain scale (effectively the outer time scale of the turbulent cascade), are presented in table 1. For the cases of over-strong turbulence
$t_{2}$
, normalized to the linear kinetic Alfvén wave period at the domain scale (effectively the outer time scale of the turbulent cascade), are presented in table 1. For the cases of over-strong turbulence
![]() $\unicode[STIX]{x1D712}>1$
, the saturation time
$\unicode[STIX]{x1D712}>1$
, the saturation time
![]() $t_{2}$
is relatively constant, with a value between one-quarter and one-third of the domain-scale kinetic Alfvén wave period. As the turbulence weakens in the regime
$t_{2}$
is relatively constant, with a value between one-quarter and one-third of the domain-scale kinetic Alfvén wave period. As the turbulence weakens in the regime
![]() $\unicode[STIX]{x1D712}<1$
, the saturation time
$\unicode[STIX]{x1D712}<1$
, the saturation time
![]() $t_{2}$
increases monotonically as the strength of the turbulence
$t_{2}$
increases monotonically as the strength of the turbulence
![]() $\unicode[STIX]{x1D712}$
decreases, as expected theoretically (Sridhar & Goldreich Reference Sridhar and Goldreich1994; Howes, TenBarge & Dorland Reference Howes, TenBarge and Dorland2011a
).
$\unicode[STIX]{x1D712}$
decreases, as expected theoretically (Sridhar & Goldreich Reference Sridhar and Goldreich1994; Howes, TenBarge & Dorland Reference Howes, TenBarge and Dorland2011a
).
2.2 Stochasticity of magnetic field lines
Here we describe the development of the stochasticity of the magnetic field lines in gyrokinetic turbulence as a function of the time-averaged nonlinearity parameter
![]() $\overline{\unicode[STIX]{x1D712}}$
. To study the magnetic field stochasticity, we employ Poincaré recurrence plots derived from snapshots of the magnetic field at different chosen times in the evolution of the turbulence simulations listed in table 1.
$\overline{\unicode[STIX]{x1D712}}$
. To study the magnetic field stochasticity, we employ Poincaré recurrence plots derived from snapshots of the magnetic field at different chosen times in the evolution of the turbulence simulations listed in table 1.

Figure 4. The time evolution of: (a) the perpendicular magnetic energy spectrum
![]() $E_{\bot }$
at
$E_{\bot }$
at
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{i}=20$
,
$k_{\bot }\unicode[STIX]{x1D70C}_{i}=20$
,
![]() $E_{\bot }$
(a,b) the spectral index
$E_{\bot }$
(a,b) the spectral index
![]() $\unicode[STIX]{x1D6FC}$
that corresponds to function
$\unicode[STIX]{x1D6FC}$
that corresponds to function
![]() $C(k_{\bot }\unicode[STIX]{x1D70C}_{i})^{\unicode[STIX]{x1D6FC}}\exp (-k_{\bot }\unicode[STIX]{x1D70C}_{e})$
fit to
$C(k_{\bot }\unicode[STIX]{x1D70C}_{i})^{\unicode[STIX]{x1D6FC}}\exp (-k_{\bot }\unicode[STIX]{x1D70C}_{e})$
fit to
![]() $E_{\bot }(k_{\bot })$
, (c) the normalized total heating rate,
$E_{\bot }(k_{\bot })$
, (c) the normalized total heating rate,
![]() ${\hat{H}}=H/P_{in}$
, the normalized rate of change of energy of turbulent fluctuations
${\hat{H}}=H/P_{in}$
, the normalized rate of change of energy of turbulent fluctuations
![]() ${\hat{W}}={\dot{W}}/P_{in}$
(
${\hat{W}}={\dot{W}}/P_{in}$
(
![]() ${\dot{W}}=-\text{d}W/\text{d}t$
) and the sum
${\dot{W}}=-\text{d}W/\text{d}t$
) and the sum
![]() ${\hat{H}}+{\hat{W}}$
, where
${\hat{H}}+{\hat{W}}$
, where
![]() $P_{in}$
is the power input into the plasma by the Langevin antenna driving. Columns from left to right are for Run 5 (
$P_{in}$
is the power input into the plasma by the Langevin antenna driving. Columns from left to right are for Run 5 (
![]() $\overline{\unicode[STIX]{x1D712}}=0.83$
) and Run 6 (
$\overline{\unicode[STIX]{x1D712}}=0.83$
) and Run 6 (
![]() $\overline{\unicode[STIX]{x1D712}}=0.44$
).
$\overline{\unicode[STIX]{x1D712}}=0.44$
).
To construct the Poincaré plot, we begin with the magnetic field
![]() $\boldsymbol{B}(\boldsymbol{x})$
at some time
$\boldsymbol{B}(\boldsymbol{x})$
at some time
![]() $t$
. On the perpendicular plane at one end of the simulation domain at
$t$
. On the perpendicular plane at one end of the simulation domain at
![]() $z=0$
, we specify a sparse pattern of points with the colour of each point creating a bullseye pattern, as shown in figure 5. The magnetic field line passing through each point is traced through the domain to the far end of the simulation domain at
$z=0$
, we specify a sparse pattern of points with the colour of each point creating a bullseye pattern, as shown in figure 5. The magnetic field line passing through each point is traced through the domain to the far end of the simulation domain at
![]() $z=L_{\Vert }$
, and a point is plotted there, with colour matching that of the original field line position. That field line is periodically wrapped to
$z=L_{\Vert }$
, and a point is plotted there, with colour matching that of the original field line position. That field line is periodically wrapped to
![]() $z=0$
, and the process is continued, with a coloured point plotted at each crossing at
$z=0$
, and the process is continued, with a coloured point plotted at each crossing at
![]() $z=L_{\Vert }$
. We trace through the box
$z=L_{\Vert }$
. We trace through the box
![]() $20$
times for each field line, thereby plotting 20 coloured points on the plane for each field line. A fourth-order Runge–Kutta method with adaptive step size is used to trace each field line by integrating the ordinary differential equation
$20$
times for each field line, thereby plotting 20 coloured points on the plane for each field line. A fourth-order Runge–Kutta method with adaptive step size is used to trace each field line by integrating the ordinary differential equation
![]() $\text{d}\boldsymbol{r}/\text{d}l=\hat{\boldsymbol{b}}(\boldsymbol{x})$
, where
$\text{d}\boldsymbol{r}/\text{d}l=\hat{\boldsymbol{b}}(\boldsymbol{x})$
, where
![]() $\hat{\boldsymbol{b}}(\boldsymbol{x})=\boldsymbol{B}(\boldsymbol{x})/|\boldsymbol{B}(\boldsymbol{x})|$
. If the field line passes through the boundaries of the simulation domain in the
$\hat{\boldsymbol{b}}(\boldsymbol{x})=\boldsymbol{B}(\boldsymbol{x})/|\boldsymbol{B}(\boldsymbol{x})|$
. If the field line passes through the boundaries of the simulation domain in the
![]() $x$
or
$x$
or
![]() $y$
directions, it is periodically wrapped to the opposite boundary.
$y$
directions, it is periodically wrapped to the opposite boundary.

Figure 5. Coloured points represent the coordinates of the starting points in the
![]() $z=0$
plane for tracing field lines to generate Poincaré recurrence plots.
$z=0$
plane for tracing field lines to generate Poincaré recurrence plots.

Figure 6. Poincaré recurrence plots for over-strong and strong turbulence in Runs 1–4 at the times indicated. The corresponding time-averaged nonlinearity parameters are
![]() $\overline{\unicode[STIX]{x1D712}}=4.9$
(a),
$\overline{\unicode[STIX]{x1D712}}=4.9$
(a),
![]() $\overline{\unicode[STIX]{x1D712}}=3.4$
(b),
$\overline{\unicode[STIX]{x1D712}}=3.4$
(b),
![]() $\overline{\unicode[STIX]{x1D712}}=1.6$
(c) and
$\overline{\unicode[STIX]{x1D712}}=1.6$
(c) and
![]() $\overline{\unicode[STIX]{x1D712}}=1.3$
(d).
$\overline{\unicode[STIX]{x1D712}}=1.3$
(d).

Figure 7. Poincaré recurrence plots for weak turbulence in Runs 5–7 at the times indicated. The corresponding time-averaged nonlinearity parameters are
![]() $\overline{\unicode[STIX]{x1D712}}=0.83$
(a),
$\overline{\unicode[STIX]{x1D712}}=0.83$
(a),
![]() $\overline{\unicode[STIX]{x1D712}}=0.44$
(b) and
$\overline{\unicode[STIX]{x1D712}}=0.44$
(b) and
![]() $\overline{\unicode[STIX]{x1D712}}=0.14$
(c).
$\overline{\unicode[STIX]{x1D712}}=0.14$
(c).
The Poincaré plots for Runs 1–4 are presented in figure 6 and for Runs 5–7 in figure 7. Stochasticity of the magnetic field is qualitatively assessed by the appearance of the Poincaré recurrence plots: a regular pattern of colours indicates a non-stochastic field, whereas a scrambling of the different colours indicates a stochastic field. In some cases, regions of the domain display a stochastic field while other regions appear more well ordered.
From the Poincaré plots presented in figures 6 and 7, we make the following observations. Early in the evolution at
![]() $t\ll t_{2}$
, when the turbulence is still not well developed and little energy has cascaded to small scales to generate a broadband turbulent spectrum, the Poincaré plots for all cases show a well-ordered pattern with no indication of stochasticity. After the turbulent cascade has saturated, at times
$t\ll t_{2}$
, when the turbulence is still not well developed and little energy has cascaded to small scales to generate a broadband turbulent spectrum, the Poincaré plots for all cases show a well-ordered pattern with no indication of stochasticity. After the turbulent cascade has saturated, at times
![]() $t>t_{2}$
, the over-strong and strong turbulence cases in Runs 1–4 with
$t>t_{2}$
, the over-strong and strong turbulence cases in Runs 1–4 with
![]() $\overline{\unicode[STIX]{x1D712}}\gtrsim 1$
all show that the magnetic field lines have become completely stochastic throughout the domain. For the weaker turbulence cases of Runs 5–7 with
$\overline{\unicode[STIX]{x1D712}}\gtrsim 1$
all show that the magnetic field lines have become completely stochastic throughout the domain. For the weaker turbulence cases of Runs 5–7 with
![]() $\overline{\unicode[STIX]{x1D712}}<1$
, a remnant of order persists in the Poincaré plots even at
$\overline{\unicode[STIX]{x1D712}}<1$
, a remnant of order persists in the Poincaré plots even at
![]() $t\sim t_{2}$
when the turbulent cascade has saturated. At sufficiently long times
$t\sim t_{2}$
when the turbulent cascade has saturated. At sufficiently long times
![]() $t\gg t_{2}$
, one sees the eventual development of a fully stochastic magnetic field throughout the domain for Run 5 with
$t\gg t_{2}$
, one sees the eventual development of a fully stochastic magnetic field throughout the domain for Run 5 with
![]() $\overline{\unicode[STIX]{x1D712}}=0.83$
and Run 6 with
$\overline{\unicode[STIX]{x1D712}}=0.83$
and Run 6 with
![]() $\overline{\unicode[STIX]{x1D712}}=0.44$
. In contrast, the very weakest turbulence case with
$\overline{\unicode[STIX]{x1D712}}=0.44$
. In contrast, the very weakest turbulence case with
![]() $\overline{\unicode[STIX]{x1D712}}=0.14$
in Run 7 shows persistent regions of order, even at long times
$\overline{\unicode[STIX]{x1D712}}=0.14$
in Run 7 shows persistent regions of order, even at long times
![]() $t>10t_{2}$
. Therefore, it seems that there is indeed a minimum amplitude threshold
$t>10t_{2}$
. Therefore, it seems that there is indeed a minimum amplitude threshold
![]() $\unicode[STIX]{x1D712}_{thresh}$
for the development of a completely stochastic magnetic field within the saturation time interval
$\unicode[STIX]{x1D712}_{thresh}$
for the development of a completely stochastic magnetic field within the saturation time interval
![]() $t_{2}<t<13t_{2}$
, with order persisting for cases with nonlinear parameters
$t_{2}<t<13t_{2}$
, with order persisting for cases with nonlinear parameters
![]() $\unicode[STIX]{x1D712}\lesssim \unicode[STIX]{x1D712}_{thresh}\sim 0.1$
.
$\unicode[STIX]{x1D712}\lesssim \unicode[STIX]{x1D712}_{thresh}\sim 0.1$
.
2.3 Separation of the magnetic field lines
The stochasticity is not the only feature that characterizes the magnetic field line wander in plasma turbulence. Two adjacent magnetic field lines may also separate from one another as we follow along one of the field lines. This magnetic field line separation may significantly impact the propagation of energetic particles in a turbulent plasma. Here we investigate the separation of stochastic magnetic field lines caused by plasma turbulence as a function of the nonlinearity parameter
![]() $\unicode[STIX]{x1D712}$
using gyrokinetic simulations (listed in table 1). We consider only Runs 1–6, excluding Run 7 as the magnetic field lines are not fully stochastic at the saturation phase of that simulation run.
$\unicode[STIX]{x1D712}$
using gyrokinetic simulations (listed in table 1). We consider only Runs 1–6, excluding Run 7 as the magnetic field lines are not fully stochastic at the saturation phase of that simulation run.

Figure 8. Sketch describing how field lines pass through an extended domain built of six simulation boxes, showing the tracing of several wandering magnetic field lines up to distance
![]() $z=2L_{\Vert }$
.
$z=2L_{\Vert }$
.
To explore the separation of magnetic field lines, we assume an extended domain built up from the periodic extension of the single gyrokinetic simulation domain of size
![]() $L_{\bot }\times L_{\bot }\times L_{\Vert }$
. The magnetic field is initially defined by simulation over the ranges
$L_{\bot }\times L_{\bot }\times L_{\Vert }$
. The magnetic field is initially defined by simulation over the ranges
![]() $0\leqslant z\leqslant L_{\Vert }$
and
$0\leqslant z\leqslant L_{\Vert }$
and
![]() $0\leqslant x,y\leqslant L_{\bot }$
. To track the magnetic field lines in the extended spatial domain beyond these limits, we begin at a point in the
$0\leqslant x,y\leqslant L_{\bot }$
. To track the magnetic field lines in the extended spatial domain beyond these limits, we begin at a point in the
![]() $z=0$
plane and trace along the magnetic field line passing through that point (using the fourth-order Runge–Kutta method with adaptive step size) in the
$z=0$
plane and trace along the magnetic field line passing through that point (using the fourth-order Runge–Kutta method with adaptive step size) in the
![]() $+\hat{\boldsymbol{z}}$
direction. When the field line reaches the end of the single simulation domain at
$+\hat{\boldsymbol{z}}$
direction. When the field line reaches the end of the single simulation domain at
![]() $z=L_{\Vert }$
, it enters an identical domain periodically extended to
$z=L_{\Vert }$
, it enters an identical domain periodically extended to
![]() $z>L_{\Vert }$
, as depicted in figure 8. If the magnetic field line exits through the side of the domain at
$z>L_{\Vert }$
, as depicted in figure 8. If the magnetic field line exits through the side of the domain at
![]() $x,y<0$
or
$x,y<0$
or
![]() $x,y>L_{\bot }$
, it is not periodically wrapped to the opposite side but instead extended into a periodically continued extended domain in the same direction, as shown in figure 8. To be clear, the vector magnetic field in each of the six rectangular black boxes in figure 8 is identical, derived from a single time snapshot of the gyrokinetic simulation.
$x,y>L_{\bot }$
, it is not periodically wrapped to the opposite side but instead extended into a periodically continued extended domain in the same direction, as shown in figure 8. To be clear, the vector magnetic field in each of the six rectangular black boxes in figure 8 is identical, derived from a single time snapshot of the gyrokinetic simulation.
To investigate the separation of magnetic field lines, we initially select a large number of field lines uniformly distributed within a circular region in
![]() $(x,y)$
plane at
$(x,y)$
plane at
![]() $z=0$
, (their uniform distribution is depicted in side projection in figure 9
c). These field lines are each followed through the extended simulation box (figure 9
b), after which their distribution appears to be well fit by a Gaussian distribution (figure 9
a, blue line) at
$z=0$
, (their uniform distribution is depicted in side projection in figure 9
c). These field lines are each followed through the extended simulation box (figure 9
b), after which their distribution appears to be well fit by a Gaussian distribution (figure 9
a, blue line) at
![]() $z=3L_{\Vert }$
. The full width at half-maximum (FWHM) of the Gaussian function represents the mean separation
$z=3L_{\Vert }$
. The full width at half-maximum (FWHM) of the Gaussian function represents the mean separation
![]() $\langle (\unicode[STIX]{x1D6FF}r)\rangle$
of the field line at given distance
$\langle (\unicode[STIX]{x1D6FF}r)\rangle$
of the field line at given distance
![]() $z=n\times L_{\Vert }$
. For example, in figure 10 we plot the distribution of the field lines (stars) in
$z=n\times L_{\Vert }$
. For example, in figure 10 we plot the distribution of the field lines (stars) in
![]() $(x,y)$
plane at
$(x,y)$
plane at
![]() $z=12L_{\Vert }$
for Run 3 (at time
$z=12L_{\Vert }$
for Run 3 (at time
![]() $t/t_{l}=3.6$
), showing that the distribution of the field lines is well fit by a Gaussian function (blue solid line). Here it is worth mentioning that the centre of the ensemble of the field lines in the
$t/t_{l}=3.6$
), showing that the distribution of the field lines is well fit by a Gaussian function (blue solid line). Here it is worth mentioning that the centre of the ensemble of the field lines in the
![]() $x$
–
$x$
–
![]() $y$
plane is changing with distance
$y$
plane is changing with distance
![]() $z$
. The centre position of the field lines at a given distance
$z$
. The centre position of the field lines at a given distance
![]() $z$
can be calculated as the average of all field line positions in
$z$
can be calculated as the average of all field line positions in
![]() $x$
–
$x$
–
![]() $y$
plane at distance
$y$
plane at distance
![]() $z$
. The distributions of the field lines (see, e.g. figures 9 and 10) are estimated with respect to this moving centre. In our analysis we focus only on the spread of the magnetic field lines.
$z$
. The distributions of the field lines (see, e.g. figures 9 and 10) are estimated with respect to this moving centre. In our analysis we focus only on the spread of the magnetic field lines.

Figure 9. An initially uniform distribution of field lines within a small circle in the plane at
![]() $z=0$
(c) wanders through the simulation domain in Run 3 (b) to generate a Gaussian distribution at
$z=0$
(c) wanders through the simulation domain in Run 3 (b) to generate a Gaussian distribution at
![]() $z=3L_{\Vert }$
(a).
$z=3L_{\Vert }$
(a).

Figure 10. For Run 3 with
![]() $\overline{\unicode[STIX]{x1D712}}=1.6$
, the binned distribution of the field lines (asterisks) at
$\overline{\unicode[STIX]{x1D712}}=1.6$
, the binned distribution of the field lines (asterisks) at
![]() $z=12L_{\Vert }$
versus the normalized separation length
$z=12L_{\Vert }$
versus the normalized separation length
![]() $r/\unicode[STIX]{x1D70C}_{i}$
, where
$r/\unicode[STIX]{x1D70C}_{i}$
, where
![]() $r=\sqrt{x^{2}+y^{2}}$
. The separation distance is divided into 11 bins. The distribution is fit to a Gaussian function with a FWHM
$r=\sqrt{x^{2}+y^{2}}$
. The separation distance is divided into 11 bins. The distribution is fit to a Gaussian function with a FWHM
![]() $\langle \unicode[STIX]{x1D6FF}r\rangle$
.
$\langle \unicode[STIX]{x1D6FF}r\rangle$
.
Using this method to trace the magnetic field line separation for Runs 1–6 in table 1, we compute directly the mean square displacement
![]() $\langle (\unicode[STIX]{x1D6FF}r)^{2}\rangle$
as a function of
$\langle (\unicode[STIX]{x1D6FF}r)^{2}\rangle$
as a function of
![]() $z/L_{\Vert }$
at different evolution times within the saturation phase of each simulation run. Note the we do not fit the FWHM of the best fit Gaussian, but rather calculate directly the mean square displacement
$z/L_{\Vert }$
at different evolution times within the saturation phase of each simulation run. Note the we do not fit the FWHM of the best fit Gaussian, but rather calculate directly the mean square displacement
![]() $\langle (\unicode[STIX]{x1D6FF}r)^{2}\rangle$
of the magnetic field line distribution in order to account for any skewness in the resulting distribution that may prevent a good Gaussian fit. We fit the computed mean square displacement
$\langle (\unicode[STIX]{x1D6FF}r)^{2}\rangle$
of the magnetic field line distribution in order to account for any skewness in the resulting distribution that may prevent a good Gaussian fit. We fit the computed mean square displacement
![]() $\langle (\unicode[STIX]{x1D6FF}r)^{2}\rangle$
by the power-law function
$\langle (\unicode[STIX]{x1D6FF}r)^{2}\rangle$
by the power-law function
where we expect the amplitude factor
![]() $A(\unicode[STIX]{x1D712})$
and the power-law exponent
$A(\unicode[STIX]{x1D712})$
and the power-law exponent
![]() $p(\unicode[STIX]{x1D712})$
both to be a function of the nonlinearity parameter
$p(\unicode[STIX]{x1D712})$
both to be a function of the nonlinearity parameter
![]() $\unicode[STIX]{x1D712}$
. Note that an exponent of
$\unicode[STIX]{x1D712}$
. Note that an exponent of
![]() $p=1$
corresponds to a diffusive behaviour of the field line separation, while
$p=1$
corresponds to a diffusive behaviour of the field line separation, while
![]() $p>1$
indicates a superdiffusive process and
$p>1$
indicates a superdiffusive process and
![]() $p<1$
indicates a subdiffusive process.
$p<1$
indicates a subdiffusive process.

Figure 11. For Runs 1–6, plots of the mean square separation
![]() $\langle \unicode[STIX]{x1D6FF}r^{2}\rangle$
versus distance
$\langle \unicode[STIX]{x1D6FF}r^{2}\rangle$
versus distance
![]() $z/L_{\Vert }$
at four different evolution times. The solid curves are the corresponding power-law fitting functions, with coefficients denoted.
$z/L_{\Vert }$
at four different evolution times. The solid curves are the corresponding power-law fitting functions, with coefficients denoted.

Figure 12. (a) The mean value of the amplitude coefficient
![]() $\overline{A}$
versus the time-averaged nonlinearity parameter
$\overline{A}$
versus the time-averaged nonlinearity parameter
![]() $\overline{\unicode[STIX]{x1D712}}$
. The blue line is the corresponding power-law exponent fitting curve
$\overline{\unicode[STIX]{x1D712}}$
. The blue line is the corresponding power-law exponent fitting curve
![]() $\overline{A}(\overline{\unicode[STIX]{x1D712}})=0.3\exp (1.1\overline{\unicode[STIX]{x1D712}})$
. (b) The average value of exponent
$\overline{A}(\overline{\unicode[STIX]{x1D712}})=0.3\exp (1.1\overline{\unicode[STIX]{x1D712}})$
. (b) The average value of exponent
![]() $\overline{p}$
versus the time-averaged nonlinearity parameter
$\overline{p}$
versus the time-averaged nonlinearity parameter
![]() $\overline{\unicode[STIX]{x1D712}}$
. The red line is the corresponding fitting curve
$\overline{\unicode[STIX]{x1D712}}$
. The red line is the corresponding fitting curve
![]() $\overline{p}=1.46-0.82\exp (-0.80\overline{\unicode[STIX]{x1D712}})$
. The green horizontal line corresponds to value
$\overline{p}=1.46-0.82\exp (-0.80\overline{\unicode[STIX]{x1D712}})$
. The green horizontal line corresponds to value
![]() $\overline{p}=1$
which is associated with a standard diffusive process. Vertical and horizontal error bars correspond to standard deviations.
$\overline{p}=1$
which is associated with a standard diffusive process. Vertical and horizontal error bars correspond to standard deviations.
In figure 11, we plot the results of this analysis of the magnetic field line separation, including the values of the fitting parameters
![]() $A$
and
$A$
and
![]() $p$
. For each simulation run, we plot the results of
$p$
. For each simulation run, we plot the results of
![]() $\langle (\unicode[STIX]{x1D6FF}r)^{2}\rangle$
as a function of the distance along the equilibrium magnetic field
$\langle (\unicode[STIX]{x1D6FF}r)^{2}\rangle$
as a function of the distance along the equilibrium magnetic field
![]() $z/L_{\Vert }$
at four different representative times after the turbulent cascade has saturated. Note that, in addition to the time-averaged nonlinearity parameter
$z/L_{\Vert }$
at four different representative times after the turbulent cascade has saturated. Note that, in addition to the time-averaged nonlinearity parameter
![]() $\overline{\unicode[STIX]{x1D712}}$
given for each run in table 1, we also compute the instantaneous nonlinearity parameter
$\overline{\unicode[STIX]{x1D712}}$
given for each run in table 1, we also compute the instantaneous nonlinearity parameter
![]() $\unicode[STIX]{x1D712}$
at each of the chosen times in figure 11.
$\unicode[STIX]{x1D712}$
at each of the chosen times in figure 11.
From the results in figure 11, we find the following general properties about the separation of magnetic fields lines as a function of the turbulence amplitudes
![]() $\unicode[STIX]{x1D712}$
. First, the amplitude of the field line separation, parameterized by the coefficient
$\unicode[STIX]{x1D712}$
. First, the amplitude of the field line separation, parameterized by the coefficient
![]() $A$
, generally increases monotonically with the time-averaged nonlinearity parameter
$A$
, generally increases monotonically with the time-averaged nonlinearity parameter
![]() $\overline{\unicode[STIX]{x1D712}}$
. However, it does not always follow that a larger instantaneous value of the nonlinearity parameter
$\overline{\unicode[STIX]{x1D712}}$
. However, it does not always follow that a larger instantaneous value of the nonlinearity parameter
![]() $\unicode[STIX]{x1D712}$
will yield a larger value of the coefficient
$\unicode[STIX]{x1D712}$
will yield a larger value of the coefficient
![]() $A$
. This finding suggests that the amplitude of the field line separation may indeed depend not only on the nonlinearity parameter, but also on the history of the turbulent tangling of the magnetic field. Therefore, to determine the functional forms of the amplitude
$A$
. This finding suggests that the amplitude of the field line separation may indeed depend not only on the nonlinearity parameter, but also on the history of the turbulent tangling of the magnetic field. Therefore, to determine the functional forms of the amplitude
![]() $A(\unicode[STIX]{x1D712})$
and the power-law exponent
$A(\unicode[STIX]{x1D712})$
and the power-law exponent
![]() $p(\unicode[STIX]{x1D712})$
requires a statistical approach, effectively leading us to determine averaged values of these parameters as a function of the averaged nonlinearity parameter,
$p(\unicode[STIX]{x1D712})$
requires a statistical approach, effectively leading us to determine averaged values of these parameters as a function of the averaged nonlinearity parameter,
![]() $\overline{A}(\overline{\unicode[STIX]{x1D712}})$
and
$\overline{A}(\overline{\unicode[STIX]{x1D712}})$
and
![]() $\overline{p}(\overline{\unicode[STIX]{x1D712}})$
.
$\overline{p}(\overline{\unicode[STIX]{x1D712}})$
.
Another important conclusion regards the power-law scaling exponent
![]() $p$
of the field line separation as a function of the nonlinearity parameter
$p$
of the field line separation as a function of the nonlinearity parameter
![]() $\unicode[STIX]{x1D712}$
. Again, in general, we find a larger exponent
$\unicode[STIX]{x1D712}$
. Again, in general, we find a larger exponent
![]() $p$
for larger values of the time-averaged nonlinearity parameter
$p$
for larger values of the time-averaged nonlinearity parameter
![]() $\overline{\unicode[STIX]{x1D712}}$
. For the cases of over-strong and strong turbulence in Runs 1–4 with
$\overline{\unicode[STIX]{x1D712}}$
. For the cases of over-strong and strong turbulence in Runs 1–4 with
![]() $\overline{\unicode[STIX]{x1D712}}>1$
, the field line separation appears to follow a superdiffusive scaling,
$\overline{\unicode[STIX]{x1D712}}>1$
, the field line separation appears to follow a superdiffusive scaling,
![]() $p>1$
, as a function of
$p>1$
, as a function of
![]() $z$
; in contrast, for the weak turbulence cases Runs 5 and 6, it follows a subdiffusive scaling,
$z$
; in contrast, for the weak turbulence cases Runs 5 and 6, it follows a subdiffusive scaling,
![]() $p<1$
.
$p<1$
.
To quantitatively describe the field line separation as a function of the time-averaged nonlinearity parameter
![]() $\overline{\unicode[STIX]{x1D712}}$
, we compute the mean values of the amplitude coefficient
$\overline{\unicode[STIX]{x1D712}}$
, we compute the mean values of the amplitude coefficient
![]() $\overline{A}$
and the exponent
$\overline{A}$
and the exponent
![]() $\overline{p}$
for each of the simulation Runs 1–6. We compute the mean and standard deviation for
$\overline{p}$
for each of the simulation Runs 1–6. We compute the mean and standard deviation for
![]() $\overline{A}$
and
$\overline{A}$
and
![]() $\overline{p}$
by averaging over the four values of
$\overline{p}$
by averaging over the four values of
![]() $p$
and
$p$
and
![]() $A$
shown in figure 11. We plot in figure 12 the average values
$A$
shown in figure 11. We plot in figure 12 the average values
![]() $\overline{A}$
(a) and
$\overline{A}$
(a) and
![]() $\overline{p}$
(b) as a function of the time-averaged nonlinearity parameter
$\overline{p}$
(b) as a function of the time-averaged nonlinearity parameter
![]() $\overline{\unicode[STIX]{x1D712}}$
. Uncertainties in figure 12 are given by the standard deviation of each of these averaged quantities.
$\overline{\unicode[STIX]{x1D712}}$
. Uncertainties in figure 12 are given by the standard deviation of each of these averaged quantities.
Figure 12(a) clearly shows that
![]() $\overline{A}$
nonlinearly increases with increasing
$\overline{A}$
nonlinearly increases with increasing
![]() $\overline{\unicode[STIX]{x1D712}}$
indicating more spreading of magnetic field in strong turbulence than in weak turbulence. The data are fit to an exponential form
$\overline{\unicode[STIX]{x1D712}}$
indicating more spreading of magnetic field in strong turbulence than in weak turbulence. The data are fit to an exponential form
with best fit values
![]() $\overline{a}_{0}=0.3$
and
$\overline{a}_{0}=0.3$
and
![]() $\overline{b}_{0}=1.1$
.
$\overline{b}_{0}=1.1$
.
Figure 12(b) displays the dependence of the mean exponent
![]() $\overline{p}$
on the time-averaged nonlinearity parameter
$\overline{p}$
on the time-averaged nonlinearity parameter
![]() $\overline{\unicode[STIX]{x1D712}}$
. We fit this behaviour to the functional form
$\overline{\unicode[STIX]{x1D712}}$
. We fit this behaviour to the functional form
where the best fit yields values
![]() $\overline{p}_{0}=1.46$
,
$\overline{p}_{0}=1.46$
,
![]() $\overline{p}_{1}=0.82$
and
$\overline{p}_{1}=0.82$
and
![]() $C_{1}=-0.80$
. Based on this statistically averaged functional form, we conclude that the diffusion approximation is a reasonable model for turbulence with a nonlinearity parameter
$C_{1}=-0.80$
. Based on this statistically averaged functional form, we conclude that the diffusion approximation is a reasonable model for turbulence with a nonlinearity parameter
![]() $\overline{\unicode[STIX]{x1D712}}=1.\pm 0.15$
.
$\overline{\unicode[STIX]{x1D712}}=1.\pm 0.15$
.
3 Discussion and conclusions
In this investigation, we have explored the saturation of the turbulent cascade, the development of stochasticity due to turbulent tangling of the magnetic field lines and the separation of field lines through the turbulent dynamics using nonlinear gyrokinetic simulations of weakly collisional plasma turbulence, relevant to many turbulent space and astrophysical plasma environments. We focus on the sub-ion range of kinetic Alfvén wave turbulence, corresponding to the dissipation range of turbulence in the solar wind, over the range
![]() $5\leqslant k_{\bot }\unicode[STIX]{x1D70C}_{i}\leqslant 105$
, or
$5\leqslant k_{\bot }\unicode[STIX]{x1D70C}_{i}\leqslant 105$
, or
![]() $0.12\leqslant k_{\bot }\unicode[STIX]{x1D70C}_{e}\leqslant 2.5$
. The motivation for beginning this methodical investigation of magnetic field line wander in plasma turbulence with the small-scale end of the turbulent spectrum is that the kinetic physical mechanisms, including collisionless damping and collisionless magnetic reconnection, are resolved properly by our gyrokinetic simulations as long as we resolve wavenumbers
$0.12\leqslant k_{\bot }\unicode[STIX]{x1D70C}_{e}\leqslant 2.5$
. The motivation for beginning this methodical investigation of magnetic field line wander in plasma turbulence with the small-scale end of the turbulent spectrum is that the kinetic physical mechanisms, including collisionless damping and collisionless magnetic reconnection, are resolved properly by our gyrokinetic simulations as long as we resolve wavenumbers
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{e}\sim 2$
(Howes et al.
Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006; Numata et al.
Reference Numata, Howes, Tatsuno, Barnes and Dorland2010; TenBarge et al.
Reference TenBarge, Howes and Dorland2013). Our focus is to understand the properties of magnetic field line wander as a function of the amplitude of the turbulence, parameterized here by the dimensionless nonlinearity parameter
$k_{\bot }\unicode[STIX]{x1D70C}_{e}\sim 2$
(Howes et al.
Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006; Numata et al.
Reference Numata, Howes, Tatsuno, Barnes and Dorland2010; TenBarge et al.
Reference TenBarge, Howes and Dorland2013). Our focus is to understand the properties of magnetic field line wander as a function of the amplitude of the turbulence, parameterized here by the dimensionless nonlinearity parameter
![]() $\unicode[STIX]{x1D712}$
, approximately a measure of the linear wave period to the nonlinear energy transfer time scale. We perform here a set of seven simulations with time-averaged nonlinearity parameter
$\unicode[STIX]{x1D712}$
, approximately a measure of the linear wave period to the nonlinear energy transfer time scale. We perform here a set of seven simulations with time-averaged nonlinearity parameter
![]() $\overline{\unicode[STIX]{x1D712}}$
varying from over-strong turbulence with
$\overline{\unicode[STIX]{x1D712}}$
varying from over-strong turbulence with
![]() $\overline{\unicode[STIX]{x1D712}}=4.9$
, to critically balance, strong turbulence with
$\overline{\unicode[STIX]{x1D712}}=4.9$
, to critically balance, strong turbulence with
![]() $\overline{\unicode[STIX]{x1D712}}=1.3$
to weak turbulence with
$\overline{\unicode[STIX]{x1D712}}=1.3$
to weak turbulence with
![]() $\overline{\unicode[STIX]{x1D712}}=0.14$
.
$\overline{\unicode[STIX]{x1D712}}=0.14$
.
First, we have investigated the development and saturation of the turbulent cascade, beginning with uniform, straight magnetic field conditions driven by an antenna that creates counterpropagating kinetic Alfvén waves at the domain scale. Nonlinear interactions between the counterpropagating kinetic Alfvén waves efficiently transfer energy to small scales, generating a broadband turbulent cascade of magnetic field and plasma bulk flow fluctuations. For all values of
![]() $\overline{\unicode[STIX]{x1D712}}$
, we find the development of the cascade is characterized by two time scales
$\overline{\unicode[STIX]{x1D712}}$
, we find the development of the cascade is characterized by two time scales
![]() $t_{1}$
and
$t_{1}$
and
![]() $t_{2}$
. At time
$t_{2}$
. At time
![]() $t_{1}$
, the small-scale modes reach sufficient amplitudes to interact nonlinearly and transfer their energy to yet smaller-scale modes. In the time interval,
$t_{1}$
, the small-scale modes reach sufficient amplitudes to interact nonlinearly and transfer their energy to yet smaller-scale modes. In the time interval,
![]() $t_{1}<t<t_{2}$
, the normalized rate of energy increase in the plasma due to driving
$t_{1}<t<t_{2}$
, the normalized rate of energy increase in the plasma due to driving
![]() ${\dot{W}}/P_{in}$
is overtaken by the rate of heating due to dissipation
${\dot{W}}/P_{in}$
is overtaken by the rate of heating due to dissipation
![]() $H/P_{in}$
, indicating the approach to saturation. At the saturation time
$H/P_{in}$
, indicating the approach to saturation. At the saturation time
![]() $t_{2}$
, the spectral index of the perpendicular magnetic energy spectrum
$t_{2}$
, the spectral index of the perpendicular magnetic energy spectrum
![]() $\unicode[STIX]{x1D6FC}$
reaches a statistically steady value and the rate of heating
$\unicode[STIX]{x1D6FC}$
reaches a statistically steady value and the rate of heating
![]() $H/P_{in}$
dominates over the rate of energy increase in the turbulent plasma
$H/P_{in}$
dominates over the rate of energy increase in the turbulent plasma
![]() ${\dot{W}}/P_{in}$
, indicating that all of the input power is collisionally dissipated, heating the plasma irreversibly.
${\dot{W}}/P_{in}$
, indicating that all of the input power is collisionally dissipated, heating the plasma irreversibly.
Next, we have studied the development of stochasticity of the magnetic field lines as a function of the time-averaged nonlinearity parameter
![]() $\overline{\unicode[STIX]{x1D712}}$
using Poincaré recurrence plots. We find that for over-strong and strong turbulence cases with
$\overline{\unicode[STIX]{x1D712}}$
using Poincaré recurrence plots. We find that for over-strong and strong turbulence cases with
![]() $\overline{\unicode[STIX]{x1D712}}\gtrsim 1$
, the magnetic field lines have become completely stochastic throughout the domain for
$\overline{\unicode[STIX]{x1D712}}\gtrsim 1$
, the magnetic field lines have become completely stochastic throughout the domain for
![]() $t\geqslant t_{2}$
. For weaker turbulence cases with
$t\geqslant t_{2}$
. For weaker turbulence cases with
![]() $\overline{\unicode[STIX]{x1D712}}<1$
, a remnant of order persists in the Poincaré plots even at
$\overline{\unicode[STIX]{x1D712}}<1$
, a remnant of order persists in the Poincaré plots even at
![]() $t\sim t_{2}$
when the turbulent cascade has saturated. Over a much longer time
$t\sim t_{2}$
when the turbulent cascade has saturated. Over a much longer time
![]() $t\gg t_{2}$
, the turbulent magnetic field lines become fully stochastic if the turbulent amplitude exceeds a threshold value
$t\gg t_{2}$
, the turbulent magnetic field lines become fully stochastic if the turbulent amplitude exceeds a threshold value
![]() $\unicode[STIX]{x1D712}_{thresh}\sim 0.1$
. For yet weaker turbulence with
$\unicode[STIX]{x1D712}_{thresh}\sim 0.1$
. For yet weaker turbulence with
![]() $\unicode[STIX]{x1D712}\lesssim 0.1$
, ordered regions of simulation domain persist, indicating that a fully stochastic magnetic field does not arise below this amplitude threshold over the course of the saturation time interval
$\unicode[STIX]{x1D712}\lesssim 0.1$
, ordered regions of simulation domain persist, indicating that a fully stochastic magnetic field does not arise below this amplitude threshold over the course of the saturation time interval
![]() $t_{2}<t<13t_{2}$
.
$t_{2}<t<13t_{2}$
.
Finally, we quantified the mean square displacement of magnetic field lines in the turbulent magnetic field with a functional form
![]() $\langle (\unicode[STIX]{x1D6FF}r)^{2}\rangle =A(z/L_{\Vert })^{p}$
, where we expect the amplitude factor
$\langle (\unicode[STIX]{x1D6FF}r)^{2}\rangle =A(z/L_{\Vert })^{p}$
, where we expect the amplitude factor
![]() $A(\unicode[STIX]{x1D712})$
and the power-law exponent
$A(\unicode[STIX]{x1D712})$
and the power-law exponent
![]() $p(\unicode[STIX]{x1D712})$
both to be a function of the nonlinearity parameter
$p(\unicode[STIX]{x1D712})$
both to be a function of the nonlinearity parameter
![]() $\unicode[STIX]{x1D712}$
. Statistical determinations of these two parameters yield the best fit results for the amplitude coefficient
$\unicode[STIX]{x1D712}$
. Statistical determinations of these two parameters yield the best fit results for the amplitude coefficient
![]() $\overline{A}(\overline{\unicode[STIX]{x1D712}})=\overline{a}_{0}\exp (\overline{b}_{0}\overline{\unicode[STIX]{x1D712}})$
for
$\overline{A}(\overline{\unicode[STIX]{x1D712}})=\overline{a}_{0}\exp (\overline{b}_{0}\overline{\unicode[STIX]{x1D712}})$
for
![]() $0.14\leqslant \overline{\unicode[STIX]{x1D712}}\leqslant 4.9$
(with
$0.14\leqslant \overline{\unicode[STIX]{x1D712}}\leqslant 4.9$
(with
![]() $\overline{a_{0}}=0.3$
, and
$\overline{a_{0}}=0.3$
, and
![]() $\overline{b_{0}}=1.1$
) and the power-law exponent
$\overline{b_{0}}=1.1$
) and the power-law exponent
![]() $\overline{p}(\overline{\unicode[STIX]{x1D712}})=\overline{p}_{0}-\overline{p}_{1}\exp C_{1}\overline{\unicode[STIX]{x1D712}}$
with
$\overline{p}(\overline{\unicode[STIX]{x1D712}})=\overline{p}_{0}-\overline{p}_{1}\exp C_{1}\overline{\unicode[STIX]{x1D712}}$
with
![]() $\overline{p}_{0}=1.46$
,
$\overline{p}_{0}=1.46$
,
![]() $\overline{p}_{1}=0.82$
and
$\overline{p}_{1}=0.82$
and
![]() $C_{1}=-0.80$
, as shown in figure 12.
$C_{1}=-0.80$
, as shown in figure 12.
The analysis of magnetic field stochasticity using Poincaré plots for the magnetic field tracing has been also used in plasma fusions (Wang et al. Reference Wang, Nevins, Candy, Hatch, Terry and Guttenfelder2011; Pueschel et al. Reference Pueschel, Hatch, Görler, Nevins, Jenko, Terry and Told2013). For example, Pueschel et al. (Reference Pueschel, Hatch, Görler, Nevins, Jenko, Terry and Told2013) have implemented the radial displacement of the field lines as a function of the number of poloidal turns to estimate the field line diffusivity. The authors found that the magnetic field lines follow a diffusive law after a few tens of poloidal turns. Although the geometry of the background field in our analysis is different from the one used in the work of Pueschel et al. (Reference Pueschel, Hatch, Görler, Nevins, Jenko, Terry and Told2013), we also found that the field lines may obey a diffusive law in gyrokinetic turbulence if the nonlinearity parameter is approximately 1 as shown in figure 12.
Furthermore, studies of the effect of magnetic field stochasticity on zonal flows in plasma fusion have shown that the normalized critical value
![]() $\unicode[STIX]{x1D6FD}_{crit}^{NZT}$
of the electron normalized plasma pressure for non-zonal transition (NZT) depends on the amplitude of the magnetic field fluctuations (see e.g. Pueschel et al.
Reference Pueschel, Terry and Hatch2014). The authors found that a strong driving (or higher background gradients) leads to higher radial displacement of magnetic field lines as a result of magnetic field stochasticity. As a consequence, the NZT can occur for relatively smaller values of
$\unicode[STIX]{x1D6FD}_{crit}^{NZT}$
of the electron normalized plasma pressure for non-zonal transition (NZT) depends on the amplitude of the magnetic field fluctuations (see e.g. Pueschel et al.
Reference Pueschel, Terry and Hatch2014). The authors found that a strong driving (or higher background gradients) leads to higher radial displacement of magnetic field lines as a result of magnetic field stochasticity. As a consequence, the NZT can occur for relatively smaller values of
![]() $\unicode[STIX]{x1D6FD}_{crit}^{NZT}$
. The increase in the turbulence amplitude will cause more separation of the magnetic field lines in gyrokinetic turbulence as found in our paper.
$\unicode[STIX]{x1D6FD}_{crit}^{NZT}$
. The increase in the turbulence amplitude will cause more separation of the magnetic field lines in gyrokinetic turbulence as found in our paper.
The nonlinearity parameter was also found to be a crucial for development of the magnetic field wander in MHD turbulence. It has been demonstrated that the magnetic stochasticity in weak MHD turbulence (when the nonlinearity parameter is less than 1) does not fully develop (Eyink, Lazarian & Vishniac Reference Eyink, Lazarian and Vishniac2011). However, as the turbulent cascade proceeds and the nonlinearity parameter is close to unity, the spontaneous stochasticity of magnetic field lines is induced in MHD turbulence and the rate of magnetic reconnection is altered (Eyink Reference Eyink2011).
As mentioned above, to better describe the energetic particle propagation we need a realistic model of turbulence and an accurate transport theory. If we assume that the gyrocentres of the energetic charged particles follow magnetic field lines then the cross-field transport of these particles is governed by the perpendicular spread of magnetic field lines. In this limit, if the magnetic field lines are diffusive, then the perpendicular diffusion coefficient of the energetic particles can be given as
![]() $\unicode[STIX]{x1D705}_{\bot }=vD_{FL}$
(Jokipii Reference Jokipii1966), where
$\unicode[STIX]{x1D705}_{\bot }=vD_{FL}$
(Jokipii Reference Jokipii1966), where
![]() $D_{FL}=\langle (\unicode[STIX]{x1D6FF}r)^{2}\rangle /2z$
is the magnetic field diffusion coefficient and
$D_{FL}=\langle (\unicode[STIX]{x1D6FF}r)^{2}\rangle /2z$
is the magnetic field diffusion coefficient and
![]() $v$
is the velocity of the energetic particles. For instance, in our analysis we found that the magnetic field lines are nearly diffusive in critically balance gyrokinetic turbulence (when
$v$
is the velocity of the energetic particles. For instance, in our analysis we found that the magnetic field lines are nearly diffusive in critically balance gyrokinetic turbulence (when
![]() $\overline{\unicode[STIX]{x1D712}}=1$
), and we get
$\overline{\unicode[STIX]{x1D712}}=1$
), and we get
![]() $D_{FL}=\langle (\unicode[STIX]{x1D6FF}r)^{2}\rangle /2z\simeq \unicode[STIX]{x1D70C}_{i}^{2}\overline{A}(\overline{\unicode[STIX]{x1D712}}=1)/L_{\Vert }$
, and thus the particle cross-field transport coefficient
$D_{FL}=\langle (\unicode[STIX]{x1D6FF}r)^{2}\rangle /2z\simeq \unicode[STIX]{x1D70C}_{i}^{2}\overline{A}(\overline{\unicode[STIX]{x1D712}}=1)/L_{\Vert }$
, and thus the particle cross-field transport coefficient
![]() $\unicode[STIX]{x1D705}_{\bot }\simeq v\unicode[STIX]{x1D70C}_{i}^{2}\overline{A}/2L_{\Vert }$
. In this case, the value of
$\unicode[STIX]{x1D705}_{\bot }\simeq v\unicode[STIX]{x1D70C}_{i}^{2}\overline{A}/2L_{\Vert }$
. In this case, the value of
![]() $D_{FL}$
is approximately
$D_{FL}$
is approximately
![]() $0.3$
in units of
$0.3$
in units of
![]() $L_{\bot }^{2}/L_{\Vert }$
(with
$L_{\bot }^{2}/L_{\Vert }$
(with
![]() $L_{\bot }=2\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{i}/5$
) when
$L_{\bot }=2\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{i}/5$
) when
![]() $\overline{\unicode[STIX]{x1D712}}=1$
in gyrokinetic turbulence simulation. This value is close to the one of
$\overline{\unicode[STIX]{x1D712}}=1$
in gyrokinetic turbulence simulation. This value is close to the one of
![]() $D_{FL}\simeq 0.33$
estimated for critically balance reduced MHD turbulence (Ruffolo & Matthaeus Reference Ruffolo and Matthaeus2013; Snodin et al.
Reference Snodin, Ruffolo, Oughton, Servidio and Matthaeus2013).
$D_{FL}\simeq 0.33$
estimated for critically balance reduced MHD turbulence (Ruffolo & Matthaeus Reference Ruffolo and Matthaeus2013; Snodin et al.
Reference Snodin, Ruffolo, Oughton, Servidio and Matthaeus2013).
In heliospheric plasma, the diffusion of the solar energetic particles in the interplanetary medium is affected by solar wind turbulence. During their transit from the Sun’s atmosphere to the outer heliosphere the solar energetic particles go through varying conditions of solar wind plasma, for example, the plasma
![]() $\unicode[STIX]{x1D6FD}$
and the ratio ion-to-electron temperature
$\unicode[STIX]{x1D6FD}$
and the ratio ion-to-electron temperature
![]() $T_{i}/T_{e}$
vary with heliocentric distance. The variation of these plasma parameters can be crucial for the amount of the perpendicular displacement of the magnetic field lines. For instance, in fusion plasmas, it has been shown that the related stochasticity parameter varies with respect to the plasma
$T_{i}/T_{e}$
vary with heliocentric distance. The variation of these plasma parameters can be crucial for the amount of the perpendicular displacement of the magnetic field lines. For instance, in fusion plasmas, it has been shown that the related stochasticity parameter varies with respect to the plasma
![]() $\unicode[STIX]{x1D6FD}$
in gyrokinetic turbulence in CYCLONE base case plasmas Pueschel et al. (Reference Pueschel, Hatch, Görler, Nevins, Jenko, Terry and Told2013).
$\unicode[STIX]{x1D6FD}$
in gyrokinetic turbulence in CYCLONE base case plasmas Pueschel et al. (Reference Pueschel, Hatch, Görler, Nevins, Jenko, Terry and Told2013).
In the future work, we will employ direct numerical simulations of plasma turbulence to determine how the properties of the magnetic field line wander vary with the plasma parameters, such as the plasma
![]() $\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FD}$
and
![]() $T_{i}/T_{e}$
(as the turbulence dissipation and magnetic reconnection strongly depend on these plasma parameters), and with the parameters of the turbulence, such as the length scale range characterized by
$T_{i}/T_{e}$
(as the turbulence dissipation and magnetic reconnection strongly depend on these plasma parameters), and with the parameters of the turbulence, such as the length scale range characterized by
![]() $k_{\bot 0}\unicode[STIX]{x1D70C}_{i}$
.
$k_{\bot 0}\unicode[STIX]{x1D70C}_{i}$
.
Acknowledgements
The work has been supported by NSF CAREER Award AGS-1054061 and NASA NNX10AC91G.