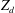1 Introduction
The study of solitons in dusty plasmas with variable temperatures starting in the last century has attained at present a high stage of investigation. Starting from the simple stage of two component plasmas, studies are extended to multi-component plasmas with the insertion of various characteristic effects. There are many investigations with isothermal and non-isothermal electrons without consideration of pressure variations. But the astrophysical and space environments are found to be occupied by dusty plasmas which are known from many space probes. In planetary rings (Shukla & Silin Reference Shukla and Silin1992), the Earth’s magnetosphere (Vette Reference Vette1970; Tokar & Gary Reference Tokar and Gary1984), neighbourhood of stars (Shukla & Mamun Reference Shukla and Mamun2002) and in cometary tails (Chow, Mendis & Rosenberg Reference Chow, Mendis and Rosenberg1993; Mendis & Rosenberg Reference Mendis and Rosenberg1994), the effect of dust particles are nicely described. The presence of dust particles is found to drastically change the properties of solitary waves of space (Rao, Shukla & Yu Reference Rao, Shukla and Yu1990; Shukla & Silin Reference Shukla and Silin1992; Verheest Reference Verheest1992; Barkan, Marlino & D’Angelo Reference Barkan, Marlino and D’Angelo1995; Mamun, Cairns & D’Angelo Reference Mamun, Cairns and D’Angelo1996; Mamun Reference Mamun1999; Shukla & Mamun Reference Shukla and Mamun2002) and laboratory (Nakamura, Bailung & Shukla Reference Nakamura, Bailung and Shukla1999; Ghosh et al. Reference Ghosh, Sarkar, Khan and Gupta2000; Nakamura & Sarma Reference Nakamura and Sarma2001; Shahmansouri & Tribeche Reference Shahmansouri and Tribeche2014) plasmas.
In most studies, the variable temperature of the plasma is found to be neglected as inclusion of temperature variation in the plasma demands the additional pressure variation equation of the state in the set of governing equations. Kalita & Barman (Reference Kalita and Barman1995) have investigated the existence of solitary waves in multi-component un-magnetized plasmas with pressure variations for the ions, negative ions and isothermal electrons. Chatterjee & Roychoudhury (Reference Chatterjee and Roychoudhury1994) have reported the role of ion temperature in the formation of solitary waves in plasmas with relativistic ions under variable pressure and non-relativistic electrons. Usually, solitary waves of small amplitude are studied through the Korteweg–de Vries (KdV) and modified Korteweg–de Vries (MKdV) equations. Das, Singh & Singh (Reference Das, Singh and Singh1996) have studied KdV and MKdV ion acoustic solitons in unmagnetized plasmas with free and trapped electrons of different temperatures supported by a uniform ionization rate.
In many investigations, dust acoustic (DA) waves are studied in plasmas with the dust momentum fluid equations (Rao et al. Reference Rao, Shukla and Yu1990; Mamun Reference Mamun1998, Reference Mamun1999; Baluku & Helberg Reference Baluku and Helberg2008; Verheest & Pillay Reference Verheest and Pillay2008; Ghosh et al. Reference Ghosh, Choudhury, Sarkar, Khan and Gupta2001; Asgari, Muniandy & Wong Reference Asgari, Muniandy and Wong2013) considering a Boltzmann distribution, Cairns distribution (Cairns et al. Reference Cairns, Mamun, Bingham, Dendy, Boström, Nairn and Shukla1995) of the electrons and ions or non-thermal electrons or ions and a kappa distribution of the electrons. Rosengberg (Reference Rosengberg1993) has discussed the excitation of dust acoustic wave modes caused by ions and electrons streaming through dust grains which are even essential for instability studies. The existence of dust acoustic solitary waves is shown by Rouchoudhury & Mukherjee (Reference Rouchoudhury and Mukherjee1997) under the restriction of finite dust temperature. Rosengberg & Krall (Reference Rosengberg and Krall1996) have reported that dust temperature is important for the thermalization of ions or orbital effects. The effects of finite dust temperature and dust charge fluctuation on DA waves are studied by EL-Labony & EL-Taibany (Reference EL-Labony and EL-Taibany2003). Pakzad (Reference Pakzad2009) has studied DA solitary waves through the pseudo-potential method taking a non-thermal distribution of ions as variable. The dust ion acoustic (DIA) Gardner soliton is established by Masud, Asaduzzaman & Mamun (Reference Masud, Asaduzzaman and Mamun2012) in obliquely propagating magnetized dusty plasma employing the Zakharov–Kuznetsov (ZK) equation. Asgari et al. (Reference Asgari, Muniandy and Wong2013) have studied DIA waves with a non-thermal Cairns-like distribution of the ions in the plasma. In the presence of massive stationary dust in the background plasma, the lighter particles, electrons and ions, suffer appreciable initial drift. These initial values are found to characteristically change the growth of solitons in this present investigation. In dust ion acoustic solitons with dust as a stationary background, for slow perturbations, small amplitude waves need to be described by the KdV equation, essential particularly for a multi-component plasma. To incorporate higher-order nonlinearity for an in-depth study into the plasma scenario, it is desirable to employ the MKdV equations.
Kopnin et al. (Reference Kopnin, Kosarev, Popel and Yu2005) have pointed out that the dust grain charging process is described in terms of the so-called orbit motion (Barnes et al. Reference Barnes, Keller, Forster, O’Neill and Coultas1992). Therefore with dust as a stationary background, dust charge may be constant (Kundu & Mamun Reference Kundu and Mamun2012) and so it is ‘dust ion acoustic’. In dust acoustic solitons with mobile dust, variable dust charges are being considered although it is questionable for conservation of mass. In the presence of the massive dust particles in a space plasma, the DIA (or DA) waves are expected to form low frequency waves. A behavioural study of the properties of these waves, in particular solitary waves or solitons moving with constant but low speed, can be readily tapped for information by space probes. For complete determination of phase space (position, velocity out of any form) mapping of dust particles in the plasmas surrounding space bodies such as the Moon or Mars – through Spectrometer and ‘Imager’ –have been investigated in space missions such as ASPERA (automatic space plasma experiment with a rotating analyser) on the Phobos satellite. This is described in the works of Kalita & Kalita (Reference Kalita and Kalita2016).
This paper is organized as follows: the introduction is given in § 1, the basic equations in § 2, the validity condition for the neglect of charge variation in support of a conservative system in § 3, derivation of the Korteweg–de Vries and the modified Korteweg–de Vries equations in § 4, solitary wave solutions of the Korteweg–de Vries and the modified Korteweg–de Vries equations in § 5 and the discussion is in § 6. The references are included at the end.
2 Basic equations
In this model, we consider variable pressure in both the ion and electron components in the presence of immobile negatively charged dust particles in the plasma. The dynamics of dust ion acoustic (DIA) waves propagating in such a system of dusty plasma is described by means of the equations for conservation of mass, conservation of momentum and pressure variations (or temperatures) of both the ion and electron species. They are supplemented by the Poisson equation with immobile dust.
For ions,
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}n_{i}}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}(n_{i}v_{i})=0 & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}v_{i}}{\unicode[STIX]{x2202}t}+v_{i}\frac{\unicode[STIX]{x2202}v_{i}}{\unicode[STIX]{x2202}x}+\frac{\unicode[STIX]{x1D6FC}}{n_{i}}\frac{\unicode[STIX]{x2202}p_{i}}{\unicode[STIX]{x2202}x}=-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}{\unicode[STIX]{x2202}x} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}p_{i}}{\unicode[STIX]{x2202}t}+v_{i}\frac{\unicode[STIX]{x2202}p_{i}}{\unicode[STIX]{x2202}x}+3p_{i}\frac{\unicode[STIX]{x2202}v_{i}}{\unicode[STIX]{x2202}x}=0 & \displaystyle\end{eqnarray}$$
for electrons,
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}n_{e}}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}(n_{e}v_{e})=0 & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}v_{e}}{\unicode[STIX]{x2202}t}+v_{e}\frac{\unicode[STIX]{x2202}v_{e}}{\unicode[STIX]{x2202}x}=\frac{1}{Q}\left(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}{\unicode[STIX]{x2202}x}-\frac{1}{n_{e}}\frac{\unicode[STIX]{x2202}p_{e}}{\unicode[STIX]{x2202}x}\right), & \displaystyle\end{eqnarray}$$
where
$Q=m_{e}/m_{i},~m_{e}$
and
$m_{i}$
being the masses of electrons and ions respectively
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}p_{e}}{\unicode[STIX]{x2202}t}+v_{e}\frac{\unicode[STIX]{x2202}p_{e}}{\unicode[STIX]{x2202}x}+3p_{e}\frac{\unicode[STIX]{x2202}v_{e}}{\unicode[STIX]{x2202}x}=0 & \displaystyle\end{eqnarray}$$
and the Poisson equation
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D711}}{\unicode[STIX]{x2202}x^{2}}=n_{e}+Z_{d}n_{d}-n_{i},\end{eqnarray}$$
where
$v_{i}$
,
$v_{e}$
;
$n_{i}$
,
$n_{e}$
and
$p_{i}$
,
$p_{e}$
are velocities, densities and pressures of the positive ions and electrons respectively,
$Z_{d}$
is the number of charges contained in a dust grain,
$n_{d}$
is the density of dust charges and
$\unicode[STIX]{x1D711}$
is the electrostatic potential.
3 Validity condition for the neglect of charge variation in support of a conservative system
In most of the dynamical scenarios, we are concerned with a conservative system. Kundu & Mamun (Reference Kundu and Mamun2012) have reported that the omission of dust charge fluctuations and the ion–neutral collision frequency is valid as long as the DIA wave frequency is not comparable to the dust charging frequency and ion neutral collision frequency. Here ‘comparable to’ means ‘remaining always smaller’ because the DIA is a wave but charges are particles. The investigation of an actual comparable stage is beyond the scope of the paper. Under this assumption, the charge variation in DIA waves for variation of pressures with time can be ignored for the reason mentioned below.
An essential feature of dust ion acoustic waves is that they can exist at
$T_{e}\approx T_{i}$
(Shukla & Silin Reference Shukla and Silin1992; Nakamura et al.
Reference Nakamura, Bailung and Shukla1999; Popel, Golubo’ & Losseva Reference Popel, Golubo’ and Losseva2001; Popel et al.
Reference Popel, Andreev, Gisko, Golubo’ and Losseva2004).
From (2.3) of the ions in this model of plasma, we get
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}(n_{i}T_{i})+v_{i}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}(n_{i}T_{i})+3n_{i}T_{i}\frac{\unicode[STIX]{x2202}v_{i}}{\unicode[STIX]{x2202}x}=0,\quad \text{putting }p_{i}=n_{i}KT_{i}. & & \displaystyle\end{eqnarray}$$
Using the equation of continuity (2.1), it can be simplified to give
$$\begin{eqnarray}\frac{1}{T_{i}}\frac{\unicode[STIX]{x2202}T_{i}}{\unicode[STIX]{x2202}t}+\frac{v_{i}}{T_{i}}\frac{\unicode[STIX]{x2202}T_{i}}{\unicode[STIX]{x2202}x}=-2\frac{\unicode[STIX]{x2202}v_{i}}{\unicode[STIX]{x2202}x}.\end{eqnarray}$$
Also, from the pressure variation (2.6) of the electrons and the equation of continuity (2.4), we can similarly get
$$\begin{eqnarray}\frac{1}{T_{e}}\frac{\unicode[STIX]{x2202}T_{e}}{\unicode[STIX]{x2202}t}+\frac{v_{e}}{T_{e}}\frac{\unicode[STIX]{x2202}T_{e}}{\unicode[STIX]{x2202}x}=-2\frac{\unicode[STIX]{x2202}v_{e}}{\unicode[STIX]{x2202}x}.\end{eqnarray}$$
Equations (3.2) and (3.3) gives for
$T_{e}\approx T_{i}=T\,(\text{approx.})$
$$\begin{eqnarray}\frac{1}{T}(v_{i}-v_{e})\frac{\unicode[STIX]{x2202}T}{\unicode[STIX]{x2202}x}=-2\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}(v_{i}-v_{e}).\end{eqnarray}$$
After integration, it gives
$$\begin{eqnarray}\frac{(v_{e}-v_{i})}{(v_{e0}-v_{i0})}=\sqrt{\frac{T_{0}}{T}}\quad \text{so that }v_{e}-v_{i}=\frac{\unicode[STIX]{x1D706}}{\sqrt{T}},\end{eqnarray}$$
where
$\unicode[STIX]{x1D706}=(v_{e0}-v_{i0})\sqrt{T_{0}}\neq 0$
with initial streaming velocity
$v_{e0}$
of the electrons,
$v_{i0}$
of the ions (shown in the next section) and pressure
$T_{0}$
at that instant. In (3.5),
$(v_{e}-v_{i})$
represents relative velocity of the electrons with respect to the ions at any instant.
Kopnin et al. (Reference Kopnin, Kosarev, Popel and Yu2005) have reported that for negative dust charge
$q_{d}=-Z_{d}e$
, only electrons with velocities such that
$|\boldsymbol{v}|>[(2(-e)q_{d})/am_{e}]^{1/2}=[(2\text{e}^{2}Z_{d})/am_{e}]^{1/2}$
(‘
$a$
’ is the grain size and ‘
$m_{e}$
’ is the electron mass) can reach the grain surfaces, while the ions are free of this constraint. Under this circumstance, the ions are free from recombination with the grain surfaces. Besides, there is every possibility to admit the condition
$(|\boldsymbol{v}|=)v_{e}=v_{i}+\unicode[STIX]{x1D706}/\sqrt{T}<[(2\text{e}^{2}Z_{d})/am_{e}]^{1/2}$
for smaller relative velocity of electrons
$v_{e}$
and higher values of
$T$
(both feasible) so that the electrons also cannot reach the grain surfaces. Therefore, in this sense, electrons also are free of recombination with the grain surfaces. Hence, the general conservative system will continue to hold good in such a system of dusty plasmas under the consideration
$T_{e}\approx T_{i}$
.
4 Derivation of the Korteweg–de Vries and the modified Korteweg–de Vries equations
To derive the KdV equation from the set of (2.1)–(2.7), we use the stretched variables,
$$\begin{eqnarray}\unicode[STIX]{x1D709}=\unicode[STIX]{x1D700}^{1/2}(x-Vt),\quad \unicode[STIX]{x1D70F}=\unicode[STIX]{x1D700}^{3/2}Vt,\end{eqnarray}$$
with the phase velocity
$V$
of the waves. We expand the flow variables asymptotically about the equilibrium state in terms of the smallness parameter
$\unicode[STIX]{x1D700}$
as
$$\begin{eqnarray}\left.\begin{array}{@{}l@{}}n_{i}=n_{i0}+\unicode[STIX]{x1D700}n_{i1}+\unicode[STIX]{x1D700}^{2}n_{i2}+\cdots \\ n_{e}=n_{e0}+\unicode[STIX]{x1D700}n_{e1}+\unicode[STIX]{x1D700}^{2}n_{e2}+\cdots \\ v_{i}=v_{i0}+\unicode[STIX]{x1D700}v_{i1}+\unicode[STIX]{x1D700}^{2}v_{i2}+\cdots \\ v_{e}=v_{e0}+\unicode[STIX]{x1D700}v_{e1}+\unicode[STIX]{x1D700}^{2}v_{e2}+\cdots \\ \unicode[STIX]{x1D711}=\unicode[STIX]{x1D700}\unicode[STIX]{x1D711}_{1}+\unicode[STIX]{x1D700}^{2}\unicode[STIX]{x1D711}_{2}+\cdots \\ p_{i}=p_{i0}+\unicode[STIX]{x1D700}p_{i1}+\unicode[STIX]{x1D700}^{2}p_{i2}+\cdots \\ p_{e}=p_{e0}+\unicode[STIX]{x1D700}p_{e1}+\unicode[STIX]{x1D700}^{2}p_{e2}+\cdots \end{array}\right\}.\end{eqnarray}$$
Following the standard perturbation method with the use of transformation (4.1), expansions (4.2) in the normalized set of (2.1)–(2.6), we equate the coefficients of
$\unicode[STIX]{x1D700}$
-order equations and after integration use the boundary conditions,
$$\begin{eqnarray}\displaystyle n_{i1}=0,\quad n_{e1}=0;\quad v_{i1}=0,\quad v_{e1}=0\quad \text{and}\quad \unicode[STIX]{x1D711}_{1}=0\quad \text{at }|\unicode[STIX]{x1D709}|\rightarrow \infty & & \displaystyle\end{eqnarray}$$
to get the following first-order perturbed quantities:
$$\begin{eqnarray}\left.\begin{array}{@{}l@{}}\displaystyle v_{i1}=-\frac{(v_{i0}-V)}{\left(v_{i0}-V\right)^{2}-3\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D711}_{1},\quad p_{i1}=\frac{3p_{i0}}{\left(v_{i0}-V\right)^{2}-3\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D711}_{1},\\[10.0pt] \displaystyle n_{i1}=\frac{n_{i0}}{\left(v_{i0}-V\right)^{2}-3\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D711}_{1},\quad v_{e1}=\frac{\left(v_{e0}-V\right)}{Q\left(v_{e0}-V\right)^{2}-3}\unicode[STIX]{x1D711}_{1},\\[12.0pt] \displaystyle n_{e1}=-\frac{n_{e0}\left(v_{e0}-V\right)}{Q\left(v_{e0}-V\right)^{2}-3}\unicode[STIX]{x1D711}_{1},\quad p_{e1}=-\frac{3p_{e0}}{Q\left(v_{e0}-V\right)^{2}-3}\unicode[STIX]{x1D711}_{1}\end{array}\right\}.\end{eqnarray}$$
Also, using expansion (4.2) in (2.7), we get
$$\begin{eqnarray}n_{e0}+Z_{d}n_{d0}-n_{i0}=0\quad \text{or},\quad \frac{n_{e0}}{n_{i0}}=1-Z_{d}\unicode[STIX]{x1D70E},\quad \text{where }\unicode[STIX]{x1D70E}=\frac{n_{d0}}{n_{i0}},\frac{p_{i0}}{n_{i0}}=1\end{eqnarray}$$
and
$$\begin{eqnarray}n_{e1}-n_{i1}=0.\end{eqnarray}$$
Using the first-order quantities in (4.6), the phase velocity equation for
$V$
is obtained as
$$\begin{eqnarray}\displaystyle \left(1-Z_{d}\unicode[STIX]{x1D70E}+Q\right)V^{2}-2\{v_{i0}(1-Z_{d}\unicode[STIX]{x1D70E})+Qv_{e0}\}V+\{(1-Z_{d}\unicode[STIX]{x1D70E})(v_{i0}^{2}-3\unicode[STIX]{x1D6FC})+Qv_{e0}^{2}-3\}=0 & & \displaystyle \nonumber\\ \displaystyle . & & \displaystyle\end{eqnarray}$$
Using relation (4.4) in the
$\unicode[STIX]{x1D700}^{2}$
-order equations (not shown here), we get the KdV equation
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}+p\unicode[STIX]{x1D711}_{1}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}+q\frac{\unicode[STIX]{x2202}^{3}\unicode[STIX]{x1D711}_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}^{3}}=0,\end{eqnarray}$$
where
$$\begin{eqnarray}\left.\begin{array}{@{}l@{}}\displaystyle p=\frac{BL_{1}(1-Z_{d}\unicode[STIX]{x1D70E})(B_{1}L_{1}+4K_{1}M_{1}+2K_{1})-B_{1}L(BL+4\unicode[STIX]{x1D6FC}KM+2K)}{VBL_{1}(1-Z_{d}\unicode[STIX]{x1D70E})(1+M_{1}+QB_{1}K_{1})+VB_{1}L(1+\unicode[STIX]{x1D6FC}M+BK)}\\[10.0pt] \displaystyle q=-\frac{BB_{1}}{n_{i0}\{VBL_{1}(1-Z_{d}\unicode[STIX]{x1D70E})(1+M_{1}+QB_{1}K_{1})+VB_{1}L(1+\unicode[STIX]{x1D6FC}M+BK)\}}\end{array}\right\},\end{eqnarray}$$
with
$K=B/F,L=1/F,M=3/F,K_{1}=B_{1}/F_{1},L_{1}=1/F_{1},M_{1}=3/F_{1},F=B^{2}-3\unicode[STIX]{x1D6FC},F_{1}=QB_{1}^{2}-3,B_{1}=v_{eo}-V,B=v_{io}-V$
.
For higher-order nonlinearity and to derive the MKdV equation from the set of (2.1)–(2.6), we introduce the new stretched variables,
$$\begin{eqnarray}\unicode[STIX]{x1D709}=\unicode[STIX]{x1D700}(x-Vt),\quad \unicode[STIX]{x1D70F}=\unicode[STIX]{x1D700}^{3}Vt,\quad \text{where }V\text{ is phase velocity of the waves}.\end{eqnarray}$$
Using these new stretched variables (4.10) and expansions (4.2) in (2.1)–(2.6) and after putting the first-order quantities in (4.6), we get the same phase velocity (4.7) for the phase velocity
$V$
. The new second-order equations subject to the boundary conditions
$$\begin{eqnarray}\displaystyle n_{i2}=n_{e2}=0;\quad v_{i2}=v_{e2}=0,\quad p_{i2}=p_{e2}=0\quad \text{and}\quad \unicode[STIX]{x1D711}_{2}=0\quad \text{at}~|\unicode[STIX]{x1D709}|\rightarrow \infty & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
after integration, produce the following results
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle v_{i2}=-R\unicode[STIX]{x1D711}_{1}^{2}-K\unicode[STIX]{x1D711}_{2},\quad n_{i2}=n_{i0}S\unicode[STIX]{x1D711}_{1}^{2}+n_{i0}L\unicode[STIX]{x1D711}_{2},\quad p_{i2}=n_{i0}T\unicode[STIX]{x1D711}_{1}^{2}+n_{i0}M\unicode[STIX]{x1D711}_{2},\\[5.0pt] \displaystyle v_{e2}=-R_{1}\unicode[STIX]{x1D711}_{1}^{2}+K_{1}\unicode[STIX]{x1D711}_{2},\quad n_{e2}=n_{e0}S_{1}\unicode[STIX]{x1D711}_{1}^{2}-n_{e0}L_{1}\unicode[STIX]{x1D711}_{2},\quad p_{e2}=n_{e0}T_{1}\unicode[STIX]{x1D711}_{1}^{2}-n_{e0}M_{1}\unicode[STIX]{x1D711}_{2},\end{array}\right\} & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle R=\frac{KL}{2}+\frac{2\unicode[STIX]{x1D6FC}KM}{F},\quad S=\frac{n_{i0}L}{2F}+\frac{n_{i0}K}{B}\left(\frac{2\unicode[STIX]{x1D6FC}M}{F}+L\right),\\[10.0pt] \displaystyle T=\frac{3p_{i0}L}{2F}+\frac{3p_{i0}KM}{B}\left(\frac{3\unicode[STIX]{x1D6FC}}{F}+1\right),\quad R_{1}=\frac{K_{1}L_{1}}{2}+\frac{2K_{1}M_{1}}{F_{1}},\\[10.0pt] \displaystyle S_{1}=\frac{n_{e0}L_{1}}{2F_{1}}+\frac{n_{e0}K_{1}}{B_{1}}\left(\frac{2M_{1}}{F_{1}}+L_{1}\right),\quad T_{1}=\frac{3p_{e0}L_{1}}{2F_{1}}+\frac{3p_{e0}K_{1}M_{1}}{B_{1}}\left(\frac{3}{F_{1}}+1\right)\end{array}\right\}\end{eqnarray}$$
Putting the values of
$n_{i2},n_{e2}$
in the second-order Poisson equation
$n_{i2}-n_{e2}=0$
, we get the following equation
$$\begin{eqnarray}(1-Z_{d}\unicode[STIX]{x1D70E})S_{1}-S=0.\end{eqnarray}$$
From the third-order equations in
$\unicode[STIX]{x1D700}$
, we get
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle B\frac{\unicode[STIX]{x2202}n_{i3}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}+n_{i0}\frac{\unicode[STIX]{x2202}v_{i3}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}+n_{i0}VL\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}-3n_{i0}(RL+KS)\unicode[STIX]{x1D711}_{1}^{2}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}-2n_{i0}KL\frac{\unicode[STIX]{x2202}(\unicode[STIX]{x1D711}_{1}\unicode[STIX]{x1D711}_{2})}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle n_{i0}B\frac{\unicode[STIX]{x2202}v_{i3}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}+\unicode[STIX]{x1D6FC}\frac{\unicode[STIX]{x2202}p_{i3}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}-n_{i0}VK\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}+n_{i0}L\frac{\unicode[STIX]{x2202}(\unicode[STIX]{x1D711}_{1}\unicode[STIX]{x1D711}_{2})}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}+n_{i0}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{3}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle B\frac{\unicode[STIX]{x2202}p_{i3}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}+3p_{i0}\frac{\unicode[STIX]{x2202}v_{i3}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}+p_{i0}VM\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}-n_{i0}(5KT+7RM)\unicode[STIX]{x1D711}_{1}^{2}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}-4p_{i0}KM\frac{\unicode[STIX]{x2202}(\unicode[STIX]{x1D711}_{1}\unicode[STIX]{x1D711}_{2})}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}=0,\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle B_{1}\frac{\unicode[STIX]{x2202}n_{e3}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}+n_{e0}\frac{\unicode[STIX]{x2202}v_{e3}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}+n_{e0}VL_{1}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}-3n_{e0}(R_{1}L_{1}+K_{1}S_{1})\unicode[STIX]{x1D711}_{1}^{2}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}-2n_{20}K_{1}L_{1}\frac{\unicode[STIX]{x2202}(\unicode[STIX]{x1D711}_{1}\unicode[STIX]{x1D711}_{2})}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}=0,\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle n_{e0}B_{1}\frac{\unicode[STIX]{x2202}v_{e3}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}+\frac{\unicode[STIX]{x2202}p_{e3}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}-n_{e0}QVK_{1}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}+n_{e0}L_{1}\frac{\unicode[STIX]{x2202}(\unicode[STIX]{x1D711}_{1}\unicode[STIX]{x1D711}_{2})}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}-n_{e0}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{3}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle B_{1}\frac{\unicode[STIX]{x2202}p_{e3}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}+3p_{e0}\frac{\unicode[STIX]{x2202}v_{e3}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}-p_{e0}VM_{1}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad +\,n_{e0}(5K_{1}T_{1}+7R_{1}M_{1})\unicode[STIX]{x1D711}_{1}^{2}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}-4p_{e0}K_{1}M_{1}\frac{\unicode[STIX]{x2202}(\unicode[STIX]{x1D711}_{1}\unicode[STIX]{x1D711}_{2})}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D711}_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}^{2}}=n_{e3}-n_{i3}.\end{eqnarray}$$
On differentiation of (4.21), we get
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}^{3}\unicode[STIX]{x1D711}_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}^{3}}=\frac{\unicode[STIX]{x2202}n_{e3}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}-\frac{\unicode[STIX]{x2202}n_{i3}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}.\end{eqnarray}$$
Putting the values of
$\unicode[STIX]{x2202}n_{e3}/\unicode[STIX]{x2202}\unicode[STIX]{x1D709}$
and
$\unicode[STIX]{x2202}n_{i3}/\unicode[STIX]{x2202}\unicode[STIX]{x1D709}$
determined from relations (4.15)–(4.20), in (4.22) and using (4.14), we get the MKdV equation
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}+p^{\prime }\unicode[STIX]{x1D711}_{1}^{2}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}+q^{\prime }\frac{\unicode[STIX]{x2202}^{3}\unicode[STIX]{x1D711}_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}^{3}}=0,\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}rcl@{}}\displaystyle p^{\prime }\hspace{3.0pt} & =\hspace{3.0pt} & \displaystyle -\frac{[(1-Z_{d}\unicode[STIX]{x1D70E})\{BB_{1}L_{1}S_{1}+BL_{1}(5K_{1}T_{1}+7M_{1}R_{1})+3B(K_{1}S_{1}+L_{1}R_{1})\}]}{(1-Z_{d}\unicode[STIX]{x1D70E})\{BVL_{1}(QB_{1}K_{1}+M_{1})+BVL_{1}\}+B_{1}VL(BK+\unicode[STIX]{x1D6FC}M)+B_{1}VL}\\[10.0pt] \hspace{3.0pt} & \hspace{3.0pt} & \displaystyle +\,\frac{[\{BB_{1}LS+\unicode[STIX]{x1D6FC}B_{1}L(5KT+7MR)+3B_{1}(RL+KS)\}]}{(1-Z_{d}\unicode[STIX]{x1D70E})\{BVL_{1}(QB_{1}K_{1}+M_{1})+BVL_{1}\}+B_{1}VL(BK+\unicode[STIX]{x1D6FC}M)+B_{1}VL}\\[10.0pt] \displaystyle q^{\prime }\hspace{3.0pt} & =\hspace{3.0pt} & \displaystyle -\frac{BB_{1}}{n_{i0}[(1-Z_{d}\unicode[STIX]{x1D70E})\{BVL_{1}(QB_{1}K_{1}+M_{1})+BVL_{1}\}+B_{1}VL(BK+\unicode[STIX]{x1D6FC}M)+B_{1}VL]}\end{array}\right\}. & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
5 Solitary wave solutions of the Korteweg–de Vries and the modified Korteweg–de Vries equations
Introducing the transformation
$\unicode[STIX]{x1D702}=\unicode[STIX]{x1D709}-C_{1}\unicode[STIX]{x1D70F}$
where
$C_{1}$
is the soliton speed in the linear
$\unicode[STIX]{x1D702}$
-space and using the boundary conditions
$\unicode[STIX]{x1D711}_{1}=\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{1}/\unicode[STIX]{x2202}\unicode[STIX]{x1D702}=\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D711}_{1}/\unicode[STIX]{x2202}\unicode[STIX]{x1D702}^{2}=0$
as
$|\unicode[STIX]{x1D702}|\rightarrow 0$
, we get the solution of the KdV (4.8) as
$$\begin{eqnarray}\unicode[STIX]{x1D711}_{1}=\unicode[STIX]{x1D711}_{0}\sec h^{2}\left(\frac{\unicode[STIX]{x1D702}}{\unicode[STIX]{x1D6E5}}\right).\end{eqnarray}$$
The amplitude and the width of the solitary waves are respectively given by
$\unicode[STIX]{x1D711}_{0}=3C_{1}/p$
and
$\unicode[STIX]{x1D6E5}=\sqrt{4q/C_{1}}$
,
$C_{1}$
is soliton speed.
Using the same transformation and integrating the MKdV (4.23) subject to the boundary conditions
$\unicode[STIX]{x1D711}_{1}=\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D711}_{1}/\unicode[STIX]{x2202}\unicode[STIX]{x1D702}^{2}=0$
as
$|\unicode[STIX]{x1D702}|\rightarrow \pm \infty$
, the solution is obtained as
$$\begin{eqnarray}\unicode[STIX]{x1D711}_{1}^{\prime }=\unicode[STIX]{x1D711}_{0}^{\prime }\sec h\left(\frac{\unicode[STIX]{x1D702}}{\unicode[STIX]{x1D6E5}_{1}}\right).\end{eqnarray}$$
The amplitude and the width of the solitary waves represented by the MKdV equations (4.23) are respectively given by
$\unicode[STIX]{x1D711}_{0}^{\prime }=\sqrt{6C_{1}/p^{\prime }}$
and
$\unicode[STIX]{x1D6E5}_{1}=\sqrt{q^{\prime }/C_{1}}$
,
$C_{1}$
being the soliton speed.
6 Discussion
In this model of a dusty plasma with variable pressure in both the ions and electrons, compressive solitons in most cases and rarefactive solitons in some cases based on parametric domains are shown to exist in the presence of stationary dust particles in the plasma. To trace out a curve, the points for a graph are plotted corresponding to each
$v_{e0}$
(as for example in figure 1) and for all the values of
$v_{i0}$
to yield the unique value of the amplitude
$\unicode[STIX]{x1D711}_{0}=3C_{1}/p$
. This principle is adopted for all cases of the graphs.
The amplitudes of the compressive solitons for small
$v_{i0}<5$
starting with reasonable magnitudes sharply decrease to smaller values for each streaming
$v_{e0}$
of electrons and increase thereafter to a critical
$v_{i0}\approx 12$
for
$Z_{d}=270$
(figure 1). The graphs of the soliton amplitudes reflect an interesting characteristic behaviour. The soliton of smallest amplitude for
$v_{e0}=25$
further increases to a maximum after crossing the critical position of
$v_{i0}$
just to decrease thereafter. Contrary to this, the soliton of highest amplitude attained before the critical value of
$v_{i0}\approx 12$
at
$v_{e0}=5$
decreases after the critical
$v_{i0}$
without growing to a maximum. Similar characteristic behaviour of amplitudes is reflected corresponding to two other values of
$v_{e0}=7.5$
, 10 also. Computationally, it is found that all
$\unicode[STIX]{x1D711}_{\text{max}}$
for all electron streaming velocities (
$5<v_{e0}<25$
) lie between
$12\leqslant v_{i0}\leqslant 17.5$
. In conformity with the decrease and increase in amplitudes of compressive and decrease in rarefactive solitons, the growth pattern is reflected in figure 1(b) corresponding to figure 1(a). Further, the dependence of the amplitude growth pattern of compressive solitons on electron and ion streaming can also be observed in figure 1(b).
Figure 1. Amplitudes of compressive and rarefactive KdV solitons versus ion streaming speed
$v_{i0}$
for fixed
$v_{e0}=5(\text{i}),7.5(\text{ii}),10(\text{iii}),12.5(\text{iv})\ldots 25(\text{ix}),\unicode[STIX]{x1D70E}=0.001,Z_{d}=270$
and
$\unicode[STIX]{x1D6FC}=0.1$
.
The widths of the compressive KdV solitons (corresponding to the amplitudes of figure 1) become very great (i.e. waves are flat) for solitons in the upper range of
$v_{e0}\approx 25$
lying within the lower range of
$v_{i0}$
. Of course, these flat waves are seen to be produced within the vicinity of
$v_{i0}=5$
. Widths of sharp amplitudes mostly of rarefactive character related to the corresponding
$v_{i0}$
of figure 1(a) are found in the vicinity of
$v_{i0}=25$
. The flatness of the width shown in figure 2(a) is convincingly represented in figure 2(b). Besides, the clear flatness of waves reflecting bigger widths are shown in figure 2(b) for smaller values of
$v_{i0}$
corresponding to higher values of
$v_{e0}$
.
Figure 2. Width of compressive and rarefactive KdV solitons versus ion streaming speed
$v_{i0}$
for fixed
$v_{e0}=5(\text{i}),7.5(\text{ii}),10(\text{iii}),12.5(\text{iv})\ldots 25(\text{ix}),\unicode[STIX]{x1D70E}=0.001,Z_{d}=270$
and
$\unicode[STIX]{x1D6FC}=0.1$
.
The characteristic of slightly decreasing convex growth of only compressive KdV solitons tends to zero as
$v_{e0}$
increases for
$v_{i0}=2(\text{i}),3(\text{ii}),4(\text{iii}),5(\text{iv}),6(\text{v}),Z_{d}=270$
(fixed) and for some value of
$v_{e0}$
in its range (figure 3
a). Of course in all cases, the amplitudes diminish with
$v_{e0}$
. Contrary to this, the amplitudes of only compressive KdV solitons grow quite linearly to high amplitudes (figure 3
a) subject to the limitation of KdV solitons. Interestingly, the dual linear growth of rarefactive turning to compressive KdV solitons follows the same pattern with the exception that the amplitudes of rarefactive solitons decreases from higher values to lower values (figure 3(a), xi, xii, xiii) but for the compressive part it reflects just the opposite character. The dual characteristic representations of compressive and rarefactive solution amplitudes are shown in figure 3(b). The amplitudes of the corresponding MKdV solitons (figure 3
c) are found to decrease concavely (unlike KdV solitons figure 3
a) with
$v_{e0}$
for different
$v_{i0}=0.5$
(i), 1(ii), 1.5(iii), 2(iv), 2.5(v). The range of
$v_{e0}$
for the existence of MKdV soliton in this case is reduced to
$v_{e0}=18$
for
$v_{i0}=2.5$
when
$\unicode[STIX]{x1D6FC}=0.8$
which does not exist for
$\unicode[STIX]{x1D6FC}0.1$
within the limit.
Figure 3. (a,b) Amplitudes of compressive and rarefactive KdV solitons versus electron streaming speed
$v_{e0}$
for fixed
$v_{i0}=2(\text{i})$
, 3(ii), 4(iii), 5(iv)
$\ldots$
26(xiii),
$\unicode[STIX]{x1D70E}=0.001$
,
$Z_{d}=270$
and
$\unicode[STIX]{x1D6FC}=0.1$
. (c) Amplitudes of compressive MKdV solitons versus electron streaming speed
$v_{e0}$
for fixed
$v_{i0}=0.5(\text{i})$
, 1(ii), 1.5(iii), 2(iv), 2.5(v),
$\unicode[STIX]{x1D70E}=0.001$
,
$Z_{d}=270$
and
$\unicode[STIX]{x1D6FC}=0.8$
.
For small streaming speed values of ions
$v_{i0}=0.1(\text{i})\ldots 1.5(\text{viii}),$
the small amplitude compressive KdV solitons are found to convexly diminish to zero with
$v_{e0}$
at
$v_{e0}\leqslant 70$
for
$Z_{d}=500,\unicode[STIX]{x1D70E}=0.001,\unicode[STIX]{x1D6FC}=0.1$
(figure 4
a). After diminishing to zero, the solitons become rarefactive when the electron streaming speed exceeds (
$v_{e0}>$
) 80. The small amplitude KdV compressive solitons have attained relatively high amplitudes against each small value of
$v_{i0}=0.1(\text{i}),0.3(\text{ii}),0.5(\text{iii}),0.7(\text{iv})\ldots 1.3(\text{vii}),1.5(\text{viii})$
corresponding to respective values of
$v_{e0}$
but in its lower regimes (figure 4
a). The compressive character of the KdV solitons is rightly forced to extinction when the electrons initial streaming speed attains a very high value supplemented by the high negative dust charge
$Z_{d}$
against very small ion initial streaming speed
$v_{i0}<1.5$
. Further, it appears to generate rarefactive solitons, indicating attainment of high amplitudes. The complex representation is seen in figure 4(b). The KdV solitons are restricted to a small amplitude limit less than 1. For the small ion streaming speed
$v_{i0}<1.5$
, the electron streaming speed
$v_{\text{e0}}$
, exceeding 100 in this case, dominates imbibing to cross the limit of existence (from computation work). Moreover, the nonlinear coefficient
$p=0$
identifies the region of non-existence of KdV solitons (
$\unicode[STIX]{x1D711}_{0}=3c/p$
) in the vicinity of
$v_{\text{e0}}=100$
which keeps open the search for the MKdV solitons. This causes the sudden change of amplitudes indicating growth to infinity.
Figure 4. Amplitudes of compressive KdV solitons versus electron streaming speed
$v_{e0}$
for fixed
$v_{i0}=0.1(\text{i}),0.3(\text{ii}),0.5(\text{iii}),0.7(\text{iv})\ldots 1.3(\text{vii}),1.5(\text{viii}),\unicode[STIX]{x1D70E}=0.001,Z_{d}=500$
and
$\unicode[STIX]{x1D6FC}=0.1$
.
The MKdV compressive solitons are found to exist against very small values of initial streaming speed of the ions
$v_{i0}=0.1(\text{i}),0.2,1.3(\text{vii})$
but not for greater values of electron streaming speed (figure 5) for
$Z_{d}=500,\unicode[STIX]{x1D70E}=0.001,\unicode[STIX]{x1D6FC}=0.1$
unlike the existence of KdV solitons of both kinds (figure 4). Besides, the only compressive KdV solitons appear to vanish (convexly) in a shorter interval
$v_{e0}\leqslant 30$
(figure 3) but the MKdV solitons appear to vanish (concavely) at a much expanded upper limit of
$v_{e0}\leqslant 70$
(figure 5). For the same set of parametric values, the amplitudes of both compressive and rarefactive KdV solitons (figure 4) are much smaller than those of MKdV compressive solitons (figure 5).
Figure 5. Amplitudes of compressive MKdV solitons versus electron streaming speed
$v_{e0}$
for fixed
$v_{i0}=0.1(\text{i}),0.3(\text{ii}),0.5(\text{iii}),0.7(\text{iv})\ldots 1.3(\text{vii}),\unicode[STIX]{x1D70E}=0.001,Z_{d}=500$
and
$\unicode[STIX]{x1D6FC}=0.1$
.
Further, with the inclusion of higher-order nonlinearity in the resulting MKdV equation, only compressive solitons of much higher amplitudes are found to exist but in a contracted range of
$v_{e0}$
(figure 5) from either side corresponding to the same set of values of
$v_{i0}$
(figure 4
a). In growth of amplitudes, it appears to disregard the effects of higher electron streaming speed and negative dust charges
$Z_{d}$
in this situation.
The amplitudes of the compressive KdV solitons are found to increase uniformly but nonlinearly (figure 6) with
$Z_{d}$
corresponding to each value of small ion streaming speed
$v_{i0}=0.1(\text{i}),0.3(\text{ii}),0.5(\text{iii}),0.7(\text{iv}),0.9(\text{v}),v_{e0}=5,\unicode[STIX]{x1D70E}=0.001,\unicode[STIX]{x1D6FC}=0.1$
. The increase of the number of dust charges
$Z_{d}$
is seen to contribute in intensive growth of amplitudes of compressive KdV solitons. It appears that the flux of negative dust charges at large numbers to the plasma compound compresses the plasma state taking the advantage of small pairs of ions and electrons streaming. The smaller the value of the ion streaming speed the smaller is the amplitude of the compressive solitons but at its higher value supplemented by high accumulation of negative dust charges
$Z_{d}$
from the dust component, the growth becomes much higher turning the amplitude smaller after some stage of
$Z_{d}$
.
Figure 6. Amplitudes of compressive KdV solitons versus
$Z_{d}$
for fixed
$v_{i0}=0.1(\text{i}),0.3(\text{ii}),0.5(\text{iii}),0.7(\text{iv}),0.9(\text{v}),\unicode[STIX]{x1D70E}=0.001,v_{e0}=5$
and
$\unicode[STIX]{x1D6FC}=0.1$
.
The amplitudes of the only compressive MKdV solitons are found to increase quite nonlinearly with
$v_{i0}$
(figure 7) for high values of electron streaming speeds
$v_{e0}=31(\text{i}),33(\text{ii})\ldots 49(x)$
and
$Z_{d}=90,\unicode[STIX]{x1D70E}=0.001,\unicode[STIX]{x1D6FC}=0.1$
. Smaller value of
$v_{e0}$
like 31(i) is seen to produce high amplitude MKdV compressive solitons throughout the range of
$v_{i0}$
. Due to higher-order nonlinearity, the nonlinear monotonic growth of amplitudes of MKdV solitons, we observe, is rather supported by the almost equal streaming pairs of ions and electrons for relatively small
$Z_{d}=90$
.
Figure 7. Amplitudes of compressive MKdV solitons versus electron streaming speed
$v_{i0}$
for fixed
$v_{e0}=31(\text{i}),33(\text{ii}),35(\text{iii}),37(\text{iv})\ldots 49(\text{x}),\unicode[STIX]{x1D70E}=0.001,Z_{d}=90$
and
$\unicode[STIX]{x1D6FC}=0.1$
.
For small ion streaming speed, namely
$v_{i0}=0.1(\text{i}),0.15(\text{ii}),0.2(\text{iii}),0.25(\text{iv}),0.3(\text{v}),$
the amplitudes of the compressive MKdV solitons slowly increase from linear (for small
$Z_{d}$
) to nonlinear as
$Z_{d}$
increases for fixed
$v_{e0}=20,\unicode[STIX]{x1D70E}=0.001,\unicode[STIX]{x1D6FC}=0.8$
(figure 8). Of course, the smaller the value of
$v_{i0}(=0.1)$
, the higher are the values of soliton amplitude in the whole lower range of
$Z_{d}$
, which are found to be gradually higher in the upper range (here) of
$Z_{d}$
.
Figure 8. Amplitudes of compressive MKdV solitons versus
$Z_{d}$
for fixed
$v_{i0}=0.1(\text{i}),0.15(\text{ii}),0.2(\text{iii})\ldots 0.3(\text{v}),\unicode[STIX]{x1D70E}=0.001,v_{e0}=20$
and
$\unicode[STIX]{x1D6FC}=0.8$
.
Corresponding to the higher value of
$v_{i0}=78$
but in the higher range of electron streaming speed
$v_{e0}=176(\text{i}),178(\text{ii})\ldots 194(\text{x}),$
the amplitudes of compressive MKdV solitons remain almost constant (figure 9) for the entire range of
$Z_{d}$
including its higher range (figure 9
a). The linear growth of amplitudes is clear in figure 9(b). Comparing the results of (figure 8) and (figure 9
a), it is observed, that the growth of amplitude of the compressive soliton (in case of higher-order nonlinearity) is dependent on the initial streaming speed of
$v_{e0},v_{i0}$
and
$Z_{d}$
. In contrast to earlier figures of KdV soliton amplitudes, the MKdV soliton amplitudes are found not to be much dependent on
$Z_{d}$
and
$v_{e0}$
, rather it is submissive to higher-order nonlinearity.
Figure 9. Amplitudes of compressive MKdV solitons versus
$Z_{d}$
for fixed
$v_{e0}=176(\text{i}),178(\text{ii}),180(\text{iii})\ldots 194(\text{x}),\unicode[STIX]{x1D70E}=0.001,v_{i0}=78$
and
$\unicode[STIX]{x1D6FC}=0.1$
.
The nature of amplitude growth of KdV compressive solitons with temperature
$\unicode[STIX]{x1D6FC}$
remains almost constant for all
$v_{i0}$
. For
$v_{i0}=0.2(\text{i}){-}0.8(\text{iv})$
small amplitudes of the compressive solitons are seen to increase up to some
$\unicode[STIX]{x1D6FC}$
but for
$v_{i0}=1(\text{v}){-}2(\text{x})$
, it is seen (figure 10) that the amplitudes of solitons remain constant, becoming smaller and smaller after some
$\unicode[STIX]{x1D6FC}$
. But the small amplitude solitons reflect increasing growth with
$\unicode[STIX]{x1D6FC}$
for all
$v_{i0}\leqslant 1$
.
Figure 10. Amplitudes of compressive KdV solitons versus
$\unicode[STIX]{x1D6FC}$
for fixed
$v_{i0}=0.2(\text{i}),0.4(\text{ii}),0.6(\text{iii}),0.8(\text{iv})\ldots 2(\text{x}),\unicode[STIX]{x1D70E}=0.001$
and
$Z_{d}=200$
.
The parametric limitations of the parameters
$v_{i0},v_{e0},Z_{d},\unicode[STIX]{x1D6FC},$
required for the existence of DIA waves in plasmas under the small amplitude consideration (
${<}$
1 for the perturbative method) and variable temperatures are shown almost in all figures in this investigation. These are quite new results in this direction.
One of the primary objectives of space probes is to investigate the properties of the dust surrounding space bodies like the Moon or Mars. The dust acoustic waves are basically low frequency waves in plasmas and for stationary background mapping of the massive dust particles, spectrometer insertion into a space vehicle is rather more convenient. For the flux of solar flares, solar winds in interplanetary space at high altitudes, the temperature of the ions and electrons vary causing release of charge (negative or positive) to stationary dust and the system turns into one of higher-order nonlinearity inviting the MKdV equation for steady waves. The temperature variations of the plasma species posing behavioural changes of the dust in DIA waves may be helpful from our studies to know the character of the dust in space probes. Further, the proposed information of the parameters may be of great help for experimentalists in using the Q-machine.
The plasma scenario is greatly affected by frequent bursts of solar winds of different kinds and magnetic storms. The nonlinearity developed in space plasmas due to various factors creates hazards to space vehicles and probes. The study of nonlinear DIA waves in the presence of dust predicting the character of plasma parameters in space, which are a kind of slow and stable waves, may be a great help to meet these hazards in some extent.
Though not exactly similar, Verheest, Olivier & Hereman (Reference Verheest, Olivier and Hereman2016) have recently shown a comparative and nice representative structure of KdV and MKdV solitons in plasmas but with quartic nonlinearity for the latter.
The characteristic change of the DIA waves shown in the discussion, subject to variations of pressure, is the important highlight of our investigation.
Acknowledgements
The Author B.C.K. has acknowledged with sincere gratitude the University of Grants Commission (UGC), Govt. of India for granting Professor-Emeritus Fellowship award to pursue future research for two years. Further the authors are grateful to the referees for constructive suggestions in the manuscript.
