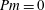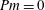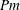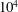1 Introduction
In recent years instabilities in rotating conducting fluids under the influence of magnetic fields have become of high interest. Especially in view of astrophysical applications, the consideration of non-uniform rotational rates
$\unicode[STIX]{x1D6FA}$
with
$\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D6FA}(R)$
is relevant with
$R$
the distance from the rotation axis. It has been known for a long time that differential rotation with negative shear (
$\text{d}\unicode[STIX]{x1D6FA}/\text{d}R<0$
, ‘sub-rotation’) becomes unstable under the influence of an axial field (Velikhov Reference Velikhov1959; Balbus & Hawley Reference Balbus and Hawley1991). When considered separately, both ingredients of this magnetorotational instability (MRI), i.e. the axial field and also the rotation, are stable. The full system proves to be unstable if and only if the fluid is sub-rotating. For ideal fluids the criterion of stability against axisymmetric perturbations of differential rotation under the presence of toroidal fields
$B_{\unicode[STIX]{x1D719}}$
reads
$$\begin{eqnarray}\frac{1}{R^{3}}\frac{\text{d}}{\text{d}R}(R^{2}\unicode[STIX]{x1D6FA})^{2}-\frac{R}{\unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D70C}}\frac{\text{d}}{\text{d}R}\left(\frac{B_{\unicode[STIX]{x1D719}}}{R}\right)^{2}>0,\end{eqnarray}$$
where
$\unicode[STIX]{x1D707}_{0}$
is the magnetic permeability and
$\unicode[STIX]{x1D70C}$
the mass density (Michael Reference Michael1954).
The stability problem of toroidal fields plus differential rotation in a cylindrical geometry has been studied by several authors often considering the fluid as ideal and/or the perturbations as axisymmetric (Chandrasekhar Reference Chandrasekhar1961; Gotoh Reference Gotoh1962; Howard & Gupta Reference Howard and Gupta1962; Chanmugam Reference Chanmugam1979; Fearn Reference Fearn1984; Balbus & Hawley Reference Balbus and Hawley1992; Knobloch Reference Knobloch1992; Dubrulle & Knobloch Reference Dubrulle and Knobloch1993; Ogilvie & Pringle Reference Ogilvie and Pringle1996; Terquem & Papaloizou Reference Terquem and Papaloizou1996; Pessah & Psaltis Reference Pessah and Psaltis2005; Shalybkov Reference Shalybkov2006). In view of possible experiments, in the present paper the perturbations are considered as non-axisymmetric, existing in a diffusive fluid under the influence of a current-free toroidal magnetic field.
After (1.1), solid-body rotation and rotation laws with positive shear (
$\text{d}\unicode[STIX]{x1D6FA}/\text{d}R>0$
, ‘super-rotation’) are stabilized by the magnetic field unless the field strongly increases outwards. The profiles
$B_{\unicode[STIX]{x1D719}}\propto 1/R$
(current free between the cylinders) and
$B_{\unicode[STIX]{x1D719}}\propto R$
(
$z$
-pinch, homogeneous axial electric current) cannot destabilize rotation increasing radially if only axisymmetric perturbations are considered. It has even been demonstrated that for fields with
$B_{\unicode[STIX]{x1D719}}\propto 1/R$
all Taylor–Couette flows are stable against axisymmetric perturbations (Herron & Soliman Reference Herron and Soliman2006). The azimuthal magnetorotational instability (AMRI) of differential rotation plus azimuthal fields that are current free between the cylinders is thus basically non-axisymmetric. Standard MRI and AMRI have in common that, in both cases, the magnetic background fields are force free and the combination of two stable components leads to instability. If the azimuthal magnetic field is not current free and axial electric background currents exist, we speak about Tayler instability (TI), which even exists without any rotation.
Taylor–Couette flows with positive shear are the prototype hydrodynamic stability for moderate Reynolds numbers (Wendt Reference Wendt1933; Schultz-Grunow Reference Schultz-Grunow1959). For finite, but very large, Reynolds numbers, the existence of a linear instability for super-rotating Taylor–Couette flow has been reported recently (Deguchi Reference Deguchi2017). All the more surprising is the finding that weak and stable magnetic azimuthal fields can also destabilize flows with radially increasing
$\unicode[STIX]{x1D6FA}$
of rather low Reynolds number if non-axisymmetric perturbations are taken into account (Stefani & Kirillov Reference Stefani and Kirillov2015; Rüdiger et al.
Reference Rüdiger, Schultz, Gellert and Stefani2016). Even in this particular combination of two highly stable ingredients the resulting MHD flow becomes unstable. We shall also demonstrate that the radial profile of the fields – if not too steep – does not play an important role for the question of stability or instability. On the other hand, the new instability is a double-diffusive phenomenon as it does not appear if the molecular viscosity and the molecular magnetic resistivity are equal. Contrary to AMRI, the standard MRI with axial magnetic fields and differential rotation with negative shear has no counterpart for positive shear.
The equations of the problem are
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{U}}{\unicode[STIX]{x2202}t}+(\boldsymbol{U}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{U}=-\frac{1}{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D735}P+\unicode[STIX]{x1D708}\unicode[STIX]{x0394}\boldsymbol{U}+\frac{1}{\unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D70C}}\text{curl}\,\boldsymbol{B}\times \boldsymbol{B}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{B}}{\unicode[STIX]{x2202}t}=\text{curl}(\boldsymbol{U}\times \boldsymbol{B})+\unicode[STIX]{x1D702}\unicode[STIX]{x0394}\boldsymbol{B}, & \displaystyle\end{eqnarray}$$
with
$\operatorname{div}\boldsymbol{U}=\operatorname{div}\boldsymbol{B}=0$
for an incompressible fluid.
$\boldsymbol{U}$
is the velocity,
$\boldsymbol{B}$
the magnetic field vector,
$P$
the pressure,
$\unicode[STIX]{x1D708}$
the kinematic viscosity and
$\unicode[STIX]{x1D702}$
is the magnetic resistivity. The basic state in the cylindrical system with the coordinates (
$R,\unicode[STIX]{x1D719},z$
) is
$U_{R}=U_{z}=B_{R}=B_{z}=0$
for the poloidal components and
$\unicode[STIX]{x1D6FA}=a_{\unicode[STIX]{x1D6FA}}+b_{\unicode[STIX]{x1D6FA}}/R^{2}$
for the rotation law with the constants
$$\begin{eqnarray}\displaystyle a_{\unicode[STIX]{x1D6FA}}=\frac{\unicode[STIX]{x1D707}-r_{\text{in}}^{2}}{1-r_{\text{in}}^{2}}\unicode[STIX]{x1D6FA}_{\text{in}},\quad b_{\unicode[STIX]{x1D6FA}}=\frac{1-\unicode[STIX]{x1D707}}{1-r_{\text{in}}^{2}}\unicode[STIX]{x1D6FA}_{\text{in}}R_{\text{in}}^{2}. & & \displaystyle\end{eqnarray}$$
Here
$r_{\text{in}}=R_{\text{in}}/R_{\text{out}}$
is the ratio of the inner cylinder radius
$R_{\text{in}}$
and the outer cylinder radius
$R_{\text{out}}$
.
$\unicode[STIX]{x1D6FA}_{\text{in}}$
and
$\unicode[STIX]{x1D6FA}_{\text{out}}$
are the angular velocities of the inner and outer cylinders, respectively. With the definition
$$\begin{eqnarray}\unicode[STIX]{x1D707}=\frac{\unicode[STIX]{x1D6FA}_{\text{out}}}{\unicode[STIX]{x1D6FA}_{\text{in}}}\end{eqnarray}$$
super-rotation is represented by
$\unicode[STIX]{x1D707}>1$
.
For the magnetic field the stationary solution is
$$\begin{eqnarray}\displaystyle B_{\unicode[STIX]{x1D719}}=a_{B}R+\frac{b_{B}}{R}. & & \displaystyle\end{eqnarray}$$
The radial magnetic profile
$B_{\unicode[STIX]{x1D719}}\propto R$
is due to an applied homogeneous axial electric current while
$B_{\unicode[STIX]{x1D719}}\propto 1/R$
is current free in the fluid. We define
$\unicode[STIX]{x1D707}_{B}=B_{\text{out}}/B_{\text{in}}$
. The current-free field is then given by
$\unicode[STIX]{x1D707}_{B}=r_{\text{in}}$
and the field in the
$z$
-pinch is
$\unicode[STIX]{x1D707}_{B}=1/r_{\text{in}}$
. Almost always in the present paper a narrow gap with
$r_{\text{in}}=0.9$
is considered.
The dimensionless physical parameters of the system are the magnetic Prandtl number
$Pm$
, the Hartmann number
$Ha$
and the Reynolds number
$Re$
, i.e.
$$\begin{eqnarray}\displaystyle Pm=\frac{\unicode[STIX]{x1D708}}{\unicode[STIX]{x1D702}},\quad Ha=\frac{B_{\text{in}}D}{\sqrt{\unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D70C}\unicode[STIX]{x1D708}\unicode[STIX]{x1D702}}},\quad Re=\frac{\unicode[STIX]{x1D6FA}_{\text{out}}D^{2}}{\unicode[STIX]{x1D708}}. & & \displaystyle\end{eqnarray}$$
The magnetic Reynolds number is
$Rm=Pm\cdot Re$
. The parameters combine to the magnetic Mach number
$$\begin{eqnarray}\displaystyle Mm=\frac{R_{\text{out}}}{D}\frac{\sqrt{Pm}Re}{Ha}, & & \displaystyle\end{eqnarray}$$
indicating whether the rotation energy dominates the magnetic energy or not. The parameter
$D=R_{\text{out}}-R_{\text{in}}$
is the gap width. The Hartmann number is defined by the magnetic field on the inner wall where it is maximal. If the Reynolds number is defined with the rotation rate of the outer cylinder, then
$Re/\unicode[STIX]{x1D707}$
describes the Reynolds number of the inner cylinder.
$\unicode[STIX]{x1D707}=\infty$
gives a model where the inner cylinder rests.
The variables
$\boldsymbol{U}$
,
$\boldsymbol{B}$
and
$P$
are split into mean and fluctuating components, i.e.
$\boldsymbol{U}=\bar{\boldsymbol{U}}+\boldsymbol{u}$
,
$\boldsymbol{B}=\bar{\boldsymbol{B}}+\boldsymbol{b}$
and
$P=\bar{P}+p$
. The bars from the variables are immediately dropped, so that the uppercase letters
$\boldsymbol{U}$
,
$\boldsymbol{B}$
and
$P$
represent the background quantities. By developing the disturbances
$\boldsymbol{u}$
,
$p$
and
$\boldsymbol{b}$
into normal modes the solutions of the linearized magnetohydrodynamics (MHD) equations
$$\begin{eqnarray}[\boldsymbol{u},\boldsymbol{b},p]=[\boldsymbol{u}(R),\boldsymbol{b}(R),p(R)]\text{e}^{\text{i}(\unicode[STIX]{x1D714}t+kz+m\unicode[STIX]{x1D719})},\end{eqnarray}$$
are considered for axially unbounded cylinders. Here
$k$
is the axial wavenumber of the perturbation,
$m$
its azimuthal wavenumber and
$\unicode[STIX]{x1D714}$
the complex frequency including growth rate as its imaginary part and a drift frequency
$\unicode[STIX]{x1D714}_{\text{dr}}$
as its real part. A linear code is used to solve the resulting set of linearized ordinary differential equations for the radial functions of flow, field and pressure fluctuations. The solutions are optimized with respect to the Reynolds number for given Hartmann number by varying the wavenumber. Only solutions for
$m=1$
are here discussed. The hydrodynamic boundary conditions at the cylinder walls are the rigid ones, i.e.
$u_{R}=u_{\unicode[STIX]{x1D719}}=u_{z}=0$
. The cylinders are assumed to be perfectly conducting or – in a few cases – insulating. For the conducting walls the fluctuations
$\boldsymbol{b}$
must fulfil
$\text{d}b_{\unicode[STIX]{x1D719}}/\text{d}R+b_{\unicode[STIX]{x1D719}}/R=b_{R}=0$
at
$R_{\text{in}}$
and
$R_{\text{out}}$
so that ten boundary conditions exist for the set of ten differential equations. For
$B_{z}=0$
one can easily show that the system is degenerate under the transformation
$m\rightarrow -m$
so that all eigenvalues (for specific
$Re$
and
$Ha$
) are valid for each pair
$m=\pm 1$
.
2 Azimuthal magnetorotational instability
Consider rotation laws where the outer cylinder rotates with higher frequency than the inner cylinder. For the small magnetic Prandtl number of
$Pm=10^{-5}$
figure 1 presents the lines of marginal instability (i.e. for vanishing growth rate) for the two rotation profiles with
$\unicode[STIX]{x1D707}=1.9$
and
$\unicode[STIX]{x1D707}=2.3$
for a narrow gap with
$r_{\text{in}}=0.9$
. The magnetic field between the perfectly conducting cylinders is fixed to the vacuum type,
$B_{\unicode[STIX]{x1D719}}\propto 1/R$
. The form of the resulting neutral lines corresponds to the well-known form for sub-rotation as a tilted cone with both branches having a positive slope (Hollerbach, Teeluck & Rüdiger Reference Hollerbach, Teeluck and Rüdiger2010; Rüdiger, Kitchatinov & Hollerbach Reference Rüdiger, Kitchatinov and Hollerbach2013). Absolute minima of the Hartmann number and the Reynolds number exist, below which the rotation law is stable. Above the minima the instability domain is always limited by two critical values of the Hartmann number or the Reynolds number. For a given supercritical Reynolds number there is a minimum magnetic field for the instability and there is a maximum magnetic field destructing the instability. Also the Reynolds number can be too small or too large for a given Hartmann number. Above the upper branch of the instability curve the rotational shear is too strong to support non-axisymmetric perturbations. Here we are in particular interested in the values of the absolute minimum
$Ha_{\min }$
of the Hartmann number for neutral stability in order to discuss the possibility of laboratory experiments. Without magnetic field the flow is stable while the vertical dotted lines in figure 1 characterize the minimum magnetic field via
$Ha_{\text{min}}$
.
Figure 1. Instability cones for two rotation profiles with
$\unicode[STIX]{x1D707}=1.9$
and
$\unicode[STIX]{x1D707}=2.3$
. By the vertical dotted lines the minimum Hartmann numbers
$Ha_{\min }$
are defined.
$\unicode[STIX]{x1D707}_{B}=r_{\text{in}}=0.9$
,
$m=\pm 1$
,
$Pm=10^{-5}$
. The stability lines are also valid for
$Pm=0$
. Perfectly conducting cylinders.
Figure 2. The axial wavenumber
$kD$
(a) and the drift frequency
$\unicode[STIX]{x1D714}_{\text{dr}}/\unicode[STIX]{x1D6FA}_{\text{out}}$
(b) along the lines of marginal instability for
$Pm=10^{-5}$
(
$\unicode[STIX]{x1D707}=5,2.3,1.9$
, from left to right) and
$Pm=10$
(
$\unicode[STIX]{x1D707}=5$
).
$\unicode[STIX]{x1D707}_{B}=r_{\text{in}}=0.9$
,
$m=\pm 1$
. Perfectly conducting cylinders.
Figure 2(a) gives the optimized axial wavenumbers of the instability normalized with the gap width
$D$
along the two branches of instability for small and large
$Pm$
. The axial cell size is
$\unicode[STIX]{x1D6FF}z\simeq \unicode[STIX]{x03C0}D/k$
. Cells with
$k<\unicode[STIX]{x03C0}$
are thus prolate while cells with
$k>\unicode[STIX]{x03C0}$
are oblate with respect to the rotation axis. The limit
$k=\unicode[STIX]{x03C0}$
for nearly circular cells is marked by a horizontal dotted line. The plot demonstrates that the cell geometry strongly depends on the magnetic Prandtl number. For small
$Pm$
also the wavenumbers are small hence the cells are prolate or circular in the (
$R,z$
) plane. Along the strong-field (lower) branch of the instability cone the axial wavenumbers exceed those of the low-field (upper) branch where the cells are rather long in axial direction. For
$Pm\gg 1$
, however, the wavenumbers at both branches of the cone are larger than
$\unicode[STIX]{x03C0}$
so that the cells are always very flat.
Also the drift rates possess a strong
$Pm$
-dependence. The drift values as given in figure 2(b) are the real parts
$\unicode[STIX]{x1D714}_{\text{dr}}$
of the frequency
$\unicode[STIX]{x1D714}$
of the Fourier mode of the instability normalized with the rotation rate of the outer cylinder. Because of
$$\begin{eqnarray}\frac{\dot{\unicode[STIX]{x1D719}}}{\unicode[STIX]{x1D6FA}_{\text{out}}}=-\frac{\unicode[STIX]{x1D714}_{\text{dr}}}{m\unicode[STIX]{x1D6FA}_{\text{out}}}\end{eqnarray}$$
the azimuthal migration
$\dot{\unicode[STIX]{x1D719}}$
has the opposite sign of
$\unicode[STIX]{x1D714}_{\text{dr}}$
. For AMRI with negative shear we always found that the pattern migrates for all
$Pm$
in positive
$\unicode[STIX]{x1D719}$
-direction (Rüdiger et al.
Reference Rüdiger, Gellert, Schultz, Hollerbach and Stefani2014). For Tayler instability under the influence of radially increasing rotation the situation is more complicated as the pattern counter-rotates for small
$Pm$
while it co-rotates for
$Pm>1$
. Figure 2 shows similar results. For small
$Pm$
positive
$\unicode[STIX]{x1D714}_{\text{dr}}$
occur and the perturbation pattern indeed rotates retrograde. Large
$Pm$
provide negative drift values hence the pattern migrates in the direction of the rotation. For
$\unicode[STIX]{x1D714}_{\text{dr}}/\unicode[STIX]{x1D6FA}_{\text{out}}=-1$
the pattern rotates just as the outer cylinder.
To see the influence of the boundary condition figure 3(a) gives the stability map for
$\unicode[STIX]{x1D707}=5$
for the two cases with perfectly conducting walls and insulating boundary conditions. The small magnetic Prandtl number of
$Pm=10^{-5}$
characterizes liquid sodium. For vacuum boundaries the rotation laws are much more stable than for perfectly conducting conditions. Note that
$Ha_{\min }$
for insulating cylinders exceed the values of
$Ha_{\min }$
for perfectly conducting cylinders by a factor of 4. Also for AMRI with negative shear the critical Hartmann numbers and the Reynolds numbers for vacuum conditions strictly lie above the values for perfectly conducting conditions. One finds from figures 1–3 the expected trend with
$\unicode[STIX]{x1D707}$
for the minimum Hartmann number. For perfectly conducting boundaries and
$Pm=10^{-5}$
it decreases from
$Ha_{\min }\simeq 700$
for the flat rotation law with
$\unicode[STIX]{x1D707}=1.9$
to
$Ha_{\min }\simeq 200$
for the steeper rotation law with
$\unicode[STIX]{x1D707}=5$
. Below we shall discuss whether the reduction of
$Ha_{\min }$
by growing rotation ratio
$\unicode[STIX]{x1D707}$
is continued or not for
$\unicode[STIX]{x1D707}\rightarrow \infty$
, i.e. for stationary inner cylinder.
Figure 3. Stability maps for
$\unicode[STIX]{x1D707}=5$
for perfectly conducting cylinders for
$Pm=10^{-5}$
(a) and
$Pm\gg 1$
(b). The lines for
$Pm=100$
and
$Pm=1000$
are almost indistinguishable. Panel (a) also contains the line of neutral stability for insulating cylinders; the curve for
$Pm=10$
(b) holds for insulating and perfectly conducting boundary conditions. Solutions for
$Pm=1$
do not exist.
$Mm<1$
for all curves.
$\unicode[STIX]{x1D707}_{B}=r_{\text{in}}=0.9$
.
Figure 3(b) demonstrates instability also for
$Pm\gg 1$
. The stability curves for
$Pm=10$
,
$Pm=100$
and
$Pm=1000$
are given for perfectly conducting boundary conditions in the
$Ha,Rm$
plane with
$Rm$
as the magnetic Reynolds number. Note that in this representation the minimum values for Hartmann number and magnetic Reynolds number hardly depend on
$Pm$
. For
$Pm\rightarrow \infty$
the critical rotation rate appears to scale with
$Rm$
. The curve for
$Pm=10$
simultaneously holds for the boundary conditions of both perfectly conducting and insulating cylinders. For
$Pm>1$
the large gaps between these curves known for
$Pm<1$
disappear. The role of the boundary conditions for the excitation of the instability strongly depends on the choice of the magnetic Prandtl number.
3 Role of the magnetic Prandtl number
We should also be interested to model containers with resting inner cylinder described by
$\unicode[STIX]{x1D707}\rightarrow \infty$
which our code approximates for very high
$\unicode[STIX]{x1D707}$
-values. One finds that already
$\unicode[STIX]{x1D707}=128$
gives an excellent approximation of this rotation law. Figure 4(a) presents essential parts of the instability cones for
$\unicode[STIX]{x1D707}=128$
for decreasing magnetic Prandtl numbers in the
$(Ha,Re)$
plane. For small
$Pm$
the curves perfectly coincide. The eigensolutions for neutral stability, therefore, scale with
$Re$
and
$Ha$
for
$Pm\rightarrow 0$
. Hence, the numerical values of
$Ha$
and
$Re$
calculated with the inductionless approximation
$Pm=0$
can also be used for the small magnetic Prandtl numbers of gallium (
$Pm\simeq 10^{-6}$
) or even liquid sodium (
$Pm\simeq 10^{-5}$
). This approximation only models the relation
$\unicode[STIX]{x1D708}\ll \unicode[STIX]{x1D702}$
, it does not mean that
$\unicode[STIX]{x1D708}=0$
(Roberts Reference Roberts1967). Below we shall demonstrate that the curves of neutral stability always scale with
$Ha$
and
$Re$
within this approximation. Note also how clear in figure 4(a) the minimum Hartmann number
$Ha_{\min }$
stands at a constant value for the various small
$Pm$
.
Figure 4. (a) Lines of neutral stability in the (
$Ha,Re$
) plane for various magnetic Prandtl numbers (marked) for almost stationary inner cylinder. For small
$Pm$
the lines coincide. Their minimum Hartmann number is
$Ha_{\min }\simeq 147$
. Stars denote the
$Ha_{\min }$
. (b) Growth rate normalized with
$\unicode[STIX]{x1D6FA}_{\text{out}}$
for
$Re=1000$
and three magnetic Prandtl numbers as indicated.
$\unicode[STIX]{x1D707}_{B}=r_{\text{in}}=0.9$
,
$\unicode[STIX]{x1D707}=128$
. Perfectly conducting cylinders.
For applications also the growth rates of the instability as the negative imaginary part of the Fourier frequency are relevant. They are normalized with the rotation rate
$\unicode[STIX]{x1D6FA}_{\text{out}}$
of the outer cylinder for a fixed Reynolds number and for almost-stationary inner cylinder by figure 4(b). The common Reynolds number
$Re=1000$
is the maximal value in (a). By definition the growth rates vanish for the marginal values of the Hartmann number. For
$\unicode[STIX]{x1D714}_{\text{gr}}/\unicode[STIX]{x1D6FA}_{\text{out}}=1$
the growth time relative to the rotation time (of the outer cylinder) is
$\unicode[STIX]{x1D70F}_{\text{gr}}/\unicode[STIX]{x1D70F}_{\text{rot}}=1/2\unicode[STIX]{x03C0}$
. We find for supercritical magnetic fields finite values of order 0.2 leading to the typical relation
$\unicode[STIX]{x1D70F}_{\text{gr}}\simeq \unicode[STIX]{x1D70F}_{\text{rot}}$
. The
$Pm$
-dependence is only weak and disappears for
$Pm\rightarrow 0$
. The lines converge for sufficiently small magnetic Prandtl number. Rotation with radially increasing frequency, therefore, magnetically decays and grows with the time scale of rotation itself – similar to the other forms of magnetorotational instability.
Figure 5 gives the minimum Hartmann number
$Ha_{\min }$
together with the associated Reynolds numbers for strong (
$\unicode[STIX]{x1D707}=128$
) positive shear in dependence on
$Pm$
. One finds convergence for both eigenvalues for
$Pm\rightarrow 0$
. The curves basically scale with
$Ha$
and
$Re$
for
$Pm\rightarrow 0$
in both cases.
Figure 5. Minimum Hartmann number
$Ha_{\min }$
and the corresponding Reynolds numbers (
$Pm<1$
) and magnetic Reynolds numbers (
$Pm>1$
) dependence on
$Pm$
for
$\unicode[STIX]{x1D707}=128$
. For
$Pm=1$
solutions with positive growth rates do not exist.
$\unicode[STIX]{x1D707}_{B}=r_{\text{in}}=0.9$
. Perfectly conducting cylinders.
For
$Pm<1$
the Reynolds number takes a minimum at
$Pm\simeq 0.1$
. For even larger
$Pm$
it grows to infinity if
$Pm\rightarrow 1$
. No solution for
$Pm=1$
exists. For even larger
$Pm$
, however, the instability is reanimated with Hartmann numbers of the same order as for
$Pm<1$
and rather low magnetic Reynolds numbers. Even for large magnetic Prandtl numbers the magnetic Mach number remains smaller than unity. Instabilities which only exist for
$\unicode[STIX]{x1D708}\neq \unicode[STIX]{x1D702}$
belong to the class of double-diffusive instabilities (Acheson Reference Acheson1978). They do not appear for
$Pm=1$
what possibly means that they do not exist in ideal fluids. Stefani & Kirillov (Reference Stefani and Kirillov2015) derived eigenvalues for rotation laws with positive shear and for
$Pm=0$
in a short-wave approximation without boundary conditions, demonstrating the local character of the instability.
In figure 5 the eigenvalues
$Re$
and
$Ha$
do not depend on
$Pm$
if
$Pm\rightarrow 0$
. The question is whether the global equation system for the perturbations also possesses solutions for
$Pm=0$
for all
$\unicode[STIX]{x1D707}>1$
or not. We already know that AMRI solutions with negative shear do exist for
$Pm=0$
but only for flows close to the Rayleigh line with
$\unicode[STIX]{x1D707}\leqslant 0.3$
(Hollerbach et al.
Reference Hollerbach, Teeluck and Rüdiger2010). We ask whether such a limit also exists for super-rotation. The standard MRI (with axial fields) for all (negative) shear values does not exist for
$Pm=0$
(Chandrasekhar Reference Chandrasekhar1961). For
$Pm\rightarrow 0$
it scales with the magnetic Reynolds number
$Rm$
leading for small
$Pm$
to very large Reynolds numbers. This is the explanation that the experimental realization of the standard MRI is still an existing challenge.
The dimensionless and linearized equations for the evolution of the flow, field and pressure perturbations in the inductionless (or ‘quasistationary’) approximation for
$Pm=0$
are
$$\begin{eqnarray}\displaystyle Re\left(\frac{\unicode[STIX]{x2202}\boldsymbol{u}}{\unicode[STIX]{x2202}t}+(\boldsymbol{U}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{u}+(\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{U}\right)=-\unicode[STIX]{x1D735}p+\unicode[STIX]{x0394}\boldsymbol{u}+Ha^{2}(\text{curl}\,\boldsymbol{b}\times \boldsymbol{B}+\text{curl}\,\boldsymbol{B}\times \boldsymbol{b})\qquad & & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\text{curl}(\boldsymbol{u}\times \boldsymbol{B})+\unicode[STIX]{x0394}\boldsymbol{b}=0,\end{eqnarray}$$
together with
$\operatorname{div}\boldsymbol{u}=\operatorname{div}\boldsymbol{b}=0$
. The fluctuating and mean magnetic fields are normalized with a characteristic scale
$B_{0}$
of the background field. The background flow
$\boldsymbol{U}$
is normalized with a characteristic flow amplitude
$U_{0}$
, the flow perturbations with
$\unicode[STIX]{x1D702}/D$
and the time with
$D/U_{0}$
. Obviously, the eigenvalues of the system are
$Re$
and
$Ha$
.
The equation system (3.1) and (3.2) is numerically solved with the boundary conditions as described above. Figure 6 shows that for rotation with sufficiently large positive shear
$\unicode[STIX]{x1D707}>\unicode[STIX]{x1D707}_{\text{crit}}>1$
solutions for
$Pm=0$
indeed exist for both sorts of boundary conditions. For perfectly conducting boundaries the dotted vertical line at
$\unicode[STIX]{x1D707}_{\text{crit}}=1.8$
appears as a lower bound for the eigensolutions. As indicated by black dots, for
$Pm=10^{-5}$
solutions also exist for
$\unicode[STIX]{x1D707}<\unicode[STIX]{x1D707}_{\text{crit}}$
but only for very large Reynolds and Hartmann numbers. It is a similar situation as for negative shear where solutions for
$\unicode[STIX]{x1D707}\gtrsim 0.3$
only exist for finite
$Pm$
with very large Reynolds numbers. Note that the lower bounds
$\unicode[STIX]{x1D707}_{\text{crit}}$
are much harder to extrapolate for insulating boundary conditions than for perfectly conducting ones.
After figure 1 the global solution with
$\unicode[STIX]{x1D707}=1.9$
and for
$Pm=10^{-5}$
requires much higher Hartmann numbers and Reynolds numbers than the steeper rotation law with
$\unicode[STIX]{x1D707}=2.3$
. Formally, the critical values for
$\unicode[STIX]{x1D707}=1$
(rigid rotation) are infinite. It is not surprising that both Reynolds numbers and Hartmann numbers are growing for
$\unicode[STIX]{x1D707}\rightarrow 1$
. For
$Pm=0$
, however, no solution for
$\unicode[STIX]{x1D707}<1.9$
has been found. The curves for
$Pm=0$
indeed suggest the existence of the lower limit
$\unicode[STIX]{x1D707}_{\text{crit}}>1$
where the eigenvalues become infinite. Obviously, finite values of the magnetic resistivity stabilize too flat rotation laws with positive shear in the sense as Liu et al. (Reference Liu, Goodman, Herron and Ji2006) found for the axisymmetric modes of helical magnetorotational instability within the inductionless short-wave approximation.
Figure 6.
$Ha_{\min }$
(a), the corresponding Reynolds numbers (b) versus the shear number
$\unicode[STIX]{x1D707}$
for insulating cylinders (blue,
$Pm=0$
) and perfectly conducting cylinders (red,
$Pm=0$
,
$Pm=10^{-5}$
). The vertical dotted lines mark shear of
$\unicode[STIX]{x1D707}_{\text{crit}}=1.8$
. For
$Pm=0$
no solution for
$\unicode[STIX]{x1D707}<1.9$
(red dot) has been found. The dark dot represents the last known solution at
$\unicode[STIX]{x1D707}=1.7$
for
$Pm=10^{-5}$
. Note the crossing of the Reynolds number lines for
$\unicode[STIX]{x1D707}\approx 8$
.
$m=\pm 1$
,
$r_{\text{in}}=0.9$
.
For conducting boundaries also the curves for
$Pm=10^{-5}$
in figure 6 are given showing nearly perfect coincidence with the curve for
$Pm=0$
. The two lines hardly can be distinguished by eyes. The results of calculations in the inductionless approximation can thus be assumed as valid for liquid metals with their small
$Pm$
. Note also that for perfectly conducting cylinders much weaker magnetic fields than for insulating cylinders are needed for the instability onset. For large values of
$\unicode[STIX]{x1D707}$
the ratio of the
$Ha_{\min }$
for insulating and perfectly conducting boundaries is approximately 2.5. The same is true with respect to the Reynolds number but only for small
$\unicode[STIX]{x1D707}$
(flat rotation laws) while for large
$\unicode[STIX]{x1D707}$
(steep rotation laws) the critical Reynolds numbers for vacuum conditions are smaller than for conducting boundary conditions. This behaviour of the eigenvalues is already known from standard MRI of quasi-Keplerian rotation laws with axial fields for different boundary conditions.
We seek the azimuthal drift rates
$\unicode[STIX]{x1D714}_{\text{dr}}/\unicode[STIX]{x1D6FA}_{\text{out}}$
of the solution with the lowest Hartmann number. In figure 2(b) these values for
$Pm=10^{-5}$
only slightly vary with
$\unicode[STIX]{x1D707}$
for
$\unicode[STIX]{x1D707}\leqslant 5$
. Figure 7 also shows the azimuthal drift measured in terms of the outer rotation rate which hardly depends on the shear or the magnetic Prandtl number but its numerical value basically depends on the boundary condition. For both boundary conditions and for small
$Pm$
the instability pattern rotates retrograde. The amount of this migration basically depends on the material of the cylinders. The rotation rate of the inner cylinder does not at all influence the azimuthal migration of the pattern.
Figure 7. Same as in figure 6 but for the drift rate
$\unicode[STIX]{x1D714}_{\text{dr}}/\unicode[STIX]{x1D6FA}_{\text{out}}$
.
4 Electric currents
It remains to discuss the influence of the size of the gap between the cylinders on the excitation conditions and the axial electric current which produces the minimum Hartmann numbers.
A Taylor–Couette flow with resting inner cylinder is clearly the most simple model for super-rotating fluids. As it also forms the steepest radial profile one expects for this configuration the lowest Hartmann numbers. From figure 6 we find, however, that both Reynolds and Hartmann numbers for
$\unicode[STIX]{x1D707}\rightarrow \infty$
are well represented by the solutions already for
$\unicode[STIX]{x1D707}=128$
and that perfectly conducting boundaries always lead to the least numerical values. Figure 8 provides the results for variation of the gap width for
$Pm=0$
and for
$0.7\leqslant r_{\text{in}}<1$
. The Hartmann number for perfectly conducting boundaries has a minimum close to
$r_{\text{in}}=0.9$
. In order to transform the values to the axial electric current within the inner cylinder the relation
$I_{\text{axis}}=5R_{\text{in}}B_{\text{in}}$
(see Rüdiger et al.
Reference Rüdiger, Kitchatinov and Hollerbach2013) can be written as
$$\begin{eqnarray}\displaystyle I_{\text{axis}}=5\frac{R_{\text{in}}}{D}Ha\sqrt{\unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D70C}\unicode[STIX]{x1D708}\unicode[STIX]{x1D702}}, & & \displaystyle\end{eqnarray}$$
where the axial currents are measured in ampere. The numerical values are given as the thick dashed line in figure 8. The result is that the minimum electric current is 26.1 kA for liquid sodium as the conducting fluidFootnote 1 with a gap width of 0.25.
Figure 8.
$Ha_{\min }$
(thick solid line) and corresponding Reynolds number (thin solid line) versus
$r_{\text{in}}$
. The necessary axial electric current
$I_{\text{axis}}$
(thick dashed line, in kA) and rotation frequency
$f$
of the outer cylinder (thin dashed line, in Hz) are also given for sodium as the conducting fluid.
$R_{\text{out}}=5~\text{cm}$
,
$\unicode[STIX]{x1D707}=128$
,
$m=\pm 1$
,
$Pm=0$
. Perfectly conducting cylinders.
The Reynolds numbers associated with the minimal Hartmann numbers given in figure 8 are moderate enough to ensure laminar flows in non-magnetic experiments (see Balbus Reference Balbus2011). For stationary inner cylinders with
$r_{\text{in}}=0.92$
Schultz-Grunow (Reference Schultz-Grunow1959) found stable solutions for Reynolds numbers not exceeding 40.000, in agreement with the data of Taylor (Reference Taylor1936). Burin & Czarnocki (Reference Burin and Czarnocki2012) discussed in detail the phenomena of subcritical transition to turbulence in Taylor–Couette flows by finite disturbances. The experiment described by Seilmayer et al. (Reference Seilmayer, Galindo, Gerbeth, Gundrum, Stefani, Gellert, Rüdiger, Schultz and Hollerbach2014) to realize the current-free AMRI for negative shear worked with
$r_{\text{in}}=0.5$
(with outer radius 8 cm) and a Reynolds number of 2956 without indication of any non-magnetic instability within the container. Flows with positive shears are even more stable.
Figure 9. Same as in figure 8 but for the axial wavenumber
$kD$
(a) and the azimuthal drift rate
$\unicode[STIX]{x1D714}_{\text{dr}}/\unicode[STIX]{x1D6FA}_{\text{out}}$
(b).
For increasing gap width the Reynolds number continuously grows. However, the rotation frequency
$f=\unicode[STIX]{x1D6FA}_{\text{out}}/2\unicode[STIX]{x03C0}$
possesses a minimum at
$r_{\text{in}}=0.8$
. For liquid sodium (
$\unicode[STIX]{x1D708}=7.1\cdot 10^{-3}~\text{cm}^{2}~\text{s}^{-1}$
) and (say)
$R_{\text{out}}=5~\text{cm}$
one obtains
$f=9.3~\text{Hz}$
. For wider gaps both the critical Reynolds number and Hartmann number rapidly increase. For
$r_{\text{in}}=0.66$
we did not find any instability assuming
$Re<15.000$
. Note that the size of the container does not influence the needed electric current for instability but the fractional gap width does.
The eigenvalues given in figure 8 are also characterized by associated axial wavenumbers and azimuthal drift rates. The dependencies of these values on
$r_{\text{in}}$
are not strong. For not too narrow gaps the cells are hardly elongated with the rotation axis and the azimuthal migration (2.1) of the instability pattern is always negative, becoming (slightly) slower for wider gaps (figure 9). With the used normalizations both the axial wavenumber and the drift rates linearly grow with the value of
$r_{\text{in}}$
; they are maximal for
$r_{\text{in}}\rightarrow 1$
.
Figure 10. Same as in figure 5 but for
$r_{\text{in}}=0.75$
. For
$Pm=10^{-5}$
the Hartmann number is
$Ha_{\min }=211.8$
and the Reynolds number is
$Re=5360$
. Between
$Pm\simeq 10^{-3}$
and
$Pm=1$
the values rapidly grow to
$\infty$
.
$\unicode[STIX]{x1D707}=128$
,
$\unicode[STIX]{x1D707}_{B}=r_{\text{in}}=0.75$
. Perfectly conducting cylinders.
For the container with
$r_{\text{in}}=0.75$
, which after figure 8 requires the minimum axial electric current for excitation, the figure 10 again demonstrates the independence of Hartmann number and Reynolds number of the magnetic Prandtl number. Neither value depend on
$Pm$
for
$Pm\lesssim 10^{-5}$
. It is indeed allowed to use for the critical values of
$Ha_{\min }$
and
$Re$
the results of the inductionless approximation for liquid metals such as mercury, gallium and sodium as the conducting fluids. The magnetic Mach number (1.8) for the largest
$Pm$
in figure 10 is of order unity but for smaller
$Pm$
– as for all instabilities which scale with
$Ha$
and
$Re$
for
$Pm\rightarrow 0$
– the magnetic Mach number is much smaller than unity.
After (4.1) the electric currents needed for neutral stability behave like the numerical values of the material expression
$\sqrt{\unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D70C}\unicode[STIX]{x1D708}\unicode[STIX]{x1D702}}$
which mainly runs with
$\sqrt{\unicode[STIX]{x1D70C}}$
as for the mentioned liquid metals the averaged diffusivity
$\sqrt{\unicode[STIX]{x1D708}\unicode[STIX]{x1D702}}\approx \text{const}$
. It is thus clear that experiments for liquid sodium require the weakest electric currents.
So far we did not vary the radial profile of the magnetic background field. One of the questions is how sensitively the described instability reacts in the presence of axial electric currents within the fluid. The Tayler instability of the
$z$
-pinch with
$B_{\unicode[STIX]{x1D719}}\propto R$
– which for
$Ha=Ha_{0}$
is unstable against non-axisymmetric perturbations for all
$Pm$
even without rotation – is supported by super-rotation unless
$Pm=1$
so that even subcritical Hartmann numbers
$Ha<Ha_{0}$
exist (Rüdiger et al.
Reference Rüdiger, Schultz, Gellert and Stefani2016). Similar to our above results, the azimuthal migration of the non-axisymmetric instability pattern depends on
$Pm$
. Also here the pattern counter-rotates for
$Pm\ll 1$
and it co-rotates for
$Pm\gg 1$
.
Figure 11. Stability map for resting inner cylinder. The radial profiles of the background fields vary from
$\unicode[STIX]{x1D707}_{B}=1/r_{\text{in}}$
(TI, thick lines) to
$\unicode[STIX]{x1D707}_{B}=r_{\text{in}}$
(AMRI, thin lines) and for
$Pm=0.02$
(blue) and
$Pm=10^{-5}$
(red).
$Ha_{0}=332$
for all
$Pm$
. Note the coincidence of the upper branches for large Reynolds numbers.
$r_{\text{in}}=0.9$
, perfectly conducting boundaries.
In addition for the current-free field
$B_{\unicode[STIX]{x1D719}}\propto 1/R$
figure 11 also yields the stability lines for the field
$B_{\unicode[STIX]{x1D719}}\propto R$
for two different magnetic Prandtl numbers. The instability for
$Re=0$
appears at
$Ha_{0}$
(Tayler Reference Tayler1957, Reference Tayler1973; Vandakurov Reference Vandakurov1972; Seilmayer et al.
Reference Seilmayer, Stefani, Gundrum, Weier, Gerbeth, Gellert and Rüdiger2012) which does not depend on
$Pm$
(Rüdiger & Schultz Reference Rüdiger and Schultz2010). For large Reynolds numbers only small differences of the lines of marginal instability exist for the two radial profiles. The minimum Hartmann numbers for instability are slightly reduced by the electric currents,
$Ha_{\min }<Ha_{0}$
, but the differences are small. The main result is that the magnetically induced instability of super-rotating Taylor–Couette flows with narrow gaps is only slightly influenced by the applied radial field profile. The upper branches in figure 11 demonstrate this phenomenon for two different magnetic Prandtl numbers. One can even consider the field as uniform between the cylinders (Edmonds Reference Edmonds1958). The magnetic field only acts as a catalyst for the instability.
To visualize the shape of the instability pattern a nonlinear spectral code is used which has been developed from the hydrodynamic code of described by Fournier et al. (Reference Fournier, Bunge, Hollerbach and Vilotte2004) and which works with the expansion of the solution after azimuthal Fourier modes. Figure 12 demonstrates that the resulting patterns of the instabilities for resting inner cylinder and for
$Pm=0.02$
only slightly differ in dependence on the existence of axial electric background currents. The isolines of the radial magnetic field component are given showing different helicities of the two cases (for the given sign of the electric current) and the axial wavelength in (a) exceeds that of the instability model in panel (b).
The two examples in figure 12 have identical supercritical Reynolds number and Hartmann number. In panel (b) a uniform axial electric current exists in the fluid between the cylinders so that the pattern belongs to the Tayler instability (under the influence of differential rotation). The electric current is missing in (a) but the cell structure is very similar. For strong super-rotation the two instabilities appear to fuse and both instabilities are hard to distinguish unless
$Pm=1$
.
Figure 12. Isolines of the radial magnetic field component for instability without axial electric current between the cylinders (
$\unicode[STIX]{x1D707}_{B}=r_{\text{in}}$
, a) and with axial electric current (
$\unicode[STIX]{x1D707}_{B}=1/r_{\text{in}}$
, b). Resting inner cylinder.
$Ha=300$
,
$r_{\text{in}}=0.9$
,
$Re=155$
,
$Pm=0.02$
, perfectly conducting boundaries.
5 Conclusions
In an earlier paper we have shown that Taylor–Couette flows with radially increasing rotation can become unstable against non-axisymmetric perturbations in the presence of sufficiently strong azimuthal magnetic fields which are due to a homogeneous electric current (Rüdiger et al.
Reference Rüdiger, Schultz, Gellert and Stefani2016). The present paper leads to the conclusion that such instability also exists if the field between the cylinders is current free. At least for small
$Pm$
under the influence of differential rotation the differences between both instabilities become very small. Both instabilities appear for
$Pm\neq 1$
while the sign of the azimuthal pattern drift strongly differs for
$Pm\ll 1$
and
$Pm\gg 1$
. For
$Pm=1$
rotation with positive shear stabilizes TI and completely suppresses the instability of current-free fields. Solutions for AMRI only exist if the molecular viscosity and the microscopic magnetic diffusivity strongly differ, hence solutions do not exist for
$Pm=1$
which is characteristic of double-diffusive instabilities.
An important difference to the standard magnetorotational instability with axial fields (which only exists for negative shear) is that the new instability also appears in the inductionless approximation with
$Pm=0$
for sufficiently large positive shear. The numerical calculations suggest a lower limit of
$\unicode[STIX]{x1D707}_{\text{crit}}=1.8$
. For finite but small magnetic Prandtl numbers solutions exist even below this limit but with very large Reynolds numbers. The consequence is that for finite but small magnetic Prandtl numbers the solutions for
$\unicode[STIX]{x1D707}>\unicode[STIX]{x1D707}_{\text{crit}}$
scale with
$Re$
and
$Ha$
almost independent of
$Pm$
. This gives the chance to probe the numerical results by experiments in the laboratory by use of liquid metals with their extremely low magnetic Prandtl numbers. For the optimal gap width of 0.25 and for liquid sodium as the conducting fluid the minimal axial current is 26.1 kA and the rotation frequency is approximately 10 Hz (for
$R_{\text{out}}=5~\text{cm}$
). These numbers should be suitable for experiments. However, in view of the significant differences of
$Ha_{\min }$
for perfectly conducting and insulating boundaries (figure 6) any real experiment with sodium flowing between (for example) copper walls remains to be carefully predicted.
