Optimal funding of defined benefit pension plans

DONATIEN HAINAUT; GRISELDA DEELSTRA

doi:10.1017/S1474747210000016

Optimal funding of defined benefit pension plans

Published online by Cambridge University Press: 25 June 2010

DONATIEN HAINAUT and

GRISELDA DEELSTRA

Show author details

DONATIEN HAINAUT: Affiliation:
ESC Rennes Business School, Rennes, France (e-mail: donatien.hainaut@esc-rennes.fr)
GRISELDA DEELSTRA: Affiliation:
Dpt des Mathématiques, Université Libre de Bruxelles, Belgium (e-mail: griselda.deelstra@ulb.ac.be)

Article contents

Abstract
Introduction
The financial market
The pension fund
The deflator and the fair value of liabilities
The optimization problem
The martingale solution
Example
Conclusion
References

Rights & Permissions

Abstract

In this paper, we address the issue of determining the optimal contribution rate of a defined benefit pension fund. The affiliate's mortality is modelled by a jump process and the benefits paid at retirement are function of the evolution of future salaries. Assets of the fund are invested in cash, stocks, and a rolling bond. Interest rates are driven by a Vasicek model. The objective is to minimize both the quadratic spread between the contribution rate and the normal cost, and the quadratic spread between the terminal wealth and the mathematical reserve required to cover benefits. The optimization is done under a budget constraint that guarantees the actuarial equilibrium between the current asset and future contributions and benefits. The method of resolution is based on the Cox–Huang approach and on dynamic programming.

Type: Articles
Information: Journal of Pension Economics & Finance , Volume 10 , Issue 1 , January 2011 , pp. 31 - 52

DOI: https://doi.org/10.1017/S1474747210000016 [Opens in a new window]
Copyright: Copyright © Cambridge University Press 2010

1 Introduction

There mainly exist two categories of pension funds: the defined contribution pension plan and the defined benefit pension plan. In the first one, the financial risk is born by the affiliate – in case of poor performance of assets, his savings may be insufficient to maintain his standard of living at retirement – whereas in a defined benefit pension plan, the risk is born by the pension funds – whatsoever the return of assets, benefits paid to pensioners are proportional to his salary. In this context, the choice of the investment policy and of the contribution pattern is hence crucial for the agent financing the fund.

Defined benefit pension plans have been extensively studied in the literature. Some authors like Sundaresan and Zapatero (Reference Sundaresan and Zapatero1997) argue that the investor should maximize the expected utility of the surplus of assets over the liabilities of the fund. However, especially from the employer's point of view, and it is the employer who pays for the defined benefit pension plan of his employees, the important issue is to find a contribution process which has small fluctuations and which leads as exactly as possible to the value of the mathematical reserve necessary for covering the liabilities promised in the pension plan. Therefore, a whole branch of papers has studied the minimization of a loss function of contributions and the wealth to be obtained. In the papers of, for example, Haberman and Sung (Reference Haberman and Sung1994, Reference Haberman and Sung2005), Boulier et al. (Reference Boulier, Trussant and Florens1995), Josa-Fombellida and Rincon-Zapatero (Reference Josa-Fombellida and Rincon-Zapatero2004, Reference Josa-Fombellida and Rincon-Zapatero2006), the fund manager keeps the value of the assets as close as possible to liabilities by controlling the level of contributions. Cairns (Reference Cairns1995, Reference Cairns2000) has discussed the role of objectives in selecting an asset allocation strategy and has analysed some current problems faced by defined benefit pension funds. Huang and Cairns (Reference Huang and Cairns2006) have studied the optimal contribution rate for defined benefit pension plans when interest rates are stochastic.

The most novel features of our work are the modelling of the affiliates' mortality by a jump process, and the use of stochastic interest rates and salaries. Furthermore, we minimize both contribution adjustments and a terminal surplus. By contribution adjustment, we mean the spread between the sponsor's contribution and the normal cost; whereas the terminal surplus is here defined as the difference between the terminal wealth and the fair value of liabilities at retirement. The optimization is done under a budget constraint that ensures the actuarial equilibrium between the current assets and future deflated cash flows and with initial negative unfunded liabilities. The objective function in the optimization problem further contains some weighting expressing the importance given to the minimization of contribution adjustments and of the terminal surplus. Numerical results will show that the optimal contribution process depends on the weights corresponding to the minimization of the surplus variation in comparison with the weight corresponding to the minimization of the contribution fluctuations.

In this paper, we deal with the difficulty that the presence of stochastic salary and mortality entails that the market is incomplete. The set of equivalent martingale measures counts therefore more than one element and we need to fix the deflator used by the insurer to value liabilities in order to apply the Cox and Huang (Reference Cox and Huang1989) martingale method, which is well adapted to deal with the presence of wealth constraints. Furthermore, it does not require the Markov properties of state processes and controls. This approach was used in a dynamic Bayesian learning setting by Brennan and Xia (Reference Brennan and Xia2002) and translates in fact common practice of actuaries, who traditionally already used security adjustments, which means that they already chose a certain probability measure to work under. A more annoying implication of the incompleteness implied by the salary and mortality risk is that the optimal target wealth process found by the martingale method is not fully replicable. However, it is possible to determine the investment strategy replicating at best this solution by using the dynamic programming principle as in Hainaut and Devolder (Reference Hainaut and Devolder2007a,Reference Hainaut and Devolderb), which are both studies of asset allocation of deterministic insurance liabilities with a stochastic mortality risk.

The outline of this paper is as follows. Sections 2 and 3 respectively present the financial market and the defined benefit pension plans. In Section 4, the form of the deflator is discussed. Section 5 introduces the optimization problem, and, in Section 6, we propose a solution. Section 7 contains a numerical illustration and the last section concludes.

2 The financial market

In this section, we introduce the market structure of our model and define the dynamics of interest rates and asset values. The uncertainty involved by the financial market is described by a two-dimensional standard Brownian motion $W_{t}^{P^{\hskip1 f} } \equals \lpar {W_{t}^{r\comma P^{\hskip1 f} } \comma W_{t}^{S\comma P^{\hskip1 f} } } \rpar^{\prime}$ defined on a complete probability space (Ω^f, F ^f, P ^f). F ^f is the filtration generated by $W_{t}^{P^{\hskip1 f} }$

$F^{\hskip1 f} \equals \!\mathop {\left( {F_{t}^{\hskip1 f} } \right)}\nolimits_{t} \equals \sigma \left\{ {\left( {W_{u}^{r\comma P^{\hskip1 f} } \comma W_{u}^{S\comma P^{\hskip1 f} } } \right)\colon u\leqslant t} \right\}.$

P ^f represents the historical financial probability measure. The two Wiener processes $W_{t}^{r\comma P^{\hskip1 f} }$ and $W_{t}^{S\comma P^{\hskip1 f} }$ are independent. The financial market is complete and there exists therefore a unique equivalent measure under which the discounted prices of assets are martingales. This risk neutral measure is denoted by Q ^f. The assets of the defined benefit pension fund are invested in cash, rolling bonds, and stocks. The return of cash is the risk free rate r _t and is modelled by an Ornstein–Uhlenbeck process (Vasicek model)

(1)

$dr_{t} \equals a.\lpar b \minus r_{t} \rpar.dt \plus \sigma _{r}.dW_{t}^{r\comma P^{\hskip1 f} }.$

The constant parameters a, b, and σ_r are respectively the speed of mean reversion, the level of mean reversion, and the volatility of r _t. The Vasicek model provides a convenient and tractable way for modelling interest rates, even if there is a small probability of having negative interest rates. Let λ_r be a negative constant being the market price of risk and so implying the dynamics of r _t under the risk neutral measure Q ^f. Indeed, under Q ^f the risk free rate is the solution of the following SDE (Smart Development Environment)

(2)

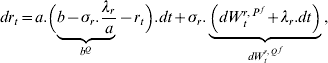
$dr_{t} \equals a.\Big(\! \underbrace {b \minus \sigma _{r}.{{\lambda _{r} } \over a}}_{b^{Q} } \minus r_{t} \Big).dt \plus \sigma _{r}.\underbrace {\left( {dW_{t}^{r\comma P^{\hskip1 f} } \plus \lambda _{r}.dt} \right)}_{dW_{t}^{{r\comma Q^{\hskip1 f} }} }\comma$

where $W_{t}^{r\comma Q^{\hskip1 f} }$ is a Wiener process under Q ^f.

The second category of assets is a rolling bond of maturity K whose price is denoted R _t^K. This bond is a zero coupon bond continuously rebalanced in order to keep a constant maturity and its price obeys the dynamics

$\eqalign{ {{dR_{t}^{K} } \over {R_{t}^{K} }} \equals \tab r_{t}.dt \minus \sigma _{r}.n\lpar K\rpar.\left( {dW_{t}^{r\comma P^{\hskip1 f} } \plus \lambda _{r}.dt} \right) \tab\cr \equals \tab r_{t}.dt \minus \sigma _{r}.n\lpar K\rpar.dW_{t}^{r\comma Q^{\hskip1 f} } \cr}$

where n(K) is a function of the maturity K

$n\lpar K\rpar \equals {1 \over a}.\left( {1 \minus e^{ \minus a.K} } \right).$

Note that the risk premium of the rolling bond is denoted by ν_R=−σ_r.n(K).λ_r.

The last kind of assets available on the financial market is a stock. Its price process S _t is modelled by a geometric Brownian motion and is correlated with the interest rate fluctuations

$\eqalign{ {{dS_{t} } \over {S_{t} }} \equals \tab r_{t}.dt \plus \sigma _{Sr}.\left( {dW_{t}^{r\comma P^{\hskip1 f} } \plus \lambda _{r}.dt} \right) \plus \sigma _{S}.\left( {dW_{t}^{S\comma P^{\hskip1 f} } \plus \lambda _{S}.dt} \right) \tab \cr \equals \tab r_{t}.dt \plus \sigma _{Sr}.dW_{t}^{r\comma Q^{\hskip1 f} } \plus \sigma _{S}.dW_{t}^{S\comma Q^{\hskip1 f} }. \cr}$

The constant parameters σ_Sr, σ_S, and λ_S denote respectively the correlation between stocks and the risk free interest rates, the embedded volatility of the stocks, and the market price of risk parameter. The stock risk premium is defined by ν_S=σ_Sr.λ_r+σ_S.λ_s. The correlation between the share price process and interest rates is crucial in the context of long-term asset-liability management. This point was highlighted in the work of Wilkie (Reference Wilkie1986, Reference Wilkie1995) in his discrete-time stochastic investment model. Chan (Reference Chan1997) has developed a continuous time version of this stochastic investment model.

3 The pension fund

The pension plan considered in this work provides benefits to affiliates that are defined in terms of a member's final salary. For the sake of simplicity, we assume that the pension fund counts initially n _x members of the same age x and earning the same salary, denoted (A _t)_t. All members retire at the age x+T and, in case of death, no benefits are paid. The evolution of the individual salary is stochastic and correlated to the financial market. More precisely, we suppose that the dynamics of an affiliate's salary are defined by the following SDE

(3)

${{dA_{t} } \over {A_{t} }} \equals \mu _{A} \lpar t\rpar.dt \plus \sigma _{Ar} dW_{t}^{r\comma P^{\hskip1 f} } \plus \sigma _{AS} dW_{t}^{S\comma P^{\hskip1 f} } \plus \sigma _{A}.dW_{t}^{A\comma P^{a} }$

where μ_A(t) is the average growth of the salary and $W_{t}^{A\comma P^{a} }$ is a Wiener process that represents the intrinsic randomness of the salary and is independent from $W_{t}^{r\comma P^{\hskip1 f} }$ and $W_{t}^{S\comma P^{\hskip1 f} }$ . As this salary risk is not traded, $W_{t}^{A\comma P^{a} }$ is a source of incompleteness. We will come back to this point in the next section. The constants σ_Ar and σ_AS model the correlation of the salary with respectively interest rates and stocks; and σ_A denotes the embedded wage volatility. $W_{t}^{A\comma P^{a} }$ is defined on a probability space (Ω^a, F ^a, P ^a), where F ^a is the filtration generated by $W_{t}^{A\comma P^{a} }$ .

Benefits are defined in terms of the salary at retirement date. Each pensioner will receive a continuous annuity, whose rate B is a fraction, α of the last wage

$B \equals A_{T}.\alpha .$

These benefits are financed during the accumulation phase. c _t is the contribution rate made by the sponsor to the funding process at time t.

The fair value of liabilities will be discussed in the next section. We now detail the jump process, modelling the mortality of the covered employees. The mortality process is defined as in Møller (Reference Møller1998) on a probability space (Ω^m, F ^m, P ^m) and is assumed to be independent from the filtration generated by $W_{t}^{r\comma P^{\hskip1 f} }$ , $W_{t}^{S\comma P^{\hskip1 f} }$ , $W_{t}^{A\comma P^{a} }$ . The remaining lifetimes of the affiliates are exponential random variables, denoted T ₁, T ₂, …, $T_{n_{x}}$ and their hazard rate (namely the mortality rate), at time t, is given by μ(x+t). N _t is the total number of deaths observed till time t

$N_{t} \equals \mathop{\sum}\limits_{i \equals \setnum{1}}^{n_{x} } I\lpar T_{i} \leqslant t\rpar$

where I(.) is an indicator function. The filtration F ^m is generated by N _t and the expectation of the infinitesimal variation of N _t verifies

$E\left( {dN_{t} \vert F_{t \minus }^{m} } \right) \equals \lpar n_{x} \minus N_{t \minus } \rpar.\mu \lpar x \plus t\rpar.dt .$

As the mortality is not traded in our model, this is a second source of incompleteness. The compensated process M _t of the mortality process is defined as follows

$M_{t} \equals N_{t} \minus \int_{\setnum{0}}^{t} \!\lpar n_{x} \minus N_{u \minus } \rpar.\mu \lpar x \plus u\rpar.du$

and M _t is a martingale under the historical measure P ^m. The expected number of survivors under P ^m is equal to the current number of survivors times a survival probability

$\openup0\eqalign{ E\left( {\lpar n_{x} \minus N_{s} \rpar \vert F_{t}^{m} } \right) \tab \equals E\left( {\mathop{\sum}\limits_{i \equals \setnum{1}}^{n_{x} } I\lpar T_{i} \gt s\rpar \vert F_{t}^{m} } \right) \cr \tab \equals \mathop{\sum}\limits_{T_{i} \gt s} E\left( {I\lpar T_{i} \gt s\rpar \vert F_{t}^{m} } \right) \cr \tab \equals \lpar n_{x} \minus N_{t} \rpar .\underbrace {\exp\left(\!\! { \minus \!\int_{t}^{s} \mu \lpar x \plus u\rpar .du} \right)}_{_{{s \minus t}} \, p_{{x \plus t}} }. \cr}$

_s−tp _x+t is the actuarial notation for the probability that an individual of age x+t survives till age x+s.

4 The deflator and the fair value of liabilities

Let (Ω, F, P) be the probability space resulting from the product of the financial, wage, and mortality probability spaces

$\rmOmega \equals \rmOmega ^{\hskip1 f} \times \rmOmega ^{a} \times \rmOmega ^{m} \quad F \equals F^{\hskip1 f} \otimes F^{a} \otimes F^{m} \vee N\quad P \equals P^{\hskip1 f} \times P^{a} \times P^{m}$

where the sigma algebra N is generated by all subsets of null sets from F ^f⊗F ^a⊗F ^m. The prices of pension fund liabilities are defined on (Ω, F, P). In this setting, the market of pension fund liabilities is incomplete, owing to the presence of two unhedgeable risks: the salary risk and the mortality risk. It entails that prices may differ from one insurance company to another. The next subsections describe the insurer's deflator that is here composed of three elements called the financial, wage, and actuarial deflators, and is an extension of the deflators used in Hainaut and Devolder (Reference Hainaut and Devolder2007b).

4.1 Financial deflator

The completeness of the financial market entails that there exists one unique equivalent measure, namely the risk neutral measure, under which the discounted prices of assets are martingales. This measure is denoted Q ^f and is defined by the following Radon–Nikodym derivative

$\mathop {\left( {{{dQ^{\hskip1 f} } \over {dP^{\hskip1 f} }}} \,\right)}\nolimits_{t} \equals \exp\left(\! { \minus {1 \over 2}.\int_{\setnum{0}}^{t} \vert \vert \rmLambda ^{\hskip1 f} \vert \vert ^{\setnum{2}}.du \minus \int_{\setnum{0}}^{t} \rmLambda ^{\hskip1 f}.dW_{u}^{P^{\hskip1 f} } } \right)$

where Λ^f=(λ_r, λ_S). The dynamics of the assets under Q ^f have been discussed in Section 2. The financial deflator H ^f(t, s) at time t for a cash flow to be paid at time t⩽s is equal to the product of the discount factor and of the Radon–Nykodym derivative

$\eqalign{ H^{\hskip1 f} \lpar t\comma s\rpar \equals \tab {{\exp\left(\! { \minus \int_{\setnum{0}}^{s} r_{u}.du} \right).\mathop {\left( {{\textstyle{{dQ^{\hskip1 f} } \over {dP^{\hskip1 f} }}}} \right)}\nolimits_{s} } \over {\exp\left(\! { \minus \int_{\setnum{0}}^{t} r_{u}.du} \right).\mathop {\left( {{\textstyle{{dQ^{\hskip1 f} } \over {dP^{\hskip1 f} }}}} \right)}\nolimits_{t} }} \tab \cr \equals \tab \exp\left(\! { \minus \int_{t}^{s} r_{u}.du \minus {1 \over 2}.\int_{t}^{s} \vert \vert \rmLambda ^{\hskip1 f} \vert \vert ^{\setnum{2}}.du \minus \int_{t}^{s} \rmLambda ^{\hskip1 f}.dW_{u}^{P^{\hskip1 f} } } \right). \cr}$

4.2 The wage deflator

As the intrinsic salary risk is not traded, the market of pension fund liabilities is incomplete, and for any F ^a adapted process λ_a,t, an equivalent probability measure $Q^{a\comma \lambda _{a} }$ can be defined by the following Radon–Nikodym derivative

$\mathop {\left( {{{dQ^{a\comma \lambda _{a} } } \over {dP^{a} }}} \right)}\nolimits_{\!\!t}\! \equals \exp\left(\! { \minus {1 \over 2}.\int_{\setnum{0}}^{t} \vert \lambda _{a\comma u} \vert ^{\setnum{2}}.du \minus \int_{\setnum{0}}^{t} \lambda _{a\comma u}.dW_{u}^{A\comma P^{a} } } \right)$

and by Girsanov Theorem under $Q^{a\comma \lambda _{a} }$ , $dW_{u}^{A\comma Q^{{a\comma \lambda _{a} }} } \equals dW_{u}^{A\comma P^{a} } \plus \lambda _{a\comma u}.du$ is a F _a-Brownian motion. For the sake of simplicity, λ_a,u is assumed to be constant and denoted λ_a in the sequel. The dynamics of the salary process under $Q^{\hskip1 f} \times Q^{a\comma \lambda _{a} }$ is

(4)

${{dA_{t} } \over {A_{t} }} \equals \underbrace {\left( {\mu _{A} \lpar t\rpar \minus \sigma _{Ar}.\lambda _{r} \minus \sigma _{AS}.\lambda _{S} \minus \sigma _{A}.\lambda _{a} } \right)}_{\mu _{A}^{Q} \lpar t\rpar }.dt \plus \sigma _{Ar} dW_{t}^{r\comma Q^{\hskip1 f} } \plus \sigma _{AS} dW_{t}^{S\comma Q^{\hskip1 f} } \plus \sigma _{A}.dW_{t}^{A\comma Q^{{a\comma \lambda _{a} }} }$

and H ^a(t, s) denotes the wage deflator at instant t, for a payment occurring at time s⩾t

$H^{a} \lpar t\comma s\rpar \equals {{\mathop {\left( {{\textstyle{{dQ^{a\comma \lambda _{a} } } \over {dP^{a} }}}} \right)}\nolimits_{\!s} } \over {\mathop {\left( {{\textstyle{{dQ^{a\comma \lambda _{a} } } \over {dP^{a} }}}} \right)}\nolimits_{\!\!t} }} \equals \exp\left(\! { \minus {1 \over 2}.\int_{t}^{s} \vert \lambda _{a\comma u} \vert ^{\setnum{2}}.du \minus \int_{t}^{s} \lambda _{a\comma u}.dW_{u}^{A\comma P^{a} } } \right).$

Notice that the discount factor does not appear in the definition of H ^a(t, s) since it was introduced when defining H ^f(t, s).

4.3 The actuarial deflator

The second source of incompleteness is the mortality risk. For any F ^m-predictable process h _s, such that h _s>−1, an equivalent actuarial measure Q ^m,h is defined by a solution of the SDE

(5)

$\eqalign{ d\mathop {\left( {{{dQ^{m\comma h} } \over {dP^{m} }}} \right)}\nolimits_{\!\!t} \tab \equals \mathop {\left( {{{dQ^{m\comma h} } \over {dP^{m} }}} \right)}\nolimits_{\!\!t}.h_{t}.d\left( {N_{t} \minus \int_{\setnum{0}}^{t} \left( {n_{x} \minus N_{u \minus } } \right).\mu \lpar x \plus u\rpar.du} \right) \cr \tab \equals \mathop {\left( {{{dQ^{m\comma h} } \over {dP^{m} }}} \right)}\nolimits_{\!\!t}.h_{t}.dM_{t} \cr}$

and we have the property that the process M _t^m,h defined by

$M_{t}^{m\comma h} \equals N_{t} \minus \int_{\setnum{0}}^{t} \left( {n_{x} \minus N_{u \minus } } \right).\mu \lpar x \plus u\rpar.\lpar 1 \plus h_{u} \rpar.du$

is a martingale under Q ^m,h. We adopt the notation λ_N,u=(n _x−N _u−).μ(x+u) for the intensity of jumps. The solution of the SDE (5) is (for details, see Duffie, Reference Duffie2001: Appendix I on counting processes)

$\eqalign{ \mathop {\left( {{{dQ^{m\comma h} } \over {dP^{m} }}} \right)}\nolimits_{\!\!t} \equals \tab \prod\limits_{T_{i} \leqslant t} \,\left( {1 \plus h_{T_{i} } } \right).\exp\left(\! { \minus\!\! \int_{\setnum{0}}^{t}\! h_{u}.\lambda _{N\comma u}.du} \right) \tab\cr \equals \tab\exp\left( {\int_{\setnum{0}}^{t}\! \ln\left( {1 \plus h_{u} } \right).dN_{u} \minus \int_{\setnum{0}}^{t} \! h_{u}.\lambda _{N\comma u}.du} \right) \cr}$

and H ^m(t, s) denotes the actuarial deflator at instant t, for a payment occurring at time s⩾t, defined by

(6)

$H^{m} \lpar t\comma s\rpar \equals {{\mathop {\left( {{\textstyle{{dQ^{m\comma h} } \over {dP^{m} }}}} \right)}\nolimits_{\!s} } \over {\mathop {\left( {{\textstyle{{dQ^{m\comma h} } \over {dP^{m} }}}} \right)}\nolimits_{\!\!t} }} \equals \exp\left( {\int_{t}^{s}\! \ln\lpar 1 \plus h_{u} \rpar.dN_{u} \minus \!\!\int_{t}^{s}\! h_{u}.\lambda _{N\comma u}.du} \right).$

Under Q ^m,h, the expected number of survivors at time s is equal to the number of survivors at time t multiplied by a modified probability of survival _s−tp _x+t^h

$E^{Q^{{m\comma h}} } \left( {\lpar n_{x} \minus N_{s} \rpar \vert F_{t}^{\,m} } \right) \equals \lpar n_{x} \minus N_{t} \rpar.\underbrace {\exp\left(\!\! { \minus\!\! \int_{t}^{s}\! \mu \lpar x \plus u\rpar.\lpar 1 \plus h_{u} \rpar.du} \right)}_{_{{s \minus t}} \, p_{{x \plus t}}^{h} }.$

In the sequel of this work, we pay attention to a constant process h _u=h. The reason motivating this choice is that, in this particular case, some interesting analytic results can be presented. Remark that if h>0, h can be seen as a security margin against an adverse evolution of the mortality or as the price of mortality risk.

4.4 The deflator and the price of liabilities

The deflator used to price liabilities, written H(t, s) is in our settings the product of the financial, wage, and mortality deflators

(7)

$H\lpar t\comma s\rpar \equals {{\exp\left( {\! \minus\!\! \int_{\setnum{0}}^{s} r_{u}.du} \right)} \over {\exp\left( {\! \minus\!\! \int_{\setnum{0}}^{t} r_{u}.du} \right)}}.{{\mathop {\left( {{\textstyle{{dQ^{\hskip1 f} } \over {dP^{\hskip1 f} }}}} \right)}\nolimits_{\!\!s} } \over {\mathop {\left( {{\textstyle{{dQ^{\hskip1 f} } \over {dP^{\hskip1 f} }}}} \right)}\nolimits_{\!\!t} }}.{{\mathop {\left( {{\textstyle{{dQ^{a\comma \lambda _{a} } } \over {dP^{a} }}}} \right)}\nolimits_{\!\!s} } \over {\mathop {\left( {{\textstyle{{dQ^{a\comma \lambda _{a} } } \over {dP^{a} }}}} \right)}\nolimits_{\!\!t} }}.{{\mathop {\left( {{\textstyle{{dQ^{m\comma h} } \over {dP^{m} }}}} \right)}\nolimits_{\!\!s} } \over {\mathop {\left( {{\textstyle{{dQ^{m\comma h} } \over {dP^{m} }}}} \right)}\nolimits_{\!\!t} }}.$

The pricing of pension fund liabilities is hence done under a probability measure Q, equivalent to P, which is equal to the product of Q ^f, Q ^a, and Q ^m. Q is thus defined by the deflator H(t, s), which depends on the particular choice of h and λ_a, which are decided by the insurer and depend on the way he evaluates the mortality risk and salary risk.

Remark that the expectation of the deflator H(t, s) is equal to the price of a zero coupon bond paying one unit at time s, denoted B(t, s)

$\eqalign{ B\lpar t\comma s\rpar \equals \tab E\left( {H\lpar t\comma s\rpar \vert F_{t} } \right) \tab\cr \equals \tab E^{Q} \left( {e^{ \minus \int_{t}^{s} r_{u}.du} \vert F_{t} } \right). \cr}$

The analytic expression of B(t, s) is recalled in Appendix A. The fair value at time t of the liabilities at the date of retirement, denoted L _t, is defined as the expectation of the deflated value of future contributions and benefits. L _t will be used in the sequel to state the optimization problem. In particular, if T ^m is the maximum time horizon of the insurer's commitments, L _t is equal to

$L_{t} \equals E\left(\! { \minus \int_{t}^{T}\! H\lpar t\comma s\rpar.c_{s}.ds \plus\! \int_{T}^{T^{m} }\! H\lpar t\comma s\rpar.\left( {n_{x} \minus N_{s} } \right).B.ds\vert F_{t} } \right).$

Generally, the minimum value of asset that the fund must hold to ensure his solvency is set larger than or equal to L _t (this minimum depends evidently on the local regulation).

5 The optimization problem

As motivated in the introduction, the insurer's objective is to minimize the quadratic spread between the contribution rate and a constant target one (namely the normal cost) and to minimize the deviation of the terminal target asset from the mathematical reserve required to cover benefits at the date of retirement. The normal cost, denoted NC, is the contribution rate allowing equality between expected assets and liabilities under the chosen risk neutral measure Q

$NC \equals {{E^{Q} \Big( {e^{ \minus\! \int_{\setnum{0}}^{T} r_{u}.du}.L_{T} \vert F_{\setnum{0}} } \Big)} \over {E^{Q} \Big( {\int_{\setnum{0}}^{T} e^{ \minus\! \int_{\setnum{0}}^{s} r_{u}.du}.ds\vert F_{\setnum{0}} } \Big)}} \equals {{E\left( {H\lpar 0\comma T\rpar.L_{T} \vert F_{\setnum{0}} } \right)} \over {E\Big( {\int_{\setnum{0}}^{T} H\lpar 0\comma s\rpar.ds\vert F_{\setnum{0}} } \Big)}}.$

The market being incomplete, the normal cost depends on the safety margins, h and λ_a, which are set by the insurer in deflators (7), to appraise the mortality and salary risks. The target total asset is denoted $\mathop {\tilde{X}}\nolimits_{T}$ . Following Brennan and Xia (Reference Brennan and Xia2002), we will use the Cox–Huang method and minimize first with respect to the contributions and the associated terminal target wealth. As done by Josa-Fombellida and Rincon–Zapatero (Reference Josa-Fombellida and Rincon-Zapatero2004), we define the value function as follows

(8)

$\eqalign{ \tab V\lpar t\comma x\comma n\comma a\rpar \equals \cr\tab\quad\mathop {\rm min}\limits_{c_{t} \comma \mathop {\tilde{X}}\nolimits_{T}\; \in\; A_{t} \lpar x\rpar } E\left[ {\int_{t}^{T} u_{\setnum{1}} .{\left( {c_{s} \minus NC} \right)}^{\setnum{2}} .ds \plus u_{\setnum{2}} .\lpar {\tilde{X}}\nolimits_{T} \minus L_{T} \rpar ^{\setnum{2}} \>\vert \>\underbrace {\mathop {\tilde{X}}\nolimits_{t} \equals x\comma \>N_{t} \equals n\comma \>A_{t} \equals a}_{F_{t} }} \right]\!\comma \cr}$

where u ₁ and u ₂ are constant weights. We draw the attention of the reader on the fact that the specification (8) implies that the fund manager assigns the same importance to over and under deviations of the fund's assets and contributions from their respective targets. This kind of objective is particularly well adapted if a fund manager considers that a low volatility of contribution rates and terminal wealth is a sign of good management. The contribution rate and the target wealth are chosen in a set A _t(x) which is delimited by a constraint ensuring the actuarial equilibrium between future deflated cash flows and the current asset x.

(9)

$\!\!\!\!\!\!\!{ A_{t} \lpar x\rpar \equals \tab \bigg\{ {\left( {\mathop {\left( {c_{s} } \right)}\nolimits_{s \;\in\; \lsqb t\comma T\rsqb } \comma {\tilde{X}}\nolimits_{T} } \right)such\>that} \ \tab\cr \tab\left. { E\bigg(\! { \minus \!\int_{t}^{T}\! H\lpar t\comma s\rpar .c_{s} .ds \plus H\lpar t\comma T\rpar .\mathop {\tilde{X}}\nolimits_{T} \vert F_{t} } \bigg)\leqslant x} \bigg\}. \cr}$

In the sequel, this constraint is called the budget constraint. However, as the market is incomplete, the fact that $\mathop {\tilde{X}}\nolimits_{T}$ belongs to A _t(x) does not guarantee that it is replicable by an adapted investment policy. This is the reason why we use the terminology of ‘target’ terminal wealth, denoted by $\mathop {\tilde{X}}\nolimits_{T}$ . This point is detailed in Subsection 6.2, in which we introduce also a replicable wealth X _T at time of retirement.

6 The martingale solution

6.1 Optimal contribution rate and wealth

In this section, we solve the optimization problem (8)–(9). Let y _t∊R ⁺ be the Lagrange multiplier associated to the budget constraint at instant t. The Lagrangian is defined by

(10)

$\openup2\eqalign{\! L\left( {t\comma x\comma n\comma a\comma {\left( {c_{s} } \right)}\nolimits_{s} \comma \, {\tilde{X}}_{T} \comma \, y_{t} } \right) \equals \tab E\left( {\int_{t}^{T} u_{\setnum{1}}. {\left( {c_{s} \minus NC} \right)}\nolimits^{\setnum{2}}.ds \plus u_{\setnum{2}}.\lpar \mathop {\tilde{X}}\nolimits_{T} \minus L_{T} \rpar ^{\setnum{2}} \vert F_{t} } \right)\cr \tab\! \minus y_{t}.\left( \!{x \minus E\left(\! {\! \minus\! \int_{t}^{T} H\lpar t\comma s\rpar.c_{s}.ds \plus H\lpar t\comma T\rpar.\mathop {\tilde{X}}\nolimits_{T} \vert F_{t} } \right)}\!\! \right). \cr}$

A sufficient condition to obtain an optimal contribution rate (c _s*)_s∊[t,T] and an optimal target wealth $\mathop {\tilde{X}}\nolimits_{T}{ \hskip-5\vskip-2\ast }$ is the existence of an optimal Lagrange multiplier y _t*>0 such that the couple $\left( {\lpar c_{s}{\! \ast } \rpar _{s\; \in\; \lsqb t\comma T\rsqb } \comma\, {\tilde{X}}_{T}{\hskip-5\vskip-2 \ast } } \right)$ is a saddle point of the Lagrangian. The value function may therefore be reformulated as

(11)

$\eqalign{ V\lpar t\comma x\comma n\comma a\rpar \equals \tab {\rm sup}\limits_{y_{t} \;\in\; R^{ \plus } } \left( {\mathop {\inf}\limits_{\lpar c_{s} \rpar _{s} \comma \, {\tilde{X}}\nolimits_{T} } L\left( {t\comma x\comma n\comma a\comma {\left( {c_{s} } \right)}_{s} \comma \, {\tilde{X}}_{T} \comma y_{t} } \right)} \right) \tab \cr \equals \tab {\rm sup}\limits_{y_{t} \;\in\; R^{ \plus } } \;\tilde{V}\lpar t\comma x\comma n\comma a\comma y_{t} \rpar \cr}$

and

$V\lpar t\comma x\comma n\comma a\rpar \equals \tilde{V}\lpar t\comma x\comma n\comma a\comma y_{t}{ \ast } \rpar.$

It can be proved under technical conditions (see Karatzas and Shreve, Reference Karatzas and Shreve1998, for details) that the optimal contribution rate and target wealth are

(12)

$c_{s}{\!\! \ast } \equals y_{t}{ \!\ast }.H\lpar t\comma s\rpar.{1 \over {2.u_{\setnum{1}} }} \plus NC$

(13)

$\mathop {\tilde{X}}\nolimits_{T}{ \hskip-5\vskip-1\ast } \equals \minus y_{t}{ \hskip-2.2\vskip-0\ast }.H\lpar t\comma T\rpar.{1 \over {2.u_{\setnum{2}} }} \plus L_{T}.$

Formally, c _s* and ${\tilde{X}}_{T}{ \hskip-3\vskip-2\ast }$ are obtained by offsetting the derivatives of equation (10) with respect to c _s and X _T. The optimal Lagrange multiplier, y _t*, is such that the budget constraint (9) is binding

(14)

$y_{t}{ \!\ast } \equals {{E\left( {H\lpar t\comma T\rpar.L_{T} \vert F_{t} } \right) \minus x \minus NC.\int_{t}^{T} E\left( {H\lpar t\comma s\rpar \vert F_{t} } \right)ds} \over {{\textstyle{1 \over {2.u_{\setnum{1}} }}}.\int_{t}^{T} E\left( {H\lpar t\comma s\rpar ^{\setnum{2}} \vert F_{t} } \right)ds \plus {\textstyle{1 \over {2.u_{\setnum{2}} }}}.E\left( {H\lpar t\comma T\rpar ^{\setnum{2}} \vert F_{t} } \right)}}.$

The numerator of (14) is precisely the part of the benefits that are not yet financed: the expected fair value of reserves less the current asset and less the normal cost times a financial annuity. This quantity is called unfunded liabilities in the sequel of this paper and noted as follows

(15)

$UL_{t} \equals E\left( {H\lpar t\comma T\rpar.L_{T} \vert F_{t} } \right) \minus x \minus NC.\underbrace {\int_{t}^{T}\! E\left( {H\lpar t\comma s\rpar \vert F_{t} } \right)ds}_{\mathop {\bar{a}}\nolimits_{{t\comma T}} }\comma$

where ${\bar{a}}\nolimits_{t\comma T}$ is a financial annuity of maturity T−t. The Lagrange multiplier, being positive, implies that the unfunded liabilities must remain positive. Therefore, according to equation (13), the optimal target wealth at the date of retirement is lower than the mathematical reserve required to cover the liabilities at that date ( $\tilde{X}_{T}{\hskip-3.4\vskip-2 \ast } \leqslant L_{T}$ ). The positivity of the Lagrange multiplier also implies that, according to equation (12), the optimal contribution rate is always higher that the normal cost. We draw the attention of the reader to the fact that those observations are valid only if we can replicate the optimal target wealth $\tilde{X}_{T}{\hskip-3.4\vskip-2 \ast }$ by an adapted investment policy. However, in practice, that is not the case given that $\tilde{X}_{T}{\hskip-3.4\vskip-2 \ast }$ depends on L _T, and then on mortality and wage risks that are not hedgeable. In the next section, we will propose an investment strategy, replicating at best the optimal wealth process $\tilde{X}_{T}{\hskip-3.4\vskip-2 \ast }$ . In the example proposed in Section 7, we will see that this strategy may lead to negative unfunded liabilities (a surplus of assets above liabilities) and hence to a negative Lagrange multiplier. In this case, it means that the optimal target wealth $\tilde{X}_{T}{ \hskip-3.4\vskip-2\ast }$ minimizes the value function under the equality constraint

$E\left(\! { \minus \int_{t}^{T} H\lpar t\comma s\rpar.c_{s}.ds \plus H\lpar t\comma T\rpar.\mathop {\tilde{X}}\nolimits_{T} \vert F_{t} } \right) \equals x$

rather than under the initial inequality constraint defined in equation (9). For an equality constraint, the Lagrange multiplier may indeed be negative or positive.

If we insert (12) and (13) in the objective (8), the value function is rewritten in terms of unfunded liabilities

(16)

$V\lpar t\comma x\comma n\comma a\rpar \equals {{UL_{t}^{\setnum{2}} } \over {{\textstyle{1 \over {u_{\setnum{1}} }}}.\int_{t}^{T} E\left( {H\lpar t\comma s\rpar ^{\setnum{2}} \vert F_{t} } \right)ds \plus {\textstyle{1 \over {u_{\setnum{2}} }}}.E\left( {H\lpar t\comma T\rpar ^{\setnum{2}} \vert F_{t} } \right)}}$

The following propositions detail the expectations intervening in the calculation of the Lagrange multiplier (14) and of the value function (16).

Proposition 1. Under the assumptions that interest rates follow ( 1), that the deflator is defined by ( 7), and that the process defining the actuarial measure Q^m,h is constant, h_t=h with $h \gt \!\minus {\textstyle{1 \over 2}}$ , the conditional expectation of the square of the deflator is equal to

$\eqalign{ E\left( {H\lpar t\comma s\rpar ^{\setnum{2}} \vert F_{t} } \right) \equals \tab \exp\left( {\int_{t}^{s} \left( {\lambda _{r}^{\setnum{2}} \plus \lambda _{S}^{\setnum{2}} \plus \lambda _{a}^{\setnum{2}} } \right).du} \right)\comma \cr \tab \exp\left(\! { \minus \beta ^{\tilde{P}}.\lpar s \minus t\rpar \plus n\lpar s \minus t\rpar.\lpar \beta ^{\tilde{P}} \minus 2.r_{t} \rpar \minus {{\sigma _{r}^{\setnum{2}} } \over a}.n\lpar s \minus t\rpar ^{\setnum{2}} } \right)\comma \cr \tab \mathop{\sum}\limits_{n \equals \setnum{1}}^{n_{x} \minus N_{t} } \,{{\lpar n_{x} \minus N_{t} \rpar \exclam } \over {\lpar n_{x} \minus N_{t} \minus n\rpar \exclam \>n\exclam }}\left( {k^{n}.\mathop {\left( {_{s \minus t} p_{x \plus t}^{\setnum{2}h} } \right)}\nolimits^{n_{x} \minus N_{t} \minus n}.\mathop {\left( {1 \minus _{s \minus t} p_{x \plus t}^{\setnum{2}h} } \right)}\nolimits^{n} } \right) \cr}$

where $\beta ^{\tilde{P}}$ and k are constant and defined by

$\beta ^{\tilde{P}} \equals 2.b \minus 4.{{\sigma _{r}.\lambda _{r} } \over a} \minus 2.{{\sigma _{r}^{\setnum{2}} } \over {a^{\setnum{2}} }}$

$k \equals {{\mathop {\lpar 1 \plus h\rpar }\nolimits^{\setnum{2}} } \over {\lpar 1 \plus 2.h\rpar }}$

_s−tp _x+t^2his a probability of survival under a modified measure of probability

$_{s \minus t} \, p_{x \plus t}^{\setnum{2}h} \tab \equals \tab \exp\left(\! { \minus \int_{t}^{s} \mu \lpar x \plus u\rpar.\lpar 1 \plus 2.h\rpar.du} \right)$

and n(s−t) is a positive decreasing function, null when s=t

(17)

$n\lpar s \minus t\rpar \equals {{1 \minus e^{ \minus a\lpar s \minus t\rpar } } \over a}$

The proof is provided in Appendix B.

Proposition 2. The expectation of the deflated value of liabilities, at time t⩽T, is

$E\left( {H\lpar t\comma T\rpar.L_{T} \vert F_{t} } \right) \equals \lpar n_{x} \minus N_{t} \rpar.\alpha.\int_{t}^{T} {_{s \minus t}\, p}_{x \plus t}^{h}.E^{Q} \left( {e^{ \minus \int_{t}^{T} r_{u}.du}.A_{T}.B\lpar T\comma s\rpar \vert F_{t} } \right).ds$

where

${ E^{Q} \left( {e^{ \minus \int_{t}^{T} r_{u}.du}.A_{T}.B\lpar T\comma s\rpar \vert F_{t} } \right) \equals \tab A_{t}.e^{\int_{t}^{T} \mu _{A}^{Q} \lpar u\rpar.du}.B\lpar t\comma s\rpar \tab\cr \tab .e^{\left( {{\textstyle{{\sigma _{{Ar}}.\sigma _{r} } \over a}}.\left(\! { \minus \lpar T \minus t\rpar \plus n\lpar s \minus t\rpar \minus n\lpar s \minus T\rpar } \right)} \right)} \cr}$

and n(s−t) is defined by equation (17).

The proof is detailed in Appendix C. Note that, in the example detailed in Section 7, the integrals $\int_{t}^{T} E\left( {H\lpar t\comma s\rpar ^{\setnum{2}} \vert F_{t} } \right)ds$ and $\int_{t}^{T} {_{s \minus t}\, p}_{x \plus t}^{h}.E^{Q} \Big( {e^{ \minus \int_{t}^{T} r_{u}.du}.A_{T}.B\lpar T\comma s\rpar \vert F_{t} } \Big).ds$ are computed numerically.

6.2 The best replicating strategy

We now turn to the issue that the optimal target wealth $\mathop {\tilde{X}}\nolimits{\vskip-1 \ast }_{\!\!\!\!T}$ is in general not hedgeable due to the incompleteness of the market caused by mortality and salary risk. From the previous section, we recall that $\mathop {\tilde{X}}\nolimits{\vskip-1 \ast }_{\!\!\!\!T}$ depends on L _T, which has the following expression

$\openup3\eqalign{ L_{T} \equals \tab E\left( {\int_{T}^{Tm}\! H\lpar T\comma s\rpar.\left( {n_{x} \minus N_{s} } \right).B.ds\vert F_{T} } \right) \cr \tab \hskip-10\equals \left( {n_{x} \minus N_{T} } \right).\alpha.A_{T}.\int_{T}^{Tm} {_{s \minus T}\, p}_{x \plus T}^{h}.B\lpar T\comma s\rpar.ds. \cr}$

As L _T is a function both of the mortality N _T and of the salary A _T, which are not replicable, it is easily seen that ${\tilde{X}}\nolimits_{T}{\hskip-3\vskip-2 \ast }$ is not hedgeable. However, it is possible to find the investment strategy replicating at best this process. We refer the interested readers to Hainaut and Devolder (Reference Hainaut and Devolder2007a), in which two conceivable ways to establish the best investment policy are studied in order to determine the optimal asset allocation in case of pure endowment insurance contracts. Our reasoning in this paper is based on dynamic programming (see e.g. Fleming and Rishel Reference Fleming and Rishel1975 for details) and is also applied in Hainaut and Devolder (Reference Hainaut and Devolder2007b), which is a study of the dividend policy and the asset allocation of a portfolio of life insurance policies with predetermined contributions and benefits.

Let A _t^π(x) be the set of replicable wealth processes. If (π_t^S, π_t^R) denote respectively the fraction of the wealth invested in stocks and rolling bonds, A _t^π(x) is defined as follows

$\eqalign{ A_{t}^{\pi } \lpar x\rpar \equals \tab \bigg\{ {\left( {\mathop {\left( {c_{s} } \right)}\nolimits_{s \;\in\; \lsqb t\comma T\rsqb } \comma \,X_{T} } \right)\vert \exists \>\lpar \pi _{t}^{S} \rpar _{t} \;\lpar \pi _{t}^{R} \rpar _{t} \quad F_{t} \minus adapted\colon } \right. \cr \tab e^{ \minus \int_{t}^{T} r_{s}.ds}.X_{T} \equals x \plus \int_{t}^{T} e^{ \minus \int_{t}^{s} r_{u}.du}.c_{s}.ds \cr \tab \left. { \plus \int_{t}^{T} e^{ \minus \int_{t}^{s} r_{u}.du}.\pi _{s}^{S}.X_{s}.dS_{s} \plus \int_{t}^{T} e^{ \minus \int_{t}^{s} r_{u}.du}.\pi _{s}^{R}.X_{s}.dR_{s}^{K} } \bigg\}. \cr}$

By definition, the set A _t^π(x) is included in A _t(x) and the dynamics of the replicable wealth process are such that

$\eqalign{ dX_{t} \equals \tab \left( {\left( {r_{t} \plus \pi _{t}^{S}.\nu _{S} \plus \pi _{t}^{R}.\nu _{R} } \right).X_{t} \plus c_{t} } \right).dt \plus \pi _{t}^{S}.\sigma _{S}.X_{t}.dW_{t}^{S\comma P^{\hskip1 f} } \cr \tab \plus \left( {\pi _{t}^{S}.\sigma _{Sr} \minus \pi _{t}^{R}.\sigma _{r}.n\lpar K\rpar } \right).X_{t}.dW_{t}^{r\comma P^{\hskip1 f} }. \cr}$

For a small step of time Δt, the dynamic programming principle states that

(18)

$\!\!\eqalign{ V\lpar t\comma x\comma n\comma a\rpar \tab \equals E\left[ {\int_{t}^{t \plus \rmDelta t} u_{\setnum{1}}. {\left( {c_{s}^{\ast } \minus NC} \right)}\nolimits^{\setnum{2}}.ds \plus V\left( {t \plus \rmDelta t\comma \mathop {\tilde{X}}\nolimits_{t \plus \rmDelta t}^{\ast } \comma N_{t \plus \rmDelta t} \comma A_{t \plus \rmDelta t} } \right)\>\vert \>F_{t} } \right] \cr \tab \equals \mathop {\inf }\limits_{c_{t} \comma \tilde{X}_{t} \;\in\; A_{t} \lpar x\rpar } E\left[ {\int_{t}^{t \plus \rmDelta t} \!u_{\setnum{1}}.\!\mathop {\left( {c_{s} \minus NC} \right)}\nolimits^{\setnum{2}}\!.ds \plus V\left( {t \plus \rmDelta t\comma \tilde{X}_{t \plus \rmDelta t} \comma N_{t \plus \rmDelta t} \comma A_{t \plus \rmDelta t} } \right)\>\vert \>F_{t} } \right]. \cr}$

The process $\mathop {\left( {\mathop {\tilde{X}}\nolimits_{t}{ \hskip-3\vskip-2\ast } } \right)}\nolimits_{t}$ being the optimal target wealth (13), any other couple $\big( \big( {c_{t}{\!\ast } } \big)_{t} \comma X_{T} \big) \in A_{t}^{\pi } \lpar x\rpar \subset A_{t} \lpar x\rpar$ verifies the inequality

(19)

$V\lpar t\comma x\comma n\comma a\rpar \leqslant E\left[ {\int_{t}^{t \plus \rmDelta t} u_{\setnum{1}}. {\left( {c_{s}{ \!\!\ast } \minus NC} \right)}\nolimits^{\setnum{2}}.ds \plus V\left( {t \plus \rmDelta t\comma X_{t \plus \rmDelta t} \comma N_{t \plus \rmDelta t} \comma A_{t \plus \rmDelta t} } \right)\>\vert \>F_{t} } \right].$

A proof of the dynamic programming principle may be found in Yong and Zhou (Reference Yong and Zhou1999, page 180, theorem 3.3). The closest replicable process to $\mathop {\left( { {\tilde{X}}\nolimits_{t}{\hskip-2\vskip-2 \ast } } \right)}\nolimits_{t}$ is the one minimizing the right-hand term of the inequality (19). Indeed, the value function V(t, x, n, a) is quadratic and then locally Lipschitz

$\forall O \subset R\comma \>\exists C^{O} \;\in\; R^{ \plus } \>\vert \>x_{\setnum{1}} \comma x_{\setnum{2}} \;\in\; O\>\left\vert {V\lpar t\comma x_{\setnum{1}} \comma n\comma a\rpar \minus V\lpar t\comma x_{\setnum{2}} \comma n\comma a\rpar } \right\vert\leqslant C^{O}.\vert x_{\setnum{1}} \minus x_{\setnum{2}} \vert$

And if t+Δt is the first exit time of $\mathop {\tilde{X}}\nolimits{\hskip-0\vskip-1 \ast }_{\!\!\!\!\!t \plus \rmDelta t}$ or X _t+Δt from an interval O round x, the difference between the right-hand sides of (18) and (19) is bounded around x, as follows

$\eqalign{ 0\leqslant \tab E\left[ {V\left( {t \plus \rmDelta t\comma X_{t \plus \rmDelta t} \comma N_{t \plus \rmDelta t} \comma A_{t \plus \rmDelta t} } \right) \minus V\left( {t \plus \rmDelta t\comma \mathop {\tilde{X}}\nolimits{ \vskip-1\ast }_{\!\!\!\!t \plus \rmDelta t} \comma N_{t \plus \rmDelta t} \comma A_{t \plus \rmDelta t} } \right)\>\vert \>F_{t} } \right] \comma \cr \leqslant \tab E\left[ {C^{O}.\left\vert {X_{t \plus \rmDelta t} \minus \mathop {\tilde{X}}\nolimits{\vskip-1 \ast }_{\!\!\!\!t \plus \rmDelta t} } \right\vert\>\vert \>F_{t} } \right] \cr}$

where C ^O is constant. Minimizing $E\left[ {\left\vert {X_{t \plus \rmDelta t} \minus \mathop {\tilde{X}}\nolimits{ \vskip-1\ast }_{\!\!\!\!t \plus \rmDelta t} } \right\vert\>\vert \>F_{t} } \right]$ is therefore equivalent to minimizing the right-hand term of (19). The Ito's lemma for jump processes (see for e.g. Øksendal and Sulem 2004, chapter 1), leads to the following expression for the expectation of the value function at time t+Δt

$\eqalign{\tab E\left( {V\lpar t \plus \rmDelta t\comma X_{t \plus \rmDelta t} \comma N_{t \plus \rmDelta t} \comma A_{t \plus \rmDelta t} \rpar \vert F_{t} } \right) \equals \cr\tab\quad V \lpar t\comma x\comma n\comma a\rpar \plus E\left( {\int_{t}^{t \plus \rmDelta t} G^{\pi } \lpar s\comma X_{s} \comma N_{s} \comma A_{s} \rpar.ds\vert F_{t} } \right) \cr\tab \!\quad \plus E\left( {\int_{t}^{t \plus \rmDelta t} \left( {V\lpar s\comma X_{s} \comma N_{s} \comma A_{s} \rpar \minus V\lpar s\comma X_{s} \comma N_{s \minus } \comma A_{s} \rpar } \right).dN_{s} \vert F_{t} } \right) \cr}$

where G ^π(s, X _s, N _s, A _s) is the generator of the value function

$\!\!\eqalign{ G^{\pi } \lpar s\comma X_{s} \comma N_{s} \comma A_{s} \rpar \equals \tab V_{s} \plus a.\lpar b \minus r_{s} \rpar .V_{r} \plus \mu _{A} \lpar s\rpar .A_{s} .V_{A} \cr\tab \!\!\plus {1 \over 2}.\sigma _{r}^{\setnum{2}} .V_{rr} \plus {1 \over 2}.A_{s}^{\setnum{2}} .\lpar \sigma _{A}^{\setnum{2}} \plus \sigma _{Ar}^{\setnum{2}} \plus \sigma _{AS}^{\setnum{2}} \rpar .V_{AA} \plus \sigma _{Ar} .A_{s} .\sigma _{r} .V_{Ar} \cr\tab\!\! \plus X_{s} .A_{s} .\left( {\sigma _{AS} .\pi _{s}^{S} .\sigma _{S} \plus \sigma _{Ar} .\left( {\pi _{s}^{S} .\sigma _{Sr} \minus \pi _{s}^{R} .\sigma _{r} .n\lpar K\rpar } \right)} \right).V_{XA} \cr\tab\!\! \plus \left(\! {\left( {r_{s}\hskip-.5 \plus\hskip-.5 \pi _{s}^{S} .\nu _{S} \hskip-.5\plus\hskip-.5 \pi _{s}^{R} .\nu _{R} } \right).X_{s}\hskip-.5 \plus \hskip-.5 c_{s}{ \ast } } \right).V_{X}\hskip-.5 \plus\hskip-.5 X_{s} .\sigma _{r} .\left( {\pi _{s}^{S} .\sigma _{Sr}\hskip-.5 \minus\hskip-.5 \pi _{s}^{R} .\sigma _{r} .n\lpar K\rpar }\hskip-1 \right).V_{Xr} \cr\tab\!\! \plus {1 \over 2}.X_{s}^{\setnum{2}} .\left( \!{\mathop {\left( {\pi _{s}^{S} .\sigma _{S} } \right)}\nolimits^{\setnum{2}} \plus \mathop {\left( {\pi _{s}^{S} .\sigma _{Sr} \minus \pi _{s}^{R} .\sigma _{r} .n\lpar K\rpar } \right)}\nolimits^{\setnum{2}} } \right).V_{XX} . \cr}$

V _s, V _X, V _r, V _A, V _XX, V _Xr, V _XA, V _rr, V _AA are partial derivatives of first and second orders with respect to time, fund, wage, and interest rate. When Δt tends to zero, minimizing the right-hand term of the inequality (19) is equivalent to minimizing the generator G ^π(s, X, N _s, A _s). The investment strategy replicating at best the process ${\tilde{X}}\nolimits_{t}{ \vskip-1\! \ast }$ is then obtained by deriving G ^π(t, X _t, N _t, A _t) with respect to π_t^s and π_t^R

(20)

$\pi _{t}^{S \ast } \tab \equals \left(\! \! { \minus {{\nu _{R}.\sigma _{Sr} } \over {\sigma _{S}^{\setnum{2}}.\sigma _{r}.n\lpar K\rpar }} \minus {{\nu _{S} } \over {\sigma _{S}^{\setnum{2}} }}} \right).{{V_{X} } \over {V_{XX} }}.{1 \over {X_{t} }} \minus {{\sigma _{AS} } \over {\sigma _{S} }}.{{V_{XA} } \over {V_{XX} }}.{{A_{t} } \over {X_{t} }}$

(21)

$\eqalign{ \pi _{t}^{R \ast } \equals \tab \left(\! \! { \minus {{\nu _{S}.\sigma _{Sr} } \over {\sigma _{S}^{\setnum{2}}.\sigma _{r}.n\lpar K\rpar }} \minus {{\nu _{R} } \over {\sigma _{r}^{\setnum{2}}.n\lpar K\rpar ^{\setnum{2}} }}.\left( {1 \plus {{\sigma _{Sr}^{\setnum{2}} } \over {\sigma _{S}^{\setnum{2}} }}} \right)}\! \! \right).{{V_{X} } \over {V_{XX} }}.{1 \over {X_{t} }} \cr \tab\plus \left( {{{\sigma _{Ar} } \over {\sigma _{r}.n\lpar K\rpar }} \minus {{\sigma _{AS}.\sigma _{Sr} } \over {\sigma _{S}.\sigma _{r}.n\lpar K\rpar }}} \right){{V_{XA} } \over {V_{XX} }}.{{A_{t} } \over {X_{t} }} \plus {1 \over {n\lpar K\rpar }}.{{V_{Xr} } \over {V_{XX} }}.{1 \over {X_{t} }}. \cr}$

As the value function is known (see expression (16)), it suffices to derive it with respect to X _t, r _t, and A _t to obtain the optimal part of the funds invested in stocks and bonds

(23)

$\eqalign{ \pi _{t}^{S \ast } \equals \tab \left( {{{\nu _{R}.\sigma _{Sr} } \over {\sigma _{S}^{\setnum{2}}.\sigma _{r}.n\lpar K\rpar }} \plus {{\nu _{S} } \over {\sigma _{S}^{\setnum{2}} }}} \right).{{UL_{t} } \over {X_{t} }} \plus {{\sigma _{AS} } \over {\sigma _{S} }}.{{E\left( {H\lpar t\comma T\rpar.L_{T} \vert F_{t} } \right)} \over {X_{t} }} \cr \pi _{t}^{R \ast } \equals \tab \left( {{{\nu _{S}.\sigma _{Sr} } \over {\sigma _{S}^{\setnum{2}}.\sigma _{r}.n\lpar K\rpar }} \plus {{\nu _{R} } \over {\sigma _{r}^{\setnum{2}}.n\lpar K\rpar ^{\setnum{2}} }}.\left( {1 \plus {{\sigma _{Sr}^{\setnum{2}} } \over {\sigma _{S}^{\setnum{2}} }}} \right)} \right).{{UL_{t} } \over {X_{t} }} \cr \tab \minus \left( {{{\sigma _{Ar} } \over {\sigma _{r}.n\lpar K\rpar }} \minus {{\sigma _{AS}.\sigma _{Sr} } \over {\sigma _{S}.\sigma _{r}.n\lpar K\rpar }}} \right).{{E\left( {H\lpar t\comma T\rpar.L_{T} \vert F_{t} } \right)} \over {X_{t} }} \cr \tab \plus \underbrace {{1 \over {n\lpar K\rpar }}.{{V_{Xr} } \over {V_{XX} }}.{1 \over {X_{t} }}}_{correction\>term}. \cr \cr}$

The correction term has no simple analytic expression

$\openup2\eqalign{ {1 \over {n\lpar K\rpar }}.{{V_{Xr} } \over {V_{XX} }}.{1 \over {X_{t} }} \equals \tab {1 \over {n\lpar K\rpar.X_{t} }}.\left( {NC.\int_{t}^{T} {{\partial B\lpar t\comma s\rpar } \over {\partial r_{t} }}.ds \minus {{\partial E\left( {H\lpar t\comma T\rpar.L_{T} \vert F_{t} } \right)} \over {\partial r_{t} }}} \right) \cr \tab\plus {{UL_{t} } \over {n\lpar K\rpar.X_{t} }}.{{\left( {{\textstyle{1 \over {u_{\setnum{1}} }}}.\int_{t}^{T} {\textstyle{{\partial E\left( {H\lpar t\comma s\rpar ^{\setnum{2}} \vert F_{t} } \right)} \over {\partial r_{t} }}}ds \plus {\textstyle{1 \over {u_{\setnum{2}} }}}.{\textstyle{{\partial E\left( {H\lpar t\comma T\rpar ^{\setnum{2}} \vert F_{t} } \right)} \over {\partial r_{t} }}}ht } \right)} \over {\mathop {\left( {{\textstyle{1 \over {u_{\setnum{1}} }}}.\int_{t}^{T} E\left( {H\lpar t\comma s\rpar ^{\setnum{2}} \vert F_{t} } \right)ds \plus {\textstyle{1 \over {u_{\setnum{2}} }}}.E\left( {H\lpar t\comma T\rpar ^{\setnum{2}} \vert F_{t} } \right)} \right)}\nolimits^{\setnum{2}} }} \cr}$

where

$\eqalign{ {{\partial B\lpar t\comma s\rpar } \over {\partial r_{t} }} \equals \tab \minus n\lpar s \minus t\rpar.B\lpar t\comma s\rpar \cr {{\partial E\left( {H\lpar t\comma s\rpar ^{\setnum{2}} \vert F_{t} } \right)} \over {\partial r_{t} }} \equals \tab \minus 2.n\lpar s \minus t\rpar.E\left( {H\lpar t\comma s\rpar ^{\setnum{2}} \vert F_{t} } \right) \cr}$

$\eqalign{\tab {{\partial E\left( {H\lpar t\comma T\rpar.L_{T} \vert F_{t} } \right)} \over {\partial r_{t} }} \equals \cr\tab\qquad \minus \lpar n_{x} \minus N_{t} \rpar.\alpha.\int_{t}^{T} _{s \minus t} p_{x \plus s}^{h}.n\lpar T \minus s\rpar.E^{Q} \left( {e^{ \minus \int_{t}^{T} r_{u}.du}.A_{T}.B\lpar T\comma s\rpar \vert F_{t} } \right).ds. \cr}$

An interesting characteristic of this correction term is that it tends to zero when t→T. Indeed, all terms intervening in the numerator of the correction term are integrals or function of n(T−t), which tend to zero when t→T.

The economic significance of the investment strategy proposed may be summarized as follows:

(1) In a first stage, we define an optimal wealth process $\left( {\mathop {\tilde{X}}\nolimits_{t}{\!\!\vskip-1 \ast } } \right)_{t}$ that is not replicable by an adapted investment strategy, given that it depends upon the mortality and wages, which are not traded in our model (see equations (13) and (14)).
(2) In a second stage, we propose a strategy of investment/contribution as close as possible to the optimal solution. As close as possible, in the sense that the wealth process (X _t)_t minimizes locally $E\left[ {\left\vert {X_{t \plus \rmDelta t} \minus \mathop {\tilde{X}}\nolimits{ \vskip-1\ast }_{\!\!\!\!t \plus \rmDelta t} } \right\vert\>\vert \>F_{t} } \right]$ .

Note that Nielsen (Reference Nielsen2005) has adopted a similar approach. He has first solved by the martingale approach a problem of utility maximization, in an incomplete market, due to the presence of mortality. The optimal wealth process found in this way is, as in our case, not replicable. Nielsen has next calculated the local risk minimizing strategy following at best this target wealth process.

7 Example

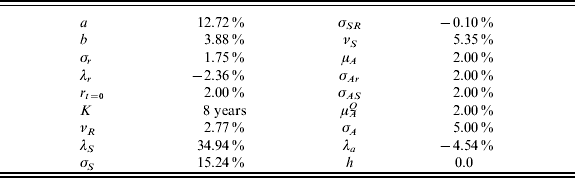
We consider a male population, age 50, of n ₅₀=10000 affiliates, and who earns a wage A _t=0 of 2500 Euro. We assume that all individuals retire at 65 years and receive till their death a continuous annuity equal to α=20% of their last salary A _T. Market parameters are presented in the Table 1.

Table 1. Parameters

The normal cost is set to

$NC \equals {{E\left( {H\lpar 0\comma T\rpar.L_{T} \vert F_{\setnum{0}} } \right)} \over {\mathop {\bar{a}}\nolimits_{\setnum{0}\comma T} }} \equals 26.763\>Eur .$

According to equation (16), this is the normal cost, minimizing the value function at time t=0 (indeed, it implies that UL _t=0=0 since the initial wealth is null at t=0). Three choices of weights u ₁, u ₂ are tested. In the first test, the asset manager seeks mainly to limit the volatility of the contribution rate: u ₁=1, u ₂=0.1. In the second case studied, u ₁ and u ₂ are set equal to one. In the last test, the aim is mainly to limit the volatility of the terminal surplus: u ₁=1, u ₂=10. We have opted for Monte Carlo simulations. Five thousand sample paths are generated for each test and the discretization step of time Δt is set to one year (contributions and asset allocation are both changed once a year). In Figures 1 and 2, we compare respectively the average contribution rates and the average negative unfunded liabilities (−UL _t, which is equal at time T to the terminal surplus, see equation (15)). These negative unfunded liabilities may be seen as the surplus of assets owned by the fund.

The unfunded liabilities are on average negative. According to equation (14), it means that on average the Lagrange multiplier is negative and that the investment/contribution strategy is suboptimal for the optimization problem (8). In fact, it means that the optimal target wealth $\mathop {\tilde{X}}\nolimits{\vskip-1.5 \ast }_{\!\!\!\!T}$ minimizes the value function under the equality constraint

$E\left(\!\! { \minus \int_{t}^{T} \!H\lpar t\comma s\rpar.c_{s}.ds \plus H\lpar t\comma T\rpar.\mathop {\tilde{X}}\nolimits_{T} \vert F_{t} } \right) \equals x$

rather than under the initial inequality constraint defined in equation (9). For an equality constraint, the Lagrange multiplier may indeed be negative or positive.

As mentioned in Section 6.1, this results from the fact that the proposed investment strategy does not perfectly replicate the optimal wealth process $\mathop {\tilde{X}}\nolimits{ \vskip-1\ast }_{\!\!\!\!t}$ , equation (13), owing to the presence of unhedgeable risks. As mentioned earlier, the followed strategy is however as close as possible to the non-replicable optimal one, solution (8).

Fig. 1. Contribution rates

Fig. 2. −UL _t (% of the fund)

For each set of weights, the contribution rate decreases on average. The higher is the weight u ₂ granted to minimize the terminal surplus variation, the higher is the decrease of the contribution rate and the lower is the average negative unfunded liabilities.

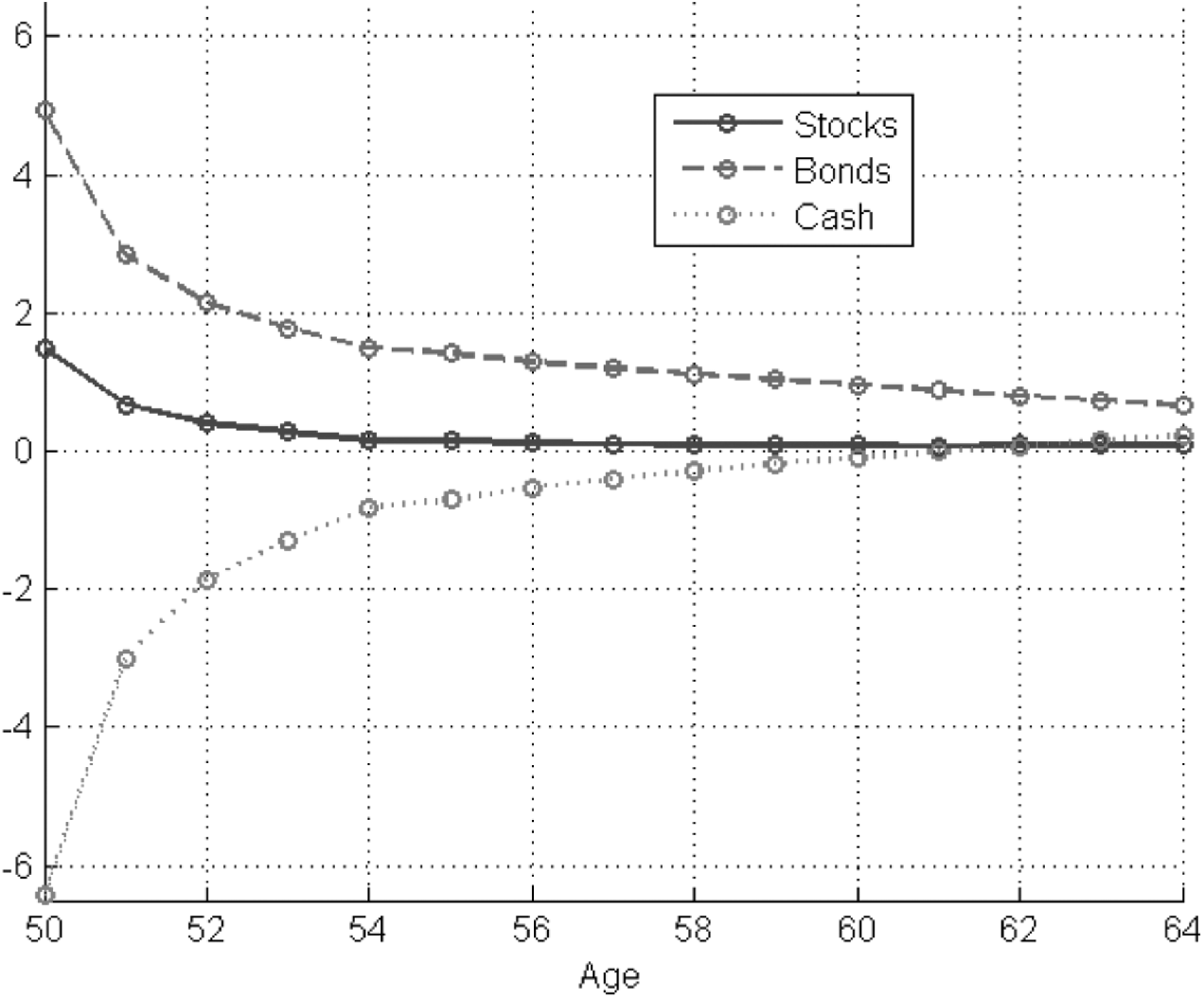
In Figure 3 depicts the evolution of the average asset allocation for u ₁=1 and u ₂=0.1 as obtained in equations (22) and (23). Over the first nine years, huge amounts of cash are borrowed and invested in stocks and bonds. This short position in cash is reduced with time. One year before T, the asset allocation is as follows: 68.3% in bonds, 21.3% in cash, and 10.4% in stocks. We also observe that weights mainly influence the contribution rate and the terminal surplus: the average asset allocation for the two other sets of weights are nearly identical to the one displayed in Figure 3.

Fig. 3. Asset mix for u ₁=1 and u ₂=10

8 Conclusion

In this paper, we have investigated a model for defined benefit pension plans, which incorporates stochastic interest rates, mortality, and salary. In particular, we have studied the problem of pension funds from the perspective of an asset manager who wishes to minimize the deviation of contributions and terminal surplus from target ones, under a budget constraint and using a quadratic criterion.

The presence of stochastic mortality and salary entails that the market of pension fund liabilities is incomplete and the set of deflators used to valuate liabilities counts more than one element. In order to apply the Cox and Huang martingale method, it is then necessary to choose a deflator that reflects the pricing preferences of the fund manager. This assumption is not really impeding and corresponds to the actuarial practice. Another problem of the market incompleteness is that the optimal wealth process found by the martingale approach is not perfectly replicable. However, we can find the optimal investment hedging this process at best by a reasoning based on the dynamic programming principle.

We have seen that the optimal contribution rate is the sum of the normal cost and of the unfunded liabilities amortized by a factor, the function of the market conditions. The optimal investment strategy also depends on the unfunded liabilities; in particular: for initial negative unfunded liabilities, the optimal target wealth will be larger than the mathematical reserve at retirement date necessary to cover the promised liabilities. An illustrative example has been given which shows the dependence between the contribution rate and the weights respectively, given to the minimization of the contribution risk and of the surplus risk.

Appendix A

As mentioned early in Section 4, the expected value of the deflator, E(H(t, s)|F _t), is the price of a zero coupon bond B(t, s), because of independency of $W_{u}^{r\comma P^{\hskip1 f} }$ , $W_{t}^{S\comma P^{\hskip1 f} }$ , and $W_{t}^{A\comma P^{a} }$ . If interest rates are driven by a Vasicek model (for details on this model, we refer to Cairns Reference Cairns2004), the price of a zero coupon bond is given by

(24)

$B\lpar t\comma s\rpar \equals \exp\left(\! { \minus \beta.\lpar s \minus t\rpar \plus n\lpar s \minus t\rpar.\lpar \beta \minus r_{t} \rpar \minus {{\sigma _{r}^{\setnum{2}} } \over {4.a}}.n\lpar s \minus t\rpar ^{\setnum{2}} } \right)$

where

(25)

$\beta \equals b^{Q} \minus {{\sigma _{r}^{\setnum{2}} } \over {2.a^{\setnum{2}} }} \equals b \minus \sigma _{r}.{{\lambda _{r} } \over a} \minus {{\sigma _{r}^{\setnum{2}} } \over {2.a^{\setnum{2}} }}$

and n(s−t) is a positive decreasing function, null when s=t

$n\lpar s \minus t\rpar \equals {1 \over a}.\left( {1 \minus e^{ \minus a.\lpar s \minus t\rpar } } \right).$

The derivative of the bond price with respect to r _t, used in paragraph 2 to calculate the correction term of the optimal bonds strategy (23), is

${{\partial B\lpar t\comma s\rpar } \over {\partial r_{t} }} \equals \minus n\lpar s \minus t\rpar.B\lpar t\comma s\rpar.$

Appendix B

This appendix presents the proof of the proposition 1. The deflator (7) can be rewritten as follows

$\eqalign{ H\lpar t\comma s\rpar \equals \tab \exp\left(\! { \minus \int_{t}^{s}\! r_{u}.du \minus {1 \over 2}.\int_{t}^{s}\! \vert \vert \rmLambda \vert \vert ^{\setnum{2}}.du \minus \int_{t}^{s} \!\rmLambda.dW_{u}^{P} } \right). \cr \tab \exp\left( {\int_{t}^{s} \ln\left( {1 \plus h} \right).dN_{u} \minus \int_{t}^{s} h.\lambda _{N\comma u}.du} \right) \cr}$

where Λ=(λ_r, λ_S, λ_a) and $W_{u}^{P} \equals \left( {W_{u}^{r\comma P^{\hskip1 f} } \comma W_{u}^{S\comma P^{\hskip1 f} } \comma W_{u}^{A\comma P^{a} } } \right)\prime$ . E ^P(H(t, s)²|F _t) can therefore be decomposed in two independent terms called the financial and actuarial components, which are next calculated separately

(26)

$\eqalign{ E^{P} \left( {H\lpar t\comma s\rpar ^{\setnum{2}} \vert F_{t} } \right) \equals \tab \underbrace {E^{P} \left( {\exp\left(\! { \minus 2.\int_{t}^{s} \!r_{u}.du \minus \int_{t}^{s}\! \vert \vert \rmLambda \vert \vert ^{\setnum{2}}.du \minus 2.\int_{t}^{s}\! \rmLambda.dW_{u}^{P} } \right)\vert F_{t} } \right)}_{Financial\>component} \cr \tab\underbrace {E^{P} \left( {\exp \left( {\int_{t}^{s}\! \ln \lpar \lpar 1 \plus h\rpar ^{\setnum{2}} \rpar.dN_{u} \minus \int_{t}^{s} 2.h.\lambda _{N\comma u}.du} \right)\vert F_{t} } \right)}_{Actuarial\>component} \cr}$

Calculation of the financial component

The following random variable defines a change of measure from P to $\tilde{P}$

$\mathop {\left( {{{d\tilde{P}} \over {dP}}} \right)}\nolimits_{t} \equals \exp\left(\! { \minus \int_{\setnum{0}}^{t}\! 2.\rmLambda .dW_{u}^{P} \minus {1 \over 2}.\int_{\setnum{0}}^{t} \vert \vert 2.\rmLambda \vert \vert ^{\setnum{2}} .du} \right)$

and under $\tilde{P}$ , the following elements are Brownian motions

$d {\tilde{W}}\nolimits_{u}^{r\comma \tilde{P}} \equals dW_{u}^{r\comma P^{\hskip1 f} } \plus 2.\lambda _{r}.du$

$d {\tilde{W}}\nolimits_{u}^{S\comma \tilde{P}} \equals dW_{u}^{S\comma P^{\hskip1 f} } \plus 2.\lambda _{S}.du$

$d {\tilde{W}}\nolimits_{u}^{A\comma \tilde{P}} \equals dW_{u}^{A\comma P^{a} } \plus 2.\lambda _{a}.du.$

The financial component of (26) becomes

$\eqalign{\tab E^{P} \left( {\exp\left(\! { \minus 2.\int_{t}^{s} r_{u}.du \minus \int_{t}^{s} \vert \vert \rmLambda \vert \vert ^{\setnum{2}}.du \minus 2.\int_{t}^{s} \rmLambda.dW_{u}^{P} } \right)\vert F_{t} } \right) \cr \tab \quad \equals \exp\left( {\int_{t}^{s} \vert \vert \rmLambda \vert \vert ^{\setnum{2}}.du} \right).E^{\tilde{P}} \left( {e^{ \minus \int_{t}^{s} \setnum{2}.r_{u}.du} \vert F_{t} } \right) \cr}$

and as 2.r _u has mean reverting dynamics under $\tilde{P}$

$d\left( {2.r_{u} } \right) \equals a.\left( {2.b \minus 4.{{\sigma _{r}.\lambda _{r} } \over a} \minus 2.r_{u} } \right).dt \plus 2.\sigma _{r}.d {\tilde{W}}\nolimits_{u}^{r\comma \tilde{P}} \comma$

it suffices to apply the Vasicek's formula to obtain that

$E^{\tilde{P}} \left( {e^{ \minus \int_{t}^{s} \setnum{2}.r_{u}.du} \vert F_{t} } \right) \equals \exp\left(\! { \minus \beta ^{\tilde{P}}.\lpar s \minus t\rpar \plus n\lpar s \minus t\rpar.\lpar \beta ^{\tilde{P}} \minus 2.r_{t} \rpar \minus {{\sigma _{r}^{\setnum{2}} } \over a}.n\lpar s \minus t\rpar ^{\setnum{2}} } \right)$

where

$\beta ^{\tilde{P}} \equals 2.b \minus 4.{{\sigma _{r}.\lambda _{r} } \over a} \minus 2.{{\sigma _{r}^{\setnum{2}} } \over {a^{\setnum{2}} }}$

and

$n\lpar s \minus t\rpar \equals {1 \over a}.\left( {1 \minus e^{ \minus a.\lpar s \minus t\rpar } } \right).$

Calculation of the actuarial component

By the assumption that $h \gt \minus {\textstyle{1 \over 2}}$ , it is possible to define a positive constant k

$k \equals {{\mathop {\left( {1 \plus h} \right)}\nolimits^{\setnum{2}} } \over {\left( {1 \plus 2.h} \right)}}$

such that the actuarial component of equation (26) can be rewritten as

(27)

$\openup2\eqalign{ \tab E^{P} \left( {\exp\left( {\int_{t}^{s} \ln\left( {\mathop {\left( {1 \plus h} \right)}\nolimits^{\setnum{2}} } \right).dN_{u} \minus \int_{t}^{s} 2.h.\lambda _{N\comma u}.du} \right)\vert F_{t} } \right) \cr \tab \quad \equals E^{Q^{{m\comma \setnum{2}.h}} } \left( {\exp\left( {\int_{t}^{s} \ln\lpar k\rpar.dN_{u} } \right).\underbrace {\exp\left( {\int_{t}^{s} \ln\left( {1 \plus 2.h} \right).dN_{u} \minus \int_{t}^{s} 2.h.\lambda _{N\comma u}.du} \right)}_{}\vert F_{t} } \right) \cr \tab\!\qquad\times{{dQ^{m\comma \setnum{2}.h} } \over {dP^{m} }} \hskip0}\hskip-12\vskip44$

The term ${\textstyle{{dQ^{m\comma \setnum{2}.h} } \over {dP^{m} }}}$ defines a new actuarial measure Q ^m,2.h, under which the following centered process

$M_{t}^{m\comma \setnum{2}.h} \equals N_{t} \minus \int_{\setnum{0}}^{t} \lpar n_{x} \minus N_{u \minus } \rpar.\mu \lpar x \plus u\rpar.\lpar 1 \plus 2.h\rpar.du$

is a martingale. The expected number of survivors at time s, conditional to instant t is given by

$E^{Q^{{m\comma \setnum{2}.h}} } \left( {\lpar n_{x} \minus N_{s} \rpar \vert F_{t} } \right) \equals \lpar n_{x} \minus N_{t} \rpar.\underbrace {\exp\left(\! { \minus \int_{t}^{s} \mu \lpar x \plus u\rpar.\lpar 1 \plus 2.h\rpar.du} \right)}_{_{{s \minus t}} \, p_{{x \plus t}}^{{\setnum{2}.h}} }.$

Equation (27) is finally rewritten as the expectation under Q ^m,2.h of a constant k to the power N _s−N _t, the number of deaths

$E^{P} \left( {\exp\left( {\int_{t}^{s} \ln\left( {\mathop {\left( {1 \plus h} \right)}\nolimits^{\setnum{2}} } \right).dN_{u} \minus \int_{t}^{s} 2.h.\lambda _{N\comma u}.du} \right)\vert F_{t} } \right) \tab \equals \tab E^{Q^{{m\comma \setnum{2}.h}} } \left( {k^{N_{s} \minus N_{t} } \vert F_{t} } \right).$

Under Q ^m,2.h, the probability of observing n deceases in the interval of time (t, s) is a binomial variable of parameters (n _x−N _t, 1−_s−tp _x+t^2.h). The expected value of $k^{N_{s} \minus N_{t} }$ is then computable by the following formula

$\eqalign{ \tab E^{P} \left( {\exp\left( {\int_{t}^{s} \ln\left( {\mathop {\left( {1 \plus h} \right)}\nolimits^{\setnum{2}} } \right).dN_{u} \minus \int_{t}^{s} 2.h.\lambda _{N\comma u}.du} \right)\vert F_{t} } \right) \equals E^{Q^{{m\comma \setnum{2}.h}} } \left( {k^{N_{s} \minus N_{t} } \vert F_{t} } \right) \cr \tab \quad \equals \mathop{\sum}\limits_{n \equals \setnum{1}}^{n_{x} \minus N_{t} } {{\lpar n_{x} \minus N_{t} \rpar \exclam } \over {\lpar n_{x} \minus N_{t} \minus n\rpar \exclam \>n\exclam }}\left( {k^{n}.\mathop {\left( {_{s \minus t} p_{x \plus t}^{\setnum{2}.h} } \right)}\nolimits^{n_{x} \minus N_{t} \minus n}.\mathop {\left( {1 \minus _{s \minus t} \, p_{x \plus t}^{\setnum{2}.h} } \right)}\nolimits^{n} } \right).}$

Appendix C

The independence between mortality and the other random variables of our model entails that the fair value of the pension fund liabilities is

$\eqalign{ L_{T} \equals \tab E\left( {\int_{T}^{Tm} H\lpar T\comma s\rpar.\left( {n_{x} \minus N_{s} } \right).B.ds\vert F_{T} } \right) \cr\equals\tab \left( {n_{x} \minus N_{T} } \right).\alpha.A_{T}.\int_{T}^{Tm} _{s \minus T} p_{x \plus T}^{h}.B\lpar T\comma s\rpar.ds \cr}$

and that the expectation at time t⩽T of L _T equals

$\eqalign{ E\left( {H\lpar t\comma T\rpar.L_{T} \vert F_{t} } \right) \equals \alpha.\left( {n_{x} \minus N_{t} } \right).\int_{T}^{Tm} _{s \minus t} p_{x \plus t}^{h}.E^{Q} \left( {e^{ \minus \int_{t}^{T} r_{u}.du}.A_{T}.B\lpar T\comma s\rpar \vert F_{t} } \right).ds. \cr}$

The sequel of this paragraph focuses then on the calculation of $E^{Q} \big( {e^{ \minus \int_{t}^{T} r_{u}.du}.A_{T}.B\lpar T\comma s\rpar \vert F_{t} } \big)$ . This step is based on the following four observations. Firstly, A _T is the Dolean–Dade exponential, solution of the SDE (4)

(28)

$\eqalign{A_{T} \equals \tab A_{t}.\exp\left( {\int_{t}^{T} \left( {\mu _{A}^{Q} \lpar u\rpar \minus {{\sigma _{Ar}^{\setnum{2}} } \over 2} \minus {{\sigma _{AS}^{\setnum{2}} } \over 2} \minus {{\sigma _{A}^{\setnum{2}} } \over 2}} \right)du} \right) \cr \tab .\exp\left( { \plus \int_{t}^{T} \sigma _{A}.dW_{u}^{A\comma Q^{{a\comma \lambda _{a} }} } \plus \int_{t}^{T} \sigma _{Ar} dW_{u}^{r\comma Q^{\hskip1 f} } \plus \int_{t}^{T} \sigma _{AS} dW_{u}^{S\comma Q^{\hskip1 f} } } \right). \cr}$

Secondly, as detailed in Appendix A, the price of a zero coupon bond is given by

(29)

$B\lpar T\comma s\rpar \equals \exp\left(\! { \minus \beta.\lpar s \minus T\rpar \plus n\lpar s \minus T\rpar.\lpar \beta \minus r_{T} \rpar \minus {{\sigma _{r}^{\setnum{2}} } \over {4.a}}.n\lpar s \minus T\rpar ^{\setnum{2}} } \right) \comma$

where β is defined by equation (25). The last useful elements are related to the fact that interest rates are Gaussian in the Vasicek model

(30)

$r_{T} \tab \equals \left( {1 \minus e^{ \minus a.\lpar T \minus t\rpar } } \right).b^{Q} \plus e^{ \minus a.\lpar T \minus t\rpar }.r_{t} \plus \int_{t}^{T} \sigma _{r}.e^{ \minus a.\lpar T \minus u\rpar }.dW_{u}^{r\comma Q^{\hskip1 f} }$

(31)

$\int_{t}^{T} r_{u} du \equals b^{Q}.\lpar T \minus t\rpar \plus \lpar r_{t} \minus b^{Q} \rpar.n\lpar T \minus t\rpar \plus \sigma _{r}.\int_{t}^{T} n\lpar T \minus u\rpar.dW_{u}^{r\comma Q^{\hskip1 f} }.$

The proof of such results can be found in Cairns (Reference Cairns2004: Appendix B). Combining expressions (28), (29), (30), and (31) allows us to rewrite $e^{ \minus \int_{t}^{T} r_{u}.du}.A_{T}.B\lpar T\comma s\rpar$ as an exponential of independent normal random variables and the calculation of $E^{Q} \big( {e^{ \minus \int_{t}^{T} r_{u}.du}.A_{T}.B\lpar T\comma s\rpar \vert F_{t} } \big)$ directly results from the expectation of lognormal variables.

Appendix D

In the example presented in this paper, mortality rates obey to a Gompertz–Makeham distribution. The parameters are those defined by the Belgian regulator for the pricing of a life insurance purchased by a man. For an individual of age x, the mortality rate is

$\eqalign{\mu \lpar x\rpar \equals a_{\mu } \plus b_{\mu }.c^{x} \quad \quad a_{\mu } \equals \minus \ln\lpar s_{\mu } \rpar \quad \quad b_{\mu } \equals \ln\lpar g_{\mu } \rpar.\ln\lpar c_{\mu } \rpar}$

where the parameters s _μ, g _μ, c _μ take the values shown in the Table 2.

Table 2. Belgian legal mortality, for life insurance products and for a male population

References

Boulier, J. F., Trussant, E., and Florens, D. (1995) A dynamic model for pension fund management. Proceedings of the 5th AFIR International Symposium, Brussels, Vol 1, 361–384.Google Scholar

Brennan, M. J. and Xia, Y. (2002) Dynamic asset allocation under inflation. The Journal of Finance, 57(3): 1201–1238.CrossRef Google Scholar

Cairns, A. J. G. (1995) Pension funding in a stochastic environment: the role of objectives in selecting an asset allocation strategy. Proceedings of the 5th AFIR International Symposium, Brussels, Vol 1, 429–453.Google Scholar

Cairns, A. J. G. (2000) Some notes on the dynamics and optimal control of stochastic pension fund models in continuous time. ASTIN Bulletin, 30(1): 19–55.Google Scholar

Cairns, A. (2004) Interest Rate Models: An Introduction. Princeton, NJ: Princeton University Press.Google Scholar

Chan, T. (1997) Some applications of Lévy processes to stochastic investment models. ASTIN Bulletin, 28: 77–93.CrossRef Google Scholar

Cox, J. and Huang, C. F. (1989) Optimal consumption and portfolio policies when asset prices follow a diffusion process. Journal of Economic Theory, 49: 33–83.Google Scholar

Duffie, D. (2001) Dynamic Asset Pricing Theory. Third edition. Princeton, NJ: Princeton University Press.Google Scholar

Fleming, W. and Rishel, R. (1975) Deterministic and Stochastic Optimal Control. New York: Springer-Verlag.Google Scholar

Haberman, S. and Sung, J. H. (1994) Dynamic approaches to pension funding. Insurance: Mathematics and Economics, 15: 151–162.Google Scholar

Haberman, S. and Sung, J. H. (2005) Optimal pension funding dynamics over infinite control horizon when stochastic rates of return are stationary. Insurance: Mathematics and Economics, 36: 103–116.Google Scholar

Hainaut, D. and Devolder, P. (2007a) A martingale approach applied to the management of life insurances. ICFAI Journal of Risk and Insurance, 4.Google Scholar

Hainaut, D. and Devolder, P. (2007b) Management of a pension funds under stochastic mortality and interest rates. Insurance: Mathematics and economics, 41.Google Scholar

Huang, H.-C. and Cairns, A. J. G. (2006) On the control of defined-benefit pension plans. Insurance: Mathematics and Economics, 38: 113–131.Google Scholar

Josa-Fombellida, R. and Rincon-Zapatero, J. P. (2004) Optimal risk management in defined benefit stochastic pension funds. Insurance: Mathematics and Economics, 34: 489–503.Google Scholar

Josa-Fombellida, R. and Rincon-Zapatero, J. P. (2006) Optimal investment decisions with a liability: the case of defined benefits pension plans. Insurance: Mathematics and Economics, 36: 81–98.Google Scholar

Karatzas, I. and Shreve, S. (1998) Methods of Mathematical Finance. New York: Springer-Verlag.Google Scholar

Møller, T. (1998) Risk minimizing hedging strategies for unit-linked life insurance contracts. ASTIN Bulletin, 28(1): 17–47.Google Scholar

Nielsen, P. H. (2005) Utility maximization and risk minimization in life and pension insurance. Finance and Stochastics, 10(1): 75–97.Google Scholar

Øksendal, B. and Sulem, A. (2004) Applied Stochastic Control of Jump Diffusions. New York: Springer-Verlag.Google Scholar

Sundaresan, S. and Zapatero, F. (1997) Valuation, optimal asset allocation and retirement incentives of pension plans. The Review of Financial Studies, 10(3): 631–660.Google Scholar

Wilkie, A. D. (1986) A stochastic investment model for actuarial use. TFA, 39: 341–403.Google Scholar

Wilkie, A. D. (1995) More on a stochastic asset model for actuarial use. Bristish Actuarial Journal, 1: 777–964.Google Scholar

Yong, J. and Zhou, X. Y. (1999) Stochastic Controls: Hamiltonian Systems and HJB Equations. New York: Springer-Verlag.Google Scholar

Table 1. Parameters

Fig. 1. Contribution rates

Fig. 2. −ULt (% of the fund)

Fig. 3. Asset mix for u1=1 and u2=10

Table 2. Belgian legal mortality, for life insurance products and for a male population

Article contents

Optimal funding of defined benefit pension plans

Abstract

1 Introduction

2 The financial market

3 The pension fund

4 The deflator and the fair value of liabilities

4.1 Financial deflator

4.2 The wage deflator

4.3 The actuarial deflator

4.4 The deflator and the price of liabilities

5 The optimization problem

6 The martingale solution

6.1 Optimal contribution rate and wealth

6.2 The best replicating strategy

7 Example

8 Conclusion

Appendix A

Appendix B

Calculation of the financial component

Calculation of the actuarial component

Appendix C

Appendix D

References

Save article to Kindle

Save article to Dropbox

Save article to Google Drive

Reply to: Submit a response

Your details

You have entered the maximum number of contributors

Conflicting interests