The Pension Benefit Guaranty Corporation (PBGC) is an agency of the U.S. federal government that insures private sector defined benefit (DB) pension plans, when an employer becomes insolvent and is unable to pay the pension liabilities. When a plan is terminated, the PBGC takes over the plan assets and pays vested employees their future benefits up to certain limits (trusteed plans). For this insurance coverage, the employers of the ongoing plans (non-trusteed) must pay fixed/variable premiums to the PBGC. In principle, the insurance premiums collected by the PBGC should be sufficient to cover the potential losses; this would ensure that PBGC could pay the insured benefits of terminated pension plan without additional external funding (e.g., from the taxpayers). Therefore, the risk exposure of the PBGC from insuring DB pension plans arises from two sources: the probability of employer insolvencies; and the terminating plans’ funding status (the excess of the value of the insured plan liabilities over the plan assets).
My comments here focus on only the second component, namely the impact of the plan underfunding for the operation of the PBGC. When a DB plan is fully funded (i.e., the value of plan assets is equal to the value of the plan liability), the PBGC's risk exposure for an ongoing plan is low even if the plan sponsor becomes insolvent. For this reason, the questions most pertinent to the PBGC are: what key risk factors can produce underfunding in a DB pension plan, and how can these risk factors be quantified?
In what follows, we explore the most important risk factors that produce DB pension underfunding, namely, investment risk and liability risk. These are interrelated and must be considered simultaneously in order to quantify the risk exposure of a DB pension plan (Hustead and Mitchell, Reference Hustead, Mitchell, Mitchell and Hustead2001). Therefore researchers and practitioners have argued that there is a need for an integrated risk management model – also referred as Integrated Asset/Liability Model – to better understand DB pension plan funding risk. We also examine the Pension Insurance Modeling System (PIMS) developed by the PBGC in terms of its own use of some of the building blocks of an integrated risk management model.
The PIMS uses detailed information on liabilities of terminated and ongoing plans. It also implements a wide range of detailed legal rules, i.e., contribution requirements from the Pension Protection Act (PPA), rules from the U.S. tax code, and the way that fixed/variable PBGC-premiums are calculated. It also includes simple management rules on how the assets of the terminated and ongoing plans are invested.Footnote 1 Based on seven key stochastic variables,Footnote 2 PIMS specifies for each simulation path i = 1,…. I and time period t = 1, …., T for each ongoing plan m = 1, …, M and n = 1, …, N terminated planFootnote 3:
1. the funding status (value of plan assets minus actuarial value of plan liabilities),
2. the cash flows from assets, the premiums paid to PBGC from ongoing plans, and the benefits paid to retirees of terminated plans,
3. the probability of insolvency for ongoing plans.
Consequently, PIMS considers both pure and parameter risk in the simulation procedure. The resulting simulations produce a wide range of potential future outcomes of claims. These outcomes are reported in various summary statistics; for example, as distributions over time (using quantiles and averages) and/or as a stochastic present value of PBGC net financial position using the riskless interest rate to discount (on each path) future payments.
Overall, we can conclude that the PBGC has developed a complex, reasonably sensible, and defensible stochastic model to predict the probability distribution of potential future losses for PBGC from both terminated and ongoing DB plans. Additionally, we outline two key areas where extensions of PIMS may be valuable in the future to incorporate systematic mortality risk in the liability part of the model, and to model the complete term structure of interest rate instead of only a single interest rate (30-year government bonds). Besides these two areas, the model should be expanded to include not only equity and bonds, but also real estate and alternative investments. And finally, the Conditional Value-at-Risk (CVaR) metric may be a useful way to communicate the model outcomes.
Liability risk
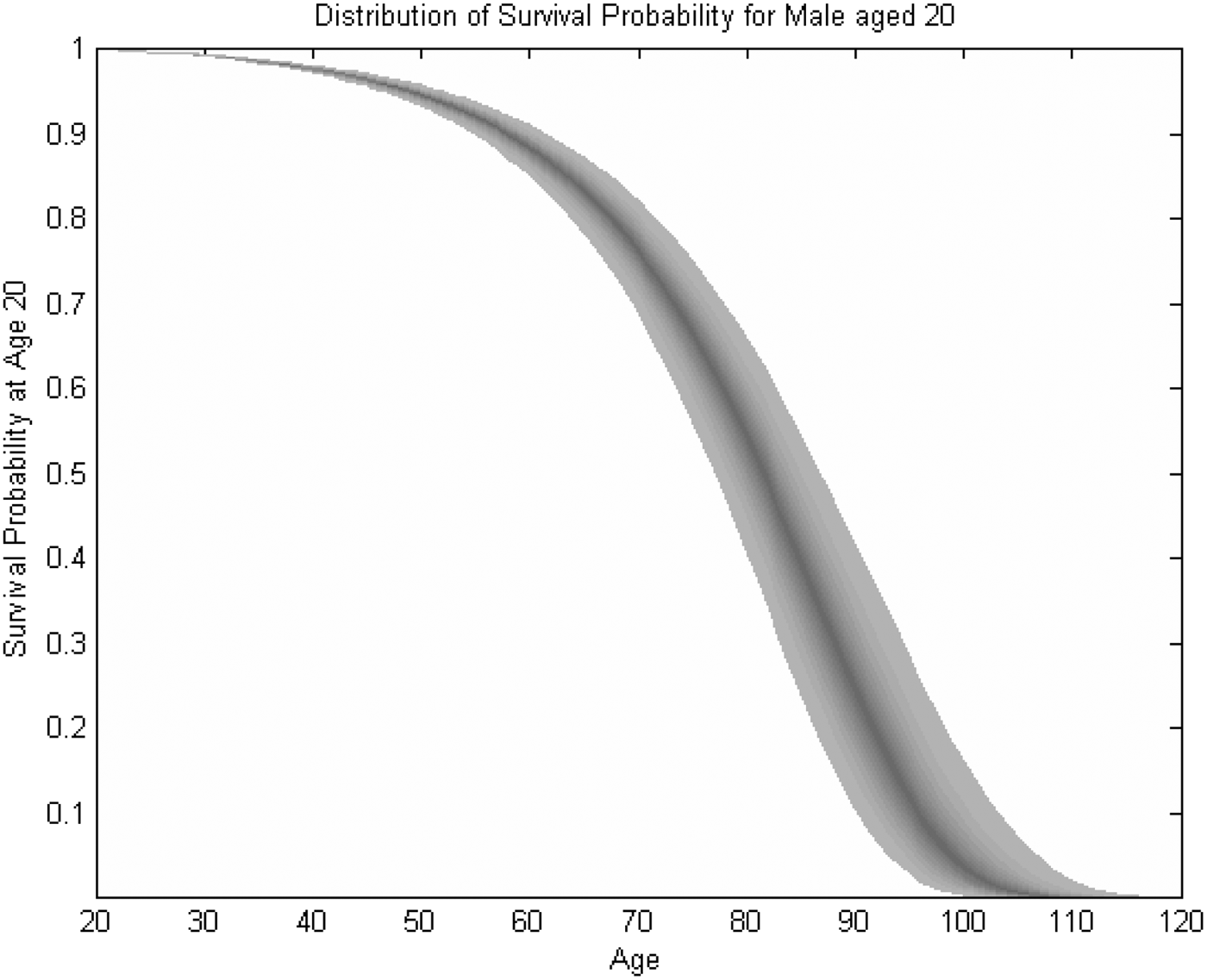
DB-plan liabilities evolve as a function of various demographic assumptions, economic assumptions, and assumptions about future benefit flows. The actuarial profession has established well-developed standards on how to set and work with such assumptions when evaluating the current liabilities of a pension plan. Yet the future realizations of these factors may differ from expectations, and/or the assumption may change which results in fluctuations in the value of the plan liabilities (liability risk). For example, actuaries use a specific mortality table to specify the present value of future benefits. But realized mortality rates for a specific pension plan could be higher or lower than those of the assumed mortality table. Such uncertainty is referred as idiosyncratic mortality risk. In addition, mortality can also change systematically because of unexpected improvements in survival probabilities (systematic mortality risk). Research shows that especially for long-term liabilities like pension benefits, systematic mortality risk is an important and often underestimated risk factor.Footnote 4Figure 1 illustrates the impact of systematic mortality risk,Footnote 5 indicating that the probability of living to advanced ages exhibits significant dispersion. For example, the probability of attaining age 80 spans the range from 45 to 65%, with a median of 56%. Thus the range of the expected lifetime remaining from age 20 varies between 53.1 and 67.2 years, with a median of 59.5 years. Hence a stochastic mortality model shows that future survival rates and years of life remaining are likely to substantially exceed those derived from the deterministic scenario.

Figure 1. Systematic mortality risk: Distribution of survival probability: Age-20 male.
To indicate the economic cost of stochastic mortality, one can calculate the age-dependent implied loadings for pre-selected confidence levels that an insurance company or a pension fund must charge for providing lifelong annuity benefits. For each initial age, these are derived by sampling 10,000,000 realizations of the stochastic mortality process for a deferred annuity (until 67), and then by calculating the required premium with respect to a certain solvency confidence level (see Maurer et al. Reference Maurer, Mitchell, Rogalla and Kartashov2013).
Figure 2 shows that premium increases which take into account the stochastic mortality can be substantial, especially for younger annuitants. For example, providers must charge 20-year-old females loadings of about 32% on the top of the actuarially fair premium, to maintain a 99.99% solvency confidence level. At the 90% confidence level, loadings must amount to over 10% for this age group. At later ages, the dispersion of possible future mortality outcome decreases and so does the implied loading. Nevertheless, at age 66, the loadings that are required to meet the 99.99% (90%) confidence level still amount to about 14% (5%).
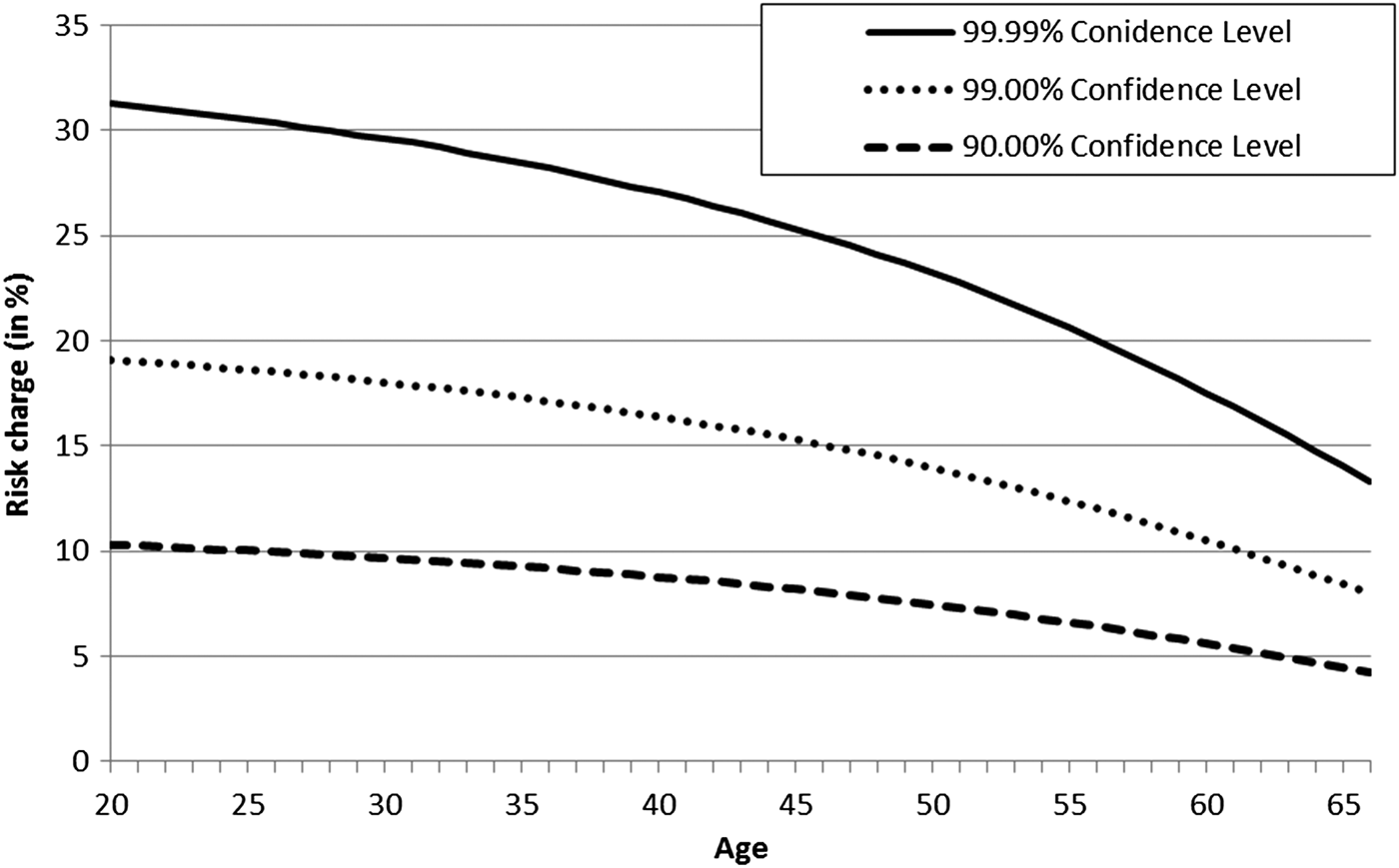
Figure 2. Stochastic mortality and risk charges for annuity benefits.
Assumptions in the PIMS model
Overall, the liability section of PIMS relies on professional actuarial standards for evaluating the current liabilities of the DB pension plans they insure. In addition, the PIMS model provides a methodology to project the uncertainty of the future liabilities by varying population dynamics (firm employment), interest rates, and benefit growth.Footnote 6 To discount future liabilities, PIMS uses the yield for corporate bonds. The corporate bond yield is a function of the (simulated) nominal interest rate for government bond plus a spread and an adjustment factor. Owing to their long-term character, pension liabilities have a long duration and therefore are sensitive to the discount rate selected. There is an ongoing debate, whether a (higher) discount rate other than the yield for (quasi) risk-free government bonds is appropriateFootnote 7.
Systematic mortality risk is still not incorporated in the PIMS model. Yet a large literature, developed over the last two decades, explores the uncertain evolution of human mortality rates.Footnote 8 In their seminal work, Lee and Carter, (Reference Lee and Carter1992) introduced a discrete-time one-factor model for the central death rate. Although this model was able to trace the time trend in mortality, the one-factor approach implied perfect correlation of mortality innovations over all ages, an implication contradicted by empirical evidence (see Maurer et al. Reference Maurer, Mitchell, Rogalla and Kartashov2013, p. 651). Subsequent stochastic mortality models try to overcome this drawback by employing a multi-factor approach (e.g., Renshaw and Haberman Reference Renshaw and Haberman2003; Cairns et al. Reference Cairns, Blake and Dowd2006b). Currently, the parsimonious two-factor modelFootnote 9 by Cairns, Blake, and Dowd is widely used as a model for stochastic mortality.
Investment risk
General aspects
The pension plan assets are invested in various categories, e.g., stocks, fixed income instruments, real estate, and alternative investments. The future returns of these assets typically fluctuate over time and could be lower than the assumed interest rate used to discount future benefits (investment risk). Fluctuating interest rates (a spot rate curve) are particularly important, because they simultaneously affect the development of the plan assets and the evaluation of plan liabilities. Therefore it is necessary to model the long run stochastic dynamics of interest rates and future returns on the various assets accumulated in the pension plan. Various models are documented in the literature,Footnote 10 which also notes that the modeling of illiquid assets (e.g., real estate or alternative assets) represents a big challenge.Footnote 11
Specific comments on the PIMS model
Currently PIMS uses a Value-at-Risk(VAR) approach to model two asset classes: risky stocks and bonds. The returns for the bonds (interest and capital gains) depend on the development of the nominal interest rate and a duration adjustment for capital gains. Stock returns are modeled independent and identically distributed. The return on corporate bonds is assumed to depend on the interest rate level adjusted for a possible (but certain) spread. The model parameters are calibrated using U.S. data. Additional assets such as real estate or alternative assets are not included in the model. The range of asset holdings for the specific pension plans is approximated using historical Form 5,500 information. PIMS also allows plans to smooth asset values within the context of the minimum PPA funding rules. Plan assets of PPGC are invested first in long-term bonds (and T-bills) to immunize the liabilities and for the trust fund equity investments, they are allowed within limits.
Overall, the PIMS investment model is a reasonable approach, providing a good compromise between the tractability of the model (length, time of running the code, and calibration of model parameters) and the need to use plan specific information. Useful extensions would include additional asset classes (e.g., real estate), the modeling of uncertainty of the spread for corporate bonds, and (most important) a complete term structure model for nominal interest rates.
Integrating assets and liabilities: the key importance of the interest rate
Besides the budget equations and the correlations of (the residuals of) the stochastic variables, the nominal interest rate is of key importance for PIMS. The nominal interest rate enters in the following components in the PIMS model in several ways:
1. actuarial valuation of liabilities of terminated/ongoing plans,Footnote 12
2. minimum contribution rules according to PPA rules,
3. specifying the return on plan assets for ongoing plans (stock and bonds)
4. specifying the return PBGC assets for terminated plans (stock and bonds),
5. yield for corporate bonds = (i + spread)*adj. factor
6. inflation rate = (1 + i)/(1 + fix real interest rate) −1,
7. nominal benefit (wage) growths (since inflation is related to the nominal interest rate),
8. calculation of the stochastic present value of PBGC claims.
In the current version of PIMS, the nominal interest is modeled and calibrated as a single stochastic variable for U.S. government bonds with a maturity of 30 years. Such an approach does not allow for any variation in the shape (curvature) of the term structure, nor does it include any uncertainty in credit spreads. This is not the state of the art in Asset-Liability-Modeling (ALM), nor it is consistent with empirical fluctuations of the term structure. For example, the current term structure is very steep (0% for T-bills and 3% for 30 maturities). Given the key importance of the interest rate for PIMS using only one single random variable may be too parsimonious. One way to extend PIMS would model the complete term structure of interest rates. Such a term structure can be used to discount future benefitsFootnote 13 and also to model the development of fixed income assets in terminated and ongoing plans. Various (arbitrage free) term structure models (including procedure to calibrate the parameters) are availableFootnote 14.
Communication of outcomes: CVaR
One outcome from the PIMS model is the distribution of the stochastic present values of the agency's future net positions using a 10-year horizon (except for the 20-year probability of PBGC insolvency). One way to communicate this distribution by a risk measure is to use the CVaR of pension cost at a certain confidence level x (e.g., 95%). The x%-CVaR is defined as the expected present value of total future net liabilities under the condition that its ralization exceeds the VAR for that confidence level. The CVaR risk metric is in many ways superior to the more widely-used VaR measure, i.e., the costs that will not be exceeded with a given probability. In particular, the CVaR focuses attention on a given percentile of a loss distribution, and it also accounts for the magnitude of losses in the distributional tails beyond this percentile (cf Maurer et al. Reference Maurer, Mitchell, Rogalla, Mitchell and Anderson2009)Footnote 15. The CVaR risk metric could be a promising way to communicate risk to policymakers. In addition, this risk measure is consistent with important theoretical properties (e.g., it is a coherent risk measure).
Figure 3 illustrates the CVaR of the (stochastic) present value of costs for different investment strategies that might be used to fund the benefits of a DB pension plan.Footnote 16 The range of the optimal portfolio is substantially smaller than for pure equity or bond investments, whereas investing only in real estate would result in an even smaller range. The overall level of costs resulting from following the optimal strategy is also substantially lower, compared to the pure real estate investment case. Figure 3 illustrates the benefit of diversification to minimize the worst-case risk of pension costs represented with the CVaR.

Figure 3. Illustration of CVaR to communicate the range of pension costs.
Conclusions
Overall, the PIMS model is an important tool for modeling the liability risk of pension plans insured by PBGC. There is, to my knowledge, no other documented model available that can do a comparable job. Nevertheless, there are several opportunities for extensions:
a) incorporating systematic mortality risk,
b) incorporation of a stochastic investment model for the major asset classes beyond stocks and bonds (including real estate),
c) modeling of the full term structure of interest rate.
Appendix
See Appendix Figure A.1.

Figure A.1. General structure of integrated ALM models.