2. ORIGINS OF GPS IONOSPHERIC DELAY

The GPS ionospheric delay is originated by the complex dynamics of space weather (Davis, Reference Davis1991, Parkinson and Spilker Jr, Reference Parkinson and Spilker1996). This is a common name for a plethora of physical and chemical processes taking place in the vast space between the Sun and the Earth, commonly known as the Solar-Terrestrial Environment (STE) (Davis, Reference Davis1991, Parkinson and Spilker Jr, Reference Parkinson and Spilker1996), shown on Figure 1.

Figure 1. Solar-terrestrial environment.

Powerful bursts of energy and matter expelled from the Sun are frequently observed during the intervals of increased solar activity. Particles and radiations expelled from the Sun form the solar wind, which can move towards the Earth. Particularly strong solar wind blowing towards the Earth generally causes two fundamental effects to the Earth's environment (Davis, Reference Davis1991):

• • disruption of the Earth's magnetic (geomagnetic) field

• • disturbance of the vertical distribution of ionised particles (vertical profile) in the ionosphere.

Disruptions of the geomagnetic field, caused by space weather, appear as measurable and usually noticeable changes in the geomagnetic field's strength and orientation. Such disturbances are commonly known as geomagnetic storms (Davis, Reference Davis1991). Variations of the horizontal component of the geomagnetic field caused by geomagnetic storms affect various navigation devices, including magnetic compasses.

Ionospheric disturbances appear as sudden and marked natural variations of the vertical distribution of charged particles' density (vertical ionospheric profile) (Davis, Reference Davis1991). These variations affect the propagation of radio waves (including the signals from GPS satellites), causing delays and thus worsening GPS positioning performance. Stronger disturbances are referred to as ionospheric storms (Davis, Reference Davis1991, Parkinson and Spilker Jr, Reference Parkinson and Spilker1996, Klobuchar, Reference Klobuchar1987). Ionospheric storms are usually closely correlated with geomagnetic storms.

The variability of the vertical ionospheric profile has a direct impact on the GPS ionospheric delay (Davis, Reference Davis1991). Satellite positioning signal propagating through the ionosphere encounters a charge particle density described by the Total Electron Content (TEC) (Davis, Reference Davis1991, Klobuchar, Reference Klobuchar1987, Parkinson and Spilker Jr, Reference Parkinson and Spilker1996):

(1)

where:

• N(h) … vertical ionospheric profile

• h … height above the Earth's surface in [km]

The TEC value directly determines the equivalent GPS ionosphere delay (in metres), expressed as (Davis, Reference Davis1991, Klobuchar, Reference Klobuchar1987, Parkinson and Spilker Jr, Reference Parkinson and Spilker1996):

(2)

where:

• d _t … equivalent GPS ionospheric delay in [m]

• f … radio wave frequency (for single-frequency GPS receiver: 1575·42 MHz)

Space weather affects the ionosphere which, through TEC, has a direct impact on the GPS ionospheric delay, so ionospheric disturbances will cause variations in GPS ionospheric delay ((Davis, Reference Davis1991, Klobuchar, Reference Klobuchar1987, Parkinson and Spilker Jr, Reference Parkinson and Spilker1996). The intensity and frequency of appearance of both geomagnetic and ionospheric storms depend on various factors, among them (Davis, Reference Davis1991):

• • recent and current space weather conditions

• • season of the year

• • time of the day

• • geographical area (polar, equatorial, or mid-latitudes)

Each of these factors adds a particular signature to the GPS ionospheric dynamics. Numerous experimental studies of the ionosphere have revealed certain patterns in TEC dynamics such as common daily variations of the GPS ionospheric delay. (Davis, Reference Davis1991, Klobuchar, Reference Klobuchar1987, Parkinson and Spilker Jr, Reference Parkinson and Spilker1996, Filjar, Reference Filjar2008, Filjar et al, Reference Filjar, Kitarović and Lakoš2007, Filjar and Kos, Reference Filjar and T2006). The daily variations of GPS ionospheric delay can be represented by a composite model encompassing bias (DC night-time component) and a cosine component (with a peak around 14.00 hours, local time) (Klobuchar, Reference Klobuchar1987, Parkinson and Spilker Jr, Reference Parkinson and Spilker1996, Misra and Enge, Reference Misra and P2004). This pattern of the GPS ionospheric delay has been explored in the standard (or Klobuchar) GPS ionospheric delay model (Klobuchar, Reference Klobuchar1987, Parkinson and Spilker Jr, Reference Parkinson and Spilker1996, Mira and Enge).

3. CLASSICAL DECOMPOSITION OF A COMPOSITE SIGNAL

Mathematical theory provides a robust method for the decomposition of an observed signal into the following components (Williams, Reference Williams1987, Brockwell and Davis, Reference Brockwell and Davis2002, Trauth, Reference Trauth2007, Falk et al, Reference Falk2006):

• • trend

• • cyclicity

• • seasonality

• • residual stochastic signal

In general terms, trend can be assumed as a combination of a bias, linearly increasing and linearly decreasing functions, where all components do not necessarily appear. In the case of GPS ionospheric delay, trend can be assumed as a constant bias (DC component) representing a night-time GPS ionospheric delay (Klobuchar, Reference Klobuchar1987, Parkinson and Spilker Jr, Reference Parkinson and Spilker1996).

Cyclicity in a composite signal refers to a component that varies through the course of a basic time period by the sine law. Apparently, there is a cosine component of the GPS ionospheric delay during the day-time hours (Klobuchar, Reference Klobuchar1987, Davis, Reference Davis1991, Parkinson and Spilker Jr, Reference Parkinson and Spilker1996).

Seasonality refers to repeatable changes of the signal during the broadened period of time including more basic time periods (for instance, season of the year containing a number of days). In case of GPS ionospheric delay, season of the year and day-to-day changes in GPS ionospheric delay dynamics should be explored (Davis, Reference Davis1991, Parkinson and Spilker Jr, Reference Parkinson and Spilker1996).

The residual stochastic signal is always present in the decomposed signal, and usually reflects the influence of an un-modelled contribution of the original signal, as well as measurement errors. In contrast to previous components, which can be modelled by common linear mathematical functions, residual stochastic signal should be treated either as deterministic or chaotic, and modelled in accordance with initial presumptions of its nature (Williams, Reference Williams1997, Brockwell and Davis, Reference Brockwell and Davis2002, Trauth, Reference Trauth2007).

4. DECOMPOSITION OF GPS IONOSPHERIC DELAY DURING QUIET SPACE WEATHER CONDITIONS

Classical decomposition is the foundation of the standard (Klobuchar) GPS ionospheric model. The same initial approach has been used in analysis of local behaviour of GPS ionospheric delay in the northern Adriatic area. A case study explored the properties of the composite daily GPS ionospheric delay signal in periods of quiet space weather conditions. Two periods in 2007 were chosen when there were markedly quiet space weather conditions and daily GPS ionospheric delay data sets for a Croatian coastal region of the northern Adriatic (ϕ=45°N, λ=15°E) were retrieved from an internet archive for use in model development.

4.1. Data collection methodology

GPS ionospheric delay data were taken from the internet archive (AIUB, 2008). Data for a given position in the northern Adriatic were extrapolated from the real observation taken at reference sites that cover the whole of Europe. In order to confirm that data sets were taken during quiet space weather conditions, a review of space weather data was conducted (Filjar, Reference Filjar2008). The time series of common space weather parameters (sunspot number, solar flux and planetary Ap geomagnetic index)(NOAA NGDC, 2008) were explored. Analysis of space weather indices values revealed two significant periods of quiet space weather conditions in 2007, as shown on Figure 2:

• • days 251–260 (in Summer 2007)

• • days 357–365 (in Winter 2007)

Figure 2. Space weather conditions in 2007 (data courtesy NOAA NGDC).

4.2. Modelling actual (observed) GPS ionospheric delay data

It was assumed that the observed GPS ionospheric delay could be decomposed into a set of common components, as stated in Section 3 (Williams, Reference Williams1997, Trauth, Reference Trauth2007, Brockwell and Davis, Reference Brockwell and Davis2002). It was also assumed that daily GPS ionospheric delay data sets of the same season of the year have similar seasonal properties. This allowed for separation of Summer 2007 and Winter 2007 data sets, and the production of summer-time and winter-time GPS ionospheric delay data models for quiet space weather conditions in the northern Adriatic. Furthermore, it was assumed that the GPS ionospheric delay trend could be modelled as a DC component related to the night-time GPS ionospheric delay value (Klobuchar, Reference Klobuchar1987, Misra and Enge, Reference Misra and P2004). In addition, daily variation of GPS ionospheric delay has been presumed to follow the cosine law, biased by the night-GPS ionospheric delay value (Klobuchar, Reference Klobuchar1987, Parkinson and Spilker Jr, Reference Parkinson and Spilker1996). All above-mentioned presumptions are valid for both summer- and winter-time decomposition models. Two seasonal models are distinguished by duration of daylight. In summer, daylight lasts longer than in winter, so the daytime interval for summer was set as 06.00–22.00, local time and for winter as 08.00–20.00, local time).

Using the least-square method, model parameters a ₀ and a ₁ were determined and averages were computed for both summer-time and winter-time data sets. See Tables 1 and 2. The residual GPS ionospheric delay sets were simply calculated by subtracting bias and daily cosine components from the observed composite GPS ionospheric delay sets. Figure 3 shows the decomposition process in action (comparison between real and modelled value, and time series of residual GPS ionospheric delay data, respectively) for day 251 in 2007.

Figure 3. Day 251 in 2007.

Table 1. Model of the actual Summer daily GPS ionospheric delay (Summer 2007).

Table 2. Model of the observed Winter daily GPS ionospheric delay (Winter 2007).

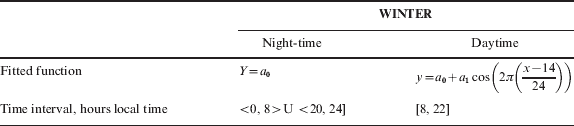
4.3. Classical decomposition and residual GPS ionospheric delay in Summer 2007 quiet space weather conditions

Figure 4 shows the time series of observed and modelled daily GPS ionospheric delay data and the residual GPS ionospheric data, collected during Summer 2007. Observed data sets show two characteristic daily maximums, the first around 11.00 local time, the other around 16.30 hrs. The decomposition model used one local maximum (around 14.00 local time) as a result of cosine-based model of daily variation of GPS ionospheric delay model. This results in a systematic error, providing two artificial maxima of the residual GPS ionospheric delay time series.

Figure 4. Composite observed GPS ionospheric delay and its components (summer-time model and residuals) in quiet space weather conditions, northern Adriatic, for days 251–260, Summer 2007 (y-axis in [m], x-axis in [h], local time).

Furthermore, the long-lasting daily ionisation impact has been strong enough to keep the night-time GPS ionospheric delay values from a constant. This caused variations in residual GPS ionospheric delay that can also be considered at least partly artificial.

Identified systematic errors are clearly visible on the histogram of summer-time residual GPS ionospheric time delays (Figure 5). The bimodal distribution of these delays is the result of the presumption of a single daily maximum of GPS ionospheric delay, instead of two. Nevertheless, residual GPS ionospheric delays remain reasonably limited in interval [−0·4 m, 0·4 m], proving the value of the summer-time quiet space weather local model of GPS ionospheric delay.

Figure 5. Histogram of residual GPS ionospheric time delay during quiet space weather conditions, northern Adriatic, days 251–260, Summer 2007 (y-axis in number of observations, x-axis in GPS ionospheric delay values in [m])

4.4. Classical decomposition and residual GPS ionospheric delay in Winter 2007 quiet space weather conditions

Figure 6 shows the time series of observed and modelled daily GPS ionospheric delay data and residual GPS ionospheric data, collected during Winter 2007. In contrast to summer-time time series, data sets observed in Winter 2007 show one clearly defined daily maximum, around 14.00 local time. This results in reduced systematic error, compared with the analysis of the summer-time GPS ionospheric delays.

Figure 6. Composite GPS ionospheric delay and its components (winter-time model and residuals) in quiet space weather conditions, northern Adriatic, for days 357–365, Winter 2007 (y-axis in [m], x-axis in [h], local time.)

Since the daily ionisation lasts considerably less than in summer, winter night-time GPS ionospheric delays tend to decrease more linearly and reach the lowest value around dawn. The winter-time dawn GPS ionospheric delay appears to be considerably lower than the correspondent value in summer. DC component approximation of the winter night-time GPS ionospheric delays causes a systematic error around the dawn, as is evident from Figure 6. This error resulted in a histogram of residual GPS ionospheric delays expressing a clear negative skewness (Figure 7). Again, residual GPS ionospheric delays remain reasonably limited in interval [−0·4 m, 0·4 m], proving the value of the winter-time quiet space weather local model of GPS ionospheric delay.

Figure 7. Histogram of residual GPS ionospheric time delay during quiet space weather conditions, northern Adriatic, days 357–365, Winter 2007 (y-axis in number of observations, x-axis in GPS ionospheric delay values in [m])

6. CONCLUSION AND FUTURE WORK

This article presents the results of GPS ionospheric delay analysis for data taken during quiet space weather conditions in different seasons of the year 2007 in the northern Adriatic. Several patterns in daily GPS ionospheric delay variability have been observed, including the existence of two maxima per day during summer and linear variability of the night-time GPS ionospheric delay during winter.

Klobuchar-like local quiet space weather models of daily variations of GPS ionospheric delay have been developed for the northern Adriatic area and for two seasons of the year (summer and winter). Their performance has been indirectly validated through examination of statistical properties of residual GPS ionospheric delay. The developed models of GPS ionospheric delay dynamics are to be used in various GPS-based solutions in the northern Adriatic, including maritime traffic (merchant, military and recreational), road traffic and personal (tourist) navigation.

The analysis has provided better insight into local GPS ionospheric delay variation patterns. The revealed issues will be used in transition of Klobuchar-like models towards non-Klobuchar models of local GPS ionospheric delay in quiet space weather conditions for the northern Adriatic. These are to be validated through several experimental campaigns in the region in different seasons of the year and during periods of quiet space weather conditions.