1. INTRODUCTION
Today, Global Navigation Satellite Systems (GNSS), such as the Global Positioning System (GPS) of the United States of America (USA) and the Beidou System of China, are widely utilised in the navigation of near-Earth spacecraft. However, due to the geometry of GNSS, these systems are not available for space explorations to the Moon and beyond. With the growing number of deep-space missions, many autonomous navigation technologies are being developed. For example, a celestial navigation method using optical measurement was proposed in Synnott et al. (Reference Synnott, Donegan, Riedel and Stuve1986). This technique was successfully employed in the Deep Space-1 mission (Riedel et al., Reference Riedel, Bhaskaran, Synnott, Desai, Bollman, Dumont, Halsell, Han, Kennedy, Null, Owen, Werner and Williams1997). Hill et al. (Reference Hill, Lo and Born2005a; Reference Hill, Born and Lo2005b) designed a novel navigation system that consists of Earth-Moon libration point satellites, known as “Liaison Navigation”. The coverage ability and orbit determination performance of this system were analysed in Zhang and Xu (Reference Zhang and Xu2014). In addition, X-ray pulsar-based navigation system has also attracted the attention of many researchers. In this technique, remote neutron stars – pulsars – serve as lighthouses for spacecraft throughout the solar system.
Recent years have witnessed significant developments in X-ray pulsar-based navigation technology. Pulsar databases and pulse-timing models as well as orbit determination algorithms have been extensively studied. Some engineering verification experiments have been carried out, such as the Station Explorer for X-ray Timing and Navigation Technology (SEXTANT) on board the International Space Station (Winternitz et al., Reference Winternitz, Hassouneh, Mitchell, Valdez, Price, Semper, Yu, Ray, Wood, Arzoumanian and Gendreau2015; Reference Winternitz, Mitchell, Hassouneh, Valdez, Price, Semper and Gendreau2016) and the experiments on board the TianGong-2 Spacelab (Zheng et al., Reference Zheng, Ge, Han, Wang, Chen, Lu, Bao, Chai, Dong, Feng and He2017).
The accuracy in an X-ray pulsar-based navigation system depends mainly on the accuracy of pulse phase estimation. Many algorithms have been designed to estimate the phase delay in a pulsar's signal. In a report for the European Space Agency (Sala et al., Reference Sala, Urruela, Villares, Estalella and Paredes2004), a maximum likelihood method was described to estimate phase delay, which provides unbiased minimum variance estimation by maximising a log-likelihood function. In Emadzadeh et al. (Reference Emadzadeh, Golshan and Speyer2009), as well as Emadzadeh and Speyer (Reference Emadzadeh and Speyer2010), an epoch folding process was established to recover the rate function from photons' Times-Of-Arrival (TOAs). They also proposed a nonlinear least-squares estimator to evaluate pulse phase. Emadzadeh and Speyer (Reference Emadzadeh and Speyer2011a) introduced a cross-correlation method for pulse phase estimation. This cross-correlation algorithm estimates the pulse phase by computing the cross-correlation function between a recovered rate function and a standard rate function. With the help of fast Fourier transformation, the computational complexity of the cross-correlation approach is less than the complexities of the maximum likelihood method and the least squares estimator. In Rinauro et al. (Reference Rinauro, Colonnese and Scarano2013), Lin and Xu (Reference Lin and Xu2015) as well as Xue et al. (Reference Xue, Li, Sun and Fang2016), different versions of Fourier Transform-based algorithms, with lower computational complexities, were proposed. In addition, some researchers developed techniques that can estimate both pulse phase and Doppler effect. In Zhang et al. (Reference Zhang, Xu and Xie2011), Zhang and Xu (Reference Zhang and Xu2011) and Zhang et al. (Reference Zhang, Xu, Jiao, Shen and Sun2014), the authors employed Gaussian component decomposition to express the pulse profile and derived a minimum entropy method to estimate the spacecraft's position and velocity. Liu et al. (Reference Liu, Fang, Wu and Kang2014) proposed a non-linear constraint least squares method. In this method, the Doppler effect can be evaluated by the variation of TOAs and both position and velocity can be estimated. Yu et al. (Reference Yu, Xu, Feng, He and Ye2015) gave an optimisation algorithm based on the sparse representation of the pulse profile to evaluate the pulse phase and Doppler frequency. Liu et al. (Reference Liu, Wu, Xiong, Fang and Liu2017) suggested using the near-maximum likelihood and least squares methods to estimate the position and velocity of spacecraft.
In reality, however, due to the intrinsic faintness of most pulsars, the Signal-to-Noise Ratios (SNR) for most pulsars are quite low. As a consequence, compared with the accuracy available from navigation systems using Satellite-to-Satellite Tracking data, such as GPS and “Liaison Navigation”, the accuracy of positioning using pulsars is relatively low. For example, as estimated in Sheikh et al. (Reference Sheikh, Pines, Ray, Wood, Lovellette and Wolff2006), with a detector of area 1 m 2 and observation time of 100 s, pulsar B1937 + 21 can only provide a range measurement with an accuracy of about 200 m. In comparison, the accuracy of the range measurement in “Liaison Navigation” can reach tens of metres (Zhang and Xu, Reference Zhang and Xu2015). Therefore, how to improve the accuracy in X-ray pulsar-based navigation system requires further study.
This paper proposes a novel algorithm combining an epoch folding procedure and cross-correlation method with the idea of “averaging multiple measurements”. In the measurements with random error, the accuracy can be improved by taking multiple measurements and calculating the average as the final result. By sampling the time tags of accumulated photons, the pulse phase is estimated many times with the epoch folding process and cross-correlation algorithm, and then the results are gathered to give a final estimation by weighted averaging, where the “cross-correlation value” serves as weight. Two explanations as to how this method can improve accuracy are also provided: an SNR-based explanation and an “error-difference trade-off” explanation. Numerical simulations show that this method can achieve a higher accuracy of pulse phase estimation.
The remainder of the paper is organised as follows: Section 2 reviews the epoch folding process and the cross-correlation method in an X-ray pulsar-based navigation system. In Section 3, a description of the proposed algorithm is presented. Section 4 gives two explanations on this method's mechanism. Two numerical simulations are introduced in Section 5 to validate the performance of the proposed algorithm. Section 6 provides concluding remarks.
2. A REVIEW OF EPOCH FOLDING AND CROSS-CORRELATION
2.1. Pulse phase estimation in an X-ray pulsar-based navigation system
Pulse phase is a key measurement in an X-ray pulsar-based navigation system as pulse phase delay provides information on the position of the spacecraft. However, due to the intrinsic faintness of the signals from X-ray pulsars, pulse phase cannot be measured directly. In the observations of pulsars, the X-ray detector collects the photons and records the TOAs. Pulse phase is estimated using these time tags of arriving photons.
In a pulsar timing model, in order to describe the rate of photon arrival, an overall rate function λ(t) is defined by (Sala et al., Reference Sala, Urruela, Villares, Estalella and Paredes2004):
$$\lambda\lpar t\rpar =\lambda_{b}+\lambda_{s}h\lpar \varphi\lpar t\rpar \rpar $$where λ b is called the background arrival rate, λ s represents the source arrival rate, h(φ) is the periodic pulsar profile and φ(t) is the phase of the pulsar signal.
The event of the arriving X-ray photons from a pulsar is a stochastic process and it is usually modelled as a nonhomogeneous Poisson process. The number of received photons from a source in a certain interval is a random variable with a Poisson distribution. The probability of receiving k photons from a pulsar in a given interval (t 1, t 2) is described as (Emadzadeh and Speyer, Reference Emadzadeh and Speyer2011b):
$$P\lpar k\semicolon \; t_1\comma \; t_2\rpar =\displaystyle{{1}\over{k!}}\left(\vint_{t_1}^{t_2}\lambda\lpar \xi\rpar {\rm d}\xi\right)^{k} \exp\left(-\vint_{t_1}^{t_2}\lambda\lpar \xi\rpar {\rm d}\xi\right)$$The X-ray detector outputs the time tags of photon arrival. Pulse phase estimation is the process that estimates the phase φ(t) of given photon TOAs.
2.2. Epoch folding procedure
Epoch folding is usually the first step in evaluating the pulse phase. In this subsection, a brief review of the epoch folding procedure is given.
Epoch folding is the process that recovers the X-ray pulsar rate function from the measured photons' arrival time. This procedure is formulated mathematically in Emadzadeh and Speyer (2009).
Assume that a pulsar is continually observed for N p pulsar periods, and a pulsar period is equally divided into N b bins. The length of each bin is T b = P/N b, where P represents the period of the pulsar. Let c(t i) denote the number of photons in the i-th bin whose centre is t i, then the empirical rate function can be expressed as:
$$\hat{\lambda}\lpar t_i\rpar =\displaystyle{{1}\over{N_PT_b}}\sum_{j=1}^{N_P}c_j\lpar t_i\rpar $$and it can be proven that for a long observation time T obs:
$$\hat{\lambda}\lpar t_i\rpar =\lambda\lpar t_i\rpar +w\lpar t_i\rpar $$where w(t i) is an uncorrelated noise that satisfies:
$$E\lsqb w\lpar t_i\rpar \rsqb = 0 $$
$${\rm var}\lsqb w\lpar t_i\rpar \rsqb = \displaystyle{{N_b}\over{T_{obs}}}\lambda\lpar t_i\rpar $$where E[] is the expectation operator, and var[] is the variance operator.
2.3. Cross-correlation estimator
In this subsection, the process of cross-correlation is reviewed.
Cross-correlation, also known as sliding dot product, is a function of the displacement between two signals. It is very useful for determining the time delay between two signals. After calculating the cross-correlation between two signals, the maximum of the cross-correlation function indicates the point in time where these signals are best aligned.
In a pulsar-based navigation system, the cross-correlation estimator maximises the cross-correlation function of the standard rate function and the empirical rate function (Emadzadeh, et al., 2011a), which can be formulated as:
$$C\lpar \varphi\rpar =\vint_{-\infty}^{\infty}\lambda^{\ast}\lpar t\semicolon \; \varphi\rpar \hat{\lambda}\lpar t\rpar dt $$
where the empirical rate function 
$\hat{\lambda}\lpar t\rpar $ is usually obtained in an epoch folding procedure.
The estimation of phase delay is computed by:
$$\hat{\varphi}={\rm arg\,\ max}\ C\lpar \varphi\rpar $$In practice, a Discrete Fourier Transform (DFT) is usually employed to compute the cross-correlation function. The input and output of the DFT are both finite discrete sequences. If the input sequence is one cycle of a periodic signal, the DFT yields the discrete samples of one discrete-time Fourier transform cycle. The DFT sequence X(k) of a signal in a time domain x(n) is defined as:
$$X\lpar k\rpar =DFT\lsqb x\lpar n\rpar \rsqb =\sum_{n=0}^{N-1}x\lpar n\rpar e^{-j\left(\displaystyle{{2\pi}\over{N}}\right)nk} $$where N is the length of the sequence x(n), and j 2 = −1.
The empirical rate function 
$\hat{\lambda}\lpar t\rpar $ is usually obtained in an epoch folding process, hence it is a discrete sequence with a length of N b. We use symbol 
$\hat{\lambda}\lpar n\rpar $ to express the discrete empirical rate sequence. The standard rate function λ(t) is also discretised as a sequence with length N b, which is expressed as λ(n). The cross-correlation can be computed by:
$$\eqalign{\Lambda_1\lpar k\rpar & =DFT\lsqb \lambda\lpar n\rpar \rsqb \comma \; \, \Lambda_2\lpar k\rpar =DFT\lsqb \hat{\lambda}\lpar n\rpar \rsqb \cr C\lpar n\rpar & = IDFT\lsqb \Lambda_1\lpar k\rpar \ast \Lambda_2^{\ast}\lpar k\rpar \rsqb }$$where DFT[·] and IDFT[·] denote the operation of the DFT and inverse DFT respectively. They are usually computed with the aid of a fast Fourier transform (Proakis and Manolakis, Reference Proakis and Manolakis1996).
3. SAMPLING AND WEIGHTED AVERAGING-BASED METHOD
In this section an algorithm based on sampling and weighted averaging is proposed. The method of averaging multiple measurements is widely utilised for measurements with random error.
Assume the true value of pulse phase is φ and N independent measurements φ i are taken, where i = 1, 2… N. Let 
$\bar{\varphi}$ denote the average of these measurements. 
$\bar{\varphi}$ is an unbiased estimator of φ:
$$E\lsqb \bar{\varphi}\rsqb =\varphi $$According to Hoeffding's inequality (Hoeffding, Reference Hoeffding1963):
$$P\lpar \vert \bar{\varphi}-\varphi\vert \geq v\rpar =P\lpar \vert \bar{\varphi}-E\lsqb \bar{\varphi}\rsqb \vert \geq v\rpar \leq 2e^{-2Nv^2} $$ Equation (12) means that the probability of the event that the difference between 
$\bar{\varphi}$ and φ is larger than any positive number v declines exponentially as the number of measurements N increases. In the case that the qualities vary in different measurements or we have different confidence in different measurements, a weighted averaging method is commonly used.
As stated in previous sections, pulse phase is estimated from the TOAs of arriving photons. With the constraints in observation time and the area of the detector, the number of received photons cannot be easily increased. Nevertheless, we can generate multiple measurements in pulse phase by simple random sampling in the set of TOAs.
Let S U represent the universal set of all arriving photons' time tags. Several subsets S 1, S 2, …, S n are obtained by simple random sampling in S U, where the sampling rate is determined in advance. For each subset S i of TOAs, the epoch folding process provides an empirical rate function 
$\hat{\lambda}_{i}$ and different estimations of pulse phase 
$\hat{\varphi}_{i}$ can be obtained by the cross-correlation method.
We define “cross-correlation value” V C as the maximum of the cross-correlation function as:
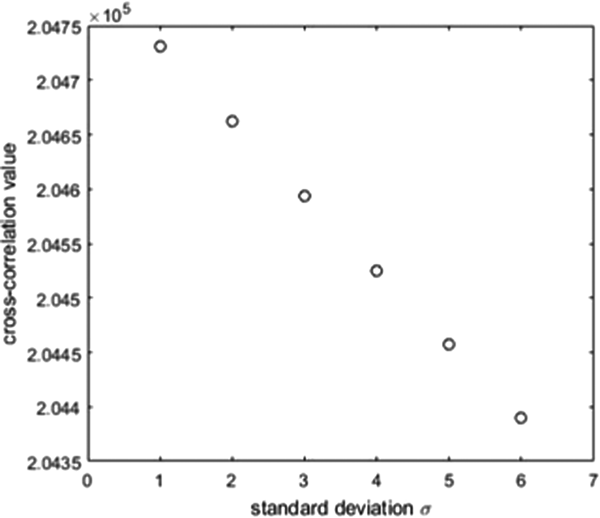
$$V_C=\max C \lpar \varphi\rpar $$The cross-correlation value describes the similarity between two signals after being aligned in the time axis. For example, the cross-correlation between x(n) = 10sin(n) and y(n) = x(n) + w(n) is computed where w(n) is a Gaussian noise with zero mean and standard deviation σ. The difference between y(n) and x(n) increases as σ rises. Figure 1 displays the cross-correlation value versus the standard deviation in noise.
Figure 1. Cross-correlation value versus standard deviation in noise.
Figure 1 shows that the cross-correlation value V C declines as the standard deviation σ in noise grows. The cross-correlation value can be an indicator of the similarity between two signals.
In a pulsar-based navigation system, for each subset S i of time tags, a cross-correlation between empirical rate function 
$\hat{\lambda}_{i}$ and the standard rate function is performed. The computed cross-correlation value V Ci indicates the quality of corresponding estimation 
$\hat{\varphi}_{i}$ and serves as the weight in the weighted average. Lastly, the final estimation 
$\hat{\varphi}$ of pulse phase is calculated as the weighted average of the estimations:
$$\hat{\varphi}=\displaystyle{{\sum_{i=1}^{n}V_{Ci}\hat{\varphi}_i}\over{\sum_{i=1}^{n}V_{Ci}}} $$The scheme of the proposed method is summarised as:
(a) The X-ray detector collects photons and the universal set S U of TOAs is obtained.
(b) With a prior defined sampling rate, the subsets S 1, S 2, …, S n are obtained by simple random sampling from S U based on the number of photons.
(c) For each subset S i of TOAs, an empirical rate function
$\hat{\lambda}_{i}$ is obtained by the epoch folding procedure.(d) The cross-correlation function between the standard rate function λ(t) and the empirical rate function
$\hat{\lambda}_{i}$ is computed using Equation (10), the pulse phase $\hat{\varphi}_{i}$ is evaluated using Equation (8), and the cross-correlation value V Ci is obtained from Equation (13).(e) The final estimation
$\hat{\varphi}$ of pulse phase is obtained by performing weighted averaging using Equation (14).
4. EXPLANATIONS OF THE MECHANISM OF THE PROPOSED METHOD
This section provides two explanations as to why the proposed algorithm can improve the accuracy of pulse phase estimation.
4.1. SNR-based explanation
Sheikh et al. (Reference Sheikh, Pines, Ray, Wood, Lovellette and Wolff2006) revealed that the relation between pulse TOA accuracy and SNR can be expressed as:
$$\sigma_{TOA}=\displaystyle{{W}\over{2SNR}} $$where σ TOA denotes the standard deviation in pulse TOA estimation and W, called Half-Width Half-Maximum, is defined as one-half the pulse width. The accuracy in range measurement can be written as:
$$\sigma_{range}=c\sigma_{TOA} $$where c denotes the speed of light.
Equations (15) and (16) mean that accuracy is improved as SNR rises.
SNR can be determined as:
$$\eqalign{SNR & =\displaystyle{{N_{Spulsed}}\over{\sqrt{\lpar N_B+N_{Snonpulsed}\rpar +N_{Spulsed}}}} \cr & =\displaystyle{{\lambda_s A_d p_f t_{obs}}\over{\sqrt{\lsqb \lambda_b+\lambda_s\lpar 1-p_f\rpar \rsqb A_dt_{obs}Wf_s+\lambda_s A_d p_f t_{obs}}}}} $$where N Spulsed, N Snonpulsed and N B represent the number of photons that are emitted from a pulsed pulsar, a non-pulsed pulsar and background radiation respectively, the pulse fraction p f is defined as the percentage of the source flux that is pulsed, A d represents the area of X-ray detector and f s = 1/P is the frequency of the observed pulsar.
The flux in the band 2-10 keV of some X-ray pulsars are listed in Table 1 (Sheikh, Reference Sheikh2005). In comparison, the flux in the 2–10 keV band of X-ray background noise is about 0·005 ph/cm 2/s. It can be seen from Table 1 that except for pulsar B0531 + 21, the SNRs for most pulsars are quite low, hampering any improvement in accuracy.
Table 1. Flux of some X-ray pulsars.
Due to the indistinguishability of photons, the X-ray detector cannot tell whether a received X-ray photon is emitted by a pulsar or from background radiation. In order to improve SNR, one way is to increase the number of arriving photons, that is, to increase the area of the X-ray detector or to elongate observation time.
The proposed algorithm increases SNR in another way. As the time tags of received photons are sampled randomly, the ratio of photons emitted from a pulsed pulsar may increase or decrease after sampling, resulting in a relatively higher SNR or a lower SNR. A subset of TOAs with a higher SNR is more likely to align better with the standard rate function λ(t). As stated above, the cross-correlation value measures the similarity between two signals. Therefore, a subset with a higher SNR is more likely to have a larger weight in weighted averaging. As a result, although the sampling process reduces the number of photons involved in each estimation of pulse phase, the overall SNR of the final estimation can be improved by weighted averaging.
4.2. Error-difference trade-off
This subsection provides a statistical explanation of the mechanism of the proposed algorithm. Let 
$\hat{\varphi}_{i}\lpar S_{i}\rpar $ represent the estimation of the pulse phase on subset S i, and w i denotes the normalised weight for 
$\hat{\varphi}_{i}\lpar S_{i}\rpar $. The final estimation of pulse phase 
$\hat{\varphi}$ is written as:
$$\hat{\varphi}=\sum_{i=1}^n w_i\hat{\varphi}_i\lpar S_i\rpar $$Define the difference between i-th estimation and final estimation as:
$$D_i=\lpar \hat{\varphi}_i-\hat{\varphi}\rpar ^2 $$and the “overall difference” is defined as the weighted average of all differences:
$$\overline{D}=\sum_{i=1}^n w_i\lpar \hat{\varphi}_i-\hat{\varphi}\rpar ^2 $$ Express the true pulse phase as φ, then the squared error of each estimation 
$\hat{\varphi}_{i}$ is calculated by:
$$E\lpar \hat{\varphi}_i\rpar =\lpar \varphi-\hat{\varphi}_i\rpar ^2 $$ Define the weighted average of 
$E\lpar \hat{\varphi}_{i}\rpar $ as “overall error”:
$$\overline{E}\lpar \hat{\varphi}_i\rpar =\sum_{i=1}^n w_i E\lpar \hat{\varphi}_i\rpar $$The squared error of the final estimation is:
$$E\lpar \hat{\varphi}\rpar =\lpar \varphi-\hat{\varphi}\rpar ^2 $$It can be proven that:
$$E\lpar \hat{\varphi}\rpar =\overline{E}\lpar \hat{\varphi}_i\rpar -\overline{D}$$Proof:
$$\eqalign{\overline{D} &=\sum_{i=1}^{n}w_i\lpar \hat{\varphi}_i-\hat{\varphi}\rpar ^2 \cr &=\sum_{i=1}^{n}w_i\lpar \hat{\varphi}_i-\varphi+\varphi-\hat{\varphi}\rpar ^2 \cr &=\sum_{i=1}^{n}w_i\lpar \hat{\varphi}_i-\varphi\rpar ^2+\sum_{i=1}^{n}w_i \lpar \varphi-\hat{\varphi}\rpar ^2+2\sum_{i=1}^{n}w_i\lpar \hat{\varphi}_i-\varphi\rpar \lpar \varphi-\hat{\varphi}\rpar \cr &=\sum_{i=1}^{n}w_i\lpar \hat{\varphi}_i-\varphi\rpar ^2+\lpar \varphi-\hat{\varphi}\rpar ^2+2\left(\sum_{i=1}^{n}w_i\hat{\varphi}_i-\varphi\right)\lpar \varphi-\hat{\varphi}\rpar \cr &=\sum_{i=1}^{n}w_i\lpar \hat{\varphi}_i-\varphi\rpar ^2+\lpar \varphi-\hat{\varphi}\rpar ^2+2\lpar \hat{\varphi}-\varphi\rpar \lpar \varphi-\hat{\varphi}\rpar \cr &=\sum_{i=1}^{n}w_i\lpar \hat{\varphi}_i-\varphi\rpar ^2-\lpar \varphi-\hat{\varphi}\rpar ^2 \cr &=\overline{E}\lpar \hat{\varphi}_i\rpar -E\lpar \hat{\varphi}\rpar } $$ Equation (24) means that the squared error in final estimation 
$E\lpar \hat{\varphi}\rpar $ equals the weighted average of errors in each estimation substituting the weighted average of differences, that is:
$$error\, in\, final\, estimation\, =\, overall\, error\, -\, overall\, difference $$In order to improve the accuracy in final pulse phase estimation, we can either decrease the “overall error” or increase the “overall difference”. The first path means that we should reduce the error in every estimation on subset S i, whereas the second path means that we are supposed to increase the difference between different estimations. In order to decrease the overall error, we should increase the number of photons in each subset so that the SNR in each subset gets larger and the accuracy in each estimation improves. On the other hand, to increase the difference between different subsets, the number of photons in each subset should be reduced so that the sampled subsets are different from each other.
These two paths cannot be realised simultaneously. As the sampling rate increases, the error in every estimation can be diminished because more TOAs of arriving photons are considered. However, the difference between different subsets, thus the “overall difference” will be reduced as sampled subsets tend to be the same. In contrast, if we reduce the sampling rate, the difference in estimations would increase but the accuracy in these estimations would decline. Therefore, the choice of sampling rate is a trade-off between “overall error” and “overall difference”. With a properly chosen sampling rate, the accuracy in final estimation can be improved.
5. NUMERICAL SIMULATION
In this section, two numerical simulations are presented to validate the performance of the proposed algorithm.
In the simulations, pulsars B0531 + 21 and J1420-6048 were chosen to be observed. Table 2 lists the parameters of these pulsars. The parameters of these pulsars were obtained from the Australia Telescope National Facility (ATNF) pulsar database (Manchester et al., Reference Manchester, Hobbs, Teoh and Hobbs2005; D'Amico et al., Reference D'Amico, Kaspi, Manchester, Camilo, Lyne, Possenti, Stairs, Kramer, Crawford and Bell2001; Sheikh, Reference Sheikh2005).
Table 2. Parameters of the observed pulsars.
In the first simulation, pulsar B0531 + 21 was observed. The area of the X-ray detector is set to 100 cm2 and the observation time was 212 s. A Monte-Carlo simulation repeated 200 times was performed. Pulse phase was estimated with different sampling rates and different sampling times. The averaged errors in pulse TOA estimations are presented in Table 3. As a comparison, the averaged error with only epoch folding and cross-correlation (non-sampling) is 
$2\cdot53\times10^{-6}$ s.
Table 3. Averaged errors (seconds) in pulse TOA estimations (B0531 + 21).
Table 3 indicates that the accuracy of pulse phase estimations with a sampling rate of 0·7 and 0·9 is better than a non-sampling result. The best result, which is about 5·5% improved from the non-sampling result, is obtained by sampling 90 times with a sampling rate of 0·9.
Figure 2 is an error bar plot displaying the average and standard deviation in the results with sampling rate 0·9. The line in the figure exhibits the averaged error, whereas the bars show the standard deviation of errors. As a comparison, the non-sampling result is plotted as sampling times = 0. It is obvious in Figure 2 that the standard deviation of errors reduces as sampling times grow, and all results with sampling are better than non-sampling results.
Figure 2. Results with sampling rate 0·9.
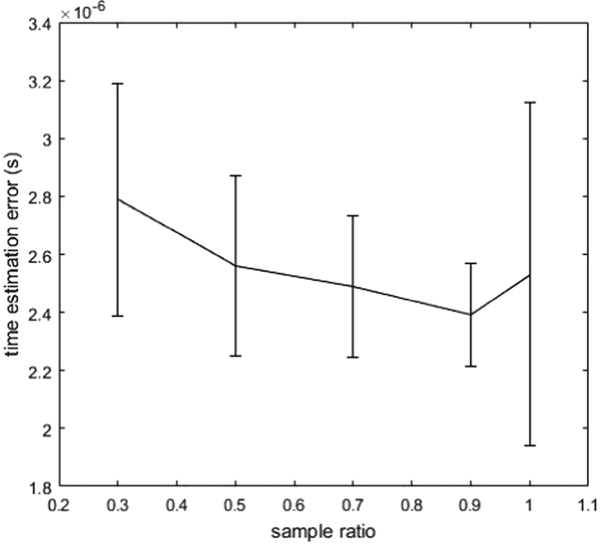
Figure 3 demonstrates the average and standard deviation in the results with sampling times 90. The non-sampling result is plotted as sampling rate = 1 for comparison. It can be seen that both the average and standard deviation of errors decline as the sampling rate increases.
Figure 3. Results with sampling time 90.
In the second simulation, pulsar J1420-6048 is observed with an X-ray detector of area 1 m2 and observation time 600 s. Again, we ran a Monte-Carlo simulation with 200 repetitions. Pulse phase is estimated with different sampling rate and different sampling times. Table 4 lists the averaged errors in pulse TOA estimation. As a comparison, the averaged error with only epoch folding and cross-correlation (non-sampling) is 
$4\cdot02\times10^{-5}$ s.
Table 4. Averaged errors (seconds) in pulse TOA estimations (J1420-6048).
It can be seen from Table 4 that most results with sampling are more accurate than the results with no sampling. The average error with sampling rate 0·3 and sampling times 50 is 
$2\cdot16\times10^{-5}$ s, about 46·3% less than the non-sampling results.
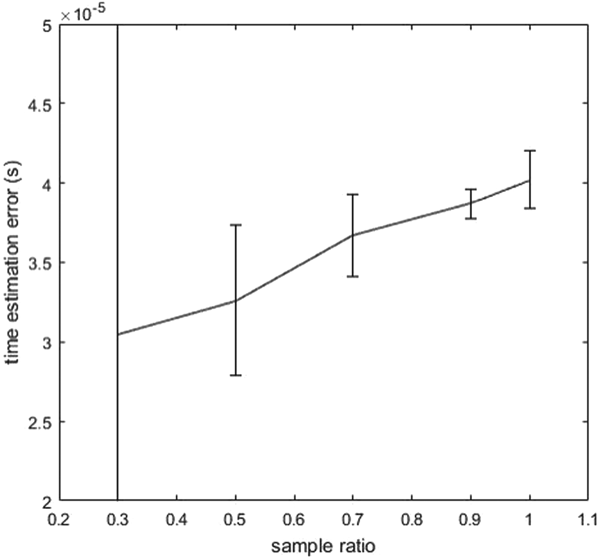
Figure 4 demonstrates the average and standard deviation in the results with sampling rate 0·9. Again, the line in the figure expresses the averaged error, whereas the bars show the standard deviation of errors. For comparison, the non-sampling result is plotted as sampling times = 0. The standard deviation of errors declines when sampling times rise, and all results with sampling are better than non-sampling results.
Figure 4. Results with sampling rate 0·9.
Figure 5 exhibits the average and standard deviation in the results with sampling 90 times. The non-sampling result is plotted as sampling rate = 1 as a comparison. It can also be seen that the standard deviation of errors decreases as sampling rate increases, and all results with sampling are better than non-sampling results. However, in contrast to the tendency shown in Figure 3, here the average error grows with sampling rate.
Figure 5. Results with sampling times 90.
The performances in these simulations seem different as the best sampling rate is 0·9 for pulsar B0531 + 21 and 0·3 for pulsar J1420-6048. It is assumed that for pulsars with a relatively high SNR (such as B0531 + 21), a low sampling rate will largely decrease SNR in each subset and increase the error in each estimation, while the difference between estimations does not increase that much. For pulsars such as J1420-6048, since their SNRs are relatively low, the decrease in SNR is not severe with a low sampling rate and the accuracy is improved with the increase in difference. As yet, the authors have not worked out a quantitative explanation on this phenomenon because it is hard to model the relationship between overall difference and sampling rate. Nevertheless, in numerical experiments it has been found that the best sampling rate is fixed for certain pulsars, so the sampling rate can be determined by grid-search experiments in advance.
6. CONCLUSION
This paper focuses on improving the accuracy in pulse phase estimation in X-ray pulsar-based navigation. Based on traditional epoch folding processes, a cross-correlation method and the idea of “averaging multiple measurements”, a new algorithm is proposed that can improve the accuracy of pulse phase estimation. In the method proposed, multiple estimations of pulse phase are generated by sampling the universal set of TOAs and these estimations are gathered to give a final estimation by weighted averaging. Cross-correlation values are employed as weights to achieve a higher overall SNR. Two explanations, an SNR-based explanation and an error-difference trade-off explanation, are provided. Numerical simulations validate that the accuracy in pulse phase estimation can be improved with the proposed algorithm.
The selection of sampling rate remains a problem. Since it is a “trade-off between error and difference”, it cannot be simply stated “the larger the better” or “the smaller the better”. Numerical simulations show that the best sampling rate is fixed for certain pulsars, so it is recommended to determine a sampling rate by grid-search experiments in advance. As yet it has not been possible to provide any systematic approach on the choice of sampling rate because it is hard to model the relationship between the overall difference and the sampling rate. This question is worthy of further research.
ACKNOWLEDGMENTS
This work was carried out with financial support from the National Basic Research Program 973 of China (No. 2015CB857100) and National Defense Scientific Research Fund (No. 2016110C019).
