1. INTRODUCTION
Fast high precision relative Global Navigation Satellite System (GNSS) positioning is very important to various applications, such as navigation, surveying, geodesy and geophysics. Ambiguity resolution is the key to achieve these purposes. It has been a continuing challenge to determine and fix the GNSS carrier-phase ambiguity, especially for medium- and long-distance baselines. With dual-frequency Global Positioning System (GPS) bands, it is almost impossible to achieve fast ambiguity resolution of medium- and long-distance baselines mainly due to the ionospheric and tropospheric effects in the past research.
As an important error source, the ionospheric effect can vary rapidly from a few metres to more than twenty metres within one day and it is difficult to model the ionospheric effects due to complicated physical interactions among the geomagnetic field and solar activities (Xu, Reference Xu2003). However, as the ionosphere is a dispersive medium, its first-order effect can be corrected with observations of multiple frequency bands and the remaining high-order effect can be generally neglected.
Unlike the ionosphere, the troposphere is a non-dispersive medium at GPS or BeiDou carrier frequencies. In past research, several tropospheric models have been established, such as the Modified Saastamoinen Model (Saastamoinen, Reference Saastamoinen1972; Reference Saastamoinen1973), the Modified Hopfield Model (Hopfield, Reference Hopfield1969; Reference Hopfield1970; Reference Hopfield1972). These can correct up to 90% of the tropospheric effect. But for ambiguity resolution of medium- and long-distance baselines, the remaining part cannot be neglected and should be taken into account. Generally, in the mathematical models, the tropospheric delay in the zenith direction will be treated as an unknown parameter and will be assumed to be stable over a short time, for example, within two hours. A mapping function will be used to combine the delay in the zenith direction and those in the signal-transmitting path.
With the modernization of GPS and the launch of the BeiDou system, observations of triple-frequency bands will be available. Therefore, ionospheric effect will not be a serious problem for ambiguity resolution while tropospheric effect becomes the main obstacle to ambiguity resolution of medium- and long-distance baselines.
In the past 15 years, the three-dimensional numerical weather prediction (NWP) model has become an important research aspect (Schüler, Reference Schüler2006; Jensen and Ovstedal, Reference Jensen and Ovstedal2008; Ibrahim and Rabbany, Reference Ibrahim and El-Rabbany2009). Recently, several NWP models have been established in many countries and areas around the world, such as North America (Ibrahim and Rabbany, Reference Ibrahim and El-Rabbany2009), Japan and Germany (Ghoddousi-Fard et al., Reference Ghoddousi-Fard, Dare and Langley2009; Böhm et al., Reference Böhm, Hobiger, Ichikawa, Kondo, Koyama, Pany, Schuh and Teke2010), Poland (Wielgosz et al., Reference Wielgosz, Cellmer, Rzepecka and Grejner-Brzezinska2008), Australia (Fu, Reference Fu2008), USA (Gutman and Benjamin, Reference Gutman and Benjamin2001; Ahn et al., Reference Ahn, Lachapele, Skone, Gutman and Sahm2006; Byun and Bar-Sever, Reference Byun. and Bar-Sever2009) and this can provide much more accurate corrections compared to conventional models, such as the Modified Hopfield Model and the Modified Saastamoinen Model. The accuracy of the predicted zenith path delay will depend on the resolution of the model and it can reach up to 3 cm level with a horizontal resolution of 1°×1° and a vertical resolution of 23 pressure layers up to 20 mbar (Andrei and Chen, Reference Andrei and Chen2009). So after correction with the NWP model, the remaining tropospheric effect may be able to be neglected after double-differencing.
With the launch of the BeiDou system, triple-frequency band GNSS observations are available for the first time. This research aims to test the ambiguity resolution performance with BeiDou triple-frequency band observations for medium- and long-distance baselines: 45 km, 70 km and 100 km. For the tropospheric effect, two different mathematical models are compared. First, the zenith tropospheric delay is estimated as an unknown parameter. Second, the tropospheric effect is corrected and the remaining part is neglected. In our experiment, as there is no NWP model available, the zenith tropospheric delay is estimated with the Precise Point Processing (PPP) technique and used to correct the tropospheric effect.
In addition, as BeiDou observations may have obvious multipath effects and large noise at low elevation angles, even around or higher than 15° (Cheng et al., Reference Cheng, Li and Mi2013), the ambiguity resolution performance is investigated with different cut-off elevation angles. At the end, the ambiguity resolution performance is tested with combined Beidou and GPS.
2. BEIDOU SYSTEM
The BeiDou Navigation Satellite System (BDS) is a Chinese satellite navigation system. It consists of two separate satellite constellations – a limited test system that has been operating since 2000, and a full-scale global navigation system, that is currently under construction.
The second generation of the system officially called the BeiDou Satellite Navigation System and also known as COMPASS or BeiDou-2, is under construction as of January 2013. BeiDou-2 will be a constellation of 35 satellites, which include five geostationary Earth orbit satellites (GEO) for backward compatibility with BeiDou-1, and 30 non-geostationary satellites (27 in medium earth orbit (MEO) and three in inclined geosynchronous orbit (IGSO)), that will offer complete coverage of the globe (BDS, 2012).
The BDS signals are code division multiple access (CDMA) signals similar to those of GPS and Galileo. Table 1 lists the available observation codes of BeiDou, which includes three frequency bands: B1, B2 and B3 (RINEX 3.02, 2013).
Table 1. BeiDou observation codes.
During the experimental period of this research around 19 April 2013, 14 satellites could be observed, including five GEO (PRN: 01, 02, 03, 04, 05), five IGSO (PRN: 06, 07, 08, 09, 10) and four MEO (PRN: 11, 12, 13, 14).
The China Geodetic Coordinate System 2000 (CGCS2000) is a geocentric coordinate system associated with an earth ellipsoid defined slightly differently from the GRS80 (Geodetic Reference System 1980) and WGS84 (World Geodetic System 1984). CGCS2000 is referred to ITRF97 (International Terrestrial Reference Frame 1997) at the epoch of 2000·0 (Wei, Reference Wei2008; Cheng et al., Reference Cheng, Wen, Cheng and Wang2009).
CGCS2000 is compatible to WGS84 and is the same as WGS84 in origin, scale, orientation and time evolution. Among the four defining parameters of the CGCS2000 ellipsoid, semi-major axis a, flattening f, Earth's gravitational constant GM and angular velocity of the Earth ω, f. and ω are slightly different from that of WGS84. For WGS84, f is 1/298·257223563. For CGCS2000, f is 1/298·257222101. For WGS84, ω is 7·2921158553E-5, for CGCS2000, ω is 7·2921150E-5 (Wei, Reference Wei2008; Cheng et al., Reference Cheng, Wen, Cheng and Wang2009).
The BDS time reference (BeiDou System Time), named BDT, is based on atomic time. Similar to GPS time, BDS time is a continuous time scale, which does not introduce any leap seconds. The BDS timing system starts from UTC 00:00:00, 1 January 2006 which is 14 seconds different from GPS time (i.e. GPST=BDT +14) (Dong et al., Reference Dong, Li and Wu2007; BDS, 2012).
3. MATHEMATICAL MODELS
The code and carrier phase measurements from a BeiDou satellite p to receiver m. at epoch te can be formulated as (Leick, Reference Leick2004):
$$\eqalign{{\rm P}_{{\rm m},{\rm i}}^{\rm p} ({\rm t}_{\rm e} ) = & {\rm \rho} _{\rm m}^{\rm p} ({\rm t}_{\rm e} ) + {\rm c(\delta t}^{\rm p} ({\rm t}_{\rm e} ) - {\rm \delta t}_{\rm m} ({\rm t}_{\rm e} )) + {\rm \delta} _{{\rm ion},{\rm m},{\rm i}}^{\rm p} ({\rm t}_{\rm e} ) + {\rm F}_{\rm m}^{\rm p} ({\rm t}_{\rm e} ){\rm Z}_{{\rm trop},{\rm m}} ({\rm t}_{\rm e} ) + {\rm \varepsilon} _{{\rm p},{\rm m}}^{\rm p} ({\rm t}_{\rm e} )} $$
$$\eqalign{{\rm \varphi} _{{\rm m},{\rm i}}^{\rm p} ({\rm t}_{\rm e} ) = & {\rm \rho} _{\rm m}^{\rm p} ({\rm t}_{\rm e} ) + {\rm c(\delta t}^{\rm p} ({\rm t}_{\rm e} ) - {\rm \delta t}_{\rm m} ({\rm t}_{\rm e} )) + {\rm \lambda} _{\rm i} {\rm N}_{{\rm m},{\rm i}}^{\rm p} - {\rm \delta} _{{\rm ion},{\rm m},{\rm i}}^{\rm p} ({\rm t}_{\rm e} ) + {\rm F}_{{\rm m},{\rm i}}^{\rm p} ({\rm t}_{\rm e} ){\rm Z}_{{\rm trop},{\rm m}} ({\rm t}_{\rm e} ) + {\rm \varepsilon} _{{\rm \varphi}, {\rm m}}^{\rm p} ({\rm t}_{\rm e} )} $$where i=1, 2, 3, corresponds to the three frequency bands; Pm,ip is the code measurement; φm,ip is the carrier phase measurement in distance; ρmp is the geometric distance from the satellite p to the receiver m; c is the light speed; δtp and δtm is the clock error of the satellite and the receiver; δion,m,ip is the ionospheric delay; Ztrop,m is the zenith tropospheric delay; Fmp. is the corresponding mapping function of tropospheric delay; εP,mp. and εφ,mp are the other error sources, such as multipath, observation noise and satellite orbital error; Nm,ip. is the integer ambiguity parameter and λi is the corresponding wavelength.
After linearization and double-differencing between stations m and n and satellites p and q, there is (Parkinson and Spilker, Reference Parkinson and Spilker1996):
$$\eqalign{\Delta \nabla {\rm P}_{{\rm mn},{\rm i}}^{{\rm pq}} ({\rm t}_{\rm e} ) = & {\rm a}_{{\rm mn}} \Delta {\rm x}_{{\rm mn}} + {\rm b}_{{\rm mn}} \Delta {\rm y}_{{\rm mn}} + {\rm c}_{{\rm mn}} \Delta {\rm z}_{{\rm mn}} + \Delta \nabla \delta _{{\rm ion,mn,i}}^{{\rm pq}} ({\rm t}_{\rm e} ) \cr & + \Delta \nabla {\rm F}_{{\rm mn}}^{{\rm pq}} ({\rm t}_{\rm e} ){\rm Z}_{{\rm trop}} ({\rm t}_{\rm e} ) + \Delta \nabla \varepsilon _{{\rm P,mn}}^{{\rm pq}} ({\rm t}_{\rm e} )} $$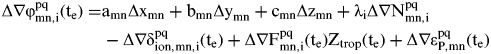
$$\eqalign{\Delta \nabla {\rm \varphi} _{{\rm mn},{\rm i}}^{{\rm pq}} ({\rm t}_{\rm e} ) = & {\rm a}_{{\rm mn}} \Delta {\rm x}_{{\rm mn}} + {\rm b}_{{\rm mn}} \Delta {\rm y}_{{\rm mn}} + {\rm c}_{{\rm mn}} \Delta {\rm z}_{{\rm mn}} + {\rm \lambda} _{\rm i} \Delta \nabla {\rm N}_{{\rm mn},{\rm i}}^{{\rm pq}} \cr & - \Delta \nabla {\rm \delta} _{{\rm ion},{\rm mn},{\rm i}}^{{\rm pq}} ({\rm t}_{\rm e} ) + \Delta \nabla {\rm F}_{{\rm mn},{\rm i}}^{{\rm pq}} ({\rm t}_{\rm e} ){\rm Z}_{{\rm trop}} ({\rm t}_{\rm e} ) + \Delta \nabla {\rm \varepsilon} _{{\rm P},{\rm mn}}^{{\rm pq}} ({\rm t}_{\rm e} )} $$where (Δxmn, Δymn, Δzmn) is the correction to the coordinate difference between stations m & n and amn, bmn and cmn are the corresponding coefficients. Note that, in forming Equations (3) and (4), zenith tropospheric delay at stations m and n is assumed to be the same and denoted as Ztrop. For satellites p and q and stations m and n, the double-differenced observation equations at epoch te will become:
$$\left\{ {\matrix{ {A_{mn}^{\,pq} {\rm X + d}_1 \Delta \nabla {\rm \delta} _{{\rm ion,mn}}^{{\rm pq}} ({\rm t}_{\rm e} ) + \Delta \nabla {\rm F}_{{\rm mn}}^{{\rm pq}} ({\rm t}_{\rm e} ){\rm Z}_{{\rm trop}} ({\rm t}_{\rm e} ) = \Delta \nabla {\rm P}_{{\rm mn,1}}^{{\rm pq}} ({\rm t}_{\rm e} )} \cr {A_{mn}^{\,pq} {\rm X + d}_2 \Delta \nabla {\rm \delta} _{{\rm ion,mn}}^{{\rm pq}} ({\rm t}_{\rm e} ) + \Delta \nabla {\rm F}_{{\rm mn}}^{{\rm pq}} ({\rm t}_{\rm e} ){\rm Z}_{{\rm trop}} ({\rm t}_{\rm e} ) = \Delta \nabla {\rm P}_{{\rm mn,2}}^{{\rm pq}} ({\rm t}_{\rm e} )} \cr {A_{mn}^{\,pq} {\rm X + d}_3 \Delta \nabla {\rm \delta} _{{\rm ion,mn}}^{{\rm pq}} ({\rm t}_{\rm e} ) + \Delta \nabla {\rm F}_{{\rm mn}}^{{\rm pq}} ({\rm t}_{\rm e} ){\rm Z}_{{\rm trop}} ({\rm t}_{\rm e} ) = \Delta \nabla {\rm P}_{{\rm mn,3}}^{{\rm pq}} ({\rm t}_{\rm e} )} \cr {A_{mn}^{\,pq} {\rm X}{\rm -} {\rm d}_1 \Delta \nabla {\rm \delta} _{{\rm ion,mn}}^{{\rm pq}} ({\rm t}_{\rm e} ) + \Delta \nabla {\rm F}_{{\rm mn}}^{{\rm pq}} ({\rm t}_{\rm e} ){\rm Z}_{{\rm trop}} ({\rm t}_{\rm e} ) + {\rm \lambda} _1 \Delta \nabla {\rm N}_{{\rm mn,1}}^{{\rm pq}} = \Delta \nabla {\rm \varphi} _{{\rm mn,1}}^{{\rm pq}} ({\rm t}_{\rm e} )} \cr {A_{mn}^{\,pq} {\rm X}{\rm -} {\rm d}_2 \Delta \nabla {\rm \delta} _{{\rm ion,mn}}^{{\rm pq}} ({\rm t}_{\rm e} ) + \Delta \nabla {\rm F}_{{\rm mn}}^{{\rm pq}} ({\rm t}_{\rm e} ){\rm Z}_{{\rm trop}} ({\rm t}_{\rm e} ) + {\rm \lambda} _2 \Delta \nabla {\rm N}_{{\rm mn,2}}^{{\rm pq}} = \Delta \nabla {\rm \varphi} _{{\rm mn,2}}^{{\rm pq}} ({\rm t}_{\rm e} )} \cr {A_{mn}^{\,pq} {\rm X}{\rm -} {\rm d}_3 \Delta \nabla {\rm \delta} _{{\rm ion,mn}}^{{\rm pq}} ({\rm t}_{\rm e} ) + \Delta \nabla {\rm F}_{{\rm mn}}^{{\rm pq}} ({\rm t}_{\rm e} ){\rm Z}_{{\rm trop}} ({\rm t}_{\rm e} ) + {\rm \lambda} _3 \Delta \nabla {\rm N}_{{\rm mn,3}}^{{\rm pq}} = \Delta \nabla {\rm \varphi} _{{\rm mn,1}}^{{\rm pq}} ({\rm t}_{\rm e} )} \cr}} \right.$$where A mnpq=(amn, bmn, cmn); di (i=1, 2, 3) are the coefficients of ionospheric delay and d1=1 for frequency bands B1; X is (Δxmn, Δymn, Δzmn).
In the above equations, satellite and receiver related errors are cancelled, including the satellite and receiver clock errors and satellite orbital error. For short baselines (<30 km), the remaining ionospheric and tropospheric delays after double-differencing can be neglected generally. But for medium- or long-distance baselines, they should be taken into account in the observation equations.
Then, all observation equations of epoch te can be denoted as:
$$\left\{{\matrix{ {{\rm AI} + {\rm BX} + {\rm CT} = {\rm L}_{{\rm code}}} \cr {{\rm AI} + {\rm BX} + {\rm CT} + {\rm DN} = {\rm L}_{{\rm phase}}} \cr}} \right.$$where Lcode and Lphase are double-differenced code and carrier phase measurements; I is the double-differenced ionospheric delays; X is (Δxmn, Δymn, Δzmn); T is the zenith tropospheric delay; N is the double-differenced integer ambiguity parameters and A, B, C and D are the corresponding coefficients.
If the tropospheric effect can be corrected with NWP model or other methods, the above equations will become:
$$\left\{ {\matrix{ {{\rm AI} + {\rm BX} = {\rm L}_{{\rm code}}} \cr {{\rm AI} + {\rm BX} + {\rm DN} = {\rm L}_{{\rm phase}}} \cr}} \right.$$For composing the weight matrix, the sigma of carrier phase noise is set to 3 mm same as GPS. As multipath of BeiDou code measurements is obvious (Cheng et al., Reference Cheng, Li and Mi2013), the sigma of code noise is set to 0·5 m instead of 0·3 m as GPS.
In order to solve the above equations, ionospheric parameters will be equivalently eliminated every epoch (Xu, Reference Xu2003). After that, the sequential least-squares adjustment method can be used to obtain the float ambiguity solution and the LAMBDA method (Teunissen, Reference Teunissen1995) can be employed to obtain the integer ambiguity candidate corresponding to the minimum quadratic form of the residuals.
In past research, many ambiguity resolution validation methods have been discussed and suggested (Euler and Schaffrin, Reference Euler and Schaffrin1991; Wang et al., Reference Wang, Stewart and Tsakiri1998; Reference Wang, Stewart and Tsakiri2000; Leick, Reference Leick2004; Ji et al., Reference Ji, Chen, Ding, Chen, Zhao and Hu2010). In this research, the popular R-ratio (Euler and Schaffrin, Reference Euler and Schaffrin1991; Leick, Reference Leick2004) is used and a threshold value is set to two.
4. NUMERICAL RESULTS
To investigate the ambiguity resolution performance of BeiDou medium- and long-distance baselines, experimental data were collected on 1 May 2013 and three Trimble NetR9 receivers were used at stations HK01, HK02 and HK03 with coordinates around 40°N, 100°E. Both GPS and BeiDou observations were collected from 00:00:00 to 23:59:59 (GPS time) and the sample interval was 15 seconds.
Three baselines can be formed, including HK01-HK02 (about 45 km), HK01-HK03 (about 70 km) and HK02-HK03 (about 100 km).
The observed satellites include BeiDou satellites from PRN 1 to 14. But for PRN 13 and 14, only observations of two frequency bands (B1 and B2) were available. No broadcast ephemeris and precise ephemeris (normally provided by Wuhan University) was available for satellites PRN 2 and 5. The BeiDou satellites used in data processing and their observation periods are shown in Figure 1, including: three GEO (PRN 1, 3, 4), five IGSO (PRN 6, 7, 8, 9, 10) and two MEO (PRN 11, 12).
Figure 1. BeiDou satellites used in data processing and their observation time.
4.1. Results with cutoff elevation angle 15°
The data was first processed with the mathematical model of Equation (6) every hour from 01:00:00 to 21:00:00 (GPS time) with a cut-off elevation angle 15° for all the three baselines. If the required time exceeds four hours, it will be regarded as failed. Figure 2 shows the time required to reach an R-ratio value of two and all ambiguity resolutions are correct.
Figure 2. Time required fixing ambiguity with a cut-off elevation angle 15° and without tropospheric parameter.
From the figure, we can see that the required time differs greatly from several minutes to about three hours. From 14:00:00 to 21:00:00 (GPS time), almost all failed except for 17:00:00 for baseline HK01-HK02. Figure 3 shows a sample failed case at 17:00:00 (GPS time) of baseline HK01-HK02 and we can see that the ratio value is only slightly larger than 1·0 for all three hours. The possible reasons for the failed cases may be due to bad observation quality. But there may be another reason, that is, the change of the satellite geometry is not enough as most of them are geostationary.
Figure 3. Sample failed case at 15:00:00 of baseline HK01-HK02.
4.2. Compare different cut-off elevation angles
To investigate the reason for the failed cases, different cut-off elevation angles are tested from 15° to 40° every 5° for baseline HK01-HK03 based on the mathematical model of Equation (6). Table 2 shows the time required to fix ambiguities with different cut-off elevation angles. We can see that with a cut-off elevation angle of 20°, the performance is obviously better than that of 15° and there is no failed case. The performances from 20° to 40° are similar and the average times are all around 45 minutes. As we know, the number of observed satellites will decrease with the increase of the cut-off elevation angle, which will be disadvantageous to final positioning results; a cut-off elevation angle of 20° is the best choice.
Table 2. Time required fixing ambiguities with different cut-off elevation angles. (unit: minute)
4.3. Ambiguity resolution performance with and without tropospheric parameter
The performances with cut-off elevation angle of 20° are investigated with the two mathematical models of Equations (5) and (6) for all three baselines. Figures 4 and 5 show the time required and Table 3 gives the average required time.
Figure 4. Time required fixing ambiguities for mathematical model of Equation (5) with cut-off elevation angle of 20°.
Figure 5. Time required fixing ambiguities for mathematical model of Equation (6) with cut-off elevation angle of 20°.
Table 3. Average time required fixing ambiguities. (unit: minute)
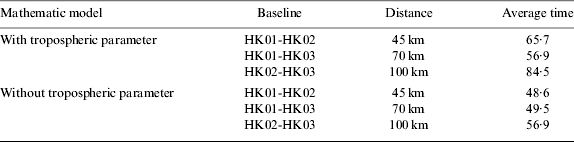
From the two figures, we can see that the required time still differs greatly from several minutes to about three hours and there is no failed case for all three baselines and both models. Comparing the performance of the three baselines, the time required has no great difference generally and the average required time is also similar for the two models. Comparing the performance of the two models, we can find that the required time of Equation (6) is generally less than that of Equation (5) and the average time required of Equation (6) in Table 3 is also less than that of Equation (5).
4.4. BeiDou alone vs BeiDou and GPS
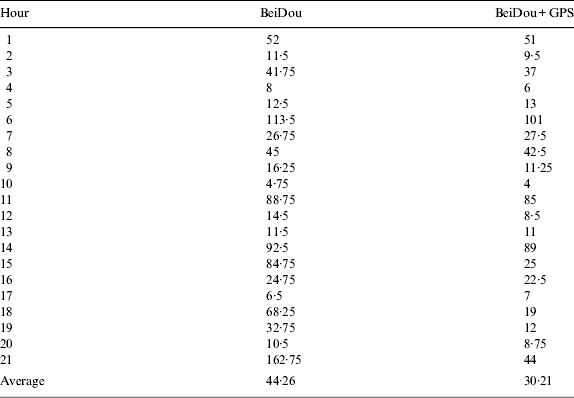
In this section, the performance with combined BeiDou and GPS is investigated and compared to that of BeiDou alone and only ambiguities of BeiDou satellites are fixed. The cut-off elevation angle is 20°, the mathematical model used is Equation (6) and only baseline HK01-HK03 (70 km) is tested. Table 4 shows the time required for BeiDou alone and BeiDou and GPS. We can see that the required time of BeiDou and GPS is generally less than that of BeiDou alone, which shows that GPS observations are beneficial to the ambiguity resolution of BeiDou. The possible reason may be that GPS observations are helpful to float the BeiDou ambiguity solution.
Table 4. Time required fixing ambiguities with the cutoff elevation angle 20° and the model of Equation (6). (unit: minute)
5. CONCLUSIONS
In this research, ambiguity resolution performance with triple-frequency BeiDou bands is investigated for baselines of 45 km, 70 km and 100 km. Experimental results clearly show that with observations of triple-frequency bands, ambiguity of medium- or long-distance can be fixed. The results also show that:
• The test results with different cut-off elevation angle show that the performance with 20° is much better than that of 15°;
• The performance with tropospheric effect corrected is slightly better than that with tropospheric effect as an estimated parameter;
• Dual-frequency band GPS observations will benefit ambiguity resolution performance;
• The performances are similar for baselines with different distances;
• The time required for fixing ambiguities differs greatly with at different tested times and the average required time is around 45 minutes.
The results of this research will benefit us for further research to improve the ambiguity resolution performance. For our further work, we need to analyse the reason for the obvious variation of the fixing time required. The possible reasons may be slow geometry change of geostationary satellites as the satellite geometry change is important to ambiguity resolution. Another possible reason may be that the stochastic model used is not optimal. BeiDou and GPS are different in some aspects. BeiDou has various types of satellites, including: GEO, IGSO and MEO. Every type of satellite may have its own characteristics, such as multipath and noise levels. BeiDou and GPS also have different frequency bands. It is for future research to investigate how to improve the ambiguity resolution performance for medium- and long-distance baselines based on the different characteristics of BeiDou.
ACKNOWLEDGEMENT
The research was substantially supported by the Fundamental Research Funds for the Central Universities (Grant No. 14CX02036A, 14CX02033A, 14CX02039A and 11CX05015A), funded by Hong Kong RGC General Research fund (A/C: PolyU 5131/10E), National Natural Science Foundation of China (Grant No. 40974004, 41274011, 41274006 and 41001250) and Natural Science Foundation of Shandong Province, China (Grant No. ZR2012DM010 and ZR2011DQ011).
