Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-02-05T23:46:42.310Z Has data issue: false hasContentIssue false
  • English
  • Français

A Comparison of Outlier Detection Procedures and Robust Estimation Methods in GPS Positioning

Published online by Cambridge University Press:  07 October 2009

Nathan L. Knight  and
Jinling Wang
Nathan L. Knight*
Affiliation:
(The University of New South Wales, Sydney, Australia)
Jinling Wang
Affiliation:
(The University of New South Wales, Sydney, Australia)
*
(Email: N.Knight@student.unsw.edu.au)
Rights & Permissions [Opens in a new window]

Abstract

With more satellite systems becoming available there is currently a need for Receiver Autonomous Integrity Monitoring (RAIM) to exclude multiple outliers. While the single outlier test can be applied iteratively, in the field of statistics robust methods are preferred when multiple outliers exist. This study compares the outlier test and numerous robust methods with simulated GPS measurements to identify which methods have the greatest ability to correctly exclude outliers. It was found that no method could correctly exclude outliers 100% of the time. However, for a single outlier the outlier test achieved the highest rates of correct exclusion followed by the MM-estimator and the L1-norm. As the number of outliers increased MM-estimators and the L1-norm obtained the highest rates of normal exclusion, which were up to ten percent higher than the outlier test.

Keywords

RAIMOutliersRobustIntegrity
Type
Research Article
Information
The Journal of Navigation , Volume 62 , Issue 4 , October 2009 , pp. 699 - 709
Copyright
Copyright © The Royal Institute of Navigation 2009

1. INTRODUCTION

There is currently a need for Receiver Autonomous Integrity Monitoring (RAIM) to identify multiple outliers. This is due to the fact that two or more simultaneous satellite failures are likely. Particularly, in less than ideal environments, multiple outliers are more frequent due to the additional affects of non line of sight multipath.

There are two different strategies to mitigate the presence of outliers in RAIM. The first is to identify outliers using outlier tests, and then reject the largest observation (Sturza, Reference Sturza1988; Lee, Reference Lee1986; Brenner, Reference Brenner1990; Pervan et al., Reference Pervan, Lawrence, Cohen and Parkinson1996; Parkinson and Axelrad, Reference Parkinson and Axelrad1988). If multiple outliers exist then the single outlier test is applied iteratively until all outliers have been removed (Kelly, Reference Kelly1998, Hewitson and Wang, Reference Hewitson and Wang2006). The second method is to use robust methods that retain all observations but either down-weight suspect observations or minimise alternatives to the sum of the squared residuals (Wang and Wang, Reference Wang and Wang2007).

When multiple outliers exist, statisticians frequently use robust methods since ordinary least squares are non-robust (Andersen, Reference Andersen2008). It is for this reason that outlier diagnostics are required to identify outliers that have substantially influenced the estimated parameters. However, robust methods are designed so that the estimators are resistant to the influence of outliers.

It is also claimed that robust methods are good for automated processing (Kuter et al., Reference Kuter, Nachtsheim, Neter and Li2005) as required for RAIM. This is due to the ease of application of robust methods, requiring no outlier diagnostics that can be very complex and time consuming for multiple outliers.

Another desirable characteristic of many robust methods is the bounded influence of leverage observations (Rousseeuw and Leroy, Reference Rousseeuw and Leroy1987). Leverage observations are pseudoranges that have a high potential to influence the estimated parameters. In RAIM, due to the method of least squares having an unbounded influence, leverage observations are controlled by monitoring protection levels to ensure that they are within the requirements of the application. This means that monitoring protection levels may be unnecessary for robust methods.

There are currently a large number of robust methods to choose from including the Danish Method (Krarup et al., Reference Krarup, Kubik and Juhl1980), least absolute values method (Edgeworth, Reference Edgeworth1887), Least Median Squares (Rousseeuw, Reference Rousseeuw1984), Least Trimmed Squares (Rousseeuw, Reference Rousseeuw1984), R-estimators (Jaeckel, Reference Jaeckel1972), M-estimators (Huber, Reference Huber1964), Generalised M-estimators (Hampel et al., Reference Hampel, Ronchetti, Rousseeuw and Stahel1986), IGGIII estimators (Yang Reference Yang, Cheng, Shum and Tapley1999), S-estimators (Yohai and Rousseeuw, Reference Rousseeuw1984), and MM-estimators (Yohai, Reference Yohai1987).

As this is the case then should a robust method be used for RAIM? Ideally, the RAIM method chosen should be capable of handling multiple outliers. It should be resistant to the influence of leverage observations. The method should also be resilient to the effects of incorrect exclusion where only some of the outliers are identified and wrong exclusion where a correct observation is identified. If neither incorrect exclusion nor wrong exclusion occurs then it is a correct exclusion as all of the outliers and only the outliers have been excluded.

The ability of an estimator to resist multiple outliers is given by the breakdown point. This is a global measure of the percentage of outliers that can be tolerated without producing an arbitrary result. However, the breakdown points as given by Hampel (Reference Hampel1971) and Donoho and Huber (Reference Donoho, Huber, Bickel, Doksum and Hodges1983) are asymptotic and do not give any information on the reliability of the methods to correctly exclude outliers. In addition, the breakdown point does not take into account outlier tests that effectively increase the breakdown point.

As a result of this, it is the intention of this study to compare the abilities of the outlier test and robust methods to correctly exclude outliers in single point positioning. The comparison is based on the number of outliers present and the size of the outliers. An analysis is made of what has occurred in the times that the methods do not correctly exclude the outliers.

2. THE OUTLIER TEST

The linear model used to find the positioning solution is given by:

(1)
v \equals A\hat{x} \minus \ell

where v is the matrix of residuals, A is the design matrix, \hat{x} is the matrix of parameters solved for and ℓ is the measurement matrix. The variance covariance matrix, Σ of the pseudoranges is given by:

(2)
\Sigma \equals \sigma _{\setnum{0}}\,\! ^{\setnum{2}} Q \equals \sigma _{\setnum{0}}\,\!^{\setnum{2}} P^{ \minus \setnum{1}}

where σ02 is the a priori variance factor, Q is the cofactor matrix, and P is the weight matrix.

The studentised outlier test is given by (Baarda, Reference Baarda1968; Hewitson et al., Reference Hewitson, Lee and Wang2004):

(3)
w_{i} \equals {{\vert h_{i}\,\!^{\rm T} Pv\vert } \over {\sigma _{\setnum{0}} \sqrt {h_{i}\,\! ^{\rm T} PQ_{v} Ph_{i} } }}

where h is [0…1…0]T with the i th element equal to one, and Q v is the cofactor matrix of the estimated residuals given by:

(4)
Q_{v} \equals P^{ \minus \setnum{1}} \minus A\lpar A^{\rm T} PA\rpar ^{ \minus \setnum{1}} A^{\rm T}

The pseudorange with the largest test statistic greater than the threshold is considered an outlier. In this study, it is assumed that the measurements are uncorrelated and their weights are defined by the squared sine of the satellite elevation angles.

3. ROBUST METHODS

3.1. The Danish Method

The Danish method was proposed by Krarup (Krarup et al., Reference Krarup, Kubik and Juhl1980) and is purely heuristic with no rigorous statistical theory. The method works by carrying out a least squares adjustment using the a priori weight matrix. Then the process is repeated iteratively altering the weight matrix according to (Caspary, Reference Caspary1987):

(5)
\lpar P_{ii} \rpar _{k \plus \setnum{1}} \equals \left\{ {\matrix{ {\lpar P_{ii} \rpar _{k} } \hfill \tab {\vert \lpar v_{i} \rpar _{k} \vert \les c\sigma _{\setnum{0}} \sqrt {Q_{ii} } } \hfill \cr {\lpar P_{ii} \rpar _{k} {\rm e}^{ \big ( \minus {{\vert \lpar v_{i} \rpar _{k} \vert } \over {c\sigma _{\setnum{0}} \sqrt {Q_{{ii}} } }}\big ) } } \hfill \tab {\vert \lpar v_{i} \rpar _{k} \vert \gt c\sigma _{\setnum{0}} \sqrt {Q_{ii} } } \hfill \cr} } \right.

where k is the number of iterations, and c is a constant usually set between two and three. The process is continued until convergence is achieved. The outliers then have zero weights and the size of the residuals represents the magnitude of the outlier. The estimated parameters are either left as is or the outliers are discarded and a new least squares solution is obtained using the a priori weights.

3.2. Least Absolute Values

The least absolute values method, otherwise known as the L1-norm was proposed by Edgeworth (Reference Edgeworth1887). The L1-norm is found by minimising the sum of the absolute weighted residuals.

(6)
{\rm Min}\sum\limits_{i \equals \setnum{1}}^{n} {\left\vert {{{v_{i} } \over {\sqrt {Q_{ii} } }}} \right\vert}

By not squaring the residuals, there is less emphasis on the outliers than would be the case with the least squares.

3.3. Least Median Squares

The Least Median Squares (LMS) was developed by Rousseeuw (Reference Rousseeuw1984). It is characterised by solving the linear model by minimising the median of the weighted residuals squared.

(7)
{\rm Min}\left( {{\rm Median}\left( {{{v_{i} \hskip 2\! ^{\setnum{2}} } \over {Q_{ii} }}} \right)} \right)

3.4. Least Trimmed Squares

The Least Trimmed Squares (LTS) method was also developed by Rousseeuw (Reference Rousseeuw1984). It is close to ordinary least squares except that the largest weighted squared residuals are excluded from the summation to be minimised,

(8)
{\rm Min}\sum\limits_{i \equals \setnum{1}}^{u} {{{v_{i}\hskip 2\! ^{\setnum{2}} } \over {Q_{ii} }}}

where u is the number of residuals included in the summation. It has been suggested to set u=n(1−α)+1 where α is the percentage of residuals to be trimmed from the summation. However to achieve maximum robustness u should be set to n/2.

3.5. R-Estimators

Jaeckel (Reference Jaeckel1972) proposed the R-estimators that are based on the rank of the residuals. The linear equation is solved by minimising the sum of the scored ranked weighted residuals:

(9)
{\rm Min}\sum\limits_{i \equals \setnum{1}}^{n} {a\lpar R_{i} \rpar {{v_{i} } \over {\sqrt {Q_{ii} } }}}

where R i is the rank of the weighted residuals, and a(i) is the score function given by:

(10)
a\lpar i\rpar \equals {\rm Min}\left( {c_{R} \comma {\rm Max}\left( {\rmPhi ^{ \minus \setnum{1}} \left( {{i \over {n \plus 1}}} \right)\comma \minus c_{R} } \right)} \right)

where Φ−1 is the inverse of the normal probability density function, and c R is a constant.

3.6. M-Estimators

The M-estimators were first proposed by Huber (Reference Huber1964) and are based on minimising a function of the residuals:

(11)
{\rm Min}\sum\limits_{i \equals \setnum{1}}^{n} {\rho \lpar v_{i} \rpar }

where ρ is a symmetric function with a unique minimum at zero. By differentiating Equation (11) with respect to the parameters yields:

(12)
\sum\limits_{i \equals \setnum{1}}^{n} {\varphi \left( {{{v_{i} } \over {\hat{\sigma }_{\setnum{0}} }}} \right)} A_{i} \equals 0

where ϕ is the derivative of ρ and the residuals have been scaled. The ϕ is replaced by an appropriate weight function that increases as the size of the residuals increases:

(13)
\lpar P_{ii} \rpar _{k \plus \setnum{1}} \equals \left\{ {\matrix{ 1 \hfill \tab {\displaystyle{{\vert \lpar v_{i} \rpar _{k} \vert } \over {\hat{\sigma }_{\setnum{0}} }}\les 1\!{\cdot}\!345} \hfill \cr {\displaystyle{{1\!{\cdot}\!345} \over {\vert \lpar v_{i} \rpar _{k} \sol \hat{\sigma }_{\setnum{0}} \vert }}} \hfill \tab {\displaystyle{{\vert \lpar v_{i} \rpar _{k} \vert } \over {\hat{\sigma }_{\setnum{0}} }} \gt 1\!{\cdot}\!345} \hfill \cr} } \right.

where \hat{\sigma }_{\setnum{0}} is the a posteriori scale factor given by the robust estimator:

(14)
\hat{\sigma }_{\setnum{0}} \equals {1 \over {0\!{\cdot}\!6745}}{\rm Median}\lpar \vert v_{i} \minus {\rm Median}\lpar v_{i} \rpar \vert \rpar

Due to the difficulty in solving Equation (12) initiative re-weighted least squares is used. An initial adjustment is carried out with the least squares using the a priori weight matrix. Then the weight matrix is altered in the following iterations by Equation (13) until convergence.

3.7. Generalised M-Estimators

Since M-estimates fail to account for leverage observations, Mallows proposed Generalised M-estimators (Hampel et al., Reference Hampel, Ronchetti, Rousseeuw and Stahel1986). The Generalised M-estimators are given by:

(15)
\sum\limits_{i \equals \setnum{1}}^{n} {\sqrt {\lpar Q_{v} P\rpar _{ii} } \varphi \left( {{{v_{i} } \over {\hat{\sigma }_{\setnum{0}} }}} \right)} A_{i} \equals 0

where leverage observations are down weighted according to their redundancy number. However, this is only valid when the measurements are uncorrelated, otherwise the redundancy number may become negative values (Wang and Chen, Reference Wang and Chen1994a, Reference Wang and Chenb). To solve Equation (15) an initial adjustment is carried out with the least squares using the a priori weight matrix. Then the weight matrix is updated in the following iterations by:

(16)
\lpar P_{ii} \rpar _{k \plus \setnum{1}} \equals \left\{ {\matrix{ {\sqrt {\lpar Q_{v} P\rpar _{ii} } } \hfill \tab {\displaystyle{{\vert \lpar v_{i} \rpar _{k} \vert } \over {\hat{\sigma }_{\setnum{0}} }}\les 1\!{\cdot}\!345} \hfill \cr {\displaystyle{{1\!{\cdot}\!345\sqrt {\lpar Q_{v} P\rpar _{ii} } } \over {\vert \lpar v_{i} \rpar _{k} \sol \hat{\sigma }_{\setnum{0}} \vert }}} \hfill \tab {\displaystyle{{\vert \lpar v_{i} \rpar _{k} \vert } \over {\hat{\sigma }_{\setnum{0}} }} \gt 1\!{\cdot}\!345} \hfill \cr} } \right.

until convergence is achieved.

3.8. IGGIII

The IGGIII is similar to M-estimation except that the weight function is given by (Yang Reference Yang, Cheng, Shum and Tapley1999):

(17)
\lpar P_{ii} \rpar _{k \plus \setnum{1}} \equals \left\{ {\matrix{ {P_{ii} } \hfill \tab {\vert \bar{v}_{i} \vert \les 1\!{\cdot}\!345} \hfill \cr \displaystyle{P_{ii} {{1\!{\cdot}\!345} \over {\vert \bar{v}_{i} \vert }}\left( {{{3 \minus \vert \bar{v}_{i} \vert } \over {3 \minus 1\!{\cdot}\!345}}} \right)^{\setnum{2}} } \hfill \tab {1\!{\cdot}\!345 \lt \vert \bar{v}_{i} \vert \les 3} \hfill \cr 0 \hfill \tab {\vert \bar{v}_{i} \vert \gt 3} \hfill \cr} } \right.

where the studentised residuals, \bar{v}_{i} are used to adjust the weights.

3.9. S-Estimators

The least median squares and the least trimmed squares are defined by minimising a robust measure of the scatter of the residuals. Yohai and Rousseeuw (Reference Rousseeuw1984) generalised this to the S-estimators that minimise the dispersion of the residuals:

(18)
{\rm Min}\ \hat{\sigma }_{\setnum{0}} \lpar v_{\setnum{1}} \comma v_{\setnum{2}} \comma \ldots v_{n} \rpar

Rather than minimise the variance of the residuals, robust S-estimators minimise a robust M-estimate,

(19)
{1 \over n}\sum\limits_{i \equals \setnum{1}}^{n} {\varphi \left( {{{v_{i} } \over {\hat{\sigma }_{\setnum{0}} }}} \right)} \equals b

where ϕ is replaced by an appropriate weight function.

3.10. MM-Estimators

Yohai (Reference Yohai1987) proposed the MM-estimator, which combines the S-estimator and the M-estimator. The procedure is to obtain initial estimators using the S-estimator. Then the residuals from the S-estimator are used to determine the scale factor, \hat{\sigma }_{\setnum{0}}. The scale factor is then held constant during consecutive iterations of the M-estimator, starting with the final S-estimation parameters. The MM-estimator can also be found using the method of least median squares in place of the S-estimator.

4. THE METHOD OF COMPARISON

To compare the outlier test and robust estimation methods 24-hours of GPS data was simulated with the number of satellites and PDOP as displayed in Figure 1. Outliers were injected into the pseudoranges and the success rates of the outlier test and robust methods were recorded.

Figure 1. Number of satellites and PDOP.

4.1. Outlier Definition

An outlier is a piece of data that is suspected to be incorrect due to the remote probability that it is in fact correct (Ferguson, Reference Ferguson1961). In this study, the point at which a pseudorange becomes an outlier is considered to be at three standard deviations. This corresponds to a 0·27% chance of a pseudorange being incorrectly identified as an outlier.

The three standard deviation definition of an outlier was also primarily chosen since there is no pre-defined point at which robust estimators start to reduce the influence of outliers on the estimated parameters. However, outlier tests only start to reject outliers once the pre-defined threshold of an outlier has been breached. Since it is generally considered that a residual greater than three standard deviations is an outlier, and it is most likely that the robust methods would have significantly reduced the influence of residuals of this magnitude, then the three standard deviation definition was chosen.

4.2. Outlier Simulation

Outliers of varying size and number were injected into the pseudoranges. This was done for zero, one, and two outliers. The sizes of the outliers were randomly generated in two categories between three and six standard deviations and between six and nine standard deviations. The simulated outliers were then randomly added to or subtracted from the pseudoranges.

4.3. Testing Method

The outlier test and the robust methods were tested with the simulated GPS data. To ensure that the correct solution could be obtained, only epochs with five satellites plus at least the number of simulated outliers were used. To correspond with the definition of an outlier at three standard deviations the threshold for the outlier test was set at three. In addition, the constant value, c in the Danish method was also set to three, and at the end of the adjustment the outliers with significantly small weights (i.e. <1e−6) were discarded and a new Least Squares adjustment using the a priori weight matrix was used. To achieve the maximum robustness for the Least Trimmed Squares method, u was set to n/2 and for the R-estimator, c R was set to 0·68.

4.4. Breakdown of the Results

After the outlier test and robust methods were tested, the estimated parameters were then used to determine the residuals for all of the pseudoranges. If a residual was greater than three standard deviations then it was considered that the pseudorange was excluded as a suspected outlier. Similarly, if a residual was less than three standard deviations then it was considered that the method had identified the pseudorange as correct.

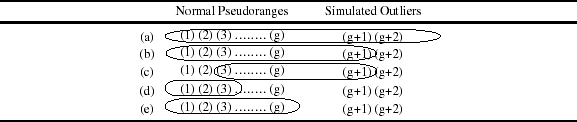
Based on the comparison of the pseudoranges excluded and the pseudoranges that contained simulated outliers the estimated parameters were categorised as shown in Table 1 where g is the number of normal pesudoranges, and the scenarios are:

  1. (a) None of the outliers were excluded

  2. (b) Some of the outliers were excluded

  3. (c) Some of the outliers were excluded and some normal pseudoranges were also excluded

  4. (d) All of the outliers were excluded and some normal pseudoranges were also excluded

  5. (e) Correct exclusion, where all of the outliers were excluded and none of the normal pseudoranges were excluded

Table 1. Scenarios of selected pseudoranges for two outliers.

5. RESULTS

The comparisons of the methods for zero, one, and two outliers are displayed in Tables 2, 3 and 4 respectively.

Table 2. Comparison for zero outliers.

Table 3. Comparison for one outlier.

Table 4. Comparison for two outliers.

6. DISCUSSION

From Table 2 for the case of zero outliers it can be seen that all of the results are in the (e) and (d) categories since there were no outliers present. The Danish method was the only method to achieve 100% correct exclusion, closely followed by the outlier test. For the outlier test, it is generally undesirable to have a high amount of category (d) as it can lead to the positioning solution being unavailable if there are only a small number of satellites (Wang and Ober, Reference Wang and Ober2009). However, this will become less of a concern as the number of satellites increases. In comparison to the robust methods that have a correct exclusion rate of approximately ninety percent and a category (d) rate of approximately ten percent, this could be considered a failure of the robust methods. However, while exclusion of normal pseudoranges is less than desired, as it does not utilise all normal pseudoranges, it is still a satisfactory result as the positing solution only uses normal pseudoranges.

One of the reasons for the robust methods having a high rate of excluding normal pseudoranges is believed to be due to their characteristic of bounded influence. If a pseudorange has a high protection level, otherwise known as a leverage observation, then it has a high potential to influence the estimated parameters. It is only when the addition or removal of the observation causes a substantial change in the estimated parameters that it becomes influential (Andersen, Reference Andersen2008). By bounding the influence of observations, the robust methods retain leverage observations that have little influence but reject observations with high influence. As can be seen from Table 2 if an observation is highly influential it does not necessarily mean that it is an outlier. It is expected that as the number of satellites increase the frequency of highly influential observations decreases.

For a single outlier in Table 3, category (b) is zero since for some outliers to be excluded multiple outliers must exist.

From Tables 3 and 4 it can be seen that no method has achieved 100% correct exclusion for a single or multiple outliers. For a single outlier the outlier test provided the highest rates of correct exclusion followed by the L1-norm and MM-estimators. However, as the level of contamination increases the outlier test starts to produce average results while MM-estimators and the L1-norm start to achieve the highest rates of correct exclusion. R-estimators have the lowest rates of correct exclusion for all levels contamination.

When the less than desirable, but acceptable result of scenario (d) is taken into account in addition to correct exclusion (i.e. (d)+(e)) a 100% success rate is still not achieved. The R-estimator now has the highest rates of success followed by MM-estimators, and the L1-norm. The Danish method now has the poorest rates of success. The R-estimator on this measure has remarkable results particularly for high levels of contamination due to the very high levels of successfully selecting a subset of normal pseudoranges.

In comparison to the robust methods, the outlier test has higher levels of category (b) and reasonable levels of category (a). In addition, the outlier test has lower levels of category (d). This appears to be due to the outlier tests' reluctance to reject observations compared to the robust methods.

All the methods tested are prone to the five different scenarios. It can be stated that generally clear relationships between the five categories and the number and magnitude of outliers exist. As the number of outliers increases the amount of (b) and (c) increases, while (a), (d) and correct exclusion decreases. When the magnitudes of the outliers increase the percentages of (c), (d) and correct exclusion increases, whereas (a) and (b) decreases.

From the breakdown of the results it can also be seen how the conventional outlier test results would have changed if additional methods were employed. If observations with high leverage were removed then it would have resulted in a slight decrease in the amount of correct exclusion and a corresponding increase in (d). This is because the majority of pseudoranges that have been rejected are normal. Another strategy to improve the results of outlier tests is to replace pseudoranges one at a time in the order of rejection and retest in case a normal pseudorange has been incorrectly excluded. However, this strategy only has the potential to reduce category (d), which in this paper has a maximum value of one percent and hence results in a very minor improvement.

It was also found that the robust methods are easier to apply than the outlier tests that require complex diagnostics. However since the robust methods cannot be uniquely solved for, time consuming search methods must be employed.

7. CONCLUSION

There is an increasing requirement of RAIM to identify and exclude multiple outliers. To meet this requirement there are numerous options including the outlier test and robust methods consisting of the Danish method, Least Absolute Values method, Least Median Squares, Least Trimmed Squares, R-estimators, M-estimators, Generalised M-estimators, IGGIII estimators, S-estimators, and MM-estimators.

However, despite this it has been found that no method correctly identifies all outliers in all situations even for a single outlier, let alone if multiple outliers exist. This demonstrates that the mitigation of outliers for a 100% success rate is a very challenging task. From the results, the outlier test achieves the highest rates of correct exclusion for a single outlier. However, as the level of contamination increases the robust methods of the MM-estimators and the L1-norm achieved the highest rates of correct exclusion. If the rejection of normal observations in addition to the outliers is considered acceptable then the R-estimator has the highest rates of success followed by the MM-estimators and the L1-norm. However the difference between the success rates of the outlier test and the robust methods are at most of the order of 10%. The exception to this is the R-estimator, which produces significantly higher success rates at increased levels of contamination and hence warrants further investigation.

It can be stated generally that as the number of outliers increases, the percentages of correct exclusion decreases. When the magnitudes of the outliers increase, the percentages of correct exclusion increase.

It was also found that all the methods tested are prone to the five different scenarios. In comparison to the robust methods, the outlier test has higher levels of partially excluding some outliers and lower levels of excluding some normal pseudoranges in addition to the outliers.

Some of the differences between the robust methods and the conventional outlier tests are believed to be due to the robust methods' property of bounded influence. Hence, the conventional outlier test results may be improved if the influences of pseudoranges are bounded.

Even though the robust methods obtain higher rates of success when multiple outliers exist, the computational intensity of the methods is an issue to be addressed for the real time application of RAIM. One way of increasing the reliability of outlier identification that is practical is through a dynamic model as demonstrated by Hewitson and Wang (Reference Hewitson and Wang2007).

References

REFERENCES

Andersen, R. (2008) Modern Methods for Robust Regression. Sage Publications, London.CrossRefGoogle Scholar
Baarda, W. (1968) A Testing procedure for use in geodetic networks. Netherlands Geodetic Commission, Publications on Geodesy, New Series 2, No. 5, Delft, Netherlands.CrossRefGoogle Scholar
Brenner, M. (1990) Implementation of a RAIM Monitor in a GPS Receiver and an Integrated GPS/INS. Proceedings of ION GPS 1990, 19–21 September 1990, Colorado Springs, Colorado, 397–414.Google Scholar
Caspary, W. F. (1987) Concepts of Network and Deformation Analysis. Monograph 11, School of Geomatic Engineering, The University of New South Wales, Sydney.Google Scholar
Donoho, D. L. and Huber, P. J. (1983) The Notion of Breakdown Point. A Festschrift For Erich L. Lehmann, Editors Bickel, P. J., Doksum, K. and Hodges, J. L., Wadsworth, Belmont, California, 157–185.Google Scholar
Edgeworth, F. Y. (1887) On Observations Relating to Several Quantities. Hermathena, 6, 279–285.Google Scholar
Ferguson, T. S. (1961) On the Rejection of Outliers. Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, California, 1, 253–287.Google Scholar
Hampel, F. R. (1971) A General Qualitative Definition of Robustness. The Annals of Mathematical Statistics, 42, 1887–1896.CrossRefGoogle Scholar
Hampel, F. R., Ronchetti, E. Z., Rousseeuw, P. J. and Stahel, W. A. (1986) Robust Statistics: The Approach Based on Influence Functions. Wiley, New York.Google Scholar
Hewitson, S. and Wang, J. (2006) GNSS Receiver Autonomous Integrity Monitoring (RAIM) Performance Analysis. GPS Solutions, 10(3), 155–170.CrossRefGoogle Scholar
Hewitson, S. and Wang, J. (2007) GNSS Receiver Autonomous Integrity Monitoring with a Dynamic Model. Journal of Navigation, 60(2), 247–263.CrossRefGoogle Scholar
Hewitson, S.Lee, H. K. and Wang, J. (2004) Localizability Analysis for GPS/Galileo Receiver Autonomus Integrity Monitoring. Journal of Navigation, 57(2), 245–259.CrossRefGoogle Scholar
Huber, P. J. (1964) Robust Estimation of Location Parameters. Annals of Mathematical Statistics, 35, 73–101.CrossRefGoogle Scholar
Jaeckel, L. A. (1972) Estimating Regression Coefficients by Minimising the Dispersion of the Residuals. Annals of Mathematical Statistics, 43, 1449–1458.CrossRefGoogle Scholar
Kelly, R. J. (1998) The Linear Model, RNP, and the Near-Optimum Fault Detection and Exclusion Algorithm. Global Positioning System: Papers Published in NAVIGATION, The Institute of Navigation, Fairfax, Virginia, 5, 227–260.Google Scholar
Krarup, T., Kubik, K. and Juhl, J. (1980) Götterdämmerung Over Least Squares. Proceedings of International Society for Photogrammetry 14th Congress, Hamburg, 370–378.Google Scholar
Kuter, M. H., Nachtsheim, C. J., Neter, J. and Li, W. (2005) Applied Linear Statistical Models. 5th Edn., McGraw-Hill Irwin, New York.Google Scholar
Lee, Y. C. (1986) Analysis of Range and Position Comparison Methods as a Means to Provide GPS Integrity in the User Receiver. Global Positioning System: Papers Published in NAVIGATION, The Institute of Navigation, Fairfax, Virginia, 5, 5–19.Google Scholar
Parkinson, B. W. and Axelrad, P. (1988) Autonomous GPS Integrity Monitoring Using the Pseudorange Residual. Navigation, 35(2), 49–68.CrossRefGoogle Scholar
Pervan, B. S., Lawrence, D. G., Cohen, C. E. and Parkinson, B. W. (1996) Parity Space Methods For Autonomous Fault Detection and Exclusion Algorithms Using Carrier Phase. Proceedings of ION PLANS 1996, 22–16 April 1996, Atlanta, Georgia, 649–656.Google Scholar
Rousseeuw, P. J. (1984) Least Median of Squares Regression. Journal of the American Statistical Association, 79, 871–880.CrossRefGoogle Scholar
Rousseeuw, P. J. and Leroy, A. M. (1987) Robust Regression and Outlier Detection. John Wiley and Sons, New York.CrossRefGoogle Scholar
Sturza, M. A. (1988) Navigation system Integrity Monitoring Using Redundant Measurements. Navigation, 35(4), 69–87.CrossRefGoogle Scholar
Wang, J. and Chen, Y. Q. (1994a) On the Reliability Measures of Observations. Acta Geodaetica et Cartographica Sinica (English Edition), Journal of Chinese Society of Geodesy, Photogrammetry and Cartography, 42–51.Google Scholar
Wang, J. and Chen, Y. Q. (1994b) On the Localizability of Blunders in Correlated Coordinates of Junction Points in Densification Networks. Australian Journal of Geodesy, Photogrammetry and Surveying, 60, 109–119.Google Scholar
Wang, J. and Ober, P. B. (2009) On the Availability of Fault Detection and Exclusion in GNSS Receiver Autonomous Integrity Monitoring. Journal of Navigation, 62(2), 1–11.CrossRefGoogle Scholar
Wang, J. and Wang, J. (2007) Mitigation the Effects of Multiple Outliers on GNSS Navigation with M-Estimation Schemes. Proceedings of IGNSS Symposium 2007, 4–6 December 2007, Sydney, 1–9.Google Scholar
Yang, Y., Cheng, M. K., Shum, C. K. and Tapley, B. D. (1999) Robust Estimation of Systematic Errors of Satellite Laser Range. Journal of Geodesy, 73, 345–349.CrossRefGoogle Scholar
Yohai, V. J. (1987) High Breakdown Point and High Efficiency Robust Estimates for Regression. The Annals of Statistics, 15, 642–656.CrossRefGoogle Scholar
Yohai, V. J. and Rousseeuw, P. J. (1984) Robust and Nonlinear Time Series Analysis. Lecture Notes in Statistics, No. 26, Editors Franke, J., Härdle, W. and Martin, D., Springer-Verlag, New York, 256–272.Google Scholar
Figure 0

Figure 1. Number of satellites and PDOP.

Figure 1

Table 1. Scenarios of selected pseudoranges for two outliers.

Figure 2

Table 2. Comparison for zero outliers.

Figure 3

Table 3. Comparison for one outlier.

Figure 4

Table 4. Comparison for two outliers.