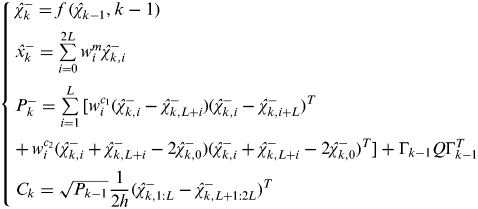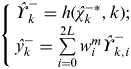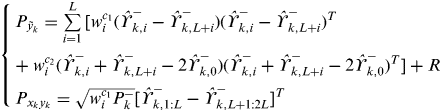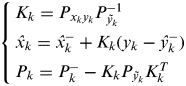2. THE CDRTSS ALGORITHM

The ERTSS and CDRTSS possess the same form and are all derived from a R-T-S smoother. In the R-T-S smoother, the data is first processed by the forward filter, and then a backward recursion is used to compute the smoothing results based on the forward filtering outputs. The ERTSS has been discussed in several literatures and can be found in Simon (Reference Simon2006). In this section, a brief introduction of CDRTSS is presented.

Consider the following nonlinear system:

(1)$$\left\{ \matrix{x_k = f\,(x_{k - 1}, k - 1) + \Gamma _{k - 1} w_{k - 1} \cr z_k = h(x_k, k) + v_k } \right.$$

where x _k is the state vector and z _k is the measurement vector. f(·) is the dynamic model function and h(·) is the measurement model function. The process noise w _k−1 and the measurement noise v _k are assumed to be Gaussian white noise with covariance Q _k−1 and R _k−1 respectively.

The forward process part of CDRTSS is a standard CDKF algorithm. Based on Stirling's interpolation formula, CDKF utilizes the prior distribution to create 2L+1 (L is the state dimension) sigma points and then captures the posterior distribution by propagating the sigma-points through the dynamic and measurement models. The CDKF algorithm is given as follows (Ito and Xiong, Reference Ito and Xiong2000; Van der Merwe et al., Reference Van der Merwe, Wan and Julier2004):

Initialization:

(2)$$\hat x = E[x_0 ],P_{x_0} = E[(x_0 - \hat x)(x_0 - \hat x)^T ]$$

1. (1) Calculate sigma-points for time-update

   (3)$$\hat \chi _{k - 1} = [\matrix{ {\hat x_{k - 1}} & {\hat x_{k - 1} + h\sqrt {P_{k - 1}}} & {\hat x_{k - 1} - h\sqrt {P_{k - 1}}} \cr} ]$$

2. (2) Time-update equations

   (4)$$\left\{ \matrix{\hat \chi _k^ - = f\,(\hat \chi _{k - 1}, k - 1) \cr \hat x_k^ - = \sum\limits_{i = 0}^{2L} {w_i^m \hat \chi _{k,i}^ -} \cr P_k^ - = \sum\limits_{i = 1}^L {[w_i^{c_1} (\hat \chi _{k,i}^ - - \hat \chi _{k,L + i}^ - )(\hat \chi _{k,i}^ - - \hat \chi _{k,i + L}^ - )^T} \cr +\, w_i^{c_2} (\hat \chi _{k,i}^ - + \hat \chi _{k,L + i}^ - - 2\hat \chi _{k,0}^ - )(\hat \chi _{k,i}^ - + \hat \chi _{k,L + i}^ - - 2\hat \chi _{k,0}^ - )^T ] + \Gamma _{k - 1} Q\Gamma _{k - 1}^T \cr C_k = \sqrt {P_{k - 1}} \displaystyle{1 \over {2h}}(\hat \chi _{k,1:L}^ - - \hat \chi _{k,L + 1:2L}^ - )^T } \right.$$

3. (3) Calculate sigma points for measurement-update

   (5)$$\hat \chi _k^{ - *} = [\matrix{ {\hat x_k^ -} & {\hat x_k^ - + h\sqrt {P_k^ -}} & {\hat x_k^ - - h\sqrt {P_k^ -}} \cr} ]$$

4. (4) Measurement-update equations

   (6)$$\left\{ \matrix{ \hat \Upsilon _k^ - = h(\hat \chi _k^{ - *}, k); \cr \hat y_k^ - = \sum\limits_{i = 0}^{2L} {w_i^m \hat \Upsilon _{k,i}^ -} } \right.$$
   (7)$$\left\{ \matrix{P_{\tilde y_k} = \sum\limits_{i = 1}^L {[w_i^{c_1} (\hat \Upsilon _{k,i}^ - - \hat \Upsilon _{k,L + i}^ - )(\hat \Upsilon _{k,i}^ - - \hat \Upsilon _{k,L + i}^ - )^T} \cr + \hskip-6pt\mathop {}\limits^{} \mathop {}\limits^{} \mathop {}\limits^{} \mathop {}\limits^{} w_i^{c_2} (\hat \Upsilon _{k,i}^ - + \hat \Upsilon _{k,L + i}^ - - 2\hat \Upsilon _{k,0}^ - )(\hat \Upsilon _{k,i}^ - + \hat \Upsilon _{k,L + i}^ - - 2\hat \Upsilon _{k,0}^ - )^T ] + R \cr P_{x_k y_k} = \sqrt {w_i^{c_1} P_k^ -} [\hat \Upsilon _{k,1:L}^ - - \hat \Upsilon _{k,L + 1:2L}^ - ]^T } \right.$$
   (8)$$\left\{ \matrix{K_k = P_{x_k y_k} P_{\tilde y_k} ^{ - 1} \cr \hat x_k = \hat x_k^ - + K_k (y_k - \hat y_k^ - ) \cr P_k = P_k^ - - K_k P_{\tilde y_k} K_k^T } \right.$$

where the weights of each sigma-point are w ₀^m=(h ²−L)/h ², w ₀^m=1/(2h ²), $w_i^{c_1} = 1/(4h^2 )$, $w_i^{c_2} = (h^2 - 1)/(4h^4 )$ . h⩾1 is the scalar central difference interval size which determines the spread of the sigma points around the prior mean, and its optimal value is $\sqrt 3 $ for Gaussian distribution. The cross-covariance C _k between $\hat x_{k - 1} $ and $\hat x_k^ - $ is calculated for the backward process part.

During the processing of CDKF, the predicted state $\hat x_k^ - $, estimated state $\hat x_k $, predicted covariance $P_k^ - $, estimated covariance P _k and the cross-covariance C _k need to be stored at each filtering point for late backward recursion.

After the filtering estimates have been computed, the smoothed state estimation and its covariance can be computed using the following backward recursion (for n=N−1…0) (Sarkka and Hartikainen, Reference Sarkka and Hartikainen2010):

(9)$$\left\{ \matrix{K_k^S = C_{k + 1} (P_{k + 1}^ - )^{ - 1} \cr \hat x_k^S = \hat x_k + K_k^S (\hat x_{k + 1}^S - \hat x_{k + 1}^ - ) \cr P_k^S = P_k + K_k^S (P_{k + 1}^S - P_{k + 1}^ - )(K_k^S ) } \right.$$

Where the smoothing distribution and filtering distribution of the last time step N are the same, $\hat x_N^S = \hat x_N $ and P _N^S=P _N.

3. CDRTSS FOR THE SINS/GPS INTEGRATED SYSTEM

3.1. SINS error model

The SINS error model, which is the foundation of the integrated SINS/GPS system, is established in this subsection. It includes the differential equation of attitude, velocity and position error (Goshen-Meskin and Bar-Itzhack, Reference Goshen-Meskin and Bar-Itzhack1992). The coordinate frames used in this paper include the geocentric inertial frame (i-frame), earth-centered earth fixed frame (e-frame), navigation frame (n-frame), platform frame (p-frame) and body frame (b-frame). A detailed description of these coordinate frames is in Farrell and Barth (Reference Farrell and Barth1998), and Crassidis (Reference Crassidis2006).

The differential equation of attitude error is given by (Groves, Reference Groves2008):

(10)$$\dot \phi = (I - C_n^p )\omega _{in}^n + \delta \omega _{in}^n - \hat C_b^n \varepsilon ^b $$

where $\phi = [\matrix{ {\phi _E} & {\phi _N} & {\phi _U} \cr} ]^T $ denotes the attitude error angle. The C _n^p is the direction cosine matrix (DCM) between the p-frame and the n-frame. ω _inⁿ is the rotation velocity vector of n-frame relative to i-frame expressed in n-frame, and δω _inⁿ is the error of ω _inⁿ. C _bⁿ is the DCM between the n-frame and the b-frame, meanwhile $\hat C_b^n $ is the estimate of C _bⁿ. $\varepsilon ^b = [\matrix{ {\varepsilon _x} & {\varepsilon _y} & {\varepsilon _z} \cr} ]^T $ is the gyro drifts in the b-frame. (I−C _n^p)ω _inⁿ is the nonlinear term of attitude error equation.

The differential equation of the velocity can be described as follows:

(11)$$\delta \dot V = (I - C_p^n )\hat C_b^n {\rm \hat f}^{\rm b} - (2\omega _{ie}^n + \omega _{en}^n ) \times \delta V - (2\delta \omega _{ie}^n + \delta \omega _{en}^n ) \times V + C_b^n \nabla ^b $$

where $V = [\matrix{ {V_E} & {V_N} & {V_U} \cr} ]^T $ is the velocity vector, and δV is the velocity error vector. ${\rm \hat f}^b $ is the specific force measured by the accelerometers expressed in the b-frame. ω _ieⁿ is the rotation rate from the e-frame relative to the i-frame expressed in the n-frame and ω _enⁿ is the rotation rate from the n-frame relative to the e-frame expressed in the n-frame. δω _ieⁿ and δω _enⁿ are the error of ω _ieⁿ and ω _enⁿ, respectively. ∇^b is the bias of the accelerometer measurement expressed in the b-frame. $(I - C_p^n )\hat C_b^n {\rm \hat f}^{\rm b} $ is the nonlinear term of velocity error equation.

The differential equation of position error is given by:

(12)$$\left\{ \matrix{\delta \dot L = - \displaystyle{{V_N} \over {\left( {R_M + h} \right)^2}} \delta h + \displaystyle{1 \over {R_M + h}}\delta V_N \cr \delta \dot \lambda = - \displaystyle{{V_E \sin L} \over {\left( {R_N + h} \right)\cos ^2 L}}\delta L - \displaystyle{{V_E} \over {\left( {R_N + h} \right)^2 \cos L}}\delta h + \displaystyle{1 \over {\left( {R_N + h} \right)\cos L}}\delta V_E \cr \delta \dot h = \delta V_U } \right.$$

where δL, δλ, δh are the errors of latitude, longitude and height, respectively. R _M and R _N are the main curvature radii along the meridian and the vertical plane of meridian, respectively.

3.2. Design of the CDRTSS for integrated SINS/GPS system

As we can see from Equations (10) and (11), the SINS error model is related to the gyro drift ε and the accelerometer bias ∇. To achieve better SINS error estimation accuracy, the gyroscope drift and accelerometer bias must be considered. The gyroscope drift and accelerometer bias can be approximated as random noise, which includes a random constant process and a white Gaussian process. The constant drift and bias of the gyro and the accelerometer as well as the SINS errors are selected as the state vector. The random noise of the gyro and accelerometer are estimated as the model error. The state vector is as follows: x=[ϕ _E ϕ _N ϕ _U ϕ _E δV _E δV _N δV _U δL δλ δH ε _x ε _y ε _z ∇_x ∇_y ∇_z]^T. ε _x, ε _y, ε_z, ∇_x, ∇_y, ∇_z, are the constant drift and bias of the gyro and accelerometer in x, y and z directions respectively, which can be modelled by $\dot \varepsilon = 0,\;\dot \nabla = 0$. The continued system model of SINS/GPS is formed as $\dot x(t) = f\,(x,t) + Gw(t)$, where $w = [\matrix{ {w_{\varepsilon _x}} & {w_{\varepsilon _y}} & {w_{\varepsilon _z}} & {w_{\nabla _x}} & {w_{\nabla _y}} & {w_{\nabla _z}} \cr} ]$ represents the gyro and accelerometer random noise with E[ww^T]=Q. Matrix G is given by:

$${\rm G} = \left[ {\matrix{ {\hat C_b^n} & {0_{3 \times 3}} \cr {0_{3 \times 3}} & {\hat C_b^n} \cr {0_{9 \times 3}} & {0_{9 \times 3}} \cr}} \right]$$

To transfer the continued model to discrete model, a four-step Runge-Kutta numerical solution is utilized in this paper. The observation vector is defined by $z = \left[ {\matrix{ {\delta V_E^'} & {\delta V_N^'} & {\delta V_U^'} & {\delta L^'} & {\delta \lambda ^'} & {\delta h^'} \cr}} \right]^T $. $\delta V_E^' $, $\delta V_N^' $, $\delta V_U^' $ represent the differences of the east velocity, north velocity and up velocity between the measurements of SINS and the GPS, respectively. $\delta L$, $\delta \lambda ^' $, $\delta h^' $ represent the differences between the latitude, longitude, and height calculated from SINS and GPS outputs respectively. The observation noise $v = [\matrix{ {v_{\delta V_E^'}} & {v_{\delta V_N^'}} & {v_{\delta V_U^'}} & {v_{\delta L}} & {v_{\delta \lambda ^'}} & {v_{\delta h^'}} \cr} ]^T $ represents GPS velocity and position measurement noises, and the observation matrix H is given by:

$$H = \left[ {\matrix{ {0_{3 \times 3}} & {diag\left\{ {1,1,1} \right\}} & {0_{3 \times 3}} & {0_{3 \times 6}} \cr {0_{3 \times 3}} & {0_{3 \times 3}} & {diag\left\{ {R_M + h,(R_N + h)\cos L,1} \right\}} & {0_{3 \times 6}} \cr}} \right]$$

Since the measurement model is linear, the formulation of CDKF in Equations (5, 6, 7) can be simplified as follows:

(13)$$\left\{ \matrix{\hat y_k = H_k \hat x_k^ - \cr P_{yy} = P_k^ - H_k^T \cr P_{xy} = H_k P_k^ - H_k^T + R_k } \right.$$

Figure 1 shows the computation procedure diagram of an integrated SINS/GPS system using CDRTSS.

Figure 1. The computation procedure diagram of SINS/GPS integrated system using CDRTSS.

In summary, the CDRTSS used for SINS/GPS integrated post-processing can be divided into two parts: the filter solution and the smoother solution. The relationship of these two parts based on the synthesis of numerical simulation results is shown in Figure 2. In the whole process of SINS/GPS integration, the filter and smoother are computed at the GPS sampling rate, and the strapdown navigator is computed at the SINS sampling rate. In general, the sampling rate of SINS is higher than that of GPS.

Figure 2. Relation between filter solution and smoother solution of CDRTSS.

From Figure 2, it can be seen that the strapdown computing error grows with time during the interval of GPS data. Once the GPS data arrives, the slowly growing errors in the strapdown navigator can thus be limited by the feedback correction of filter and smoother. In the filtering solution, the V^F, P^F and A^F (denoting the velocity, position and attitude results of integration using filtering, respectively) would be corrected by using ${\bi \hat x}_{\,f,k} $ (the state estimate of CDKF) at every filtering point. After the correction, ${\bi \hat x}_{\,f,k} $ should be set to zero. In the smoothing solution, V^S, P^S and A^S (denoting the velocity, position and attitude results of integration using smoothing, respectively) should be corrected by using ${\bi \hat x}_{s,k} $ (the state estimate of smoothing) at every smoothing point. The corrected velocity, position and attitude are regarded as the initial value of strapdown computation after every estimate point.

4. SIMULATION AND ANALYSIS

To test and analyse the performance of CDRTSS, numerical simulations based on the simulated flight trajectory of an integrated SINS/GPS system have been conducted in this section.

4.1. Simulation design

In this subsection, a typical sequential U-form imaging flight trajectory with an S-manoeuvre at the beginning is used, as shown in Figure 3. The initial position is Latitude 40°N, Longitude 116°E and 500 m in height. The initial heading is 040° and the velocity is 100 m/s during the flight. Firstly, the aircraft flies 100 s in a straight line, and after that there is an S-manoeuvre with 60° increase (100 s) and decrease (100 s) in heading direction. Then the aircraft flies 400 s straight before turning 180° clockwise in 200 s, and finally it flies 400 s straight again.

Figure 3. Trajectory of simulation.

The errors of sensors in SINS/GPS integration are as follows: the gyro bias and white noise are all 0·2°/h, the accelerometer bias is 100 μg and the accelerometer white noise is 50 μg, the horizontal position noise is 0·1 m, the vertical position noise is 0·15 m, the horizontal velocity noise is 0·03 m/s, and the vertical velocity noise is 0·05 m/s. There is no outage in GPS data.

To test the performance of the CDRTSS and analyse the effect of different initial attitude errors on the precision of the integrated SINS/GPS estimation, three conditions with 10°, 20° and 30° initial attitude errors (the initial attitude includes heading, pitch, and roll) are designed, and the simulated data are processed by ERTSS and CDRTSS respectively.

4.2. Simulation results and analysis

The attitude estimate errors of CDRTSS and ERTSS in three conditions mentioned in Section 4.1 are shown in Figures 4, 5, 6. Moreover, the performance of CDRTSS and ERTSS with initial attitude error of 30° for a Monte-Carlo run of 100 randomly initialized experiments is summarized and compared in Table 1. Figure 4 illustrates that there is no distinct difference between the performance of the ERTSS and CDRTSS with 10° initial attitude error. Along with the initial attitude error increase, it is obvious that the CDRTSS gives better results than the ERTSS. Furthermore, the mean standard deviation (E[STD]) of attitude errors using the CDRTSS algorithm shown in Table 1 is much smaller than that of ERTSS, validating the superiority of the CDRTSS.

Figure 4. Estimated attitude error with 10° initial attitude error.

Figure 5. Estimated attitude error with 20° initial attitude error.

Figure 6. Estimated attitude error with 30° initial attitude error.

Table 1. The mean STD of attitude error for 100 Monte-Carlo simulations (deg).

5. FLIGHT TEST AND DISCUSSION

The simulation tests, given in Section 4, have shown that the CDRTSS can obtain a better performance over ERTSS. How about the real application result of the CDRTSS? In this section, flight data will be used to validate the effectiveness of CDRTSS.

A two-hour flight test was carried out in a calibration field in Pingdingshan, China. This area has a large number of ground control points with their actual positions known in advance, which makes it possible to calculate the actual attitude and position of the aircraft through the photos it takes. The SINS/GPS integrated system is carried on an ultra-light A2C aircraft with the GPS antenna fixed on the top (seen in Figure 7(a)). The IMU (TXD10-A2) and the camera are placed in the cabin of the aircraft (see Figure 7(b)).

Figure 7. The test platform. (a) The A2C aircraft. (b) Sensor installation on the aircraft.

The integrated SINS/GPS system developed by Beihang University is used in the flight test, which consists of the Dynamically Tuned Gyroscope (DTG)-based IMU and the Trimble 5700 dual-frequency GPS receiver. The IMU comprises two HT-A3 dynamically tuned gyroscopes (HT-A3 precision strapdown flexible gyroscope, 1999) and three JHT-I-B quartz accelerometers (Jht-i-b quartz accelerometers, 1998). The sampling rates of the IMU and GPS are 100 Hz and 10 Hz respectively. The gyro constant and random drifts are 0·1°/h and the accelerometer constant and random biases are 100 μg. The post-processed position and velocity precision of GPS is 10 mm+1·5 ppm and 0·01 m/s respectively. During the flight, the original output data of the integrated SINS/GPS system are stored by the PCS fixed in the cabin.

Figure 8(a) shows the trajectory of the flight measured by GPS. Point A in Figure 8(b) can be seen as the time that the IMU started up and the imaging area is marked by the dashed line. There are four image segments, including about 2000s data. Each segment has a series of discrete image dots. Currently, the aero-triangulation method is recognized as a better way to calibrate the navigation data processed by SINS/GPS integration (Toth, Reference Toth2002). In this flight test, the position and attitude information of higher precision are provided by Chinese Academy of Surveying and Mapping, which is computed by the aero-triangulation method with the well-signalized ground control points and the imaging data. This flight test was in good conditions with the sky very clear. This all ensures that aero-triangulation can obtain maximum positioning and attitude accuracy that can be used as the reference for SINS/GPS integration. In the in-flight startup case, the GPS can provide initial position and velocity information for the aircraft. In general, the approximate value of the initial heading can be acquired through the east and north velocity information from GPS. However, the accurate initial heading still remains unknown due to the existence of the drift angle induced by the wind speed and other factors. According to other flight tests, the drift angle is around 10° in fine weather and these values will increase in worse conditions. So we consider different cases with heading misalignment ranging from 5° to 30° increased by 5° steps. Moreover, there is no large pitch and roll during the preparation period, based on the many flight tests conducted. Hence, the maximal values of pitch and roll are both about 5° for this aircraft. Here, the pitch and roll can be initialized to zero and the misalignment is assumed to be 5°.

Figure 8. Flight trajectory. (a) three-dimensional trajectory. (b) two-dimensional trajectory.

Figures 9 and 10 show the STD of latitude, longitude and altitude error with different initial heading errors using CDRTSS and ERTSS. From the figures, it can be seen that the estimated error of position using ERTSS climbs with the increase of initial heading error, whereas the performance of CDRTSS is very stable. Also, the precision of the positioning estimate of CDRTSS is better than that of ERTSS.

Figure 9. The STD of latitude and longitude error with different initial heading error.

Figure 10. The STD of altitude error with different initial heading error.

Figure 11 shows the STD of the pitch and roll error with different initial heading errors using CDRTSS and ERTSS. It can be seen that the STD of pitch and roll error using these two methods are very close and small due to high observability and the small initial horizontal misalignment error. The STD of the heading error shown in Figure 12 illustrates that the STD of heading error using CDRTSS is smaller and much more stable than that of ERTSS, which is further displayed in Table 2.

Figure 11. The STD of pitch and roll error with different initial heading error.

Figure 12. The STD of heading error with different initial heading error.

Table 2. STD of heading error in different cases (deg).

From the figures and tables above, it can be seen that the positioning precision of CDRTSS can be improved by several millimetres, while the heading precision can be improved by several percent of a degree. So, the remnant heading error (the absolute error subtracting the mean error) with 30° heading misalign is shown in Figure 13. It can be seen that the amplitude of CDRTSS is smaller than that of ERTSS and it is obvious that CDRTSS has great advantages over ERTSS. Undoubtedly, it is more effective.

Figure 13. The remnant heading error with 30° initial heading error.