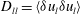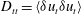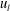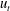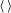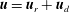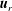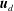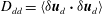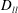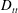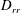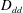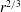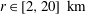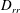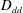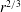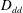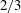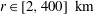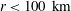Contents
Rapids
The other optimal Stokes drag profile
-
- Published online by Cambridge University Press:
- 27 November 2014, R3
-
- Article
- Export citation
-
The lowest drag shape of fixed volume in Stokes flow has been known for some 40 years. It is front–back symmetric and similar to an American football with ends tangent to a cone of
$60^{\circ }$. The analogous convex axisymmetric shape of fixed surface area, which may be of interest for particle design in chemistry and colloidal science, is characterised in this paper. This ‘other’ optimal shape has a surface vorticity proportional to the mean surface curvature, which is used with a local analysis of the flow near the tip to show that the front and rear ends are tangent to a cone of angle 
$30.8^{\circ }$. Using the boundary element method, we numerically represent the shape by expanding its tangent angle in terms decaying odd Legendre modes, and show that it has 11.3 % lower drag than a sphere of equal surface area, significantly more pronounced than for the fixed-volume optimal.
A Helmholtz decomposition of structure functions and spectra calculated from aircraft data
-
- Published online by Cambridge University Press:
- 03 December 2014, R4
-
- Article
- Export citation
-
Longitudinal and transverse structure functions,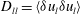
$D_{ll}=\langle {\it\delta}u_{l}{\it\delta}u_{l}\rangle$ and 
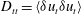$D_{tt}=\langle {\it\delta}u_{t}{\it\delta}u_{t}\rangle$, can be calculated from aircraft data. Here, 
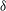${\it\delta}$ denotes the increment between two points separated by a distance 
$r$,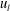 
$u_{l}$ and 
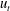$u_{t}$ the velocity components parallel and perpendicular to the aircraft track respectively and 
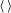$\langle \,\rangle$ an average. Assuming statistical axisymmetry and making a Helmholtz decomposition of the horizontal velocity, 
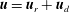$\boldsymbol{u}=\boldsymbol{u}_{r}+\boldsymbol{u}_{d}$, where 
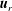$\boldsymbol{u}_{r}$ is the rotational and 
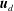$\boldsymbol{u}_{d}$ the divergent component of the velocity, we derive expressions relating the structure functions 
$D_{rr}=\langle {\it\delta}\boldsymbol{u}_{r}\boldsymbol{\cdot }{\it\delta}\boldsymbol{u}_{r}\rangle$ and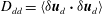 
$D_{dd}=\langle {\it\delta}\boldsymbol{u}_{d}\boldsymbol{\cdot }{\it\delta}\boldsymbol{u}_{d}\rangle$ to 
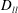$D_{ll}$ and 
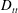$D_{tt}$. Corresponding expressions are also derived in spectral space. The decomposition is applied to structure functions calculated from aircraft data. In the lower stratosphere, 
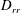$D_{rr}$ and 
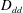$D_{dd}$ both show a nice 
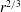$r^{2/3}$-dependence for 
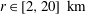$r\in [2,20]\ \text{km}$. In this range, the ratio between rotational and divergent energy is a little larger than unity, excluding gravity waves as the principal agent behind the observations. In the upper troposphere, 
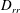$D_{rr}$ and 
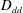$D_{dd}$ show no clean 
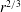$r^{2/3}$-dependence, although the overall slope of 
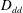$D_{dd}$ is close to 
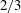$2/3$ for 
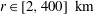$r\in [2,400]\ \text{km}$. The ratio between rotational and divergent energy is approximately three for 
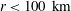$r<100\ \text{km}$, excluding gravity waves also in this case. We argue that the possible errors in the decomposition at scales of the order of 10 km are marginal.
Liquid clustering and capillary pressure in granular media
-
- Published online by Cambridge University Press:
- 03 December 2014, R5
-
- Article
- Export citation
Gyrotaxis in uniform vorticity
-
- Published online by Cambridge University Press:
- 04 December 2014, R6
-
- Article
- Export citation
-
Analysis of bioconvection in dilute suspensions of bottom-heavy but randomly swimming micro-organisms is commonly based on a model introduced in 1990. This couples the Navier–Stokes equations, the cell conservation equation and the Fokker–Planck equation (FPE) for the probability density function for a cell’s swimming direction
$\boldsymbol{p}$, which balances rotational diffusion against viscous and gravitational torques. The results have shown qualitative agreement with observation, but the model has not been subjected to direct quantitative testing in a controlled experiment. Here, we consider a simple configuration in which the suspension is contained in a circular cylinder of radius 
$R$, which rotates at angular velocity 
${\rm\Omega}$ about a horizontal axis. We solve the FPE and calculate the cells’ mean swimming velocity, which proves to be horizontal when 
$B{\rm\Omega}\gg 1$, where 
$B$ is the gyrotactic reorientation time scale. Then we compute the cell concentration distribution, which is non-uniform only in a thin boundary layer near the cylinder wall when 
${\it\beta}^{2}={\rm\Omega}R^{2}/D\gg 1$, where 
$D$ is the cells’ translational diffusivity. The fact that cells are denser than water means that this concentration distribution drives a perturbation to the underlying solid-body rotational flow which can be calculated analytically. The predictions of the theory are evaluated in terms of a proposed experimental realisation of the configuration, using suspensions of the alga Chlamydomonas nivalis or Chlamydomonas reinhardtii or the algal colony Volvox.
Front Cover (OFC, IFC) and matter
FLM volume 762 Cover and Front matter
-
- Published online by Cambridge University Press:
- 16 December 2014, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
FLM volume 762 Cover and Back matter
-
- Published online by Cambridge University Press:
- 16 December 2014, pp. b1-b3
-
- Article
-
- You have access
- Export citation