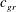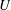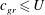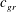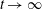1. Introduction
The representation of motion as the sum of slow quasi-geostrophic (QG) and fast ageostrophic (AG) components forms the basis of several interrelated concepts of geophysical fluid dynamics: geostrophic adjustment, balanced models, slow and fast manifolds, and the initialization problem (see e.g. Reznik & Zeitlin Reference Reznik and Zeitlin2007, and references therein). Almost all works on this subject treat the slow and fast components separately. A large (probably the major) part of the vast literature is devoted to balance models that govern the slow motion in the absence of fast waves. These models are derived from the full dynamical equations by filtering the fast waves under the assumption of slowness of motion (see e.g. Hoskins Reference Hoskins1975; Leith Reference Leith1980; Gent & McWilliams Reference Gent and McWilliams1983; Pedlosky Reference Pedlosky1984; Allen Reference Allen1993; Warn et al. Reference Warn, Bokhove, Shepherd and Vallis1995; Mohebalhojeh & Dritschell Reference Mohebalhojeh and Dritschell2001, and references therein). On the other hand, there are a number of works on the dynamics of fast waves propagating in a prescribed slow flow (see e.g. Young & Ben Jelloul Reference Young and Ben Jelloul1997; Balmforth, Llewellyn Smith & Young Reference Balmforth, Llewellyn Smith and Young1998; Balmforth & Young Reference Balmforth and Young1999; Klein & Llewellyn-Smith Reference Klein and Llewellyn-Smith2001; Klein, Llewellyn-Smith & Lapeyre Reference Klein, Llewellyn-Smith and Lapeyre2004).
One aim of this paper is to study both the slow and fast components when the fast component is not assumed to be small in comparison with the slow one, and both components evolve freely from an arbitrary initial state. An important part of this general problem is the geostrophic adjustment, which can be determined as the long-term evolution of an arbitrary spatially localized perturbation in a rotating fluid (cf. McWilliams Reference McWilliams2006). The evolution is conditioned by radiating fast inertia–gravity waves propagating away from the initial perturbation domain and leaving behind them a spatially localized flow, which in the leading order does not contain the fast waves capable of radiating away. Generally, in the nonlinear case this residual flow is not necessarily the QG slow one – it can contain trapped AG fast modes (inertial oscillations). The nonlinear QG–AG splitting was examined in a number of papers by the present author with various co-authors (Reznik, Zeitlin & Ben Jelloul Reference Reznik, Zeitlin and Ben Jelloul2001; Reznik & Grimshaw Reference Reznik and Grimshaw2002; Zeitlin, Reznik & Ben Jelloul Reference Zeitlin, Reznik and Ben Jelloul2003; Reznik & Sutyrin Reference Reznik and Sutyrin2005; Reznik Reference Reznik2013, Reference Reznik2014a ,Reference Reznik b ) and this study is a development of these works.
In a ‘pure’ form the QG–AG splitting occurs in the linear approximation when the QG component is geostrophic and time-independent, and the AG one consists of linear waves. In this case the geostrophic component is determined only by the initial potential vorticity (PV) and geostrophic relationships and can be found without solving an initial problem (see e.g. Reznik et al.
Reference Reznik, Zeitlin and Ben Jelloul2001; Zeitlin et al.
Reference Zeitlin, Reznik and Ben Jelloul2003). If the initial state is localized, then the linear waves decay because of dispersion and the system tends to the geostrophic state: geostrophic adjustment occurs. The typical time
![]() $T_{w}$
of the adjustment is determined as the ratio
$T_{w}$
of the adjustment is determined as the ratio
![]() $T_{w}=L/c_{g}$
, where
$T_{w}=L/c_{g}$
, where
![]() $L$
is the horizontal scale of the initial perturbation and
$L$
is the horizontal scale of the initial perturbation and
![]() $c_{g}$
is the typical group velocity of radiated waves.
$c_{g}$
is the typical group velocity of radiated waves.
The effect of nonlinearity on the geostrophic splitting depends on the Rossby number
![]() $\mathit{Ro}=U/fL$
, where
$\mathit{Ro}=U/fL$
, where
![]() $U$
is the scale of horizontal velocity and
$U$
is the scale of horizontal velocity and
![]() $f$
is the Coriolis parameter. At small Rossby number
$f$
is the Coriolis parameter. At small Rossby number
![]() $\mathit{Ro}\ll 1$
(fast rotation), the QG component changes slowly (as compared to the inertial time
$\mathit{Ro}\ll 1$
(fast rotation), the QG component changes slowly (as compared to the inertial time
![]() $1/f$
) on the advective time
$1/f$
) on the advective time
![]() $T_{a}=O(1/\mathit{Ro}f)$
and the scenario of the adjustment depends on the relationship between the times
$T_{a}=O(1/\mathit{Ro}f)$
and the scenario of the adjustment depends on the relationship between the times
![]() $T_{a}$
and
$T_{a}$
and
![]() $T_{w}$
. In the case
$T_{w}$
. In the case
![]() $T_{w}\ll T_{a}$
, the group velocity
$T_{w}\ll T_{a}$
, the group velocity
![]() $c_{g}$
greatly exceeds the flow velocity
$c_{g}$
greatly exceeds the flow velocity
![]() $U$
, i.e. the waves rapidly radiate away from the initial perturbation, leaving behind them the residual QG flow slowly changing on the advective time and not affecting the waves in the leading order. If, however,
$U$
, i.e. the waves rapidly radiate away from the initial perturbation, leaving behind them the residual QG flow slowly changing on the advective time and not affecting the waves in the leading order. If, however,
![]() $T_{w}\geqslant T_{a}$
and, therefore,
$T_{w}\geqslant T_{a}$
and, therefore,
![]() $c_{g}\leqslant U$
, then the waves can effectively interact with the geostrophic mode (see e.g. Reznik et al.
Reference Reznik, Zeitlin and Ben Jelloul2001; Zeitlin et al.
Reference Zeitlin, Reznik and Ben Jelloul2003).
$c_{g}\leqslant U$
, then the waves can effectively interact with the geostrophic mode (see e.g. Reznik et al.
Reference Reznik, Zeitlin and Ben Jelloul2001; Zeitlin et al.
Reference Zeitlin, Reznik and Ben Jelloul2003).
For large Rossby numbers
![]() $\mathit{Ro}\geqslant 1$
(moderate rotation and strong nonlinearity), a general theory of geostrophic splitting is still lacking: it is unclear under what conditions (if any) strongly nonlinear motion can be represented as a superposition of slow component and radiating fast waves. However, on the assumption of splitting, the final balanced state can be calculated for some symmetric initial perturbations (for example, one-dimensional or axisymmetric) using Lagrangian conservation of PV, absolute or angular momentum, and mass – see the pioneering work by Rossby (Reference Rossby1938) and, for example, that by McWilliams (Reference McWilliams1988, Reference McWilliams2006) and Kalashnick (Reference Kalashnick2004).
$\mathit{Ro}\geqslant 1$
(moderate rotation and strong nonlinearity), a general theory of geostrophic splitting is still lacking: it is unclear under what conditions (if any) strongly nonlinear motion can be represented as a superposition of slow component and radiating fast waves. However, on the assumption of splitting, the final balanced state can be calculated for some symmetric initial perturbations (for example, one-dimensional or axisymmetric) using Lagrangian conservation of PV, absolute or angular momentum, and mass – see the pioneering work by Rossby (Reference Rossby1938) and, for example, that by McWilliams (Reference McWilliams1988, Reference McWilliams2006) and Kalashnick (Reference Kalashnick2004).
For spatially periodic flows, the theory of geostrophic splitting was also developed (see e.g. Embid & Majda Reference Embid and Majda1996; Babin, Mahalov & Nikolaenko Reference Babin, Mahalov and Nikolaenko1998; Wingate et al.
Reference Wingate, Embid, Holmes-Cerfon and Taylor2011, and references therein). For small Rossby number, the spatially periodic motion, too, is split into the slow QG and fast wave components, and the fast–fast interactions (i.e. interactions between the fast waves) do not make a contribution to the slow component, at least on times
![]() $O(1/f\mathit{Ro})$
(longer times were not considered), despite the fact that in periodic geometry the waves cannot ‘escape’. Unlike the localized flow, in the periodic case the fast waves are coupled to the slow flow regardless of the relationship between the group velocity
$O(1/f\mathit{Ro})$
(longer times were not considered), despite the fact that in periodic geometry the waves cannot ‘escape’. Unlike the localized flow, in the periodic case the fast waves are coupled to the slow flow regardless of the relationship between the group velocity
![]() $c_{g}$
and the slow flow velocity
$c_{g}$
and the slow flow velocity
![]() $U$
.
$U$
.
Another aim of the paper is to show that no rotation or stratification are necessary for the splitting of motion into slow and wave components; splitting can take place in any physical system meeting the simple general constraints formulated in § 2. By analogy with the geostrophic adjustment described above, the splitting will be called wave adjustment. Two key elements are needed for wave adjustment to exist in a linear system: linear invariants and linear waves harmonically depending on time. The invariants are determined by initial conditions and are not affected by the waves, which are characterized by zero linear invariants. The evolution of such a system can be represented in a natural way as the sum of a stationary component with non-zero invariants and a non-steady wave part with zero invariants. If the governing equations of the system are perturbed by a small perturbation (linear or nonlinear), then the stationary component ceases to be time-independent and slowly changes in time. Under some conditions, the slow component can be described by a closed set of equations, which can be naturally called the balanced equations.
In §§ 3–5 various scenarios of the wave adjustment in different hydrodynamic systems are presented using full three-dimensional equations without the shallow-water and hydrostatic approximations. In all cases the flow is assumed to be spatially localized. Each scenario is illustrated by a simple example supplemented with a brief discussion of similar situations. The simplest case of non-rotating barotropic fluid layer with free surface is considered in § 3. The same layer with rotation is examined in § 4. A non-rotating stratified fluid layer between two rigid lids is analysed in § 5. In each case we obtain corresponding invariants of linearized equations, analyse the linear adjustment and examine the effect of small nonlinearity. Section 6 contains a summary and conclusions. Some technical details are relegated to appendices A–C.
2. General analysis
In this section we consider a general physical system characterized by the state vector
![]() $\boldsymbol{f}=(f_{1},f_{2},\ldots ,f_{n})(\boldsymbol{x},t)$
consisting of
$\boldsymbol{f}=(f_{1},f_{2},\ldots ,f_{n})(\boldsymbol{x},t)$
consisting of
![]() $n$
physical parameters that depend on the space point
$n$
physical parameters that depend on the space point
![]() $\boldsymbol{x}=(x,y,z)$
and the time
$\boldsymbol{x}=(x,y,z)$
and the time
![]() $t$
. In § 2.1 linear dynamics is discussed, in § 2.2 weak nonlinearity and balanced models are examined.
$t$
. In § 2.1 linear dynamics is discussed, in § 2.2 weak nonlinearity and balanced models are examined.
2.1. Linear invariants and waves
In the linear approximation let the system obey the equation
where
![]() $\unicode[STIX]{x1D647}$
and
$\unicode[STIX]{x1D647}$
and
![]() $\unicode[STIX]{x1D64D}$
are some linear matrix operators,
$\unicode[STIX]{x1D64D}$
are some linear matrix operators,
![]() $\unicode[STIX]{x1D647}$
being independent of the time
$\unicode[STIX]{x1D647}$
being independent of the time
![]() $t$
. For simplicity let the state vector
$t$
. For simplicity let the state vector
![]() $\boldsymbol{f}$
satisfy the homogeneous boundary condition at time-independent boundary
$\boldsymbol{f}$
satisfy the homogeneous boundary condition at time-independent boundary
![]() ${\it\Gamma}$
,
${\it\Gamma}$
,
and the initial condition,
The linear operator
![]() $\boldsymbol{B}$
can depend on time; here and below the subscript ‘
$\boldsymbol{B}$
can depend on time; here and below the subscript ‘
![]() $I$
’ denotes initial values.
$I$
’ denotes initial values.
Our consideration is based on the two following assumptions.
(i) There exists a time-independent linear operator
![]() $\unicode[STIX]{x1D648}\neq 0$
that nullifies the right-hand side of (2.1), i.e.
$\unicode[STIX]{x1D648}\neq 0$
that nullifies the right-hand side of (2.1), i.e.
In this case in view of the time independence of
![]() $\unicode[STIX]{x1D647}$
and
$\unicode[STIX]{x1D647}$
and
![]() $\unicode[STIX]{x1D648}$
, (2.1) possesses the linear invariant
$\unicode[STIX]{x1D648}$
, (2.1) possesses the linear invariant
since
The operator
![]() $\unicode[STIX]{x1D648}$
will be called the invariant operator. The value of the invariant
$\unicode[STIX]{x1D648}$
will be called the invariant operator. The value of the invariant
![]() ${\it\Lambda}$
is determined by the initial conditions (2.2b
):
${\it\Lambda}$
is determined by the initial conditions (2.2b
):
(ii) The equations (2.1) and (2.2a ) possess harmonic wave solutions of the form
The key point is that for the wave solution (2.7) the linear invariant (2.4) is identically zero since the product
![]() $\unicode[STIX]{x1D648}\unicode[STIX]{x1D647}$
is linear and time-independent; therefore we have
$\unicode[STIX]{x1D648}\unicode[STIX]{x1D647}$
is linear and time-independent; therefore we have
Physically, this means that the waves do not transport and affect the invariant
![]() ${\it\Lambda}$
.
${\it\Lambda}$
.
In this case it is natural to represent the solution
![]() $\boldsymbol{f}$
to the problem (2.1) and (2.2) as a sum of two solutions:
$\boldsymbol{f}$
to the problem (2.1) and (2.2) as a sum of two solutions:
The stationary solution
![]() $\boldsymbol{f}=\bar{\boldsymbol{f}}(\boldsymbol{x})$
possesses the non-zero invariant
$\boldsymbol{f}=\bar{\boldsymbol{f}}(\boldsymbol{x})$
possesses the non-zero invariant
![]() ${\it\Lambda}$
and satisfies the equations
${\it\Lambda}$
and satisfies the equations
and the solution
![]() $\tilde{\boldsymbol{f}}$
obeys (2.1) and has the zero invariant, i.e.
$\tilde{\boldsymbol{f}}$
obeys (2.1) and has the zero invariant, i.e.
If the system of waves (2.7) is complete, then the solution
![]() $\tilde{\boldsymbol{f}}$
is a linear superposition of these waves; therefore it is natural to call
$\tilde{\boldsymbol{f}}$
is a linear superposition of these waves; therefore it is natural to call
![]() $\tilde{\boldsymbol{f}}$
the wave component. We now introduce the time average
$\tilde{\boldsymbol{f}}$
the wave component. We now introduce the time average
and assume the operators
![]() $\unicode[STIX]{x1D64D}$
and
$\unicode[STIX]{x1D64D}$
and
![]() $\boldsymbol{B}$
to be such that
$\boldsymbol{B}$
to be such that
This takes place, for example, if
![]() $\unicode[STIX]{x1D64D}$
and
$\unicode[STIX]{x1D64D}$
and
![]() $\boldsymbol{B}$
are either time-independent or include only time derivatives (as in the examples below). In this case, averaging (2.11) in time, we obtain
$\boldsymbol{B}$
are either time-independent or include only time derivatives (as in the examples below). In this case, averaging (2.11) in time, we obtain
The system (2.14) coincides with (2.10) for
![]() ${\it\Lambda}=0$
. Therefore if the problem (2.10) has a unique solution, then we have from (2.14) that
${\it\Lambda}=0$
. Therefore if the problem (2.10) has a unique solution, then we have from (2.14) that
i.e. the wave solution oscillates near the stationary one. If the waves (2.7) are able to radiate away from the initial perturbation domain, then the wave component
![]() $\tilde{\boldsymbol{f}}$
gradually decays at any fixed point
$\tilde{\boldsymbol{f}}$
gradually decays at any fixed point
![]() $\boldsymbol{x}$
and the solution (2.9) tends to the stationary component
$\boldsymbol{x}$
and the solution (2.9) tends to the stationary component
![]() $\bar{\boldsymbol{f}}$
with increasing time – so-called wave adjustment takes place.
$\bar{\boldsymbol{f}}$
with increasing time – so-called wave adjustment takes place.
Thus the sufficient condition for the state vector
![]() $\boldsymbol{f}$
of the linear system to split into stationary and oscillating parts is that the system possesses linear invariants and a complete set of linear waves.
$\boldsymbol{f}$
of the linear system to split into stationary and oscillating parts is that the system possesses linear invariants and a complete set of linear waves.
An alternative way of achieving the linear fast–slow splitting exploits the decomposition of the state vector into normal modes of the system considered. If the normal modes can be divided into two sets consisting, respectively, of slow (low-frequency) modes and fast (high-frequency) modes, then the state vector can be decomposed into the slow and fast components, which are the vector’s projections onto the slow and fast sets, respectively (Leith Reference Leith1980; Salmon Reference Salmon1998). This kind of splitting is used as a first step in initialization (see e.g. Leith Reference Leith1980; Daley Reference Daley1981; Temperton Reference Temperton1988). This way is more general than the way that we use because it works in the absence of linear invariants, too. The price paid for this universality is that dynamical equations should be represented in phase space (space of the normal modes) instead of the physical one. Such a representation may be useful for numerical modelling, but for our analytical treatment the equations in physical space are much more convenient. The splitting in physical space based on linear invariants also was used for initialization (Temperton Reference Temperton1988) and for derivation of balanced models (Lynch Reference Lynch1989) as applied to the rotating shallow-water (RSW) model.
2.2. Weak nonlinearity and balanced models
We now consider the perturbed model (2.1) written in a non-dimensional form:
The term
![]() ${\it\varepsilon}\unicode[STIX]{x1D649}\boldsymbol{f}$
is a small perturbation,
${\it\varepsilon}\unicode[STIX]{x1D649}\boldsymbol{f}$
is a small perturbation,
![]() $\unicode[STIX]{x1D649}$
is a linear or nonlinear operator, which can depend on
$\unicode[STIX]{x1D649}$
is a linear or nonlinear operator, which can depend on
![]() ${\it\varepsilon}$
, and the boundary and initial conditions (2.2a,b
) are assumed to be
${\it\varepsilon}$
, and the boundary and initial conditions (2.2a,b
) are assumed to be
![]() ${\it\varepsilon}$
-independent. Applying the invariant operator
${\it\varepsilon}$
-independent. Applying the invariant operator
![]() $\unicode[STIX]{x1D648}$
to (2.16) one obtains
$\unicode[STIX]{x1D648}$
to (2.16) one obtains
i.e. the ‘former’ linear invariant
![]() $\unicode[STIX]{x1D648}\unicode[STIX]{x1D647}\,\boldsymbol{f}$
ceases to be invariant but changes slowly in time. There are two time scales in the system – the slow one
$\unicode[STIX]{x1D648}\unicode[STIX]{x1D647}\,\boldsymbol{f}$
ceases to be invariant but changes slowly in time. There are two time scales in the system – the slow one
![]() ${\sim}1/{\it\varepsilon}$
and the fast one
${\sim}1/{\it\varepsilon}$
and the fast one
![]() ${\sim}1$
. Therefore, a solution to the problem is sought in the form of a multiple-time-scale asymptotic expansion:
${\sim}1$
. Therefore, a solution to the problem is sought in the form of a multiple-time-scale asymptotic expansion:
where
![]() $T_{n},~n=1,2,\ldots$
, are the slow times.
$T_{n},~n=1,2,\ldots$
, are the slow times.
Substitution of (2.18) into (2.16) gives in the lowest order:
Applying the invariant operator
![]() $\unicode[STIX]{x1D648}$
to (2.19), one obtains that the quantity
$\unicode[STIX]{x1D648}$
to (2.19), one obtains that the quantity
![]() $\unicode[STIX]{x1D648}\unicode[STIX]{x1D647}\,\boldsymbol{f}^{(0)}$
does not depend on the fast time
$\unicode[STIX]{x1D648}\unicode[STIX]{x1D647}\,\boldsymbol{f}^{(0)}$
does not depend on the fast time
![]() $t$
:
$t$
:
We now represent
![]() $\boldsymbol{f}^{(0)}$
as a sum of slow and fast components (cf. (2.9)),
$\boldsymbol{f}^{(0)}$
as a sum of slow and fast components (cf. (2.9)),
which obey the equations (cf. (2.10) and (2.11))
Initial conditions for
![]() $\bar{\boldsymbol{f}}^{(0)}$
and
$\bar{\boldsymbol{f}}^{(0)}$
and
![]() $\tilde{\boldsymbol{f}}^{(0)}$
are determined from the equations following from (2.22) and (2.23):
$\tilde{\boldsymbol{f}}^{(0)}$
are determined from the equations following from (2.22) and (2.23):
The function
![]() ${\it\Lambda}(\boldsymbol{x},T_{1})$
in (2.22b
) has yet to be found; the slow evolution is determined from boundedness of the first-order correction, which obeys the equation
${\it\Lambda}(\boldsymbol{x},T_{1})$
in (2.22b
) has yet to be found; the slow evolution is determined from boundedness of the first-order correction, which obeys the equation
where
![]() $\unicode[STIX]{x1D649}^{(0)}$
is the lowest-order term in the expansion of the operator
$\unicode[STIX]{x1D649}^{(0)}$
is the lowest-order term in the expansion of the operator
![]() $\unicode[STIX]{x1D649}$
in
$\unicode[STIX]{x1D649}$
in
![]() ${\it\varepsilon}$
. We now apply the invariant operator to (2.25), taking into account (2.22) and (2.23):
${\it\varepsilon}$
. We now apply the invariant operator to (2.25), taking into account (2.22) and (2.23):
It readily follows from (2.26) that the first-order correction
![]() $\boldsymbol{f}^{(1)}$
is bounded in the fast time
$\boldsymbol{f}^{(1)}$
is bounded in the fast time
![]() $t$
if
$t$
if
where the angle brackets denote time averaging (2.12).
Equation (2.27) determines the slow evolution of the zero-order invariant
![]() $\unicode[STIX]{x1D648}\unicode[STIX]{x1D647}\bar{\boldsymbol{f}}^{(0)}$
. To close the problem for
$\unicode[STIX]{x1D648}\unicode[STIX]{x1D647}\bar{\boldsymbol{f}}^{(0)}$
. To close the problem for
![]() $\bar{\boldsymbol{f}}^{(0)}$
, one should express
$\bar{\boldsymbol{f}}^{(0)}$
, one should express
![]() $\langle \unicode[STIX]{x1D648}\unicode[STIX]{x1D649}^{(0)}\boldsymbol{f}^{(0)}\rangle$
in terms of
$\langle \unicode[STIX]{x1D648}\unicode[STIX]{x1D649}^{(0)}\boldsymbol{f}^{(0)}\rangle$
in terms of
![]() $\bar{\boldsymbol{f}}^{(0)}$
; in this case
$\bar{\boldsymbol{f}}^{(0)}$
; in this case
![]() $\bar{\boldsymbol{f}}^{(0)}$
could be determined from (2.22a
) and (2.27). It is unlikely that the problem can be solved in the general case, but if one assumes that the wave component
$\bar{\boldsymbol{f}}^{(0)}$
could be determined from (2.22a
) and (2.27). It is unlikely that the problem can be solved in the general case, but if one assumes that the wave component
![]() $\tilde{\boldsymbol{f}}^{(0)}$
can be neglected, at least, on times
$\tilde{\boldsymbol{f}}^{(0)}$
can be neglected, at least, on times
![]() ${\sim}1/{\it\varepsilon}$
, i.e.
${\sim}1/{\it\varepsilon}$
, i.e.
then the time evolution of the slow component is described by the equation
In addition,
![]() $\bar{\boldsymbol{f}}^{(0)}$
should obey the corresponding boundary conditions and equations (2.24a,b
), which filter out the fast waves from the initial field
$\bar{\boldsymbol{f}}^{(0)}$
should obey the corresponding boundary conditions and equations (2.24a,b
), which filter out the fast waves from the initial field
![]() $\boldsymbol{f}_{I}$
. The set of equations (2.22a
), (2.29) and (2.24a,b
) and the boundary conditions determine the balanced model (in which the fast waves are absent) related to the system (2.16).
$\boldsymbol{f}_{I}$
. The set of equations (2.22a
), (2.29) and (2.24a,b
) and the boundary conditions determine the balanced model (in which the fast waves are absent) related to the system (2.16).
Of course, the important question is under what conditions (2.28) is valid. Analysis of various examples from fluid dynamics shows that (2.28) is fulfilled (as could be expected) if the fast waves are absent in initial fields or their group speeds greatly exceed the velocities typical of the slow component. The corresponding scenario of wave adjustment will be referred to as ‘fast radiation’ (see § 3). More surprisingly, (2.28) is valid also if the group speeds are of the order of or smaller than the slow velocities. In this case the waves are trapped by the slow component but their self-interaction gives no contribution to the left-hand side of (2.28), at least, on times
![]() ${\sim}1/{\it\varepsilon}$
. The scenario of such adjustment will be called ‘nonlinear trapping’ (see § 4). In § 5 we consider the situation when non-stationary boundary layers arise near the boundary
${\sim}1/{\it\varepsilon}$
. The scenario of such adjustment will be called ‘nonlinear trapping’ (see § 4). In § 5 we consider the situation when non-stationary boundary layers arise near the boundary
![]() ${\it\Gamma}$
or inside the motion domain at large times
${\it\Gamma}$
or inside the motion domain at large times
![]() $t$
in the linear problem (2.1) and (2.2). Each boundary layer consists of an infinite number of very short harmonic waves (2.7) with vanishingly small group speeds; therefore the corresponding scenario of adjustment is called ‘imperfect splitting’.
$t$
in the linear problem (2.1) and (2.2). Each boundary layer consists of an infinite number of very short harmonic waves (2.7) with vanishingly small group speeds; therefore the corresponding scenario of adjustment is called ‘imperfect splitting’.
In the theory developed we have used the basic equations in the operator form (2.1), (2.2) and (2.16). This is convenient for general theory but for ‘practical’ calculations in the examples considered below the matrix operators
![]() $\unicode[STIX]{x1D647}$
,
$\unicode[STIX]{x1D647}$
,
![]() $\unicode[STIX]{x1D64D}$
and
$\unicode[STIX]{x1D64D}$
and
![]() $\unicode[STIX]{x1D649}$
are too cumbersome and we examine the equations written in ‘standard’ form. Operator forms of the models in use are given in appendix A.
$\unicode[STIX]{x1D649}$
are too cumbersome and we examine the equations written in ‘standard’ form. Operator forms of the models in use are given in appendix A.
3. ‘Fast radiation’ scenario: barotropic fluid layer with free surface
In this section we examine the ‘fast radiation’ scenario using the non-rotating barotropic fluid layer with a free surface (figure 1) as an example. This is probably the simplest hydrodynamic system in which the wave adjustment occurs without rotation and stratification.

Figure 1. Wave adjustment of non-rotating barotropic layer. (a) Schematic representation of the layer; (b) schematic representation of the adjustment. Here 3D means three-dimensional motion, and gw are the surface gravity waves.
3.1. Statement of the problem
The corresponding equations of motion are written in the form:
Here
![]() $\boldsymbol{u}=(u,v,w)$
is the velocity, with components
$\boldsymbol{u}=(u,v,w)$
is the velocity, with components
![]() $u,v,w$
along the axes
$u,v,w$
along the axes
![]() $x,y,z$
, respectively;
$x,y,z$
, respectively;
![]() $p$
is the deviation of pressure from the hydrostatic one divided by the fluid density. At the free surface
$p$
is the deviation of pressure from the hydrostatic one divided by the fluid density. At the free surface
![]() $z={\it\varsigma}$
and bottom
$z={\it\varsigma}$
and bottom
![]() $z=-H$
the dynamic and kinematic conditions are fulfilled:
$z=-H$
the dynamic and kinematic conditions are fulfilled:
The velocity and elevation are given at the initial moment
![]() $t=0$
:
$t=0$
:
In what follows all fields are assumed to decay at infinity, i.e. as
![]() $\sqrt{x^{2}+y^{2}}\rightarrow \infty$
.
$\sqrt{x^{2}+y^{2}}\rightarrow \infty$
.
3.2. Linear invariants and waves
In the linearized problem (3.1) and (3.2),
the vorticity vector
![]() $\text{curl }\boldsymbol{u}=({\it\Omega}^{x},{\it\Omega}^{y},{\it\Omega}^{z})$
is conserved in view of (3.3a
), i.e. there are three linear invariants:
$\text{curl }\boldsymbol{u}=({\it\Omega}^{x},{\it\Omega}^{y},{\it\Omega}^{z})$
is conserved in view of (3.3a
), i.e. there are three linear invariants:
Following § 2, we represent the solution in the form (2.9), i.e.
where the stationary solution
![]() $(\bar{\boldsymbol{u}},\bar{p},\bar{{\it\varsigma}})$
obeys the equations
$(\bar{\boldsymbol{u}},\bar{p},\bar{{\it\varsigma}})$
obeys the equations
and the boundary conditions
For the wave solution
![]() $(\tilde{\boldsymbol{u}},p,{\it\varsigma})$
we have
$(\tilde{\boldsymbol{u}},p,{\it\varsigma})$
we have
To find the stationary solution, one obtains the vertical velocity
![]() $\bar{w}$
from the equation
$\bar{w}$
from the equation
![]() ${\rm\Delta}\bar{w}={\it\Omega}_{Iy}^{x}-{\it\Omega}_{Ix}^{y}$
and boundary conditions (3.6d
), and then the horizontal velocities from the equations
${\rm\Delta}\bar{w}={\it\Omega}_{Iy}^{x}-{\it\Omega}_{Ix}^{y}$
and boundary conditions (3.6d
), and then the horizontal velocities from the equations
![]() ${\rm\Delta}_{2}\bar{u}=-\bar{w}_{xz}-{\it\Omega}_{Iy}^{z}$
and
${\rm\Delta}_{2}\bar{u}=-\bar{w}_{xz}-{\it\Omega}_{Iy}^{z}$
and
![]() ${\rm\Delta}_{2}\bar{v}=-\bar{w}_{yz}+{\it\Omega}_{Ix}^{z}$
, where
${\rm\Delta}_{2}\bar{v}=-\bar{w}_{yz}+{\it\Omega}_{Ix}^{z}$
, where
![]() ${\rm\Delta}=\partial _{xx}+\partial _{yy}+\partial _{zz}$
and
${\rm\Delta}=\partial _{xx}+\partial _{yy}+\partial _{zz}$
and
![]() ${\rm\Delta}_{2}=\partial _{xx}+\partial _{yy}$
. Knowing the stationary component one can determine the initial conditions for the wave component:
${\rm\Delta}_{2}=\partial _{xx}+\partial _{yy}$
. Knowing the stationary component one can determine the initial conditions for the wave component:
In view of (3.7c
) the system (3.7a,b,d,e
) can be represented in terms of the potential
![]() ${\it\Phi}$
:
${\it\Phi}$
:
The solution for the potential is written as a superposition of the irrotational surface gravity waves,
where the Fourier amplitude
![]() $A({\bf\kappa})$
is determined by the initial conditions (3.8) and
$A({\bf\kappa})$
is determined by the initial conditions (3.8) and
![]() $\boldsymbol{x}_{2}=(x,y)$
. If the initial fields are localized in space, then
$\boldsymbol{x}_{2}=(x,y)$
. If the initial fields are localized in space, then
![]() ${\it\Phi}$
decays at a fixed point
${\it\Phi}$
decays at a fixed point
![]() $x,y$
as
$x,y$
as
![]() $t\rightarrow \infty$
because of geometrical scattering and dispersion of the waves:
$t\rightarrow \infty$
because of geometrical scattering and dispersion of the waves:
Thus in the process of wave adjustment the system tends with increasing time to the vortical three-dimensional stationary state
![]() $(\bar{\boldsymbol{u}},\bar{p},\bar{{\it\varsigma}})$
specified by (3.4) and (3.6). Importantly, the stationary residual flow does not perturb the free surface in view of (3.6a,d
) (see figure 1).
$(\bar{\boldsymbol{u}},\bar{p},\bar{{\it\varsigma}})$
specified by (3.4) and (3.6). Importantly, the stationary residual flow does not perturb the free surface in view of (3.6a,d
) (see figure 1).
3.3. Weak nonlinearity and balanced equations
We now write the system (3.1) and (3.2) in non-dimensional form using the scales of length
![]() $L=H$
, time
$L=H$
, time
![]() $T=L/\sqrt{gH}$
, velocity
$T=L/\sqrt{gH}$
, velocity
![]() $U$
, pressure
$U$
, pressure
![]() $U\sqrt{gH}$
and elevation
$U\sqrt{gH}$
and elevation
![]() ${\it\varepsilon}H$
, where
${\it\varepsilon}H$
, where
![]() ${\it\varepsilon}=U/\sqrt{gH}$
:
${\it\varepsilon}=U/\sqrt{gH}$
:
Let the nonlinearity be weak, i.e. the parameter
![]() ${\it\varepsilon}\ll 1$
. According to § 2 the solution is sought in the asymptotic form (2.18) and the lowest-order solution
${\it\varepsilon}\ll 1$
. According to § 2 the solution is sought in the asymptotic form (2.18) and the lowest-order solution
![]() $(\boldsymbol{u}^{(0)},p^{(0)},{\it\varsigma}^{(0)})$
obeys equations coinciding with (3.3) in which
$(\boldsymbol{u}^{(0)},p^{(0)},{\it\varsigma}^{(0)})$
obeys equations coinciding with (3.3) in which
![]() $g$
and
$g$
and
![]() $H$
are replaced by 1. Therefore the formulae (3.4)–(3.11) are valid (mutatis mutandis) for the lowest-order solution if we assume that the invariants
$H$
are replaced by 1. Therefore the formulae (3.4)–(3.11) are valid (mutatis mutandis) for the lowest-order solution if we assume that the invariants
![]() ${\it\Omega}^{x}$
,
${\it\Omega}^{x}$
,
![]() ${\it\Omega}^{y}$
and
${\it\Omega}^{y}$
and
![]() ${\it\Omega}^{z}$
in (3.6) and the amplitude
${\it\Omega}^{z}$
in (3.6) and the amplitude
![]() $A$
in (3.10) depend on the slow time, i.e.
$A$
in (3.10) depend on the slow time, i.e.
As in § 2, this dependence is determined from the boundedness of higher-order corrections.
For the first-order correction
![]() $(\boldsymbol{u}^{(1)},p^{(1)},{\it\varsigma}^{(1)})$
we have
$(\boldsymbol{u}^{(1)},p^{(1)},{\it\varsigma}^{(1)})$
we have
Applying the curl operator to (3.15) one finds
The fast time averaging (2.12) of (3.16a ) taking into account the asymptotic equation (3.11) gives
Equation (3.17) describes the evolution of the slow vortex component and should be solved for the initial conditions coinciding with the stationary component
![]() $\bar{\boldsymbol{u}}$
of the linear problem (3.6) and (3.4) considered above. In addition, the boundary conditions (3.6d
) should be satisfied:
$\bar{\boldsymbol{u}}$
of the linear problem (3.6) and (3.4) considered above. In addition, the boundary conditions (3.6d
) should be satisfied:
Equation (3.17) together with the no-flux boundary condition (3.18) and initial conditions constitute a closed balanced model for calculation of the slow vortex component of motion. Analysis of the fast first-order component (very similar to that in Reznik et al. (Reference Reznik, Zeitlin and Ben Jelloul2001)) shows that the amplitude (3.14b
) does not depend on the slow time
![]() $T_{1}$
, i.e. it can be considered as constant on times
$T_{1}$
, i.e. it can be considered as constant on times
![]() $t\sim 1/{\it\varepsilon}$
.
$t\sim 1/{\it\varepsilon}$
.
In view of (3.18) the lowest-order vortex component does not perturb the free surface on times
![]() $t\sim 1/{\it\varepsilon}$
(see figure 1). Time averaging of (3.15) gives the equation for
$t\sim 1/{\it\varepsilon}$
(see figure 1). Time averaging of (3.15) gives the equation for
![]() $\bar{p}^{(1)}$
:
$\bar{p}^{(1)}$
:
Knowing
![]() $\bar{p}^{(1)}$
one can find the slow part of the first-order elevation correction
$\bar{p}^{(1)}$
one can find the slow part of the first-order elevation correction
![]() $\bar{{\it\varsigma}}^{(1)}=\bar{p}^{(1)}(x,y,0,T_{1})$
, which, generally, is non-zero, i.e. the first-order slow component of motion contributes to the elevation. In turn, the first-order fast component ceases to be irrotational, as readily follows from the vortex equation (3.16a
).
$\bar{{\it\varsigma}}^{(1)}=\bar{p}^{(1)}(x,y,0,T_{1})$
, which, generally, is non-zero, i.e. the first-order slow component of motion contributes to the elevation. In turn, the first-order fast component ceases to be irrotational, as readily follows from the vortex equation (3.16a
).
Thus the nonlinear wave adjustment in a non-rotating homogeneous fluid with free surface follows the ‘fast radiation’ scenario when the leading-order slow and wave components evolve independently of one another, at least on times
![]() ${\sim}1/{\it\varepsilon}$
. This takes place because the assumed smallness of the nonlinearity parameter
${\sim}1/{\it\varepsilon}$
. This takes place because the assumed smallness of the nonlinearity parameter
![]() ${\it\varepsilon}$
means that the typical fluid particle velocity
${\it\varepsilon}$
means that the typical fluid particle velocity
![]() $U$
is small as compared to the typical group speed
$U$
is small as compared to the typical group speed
![]() $\sqrt{gH}$
of surface gravity waves. In this case the waves rapidly radiate away from the initial perturbation and do not interact effectively with the slow component. We have considered the case
$\sqrt{gH}$
of surface gravity waves. In this case the waves rapidly radiate away from the initial perturbation and do not interact effectively with the slow component. We have considered the case
![]() $L=H$
; analysis of the long-wave motion
$L=H$
; analysis of the long-wave motion
![]() $L\gg H$
(not given here) also confirms the validity of this scenario. In the short-wave case
$L\gg H$
(not given here) also confirms the validity of this scenario. In the short-wave case
![]() $L\ll H$
, in view of (3.10c
) the frequency
$L\ll H$
, in view of (3.10c
) the frequency
![]() ${\it\sigma}\sim \sqrt{g/L}$
and the group speed
${\it\sigma}\sim \sqrt{g/L}$
and the group speed
![]() $c_{gr}\sim \sqrt{gL}$
, i.e.
$c_{gr}\sim \sqrt{gL}$
, i.e.
![]() ${\it\sigma}$
increases and
${\it\sigma}$
increases and
![]() $c_{gr}$
decreases with decreasing
$c_{gr}$
decreases with decreasing
![]() $L$
. However, the typical phase speed
$L$
. However, the typical phase speed
![]() ${\it\sigma}L$
is of the order of
${\it\sigma}L$
is of the order of
![]() $c_{gr}$
and the nonlinearity parameter here is equal to
$c_{gr}$
and the nonlinearity parameter here is equal to
![]() $U/\sqrt{gL}$
. Smallness of the parameter means again that the wave group speed greatly exceeds the typical velocity
$U/\sqrt{gL}$
. Smallness of the parameter means again that the wave group speed greatly exceeds the typical velocity
![]() $U$
, similarly to the case
$U$
, similarly to the case
![]() $L\geqslant H$
. Therefore one can think (we did not examine this case in detail) that the ‘fast radiation’ scenario takes place in the short-wave limit too.
$L\geqslant H$
. Therefore one can think (we did not examine this case in detail) that the ‘fast radiation’ scenario takes place in the short-wave limit too.
Note that, in the absence of rotation, the frequencies of the gravity waves are not bounded from below; the dispersion relation (3.10c
) gives for long waves
![]() ${\it\sigma}\cong \sqrt{gH}{\it\kappa}$
for
${\it\sigma}\cong \sqrt{gH}{\it\kappa}$
for
![]() ${\it\kappa}\rightarrow 0$
, i.e. there is no frequency gap between the waves and the stationary flow in this case. Nevertheless, the fast time average works well. The point is that the result of the averaging depends strongly on the structure of the initial perturbation. If the perturbation is localized, then the contribution of very long waves with very small frequencies to its Fourier integral is vanishingly small and the wave part tends to zero with increasing time at a fixed point of space. In moving coordinates the wave perturbation can be non-decaying, for example in the case of one-dimensional non-dispersive waves any localized perturbation propagates at a constant speed, conserving its shape. Obviously, the time average of such a wave perturbation at a fixed space point is zero. A similar situation takes place for the geostrophic adjustment in RSW on a half-plane with rigid lateral boundary (Reznik & Grimshaw Reference Reznik and Grimshaw2002; Reznik & Sutyrin Reference Reznik and Sutyrin2005) where the wave spectrum contains Kelvin waves whose frequency tends to zero in the long-wave limit.
${\it\kappa}\rightarrow 0$
, i.e. there is no frequency gap between the waves and the stationary flow in this case. Nevertheless, the fast time average works well. The point is that the result of the averaging depends strongly on the structure of the initial perturbation. If the perturbation is localized, then the contribution of very long waves with very small frequencies to its Fourier integral is vanishingly small and the wave part tends to zero with increasing time at a fixed point of space. In moving coordinates the wave perturbation can be non-decaying, for example in the case of one-dimensional non-dispersive waves any localized perturbation propagates at a constant speed, conserving its shape. Obviously, the time average of such a wave perturbation at a fixed space point is zero. A similar situation takes place for the geostrophic adjustment in RSW on a half-plane with rigid lateral boundary (Reznik & Grimshaw Reference Reznik and Grimshaw2002; Reznik & Sutyrin Reference Reznik and Sutyrin2005) where the wave spectrum contains Kelvin waves whose frequency tends to zero in the long-wave limit.
The ‘fast radiation’ scenario also occurs in one- and two-layer RSW models if the dominating horizontal scale
![]() $L$
is smaller than or of the order of the corresponding Rossby scale
$L$
is smaller than or of the order of the corresponding Rossby scale
![]() $L_{R}$
(for details, see Reznik et al.
Reference Reznik, Zeitlin and Ben Jelloul2001; Zeitlin et al.
Reference Zeitlin, Reznik and Ben Jelloul2003). In the next section we will see that a different wave adjustment scenario is realized in this scale range in a three-dimensional homogeneous rotating fluid.
$L_{R}$
(for details, see Reznik et al.
Reference Reznik, Zeitlin and Ben Jelloul2001; Zeitlin et al.
Reference Zeitlin, Reznik and Ben Jelloul2003). In the next section we will see that a different wave adjustment scenario is realized in this scale range in a three-dimensional homogeneous rotating fluid.
4. ‘Nonlinear trapping’ scenario: rotating barotropic layer
In this section the ‘nonlinear trapping’ scenario is examined using a uniformly rotating three-dimensional barotropic fluid layer with a free surface (figure 2) as a model. The rotation drastically changes both the linear invariants and the wave spectrum: in a rotating fluid only one non-local linear invariant exists and gyroscopic waves appear in addition to the gravity ones. The gyroscopic waves are characterized by small group speeds in a physically relevant range of scales and can be trapped by the slow component of motion.

Figure 2. Wave adjustment of the rotating barotropic layer. (a) Schematic representation of the layer; (b) schematic representation of the adjustment. Here
![]() $\text{QG}+\text{IO}$
means that the residual flow consists of QG two-dimensional flow and inertial oscillations.
$\text{QG}+\text{IO}$
means that the residual flow consists of QG two-dimensional flow and inertial oscillations.
4.1. Statement of the problem
Let the barotropic layer considered above rotate at a constant angular speed
![]() ${\it\Omega}=f/2$
as shown in figure 2. The modified equations of motion are written as follows (see also appendix A):
${\it\Omega}=f/2$
as shown in figure 2. The modified equations of motion are written as follows (see also appendix A):
The boundary and initial conditions (3.2) remain unchanged. Here
![]() $\boldsymbol{e}_{\boldsymbol{z}}$
is the vertical unit vector.
$\boldsymbol{e}_{\boldsymbol{z}}$
is the vertical unit vector.
4.2. Linear invariants and waves
Without nonlinear terms equations (4.1) and (3.2a−c ) take the form (cf. (3.3)):
The system (4.2) conserves the non-local invariant
![]() ${\it\Pi}$
, which can be naturally treated as a PV for a rotating three-dimensional barotropic layer with free surface:
${\it\Pi}$
, which can be naturally treated as a PV for a rotating three-dimensional barotropic layer with free surface:
In the representation (3.5) the stationary part now obeys the geostrophic relations
and is determined from the equation following from (4.3) and (4.4),
The wave component in (3.5) is a solution to the system (4.2) with the zero invariant (4.3) and is a superposition of the wave harmonics
where the amplitudes
![]() $U$
,
$U$
,
![]() $V$
,
$V$
,
![]() $W$
,
$W$
,
![]() $P$
and
$P$
and
![]() $Z$
depend on
$Z$
depend on
![]() $z$
and
$z$
and
![]() ${\bf\kappa}(k,l)$
. Substitution of (4.6) into (4.2) and exclusion of
${\bf\kappa}(k,l)$
. Substitution of (4.6) into (4.2) and exclusion of
![]() $U$
,
$U$
,
![]() $V$
,
$V$
,
![]() $P$
and
$P$
and
![]() $Z$
gives the following eigenvalue problem for
$Z$
gives the following eigenvalue problem for
![]() $W(z)$
and
$W(z)$
and
![]() ${\it\sigma}$
:
${\it\sigma}$
:
where
![]() $q={\it\sigma}{\it\kappa}/\sqrt{|{\it\sigma}^{2}-f^{2}|}$
. The wave spectrum consists of super-inertial gravity waves with the eigenfunctions and dispersion relation
$q={\it\sigma}{\it\kappa}/\sqrt{|{\it\sigma}^{2}-f^{2}|}$
. The wave spectrum consists of super-inertial gravity waves with the eigenfunctions and dispersion relation
and sub-inertial gyroscopic waves for which
In the case of low frequencies
one obtains the following approximate dispersion relations:
For typical geophysical parameters
![]() $f=10^{-4}~\text{s}^{-1}$
and
$f=10^{-4}~\text{s}^{-1}$
and
![]() $H=10^{5}~\text{cm}$
, we have
$H=10^{5}~\text{cm}$
, we have
![]() $f^{2}H/g=10^{-6}\ll 1$
, and therefore for gyroscopic waves whose frequencies obey (4.9c
) the dispersion relation (4.11b
) is a good approximation throughout the range of wavenumbers. This is not the case for the gravity waves since (4.11a
) is fulfilled only for the long waves with wavenumbers
$f^{2}H/g=10^{-6}\ll 1$
, and therefore for gyroscopic waves whose frequencies obey (4.9c
) the dispersion relation (4.11b
) is a good approximation throughout the range of wavenumbers. This is not the case for the gravity waves since (4.11a
) is fulfilled only for the long waves with wavenumbers
For the gravity waves with moderate and short wavelengths we have
![]() ${\it\sigma}^{g}\gg f$
and the dispersion relation (4.8b
) takes the form (3.10c
):
${\it\sigma}^{g}\gg f$
and the dispersion relation (4.8b
) takes the form (3.10c
):
In the range of horizontal scales from
![]() $H$
to the Rossby scale
$H$
to the Rossby scale
![]() $L_{R}=\sqrt{gH}/f$
,
$L_{R}=\sqrt{gH}/f$
,
one obtains from (4.11) and (4.13) the following estimates for the group velocities of the gravity and gyroscopic waves:
4.3. Weak nonlinearity and balanced equations
Nonlinear effects are considered in the long-wave approximation when
There exist three time scales in the problem:
Here
![]() $T^{g}$
,
$T^{g}$
,
![]() $T^{r}$
and
$T^{r}$
and
![]() $T^{ad}$
are the typical times of gravity waves, rotation and advection, respectively; the Rossby number
$T^{ad}$
are the typical times of gravity waves, rotation and advection, respectively; the Rossby number
![]() ${\it\varepsilon}=U/fL$
is assumed to be small,
${\it\varepsilon}=U/fL$
is assumed to be small,
We now write (4.1) in non-dimensional form. In the range (4.16a
),
![]() $T^{g}\leqslant T^{r}$
, and therefore
$T^{g}\leqslant T^{r}$
, and therefore
![]() $T^{g}$
is chosen as the time scale. Also we use the scales of horizontal and vertical velocities
$T^{g}$
is chosen as the time scale. Also we use the scales of horizontal and vertical velocities
![]() $U$
and
$U$
and
![]() $W={\it\delta}U$
, pressure
$W={\it\delta}U$
, pressure
![]() $U\sqrt{gH}$
and elevation
$U\sqrt{gH}$
and elevation
![]() ${\it\varepsilon}BH$
, where
${\it\varepsilon}BH$
, where
![]() $B=L/L_{R}\leqslant 1$
. The resulting equations are written as
$B=L/L_{R}\leqslant 1$
. The resulting equations are written as
The boundary conditions (3.2a−c ) take the form
There are two small parameters
![]() ${\it\varepsilon}$
and
${\it\varepsilon}$
and
![]() ${\it\delta}$
in (4.19) and (4.20). We put
${\it\delta}$
in (4.19) and (4.20). We put
which, in view of (4.15), is equivalent to the assumption
![]() $U\geqslant {\it\delta}fH\sim c_{gr}^{gir}$
. Since
$U\geqslant {\it\delta}fH\sim c_{gr}^{gir}$
. Since
![]() $B\leqslant 1$
and, therefore,
$B\leqslant 1$
and, therefore,
![]() ${\it\varepsilon}B=U/\sqrt{gH}\ll 1$
, this choice of scales means that
${\it\varepsilon}B=U/\sqrt{gH}\ll 1$
, this choice of scales means that
i.e. the typical flow velocity is much smaller than the group speed of gravity waves and exceeds the group speed of gyroscopic waves. Therefore, as we will see (cf. § 3), the balanced slow component affects weakly the gravity waves and strongly the gyroscopic ones.
The solution is again sought in the asymptotic form (2.18). Here only results are given; details can be found in appendix B. The lowest-order equations are a simplified version of the set (4.2), and (4.3) takes the form
The slow solution
![]() $(\bar{\boldsymbol{u}}^{(0)},\bar{p}^{(0)},\bar{{\it\varsigma}}^{(0)})$
in the representation (2.21) obeys the geostrophic equations analogous to (4.4),
$(\bar{\boldsymbol{u}}^{(0)},\bar{p}^{(0)},\bar{{\it\varsigma}}^{(0)})$
in the representation (2.21) obeys the geostrophic equations analogous to (4.4),
and the non-dimensional version of (4.5),
The wave solution
![]() $(\tilde{\boldsymbol{u}}^{(0)},\tilde{p}^{(0)},\tilde{{\it\varsigma}}^{(0)})$
is characterized by the zero invariant (4.23), i.e.
$(\tilde{\boldsymbol{u}}^{(0)},\tilde{p}^{(0)},\tilde{{\it\varsigma}}^{(0)})$
is characterized by the zero invariant (4.23), i.e.
and can be written as the sum
The first term on the right-hand side of (4.27) describes the long gravity waves with depth-independent horizontal velocities:
The elevation
![]() $\tilde{{\it\varsigma}}^{(0)}$
obeys the Klein–Gordon equation:
$\tilde{{\it\varsigma}}^{(0)}$
obeys the Klein–Gordon equation:
The second term on the right-hand side of (4.27) corresponds to the inertial oscillations (i.e. long gyroscopic waves) in which the pressure, elevation and depth-averaged horizontal velocities are zero:
For localized initial fields the gravity waves decay at a fixed point
![]() $x,y$
proportionally to
$x,y$
proportionally to
![]() $1/t$
because of the dispersion (see e.g. Reznik et al.
Reference Reznik, Zeitlin and Ben Jelloul2001):
$1/t$
because of the dispersion (see e.g. Reznik et al.
Reference Reznik, Zeitlin and Ben Jelloul2001):
At the same time the inertial oscillations do not propagate (in this approximation) and remain to be localized in the initial perturbation domain.
Knowing the PV
![]() ${\it\Pi}^{(0)}(x,y,T_{1},\ldots )$
and the amplitude of inertial oscillations
${\it\Pi}^{(0)}(x,y,T_{1},\ldots )$
and the amplitude of inertial oscillations
![]() $A(x,y,z,T_{1},\ldots )$
, one can calculate all other fields. Slow evolution of
$A(x,y,z,T_{1},\ldots )$
, one can calculate all other fields. Slow evolution of
![]() ${\it\Pi}^{(0)}$
and
${\it\Pi}^{(0)}$
and
![]() $A$
is determined from the condition of boundedness of the first-order solution (see appendix B).
$A$
is determined from the condition of boundedness of the first-order solution (see appendix B).
The evolution equation for the slow QG component is written for the geostrophic streamfunction
![]() $\bar{{\it\psi}}^{(0)}$
:
$\bar{{\it\psi}}^{(0)}$
:
where
![]() $\text{J}$
is the Jacobian. Equations (4.32) together with the initial streamfunction
$\text{J}$
is the Jacobian. Equations (4.32) together with the initial streamfunction
![]() $\bar{{\it\psi}}_{I}^{(0)}$
(which is determined as the solution of (4.25) with the right-hand side equal to
$\bar{{\it\psi}}_{I}^{(0)}$
(which is determined as the solution of (4.25) with the right-hand side equal to
![]() ${\it\Pi}_{I}$
in (4.3)) constitute the balanced model for the rotating layer. Obviously, (4.32) express conservation of the QG PV
${\it\Pi}_{I}$
in (4.3)) constitute the balanced model for the rotating layer. Obviously, (4.32) express conservation of the QG PV
![]() ${\it\Pi}^{(0)}$
and coincide exactly with the corresponding equations derived in the model of RSW (see e.g. Reznik et al.
Reference Reznik, Zeitlin and Ben Jelloul2001), in which the horizontal velocities and pressure are assumed to be
${\it\Pi}^{(0)}$
and coincide exactly with the corresponding equations derived in the model of RSW (see e.g. Reznik et al.
Reference Reznik, Zeitlin and Ben Jelloul2001), in which the horizontal velocities and pressure are assumed to be
![]() $z$
-independent, i.e. the gyroscopic waves (4.30) are neglected.
$z$
-independent, i.e. the gyroscopic waves (4.30) are neglected.
The equation describing the slow evolution of the inertial oscillation amplitude
![]() $A$
on times
$A$
on times
![]() $t\sim 1/{\it\varepsilon}$
has the form:
$t\sim 1/{\it\varepsilon}$
has the form:
Without the last term on the left-hand side of (4.33) we have
i.e. the inertial oscillations are trapped by the slow QG component. The term proportional to
![]() ${\it\delta}^{2}/{\it\varepsilon}$
counteracts the trapping and arises due to slow dispersion of the long gyroscopic waves. The dispersion is effective on times
${\it\delta}^{2}/{\it\varepsilon}$
counteracts the trapping and arises due to slow dispersion of the long gyroscopic waves. The dispersion is effective on times
![]() $t\sim 1/{\it\varepsilon}$
if
$t\sim 1/{\it\varepsilon}$
if
![]() ${\it\delta}^{2}/{\it\varepsilon}\sim 1$
or, in the dimensional form,
${\it\delta}^{2}/{\it\varepsilon}\sim 1$
or, in the dimensional form,
i.e. the group speed of inertial oscillations and the typical QG velocity are of the same order.
In the barotropic, two-layer and stably continuously stratified RSW models, only gravity waves exist, the gyroscopic ones are absent, but the ‘nonlinear trapping’ scenario occurs if the dominating horizontal scale
![]() $L$
greatly exceeds the corresponding Rossby scale
$L$
greatly exceeds the corresponding Rossby scale
![]() $L_{R}$
(Reznik et al.
Reference Reznik, Zeitlin and Ben Jelloul2001; Zeitlin et al.
Reference Zeitlin, Reznik and Ben Jelloul2003). Physically, this is due to the fact that the surface and internal gravity waves with
$L_{R}$
(Reznik et al.
Reference Reznik, Zeitlin and Ben Jelloul2001; Zeitlin et al.
Reference Zeitlin, Reznik and Ben Jelloul2003). Physically, this is due to the fact that the surface and internal gravity waves with
![]() $L\gg L_{R}$
are close to inertial oscillations with small group speeds (see e.g. (4.11a
)).
$L\gg L_{R}$
are close to inertial oscillations with small group speeds (see e.g. (4.11a
)).
Surprisingly, the fast inertial oscillations, being trapped by the slow component, do not contribute to the latter on times
![]() ${\sim}1/{\it\varepsilon}$
as readily seen from (4.32). Self-interaction of the oscillations gives a contribution to the first-order PV equation (B 7) only on a double inertial frequency; the corresponding terms with zero frequency cancel each other. The same is valid in the RSW models (Reznik et al.
Reference Reznik, Zeitlin and Ben Jelloul2001; Zeitlin et al.
Reference Zeitlin, Reznik and Ben Jelloul2003), in a three-dimensional rotating barotropic fluid confined between two rigid lids (Reznik Reference Reznik2014a
) and in a rotating stably neutrally stratified (SNS) fluid (Reznik Reference Reznik2014b
). In the RSW models, the trapped oscillations do not affect the slow motion even on longer times
${\sim}1/{\it\varepsilon}$
as readily seen from (4.32). Self-interaction of the oscillations gives a contribution to the first-order PV equation (B 7) only on a double inertial frequency; the corresponding terms with zero frequency cancel each other. The same is valid in the RSW models (Reznik et al.
Reference Reznik, Zeitlin and Ben Jelloul2001; Zeitlin et al.
Reference Zeitlin, Reznik and Ben Jelloul2003), in a three-dimensional rotating barotropic fluid confined between two rigid lids (Reznik Reference Reznik2014a
) and in a rotating stably neutrally stratified (SNS) fluid (Reznik Reference Reznik2014b
). In the RSW models, the trapped oscillations do not affect the slow motion even on longer times
![]() ${\sim}1/{\it\varepsilon}^{2}$
. At the same time, in a three-dimensional rotating fluid, the long gyroscopic waves affect the slow component on times
${\sim}1/{\it\varepsilon}^{2}$
. At the same time, in a three-dimensional rotating fluid, the long gyroscopic waves affect the slow component on times
![]() ${\sim}1/{\it\varepsilon}^{2}$
(Reznik Reference Reznik2014a
).
${\sim}1/{\it\varepsilon}^{2}$
(Reznik Reference Reznik2014a
).
5. ‘Imperfect splitting’ scenario: continuously stratified fluid layer
In this section we present the ‘imperfect splitting’ scenario, which in the simplest case occurs in a continuously stratified fluid confined between two rigid lids (figure 3). The wave adjustment in this model is accompanied by non-stationary boundary layers arising near the surface and bottom at large times. Each boundary layer consists of an infinite number of wave modes with vanishingly small group speeds, and complete splitting of motion into fast and slow components is impossible even in the linear approximation.

Figure 3. Wave adjustment of the stratified layer. (a) Schematic representation of the layer; (b) schematic representation of the adjustment. Here the domains between the rigid boundaries and horizontal dashed lines represent the non-stationary boundary layers with thickness
![]() ${\sim}1/t$
.
${\sim}1/t$
.
5.1. Statement of the problem
We now consider a layer of continuously stratified fluid of constant depth
![]() $H$
confined between two rigid lids
$H$
confined between two rigid lids
![]() $z=0,-H$
(figure 3). In the Boussinesq approximation, the system is described by the equations (see also appendix A)
$z=0,-H$
(figure 3). In the Boussinesq approximation, the system is described by the equations (see also appendix A)
with the no-flux boundary conditions and initial conditions
Here
![]() $b=g{\it\rho}/{\it\rho}_{0}$
is the buoyancy,
$b=g{\it\rho}/{\it\rho}_{0}$
is the buoyancy,
![]() ${\it\rho}/{\it\rho}_{0}$
and
${\it\rho}/{\it\rho}_{0}$
and
![]() $p$
are the variations of density and pressure from their hydrostatic profiles divided by the reference density
$p$
are the variations of density and pressure from their hydrostatic profiles divided by the reference density
![]() ${\it\rho}_{0}$
, and
${\it\rho}_{0}$
, and
![]() $N$
is the buoyancy frequency.
$N$
is the buoyancy frequency.
5.2. Linear invariants and linear waves
The linearized system (5.1),
conserves the vertical component of vorticity,
and, in view of (5.3b
) and (5.2), the buoyancy at the boundaries
![]() $z=0,-H$
,
$z=0,-H$
,
In the corresponding representation (2.9), the stationary solution obeys the equations
Assuming the fields to decay at infinity in any horizontal plane, one finds that
where the streamfunction
![]() $\bar{{\it\psi}}$
is found from the equation
$\bar{{\it\psi}}$
is found from the equation
following from (5.6c ) and (5.4).
Lighthill (Reference Lighthill1996) examined the linear wave adjustment of localized perturbation in an unbounded (vertically and horizontally) stratified ocean and showed that the motion is split into a steady vortical flow obeying (5.6)–(5.8) and radiated internal waves propagating away from the initial perturbation. In our case the fluid is bounded by two rigid lids, which results in the existence of two additional ‘boundary’ invariants (5.5) absent in the vertically unbounded fluid. These invariants are not used when determining the stationary solution (5.7), which does not satisfy (5.5) if the initial buoyancy
![]() $b_{I}$
is non-zero at the boundaries. In this case the time-independent non-zero boundary conditions (5.5) should be satisfied by the wave part of the solution
$b_{I}$
is non-zero at the boundaries. In this case the time-independent non-zero boundary conditions (5.5) should be satisfied by the wave part of the solution
![]() $\tilde{\boldsymbol{u}}=(\tilde{u} ,\tilde{v},w),p,b$
, which obeys the equations
$\tilde{\boldsymbol{u}}=(\tilde{u} ,\tilde{v},w),p,b$
, which obeys the equations
As a rule, the equations of internal waves (5.9) and (5.10) are reduced to a problem for the vertical velocity
![]() $w$
(see e.g. Miropol’sky Reference Miropol’sky2001). From (5.9a–c
) one derives the equation
$w$
(see e.g. Miropol’sky Reference Miropol’sky2001). From (5.9a–c
) one derives the equation
which should be solved under the no-flux conditions (5.10a ) and initial conditions
The initial field
![]() ${\dot{w}}_{I}$
in (5.12a
) can be expressed in terms of
${\dot{w}}_{I}$
in (5.12a
) can be expressed in terms of
![]() $u_{I}$
,
$u_{I}$
,
![]() $v_{I}$
and
$v_{I}$
and
![]() $b_{I}$
(see e.g. Reznik Reference Reznik2013).
$b_{I}$
(see e.g. Reznik Reference Reznik2013).
The solution to the problem (5.11), (5.10a
) and (5.12a
) is well known (see e.g. Miropol’sky Reference Miropol’sky2001). The velocity
![]() $w$
is written as the Fourier integral in the horizontal coordinates,
$w$
is written as the Fourier integral in the horizontal coordinates,
and for the Fourier amplitude
![]() ${\hat{w}}$
we have
${\hat{w}}$
we have
Here and below the hat denotes the corresponding Fourier amplitude. The solution for
![]() ${\hat{w}}$
can be written as the series
${\hat{w}}$
can be written as the series
where
![]() $G_{n}$
and
$G_{n}$
and
![]() ${\it\lambda}_{n}$
are the eigenfunctions and eigenvalues of the Sturm–Liouville problem:
${\it\lambda}_{n}$
are the eigenfunctions and eigenvalues of the Sturm–Liouville problem:
In the case
![]() $N=\text{const.}$
we have
$N=\text{const.}$
we have
In view of the conditions
the coefficients
![]() ${\hat{w}}_{In}$
and
${\hat{w}}_{In}$
and
![]() $\hat{{\dot{w}}}_{In}$
decay rapidly with increasing
$\hat{{\dot{w}}}_{In}$
decay rapidly with increasing
![]() $n$
:
$n$
:
Since
![]() ${\it\sigma}_{n}=O(n^{-1}),~n\rightarrow \infty$
, the series (5.15a
) converges absolutely and uniformly in the domain
${\it\sigma}_{n}=O(n^{-1}),~n\rightarrow \infty$
, the series (5.15a
) converges absolutely and uniformly in the domain
![]() $[-H\leqslant z\leqslant 0]\times [0\leqslant t\leqslant \infty ]$
. Solutions for the horizontal velocities
$[-H\leqslant z\leqslant 0]\times [0\leqslant t\leqslant \infty ]$
. Solutions for the horizontal velocities
![]() $\tilde{u} ,\tilde{v}$
and pressure
$\tilde{u} ,\tilde{v}$
and pressure
![]() $p$
are given in appendix C.
$p$
are given in appendix C.
The problem for the buoyancy is conveniently reduced to the form
where
![]() $c=b/N^{2}$
is the normalized buoyancy and
$c=b/N^{2}$
is the normalized buoyancy and
![]() $c_{I}=b_{I}/N^{2}$
. If the initial buoyancy is zero at the boundaries, i.e.
$c_{I}=b_{I}/N^{2}$
. If the initial buoyancy is zero at the boundaries, i.e.
![]() $b_{I}|_{z=0,-H}=0$
, then (5.20) is analogous to the problem (5.11) and (5.12) and the buoyancy Fourier amplitude can be represented as an absolutely and uniformly converging series of the form (5.15). However, for
$b_{I}|_{z=0,-H}=0$
, then (5.20) is analogous to the problem (5.11) and (5.12) and the buoyancy Fourier amplitude can be represented as an absolutely and uniformly converging series of the form (5.15). However, for
the situation becomes somewhat more complicated. First, in view of (5.20a
), the time average
![]() $\langle c\rangle =0$
inside the interval
$\langle c\rangle =0$
inside the interval
![]() $[-H,0]$
, but
$[-H,0]$
, but
![]() $\langle c\rangle \neq 0$
at the boundaries by virtue of (5.20b
) and (5.21). Second, the vertical gradients of horizontal velocities grow linearly in time near the boundaries since it readily follows from (5.9a,b
) and (5.10) that
$\langle c\rangle \neq 0$
at the boundaries by virtue of (5.20b
) and (5.21). Second, the vertical gradients of horizontal velocities grow linearly in time near the boundaries since it readily follows from (5.9a,b
) and (5.10) that
These peculiarities indicate that in close vicinities of the boundaries the solutions for
![]() $\tilde{u} ,\tilde{v},c$
have a boundary-layer structure when, for example, near
$\tilde{u} ,\tilde{v},c$
have a boundary-layer structure when, for example, near
![]() $z=0$
the normalized buoyancy
$z=0$
the normalized buoyancy
![]() $c$
at large times is represented as
$c$
at large times is represented as
where the right-hand side tends to zero at any
![]() $z<0$
,
$z<0$
,
![]() $t\rightarrow \infty$
but
$t\rightarrow \infty$
but
![]() $c(x,y,0)\neq 0$
.
$c(x,y,0)\neq 0$
.
To understand better the physics of the boundary layer, we consider the solution to (5.20) in terms of the Fourier amplitude
![]() ${\hat{c}}$
, which can be written in the forms (see appendix C)
${\hat{c}}$
, which can be written in the forms (see appendix C)
or
In the case (5.21) we have (appendix C)
and therefore the terms of the series in (5.24) behave as
![]() $O(n^{-3})$
,
$O(n^{-3})$
,
![]() $n\rightarrow \infty$
, at a fixed
$n\rightarrow \infty$
, at a fixed
![]() $t$
, i.e. the series converges absolutely and uniformly in the domain
$t$
, i.e. the series converges absolutely and uniformly in the domain
![]() $[-H,0]\times [0,T_{0}]$
, where
$[-H,0]\times [0,T_{0}]$
, where
![]() $T_{0}$
is an arbitrary finite time. However, the convergence gets worse with increasing time
$T_{0}$
is an arbitrary finite time. However, the convergence gets worse with increasing time
![]() $t$
since in (5.24) the terms
$t$
since in (5.24) the terms
![]() ${\hat{c}}_{In}[\cos ({\it\sigma}_{n}t)-1]\sim t^{2}/n^{3}$
and
${\hat{c}}_{In}[\cos ({\it\sigma}_{n}t)-1]\sim t^{2}/n^{3}$
and
![]() $({\hat{w}}_{In}/{\it\sigma}_{n})\sin ({\it\sigma}_{n}t)\sim t/n^{3}$
as
$({\hat{w}}_{In}/{\it\sigma}_{n})\sin ({\it\sigma}_{n}t)\sim t/n^{3}$
as
![]() $n\rightarrow \infty$
. The series (5.25) has the same form as (5.15) but it converges much slower because of (5.26). Any partial sum in the series has zero time average (2.12); the sum does not have ‘boundary layer’ form (5.23) and its contribution to the corresponding Fourier integral of the form (5.13) for
$n\rightarrow \infty$
. The series (5.25) has the same form as (5.15) but it converges much slower because of (5.26). Any partial sum in the series has zero time average (2.12); the sum does not have ‘boundary layer’ form (5.23) and its contribution to the corresponding Fourier integral of the form (5.13) for
![]() $c$
tends to zero with increasing time because of dispersion. This means that the non-stationary boundary layers developing at large times near the surface and bottom arise as a result of joint impact of the low-frequency wave harmonics with numbers
$c$
tends to zero with increasing time because of dispersion. This means that the non-stationary boundary layers developing at large times near the surface and bottom arise as a result of joint impact of the low-frequency wave harmonics with numbers
![]() $1\ll n\leqslant \infty$
in the series (5.24) and (5.25), characterized by a very weak dispersion.
$1\ll n\leqslant \infty$
in the series (5.24) and (5.25), characterized by a very weak dispersion.
5.3. Non-stationary boundary layer
To describe the buoyancy at large times, one uses the new variable (cf. Il’in Reference Il’in1970, Reference Il’in1972; Kamenkovich & Kamenkovich Reference Kamenkovich and Kamenkovich1993)
The meaning of the variable
![]() $C$
is that the contribution of the rapidly oscillating part of the field
$C$
is that the contribution of the rapidly oscillating part of the field
![]() $c$
to
$c$
to
![]() $C$
becomes negligible at large times
$C$
becomes negligible at large times
![]() $t\gg 1$
, as seen from (5.25). Equations (5.20) are rewritten in non-dimensional form using the length scale
$t\gg 1$
, as seen from (5.25). Equations (5.20) are rewritten in non-dimensional form using the length scale
![]() $H$
and the time scale
$H$
and the time scale
![]() $1/N$
:
$1/N$
:
For simplicity,
![]() $N$
is assumed to be constant.
$N$
is assumed to be constant.
Let us consider the problem (5.28) at large times. Outside the boundary layers the vertical scale is assumed to be of the order of the layer depth and the solution here is sought in the following asymptotic form:
Substitution of (5.29) into (5.28a ) gives
Generally,
![]() $C_{1}/t$
does not satisfy the boundary conditions (5.28b
); this discrepancy is corrected by boundary layers confined to narrow vicinities near the boundaries. The solution near
$C_{1}/t$
does not satisfy the boundary conditions (5.28b
); this discrepancy is corrected by boundary layers confined to narrow vicinities near the boundaries. The solution near
![]() $z=0$
is sought in the form of the expansion
$z=0$
is sought in the form of the expansion
where
![]() ${\it\xi}$
is the boundary layer stretched variable.
${\it\xi}$
is the boundary layer stretched variable.
In the leading order we have the equation
where the superscripts and primes mean differentiation with respect to
![]() ${\it\xi}$
. The function
${\it\xi}$
. The function
![]() $D_{0}$
should satisfy the boundary conditions
$D_{0}$
should satisfy the boundary conditions
The corresponding equations for the Fourier amplitude
![]() $\hat{D}_{0}$
are written as
$\hat{D}_{0}$
are written as
The solution to (5.34) has the form (Kamke Reference Kamke1976)
where here and below
![]() $\text{J}_{n}$
is the Bessel function of
$\text{J}_{n}$
is the Bessel function of
![]() $n$
th order. The lowest-order normalized buoyancy and vertical velocity are found from (5.27b
), (5.35) and (5.9b
) as
$n$
th order. The lowest-order normalized buoyancy and vertical velocity are found from (5.27b
), (5.35) and (5.9b
) as
Using (5.36b ) and (5.9c,d ) we find the Fourier amplitudes of the lowest-order boundary layer horizontal velocities:
One can readily check that (5.37) agrees with (5.22) and the horizontal boundary layer velocity is time-independent at
![]() $z=0$
. The boundary layer near the bottom
$z=0$
. The boundary layer near the bottom
![]() $z=-H$
is analysed in the same way.
$z=-H$
is analysed in the same way.
5.4. Weak nonlinearity and balanced equations
We now write (5.1) in non-dimensional form using the scales of length
![]() $L=H$
, time
$L=H$
, time
![]() $T=1/N_{0}$
, velocity
$T=1/N_{0}$
, velocity
![]() $U$
, pressure
$U$
, pressure
![]() $UHN_{0}$
and buoyancy
$UHN_{0}$
and buoyancy
![]() $UN_{0}$
:
$UN_{0}$
:
Here
![]() $N_{0}$
is the typical buoyancy frequency and the nonlinearity parameter
$N_{0}$
is the typical buoyancy frequency and the nonlinearity parameter
![]() ${\it\varepsilon}$
is assumed to be small:
${\it\varepsilon}$
is assumed to be small:
The boundary and initial conditions (5.2) keep their form with
![]() $H$
replaced by 1.
$H$
replaced by 1.
Again, the solution is sought in the asymptotic form (2.18); details are given in appendix C. The lowest-order solution
![]() $(u^{(0)},v^{(0)},w^{(0)},b^{(0)},p^{(0)})$
obeys the linear equations (5.3) and conditions (5.2), and therefore the slow component of the solution
$(u^{(0)},v^{(0)},w^{(0)},b^{(0)},p^{(0)})$
obeys the linear equations (5.3) and conditions (5.2), and therefore the slow component of the solution
![]() $\bar{u}^{(0)}(\boldsymbol{x},T_{1},\ldots ),\ldots$
satisfies (5.6) and (5.7),
$\bar{u}^{(0)}(\boldsymbol{x},T_{1},\ldots ),\ldots$
satisfies (5.6) and (5.7),
and (5.8) takes the form
The initial conditions for the slow component follow from (5.41):
The buoyancy at
![]() $z=0,-1$
also depends on the slow time
$z=0,-1$
also depends on the slow time
![]() $T_{1}$
, i.e. instead of (5.5) we have
$T_{1}$
, i.e. instead of (5.5) we have
The functions
![]() $b_{0,-1}$
are known only at the initial moment:
$b_{0,-1}$
are known only at the initial moment:
The dependence of
![]() ${\it\Omega}^{z}$
and
${\it\Omega}^{z}$
and
![]() $b_{0,-1}$
on
$b_{0,-1}$
on
![]() $T_{1}$
is determined from the condition of boundedness of first-order fields (see appendix C).
$T_{1}$
is determined from the condition of boundedness of first-order fields (see appendix C).
The lowest-order wave component is described by (5.9) and (5.10); in this case the solution (5.15) for the vertical velocity remains unchanged, at least up to times
![]() $t=O(1/{\it\varepsilon})$
(see Reznik et al.
Reference Reznik, Zeitlin and Ben Jelloul2001). As for the buoyancy and horizontal velocity, the representations (5.24), (5.25) and (C 3b
) remain relevant for
$t=O(1/{\it\varepsilon})$
(see Reznik et al.
Reference Reznik, Zeitlin and Ben Jelloul2001). As for the buoyancy and horizontal velocity, the representations (5.24), (5.25) and (C 3b
) remain relevant for
![]() $t\ll 1/{\it\varepsilon}$
; for
$t\ll 1/{\it\varepsilon}$
; for
![]() $t=O(1/{\it\varepsilon})$
the solution for the boundary layer becomes relevant, with the quantities
$t=O(1/{\it\varepsilon})$
the solution for the boundary layer becomes relevant, with the quantities
![]() $b_{I}|_{z=0,-1}$
replaced by
$b_{I}|_{z=0,-1}$
replaced by
![]() $b_{0,-1}(x,y,T_{1},\ldots )$
in (5.22), (5.36b
) and (5.37), and
$b_{0,-1}(x,y,T_{1},\ldots )$
in (5.22), (5.36b
) and (5.37), and
![]() $c_{I}|_{z=0,-1}$
replaced by
$c_{I}|_{z=0,-1}$
replaced by
![]() $b_{0,-1}/N^{2}|_{z=0,-1}$
in (5.28b
), (5.33a
), (5.34b
), (5.35) and (5.36a
).
$b_{0,-1}/N^{2}|_{z=0,-1}$
in (5.28b
), (5.33a
), (5.34b
), (5.35) and (5.36a
).
The streamfunction
![]() $\bar{{\it\psi}}$
obeys the equation for two-dimensional hydrodynamics,
$\bar{{\it\psi}}$
obeys the equation for two-dimensional hydrodynamics,
while the surface buoyancy is described by the equations
The ‘wave’ velocities
![]() $\tilde{u} _{0}$
and
$\tilde{u} _{0}$
and
![]() $\tilde{v}_{0}$
do not depend on the fast time at the boundaries in view of (5.37) and in terms of the Fourier amplitudes are given by
$\tilde{v}_{0}$
do not depend on the fast time at the boundaries in view of (5.37) and in terms of the Fourier amplitudes are given by
Equations (5.45) and (5.46) determine the evolution of the slow component and should be solved under the initial conditions following from (5.42a
) for the streamfunction and from (5.43) and (5.44) for the boundary buoyancy. The slow vertical velocity
![]() $\bar{w}^{(0)}$
is zero in view of (5.40a
), and therefore the slow motion is quasi-two-dimensional, i.e. the motion at any plane
$\bar{w}^{(0)}$
is zero in view of (5.40a
), and therefore the slow motion is quasi-two-dimensional, i.e. the motion at any plane
![]() $z=z_{0}=\text{const.}$
does not depend on the motion at other planes, whereas the motions at different horizons differ from one another if the initial vorticity
$z=z_{0}=\text{const.}$
does not depend on the motion at other planes, whereas the motions at different horizons differ from one another if the initial vorticity
![]() ${\it\Omega}_{I}^{z}$
varies with
${\it\Omega}_{I}^{z}$
varies with
![]() $z$
.
$z$
.
During the wave adjustment (see figure 3) the wave parts of the vertical velocity and pressure decay with increasing time at any fixed point
![]() $x$
,
$x$
,
![]() $y$
,
$y$
,
![]() $z$
. As for the buoyancy and wave part of the horizontal velocity, they turn out to be confined to the non-stationary boundary layers near the surface and bottom at large times. Thus any localized initial perturbation tends with increasing time to the sum of a quasi-two-dimensional state determined by the vortex equation (5.45) and the boundary layer fields. The boundary layers are characterized by sharp vertical gradients of the buoyancy and horizontal velocity growing proportionally to the time
$z$
. As for the buoyancy and wave part of the horizontal velocity, they turn out to be confined to the non-stationary boundary layers near the surface and bottom at large times. Thus any localized initial perturbation tends with increasing time to the sum of a quasi-two-dimensional state determined by the vortex equation (5.45) and the boundary layer fields. The boundary layers are characterized by sharp vertical gradients of the buoyancy and horizontal velocity growing proportionally to the time
![]() $t$
; the layer thicknesses decrease proportionally to
$t$
; the layer thicknesses decrease proportionally to
![]() $t$
. The time dependence of the buoyancy and wave horizontal velocities slows down when approaching the boundaries; at the boundaries the quantities do not depend on the fast time
$t$
. The time dependence of the buoyancy and wave horizontal velocities slows down when approaching the boundaries; at the boundaries the quantities do not depend on the fast time
![]() $t$
. It is impossible to split the slow and wave components even in the linear approximation; therefore we call this the ‘imperfect splitting’ scenario.
$t$
. It is impossible to split the slow and wave components even in the linear approximation; therefore we call this the ‘imperfect splitting’ scenario.
The same scenario takes place for the wave adjustment in an SNS fluid consisting of a stratified upper layer and a homogeneous lower layer, the density and other fields being continuous at the interface between the layers (Reznik Reference Reznik2013). In this model the vertical component of vorticity is invariant in the upper layer and the full three-dimensional vorticity components are invariants in the lower one. Generally, the stationary solution related to these invariants is discontinuous at the interface between the layers. The result of this is that, in parallel with the boundary layers near rigid surface, an internal boundary layer arises at large times near the interface between the stratified and homogeneous fluids. The layer is characterized by sharp vertical gradients of the horizontal velocity.
Dissipation can be important in these domains with sharp gradients. As noted by an anonymous reviewer, ‘In the presence of dissipation, mean flow can be generated due to the dissipative operator’. Probably, in our case the dissipation will transform the non-stationary boundary layers into stationary ones, and, in doing so, contributes to the slow flow. This interesting and important effect will be considered elsewhere.
5.5. Effects of rotation
Linearized equations of a rotating stratified fluid have the form (cf. (4.2) and (5.3)):
The boundary and initial conditions (5.2) remain unchanged. The conserved quantity here is the PV,
The stationary geostrophic solution is expressed in terms of the geostrophic streamfunction
![]() $\bar{{\it\psi}}$
as
$\bar{{\it\psi}}$
as
determined from the equation
following from (5.48) and (5.49). The conservation of boundary buoyancy (5.5) gives here the boundary conditions for (5.50):
That is, in the rotating case, the stationary solution and conditions (5.5) do not ‘contradict’ each other unlike in the non-rotating fluid.
Nevertheless, non-stationary boundary layers arise too in the rotating fluid. It follows from (5.47) and (5.5) that, at the boundaries
![]() $z=0,-H$
(M. V. Kalashnik, private communication),
$z=0,-H$
(M. V. Kalashnik, private communication),
whence one obtains that
Thus for
![]() $U_{Iz}|_{z=0,-H}\neq 0$
and/or
$U_{Iz}|_{z=0,-H}\neq 0$
and/or
![]() ${\rm\nabla}_{2}b_{I}|_{z=0,-H}\neq 0$
inertial oscillations proportional to
${\rm\nabla}_{2}b_{I}|_{z=0,-H}\neq 0$
inertial oscillations proportional to
![]() $\text{e}^{-\text{i}ft}$
are generated in the vertical gradient of the horizontal velocity at the boundaries. Let us multiply (5.9) and (5.10a
) by the harmonic
$\text{e}^{-\text{i}ft}$
are generated in the vertical gradient of the horizontal velocity at the boundaries. Let us multiply (5.9) and (5.10a
) by the harmonic
![]() $\text{e}^{\pm \text{i}ft}$
and apply the time averaging (2.12) to the resulting equations. A simple investigation of the obtained system shows (see e.g. Reznik Reference Reznik2014b
) that inertial oscillations localized in the horizontal plane are prohibited inside a stably stratified fluid, i.e.
$\text{e}^{\pm \text{i}ft}$
and apply the time averaging (2.12) to the resulting equations. A simple investigation of the obtained system shows (see e.g. Reznik Reference Reznik2014b
) that inertial oscillations localized in the horizontal plane are prohibited inside a stably stratified fluid, i.e.
Therefore near the boundaries
![]() $z=0,-H$
at large times boundary layers should arise that provide a transition from the ‘boundary’ motion (5.53) to the motion in the inner domain. A description of the boundary layers is given in Reznik (Reference Reznik2014b
).
$z=0,-H$
at large times boundary layers should arise that provide a transition from the ‘boundary’ motion (5.53) to the motion in the inner domain. A description of the boundary layers is given in Reznik (Reference Reznik2014b
).
In a rotating SNS fluid the boundary layer near the interface is more intense than that near the rigid boundaries; the layer prevents penetration into the stably stratified upper fluid of ‘prohibited’ inertial oscillations (long sub-inertial gyroscopic waves) which occur in the homogeneous fluid and cannot exist in the stratified one (Reznik Reference Reznik2014b ).
6. Summary and conclusions
We have shown that the geostrophic and hydrostatic adjustments can be considered as particular cases of the more general wave adjustment which takes place in a physical system (not necessarily a hydrodynamic one) possessing in the linear approximation linear invariants and linear wave solutions harmonically depending on time. The waves are characterized by zero linear invariants, i.e. they do not transport and affect the invariants. As a result, any solution of the linearized system is represented in a unique way as the sum of a time-independent solution with non-zero invariants and a non-steady wave solution with zero invariants. If the waves are able to propagate away from the initial perturbation domain, then with increasing time any localized initial perturbation tends to the stationary solution which can be determined using the invariants without solving an initial problem.
If the system is slightly perturbed (for example by weak nonlinearity), then the state vector of the system is split into a component that is slowly evolving in time and a fast wave component. If the waves are absent in the initial state or rapidly radiate away, then at large times the system is described by the so-called balanced model, which is presented here in most general operator form.
Various scenarios of wave adjustment are demonstrated with fairly simple hydrodynamic examples. The simplest ‘fast radiation’ scenario occurs when the waves rapidly (their group speed
![]() $c_{gr}$
greatly exceeds the slow flow velocity
$c_{gr}$
greatly exceeds the slow flow velocity
![]() $U$
) radiate away from the initial perturbation and do not interact effectively with the slow component. As a result, at large times, after the waves have propagated away, the motion is slow and described by a balanced model. The scenario is illustrated by the example of three-dimensional non-rotating barotropic flow with a free surface. In this case, in the linear approximation, three components of the vortex are conserved and the wave adjustment results in a slowly changing (in time) three-dimensional vortex motion with zero pressure, which spreads across the whole depth of the fluid but does not perturb the free surface.
$U$
) radiate away from the initial perturbation and do not interact effectively with the slow component. As a result, at large times, after the waves have propagated away, the motion is slow and described by a balanced model. The scenario is illustrated by the example of three-dimensional non-rotating barotropic flow with a free surface. In this case, in the linear approximation, three components of the vortex are conserved and the wave adjustment results in a slowly changing (in time) three-dimensional vortex motion with zero pressure, which spreads across the whole depth of the fluid but does not perturb the free surface.
The ‘fast radiation’ scenario takes place in the hydrostatic adjustment in an unbounded stratified fluid (Lighthill Reference Lighthill1996), in wave adjustment in shallow-water models (one and many layers), and in geostrophic adjustment of RSW if the dominating horizontal scale
![]() $L$
is smaller than or of the order of the Rossby scale
$L$
is smaller than or of the order of the Rossby scale
![]() $L_{R}$
(Obukhov Reference Obukhov1949; Monin & Obukhov Reference Monin and Obukhov1958; Reznik et al.
Reference Reznik, Zeitlin and Ben Jelloul2001; Reznik & Grimshaw Reference Reznik and Grimshaw2002; Zeitlin et al.
Reference Zeitlin, Reznik and Ben Jelloul2003; Reznik & Sutyrin Reference Reznik and Sutyrin2005).
$L_{R}$
(Obukhov Reference Obukhov1949; Monin & Obukhov Reference Monin and Obukhov1958; Reznik et al.
Reference Reznik, Zeitlin and Ben Jelloul2001; Reznik & Grimshaw Reference Reznik and Grimshaw2002; Zeitlin et al.
Reference Zeitlin, Reznik and Ben Jelloul2003; Reznik & Sutyrin Reference Reznik and Sutyrin2005).
The more complicated ‘nonlinear trapping’ scenario occurs when oscillations with group speed
![]() $c_{gr}$
smaller than or of the order of the slow flow velocity
$c_{gr}$
smaller than or of the order of the slow flow velocity
![]() $U$
are present in the wave spectrum. A fairly simple example of this situation is the geostrophic adjustment of a three-dimensional rotating barotropic layer with a free surface. There is only one non-local linear invariant (PV) in this case. The slow component of motion is QG and depth-independent. The wave spectrum consists of surface gravity waves that rapidly radiate away and gyroscopic waves that in the long-wave approximation
$U$
are present in the wave spectrum. A fairly simple example of this situation is the geostrophic adjustment of a three-dimensional rotating barotropic layer with a free surface. There is only one non-local linear invariant (PV) in this case. The slow component of motion is QG and depth-independent. The wave spectrum consists of surface gravity waves that rapidly radiate away and gyroscopic waves that in the long-wave approximation
![]() $L\gg H$
are inertial oscillations modulated by a slowly changing amplitude and characterized by a moderate group speed
$L\gg H$
are inertial oscillations modulated by a slowly changing amplitude and characterized by a moderate group speed
![]() $c_{gr}\leqslant U$
. The motion after nonlinear wave adjustment is a superposition of the slow QG component and the inertial oscillations trapped by this component. An analogous scenario takes place for the geostrophic adjustment in a three-dimensional rotating homogeneous layer if
$c_{gr}\leqslant U$
. The motion after nonlinear wave adjustment is a superposition of the slow QG component and the inertial oscillations trapped by this component. An analogous scenario takes place for the geostrophic adjustment in a three-dimensional rotating homogeneous layer if
![]() $L\gg H$
(Reznik Reference Reznik2014a
), and in the RSW models when
$L\gg H$
(Reznik Reference Reznik2014a
), and in the RSW models when
![]() $L\gg L_{R}$
and all waves are close to inertial oscillations (Reznik et al.
Reference Reznik, Zeitlin and Ben Jelloul2001; Zeitlin et al.
Reference Zeitlin, Reznik and Ben Jelloul2003).
$L\gg L_{R}$
and all waves are close to inertial oscillations (Reznik et al.
Reference Reznik, Zeitlin and Ben Jelloul2001; Zeitlin et al.
Reference Zeitlin, Reznik and Ben Jelloul2003).
Stratification in the presence of boundaries introduces a new element into the wave adjustment. At large times near the surface and bottom there arise narrow boundary layers whose thicknesses tend to zero and the vertical gradients of physical parameters in the layers tend to infinity as
![]() $t\rightarrow \infty$
. The layer consists of an infinite number of internal wave modes with large vertical numbers
$t\rightarrow \infty$
. The layer consists of an infinite number of internal wave modes with large vertical numbers
![]() $n\gg 1$
. The group speeds of the modes are very small and tend to zero as
$n\gg 1$
. The group speeds of the modes are very small and tend to zero as
![]() $n\rightarrow \infty$
. In such a system a complete splitting of motion into fast and slow components is impossible even in the linear approximation; therefore we called this the ‘incomplete splitting’ scenario. In an SNS fluid, in parallel with the boundary layers near the surface and bottom, analogous boundary layers arise near the interface between stratified and homogeneous fluids (Reznik Reference Reznik2013, Reference Reznik2014b
).
$n\rightarrow \infty$
. In such a system a complete splitting of motion into fast and slow components is impossible even in the linear approximation; therefore we called this the ‘incomplete splitting’ scenario. In an SNS fluid, in parallel with the boundary layers near the surface and bottom, analogous boundary layers arise near the interface between stratified and homogeneous fluids (Reznik Reference Reznik2013, Reference Reznik2014b
).
Summarizing, one can state that the above scenarios describe, at least, the majority of known cases of wave adjustment.
Acknowledgement
This work was funded by the Russian Science Foundation grant no. 14-50-00095.
Appendix A. Operator forms
In the non-rotating fluid described by (3.1) and (3.2) the state vector consists of five parameters,
and the system can be rewritten in the operator form
 $$\begin{eqnarray}\unicode[STIX]{x1D647}=\left(\begin{array}{@{}ccccc@{}}1 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1\end{array}\right),\quad \unicode[STIX]{x1D64D}=\left(\begin{array}{@{}ccccc@{}}0 & 0 & 0 & -\partial _{x} & 0\\ 0 & 0 & 0 & -\partial _{y} & 0\\ 0 & 0 & 0 & -\partial _{z} & 0\\ \partial _{x} & \partial _{y} & \partial _{z} & 0 & 0\\ 0 & 0 & \boldsymbol{J}\partial _{z} & 0 & 0\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D647}=\left(\begin{array}{@{}ccccc@{}}1 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1\end{array}\right),\quad \unicode[STIX]{x1D64D}=\left(\begin{array}{@{}ccccc@{}}0 & 0 & 0 & -\partial _{x} & 0\\ 0 & 0 & 0 & -\partial _{y} & 0\\ 0 & 0 & 0 & -\partial _{z} & 0\\ \partial _{x} & \partial _{y} & \partial _{z} & 0 & 0\\ 0 & 0 & \boldsymbol{J}\partial _{z} & 0 & 0\end{array}\right),\end{eqnarray}$$
 $$\begin{eqnarray}\unicode[STIX]{x1D649}=\left(\!\begin{array}{@{}ccccc@{}}-\boldsymbol{u}\boldsymbol{{\rm\nabla}} & 0 & 0 & 0 & 0\\ 0 & -\boldsymbol{u}\boldsymbol{{\rm\nabla}} & 0 & 0 & 0\\ 0 & 0 & -\boldsymbol{u}\boldsymbol{{\rm\nabla}} & 0 & 0\\ 0 & 0 & 0 & 0 & 0\\ 0 & 0 & \boldsymbol{J}_{{\it\varsigma}}\partial _{z} & 0 & -\boldsymbol{u}_{{\it\varsigma}}\boldsymbol{{\rm\nabla}}_{2}\end{array}\!\right),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D649}=\left(\!\begin{array}{@{}ccccc@{}}-\boldsymbol{u}\boldsymbol{{\rm\nabla}} & 0 & 0 & 0 & 0\\ 0 & -\boldsymbol{u}\boldsymbol{{\rm\nabla}} & 0 & 0 & 0\\ 0 & 0 & -\boldsymbol{u}\boldsymbol{{\rm\nabla}} & 0 & 0\\ 0 & 0 & 0 & 0 & 0\\ 0 & 0 & \boldsymbol{J}_{{\it\varsigma}}\partial _{z} & 0 & -\boldsymbol{u}_{{\it\varsigma}}\boldsymbol{{\rm\nabla}}_{2}\end{array}\!\right),\end{eqnarray}$$
The corresponding invariant operators have the form:
In the rotating layer described by (4.1) and (4.2), the state vector (A 1) remains unchanged, the operators
![]() $\unicode[STIX]{x1D647}$
and
$\unicode[STIX]{x1D647}$
and
![]() $\unicode[STIX]{x1D649}$
in the operator form (A 2) coincide with (A 3a,b
), and
$\unicode[STIX]{x1D649}$
in the operator form (A 2) coincide with (A 3a,b
), and
![]() $\unicode[STIX]{x1D64D}$
is modified as follows:
$\unicode[STIX]{x1D64D}$
is modified as follows:
 $$\begin{eqnarray}\unicode[STIX]{x1D64D}=\left(\begin{array}{@{}ccccc@{}}0 & f & 0 & -\partial _{x} & 0\\ -f & 0 & 0 & -\partial _{y} & 0\\ 0 & 0 & 0 & -\partial _{z} & 0\\ \partial _{x} & \partial _{y} & \partial _{z} & 0 & 0\\ 0 & 0 & \boldsymbol{J}\partial _{z} & 0 & 0\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D64D}=\left(\begin{array}{@{}ccccc@{}}0 & f & 0 & -\partial _{x} & 0\\ -f & 0 & 0 & -\partial _{y} & 0\\ 0 & 0 & 0 & -\partial _{z} & 0\\ \partial _{x} & \partial _{y} & \partial _{z} & 0 & 0\\ 0 & 0 & \boldsymbol{J}\partial _{z} & 0 & 0\end{array}\right).\end{eqnarray}$$
The modification of
![]() $\unicode[STIX]{x1D64D}$
results in the existence here of only one non-local invariant operator instead of the three operators in (A4):
$\unicode[STIX]{x1D64D}$
results in the existence here of only one non-local invariant operator instead of the three operators in (A4):
In the stratified case described by (5.1) and (5.2) the state vector
![]() $\boldsymbol{f}$
has the form
$\boldsymbol{f}$
has the form
![]() $\boldsymbol{f}=(u,v,w,p,b)$
; in the operator form (A 2) the operator
$\boldsymbol{f}=(u,v,w,p,b)$
; in the operator form (A 2) the operator
![]() $\unicode[STIX]{x1D647}$
coincides with (A3a
) and
$\unicode[STIX]{x1D647}$
coincides with (A3a
) and
![]() $\unicode[STIX]{x1D64D}$
and
$\unicode[STIX]{x1D64D}$
and
![]() $\unicode[STIX]{x1D649}$
take the form:
$\unicode[STIX]{x1D649}$
take the form:
 $$\begin{eqnarray}\unicode[STIX]{x1D64D}=\left(\begin{array}{@{}ccccc@{}}0 & 0 & 0 & -\partial _{x} & 0\\ 0 & 0 & 0 & -\partial _{y} & 0\\ 0 & 0 & 0 & -\partial _{z} & -1\\ \partial _{x} & \partial _{y} & \partial _{z} & 0 & 0\\ 0 & 0 & N^{2} & 0 & 0\end{array}\right)\!,\quad \unicode[STIX]{x1D649}=\left(\begin{array}{@{}ccccc@{}}-\boldsymbol{u}\boldsymbol{{\rm\nabla}} & 0 & 0 & 0 & 0\\ 0 & -\boldsymbol{u}\boldsymbol{{\rm\nabla}} & 0 & 0 & 0\\ 0 & 0 & -\boldsymbol{u}\boldsymbol{{\rm\nabla}} & 0 & 0\\ 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & -\boldsymbol{u}\boldsymbol{{\rm\nabla}}\end{array}\right)\!.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D64D}=\left(\begin{array}{@{}ccccc@{}}0 & 0 & 0 & -\partial _{x} & 0\\ 0 & 0 & 0 & -\partial _{y} & 0\\ 0 & 0 & 0 & -\partial _{z} & -1\\ \partial _{x} & \partial _{y} & \partial _{z} & 0 & 0\\ 0 & 0 & N^{2} & 0 & 0\end{array}\right)\!,\quad \unicode[STIX]{x1D649}=\left(\begin{array}{@{}ccccc@{}}-\boldsymbol{u}\boldsymbol{{\rm\nabla}} & 0 & 0 & 0 & 0\\ 0 & -\boldsymbol{u}\boldsymbol{{\rm\nabla}} & 0 & 0 & 0\\ 0 & 0 & -\boldsymbol{u}\boldsymbol{{\rm\nabla}} & 0 & 0\\ 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & -\boldsymbol{u}\boldsymbol{{\rm\nabla}}\end{array}\right)\!.\end{eqnarray}$$
The invariant operator in this case corresponds to conservation of the vertical component of vorticity:
Appendix B. Nonlinear wave adjustment of a rotating barotropic layer
The asymptotic solution to (4.19) and (4.20) has the form (2.18) in which the state vector
![]() $\boldsymbol{f}$
is given by (A 1). In the lowest and first orders we have
$\boldsymbol{f}$
is given by (A 1). In the lowest and first orders we have
Excluding
![]() $p^{(0)}$
from (B 1a,b
), integrating the derived equation over the depth and using (B 2a,b
), one obtains the invariant (4.23), which takes the form (4.25) being expressed in terms of the slow solution (4.24). The fast wave part of the solution
$p^{(0)}$
from (B 1a,b
), integrating the derived equation over the depth and using (B 2a,b
), one obtains the invariant (4.23), which takes the form (4.25) being expressed in terms of the slow solution (4.24). The fast wave part of the solution
![]() $(\tilde{\boldsymbol{u}}^{(0)},\tilde{p}^{(0)},\tilde{{\it\varsigma}}^{(0)})$
is described by (B 1) and (B 2a,b
):
$(\tilde{\boldsymbol{u}}^{(0)},\tilde{p}^{(0)},\tilde{{\it\varsigma}}^{(0)})$
is described by (B 1) and (B 2a,b
):
with the zero invariant (4.26). To find the solution (4.27) one integrates (B 1a,b,d
) over the depth taking into account (B 2a,b
). As a result, one obtains a closed system for
![]() $\tilde{u} ^{(g)}$
,
$\tilde{u} ^{(g)}$
,
![]() $\tilde{v}^{(g)}$
and
$\tilde{v}^{(g)}$
and
![]() $\tilde{{\it\varsigma}}^{(0)}$
, which is readily reduced to (4.29) using (4.26). Subtracting the integrated equations from (B 1a,b,d
) gives simple equations for the inertial oscillations
$\tilde{{\it\varsigma}}^{(0)}$
, which is readily reduced to (4.29) using (4.26). Subtracting the integrated equations from (B 1a,b,d
) gives simple equations for the inertial oscillations
![]() $(\hat{\boldsymbol{u}},0,0)$
, which have a zero pressure in the lowest order and are given by (4.30).
$(\hat{\boldsymbol{u}},0,0)$
, which have a zero pressure in the lowest order and are given by (4.30).
Slow evolution of the PV
![]() ${\it\Pi}^{(0)}$
and the amplitude of the inertial oscillations
${\it\Pi}^{(0)}$
and the amplitude of the inertial oscillations
![]() $A$
is determined from the boundedness of the first-order solution. Excluding
$A$
is determined from the boundedness of the first-order solution. Excluding
![]() $p^{(1)}$
from (B 3a,b
) and integrating the resulting equation over
$p^{(1)}$
from (B 3a,b
) and integrating the resulting equation over
![]() $z$
from −1 to 0 one obtains
$z$
from −1 to 0 one obtains
where
We now apply the fast time average (2.12) to (B 7) and use the representations (2.21), (4.24), (4.27) and (4.30) and the asymptotics (4.31) to derive the evolution equation for the slow QG component:
where
![]() $\text{J}$
is the Jacobian.
$\text{J}$
is the Jacobian.
To derive the equation for the amplitude
![]() $A$
we integrate (B 3a,b
) over
$A$
we integrate (B 3a,b
) over
![]() $z$
from −1 to 0 and subtract the resulting equations from (B 3a,b
). As a result we have
$z$
from −1 to 0 and subtract the resulting equations from (B 3a,b
). As a result we have
where
The solution
![]() $\hat{U} ^{(1)}$
is bounded for
$\hat{U} ^{(1)}$
is bounded for
![]() $t\rightarrow \infty$
if the right-hand side of (B 10a
) does not contain resonance terms proportional to
$t\rightarrow \infty$
if the right-hand side of (B 10a
) does not contain resonance terms proportional to
![]() $\text{e}^{-\text{i}Bt}$
. It follows from (B 3c
) that
$\text{e}^{-\text{i}Bt}$
. It follows from (B 3c
) that
Using (B 11), (4.24) and (4.30), one can readily show that the resonance terms are absent under the condition (4.33).
Appendix C. Wave adjustment in a stratified fluid
To determine the horizontal velocities
![]() $\tilde{u} ,\tilde{v}$
and the pressure
$\tilde{u} ,\tilde{v}$
and the pressure
![]() $p$
, it is convenient to introduce the potential
$p$
, it is convenient to introduce the potential
![]() ${\it\Phi}$
in view of (5.9d
) so that
${\it\Phi}$
in view of (5.9d
) so that
The relations between the Fourier amplitudes
![]() $\hat{\tilde{u} },\hat{\tilde{v}},\hat{p}$
and
$\hat{\tilde{u} },\hat{\tilde{v}},\hat{p}$
and
![]() ${\hat{w}}$
simply follow from (C 1):
${\hat{w}}$
simply follow from (C 1):
In view of (5.19) the series (5.15a
) can be differentiated with respect to
![]() $z$
, and therefore the amplitudes
$z$
, and therefore the amplitudes
![]() $\hat{\tilde{u} }$
,
$\hat{\tilde{u} }$
,
![]() $\hat{\tilde{v}}$
and
$\hat{\tilde{v}}$
and
![]() $\hat{p}$
are also represented as the following series:
$\hat{p}$
are also represented as the following series:
To solve the problem (5.20) for the buoyancy we write
![]() $c$
as the sum
$c$
as the sum
where
![]() $g$
is the solution to the problem:
$g$
is the solution to the problem:
In terms of Fourier amplitudes one finds from (C 4) and (C 5) that
For
![]() $N=\text{const.}$
we have
$N=\text{const.}$
we have
whence the estimate (5.26) follows. For
![]() $N\neq \text{const.}$
the estimate (5.26) is also valid; to show that, one should use the asymptotics of
$N\neq \text{const.}$
the estimate (5.26) is also valid; to show that, one should use the asymptotics of
![]() $G_{n},{\it\lambda}_{n}$
for large
$G_{n},{\it\lambda}_{n}$
for large
![]() $n$
(e.g. Morse & Feshbach Reference Morse and Feshbach1953).
$n$
(e.g. Morse & Feshbach Reference Morse and Feshbach1953).
The solution to the nonlinear problem (5.38) is sought in the asymptotic form (2.18). In the first two approximations we have:
As before, the lowest-order linear system (C 8) and (C 9) coincides (mutatis mutandis) with the linearized system (5.1) and (5.2). Correspondingly, the slow component in the representation (2.21) satisfies (5.6) and (5.7), and (5.8) transforms into (5.41), whence the initial slow fields (5.42) are determined.
To determine the slow evolution of
![]() ${\it\Omega}^{z}$
we obtain an equation for the vertical component of vorticity from (C 10a
) for the horizontal velocities
${\it\Omega}^{z}$
we obtain an equation for the vertical component of vorticity from (C 10a
) for the horizontal velocities
![]() $u^{(1)}$
and
$u^{(1)}$
and
![]() $v^{(1)}$
:
$v^{(1)}$
:
where
![]() ${\it\Omega}^{(0,1)}=v_{x}^{(0,1)}-u_{y}^{(0,1)}$
. Applying to (C 12) the time averaging (2.12) and using the fact that the fast waves decay at a fixed point because of dispersion (see e.g. Zeitlin et al.
Reference Zeitlin, Reznik and Ben Jelloul2003) one arrives at (5.45).
${\it\Omega}^{(0,1)}=v_{x}^{(0,1)}-u_{y}^{(0,1)}$
. Applying to (C 12) the time averaging (2.12) and using the fact that the fast waves decay at a fixed point because of dispersion (see e.g. Zeitlin et al.
Reference Zeitlin, Reznik and Ben Jelloul2003) one arrives at (5.45).
Slow evolution of the surface buoyancy invariants (5.5) follows from (C 10b
) written at
![]() $z=0,-1$
:
$z=0,-1$
:
Taking into account (5.37) averaging (C 13) over the fast time gives (5.46).