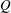1. Introduction
Similarly to the flows around circular cylinders and spheres, the flow past an inclined plate is important in many fluid dynamics applications. However, compared with the flow around those more-studied bodies, the wake behind an inclined plate displays higher complexity, with increased vorticity transport into the wake, asymmetry introduced by the inclination angle and critical transitions occurring at substantially lower Reynolds numbers.
For a two-dimensional normal flat plate, Thompson et al. (Reference Thompson, Hourigan, Ryan and Sheard2006, Reference Thompson, Radi, Rao, Sheridan and Hourigan2014) showed that the initial three-dimensional wake transition occurs at a Reynolds number of
$\mathit{Re}_{c}\simeq 115$
. Indeed, even at such relatively low Reynolds numbers, the two-dimensional wake is quite different from that of a circular cylinder, with the familiar von Kármán wake undergoing a very rapid transition to a two-layered wake within a few diameters downstream (Johnson, Thompson & Hourigan Reference Johnson, Thompson and Hourigan2004; Thompson et al.
Reference Thompson, Hourigan, Ryan and Sheard2006; Saha Reference Saha2007, Reference Saha2013). This first three-dimensional transition is quasi-periodic (QP), i.e. the period of the three-dimensional mode is incommensurate with the two-dimensional shedding frequency. A QP mode has been observed in the circular cylinder wake (Blackburn & Lopez Reference Blackburn and Lopez2003), although the base two-dimensional wake state is quite different in this case. In addition, a further three-dimensional equi-period mode becomes unstable on the unperturbed two-dimensional base flow at
$\mathit{Re}\simeq 140$
. Despite the persistence of these transitions, the flow still remains reasonably two-dimensional for higher Reynolds numbers, perhaps up to
$\mathit{Re}\simeq 200$
(Radi et al.
Reference Radi, Thompson, Sheridan and Hourigan2013). Beyond this Reynolds number range, when the wake is fully three-dimensional, numerical simulations of Najjar & Balachandar (Reference Najjar and Balachandar1998) showed that at
$\mathit{Re}=250$
the formation of streamwise and spanwise wake vortices featured a low-frequency unsteadiness.
The flows over inclined plates for a series of angles of attack were analysed by Zhang, Liu & Lu (Reference Zhang, Liu and Lu2009), Chen, Colonius & Taira (Reference Chen, Colonius and Taira2010) and Yang et al. (Reference Yang, Pettersen, Andersson and Narasimhamurthy2011). On this basis, flows modified by special inlet conditions, such as incident coherent gusts (Afgan et al. Reference Afgan, Benhamadouche, Han, Sagaut and Laurence2013), were studied, and it was conjectured that the thickness of the body plays a key role in the development of the complex wake behind inclined bluff bodies.
In addition to purely two-dimensional plates, interest has also been focused on finite aspect-ratio plates with tapered edges (Narasimhamurthy, Andersson & Pettersen Reference Narasimhamurthy, Andersson and Pettersen2008; Khaledi, Narasimhamurthy & Andersson Reference Khaledi, Narasimhamurthy and Andersson2009). According to those studies, the Strouhal number in the wake of a tapered plate was distinctly lower than in the wake of an equivalent two-dimensional plate, whereas the base pressure coefficient was substantially higher. They revealed a pressure-driven spanwise secondary motion in the near wake, in both the steady laminar case and the turbulent case.
With the growing interest in micro-aerial vehicles (MAVs), the flow around inclined low-aspect-ratio wings (plates) at low Reynolds number has attracted increasing attention over the last decade. For instance, the flapping of Drosophila melanogaster (fruit fly) wings has a characteristic Reynolds number of approximately 100 and the associated flow has been studied by a number of researchers (e.g. Lentick & Dickinson Reference Lentick and Dickinson2009; Harbig, Sheridan & Thompson Reference Harbig, Sheridan and Thompson2013a ,Reference Harbig, Sheridan and Thompson b , Reference Harbig, Sheridan and Thompson2014). The flow fields around airfoils (Hamdani & Sun Reference Hamdani and Sun2000), delta wings (Gordnier & Visbal Reference Gordnier and Visbal2003; Gursul, Gordnier & Visbal Reference Gursul, Gordnier and Visbal2005) and MAV wings (Viieru et al. Reference Viieru, Albertani, Shyy and Ifju2005) have been experimentally modelled and numerical investigated, characterising the flows and examining the wake physics. Notably, in a wind-tunnel study, Torres & Mueller (Reference Torres and Mueller2004) documented the aerodynamic performance of 28 different planforms based on four shapes with different aspect ratios, including the rectangle and ellipse. Subsequently, an analysis of different wing shapes was provided by Taira, Dickson & Colonius (Reference Taira, Dickson and Colonius2007). They compared the force on plates with the same area but different shapes (rectangular, elliptic, semicircular and delta shaped). It was surmised that the addition of curvature along the leading edge delayed the separation of the leading-edge vortex, which increased the potential lift. Following that study, the flows over rectangular plates under actuation (Taira et al. Reference Taira, Dickson and Colonius2007) and periodic excitation (Taira et al. Reference Taira, Rowley, Colonius and Williams2010) were investigated as a means to control the flow.
Experimental methods based on flow visualisation and particle image velocimetry (PIV) have also played an important role in related studies, especially in research on rotating and flapping wing models. For example, Birch (Reference Birch2004) employed a dynamically scaled robot to investigate the forces and flows created by a flapping wing, Lam & Leung (Reference Lam and Leung2005) carried out experiments in a wind tunnel to capture the wake vortices using PIV, Buchholz & Smits (Reference Buchholz and Smits2008) used PIV in a water channel to quantify the vorticity fields in the wake of a pitching panel, Liu & Hsiao (Reference Liu and Hsiao2012) used wind-tunnel smoke visualisation to realise the wingtip vortices and post-stall characteristics of low-aspect-ratio wings and Pitt Ford & Babinsky (Reference Pitt Ford and Babinsky2013) explored the leading-edge vortex structure and lift coefficient with dye flow visualisation, PIV and force measurements. At the same time, tufts have been employed to reveal surface skin friction patterns at the plate surface (Gresham, Wang & Gursul Reference Gresham, Wang and Gursul2009; Shields & Mohseni Reference Shields and Mohseni2012).
Compared with rectangular plates and delta wings, trapezoidal plates add increased geometric complexity, with the leading edge and swept edges at different lengths and angles. It was observed that additional vortices could be created along the swept edges in low-Strouhal-number conditions or for high taper angles (Green, Rowley & Smits Reference Green, Rowley and Smits2011). The swept-edge structures were conjectured to add to the complex three-dimensional flow near the tips of the panel. Rotating trapezoidal plates have been studied using dye visualisation and PIV by DeVoria & Ringuette (Reference DeVoria and Ringuette2012), providing a database of results at different stall positions and sweep angles.
The present study focuses on the body forces and wake characteristics of trapezoidal plates as a function of the parameters defining the geometry. The motivation is to understand the interaction between the trailing vortical wake structures induced by the swept edges, and those produced from leading- and trailing-edge shedding, whether, and if so how, this leads to unsteadiness, and to correlate this back to the time-dependent forces on the plate. Essentially, this study is an extension of that of Taira & Colonius (Reference Taira and Colonius2009), where their focus was mostly on rectangular planforms. The use of trapezoidal plates, rather than rectangular plates, essentially allows a higher degree of variation between the different vortex systems. In general, the interaction between these two vortex systems is important in a variety of three-dimensional flows, for instance in the wake of an Ahmed body, representing a generic model of a hatchback vehicle (Ahmed Reference Ahmed1981; Ahmed, Ramm & Faitin Reference Ahmed, Ramm and Faitin1984). Moreover, recent experimental work shows that variation of the width to height ratio of an Ahmed body causes a significant change in the interaction between the von Kármán-like wake vortices and the C-pillar trailing vortices, resulting in a switch from a low- to a high-drag state (McQueen, Venning & Sheridan Reference McQueen, Venning and Sheridan2014; Venning et al. Reference Venning, Lo Jacono, Burton, Thompson and Sheridan2015).
This study is conducted using full three-dimensional numerical simulations, which allows a detailed analysis of the time-resolved three-dimensional nature of the induced flows.
2. Methodology
2.1. Model description
The fully three-dimensional incompressible flow past an infinitesimally thin inclined trapezoidal plate is considered, as shown in figure 1. The dimensions
$L_{l}$
and
$L_{t}$
represent the lengths of the leading and trailing edges respectively. The plate is placed at an angle of attack (or inclination) to the flow; this angle is denoted by
${\it\alpha}$
, as shown in figure 1(a). The other important parameter is the taper angle of the side edges of the plate,
${\it\Lambda}$
. The chord,
$c$
, is related to the other plate lengths and the taper angle through
$c=(L_{t}-L_{l})\cot ({\it\Lambda})/2$
. The non-dimensional taper ratio,
$\mathit{TR}$
, is defined as
$(L_{t}-L_{l})/L_{t}$
. Thus, a rectangular plate can be thought of as a trapezoidal plate with
$\mathit{TR}=0$
, and similarly a triangular plate corresponds to
$\mathit{TR}=1$
. The other important non-dimensional parameter is the Reynolds number defined as
$\mathit{Re}=u_{\infty }c/{\it\nu}$
, where
$u_{\infty }$
is the free-stream velocity and
${\it\nu}$
is the kinematic viscosity.
Figure 1. (a) Three-dimensional view of the flow geometry showing the position of the plate within the computational domain. (b) Schematic showing key dimensions and parameters of the flow set-up. Only the
$y{-}z$
domain cross-section is shown; this extends
$L_{x}$
in the
$x$
direction (into the page). (c) The plate geometry and dimensions.
Simulations are performed in a large rectangular box, typically of size of (at least)
$(L_{x}\times L_{y}\times L_{z}=)~8c\times 6c\times 12c$
in the spanwise (
$x$
), vertical (
$y$
) and streamwise (
$z$
) directions. Thus, the blockage ratio, i.e. frontal plate area to computational domain cross-section, is restricted to only a few percent with the exact value a function of the plate geometry. The inflow plane is located
$4c$
upstream of the midpoint of the plate, so the outflow length is typically
$8c$
.
Several different definitions of the aspect ratio of non-rectangular plates have been introduced previously. A common definition is
$AR=b_{max}^{2}/S$
, where
$S$
is the plate area and
$b_{max}$
is the maximum span (Sfakiotakis, Lane & Davies Reference Sfakiotakis, Lane and Davies1999). This definition has been widely used (Dong, Mittal & Najjar Reference Dong, Mittal and Najjar2006; Ringuette, Milano & Gharib Reference Ringuette, Milano and Gharib2007; DeVoria & Ringuette Reference DeVoria and Ringuette2012), but it does not appear to be useful for the current study. Because the focus of this paper is on the difference in wake behaviour as the leading-edge to angled-edge shedding is varied, we have adopted the simpler definition that
$AR$
is the ratio of the maximum span to chord (
$AR=b_{max}/c\equiv L_{t}/c$
), as was used by Green et al. (Reference Green, Rowley and Smits2011).
Spatial and temporal results reported in this paper are generally given in terms of non-dimensional units. Lengths are normalised by the plate chord and time is normalised using the chord and free-stream velocity, i.e. the non-dimensional time
$t=t_{d}/T$
,
$T=c/u_{\infty }$
, with
$t_{d}$
the actual flow time.
Eighteen different plate geometries are studied, as listed in table 1. Plates 1–6 maintain the same plate area (
$1~\text{unit}^{2}$
), but with varying aspect ratios and taper angles. Plate 6 is a triangular plate of
$AR=2$
. Plates 7–11 have
$AR=2$
, with the taper angle varied between
$0^{\circ }$
and
$40^{\circ }$
; plates 12–18 have
$AR=4$
, with the taper angle varied between
$0^{\circ }$
and
$60^{\circ }$
.
Table 1. Model dimensions.
2.2. Numerical methodology
The non-dimensionalised fully three-dimensional Navier–Stokes equations are integrated numerically to study the flow structure for
$\mathit{Re}=300$
and 500. These choices were made for two reasons. First, this allows a direct comparison of predictions with those of Taira & Colonius (Reference Taira and Colonius2009) for cases with identical plate geometries. Second, it was decided to study the wake flows at sufficiently low Reynolds numbers so that the saturated wakes were dominated by the initial wake instabilities, allowing easier interpretation of the wake flow behaviour, rather than at higher Reynolds number where the flow structures are less clean. It will be seen that at
$\mathit{Re}=300$
the time-dependent wake structures are relatively weak, while at
$\mathit{Re}=500$
they are much stronger.
The parallelised commercial software Fluent 14.0/14.5 from the ANSYS package is used for the simulations. The key features of the numerical algorithms are now briefly described. The momentum equations are advanced using a second-order upwind difference scheme and the temporal discretisation is based on a second-order (semi-) implicit approach. The equations are discretised in space using the finite-volume method, with all variables defined at the cell centres. The incompressible segregated solver based on the SIMPLEC method to enforce continuity is used. For the infinitesimally thin rectangular and trapezoidal plate models studied, the mesh consists of hexahedral cells over the entire domain. For the single triangular plate geometry, triangular prisms are used to build the mesh in the neighbourhood of the plate, and hexahedral cells extend the mesh out to the domain boundaries. Grid compression is applied towards the plate to capture the higher gradients in those regions. While the time stepping method is semi-implicit, the maximum Courant (CFL) number is restricted to unity, which ensures good temporal resolution of the time-varying flows.
In terms of boundary conditions, at the inlet a uniform free-stream velocity profile (
$u_{z}=u_{\infty }$
,
$u_{x}=u_{y}=0$
) is imposed. The usual no-slip condition is prescribed at the plate surface and the outer domain boundaries are set to be free-slip surfaces. At the outlet, the pressure is set to be constant, and the normal velocity gradient is set to zero.
In the discussions that follow, the forces on the plate are non-dimensionalised to give lift, drag and spanwise force coefficients:
$C_{l}=F_{y}/(({\it\rho}u_{\infty }^{2}A)/2)$
,
$C_{d}=F_{z}/(({\it\rho}u_{\infty }^{2}A)/2)$
. In these equations,
${\it\rho}$
is the fluid density and
$A$
is the plate area. The vorticity is defined as
${\bf\omega}=({\it\omega}_{x},{\it\omega}_{y},{\it\omega}_{z})=\boldsymbol{{\rm\nabla}}\times \boldsymbol{u}$
, with
$\boldsymbol{u}$
the fluid velocity.
For the analysis, the vortical flow structures in the wake are characterised by plotting surfaces of constant
$Q$
(Hunt, Wray & Moin Reference Hunt, Wray and Moin1988), which is defined by
$$\begin{eqnarray}Q\equiv {\textstyle \frac{1}{2}}(\Vert {\it\bf\Omega}\Vert ^{2}-\Vert \unicode[STIX]{x1D64E}\Vert ^{2}),\end{eqnarray}$$
where
${\it\Omega}_{ij}$
and
$\unicode[STIX]{x1D61A}_{ij}$
represent the anti-symmetric and symmetric parts of the rate-of-strain tensor.
For the cases resulting in periodic wake flows, Fourier analysis was used to investigate the frequency information of the flow. Fast Fourier transform routines based on the Cooley–Tukey algorithm (Cooley & Tukey Reference Cooley and Tukey1965) from MATLAB were used to produce power spectra for each lift/drag coefficient time trace. The power spectra reveal the relative energy content of each frequency component, and hence the important frequencies can be identified. The frequencies (
$f$
) are non-dimensionalised by the projected chord length and the free-stream velocity to give equivalent Strouhal numbers, i.e.
$\mathit{St}=fc\sin {\it\alpha}/u_{\infty }$
.
2.3. Validation
Prior to undertaking the simulations, the effects of mesh resolution and domain size are investigated. After preliminary studies, two meshes were constructed to investigate the effect of mesh resolution for the
$AR=2$
rectangular plate. These consisted of
$162\times 132\times 148=3160\,000$
cells (mesh 1) and
$196\times 148\times 172=4990\,000$
cells (mesh 2). The cell size at the plate surface was decreased from
$0.025c$
for mesh 1 to
$0.02c$
for mesh 2. The quantitative effect of mesh resolution was investigated through the time evolution of the lift and drag coefficients. These are shown in figure 2. Clearly, there are slight differences between the curves but the positions and amplitudes of the peaks and troughs match well between the two meshes. At the final time, where the force curves are beginning to asymptote, the difference between the force coefficients provides an indication of spatial accuracy. Since the method is second order in space, through Richardson extrapolation, the difference in the final lift coefficients (
${\rm\Delta}C_{D}\simeq 4\,\%$
) can be extrapolated to give an approximate error estimate for mesh 2 of
$16/9\times 4\,\%\simeq 8\,\%$
. The estimated error for the drag is similar. While these projected errors are not ideal, this is a large parametric study to characterise a complex three-dimensional flow with fine-scale wake flow structures and thin separating shear layers requiring long integration times. These factors place a considerable strain on computational resources and hence it was decided that mesh 2 would provide a good compromise between accuracy and the ability to undertake a comprehensive parameter study, remembering, of course, that the force evolution curves indicate that the essential flow behaviour is still well captured.
Figure 2. Force coefficient evolution comparisons for the grid-resolution/domain-size study. The solid black line represents mesh 1, the solid grey line represents mesh 2 and the dashed black line represents mesh 3: (a) lift coefficient, (b) drag coefficient.
The effect of blockage was also investigated by constructing a mesh based on the resolution of mesh 2, but with the cross-sectional domain size increased from
$8c\times 6c$
to
$10c\times 10c$
, i.e. approximately reducing blockage by a factor of two. This mesh is referred to as mesh 3. For the
$AR=2$
rectangular cylinder, the area blockage ratio is reduced from approximately 4 % to 2 %. This effect is again shown in figure 2. Once more, the peaks, troughs and overall time behaviour are very similar between meshes 2 and 3. The difference between the final lift and drag values indicates a projected blockage error of approximately 4 % for mesh 2, as expected. Thus, for most of the simulation results reported in this paper, meshes based on the resolution of mesh 2 were used.
Figure 3. Comparison of the spanwise vorticity field at midspan for the
$AR=2$
rectangular plate at
${\it\alpha}=30^{\circ }$
and
$\mathit{Re}=100$
for (a)
$t=1.5$
and (b)
$t=7.5$
. Left: experimental results from Taira & Colonius (Reference Taira and Colonius2009) using DPIV; middle: simulations from Taira & Colonius (Reference Taira and Colonius2009); right: simulations from the present study. It should be noted that both the colourmaps and contour levels are only approximately equivalent.
To validate numerical predictions against previously published results, predictions are compared with those from numerical simulations and oil tow-tank experiments of Taira & Colonius (Reference Taira and Colonius2009). Again, the flow around an
$AR=2$
rectangular plate at an inclination angle of
${\it\alpha}=30^{\circ }$
is taken for comparison, but in this case the study was conducted at the much lower Reynolds number of 100. The vorticity field snapshots at different integration times from the present simulation are very close to both the numerical and the experimental results of Taira & Colonius (Reference Taira and Colonius2009), as can seen from figure 3. For a more quantitative comparison, the lift and drag coefficients were compared. Figure 4 shows the lift coefficients obtained from simulations and experiments of Taira & Colonius (Reference Taira and Colonius2009) compared with our predictions. The agreement between the oil tow-tank results is very good except for a slight underprediction for high inclination angles (
${\it\alpha}=70^{\circ }$
and
$80^{\circ }$
) and close to
${\it\alpha}=30^{\circ }$
, where, for the latter case, the numerical prediction for both meshes is about 5 % above the experimental result. Interestingly, this discrepancy at
$30^{\circ }$
remains even after the mesh is adaptively refined based on the magnitude of the local velocity gradient, doubling the total number of cells to approximately 10 million. In terms of the comparison with the simulations of Taira & Colonius (Reference Taira and Colonius2009), the match is very good over the entire domain, again except in the neighbourhood of
$30^{\circ }$
, where the Taira & Colonius (Reference Taira and Colonius2009) simulations show the opposite trend and underpredict the experimental result by approximately a similar amount. Over most of the range of
${\it\alpha}$
, the agreement between the different sets of results is much closer. It should be noted also that the force predictions from the two different meshes used for the current simulations are generally within approximately 1 % of each other. Of course, the experimental results have inherent uncertainty, such as from the influence from the mechanism for holding the plate in place. In addition, the numerical simulations of Taira & Colonius (Reference Taira and Colonius2009) employed a force-based immersed boundary method, which is different from the approach used here. In any case, the comparison provides reasonable confidence in the validity of the current numerical predictions.
Figure 4. Comparison of the lift (a) and drag (b) predictions at
$\mathit{Re}=100$
for an
$AR=2$
rectangular plate with experimental and numerical results from Taira & Colonius (Reference Taira and Colonius2009) as a function of angle of attack
${\it\alpha}$
.
Figure 5 displays the comparison of force coefficients against the numerical predictions of Taira & Colonius (Reference Taira and Colonius2009). The flows over the rectangular plates of
$AR=2$
and
$AR=4$
at various attack angles are considered. Good agreement is observed with the maximum lift coefficients. The comparison for averaged lift and averaged drag is less good, but some of the differences are probably due to the effect of different sampling windows for not perfectly periodic signals. Despite these uncertainties, the overall comparison is favourable, providing confidence to continue with further simulations.
Figure 5. Comparisons with the simulations from Taira & Colonius (Reference Taira and Colonius2009) for the forces on
$AR=2$
(triangles) and 4 (squares) rectangular plates at
$\mathit{Re}=300$
. The filled symbols correspond to the current simulations and the open symbols to those of Taira & Colonius (Reference Taira and Colonius2009): (a) maximum lift coefficient, (b) average lift coefficient at large times, (c) average drag coefficient at large times.
3. Results and discussion
3.1. Constant area plates:
$\mathit{Re}=500$
3.1.1. Lift and drag forces
We begin by surveying the force coefficients exerted on plates for a series of taper ratios for the same plate area, i.e. plates 1–5 and plate 6 of table 1. Figure 6 shows the lift and drag coefficients for selected angles of attack in the critical range:
${\it\alpha}=30^{\circ }$
and
$40^{\circ }$
, for
$\mathit{Re}=500$
. The asymptotic behaviour of the complete set is provided in table 2.
Figure 6. Time histories of force coefficients on flat plates of different taper ratios (
$\mathit{TR}$
) at
$\mathit{Re}=500$
for a range of angles of attack. (a) Lift coefficient,
${\it\alpha}=30^{\circ }$
. (b) Drag coefficient,
${\it\alpha}=30^{\circ }$
. (c) Lift coefficient,
${\it\alpha}=40^{\circ }$
. (d) Drag coefficient,
${\it\alpha}=40^{\circ }$
.
Table 2. Result summary for plates with constant area.
For trapezoidal plates with
${\it\alpha}=30^{\circ }$
and
$\mathit{TR}=0.4$
, 0.6, 0.8 and 1, the lift and drag evolved to asymptotically steady values over a long time. The leading edge in these models is relatively short so that leading-edge vortex shedding is suppressed or at least restricted, which allows the vortex sheets from the swept edges to roll up into trailing vortices that convect downstream without oscillation. The force coefficients on the rectangular plate with the longest leading edge develop a regular period at long times. However, for the trapezoidal plates with
${\it\alpha}=30^{\circ }$
and
$\mathit{TR}=0.2$
, after a sufficiently long transient development, the forces develop small periodic fluctuations with a period close to that seen for the
$\mathit{TR}=0$
rectangular plate, as shown in figure 6(a,b).
If the angle of attack is increased to 40° (see figure 6
c,d), the forces on most of the plates, except the triangular plate, fluctuate with similar periods. It is also clear that the maxima of the lift and drag coefficients over the initial transient period strictly decrease with a reduction of taper ratio. In addition, these flows spend significantly different times prior to entering the QP asymptotic state. This time is denoted by
$t_{m}$
, i.e. the time to reach a mature state.
Some characteristics of the force coefficients are shown in figure 7. Figure 7(a) shows that the maximum lift for the
$\mathit{TR}=0.8$
trapezoidal plate is larger than for any of the other plates over all angles of attack. The maximum lift decreases with decreasing taper ratio, as pointed out above. At increasing angle of attack, the difference in maximum lift between the different plates reduces.
Figure 7. Characteristic force behaviour of the constant-area trapezoidal plates at
$\mathit{Re}=500$
. The rectangular plate (
$\mathit{TR}=0$
) is plotted with hollow squares,
$\mathit{TR}=0.2$
with circles,
$\mathit{TR}=0.4$
with triangles,
$\mathit{TR}=0.6$
with diamonds and
$\mathit{TR}=0.8$
with filled squares: (a) Time-averaged lift coefficient at large times, (b) Time-averaged drag coefficient at large times, (c) maximum lift coefficient, (d) time-averaged lift-to-drag ratio at large times.
For the averaged lift-to-drag ratio shown in figure 7(d), the highest values occurred at
${\it\alpha}=20^{\circ }$
. As reported by Taira & Colonius (Reference Taira and Colonius2009), the average lift-to-drag ratio at large times for an
$AR=1$
rectangular plate reaches its maximum at
${\it\alpha}\simeq 20^{\circ }$
; however, for
$AR=2$
, this occurs at
${\it\alpha}=15^{\circ }$
. For the trapezoidal plate with
$\mathit{TR}=0.8$
,
$AR=1.66$
, and the average lift-to-drag ratio at
${\it\alpha}=10^{\circ }$
is very close to the
${\it\alpha}=20^{\circ }$
value. Indeed, for low angles of attack (
${\it\alpha}\leqslant 20^{\circ }$
) the results show considerable variation, indicating a dependence on
$AR$
. At angles greater than
$20^{\circ }$
, the average lift-to-drag ratio is effectively independent of both
$\mathit{TR}$
and
$AR$
. Figure 7(a,b) shows that this independence holds for the individual time-averaged lift and drag coefficients for this range of angles of attack too.
Figure 8 depicts the characteristic times for the lift coefficient histories where all the cases are run from the same initial conditions, with no imposed noise and initial values determined by the free-stream velocity. The time at which the maximum lift is achieved is denoted by
$t^{\ast }$
. This is presented for a range of
${\it\alpha}$
. Similarly to the finding for rectangular plates,
$t^{\ast }$
for trapezoidal plates falls into the range 0.94–2.08. This is in broad agreement with Taira & Colonius (Reference Taira and Colonius2009), who found that for rectangular planforms the average time after startup was approximately 1.7, with some spread about this value. For all trapezoidal plates at the various angles of attack studied here, a smaller
$\mathit{TR}$
results in a larger
$t^{\ast }$
. One possible interpretation of this is that the maximum lift is achieved by the accumulation of leading-edge vorticity prior to shedding, whereby the longer leading edge of smaller
$\mathit{TR}$
plates allows an increased time to accumulate vorticity before end effects assist in causing shedding.
Figure 8. Characteristic times for the lift coefficient for different plates at various angles of attack. The rectangular plate (
$\mathit{TR}=0$
) is plotted with hollow squares,
$\mathit{TR}=0.2$
with circles,
$\mathit{TR}=0.4$
with triangles,
$\mathit{TR}=0.6$
with diamonds and
$\mathit{TR}=0.8$
with filled squares. (a) The time at which the lift is a maximum,
$t^{\ast }$
. (b) The time at which the lift becomes unsteady,
$t_{m}$
.
The other time,
$t_{m}$
, is defined as the (approximate) time at which the lift history enters into an unsteady final state. Its value follows the rule that on trapezoidal plates for
$\mathit{TR}$
between 0.2 and 0.8, higher
$\mathit{TR}$
implies smaller
$t_{m}$
. Despite this,
$t_{m}$
for the rectangular plate (
$\mathit{TR}=0$
) is always smaller than for the
$\mathit{TR}=0.2$
trapezoidal plate. While these times are likely to be strongly influenced by the effective numerical noise in the simulations, the relative times should reflect the growth rate of the instability triggering the oscillatory state.
3.1.2. Vortex-shedding mechanism: plate area
$=1$
,
$\mathit{Re}=500$
Isosurfaces of
$Q=10$
behind constant aspect-ratio plates 1–6 (
$\text{area}=1$
) are depicted in figure 9 to highlight the vortex-shedding mechanism. These visualisations correspond to the
${\it\alpha}=40^{\circ }$
models at
$t=70$
and
$\mathit{Re}=500$
. The isosurfaces are coloured by streamwise vorticity (
${\it\omega}_{z}$
) in the range of
$-0.04{-}0.04$
.
Figure 9. Top-down angled view of the isosurface of
$Q=10$
coloured by streamwise vorticity to highlight the vortex structures in the wake of
$\text{area}=1$
plates 1–6 at
${\it\alpha}=40^{\circ }$
,
$\mathit{Re}=500$
and
$t=70$
: (a)
$\mathit{TR}=0$
; (b)
$\mathit{TR}=0.2$
; (c)
$\mathit{TR}=0.4$
; (d)
$\mathit{TR}=0.6$
; (e)
$\mathit{TR}=0.8$
; (f)
$\mathit{TR}=1$
. These structures are similar to those observed from a sphere.
In all plates except the triangular model, the flows over the swept edges roll up and interact with the leading-edge vortex. As the
$\mathit{TR}$
decreases, the leading edge is lengthened, and the swept edges and trailing edge are shortened accordingly. The shed leading-edge vortices gradually become more dominant in the downstream flow, an effect of which is to narrow the opening of the vortex rings. For the triangular model (figure 9
f), most of the wake vorticity is due to the sheet flow over the swept edges, and its forming wake vortex loops have the widest openings.
3.2. Constant aspect-ratio plates
3.2.1. Vortex-shedding mechanisms and the relationship to lift force:
$AR=2$
For the constant area plates discussed above, when the taper ratio is changed, both
$AR$
and
${\it\Lambda}$
(°) need to be varied to achieve this. This complicates the analysis of the relationship between the flow characteristics and the geometric parameters. Hence the following discussion focuses on constant aspect-ratio plates.
The lift coefficients of different plates with
$AR=2$
are plotted in figure 10. Corresponding
$Q$
isosurfaces coloured by streamwise vorticity at marked times are displayed in figure 11 for the
${\it\Lambda}=10^{\circ }$
case at
${\it\alpha}=30^{\circ }$
. The asymptotic behaviours of the full set at the two Reynolds numbers investigated are provided in tables 3 and 4. When
$\mathit{Re}=500$
, the wakes displays stronger wake structures and are generally more chaotic than those at the lower Reynolds number. Thus, the lower Reynolds number cases at
$\mathit{Re}=300$
allow a less complicated analysis and interpretation of the cleaner flows than the similar but more chaotic flows at higher Reynolds number, and are the main focus of this section.
Figure 10. Lift coefficients for flow over
$AR=2$
flat plates at
$\mathit{Re}=300$
. (a) Here,
${\it\Lambda}=0^{\circ }$
, 10°, 20°, 30° and 40° at
${\it\alpha}=30^{\circ }$
. (b) Periodic flows:
${\it\Lambda}=0^{\circ }$
at
${\it\alpha}=25^{\circ }$
;
${\it\Lambda}=10^{\circ }$
, 20°at
${\it\alpha}=30^{\circ }$
;
${\it\Lambda}=30^{\circ }$
, 40° at
${\it\alpha}=40^{\circ }$
. (c) Long-time lift variation for
${\it\Lambda}=10^{\circ }$
,
${\it\alpha}=30^{\circ }$
. (d) Long-time lift variation for
${\it\Lambda}=20^{\circ }$
,
${\it\alpha}=30^{\circ }$
.
Figure 11. Top row: top-down angled view of the isosurface for
$Q=10$
coloured by streamwise vorticity behind an
$AR=2$
trapezoidal plate at
${\it\Lambda}=10^{\circ }$
,
${\it\alpha}=30^{\circ }$
and
$\mathit{Re}=300$
. Bottom row: corresponding spanwise vorticity plots in the centre plane showing the leading-edge shedding that is associated with the observed lift coefficient variation. The surfaces correspond to the times marked in figure 10(c): (a)
$t_{1}$
; (b)
$t_{2}$
; (c)
$t_{3}$
; (d)
$t_{4}$
.
Table 3. Result summary for plates with the same aspect ratio (
$AR=2,\mathit{Re}=300$
).
Table 4. Result summary for plates with the same aspect ratio (
$AR=2,\mathit{Re}=500$
).
At
${\it\alpha}=30^{\circ }$
and
$\mathit{Re}=300$
, the wakes of plates with
${\it\Lambda}=0^{\circ }$
,
$10^{\circ }$
and
$20^{\circ }$
are unsteady. The flow over the rectangular plate is aperiodic and the remaining two plates have periodic (or near-periodic) wakes. As depicted in the lift traces, the first maximum occurs at almost the same time. However, compared with the lift trace for the rectangular plate, those for the trapezoidal plates lack the second peak, which occurs when the leading-edge hairpin vortex first detaches at approximately
$t=8$
. One possible reason why this occurs for trapezoidal plates is that the leading-edge shedding is interfered with by the vortex structures from the rollup over the swept edges, especially as the leading-edge vortex intensity is weak relative to the trailing vortices. This seems to limit the magnitude of the lift from trapezoidal plates.
With an increase in taper angle, the plate area is reduced and the fluctuations are generally also reduced. In the lift coefficient trace for the plate with
${\it\Lambda}=20^{\circ }$
(figure 10
d), the signal asymptotes to a near-periodic state, although of amplitude less than 0.02, i.e. only 3 % of the mean lift. This fluctuation is barely observable in figure 10(a).
Figure 10(b) shows cases that evolve to near-periodic lift signals for plates with
$AR=2$
. For the rectangular plate (
${\it\Lambda}=0^{\circ }$
), periodic flow first occurs at
${\it\alpha}=25^{\circ }$
. The periods are similar for each of these cases.
Figure 10(c,d) shows that there are some common features of both shedding cycles: both periods are close to 11 and there are two peaks within each period. The amplitude of the lift fluctuations for the plate with the longer leading edge is approximately twice that for the shorter one. As listed in table 3, the dominant frequencies in these cases of trapezoidal plates with
${\it\Lambda}=10^{\circ }$
and
${\it\Lambda}=20^{\circ }$
at
${\it\alpha}=30^{\circ }$
are found to be particularly low. The corresponding dominant Strouhal numbers are only 0.096 and 0.087 respectively. In fact, the time traces of the lift signals show that they actually repeat over two of these cycles. Thus, there appears to be weak period doubling in both cases.
The constant
$Q$
isosurfaces illustrate the shedding characteristics directly. As shown in figure 11(a–c), which corresponds to a high lift state, the hairpin vortex that forms from the leading-edge separation zone has completely formed and advects downstream. There are some differences in vortex structures that have rolled up from the swept edges and the vortex arch structure at the back of the plate (see figure 11
a). Relative to figure 11(d), the vortex arch is more fully formed and/or closer to the plate surface in the other higher lift cases, and since it should be associated with a low core pressure, the proximity to the back surface and the increased strength presumably explain the higher force for the first three panels. The situation is further elucidated through the corresponding spanwise vorticity plots in the centre plane, shown below each
$Q$
isosurface. In figure 11(b), it is clear that the leading-edge vortex is forming and strengthening, moving towards a state at which it will shed. However, figure 11(c) indicates that the shedding does not take place, seemingly through the interaction of the trailing-edge shedding. Thus the next shedding cycle is considerably delayed, leading to a much longer period cycle than in the larger
${\it\alpha}$
cases. It can be seen in figure 11(d) that the leading-edge vortex is just starting to roll up into a new leading-edge vortex, marking the beginning of a new shedding cycle.
For the trapezoidal plate with
${\it\Lambda}=20^{\circ }$
, the oscillatory behaviour is even weaker. There is a very long time before the lift begins to even regularly fluctuate, and then the fluctuation amplitude is only slightly more than 1 % of the mean lift. This is presumably because of the reduced relative span of the leading edge, weakening the leading-edge shedding that is mainly responsible for the lift periodicity.
At this small angle of attack (i.e.
$30^{\circ }$
), the vertical distance between the leading edge and the trailing edge is very short and the vortex arch, which feeds the upward-bending vortex hairpins as they are released and advect downstream, is weak relative to cases at a larger angle of attack. Thus, this means that the wake formation is dominated by the formation and rollup of the trailing vortices from the swept edges, and this appears to be a steady process, at least at low Reynolds numbers. Hence, again, these cases lead to little fluctuation of the asymptotic lift signal. This inclination angle results in a transitional state between steady flow and larger amplitude periodic flow. However, true periodic flow only results from a particular combination of planform, angle of attack and Reynolds number. For the cases that have just been examined, periodic flow is suppressed on increasing the angle of attack.
For a rectangular plate, figure 12 highlights the vortex structure together with streamlines, corresponding to times when the lift trace shows peaks and troughs. The biggest noticeable difference between the two states is in the shedding process of the leading-edge vortex: the lift is maximal when the arch vortex, which forms into the upward-bending wake hairpins, begins to shed, while the lift is minimal while this arch vortex is still growing and forming. This situation is confirmed by the streamline plots in figure 12(c,d). These show that at maximum lift, there is considerable swirling flow at the back of the plate associated with the release of the hairpin vortex structure into the wake, while figure 12(d) shows that this is not the case while the vortex arch is still forming. (This swirling flow is associated with lower pressure, and hence increased lift.)
Figure 12. Isosurfaces of
$Q=10$
together with streamlines over the
$AR=2$
rectangular plate at two times corresponding to a peak and a trough in the lift signal at
$\mathit{Re}=300$
: (a) isosurface for
${\it\Lambda}=0^{\circ }$
,
${\it\alpha}=30^{\circ }$
,
$C_{L}$
peak, (b) isosurface for
${\it\Lambda}=0^{\circ }$
,
${\it\alpha}=30^{\circ }$
,
$C_{L}$
trough, (c) streamlines,
$C_{L}$
peak, (d) streamlines,
$C_{L}$
trough.
For the increasingly swept-edge trapezoidal plates of
${\it\Lambda}=30^{\circ }$
and
$40^{\circ }$
(see figure 13), the hairpins/vortex loops that form and shed into the wake are generated when the angle of attack is increased to
$40^{\circ }$
. In this case, the hairpins bend downwards and are formed from the combined leading-edge shedding and swept-edge trailing vortices. These two vortex systems are no longer separate, as was the case for lower sweep angles (and/or longer leading edges). In these two cases, the fluctuation amplitude of the lift signal reaches approximately 6 % of the mean, considerably larger than for the lower taper-angle cases discussed above.
Figure 13. Isosurfaces of
$Q=10$
showing the flow structure behind different
$AR=2$
trapezoidal plates at different inclinations at
$\mathit{Re}=300$
. The images correspond to either peaks or troughs in the lift trace: (a)
${\it\Lambda}=30^{\circ }$
,
${\it\alpha}=40^{\circ }$
,
$C_{L}$
peak; (b)
${\it\Lambda}=30^{\circ }$
,
${\it\alpha}=40^{\circ }$
,
$C_{L}$
trough; (c)
${\it\Lambda}=40^{\circ }$
,
${\it\alpha}=40^{\circ }$
,
$C_{L}$
peak; (d)
${\it\Lambda}=40^{\circ }$
,
${\it\alpha}=40^{\circ }$
,
$C_{L}$
trough.
Views of streamlines starting from close to the edges of the trapezoidal plates are shown in figures 14–16 at times when the lift is maximal and minimal. The lines are coloured by red, blue, green and yellow to allow the downstream flows over the leading edge, trailing edge, left swept edge and right swept edge respectively to be distinguished. For the cases of
${\it\Lambda}=10^{\circ }{-}20^{\circ }$
,
${\it\alpha}=30^{\circ }$
and
${\it\Lambda}=30^{\circ }{-}40^{\circ }$
,
${\it\alpha}=40^{\circ }$
, as shown in figure 10(b), the force coefficients on these plates fluctuate periodically in the asymptotic state. Consistent with this, the corresponding streamlines show both bilateral symmetry and periodicity (see figures 14
a,b,e,f and 15). Although these visualisations only represent instantaneous views of the wakes rather than particle tracers, two broad types of periodic unsteady flow can be inferred from these sets of instantaneous streamline plots. When the taper angle is small (i.e.
${\it\Lambda}=10^{\circ }{-}20^{\circ }$
), these plots suggest that the fluid passing the swept edges gets fed into the wake as two laterally separated trailing vortices, while the fluid passing over the leading edge rolls up into a semi-persistent attached vortical structure, which feeds fluid outwards from the centre into those trailing vortices. The streamlines originating near the trailing edge also show this lateral displacement of fluid axial motion along the vortex core into the trailing vortices. At the larger taper angles,
${\it\Lambda}=30^{\circ }{-}40^{\circ }$
, the situation is distinctly different. In this case, the streamlines suggest much less lateral displacement of fluid outwards. In addition, there is no longer a large lateral separation of the trailing vortices. Similarly to the rectangular plate, the lift is a maximum when the spanwise aligned vortex formed from fluid passing over the leading edge is just about to shed, while the minimum lift occurs when the trailing-edge vortex forms (in particular, see figure 16
b,d,f,h).
Figure 14. Streamlines over
$AR=2$
trapezoidal plates with the same taper angle at different angles of attack, at the times corresponding to the peak lift and troughs, at
$\mathit{Re}=300$
: (a)
${\it\Lambda}=10^{\circ }$
,
${\it\alpha}=30^{\circ }$
,
$C_{L}$
peak; (b)
${\it\Lambda}=10^{\circ }$
,
${\it\alpha}=30^{\circ }$
,
$C_{L}$
trough; (c)
${\it\Lambda}=10^{\circ }$
,
${\it\alpha}=40^{\circ }$
,
$C_{L}$
peak; (d)
${\it\Lambda}=10^{\circ }$
,
${\it\alpha}=40^{\circ }$
,
$C_{L}$
trough; (e)
${\it\Lambda}=20^{\circ }$
,
${\it\alpha}=30^{\circ }$
,
$C_{L}$
peak; (f)
${\it\Lambda}=20^{\circ }$
,
${\it\alpha}=30^{\circ }$
,
$C_{L}$
trough; (g)
${\it\Lambda}=20^{\circ }$
,
${\it\alpha}=40^{\circ }$
,
$C_{L}$
peak; (h)
${\it\Lambda}=20^{\circ }$
,
${\it\alpha}=40^{\circ }$
,
$C_{L}$
trough.
Figure 15. Streamlines over
$AR=2$
trapezoidal plates at
${\it\alpha}=40^{\circ }$
, at the times corresponding to the peak lift and troughs, at
$\mathit{Re}=300$
: (a)
${\it\Lambda}=30^{\circ }$
,
${\it\alpha}=40^{\circ }$
,
$C_{L}$
peak; (b)
${\it\Lambda}=30^{\circ }$
,
${\it\alpha}=40^{\circ }$
,
$C_{L}$
trough; (c)
${\it\Lambda}=40^{\circ }$
,
${\it\alpha}=40^{\circ }$
,
$C_{L}$
peak; (d)
${\it\Lambda}=40^{\circ }$
,
${\it\alpha}=40^{\circ }$
,
$C_{L}$
trough.
Figure 16. The side view of the streamlines over
$AR=2$
trapezoidal plates, at times corresponding to the peak lift and troughs, at
$\mathit{Re}=300$
: (a)
${\it\Lambda}=10^{\circ }$
,
${\it\alpha}=40^{\circ }$
,
$C_{L}$
peak; (b)
${\it\Lambda}=10^{\circ }$
,
${\it\alpha}=40^{\circ }$
,
$C_{L}$
trough; (c)
${\it\Lambda}=20^{\circ }$
,
${\it\alpha}=40^{\circ }$
,
$C_{L}$
peak; (d)
${\it\Lambda}=20^{\circ }$
,
${\it\alpha}=40^{\circ }$
,
$C_{L}$
trough; (e)
${\it\Lambda}=30^{\circ }$
,
${\it\alpha}=40^{\circ }$
,
$C_{L}$
peak; (f)
${\it\Lambda}=30^{\circ }$
,
${\it\alpha}=40^{\circ }$
,
$C_{L}$
trough; (g)
${\it\Lambda}=40^{\circ }$
,
${\it\alpha}=40^{\circ }$
,
$C_{L}$
peak; (h)
${\it\Lambda}=40^{\circ }$
,
${\it\alpha}=40^{\circ }$
,
$C_{L}$
trough.
3.2.2. Analysis of
$AR=4$
trapezoidal plates
Plates with
$AR=4$
are considered to examine the effect of aspect ratio. The asymptotic behaviours of this set of plates at
$\mathit{Re}=300$
are provided in table 5, including the measured Strouhal numbers when the wake is periodic. Compared with the flows over the smaller aspect ratio
$AR=2$
plates, these wakes show increased fluctuations at lower angles of attack (
${\it\alpha}>20^{\circ }$
). The dominant Strouhal number for most of these cases lies in the range
$\mathit{St}\in [0.13,0.19]$
.
Figure 17. Isosurfaces of
$Q=10$
coloured by streamwise vorticity for the trapezoidal plates with
${\it\Lambda}=20^{\circ }$
at a range of angles of attack. Here,
$AR=4$
,
$\mathit{Re}=300$
: (a) Lift peak,
${\it\alpha}=20^{\circ }$
, (b) Lift peak,
${\it\alpha}=30^{\circ }$
, (c) Lift peak,
${\it\alpha}=40^{\circ }$
, (d) Lift trough,
${\it\alpha}=20^{\circ }$
, (e) Lift trough,
${\it\alpha}=30^{\circ }$
, (f) Lift trough,
${\it\alpha}=40^{\circ }$
.
Table 5. Result summary for plates with the same aspect ratio (
$AR=4,\mathit{Re}=300$
).
Constant
$Q$
isosurfaces and spanwise vorticity contours
$0.75c$
downstream of the plate centres for the
$AR=4$
trapezoidal plates are displayed in figures 17–20 for
${\it\Lambda}=20^{\circ }$
(17 and 18) and
${\it\Lambda}=50^{\circ }$
(19 and 20). Figures 18 and 20 additionally show the streamlines within the cross-stream plane. These show that the direction of swirl of the streamwise vortices internal to the swept-edge vortices changes during the lift cycle, at least for
${\it\alpha}\leqslant 30^{\circ }$
. Similarly to the lower angle of attack
$AR=2$
plates, the isosurface plots for the larger aspect ratios show that the near wake consists of effectively independent shedding of trailing vortices from the swept edges together with shedding originating from the leading and trailing edges. As the angle of attack is increased to
$30^{\circ }$
, the shed hairpins are recognisably upward-facing. This contrasts with the situation for the
$AR=4$
plate with
${\it\Lambda}=50^{\circ }$
, where there is no longer a distinction between the trailing swept-edge vortices and the internal hairpins, as is shown in figure 19. This is presumably due to the higher circulation from the swept-edge vortices and reduced leading-edge vorticity from the shorter leading edge, which couple together to produce the different behaviour. While the wake is complex, there are distinct downward-facing hairpins entering the wake, especially noticeable at the highest angle of attack (e.g. see figure 19
f).
Figure 18. Cross-stream view showing coloured contours of spanwise vorticity with overlaid streamlines in a plane
$0.75c$
downstream from the midpoint of the plate. The geometry is a trapezoidal plate with
${\it\Lambda}=20^{\circ }$
. Here,
$AR=4$
,
$\mathit{Re}=300$
: (a) lift peak,
${\it\alpha}=20^{\circ }$
, (b) lift peak,
${\it\alpha}=30^{\circ }$
, (c) lift peak,
${\it\alpha}=40^{\circ }$
, (d) lift trough,
${\it\alpha}=20^{\circ }$
, (e) lift trough,
${\it\alpha}=30^{\circ }$
, (f) lift trough,
${\it\alpha}=40^{\circ }$
.
Figure 19. Isosurfaces coloured by streamwise vorticity for the trapezoidal plates with
${\it\Lambda}=50^{\circ }$
at a range of angles of attack. Here,
$AR=4$
,
$\mathit{Re}=300$
. The isosurfaces are extracted for
$Q=4$
in (a,d) and
$Q=10$
in (b,c,e,f): (a) lift peak,
${\it\alpha}=20^{\circ }$
, (b) lift peak,
${\it\alpha}=30^{\circ }$
, (c) lift peak,
${\it\alpha}=40^{\circ }$
, (d) lift trough,
${\it\alpha}=20^{\circ }$
, (e) lift trough,
${\it\alpha}=30^{\circ }$
, (f) lift trough,
${\it\alpha}=40^{\circ }$
.
Figure 20. Cross-stream view showing coloured contours of spanwise vorticity with overlaid streamlines in a plane
$0.75c$
downstream from the midpoint of the plate. The geometry is a trapezoidal plate with
${\it\Lambda}=50^{\circ }$
,
$AR=4$
,
$\mathit{Re}=300$
: (a) lift peak,
${\it\alpha}=20^{\circ }$
, (b) lift peak,
${\it\alpha}=30^{\circ }$
, (c) lift peak,
${\it\alpha}=40^{\circ }$
, (d) lift trough,
${\it\alpha}=20^{\circ }$
, (e) lift trough,
${\it\alpha}=30^{\circ }$
, (f) lift trough,
${\it\alpha}=40^{\circ }$
.
3.3. Aperiodic wake behaviour
At higher angles of attack, tables 3–5 indicate that the wakes become aperiodic. The aperiodicity becomes stronger as the Reynolds number is increased. This can be attributed to loss of centre plane reflection symmetry in the wake, as was found in the study of Taira & Colonius (Reference Taira and Colonius2009). In fact, for lower angles of attack and Reynolds numbers, the loss of wake symmetry is relatively minor and is not easily detectable in the
$Q$
isosurface plots, although it is clear in instantaneous streamline plots. As an example of an aperiodic wake state, figure 21 displays
$Q$
isosurfaces coloured by streamwise vorticity for the
$AR=4$
plate with
${\it\Lambda}=20^{\circ }$
,
${\it\alpha}=40^{\circ }$
at
$\mathit{Re}=500$
, where the loss of wake symmetry is clear.
Figure 21. Isosurface of
$Q=10$
for an
$AR=4$
trapezoidal plate with
${\it\Lambda}=20$
,
${\it\alpha}=40$
, at
$\mathit{Re}=500$
, clearly showing loss of wake symmetry.
3.4. Frequency analysis and stability of the wake
Additional analysis is made of the behaviour of the force coefficients at large times. For all the plates, after the decay of the initial transients generated by the impulsive start, the wake reaches either a steady or an unsteady state. Increased angle of attack tends to increase the unsteadiness. For rectangular plates at
$\mathit{Re}=300$
, the lift signal shows periodic characteristics when the angle of attack reaches
$25^{\circ }$
, with the dominant frequency found to be approximately
$\mathit{St}=0.12$
(figure 22
a); this conforms to previous studies (Taira et al.
Reference Taira, Dickson and Colonius2007). When the angle of attack is increased to
$30^{\circ }$
, the flows over the smaller taper-angle plates become periodic as well (
${\it\Lambda}=10^{\circ },~20^{\circ }$
, figure 10
c,d). The periodicity appears to be mostly associated with shedding of the leading-edge vortex and the corresponding Strouhal number is much smaller (approximately 0.05, see figure 22
c,d). The characteristic Strouhal number increases with increasing angle of attack (see figure 22
e,f).
Figure 22. The power spectral density of lift traces on the plates of
$AR=2$
,
$\mathit{Re}=300$
.
When the angle of attack is increased to
$40^{\circ }$
, together with an increase in taper angle, the vortical flows over the swept edges interact with the leading-edge vortices. Vortex hairpins develop and gradually dominate the wake flow (figure 13). The Strouhal number increases to the vicinity of 0.18 (see figure 22
g,h). In these cases with higher taper angle, the plate area is reduced, and the corresponding Strouhal number is larger.
Figures 23 and 24 show the power spectra of the lift traces on larger aspect-ratio
$AR=4$
plates at
${\it\alpha}=20^{\circ }$
and
${\it\alpha}=30^{\circ }$
. These plots demonstrate that the dominant Strouhal numbers are approximately 0.14 when the flows are in a stable periodic state. However, for taper angle/angle of attack, when the wake periodicity is due to leading-edge vortices only, the dominant Strouhal number is again reduced. For a case such as shown in figure 23(f), the dominant Strouhal number is less than 0.1.
Figure 23. The power spectral density of lift traces on the plates of
$AR=4$
,
${\it\alpha}=20^{\circ }$
,
$\mathit{Re}=300$
.
Figure 24. The power spectral density of lift traces on the plates of
$AR=4$
,
${\it\alpha}=30^{\circ }$
,
$\mathit{Re}=300$
.
In order to illustrate this contrast, the lift traces and corresponding power spectra for a single plate (
$AR=4$
,
${\it\Lambda}=50^{\circ }$
) at various angles of attack (
${\it\alpha}=20^{\circ },~30^{\circ }$
and
$40^{\circ }$
) are plotted in figure 25, where the changes to the lift signal and dominant Strouhal number can be directly observed.
Figure 25. The power spectral density of lift traces on the trapezoidal plates of
$AR=4$
,
${\it\Lambda}=50^{\circ }$
${\it\alpha}=30^{\circ }$
,
$\mathit{Re}=300$
. (a) Lift trace. (b) Power spectral density of the lift traces.
3.5. Wake state dependence on Reynolds number and aspect ratio
Although tables 3–5 indicate the observed asymptotic wake states for trapezoidal plates as the taper angle and angle of attack vary, it is worth consolidating the data into parameter maps to explicitly highlight the effects of changing the Reynolds number and aspect ratio. This has been done in figure 26. Figure 26(b), the reference parameter map, shows, as has been discussed, that an increase in the angle of attack results in the wake state changing from steady to periodic to aperiodic. This is expected given that the Reynolds number is based on the chord of the plate rather than the height normal to the flow. Thus, higher
${\it\alpha}$
will result in stronger leading and trailing wake vortices leading to stronger interaction and shedding. On the other hand, increasing the taper angle is equivalent to reducing the length of the leading edge relative to the trailing edge, which in turn will weaken the leading-edge shedding resulting in a delay of the two transitions to higher angles of attack. Comparison with figure 26(a) shows the shift in the transition boundaries as the Reynolds number is increased from
$\mathit{Re}=300$
to 500. The overall effect is to shift the two transitions to smaller angles of attack by approximately
$10^{\circ }$
. This is consistent with the previous discussion. A comparison with figure 26(c) shows the effect of increasing the aspect ratio from 2 to 4 at a fixed Reynolds number of 300. The increased aspect ratio results in a lowering of the aspect ratio for steady to periodic transition, with the periodic state occurring over a larger range of
${\it\alpha}$
than for the smaller aspect-ratio case – approximately
$20^{\circ }$
rather than
$10^{\circ }$
. The effect of the taper angle is less strong in this case, reflecting the fact that physically the wake state might be expected to scale more strongly with the ratio of the leading- to trailing-edge length. It should be noted that the vertical range for each of these maps covers purely rectangular plates at the lower end to triangular plates at the upper end.
Figure 26. Wake state as a function of taper angle (
${\it\Lambda}$
) and angle of attack (
${\it\alpha}$
) for trapezoidal plates. The reference parameter map (b) shows the wake state (steady, open symbols; periodic, half-filled symbols; aperiodic, filled symbols) for fixed
$\mathit{Re}=300$
and
$AR=2$
. The transition boundaries are only approximate. The parameter map (a) shows the effect of increasing the Reynolds number from
$\mathit{Re}=300$
to 500, and (c) shows the effect of changing the aspect ratio from
$AR=2$
to 4.
4. Conclusion
The low-Reynolds-number wake flows over inclined trapezoidal plates with various planforms have been computed. The eighteen different plate geometries investigated fall into three broad sets. For the first, the aspect ratio is fixed at 4, with the taper angle taking values between
$0^{\circ }$
and
$60^{\circ }$
. The second set is similar but the aspect ratio is fixed at
$AR=2$
. This includes an
$AR=2$
triangular plate. The third set incorporates plates with constant area, changing aspect ratio and taper angle to allow this constraint.
The evolution of the force coefficients on plates with the same area was studied first. The taper ratio and angle of attack were found to have a significant influence on the wake stability and asymptotic forces experienced by the body. Smaller taper ratios result in lower maximum lift, while an increase in the angle of attack results in a reduction in the difference between the maximum lift generated for the different plates. The set of plates was also compared in terms of two characteristic times:
$t^{\ast }$
, the time at which the maximum lift is achieved, and
$t_{m}$
, the time at which the lift signal enters the asymptotic state. (It is likely that
$t^{m}$
will be a function of numerical or experimental noise, since the transition from a steady to an unsteady wake is presumably caused by a linear instability. The initial amplitude of the instability is a function of the initial noise level. However, the order of
$t^{m}$
between the different geometries is likely to remain the same for the same initial noise level.) Similarly to the rectangular plate, the
$t^{\ast }$
values for trapezoidal plates were approximately 1.7 (Taira & Colonius Reference Taira and Colonius2009). For trapezoidal plates with
$\mathit{TR}$
varying between 0.2 and 0.8, higher
$\mathit{TR}$
resulted in smaller
$t_{m}$
. However, this trend did not continue for the purely rectangular plate (
$\mathit{TR}=0$
). For that case
$t_{m}$
was always smaller than for the closest trapezoidal plate with
$\mathit{TR}=0.2$
. Interestingly, the asymptotic lift-to-drag ratio of plates with the same area is independent to within a few percent of the taper angle for angles of attack of
$20^{\circ }$
or above.
To study the vortex-shedding mechanism, constant
$Q$
isosurfaces together with streamlines in the cross-stream plane just downstream of the trailing edge were employed. For the plates with the same area, a decrease in
$\mathit{TR}$
is associated with an increase in the leading-edge length, and the swept-edge and trailing-edge lengths are reduced. This changes the vortical wake structures somewhat, and in particular, narrows the opening of the vortex loops.
Two kinds of periodic unsteady flow are found in the
$AR=2$
plate models. At the smaller angles of attack (
${\it\alpha}<30^{\circ }$
), the wake consists of two sets of longitudinal vortex structures: those associated with the rollup over the swept edges and those that originate from leading- and trailing-edge shedding. These two vortex systems shed into the wake relatively independently, with the low-amplitude periodicity due to the latter source. This behaviour occurs for small taper angles (
${\it\Lambda}=10^{\circ }$
,
$20^{\circ }$
). The shedding frequency in this state is particularly low, with a corresponding Strouhal number of approximately 0.09. Indeed, the wake only strictly repeats after two cycles. Another form of wake appears at increased angles of attack (
$40^{\circ }$
). In these cases, the flows over the swept edge interact strongly with the leading-edge vortices. This produces a regular stream of vortex loops which are shed into the wake. The Strouhal number associated with this type of shedding is considerably larger at approximately 0.18. As the Reynolds number or angle of attack is increased, the wake loses centre plane reflection symmetry, similarly to what is observed for a sphere wake on increasing the Reynolds number (Mittal Reference Mittal1999). This is subtle at the lower Reynolds number studied, but leads to considerable wake distortion at the higher Reynolds numbers, as shown in figure 21.
For the
$AR=4$
plate models, similarly to the low-angle-of-attack
$AR=2$
trapezoidal plate, the constant
$Q$
isosurfaces show that the wake consists of effectively independent shedding of trailing vortices from the swept edges together with shedding originating from the leading and trailing edges. As the angle of attack is increased to
$30^{\circ }$
, the shed hairpins are recognisably upward-facing. The corresponding Strouhal number is approximately 0.14. Yet when the taper angle is increased to
${\it\Lambda}=50^{\circ }$
at very small angles of attack (
$20^{\circ }$
), there is no longer a distinction between the trailing swept-edge vortices and internal hairpins. For this case, the corresponding Strouhal number is approximately 0.07, and the fluctuations tend to flatten out at very large times.
Apart from the aperiodic cases, where the wake becomes asymmetric relative to the vertical centre plane, the leading-edge vortices and swept-edge trailing vortices interact only relatively weakly near the plate surface. In particular, there appears to be little transport of spanwise vorticity along the leading-edge vortex cores towards the swept-edge trailing vortices to delay separation, as was also observed by Taira & Colonius (Reference Taira and Colonius2009) in their rectangular plate studies. They also considered some plates with curved leading edges to induce spanwise flow, but again the spanwise flow of vorticity was insufficient to prevent/delay leading-edge vortex shedding, as is observed for rotating wing planforms, e.g. Birch (Reference Birch2004) and Harbig et al. (Reference Harbig, Sheridan and Thompson2013b ). As has been previously pointed out by Taira & Colonius (Reference Taira and Colonius2009) and others, strong spanwise flows seem to require wing rotation.
Acknowledgements
This work was supported by a National Natural Science Foundation of China grant (No. 51206141) awarded to the first author. We would also like to acknowledge financial support from an Australian Research Council Linkage Project Grant (LP0991170). We are thankful to Dr D. Parkin and Dr R. Harbig for the enlightening discussions.
