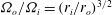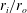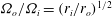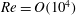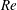1 Introduction
In the past decade or so there has been much controversy about the transition to turbulence in laboratory experiments on centrifugally stable Taylor–Couette flow (Balbus Reference Balbus2011). The motivation behind these experiments has been to uncover physical mechanisms to explain the origin of turbulence in accretion disks where, in the simplest model of a non-self-gravitating disk, the angular velocity
${\it\Omega}\sim r^{-3/2}$
decreases with the radius
$r$
while the angular momentum
$L=r^{2}{\it\Omega}\sim r^{1/2}$
increases: so-called Keplerian flow. This flow is centrifugally stable according to Rayleigh’s criterion (Rayleigh Reference Rayleigh1917). The connection with Taylor–Couette flow (Zeldovich Reference Zeldovich1981) lies in the fact that a similar ‘Rayleigh-stable’ flow can be set up by appropriate motion of the inner and outer cylinders. Specifically, if we define the ratios
${\it\eta}:=r_{i}/r_{o}$
and
${\it\mu}:={\it\Omega}_{o}/{\it\Omega}_{i}$
, where the inner (respectively outer) cylinder at
$r=r_{i}$
(respectively
$r=r_{o}$
) rotates at
${\it\Omega}_{i}$
(respectively
${\it\Omega}_{o}$
), see figure 1, then the angular velocity in the interior is
$$\begin{eqnarray}{\it\Omega}_{TC}=\frac{{\it\Omega}_{i}}{1-{\it\eta}^{2}}\biggl[{\it\mu}-{\it\eta}^{2}+(1-{\it\mu})\frac{r_{i}^{2}}{r^{2}}\biggr],\end{eqnarray}$$
with ‘quasi-Keplerian’ flows,
$\text{d}|{\it\Omega}|/\text{d}r<0$
and
$\text{d}|L|/\text{d}r>0$
, corresponding to the parameter range
$$\begin{eqnarray}{\it\eta}^{2}<{\it\mu}<1.\end{eqnarray}$$
In the presence of an axial magnetic field, quasi-Keplerian Taylor–Couette flow (Velikhov Reference Velikhov1959; Chandrasekhar Reference Chandrasekhar1960) and accretion disks (Balbus & Hawley Reference Balbus and Hawley1991, Reference Balbus and Hawley1998) are known to be prone to the magnetorotational instability. However, this linear instability mechanism cannot operate in weakly ionized accretion disks, which led to the hypothesis (Richard & Zahn Reference Richard and Zahn1999) that disk turbulence is the result of a finite-amplitude instability of Keplerian flow. Subsequently, a number of experiments were aimed at assessing this subcritical transition scenario in the laboratory.
Figure 1. Partially stratified Taylor–Couette set-up: the flow is linearly stratified in the axial direction
$z$
near the end plates (the colour scheme is indicative of temperature). In this paper, the end plates are attached to the outer cylinder. Rather than the total density,
${\it\rho}$
denotes the deviation with respect to a reference value
${\it\rho}_{0}$
.
Unfortunately, this deceptively simple idea has proven hard to implement in practice (leaving aside unreachable values of the Reynolds number,
$Re>10^{9}$
, in accretion disks (Turner et al.
Reference Turner, Fromang, Gammie, Klahr, Lesur, Wardle and Bai2014)) because of significant effects caused by the top and bottom boundaries necessary to contain the fluid. As explained by Czarny et al. (Reference Czarny, Serre, Bontoux and Lueptow2003), the no-slip boundary condition disturbs the balance between the centrifugal force and the radial pressure gradient that prevails in the interior. This force imbalance leads to Ekman layers on the end plates and, consequently, to a radial flow there, which in turn drives a global meridional circulation. In the centrifugally stable regime, Avila et al. (Reference Avila, Grimes, Lopez and Marques2008) showed that the two symmetric recirculation cells are able to penetrate deep into the flow and merge at the equator (defined as the plane
$z=0$
in figure 1) to form an unstable radial jet (this will be discussed further in § 4.1.1). This experimental artefact clearly compromises the analogy between Taylor–Couette flow and accretion disks, and, as a result, various strategies have been implemented to minimize these end effects. The Princeton group (Ji et al.
Reference Ji, Burin, Schartman and Goodman2006) split their endcaps into two independent rings, creating a piecewise constant angular velocity profile at the top and bottom boundaries, and reported that the flow was ‘essentially steady’ up to
$Re=O(10^{6})$
. On the other hand, the Maryland group (Paoletti & Lathrop Reference Paoletti and Lathrop2011) split the inner cylinder of their large-aspect-ratio apparatus into three parts, sensing the torque only on the central section. Their measurements were in contradiction with the findings of Ji et al. (Reference Ji, Burin, Schartman and Goodman2006) and suggested turbulence at similarly high Reynolds number. Later, Avila (Reference Avila2012) reproduced the experiments numerically and found both set-ups to be linearly unstable and already turbulent at
$Re=O(10^{3})$
, because of instabilities stemming from the end plates. The Princeton group (Edlund & Ji Reference Edlund and Ji2014) recently reported new experiments on a modified device (one independent ring surrounded by end plates attached to the inner and outer cylinders), showing that these instabilities could be avoided in a narrow range of operating parameters. Using laser-Doppler velocimetry, the Princeton authors demonstrated agreement of their velocity profiles with (1.1) and also confirmed stability of the flow with respect to finite-amplitude perturbations at
$Re=O(10^{6})$
. Recent numerical results by Ostilla-Mónico et al. (Reference Ostilla-Mónico, Verzicco, Grossmann and Lohse2014), based on axially periodic direct numerical simulations for
$Re$
up to
$O(10^{5})$
, also seem to indicate nonlinear stability of quasi-Keplerian flows.
In this work, we propose a new approach directed at reducing end effects in experiments. Our strategy consists of adding stably stratified layers near the top and bottom plates while leaving the equatorial part of the flow unstratified, as shown in figure 1. The idea is that the stratified layers should suppress vertical motion and therefore act as ‘buffer zones’ isolating our hydrodynamic model of an accretion disk at the centre of the cylinder from the undesired flow induced by the end plates. Of course, this approach is only useful if stratification does not introduce any linear instabilities into the problem. In the absence of axial boundaries, stratified Taylor–Couette flow is known to be prone to the stratorotational instability (SRI) (so named by Dubrulle et al. (Reference Dubrulle, Marié, Normand, Richard, Hersant and Zahn2005)) caused by the resonance between boundary-trapped inertia–gravity waves. Originally discovered by Molemaker, McWilliams & Yavneh (Reference Molemaker, McWilliams and Yavneh2001) and Yavneh, McWilliams & Molemaker (Reference Yavneh, McWilliams and Molemaker2001), the instability was theoretically predicted to develop for any value of
${\it\mu}<1$
(cyclonic regime) in the inviscid small-gap limit. Shalybkov & Rüdiger (Reference Shalybkov and Rüdiger2005) and Rüdiger & Shalybkov (Reference Rüdiger and Shalybkov2009) later extended these results to the wide-gap and viscous case with the help of numerical methods. These authors showed that the instability range was narrower than initially thought, as the SRI could only be found for a very limited range of rotation ratios
${\it\mu}$
beyond
${\it\eta}$
, if at all, depending on the radius ratio and stratification. In parallel, Le Bars & Le Gal (Reference Le Bars and Le Gal2007) verified their predictions experimentally, providing the first evidence of the existence of the SRI. Given the development of the SRI in ‘fully’ stratified flows, the effect of the stratified layers on the global stability of the axisymmetric base flow is systematically assessed in this work.
The plan of the paper is as follows. In § 2, we introduce the governing equations of the problem, and then present the numerical and experimental methods in § 3. In § 4, the effects of stratification ‘strength’ and layer thickness are assessed for different rotation ratios. In § 5, we discuss the physical mechanisms responsible for the generation and suppression of meridional flow, the limits of our numerical model, and ultimately the nonlinear stability of the optimally controlled flow. Finally, § 6 summarizes our main results.
Figure 2. (a) Convergence of the spectral coefficients
$\hat{U} _{ij}$
of the radial velocity component, for
${\it\mu}={\it\eta}^{1/2}$
,
${\it\alpha}=0.5$
and
$Ri_{l}=2$
. (b) Maximum radial velocity at the equator for
${\it\eta}=0.5$
,
${\it\Gamma}=6$
,
${\it\mu}=1$
, fixed end plates and no stratification. The solid line shows the data digitized from Avila et al. (Reference Avila, Grimes, Lopez and Marques2008) and the dots show the present code.
2 Governing equations
The dimensional parameters of the problem are defined in figure 1. There are seven independent non-dimensional parameters specifying the problem. The geometry of the container requires two:
$$\begin{eqnarray}{\it\eta}:={\displaystyle \frac{r_{i}}{r_{o}}}\quad \text{and}\quad {\it\Gamma}:={\displaystyle \frac{h}{d}},\end{eqnarray}$$
where
$h$
and
$d:=r_{o}-r_{i}$
are respectively the height of the cylinders and the radial gap between them. In all computations and experiments, the radius ratio and aspect ratio are set to
${\it\eta}=0.417$
and
${\it\Gamma}=3$
(except for validation, cf. figure 2
b). The rotation and shear imposed on the fluid are quantified by the Reynolds number and rotation ratio
$$\begin{eqnarray}Re:=\frac{r_{i}{\it\Omega}_{i}d}{{\it\nu}}\quad \text{and}\quad {\it\mu}:={\displaystyle \frac{{\it\Omega}_{o}}{{\it\Omega}_{i}}},\end{eqnarray}$$
where
${\it\nu}$
is the kinematic viscosity. The quasi-Keplerian range
${\it\eta}^{2}<{\it\mu}<1$
is bordered by solid-body rotation (no shear)
${\it\mu}=1$
and the so-called ‘Rayleigh line’
${\it\mu}={\it\eta}^{2}$
where the angular momentum is constant over radius. Three more non-dimensional numbers are required to describe the stratification. Let
${\it\rho}_{\mathit{tot}}$
denote the density field and
${\it\rho}:={\it\rho}_{\mathit{tot}}-{\it\rho}_{0}$
be the deviation with respect to the reference value
${\it\rho}_{0}:={\it\rho}_{tot}\,(z=0,t=0)$
, such that
${\it\rho}$
is initially antisymmetric with respect to
$z$
. The initial buoyancy frequency within the layers is
$N:=\sqrt{-(g/{\it\rho}_{0})\partial {\it\rho}/\partial z}$
, where
$g$
denotes gravity. The strength of the initial stratification is quantified by the local Richardson number
$$\begin{eqnarray}Ri_{l}:=N^{2}/{\it\Omega}_{i}^{2}.\end{eqnarray}$$
The ratio of the momentum diffusion coefficient
${\it\nu}$
to the density diffusion coefficient
${\it\kappa}$
is either the Prandtl number
$Pr$
for thermal stratification or the Schmidt number
$Sc$
for salt stratification,
$$\begin{eqnarray}Pr,Sc:={\displaystyle \frac{{\it\nu}}{{\it\kappa}}}.\end{eqnarray}$$
The momentum and density diffusion time scales across the gap
$d$
are given by
${\it\tau}_{{\it\nu}}:=d^{2}/{\it\nu}$
and
${\it\tau}_{{\it\kappa}}:=d^{2}/{\it\kappa}$
. Finally, the stratified fraction
$$\begin{eqnarray}0\leqslant {\it\alpha}:={\displaystyle \frac{l}{h}}\leqslant 1\end{eqnarray}$$
is defined as the ratio between the thickness
$l/2$
of each stratified layer and the half-height
$h/2$
of the apparatus. With these definitions, the buoyancy frequency can be expressed as
$N=\sqrt{g{\rm\Delta}{\it\rho}/({\it\rho}_{0}{\it\alpha}{\it\Gamma}d)}$
.
The flow is governed by the incompressible Navier–Stokes equations in the Boussinesq approximation, relying on the assumption that
${\rm\Delta}{\it\rho}/{\it\rho}_{0}\ll 1$
and that curvature of the isopycnals due to centrifugal effects can be neglected. In the following, we choose
$d$
,
$r_{i}{\it\Omega}_{i}$
and
${\rm\Delta}{\it\rho}$
as typical length, velocity and density scales in order to obtain non-dimensional quantities. In cylindrical coordinates
$(r,{\it\theta},z)$
, the dynamical equations for the velocity
$\boldsymbol{u}=u\boldsymbol{e}_{r}+v\boldsymbol{e}_{{\it\theta}}+w\boldsymbol{e}_{z}$
and density
${\it\rho}$
read
$$\begin{eqnarray}\displaystyle & \displaystyle \partial _{t}u+u\partial _{r}u+{\displaystyle \frac{v}{r}}\partial _{{\it\theta}}u+w\partial _{z}u-{\displaystyle \frac{v^{2}}{r}}=-\partial _{r}p+{\displaystyle \frac{1}{Re}}\left({\rm\nabla}^{2}u-{\displaystyle \frac{u}{r^{2}}}-{\displaystyle \frac{2}{r^{2}}}\partial _{{\it\theta}}v\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \partial _{t}v+u\partial _{r}v+{\displaystyle \frac{v}{r}}\partial _{{\it\theta}}v+w\partial _{z}v+{\displaystyle \frac{uv}{r}}=-{\displaystyle \frac{1}{r}}\partial _{{\it\theta}}p+{\displaystyle \frac{1}{Re}}\left({\rm\nabla}^{2}v-{\displaystyle \frac{v}{r^{2}}}+{\displaystyle \frac{2}{r^{2}}}\partial _{{\it\theta}}u\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \partial _{t}w+u\partial _{r}w+{\displaystyle \frac{v}{r}}\partial _{{\it\theta}}w+w\partial _{z}w=-\partial _{z}p+{\displaystyle \frac{1}{Re}}{\rm\nabla}^{2}w-Ri_{g}{\it\rho}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \partial _{t}{\it\rho}+u\partial _{r}{\it\rho}+{\displaystyle \frac{v}{r}}\partial _{{\it\theta}}{\it\rho}+w\partial _{z}{\it\rho}={\displaystyle \frac{1}{Re\,Sc}}{\rm\nabla}^{2}{\it\rho}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}{\rm\nabla}^{2}:=\partial _{rr}^{2}+{\displaystyle \frac{1}{r}}\partial _{r}+\frac{1}{r^{2}}\partial _{{\it\theta}{\it\theta}}^{2}+\partial _{zz}^{2}\end{eqnarray}$$
is the scalar Laplacian operator,
$p:={\it\Pi}/{\it\rho}_{0}+gz$
is a potential based on the pressure
${\it\Pi}$
, and finally
$$\begin{eqnarray}Ri_{g}:={\it\alpha}{\it\Gamma}{\displaystyle \frac{(1-{\it\eta})^{2}}{{\it\eta}^{2}}}Ri_{l}\end{eqnarray}$$
is a global Richardson number (created in the equations by the choice of reference scales).
In strongly rotating flows, ‘centrifugal buoyancy’ can be taken into account by including the nonlinear term
$({\rm\Delta}{\it\rho}/{\it\rho}_{0}){\it\rho}(\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})\boldsymbol{u}$
in the convective derivative (Lopez, Marques & Avila Reference Lopez, Marques and Avila2013). This term is
$O({\rm\Delta}{\it\rho}/{\it\rho}_{0})$
with our choice of reference scales, whereas the usual buoyancy term related to gravity is
$O(Ri_{g})$
. In the present study,
$Ri_{g}\gg {\rm\Delta}{\it\rho}/{\it\rho}_{0}$
(see the parameter values in table 1), which justifies the use of the traditional Boussinesq approximation. The incompressibility constraint can be written as
$$\begin{eqnarray}\partial _{r}u+{\displaystyle \frac{u}{r}}+{\displaystyle \frac{1}{r}}\partial _{{\it\theta}}v+\partial _{z}w=0.\end{eqnarray}$$
The meridional velocity
$\boldsymbol{u}_{\bot }:=(u,w)$
vanishes at the boundaries whereas the zonal component satisfies
$$\begin{eqnarray}v=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if }r=r_{i}^{\star },~|z|\leqslant {\it\Gamma}/2,\\ {\it\mu}/{\it\eta}\quad & \text{if }r=r_{o}^{\star },~|z|\leqslant {\it\Gamma}/2,\\ {\it\mu}(r/r_{i}^{\star })\quad & \text{if }r_{i}^{\star }<r\leqslant r_{o}^{\star },~|z|={\it\Gamma}/2,\end{array}\right.\end{eqnarray}$$
where
$r_{i}^{\star }={\it\eta}/(1-{\it\eta})$
and
$r_{o}^{\star }=1/(1-{\it\eta})$
denote respectively the non-dimensional inner and outer radii. Finally, we impose the piecewise-linear density profile
$$\begin{eqnarray}{\it\rho}=\left\{\begin{array}{@{}ll@{}}-{\displaystyle \frac{1}{2{\it\alpha}}}\biggl[{\displaystyle \frac{2z}{{\it\Gamma}}}-(1-{\it\alpha})\biggr]\quad & \text{if }1-{\it\alpha}\leqslant 2z/{\it\Gamma}\leqslant 1,\\ -{\displaystyle \frac{1}{2{\it\alpha}}}\biggl[{\displaystyle \frac{2z}{{\it\Gamma}}}+(1-{\it\alpha})\biggr]\quad & \text{if }1-{\it\alpha}\leqslant -2z/{\it\Gamma}\leqslant 1,\\ 0\quad & \text{otherwise},\end{array}\right.\end{eqnarray}$$
either initially in the volume in the case of salt stratification, or at the boundaries at all times in the case of temperature stratification. Indeed, in the former case, the density satisfies no-flux (Neumann) boundary conditions at the walls,
$\partial _{n}{\it\rho}=0$
(where
$\partial _{n}$
denotes the wall-normal derivative), whereas in the latter case, the temperature on the walls can be controlled such that (2.11) holds for all time there (Dirichlet boundary conditions).
Table 1. Comparison between numerical and experimental control parameters. For the stratified experiment with
${\it\alpha}=0.5$
,
$Ri_{l}=2$
, and the larger value of
$Re=14\,000$
,
$Ri_{g}\approx 6$
and
${\rm\Delta}{\it\rho}/{\it\rho}_{0}\approx 0.04$
, so the condition
$Ri_{g}\gg {\rm\Delta}{\it\rho}/{\it\rho}_{0}$
is well satisfied. ‘Centrifugal buoyancy’ is therefore expected to be negligible compared with ‘gravitational buoyancy’, justifying the use of the Boussinesq approximation.
3 Methods
3.1 Numerical methods
In the following, the flow variables are jointly written as
$\boldsymbol{q}:=(\boldsymbol{u},p,{\it\rho})$
. Base flow quantities are denoted with capital letters or subscript ‘
$B$
’ for Greek characters, hence
$\boldsymbol{Q}=(\boldsymbol{U},P,{\it\rho}_{B})$
. Perturbations with respect to the base flow are denoted
$\boldsymbol{q}^{\prime }:=\boldsymbol{q}-\boldsymbol{Q}$
.
3.1.1 Temperature stratification: steady base flows
In the case of temperature stratification, the base flow is steady, axisymmetric and has the
$z$
-symmetry
$$\begin{eqnarray}\mathscr{Z}:(U,V,W,P,{\it\rho}_{B})(r,z)\,\rightarrow \,(U,V,-W,P,-{\it\rho}_{B})(r,-z)\end{eqnarray}$$
as a consequence of the Boussinesq approximation and the imposed boundary conditions. Each field was discretized using a double expansion of Chebyshev polynomials,
$$\begin{eqnarray}Q(r,z)=\mathop{\sum }_{i=0,j=0}^{I,J}\hat{Q}_{ij}T_{i}\left(2(r-r_{i}^{\star })-1\right){\it\Phi}_{j}\left(2z/{\it\Gamma}\right),\end{eqnarray}$$
where
$T_{i}(x):=\cos (\text{i}\cos ^{-1}x)$
and
${\it\Phi}_{j}(x):=T_{2j}(x)$
or
$T_{2j+1}(x)$
, depending on whether the field
$Q$
is symmetric or antisymmetric in
$z$
. Because of the absence of boundary conditions on
$P$
, the corresponding expansion (3.2) was truncated at order
$(I-2,J-1)$
instead of
$(I,J)$
in this case (see Peyret Reference Peyret2002). The governing equations were solved directly in the physical space using a collocation method. Discontinuities in (2.10) (at
$r=r_{i}^{\star }$
for
$|2z/{\it\Gamma}|=1$
) and (2.11) (at
$|2z/{\it\Gamma}|=1-{\it\alpha}$
) were smoothed in order to preserve spectral accuracy. This was achieved by introducing a small length scale
${\it\delta}$
, following Lopez & Shen (Reference Lopez and Shen1998), and defining new boundary conditions for the azimuthal velocity
$$\begin{eqnarray}V=\frac{r}{r_{i}^{\star }}\left[{\it\mu}+(1-{\it\mu})\exp \left(-\frac{r-r_{i}^{\star }}{{\it\delta}}\right)\right]\end{eqnarray}$$
and density
${\it\rho}_{B}$
, by integration of
$$\begin{eqnarray}\partial _{z}{\it\rho}_{B}=-{\displaystyle \frac{1}{2{\it\alpha}{\it\Gamma}}}\left[2+\text{tanh}\left({\displaystyle \frac{z-{\it\Gamma}/2(1-{\it\alpha})}{{\it\delta}}}\right)-\text{tanh}\left({\displaystyle \frac{z+{\it\Gamma}/2(1-{\it\alpha})}{{\it\delta}}}\right)\right]\end{eqnarray}$$
with respect to
$z$
. A value of
${\it\delta}=0.006$
was taken for the computations, following Avila et al. (Reference Avila, Grimes, Lopez and Marques2008). Solutions were computed by Newton–Raphson iteration until the residuals
$\Vert Q^{n+1}-Q^{n}\Vert _{\infty }/\Vert Q^{n}\Vert _{\infty }$
converged below
$10^{-8}$
for each component
$Q$
of
$\boldsymbol{Q}$
. All base flow computations were performed with
$(I,J)=(101,150)$
, ensuring that the trailing coefficients were always between four and five orders of magnitude lower than the maximum coefficient. Figure 2(a) shows a typical ‘spectral’ convergence of the coefficients of (3.2). The solver was also validated against results from Avila et al. (Reference Avila, Grimes, Lopez and Marques2008) (see figure 2
b) and Abshagen et al. (Reference Abshagen, Heise, Pfister and Mullin2010).
3.1.2 Linear stability
We investigated the linear stability of the base flows computed using temperature boundary conditions. As
$\boldsymbol{Q}$
is steady and axisymmetric, infinitesimal perturbations can be expressed as a superposition of normal modes of the form
$\boldsymbol{q}^{\prime }=\tilde{\boldsymbol{q}}^{\prime }(r,z)\exp [\text{i}(m{\it\theta}-{\it\omega}t)]$
, with azimuthal mode number
$m$
and complex frequency
${\it\omega}$
. These modes either share the
$z$
-symmetry (3.1) of the base flow, so that
$\mathscr{Z}\boldsymbol{q}^{\prime }=\boldsymbol{q}^{\prime }$
, or are antisymmetric under the action of
$\mathscr{Z}:\mathscr{Z}\boldsymbol{q}^{\prime }=-\boldsymbol{q}^{\prime }$
. Substituting the normal mode form into the Navier–Stokes equations (2.6)–(2.11) linearized about
$\boldsymbol{Q}$
leads to a generalized eigenvalue problem in
${\it\omega}$
and
$\boldsymbol{q}^{\prime }$
. Following Leclercq, Pier & Scott (Reference Leclercq, Pier and Scott2013), this problem was reduced to a much smaller standard eigenvalue problem by eliminating the pressure, boundary points and one velocity component (
$\tilde{w}^{\prime }$
if
$m=0$
and
$\tilde{v}^{\prime }$
otherwise), and then solved using standard LAPACK and ARPACK++ routines. The solver was validated against figure 6 of Avila et al. (Reference Avila, Grimes, Lopez and Marques2008), with perfect agreement between our computed values of critical
$Re$
and values digitized from the plot for
${\it\Gamma}=3,4,6$
and the various values of
$m$
shown.
3.1.3 Salt stratification: quasisteady base flows
In the case of salt stratification, the no-flux boundary conditions lead to a very slow relaxation of the density field to an eventually unstratified state. The time scale of density diffusion
${\it\tau}_{{\it\kappa}}$
is larger than 5 months in our apparatus, however, so that the laboratory experiments are quasisteady after a few momentum diffusion times (
${\it\tau}_{{\it\nu}}\sim 5~\text{h}~30~\text{min}$
). The resulting time-dependent base flow is also axisymmetric and invariant under the action of
$\mathscr{Z}$
. In order to compute these solutions, a time stepper was developed with no-flux boundary conditions on the density
$\partial _{n}{\it\rho}_{B}=0$
, as in the experiments. The flow was taken initially at rest with a stratification profile given by (3.4) at any radial position. The cylinders and end plates were then accelerated to their final rotation speed over a few periods
${\it\tau}=0.05{\it\tau}_{{\it\nu}}$
, by multiplying the boundary condition (3.3) by the factor
$(1-\exp [-t/{\it\tau}])$
. A streamfunction–vorticity formulation was used and spectral expansions of the form given in (3.2) were again used to discretize the problem (see Peyret Reference Peyret2002, pp. 188–195). Nonlinear terms were treated explicitly with a second-order extrapolation (Adams–Bashforth), whereas the diffusion terms were treated implicitly (backward differentiation). Incompressibility was enforced with an influence matrix. Helmholtz and Poisson problems were solved using a full diagonalization method. The code was validated by applying Dirichlet boundary conditions (3.4) on the density and checking consistency with solutions given by the Newton–Raphson solver.
3.2 Experimental methods
Experiments were conducted in a Taylor–Couette tank of height
$50$
cm with
$(r_{i},r_{o})=(10,24)$
cm, resulting in a radius ratio
${\it\eta}=0.417$
. The tank was filled to a depth
$h=42\pm 2$
cm, giving an aspect ratio
${\it\Gamma}=3\pm 0.14$
. The top and bottom boundaries both rotated with the outer cylinder. A transparent perspex lid, placed in contact with the fluid in the annulus, was fixed to the outer cylinder after filling and formed the top end plate, while the bottom end plate was securely attached to the rotating table forming the base of the tank. The inner cylinder was driven independently from above by a mounted motor unit, at its maximum rotation rate
${\it\Omega}_{i}=1\pm 0.03$
rad s
$^{-1}$
for all experiments. The rotation rate
${\it\Omega}_{o}$
of the rotating table was varied to achieve the desired value of
${\it\mu}$
.
The experiments began by filling the tank to the desired stratification using two computer-controlled peristaltic pumps. The two pumps were connected to different reservoirs of fluid, one of relatively dense NaCl solution and the other of fresh water, both of which had been deaerated using vacuum cylinders to reduce unwanted air coming out of the solution during the course of an experiment and hindering the visualization. The reservoirs also sat out for approximately one day to equilibrate with the ambient temperature conditions of the laboratory. The densities of the two reservoirs were measured just prior to filling using an Anton Paar DMA5000 density meter with a resolution of
$10^{-6}~\text{g}~\text{cm}^{-3}$
. After filling, a conductivity probe was then traversed through the depth of the tank to measure the resulting stratification. Due to the long filling time (
${\sim}1{-}2$
h), the flow rates in the pumps could deviate during the filling procedure, resulting in a small error in the desired fill height (
$\pm 5\,\%$
). We do not expect this small change in aspect ratio to alter the overall flow patterns observed.
To reduce the impact of any initial transient, the cylinders were slowly ramped up over 8 h (
${\sim}1.5{\it\tau}_{{\it\nu}}$
), with the rotation ratio
${\it\mu}$
held constant during the course of the ramp. After the initial ramp period, the cylinder rotation rates were held constant for another momentum diffusion time before acquiring any raw images for particle image velocimetry (PIV). After the raw images had been acquired, the cylinders were both ramped down to rest over a momentum diffusion time to minimize unwanted shear before taking a final density profile using the conductivity probe.
To monitor the behaviour of the stratified layers, shadowgraph images were automatically recorded at 30 min intervals during the experiment. To enable simultaneous capture of PIV and shadowgraph images, the inner cylinder was painted white except for a black band that spanned
$z=-9$
cm to
$z=10$
cm. A slide projector positioned approximately 3 m from the tank illuminated the flow and projected refractive index variations onto the white regions of the inner cylinder, which were then recorded using a Uniq Vision UP1830-12B 1 megapixel resolution camera.
Raw images for PIV were captured using a 4 megapixel Dalsa Falcon 2 camera at 160 fps for 30 s (
${\sim}5$
rotation periods of the inner cylinder). The camera was mounted directly above the apparatus, viewing down through the top transparent end plate. The flow was seeded using
$20~{\rm\mu}\text{m}$
diameter polyamide particles and illuminated using a 700 W arc lamp. The resulting light sheet was approximately 3 mm thick and was horizontally orientated, so all velocity data are in the
$(r,{\it\theta})$
plane. For all of the data reported here, the light sheet was positioned at
$z=0\pm 1$
cm, so data were acquired in the centre of the unstratified region. The region illuminated and captured by the camera was
$14~\text{cm}\times 3~\text{cm}$
, which corresponded to 1800 pixels
$\times$
400 pixels. The PIV was analysed using DigiFlow (Dalziel et al.
Reference Dalziel, Carr, Sveen and Davies2007), with an interrogation window size of 32 pixels
$\times$
32 pixels and an overlap of 50 %, which resulted in a spatial resolution of
${\sim}1.24$
mm. The error in particle displacement was
${\sim}0.02$
of a pixel, which gives an error in velocity of
${\sim}0.25~\text{mm}~\text{s}^{-1}$
(
${\sim}0.025\,\%$
of
$r_{i}{\it\Omega}_{i}$
).
4 Mitigating end effects with stratification
Table 1 summarizes the values of the different control parameters taken in our experiments and computations. Two rotation ratios were considered in both: a ‘high-shear’ (HS) value where
${\it\mu}={\it\eta}^{3/2}$
and a ‘low-shear’ (LS) one where
${\it\mu}={\it\eta}^{1/2}$
. We recall that the quasi-Keplerian range is
${\it\eta}^{2}<{\it\mu}<1$
, with the upper limit
${\it\mu}=1$
corresponding to uniform rotation and therefore no shear. Here, we use the terms ‘low’ and ‘high’ only to distinguish the two cases by comparison with one another, but note that arbitrarily large shear rates can be achieved even in the LS case, by setting
$Re$
to a large enough value.
Because of our underlying objective of investigating the existence of turbulence in quasi-Keplerian flow, we indeed chose to maximize the value of the Reynolds number in the experiments, leading to
$Re=14\,000$
with our set-up. However, accurate computations could not be achieved at this large value of
$Re$
in a reasonable time frame with our serial codes, so an upper limit of
$Re=5000$
was taken for these.
Salt was used to generate stratification in the experiments, so the density field satisfied no-flux boundary conditions at the walls and the Schmidt number was
$Sc\approx 700$
. However, for reasons that will be discussed further in § 5.3, we chose to model the experiment with Dirichlet boundary conditions at the walls, instead of Neumann conditions. In practice, this would correspond to imposing a temperature profile at the walls, which would lead to much quicker density diffusion, as heat diffuses more rapidly than salt in fresh water (
$Pr\approx 7$
instead of
$Sc\approx 700$
). This other discrepancy will be discussed in § 5.2. Put simply, these modelling choices for stratification made our equations much more amenable to numerical computation than if actual experimental settings were taken.
The computed meridional and zonal base flows are presented in figures 3 and 4 for the two shear cases and three choices of stratification: no stratification (
${\it\alpha}=0$
), full stratification (
${\it\alpha}=1$
) and partial stratification (
$0<{\it\alpha}<1$
). Each case is discussed in more detail in the following subsections.
Figure 3. Base flow for the HS case
${\it\mu}={\it\eta}^{3/2}$
. (a–c) Meridional flow
$\boldsymbol{U}_{\bot }=(U,W)$
: streamlines (
${\rm\Delta}{\it\psi}=10^{-3}$
) and colourmap of the norm
$\Vert \boldsymbol{U}_{\bot }\Vert$
. (d–f) Azimuthal velocity
$V$
: colourmap and contours of
$V$
(
${\rm\Delta}V=0.05$
). The dotted lines in (b,e) indicate the limit of the stratified layers. In this figure and hereafter, the left (respectively right) boundary corresponds to the inner (respectively outer) cylinder; (a,d)
${\it\alpha}=0$
, (b,e)
${\it\alpha}=0.5$
, (c,f)
${\it\alpha}=1$
.
Figure 4. Base flow in the LS case
${\it\mu}={\it\eta}^{1/2}$
. The same as figure 3, except that here
${\rm\Delta}{\it\psi}=2.5\times 10^{-4}$
.
Figure 5. Structure of the most unstable linear mode for
${\it\mu}={\it\eta}^{3/2}$
,
$Re=1500$
and (a)
${\it\alpha}=0$
(
$m=2$
, symmetric under
$\mathscr{Z}$
), (b)
${\it\alpha}=0.5$
(
$m=1$
, antisymmetric under
$\mathscr{Z}$
), (c)
${\it\alpha}=1$
(
$m=1$
, symmetric under
$\mathscr{Z}$
). The production of perturbation energy (kinetic
$+$
potential) over the volume
$\mathscr{V}$
of the container can be expressed as
$\mathscr{P}_{\mathscr{V}}=-\int _{\mathscr{V}}\boldsymbol{u}^{\prime }\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{U}\boldsymbol{\cdot }\boldsymbol{u}^{\prime }\,\text{d}\mathscr{V}$
. We introduce the density
$\widetilde{\mathscr{P}}(r,z)$
by writing
$\mathscr{P}_{\mathscr{V}}$
as
$4{\rm\pi}\text{e}^{\text{i}2{\it\omega}_{\mathit{i}}t}\int \widetilde{\mathscr{P}}(r,z)r\,\text{d}r\,\text{d}z$
. The quantity
$r\widetilde{\mathscr{P}}(r,z)$
indicates the distribution of positive production of perturbation energy in the meridional plane, averaged over
${\it\theta}$
. Contour lines:
${\rm\Delta}\log _{10}[r\widetilde{\mathscr{P}}(r,z)]=0.25$
. The dotted lines in (b) mark the limits of the stratified layers. The resolution here is
$(I,J)=(67\,100)$
.
4.1 Unstratified case:
${\it\alpha}=0$
4.1.1 ‘High-shear case’
${\it\mu}={\it\eta}^{3/2}$
In the absence of stratification, the meridional circulation for the HS case penetrates deep into the flow and causes a strong distortion of the azimuthal flow field, as can be seen in figure 3(a). The driving mechanism is a broken balance between centrifugal force and pressure gradient at the end plates caused by the no-slip boundary condition (Czarny et al.
Reference Czarny, Serre, Bontoux and Lueptow2003). The inward radial flow at the endcaps is then redirected to the equatorial region through Stewartson layers once it reaches the inner cylinder. This leads to the formation of two meridional recirculation cells that merge at the equator into a strong outward radial jet (Avila et al.
Reference Avila, Grimes, Lopez and Marques2008). The jet redistributes angular momentum along
$r$
, leading to a locally centrifugally unstable angular momentum profile, i.e.
$\text{d}|L|/\text{d}r<0$
for
$0\lesssim r-r_{i}^{\star }\lesssim 0.63$
and
$z=0$
. The structure of the resulting global mode linear instability is represented in figure 5(a). In the experiment, this instability develops into turbulent motion, characterized by high levels of velocity fluctuations in the equatorial plane:
$\sqrt{\overline{{\it\delta}u^{2}+{\it\delta}v^{2}}}/\overline{v}$
up to 5–6 % near the inner cylinder (
$\overline{(\cdot )}$
denotes temporal average and
${\it\delta}\boldsymbol{u}$
is the fluctuation with respect to the mean,
${\it\delta}\boldsymbol{u}:=\boldsymbol{u}-\overline{\boldsymbol{u}}$
), as shown by the dashed line in figure 6. Turbulence tends to homogenize angular momentum in centrifugally unstable regions, explaining the deviation between the computed base flow (dashed line) and the time-averaged azimuthal velocity (solid line with markers) for
$0\lesssim r-r_{i}^{\star }\lesssim 0.7$
in figure 7(a).
Figure 6. Particle image velocimetry measurements of the horizontal turbulence intensity at the equator, in the absence of stratification. Comparison between the HS case (dashed red line) and the LS case (solid black line).
4.1.2 ‘Low-shear case’
${\it\mu}={\it\eta}^{1/2}$
Although the end plates generate large-scale meridional circulation in the LS case, the symmetric cells in figure 4(a) do not appear to reach the equator. As a result, the axial homogeneity of the zonal flow
$V$
is preserved across
$z=0$
and the flow is numerically found to be linearly stable. Correlatively, the velocity fluctuations in the experiments remain small, with
$\sqrt{\overline{{\it\delta}u^{2}+{\it\delta}v^{2}}}/\overline{v}\sim 1\,\%$
at the equator (solid line in figure 6). In fact, apart from rapid variations in boundary layers near the end plates, the azimuthal velocity seems to be virtually independent of
$z$
across the entire container. However, a closer look at the radial profile of
$\overline{v}$
in figure 7(b) shows significant differences between the experiments (solid line with markers) and the ideal Taylor–Couette solution (thick solid line). This mismatch can be interpreted as a manifestation of the Taylor–Proudman theorem in rapidly rotating flows, as explained in Hollerbach & Fournier (Reference Hollerbach and Fournier2004). Indeed, in the LS case, the Rossby number (defined as in Hollerbach & Fournier (Reference Hollerbach and Fournier2004) and Paoletti & Lathrop (Reference Paoletti and Lathrop2011))
$Ro:=({\it\Omega}_{i}-{\it\Omega}_{o})/{\it\Omega}_{o}=(1-{\it\mu})/{\it\mu}$
is small (
$Ro\approx 0.55$
for
${\it\eta}=0.417$
) and the flow is not very far from geostrophic balance. It is therefore nearly invariant along the axial direction and is controlled by Ekman pumping at the end plates. Thus, despite weak meridional circulation and stability, experiments in the LS case do not yield the desired Taylor–Couette solution (1.1).
4.2 Fully stratified case:
${\it\alpha}=1$
In this section, we investigate the effect of stratification across the entire container. The choice of
$Ri_{l}=2$
for the stratified cases in figures 3–5 will be justified later in § 4.3.
4.2.1 ‘High-shear case’
${\it\mu}={\it\eta}^{3/2}$
The addition of stratification in our axisymmetric computations results in a dramatic reduction in meridional circulation and subsequent zonal flow distortion for the HS case, as can be seen in figure 3(c). Apart from boundary layers at the end plates and a small ‘eddy’ trapped in the inner corners, the magnitude of
$\boldsymbol{U}_{\bot }$
has dropped to less than 0.1 % of the inner cylinder velocity everywhere in the flow. As a result, the azimuthal flow now weakly depends on
$z$
in the equatorial region and solution (1.1) (thick solid red line) is almost perfectly recovered at
$z=0$
, as can be seen in figure 7(a) (dashed–dotted blue line).
Figure 7. Azimuthal velocity profiles at the equator for (a) the HS and (b) the LS case. The solid red lines show the axially invariant Taylor–Couette solution (1.1), the dashed blue lines show the computed values in the unstratified case, the dashed–dotted blue lines show the computed base flows in the fully stratified case
$({\it\alpha},Ri_{l})=(1,2)$
and the solid black line with markers show the time-averaged profiles in the unstratified case, from PIV measurements. There is a small discrepancy in the measured velocity profile due to experimental error (
${<}5\,\%$
) in setting the rotation rate of the cylinders.
However, despite the fully stratified solutions being significantly closer to the base flow, the computed axisymmetric solution cannot actually be observed in an experiment as the flow is, again, subject to a linear instability. The structure of the most unstable mode, shown for
$Re=1500$
in figure 5(c), is clearly reminiscent of the SRI as described in Shalybkov & Rüdiger (Reference Shalybkov and Rüdiger2005) and Rüdiger & Shalybkov (Reference Rüdiger and Shalybkov2009): the mode is non-axisymmetric and almost axially periodic, with an axial wavelength smaller than the gap (for infinite cylinders, Shalybkov & Rüdiger (Reference Shalybkov and Rüdiger2005) found the scaling
${\it\lambda}\sim Ri_{l}^{-1/2}$
for the critical axial wavelength
${\it\lambda}$
). However, the production of total disturbance energy is localized near the inner cylinder, which suggests that the instability mechanism for our wide-gap configuration
${\it\eta}=0.417$
is closer to the radiative mechanism of Le Dizès & Riedinger (Reference Le Dizès and Riedinger2010) for
${\it\eta}\rightarrow 0$
than to a resonance between boundary-trapped inertia–gravity waves, as discussed by Molemaker et al. (Reference Molemaker, McWilliams and Yavneh2001) in the limit
${\it\eta}\rightarrow 1$
.
4.2.2 ‘Low-shear case’
${\it\mu}={\it\eta}^{1/2}$
In the LS case, the effect of stratification on the base flow is similarly beneficial: the meridional flow is negligible except in boundary layers, and the azimuthal velocity is not only almost axially invariant, but also very close to the theoretical solution (1.1) (see figure 7(b); dashed–dotted blue line for the base flow and thick solid red line for the Taylor–Couette solution).
However, a crucial difference with the HS case is that the base flow now remains stable. This is consistent with the predictions of Shalybkov & Rüdiger (Reference Shalybkov and Rüdiger2005) and Rüdiger & Shalybkov (Reference Rüdiger and Shalybkov2009), who showed that stratified Taylor–Couette flow between infinite cylinders is generally stable for
${\it\mu}<{\it\eta}$
. For the HS case, the presence of end plates does not seem to impact the structure of the mode far from the end plates (see 5
c). Therefore, it may not be surprising to obtain good agreement with theoretical results obtained for an axially invariant base flow in the LS case too.
4.3 Partially stratified case:
$0<{\it\alpha}<1$
The promising numerical results of section § 4.2 indicate that stratification is quite powerful at suppressing large meridional circulation cells, which in turn leads to azimuthal velocity profiles close to (1.1). However, the end goal of our investigation is to probe the possibility of purely hydrodynamic turbulence, so the central portion of the apparatus needs to be left unstratified and avoid contamination by the SRI.
Our control strategy hence relies on two parameters: the stratified fraction
${\it\alpha}$
and the local Richardson number
$Ri_{l}$
. The effect of these two parameters on the departure of computed solutions with respect to (1.1) is shown in figure 8 in the LS case (the results are qualitatively similar for the HS case). The relative difference between computed and ideal solutions is averaged over a volume spanning half of the unstratified region and centred about the equator. More specifically, we introduce zonal and meridional deviations,
$$\begin{eqnarray}{\it\Delta}_{V}:=\langle (V-V_{TC})/V_{TC}\rangle _{\mathscr{V}}\quad \text{and}\quad {\it\Delta}_{\bot }:=\langle \Vert \boldsymbol{U}_{\bot }\Vert /V_{TC}\rangle _{\mathscr{V}},\end{eqnarray}$$
where
$V_{TC}:=r{\it\Omega}_{TC}$
,
$$\begin{eqnarray}\langle (\cdot )\rangle _{\mathscr{V}}:=\left({\displaystyle \frac{1}{\mathscr{V}}}\int _{\mathscr{V}}(\cdot )^{2}\,\text{d}\mathscr{V}\right)^{1/2}\end{eqnarray}$$
and
$$\begin{eqnarray}\mathscr{V}:=\left\{(r,{\it\theta},z)\in [r_{i}^{\star },r_{o}^{\star }]\times [0,2{\rm\pi}[\,\times \left[-{\displaystyle \frac{{\it\Gamma}(1-{\it\alpha})}{4}},{\displaystyle \frac{{\it\Gamma}(1-{\it\alpha})}{4}}\right]\right\}.\end{eqnarray}$$
It appears that both quantities decrease rapidly as
$Ri_{l}$
increases in the range
$0<Ri_{l}\leqslant 5$
. The meridional deviation
${\it\Delta}_{\bot }$
even drops by nearly one order of magnitude within the range
$0<Ri_{l}<1$
. Increasing
$Ri_{l}$
further has virtually no effect on
$\boldsymbol{U}_{\bot }$
but keeps improving
$V$
. Similarly, the thickness of the layers does not seem to be critical to the suppression of the meridional flow, as long as
$Ri_{l}\gtrsim 1$
. However, thick layers are more efficient at correcting the azimuthal velocity profile, as long as the unstratified zone does not become shallow. Indeed, when
${\it\alpha}\geqslant 5/6$
, the depth of the unstratified zone becomes lower than half of the gap width and the flow is no longer axially homogeneous in this region. This has a negative impact on the deviations, which start to increase again with
${\it\alpha}$
and
$Ri_{l}$
.
Figure 8. (a) Relative azimuthal deviation
${\it\Delta}_{V}$
and (b) relative meridional deviation
${\it\Delta}_{\bot }$
as functions of
$Ri_{l}$
, for various values of
${\it\alpha}$
, in the LS case.
In this section, we choose to study the case
$({\it\alpha},Ri_{l})=(0.5,2)$
, which appears to be a good compromise for various reasons: the deviations
${\it\Delta}_{V}$
and
${\it\Delta}_{\bot }$
are both small, the aspect ratio of the unstratified zone
${\it\Gamma}(1-{\it\alpha})=1.5$
is larger than 1 and finally this combination is easily achieved experimentally since
${\rm\Delta}{\it\rho}/{\it\rho}_{0}\approx 4\,\%$
for
$Re=14\,000$
. This justifies a posteriori the choice of
$Ri_{l}=2$
to illustrate the fully stratified case in § 4.2. The density field corresponding to this parameter combination is shown in figure 9 for the HS and LS cases. In both, the isopycnals are almost horizontal, indicating that the stratification is ‘strong enough’ to avoid overturning by the meridional circulation, except at the inner corners (more details will be provided in § 5.1).
Figure 9. The base flow density field
${\it\rho}_{B}$
in (a) the HS case (unstable),
${\it\mu}={\it\nu}^{3/2}$
, and (b) the LS case (stable),
${\it\mu}={\it\nu}^{1/2}$
;
$({\it\alpha},Ri_{l})=(0.5,2)$
. The dotted lines mark the limits of the stratified layers. The density step between solid lines is 0.05 and between dashed lines is
$5\times 10^{-3}$
.
4.3.1 ‘High-shear case’
${\it\mu}={\it\eta}^{3/2}$
There is barely any noticeable difference between the computed meridional flow fields in the fully and partially stratified cases in figure 3(b,c). Apart from boundary layers in the unstratified region for
${\it\alpha}=0.5$
, the two fields are almost indistinguishable, confirming that partial stratification efficiently suppresses
$\boldsymbol{U}_{\bot }$
even when
${\it\alpha}\neq 1$
. The azimuthal velocity is also remarkably homogeneous along the axial direction in the unstratified zone, but unfortunately the computed base flow is linearly unstable. The production of energy of the most unstable mode, displayed in figure 5(b) for
$Re=1500$
, is precisely localized within the stratified layers. Moreover, the distribution of this quantity is very similar to that of the fully stratified flow in the same region. Therefore, we conclude that the mode is subject to an SRI mode localized inside the layers.
Experimentally, this instability leads to the braid pattern visible in the spatiotemporal shadowgraph of figure 10(a). This pattern corresponds to the nonlinear interaction of two helical modes of opposite ‘handedness’, which are destabilized simultaneously because of symmetry. In the long term, this secondary flow generates mixing and destroys the initial density profile, as can be seen in figure 10(b).
Figure 10. Instability of the stratified layers in the HS case with
$({\it\alpha},Ri_{l})=(0.5,2)$
. (a) Spatiotemporal diagram of shadowgraph. (b) Density profiles (deviation with respect to the mean
${\it\rho}_{0}$
, non-dimensionalized by
${\it\rho}_{0}$
) at mid-gap
$r=1/2(r_{i}^{\star }+r_{o}^{\star })$
from conductivity measurements, at
$t=0$
(solid line) and
$t=40$
h (dashed line). The SRI destroys the initial density profile in a few diffusion time units.
4.3.2 ‘Low-shear case’
${\it\mu}={\it\eta}^{1/2}$
The effect of partial stratification on the base flow in the LS case is similar to that observed for the HS case. The meridional flow is suppressed in the unstratified zone, including within the boundary layer running along the inner cylinder, as
$|z|\rightarrow 0$
. The azimuthal velocity is virtually axially homogeneous in the unstratified region, but contrary to the unstratified case, the radial profile now closely matches the ideal solution (1.1), as illustrated in figure 11.
For LS, no instability is found (numerically tested up to
$Re=5000$
and experimentally up to 14 000) in either the fully or the partially stratified case. This result is consistent with the analysis of Rüdiger & Shalybkov (Reference Rüdiger and Shalybkov2009), who always found linear stability at
${\it\mu}={\it\eta}^{1/2}$
(these authors investigated the range
$0.3\leqslant {\it\eta}\leqslant 0.78$
and
$0.2\leqslant Ri_{l}\leqslant 4$
).
In conclusion, it appears that the partially stratified LS case
$({\it\alpha},Ri_{l})=(0.5,2)$
corresponds to a ‘sweet spot’ where stratification efficiently mitigates end effects without introducing any additional instability mechanism. It is also a realistic set of parameters for an experiment since it only requires
${\rm\Delta}{\it\rho}/{\it\rho}_{0}\approx 4\,\%$
for
$Re=14\,000$
.
Figure 11. Comparison between the azimuthal velocity profile at the equator with and without control in the LS case. The thick solid red line shows the ideal Taylor–Couette solution (1.1), the solid black line with markers shows the time averages from experiments (circles, unstratified; squares, partially stratified
$({\it\alpha},Ri_{l})=(0.5,2)$
) and the blue dashed/dashed–dotted lines show the computed base flows for the unstratified case/partially stratified case
$({\it\alpha},Ri_{l})=(0.5,2)$
. Additional measurements at
$z\approx {\it\Gamma}/6(1-{\it\alpha})$
in the partially stratified case yielded a mean velocity profile nearly indistinguishable from that at
$z\approx 0$
, hence very close to ideality too. This confirms the effectiveness of the control strategy across a large portion of the volume bounded by the stratified layers.
5 Discussion
5.1 Physical mechanism
To understand why end plates create meridional flow, consider the transport equation for the azimuthal vorticity
${\it\zeta}:=\partial _{z}u-\partial _{r}w$
. For the axisymmetric and steady base flow, this equation can be written as
$$\begin{eqnarray}\left[\left(U\partial _{r}+W\partial _{z}-{\displaystyle \frac{U}{r}}\right)-{\displaystyle \frac{1}{Re}}\left({\rm\nabla}^{2}-{\displaystyle \frac{1}{r^{2}}}\right)\right]{\it\zeta}_{B}=\partial _{z}\left({\displaystyle \frac{V^{2}}{r}}\right)+Ri_{g}\partial _{r}{\it\rho}_{B}.\end{eqnarray}$$
In the absence of end plates and stratification, the right-hand side of (5.1) is exactly zero, and the basic flow solution satisfies
${\it\zeta}_{B}=0$
, which implies that there is no meridional flow. In this case, the cyclostrophic balance
$V^{2}/r=\text{d}P/\text{d}r$
is satisfied everywhere in the flow. When end plates are added, the boundary condition on the azimuthal velocity disrupts this equilibrium (Czarny et al.
Reference Czarny, Serre, Bontoux and Lueptow2003) and a now non-vanishing torque term
$\partial _{z}(V^{2}/r)\neq 0$
(due to an inhomogeneous centrifugal force along
$z$
) generates meridional vorticity. When stratification is added, the baroclinic torque
$Ri_{g}\partial _{r}{\it\rho}_{B}$
counteracts this effect, leaving the flow virtually free of meridional vorticity when the right-hand side becomes negligible. If we estimate that
$r\approx 1/2(r_{i}^{\star }+r_{o}^{\star })=1/2(1+{\it\eta})/(1-{\it\eta})$
,
$V\approx 1$
and
$\partial _{z}=O(d/(l/2))=O(2/({\it\alpha}{\it\Gamma}))$
, this occurs for
$$\begin{eqnarray}Ri_{l}\approx {\displaystyle \frac{4{\it\eta}^{2}}{({\it\alpha}{\it\Gamma})^{2}(1-{\it\eta}^{2})\partial _{r}{\it\rho}_{B}}}.\end{eqnarray}$$
This expression confirms that thick layers, i.e. large
${\it\alpha}{\it\Gamma}$
, are more efficient at suppressing meridional motion, as they require a lower value of
$Ri_{l}$
. There are indeed two reasons to try to minimize the required value for
$Ri_{l}$
in experiments. First,
$Ri_{l}\propto {\it\Omega}_{i}^{-2}$
decreases rapidly with increasing
$Re\propto {\it\Omega}_{i}$
at fixed buoyancy frequency
$N$
. Second, the maximum buoyancy frequency
$N$
is set by saturation of salt into water at
${\rm\Delta}{\it\rho}/{\it\rho}_{0}\approx 20\,\%$
, limiting in turn the maximum
$Ri_{l}\propto N^{2}\propto {\rm\Delta}{\it\rho}/{\it\rho}_{0}$
. Therefore, thick layers are helpful when trying to maximize
$Re$
in an experiment while satisfying (5.2). As discussed in § 4.3, this only remains true as long as the aspect ratio of the unstratified zone
${\it\Gamma}(1-{\it\alpha})$
does not become small.
By estimating an upper bound for
$\partial _{r}{\it\rho}_{B}$
it is also possible to evaluate a lower bound for
$Ri_{l}$
. Looking at the density field in figure 9, we observe that the isopycnals are approximately straight lines in the meridional plane, except at the inner corners. In dimensional units, the radial density gradient must therefore be lower than
${\rm\Delta}{\it\rho}/(2d)$
, since, by definition, the initial density jump across one layer is equal to
${\rm\Delta}{\it\rho}/2$
. This leads to the non-dimensional estimate
$\partial _{r}{\it\rho}<1/2$
. For
${\it\alpha}=0.5$
,
${\it\eta}=0.417$
and
${\it\Gamma}=3$
, we obtain the upper bound
$Ri_{l}>0.75$
, which is consistent with the observation that
${\it\Delta}_{\bot }$
is nearly constant beyond that value in figure 8.
Finally, we note that in the case of Dirichlet boundary conditions on the density, the baroclinic term is infinitesimally small in the vicinity of the end plates, making it impossible to fully cancel the centrifugal torque term. This centrifugal torque is large in the vicinity of the inner corners because of the sharp vertical variation in
$V$
, explaining the locally higher levels of
$\Vert \boldsymbol{U}_{\bot }\Vert$
.
5.2 Effect of Prandtl number
Figure 12 shows the impact of the Prandtl number on the deviations
${\it\Delta}_{V}$
and
${\it\Delta}_{\bot }$
defined in (4.1). It appears that larger
$Pr$
leads to a significant reduction in both quantities, following approximate power laws
${\it\Delta}_{V}\propto Pr^{-0.47}$
and
${\it\Delta}_{\bot }\propto Pr^{-0.7}$
in the range
$Pr\in [1,46]$
for
$Re=5000$
. This behaviour suggests that stratification with salt (
$Sc\approx 700$
) ought to be more efficient than stratification with temperature (
$Pr\approx 7$
), ignoring the differing boundary conditions. This observation suggests that our numerical model overestimates the departure of the experiment from (1.1), as can also be seen in figure 11. This result reinforces our confidence in the effectiveness of our method.
Figure 12. The effect of the Prandtl number on the deviations
${\it\Delta}_{V}$
and
${\it\Delta}_{\bot }$
for the HS case
${\it\mu}={\it\eta}^{3/2}$
,
${\it\alpha}=0.5$
and
$Ri_{l}=2$
.
5.3 Effect of no-flux boundary conditions on density
Aside from the difference in Reynolds numbers, the only remaining discrepancy between the model and the experiment lies in the boundary conditions for the density. In our model, we assumed that stratification was permanently forced by applying a temperature profile at the walls, whereas in the experiments, the density is only controlled at
$t=0$
. In the experiment, a piecewise-linear density profile of the form (2.11) is set initially, but it is subject to no-flux boundary conditions
$\partial _{n}{\it\rho}_{B}$
at all times. Because of mass diffusion, the only possible steady-state solution is unfortunately unstratified. Yet, given the large value of the Schmidt number
$Sc={\it\nu}/{\it\kappa}\approx 700$
in the experiment, there is a separation of time scales between momentum diffusion
${\it\tau}_{{\it\nu}}=d^{2}/{\it\nu}$
and mass diffusion
${\it\tau}_{{\it\kappa}}=d^{2}/{\it\kappa}$
, which translates into a quasisteady evolution of the flow after a few units of
${\it\tau}_{{\it\nu}}$
. However, simulation of such large
$Sc$
flows proves computationally expensive as the corresponding separation of length scales is also large. Indeed, if we estimate the smallest inhomogeneity scale in the flow to be given by the Batchelor (Reference Batchelor1959) scale (formally defined for a stratified turbulent flow)
$L_{B}\sim Sc^{-1/2}$
(or
$L_{B}\sim Pr^{-1/2}$
for temperature), we expect it to be one order of magnitude smaller for
$Sc=700$
than for
$Pr=7$
. The resulting increase in computational cost did not allow us to perform the calculations in a reasonable time frame with the present codes.
However, it is in principle possible to satisfy the separation of time scales
${\it\tau}_{{\it\kappa}}/{\it\tau}_{{\it\nu}}=Sc\gg 1$
without taking
$Sc$
as large as 700. One might hope that a lower value of
$Sc$
, for instance
$Sc=30$
, would suffice. Figure 13 shows that this is not the case. Indeed, the discontinuity of
$V$
in the corners leads to local overturning of the density field, and hence strongly curved isopycnals (see figure 9). As a result, the mass diffusion term in (2.6d
) is not negligible in these corners, despite the small prefactor
$(Re\,Sc)^{-1}\approx 7\times 10^{-6}$
. Therefore, the rate of expansion of the meridional circulation cannot be approximated by
${\it\tau}_{{\it\kappa}}^{-1}$
, as the inhomogeneity length scale in the corners is much smaller than
$d$
. We conclude that it is not possible to compute quasisteady solutions even for Schmidt numbers in the range
$1\ll Sc\ll 700$
. This prohibits the use of linear stability analysis and motivates the use of Dirichlet (temperature) boundary conditions in our model.
Figure 13. Meridional flow in the case of no-flux boundary conditions on density; HS case,
$Re=1000$
,
${\it\alpha}=0.5$
,
$Ri_{l}=2$
and
$Sc=30$
, for (a)
$t=0.5$
, (b)
$t=2$
, (c)
$t=10$
. The unit of time here is the density diffusion time
${\it\tau}_{{\it\nu}}=d^{2}/{\it\nu}$
. Despite a large Schmidt number, there is no separation of time scales between diffusion of momentum and diffusion of density, leading to a rapid expansion of the meridional circulation. The contours and colourmap are the same as in figure 3(a–c) (here
${\rm\Delta}{\it\psi}=10^{-3}$
). The dotted lines indicate the limit of the stratified layers at
$t=0$
.
Despite an inadequate separation of time scales, it is worth noting that the aspect of the solution at the inner corners in the initial stages of our simulation with Neumann (salt) boundary conditions (see figure 13(a) for
$t=0.5{\it\tau}_{{\it\nu}}$
) is quite similar to the equivalent steady flow in figure 3(b). This observation strengthens our confidence in the ability of the model with Dirichlet boundary conditions to capture the dynamics of the experiment.
5.4 Seeking subcritical transition to turbulence
After demonstrating that the parameter combination
$(\ln {\it\mu}/\ln {\it\eta},{\it\alpha},Ri_{l})=(0.5,0.5,2)$
satisfies all of the constraints set forth in the introduction, we probed the possibility of sustained turbulence in the unstratified zone by carrying out a series of experiments.
In our first experiment, the flow was perturbed impulsively by reducing the inner cylinder rotation rate by 75 % in approximately 1 s. A first PIV measurement was taken then (defining
$t=0$
), before
${\it\Omega}_{i}$
was ramped back up to its final value over the course of 1 min (approximately 10 inner cylinder rotation periods). A second measurement was made 30 min later, at
$t\approx {\it\tau}_{{\it\nu}}/10$
. Figure 14 shows the deviation from the unperturbed state
$\boldsymbol{q}_{\infty }$
(time-averaged azimuthal profile
$\overline{v}_{\infty }$
shown in figure 11), measured by
${\it\Delta}_{\infty }:=\sqrt{\overline{u^{2}+(v-\overline{v}_{\infty })^{2}}}/\overline{v}_{\infty }$
, at both instants. At
$t=0$
(dashed line), the perturbation extends radially over a distance
$d^{\prime }\approx d/10$
, corresponding to an effective diffusion time
${\it\tau}_{{\it\nu}}^{\prime }=d^{\prime 2}/{\it\nu}\approx {\it\tau}_{{\it\nu}}/100$
. At
$t\approx {\it\tau}_{{\it\nu}}/10\approx 10{\it\tau}_{{\it\nu}}^{\prime }$
(solid line), the perturbation has completely diffused and the flow has relaxed to its unperturbed laminar state, as indicated by the low value of
${\it\Delta}_{\infty }\approx 1\,\%$
over the entire radial range.
In addition to that, we also tried to trigger subcritical transition to turbulence using two types of non-axisymmetric perturbations. After the spin-up procedure, a turbulent radial jet was introduced at the equator using a syringe and a needle of diameter 1 mm. The needle was introduced into the flow through a hole in the top end plate before passing through the upper stratified region to reach the unstratified core. No discernible mixing was introduced in the stratified region throughout this procedure. The perturbation velocity in the jet was approximately 7 % of the inner cylinder velocity, but sustained turbulence was not triggered, with the flow relaminarizing within 30 min. The second non-axisymmetric perturbation involved the same needle set-up, but this time fluid was removed from the unstratified core region to induce vortex stretching. Once again, no sustainable turbulence was generated using this method.
All of these observations show the robustness of the laminar flow with respect to finite-amplitude perturbations, and indicate its nonlinear stability at
$Re=O(10^{4})$
and
${\it\mu}={\it\eta}^{1/2}$
. This conclusion is consistent with recent numerical and experimental results by Ostilla-Mónico et al. (Reference Ostilla-Mónico, Verzicco, Grossmann and Lohse2014) and Edlund & Ji (Reference Edlund and Ji2014), at even higher Reynolds number and larger rotation ratios. The first authors used axially periodic direct numerical simulation (with no stratification), and could not find any evidence of a self-sustaining process up to
$Re=O(10^{5})$
with
${\it\mu}={\it\eta}^{3/2}$
. Similarly, the latter authors, from the Princeton group, found robust decay of various types of initial perturbations in their enhanced split-ring apparatus (HTX device) at
$Re$
even greater than
$10^{6}$
, with
${\it\mu}={\it\eta}^{1.8}$
.
Figure 14. The deviation
${\it\Delta}_{\infty }$
from the unperturbed state at the equator when searching for subcritical transition to turbulence. The dashed curve shows a measure of
${\it\Delta}_{\infty }$
right after applying the perturbation and the solid line corresponds to the deviation 30 min later. For this forcing at
$Re=O(10^{4})$
, turbulence is not triggered in the unstratified zone, as is evident from the low values of
${\it\Delta}_{\infty }\approx 1\,\%$
rapidly reached.
6 Conclusions
In this work we have confirmed both experimentally and numerically the severe effect that end plates have on the interior of Taylor–Couette flow in the quasi-Keplerian regime. In the ‘high-shear case’
${\it\mu}={\it\eta}^{3/2}$
, two symmetric recirculation cells are generated in the meridional plane; these merge at the equator to form a strong radial jet. This jet redistributes angular momentum, causing the flow to become turbulent through a linear instability. In the ‘low-shear case’
${\it\mu}={\it\eta}^{1/2}$
, the meridional flow is weaker, and there is no radial jet at the equator for the same value of
$Re$
. Despite remaining approximately invariant along the axial direction, the azimuthal flow is however significantly disturbed by the presence of end plates and deviates from the ‘ideal’ Taylor–Couette solution corresponding to an axially unbounded system.
We have then examined how stable stratification can be judiciously used to mitigate these end effects in order to recover ‘ideal’ Taylor–Couette flow. When stratification is added across the full height, axisymmetric meridional flow is only able to develop in boundary layers near the end plates, and recirculation becomes essentially confined to the inner corners, where the azimuthal velocity is discontinuous. Everywhere else in the flow, the deviation with respect to the ideal velocity profile drops significantly. The physical mechanism behind this passive control method is the competition between the ‘centrifugal’ torque term
$\partial _{z}(v^{2}/r)$
responsible for the generation of azimuthal vorticity and the baroclinic torque
$Ri_{g}\partial _{r}{\it\rho}$
acting against it. This mechanism is robust enough that similar enhancement of the base flow in the equatorial region can be achieved even when stratification is restricted to layers adjacent to the top and bottom end plates. As long as the stable stratification is strong enough, typically
$1<Ri_{l}<5$
, and neither the stratified nor the unstratified layers are too shallow (typically
${\it\alpha}\approx 0.5$
for
${\it\Gamma}=3$
), the control of the base flow is effective.
One obvious advantage of the approach is that it is much easier to implement than complex designs such as split endcaps (Ji et al.
Reference Ji, Burin, Schartman and Goodman2006; Edlund & Ji Reference Edlund and Ji2014) or a split inner cylinder (Paoletti & Lathrop Reference Paoletti and Lathrop2011). By simply adding salt in varying concentration to the working fluid, we managed to significantly mitigate end effects and recover the Couette flow solution around the equator
$z=0$
.
However, like any other control method, this approach has its limits. First, the method is only applicable to rotation ratios in the range
${\it\eta}\lesssim {\it\mu}<1$
, corresponding to the least-sheared configurations in the quasi-Keplerian range
${\it\eta}^{2}<{\it\mu}<1$
. When
${\it\mu}<{\it\eta}$
, the SRI develops in the stratified layers, despite the presence of the unstratified region and end plates. This instability destroys the initial density profile, rendering the method ineffective. Second, application of the method at very high Reynolds number, of the order of
$10^{6}$
or more, is challenging due to the eventual saturation of water by salt. For example, taking
$Ri_{l}=2$
,
${\rm\Delta}{\it\rho}/{\it\rho}_{0}\approx 20\,\%$
(saturation threshold for salt in water) and a layer height of 0.75 gap (corresponding to
${\it\alpha}{\it\Gamma}=1.5$
as in § 4.3), means that reaching
$Re=10^{6}$
would require a huge tank of outer radius
$r_{o}\approx 2~\text{m}$
or more.
This aside, we have successfully demonstrated the applicability of the method at
$Re=O(10^{4})$
for the rotation ratio
${\it\mu}={\it\eta}^{1/2}$
, and found turbulence decay following several types of large-amplitude disturbances. This result is consistent with the most recent numerical (Ostilla-Mónico et al.
Reference Ostilla-Mónico, Verzicco, Grossmann and Lohse2014) and experimental (Edlund & Ji Reference Edlund and Ji2014) investigations at respectively
$Re=O(10^{5})$
and
$Re=O(10^{6})$
, and hence further strengthens the view that extra physics beyond that of a simple rotating shear flow is needed to explain the inferred turbulence in weakly ionized accretion disks (see Turner et al. (Reference Turner, Fromang, Gammie, Klahr, Lesur, Wardle and Bai2014) for a recent review of other possible instability mechanisms).
Acknowledgement
We gratefully acknowledge the support of EPSRC under grant EP/K034529/1. The data associated with this study are made available at https://www.repository.cam.ac.uk/handle/1810/253344.
