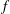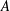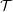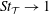1 Introduction
Almost all aquatic and flying animals generate thrust via the oscillatory motion of foil-like body parts (for example, tails, fins, etc.). Moreover, flapping foil systems are often associated with high efficiency and strong side forces, ideal for manoeuvring (Read, Hover & Triantafyllou Reference Read, Hover and Triantafyllou2003). Thus, many studies have focused on the analysis and implementation of these biological configurations into man-made designs (Triantafyllou, Techet & Hover Reference Triantafyllou, Techet and Hover2004; Wang Reference Wang2005; Fish & Lauder Reference Fish and Lauder2006), although the underlying physics is still not clearly understood.
Here we aim to determine the drag-to-thrust wake transition of these flapping mechanisms via the analysis of the vortex pattern development. Assuming foil undulations above the lock-in frequency (Vial, Bellon & Hernández Reference Vial, Bellon and Hernández2004; Thiria, Goujon-Durand & Wesfreid Reference Thiria, Goujon-Durand and Wesfreid2006) we observe at least three basic wake patterns (Von Kármán Reference Von Kármán1935): the classic Bénard von Kármán (Bvk) street, where
$U_{wake}<U_{\infty }$
(figure 1
a); the neutral line, where
$U_{wake}\sim U_{\infty }$
(figure 1
b); and the reversed BvK wake, where
$U_{wake}>U_{\infty }$
(figure 1
c). The latter is synonymous with the drag-to-thrust wake transition, although a lag exists between this phenomenon and the foil’s overall transition towards thrust. This is due to the fact that a weak velocity surplus cannot overcome profile drag or velocity fluctuations and pressure differences within the control volume (Streitlien & Triantafyllou Reference Streitlien and Triantafyllou1998; Ramamurti & Sandberg Reference Ramamurti and Sandberg2001; Bohl & Koochesfahani Reference Bohl and Koochesfahani2009).
Figure 1. Drag-to-thrust transition within the wake of a symmetric flapping foil. (a) BvK street, (b) Neutral line, (c) reversed BvK wake.
As the driving factors of BvK reversal we typically consider the oscillating amplitude and the oscillating frequency
$f$
of the kinematics (Koochesfahani Reference Koochesfahani1989). The former is expressed by the trailing-edge (TE) peak-to-peak amplitude
$A$
. In dimensionless terms it is often normalised by the thickness
$D$
or the chord length
${\mathcal{C}}$
of the foil. In a similar fashion the frequency is often expressed as a reduced frequency
$k=U_{\infty }/(f{\mathcal{C}})$
(Birnbaum Reference Birnbaum1924), a thickness-based Strouhal number
$Sr=(fD)/U_{\infty }$
(GodoyDiana et al. Reference Godoy-Diana, Marais, Aider and Wesfreid2009) or a chord-length-based Strouhal number
$St_{{\mathcal{C}}}=1/k$
(Cleaver, Wang & Gursul Reference Cleaver, Wang and Gursul2012). Triantafyllou, Triantafyllou & Gopalkrishnan (Reference Triantafyllou, Triantafyllou and Gopalkrishnan1991) suggested a modified amplitude-based Strouhal number
$St_{A}=(fA)/U_{\infty }$
. By including both the frequency and the amplitude of oscillation,
$St_{A}$
can potentially characterise the BvK reversal by a single factor, as opposed to
$k$
,
$Sr$
and
$St_{{\mathcal{C}}}$
. Studies of Anderson et al. (Reference Anderson, Streitlien, Barrett and Triantafyllou1998) and Read et al. (Reference Read, Hover and Triantafyllou2003) showed that optimal efficiency occurs for a short range of
$St_{A}\sim [0.2,0.4]$
. This was also supported by Triantafyllou, Triantafyllou & Grosenbaugh (Reference Triantafyllou, Triantafyllou and Grosenbaugh1993) and Taylor, Nudds & Thomas (Reference Taylor, Nudds and Thomas2003), who observed that the majority of natural fliers and swimmers prefer to cruise within this range. According to Andersen et al. (Reference Andersen, Bohr, Schnipper and Walther2017), BvK reversal occurs at different
$St_{A}$
values for pure heave and pure pitch. Therefore,
$St_{A}$
cannot be regarded as an expression of self-similarity.
The fundamental problem is that characterising the motion only by the amplitude fails to capture the contribution of the other points of the foil. This becomes important when the heaving component is significant, resulting in the generation of strong leading edge vortices (LEV) which travel downstream and blend with the trailing-edge vortices (TEV). Instead, we need to take into account the length of the entire path travelled in a period rather than the maximum distance from equilibrium.
In this study, we formulate a novel length scale, which characterises the Bvk reversal of harmonically flapping foils. Two-dimensional simulations are conducted at a Reynolds number of
$Re=1173$
for a rigid NACA0016 profile and three basic harmonic kinematics: pure heave, pure pitch and heave–pitch coupling. Additional higher-Reynolds-number simulations (
$Re=11\,730$
) are used to quantify the Reynolds number effects. The influence of different pivot points is examined for pure pitch and coupled motions. In addition, we analyse the impact of different maximum effective angles of attack on coupled kinematics. Finally, we develop a new metric based on the chordwise-averaged path travelled by the foil, in order to determine BvK wake reversal for a vast range of harmonic motions.
1.1 Geometry and kinematics
We consider a rigid NACA0016 with a thickness
$D=0.16{\mathcal{C}}$
. The foil performs simple harmonic oscillations around a stationary equilibrium position, against a uniform free stream velocity
$U_{x}=U_{\infty }$
. The lateral direction of every point along this chordline is denoted with
$y(t,s)$
. Here
$t$
is the time and
$s$
is the
${\mathcal{C}}$
-normalised coordinate along the chord, ranging from 0 at LE to 1 at TE. Pure pitch (see figure 2
b) is modelled as a sinusoidal rotation about a specified pivot point along the chordline (
$s={\mathcal{P}}$
, where
${\mathcal{P}}$
is the non-dimensional distance between the LE and the pivot point along the chordline) and pure heave (see figure 2
a) as a sinusoidal lateral translation of the entire chordline. Coupled motion (see figure 2
c) occurs by the superposition of these pure motions:
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle y_{c}(t,s)=y_{h}(t,s)+y_{\unicode[STIX]{x1D703}}(t,s)\quad \text{where}\\ \displaystyle y_{h}(t,1)=h_{0}\sin (2f\unicode[STIX]{x03C0}t),\quad y_{\unicode[STIX]{x1D703}}(t,1)=(1-{\mathcal{P}}){\mathcal{C}}\sin (\unicode[STIX]{x1D703}(t))\quad \text{and}\\ \displaystyle \unicode[STIX]{x1D703}(t)=\unicode[STIX]{x1D703}_{0}\sin (2f\unicode[STIX]{x03C0}t+\unicode[STIX]{x1D713}).\end{array}\right\}\end{eqnarray}$$
Here
$\unicode[STIX]{x1D703}(t)$
is the instantaneous value of pure pitch whilst
$h_{0}$
and
$\unicode[STIX]{x1D703}_{0}$
are the amplitudes of pure heave and pure pitch, respectively. The phase difference between pitch and heave is expressed as
$\unicode[STIX]{x1D713}$
. Here
$\unicode[STIX]{x1D713}=90^{\circ }$
, because this value is considered optimal in terms of propulsive efficiency (Platzer & Jones Reference Platzer and Jones2008).
Another important kinematic parameter in coupled motions is the effective angle of attack
$\unicode[STIX]{x1D6FC}_{eff}(t)$
, which is the summation of the instantaneous pitch angle
$\unicode[STIX]{x1D703}(t)$
and the heave-induced angle of attack. Thus, for
$\unicode[STIX]{x1D713}=90^{\circ }$
, the amplitude of
$\unicode[STIX]{x1D6FC}_{eff}(t)$
is
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}=\arctan \frac{2\unicode[STIX]{x03C0}fh_{0}}{U_{\infty }}-\unicode[STIX]{x1D703}_{0}.\end{eqnarray}$$
In this study, we differentiate coupled motions by varying
${\mathcal{P}}$
and
$\unicode[STIX]{x1D6FC}$
while keeping
$\unicode[STIX]{x1D713}=90^{\circ }$
.
Figure 2. Foil kinematics, geometry and coordinate system. (a) Pure heave, (b) pure pitch, (c) coupled motion.
1.2 Dimensionless parameters
Three non-dimensional parameters are used to describe the interaction between the oscillating foil and the free stream: the Reynolds number based on chord length,
$Re=U_{\infty }{\mathcal{C}}/\unicode[STIX]{x1D708}$
(where
$\unicode[STIX]{x1D708}$
is the kinematic viscosity), the thickness-based Strouhal number,
$Sr$
, and the non-dimensional TE amplitude (
$A_{D}$
):
$$\begin{eqnarray}Sr=\frac{Df}{U_{\infty }},\quad A_{D}=\frac{2y_{c}(t_{max},1)}{D}.\end{eqnarray}$$
Thus,
$St_{A}=SrA_{D}$
and can be understood as the ratio between the speed of the foil trailing edge and
$U_{\infty }$
(Godoy-Diana et al.
Reference Godoy-Diana, Marais, Aider and Wesfreid2009).
The thrust coefficient
$C_{t}$
is expressed by simply normalising the total force acting on the
$x$
axis by the dynamic pressure of the free stream. Time-averaged quantities are presented with an overbar to distinguish them from their instantaneous counterparts.
$$\begin{eqnarray}C_{t}=\frac{F_{x}}{{\textstyle \frac{1}{2}}\unicode[STIX]{x1D70C}U_{\infty }^{2}{\mathcal{C}}}.\end{eqnarray}$$
1.3 Computational method
The CFD solver chosen for this study can simulate complex geometries and moving boundaries for a wide range of Reynolds numbers in two- and three-dimensional domains, by utilising the boundary data immersion method (BDIM) (Weymouth & Yue Reference Weymouth and Yue2011). BDIM solves the viscous time-dependent Navier–Stokes equations and simulates the entire domain by combining the moving body and the ambient fluid through a kernel function. This technique has quadratic convergence and has been validated for flapping foil simulations over a wide range of kinematics (Maertens & Weymouth Reference Maertens and Weymouth2015; Polet, Rival & Weymouth Reference Polet, Rival and Weymouth2015).
The mesh configuration is a rectangular Cartesian grid with a dense uniform grid near the body and in the near wake, and exponential grid stretching used in the far-field, and the numerical domain uses a uniform inflow, zero-gradient outflow and free-slip conditions on the upper and lower boundaries. Furthermore, no-slip boundary conditions are used on the oscillating foil. Mesh density is expressed in terms of grid points per chord. A uniform grid of
$\unicode[STIX]{x1D6FF}x=\unicode[STIX]{x1D6FF}y={\mathcal{C}}/192$
is used for the results in this work, based on the results of the convergence study shown in table 1.
Table 1. Computational statistics of grid convergence for a harmonically flapping foil.
2 Results and discussion
2.1 Wake comparison of different kinematics
According to Godoy-Diana, Aider & Wesfreid (Reference Godoy-Diana, Aider and Wesfreid2008), the Reynolds number range of naturally occurring flapping foils is
$100<Re<10\,000$
. In this study, most simulations are conducted for
$Re=1173$
to be within this range and to enable comparison with the experiments of Godoy-Diana et al. (Reference Godoy-Diana, Marais, Aider and Wesfreid2009). Additional simulations are conducted for selected cases at
$Re=11\,730$
to examine the effects of higher Reynolds number. The pivot points tested for pure pitch and coupling are
${\mathcal{P}}=0$
and 0.25. The coupled motion is also tested for three values of
$\unicode[STIX]{x1D6FC}=5^{\circ }$
,
$10^{\circ }$
and
$20^{\circ }$
.
We analyse the wake patterns and resultant hydrodynamic loads for the above-mentioned kinematics. Various stages of the wake development can be seen in figure 3 for pure heave, pure pitch for
${\mathcal{P}}=0.25$
and coupled motion for
${\mathcal{P}}=0.25$
and
$\unicode[STIX]{x1D6FC}=10^{\circ }$
. The transition from the BvK (third row) to the neutral wake where vortices are shed in-line (fourth row) and later the reversed BvK (fifth and sixth rows) is in agreement with literature (Koochesfahani Reference Koochesfahani1989; Godoy-Diana et al.
Reference Godoy-Diana, Marais, Aider and Wesfreid2009; Andersen et al.
Reference Andersen, Bohr, Schnipper and Walther2017). At lower
$Sr{-}A_{D}$
combinations, more complicated wake patterns (for example, 2P wakes (Williamson & Roshko Reference Williamson and Roshko1988)) at the first row of figure 3 are in accordance with those observed by Andersen et al. (Reference Andersen, Bohr, Schnipper and Walther2017) for wedge-type foils. At such low
$Sr{-}A_{D}$
combinations, coupled motions are dominated by one of the two modes – for example, for
$Sr=0.01$
, the heaving contribution to the foil displacement is less than 35 % for all the coupled cases studied.
Figure 3. Contour plots of normalised instantaneous vorticity magnitude of the 30th cycle at
$Sr=0.15$
and
$Re=1173$
, for (a) pure heave at
$A_{D}\sim [0.5{-}0.1]$
, (b) pitch at
${\mathcal{P}}=0$
and
$A_{D}\sim [0.82{-}1.3]$
and (c) coupled motion at
${\mathcal{P}}=0$
,
$\unicode[STIX]{x1D6FC}=10^{\circ }$
and
$A_{D}\sim [1.02{-}1.4]$
. Drag regime ▾, neutral state ●, thrust-producing flow ▴.
Among the three kinematic test cases, significant discrepancies can be seen in close proximity to the foil, most notably at the LE. The deep stall (high
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FF}t$
across the chord) experienced by the pure heaving foil generates LEVs of sizes comparable to the TEVs which travel across the chord and blend with the wake. A closer look at figure 3(c) reveals that the coupled motion generates the smallest amount of dynamic separation among the three cases. Finally, as seen in the last row of figure 3, even when the BvK street is fully reversed, some cases exist within the drag-producing regime. This lag is expected since a weak propulsive wake is not enough to overcome the profile drag or to compensate for the velocity fluctuations and pressure differences that exist within the control volume (Streitlien & Triantafyllou Reference Streitlien and Triantafyllou1998; Ramamurti & Sandberg Reference Ramamurti and Sandberg2001; Bohl & Koochesfahani Reference Bohl and Koochesfahani2009).
Figure 4 shows the best-fit curve that isolates the neutral line (where
$U_{wake}\sim U_{\infty }$
), for the different harmonics. These best-fit curves are reproduced in figure 5(a) in order to compare this neutral line across different kinematics. Although the
$Sr{-}A_{D}$
phase diagram is suitable to examine a specific kinematics, it is clear that this does not universally describe wake transitions. This is the result of the unique interactions between LEVs and TEVs that are specific to the motion type. Consequently, this demonstrates the need for a self-similar classification of the oscillating amplitude to accurately determine wake development.
Figure 4.
$A_{D}{-}Sr$
wake map for various kinematics at
$Re=1173$
for (a) pure heave, (b) pure pitch at
${\mathcal{P}}=0.25$
, (c) pure pitch at
${\mathcal{P}}=0$
and (d) coupled motion at
${\mathcal{P}}=0$
and
$\unicode[STIX]{x1D6FC}=20^{\circ }$
. Black dots: BvK street. Grey dots: reversed BvK wake. White dots: wake symmetry breaking. The dashed black curves correspond to the best-fit curves of the neutral line.
Figure 5. Comparison of neutral line best-fit curves for various kinematics on a
$Sr{-}A_{D}$
phase space (a) and a
$Sr{-}{\mathcal{T}}_{D}$
phase space (b) at
$Re=1173$
. Here
${\mathcal{T}}_{D}$
is the thickness-normalised
${\mathcal{T}}$
.
2.2 An alternative length scale
Fundamentally, the foil generates thrust force by displacing and accelerating fluid out of its path as it moves through its prescribed trajectory. The quantity of fluid displaced is dependent on the path length travelled by the foil over one period of oscillation. Thus, a proper indicator of the wake’s drag-to-thrust transition should reflect the length of this curve.
To quantify the aforementioned distance, we compare different length approximations of the path length (
${\mathcal{L}}$
) covered by the TE in one non-dimensional period for a heaving foil. We estimate this length in three different ways: (i) step motion, (ii) square wave and (iii) sine wave. As shown in figure 6(a) (red curve), the step motion definition is equivalent to the use of
$A$
to capture the covered length. As we see in figure 6(b), the square wavelength
$Sq$
captures
$A$
in the vertical direction but also the streamwise length (
$U_{\infty }/f$
) traversed by TE in one period. Finally, the trajectory length
$Tr$
of the sine wave (see figure 6
c) captures the exact
${\mathcal{L}}$
traversed by the TE over the entire period:
$$\begin{eqnarray}T_{r}=\int _{0}^{1/f}\sqrt{{\dot{x}}^{2}(t,1)+{\dot{y}}^{2}(t,1)}\,\text{d}t,\end{eqnarray}$$
where
${\dot{x}}$
is the horizontal velocity of the foil, which is approximately
$U_{\infty }$
for small amplitude motions.
Figure 6. Best-fit curves of the neutral line of various harmonic kinematics plotted on
$A_{D}-1/Sr$
(a),
$Sq_{D}-1/Sr$
(b),
$Tr_{D}-1/Sr$
(c) and
${\mathcal{T}}_{D}-1/Sr$
(d) at
$Re=1173$
and
$Re=11\,730$
. Each point on the
$y$
axis expresses the thickness-normalised length of the curve (red) of the corresponding approximation of the path traversed by the foil within one cycle.
The utility of these three metrics is estimated via the agreement (collapse) of the neutral curves for different types of motions in the
$f-{\mathcal{L}}$
domain. Here,
${\mathcal{L}}$
is normalised by
$D$
, and this is done so that
$f$
can be expressed by
$Sr$
at the same domain. Again, figures 6(a), 6(b) and 6(c) show the neutral lines for different kinematics in
${\mathcal{L}}_{D}-1/Sr$
domains for the aforementioned types of
${\mathcal{L}}_{D}$
– namely,
$A_{D}$
,
$Sq_{D}$
and
$Tr_{D}$
, respectively. The frequency is represented in the inverse form so that a power law between amplitude and frequency is depicted by a straight line. Since previous studies suggest that BvK reversal depends solely on
$St_{A}$
, we expect a collapse of the neutral line curves of different kinematics when plotted on an
$A_{D}-1/Sr$
chart. However, as seen in figure 6(a), these curves are heavily dependent on kinematics. On the other hand, as we move towards
$Tr$
(which accurately represents the trajectory length) the collapse of the various neutral line curves is significantly improved (see figure 6
c).
$Tr$
is suitable for characterising heave-dominant kinematics since the motion of the entire chord can be represented just by the path traversed by the TE. However,
$Tr$
fails to capture the effects of a chordwise gradient
$A$
present in pitch-dominated motions, since most of the lateral motion is downstream of the pivot point for
${\mathcal{P}}<0.5$
(see figure 3
b). This means that
$Tr$
overestimates the displaced fluid for these particular cases, and therefore it is still dependent on kinematics (see figure 6
c). The effect of the pitching component can be incorporated into the metric by calculating the average trajectory length covered by the entire foil (chord) over one period:
$$\begin{eqnarray}{\mathcal{T}}=\bar{{\mathcal{L}}}=\int _{0}^{1}\int _{0}^{1/f}\sqrt{{\dot{x}}^{2}(t,s)+{\dot{y}}^{2}(t,s)}\,\text{d}t\,\text{d}s,\end{eqnarray}$$
where
$s$
is the coordinate along the chord, with
$s=0$
at LE and
$s=1$
at the TE.
The
$D$
-normalised chord-averaged trajectory length
${\mathcal{T}}_{D}$
is plotted versus
$1/Sr$
in figure 6(d). The new metric demonstrates remarkable collapse of different kinematics on the curve corresponding to the neutral line of pure heave (where
$Tr_{D}={\mathcal{T}}_{D}$
). Interestingly this curve follows the diagonal of a square, and as we move towards more inviscid flows it can be expressed as
${\mathcal{T}}_{D}\cdot Sr\approx \,\text{const}\,\rightarrow 1$
. More specifically for
$Re=1173$
,
${\mathcal{T}}_{D}Sr\approx 1.035$
, while for
$Re=11\,730$
,
${\mathcal{T}}_{D}Sr\approx 1.015$
. This product represents the average speed of the foil over one period. Thus, the area in the lower right half of the straight line represents the zone where this average speed is less than
$U_{\infty }$
, while the upper left is where the speed is larger than
$U_{\infty }$
. This provides a very simple physical interpretation of the
$1/f-{\mathcal{T}}$
phase space where, in order for the foil to produce thrust, the kinematics has to be tuned in such a way that the chord-averaged speed of the foil along the path over one period must be faster than the free stream. In other words, a path-length-based Strouhal number (
$St_{{\mathcal{T}}}=f{\mathcal{T}}/U_{\infty }$
) should be greater than 1. As the value of
$St_{{\mathcal{T}}}$
increases further beyond 1, the wake of the foil becomes stronger, producing higher and higher values of thrust.
The universality of the new length scale is evaluated by further examining the agreement of neutral line curves for various kinematic factors such as
$f$
,
${\mathcal{P}}$
,
$\unicode[STIX]{x1D6FC}$
. Figure 5(b) shows all the kinematic options where a collapse was demonstrated. The agreement among these curves deteriorates for
$Sr<0.15$
or
$Sr>0.35$
, perhaps due to the limitations of using two-dimensional numerical simulations. This is consistent with the observations of Mittal & Balachandar (Reference Mittal and Balachandar1995), who found that two-dimensional simulations might result in large force fluctuations and erroneous wake patterns. Additionally non-periodic wakes have been observed for pure pitch motion at
${\mathcal{P}}>0.6$
which could also contribute to the poor collapse. As
$\unicode[STIX]{x1D6FC}$
is essentially an indicator of the heave to pitch ratio, within a coupled motion case it has no real effect on periodicity, at least up to
$\unicode[STIX]{x1D6FC}=20^{\circ }$
, and thus the coupled motions presented here agree well with the pure pitch and heave test cases. Clearly, the new metric sets a threshold for the drag-to-thrust wake transition of two-dimensional flapping foils for the entire range of kinematics, provided that the resultant wake is periodic.
3 Conclusions
Two-dimensional simulations were conducted for a rigid flapping NACA0016 profile at low- and high-Reynolds-number incompressible flow. The wake development towards a reversed BvK street was examined for a variety of harmonic motions, amplitudes and frequencies. At very low amplitudes and frequencies, 2P wake patterns were observed for the coupled motions, in agreement with either the pure heave or the pure pitch cases. This is due to the fact that at such low
$Sr{-}A_{D}$
combinations the coupled motions are dominated by either the heaving or the pitching component.
In dimensionless amplitude–period maps, various length scales were evaluated with respect to the neutral line of different motion types. It was revealed that the relationship between
$A_{D}$
and the period is nonlinear since the maximum distance from equilibrium cannot properly characterise the displaced volume (or area) required to overcome the drag forces. This is solved by calculating the length of the path traversed by the foil over one period of oscillation.
On a
$1/Sr-Tr_{D}$
graph, the neutral line of pure heave forms a linear curve. Since
$U_{foil}=Tr_{D}/(1/Sr)$
, this means that thrust is achieved when
$U_{foil}>U_{\infty }$
. Furthermore, the dimensionless chord-averaged trajectories per cycle
${\mathcal{T}}_{D}$
of all motion types tested collapse upon the pure heaving case. In other words, the neutral lines of all test cases collapse on a trajectory-based Strouhal
$St_{{\mathcal{T}}}\rightarrow 1$
. Thus the new metric can serve as a universal length scale that captures the BvK reversal for every combination of harmonic two-dimensional kinematics.
This novel method allows us to parametrise drag-to-thrust wake transition of a simple two-dimensional harmonically oscillating body via the chosen kinematics without the use of complex fluid dynamic equations. Knowing the onset of thrust for a flapping foil via a single parameter can significantly reduce the effort of designing sufficient biomimetic propulsors. Moreover, it will enable scientists and engineers to describe and/or confirm observations regarding the thrust-generating strategies and evolution of natural flyers and swimmers.
Acknowledgements
This research was supported financially by the Office of Naval Research award no. N62909-18-1-2091 and the Engineering and Physical Sciences Research Council doctoral training award (1789955). All data supporting this study are openly available from the University of Southampton repository at https://doi.org/10.5258/SOTON/D0905.
