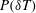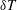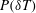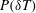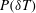1 Introduction
Mixing of a passive scalar field, such as temperature or concentration, by a chaotic velocity field is a common phenomenon in nature and technology. It is relevant to many practical applications ranging from transport and chemical reactions to design and operation of mixing equipment in various industrial processes of polymers, minerals, fine chemicals, paints, cosmetics, food, water and waste water treatment (Ottino Reference Ottino1989; Paul, Atiemo-Obeng & Kresta Reference Paul, Atiemo-Obeng and Kresta2004; Dimotakis Reference Dimotakis2005). When the fluid motion is turbulent, the repeated action of advection and stretching is known to create convoluted spatial structures, characterized by elongated lamellae (in two dimensions) or sheets (in three dimensions) with a wide range of self-similar scales, which promote mixing for diffusive transfer at the smallest length scale and reduction of mixing times (Ottino Reference Ottino1989; Sreenivasan, Ramshankar & Meneveau Reference Sreenivasan, Ramshankar and Meneveau1989; Procaccia et al. Reference Procaccia, Ching, Constantin, Kadanoff, Libchaber and Wu1991; Villermaux Reference Villermaux2012). In the past decades, there has been a large number of theoretical (Procaccia & Zeitak Reference Procaccia and Zeitak1989, Reference Procaccia and Zeitak1990; She & Orszag Reference She and Orszag1991; Sreenivasan Reference Sreenivasan1991; Grossmann & Lohse Reference Grossmann and Lohse1992; Benzi et al. Reference Benzi, Ciliberto, Tripiccione, Baudet, Massaioli and Succi1993; Grossmann & Lohse Reference Grossmann and Lohse1993; She & Léveque Reference She and Léveque1994; Chertkov et al. Reference Chertkov, Falkovich, Kolokolov and Lebedev1995; Gawȩdzki & Kupiainen Reference Gawȩdzki and Kupiainen1995; Shraiman & Siggia Reference Shraiman and Siggia1995a ,Reference Shraiman and Siggia b ; Cao & Chen Reference Cao and Chen1997; Ching & Chau Reference Ching and Chau2001; Ching Reference Ching2007; Arnèodo et al. Reference Arnèodo, Benzi, Berg, Biferale, Bodenschatz, Busse, Calzavarini, Castaing, Cencini and Chevillard2008), numerical (Cao, Chen & Sreenivasan Reference Cao, Chen and Sreenivasan1996; Kerr Reference Kerr1996; Calzavarini, Toschi & Tripiccione Reference Calzavarini, Toschi and Tripiccione2002; Camussi & Verzicco Reference Camussi and Verzicco2004; Ching, Guo & Lo Reference Ching, Guo and Lo2008) and experimental (Wu et al. Reference Wu, Kadanoff, Libchaber and Sano1990; Procaccia et al. Reference Procaccia, Ching, Constantin, Kadanoff, Libchaber and Wu1991; Solomon & Gollub Reference Solomon and Gollub1991; Tong & Shen Reference Tong and Shen1992; Benzi et al. Reference Benzi, Tripiccione, Massaioli, Succi and Cilibertoi1994; Cioni, Ciliberto & Sommeria Reference Cioni, Ciliberto and Sommeria1995; Takeshita et al. Reference Takeshita, Segawa, Glazier and Sano1996; Ashkenazi & Steinberg Reference Ashkenazi and Steinberg1999; Zhou & Xia Reference Zhou and Xia2001; Skrbek et al. Reference Skrbek, Niemela, Sreenivasan and Donnelly2002; Mashiko et al. Reference Mashiko, Tsuji, Mizuno and Sano2004) studies of small-scale velocity and temperature fluctuations in turbulent flows. Details about these studies have been reviewed by Sreenivasan (Reference Sreenivasan1991), Siggia (Reference Siggia1994), Warhaft (Reference Warhaft2000), Biferale & Procaccia (Reference Biferale and Procaccia2005), Ishihara, Gotoh & Kaneda (Reference Ishihara, Gotoh and Kaneda2009), Lohse & Xia (Reference Lohse and Xia2010), Chillá & Schumacher (Reference Chillá and Schumacher2012).
Many experimental studies focused on the structure functions,
![]() $\langle \unicode[STIX]{x1D6FF}T_{r}^{n}\rangle$
, of temperature increment
$\langle \unicode[STIX]{x1D6FF}T_{r}^{n}\rangle$
, of temperature increment
![]() $\unicode[STIX]{x1D6FF}T_{r}=T(x+r)-T(x)$
between two points separated by a distance
$\unicode[STIX]{x1D6FF}T_{r}=T(x+r)-T(x)$
between two points separated by a distance
![]() $r$
, aimed at testing the anomalous scaling (He, Shang & Tong Reference He, Shang and Tong2014). Some of the experiments were carried out in turbulent Rayleigh–Bénard convection (RBC) (Siggia Reference Siggia1994; Kadanoff Reference Kadanoff2001; Lohse & Xia Reference Lohse and Xia2010), in which a confined fluid layer of thickness
$r$
, aimed at testing the anomalous scaling (He, Shang & Tong Reference He, Shang and Tong2014). Some of the experiments were carried out in turbulent Rayleigh–Bénard convection (RBC) (Siggia Reference Siggia1994; Kadanoff Reference Kadanoff2001; Lohse & Xia Reference Lohse and Xia2010), in which a confined fluid layer of thickness
![]() $H$
is heated from below and cooled from the top with a constant vertical temperature gradient parallel to gravity. When the temperature difference
$H$
is heated from below and cooled from the top with a constant vertical temperature gradient parallel to gravity. When the temperature difference
![]() $\unicode[STIX]{x0394}T$
across the fluid layer or its dimensionless expression, the Rayleigh number
$\unicode[STIX]{x0394}T$
across the fluid layer or its dimensionless expression, the Rayleigh number
![]() $Ra$
, is sufficiently large, the bulk fluid becomes turbulent and heat is transported predominantly by convection. In addition to the study of the intermittent behaviour of temperature increment
$Ra$
, is sufficiently large, the bulk fluid becomes turbulent and heat is transported predominantly by convection. In addition to the study of the intermittent behaviour of temperature increment
![]() $\unicode[STIX]{x1D6FF}T_{r}$
, the study of amplitude fluctuations of the local temperature at a fixed point is also of great interest. For example, an intriguing feature of RBC is the continuing appearance of large fluctuations in the temperature field, which do not follow the Gaussian statistics (Kadanoff Reference Kadanoff2001). Instead, the measured probability density function (PDF)
$\unicode[STIX]{x1D6FF}T_{r}$
, the study of amplitude fluctuations of the local temperature at a fixed point is also of great interest. For example, an intriguing feature of RBC is the continuing appearance of large fluctuations in the temperature field, which do not follow the Gaussian statistics (Kadanoff Reference Kadanoff2001). Instead, the measured probability density function (PDF)
![]() $P(\unicode[STIX]{x1D6FF}T)$
of temperature fluctuations
$P(\unicode[STIX]{x1D6FF}T)$
of temperature fluctuations
![]() $\unicode[STIX]{x1D6FF}T$
from the local mean value was found to have an exponential tail, which falls off much slower than a Gaussian (see figure 5
d). Such an exponential PDF was observed in a wide dynamic range with
$\unicode[STIX]{x1D6FF}T$
from the local mean value was found to have an exponential tail, which falls off much slower than a Gaussian (see figure 5
d). Such an exponential PDF was observed in a wide dynamic range with
![]() $Ra$
varied from
$Ra$
varied from
![]() $4\times 10^{7}$
up to
$4\times 10^{7}$
up to
![]() $10^{15}$
and in various convecting fluids, such as low-temperature helium gas (Castaing et al.
Reference Castaing, Gunaratne, Heslot, Kadanoff, Libchaber, Thomae, Wu, Zaleski and Zanetti1988; Sano, Wu & Libchber Reference Sano, Wu and Libchber1989; Niemela et al.
Reference Niemela, Skrbek, Sreenivasan and Donnelly2000), mercury (Gollub et al.
Reference Gollub, Clarke, Gharib, Lane and Mesquita1991), sulphur hexafluoride gas (Belmonte, Tilgner & Libchaber Reference Belmonte, Tilgner and Libchaber1994), fluorocarbon FC72 (Wei & Ahlers Reference Wei and Ahlers2016) and water (Du & Tong Reference Du and Tong2001; Zhou & Xia Reference Zhou and Xia2002; He, Tong & Xia Reference He, Tong and Xia2007).
$10^{15}$
and in various convecting fluids, such as low-temperature helium gas (Castaing et al.
Reference Castaing, Gunaratne, Heslot, Kadanoff, Libchaber, Thomae, Wu, Zaleski and Zanetti1988; Sano, Wu & Libchber Reference Sano, Wu and Libchber1989; Niemela et al.
Reference Niemela, Skrbek, Sreenivasan and Donnelly2000), mercury (Gollub et al.
Reference Gollub, Clarke, Gharib, Lane and Mesquita1991), sulphur hexafluoride gas (Belmonte, Tilgner & Libchaber Reference Belmonte, Tilgner and Libchaber1994), fluorocarbon FC72 (Wei & Ahlers Reference Wei and Ahlers2016) and water (Du & Tong Reference Du and Tong2001; Zhou & Xia Reference Zhou and Xia2002; He, Tong & Xia Reference He, Tong and Xia2007).
In a more recent experiment, He, Wang & Tong (Reference He, Wang and Tong2018) showed with solid experimental evidence that the exponential PDF in RBC is generated by the thermal plumes, which can be uniquely characterized by the local thermal dissipation rate
![]() $\unicode[STIX]{x1D716}(t)\equiv \unicode[STIX]{x1D705}[\unicode[STIX]{x1D735}T(t)]^{2}$
. The thermal plumes are intermittently emitted from the thermal boundary layers (BLs) and carry temperature fluctuations from the BLs to the bulk region of the flow (Siggia Reference Siggia1994; Kadanoff Reference Kadanoff2001). Because of rapid mixing and advection of warm and cold plumes passing through the central region of the convection cell, the local thermal dissipation rate has a broad distribution
$\unicode[STIX]{x1D716}(t)\equiv \unicode[STIX]{x1D705}[\unicode[STIX]{x1D735}T(t)]^{2}$
. The thermal plumes are intermittently emitted from the thermal boundary layers (BLs) and carry temperature fluctuations from the BLs to the bulk region of the flow (Siggia Reference Siggia1994; Kadanoff Reference Kadanoff2001). Because of rapid mixing and advection of warm and cold plumes passing through the central region of the convection cell, the local thermal dissipation rate has a broad distribution
![]() $f(\unicode[STIX]{x1D716})$
(He & Tong Reference He and Tong2009). Owing to this dynamic heterogeneity in
$f(\unicode[STIX]{x1D716})$
(He & Tong Reference He and Tong2009). Owing to this dynamic heterogeneity in
![]() $\unicode[STIX]{x1D716}$
, the temperature PDF
$\unicode[STIX]{x1D716}$
, the temperature PDF
![]() $P(\unicode[STIX]{x1D6FF}T)$
can be written as
$P(\unicode[STIX]{x1D6FF}T)$
can be written as
where
![]() $G(\unicode[STIX]{x1D6FF}T|\unicode[STIX]{x1D716})$
is the conditional PDF of temperature fluctuations when
$G(\unicode[STIX]{x1D6FF}T|\unicode[STIX]{x1D716})$
is the conditional PDF of temperature fluctuations when
![]() $\unicode[STIX]{x1D716}$
is held constant. The measured
$\unicode[STIX]{x1D716}$
is held constant. The measured
![]() $G(\unicode[STIX]{x1D6FF}T|\unicode[STIX]{x1D716})$
was found to be of Gaussian form
$G(\unicode[STIX]{x1D6FF}T|\unicode[STIX]{x1D716})$
was found to be of Gaussian form
and its variance
![]() $\unicode[STIX]{x1D70E}_{T}^{2}$
for different values of
$\unicode[STIX]{x1D70E}_{T}^{2}$
for different values of
![]() $\unicode[STIX]{x1D716}$
follows an exponential distribution. The convolution of the two distribution functions gives rise to the exponential PDF
$\unicode[STIX]{x1D716}$
follows an exponential distribution. The convolution of the two distribution functions gives rise to the exponential PDF
![]() $P(\unicode[STIX]{x1D6FF}T)$
. This work thus provided a direct link between the coherent structures in the convective flow (thermal plumes) and statistics of local temperature fluctuations.
$P(\unicode[STIX]{x1D6FF}T)$
. This work thus provided a direct link between the coherent structures in the convective flow (thermal plumes) and statistics of local temperature fluctuations.
In this paper, we report a systematic study of spatial variations of the temperature PDF
![]() $P(\unicode[STIX]{x1D6FF}T)$
in two different closed convection cells, which provide a unique spatial distribution of thermal plumes neither homogeneous nor isotropic (Shang et al.
Reference Shang, Qiu, Tong and Xia2003). This steady-state distribution of thermal plumes and the resulting large-scale velocity field with a single-rotation-roll symmetry allow us to probe distinct changes of the functional form of
$P(\unicode[STIX]{x1D6FF}T)$
in two different closed convection cells, which provide a unique spatial distribution of thermal plumes neither homogeneous nor isotropic (Shang et al.
Reference Shang, Qiu, Tong and Xia2003). This steady-state distribution of thermal plumes and the resulting large-scale velocity field with a single-rotation-roll symmetry allow us to probe distinct changes of the functional form of
![]() $P(\unicode[STIX]{x1D6FF}T)$
in four different flow regions, namely, the thermal boundary layer, mixing zone, turbulent bulk region and cell centre, by moving the temperature probe from the bottom to the centre of the convection cell along its central axis. A central finding of this investigation is that temperature fluctuations in the four flow regions are all made from two independent sources, namely,
$P(\unicode[STIX]{x1D6FF}T)$
in four different flow regions, namely, the thermal boundary layer, mixing zone, turbulent bulk region and cell centre, by moving the temperature probe from the bottom to the centre of the convection cell along its central axis. A central finding of this investigation is that temperature fluctuations in the four flow regions are all made from two independent sources, namely,
where
![]() $\unicode[STIX]{x1D6FF}T_{B}(t)$
denotes temperature fluctuations from the (turbulent) background, which obeys Gaussian statistics, and
$\unicode[STIX]{x1D6FF}T_{B}(t)$
denotes temperature fluctuations from the (turbulent) background, which obeys Gaussian statistics, and
![]() $\unicode[STIX]{x1D6FF}T_{P}(t)$
represents those resulting from the thermal plumes with an exponential distribution. As a result, the temperature PDF
$\unicode[STIX]{x1D6FF}T_{P}(t)$
represents those resulting from the thermal plumes with an exponential distribution. As a result, the temperature PDF
![]() $P(\unicode[STIX]{x1D6FF}T)$
is well described by a convolution of the two modes of fluctuations with a relative strength, which varies among the four different flow regions. While the decomposition of fluctuation modes has been proposed in various forms in previous studies (Procaccia et al.
Reference Procaccia, Ching, Constantin, Kadanoff, Libchaber and Wu1991; Naert et al.
Reference Naert, Castaing, Chabaud, Htbral and Peinke1998; Grossmann & Lohse Reference Grossmann and Lohse2004; Wilczek Reference Wilczek2016; Le Borgne et al.
Reference Le Borgne, Huck, Dentz and Villermaux2017; He et al.
Reference He, Wang and Tong2018), it is the first time that these ideas are systematically tested in a well-characterized turbulent system with a solid experimental support.
$P(\unicode[STIX]{x1D6FF}T)$
is well described by a convolution of the two modes of fluctuations with a relative strength, which varies among the four different flow regions. While the decomposition of fluctuation modes has been proposed in various forms in previous studies (Procaccia et al.
Reference Procaccia, Ching, Constantin, Kadanoff, Libchaber and Wu1991; Naert et al.
Reference Naert, Castaing, Chabaud, Htbral and Peinke1998; Grossmann & Lohse Reference Grossmann and Lohse2004; Wilczek Reference Wilczek2016; Le Borgne et al.
Reference Le Borgne, Huck, Dentz and Villermaux2017; He et al.
Reference He, Wang and Tong2018), it is the first time that these ideas are systematically tested in a well-characterized turbulent system with a solid experimental support.
The remainder of the paper is organized as follows. We first describe the experimental methods in § 2. Experimental results are presented in § 3. Further theoretical analyses are given in § 4. Finally, the work is summarized in § 5.
2 Experiment
The experimental apparatus and procedures used in this experiment are similar to those described previously (He & Tong Reference He and Tong2009; Wang, He & Tong Reference Wang, He and Tong2016; Wang et al.
Reference Wang, Xu, He, Yik, Wang, Schumacher and Tong2018b
), and here we only mention some key points. The experiment is conducted in two convection cells with different geometries. One of them is a vertical thin disk with its circular cross-section aligned parallel to gravity, as shown in figure 1(a). The cell has a diameter
![]() $D=188~\text{mm}$
and thickness
$D=188~\text{mm}$
and thickness
![]() $L=20~\text{mm}$
, and thus the corresponding aspect ratio is
$L=20~\text{mm}$
, and thus the corresponding aspect ratio is
![]() $\unicode[STIX]{x1D6E4}\equiv L/D\simeq 0.1$
. The top and bottom
$\unicode[STIX]{x1D6E4}\equiv L/D\simeq 0.1$
. The top and bottom
![]() $1/3$
of the circular side wall are made of copper of 8 mm in thickness. The surface of the copper plates in contact with the convecting fluid is electroplated with a thin layer of nickel. The remaining
$1/3$
of the circular side wall are made of copper of 8 mm in thickness. The surface of the copper plates in contact with the convecting fluid is electroplated with a thin layer of nickel. The remaining
![]() $1/3$
of the side wall on both sides is made of transparent Plexiglas of 18 mm in thickness. The two flat end walls of the cell are also made of the same type of Plexiglas. Two silicon rubber film heaters connected in parallel are sandwiched on the back side of the bottom conducting plate to provide constant and uniform heating. The top copper plate is in contact with a cooling chamber consisting of two water channels. The temperature of the top plate is maintained by a temperature-controlled circulator (NESLAB, RTE740), which circulates cooling water with a temperature stability of 10 mK. The temperature of the top and bottom plates is measured at a rate of 2 Hz by calibrated thermistors with an accuracy of 5 mK. They are embedded in each plate at a distance of 1 mm away from the surface of the conducting plate. This cell was used in the previous convection experiments (Song, Villermaux & Tong Reference Song, Villermaux and Tong2011; Wang et al.
Reference Wang, He and Tong2016, Reference Wang, Lai, Song and Tong2018a
,Reference Wang, Xu, He, Yik, Wang, Schumacher and Tong
b
).
$1/3$
of the side wall on both sides is made of transparent Plexiglas of 18 mm in thickness. The two flat end walls of the cell are also made of the same type of Plexiglas. Two silicon rubber film heaters connected in parallel are sandwiched on the back side of the bottom conducting plate to provide constant and uniform heating. The top copper plate is in contact with a cooling chamber consisting of two water channels. The temperature of the top plate is maintained by a temperature-controlled circulator (NESLAB, RTE740), which circulates cooling water with a temperature stability of 10 mK. The temperature of the top and bottom plates is measured at a rate of 2 Hz by calibrated thermistors with an accuracy of 5 mK. They are embedded in each plate at a distance of 1 mm away from the surface of the conducting plate. This cell was used in the previous convection experiments (Song, Villermaux & Tong Reference Song, Villermaux and Tong2011; Wang et al.
Reference Wang, He and Tong2016, Reference Wang, Lai, Song and Tong2018a
,Reference Wang, Xu, He, Yik, Wang, Schumacher and Tong
b
).

Figure 1. Sketch of the experimental set-up for the measurement of local temperature fluctuations at different locations along the central axis of (a) the vertical thin disk and (b) the
![]() $\unicode[STIX]{x1D6E4}=1$
upright cylinder. The black arrows indicate the direction of the large-scale circulation.
$\unicode[STIX]{x1D6E4}=1$
upright cylinder. The black arrows indicate the direction of the large-scale circulation.
The second cell is an upright cylinder, as shown in figure 1(b). The inner diameter of the cell is
![]() $D_{up}=19.0~\text{cm}$
and its height is
$D_{up}=19.0~\text{cm}$
and its height is
![]() $H=19.0~\text{cm}$
. The corresponding aspect ratio of the cell is
$H=19.0~\text{cm}$
. The corresponding aspect ratio of the cell is
![]() $\unicode[STIX]{x1D6E4}\equiv D_{up}/H=1$
. The side wall of the cell is made of a transparent Plexiglas ring with a wall thickness of 6 mm. The top and bottom plates of the cell are made of brass and their surfaces are electroplated with a thin layer of gold. The Plexiglas ring side wall is sandwiched between the two plates and is sealed to the top and bottom plates via two rubber O-rings. Except for the difference in shape, all other aspects of the cell, such as the heating (cooling) of the bottom (top) plate and temperature measurement of the conducting plates, remain the same as those for the vertical thin disk. The temperature standard deviation of the top and bottom plates is found to be within
$\unicode[STIX]{x1D6E4}\equiv D_{up}/H=1$
. The side wall of the cell is made of a transparent Plexiglas ring with a wall thickness of 6 mm. The top and bottom plates of the cell are made of brass and their surfaces are electroplated with a thin layer of gold. The Plexiglas ring side wall is sandwiched between the two plates and is sealed to the top and bottom plates via two rubber O-rings. Except for the difference in shape, all other aspects of the cell, such as the heating (cooling) of the bottom (top) plate and temperature measurement of the conducting plates, remain the same as those for the vertical thin disk. The temperature standard deviation of the top and bottom plates is found to be within
![]() $1\,\%$
of
$1\,\%$
of
![]() $\unicode[STIX]{x0394}T$
used in the experiment. This cell was also used in previous convection experiments (He & Tong Reference He and Tong2009; He, Ching & Tong Reference He, Ching and Tong2011; Wang et al.
Reference Wang, Xu, He, Yik, Wang, Schumacher and Tong2018b
).
$\unicode[STIX]{x0394}T$
used in the experiment. This cell was also used in previous convection experiments (He & Tong Reference He and Tong2009; He, Ching & Tong Reference He, Ching and Tong2011; Wang et al.
Reference Wang, Xu, He, Yik, Wang, Schumacher and Tong2018b
).
In the experiment, the entire convection cell is placed inside a square thermostat box, whose temperature matches the mean temperature of the bulk fluid (maintained at
![]() $40\pm 0.1\,^{\circ }\text{C}$
), in order to prevent heat exchange between the convecting fluid and the surroundings. The Rayleigh number
$40\pm 0.1\,^{\circ }\text{C}$
), in order to prevent heat exchange between the convecting fluid and the surroundings. The Rayleigh number
![]() $Ra$
for the thin disk is defined as
$Ra$
for the thin disk is defined as
![]() $Ra\equiv \unicode[STIX]{x1D713}g\unicode[STIX]{x0394}TD^{3}/(\unicode[STIX]{x1D708}\unicode[STIX]{x1D705})$
, where
$Ra\equiv \unicode[STIX]{x1D713}g\unicode[STIX]{x0394}TD^{3}/(\unicode[STIX]{x1D708}\unicode[STIX]{x1D705})$
, where
![]() $g$
is the gravitational acceleration,
$g$
is the gravitational acceleration,
![]() $\unicode[STIX]{x0394}T$
is the vertical temperature difference across the cell and
$\unicode[STIX]{x0394}T$
is the vertical temperature difference across the cell and
![]() $\unicode[STIX]{x1D713}$
,
$\unicode[STIX]{x1D713}$
,
![]() $\unicode[STIX]{x1D708}$
and
$\unicode[STIX]{x1D708}$
and
![]() $\unicode[STIX]{x1D705}$
are, respectively, the thermal expansion coefficient, viscous and thermal diffusivity of the convecting fluid. For the upright cylinder, the cell height
$\unicode[STIX]{x1D705}$
are, respectively, the thermal expansion coefficient, viscous and thermal diffusivity of the convecting fluid. For the upright cylinder, the cell height
![]() $H$
is used to replace
$H$
is used to replace
![]() $D$
. The Prandtl number
$D$
. The Prandtl number
![]() $Pr$
is defined as
$Pr$
is defined as
![]() $Pr\equiv \unicode[STIX]{x1D708}/\unicode[STIX]{x1D705}$
. Two working fluids are used in the experiment. For the thin disk, a 20 wt. % aqueous solution of glycerin with
$Pr\equiv \unicode[STIX]{x1D708}/\unicode[STIX]{x1D705}$
. Two working fluids are used in the experiment. For the thin disk, a 20 wt. % aqueous solution of glycerin with
![]() $Pr=7.6$
is used. For the upright cylinder, both distilled water with
$Pr=7.6$
is used. For the upright cylinder, both distilled water with
![]() $Pr=4.4$
and the 20 wt. % aqueous solution of glycerin with
$Pr=4.4$
and the 20 wt. % aqueous solution of glycerin with
![]() $Pr=7.6$
are used. In the experiment, the temperature
$Pr=7.6$
are used. In the experiment, the temperature
![]() $T_{b}$
of the bottom heating plate is varied in the range
$T_{b}$
of the bottom heating plate is varied in the range
![]() $42.4\lesssim T_{b}\lesssim 60.2\,^{\circ }\text{C}$
, and the temperature
$42.4\lesssim T_{b}\lesssim 60.2\,^{\circ }\text{C}$
, and the temperature
![]() $T_{t}$
of the top cooling plate is varied in the range
$T_{t}$
of the top cooling plate is varied in the range
![]() $13.8\lesssim T_{t}\lesssim 37.8\,^{\circ }\text{C}$
. Correspondingly,
$13.8\lesssim T_{t}\lesssim 37.8\,^{\circ }\text{C}$
. Correspondingly,
![]() $Ra$
is varied in the range
$Ra$
is varied in the range
![]() $9\times 10^{8}\lesssim Ra\lesssim 1.2\times 10^{10}$
and
$9\times 10^{8}\lesssim Ra\lesssim 1.2\times 10^{10}$
and
![]() $Pr$
is fixed for a given fluid. The black arrows in figure 1 show the direction of the large-scale circulation (LSC). To pin down the azimuthal motion of the LSC in the upright cylinder, the cylindrical cell is tilted slightly at a small angle (
$Pr$
is fixed for a given fluid. The black arrows in figure 1 show the direction of the large-scale circulation (LSC). To pin down the azimuthal motion of the LSC in the upright cylinder, the cylindrical cell is tilted slightly at a small angle (
![]() ${<}1^{\circ }$
) by adjusting the levelling plate of the cell. It has been shown (Ahlers, Brown & Nikolaenko Reference Ahlers, Brown and Nikolaenko2006a
) that such a small tilt to the
${<}1^{\circ }$
) by adjusting the levelling plate of the cell. It has been shown (Ahlers, Brown & Nikolaenko Reference Ahlers, Brown and Nikolaenko2006a
) that such a small tilt to the
![]() $\unicode[STIX]{x1D6E4}=1$
upright cylinder does not affect the convective flow very much, as the single-roll structure of the LSC is quite stable in the
$\unicode[STIX]{x1D6E4}=1$
upright cylinder does not affect the convective flow very much, as the single-roll structure of the LSC is quite stable in the
![]() $\unicode[STIX]{x1D6E4}=1$
cell (Qiu & Tong Reference Qiu and Tong2001). The LSC structure in the
$\unicode[STIX]{x1D6E4}=1$
cell (Qiu & Tong Reference Qiu and Tong2001). The LSC structure in the
![]() $\unicode[STIX]{x1D6E4}=0.5$
upright cylinder, however, is more sensitive to the cell tilt and so are the temperature fluctuations (Chillá et al.
Reference Chillá, Rastello, Chaumat and Castaing2004).
$\unicode[STIX]{x1D6E4}=0.5$
upright cylinder, however, is more sensitive to the cell tilt and so are the temperature fluctuations (Chillá et al.
Reference Chillá, Rastello, Chaumat and Castaing2004).
The local fluid temperature is measured using a glass-encapsulated thermistor of diameter 0.17 mm with an accuracy of 5 mK (AB6E3-B05KA202R). Details about the temperature calibration and measurements have been reported elsewhere (He & Tong Reference He and Tong2009). To guide the two thermistors into the thin disk, we install a horizontal and a vertical stainless steel tube in the cell, as shown in figure 1(a). The horizontal tube is fixed to measure the mean temperature
![]() $T_{0}$
at the cell centre. The vertical tube is used to measure the temperature time series data
$T_{0}$
at the cell centre. The vertical tube is used to measure the temperature time series data
![]() $T(t)$
with varying distance
$T(t)$
with varying distance
![]() $z$
away from the centre of the bottom plate. The vertical tube is mounted on a translational stage, which is controlled by a stepping motor with a position resolution of 50
$z$
away from the centre of the bottom plate. The vertical tube is mounted on a translational stage, which is controlled by a stepping motor with a position resolution of 50
![]() $\unicode[STIX]{x03BC}$
m. The measurements of
$\unicode[STIX]{x03BC}$
m. The measurements of
![]() $T_{0}$
and
$T_{0}$
and
![]() $T(t)$
are made, respectively, at the sampling rates of 2 Hz and 15 Hz. Typically, we take 1 h long time series data (
$T(t)$
are made, respectively, at the sampling rates of 2 Hz and 15 Hz. Typically, we take 1 h long time series data (
![]() $5.4\times 10^{4}$
data points) at each location of
$5.4\times 10^{4}$
data points) at each location of
![]() $z$
for the measurement of
$z$
for the measurement of
![]() $T(t)$
. The measurement of temperature fluctuations in the upright cylinder is made in a similar way, except that a vertical tube is installed to measure
$T(t)$
. The measurement of temperature fluctuations in the upright cylinder is made in a similar way, except that a vertical tube is installed to measure
![]() $T_{0}$
, as shown in figure 1(b).
$T_{0}$
, as shown in figure 1(b).
3 Experimental results
3.1 Turbulent temperature fluctuations in the thin disk
Figure 2(a) shows the evolution of the measured local temperature variations
![]() $T(t)$
for four different values of distance
$T(t)$
for four different values of distance
![]() $z$
away from the centre of the bottom plate, and at a fixed value of
$z$
away from the centre of the bottom plate, and at a fixed value of
![]() $Ra=5.3\times 10^{9}$
and
$Ra=5.3\times 10^{9}$
and
![]() $Pr=7.6$
in the thin disk. Figure 2(b) shows the corresponding PDFs of the measured
$Pr=7.6$
in the thin disk. Figure 2(b) shows the corresponding PDFs of the measured
![]() $T(t)$
in figure 2(a). In a recent experiment and direct numerical simulation, we have shown that there is a well-developed thermal BL near the bottom (top) conducting plate of the thin disk cell. A typical value of the BL thickness
$T(t)$
in figure 2(a). In a recent experiment and direct numerical simulation, we have shown that there is a well-developed thermal BL near the bottom (top) conducting plate of the thin disk cell. A typical value of the BL thickness
![]() $\unicode[STIX]{x1D6FF}$
at this
$\unicode[STIX]{x1D6FF}$
at this
![]() $Ra$
is
$Ra$
is
![]() $\unicode[STIX]{x1D6FF}\simeq 0.55~\text{mm}$
. Heat transport inside the BL is accomplished mainly by thermal diffusion, which establishes a large mean temperature gradient across the BL. In the region outside the BL, however, heat transport is dominated by turbulent convection and the mean temperature along the central axis of the bulk region is approximately constant. At
$\unicode[STIX]{x1D6FF}\simeq 0.55~\text{mm}$
. Heat transport inside the BL is accomplished mainly by thermal diffusion, which establishes a large mean temperature gradient across the BL. In the region outside the BL, however, heat transport is dominated by turbulent convection and the mean temperature along the central axis of the bulk region is approximately constant. At
![]() $z=0.2~\text{mm}$
which is in the inner region of the BL, the measured
$z=0.2~\text{mm}$
which is in the inner region of the BL, the measured
![]() $T(t)$
(black curve in figure 2
a) reveals large symmetric fluctuations, and thus their PDF (black squares in figure 2
b) has a symmetric shape with a broad width. In addition, the measured mean temperature
$T(t)$
(black curve in figure 2
a) reveals large symmetric fluctuations, and thus their PDF (black squares in figure 2
b) has a symmetric shape with a broad width. In addition, the measured mean temperature
![]() $\langle T\rangle$
at this location is much larger than that at the other three positions.
$\langle T\rangle$
at this location is much larger than that at the other three positions.

Figure 2. (a) Evolution of the measured local temperature variations
![]() $T(t)$
for 4 different values of distance
$T(t)$
for 4 different values of distance
![]() $z$
away from the centre of the bottom plate (bottom to top):
$z$
away from the centre of the bottom plate (bottom to top):
![]() $z=0.2~\text{mm}$
(black curve),
$z=0.2~\text{mm}$
(black curve),
![]() $z=4.9~\text{mm}$
(red curve),
$z=4.9~\text{mm}$
(red curve),
![]() $z=61.6~\text{mm}$
(green curve) and
$z=61.6~\text{mm}$
(green curve) and
![]() $z=94.0~\text{mm}$
(blue curve). The measurements are made in the thin disk at
$z=94.0~\text{mm}$
(blue curve). The measurements are made in the thin disk at
![]() $Ra=5.3\times 10^{9}$
and
$Ra=5.3\times 10^{9}$
and
![]() $Pr=7.6$
(20 wt. % aqueous solution of glycerin). (b) Corresponding PDFs of the measured
$Pr=7.6$
(20 wt. % aqueous solution of glycerin). (b) Corresponding PDFs of the measured
![]() $T(t)$
in (a) at
$T(t)$
in (a) at
![]() $z=0.2~\text{mm}$
(black squares),
$z=0.2~\text{mm}$
(black squares),
![]() $z=4.9~\text{mm}$
(red circles),
$z=4.9~\text{mm}$
(red circles),
![]() $z=61.6~\text{mm}$
(green up triangles) and
$z=61.6~\text{mm}$
(green up triangles) and
![]() $z=94.0~\text{mm}$
(blue down triangles).
$z=94.0~\text{mm}$
(blue down triangles).
At
![]() $z=4.9~\text{mm}$
which is outside the BL and in the mixing zone (Wang et al.
Reference Wang, He and Tong2016), the measured
$z=4.9~\text{mm}$
which is outside the BL and in the mixing zone (Wang et al.
Reference Wang, He and Tong2016), the measured
![]() $T(t)$
(red curve in figure 2
a) reveals large temperature spikes in one direction, resulting from warm thermal plumes passing through the measuring position. These warm plumes are intermittently emitted from the bottom BL. In addition to the hot spikes, the measured
$T(t)$
(red curve in figure 2
a) reveals large temperature spikes in one direction, resulting from warm thermal plumes passing through the measuring position. These warm plumes are intermittently emitted from the bottom BL. In addition to the hot spikes, the measured
![]() $T(t)$
also shows small continuous fluctuations resulting from the turbulent background. As shown in figure 2(b), the intermittent temperature spikes in the time series
$T(t)$
also shows small continuous fluctuations resulting from the turbulent background. As shown in figure 2(b), the intermittent temperature spikes in the time series
![]() $T(t)$
give rise to an exponential tail in the corresponding temperature PDF
$T(t)$
give rise to an exponential tail in the corresponding temperature PDF
![]() $P(T)$
(red circles with
$P(T)$
(red circles with
![]() $T\gtrsim 41\,^{\circ }\text{C}$
). The small background fluctuations, on the other hand, produce a symmetric peak in the measured
$T\gtrsim 41\,^{\circ }\text{C}$
). The small background fluctuations, on the other hand, produce a symmetric peak in the measured
![]() $P(T)$
.
$P(T)$
.
By increasing
![]() $z$
further into the turbulent bulk region, the warm plumes are mixed and dissipated by the flow field. As a result, the intermittent spikes in
$z$
further into the turbulent bulk region, the warm plumes are mixed and dissipated by the flow field. As a result, the intermittent spikes in
![]() $T(t)$
and the asymmetric tail in the resulting
$T(t)$
and the asymmetric tail in the resulting
![]() $P(T)$
gradually diminish. The green curve in figure 2(a) and green up triangles in figure 2(b) show an example at
$P(T)$
gradually diminish. The green curve in figure 2(a) and green up triangles in figure 2(b) show an example at
![]() $z=61.8~\text{mm}$
. In addition, the standard deviation of temperature fluctuations also decreases with increasing
$z=61.8~\text{mm}$
. In addition, the standard deviation of temperature fluctuations also decreases with increasing
![]() $z$
. Finally, at the cell centre (
$z$
. Finally, at the cell centre (
![]() $z=94.0~\text{mm}$
), the standard deviation of temperature fluctuations becomes the smallest (blue curve in figure 2
a), and the resulting
$z=94.0~\text{mm}$
), the standard deviation of temperature fluctuations becomes the smallest (blue curve in figure 2
a), and the resulting
![]() $P(T)$
shows the smallest width (blue down triangles in figure 2
b). Because of the reflection symmetry at the cell centre, the measured
$P(T)$
shows the smallest width (blue down triangles in figure 2
b). Because of the reflection symmetry at the cell centre, the measured
![]() $P(T)$
has a symmetric shape as expected. An interesting feature shown in figure 2(b) is that once outside the thermal BL, both the peak position and left side of the peak of all the measured
$P(T)$
has a symmetric shape as expected. An interesting feature shown in figure 2(b) is that once outside the thermal BL, both the peak position and left side of the peak of all the measured
![]() $P(T)$
remain unchanged with
$P(T)$
remain unchanged with
![]() $z$
. This result suggests that temperature fluctuations in the bulk region outside the BL have a fairly uniform turbulent background (Zhou & Xia Reference Zhou and Xia2013).
$z$
. This result suggests that temperature fluctuations in the bulk region outside the BL have a fairly uniform turbulent background (Zhou & Xia Reference Zhou and Xia2013).

Figure 3. Sketch of the four flow regions in the thin disk cell, namely, boundary layer (BL,
![]() $z\lesssim 2\unicode[STIX]{x1D6FF}$
), mixing zone (
$z\lesssim 2\unicode[STIX]{x1D6FF}$
), mixing zone (
![]() $0.01\lesssim z/D\lesssim 0.1$
), turbulent bulk (
$0.01\lesssim z/D\lesssim 0.1$
), turbulent bulk (
![]() $0.1\lesssim z/D\leqslant 0.5$
) and cell centre (
$0.1\lesssim z/D\leqslant 0.5$
) and cell centre (
![]() $z/D=0.5$
). The vertical dashed line shows the central
$z/D=0.5$
). The vertical dashed line shows the central
![]() $z$
-axis of the cell. The BL can be further divided into an inner region (
$z$
-axis of the cell. The BL can be further divided into an inner region (
![]() $z\lesssim 0.6\unicode[STIX]{x1D6FF}$
) and an outer region (
$z\lesssim 0.6\unicode[STIX]{x1D6FF}$
) and an outer region (
![]() $0.6\unicode[STIX]{x1D6FF}\lesssim z\lesssim 2\unicode[STIX]{x1D6FF}$
), in which thermal plumes start to form. The black arrow indicates the direction of the large-scale circulation.
$0.6\unicode[STIX]{x1D6FF}\lesssim z\lesssim 2\unicode[STIX]{x1D6FF}$
), in which thermal plumes start to form. The black arrow indicates the direction of the large-scale circulation.
Figure 3 shows a sketch of the four flow regions in the thin disk cell, as discussed above. In particular, the BL can be further divided into two sub-regions: inner and outer regions. In the inner region of the BL (
![]() $z\lesssim 0.6\unicode[STIX]{x1D6FF}$
), the mean value of the local temperature decreases linearly with distance
$z\lesssim 0.6\unicode[STIX]{x1D6FF}$
), the mean value of the local temperature decreases linearly with distance
![]() $z$
and heat is transported primarily by diffusion. In the outer region of the BL (
$z$
and heat is transported primarily by diffusion. In the outer region of the BL (
![]() $0.6\unicode[STIX]{x1D6FF}\lesssim z\lesssim 2\unicode[STIX]{x1D6FF}$
), the mean value of the local temperature gradually approaches a constant value and thermal plumes start to form. These thermal plumes are emitted intermittently into the mixing zone (
$0.6\unicode[STIX]{x1D6FF}\lesssim z\lesssim 2\unicode[STIX]{x1D6FF}$
), the mean value of the local temperature gradually approaches a constant value and thermal plumes start to form. These thermal plumes are emitted intermittently into the mixing zone (
![]() $0.01\lesssim z/D\lesssim 0.1$
) outside the BL and then are carried away by the LSC (as marked by the black arrow in figure 3). Because of turbulent mixing and thermal dissipation, the thermal plumes in the turbulent bulk region (
$0.01\lesssim z/D\lesssim 0.1$
) outside the BL and then are carried away by the LSC (as marked by the black arrow in figure 3). Because of turbulent mixing and thermal dissipation, the thermal plumes in the turbulent bulk region (
![]() $0.1\lesssim z/D\lesssim 0.5$
) become less energetic and fewer in number compared with those in the mixing zone.
$0.1\lesssim z/D\lesssim 0.5$
) become less energetic and fewer in number compared with those in the mixing zone.

Figure 4. Measured PDF
![]() $P(\unicode[STIX]{x1D6FF}T)$
of the normalized temperature fluctuation
$P(\unicode[STIX]{x1D6FF}T)$
of the normalized temperature fluctuation
![]() $\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
for different values of
$\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
for different values of
![]() $Ra$
with a fixed value
$Ra$
with a fixed value
![]() $Pr=7.6$
(20 wt. % aqueous solution of glycerin). The measurements are made in the thin disk and in four different regions of distance
$Pr=7.6$
(20 wt. % aqueous solution of glycerin). The measurements are made in the thin disk and in four different regions of distance
![]() $z$
away from the bottom plate: (a)
$z$
away from the bottom plate: (a)
![]() $z/\unicode[STIX]{x1D6FF}\lesssim 0.62$
(inner region of the BL), (b)
$z/\unicode[STIX]{x1D6FF}\lesssim 0.62$
(inner region of the BL), (b)
![]() $z/D\simeq 0.026$
(mixing zone), (c)
$z/D\simeq 0.026$
(mixing zone), (c)
![]() $z/D\simeq 0.33$
and (d)
$z/D\simeq 0.33$
and (d)
![]() $z/D=0.5$
(cell centre). The dashed lines in (a–d) show the Gaussian function given in (3.1). The solid line in (b) shows a fit of (4.8) to the data points with
$z/D=0.5$
(cell centre). The dashed lines in (a–d) show the Gaussian function given in (3.1). The solid line in (b) shows a fit of (4.8) to the data points with
![]() $\unicode[STIX]{x1D6FC}_{1}=0.25\pm 0.05$
and
$\unicode[STIX]{x1D6FC}_{1}=0.25\pm 0.05$
and
![]() $\unicode[STIX]{x1D6FD}=0.1\pm 0.03$
. The solid line in (c) shows a fit (4.6) to the data points with
$\unicode[STIX]{x1D6FD}=0.1\pm 0.03$
. The solid line in (c) shows a fit (4.6) to the data points with
![]() $\unicode[STIX]{x1D6FC}_{1}=1.1\pm 0.2$
. The solid line in (d) is a fit of (4.11) to the data points with
$\unicode[STIX]{x1D6FC}_{1}=1.1\pm 0.2$
. The solid line in (d) is a fit of (4.11) to the data points with
![]() $\unicode[STIX]{x1D6FC}=1.7\pm 0.3$
.
$\unicode[STIX]{x1D6FC}=1.7\pm 0.3$
.
We now discuss the scaling properties of the measured PDF
![]() $P(\unicode[STIX]{x1D6FF}T)$
of temperature fluctuations
$P(\unicode[STIX]{x1D6FF}T)$
of temperature fluctuations
![]() $\unicode[STIX]{x1D6FF}T$
from the mean value with varying values of
$\unicode[STIX]{x1D6FF}T$
from the mean value with varying values of
![]() $z$
and
$z$
and
![]() $Ra$
. Here
$Ra$
. Here
![]() $\unicode[STIX]{x1D6FF}T=T(t)-\langle T\rangle$
with
$\unicode[STIX]{x1D6FF}T=T(t)-\langle T\rangle$
with
![]() $\langle T\rangle$
being the local mean temperature. It is found that the temperature PDFs obtained at a fixed value of
$\langle T\rangle$
being the local mean temperature. It is found that the temperature PDFs obtained at a fixed value of
![]() $z$
and different values of
$z$
and different values of
![]() $Ra$
can all be brought into coincidence, by normalizing
$Ra$
can all be brought into coincidence, by normalizing
![]() $\unicode[STIX]{x1D6FF}T$
by its root mean square (r.m.s.) value
$\unicode[STIX]{x1D6FF}T$
by its root mean square (r.m.s.) value
![]() $\unicode[STIX]{x1D70E}_{T}$
. Plots of
$\unicode[STIX]{x1D70E}_{T}$
. Plots of
![]() $P(\unicode[STIX]{x1D6FF}T)$
versus
$P(\unicode[STIX]{x1D6FF}T)$
versus
![]() $\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
remain unchanged in the
$\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
remain unchanged in the
![]() $Ra$
range studied and only
$Ra$
range studied and only
![]() $\unicode[STIX]{x1D70E}_{T}$
changes with
$\unicode[STIX]{x1D70E}_{T}$
changes with
![]() $Ra$
. Figure 4 shows the measured
$Ra$
. Figure 4 shows the measured
![]() $P(\unicode[STIX]{x1D6FF}T)$
as a function of
$P(\unicode[STIX]{x1D6FF}T)$
as a function of
![]() $\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
for different values of
$\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
for different values of
![]() $Ra$
in four regions of
$Ra$
in four regions of
![]() $z$
. It is seen that the measured
$z$
. It is seen that the measured
![]() $P(\unicode[STIX]{x1D6FF}T)$
in each region of
$P(\unicode[STIX]{x1D6FF}T)$
in each region of
![]() $z$
has a unique functional form independent of
$z$
has a unique functional form independent of
![]() $Ra$
.
$Ra$
.
Figure 4(a) shows the measured
![]() $P(\unicode[STIX]{x1D6FF}T)$
as a function of normalized temperature fluctuations
$P(\unicode[STIX]{x1D6FF}T)$
as a function of normalized temperature fluctuations
![]() $\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
when
$\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
when
![]() $z$
is in the inner region of the BL with
$z$
is in the inner region of the BL with
![]() $z/\unicode[STIX]{x1D6FF}\lesssim 0.62$
, where the mean temperature gradient is almost constant. It is seen that all of the measured PDFs
$z/\unicode[STIX]{x1D6FF}\lesssim 0.62$
, where the mean temperature gradient is almost constant. It is seen that all of the measured PDFs
![]() $P(\unicode[STIX]{x1D6FF}T)$
can be well described by a Gaussian function (dashed line)
$P(\unicode[STIX]{x1D6FF}T)$
can be well described by a Gaussian function (dashed line)
and only
![]() $\unicode[STIX]{x1D70E}_{T}$
changes with
$\unicode[STIX]{x1D70E}_{T}$
changes with
![]() $z$
. For RBC in an rectangular cell, the measured
$z$
. For RBC in an rectangular cell, the measured
![]() $P(\unicode[STIX]{x1D6FF}T)$
inside the BL was also found to have a similar Gaussian form (Zhou & Xia Reference Zhou and Xia2013). In the outer region of the BL with
$P(\unicode[STIX]{x1D6FF}T)$
inside the BL was also found to have a similar Gaussian form (Zhou & Xia Reference Zhou and Xia2013). In the outer region of the BL with
![]() $0.62\lesssim z/\unicode[STIX]{x1D6FF}\lesssim 2$
, while plots of
$0.62\lesssim z/\unicode[STIX]{x1D6FF}\lesssim 2$
, while plots of
![]() $P(\unicode[STIX]{x1D6FF}T)$
versus
$P(\unicode[STIX]{x1D6FF}T)$
versus
![]() $\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
remain unchanged with
$\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
remain unchanged with
![]() $Ra$
at a fixed value of
$Ra$
at a fixed value of
![]() $z/\unicode[STIX]{x1D6FF}$
, the shapes of the measured
$z/\unicode[STIX]{x1D6FF}$
, the shapes of the measured
![]() $P(\unicode[STIX]{x1D6FF}T)$
for different values of
$P(\unicode[STIX]{x1D6FF}T)$
for different values of
![]() $z$
start to show systematic deviations from the Gaussian function. These deviations cause the measured
$z$
start to show systematic deviations from the Gaussian function. These deviations cause the measured
![]() $P(\unicode[STIX]{x1D6FF}T)$
to become asymmetric and skewed toward the positive side of
$P(\unicode[STIX]{x1D6FF}T)$
to become asymmetric and skewed toward the positive side of
![]() $\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
with the skewness increasing with
$\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
with the skewness increasing with
![]() $z$
.
$z$
.
When
![]() $z$
moves beyond the BL region (
$z$
moves beyond the BL region (
![]() $z/\unicode[STIX]{x1D6FF}\gtrsim 2$
or equivalently
$z/\unicode[STIX]{x1D6FF}\gtrsim 2$
or equivalently
![]() $z/D\gtrsim 0.01$
), the BL thickness
$z/D\gtrsim 0.01$
), the BL thickness
![]() $\unicode[STIX]{x1D6FF}$
is no longer the scaling length. Instead, the normalized variance profile
$\unicode[STIX]{x1D6FF}$
is no longer the scaling length. Instead, the normalized variance profile
![]() $\unicode[STIX]{x1D70E}_{T}^{2}(z)/(\unicode[STIX]{x1D70E}_{T}^{2})_{0}$
, with
$\unicode[STIX]{x1D70E}_{T}^{2}(z)/(\unicode[STIX]{x1D70E}_{T}^{2})_{0}$
, with
![]() $(\unicode[STIX]{x1D70E}_{T}^{2})_{0}$
being the maximal value of
$(\unicode[STIX]{x1D70E}_{T}^{2})_{0}$
being the maximal value of
![]() $\unicode[STIX]{x1D70E}_{T}^{2}$
, was found to scale with
$\unicode[STIX]{x1D70E}_{T}^{2}$
, was found to scale with
![]() $z/D$
in the range
$z/D$
in the range
![]() $0.01\lesssim z/D\lesssim 0.1$
(mixing zone) (Wang et al.
Reference Wang, He and Tong2016, Reference Wang, Xu, He, Yik, Wang, Schumacher and Tong2018b
). Figure 4(b) shows an example of the measured
$0.01\lesssim z/D\lesssim 0.1$
(mixing zone) (Wang et al.
Reference Wang, He and Tong2016, Reference Wang, Xu, He, Yik, Wang, Schumacher and Tong2018b
). Figure 4(b) shows an example of the measured
![]() $P(\unicode[STIX]{x1D6FF}T)$
in the mixing zone for different values of
$P(\unicode[STIX]{x1D6FF}T)$
in the mixing zone for different values of
![]() $Ra$
. The measurements are made at approximately the same position with
$Ra$
. The measurements are made at approximately the same position with
![]() $z/D\simeq 0.026$
. All of the PDFs collapse onto a single curve, which has a Gaussian-like main portion (dashed line) for small temperature fluctuations (
$z/D\simeq 0.026$
. All of the PDFs collapse onto a single curve, which has a Gaussian-like main portion (dashed line) for small temperature fluctuations (
![]() $\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}\lesssim 1$
) and a long exponential tail for large temperature fluctuations (
$\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}\lesssim 1$
) and a long exponential tail for large temperature fluctuations (
![]() $\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}\gtrsim 2$
). As shown in figure 2(a) (red curve), the long exponential tail is caused by the warm plumes, which are intermittently emitted from the bottom BL and pass through the measuring position. For other values of
$\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}\gtrsim 2$
). As shown in figure 2(a) (red curve), the long exponential tail is caused by the warm plumes, which are intermittently emitted from the bottom BL and pass through the measuring position. For other values of
![]() $z$
in the mixing zone, the measured PDFs
$z$
in the mixing zone, the measured PDFs
![]() $P(\unicode[STIX]{x1D6FF}T)$
retain the same characteristic shape as that shown in figure 4(b), but they vary slightly with
$P(\unicode[STIX]{x1D6FF}T)$
retain the same characteristic shape as that shown in figure 4(b), but they vary slightly with
![]() $z$
so that plots of
$z$
so that plots of
![]() $P(\unicode[STIX]{x1D6FF}T)$
versus
$P(\unicode[STIX]{x1D6FF}T)$
versus
![]() $\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
do not overlap with each other.
$\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
do not overlap with each other.
As
![]() $z$
is further moved to the bulk region, with the values of
$z$
is further moved to the bulk region, with the values of
![]() $z$
being larger than the cell thickness (
$z$
being larger than the cell thickness (
![]() $0.1\lesssim z/D\lesssim 0.4$
), the shape of the measured PDFs
$0.1\lesssim z/D\lesssim 0.4$
), the shape of the measured PDFs
![]() $P(\unicode[STIX]{x1D6FF}T)$
changes to another form due to the strong mixing in this region. Figure 4(c) shows an example of the measured
$P(\unicode[STIX]{x1D6FF}T)$
changes to another form due to the strong mixing in this region. Figure 4(c) shows an example of the measured
![]() $P(\unicode[STIX]{x1D6FF}T)$
in this region for different values of
$P(\unicode[STIX]{x1D6FF}T)$
in this region for different values of
![]() $Ra$
. The measurements are made at approximately the same position with
$Ra$
. The measurements are made at approximately the same position with
![]() $z/D\simeq 0.33$
. All of the PDFs collapse onto a single curve, which has a Gaussian-like main portion (dashed line) for small temperature fluctuations (
$z/D\simeq 0.33$
. All of the PDFs collapse onto a single curve, which has a Gaussian-like main portion (dashed line) for small temperature fluctuations (
![]() $\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}\lesssim 1.5$
) and an asymmetric tail which smoothly evolves to an exponential shape for large temperature fluctuations (
$\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}\lesssim 1.5$
) and an asymmetric tail which smoothly evolves to an exponential shape for large temperature fluctuations (
![]() $\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}\gtrsim 2.5$
).
$\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}\gtrsim 2.5$
).
As
![]() $z$
moves toward the central region of the cell (
$z$
moves toward the central region of the cell (
![]() $0.4\lesssim z/D\lesssim 0.5$
), temperature fluctuations become more and more symmetric and so does the measured
$0.4\lesssim z/D\lesssim 0.5$
), temperature fluctuations become more and more symmetric and so does the measured
![]() $P(\unicode[STIX]{x1D6FF}T)$
. Figure 4(d) shows the measured PDFs
$P(\unicode[STIX]{x1D6FF}T)$
. Figure 4(d) shows the measured PDFs
![]() $P(\unicode[STIX]{x1D6FF}T)$
at the cell centre with different values of
$P(\unicode[STIX]{x1D6FF}T)$
at the cell centre with different values of
![]() $Ra$
. Again, all of the measured PDFs collapse onto a single curve, which is symmetric and has a Gaussian cap (dashed line) for small temperature fluctuations
$Ra$
. Again, all of the measured PDFs collapse onto a single curve, which is symmetric and has a Gaussian cap (dashed line) for small temperature fluctuations
![]() $-2.5\lesssim \unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}\lesssim 2.5$
and an exponential-like tail which falls off slower than a Gaussian.
$-2.5\lesssim \unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}\lesssim 2.5$
and an exponential-like tail which falls off slower than a Gaussian.
3.2 Turbulent temperature fluctuations in the
 $\unicode[STIX]{x1D6E4}=1$
upright cylinder
$\unicode[STIX]{x1D6E4}=1$
upright cylinder
We now examine the scaling properties of the measured
![]() $P(\unicode[STIX]{x1D6FF}T)$
in the
$P(\unicode[STIX]{x1D6FF}T)$
in the
![]() $\unicode[STIX]{x1D6E4}=1$
upright cylinder. Similar to the situation in the thin disk, once
$\unicode[STIX]{x1D6E4}=1$
upright cylinder. Similar to the situation in the thin disk, once
![]() $\unicode[STIX]{x1D6FF}T$
is normalized by its r.m.s. value
$\unicode[STIX]{x1D6FF}T$
is normalized by its r.m.s. value
![]() $\unicode[STIX]{x1D70E}_{T}$
, the temperature PDFs obtained at a fixed value of
$\unicode[STIX]{x1D70E}_{T}$
, the temperature PDFs obtained at a fixed value of
![]() $z$
and different values of
$z$
and different values of
![]() $Ra$
all fall onto a single master curve. Figure 5 shows the measured
$Ra$
all fall onto a single master curve. Figure 5 shows the measured
![]() $P(\unicode[STIX]{x1D6FF}T)$
as a function of
$P(\unicode[STIX]{x1D6FF}T)$
as a function of
![]() $\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
for different values of
$\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
for different values of
![]() $Ra$
with fixed
$Ra$
with fixed
![]() $Pr=4.4$
(water). The measurements are made in four representative regions of distance
$Pr=4.4$
(water). The measurements are made in four representative regions of distance
![]() $z$
away from the bottom plate. In each region of
$z$
away from the bottom plate. In each region of
![]() $z$
, the measured
$z$
, the measured
![]() $P(\unicode[STIX]{x1D6FF}T)$
has a unique functional form, which remains unchanged with
$P(\unicode[STIX]{x1D6FF}T)$
has a unique functional form, which remains unchanged with
![]() $Ra$
in the
$Ra$
in the
![]() $Ra$
range studied. In the inner region of the BL with
$Ra$
range studied. In the inner region of the BL with
![]() $z/\unicode[STIX]{x1D6FF}\lesssim 0.46$
, the measured
$z/\unicode[STIX]{x1D6FF}\lesssim 0.46$
, the measured
![]() $P(\unicode[STIX]{x1D6FF}T)$
, as shown in figure 5(a), can also be well described by the Gaussian function given in (3.1) (dashed line).
$P(\unicode[STIX]{x1D6FF}T)$
, as shown in figure 5(a), can also be well described by the Gaussian function given in (3.1) (dashed line).
In a recent experiment, Wang et al. (Reference Wang, Xu, He, Yik, Wang, Schumacher and Tong2018b
) reported that a mixing zone exists outside the BL in the
![]() $\unicode[STIX]{x1D6E4}=1$
upright cylinder in the range of
$\unicode[STIX]{x1D6E4}=1$
upright cylinder in the range of
![]() $0.04\lesssim z/H\lesssim 0.3$
for
$0.04\lesssim z/H\lesssim 0.3$
for
![]() $Pr=4.4$
and
$Pr=4.4$
and
![]() $0.06\lesssim z/H\lesssim 0.3$
for
$0.06\lesssim z/H\lesssim 0.3$
for
![]() $Pr=7.6$
. Two characteristic forms of
$Pr=7.6$
. Two characteristic forms of
![]() $P(\unicode[STIX]{x1D6FF}T)$
are observed in the mixing zone. Figure 5(b) shows a characteristic form of
$P(\unicode[STIX]{x1D6FF}T)$
are observed in the mixing zone. Figure 5(b) shows a characteristic form of
![]() $P(\unicode[STIX]{x1D6FF}T)$
in the inner region of the mixing zone (
$P(\unicode[STIX]{x1D6FF}T)$
in the inner region of the mixing zone (
![]() $0.04\lesssim z/H\lesssim 0.07$
) for different values of
$0.04\lesssim z/H\lesssim 0.07$
) for different values of
![]() $Ra$
and
$Ra$
and
![]() $Pr\simeq 4.4$
. The shape of the measured
$Pr\simeq 4.4$
. The shape of the measured
![]() $P(\unicode[STIX]{x1D6FF}T)$
in this region is similar to that in the thin disk, namely, all the PDFs have a Gaussian-like main portion (dashed line) for small temperature fluctuations (
$P(\unicode[STIX]{x1D6FF}T)$
in this region is similar to that in the thin disk, namely, all the PDFs have a Gaussian-like main portion (dashed line) for small temperature fluctuations (
![]() $\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}\lesssim 1$
) and a long exponential tail for large temperature fluctuations (
$\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}\lesssim 1$
) and a long exponential tail for large temperature fluctuations (
![]() $\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}\gtrsim 2$
). In the outer region of the mixing zone (
$\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}\gtrsim 2$
). In the outer region of the mixing zone (
![]() $0.1\lesssim z/H\lesssim 0.3$
), the measured
$0.1\lesssim z/H\lesssim 0.3$
), the measured
![]() $P(\unicode[STIX]{x1D6FF}T)$
has a new characteristic form, which is not observed in the thin disk. Figure 5(c) shows an example of the measured
$P(\unicode[STIX]{x1D6FF}T)$
has a new characteristic form, which is not observed in the thin disk. Figure 5(c) shows an example of the measured
![]() $P(\unicode[STIX]{x1D6FF}T)$
in this region. All of the PDFs for different values of
$P(\unicode[STIX]{x1D6FF}T)$
in this region. All of the PDFs for different values of
![]() $Ra$
collapse onto a single curve, which has a Gaussian cap (dashed line) for small temperature fluctuations (
$Ra$
collapse onto a single curve, which has a Gaussian cap (dashed line) for small temperature fluctuations (
![]() $-1\lesssim \unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}\lesssim 1$
) and two asymmetric exponential tails for larger temperature fluctuations. For the tail with
$-1\lesssim \unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}\lesssim 1$
) and two asymmetric exponential tails for larger temperature fluctuations. For the tail with
![]() $\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}\lesssim -1$
, it smoothly connects to the Gaussian cap and we believe that it results from the cold plumes passing through the measuring position. There is an abrupt change in the local slope of the measured
$\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}\lesssim -1$
, it smoothly connects to the Gaussian cap and we believe that it results from the cold plumes passing through the measuring position. There is an abrupt change in the local slope of the measured
![]() $P(\unicode[STIX]{x1D6FF}T)$
between the Gaussian cap and the exponential tail with
$P(\unicode[STIX]{x1D6FF}T)$
between the Gaussian cap and the exponential tail with
![]() $\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}\gtrsim 2$
. This result indicates that the properties of the cold and warm plumes in the outer region of the mixing zone are different.
$\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}\gtrsim 2$
. This result indicates that the properties of the cold and warm plumes in the outer region of the mixing zone are different.
When
![]() $z$
moves into the bulk region (
$z$
moves into the bulk region (
![]() $0.3\lesssim z/H\lesssim 0.5$
), the measured
$0.3\lesssim z/H\lesssim 0.5$
), the measured
![]() $P(\unicode[STIX]{x1D6FF}T)$
has a small Gaussian cap with two smooth but asymmetric exponential tails (not shown here). As
$P(\unicode[STIX]{x1D6FF}T)$
has a small Gaussian cap with two smooth but asymmetric exponential tails (not shown here). As
![]() $z$
moves toward the cell centre (
$z$
moves toward the cell centre (
![]() $z/H=0.5$
), the asymmetry between the two exponential tails reduces and finally vanishes at the cell centre. Figure 5(d) shows the measured PDFs
$z/H=0.5$
), the asymmetry between the two exponential tails reduces and finally vanishes at the cell centre. Figure 5(d) shows the measured PDFs
![]() $P(\unicode[STIX]{x1D6FF}T)$
at the cell centre for different values of
$P(\unicode[STIX]{x1D6FF}T)$
at the cell centre for different values of
![]() $Ra$
. Except for a small round-off near the origin, all of the PDFs are symmetric and have a long exponential tail (solid line) on each side of the distribution with its amplitude varied by more than 4 decades, which falls off much slower than a Gaussian (Kadanoff Reference Kadanoff2001). The exponential PDF
$Ra$
. Except for a small round-off near the origin, all of the PDFs are symmetric and have a long exponential tail (solid line) on each side of the distribution with its amplitude varied by more than 4 decades, which falls off much slower than a Gaussian (Kadanoff Reference Kadanoff2001). The exponential PDF
![]() $P(\unicode[STIX]{x1D6FF}T)$
was also observed in the previous convection experiments with
$P(\unicode[STIX]{x1D6FF}T)$
was also observed in the previous convection experiments with
![]() $Ra$
varied in a wide range from
$Ra$
varied in a wide range from
![]() $4\times 10^{7}$
up to
$4\times 10^{7}$
up to
![]() $10^{15}$
and in various convecting fluids (Castaing et al.
Reference Castaing, Gunaratne, Heslot, Kadanoff, Libchaber, Thomae, Wu, Zaleski and Zanetti1988; Sano et al.
Reference Sano, Wu and Libchber1989; Gollub et al.
Reference Gollub, Clarke, Gharib, Lane and Mesquita1991; Solomon & Gollub Reference Solomon and Gollub1991; Belmonte et al.
Reference Belmonte, Tilgner and Libchaber1994; Niemela et al.
Reference Niemela, Skrbek, Sreenivasan and Donnelly2000; Du & Tong Reference Du and Tong2001; Zhou & Xia Reference Zhou and Xia2002; He et al.
Reference He, Tong and Xia2007; Wei & Ahlers Reference Wei and Ahlers2016).
$10^{15}$
and in various convecting fluids (Castaing et al.
Reference Castaing, Gunaratne, Heslot, Kadanoff, Libchaber, Thomae, Wu, Zaleski and Zanetti1988; Sano et al.
Reference Sano, Wu and Libchber1989; Gollub et al.
Reference Gollub, Clarke, Gharib, Lane and Mesquita1991; Solomon & Gollub Reference Solomon and Gollub1991; Belmonte et al.
Reference Belmonte, Tilgner and Libchaber1994; Niemela et al.
Reference Niemela, Skrbek, Sreenivasan and Donnelly2000; Du & Tong Reference Du and Tong2001; Zhou & Xia Reference Zhou and Xia2002; He et al.
Reference He, Tong and Xia2007; Wei & Ahlers Reference Wei and Ahlers2016).

Figure 5. Measured PDF
![]() $P(\unicode[STIX]{x1D6FF}T)$
of the normalized temperature fluctuation
$P(\unicode[STIX]{x1D6FF}T)$
of the normalized temperature fluctuation
![]() $\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
for different values of
$\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
for different values of
![]() $Ra$
with a fixed value
$Ra$
with a fixed value
![]() $Pr=4.4$
(water). The measurements are made in the
$Pr=4.4$
(water). The measurements are made in the
![]() $\unicode[STIX]{x1D6E4}=1$
upright cylinder and in four representative regions of distance
$\unicode[STIX]{x1D6E4}=1$
upright cylinder and in four representative regions of distance
![]() $z$
away from the bottom plate centre: (a)
$z$
away from the bottom plate centre: (a)
![]() $z/\unicode[STIX]{x1D6FF}\lesssim 0.46$
(inner region of the BL), (b)
$z/\unicode[STIX]{x1D6FF}\lesssim 0.46$
(inner region of the BL), (b)
![]() $z/H=0.05$
(inner mixing zone), (c)
$z/H=0.05$
(inner mixing zone), (c)
![]() $z/H=0.16$
(outer mixing zone) and (d)
$z/H=0.16$
(outer mixing zone) and (d)
![]() $z/H=0.5$
(cell centre). The dashed lines in (a–c) show a Gaussian function given in (3.1). The solid line in (b) shows a fit of (4.8) to the data points with
$z/H=0.5$
(cell centre). The dashed lines in (a–c) show a Gaussian function given in (3.1). The solid line in (b) shows a fit of (4.8) to the data points with
![]() $\unicode[STIX]{x1D6FC}_{1}=0.31\pm 0.06$
and
$\unicode[STIX]{x1D6FC}_{1}=0.31\pm 0.06$
and
![]() $\unicode[STIX]{x1D6FD}=0.18\pm 0.05$
. The solid line in (c) shows a fit of (4.13) to the data points with
$\unicode[STIX]{x1D6FD}=0.18\pm 0.05$
. The solid line in (c) shows a fit of (4.13) to the data points with
![]() $\unicode[STIX]{x1D6FC}_{1}=0.33\pm 0.06$
,
$\unicode[STIX]{x1D6FC}_{1}=0.33\pm 0.06$
,
![]() $\unicode[STIX]{x1D6FC}_{2}=0.92\pm 0.15$
and
$\unicode[STIX]{x1D6FC}_{2}=0.92\pm 0.15$
and
![]() $\unicode[STIX]{x1D6FD}=0.18\pm 0.05$
. The solid line in (d) is a fit of (4.11) to the data points with
$\unicode[STIX]{x1D6FD}=0.18\pm 0.05$
. The solid line in (d) is a fit of (4.11) to the data points with
![]() $\unicode[STIX]{x1D6FC}=0.30\pm 0.06$
.
$\unicode[STIX]{x1D6FC}=0.30\pm 0.06$
.
Figure 6 shows
![]() $P(\unicode[STIX]{x1D6FF}T)$
as a function of
$P(\unicode[STIX]{x1D6FF}T)$
as a function of
![]() $\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
for different values of
$\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
for different values of
![]() $Ra$
with fixed
$Ra$
with fixed
![]() $Pr=7.6$
(20 wt. % aqueous solution of glycerin). It is seen that the measured PDFs
$Pr=7.6$
(20 wt. % aqueous solution of glycerin). It is seen that the measured PDFs
![]() $P(\unicode[STIX]{x1D6FF}T)$
in the four representative regions of
$P(\unicode[STIX]{x1D6FF}T)$
in the four representative regions of
![]() $z$
for the 20 wt. % glycerin solution have similar behaviours to those as shown in figure 5 for water. At a fixed location
$z$
for the 20 wt. % glycerin solution have similar behaviours to those as shown in figure 5 for water. At a fixed location
![]() $z$
, the measured PDFs
$z$
, the measured PDFs
![]() $P(\unicode[STIX]{x1D6FF}T)$
with different values of
$P(\unicode[STIX]{x1D6FF}T)$
with different values of
![]() $Ra$
all fall onto a single master curve, which remains unchanged with
$Ra$
all fall onto a single master curve, which remains unchanged with
![]() $Ra$
in the
$Ra$
in the
![]() $Ra$
range studied. The shape of
$Ra$
range studied. The shape of
![]() $P(\unicode[STIX]{x1D6FF}T)$
continuously evolves with
$P(\unicode[STIX]{x1D6FF}T)$
continuously evolves with
![]() $z$
, from a Gaussian form in the inner region of the BL to an exponential form at the cell centre. For the two working fluids used in the experiment, previous studies (Wu & Libchaber Reference Wu and Libchaber1991; Zhang, Childress & Libchaber Reference Zhang, Childress and Libchaber1997; Chillá et al.
Reference Chillá, Rastello, Chaumat and Castaing2004; Ahlers et al.
Reference Ahlers, Brown, Araujo, Funfschilling, Grossmann and Lohse2006b
) have shown that the non-Oberbeck–Boussinesq (NOB) effect of distilled water is very weak. The 20 wt. % aqueous solution of glycerin, on the other hand, has a stronger NOB effect, as its viscosity depends sensitively on the fluid temperature. It is seen from figures 5 and 6 that the four distinct forms of the measured
$z$
, from a Gaussian form in the inner region of the BL to an exponential form at the cell centre. For the two working fluids used in the experiment, previous studies (Wu & Libchaber Reference Wu and Libchaber1991; Zhang, Childress & Libchaber Reference Zhang, Childress and Libchaber1997; Chillá et al.
Reference Chillá, Rastello, Chaumat and Castaing2004; Ahlers et al.
Reference Ahlers, Brown, Araujo, Funfschilling, Grossmann and Lohse2006b
) have shown that the non-Oberbeck–Boussinesq (NOB) effect of distilled water is very weak. The 20 wt. % aqueous solution of glycerin, on the other hand, has a stronger NOB effect, as its viscosity depends sensitively on the fluid temperature. It is seen from figures 5 and 6 that the four distinct forms of the measured
![]() $P(\unicode[STIX]{x1D6FF}T)$
in the four flow regions remain approximately the same in the two working fluids, suggesting that the characteristic behaviours of the measured
$P(\unicode[STIX]{x1D6FF}T)$
in the four flow regions remain approximately the same in the two working fluids, suggesting that the characteristic behaviours of the measured
![]() $P(\unicode[STIX]{x1D6FF}T)$
are not influenced very much by the NOB effect.
$P(\unicode[STIX]{x1D6FF}T)$
are not influenced very much by the NOB effect.

Figure 6. Measured PDF
![]() $P(\unicode[STIX]{x1D6FF}T)$
as a function of
$P(\unicode[STIX]{x1D6FF}T)$
as a function of
![]() $\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
for different values of
$\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
for different values of
![]() $Ra$
with a fixed value
$Ra$
with a fixed value
![]() $Pr=7.6$
(20 wt. % aqueous solution of glycerin). The measurements are made in the
$Pr=7.6$
(20 wt. % aqueous solution of glycerin). The measurements are made in the
![]() $\unicode[STIX]{x1D6E4}=1$
upright cylinder and in four representative regions of distance
$\unicode[STIX]{x1D6E4}=1$
upright cylinder and in four representative regions of distance
![]() $z$
away from the bottom plate: (a)
$z$
away from the bottom plate: (a)
![]() $z/\unicode[STIX]{x1D6FF}\lesssim 0.52$
(inner region of the BL), (b)
$z/\unicode[STIX]{x1D6FF}\lesssim 0.52$
(inner region of the BL), (b)
![]() $z/H=0.062$
(inner mixing zone), (c)
$z/H=0.062$
(inner mixing zone), (c)
![]() $z/H=0.18$
(outer mixing zone) and (d)
$z/H=0.18$
(outer mixing zone) and (d)
![]() $z/H=0.5$
(cell centre). The dashed lines in (a–c) show a Gaussian function given in (3.1). The solid line in (b) shows a fit of (4.8) to the data points with
$z/H=0.5$
(cell centre). The dashed lines in (a–c) show a Gaussian function given in (3.1). The solid line in (b) shows a fit of (4.8) to the data points with
![]() $\unicode[STIX]{x1D6FC}_{1}=0.24\pm 0.04$
and
$\unicode[STIX]{x1D6FC}_{1}=0.24\pm 0.04$
and
![]() $\unicode[STIX]{x1D6FD}=0.10\pm 0.03$
. The solid line in (c) shows a fit of (4.13) to the data points with
$\unicode[STIX]{x1D6FD}=0.10\pm 0.03$
. The solid line in (c) shows a fit of (4.13) to the data points with
![]() $\unicode[STIX]{x1D6FC}_{1}=0.30\pm 0.05$
,
$\unicode[STIX]{x1D6FC}_{1}=0.30\pm 0.05$
,
![]() $\unicode[STIX]{x1D6FC}_{2}=1.05\pm 0.2$
and
$\unicode[STIX]{x1D6FC}_{2}=1.05\pm 0.2$
and
![]() $\unicode[STIX]{x1D6FD}=0.10\pm 0.03$
. The solid line in (d) is a fit of (4.11) to the data points with
$\unicode[STIX]{x1D6FD}=0.10\pm 0.03$
. The solid line in (d) is a fit of (4.11) to the data points with
![]() $\unicode[STIX]{x1D6FC}=0.20\pm 0.04$
.
$\unicode[STIX]{x1D6FC}=0.20\pm 0.04$
.
4 Further theoretical analysis
Based on the above experimental results, we now derive expressions of the temperature PDF
![]() $P(\unicode[STIX]{x1D6FF}T)$
in different regions. We assume that temperature fluctuations in the convecting fluid are made from two independent sources, as shown in (1.3). The turbulent background is assumed to be homogeneous, so that
$P(\unicode[STIX]{x1D6FF}T)$
in different regions. We assume that temperature fluctuations in the convecting fluid are made from two independent sources, as shown in (1.3). The turbulent background is assumed to be homogeneous, so that
![]() $\unicode[STIX]{x1D6FF}T_{B}(t)$
is homogeneous both in space and time and has a Gaussian distribution
$\unicode[STIX]{x1D6FF}T_{B}(t)$
is homogeneous both in space and time and has a Gaussian distribution
where
![]() $\unicode[STIX]{x1D70E}_{B}$
is the r.m.s. value of
$\unicode[STIX]{x1D70E}_{B}$
is the r.m.s. value of
![]() $\unicode[STIX]{x1D6FF}T_{B}(t)$
. Because thermal plumes have a non-uniform spatial distribution in the convection cell,
$\unicode[STIX]{x1D6FF}T_{B}(t)$
. Because thermal plumes have a non-uniform spatial distribution in the convection cell,
![]() $\unicode[STIX]{x1D6FF}T_{P}(t)$
can be further divided into
$\unicode[STIX]{x1D6FF}T_{P}(t)$
can be further divided into
![]() $\unicode[STIX]{x1D6FF}T_{P}^{h}(t)$
for warm plumes near the bottom conducting plate and
$\unicode[STIX]{x1D6FF}T_{P}^{h}(t)$
for warm plumes near the bottom conducting plate and
![]() $\unicode[STIX]{x1D6FF}T_{P}^{c}(t)$
for cold plumes near the top conducting plate. As mentioned in Introduction, the conditional PDF for temperature fluctuations resulting from thermal plumes alone has a simple exponential form (He et al.
Reference He, Wang and Tong2018). Therefore, the PDFs for
$\unicode[STIX]{x1D6FF}T_{P}^{c}(t)$
for cold plumes near the top conducting plate. As mentioned in Introduction, the conditional PDF for temperature fluctuations resulting from thermal plumes alone has a simple exponential form (He et al.
Reference He, Wang and Tong2018). Therefore, the PDFs for
![]() $\unicode[STIX]{x1D6FF}T_{P}^{h}(t)$
and
$\unicode[STIX]{x1D6FF}T_{P}^{h}(t)$
and
![]() $\unicode[STIX]{x1D6FF}T_{P}^{c}(t)$
can be expressed, respectively, as
$\unicode[STIX]{x1D6FF}T_{P}^{c}(t)$
can be expressed, respectively, as
and
where
![]() $\unicode[STIX]{x1D70E}_{h}$
and
$\unicode[STIX]{x1D70E}_{h}$
and
![]() $\unicode[STIX]{x1D70E}_{c}$
are, respectively, the r.m.s. value of
$\unicode[STIX]{x1D70E}_{c}$
are, respectively, the r.m.s. value of
![]() $\unicode[STIX]{x1D6FF}T_{P}^{h}(t)$
and
$\unicode[STIX]{x1D6FF}T_{P}^{h}(t)$
and
![]() $\unicode[STIX]{x1D6FF}T_{P}^{c}(t)$
. The condition
$\unicode[STIX]{x1D6FF}T_{P}^{c}(t)$
. The condition
![]() $\unicode[STIX]{x1D6FF}T_{P}^{h}\geqslant 0$
applies for warm plumes and
$\unicode[STIX]{x1D6FF}T_{P}^{h}\geqslant 0$
applies for warm plumes and
![]() $\unicode[STIX]{x1D6FF}T_{P}^{c}\leqslant 0$
applies for cold plumes, which state that the thermal plumes are fluid particles with their temperature warmer (or colder) than the surroundings.
$\unicode[STIX]{x1D6FF}T_{P}^{c}\leqslant 0$
applies for cold plumes, which state that the thermal plumes are fluid particles with their temperature warmer (or colder) than the surroundings.
In the lower half of the bulk region, one finds more warm plumes than cold plumes. In this case, the local temperature fluctuation can be expressed as
and its PDF is a convolution of (4.1) and (4.2) with
 $$\begin{eqnarray}\displaystyle P(\unicode[STIX]{x1D6FF}T) & = & \displaystyle \int _{0}^{+\infty }P_{B}(\unicode[STIX]{x1D6FF}T-\unicode[STIX]{x1D6FF}T_{P}^{h})P_{h}(\unicode[STIX]{x1D6FF}T_{P}^{h})\,\text{d}(\unicode[STIX]{x1D6FF}T_{P}^{h})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2\unicode[STIX]{x1D70E}_{h}}e^{[(1/2)(\unicode[STIX]{x1D70E}_{B}/\unicode[STIX]{x1D70E}_{h})^{2}-\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{h}-1]}\text{erfc}\left(\frac{\unicode[STIX]{x1D70E}_{B}^{2}/\unicode[STIX]{x1D70E}_{h}-\unicode[STIX]{x1D6FF}T-\unicode[STIX]{x1D70E}_{h}}{\sqrt{2}\unicode[STIX]{x1D70E}_{B}}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P(\unicode[STIX]{x1D6FF}T) & = & \displaystyle \int _{0}^{+\infty }P_{B}(\unicode[STIX]{x1D6FF}T-\unicode[STIX]{x1D6FF}T_{P}^{h})P_{h}(\unicode[STIX]{x1D6FF}T_{P}^{h})\,\text{d}(\unicode[STIX]{x1D6FF}T_{P}^{h})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2\unicode[STIX]{x1D70E}_{h}}e^{[(1/2)(\unicode[STIX]{x1D70E}_{B}/\unicode[STIX]{x1D70E}_{h})^{2}-\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{h}-1]}\text{erfc}\left(\frac{\unicode[STIX]{x1D70E}_{B}^{2}/\unicode[STIX]{x1D70E}_{h}-\unicode[STIX]{x1D6FF}T-\unicode[STIX]{x1D70E}_{h}}{\sqrt{2}\unicode[STIX]{x1D70E}_{B}}\right),\end{eqnarray}$$
where
![]() $\text{erfc}(x)$
is the complementary error function. Similar convolution was also used in the study of scaler mixing (Le Borgne et al.
Reference Le Borgne, Huck, Dentz and Villermaux2017). In (4.5), we have dropped off the mean value of
$\text{erfc}(x)$
is the complementary error function. Similar convolution was also used in the study of scaler mixing (Le Borgne et al.
Reference Le Borgne, Huck, Dentz and Villermaux2017). In (4.5), we have dropped off the mean value of
![]() $\unicode[STIX]{x1D6FF}T$
so that
$\unicode[STIX]{x1D6FF}T$
so that
![]() $P(\unicode[STIX]{x1D6FF}T)$
has a zero mean. The mean value of
$P(\unicode[STIX]{x1D6FF}T)$
has a zero mean. The mean value of
![]() $\unicode[STIX]{x1D6FF}T$
represents the contribution of thermal plumes to the mean temperature field, which is small but spatially heterogeneous. As the focus of this paper is on local temperature fluctuations, we will not consider the local mean value of
$\unicode[STIX]{x1D6FF}T$
represents the contribution of thermal plumes to the mean temperature field, which is small but spatially heterogeneous. As the focus of this paper is on local temperature fluctuations, we will not consider the local mean value of
![]() $\unicode[STIX]{x1D6FF}T$
in the rest of our analysis. From (4.5), one can show that
$\unicode[STIX]{x1D6FF}T$
in the rest of our analysis. From (4.5), one can show that
![]() $P(\unicode[STIX]{x1D6FF}T)$
has a r.m.s. value of
$P(\unicode[STIX]{x1D6FF}T)$
has a r.m.s. value of
![]() $\unicode[STIX]{x1D70E}_{T}=(\unicode[STIX]{x1D70E}_{B}^{2}+\unicode[STIX]{x1D70E}_{h}^{2})^{1/2}$
. With the normalized variable
$\unicode[STIX]{x1D70E}_{T}=(\unicode[STIX]{x1D70E}_{B}^{2}+\unicode[STIX]{x1D70E}_{h}^{2})^{1/2}$
. With the normalized variable
![]() $\unicode[STIX]{x1D709}=\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
, equation (4.5) can be rewritten as
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
, equation (4.5) can be rewritten as
where
![]() $\unicode[STIX]{x1D6FC}_{1}=\unicode[STIX]{x1D70E}_{B}/\unicode[STIX]{x1D70E}_{h}$
. The solid line in figure 4(c) shows a fit of (4.6) to the data points with
$\unicode[STIX]{x1D6FC}_{1}=\unicode[STIX]{x1D70E}_{B}/\unicode[STIX]{x1D70E}_{h}$
. The solid line in figure 4(c) shows a fit of (4.6) to the data points with
![]() $\unicode[STIX]{x1D6FC}_{1}=1.1\pm 0.2$
as a fitting parameter. Excellent agreement is found between the theoretical prediction and experimental data. The obtained value of
$\unicode[STIX]{x1D6FC}_{1}=1.1\pm 0.2$
as a fitting parameter. Excellent agreement is found between the theoretical prediction and experimental data. The obtained value of
![]() $\unicode[STIX]{x1D6FC}_{1}=1.1$
suggests that the two fluctuation sources have comparable r.m.s. values in the bulk region of the thin disk.
$\unicode[STIX]{x1D6FC}_{1}=1.1$
suggests that the two fluctuation sources have comparable r.m.s. values in the bulk region of the thin disk.

Figure 7. Comparison of the measured power spectra
![]() $P_{T}(f)$
of local temperature fluctuations
$P_{T}(f)$
of local temperature fluctuations
![]() $\unicode[STIX]{x1D6FF}T(t)$
in three representative regions of distance
$\unicode[STIX]{x1D6FF}T(t)$
in three representative regions of distance
![]() $z$
away from the bottom plate:
$z$
away from the bottom plate:
![]() $z/D=0.026$
(mixing zone, black curve),
$z/D=0.026$
(mixing zone, black curve),
![]() $z/D=0.33$
(bulk region, red curve) and
$z/D=0.33$
(bulk region, red curve) and
![]() $z/D=0.5$
(cell centre, blue curve). The measurements are conducted at
$z/D=0.5$
(cell centre, blue curve). The measurements are conducted at
![]() $Ra=5.3\times 10^{9}$
and
$Ra=5.3\times 10^{9}$
and
![]() $Pr=7.6$
in the thin disk. For clarity, the measured
$Pr=7.6$
in the thin disk. For clarity, the measured
![]() $P_{T}(f)$
is shifted vertically.
$P_{T}(f)$
is shifted vertically.
In the above, the two signals
![]() $\unicode[STIX]{x1D6FF}T_{B}(t)$
and
$\unicode[STIX]{x1D6FF}T_{B}(t)$
and
![]() $\unicode[STIX]{x1D6FF}T_{P}^{h}(t)$
are assumed to be continuous in time. However, this is not always the case. For example, it was reported (Song et al.
Reference Song, Villermaux and Tong2011) that warm plumes emit periodically from the lower BL to the mixing zone, so that
$\unicode[STIX]{x1D6FF}T_{P}^{h}(t)$
are assumed to be continuous in time. However, this is not always the case. For example, it was reported (Song et al.
Reference Song, Villermaux and Tong2011) that warm plumes emit periodically from the lower BL to the mixing zone, so that
![]() $\unicode[STIX]{x1D6FF}T_{P}^{h}(t)$
in this region is not continuous in time. Figure 7 shows a comparison of the measured power spectra
$\unicode[STIX]{x1D6FF}T_{P}^{h}(t)$
in this region is not continuous in time. Figure 7 shows a comparison of the measured power spectra
![]() $P_{T}(f)$
of
$P_{T}(f)$
of
![]() $\unicode[STIX]{x1D6FF}T(t)$
in three representative regions of the thin disk cell. It is seen that in the mixing zone (
$\unicode[STIX]{x1D6FF}T(t)$
in three representative regions of the thin disk cell. It is seen that in the mixing zone (
![]() $z/D=0.026$
), the measured
$z/D=0.026$
), the measured
![]() $P_{T}(f)$
(black curve) reveals a peak at
$P_{T}(f)$
(black curve) reveals a peak at
![]() $f\simeq 0.02~\text{Hz}$
, indicating a periodic emission of warm plumes from the lower BL (Song et al.
Reference Song, Villermaux and Tong2011). The frequency peak in
$f\simeq 0.02~\text{Hz}$
, indicating a periodic emission of warm plumes from the lower BL (Song et al.
Reference Song, Villermaux and Tong2011). The frequency peak in
![]() $P_{T}(f)$
gradually diminishes with increasing
$P_{T}(f)$
gradually diminishes with increasing
![]() $z$
and eventually vanishes in the bulk region (red curve) and at the cell centre (blue curve), as a result of turbulent mixing and plume–plume interactions, which smear out the coherence of plume emission. This finding suggests that at certain times
$z$
and eventually vanishes in the bulk region (red curve) and at the cell centre (blue curve), as a result of turbulent mixing and plume–plume interactions, which smear out the coherence of plume emission. This finding suggests that at certain times
![]() $t$
,
$t$
,
![]() $\unicode[STIX]{x1D6FF}T_{P}^{h}(t)\simeq 0$
and
$\unicode[STIX]{x1D6FF}T_{P}^{h}(t)\simeq 0$
and
![]() $\unicode[STIX]{x1D6FF}T(t)\simeq \unicode[STIX]{x1D6FF}T_{B}(t)$
. To characterize this temporal intermittency in the mixing zone, we introduce two duty cycle parameters with
$\unicode[STIX]{x1D6FF}T(t)\simeq \unicode[STIX]{x1D6FF}T_{B}(t)$
. To characterize this temporal intermittency in the mixing zone, we introduce two duty cycle parameters with
![]() $\unicode[STIX]{x1D6FD}$
being used to describe the probability for
$\unicode[STIX]{x1D6FD}$
being used to describe the probability for
![]() $\unicode[STIX]{x1D6FF}T(t)=\unicode[STIX]{x1D6FF}T_{B}(t)+\unicode[STIX]{x1D6FF}T_{P}^{h}(t)$
and
$\unicode[STIX]{x1D6FF}T(t)=\unicode[STIX]{x1D6FF}T_{B}(t)+\unicode[STIX]{x1D6FF}T_{P}^{h}(t)$
and
![]() $1-\unicode[STIX]{x1D6FD}$
for the probability that
$1-\unicode[STIX]{x1D6FD}$
for the probability that
![]() $\unicode[STIX]{x1D6FF}T(t)=\unicode[STIX]{x1D6FF}T_{B}(t)$
. In this case, the PDF of
$\unicode[STIX]{x1D6FF}T(t)=\unicode[STIX]{x1D6FF}T_{B}(t)$
. In this case, the PDF of
![]() $\unicode[STIX]{x1D6FF}T(t)$
can be written as
$\unicode[STIX]{x1D6FF}T(t)$
can be written as
 $$\begin{eqnarray}\displaystyle P(\unicode[STIX]{x1D6FF}T) & = & \displaystyle (1-\unicode[STIX]{x1D6FD})P_{B}(\unicode[STIX]{x1D6FF}T)+\unicode[STIX]{x1D6FD}\int _{0}^{+\infty }P_{B}(\unicode[STIX]{x1D6FF}T-\unicode[STIX]{x1D6FF}T_{P}^{h})P_{h}(\unicode[STIX]{x1D6FF}T_{P}^{h})\,\text{d}(\unicode[STIX]{x1D6FF}T_{P}^{h})\nonumber\\ \displaystyle & = & \displaystyle \frac{1-\unicode[STIX]{x1D6FD}}{\sqrt{2\unicode[STIX]{x03C0}}\unicode[STIX]{x1D70E}_{B}}e^{[-(\unicode[STIX]{x1D6FF}T+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D70E}_{h})^{2}/(2\unicode[STIX]{x1D70E}_{B}^{2})]}+\frac{\unicode[STIX]{x1D6FD}}{2\unicode[STIX]{x1D70E}_{h}}e^{[(1/2)(\unicode[STIX]{x1D70E}_{B}/\unicode[STIX]{x1D70E}_{h})^{2}-\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{h}-\unicode[STIX]{x1D6FD}]}\text{erfc}\left(\frac{\unicode[STIX]{x1D70E}_{B}^{2}/\unicode[STIX]{x1D70E}_{h}-\unicode[STIX]{x1D6FF}T-\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D70E}_{h}}{\sqrt{2}\unicode[STIX]{x1D70E}_{B}}\right).\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P(\unicode[STIX]{x1D6FF}T) & = & \displaystyle (1-\unicode[STIX]{x1D6FD})P_{B}(\unicode[STIX]{x1D6FF}T)+\unicode[STIX]{x1D6FD}\int _{0}^{+\infty }P_{B}(\unicode[STIX]{x1D6FF}T-\unicode[STIX]{x1D6FF}T_{P}^{h})P_{h}(\unicode[STIX]{x1D6FF}T_{P}^{h})\,\text{d}(\unicode[STIX]{x1D6FF}T_{P}^{h})\nonumber\\ \displaystyle & = & \displaystyle \frac{1-\unicode[STIX]{x1D6FD}}{\sqrt{2\unicode[STIX]{x03C0}}\unicode[STIX]{x1D70E}_{B}}e^{[-(\unicode[STIX]{x1D6FF}T+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D70E}_{h})^{2}/(2\unicode[STIX]{x1D70E}_{B}^{2})]}+\frac{\unicode[STIX]{x1D6FD}}{2\unicode[STIX]{x1D70E}_{h}}e^{[(1/2)(\unicode[STIX]{x1D70E}_{B}/\unicode[STIX]{x1D70E}_{h})^{2}-\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{h}-\unicode[STIX]{x1D6FD}]}\text{erfc}\left(\frac{\unicode[STIX]{x1D70E}_{B}^{2}/\unicode[STIX]{x1D70E}_{h}-\unicode[STIX]{x1D6FF}T-\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D70E}_{h}}{\sqrt{2}\unicode[STIX]{x1D70E}_{B}}\right).\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
In (4.7)
![]() $P(\unicode[STIX]{x1D6FF}T)$
has a r.m.s. value
$P(\unicode[STIX]{x1D6FF}T)$
has a r.m.s. value
![]() $\unicode[STIX]{x1D70E}_{T}=(\unicode[STIX]{x1D70E}_{B}^{2}+(2\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FD}^{2})\unicode[STIX]{x1D70E}_{h}^{2})^{1/2}$
. With the normalized variable
$\unicode[STIX]{x1D70E}_{T}=(\unicode[STIX]{x1D70E}_{B}^{2}+(2\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FD}^{2})\unicode[STIX]{x1D70E}_{h}^{2})^{1/2}$
. With the normalized variable
![]() $\unicode[STIX]{x1D709}=\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
, equation (4.7) can be rewritten as
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
, equation (4.7) can be rewritten as
where
![]() $\unicode[STIX]{x1D6FE}=(\unicode[STIX]{x1D6FC}_{1}^{2}+2\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FD}^{2})^{1/2}$
.
$\unicode[STIX]{x1D6FE}=(\unicode[STIX]{x1D6FC}_{1}^{2}+2\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FD}^{2})^{1/2}$
.
It is found that the theoretical prediction given in (4.8) can well describe the experimental results in the mixing zone of both the thin disk cell and upright cylinder. The solid line in figure 4(b) shows a fit of (4.8) to the data points with
![]() $\unicode[STIX]{x1D6FC}_{1}=0.25\pm 0.05$
and
$\unicode[STIX]{x1D6FC}_{1}=0.25\pm 0.05$
and
![]() $\unicode[STIX]{x1D6FD}=0.1\pm 0.03$
as two fitting parameters. The solid line in figure 5(b) shows a fit of (4.8) to the data points in the inner mixing zone of the
$\unicode[STIX]{x1D6FD}=0.1\pm 0.03$
as two fitting parameters. The solid line in figure 5(b) shows a fit of (4.8) to the data points in the inner mixing zone of the
![]() $\unicode[STIX]{x1D6E4}=1$
upright cylinder filled with water (
$\unicode[STIX]{x1D6E4}=1$
upright cylinder filled with water (
![]() $Pr=4.4$
) using
$Pr=4.4$
) using
![]() $\unicode[STIX]{x1D6FC}_{1}=0.31\pm 0.06$
and
$\unicode[STIX]{x1D6FC}_{1}=0.31\pm 0.06$
and
![]() $\unicode[STIX]{x1D6FD}=0.18\pm 0.05$
as two fitting parameters. Similarly, the solid line in figure 6(b) shows a fit of (4.8) to the data points in the inner mixing zone of the
$\unicode[STIX]{x1D6FD}=0.18\pm 0.05$
as two fitting parameters. Similarly, the solid line in figure 6(b) shows a fit of (4.8) to the data points in the inner mixing zone of the
![]() $\unicode[STIX]{x1D6E4}=1$
upright cylinder filled with the 20 wt. % aqueous solution of glycerin (
$\unicode[STIX]{x1D6E4}=1$
upright cylinder filled with the 20 wt. % aqueous solution of glycerin (
![]() $Pr=7.6$
) using
$Pr=7.6$
) using
![]() $\unicode[STIX]{x1D6FC}_{1}=0.24\pm 0.04$
and
$\unicode[STIX]{x1D6FC}_{1}=0.24\pm 0.04$
and
![]() $\unicode[STIX]{x1D6FD}=0.1\pm 0.03$
.
$\unicode[STIX]{x1D6FD}=0.1\pm 0.03$
.
When the measuring position
![]() $z$
moves to the cell centre, both warm and cold plumes contribute to temperature fluctuations. In this case, the local temperature fluctuation can be expressed as
$z$
moves to the cell centre, both warm and cold plumes contribute to temperature fluctuations. In this case, the local temperature fluctuation can be expressed as
and its PDF can be written as
 $$\begin{eqnarray}\displaystyle P(\unicode[STIX]{x1D6FF}T) & = & \displaystyle \int _{-\infty }^{0}\int _{0}^{+\infty }P_{B}(T-\unicode[STIX]{x1D6FF}T_{P}^{h}-\unicode[STIX]{x1D6FF}T_{P}^{c})P_{h}(\unicode[STIX]{x1D6FF}T_{P}^{h})P_{c}(\unicode[STIX]{x1D6FF}T_{P}^{c})\text{d}(\unicode[STIX]{x1D6FF}T_{P}^{h})\,\text{d}(\unicode[STIX]{x1D6FF}T_{P}^{c})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{4\unicode[STIX]{x1D70E}_{P}}e^{(\unicode[STIX]{x1D70E}_{B}/\unicode[STIX]{x1D70E}_{P})^{2}/2}\left[e^{\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{P}}\text{erfc}\left(\frac{\unicode[STIX]{x1D70E}_{B}^{2}+\unicode[STIX]{x1D6FF}T\unicode[STIX]{x1D70E}_{P}}{\sqrt{2}\unicode[STIX]{x1D70E}_{P}\unicode[STIX]{x1D70E}_{B}}\right)+e^{-\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{P}}\text{erfc}\left(\frac{\unicode[STIX]{x1D70E}_{B}^{2}-\unicode[STIX]{x1D6FF}T\unicode[STIX]{x1D70E}_{P}}{\sqrt{2}\unicode[STIX]{x1D70E}_{P}\unicode[STIX]{x1D70E}_{B}}\right)\right],\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P(\unicode[STIX]{x1D6FF}T) & = & \displaystyle \int _{-\infty }^{0}\int _{0}^{+\infty }P_{B}(T-\unicode[STIX]{x1D6FF}T_{P}^{h}-\unicode[STIX]{x1D6FF}T_{P}^{c})P_{h}(\unicode[STIX]{x1D6FF}T_{P}^{h})P_{c}(\unicode[STIX]{x1D6FF}T_{P}^{c})\text{d}(\unicode[STIX]{x1D6FF}T_{P}^{h})\,\text{d}(\unicode[STIX]{x1D6FF}T_{P}^{c})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{4\unicode[STIX]{x1D70E}_{P}}e^{(\unicode[STIX]{x1D70E}_{B}/\unicode[STIX]{x1D70E}_{P})^{2}/2}\left[e^{\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{P}}\text{erfc}\left(\frac{\unicode[STIX]{x1D70E}_{B}^{2}+\unicode[STIX]{x1D6FF}T\unicode[STIX]{x1D70E}_{P}}{\sqrt{2}\unicode[STIX]{x1D70E}_{P}\unicode[STIX]{x1D70E}_{B}}\right)+e^{-\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{P}}\text{erfc}\left(\frac{\unicode[STIX]{x1D70E}_{B}^{2}-\unicode[STIX]{x1D6FF}T\unicode[STIX]{x1D70E}_{P}}{\sqrt{2}\unicode[STIX]{x1D70E}_{P}\unicode[STIX]{x1D70E}_{B}}\right)\right],\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D70E}_{P}\equiv \unicode[STIX]{x1D70E}_{h}=\unicode[STIX]{x1D70E}_{c}$
, because the system is symmetric at the cell centre. In (4.10),
$\unicode[STIX]{x1D70E}_{P}\equiv \unicode[STIX]{x1D70E}_{h}=\unicode[STIX]{x1D70E}_{c}$
, because the system is symmetric at the cell centre. In (4.10),
![]() $P(\unicode[STIX]{x1D6FF}T)$
has a r.m.s. value
$P(\unicode[STIX]{x1D6FF}T)$
has a r.m.s. value
![]() $\unicode[STIX]{x1D70E}_{T}=(\unicode[STIX]{x1D70E}_{B}^{2}+2\unicode[STIX]{x1D70E}_{P}^{2})^{1/2}$
. With the normalized variable
$\unicode[STIX]{x1D70E}_{T}=(\unicode[STIX]{x1D70E}_{B}^{2}+2\unicode[STIX]{x1D70E}_{P}^{2})^{1/2}$
. With the normalized variable
![]() $\unicode[STIX]{x1D709}=\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
, equation (4.10) can be rewritten as
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
, equation (4.10) can be rewritten as
 $$\begin{eqnarray}\displaystyle P(\unicode[STIX]{x1D709};\unicode[STIX]{x1D6FC}) & = & \displaystyle \frac{\sqrt{\unicode[STIX]{x1D6FC}^{2}+2}}{4}e^{\unicode[STIX]{x1D6FC}^{2}/2}\left[e^{\unicode[STIX]{x1D709}\sqrt{\unicode[STIX]{x1D6FC}^{2}+2}}\text{erfc}\left(\frac{\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D709}\sqrt{\unicode[STIX]{x1D6FC}^{2}+2}}{\sqrt{2}\unicode[STIX]{x1D6FC}}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \left.+e^{-\unicode[STIX]{x1D709}\sqrt{\unicode[STIX]{x1D6FC}^{2}+2}}\text{erfc}\left(\frac{\unicode[STIX]{x1D6FC}^{2}-\unicode[STIX]{x1D709}\sqrt{\unicode[STIX]{x1D6FC}^{2}+2}}{\sqrt{2}\unicode[STIX]{x1D6FC}}\right)\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P(\unicode[STIX]{x1D709};\unicode[STIX]{x1D6FC}) & = & \displaystyle \frac{\sqrt{\unicode[STIX]{x1D6FC}^{2}+2}}{4}e^{\unicode[STIX]{x1D6FC}^{2}/2}\left[e^{\unicode[STIX]{x1D709}\sqrt{\unicode[STIX]{x1D6FC}^{2}+2}}\text{erfc}\left(\frac{\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D709}\sqrt{\unicode[STIX]{x1D6FC}^{2}+2}}{\sqrt{2}\unicode[STIX]{x1D6FC}}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \left.+e^{-\unicode[STIX]{x1D709}\sqrt{\unicode[STIX]{x1D6FC}^{2}+2}}\text{erfc}\left(\frac{\unicode[STIX]{x1D6FC}^{2}-\unicode[STIX]{x1D709}\sqrt{\unicode[STIX]{x1D6FC}^{2}+2}}{\sqrt{2}\unicode[STIX]{x1D6FC}}\right)\right],\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D70E}_{B}/\unicode[STIX]{x1D70E}_{P}$
. Equation (4.11) is a symmetric function of
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D70E}_{B}/\unicode[STIX]{x1D70E}_{P}$
. Equation (4.11) is a symmetric function of
![]() $\unicode[STIX]{x1D709}$
with the exponential distribution (
$\unicode[STIX]{x1D709}$
with the exponential distribution (
![]() $\unicode[STIX]{x1D6FC}=0$
) and Gaussian distribution (
$\unicode[STIX]{x1D6FC}=0$
) and Gaussian distribution (
![]() $\unicode[STIX]{x1D6FC}=+\infty$
) being its two asymptotic forms.
$\unicode[STIX]{x1D6FC}=+\infty$
) being its two asymptotic forms.
It is found that the theoretical prediction given in (4.11) can well describe the experimental results at the centre of both convection cells. The solid line in figure 4(d) shows a fit of (4.11) to the data points in the thin disk with
![]() $\unicode[STIX]{x1D6FC}=1.7\pm 0.3$
as a fitting parameter. The solid line in figure 5(d) shows a fit of (4.11) to the data points at the centre of the
$\unicode[STIX]{x1D6FC}=1.7\pm 0.3$
as a fitting parameter. The solid line in figure 5(d) shows a fit of (4.11) to the data points at the centre of the
![]() $\unicode[STIX]{x1D6E4}=1$
upright cylinder filled with water (
$\unicode[STIX]{x1D6E4}=1$
upright cylinder filled with water (
![]() $Pr=4.4$
) using
$Pr=4.4$
) using
![]() $\unicode[STIX]{x1D6FC}=0.30\pm 0.06$
. Similarly, the solid line in figure 6(d) shows a fit of (4.11) to the data points at the centre of the
$\unicode[STIX]{x1D6FC}=0.30\pm 0.06$
. Similarly, the solid line in figure 6(d) shows a fit of (4.11) to the data points at the centre of the
![]() $\unicode[STIX]{x1D6E4}=1$
upright cylinder filled with the 20 wt. % aqueous solution of glycerin (
$\unicode[STIX]{x1D6E4}=1$
upright cylinder filled with the 20 wt. % aqueous solution of glycerin (
![]() $Pr=7.6$
) using
$Pr=7.6$
) using
![]() $\unicode[STIX]{x1D6FC}=0.20\pm 0.04$
.
$\unicode[STIX]{x1D6FC}=0.20\pm 0.04$
.

Figure 8. Measured temperature PDF
![]() $P(\unicode[STIX]{x1D6FF}T)$
as a function of
$P(\unicode[STIX]{x1D6FF}T)$
as a function of
![]() $\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
for different values of
$\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
for different values of
![]() $Ra$
and at a fixed value of
$Ra$
and at a fixed value of
![]() $Pr=4.4$
(a) and
$Pr=4.4$
(a) and
![]() $Pr=7.6$
(b). The measurements are conducted at the centre of the
$Pr=7.6$
(b). The measurements are conducted at the centre of the
![]() $\unicode[STIX]{x1D6E4}=1$
upright cylinder, and the data in (a) and (b) are the same as those shown in figure 5(d) and figure 6(d), respectively. For clarity, the measured PDFs are plotted on a linear scale showing an expanded view of the round-off cap region near
$\unicode[STIX]{x1D6E4}=1$
upright cylinder, and the data in (a) and (b) are the same as those shown in figure 5(d) and figure 6(d), respectively. For clarity, the measured PDFs are plotted on a linear scale showing an expanded view of the round-off cap region near
![]() $\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}\simeq 0$
. The solid lines are the fits of (4.11) to the data points with
$\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}\simeq 0$
. The solid lines are the fits of (4.11) to the data points with
![]() $\unicode[STIX]{x1D6FC}=0.30\pm 0.06$
(a) and
$\unicode[STIX]{x1D6FC}=0.30\pm 0.06$
(a) and
![]() $\unicode[STIX]{x1D6FC}=0.20\pm 0.04$
(b). The horizontal dashed line shows the expected peak value
$\unicode[STIX]{x1D6FC}=0.20\pm 0.04$
(b). The horizontal dashed line shows the expected peak value
![]() $1/\sqrt{2\unicode[STIX]{x03C0}}$
for a normalized Gaussian distribution, and the horizontal dotted line shows the expected peak value
$1/\sqrt{2\unicode[STIX]{x03C0}}$
for a normalized Gaussian distribution, and the horizontal dotted line shows the expected peak value
![]() $1/\sqrt{2}$
for a normalized exponential distribution.
$1/\sqrt{2}$
for a normalized exponential distribution.
While the effect of background fluctuations at the cell centre is relatively small, it nevertheless provides a measurable mixing effect to smear out the distribution of thermal plumes. Mathematically, a pure exponential distribution has a normalized form,
![]() $P(\unicode[STIX]{x1D709})=(1/\sqrt{2})\exp (-\sqrt{2}|\unicode[STIX]{x1D709}|)$
, so that its peak value at
$P(\unicode[STIX]{x1D709})=(1/\sqrt{2})\exp (-\sqrt{2}|\unicode[STIX]{x1D709}|)$
, so that its peak value at
![]() $\unicode[STIX]{x1D709}=0$
is
$\unicode[STIX]{x1D709}=0$
is
![]() $P_{max}=1/\sqrt{2}\simeq 0.707$
. On the other hand, the peak value of a normalized Gaussian distribution is
$P_{max}=1/\sqrt{2}\simeq 0.707$
. On the other hand, the peak value of a normalized Gaussian distribution is
![]() $P_{max}=1/\sqrt{2\unicode[STIX]{x03C0}}\simeq 0.399$
. Figure 8 shows a magnified view of the measured
$P_{max}=1/\sqrt{2\unicode[STIX]{x03C0}}\simeq 0.399$
. Figure 8 shows a magnified view of the measured
![]() $P(\unicode[STIX]{x1D6FF}T)$
near the origin. It is seen that all the measured values of
$P(\unicode[STIX]{x1D6FF}T)$
near the origin. It is seen that all the measured values of
![]() $P_{max}$
for different values of
$P_{max}$
for different values of
![]() $Ra$
and
$Ra$
and
![]() $Pr$
are in between
$Pr$
are in between
![]() $1/\sqrt{2}$
(dotted lines) and
$1/\sqrt{2}$
(dotted lines) and
![]() $1/\sqrt{2\unicode[STIX]{x03C0}}$
(dashed lines), indicating the existence of a Gaussian component. In a physical system, this Gaussian component at the origin precludes the non-analytic sharp peak of the exponential distribution (Wei & Ahlers Reference Wei and Ahlers2016).
$1/\sqrt{2\unicode[STIX]{x03C0}}$
(dashed lines), indicating the existence of a Gaussian component. In a physical system, this Gaussian component at the origin precludes the non-analytic sharp peak of the exponential distribution (Wei & Ahlers Reference Wei and Ahlers2016).
Equation (4.11) can well describe the temperature PDFs obtained not only from the above experiments but also from previous experiments (Wu & Libchaber Reference Wu and Libchaber1992; Du & Tong Reference Du and Tong2001). Figure 9 shows the measured
![]() $P(\unicode[STIX]{x1D6FF}T)$
as a function of
$P(\unicode[STIX]{x1D6FF}T)$
as a function of
![]() $\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
for a low-temperature (5 K) helium gas (
$\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
for a low-temperature (5 K) helium gas (
![]() $Pr=0.7$
) over a range of
$Pr=0.7$
) over a range of
![]() $Ra$
. The measurements were conducted at the centre of a
$Ra$
. The measurements were conducted at the centre of a
![]() $\unicode[STIX]{x1D6E4}=0.5$
upright cylinder (Wu & Libchaber Reference Wu and Libchaber1992). The solid line shows a fit of (4.11) to the data points with
$\unicode[STIX]{x1D6E4}=0.5$
upright cylinder (Wu & Libchaber Reference Wu and Libchaber1992). The solid line shows a fit of (4.11) to the data points with
![]() $\unicode[STIX]{x1D6FC}=1.2\pm 0.2$
as a fitting parameter. Similar measurements at the centre of a
$\unicode[STIX]{x1D6FC}=1.2\pm 0.2$
as a fitting parameter. Similar measurements at the centre of a
![]() $\unicode[STIX]{x1D6E4}=6.7$
upright cylinder with
$\unicode[STIX]{x1D6E4}=6.7$
upright cylinder with
![]() $Pr=0.7$
(Wu & Libchaber Reference Wu and Libchaber1992) are also found to be well described by (4.11) with
$Pr=0.7$
(Wu & Libchaber Reference Wu and Libchaber1992) are also found to be well described by (4.11) with
![]() $\unicode[STIX]{x1D6FC}=1.5\pm 0.3$
(not shown here). These results further confirm that our model is quite general and can be used to describe temperature PDFs in a closed convection cell with different aspect ratios and filled with a working fluid with different values of
$\unicode[STIX]{x1D6FC}=1.5\pm 0.3$
(not shown here). These results further confirm that our model is quite general and can be used to describe temperature PDFs in a closed convection cell with different aspect ratios and filled with a working fluid with different values of
![]() $Ra$
and
$Ra$
and
![]() $Pr$
.
$Pr$
.
Finally, we consider a general case described in (4.9), in which
![]() $\unicode[STIX]{x1D6FF}T_{P}^{h}(t)$
is intermittent with its duty ratio being
$\unicode[STIX]{x1D6FF}T_{P}^{h}(t)$
is intermittent with its duty ratio being
![]() $\unicode[STIX]{x1D6FD}$
. The corresponding PDF
$\unicode[STIX]{x1D6FD}$
. The corresponding PDF
![]() $P(\unicode[STIX]{x1D6FF}T)$
is given as
$P(\unicode[STIX]{x1D6FF}T)$
is given as
 $$\begin{eqnarray}\displaystyle P(\unicode[STIX]{x1D6FF}T) & = & \displaystyle (1-\unicode[STIX]{x1D6FD})\int _{-\infty }^{\unicode[STIX]{x1D70E}_{c}}P_{B}(\unicode[STIX]{x1D6FF}T-\unicode[STIX]{x1D6FF}T_{P}^{c})P_{c}(\unicode[STIX]{x1D6FF}T_{P}^{c})\,\text{d}(\unicode[STIX]{x1D6FF}T_{P}^{c})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D6FD}\int _{-\infty }^{\unicode[STIX]{x1D70E}_{c}}\int _{-\unicode[STIX]{x1D70E}_{h}}^{+\infty }P_{B}(\unicode[STIX]{x1D6FF}T-\unicode[STIX]{x1D6FF}T_{P}^{h}-\unicode[STIX]{x1D6FF}T_{P}^{c})P_{h}(\unicode[STIX]{x1D6FF}T_{P}^{h})P_{c}(\unicode[STIX]{x1D6FF}T_{P}^{c})\,\text{d}(\unicode[STIX]{x1D6FF}T_{P}^{h})\,\text{d}(\unicode[STIX]{x1D6FF}T_{P}^{c})\nonumber\\ \displaystyle & = & \displaystyle \frac{1-\unicode[STIX]{x1D6FD}}{2\unicode[STIX]{x1D70E}_{c}}e^{[(\unicode[STIX]{x1D70E}_{B}/\unicode[STIX]{x1D70E}_{c})^{2}/2+(\unicode[STIX]{x1D6FF}T+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D70E}_{h})/\unicode[STIX]{x1D70E}_{c}-1]}\text{erfc}\left(\frac{\unicode[STIX]{x1D70E}_{B}^{2}+(\unicode[STIX]{x1D6FF}T+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D70E}_{h}-\unicode[STIX]{x1D70E}_{c})\unicode[STIX]{x1D70E}_{c}}{\sqrt{2}\unicode[STIX]{x1D70E}_{B}\unicode[STIX]{x1D70E}_{c}}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x1D6FD}}{2(\unicode[STIX]{x1D70E}_{h}+\unicode[STIX]{x1D70E}_{c})}e^{[(\unicode[STIX]{x1D70E}_{B}/\unicode[STIX]{x1D70E}_{h})^{2}/2-(\unicode[STIX]{x1D6FF}T-\unicode[STIX]{x1D70E}_{c})/\unicode[STIX]{x1D70E}_{h}-\unicode[STIX]{x1D6FD}]}\text{erfc}\left(\frac{\unicode[STIX]{x1D70E}_{B}^{2}-(\unicode[STIX]{x1D6FF}T+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D70E}_{h}-\unicode[STIX]{x1D70E}_{c})\unicode[STIX]{x1D70E}_{h}}{\sqrt{2}\unicode[STIX]{x1D70E}_{B}\unicode[STIX]{x1D70E}_{h}}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x1D6FD}}{2(\unicode[STIX]{x1D70E}_{h}+\unicode[STIX]{x1D70E}_{c})}e^{[(\unicode[STIX]{x1D70E}_{B}/\unicode[STIX]{x1D70E}_{c})^{2}/2+(\unicode[STIX]{x1D6FF}T+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D70E}_{h})/\unicode[STIX]{x1D70E}_{c}-1]}\text{erfc}\left(\frac{\unicode[STIX]{x1D70E}_{B}^{2}+(\unicode[STIX]{x1D6FF}T+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D70E}_{h}-\unicode[STIX]{x1D70E}_{c})\unicode[STIX]{x1D70E}_{c}}{\sqrt{2}\unicode[STIX]{x1D70E}_{B}\unicode[STIX]{x1D70E}_{c}}\right).\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P(\unicode[STIX]{x1D6FF}T) & = & \displaystyle (1-\unicode[STIX]{x1D6FD})\int _{-\infty }^{\unicode[STIX]{x1D70E}_{c}}P_{B}(\unicode[STIX]{x1D6FF}T-\unicode[STIX]{x1D6FF}T_{P}^{c})P_{c}(\unicode[STIX]{x1D6FF}T_{P}^{c})\,\text{d}(\unicode[STIX]{x1D6FF}T_{P}^{c})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D6FD}\int _{-\infty }^{\unicode[STIX]{x1D70E}_{c}}\int _{-\unicode[STIX]{x1D70E}_{h}}^{+\infty }P_{B}(\unicode[STIX]{x1D6FF}T-\unicode[STIX]{x1D6FF}T_{P}^{h}-\unicode[STIX]{x1D6FF}T_{P}^{c})P_{h}(\unicode[STIX]{x1D6FF}T_{P}^{h})P_{c}(\unicode[STIX]{x1D6FF}T_{P}^{c})\,\text{d}(\unicode[STIX]{x1D6FF}T_{P}^{h})\,\text{d}(\unicode[STIX]{x1D6FF}T_{P}^{c})\nonumber\\ \displaystyle & = & \displaystyle \frac{1-\unicode[STIX]{x1D6FD}}{2\unicode[STIX]{x1D70E}_{c}}e^{[(\unicode[STIX]{x1D70E}_{B}/\unicode[STIX]{x1D70E}_{c})^{2}/2+(\unicode[STIX]{x1D6FF}T+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D70E}_{h})/\unicode[STIX]{x1D70E}_{c}-1]}\text{erfc}\left(\frac{\unicode[STIX]{x1D70E}_{B}^{2}+(\unicode[STIX]{x1D6FF}T+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D70E}_{h}-\unicode[STIX]{x1D70E}_{c})\unicode[STIX]{x1D70E}_{c}}{\sqrt{2}\unicode[STIX]{x1D70E}_{B}\unicode[STIX]{x1D70E}_{c}}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x1D6FD}}{2(\unicode[STIX]{x1D70E}_{h}+\unicode[STIX]{x1D70E}_{c})}e^{[(\unicode[STIX]{x1D70E}_{B}/\unicode[STIX]{x1D70E}_{h})^{2}/2-(\unicode[STIX]{x1D6FF}T-\unicode[STIX]{x1D70E}_{c})/\unicode[STIX]{x1D70E}_{h}-\unicode[STIX]{x1D6FD}]}\text{erfc}\left(\frac{\unicode[STIX]{x1D70E}_{B}^{2}-(\unicode[STIX]{x1D6FF}T+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D70E}_{h}-\unicode[STIX]{x1D70E}_{c})\unicode[STIX]{x1D70E}_{h}}{\sqrt{2}\unicode[STIX]{x1D70E}_{B}\unicode[STIX]{x1D70E}_{h}}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x1D6FD}}{2(\unicode[STIX]{x1D70E}_{h}+\unicode[STIX]{x1D70E}_{c})}e^{[(\unicode[STIX]{x1D70E}_{B}/\unicode[STIX]{x1D70E}_{c})^{2}/2+(\unicode[STIX]{x1D6FF}T+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D70E}_{h})/\unicode[STIX]{x1D70E}_{c}-1]}\text{erfc}\left(\frac{\unicode[STIX]{x1D70E}_{B}^{2}+(\unicode[STIX]{x1D6FF}T+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D70E}_{h}-\unicode[STIX]{x1D70E}_{c})\unicode[STIX]{x1D70E}_{c}}{\sqrt{2}\unicode[STIX]{x1D70E}_{B}\unicode[STIX]{x1D70E}_{c}}\right).\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
In (4.12),
![]() $P(\unicode[STIX]{x1D6FF}T)$
has a r.m.s. value
$P(\unicode[STIX]{x1D6FF}T)$
has a r.m.s. value
![]() $\unicode[STIX]{x1D70E}_{T}=(\unicode[STIX]{x1D70E}_{B}^{2}+\unicode[STIX]{x1D70E}_{c}^{2}+(2\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FD}^{2})\unicode[STIX]{x1D70E}_{h}^{2})^{1/2}$
. With the normalized variable
$\unicode[STIX]{x1D70E}_{T}=(\unicode[STIX]{x1D70E}_{B}^{2}+\unicode[STIX]{x1D70E}_{c}^{2}+(2\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FD}^{2})\unicode[STIX]{x1D70E}_{h}^{2})^{1/2}$
. With the normalized variable
![]() $\unicode[STIX]{x1D709}=\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
, equation (4.12) can be rewritten as
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
, equation (4.12) can be rewritten as
 $$\begin{eqnarray}\displaystyle P(\unicode[STIX]{x1D709};\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FD}) & = & \displaystyle \frac{(1-\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D6FE}_{2}}{2}e^{[\unicode[STIX]{x1D6FC}_{2}^{2}/2+\unicode[STIX]{x1D6FE}_{2}\unicode[STIX]{x1D709}+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}_{2}/\unicode[STIX]{x1D6FC}_{1}-1]}\text{erfc}\left(\frac{\unicode[STIX]{x1D6FC}_{2}^{2}+\unicode[STIX]{x1D6FE}_{2}\unicode[STIX]{x1D709}+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}_{2}/\unicode[STIX]{x1D6FC}_{1}-1}{\sqrt{2}\unicode[STIX]{x1D6FC}_{2}}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FE}_{2}}{2(\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2})}e^{[\unicode[STIX]{x1D6FC}_{1}^{2}/2-\unicode[STIX]{x1D6FE}_{1}\unicode[STIX]{x1D709}+\unicode[STIX]{x1D6FC}_{1}/\unicode[STIX]{x1D6FC}_{2}-\unicode[STIX]{x1D6FD}]}\text{erfc}\left(\frac{\unicode[STIX]{x1D6FC}_{1}^{2}-\unicode[STIX]{x1D6FE}_{1}\unicode[STIX]{x1D709}+\unicode[STIX]{x1D6FC}_{1}/\unicode[STIX]{x1D6FC}_{2}-\unicode[STIX]{x1D6FD}}{\sqrt{2}\unicode[STIX]{x1D6FC}_{1}}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FE}_{2}}{2(\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2})}e^{[\unicode[STIX]{x1D6FC}_{2}^{2}/2+\unicode[STIX]{x1D6FE}_{2}\unicode[STIX]{x1D709}+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}_{2}/\unicode[STIX]{x1D6FC}_{1}-1]}\text{erfc}\left(\frac{\unicode[STIX]{x1D6FC}_{2}^{2}+\unicode[STIX]{x1D6FE}_{2}\unicode[STIX]{x1D709}+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}_{2}/\unicode[STIX]{x1D6FC}_{1}-1}{\sqrt{2}\unicode[STIX]{x1D6FC}_{2}}\right),\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P(\unicode[STIX]{x1D709};\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FD}) & = & \displaystyle \frac{(1-\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D6FE}_{2}}{2}e^{[\unicode[STIX]{x1D6FC}_{2}^{2}/2+\unicode[STIX]{x1D6FE}_{2}\unicode[STIX]{x1D709}+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}_{2}/\unicode[STIX]{x1D6FC}_{1}-1]}\text{erfc}\left(\frac{\unicode[STIX]{x1D6FC}_{2}^{2}+\unicode[STIX]{x1D6FE}_{2}\unicode[STIX]{x1D709}+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}_{2}/\unicode[STIX]{x1D6FC}_{1}-1}{\sqrt{2}\unicode[STIX]{x1D6FC}_{2}}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FE}_{2}}{2(\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2})}e^{[\unicode[STIX]{x1D6FC}_{1}^{2}/2-\unicode[STIX]{x1D6FE}_{1}\unicode[STIX]{x1D709}+\unicode[STIX]{x1D6FC}_{1}/\unicode[STIX]{x1D6FC}_{2}-\unicode[STIX]{x1D6FD}]}\text{erfc}\left(\frac{\unicode[STIX]{x1D6FC}_{1}^{2}-\unicode[STIX]{x1D6FE}_{1}\unicode[STIX]{x1D709}+\unicode[STIX]{x1D6FC}_{1}/\unicode[STIX]{x1D6FC}_{2}-\unicode[STIX]{x1D6FD}}{\sqrt{2}\unicode[STIX]{x1D6FC}_{1}}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FE}_{2}}{2(\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2})}e^{[\unicode[STIX]{x1D6FC}_{2}^{2}/2+\unicode[STIX]{x1D6FE}_{2}\unicode[STIX]{x1D709}+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}_{2}/\unicode[STIX]{x1D6FC}_{1}-1]}\text{erfc}\left(\frac{\unicode[STIX]{x1D6FC}_{2}^{2}+\unicode[STIX]{x1D6FE}_{2}\unicode[STIX]{x1D709}+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}_{2}/\unicode[STIX]{x1D6FC}_{1}-1}{\sqrt{2}\unicode[STIX]{x1D6FC}_{2}}\right),\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
with
![]() $\unicode[STIX]{x1D6FC}_{1}=\unicode[STIX]{x1D70E}_{B}/\unicode[STIX]{x1D70E}_{h}$
,
$\unicode[STIX]{x1D6FC}_{1}=\unicode[STIX]{x1D70E}_{B}/\unicode[STIX]{x1D70E}_{h}$
,
![]() $\unicode[STIX]{x1D6FC}_{2}=\unicode[STIX]{x1D70E}_{B}/\unicode[STIX]{x1D70E}_{c}$
,
$\unicode[STIX]{x1D6FC}_{2}=\unicode[STIX]{x1D70E}_{B}/\unicode[STIX]{x1D70E}_{c}$
,
![]() $\unicode[STIX]{x1D6FE}_{1}=(\unicode[STIX]{x1D6FC}_{1}^{2}+\unicode[STIX]{x1D6FC}_{1}^{2}/\unicode[STIX]{x1D6FC}_{2}^{2}+2\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FD}^{2})^{1/2}$
and
$\unicode[STIX]{x1D6FE}_{1}=(\unicode[STIX]{x1D6FC}_{1}^{2}+\unicode[STIX]{x1D6FC}_{1}^{2}/\unicode[STIX]{x1D6FC}_{2}^{2}+2\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FD}^{2})^{1/2}$
and
![]() $\unicode[STIX]{x1D6FE}_{2}=(\unicode[STIX]{x1D6FC}_{2}^{2}+(2\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FD}^{2})\unicode[STIX]{x1D6FC}_{2}^{2}/\unicode[STIX]{x1D6FC}_{1}^{2}+1)^{1/2}$
.
$\unicode[STIX]{x1D6FE}_{2}=(\unicode[STIX]{x1D6FC}_{2}^{2}+(2\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FD}^{2})\unicode[STIX]{x1D6FC}_{2}^{2}/\unicode[STIX]{x1D6FC}_{1}^{2}+1)^{1/2}$
.
Equation (4.13) is the most general form of
![]() $P(\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T})$
and includes the asymptotic cases given by (4.6), (4.8) and (4.11). In the case
$P(\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T})$
and includes the asymptotic cases given by (4.6), (4.8) and (4.11). In the case
![]() $\unicode[STIX]{x1D6FC}_{2}=+\infty$
and
$\unicode[STIX]{x1D6FC}_{2}=+\infty$
and
![]() $\unicode[STIX]{x1D6FD}=1$
, equation (4.13) reduces to (4.6). In the case
$\unicode[STIX]{x1D6FD}=1$
, equation (4.13) reduces to (4.6). In the case
![]() $\unicode[STIX]{x1D6FC}_{2}=+\infty$
, equation (4.13) reduces to (4.8). In the case
$\unicode[STIX]{x1D6FC}_{2}=+\infty$
, equation (4.13) reduces to (4.8). In the case
![]() $\unicode[STIX]{x1D6FC}_{1}=\unicode[STIX]{x1D6FC}_{2}=\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}_{1}=\unicode[STIX]{x1D6FC}_{2}=\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}=1$
, equation (4.13) reduces to (4.11). It is found that (4.13) can well describe the measured
$\unicode[STIX]{x1D6FD}=1$
, equation (4.13) reduces to (4.11). It is found that (4.13) can well describe the measured
![]() $P(\unicode[STIX]{x1D6FF}T)$
in the outer mixing zone of the
$P(\unicode[STIX]{x1D6FF}T)$
in the outer mixing zone of the
![]() $\unicode[STIX]{x1D6E4}=1$
upright cylinder, in which cold plumes are continuous (far away from the upper cooling plate and thus lose their intermittency) and warm plumes are highly intermittent (close to the lower heating plate). The solid line in figure 5(c) shows a fit of (4.13) to the data points in the outer mixing zone of the
$\unicode[STIX]{x1D6E4}=1$
upright cylinder, in which cold plumes are continuous (far away from the upper cooling plate and thus lose their intermittency) and warm plumes are highly intermittent (close to the lower heating plate). The solid line in figure 5(c) shows a fit of (4.13) to the data points in the outer mixing zone of the
![]() $\unicode[STIX]{x1D6E4}=1$
upright cylinder filled with water (
$\unicode[STIX]{x1D6E4}=1$
upright cylinder filled with water (
![]() $Pr=4.4$
) using
$Pr=4.4$
) using
![]() $\unicode[STIX]{x1D6FC}_{1}=0.33\pm 0.06$
,
$\unicode[STIX]{x1D6FC}_{1}=0.33\pm 0.06$
,
![]() $\unicode[STIX]{x1D6FC}_{2}=0.92\pm 0.15$
and
$\unicode[STIX]{x1D6FC}_{2}=0.92\pm 0.15$
and
![]() $\unicode[STIX]{x1D6FD}=0.18\pm 0.05$
. Similarly, the solid line in figure 6(c) shows a fit of (4.13) to the data points in the outer mixing zone of the
$\unicode[STIX]{x1D6FD}=0.18\pm 0.05$
. Similarly, the solid line in figure 6(c) shows a fit of (4.13) to the data points in the outer mixing zone of the
![]() $\unicode[STIX]{x1D6E4}=1$
upright cylinder filled with the 20 wt. % aqueous solution of glycerin (
$\unicode[STIX]{x1D6E4}=1$
upright cylinder filled with the 20 wt. % aqueous solution of glycerin (
![]() $Pr=7.6$
) using
$Pr=7.6$
) using
![]() $\unicode[STIX]{x1D6FC}_{1}=0.30\pm 0.05$
,
$\unicode[STIX]{x1D6FC}_{1}=0.30\pm 0.05$
,
![]() $\unicode[STIX]{x1D6FC}_{2}=1.05\pm 0.2$
and
$\unicode[STIX]{x1D6FC}_{2}=1.05\pm 0.2$
and
![]() $\unicode[STIX]{x1D6FD}=0.10\pm 0.03$
.
$\unicode[STIX]{x1D6FD}=0.10\pm 0.03$
.

Figure 9. Measured temperature PDF
![]() $P(\unicode[STIX]{x1D6FF}T)$
as a function of
$P(\unicode[STIX]{x1D6FF}T)$
as a function of
![]() $\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
at the centre of a
$\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
at the centre of a
![]() $\unicode[STIX]{x1D6E4}=0.5$
upright cylinder (red line). The measurements were conducted at a fixed value of
$\unicode[STIX]{x1D6E4}=0.5$
upright cylinder (red line). The measurements were conducted at a fixed value of
![]() $Pr=0.7$
(a low-temperature helium gas) in the
$Pr=0.7$
(a low-temperature helium gas) in the
![]() $Ra$
range from
$Ra$
range from
![]() $4\times 10^{9}$
to
$4\times 10^{9}$
to
![]() $6\times 10^{14}$
. The data are taken from figure 1(b) in Wu & Libchaber (Reference Wu and Libchaber1992). The solid line shows a fit of (4.11) to the data points with
$6\times 10^{14}$
. The data are taken from figure 1(b) in Wu & Libchaber (Reference Wu and Libchaber1992). The solid line shows a fit of (4.11) to the data points with
![]() $\unicode[STIX]{x1D6FC}=1.2\pm 0.2$
. The dashed and dotted lines show, respectively, a simple exponential distribution function and a Gaussian distribution function for comparison.
$\unicode[STIX]{x1D6FC}=1.2\pm 0.2$
. The dashed and dotted lines show, respectively, a simple exponential distribution function and a Gaussian distribution function for comparison.
Table 1. Obtained values of the parameters
![]() $\unicode[STIX]{x1D6FC}_{1}$
,
$\unicode[STIX]{x1D6FC}_{1}$
,
![]() $\unicode[STIX]{x1D6FC}_{2}$
and
$\unicode[STIX]{x1D6FC}_{2}$
and
![]() $\unicode[STIX]{x1D6FD}$
in (4.13) for three different flow regions in the two convection cells. The numbers with an error bar indicate the fitted values with a fitting uncertainty and those without an error bar are the expected values in theory.
$\unicode[STIX]{x1D6FD}$
in (4.13) for three different flow regions in the two convection cells. The numbers with an error bar indicate the fitted values with a fitting uncertainty and those without an error bar are the expected values in theory.

Table 1 gives a summary of the final fitting results obtained in the two convection cells. It is seen that the fitted values of
![]() $\unicode[STIX]{x1D6FC}_{1}=\unicode[STIX]{x1D70E}_{B}/\unicode[STIX]{x1D70E}_{h}$
in the thin disk cell increase monotonically, as the measuring position
$\unicode[STIX]{x1D6FC}_{1}=\unicode[STIX]{x1D70E}_{B}/\unicode[STIX]{x1D70E}_{h}$
in the thin disk cell increase monotonically, as the measuring position
![]() $z$
moves from the mixing zone to the cell centre (see figure 3). This result suggests that the contribution of warm plumes to the local temperature fluctuations decreases with increasing
$z$
moves from the mixing zone to the cell centre (see figure 3). This result suggests that the contribution of warm plumes to the local temperature fluctuations decreases with increasing
![]() $z$
, as expected. However, the fitted values of
$z$
, as expected. However, the fitted values of
![]() $\unicode[STIX]{x1D6FC}_{1}$
in the upright cylinder do not change much in the three different flow regions. The fitted values of
$\unicode[STIX]{x1D6FC}_{1}$
in the upright cylinder do not change much in the three different flow regions. The fitted values of
![]() $\unicode[STIX]{x1D6FC}_{1}$
in the turbulent bulk region and at the centre of the upright cylinder are much smaller than those obtained in the thin disk. These findings indicate that the effect of thermal plumes in the upright cylinder is much larger than that in the thin disk. This is because the quasi-two-dimensional LSC in the thin disk is more stable than the LSC in the upright cylinder, which gives rise to a more organized spatial distribution of thermal plumes, reducing their probabilities to go through the bulk region. Such an aspect-ratio-dependent
$\unicode[STIX]{x1D6FC}_{1}$
in the turbulent bulk region and at the centre of the upright cylinder are much smaller than those obtained in the thin disk. These findings indicate that the effect of thermal plumes in the upright cylinder is much larger than that in the thin disk. This is because the quasi-two-dimensional LSC in the thin disk is more stable than the LSC in the upright cylinder, which gives rise to a more organized spatial distribution of thermal plumes, reducing their probabilities to go through the bulk region. Such an aspect-ratio-dependent
![]() $P(\unicode[STIX]{x1D6FF}T)$
at the cell centre was also reported previously by Solomon & Gollub (Reference Solomon and Gollub1991).
$P(\unicode[STIX]{x1D6FF}T)$
at the cell centre was also reported previously by Solomon & Gollub (Reference Solomon and Gollub1991).
It is also seen that the fitted value of
![]() $\unicode[STIX]{x1D6FD}$
at
$\unicode[STIX]{x1D6FD}$
at
![]() $Pr=7.6$
is
$Pr=7.6$
is
![]() $\unicode[STIX]{x1D6FD}=0.1$
, which indicates that the warm plumes are active for only 10 % of the measuring time, so that they are highly intermittent in the mixing zone. The fact that the obtained value of
$\unicode[STIX]{x1D6FD}=0.1$
, which indicates that the warm plumes are active for only 10 % of the measuring time, so that they are highly intermittent in the mixing zone. The fact that the obtained value of
![]() $\unicode[STIX]{x1D6FD}$
in the thin disk is the same as that in the upright cylinder suggests that the fitted value of
$\unicode[STIX]{x1D6FD}$
in the thin disk is the same as that in the upright cylinder suggests that the fitted value of
![]() $\unicode[STIX]{x1D6FD}=0.1$
is not sensitive to the changes of cell geometry and
$\unicode[STIX]{x1D6FD}=0.1$
is not sensitive to the changes of cell geometry and
![]() $Ra$
. Table 1 also reveals that the fitted values of
$Ra$
. Table 1 also reveals that the fitted values of
![]() $\unicode[STIX]{x1D6FC}_{1}$
and
$\unicode[STIX]{x1D6FC}_{1}$
and
![]() $\unicode[STIX]{x1D6FD}$
in the upright cylinder decrease slightly with increasing
$\unicode[STIX]{x1D6FD}$
in the upright cylinder decrease slightly with increasing
![]() $Pr$
. This is because the thermal plumes in the mixing zone become more coherent with increasing
$Pr$
. This is because the thermal plumes in the mixing zone become more coherent with increasing
![]() $Pr$
. Here ‘coherent’ has two meanings. First, because the warm plumes at larger
$Pr$
. Here ‘coherent’ has two meanings. First, because the warm plumes at larger
![]() $Pr$
have a longer lifetime, they are relatively hotter than the warm plumes at lower
$Pr$
have a longer lifetime, they are relatively hotter than the warm plumes at lower
![]() $Pr$
(at the same position
$Pr$
(at the same position
![]() $z$
). As a result, the plume-induced temperature fluctuations have a larger amplitude, leading to a smaller value of
$z$
). As a result, the plume-induced temperature fluctuations have a larger amplitude, leading to a smaller value of
![]() $\unicode[STIX]{x1D6FC}_{1}$
at larger
$\unicode[STIX]{x1D6FC}_{1}$
at larger
![]() $Pr$
. Second, because the thermal plumes at larger
$Pr$
. Second, because the thermal plumes at larger
![]() $Pr$
are more localized in space (less thermal diffusion) and move faster (more buoyant), they have a shorter time passing through the temperature probe and thus a smaller value of
$Pr$
are more localized in space (less thermal diffusion) and move faster (more buoyant), they have a shorter time passing through the temperature probe and thus a smaller value of
![]() $\unicode[STIX]{x1D6FD}$
.
$\unicode[STIX]{x1D6FD}$
.
5 Summary
We have carried out a systematic study of spatial variations of the PDF
![]() $P(\unicode[STIX]{x1D6FF}T)$
for temperature fluctuations
$P(\unicode[STIX]{x1D6FF}T)$
for temperature fluctuations
![]() $\unicode[STIX]{x1D6FF}T$
in turbulent Rayleigh–Bénard convection. The local temperature measurements were made along the central axis of two closed convection cells: one is a thin circular disk cell and the other is an upright cylinder of aspect ratio unity. In the experiment, the Rayleigh number
$\unicode[STIX]{x1D6FF}T$
in turbulent Rayleigh–Bénard convection. The local temperature measurements were made along the central axis of two closed convection cells: one is a thin circular disk cell and the other is an upright cylinder of aspect ratio unity. In the experiment, the Rayleigh number
![]() $Ra$
was varied in the range between
$Ra$
was varied in the range between
![]() $9\times 10^{8}$
and
$9\times 10^{8}$
and
![]() $1.2\times 10^{10}$
with two fixed Prandtl numbers
$1.2\times 10^{10}$
with two fixed Prandtl numbers
![]() $Pr=4.4$
and
$Pr=4.4$
and
![]() $Pr=7.6$
. The measured
$Pr=7.6$
. The measured
![]() $P(\unicode[STIX]{x1D6FF}T)$
reveals distinct changes in four different flow regions in the lower half of the cell, namely, the thermal BL near the bottom conducting place, mixing zone outside the BL, lower turbulent bulk region and cell centre. Because of the symmetry of the cell shape, one expects that similar regions exist in the upper half of the cell. These distinct changes in the functional form of
$P(\unicode[STIX]{x1D6FF}T)$
reveals distinct changes in four different flow regions in the lower half of the cell, namely, the thermal BL near the bottom conducting place, mixing zone outside the BL, lower turbulent bulk region and cell centre. Because of the symmetry of the cell shape, one expects that similar regions exist in the upper half of the cell. These distinct changes in the functional form of
![]() $P(\unicode[STIX]{x1D6FF}T)$
remain unchanged for different values of
$P(\unicode[STIX]{x1D6FF}T)$
remain unchanged for different values of
![]() $Ra$
and
$Ra$
and
![]() $Pr$
, once the normalized temperature fluctuation
$Pr$
, once the normalized temperature fluctuation
![]() $\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
is used as the scaling variable. Here
$\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
is used as the scaling variable. Here
![]() $\unicode[STIX]{x1D70E}_{T}$
is the r.m.s. value of
$\unicode[STIX]{x1D70E}_{T}$
is the r.m.s. value of
![]() $\unicode[STIX]{x1D6FF}T$
.
$\unicode[STIX]{x1D6FF}T$
.
In the inner region of the BL, where the mean temperature gradient remains approximately constant, the measured
![]() $P(\unicode[STIX]{x1D6FF}T)$
has a Gaussian form in both convection cells. In the mixing zone outside the BL, the measured
$P(\unicode[STIX]{x1D6FF}T)$
has a Gaussian form in both convection cells. In the mixing zone outside the BL, the measured
![]() $P(\unicode[STIX]{x1D6FF}T)$
in the thin disk cell has a Gaussian shape in the main body but with an exponential tail for large positive values of
$P(\unicode[STIX]{x1D6FF}T)$
in the thin disk cell has a Gaussian shape in the main body but with an exponential tail for large positive values of
![]() $\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
. Such an exponential tail is caused by the periodic emission of warm plumes from the bottom BL, which also gives rise to an abrupt change in the local slope of the measured exponential tail of
$\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
. Such an exponential tail is caused by the periodic emission of warm plumes from the bottom BL, which also gives rise to an abrupt change in the local slope of the measured exponential tail of
![]() $P(\unicode[STIX]{x1D6FF}T)$
. A similar
$P(\unicode[STIX]{x1D6FF}T)$
. A similar
![]() $P(\unicode[STIX]{x1D6FF}T)$
is also found in the upright cylinder. In the outer region of the mixing zone, the measured
$P(\unicode[STIX]{x1D6FF}T)$
is also found in the upright cylinder. In the outer region of the mixing zone, the measured
![]() $P(\unicode[STIX]{x1D6FF}T)$
in the upright cylinder evolves to a new shape containing two asymmetric exponential tails for large absolute values of
$P(\unicode[STIX]{x1D6FF}T)$
in the upright cylinder evolves to a new shape containing two asymmetric exponential tails for large absolute values of
![]() $\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
. This new shape of
$\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
. This new shape of
![]() $P(\unicode[STIX]{x1D6FF}T)$
is not observed in the thin disk cell. In the lower turbulent bulk region of both convection cells, the abrupt change in the local slope of the measured exponential tail of
$P(\unicode[STIX]{x1D6FF}T)$
is not observed in the thin disk cell. In the lower turbulent bulk region of both convection cells, the abrupt change in the local slope of the measured exponential tail of
![]() $P(\unicode[STIX]{x1D6FF}T)$
disappears, suggesting that the effect of the periodic emission of thermal plumes is diminished. In this case, the measured
$P(\unicode[STIX]{x1D6FF}T)$
disappears, suggesting that the effect of the periodic emission of thermal plumes is diminished. In this case, the measured
![]() $P(\unicode[STIX]{x1D6FF}T)$
in the thin disk has a Gaussian shape in the main body and a smooth exponential tail for large positive values of
$P(\unicode[STIX]{x1D6FF}T)$
in the thin disk has a Gaussian shape in the main body and a smooth exponential tail for large positive values of
![]() $\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
. The measured
$\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
. The measured
![]() $P(\unicode[STIX]{x1D6FF}T)$
in the upright cylinder has a Gaussian cap and two asymmetric but smooth exponential tails for large absolute values of
$P(\unicode[STIX]{x1D6FF}T)$
in the upright cylinder has a Gaussian cap and two asymmetric but smooth exponential tails for large absolute values of
![]() $\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
. At the centre of both convection cells, because of the symmetry of the convection cell, the measured
$\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
. At the centre of both convection cells, because of the symmetry of the convection cell, the measured
![]() $P(\unicode[STIX]{x1D6FF}T)$
has a symmetric shape with a Gaussian cap for small absolute values of
$P(\unicode[STIX]{x1D6FF}T)$
has a symmetric shape with a Gaussian cap for small absolute values of
![]() $\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
and two long exponential tails for large absolute values of
$\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
and two long exponential tails for large absolute values of
![]() $\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
.
$\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D70E}_{T}$
.
Based on the above experimental findings, we proposed a theoretical model which assumes that temperature fluctuations in different regions of the convection cell are all made from two independent sources, namely, a homogeneous background which obeys Gaussian statistics and non-uniform thermal plumes with an exponential distribution. As a result, the temperature PDF
![]() $P(\unicode[STIX]{x1D6FF}T)$
is uniquely described by a convolution of the two modes of fluctuations with a relative strength, which varies among the four different flow regions. The predicted analytic expressions of
$P(\unicode[STIX]{x1D6FF}T)$
is uniquely described by a convolution of the two modes of fluctuations with a relative strength, which varies among the four different flow regions. The predicted analytic expressions of
![]() $P(\unicode[STIX]{x1D6FF}T)$
, as shown in (4.6), (4.8), (4.11) and (4.13), agree well with the experimental results obtained in the present experiment and also in previous experiments. Our model thus provides a unique theoretical framework with a common set of parameters to quantitatively describe the effect of turbulent background, thermal plumes and their spatio-temporal intermittency on the temperature PDF
$P(\unicode[STIX]{x1D6FF}T)$
, as shown in (4.6), (4.8), (4.11) and (4.13), agree well with the experimental results obtained in the present experiment and also in previous experiments. Our model thus provides a unique theoretical framework with a common set of parameters to quantitatively describe the effect of turbulent background, thermal plumes and their spatio-temporal intermittency on the temperature PDF
![]() $P(\unicode[STIX]{x1D6FF}T)$
. Such an understanding of turbulent fluctuations with decomposition of fluctuation modes based on the coherent structures in the flow is very useful not only for the study of temperature fluctuations in turbulent thermal convection but also for the understanding of turbulent mixing problems of practical interest.
$P(\unicode[STIX]{x1D6FF}T)$
. Such an understanding of turbulent fluctuations with decomposition of fluctuation modes based on the coherent structures in the flow is very useful not only for the study of temperature fluctuations in turbulent thermal convection but also for the understanding of turbulent mixing problems of practical interest.
Acknowledgements
This work was supported in part by the Hong Kong Research Grants Council under grant nos 16306418 (P.T.) and 16302718 (P.T.). X.H. acknowledges the support of the National Natural Science Foundation of China under grant no. 11772111 and Shenzhen Startup Funds no. CB11409001 and Shenzhen Overseas Talent Project no. CB24405026.