3.1. Type 1

Figure 3(a) shows vertical profiles of the streamwise components $\overline {u'c'}$ and $\partial \bar {c} / \partial x$ for $r=1$. These are located at $x/D=5$ on the centreline ($z/D=0$). There is a region, marked in grey, where both $\overline {u'c'} < 0$ and $\partial \bar {c} / \partial x < 0$. Figure 3(b) presents profiles of the mean streamwise velocity and concentration, $\bar {u}$ and $\bar {c}$, in the same location. It shows that the region with implied streamwise counter gradient transport is located just above the jet centreline, which is a similar observation to that of Schreivogel et al. (Reference Schreivogel, Abram, Fond, Straußwald, Beyrau and Pfitzner2016) and Bodart et al. (Reference Bodart, Coletti, Bermejo-Moreno and Eaton2013). Here, the likely cause of that phenomenon is not turbulent motion in the $x$-direction, but instead turbulent motion in the $y$-direction. In the grey area turbulent eddies of sufficiently small size that bring fluid from above ($v' < 0$) tend to bring weaker concentration ($c' < 0$) and higher streamwise velocity ($u' > 0$) since locally $\partial \bar {c} / \partial y < 0$ and $\partial \bar {u} / \partial y > 0$. Similarly, eddies that bring fluid from below ($v' > 0$) correlate $c' > 0$ with $u' < 0$. That causes $\overline {u'c'}$ to be negative, which implies negative diffusivity since $\partial \bar {c} / \partial x < 0$.

Figure 3. Vertical profiles at $x/D=5$ and $z/D=0$ from the $r=1$ (a,b) and $r=2$ (c,d) LES. (a,c) Streamwise turbulent scalar flux and mean concentration gradient. (b,d) Mean streamwise velocity and concentration. The grey area shows a region of implied negative diffusivity in the streamwise direction. $(a)$ $r=1$. $(b)$ $r=1$. $(c)$ $r=2$. $(d)$ $r=2$.

The same phenomenon manifests itself in higher velocity ratio jets, with slight differences. Figure 3(c) shows vertical profiles at $x/D=5$ and $z/D=0$ from the $r=2$ LES. As is clear in figure 3(d), the jet core is faster than the free stream flow, so the $y$ gradients of mean streamwise velocity and mean scalar gradient are roughly aligned in the top half of the jet, unlike when $r=1$. Through a similar argument as before, vertical turbulent transport produces positive $\overline {u'c'}$ in that region. Thus, the perceived negative diffusivity region should occur when $\partial \bar {c} / \partial x > 0$. The streamwise mean scalar gradient is controlled by two main, competing effects: the spreading of the jet (which causes the concentration in the core to decrease), and the fact that the jet as a whole is moving up, away from the wall. Positive mean concentration streamwise gradients do not happen immediately above the jet centreline, but instead are present further up in the windward shear layer, as seen in figure 3(c). So, the grey band is located higher up and is wider when compared to the one shown in figure 3(a) for $r=1$.

To support these explanations, consider figures 4(a) and 4(b). They show three differently averaged profiles of $\overline {u'c'}$ in the same location as shown in figure 3 for $r=1$ and $r=2$. For the solid line, the quantity $u'c'$ is averaged over all available time steps to produce the same quantity shown in figures 3(a) and 3(c). For the other two lines, the average is conditioned on the local value of the magnitude of the vertical velocity fluctuation, $|v'|$, at the centre of the grey band ($y/D=0.91$ and $y/D=2$, respectively). The average is taken either when $|v'|$ is high (top 20 % of samples) or low (bottom 20 % of samples). Away from the shaded region, the three lines converge as expected since the value of $v'$ is uncorrelated with $u'c'$ at long distances. However, in the grey band, the three lines are significantly different: $\overline {u'c'}$ has much higher magnitude when $|v'|$ is high, and much smaller magnitude when $|v'|$ is low. This shows that vertical transport indeed plays an important role in setting the value of $\overline {u'c'}$ in this region and that events of high $|v'|$ accentuate the perceived negative diffusivity in the streamwise direction.

Figure 4. Vertical profiles at $x/D=5$ and $z/D=0$ of $\overline {u'c'}$ from the LES. Different averages are performed: unconditional or conditioned on high/low values of $|v'|$ at the centre of the grey band. $(a)$ $r=1$. $(b)$ $r=2$.

To investigate the behaviour of $\overline {u'_i c'}$ in more detail, it is useful to examine its transport equation, shown in (3.1). This equation is exact, and can be derived by multiplying $u'_i$ to the (unaveraged) scalar transport equation and $c'$ to the (unaveraged) Navier–Stokes equation, adding the results, and performing a time average. Capital letters $U$ and $C$ stand for time averages exactly like overbars (thus, $\bar {c} = C$), but are used here for a leaner notation. Here $\delta _{ij}$ is the Kronecker delta and $\alpha$ is the molecular diffusivity of the scalar, so $\alpha = \nu / Sc$. Note that these equations are mostly analogous to the Reynolds stress transport equations. Term A is the advection due to the mean velocity. Term I is the production term and shows how mean velocity and scalar gradients can locally generate $\overline {u'_i c'}$. Term II is the viscous destruction term. Term III consists of different mechanisms of turbulent transport, and term IV is a source term due to the pressure-scalar gradient correlation. For more details and modelling ideas, consult Younis, Speziale & Clark (Reference Younis, Speziale and Clark2005). The equation is

(3.1)\begin{align} \frac{\partial \overline{u'_i c'}}{\partial t} + \overbrace{ \frac{ \partial \left( U_j \overline{u'_i c'}\right) }{\partial x_j}}^{A} &= \overbrace{-\overline{u'_j c'} \frac{\partial U_i}{\partial x_j} - \overline{u'_j u'_i} \frac{\partial C}{\partial x_j}}^{I} \overbrace{ - (\nu + \alpha)\overline{\frac{\partial c'}{\partial x_j} \frac{\partial u'_i}{\partial x_j}}}^{II}\nonumber\\ &\qquad \overbrace{-\frac{\partial}{\partial x_j} \left( \overline{u'_j u'_i c'} + \frac{\overline{p'c'}}{\rho} \delta_{ij} - \alpha \overline{u'_i \frac{\partial c'}{\partial x_j}} - \nu \overline{c' \frac{\partial u'_i}{\partial x_j}} \right)}^{III} \overbrace{+ \overline{\frac{p'}{\rho} \frac{\partial c'}{\partial x_i}}}^{IV}. \end{align}

As further evidence that vertical velocity and concentration gradients are responsible for the streamwise negative diffusivity shown in figure 3, we consider the production terms of (3.1) for $\overline {u'c'}$. In figure 5 vertical profiles of the six different components of term I are shown. Note that the GDH considers only the effects of the mean concentration gradient in the $x$-direction on $\overline {u'c'}$, which is reflected on the production term $-\overline {u'u'} ({\partial C}/{\partial x})$. However, in the regions where counter gradient transport is observed, the production term is dominated by the components containing the vertical gradients: $-\overline {v'c'} ({\partial U}/{\partial y})$ and $-\overline {u'v'} ({\partial C}/{\partial y})$. These terms are indeed negative in figure 5(a) and positive in figure 5(b), which explains the sign of $\overline {u'c'}$ in the grey regions.

Figure 5. Vertical profiles of different components of the $\overline {u'c'}$ production term (marked as I in (3.1)). The profiles are shown at $x/D=5$, $z/D=0$ and the grey band represents the area of negative diffusivity. Terms are non-dimensionalized by $U_c$ and $D$. $(a)$ $r=1$. $(b)$ $r=2$.

There is one important caveat in our discussion of type 1 counter gradient transport. In shear flows the resulting mean scalar concentration is not a strong function of the modelled $\overline {u'c'}$ since the mean advection typically dominates the scalar transport in the streamwise direction. This point is discussed in more detail in appendix A. So, a turbulence model that fails to capture this phenomenon might still produce acceptable mean scalar field results in jets in crossflow. We believe the present analysis is still relevant for two reasons. First, it builds physical understanding of the turbulent transport in 3-D jets in crossflow by showing a concrete instance of the failure of the GDH and explaining the underlying cause. Such understanding is necessary to design improved and robust mixing models, and could be useful to interpret turbulence results in other flows as well. Second, in different contexts the correct prediction of these type 1 transport regions might be more relevant. For example, cross-gradient transport could be more important in different 3-D turbulent flows; or the quantity of interest might not be the mean scalar field, and instead be more sensitive to the streamwise scalar flux.

3.2. Type 2

A second region where counter gradient transport is present is near the wall, right after injection. In this case, negative diffusivity is observed in the vertical component: both $\overline {v'c'}$ and $\partial \bar {c} / \partial y$ are positive there. Figures 6(a) and 6(b) show vertical profiles at $x/D=2$ and $x/D=5$ for both $r=1$ and $r=2$, with grey bands indicating counter gradient transport regions. In general, it seems that the simple GDH could be useful: the solid lines approximately track the negated dashed lines throughout most of the plot, so a moderately non-uniform diffusivity could model $\overline {v'c'}$. However, this pattern breaks down close to the wall in all cases, where $\overline {v'c'}$ either has the same sign as $\partial \bar {c} / \partial y$ or is much smaller in magnitude than expected.

Figure 6. Vertical profiles at the centreplane of the $y$-component of scalar gradient and turbulent scalar flux. The grey band indicates regions where both have the same sign; for $r=2$ and $x/D=5$, no consistent region of counter gradient transport is observed (thus, no grey band), but $\overline {v'c'}$ is very near zero close to the wall. $(a)$ $r=1$. $(b)$ $r=2$.

The first hypothesis to explain this instance of counter gradient transport is that it is similar in nature to the one described before, i.e. that gradients in directions orthogonal to $y$ cause a positive correlation between $v'$ and $c'$. However, this is not the case. Averages that are conditional on $u'$ or $w'$ are inconclusive, and the $\overline {v'c'}$ production term is dominated by mean gradients in the $y$-direction. So, the negative diffusivity observed in figure 6 is caused by a different physical mechanism. To help explain it, figure 7 shows a complete budget of $\overline {v'c'}$, with vertical profiles of all terms of (3.1).

Figure 7. Terms from (3.1) in the channel centreline, non-dimensionalized using $D$ and $U_c$. For $r=1$, the zoomed in version shows $0 < y/D < 0.25$. For $r=2$, it shows $0 < y/D < 0.3$. The grey band indicates counter gradient transport in the vertical direction. $(a)$ $r=1$, $x/D=2$. $(b)$ $r=1$, $x/D=5$. $(c)$ $r=2$, $x/D=2$. $(d)$ $r=2$, $x/D=5$.

As the plots show, the production term is consistently negative in the grey band, which means that local effects act as a sink and, therefore, favour a negative value of $\overline {v'c'}$. Since the resulting scalar flux is positive, other effects are overwhelming the production. In particular, close to injection ($x/D=2$), term III is the most positive term. This is the turbulent transport of $\overline {v'c'}$, which unlike the production is inherently non-local. The breakdown of term III (not shown) shows that the molecular terms are negligible throughout the domain, and close to the wall the pressure-scalar correlation is dominant. This suggests that non-local turbulent effects, chiefly through fluctuating pressure, are responsible for generating a positive correlation between $v'$ and $c'$ in this region. Physically, this could be explained by the large scale stirring mentioned by Bodart et al. (Reference Bodart, Coletti, Bermejo-Moreno and Eaton2013): turbulent eddies with much larger length scales than the length scales over which $\partial \bar {c} / \partial {y}$ varies act in those regions, meaning that they can induce turbulent fluctuations that cannot be explained by local information. Note, however, that Bodart et al. (Reference Bodart, Coletti, Bermejo-Moreno and Eaton2013) pointed out locations of type 1 counter gradient transport in their data but provided a physical reasoning that is more appropriate for type 2.

Another interesting observation is on the role of mean flow advection (term A) in the balance. Since A is on the left-hand side of (3.1), a positive value represents a net outflow and a negative value represents a net inflow. Even though term A is not as important as some other terms in the grey band, it seems to enter the balance as a net outflow at $x/D=2$ and as a net inflow at $x/D=5$ for both velocity ratios. Since this is mostly due to mean streamwise advection, it suggests that non-local effects generate a positive $\overline {v'c'}$ close to the wall right after injection, which then is advected downstream. In other words, those non-local effects are not as strong at $x/D=5$, but $\overline {v'c'}$ remains positive there partly because it is being advected from upstream (i.e. due to memory effects). This explanation is consistent with figure 6: the positive $\overline {v'c'}$ close to the wall is more intense and concentrated at $x/D=2$, and it is more diffuse at $x/D=5$.

3.3. Three-dimensional perspective

In the previous subsections we highlighted locations where a particular component of the turbulent scalar flux had the same sign as the equivalent component of the mean scalar gradient. We did so for two reasons. First, that is how many previous authors reported counter gradient transport in this flow. For example, Muppidi & Mahesh (Reference Muppidi and Mahesh2008), Bodart et al. (Reference Bodart, Coletti, Bermejo-Moreno and Eaton2013) and Schreivogel et al. (Reference Schreivogel, Abram, Fond, Straußwald, Beyrau and Pfitzner2016) noted regions where $\overline {u'c'}$ and $\partial \bar {c} / \partial x$ have the same sign, while Salewski et al. (Reference Salewski, Stankovic and Fuchs2008) and Milani & Eaton (Reference Milani and Eaton2018) highlighted regions where $\overline {v'c'}$ and $\partial \bar {c} / \partial y$ have the same sign; their results are consistent with the locations and mechanisms we explained as type 1 and type 2, respectively. Second, starting with a one-dimensional perspective permits an easier visualization of the turbulent scalar flux transport equation budgets as done in figures 5 and 7. However, despite providing useful insights, that methodology is dependent on the particular choice of axis; in fact, unless the mean scalar gradient and the negative turbulent scalar flux vectors are perfectly aligned, it is possible to construct a coordinate frame where one of the components will indicate apparent counter gradient transport. So, in this subsection we study the same locations by considering the angle between the vectors $-\overline {u_i'c'}$ and ${\partial \bar {c}}/{\partial x_i}$, given by $\theta$ in (3.2). This measure takes all of the 3-D information into account and is independent of the choice of axis. In places where the simple GDH of (1.2) is valid exactly, we should have $\theta = 0$; in places of ‘true’ counter gradient transport, $\theta > 90^{\circ }$. The angle $\theta$ is given by

(3.2)\begin{equation} \theta = \arccos{\left(\dfrac{-\overline{u_i'c'} \dfrac{\partial \bar{c}}{\partial x_i} }{\sqrt{\overline{u_i'c'} \ \overline{u_i'c'}} \sqrt{\dfrac{\partial \bar{c}}{\partial x_i} \dfrac{\partial \bar{c}}{\partial x_i}}}\right)}. \end{equation}

Figure 8(a,b) shows colour contours of the angle $\theta$ in the $r=1$ LES. Figures 8(c,d) and 8(e,f) contain the same planes showing the regions of type 1 and type 2, respectively, as described previously. In general, the angle $\theta$ is highest close to the wall, whose presence induces strong anisotropy into the turbulent mixing. Interestingly, there are key differences between type 1 and type 2 regions identified previously. On the windward shear layer, where cross-gradient effects give rise to type 1 transport, the overall misalignment indicated by $\theta$ is not too high, with angles between $20^{\circ }$ and $50^{\circ }$ being common. On the other hand, regions of type 2 transport shown in figure 8(e,f) coincide with severe misalignment of $-\overline {u_i'c'}$ and ${\partial \bar {c}}/{\partial x_i}$, and in such areas the angle $\theta$ is frequently higher than $90^{\circ }$. This shows that type 1 transport, caused mainly by local effects, actually translates to a consistent but small misalignment between the vectors when seen in three dimensions. The non-equilibrium, non-local causes of type 2 transport actually lead to a more than $90^{\circ }$ misalignment between the flux and gradient vectors in three dimensions, which can be seen as a ‘true’ counter gradient transport that is independent of the coordinate frame. Figure 9, which presents the same plots for the $r=2$ dataset, leads to similar conclusions.

Figure 8. Counter gradient transport in the $r=1$ case. (a,c,e) Centreplanes ($z=0$) and (b,d,f) axial planes at $x/D=2$. Lines indicate isocontours of $\bar {c}=0.2, 0.4, 0.6, 0.8$. (a,b) Contains colour contours of $\theta$ in degrees. (c,d) Shows, in red, places where $\overline {u'c'} ({\partial \bar {c}}/{\partial x}) > 0$ (with arrows highlighting type 1 transport). (e,f) Identifies regions where $\overline {v'c'} ({\partial \bar {c}}/{\partial y}) > 0$ (with arrows highlighting type 2 transport).

Figure 9. Counter gradient transport in the $r=2$ case. Same description as figure 8.

From a modelling perspective, regions where $\theta$ is significantly above zero cannot be well captured with the simple GDH of (1.2) irrespective of the diffusivity chosen. Moving to a tensor diffusivity $D_{ij}$, as shown in (1.3), can capture cross-gradient effects (since turbulent transport in the $x$-direction can be a function of the $y$ gradient) and would thus be expected to model well the turbulent mixing in regions of type 1. This is further supported by the fact that $\theta$ in those regions is less than $90^{\circ }$, so the matrix diffusivity $D_{ij}$ is only required to rotate the concentration gradient vector by an acute angle. Thus, a positive semi-definite matrix $D_{ij}$ can be used, guaranteeing numerical stability. In locations where type 2 transport is found, the non-local effects on $\overline {u_i'c'}$ preclude a purely local model, such as (1.3), from capturing all the relevant physics. Even if a diffusivity $D_{ij}$ where chosen such that $\overline {u_i'c'}$ is matched, that matrix would not be positive semi-definite since $\theta > 90^{\circ }$ in those areas. Therefore, the equation would be numerically unstable, akin to using a negative value of $\alpha _t$ in (1.2). For locations of type 2 counter gradient transport, only a non-local model, based potentially on solving separate transport equations for $\overline {u_i'c'}$, could hope to reproduce the appropriate physics.

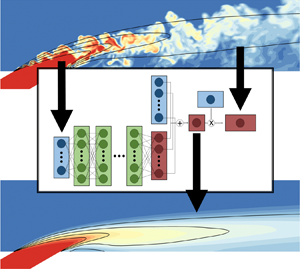
4.1. Tensor basis neural network for scalar flux modelling

Given the promise of the tensor basis neural network proposed by Ling et al. (Reference Ling, Kurzawski and Templeton2016a), we would like to use a similar method to model the vector $\overline {\boldsymbol {u}'c'}$. In summary, we aim to employ a neural network architecture that is designed to respect rotational invariance while predicting a tensorial output. However, the architecture described in Ling et al. (Reference Ling, Kurzawski and Templeton2016a) is designed to prescribe the Reynolds stress anisotropy tensor $\boldsymbol{\mathsf{B}}$, which is a symmetric and traceless second-order tensor. The approach must be modified for the turbulent scalar flux vector $\overline {\boldsymbol {u}'c'}$, which does not have those characteristics.

We start by assuming that the turbulent scalar flux is a general vector-valued function of the mean velocity and scalar gradients, $\boldsymbol {\nabla } \bar {\boldsymbol {u}}$ and $\boldsymbol {\nabla } \bar {c}$. The velocity gradient tensor is split into a symmetric and an anti-symmetric part, $\boldsymbol{\mathsf{S}}$ and $\boldsymbol{\mathsf{R}}$, respectively, such that $\boldsymbol {\nabla } \bar {\boldsymbol {u}} = \boldsymbol{\mathsf{S}} + \boldsymbol{\mathsf{R}}$. As is done in previous work that models turbulent scalar fluxes (Milani et al. Reference Milani, Ling, Saez-Mischlich, Bodart and Eaton2018), two additional dimensionless quantities are also used to regress $\overline {\boldsymbol {u}'c'}$: the Reynolds number based on wall distance, $Re_d = \sqrt {k}d/\nu$, and the eddy viscosity ratio, $\nu _t / \nu$, where $d$ is the distance to the nearest wall, $k$ is the turbulent kinetic energy and $\nu _t$ is the eddy viscosity from a baseline turbulence model. So, the functional dependence is

(4.1)\begin{equation} -\overline{\boldsymbol{u}'c'} = \boldsymbol{f}(\boldsymbol{\mathsf{S}}, \boldsymbol{\mathsf{R}}, \boldsymbol{\nabla} \bar{c}, \nu_t / \nu, Re_d). \end{equation}

Note that the model in (4.1) depends on a baseline turbulence model for the momentum equations, which provides field quantities such as $k$ and $\nu _t$. This is a design choice that makes the model more usable in practice, since one would not have access to high-fidelity simulation values for these quantities in a practical RANS simulation. A similar approach was taken by other authors who worked in scalar flux modelling with machine learning techniques (e.g. Sandberg et al. Reference Sandberg, Tan, Weatheritt, Ooi, Haghiri, Michelassi and Laskowski2018; Sotgiu et al. Reference Sotgiu, Weigand and Semmler2018). As is done in Ling et al. (Reference Ling, Kurzawski and Templeton2016a), (4.1) is cast as a summation of an appropriate tensor basis, where each basis element is a vector and is multiplied by a scalar factor $g^{(n)}$. This quantity, in turn, can be an arbitrary function of invariants $\lambda _j$, which are scalar quantities derived from the tensors $\boldsymbol{\mathsf{S}}$, $\boldsymbol{\mathsf{R}}$ and $\boldsymbol {\nabla } \bar {c}$ that are reference frame independent. Thus, $\overline {\boldsymbol {u}'c'}$ becomes

(4.2)\begin{equation} -\overline{\boldsymbol{u}'c'} = \sum_{n=1}^{6}g^{(n)}(\lambda_1, \lambda_2,\ldots, \lambda_{15}) \boldsymbol{t}^{(n)}. \end{equation}

When the function is written in this form, it is guaranteed to be unchanged under any coordinate frame rotation and reflection as explained in Ling et al. (Reference Ling, Kurzawski and Templeton2016a). The neural network's eventual goal will be to approximate the functions $g^{(n)}(\lambda _1, \lambda _2,\ldots , \lambda _{15})$.

For this problem, we cannot use the same basis and invariants used in Pope (Reference Pope1975) or Ling et al. (Reference Ling, Kurzawski and Templeton2016a), since the quantity of interest is a vector ($\overline {\boldsymbol {u}'c'}$) that depends upon one symmetric matrix ($\boldsymbol{\mathsf{S}}$), one anti-symmetric matrix ($\boldsymbol{\mathsf{R}}$) and one vector ($\boldsymbol {\nabla } \bar {c}$). Turning to the review of Zheng (Reference Zheng1994), one can find the appropriate vector basis, given as

(4.3)\begin{equation} \left. \begin{gathered} \boldsymbol{t}^{(1)} = \boldsymbol{\nabla} \bar{c}, \quad \boldsymbol{t}^{(2)} = \boldsymbol{\mathsf{S}} \boldsymbol{\nabla} \bar{c}, \quad \boldsymbol{t}^{(3)} = \boldsymbol{\mathsf{R}} \boldsymbol{\nabla} \bar{c},\\ \boldsymbol{t}^{(4)} = \boldsymbol{\mathsf{S}}^2 \boldsymbol{\nabla} \bar{c}, \quad \boldsymbol{t}^{(5)} = \boldsymbol{\mathsf{R}}^2 \boldsymbol{\nabla} \bar{c}, \quad \boldsymbol{t}^{(6)} = \left( \boldsymbol{\mathsf{S}}\boldsymbol{\mathsf{R}} + \boldsymbol{\mathsf{R}}\boldsymbol{\mathsf{S}} \right)\boldsymbol{\nabla} \bar{c}, \end{gathered} \right\} \end{equation}

and the appropriate invariants for the incompressible case, given as

(4.4)\begin{equation} \left. \begin{gathered} \lambda_1 = \textrm{tr}(\boldsymbol{\mathsf{S}}^2), \quad \lambda_2 = \textrm{tr}(\boldsymbol{\mathsf{S}}^3), \quad \lambda_3 = \textrm{tr}(\boldsymbol{\mathsf{R}}^2), \quad \lambda_4 = \textrm{tr}(\boldsymbol{\mathsf{S}}\boldsymbol{\mathsf{R}}^2), \quad \lambda_5 = \textrm{tr}(\boldsymbol{\mathsf{S}}^2\boldsymbol{\mathsf{R}}^2),\\ \lambda_6 = \textrm{tr}(\boldsymbol{\mathsf{S}}^2\boldsymbol{\mathsf{R}}^2\boldsymbol{\mathsf{S}}\boldsymbol{\mathsf{R}}) , \quad \lambda_7 = \boldsymbol{\nabla} \bar{c}^T\boldsymbol{\nabla} \bar{c}, \quad \lambda_8 = \boldsymbol{\nabla} \bar{c}^T\boldsymbol{\mathsf{S}}\boldsymbol{\nabla} \bar{c}, \quad \lambda_9 = \boldsymbol{\nabla} \bar{c}^T\boldsymbol{\mathsf{S}}^2\boldsymbol{\nabla} \bar{c},\\ \lambda_{10} = \boldsymbol{\nabla} \bar{c}^T\boldsymbol{\mathsf{R}}^2\boldsymbol{\nabla} \bar{c}, \quad \lambda_{11} = \boldsymbol{\nabla} \bar{c}^T\boldsymbol{\mathsf{S}}\boldsymbol{\mathsf{R}}\boldsymbol{\nabla} \bar{c}, \quad \lambda_{12} = \boldsymbol{\nabla} \bar{c}^T\boldsymbol{\mathsf{S}}^2\boldsymbol{\mathsf{R}}\boldsymbol{\nabla} \bar{c},\\ \lambda_{13} = \boldsymbol{\nabla} \bar{c}^T\boldsymbol{\mathsf{R}}\boldsymbol{\mathsf{S}}\boldsymbol{\mathsf{R}}^2\boldsymbol{\nabla} \bar{c}, \quad \lambda_{14} = Re_d, \quad \lambda_{15} = \nu_t / \nu. \end{gathered} \right\} \end{equation}

Note that the first 13 invariants are obtained from the tensor inputs, and the last two are purely the scalar quantities $Re_d$ and $\nu _t / \nu$ (which are automatically invariant to the choice of coordinate frame). In (4.3) and (4.4) products denote standard matrix-matrix or matrix-vector products, and $\textrm {tr}()$ denotes the trace of a matrix.

Under this formulation, given a vector basis and the invariants, the neural network directly prescribes the vector $\overline {\boldsymbol {u}'c'}$ whose divergence acts as a source term in the Reynolds averaged scalar transport equation. As discussed in Wu et al. (Reference Wu, Xiao, Sun and Wang2019), such an approach can lead to an ill conditioned equation, which is difficult to solve numerically. To mitigate this, they suggest that whenever possible data-driven closures should aim to predict diffusivity coefficients instead of source terms. With that in mind, we note that all basis elements shown in (4.3) consist of a matrix multiplying the mean concentration gradient. So, we can define a different basis $\boldsymbol{\mathsf{T}}^{(n)}$ where $\boldsymbol {t}^{(n)} = \boldsymbol{\mathsf{T}}^{(n)} \boldsymbol {\nabla } \bar {c}$. Thus, we rewrite (4.2) as

(4.5)\begin{equation} -\overline{\boldsymbol{u}'c'} = \overbrace{\left[ \sum_{n=1}^{6}g^{(n)}(\lambda_1, \lambda_2,\ldots, \lambda_{15}) \boldsymbol{\mathsf{T}}^{(n)} \right]}^{\boldsymbol{\mathsf{D}}} \boldsymbol{\nabla} \bar{c}, \end{equation}

with the matrix part of the basis given by

(4.6)\begin{equation} \left. \begin{gathered} \boldsymbol{\mathsf{T}}^{(1)} = \boldsymbol{\mathsf{I}}, \quad \boldsymbol{\mathsf{T}}^{(2)} = \boldsymbol{\mathsf{S}}, \quad \boldsymbol{\mathsf{T}}^{(3)} = \boldsymbol{\mathsf{R}},\\ \boldsymbol{\mathsf{T}}^{(4)} = \boldsymbol{\mathsf{S}}^2, \quad \boldsymbol{\mathsf{T}}^{(5)} = \boldsymbol{\mathsf{R}}^2, \quad \boldsymbol{\mathsf{T}}^{(6)} = \boldsymbol{\mathsf{S}}\boldsymbol{\mathsf{R}} + \boldsymbol{\mathsf{R}}\boldsymbol{\mathsf{S}}, \end{gathered} \right\} \end{equation}

where $\boldsymbol{\mathsf{I}}$ is the $3\times 3$ identity matrix.

In (4.5) the term in square brackets is naturally interpreted as a $3\times 3$ turbulent diffusivity matrix $\boldsymbol{\mathsf{D}}$. Thus, we recover an equation of the same form as (1.3) that is amenable to be learned via a neural network with embedded rotational invariance.

Before the full model architecture is discussed, there remains the issue of non-dimensionalization. To obtain relevant scales and values for the eddy viscosity $\nu _t$, a baseline turbulence model is run on the original mesh utilizing the frozen mean velocity field from the LES calculation. Any model that yields length and time scales and a value for the eddy viscosity could be employed with the current framework; in the present paper we use the realizable $k-\epsilon$ model of Shih, Zhu & Lumley (Reference Shih, Zhu and Lumley1995). So, given the mean LES velocity and pressure fields, the transport equations for $k$ and $\epsilon$ are solved, which also generates $\nu _t$ as a by-product. This approach to non-dimensionalization has been used by others such as Sandberg et al. (Reference Sandberg, Tan, Weatheritt, Ooi, Haghiri, Michelassi and Laskowski2018) and Milani et al. (Reference Milani, Ling and Eaton2020). Then, $\boldsymbol{\mathsf{S}}$, $\boldsymbol{\mathsf{R}}$ and $\boldsymbol {\nabla } \bar {c}$ in (4.4) and (4.6) are non-dimensionalized using local values of $k$ and $\epsilon$ before being fed as inputs to the network. To guarantee that the neural network maps from dimensionless inputs to a dimensionless output, a non-dimensional diffusivity tensor $\boldsymbol{\mathsf{D}}^*$ is explicitly introduced as $\boldsymbol{\mathsf{D}} = \nu _t \boldsymbol{\mathsf{D}}^*$.

The architecture proposed, henceforth referred to as tensor basis neural network for scalar flux modelling, or TBNN-s, is presented in figure 10. The network receives as inputs the mean flow invariants (listed in (4.4)) non-dimensionalized by $k$ and $\epsilon$ and processes them through a sequence of hidden layers. These are fully connected layers, which sequentially perform a linear transformation (matrix multiplication plus an offset) followed by a nonlinear activation function (the simple rectified linear unit, or ReLU, is employed). The last hidden layer does not use a ReLU function and transforms its inputs into a six-dimensional vector containing the values of $g^{(n)}$, the dimensionless basis coefficients. Note that the hidden layers are responsible for explicitly providing the functions $g^{(n)}(\lambda _1,\ldots , \lambda _{15})$ and contain all the tuneable parameters of the model, which are learned from training data. Then, the coefficients $g^{(n)}$ multiply elementwise their respective dimensionless basis tensor $\boldsymbol{\mathsf{T}}^{(n)}$ shown in (4.6) and the result is summed producing the dimensionless diffusivity matrix $\boldsymbol{\mathsf{D}}^*$. Finally, the diffusivity is made dimensional via multiplication by $\nu _t$ and its matrix-vector product with the mean scalar gradient produces $-\overline {\boldsymbol {u}'c'}$.

Figure 10. Schematic of TBNN-s architecture. Blue cells represent inputs to the network, green cells represent the hidden layers containing tuneable parameters and red cells denote different levels of outputs.

Note that this modelling framework is similar to that of Weatheritt et al. (Reference Weatheritt, Zhao, Sandberg, Mizukami and Tanimoto2020), who also expanded the turbulent scalar flux vector as a sum of tensor basis that maintains rotational invariance. Our model has two key differences. First, we use a deep neural network to approximate the functions $g^{(n)}(\lambda _i)$, while Weatheritt et al. (Reference Weatheritt, Zhao, Sandberg, Mizukami and Tanimoto2020) use gene expression programming, a different regression tool (see Weatheritt et al. (Reference Weatheritt, Sandberg, Ling, Saez and Bodart2017) for a discussion of their differences). Second, their basis also involves the Reynolds stress tensor. In theory this allows for more accurate representation of the scalar flux, as they confirm. However, in a typical RANS framework one does not have access to the true values of the Reynolds stress; as such, we preferred to develop models that are based solely on the mean velocity gradient. In future work it would be useful to compare their model to ours under the same conditions in order to analyse strengths and weaknesses of different data-driven turbulence modelling strategies.

4.2. Loss function and implementation

Neural networks are trained via gradient descent-like algorithms. A loss function $J$ is defined to capture how inadequate the present solution is compared to the known results from training data. Given multiple batches of training data, the loss function is calculated together with its gradient with respect to each trainable parameter. The gradient, a key component for training neural networks, is calculated using backpropagation, which is sequential application of the chain rule starting at the loss function $J$ and progressing back through the layers all the way to the first hidden layer. For backpropagation to work, every operation defined in the network must be differentiable which is the case for figure 10. Note that the loss function is defined based on the mismatch between the predicted value of the turbulent scalar flux, $\overline {\boldsymbol {u}'c'}_{PRED}$, and the turbulent scalar flux given in the training data, $\overline {\boldsymbol {u}'c'}_{LES}$. We experimented with a few different options, including the common sum of squared differences and sum of absolute differences:

(4.7)\begin{gather} J_{L1} = \frac{1}{N_{data}} \sum_{i=1}^{N_{data}} \|\overline{\boldsymbol{u}'c'}^{(i)}_{PRED} - \overline{\boldsymbol{u}'c'}^{(i)}_{LES} \|_1, \end{gather}

(4.8)\begin{gather} J_{L2} = \frac{1}{N_{data}} \sum_{i=1}^{N_{data}} \|\overline{\boldsymbol{u}'c'}^{(i)}_{PRED} - \overline{\boldsymbol{u}'c'}^{(i)}_{LES} \|^2_2. \end{gather}

Here $\| \ \|_1$ indicates vector 1-norm, $\| \ \|_2$ indicates vector 2-norm, $N_{data}$ is the number of data points over which the loss is computed and a superscript $i$ indicates the $i$-th training point. These definitions of the loss have the disadvantage that they depend on a particular non-dimensionalization and scaling to compare points from different datasets and different locations from the same dataset. Instead, if we desire a loss function whose gradient with respect to model parameters is independent of the scaling used, the mean of the natural logarithms of the vector norms is a possible choice:

(4.9)\begin{equation} J_{log} = \frac{1}{N_{data}} \sum_{i=1}^{N_{data}} \log \left( \frac{\|\overline{\boldsymbol{u}'c'}^{(i)}_{PRED} - \overline{\boldsymbol{u}'c'}^{(i)}_{LES} \|_2}{\| \overline{\boldsymbol{u}'c'}^{(i)}_{LES} \|_2} \right). \end{equation}

In (4.9) the factor that scales the loss at each point is the $\| \overline {\boldsymbol {u}'c'}^{(i)}_{LES} \|_2$ in the denominator. Because the logarithm of the ratio becomes a difference of logarithms, this term vanishes when the gradient of $J_{log}$ with respect to the neural network parameters is calculated. This scaling is chosen so that the loss attains readily interpretable values (for example, a loss around 0 indicates that the vectorial discrepancy between predicted and given scalar fluxes has roughly the same norm as the LES scalar flux itself).

We experimented with the three loss definitions shown in (4.7), (4.8) and (4.9). The results on the mean scalar field $\bar {c}$ were similar among the three, so a comparison will not be shown for brevity. For the results in the present paper, the function $J_{log}$ of (4.9) is employed. We also added an L2 regularization term to the loss, which penalizes high magnitude parameters in the model. This is commonly done to prevent overfitting. The loss is optimized with a widely used algorithm based on stochastic gradient descent, called adaptive moment estimation (Adam) from Kingma & Ba (Reference Kingma and Ba2014). Part of the reason for the current popularity of this method is that it has been shown to be reasonably robust to the choice of hyperparameters, especially the learning rate.

To choose the different hyperparameters for the TBNN-s, we used validation points that were not used during training. Milani et al. (Reference Milani, Gunady, Ching, Banko, Elkins and Eaton2019a) presents data on the geometry of figure 1 for a third value of velocity ratio, $r=1.5$. In the current paper the TBNN-s is trained exclusively on the $r=2$ dataset and the hyperparameters are chosen such that good values of the loss function are obtained on points taken from the $r=1.5$ case. We observed that the quality of the model generated is not a strong function of the hyperparameters considered within a reasonable range. Besides, the validation aims to find hyperparameters that minimize the loss in (4.9), when the true test for the model is how well it predicts the mean scalar field $\bar {c}$ after the Reynolds averaged equations are solved. Thus, not much emphasis should be placed on the specific choice of hyperparameters, and we picked a set that performed well on the validation set after manual tuning. In the current work we use a learning rate of $10^{-3}$ and other default parameters for Adam; we employ 10 hidden layers with 30 nodes each, roughly in line with the network size of Ling et al. (Reference Ling, Kurzawski and Templeton2016a); we use an L2 regularization strength of $10^{-2}$; we use an additional regularization method called dropout (Srivastava et al. Reference Srivastava, Hinton, Krizhevsky, Sutskever and Salakhutdinov2014) with a drop probability of $0.2$; and the batch size in which training data is fed into the Adam optimizer is 50. Training a neural network is not a deterministic exercise because results depend on a random initialization and on the stochastic nature of the optimization algorithm. To mitigate this, several training runs were executed with the same hyperparameters and the network that was saved and employed in this paper is the one that, at any point during each training procedure, produced the minimum loss in the validation set.

The network as shown in figure 10 is implemented in Python using the Tensorflow package (Abadi et al. Reference Abadi, Agarwal, Barham, Brevdo, Chen, Citro, Corrado, Davis, Dean and Devin2016) and the code can be found online in the following GitHub repository: https://github.com/pmmilani/tbnns. The TBNN-s discussed in following subsections was trained on 100k randomly sample points from the inclined jet in crossflow with $r=2$. Only points where the mean scalar gradient is significant ($\|\boldsymbol {\nabla } \bar {c}\|_2 / (\epsilon / k^{1.5}) > 10^{-3}$) are considered at training time.