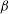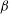1 Introduction
The aim of this paper is to analyse zonostrophic instability and transport in planar forced magnetohydrodynamic (MHD) systems. The term zonostrophic turbulence or zonation was introduced in Galperin et al. (Reference Galperin, Sukoriansky, Dikovskaya, Read, Yamazaki and Wordsworth2006), referring to the generation of strong zonal flows or jets in two-dimensional turbulent flow driven by an external body force. Srinivasan & Young (Reference Srinivasan and Young2012) discuss the interaction of mean flows and eddies in forced fluid dynamical systems, and term the formation of jets ‘zonostrophic instability’. Such jets are widely observed in the Earth’s atmosphere and oceans, in the laboratory and in simulations, and most famously in the banded structures of Jupiter; see, for example, Vallis & Maltrud (Reference Vallis and Maltrud1993), Heimpel, Aurnou & Wicht (Reference Heimpel, Aurnou and Wicht2005), Rotvig & Jones (Reference Rotvig and Jones2006), Read et al. (Reference Read, Yamazaki, Lewis, Williams, Wordsworth, Miki-Yamazaki, Sommeria, Didelle and Fincham2007), Scott & Polvani (Reference Scott and Polvani2007), Berloff, Kamenkovich & Pedlosky (Reference Berloff, Kamenkovich and Pedlosky2009) and Galperin et al. (Reference Galperin, Young, Sukoriansky, Dikovskaya, Read, Lancaster and Armstrong2014). With the identification of this robust fluid dynamical phenomenon goes an ever-expanding literature which we can only outline in what follows.
Instability of a forced fluid flow to large-scale zonal flows was first identified in the classic work of Meshalkin & Sinai (Reference Meshalkin and Sinai1961), who considered Kolmogorov flow
![]() $\boldsymbol{u}=(0,\sin x)$
in the plane, with viscous dissipation balanced by an imposed body force. Above a critical Reynolds number
$\boldsymbol{u}=(0,\sin x)$
in the plane, with viscous dissipation balanced by an imposed body force. Above a critical Reynolds number
![]() $\mathit{Re}_{c}=2^{-1/2}$
, the flow becomes unstable to
$\mathit{Re}_{c}=2^{-1/2}$
, the flow becomes unstable to
![]() $x$
-directed sinusoidal motion, whose scale diverges as
$x$
-directed sinusoidal motion, whose scale diverges as
![]() $\mathit{Re}_{c}$
is approached from above. Extensions incorporate the effect of nonlinearity in a multiple-scale framework, and a
$\mathit{Re}_{c}$
is approached from above. Extensions incorporate the effect of nonlinearity in a multiple-scale framework, and a
![]() ${\it\beta}$
-effect corresponding to an imposed background vorticity gradient; see Frisch, Legras & Villone (Reference Frisch, Legras and Villone1996) and Manfroi & Young (Reference Manfroi and Young1998, Reference Manfroi and Young2002). In the case of zonostrophic instability of a Kolmogorov flow, the principal effect of nonlinearity is that the zonal flows evolve to increasing spatial scales, a process that is then halted if the parameter
${\it\beta}$
-effect corresponding to an imposed background vorticity gradient; see Frisch, Legras & Villone (Reference Frisch, Legras and Villone1996) and Manfroi & Young (Reference Manfroi and Young1998, Reference Manfroi and Young2002). In the case of zonostrophic instability of a Kolmogorov flow, the principal effect of nonlinearity is that the zonal flows evolve to increasing spatial scales, a process that is then halted if the parameter
![]() ${\it\beta}$
is non-zero.
${\it\beta}$
is non-zero.
It became apparent that zonostrophic instability is widespread in rotating physical systems, and in laboratory and numerical simulations, and is broadly independent of the way in which the fluid is driven, for example an imposed body force in a simulation, or convection in a giant planet. With this, further theoretical understanding developed. One route is based on the conservation of potential vorticity (PV) in ideal flows, leading to an understanding of the development of zonal flows in terms of what is known as the PV Phillips effect (Dritschel & McIntyre Reference Dritschel and McIntyre2008). Flow evolution naturally leads to inhomogeneities as PV mixing tends to be suppressed in regions of high PV gradient. This negative viscosity or anti-friction effect, maintaining and sharpening gradients, is further studied in high-Reynolds-number simulations (Dritschel & Scott Reference Dritschel and Scott2011; Scott & Dritschel Reference Scott and Dritschel2012) and variational principles used to generate possible jet-like structures (Dunkerton & Scott Reference Dunkerton and Scott2008). In these studies there is the assumption that, although the true system is forced and dissipative, these are weak or lower-order effects, and it is the ideal evolution or at least the corresponding conservation laws that determines the evolution of zonal flows. We will not discuss these approaches further, noting that in MHD systems conservation of PV is lost, and so these tools are not available in any case.
A second theoretical approach is based on a more detailed modelling of the dynamics, mostly in the framework of the quasi-linear approximation. This incorporates a mean zonal flow (independent of
![]() $x$
, say) and forced waves (with zero average in
$x$
, say) and forced waves (with zero average in
![]() $x$
) whose evolution is linearised about this mean flow. The waves exert mean Reynolds stresses, and with these the mean flow can itself evolve, on a slower time scale than that of the waves. What is neglected is the interactions of waves giving smaller-scale waves, in other words the beginning of a turbulent cascade. In the context of zonostrophic instability, these ideas and applications are developed in the stochastic structural stability theory of Farrell & Iouannou (Reference Farrell and Iouannou2003, Reference Farrell and Iouannou2006, Reference Farrell and Iouannou2008), Bakas & Iouannou (Reference Bakas and Iouannou2011, Reference Bakas and Iouannou2013, Reference Bakas and Iouannou2014) and Constantinou, Farrell & Iouannou (Reference Constantinou, Farrell and Iouannou2014). Here, coupled equations for mean flow and waves, with additional stochastic forcing, are solved numerically in a variety of systems, showing robust jet formation, and the quasi-linear theory is validated against direct simulations. Further approximations that bring in higher-order corrections, so-called direct statistical simulation, are developed in Tobias, Dagon & Marston (Reference Tobias, Dagon and Marston2011).
$x$
) whose evolution is linearised about this mean flow. The waves exert mean Reynolds stresses, and with these the mean flow can itself evolve, on a slower time scale than that of the waves. What is neglected is the interactions of waves giving smaller-scale waves, in other words the beginning of a turbulent cascade. In the context of zonostrophic instability, these ideas and applications are developed in the stochastic structural stability theory of Farrell & Iouannou (Reference Farrell and Iouannou2003, Reference Farrell and Iouannou2006, Reference Farrell and Iouannou2008), Bakas & Iouannou (Reference Bakas and Iouannou2011, Reference Bakas and Iouannou2013, Reference Bakas and Iouannou2014) and Constantinou, Farrell & Iouannou (Reference Constantinou, Farrell and Iouannou2014). Here, coupled equations for mean flow and waves, with additional stochastic forcing, are solved numerically in a variety of systems, showing robust jet formation, and the quasi-linear theory is validated against direct simulations. Further approximations that bring in higher-order corrections, so-called direct statistical simulation, are developed in Tobias, Dagon & Marston (Reference Tobias, Dagon and Marston2011).
To obtain analytical results for zonostrophic instability, Srinivasan & Young (Reference Srinivasan and Young2012) write the problem for forced flows on a
![]() ${\it\beta}$
-plane in terms of correlation functions in the presence of a weak zonal flow. They then exploit translational symmetry to obtain an exact implicit equation for the instability growth rate, which can be solved numerically to give windows of
${\it\beta}$
-plane in terms of correlation functions in the presence of a weak zonal flow. They then exploit translational symmetry to obtain an exact implicit equation for the instability growth rate, which can be solved numerically to give windows of
![]() $y$
-wavenumbers
$y$
-wavenumbers
![]() $K$
that can be destabilised. Interestingly, they find that a destabilising effect linked to the parameter
$K$
that can be destabilised. Interestingly, they find that a destabilising effect linked to the parameter
![]() ${\it\beta}$
acts as a negative effective hyperviscosity for large-scale modes, in other words gives a contribution to the growth rate proportional to
${\it\beta}$
acts as a negative effective hyperviscosity for large-scale modes, in other words gives a contribution to the growth rate proportional to
![]() $K^{4}$
for wavenumber
$K^{4}$
for wavenumber
![]() $K\ll 1$
. This is when the system is forced isotropically, whereas for an anisotropic driving, there can be a negative effective viscosity effect, proportional to
$K\ll 1$
. This is when the system is forced isotropically, whereas for an anisotropic driving, there can be a negative effective viscosity effect, proportional to
![]() $K^{2}$
and independent of
$K^{2}$
and independent of
![]() ${\it\beta}$
(as per the original Kolmogorov flow above); see Bakas & Iouannou (Reference Bakas and Iouannou2013), Srinivasan & Young (Reference Srinivasan and Young2014), and references therein. We stress that these transport effects emerge from the averaged equations for mean zonal flows. As such, we are referring only to large-scale modes
${\it\beta}$
(as per the original Kolmogorov flow above); see Bakas & Iouannou (Reference Bakas and Iouannou2013), Srinivasan & Young (Reference Srinivasan and Young2014), and references therein. We stress that these transport effects emerge from the averaged equations for mean zonal flows. As such, we are referring only to large-scale modes
![]() $K\ll 1$
, and any
$K\ll 1$
, and any
![]() $K^{2}$
or
$K^{2}$
or
![]() $K^{4}$
dispersion relation for the growth rate as a function of
$K^{4}$
dispersion relation for the growth rate as a function of
![]() $K$
must be brought down by further terms as
$K$
must be brought down by further terms as
![]() $K$
increases (cf. Sukoriansky, Galperin & Chekhlov Reference Sukoriansky, Galperin and Chekhlov1999). It is worth noting that in these studies the forced small-scale disturbances are damped (by bottom friction or viscosity): they dissipate soon after being created and after depositing any Reynolds stress on the mean flow. In this sense, the set-up is diametrically opposite to the theories based on PV conservation in ideal flow. Extension of the quasi-linear theory to the case where the waves are forced but only weakly damped raises new challenges. In particular, in the equation for the small-scale waves, some quantities converge in the inviscid limit, and others diverge (for example enstrophy). This is studied by Bouchet & Morita (Reference Bouchet and Morita2010), Bouchet, Nardini & Tangarife (Reference Bouchet, Nardini and Tangarife2013, Reference Bouchet, Nardini and Tangarife2014) and Bedrossian & Masmoudi (Reference Bedrossian and Masmoudi2015) for
$K$
increases (cf. Sukoriansky, Galperin & Chekhlov Reference Sukoriansky, Galperin and Chekhlov1999). It is worth noting that in these studies the forced small-scale disturbances are damped (by bottom friction or viscosity): they dissipate soon after being created and after depositing any Reynolds stress on the mean flow. In this sense, the set-up is diametrically opposite to the theories based on PV conservation in ideal flow. Extension of the quasi-linear theory to the case where the waves are forced but only weakly damped raises new challenges. In particular, in the equation for the small-scale waves, some quantities converge in the inviscid limit, and others diverge (for example enstrophy). This is studied by Bouchet & Morita (Reference Bouchet and Morita2010), Bouchet, Nardini & Tangarife (Reference Bouchet, Nardini and Tangarife2013, Reference Bouchet, Nardini and Tangarife2014) and Bedrossian & Masmoudi (Reference Bedrossian and Masmoudi2015) for
![]() ${\it\beta}=0$
, and it is established that the quasi-linear model is valid in the limit of zero dissipation for the waves. The formation of zonal flows is further viewed as a problem in pattern formation in Newton, Kim & Liu (Reference Newton, Kim and Liu2013) and Parker & Krommes (Reference Parker and Krommes2013, Reference Parker and Krommes2014), and studied by means of a Ginzburg–Landau equation which incorporates further nonlinear terms.
${\it\beta}=0$
, and it is established that the quasi-linear model is valid in the limit of zero dissipation for the waves. The formation of zonal flows is further viewed as a problem in pattern formation in Newton, Kim & Liu (Reference Newton, Kim and Liu2013) and Parker & Krommes (Reference Parker and Krommes2013, Reference Parker and Krommes2014), and studied by means of a Ginzburg–Landau equation which incorporates further nonlinear terms.
Our principal focus is the MHD problem: how are processes of zonostrophic instability on a
![]() ${\it\beta}$
-plane modified in the presence of a magnetic field (taken to point in the zonal direction)? Although our focus is not on applications, we mention that in the Earth’s core as well as astrophysical bodies, magnetic fields interact with turbulence, rotation and shear. An example is the solar tachocline, where the interaction of magnetic field, shear and convection remains poorly understood (see, e.g., Hughes, Rosner & Weiss Reference Hughes, Rosner and Weiss2007), while dynamo action in the presence of zonal flows is studied in Aubert (Reference Aubert2005), Yadav et al. (Reference Yadav, Gastine, Christensen and Reiners2015), and references therein. There are few studies of the role of magnetic field in zonostrophic instability; however, Diamond et al. (Reference Diamond, Itoh, Itoh, Silvers, Hughes, Rosner and Weiss2007) argue that in turbulent regimes magnetic fields will have the effect of suppressing any inverse cascade of energy that would result in zonal flows, while Tobias, Hughes & Diamond (Reference Tobias, Hughes and Diamond2012) find computationally that even a weak magnetic field
${\it\beta}$
-plane modified in the presence of a magnetic field (taken to point in the zonal direction)? Although our focus is not on applications, we mention that in the Earth’s core as well as astrophysical bodies, magnetic fields interact with turbulence, rotation and shear. An example is the solar tachocline, where the interaction of magnetic field, shear and convection remains poorly understood (see, e.g., Hughes, Rosner & Weiss Reference Hughes, Rosner and Weiss2007), while dynamo action in the presence of zonal flows is studied in Aubert (Reference Aubert2005), Yadav et al. (Reference Yadav, Gastine, Christensen and Reiners2015), and references therein. There are few studies of the role of magnetic field in zonostrophic instability; however, Diamond et al. (Reference Diamond, Itoh, Itoh, Silvers, Hughes, Rosner and Weiss2007) argue that in turbulent regimes magnetic fields will have the effect of suppressing any inverse cascade of energy that would result in zonal flows, while Tobias, Hughes & Diamond (Reference Tobias, Hughes and Diamond2012) find computationally that even a weak magnetic field
![]() $B_{0}$
can suppress the instability with a threshold
$B_{0}$
can suppress the instability with a threshold
![]() $B_{0}^{2}\propto {\it\eta}$
, the magnetic diffusivity. A similar suppression is found in the presence of ambient shear
$B_{0}^{2}\propto {\it\eta}$
, the magnetic diffusivity. A similar suppression is found in the presence of ambient shear
![]() ${\it\Omega}_{0}$
by Srinivasan & Young (Reference Srinivasan and Young2014) and Hsu & Diamond (Reference Hsu and Diamond2015). Although there has been little work on zonal flow generation in the presence of magnetic fields, there have been many studies on the modification of transport processes and subsequent generation of magnetic fields, particularly by dynamo action in three dimensions (e.g. Zheligovsky Reference Zheligovksy2011), which we will not review here. Very relevant to us, however, are studies of the modification of transport effects in forced two-dimensional flows threaded by magnetic fields. Chechkin (Reference Chechkin1999) determines transport effects in terms of the correlation properties of random small-scale fields, and shows that the effective viscosity can change sign. In a series of papers, Leprovost & Kim (Reference Leprovost and Kim2008a
,Reference Leprovost and Kim
b
, Reference Leprovost and Kim2009) determine the effective magnetic diffusivity and viscosity in the limits of strong and weak magnetic field and imposed shear flow; also identified is an additional coupling term in the averaged Navier–Stokes equation related to the gradient of the zonal magnetic field. Keating & Diamond (Reference Keating and Diamond2008) determine transport effects for turbulent MHD flow on a
${\it\Omega}_{0}$
by Srinivasan & Young (Reference Srinivasan and Young2014) and Hsu & Diamond (Reference Hsu and Diamond2015). Although there has been little work on zonal flow generation in the presence of magnetic fields, there have been many studies on the modification of transport processes and subsequent generation of magnetic fields, particularly by dynamo action in three dimensions (e.g. Zheligovsky Reference Zheligovksy2011), which we will not review here. Very relevant to us, however, are studies of the modification of transport effects in forced two-dimensional flows threaded by magnetic fields. Chechkin (Reference Chechkin1999) determines transport effects in terms of the correlation properties of random small-scale fields, and shows that the effective viscosity can change sign. In a series of papers, Leprovost & Kim (Reference Leprovost and Kim2008a
,Reference Leprovost and Kim
b
, Reference Leprovost and Kim2009) determine the effective magnetic diffusivity and viscosity in the limits of strong and weak magnetic field and imposed shear flow; also identified is an additional coupling term in the averaged Navier–Stokes equation related to the gradient of the zonal magnetic field. Keating & Diamond (Reference Keating and Diamond2008) determine transport effects for turbulent MHD flow on a
![]() ${\it\beta}$
-plane using weak turbulence theory and find that the combination of these two effects can lead to an increase in the effective magnetic diffusivity.
${\it\beta}$
-plane using weak turbulence theory and find that the combination of these two effects can lead to an increase in the effective magnetic diffusivity.
Our goal is to present a study of transport and zonostrophic instability in MHD flow on a
![]() ${\it\beta}$
-plane, in which we go from the governing equations and forcing, through calculations of transport coefficients, to plots of instability thresholds and equilibrium profiles. We also incorporate ambient shear into the system we study, given by a parameter
${\it\beta}$
-plane, in which we go from the governing equations and forcing, through calculations of transport coefficients, to plots of instability thresholds and equilibrium profiles. We also incorporate ambient shear into the system we study, given by a parameter
![]() ${\it\Omega}_{0}$
. We work in the quasi-linear framework and additionally assume a scale separation between the waves and the zonal flow, to allow analytical progress. Although our study builds on earlier work, it is distinguished by, first, a framework that easily allows different forms of molecular diffusive/viscous terms, although we always use the Laplacian in our results (rather than molecular hyperdiffusion/hyperviscosity), and, second, in the range of physical effects considered, ultimately parameterised by
${\it\Omega}_{0}$
. We work in the quasi-linear framework and additionally assume a scale separation between the waves and the zonal flow, to allow analytical progress. Although our study builds on earlier work, it is distinguished by, first, a framework that easily allows different forms of molecular diffusive/viscous terms, although we always use the Laplacian in our results (rather than molecular hyperdiffusion/hyperviscosity), and, second, in the range of physical effects considered, ultimately parameterised by
![]() $B_{0}$
,
$B_{0}$
,
![]() ${\it\Omega}_{0}$
,
${\it\Omega}_{0}$
,
![]() ${\it\beta}$
and a diffusion/viscosity parameter
${\it\beta}$
and a diffusion/viscosity parameter
![]() ${\it\lambda}$
. With this go two caveats: we do not attempt to verify the results by means of full simulations in this paper, and we indeed recognise that quasi-linear theory may in many regimes be only a qualitative guide to the behaviour realised in the full nonlinear fluid system.
${\it\lambda}$
. With this go two caveats: we do not attempt to verify the results by means of full simulations in this paper, and we indeed recognise that quasi-linear theory may in many regimes be only a qualitative guide to the behaviour realised in the full nonlinear fluid system.
The paper is structured as follows. In § 2 we set out the governing equations and the quasi-linear system we will study. We take the driving of the flow, in the
![]() $(x,y)$
-plane, to be as basic as possible, a periodic excitation of a wave proportional to
$(x,y)$
-plane, to be as basic as possible, a periodic excitation of a wave proportional to
![]() $\text{e}^{\text{i}mx}$
with a random phase; note that this driving is anisotropic, which has implications for the transport effects that emerge. In § 3 we focus on the purely hydrodynamic problem, and determine the feedback on the mean flow from a wave, both numerically and analytically. We identify that zonostrophic instability can occur at large scales through a negative effective viscosity term that emerges in the equation for large-scale zonal flow. We also determine how the instability is suppressed by an ambient shear
$\text{e}^{\text{i}mx}$
with a random phase; note that this driving is anisotropic, which has implications for the transport effects that emerge. In § 3 we focus on the purely hydrodynamic problem, and determine the feedback on the mean flow from a wave, both numerically and analytically. We identify that zonostrophic instability can occur at large scales through a negative effective viscosity term that emerges in the equation for large-scale zonal flow. We also determine how the instability is suppressed by an ambient shear
![]() ${\it\Omega}_{0}$
and solve for equilibrium profiles, in which a steady large-scale flow exhibiting a vorticity step is maintained as a result of the varying effective viscosity. We then incorporate a passive scalar field in § 4 and determine the corresponding modifications to passive scalar diffusion and profiles. In these sections we make contact with related studies by Srinivasan & Young (Reference Srinivasan and Young2012, Reference Srinivasan and Young2014) and Hsu & Diamond (Reference Hsu and Diamond2015) with reference to negative effective viscosity effects, ambient shear and passive scalar evolution, as detailed in the text. Section 5 is devoted to the MHD problem, introducing the Lorentz force to the framework developed in earlier sections. The problem becomes much more complicated, but with a mixture of analytical development and numerical evaluation, we produce thresholds for instabilities in the presence of magnetic fields, shear and
${\it\Omega}_{0}$
and solve for equilibrium profiles, in which a steady large-scale flow exhibiting a vorticity step is maintained as a result of the varying effective viscosity. We then incorporate a passive scalar field in § 4 and determine the corresponding modifications to passive scalar diffusion and profiles. In these sections we make contact with related studies by Srinivasan & Young (Reference Srinivasan and Young2012, Reference Srinivasan and Young2014) and Hsu & Diamond (Reference Hsu and Diamond2015) with reference to negative effective viscosity effects, ambient shear and passive scalar evolution, as detailed in the text. Section 5 is devoted to the MHD problem, introducing the Lorentz force to the framework developed in earlier sections. The problem becomes much more complicated, but with a mixture of analytical development and numerical evaluation, we produce thresholds for instabilities in the presence of magnetic fields, shear and
![]() ${\it\beta}$
-effect. Finally, § 6 offers conclusions and future directions.
${\it\beta}$
-effect. Finally, § 6 offers conclusions and future directions.
2 Governing equations
Our starting point is two-dimensional MHD flow on a
![]() ${\it\beta}$
-plane, with governing equations
${\it\beta}$
-plane, with governing equations
Here,
![]() ${\it\psi}$
is the stream function and
${\it\psi}$
is the stream function and
![]() $a$
is the vector potential, with flow
$a$
is the vector potential, with flow
![]() $\boldsymbol{u}=(\partial _{y}{\it\psi},-\partial _{x}{\it\psi})$
and magnetic field
$\boldsymbol{u}=(\partial _{y}{\it\psi},-\partial _{x}{\it\psi})$
and magnetic field
![]() $\boldsymbol{b}=(\partial _{y}a,-\partial _{x}a)$
(measured in units of velocity). We have also included a passive scalar
$\boldsymbol{b}=(\partial _{y}a,-\partial _{x}a)$
(measured in units of velocity). We have also included a passive scalar
![]() ${\it\sigma}$
, which obeys the same equation as the vector potential but with no Lorentz feedback term. The vorticity and current are given by
${\it\sigma}$
, which obeys the same equation as the vector potential but with no Lorentz feedback term. The vorticity and current are given by
All fields are functions of
![]() $(x,y,t)$
, and
$(x,y,t)$
, and
![]() $\text{J}$
denotes the usual Jacobian with respect to the
$\text{J}$
denotes the usual Jacobian with respect to the
![]() $(x,y)$
coordinates. In (2.1) the flow is driven by the source term
$(x,y)$
coordinates. In (2.1) the flow is driven by the source term
![]() $s$
, the curl of a body force, which generates vorticity in the fluid, and which we prescribe below.
$s$
, the curl of a body force, which generates vorticity in the fluid, and which we prescribe below.
2.1 Non-dimensionalisation
To identify the parameters involved, it is helpful to write the governing equations in a non-dimensional form. The external input to the system is the vorticity source term
![]() $s(x,y,t)$
, and we take it to have magnitude
$s(x,y,t)$
, and we take it to have magnitude
![]() $\mathscr{S}$
and act on a spatial scale
$\mathscr{S}$
and act on a spatial scale
![]() $\mathscr{L}$
. We choose to use the length scale
$\mathscr{L}$
. We choose to use the length scale
![]() $\mathscr{L}$
and the time scale
$\mathscr{L}$
and the time scale
![]() $\mathscr{T}\equiv \mathscr{S}^{-1/2}$
to non-dimensionalise the problem, rescaling quantities such as
$\mathscr{T}\equiv \mathscr{S}^{-1/2}$
to non-dimensionalise the problem, rescaling quantities such as
This recovers (2.1)–(2.4) in a dimensionless form, adorned with daggers. The system is then characterised by the dimensionless parameters, the Grashof number
![]() $\mathit{Gr}$
and the source Rhines number
$\mathit{Gr}$
and the source Rhines number
![]() $\mathit{Rh}_{s}$
, given by
$\mathit{Rh}_{s}$
, given by
as well as Prandtl and magnetic Prandtl numbers giving the ratios of the appropriate diffusivities, and the functional form of the source term
![]() $s$
. It should be noted that
$s$
. It should be noted that
![]() $\mathit{Rh}_{s}$
is here based on the source strength rather than on the actual flow velocities realised, whereas the usual Rhines number
$\mathit{Rh}_{s}$
is here based on the source strength rather than on the actual flow velocities realised, whereas the usual Rhines number
![]() $\mathit{Rh}=\mathscr{U}/{\it\beta}\mathscr{L}^{2}$
, like the Reynolds number
$\mathit{Rh}=\mathscr{U}/{\it\beta}\mathscr{L}^{2}$
, like the Reynolds number
![]() $\mathit{Re}=\mathscr{L}\mathscr{U}/{\it\nu}$
, would be a diagnostic depending on the flow velocities
$\mathit{Re}=\mathscr{L}\mathscr{U}/{\it\nu}$
, would be a diagnostic depending on the flow velocities
![]() $\mathscr{U}$
that emerge in the forced system (Rhines Reference Rhines1975).
$\mathscr{U}$
that emerge in the forced system (Rhines Reference Rhines1975).
As a key simplification in this study we will take all the diffusivities to be equal,
so the Prandtl numbers are unity, and we use the neutral quantity
![]() ${\it\lambda}^{\dagger }$
to denote any diffusivity or viscosity in what follows. This is both to make analytical progress and to reduce the number of parameters involved, making our study more manageable. For ease of notation it is also convenient to use the dimensionless parameters
${\it\lambda}^{\dagger }$
to denote any diffusivity or viscosity in what follows. This is both to make analytical progress and to reduce the number of parameters involved, making our study more manageable. For ease of notation it is also convenient to use the dimensionless parameters
![]() $\{{\it\lambda}^{\dagger },{\it\beta}^{\dagger }\}$
in what follows rather than
$\{{\it\lambda}^{\dagger },{\it\beta}^{\dagger }\}$
in what follows rather than
![]() $\{\mathit{Gr},\mathit{Rh}_{s}\}$
. From now on we will also drop the daggers on non-dimensional quantities, and so the key parameters at the outset are simply
$\{\mathit{Gr},\mathit{Rh}_{s}\}$
. From now on we will also drop the daggers on non-dimensional quantities, and so the key parameters at the outset are simply
![]() $\{{\it\lambda},{\it\beta}\}$
, with the source
$\{{\it\lambda},{\it\beta}\}$
, with the source
![]() $s$
taken of length scale and magnitude of order unity.
$s$
taken of length scale and magnitude of order unity.
2.2 Quasi-linear approximation
Table 1. Mean and fluctuating fields (the second of each pair has had the pure advection term
![]() $\text{e}^{-\text{i}mU(y)t}$
removed).
$\text{e}^{-\text{i}mU(y)t}$
removed).

We adopt the quasi-linear approximation in which we take a mean or background flow and magnetic field independent of
![]() $x$
, namely
$x$
, namely
and assume that these are quasi-steady, varying on a longer time scale than that of the fluctuating fields, namely those fields with a non-trivial
![]() $x$
-dependence. We need then to define the source term
$x$
-dependence. We need then to define the source term
![]() $s$
that creates disturbances, evolving according to linear dynamics, linearised about the background profile (2.8). We take first the specific case of a delta-function (in time) source of vorticity that is a single Fourier mode in
$s$
that creates disturbances, evolving according to linear dynamics, linearised about the background profile (2.8). We take first the specific case of a delta-function (in time) source of vorticity that is a single Fourier mode in
![]() $x$
,
$x$
,
In the quasi-linear approximation we break fields into mean and fluctuating components, as summarised in table 1,
and retain only the leading harmonics shown. We refer to an evolving
![]() $\text{e}^{\text{i}mx}$
disturbance as a wave (even in regimes where it may be heavily damped), and this obeys linear equations
$\text{e}^{\text{i}mx}$
disturbance as a wave (even in regimes where it may be heavily damped), and this obeys linear equations
with initial conditions from (2.9),
A prime here denotes the
![]() $y$
-derivative of any mean field, these being related as shown in table 1.
$y$
-derivative of any mean field, these being related as shown in table 1.
The feedback on the mean fields in (2.10) from the waves via the quadratic terms in (2.1)–(2.3) is retained, and this can be written in terms of fluxes
from Reynolds and Lorentz stresses in (2.16), and from advection of vector potential and scalar fluctuations in (2.17). Over the lifetime of a wave, the feedback on the mean flow from any one of these fluxes is given by the integral
Here and elsewhere we find it convenient to use
![]() $\mathit{Z}$
as a place-holder: it can be
$\mathit{Z}$
as a place-holder: it can be
![]() $R$
,
$R$
,
![]() $L$
,
$L$
,
![]() $M$
or
$M$
or
![]() $P$
as in (2.16), (2.17), or involve further symbols later on.
$P$
as in (2.16), (2.17), or involve further symbols later on.
We have (2.11)–(2.15) for a single wave launched at
![]() $t=0$
and the feedback (2.16)–(2.18) on the mean fields as the wave evolves and dissipates. As this effect must be weak in any quasi-linear set-up, we now incorporate a stream of such waves, replacing (2.9) by the renewing source
$t=0$
and the feedback (2.16)–(2.18) on the mean fields as the wave evolves and dissipates. As this effect must be weak in any quasi-linear set-up, we now incorporate a stream of such waves, replacing (2.9) by the renewing source
in which at each unit of time vorticity is introduced into the flow with random independent phases
![]() ${\it\mu}_{j}$
uniformly distributed over
${\it\mu}_{j}$
uniformly distributed over
![]() $[-{\rm\pi},{\rm\pi}]$
. Given the random phases, in a time average (or ensemble average) all waves contribute independently to the quadratic fluxes. The equations for the mean fields then become
$[-{\rm\pi},{\rm\pi}]$
. Given the random phases, in a time average (or ensemble average) all waves contribute independently to the quadratic fluxes. The equations for the mean fields then become
where it is convenient to combine Reynolds and Lorentz terms via
It should be noted that the term
![]() $\mathscr{F}_{\mathit{K}}$
would also appear in a mean momentum equation, as per (3.18) below, but we usually prefer to remain within a vorticity–stream-function formulation.
$\mathscr{F}_{\mathit{K}}$
would also appear in a mean momentum equation, as per (3.18) below, but we usually prefer to remain within a vorticity–stream-function formulation.
2.3 Summary and comments
The quasi-linear system that we will consider is well established in the literature and consists of solving (2.11)–(2.15) for general mean profiles
![]() $U$
,
$U$
,
![]() $B$
and
$B$
and
![]() ${\it\Sigma}$
, and then determining the feedback on each mean field through the fluxes (2.16)–(2.18) that feed into (2.20)–(2.22). Several comments are in order.
${\it\Sigma}$
, and then determining the feedback on each mean field through the fluxes (2.16)–(2.18) that feed into (2.20)–(2.22). Several comments are in order.
(i) Given the renewing source (2.19), (2.20)–(2.21) for the mean fields are only valid on time scales
![]() $t\gg 1$
, that is over many waves launched into the flow. Furthermore, the quasi-linear approximation (as we use it) keeps the mean fields
$t\gg 1$
, that is over many waves launched into the flow. Furthermore, the quasi-linear approximation (as we use it) keeps the mean fields
![]() $U$
and
$U$
and
![]() $B$
steady while we solve (2.11)–(2.15) and compute the integrated fluxes in (2.18). There is thus a key consistency condition, that the time scale of evolution of the mean fields in (2.20)–(2.22) be greater than that over which the waves contribute to the integrated fluxes (2.18), as stressed by Bouchet & Morita (Reference Bouchet and Morita2010). This consistency condition needs to be assessed as any quasi-linear model is developed.
$B$
steady while we solve (2.11)–(2.15) and compute the integrated fluxes in (2.18). There is thus a key consistency condition, that the time scale of evolution of the mean fields in (2.20)–(2.22) be greater than that over which the waves contribute to the integrated fluxes (2.18), as stressed by Bouchet & Morita (Reference Bouchet and Morita2010). This consistency condition needs to be assessed as any quasi-linear model is developed.
(ii) One of the features of this study is keeping the source term (2.19) as tractable as possible without too much loss of generality. Regarding this, we note that we could have introduced a more general time dependence, for example involving a stationary random process with a given correlation function (decaying on a time scale shorter than that of the evolution of the mean fields), for example delta-correlated. However, doing so would increase complexity for us without adding greatly to generality. In fact, we can note that the problem as formulated in (2.11)–(2.15) gives the Green’s function for waves, and the effect of a more general time dependence of the source
![]() $s$
could thus be obtained by integration.
$s$
could thus be obtained by integration.
(iii) Likewise, we have considered a single source mode with wavenumber
![]() $m$
in (2.19); we treat
$m$
in (2.19); we treat
![]() $m$
as a parameter (though strictly it could be scaled to
$m$
as a parameter (though strictly it could be scaled to
![]() $m=1$
in our non-dimensionalisation). More generally, we could consider modes of the form
$m=1$
in our non-dimensionalisation). More generally, we could consider modes of the form
![]() $\text{e}^{\text{i}mx+\text{i}ny}$
and arbitrary sums of such modes, for example forming an isotropic or ring forcing as used in many other studies. However, because of shearing in the gradients
$\text{e}^{\text{i}mx+\text{i}ny}$
and arbitrary sums of such modes, for example forming an isotropic or ring forcing as used in many other studies. However, because of shearing in the gradients
![]() $U^{\prime }$
of the mean flow, a more general mode
$U^{\prime }$
of the mean flow, a more general mode
![]() $\text{e}^{\text{i}mx+\text{i}ny}$
simply corresponds to a shift in time of the mode
$\text{e}^{\text{i}mx+\text{i}ny}$
simply corresponds to a shift in time of the mode
![]() $\text{e}^{\text{i}mx}$
, and so our analysis could be extended, creating additional complexity in integrating over angles but without any fundamental changes. We should remark though that our forcing is anisotropic, in contrast to some other studies, and this is known to enhance instabilities leading to zonal flows, by selecting a preferred direction in the system, as discussed in Srinivasan & Young (Reference Srinivasan and Young2012) and Bakas & Iouannou (Reference Bakas and Iouannou2013).
$\text{e}^{\text{i}mx}$
, and so our analysis could be extended, creating additional complexity in integrating over angles but without any fundamental changes. We should remark though that our forcing is anisotropic, in contrast to some other studies, and this is known to enhance instabilities leading to zonal flows, by selecting a preferred direction in the system, as discussed in Srinivasan & Young (Reference Srinivasan and Young2012) and Bakas & Iouannou (Reference Bakas and Iouannou2013).
(iv) We have not discussed the strength of the background flow
![]() $U$
, scalar field
$U$
, scalar field
![]() ${\it\Sigma}$
or magnetic field
${\it\Sigma}$
or magnetic field
![]() $B$
. In fact, the status of these is rather different. A background flow
$B$
. In fact, the status of these is rather different. A background flow
![]() $U$
can grow from a seed through zonostrophic instability, and so we cannot set its scale at the outset. For passive scalar transport, the magnitude of the background gradient
$U$
can grow from a seed through zonostrophic instability, and so we cannot set its scale at the outset. For passive scalar transport, the magnitude of the background gradient
![]() ${\it\Sigma}^{\prime }$
is a constant that can be set arbitrarily. The strength of a mean magnetic field (that is,
${\it\Sigma}^{\prime }$
is a constant that can be set arbitrarily. The strength of a mean magnetic field (that is,
![]() $B$
averaged over the
$B$
averaged over the
![]() $y$
-coordinate) is another constant that must be set initially and will introduce a further parameter into the problem. It should be noted that given our present non-dimensionalisation (2.5), the magnetic field strength
$y$
-coordinate) is another constant that must be set initially and will introduce a further parameter into the problem. It should be noted that given our present non-dimensionalisation (2.5), the magnetic field strength
![]() $B$
is measured relative to the velocity strength, corresponding to an inverse magnetic Mach number.
$B$
is measured relative to the velocity strength, corresponding to an inverse magnetic Mach number.
(v) Our primary focus will be on
![]() ${\rm\nabla}^{2}$
dissipation (we refer to this as molecular dissipation) in the development from (2.1)–(2.3), but we will below remark briefly on more general forms of dissipation, using
${\rm\nabla}^{2}$
dissipation (we refer to this as molecular dissipation) in the development from (2.1)–(2.3), but we will below remark briefly on more general forms of dissipation, using
![]() $-{\it\lambda}_{r}(-{\rm\nabla}^{2})^{r}{\it\omega}$
in (2.1), and likewise for
$-{\it\lambda}_{r}(-{\rm\nabla}^{2})^{r}{\it\omega}$
in (2.1), and likewise for
![]() $a$
and
$a$
and
![]() ${\it\sigma}$
. The case
${\it\sigma}$
. The case
![]() $r=0$
is bottom drag,
$r=0$
is bottom drag,
![]() $r\geqslant 2$
is hyperviscosity (or hyperdiffusion) and
$r\geqslant 2$
is hyperviscosity (or hyperdiffusion) and
![]() $r=1$
,
$r=1$
,
![]() ${\it\lambda}_{1}\equiv {\it\lambda}$
is standard viscous dissipation. We stress that these are the ‘molecular’ effects – in other words terms that we introduce into the governing equations, to be distinguished from the ‘effective’ transport effects, for example
${\it\lambda}_{1}\equiv {\it\lambda}$
is standard viscous dissipation. We stress that these are the ‘molecular’ effects – in other words terms that we introduce into the governing equations, to be distinguished from the ‘effective’ transport effects, for example
![]() ${\it\nu}_{\mathit{eff}}$
,
${\it\nu}_{\mathit{eff}}$
,
![]() ${\it\kappa}_{\mathit{eff}}$
, that emerge from our analysis below.
${\it\kappa}_{\mathit{eff}}$
, that emerge from our analysis below.
3 Hydrodynamic transport
Although the purely hydrodynamic problem has been well explored in the literature, it is naturally a starting point for the MHD problem. In order to set the scene, give a point of comparison, and establish scalings for the MHD problem, we sketch this case. We need to solve for waves on a given profile
![]() $U$
, from (2.11),
$U$
, from (2.11),
3.1 Multiple-scale formulation
We first apply a transformation to absorb the advective term,
and obtain
with
![]() $\mathscr{L}$
denoting the Laplacian operator,
$\mathscr{L}$
denoting the Laplacian operator,
The flux (2.16) may then be written as
It should be noted that the leading-order term in
![]() ${\it\zeta}$
from (3.4), which is a purely real multiple
${\it\zeta}$
from (3.4), which is a purely real multiple
![]() $m^{2}(1+{\it\Omega}^{2}t^{2})$
of
$m^{2}(1+{\it\Omega}^{2}t^{2})$
of
![]() ${\it\phi}$
, does not contribute to the flux
${\it\phi}$
, does not contribute to the flux
![]() $F_{\mathit{R}}$
. This absence of a phase shift between the two fields means that a vorticity disturbance on an exactly linear shear flow
$F_{\mathit{R}}$
. This absence of a phase shift between the two fields means that a vorticity disturbance on an exactly linear shear flow
![]() ${\it\Omega}=\text{const.}$
cannot contribute a mean Reynolds stress: it is higher-order terms that need to be included, involving gradients of
${\it\Omega}=\text{const.}$
cannot contribute a mean Reynolds stress: it is higher-order terms that need to be included, involving gradients of
![]() ${\it\Omega}$
.
${\it\Omega}$
.
The development so far is exact (within the quasi-linear approximation), and to make further progress we take the case when the mean or background flow varies on a large scale
![]() $Y$
, setting
$Y$
, setting
with
![]() ${\it\varepsilon}\ll 1$
. We now write
${\it\varepsilon}\ll 1$
. We now write
![]() ${\it\Omega}=-U^{\prime }$
, using the prime to denote a
${\it\Omega}=-U^{\prime }$
, using the prime to denote a
![]() $Y$
-derivative of any background field. Here and elsewhere we suppress the (slow) time dependence of the background field, governed by (3.12) below. (It should be noted that the correlation function approach of Srinivasan & Young (Reference Srinivasan and Young2012) does not assume scale separation.)
$Y$
-derivative of any background field. Here and elsewhere we suppress the (slow) time dependence of the background field, governed by (3.12) below. (It should be noted that the correlation function approach of Srinivasan & Young (Reference Srinivasan and Young2012) does not assume scale separation.)
We now adopt the scalings
These give for the wave evolution on the
![]() $T$
time scale
$T$
time scale
with
The equation (2.20) for mean fields takes the form
and these fields develop on the long time scale
![]() $\mathscr{T}={\it\varepsilon}^{2}T$
, where as a consequence of the new scalings in (3.8), the equation
$\mathscr{T}={\it\varepsilon}^{2}T$
, where as a consequence of the new scalings in (3.8), the equation
now replaces (2.18) for any label
![]() $\mathit{Z}$
.
$\mathit{Z}$
.
Equations (3.9)–(3.13) are the ones we wish to expand and study asymptotically for small
![]() ${\it\varepsilon}$
. The rationale for the above choice of scaling in (3.7), (3.8) is to retain as many terms at leading order as possible in (3.9)–(3.13). It should be noted that from (3.7), the strength of the waves, and so the strength of the original driving force, is being reduced as
${\it\varepsilon}$
. The rationale for the above choice of scaling in (3.7), (3.8) is to retain as many terms at leading order as possible in (3.9)–(3.13). It should be noted that from (3.7), the strength of the waves, and so the strength of the original driving force, is being reduced as
![]() ${\it\varepsilon}\rightarrow 0$
, to balance the viscous term in (3.12) for the mean fields. For more general dissipation the scalings would be as above except for
${\it\varepsilon}\rightarrow 0$
, to balance the viscous term in (3.12) for the mean fields. For more general dissipation the scalings would be as above except for
and give rise to the same set of equations with only modifications to the definition of
![]() $\mathscr{L}$
in (3.10). For
$\mathscr{L}$
in (3.10). For
![]() $r=0$
(linear drag) there is no separation of scales between
$r=0$
(linear drag) there is no separation of scales between
![]() $\mathscr{T}$
and
$\mathscr{T}$
and
![]() $T$
, and so the consistency condition discussed in the first comment of § 2.3 would not be satisfied: mean flow and waves would be damped on the same time scale (at least, unless some further limit were taken, or perhaps some combination of damping effects employed).
$T$
, and so the consistency condition discussed in the first comment of § 2.3 would not be satisfied: mean flow and waves would be damped on the same time scale (at least, unless some further limit were taken, or perhaps some combination of damping effects employed).
3.2 Numerical solution

Figure 1. Simulation of waves with
![]() ${\it\beta}=0$
,
${\it\beta}=0$
,
![]() $m=1$
,
$m=1$
,
![]() ${\it\varepsilon}=0.1$
,
${\it\varepsilon}=0.1$
,
![]() ${\it\lambda}=0$
and
${\it\lambda}=0$
and
![]() $U=\cos Y$
. In (a)
$U=\cos Y$
. In (a)
![]() $\text{Re}\,{\it\omega}$
, (b)
$\text{Re}\,{\it\omega}$
, (b)
![]() $\text{Re}\,{\it\psi}$
and (c)
$\text{Re}\,{\it\psi}$
and (c)
![]() $F_{R}$
are plotted in the
$F_{R}$
are plotted in the
![]() $(T,Y)$
-plane. In (d)
$(T,Y)$
-plane. In (d)
![]() $F_{R}(Y,T)$
is shown as a function of
$F_{R}(Y,T)$
is shown as a function of
![]() $Y$
for
$Y$
for
![]() $T=0.1,0.2,\ldots ,1$
(solid, innermost to outermost curve), with
$T=0.1,0.2,\ldots ,1$
(solid, innermost to outermost curve), with
![]() $U(Y)$
(dashed).
$U(Y)$
(dashed).
Before undertaking further analysis, it is worth gaining some intuition by simulating the system we have so far for the linear waves
![]() ${\it\omega}(Y,T)$
,
${\it\omega}(Y,T)$
,
![]() ${\it\psi}(Y,T)$
. The system may be written as
${\it\psi}(Y,T)$
. The system may be written as
equivalent to (3.9), (3.10), with here
A run with
![]() ${\it\beta}=0$
,
${\it\beta}=0$
,
![]() ${\it\varepsilon}=0.1$
and
${\it\varepsilon}=0.1$
and
![]() $U=\cos Y$
is shown in figure 1: (a,b) show the real part of the vorticity
$U=\cos Y$
is shown in figure 1: (a,b) show the real part of the vorticity
![]() ${\it\omega}$
and stream function
${\it\omega}$
and stream function
![]() ${\it\psi}$
respectively, in the
${\it\psi}$
respectively, in the
![]() $(T,Y)$
-plane. We have taken zero viscosity,
$(T,Y)$
-plane. We have taken zero viscosity,
![]() ${\it\lambda}=0$
; otherwise we would simply see a damping effect. Away from the maxima of
${\it\lambda}=0$
; otherwise we would simply see a damping effect. Away from the maxima of
![]() $|U|$
at
$|U|$
at
![]() $Y=0$
,
$Y=0$
,
![]() $\pm {\rm\pi}$
(where
$\pm {\rm\pi}$
(where
![]() ${\it\Omega}=0$
) the vorticity gains finer scales and the stream function is suppressed. The flux
${\it\Omega}=0$
) the vorticity gains finer scales and the stream function is suppressed. The flux
![]() $F_{\mathit{R}}$
is shown in (c) and develops (red) peaks and (blue) troughs for large
$F_{\mathit{R}}$
is shown in (c) and develops (red) peaks and (blue) troughs for large
![]() $T$
.
$T$
.
The short-time evolution of flux
![]() $F_{\mathit{R}}(Y,T)$
is shown in (d) for
$F_{\mathit{R}}(Y,T)$
is shown in (d) for
![]() $T=0.1,0.2,\ldots ,1$
(solid), going from the innermost (smoothest) curve to the outermost one. Figure 1(d) contains key information as we can write from (3.12) for the mean velocity
$T=0.1,0.2,\ldots ,1$
(solid), going from the innermost (smoothest) curve to the outermost one. Figure 1(d) contains key information as we can write from (3.12) for the mean velocity
and here
![]() $U=\cos Y$
is shown dashed in figure 1(d). Thus, the short-time effect of the flux
$U=\cos Y$
is shown dashed in figure 1(d). Thus, the short-time effect of the flux
![]() $F_{\mathit{R}}$
(as it contributes to
$F_{\mathit{R}}$
(as it contributes to
![]() $\mathscr{F}_{\mathit{R}}$
) is to reinforce the original flow
$\mathscr{F}_{\mathit{R}}$
) is to reinforce the original flow
![]() $U$
, which is precisely the effect leading to zonostrophic instability. If there is sufficient viscous damping, then only the short-time feedback is relevant, and below we will recover this effect, which naturally is well documented in the literature (e.g. Srinivasan & Young Reference Srinivasan and Young2012).
$U$
, which is precisely the effect leading to zonostrophic instability. If there is sufficient viscous damping, then only the short-time feedback is relevant, and below we will recover this effect, which naturally is well documented in the literature (e.g. Srinivasan & Young Reference Srinivasan and Young2012).
For greater times, the feedback from the flux
![]() $F_{\mathit{R}}$
becomes more oscillatory in
$F_{\mathit{R}}$
becomes more oscillatory in
![]() $Y$
, changing sign in places with respect to the original
$Y$
, changing sign in places with respect to the original
![]() $U=\cos Y$
profile, as seen in figure 1(c,d). This is investigated further below, but there is an indication that the effect of the feedback is to sharpen any pre-existing profile, increasing the flow where
$U=\cos Y$
profile, as seen in figure 1(c,d). This is investigated further below, but there is an indication that the effect of the feedback is to sharpen any pre-existing profile, increasing the flow where
![]() ${\it\Omega}=-U^{\prime }=0$
and flattening the flow profile where
${\it\Omega}=-U^{\prime }=0$
and flattening the flow profile where
![]() $U=0$
and
$U=0$
and
![]() $|{\it\Omega}|$
is maximal. It should be noted that a tendency to sharpen shear profiles is found in weakly damped vortex dynamics simulations by Dritschel & McIntyre (Reference Dritschel and McIntyre2008), and by Kim & MacGregor (Reference Kim and MacGregor2003) in a study of gravity waves in stratified fluid, together with a bifurcation to an oscillatory state.
$|{\it\Omega}|$
is maximal. It should be noted that a tendency to sharpen shear profiles is found in weakly damped vortex dynamics simulations by Dritschel & McIntyre (Reference Dritschel and McIntyre2008), and by Kim & MacGregor (Reference Kim and MacGregor2003) in a study of gravity waves in stratified fluid, together with a bifurcation to an oscillatory state.
3.3 Multiple-scale expansion
We now return to the development in § 3.1 and approximate. We expand quantities in powers of
![]() ${\it\varepsilon}$
, for example,
${\it\varepsilon}$
, for example,
and the leading-order equations (3.9), (3.10) take the form
The accelerated decay through the
![]() $T^{3}$
term in the exponential is known as the shear–diffuse mechanism (Bernoff & Lingevitch Reference Bernoff and Lingevitch1994) responsible for flux expulsion in kinematic magnetic field evolution (Weiss Reference Weiss1966). This gives a first-order ordinary differential equation (ODE) with respect to
$T^{3}$
term in the exponential is known as the shear–diffuse mechanism (Bernoff & Lingevitch Reference Bernoff and Lingevitch1994) responsible for flux expulsion in kinematic magnetic field evolution (Weiss Reference Weiss1966). This gives a first-order ordinary differential equation (ODE) with respect to
![]() $T$
, with the solution
$T$
, with the solution
The expansion gives us functions of
![]() ${\it\Omega}T$
rather than
${\it\Omega}T$
rather than
![]() $T$
, and so it is convenient to call this
$T$
, and so it is convenient to call this
![]() ${\it\tau}$
and to try to reduce the number of parameters involved. We set
${\it\tau}$
and to try to reduce the number of parameters involved. We set
in terms of which we have the more compact form
We will for simplicity and without loss of generality consider points
![]() $Y$
in the profile where
$Y$
in the profile where
![]() ${\it\Omega}>0$
, so that
${\it\Omega}>0$
, so that
![]() ${\it\tau}\in [0,\infty ]$
; the final results are nonetheless correct also for
${\it\tau}\in [0,\infty ]$
; the final results are nonetheless correct also for
![]() ${\it\Omega}<0$
. Behaviour at points where
${\it\Omega}<0$
. Behaviour at points where
![]() ${\it\Omega}=0$
can be established by letting
${\it\Omega}=0$
can be established by letting
![]() ${\it\Omega}\rightarrow 0$
; although this need not detain us here, we make some further comments and qualifications in appendix A.
${\it\Omega}\rightarrow 0$
; although this need not detain us here, we make some further comments and qualifications in appendix A.
We then obtain the leading-order flux from (3.11) as a function of time,
(we have simply dropped the term of order
![]() ${\it\varepsilon}$
in (3.11), but not further complicated the notation), with
${\it\varepsilon}$
in (3.11), but not further complicated the notation), with
The leading-order integral may be written as
where we set, for any label
![]() $\mathit{Z}$
,
$\mathit{Z}$
,
It should be noted that
![]() $h_{\mathit{R}}=h_{\mathit{R}}(\hat{{\it\lambda}})$
only, and in fact
$h_{\mathit{R}}=h_{\mathit{R}}(\hat{{\it\lambda}})$
only, and in fact
![]() $\hat{{\it\beta}}$
has dropped out of the calculations. The large-scale equation is now
$\hat{{\it\beta}}$
has dropped out of the calculations. The large-scale equation is now
with an effective viscosity
![]() ${\it\nu}_{\mathit{eff}}({\it\Omega},{\it\lambda})$
identified and arising from the externally forced waves. This term emerges from the two-scale analysis with the expected form, in other words giving transport of the large-scale vorticity field
${\it\nu}_{\mathit{eff}}({\it\Omega},{\it\lambda})$
identified and arising from the externally forced waves. This term emerges from the two-scale analysis with the expected form, in other words giving transport of the large-scale vorticity field
![]() ${\it\Omega}(Y,\mathscr{T})$
. It should be noted, however, that although the underlying molecular viscosity
${\it\Omega}(Y,\mathscr{T})$
. It should be noted, however, that although the underlying molecular viscosity
![]() ${\it\lambda}$
is always positive and so dissipative in effect, given that we have averaged over the vorticity equation with an imposed body force present, there is no reason why the effective (or ‘renormalised’) viscosity
${\it\lambda}$
is always positive and so dissipative in effect, given that we have averaged over the vorticity equation with an imposed body force present, there is no reason why the effective (or ‘renormalised’) viscosity
![]() ${\it\nu}_{\mathit{eff}}$
need be positive, and generally it is not, this being the origin of zonostrophic instability in this system.
${\it\nu}_{\mathit{eff}}$
need be positive, and generally it is not, this being the origin of zonostrophic instability in this system.
To summarise, (3.24) gives the instantaneous feedback
![]() $F_{\mathit{R}}$
from the wave to the mean flow, coded in the function
$F_{\mathit{R}}$
from the wave to the mean flow, coded in the function
![]() $f_{\mathit{R}}({\it\tau},\hat{{\it\lambda}})$
in (3.25) with the damping factor
$f_{\mathit{R}}({\it\tau},\hat{{\it\lambda}})$
in (3.25) with the damping factor
![]() $D^{2}$
. The integrated effect is found in
$D^{2}$
. The integrated effect is found in
![]() $h_{\mathit{R}}(\hat{{\it\lambda}})$
and gives the effective viscosity in (3.26); the parameter
$h_{\mathit{R}}(\hat{{\it\lambda}})$
and gives the effective viscosity in (3.26); the parameter
![]() $\hat{{\it\beta}}$
plays no role at this order (cf. Srinivasan & Young Reference Srinivasan and Young2012, Reference Srinivasan and Young2014). Figure 2(a) shows
$\hat{{\it\beta}}$
plays no role at this order (cf. Srinivasan & Young Reference Srinivasan and Young2012, Reference Srinivasan and Young2014). Figure 2(a) shows
![]() $D^{2}f_{\mathit{R}}$
as a function of
$D^{2}f_{\mathit{R}}$
as a function of
![]() ${\it\tau}$
in the inviscid limit,
${\it\tau}$
in the inviscid limit,
![]() $\hat{{\it\lambda}}=0$
, and for increasing values of
$\hat{{\it\lambda}}=0$
, and for increasing values of
![]() $\hat{{\it\lambda}}$
. Focusing on the inviscid case (outermost curve), it is worth noting that the feedback changes sign at
$\hat{{\it\lambda}}$
. Focusing on the inviscid case (outermost curve), it is worth noting that the feedback changes sign at
![]() ${\it\tau}=3^{-1/2}$
. The effect of increasing the damping,
${\it\tau}=3^{-1/2}$
. The effect of increasing the damping,
![]() $\hat{{\it\lambda}}>0$
(inner curves), is primarily to suppress
$\hat{{\it\lambda}}>0$
(inner curves), is primarily to suppress
![]() $f_{\mathit{R}}$
at ever earlier times. Figure 2(b) shows
$f_{\mathit{R}}$
at ever earlier times. Figure 2(b) shows
![]() $h_{\mathit{R}}(\hat{{\it\lambda}})$
, which is the total integrated flux. We have
$h_{\mathit{R}}(\hat{{\it\lambda}})$
, which is the total integrated flux. We have
![]() $h_{\mathit{R}}(0)=1$
while for small
$h_{\mathit{R}}(0)=1$
while for small
![]() $\hat{{\it\lambda}}$
the effective viscosity is positive, corresponding to the damping of the mean flow. At
$\hat{{\it\lambda}}$
the effective viscosity is positive, corresponding to the damping of the mean flow. At
![]() $\hat{{\it\lambda}}\simeq 0.95$
,
$\hat{{\it\lambda}}\simeq 0.95$
,
![]() $h_{\mathit{R}}$
changes sign, and for larger
$h_{\mathit{R}}$
changes sign, and for larger
![]() $\hat{{\it\lambda}}$
it is negative and so destabilising. For large
$\hat{{\it\lambda}}$
it is negative and so destabilising. For large
![]() $\hat{{\it\lambda}}$
the integral (3.27) is effectively cut off at times
$\hat{{\it\lambda}}$
the integral (3.27) is effectively cut off at times
![]() ${\it\tau}=O(\hat{{\it\lambda}}^{-1})$
and we can expand the functions
${\it\tau}=O(\hat{{\it\lambda}}^{-1})$
and we can expand the functions
![]() $D$
and
$D$
and
![]() $f_{\mathit{R}}$
as power series in
$f_{\mathit{R}}$
as power series in
![]() ${\it\tau}$
, giving
${\it\tau}$
, giving
also shown in figure 2(b) (dashed curve).
Let us now relate this detailed calculation back to the bigger picture, for example as in the simulations in figure 1. For good scale separation,
![]() ${\it\varepsilon}\ll 1$
, at each
${\it\varepsilon}\ll 1$
, at each
![]() $Y$
the flow is locally shearing, as given by the value of
$Y$
the flow is locally shearing, as given by the value of
![]() ${\it\Omega}(Y)$
. The subsequent evolution of a wave is determined by the key parameter
${\it\Omega}(Y)$
. The subsequent evolution of a wave is determined by the key parameter
![]() $\hat{{\it\lambda}}$
and occurs on a time scale
$\hat{{\it\lambda}}$
and occurs on a time scale
![]() ${\it\tau}$
; see (3.22). The evolution on the
${\it\tau}$
; see (3.22). The evolution on the
![]() ${\it\tau}$
time scale is damped by the factor
${\it\tau}$
time scale is damped by the factor
![]() $D$
, which occurs at
$D$
, which occurs at
![]() ${\it\tau}=O(\hat{{\it\lambda}}^{-1})$
for large
${\it\tau}=O(\hat{{\it\lambda}}^{-1})$
for large
![]() $\hat{{\it\lambda}}$
, or at
$\hat{{\it\lambda}}$
, or at
![]() ${\it\tau}=O(\hat{{\it\lambda}}^{-1/3})$
for small
${\it\tau}=O(\hat{{\it\lambda}}^{-1/3})$
for small
![]() $\hat{{\it\lambda}}$
, by the shear–diffuse mechanism. For small
$\hat{{\it\lambda}}$
, by the shear–diffuse mechanism. For small
![]() ${\it\varepsilon}$
, this is all that is needed to recreate the evolution of
${\it\varepsilon}$
, this is all that is needed to recreate the evolution of
![]() $F_{\mathit{R}}$
in figure 1(c,d), and for each
$F_{\mathit{R}}$
in figure 1(c,d), and for each
![]() $Y$
good agreement can be shown between the evolution in time
$Y$
good agreement can be shown between the evolution in time
![]() $T$
in this figure, and in the analysis above based on the local ODE (3.20).
$T$
in this figure, and in the analysis above based on the local ODE (3.20).

Figure 2. (a) Plot of
![]() $D^{2}f_{\mathit{R}}$
as a function of
$D^{2}f_{\mathit{R}}$
as a function of
![]() ${\it\tau}$
for
${\it\tau}$
for
![]() $\hat{{\it\lambda}}=0,0.1,0.2,0.4,\ldots ,3.2$
(from outermost to innermost curve). (b) Plot of
$\hat{{\it\lambda}}=0,0.1,0.2,0.4,\ldots ,3.2$
(from outermost to innermost curve). (b) Plot of
![]() $h_{\mathit{R}}$
as a function of
$h_{\mathit{R}}$
as a function of
![]() $\hat{{\it\lambda}}$
(solid) and the approximation (3.29) (dashed).
$\hat{{\it\lambda}}$
(solid) and the approximation (3.29) (dashed).
It should be noted that in a profile with varying
![]() ${\it\Omega}$
, the local parameter
${\it\Omega}$
, the local parameter
![]() $\hat{{\it\lambda}}$
will also vary. Taking
$\hat{{\it\lambda}}$
will also vary. Taking
![]() ${\it\Omega}$
bounded, if
${\it\Omega}$
bounded, if
![]() ${\it\lambda}\gg 1$
then the waves are always in a viscous regime,
${\it\lambda}\gg 1$
then the waves are always in a viscous regime,
![]() $\hat{{\it\lambda}}\gg 1$
, whereas if
$\hat{{\it\lambda}}\gg 1$
, whereas if
![]() ${\it\lambda}$
is small, at different locations
${\it\lambda}$
is small, at different locations
![]() $Y$
the waves may effectively be in a low-viscosity,
$Y$
the waves may effectively be in a low-viscosity,
![]() $\hat{{\it\lambda}}\ll 1$
, or a viscous,
$\hat{{\it\lambda}}\ll 1$
, or a viscous,
![]() $\hat{{\it\lambda}}\gg 1$
, regime. In a viscous regime we have
$\hat{{\it\lambda}}\gg 1$
, regime. In a viscous regime we have
This destabilising negative viscosity term corresponds to the instability of the original steady Kolmogorov flow discussed in Meshalkin & Sinai (Reference Meshalkin and Sinai1961), and follows from the anisotropy of the forcing as discussed, for example, in Srinivasan & Young (Reference Srinivasan and Young2014). The inverse power of
![]() ${\it\lambda}$
shows the effect of large viscosity in cutting off the feedback on the mean flow, corresponding to capturing the short-time behaviour seen in figure 1(d). This result is key to zonostrophic instability, in which
${\it\lambda}$
shows the effect of large viscosity in cutting off the feedback on the mean flow, corresponding to capturing the short-time behaviour seen in figure 1(d). This result is key to zonostrophic instability, in which
![]() ${\it\Omega}\simeq 0$
initially everywhere. No matter what the molecular value of
${\it\Omega}\simeq 0$
initially everywhere. No matter what the molecular value of
![]() ${\it\lambda}>0$
is, the limit
${\it\lambda}>0$
is, the limit
![]() $\hat{{\it\lambda}}\gg 1$
and the result (3.30) are then appropriate, with the destabilising effect of a negative effective viscosity arising from the negative values of
$\hat{{\it\lambda}}\gg 1$
and the result (3.30) are then appropriate, with the destabilising effect of a negative effective viscosity arising from the negative values of
![]() $f_{\mathit{R}}$
for short times and so of
$f_{\mathit{R}}$
for short times and so of
![]() $h_{\mathit{R}}$
for large
$h_{\mathit{R}}$
for large
![]() $\hat{{\it\lambda}}$
; see figure 2.
$\hat{{\it\lambda}}$
; see figure 2.
We remark that even if we applied molecular hyperviscosity (i.e. hyperdiffusion) to the waves (end of § 2.3), which would lead to modified forms of
![]() $D$
and
$D$
and
![]() $\mathscr{L}$
, we would still recover effective viscosity for the large-scale fields, in other words via a term of the form
$\mathscr{L}$
, we would still recover effective viscosity for the large-scale fields, in other words via a term of the form
![]() $\partial _{Y}({\it\nu}_{\mathit{eff}}\partial _{Y}{\it\Omega})$
. Whereas negative effective viscosity leads to an ill-posed problem if it is only balanced by weaker positive molecular viscosity, having molecular hyperviscosity recovers a sensible problem for the large-scale fields, for example to integrate numerically. We leave this for future study, noting that molecular hyperviscosity should only be introduced with considerable caution: see Sukoriansky et al. (Reference Sukoriansky, Galperin and Chekhlov1999) in the case of turbulence and Zhang & Jones (Reference Zhang and Jones1997) for rapidly rotating convection.
$\partial _{Y}({\it\nu}_{\mathit{eff}}\partial _{Y}{\it\Omega})$
. Whereas negative effective viscosity leads to an ill-posed problem if it is only balanced by weaker positive molecular viscosity, having molecular hyperviscosity recovers a sensible problem for the large-scale fields, for example to integrate numerically. We leave this for future study, noting that molecular hyperviscosity should only be introduced with considerable caution: see Sukoriansky et al. (Reference Sukoriansky, Galperin and Chekhlov1999) in the case of turbulence and Zhang & Jones (Reference Zhang and Jones1997) for rapidly rotating convection.
3.4 Zonostrophic instability
At the end of the last section we indicated the origin of zonostrophic instability through the negative sign in (3.30). We study this in the more general context of a uniform background shear flow. Consider again (3.28) and think of
![]() ${\it\nu}_{\mathit{eff}}={\it\nu}_{\mathit{eff}}({\it\Omega},{\it\lambda})$
in general. A solution is simply steady uniform vorticity
${\it\nu}_{\mathit{eff}}={\it\nu}_{\mathit{eff}}({\it\Omega},{\it\lambda})$
in general. A solution is simply steady uniform vorticity
![]() ${\it\Omega}(Y,\mathscr{T})={\it\Omega}_{0}=\text{const.}$
, that is uniform shear
${\it\Omega}(Y,\mathscr{T})={\it\Omega}_{0}=\text{const.}$
, that is uniform shear
![]() $U=-{\it\Omega}_{0}Y$
, and we can investigate the stability of this solution to perturbations.
$U=-{\it\Omega}_{0}Y$
, and we can investigate the stability of this solution to perturbations.
We replace
![]() ${\it\Omega}\rightarrow {\it\Omega}_{0}+{\it\Omega}$
in (3.28) with now
${\it\Omega}\rightarrow {\it\Omega}_{0}+{\it\Omega}$
in (3.28) with now
![]() ${\it\Omega}\ll 1$
to give
${\it\Omega}\ll 1$
to give
at leading order. Seeking a normal mode in
![]() ${\it\Omega}$
proportional to
${\it\Omega}$
proportional to
![]() $\exp (PK^{2}\mathscr{T}+\text{i}KY)$
gives the (scaled) growth rate
$\exp (PK^{2}\mathscr{T}+\text{i}KY)$
gives the (scaled) growth rate
![]() $P$
as
$P$
as
The last term
![]() $-{\it\lambda}$
is the damping effect of molecular viscosity, and the nature of any instability is again clear as the result of a negative effective viscosity, taking place if
$-{\it\lambda}$
is the damping effect of molecular viscosity, and the nature of any instability is again clear as the result of a negative effective viscosity, taking place if
![]() ${\it\nu}_{\mathit{eff}}$
is negative and large enough. We first consider when
${\it\nu}_{\mathit{eff}}$
is negative and large enough. We first consider when
![]() ${\it\Omega}_{0}=0$
, in which case we insert the large-
${\it\Omega}_{0}=0$
, in which case we insert the large-
![]() $\hat{{\it\lambda}}$
expansion (3.30) to obtain
$\hat{{\it\lambda}}$
expansion (3.30) to obtain
We have zonostrophic instability if
![]() $P>0$
, which amounts to the condition
$P>0$
, which amounts to the condition
![]() $m^{2}{\it\lambda}<2^{-1/3}$
.
$m^{2}{\it\lambda}<2^{-1/3}$
.

Figure 3. Contour plot of
![]() $m^{2}P$
(3.32) in the
$m^{2}P$
(3.32) in the
![]() $(m^{2}{\it\lambda},{\it\Omega}_{0})$
-plane. Contours increase from
$(m^{2}{\it\lambda},{\it\Omega}_{0})$
-plane. Contours increase from
![]() $m^{2}P=0$
(outermost) in steps of 0.1 to
$m^{2}P=0$
(outermost) in steps of 0.1 to
![]() $m^{2}P=10$
(bottom left corner).
$m^{2}P=10$
(bottom left corner).
For the more general case of a uniform background vorticity distribution
![]() ${\it\Omega}_{0}\neq 0$
, the relative size of
${\it\Omega}_{0}\neq 0$
, the relative size of
![]() ${\it\Omega}_{0}$
and
${\it\Omega}_{0}$
and
![]() ${\it\lambda}$
is important through the value
${\it\lambda}$
is important through the value
![]() $\hat{{\it\lambda}}=m^{2}{\it\lambda}/{\it\Omega}_{0}$
in (3.32). We cannot evaluate
$\hat{{\it\lambda}}=m^{2}{\it\lambda}/{\it\Omega}_{0}$
in (3.32). We cannot evaluate
![]() $h_{\mathit{R}}$
analytically in general, but we can easily do so numerically, and figure 3 shows a contour plot of
$h_{\mathit{R}}$
analytically in general, but we can easily do so numerically, and figure 3 shows a contour plot of
![]() $m^{2}P$
in the
$m^{2}P$
in the
![]() $(m^{2}{\it\lambda},{\it\Omega}_{0})$
-plane. The outer contour gives
$(m^{2}{\it\lambda},{\it\Omega}_{0})$
-plane. The outer contour gives
![]() $P=0$
, and outside this
$P=0$
, and outside this
![]() $P<0$
. Along the horizontal axis
$P<0$
. Along the horizontal axis
![]() ${\it\Omega}_{0}=0$
the result (3.33) holds. For increasing
${\it\Omega}_{0}=0$
the result (3.33) holds. For increasing
![]() ${\it\Omega}_{0}$
, zonostrophic instability is suppressed (Srinivasan & Young Reference Srinivasan and Young2014; Hsu & Diamond Reference Hsu and Diamond2015), being restricted to a finite range of viscosities
${\it\Omega}_{0}$
, zonostrophic instability is suppressed (Srinivasan & Young Reference Srinivasan and Young2014; Hsu & Diamond Reference Hsu and Diamond2015), being restricted to a finite range of viscosities
![]() $m^{2}{\it\lambda}$
bounded above zero, and turns off completely for
$m^{2}{\it\lambda}$
bounded above zero, and turns off completely for
![]() ${\it\Omega}_{0}$
greater than approximately 0.25. It should be noted that the suppression of instability by shear is also evident in the sign of the second correction term in (3.29). The value of
${\it\Omega}_{0}$
greater than approximately 0.25. It should be noted that the suppression of instability by shear is also evident in the sign of the second correction term in (3.29). The value of
![]() $m^{2}P$
diverges as
$m^{2}P$
diverges as
![]() ${\it\lambda}\rightarrow 0$
,
${\it\lambda}\rightarrow 0$
,
![]() ${\it\Omega}_{0}\rightarrow 0$
(bottom left, where the contours accumulate), and in fact the contours accumulate near the origin on the line given by
${\it\Omega}_{0}\rightarrow 0$
(bottom left, where the contours accumulate), and in fact the contours accumulate near the origin on the line given by
![]() $m^{2}{\it\lambda}/{\it\Omega}_{0}\simeq 0.95$
, on which
$m^{2}{\it\lambda}/{\it\Omega}_{0}\simeq 0.95$
, on which
![]() $h_{\mathit{R}}$
changes sign.
$h_{\mathit{R}}$
changes sign.
3.5 Equilibrium profiles
We cannot readily time step (3.28) numerically: as
![]() ${\it\nu}_{\mathit{eff}}$
can change sign this is ill-posed without some additional cutoff for short wavelengths (on the
${\it\nu}_{\mathit{eff}}$
can change sign this is ill-posed without some additional cutoff for short wavelengths (on the
![]() $Y$
scale). Incorporation of a cutoff would not be unreasonable given that the theory is based on scale separation and a threshold can be determined in related models that allow zonostrophic instability on arbitrary scales (Srinivasan & Young Reference Srinivasan and Young2012). For example, negative effective viscosity at large scale can be cut off by positive effective hyperviscosity at smaller scales (and Sukoriansky et al. (Reference Sukoriansky, Galperin and Chekhlov1999) argue that in two-dimensional turbulence these effects also need to be time-dependent to simulate subgrid-scale motion). We defer these considerations to future study, and here note that although we cannot integrate (3.28) explicitly, we can seek equilibrium profiles, that is, mean field profiles independent of the time scale
$Y$
scale). Incorporation of a cutoff would not be unreasonable given that the theory is based on scale separation and a threshold can be determined in related models that allow zonostrophic instability on arbitrary scales (Srinivasan & Young Reference Srinivasan and Young2012). For example, negative effective viscosity at large scale can be cut off by positive effective hyperviscosity at smaller scales (and Sukoriansky et al. (Reference Sukoriansky, Galperin and Chekhlov1999) argue that in two-dimensional turbulence these effects also need to be time-dependent to simulate subgrid-scale motion). We defer these considerations to future study, and here note that although we cannot integrate (3.28) explicitly, we can seek equilibrium profiles, that is, mean field profiles independent of the time scale
![]() $\mathscr{T}$
. Integrating (3.28) once, we can write
$\mathscr{T}$
. Integrating (3.28) once, we can write
with a constant
![]() $C$
. To plot solutions it is convenient to reduce the number of parameters by setting
$C$
. To plot solutions it is convenient to reduce the number of parameters by setting
so that we solve
to obtain a family of solutions depending on only one parameter
![]() $\tilde{{\it\lambda}}$
.
$\tilde{{\it\lambda}}$
.
Now we numerically integrate (3.36) over a range of
![]() ${\tilde{Y}}$
with
${\tilde{Y}}$
with
![]() $\tilde{{\it\Omega}}$
passing through
$\tilde{{\it\Omega}}$
passing through
![]() $\tilde{{\it\Omega}}=0$
; this gives a family of profiles depicted in figure 4(a) for
$\tilde{{\it\Omega}}=0$
; this gives a family of profiles depicted in figure 4(a) for
![]() $\tilde{{\it\Omega}}$
and (b) for
$\tilde{{\it\Omega}}$
and (b) for
![]() $\tilde{U}$
. It turns out that we cannot obtain sensible solutions unless the effective viscosity
$\tilde{U}$
. It turns out that we cannot obtain sensible solutions unless the effective viscosity
![]() $[\cdots ]$
in (3.36) remains positive, and this restricts
$[\cdots ]$
in (3.36) remains positive, and this restricts
![]() $\tilde{{\it\lambda}}^{-3}<2$
. This is equivalent to being below the threshold for zonostrophic instability (without background uniform shear) in (3.33). As
$\tilde{{\it\lambda}}^{-3}<2$
. This is equivalent to being below the threshold for zonostrophic instability (without background uniform shear) in (3.33). As
![]() $\tilde{{\it\lambda}}^{-3}$
is made closer to 2, we have a lower effective viscosity in a region close to
$\tilde{{\it\lambda}}^{-3}$
is made closer to 2, we have a lower effective viscosity in a region close to
![]() $\tilde{{\it\Omega}}=0$
, and so the scope to sustain larger gradients of
$\tilde{{\it\Omega}}=0$
, and so the scope to sustain larger gradients of
![]() $\tilde{{\it\Omega}}$
. This is seen in figure 4(a), while (b) shows the increasing sharpness of the
$\tilde{{\it\Omega}}$
. This is seen in figure 4(a), while (b) shows the increasing sharpness of the
![]() $\tilde{U}$
profile and (c) shows the corresponding dip in the total viscosity, i.e.
$\tilde{U}$
profile and (c) shows the corresponding dip in the total viscosity, i.e.
![]() ${\it\lambda}+{\it\nu}_{\mathit{eff}}$
, to a small but positive value.
${\it\lambda}+{\it\nu}_{\mathit{eff}}$
, to a small but positive value.
Using (3.29) we can also obtain the approximate form of the
![]() $\tilde{{\it\Omega}}$
profile as an inverse cubic,
$\tilde{{\it\Omega}}$
profile as an inverse cubic,
and in the limit
![]() $\hat{{\it\lambda}}^{-3}\rightarrow 2$
we obtain profiles
$\hat{{\it\lambda}}^{-3}\rightarrow 2$
we obtain profiles
(up to appropriate additive constants).

Figure 4. Plots of equilibrium profiles found by integrating the ODEs (3.36). Here,
![]() $2-\tilde{{\it\lambda}}^{-3}=1$
,
$2-\tilde{{\it\lambda}}^{-3}=1$
,
![]() $1/2$
,
$1/2$
,
![]() $1/4,\ldots ,1/16$
, and as
$1/4,\ldots ,1/16$
, and as
![]() $\tilde{{\it\lambda}}^{-3}$
approaches the value 2, smaller-scale structure is evident in the curves for (a)
$\tilde{{\it\lambda}}^{-3}$
approaches the value 2, smaller-scale structure is evident in the curves for (a)
![]() $\tilde{{\it\Omega}}({\tilde{Y}})$
(reading up the curves), (b)
$\tilde{{\it\Omega}}({\tilde{Y}})$
(reading up the curves), (b)
![]() $\tilde{U} ({\tilde{Y}})$
(down) and (c)
$\tilde{U} ({\tilde{Y}})$
(down) and (c)
![]() $\tilde{{\it\lambda}}^{-3}\tilde{{\it\Omega}}^{-2}\,h_{\mathit{R}}(\tilde{{\it\Omega}}^{-1})+1$
(down, on the left-hand side).
$\tilde{{\it\lambda}}^{-3}\tilde{{\it\Omega}}^{-2}\,h_{\mathit{R}}(\tilde{{\it\Omega}}^{-1})+1$
(down, on the left-hand side).
4 Passive scalar and kinematic magnetic field transport
As a useful intermediate step before tackling the full MHD problem, but also of interest in its own right, we consider passive scalar evolution; related work including bounds on effective diffusivities may be found in Srinivasan & Young (Reference Srinivasan and Young2014), when the vorticity is damped by a bottom drag term
![]() $-{\it\lambda}_{0}{\it\omega}$
and likewise the passive scalar field, i.e. via a term
$-{\it\lambda}_{0}{\it\omega}$
and likewise the passive scalar field, i.e. via a term
![]() $-{\it\lambda}_{0}{\it\sigma}$
. Naturally, for us the passive scalar could be the vector potential of a weak magnetic field, in a kinematic regime; see (2.2), (2.3) and below.
$-{\it\lambda}_{0}{\it\sigma}$
. Naturally, for us the passive scalar could be the vector potential of a weak magnetic field, in a kinematic regime; see (2.2), (2.3) and below.
4.1 Multiple-scale formulation
We follow the discussion at the beginning of § 3 and set
![]() ${\it\sigma}(y,t)=\text{e}^{-\text{i}mU(y)t}\,c(y,t)$
. With the scalings
${\it\sigma}(y,t)=\text{e}^{-\text{i}mU(y)t}\,c(y,t)$
. With the scalings
(and
![]() $Y$
,
$Y$
,
![]() $T$
as before), we obtain from (2.13)
$T$
as before), we obtain from (2.13)
for the waves and
for the mean field, from (2.22). The scalings for the fluxes in (4.2) differ from those earlier in (3.8) because
does not have the same leading-order cancellation as that seen for
![]() $F_{\mathit{R}}$
, discussed below (3.5). Although the equations for vorticity and a passive scalar have similarities, this is one key difference, the other being that the vorticity equation includes an explicit source term, the external forcing, where for a passive scalar there is no source, only a background gradient.
$F_{\mathit{R}}$
, discussed below (3.5). Although the equations for vorticity and a passive scalar have similarities, this is one key difference, the other being that the vorticity equation includes an explicit source term, the external forcing, where for a passive scalar there is no source, only a background gradient.
The leading-order passive scalar problem is easily integrated, using (3.23),
(with
![]() $D$
defined in (3.22)), and we may write the integrated flux as
$D$
defined in (3.22)), and we may write the integrated flux as
with
![]() $h_{\mathit{P}}=h_{\mathit{P}}(\hat{{\it\lambda}},\hat{{\it\beta}})$
from (3.27). This appears in the large-scale passive scalar transport equation
$h_{\mathit{P}}=h_{\mathit{P}}(\hat{{\it\lambda}},\hat{{\it\beta}})$
from (3.27). This appears in the large-scale passive scalar transport equation

Figure 5. Plot of (a)
![]() $f_{\mathit{P}}$
as a function of
$f_{\mathit{P}}$
as a function of
![]() ${\it\tau}$
and (b)
${\it\tau}$
and (b)
![]() $h_{\mathit{P}}$
as a function of
$h_{\mathit{P}}$
as a function of
![]() $\hat{{\it\lambda}}$
. In each plot the values are
$\hat{{\it\lambda}}$
. In each plot the values are
![]() $\hat{{\it\beta}}=0,1,\ldots ,5$
, reading down the curves on the left.
$\hat{{\it\beta}}=0,1,\ldots ,5$
, reading down the curves on the left.
As in the previous section, with similar notation, the function
![]() $f_{\mathit{P}}$
gives the instantaneous flux of the passive scalar (from a uniform background) in the presence of a wave initiated by the external forcing at
$f_{\mathit{P}}$
gives the instantaneous flux of the passive scalar (from a uniform background) in the presence of a wave initiated by the external forcing at
![]() $T=0$
. Unlike in the previous section,
$T=0$
. Unlike in the previous section,
![]() $f_{\mathit{P}}$
depends on the parameter
$f_{\mathit{P}}$
depends on the parameter
![]() $\hat{{\it\beta}}$
as well as the rescaled time
$\hat{{\it\beta}}$
as well as the rescaled time
![]() ${\it\tau}$
, but not on
${\it\tau}$
, but not on
![]() $\hat{{\it\lambda}}$
. Figure 5(a) shows
$\hat{{\it\lambda}}$
. Figure 5(a) shows
![]() $f_{P}$
for varying values of
$f_{P}$
for varying values of
![]() $\hat{{\it\beta}}$
; as this parameter is increased the profile becomes increasingly oscillatory and the integrated transport is reduced. This is shown in figure 5(b) depicting
$\hat{{\it\beta}}$
; as this parameter is increased the profile becomes increasingly oscillatory and the integrated transport is reduced. This is shown in figure 5(b) depicting
![]() $h_{\mathit{P}}$
as a function of
$h_{\mathit{P}}$
as a function of
![]() $\hat{{\it\lambda}}$
for various values of
$\hat{{\it\lambda}}$
for various values of
![]() $\hat{{\it\beta}}$
, showing the suppression of transport as the
$\hat{{\it\beta}}$
, showing the suppression of transport as the
![]() ${\it\beta}$
-effect is increased (see, e.g., Srinivasan & Young Reference Srinivasan and Young2014) and the flows become more wave-like in nature. We also note that
${\it\beta}$
-effect is increased (see, e.g., Srinivasan & Young Reference Srinivasan and Young2014) and the flows become more wave-like in nature. We also note that
4.2 Equilibrium profiles
Although in figure 5 we see variation in the transport of the passive scalar as
![]() $\hat{{\it\lambda}}$
and
$\hat{{\it\lambda}}$
and
![]() $\hat{{\it\beta}}$
are varied, the effect on the equilibrium passive scalar profiles turns out not to be as dramatic as for the vorticity transport in § 3.5. The steady-state version of (4.9) is
$\hat{{\it\beta}}$
are varied, the effect on the equilibrium passive scalar profiles turns out not to be as dramatic as for the vorticity transport in § 3.5. The steady-state version of (4.9) is
where the constant
![]() $C_{{\it\Sigma}}$
would be fixed by the overall gradient of the passive scalar across the system. We rescale
$C_{{\it\Sigma}}$
would be fixed by the overall gradient of the passive scalar across the system. We rescale
together with (3.35), so that we can write from (4.11)
To obtain a passive scalar profile we first fix
![]() $\tilde{{\it\lambda}}^{-3}=2-1/16$
, giving the sharpest
$\tilde{{\it\lambda}}^{-3}=2-1/16$
, giving the sharpest
![]() $\tilde{{\it\Omega}}$
profile depicted in figure 4(a). We then integrate (4.13) for any value of
$\tilde{{\it\Omega}}$
profile depicted in figure 4(a). We then integrate (4.13) for any value of
![]() $\tilde{{\it\beta}}$
, and the resulting values of
$\tilde{{\it\beta}}$
, and the resulting values of
![]() $\tilde{{\it\Sigma}}({\tilde{Y}})$
are shown in figure 6(a) for
$\tilde{{\it\Sigma}}({\tilde{Y}})$
are shown in figure 6(a) for
![]() $\tilde{{\it\beta}}=0,1,\ldots ,5$
, reading up the curves. There is little effect on sharpening the passive scalar profiles in (a), although the plots of the gradient
$\tilde{{\it\beta}}=0,1,\ldots ,5$
, reading up the curves. There is little effect on sharpening the passive scalar profiles in (a), although the plots of the gradient
![]() $\partial _{{\tilde{Y}}}\tilde{{\it\Sigma}}$
in (b) show more structure. It should be noted that if the passive scalar is the vector potential of a kinematic magnetic field, then figure 5(b) represents the field itself, reduced to approximately half the exterior value within the step for
$\partial _{{\tilde{Y}}}\tilde{{\it\Sigma}}$
in (b) show more structure. It should be noted that if the passive scalar is the vector potential of a kinematic magnetic field, then figure 5(b) represents the field itself, reduced to approximately half the exterior value within the step for
![]() ${\it\beta}=0$
. This may be thought of as a process of flux expulsion (Weiss Reference Weiss1966), from regions of stronger motion corresponding to greater effective scalar diffusivity.
${\it\beta}=0$
. This may be thought of as a process of flux expulsion (Weiss Reference Weiss1966), from regions of stronger motion corresponding to greater effective scalar diffusivity.

Figure 6. Plots of equilibrium scalar profiles by integrating the ODE (4.13). Here,
![]() $2-\tilde{{\it\lambda}}^{-3}=1/16$
. For values of
$2-\tilde{{\it\lambda}}^{-3}=1/16$
. For values of
![]() $\tilde{{\it\beta}}=0,1,\ldots ,5$
, in (a)
$\tilde{{\it\beta}}=0,1,\ldots ,5$
, in (a)
![]() $\tilde{{\it\Sigma}}({\tilde{Y}})$
(reading up the curves) and in (b)
$\tilde{{\it\Sigma}}({\tilde{Y}})$
(reading up the curves) and in (b)
![]() $\partial _{{\tilde{Y}}}\tilde{{\it\Sigma}}$
(reading up) are plotted against
$\partial _{{\tilde{Y}}}\tilde{{\it\Sigma}}$
(reading up) are plotted against
![]() ${\tilde{Y}}$
.
${\tilde{Y}}$
.
Somewhat paradoxically then, a step jump can be supported in the vorticity profile of figure 4(a), whereas a passive scalar profile remains relatively unperturbed. Of course, different types of transport are involved, and whereas the effective viscosity can become negative and nearly cancel out the molecular viscosity to allow a jump, the same is not true for the passive scalar (or vector potential). Further investigations for the case of different values of the scalar diffusivity and viscosity in (2.7) would be of interest, but the governing ODEs would need to be solved numerically.
5 Magnetohydrodynamic transport
We now return to the full MHD problem given in § 2.2, armed with the above discussion of the hydrodynamic and passive scalar/kinematic magnetic field cases. The scalings remain the same for the vorticity as in § 3, and for the vector potential the development follows that for the passive scalar in § 4, though naturally we now have the Lorentz force coupling. We will drop further mention of the passive scalar from the discussion.
5.1 Multiple-scale formulation
We again remove the fast advection terms in (2.11), (2.12), by setting
(as listed in table 1), to obtain
with corresponding fluxes
![]() $F_{\mathit{R}}$
in (3.5),
$F_{\mathit{R}}$
in (3.5),
For the large-scale expansion we replace
As before, we adopt
![]() $Y={\it\varepsilon}y$
,
$Y={\it\varepsilon}y$
,
![]() $T={\it\varepsilon}t$
,
$T={\it\varepsilon}t$
,
![]() $\mathscr{T}={\it\varepsilon}^{3}t$
, as well as the replacements
$\mathscr{T}={\it\varepsilon}^{3}t$
, as well as the replacements
referring to the small-scale fields, and
with the large-scale equations
recalling (2.23). The flux
![]() $F_{\mathit{R}}$
is given in (3.11); we gain a similar term from the Lorentz force,
$F_{\mathit{R}}$
is given in (3.11); we gain a similar term from the Lorentz force,
and
![]() $F_{\mathit{M}}$
remains as in (5.6).
$F_{\mathit{M}}$
remains as in (5.6).
5.2 Numerical solution
Again, before embarking on analysis, we present a simulation of the full wave problem with
![]() ${\it\beta}=0$
,
${\it\beta}=0$
,
![]() ${\it\varepsilon}=0.1$
,
${\it\varepsilon}=0.1$
,
![]() $U=\cos Y$
and a constant field
$U=\cos Y$
and a constant field
![]() $B=2$
. The exact rescaled equations are
$B=2$
. The exact rescaled equations are
(The fluxes
![]() $F_{\mathit{R}}$
,
$F_{\mathit{R}}$
,
![]() $F_{\mathit{L}}$
are rescaled as in (3.17) whereas
$F_{\mathit{L}}$
are rescaled as in (3.17) whereas
![]() $F_{\mathit{P}}$
is not.) Figure 7 shows the real parts of the fields
$F_{\mathit{P}}$
is not.) Figure 7 shows the real parts of the fields
![]() ${\it\omega},{\it\psi},j,a$
as functions of
${\it\omega},{\it\psi},j,a$
as functions of
![]() $(T,Y)$
in (a–d), with the corresponding fluxes in (e–h). As well as the general decrease in scale as
$(T,Y)$
in (a–d), with the corresponding fluxes in (e–h). As well as the general decrease in scale as
![]() $T$
increases, one can clearly see the presence of oscillations, Alfvén waves, in which energy is transferred between the fluid flow and the magnetic field in (a–d). With these are oscillations in the instantaneous fluxes giving the feedback on the mean flow and field.
$T$
increases, one can clearly see the presence of oscillations, Alfvén waves, in which energy is transferred between the fluid flow and the magnetic field in (a–d). With these are oscillations in the instantaneous fluxes giving the feedback on the mean flow and field.

Figure 7. Simulation of waves with
![]() ${\it\beta}=0$
,
${\it\beta}=0$
,
![]() $m=1$
,
$m=1$
,
![]() ${\it\varepsilon}=0.1$
,
${\it\varepsilon}=0.1$
,
![]() ${\it\lambda}=0$
,
${\it\lambda}=0$
,
![]() $U=\cos Y$
and
$U=\cos Y$
and
![]() $B=2$
. In (a)
$B=2$
. In (a)
![]() $\text{Re}\,{\it\omega}$
, (b)
$\text{Re}\,{\it\omega}$
, (b)
![]() $\text{Re}\,{\it\psi}$
, (c)
$\text{Re}\,{\it\psi}$
, (c)
![]() $\text{Re}\,j$
, (d)
$\text{Re}\,j$
, (d)
![]() $\text{Re}\,a$
, (e)
$\text{Re}\,a$
, (e)
![]() $F_{\mathit{R}}$
, (f)
$F_{\mathit{R}}$
, (f)
![]() $F_{\mathit{L}}$
, (g)
$F_{\mathit{L}}$
, (g)
![]() $F_{\mathit{K}}$
and (h)
$F_{\mathit{K}}$
and (h)
![]() $F_{\mathit{M}}$
are plotted in the
$F_{\mathit{M}}$
are plotted in the
![]() $(T,Y)$
-plane.
$(T,Y)$
-plane.
5.3 Multiple-scale expansion
To analyse the complicated picture emerging in figure 7, we again expand all small-scale fields in powers of
![]() ${\it\varepsilon}$
to yield the leading-order wave equations, from (5.10), (5.11),
${\it\varepsilon}$
to yield the leading-order wave equations, from (5.10), (5.11),
These are to be solved with initial conditions from (2.15) and the results fed into the mean equations via fluxes (dropping the terms of order
![]() ${\it\varepsilon}$
),
${\it\varepsilon}$
),
Unfortunately, the above ODEs (5.18)–(5.20) are not soluble analytically in simple terms (that is, without recourse to so-called Heun functions). They can be solved approximately in the limit of strong and weak shear as measured by
![]() $\hat{B}$
below (Leprovost & Kim Reference Leprovost and Kim2009) to obtain expressions for the effective transport coefficients for the case of isotropic driving.
$\hat{B}$
below (Leprovost & Kim Reference Leprovost and Kim2009) to obtain expressions for the effective transport coefficients for the case of isotropic driving.
In the first instance we wish to proceed without approximation. We first rescale and remove the diffusive decay by setting
with the damping term
![]() $D$
given in (3.22), to leave equations for sheared Alfvén waves,
$D$
given in (3.22), to leave equations for sheared Alfvén waves,
Although we cannot solve the ODEs, we proceed for the moment as if we knew the solution with all quantities expressed as functions of
![]() $(T,{\it\Omega},B,{\it\beta})$
. We would then evaluate the fluxes by differentiating these expressions, and could write the instantaneous fluxes in the form
$(T,{\it\Omega},B,{\it\beta})$
. We would then evaluate the fluxes by differentiating these expressions, and could write the instantaneous fluxes in the form
It should be noted that, crucially, the fluxes depend on
![]() $Y$
not only through gradients of the vorticity profile
$Y$
not only through gradients of the vorticity profile
![]() ${\it\Omega}^{\prime }$
(as in the hydrodynamic problem earlier) but also through the gradients
${\it\Omega}^{\prime }$
(as in the hydrodynamic problem earlier) but also through the gradients
![]() $B^{\prime }$
in the magnetic field profile. This feature, discussed by Chechkin (Reference Chechkin1999), Kim (Reference Kim2007) and Leprovost & Kim (Reference Leprovost and Kim2009), creates additional complexity in the MHD problem.
$B^{\prime }$
in the magnetic field profile. This feature, discussed by Chechkin (Reference Chechkin1999), Kim (Reference Kim2007) and Leprovost & Kim (Reference Leprovost and Kim2009), creates additional complexity in the MHD problem.
Following through with similar notation to § 3.3, the functions
![]() $f_{\mathit{Z}}$
encapsulate all of the interesting time evolution of the fluxes, and this may be most conveniently expressed by first extending the definitions in (3.22) to include
$f_{\mathit{Z}}$
encapsulate all of the interesting time evolution of the fluxes, and this may be most conveniently expressed by first extending the definitions in (3.22) to include
We may then write all of the functions in terms of
![]() ${\it\tau}$
and three parameters
${\it\tau}$
and three parameters
![]() $\hat{B}$
,
$\hat{B}$
,
![]() $\hat{{\it\beta}}$
and
$\hat{{\it\beta}}$
and
![]() $\hat{{\it\lambda}}$
, with
$\hat{{\it\lambda}}$
, with
Here, the functions
![]() $f_{{\it\Omega}\mathit{R}}$
and
$f_{{\it\Omega}\mathit{R}}$
and
![]() $f_{{\it\Omega}\mathit{L}}$
capture the effect of a vorticity gradient
$f_{{\it\Omega}\mathit{L}}$
capture the effect of a vorticity gradient
![]() ${\it\Omega}^{\prime }$
on the Reynolds stress and Lorentz force, while
${\it\Omega}^{\prime }$
on the Reynolds stress and Lorentz force, while
![]() $f_{B\mathit{R}}$
and
$f_{B\mathit{R}}$
and
![]() $f_{B\mathit{L}}$
give the effect in the Navier–Stokes equation of a gradient of background magnetic field
$f_{B\mathit{L}}$
give the effect in the Navier–Stokes equation of a gradient of background magnetic field
![]() $B^{\prime }$
. The transport of scalar vector potential
$B^{\prime }$
. The transport of scalar vector potential
![]() $A$
is linked to
$A$
is linked to
![]() $B=A^{\prime }$
through the
$B=A^{\prime }$
through the
![]() $f_{\mathit{M}}$
term.
$f_{\mathit{M}}$
term.
We now extend the convention in (2.23), so that
![]() $\mathit{Z}_{\mathit{K}}=\mathit{Z}_{\mathit{R}}-\mathit{Z}_{\mathit{L}}$
for any quantity
$\mathit{Z}_{\mathit{K}}=\mathit{Z}_{\mathit{R}}-\mathit{Z}_{\mathit{L}}$
for any quantity
![]() $\mathit{Z}$
, and express the integrated fluxes in terms of transport coefficients
$\mathit{Z}$
, and express the integrated fluxes in terms of transport coefficients
![]() ${\it\nu}_{\mathit{eff}}$
,
${\it\nu}_{\mathit{eff}}$
,
![]() ${\it\chi}_{\mathit{eff}}$
and
${\it\chi}_{\mathit{eff}}$
and
![]() ${\it\eta}_{\mathit{eff}}$
,
${\it\eta}_{\mathit{eff}}$
,
This leads to coupled large-scale equations
with (making use of (3.27))
We have reached the end of an analytical development for the MHD problem mirroring that for the hydrodynamic framework in § 3.3. If we could solve the ODEs (5.23) explicitly to obtain
![]() $\hat{{\it\zeta}}_{0},\hat{{\it\phi}}_{0},\hat{{\it\alpha}}_{0},\hat{{\it\gamma}}_{0}$
, taken as functions of
$\hat{{\it\zeta}}_{0},\hat{{\it\phi}}_{0},\hat{{\it\alpha}}_{0},\hat{{\it\gamma}}_{0}$
, taken as functions of
![]() $(T,{\it\Omega},B,{\it\beta})$
, we would then calculate the functions
$(T,{\it\Omega},B,{\it\beta})$
, we would then calculate the functions
![]() $f_{\mathit{Z}}$
in (5.28)–(5.32), differentiating quantities as needed. Although we cannot solve these ODEs analytically in general, we can do so numerically, and in fact we can add to these ODEs further equations for derivatives such as
$f_{\mathit{Z}}$
in (5.28)–(5.32), differentiating quantities as needed. Although we cannot solve these ODEs analytically in general, we can do so numerically, and in fact we can add to these ODEs further equations for derivatives such as
![]() ${\it\Omega}\partial _{{\it\Omega}}|\hat{{\it\zeta}}_{0}|^{2}$
or
${\it\Omega}\partial _{{\it\Omega}}|\hat{{\it\zeta}}_{0}|^{2}$
or
![]() $B\partial _{B}|\hat{{\it\zeta}}_{0}|^{2}$
. We relegate these uninspiring details to (B 1)–(B 6) in appendix B.
$B\partial _{B}|\hat{{\it\zeta}}_{0}|^{2}$
. We relegate these uninspiring details to (B 1)–(B 6) in appendix B.

Figure 8. Plots of
![]() $f_{{\it\Omega}\mathit{R}}$
(solid),
$f_{{\it\Omega}\mathit{R}}$
(solid),
![]() $f_{{\it\Omega}\mathit{L}}$
(dashed) and
$f_{{\it\Omega}\mathit{L}}$
(dashed) and
![]() $f_{{\it\Omega}\mathit{K}}$
(dotted) as functions of
$f_{{\it\Omega}\mathit{K}}$
(dotted) as functions of
![]() ${\it\tau}$
for
${\it\tau}$
for
![]() $\hat{{\it\lambda}}=\hat{{\it\beta}}=0$
and (a)
$\hat{{\it\lambda}}=\hat{{\it\beta}}=0$
and (a)
![]() $\hat{B}=0.5$
and (b)
$\hat{B}=0.5$
and (b)
![]() $\hat{B}=2.0$
.
$\hat{B}=2.0$
.

Figure 9. Plots of
![]() $f_{B\mathit{R}}$
(solid),
$f_{B\mathit{R}}$
(solid),
![]() $f_{B\mathit{L}}$
(dashed) and
$f_{B\mathit{L}}$
(dashed) and
![]() $f_{B\mathit{K}}$
(dotted) as functions of
$f_{B\mathit{K}}$
(dotted) as functions of
![]() ${\it\tau}$
for
${\it\tau}$
for
![]() $\hat{{\it\lambda}}=\hat{{\it\beta}}=0$
and (a)
$\hat{{\it\lambda}}=\hat{{\it\beta}}=0$
and (a)
![]() $\hat{B}=0.5$
and (b)
$\hat{B}=0.5$
and (b)
![]() $\hat{B}=2.0$
.
$\hat{B}=2.0$
.

Figure 10. Plots of
![]() $f_{M}$
as a function of
$f_{M}$
as a function of
![]() ${\it\tau}$
for
${\it\tau}$
for
![]() $\hat{{\it\lambda}}=\hat{{\it\beta}}=0$
and (a)
$\hat{{\it\lambda}}=\hat{{\it\beta}}=0$
and (a)
![]() $\hat{B}=0.5$
and (b)
$\hat{B}=0.5$
and (b)
![]() $\hat{B}=2.0$
.
$\hat{B}=2.0$
.
With this set-up, figures 8–10 show the transport terms
![]() $f_{\mathit{Z}}$
as functions of
$f_{\mathit{Z}}$
as functions of
![]() ${\it\tau}$
for
${\it\tau}$
for
![]() $\hat{{\it\lambda}},\hat{{\it\beta}}=0$
and values
$\hat{{\it\lambda}},\hat{{\it\beta}}=0$
and values
![]() $\hat{B}=0.5$
and 2. The results for
$\hat{B}=0.5$
and 2. The results for
![]() $f_{{\it\Omega}\mathit{R}}$
(solid) in figure 8 may be compared with
$f_{{\it\Omega}\mathit{R}}$
(solid) in figure 8 may be compared with
![]() $f_{\mathit{R}}$
(outer curve) in figure 2(a); it is clear how increasing
$f_{\mathit{R}}$
(outer curve) in figure 2(a); it is clear how increasing
![]() $\hat{B}$
gives rise to oscillations in these fluxes because of Alfvén waves. Likewise,
$\hat{B}$
gives rise to oscillations in these fluxes because of Alfvén waves. Likewise,
![]() $f_{\mathit{M}}$
in figure 10 may be compared with
$f_{\mathit{M}}$
in figure 10 may be compared with
![]() $f_{\mathit{P}}$
for a passive scalar in figure 5(a) (outer curve).
$f_{\mathit{P}}$
for a passive scalar in figure 5(a) (outer curve).

Figure 11. Plots of (a)
![]() $\hat{{\it\lambda}}^{2}h_{{\it\Omega}\mathit{R}}$
, (b)
$\hat{{\it\lambda}}^{2}h_{{\it\Omega}\mathit{R}}$
, (b)
![]() $\hat{{\it\lambda}}^{2}h_{{\it\Omega}\mathit{L}}$
, (c)
$\hat{{\it\lambda}}^{2}h_{{\it\Omega}\mathit{L}}$
, (c)
![]() $\hat{{\it\lambda}}^{2}h_{{\it\Omega}\mathit{K}}$
, (d)
$\hat{{\it\lambda}}^{2}h_{{\it\Omega}\mathit{K}}$
, (d)
![]() $\hat{{\it\lambda}}^{2}h_{B\mathit{R}}$
, (e)
$\hat{{\it\lambda}}^{2}h_{B\mathit{R}}$
, (e)
![]() $\hat{{\it\lambda}}^{2}h_{B\mathit{L}}$
, (f)
$\hat{{\it\lambda}}^{2}h_{B\mathit{L}}$
, (f)
![]() $\hat{{\it\lambda}}^{2}h_{B\mathit{K}}$
, (g)
$\hat{{\it\lambda}}^{2}h_{B\mathit{K}}$
, (g)
![]() $\hat{{\it\lambda}}^{2}h_{\mathit{M}}$
, (h)
$\hat{{\it\lambda}}^{2}h_{\mathit{M}}$
, (h)
![]() $\hat{{\it\lambda}}^{2}m^{3}{\it\Omega}B({\it\eta}_{\mathit{eff}}+B\,\partial _{B}{\it\eta}_{\mathit{eff}})$
(see (B 11)) and (i)
$\hat{{\it\lambda}}^{2}m^{3}{\it\Omega}B({\it\eta}_{\mathit{eff}}+B\,\partial _{B}{\it\eta}_{\mathit{eff}})$
(see (B 11)) and (i)
![]() $\hat{{\it\lambda}}^{2}m^{3}{\it\Omega}^{2}\,\partial _{{\it\Omega}}{\it\eta}_{\mathit{eff}}$
(see (B 12)) as functions of
$\hat{{\it\lambda}}^{2}m^{3}{\it\Omega}^{2}\,\partial _{{\it\Omega}}{\it\eta}_{\mathit{eff}}$
(see (B 12)) as functions of
![]() $\hat{{\it\lambda}}$
for
$\hat{{\it\lambda}}$
for
![]() $\hat{B}=0$
, 1, 2, 3, 4 (solid) and 5 (dashed), with
$\hat{B}=0$
, 1, 2, 3, 4 (solid) and 5 (dashed), with
![]() $\hat{{\it\beta}}=0$
.
$\hat{{\it\beta}}=0$
.
We now begin to suffer from the presence of too many parameters in the problem and struggle to plot the dependence of quantities
![]() $f_{\mathit{Z}}({\it\tau},\hat{B},\hat{{\it\beta}},\hat{{\it\lambda}})$
. However, the quantities
$f_{\mathit{Z}}({\it\tau},\hat{B},\hat{{\it\beta}},\hat{{\it\lambda}})$
. However, the quantities
![]() $\hat{{\it\lambda}}^{2}h_{\mathit{Z}}(\hat{B},\hat{{\it\beta}},\hat{{\it\lambda}})$
(the prefactor chosen to show the clearest structure) are plotted as functions of
$\hat{{\it\lambda}}^{2}h_{\mathit{Z}}(\hat{B},\hat{{\it\beta}},\hat{{\it\lambda}})$
(the prefactor chosen to show the clearest structure) are plotted as functions of
![]() $\hat{{\it\lambda}}$
for
$\hat{{\it\lambda}}$
for
![]() $\hat{{\it\beta}}=0$
and different values of
$\hat{{\it\beta}}=0$
and different values of
![]() $\hat{B}$
in figure 11. The values are
$\hat{B}$
in figure 11. The values are
![]() $\hat{B}=0$
,
$\hat{B}=0$
,
![]() $1,\ldots ,5$
, with the last curve dashed to mark it out. Where there are straight lines, this reflects the lack of coupling in the non-magnetic case
$1,\ldots ,5$
, with the last curve dashed to mark it out. Where there are straight lines, this reflects the lack of coupling in the non-magnetic case
![]() $\hat{B}=0$
. Some effects can clearly be seen, for example the effect of magnetic field is to suppress transport of
$\hat{B}=0$
. Some effects can clearly be seen, for example the effect of magnetic field is to suppress transport of
![]() $A$
, via suppression of
$A$
, via suppression of
![]() ${\it\eta}_{\mathit{eff}}$
or
${\it\eta}_{\mathit{eff}}$
or
![]() $h_{\mathit{M}}$
, depicted in figure 11(g). These curves have been carefully confirmed against analytical approximations (see appendix B) for varying values of
$h_{\mathit{M}}$
, depicted in figure 11(g). These curves have been carefully confirmed against analytical approximations (see appendix B) for varying values of
![]() $\hat{B},\hat{{\it\lambda}},\hat{{\it\beta}}\gg 1$
as a partial check on our analysis and coding.
$\hat{B},\hat{{\it\lambda}},\hat{{\it\beta}}\gg 1$
as a partial check on our analysis and coding.
5.4 Zonostrophic instability
Although any calculations become somewhat opaque at this point, as we can only evaluate many quantities numerically, we can still press on to study zonostrophic instability for the MHD system, based on the large-scale equations (5.34), (5.35). These are complicated as we have three effective transport terms, which themselves depend on the local vorticity
![]() ${\it\Omega}$
and magnetic field
${\it\Omega}$
and magnetic field
![]() $B$
.
$B$
.
We therefore think of the coefficients
![]() ${\it\nu}_{\mathit{eff}},{\it\chi}_{\mathit{eff}},{\it\eta}_{\mathit{eff}}$
as functions of
${\it\nu}_{\mathit{eff}},{\it\chi}_{\mathit{eff}},{\it\eta}_{\mathit{eff}}$
as functions of
![]() $({\it\Omega},B,{\it\beta},{\it\lambda})$
and linearise (5.34), (5.35) about a state of constant vorticity
$({\it\Omega},B,{\it\beta},{\it\lambda})$
and linearise (5.34), (5.35) about a state of constant vorticity
![]() ${\it\Omega}_{0}$
and field
${\it\Omega}_{0}$
and field
![]() $B_{0}$
. We thus replace
$B_{0}$
. We thus replace
where now
![]() ${\it\Omega}$
,
${\it\Omega}$
,
![]() $B=A^{\prime }$
and
$B=A^{\prime }$
and
![]() $A$
are small quantities. We then obtain
$A$
are small quantities. We then obtain
where the coefficients and their derivatives are evaluated at
![]() $({\it\Omega},B)=({\it\Omega}_{0},B_{0})$
. In general, the equations are completely coupled, and if we seek a mode with
$({\it\Omega},B)=({\it\Omega}_{0},B_{0})$
. In general, the equations are completely coupled, and if we seek a mode with
![]() $({\it\Omega},B)$
proportional to
$({\it\Omega},B)$
proportional to
![]() $\exp (PK^{2}\mathscr{T}+\text{i}KY)$
we find growth rates
$\exp (PK^{2}\mathscr{T}+\text{i}KY)$
we find growth rates
![]() $P$
satisfying
$P$
satisfying
where
![]() $\unicode[STIX]{x1D644}$
is the identity matrix.
$\unicode[STIX]{x1D644}$
is the identity matrix.
We wish to investigate instabilities as a function of
![]() $({\it\Omega}_{0},B_{0},{\it\beta},{\it\lambda})$
, and we commence by setting
$({\it\Omega}_{0},B_{0},{\it\beta},{\it\lambda})$
, and we commence by setting
![]() ${\it\beta}=0$
and
${\it\beta}=0$
and
![]() ${\it\Omega}_{0}=0$
, no background shear. This is a major simplification, because for given
${\it\Omega}_{0}=0$
, no background shear. This is a major simplification, because for given
![]() ${\it\lambda}$
,
${\it\lambda}$
,
![]() $B_{0}$
, we use the limiting expressions for
$B_{0}$
, we use the limiting expressions for
![]() ${\it\Omega}_{0}\rightarrow 0$
, that is for
${\it\Omega}_{0}\rightarrow 0$
, that is for
![]() $\hat{{\it\lambda}},\hat{B}\gg 1$
. We are again effectively in a viscous regime (on the
$\hat{{\it\lambda}},\hat{B}\gg 1$
. We are again effectively in a viscous regime (on the
![]() ${\it\tau}$
time scale) in which the exponential damping effect of the diffusion terms is dominant, for
${\it\tau}$
time scale) in which the exponential damping effect of the diffusion terms is dominant, for
![]() ${\it\tau}=O(\hat{{\it\lambda}}^{-1})\ll 1$
. On this time scale
${\it\tau}=O(\hat{{\it\lambda}}^{-1})\ll 1$
. On this time scale
![]() $\hat{B}{\it\tau}=O(1)$
also and so we need to use
$\hat{B}{\it\tau}=O(1)$
also and so we need to use
as leading-order approximations to solutions of (5.23) (see appendix B). (It should be noted that a straightforward Maclaurin expansion in powers of
![]() ${\it\tau}$
is not satisfactory as this series becomes non-uniform when
${\it\tau}$
is not satisfactory as this series becomes non-uniform when
![]() $\hat{B}{\it\tau}=O(1)$
; our series is valid provided only that
$\hat{B}{\it\tau}=O(1)$
; our series is valid provided only that
![]() $\hat{B}{\it\tau}^{2}\ll 1$
.) This gives expressions for the
$\hat{B}{\it\tau}^{2}\ll 1$
.) This gives expressions for the
![]() $h_{\mathit{Z}}$
that we do not set out here, but that have been used to check the numerical calculations in figure 11. More interestingly, we obtain
$h_{\mathit{Z}}$
that we do not set out here, but that have been used to check the numerical calculations in figure 11. More interestingly, we obtain
valid for fixed
![]() ${\it\lambda}$
and
${\it\lambda}$
and
![]() $B$
with
$B$
with
![]() ${\it\Omega}\rightarrow 0$
, at leading order.
${\it\Omega}\rightarrow 0$
, at leading order.

Figure 12. Contour plot of
![]() $m^{2}P$
(5.43) in the
$m^{2}P$
(5.43) in the
![]() $(m^{2}{\it\lambda},mB_{0})$
-plane for
$(m^{2}{\it\lambda},mB_{0})$
-plane for
![]() ${\it\Omega}_{0}={\it\beta}=0$
. Contours increase from
${\it\Omega}_{0}={\it\beta}=0$
. Contours increase from
![]() $m^{2}P=0$
(outermost) in steps of 0.1 to
$m^{2}P=0$
(outermost) in steps of 0.1 to
![]() $m^{2}P=10$
.
$m^{2}P=10$
.
Turning to (5.40), at
![]() ${\it\Omega}={\it\Omega}_{0}=0$
both diagonal entries vanish, and in addition for the bottom right entry
${\it\Omega}={\it\Omega}_{0}=0$
both diagonal entries vanish, and in addition for the bottom right entry
![]() ${\it\eta}_{\mathit{eff}}+B\partial _{B}{\it\eta}_{\mathit{eff}}=-{\it\nu}_{\mathit{eff}}$
at this order. Thus, we are left with explicit expressions for the growth rates,
${\it\eta}_{\mathit{eff}}+B\partial _{B}{\it\eta}_{\mathit{eff}}=-{\it\nu}_{\mathit{eff}}$
at this order. Thus, we are left with explicit expressions for the growth rates,
The corresponding growth rate contours for
![]() $m^{2}P\geqslant 0$
are depicted in figure 12. The lower set of contours, intersecting the horizontal axis, are for the first set of eigenvalues in (5.43) and correspond to the hydrodynamic zonostrophic instability in § 3.4, modified by the magnetic field. This has a suppressing effect, switching off the instability for
$m^{2}P\geqslant 0$
are depicted in figure 12. The lower set of contours, intersecting the horizontal axis, are for the first set of eigenvalues in (5.43) and correspond to the hydrodynamic zonostrophic instability in § 3.4, modified by the magnetic field. This has a suppressing effect, switching off the instability for
![]() $mB_{0}$
larger than approximately 0.34, in at least qualitative agreement with the results of Tobias et al. (Reference Tobias, Hughes and Diamond2012).
$mB_{0}$
larger than approximately 0.34, in at least qualitative agreement with the results of Tobias et al. (Reference Tobias, Hughes and Diamond2012).
The second set of eigenvalues in (5.43) gives contours intersecting the vertical axis in figure 12. This is a magnetically driven instability, in which the variations of diffusivity
![]() ${\it\eta}_{\mathit{eff}}$
with
${\it\eta}_{\mathit{eff}}$
with
![]() $B$
lead to the tendency of the field to segregate into regions of weaker and stronger
$B$
lead to the tendency of the field to segregate into regions of weaker and stronger
![]() $B$
. The effect of removing the field from regions of overturning motion is known as flux expulsion (Weiss Reference Weiss1966); in such regions the Lorentz force feedback is then reduced, increasing the fluid flows and so enhancing the flux expulsion, giving a runaway effect. The zonostrophic instability is restricted to a range of
$B$
. The effect of removing the field from regions of overturning motion is known as flux expulsion (Weiss Reference Weiss1966); in such regions the Lorentz force feedback is then reduced, increasing the fluid flows and so enhancing the flux expulsion, giving a runaway effect. The zonostrophic instability is restricted to a range of
![]() ${\it\lambda}$
values for
${\it\lambda}$
values for
![]() $B_{0}=0$
, whereas the magnetic flux expulsion instability occurs for any
$B_{0}=0$
, whereas the magnetic flux expulsion instability occurs for any
![]() $B_{0}$
as
$B_{0}$
as
![]() ${\it\lambda}\rightarrow 0$
. It should be noted that this latter instability does not correspond to a sign change in
${\it\lambda}\rightarrow 0$
. It should be noted that this latter instability does not correspond to a sign change in
![]() ${\it\chi}_{\mathit{eff}}$
, which would be impossible as the effective diffusivity arises from advection–diffusion of
${\it\chi}_{\mathit{eff}}$
, which would be impossible as the effective diffusivity arises from advection–diffusion of
![]() $A$
, but is seen in (5.40) to emerge from the variation of
$A$
, but is seen in (5.40) to emerge from the variation of
![]() ${\it\chi}_{\mathit{eff}}$
with respect to changes in the magnetic field
${\it\chi}_{\mathit{eff}}$
with respect to changes in the magnetic field
![]() $B$
.
$B$
.

Figure 13. Contour plot of
![]() $m^{2}P$
from (5.40) in the
$m^{2}P$
from (5.40) in the
![]() $(m^{2}{\it\lambda},mB_{0})$
-plane for
$(m^{2}{\it\lambda},mB_{0})$
-plane for
![]() ${\it\beta}=0$
and (a,b)
${\it\beta}=0$
and (a,b)
![]() ${\it\Omega}_{0}=0.1$
and (c,d)
${\it\Omega}_{0}=0.1$
and (c,d)
![]() ${\it\Omega}_{0}=0.2$
. In (a,c) the real part of
${\it\Omega}_{0}=0.2$
. In (a,c) the real part of
![]() $m^{2}P$
is shown and in (b,d) the imaginary part. Contours increase from
$m^{2}P$
is shown and in (b,d) the imaginary part. Contours increase from
![]() $m^{2}P=0$
(outermost) in steps of 0.1 to 10.
$m^{2}P=0$
(outermost) in steps of 0.1 to 10.
From this calculation we can now include a background shear, linearising about
![]() $({\it\Omega}_{0},B_{0})$
with
$({\it\Omega}_{0},B_{0})$
with
![]() ${\it\Omega}_{0}>0$
. As in § 3.4, we can no longer evaluate the quantities
${\it\Omega}_{0}>0$
. As in § 3.4, we can no longer evaluate the quantities
![]() ${\it\nu}_{\mathit{eff}}$
,
${\it\nu}_{\mathit{eff}}$
,
![]() ${\it\chi}_{\mathit{eff}}$
and
${\it\chi}_{\mathit{eff}}$
and
![]() ${\it\eta}_{\mathit{eff}}$
analytically to obtain values of
${\it\eta}_{\mathit{eff}}$
analytically to obtain values of
![]() $P$
from (5.40), and so we compute them numerically. Figure 13 shows the contour plot of
$P$
from (5.40), and so we compute them numerically. Figure 13 shows the contour plot of
![]() $m^{2}P$
for (a,b)
$m^{2}P$
for (a,b)
![]() ${\it\Omega}_{0}=0.1$
and (c,d) 0.2. The real parts of
${\it\Omega}_{0}=0.1$
and (c,d) 0.2. The real parts of
![]() $m^{2}P$
are shown in (a,c), and these reveal that shear tends to suppress both types of instability. Interestingly though, there emerges near to the line
$m^{2}P$
are shown in (a,c), and these reveal that shear tends to suppress both types of instability. Interestingly though, there emerges near to the line
![]() $mB_{0}=m^{2}{\it\lambda}$
a region of oscillatory instability, with a pair of complex conjugate values of
$mB_{0}=m^{2}{\it\lambda}$
a region of oscillatory instability, with a pair of complex conjugate values of
![]() $m^{2}P$
, whose imaginary parts are depicted in (b,d). This suggests emergence of a coupled instability through overstability. This can be seen to some extent in our analysis: in (5.40), the product
$m^{2}P$
, whose imaginary parts are depicted in (b,d). This suggests emergence of a coupled instability through overstability. This can be seen to some extent in our analysis: in (5.40), the product
![]() ${\it\chi}_{\mathit{eff}}B_{0}\partial _{{\it\Omega}}{\it\eta}_{\mathit{eff}}$
is negative (near
${\it\chi}_{\mathit{eff}}B_{0}\partial _{{\it\Omega}}{\it\eta}_{\mathit{eff}}$
is negative (near
![]() $mB_{0}=m^{2}{\it\lambda}$
) in our analytical approximation, from (5.42), (B 10). It also corresponds to the product of the quantities shown in figure 11(f,i) being negative, at least for small
$mB_{0}=m^{2}{\it\lambda}$
) in our analytical approximation, from (5.42), (B 10). It also corresponds to the product of the quantities shown in figure 11(f,i) being negative, at least for small
![]() $B$
. Therefore, if the actual diagonal terms are small, the off-diagonal terms can give an imaginary part in
$B$
. Therefore, if the actual diagonal terms are small, the off-diagonal terms can give an imaginary part in
![]() $m^{2}P$
. The oscillatory eigenvalue could be considered as resulting from a resonance between the two instabilities in figure 12.
$m^{2}P$
. The oscillatory eigenvalue could be considered as resulting from a resonance between the two instabilities in figure 12.

Figure 14. Contour plot of
![]() $m^{2}P$
(3.32) in the
$m^{2}P$
(3.32) in the
![]() $(m^{2}{\it\lambda},mB_{0})$
-plane for
$(m^{2}{\it\lambda},mB_{0})$
-plane for
![]() ${\it\Omega}_{0}=0$
and (a,b)
${\it\Omega}_{0}=0$
and (a,b)
![]() ${\it\beta}=0.2$
and (c,d)
${\it\beta}=0.2$
and (c,d)
![]() ${\it\beta}=0.4$
. In (a,c) contours for the zonostrophic instability are shown and in (b,d) contours of the magnetic segregation instability. Contours increase from
${\it\beta}=0.4$
. In (a,c) contours for the zonostrophic instability are shown and in (b,d) contours of the magnetic segregation instability. Contours increase from
![]() $m^{2}P=0$
(outermost) in steps of 0.1 to 10.
$m^{2}P=0$
(outermost) in steps of 0.1 to 10.
The other effect we can include is that of a background vorticity gradient,
![]() ${\it\beta}\neq 0$
. We turn off the background shear,
${\it\beta}\neq 0$
. We turn off the background shear,
![]() ${\it\Omega}_{0}=0$
, and reintroduce the parameter
${\it\Omega}_{0}=0$
, and reintroduce the parameter
![]() $\hat{{\it\beta}}$
. The corresponding transport coefficients may be computed, as we are again in the limit
$\hat{{\it\beta}}$
. The corresponding transport coefficients may be computed, as we are again in the limit
![]() $\hat{{\it\lambda}},\hat{{\it\beta}},\hat{B}\gg 1$
as
$\hat{{\it\lambda}},\hat{{\it\beta}},\hat{B}\gg 1$
as
![]() ${\it\Omega}_{0}\rightarrow 0$
, and these are given in (B 14)–(B 16). The off-diagonal elements are again zero (at this order) in the matrix (5.40), and so the problem decouples to eigenvalues given by the diagonal entries only. Figure 14 shows plots of the zonostrophic modes in (a,c) and the magnetic flux expulsion modes in (b,d) for
${\it\Omega}_{0}\rightarrow 0$
, and these are given in (B 14)–(B 16). The off-diagonal elements are again zero (at this order) in the matrix (5.40), and so the problem decouples to eigenvalues given by the diagonal entries only. Figure 14 shows plots of the zonostrophic modes in (a,c) and the magnetic flux expulsion modes in (b,d) for
![]() ${\it\beta}=0.2$
and 0.4. The effect of increasing
${\it\beta}=0.2$
and 0.4. The effect of increasing
![]() ${\it\beta}$
is to suppress the magnetic instability, panels (b,d). However, the zonostrophic instability contours now embrace the vertical axis. The combined effect of the magnetic field
${\it\beta}$
is to suppress the magnetic instability, panels (b,d). However, the zonostrophic instability contours now embrace the vertical axis. The combined effect of the magnetic field
![]() $B_{0}$
and
$B_{0}$
and
![]() ${\it\beta}$
is to enhance the zonostrophic instability, particularly for small viscosity. This can be contrasted with figure 12 for
${\it\beta}$
is to enhance the zonostrophic instability, particularly for small viscosity. This can be contrasted with figure 12 for
![]() ${\it\beta}=0$
, where the zonostrophic contours remain below the line
${\it\beta}=0$
, where the zonostrophic contours remain below the line
![]() $m^{2}{\it\lambda}=mB_{0}$
. There is supporting evidence of enhanced instability in full numerical simulations (Durston Reference Durston2015).
$m^{2}{\it\lambda}=mB_{0}$
. There is supporting evidence of enhanced instability in full numerical simulations (Durston Reference Durston2015).
Finally, we note that the effective terms
![]() ${\it\nu}_{\mathit{eff}}$
and
${\it\nu}_{\mathit{eff}}$
and
![]() ${\it\chi}_{\mathit{eff}}$
include contributions from both the Reynolds stress and Lorentz force terms. These contributions can be expressed as
${\it\chi}_{\mathit{eff}}$
include contributions from both the Reynolds stress and Lorentz force terms. These contributions can be expressed as
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle {\it\lambda}_{\mathit{eff}\,\mathit{R}}=-\frac{2{\it\lambda}^{4}+m^{-2}{\it\lambda}^{2}B^{2}+m^{-4}B^{4}}{4m^{6}{\it\lambda}^{2}({\it\lambda}^{2}+m^{-2}B^{2})^{2}},\\ \displaystyle {\it\lambda}_{\mathit{eff}\,\mathit{L}}=-\frac{m^{-2}B^{2}(3{\it\lambda}^{2}+m^{-2}B^{2})}{4m^{6}{\it\lambda}^{2}({\it\lambda}^{2}+m^{-2}B^{2})^{2}},\\ \displaystyle {\it\chi}_{\mathit{eff}\,\mathit{R}}=-{\it\chi}_{\mathit{eff}\,\mathit{L}}={\textstyle \frac{1}{2}}{\it\chi}_{\mathit{eff}}.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle {\it\lambda}_{\mathit{eff}\,\mathit{R}}=-\frac{2{\it\lambda}^{4}+m^{-2}{\it\lambda}^{2}B^{2}+m^{-4}B^{4}}{4m^{6}{\it\lambda}^{2}({\it\lambda}^{2}+m^{-2}B^{2})^{2}},\\ \displaystyle {\it\lambda}_{\mathit{eff}\,\mathit{L}}=-\frac{m^{-2}B^{2}(3{\it\lambda}^{2}+m^{-2}B^{2})}{4m^{6}{\it\lambda}^{2}({\it\lambda}^{2}+m^{-2}B^{2})^{2}},\\ \displaystyle {\it\chi}_{\mathit{eff}\,\mathit{R}}=-{\it\chi}_{\mathit{eff}\,\mathit{L}}={\textstyle \frac{1}{2}}{\it\chi}_{\mathit{eff}}.\end{array}\right\}\end{eqnarray}$$
Thus, whereas two terms contribute equally and additively to
![]() ${\it\chi}_{\mathit{eff}}$
, for the effective viscosity there is a leading-order cancellation for large magnetic field
${\it\chi}_{\mathit{eff}}$
, for the effective viscosity there is a leading-order cancellation for large magnetic field
![]() $B\gg m{\it\lambda}$
. The effect of the Lorentz force in cancelling Reynolds stresses for strong magnetic fields, and the overall suppression of transport for large
$B\gg m{\it\lambda}$
. The effect of the Lorentz force in cancelling Reynolds stresses for strong magnetic fields, and the overall suppression of transport for large
![]() $B$
evident in (5.42) are discussed in Leprovost & Kim (Reference Leprovost and Kim2009).
$B$
evident in (5.42) are discussed in Leprovost & Kim (Reference Leprovost and Kim2009).
5.5 Equilibrium profiles
Finally, we consider steady equilibrium profiles in the full MHD system. For a steady profile we have
In addition to (3.35), (4.12), we rescale
here,
![]() $A$
is analogous to the passive scalar in (4.12). Making use of (5.36), we obtain the equations
$A$
is analogous to the passive scalar in (4.12). Making use of (5.36), we obtain the equations
with now the functions
which we have to evaluate numerically. It should be noted that here
![]() $\tilde{B}(Y)$
gives the magnetic field profile, but
$\tilde{B}(Y)$
gives the magnetic field profile, but
![]() $\tilde{B}_{0}$
is a constant, a measure of the average field strength in the system. Given values for the parameters
$\tilde{B}_{0}$
is a constant, a measure of the average field strength in the system. Given values for the parameters
![]() $\tilde{{\it\lambda}}$
,
$\tilde{{\it\lambda}}$
,
![]() $\tilde{{\it\beta}}$
and
$\tilde{{\it\beta}}$
and
![]() $\tilde{B}_{0}$
, integrating the differential algebraic system (5.49)–(5.51) determines profiles for the fields.
$\tilde{B}_{0}$
, integrating the differential algebraic system (5.49)–(5.51) determines profiles for the fields.

Figure 15. Plots of equilibrium profiles by integrating the ODEs (5.49)–(5.51) with
![]() $2-\tilde{{\it\lambda}}^{-3}=1/16$
. Panel (a) shows
$2-\tilde{{\it\lambda}}^{-3}=1/16$
. Panel (a) shows
![]() $\tilde{{\it\Omega}}$
(reading down the curves) and (b) shows
$\tilde{{\it\Omega}}$
(reading down the curves) and (b) shows
![]() $\tilde{B}$
(reading up on the left side) for
$\tilde{B}$
(reading up on the left side) for
![]() $\tilde{{\it\beta}}=0$
and
$\tilde{{\it\beta}}=0$
and
![]() $\tilde{B}_{0}=0,0.2,\ldots ,1$
. Panel (c) shows
$\tilde{B}_{0}=0,0.2,\ldots ,1$
. Panel (c) shows
![]() $\tilde{{\it\Omega}}$
(reading up) and (d) shows
$\tilde{{\it\Omega}}$
(reading up) and (d) shows
![]() $\tilde{B}$
(reading up) for
$\tilde{B}$
(reading up) for
![]() $\tilde{B}_{0}=1$
and
$\tilde{B}_{0}=1$
and
![]() $\tilde{{\it\beta}}=0,1,\ldots ,5$
.
$\tilde{{\it\beta}}=0,1,\ldots ,5$
.
We illustrate some profiles in figure 15. It should be noted that in the limit
![]() $\tilde{B}_{0}=0$
, we regain the decoupled hydrodynamic and passive scalar problem, with profiles shown in figures 4(a) and 6(b). With this in mind, in figure 15(a,b) we show the profiles
$\tilde{B}_{0}=0$
, we regain the decoupled hydrodynamic and passive scalar problem, with profiles shown in figures 4(a) and 6(b). With this in mind, in figure 15(a,b) we show the profiles
![]() $\tilde{{\it\Omega}}({\tilde{Y}})$
and
$\tilde{{\it\Omega}}({\tilde{Y}})$
and
![]() $\tilde{B}({\tilde{Y}})$
respectively, where we start with
$\tilde{B}({\tilde{Y}})$
respectively, where we start with
![]() $\tilde{B}_{0}=0$
and
$\tilde{B}_{0}=0$
and
![]() $\hat{{\it\lambda}}^{-3}=2-(1/16)$
(close to the threshold for zonostrophic instability). This gives the sharpest profiles for
$\hat{{\it\lambda}}^{-3}=2-(1/16)$
(close to the threshold for zonostrophic instability). This gives the sharpest profiles for
![]() $\tilde{{\it\Omega}}$
and
$\tilde{{\it\Omega}}$
and
![]() $\tilde{B}$
as in the earlier figures, and as the parameter
$\tilde{B}$
as in the earlier figures, and as the parameter
![]() $\tilde{B}_{0}$
is increased we observe smoother curves: the step in vorticity and the effect of flux expulsion are smoothed out in the presence of increasing magnetic fields. This could also be viewed as the effect of increasing magnetic field in moving the point in parameter space away from the threshold for zonostrophic instability (see figure 12), and indeed if
$\tilde{B}_{0}$
is increased we observe smoother curves: the step in vorticity and the effect of flux expulsion are smoothed out in the presence of increasing magnetic fields. This could also be viewed as the effect of increasing magnetic field in moving the point in parameter space away from the threshold for zonostrophic instability (see figure 12), and indeed if
![]() $\hat{{\it\lambda}}$
is also adjusted, the profiles can be steepened again for non-zero magnetic field (not shown).
$\hat{{\it\lambda}}$
is also adjusted, the profiles can be steepened again for non-zero magnetic field (not shown).
We continue to fix
![]() $\hat{{\it\lambda}}^{-3}=2-(1/16)$
, take
$\hat{{\it\lambda}}^{-3}=2-(1/16)$
, take
![]() $\tilde{B}_{0}=1$
giving the two sharpest profiles in figure 15(a,b), and then consider the effects of increasing
$\tilde{B}_{0}=1$
giving the two sharpest profiles in figure 15(a,b), and then consider the effects of increasing
![]() $\tilde{{\it\beta}}$
in figure 15(c,d). Interestingly, the effect of increasing
$\tilde{{\it\beta}}$
in figure 15(c,d). Interestingly, the effect of increasing
![]() $\tilde{{\it\beta}}$
is to sharpen the vorticity profile again, while the magnetic field profile becomes smoother. The behaviour of the magnetic field profile is very similar to that of the analogous passive scalar gradient in figure 6(b). However, the sharpening of the vorticity profile is not observed in the purely hydrodynamic system, and in that case there is actually no dependence on
$\tilde{{\it\beta}}$
is to sharpen the vorticity profile again, while the magnetic field profile becomes smoother. The behaviour of the magnetic field profile is very similar to that of the analogous passive scalar gradient in figure 6(b). However, the sharpening of the vorticity profile is not observed in the purely hydrodynamic system, and in that case there is actually no dependence on
![]() $\tilde{{\it\beta}}$
for vorticity profiles. Therefore, we observe that the magnetic field has a catalysing effect: its presence allows the
$\tilde{{\it\beta}}$
for vorticity profiles. Therefore, we observe that the magnetic field has a catalysing effect: its presence allows the
![]() ${\it\beta}$
-effect to sharpen the vorticity profile. This is in line with the earlier discussion of zonostrophic instabilities: the combination of
${\it\beta}$
-effect to sharpen the vorticity profile. This is in line with the earlier discussion of zonostrophic instabilities: the combination of
![]() ${\it\beta}$
-effect and magnetic field can be destabilising, leading to the increased areas of zonostrophic instability in figure 14(a,c).
${\it\beta}$
-effect and magnetic field can be destabilising, leading to the increased areas of zonostrophic instability in figure 14(a,c).
6 Discussion
In this paper we have considered forced two-dimensional flows in the presence of shear,
![]() ${\it\beta}$
-effect, magnetic field and viscous damping. We have used a driving with a very basic structure in the interests of the analytical development, and discussed the hydrodynamic, passive scalar and magnetic field problems in turn. We have made contact with results elsewhere in the literature for hydrodynamic and passive scalar cases, although frequently other studies differ in significant aspects, for example in the type of dissipation or type of forcing. In particular, the molecular dissipation used here is always Fickian diffusion, i.e. controlled by a Laplacian,
${\it\beta}$
-effect, magnetic field and viscous damping. We have used a driving with a very basic structure in the interests of the analytical development, and discussed the hydrodynamic, passive scalar and magnetic field problems in turn. We have made contact with results elsewhere in the literature for hydrodynamic and passive scalar cases, although frequently other studies differ in significant aspects, for example in the type of dissipation or type of forcing. In particular, the molecular dissipation used here is always Fickian diffusion, i.e. controlled by a Laplacian,
![]() $+{\it\lambda}{\rm\nabla}^{2}{\it\omega}$
; this brings in more subtle ‘shear–diffuse’ mechanisms than for the commonly used bottom drag
$+{\it\lambda}{\rm\nabla}^{2}{\it\omega}$
; this brings in more subtle ‘shear–diffuse’ mechanisms than for the commonly used bottom drag
![]() $-{\it\lambda}_{0}{\it\omega}$
, but complicates analysis (and leaves some mathematical questions unresolved, as indicated in appendix A). For future study, it would also be interesting to relax the requirement that all diffusivities are equal in (2.7).
$-{\it\lambda}_{0}{\it\omega}$
, but complicates analysis (and leaves some mathematical questions unresolved, as indicated in appendix A). For future study, it would also be interesting to relax the requirement that all diffusivities are equal in (2.7).
Key novel results that we have obtained in the MHD problem are (i) quantifying the effect of the magnetic field in suppressing zonostrophic instability (discussed in Diamond et al. (Reference Diamond, Itoh, Itoh, Silvers, Hughes, Rosner and Weiss2007) and observed numerically by Tobias et al. (Reference Tobias, Hughes and Diamond2012)) and (ii) the presence of a further magnetic flux expulsion instability (figure 12), (iii) the suppression of these instabilities in the presence of shear (figure 13), (iv) the prediction of resonance leading to instability through overstability (figure 14) and (v) that the combination of magnetic field and
![]() ${\it\beta}$
-effect can be destablising in situations where neither individually drives an instability (figure 15). This latter effect is also identified in a study of transport by Keating & Diamond (Reference Keating and Diamond2008). We have also obtained a range of equilibrium profiles, representing steady-state solutions in which the profile is governed by the effective transport coefficients, themselves nonlinear functions of the fields. These show vorticity steps and related features in passive scalar and magnetic fields.
${\it\beta}$
-effect can be destablising in situations where neither individually drives an instability (figure 15). This latter effect is also identified in a study of transport by Keating & Diamond (Reference Keating and Diamond2008). We have also obtained a range of equilibrium profiles, representing steady-state solutions in which the profile is governed by the effective transport coefficients, themselves nonlinear functions of the fields. These show vorticity steps and related features in passive scalar and magnetic fields.
In terms of the limitations and context of our work (and so directions for future study), clearly a major consideration is that it is based on the quasi-linear approximation, and while we have explored this in some depth, we have not in this paper attempted to verify predictions by full numerical simulations; see Tobias et al. (Reference Tobias, Hughes and Diamond2012) and the preliminary results presented in Durston (Reference Durston2015). While there are several studies that show the utility of the quasi-linear approximation (e.g. Srinivasan & Young Reference Srinivasan and Young2012; Constantinou et al.
Reference Constantinou, Farrell and Iouannou2014), and while this approximation would certainly be valid in some parameter regimes (as per our scalings in
![]() ${\it\varepsilon}$
early in the paper), we recognise that the approach may principally be useful as a qualitative rather than quantitative guide to behaviour in full nonlinear simulations. We have also assumed scale separation between waves and mean flows, and this can be relaxed by using the correlation function formulation developed by Srinivasan & Young (Reference Srinivasan and Young2012) and discussed by Bakas & Iouannou (Reference Bakas and Iouannou2013). This remains to be explored in the magnetic problem, together with the Ginzburg–Landau formulation of Parker & Krommes (Reference Parker and Krommes2013, Reference Parker and Krommes2014).
${\it\varepsilon}$
early in the paper), we recognise that the approach may principally be useful as a qualitative rather than quantitative guide to behaviour in full nonlinear simulations. We have also assumed scale separation between waves and mean flows, and this can be relaxed by using the correlation function formulation developed by Srinivasan & Young (Reference Srinivasan and Young2012) and discussed by Bakas & Iouannou (Reference Bakas and Iouannou2013). This remains to be explored in the magnetic problem, together with the Ginzburg–Landau formulation of Parker & Krommes (Reference Parker and Krommes2013, Reference Parker and Krommes2014).
We also note that the forcing chosen is anisotropic, and it is known that in the purely hydrodynamic problem the feedback on the mean flow is switched off completely in the case of an isotropic driving with
![]() ${\it\beta}=0$
. This is explored in a number of papers, most recently by Srinivasan & Young (Reference Srinivasan and Young2014) who discuss the effects of a family of forcings going from isotropic to anisotropic. In our hydrodynamic set-up we also gain feedback at leading order in our expansions which arises through the anisotropy of the driving and which is independent of
${\it\beta}=0$
. This is explored in a number of papers, most recently by Srinivasan & Young (Reference Srinivasan and Young2014) who discuss the effects of a family of forcings going from isotropic to anisotropic. In our hydrodynamic set-up we also gain feedback at leading order in our expansions which arises through the anisotropy of the driving and which is independent of
![]() ${\it\beta}$
. It would be interesting to rework the study for an isotropic driving and pick up the effect of
${\it\beta}$
. It would be interesting to rework the study for an isotropic driving and pick up the effect of
![]() ${\it\beta}$
, known to be a term of the form
${\it\beta}$
, known to be a term of the form
![]() ${\it\beta}^{2}{\it\Omega}^{\prime \prime \prime \prime }$
in the large-scale vorticity equation (Srinivasan & Young Reference Srinivasan and Young2012; Bakas & Iouannou Reference Bakas and Iouannou2013). This would involve taking our systematic expansion down two further orders, a significant task. With this, though, we note that the equilibrium profiles we obtain show only a single vorticity step (figure 4), and so tell us nothing about the important question of the natural spacing between steps in a periodic profile on a
${\it\beta}^{2}{\it\Omega}^{\prime \prime \prime \prime }$
in the large-scale vorticity equation (Srinivasan & Young Reference Srinivasan and Young2012; Bakas & Iouannou Reference Bakas and Iouannou2013). This would involve taking our systematic expansion down two further orders, a significant task. With this, though, we note that the equilibrium profiles we obtain show only a single vorticity step (figure 4), and so tell us nothing about the important question of the natural spacing between steps in a periodic profile on a
![]() ${\it\beta}$
-plane; perhaps bringing in a
${\it\beta}$
-plane; perhaps bringing in a
![]() ${\it\beta}^{2}{\it\Omega}^{\prime \prime \prime \prime }$
term would give this information. Although one can argue about whether the driving in a ‘real’ fluid system would be isotropic or not, this is perhaps somewhat philosophical, and it would be more interesting to explore systems driven by convection (e.g. Morin & Dormy Reference Morin and Dormy2004; Rotvig & Jones Reference Rotvig and Jones2006; Read et al.
Reference Read, Jacoby, Rogberg, Wordsworth, Yamazaki, Miki-Yamazaki, Young, Sommeria, Didelle and Viboud2015) or some other natural instability, rather than an externally imposed body force. Finally, we acknowledge that the study here is somewhat far from immediate application. Perhaps the most relevant zone for the interaction of magnetic fields and waves in the
${\it\beta}^{2}{\it\Omega}^{\prime \prime \prime \prime }$
term would give this information. Although one can argue about whether the driving in a ‘real’ fluid system would be isotropic or not, this is perhaps somewhat philosophical, and it would be more interesting to explore systems driven by convection (e.g. Morin & Dormy Reference Morin and Dormy2004; Rotvig & Jones Reference Rotvig and Jones2006; Read et al.
Reference Read, Jacoby, Rogberg, Wordsworth, Yamazaki, Miki-Yamazaki, Young, Sommeria, Didelle and Viboud2015) or some other natural instability, rather than an externally imposed body force. Finally, we acknowledge that the study here is somewhat far from immediate application. Perhaps the most relevant zone for the interaction of magnetic fields and waves in the
![]() ${\it\beta}$
-plane setting is the solar tachocline (e.g. Hughes et al.
Reference Hughes, Rosner and Weiss2007). The tachocline includes other physical processes, for example stratification, and its origin and persistence are not well understood, but nonetheless Diamond et al. (Reference Diamond, Itoh, Itoh, Silvers, Hughes, Rosner and Weiss2007) argue that understanding of
${\it\beta}$
-plane setting is the solar tachocline (e.g. Hughes et al.
Reference Hughes, Rosner and Weiss2007). The tachocline includes other physical processes, for example stratification, and its origin and persistence are not well understood, but nonetheless Diamond et al. (Reference Diamond, Itoh, Itoh, Silvers, Hughes, Rosner and Weiss2007) argue that understanding of
![]() ${\it\beta}$
-plane MHD is important for basic understanding of the interaction of forced Rossby and Alfvén waves, and the present paper has aimed to elaborate such processes, albeit within the quasi-linear approximation.
${\it\beta}$
-plane MHD is important for basic understanding of the interaction of forced Rossby and Alfvén waves, and the present paper has aimed to elaborate such processes, albeit within the quasi-linear approximation.
Acknowledgements
We thank E.-J. Kim for references and valuable comments on an earlier draft, S. Tobias for illuminating discussions and for sharing results with us prior to formal publication, and the referees for useful comments and references. We are grateful to the EPSRC for funding S.D. via a DTG research studentship.
Appendix A. Local analysis near
 ${\it\Omega}=0$
${\it\Omega}=0$
A.1 Non-uniformity as
 ${\it\lambda}\rightarrow 0$
${\it\lambda}\rightarrow 0$
In this appendix we pick up questions about the approximations we have used, at points where
![]() ${\it\Omega}$
goes to zero. We focus on the purely hydrodynamic formulation, where our starting point is the framework and exact solutions in § 3.3, but similar remarks would apply for the MHD case. Our analysis in § 3.3 is based on
${\it\Omega}$
goes to zero. We focus on the purely hydrodynamic formulation, where our starting point is the framework and exact solutions in § 3.3, but similar remarks would apply for the MHD case. Our analysis in § 3.3 is based on
![]() $Y$
,
$Y$
,
![]() $T$
,
$T$
,
![]() ${\it\lambda}$
and
${\it\lambda}$
and
![]() ${\it\beta}$
all being of order unity. With
${\it\beta}$
all being of order unity. With
![]() ${\it\lambda}>0$
taken of order unity, any wave is damped on a time scale of
${\it\lambda}>0$
taken of order unity, any wave is damped on a time scale of
![]() $T$
, and so we do not care about the expansions perhaps becoming non-uniform beyond this point – there would be only a negligible contribution to fluxes. With this, we note that references to the ‘inviscid’ limit in the text above must be understood in these terms: one fixes
$T$
, and so we do not care about the expansions perhaps becoming non-uniform beyond this point – there would be only a negligible contribution to fluxes. With this, we note that references to the ‘inviscid’ limit in the text above must be understood in these terms: one fixes
![]() ${\it\lambda}>0$
to a value, however small, and then the results are valid for that fixed value, as
${\it\lambda}>0$
to a value, however small, and then the results are valid for that fixed value, as
![]() ${\it\varepsilon}\rightarrow 0$
, i.e. in the limit of large scale separation.
${\it\varepsilon}\rightarrow 0$
, i.e. in the limit of large scale separation.
To confirm this, and to see what happens when we try to relax these conditions, consider the key approximation, from (3.10),
Clearly, the main problem that could arise is at points, or in regions, where
![]() ${\it\Omega}=0$
(particularly given our scaling out of
${\it\Omega}=0$
(particularly given our scaling out of
![]() ${\it\Omega}$
in (3.22)). However (with
${\it\Omega}$
in (3.22)). However (with
![]() $T=O(1)$
), the term
$T=O(1)$
), the term
![]() ${\it\varepsilon}{\it\Omega}^{\prime }T\,{\it\phi}$
remains uniformly small compared with the right-hand side. It is perhaps more revealing to substitute the leading-order solution
${\it\varepsilon}{\it\Omega}^{\prime }T\,{\it\phi}$
remains uniformly small compared with the right-hand side. It is perhaps more revealing to substitute the leading-order solution
![]() ${\it\phi}_{0}$
taken from (3.21) into the third term, with
${\it\phi}_{0}$
taken from (3.21) into the third term, with
 $$\begin{eqnarray}\displaystyle {\it\varepsilon}{\it\Omega}T\partial _{Y}{\it\phi}_{0} & = & \displaystyle {\it\varepsilon}{\it\Omega}T\left[\frac{-2{\it\Omega}{\it\Omega}^{\prime }T^{2}}{1+{\it\Omega}^{2}T^{2}}-\frac{2}{3}m^{2}{\it\lambda}{\it\Omega}{\it\Omega}^{\prime }T^{3}\right.\nonumber\\ \displaystyle & & \displaystyle +\,\left.\frac{\text{i}{\it\beta}}{m}\left(-\frac{{\it\Omega}^{\prime }}{{\it\Omega}^{2}}\tan ^{-1}{\it\Omega}T+\frac{{\it\Omega}^{\prime }T}{{\it\Omega}(1+{\it\Omega}^{2}T^{2})}\right)\right]{\it\phi}_{0}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\varepsilon}{\it\Omega}T\partial _{Y}{\it\phi}_{0} & = & \displaystyle {\it\varepsilon}{\it\Omega}T\left[\frac{-2{\it\Omega}{\it\Omega}^{\prime }T^{2}}{1+{\it\Omega}^{2}T^{2}}-\frac{2}{3}m^{2}{\it\lambda}{\it\Omega}{\it\Omega}^{\prime }T^{3}\right.\nonumber\\ \displaystyle & & \displaystyle +\,\left.\frac{\text{i}{\it\beta}}{m}\left(-\frac{{\it\Omega}^{\prime }}{{\it\Omega}^{2}}\tan ^{-1}{\it\Omega}T+\frac{{\it\Omega}^{\prime }T}{{\it\Omega}(1+{\it\Omega}^{2}T^{2})}\right)\right]{\it\phi}_{0}.\end{eqnarray}$$
As
![]() ${\it\Omega}$
tends to zero with
${\it\Omega}$
tends to zero with
![]() $T=O(1)$
, this remains uniformly small with respect to the right-hand side of (A 1). This is reassuring but not unexpected.
$T=O(1)$
, this remains uniformly small with respect to the right-hand side of (A 1). This is reassuring but not unexpected.
More interestingly, suppose that we imagine now reducing
![]() ${\it\lambda}$
, being interested in the inviscid limit for a fixed scale separation
${\it\lambda}$
, being interested in the inviscid limit for a fixed scale separation
![]() ${\it\varepsilon}\ll 1$
. In fact, let us set
${\it\varepsilon}\ll 1$
. In fact, let us set
![]() ${\it\lambda}=0$
, and consider the approximation (A 1). For definiteness we consider a locally quadratic profile
${\it\lambda}=0$
, and consider the approximation (A 1). For definiteness we consider a locally quadratic profile
i.e. a generic zero-crossing of the vorticity profile. First, we take the term
![]() ${\it\varepsilon}{\it\Omega}^{\prime }T\,{\it\phi}_{0}$
in (A 1): this becomes of comparable size to the right-hand side when
${\it\varepsilon}{\it\Omega}^{\prime }T\,{\it\phi}_{0}$
in (A 1): this becomes of comparable size to the right-hand side when
We can now revisit the terms in (A 2). The first term on the right-hand side of (A 2) also becomes comparable to the right-hand side of (A 1) when (A 4) holds. Other terms in (A 2) involve
![]() ${\it\lambda}$
and
${\it\lambda}$
and
![]() ${\it\beta}$
, and so we imagine increasing these from zero: given the scalings (A 4) these terms begin to become comparable with the right-hand side of (A 1) when
${\it\beta}$
, and so we imagine increasing these from zero: given the scalings (A 4) these terms begin to become comparable with the right-hand side of (A 1) when
To summarise, we have developed theory for
![]() ${\it\lambda}=O(1)$
(
${\it\lambda}=O(1)$
(
![]() ${\it\lambda}>0$
) and
${\it\lambda}>0$
) and
![]() ${\it\varepsilon}\rightarrow 0$
. If we wish to gain a uniform approximation that includes
${\it\varepsilon}\rightarrow 0$
. If we wish to gain a uniform approximation that includes
![]() ${\it\lambda}=0$
for
${\it\lambda}=0$
for
![]() ${\it\varepsilon}\rightarrow 0$
, then we need to investigate regions of non-uniformity given by (A 4). At the same time we could bring in
${\it\varepsilon}\rightarrow 0$
, then we need to investigate regions of non-uniformity given by (A 4). At the same time we could bring in
![]() ${\it\lambda}$
and
${\it\lambda}$
and
![]() ${\it\beta}$
with the appropriate scalings being (A 5).
${\it\beta}$
with the appropriate scalings being (A 5).
A.2 Long-time expansion
We now develop some theory based on these new scalings. It is convenient to return to the original equations (2.11) with (2.14) (and no magnetic field or scalar transport). We replace
corresponding to (A 5). Looking at (A 4) we see that this corresponds to using
![]() $(y,T)$
coordinates with
$(y,T)$
coordinates with
![]() $y=O(1)$
(the original
$y=O(1)$
(the original
![]() $y$
) and
$y$
) and
![]() $T={\it\varepsilon}^{2}t$
. The quadratic profile (A 3) becomes
$T={\it\varepsilon}^{2}t$
. The quadratic profile (A 3) becomes
with
![]() ${\it\alpha}$
a constant; in this section
${\it\alpha}$
a constant; in this section
![]() ${\it\alpha},a,b,f,g,h,T$
are recycled and have no connection with these quantities in earlier sections. With these replacements the governing equations are simply
${\it\alpha},a,b,f,g,h,T$
are recycled and have no connection with these quantities in earlier sections. With these replacements the governing equations are simply
with
![]() $\tilde{{\it\beta}}={\it\beta}-2{\it\alpha}$
. This is the full inner problem, and may be solved numerically (Durston Reference Durston2015).
$\tilde{{\it\beta}}={\it\beta}-2{\it\alpha}$
. This is the full inner problem, and may be solved numerically (Durston Reference Durston2015).
For further analytical progress, though, we approximate
![]() $-m^{2}+\partial _{y}^{2}\simeq \partial _{y}^{2}$
for large gradients (as we will discuss later), giving
$-m^{2}+\partial _{y}^{2}\simeq \partial _{y}^{2}$
for large gradients (as we will discuss later), giving
Following Bajer, Bassom & Gilbert (Reference Bajer, Bassom and Gilbert2001), we seek a solution of the form
where the
![]() $M$
are Kummer functions (see the NIST handbook, Olver et al.
Reference Olver, Lozier, Boisvert and Clark2010) with parameters
$M$
are Kummer functions (see the NIST handbook, Olver et al.
Reference Olver, Lozier, Boisvert and Clark2010) with parameters
![]() $a$
,
$a$
,
![]() $b$
and argument
$b$
and argument
![]() $s$
. Equation (A 9b
) is satisfied provided that (NIST 13.2.1, 13.3.17)
$s$
. Equation (A 9b
) is satisfied provided that (NIST 13.2.1, 13.3.17)
The value of
![]() $b$
indicates that we could instead express what follows in terms of parabolic cylinder functions. Equation (A 9a
) becomes
$b$
indicates that we could instead express what follows in terms of parabolic cylinder functions. Equation (A 9a
) becomes
Now we express (NIST 13.3.17, 13.3.19),
for the terms on the right-hand side of (A 9) and gather terms in
![]() $M$
,
$M$
,
![]() $sM$
and
$sM$
and
![]() $sM^{\prime }$
, all taken as functions of
$sM^{\prime }$
, all taken as functions of
![]() $(a+1,b,s)$
. This yields three equations which may be simplified using (A 11) to give respectively
$(a+1,b,s)$
. This yields three equations which may be simplified using (A 11) to give respectively
Equation (A 16) fixes values of
![]() $a$
with
$a$
with
and we have (taking
![]() ${\it\alpha}>0$
for definiteness)
${\it\alpha}>0$
for definiteness)
and then
We thus obtain exact solutions of the partial differential equations (A 9) describing the evolution of waves subject to the flow,
![]() ${\it\beta}$
-effect and viscosity. It should be noted that for small viscosity,
${\it\beta}$
-effect and viscosity. It should be noted that for small viscosity,
![]() ${\it\mu}\ll 1$
, and
${\it\mu}\ll 1$
, and
![]() $\mathscr{T}\ll {\it\mu}^{-1}$
(before viscosity acts), we have
$\mathscr{T}\ll {\it\mu}^{-1}$
(before viscosity acts), we have
![]() $f\simeq m{\it\alpha}T$
. Using the large-
$f\simeq m{\it\alpha}T$
. Using the large-
![]() $s$
asymptotics for
$s$
asymptotics for
![]() $M$
, namely (NIST 13.7.2),
$M$
, namely (NIST 13.7.2),
we obtain for large
![]() $s$
$s$
This should then be matched with the outer solutions in § 3.3, although it may be that the terms neglected in going from (A 8) to (A 9) have to be reincorporated. It should be noted that in the case
![]() $\tilde{{\it\beta}}=0$
, when the
$\tilde{{\it\beta}}=0$
, when the
![]() ${\it\beta}$
effect precisely cancels out the vorticity gradient from the flow,
${\it\beta}$
effect precisely cancels out the vorticity gradient from the flow,
![]() ${\it\omega}$
evolves like a passive scalar, and the root
${\it\omega}$
evolves like a passive scalar, and the root
![]() $a=-1/2$
correctly gives
$a=-1/2$
correctly gives
![]() $|{\it\omega}|^{2}$
constant in (A 23). We leave this topic for further investigation, the aim being to obtain a complete (and useful) description of the evolution of waves and feedback outlined in § 3.3, valid for good scale separation
$|{\it\omega}|^{2}$
constant in (A 23). We leave this topic for further investigation, the aim being to obtain a complete (and useful) description of the evolution of waves and feedback outlined in § 3.3, valid for good scale separation
![]() ${\it\varepsilon}\ll 1$
uniformly in
${\it\varepsilon}\ll 1$
uniformly in
![]() ${\it\lambda}\geqslant 0$
.
${\it\lambda}\geqslant 0$
.
Appendix B. Magnetohydrodynamic formulation
In this appendix we give some of the less interesting calculations related to the MHD problem in § 5. First, we use (5.23) to obtain a fourth-order real system written symbolically as
where
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\mathscr{V}(T,{\it\Omega},B,{\it\beta})=\left(\begin{array}{@{}c@{}}|\hat{{\it\zeta}}_{0}|^{2}\\ |\hat{{\it\alpha}}_{0}|^{2}\\ \text{i}(\hat{{\it\zeta}}_{0}^{\ast }\hat{{\it\alpha}}_{0}-\hat{{\it\zeta}}_{0}\hat{{\it\alpha}}_{0}^{\ast })\\ \hat{{\it\zeta}}_{0}^{\ast }\hat{{\it\alpha}}_{0}+\hat{{\it\zeta}}_{0}\hat{{\it\alpha}}_{0}^{\ast }\end{array}\right),\\ \mathscr{M}({\it\tau},B,{\it\beta})=\left(\begin{array}{@{}cccc@{}}0 & 0 & mB\mathscr{S}^{-1} & 0\\ 0 & 0 & -mB\mathscr{S} & 0\\ -2mB\mathscr{S} & 2mB\mathscr{S}^{-1} & 0 & m^{-1}{\it\beta}\mathscr{S}\\ 0 & 0 & -m^{-1}{\it\beta}\mathscr{S} & 0\end{array}\right),\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\mathscr{V}(T,{\it\Omega},B,{\it\beta})=\left(\begin{array}{@{}c@{}}|\hat{{\it\zeta}}_{0}|^{2}\\ |\hat{{\it\alpha}}_{0}|^{2}\\ \text{i}(\hat{{\it\zeta}}_{0}^{\ast }\hat{{\it\alpha}}_{0}-\hat{{\it\zeta}}_{0}\hat{{\it\alpha}}_{0}^{\ast })\\ \hat{{\it\zeta}}_{0}^{\ast }\hat{{\it\alpha}}_{0}+\hat{{\it\zeta}}_{0}\hat{{\it\alpha}}_{0}^{\ast }\end{array}\right),\\ \mathscr{M}({\it\tau},B,{\it\beta})=\left(\begin{array}{@{}cccc@{}}0 & 0 & mB\mathscr{S}^{-1} & 0\\ 0 & 0 & -mB\mathscr{S} & 0\\ -2mB\mathscr{S} & 2mB\mathscr{S}^{-1} & 0 & m^{-1}{\it\beta}\mathscr{S}\\ 0 & 0 & -m^{-1}{\it\beta}\mathscr{S} & 0\end{array}\right),\end{array}\right\}\end{eqnarray}$$
![]() $\mathscr{S}=(1+{\it\tau}^{2})^{-1}$
and
$\mathscr{S}=(1+{\it\tau}^{2})^{-1}$
and
![]() ${\it\tau}={\it\Omega}T$
as usual. We consider
${\it\tau}={\it\Omega}T$
as usual. We consider
![]() $\mathscr{V}=\mathscr{V}(T,{\it\Omega},B,{\it\beta})$
, and differentiating gives supplementary ODEs for
$\mathscr{V}=\mathscr{V}(T,{\it\Omega},B,{\it\beta})$
, and differentiating gives supplementary ODEs for
![]() $B\partial _{B}\mathscr{V}$
and
$B\partial _{B}\mathscr{V}$
and
![]() ${\it\Omega}\partial _{{\it\Omega}}\mathscr{V}$
,
${\it\Omega}\partial _{{\it\Omega}}\mathscr{V}$
,
which may be written, after a change of variable to
![]() ${\it\tau}$
, as
${\it\tau}$
, as
To calculate the fluxes
![]() $f_{\mathit{Z}}$
in (5.28)–(5.32) numerically, we integrate the ODEs (B 1) together with (B 5), (B 6) in terms of
$f_{\mathit{Z}}$
in (5.28)–(5.32) numerically, we integrate the ODEs (B 1) together with (B 5), (B 6) in terms of
![]() ${\it\tau}$
for initial conditions
${\it\tau}$
for initial conditions
![]() $\mathscr{V}=(1,0,0,0)$
, independent of
$\mathscr{V}=(1,0,0,0)$
, independent of
![]() ${\it\Omega}$
and
${\it\Omega}$
and
![]() $B$
. We then extract any information needed at time
$B$
. We then extract any information needed at time
![]() ${\it\tau}$
, for example for the figures 8–10. The resulting numerical procedures were checked by computing derivatives numerically, and against analytical approximations below. It should be noted that quantities such as
${\it\tau}$
, for example for the figures 8–10. The resulting numerical procedures were checked by computing derivatives numerically, and against analytical approximations below. It should be noted that quantities such as
![]() $h_{\mathit{Z}}$
were computed by incorporating in the system further ODEs of the form
$h_{\mathit{Z}}$
were computed by incorporating in the system further ODEs of the form
![]() $\text{d}h_{\mathit{Z}}^{\dagger }/\text{d}{\it\tau}=D^{2}f_{\mathit{Z}}$
with
$\text{d}h_{\mathit{Z}}^{\dagger }/\text{d}{\it\tau}=D^{2}f_{\mathit{Z}}$
with
![]() $h_{\mathit{Z}}^{\dagger }(0)=0$
and evaluating
$h_{\mathit{Z}}^{\dagger }(0)=0$
and evaluating
![]() $h_{\mathit{Z}}=h_{\mathit{Z}}^{\dagger }({\it\tau})$
for
$h_{\mathit{Z}}=h_{\mathit{Z}}^{\dagger }({\it\tau})$
for
![]() ${\it\tau}$
large enough that
${\it\tau}$
large enough that
![]() $D^{2}$
is sufficiently small.
$D^{2}$
is sufficiently small.
We now turn to the calculations involving instabilities in § 5.4 and outline parts omitted from the main text. First, equations (5.23) may be expanded as
and then solutions can be developed perturbatively by bringing in successively higher powers of
![]() ${\it\tau}$
. This gives, for
${\it\tau}$
. This gives, for
![]() $\hat{{\it\beta}}=0$
,
$\hat{{\it\beta}}=0$
,
The leading-order terms have been presented in (5.41) and give rise to the formulae (5.42) in due course; we omit the details. The second-order terms are interesting as they determine
![]() ${\it\eta}_{\mathit{eff}}$
to better accuracy, namely
${\it\eta}_{\mathit{eff}}$
to better accuracy, namely
and so give values for
![]() $B\partial _{{\it\Omega}}{\it\eta}_{\mathit{eff}}$
, which otherwise vanishes at leading order.
$B\partial _{{\it\Omega}}{\it\eta}_{\mathit{eff}}$
, which otherwise vanishes at leading order.
It should be noted that in the numerical calculations leading to figure 13(b,c), we differentiate
![]() ${\it\eta}_{\mathit{eff}}$
analytically before computing (5.40), with evaluation of the following integrals numerically:
${\it\eta}_{\mathit{eff}}$
analytically before computing (5.40), with evaluation of the following integrals numerically:
 $$\begin{eqnarray}\displaystyle B\partial _{{\it\Omega}}{\it\eta}_{\mathit{eff}} & = & \displaystyle m^{-3}{\it\Omega}^{-2}\int _{0}^{\infty }D^{2}(1+{\it\tau}^{2})^{-1}\left[2{\it\tau}^{2}(1+{\it\tau}^{2})^{-1}+\frac{4}{3}\hat{{\it\lambda}}{\it\tau}^{3}-{\it\Omega}\partial _{{\it\Omega}}\right]\nonumber\\ \displaystyle & & \displaystyle \times \,\text{i}(\hat{{\it\zeta}}_{0}^{\ast }\hat{{\it\alpha}}_{0}-\hat{{\it\zeta}}_{0}\hat{{\it\alpha}}_{0}^{\ast })\,\text{d}{\it\tau}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle B\partial _{{\it\Omega}}{\it\eta}_{\mathit{eff}} & = & \displaystyle m^{-3}{\it\Omega}^{-2}\int _{0}^{\infty }D^{2}(1+{\it\tau}^{2})^{-1}\left[2{\it\tau}^{2}(1+{\it\tau}^{2})^{-1}+\frac{4}{3}\hat{{\it\lambda}}{\it\tau}^{3}-{\it\Omega}\partial _{{\it\Omega}}\right]\nonumber\\ \displaystyle & & \displaystyle \times \,\text{i}(\hat{{\it\zeta}}_{0}^{\ast }\hat{{\it\alpha}}_{0}-\hat{{\it\zeta}}_{0}\hat{{\it\alpha}}_{0}^{\ast })\,\text{d}{\it\tau}.\end{eqnarray}$$
For
![]() $\hat{{\it\beta}}\neq 0$
solutions to (B 7) (just at leading order) are
$\hat{{\it\beta}}\neq 0$
solutions to (B 7) (just at leading order) are
(cf. Keating & Diamond Reference Keating and Diamond2008) from which we can obtain
where we have abbreviated (in this appendix only)