2.1 Boundary conditions

2.1.1 Translating cylinder with a rough or no-slip surface

For a no-slip cylinder moving in the $x$ -direction with unit speed (i.e. dimensional speed ${\mathcal{U}}$ ), we impose

(2.6) $$\begin{eqnarray}\displaystyle (u,v)=(\cos \unicode[STIX]{x1D703},-\sin \unicode[STIX]{x1D703})\quad \text{at }r=1. & & \displaystyle\end{eqnarray}$$

Both velocity conditions cannot be applied in ideal plasticity. Instead, a prescribed normal velocity forces plastic deformation with tangential slip along the boundary of the cylinder. At finite, but large Bingham number, one expects any such slip to become smoothed over viscous boundary layers wherein the shear stress dominates the other stress components. If this turns out to be the case, no-slip is equivalent to the local stress condition $|\unicode[STIX]{x1D70F}_{r\unicode[STIX]{x1D703}}|\sim Bi$ , which is the fully rough surface condition used in plasticity theory.

2.1.2 Translation with slip

If the surface of the cylinder is partially rough, with a roughness factor $\unicode[STIX]{x1D71A}\in [0,1]$ , the boundary condition to be imposed is

(2.7a,b ) $$\begin{eqnarray}\displaystyle u=\cos \unicode[STIX]{x1D703}\quad \text{and}\quad \unicode[STIX]{x1D70F}_{r\unicode[STIX]{x1D703}}=\unicode[STIX]{x1D71A}Bi\;\text{sgn}(y)\quad \text{at }r=1 & & \displaystyle\end{eqnarray}$$

(Randolph & Houlsby Reference Randolph and Houlsby1984; Martin & Randolph Reference Martin and Randolph2006); setting $\unicode[STIX]{x1D71A}=1$ corresponds to a fully rough cylinder, and $\unicode[STIX]{x1D71A}=0$ to a perfectly smooth, or free-slip, cylinder. Although it is not necessarily a natural boundary condition for a fluid, the second condition in (2.7) is equivalent to the rate-independent limit of the Mooney-type slip law

(2.8) $$\begin{eqnarray}\displaystyle v(1,\unicode[STIX]{x1D703})+\sin \unicode[STIX]{x1D703}=A(|\unicode[STIX]{x1D70F}_{r\unicode[STIX]{x1D703}}|-\unicode[STIX]{x1D70F}_{w})^{q}\;\text{sgn}(\unicode[STIX]{x1D70F}_{r\unicode[STIX]{x1D703}}), & & \displaystyle\end{eqnarray}$$

for some parameters $A$ , $q$ and wall stress threshold $\unicode[STIX]{x1D70F}_{w}=\unicode[STIX]{x1D71A}Bi$ . Such slip laws are common when modelling effective slip due to surface interactions in many suspensions (e.g. Barnes (Reference Barnes1995); see also Ozogul et al. (Reference Ozogul, Jay and Magnin2015)).

2.1.3 Squirming surface motions

For a model squirmer, we again impose the surface velocity, this time in the frame of the cylinder, and select ${\mathcal{U}}$ as its characteristic scale. The speed of the cylinder with respect to the ambient fluid then becomes $U_{s}$ . We consider purely tangential squirming motions and set

(2.9) $$\begin{eqnarray}\displaystyle (u,v)=(U_{s}\cos \unicode[STIX]{x1D703},V_{p}(\unicode[STIX]{x1D703})-U_{s}\sin \unicode[STIX]{x1D703})\quad \text{at }r=1, & & \displaystyle\end{eqnarray}$$

where $(0,V_{p})$ represents the prescribed surface velocity. For specific examples, we adopt previously employed models of treadmilling cilia given by

(2.10) $$\begin{eqnarray}\displaystyle V_{p}(\unicode[STIX]{x1D703})=\sin n\unicode[STIX]{x1D703}+a\sin m\unicode[STIX]{x1D703}, & & \displaystyle\end{eqnarray}$$

with integers $n$ and $m\neq 1$ . Notable conventional models include the simplest case, with $(n,a)=(1,0)$ , or employ $(n,m)=(1,2)$ with $a<0$ giving a ‘pusher’ and $a>0$ a ‘puller’ (based on the distribution of $V_{p}(\unicode[STIX]{x1D703})$ ). Note that, although one can generate solutions for any $U_{s}$ , the swimming speed of a free locomotor is set by the requirement that the net force on the cylinder in the $x$ -direction should vanish; i.e. $F_{x}=0$ in (2.5).

Finally, we also consider a limited number of examples in which we replace (2.9) with a squirming motion normal to the cylinder surface,

(2.11) $$\begin{eqnarray}\left.(u,v)\right|_{r=1}=(U_{s}\cos \unicode[STIX]{x1D703}-U_{p}(\unicode[STIX]{x1D703}),-U_{s}\sin \unicode[STIX]{x1D703}),\quad \text{with }U_{p}=\cos n\unicode[STIX]{x1D703}+a\cos m\unicode[STIX]{x1D703}.\end{eqnarray}$$

Although Blake also considered normal surface velocities, he took these as components of propagating wave-like motions, unlike the steady model in (2.11), which is closer to the propulsion mechanism discussed by Spagnolie & Lauga (Reference Spagnolie and Lauga2010).

2.2 Numerical method

We solve the governing equations using the augmented Lagrangian scheme summarized by Hewitt & Balmforth (Reference Hewitt and Balmforth2017). In brief, after the elimination of the pressure from the momentum equations (2.1b )–(2.1c ) and the introduction of a stream function $\unicode[STIX]{x1D713}(r,\unicode[STIX]{x1D703})$ such that

(2.12) $$\begin{eqnarray}\displaystyle & \displaystyle (u,v)=\left(\frac{1}{r}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}},-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}r}\right), & \displaystyle\end{eqnarray}$$

we must solve the biharmonic-like problem

(2.13) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FB}^{4}\unicode[STIX]{x1D713}=Bi\left[\left(\frac{1}{r}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}}r{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}}+\frac{2}{r}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}}-\frac{1}{r^{2}}{\displaystyle \frac{\unicode[STIX]{x2202}^{2}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}^{2}}}\right)\frac{\dot{\unicode[STIX]{x1D6FE}}_{r\unicode[STIX]{x1D703}}}{\dot{\unicode[STIX]{x1D6FE}}}-\frac{2}{r}\left({\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}}+\frac{1}{r}\right){\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}}\frac{\dot{\unicode[STIX]{x1D6FE}}_{rr}}{\dot{\unicode[STIX]{x1D6FE}}}\right], & \displaystyle\end{eqnarray}$$

over the yielded regions $\dot{\unicode[STIX]{x1D6FE}}>0$ . This is achieved by means of an iterative scheme in which one solves, at each step, a linear biharmonic equation over the whole domain (both yielded and plugged) and a nonlinear algebraic problem that incorporates the constitutive law.

We work on the domain $0\leqslant \unicode[STIX]{x1D703}\leqslant \unicode[STIX]{x03C0}$ , with symmetry conditions at $\unicode[STIX]{x1D703}=0,\unicode[STIX]{x03C0}$ . The stress invariant decays away from the cylinder, and must eventually fall below the yield stress. We therefore choose a sufficiently large computational domain to contain all the yielded fluid, and set $(u,v)=(0,0)$ at the edge. If both velocity components are also specified on the surface of the cylinder, the boundary conditions there can be implemented directly in terms of the stream function and its derivatives. The boundary condition in (2.7b ), however, imposes the shear stress, which is problematic as the iterative solution of (2.13) requires conditions involving the stream function. To surmount this difficulty, we replace (2.7b ) by the condition $\dot{\unicode[STIX]{x1D6FE}}_{r\unicode[STIX]{x1D703}}=\unicode[STIX]{x1D71A}\dot{\unicode[STIX]{x1D6FE}}\,\text{sgn}(y)$ at $r=1$ , which reduces to (2.7b ) where the fluid surface is yielded. If, however, the boundary is plugged, the two conditions are not equivalent. To avoid this inconsistency, in the corresponding computations we used a common regularized constitutive model $\unicode[STIX]{x1D70F}_{ij}=\dot{\unicode[STIX]{x1D6FE}}_{ij}[1+\dot{\unicode[STIX]{x1D6FE}}^{-1}Bi(1-e^{-m\dot{\unicode[STIX]{x1D6FE}}})]$ , which reproduces the Bingham law in (2.2) for $\dot{\unicode[STIX]{x1D6FE}}\gg m^{-1}$ , with $m=10^{4}$ (this choice of $m$ was sufficiently high that the solutions match those for the unregularized law over the yielded regions, and are insensitive to the precise value of $m$ ). Now the fluid is forced to yield everywhere, the boundary is never plugged, and the alternative boundary condition is always equivalent to (2.7b ).

The linear biharmonic equation is solved by exploiting a Fourier sine series in $\unicode[STIX]{x1D703}$ , and second-order finite differences in the radial direction. The numerical resolution was chosen to be sufficient to resolve the smallest scales of the problem: the radial grid size was at most $0.003$ , and at least $512$ Fourier modes in $\unicode[STIX]{x1D703}$ were used. In some of our computations at the highest Bingham numbers, we used a stretched grid in the radial direction to enhance the resolution in boundary layers near the cylinder’s surface.

2.3 Ideal plasticity

In the limit $Bi\rightarrow \infty$ , one expects that the viscous stresses become insignificant in comparison to the yield stress outside any boundary layers, implying that yielded material deforms at the yield stress, with $\unicode[STIX]{x1D70F}_{ij}=Bi\dot{\unicode[STIX]{x1D6FE}}_{ij}/\dot{\unicode[STIX]{x1D6FE}}$ . In Cartesian coordinates $(x,y)$ , the stress components can then be written in terms of a local slip angle $\unicode[STIX]{x1D717}$ as $(\unicode[STIX]{x1D70F}_{xx},\unicode[STIX]{x1D70F}_{xy})=Bi(-\sin 2\unicode[STIX]{x1D717},\cos 2\unicode[STIX]{x1D717})$ . Upon substituting the stress components into the momentum equations $(\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D749}=\unicode[STIX]{x1D735}p)$ , the equations are hyperbolic in $p$ and $\unicode[STIX]{x1D717}$ with the characteristics of the stress field following the sliplines (Prager & Hodge Reference Prager and Hodge1951),

(2.14) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}\text{-lines:}\quad \frac{\text{d}y}{\text{d}x}=\tan \unicode[STIX]{x1D717},\quad p+2Bi\unicode[STIX]{x1D717}=\text{constant}, & & \displaystyle\end{eqnarray}$$

(2.15) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FD}\text{-lines:}\quad \frac{\text{d}y}{\text{d}x}=-\cot \unicode[STIX]{x1D717},\quad p-2Bi\unicode[STIX]{x1D717}=\text{constant.} & & \displaystyle\end{eqnarray}$$

The angle $\unicode[STIX]{x1D717}$ is the anticlockwise angle of the $\unicode[STIX]{x1D6FC}$ -line as measured from the $x$ -axis. The sliplines are a set of mutually orthogonal lines along which the shear stress is the maximum and the normal stresses are zero. In other words, if $\unicode[STIX]{x1D64D}(\unicode[STIX]{x1D717})$ denotes the rotation matrix, then,

(2.16) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D64D}(\unicode[STIX]{x1D717})\unicode[STIX]{x1D749}\unicode[STIX]{x1D64D}(\unicode[STIX]{x1D717})^{\text{T}}=\left[\begin{array}{@{}cc@{}}0 & \pm Bi\\ \pm Bi & 0\end{array}\right]. & \displaystyle\end{eqnarray}$$

The components of the velocity field along the sliplines $(u_{\unicode[STIX]{x1D6FC}},u_{\unicode[STIX]{x1D6FD}})$ satisfy

(2.17) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}u_{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x2202}s_{\unicode[STIX]{x1D6FC}}}=\frac{\unicode[STIX]{x2202}u_{\unicode[STIX]{x1D6FD}}}{\unicode[STIX]{x2202}s_{\unicode[STIX]{x1D6FD}}}=0, & \displaystyle\end{eqnarray}$$

where $s_{\unicode[STIX]{x1D6FC}}$ and $s_{\unicode[STIX]{x1D6FD}}$ are the arclengths along the respective sliplines. That is, the component of the velocity directed along a particular slipline must be constant.

The plasticity problem can also be formulated in variational terms to establish the following two useful results (Prager & Hodge Reference Prager and Hodge1951): first, if the velocity field is not simultaneously calculated, slipline fields that satisfy (2.14) and (2.15), together with any stress boundary conditions, constrain the true solution by providing strict lower bounds on the drag force on the cylinder. Second, trial velocity fields that satisfy the surface velocity and incompressibility conditions, but not the stress relations, place upper bounds on the drag force (given that the associated dissipation rate must balance the power input required to overcome the drag). Such upper bounds can be improved by posing trial velocity fields guided by the slipline fields. Indeed, if the lower and upper bounds then match, the stress and the velocity fields must correspond to those of the actual solution. Note that, in the slipline stress analysis, one must further demonstrate that there is an admissible stress distribution inside any rigid plugs that satisfies both the force balance equations and yield criterion ( $\unicode[STIX]{x1D70F}<Bi$ ).

Randolph & Houlsby (Reference Randolph and Houlsby1984) exploited these bounding principles for a fully rough cylinder driven through a perfectly plastic medium. In particular, they constructed a slipline solution and a matching velocity field for which the upper and lower bounds agreed. They further showed that an admissible stress distribution could be found for all the unyielded regions. Hence, their construction provides the true plastic solution. For partially rough cylinders, however, their trial velocity field was not consistent with the slipline solution over part of the yielded region, and the correct computation of the upper bound leaves a mismatch with the lower bound (Murff et al. Reference Murff, Wagner and Randolph1989). This led Martin & Randolph (Reference Martin and Randolph2006) to suggest an alternative trial velocity field, associated with a different slipline solution, that lay closer to, but not coincident with, the lower bound. The true solution for partially rough cylinders has therefore not been previously identified.

3.1 Randolph and Houlsby’s slipline solution

In detail and for the upper half of the solution, the slipline pattern (figure 1 b) consists of a semi-circular centred fan at the top of the cylinder with centre $A$ at $(0,1)$ and radius $1+\unicode[STIX]{x03C0}/4$ . The $\unicode[STIX]{x1D6FD}$ -lines form the spokes and the $\unicode[STIX]{x1D6FC}$ -lines form the circular arcs. The $\unicode[STIX]{x1D6FC}$ -lines are continued below the line $AD$ by the involutes of the cylinder, and the $\unicode[STIX]{x1D6FD}$ -lines become tangents. The construction of the involutes ensures that the stress field satisfies the fully rough boundary condition, $\unicode[STIX]{x1D70F}_{r\unicode[STIX]{x1D703}}=Bi$ , on the cylinder surface. The limiting $\unicode[STIX]{x1D6FD}$ -lines $BC$ and $B^{\prime }C^{\prime }$ intersect the $x$ -axis at $45^{\circ }$ , as demanded by symmetry, which isolates the triangular plugs capping the front and back of the cylinder. The $\unicode[STIX]{x1D6FC}$ -line $CDGD^{\prime }C^{\prime }$ determines the outermost yield surface.

The velocity field associated with the slipline pattern is directed purely along the $\unicode[STIX]{x1D6FC}$ -lines (and so, in this case, the streamlines are $\unicode[STIX]{x1D6FC}$ -lines): the involutes beginning along $BC$ have $v_{\unicode[STIX]{x1D6FC}}=1/\sqrt{2}$ , whereas those that begin at the cylinder along $AB$ have $v_{\unicode[STIX]{x1D6FC}}=\cos \unicode[STIX]{x1D703}$ . At the base of both sets of sliplines, there is a velocity jump tangential to $ABC$ . Similarly, along the outermost yield surface $CDGD^{\prime }C^{\prime }$ , another velocity jump arises. In the viscoplastic computation, all these discontinuities become broadened into thin boundary layers with enhanced shear rate (see figure 1(a), or figure 14 in appendix A, for a magnification of the boundary layer attached to the cylinder). The thickness of these layers is expected to scale with either $Bi^{-1/3}$ or $Bi^{-1/2}$ (Balmforth et al. Reference Balmforth, Craster, Hewitt, Hormozi and Maleki2017), but otherwise they leave no enduring viscous disfigurement of the plastic solution.

Along the $\unicode[STIX]{x1D6FD}$ -lines, the Riemann invariant is $p-2Bi\unicode[STIX]{x1D717}$ . If we set $p=0$ along the vertical symmetry line at $x=0$ , this implies $p=2Bi(\unicode[STIX]{x03C0}-\unicode[STIX]{x1D717})$ throughout the deformed region, and so the pressure on the surface of the cylinder is given by

(3.1) $$\begin{eqnarray}\displaystyle p(1,\unicode[STIX]{x1D703})=\left\{\begin{array}{@{}ll@{}}2Bi(\unicode[STIX]{x03C0}-\unicode[STIX]{x1D703}), & \unicode[STIX]{x03C0}/4<\unicode[STIX]{x1D703}<\unicode[STIX]{x03C0}/2,\\ 2Bi(\unicode[STIX]{x03C0}-\unicode[STIX]{x1D703})-2Bi\unicode[STIX]{x03C0}, & \unicode[STIX]{x03C0}/2<\unicode[STIX]{x1D703}<3\unicode[STIX]{x03C0}/4,\end{array}\right. & & \displaystyle\end{eqnarray}$$

which jumps by $2\unicode[STIX]{x03C0}Bi$ at the centre of the fan.

With the stresses implied by the slipline pattern, we may integrate over the contour $CBAB^{\prime }C^{\prime }$ to determine the net horizontal force on the upper half of the cylinder $F_{x}$ (although the stress field is not prescribed over the plugs, the net force on these regions must vanish, and so the horizontal force along $BC$ or $B^{\prime }C^{\prime }$ must equal that along the corresponding plugged section of the cylinder’s surface). We then find the drag coefficient (Randolph & Houlsby Reference Randolph and Houlsby1984),

(3.2) $$\begin{eqnarray}\displaystyle & \displaystyle C_{d}=-\frac{F_{x}}{2Bi}=2(\unicode[STIX]{x03C0}+2\sqrt{2})\simeq 11.94. & \displaystyle\end{eqnarray}$$

3.2 The residual plugs

The rotating plugs of the viscoplastic computation in figure 1(a) are centred at the fans of the slipline solution and are attached to the viscous boundary layer buffering the cylinder surface. Since the viscous stress is prominent in that boundary layer, the question arises as to how the pressure jump at the centre of the fan becomes smoothed and whether this prompts a permanent adjustment of the slipline solution that explains the rotating plugs. Indeed, both Tokpavi et al. (Reference Tokpavi, Magnin and Jay2008) and Chaparian & Frigaard (Reference Chaparian and Frigaard2017) have suggested that these features are permanent for $Bi\rightarrow \infty$ . Such a conclusion is problematic as it implies that the viscoplastic theory does not converge to perfect plasticity.

The current computations suggest an alternative perspective: the rotating plugs correspond to a persistent effect that arises from the pressure discontinuity of the slipline solution at the centre of the centred fans. Because fluid flows through the pressure gradient here, the discontinuity must necessarily become smoothed by viscous stresses over a narrow window of angles $\unicode[STIX]{x1D703}$ surrounding $A$ . The angular scale of this smoothing region turns out to be relatively wide (in comparison to the viscous boundary layers), scaling very weakly with $Bi$ ; see figures 2 and 3(d). Moreover, to accommodate the smoothing of the pressure over this scale (which is too wide to allow any viscous adjustments), the overlying plastic flow must plug up, thereby creating the persistent features. Crucially, the size of the plug therefore asymptotically decreases to zero, albeit extremely slowly, as $Bi\rightarrow \infty$ (see figure 3 a; we find, in particular, that the radius decreases like $Bi^{-3/28}$ ). Consequently, the drag coefficient should approach the prediction in (3.2) for $Bi\rightarrow \infty$ , as illustrated by the numerical results (figure 4 a).

Figure 2. Pressure variation over the cylinder scaled by $Bi$ , for the Bingham numbers indicated. The dashed line corresponds to the pressure of the slipline solution given by (3.1). The inset shows $p/Bi$ against $(\unicode[STIX]{x1D703}-\unicode[STIX]{x03C0}/2)Bi^{1/7}$ .

Figure 3. Scaling data for the residual rotating plug against $Bi$ , showing (a) the plug radius $y_{p}-1$ (where $(0,y_{p})$ is the the top of the plug), (b) the rotation rate $\unicode[STIX]{x1D714}$ , (c) the boundary layer thickness at $\unicode[STIX]{x1D703}=\frac{1}{2}\unicode[STIX]{x03C0}$ and $\frac{1}{3}\unicode[STIX]{x03C0}$ , and (d) the angular size of the smoothing region, estimated by the location $\hat{\unicode[STIX]{x1D703}}_{\ast }$ for which $p=\frac{1}{2}Bi$ . The dashed lines indicate the expected scalings according to the boundary-layer theory of appendix A.

Figure 4. (a) Drag coefficient $C_{d}$ against $Bi$ for computations using a no-slip boundary condition (red circles) or the plastic slip law in (2.7) with $\unicode[STIX]{x1D71A}=1$ (blue stars). The dashed line shows (3.2). (b) Plots of $\log _{10}\dot{\unicode[STIX]{x1D6FE}}$ and streamlines for two solutions at $Bi=2^{8}$ ; the upper half shows the no-slip cylinder, and the lower half the cylinder with (2.7) and $\unicode[STIX]{x1D71A}=1$ .

A number of other numerical results are shown in figure 3, including the rotation rate of the plug and the thickness of the boundary layer against the cylinder. Notably, directly under the plug, the boundary layer is thinned by the presence of the smoothing region, scaling with $Bi^{-4/7}$ . Beyond this region, the boundary layer has a thickness of $O(Bi^{-1/2})$ , as expected from viscoplastic boundary-layer theory (Balmforth et al. Reference Balmforth, Craster, Hewitt, Hormozi and Maleki2017). The thinner boundary-layer scaling near $A$ is in disagreement with the conclusions of Tokpavi et al. (Reference Tokpavi, Magnin and Jay2008), although the difference between $-1/2$ and $-4/7$ is small (these authors actually find a scaling of $-0.53$ ). A boundary-layer theory in support of the observed scalings and the overall phenomenology of the rotating plug is provided in appendix A.

A key feature of the boundary-layer theory is that the slowly converging scalings of the rotating plug arise from the interplay between the flow within the boundary layer and the overlying plastic deformation. The important role played by the boundary layer therefore implies that the passage to the plastic limit should be different if that sharp feature is not present. Indeed, when we recompute the solutions using the slip law outlined in § 2.1.2 (with $\unicode[STIX]{x1D71A}=1$ , corresponding to a fully rough surface), the boundary layers against the cylinder are removed as all the tangential slip that is required for the adjacent perfectly plastic deformation can be taken up along the boundary itself. No slowly shrinking plugs then appear at the centre of the fans whatsoever and the convergence to the plastic limit is noticeably accelerated (see figure 4).

4.1 The Martin and Randolph slipline solution and upper bound

As for Randolph and Houlsby’s slipline field shown in figure 1, the pattern proposed by Martin & Randolph (Reference Martin and Randolph2006) consists of centred fans and involutes that leave a triangular plug at the front and back of the cylinder. However, the centres of fans are now displaced off the surface and the cores of the fans are replaced by the rigidly rotating plugs. Focussing on the upper right half of the pattern, the fan is centred at point $P$ and occupies the region $EFDGI$ in figure 5. The rotating plug spans $AEI$ . The involutes that extend the $\unicode[STIX]{x1D6FC}$ -lines from the fan into $EBCDF$ correspond to $\unicode[STIX]{x1D6FD}$ -lines that are tangent to an inner circle centred at $O$ with radius

(4.1) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D706}=\cos \left(\frac{\cos ^{-1}\unicode[STIX]{x1D71A}}{2}\right). & \displaystyle\end{eqnarray}$$

This choice for $\unicode[STIX]{x1D706}$ ensures that the $\unicode[STIX]{x1D6FC}$ -lines meet the surface of the cylinder at an angle $(\unicode[STIX]{x03C0}/4-\unicode[STIX]{x1D6E5}/2)$ , where $\unicode[STIX]{x1D6E5}=\sin ^{-1}\unicode[STIX]{x1D71A}$ , in line with the boundary condition (2.7b ) on $EB$ , $|\unicode[STIX]{x1D70F}_{r\unicode[STIX]{x1D703}}|/Bi=\unicode[STIX]{x1D71A}$ . In other words, the unwrapping of the $\unicode[STIX]{x1D6FD}$ -lines from the inner circle ensures that the slip condition is satisfied along the yielded boundary of the cylinder, and follows Randolph and Houlsby’s original generalization of figure 1 for $\unicode[STIX]{x1D71A}<1$ . The main difference between their generalization and the construction of Martin and Randolph is the introduction of the rigidly rotating plugs at the cores of the fans. Such plugs are permitted because any slipline can be taken as a yield surface and the normal velocity across the sliding, unyielded boundary can be made continuous by demanding that the rotation rate of the plugs is $\sin \unicode[STIX]{x1D6FD}_{2}/\unicode[STIX]{x1D706}$ , where $\unicode[STIX]{x03C0}-\unicode[STIX]{x1D6FD}_{2}$ dictates the angular extent of the fan (the angle between $IPE$ ). The introduction of the plugs then shifts the centre of the fan $P$ so that it lies a vertical distance $\unicode[STIX]{x1D706}/\sin \unicode[STIX]{x1D6FD}_{2}$ above $O$ .

Again, the velocity field over the plastic region is prescribed by $v_{\unicode[STIX]{x1D6FD}}=0$ and matching $v_{\unicode[STIX]{x1D6FC}}$ with the normal velocity to the contour $EBC$ . Velocity jumps thereby occur along the $\unicode[STIX]{x1D6FC}$ -lines $BFH$ and $CDG$ , which broaden into the prominent viscoplastic shear layers of the computations in figure 5, and fluid slides along the cylinder boundary $AEB$ .

Figure 6. Upper and lower bounds derived from Martin and Randolph’s slipline solution (solid blue and black lines, respectively) for the values of $\unicode[STIX]{x1D71A}$ indicated; the circles indicate the minimum of the upper bound, which coincides with the intersection with the lower bound. For $\unicode[STIX]{x1D6FD}_{2}$ less than this minimum, the lower bound exceeds the upper bound and is thus spurious (shown dashed). For $\unicode[STIX]{x1D6FD}_{2}>\frac{1}{2}\unicode[STIX]{x03C0}$ , the velocity and stress fields become inconsistent, as in the original Randolph and Houlsby construction (the corresponding bounds are shown by dotted lines). The red stars show the extrapolated values for $Bi\rightarrow \infty$ of the drag and angle $\unicode[STIX]{x1D6FD}_{2}$ from numerical computations. For the latter, the rotation rate of the rigid plugs, $\sin \unicode[STIX]{x1D6FD}_{2}/\unicode[STIX]{x1D706}$ , provides a convenient means for estimating the angle $\unicode[STIX]{x1D6FD}_{2}$ from the numerical solutions without tracing yield surfaces (which are sensitive to numerical errors).

Martin and Randolph treat the angle $\unicode[STIX]{x1D6FD}_{2}$ as an optimization parameter that can be adjusted to vary the upper bound on the drag force computed from the net dissipation rate incurred by the velocity field. The smallest possible drag coefficient provides the best upper bound, as illustrated in figure 6, which plots the upper bound against $\unicode[STIX]{x1D6FD}_{2}$ for a number of choices of the roughness factor $\unicode[STIX]{x1D71A}$ . (Martin and Randolph also include the inclination of the triangular plug and the radius $\unicode[STIX]{x1D706}$ as further optimization parameters; these turn out to be optimized by the choices of $45^{\circ }$ and (4.1), respectively, both of which are in any case demanded by the boundary and symmetry conditions.) Note that, as $\unicode[STIX]{x1D6FD}_{2}\rightarrow \frac{1}{2}\unicode[STIX]{x03C0}+\cos ^{-1}\unicode[STIX]{x1D706}$ , the rotating plug disappears and the slipline construction reduces to that of Randolph & Houlsby (Reference Randolph and Houlsby1984).

4.2 Lower bound and torque balance

Although Martin and Randolph did not do so, the stress field of the slipline solution can also be used to compute the drag force which, in principle, sets a complementary lower bound. For this task, we again set $p=0$ along the y-axis, implying $p=2Bi\unicode[STIX]{x03C0}-2Bi\unicode[STIX]{x1D717}$ in the regions of deformation. With that pressure field and the known slipline angle, we may then calculate the drag force on the cylinder by integrating over the contour $IEBC$ . The details of this calculation are provided in appendix B.1. This calculation is incomplete, however, because we do not extend the stress field into the plugs to demonstrate that an admissible solution that satisfies the yield condition exists there. Nevertheless, the construction of Randolph and Houlsby can be used to find admissible stress fields for both the triangular plugs at the front and back of the cylinder and the surrounding stagnant plug. The only missing piece of the puzzle is therefore the establishment of an admissible stress distribution for the rotating plugs.

Modulo this limitation, the implied lower bound on $C_{d}$ is also plotted in figure 6 for comparison with the upper bound. The lower bound passes through the upper bound at exactly its minimum. That is, the upper bound and lower bounds match each other at the optimal choice for $\unicode[STIX]{x1D6FD}_{2}$ , which suggests that the corresponding slipline solution is the actual true solution. However, for smaller values of $\unicode[STIX]{x1D6FD}_{2}$ (indicated by dot-dashed lines in the figure), the lower bound calculation yields a higher value than the upper bound, which is not possible. This flaw must have its origin in the lack of an admissible stress field for the rotating plugs.

The slipline construction also shares the same issue of incompatibility suffered by the original Randolph and Houlsby solution (which must be the case, given that the construction reduces to this solution in the limit $\unicode[STIX]{x1D6FD}_{2}\rightarrow \frac{1}{2}\unicode[STIX]{x03C0}+\cos ^{-1}\unicode[STIX]{x1D706}$ ): for $\unicode[STIX]{x1D6FD}_{2}>\frac{1}{2}\unicode[STIX]{x03C0}$ the shear stresses along the $\unicode[STIX]{x1D6FC}$ -lines are not consistent with the corresponding shear rates everywhere throughout the deforming region. Nevertheless, this inconsistency does not affect the optimal solution for $\unicode[STIX]{x1D6FD}_{2}$ .

More light can be shed on the rotating plug by considering the balance of torques acting on this region (appendix B.2). In particular, and with reference to figure 5(b), the upper plug is the crescent formed from the two circular arcs $EAE^{\prime }$ and $EIE^{\prime }$ . Along these arcs, the shear stresses are $\unicode[STIX]{x1D71A}Bi$ and $-Bi$ , respectively, which imply the torques $T_{EAE^{\prime }}=2\unicode[STIX]{x1D71A}Bi(\frac{1}{2}\unicode[STIX]{x03C0}-\unicode[STIX]{x1D703}_{E})$ and $T_{EIE^{\prime }}=-2r_{EI}^{2}Bi(\unicode[STIX]{x03C0}-\unicode[STIX]{x1D6FD}_{2})$ , acting about the centres of the respective circles (i.e. $P$ and $O$ ). Here, $\unicode[STIX]{x1D703}_{E}=\unicode[STIX]{x1D6FD}_{2}-\frac{1}{4}\unicode[STIX]{x03C0}+\frac{1}{2}\unicode[STIX]{x1D6E5}$ is the polar angle of point $E$ and $r_{EI}=\unicode[STIX]{x1D706}\cot \unicode[STIX]{x1D6FD}_{2}+\sqrt{1-\unicode[STIX]{x1D706}^{2}}$ is the radius of the circular arc $EIE^{\prime }$ . In addition to these torques, the difference between the two horizontal forces on the arcs provides a moment that also acts on the plug. This moment is $-\unicode[STIX]{x1D706}F_{EIE^{\prime }}/\sin \unicode[STIX]{x1D6FD}_{2}$ , if $F_{EIE^{\prime }}$ is the horizontal force on the section $EIE^{\prime }$ , which must be equal and opposite to the force on $EAE^{\prime }$ if the plug is in force balance. But $F_{EAE^{\prime }}=2F_{AE}$ , where $F_{AE}=-r_{EI}Bi[2(\unicode[STIX]{x03C0}-\unicode[STIX]{x1D6FD}_{2})\cos \unicode[STIX]{x1D6FD}_{2}+\sin \unicode[STIX]{x1D6FD}_{2}]$ is the force on the section $AE$ (see appendix B.1). Hence, the rotating plug is free of torques if $T_{EIE^{\prime }}-T_{EAE^{\prime }}-2\unicode[STIX]{x1D706}F_{AE}/\sin \unicode[STIX]{x1D6FD}_{2}=0$ , or

(4.2) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D71A}\left({\textstyle \frac{3}{4}}\unicode[STIX]{x03C0}-\unicode[STIX]{x1D6FD}_{2}+{\textstyle \frac{1}{2}}\unicode[STIX]{x1D6E5}\right)+[(\unicode[STIX]{x03C0}-\unicode[STIX]{x1D6FD}_{2})(\sqrt{1-\unicode[STIX]{x1D706}^{2}}-\unicode[STIX]{x1D706}\cot \unicode[STIX]{x1D6FD}_{2})-\unicode[STIX]{x1D706}](\unicode[STIX]{x1D706}\cot \unicode[STIX]{x1D6FD}_{2}+\sqrt{1-\unicode[STIX]{x1D706}^{2}})=0. & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$

This condition picks out a unique value for $\unicode[STIX]{x1D6FD}_{2}$ which coincides exactly with the optimal value. We conclude that there cannot be an admissible stress field for the rotating plug, except potentially at the torque-free value of $\unicode[STIX]{x1D6FD}_{2}$ . Thus, Martin and Randolph’s slipline field with this choice is the only candidate for the true plastic solution. This conclusion is supported by the numerical computations, which match the predictions of the slipline theory for a variety of choices for the roughness parameter $\unicode[STIX]{x1D71A}$ (see figures 5 and 6), and which explicitly construct admissible stress solutions for the rotating plug. Thus, the combination of slipline theory and numerical computation provides evidence that the slipline patterns of figure 5 are the actual perfectly plastic solutions.

5.1 Newtonian limit

As described by Blake (Reference Blake1971b ), it is straightforward to solve the Stokes problem in the Newtonian limit to furnish the stream function,

(5.1) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}=\unicode[STIX]{x1D713}_{0}=U_{s}r\sin \unicode[STIX]{x1D703}+{\textstyle \frac{1}{2}}(r^{-n}-r^{2-n})\sin n\unicode[STIX]{x1D703}+{\textstyle \frac{1}{2}}a(r^{-m}-r^{2-m})\sin m\unicode[STIX]{x1D703}, & & \displaystyle\end{eqnarray}$$

for the prescribed tangential surface motion. This result incorporates the Stokes paradox in that there is no bounded solution for $r\rightarrow \infty$ unless $U_{s}=\frac{1}{2}$ and $n=1$ . Moreover, the solution implies that $F_{x}$ in (2.5) is identically zero. A similar result holds if the normal surface velocity is prescribed (Blake Reference Blake1971b ).

Following Hewitt & Balmforth (Reference Hewitt and Balmforth2018), we may proceed beyond this leading solution and compute the correction prompted by the yield stress using perturbation theory. In the vicinity of the cylinder ( $r=O(1)$ ) this correction is forced by the need to match the solution with that in the far field ( $r\gg 1$ ), as in the classical resolution of the Stokes paradox by the inclusion of inertia. Here, however, the far field region is controlled by the yield stress. In particular, balancing the two sides of (2.13) for $r\gg 1$ , we must have that $\unicode[STIX]{x1D713}=O(r^{2}Bi)$ in the far field. But, provided $U_{s}\neq \frac{1}{2}\unicode[STIX]{x1D6FF}_{n1}$ , $\unicode[STIX]{x1D713}_{0}$ grows like $r$ . Hence, the far-field balance demands that $r=O(Bi^{-1})$ . Moreover, the yield stress eventually arrests motion here, limiting the flow to a yielded region with a radial extent of $O(Bi^{-1})$ .

The correction to the near-field solution again satisfies the biharmonic equation and is proportional to $2r\log r-r+r^{-1}$ , in view of the boundary conditions on the cylinder and the need to discard terms that grow any more rapidly with $r$ (Hinch Reference Hinch1991). This correction breaks asymptotic order and becomes of comparable size to $\unicode[STIX]{x1D713}_{0}$ as one enters the far field, leading to the estimate, $\unicode[STIX]{x1D713}-\unicode[STIX]{x1D713}_{0}=O((U_{s}-\unicode[STIX]{x1D6FF}_{n1})/\log Bi^{-1})$ . Hence, the horizontal drag force, which is dictated by the correction, can be calculated and the match to the far field demands

(5.2) $$\begin{eqnarray}\displaystyle & \displaystyle F_{x}=-4\unicode[STIX]{x03C0}\frac{(U_{s}-\frac{1}{2}\unicode[STIX]{x1D6FF}_{n1})}{\log Bi^{-1}}. & \displaystyle\end{eqnarray}$$

Evidently, the cylinder is force-free to leading order when $U_{s}=\frac{1}{2}\unicode[STIX]{x1D6FF}_{n1}$ , which is the locomotion speed of a free swimmer in the limit $Bi\rightarrow 0$ . Thus, in the Newtonian limit, surface motions without a $\sin \unicode[STIX]{x1D703}$ component cannot swim. Note that, because the stream function decays more rapidly when $U_{s}-\frac{1}{2}\unicode[STIX]{x1D6FF}_{n1}\rightarrow 0$ , all the preceding scalings must change for the force-free case.

5.2 Symmetries

With the surface velocity condition $V_{p}=\sin n\unicode[STIX]{x1D703}+a\sin m\unicode[STIX]{x1D703}$ , the problem can inherit spatial symmetries that constrain the solutions. First, if the driving angular velocity pattern contains multiple lines of reflection symmetry, then the problem with $U_{s}=0$ is invariant under a set of finite angular rotations. This implies that the driving pattern possesses no preferred swimming direction and force-free states with $U_{s}=0$ exist whatever the Bingham number. Single mode patterns with $n>1$ and $a=0$ are of this type.

Second, when $m$ is even and $n$ is odd, the equations and boundary conditions are invariant under the transformation, $(U_{s},a,\unicode[STIX]{x1D703},u,v,\unicode[STIX]{x1D713})\rightarrow (U_{s},-a,\unicode[STIX]{x03C0}-\unicode[STIX]{x1D703},-u,v,\unicode[STIX]{x1D713})$ . This implies that, given a solution with a certain $U_{s}$ and $V_{p}=\sin n\unicode[STIX]{x1D703}+a\sin m\unicode[STIX]{x1D703}$ , one can generate another solution with the same translation speed but driving pattern $V_{p}=\sin n\unicode[STIX]{x1D703}-a\sin m\unicode[STIX]{x1D703}$ ; the two solutions are symmetrical under reflection about $\unicode[STIX]{x1D703}=\frac{1}{2}\unicode[STIX]{x03C0}$ . Consequently, the force-free swimming speed is independent of the sign of $a$ . Similarly, the transformation $(U_{s},a,\unicode[STIX]{x1D703},u,v,\unicode[STIX]{x1D713})\rightarrow (-U_{s},-a,\unicode[STIX]{x03C0}-\unicode[STIX]{x1D703},u,-v,-\unicode[STIX]{x1D713})$ again leaves the system invariant if $m$ is odd and $n$ is even. Thus, in this case, for a swimmer with $(a,U_{s})$ , there is another with $(-a,-U_{s})$ .

Finally, for the alternative driving pattern $U_{p}=\cos n\unicode[STIX]{x1D703}+a\sin m\unicode[STIX]{x1D703}$ in (2.11) with $(n,a)=(1,0)$ , if we set $U_{s}=1-\hat{U} _{s}$ , the boundary condition becomes $(u,v)_{r=1}=(\hat{U} _{s}\cos \unicode[STIX]{x1D703},\sin \unicode[STIX]{x1D703}-\hat{U} _{s}\sin \unicode[STIX]{x1D703})$ . But this is identical to the driving pattern in (2.9) for $V_{p}=\sin \unicode[STIX]{x1D703}$ and translation speed $\hat{U} _{s}$ . In other words, these particular squirmer solutions are identical, except for the switch in translation speed.

5.3 Numerical results

To gain a broader perspective on the problem, we now solve the system of equations numerically, calculating solutions with different (fixed) translation speeds $U_{s}$ and Bingham numbers $Bi$ , for a variety of driving patterns. To begin, we consider the simplest case, with $(n,a)=(1,0)$ (figure 7). The most obvious feature of the computed flow patterns is their similarity to those around translating cylinders: in all but the example with highest translation speed in figure 7, the flow is localized to a region with a radial extent that is comparable to the diameter of the cylinder, and prominent recirculation cells with embedded rotating plugs appear above and below. In fact, at higher Bingham number, the organization of the flow looks identical to the Randolph and Houlsby slipline pattern (figure 1), with simply a different velocity distribution along the $\unicode[STIX]{x1D6FC}$ -lines. Notably, the tangential surface forcing strengthens the boundary layers which are now able to adjust the plastic deformation beyond. As a result, the rotating plugs continue to widen with increasing $Bi$ and become permanent in the plastic limit. The collapse to the Randolph and Houlsby stress field is reflected in the drag coefficient, which equilibrates to $C_{d}=-(2\unicode[STIX]{x03C0}+4\sqrt{2})$ for $U_{s}\lesssim 0.16Bi^{-1/2}$ at high $Bi$ (figure 7 g). With higher translation speeds, however, the extent of the yielded region abruptly decreases, with all deformation becoming consumed by the boundary layer around the cylinder for $Bi\gg 1$ (figure 7 f). The switch in flow pattern prompts a fall in the magnitude of the drag coefficient, which passes through zero at a critical value, $U_{s}^{ff}$ , corresponding to the locomotion speed of a swimmer moving under its own power.

Figure 7. Squirmer solutions for $(n,a)=(1,0)$ showing density plots of $\log _{10}\dot{\unicode[STIX]{x1D6FE}}$ overlain by streamlines (blue), with (a–c) $Bi=1$ and (d–f) $Bi=2^{8}$ , for $U_{s}Bi^{1/2}\approx [0,0.1,0.38]$ , respectively. In (f), the full circle has the scale of the axes as in (d) and (e), whereas the quarter circle shown in the inset is a magnification to highlight the thin boundary layer. (g) Drag coefficients $C_{d}$ against scaled translation speed $Bi^{1/2}U_{s}$ , from simulations with the Bingham numbers indicated, together with the asymptotic predictions for $Bi\gg 1$ from the Randolph and Houlsby slipline solution (§ 3) and the boundary-layer analysis of § 5.4 (dashed black lines).

Figure 8. Squirmer solutions showing $\log _{10}\dot{\unicode[STIX]{x1D6FE}}$ at $Bi=2^{8}$ for (a–c) $n=3$ , $m=0$ and (d–f) $n=5,m=0$ with the imposed swimming speed (a,d) $U_{s}=-0.015$ , (b,e) $U_{s}=0$ and (c,f) $U_{s}=0.015$ . (g) The variation of the drag coefficient $C_{d}$ with $U_{s}$ for $n=3$ (blue stars) and $n=5$ (red squares); the dashed line, with $C_{d}=0$ , is the required value for $U_{s}=0$ .

Flow fields around single-mode squirmers with higher $n$ are shown in figure 8. As expected from the symmetries of the problem, the drag coefficient for these solutions vanishes only for $U_{s}=0$ , precluding locomotion at any $Bi$ (see § 5.2). In the force-free states, the flow patterns take the form of a straightforward geometrical generalization of the Randolph and Houlsby slipline field, containing a network of $2n$ centred fans with angular extent $\unicode[STIX]{x03C0}(\frac{1}{2}+n^{-1})$ and triangular plugs attached to the cylinder. These solutions become distorted by translation, but the patchwork of attached plugs and rotating fans persists, with broader seams of more complicated plastic deformation. Again, the fans contain persistent plugs, sometimes becoming displaced from the cylinder surface in the manner of the Martin and Randolph slipline field.

The force-free swimming states can be computed directly by employing an interval-bisection algorithm to vary $U_{s}$ until $C_{d}=0$ . Figure 9(a–h) shows the output of this algorithm for both the simple swimmer with $(n,a)=(1,0)$ , and for pushers and pullers with $(n,m)=(1,2)$ and varying $a$ . As discussed in § 5.2, since $n$ is odd and $m$ is even in this case, the solutions with $a<0$ are reflections of those with $a>0$ about the vertical axis, with the same swimming speed. Thus, as in the Newtonian limit, these pushers and pullers always travel at equal speeds. In all cases, the swimming speed converges to the Newtonian limit $U_{s}=\frac{1}{2}$ for $Bi\rightarrow 0$ (see § 5.1 and Blake (Reference Blake1971b )). At large yield stress, the swimming speeds instead decline as $U_{s}\sim Bi^{-1/2}$ (see figure 9 i). The corresponding force-free flow patterns remain confined to the surface boundary layers at low values of $a$ . But when this parameter is larger, the states becomes less confined and again adopt a wider scale pattern of plastic deformation with the form of a patchwork of triangular plugs and fans, much like the slipline solutions of §§ 3 and 4 (see figure 9 h). Such patterns are not, however, the only possibility; figure 9(g), for example, displays a swimmer in which closer examination reveals curved sliplines that peel off the surface boundary layer, and incorporate a non-circular fan pinned at the centre of circulation.

Figure 9. Force-free squirmer solutions for surface velocities $n=1$ , $m=2$ and (a–d) $Bi=1$ and (e–h) $Bi=2^{8}$ , showing $\log _{10}\dot{\unicode[STIX]{x1D6FE}}$ and streamlines (blue) for (a,e) $a=0$ , (b,f) $a=0.25$ , (c,g) $a=1$ and (d,h) $a=2$ . The colour bar is the same as in figure 8. (i) The corresponding swimming speeds. (j) The same data for $a=0$ and $a=0.25$ only, together with the predictions of the boundary-layer theory (§ 5.4, dashed).

Force-free pushers and pullers with $(n,m)=(1,3)$ are shown in figure 10(a–f). In this case, since $m$ and $n$ are both odd, the $a\rightarrow -a$ symmetry is lost (although the flow patterns remain symmetrical about the $y$ -axis) and the swimming speed depends on the sign of $a$ . Regardless of this, however, the flow is again confined to the surface boundary layers for lower values of $a$ , and features larger-scale plastic deformation for higher $a$ , with the swimming speed scaling as $U_{s}\sim Bi^{-1/2}$ in the plastic limit and converging to $U_{s}=\frac{1}{2}$ for $Bi\rightarrow 0$ .

A less expected result is shown in figure 11, which displays flow fields and swimming speeds for a swimmer with $(n,m)=(2,3)$ . In the Newtonian limit, such a mixed-mode driving pattern cannot provide propulsion as it does not contain a $\sin \unicode[STIX]{x1D703}$ component. Moreover, swimming is not possible with either of the $n=2$ and $m=3$ components individually. With a finite yield-stress, however, propulsion becomes possible, and the swimmer reaches a maximum speed at an intermediate value of $Bi$ (figure 11 c; again, the symmetry of the driving pattern implies that $U_{s}$ does not depend on the sign of $a$ ).

Figure 10. Force-free squirmer solutions with $(n,m)=(1,3)$ and $Bi=2^{8}$ showing $\log _{10}\dot{\unicode[STIX]{x1D6FE}}$ for (a) $a=0.25$ , (b) $a=-0.25$ , (c) $a=1$ , (d) $a=-1$ , (e) $a=2$ and (f) $a=-2$ . The bottom row (g–i) shows the variation of the swimming speed with $Bi$ for (g) $a=\pm 0.25$ , (h) $a=\pm 1$ and (i) $a=\pm 2$ . The dashed line shows the asymptotic prediction from (5.15) for $a=0.25$ and $Bi\gg 1$ .

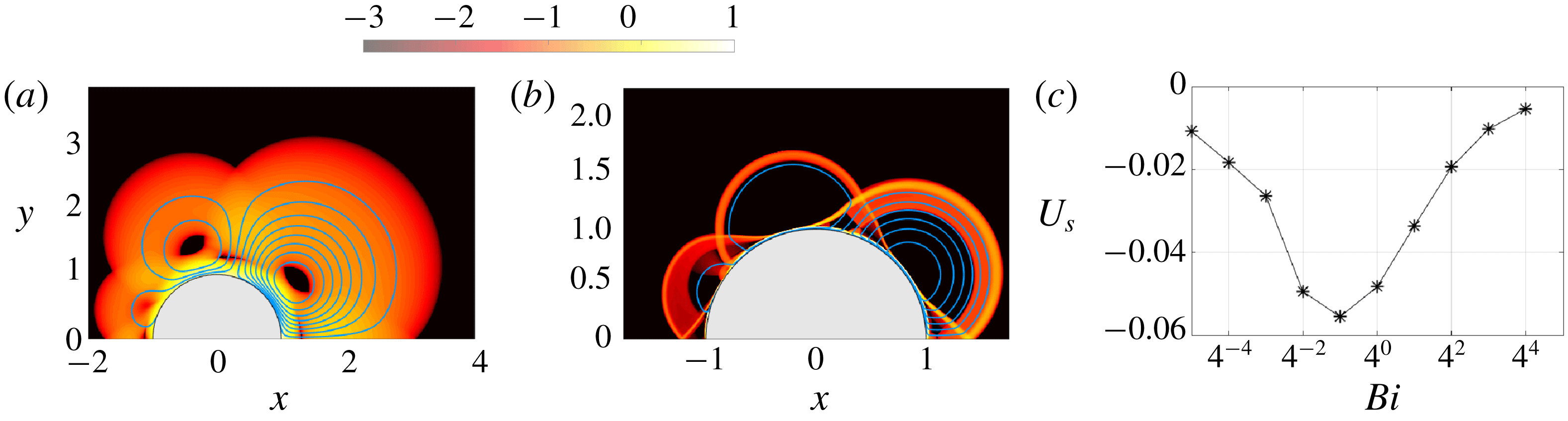
Figure 11. Force-free squirmer solutions for $(n,m)=(2,3)$ and $a=1$ showing $\log _{10}\dot{\unicode[STIX]{x1D6FE}}$ for (a) $Bi=1$ and (b) $Bi=2^{8}$ . (c) The variation of the force-free swimming speed $U_{s}$ with $Bi$ .

Finally, we report an example exploiting the prescribed normal surface velocity in (2.11), rather than the tangential motions previously discussed. As argued in § 5.2, the simplest example of this model with $n=1$ and $a=0$ is equivalent to the squirmer with the tangential surface velocity $V_{p}=\sin \unicode[STIX]{x1D703}$ , but for the switch in translation speed $U_{s}\rightarrow 1-U_{s}$ . Hence, all the results in figures 7 and 9 immediately carry over, although the switch in $U_{s}$ implies a very different limit for the force-free swimming speed for $Bi\gg 1$ . Additional results for $m=2$ and varying $a$ are displayed in figure 12. When $a$ is not small, the swimmer is no longer equivalent to a squirmer with tangential surface velocity; larger-scale patterns of plastic deformation develop with both curved sliplines, centred fans and constant-stress triangles. The swimming speed now converges to an $a$ -dependent constant for $Bi\rightarrow \infty$ (the Newtonian limit is again $U_{s}\rightarrow \frac{1}{2}$ ).

Figure 12. Force-free squirmer solutions showing $\log _{10}\dot{\unicode[STIX]{x1D6FE}}$ for the normal surface velocity condition (2.11) with (a) $a=0.1$ , (b) $0.25$ and (c) 1, at $Bi=2^{8}$ . (d) The variation of the swimming speed with $Bi$ .

5.4 Boundary-layer theory

5.4.1 Boundary-layer structure

When flow becomes confined to the boundary layer attached to the cylinder, as in figures 9(e,f) and 10(a,b), we rescale the variables to describe that narrow region (cf. appendix A) as follows:

(5.3a-d ) $$\begin{eqnarray}\displaystyle r=1+Bi^{-1/2}\unicode[STIX]{x1D702},\quad [u,U_{s}]=Bi^{-1/2}[U(\unicode[STIX]{x1D702},\unicode[STIX]{x1D703}),U_{1}],\quad v=V(\unicode[STIX]{x1D702},\unicode[STIX]{x1D703}),\quad p=BiP(\unicode[STIX]{x1D702},\unicode[STIX]{x1D703}). & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$

At leading order, local force balance then demands

(5.4a,b ) $$\begin{eqnarray}\displaystyle P_{\unicode[STIX]{x1D702}}=0\quad \text{and}\quad V_{\unicode[STIX]{x1D702}\unicode[STIX]{x1D702}}+2\text{ sgn }(V_{\unicode[STIX]{x1D702}})=P_{\unicode[STIX]{x1D703}}. & & \displaystyle\end{eqnarray}$$

In terms of the rescaled variables, the boundary conditions in (2.9) become

(5.5a,b ) $$\begin{eqnarray}\displaystyle V(0,\unicode[STIX]{x1D703})\sim V_{p}(\unicode[STIX]{x1D703})\quad \text{and}\quad U(0,\unicode[STIX]{x1D703})=U_{1}\cos \unicode[STIX]{x1D703}, & & \displaystyle\end{eqnarray}$$

whereas the match to the surrounding plug at the yield surface, $\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}_{b}(\unicode[STIX]{x1D703})$ , demands that

(5.6) $$\begin{eqnarray}\displaystyle & \displaystyle V(\unicode[STIX]{x1D702}_{b},\unicode[STIX]{x1D703})=V_{\unicode[STIX]{x1D702}}(\unicode[STIX]{x1D702}_{b},\unicode[STIX]{x1D703})=U(\unicode[STIX]{x1D702}_{b},\unicode[STIX]{x1D703})=0. & \displaystyle\end{eqnarray}$$

We therefore find the velocity profile,

(5.7) $$\begin{eqnarray}\displaystyle & \displaystyle V=V_{p}(\unicode[STIX]{x1D703})\left(1-\frac{\unicode[STIX]{x1D702}}{\unicode[STIX]{x1D702}_{b}}\right)^{2}, & \displaystyle\end{eqnarray}$$

with

(5.8) $$\begin{eqnarray}\displaystyle & \displaystyle P_{\unicode[STIX]{x1D703}}=2\left(\frac{|V_{p}|}{\unicode[STIX]{x1D702}_{b}^{2}}-1\right)\;\text{sgn}(V_{p}). & \displaystyle\end{eqnarray}$$

The integral of the leading-order continuity equation, $V_{\unicode[STIX]{x1D703}}+U_{\unicode[STIX]{x1D702}}\sim 0$ across the boundary layer now furnishes

(5.9) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\left[\frac{\unicode[STIX]{x1D702}_{b}V_{p}(\unicode[STIX]{x1D703})}{3}\right]-U_{1}\cos \unicode[STIX]{x1D703}=0. & \displaystyle\end{eqnarray}$$

Focussing on surface motions that are up–down antisymmetric with $V_{p}(0)=V_{p}(\unicode[STIX]{x03C0})=0$ , we now find the boundary-layer profile,

(5.10) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D702}_{b}(\unicode[STIX]{x1D703})=\frac{3U_{1}\sin \unicode[STIX]{x1D703}}{V_{p}(\unicode[STIX]{x1D703})}. & \displaystyle\end{eqnarray}$$

This thickness is only positive when the angular surface motion $V_{p}(\unicode[STIX]{x1D703})$ is directed opposite to the sense of translation, $\text{sgn}(U_{s})$ . Otherwise, the balances implied by the scalings in (5.3) are not consistent, which we interpret to signify that the flow cannot be confined to the surface boundary layer. Indeed, the numerical solutions in § 5.3 display larger-scale flow patterns at large $Bi$ whenever $U_{s}/V_{p}<0$ .

Figure 13 compares the predictions of (5.10) with some of the measured yield surfaces of the numerical solution with confined flow patterns. In the simple case with $V_{p}(\unicode[STIX]{x1D703})=\sin \unicode[STIX]{x1D703}$ (figure 13 a), the boundary layer has the constant width, $\unicode[STIX]{x1D702}_{b}=(r_{p}-1)Bi^{1/2}=\sqrt{\unicode[STIX]{x03C0}/2}$ , where $r_{p}$ is the radius of the yield surface. The yield surfaces of the computations are indeed relatively flat and compare well with the prediction, except close to the front and back of the cylinder where the boundary-layer thickness sharply declines over further ‘corner regions’. For squirmers with $V_{p}=\sin \unicode[STIX]{x1D703}+a\sin m\unicode[STIX]{x1D703}$ , the boundary-layer thickness varies with position; again the predictions match well with numerical results except for the adjustments at the front and back (figure 13(b,c)).

Figure 13. Boundary-layer thicknesses of squirmers for (a) $(n,a)=(1,0)$ , (b) $(n,m,a)=(1,2,0.25)$ and (c) $(n,m,a)=(1,3,0.25)$ , with $Bi=2^{6}$ (black), $Bi=2^{8}$ (blue), $Bi=2^{10}$ (red) and $Bi=2^{12}$ (green). The prediction from (5.10) is shown by dashed lines.

For $V_{p}U_{1}<0$ , the emergence of plastic deformation outside the boundary layer (with $(u,v)\sim O(Bi^{-1/2})$ ) modifies the final boundary condition in (5.5), and therefore the flux balance in (5.9). The resulting flow into or out of the boundary layer then maintains a boundary layer of finite thickness. Importantly, however, the scalings of the boundary layer in (5.3), do not change although one must now complete the solution by matching to the adjacent region of perfectly plastic deformation (which we avoid here).

5.4.2 Drag force and swimming speed

Given the surface pressure $BiP$ and tangential shear stress $Bi\;\text{sgn}(V_{\unicode[STIX]{x1D702}})=-Bi\;\text{sgn}(V_{p})$ , the net horizontal force on the swimmer is given by

(5.11) $$\begin{eqnarray}F_{x}=-Bi\int _{-\unicode[STIX]{x03C0}}^{\unicode[STIX]{x03C0}}[P\cos \unicode[STIX]{x1D703}-\text{sgn}(V_{p})\sin \unicode[STIX]{x1D703}]\,\text{d}\unicode[STIX]{x1D703}=2Bi\int _{0}^{\unicode[STIX]{x03C0}}\left(\frac{2|V_{p}|^{3}}{9U_{1}^{2}\sin \unicode[STIX]{x1D703}}-\sin \unicode[STIX]{x1D703}\right)\text{sgn}(V_{p})\,\text{d}\unicode[STIX]{x1D703}.\end{eqnarray}$$

The drag therefore vanishes for

(5.12) $$\begin{eqnarray}\displaystyle & \displaystyle U_{s}^{ff}=\frac{Bi^{-1/2}}{3}\sqrt{2\int _{0}^{\unicode[STIX]{x03C0}}\frac{V_{p}(\unicode[STIX]{x1D703})^{3}}{\sin \unicode[STIX]{x1D703}}\,\text{d}\unicode[STIX]{x1D703}}\left[\int _{0}^{\unicode[STIX]{x03C0}}\sin \unicode[STIX]{x1D703}\;\text{sgn}(V_{p})\,\text{d}\unicode[STIX]{x1D703}\right]^{-1/2}, & \displaystyle\end{eqnarray}$$

furnishing an asymptotic prediction of the locomotion speed of the force-free swimmer.

The drag from (5.11) also increases with decreasing translation speed $U_{s}$ , diverging for $U_{s}\rightarrow 0$ , and must therefore exceed that associated with the Randolph and Houlsby slipline solution below some threshold in $U_{s}$ . We interpret the crossover to correspond to the switch from the confined flow pattern to larger-scale plastic deformation. The deconfinement of the flow must therefore occur for

(5.13) $$\begin{eqnarray}\displaystyle U_{s}=U_{s}^{ff}\left\{1+2(\unicode[STIX]{x03C0}+2\sqrt{2})\left[\int _{0}^{\unicode[STIX]{x03C0}}\sin \unicode[STIX]{x1D703}\;\text{sgn}(V_{p})\,\text{d}\unicode[STIX]{x1D703}\right]^{-1}\right\}^{-1/2}. & & \displaystyle\end{eqnarray}$$

For the simplest case with $V_{p}=\sin \unicode[STIX]{x1D703}$ ( $n=1$ , $a=0$ ), the drag coefficient implied by (5.11) is

(5.14) $$\begin{eqnarray}\displaystyle & \displaystyle C_{d}=-\frac{F_{x}}{2Bi}=2-\frac{\unicode[STIX]{x03C0}}{9U_{1}^{2}}, & \displaystyle\end{eqnarray}$$

which is compared to the numerical results in figure 7(g); the switch in flow pattern for (5.13) also matches satisfyingly with the abrupt drop in the magnitude of $C_{d}$ in the numerical solutions. The corresponding force-free swimmer has $U_{s}^{ff}=\sqrt{\unicode[STIX]{x03C0}/18}Bi^{-1/2}$ , which again compares well with the numerical results (figure 7 g).

For squirmers with $V_{p}=\sin \unicode[STIX]{x1D703}+a\sin m\unicode[STIX]{x1D703}$ , the swimming speed is

(5.15) $$\begin{eqnarray}\displaystyle U_{s}^{ff}=\left\{\begin{array}{@{}ll@{}}{\textstyle \frac{1}{3}}Bi^{-1/2}\sqrt{{\textstyle \frac{1}{2}}\unicode[STIX]{x03C0}(1+3a^{2})}, & m\text{ even,}\\[12.0pt] {\textstyle \frac{1}{3}}Bi^{-1/2}\sqrt{{\textstyle \frac{1}{2}}\unicode[STIX]{x03C0}(1+3a^{2}+a^{3})}, & m\text{ odd,}\end{array}\right. & & \displaystyle\end{eqnarray}$$

provided the boundary-layer thickness remains finite everywhere, which demands that $a<m^{-1}$ for $m$ even and $a\lesssim \sin (3\unicode[STIX]{x03C0}/2m)$ for $m$ odd. Figures 9(j) and 10(g) include the predictions in (5.15).

Note that the prediction for the swimming speed in (5.12) relies on the solutions in (5.8) and (5.10), which fail when flow is no longer confined to the boundary layer. Nevertheless, because the scalings of the problem do not change in that situation, the swimming speed still scales with $Bi^{-1/2}$ , as seen in the numerical computations (e.g. figure 9 i). The match to the surrounding plastic deformation, however, determines the coefficient $U_{1}$ .