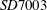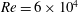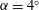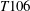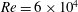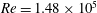1 Introduction
Understanding of boundary layer separation, transition to turbulence and reattachment of the turbulent boundary layer is of great importance for many applications ranging from diffusers and turbine blades to micro air vehicles and unmanned air vehicles. Despite many experimental and numerical studies, improving the efficiency of engineering designs remains challenging due to the lack of predictive and controlling capabilities and requires further investigations to complement our current understanding.
Laminar separation typically occurs in the low-Reynolds-number regime, for example in the flow over an airfoil at incidence or in the flow over a flat plate with a prescribed suction profile as the upper boundary condition. On the upper surface, the boundary layer remains laminar beyond the point of minimum surface pressure and into the pressure recovery region, where the adverse pressure gradient opposes the flow and causes its detachment. Downstream of the separation point, the highly unstable separated shear layer transitions to turbulence. Subsequently, at sufficiently high Reynolds numbers or low angles of attack, the turbulent flow promotes momentum transfer in the wall-normal direction and causes reattachment of the boundary layer, thus closing the so-called laminar separation bubble (LSB). The later the reattachment happens, the bigger the LSB and the larger the loss of lift and the increase in drag. In the limit of no reattachment and complete separation, the airfoil is said to be in a stall condition with poor aerodynamic performance. Thus, optimizing performance requires understanding and control of these mechanisms.
Recent studies were focused on the mechanism of transition to turbulence, with special attention paid to understanding the stability features of LSBs, including the role of primary and secondary instabilities in the transition process. While it was shown theoretically and experimentally by Gaster (Reference Gaster1963) and Dovgal, Kozlov & Michalke (Reference Dovgal, Kozlov and Michalke1994) that viscous instabilities, such as Tollmien–Schlichting (T–S) waves (see e.g. Schlichting et al. Reference Schlichting, Gersten, Krause, Oertel and Mayes1960; Ho & Huerre Reference Ho and Huerre1984), amplify upstream disturbances in the laminar part of the bubble, inviscid instabilities, e.g. of Kelvin–Helmholtz (K–H) type, play the dominant role in the amplification of disturbances in the free shear layer of the separation bubble and thus in the transition to turbulence (Ahuja & Burrin Reference Ahuja and Burrin1984; Watmuff Reference Watmuff1999; Yang & Voke Reference Yang and Voke2001; Lang, Rist & Wagner Reference Lang, Rist and Wagner2004; Yarusevych, Sullivan & Kawall Reference Yarusevych, Sullivan and Kawall2006; Yarusevych, Kawall & Sullivan Reference Yarusevych, Kawall and Sullivan2008; Hain, Kähler & Radespiel Reference Hain, Kähler and Radespiel2009).
One of the first direct numerical simulations (DNS) of transition over a flat plate, induced by a prescribed suction profile as the upper boundary condition, was performed by Alam & Sandham (Reference Alam and Sandham2000). Before the transition, a staggered formation of
![]() $\unicode[STIX]{x1D6EC}$
vortices was observed. Based on linear stability analysis, it was concluded that the transition process was driven by convective instability (disturbances grow in space) rather than by absolute instability (disturbances grow in time and spread everywhere). In contrast, Spalart & Strelets (Reference Spalart and Strelets2000) performed a DNS with the same set-up and observed transition of an unforced LSB with negligible T–S instabilities and no distinct regions of primary or secondary instabilities, leading to a rapid three-dimensionality.
$\unicode[STIX]{x1D6EC}$
vortices was observed. Based on linear stability analysis, it was concluded that the transition process was driven by convective instability (disturbances grow in space) rather than by absolute instability (disturbances grow in time and spread everywhere). In contrast, Spalart & Strelets (Reference Spalart and Strelets2000) performed a DNS with the same set-up and observed transition of an unforced LSB with negligible T–S instabilities and no distinct regions of primary or secondary instabilities, leading to a rapid three-dimensionality.
Marxen et al. (Reference Marxen, Lang, Rist and Wagner2003) investigated LSBs over a flat plate by means of experiment and DNS using periodic two-dimensional disturbances upstream of the separation along with a spanwise array of spacers to trigger transition. It was observed that vortices were formed due to the roll-up of the separated shear layer, which eventually broke down to turbulence.
Subsequent investigations in Marxen, Rist & Wagner (Reference Marxen, Rist and Wagner2004) concluded that the transition was driven by convective amplification of a two-dimensional T–S wave, and that the dominant mechanism behind transition is an absolute secondary instability as proposed by Rist, Maucher & Wagner (Reference Rist, Maucher and Wagner1996), Maucher, Rist & Wagner (Reference Maucher, Rist and Wagner1997, Reference Maucher, Rist and Wagner1999) and Rist & Maucher (Reference Rist and Maucher2002), for which the growth of two-dimensional disturbances via viscous T–S instability upstream of the separation point undergoes a gradual transition to inviscid K–H-type amplification. The dominant downstream travelling waves quickly saturate and form large, downstream-propagating spanwise vortices. Besides this convective spatial growth, the existence of an additional temporal amplification has been observed experimentally, theoretically and numerically by Gaster (Reference Gaster1992, Reference Gaster2006), Alam & Sandham (Reference Alam and Sandham2000) and Maucher (Reference Maucher2002), among others.
In the work of Jones, Sandberg & Sandham (Reference Jones, Sandberg and Sandham2008) it was shown that although classical linear stability theory of the time-averaged flow fields suggests convective instability (Boutilier & Yarusevych Reference Boutilier and Yarusevych2012a
) with no evidence of absolute instability, removing the forcing still leads to self-sustained turbulence. They concluded, based on three-dimensional simulations resolving the linear response, that transition occurs by absolute instability of two-dimensional vortex shedding within the shear layer in the absence of convectively driven transition. Further studies on flat plates and airfoils have shown the vortex roll-up occurring in the separated shear layer at the frequency of dominant disturbance amplification with downstream vortex pairing for some flow conditions (Watmuff Reference Watmuff1999; Lang et al.
Reference Lang, Rist and Wagner2004; Burgmann, Dannemann & Schröder Reference Burgmann, Dannemann and Schröder2008; Zhang, Hain & Kähler Reference Zhang, Hain and Kähler2008; Hain et al.
Reference Hain, Kähler and Radespiel2009; Yarusevych, Sullivan & Kawall Reference Yarusevych, Sullivan and Kawall2009). In the work by Burgmann et al. (Reference Burgmann, Dannemann and Schröder2008), time-resolved measurements of the velocity field over the
![]() $SD7003$
airfoil revealed several types of coherent vortical structures developing during transition. Qualitative differences in these structures compared to the flow over flat plates, such as in Watmuff (Reference Watmuff1999) and Lang et al. (Reference Lang, Rist and Wagner2004), were observed and attributed to a dependence of the transition behaviour on surface curvature as well as a dependence of the development of the coherent structures on the flow conditions. In Kurelek, Lambert & Yarusevych (Reference Kurelek, Lambert and Yarusevych2016) it was further demonstrated that the newly coalesced (due to vortex pairing) shear layer vortices, characterized by an initially high spanwise coherence, undergo rapid spanwise deformations and subsequently break down to smaller structures in the vicinity of the reattachment point.
$SD7003$
airfoil revealed several types of coherent vortical structures developing during transition. Qualitative differences in these structures compared to the flow over flat plates, such as in Watmuff (Reference Watmuff1999) and Lang et al. (Reference Lang, Rist and Wagner2004), were observed and attributed to a dependence of the transition behaviour on surface curvature as well as a dependence of the development of the coherent structures on the flow conditions. In Kurelek, Lambert & Yarusevych (Reference Kurelek, Lambert and Yarusevych2016) it was further demonstrated that the newly coalesced (due to vortex pairing) shear layer vortices, characterized by an initially high spanwise coherence, undergo rapid spanwise deformations and subsequently break down to smaller structures in the vicinity of the reattachment point.
The flow development near the reattachment point has shown significant variations depending on the surface geometry and the operating conditions. Under certain conditions, the reattachment process appears relatively steady with no shedding of large coherent spanwise vortices (Balzer & Fasel Reference Balzer and Fasel2010), while in other cases it was observed to be an unsteady process accompanied by vortex shedding. The unsteady reattachment behaviour is called bubble flapping and was observed both experimentally and numerically, with a frequency below the one of the primary K–H instabilities (see e.g. Watmuff Reference Watmuff1999; Boiko et al. Reference Boiko, Grek, Dovgal and Kozlov2002; Rist & Maucher Reference Rist and Maucher2002; Lang et al. Reference Lang, Rist and Wagner2004; Burgmann et al. Reference Burgmann, Dannemann and Schröder2008; Hain et al. Reference Hain, Kähler and Radespiel2009; Jones, Sandberg & Sandham Reference Jones, Sandberg and Sandham2010; Marxen & Rist Reference Marxen and Rist2010). To explain the cause of bubble flapping, various authors pointed at the absolute secondary instability mechanisms of the shed vortices to three-dimensional disturbances (Jones et al. Reference Jones, Sandberg and Sandham2008), at acoustic feedback mechanisms (Jones et al. Reference Jones, Sandberg and Sandham2010; Jones & Sandberg Reference Jones and Sandberg2011) and at a viscous–inviscid coupling interacting with varying levels of free-stream turbulence (Marxen & Rist Reference Marxen and Rist2010). As shown by e.g. Wissink & Rodi (Reference Wissink and Rodi2004), on performing a DNS on a flat plate with different free-stream disturbances, a larger disturbance leads to a smaller bubble size, while the reattachment point is moved upstream. Similarly, Jones et al. (Reference Jones, Sandberg and Sandham2008) observed a large decrease of the bubble size when forcing was applied, leading to a significant increase of aerodynamic performance for the NACA0012 airfoil.
Due to the lack of a comprehensive picture (Boutilier & Yarusevych Reference Boutilier and Yarusevych2012b ) of the instability mechanisms at play during transition, it is inherently difficult to model these phenomena. In the work of Spalart & Strelets (Reference Spalart and Strelets2000), the accuracy of various Reynolds-averaged Navier–Stokes (RANS) turbulence models was assessed. Although the results obtained by the Spalart–Allmaras model showed reasonable agreement with the DNS, large discrepancies between the models and the reference case were observed. In particular, more sensitive quantities such as the skin friction coefficient showed significant deviations. Minor improvements of various RANS models were reported in the works of Papanicolaou & Rodi (Reference Papanicolaou and Rodi1999), Hadzic & Hanjalic (Reference Hadzic and Hanjalic2000) and Howard, Alam & Sandham (Reference Howard, Alam and Sandham2000). In recent years, large-eddy simulations (LES) for transitional flows have become increasingly popular (see e.g. Wilson & Pauley Reference Wilson and Pauley1998; Yang & Voke Reference Yang and Voke2001; Roberts & Yaras Reference Roberts and Yaras2006; Eisenbach & Friedrich Reference Eisenbach and Friedrich2008; Xu, Sullivan & Paraschivoiu Reference Xu, Sullivan and Paraschivoiu2010; Cadieux et al. Reference Cadieux, Domaradzki, Sayadi and Bose2014). While accurate results were reported for implicit LES, relying on high-order schemes for spatial derivatives to capture transition, combined with filtering for stabilization (see e.g. Galbraith & Visbal Reference Galbraith and Visbal2008; Visbal Reference Visbal2009; Zhou & Wang Reference Zhou and Wang2010), the recent work of Cadieux & Domaradzki (Reference Cadieux and Domaradzki2015) highlights the importance of appropriate subgrid-scale modelling by a comparison of dynamic Smagorinsky, truncated Navier–Stokes and no-model under-resolved DNS.
The motivation of the present study is to assess the recently developed entropy-based lattice Boltzmann models with respect to capturing the subtle mechanisms of transitional flows. Despite the fact that lattice Boltzmann methods (LBM) are becoming increasingly popular due to their efficiency and simplicity, stability and accuracy issues have obstructed applications to complex flows for a long time. These issues have been overcome by entropy-based LBM, which has shown encouraging results for resolved and, due to its built-in subgrid features, also coarse grid simulations (Karlin, Ferrante & Öttinger Reference Karlin, Ferrante and Öttinger1999; Karlin, Bösch & Chikatamarla Reference Karlin, Bösch and Chikatamarla2014; Bösch, Chikatamarla & Karlin Reference Bösch, Chikatamarla and Karlin2015b ; Dorschner et al. Reference Dorschner, Bösch, Chikatamarla, Boulouchos and Karlin2016a ; Dorschner, Chikatamarla & Karlin Reference Dorschner, Chikatamarla and Karlin2016b ). In spite of validation in both laminar and turbulent flow regimes, the transition to turbulence, which not only depends on accurate prediction of the bulk flow but also is highly sensitive to the implementation of the boundary conditions, has received little attention so far in the realm of LBM. However, to establish LBM as a predictive method for engineering applications, it is of great importance to also assess the accuracy of LBM in the transitional flow regime.
The paper is organized as follows. In § 2, a brief review of entropy-based lattice Boltzmann methods is presented. Subsequently, in § 3, we consider the flow past the
![]() $SD7003$
airfoil at an angle of attack
$SD7003$
airfoil at an angle of attack
![]() $\unicode[STIX]{x1D6FC}=4^{\circ }$
and a chord Reynolds number of
$\unicode[STIX]{x1D6FC}=4^{\circ }$
and a chord Reynolds number of
![]() $Re=6\times 10^{4}$
. Moreover, in order to test the model’s performance for highly curved geometries, simulations of the flow in a low-pressure turbine passage for different Reynolds numbers and free-stream turbulence intensities are performed and, where available, compared to DNS and experimental data. Results are discussed in § 4.
$Re=6\times 10^{4}$
. Moreover, in order to test the model’s performance for highly curved geometries, simulations of the flow in a low-pressure turbine passage for different Reynolds numbers and free-stream turbulence intensities are performed and, where available, compared to DNS and experimental data. Results are discussed in § 4.
2 Entropic multi-relaxation time lattice Boltzmann models
The LBM is a promising approach to computational fluid dynamics (CFD) with applications in various regimes, such as turbulence or multiphase, thermal, compressible and micro-flows among others (Succi Reference Succi2015). While conventional CFD discretizes the governing equations directly, the LBM employs discretized particle distribution functions (populations)
![]() $f_{i}(\boldsymbol{x},t)$
, which are designed to recover the Navier–Stokes equations in the hydrodynamic limit (Higuera & Jimenez Reference Higuera and Jimenez1989; Higuera & Succi Reference Higuera and Succi1989; Higuera, Succi & Benzi Reference Higuera, Succi and Benzi1989). Each population is associated with a discrete velocity
$f_{i}(\boldsymbol{x},t)$
, which are designed to recover the Navier–Stokes equations in the hydrodynamic limit (Higuera & Jimenez Reference Higuera and Jimenez1989; Higuera & Succi Reference Higuera and Succi1989; Higuera, Succi & Benzi Reference Higuera, Succi and Benzi1989). Each population is associated with a discrete velocity
![]() $\boldsymbol{c}_{i},i=1,\ldots ,Q$
, and these velocity vectors span a regularly spaced lattice and thus allow for a highly efficient stream–collide algorithm with exact propagation and easy parallelizability due to local nonlinearity.
$\boldsymbol{c}_{i},i=1,\ldots ,Q$
, and these velocity vectors span a regularly spaced lattice and thus allow for a highly efficient stream–collide algorithm with exact propagation and easy parallelizability due to local nonlinearity.
In recent years, the development of LBM has made significant advances. In particular, stability issues have been overcome by the development of collision models beyond the original lattice Bhatnagar–Gross–Krook (LBGK) model. While on the one hand, the inclusion of explicit turbulence models (see e.g. Chen et al.
Reference Chen, Kandasamy, Orszag, Shock, Succi and Yakhot2003; Malaspinas & Sagaut Reference Malaspinas and Sagaut2012) has shown success, the class of parameter-free entropic lattice Boltzmann models (ELBM) has achieved accurate results for both resolved and under-resolved simulations. In particular, the notion of a discretized entropy function
![]() $H$
was introduced in Karlin et al. (Reference Karlin, Ferrante and Öttinger1999) and used to determine the relaxation of the population consistent with the second law of thermodynamics, resulting in a nonlinearly stable scheme. A key component of ELBM is the adaptive relaxation of the populations in both space and time (see e.g. Dorschner et al. (Reference Dorschner, Frapolli, Chikatamarla and Karlin2016c
) for a recent discussion on the topic in the context of multi-domain simulations).
$H$
was introduced in Karlin et al. (Reference Karlin, Ferrante and Öttinger1999) and used to determine the relaxation of the population consistent with the second law of thermodynamics, resulting in a nonlinearly stable scheme. A key component of ELBM is the adaptive relaxation of the populations in both space and time (see e.g. Dorschner et al. (Reference Dorschner, Frapolli, Chikatamarla and Karlin2016c
) for a recent discussion on the topic in the context of multi-domain simulations).
Recently, this notion has been extended to multi-relaxation time (MRT) lattice Boltzmann models. Generally, MRT models exploit the high dimensionality of the kinetic system to choose the relaxation of higher-order, non-hydrodynamic moments in order to stabilize the scheme. For a long time, this was done by tuning the corresponding relaxation parameters (see e.g. d’Humieres Reference d’Humieres1992; Latt & Chopard Reference Latt and Chopard2006). In Karlin et al. (Reference Karlin, Bösch and Chikatamarla2014), the so-called Karlin–Bösch–Chikatamarla (KBC) model was introduced, where this issue was resolved by invoking the notion of entropy to choose the relaxation adaptively, which leads to enhanced stability and accuracy (Karlin et al. Reference Karlin, Bösch and Chikatamarla2014; Bösch et al. Reference Bösch, Chikatamarla and Karlin2015b ).
The derivation of the KBC model was already discussed in Karlin et al. (Reference Karlin, Bösch and Chikatamarla2014), Bösch et al. (Reference Bösch, Chikatamarla and Karlin2015b
) and Dorschner et al. (Reference Dorschner, Bösch, Chikatamarla, Boulouchos and Karlin2016a
); here we state the main steps and restrict ourselves to the isothermal case using the standard
![]() $D3Q27$
lattice.
$D3Q27$
lattice.
The general lattice Boltzmann equation for the population
![]() $f_{i}(\boldsymbol{x},t)$
is given by
$f_{i}(\boldsymbol{x},t)$
is given by
where the streaming step is given by the left-hand side and the post-collision state
![]() $f_{i}^{\prime }$
is represented on the right-hand side by a convex linear combination of
$f_{i}^{\prime }$
is represented on the right-hand side by a convex linear combination of
![]() $f_{i}(\boldsymbol{x},t)$
and the mirror state
$f_{i}(\boldsymbol{x},t)$
and the mirror state
![]() $f_{i}^{mirr}(\boldsymbol{x},t)$
.
$f_{i}^{mirr}(\boldsymbol{x},t)$
.
The KBC model, as used in all simulations in this paper, represents the population
![]() $f_{i}$
in terms of its natural moments as the sum of a kinematic part
$f_{i}$
in terms of its natural moments as the sum of a kinematic part
![]() $k_{i}$
, a shear part
$k_{i}$
, a shear part
![]() $s_{i}$
and the remaining higher-order moments
$s_{i}$
and the remaining higher-order moments
![]() $h_{i}$
:
$h_{i}$
:
The mirror state is defined as
where
![]() $s_{i}^{eq}$
and
$s_{i}^{eq}$
and
![]() $h_{i}^{eq}$
denote
$h_{i}^{eq}$
denote
![]() $s_{i}$
and
$s_{i}$
and
![]() $h_{i}$
evaluated at equilibrium. The equilibrium
$h_{i}$
evaluated at equilibrium. The equilibrium
![]() $f^{eq}$
is defined as the minimum of the entropy function
$f^{eq}$
is defined as the minimum of the entropy function
subject to the local conservation laws for mass and momentum
where the weights
![]() $W_{i}$
are lattice-specific constants. Finally, minimizing the
$W_{i}$
are lattice-specific constants. Finally, minimizing the
![]() $H$
function in the post-collision state yields the relaxation parameter
$H$
function in the post-collision state yields the relaxation parameter
where
![]() $\unicode[STIX]{x0394}s_{i}=s_{i}-s_{i}^{eq}$
and
$\unicode[STIX]{x0394}s_{i}=s_{i}-s_{i}^{eq}$
and
![]() $\unicode[STIX]{x0394}h_{i}=h_{i}-h_{i}^{eq}$
indicate the deviation from equilibrium and the entropic scalar product is given by
$\unicode[STIX]{x0394}h_{i}=h_{i}-h_{i}^{eq}$
indicate the deviation from equilibrium and the entropic scalar product is given by
![]() $\langle X|Y\rangle =\sum _{i}(X_{i}Y_{i}/f_{i}^{eq})$
.
$\langle X|Y\rangle =\sum _{i}(X_{i}Y_{i}/f_{i}^{eq})$
.
The KBC model recovers the Navier–Stokes equations in the hydrodynamic limit, where the parameter
![]() $\unicode[STIX]{x1D6FD}$
in (2.1) is related to the viscosity as
$\unicode[STIX]{x1D6FD}$
in (2.1) is related to the viscosity as
where
![]() $c_{s}=1/\sqrt{3}$
is the lattice speed of sound.
$c_{s}=1/\sqrt{3}$
is the lattice speed of sound.
Finally, we mention that the transitional flows considered in this paper are sensitive to the wall boundary conditions and spurious artefacts can occur for an inappropriate choice. In the LBM framework, various propositions exist, among which only a few have been shown to be stable and accurate for both resolved and under-resolved simulations. To that end, we use the boundary condition as detailed in Dorschner et al. (Reference Dorschner, Chikatamarla, Bösch and Karlin2015, Reference Dorschner, Chikatamarla and Karlin2016b ), which was validated for various flow set-ups including channel flow, the flow in engine-like geometries and self-propelled swimmers. Other boundary conditions used in the simulations include inflow, outflow, free-stream and periodic boundary conditions. Unless stated otherwise, we implement these boundary conditions as follows: the inflow is prescribed using equilibrium populations with unit density. For the outflow boundary, we employ the no boundary condition. The free-stream or free-slip boundary condition reflects the population with respect to the wall normal and is used to mimic an open space. The periodic boundaries are directly applied within the advection step.
3 Flow separation and transition to turbulence
In this section, we investigate two cases to test the accuracy of KBC models. In the first instance, we consider the flow over the
![]() $SD7003$
airfoil at angle of attack
$SD7003$
airfoil at angle of attack
![]() $\unicode[STIX]{x1D6FC}=4^{\circ }$
and Reynolds number
$\unicode[STIX]{x1D6FC}=4^{\circ }$
and Reynolds number
![]() $Re=6\times 10^{4}$
based on the chord length
$Re=6\times 10^{4}$
based on the chord length
![]() $c$
and the inflow velocity
$c$
and the inflow velocity
![]() $U_{\infty }$
. The second test case is regarding the flow in a low-pressure turbine passage composed of
$U_{\infty }$
. The second test case is regarding the flow in a low-pressure turbine passage composed of
![]() $T106A$
airfoils at Reynolds numbers of
$T106A$
airfoils at Reynolds numbers of
![]() $Re=6\times 10^{4}$
and
$Re=6\times 10^{4}$
and
![]() $Re=1.48\times 10^{5}$
based on the axial chord and the inflow velocity.
$Re=1.48\times 10^{5}$
based on the axial chord and the inflow velocity.
As stated in Cadieux & Domaradzki (Reference Cadieux and Domaradzki2015) and also confirmed by our simulations, the key to obtaining accurate results, in agreement with experiment, is to resolve the reverse flow region near the wall and the shear layer which transitions to turbulence. Despite the efficiency of the LBM, this is an intractable task for a uniform resolution. To remedy this issue we employ the multi-domain grid refinement technique as proposed and validated for various set-ups in our recent publication (Dorschner et al. Reference Dorschner, Frapolli, Chikatamarla and Karlin2016c ).
3.1 Transitional flow past SD7003 airfoil
3.1.1 Numerical set-up
The numerical set-up is identical to the experimental and numerical studies of Ol et al. (Reference Ol, McCauliffe, Hanff, Scholz and Kaehler2005), Galbraith & Visbal (Reference Galbraith and Visbal2008) and Zhou & Wang (Reference Zhou and Wang2010) to allow a direct comparison with the results obtained by the KBC model.
The experimental investigations of Ol et al. (Reference Ol, McCauliffe, Hanff, Scholz and Kaehler2005) were conducted in order to assess the suitability of three different test facilities, namely, a low turbulence wind tunnel (Technical University of Braunschweig (TU-BS) Low-Noise Wind Tunnel), a water tunnel (Air Force Research Laboratory (AFRL) Free-Surface Water Tunnel) and a tow tank (Institute for Aerospace Research (IAR) Tow Tank). While good agreement was found for IAR and TU-BS, the AFRL facility showed significantly earlier separation and reattachment, and was not able to resolve reverse flow in the bubble. The numerical study of Galbraith & Visbal (Reference Galbraith and Visbal2008) was conducted to test the capabilities of implicit large-eddy simulations (ILES) to capture the LSB mechanism accurately. The use of high-order compact schemes for spatial derivatives and a Pade-type low-pass filter for stability has yielded accurate predictions of LSB for various operating points. In a similar fashion, Zhou & Wang (Reference Zhou and Wang2010) employed an implicit LES using a high-order spectral difference method to capture the LSB.
In our study and in accordance with Galbraith & Visbal (Reference Galbraith and Visbal2008) and Zhou & Wang (Reference Zhou and Wang2010), we use a uniform inlet velocity with no inflow disturbances. A small perturbation at the beginning of the simulation is introduced to initiate vortex shedding. All statistical quantities are recorded after an initial transient of
![]() $t=15c/U_{\infty }$
and collected for another
$t=15c/U_{\infty }$
and collected for another
![]() $t=45c/U_{\infty }$
until statistically stationary conditions have been reached. The solutions are obtained on a computational domain of
$t=45c/U_{\infty }$
until statistically stationary conditions have been reached. The solutions are obtained on a computational domain of
![]() $10c\times 5c\times 0.2c$
for the stream, pitch and spanwise directions, respectively. Periodic boundary conditions are applied in the spanwise direction, while free-stream boundary conditions are prescribed in the pitchwise direction. The computational domain is refined with five levels, where the coarsest level resolves the airfoil with
$10c\times 5c\times 0.2c$
for the stream, pitch and spanwise directions, respectively. Periodic boundary conditions are applied in the spanwise direction, while free-stream boundary conditions are prescribed in the pitchwise direction. The computational domain is refined with five levels, where the coarsest level resolves the airfoil with
![]() $c=100$
lattice points to ensure enough spatial extent to represent the reverse flow region accurately. As shown in figure 1, the refinement patches are located closely around the airfoil to minimize computational cost. Based on the maximum wall shear stress in the reattachment zone, the resolution in wall units amounts to
$c=100$
lattice points to ensure enough spatial extent to represent the reverse flow region accurately. As shown in figure 1, the refinement patches are located closely around the airfoil to minimize computational cost. Based on the maximum wall shear stress in the reattachment zone, the resolution in wall units amounts to
![]() $\unicode[STIX]{x0394}y^{+}\approx 2.1$
at the finest level, which is similar to the ILES study of Zhou & Wang (Reference Zhou and Wang2010) with
$\unicode[STIX]{x0394}y^{+}\approx 2.1$
at the finest level, which is similar to the ILES study of Zhou & Wang (Reference Zhou and Wang2010) with
![]() $\unicode[STIX]{x0394}y^{+}\approx 2.5$
using high-order spectral differences. As an additional verification of sufficient resolution, a snapshot of the spatial distribution of the stabilizer
$\unicode[STIX]{x0394}y^{+}\approx 2.5$
using high-order spectral differences. As an additional verification of sufficient resolution, a snapshot of the spatial distribution of the stabilizer
![]() $\unicode[STIX]{x1D6FE}$
is shown in figure 2. It has been shown in Bösch, Chikatamarla & Karlin (Reference Bösch, Chikatamarla and Karlin2015a
), Bösch et al. (Reference Bösch, Chikatamarla and Karlin2015b
) and Dorschner et al. (Reference Dorschner, Frapolli, Chikatamarla and Karlin2016c
) that the value of
$\unicode[STIX]{x1D6FE}$
is shown in figure 2. It has been shown in Bösch, Chikatamarla & Karlin (Reference Bösch, Chikatamarla and Karlin2015a
), Bösch et al. (Reference Bösch, Chikatamarla and Karlin2015b
) and Dorschner et al. (Reference Dorschner, Frapolli, Chikatamarla and Karlin2016c
) that the value of
![]() $\unicode[STIX]{x1D6FE}$
is directly related to the degree of under-resolution and that
$\unicode[STIX]{x1D6FE}$
is directly related to the degree of under-resolution and that
![]() $\unicode[STIX]{x1D6FE}$
automatically tends towards the LBGK value
$\unicode[STIX]{x1D6FE}$
automatically tends towards the LBGK value
![]() $\unicode[STIX]{x1D6FE}_{lim}=2$
in the limit of a fully resolved simulation. Therefore, the deviation of the stabilizer from its limit value indicates under-resolution. Figure 2 shows the expected small deviations from
$\unicode[STIX]{x1D6FE}_{lim}=2$
in the limit of a fully resolved simulation. Therefore, the deviation of the stabilizer from its limit value indicates under-resolution. Figure 2 shows the expected small deviations from
![]() $\unicode[STIX]{x1D6FE}_{lim}=2$
at the finest grid level, suggesting negligible numerical diffusion. This assertion will be further investigated through comparison to reference data.
$\unicode[STIX]{x1D6FE}_{lim}=2$
at the finest grid level, suggesting negligible numerical diffusion. This assertion will be further investigated through comparison to reference data.

Figure 1. Multi-domain block refinement for the flow past the
![]() $SD7003$
airfoil along with a slice of instantaneous streamwise velocity.
$SD7003$
airfoil along with a slice of instantaneous streamwise velocity.

Figure 2. Instantaneous snapshot of the spatial distribution of the stabilizer
![]() $\unicode[STIX]{x1D6FE}$
.
$\unicode[STIX]{x1D6FE}$
.

Figure 3. Isosurfaces of the Q-criterion (Q
![]() $=$
4) coloured by normalized streamwise velocity for the simulation of the
$=$
4) coloured by normalized streamwise velocity for the simulation of the
![]() $SD7003$
airfoil at an angle of attack
$SD7003$
airfoil at an angle of attack
![]() $\unicode[STIX]{x1D6FC}=4^{\circ }$
and a Reynolds number
$\unicode[STIX]{x1D6FC}=4^{\circ }$
and a Reynolds number
![]() $Re=6\times 10^{4}$
.
$Re=6\times 10^{4}$
.

Figure 4. Average pressure coefficient
![]() $\overline{C_{p}}$
over the upper and lower surfaces of the
$\overline{C_{p}}$
over the upper and lower surfaces of the
![]() $SD7003$
airfoil. Here and in the following, the symbols represent sampled values along the chord for clarity.
$SD7003$
airfoil. Here and in the following, the symbols represent sampled values along the chord for clarity.

Figure 5. Average skin friction coefficient
![]() $\overline{C_{f}}$
over the upper and lower surfaces of the
$\overline{C_{f}}$
over the upper and lower surfaces of the
![]() $SD7003$
airfoil.
$SD7003$
airfoil.
3.1.2 Results
In order to gain insight into the coherent flow structures in the LSB, we present an instantaneous snapshot of isosurfaces of the Q-criterion coloured by streamwise velocity in figure 3. As expected, starting from the leading edge, the flow remains laminar and further downstream it separates due to the adverse pressure gradient on the suction side of the airfoil. Instabilities, forming a corrugated flow pattern, and interaction with the small-scale structures in the recirculation zone can be observed at the end of the laminar shear layer. Further downstream, spanwise distortion leads to fully three-dimensional structures, indicating the transitional region, followed by fine-scale turbulence.
Beyond the visual inspection, one can quantify separation, transition and reattachment by computing the mean pressure coefficient
![]() $\overline{C_{p}}=(\overline{p}-p_{\infty })/(1/2\unicode[STIX]{x1D70C}_{\infty }u_{\infty }^{2})$
and the mean skin friction coefficient
$\overline{C_{p}}=(\overline{p}-p_{\infty })/(1/2\unicode[STIX]{x1D70C}_{\infty }u_{\infty }^{2})$
and the mean skin friction coefficient
![]() $\overline{C_{f}}=\overline{\unicode[STIX]{x1D70F}}/(1/2\unicode[STIX]{x1D70C}_{\infty }u_{\infty }^{2})$
on the airfoil surface as shown in figures 4 and 5, respectively. Here, the mean wall shear stress is denoted by
$\overline{C_{f}}=\overline{\unicode[STIX]{x1D70F}}/(1/2\unicode[STIX]{x1D70C}_{\infty }u_{\infty }^{2})$
on the airfoil surface as shown in figures 4 and 5, respectively. Here, the mean wall shear stress is denoted by
![]() $\overline{\unicode[STIX]{x1D70F}}$
.
$\overline{\unicode[STIX]{x1D70F}}$
.
The distribution of the mean pressure coefficient over the suction side of the airfoil surface can be used to extract various characteristics of the LSB. As seen in figure 4, the point of minimum pressure is followed by a pressure plateau, which has been shown to occur near the separated flow region (Tani Reference Tani1964; Boutilier & Yarusevych Reference Boutilier and Yarusevych2012b
). Consequently, the separation point
![]() $x_{s}$
and transition location
$x_{s}$
and transition location
![]() $x_{t}$
can be identified as the start and the end of the pressure plateau (O’meara & Mueller Reference O’meara and Mueller1987). Similarly, the reattachment point
$x_{t}$
can be identified as the start and the end of the pressure plateau (O’meara & Mueller Reference O’meara and Mueller1987). Similarly, the reattachment point
![]() $x_{r}$
can be estimated as the point at the end of the enhanced rate of pressure recovery downstream of the transition point. These definitions are commonly used to experimentally obtain LSB characteristics by linearly fitting the surface pressure data (Gerakopulos, Boutilier & Yarusevych Reference Gerakopulos, Boutilier and Yarusevych2010; Boutilier & Yarusevych Reference Boutilier and Yarusevych2012b
). A first indication that the KBC model is able to accurately predict the mean bubble size characteristics is given by the excellent match of the
$x_{r}$
can be estimated as the point at the end of the enhanced rate of pressure recovery downstream of the transition point. These definitions are commonly used to experimentally obtain LSB characteristics by linearly fitting the surface pressure data (Gerakopulos, Boutilier & Yarusevych Reference Gerakopulos, Boutilier and Yarusevych2010; Boutilier & Yarusevych Reference Boutilier and Yarusevych2012b
). A first indication that the KBC model is able to accurately predict the mean bubble size characteristics is given by the excellent match of the
![]() $\overline{C_{p}}$
distribution with the high-order implicit LES of Galbraith & Visbal (Reference Galbraith and Visbal2008) and Zhou & Wang (Reference Zhou and Wang2010).
$\overline{C_{p}}$
distribution with the high-order implicit LES of Galbraith & Visbal (Reference Galbraith and Visbal2008) and Zhou & Wang (Reference Zhou and Wang2010).
On the other hand, computing the skin friction on the airfoil surface gives another meaningful way to determine the average geometrical properties of the LSB. The separation and reattachment points can be inferred from the location of zero skin friction. While the first root with a negative gradient indicates separation, reattachment happens further downstream at zero skin friction and a positive gradient. From this analysis, we report
![]() $x_{s}$
and
$x_{s}$
and
![]() $x_{r}$
along with the reference data in table 1. It is apparent that excellent agreement with the experimental data is obtained. As was mentioned above, the AFRL facility is an outlier of the experimental studies but is still reported for completeness. Furthermore, the agreement with both ILES results is reasonable. From the skin friction plot one can see that the KBC model predicts a considerably later separation as compared to the ILES but matches the experimental data. Nonetheless, the location of minimum skin friction and the reattachment location agree well with the ILES results from Zhou & Wang (Reference Zhou and Wang2010).
$x_{r}$
along with the reference data in table 1. It is apparent that excellent agreement with the experimental data is obtained. As was mentioned above, the AFRL facility is an outlier of the experimental studies but is still reported for completeness. Furthermore, the agreement with both ILES results is reasonable. From the skin friction plot one can see that the KBC model predicts a considerably later separation as compared to the ILES but matches the experimental data. Nonetheless, the location of minimum skin friction and the reattachment location agree well with the ILES results from Zhou & Wang (Reference Zhou and Wang2010).

Figure 6. Determination of the onset to transition. (a) Distribution of Reynolds shear stress
![]() $-u^{\prime }w^{\prime }/u_{\infty }^{2}$
with a threshold of
$-u^{\prime }w^{\prime }/u_{\infty }^{2}$
with a threshold of
![]() $0.001$
. (b) Reynolds shear stress value plotted along the line of maximum shear stress.
$0.001$
. (b) Reynolds shear stress value plotted along the line of maximum shear stress.
Table 1. Comparison of the LSB properties for the flow over the
![]() $SD7003$
airfoil, where
$SD7003$
airfoil, where
![]() $Tu$
denotes the turbulence intensity of the inflow.
$Tu$
denotes the turbulence intensity of the inflow.


Figure 7. Mean velocity profiles at
![]() $x/c=0.1{-}0.5$
.
$x/c=0.1{-}0.5$
.
Finally, in order to identify the mean location of transition, Reynolds shear stresses are considered. In figure 6(a), the distribution of Reynolds shear stress
![]() $-u^{\prime }w^{\prime }/U_{\infty }^{2}$
is shown with a threshold of
$-u^{\prime }w^{\prime }/U_{\infty }^{2}$
is shown with a threshold of
![]() $0.001$
. The commonly used criterion for the transition onset is the region which exceeds this threshold as these stresses describe the transport of momentum into the boundary layer (Ol et al.
Reference Ol, McCauliffe, Hanff, Scholz and Kaehler2005; Yuan et al.
Reference Yuan, Khalid, Windte, Scholz and Radespiel2005; Burgmann et al.
Reference Burgmann, Dannemann and Schröder2008). Different criteria, such as the shape factor
$0.001$
. The commonly used criterion for the transition onset is the region which exceeds this threshold as these stresses describe the transport of momentum into the boundary layer (Ol et al.
Reference Ol, McCauliffe, Hanff, Scholz and Kaehler2005; Yuan et al.
Reference Yuan, Khalid, Windte, Scholz and Radespiel2005; Burgmann et al.
Reference Burgmann, Dannemann and Schröder2008). Different criteria, such as the shape factor
![]() $H_{12}$
(defined as the ratio of the displacement thickness and the momentum thickness) or the deviation from exponential growth, were identified and are in good agreement with each other (Lang et al.
Reference Lang, Rist and Wagner2004; McAuliffe & Yaras Reference McAuliffe and Yaras2005). In figure 6(b), the Reynolds shear stress value is plotted along the line of maximum shear stress, which allows us to accurately extract the transition point as the point exceeding the threshold of
$H_{12}$
(defined as the ratio of the displacement thickness and the momentum thickness) or the deviation from exponential growth, were identified and are in good agreement with each other (Lang et al.
Reference Lang, Rist and Wagner2004; McAuliffe & Yaras Reference McAuliffe and Yaras2005). In figure 6(b), the Reynolds shear stress value is plotted along the line of maximum shear stress, which allows us to accurately extract the transition point as the point exceeding the threshold of
![]() $0.001$
. The agreement with all reference data is excellent (see table 1).
$0.001$
. The agreement with all reference data is excellent (see table 1).
The mean velocity profiles along the chord line in the wall-normal direction are compared to the ILES by Zhou & Wang (Reference Zhou and Wang2010) in figure 7. The evolution from the attached shear layer to the detachment is clearly visible and the separation location is in line with its evaluation using the mean skin friction coefficient
![]() $\overline{C_{f}}$
. In agreement with the previously observed deviations of the skin friction distribution over the airfoil surface, the ILES predicts earlier separation compared to both experiment and the present simulation. Nonetheless, the agreement between KBC and ILES is reasonable.
$\overline{C_{f}}$
. In agreement with the previously observed deviations of the skin friction distribution over the airfoil surface, the ILES predicts earlier separation compared to both experiment and the present simulation. Nonetheless, the agreement between KBC and ILES is reasonable.

Figure 8. Spectra of fluctuating streamwise velocity along the spanwise direction.

Figure 9. Power spectral density (PSD) for two observer points, one within the bubble and one in the near wake. (a) Power spectral density in the LSB at
![]() $x/c\approx 0.53$
. (b) Power spectral density in the near wake.
$x/c\approx 0.53$
. (b) Power spectral density in the near wake.
Next, we investigate the spanwise flow development. The recent experimental study of the flow over a NACA0018 airfoil by Kurelek et al. (Reference Kurelek, Lambert and Yarusevych2016) suggests that newly coalesced shear layer vortices possess a relatively high spanwise coherence and undergo a rapid spanwise deformation, which eventually leads to a break down into small-scale structures in the reattachment zone. To quantify this behaviour with the present simulation, spanwise wavelength statistics are extracted by computing the spectra of streamwise velocity fluctuations
![]() $u^{\prime }u^{\prime }$
along the spanwise direction for various chordwise locations within the LSB at a constant wall-normal distance of
$u^{\prime }u^{\prime }$
along the spanwise direction for various chordwise locations within the LSB at a constant wall-normal distance of
![]() $y/c=0.00625$
. The corresponding spectra are reported in figure 8. Starting beyond the separation point at
$y/c=0.00625$
. The corresponding spectra are reported in figure 8. Starting beyond the separation point at
![]() $x/c=0.4$
, one can observe that the maximum corresponds to the spanwise extent, thereby confirming the two-dimensionality of the main vortices. At the mean transition location
$x/c=0.4$
, one can observe that the maximum corresponds to the spanwise extent, thereby confirming the two-dimensionality of the main vortices. At the mean transition location
![]() $x/c=0.55$
, a steep increase at
$x/c=0.55$
, a steep increase at
![]() $\unicode[STIX]{x1D706}/c\approx 0.01$
is followed by a plateau of dominant wavelengths ranging from
$\unicode[STIX]{x1D706}/c\approx 0.01$
is followed by a plateau of dominant wavelengths ranging from
![]() $\unicode[STIX]{x1D706}/c\approx 0.03$
to
$\unicode[STIX]{x1D706}/c\approx 0.03$
to
![]() $\unicode[STIX]{x1D706}/c\approx 0.1$
. This characteristic behaviour is identical to what was observed by Kurelek et al. (Reference Kurelek, Lambert and Yarusevych2016) and implies three-dimensional vortex structures and weak spatial periodicity. Beyond transition onset at
$\unicode[STIX]{x1D706}/c\approx 0.1$
. This characteristic behaviour is identical to what was observed by Kurelek et al. (Reference Kurelek, Lambert and Yarusevych2016) and implies three-dimensional vortex structures and weak spatial periodicity. Beyond transition onset at
![]() $x/c=0.615$
, the breakdown into small structures is evidenced by a broadening of the aforementioned plateau and an increase of the spectra at lower wavelengths. At the average reattachment point
$x/c=0.615$
, the breakdown into small structures is evidenced by a broadening of the aforementioned plateau and an increase of the spectra at lower wavelengths. At the average reattachment point
![]() $x/c=0.68$
, the spectra practically overlap and only a minor increase at higher wavelengths is observed, suggesting a rather fast breakdown. These results agree well with the experimental study of Kurelek et al. (Reference Kurelek, Lambert and Yarusevych2016) and therefore confirm that the KBC model is able to capture the spanwise evolution of the flow.
$x/c=0.68$
, the spectra practically overlap and only a minor increase at higher wavelengths is observed, suggesting a rather fast breakdown. These results agree well with the experimental study of Kurelek et al. (Reference Kurelek, Lambert and Yarusevych2016) and therefore confirm that the KBC model is able to capture the spanwise evolution of the flow.
Finally, the time-resolved KBC simulation allows us to study the LSB dynamics. The power spectral density of the streamwise velocity fluctuations is shown in figure 9 for two observer points, one within the LSB at
![]() $x/c\approx 0.53$
and the other in the near wake. Despite the fact that more frequencies are present in the near wake, both observer points display a dominant vortex shedding frequency at a Strouhal number
$x/c\approx 0.53$
and the other in the near wake. Despite the fact that more frequencies are present in the near wake, both observer points display a dominant vortex shedding frequency at a Strouhal number
![]() $St_{vs}=f\sin (\unicode[STIX]{x1D6FC})c/U_{\infty }\approx 0.38$
. In order to assess if the reattachment behaviour is steady or if bubble flapping occurs, the normalized bubble length
$St_{vs}=f\sin (\unicode[STIX]{x1D6FC})c/U_{\infty }\approx 0.38$
. In order to assess if the reattachment behaviour is steady or if bubble flapping occurs, the normalized bubble length
![]() $l/c$
, which is computed through the instantaneous
$l/c$
, which is computed through the instantaneous
![]() $C_{f}$
distribution, is monitored over the course of the simulation (see figure 10
a). A highly unsteady reattachment behaviour with various frequency contributions is evident and the bubble length fluctuates as much as
$C_{f}$
distribution, is monitored over the course of the simulation (see figure 10
a). A highly unsteady reattachment behaviour with various frequency contributions is evident and the bubble length fluctuates as much as
![]() $0.15l/c$
from its mean value. By employing spectral analysis and plotting the power spectral density of the bubble length (see figure 10
b), various dominant frequencies are revealed. On the one hand, the vortex shedding frequency at
$0.15l/c$
from its mean value. By employing spectral analysis and plotting the power spectral density of the bubble length (see figure 10
b), various dominant frequencies are revealed. On the one hand, the vortex shedding frequency at
![]() $St_{vs}$
is observed as in the analysis above. On the other hand, other dominant frequencies at lower Strouhal numbers, namely
$St_{vs}$
is observed as in the analysis above. On the other hand, other dominant frequencies at lower Strouhal numbers, namely
![]() $St\approx 0.09$
and
$St\approx 0.09$
and
![]() $St\approx 0.02$
, are superimposed. As mentioned in the introduction, similar behaviour was observed numerically and experimentally (see e.g. Watmuff Reference Watmuff1999; Boiko et al.
Reference Boiko, Grek, Dovgal and Kozlov2002; Rist & Maucher Reference Rist and Maucher2002; Lang et al.
Reference Lang, Rist and Wagner2004; Burgmann et al.
Reference Burgmann, Dannemann and Schröder2008; Hain et al.
Reference Hain, Kähler and Radespiel2009; Jones et al.
Reference Jones, Sandberg and Sandham2010; Marxen & Rist Reference Marxen and Rist2010). While the bubble flapping effect is confirmed by the present simulation, the cause of the low-frequency contribution is controversial in the literature and deserves further investigation in future work.
$St\approx 0.02$
, are superimposed. As mentioned in the introduction, similar behaviour was observed numerically and experimentally (see e.g. Watmuff Reference Watmuff1999; Boiko et al.
Reference Boiko, Grek, Dovgal and Kozlov2002; Rist & Maucher Reference Rist and Maucher2002; Lang et al.
Reference Lang, Rist and Wagner2004; Burgmann et al.
Reference Burgmann, Dannemann and Schröder2008; Hain et al.
Reference Hain, Kähler and Radespiel2009; Jones et al.
Reference Jones, Sandberg and Sandham2010; Marxen & Rist Reference Marxen and Rist2010). While the bubble flapping effect is confirmed by the present simulation, the cause of the low-frequency contribution is controversial in the literature and deserves further investigation in future work.

Figure 10. LSB dynamics. (a) Evolution of the bubble size. (b) Power spectral density for the bubble size.
Summarizing, we have shown that the parameter-free KBC model supplied with the boundary conditions as in Dorschner et al. (Reference Dorschner, Chikatamarla, Bösch and Karlin2015, Reference Dorschner, Chikatamarla and Karlin2016b ) is able to accurately predict the boundary layer separation, transition to turbulence and reattachment of the turbulent boundary layer. Thus, it provides a simple and efficient alternative to conventional modelling approaches such as LES. It also needs to be stressed that to accurately capture the transition phenomena it is necessary to resolve the recirculation region for which grid refinement is crucial to keep the computational cost reasonable.
3.2 Flow in a low-pressure turbine passage
In this section, the flow in a low-pressure turbine passage is considered. Similar to the flow past the
![]() $SD7003$
airfoil in the previous section, low-pressure turbines typically operate at relatively low Reynolds and Mach numbers. Under these conditions, depending on the geometry and the inflow, a LSB might occur. Note that, while in general compressibility effects may not be neglected for industrial applications, insight into LSB dynamics can already be gained in the incompressible flow regime (Zhang et al.
Reference Zhang, Zou, Qi, Ye and Wang2015; Bigoni et al.
Reference Bigoni, Vagnoli, Arts and Verstraete2016). The present set-up is distinctly different from the previous case of the
$SD7003$
airfoil in the previous section, low-pressure turbines typically operate at relatively low Reynolds and Mach numbers. Under these conditions, depending on the geometry and the inflow, a LSB might occur. Note that, while in general compressibility effects may not be neglected for industrial applications, insight into LSB dynamics can already be gained in the incompressible flow regime (Zhang et al.
Reference Zhang, Zou, Qi, Ye and Wang2015; Bigoni et al.
Reference Bigoni, Vagnoli, Arts and Verstraete2016). The present set-up is distinctly different from the previous case of the
![]() $SD7003$
airfoil as it allows for blockage and curvature effects, as well as the unsteady wake of the blade, which can have a significant influence on the LSB and the onset of transition. In particular, the flow is redirected by more than
$SD7003$
airfoil as it allows for blockage and curvature effects, as well as the unsteady wake of the blade, which can have a significant influence on the LSB and the onset of transition. In particular, the flow is redirected by more than
![]() $100^{\circ }$
and accelerated to approximately double its inflow value, leading to a large streamwise straining where its principal axes vary spatially, as observed by Wu & Durbin (Reference Wu and Durbin2001).
$100^{\circ }$
and accelerated to approximately double its inflow value, leading to a large streamwise straining where its principal axes vary spatially, as observed by Wu & Durbin (Reference Wu and Durbin2001).
Various experimental investigations have been conducted to study LSBs in low-pressure turbines (LPTs) (Mayle Reference Mayle1991; Schulte & Hodson Reference Schulte and Hodson1994; Engber & Fottner Reference Engber and Fottner1996; Schulte & Hodson Reference Schulte and Hodson1998; Hodson Reference Hodson2000; Sieverding Reference Sieverding2000; Hilgenfeld, Stadtmüller & Fottner Reference Hilgenfeld, Stadtmüller and Fottner2002; Stieger & Hodson Reference Stieger and Hodson2003). Considering the full rotor/stator arrangement in real turbine cascades, the incoming flow is highly unsteady, with wakes generated by the preceding row of blades. In the work of Schulte & Hodson (Reference Schulte and Hodson1994), a significant effect of a periodically passing turbulent inflow wake on the LSB and thus performance was observed. Combined with hot-film measurements (Schulte & Hodson Reference Schulte and Hodson1998), it was concluded that separation is periodically suppressed by the turbulent incoming wake and the subsequent calmed region with their full velocity profiles (see also Stieger & Hodson Reference Stieger and Hodson2003).
On the numerical side, the increasing computing power and the relatively low Reynolds and Mach numbers in LPTs allow for DNS (see e.g. Wu et al. Reference Wu, Jacobs, Hunt and Durbin1999; Wu & Durbin Reference Wu and Durbin2001). Noteworthy is the DNS study of Wu & Durbin (Reference Wu and Durbin2001), who investigated the bypass transition due to a periodic, turbulent inflow wake, which was used to generate large free-stream disturbances.
On the modelling side, the lack of accuracy of RANS models (Raverdy et al. Reference Raverdy, Mary, Sagaut and Liamis2003) led to an increasing number of LES studies of LSBs in LPTs, focusing again on the boundary layer–wake interference (Mittal, Venkatasubramanian & Najjar Reference Mittal, Venkatasubramanian and Najjar2001; Michelassi, Wissink & Rodi Reference Michelassi, Wissink and Rodi2002, Reference Michelassi, Wissink and Rodi2003; Rodi Reference Rodi2006). The results of these LES are encouraging, but uncertainties remain and high resolution is needed to capture all features of the transition. In the LES study of Michelassi et al. (Reference Michelassi, Wissink and Rodi2003) for example, significant discrepancies with the reference DNS are observed, where the LES was not capable of fully reproducing the transition location (delayed transition) and skin friction coefficient. These discrepancies are attributed to the resolution near the boundary and also in the bulk, which is not able to account for the fine-scale structures convected by the wake and thus to trigger transition.
In this paper, analogous to Raverdy et al. (Reference Raverdy, Mary, Sagaut and Liamis2003), we focus on the flow past the turbine blade without an inflow wake. To analyse the effect of Reynolds number and free-stream turbulence, we conduct simulations at Reynolds numbers of
![]() $Re=6\times 10^{4}$
and
$Re=6\times 10^{4}$
and
![]() $Re=1.48\times 10^{5}$
with imposed free-stream turbulence intensities in the range
$Re=1.48\times 10^{5}$
with imposed free-stream turbulence intensities in the range
![]() $Tu=0{-}10\,\%$
.
$Tu=0{-}10\,\%$
.
3.3 Numerical set-up
The simulation set-up is identical to the DNS of Wu & Durbin (Reference Wu and Durbin2001), who conducted incompressible flow simulations with and without a turbulent inflow wake. For comparison with experiment, the study of Engber & Fottner (Reference Engber and Fottner1996), who carried out various experiments for different inflow disturbances and Reynolds numbers (but no turbulent wake), is considered.
The set-up consists of a single
![]() $T106$
low-pressure turbine blade, which is periodically repeated in the pitchwise direction to mimic the full turbine passage. The distance between two consecutive blade profiles is given by the normalized pitch
$T106$
low-pressure turbine blade, which is periodically repeated in the pitchwise direction to mimic the full turbine passage. The distance between two consecutive blade profiles is given by the normalized pitch
![]() $g/C_{ax}=0.93$
, where
$g/C_{ax}=0.93$
, where
![]() $C_{ax}$
denotes the axial chord. The Reynolds number is based on the mean inflow velocity and the axial chord. The computational domain is chosen as
$C_{ax}$
denotes the axial chord. The Reynolds number is based on the mean inflow velocity and the axial chord. The computational domain is chosen as
![]() $[-C_{ax},3C_{ax}]\times [-0.5g,0.5g]\times [-0.1C_{ax},0.1C_{ax}]$
for the stream, pitch and spanwise directions, where the turbine blade is located at the origin. The computational cost is reduced by using three levels of grid refinement, where the coarsest level resolves the turbine blade with
$[-C_{ax},3C_{ax}]\times [-0.5g,0.5g]\times [-0.1C_{ax},0.1C_{ax}]$
for the stream, pitch and spanwise directions, where the turbine blade is located at the origin. The computational cost is reduced by using three levels of grid refinement, where the coarsest level resolves the turbine blade with
![]() $C_{ax}=300$
lattice points (see figure 11). In the case of full transition, this yields a maximum effective grid spacing of
$C_{ax}=300$
lattice points (see figure 11). In the case of full transition, this yields a maximum effective grid spacing of
![]() $\unicode[STIX]{x0394}y^{+}\approx 0.25$
within the separation bubble and
$\unicode[STIX]{x0394}y^{+}\approx 0.25$
within the separation bubble and
![]() $\unicode[STIX]{x0394}y^{+}\approx 2.1$
in the turbulent boundary layer at the trailing edge.
$\unicode[STIX]{x0394}y^{+}\approx 2.1$
in the turbulent boundary layer at the trailing edge.
Periodic boundary conditions are applied in the pitch and spanwise directions. The exit flow has a designed angle of
![]() $-63.2^{\circ }$
with the
$-63.2^{\circ }$
with the
![]() $x$
axis and we employ convective boundary conditions at the outlet. Regarding the inflow, simulations with uniform and turbulent inflow conditions at an inlet angle of
$x$
axis and we employ convective boundary conditions at the outlet. Regarding the inflow, simulations with uniform and turbulent inflow conditions at an inlet angle of
![]() $37.7^{\circ }$
are presented.
$37.7^{\circ }$
are presented.
In order to generate the inflow turbulence, a method similar to that in Zhang et al. (Reference Zhang, Zou, Qi, Ye and Wang2015) was adopted, where a frozen homogeneous isotropic turbulence field within a periodic box of spanwise length is superimposed onto the mean flow at the inlet angle. The box is duplicated to fill the entire inflow plane and advected with the inflow velocity to mimic time-varying fluctuations. The initial turbulence field is computed using a synthetic kinematic simulation (Fung et al.
Reference Fung, Hunt, Malik and Perkins1992), where the solenoidal velocity field is described as a superposition of a finite number of random Fourier modes according to an energy spectrum of the form
![]() $E(k)=Ak^{4}\exp (-2k^{2}/k_{0}^{2})$
. The constant
$E(k)=Ak^{4}\exp (-2k^{2}/k_{0}^{2})$
. The constant
![]() $A$
and the wavenumber of the spectrum peak
$A$
and the wavenumber of the spectrum peak
![]() $k_{0}$
are chosen in accordance with the prescribed turbulence intensity.
$k_{0}$
are chosen in accordance with the prescribed turbulence intensity.

Figure 11. Computational set-up for the flow over an
![]() $T106$
turbine blade.
$T106$
turbine blade.

Figure 12. Flow in low-pressure turbine passage at
![]() $Re=1.48\times 10^{5}$
, visualized by vorticity isosurfaces coloured by streamwise velocity. (a) Uniform inflow. (b) Turbulent inflow.
$Re=1.48\times 10^{5}$
, visualized by vorticity isosurfaces coloured by streamwise velocity. (a) Uniform inflow. (b) Turbulent inflow.

Figure 13. Distribution of the mean pressure coefficient over the axial chord of the
![]() $T106$
turbine blade at
$T106$
turbine blade at
![]() $Re=1.48\times 10^{5}$
.
$Re=1.48\times 10^{5}$
.
3.4 Results
First, for the purpose of validation, we consider the high-Reynolds-number case of
![]() $Re=1.48\times 10^{5}$
with a uniform inflow and a turbulent inflow with
$Re=1.48\times 10^{5}$
with a uniform inflow and a turbulent inflow with
![]() $Tu=0.2\,\%$
. A snapshot of the flow in the periodically completed turbine passage is visualized in figure 12 using vorticity isosurfaces, coloured by streamwise velocity. The distribution of the pressure coefficient over both the suction and the pressure sides of the turbine blade is shown in figure 13 along with the reference data for the uniform and turbulent inflow. On the suction side, a favourable pressure gradient accelerates the flow until the adverse pressure gradient downstream of
$Tu=0.2\,\%$
. A snapshot of the flow in the periodically completed turbine passage is visualized in figure 12 using vorticity isosurfaces, coloured by streamwise velocity. The distribution of the pressure coefficient over both the suction and the pressure sides of the turbine blade is shown in figure 13 along with the reference data for the uniform and turbulent inflow. On the suction side, a favourable pressure gradient accelerates the flow until the adverse pressure gradient downstream of
![]() $x/C_{ax}\approx 0.6$
causes a deceleration. On the pressure side, the pressure gradient is nearly zero until
$x/C_{ax}\approx 0.6$
causes a deceleration. On the pressure side, the pressure gradient is nearly zero until
![]() $x/C_{ax}\approx 0.5$
, where a steep pressure gradient accelerates the flow up to the trailing edge.
$x/C_{ax}\approx 0.5$
, where a steep pressure gradient accelerates the flow up to the trailing edge.
The comparison of the simulated pressure coefficient with the experimental and numerical data in figure 13 shows good agreement. On the pressure side, only marginal discrepancies between all data are observed. On the suction side, due to the different inflow conditions, the discrepancies are larger. The influence of the wake for the DNS data becomes apparent in the aft of the blade, where the pressure is increasing at
![]() $x/C_{ax}\approx 0.85$
compared to the uniform inlet. Similarly, minor deviations between the different inflow disturbances can be observed for the experimental data and the present simulation.
$x/C_{ax}\approx 0.85$
compared to the uniform inlet. Similarly, minor deviations between the different inflow disturbances can be observed for the experimental data and the present simulation.
To further investigate the effect of the inflow disturbances, a close-up image zoomed in from the top in figure 14 shows the isosurfaces of the Q-criterion coloured by the normalized streamwise velocity. Both simulations exhibit
![]() $\unicode[STIX]{x1D6EC}$
-type vortices at the initial stage, which subsequently develop into hairpin-type vortices. While for the simulation using a uniform inflow, these flow structures are relatively well ordered in staggered formation, the hairpin vortices for the case with a turbulent inlet are more pronounced with a higher degree of disorder.
$\unicode[STIX]{x1D6EC}$
-type vortices at the initial stage, which subsequently develop into hairpin-type vortices. While for the simulation using a uniform inflow, these flow structures are relatively well ordered in staggered formation, the hairpin vortices for the case with a turbulent inlet are more pronounced with a higher degree of disorder.
However, as indicated by the distributions of the pressure and skin friction coefficient over the airfoil surfaces, the influence of free-stream turbulence is minor in terms of the aerodynamic quantities. In fact, the integral effects, as manifested by the drag and lift coefficients, are insignificant with deviations of less than
![]() $0.25\,\%$
and
$0.25\,\%$
and
![]() $0.01\,\%$
, respectively. While the rapid increase of the skin friction coefficient as shown in figure 15 indicates a starting transition process, full transition, as defined by the Reynolds stress criteria used above, is triggered by neither uniform nor turbulent inflow conditions. Moreover, as indicated by the skin friction coefficient and in line with DNS and LES results (Wu & Durbin Reference Wu and Durbin2001; Rodi Reference Rodi2006), the mean flow does not separate. This is in contrast to the LES by Raverdy et al. (Reference Raverdy, Mary, Sagaut and Liamis2003), who reported a fully developed LSB, albeit at a lower nominal Reynolds number of
$0.01\,\%$
, respectively. While the rapid increase of the skin friction coefficient as shown in figure 15 indicates a starting transition process, full transition, as defined by the Reynolds stress criteria used above, is triggered by neither uniform nor turbulent inflow conditions. Moreover, as indicated by the skin friction coefficient and in line with DNS and LES results (Wu & Durbin Reference Wu and Durbin2001; Rodi Reference Rodi2006), the mean flow does not separate. This is in contrast to the LES by Raverdy et al. (Reference Raverdy, Mary, Sagaut and Liamis2003), who reported a fully developed LSB, albeit at a lower nominal Reynolds number of
![]() $Re=1.1\times 10^{5}$
and a uniform inflow.
$Re=1.1\times 10^{5}$
and a uniform inflow.

Figure 14. Snapshot of isosurfaces of the Q-criterion (
![]() $\text{Q}=200$
) coloured by normalized streamwise velocity at
$\text{Q}=200$
) coloured by normalized streamwise velocity at
![]() $Re=1.48\times 10^{5}$
: (a)
$Re=1.48\times 10^{5}$
: (a)
![]() $Tu=0\,\%$
; (b)
$Tu=0\,\%$
; (b)
![]() $Tu=0.2\,\%$
.
$Tu=0.2\,\%$
.

Figure 15. Distribution of the mean skin friction coefficient over the axial chord on the suction side of the
![]() $T106$
turbine blade at
$T106$
turbine blade at
![]() $Re=1.48\times 10^{5}$
.
$Re=1.48\times 10^{5}$
.

Figure 16. Snapshot of isosurfaces of the Q-criterion (Q
![]() $=$
110) coloured by normalized streamwise velocity at
$=$
110) coloured by normalized streamwise velocity at
![]() $Re=6\times 10^{4}$
: (a)
$Re=6\times 10^{4}$
: (a)
![]() $Tu=0\,\%$
; (b)
$Tu=0\,\%$
; (b)
![]() $Tu=5\,\%$
. (c)
$Tu=5\,\%$
. (c)
![]() $Tu=10\,\%$
.
$Tu=10\,\%$
.
To investigate this discrepancy, another set of simulations was run with the same Reynolds number
![]() $Re=1.1\times 10^{5}$
as in Raverdy et al. (Reference Raverdy, Mary, Sagaut and Liamis2003). However, the change in Reynolds number had only a marginal effect and no transition or mean flow separation was observed, also not under turbulent inflow conditions with
$Re=1.1\times 10^{5}$
as in Raverdy et al. (Reference Raverdy, Mary, Sagaut and Liamis2003). However, the change in Reynolds number had only a marginal effect and no transition or mean flow separation was observed, also not under turbulent inflow conditions with
![]() $Tu=0.2\,\%$
. Thus, similar to Zhang et al. (Reference Zhang, Zou, Qi, Ye and Wang2015), we decreased the Reynolds number to
$Tu=0.2\,\%$
. Thus, similar to Zhang et al. (Reference Zhang, Zou, Qi, Ye and Wang2015), we decreased the Reynolds number to
![]() $Re=6\times 10^{4}$
, thereby stipulating mean flow separation on the airfoil, and studied three cases with varying free-stream turbulence intensities,
$Re=6\times 10^{4}$
, thereby stipulating mean flow separation on the airfoil, and studied three cases with varying free-stream turbulence intensities,
![]() $Tu=\{0\,\%,5\,\%,10\,\%\}$
. The corresponding instantaneous snapshots showing isosurfaces of the Q-criterion, zoomed in from the top view onto the trailing edge of the blade, are shown in figure 16. It is apparent that for uniform inflow as in figure 16(a), the flow separates as shown by the two-dimensional vortex structures in the aft of the blade. However, turbulent structures are only developing in the wake of the blade and no natural transition occurs on the blade surface. The cases with a free-stream turbulence of
$Tu=\{0\,\%,5\,\%,10\,\%\}$
. The corresponding instantaneous snapshots showing isosurfaces of the Q-criterion, zoomed in from the top view onto the trailing edge of the blade, are shown in figure 16. It is apparent that for uniform inflow as in figure 16(a), the flow separates as shown by the two-dimensional vortex structures in the aft of the blade. However, turbulent structures are only developing in the wake of the blade and no natural transition occurs on the blade surface. The cases with a free-stream turbulence of
![]() $Tu=5\,\%$
and
$Tu=5\,\%$
and
![]() $Tu=10\,\%$
are shown in figure 16(b,c), respectively. It can be seen that transition is triggered for both cases, and is initiated by the formation of
$Tu=10\,\%$
are shown in figure 16(b,c), respectively. It can be seen that transition is triggered for both cases, and is initiated by the formation of
![]() $\unicode[STIX]{x1D6EC}$
-type vortices, similar to the high-Reynolds-number case. Further downstream these vortices develop into hairpin-type vortices, which eventually break down into fine-scale turbulence past the blade. This is in contrast to the high-Reynolds-number case, for which the boundary layer remains attached without transition to turbulence. On the other hand, in the present low-Reynolds-number cases with free-stream turbulence, separated-flow transition is observed.
$\unicode[STIX]{x1D6EC}$
-type vortices, similar to the high-Reynolds-number case. Further downstream these vortices develop into hairpin-type vortices, which eventually break down into fine-scale turbulence past the blade. This is in contrast to the high-Reynolds-number case, for which the boundary layer remains attached without transition to turbulence. On the other hand, in the present low-Reynolds-number cases with free-stream turbulence, separated-flow transition is observed.

Figure 17. Average skin friction coefficient over the suction side of the
![]() $T106$
blade for varying free-stream turbulence intensities at
$T106$
blade for varying free-stream turbulence intensities at
![]() $Re=6\times 10^{4}$
.
$Re=6\times 10^{4}$
.

Figure 18. Average pressure coefficient over the suction side of the
![]() $T106$
blade for varying free-stream turbulence intensities at
$T106$
blade for varying free-stream turbulence intensities at
![]() $Re=6\times 10^{4}$
.
$Re=6\times 10^{4}$
.
The effect of free-stream turbulence on the geometrical properties of the LSB is investigated next. In figure 17 we present the skin friction coefficient for all turbulence intensities. As in Zhang et al. (Reference Zhang, Zou, Qi, Ye and Wang2015), we observe that the separation location is affected by the level of free-stream turbulence and moves downstream with increasing
![]() $Tu$
. In addition, the reattachment location moves upstream with increasing
$Tu$
. In addition, the reattachment location moves upstream with increasing
![]() $Tu$
, thereby reducing the extent of the entire LSB and improving aerodynamic performance. It is worth pointing out that figure 17 also shows that the effect of LSB size reduction is nonlinear with respect to
$Tu$
, thereby reducing the extent of the entire LSB and improving aerodynamic performance. It is worth pointing out that figure 17 also shows that the effect of LSB size reduction is nonlinear with respect to
![]() $Tu$
. This effect mainly stems from the nonlinear upstream shift of the reattachment location rather than the separation location, which appears to behave more linearly. Similar behaviour is shown by the mean pressure coefficient over the suction side of the airfoil in figure 18, where the pressure plateau is most pronounced for the uniform inflow case, suggesting the largest LSB. All geometrical quantities of the LSB are tabulated in table 2, where we define the onset to transition
$Tu$
. This effect mainly stems from the nonlinear upstream shift of the reattachment location rather than the separation location, which appears to behave more linearly. Similar behaviour is shown by the mean pressure coefficient over the suction side of the airfoil in figure 18, where the pressure plateau is most pronounced for the uniform inflow case, suggesting the largest LSB. All geometrical quantities of the LSB are tabulated in table 2, where we define the onset to transition
![]() $x_{t}$
as above using a threshold of
$x_{t}$
as above using a threshold of
![]() $u^{\prime }w^{\prime }/u_{\infty }^{2}\approx 0.001$
. Investigating the flow field in more detail, we report the mean and root-mean-square (r.m.s.) streamwise velocity profiles (tangential to the blade surface on the suction side) for
$u^{\prime }w^{\prime }/u_{\infty }^{2}\approx 0.001$
. Investigating the flow field in more detail, we report the mean and root-mean-square (r.m.s.) streamwise velocity profiles (tangential to the blade surface on the suction side) for
![]() $x/C_{ax}=0.88{-}0.99$
in steps of
$x/C_{ax}=0.88{-}0.99$
in steps of
![]() $0.1C_{ax}$
as a function of the normal distance
$0.1C_{ax}$
as a function of the normal distance
![]() $n/C_{ax}$
in figure 19. The average velocity profiles in figure 19(a) confirm the visual impression from the instantaneous snapshots of a pronounced separation for the case without free-stream turbulence. For the cases including free-stream turbulence, separation is less distinct and a smaller shear layer thickness with a clear reattachment zone can be observed. Also for the mean velocity, the trend of earlier reattachment with increasing
$n/C_{ax}$
in figure 19. The average velocity profiles in figure 19(a) confirm the visual impression from the instantaneous snapshots of a pronounced separation for the case without free-stream turbulence. For the cases including free-stream turbulence, separation is less distinct and a smaller shear layer thickness with a clear reattachment zone can be observed. Also for the mean velocity, the trend of earlier reattachment with increasing
![]() $Tu$
is obvious. The fluctuations of the streamwise velocity component are presented in figure 19(b). In the case of uniform inflow, mild fluctuations within the separated region indicate the unsteady two-dimensional vortex rolls, whereas relatively sharp peaks of r.m.s. values are measured within the reattachment zone, which are confined to the near-wall region up to a normal distance of
$Tu$
is obvious. The fluctuations of the streamwise velocity component are presented in figure 19(b). In the case of uniform inflow, mild fluctuations within the separated region indicate the unsteady two-dimensional vortex rolls, whereas relatively sharp peaks of r.m.s. values are measured within the reattachment zone, which are confined to the near-wall region up to a normal distance of
![]() $n/C_{ax}\approx 0.005$
. In contrast, in the case of free-stream turbulence, no vortex rolls are observed in the separation zone and the reattachment region exhibits a much broader plateau due to transition, as compared to the uniform case. This is in line with what is observed in the literature (see e.g. Raverdy et al.
Reference Raverdy, Mary, Sagaut and Liamis2003).
$n/C_{ax}\approx 0.005$
. In contrast, in the case of free-stream turbulence, no vortex rolls are observed in the separation zone and the reattachment region exhibits a much broader plateau due to transition, as compared to the uniform case. This is in line with what is observed in the literature (see e.g. Raverdy et al.
Reference Raverdy, Mary, Sagaut and Liamis2003).

Figure 19. Streamwise velocity profiles (tangent to the suction side of the blade surface) as a function of the normal distance for
![]() $x/C_{ax}=0.88{-}0.99$
in steps of
$x/C_{ax}=0.88{-}0.99$
in steps of
![]() $0.1C_{ax}$
at
$0.1C_{ax}$
at
![]() $Re=6\times 10^{4}$
. (a) Mean streamwise velocity. (b) The r.m.s. streamwise velocity. For the legend see figure 18.
$Re=6\times 10^{4}$
. (a) Mean streamwise velocity. (b) The r.m.s. streamwise velocity. For the legend see figure 18.
Table 2. Comparison of LSB properties for the flow over the
![]() $T106$
blade for different free-stream turbulence intensities at
$T106$
blade for different free-stream turbulence intensities at
![]() $Re=6\times 10^{4}$
.
$Re=6\times 10^{4}$
.

4 Concluding remarks
Due to the lack of a comprehensive understanding of the mechanisms at play during the formation of a LSB, increasing the performance of engineering devices requires simple and efficient predictive tools. In this work, we presented a detailed investigation of entropic multi-relaxation time models and their application to transitional flows. The simulations show that the KBC model, together with Grad’s boundary conditions, is capable of accurately capturing all features of LSB including separation, transition and unsteady reattachment. Although the implicit subgrid features of the KBC allow for a relatively coarse mesh resolution (Dorschner et al. Reference Dorschner, Bösch, Chikatamarla, Boulouchos and Karlin2016a ), accurate results were only achieved by resolving the reverse flow region on the airfoil surface. To meet these resolution requirements, an appropriate grid refinement technique is crucial.
Thus, we have shown that the KBC model in combination with appropriate boundary conditions and grid refinement strategies is a robust, parameter-free and accurate alternative method for studying complex flows of engineering interest, where a simple grid refinement study is sufficient to ensure the validity of the simulation.
Acknowledgements
This work was supported by the European Research Council (ERC) Advanced grant no. 291094-ELBM and the ETH-32-14-2 grant. The computational resources at the Swiss National Super Computing Center CSCS were provided under the grants s492 and s630.