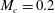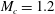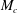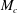1 Introduction
Free shear layer flows and associated turbulence have been extensively studied using analytical, experimental and numerical techniques for several decades. The planar mixing layer is the simplest of them with a modal instability, devoid of the complexities of most other shear flows. As Mach number of the flow increases, compressibility effects become significant and begin to influence the flow dynamics. These effects in a mixing layer are quantified by the convective Mach number,
![]() $M_{c}=(U_{1}-U_{2})/(c_{1}+c_{2})$
, where
$M_{c}=(U_{1}-U_{2})/(c_{1}+c_{2})$
, where
![]() $U_{1},U_{2}$
are free-stream velocities and
$U_{1},U_{2}$
are free-stream velocities and
![]() $c_{1},c_{2}$
are sonic speeds in either stream. The most notable effect of compressibility on mixing layers is the suppression of turbulence and the consequent reduction of spreading rate. The physical mechanism of turbulence suppression due to compressibility has been examined in previous works. It has also been noted that the turbulent flow structure is modified due to compressibility (Normand & Lesieur Reference Normand and Lesieur1992). The goal of the present study is to enhance the understanding of compressibility effects by characterizing the suppression mechanism in terms of local streamline topology and vortex structure.
$c_{1},c_{2}$
are sonic speeds in either stream. The most notable effect of compressibility on mixing layers is the suppression of turbulence and the consequent reduction of spreading rate. The physical mechanism of turbulence suppression due to compressibility has been examined in previous works. It has also been noted that the turbulent flow structure is modified due to compressibility (Normand & Lesieur Reference Normand and Lesieur1992). The goal of the present study is to enhance the understanding of compressibility effects by characterizing the suppression mechanism in terms of local streamline topology and vortex structure.
The reduced turbulence levels and mixing-layer spread rate at high
![]() $M_{c}$
are attributed to the suppression of pressure–strain redistribution by Pantano & Sarkar (Reference Pantano and Sarkar2002). As Mach number increases, the free-stream pressure itself decreases, leading to reduced levels of pressure fluctuations and a proportional reduction in pressure–strain correlation. Recent attempts to explain the reduction of growth rate by compressibility include a detailed analysis of vorticity and its generation near the turbulent/non-turbulent interface and the entrainment process. Jahanbakhshi & Madnia (Reference Jahanbakhshi and Madnia2016) show that the curvature of the turbulent/non-turbulent interface in mixing layers is significantly altered by compressibility, thereby leading to a reduction in entrained mass flux. Karimi & Girimaji (Reference Karimi and Girimaji2016) examine the stabilizing action of compressibility on Kelvin–Helmholtz instability and propose the existence of a dilatation interface layer (DIL) in which strong vorticity wind and unwind due to the action of pressure field. This reversal of vorticity in time reduces the growth of instability. Linear stability analysis by Sandham & Reynolds (Reference Sandham and Reynolds1990) shows that it is not just the growth rate, but the most unstable mode itself is modified by compressibility. The most unstable mode changes to oblique modes for
$M_{c}$
are attributed to the suppression of pressure–strain redistribution by Pantano & Sarkar (Reference Pantano and Sarkar2002). As Mach number increases, the free-stream pressure itself decreases, leading to reduced levels of pressure fluctuations and a proportional reduction in pressure–strain correlation. Recent attempts to explain the reduction of growth rate by compressibility include a detailed analysis of vorticity and its generation near the turbulent/non-turbulent interface and the entrainment process. Jahanbakhshi & Madnia (Reference Jahanbakhshi and Madnia2016) show that the curvature of the turbulent/non-turbulent interface in mixing layers is significantly altered by compressibility, thereby leading to a reduction in entrained mass flux. Karimi & Girimaji (Reference Karimi and Girimaji2016) examine the stabilizing action of compressibility on Kelvin–Helmholtz instability and propose the existence of a dilatation interface layer (DIL) in which strong vorticity wind and unwind due to the action of pressure field. This reversal of vorticity in time reduces the growth of instability. Linear stability analysis by Sandham & Reynolds (Reference Sandham and Reynolds1990) shows that it is not just the growth rate, but the most unstable mode itself is modified by compressibility. The most unstable mode changes to oblique modes for
![]() $M_{c}>0.6$
, leading to strongly three-dimensional structures at higher Mach numbers. Karimi & Girimaji (Reference Karimi and Girimaji2017) also exhibit the effect of perturbation orientation on instability growth in compressible mixing layers. It is demonstrated that the degree of stabilization decreases with increasing obliqueness. Bertsch, Suman & Girimaji (Reference Bertsch, Suman and Girimaji2012) investigate the effects of flow-thermodynamic interactions in compressible homogeneous shear flows by examining the evolution of pressure fluctuations. The analysis suggests that in spatio-temporally developing flows, compressibility effects diminish with time (or distance). Thus, compressibility effects are most severe in the transient stages of flow evolution. In this paper, we address the effects of compressibility on the turbulence statistics and examine the role of pressure and inertia effects during the transient evolution of mixing layers.
$M_{c}>0.6$
, leading to strongly three-dimensional structures at higher Mach numbers. Karimi & Girimaji (Reference Karimi and Girimaji2017) also exhibit the effect of perturbation orientation on instability growth in compressible mixing layers. It is demonstrated that the degree of stabilization decreases with increasing obliqueness. Bertsch, Suman & Girimaji (Reference Bertsch, Suman and Girimaji2012) investigate the effects of flow-thermodynamic interactions in compressible homogeneous shear flows by examining the evolution of pressure fluctuations. The analysis suggests that in spatio-temporally developing flows, compressibility effects diminish with time (or distance). Thus, compressibility effects are most severe in the transient stages of flow evolution. In this paper, we address the effects of compressibility on the turbulence statistics and examine the role of pressure and inertia effects during the transient evolution of mixing layers.
In recent years, characterization of turbulence and turbulent mechanisms using local streamline topology has gained much popularity (Chong, Perry & Cantwell Reference Chong, Perry and Cantwell1990). Soria et al. (Reference Soria, Sondergaard, Cantwell, Chong and Perry1994) studied the local topology in incompressible mixing layers using this technique and identify flow features such as vortex sheets and vortex tubes. Compressibility effects on local flow topology were examined by Suman & Girimaji (Reference Suman and Girimaji2010) in decaying isotropic turbulence. Although the Mach number has little effect, the topology was found to be sensitive to local dilatation. Vaghefi & Madnia (Reference Vaghefi and Madnia2015) observe that the topology in the vicinity of a turbulent/non-turbulent interface is different from that in the turbulent core of a mixing layer and that vorticity is concentrated in specific topologies.
Vortical eddy structures play a key role in many turbulent flows, but a comprehensive examination of these structures is rendered difficult due to the lack of a formal mathematical basis for identifying them. There have been attempts to define a vortex using both Eulerian and Lagrangian approaches (Epps Reference Epps2017). Several vortex identification techniques using velocity gradient tensor have been proposed over the years, of which the
![]() $Q$
-criterion by Hunt, Wray & Moin (Reference Hunt, Wray and Moin1988) and the
$Q$
-criterion by Hunt, Wray & Moin (Reference Hunt, Wray and Moin1988) and the
![]() $\unicode[STIX]{x1D706}_{2}$
-criterion by Jeong & Hussain (Reference Jeong and Hussain1995) are widely used. Tian et al. (Reference Tian, Gao, Dong and Liu2018) propose a vector quantity to identify vortical structures in the flow field, which not only quantifies the local strength of rotation of a fluid element but also provides the direction of rotation. Vortex identification techniques help to elucidate the large-scale structures in the flow field. Compressibility effects on flow structures and their relation to turbulence statistics in compressible boundary layers are examined by Normand & Lesieur (Reference Normand and Lesieur1992), Wang & Lu (Reference Wang and Lu2012). The large-scale organization in mixing layers is influenced by the compressibility as observed by Sandham & Reynolds (Reference Sandham and Reynolds1990) and Sandham & Reynolds (Reference Sandham and Reynolds1991). At high
$\unicode[STIX]{x1D706}_{2}$
-criterion by Jeong & Hussain (Reference Jeong and Hussain1995) are widely used. Tian et al. (Reference Tian, Gao, Dong and Liu2018) propose a vector quantity to identify vortical structures in the flow field, which not only quantifies the local strength of rotation of a fluid element but also provides the direction of rotation. Vortex identification techniques help to elucidate the large-scale structures in the flow field. Compressibility effects on flow structures and their relation to turbulence statistics in compressible boundary layers are examined by Normand & Lesieur (Reference Normand and Lesieur1992), Wang & Lu (Reference Wang and Lu2012). The large-scale organization in mixing layers is influenced by the compressibility as observed by Sandham & Reynolds (Reference Sandham and Reynolds1990) and Sandham & Reynolds (Reference Sandham and Reynolds1991). At high
![]() $M_{c}$
, the spanwise roller structures are mostly absent, and the vortical structures are elongated in the streamwise direction, which leads to different mixing characteristics. Jahanbakhshi, Vaghefi & Madnia (Reference Jahanbakhshi, Vaghefi and Madnia2015) find that the interaction of intense vorticity structures with the turbulent/non-turbulent interface is crucial to vorticity transport in compressible mixing layers. In direct numerical simulations (DNS) of spatially evolving mixing layers by Zhou, He & Shen (Reference Zhou, He and Shen2012), it is observed that
$M_{c}$
, the spanwise roller structures are mostly absent, and the vortical structures are elongated in the streamwise direction, which leads to different mixing characteristics. Jahanbakhshi, Vaghefi & Madnia (Reference Jahanbakhshi, Vaghefi and Madnia2015) find that the interaction of intense vorticity structures with the turbulent/non-turbulent interface is crucial to vorticity transport in compressible mixing layers. In direct numerical simulations (DNS) of spatially evolving mixing layers by Zhou, He & Shen (Reference Zhou, He and Shen2012), it is observed that
![]() $\unicode[STIX]{x1D6EC}$
-structures in the flow field evolve to hairpin vortices which eventually break down to slender vortices before the flow reaches a self-similar state. Pirozzoli et al. (Reference Pirozzoli, Bernardini, Marié and Grasso2015) also observe that a spanwise coherence in flow structures makes way for skewed eddies in the flow which align in the flow direction. Reynolds stress and mean velocity profiles in these cases also evolve with time and are related to the evolution of large-scale structures. In compressible homogeneous shear flow, production and turbulent kinetic energy are predominant in strain-dominated topologies, as shown by Ma & Xiao (Reference Ma and Xiao2016) using conditional statistics of DNS data. While the changes in flow structures due to compressibility have been studied to a reasonable extent, the relation between vortex-structure modification and changes in flow mechanisms is yet to be clearly established.
$\unicode[STIX]{x1D6EC}$
-structures in the flow field evolve to hairpin vortices which eventually break down to slender vortices before the flow reaches a self-similar state. Pirozzoli et al. (Reference Pirozzoli, Bernardini, Marié and Grasso2015) also observe that a spanwise coherence in flow structures makes way for skewed eddies in the flow which align in the flow direction. Reynolds stress and mean velocity profiles in these cases also evolve with time and are related to the evolution of large-scale structures. In compressible homogeneous shear flow, production and turbulent kinetic energy are predominant in strain-dominated topologies, as shown by Ma & Xiao (Reference Ma and Xiao2016) using conditional statistics of DNS data. While the changes in flow structures due to compressibility have been studied to a reasonable extent, the relation between vortex-structure modification and changes in flow mechanisms is yet to be clearly established.
The objective of this work is to develop further insight into the turbulence suppression due to compressibility effects in high-speed mixing layers. Specifically, we seek to characterize the suppression mechanism conditioned on local streamline topology and vortical structure. To this end, we undertake the following tasks:
(i) Perform mixing-layer simulations over a range of Mach numbers that encompasses incompressible and compressible flow regimes.
(ii) Reaffirm the suppression of turbulence and mixing-layer spread rate with increasing Mach number.
(iii) Establish the changes, with increasing Mach number, in pressure–strain correlation, turbulence shear stress and kinetic energy production processes when conditioned upon local streamline topology.
(iv) Examine the changes in vortex structure with increasing Mach numbers. We quantify the change in topology by means of the vortex field structure.
Flow configuration and simulation parameters are summarized in § 2. The main results, including the evolution of turbulent quantities and topology effects, are discussed in § 3, followed by conclusions in § 4.
2 Numerical set-up
We perform simulations of temporally evolving mixing layers in a cuboid domain, shown in figure 1, with free-stream velocities in the
![]() $\pm x_{1}$
direction. The streamwise velocity is a function of the transverse location
$\pm x_{1}$
direction. The streamwise velocity is a function of the transverse location
![]() $(x_{2})$
. The domain, of dimension
$(x_{2})$
. The domain, of dimension
![]() $L_{1}\times L_{2}\times L_{3}$
(see table 1), is discretized uniformly into
$L_{1}\times L_{2}\times L_{3}$
(see table 1), is discretized uniformly into
![]() $512\times 256\times 128$
grid points with periodic boundary conditions in the streamwise
$512\times 256\times 128$
grid points with periodic boundary conditions in the streamwise
![]() $(x_{1})$
and spanwise
$(x_{1})$
and spanwise
![]() $(x_{3})$
directions. In the transverse direction, stress-free boundary conditions are applied. A discussion on domain independence and grid convergence is given in § A.2.
$(x_{3})$
directions. In the transverse direction, stress-free boundary conditions are applied. A discussion on domain independence and grid convergence is given in § A.2.

Figure 1. Schematic of the computational domain with mean velocity profile.
Table 1. Key non-dimensional parameters at the end of the simulations for different cases.

Simulations are performed for five different values of convective Mach number,
![]() $M_{c}=(0.2,0.5,0.75,0.9,1.2)$
. The lowest
$M_{c}=(0.2,0.5,0.75,0.9,1.2)$
. The lowest
![]() $M_{c}$
case corresponds to a nearly incompressible case, while the two higher Mach number cases have significant compressibility effects involved. A key parameter used for initializing the flow field is the initial momentum thickness,
$M_{c}$
case corresponds to a nearly incompressible case, while the two higher Mach number cases have significant compressibility effects involved. A key parameter used for initializing the flow field is the initial momentum thickness,
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}_{0}}$
. The Reynolds number of the flow is defined based on free-stream velocity difference and momentum thickness
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}_{0}}$
. The Reynolds number of the flow is defined based on free-stream velocity difference and momentum thickness
![]() $(Re=\unicode[STIX]{x1D70C}_{\infty }\unicode[STIX]{x0394}U\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}_{0}}/\unicode[STIX]{x1D707})$
. For all cases considered here initial
$(Re=\unicode[STIX]{x1D70C}_{\infty }\unicode[STIX]{x0394}U\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}_{0}}/\unicode[STIX]{x1D707})$
. For all cases considered here initial
![]() $Re=160$
. Many authors have used
$Re=160$
. Many authors have used
![]() $Re\approx 200$
(Jahanbakhshi et al.
Reference Jahanbakhshi, Vaghefi and Madnia2015; Vaghefi & Madnia Reference Vaghefi and Madnia2015) in their simulations, and the Reynolds number used in the present simulations is well documented (Pantano & Sarkar Reference Pantano and Sarkar2002; Foysi & Sarkar Reference Foysi and Sarkar2010; Hadjadj, Yee & Sjögreen Reference Hadjadj, Yee and Sjögreen2012). Mean streamwise velocity has a hyperbolic tangent profile given by
$Re\approx 200$
(Jahanbakhshi et al.
Reference Jahanbakhshi, Vaghefi and Madnia2015; Vaghefi & Madnia Reference Vaghefi and Madnia2015) in their simulations, and the Reynolds number used in the present simulations is well documented (Pantano & Sarkar Reference Pantano and Sarkar2002; Foysi & Sarkar Reference Foysi and Sarkar2010; Hadjadj, Yee & Sjögreen Reference Hadjadj, Yee and Sjögreen2012). Mean streamwise velocity has a hyperbolic tangent profile given by
and the other two components are set to zero. Temperature follows the Crocco–Busemann relation (White Reference White2006) for compressible shear layers,
where
![]() $\tilde{u_{1}}$
and
$\tilde{u_{1}}$
and
![]() $\tilde{T}$
are Favre-averaged quantities defined in the next section. The pressure field is uniform, and the density field is obtained from the ideal gas equation of state. Three-dimensional perturbations are added to the mean velocity field to accelerate the transition to turbulence. Perturbations are generated using a digital filter method, which has been successfully employed in the computation of temporally evolving mixing layers by Vaghefi & Madnia (Reference Vaghefi and Madnia2015). By this method, three-dimensional perturbations are generated based on a prescribed length scale and Reynolds stress profile. A spatially correlated perturbation field, rather than white noise, is obtained by employing this technique. We used initial vorticity thickness
$\tilde{T}$
are Favre-averaged quantities defined in the next section. The pressure field is uniform, and the density field is obtained from the ideal gas equation of state. Three-dimensional perturbations are added to the mean velocity field to accelerate the transition to turbulence. Perturbations are generated using a digital filter method, which has been successfully employed in the computation of temporally evolving mixing layers by Vaghefi & Madnia (Reference Vaghefi and Madnia2015). By this method, three-dimensional perturbations are generated based on a prescribed length scale and Reynolds stress profile. A spatially correlated perturbation field, rather than white noise, is obtained by employing this technique. We used initial vorticity thickness
![]() $(\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714}_{0}}\approx 4\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}_{0}})$
as length scale and Gaussian profiles for Reynolds stress components, with peak values of stress components from the nearly incompressible case of Pantano & Sarkar (Reference Pantano and Sarkar2002). All simulations are initialized with the same perturbation velocity field to minimize differences due to initial condition effects on the transient evolution of the mixing layer. Therefore, any difference in the evolution of the mixing layer is the varying response of the system relaxing from these initial conditions and is due to compressibility, as
$(\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714}_{0}}\approx 4\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}_{0}})$
as length scale and Gaussian profiles for Reynolds stress components, with peak values of stress components from the nearly incompressible case of Pantano & Sarkar (Reference Pantano and Sarkar2002). All simulations are initialized with the same perturbation velocity field to minimize differences due to initial condition effects on the transient evolution of the mixing layer. Therefore, any difference in the evolution of the mixing layer is the varying response of the system relaxing from these initial conditions and is due to compressibility, as
![]() $M_{c}$
is the only parameter which varies across the different cases.
$M_{c}$
is the only parameter which varies across the different cases.
A finite volume gas-kinetic scheme which solves the Bhatnagar–Gross–Krook (BGK)-Boltzmann equation is used for computations (Xu, Mao & Tang Reference Xu, Mao and Tang2005). The scheme employs a second-order approximation for the variation of particle velocity distribution function in space. For the simulation of turbulent flows, Kumar, Girimaji & Kerimo (Reference Kumar, Girimaji and Kerimo2013) observed that macroscopic variable reconstruction using weighted essentially non-oscillatory (WENO) schemes enable the resolution of sharp discontinuities like shocklets without compromising on the accuracy in smooth flow regions. Following their work, a fifth-order WENO reconstruction is used to calculate cell interface quantities. To enable simulations for gases with
![]() $Pr\neq 1$
, a Prandtl number correction, proposed by May, Srinivasan & Jameson (Reference May, Srinivasan and Jameson2007), is employed. Time step is determined according to the Courant–Friedrichs–Lewy (CFL) criterion using macroscopic flow variables. A brief discussion on the numerical scheme is given in § A.1.
$Pr\neq 1$
, a Prandtl number correction, proposed by May, Srinivasan & Jameson (Reference May, Srinivasan and Jameson2007), is employed. Time step is determined according to the Courant–Friedrichs–Lewy (CFL) criterion using macroscopic flow variables. A brief discussion on the numerical scheme is given in § A.1.
3 Results
The turbulent statistics are discussed for different cases to understand how they vary with convective Mach number, which is a measure of compressibility. Following that, we analyse how these statistics are distributed across different topologies in the flow, in an attempt to explain how changes in topology with Mach number influence the turbulent statistics. A density weighted averaging in homogeneous
![]() $x_{1}x_{3}$
plane is used to obtain mean velocity and temperature. Mean density and pressure fields are obtained by Reynolds averaging. We use the conventional notations for Reynolds
$x_{1}x_{3}$
plane is used to obtain mean velocity and temperature. Mean density and pressure fields are obtained by Reynolds averaging. We use the conventional notations for Reynolds
![]() $(\overline{[.]})$
and Favre
$(\overline{[.]})$
and Favre
![]() $(\tilde{[.]})$
averaged quantities and respective fluctuations (
$(\tilde{[.]})$
averaged quantities and respective fluctuations (
![]() $[.]^{\prime }$
and
$[.]^{\prime }$
and
![]() $[.]^{\prime \prime }$
) from averages, as given in equation (3.1).
$[.]^{\prime \prime }$
) from averages, as given in equation (3.1).
3.1 Validation
Our computational results are validated by comparing the temporal evolution of the mixing-layer width with existing experimental and numerical data. Suppression of mixing-layer growth rate by compressibility is a well-known phenomenon, and a vast majority of the literature on compressible mixing layers focuses on this aspect. We use momentum thickness
![]() $(\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}})$
, an integral quantity, to quantify the extent of the shear layer. Evolution of momentum thickness, normalized by its initial value
$(\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}})$
, an integral quantity, to quantify the extent of the shear layer. Evolution of momentum thickness, normalized by its initial value
![]() $(\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}_{0}})$
, with time
$(\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}_{0}})$
, with time
![]() $(\unicode[STIX]{x1D70F}=\unicode[STIX]{x0394}Ut/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}_{0}})$
is shown in figure 2(a) for different
$(\unicode[STIX]{x1D70F}=\unicode[STIX]{x0394}Ut/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}_{0}})$
is shown in figure 2(a) for different
![]() $M_{c}$
. After an initial transient period, the mixing layer has a self-similar evolution characterized by a linear growth of momentum thickness. The linear growth rates, which reduce with Mach number, are shown in figure 2(b). Self-similar growth rate,
$M_{c}$
. After an initial transient period, the mixing layer has a self-similar evolution characterized by a linear growth of momentum thickness. The linear growth rates, which reduce with Mach number, are shown in figure 2(b). Self-similar growth rate,
![]() $\dot{\unicode[STIX]{x1D6FF}}$
, normalized by the incompressible growth rate
$\dot{\unicode[STIX]{x1D6FF}}$
, normalized by the incompressible growth rate
![]() $(\dot{\unicode[STIX]{x1D6FF}}_{inc})$
is plotted along the vertical axis against convective Mach number on the horizontal axis. Growth rate at the lowest
$(\dot{\unicode[STIX]{x1D6FF}}_{inc})$
is plotted along the vertical axis against convective Mach number on the horizontal axis. Growth rate at the lowest
![]() $M_{c}$
is chosen as the incompressible growth rate and is estimated to be
$M_{c}$
is chosen as the incompressible growth rate and is estimated to be
![]() $\dot{\unicode[STIX]{x1D6FF}}_{inc}=0.0167$
, which is in good agreement with the accepted value of
$\dot{\unicode[STIX]{x1D6FF}}_{inc}=0.0167$
, which is in good agreement with the accepted value of
![]() $\dot{\unicode[STIX]{x1D6FF}}_{inc}=0.0160$
(Pantano & Sarkar Reference Pantano and Sarkar2002). The self-similar growth rates for different
$\dot{\unicode[STIX]{x1D6FF}}_{inc}=0.0160$
(Pantano & Sarkar Reference Pantano and Sarkar2002). The self-similar growth rates for different
![]() $M_{c}$
are compared with the empirical models of Birch & Eggers (Reference Birch and Eggers1972), Slessor, Zhuang & Dimotakis (Reference Slessor, Zhuang and Dimotakis2000) and Barone, Oberkampf & Blottner (Reference Barone, Oberkampf and Blottner2006) in figure 2(b). Growth rates from several numerical simulations are also compared in the same figure, and they show a scattered behaviour, which is attributed to differences in initial conditions and the reference value chosen as the incompressible growth rate. As further validation of our results, we show the evolution of anisotropy tensor for different
$M_{c}$
are compared with the empirical models of Birch & Eggers (Reference Birch and Eggers1972), Slessor, Zhuang & Dimotakis (Reference Slessor, Zhuang and Dimotakis2000) and Barone, Oberkampf & Blottner (Reference Barone, Oberkampf and Blottner2006) in figure 2(b). Growth rates from several numerical simulations are also compared in the same figure, and they show a scattered behaviour, which is attributed to differences in initial conditions and the reference value chosen as the incompressible growth rate. As further validation of our results, we show the evolution of anisotropy tensor for different
![]() $M_{c}$
in figure 3. The anisotropy tensor
$M_{c}$
in figure 3. The anisotropy tensor
![]() $(b_{ij})$
is defined as
$(b_{ij})$
is defined as
where
![]() $\bar{R}_{ij}$
and
$\bar{R}_{ij}$
and
![]() $\bar{K}$
are respectively Reynolds stress and turbulent kinetic energy integrated across the mixing layer. The evolution of anisotropy tensor
$\bar{K}$
are respectively Reynolds stress and turbulent kinetic energy integrated across the mixing layer. The evolution of anisotropy tensor
![]() $(b_{11},b_{22},b_{12})$
at
$(b_{11},b_{22},b_{12})$
at
![]() $M_{c}=0.20,0.75$
and
$M_{c}=0.20,0.75$
and
![]() $1.20$
from our computations are compared against the results of Pantano & Sarkar (Reference Pantano and Sarkar2002). However, their computations are for different Mach numbers, and our results are compared against the evolution of anisotropy for
$1.20$
from our computations are compared against the results of Pantano & Sarkar (Reference Pantano and Sarkar2002). However, their computations are for different Mach numbers, and our results are compared against the evolution of anisotropy for
![]() $M_{c}=0.3,0.7$
and
$M_{c}=0.3,0.7$
and
![]() $1.1$
from Pantano & Sarkar (Reference Pantano and Sarkar2002). The mean velocity gradient is negative according to equation (2.1), which implies that the Reynolds shear stress
$1.1$
from Pantano & Sarkar (Reference Pantano and Sarkar2002). The mean velocity gradient is negative according to equation (2.1), which implies that the Reynolds shear stress
![]() $R_{12}$
, and hence
$R_{12}$
, and hence
![]() $b_{12}$
, is positive in our simulations. Anisotropy peaks during the initial period before it settles down to a lower value, which increases marginally with
$b_{12}$
, is positive in our simulations. Anisotropy peaks during the initial period before it settles down to a lower value, which increases marginally with
![]() $M_{c}$
. While the late time anisotropy levels from our computations match well with those in the literature, there is a difference in the peak values. This can be attributed to the differences in setting up the initial perturbation field. The peak value of
$M_{c}$
. While the late time anisotropy levels from our computations match well with those in the literature, there is a difference in the peak values. This can be attributed to the differences in setting up the initial perturbation field. The peak value of
![]() $u_{1rms}^{\prime \prime }/u_{2rms}^{\prime \prime }$
for M02 is
$u_{1rms}^{\prime \prime }/u_{2rms}^{\prime \prime }$
for M02 is
![]() $1.24$
, which is in agreement with previous numerical experiments (Gatski & Bonnet Reference Gatski and Bonnet2013).
$1.24$
, which is in agreement with previous numerical experiments (Gatski & Bonnet Reference Gatski and Bonnet2013).

Figure 2. (a) Evolution of momentum thickness for various
![]() $M_{c}$
. (b) Comparison of linear growth rates at different Mach numbers with different numerical databases and empirical models. ▾, Papamoschou & Roshko (Reference Papamoschou and Roshko1988); ▪, Freund, Lele & Moin (Reference Freund, Lele and Moin2000); ♦, Pantano & Sarkar (Reference Pantano and Sarkar2002); ▵, Fu & Li (Reference Fu and Li2006); ▿, Foysi & Sarkar (Reference Foysi and Sarkar2010); ▫, Hadjadj et al. (Reference Hadjadj, Yee and Sjögreen2012); ○, Vaghefi et al. (Reference Vaghefi, Nik, Pisciuneri and Madnia2013); (- - -), Birch & Eggers (Reference Birch and Eggers1972); (
$M_{c}$
. (b) Comparison of linear growth rates at different Mach numbers with different numerical databases and empirical models. ▾, Papamoschou & Roshko (Reference Papamoschou and Roshko1988); ▪, Freund, Lele & Moin (Reference Freund, Lele and Moin2000); ♦, Pantano & Sarkar (Reference Pantano and Sarkar2002); ▵, Fu & Li (Reference Fu and Li2006); ▿, Foysi & Sarkar (Reference Foysi and Sarkar2010); ▫, Hadjadj et al. (Reference Hadjadj, Yee and Sjögreen2012); ○, Vaghefi et al. (Reference Vaghefi, Nik, Pisciuneri and Madnia2013); (- - -), Birch & Eggers (Reference Birch and Eggers1972); (

Figure 3. Evolution of anisotropy tensor for (a)
![]() $M_{c}=0.20$
, (b)
$M_{c}=0.20$
, (b)
![]() $M_{c}=0.75$
and (c)
$M_{c}=0.75$
and (c)
![]() $M_{c}=1.20$
. Dashed lines in (a–c) correspond to anisotropy levels at
$M_{c}=1.20$
. Dashed lines in (a–c) correspond to anisotropy levels at
![]() $M_{c}=0.3,0.7$
$M_{c}=0.3,0.7$
![]() $1.1$
reported by Pantano & Sarkar (Reference Pantano and Sarkar2002).
$1.1$
reported by Pantano & Sarkar (Reference Pantano and Sarkar2002).
It is important that the small scales are resolved in turbulent flow computations. If the smallest length scale in the flow, which is the Kolmogorov length scale, is of the same order as the grid size then the scales are sufficiently resolved. The Kolmogorov scale
![]() $(l_{\unicode[STIX]{x1D702}})$
is a function of turbulent energy dissipation and kinematic viscosity and takes the smallest value where dissipation is maximum, which is at the centreline of the mixing layer. In table 1, we report the Reynolds number based on vorticity thickness
$(l_{\unicode[STIX]{x1D702}})$
is a function of turbulent energy dissipation and kinematic viscosity and takes the smallest value where dissipation is maximum, which is at the centreline of the mixing layer. In table 1, we report the Reynolds number based on vorticity thickness
![]() $(Re_{\unicode[STIX]{x1D714}};\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714}}=\unicode[STIX]{x0394}U/(\text{d}\tilde{u} _{1}/\text{d}x_{2})_{max})$
, Taylor microscale Reynolds number
$(Re_{\unicode[STIX]{x1D714}};\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714}}=\unicode[STIX]{x0394}U/(\text{d}\tilde{u} _{1}/\text{d}x_{2})_{max})$
, Taylor microscale Reynolds number
![]() $(Re_{\unicode[STIX]{x1D706}}=2K\sqrt{5/3\unicode[STIX]{x1D708}\unicode[STIX]{x1D716}})$
, turbulent Mach number
$(Re_{\unicode[STIX]{x1D706}}=2K\sqrt{5/3\unicode[STIX]{x1D708}\unicode[STIX]{x1D716}})$
, turbulent Mach number
![]() $(M_{t}=\sqrt{2\bar{\unicode[STIX]{x1D70C}}K/\unicode[STIX]{x1D6FE}\bar{p}})$
and Kolmogorov length scale
$(M_{t}=\sqrt{2\bar{\unicode[STIX]{x1D70C}}K/\unicode[STIX]{x1D6FE}\bar{p}})$
and Kolmogorov length scale
![]() $(l_{\unicode[STIX]{x1D702}}/\unicode[STIX]{x1D6FF})$
at the end of the simulation for each case. The grid size
$(l_{\unicode[STIX]{x1D702}}/\unicode[STIX]{x1D6FF})$
at the end of the simulation for each case. The grid size
![]() $(\unicode[STIX]{x1D6E5})$
, shown to be comparable with Kolmogorov scales, is small enough to resolve all the scales. We also compute the integral length scale
$(\unicode[STIX]{x1D6E5})$
, shown to be comparable with Kolmogorov scales, is small enough to resolve all the scales. We also compute the integral length scale
![]() $(l_{1})$
, defined as
$(l_{1})$
, defined as
where the separation
![]() $(\unicode[STIX]{x1D6FF})$
is along the streamwise direction
$(\unicode[STIX]{x1D6FF})$
is along the streamwise direction
![]() $(\hat{e}_{1})$
. At the end of the simulation, it is observed that the large scales, quantified by
$(\hat{e}_{1})$
. At the end of the simulation, it is observed that the large scales, quantified by
![]() $l_{1}$
, are very small compared to domain length, thereby ensuring that the computations are not contaminated by domain size. A comparison of
$l_{1}$
, are very small compared to domain length, thereby ensuring that the computations are not contaminated by domain size. A comparison of
![]() $M_{t}$
at the centreline, a measure of compressibility, for the different cases shows that compressibility effects are negligible for the two low
$M_{t}$
at the centreline, a measure of compressibility, for the different cases shows that compressibility effects are negligible for the two low
![]() $M_{c}$
cases. Turbulent Mach number increases with
$M_{c}$
cases. Turbulent Mach number increases with
![]() $M_{c}$
, but the increase is not proportional to that in the convective Mach number.
$M_{c}$
, but the increase is not proportional to that in the convective Mach number.
3.2 Evolution of turbulent statistics
In the present study, we focus on the initial evolution of the mixing layers, during which the effects of compressibility, being significant, manifest in the slow growth of momentum thickness. Our objective is to investigate how compressibility changes different turbulent statistics during this initial period. The statistics reported in this work correspond to time,
![]() $\unicode[STIX]{x1D70F}<400$
. Turbulent statistics in mixing layers are a function of the transverse direction,
$\unicode[STIX]{x1D70F}<400$
. Turbulent statistics in mixing layers are a function of the transverse direction,
![]() $x_{2}$
, at any given instant of time. To enable comparison during transient evolution of the mixing layer, we use an averaged value for turbulent quantities defined as
$x_{2}$
, at any given instant of time. To enable comparison during transient evolution of the mixing layer, we use an averaged value for turbulent quantities defined as
 $$\begin{eqnarray}\displaystyle F(t)=\frac{\displaystyle \int f(t,x_{2})\,\text{d}x_{2}}{\displaystyle \int \text{d}x_{2}}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F(t)=\frac{\displaystyle \int f(t,x_{2})\,\text{d}x_{2}}{\displaystyle \int \text{d}x_{2}}, & & \displaystyle\end{eqnarray}$$
where
![]() $f(t,x_{2})$
is any turbulent statistic varying along the transverse direction and
$f(t,x_{2})$
is any turbulent statistic varying along the transverse direction and
![]() $F(t)$
is the corresponding averaged quantity. However, the definition does not hold any physical meaning if a quantity takes both positive and negative values across the shear layer and caution must be exercised while employing this method to various turbulent statistics. For example, the transport terms in the kinetic energy budget cannot be quantified using such an integrated value.
$F(t)$
is the corresponding averaged quantity. However, the definition does not hold any physical meaning if a quantity takes both positive and negative values across the shear layer and caution must be exercised while employing this method to various turbulent statistics. For example, the transport terms in the kinetic energy budget cannot be quantified using such an integrated value.
The Reynolds stress
![]() $(R_{ij}=\widetilde{u_{i}^{\prime \prime }u_{j}^{\prime \prime }})$
transport equation for compressible turbulent flows is given by
$(R_{ij}=\widetilde{u_{i}^{\prime \prime }u_{j}^{\prime \prime }})$
transport equation for compressible turbulent flows is given by
where
where
![]() $K=\frac{1}{2}\widetilde{u_{i}^{\prime \prime }u_{i}^{\prime \prime }}$
and the other terms
$K=\frac{1}{2}\widetilde{u_{i}^{\prime \prime }u_{i}^{\prime \prime }}$
and the other terms
![]() ${\mathcal{P}},\unicode[STIX]{x1D6F1},\unicode[STIX]{x1D716},{\mathcal{M}}$
and
${\mathcal{P}},\unicode[STIX]{x1D6F1},\unicode[STIX]{x1D716},{\mathcal{M}}$
and
![]() $T_{k}$
are similarly obtained from equations (3.6a–e
), respectively.
$T_{k}$
are similarly obtained from equations (3.6a–e
), respectively.
Figures 4–6 show the evolution of turbulent kinetic energy, turbulent stress components and their budgets for cases M2, M7 and M12. Reynolds stress components and turbulent kinetic energy are normalized by
![]() $\unicode[STIX]{x0394}U^{2}$
and budget quantities by
$\unicode[STIX]{x0394}U^{2}$
and budget quantities by
![]() $\unicode[STIX]{x0394}U^{3}/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}(t)$
. Only the dominant source (positive) and sink (negative) terms in the respective budget equations are shown in the plots. Evolution of averaged turbulent kinetic energy across the shear layer, for different
$\unicode[STIX]{x0394}U^{3}/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}(t)$
. Only the dominant source (positive) and sink (negative) terms in the respective budget equations are shown in the plots. Evolution of averaged turbulent kinetic energy across the shear layer, for different
![]() $M_{c}$
, is given in figure 4(a). Along the horizontal axis is non-dimensional time
$M_{c}$
, is given in figure 4(a). Along the horizontal axis is non-dimensional time
![]() $(\unicode[STIX]{x1D70F})$
and along the vertical axis is averaged turbulent kinetic energy. For all cases, turbulent energy increases with time, but at slower rates for higher Mach numbers. This means that the turbulent fluctuations are suppressed by compressibility and this is in agreement with our knowledge of compressible mixing layers. The reason for the suppression can be understood by comparing the budgets of turbulent kinetic energy. The major contributions to the kinetic energy budget are from the production
$(\unicode[STIX]{x1D70F})$
and along the vertical axis is averaged turbulent kinetic energy. For all cases, turbulent energy increases with time, but at slower rates for higher Mach numbers. This means that the turbulent fluctuations are suppressed by compressibility and this is in agreement with our knowledge of compressible mixing layers. The reason for the suppression can be understood by comparing the budgets of turbulent kinetic energy. The major contributions to the kinetic energy budget are from the production
![]() $({\mathcal{P}})$
, dissipation
$({\mathcal{P}})$
, dissipation
![]() $(\unicode[STIX]{x1D716})$
and transport of turbulent fluctuations
$(\unicode[STIX]{x1D716})$
and transport of turbulent fluctuations
![]() $(T_{k})$
. Production of kinetic energy is the only source and dissipation by molecular viscosity is the only sink in the kinetic energy budget. Turbulent, molecular and pressure transports only redistribute energy in the transverse direction, while pressure dilatation
$(T_{k})$
. Production of kinetic energy is the only source and dissipation by molecular viscosity is the only sink in the kinetic energy budget. Turbulent, molecular and pressure transports only redistribute energy in the transverse direction, while pressure dilatation
![]() $(\unicode[STIX]{x1D6F1})$
and fluctuating mass flux contributions
$(\unicode[STIX]{x1D6F1})$
and fluctuating mass flux contributions
![]() $(M)$
are negligible for all the cases considered here. Turbulent kinetic energy production and dissipation are shown in figure 4(b). With an increase in
$(M)$
are negligible for all the cases considered here. Turbulent kinetic energy production and dissipation are shown in figure 4(b). With an increase in
![]() $M_{c}$
, energy production decreases and the changes in the dissipation of energy are not as large as those in production. Therefore, the difference in energy levels arises from a reduced level of production at higher convective Mach number. In a temporally evolving mixing layer, the only non-zero component in the mean velocity gradient tensor is
$M_{c}$
, energy production decreases and the changes in the dissipation of energy are not as large as those in production. Therefore, the difference in energy levels arises from a reduced level of production at higher convective Mach number. In a temporally evolving mixing layer, the only non-zero component in the mean velocity gradient tensor is
![]() $\text{d}\tilde{u} _{1}/\text{d}x_{2}$
, and hence the turbulent stress responsible for the production is
$\text{d}\tilde{u} _{1}/\text{d}x_{2}$
, and hence the turbulent stress responsible for the production is
![]() $R_{12}~(=\widetilde{u_{1}^{\prime \prime }u_{2}^{\prime \prime }})$
according to (3.6a
).
$R_{12}~(=\widetilde{u_{1}^{\prime \prime }u_{2}^{\prime \prime }})$
according to (3.6a
).

Figure 4. (a) Evolution of averaged turbulent kinetic energy with time:
A detailed examination of the budgets of
![]() $R_{12}$
indicates that the dominant source and sink are respectively production by mean flow gradient
$R_{12}$
indicates that the dominant source and sink are respectively production by mean flow gradient
![]() $({\mathcal{P}}_{12}=R_{22}\,\text{d}\tilde{u} _{1}/\text{d}x_{2})$
and destruction by pressure–strain rate covariance
$({\mathcal{P}}_{12}=R_{22}\,\text{d}\tilde{u} _{1}/\text{d}x_{2})$
and destruction by pressure–strain rate covariance
![]() $(\unicode[STIX]{x1D6F1}_{12}=\overline{p^{\prime }(\text{d}u_{1}^{\prime \prime }/\text{d}x_{2}+\text{d}u_{2}^{\prime \prime }/\text{d}x_{1})})$
. The budget equation may be obtained from equation (3.5) by substituting
$(\unicode[STIX]{x1D6F1}_{12}=\overline{p^{\prime }(\text{d}u_{1}^{\prime \prime }/\text{d}x_{2}+\text{d}u_{2}^{\prime \prime }/\text{d}x_{1})})$
. The budget equation may be obtained from equation (3.5) by substituting
![]() $i=1$
and
$i=1$
and
![]() $j=2$
. Viscous dissipation of turbulent shear stress is negligible compared to production and pressure–strain covariance. The time-varying budget terms, in figure 5(a), show that the production of turbulent shear stress decreases with increase in Mach number. There exists a balance between shear stress production and pressure–strain correlation during the very early stages of evolution. This regime is characterized by a balance between pressure and inertia effects, according to Bertsch et al. (Reference Bertsch, Suman and Girimaji2012), resulting in stabilization of kinetic energy growth. Though the pressure–strain covariance also changes with compressibility, we focus on the stress production because any reduction in source term directly reflects on the shear stress itself. Transverse velocity fluctuations, in the form of
$j=2$
. Viscous dissipation of turbulent shear stress is negligible compared to production and pressure–strain covariance. The time-varying budget terms, in figure 5(a), show that the production of turbulent shear stress decreases with increase in Mach number. There exists a balance between shear stress production and pressure–strain correlation during the very early stages of evolution. This regime is characterized by a balance between pressure and inertia effects, according to Bertsch et al. (Reference Bertsch, Suman and Girimaji2012), resulting in stabilization of kinetic energy growth. Though the pressure–strain covariance also changes with compressibility, we focus on the stress production because any reduction in source term directly reflects on the shear stress itself. Transverse velocity fluctuations, in the form of
![]() $R_{22}$
, are responsible for the production of turbulent shear stress. The dependence is evident from the reduction in transverse velocity fluctuations with
$R_{22}$
, are responsible for the production of turbulent shear stress. The dependence is evident from the reduction in transverse velocity fluctuations with
![]() $M_{c}$
, as seen in figure 5(b). Transverse fluctuations are also stabilized during the very early stages before they start to grow; the onset of which is delayed by compressibility. Thus, lower
$M_{c}$
, as seen in figure 5(b). Transverse fluctuations are also stabilized during the very early stages before they start to grow; the onset of which is delayed by compressibility. Thus, lower
![]() $R_{12}$
at higher Mach numbers is due to the reduced intensity of transverse fluctuations as well as the stabilization arising from the balance between the pressure–strain correlation and inertia effects.
$R_{12}$
at higher Mach numbers is due to the reduced intensity of transverse fluctuations as well as the stabilization arising from the balance between the pressure–strain correlation and inertia effects.

Figure 5. (a) Production of Reynolds shear stress (filled symbols) and pressure rate of strain correlation,
![]() $\unicode[STIX]{x1D6F1}_{12}$
(open symbols) at different Mach numbers;
$\unicode[STIX]{x1D6F1}_{12}$
(open symbols) at different Mach numbers;

Figure 6. Redistribution terms in the budget of turbulent normal stresses: (a)
![]() $\unicode[STIX]{x1D6F1}_{11}$
; (b) ——,
$\unicode[STIX]{x1D6F1}_{11}$
; (b) ——,
![]() $\unicode[STIX]{x1D6F1}_{22}$
and - - -,
$\unicode[STIX]{x1D6F1}_{22}$
and - - -,
![]() $\unicode[STIX]{x1D6F1}_{33}$
. The plots are for three different cases:
$\unicode[STIX]{x1D6F1}_{33}$
. The plots are for three different cases:
The direct production of turbulent fluctuations by the mean flow gradient contributes only to the streamwise fluctuations. In other words, production of
![]() $R_{22}$
and
$R_{22}$
and
![]() $R_{33}$
by the mean velocity gradient is zero since
$R_{33}$
by the mean velocity gradient is zero since
![]() $\tilde{u} _{2}$
and
$\tilde{u} _{2}$
and
![]() $\tilde{u} _{3}$
are zero. The dominant source in the budget of transverse and spanwise fluctuations is pressure–strain rate covariance. In the turbulent energy budget, pressure dilatation (which is the trace of the pressure–strain rate tensor) is negligible in our computations
$\tilde{u} _{3}$
are zero. The dominant source in the budget of transverse and spanwise fluctuations is pressure–strain rate covariance. In the turbulent energy budget, pressure dilatation (which is the trace of the pressure–strain rate tensor) is negligible in our computations
![]() $(\unicode[STIX]{x1D6F1}_{kk}=0)$
, even when shocklets are observed in the flow field at
$(\unicode[STIX]{x1D6F1}_{kk}=0)$
, even when shocklets are observed in the flow field at
![]() $M_{c}=1.20$
. The diagonal components of the pressure–strain rate tensor are not zero, but balance each other such that
$M_{c}=1.20$
. The diagonal components of the pressure–strain rate tensor are not zero, but balance each other such that
![]() $\unicode[STIX]{x1D6F1}_{11}\approx -(\unicode[STIX]{x1D6F1}_{22}+\unicode[STIX]{x1D6F1}_{33})$
. This is often referred to as the redistribution of energy by pressure–strain rate covariance (Pope Reference Pope2000). It can be perceived as
$\unicode[STIX]{x1D6F1}_{11}\approx -(\unicode[STIX]{x1D6F1}_{22}+\unicode[STIX]{x1D6F1}_{33})$
. This is often referred to as the redistribution of energy by pressure–strain rate covariance (Pope Reference Pope2000). It can be perceived as
![]() $\unicode[STIX]{x1D6F1}_{11}$
extracting some amount of energy from streamwise velocity fluctuations and redistributing that to the other two fluctuating velocity components.
$\unicode[STIX]{x1D6F1}_{11}$
extracting some amount of energy from streamwise velocity fluctuations and redistributing that to the other two fluctuating velocity components.
The values of diagonal terms in
![]() $\unicode[STIX]{x1D6F1}_{ij}$
, averaged in the transverse direction according to (3.4), varies with time, and their evolution is given in figure 6. The individual components of the covariance tensor are normalized by the streamwise fluctuation production
$\unicode[STIX]{x1D6F1}_{ij}$
, averaged in the transverse direction according to (3.4), varies with time, and their evolution is given in figure 6. The individual components of the covariance tensor are normalized by the streamwise fluctuation production
![]() $({\mathcal{P}}_{11})$
, which enables us to compare the efficiency of pressure–strain covariance in redistributing the available energy among different velocity components. Irrespective of Mach number, the redistribution to transverse and spanwise fluctuations are approximately equal, and the turbulence is expected to have an axisymmetric structure. There is no equipartition of energy between transverse fluctuations and internal energy as observed by Lavin et al. (Reference Lavin, Girimaji, Suman and Yu2012) for homogeneous shear turbulence, but the energy is almost equally distributed between transverse and streamwise fluctuating components. The magnitudes of diagonal components of pressure–strain covariance, namely
$({\mathcal{P}}_{11})$
, which enables us to compare the efficiency of pressure–strain covariance in redistributing the available energy among different velocity components. Irrespective of Mach number, the redistribution to transverse and spanwise fluctuations are approximately equal, and the turbulence is expected to have an axisymmetric structure. There is no equipartition of energy between transverse fluctuations and internal energy as observed by Lavin et al. (Reference Lavin, Girimaji, Suman and Yu2012) for homogeneous shear turbulence, but the energy is almost equally distributed between transverse and streamwise fluctuating components. The magnitudes of diagonal components of pressure–strain covariance, namely
![]() $\unicode[STIX]{x1D6F1}_{11},\unicode[STIX]{x1D6F1}_{22}$
and
$\unicode[STIX]{x1D6F1}_{11},\unicode[STIX]{x1D6F1}_{22}$
and
![]() $\unicode[STIX]{x1D6F1}_{33}$
, decrease with increasing
$\unicode[STIX]{x1D6F1}_{33}$
, decrease with increasing
![]() $M_{c}$
, especially during the early stages. Therefore it is evident that redistribution is less efficient as compressibility effects become significant.
$M_{c}$
, especially during the early stages. Therefore it is evident that redistribution is less efficient as compressibility effects become significant.

Figure 7. (a) Change in mean internal energy in the mixing layer with time. (b) Evolution of averaged thermodynamic potential energy;
The evolution of averaged internal energy in the mixing layer is shown in figure 7(a). We report the change in mean internal energy from its initial value
![]() $(\unicode[STIX]{x0394}E=c_{v}[\tilde{T}-\tilde{T}_{0}])$
, normalized by the initial fluctuation kinetic energy. The internal energy increases with time primarily due to the energy transfer from kinetic energy by viscous dissipation. In compressible turbulent flows, there is energy transfer to the internal mode by dilatational effects, including dilatational dissipation and pressure dilatation in addition to the incompressible viscous dissipation (Lele Reference Lele1994). Internal energy increases more rapidly for lower
$(\unicode[STIX]{x0394}E=c_{v}[\tilde{T}-\tilde{T}_{0}])$
, normalized by the initial fluctuation kinetic energy. The internal energy increases with time primarily due to the energy transfer from kinetic energy by viscous dissipation. In compressible turbulent flows, there is energy transfer to the internal mode by dilatational effects, including dilatational dissipation and pressure dilatation in addition to the incompressible viscous dissipation (Lele Reference Lele1994). Internal energy increases more rapidly for lower
![]() $M_{c}$
, which implies that the dilatational effects are negligible and transfer is mainly through viscous dissipation, which decreases when
$M_{c}$
, which implies that the dilatational effects are negligible and transfer is mainly through viscous dissipation, which decreases when
![]() $M_{c}$
increases, as seen in figure 4(b). However, the thermodynamic potential energy, defined by
$M_{c}$
increases, as seen in figure 4(b). However, the thermodynamic potential energy, defined by
![]() $E_{T}=\overline{p^{\prime 2}}/\unicode[STIX]{x1D6FE}\bar{p}$
, exhibits different behaviour. Sarkar et al. (Reference Sarkar, Erlebacher, Hussaini and Kreiss1991) and Lee & Girimaji (Reference Lee and Girimaji2013) used this quantity to quantify the energy associated with thermodynamic fluctuations. The evolution of average
$E_{T}=\overline{p^{\prime 2}}/\unicode[STIX]{x1D6FE}\bar{p}$
, exhibits different behaviour. Sarkar et al. (Reference Sarkar, Erlebacher, Hussaini and Kreiss1991) and Lee & Girimaji (Reference Lee and Girimaji2013) used this quantity to quantify the energy associated with thermodynamic fluctuations. The evolution of average
![]() $E_{T}$
in the shear layer is shown in figure 7(b). The potential energy increases with
$E_{T}$
in the shear layer is shown in figure 7(b). The potential energy increases with
![]() $M_{c}$
, which implies that even though the energy transfer from kinetic mode to internal mode decreases with compressibility, there is an increase in energy transfer to thermodynamic fluctuations.
$M_{c}$
, which implies that even though the energy transfer from kinetic mode to internal mode decreases with compressibility, there is an increase in energy transfer to thermodynamic fluctuations.
Pantano & Sarkar (Reference Pantano and Sarkar2002) attributed the lower levels of production to a decrease in pressure–strain term with increasing
![]() $M_{c}$
in their self-similar analysis. They also noted that the decrease in
$M_{c}$
in their self-similar analysis. They also noted that the decrease in
![]() $\unicode[STIX]{x1D6F1}_{11}$
is similar to that in pressure fluctuations with increasing compressibility. The present study shows that the initial evolution of the mixing layer is also characterized by differences in the redistribution of energy by pressure–strain rate covariance, as they are in the self-similar regime. The pressure–strain correlation and root mean square of pressure fluctuations at the centreline for different convective Mach numbers at
$\unicode[STIX]{x1D6F1}_{11}$
is similar to that in pressure fluctuations with increasing compressibility. The present study shows that the initial evolution of the mixing layer is also characterized by differences in the redistribution of energy by pressure–strain rate covariance, as they are in the self-similar regime. The pressure–strain correlation and root mean square of pressure fluctuations at the centreline for different convective Mach numbers at
![]() $\unicode[STIX]{x1D70F}=200$
are shown in figure 8. The quantities are normalized by the incompressible
$\unicode[STIX]{x1D70F}=200$
are shown in figure 8. The quantities are normalized by the incompressible
![]() $(M_{c}=0.20)$
value. There is a direct correlation between redistribution and pressure fluctuations. Pantano & Sarkar (Reference Pantano and Sarkar2002) observed similar trends in the self-similar regime. Thus, the reduced redistribution during the transient evolution is caused by the suppression of pressure fluctuations by compressibility. Apart from the variations in redistribution, we also observe that there is a stabilization of turbulent shear stress growth due to the balance between stress production and pressure–strain correlation when compressibility effects are significant.
$(M_{c}=0.20)$
value. There is a direct correlation between redistribution and pressure fluctuations. Pantano & Sarkar (Reference Pantano and Sarkar2002) observed similar trends in the self-similar regime. Thus, the reduced redistribution during the transient evolution is caused by the suppression of pressure fluctuations by compressibility. Apart from the variations in redistribution, we also observe that there is a stabilization of turbulent shear stress growth due to the balance between stress production and pressure–strain correlation when compressibility effects are significant.

Figure 8. Pressure–strain correlation and pressure fluctuation at different
![]() $M_{c}$
, normalized by the incompressible value.
$M_{c}$
, normalized by the incompressible value.
3.3 Topological considerations
Turbulent statistics can be influenced by variations in topology. We use the
![]() $Q$
-criterion to classify the topology of the flow into two distinct categories (Hunt et al.
Reference Hunt, Wray and Moin1988). The second invariant
$Q$
-criterion to classify the topology of the flow into two distinct categories (Hunt et al.
Reference Hunt, Wray and Moin1988). The second invariant
![]() $(Q)$
of the velocity gradient tensor is given by
$(Q)$
of the velocity gradient tensor is given by
In the above,
![]() $\unicode[STIX]{x1D61A}_{ij}=[\unicode[STIX]{x1D735}u^{\prime \prime }+\unicode[STIX]{x1D735}u^{\prime \prime \text{T}}]/2$
and
$\unicode[STIX]{x1D61A}_{ij}=[\unicode[STIX]{x1D735}u^{\prime \prime }+\unicode[STIX]{x1D735}u^{\prime \prime \text{T}}]/2$
and
![]() $\unicode[STIX]{x1D6FA}_{ij}=[\unicode[STIX]{x1D735}u^{\prime \prime }-\unicode[STIX]{x1D735}u^{\prime \prime \text{T}}]/2$
are respectively the symmetric and anti-symmetric parts of the deviatoric strain rate tensor,
$\unicode[STIX]{x1D6FA}_{ij}=[\unicode[STIX]{x1D735}u^{\prime \prime }-\unicode[STIX]{x1D735}u^{\prime \prime \text{T}}]/2$
are respectively the symmetric and anti-symmetric parts of the deviatoric strain rate tensor,
![]() $\unicode[STIX]{x1D735}u^{\prime \prime }=u_{i,j}^{\prime \prime }-u_{k,k}^{\prime \prime }\unicode[STIX]{x1D6FF}_{ij}/3$
. The criterion, originally developed for incompressible flows, is valid for compressible flows only when the invariant is obtained for deviatoric part of velocity gradient tensor (Kolár Reference Kolár2009). Local flow structure is classified according to the numerical value of
$\unicode[STIX]{x1D735}u^{\prime \prime }=u_{i,j}^{\prime \prime }-u_{k,k}^{\prime \prime }\unicode[STIX]{x1D6FF}_{ij}/3$
. The criterion, originally developed for incompressible flows, is valid for compressible flows only when the invariant is obtained for deviatoric part of velocity gradient tensor (Kolár Reference Kolár2009). Local flow structure is classified according to the numerical value of
![]() $Q$
. According to the criterion, a positive value of
$Q$
. According to the criterion, a positive value of
![]() $Q$
indicates that the flow is locally vortex-dominated and negative values indicate strain-dominated regions. In the present work, the topology is determined using the fluctuating quantities, since for the mean field
$Q$
indicates that the flow is locally vortex-dominated and negative values indicate strain-dominated regions. In the present work, the topology is determined using the fluctuating quantities, since for the mean field
![]() $Q$
turns out to be zero. In this section, we analyse various turbulent statistics conditioned on the value of
$Q$
turns out to be zero. In this section, we analyse various turbulent statistics conditioned on the value of
![]() $\bar{Q}=Q/Q_{rms}$
to study how changes in local flow topology due to compressibility manifests on turbulent statistics. An average in the homogeneous plane is used for the root mean square (r.m.s.) calculation. The sample used to calculate the conditional statistics is the region
$\bar{Q}=Q/Q_{rms}$
to study how changes in local flow topology due to compressibility manifests on turbulent statistics. An average in the homogeneous plane is used for the root mean square (r.m.s.) calculation. The sample used to calculate the conditional statistics is the region
![]() $-2\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}\leqslant x_{2}\leqslant 2\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}$
, which constitutes the turbulent core of the mixing layer. Extreme events,
$-2\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}\leqslant x_{2}\leqslant 2\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}$
, which constitutes the turbulent core of the mixing layer. Extreme events,
![]() $|\bar{Q}|\gg 1$
, are not discussed here. Various quantities from each spatial location are put into different bins based on the local value of
$|\bar{Q}|\gg 1$
, are not discussed here. Various quantities from each spatial location are put into different bins based on the local value of
![]() $\bar{Q}$
and conditional averages for different
$\bar{Q}$
and conditional averages for different
![]() $\bar{Q}$
are obtained by averaging the data in respective bins.
$\bar{Q}$
are obtained by averaging the data in respective bins.
Distribution of turbulence among different flow topologies is given by the turbulent kinetic energy conditioned on
![]() $\bar{Q}$
, as in figure 9. The figure shows the variation of the conditional mean of
$\bar{Q}$
, as in figure 9. The figure shows the variation of the conditional mean of
![]() $u_{k}^{\prime \prime }u_{k}^{\prime \prime }$
, normalized by
$u_{k}^{\prime \prime }u_{k}^{\prime \prime }$
, normalized by
![]() $2K(y)$
, with
$2K(y)$
, with
![]() $\bar{Q}$
. For negative values of
$\bar{Q}$
. For negative values of
![]() $\bar{Q}$
, the conditioned turbulent kinetic energy is higher than the overall turbulent kinetic energy. There is a sharp drop in the conditional mean as
$\bar{Q}$
, the conditioned turbulent kinetic energy is higher than the overall turbulent kinetic energy. There is a sharp drop in the conditional mean as
![]() $\bar{Q}$
increases from zero. This implies that the turbulent fluctuations are more intense in shear-dominated regions, and their relative contribution towards overall kinetic energy is higher. The conditional mean remains nearly constant in the strain-dominated regions, and they are less influenced by changes in
$\bar{Q}$
increases from zero. This implies that the turbulent fluctuations are more intense in shear-dominated regions, and their relative contribution towards overall kinetic energy is higher. The conditional mean remains nearly constant in the strain-dominated regions, and they are less influenced by changes in
![]() $M_{c}$
. In vortex-dominated regions, the normalized conditional kinetic energy has values less than unity and decreases as
$M_{c}$
. In vortex-dominated regions, the normalized conditional kinetic energy has values less than unity and decreases as
![]() $\bar{Q}$
increases in the compressible flow regime (large
$\bar{Q}$
increases in the compressible flow regime (large
![]() $M_{c}$
). As
$M_{c}$
). As
![]() $M_{c}$
increases, the conditional mean for a given
$M_{c}$
increases, the conditional mean for a given
![]() $\bar{Q}$
decreases in vortex-dominated regions. At the highest Mach number considered, the conditional mean is only approximately 0.60 times the turbulent kinetic energy in vortex-dominated regions. Thus, vortex-dominated regions have less turbulence intensity, and in the absence of these flow structures, the overall turbulent kinetic energy would have been higher owing to higher intensities in strain-dominated regions. For the range of turbulent Mach numbers in our study, it is safe to conclude that there is a preferential distribution of turbulent kinetic energy in regions of negative
$\bar{Q}$
decreases in vortex-dominated regions. At the highest Mach number considered, the conditional mean is only approximately 0.60 times the turbulent kinetic energy in vortex-dominated regions. Thus, vortex-dominated regions have less turbulence intensity, and in the absence of these flow structures, the overall turbulent kinetic energy would have been higher owing to higher intensities in strain-dominated regions. For the range of turbulent Mach numbers in our study, it is safe to conclude that there is a preferential distribution of turbulent kinetic energy in regions of negative
![]() $\bar{Q}$
.
$\bar{Q}$
.

Figure 9. Conditional mean of turbulent kinetic energy,
![]() $K_{Q}=\langle u_{k}^{\prime \prime }u_{k}^{\prime \prime }|\bar{Q}\rangle /2K$
, representing spatial distribution of turbulent energy among different topologies, for different cases at
$K_{Q}=\langle u_{k}^{\prime \prime }u_{k}^{\prime \prime }|\bar{Q}\rangle /2K$
, representing spatial distribution of turbulent energy among different topologies, for different cases at
![]() $\unicode[STIX]{x1D70F}=300$
.
$\unicode[STIX]{x1D70F}=300$
.
We have already observed in § 3.2 that differences in turbulent kinetic energy with compressibility arise from reduced levels of production. Ma & Xiao (Reference Ma and Xiao2016) showed that the turbulent kinetic energy production is more in strain-dominated regions, in the case of homogeneous turbulent shear flows. In our simulations, mixing layer evolves in such a way that turbulent energy production is due to Reynolds shear stress,
![]() $R_{12}$
, as discussed earlier. So any influence of local flow structure on energy production must be evident from a conditioned average of
$R_{12}$
, as discussed earlier. So any influence of local flow structure on energy production must be evident from a conditioned average of
![]() $\unicode[STIX]{x1D70C}u_{1}^{\prime \prime }u_{2}^{\prime \prime }$
. The conditional mean of turbulent shear stress, normalized by
$\unicode[STIX]{x1D70C}u_{1}^{\prime \prime }u_{2}^{\prime \prime }$
. The conditional mean of turbulent shear stress, normalized by
![]() $\bar{\unicode[STIX]{x1D70C}}(y)R_{12}(y)$
is shown in figure 10. There is a stronger co-variance of fluctuating streamwise and transverse velocities in regions dominated by strain which means those regions produce more fluctuating energy than vortex-dominated regions. For the nearly incompressible case (M2), the conditional mean gradually decreases as
$\bar{\unicode[STIX]{x1D70C}}(y)R_{12}(y)$
is shown in figure 10. There is a stronger co-variance of fluctuating streamwise and transverse velocities in regions dominated by strain which means those regions produce more fluctuating energy than vortex-dominated regions. For the nearly incompressible case (M2), the conditional mean gradually decreases as
![]() $\bar{Q}$
increases from negative values to positive values. For moderate
$\bar{Q}$
increases from negative values to positive values. For moderate
![]() $M_{c}$
(M5 and M7), the conditional mean is nearly constant for
$M_{c}$
(M5 and M7), the conditional mean is nearly constant for
![]() $\bar{Q}<0$
, peaks at
$\bar{Q}<0$
, peaks at
![]() $\bar{Q}=0$
and monotonically decreases beyond that. For the larger Mach numbers, the conditional turbulent stress increases with
$\bar{Q}=0$
and monotonically decreases beyond that. For the larger Mach numbers, the conditional turbulent stress increases with
![]() $\bar{Q}$
in the strain-dominated regions, reaches a maximum at
$\bar{Q}$
in the strain-dominated regions, reaches a maximum at
![]() $\bar{Q}=0$
and decreases as
$\bar{Q}=0$
and decreases as
![]() $\bar{Q}$
increases in the vortex-dominated regions. Most of the production happens at small negative values of
$\bar{Q}$
increases in the vortex-dominated regions. Most of the production happens at small negative values of
![]() $\bar{Q}$
. However, at all
$\bar{Q}$
. However, at all
![]() $M_{c}$
, the conditional mean has higher values in strain-dominated regions than that in vortex-dominated regions. Similar to turbulent kinetic energy, the shear stress also decreases as
$M_{c}$
, the conditional mean has higher values in strain-dominated regions than that in vortex-dominated regions. Similar to turbulent kinetic energy, the shear stress also decreases as
![]() $M_{c}$
increases for a given positive value of
$M_{c}$
increases for a given positive value of
![]() $\bar{Q}$
. Thus structures which are strongly dominated by vortex-like motions are less efficient in extracting energy from mean flow to turbulence. The spatial distribution of production explains the higher turbulence intensity in strain-dominated regions. The observation relating energy production and the fluctuating velocity gradient in compressible mixing layers was hitherto unknown.
$\bar{Q}$
. Thus structures which are strongly dominated by vortex-like motions are less efficient in extracting energy from mean flow to turbulence. The spatial distribution of production explains the higher turbulence intensity in strain-dominated regions. The observation relating energy production and the fluctuating velocity gradient in compressible mixing layers was hitherto unknown.

Figure 10. Turbulent shear stress conditioned on the value of
![]() $\bar{Q}$
,
$\bar{Q}$
,
![]() $R_{12|Q}=\langle \unicode[STIX]{x1D70C}u_{1}^{\prime \prime }u_{2}^{\prime \prime }|\bar{Q}\rangle /\bar{\unicode[STIX]{x1D70C}}R_{12}$
, for different convective Mach numbers at
$R_{12|Q}=\langle \unicode[STIX]{x1D70C}u_{1}^{\prime \prime }u_{2}^{\prime \prime }|\bar{Q}\rangle /\bar{\unicode[STIX]{x1D70C}}R_{12}$
, for different convective Mach numbers at
![]() $\unicode[STIX]{x1D70F}=300$
.
$\unicode[STIX]{x1D70F}=300$
.
The Reynolds shear stress,
![]() $R_{12}$
, represents turbulent transport of fluctuating streamwise momentum
$R_{12}$
, represents turbulent transport of fluctuating streamwise momentum
![]() $(\unicode[STIX]{x1D70C}u_{1}^{\prime \prime })$
by transverse fluctuations
$(\unicode[STIX]{x1D70C}u_{1}^{\prime \prime })$
by transverse fluctuations
![]() $(u_{2}^{\prime \prime })$
. Conditioned statistics in figure 10 imply that vortex-dominated regions do not transport as much fluctuating momentum as strain-dominated regions do. A closer look at flow structure in regions of strong positive
$(u_{2}^{\prime \prime })$
. Conditioned statistics in figure 10 imply that vortex-dominated regions do not transport as much fluctuating momentum as strain-dominated regions do. A closer look at flow structure in regions of strong positive
![]() $\bar{Q}$
makes apparent how local flow topology affects turbulent stress. Figure 11 shows the streamline pattern around a tube-like structure with
$\bar{Q}$
makes apparent how local flow topology affects turbulent stress. Figure 11 shows the streamline pattern around a tube-like structure with
![]() $\bar{Q}=1.1$
for
$\bar{Q}=1.1$
for
![]() $M_{c}=0.75$
at
$M_{c}=0.75$
at
![]() $\unicode[STIX]{x1D70F}=200$
. Streamlines are coloured by
$\unicode[STIX]{x1D70F}=200$
. Streamlines are coloured by
![]() $sgn(u_{1}^{\prime \prime }u_{2}^{\prime \prime })$
, solid red for positive values and dashed blue for negative values. The streamlines are helical near the vortex-dominated region, swirling around the tube-like structure. Such helical streamlines are characteristic of vortex-dominated regions. Moving along the helical streamline, the product
$sgn(u_{1}^{\prime \prime }u_{2}^{\prime \prime })$
, solid red for positive values and dashed blue for negative values. The streamlines are helical near the vortex-dominated region, swirling around the tube-like structure. Such helical streamlines are characteristic of vortex-dominated regions. Moving along the helical streamline, the product
![]() $u_{1}^{\prime \prime }u_{2}^{\prime \prime }$
alternates between positive and negative values. Therefore, any net positive contributions to
$u_{1}^{\prime \prime }u_{2}^{\prime \prime }$
alternates between positive and negative values. Therefore, any net positive contributions to
![]() $R_{12}$
from these regions are small and turbulent transport of fluctuating momentum is less compared to regions where such helical streamlines are absent. This kind of flow pattern is more likely to diminish turbulent production when these streamlines are aligned with their axes along the streamwise direction. Helical streamlines with their axes inclined away from the streamwise direction may contribute significantly to the turbulent shear stress and thus the energy production. A better understanding of the inclination of such streamlines is given by an in-depth analysis of the structure of the vortex field in § 3.4. Although the streamline pattern shown in figure 11 is instantaneous, we have observed several such patterns in the flow field for all the cases, and all helical streamlines are found in the regions of positive
$R_{12}$
from these regions are small and turbulent transport of fluctuating momentum is less compared to regions where such helical streamlines are absent. This kind of flow pattern is more likely to diminish turbulent production when these streamlines are aligned with their axes along the streamwise direction. Helical streamlines with their axes inclined away from the streamwise direction may contribute significantly to the turbulent shear stress and thus the energy production. A better understanding of the inclination of such streamlines is given by an in-depth analysis of the structure of the vortex field in § 3.4. Although the streamline pattern shown in figure 11 is instantaneous, we have observed several such patterns in the flow field for all the cases, and all helical streamlines are found in the regions of positive
![]() $\bar{Q}$
. Not all regions of positive
$\bar{Q}$
. Not all regions of positive
![]() $\bar{Q}$
, however, have a helical streamline pattern.
$\bar{Q}$
, however, have a helical streamline pattern.

Figure 11. Streamlines around a vortex-dominated tube-like structure in the flow. The structure is contour of
![]() $\bar{Q}=1.1$
from an instantaneous snapshot of the flow field at
$\bar{Q}=1.1$
from an instantaneous snapshot of the flow field at
![]() $\unicode[STIX]{x1D70F}=200$
for
$\unicode[STIX]{x1D70F}=200$
for
![]() $M_{c}=0.75$
. Solid parts of the streamline indicate that
$M_{c}=0.75$
. Solid parts of the streamline indicate that
![]() $u_{1}^{\prime \prime }u_{2}^{\prime \prime }$
is positive in those regions and dashed lines indicate that the product is negative.
$u_{1}^{\prime \prime }u_{2}^{\prime \prime }$
is positive in those regions and dashed lines indicate that the product is negative.
Turbulent kinetic energy production in simple shear flows is linked to redistribution effects of the pressure–strain correlation tensor
![]() $(\unicode[STIX]{x1D6F1}_{ij})$
, as described in § 3.2. Turbulent stress, responsible for energy production in mixing layers, depends on transverse velocity fluctuations, which are produced by redistribution of energy by diagonal components of
$(\unicode[STIX]{x1D6F1}_{ij})$
, as described in § 3.2. Turbulent stress, responsible for energy production in mixing layers, depends on transverse velocity fluctuations, which are produced by redistribution of energy by diagonal components of
![]() $\unicode[STIX]{x1D6F1}_{ij}$
. We observed that compressibility reduces redistribution by
$\unicode[STIX]{x1D6F1}_{ij}$
. We observed that compressibility reduces redistribution by
![]() $\unicode[STIX]{x1D6F1}_{ij}$
. Therefore, it is imperative to investigate the effects of local flow topology on energy redistribution. Redistribution of kinetic energy depends on the local flow structure, as shown in figure 12, where we plot conditional average
$\unicode[STIX]{x1D6F1}_{ij}$
. Therefore, it is imperative to investigate the effects of local flow topology on energy redistribution. Redistribution of kinetic energy depends on the local flow structure, as shown in figure 12, where we plot conditional average
![]() $\unicode[STIX]{x1D6F1}_{11|Q}=\langle -p^{\prime }\unicode[STIX]{x2202}u_{1}^{\prime \prime }/\unicode[STIX]{x2202}x_{1}|\bar{Q}\rangle /(K\unicode[STIX]{x0394}U/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}})$
against
$\unicode[STIX]{x1D6F1}_{11|Q}=\langle -p^{\prime }\unicode[STIX]{x2202}u_{1}^{\prime \prime }/\unicode[STIX]{x2202}x_{1}|\bar{Q}\rangle /(K\unicode[STIX]{x0394}U/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}})$
against
![]() $\bar{Q}$
. The quantity on the vertical axis represents the rate of energy extraction from streamwise fluctuations by pressure–strain covariance, which then is redistributed between the transverse and spanwise fluctuating components. The conditional mean is minimum for
$\bar{Q}$
. The quantity on the vertical axis represents the rate of energy extraction from streamwise fluctuations by pressure–strain covariance, which then is redistributed between the transverse and spanwise fluctuating components. The conditional mean is minimum for
![]() $\bar{Q}=0$
, but increases as the topology become either strain dominated or vortex dominated. However, the strain-dominated regions have higher values for the conditional mean than vortex-dominated regions and the difference increases with
$\bar{Q}=0$
, but increases as the topology become either strain dominated or vortex dominated. However, the strain-dominated regions have higher values for the conditional mean than vortex-dominated regions and the difference increases with
![]() $M_{c}$
. Thus strain-dominated regions, where
$M_{c}$
. Thus strain-dominated regions, where
![]() $\bar{Q}<0$
, are significantly more effective in transferring energy from streamwise fluctuations to the other directions. Redistribution by pressure–strain in vortex-dominated regions is comparatively less, especially at higher Mach numbers. These differences contribute to the preferential distribution of production and kinetic energy discussed above.
$\bar{Q}<0$
, are significantly more effective in transferring energy from streamwise fluctuations to the other directions. Redistribution by pressure–strain in vortex-dominated regions is comparatively less, especially at higher Mach numbers. These differences contribute to the preferential distribution of production and kinetic energy discussed above.

Figure 12. Conditional average of pressure–strain covariance
![]() $\unicode[STIX]{x1D6F1}_{11|Q}=\langle -p^{\prime }(\unicode[STIX]{x2202}u_{1}^{\prime \prime }/\unicode[STIX]{x2202}x_{1})|\bar{Q}\rangle /(K\unicode[STIX]{x0394}U/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}})$
in the turbulent mixing layer at different convective Mach numbers.
$\unicode[STIX]{x1D6F1}_{11|Q}=\langle -p^{\prime }(\unicode[STIX]{x2202}u_{1}^{\prime \prime }/\unicode[STIX]{x2202}x_{1})|\bar{Q}\rangle /(K\unicode[STIX]{x0394}U/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}})$
in the turbulent mixing layer at different convective Mach numbers.
The turbulent kinetic energy has a dependence on local flow structure, which is due to a preferential distribution of energy production and redistribution. However, the preferential distribution of kinetic energy and production exist at all Mach numbers in our study. Therefore it is difficult to explain reduced turbulence levels at higher Mach numbers based on conditional statistics alone. However, the probability density function (PDF) of
![]() $\bar{Q}$
shows that the flow topology is changed by compressibility. Figure 13 compares the PDF of
$\bar{Q}$
shows that the flow topology is changed by compressibility. Figure 13 compares the PDF of
![]() $\bar{Q}$
for
$\bar{Q}$
for
![]() $M_{c}=0.20$
and
$M_{c}=0.20$
and
![]() $1.20$
. At higher convective Mach numbers, the probability of the occurrence of positive values of
$1.20$
. At higher convective Mach numbers, the probability of the occurrence of positive values of
![]() $\bar{Q}$
is higher than that in lower Mach number cases. The fraction of the shear layer which has a locally vortex-dominated topology, calculated by the area under PDF curve for
$\bar{Q}$
is higher than that in lower Mach number cases. The fraction of the shear layer which has a locally vortex-dominated topology, calculated by the area under PDF curve for
![]() $\bar{Q}$
, for different cases is listed in table 2. At any given instant of time or mixing-layer width, the fraction of the shear layer with vortex-dominated structures increases with convective Mach number. Nevertheless, strain-dominated regions are more prominent than vortex-dominated regions at all Mach numbers, according to the values in table 2. The lower turbulent kinetic energy at higher Mach numbers can thus be attributed to the higher fraction of vortex-dominated regions which are less efficient in kinetic energy production and redistribution. The differences in topology tend to even out at later times and any differences in turbulent statistics due to differences in local flow structure are expected to be small during the late time and self-similar evolution of the mixing layer. In addition to the pressure dilatation effects, a vortex-dominated topology also contributes towards lower levels of turbulence as convective Mach number increases.
$\bar{Q}$
, for different cases is listed in table 2. At any given instant of time or mixing-layer width, the fraction of the shear layer with vortex-dominated structures increases with convective Mach number. Nevertheless, strain-dominated regions are more prominent than vortex-dominated regions at all Mach numbers, according to the values in table 2. The lower turbulent kinetic energy at higher Mach numbers can thus be attributed to the higher fraction of vortex-dominated regions which are less efficient in kinetic energy production and redistribution. The differences in topology tend to even out at later times and any differences in turbulent statistics due to differences in local flow structure are expected to be small during the late time and self-similar evolution of the mixing layer. In addition to the pressure dilatation effects, a vortex-dominated topology also contributes towards lower levels of turbulence as convective Mach number increases.

Figure 13. Probability density function of
![]() $\bar{Q}$
in the turbulent shear layer for
$\bar{Q}$
in the turbulent shear layer for
![]() $M_{c}=0.20\text{ and }1.20$
at
$M_{c}=0.20\text{ and }1.20$
at
![]() $\unicode[STIX]{x1D70F}=300$
. Data correspond to
$\unicode[STIX]{x1D70F}=300$
. Data correspond to
![]() $-2\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}\leqslant x_{2}\leqslant 2\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}$
.
$-2\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}\leqslant x_{2}\leqslant 2\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}$
.
Table 2. Percentage of vortex-dominated regions in the turbulent shear layer, estimated from the probability density function of
![]() $\bar{Q}$
, for different cases. The changes in topology with time (top) and growth of the mixing-layer thickness (bottom) for different cases show that higher
$\bar{Q}$
, for different cases. The changes in topology with time (top) and growth of the mixing-layer thickness (bottom) for different cases show that higher
![]() $M_{c}$
has more vortex-dominated regions in the flow field.
$M_{c}$
has more vortex-dominated regions in the flow field.

3.4 Vortex vectors
In § 3.3, the
![]() $Q$
-criterion was used to identify the vortex-dominated regions and the reported statistics were conditioned on the value of
$Q$
-criterion was used to identify the vortex-dominated regions and the reported statistics were conditioned on the value of
![]() $Q$
, a scalar. Vortex identification using the
$Q$
, a scalar. Vortex identification using the
![]() $Q$
-criterion lacks information on the direction of rotation, or on the orientation of these vortex-dominated structures. Recently, Tian et al. (Reference Tian, Gao, Dong and Liu2018) (from now on TGDL18) defined a quantity called the vortex vector which not only identifies vortex-dominated regions but also gives the direction of rotation of the fluid element locally. In this section, we apply their definition of the vortex vector to our DNS data to analyse the effects of compressibility.
$Q$
-criterion lacks information on the direction of rotation, or on the orientation of these vortex-dominated structures. Recently, Tian et al. (Reference Tian, Gao, Dong and Liu2018) (from now on TGDL18) defined a quantity called the vortex vector which not only identifies vortex-dominated regions but also gives the direction of rotation of the fluid element locally. In this section, we apply their definition of the vortex vector to our DNS data to analyse the effects of compressibility.
At any point in the flow field, TGDL18 defines a local rotation axis relative to which fluid has rotational motion in the plane orthogonal to the axis. Let us denote this local rotation axis by
![]() $z$
, and let
$z$
, and let
![]() $xy$
be the plane orthogonal to this axis. Then
$xy$
be the plane orthogonal to this axis. Then
![]() $xyz$
is an orthogonal coordinate system which varies from point to point due to the change in orientation of the local rotation axis. By definition, there is no rotational motion of the fluid element in any plane other than
$xyz$
is an orthogonal coordinate system which varies from point to point due to the change in orientation of the local rotation axis. By definition, there is no rotational motion of the fluid element in any plane other than
![]() $xy$
. This requires that the local velocity field
$xy$
. This requires that the local velocity field
![]() $\boldsymbol{V}=(u,v,w)$
in the local orthogonal coordinate system satisfies
$\boldsymbol{V}=(u,v,w)$
in the local orthogonal coordinate system satisfies
![]() $\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}z=0$
and
$\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}z=0$
and
![]() $\unicode[STIX]{x2202}v/\unicode[STIX]{x2202}z=0$
. These are necessary and sufficient conditions for
$\unicode[STIX]{x2202}v/\unicode[STIX]{x2202}z=0$
. These are necessary and sufficient conditions for
![]() $z$
to be the local rotation axis. The unit vector along
$z$
to be the local rotation axis. The unit vector along
![]() $z$
in the general reference frame is given by
$z$
in the general reference frame is given by
![]() $\boldsymbol{r}=r_{1}\hat{e}_{1}+r_{2}\hat{e}_{2}+r_{3}\hat{e}_{3}$
, where
$\boldsymbol{r}=r_{1}\hat{e}_{1}+r_{2}\hat{e}_{2}+r_{3}\hat{e}_{3}$
, where
![]() $\hat{e}_{1},\hat{e}_{2}$
and
$\hat{e}_{1},\hat{e}_{2}$
and
![]() $\hat{e}_{3}$
are unit vectors in the general reference frame along the
$\hat{e}_{3}$
are unit vectors in the general reference frame along the
![]() $x_{1},x_{2}$
and
$x_{1},x_{2}$
and
![]() $x_{3}$
directions respectively. The vector
$x_{3}$
directions respectively. The vector
![]() $\boldsymbol{r}$
at each point is obtained by solving the following equations,
$\boldsymbol{r}$
at each point is obtained by solving the following equations,
where
![]() $\unicode[STIX]{x1D63C}$
is the orthogonal transformation matrix. The transformation matrix is a function of the local rotation axis and is given by
$\unicode[STIX]{x1D63C}$
is the orthogonal transformation matrix. The transformation matrix is a function of the local rotation axis and is given by
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D63C}=\left[\begin{array}{@{}ccc@{}}\displaystyle \frac{r_{2}^{2}+r_{3}^{2}+r_{3}}{1+r_{3}} & \displaystyle -\frac{r_{1}r_{2}}{1+r_{3}} & -r_{1}\\ \displaystyle -\frac{r_{1}r_{2}}{1+r_{3}} & \displaystyle \frac{r_{1}^{2}+r_{3}^{2}+r_{3}}{1+r_{3}} & -r_{2}\\ \displaystyle r_{1} & r_{2} & r_{3}\end{array}\right]. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D63C}=\left[\begin{array}{@{}ccc@{}}\displaystyle \frac{r_{2}^{2}+r_{3}^{2}+r_{3}}{1+r_{3}} & \displaystyle -\frac{r_{1}r_{2}}{1+r_{3}} & -r_{1}\\ \displaystyle -\frac{r_{1}r_{2}}{1+r_{3}} & \displaystyle \frac{r_{1}^{2}+r_{3}^{2}+r_{3}}{1+r_{3}} & -r_{2}\\ \displaystyle r_{1} & r_{2} & r_{3}\end{array}\right]. & & \displaystyle\end{eqnarray}$$
Since
![]() $\unicode[STIX]{x1D735}\boldsymbol{u}$
is known, equation (3.10) becomes a system of nonlinear equations with
$\unicode[STIX]{x1D735}\boldsymbol{u}$
is known, equation (3.10) becomes a system of nonlinear equations with
![]() $r_{1},r_{2}$
and
$r_{1},r_{2}$
and
![]() $r_{3}$
as unknowns. This set of equations are solved using the Newton–Raphson method, with local vorticity direction as an initial guess.
$r_{3}$
as unknowns. This set of equations are solved using the Newton–Raphson method, with local vorticity direction as an initial guess.
The conditions imposed to define the local rotation axis only imply that there is no rotation around the other axes in the orthogonal reference frame, but they do not mean that the fluid element is rotating about the
![]() $z$
-axis. The rotation of the fluid also needs to be quantified. The fluid element is deemed to be rotational depending on the values of
$z$
-axis. The rotation of the fluid also needs to be quantified. The fluid element is deemed to be rotational depending on the values of
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
, which are defined as follows,
$\unicode[STIX]{x1D6FD}$
, which are defined as follows,
The fluid element has a rotational deformation only when
![]() $\unicode[STIX]{x1D6FD}^{2}>\unicode[STIX]{x1D6FC}^{2}$
and then the strength of rotation is defined as
$\unicode[STIX]{x1D6FD}^{2}>\unicode[STIX]{x1D6FC}^{2}$
and then the strength of rotation is defined as
 $$\begin{eqnarray}\displaystyle R_{z}=\left\{\begin{array}{@{}ll@{}}2(\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FC}), & \unicode[STIX]{x1D6FD}^{2}-\unicode[STIX]{x1D6FC}^{2}>0,\unicode[STIX]{x1D6FD}>0,\\ 2(\unicode[STIX]{x1D6FD}+\unicode[STIX]{x1D6FC}), & \unicode[STIX]{x1D6FD}^{2}-\unicode[STIX]{x1D6FC}^{2}>0,\unicode[STIX]{x1D6FD}<0,\\ 0, & \unicode[STIX]{x1D6FD}^{2}-\unicode[STIX]{x1D6FC}^{2}\leqslant 0.\end{array}\right. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R_{z}=\left\{\begin{array}{@{}ll@{}}2(\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FC}), & \unicode[STIX]{x1D6FD}^{2}-\unicode[STIX]{x1D6FC}^{2}>0,\unicode[STIX]{x1D6FD}>0,\\ 2(\unicode[STIX]{x1D6FD}+\unicode[STIX]{x1D6FC}), & \unicode[STIX]{x1D6FD}^{2}-\unicode[STIX]{x1D6FC}^{2}>0,\unicode[STIX]{x1D6FD}<0,\\ 0, & \unicode[STIX]{x1D6FD}^{2}-\unicode[STIX]{x1D6FC}^{2}\leqslant 0.\end{array}\right. & & \displaystyle\end{eqnarray}$$
With the local rotation axis and strength of rotation known, the vortex vector at any point in the flow field is given by
The vortex vector represents the magnitude and direction of the local fluid rotation and a connected region where
![]() $\boldsymbol{R}\neq 0$
is a vortex. Rigorous mathematical proofs for the definitions can be found in Liu et al. (Reference Liu, Gao, Tian and Dong2018).
$\boldsymbol{R}\neq 0$
is a vortex. Rigorous mathematical proofs for the definitions can be found in Liu et al. (Reference Liu, Gao, Tian and Dong2018).
We employ this method to find the vortex vectors and identify vortices in the turbulent mixing layer at different
![]() $M_{c}$
. According to TGDL18, iso-surfaces of the vortex vector magnitude can be used to visualize the vortices in the flow. The vortex vector is normalized by
$M_{c}$
. According to TGDL18, iso-surfaces of the vortex vector magnitude can be used to visualize the vortices in the flow. The vortex vector is normalized by
![]() $\unicode[STIX]{x0394}U/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}_{0}}$
in this study. For the conditional statistical analysis in the previous section, the
$\unicode[STIX]{x0394}U/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}_{0}}$
in this study. For the conditional statistical analysis in the previous section, the
![]() $Q$
-criterion was used to identify vortex-dominated regions. In figure 14, we compare the visualization of vortices in the flow field using the
$Q$
-criterion was used to identify vortex-dominated regions. In figure 14, we compare the visualization of vortices in the flow field using the
![]() $Q$
-criterion and vortex vector. Figure 14(a) shows contours of
$Q$
-criterion and vortex vector. Figure 14(a) shows contours of
![]() $\hat{Q}=0.07$
and figure 14(b) shows the iso-surfaces of
$\hat{Q}=0.07$
and figure 14(b) shows the iso-surfaces of
![]() $|\boldsymbol{R}|=0.05$
for
$|\boldsymbol{R}|=0.05$
for
![]() $M_{c}=0.75$
at time
$M_{c}=0.75$
at time
![]() $\unicode[STIX]{x1D70F}=200$
. The iso-surfaces in the latter are qualitatively similar to the contours of
$\unicode[STIX]{x1D70F}=200$
. The iso-surfaces in the latter are qualitatively similar to the contours of
![]() $\hat{Q}$
, albeit there are differences in small-scale structure. The large-scale structures in either visualization match very well. The figures may exactly match each other if the contour values are chosen appropriately. Since the relation between the strength of rotation and the
$\hat{Q}$
, albeit there are differences in small-scale structure. The large-scale structures in either visualization match very well. The figures may exactly match each other if the contour values are chosen appropriately. Since the relation between the strength of rotation and the
![]() $Q$
value is unknown at this point of time, it is not possible to predict the value of
$Q$
value is unknown at this point of time, it is not possible to predict the value of
![]() $\hat{Q}$
which exactly matches the iso-surfaces for a given value of rotation strength. Nevertheless, it is safe to assume that the vortex-dominated regions identified by the
$\hat{Q}$
which exactly matches the iso-surfaces for a given value of rotation strength. Nevertheless, it is safe to assume that the vortex-dominated regions identified by the
![]() $Q$
-criterion are regions of finite rotation strength.
$Q$
-criterion are regions of finite rotation strength.

Figure 14. Visualization of vortical structures in a turbulent mixing layer using the
![]() $Q$
-criterion and vortex vector. The figures are instantaneous snapshots for
$Q$
-criterion and vortex vector. The figures are instantaneous snapshots for
![]() $M_{c}=0.75$
at
$M_{c}=0.75$
at
![]() $\unicode[STIX]{x1D70F}=200$
. (a) Contours of
$\unicode[STIX]{x1D70F}=200$
. (a) Contours of
![]() $\hat{Q}=0.07$
, where
$\hat{Q}=0.07$
, where
![]() $\hat{Q}$
is the value of
$\hat{Q}$
is the value of
![]() $Q$
normalized by
$Q$
normalized by
![]() $(\unicode[STIX]{x0394}U/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}_{0}})^{2}$
. (b) Iso-surfaces of normalized
$(\unicode[STIX]{x0394}U/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}_{0}})^{2}$
. (b) Iso-surfaces of normalized
![]() $|\boldsymbol{R}|=0.05$
.
$|\boldsymbol{R}|=0.05$
.
Vortex vector also gives the direction of rotation, which the
![]() $Q$
-criterion does not. The vector is directed along the local rotational axis defined earlier. Figure 15(a) shows the vortex vectors on a hairpin vortex core, identified using rotation strength, in the flow field. The hairpin vortex is one of several similar structures in figure 14(b) and is isolated by magnifying the same figure. The vortex vectors show the direction of rotation at each point, and their length is proportional to the magnitude of the vortex vector. These vortex vectors align with the identified vortex core structure and indicate the direction of local rotation axis at each point. The fluid element rotates about the vortex vector in a plane perpendicular to it. In fluid mechanics, the lines formed by the vorticity vector is referred to as vortex lines. However, TGDL18 define vortex lines as lines whose tangent at any point is along the vortex vector, not the vorticity vector, at that point. A few vortex lines in the neighbourhood of the same hairpin vortex structure are shown in figure 15(b). These vortex lines also capture the shape of the hairpin structure as good as the iso-surface of rotation strength. The lines are coloured by the local rotation strength, which helps in finding out where the rotation is strong or weak. With the
$Q$
-criterion does not. The vector is directed along the local rotational axis defined earlier. Figure 15(a) shows the vortex vectors on a hairpin vortex core, identified using rotation strength, in the flow field. The hairpin vortex is one of several similar structures in figure 14(b) and is isolated by magnifying the same figure. The vortex vectors show the direction of rotation at each point, and their length is proportional to the magnitude of the vortex vector. These vortex vectors align with the identified vortex core structure and indicate the direction of local rotation axis at each point. The fluid element rotates about the vortex vector in a plane perpendicular to it. In fluid mechanics, the lines formed by the vorticity vector is referred to as vortex lines. However, TGDL18 define vortex lines as lines whose tangent at any point is along the vortex vector, not the vorticity vector, at that point. A few vortex lines in the neighbourhood of the same hairpin vortex structure are shown in figure 15(b). These vortex lines also capture the shape of the hairpin structure as good as the iso-surface of rotation strength. The lines are coloured by the local rotation strength, which helps in finding out where the rotation is strong or weak. With the
![]() $Q$
-criterion or other vortex identification techniques, it is not possible to quantify the strength of local rotation. For example,
$Q$
-criterion or other vortex identification techniques, it is not possible to quantify the strength of local rotation. For example,
![]() $Q$
, defined by equation (3.9), is not a measure of rotation itself. It only indicates whether vorticity or strain rate is dominant. Vortex vector, on the other hand, describes both the strength and direction of local fluid rotation.
$Q$
, defined by equation (3.9), is not a measure of rotation itself. It only indicates whether vorticity or strain rate is dominant. Vortex vector, on the other hand, describes both the strength and direction of local fluid rotation.

Figure 15. Vortex vectors and vortex lines on a hairpin-like structure, identified using iso-surface of vortex strength
![]() $(|\boldsymbol{R}|=0.05)$
, in a turbulent mixing layer for
$(|\boldsymbol{R}|=0.05)$
, in a turbulent mixing layer for
![]() $M_{c}=0.75$
at
$M_{c}=0.75$
at
![]() $\unicode[STIX]{x1D70F}=200$
. (a) Vortex vectors on the vortical structure. (b) Vortex lines passing through the vortical structure coloured by the local strength of rotation.
$\unicode[STIX]{x1D70F}=200$
. (a) Vortex vectors on the vortical structure. (b) Vortex lines passing through the vortical structure coloured by the local strength of rotation.
In § 3.3, we discussed how the turbulent statistics are different in regions with vortical structures compared to those in other regions. It was found that turbulent kinetic energy production is lower in regions of positive
![]() $Q$
, and the reduction was attributed to the helical streamline patterns in the vortex-dominated regions (refer to figure 11). Changes in turbulent shear stress
$Q$
, and the reduction was attributed to the helical streamline patterns in the vortex-dominated regions (refer to figure 11). Changes in turbulent shear stress
![]() $(R_{12})$
, which are responsible for energy production, are mirrored by those in the inclination of these vortex lines with respect to the streamwise direction as explained below. Let us consider a helical streamline pattern with the axis of helix along the streamwise direction as in figure 16(a). Along the streamline, the transverse velocity changes from positive to zero to negative and vice versa. Assuming that the streamwise velocity fluctuations do not change significantly in the neighbourhood of this streamline pattern, the product of the two fluctuating velocity components also shows similar behaviour. Hence the average of this product, which is the correlation
$(R_{12})$
, which are responsible for energy production, are mirrored by those in the inclination of these vortex lines with respect to the streamwise direction as explained below. Let us consider a helical streamline pattern with the axis of helix along the streamwise direction as in figure 16(a). Along the streamline, the transverse velocity changes from positive to zero to negative and vice versa. Assuming that the streamwise velocity fluctuations do not change significantly in the neighbourhood of this streamline pattern, the product of the two fluctuating velocity components also shows similar behaviour. Hence the average of this product, which is the correlation
![]() $\overline{u_{1}^{\prime \prime }u_{2}^{\prime \prime }}$
, is not expected to have a very large magnitude. However, this behaviour changes when the axis of the helix becomes inclined to the streamwise direction, as shown in 16(b). When
$\overline{u_{1}^{\prime \prime }u_{2}^{\prime \prime }}$
, is not expected to have a very large magnitude. However, this behaviour changes when the axis of the helix becomes inclined to the streamwise direction, as shown in 16(b). When
![]() $\unicode[STIX]{x1D703}$
, the angle between the axis of the helix and streamwise direction, takes large positive or negative values, the transverse velocity along the streamline does not alternate between positive and negative values. Instead, it remains biased towards either positive or negative
$\unicode[STIX]{x1D703}$
, the angle between the axis of the helix and streamwise direction, takes large positive or negative values, the transverse velocity along the streamline does not alternate between positive and negative values. Instead, it remains biased towards either positive or negative
![]() $u_{2}^{\prime \prime }$
. For example, the helical streamline in figure 16(b) has a positive transverse velocity at almost every point of the streamline. In such a scenario, the magnitude of the correlation
$u_{2}^{\prime \prime }$
. For example, the helical streamline in figure 16(b) has a positive transverse velocity at almost every point of the streamline. In such a scenario, the magnitude of the correlation
![]() $\overline{u_{1}^{\prime \prime }u_{2}^{\prime \prime }}$
can be significantly larger than when the helix axis is along the streamwise direction. The relationship between velocity correlation and streamwise inclination is described in appendix B. Therefore, the reduced turbulent production at higher
$\overline{u_{1}^{\prime \prime }u_{2}^{\prime \prime }}$
can be significantly larger than when the helix axis is along the streamwise direction. The relationship between velocity correlation and streamwise inclination is described in appendix B. Therefore, the reduced turbulent production at higher
![]() $M_{c}$
in vortex-dominated regions can be explained by quantifying the inclination of helical streamlines with the streamwise direction.
$M_{c}$
in vortex-dominated regions can be explained by quantifying the inclination of helical streamlines with the streamwise direction.

Figure 16. (a) Schematic diagram of a helical streamline with axis of helix along streamwise direction. Correlation
![]() $\overline{u_{1}^{\prime \prime }u_{2}^{\prime \prime }}$
is very small in this case. (b) Streamline with axis at an angle
$\overline{u_{1}^{\prime \prime }u_{2}^{\prime \prime }}$
is very small in this case. (b) Streamline with axis at an angle
![]() $\unicode[STIX]{x1D703}$
to the streamwise direction. Since
$\unicode[STIX]{x1D703}$
to the streamwise direction. Since
![]() $u_{2}^{\prime \prime }$
at most points along the streamline is positive,
$u_{2}^{\prime \prime }$
at most points along the streamline is positive,
![]() $\overline{u_{1}^{\prime \prime }u_{2}^{\prime \prime }}$
is significantly large. For details refer to appendix B.
$\overline{u_{1}^{\prime \prime }u_{2}^{\prime \prime }}$
is significantly large. For details refer to appendix B.

Figure 17. Vortical structures in the turbulent mixing-layer flow field identified using the
![]() $Q$
-criterion and the streamline pattern around the vortical structures for different cases. The streamlines are generated by seeding random points on the surface of the tube-like structures. The arrows are vortex vectors which are along the axis of the helical streamlines.
$Q$
-criterion and the streamline pattern around the vortical structures for different cases. The streamlines are generated by seeding random points on the surface of the tube-like structures. The arrows are vortex vectors which are along the axis of the helical streamlines.
The vortex vector can, by evidence, not only identify but also describe the orientation of the vortical structures in the flow field. Vortex vector is oriented along the local rotation axis defined earlier, which also coincides with the axis of any helical streamlines present in the region. Vortex-dominated regions, identified using the
![]() $Q$
-criterion, in the flow field for three different Mach numbers are shown in figure 17. The streamlines around vortex-dominated regions have a helical pattern with axis along the filament-like structures. The streamlines are generated by seeding at points very close to the iso-surfaces. At higher
$Q$
-criterion, in the flow field for three different Mach numbers are shown in figure 17. The streamlines around vortex-dominated regions have a helical pattern with axis along the filament-like structures. The streamlines are generated by seeding at points very close to the iso-surfaces. At higher
![]() $M_{c}$
, the streamlines spiral more than that at lower Mach numbers. Vortex vectors are also shown in the figure and are parallel to the axis of the helical streamline shown. Thus the orientation of helical streamlines in the flow field can be quantified using vortex vectors.
$M_{c}$
, the streamlines spiral more than that at lower Mach numbers. Vortex vectors are also shown in the figure and are parallel to the axis of the helical streamline shown. Thus the orientation of helical streamlines in the flow field can be quantified using vortex vectors.
3.5 Structure of vortex field
In the turbulent mixing layer, there are several regions where helical streamlines are present, especially in vortex-dominated regions. The orientation of such streamlines can be revealed by a statistical analysis of the vortex vector. Similar analyses of vorticity fields have been performed for turbulent channel flows by Moin & Kim (Reference Moin and Kim1985) and for incompressible homogeneous shear turbulence by Rogers & Moin (Reference Rogers and Moin1987). The orientation of vortex vectors with respect to the streamwise direction is of particular interest due to the reasons discussed earlier. The angle between the vortex vector and streamwise direction can be calculated from the scalar product of the vortex vector and the unit vector along the streamwise direction. Similarly, the orientations with respect to the transverse and spanwise directions are also given by scalar products. Thus the orientation of the vortex vector is defined by
where
![]() $\unicode[STIX]{x1D703},\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D703},\unicode[STIX]{x1D719}$
and
![]() $\unicode[STIX]{x1D713}$
are respectively the angles made by the vortex vector with the positive streamwise, transverse and spanwise directions. A statistical analysis based on the PDF or joint probability density functions (JPDF) of these angles in the turbulent mixing layer provides information on the orientation of the vortex vectors. The JPDFs for different
$\unicode[STIX]{x1D713}$
are respectively the angles made by the vortex vector with the positive streamwise, transverse and spanwise directions. A statistical analysis based on the PDF or joint probability density functions (JPDF) of these angles in the turbulent mixing layer provides information on the orientation of the vortex vectors. The JPDFs for different
![]() $M_{c}$
enable us to study how compressibility changes the vortical structures in mixing layers. We analyse the joint probability density function of the cosine of the angles, pairing them with each other, to understand how the vortex vectors are oriented when they are projected onto spanwise, streamwise and transverse planes. Only the points which are in the core of the turbulent mixing layer, that is
$M_{c}$
enable us to study how compressibility changes the vortical structures in mixing layers. We analyse the joint probability density function of the cosine of the angles, pairing them with each other, to understand how the vortex vectors are oriented when they are projected onto spanwise, streamwise and transverse planes. Only the points which are in the core of the turbulent mixing layer, that is
![]() $-2\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}\leqslant x_{2}\leqslant 2\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}$
, are used for the analysis. Points which are locally irrotational are omitted because the vortex vector has zero magnitude at those points. For the analysis, the cosines of the angles, instead of the angles themselves, are used.
$-2\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}\leqslant x_{2}\leqslant 2\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}$
, are used for the analysis. Points which are locally irrotational are omitted because the vortex vector has zero magnitude at those points. For the analysis, the cosines of the angles, instead of the angles themselves, are used.
For mixing layers, the joint probability density function for
![]() $\cos \unicode[STIX]{x1D703}$
and
$\cos \unicode[STIX]{x1D703}$
and
![]() $\cos \unicode[STIX]{x1D719}$
is more important than the other two in understanding the relation between vortex vector orientation and turbulence production. The JPDF, denoted henceforth by
$\cos \unicode[STIX]{x1D719}$
is more important than the other two in understanding the relation between vortex vector orientation and turbulence production. The JPDF, denoted henceforth by
![]() $P(\unicode[STIX]{x1D703},\unicode[STIX]{x1D719})$
, reflects the orientation of vortex vectors projected onto a spanwise plane. A JPDF analysis of vorticity components in turbulent boundary layers was performed by Ong & Wallace (Reference Ong and Wallace1998), where they observed significant changes in the JPDFs of vorticity components at different transverse locations. Moin & Kim (Reference Moin and Kim1985) also observed that the structure of the vorticity field depends on the distance from the wall in turbulent channel flows. Therefore, a similar study is undertaken here to see if there is any dependence of vortex vector orientations on the transverse location by examining the statistics at different
$P(\unicode[STIX]{x1D703},\unicode[STIX]{x1D719})$
, reflects the orientation of vortex vectors projected onto a spanwise plane. A JPDF analysis of vorticity components in turbulent boundary layers was performed by Ong & Wallace (Reference Ong and Wallace1998), where they observed significant changes in the JPDFs of vorticity components at different transverse locations. Moin & Kim (Reference Moin and Kim1985) also observed that the structure of the vorticity field depends on the distance from the wall in turbulent channel flows. Therefore, a similar study is undertaken here to see if there is any dependence of vortex vector orientations on the transverse location by examining the statistics at different
![]() $x_{2}$
. Figure 18 shows
$x_{2}$
. Figure 18 shows
![]() $P(\unicode[STIX]{x1D703},\unicode[STIX]{x1D719})$
at three transverse locations, viz
$P(\unicode[STIX]{x1D703},\unicode[STIX]{x1D719})$
at three transverse locations, viz
![]() $x_{2}=0,\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}},2\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}$
, for
$x_{2}=0,\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}},2\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}$
, for
![]() $M_{c}=0.20$
. These plots correspond to the non-dimensional time
$M_{c}=0.20$
. These plots correspond to the non-dimensional time
![]() $\unicode[STIX]{x1D70F}=200$
. The figures show contours of
$\unicode[STIX]{x1D70F}=200$
. The figures show contours of
![]() $P(\unicode[STIX]{x1D703},\unicode[STIX]{x1D719})$
and the contour levels, indicated in 18(c), are the same for all the three figures. The large values of
$P(\unicode[STIX]{x1D703},\unicode[STIX]{x1D719})$
and the contour levels, indicated in 18(c), are the same for all the three figures. The large values of
![]() $P(\unicode[STIX]{x1D703},\unicode[STIX]{x1D719})$
occur in quadrants II and IV of the
$P(\unicode[STIX]{x1D703},\unicode[STIX]{x1D719})$
occur in quadrants II and IV of the
![]() $\cos \unicode[STIX]{x1D703}{-}\cos \unicode[STIX]{x1D719}$
plane with peaks around
$\cos \unicode[STIX]{x1D703}{-}\cos \unicode[STIX]{x1D719}$
plane with peaks around
![]() $\cos \unicode[STIX]{x1D703}\approx \pm 0.8$
at all three transverse locations. This implies that the orientation of vortex vectors does not change significantly from one transverse location to another. Vortex vector orientations remain independent of the transverse location at other Mach numbers studied. For further analysis and comparison across different convective Mach numbers, all the points which are in the turbulent core
$\cos \unicode[STIX]{x1D703}\approx \pm 0.8$
at all three transverse locations. This implies that the orientation of vortex vectors does not change significantly from one transverse location to another. Vortex vector orientations remain independent of the transverse location at other Mach numbers studied. For further analysis and comparison across different convective Mach numbers, all the points which are in the turbulent core
![]() $(-2\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}\leqslant x_{2}\leqslant 2\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}})$
are considered together as a single set of data. The JPDF of these angles at different
$(-2\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}\leqslant x_{2}\leqslant 2\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}})$
are considered together as a single set of data. The JPDF of these angles at different
![]() $M_{c}$
is shown in figure 19. Only three sets of results, corresponding to
$M_{c}$
is shown in figure 19. Only three sets of results, corresponding to
![]() $M_{c}=0.50$
, 0.90 and 1.20, are presented here. The JPDFs for the nearly incompressible case are very similar to that for
$M_{c}=0.50$
, 0.90 and 1.20, are presented here. The JPDFs for the nearly incompressible case are very similar to that for
![]() $M_{c}=0.50$
. The other set of results not presented here corresponds to
$M_{c}=0.50$
. The other set of results not presented here corresponds to
![]() $M_{c}=0.75$
for which the distributions closely resemble those for
$M_{c}=0.75$
for which the distributions closely resemble those for
![]() $M_{c}=0.90$
. At all three Mach numbers, the high probability regions, indicated by red colour, falls in the second and fourth quadrants of the Cartesian plane defined by
$M_{c}=0.90$
. At all three Mach numbers, the high probability regions, indicated by red colour, falls in the second and fourth quadrants of the Cartesian plane defined by
![]() $\cos \unicode[STIX]{x1D703}$
and
$\cos \unicode[STIX]{x1D703}$
and
![]() $\cos \unicode[STIX]{x1D719}$
as axes.
$\cos \unicode[STIX]{x1D719}$
as axes.

Figure 18. The JPDFs of
![]() $\cos \unicode[STIX]{x1D703}$
and
$\cos \unicode[STIX]{x1D703}$
and
![]() $\cos \unicode[STIX]{x1D719}$
at different transverse locations for
$\cos \unicode[STIX]{x1D719}$
at different transverse locations for
![]() $M_{c}=0.20$
at
$M_{c}=0.20$
at
![]() $\unicode[STIX]{x1D70F}=200$
. (a)
$\unicode[STIX]{x1D70F}=200$
. (a)
![]() $x_{2}=0$
, (b)
$x_{2}=0$
, (b)
![]() $x_{2}=\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}$
and (c)
$x_{2}=\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}$
and (c)
![]() $x_{2}=2\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}$
.
$x_{2}=2\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}$
.

Figure 19. The JPDFs,
![]() $P(\unicode[STIX]{x1D703},\unicode[STIX]{x1D719})$
, for different Mach numbers at
$P(\unicode[STIX]{x1D703},\unicode[STIX]{x1D719})$
, for different Mach numbers at
![]() $\unicode[STIX]{x1D70F}=200$
for vortex vectors in the region
$\unicode[STIX]{x1D70F}=200$
for vortex vectors in the region
![]() $-2\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}\leqslant x_{2}\leqslant 2\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}$
. (a)
$-2\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}\leqslant x_{2}\leqslant 2\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}$
. (a)
![]() $M_{c}=0.50$
, (b)
$M_{c}=0.50$
, (b)
![]() $M_{c}=0.90$
, (c)
$M_{c}=0.90$
, (c)
![]() $M_{c}=1.20$
.
$M_{c}=1.20$
.
The vector
![]() $\cos \unicode[STIX]{x1D703}\hat{e}_{1}+\cos \unicode[STIX]{x1D719}\hat{e}_{2}$
is the projection of the unit vector along
$\cos \unicode[STIX]{x1D703}\hat{e}_{1}+\cos \unicode[STIX]{x1D719}\hat{e}_{2}$
is the projection of the unit vector along
![]() $\boldsymbol{R}$
onto the spanwise plane. The angle between the projection and coordinate axes
$\boldsymbol{R}$
onto the spanwise plane. The angle between the projection and coordinate axes
![]() $x_{1}$
and
$x_{1}$
and
![]() $x_{2}$
are, respectively,
$x_{2}$
are, respectively,
These angles are not independent of each other and are related, as schematically shown in figure 20(a). The JPDFs of the direction cosines of the projected vector reveal the most probable orientations of the vortex vector on the spanwise plane. Non-zero values of JPDFs lie on the unit circle
![]() $\cos ^{2}\unicode[STIX]{x1D703}_{2D}+\cos ^{2}\unicode[STIX]{x1D719}_{2D}=1$
. The peaks occur at approximately the same orientations as they occur in figure 19 since the likely orientations of three-dimensional vectors lie close to the unit circle described by
$\cos ^{2}\unicode[STIX]{x1D703}_{2D}+\cos ^{2}\unicode[STIX]{x1D719}_{2D}=1$
. The peaks occur at approximately the same orientations as they occur in figure 19 since the likely orientations of three-dimensional vectors lie close to the unit circle described by
![]() $\cos ^{2}\unicode[STIX]{x1D703}+\cos ^{2}\unicode[STIX]{x1D719}=1$
. Hence the high probability regions fall in quadrants II and IV of the Cartesian grid defined by the cosines of the two-dimensional angles. However, since
$\cos ^{2}\unicode[STIX]{x1D703}+\cos ^{2}\unicode[STIX]{x1D719}=1$
. Hence the high probability regions fall in quadrants II and IV of the Cartesian grid defined by the cosines of the two-dimensional angles. However, since
![]() $\unicode[STIX]{x1D703}_{2D}$
and
$\unicode[STIX]{x1D703}_{2D}$
and
![]() $\unicode[STIX]{x1D719}_{2D}$
are not independent, these quadrants correspond to
$\unicode[STIX]{x1D719}_{2D}$
are not independent, these quadrants correspond to
![]() $\unicode[STIX]{x03C0}/2\leqslant \unicode[STIX]{x1D703}\leqslant \unicode[STIX]{x03C0}$
,
$\unicode[STIX]{x03C0}/2\leqslant \unicode[STIX]{x1D703}\leqslant \unicode[STIX]{x03C0}$
,
![]() $0\leqslant \unicode[STIX]{x1D719}\leqslant \unicode[STIX]{x03C0}/2$
and
$0\leqslant \unicode[STIX]{x1D719}\leqslant \unicode[STIX]{x03C0}/2$
and
![]() $3\unicode[STIX]{x03C0}/2\leqslant \unicode[STIX]{x1D703}\leqslant 2\unicode[STIX]{x03C0}$
,
$3\unicode[STIX]{x03C0}/2\leqslant \unicode[STIX]{x1D703}\leqslant 2\unicode[STIX]{x03C0}$
,
![]() $\unicode[STIX]{x03C0}\leqslant \unicode[STIX]{x1D719}\leqslant 3\unicode[STIX]{x03C0}/2$
. The orientation of the projected vectors may be uniquely defined by either
$\unicode[STIX]{x03C0}\leqslant \unicode[STIX]{x1D719}\leqslant 3\unicode[STIX]{x03C0}/2$
. The orientation of the projected vectors may be uniquely defined by either
![]() $\unicode[STIX]{x1D703}_{2D}$
or
$\unicode[STIX]{x1D703}_{2D}$
or
![]() $\unicode[STIX]{x1D719}_{2D}$
. The high probability regions fall in the shaded quadrants of figure 20(a), and the projection of vortex vectors on the spanwise plane is parallel to the position vectors of points in these quadrants of the
$\unicode[STIX]{x1D719}_{2D}$
. The high probability regions fall in the shaded quadrants of figure 20(a), and the projection of vortex vectors on the spanwise plane is parallel to the position vectors of points in these quadrants of the
![]() $x_{1}{-}x_{2}$
Cartesian plane.
$x_{1}{-}x_{2}$
Cartesian plane.

Figure 20. (a) Schematic diagram showing relation between the cosines for vectors projected onto spanwise plane. Shaded regions represent the more probable orientations of vortex vectors in terms of their direction cosines. (b) A schematic of projections of vectors which are more likely to occur in the mixing layer. Solid and dashed arrows correspond to the shaded quadrants IV and II respectively in the figure on the left.
The mixing layer is set up in such a way that the free-stream velocity is negative for positive
![]() $x_{2}$
and positive for negative
$x_{2}$
and positive for negative
![]() $x_{2}$
. Schematic diagrams of a few highly probable orientations of the vortex vector projections in the flow field are shown in figure 20(b). The solid and dashed arrows correspond to position vectors of points in quadrants II and IV, respectively, as discussed earlier. In the upper stream
$x_{2}$
. Schematic diagrams of a few highly probable orientations of the vortex vector projections in the flow field are shown in figure 20(b). The solid and dashed arrows correspond to position vectors of points in quadrants II and IV, respectively, as discussed earlier. In the upper stream
![]() $(x_{2}>0)$
, the solid arrows direct towards the centreline while dashed arrows point towards the free stream and vice versa in the lower stream. Thus the high probability orientations are, (i) either inclined away from the direction of averaged streamwise velocity and towards the edge of the shear layer (ii) or opposing the free-stream velocity but slightly inclined in such a way that the vectors point towards the centre of the shear layer. Spanwise projection of most probable orientation of the vortex vector can be found using
$(x_{2}>0)$
, the solid arrows direct towards the centreline while dashed arrows point towards the free stream and vice versa in the lower stream. Thus the high probability orientations are, (i) either inclined away from the direction of averaged streamwise velocity and towards the edge of the shear layer (ii) or opposing the free-stream velocity but slightly inclined in such a way that the vectors point towards the centre of the shear layer. Spanwise projection of most probable orientation of the vortex vector can be found using
![]() $P(\unicode[STIX]{x1D703}_{2D},\unicode[STIX]{x1D719}_{2D})$
. A similar analysis was used by Ong & Wallace (Reference Ong and Wallace1998) to find projections of vorticity filaments contributing most to the vorticity covariance in turbulent boundary layers. There are two most probable orientations for the projections which are given by the maximum of JPDF in quadrants II and IV. Using
$P(\unicode[STIX]{x1D703}_{2D},\unicode[STIX]{x1D719}_{2D})$
. A similar analysis was used by Ong & Wallace (Reference Ong and Wallace1998) to find projections of vorticity filaments contributing most to the vorticity covariance in turbulent boundary layers. There are two most probable orientations for the projections which are given by the maximum of JPDF in quadrants II and IV. Using
![]() $\unicode[STIX]{x1D703}_{2D}$
corresponding to the peak in
$\unicode[STIX]{x1D703}_{2D}$
corresponding to the peak in
![]() $P(\unicode[STIX]{x1D703}_{2D},\unicode[STIX]{x1D719}_{2D})$
at different transverse locations, line segments can be created locally for different
$P(\unicode[STIX]{x1D703}_{2D},\unicode[STIX]{x1D719}_{2D})$
at different transverse locations, line segments can be created locally for different
![]() $x_{2}$
. These line segments, with slope
$x_{2}$
. These line segments, with slope
![]() $\tan \unicode[STIX]{x1D703}_{2D}$
on the
$\tan \unicode[STIX]{x1D703}_{2D}$
on the
![]() $x_{3}$
plane, can be joined together to obtain the projection of the most probable vortex vector orientation on the spanwise plane. This line segment can also be representative of the projection of the most probable vortex structure in the flow field. The reconstructed vortex vector orientations for different
$x_{3}$
plane, can be joined together to obtain the projection of the most probable vortex vector orientation on the spanwise plane. This line segment can also be representative of the projection of the most probable vortex structure in the flow field. The reconstructed vortex vector orientations for different
![]() $M_{c}$
at
$M_{c}$
at
![]() $\unicode[STIX]{x1D70F}=100$
and
$\unicode[STIX]{x1D70F}=100$
and
![]() $300$
are shown in figure 21. The most probable orientation of the vortex vector is nearly the same for the lower Mach numbers at
$300$
are shown in figure 21. The most probable orientation of the vortex vector is nearly the same for the lower Mach numbers at
![]() $\unicode[STIX]{x1D70F}=100$
. As
$\unicode[STIX]{x1D70F}=100$
. As
![]() $M_{c}$
increases, the most likely orientation becomes closer to that of the streamwise direction. For
$M_{c}$
increases, the most likely orientation becomes closer to that of the streamwise direction. For
![]() $M_{c}=1.20$
, vortex vectors are closer to the
$M_{c}=1.20$
, vortex vectors are closer to the
![]() $x_{1}$
axis than those at other Mach numbers. This applies to not only the most probable occurrence but also most of the orientations with large probabilities as discussed below.
$x_{1}$
axis than those at other Mach numbers. This applies to not only the most probable occurrence but also most of the orientations with large probabilities as discussed below.

Figure 21. Projections of the most probable orientation of vortex vectors for different
![]() $M_{c}$
at (a)
$M_{c}$
at (a)
![]() $\unicode[STIX]{x1D70F}=100$
and (b)
$\unicode[STIX]{x1D70F}=100$
and (b)
![]() $\unicode[STIX]{x1D70F}=300$
. The solid lines are constructed from the peaks of JPDF in quadrant II and the dashed lines from the peaks in quadrant IV.
$\unicode[STIX]{x1D70F}=300$
. The solid lines are constructed from the peaks of JPDF in quadrant II and the dashed lines from the peaks in quadrant IV.
With increasing Mach number the high probability regions (indicated in red) move closer towards
![]() $\cos \unicode[STIX]{x1D703}=\pm 1$
, as seen in figure 19. The change is subtle as
$\cos \unicode[STIX]{x1D703}=\pm 1$
, as seen in figure 19. The change is subtle as
![]() $M_{c}$
increases from
$M_{c}$
increases from
![]() $0.50$
to
$0.50$
to
![]() $0.90$
but more prominent at the highest Mach number. This implies that the vortex vectors get more aligned along the streamwise direction as compressibility effects increase. The number of helical streamlines in the flow field, which are oriented in directions close to the streamwise direction, increases with increase in
$0.90$
but more prominent at the highest Mach number. This implies that the vortex vectors get more aligned along the streamwise direction as compressibility effects increase. The number of helical streamlines in the flow field, which are oriented in directions close to the streamwise direction, increases with increase in
![]() $M_{c}$
. The JPDFs at a later time
$M_{c}$
. The JPDFs at a later time
![]() $(\unicode[STIX]{x1D70F}=300)$
are shown in figure 22. The high probability regions occur at a smaller
$(\unicode[STIX]{x1D70F}=300)$
are shown in figure 22. The high probability regions occur at a smaller
![]() $|\text{cos}\,\unicode[STIX]{x1D703}|$
in comparison with figure 19. This means that the vortex vectors tend to move away from the streamwise direction as time progresses. As seen in figure 21(b), by
$|\text{cos}\,\unicode[STIX]{x1D703}|$
in comparison with figure 19. This means that the vortex vectors tend to move away from the streamwise direction as time progresses. As seen in figure 21(b), by
![]() $\unicode[STIX]{x1D70F}=300$
, the most probable orientations of the vortex vectors are less sensitive to compressibility effects, except for the largest
$\unicode[STIX]{x1D70F}=300$
, the most probable orientations of the vortex vectors are less sensitive to compressibility effects, except for the largest
![]() $M_{c}$
. In comparison with their orientations at
$M_{c}$
. In comparison with their orientations at
![]() $\unicode[STIX]{x1D70F}=100$
, the vortex vectors tend to move away from directions closer to the streamwise direction. Nevertheless, more vortex vectors at a higher
$\unicode[STIX]{x1D70F}=100$
, the vortex vectors tend to move away from directions closer to the streamwise direction. Nevertheless, more vortex vectors at a higher
![]() $M_{c}$
continue to be closer to the streamwise direction than those at a lower
$M_{c}$
continue to be closer to the streamwise direction than those at a lower
![]() $M_{c}$
. This dependence of vortex vector orientation on the convective Mach number becomes clear when the probability density function of
$M_{c}$
. This dependence of vortex vector orientation on the convective Mach number becomes clear when the probability density function of
![]() $\cos \unicode[STIX]{x1D703}$
is analysed. In figure 23, the probability density function of the magnitude of the cosine of the angle between vortex vector and streamwise direction is plotted at two different times. The vectors which are closely aligned towards the streamwise direction have larger values of
$\cos \unicode[STIX]{x1D703}$
is analysed. In figure 23, the probability density function of the magnitude of the cosine of the angle between vortex vector and streamwise direction is plotted at two different times. The vectors which are closely aligned towards the streamwise direction have larger values of
![]() $|\text{cos}\,\unicode[STIX]{x1D703}|$
and those inclined away from the streamwise direction have smaller magnitudes of
$|\text{cos}\,\unicode[STIX]{x1D703}|$
and those inclined away from the streamwise direction have smaller magnitudes of
![]() $\cos \unicode[STIX]{x1D703}$
. In figure 23(a), which is at
$\cos \unicode[STIX]{x1D703}$
. In figure 23(a), which is at
![]() $\unicode[STIX]{x1D70F}=200$
, there are more vectors which are aligned in (or opposite to) the direction of the streamwise axis at all Mach numbers. The higher the Mach number, the larger the PDF value for direction cosines close to unity, which implies that the probability of vectors being oriented in directions closer to the streamwise direction increases with
$\unicode[STIX]{x1D70F}=200$
, there are more vectors which are aligned in (or opposite to) the direction of the streamwise axis at all Mach numbers. The higher the Mach number, the larger the PDF value for direction cosines close to unity, which implies that the probability of vectors being oriented in directions closer to the streamwise direction increases with
![]() $M_{c}$
. A reverse trend can be seen at lower magnitudes of the cosines which are more likely to occur at lower convective Mach numbers. The PDF at a later time
$M_{c}$
. A reverse trend can be seen at lower magnitudes of the cosines which are more likely to occur at lower convective Mach numbers. The PDF at a later time
![]() $(\unicode[STIX]{x1D70F}=300)$
in figure 23(b) shows that while the likelihood of finding vortex vectors not close to the streamwise directions increases, there still exist more vectors which are closely aligned to the streamwise direction. The dependence of PDF on the convective Mach number also remains similar to that at earlier times. It can be inferred that the vortex vectors change their orientation as the flow evolves with more vectors getting inclined away from directions closer to the streamwise direction. For the incompressible Mach numbers, there are more vortex vectors at larger
$(\unicode[STIX]{x1D70F}=300)$
in figure 23(b) shows that while the likelihood of finding vortex vectors not close to the streamwise directions increases, there still exist more vectors which are closely aligned to the streamwise direction. The dependence of PDF on the convective Mach number also remains similar to that at earlier times. It can be inferred that the vortex vectors change their orientation as the flow evolves with more vectors getting inclined away from directions closer to the streamwise direction. For the incompressible Mach numbers, there are more vortex vectors at larger
![]() $\unicode[STIX]{x1D703}$
at earlier time instants. From figures 21 and 23, it is clear that, as time progresses, the vortical structures in the compressible cases approach the incompressible state. The solenoidal nature of velocity fluctuations in compressible shear flows during later times is observed by Bertsch et al. (Reference Bertsch, Suman and Girimaji2012). We can conclude that similar behaviour is exhibited by the flow structures too.
$\unicode[STIX]{x1D703}$
at earlier time instants. From figures 21 and 23, it is clear that, as time progresses, the vortical structures in the compressible cases approach the incompressible state. The solenoidal nature of velocity fluctuations in compressible shear flows during later times is observed by Bertsch et al. (Reference Bertsch, Suman and Girimaji2012). We can conclude that similar behaviour is exhibited by the flow structures too.

Figure 22. The JPDFs,
![]() $P(\unicode[STIX]{x1D703},\unicode[STIX]{x1D719})$
, for different Mach numbers at
$P(\unicode[STIX]{x1D703},\unicode[STIX]{x1D719})$
, for different Mach numbers at
![]() $\unicode[STIX]{x1D70F}=300$
for vortex vectors in the region
$\unicode[STIX]{x1D70F}=300$
for vortex vectors in the region
![]() $-2\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}\leqslant x_{2}\leqslant 2\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}$
. (a)
$-2\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}\leqslant x_{2}\leqslant 2\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}$
. (a)
![]() $M_{c}=0.50$
, (b)
$M_{c}=0.50$
, (b)
![]() $M_{c}=0.90$
, (c)
$M_{c}=0.90$
, (c)
![]() $M_{c}=1.20$
.
$M_{c}=1.20$
.

Figure 23. Probability density functions of absolute values of
![]() $\cos \unicode[STIX]{x1D703}$
at different
$\cos \unicode[STIX]{x1D703}$
at different
![]() $M_{c}$
. (a)
$M_{c}$
. (a)
![]() $\unicode[STIX]{x1D70F}=200$
, (b)
$\unicode[STIX]{x1D70F}=200$
, (b)
![]() $\unicode[STIX]{x1D70F}=300$
.
$\unicode[STIX]{x1D70F}=300$
.
For completeness, we also report the statistics of the other two direction cosines. Figure 24 shows the JPDF,
![]() $P(\unicode[STIX]{x1D713},\unicode[STIX]{x1D719})$
, for different Mach numbers at
$P(\unicode[STIX]{x1D713},\unicode[STIX]{x1D719})$
, for different Mach numbers at
![]() $\unicode[STIX]{x1D70F}=200$
. It can be observed that it is rare to find vortex vectors with negative values of
$\unicode[STIX]{x1D70F}=200$
. It can be observed that it is rare to find vortex vectors with negative values of
![]() $\cos \unicode[STIX]{x1D713}$
, which indicates that almost all of them have their spanwise components of vortex vector along the positive
$\cos \unicode[STIX]{x1D713}$
, which indicates that almost all of them have their spanwise components of vortex vector along the positive
![]() $x_{3}$
direction. In this work, the mixing-layer evolution is in such a way that the mean vorticity is along the positive spanwise direction. Thus the vortex vectors also tend to align in the direction of mean vorticity. The JPDF patterns are similar for the lower
$x_{3}$
direction. In this work, the mixing-layer evolution is in such a way that the mean vorticity is along the positive spanwise direction. Thus the vortex vectors also tend to align in the direction of mean vorticity. The JPDF patterns are similar for the lower
![]() $M_{c}$
, but for the highest
$M_{c}$
, but for the highest
![]() $M_{c}$
, the pattern is significantly different. At
$M_{c}$
, the pattern is significantly different. At
![]() $M_{c}=1.20$
, the probability of finding vortex vectors being oriented with very small values of
$M_{c}=1.20$
, the probability of finding vortex vectors being oriented with very small values of
![]() $\cos \unicode[STIX]{x1D713}$
and
$\cos \unicode[STIX]{x1D713}$
and
![]() $\cos \unicode[STIX]{x1D719}$
is significant, as inferred from the green patch seen on the JPDF plot near the origin. In our earlier discussions, we have observed that at this Mach number, the probability of vortex vectors being aligned very close to the streamwise axis is very large. Therefore, those vectors are characterized by very small values of direction cosines for the other two directions, and this is reflected in the JPDF plot here. The JPDF of the remaining cosine pair,
$\cos \unicode[STIX]{x1D719}$
is significant, as inferred from the green patch seen on the JPDF plot near the origin. In our earlier discussions, we have observed that at this Mach number, the probability of vortex vectors being aligned very close to the streamwise axis is very large. Therefore, those vectors are characterized by very small values of direction cosines for the other two directions, and this is reflected in the JPDF plot here. The JPDF of the remaining cosine pair,
![]() $P(\unicode[STIX]{x1D713},\unicode[STIX]{x1D703})$
is shown in figure 25. These JPDF plots also indicate that negative values of
$P(\unicode[STIX]{x1D713},\unicode[STIX]{x1D703})$
is shown in figure 25. These JPDF plots also indicate that negative values of
![]() $\cos \unicode[STIX]{x1D713}$
are not so likely, and at higher Mach numbers the high probability orientations move towards
$\cos \unicode[STIX]{x1D713}$
are not so likely, and at higher Mach numbers the high probability orientations move towards
![]() $\cos \unicode[STIX]{x1D703}=\pm 1$
. The orientations with respect to spanwise and transverse directions are also shown using the PDF of respective direction cosines in figure 26. The PDF of
$\cos \unicode[STIX]{x1D703}=\pm 1$
. The orientations with respect to spanwise and transverse directions are also shown using the PDF of respective direction cosines in figure 26. The PDF of
![]() $|\text{cos}\,\unicode[STIX]{x1D719}|$
, shown in figure 26(a), implies that as Mach number increases, there are fewer vectors aligned in the transverse direction. The orientation of vectors with respect to the
$|\text{cos}\,\unicode[STIX]{x1D719}|$
, shown in figure 26(a), implies that as Mach number increases, there are fewer vectors aligned in the transverse direction. The orientation of vectors with respect to the
![]() $x_{3}$
direction has a uniform distribution, to a moderate extent, at smaller
$x_{3}$
direction has a uniform distribution, to a moderate extent, at smaller
![]() $M_{c}$
. At the highest
$M_{c}$
. At the highest
![]() $M_{c}$
, as more and more vortices align in the streamwise direction, they are more likely to be orthogonal to the spanwise direction as indicated by the high PDF value for
$M_{c}$
, as more and more vortices align in the streamwise direction, they are more likely to be orthogonal to the spanwise direction as indicated by the high PDF value for
![]() $|\text{cos}\,\unicode[STIX]{x1D713}|\approx 0$
in figure 26(b). In the present results, the strength of rotation of vortical structures is given by the magnitude of vortex vector. Evolution of volume-averaged vortex strength for different cases is given in figure 27. The vortex strength
$|\text{cos}\,\unicode[STIX]{x1D713}|\approx 0$
in figure 26(b). In the present results, the strength of rotation of vortical structures is given by the magnitude of vortex vector. Evolution of volume-averaged vortex strength for different cases is given in figure 27. The vortex strength
![]() $(R)$
is normalized by the initial value
$(R)$
is normalized by the initial value
![]() $(R_{0})$
. Vortex strength increases as the mixing layer develops. However, the strength of rotation of fluid elements is suppressed by compressibility. The vortical structures at high
$(R_{0})$
. Vortex strength increases as the mixing layer develops. However, the strength of rotation of fluid elements is suppressed by compressibility. The vortical structures at high
![]() $M_{c}$
mixing layers align in the streamwise direction but are weaker compared to those at low
$M_{c}$
mixing layers align in the streamwise direction but are weaker compared to those at low
![]() $M_{c}$
.
$M_{c}$
.

Figure 24. The JPDFs,
![]() $P(\unicode[STIX]{x1D713},\unicode[STIX]{x1D719})$
, for different Mach numbers at
$P(\unicode[STIX]{x1D713},\unicode[STIX]{x1D719})$
, for different Mach numbers at
![]() $\unicode[STIX]{x1D70F}=300$
for vortex vectors in the region
$\unicode[STIX]{x1D70F}=300$
for vortex vectors in the region
![]() $-2\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}\leqslant x_{2}\leqslant 2\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}$
. (a)
$-2\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}\leqslant x_{2}\leqslant 2\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}$
. (a)
![]() $M_{c}=0.50$
, (b)
$M_{c}=0.50$
, (b)
![]() $M_{c}=0.90$
, (c)
$M_{c}=0.90$
, (c)
![]() $M_{c}=1.20$
.
$M_{c}=1.20$
.

Figure 25. The JPDFs,
![]() $P(\unicode[STIX]{x1D713},\unicode[STIX]{x1D703})$
, for different Mach numbers at
$P(\unicode[STIX]{x1D713},\unicode[STIX]{x1D703})$
, for different Mach numbers at
![]() $\unicode[STIX]{x1D70F}=300$
for vortex vectors in the region
$\unicode[STIX]{x1D70F}=300$
for vortex vectors in the region
![]() $-2\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}\leqslant x_{2}\leqslant 2\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}$
. (a)
$-2\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}\leqslant x_{2}\leqslant 2\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}$
. (a)
![]() $M_{c}=0.50$
, (b)
$M_{c}=0.50$
, (b)
![]() $M_{c}=0.90$
, (c)
$M_{c}=0.90$
, (c)
![]() $M_{c}=1.20$
.
$M_{c}=1.20$
.

Figure 26. Probability density functions of absolute values of (a)
![]() $\cos \unicode[STIX]{x1D719}$
and (b)
$\cos \unicode[STIX]{x1D719}$
and (b)
![]() $\cos \unicode[STIX]{x1D713}$
at different
$\cos \unicode[STIX]{x1D713}$
at different
![]() $M_{c}$
. The statistics are obtained at
$M_{c}$
. The statistics are obtained at
![]() $\unicode[STIX]{x1D70F}=200$
.
$\unicode[STIX]{x1D70F}=200$
.

Figure 27. Evolution of volume-averaged vortex strength with time for different cases. Vortex strength, the magnitude of vortex vector, is normalized by the initial value.
In summary, vortex vectors tend to align more towards the streamwise direction as compressibility effects increase. This means that there are more helical streamline patterns in the flow field, which are aligned in such a way that the axes of helices are closer to the streamwise direction. The net turbulent transport of fluctuating momentum
![]() $(\overline{u_{1}^{\prime \prime }u_{2}^{\prime \prime }})$
in those regions are less, as discussed above. Thus, more vortical structures getting aligned in the streamwise direction effectively brings down the turbulent stress
$(\overline{u_{1}^{\prime \prime }u_{2}^{\prime \prime }})$
in those regions are less, as discussed above. Thus, more vortical structures getting aligned in the streamwise direction effectively brings down the turbulent stress
![]() $R_{12}$
and decreases the turbulent kinetic energy production. Similar changes in vortical structures with compressibility have been observed by Normand & Lesieur (Reference Normand and Lesieur1992) during the transition in compressible boundary layers. The transitional flow at low Mach numbers is dominated by hairpin vortices and spanwise billows, but at high Mach numbers, they observed that there are
$R_{12}$
and decreases the turbulent kinetic energy production. Similar changes in vortical structures with compressibility have been observed by Normand & Lesieur (Reference Normand and Lesieur1992) during the transition in compressible boundary layers. The transitional flow at low Mach numbers is dominated by hairpin vortices and spanwise billows, but at high Mach numbers, they observed that there are
![]() $\unicode[STIX]{x1D6EC}$
-vortices which break up into small-scale structures. Sandham & Reynolds (Reference Sandham and Reynolds1990) reported the streamwise elongation of vortices in compressible mixing layers, as compressibility effects increase. These vortices are less intense compared to those at low
$\unicode[STIX]{x1D6EC}$
-vortices which break up into small-scale structures. Sandham & Reynolds (Reference Sandham and Reynolds1990) reported the streamwise elongation of vortices in compressible mixing layers, as compressibility effects increase. These vortices are less intense compared to those at low
![]() $M_{c}$
. The presence of more streamwise aligned vortical structures of lesser strength in our present study conforms to these results.
$M_{c}$
. The presence of more streamwise aligned vortical structures of lesser strength in our present study conforms to these results.
4 Conclusion
Direct numerical simulations of compressible mixing layers are performed for different Mach numbers, including a nearly incompressible case. The evolution of mixing-layer thickness and degree of suppression of growth rates by compressibility are in agreement with existing numerical and experimental results. The primary objective of this work is to further enhance our understanding of the effects of compressibility on the transient evolution.
In the early evolution, the following are observed for turbulent statistics.
(i) Suppression of energy production and subsequently turbulent kinetic energy by compressibility during the transient development.
(ii) There exists a balance between
 $R_{12}$
production and pressure rate of strain correlation
$R_{12}$
production and pressure rate of strain correlation
 $(\unicode[STIX]{x1D6F1}_{12})$
, which results in reduced levels of the Reynolds shear stress.
$(\unicode[STIX]{x1D6F1}_{12})$
, which results in reduced levels of the Reynolds shear stress.(iii) Compressibility also reduces the redistribution, which again causes suppression of energy production.
The present study reaffirms that the effects of compressibility vary with time and are more prominent during the transient evolution.
The topology is classified into two regions – strain dominated or vortex dominated – using the
![]() $Q$
criterion. Influence of topology on the turbulent mechanism is examined using statistics conditioned on topology, which reveals the following.
$Q$
criterion. Influence of topology on the turbulent mechanism is examined using statistics conditioned on topology, which reveals the following.
(i) Redistribution of normal Reynolds stresses is higher in strain-dominated regions as compared to vortex-dominated topologies.
(ii) This leads to reduced levels of
 $R_{12}$
and turbulent kinetic energy in vortex-dominated regions.
$R_{12}$
and turbulent kinetic energy in vortex-dominated regions.(iii) Compressibility alters local flow topology, resulting in a larger proportion of flow field having a vortex-dominated topology at higher
 $M_{c}$
.
$M_{c}$
.
Since vortex-dominated regions are less energetic, a larger proportion of the same results in the suppression of turbulent kinetic energy as
![]() $M_{c}$
increases. The volume fraction of vortex-dominated regions in the flow field approaches the incompressible value as time progresses (observed for all
$M_{c}$
increases. The volume fraction of vortex-dominated regions in the flow field approaches the incompressible value as time progresses (observed for all
![]() $M_{c}$
).
$M_{c}$
).
Application of a recently developed vortex identification technique suggests a new interpretation of the correlations between turbulent energy production and streamline topology. We find that vortex-dominated regions feature helical streamline patterns which are associated with lower levels of turbulent production. Orientations of helical streamlines are quantified using the structure of vortex vector field, which gives the magnitude and direction of rotation of fluid elements in vortex-dominated regions. A statistical analysis of vortex vector orientation in the flow field shows that
(i) vortex vector orientations depend on compressibility;
(ii) at higher
 $M_{c}$
, the vortical structures are more aligned in the streamwise direction whereas at lower
$M_{c}$
, the vortical structures are more aligned in the streamwise direction whereas at lower
 $M_{c}$
these structures align at considerably larger angles with the streamwise direction;
$M_{c}$
these structures align at considerably larger angles with the streamwise direction;(iii) the orientations of vortical structures for all
 $M_{c}$
shift to larger angles, similar to incompressible flow, with the progress in time;
$M_{c}$
shift to larger angles, similar to incompressible flow, with the progress in time;(iv) the rate at which the orientation changes is decreasing with
 $M_{c}$
.
$M_{c}$
.
Helical streamline patterns, with axes closer to the streamwise direction, are associated with small values of
![]() $\overline{u_{1}^{\prime \prime }u_{2}^{\prime \prime }}$
and hence lower turbulent energy production. Therefore, the suppression of turbulent energy production is observed to be correlated with the presence of a large number of vortical structures aligned in the streamwise direction.
$\overline{u_{1}^{\prime \prime }u_{2}^{\prime \prime }}$
and hence lower turbulent energy production. Therefore, the suppression of turbulent energy production is observed to be correlated with the presence of a large number of vortical structures aligned in the streamwise direction.
Acknowledgements
The authors acknowledge the High Performance Computing Environment Facility at IIT Madras for providing computing time on the VIRGO Super Cluster. This research was supported in part by the International Centre for Theoretical Sciences (ICTS) during a visit for participating in the programme – Turbulence from Angstroms to light years (Code: ICTS/Prog-taly2018/01). The authors thank S. K. Lele for valuable discussions during the programme.
Appendix A. Numerical scheme and convergence
A.1 BGK gas-kinetic scheme
The numerical simulations are performed using a gas-kinetic scheme. The scheme uses a finite volume formulation to solve the Boltzmann equation with the Bhatnagar–Gross–Krook model for the collision integral (Xu et al. Reference Xu, Mao and Tang2005). The BGK-Boltzmann equation is
where
![]() $f$
is velocity distribution function,
$f$
is velocity distribution function,
![]() $g$
is equilibrium distribution function,
$g$
is equilibrium distribution function,
![]() $c_{i}$
are the particle velocities and
$c_{i}$
are the particle velocities and
![]() $\unicode[STIX]{x1D70F}$
is average particle collision time. Equation (A 1) describes the evolution of the distribution function, which is a function of space
$\unicode[STIX]{x1D70F}$
is average particle collision time. Equation (A 1) describes the evolution of the distribution function, which is a function of space
![]() $x_{i}$
, time
$x_{i}$
, time
![]() $t$
, particle velocity
$t$
, particle velocity
![]() $c_{i}$
and internal variable
$c_{i}$
and internal variable
![]() $\unicode[STIX]{x1D709}$
, in the absence of any external forces. The equilibrium distribution has the Maxwellian form and is a function of flow variables as follows:
$\unicode[STIX]{x1D709}$
, in the absence of any external forces. The equilibrium distribution has the Maxwellian form and is a function of flow variables as follows:
In the above expression,
![]() $\unicode[STIX]{x1D70C}$
is the density,
$\unicode[STIX]{x1D70C}$
is the density,
![]() $U_{i}$
are the macroscopic velocities and
$U_{i}$
are the macroscopic velocities and
![]() $\unicode[STIX]{x1D706}=m/2kT$
. The last term in the exponent has the form
$\unicode[STIX]{x1D706}=m/2kT$
. The last term in the exponent has the form
![]() $\unicode[STIX]{x1D709}^{2}=\unicode[STIX]{x1D709}_{1}^{2}+\unicode[STIX]{x1D709}_{2}^{2}+\cdots +\unicode[STIX]{x1D709}_{K}^{2}$
, where
$\unicode[STIX]{x1D709}^{2}=\unicode[STIX]{x1D709}_{1}^{2}+\unicode[STIX]{x1D709}_{2}^{2}+\cdots +\unicode[STIX]{x1D709}_{K}^{2}$
, where
![]() $K$
is the total number of internal degrees of freedom for the gas molecule given by
$K$
is the total number of internal degrees of freedom for the gas molecule given by
![]() $K=(5-3\unicode[STIX]{x1D6FE})/(\unicode[STIX]{x1D6FE}-1)$
. The flow variables,
$K=(5-3\unicode[STIX]{x1D6FE})/(\unicode[STIX]{x1D6FE}-1)$
. The flow variables,
![]() $W=(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70C}\boldsymbol{U},\unicode[STIX]{x1D70C}\unicode[STIX]{x1D716})^{\text{T}}$
, are related to
$W=(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70C}\boldsymbol{U},\unicode[STIX]{x1D70C}\unicode[STIX]{x1D716})^{\text{T}}$
, are related to
![]() $f$
by
$f$
by
 $$\begin{eqnarray}\displaystyle W=\left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D70C}\\ \unicode[STIX]{x1D70C}U_{1}\\ \unicode[STIX]{x1D70C}U_{2}\\ \unicode[STIX]{x1D70C}U_{3}\\ \unicode[STIX]{x1D70C}\unicode[STIX]{x1D716}\end{array}\right)=\int \unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FC}}\,f\,\text{d}\unicode[STIX]{x1D6EF}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle W=\left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D70C}\\ \unicode[STIX]{x1D70C}U_{1}\\ \unicode[STIX]{x1D70C}U_{2}\\ \unicode[STIX]{x1D70C}U_{3}\\ \unicode[STIX]{x1D70C}\unicode[STIX]{x1D716}\end{array}\right)=\int \unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FC}}\,f\,\text{d}\unicode[STIX]{x1D6EF}, & & \displaystyle\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FC}}=(1,c_{1},c_{2},c_{3},\frac{1}{2}(c_{1}^{2}+c_{2}^{2}+c_{3}^{2}+\unicode[STIX]{x1D709}^{2}))^{\text{T}}$
are the weights and the integration is over the entire phase space
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FC}}=(1,c_{1},c_{2},c_{3},\frac{1}{2}(c_{1}^{2}+c_{2}^{2}+c_{3}^{2}+\unicode[STIX]{x1D709}^{2}))^{\text{T}}$
are the weights and the integration is over the entire phase space
![]() $\text{d}\unicode[STIX]{x1D6EF}=\text{d}c_{1}\text{d}c_{2}\text{d}c_{3}\text{d}\unicode[STIX]{x1D709}_{1}\text{d}\unicode[STIX]{x1D709}_{2}\cdots \text{d}\unicode[STIX]{x1D709}_{n}$
. Mass, momentum and energy conservation equations for compressible flows are recovered from the BGK-Boltzmann equation when
$\text{d}\unicode[STIX]{x1D6EF}=\text{d}c_{1}\text{d}c_{2}\text{d}c_{3}\text{d}\unicode[STIX]{x1D709}_{1}\text{d}\unicode[STIX]{x1D709}_{2}\cdots \text{d}\unicode[STIX]{x1D709}_{n}$
. Mass, momentum and energy conservation equations for compressible flows are recovered from the BGK-Boltzmann equation when
![]() $\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D707}/P$
. The moments of (A 1) integrated over the phase space in a numerical cell and time step
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D707}/P$
. The moments of (A 1) integrated over the phase space in a numerical cell and time step
![]() $\unicode[STIX]{x0394}t$
give
$\unicode[STIX]{x0394}t$
give
 $$\begin{eqnarray}\displaystyle W_{mnp}^{n+1}-W_{mnp}^{n} & = & \displaystyle \frac{1}{\unicode[STIX]{x0394}x_{1}\unicode[STIX]{x0394}x_{2}\unicode[STIX]{x0394}x_{3}}\int _{t^{n}}^{t^{n+1}}\left[\int (F_{m-1/2,n,p}-F_{m+1/2,n,p})\,\text{d}x_{2}\,\text{d}x_{3}\right.\nonumber\\ \displaystyle & & \displaystyle +\,\int (G_{m,n-1/2,p}-G_{m,n+1/2,p})\,\text{d}x_{1}\,\text{d}x_{3}\nonumber\\ \displaystyle & & \displaystyle +\left.\int (H_{m,n,p-1/2}-H_{m,n,p+1/2})\,\text{d}x_{1}\,\text{d}x_{2}\right]\,\text{d}t.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle W_{mnp}^{n+1}-W_{mnp}^{n} & = & \displaystyle \frac{1}{\unicode[STIX]{x0394}x_{1}\unicode[STIX]{x0394}x_{2}\unicode[STIX]{x0394}x_{3}}\int _{t^{n}}^{t^{n+1}}\left[\int (F_{m-1/2,n,p}-F_{m+1/2,n,p})\,\text{d}x_{2}\,\text{d}x_{3}\right.\nonumber\\ \displaystyle & & \displaystyle +\,\int (G_{m,n-1/2,p}-G_{m,n+1/2,p})\,\text{d}x_{1}\,\text{d}x_{3}\nonumber\\ \displaystyle & & \displaystyle +\left.\int (H_{m,n,p-1/2}-H_{m,n,p+1/2})\,\text{d}x_{1}\,\text{d}x_{2}\right]\,\text{d}t.\end{eqnarray}$$
The time-dependent fluxes
![]() $(F,G,H)$
of macroscopic quantities arise from the advection terms in the BGK-Boltzmann equation. The moments of the right-hand side collision model vanish because mass, momentum and energy are conserved during particle collisions. This leads to the compatibility condition
$(F,G,H)$
of macroscopic quantities arise from the advection terms in the BGK-Boltzmann equation. The moments of the right-hand side collision model vanish because mass, momentum and energy are conserved during particle collisions. This leads to the compatibility condition
For a cell
![]() $(m,n,p)$
, flux across a cell interface with normal in the
$(m,n,p)$
, flux across a cell interface with normal in the
![]() $x_{1}$
direction is computed by
$x_{1}$
direction is computed by
 $$\begin{eqnarray}\displaystyle \left(\begin{array}{@{}c@{}}F_{\unicode[STIX]{x1D70C}}\\ F_{\unicode[STIX]{x1D70C}U_{1}}\\ F_{\unicode[STIX]{x1D70C}U_{2}}\\ F_{\unicode[STIX]{x1D70C}U_{3}}\\ F_{\unicode[STIX]{x1D70C}\unicode[STIX]{x1D716}}\end{array}\right)=\int c_{1}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FC}}\,f(x_{1}^{m+1/2},x_{2}^{n},x_{3}^{p},t,c_{i},\unicode[STIX]{x1D709}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left(\begin{array}{@{}c@{}}F_{\unicode[STIX]{x1D70C}}\\ F_{\unicode[STIX]{x1D70C}U_{1}}\\ F_{\unicode[STIX]{x1D70C}U_{2}}\\ F_{\unicode[STIX]{x1D70C}U_{3}}\\ F_{\unicode[STIX]{x1D70C}\unicode[STIX]{x1D716}}\end{array}\right)=\int c_{1}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FC}}\,f(x_{1}^{m+1/2},x_{2}^{n},x_{3}^{p},t,c_{i},\unicode[STIX]{x1D709}). & & \displaystyle\end{eqnarray}$$
The distribution function used for computing the flux is given by the general solution of the BGK model at the cell interface, in terms of an initial distribution
![]() $f_{0}$
and the equilibrium state
$f_{0}$
and the equilibrium state
![]() $g$
. In our simulations, we use a second-order BGK scheme in which the distribution functions are linearly reconstructed around cell interfaces. For example, the distribution functions are reconstructed in the following way around the interface located at
$g$
. In our simulations, we use a second-order BGK scheme in which the distribution functions are linearly reconstructed around cell interfaces. For example, the distribution functions are reconstructed in the following way around the interface located at
![]() $x_{1}^{m+1/2}$
,
$x_{1}^{m+1/2}$
,
The coefficients
![]() $a^{l},a^{r}$
are associated with gradients of flow variables normal to the interface and
$a^{l},a^{r}$
are associated with gradients of flow variables normal to the interface and
![]() $b^{l},\ldots ,c^{r}$
with gradients tangential to the interface. Equilibrium distributions
$b^{l},\ldots ,c^{r}$
with gradients tangential to the interface. Equilibrium distributions
![]() $g^{l}$
and
$g^{l}$
and
![]() $g^{r}$
correspond to the reconstructed values of macroscopic variables on either side of the interface. Macroscopic variables are reconstructed using a weighted essentially non-oscillatory scheme following Kumar et al. (Reference Kumar, Girimaji and Kerimo2013). This enables us to resolve any sharp discontinuities like shocklets in the turbulent flow field. All simulations are carried out with
$g^{r}$
correspond to the reconstructed values of macroscopic variables on either side of the interface. Macroscopic variables are reconstructed using a weighted essentially non-oscillatory scheme following Kumar et al. (Reference Kumar, Girimaji and Kerimo2013). This enables us to resolve any sharp discontinuities like shocklets in the turbulent flow field. All simulations are carried out with
![]() $Pr=0.7$
. The Prandtl number correction is applied at the step where coefficients
$Pr=0.7$
. The Prandtl number correction is applied at the step where coefficients
![]() $a^{l},a^{r},\ldots$
are calculated. This does not change the underlying BGK scheme and is equivalent to dividing the heat flux term by the Prandtl number in a conventional Navier–Stokes solver (May et al.
Reference May, Srinivasan and Jameson2007).
$a^{l},a^{r},\ldots$
are calculated. This does not change the underlying BGK scheme and is equivalent to dividing the heat flux term by the Prandtl number in a conventional Navier–Stokes solver (May et al.
Reference May, Srinivasan and Jameson2007).
The equilibrium distribution is reconstructed as
where
![]() $g_{0}$
is the local equilibrium distribution at the interface,
$g_{0}$
is the local equilibrium distribution at the interface,
![]() $h(x)$
is the Heaviside function which is one for positive values of
$h(x)$
is the Heaviside function which is one for positive values of
![]() $x$
and zero otherwise. The coefficients are calculated from the gradients of flow variables. Coefficients
$x$
and zero otherwise. The coefficients are calculated from the gradients of flow variables. Coefficients
![]() $A^{l}$
and
$A^{l}$
and
![]() $A^{r}$
are obtained by equating the moments of non-equilibrium contributions in (A 7) to zero and
$A^{r}$
are obtained by equating the moments of non-equilibrium contributions in (A 7) to zero and
![]() $\bar{A}$
from the compatibility condition (A 5). The procedure to obtain these coefficients from gradients of flow variables can be found in Xu et al. (Reference Xu, Mao and Tang2005). After determining these parameters, the distribution function at the cell interface, which is used to compute the numerical flux, is given by
$\bar{A}$
from the compatibility condition (A 5). The procedure to obtain these coefficients from gradients of flow variables can be found in Xu et al. (Reference Xu, Mao and Tang2005). After determining these parameters, the distribution function at the cell interface, which is used to compute the numerical flux, is given by
 $$\begin{eqnarray}\displaystyle f(x_{1}^{m+1/2},x_{2}^{n},x_{3}^{p},t,c_{i},\unicode[STIX]{x1D709}) & = & \displaystyle (1-e^{-t/\unicode[STIX]{x1D70F}})g_{0}+\unicode[STIX]{x1D70F}(t/\unicode[STIX]{x1D70F}-1+e^{-t/\unicode[STIX]{x1D70F}})\bar{A}g_{0}\nonumber\\ \displaystyle & & \displaystyle +\,(\unicode[STIX]{x1D70F}(-1+e^{-t/\unicode[STIX]{x1D70F}})+te^{-t/\unicode[STIX]{x1D70F}})\nonumber\\ \displaystyle & & \displaystyle \times \,(\bar{a}^{l}h[c_{1}]\bar{a}^{r}(1-h[c_{1}])+\bar{b}c_{2}+\bar{c}c_{3})c_{1}g_{0}\nonumber\\ \displaystyle & & \displaystyle +\,e^{-t/\unicode[STIX]{x1D70F}} ([1-(t+\unicode[STIX]{x1D70F})(c_{1}a^{l}+c_{2}b^{l}+c_{3}c^{l})]h[c_{1}]g^{l}\nonumber\\ \displaystyle & & \displaystyle +\,[1-(t+\unicode[STIX]{x1D70F})(c_{1}a^{r}+c_{2}b^{r}+c_{3}c^{r})](1-h[c_{1}])g^{r}\! )\nonumber\\ \displaystyle & & \displaystyle -\,e^{-t/\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D70F}A^{l}h[c_{1}]g^{l}+\unicode[STIX]{x1D70F}A^{r}(1-h[c_{1}])g^{r}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f(x_{1}^{m+1/2},x_{2}^{n},x_{3}^{p},t,c_{i},\unicode[STIX]{x1D709}) & = & \displaystyle (1-e^{-t/\unicode[STIX]{x1D70F}})g_{0}+\unicode[STIX]{x1D70F}(t/\unicode[STIX]{x1D70F}-1+e^{-t/\unicode[STIX]{x1D70F}})\bar{A}g_{0}\nonumber\\ \displaystyle & & \displaystyle +\,(\unicode[STIX]{x1D70F}(-1+e^{-t/\unicode[STIX]{x1D70F}})+te^{-t/\unicode[STIX]{x1D70F}})\nonumber\\ \displaystyle & & \displaystyle \times \,(\bar{a}^{l}h[c_{1}]\bar{a}^{r}(1-h[c_{1}])+\bar{b}c_{2}+\bar{c}c_{3})c_{1}g_{0}\nonumber\\ \displaystyle & & \displaystyle +\,e^{-t/\unicode[STIX]{x1D70F}} ([1-(t+\unicode[STIX]{x1D70F})(c_{1}a^{l}+c_{2}b^{l}+c_{3}c^{l})]h[c_{1}]g^{l}\nonumber\\ \displaystyle & & \displaystyle +\,[1-(t+\unicode[STIX]{x1D70F})(c_{1}a^{r}+c_{2}b^{r}+c_{3}c^{r})](1-h[c_{1}])g^{r}\! )\nonumber\\ \displaystyle & & \displaystyle -\,e^{-t/\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D70F}A^{l}h[c_{1}]g^{l}+\unicode[STIX]{x1D70F}A^{r}(1-h[c_{1}])g^{r}).\end{eqnarray}$$
Flux across the interface
![]() $m+1/2$
is computed by substituting (A 9) in (A 6). A similar procedure is used to calculate fluxes
$m+1/2$
is computed by substituting (A 9) in (A 6). A similar procedure is used to calculate fluxes
![]() $G$
and
$G$
and
![]() $H$
in the other two directions.
$H$
in the other two directions.
The time advancement is included in the flux calculation according to equation (A 4) by way of an exact integration in time of the discretized distribution function. The resulting scheme is second order accurate in time, as shown in Ohwada (Reference Ohwada2002). The time step used in this integration is calculated using the CFL criterion by
where
![]() $C$
is the CFL number,
$C$
is the CFL number,
![]() ${\mathcal{V}}$
is the volume of the cell,
${\mathcal{V}}$
is the volume of the cell,
![]() $S_{k}$
is the area of the
$S_{k}$
is the area of the
![]() $k$
th face of the cell,
$k$
th face of the cell,
![]() $\unicode[STIX]{x1D706}_{c}=|U_{k}|+c_{s}$
and
$\unicode[STIX]{x1D706}_{c}=|U_{k}|+c_{s}$
and
![]() $\unicode[STIX]{x1D706}_{v}=\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D708}/Pr$
. The quantities
$\unicode[STIX]{x1D706}_{v}=\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D708}/Pr$
. The quantities
![]() $U_{k}$
and
$U_{k}$
and
![]() $c_{s}$
are the face-normal velocity and speed of sound. The stability of the scheme depends on the macroscopic flow variables as in the case of Navier–Stokes solvers (Venugopal & Girimaji Reference Venugopal and Girimaji2015).
$c_{s}$
are the face-normal velocity and speed of sound. The stability of the scheme depends on the macroscopic flow variables as in the case of Navier–Stokes solvers (Venugopal & Girimaji Reference Venugopal and Girimaji2015).
A.2 Convergence of the numerical simulations
Two additional simulations are performed to check the accuracy of the results. The additional simulations are for the largest convective Mach number to examine the effects of grid resolution and spanwise domain extent. The initial conditions for these simulations are the same as that for the case M12 reported in this work. The details of the high resolution (HR12) and larger domain (LD12) grids are given in table 3 Case LD12 has a spanwise extent twice as that in the other two cases. The domain is uniformly discretized with equal spacing in all three directions.
Table 3. Grid details for the high resolution and larger spanwise extent simulations.

The results from LD12 and HR12 simulations are compared with those of M12. The momentum thickness evolution in these simulations does not show any significant difference, as can be seen in figure 28(a). The focus of this work is the transient evolution of the mixing layer. The evolution of averaged turbulent kinetic energy, calculated using equation (3.4), is shown in figure 28(b). As in the case of momentum thickness, the turbulent kinetic energy is not influenced by the domain extent or the cell size. The Reynolds stress anisotropy also shows grid and domain independence (see figure 28 c).

Figure 28. (a) Momentum thickness evolution with time for the three simulations. (b) Evolution of turbulent kinetic energy with time. (c) Evolution of anisotropy tensor. Solid line and circles,
![]() $b_{11}$
; dashed line and squares,
$b_{11}$
; dashed line and squares,
![]() $b_{22}$
; dot-dashed line and triangles,
$b_{22}$
; dot-dashed line and triangles,
![]() $b_{12}$
. Filled and unfilled symbols correspond to LD12 and HR12 simulations, respectively.
$b_{12}$
. Filled and unfilled symbols correspond to LD12 and HR12 simulations, respectively.

Figure 29. Conditionally averaged turbulent kinetic energy for different simulations at
![]() $\unicode[STIX]{x1D70F}=340$
.
$\unicode[STIX]{x1D70F}=340$
.

Figure 30. Vorticity contours on the
![]() $x_{2}x_{3}$
plane at
$x_{2}x_{3}$
plane at
![]() $\unicode[STIX]{x1D70F}=400$
. (a) M12 and (b) LD12.
$\unicode[STIX]{x1D70F}=400$
. (a) M12 and (b) LD12.
The effects of domain extent and grid resolution on the topology dependence of the turbulent statistics are also investigated. Figure 29 shows that the shear-dominated regions have more turbulent kinetic energy than vortex-dominated regions irrespective of the domain extent and grid resolution. It is also important to show that the topology of the flow is grid converged. For this purpose, we compare the fraction of vortex-dominated topology in the flow field from different simulations. The cases M12, LD12 and HR12 respectively have 42, 43 and 41 per cent of the flow field with a vortex topology at the instant
![]() $\unicode[STIX]{x1D70F}=340$
. The contours of vorticity on the streamwise plane during the evolution of M12 and LD12 are shown in figure 30. The spanwise distributions of vortical structures are not influenced by the length of the domain. From these results, it can be seen that HR12 and LD12 simulations do not differ significantly from M12. Hence, it is concluded that the resolutions and domains used for M12 and other simulations are adequate for the present work.
$\unicode[STIX]{x1D70F}=340$
. The contours of vorticity on the streamwise plane during the evolution of M12 and LD12 are shown in figure 30. The spanwise distributions of vortical structures are not influenced by the length of the domain. From these results, it can be seen that HR12 and LD12 simulations do not differ significantly from M12. Hence, it is concluded that the resolutions and domains used for M12 and other simulations are adequate for the present work.
Appendix B. Helical streamlines and velocity correlation
Consider the parametric equation for a helix (streamline) given by
where
![]() $A$
and
$A$
and
![]() $B$
are constants. The tangent vector for this curve is
$B$
are constants. The tangent vector for this curve is
which is the local velocity. When the helical streamline has the axis along
![]() $x_{1}$
, as in figure 16(a), the components of the tangent vector are equal to the velocity components in the original coordinate system (
$x_{1}$
, as in figure 16(a), the components of the tangent vector are equal to the velocity components in the original coordinate system (
![]() $x_{1},x_{2},x_{3}$
), given by
$x_{1},x_{2},x_{3}$
), given by
The velocity correlation is obtained by the average of the product
![]() $u_{1}^{\prime \prime }u_{2}^{\prime \prime }$
. Over one period of the helix,
$u_{1}^{\prime \prime }u_{2}^{\prime \prime }$
. Over one period of the helix,
 $$\begin{eqnarray}\displaystyle \overline{u_{1}^{\prime \prime }u_{2}^{\prime \prime }}=\frac{\displaystyle \int _{0}^{2\unicode[STIX]{x03C0}}u_{1}^{\prime \prime }u_{2}^{\prime \prime }\,\text{d}t}{\displaystyle \int _{0}^{2\unicode[STIX]{x03C0}}\,\text{d}t}=\frac{\displaystyle \int _{0}^{2\unicode[STIX]{x03C0}}AB\cos t\,\text{d}t}{\displaystyle \int _{0}^{2\unicode[STIX]{x03C0}}\,\text{d}t}=0. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \overline{u_{1}^{\prime \prime }u_{2}^{\prime \prime }}=\frac{\displaystyle \int _{0}^{2\unicode[STIX]{x03C0}}u_{1}^{\prime \prime }u_{2}^{\prime \prime }\,\text{d}t}{\displaystyle \int _{0}^{2\unicode[STIX]{x03C0}}\,\text{d}t}=\frac{\displaystyle \int _{0}^{2\unicode[STIX]{x03C0}}AB\cos t\,\text{d}t}{\displaystyle \int _{0}^{2\unicode[STIX]{x03C0}}\,\text{d}t}=0. & & \displaystyle\end{eqnarray}$$
In figure 16(b), the axis of the helix is at an angle
![]() $\unicode[STIX]{x1D703}$
with respect to
$\unicode[STIX]{x1D703}$
with respect to
![]() $x_{1}$
. Velocity components in the original coordinate system
$x_{1}$
. Velocity components in the original coordinate system
![]() $(x_{1},x_{2},x_{3})$
are given by
$(x_{1},x_{2},x_{3})$
are given by
 $$\begin{eqnarray}\displaystyle \left(\begin{array}{@{}c@{}}u_{1}^{\prime \prime }\\ u_{2}^{\prime \prime }\\ u_{3}^{\prime \prime }\end{array}\right)=\left[\begin{array}{@{}ccc@{}}\cos \unicode[STIX]{x1D703} & -\sin \unicode[STIX]{x1D703} & 0\\ \sin \unicode[STIX]{x1D703} & \cos \unicode[STIX]{x1D703} & 0\\ 0 & 0 & 1\end{array}\right]\left(\begin{array}{@{}c@{}}A\\ B\cos t\\ -B\sin t\end{array}\right). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left(\begin{array}{@{}c@{}}u_{1}^{\prime \prime }\\ u_{2}^{\prime \prime }\\ u_{3}^{\prime \prime }\end{array}\right)=\left[\begin{array}{@{}ccc@{}}\cos \unicode[STIX]{x1D703} & -\sin \unicode[STIX]{x1D703} & 0\\ \sin \unicode[STIX]{x1D703} & \cos \unicode[STIX]{x1D703} & 0\\ 0 & 0 & 1\end{array}\right]\left(\begin{array}{@{}c@{}}A\\ B\cos t\\ -B\sin t\end{array}\right). & & \displaystyle\end{eqnarray}$$
Then,
for which
over a period of the helix. The velocity correlation is thus non-zero and hence also the production. This indicates that the reduction in turbulent energy production is strongly correlated with the orientation of helical streamlines.