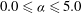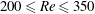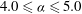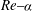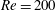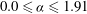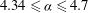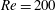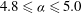1. Introduction
Imparting rotation to a circular cylinder significantly alters the flow around it. There have been several studies in the past (Ingham Reference Ingham1983; Hu et al.
Reference Hu, Sun, Yin and Tong1996; Kang, Choi & Lee Reference Kang, Choi and Lee1999; Stojković, Breuer & Durst Reference Stojković, Breuer and Durst2002; Mittal & Kumar Reference Mittal and Kumar2003; Stojković et al.
Reference Stojković, Schön, Breuer and Durst2003; Padrino & Joseph Reference Padrino and Joseph2006; El Akoury et al.
Reference El Akoury, Braza, Perrin, Harran and Hoarau2008; Pralits, Brandt & Giannetti Reference Pralits, Brandt and Giannetti2010; Pralits, Giannetti & Brandt Reference Pralits, Giannetti and Brandt2013; Rao et al.
Reference Rao, Leontini, Thompson and Hourigan2013a
,Reference Rao, Leontini, Thompson and Hourigan
b
, Reference Rao, Radi, Leontini, Thompson, Sheridan and Hourigan2014) to classify the different flow regimes based on Reynolds number,
$\mathit{Re}$
, and rate of rotation. The non-dimensional rotation rate,
${\it\alpha}$
, is defined as the ratio of the speed of the cylinder surface to the free-stream velocity. For a non-rotating cylinder, the steady two-dimensional (2D) flow becomes unstable via Hopf bifurcation, leading to the formation of a von Kármán vortex street beyond
$\mathit{Re}\sim 47$
. With rotation, the spatial symmetry of the flow along the centreline is broken. This affects the flow transitions via different mechanisms. For low
${\it\alpha}$
, the flow still loses stability via Hopf bifurcation. However, for relatively large
${\it\alpha}$
, other instabilities are observed. Hu et al. (Reference Hu, Sun, Yin and Tong1996) studied bifurcations, describing the transition from steady to a time-periodic solution. They found that imparting rotation delays the onset of vortex shedding with respect to
$\mathit{Re}$
. Kang et al. (Reference Kang, Choi and Lee1999) investigated the flow past a cylinder for
$\mathit{Re}\leqslant 160$
and
$0.0\leqslant {\it\alpha}\leqslant 2.5$
. They reported that vortex shedding is completely suppressed for
${\it\alpha}>{\it\alpha}_{L}$
, where
${\it\alpha}_{L}$
has logarithmic dependence on Reynolds number. Similar observations were also made by Barnes (Reference Barnes2000) via experiments at lower Reynolds number (
$50\leqslant \mathit{Re}\leqslant 75$
).
Stojković et al. (Reference Stojković, Breuer and Durst2002, Reference Stojković, Schön, Breuer and Durst2003) carried out 2D numerical simulations and reported that vortex shedding reappears for
$4.85\leqslant {\it\alpha}\leqslant 5.15$
at
$\mathit{Re}=100$
. This mode of vortex shedding has a frequency that is lower than that of the Kármán shedding and is referred to as mode II shedding. They presented a stability diagram demarcating boundaries of the two modes of shedding for
$60\leqslant \mathit{Re}\leqslant 200$
and
$0.0\leqslant {\it\alpha}\leqslant 6.0$
. The region between the boundaries of the two shedding regimes is associated with a steady flow. Mittal & Kumar (Reference Mittal and Kumar2003) carried out a global linear stability analysis of the 2D steady flow for
$\mathit{Re}=200$
and
$0.0\leqslant {\it\alpha}\leqslant 5.0$
. Their results from linear stability analysis are in very good agreement with results from direct time integration of the governing equations. They presented arguments based on generation of vorticity near the cylinder to explain the appearance of mode II shedding. Beyond the higher-
${\it\alpha}$
end of mode II shedding, the flow again becomes steady. The steady solutions, before and after the mode II shedding regime, are associated with different flow structures (Mittal & Kumar Reference Mittal and Kumar2003; Rao et al.
Reference Rao, Leontini, Thompson and Hourigan2013b
, Reference Rao, Radi, Leontini, Thompson, Sheridan and Hourigan2014). Mittal & Kumar (Reference Mittal and Kumar2003) reported the existence of hysteresis in achieving a steady state for
$4.8\leqslant {\it\alpha}\leqslant 5.0$
at
$\mathit{Re}=200$
. Solutions corresponding to increasing
${\it\alpha}$
(steady state I) in this regime were found to be unstable, while solutions for decreasing
${\it\alpha}$
(steady state II) were reported to be stable to small disturbances. El Akoury et al. (Reference El Akoury, Braza, Perrin, Harran and Hoarau2008) carried out numerical simulations for
$\mathit{Re}\leqslant 500$
and
$0.0\leqslant {\it\alpha}\leqslant 6.0$
. They found that the regime of
${\it\alpha}$
for which mode II occurs increases with increasing
$\mathit{Re}$
.
Despite a significant amount of research in identifying the shedding regimes encountered in flow past a rotating cylinder, very few studies have addressed the existence of three-dimensionality in these flows. For a non-rotating cylinder, spanwise instability develops in the wake beyond
$\mathit{Re}\sim 190$
. This is referred to as mode A instability (Barkley & Henderson Reference Barkley and Henderson1996; Williamson Reference Williamson1996) and has a spanwise wavelength of approximately
$4D$
. El Akoury et al. (Reference El Akoury, Braza, Perrin, Harran and Hoarau2008) performed three-dimensional (3D) numerical simulations to study the effect of rotation for
${\it\alpha}\leqslant 1.5$
. They reported that rotation attenuates the onset of 3D instabilities. For
$\mathit{Re}=200$
and
${\it\alpha}=1.5$
, the flow field was observed to be 2D. Mittal (Reference Mittal2004) reported the presence of centrifugal instabilities along the entire span of the cylinder for
${\it\alpha}=5.0$
and
$\mathit{Re}=200$
. Rao et al. (Reference Rao, Leontini, Thompson and Hourigan2013a
,Reference Rao, Leontini, Thompson and Hourigan
b
, Reference Rao, Radi, Leontini, Thompson, Sheridan and Hourigan2014) studied transition from the 2D to the 3D state using Floquet analysis for
$\mathit{Re}\leqslant 400$
and
${\it\alpha}\leqslant 7.0$
. They presented curves of marginal stability of various modes (A, B, C, D, E, E
$^{\prime }$
, F, F
$^{\prime }$
, G) associated with steady states I and II on the
$\mathit{Re}{-}{\it\alpha}$
parameter space. The eigenvalues of modes A, B, C, D, E, E
$^{\prime }$
and G are real, while modes F and F
$^{\prime }$
are associated with complex eigenvalues. Using Bayly’s (Reference Bayly1988) criteria, Rao et al. (Reference Rao, Leontini, Thompson and Hourigan2013a
,Reference Rao, Leontini, Thompson and Hourigan
b
) proposed that modes F and F
$^{\prime }$
may be responsible for centrifugal instabilities. Meena (Reference Meena2011) and Meena et al. (Reference Meena, Sidharth, Khan and Mittal2011) presented results from linear stability analysis at
$\mathit{Re}=200$
. They found that the eigenmodes associated with centrifugal instabilities beyond
${\it\alpha}=3.0$
are real. Later, Rao et al. (Reference Rao, Leontini, Thompson and Hourigan2013b
) demonstrated that mode E, for
${\it\alpha}>3.0$
, may be associated with centrifugal instability. Both modes E and F are characterized by multiple turning points on the
$\mathit{Re}{-}{\it\alpha}$
parameter space. Recently, Radi et al. (Reference Radi, Thompson, Rao, Hourigan and Sheridan2013) have presented experimental evidence of the 3D modes. A detailed review of various 3D modes for
$0\leqslant \mathit{Re}\leqslant 350$
and
$0.0\leqslant {\it\alpha}\leqslant 7.0$
has been presented by Rao et al. (Reference Rao, Radi, Leontini, Thompson, Sheridan and Hourigan2014).
In this work, we first present results for linear stability analysis of flow past a rotating cylinder. Several new modes of instability are found for
$200\leqslant \mathit{Re}\leqslant 350$
and
$4.0\leqslant {\it\alpha}\leqslant 5.0$
. Direct numerical simulations (DNS) are then carried out at
$\mathit{Re}=200$
to understand the evolution of 3D disturbances. The interaction between disturbances of different spanwise wavelengths is investigated by carrying out computations with different spanwise extent of the cylinder.
2. Formulation
2.1. Incompressible flow equations
Let
${\rm\Omega}\subset \mathbb{R}^{n_{sd}}$
and
$(0,T)$
be the spatial and temporal domains, respectively, where
$n_{sd}$
is the number of space dimensions. Let
${\rm\Gamma}$
denote the boundary of
${\rm\Omega}$
. The spatial and temporal coordinates are denoted by
$\boldsymbol{x}$
and
$t$
. The Navier–Stokes equations governing incompressible fluid flow are
$$\begin{eqnarray}\displaystyle & {\it\rho}\left({\displaystyle \frac{\partial \boldsymbol{u}}{\partial t}}+\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}\right)-\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }{\bf\sigma}=\mathbf{0}\quad \text{on }{\rm\Omega}\times (0,T), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}=0\quad \text{on }{\rm\Omega}\times (0,T). & \displaystyle\end{eqnarray}$$
${\it\rho}$
,
$\boldsymbol{u}$
and
${\bf\sigma}$
are the density, velocity and the stress tensor, respectively. The stress tensor is the sum of its isotropic and deviatoric parts, 
$$\begin{eqnarray}{\bf\sigma}=-p\unicode[STIX]{x1D644}+\unicode[STIX]{x1D64F},\quad \unicode[STIX]{x1D64F}=2{\it\mu}{\bf\varepsilon}(\boldsymbol{u}),\quad {\bf\varepsilon}(\boldsymbol{u})={\textstyle \frac{1}{2}}((\boldsymbol{{\rm\nabla}}\boldsymbol{u})+(\boldsymbol{{\rm\nabla}}\boldsymbol{u})^{\text{T}}),\end{eqnarray}$$
where
$p$
and
${\it\mu}$
are the pressure and coefficient of dynamic viscosity, respectively. The associated boundary conditions and initial conditions used for the computations are described in §§ 3–5.
2.2. Linear stability flow equations
The unsteady flow is represented as a combination of the steady state and disturbance:
$\boldsymbol{u}=\boldsymbol{U}+\boldsymbol{u}^{\prime }$
and
$p=P+p^{\prime }$
. Here
$\boldsymbol{u}^{\prime }$
and
$p^{\prime }$
are the perturbation fields of the velocity and pressure, respectively. The steady-state solution (
$\boldsymbol{U},P$
) is obtained by dropping the unsteady term in (2.1) and (2.2). It is further assumed that the disturbances are small. This permits one to linearize the equations to obtain
$$\begin{eqnarray}\displaystyle & {\it\rho}\left({\displaystyle \frac{\partial \boldsymbol{u}^{\prime }}{\partial t}}+\boldsymbol{u}^{\prime }\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{U}+\boldsymbol{U}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\prime }\right)-\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }{\bf\sigma}^{\prime }=\mathbf{0}\quad \text{on }{\rm\Omega}\times (0,T), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}^{\prime }=0\quad \text{on }{\rm\Omega}\times (0,T). & \displaystyle\end{eqnarray}$$
${\bf\sigma}^{\prime }$
is the stress tensor for the disturbance field (
$\boldsymbol{u}^{\prime },p^{\prime }$
). More details on the linearized equations of the disturbance field can be found in Mittal & Kumar (Reference Mittal and Kumar2003). The disturbances are assumed to be of the following form: 
$$\begin{eqnarray}\boldsymbol{u}^{\prime }(x,y,z,t)=\hat{\boldsymbol{u}}(x,y)\text{e}^{\text{i}{\it\beta}z}\text{e}^{{\it\lambda}t},\quad p^{\prime }(x,y,z,t)=\hat{p}(x,y)\text{e}^{\text{i}{\it\beta}z}\text{e}^{{\it\lambda}t}.\end{eqnarray}$$
Here
${\it\beta}$
is the spanwise wavenumber of the disturbance and
${\it\lambda}_{z}~(=2{\rm\pi}/{\it\beta})$
its wavelength. The eigenvalue
${\it\lambda}$
governs the stability of the base flow. In general,
${\it\lambda}$
is complex and can be represented as
${\it\lambda}={\it\lambda}_{r}+\text{i}{\it\lambda}_{i}$
where
${\it\lambda}_{r}$
and
${\it\lambda}_{i}$
are the real and imaginary parts, respectively. Here
${\it\lambda}_{i}$
represents the (circular) frequency, while
${\it\lambda}_{r}$
represents the growth rate; a positive
${\it\lambda}_{r}$
leads to instability.
2.3. Solution method
The flow equations in primitive variable form are solved via a stabilized finite element method. The numerical stabilizations are based on the streamline-upwind/Petrov–Galerkin (SUPG) and pressure-stabilizing/Petrov–Galerkin (PSPG) stabilization techniques (Tezduyar et al.
Reference Tezduyar, Mittal, Ray and Shih1992). The nonlinear equations resulting from finite element discretization are solved using the generalized minimal residual (GMRES) technique (Saad & Schultz Reference Saad and Schultz1986) in conjunction with diagonal preconditioners. Details of the numerical method can be found in our earlier work (Mittal & Kumar Reference Mittal and Kumar2003; Mittal Reference Mittal2004; Behara & Mittal Reference Behara and Mittal2009). The finite element formulation of the linear stability problem leads to a generalized eigenvalue problem of the form
$\unicode[STIX]{x1D63C}X-{\it\lambda}\unicode[STIX]{x1D63D}X=0$
, where
$\unicode[STIX]{x1D63C}$
and
$\unicode[STIX]{x1D63D}$
are non-symmetric matrices. The subspace iteration method (Stewart Reference Stewart and Miller1975) in conjunction with the shift-inverse transformation is used to solve the eigenvalue problem and to locate the eigenvalue with largest real part for different
${\it\beta}$
.
3. Problem set-up, boundary conditions and finite element mesh
For the 2D computations, the cylinder of diameter
$D$
is placed symmetrically between the two lateral walls of a rectangular domain with a blockage of
$B=2\,\%$
. The origin of the coordinate system coincides with the centre of the cylinder. The upstream and downstream boundaries are located at a distance of
$L_{u}/D=50$
and
$L_{d}/D=150$
, respectively, with respect to the origin. The finite element mesh consists of quadrilateral elements. Bilinear interpolation functions are used for both velocity and pressure. The density of elements is high near the cylinder to accurately resolve the boundary layer, and decreases radially outwards. Three meshes of different spatial resolution have been utilized in various regimes. These meshes are termed M1, M2 and M3, and consist of 16 310, 33 795 and 50 440 nodes, respectively. A detailed description of the performance of the three meshes in various flow regimes is described in appendix A. In each regime the mesh that has the lowest resolution but is adequate to resolve the corresponding flow structures is utilized. The mesh for 3D computations is generated by stacking several slices of the 2D mesh along the span of the cylinder. A parallel implementation of the stabilized finite element formulation is used for computations involving large-sized problems (Behara & Mittal Reference Behara and Mittal2009). For brevity, we introduce the notation (
$\mathit{Re},{\it\alpha}$
) to refer to any point in the
$\mathit{Re}{-}{\it\alpha}$
plane.
The following boundary conditions are employed for the DNS. A flow velocity corresponding to the rotation rate,
${\it\alpha}$
, is specified on the surface of the cylinder. Free-stream values are assigned to the velocity at the upstream boundary. At the downstream boundary the stress vector is set to zero. On the upper and lower boundaries, the component of velocity normal to and the component of the stress vector along these boundaries are prescribed a zero value. Two kinds of boundary conditions on the sidewall have been used for the computations: periodic or symmetry. The symmetry condition is imposed by prescribing the component of velocity normal to and the component of the stress vector along the boundaries a zero value. For the linear stability analysis, the boundary conditions are homogeneous versions of those used for direct time integration.
Figure 1. Flow past a rotating cylinder: curves of neutral stability of various modes associated with SSI for the parameter space investigated. The symbols used for marking the neutral curves for different modes: (a) ○, mode F; ▴, mode I; ●, mode J;
$\Box$
, mode K; (b)
$\blacksquare$
, mode H. Mode E is unstable over the entire parameter space considered in this work.
4. Overview of the various modes of instability
4.1. Neutral stability curves
Rao et al. (Reference Rao, Leontini, Thompson and Hourigan2013b
, Reference Rao, Radi, Leontini, Thompson, Sheridan and Hourigan2014) reported the existence of two steady states: steady state I (SSI) and steady state II (SSII), for
$\mathit{Re}\leqslant 400$
and
$0.0\leqslant {\it\alpha}\leqslant 7.0$
. They carried out linear stability analysis to show that the two steady states can become unstable via several 3D modes (A, B, C, D, E,
$\text{E}^{\prime }$
, F, F
$^{\prime }$
and G). The linear stability analysis in the present effort brings out additional modes of instability associated with SSI. We denote these as modes H, I, J and K. Modes I, J and K are 3D modes in the sense that they are unstable only for non-zero
${\it\beta}$
. Mode H, on the other hand, is unstable for
${\it\beta}=0$
as well. For
${\it\beta}\neq 0.0$
, the vortices are inclined to the axis of the cylinder, rendering the flow field 3D. Mode H is, therefore, a 2D mode. This will be discussed in detail in § 5.
Figure 1(a) shows the curves of neutral stability of modes I, J and K for
$200\leqslant \mathit{Re}\leqslant 350$
. The spanwise wavenumber of disturbance is varied over
$0.0\leqslant {\it\beta}\leqslant 30.0$
, where
${\it\beta}=0.0$
corresponds to a 2D disturbance. In this flow regime, modes E and F are also unstable (Rao et al.
Reference Rao, Leontini, Thompson and Hourigan2013a
,Reference Rao, Leontini, Thompson and Hourigan
b
, Reference Rao, Radi, Leontini, Thompson, Sheridan and Hourigan2014). Hence, we have included the region of instability of modes E and F in figure 1(a). In general, the flow becomes richer in terms of the number of unstable modes with increasing
${\it\alpha}$
. The regime of instability of mode H is shown in figure 1(b).
4.2. Mode characteristics
Figure 2 shows the variation of growth rate,
${\it\lambda}_{r}$
, and frequency,
${\it\lambda}_{i}$
, with wavenumber,
${\it\beta}$
, of various modes associated with SSI for
$(\mathit{Re},{\it\alpha})=(350,4.7)$
. All modes other than mode J are unstable for these parameters. The characteristic wavenumber,
${\it\beta}_{c}$
, of a mode for a set of
$(\mathit{Re},{\it\alpha})$
is defined as the spanwise wavenumber for which maximum growth rate is attained. The characteristic wavelength is inversely proportional to
${\it\beta}_{c}$
. In general, the spectrum of wavenumbers over which a mode exists varies with
$\mathit{Re}$
and/or
${\it\alpha}$
. Consequently, the characteristic wavenumber of the various modes may vary with
$\mathit{Re}$
and
${\it\alpha}$
. Among all modes, the characteristic wavenumber of mode F is the largest. We now describe in detail each of the new modes that have been discovered for SSI.
Figure 2. Flow past a rotating cylinder for
$(\mathit{Re},{\it\alpha})=(350,4.7)$
: variation of (a) growth rate and (b) frequency with wavenumber for different modes associated with SSI. For clarity, a close-up view near the bifurcation is shown. B represents the bifurcation point.
4.2.1. Mode H
The mode H instability occurs beyond
${\it\alpha}\sim 4.1$
(figure 1
b). The eigenvalues associated with this mode are complex. Hence, the instability is expected to lead the flow away from SSI via disturbances that are oscillatory in time. This mode occurs for a narrow range of wavenumbers (
$0.0\leqslant {\it\beta}\leqslant 0.3$
for
$(\mathit{Re},{\it\alpha})=(350,4.7)$
as shown in figure 2). The highest growth rate is attained for
${\it\beta}=0.0$
. As such, the characteristic wavenumber of mode H is
${\it\beta}_{c}=0.0$
. With increase in
${\it\beta}$
, the growth rate of mode H decreases till a bifurcation point is reached. We denote the bifurcation point by
$B$
. This point marks the termination of mode H and initiation of modes E and I. The location of the bifurcation point depends on
$(\mathit{Re},{\it\alpha})$
. For a fixed
$\mathit{Re}$
, with increase in rotation rate, the bifurcation occurs for lower values of
${\it\beta}$
. Figure 3 shows schematically the location of
$B$
for
${\it\alpha}=4.7$
and 5.1 at
$\mathit{Re}=325$
. The bifurcation point is indicated on curves showing the variation of growth rate and frequency with wavenumber. For
${\it\alpha}=4.7$
, the bifurcation occurs for a positive
${\it\beta}=0.3$
. It shifts towards the left on the
${\it\beta}$
axis with increase in
${\it\alpha}$
. For
${\it\alpha}=5.1$
, mode H does not exist for
${\it\beta}\geqslant 0$
and it appears as if B is located on the negative
${\it\beta}$
axis. The frequency of mode H decreases with increase in
${\it\beta}$
and is equal to zero at
$B$
. For
$200\leqslant \mathit{Re}\leqslant 350$
, mode H does not exist beyond
${\it\alpha}\simeq 5$
. Figure 4(a) shows the spanwise vorticity field and isosurfaces of spanwise vorticity of mode H for
$(\mathit{Re},{\it\alpha})=(325,4.8)$
. The instability is dominant in the wake as well as near the shoulder of the cylinder on the advancing side.
Figure 3. Flow past a rotating cylinder for
$\mathit{Re}=325$
: schematic of the variation of growth rate and frequency with wavenumber to show the bifurcations at (a)
${\it\alpha}=4.7$
and (b)
${\it\alpha}=5.1$
. B represents the bifurcation point.
Figure 4. Flow past a rotating cylinder for
$(\mathit{Re},{\it\alpha})=(325,4.8)$
: spanwise vorticity field (
${\it\omega}_{z}=\pm 0.2$
) of different modes associated with SSI. (a) Mode H (
${\it\beta}=0.0$
). (b) Mode I (
${\it\beta}=0.4$
). (c) Mode J (
${\it\beta}=8.6$
). (d) Mode K (
${\it\beta}=11.0$
). For complex modes, the vorticity field corresponding to the real part of the eigenmode is shown. Among them, modes I, J and K are prominent in the vicinity of the cylinder and/or the hyperbolic point of SSI. The regions of large perturbation associated with mode H extend into the wake as well. The flow is from left to right. The hyperbolic point is indicated by a solid dot. Also shown is the 3D construction of the modes.
4.2.2. Mode I
The mode I instability is associated with real eigenvalues. The growth rate of mode I is highest at the bifurcation point,
$B$
. With increase in
${\it\beta}$
, the growth rate of mode I decreases. Figure 5 shows the variation of characteristic wavenumber,
${\it\beta}_{c}$
, of mode I with
${\it\alpha}$
for
$\mathit{Re}=325$
. The characteristic wavenumber decreases with increase in
${\it\alpha}$
. This is attributed to the movement of the bifurcation point towards lower values of
${\it\beta}$
with increase in
${\it\alpha}$
. Beyond
${\it\alpha}\simeq 5$
, mode H ceases to exist and the characteristic wavenumber of mode I is zero. Figure 4(b) shows the spanwise vorticity field and isosurfaces of spanwise vorticity of mode I. The region of large perturbation associated with mode I is similar to mode H.
Figure 5. Flow past a rotating cylinder for
$\mathit{Re}=325$
: variation of the characteristic wavenumber of the various unstable modes with rotation rate.
4.2.3. Mode J
The mode J instability occurs in a narrow region of the parameter space for high rotation rate and
$\mathit{Re}\leqslant 250$
. The eigenvalues associated with the mode are complex. As shown in figure 1(a), the neutral stability curve of mode J has a turning point at
$(\mathit{Re},{\it\alpha})=(250,4.8)$
. The frequency of the eigenmode associated with the characteristic wavenumber does not vary with
$\mathit{Re}$
or
${\it\alpha}$
. Figure 4(c) shows the spanwise vorticity field of mode J for
$(\mathit{Re},{\it\alpha})=(325,4.8)$
. The mode grows near the cylinder as well as near the hyperbolic point. The region of large perturbation away from the cylinder appears to emanate from the hyperbolic point. This mode, therefore, may be associated with centrifugal as well as hyperbolic instability mechanisms. More analysis needs to be carried out to ascertain this.
4.2.4. Mode K
Mode K becomes unstable for large Reynolds numbers,
$\mathit{Re}\geqslant 315$
. The eigenvalues associated with the mode are complex. The neutral stability curve has a turning point at
$(\mathit{Re},{\it\alpha})=(320,4.6)$
(figure 1
a). The characteristic wavenumber of mode K decreases with
${\it\alpha}$
(figure 5). Similar to modes F and F
$^{\prime }$
, this mode grows primarily in the boundary layer over the rotating cylinder and adjacent regions of the wake (figure 4
d). Using Bayly’s (Reference Bayly1988) criteria, Rao et al. (Reference Rao, Leontini, Thompson and Hourigan2013a
,Reference Rao, Leontini, Thompson and Hourigan
b
) proposed that modes F and F
$^{\prime }$
may be associated with centrifugal instability. It is assumed that the presence of viscosity does not change the nature of the instability, but only dampens or strengthens its effect. Since modes F and K share the same base flow SSI, mode K is also expected to be associated with a centrifugal instability.
We carried out direct time integration of the governing equations to study the time evolution of mode K instability for
$(\mathit{Re},{\it\alpha})=(350,4.7)$
. Periodic boundary conditions are prescribed on the sidewalls. The computations are initiated with the eigenmode corresponding to
${\it\beta}=11.0$
superimposed on SSI. This eigenmode has the largest growth rate for mode K at
$(\mathit{Re},{\it\alpha})=(350,4.7)$
(figure 2). Figure 6 shows the variation of spanwise component of velocity at the mid-span location for one cycle of the time-periodic solution. It can be noted that the disturbance remains localized to regions near the surface of the cylinder. This further suggests that mode K is associated with centrifugal instability.
Figure 6. Flow past a rotating cylinder for
$(\mathit{Re},{\it\alpha})=(350,4.7)$
: time history of spanwise component of disturbance velocity (
$w/D=\pm 0.002$
) at the mid-span and near the surface of the cylinder,
$(x/D,y/D)=(0.0,0.75)$
, for one time period of the flow. The disturbance field corresponds to the growth of mode K instability with
${\it\beta}=11.0$
. Also shown is the spanwise component of the disturbance velocity at different time instants marked in the time history.
5. Detailed analysis of the
$\mathit{Re}=200$
flow
The results from linear stability analysis presented in § 4 and earlier studies (Rao et al.
Reference Rao, Leontini, Thompson and Hourigan2013b
, Reference Rao, Radi, Leontini, Thompson, Sheridan and Hourigan2014) show that the two steady states are associated with several unstable modes. As the disturbances evolve with time, nonlinear effects may become significant, and their evolution may depart from that predicted by linear stability analysis. In this section we present results from direct time integration of the governing equations in three dimensions to study the time evolution of the disturbances corresponding to different modes of instability. These simulations are preceded by linear stability analysis of the flow past a rotating cylinder for
$\mathit{Re}=200$
and
$0.0\leqslant {\it\alpha}\leqslant 5.0$
.
Figure 7. Flow past a rotating cylinder for
$\mathit{Re}=200$
: variation of maximum growth rate,
${\it\lambda}_{r_{max}}$
, with rotation rate,
${\it\alpha}$
, of different modes for
$0.0\leqslant {\it\alpha}\leqslant 5.0$
. Maximum growth rate is the growth rate associated with the characteristic wavenumber,
${\it\beta}_{c}$
. For clarity, only the unstable modes are shown.
5.1. The unstable eigenmodes
For the flow past a rotating cylinder at
$\mathit{Re}=200$
, SSII exists for
$4.8\leqslant {\it\alpha}\leqslant 5.0$
(Mittal & Kumar Reference Mittal and Kumar2003). Meena (Reference Meena2011), Meena et al. (Reference Meena, Sidharth, Khan and Mittal2011) and Rao et al. (Reference Rao, Leontini, Thompson and Hourigan2013b
, Reference Rao, Radi, Leontini, Thompson, Sheridan and Hourigan2014) demonstrated by linear stability analysis that SSII is stable for the entire regime. Therefore, the instability of the flow, if any, is completely determined by SSI. In this section, the linear stability of SSI is investigated for
$\mathit{Re}=200$
and
$0.0\leqslant {\it\alpha}\leqslant 5.0$
. Figure 7 shows the variation of maximum growth rate,
${\it\lambda}_{r_{max}}$
, of different modes with
${\it\alpha}$
. For a non-rotating cylinder (
${\it\alpha}=0.0$
), three modes of instability are found: mode E (Rao et al.
Reference Rao, Radi, Leontini, Thompson, Sheridan and Hourigan2014), primary wake (PW) mode and secondary wake (SW) mode. The nomenclature for the latter two has been adopted from Verma & Mittal (Reference Verma and Mittal2011). The PW and SW modes are associated with complex eigenvalues. The PW mode has the largest growth rate. This instability exists for
$0.0\leqslant {\it\alpha}\leqslant 1.91$
. The instabilities associated with the SW mode exist for
${\it\alpha}\leqslant 1.1$
. Figure 8 shows the variation of growth rate of modes PW, SW and E with
${\it\beta}$
for
${\it\alpha}=1.0$
. The growth rate of the PW and SW modes is highest for 2D perturbations (
${\it\beta}=0.0$
). With increase in
${\it\beta}$
, the growth rates of both modes decrease. It should be pointed out that the mode A instability, which exists for
$0.0\leqslant {\it\alpha}\leqslant 0.5$
(Rao et al.
Reference Rao, Leontini, Thompson and Hourigan2013a
), is obtained from Floquet analysis of the unsteady base flow. Therefore, it does not show up in the present stability analysis. The isosurfaces of spanwise vorticity of modes PW, SW and E for
${\it\beta}=0.2$
are shown in figure 9. The span of the cylinder is chosen to display exactly one wavelength of the eigenmode. All three modes are dominant in the downstream wake of the cylinder. The PW and SW modes consist of a train of vortices of alternate signs. As shown in figure 7, SSI is stable to all infinitesimal perturbations for
$1.91<{\it\alpha}<3.01$
. Mode E becomes unstable for
$0.0\leqslant {\it\alpha}\leqslant 1.91$
and
$3.01\leqslant {\it\alpha}\leqslant 5.0$
(Meena Reference Meena2011; Meena et al.
Reference Meena, Sidharth, Khan and Mittal2011; Rao et al.
Reference Rao, Leontini, Thompson and Hourigan2013b
, Reference Rao, Radi, Leontini, Thompson, Sheridan and Hourigan2014). For
$\mathit{Re}=200$
, mode H instability exists for
$4.35\leqslant {\it\alpha}\leqslant 5.0$
. Figure 10 shows isosurfaces of the spanwise component of vorticity for
${\it\alpha}=4.5$
of eigenmodes belonging to mode H. Modes I and J become unstable beyond
${\it\alpha}=4.8$
.
Figure 8. Flow past a rotating cylinder for
$(\mathit{Re},{\it\alpha})=(200,1.0)$
: variation of (a) growth rate and (b) frequency with wavenumber of modes PW, SW and E. Among them, the PW and SW modes are complex, while mode E is a real mode.
Figure 9. Flow past a rotating cylinder for
$(\mathit{Re},{\it\alpha})=(200,1.0)$
: isosurfaces of spanwise vorticity (
${\it\omega}_{z}=\pm 0.5$
) of eigenmodes corresponding to
${\it\beta}=0.2$
for modes (a) PW, (b) SW and (c) E. The span of the cylinder is chosen to display one spanwise wavelength of the eigenmode. The spanwise vorticity field in the
$x{-}y$
plane is shown at the bottom of each figure.
Figure 10. Flow past a rotating cylinder for
$(\mathit{Re},{\it\alpha})=(200,4.5)$
: spanwise component of the vorticity field for eigenmodes corresponding to (a)
${\it\beta}=0.0$
, (b)
${\it\beta}=0.2$
and (c)
${\it\beta}=0.4$
for the mode H instability. The upper row shows the isosurfaces (
${\it\omega}_{z}=\pm 0.5$
) while the lower row shows
${\it\omega}_{z}$
on the
$x{-}z$
plane located at
$y=5.63D$
. The cylinder is out of plane. Its location is indicated in broken lines.
5.2. Oblique vortex shedding
Oblique shedding in flow past a non-rotating cylinder has been reported earlier (Tritton Reference Tritton1971; Berger & Wille Reference Berger and Wille1972; Gerich & Eckelmann Reference Gerich and Eckelmann1982; Williamson Reference Williamson1989). The obliqueness of the vortices to the axis of the cylinder has been attributed to the end conditions. It is possible to manipulate the end conditions to promote parallel shedding where vortices are aligned with the axis of the cylinder. Mittal & Sidharth (Reference Mittal and Sidharth2013) showed that both parallel and oblique vortex shedding are a consequence of linearly unstable eigenmodes of SSI. They showed that parallel vortex shedding is a special case of oblique vortex shedding with
${\it\beta}=0.0$
. They carried out computations for a cylinder with finite span but periodic boundary conditions at the endwalls for the flow at
$\mathit{Re}=100$
. If the computations are initiated with an oblique eigenmode (
${\it\beta}\neq 0.0$
), the flow achieves a state where oblique vortices are shed. On the other hand, if the computations are initiated with the eigenmode corresponding to
${\it\beta}=0.0$
, the flow settles into a state of parallel vortex shedding.
We carried out DNS at
$\mathit{Re}=200$
for
${\it\alpha}=0.0$
and
${\it\alpha}=0.5$
. The computations are initiated with SSI superimposed with perturbations corresponding to the PW mode with
${\it\beta}=0.4$
. Periodic boundary conditions are employed on the endwalls enclosing the span of the cylinder. It is observed that in both cases the vortices are shed at an oblique angle. Figure 11 shows the spanwise vorticity of the initial and fully developed disturbance field. It is found that the inclination of shed vortices increases, while the vortex shedding frequency decreases when the computations are initiated with eigenmode with increased
${\it\beta}$
. This shows that for
${\it\beta}\neq 0.0$
the eigenmodes belonging to the PW mode are oblique.
Figure 11. DNS of the flow past a cylinder for
$\mathit{Re}=200$
: initial (left column) and the fully developed (right column) spanwise vorticity field (
${\it\omega}_{z}=\pm 0.5$
) of the disturbance for the unsteady flow for (a)
${\it\alpha}=0.0$
and (b)
${\it\alpha}=0.5$
. The computations are initiated with an oblique PW mode (
${\it\beta}=0.4$
). The span of the cylinder is chosen to fit one spanwise wavelength of the oblique mode. The direction of the flow is indicated by the arrow.
The spanwise vorticity field of mode H as shown in figure 12 consists of rows of vortices of alternate signs. The wake structure is similar to that of the PW mode except for an upward deflection caused by higher rotation rate. Hence, it is expected that the growth of the mode H instability with non-zero
${\it\beta}$
will also lead to oblique shedding of vortices, at least in the early stages of flow development. To test this hypothesis, we carried out DNS for
$(\mathit{Re},{\it\alpha})=(200,4.5)$
. The computations are initiated with SSI superimposed with eigenmodes for
${\it\beta}=0.0$
and 0.2. Figure 12 shows the spanwise vorticity field of the disturbance field at two time instants. While the
${\it\beta}=0.0$
eigenmode leads to parallel vortex shedding, oblique vortex shedding is observed for computations initiated with eigenmodes corresponding to non-zero
${\it\beta}$
. As has been shown earlier for non-rotating cylinder (Williamson Reference Williamson1989; Mittal & Sidharth Reference Mittal and Sidharth2013), the present work shows that, for the rotating cylinder as well, parallel shedding is a special case of oblique shedding and both modes of shedding are intrinsic to the flow. The eigenvalues associated with mode E are real. Hence, mode E instability will lead the flow away from SSI to a 3D steady state. As such, the growth of mode E instability alone will not result in either parallel or oblique shedding. However, in the presence of other instabilities, the modes are expected to interact and modify the fully developed flow. This is investigated in the next section.
Figure 12. DNS of the flow past a rotating cylinder for
$(\mathit{Re},{\it\alpha})=(200,4.5)$
: spanwise vorticity field (
${\it\omega}_{z}=\pm 0.5$
) of the disturbance for the computations initiated with mode H corresponding to (a)
${\it\beta}=0.0$
(parallel mode) and (b)
${\it\beta}=0.2$
(oblique mode). The direction of the flow is indicated by the arrow.
Figure 13. Flow past a rotating cylinder for
$(\mathit{Re},{\it\alpha})=(200,3.5)$
. (a) Variation of growth rate, with spanwise wavelength. Shown in the inset are isosurfaces of spanwise vorticity (
${\it\omega}_{z}=\pm 0.5$
) of mode E with
${\it\beta}=9.0$
, 4.5 and 2.25. (b) Time histories of lift coefficient of the fully developed flow for a cylinder of three span lengths. (c–e) The isosurfaces of spanwise vorticity (
${\it\omega}_{z}=\pm 0.5$
) for different spans at time instants marked in (b) with solid black squares for (c)
$L_{z}=0.7D$
, (d)
$L_{z}=1.4D$
and (e)
$L_{z}=2.8D$
.
5.3. Interaction between various unstable eigenmodes: effect of span
5.3.1. Rotation rate
${\it\alpha}=3.5$
: unsteady flow due to co-operation of various real eigenmodes
Figure 13(a) shows the variation of growth rate with
${\it\lambda}_{z}/D$
of the mode E instability for
${\it\alpha}=3.5$
. As shown in figure 7, mode E is the only unstable mode for
$(\mathit{Re},{\it\alpha})=(200,3.5)$
. We carry out DNS for three span lengths of the cylinder:
$L_{z}=0.7D$
,
$1.4D$
and
$2.8D$
. The computations are initialized with steady state computed for
${\it\alpha}=3.5$
superimposed with the perturbation corresponding to
${\it\beta}=9.0$
(
${\it\lambda}_{z}/D=0.7$
). We recall that mode E corresponds to a real eigenvalue/eigenmode. The maximum growth rate is for the eigenmode with
${\it\beta}=7.0$
(
${\it\lambda}_{z}/D=0.9$
). For a cylinder with
$L_{z}/D=0.7$
, as seen from figure 13(a), the only unstable eigenmode that conforms to this span is the one with
${\it\beta}=9.0$
(
${\it\lambda}_{z}/D=0.7$
). Indeed, the fully developed solution for this geometry achieves a steady state and exhibits instability with spanwise wavelength of
$0.7D$
. Figure 13(b) shows that
$C_{L}$
is constant in time, confirming the attainment of a steady state. The case of a cylinder with
$L_{z}/D=1.4$
is more interesting. The eigenmodes corresponding to
${\it\beta}=9.0$
(
${\it\lambda}_{z}/D=0.7$
) and
${\it\beta}=4.5$
(
${\it\lambda}_{z}/D=1.4$
) are the two possible unstable eigenmodes for this span. While two wavelengths of the former can fit the span, only one wavelength of the eigenmode corresponding to
${\it\beta}=4.5$
spans the length of the cylinder. Both eigenmodes are associated with identical growth rates. The fully developed flow for this situation is a time-periodic flow, as exhibited by the time history of the lift coefficient shown in figure 13(b). The flow oscillates between the two states, with the spanwise wavelength of the instability as
$0.7D$
and
$1.4D$
. For
$L_{z}/D=2.8$
, three unstable eigenmodes can fit the span,
${\it\beta}=9.0$
, 4.5 and 2.25 (
${\it\lambda}_{z}/D=0.7$
, 1.4 and 2.8). Their evolution leads to an aperiodic flow, though the wavelength of the spanwise instabilities is still governed by the two dominant eigenmodes. A larger span can accommodate more unstable wavelengths and is expected to lead to an aperiodic solution as a result of the competition between them. However, the most dominant mode is expected to be the one with the largest growth rate. These computations demonstrate the significant role of the span of the cylinder in determining the state of the flow.
5.3.2. Rotation rate
${\it\alpha}=4.5$
: interaction between modes E and H
Figure 14(a) shows the variation of the non-dimensional frequency and growth rate with
${\it\beta}$
of modes E and H for
${\it\alpha}=4.5$
. For
$(\mathit{Re},{\it\alpha})=(200,4.5)$
, modes E and H are unstable (figure 7) for
${\it\alpha}=4.5$
. While mode H is unstable for
${\it\beta}\leqslant 0.4$
(
${\it\lambda}_{z}/D\geqslant 15.71$
), mode E is unstable for
$0.6\leqslant {\it\beta}\leqslant 7.5$
(
$0.84\leqslant {\it\lambda}_{z}/D\leqslant 10.47$
). For a cylinder with span
$L_{z}/D<0.84$
, only the
${\it\beta}=0.0$
eigenmode from mode H is expected to be active. Indeed, for the 2D simulation, as well as for
$L_{z}/D=0.8$
, a low-frequency vortex shedding is observed. In the latter case, the flow is 2D and devoid of any spanwise instabilities. The mode E instability achieves the highest growth rate for
${\it\beta}=2.4$
(
${\it\lambda}_{z}/D=2.62$
). A simulation is carried out for a cylinder with span
$L_{z}/D=2.62$
. The computations are initiated with steady state for
${\it\alpha}=4.5$
, superimposed with the
${\it\beta}=2.4$
eigenmode belonging to mode E. From figure 14(a) we infer that the wavenumber of the unstable eigenmodes that can fit this span length are
${\it\beta}=0$
, 2.4, 4.8 and 7.2. The time history of the lift coefficient as well as the isosurfaces for the spanwise component of the instantaneous vorticity are shown in figure 14(b,c). The vortex shedding as well as the spanwise instabilities, which are speculated to be centrifugal in nature, coexist. The spanwise wavelength of the centrifugal instability is
$2.62D$
, which is reminiscent of the
${\it\beta}=2.4$
eigenmode. We note that mode II shedding is also present despite the growth rate of mode H being lower than that of the modes causing centrifugal instability. It is found that, as the span of the spinning cylinder is increased, the flow becomes increasingly aperiodic and complex. This is due to participation of many more unstable eigenmodes and their nonlinear interactions. The flow at
$L_{z}/D=12$
, as shown in figure 14, is one such example. Recently, Radi et al. (Reference Radi, Thompson, Rao, Hourigan and Sheridan2013) presented experimental results for
$(\mathit{Re},{\it\alpha})=(100,5.1)$
. Their preliminary investigations with a cylinder of large aspect ratio (
$L_{z}/D\sim 137$
) show that the one-sided shedding process is localized and does not occur uniformly throughout the span of the cylinder. Our results from DNS carried out on a cylinder of aspect ratio
$L_{z}/D=12$
(figure 14) agree with their observations. This is discussed further in § 5.5.
Figure 14. Flow past a rotating cylinder for
$(\mathit{Re},{\it\alpha})=(200,4.5)$
. (a) Variation of the frequency and growth rate for mode H with
${\it\beta}$
. (b) Time histories of lift coefficient of the fully developed flow obtained from direct time integrations carried out for three span lengths of the cylinder. For comparison, the result from a 2D simulation is also shown. (c) The isosurfaces of spanwise vorticity (
${\it\omega}_{z}=\pm 0.5$
), close to the instant when the lift coefficient reaches its peak value. These time instants are marked with solid squares in (b). The direction of the free-stream flow is indicated by the arrow. For the 2D computations,
${\it\omega}_{z}$
in the
$x{-}y$
plane is shown.
5.4. Solution is stable for
$4.8\leqslant {\it\alpha}\leqslant 5.0$
For
$\mathit{Re}=200$
two steady states exist for
$4.8\leqslant {\it\alpha}\leqslant 5.0$
(Mittal & Kumar Reference Mittal and Kumar2003). SSI is linearly unstable via modes E, H, I and J. On the other hand, SSII is stable to infinitesimal perturbations (Mittal & Kumar Reference Mittal and Kumar2003; Rao et al.
Reference Rao, Leontini, Thompson and Hourigan2013b
, Reference Rao, Radi, Leontini, Thompson, Sheridan and Hourigan2014). Using 2D computations, Mittal & Kumar (Reference Mittal and Kumar2003) reported that the direct time integration of the flow at
$\mathit{Re}=200$
and
$4.8\leqslant {\it\alpha}\leqslant 5.0$
leads to SSII. In this work, we present results from 3D DNS for
${\it\alpha}=5.0$
. The computations are initiated with SSI superimposed with the mode E perturbation corresponding to
${\it\beta}_{c}$
. The span of the cylinder is chosen to fit exactly one wavelength of the eigenmode. The initial perturbation as well as its evolution is shown in figure 15. Eventually, the flow settles to SSII. Computations have been carried out with various other initial conditions. In all cases, the flow achieves SSII. We therefore conclude that the flow for
${\it\alpha}\geqslant 4.8$
is devoid of instabilities and achieves a steady state. The effect of end conditions is expected to be significant (Mittal Reference Mittal2004) and has not been investigated in the present study.
Figure 15. Flow past a rotating cylinder for
$(\mathit{Re},{\it\alpha})=(200,5.0)$
. (a) Initial conditions; SSI is superimposed with the eigenmode belonging to mode E with
${\it\beta}=0.8$
. (b) Time history of the lift coefficient during flow evolution. (c) Isosurfaces of spanwise vorticity (
${\it\omega}_{z}=\pm 0.5$
) at different instants marked in time history (solid squares). The direction of the free-stream flow is indicated by the arrow.
Figure 16. Flow past a rotating cylinder for
$\mathit{Re}=200$
: time histories of lift coefficient for various rotation rates. Results from 3D computations are shown in solid lines. For comparison, results from 2D simulation (Mittal & Kumar Reference Mittal and Kumar2003) are also shown in broken lines.
Figure 17. Flow past a rotating cylinder for
$\mathit{Re}=200$
. Isosurfaces (left) of the spanwise component of vorticity (
${\it\omega}_{z}=\pm 0.5$
) at instants marked by the filled square in figure 16. Also shown (right) is the variation of the spanwise component of the velocity at
$(x/D,y/D)=(0,0.75)$
along the span. For
${\it\alpha}=3.0$
and 5.0, the fully developed flow achieves a 2D state. The cylinder axis is along the broken line. The direction of the free-stream flow is indicated by the arrow.
5.5. Direct numerical simulation
$(L_{z}/D=12,~0.0\leqslant {\it\alpha}\leqslant 5.0)$
Three-dimensional simulations are carried out for a cylinder of span
$L_{z}/D=12$
with no-slip condition on the side boundaries. Mittal & Kumar (Reference Mittal and Kumar2003), from 2D computations, found that the flow at
$\mathit{Re}=200$
is steady for
$1.91\leqslant {\it\alpha}\leqslant 4.34$
and
$4.8\leqslant {\it\alpha}\leqslant 5.0$
. Kármán shedding is observed for
${\it\alpha}<1.91$
while mode II shedding occurs for
$4.35\leqslant {\it\alpha}\leqslant 4.7$
. In accordance with earlier studies, the present computations show a Kármán vortex street, along with the mode A instability for
${\it\alpha}<0.5$
. The 2D and 3D computations yield identical results for
$0.5\leqslant {\it\alpha}\leqslant 3.0$
. Figure 16 shows the time histories of the lift coefficient for
$3.0\leqslant {\it\alpha}\leqslant 5.0$
. For comparison, the lift coefficient from 2D computations are shown as well. The isosurfaces of spanwise vorticity and the variation of the spanwise component of velocity along the span, for the fully developed flow, are shown in figure 17. The flow achieves SSI for
${\it\alpha}=3.0$
. This is consistent with the results from linear stability analysis, as shown in figure 7. For
${\it\alpha}=3.5$
, spanwise instabilities are observed in the near wake. Their appearance is attributed to the mode E instability. The flow structures are stationary and do not change significantly with time. The spanwise wavelength of the instability is
$1.2D$
approximately. This is estimated by counting the number of cycles in the variation of spanwise component of velocity (figure 17) recorded at
$(x/D,y/D)=(0,0.75)$
. Although there is no vortex shedding, small fluctuations in the time histories of the force coefficients are observed. This is due to the interactions among eigenmodes of different wavelengths. The flow at
${\it\alpha}=4.0$
is associated with stronger spanwise instabilities. This is evident from larger variations in the spanwise component of velocity along the span. The spanwise wavelength of the instability is
$2D$
, approximately. The downstream wake of the cylinder is unsteady. The unsteadiness is due to the interaction among various unstable eigenmodes of mode E. At
${\it\alpha}=4.5$
, aperiodic vortex shedding with spanwise instabilities is observed. In contrast, the 2D flow is periodic. Linear stability analysis predicts the existence of mode H and E instability for
${\it\alpha}=4.5$
. Both these modes are dominant in the vicinity of the cylinder as well as the near wake. The spanwise wavelength of the instability changes continuously along the span with time. This may be attributed to localized shedding of vortices (Radi et al.
Reference Radi, Thompson, Rao, Hourigan and Sheridan2013). It is observed that, for
$3.0\leqslant {\it\alpha}\leqslant 4.7$
, the complexity of the flow, at least in the near wake, increases with increasing
${\it\alpha}$
. This is reflected in the difference in the time histories of the lift coefficient obtained from 2D and 3D simulations. The flow at
${\it\alpha}=5.0$
is devoid of any instabilities and a 2D steady state is achieved. It corresponds to SSII. Simulations were carried out for
${\it\alpha}=5.0$
with different initial conditions, including a case where computations are initiated with SSI. In all cases the flow eventually settled to SSII.
6. Conclusions
The flow past a rotating cylinder is investigated via linear stability analysis and DNS. Building upon existing knowledge (Mittal & Kumar Reference Mittal and Kumar2003; Meena et al.
Reference Meena, Sidharth, Khan and Mittal2011; Rao et al.
Reference Rao, Leontini, Thompson and Hourigan2013a
,Reference Rao, Leontini, Thompson and Hourigan
b
, Reference Rao, Radi, Leontini, Thompson, Sheridan and Hourigan2014), several new modes of instability are found: H, I, J and K. Modes H, J and K are complex, while mode I is a real mode. The frequency,
${\it\lambda}_{i}$
, of mode H decreases with increasing
${\it\beta}$
till
${\it\lambda}_{i}$
becomes equal to zero. Beyond this value of
${\it\beta}$
, mode H bifurcates into two real modes: mode E and mode I. The growth rate of mode I decreases with further increase in
${\it\beta}$
. The regions of large perturbation associated with modes I and J indicate that these modes may be associated with hyperbolic instability. The structure of mode K suggests that this mode is associated with hyperbolic as well as centrifugal instability. A summary of the characteristics of various modes is presented in table 1.
Figure 18. Flow past a rotating cylinder for
$(\mathit{Re},{\it\alpha})=(350,4.7)$
: effect of mesh resolution on the variation of (a) growth rate and (b) frequency with wavenumber for different modes. Meshes M1, M2 and M3 consist of 16 310, 33 795 and 50 440 nodes, respectively.
Table 1. Summary of the modes showing the nature of eigenvalue (
${\it\lambda}$
) and characteristic wavenumber for
$200\leqslant \mathit{Re}\leqslant 350$
and
$0.0\leqslant {\it\alpha}\leqslant 5.0$
. The characteristic wavenumber of mode I depends strongly on Reynolds number and rotation rate.
A detailed analysis is carried out for
$\mathit{Re}=200$
to understand the evolution of 3D perturbations. Three modes of instability are reported for
$0.0\leqslant {\it\alpha}\leqslant 1.91$
. The PW and SW modes are associated with complex eigenvalues, while mode E is associated with real eigenvalues. The growth rates of the PW and SW modes decrease with increasing
${\it\beta}$
. For
${\it\beta}\neq 0.0$
, the eigenmodes belonging to PW and SW modes are oblique. It is found that the rotation of the cylinder quenches the instabilities associated with the modes PW, SW and E beyond
${\it\alpha}=1.91$
. Mode E instability reappears for
$3.01\leqslant {\it\alpha}\leqslant 5.0$
. The instabilities associated with mode H exist for
$4.8\leqslant {\it\alpha}\leqslant 5.0$
. The
${\it\beta}=0.0$
eigenmode belonging to mode H is most unstable. DNS shows that the evolution of unstable eigenmodes belonging to mode H with
${\it\beta}\neq 0.0$
leads to oblique shedding of vortices in the early stages of flow development. It is found that the span of the spinning cylinder plays a significant role in the selection of eigenmodes in the early stages of the flow development, and subsequently on the fully developed flow. In certain regimes, the span of the cylinder decides whether the flow achieves a steady, temporally periodic or aperiodic state. For
$4.8\leqslant {\it\alpha}\leqslant 5.0$
, two steady states exist: SSI and SSII. SSI is associated with unstable eigenmodes, while SSII is stable to all perturbations. It is found that, in this regime, irrespective of the initial perturbations, the flow achieves the state SSII.
Acknowledgements
The authors are grateful to Computer Center, Indian Institute of Technology Kanpur, India, for making available the High Performance Computing Facility that is set up with assistance from DST, India. The authors also acknowledge the use of computational resources at the Center for Development of Advanced Computing (CDAC), Pune, India, and computer time from the City University of New York High Performance Computing Center under NSF grants CNS-0855217, CNS-0958379 and ACI-1126113.
Appendix A. Mesh convergence
Computations have been carried out over a wide range of parameter space (
$200\leqslant \mathit{Re}\leqslant 350$
,
$0.0\leqslant {\it\alpha}\leqslant 5.0$
,
$0.0\leqslant {\it\beta}\leqslant 30.0$
). Various flow regimes have been identified. To adequately resolve the flow structures in different flow regimes, while still keeping the computational expenses as low as possible, the performance of various finite element meshes have been examined. We present the performance of three meshes M1, M2 and M3. Mesh M1 is the coarsest among the three and consists of 16 310 nodes. Meshes M2 and M3 contain 33 795 and 50 440 nodes, respectively. The computational domain as well as the structure of the mesh is identical in all cases. The difference is mostly in the density of grid points close to the cylinder. Several values of (
$\mathit{Re},{\it\alpha}$
) were considered for the mesh convergence study. Table 2 shows the effect of spatial resolution on the aerodynamic coefficients computed for the two steady states at
$(\mathit{Re},{\it\alpha})=(350,4.7)$
. The results computed using all three meshes are in very good agreement. Among all the quantities, the drag coefficient of SSI is most sensitive to the mesh resolution. While the difference between the results from M1 and M3 is 3.7 %, the difference between M2 and M3 is 1.8 %.
Table 2. Steady flow past a rotating cylinder for
$(\mathit{Re},{\it\alpha})=(350,4.7)$
: effect of mesh resolution on aerodynamic coefficients. Meshes M1, M2 and M3 consist of 16 310, 33 795 and 50 440 nodes, respectively.
Table 3. Flow past a rotating cylinder for
$(\mathit{Re},{\it\alpha})=(350,4.7)$
: effect of mesh resolution on the rightmost eigenvalue of different modes. Meshes M1, M2 and M3 consist of 16 310, 33 795 and 50 440 nodes, respectively.
Table 4. Flow past a rotating cylinder for
$(\mathit{Re},{\it\alpha})=(200,4.9)$
: effect of mesh resolution on the rightmost eigenvalue of different modes. Only unstable modes are reported. Meshes M1 and M2 consist of 16 310 and 33 795 nodes, respectively.
Figure 19. Flow past a rotating cylinder for
$(\mathit{Re},{\it\alpha})=(200,4.9)$
: effect of mesh resolution on the variation of (a) growth rate and (b) frequency with wavenumber for different modes. Meshes M1 and M2 consist of 16 310 and 33 795 nodes, respectively.
Figure 20. Flow past a rotating cylinder for
$(\mathit{Re},{\it\alpha})=(200,1.0)$
: effect of mesh resolution on the variation of (a) growth rate and (b) frequency with wavenumber for different modes. Meshes M1 and M2 consist of 16 310 and 33 795 nodes, respectively.
Figure 18 shows the effect of spatial resolution on the growth rate and frequency from linear stability analysis for
$(\mathit{Re},{\it\alpha})=(350,4.7)$
. Table 3 presents a comparison of the eigenvalues with largest real part for each of the modes that have been identified. The results with meshes M2 and M3 are in very good agreement. The maximum difference (
$0.7\,\%$
) between the results from the two is for mode F. In view of the difference being small enough, mesh M2 is employed for all the computations for
$\mathit{Re}>200$
.
Table 5. Flow past a rotating cylinder for
$(\mathit{Re},{\it\alpha})=(200,1.0)$
: effect of mesh resolution on the rightmost eigenvalue of different modes. Only unstable modes are reported. Meshes M1 and M2 consist of 16 310 and 33 795 nodes, respectively.
For the flow at
$\mathit{Re}=200$
, the mesh convergence study is carried out for various values of rotation rates (
$0.0\leqslant {\it\alpha}\leqslant 5.0$
). The results are presented for computations carried out on meshes M1 and M2. For
${\it\alpha}\leqslant 1.91$
, the various modes that are unstable are PW, SW and E. Figure 20 shows the effect of spatial resolution on the growth rate and frequency for
$(\mathit{Re},{\it\alpha})=(200,1.0)$
. Table 4 compares the eigenvalues for the modes with largest growth rate. Very good agreement is obtained in the two cases. The error in the growth rate is within 2 %. For large rotation rates (
$2.0\leqslant {\it\alpha}\leqslant 5.0$
), the steady state can become unstable via modes E, H, I and J. The variation of growth rate and frequency with spanwise wavenumber of these modes is shown in figure 19. The eigenvalues corresponding to the most unstable eigenmode is shown in table 5. The results differ within 1 %. Therefore, mesh M1 is used for all the computations for
$\mathit{Re}=200$
.
