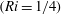1 Introduction
This study contributes to the discussion of the origin of thermohaline staircases in high-latitude regions of the World Ocean. The term thermohaline staircase describes a series of mixed layers separated by thin high-gradient interfaces, commonly observed in vertical profiles of temperature and salinity. Staircases in the Arctic and Southern Oceans are typically diffusive, with warm salty water masses located below those that are relatively cold and fresh. Diffusive staircases often exhibit remarkable spatial and temporal coherence. For instance, layers of the Beaufort Gyre staircase in the Arctic Ocean maintain their identity across hundreds of kilometres laterally and over several years of observation (e.g. Timmermans et al. Reference Timmermans, Toole, Krishfield and Winsor2008).
Despite the profound importance of staircases for high-latitude ocean dynamics (Turner Reference Turner2010; Flanagan, Lefler & Radko Reference Flanagan, Lefler and Radko2013), the physical cause of diffusive layering has not been fully explained (Kelley et al. Reference Kelley, Fernando, Gargett, Tanny and Ozsoy2003; Radko Reference Radko2013). It is generally accepted that staircases are ultimately produced and maintained by double-diffusive processes. A major challenge in the development of a complete theory of high-latitude staircases is to explain the initiation of layering and diffusive convection from smooth original distributions of temperature and salinity. The parameter range for diffusive instability in the ocean is extremely narrow (e.g. Walin Reference Walin1964; Veronis Reference Veronis1965):
where
![]() $R_{\unicode[STIX]{x1D70C}}$
is the diffusive density ratio, i.e. the ratio of vertical gradients of temperature and salinity, normalized by the expansion/contraction coefficients,
$R_{\unicode[STIX]{x1D70C}}$
is the diffusive density ratio, i.e. the ratio of vertical gradients of temperature and salinity, normalized by the expansion/contraction coefficients,
![]() $\unicode[STIX]{x1D70F}=k_{S}/k_{T}$
is the diffusivity ratio and
$\unicode[STIX]{x1D70F}=k_{S}/k_{T}$
is the diffusivity ratio and
![]() $Pr=\unicode[STIX]{x1D708}/k_{T}$
is the Prandtl number. Here,
$Pr=\unicode[STIX]{x1D708}/k_{T}$
is the Prandtl number. Here,
![]() $k_{T}$
and
$k_{T}$
and
![]() $k_{S}$
are the molecular diffusivities of temperature and salinity, and
$k_{S}$
are the molecular diffusivities of temperature and salinity, and
![]() $\unicode[STIX]{x1D708}$
is the molecular viscosity. For oceanic parameters
$\unicode[STIX]{x1D708}$
is the molecular viscosity. For oceanic parameters
![]() $(\unicode[STIX]{x1D70F}\sim 0.01,Pr\sim 10)$
, condition (1.1) reduces to
$(\unicode[STIX]{x1D70F}\sim 0.01,Pr\sim 10)$
, condition (1.1) reduces to
![]() $1<R_{\unicode[STIX]{x1D70C}}<1.1$
, and this interval lies outside the density ratio range typical for oceanic diffusive staircases
$1<R_{\unicode[STIX]{x1D70C}}<1.1$
, and this interval lies outside the density ratio range typical for oceanic diffusive staircases
![]() $(1.5<R_{\unicode[STIX]{x1D70C}}<10)$
. The typical internal wave energy and associated vertical shears in the Arctic at the staircase depth range (150–300 m) are also weak (e.g. Levine, Paulson & Morison Reference Levine, Paulson and Morison1985; Halle & Pinkel Reference Halle and Pinkel2003; Cole et al.
Reference Cole, Timmermans, Toole, Krishfield and Thwaites2014). As a result, the representative values of the Richardson number
$(1.5<R_{\unicode[STIX]{x1D70C}}<10)$
. The typical internal wave energy and associated vertical shears in the Arctic at the staircase depth range (150–300 m) are also weak (e.g. Levine, Paulson & Morison Reference Levine, Paulson and Morison1985; Halle & Pinkel Reference Halle and Pinkel2003; Cole et al.
Reference Cole, Timmermans, Toole, Krishfield and Thwaites2014). As a result, the representative values of the Richardson number
![]() $(Ri)$
, the measure of flow susceptibility to dynamic instability, are high
$(Ri)$
, the measure of flow susceptibility to dynamic instability, are high
![]() $(Ri\sim 10)$
, substantially exceeding the threshold value of
$(Ri\sim 10)$
, substantially exceeding the threshold value of
![]() $Ri=1/4$
required for dynamic instability. Hence, the background stratification is generally stable with respect to both primary diffusive and dynamic instabilities.
$Ri=1/4$
required for dynamic instability. Hence, the background stratification is generally stable with respect to both primary diffusive and dynamic instabilities.
To rationalize the propensity for layering in stably stratified waters, several hypotheses have been proposed. The applied flux mechanism (Turner & Stommel Reference Turner and Stommel1964; Kelley et al. Reference Kelley, Fernando, Gargett, Tanny and Ozsoy2003) assumes the presence of an external source of buoyancy (e.g. heating from below or, equivalently, cooling from above) which is sufficiently strong to produce top-heavy stratification in the immediate vicinity of the forcing region. The ensuing localized convection creates a well-mixed region and concurrently transfers buoyancy vertically, leading to the formation of an adjacent convecting layer. The process then repeats several times, eventually producing a multilayer staircase. The proposed scenario is actually realized in laboratory experiments, in which a staircase is created by heating the bottom of a tank filled with doubly stratified fluid (Turner & Stommel Reference Turner and Stommel1964; Fernando Reference Fernando1987). However, in the ocean interior, outside of geothermal heating zones and the subsurface mixed layer, buoyancy forcing is too weak and lacks sufficient variation with depth to consistently generate large-scale convective overturns.
Stern (Reference Stern2003) suggested that the transition from the smooth-gradient regime to the staircase configuration in a stable halocline could be initiated by lateral molecularly-driven interleaving (Holyer Reference Holyer1983), which, in turn, is contingent on the presence of horizontal temperature and salinity (
![]() $T$
–
$T$
–
![]() $S$
) gradients. What casts some doubt on the generality of this mechanism is that staircases exist throughout the Arctic diffusive zone and no correlation has been reported between the incidences of layering and the strength of lateral isopycnal gradients. Another possible pathway to thermohaline layering stems from the tendency of diffusive systems to be destabilized by fundamentally nonlinear processes (Veronis Reference Veronis1965). While Veronis’ effect undoubtedly plays a role in the transition to fully developed diffusive convection, it requires large-amplitude perturbations of unspecified origin. Thus, a complete and satisfying explanation of layering calls for some additional dynamical considerations. Furthermore, simulations in our study indicate that staircases can form spontaneously even in the absence of lateral property gradients, large-amplitude initial disturbances or external heating, which suggests that none of the aforementioned phenomena are essential for diffusive layering.
$S$
) gradients. What casts some doubt on the generality of this mechanism is that staircases exist throughout the Arctic diffusive zone and no correlation has been reported between the incidences of layering and the strength of lateral isopycnal gradients. Another possible pathway to thermohaline layering stems from the tendency of diffusive systems to be destabilized by fundamentally nonlinear processes (Veronis Reference Veronis1965). While Veronis’ effect undoubtedly plays a role in the transition to fully developed diffusive convection, it requires large-amplitude perturbations of unspecified origin. Thus, a complete and satisfying explanation of layering calls for some additional dynamical considerations. Furthermore, simulations in our study indicate that staircases can form spontaneously even in the absence of lateral property gradients, large-amplitude initial disturbances or external heating, which suggests that none of the aforementioned phenomena are essential for diffusive layering.
This paper argues for adding a new candidate to the list. We point out that even when a two-component flow is stable with respect to dynamic and diffusive instabilities individually, it may become unstable due to the interplay between shear and thermohaline effects. This conclusion is supported by a Floquet-based stability analysis for a sinusoidal velocity profile in a fluid linearly stratified in the diffusive sense. The growth rates and stability conditions are shown to be highly sensitive to the diffusivity ratio of the density components. Direct numerical simulations (DNS) indicate that the combined thermohaline–shear instabilities can indeed trigger the transition of uniformly stratified systems to well-defined staircases. In this regard, it is interesting to mention that strong large-scale shears can have adverse effects on the coherence and persistence of thermohaline staircases (e.g. Bebieva & Timmermans Reference Bebieva and Timmermans2016). Yet, somewhat counterintuitively, the vertical shear could also be essential for their generation.
Of course, destabilization driven by buoyancy diffusion is a known phenomenon which can occur even in one-component flows (e.g. Balmforth & Young Reference Balmforth and Young2002; Radko & Stern Reference Radko and Stern2011; Thorpe, Smyth & Li Reference Thorpe, Smyth and Li2013). However, in non-double-diffusive models, this effect is modest. It affects only a relatively narrow parameter range
![]() $(Ri\lesssim 1)$
and does not lead to the formation of persistent staircases. The growth rates in this extended range are much lower than those typical of Kelvin–Helmholtz instability. In contrast, the double-diffusive case is characterized by the appearance of a fundamentally new and dramatic phenomenon which bears little resemblance to either dynamic or diffusive oscillatory instabilities. Both shear and the unequal diffusivities of density components are essential, and the stability boundary can reach surprisingly high values – for instance, it could be as high as
$(Ri\lesssim 1)$
and does not lead to the formation of persistent staircases. The growth rates in this extended range are much lower than those typical of Kelvin–Helmholtz instability. In contrast, the double-diffusive case is characterized by the appearance of a fundamentally new and dramatic phenomenon which bears little resemblance to either dynamic or diffusive oscillatory instabilities. Both shear and the unequal diffusivities of density components are essential, and the stability boundary can reach surprisingly high values – for instance, it could be as high as
![]() $Ri\sim 10^{3}$
for
$Ri\sim 10^{3}$
for
![]() $R_{\unicode[STIX]{x1D70C}}=2$
. Such unrestrictive conditions are easily met in the Arctic Ocean, which lends credence to our proposition that diffusive layering could be initiated by thermohaline–shear instability.
$R_{\unicode[STIX]{x1D70C}}=2$
. Such unrestrictive conditions are easily met in the Arctic Ocean, which lends credence to our proposition that diffusive layering could be initiated by thermohaline–shear instability.
It is also interesting to note that the origin of salt-finger staircases, in which warm and salty water is located above cold and fresh, has proven to be a simpler and less controversial subject than diffusive layering. Fingering staircases are found in tropical and mid-latitude ocean regions that are already susceptible to primary (salt-finger) instabilities. These microscale perturbations produce vertical fluxes of heat and salt that are modulated by large-scale
![]() $T$
–
$T$
–
![]() $S$
gradients. The interplay between finger-driven fluxes and vertical gradients leads to the spontaneous generation of secondary double-diffusive structures – thermohaline staircases, collective instability waves and intrusions. Plausible theories of finger-driven layering based on the instability of flux-gradient laws have already been developed and numerically validated (Merryfield Reference Merryfield2000; Radko Reference Radko2003; Stellmach et al.
Reference Stellmach, Traxler, Garaud, Brummell and Radko2011; Radko Reference Radko2014). The diffusive problem considered here is very different. The static basic state in this case is linearly stable in the relevant parameter regime, and therefore even the origin of primary perturbations is uncertain.
$S$
gradients. The interplay between finger-driven fluxes and vertical gradients leads to the spontaneous generation of secondary double-diffusive structures – thermohaline staircases, collective instability waves and intrusions. Plausible theories of finger-driven layering based on the instability of flux-gradient laws have already been developed and numerically validated (Merryfield Reference Merryfield2000; Radko Reference Radko2003; Stellmach et al.
Reference Stellmach, Traxler, Garaud, Brummell and Radko2011; Radko Reference Radko2014). The diffusive problem considered here is very different. The static basic state in this case is linearly stable in the relevant parameter regime, and therefore even the origin of primary perturbations is uncertain.
The paper is organized as follows. The model set-up is described in § 2. Section 3 presents numerical evidence for spontaneous layering in shear flows that are dynamically and diffusively stable, suggesting the existence of a new type of instability. This proposition is supported by linear stability analysis based on the Floquet theory (§ 4). In § 5, we discuss the energetics – and offer physical interpretation – of the thermohaline–shear instability. The results are summarized and the conclusions are drawn in § 6.
2 Formulation
The temperature and salinity fields
![]() $(T_{tot}^{\ast },S_{tot}^{\ast })$
are separated into linear vertical background profiles
$(T_{tot}^{\ast },S_{tot}^{\ast })$
are separated into linear vertical background profiles
![]() $(T_{bg}^{\ast },S_{bg}^{\ast })$
and a departure
$(T_{bg}^{\ast },S_{bg}^{\ast })$
and a departure
![]() $(T^{\ast },S^{\ast })$
from them:
$(T^{\ast },S^{\ast })$
from them:
where
![]() $(A_{T},A_{T0},A_{S},A_{S0})$
are constants. The asterisks hereafter denote dimensional quantities and the subscripts ‘
$(A_{T},A_{T0},A_{S},A_{S0})$
are constants. The asterisks hereafter denote dimensional quantities and the subscripts ‘
![]() $tot$
’ represent the total field variables. Our focus is on the diffusive case, in which both temperature and salinity decrease upward:
$tot$
’ represent the total field variables. Our focus is on the diffusive case, in which both temperature and salinity decrease upward:
![]() $\unicode[STIX]{x2202}T_{bg}^{\ast }/\unicode[STIX]{x2202}z^{\ast }=A_{T}<0$
and
$\unicode[STIX]{x2202}T_{bg}^{\ast }/\unicode[STIX]{x2202}z^{\ast }=A_{T}<0$
and
![]() $\unicode[STIX]{x2202}S_{bg}^{\ast }/\unicode[STIX]{x2202}z^{\ast }=A_{S}<0$
. In the present version of the theory, we ignore planetary rotation, compressibility and the nonlinearity of the equation of state, which reduces the governing Boussinesq equations of motion to
$\unicode[STIX]{x2202}S_{bg}^{\ast }/\unicode[STIX]{x2202}z^{\ast }=A_{S}<0$
. In the present version of the theory, we ignore planetary rotation, compressibility and the nonlinearity of the equation of state, which reduces the governing Boussinesq equations of motion to
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \frac{\unicode[STIX]{x2202}T^{\ast }}{\unicode[STIX]{x2202}t^{\ast }}+\boldsymbol{v}_{tot}^{\ast }\boldsymbol{\cdot }\unicode[STIX]{x1D735}T^{\ast }+w_{tot}^{\ast }\frac{\unicode[STIX]{x2202}T_{bg}^{\ast }}{\unicode[STIX]{x2202}z^{\ast }}=k_{T}\unicode[STIX]{x1D6FB}^{2}T^{\ast },\\ \displaystyle \frac{\unicode[STIX]{x2202}S^{\ast }}{\unicode[STIX]{x2202}t^{\ast }}+\boldsymbol{v}_{tot}^{\ast }\boldsymbol{\cdot }\unicode[STIX]{x1D735}S^{\ast }+w_{tot}^{\ast }\frac{\unicode[STIX]{x2202}S_{bg}^{\ast }}{\unicode[STIX]{x2202}z^{\ast }}=k_{S}\unicode[STIX]{x1D6FB}^{2}S^{\ast },\\ \displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{v}_{tot}^{\ast }}{\unicode[STIX]{x2202}t^{\ast }}+\boldsymbol{v}_{tot}^{\ast }\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{v}_{tot}^{\ast }=-\frac{1}{\unicode[STIX]{x1D70C}_{0}}\unicode[STIX]{x1D735}p_{tot}^{\ast }+g(\unicode[STIX]{x1D6FC}T^{\ast }-\unicode[STIX]{x1D6FD}S^{\ast })\boldsymbol{k}+\unicode[STIX]{x1D708}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{v}_{tot}^{\ast },\\ \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{v}_{tot}^{\ast }=0,\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \frac{\unicode[STIX]{x2202}T^{\ast }}{\unicode[STIX]{x2202}t^{\ast }}+\boldsymbol{v}_{tot}^{\ast }\boldsymbol{\cdot }\unicode[STIX]{x1D735}T^{\ast }+w_{tot}^{\ast }\frac{\unicode[STIX]{x2202}T_{bg}^{\ast }}{\unicode[STIX]{x2202}z^{\ast }}=k_{T}\unicode[STIX]{x1D6FB}^{2}T^{\ast },\\ \displaystyle \frac{\unicode[STIX]{x2202}S^{\ast }}{\unicode[STIX]{x2202}t^{\ast }}+\boldsymbol{v}_{tot}^{\ast }\boldsymbol{\cdot }\unicode[STIX]{x1D735}S^{\ast }+w_{tot}^{\ast }\frac{\unicode[STIX]{x2202}S_{bg}^{\ast }}{\unicode[STIX]{x2202}z^{\ast }}=k_{S}\unicode[STIX]{x1D6FB}^{2}S^{\ast },\\ \displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{v}_{tot}^{\ast }}{\unicode[STIX]{x2202}t^{\ast }}+\boldsymbol{v}_{tot}^{\ast }\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{v}_{tot}^{\ast }=-\frac{1}{\unicode[STIX]{x1D70C}_{0}}\unicode[STIX]{x1D735}p_{tot}^{\ast }+g(\unicode[STIX]{x1D6FC}T^{\ast }-\unicode[STIX]{x1D6FD}S^{\ast })\boldsymbol{k}+\unicode[STIX]{x1D708}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{v}_{tot}^{\ast },\\ \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{v}_{tot}^{\ast }=0,\end{array}\right\} & & \displaystyle\end{eqnarray}$$
where
![]() $\boldsymbol{v}_{tot}^{\ast }=(u_{tot}^{\ast },v_{tot}^{\ast },w_{tot}^{\ast })$
is the velocity,
$\boldsymbol{v}_{tot}^{\ast }=(u_{tot}^{\ast },v_{tot}^{\ast },w_{tot}^{\ast })$
is the velocity,
![]() $p_{tot}^{\ast }$
is the dynamic pressure,
$p_{tot}^{\ast }$
is the dynamic pressure,
![]() $g$
is gravity and
$g$
is gravity and
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
are the thermal expansion and haline contraction coefficients.
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
are the thermal expansion and haline contraction coefficients.
Consider the basic state (denoted by overbars) representing unidirectional shear flow with a sinusoidal velocity profile:
It is assumed that the shear (2.3) is maintained against viscous dissipation by the externally imposed pressure gradient force
For convenience, the governing equations are non-dimensionalized using
![]() $H$
as the unit of length,
$H$
as the unit of length,
![]() $U_{0}$
as the unit of velocity and
$U_{0}$
as the unit of velocity and
![]() $H/U_{0}$
as the unit of time. The non-dimensionalization is implemented as follows:
$H/U_{0}$
as the unit of time. The non-dimensionalization is implemented as follows:
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle (u^{\ast },v^{\ast },w^{\ast })\rightarrow U_{0}(u,v,w),\quad p^{\ast }\rightarrow \unicode[STIX]{x1D70C}_{0}U_{0}^{2}p,\\ \displaystyle \unicode[STIX]{x1D6FC}T^{\ast }\rightarrow \unicode[STIX]{x1D6FC}\left|\frac{\unicode[STIX]{x2202}T_{bg}^{\ast }}{\unicode[STIX]{x2202}z^{\ast }}\right|HT,\quad \unicode[STIX]{x1D6FD}S^{\ast }\rightarrow \unicode[STIX]{x1D6FC}\left|\frac{\unicode[STIX]{x2202}T_{bg}^{\ast }}{\unicode[STIX]{x2202}z^{\ast }}\right|HS,\\ \displaystyle (x^{\ast },y^{\ast },z^{\ast })\rightarrow H(x,y,z),\quad t^{\ast }\rightarrow \frac{H}{U_{0}}t,\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle (u^{\ast },v^{\ast },w^{\ast })\rightarrow U_{0}(u,v,w),\quad p^{\ast }\rightarrow \unicode[STIX]{x1D70C}_{0}U_{0}^{2}p,\\ \displaystyle \unicode[STIX]{x1D6FC}T^{\ast }\rightarrow \unicode[STIX]{x1D6FC}\left|\frac{\unicode[STIX]{x2202}T_{bg}^{\ast }}{\unicode[STIX]{x2202}z^{\ast }}\right|HT,\quad \unicode[STIX]{x1D6FD}S^{\ast }\rightarrow \unicode[STIX]{x1D6FC}\left|\frac{\unicode[STIX]{x2202}T_{bg}^{\ast }}{\unicode[STIX]{x2202}z^{\ast }}\right|HS,\\ \displaystyle (x^{\ast },y^{\ast },z^{\ast })\rightarrow H(x,y,z),\quad t^{\ast }\rightarrow \frac{H}{U_{0}}t,\end{array}\right\} & & \displaystyle\end{eqnarray}$$
which transforms the governing equations to
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \frac{\unicode[STIX]{x2202}T}{\unicode[STIX]{x2202}t}+\boldsymbol{v}_{tot}\boldsymbol{\cdot }\unicode[STIX]{x1D735}T-w_{tot}=\frac{1}{Pe}\unicode[STIX]{x1D6FB}^{2}T,\\ \displaystyle \frac{\unicode[STIX]{x2202}S}{\unicode[STIX]{x2202}t}+\boldsymbol{v}_{tot}\boldsymbol{\cdot }\unicode[STIX]{x1D735}S-R_{\unicode[STIX]{x1D70C}}w_{tot}=\frac{\unicode[STIX]{x1D70F}}{Pe}\unicode[STIX]{x1D6FB}^{2}S,\\ \displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{v}_{tot}}{\unicode[STIX]{x2202}t}+\boldsymbol{v}_{tot}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{v}_{tot}=-\unicode[STIX]{x1D735}p_{tot}+\frac{4\unicode[STIX]{x03C0}^{2}Ri}{R_{\unicode[STIX]{x1D70C}}-1}(T-S)\boldsymbol{k}+\frac{Pr}{Pe}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{v}_{tot},\\ \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{v}_{tot}=0,\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \frac{\unicode[STIX]{x2202}T}{\unicode[STIX]{x2202}t}+\boldsymbol{v}_{tot}\boldsymbol{\cdot }\unicode[STIX]{x1D735}T-w_{tot}=\frac{1}{Pe}\unicode[STIX]{x1D6FB}^{2}T,\\ \displaystyle \frac{\unicode[STIX]{x2202}S}{\unicode[STIX]{x2202}t}+\boldsymbol{v}_{tot}\boldsymbol{\cdot }\unicode[STIX]{x1D735}S-R_{\unicode[STIX]{x1D70C}}w_{tot}=\frac{\unicode[STIX]{x1D70F}}{Pe}\unicode[STIX]{x1D6FB}^{2}S,\\ \displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{v}_{tot}}{\unicode[STIX]{x2202}t}+\boldsymbol{v}_{tot}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{v}_{tot}=-\unicode[STIX]{x1D735}p_{tot}+\frac{4\unicode[STIX]{x03C0}^{2}Ri}{R_{\unicode[STIX]{x1D70C}}-1}(T-S)\boldsymbol{k}+\frac{Pr}{Pe}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{v}_{tot},\\ \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{v}_{tot}=0,\end{array}\right\} & & \displaystyle\end{eqnarray}$$
where
 $$\begin{eqnarray}\displaystyle R_{\unicode[STIX]{x1D70C}}=\frac{\unicode[STIX]{x1D6FD}\displaystyle \frac{\unicode[STIX]{x2202}S_{bg}^{\ast }}{\unicode[STIX]{x2202}z^{\ast }}}{\unicode[STIX]{x1D6FC}\displaystyle \frac{\unicode[STIX]{x2202}T_{bg}^{\ast }}{\unicode[STIX]{x2202}z^{\ast }}} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R_{\unicode[STIX]{x1D70C}}=\frac{\unicode[STIX]{x1D6FD}\displaystyle \frac{\unicode[STIX]{x2202}S_{bg}^{\ast }}{\unicode[STIX]{x2202}z^{\ast }}}{\unicode[STIX]{x1D6FC}\displaystyle \frac{\unicode[STIX]{x2202}T_{bg}^{\ast }}{\unicode[STIX]{x2202}z^{\ast }}} & & \displaystyle\end{eqnarray}$$
is the background density ratio,
is the Richardson number,
![]() $N_{b}$
is the buoyancy frequency,
$N_{b}$
is the buoyancy frequency,
![]() $Pe=(U_{0}H)/k_{T}$
is the Peclet number,
$Pe=(U_{0}H)/k_{T}$
is the Peclet number,
![]() $\unicode[STIX]{x1D70F}=k_{S}/k_{T}$
is the diffusivity ratio and
$\unicode[STIX]{x1D70F}=k_{S}/k_{T}$
is the diffusivity ratio and
![]() $Pr=\unicode[STIX]{x1D708}/k_{T}$
is the Prandtl number. It should be noted that the Richardson number is based on the maximal shear
$Pr=\unicode[STIX]{x1D708}/k_{T}$
is the Prandtl number. It should be noted that the Richardson number is based on the maximal shear
![]() $(2\unicode[STIX]{x03C0}U_{0}/H)$
. While this convention leads to a rather cumbersome coefficient of the buoyancy term in the vertical momentum equation, it represents the most physical definition of the Richardson number. The Peclet number can also be expressed in terms of
$(2\unicode[STIX]{x03C0}U_{0}/H)$
. While this convention leads to a rather cumbersome coefficient of the buoyancy term in the vertical momentum equation, it represents the most physical definition of the Richardson number. The Peclet number can also be expressed in terms of
![]() $Ri$
and
$Ri$
and
![]() $N_{b}$
as follows:
$N_{b}$
as follows:
Representative values of the Richardson number and the buoyancy frequency in the diffusive regions of the World Ocean are
![]() $Ri\sim 1-10$
,
$Ri\sim 1-10$
,
![]() $N_{b}\sim 10^{-3}s^{-1}$
. The relevant vertical scale of the basic shear that could trigger thermohaline–shear instabilities is highly uncertain. If we assume that
$N_{b}\sim 10^{-3}s^{-1}$
. The relevant vertical scale of the basic shear that could trigger thermohaline–shear instabilities is highly uncertain. If we assume that
![]() $H\sim 1m$
, then (2.9) implies
$H\sim 1m$
, then (2.9) implies
![]() $Pe\sim 10^{3}$
, which provides very rough guidance for the exploration of the parameter space. The basic state (2.3), (2.4) reduces in non-dimensional units to
$Pe\sim 10^{3}$
, which provides very rough guidance for the exploration of the parameter space. The basic state (2.3), (2.4) reduces in non-dimensional units to
The non-dimensional perturbation velocity and pressure are defined accordingly as
3 Direct numerical simulations
Preliminary insights into thermohaline–shear destabilization were first generated from numerical solutions. The governing equations (2.6) were integrated in time using the dealiased pseudospectral method (e.g. Stern, Radko & Simeonov Reference Stern, Radko and Simeonov2001; Stellmach et al.
Reference Stellmach, Traxler, Garaud, Brummell and Radko2011) with periodic boundary conditions applied to the perturbation fields in each spatial direction. Both two- and three-dimensional DNS were performed. Double-diffusive DNS are computationally expensive, particularly for thermohaline layering experiments. In this case, it becomes necessary to resolve a wide range of dynamically significant scales – from the anticipated step height, which greatly exceeds the scale of heat dissipation, to the salinity dissipation scale, which is smaller than the heat scale by a factor of
![]() $\sqrt{\unicode[STIX]{x1D70F}}$
. In this study we consider oceanographically relevant parameters
$\sqrt{\unicode[STIX]{x1D70F}}$
. In this study we consider oceanographically relevant parameters
![]() $(Pr,\unicode[STIX]{x1D70F})=(10,0.01)$
, and such a small diffusivity ratio restricts the integration periods accessible by three-dimensional DNS. Two-dimensional DNS are certainly less demanding computationally and can be used to simulate relatively weak instabilities evolving on longer time scales. Furthermore, as will be shown here, they adequately capture key features of the nonlinear evolution of thermohaline–shear instabilities – staircase formation and subsequent layer-merging events.
$(Pr,\unicode[STIX]{x1D70F})=(10,0.01)$
, and such a small diffusivity ratio restricts the integration periods accessible by three-dimensional DNS. Two-dimensional DNS are certainly less demanding computationally and can be used to simulate relatively weak instabilities evolving on longer time scales. Furthermore, as will be shown here, they adequately capture key features of the nonlinear evolution of thermohaline–shear instabilities – staircase formation and subsequent layer-merging events.
Figure 1 presents a typical 3D simulation. The chosen parameters
![]() $(Ri,R_{\unicode[STIX]{x1D70C}},Pe)=\left(0.5,2,10^{4}\right)$
define a system that is individually stable with respect to dynamic and to diffusive instabilities. This calculation was initiated by the basic state (2.10) perturbed by small-amplitude random initial
$(Ri,R_{\unicode[STIX]{x1D70C}},Pe)=\left(0.5,2,10^{4}\right)$
define a system that is individually stable with respect to dynamic and to diffusive instabilities. This calculation was initiated by the basic state (2.10) perturbed by small-amplitude random initial
![]() $(T,S)$
distributions. The computational domain
$(T,S)$
distributions. The computational domain
![]() $(L_{x},L_{y},L_{z})=(2,1,1)$
, which corresponds to a dimensional size of
$(L_{x},L_{y},L_{z})=(2,1,1)$
, which corresponds to a dimensional size of
![]() $6~\text{m}\times 3~\text{m}\times 3~\text{m}$
, was resolved by a numerical mesh with
$6~\text{m}\times 3~\text{m}\times 3~\text{m}$
, was resolved by a numerical mesh with
![]() $768\times 384\times 384$
grid points. The evolution of this system is illustrated by a sequence of temperature perturbation snapshots (figure 1
a–f). It should be noted that the perturbation initially (figure 1
a) attains its largest values in the low-shear part of the flow
$768\times 384\times 384$
grid points. The evolution of this system is illustrated by a sequence of temperature perturbation snapshots (figure 1
a–f). It should be noted that the perturbation initially (figure 1
a) attains its largest values in the low-shear part of the flow
![]() $(z\approx 3/4)$
– one of the many features distinguishing this phenomenon from Kelvin–Helmholtz instability. This pattern gradually amplifies in time, leading to a substantial nonlinear modification of the vertical stratification and shear. As a result, the Richardson number is reduced below the critical value of
$(z\approx 3/4)$
– one of the many features distinguishing this phenomenon from Kelvin–Helmholtz instability. This pattern gradually amplifies in time, leading to a substantial nonlinear modification of the vertical stratification and shear. As a result, the Richardson number is reduced below the critical value of
![]() $Ri_{cr}=1/4$
in selected locations and becomes susceptible to Kelvin–Helmholtz instabilities. These secondary instabilities, clearly visible in figure 1(b), tend to be localized to high-shear
$Ri_{cr}=1/4$
in selected locations and becomes susceptible to Kelvin–Helmholtz instabilities. These secondary instabilities, clearly visible in figure 1(b), tend to be localized to high-shear
![]() $(z\approx 0,1/2,1)$
regions. The ensuing mixing produces a series of well-defined horizontally uniform layers (figure 1
c). While the layers formed initially are relatively thin, they merge sequentially, until there is only one well-defined layer left by
$(z\approx 0,1/2,1)$
regions. The ensuing mixing produces a series of well-defined horizontally uniform layers (figure 1
c). While the layers formed initially are relatively thin, they merge sequentially, until there is only one well-defined layer left by
![]() $t=20\,902$
(figure 1
f).
$t=20\,902$
(figure 1
f).

Figure 1. Three-dimensional DNS of layering in the dynamically and diffusively stable regime
![]() $(R_{\unicode[STIX]{x1D70C}},Ri,Pe,\unicode[STIX]{x1D70F})=(2,0.5,10^{4},0.01)$
. The instantaneous temperature perturbations are shown in (a–f) at
$(R_{\unicode[STIX]{x1D70C}},Ri,Pe,\unicode[STIX]{x1D70F})=(2,0.5,10^{4},0.01)$
. The instantaneous temperature perturbations are shown in (a–f) at
![]() $t=4012,5007,6010,7054,15\,014$
and 20 902 respectively.
$t=4012,5007,6010,7054,15\,014$
and 20 902 respectively.
The layering dynamics is revealed more clearly by the plots (figure 2) of the total horizontally averaged density profiles, which include the contribution from linear background stratification:
where
![]() $\langle \cdots \rangle$
denotes averaging in
$\langle \cdots \rangle$
denotes averaging in
![]() $(x,y)$
. These profiles demonstrate the formation of relatively homogeneous layers separated by high-gradient interfaces – structures that are suggestive of the observed thermohaline staircases. The transition from uniformly stratified to layered systems is slow, with a growth rate of
$(x,y)$
. These profiles demonstrate the formation of relatively homogeneous layers separated by high-gradient interfaces – structures that are suggestive of the observed thermohaline staircases. The transition from uniformly stratified to layered systems is slow, with a growth rate of
![]() $\unicode[STIX]{x1D706}\sim 1.5\times 10^{-3}$
, which corresponds to a dimensional time scale of several days.
$\unicode[STIX]{x1D706}\sim 1.5\times 10^{-3}$
, which corresponds to a dimensional time scale of several days.

Figure 2. The horizontally averaged density profiles for the simulation in figure 1. One can note the formation of relatively small homogeneous layers separated by high-gradient interfaces (c) and their subsequent merger (d–f).
During the early stages of the experiment (figure 1
a,b), the perturbation is relatively uniform in the
![]() $y$
-direction, which suggests that the most rapidly growing instability mode is quasi-two-dimensional and therefore the linear phase can be adequately represented by the 2D model. This proposition was readily confirmed by reproducing the foregoing simulation in two dimensions
$y$
-direction, which suggests that the most rapidly growing instability mode is quasi-two-dimensional and therefore the linear phase can be adequately represented by the 2D model. This proposition was readily confirmed by reproducing the foregoing simulation in two dimensions
![]() $(x,z)$
and observing similar evolutionary patterns. For instance, figure 3 presents an analogous two-dimensional experiment for
$(x,z)$
and observing similar evolutionary patterns. For instance, figure 3 presents an analogous two-dimensional experiment for
![]() $Ri=1$
(all other parameters were kept the same). The increase in the Richardson number results in a much lower growth rate
$Ri=1$
(all other parameters were kept the same). The increase in the Richardson number results in a much lower growth rate
![]() $(\unicode[STIX]{x1D706}\sim 2\times 10^{-4})$
, which places this case beyond the current capabilities of 3D DNS. Nevertheless, this system evolves in a very similar manner – the compact perturbation localized in the low-shear zone gradually amplifies (figure 3
a–c) and eventually transforms the uniform stratification into a well-defined staircase. As previously (cf. figure 2), the layers that are formed first are not steady but undergo a series of merging events, until there is only one step left within the limits of the computational domain. The tendency for layers to merge is a generic property of thermohaline staircases, which is realized in both diffusive and fingering configurations, in two and in three dimensions (e.g. Radko et al.
Reference Radko, Bulters, Flanagan and Campin2014a
,Reference Radko, Flanagan, Stellmach and Timmermans
b
).
$(\unicode[STIX]{x1D706}\sim 2\times 10^{-4})$
, which places this case beyond the current capabilities of 3D DNS. Nevertheless, this system evolves in a very similar manner – the compact perturbation localized in the low-shear zone gradually amplifies (figure 3
a–c) and eventually transforms the uniform stratification into a well-defined staircase. As previously (cf. figure 2), the layers that are formed first are not steady but undergo a series of merging events, until there is only one step left within the limits of the computational domain. The tendency for layers to merge is a generic property of thermohaline staircases, which is realized in both diffusive and fingering configurations, in two and in three dimensions (e.g. Radko et al.
Reference Radko, Bulters, Flanagan and Campin2014a
,Reference Radko, Flanagan, Stellmach and Timmermans
b
).

Figure 3. Two-dimensional DNS of layering for
![]() $(R_{\unicode[STIX]{x1D70C}},Ri,Pe,\unicode[STIX]{x1D70F})=(2,1,10^{4},0.01)$
. The instantaneous temperature perturbations are shown in the left panels and the horizontally averaged density profiles are on the right for
$(R_{\unicode[STIX]{x1D70C}},Ri,Pe,\unicode[STIX]{x1D70F})=(2,1,10^{4},0.01)$
. The instantaneous temperature perturbations are shown in the left panels and the horizontally averaged density profiles are on the right for
![]() $t=30\,575,49\,020,52\,118$
and 55 823 in (a–d) respectively.
$t=30\,575,49\,020,52\,118$
and 55 823 in (a–d) respectively.
The relatively slow evolution of the perturbations in figures 1–3 is consistent with our interpretation that these instabilities are being driven by the molecular diffusion of density components. Since the foregoing simulations are only weakly dissipative
![]() $(Pe=10^{4})$
, it is not surprising that the corresponding non-dimensional growth rates are also very low
$(Pe=10^{4})$
, it is not surprising that the corresponding non-dimensional growth rates are also very low
![]() $(\unicode[STIX]{x1D706}\sim 10^{-3}{-}10^{-4})$
. The reduction in the Peclet number, however, dramatically increases both the growth rates and the parameter range of thermohaline–shear instability. Figure 4, for instance, presents the simulation performed for
$(\unicode[STIX]{x1D706}\sim 10^{-3}{-}10^{-4})$
. The reduction in the Peclet number, however, dramatically increases both the growth rates and the parameter range of thermohaline–shear instability. Figure 4, for instance, presents the simulation performed for
![]() $(Pe,Ri)=(100,10)$
. The perturbation in this case amplifies much faster
$(Pe,Ri)=(100,10)$
. The perturbation in this case amplifies much faster
![]() $(\unicode[STIX]{x1D706}\sim 0.02)$
, and the Richardson number is a factor of 40 greater than the critical value of
$(\unicode[STIX]{x1D706}\sim 0.02)$
, and the Richardson number is a factor of 40 greater than the critical value of
![]() $Ri_{cr}=1/4$
suggested by classical theory for non-dissipative shear flows (Richardson Reference Richardson1920; Howard Reference Howard1961; Miles Reference Miles1961).
$Ri_{cr}=1/4$
suggested by classical theory for non-dissipative shear flows (Richardson Reference Richardson1920; Howard Reference Howard1961; Miles Reference Miles1961).

Figure 4. Two-dimensional DNS in the low-
![]() $Pe$
regime:
$Pe$
regime:
![]() $(R_{\unicode[STIX]{x1D70C}},Ri,Pe,\unicode[STIX]{x1D70F})=(2,10,10^{2},0.01)$
. The instantaneous temperature perturbations are shown in the left panels and the horizontally averaged density profiles are on the right for
$(R_{\unicode[STIX]{x1D70C}},Ri,Pe,\unicode[STIX]{x1D70F})=(2,10,10^{2},0.01)$
. The instantaneous temperature perturbations are shown in the left panels and the horizontally averaged density profiles are on the right for
![]() $t=108,311,500$
and 600 in (a–d) respectively.
$t=108,311,500$
and 600 in (a–d) respectively.
Another notable difference between the low-
![]() $Pe$
(figure 4) and high-
$Pe$
(figure 4) and high-
![]() $Pe$
(figure 3) simulations is the much larger ratio of the vertical/horizontal wavenumbers
$Pe$
(figure 3) simulations is the much larger ratio of the vertical/horizontal wavenumbers
![]() $(m/k)$
in the unstable modes. This ratio was
$(m/k)$
in the unstable modes. This ratio was
![]() $m/k\sim 2$
in high-
$m/k\sim 2$
in high-
![]() $Pe$
experiments, but the most unstable solutions were found for
$Pe$
experiments, but the most unstable solutions were found for
![]() $m/k\sim 50$
in low-
$m/k\sim 50$
in low-
![]() $Pe$
cases, a finding that is supported and rationalized by the following (§ 4) linear stability analysis. However, there are a number of similarities in the evolution of the low-
$Pe$
cases, a finding that is supported and rationalized by the following (§ 4) linear stability analysis. However, there are a number of similarities in the evolution of the low-
![]() $Pe$
system in figure 4 and high-
$Pe$
system in figure 4 and high-
![]() $Pe$
systems (e.g. figure 3) as well. The transition starts with the exponential growth of unstable perturbations (figure 4
a,b). When instabilities amplify to a level sufficient to substantially modify the vertical density and velocity gradients, they produce isolated regions that are susceptible to Kelvin–Helmholtz instability (figure 4
c). These secondary instabilities manifest themselves in the form of relatively narrow eddies, with
$Pe$
systems (e.g. figure 3) as well. The transition starts with the exponential growth of unstable perturbations (figure 4
a,b). When instabilities amplify to a level sufficient to substantially modify the vertical density and velocity gradients, they produce isolated regions that are susceptible to Kelvin–Helmholtz instability (figure 4
c). These secondary instabilities manifest themselves in the form of relatively narrow eddies, with
![]() $O(1)$
lateral extent, which are clearly visible in the late stages of the experiment (figure 4
c,d). The ensuing intense mixing generates patches of relatively uniform density separated by interfaces (figure 4
d). Since the system in figure 4 is much more dissipative than our previous examples, the staircase is not as well defined as in figures 1–3. The interfaces are diffused considerably by molecular dissipation and the mixed layers are not as homogeneous as in high-
$O(1)$
lateral extent, which are clearly visible in the late stages of the experiment (figure 4
c,d). The ensuing intense mixing generates patches of relatively uniform density separated by interfaces (figure 4
d). Since the system in figure 4 is much more dissipative than our previous examples, the staircase is not as well defined as in figures 1–3. The interfaces are diffused considerably by molecular dissipation and the mixed layers are not as homogeneous as in high-
![]() $Pe$
simulations. Nevertheless, we expect that in nature, the initiation of layering by means of thermohaline–shear instability represents only the first evolutionary stage. Layer-merging events (e.g. Radko et al.
Reference Radko, Bulters, Flanagan and Campin2014a
,Reference Radko, Flanagan, Stellmach and Timmermans
b
) can systematically increase the step heights in the staircase, concurrently increasing the effective Peclet number, and eventually produce a series of thick well-defined layers.
$Pe$
simulations. Nevertheless, we expect that in nature, the initiation of layering by means of thermohaline–shear instability represents only the first evolutionary stage. Layer-merging events (e.g. Radko et al.
Reference Radko, Bulters, Flanagan and Campin2014a
,Reference Radko, Flanagan, Stellmach and Timmermans
b
) can systematically increase the step heights in the staircase, concurrently increasing the effective Peclet number, and eventually produce a series of thick well-defined layers.

Figure 5. Two-dimensional DNS in the low-
![]() $Pe$
regime:
$Pe$
regime:
![]() $(R_{\unicode[STIX]{x1D70C}},Ri,Pe,\unicode[STIX]{x1D70F})=(2,10,10^{2},0.01)$
. The vertical extent of the computational domain is increased relative to that in figure 4 to
$(R_{\unicode[STIX]{x1D70C}},Ri,Pe,\unicode[STIX]{x1D70F})=(2,10,10^{2},0.01)$
. The vertical extent of the computational domain is increased relative to that in figure 4 to
![]() $L_{z}=64$
. The instantaneous temperature perturbations are shown for
$L_{z}=64$
. The instantaneous temperature perturbations are shown for
![]() $t=1009,2005,3500$
and 4040 in (a–d) respectively.
$t=1009,2005,3500$
and 4040 in (a–d) respectively.

Figure 6. (a) Space–time diagram of the mean density gradient for the experiment in figure 5. (b) Space–time diagram for the experiment in which
![]() $Ri=100$
; other parameters are the same as in (a).
$Ri=100$
; other parameters are the same as in (a).
Numerical support for the layer-merging hypothesis is provided by the simulation in figure 5, which is identical in all respects to the calculation in figure 4, except that the vertical size of the computational domain is now
![]() $L_{z}=64$
. As expected, the dominant vertical scale of instability modes that emerge first matches the wavelength of the basic shear (figure 5
a). These modes produce a system of horizontal layers. In time, however, layers merge sequentially and their number reduces from
$L_{z}=64$
. As expected, the dominant vertical scale of instability modes that emerge first matches the wavelength of the basic shear (figure 5
a). These modes produce a system of horizontal layers. In time, however, layers merge sequentially and their number reduces from
![]() $N=64$
at
$N=64$
at
![]() $t=1009$
(figure 5
a) to
$t=1009$
(figure 5
a) to
![]() $N=3$
at
$N=3$
at
![]() $t=4040$
(figure 5
d). The merging pattern is revealed very clearly in the space–time diagram of the horizontally averaged density gradient
$t=4040$
(figure 5
d). The merging pattern is revealed very clearly in the space–time diagram of the horizontally averaged density gradient
![]() $-\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}_{mean}/\unicode[STIX]{x2202}z$
(figure 6
a). Radko (Reference Radko2007) suggested that layered systems can exhibit two merging patterns:
$-\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}_{mean}/\unicode[STIX]{x2202}z$
(figure 6
a). Radko (Reference Radko2007) suggested that layered systems can exhibit two merging patterns:
![]() $B$
and
$B$
and
![]() $H$
modes.
$H$
modes.
![]() $B$
-mergers represent the strengthening of stronger interfaces at the expense of weaker interfaces, which gradually erode.
$B$
-mergers represent the strengthening of stronger interfaces at the expense of weaker interfaces, which gradually erode.
![]() $H$
-mergers occur when interfaces drift vertically and coalesce. Figure 6(a) indicates that both
$H$
-mergers occur when interfaces drift vertically and coalesce. Figure 6(a) indicates that both
![]() $H$
- and
$H$
- and
![]() $B$
-mergers are realized, although
$B$
-mergers are realized, although
![]() $H$
-mergers are more common. This feature is somewhat unusual since non-sheared double-diffusive systems are generally more susceptible to
$H$
-mergers are more common. This feature is somewhat unusual since non-sheared double-diffusive systems are generally more susceptible to
![]() $B$
-mergers (e.g. Radko et al.
Reference Radko, Bulters, Flanagan and Campin2014a
,Reference Radko, Flanagan, Stellmach and Timmermans
b
). Our finding that the average layer thickness greatly increases in time suggests that the effective step height is not directly controlled by the vertical shear scale
$B$
-mergers (e.g. Radko et al.
Reference Radko, Bulters, Flanagan and Campin2014a
,Reference Radko, Flanagan, Stellmach and Timmermans
b
). Our finding that the average layer thickness greatly increases in time suggests that the effective step height is not directly controlled by the vertical shear scale
![]() $(H)$
. This is an encouraging result. It opens prospects for developing theoretical models of the equilibrium-layer thickness without the explicit knowledge of the relevant wavelength of the basic shear, a quantity that is poorly constrained by observations or models. It should be noted that the non-dimensional layer thickness of
$(H)$
. This is an encouraging result. It opens prospects for developing theoretical models of the equilibrium-layer thickness without the explicit knowledge of the relevant wavelength of the basic shear, a quantity that is poorly constrained by observations or models. It should be noted that the non-dimensional layer thickness of
![]() $h\sim 20$
realized at the final stages of this experiment (figure 5
d) can be converted to dimensional values using (2.9), resulting in
$h\sim 20$
realized at the final stages of this experiment (figure 5
d) can be converted to dimensional values using (2.9), resulting in
which is broadly consistent with step sizes of diffusive staircases observed in the Arctic and Southern Oceans (e.g. Kelley et al. Reference Kelley, Fernando, Gargett, Tanny and Ozsoy2003).
Figure 6(b) presents an analogous experiment in which the Richardson number is increased to
![]() $Ri=100$
. The outcome is qualitatively similar. The spontaneous transition from uniform to stepped stratification starts with the formation of relatively thin layers, the scales of which are set by the periodicity of the background shear. These layers then undergo a series of mergers, which systematically increases the average layer thickness in the staircase. The time scale of the transition is, however, significantly longer for
$Ri=100$
. The outcome is qualitatively similar. The spontaneous transition from uniform to stepped stratification starts with the formation of relatively thin layers, the scales of which are set by the periodicity of the background shear. These layers then undergo a series of mergers, which systematically increases the average layer thickness in the staircase. The time scale of the transition is, however, significantly longer for
![]() $Ri=100$
than for
$Ri=100$
than for
![]() $Ri=10$
. The initial layering does not occur until
$Ri=10$
. The initial layering does not occur until
![]() $t=6000$
– which corresponds to a dimensional time scale of years – whereas in figure 6(a)
$t=6000$
– which corresponds to a dimensional time scale of years – whereas in figure 6(a)
![]() $(Ri=10)$
layers are already visible at
$(Ri=10)$
layers are already visible at
![]() $t=500$
.
$t=500$
.
4 Linear stability analysis
The preliminary experiments (§ 3) revealed that dynamically and double-diffusively stable flows in the ocean can be unstable with respect to mixed thermohaline–shear instability, and its nonlinear evolution can ultimately produce layered stratification. Therefore, this section offers a more systematic description of thermohaline–shear instability by means of a Floquet-based linear stability analysis.
To examine stability properties of doubly stratified shear flows, the governing equations are first linearized with respect to the basic state (2.10), resulting in
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \frac{\unicode[STIX]{x2202}T}{\unicode[STIX]{x2202}t}+\sin (2\unicode[STIX]{x03C0}z)\frac{\unicode[STIX]{x2202}T}{\unicode[STIX]{x2202}x}-w=\frac{1}{Pe}\unicode[STIX]{x1D6FB}^{2}T,\\ \displaystyle \frac{\unicode[STIX]{x2202}S}{\unicode[STIX]{x2202}t}+\sin (2\unicode[STIX]{x03C0}z)\frac{\unicode[STIX]{x2202}S}{\unicode[STIX]{x2202}x}-R_{\unicode[STIX]{x1D70C}}w=\frac{\unicode[STIX]{x1D70F}}{Pe}\unicode[STIX]{x1D6FB}^{2}S,\\ \displaystyle \frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}t}+\sin (2\unicode[STIX]{x03C0}z)\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}x}+2\unicode[STIX]{x03C0}w\cos (2\unicode[STIX]{x03C0}z)=-\frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}x}+\frac{Pr}{Pe}\unicode[STIX]{x1D6FB}^{2}u,\\ \displaystyle \frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}t}+\sin (2\unicode[STIX]{x03C0}z)\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}x}=-\frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}y}+\frac{Pr}{Pe}\unicode[STIX]{x1D6FB}^{2}v,\\ \displaystyle \frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}t}+\sin (2\unicode[STIX]{x03C0}z)\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}x}=-\frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}z}+\frac{4\unicode[STIX]{x03C0}^{2}Ri}{R_{\unicode[STIX]{x1D70C}}-1}(T-S)+\frac{Pr}{Pe}\unicode[STIX]{x1D6FB}^{2}w,\\ \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{v}=0,\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \frac{\unicode[STIX]{x2202}T}{\unicode[STIX]{x2202}t}+\sin (2\unicode[STIX]{x03C0}z)\frac{\unicode[STIX]{x2202}T}{\unicode[STIX]{x2202}x}-w=\frac{1}{Pe}\unicode[STIX]{x1D6FB}^{2}T,\\ \displaystyle \frac{\unicode[STIX]{x2202}S}{\unicode[STIX]{x2202}t}+\sin (2\unicode[STIX]{x03C0}z)\frac{\unicode[STIX]{x2202}S}{\unicode[STIX]{x2202}x}-R_{\unicode[STIX]{x1D70C}}w=\frac{\unicode[STIX]{x1D70F}}{Pe}\unicode[STIX]{x1D6FB}^{2}S,\\ \displaystyle \frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}t}+\sin (2\unicode[STIX]{x03C0}z)\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}x}+2\unicode[STIX]{x03C0}w\cos (2\unicode[STIX]{x03C0}z)=-\frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}x}+\frac{Pr}{Pe}\unicode[STIX]{x1D6FB}^{2}u,\\ \displaystyle \frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}t}+\sin (2\unicode[STIX]{x03C0}z)\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}x}=-\frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}y}+\frac{Pr}{Pe}\unicode[STIX]{x1D6FB}^{2}v,\\ \displaystyle \frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}t}+\sin (2\unicode[STIX]{x03C0}z)\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}x}=-\frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}z}+\frac{4\unicode[STIX]{x03C0}^{2}Ri}{R_{\unicode[STIX]{x1D70C}}-1}(T-S)+\frac{Pr}{Pe}\unicode[STIX]{x1D6FB}^{2}w,\\ \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{v}=0,\end{array}\right\} & & \displaystyle\end{eqnarray}$$
where the velocity and pressure perturbations are defined in (2.11). The solution is sought in the following form, suggested by the Floquet theory:
 $$\begin{eqnarray}\displaystyle \left(\begin{array}{@{}c@{}}T\\ S\\ u\\ v\\ w\\ p\end{array}\right)=\exp (\text{i}kx+\text{i}ly+\text{i}m_{f}z+\unicode[STIX]{x1D706}t)\mathop{\sum }_{n=-N}^{N}\left(\begin{array}{@{}c@{}}T_{n}\\ S_{n}\\ u_{n}\\ v_{n}\\ w_{n}\\ p_{n}\end{array}\right)\exp (2\unicode[STIX]{x03C0}\text{i}nz), & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left(\begin{array}{@{}c@{}}T\\ S\\ u\\ v\\ w\\ p\end{array}\right)=\exp (\text{i}kx+\text{i}ly+\text{i}m_{f}z+\unicode[STIX]{x1D706}t)\mathop{\sum }_{n=-N}^{N}\left(\begin{array}{@{}c@{}}T_{n}\\ S_{n}\\ u_{n}\\ v_{n}\\ w_{n}\\ p_{n}\end{array}\right)\exp (2\unicode[STIX]{x03C0}\text{i}nz), & & \displaystyle\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D706}$
is the growth rate,
$\unicode[STIX]{x1D706}$
is the growth rate,
![]() $k$
and
$k$
and
![]() $l$
are the horizontal wavenumbers, and
$l$
are the horizontal wavenumbers, and
![]() $m_{f}$
is the Floquet coefficient, which controls the fundamental wavelength in
$m_{f}$
is the Floquet coefficient, which controls the fundamental wavelength in
![]() $z$
. When (4.2) is substituted into the linear system (4.1) and the individual Fourier components are collected, the stability problem reduces to the matrix form
$z$
. When (4.2) is substituted into the linear system (4.1) and the individual Fourier components are collected, the stability problem reduces to the matrix form
where
and
![]() $\unicode[STIX]{x1D63C}$
is the
$\unicode[STIX]{x1D63C}$
is the
![]() $(12N+2)\times (12N+2)$
matrix, whose elements are functions of
$(12N+2)\times (12N+2)$
matrix, whose elements are functions of
![]() $k,l,m_{f},Pe,R_{\unicode[STIX]{x1D70C}},Ri,N$
.
$k,l,m_{f},Pe,R_{\unicode[STIX]{x1D70C}},Ri,N$
.
For each set of governing parameters, the eigenvalue with the maximum real part determines the growth rate of the most rapidly amplifying mode. The spatial pattern of the perturbation is then reconstructed from the corresponding eigenvector
![]() $\unicode[STIX]{x1D743}$
:
$\unicode[STIX]{x1D743}$
:
where
![]() $\tilde{T}$
represents the temperature distribution in the fastest growing mode. The patterns of
$\tilde{T}$
represents the temperature distribution in the fastest growing mode. The patterns of
![]() $S$
,
$S$
,
![]() $\boldsymbol{v}$
and
$\boldsymbol{v}$
and
![]() $p$
in the normal modes are reconstructed in a similar manner. Extensive experimentation with the model indicated that the most rapid growth occurs when the Floquet factor is zero. This means that the fastest growing mode of instability has the same periodicity as that of the shear, and
$p$
in the normal modes are reconstructed in a similar manner. Extensive experimentation with the model indicated that the most rapid growth occurs when the Floquet factor is zero. This means that the fastest growing mode of instability has the same periodicity as that of the shear, and
![]() $m_{f}=0$
will be used in all subsequent calculations. Likewise, testing the performance of the model for different resolutions revealed that
$m_{f}=0$
will be used in all subsequent calculations. Likewise, testing the performance of the model for different resolutions revealed that
![]() $N=100$
is sufficient for an accurate representation of the thermohaline–shear instabilities in the considered parameter range, and this value will be employed hereafter.
$N=100$
is sufficient for an accurate representation of the thermohaline–shear instabilities in the considered parameter range, and this value will be employed hereafter.
Figure 7 presents some typical experiments in which
![]() $Ri$
and
$Ri$
and
![]() $Pe$
are varied while other parameters are held constant:
$Pe$
are varied while other parameters are held constant:
![]() $(R_{\unicode[STIX]{x1D70C}},Pr,\unicode[STIX]{x1D70F})=(2,10,10^{-2})$
. The growth rate
$(R_{\unicode[STIX]{x1D70C}},Pr,\unicode[STIX]{x1D70F})=(2,10,10^{-2})$
. The growth rate
![]() $\text{Re}(\unicode[STIX]{x1D706})$
is plotted as a function of
$\text{Re}(\unicode[STIX]{x1D706})$
is plotted as a function of
![]() $(k,l)$
for
$(k,l)$
for
![]() $(Ri,Pe)=(1,10^{4}),(1,10^{2}),(10,10^{2})$
in (a–c) respectively. In all cases, the system is stable with respect to dynamic and diffusive instabilities individually. Yet, it is apparently destabilized by the interaction between weak shear and two-component stratification (figure 7
a–c). The maximal growth rate rapidly increases with decreasing
$(Ri,Pe)=(1,10^{4}),(1,10^{2}),(10,10^{2})$
in (a–c) respectively. In all cases, the system is stable with respect to dynamic and diffusive instabilities individually. Yet, it is apparently destabilized by the interaction between weak shear and two-component stratification (figure 7
a–c). The maximal growth rate rapidly increases with decreasing
![]() $Pe$
. For instance, the growth rate in the high-
$Pe$
. For instance, the growth rate in the high-
![]() $Pe$
regime (figure 7
a) is less by two orders of magnitude than in the low-
$Pe$
regime (figure 7
a) is less by two orders of magnitude than in the low-
![]() $Pe$
case (figure 7
b) for the same
$Pe$
case (figure 7
b) for the same
![]() $Ri$
. The decrease in
$Ri$
. The decrease in
![]() $Pe$
also shifts the (non-dimensional) wavelength of the fastest growing mode to much larger values. For the same
$Pe$
also shifts the (non-dimensional) wavelength of the fastest growing mode to much larger values. For the same
![]() $Pe$
, a reduction in shear (larger
$Pe$
, a reduction in shear (larger
![]() $Ri$
) results in considerably lower growth rates (cf. figure 7
b,c). It is important to emphasize that in all cases considered, the largest growth rates were always attained for
$Ri$
) results in considerably lower growth rates (cf. figure 7
b,c). It is important to emphasize that in all cases considered, the largest growth rates were always attained for
![]() $l=0$
, which means that the wave fronts of the most rapidly amplifying perturbations are aligned perpendicular to the direction of the basic current. All of these features are consistent with the observed evolution of thermohaline–shear instabilities in DNS (§ 3).
$l=0$
, which means that the wave fronts of the most rapidly amplifying perturbations are aligned perpendicular to the direction of the basic current. All of these features are consistent with the observed evolution of thermohaline–shear instabilities in DNS (§ 3).

Figure 7. The growth rates
![]() $\text{Re}(\unicode[STIX]{x1D706})$
predicted by the Floquet-based stability analysis are plotted as a function of the horizontal wavenumbers
$\text{Re}(\unicode[STIX]{x1D706})$
predicted by the Floquet-based stability analysis are plotted as a function of the horizontal wavenumbers
![]() $(k,l)$
. Calculations are presented for
$(k,l)$
. Calculations are presented for
![]() $(Ri,Pe)=(1,10^{4}),(1,10^{2}),(10,10^{2})$
in (a–c) respectively. Only positive growth rates are shown.
$(Ri,Pe)=(1,10^{4}),(1,10^{2}),(10,10^{2})$
in (a–c) respectively. Only positive growth rates are shown.
In figure 8, we plot the representative spatial pattern of the most rapidly amplifying mode for
![]() $(Ri,Pe)=(1,10^{4})$
, which was reconstructed using (4.5). The amplitude of this mode was normalized by the maximal value of the temperature perturbation, and the resulting solution is denoted by
$(Ri,Pe)=(1,10^{4})$
, which was reconstructed using (4.5). The amplitude of this mode was normalized by the maximal value of the temperature perturbation, and the resulting solution is denoted by
![]() $(\hat{T},{\hat{S}},\hat{u} ,{\hat{w}})$
. As observed in high-
$(\hat{T},{\hat{S}},\hat{u} ,{\hat{w}})$
. As observed in high-
![]() $Pe$
DNS (figures 1, 3), the unstable perturbations in the temperature and salinity fields tend to be localized to the low-shear part of the flow. Because of the symmetry of our system, there are two modes corresponding to the same (largest) growth rate: one is centred at
$Pe$
DNS (figures 1, 3), the unstable perturbations in the temperature and salinity fields tend to be localized to the low-shear part of the flow. Because of the symmetry of our system, there are two modes corresponding to the same (largest) growth rate: one is centred at
![]() $z=1/4$
and another, the mirror image of the first, at
$z=1/4$
and another, the mirror image of the first, at
![]() $z=3/4$
. In figure 9, the same calculation is performed for a low-
$z=3/4$
. In figure 9, the same calculation is performed for a low-
![]() $Pe$
case:
$Pe$
case:
![]() $(Ri,Pe)=(10,10^{2})$
. In this regime, the structure of the fastest growing normal mode is substantially different. The temperature perturbation is relatively uniform at all
$(Ri,Pe)=(10,10^{2})$
. In this regime, the structure of the fastest growing normal mode is substantially different. The temperature perturbation is relatively uniform at all
![]() $z$
-levels (figure 9
a). Salinity, on the other hand, tends to be localized in the high-shear zones
$z$
-levels (figure 9
a). Salinity, on the other hand, tends to be localized in the high-shear zones
![]() $(z\approx 0,1/2,1)$
. In both low-
$(z\approx 0,1/2,1)$
. In both low-
![]() $Pe$
and high-
$Pe$
and high-
![]() $Pe$
regimes (figures 8 and 9), the amplitude of the horizontal (vertical) velocity is largest in the high-shear (low-shear) regions.
$Pe$
regimes (figures 8 and 9), the amplitude of the horizontal (vertical) velocity is largest in the high-shear (low-shear) regions.

Figure 8. The most rapidly amplifying normal mode identified by a Floquet-based stability analysis for
![]() $(R_{\unicode[STIX]{x1D70C}},Ri,Pe,\unicode[STIX]{x1D70F})=(2,1,10^{4},0.01)$
. The perturbation is normalized by the maximal temperature value. The patterns of
$(R_{\unicode[STIX]{x1D70C}},Ri,Pe,\unicode[STIX]{x1D70F})=(2,1,10^{4},0.01)$
. The perturbation is normalized by the maximal temperature value. The patterns of
![]() $T$
,
$T$
,
![]() $S$
,
$S$
,
![]() $u$
and
$u$
and
![]() $w$
are shown in (a–d) respectively.
$w$
are shown in (a–d) respectively.

Figure 9. The same as figure 8 but for the low-
![]() $Pe$
case
$Pe$
case
![]() $(R_{\unicode[STIX]{x1D70C}},Ri,Pe,\unicode[STIX]{x1D70F})=(2,10,10^{2},0.01)$
.
$(R_{\unicode[STIX]{x1D70C}},Ri,Pe,\unicode[STIX]{x1D70F})=(2,10,10^{2},0.01)$
.
Figure 10 presents the plot of maximal growth rates, in logarithmic coordinates, as a function of
![]() $(Pe,Ri)$
for various density ratios
$(Pe,Ri)$
for various density ratios
![]() $(R_{\unicode[STIX]{x1D70C}})$
. A reduction in
$(R_{\unicode[STIX]{x1D70C}})$
. A reduction in
![]() $R_{\unicode[STIX]{x1D70C}}$
has a destabilizing effect on the system. The parameter space occupied by unstable modes tends to be very wide at low density ratios (
$R_{\unicode[STIX]{x1D70C}}$
has a destabilizing effect on the system. The parameter space occupied by unstable modes tends to be very wide at low density ratios (
![]() $R_{\unicode[STIX]{x1D70C}}=1.5$
and
$R_{\unicode[STIX]{x1D70C}}=1.5$
and
![]() $R_{\unicode[STIX]{x1D70C}}=2$
in figure 10
a,b) and contracts with the increasing
$R_{\unicode[STIX]{x1D70C}}=2$
in figure 10
a,b) and contracts with the increasing
![]() $R_{\unicode[STIX]{x1D70C}}$
(
$R_{\unicode[STIX]{x1D70C}}$
(
![]() $R_{\unicode[STIX]{x1D70C}}=10$
and
$R_{\unicode[STIX]{x1D70C}}=10$
and
![]() $R_{\unicode[STIX]{x1D70C}}=50$
in figure 10
c,d). Likewise, the thermohaline–shear instability is sensitive to the diffusivity ratio (figure 11). For
$R_{\unicode[STIX]{x1D70C}}=50$
in figure 10
c,d). Likewise, the thermohaline–shear instability is sensitive to the diffusivity ratio (figure 11). For
![]() $\unicode[STIX]{x1D70F}=0.005$
(figure 11
a) and
$\unicode[STIX]{x1D70F}=0.005$
(figure 11
a) and
![]() $\unicode[STIX]{x1D70F}=0.1$
(figure 11
b), unstable modes occupy most of the parameter space explored in figure 11. Increasing
$\unicode[STIX]{x1D70F}=0.1$
(figure 11
b), unstable modes occupy most of the parameter space explored in figure 11. Increasing
![]() $\unicode[STIX]{x1D70F}$
tends to stabilize the system. For
$\unicode[STIX]{x1D70F}$
tends to stabilize the system. For
![]() $\unicode[STIX]{x1D70F}=1$
, the dynamics of our system simplifies to that of an effectively one-component fluid, and the maximal unstable Richardson numbers reduce to the rather unremarkable interval of
$\unicode[STIX]{x1D70F}=1$
, the dynamics of our system simplifies to that of an effectively one-component fluid, and the maximal unstable Richardson numbers reduce to the rather unremarkable interval of
![]() $Ri<1$
. While being of marginal relevance for our primary objective (i.e. explaining the origin of diffusive staircases), it is interesting to examine the case in figure 11(d). This configuration
$Ri<1$
. While being of marginal relevance for our primary objective (i.e. explaining the origin of diffusive staircases), it is interesting to examine the case in figure 11(d). This configuration
![]() $(\unicode[STIX]{x1D70F}=1.5)$
represents a fluid stratified in the fingering sense (the slower diffusing component is unstably stratified) but linearly stable with respect to double diffusion
$(\unicode[STIX]{x1D70F}=1.5)$
represents a fluid stratified in the fingering sense (the slower diffusing component is unstably stratified) but linearly stable with respect to double diffusion
![]() $(R_{\unicode[STIX]{x1D70C}}>\unicode[STIX]{x1D70F})$
. Curiously, in this regime we find no evidence of new types of instability driven by a combination of shear and different molecular diffusivities of density components. Thus, thermohaline–shear destabilization appears to be an exclusively diffusive phenomenon.
$(R_{\unicode[STIX]{x1D70C}}>\unicode[STIX]{x1D70F})$
. Curiously, in this regime we find no evidence of new types of instability driven by a combination of shear and different molecular diffusivities of density components. Thus, thermohaline–shear destabilization appears to be an exclusively diffusive phenomenon.

Figure 10. The decimal logarithm of the maximal growth rate
![]() $\log _{10}(\text{Re}(\unicode[STIX]{x1D706}))$
is plotted as a function of
$\log _{10}(\text{Re}(\unicode[STIX]{x1D706}))$
is plotted as a function of
![]() $(Ri,Pe)$
for
$(Ri,Pe)$
for
![]() $R_{\unicode[STIX]{x1D70C}}=1.5,2,10$
and 50 in (a–d) respectively for
$R_{\unicode[STIX]{x1D70C}}=1.5,2,10$
and 50 in (a–d) respectively for
![]() $\unicode[STIX]{x1D70F}=0.01$
. Only the growth rates exceeding
$\unicode[STIX]{x1D70F}=0.01$
. Only the growth rates exceeding
![]() $10^{-5}$
are shown. One can note the reduction in the intensity of thermohaline–shear instability with increasing density ratio.
$10^{-5}$
are shown. One can note the reduction in the intensity of thermohaline–shear instability with increasing density ratio.

Figure 11. The decimal logarithm of the maximal growth rate
![]() $\log _{10}(\text{Re}(\unicode[STIX]{x1D706}))$
is plotted as a function of
$\log _{10}(\text{Re}(\unicode[STIX]{x1D706}))$
is plotted as a function of
![]() $(Ri,Pe)$
for
$(Ri,Pe)$
for
![]() $\unicode[STIX]{x1D70F}=0.005,0.1,1$
and 1.5 in (a–d) respectively for
$\unicode[STIX]{x1D70F}=0.005,0.1,1$
and 1.5 in (a–d) respectively for
![]() $R_{\unicode[STIX]{x1D70C}}=2$
. Only the growth rates exceeding
$R_{\unicode[STIX]{x1D70C}}=2$
. Only the growth rates exceeding
![]() $10^{-5}$
are shown. One can note the reduction in the intensity of thermohaline–shear instability with increasing diffusivity ratio.
$10^{-5}$
are shown. One can note the reduction in the intensity of thermohaline–shear instability with increasing diffusivity ratio.
5 Physical interpretation and energetics
In this section, an attempt is made to generate some insight into the dynamics of thermohaline–shear instability. One of the key questions in this regard is the ultimate source of energy required to amplify the unstable perturbations. The answer to this question is by no means obvious. The source of energy of Kelvin–Helmholtz instability is the kinetic energy of the basic shear, whereas double diffusion is driven by the release of potential energy stored in the unstably stratified density component. To identify the energy source for thermohaline–shear instabilities, the (non-dimensional) perturbation energy equation is derived as follows. First, we subtract the temperature and salinity equations in the linearized system (4.1), multiply the result by
![]() $(S-T)$
, and integrate the result over one fundamental wavelength in
$(S-T)$
, and integrate the result over one fundamental wavelength in
![]() $x$
,
$x$
,
![]() $y$
and
$y$
and
![]() $z$
to obtain the density variance equation:
$z$
to obtain the density variance equation:
Similarly, the kinetic energy equation is obtained by multiplying the
![]() $x$
,
$x$
,
![]() $y$
and
$y$
and
![]() $z$
momentum equations by
$z$
momentum equations by
![]() $u$
,
$u$
,
![]() $v$
and
$v$
and
![]() $w$
respectively, adding them, and integrating the result:
$w$
respectively, adding them, and integrating the result:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\int \frac{u^{2}+v^{2}+w^{2}}{2}\,\text{d}V+\int \frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}z}uw\,\text{d}V=\int \frac{4\unicode[STIX]{x03C0}^{2}Ri}{R_{\unicode[STIX]{x1D70C}}-1}(T-S)w\,\text{d}V\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{Pr}{Pe}\int (|\unicode[STIX]{x1D735}u|^{2}+|\unicode[STIX]{x1D735}v|^{2}+|\unicode[STIX]{x1D735}w|^{2})\,\text{d}V.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\int \frac{u^{2}+v^{2}+w^{2}}{2}\,\text{d}V+\int \frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}z}uw\,\text{d}V=\int \frac{4\unicode[STIX]{x03C0}^{2}Ri}{R_{\unicode[STIX]{x1D70C}}-1}(T-S)w\,\text{d}V\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{Pr}{Pe}\int (|\unicode[STIX]{x1D735}u|^{2}+|\unicode[STIX]{x1D735}v|^{2}+|\unicode[STIX]{x1D735}w|^{2})\,\text{d}V.\end{eqnarray}$$
Next, the density variance equation (5.1) is multiplied by
![]() $(4\unicode[STIX]{x03C0}^{2}Ri)/(R_{\unicode[STIX]{x1D70C}}-1)^{2}$
and added to the kinetic energy equation (5.2), which results in the total perturbation energy equation:
$(4\unicode[STIX]{x03C0}^{2}Ri)/(R_{\unicode[STIX]{x1D70C}}-1)^{2}$
and added to the kinetic energy equation (5.2), which results in the total perturbation energy equation:
where
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle E=\int \left(\frac{u^{2}+v^{2}+w^{2}}{2}+\frac{4\unicode[STIX]{x03C0}^{2}Ri}{(R_{\unicode[STIX]{x1D70C}}-1)^{2}}\frac{(S-T)^{2}}{2}\right)\,\text{d}V,\\ \displaystyle P_{dd}=\frac{4\unicode[STIX]{x03C0}^{2}Ri}{Pe(R_{\unicode[STIX]{x1D70C}}-1)^{2}}\int (S-T)\unicode[STIX]{x1D6FB}^{2}(\unicode[STIX]{x1D70F}S-T)\,\text{d}V,\\ \displaystyle P_{sh}=-\int \frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}z}uw\,\text{d}V,\\ \displaystyle P_{visc}=-\frac{Pr}{Pe}\int (|\unicode[STIX]{x1D735}u|^{2}+|\unicode[STIX]{x1D735}v|^{2}+|\unicode[STIX]{x1D735}w|^{2})\,\text{d}V.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle E=\int \left(\frac{u^{2}+v^{2}+w^{2}}{2}+\frac{4\unicode[STIX]{x03C0}^{2}Ri}{(R_{\unicode[STIX]{x1D70C}}-1)^{2}}\frac{(S-T)^{2}}{2}\right)\,\text{d}V,\\ \displaystyle P_{dd}=\frac{4\unicode[STIX]{x03C0}^{2}Ri}{Pe(R_{\unicode[STIX]{x1D70C}}-1)^{2}}\int (S-T)\unicode[STIX]{x1D6FB}^{2}(\unicode[STIX]{x1D70F}S-T)\,\text{d}V,\\ \displaystyle P_{sh}=-\int \frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}z}uw\,\text{d}V,\\ \displaystyle P_{visc}=-\frac{Pr}{Pe}\int (|\unicode[STIX]{x1D735}u|^{2}+|\unicode[STIX]{x1D735}v|^{2}+|\unicode[STIX]{x1D735}w|^{2})\,\text{d}V.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
The
![]() $P_{dd}$
term in (5.3) represents the production of perturbation energy by diffusion of heat and salt,
$P_{dd}$
term in (5.3) represents the production of perturbation energy by diffusion of heat and salt,
![]() $P_{sh}$
is interpreted as the production of energy by shear, and
$P_{sh}$
is interpreted as the production of energy by shear, and
![]() $P_{visc}$
is the viscous dissipation.
$P_{visc}$
is the viscous dissipation.
Finally, the individual terms in (5.3) were evaluated for the fastest growing normal modes identified using the linear analysis in § 4. Of particular interest is the relative contribution of double-diffusive, shear-driven and viscous energy production/dissipation mechanisms. The answer turned out to be regime-dependent. Figure 12 shows the variation in the energy balance for a series of Floquet-based calculations in which
![]() $Pe$
was systematically increased, whereas all other governing parameters were kept constant:
$Pe$
was systematically increased, whereas all other governing parameters were kept constant:
![]() $(R_{\unicode[STIX]{x1D70C}},Ri,\unicode[STIX]{x1D70F})=(2,1,0.01)$
. The relative contribution of various processes is quantified by plotting
$(R_{\unicode[STIX]{x1D70C}},Ri,\unicode[STIX]{x1D70F})=(2,1,0.01)$
. The relative contribution of various processes is quantified by plotting
as a function of
![]() $Pe$
. These diagnostics highlight the stark differences between the low-
$Pe$
. These diagnostics highlight the stark differences between the low-
![]() $Pe$
and high-
$Pe$
and high-
![]() $Pe$
regimes, which were evident in the DNS (§ 3) and in the linear stability analyses (§ 4). For high Peclet numbers
$Pe$
regimes, which were evident in the DNS (§ 3) and in the linear stability analyses (§ 4). For high Peclet numbers
![]() $(Pe>500)$
, the dominant balance is between the energy production by basic shear and its viscous dissipation. Nevertheless, double diffusion still accounts for a surprisingly large fraction of energy production
$(Pe>500)$
, the dominant balance is between the energy production by basic shear and its viscous dissipation. Nevertheless, double diffusion still accounts for a surprisingly large fraction of energy production
![]() $(P_{dd\,rel}=0.55{-}0.65)$
. The reason for such a high double-diffusive contribution is that much of the perturbation kinetic energy produced by shear is immediately dissipated by viscosity.
$(P_{dd\,rel}=0.55{-}0.65)$
. The reason for such a high double-diffusive contribution is that much of the perturbation kinetic energy produced by shear is immediately dissipated by viscosity.

Figure 12. The energy production/dissipation balances for various values of
![]() $Pe$
. One can note the existence of two dynamically dissimilar regimes: (i) the high-
$Pe$
. One can note the existence of two dynamically dissimilar regimes: (i) the high-
![]() $Pe$
regime
$Pe$
regime
![]() $(Pe>500)$
in which the dominant balance is between the production of the perturbation energy by shear and its viscous dissipation and (ii) the low-
$(Pe>500)$
in which the dominant balance is between the production of the perturbation energy by shear and its viscous dissipation and (ii) the low-
![]() $Pe$
regime
$Pe$
regime
![]() $(Pe<500)$
in which the energy released by the unstable basic temperature gradient is transferred directly into the perturbation field, resulting in its amplification.
$(Pe<500)$
in which the energy released by the unstable basic temperature gradient is transferred directly into the perturbation field, resulting in its amplification.
The dynamics of low-
![]() $Pe$
systems is dissimilar. The perturbation energy is produced almost entirely by double diffusion
$Pe$
systems is dissimilar. The perturbation energy is produced almost entirely by double diffusion
![]() $(P_{dd\,rel}=1.05{-}1.1)$
. The shear-driven contribution is small
$(P_{dd\,rel}=1.05{-}1.1)$
. The shear-driven contribution is small
![]() $(P_{sh\,rel}=0.01{-}0.05)$
and so is the viscous dissipation
$(P_{sh\,rel}=0.01{-}0.05)$
and so is the viscous dissipation
![]() $(-P_{visc\,rel}=0.05{-}0.15)$
. This result, however, should be interpreted with caution. Even though shear-induced effects are not strongly reflected in the energetics, it would be erroneous to conclude that they are largely irrelevant for the dynamics of thermohaline systems at low
$(-P_{visc\,rel}=0.05{-}0.15)$
. This result, however, should be interpreted with caution. Even though shear-induced effects are not strongly reflected in the energetics, it would be erroneous to conclude that they are largely irrelevant for the dynamics of thermohaline systems at low
![]() $Pe$
. On the contrary, the release of potential energy by double diffusion is only possible due to the catalytic role of shear. In the absence of shear, the smooth thermohaline stratification in the oceanographically relevant parameter regime would be linearly stable.
$Pe$
. On the contrary, the release of potential energy by double diffusion is only possible due to the catalytic role of shear. In the absence of shear, the smooth thermohaline stratification in the oceanographically relevant parameter regime would be linearly stable.
The schematic diagram in figure 13 attempts to rationalize the destabilizing tendency of shear. Before delving into the dynamics of the interaction between shear and double diffusion, let us recall the conventional interpretation of oscillatory diffusive instability. A particle initially located at the equilibrium level
![]() $(A)$
is slightly displaced (figure 13) upward into a colder and fresher region
$(A)$
is slightly displaced (figure 13) upward into a colder and fresher region
![]() $(A_{1})$
. In the absence of diffusion and friction, the particle would oscillate at the buoyancy frequency
$(A_{1})$
. In the absence of diffusion and friction, the particle would oscillate at the buoyancy frequency
![]() $(N_{b})$
. However, since heat diffuses faster than salt, the particle quickly adjusts its temperature to its new environment, but largely retains its salinity. Thus, the particle is now denser than the surrounding fluid and the buoyancy force is downward. Therefore, as the particle moves downward, it gains extra kinetic energy due to the buoyancy forcing associated with the diffusion of heat. This energy gain on the way down is slightly higher than the corresponding loss of kinetic energy on the way up (the particle is colder on the downward part of the cycle) and therefore there is a small net gain of energy in each cycle. This residual gain can, in principle, drive amplifying (overstable) oscillations. However, the oscillatory nature of diffusive instability makes it highly vulnerable to friction, and therefore its parameter range (1.1) is extremely narrow.
$(N_{b})$
. However, since heat diffuses faster than salt, the particle quickly adjusts its temperature to its new environment, but largely retains its salinity. Thus, the particle is now denser than the surrounding fluid and the buoyancy force is downward. Therefore, as the particle moves downward, it gains extra kinetic energy due to the buoyancy forcing associated with the diffusion of heat. This energy gain on the way down is slightly higher than the corresponding loss of kinetic energy on the way up (the particle is colder on the downward part of the cycle) and therefore there is a small net gain of energy in each cycle. This residual gain can, in principle, drive amplifying (overstable) oscillations. However, the oscillatory nature of diffusive instability makes it highly vulnerable to friction, and therefore its parameter range (1.1) is extremely narrow.

Figure 13. Schematic diagram illustrating the mechanism of thermohaline–shear instability. While diffusive instability is inherently oscillatory, and therefore highly susceptible to viscous damping, the presence of vertical shear allows for direct instability modes.
Let us now consider the effects of vertical shear, as indicated in figure 13. In this configuration, possibilities exist not only for oscillatory but also for direct modes of instability. After the particle is displaced upward (from point
![]() $A$
to
$A$
to
![]() $A_{1}$
) and its buoyancy is reduced, it can be advected by the shear into the downward-moving region
$A_{1}$
) and its buoyancy is reduced, it can be advected by the shear into the downward-moving region
![]() $(B_{1})$
. As a result, the downward motion there is further reinforced by buoyancy forcing. Likewise, as the particle is displaced below the equilibrium level
$(B_{1})$
. As a result, the downward motion there is further reinforced by buoyancy forcing. Likewise, as the particle is displaced below the equilibrium level
![]() $(B_{2})$
and it becomes lighter than the surrounding fluid, it can be advected by shear into the upward-moving region
$(B_{2})$
and it becomes lighter than the surrounding fluid, it can be advected by shear into the upward-moving region
![]() $(A_{2})$
. Thus, while individual Lagrangian particles in this configuration still inevitably oscillate, there is now a possibility for the direct amplification of the velocity field at any given point in space. This dynamics results in the direct – and therefore much more efficient – transfer of energy from thermal stratification into amplifying perturbations. In the direct mode, the buoyancy forcing acts continuously to amplify the perturbation, rather than alternating between reinforcing and opposing action. The absence of fast oscillations in the Eulerian velocity field implies that the proposed mechanism is also less susceptible to viscous damping. Therefore, the parameter range for thermohaline–shear instability is much wider than for diffusive convection (figures 10 and 11), and the instability conditions are readily met in the ocean.
$(A_{2})$
. Thus, while individual Lagrangian particles in this configuration still inevitably oscillate, there is now a possibility for the direct amplification of the velocity field at any given point in space. This dynamics results in the direct – and therefore much more efficient – transfer of energy from thermal stratification into amplifying perturbations. In the direct mode, the buoyancy forcing acts continuously to amplify the perturbation, rather than alternating between reinforcing and opposing action. The absence of fast oscillations in the Eulerian velocity field implies that the proposed mechanism is also less susceptible to viscous damping. Therefore, the parameter range for thermohaline–shear instability is much wider than for diffusive convection (figures 10 and 11), and the instability conditions are readily met in the ocean.
6 Discussion
Some of the most fascinating problems in instability theory arise when two independently stable processes lead to the destabilization of systems concurrently affected by both. A well-known example of this counterintuitive behaviour is the unstable system consisting of a vertically bounded uniform shear and bottom-heavy stratification, each of which is stable individually (Richardson Reference Richardson1920). Other cases that fall into the same category include the joint instability of rotating magnetic fields that are separately stable (Stern Reference Stern1963) and the instability of a stable thermal stratification in the presence of a nominally stabilizing magnetic field (Hughes & Weiss Reference Hughes and Weiss1995). Our study offers yet another example of such unexpected destabilization – dynamically and diffusively stable two-component shear flows. Linear stability analysis based on the Floquet theory demonstrates that shear flows can be unstable for surprisingly high values of the density ratio
![]() $(R_{\unicode[STIX]{x1D70C}}\sim 10)$
and Richardson number
$(R_{\unicode[STIX]{x1D70C}}\sim 10)$
and Richardson number
![]() $(Ri\sim 10^{3})$
. These values greatly exceed the individual thresholds for both dynamic and diffusive instabilities
$(Ri\sim 10^{3})$
. These values greatly exceed the individual thresholds for both dynamic and diffusive instabilities
![]() $(R_{\unicode[STIX]{x1D70C}cr},Ri_{cr})=(1.1,0.25)$
. Such a wide parameter range for thermohaline–shear instability includes typical parameters of the ocean regions characterized by thermohaline layering.
$(R_{\unicode[STIX]{x1D70C}cr},Ri_{cr})=(1.1,0.25)$
. Such a wide parameter range for thermohaline–shear instability includes typical parameters of the ocean regions characterized by thermohaline layering.
Thermohaline–shear instability exhibits many interesting and, in several ways, counterintuitive features. Depending on the parameter regime, the most rapidly amplifying unstable modes can be localized in low-shear or high-shear regions, and yet the presence of shear is absolutely essential. Thermohaline–shear instability rapidly intensifies with decreasing
![]() $Ri$
,
$Ri$
,
![]() $R_{\unicode[STIX]{x1D70C}}$
and
$R_{\unicode[STIX]{x1D70C}}$
and
![]() $\unicode[STIX]{x1D70F}$
. As with Kelvin–Helmholtz instability, the most rapidly amplifying perturbations are aligned in the direction normal to the flow. The transition to fully three-dimensional patterns occurs only at the nonlinear evolutionary stages, characterized by the appearance of secondary instabilities. Multiple lines of evidence, stemming from DNS, Floquet stability analysis and arguments based on energetics, indicate the existence of two dynamically distinct regimes, realized for low and high Peclet numbers. The low-
$\unicode[STIX]{x1D70F}$
. As with Kelvin–Helmholtz instability, the most rapidly amplifying perturbations are aligned in the direction normal to the flow. The transition to fully three-dimensional patterns occurs only at the nonlinear evolutionary stages, characterized by the appearance of secondary instabilities. Multiple lines of evidence, stemming from DNS, Floquet stability analysis and arguments based on energetics, indicate the existence of two dynamically distinct regimes, realized for low and high Peclet numbers. The low-
![]() $Pe$
regime is perhaps more interesting since its dissimilarities with one-component systems are most profound. In both low-
$Pe$
regime is perhaps more interesting since its dissimilarities with one-component systems are most profound. In both low-
![]() $Pe$
and high-
$Pe$
and high-
![]() $Pe$
cases, most of the energy required for perturbation growth is supplied by the unstably stratified density component
$Pe$
cases, most of the energy required for perturbation growth is supplied by the unstably stratified density component
![]() $(T)$
. In this regard, thermohaline–shear instability is similar to double diffusion, with shear flow playing a catalytic role in the amplification of perturbations. In the high-
$(T)$
. In this regard, thermohaline–shear instability is similar to double diffusion, with shear flow playing a catalytic role in the amplification of perturbations. In the high-
![]() $Pe$
case, however, a large amount of energy is supplied by the basic shear, but this gain is compensated by the equivalent energy loss due to viscous dissipation.
$Pe$
case, however, a large amount of energy is supplied by the basic shear, but this gain is compensated by the equivalent energy loss due to viscous dissipation.
Finally, it should be emphasized that the effects discussed in this study should not be considered as merely an example of fluid-dynamical curiosity. Fully nonlinear simulations reveal that thermohaline–shear instability can reorganize smooth
![]() $T$
–
$T$
–
![]() $S$
fields into a series of mixed layers separated by thin high-gradient interfaces. These structures are suggestive of diffusive staircases, commonly observed in high-latitude regions of the World Ocean (Arctic and Southern Oceans), which raises an intriguing question of whether the origin of staircases can be attributed to thermohaline–shear instability. In this regard, an important caveat of our analysis is the steady-state model of the background shear. The steady-state assumption made it possible to perform formal linear stability analysis in a straightforward manner and efficiently explore the parameter space. However, in the ocean, vertical fine-scale shear is largely associated with the internal wave field, and therefore it is neither steady nor unidirectional. It would be of interest to determine whether thermohaline–shear instability persists in stochastic wave-driven shears (e.g. Radko et al.
Reference Radko, Ball, Colosi and Flanagan2015) and whether it produces layering as effectively as its steady-state counterpart. Other suggestions for future research include the development of laboratory-based analogues of the presented models. Free from computational constraints, experiments could be used to explore a wider parameter range and bring additional insights into the dynamics of thermohaline–shear instability.
$S$
fields into a series of mixed layers separated by thin high-gradient interfaces. These structures are suggestive of diffusive staircases, commonly observed in high-latitude regions of the World Ocean (Arctic and Southern Oceans), which raises an intriguing question of whether the origin of staircases can be attributed to thermohaline–shear instability. In this regard, an important caveat of our analysis is the steady-state model of the background shear. The steady-state assumption made it possible to perform formal linear stability analysis in a straightforward manner and efficiently explore the parameter space. However, in the ocean, vertical fine-scale shear is largely associated with the internal wave field, and therefore it is neither steady nor unidirectional. It would be of interest to determine whether thermohaline–shear instability persists in stochastic wave-driven shears (e.g. Radko et al.
Reference Radko, Ball, Colosi and Flanagan2015) and whether it produces layering as effectively as its steady-state counterpart. Other suggestions for future research include the development of laboratory-based analogues of the presented models. Free from computational constraints, experiments could be used to explore a wider parameter range and bring additional insights into the dynamics of thermohaline–shear instability.
Acknowledgements
The author thanks E. Edwards, J. Brown and the reviewers for helpful comments. Support of the National Science Foundation (grant OCE 1334914) is gratefully acknowledged. The computing resources were supplied by the Extreme Science and Engineering Discovery Environment (XSEDE) programme, which is supported by the NSF grant number OCI-1053575.