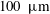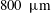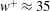1 Introduction
Much of the recent research on drag reduction in turbulent wall-bounded flows has focused on modifying the zero-slip wall boundary condition. In particular, superhydrophobic surfaces (SHS) have been shown to reduce drag in laminar and turbulent water flows by up to 50 % (Ou, Perot & Rothstein Reference Ou, Perot and Rothstein2004; Daniello, Waterhouse & Rothstein Reference Daniello, Waterhouse and Rothstein2009; Martell, Perot & Rothstein Reference Martell, Perot and Rothstein2009; Park, Park & Kim Reference Park, Park and Kim2013; Srinivasan et al. Reference Srinivasan, Choi, Park, Chhatre, Cohen and McKinley2013; Park, Sun & Kim Reference Park, Sun and Kim2014). In SHS, the surface is treated so that air can be trapped in asperities formed on the surface. This can be achieved by using a patterned surface finish (such as small grooves, micropillars or other regular structures) or a heterogenous surface finish obtained by (for example) spraying or chemical treatments, which are functionalized to have large contact angles for water, so that they preferentially hold air when submerged.
The case of SHS using simple transverse grooves is illustrated in figure 1 (the grooves in this study are longitudinal, but the concepts noted here are similar). For the flow in the regions where the water is directly in contact with the solid surface, the no-slip condition holds, and as a consequence the shear at the surface is large. In the regions where the water is flowing over a cavity filled with air, which has a viscosity approximately 50 times smaller than that of water, the interface is able to slip, and so the shear is reduced. When the local shear stress is integrated over the entire surface, a marked decrease in drag is possible.
Figure 1. Schematic of the near-wall velocity behaviour of a single-fluid system (a) and a two-fluid system (b). The presence of the second fluid creates a recirculation region, reducing the near-wall shear and drag induced by the flow.
However, SHS suffer from some significant drawbacks. The integrity of the water–air interface depends on surface tension, and so turbulent pressure fluctuations, or an increase in hydrostatic pressure associated with a change in depth, can lead to failure of the interface (Poetes et al. Reference Poetes, Holtzmann, Franze and Steiner2010; Bocquet & Lauga Reference Bocquet and Lauga2011). Similarly, a high level of shear can cause a breakdown of the interface (Samaha, Tafreshi & Gad-el Hak Reference Samaha, Tafreshi and Gad-el Hak2012). Once the cavities have been flooded with water, the surface asperities present themselves as roughness elements, causing an overall drag increase rather than the intended drag decrease (Aljallis et al. Reference Aljallis, Sarshar, Datla, Sikka, Jones and Choi2013).
In a new approach, we replace the air trapped in the surface features with a liquid that is immiscible in water, to form a liquid-infused surface (LIS) (Wong et al. Reference Wong, Kang, Tang, Smythe, Hatton, Grinthal and Aizenberg2011). Such surfaces are inherently robust to pressure changes, and so they avoid one of the major weaknesses of SHS. However, given that the infused liquid will most likely have a considerably higher viscosity compared to air, it is not obvious that such surfaces will help to reduce drag. In that respect, drag reduction has been shown to be possible in laminar flows (Solomon, Khalil & Varanasi Reference Solomon, Khalil and Varanasi2014) and in turbulent flows (Rosenberg et al. Reference Rosenberg, Van Buren, Fu and Smits2016), although the turbulent drag reduction was only approximately 10 %, considerably less than what seems to be possible with SHS.
We now present new results of drag reduction using LIS that are as high as 35 %, a level that is comparable to the drag reduction that can be achieved using SHS in the same experiment. Indications are that even higher levels may be possible in the future.
There are four primary parameters governing the performance of LIS, that stem from interrelationships between viscous stress, inertial force, buoyancy force and interfacial tension. The first is the viscosity ratio,
$N=\unicode[STIX]{x1D707}_{o}/\unicode[STIX]{x1D707}_{i}$
, where
$\unicode[STIX]{x1D707}_{o}$
and
$\unicode[STIX]{x1D707}_{i}$
are the viscosities of the external and infused fluid, respectively. Typical values for LIS are of
$O(1)$
, whereas for SHS it is approximately 50. Higher viscosity ratios result in a higher potential drag reduction (Schönecker, Baier & Hardt Reference Schönecker, Baier and Hardt2014). The second is the Reynolds number, which is the ratio of the inertial forces to the viscous forces. The Reynolds number is given by
$Re=\unicode[STIX]{x1D70C}_{o}Ud/\unicode[STIX]{x1D707}_{o}$
, where
$\unicode[STIX]{x1D70C}_{o}$
is the density of the external fluid,
$U$
is the characteristic flow velocity and
$d$
is a characteristic length scale. In our case, the characteristic velocity is the outer surface velocity and the length scale is the gap size in the Taylor–Couette apparatus. High Reynolds numbers indicate a turbulent flow (in our case the maximum Reynolds number is 10 500, which is turbulent for Taylor–Couette flows).
The other two parameters are important in maintaining the infused liquid–water interface. One is the Bond number, which is the ratio of the buoyancy force to the capillary force. When the infused and external fluids have different densities, the resulting buoyancy force can deplete the surface features by overcoming the capillary force holding the fluid in. The Bond number is given by
$Bo=(\unicode[STIX]{x1D70C}_{o}-\unicode[STIX]{x1D70C}_{i})gw^{2}/\unicode[STIX]{x1D6FE}$
, where
$w$
is the characteristic length scale of the surface asperities (which in our study is the groove width),
$\unicode[STIX]{x1D6FE}$
is the interfacial tension and
$\unicode[STIX]{x1D70C}_{0}$
and
$\unicode[STIX]{x1D70C}_{i}$
are the densities of the external and infused fluid, respectively. The other parameter is the ratio of the inertial force to the capillary force, that is, the Weber number, given by
$We=\unicode[STIX]{x1D70C}_{o}U^{2}w/\unicode[STIX]{x1D6FE}$
. When the Weber number is high, the inertia force can overcome the capillary force and allow the infused liquid to escape. For a robust LIS application, the infused and external liquids need to be immiscible, the infused liquid needs to preferentially wet the surface, and the Weber and Bond numbers need to be small to avoid failure.
Along with the properties of the impregnated fluid, the surface geometry significantly impacts drag reduction. Surfaces with larger fluid area fraction,
$a=A_{i}/A_{t}$
(where
$A_{i}$
is the surface area of the exposed infused fluid and
$A_{t}$
is the total surface area), have a higher drag reduction potential. Also, surfaces with equal fluid area fraction but larger features tend to reduce drag more (Fu et al.
Reference Fu, Mohammadi, Van Buren, Stone, Smits, Hultmark, Arenas and Leonardi2016) because fewer areas that transition from a solid to a liquid boundary will be present, and so regions where locally high stresses can occur are reduced. It should be noted that there is a lesser understood limit to the size of the features – larger wetted areas might be more susceptible to failure-inducing interfacial instabilities (Mohammadi & Smits Reference Mohammadi and Smits2016).
Here, we use surface features made by longitudinal square grooves with widths ranging from
$w=100~\unicode[STIX]{x03BC}\text{m}$
to
$800~\unicode[STIX]{x03BC}\text{m}$
. The majority of experiments were performed at a fluid area ratio
$a=50\,\%$
, though one case is shown for
$a=85\,\%$
(with
$w=400~\unicode[STIX]{x03BC}\text{m}$
). The external fluid is water, and the infused liquid is a set of alkanes, with viscosity ratios ranging from
$N=0.7$
to 3. We also consider the classical superhydrophobic (air-infused) case,
$N=50$
, for comparison purposes. The fluid properties and relevant non-dimensional parameters are summarized in table 1.
Table 1. Infused fluid properties with water as the bulk fluid. Ranges of Weber (
$We$
) and Bond (
$Bo$
) numbers are given corresponding to groove sizes of
$w=100~\unicode[STIX]{x03BC}\text{m}$
and
$800~\unicode[STIX]{x03BC}\text{m}$
and the highest Reynolds number,
$Re=10\,500$
. The viscosity ratio
$N=\unicode[STIX]{x1D707}_{o}/\unicode[STIX]{x1D707}_{i}$
.
2 Experiment
The experiment was conducted in a Taylor–Couette rheometer facility (Brabender Rheotron), illustrated in figure 2, equipped with a stainless steel outer cylinder (radius
$R_{o}=28$
mm) that rotates around the treated stationary inner cylinder (
$R_{i}=26$
mm). The gap between the two cylinders is
$d=R_{o}-R_{i}=2~\text{mm}\pm 0.013~\text{mm}$
, and the cylinder height is
$H=80$
mm, so that
$H/d=40$
. An acrylic ring, located
$500~\unicode[STIX]{x03BC}\text{m}$
above the top of the inner cylinder, minimizes the rise of the free surface of the water during rotation. As the outer cylinder rotates at angular velocity
$\unicode[STIX]{x1D714}$
, it induces a characteristic surface velocity of
$U=\unicode[STIX]{x1D714}R_{o}$
and a torque (
$T$
) on the stationary cylinder, monitored via a 25 g load cell (LCM Systems UFI) through a 25 mm lever arm. The accuracy of the load cell is
${<}\pm 0.3\,\%$
full scale, which for our experiments corresponds to a torque accuracy of
$\pm$
1–2 %, with better accuracy at higher Reynolds numbers. The load cell output signal was conditioned by a low-pass Butterworth filter and amplifier (Krohn-Hite Corporation), and each experiment is run three times independently to ensure repeatability and to gain a sense of uncertainty, which yields an average standard deviation of 2 % in torque measurements.
Figure 2. (a) Experimental set-up of the Taylor–Couette facility. Longitudinal grooves are tested with water (baseline), air (superhydrophobic) or alkane oils (liquid-infused). (b) Sample confocal microscope measurements of the smallest groove size,
$w=100~\unicode[STIX]{x03BC}\text{m}$
.
The cylinder is first dip-coated in the infused liquid, then immediately submerged in the test liquid (water) in order to limit the exposure of the infused liquid to air – the lower-viscosity alkanes are especially volatile. Because the alkane oils are less dense than water, any excess oil floats to the free surface, which is then removed to minimize impact on the experiment. It is possible that a small nanolayer of oil remains on the oleophilic outer surface of the cylinder after the dip-coating and buoyancy-driven drainage. This volume of fluid will be small with respect to the groove volume, but simulations have indicated that this nanolayer helps to keep surface asperities submerged as the fluid–fluid interface deforms, thereby improving drag reduction (Arenas et al. Reference Arenas, Bernardini, Iungo and Leonardi2016).
For liquid infusion, we created test pieces with surface features that were initially preferentially wetting to the surrounding water. A lathe was used to machine the square surface grooves, which ranged from
$w=100~\unicode[STIX]{x03BC}\text{m}$
to
$800~\unicode[STIX]{x03BC}\text{m}$
wide, and the machine accuracy was confirmed using a confocal microscope (Olympus LEXT OLS4000). To chemically treat the surface to attract alkanes, the following steps were followed: (i) plasma cleaning to remove all surface organic compounds; (ii) ultrasonic cleaning to remove remaining non-organic impurities, such as machining oil or metal chips; (iii) Boehmetization (boiling in water), following the procedure of Kim et al. (Reference Kim, Kreder, Alvarenga and Aizenberg2013), which creates a nanotextured oxide layer that enhances the surface hydrophobicity; and (iv) immersion in a solution of 1 % trichlorosilane (OTS) and 99 % heptane for 4–8 h, which covers the surface in a monolayer of polymers, resulting in a surface that is superhydrophobic, but attracting to alkane oils.
3 Results
First, we consider the baseline case, where the surface is hydrophilic and water fills the grooves. Figure 3(a) shows that, as the groove size increases, the torque at a given Reynolds number increases. Here,
$Re=\unicode[STIX]{x1D70C}_{o}Ud/\unicode[STIX]{x1D707}_{o}$
, where
$d=R_{o}-R_{i}$
. However, in this study some of the larger groove sizes are not negligible compared to the gap height. We can define an effective inner cylinder radius based on an equivalent volume of test fluid, where
$R_{eff}^{2}=R_{i}^{2}-a(R_{i}^{2}-(R_{i}-w)^{2})$
, and hence an effective gap width
$d_{eff}=d+{\mathcal{M}}(R_{i}-R_{eff})$
, where
${\mathcal{M}}=1.5$
is an empirically determined constant that tunes the importance of the grooves (for
${\mathcal{M}}=1$
the effective gap width is equal to its average value based on the equivalent volume of fluid). Figure 3(b) shows the torque
$T$
for the water-filled grooves as they vary with Reynolds numbers based on the effective gap height,
$Re^{\ast }=\unicode[STIX]{x1D70C}_{o}Ud_{eff}/\unicode[STIX]{x1D707}_{o}$
. The effective Reynolds number collapses the data reasonably well, indicating that the change in torque for the different groove sizes is mostly due to the change in the effective Reynolds number. For any particular groove size, therefore, we can use the water-filled groove case as the baseline for determining drag reduction.
Figure 3. Water-filled groove cylinder torque with Reynolds number based on (a) gap height
$d$
and (b) effective gap height
$d_{eff}$
. Groove sizes are
$w=100~\unicode[STIX]{x03BC}\text{m}$
(black),
$200~\unicode[STIX]{x03BC}\text{m}$
(dark grey),
$400~\unicode[STIX]{x03BC}\text{m}$
(light grey) and
$800~\unicode[STIX]{x03BC}\text{m}$
(white); fluid area fractions
$a=0.5$
(circles) and 0.85 (squares).
Figure 4. Cylinder torque as a function of Reynolds number for the baseline (no surface infusion), air- (superhydrophobic) and liquid-infused cases represented by their viscosity ratio,
$N$
. Here,
$a=0.5$
.
Figure 4 shows a sample set of torque measurements for a groove width of
$w=400~\unicode[STIX]{x03BC}\text{m}$
. Three test cases were studied over a range of Reynolds numbers: the baseline (water-filled,
$N=1$
) case, the superhydrophobic (air-filled,
$N=47.8$
) case and the liquid-infused (alkane-filled,
$3\geqslant N\geqslant 0.7$
) case. Generally, the torque increases with Reynolds number because at higher spin rates there is more friction drag on the inner cylinder. For this geometry, replacing the water within the grooves with air or alkanes decreases the cylinder torque at a fixed Reynolds number, with the superhydrophobic case producing the lowest drag.
The drag reduction
$DR$
is defined as the change in torque
$T$
with respect to the baseline torque
$T_{0}$
, so that
$DR=(T_{0}-T)/T_{0}$
. The results are shown in figure 5 for groove widths of
$w=100~\unicode[STIX]{x03BC}\text{m}$
to
$800~\unicode[STIX]{x03BC}\text{m}$
. For all groove sizes there is a general trend that higher viscosity ratios results in a larger drag reduction, as expected (Schönecker et al.
Reference Schönecker, Baier and Hardt2014; Fu et al.
Reference Fu, Mohammadi, Van Buren, Stone, Smits, Hultmark, Arenas and Leonardi2016). This behaviour is not entirely consistent, because there are some higher-viscosity oils that produce larger drag reduction than the lower-viscosity cases, particularly the
$w=400~\unicode[STIX]{x03BC}\text{m}$
case. This is counter-intuitive, and the most likely cause of this behaviour is surface failure of the lower-viscosity oils, possibly from the appearance of instabilities on the interface (Mohammadi & Smits Reference Mohammadi and Smits2016), although this suggestion remains to be confirmed. Unfortunately, the nature of these Taylor–Couette measurements does not allow us to assess surface failure during the experiment.
Figure 5. Drag reduction with respect to the baseline (no surface treatment) for air- (superhydrophobic) and liquid-infused cases represented by their viscosity ratio,
$N$
. Groove sizes are (a)
$w=100~\unicode[STIX]{x03BC}\text{m}$
, (b)
$200~\unicode[STIX]{x03BC}\text{m}$
, (c)
$400~\unicode[STIX]{x03BC}\text{m}$
and (d)
$800~\unicode[STIX]{x03BC}\text{m}$
. Here,
$a=0.5$
.
Figure 6. Groove width impact on drag reduction for fixed Reynolds numbers of (a)
$Re_{d}=8000$
and (b) 10 000 for air- (superhydrophobic) and liquid-infused cases. Here,
$a=0.5$
. Symbols as in figure 5.
Figure 6 shows the drag reduction at each groove size for Reynolds numbers
$Re=8000$
and 10 000. As suggested by Park et al. (Reference Park, Sun and Kim2014), we scale the groove width with the viscous length scale of the flow such that
$w^{+}=w\unicode[STIX]{x1D708}^{-1}\sqrt{\unicode[STIX]{x1D70F}_{w}/\unicode[STIX]{x1D70C}}$
, where
$\unicode[STIX]{x1D70F}_{w}=T/2\unicode[STIX]{x03C0}HR_{i}^{2}$
is the wall stress and
$\unicode[STIX]{x1D708}$
is the kinematic viscosity of water. The largest drag reduction is at
$w^{+}\approx 35$
, approaching 45 % for the air-infused case and greater than 25 % for the liquid-infused case. The location of the peak drag reduction is in good agreement with superhydrophobic results (Park et al.
Reference Park, Sun and Kim2014). Larger groove sizes produce larger drag reduction, as indicated by Park et al. (Reference Park, Park and Kim2013, Reference Park, Sun and Kim2014), and is the primary reason we achieve more substantial drag reduction than in Rosenberg et al. (Reference Rosenberg, Van Buren, Fu and Smits2016). However, for the largest groove size at the higher Reynolds numbers, the drag reduction decreases with increasing Reynolds number. Visual inspection of these cases showed that water had wetted a portion of the surface, indicating a partial surface failure under these conditions. The results from these Reynolds numbers are consistent with our entire measurement range, though it should be noted that this range is limited.
Figure 7. Drag reduction for fluid area fraction
$a=0.85$
with respect to the baseline (no surface treatment) for air- (superhydrophobic) and liquid-infused cases represented by their viscosity ratio,
$N$
(
$w=400~\unicode[STIX]{x03BC}\text{m}$
). Symbols as in figure 5.
As suggested by Fu et al. (Reference Fu, Mohammadi, Van Buren, Stone, Smits, Hultmark, Arenas and Leonardi2016), increasing the fluid area fraction
$a$
increases the level of drag reduction. Figure 5 shows results for
$a=0.5$
, and figure 7 shows results for
$a=0.85$
. At lower Reynolds numbers, we see that increasing
$a$
increases the drag reduction from approximately 25 % to up to 35 % for the liquid-infused cases at this groove width (
$400~\unicode[STIX]{x03BC}\text{m}$
).
Similar drag reduction levels have been reproduced in the MIT Taylor–Couette apparatus (Rajappan, A. & McKinley, G. H. 2017 Personal communication). In the MIT apparatus (most recently described in Saranadhi et al. (Reference Saranadhi, Chen, Kleingartner, Srinivasan, Cohen and McKinley2016)), the inner cylinder rotates while the outer one is stationary (the opposite is true for the Princeton apparatus), the gap size
$d=12.7$
mm and
$H/d=3.3$
. When comparing to a smooth cylinder as the baseline case, they see a drag reduction of up to 15 % for heptane-infused grooves,
$w=200~\unicode[STIX]{x03BC}\text{m}$
(
$w^{+}=50$
) and
$a=0.5$
, at Reynolds numbers up to
$Re=40\,000$
. This result compares well with the 18 % drag reduction shown in this study for the most similar geometry and flow condition (
$w=400~\unicode[STIX]{x03BC}\text{m}$
,
$w^{+}=40$
and
$a=0.5$
).
4 Conclusions
We demonstrated drag reduction in turbulent Taylor–Couette flow up to 35 % with liquid-infused surfaces and 45 % for superhydrophobic surfaces. Generally, the level of drag reduction increased with viscosity ratio, groove width, fluid area fraction and Reynolds number. Some cases did not follow expected trends, as when higher-viscosity fluids produced larger drag reductions, which is most likely due to surface failure. For the liquid-infused surfaces studied here, the optimum groove size was
$w^{+}\approx 35$
. For the largest grooves, the surfaces mostly failed during testing, likely because the buoyancy and inertial forces were large enough to overcome the capillary force keeping the fluid inside the grooves.
Many supporting studies are still needed, specifically in boundary layers, with finite-length grooves and at higher Reynolds numbers, to verify that these surfaces will perform under more realistic conditions.
Acknowledgements
We thank Professor T. S. Wong of Pennsylvania State University and Professor J. Aizenberg of Harvard University for their advice on chemical surface treatments. This work is funded by the Office of Naval Research through MURI grant nos. N00014-12-1-0875 and N00014-12-1-0962 (Program Manager Dr K.-H. Kim).
