1 Introduction
A rivulet is a narrow stream of liquid flowing down a solid surface and held by surface tension on its interface. The stream of water seen on an automobile windshield is the canonical example of a rivulet commonly encountered in everyday life. Rivulets have two distinct contact lines whose motion, or lack thereof, can generate a number of geometric configurations. For example, the straight rivulet has parallel contact lines, steady fully developed flow and a cylindrical meniscus (Towell & Rothfeld Reference Towell and Rothfeld1966). This base state exhibits a number of instabilities, such as droplet formation from capillary break-up (Schmuki & Laso Reference Schmuki and Laso1990), braiding (Mertens, Putkaradze & Vorobieff Reference Mertens, Putkaradze and Vorobieff2005), rivulet meandering (Nakagawa & Scott Reference Nakagawa and Scott1984; Birnir et al. Reference Birnir, Mertens, Putkaradze and Vorobieff2008a ,Reference Birnir, Mertens, Putkaradze and Vorobieff b ), rivulet splitting (Myers, Liang & Wetton Reference Myers, Liang and Wetton2004; Wilson & Duffy Reference Wilson and Duffy2005; Wilson, Sullivan & Duffy Reference Wilson, Sullivan and Duffy2011) and the development of surface waves (Schmuki & Laso Reference Schmuki and Laso1990). Gravity affects the base-state flow field of a rivulet that wets an inclined plane (Wilson & Duffy Reference Wilson and Duffy2005) or the outside of a solid cylinder (Paterson, Wilson & Duffy Reference Paterson, Wilson and Duffy2013).
A static rivulet is characterized by the absence of an axial component to the base-state velocity field. In the absence of a base flow, the rivulet is susceptible to Plateau–Rayleigh break-up (capillary instability), whereby the interface evolves into a series of individual droplets in an attempt to minimize its surface area. Plateau (Reference Plateau1863) showed the free liquid cylinder is unstable to lengths longer than its base-state circumference using a thermostatic approach and incorrectly interpreted the final drop size from this limit. Lord Rayleigh (Reference Rayleigh1879) was able to sharpen Plateau’s interpretation by computing the dispersion relation from the governing hydrodynamic equations, showing the maximal growth rate and corresponding wavenumber gave a characteristic time and size for drop formation, respectively. Davis (Reference Davis1980) has computed static stability bounds for the static rivulet, with cylindrical cap base state, under a number of contact-line conditions. In this paper, we extend the work of Davis in the same way that Rayleigh extended the work of Plateau by computing dispersion relations from which static stability is inferred and the critical wavenumber and growth rate are identified.
We consider the linear stability of the static rivulet to small disturbances that either (i) preserve the static contact angle (free) or (ii) have a fixed contact line (pinned). The static contact angle describes the wetting properties of the solid substrate and is defined through the Young–Dupré equation (Young Reference Young1805; Dupré Reference Dupré1869),
$\unicode[STIX]{x1D70E}_{sg}-\unicode[STIX]{x1D70E}_{ls}=\unicode[STIX]{x1D70E}_{lg}\cos \unicode[STIX]{x1D6FC}$
, which relates the liquid/gas
$\unicode[STIX]{x1D70E}_{lg}$
, liquid/solid
$\unicode[STIX]{x1D70E}_{ls}$
and solid/gas
$\unicode[STIX]{x1D70E}_{sg}$
surface tensions to the static contact angle
$\unicode[STIX]{x1D6FC}$
. The liquid/solid interaction, as controlled by the wetting properties and disturbance class, can affect capillary break-up in the static rivulet. We analyse these interactions in the present work. Our work is distinguished by the ability to predict the dynamics for the large contact-angle case.
Many authors have studied the stability of cylindrical interfaces under various wetting geometries. For example, Brown & Scriven (Reference Brown and Scriven1980) use a variational approach to study the pinned cylindrical fillet protruding from an infinite slot for both constant pressure and constant volume disturbances. Their static stability limit is in agreement with Davis (Reference Davis1980) in the common limit of the constant volume disturbance. Sekimoto, Oguma & Kawasaki (Reference Sekimoto, Oguma and Kawasaki1987) use variational methods to report static instabilities on horizontal substrates in two partially wetting morphologies with non-pinned contact lines, which they call ridges and holes. Alternatively, Benilov (Reference Benilov2009) uses the lubrication approximation to show that a shallow rivulet with pinned contact lines that wets the underside of a plate (pendant) is unstable to a range of axial wavenumbers. Langbein (Reference Langbein1990) studies the interior or exterior wetting of a V-groove, Roy & Schwartz (Reference Roy and Schwartz1999) analyse a number of cross-sectional containers, such as planar, V-groove, circular and elliptical, and Bostwick & Steen (Reference Bostwick and Steen2010) consider the cylindrical-cup support. For pinned disturbances, static stability is unaffected by the geometry of the solid support. In contrast, for free disturbances the curvature of the solid support affects stability in a manner which is known a priori (Bostwick & Steen Reference Bostwick and Steen2015a ).
The mobility of the contact line is known to affect both the base flow and stability of rivulets. Paterson et al. (Reference Paterson, Wilson and Duffy2013) focus on the de-pinning transition to a mobile contact line for a rivulet wetting the outside of cylinder. The presence of a streaming flow applied transversely to a rivulet on an inclined plan affects the de-pinning transition and supports the rivulet (Paterson, Wilson & Duffy Reference Paterson, Wilson and Duffy2015). For moving contact lines, one typically introduces a constitutive law that either (i) preserves the static contact angle (Davis Reference Davis1980; Hocking Reference Hocking1992; Bostwick & Steen Reference Bostwick and Steen2015b ) or (ii) relates the contact angle to the contact-line speed (Dussan Reference Dussan1979; Oron, Davis & Bankoff Reference Oron, Davis and Bankoff1997; Bonn et al. Reference Bonn, Eggers, Indekeu, Meunier and Rolley2009). Alternative models of thin film flows account for the liquid/solid interactions through a disjoining pressure that necessitate the introduction of a precursor film. Thiele & Knobloch (Reference Thiele and Knobloch2003) study transverse instabilities of rivulets on inclined substrate in the thin film limit showing the disjoining pressure is critical in understanding the localized instability near the front and back contact lines. The role of disjoining pressure, or van der Waals (vdW) forces, is further highlighted by Diez, González & Kondic (Reference Diez, González and Kondic2009), who use simulations of the thin film evolution equations to show that for micro- and nano-sized rivulets, the length scale for vdW forces yields a relationship for the critical wavenumber, as it depends upon the cross-sectional geometry. Diez, González & Kondic (Reference Diez, González and Kondic2012) verify these predictions with experiments using polydimethylsiloxane (PDMS) oils on inclined substrates.
A rivulet with an axial base flow is susceptible to kinematic-wave instabilities characteristic of thin film flows and particularly so if the rivulet is relatively flat. In a series of papers, Davis et al. study the long wavelength instabilities of the rivulet with unidirectional gravity-driven flow down a vertical plane (Weiland & Davis Reference Weiland and Davis1981; Young & Davis Reference Young and Davis1987). They report kinematic-wave instabilities for wide rivulets with immobile contact lines and capillary instability of narrow rivulets. Although their analysis is able to handle a wide range of effects and predict the varicose instability, they do not consider rivulet meandering or the sinuous instability. Alekseenko, Markovich & Shtork (Reference Alekseenko, Markovich and Shtork1996) have shown that perturbations to the base flow of a rivulet that wets the outside of a cylinder result in stationary excited waves that depend upon both the applied flow rate and frequency of excitation. Numerical simulations of the integral boundary layer model do a reasonable job of predicting the shape and dispersion relationship of these nonlinear forced waves (Aktershev & Alekseenko Reference Aktershev and Alekseenko2015; Alekseenko et al. Reference Alekseenko, Aktershev, Bobylev, Kharlamov and Markovich2015).
For the static rivulet, we show the varicose mode is unstable to a broader range of axial wavenumbers than the sinuous mode for the contact-line disturbances we consider here. Our static stability results agree well with Davis (Reference Davis1980). The dispersion relations we compute show that the relevant instability mechanism is capillary break-up; there exists a critical disturbance of maximum growth that is distinguished by a non-trivial axial wavenumber. The properties of the critical disturbance are greatly influenced by the liquid/solid interaction, as controlled by the static contact angle and mobile/immobile nature of the contact line. The pinned disturbance is relatively stabilizing compared to the free disturbance. Support geometries of a cylindrical nature, like the circular-cylinder cup and planar plate, are consistent with a quiescent cylindrical base-state interface. We show the planar support has a larger critical growth rate than the cylindrical-cup support (Bostwick & Steen Reference Bostwick and Steen2010).
Relative to capillary break-up in rivulets, rivulet meandering is less well understood but benefits from a number of experimental studies (e.g. Nakagawa & Scott Reference Nakagawa and Scott1984; Schmuki & Laso Reference Schmuki and Laso1990; Nakagawa & Scott Reference Nakagawa and Scott1992; Nakagawa & Nakagawa Reference Nakagawa and Nakagawa1996). Recent experiments by Daerr et al. (Reference Daerr, Eggers, Limat and Valade2011) and Couvreur & Daerr (Reference Couvreur and Daerr2012) demonstrate that meandering is enhanced by inertial effects from the base flow provided contact-line defects (deemed anisotropic substrate friction) can be overcome. With respect to theoretical considerations, Culkin & Davis (Reference Culkin and Davis1983) derive a stability index to measure the stabilizing effects of surface tension and de-stabilizing effects of inertia under dynamic wetting conditions. Unable to account for contact-angle hysteresis, the stability index was only marginally effective at capturing the meandering instability mechanism observed in their experiments. Kim, Kim & Kang (Reference Kim, Kim and Kang2004) use a perturbation analysis to capture the meandering instability for a rivulet base-state subject to plug flow. By balancing pressures at the contact line, they are able to derive a dispersion relation that depends upon the base-state geometry, a Weber number and wetting conditions on the contact line. The response of the fluid in terms of the disturbed interface shape is precluded from their analysis. Similarly, Grand-Piteira, Daerr & Limat (Reference Grand-Piteira, Daerr and Limat2006) derive a rivulet meandering criteria from a force balance on the contact line that incorporates contact-angle hysteresis, capillary effects and inertia from a gravity-driven base flow. They find, among other results, that the base flow is also hysteretic and thus the shape of the meandering rivulet varies only with increasing flow rate.
We report that, for free contact lines, the sinuous mode destabilizes the static rivulet with super-circular base state (
$90^{\circ }<\unicode[STIX]{x1D6FC}<180^{\circ }$
) and for a range of axial wavenumbers is the dominant instability mode. This result is new, as far as we are aware. The features of this instability are not characteristic of typical capillary break-up. Specifically, the disturbance of maximum growth rate is long wave, distinguished by an axial wavenumber
$k_{m}=0$
, for a range of contact angles
$90^{\circ }<\unicode[STIX]{x1D6FC}<150^{\circ }$
. Outside this interval, rivulet meandering
$k_{m}\neq 0$
occurs. We show that the sinuous instability is related to the walking droplet instability (Bostwick & Steen Reference Bostwick and Steen2014). The instability mechanism is illustrated through a toy problem that shows the configurational energy is lowered by decreasing both the liquid/gas and liquid/solid surface areas. We show the sinuous instability correlates with horizontal centre-of-mass motion and, thereby, suggest that the toy problem can be used to interpret rivulet meandering.
We begin this paper by defining the hydrodynamic equations that govern the motion of the rivulet interface. A normal mode expansion reduces the governing equations to a functional eigenvalue problem on linear operators, which are parametrized by the volume of the base state through the static contact angle
$\unicode[STIX]{x1D6FC}$
, and the boundary conditions at the three-phase contact line. We reduce the functional equation to a standard algebraic eigenvalue problem using a Rayleigh–Ritz procedure and compute dispersion relations. We recover the static stability limit obtained by Davis (Reference Davis1980) and report critical growth rates and wavenumbers for the varicose and sinuous modes. The sinuous instability mechanism is illustrated through a toy problem. Lastly, some concluding remarks are offered.
2 Mathematical formulation
A cylindrical interface held by uniform surface tension
$\unicode[STIX]{x1D70E}$
contacting a planar support is referred to as a rivulet. The static rivulet is a constant mean curvature
$H$
surface that satisfies the Young–Laplace equation,
$$\begin{eqnarray}p/\unicode[STIX]{x1D70E}=2H\equiv \unicode[STIX]{x1D705}_{1}+\unicode[STIX]{x1D705}_{2},\end{eqnarray}$$
which relates the principal curvatures
$\unicode[STIX]{x1D705}_{1},\unicode[STIX]{x1D705}_{2}$
to the pressure
$p$
there. When gravitational effects are neglected, the static base state is a circular arc in the
$x$
–
$y$
plane extending to infinity in the axial (
$z$
) direction, as shown in figure 1(a). The equilibrium surface
$\unicode[STIX]{x1D6E4}$
is defined parametrically,
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}X(s,z;\unicode[STIX]{x1D6FC})={\displaystyle \frac{1}{\sin (\unicode[STIX]{x1D6FC})}}\sin (s),\quad Y(s,z;\unicode[STIX]{x1D6FC})={\displaystyle \frac{1}{\sin (\unicode[STIX]{x1D6FC})}}(\cos (s)-\cos (\unicode[STIX]{x1D6FC})),\\ Z(s,z;\unicode[STIX]{x1D6FC})=z,\end{array}\right\}\end{eqnarray}$$
where
$s\in [-\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC}]$
and
$z\in [-\infty ,\infty ]$
are the arclength-like and axial coordinates, respectively. Here lengths have been scaled with respect to the base radius
$r$
and the equilibrium surface is characterized by principal curvatures
$\unicode[STIX]{x1D705}_{1}\equiv \sin \unicode[STIX]{x1D6FC},\unicode[STIX]{x1D705}_{2}\equiv 0$
. The interface is given a small disturbance
$\unicode[STIX]{x1D702}(s,z,t)$
, such that
$\boldsymbol{x}=\boldsymbol{x}_{0}(1+\unicode[STIX]{x1D716}\unicode[STIX]{x1D702})$
with
$\boldsymbol{x}_{0}$
the base state (2.2) (cf. figure 1). No domain perturbation is needed for linear problems, thus the fluid domain
$$\begin{eqnarray}D\equiv \{(x,y,z)\mid 0\leqslant x\leqslant X(s,\unicode[STIX]{x1D711};\unicode[STIX]{x1D6FC}),0\leqslant y\leqslant Y(s,\unicode[STIX]{x1D711};\unicode[STIX]{x1D6FC}),-\infty \leqslant z\leqslant \infty \}\end{eqnarray}$$
is bounded by a free surface
$\unicode[STIX]{x2202}D^{\,f}$
and a planar surface of support
$\unicode[STIX]{x2202}D^{s}$
:
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x2202}D^{\,f}\equiv \{(x,y,z)\mid x=X(s,z;\unicode[STIX]{x1D6FC}),y=Y(s,z;\unicode[STIX]{x1D6FC}),z=z\}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x2202}D^{s}\equiv \{(x,y,z)\mid y=0\}. & \displaystyle\end{eqnarray}$$
The fluid is immersed in a passive gas and the effect of gravity is neglected. In what follows we derive the governing equations for our linear stability analysis, wherein the pressure
$p$
and velocity fields
$\boldsymbol{v}$
will be associated with the disturbance fields.
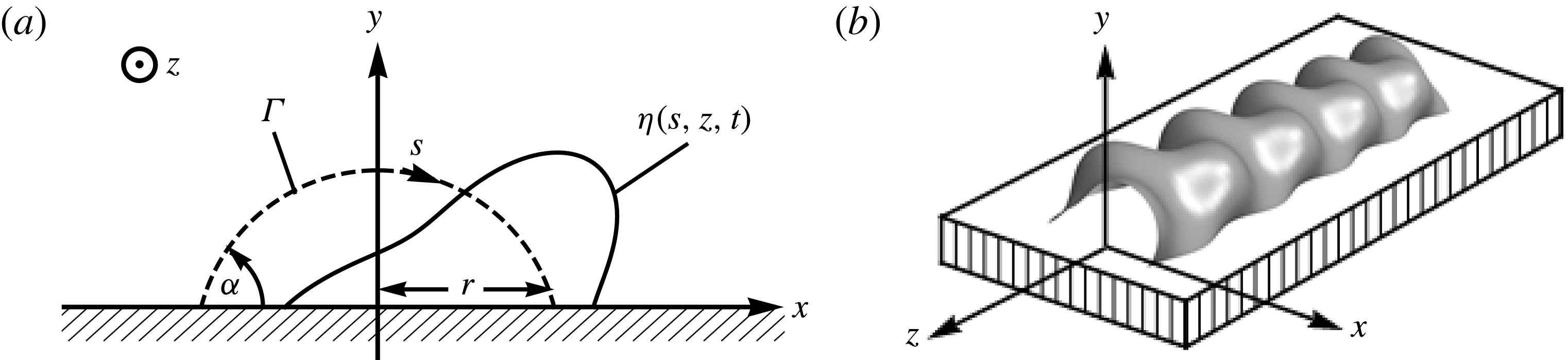
Figure 1. Definition sketch of the rivulet in (a) polar and (b) three-dimensional perspective views.
2.1 Hydrodynamic field equations
The fluid is incompressible and the flow is assumed to be irrotational. Therefore, the velocity field may be described as
$\boldsymbol{v}=-\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F9}$
, where the velocity potential
$\unicode[STIX]{x1D6F9}$
satisfies Laplace’s equation
$$\begin{eqnarray}\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D6F9}=0\end{eqnarray}$$
on the fluid domain
$D$
. Additionally, the velocity potential satisfies the no-penetration condition
$$\begin{eqnarray}\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F9}\cdot {\hat{y}}=0\end{eqnarray}$$
on the surface of support
$\unicode[STIX]{x2202}D^{s}$
(with
$\hat{n}={\hat{y}}$
) and a kinematic condition
$$\begin{eqnarray}{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F9}}{\unicode[STIX]{x2202}n}}=-{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}{\unicode[STIX]{x2202}t}}\end{eqnarray}$$
on the free surface
$\unicode[STIX]{x2202}D^{\,f}$
, which relates the normal velocity to the perturbation amplitude there. The pressure field in
$D$
for small interface disturbance is given by the linearized Bernoulli equation
$$\begin{eqnarray}p=\unicode[STIX]{x1D71A}{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F9}}{\unicode[STIX]{x2202}t}},\end{eqnarray}$$
where
$\unicode[STIX]{x1D71A}$
is the fluid density. Finally, deviations from the equilibrium surface
$\unicode[STIX]{x1D6E4}$
generate pressure gradients on
$\unicode[STIX]{x2202}D^{\,f}$
, and thereby flows, according to the linearized Young–Laplace equation
$$\begin{eqnarray}p/\unicode[STIX]{x1D70E}=-\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6E4}}\unicode[STIX]{x1D702}-(\unicode[STIX]{x1D705}_{1}^{2}+\unicode[STIX]{x1D705}_{2}^{2})\unicode[STIX]{x1D702},\end{eqnarray}$$
which is valid for small disturbances
$|\unicode[STIX]{x1D702}|\ll 1$
and their derivatives
$|\unicode[STIX]{x1D702}_{ss}|\ll 1$
, etc. The Laplace–Beltrami operator
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6E4}}$
, introduced in (2.9), is defined by functions
$\unicode[STIX]{x1D702}$
on the equilibrium surface (e.g. Kreyszig Reference Kreyszig1991),
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6E4}}\unicode[STIX]{x1D702}\equiv {\displaystyle \frac{1}{\sqrt{g}}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}u^{\unicode[STIX]{x1D707}}}}\left(\sqrt{g}g^{\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}}{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}{\unicode[STIX]{x2202}u^{\unicode[STIX]{x1D708}}}}\right),\end{eqnarray}$$
with the surface metric given by
$$\begin{eqnarray}g_{\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}}\equiv \boldsymbol{x}_{\unicode[STIX]{x1D707}}\cdot \boldsymbol{x}_{\unicode[STIX]{x1D708}}=\left(\begin{array}{@{}cc@{}}\text{csc}^{2}(\unicode[STIX]{x1D6FC}) & 0\\ 0 & 1\end{array}\right),\quad g=\text{csc}^{2}(\unicode[STIX]{x1D6FC}).\end{eqnarray}$$
Equations (2.5)–(2.9) are the linearized disturbance equations governing the motion of this inviscid fluid. To form a well-posed system of partial differential equations, the field equations are supplemented with a boundary condition on the three-phase contact line, which we discuss later.
2.2 Normal mode reduction
The following dimensionless variables are introduced:
$$\begin{eqnarray}\bar{x}=x/r,\quad \bar{\unicode[STIX]{x1D702}}=\unicode[STIX]{x1D702}/r,\quad \bar{t}=t\sqrt{{\displaystyle \frac{\unicode[STIX]{x1D70E}}{\unicode[STIX]{x1D71A}r^{3}}}},\quad \bar{\unicode[STIX]{x1D6F9}}=\unicode[STIX]{x1D6F9}\sqrt{{\displaystyle \frac{\unicode[STIX]{x1D71A}}{\unicode[STIX]{x1D70E}r}}},\quad \bar{p}=p\left({\displaystyle \frac{r}{\unicode[STIX]{x1D70E}}}\right).\end{eqnarray}$$
Here lengths are scaled by the base radius
$r$
, time with the capillary time scale
$\sqrt{\unicode[STIX]{x1D71A}r^{3}/\unicode[STIX]{x1D70E}}$
and pressure with the capillary pressure
$\unicode[STIX]{x1D70E}/r$
.
Normal modes with axial wavenumber
$k$
are written in mixed coordinates for efficiency in presentation,
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}(\boldsymbol{x},t)=\unicode[STIX]{x1D719}(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D703})\text{e}^{\unicode[STIX]{x1D6FE}t}\text{e}^{\text{i}kz},\quad \unicode[STIX]{x1D702}(s,z,t)=f(s)\text{e}^{\unicode[STIX]{x1D6FE}t}\text{e}^{\text{i}kz},\end{eqnarray}$$
where
$(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D703})$
are cylindrical coordinates. Equations (2.12) and (2.13) are then applied to the hydrodynamic field equations (2.5)–(2.9) to give
$$\begin{eqnarray}\displaystyle & \displaystyle {\displaystyle \frac{1}{\unicode[STIX]{x1D70C}}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}}\left(\unicode[STIX]{x1D70C}{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}}\right)+{\displaystyle \frac{1}{\unicode[STIX]{x1D70C}^{2}}}{\displaystyle \frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D719}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}^{2}}}-k^{2}\unicode[STIX]{x1D719}=0\quad [D], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}}{\unicode[STIX]{x2202}n}}=0\quad [\unicode[STIX]{x2202}D^{s}], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}}{\unicode[STIX]{x2202}n}}=-\unicode[STIX]{x1D706}f[\unicode[STIX]{x2202}D^{\,f}], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle f^{\prime \prime }+(1-k^{2})f=-\unicode[STIX]{x1D706}(\csc ^{2}\unicode[STIX]{x1D6FC})\unicode[STIX]{x1D719}[\unicode[STIX]{x2202}D^{\,f}]. & \displaystyle\end{eqnarray}$$
$\unicode[STIX]{x1D706}\equiv \unicode[STIX]{x1D6FE}\sqrt{\unicode[STIX]{x1D71A}r^{3}/\unicode[STIX]{x1D70E}}$
, which is parametrized by the axial wavenumber
$k$
and base-state volume via the static contact angle
$\unicode[STIX]{x1D6FC}$
. Equation (2.14a
) is Laplace’s equation written in cylindrical coordinates, equation (2.14b
) is the no-penetration condition and (2.14c
) is the kinematic condition. The dynamic pressure balance at the free surface is represented by (2.14d
), where differentiation is with respect to the arclength coordinate,
$^{\prime }=\text{d}/\text{d}s$
.3 Reduction to operator equation
The dynamic pressure balance (2.14d ) can be simplified using the kinematic condition (2.14c ) to give
$$\begin{eqnarray}\left({\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}}{\unicode[STIX]{x2202}n}}\right)^{\prime \prime }+(1-k^{2})\left({\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}}{\unicode[STIX]{x2202}n}}\right)={\displaystyle \frac{\unicode[STIX]{x1D706}^{2}}{\sin ^{2}\unicode[STIX]{x1D6FC}}}\unicode[STIX]{x1D719},\quad [\unicode[STIX]{x2202}D^{\,f}],\end{eqnarray}$$
which is recognized as an integro-differential equation that governs the motion of the interface. The solution of this inhomogeneous differential equation is parametrized by axial wavenumber
$k$
and given by
$$\begin{eqnarray}{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}}{\unicode[STIX]{x2202}n}}(s)=\hat{\unicode[STIX]{x1D706}}^{2}\int _{-\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D6FC}}G(s,\unicode[STIX]{x1D70F};k)\unicode[STIX]{x1D719}(\unicode[STIX]{x1D70F})\,\text{d}\unicode[STIX]{x1D70F},\end{eqnarray}$$
where
$\hat{\unicode[STIX]{x1D706}}\equiv \unicode[STIX]{x1D706}/\sin \unicode[STIX]{x1D6FC}$
and
$G(s,\unicode[STIX]{x1D70F};k)$
is the Green’s function or fundamental solution of the differential operator, the left-hand side of (3.1). Alternatively, one may view (3.2) as a functional eigenvalue problem for
$\hat{\unicode[STIX]{x1D706}}$
and
$\unicode[STIX]{x1D719}$
on linear operators,
$$\begin{eqnarray}M^{-1}[\unicode[STIX]{x1D719}]=\hat{\unicode[STIX]{x1D706}}^{2}K^{-1}[\unicode[STIX]{x1D719}],\end{eqnarray}$$
with
$$\begin{eqnarray}M^{-1}[\unicode[STIX]{x1D719}]\equiv {\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}}{\unicode[STIX]{x2202}n}},\quad K^{-1}[\unicode[STIX]{x1D719}]\equiv \int _{-\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D6FC}}G(s,\unicode[STIX]{x1D70F};k)\unicode[STIX]{x1D719}(\unicode[STIX]{x1D70F})\,\text{d}\unicode[STIX]{x1D70F}.\end{eqnarray}$$
3.1 Green’s function
To compute the eigenvalue spectrum of (3.2) using the operator formalism, one must construct the Green’s function or integral operator
$K^{-1}$
. We use the following representation of the Green’s function,
$$\begin{eqnarray}G(s,\unicode[STIX]{x1D70F};k)=\left\{\begin{array}{@{}ll@{}}{\displaystyle \frac{U(\unicode[STIX]{x1D70F};k)V(s;k)}{W(s;k)}}\quad & 0<s<\unicode[STIX]{x1D70F}<\unicode[STIX]{x1D6FC}\\ {\displaystyle \frac{U(s;k)V(\unicode[STIX]{x1D70F};k)}{W(s;k)}}\quad & 0<\unicode[STIX]{x1D70F}<s<\unicode[STIX]{x1D6FC},\end{array}\right.\end{eqnarray}$$
because it is amenable to a symmetric decomposition. Here
$U$
and
$V$
are the homogeneous solutions of (3.1) that satisfy the boundary conditions on the vertical mid-plane
$s=0$
and the contact line
$s=\unicode[STIX]{x1D6FC}$
, respectively. Likewise,
$W$
is the Wronskian of the solutions
$U$
and
$V$
.
3.1.1 Symmetric decomposition
We decompose the solutions of (3.2) according to their symmetry about the axis of symmetry (
$s=0$
). The varicose modes are symmetric and satisfy
$$\begin{eqnarray}\left({\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}}{\unicode[STIX]{x2202}n}}\right)^{\prime }\bigg|_{s=0}=0,\end{eqnarray}$$
while the sinuous modes are anti-symmetric and satisfy the following condition:
$$\begin{eqnarray}\left({\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}}{\unicode[STIX]{x2202}n}}\right)\bigg|_{s=0}=0.\end{eqnarray}$$
For reference, typical varicose and sinuous modes are illustrated in figure 2.
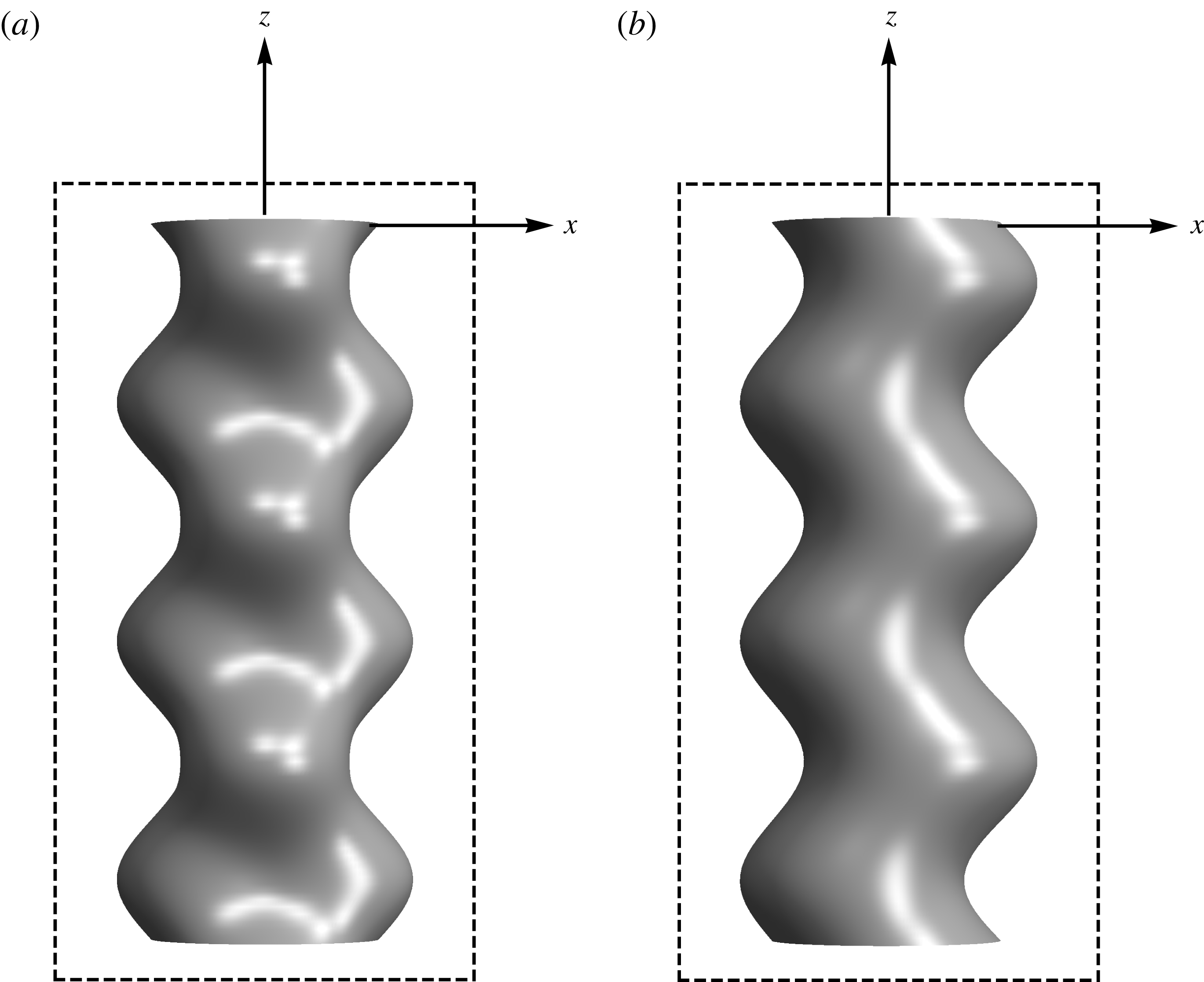
Figure 2. Top view of a three-dimensional varicose (a) and sinuous (b) mode shape.
3.1.2 Contact-line conditions
We consider two boundary conditions at the three-phase contact line, whose origin is discussed in detail in Bostwick & Steen (Reference Bostwick and Steen2015b
) and are valid for small disturbances
$|\unicode[STIX]{x1D702}|\ll 1$
. The first type has a mobile contact line that preserves the static contact angle
$\unicode[STIX]{x1D6FC}$
,
$$\begin{eqnarray}\left({\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}s}}\left({\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}}{\unicode[STIX]{x2202}n}}\right)+\cos (\unicode[STIX]{x1D6FC}){\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}}{\unicode[STIX]{x2202}n}}\right)\bigg|_{s=\unicode[STIX]{x1D6FC}}=0,\end{eqnarray}$$
and is termed the ‘free’ disturbance. The second has immobile or ‘pinned’ contact lines,
$$\begin{eqnarray}\left({\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}}{\unicode[STIX]{x2202}n}}\right)\bigg|_{s=\unicode[STIX]{x1D6FC}}=0.\end{eqnarray}$$
3.1.3
$U$
and
$V$
solutions
To distinguish between disturbances, superscripts
$f$
and
$p$
will denote the free and pinned contact-line disturbances, respectively. Similarly, a subscript
$v$
or
$s$
will distinguish the varicose from the sinuous modes.
With regards to the decomposition by symmetry, the
$U$
solutions are independent of the contact-line conditions. The varicose modes satisfy (3.6) with solution
$$\begin{eqnarray}U_{v}^{f,p}(s)=\cos (\unicode[STIX]{x1D6FD}s),\end{eqnarray}$$
with
$$\begin{eqnarray}\unicode[STIX]{x1D6FD}\equiv \sqrt{1-k^{2}}.\end{eqnarray}$$
Similarly, the sinuous modes satisfy (3.7) with solution given by
$$\begin{eqnarray}U_{s}^{f,p}(s)={\displaystyle \frac{\sin (\unicode[STIX]{x1D6FD}s)}{\unicode[STIX]{x1D6FD}}}.\end{eqnarray}$$
The
$V$
solutions are independent of the symmetry about the mid-plane. Disturbances that satisfy the free boundary condition (3.8) have the following solution,
$$\begin{eqnarray}V_{v,s}^{\,f}(s)=\cos (\unicode[STIX]{x1D6FD}s)+A\sin (\unicode[STIX]{x1D6FD}s),\end{eqnarray}$$
with
$$\begin{eqnarray}A={\displaystyle \frac{\unicode[STIX]{x1D6FD}\sin \unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}-\cos \unicode[STIX]{x1D6FC}\cos \unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6FD}\cos \unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FC}\sin \unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}}.\end{eqnarray}$$
Similarly, solutions that respect the pinned contact-line condition (3.9) are expressed as
$$\begin{eqnarray}V_{v,s}^{p}(s)=\sin \unicode[STIX]{x1D6FD}(s-\unicode[STIX]{x1D6FC}).\end{eqnarray}$$
Lastly, the Wronskians for the free (
$f$
) and pinned (
$p$
) disturbances are given by
$$\begin{eqnarray}W_{v}^{\,f}(s)=A\unicode[STIX]{x1D6FD},\quad W_{v}^{p}(s)=\unicode[STIX]{x1D6FD}\cos (\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}),\end{eqnarray}$$
for the varicose modes, and
$$\begin{eqnarray}W_{s}^{\,f}(s)=-1,\quad W_{s}^{p}(s)=\sin (\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}),\end{eqnarray}$$
for the sinuous modes, respectively.
The inverse operator
$K^{-1}$
is readily expressed by applying the appropriate solutions (
$U,V,W$
) to the Green’s function (3.5).
4 Solution of operator equation
To compute the eigenvalue spectrum of (3.3), the operator equation is reduced to a truncated set of linear algebraic equations using the variational procedure of Rayleigh–Ritz. Stationary values of the functional
$$\begin{eqnarray}\hat{\unicode[STIX]{x1D706}}^{2}={\displaystyle \frac{(M^{-1}[\unicode[STIX]{x1D719}],\unicode[STIX]{x1D719})}{(K^{-1}[\unicode[STIX]{x1D719}],\unicode[STIX]{x1D719})}},\quad \unicode[STIX]{x1D719}\in S,\end{eqnarray}$$
are the characteristic growth rates, where
$S$
is a predetermined function space. We choose this function space to satisfy Laplace’s equation (2.14a
) and the no-penetration condition (2.14b
). In this case, the minimizers of (4.1) are also solutions to the eigenvalue problem (2.14). We sketch the method here, while a more thorough illustration can be found in Bostwick & Steen (Reference Bostwick and Steen2009, Reference Bostwick and Steen2013).
4.1 Rayleigh–Ritz method
To begin, a solution series
$$\begin{eqnarray}\unicode[STIX]{x1D719}=\mathop{\sum }_{j=1}^{N}a_{j}\unicode[STIX]{x1D719}_{j},\end{eqnarray}$$
constructed from properly chosen basis functions
$\unicode[STIX]{x1D719}_{j}$
, is applied to the operator equation (3.3) and inner products are taken to generate the following algebraic eigenvalue problem,
$$\begin{eqnarray}\mathop{\sum }_{j=1}^{N}(m_{ij}-\hat{\unicode[STIX]{x1D706}}^{2}\unicode[STIX]{x1D705}_{ij})a_{j}=0_{i},\end{eqnarray}$$
with
$$\begin{eqnarray}\displaystyle & \displaystyle m_{ij}\equiv (M^{-1}[\unicode[STIX]{x1D719}_{i}],\unicode[STIX]{x1D719}_{j})=\int _{0}^{\unicode[STIX]{x1D6FC}}{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}_{i}}{\unicode[STIX]{x2202}n}}\unicode[STIX]{x1D719}_{j}\,\text{d}s, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D705}_{ij}\equiv (K^{-1}[\unicode[STIX]{x1D719}_{i}],\unicode[STIX]{x1D719}_{j})=\int _{0}^{\unicode[STIX]{x1D6FC}}\int _{0}^{\unicode[STIX]{x1D6FC}}K^{-1}[\unicode[STIX]{x1D719}_{i}]\unicode[STIX]{x1D719}_{j}\,\text{d}\unicode[STIX]{x1D70F}\,\text{d}s, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D705}_{ij} & = & \displaystyle \left(\int _{0}^{\unicode[STIX]{x1D6FC}}{\displaystyle \frac{U(s)}{W(s)}}\unicode[STIX]{x1D719}_{j}(s)\,\text{d}s\right)\left(\int _{0}^{\unicode[STIX]{x1D6FC}}V(\unicode[STIX]{x1D70F})\unicode[STIX]{x1D719}_{i}(\unicode[STIX]{x1D70F})\,\text{d}\unicode[STIX]{x1D70F}\right)\nonumber\\ \displaystyle & & \displaystyle \quad +\,\int _{0}^{\unicode[STIX]{x1D6FC}}{\displaystyle \frac{V(s)}{W(s)}}\unicode[STIX]{x1D719}_{j}(s)\int _{0}^{s}U(\unicode[STIX]{x1D70F})\unicode[STIX]{x1D719}_{i}(\unicode[STIX]{x1D70F})\,\text{d}\unicode[STIX]{x1D70F}\,\text{d}s\nonumber\\ \displaystyle & & \displaystyle \quad -\,\int _{0}^{\unicode[STIX]{x1D6FC}}{\displaystyle \frac{U(s)}{W(s)}}\unicode[STIX]{x1D719}_{j}(s)\int _{0}^{s}V(\unicode[STIX]{x1D70F})\unicode[STIX]{x1D719}_{i}(\unicode[STIX]{x1D70F})\,\text{d}\unicode[STIX]{x1D70F}\,\text{d}s.\end{eqnarray}$$
4.2 Function space
Allowable solutions of (3.3) necessarily satisfy the hydrodynamic equations (2.14). Accordingly, we choose basis functions
$\unicode[STIX]{x1D719}_{i}$
which span a function space that satisfies Laplace’s equation (2.14a
) on the fluid domain and the no-penetration condition (2.14b
) on the surface of support.
4.2.1 Varicose modes
For the varicose modes, the following basis functions span such a function space:
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{j}=\text{I}_{2(j-1)}(k\unicode[STIX]{x1D70C})\cos (2(j-1)\unicode[STIX]{x1D703}).\end{eqnarray}$$
Here
$\text{I}_{n}$
is the modified Bessel function (Arfken & Weber Reference Arfken and Weber2001). For reference, we also provide the normal derivatives of the basis functions
$\unicode[STIX]{x1D719}_{j}$
,
$$\begin{eqnarray}\displaystyle & & \displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}n}}(\text{I}_{2j}(k\unicode[STIX]{x1D70C})\cos (2j\unicode[STIX]{x1D703}))\nonumber\\ \displaystyle & & \displaystyle \quad ={\displaystyle \frac{k}{2}}[\text{I}_{2j+1}(k\unicode[STIX]{x1D70C})+\text{I}_{2j-1}(k\unicode[STIX]{x1D70C})]\cos (2j\unicode[STIX]{x1D703})(-\sin (s)\cos (\unicode[STIX]{x1D703})+\cos (s)\sin (\unicode[STIX]{x1D703}))\nonumber\\ \displaystyle & & \displaystyle \qquad -\,{\displaystyle \frac{k}{2}}[\text{I}_{2j-1}(k\unicode[STIX]{x1D70C})-\text{I}_{2j+1}(k\unicode[STIX]{x1D70C})]\sin (2j\unicode[STIX]{x1D703})(\sin (s)\sin (\unicode[STIX]{x1D703})+\cos (s)\cos (\unicode[STIX]{x1D703})),\end{eqnarray}$$
because they are needed to compute the matrix element (4.4a ). Here the normal derivative of the potential function is given in mixed coordinates for efficiency in presentation. As required by (4.4b ), the functions (4.6) and (4.7) are evaluated on the equilibrium surface through the coordinate transformations,
$$\begin{eqnarray}\unicode[STIX]{x1D70C}=\sqrt{X^{2}+Y^{2}},\quad \cos \unicode[STIX]{x1D703}={\displaystyle \frac{X}{\sqrt{X^{2}+Y^{2}}}},\quad \sin \unicode[STIX]{x1D703}={\displaystyle \frac{Y}{\sqrt{X^{2}+Y^{2}}}},\end{eqnarray}$$
with
$X=X(s;\unicode[STIX]{x1D6FC})$
and
$Y=Y(s;\unicode[STIX]{x1D6FC})$
defined in (2.2).
4.2.2 Sinuous modes
For the sinuous modes, we use the following basis functions,
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{j}=\text{I}_{2j-1}(k\unicode[STIX]{x1D70C})\sin ((2j-1)\unicode[STIX]{x1D703}),\end{eqnarray}$$
with normal derivatives given by
$$\begin{eqnarray}\displaystyle & & \displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}n}}(\text{I}_{2j}(k\unicode[STIX]{x1D70C})\sin (2j\unicode[STIX]{x1D703}))\nonumber\\ \displaystyle & & \displaystyle \quad ={\displaystyle \frac{k}{2}}[\text{I}_{2j+1}(k\unicode[STIX]{x1D70C})+\text{I}_{2j-1}(k\unicode[STIX]{x1D70C})]\sin (2j\unicode[STIX]{x1D703})(-\sin (s)\cos (\unicode[STIX]{x1D703})+\cos (s)\sin (\unicode[STIX]{x1D703}))\nonumber\\ \displaystyle & & \displaystyle \qquad +{\displaystyle \frac{k}{2}}[\text{I}_{2j-1}(k\unicode[STIX]{x1D70C})-\text{I}_{2j+1}(k\unicode[STIX]{x1D70C})]\cos (2j\unicode[STIX]{x1D703})(\sin (s)\sin (\unicode[STIX]{x1D703})+\cos (s)\cos (\unicode[STIX]{x1D703})).\end{eqnarray}$$
Once again, to compute the matrix elements (4.4b ), one evaluates the functions (4.9) and (4.10) on the equilibrium surface using the coordinate transformation (4.8).
5 Results
The eigenvalues of the matrix equation (4.3) are computed using a truncation of
$N=8$
terms in the solution series (4.2), which is sufficient to generate relative eigenvalue convergence of
$0.1\,\%$
for the results presented here. The convergence properties of eigenvalues and eigenvectors using the Ritz method are discussed in Segel (Reference Segel1987). Unstable growth rates (
$\unicode[STIX]{x1D706}^{2}>0$
) and stable oscillation frequencies (
$\unicode[STIX]{x1D706}^{2}<0$
) are reported as they depend upon the axial wavenumber
$k$
. For a given eigenvalue
$\unicode[STIX]{x1D706}^{(l)}$
with associated eigenvector
$a_{j}^{(l)}$
, the corresponding eigenfunction is the velocity potential
$$\begin{eqnarray}\unicode[STIX]{x1D719}=\mathop{\sum }_{j=1}^{N}a_{j}^{(l)}\unicode[STIX]{x1D719}_{j},\end{eqnarray}$$
which is related to the interface disturbance
$$\begin{eqnarray}f=\mathop{\sum }_{j=1}^{N}a_{j}^{(l)}{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}_{j}}{\unicode[STIX]{x2202}n}}.\end{eqnarray}$$
For a fixed mode type (varicose or sinuous), equation (4.3) has a discrete spectrum of eigenvalues
$\unicode[STIX]{x1D706}^{2}$
ordered in decreasing numerical value. This work is focused on hydrodynamic stability and, accordingly, we are primarily concerned with the eigenmode associated with the largest eigenvalue
$l=1$
, as this mode possibly exhibits instability
$\unicode[STIX]{x1D706}^{2}>0$
. The rest of the spectrum
$l>1$
displays oscillatory behaviour
$\unicode[STIX]{x1D706}^{2}<0$
. In what follows, we present results for both the varicose and sinuous modes and illustrate the differences between free and pinned disturbances.
5.1 Dispersion relations
The dependence of axial wavenumber
$k$
on the growth rate
$\unicode[STIX]{x1D706}^{2}$
is illustrated in the typical dispersion curves in figures 3 and 4. Note the free varicose mode with
$\unicode[STIX]{x1D6FC}=90^{\circ }$
can be extended via symmetry operation to the full cylinder and thus recovers the Plateau–Rayleigh result (cf. figure 3). For a given disturbance, there are a number of wavenumbers
$k\in [0,k_{s}]$
that destabilize the base state with
$k_{s}$
the static stability limit. The sinuous modes with pinned contact lines shown in figure 4 are the exception, as oscillatory behaviour persists for all wavenumbers. Each dispersion curve exhibits a fastest growing mode distinguished by wavenumber
$k_{m}$
and growth rate
$\unicode[STIX]{x1D706}_{m}^{2}$
. To summarize, the static stability limit
$k_{s}$
, critical wavenumber
$k_{m}$
and associated growth rate
$\unicode[STIX]{x1D706}_{m}^{2}$
are effective metrics to characterize the dispersion relation.
Figure 3. Free dispersion relations: growth rate
$\unicode[STIX]{x1D706}^{2}$
against axial wavenumber
$k$
for varicose (a) and sinuous (b) modes, parametrized by contact angle
$\unicode[STIX]{x1D6FC}$
. Note the Rayleigh dispersion for the liquid cylinder is recovered from the varicose mode (a) for the contact angle
$\unicode[STIX]{x1D6FC}=90^{\circ }$
.
Figure 4. Pinned dispersion relations: growth rate
$\unicode[STIX]{x1D706}^{2}$
against axial wavenumber
$k$
for varicose (a) and sinuous (b) modes, parametrized by contact angle
$\unicode[STIX]{x1D6FC}$
. The sinuous mode is always stable
$\unicode[STIX]{x1D706}^{2}<0$
and exhibits oscillations.
5.2 Static instability
The varicose modes are more unstable than the sinuous modes. Figure 5 plots the static stability limit
$k_{s}$
against contact angle
$\unicode[STIX]{x1D6FC}$
showing the varicose modes are unstable to a larger number of axial wavenumbers than the sinuous mode for both free and pinned disturbances. For reference, the free liquid cylinder is unstable to wavenumbers below the Plateau–Rayleigh limit
$k_{s}=1$
. Static stability for the varicose mode can be directly compared to that computed by Davis (Reference Davis1980). The agreement is excellent. For the free disturbance, the rivulet is unstable over the entire range of contact angles
$0^{\circ }<\unicode[STIX]{x1D6FC}<180^{\circ }$
and the instability window shrinks (enlarges) relative to the free cylinder for super-circular
$\unicode[STIX]{x1D6FC}>90^{\circ }$
(sub-circular
$\unicode[STIX]{x1D6FC}<90^{\circ }$
) base states. The limiting case
$\unicode[STIX]{x1D6FC}\rightarrow 180^{\circ }$
is the most similar to the free cylinder and highlights the role of the liquid/solid interaction; the interface must deform in a non-axisymmetric manner to satisfy the contact-line boundary condition (3.8), thus giving a stabilization
$k_{s}<1$
relative to the free cylinder. The pinned contact-line disturbance is stabilizing relative to both the free disturbance and the free cylinder, as witnessed by the smaller instability window shown in figure 5. For pinned contact lines, the varicose mode destabilizes the super-circular
$90^{\circ }<\unicode[STIX]{x1D6FC}<180^{\circ }$
base states, while the sinuous mode is always stable. Although the varicose mode is the dominant instability, the sinuous mode does exhibit instability to free disturbances when the cylindrical base state is super-circular
$90^{\circ }<\unicode[STIX]{x1D6FC}<180^{\circ }$
. The features of this instability will be discussed in a subsequent section.
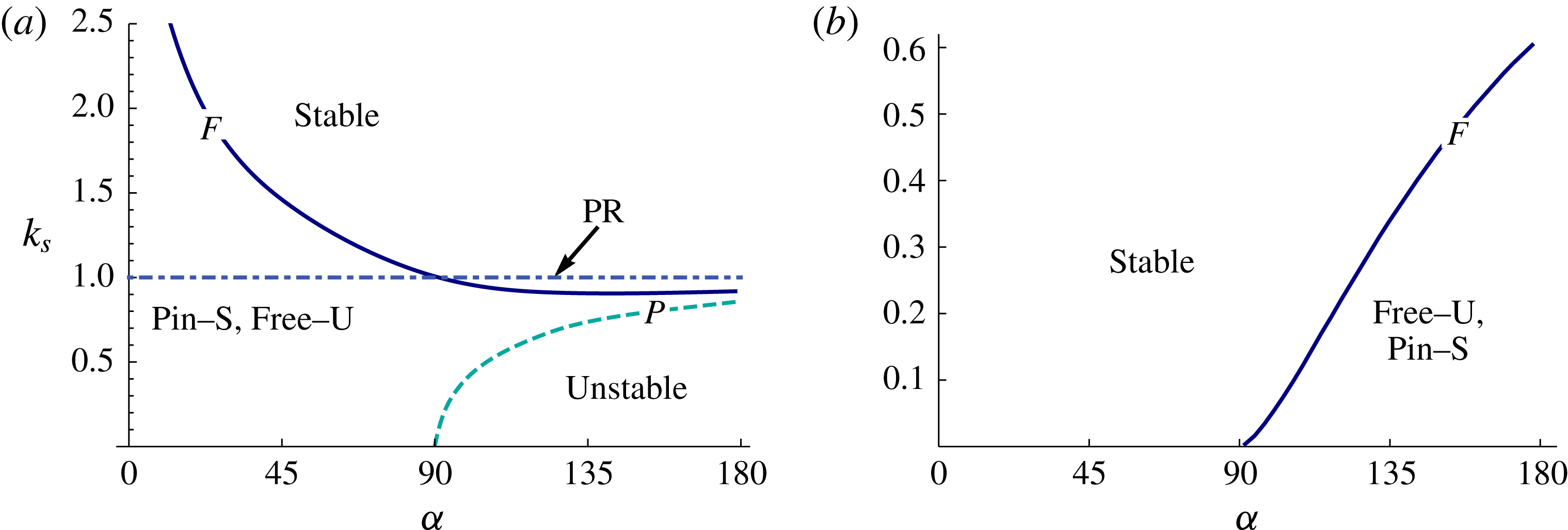
Figure 5. Free (
$F$
) and pinned (
$P$
) static stability window: critical wavenumber
$k_{s}$
, as it depends upon contact angle
$\unicode[STIX]{x1D6FC}$
, separates stable (S) from unstable (U) regions for the varicose (a) and sinuous (b) modes. Note the different vertical scales between (a) and (b) panels. The Plateau–Rayleigh (PR) limit is shown for reference. (Panel (a) reproduced from Bostwick & Steen (Reference Bostwick and Steen2015b
, figure 9b)).
5.3 Fastest growing mode
A characteristic feature of the Plateau–Rayleigh instability is the existence of a fastest growing mode shape distinguished by its axial wavenumber
$k_{m}$
and growth rate
$\unicode[STIX]{x1D706}_{m}^{2}$
. For the unconstrained Rayleigh jet (liquid cylinder), disturbances have maximum growth rate
$\unicode[STIX]{x1D706}_{m}^{2}=0.37$
at wavenumber
$k_{m}=0.69$
. Typical Plateau–Rayleigh break-up (capillary instability) characterizes the varicose modes. The critical wavenumber and growth rate are modified according to the type of disturbance and base-state geometry, as shown in figure 6. Typical varicose instability mode shapes are shown in figure 7(a,b) for free and pinned disturbances. In the limit
$\unicode[STIX]{x1D6FC}\rightarrow 180^{\circ }$
, where the rivulet contacts a planar support along a generating line, the stability results for the free and pinned disturbance are indistinguishable (cf. figures 5 and 6). Here the free disturbance has a relatively immobile contact line that degenerates into the pinned disturbance. Hence, the coincident stability results. Note the scaling length
$r$
vanishes in the limit
$\unicode[STIX]{x1D6FC}\rightarrow 0^{\circ },180^{\circ }$
.
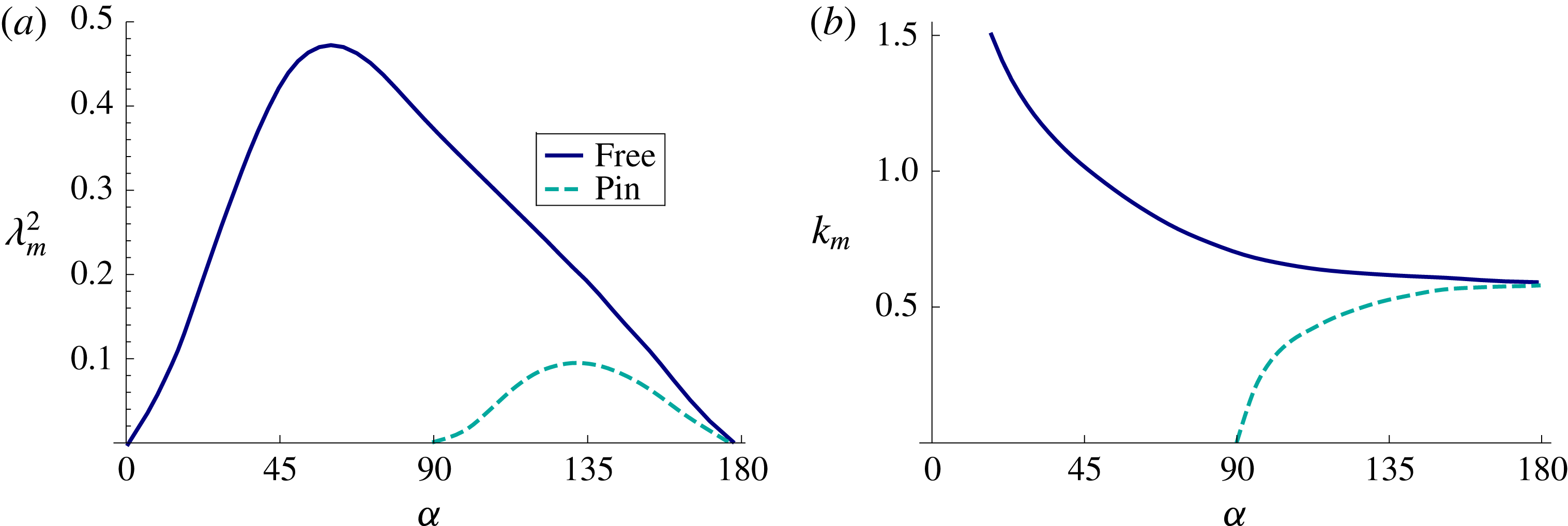
Figure 6. Fastest growing varicose mode for free and pinned disturbances: (a) growth rate
$\unicode[STIX]{x1D706}_{m}^{2}$
and (b) wavenumber
$k_{m}$
against contact angle
$\unicode[STIX]{x1D6FC}$
. The free disturbance degenerates into the pinned disturbance in the limit
$\unicode[STIX]{x1D6FC}\rightarrow 180^{\circ }$
.
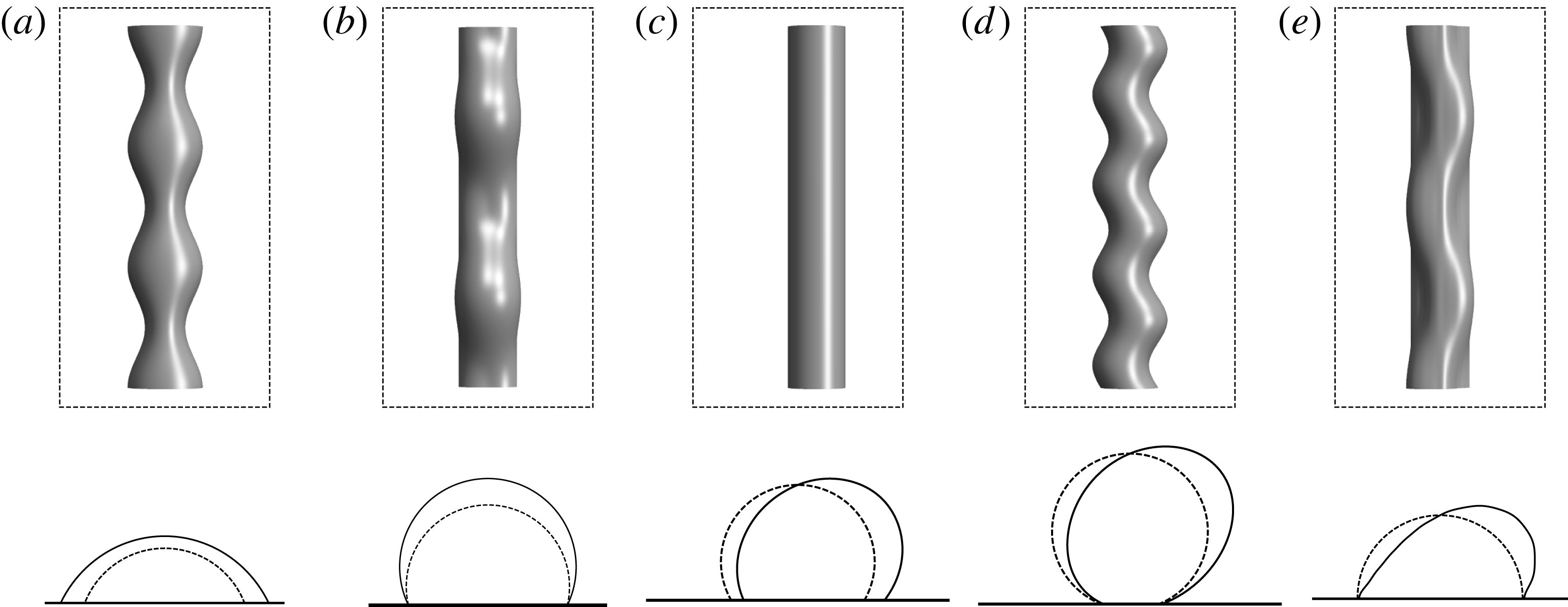
Figure 7. Typical mode shapes. (
$a,b$
) Varicose modes for (a) free
$k=3/4$
and (b) pinned
$k=1/2$
disturbances. (c–e) Sinuous modes for free (c)
$k=0$
and (d)
$k=1$
and (e) pinned
$k=1/2$
disturbances.
5.4 Effect of support geometry
Bostwick & Steen (Reference Bostwick and Steen2010) considered the linear stability of the circular segment base state with pinned contact lines in contact with a partial cylindrical-cup support. Their equilibrium configuration is similar to the one analysed here; the free surface shapes are identical but the concave support geometry differs from the planar geometry used here. For pinned disturbances, static stability is unaffected by the support geometry (Bostwick & Steen Reference Bostwick and Steen2015b
) and figure 5 encompasses both support geometries. In contrast, the growth dynamics is affected by the support geometry. Figure 8 plots the maximum instability growth rate and associated wavenumber against contact angle for the cylindrical interface with pinned contact lines in contact with a planar or cylindrical-cup support. As shown, the maximal growth rate for the interface constrained by a cylindrical-cup support, reported by Bostwick & Steen (Reference Bostwick and Steen2010), is always larger than the corresponding interface in contact with a planar support. The critical wavenumber
$k_{m}$
is unaffected by the support geometry.
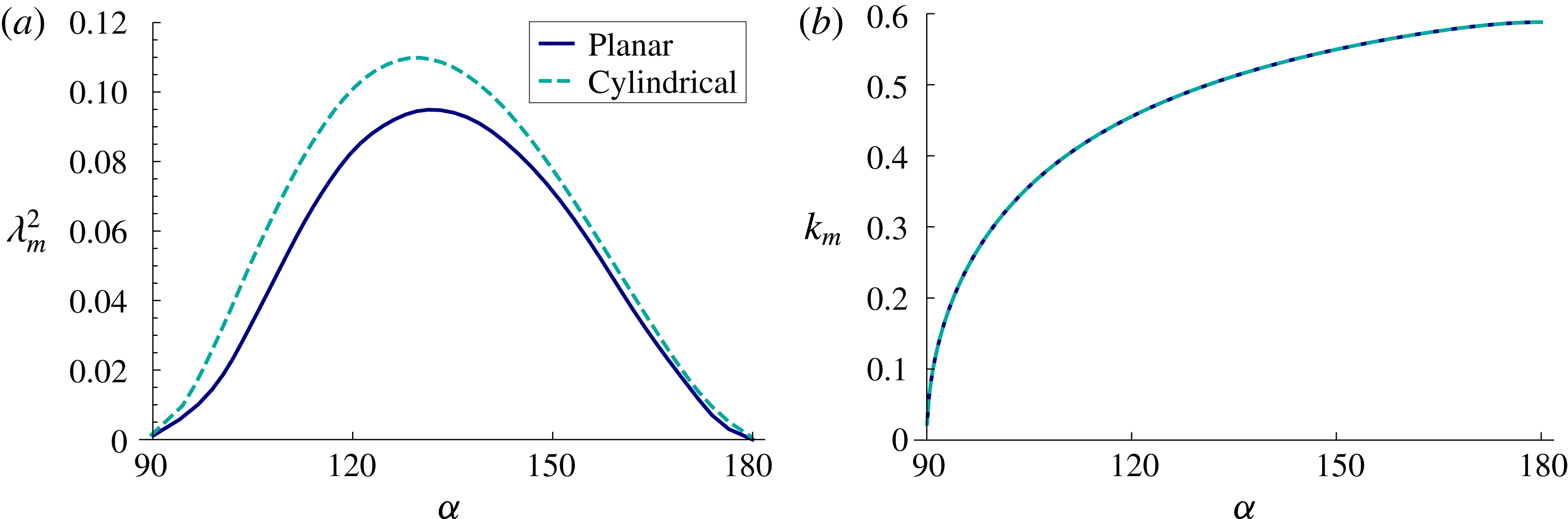
Figure 8. (a) Maximum growth rate
$\unicode[STIX]{x1D706}_{m}^{2}$
and (b) corresponding wavenumber
$k_{m}$
against contact angle
$\unicode[STIX]{x1D6FC}$
for the varicose mode with pinned contact lines, as it depends upon the support geometry. Rivulets on a (concave) cylindrical-cup support break up faster than a planar support.
5.5 Sinuous instability
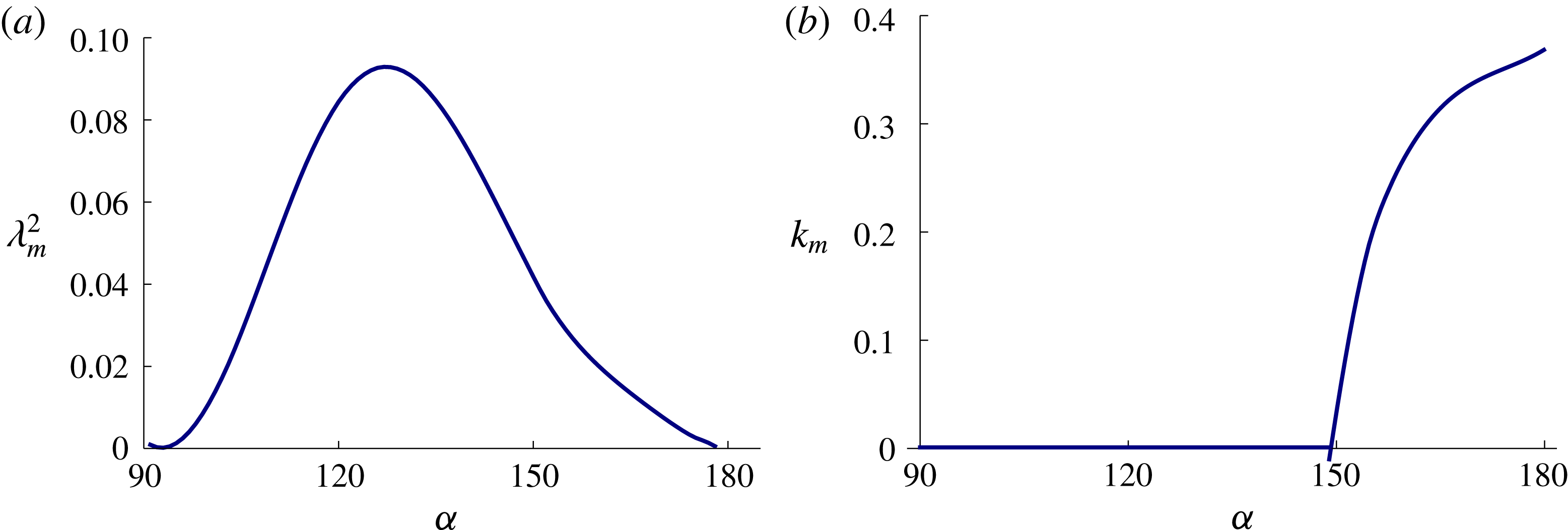
Figure 9. Free sinuous mode: (a) maximum growth rate
$\unicode[STIX]{x1D706}_{m}^{2}$
and (b) wavenumber
$k_{m}$
against contact angle
$\unicode[STIX]{x1D6FC}$
. Pinned disturbances are always stable.
The features of the sinuous instability are unlike those for the varicose instability, where typical Plateau–Rayleigh break-up dominates. Figure 9(b) shows that the critical disturbance is independent of the axial coordinate
$k_{m}=0$
for a range of base states with contact angle
$90^{\circ }<\unicode[STIX]{x1D6FC}<150^{\circ }$
. Figure 7(c) plots the critical instability mode shape from this regime. Outside this interval (
$150^{\circ }<\unicode[STIX]{x1D6FC}<180^{\circ }$
), rivulet meandering occurs as shown in figure 7(d). Recall that in Plateau–Rayleigh break-up, the instability mechanism consists of a cylindrical interface that breaks up into spherical drops in an attempt to minimize liquid/gas surface area (energy), as occurs for the varicose instability. In contrast, the sinuous instability mechanism is related to the walking droplet instability, whereby the energy is lowered by decreasing both the (i) liquid/gas and (ii) liquid/solid area (Bostwick & Steen Reference Bostwick and Steen2014). We illustrate the sinuous instability mechanism by constructing an interface shape with energy lower than that of the base-state configuration.
5.6 Mechanism of sinuous instability: toy problem
We begin with the two-dimensional drop of incompressible fluid on a solid substrate shown in figure 10(a). This is the limiting case of an interface disturbance with no axial (
$z$
) dependence. The potential energy
$E$
(per unit length) of the configuration is
$$\begin{eqnarray}E=LG-\cos (\unicode[STIX]{x1D6FC})\,LS,\end{eqnarray}$$
where
$LG$
and
$LS$
are the liquid/gas and liquid/solid surface areas (per unit length), and
$\unicode[STIX]{x1D6FC}$
is the static contact angle.
Consider the following perturbation to the circular segment with base-state radius of unity
$\boldsymbol{r}=(x(s),y(s))$
:
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle x(s)=\sin (s)(1+\unicode[STIX]{x1D716}\sin (s)+\unicode[STIX]{x1D716}^{2}x_{2}(s)),\\ \displaystyle y(s)=(\cos (s)-\cos (\unicode[STIX]{x1D6FC}))(1+\unicode[STIX]{x1D716}\sin (s))+\unicode[STIX]{x1D716}^{2}y_{2}(s),\end{array}\right\}\end{eqnarray}$$
with
$$\begin{eqnarray}x_{2}(s)=\text{const.}=\left({\displaystyle \frac{12\left(1-\cos (\unicode[STIX]{x1D6FC})+\cos (3\unicode[STIX]{x1D6FC})\right)-8\sin (2\unicode[STIX]{x1D6FC})+\sin (4\unicode[STIX]{x1D6FC})}{12(\sin (2\unicode[STIX]{x1D6FC})-2\unicode[STIX]{x1D6FC})}}\right),\end{eqnarray}$$
and
$$\begin{eqnarray}y_{2}(s)=\text{const.}=-\cos (\unicode[STIX]{x1D6FC})\sin (\unicode[STIX]{x1D6FC}).\end{eqnarray}$$
The surface is parametrized by the arclength-like coordinate
$s\in [-\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D716}^{2}\cos (\unicode[STIX]{x1D6FC}),\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D716}^{2}\cos (\unicode[STIX]{x1D6FC})]$
and the static contact angle
$\unicode[STIX]{x1D6FC}$
. Note that the circular segment base state (hereafter denoted
$0$
) is recovered by setting the perturbation amplitude
$\unicode[STIX]{x1D716}=0$
. For this incompressible fluid, the volume (per unit length) enclosed by the interface is
$$\begin{eqnarray}V=V_{0}+\mathit{O}(\unicode[STIX]{x1D716}^{3}),\quad V_{0}\equiv \unicode[STIX]{x1D6FC}-\cos (\unicode[STIX]{x1D6FC})\sin (\unicode[STIX]{x1D6FC}),\end{eqnarray}$$
with
$x_{2},y_{2}$
determined to maintain volume to
$\mathit{O}(\unicode[STIX]{x1D716}^{3})$
. The liquid/gas surface area is given by
$$\begin{eqnarray}LG=LG_{0}+\unicode[STIX]{x1D716}^{2}LG_{2},\quad LG_{0}\equiv 2\unicode[STIX]{x1D6FC},\end{eqnarray}$$
while the liquid/solid surface area is written as
$$\begin{eqnarray}LS=LS_{0}+\unicode[STIX]{x1D716}^{2}LS_{2},\quad LS_{0}\equiv 2\sin (\unicode[STIX]{x1D6FC}).\end{eqnarray}$$
Finally, we apply the liquid/gas (5.8) and liquid/solid (5.9) surface areas to the energy functional (5.3) to show that the configurational energy relative to the base state is
$$\begin{eqnarray}E-E^{0}=\unicode[STIX]{x1D716}^{2}E_{2}.\end{eqnarray}$$
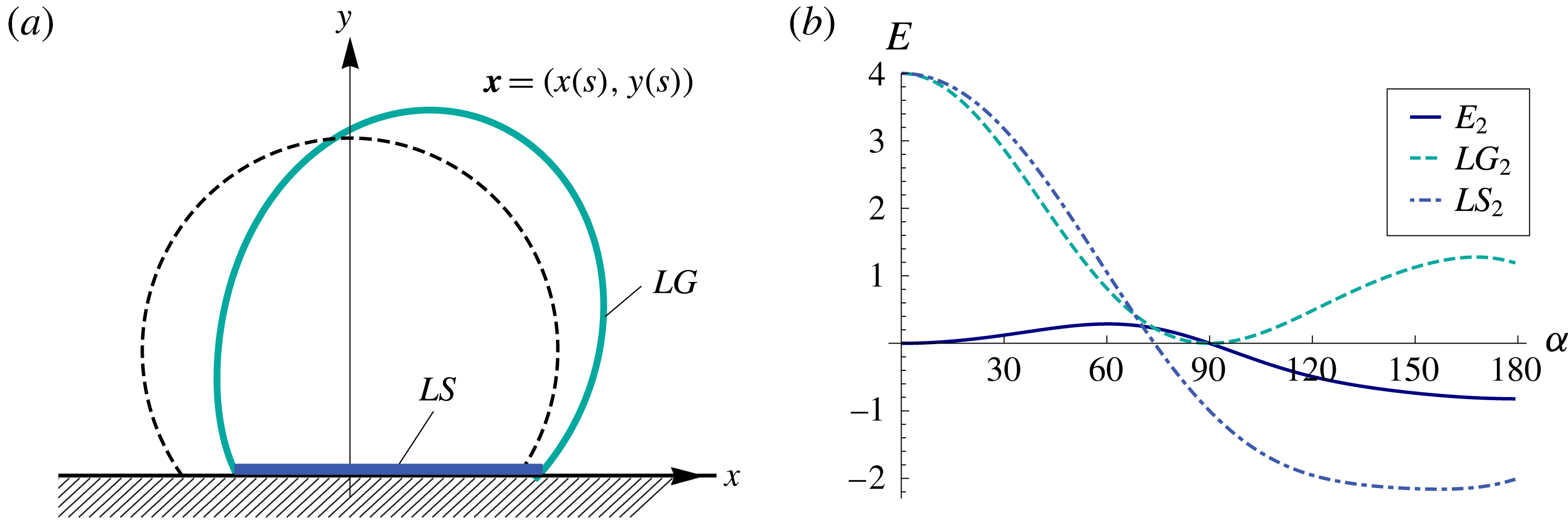
Figure 10. Sinuous instability toy model: (a) interface shape for
$\unicode[STIX]{x1D6FC}=120^{\circ }$
(
$\unicode[STIX]{x1D716}=0.29$
), and (b) decomposition of the disturbance energy
$E_{2}$
into contributions from liquid/solid
$LS_{2}$
and liquid/gas
$LG_{2}$
surface areas against contact angle
$\unicode[STIX]{x1D6FC}$
.
Figure 10(b) plots the disturbance energy
$E_{2}$
against contact angle
$\unicode[STIX]{x1D6FC}$
showing the disturbed state has lower energy than that of the circular segment for the range of contact angles
$90^{\circ }<\unicode[STIX]{x1D6FC}<180^{\circ }$
. This result is consistent with the stability diagram for the sinuous mode shown in figure 5. The decomposition of the disturbance energy
$E_{2}$
shows that the reduction of liquid/solid
$LS_{2}$
surface area overwhelms the increase in liquid/gas
$LG_{2}$
surface area to lower the total configurational energy. This instability mechanism highlights the energy competitors,
$LG$
and
$LS$
, inherent in wetting problems. Note the disturbance shape shown in figure 10(a) is asymmetric about the axis of symmetry (y-axis) and tends to displace the centre-of-mass horizontally. The resulting motion is similar to what is observed with the walking droplet instability.
In regard to our hydrodynamic stability results, the aforementioned instability mechanism certainly applies to the range of base states
$90^{\circ }<\unicode[STIX]{x1D6FC}<150^{\circ }$
whose critical disturbance is polar
$k_{m}=0$
(cf. figure 9
a). For the rivulet with base state defined by contact angle
$\unicode[STIX]{x1D6FC}>150^{\circ }$
, the critical disturbance
$k_{m}\neq 0$
involves some combination of the instability mechanism discussed in this section and traditional capillary break-up leading to rivulet meandering.
5.7 Dominant mode
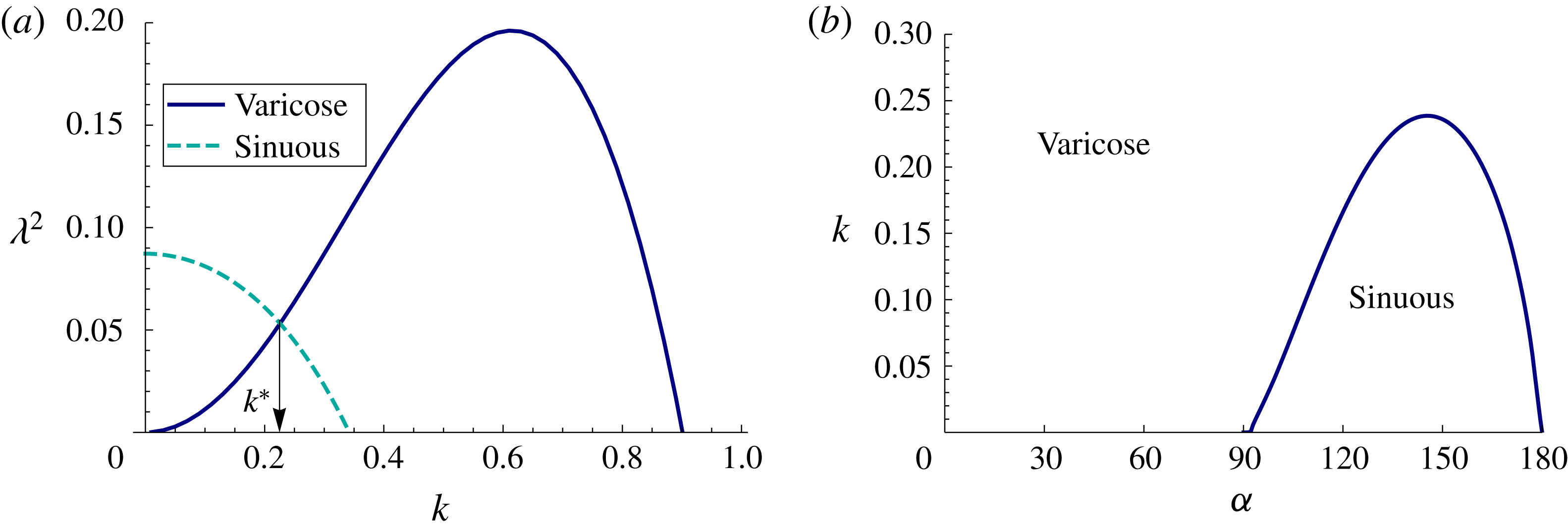
Figure 11. Dominant mode: (a) free dispersion relationship
$\unicode[STIX]{x1D706}^{2}$
against
$k$
with
$\unicode[STIX]{x1D6FC}=135^{\circ }$
shows that the sinuous mode has larger instability growth rate than the varicose mode for low wavenumber
$k<k^{\ast }$
disturbances. (b) The boundary shown in the
$k-\unicode[STIX]{x1D6FC}$
plane separates regions where varicose and sinuous modes are dominant.
For fixed axial wavenumber
$k$
, the dominant mode (largest instability growth rate) can be either the varicose or sinuous mode, despite the fact that the varicose mode always has a larger stability limit
$k_{s}$
(cf. figure 5). For example, figure 11(a) plots the free dispersion relationship
$\unicode[STIX]{x1D706}^{2}$
against
$k$
for the varicose and sinuous modes with
$\unicode[STIX]{x1D6FC}=135^{\circ }$
and shows the sinuous mode is the dominant mode for wavenumbers less than a critical value
$k<k^{\ast }$
, while the varicose mode is the dominant mode for
$k>k^{\ast }$
. The critical wavenumber
$k^{\ast }$
is plotted against the contact angle
$\unicode[STIX]{x1D6FC}$
in figure 11(b). For
$\unicode[STIX]{x1D6FC}>90^{\circ }$
, note that the sinuous mode is the dominant mode for low wavenumber disturbances, consistent with observations of rivulet meandering.
6 Concluding remarks
A number of authors have investigated the series of instabilities exhibited by fluid rivulets. In the absence of a base flow, the static rivulet is susceptible to capillary instability (Plateau–Rayleigh break-up), which can be greatly affected by the wetting conditions on the three-phase contact line. In the present work, we derive the hydrodynamic equations for static rivulets with either (i) free or (ii) pinned contact lines and report dispersion relations, as they depend upon the static contact angle. Our hydrodynamic analysis extends the static stability results of Davis (Reference Davis1980) in a manner similar to how Lord Rayleigh extended the work of Plateau on the stability of liquid cylinders. We report rates of fastest growing modes and mode shapes. We also report critical wavenumbers and stability windows – how stability limits depend on contact angle.
Solutions to the governing equations are decomposed according to their symmetry about the axis of symmetry. Using standard terminology, symmetric shapes are referred to as varicose modes and anti-symmetric shapes as sinuous modes. Static stability of the varicose modes agrees with Davis (Reference Davis1980), who considers varicose modes, since they are the more unstable of the two mode types. This is confirmed by our results. Critical disturbances and growth rates are reported for the varicose modes in figure 6, which indicate rivulets with free contact lines break up faster than those with pinned contact lines. For mobile contact lines, the instability window widens (shrinks) for rivulets with contact angle
$\unicode[STIX]{x1D6FC}<90^{\circ }$
(
$\unicode[STIX]{x1D6FC}>90^{\circ }$
) illustrating how the wetting properties of the solid substrate affect stability.
We report that the sinuous mode destabilizes the rivulet with free contact lines for super-circular base states
$90^{\circ }<\unicode[STIX]{x1D6FC}<180^{\circ }$
and is the dominant instability for a range of low axial wavenumbers. The features of this instability are not characteristic of typical capillary break-up, as long waves grow for a range of contact angles
$90^{\circ }<\unicode[STIX]{x1D6FC}<150^{\circ }$
. For
$\unicode[STIX]{x1D6FC}>150^{\circ }$
,
$k_{m}\neq 0$
and rivulet meandering occurs. The instability mechanism highlights the energy competitors (
$LG$
,
$LS$
) involved in partial wetting and lowers the configurational energy by decreasing liquid/solid surface area, while the fluid response correlates with horizontal centre-of-mass motion. Hence, cataloguing the sinuous instability is important in understanding the phenomenon of rivulet meandering. Rivulet meandering can only occur for mobile contact lines. The window of instability closes for pinned contact lines (cf. figure 5). Although we do not consider a base-state flow in our analysis, we would expect the fluid inertia to widen the instability window (destabilize) and enhance the sinuous instability (rivulet meandering). Along similar lines, viscous effects could be expected to shift the dominant modes to smaller wavenumbers consistent with bulk viscous dissipation.
Acknowledgements
P.H.S. acknowledges support by NASA grant NNX09AI83G and NSF grant CBET-1236582. We would also like to thank P. Ehrhard for useful discussions regarding stability of rivulets.
