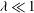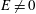1 Introduction
When a spherical drop of radius
![]() $a$
and viscosity
$a$
and viscosity
![]() $\unicode[STIX]{x1D707}_{\mathit{in}}$
is suspended in a surrounding fluid, of viscosity
$\unicode[STIX]{x1D707}_{\mathit{in}}$
is suspended in a surrounding fluid, of viscosity
![]() $\unicode[STIX]{x1D707}$
, undergoing shear or extensional flow, it will deform. Assuming incompressible Newtonian fluids under creeping flow conditions, the problem is governed by two dimensionless parameters: the capillary number
$\unicode[STIX]{x1D707}$
, undergoing shear or extensional flow, it will deform. Assuming incompressible Newtonian fluids under creeping flow conditions, the problem is governed by two dimensionless parameters: the capillary number
![]() $Ca=\unicode[STIX]{x1D707}Aa/\unicode[STIX]{x1D70E}$
and the viscosity ratio
$Ca=\unicode[STIX]{x1D707}Aa/\unicode[STIX]{x1D70E}$
and the viscosity ratio
![]() $\unicode[STIX]{x1D706}=\unicode[STIX]{x1D707}_{\mathit{in}}/\unicode[STIX]{x1D707}$
. Here
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D707}_{\mathit{in}}/\unicode[STIX]{x1D707}$
. Here
![]() $A$
is the shear or extension rate and
$A$
is the shear or extension rate and
![]() $\unicode[STIX]{x1D70E}$
is the surface tension. At
$\unicode[STIX]{x1D70E}$
is the surface tension. At
![]() $\mathit{Ca}\ll 1$
, the drop can be considered to be a slightly deformed sphere. However, in this report we shall consider slender drops only, which can be realized at
$\mathit{Ca}\ll 1$
, the drop can be considered to be a slightly deformed sphere. However, in this report we shall consider slender drops only, which can be realized at
![]() $\mathit{Ca}\gg 1$
and
$\mathit{Ca}\gg 1$
and
![]() $\unicode[STIX]{x1D706}\ll 1$
. A summary of this fundamental research topic having many industrial applications can be found in excellent reviews by Rallison (Reference Rallison1984), Stone (Reference Stone1994), and Briscoe, Lawrence & Mietus (Reference Briscoe, Lawrence and Mietus1999).
$\unicode[STIX]{x1D706}\ll 1$
. A summary of this fundamental research topic having many industrial applications can be found in excellent reviews by Rallison (Reference Rallison1984), Stone (Reference Stone1994), and Briscoe, Lawrence & Mietus (Reference Briscoe, Lawrence and Mietus1999).
Like many other topics in fluid mechanics, a slender-body theory for drops in creeping flow was first introduced by Taylor (Reference Taylor1964). He considered the deformation of a slender drop in an axisymmetric linear extensional flow, where the cross-section of the drop is circular. The theory, which was later refined by Buckmaster (Reference Buckmaster1972, Reference Buckmaster1973), Acrivos & Lo (Reference Acrivos and Lo1978), Khakhar & Ottino (Reference Khakhar and Ottino1986) and others, suggests that the slender drop has a parabolic radius profile with pointed ends. Consequently, as the capillary number increases, the drop becomes thinner, more elongated, and breaks at a critical value of
![]() $Ca\,\unicode[STIX]{x1D706}^{1/6}=0.148$
. Thus, breakup is not possible for a bubble or an inviscid drop (
$Ca\,\unicode[STIX]{x1D706}^{1/6}=0.148$
. Thus, breakup is not possible for a bubble or an inviscid drop (
![]() $\unicode[STIX]{x1D706}=0$
) in axisymmetric linear extensional creeping flow.
$\unicode[STIX]{x1D706}=0$
) in axisymmetric linear extensional creeping flow.
Several theoretical variations to the problem of a slender drop in an extensional flow have been suggested in the literature. A slender drop in a two-dimensional extensional flow, a case where the drop cross-section is not circular, was studied by Hinch & Acrivos (Reference Hinch and Acrivos1979). Evolution studies and breakup mechanisms of slender drops were treated by Hinch (Reference Hinch1980) and Favelukis, Lavrenteva & Nir (Reference Favelukis, Lavrenteva and Nir2012). Since the Reynolds number based on the length of a long and slender drop may not be so small, Acrivos & Lo (Reference Acrivos and Lo1978) and Brady & Acrivos (Reference Brady and Acrivos1982) suggested the inclusion of weak inertial effects. Howell & Siegel (Reference Howell and Siegel2004) investigated a slender non-axisymmetric drop. Booty & Siegel (Reference Booty and Siegel2005) studied the effect of an insoluble surfactant on the surface of an inviscid slender drop. Finally, Favelukis & Nir (Reference Favelukis and Nir2001) and Favelukis, Lavrenteva & Nir (Reference Favelukis, Lavrenteva and Nir2005, Reference Favelukis, Lavrenteva and Nir2006) included non-Newtonian effects outside and inside the drop, respectively.
One of the very interesting extensions to Taylor’s theory (Reference Taylor1964) can be found in the paper of Sherwood (Reference Sherwood1984), who included nonlinear terms in the extensional creeping flow and performed experiments showing the tip-streaming phenomenon. Note that today, the literature suggests that tip-streaming is caused by surfactants moving towards the tips of the drop and accumulating there (De Bruijn Reference De Bruijn1993; Janssen, Boon & Agterof Reference Janssen, Boon and Agterof1994; Eggleton, Tsai & Stebe Reference Eggleton, Tsai and Stebe2001; Renardy, Renardy & Cristini Reference Renardy, Renardy and Cristini2001). The formation of a pointed drop in a nonlinear two-dimensional extensional creeping flow was also considered by Antanovskii (Reference Antanovskii1996), since it describes better (than the linear flow) the outer flow which occurs in Taylor’s four-roller mill apparatus. It is the purpose of this report to revisit, present new results, and perform a complete stability analysis of the theoretical treatment of Sherwood (Reference Sherwood1984) on deformation and breakup of a slender drop in a nonlinear axisymmetric extensional creeping flow.
2 The governing equations
2.1 The flow outside the drop
Figure 1 shows a slender drop, positioned at the origin of a cylindrical coordinate system and embedded in an infinite incompressible Newtonian fluid, subjected to a nonlinear extensional creeping flow. The undisturbed motion suggested by Sherwood (Reference Sherwood1984) is given by
Here
![]() $p$
is the pressure, which was defined in such a way that its value at the origin is set to zero. According to Sherwood (Reference Sherwood1984), quadratic terms were excluded in order to maintain the symmetry at
$p$
is the pressure, which was defined in such a way that its value at the origin is set to zero. According to Sherwood (Reference Sherwood1984), quadratic terms were excluded in order to maintain the symmetry at
![]() $z=0$
. When
$z=0$
. When
![]() $B=0$
, the well-known simple (linear) extensional flow is recovered. Note that we define extensional flow with
$B=0$
, the well-known simple (linear) extensional flow is recovered. Note that we define extensional flow with
![]() $A>0$
; however,
$A>0$
; however,
![]() $B$
can take both positive or negative values.
$B$
can take both positive or negative values.

Figure 1. A slender drop in a nonlinear extensional flow:
![]() $R(z,t)$
is the local radius and
$R(z,t)$
is the local radius and
![]() $L(t)$
is the half-length of the drop.
$L(t)$
is the half-length of the drop.
Following Acrivos & Lo (Reference Acrivos and Lo1978), we can develop the velocity components of the disturbed motion near the slender drop:
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle v_{r}=\frac{R}{r}\frac{\unicode[STIX]{x2202}R}{\unicode[STIX]{x2202}t}+A\left\{-\left(1+3\frac{B}{A}z^{2}\right)\frac{r}{2}+\frac{R}{r}\left[\left(1+3\frac{B}{A}z^{2}\right)\frac{R}{2}+\left(1+\frac{B}{A}z^{2}\right)z\frac{\unicode[STIX]{x2202}R}{\unicode[STIX]{x2202}z}\right]\right\},\\ \displaystyle v_{z}=Az\left(1+\frac{B}{A}z^{2}\right).\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle v_{r}=\frac{R}{r}\frac{\unicode[STIX]{x2202}R}{\unicode[STIX]{x2202}t}+A\left\{-\left(1+3\frac{B}{A}z^{2}\right)\frac{r}{2}+\frac{R}{r}\left[\left(1+3\frac{B}{A}z^{2}\right)\frac{R}{2}+\left(1+\frac{B}{A}z^{2}\right)z\frac{\unicode[STIX]{x2202}R}{\unicode[STIX]{x2202}z}\right]\right\},\\ \displaystyle v_{z}=Az\left(1+\frac{B}{A}z^{2}\right).\end{array}\right\}\end{eqnarray}$$
Notice that, to a first approximation, the axial component of the velocity is not affected by the presence of a slender drop. The radial disturbed velocity can be found from the continuity equation and the kinematic condition.
Substituting the disturbed motion into the Stokes equations, we find that the leading order of the pressure outside a slender drop (
![]() $R/L\ll 1$
) is
$R/L\ll 1$
) is
2.2 The flow inside the drop
The flow inside the slender drop can be considered to be a superposition of drag flow
![]() $v_{z}$
at
$v_{z}$
at
![]() $r=R$
and a pressure flow in the opposite direction (Taylor Reference Taylor1964). Assuming an incompressible Newtonian fluid in creeping flow we easily obtain
$r=R$
and a pressure flow in the opposite direction (Taylor Reference Taylor1964). Assuming an incompressible Newtonian fluid in creeping flow we easily obtain
Here
![]() $p_{\mathit{in}}$
is the pressure inside the drop, assumed uniform at each cross-section.
$p_{\mathit{in}}$
is the pressure inside the drop, assumed uniform at each cross-section.
The volumetric flow rate, through each axial cross-section along the drop, can be found from an integral mass balance within a control volume inside the drop:
From the last equation, and after some algebraic manipulation, an expression for the internal pressure can be found:
where
![]() $p_{\mathit{in}}(0)$
is the unknown pressure at the centre of the drop. At steady state, the volumetric flow rate vanishes at every cross-section within the drop. Also, for a bubble or an inviscid drop,
$p_{\mathit{in}}(0)$
is the unknown pressure at the centre of the drop. At steady state, the volumetric flow rate vanishes at every cross-section within the drop. Also, for a bubble or an inviscid drop,
![]() $\unicode[STIX]{x1D707}_{\mathit{in}}=0$
, the pressure inside the drop is uniform, and at steady state it is also constant.
$\unicode[STIX]{x1D707}_{\mathit{in}}=0$
, the pressure inside the drop is uniform, and at steady state it is also constant.
2.3 The normal stress balance
We start this section by writing a normal stress balance at the surface of the slender drop:
where the subscripts in and out denote inside and outside of the drop respectively. Since slender drops can be realized when the viscosity of the drop is much smaller than the viscosity of the external fluid, we can neglect the normal viscous stress inside the drop.
Let all the pressures and stresses be rendered dimensionless with respect to the characteristic stress outside the drop (
![]() $\unicode[STIX]{x1D707}A$
), all the lengths with respect to the equivalent radius (
$\unicode[STIX]{x1D707}A$
), all the lengths with respect to the equivalent radius (
![]() $a$
, the radius of a sphere of an equal volume), and the time with respect to
$a$
, the radius of a sphere of an equal volume), and the time with respect to
![]() $1/A$
. Substituting the expressions for the external and internal pressures, given by (2.3) and (2.6), and the external normal stress, which can be obtained from (2.2) and Newton’s viscosity law, we arrive in a dimensionless form:
$1/A$
. Substituting the expressions for the external and internal pressures, given by (2.3) and (2.6), and the external normal stress, which can be obtained from (2.2) and Newton’s viscosity law, we arrive in a dimensionless form:
 $$\begin{eqnarray}\displaystyle & & \displaystyle p_{\mathit{in}}(0)+8\unicode[STIX]{x1D706}\int _{0}^{z}\frac{1}{R}\left[(1+Ez^{2})\frac{z}{R}+\frac{1}{R^{3}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\int _{0}^{z}R^{2}\,\text{d}z\right]\text{d}z\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{2}{R}\frac{\unicode[STIX]{x2202}R}{\unicode[STIX]{x2202}t}-2\left(1+\frac{9}{2}Ez^{2}\right)-2(1+Ez^{2})\frac{z}{R}\frac{\unicode[STIX]{x2202}R}{\unicode[STIX]{x2202}z}=\frac{1}{Ca\,R}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle p_{\mathit{in}}(0)+8\unicode[STIX]{x1D706}\int _{0}^{z}\frac{1}{R}\left[(1+Ez^{2})\frac{z}{R}+\frac{1}{R^{3}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\int _{0}^{z}R^{2}\,\text{d}z\right]\text{d}z\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{2}{R}\frac{\unicode[STIX]{x2202}R}{\unicode[STIX]{x2202}t}-2\left(1+\frac{9}{2}Ez^{2}\right)-2(1+Ez^{2})\frac{z}{R}\frac{\unicode[STIX]{x2202}R}{\unicode[STIX]{x2202}z}=\frac{1}{Ca\,R}.\end{eqnarray}$$
Equation (2.8) is governed by three dimensionless parameters: the capillary number, the viscosity ratio and the nonlinear intensity of the flow, which contrary to the other two parameters can be positive or negative:
The solution also requires three conditions: an initial drop shape:
![]() $R(z,0)$
, a radius at the end of the drop,
$R(z,0)$
, a radius at the end of the drop,
![]() $R(L,t)=0$
, and an equation for volume conservation:
$R(L,t)=0$
, and an equation for volume conservation:
Equations (2.8)–(2.10) suggest that
![]() $R\sim O(1/\mathit{Ca})$
,
$R\sim O(1/\mathit{Ca})$
,
![]() $L\sim O(\mathit{Ca}^{2})$
,
$L\sim O(\mathit{Ca}^{2})$
,
![]() $p_{\mathit{in}}(0)\sim O(1)$
, and
$p_{\mathit{in}}(0)\sim O(1)$
, and
![]() $t\sim O(1)$
. In terms of the small parameter
$t\sim O(1)$
. In terms of the small parameter
![]() $\unicode[STIX]{x1D700}=R/L\ll 1$
, the theory is valid for large capillary numbers
$\unicode[STIX]{x1D700}=R/L\ll 1$
, the theory is valid for large capillary numbers
![]() $\mathit{Ca}\sim 1/\unicode[STIX]{x1D700}^{1/3}$
, small viscosity ratios
$\mathit{Ca}\sim 1/\unicode[STIX]{x1D700}^{1/3}$
, small viscosity ratios
![]() $\unicode[STIX]{x1D706}\sim \unicode[STIX]{x1D700}^{2}$
, and a small nonlinear intensity of the flow
$\unicode[STIX]{x1D706}\sim \unicode[STIX]{x1D700}^{2}$
, and a small nonlinear intensity of the flow
![]() $E\sim \unicode[STIX]{x1D700}^{4/3}$
. From the above discussion, and following our previous report (Favelukis et al.
Reference Favelukis, Lavrenteva and Nir2006), we redefine the local radius and the coordinate
$E\sim \unicode[STIX]{x1D700}^{4/3}$
. From the above discussion, and following our previous report (Favelukis et al.
Reference Favelukis, Lavrenteva and Nir2006), we redefine the local radius and the coordinate
![]() $z$
as follows:
$z$
as follows:
![]() $y=R\,Ca$
and
$y=R\,Ca$
and
![]() $x=z/Ca^{2}$
, both having an order of magnitude of 1. Equations (2.8) and (2.10) take the following form:
$x=z/Ca^{2}$
, both having an order of magnitude of 1. Equations (2.8) and (2.10) take the following form:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle p_{\mathit{in}}(0)+8f^{6}\int _{0}^{x}\frac{1}{y}\left[(1+Gx^{2})\frac{x}{y}+\frac{1}{y^{3}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\int _{0}^{x}y^{2}\,\text{d}x\right]\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{2}{y}\frac{\unicode[STIX]{x2202}y}{\unicode[STIX]{x2202}t}-2\left(1+\frac{9}{2}Gx^{2}\right)-2(1+Gx^{2})\frac{x}{y}\frac{\unicode[STIX]{x2202}y}{\unicode[STIX]{x2202}x}=\frac{1}{y}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle p_{\mathit{in}}(0)+8f^{6}\int _{0}^{x}\frac{1}{y}\left[(1+Gx^{2})\frac{x}{y}+\frac{1}{y^{3}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\int _{0}^{x}y^{2}\,\text{d}x\right]\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{2}{y}\frac{\unicode[STIX]{x2202}y}{\unicode[STIX]{x2202}t}-2\left(1+\frac{9}{2}Gx^{2}\right)-2(1+Gx^{2})\frac{x}{y}\frac{\unicode[STIX]{x2202}y}{\unicode[STIX]{x2202}x}=\frac{1}{y}\end{eqnarray}$$
with
![]() $x_{L}=L/Ca^{2}$
. Note that the number of governing dimensionless parameters has been reduced from three (
$x_{L}=L/Ca^{2}$
. Note that the number of governing dimensionless parameters has been reduced from three (
![]() $\mathit{Ca}$
,
$\mathit{Ca}$
,
![]() $\unicode[STIX]{x1D706}$
,
$\unicode[STIX]{x1D706}$
,
![]() $E$
) to two having an order of magnitude of 1: the positive viscous strength of the flow (
$E$
) to two having an order of magnitude of 1: the positive viscous strength of the flow (
![]() $f$
) and the nonlinear strength of the flow (
$f$
) and the nonlinear strength of the flow (
![]() $G$
), which can be positive or negative:
$G$
), which can be positive or negative:
Following Hinch (Reference Hinch1980), the pressure at the centre of the drop can be obtained by combining (2.11) and (2.12):
 $$\begin{eqnarray}p_{\mathit{in}}(0)=1+\frac{\displaystyle \int _{0}^{x_{L}}\!\left(y+2Gx^{3}y{\displaystyle \frac{\unicode[STIX]{x2202}y}{\unicode[STIX]{x2202}x}}+9Gx^{2}y^{2}\right)\text{d}x-8f^{6}\!\int _{0}^{x_{L}}\!y^{2}\left\{\int _{0}^{x}\!{\displaystyle \frac{1}{y}}\left[(1+Gx^{2}){\displaystyle \frac{x}{y}}+{\displaystyle \frac{1}{y^{3}}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}\int _{0}^{x}\!y^{2}\,\text{d}x\right]\text{d}x\right\}\text{d}x}{\displaystyle \int _{0}^{x_{L}}y^{2}\,\text{d}x},\end{eqnarray}$$
$$\begin{eqnarray}p_{\mathit{in}}(0)=1+\frac{\displaystyle \int _{0}^{x_{L}}\!\left(y+2Gx^{3}y{\displaystyle \frac{\unicode[STIX]{x2202}y}{\unicode[STIX]{x2202}x}}+9Gx^{2}y^{2}\right)\text{d}x-8f^{6}\!\int _{0}^{x_{L}}\!y^{2}\left\{\int _{0}^{x}\!{\displaystyle \frac{1}{y}}\left[(1+Gx^{2}){\displaystyle \frac{x}{y}}+{\displaystyle \frac{1}{y^{3}}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}\int _{0}^{x}\!y^{2}\,\text{d}x\right]\text{d}x\right\}\text{d}x}{\displaystyle \int _{0}^{x_{L}}y^{2}\,\text{d}x},\end{eqnarray}$$
where, according to Hinch (Reference Hinch1980), the numerical integration of the last equation, for the case of an inviscid drop in creeping flow, becomes unstable if the integral in the denominator is replaced, according to (2.12), by the value
![]() $2/3$
. We found this advice to be wise here and for our previous case as well (Favelukis et al.
Reference Favelukis, Lavrenteva and Nir2012).
$2/3$
. We found this advice to be wise here and for our previous case as well (Favelukis et al.
Reference Favelukis, Lavrenteva and Nir2012).
The unknown internal pressure at the centre of the drop in (2.11) can be eliminated by differentiating the equation with respect to
![]() $x$
, to give
$x$
, to give
 $$\begin{eqnarray}\displaystyle & & \displaystyle 2\frac{\unicode[STIX]{x2202}^{2}y}{\unicode[STIX]{x2202}x\unicode[STIX]{x2202}t}-\frac{2}{y}\frac{\unicode[STIX]{x2202}y}{\unicode[STIX]{x2202}x}\frac{\unicode[STIX]{x2202}y}{\unicode[STIX]{x2202}t}+2x(1+Gx^{2})\frac{\unicode[STIX]{x2202}^{2}y}{\unicode[STIX]{x2202}x^{2}}-2\frac{x}{y}(1+Gx^{2})\left(\frac{\unicode[STIX]{x2202}y}{\unicode[STIX]{x2202}x}\right)^{2}\nonumber\\ \displaystyle & & \displaystyle \quad +\left[2(1+3Gx^{2})-\frac{1}{y}\right]\frac{\unicode[STIX]{x2202}y}{\unicode[STIX]{x2202}x}+18Gxy=8f^{6}\left[\frac{x}{y}(1+Gx^{2})+\frac{1}{y^{3}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\int _{0}^{x}y^{2}\,\text{d}x\right]\!.\qquad \quad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle 2\frac{\unicode[STIX]{x2202}^{2}y}{\unicode[STIX]{x2202}x\unicode[STIX]{x2202}t}-\frac{2}{y}\frac{\unicode[STIX]{x2202}y}{\unicode[STIX]{x2202}x}\frac{\unicode[STIX]{x2202}y}{\unicode[STIX]{x2202}t}+2x(1+Gx^{2})\frac{\unicode[STIX]{x2202}^{2}y}{\unicode[STIX]{x2202}x^{2}}-2\frac{x}{y}(1+Gx^{2})\left(\frac{\unicode[STIX]{x2202}y}{\unicode[STIX]{x2202}x}\right)^{2}\nonumber\\ \displaystyle & & \displaystyle \quad +\left[2(1+3Gx^{2})-\frac{1}{y}\right]\frac{\unicode[STIX]{x2202}y}{\unicode[STIX]{x2202}x}+18Gxy=8f^{6}\left[\frac{x}{y}(1+Gx^{2})+\frac{1}{y^{3}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\int _{0}^{x}y^{2}\,\text{d}x\right]\!.\qquad \quad\end{eqnarray}$$
The last equation needs to be solved with an initial drop shape,
![]() $y(x,0)$
, a vanishing drop radius at the end of the drop,
$y(x,0)$
, a vanishing drop radius at the end of the drop,
![]() $y(x_{L},t)=0$
, and the conservation of volume, given by (2.12).
$y(x_{L},t)=0$
, and the conservation of volume, given by (2.12).
When
![]() $G=0$
, (2.15) reduces to the one presented in the literature for simple (linear) extensional flow. Furthermore, the
$G=0$
, (2.15) reduces to the one presented in the literature for simple (linear) extensional flow. Furthermore, the
![]() $18Gxy$
term (positive or negative) on the left-hand side of (2.15) reminds us of a similar term (negative) which needs to be added when external inertia is taken into account (Favelukis et al.
Reference Favelukis, Lavrenteva and Nir2006). Thus, we anticipate that some of the results of nonlinear extensional creeping flow, when
$18Gxy$
term (positive or negative) on the left-hand side of (2.15) reminds us of a similar term (negative) which needs to be added when external inertia is taken into account (Favelukis et al.
Reference Favelukis, Lavrenteva and Nir2006). Thus, we anticipate that some of the results of nonlinear extensional creeping flow, when
![]() $G<0$
, will be similar to those of linear extensional flow under the influence of a weak amount of external inertia.
$G<0$
, will be similar to those of linear extensional flow under the influence of a weak amount of external inertia.
In the next three sections we shall revisit the results of Sherwood (Reference Sherwood1984), for the steady deformation of inviscid and viscous drops, as well as present new contributions to this interesting subject.
3 Steady state
We start this section by examining the steady-state equation (2.15), which reveals an interesting finding. Contrary to the linear extensional flow case (
![]() $G=0$
), where the local radius of the drop
$G=0$
), where the local radius of the drop
![]() $y(x)$
decreases monotonically, for
$y(x)$
decreases monotonically, for
![]() $z\geqslant 0$
, in a nonlinear extensional flow (
$z\geqslant 0$
, in a nonlinear extensional flow (
![]() $G\neq 0$
), the local radius of the drop may (or may not) achieve a maximum, besides the one at the centre of the drop.
$G\neq 0$
), the local radius of the drop may (or may not) achieve a maximum, besides the one at the centre of the drop.
3.1 The solution near the centre of the drop
At steady state, and according to (2.11), we shall follow the suggestion of Acrivos & Lo (Reference Acrivos and Lo1978) by defining the radius at the centre of the drop as follows:
Near the centre of the drop (
![]() $x\rightarrow 0$
), we assume that the local radius of the drop changes according to
$x\rightarrow 0$
), we assume that the local radius of the drop changes according to
Substituting the above definition into the steady-state equation (2.15) and neglecting terms of
![]() $O(\unicode[STIX]{x1D700}^{2})$
, results, at a first approximation, in
$O(\unicode[STIX]{x1D700}^{2})$
, results, at a first approximation, in
Together with the condition that
![]() $\unicode[STIX]{x1D700}(0)=0$
we obtain
$\unicode[STIX]{x1D700}(0)=0$
we obtain
where
![]() $C$
is an integration constant. The last two equations suggest that there is a singular point at
$C$
is an integration constant. The last two equations suggest that there is a singular point at
![]() $\unicode[STIX]{x1D708}=2$
. However, one should remember that
$\unicode[STIX]{x1D708}=2$
. However, one should remember that
![]() $\unicode[STIX]{x1D708}=2$
corresponds to an inviscid drop (
$\unicode[STIX]{x1D708}=2$
corresponds to an inviscid drop (
![]() $f=0$
) in linear (
$f=0$
) in linear (
![]() $G=0$
) extensional flow. In this case, the last term on the left-hand side and the term on the right-hand side of (3.3) vanish, so that the first terms on the right-hand side of (3.4) and (3.5) do not exist. When
$G=0$
) extensional flow. In this case, the last term on the left-hand side and the term on the right-hand side of (3.3) vanish, so that the first terms on the right-hand side of (3.4) and (3.5) do not exist. When
![]() $\unicode[STIX]{x1D708}=2$
, the solution is analytic, and we shall see later that
$\unicode[STIX]{x1D708}=2$
, the solution is analytic, and we shall see later that
![]() $C=1/800$
. When
$C=1/800$
. When
![]() $\unicode[STIX]{x1D708}>2$
, the last term on the right-hand side of (3.5) can be neglected when compared to the first term. If
$\unicode[STIX]{x1D708}>2$
, the last term on the right-hand side of (3.5) can be neglected when compared to the first term. If
![]() $\unicode[STIX]{x1D708}<2$
, the last term on the right-hand side of (3.5) is the leading one, suggesting a non-analytical solution at
$\unicode[STIX]{x1D708}<2$
, the last term on the right-hand side of (3.5) is the leading one, suggesting a non-analytical solution at
![]() $x=0$
. However, following Acrivos & Lo (Reference Acrivos and Lo1978) for the case of an inviscid drop with external inertia, the coefficient of this non-analytical term can be made to vanish by a proper choice of
$x=0$
. However, following Acrivos & Lo (Reference Acrivos and Lo1978) for the case of an inviscid drop with external inertia, the coefficient of this non-analytical term can be made to vanish by a proper choice of
![]() $\unicode[STIX]{x1D708}$
.
$\unicode[STIX]{x1D708}$
.
3.2 The solution near the end of the drop
Near the end of the drop (
![]() $x\rightarrow x_{L}$
), we assume a local radius profile of the form
$x\rightarrow x_{L}$
), we assume a local radius profile of the form
where both
![]() $M$
and
$M$
and
![]() $\unicode[STIX]{x1D6FC}$
are defined as positive. Equation (3.6) suggests three possible shapes for the end of the slender drop: a cusped end (
$\unicode[STIX]{x1D6FC}$
are defined as positive. Equation (3.6) suggests three possible shapes for the end of the slender drop: a cusped end (
![]() $\unicode[STIX]{x1D6FC}>1$
), a pointed end (
$\unicode[STIX]{x1D6FC}>1$
), a pointed end (
![]() $\unicode[STIX]{x1D6FC}=1$
) and a rounded end (
$\unicode[STIX]{x1D6FC}=1$
) and a rounded end (
![]() $\unicode[STIX]{x1D6FC}<1$
). Substituting (3.6) into the steady-state equation (2.15) reveals that only the case
$\unicode[STIX]{x1D6FC}<1$
). Substituting (3.6) into the steady-state equation (2.15) reveals that only the case
![]() $\unicode[STIX]{x1D6FC}=1$
, where the end is pointed, is possible. This finding is equivalent to the linear extensional flow case, with or without a weak amount of external inertia (Favelukis et al.
Reference Favelukis, Lavrenteva and Nir2005, Reference Favelukis, Lavrenteva and Nir2006).
$\unicode[STIX]{x1D6FC}=1$
, where the end is pointed, is possible. This finding is equivalent to the linear extensional flow case, with or without a weak amount of external inertia (Favelukis et al.
Reference Favelukis, Lavrenteva and Nir2005, Reference Favelukis, Lavrenteva and Nir2006).
At the end of the drop, the steady-state equation (2.15) reduces to
Combining the last two equations (with
![]() $\unicode[STIX]{x1D6FC}=1$
) and applying a Taylor series for
$\unicode[STIX]{x1D6FC}=1$
) and applying a Taylor series for
![]() $\unicode[STIX]{x1D700}$
around
$\unicode[STIX]{x1D700}$
around
![]() $\unicode[STIX]{x1D700}=0$
results in an algebraic equation, to which the first approximation solution is
$\unicode[STIX]{x1D700}=0$
results in an algebraic equation, to which the first approximation solution is
The following numerical results suggest that the (
![]() $+$
) solution is the correct one. This might be expected when we explore (3.8) for the limiting case of an inviscid drop (
$+$
) solution is the correct one. This might be expected when we explore (3.8) for the limiting case of an inviscid drop (
![]() $f=0$
).
$f=0$
).
Despite the discussion presented here and in the previous section, one should remember that the slender-body approximation equations may not be accurate at the centre and at end of the drop.
4 Inviscid drop
 $(\unicode[STIX]{x1D706}=0)$
$(\unicode[STIX]{x1D706}=0)$
4.1 Steady-state shapes
For a bubble or an inviscid drop,
![]() $\unicode[STIX]{x1D706}=f=0$
, the internal pressure is uniform and at steady state it is also constant. Combining the steady-state form of (2.11) with (3.1) results in
$\unicode[STIX]{x1D706}=f=0$
, the internal pressure is uniform and at steady state it is also constant. Combining the steady-state form of (2.11) with (3.1) results in
The solution of (4.1) together with the boundary condition
![]() $y(x_{L})=0$
requires a trial and error procedure in order to connect the parameters
$y(x_{L})=0$
requires a trial and error procedure in order to connect the parameters
![]() $\unicode[STIX]{x1D708}$
,
$\unicode[STIX]{x1D708}$
,
![]() $x_{L}$
and
$x_{L}$
and
![]() $G$
via the conservation of volume. The trial and error procedure can be avoided if one defines variables
$G$
via the conservation of volume. The trial and error procedure can be avoided if one defines variables
![]() $\unicode[STIX]{x1D703}=Gx^{2}$
and
$\unicode[STIX]{x1D703}=Gx^{2}$
and
![]() $\unicode[STIX]{x1D703}_{L}=Gx_{L}^{2}$
, which can be positive or negative depending on the sign of
$\unicode[STIX]{x1D703}_{L}=Gx_{L}^{2}$
, which can be positive or negative depending on the sign of
![]() $G$
. With this definition, equation (4.1) and the conservation of volume, equation (2.12), become
$G$
. With this definition, equation (4.1) and the conservation of volume, equation (2.12), become
For a choice of
![]() $\unicode[STIX]{x1D708}$
,
$\unicode[STIX]{x1D708}$
,
![]() $\unicode[STIX]{x1D703}_{L}$
can be found by solving (4.2) from
$\unicode[STIX]{x1D703}_{L}$
can be found by solving (4.2) from
![]() $y(0)=1/(2\unicode[STIX]{x1D708})$
until
$y(0)=1/(2\unicode[STIX]{x1D708})$
until
![]() $y(\unicode[STIX]{x1D703}_{L})=0$
. Then, the parameter
$y(\unicode[STIX]{x1D703}_{L})=0$
. Then, the parameter
![]() $G$
can be obtained from the conservation of volume in (4.3).
$G$
can be obtained from the conservation of volume in (4.3).
An exact solution in a closed form can be found for (4.2) and its boundary condition at the end of the drop:
 $$\begin{eqnarray}\displaystyle y & = & \displaystyle {\textstyle \frac{1}{4}}(1+\unicode[STIX]{x1D703})^{-(\unicode[STIX]{x1D708}+9/2)/2}\unicode[STIX]{x1D703}_{L}^{-\unicode[STIX]{x1D708}/2}\left[-(-\unicode[STIX]{x1D703})^{\unicode[STIX]{x1D708}/2}\unicode[STIX]{x1D703}_{L}^{\unicode[STIX]{x1D708}/2}B[-\unicode[STIX]{x1D703},-\unicode[STIX]{x1D708}/2,(\unicode[STIX]{x1D708}+9/2)/2]\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D708}/2}(-\unicode[STIX]{x1D703}_{L})^{\unicode[STIX]{x1D708}/2}B[-\unicode[STIX]{x1D703}_{L},-\unicode[STIX]{x1D708}/2,(\unicode[STIX]{x1D708}+9/2)/2]\vphantom{\unicode[STIX]{x1D703}_{L}^{\unicode[STIX]{x1D708}/2}}\right]\!,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle y & = & \displaystyle {\textstyle \frac{1}{4}}(1+\unicode[STIX]{x1D703})^{-(\unicode[STIX]{x1D708}+9/2)/2}\unicode[STIX]{x1D703}_{L}^{-\unicode[STIX]{x1D708}/2}\left[-(-\unicode[STIX]{x1D703})^{\unicode[STIX]{x1D708}/2}\unicode[STIX]{x1D703}_{L}^{\unicode[STIX]{x1D708}/2}B[-\unicode[STIX]{x1D703},-\unicode[STIX]{x1D708}/2,(\unicode[STIX]{x1D708}+9/2)/2]\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D708}/2}(-\unicode[STIX]{x1D703}_{L})^{\unicode[STIX]{x1D708}/2}B[-\unicode[STIX]{x1D703}_{L},-\unicode[STIX]{x1D708}/2,(\unicode[STIX]{x1D708}+9/2)/2]\vphantom{\unicode[STIX]{x1D703}_{L}^{\unicode[STIX]{x1D708}/2}}\right]\!,\end{eqnarray}$$
where
![]() $B$
is the incomplete beta function defined by
$B$
is the incomplete beta function defined by
Following Sherwood (Reference Sherwood1984), the solution can be obtained by expressing (4.2) as a power series in the form
where the first few coefficients are given by
A general expression for the coefficients is
 $$\begin{eqnarray}a_{k}=\frac{\displaystyle \mathop{\prod }_{j=0}^{k-1}(2j+9/2)}{\displaystyle 2\mathop{\prod }_{j=0}^{k}(\unicode[STIX]{x1D708}-2j)}.\end{eqnarray}$$
$$\begin{eqnarray}a_{k}=\frac{\displaystyle \mathop{\prod }_{j=0}^{k-1}(2j+9/2)}{\displaystyle 2\mathop{\prod }_{j=0}^{k}(\unicode[STIX]{x1D708}-2j)}.\end{eqnarray}$$
For the specific case of
![]() $j=0$
, the numerator is defined as 1. Note that
$j=0$
, the numerator is defined as 1. Note that
![]() $\unicode[STIX]{x1D708}=0,2,4,6,\ldots$
are singular points and the solution contains many branches depending on values of
$\unicode[STIX]{x1D708}=0,2,4,6,\ldots$
are singular points and the solution contains many branches depending on values of
![]() $\unicode[STIX]{x1D708}$
. Following Acrivos & Lo (Reference Acrivos and Lo1978) and Favelukis et al. (Reference Favelukis, Lavrenteva and Nir2006), we shall concentrate on solutions having low values of
$\unicode[STIX]{x1D708}$
. Following Acrivos & Lo (Reference Acrivos and Lo1978) and Favelukis et al. (Reference Favelukis, Lavrenteva and Nir2006), we shall concentrate on solutions having low values of
![]() $\unicode[STIX]{x1D708}$
, in the range
$\unicode[STIX]{x1D708}$
, in the range
![]() $0<\unicode[STIX]{x1D708}<4$
, as there we expect to find the stable solutions of physical interest.
$0<\unicode[STIX]{x1D708}<4$
, as there we expect to find the stable solutions of physical interest.
Figure 2(a) shows the deformation curve of an inviscid drop for the range
![]() $0<\unicode[STIX]{x1D708}<4$
, where 30 terms have been used in (4.6). First, let us observe the solid line, starting from the right-hand side of the plot at low
$0<\unicode[STIX]{x1D708}<4$
, where 30 terms have been used in (4.6). First, let us observe the solid line, starting from the right-hand side of the plot at low
![]() $\unicode[STIX]{x1D708}$
, large
$\unicode[STIX]{x1D708}$
, large
![]() $G$
and small
$G$
and small
![]() $x_{L}$
. As the parameter
$x_{L}$
. As the parameter
![]() $\unicode[STIX]{x1D708}$
increases, the positive
$\unicode[STIX]{x1D708}$
increases, the positive
![]() $G$
decreases and
$G$
decreases and
![]() $x_{L}$
increases, until we reach the case of an inviscid drop in creeping linear flow (
$x_{L}$
increases, until we reach the case of an inviscid drop in creeping linear flow (
![]() $\unicode[STIX]{x1D708}=2$
,
$\unicode[STIX]{x1D708}=2$
,
![]() $G=0$
,
$G=0$
,
![]() $x_{L}=20$
). Note that the literature suggests that an inviscid drop in linear extensional creeping flow is always stable and cannot be broken (Acrivos & Lo Reference Acrivos and Lo1978). As the parameter
$x_{L}=20$
). Note that the literature suggests that an inviscid drop in linear extensional creeping flow is always stable and cannot be broken (Acrivos & Lo Reference Acrivos and Lo1978). As the parameter
![]() $\unicode[STIX]{x1D708}$
continues to increase, the solid line enters a region with negative values of
$\unicode[STIX]{x1D708}$
continues to increase, the solid line enters a region with negative values of
![]() $G$
, which are very close to zero and therefore are difficult to observe in figure 2(a). The solid line turns back on itself at a bifurcation turning point (
$G$
, which are very close to zero and therefore are difficult to observe in figure 2(a). The solid line turns back on itself at a bifurcation turning point (
![]() $\unicode[STIX]{x1D708}=2.51$
), and finally terminates at
$\unicode[STIX]{x1D708}=2.51$
), and finally terminates at
![]() $\unicode[STIX]{x1D708}=4$
,
$\unicode[STIX]{x1D708}=4$
,
![]() $G=-0$
and
$G=-0$
and
![]() $x_{L}=60.0$
. An enlargement of the turning point zone is depicted in figure 2(b).
$x_{L}=60.0$
. An enlargement of the turning point zone is depicted in figure 2(b).

Figure 2. The deformation curve of an inviscid drop: (a) overall view; (b) enlargement of the turning point zone. Solid line:
![]() $\text{d}y/\text{d}x<0$
as
$\text{d}y/\text{d}x<0$
as
![]() $x\rightarrow 0$
(
$x\rightarrow 0$
(
![]() $x>0$
) with breakup point at
$x>0$
) with breakup point at
![]() $\unicode[STIX]{x1D708}=2.51$
; dashed line:
$\unicode[STIX]{x1D708}=2.51$
; dashed line:
![]() $\text{d}y/\text{d}x>0$
as
$\text{d}y/\text{d}x>0$
as
![]() $x\rightarrow 0$
(
$x\rightarrow 0$
(
![]() $x>0$
); dotted line: approximate solution. Solid circles are placed at different values of
$x>0$
); dotted line: approximate solution. Solid circles are placed at different values of
![]() $\unicode[STIX]{x1D708}$
.
$\unicode[STIX]{x1D708}$
.
Based on previous works (Acrivos & Lo Reference Acrivos and Lo1978; Favelukis et al.
Reference Favelukis, Lavrenteva and Nir2006), steady stable shapes are probably located at the lower branch (low
![]() $\unicode[STIX]{x1D708}$
) until the bifurcation turning point at
$\unicode[STIX]{x1D708}$
) until the bifurcation turning point at
![]() $\unicode[STIX]{x1D708}=2.51$
, while steady unstable shapes should be found at the upper branch and in other branches having higher values of
$\unicode[STIX]{x1D708}=2.51$
, while steady unstable shapes should be found at the upper branch and in other branches having higher values of
![]() $\unicode[STIX]{x1D708}$
which are not plotted in this figure. At the bifurcation turning point, which is considered as the breakup point, the numerical results suggest
$\unicode[STIX]{x1D708}$
which are not plotted in this figure. At the bifurcation turning point, which is considered as the breakup point, the numerical results suggest
![]() $\unicode[STIX]{x1D708}=2.51$
,
$\unicode[STIX]{x1D708}=2.51$
,
![]() $G=-9.62\times 10^{-5}$
and
$G=-9.62\times 10^{-5}$
and
![]() $x_{L}=28.7$
. We shall prove later, via a stability analysis, that our predictions are correct. Thus, contrary to the linear case (
$x_{L}=28.7$
. We shall prove later, via a stability analysis, that our predictions are correct. Thus, contrary to the linear case (
![]() $G=0$
), where the inviscid drop is always stable and breakup is not possible, the addition of nonlinear terms (
$G=0$
), where the inviscid drop is always stable and breakup is not possible, the addition of nonlinear terms (
![]() $G\neq 0$
) can cause the bubble to break. The solid lines in figure 3 show steady shapes (stable or unstable) corresponding to the solid line of figure 2. Note that all cases have a local radius which decreases monotonically (for
$G\neq 0$
) can cause the bubble to break. The solid lines in figure 3 show steady shapes (stable or unstable) corresponding to the solid line of figure 2. Note that all cases have a local radius which decreases monotonically (for
![]() $x\geqslant 0$
), and when
$x\geqslant 0$
), and when
![]() $\unicode[STIX]{x1D708}<1.68$
, the shapes also have an inflection point.
$\unicode[STIX]{x1D708}<1.68$
, the shapes also have an inflection point.
Next we discuss the dashed line in figure 2 which covers the range
![]() $2<\unicode[STIX]{x1D708}<4$
. It starts at
$2<\unicode[STIX]{x1D708}<4$
. It starts at
![]() $\unicode[STIX]{x1D708}$
just above 2 with large positive values of
$\unicode[STIX]{x1D708}$
just above 2 with large positive values of
![]() $G$
and low values of
$G$
and low values of
![]() $x_{L}$
. As the parameter
$x_{L}$
. As the parameter
![]() $\unicode[STIX]{x1D708}$
increases,
$\unicode[STIX]{x1D708}$
increases,
![]() $G$
decreases (always positive) and
$G$
decreases (always positive) and
![]() $x_{L}$
increases, until the dashed line meets the solid line at
$x_{L}$
increases, until the dashed line meets the solid line at
![]() $\unicode[STIX]{x1D708}=4$
,
$\unicode[STIX]{x1D708}=4$
,
![]() $G=+0$
and
$G=+0$
and
![]() $x_{L}=60.0$
. At the centre of the slender drop,
$x_{L}=60.0$
. At the centre of the slender drop,
![]() $\text{d}y/\text{d}x=0$
. Near the centre of the drop (
$\text{d}y/\text{d}x=0$
. Near the centre of the drop (
![]() $x\rightarrow 0$
) and if
$x\rightarrow 0$
) and if
![]() $x$
is positive, equation (3.5) with
$x$
is positive, equation (3.5) with
![]() $f=0$
suggests a negative slope,
$f=0$
suggests a negative slope,
![]() $\text{d}y/\text{d}x<0$
, for the solid line, and a positive slope,
$\text{d}y/\text{d}x<0$
, for the solid line, and a positive slope,
![]() $\text{d}y/\text{d}x>0$
, for the dashed line. Therefore, the dashed line represents steady shapes having a maximum in the local radius, besides the one at the centre of the drop (see figure 4). In the next section we shall prove through a stability analysis that these strange steady shapes are unstable. It should be noted that, contrary to the solid lines in figures 2 or 3, for these strange drops the numerical solution of the power series does not give a good prediction of the slope at the end of the drop, especially at the lower values of the parameter
$\text{d}y/\text{d}x>0$
, for the dashed line. Therefore, the dashed line represents steady shapes having a maximum in the local radius, besides the one at the centre of the drop (see figure 4). In the next section we shall prove through a stability analysis that these strange steady shapes are unstable. It should be noted that, contrary to the solid lines in figures 2 or 3, for these strange drops the numerical solution of the power series does not give a good prediction of the slope at the end of the drop, especially at the lower values of the parameter
![]() $\unicode[STIX]{x1D708}$
.
$\unicode[STIX]{x1D708}$
.

Figure 3. Steady-state shapes of inviscid drops, having
![]() $\text{d}y/\text{d}x<0$
as
$\text{d}y/\text{d}x<0$
as
![]() $x\rightarrow 0$
(
$x\rightarrow 0$
(
![]() $x>0$
), for different values of
$x>0$
), for different values of
![]() $\unicode[STIX]{x1D708}$
. Solid lines: exact solution; dotted lines: approximate solution.
$\unicode[STIX]{x1D708}$
. Solid lines: exact solution; dotted lines: approximate solution.
![]() $\unicode[STIX]{x1D708}=1$
(stable),
$\unicode[STIX]{x1D708}=1$
(stable),
![]() $\unicode[STIX]{x1D708}=2$
(stable),
$\unicode[STIX]{x1D708}=2$
(stable),
![]() $\unicode[STIX]{x1D708}=2.51$
(breakup point) and
$\unicode[STIX]{x1D708}=2.51$
(breakup point) and
![]() $\unicode[STIX]{x1D708}=3$
and (unstable).
$\unicode[STIX]{x1D708}=3$
and (unstable).

Figure 4. Steady-state shapes of inviscid drops, having
![]() $\text{d}y/\text{d}x>0$
as
$\text{d}y/\text{d}x>0$
as
![]() $x\rightarrow 0$
(
$x\rightarrow 0$
(
![]() $x>0$
), for different values of
$x>0$
), for different values of
![]() $\unicode[STIX]{x1D708}$
, according to the exact solution. All cases are unstable.
$\unicode[STIX]{x1D708}$
, according to the exact solution. All cases are unstable.
An approximate solution can be obtained by considering the first two terms of (4.6). Together with the boundary condition at the end of the drop
![]() $y(x_{L})=y(\unicode[STIX]{x1D703}_{L})=0$
, and the conservation of volume, expressed by (2.12) or (4.3), we find that
$y(x_{L})=y(\unicode[STIX]{x1D703}_{L})=0$
, and the conservation of volume, expressed by (2.12) or (4.3), we find that
Notice that the two-term approximation suggests a parabolic radius profile; therefore, it cannot represent the unstable dashed line, which is characterized by having a maximum radius, besides the one at the centre. The two-term approximation is depicted in figure 2 by the dotted line. It closely follows the solid line, especially when
![]() $\unicode[STIX]{x1D708}>2$
, and its bifurcation turning point is located at
$\unicode[STIX]{x1D708}>2$
, and its bifurcation turning point is located at
![]() $\unicode[STIX]{x1D708}=8/3=2.67$
,
$\unicode[STIX]{x1D708}=8/3=2.67$
,
![]() $G=-1.17\times 10^{-4}$
and
$G=-1.17\times 10^{-4}$
and
![]() $x_{L}=35.6$
. For the case of linear extensional flow (
$x_{L}=35.6$
. For the case of linear extensional flow (
![]() $G=0$
), equation (4.9) also represents the exact solution after substituting
$G=0$
), equation (4.9) also represents the exact solution after substituting
![]() $\unicode[STIX]{x1D708}=2$
, leading to
$\unicode[STIX]{x1D708}=2$
, leading to
![]() $x_{L}=20$
. Steady shapes of deformed drops according to the approximate solution are represented by the dotted lines in figure 3. Despite the fact that the approximate solution underestimates the half-length of the drop when
$x_{L}=20$
. Steady shapes of deformed drops according to the approximate solution are represented by the dotted lines in figure 3. Despite the fact that the approximate solution underestimates the half-length of the drop when
![]() $\unicode[STIX]{x1D708}<2$
and overestimates the half-length at
$\unicode[STIX]{x1D708}<2$
and overestimates the half-length at
![]() $\unicode[STIX]{x1D708}>2$
(see figure 3), it represents a simple and excellent alternative to the cumbersome numerical solution.
$\unicode[STIX]{x1D708}>2$
(see figure 3), it represents a simple and excellent alternative to the cumbersome numerical solution.
4.2 The stability of the solution
In this section we perform a stability analysis to small disturbances of the steady shapes in order to find the location of the stable and unstable regions. For an inviscid drop
![]() $f=0$
, and (2.15) in terms of our new variable
$f=0$
, and (2.15) in terms of our new variable
![]() $\unicode[STIX]{x1D703}=Gx^{2}$
takes the following form:
$\unicode[STIX]{x1D703}=Gx^{2}$
takes the following form:
Let a long-wave axisymmetric disturbance be defined as
Here
![]() $y_{0}$
is the steady-state solution and
$y_{0}$
is the steady-state solution and
![]() $y_{1}$
is a time-dependent small axisymmetric perturbation such that
$y_{1}$
is a time-dependent small axisymmetric perturbation such that
![]() $y_{1}\ll y_{0}$
. Combining the last two equations and neglecting terms of
$y_{1}\ll y_{0}$
. Combining the last two equations and neglecting terms of
![]() $O(y_{1}^{2})$
or higher we obtain
$O(y_{1}^{2})$
or higher we obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle 2\frac{\unicode[STIX]{x2202}^{2}y_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}\unicode[STIX]{x2202}t}-\frac{2}{y_{0}}\frac{\text{d}y_{0}}{\text{d}\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}y_{1}}{\unicode[STIX]{x2202}t}+4(1+\unicode[STIX]{x1D703})\unicode[STIX]{x1D703}\frac{\unicode[STIX]{x2202}^{2}y_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}^{2}}+\left[4(1+2\unicode[STIX]{x1D703})-\frac{8(1+\unicode[STIX]{x1D703})\unicode[STIX]{x1D703}}{y_{0}}\frac{\text{d}y_{0}}{\text{d}\unicode[STIX]{x1D703}}-\frac{1}{y_{0}}\right]\frac{\unicode[STIX]{x2202}y_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\nonumber\\ \displaystyle & & \displaystyle \quad +\left[\frac{4(1+\unicode[STIX]{x1D703})\unicode[STIX]{x1D703}}{y_{0}^{2}}\left(\frac{\text{d}y_{0}}{\text{d}\unicode[STIX]{x1D703}}\right)^{2}+\frac{1}{y_{0}^{2}}\frac{\text{d}y_{0}}{\text{d}\unicode[STIX]{x1D703}}+9\right]y_{1}=0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle 2\frac{\unicode[STIX]{x2202}^{2}y_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}\unicode[STIX]{x2202}t}-\frac{2}{y_{0}}\frac{\text{d}y_{0}}{\text{d}\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}y_{1}}{\unicode[STIX]{x2202}t}+4(1+\unicode[STIX]{x1D703})\unicode[STIX]{x1D703}\frac{\unicode[STIX]{x2202}^{2}y_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}^{2}}+\left[4(1+2\unicode[STIX]{x1D703})-\frac{8(1+\unicode[STIX]{x1D703})\unicode[STIX]{x1D703}}{y_{0}}\frac{\text{d}y_{0}}{\text{d}\unicode[STIX]{x1D703}}-\frac{1}{y_{0}}\right]\frac{\unicode[STIX]{x2202}y_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\nonumber\\ \displaystyle & & \displaystyle \quad +\left[\frac{4(1+\unicode[STIX]{x1D703})\unicode[STIX]{x1D703}}{y_{0}^{2}}\left(\frac{\text{d}y_{0}}{\text{d}\unicode[STIX]{x1D703}}\right)^{2}+\frac{1}{y_{0}^{2}}\frac{\text{d}y_{0}}{\text{d}\unicode[STIX]{x1D703}}+9\right]y_{1}=0.\end{eqnarray}$$
As always, the perturbation is described as
![]() $y_{1}=g(\unicode[STIX]{x1D703})\exp (\unicode[STIX]{x1D6FF}t)$
, where negative real values of
$y_{1}=g(\unicode[STIX]{x1D703})\exp (\unicode[STIX]{x1D6FF}t)$
, where negative real values of
![]() $\unicode[STIX]{x1D6FF}$
denote stable steady shapes while positive real values of
$\unicode[STIX]{x1D6FF}$
denote stable steady shapes while positive real values of
![]() $\unicode[STIX]{x1D6FF}$
denote unstable steady shapes. Thus, the point where the real part
$\unicode[STIX]{x1D6FF}$
denote unstable steady shapes. Thus, the point where the real part
![]() $\unicode[STIX]{x1D6FF}$
vanishes can be considered as the breakup point. Substituting this definition into (4.13) gives
$\unicode[STIX]{x1D6FF}$
vanishes can be considered as the breakup point. Substituting this definition into (4.13) gives
 $$\begin{eqnarray}\displaystyle & & \displaystyle 4(1+\unicode[STIX]{x1D703})\unicode[STIX]{x1D703}\frac{\text{d}^{2}g}{\text{d}\unicode[STIX]{x1D703}^{2}}+\left[4(1+2\unicode[STIX]{x1D703})+2\unicode[STIX]{x1D6FF}-\frac{1}{y_{0}}-\frac{8(1+\unicode[STIX]{x1D703})\unicode[STIX]{x1D703}}{y_{0}}\frac{\text{d}y_{0}}{\text{d}\unicode[STIX]{x1D703}}\right]\frac{\text{d}g}{\text{d}\unicode[STIX]{x1D703}}\nonumber\\ \displaystyle & & \displaystyle \quad +\left[\frac{4(1+\unicode[STIX]{x1D703})\unicode[STIX]{x1D703}}{y_{0}^{2}}\left(\frac{\text{d}y_{0}}{\text{d}\unicode[STIX]{x1D703}}\right)^{2}+\frac{1}{y_{0}^{2}}\frac{\text{d}y_{0}}{\text{d}\unicode[STIX]{x1D703}}+9-\frac{2\unicode[STIX]{x1D6FF}}{y_{0}}\frac{\text{d}y_{0}}{\text{d}\unicode[STIX]{x1D703}}\right]g=0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle 4(1+\unicode[STIX]{x1D703})\unicode[STIX]{x1D703}\frac{\text{d}^{2}g}{\text{d}\unicode[STIX]{x1D703}^{2}}+\left[4(1+2\unicode[STIX]{x1D703})+2\unicode[STIX]{x1D6FF}-\frac{1}{y_{0}}-\frac{8(1+\unicode[STIX]{x1D703})\unicode[STIX]{x1D703}}{y_{0}}\frac{\text{d}y_{0}}{\text{d}\unicode[STIX]{x1D703}}\right]\frac{\text{d}g}{\text{d}\unicode[STIX]{x1D703}}\nonumber\\ \displaystyle & & \displaystyle \quad +\left[\frac{4(1+\unicode[STIX]{x1D703})\unicode[STIX]{x1D703}}{y_{0}^{2}}\left(\frac{\text{d}y_{0}}{\text{d}\unicode[STIX]{x1D703}}\right)^{2}+\frac{1}{y_{0}^{2}}\frac{\text{d}y_{0}}{\text{d}\unicode[STIX]{x1D703}}+9-\frac{2\unicode[STIX]{x1D6FF}}{y_{0}}\frac{\text{d}y_{0}}{\text{d}\unicode[STIX]{x1D703}}\right]g=0.\end{eqnarray}$$
We are looking for a solution to (4.14) in the form of a power series:
where we set
![]() $c_{0}=1$
without loss of generality (Acrivos & Lo Reference Acrivos and Lo1978). We find for the first coefficients:
$c_{0}=1$
without loss of generality (Acrivos & Lo Reference Acrivos and Lo1978). We find for the first coefficients:
The conservation of volume, given by (2.12), can be differentiated with respect to time to give
The eigenvalues
![]() $\unicode[STIX]{x1D6FF}$
are determined by solving this last equation. For each
$\unicode[STIX]{x1D6FF}$
are determined by solving this last equation. For each
![]() $\unicode[STIX]{x1D708}$
there are many possible values of
$\unicode[STIX]{x1D708}$
there are many possible values of
![]() $\unicode[STIX]{x1D6FF}$
, and we are interested in
$\unicode[STIX]{x1D6FF}$
, and we are interested in
![]() $\unicode[STIX]{x1D6FF}$
with the highest real part.
$\unicode[STIX]{x1D6FF}$
with the highest real part.
In figure 5 we show the highest real value of
![]() $\unicode[STIX]{x1D6FF}$
as a function of the parameter
$\unicode[STIX]{x1D6FF}$
as a function of the parameter
![]() $\unicode[STIX]{x1D708}$
that was obtained with
$\unicode[STIX]{x1D708}$
that was obtained with
![]() $k=12$
in (4.6) and (4.15). The solid and dashed lines in this figure correspond to the solid and dashed lines in figure 2, respectively. We find that for all cases
$k=12$
in (4.6) and (4.15). The solid and dashed lines in this figure correspond to the solid and dashed lines in figure 2, respectively. We find that for all cases
![]() $\unicode[STIX]{x1D6FF}$
is real. As expected, the solid line (
$\unicode[STIX]{x1D6FF}$
is real. As expected, the solid line (
![]() $\text{d}y_{0}/\text{d}x<0$
,
$\text{d}y_{0}/\text{d}x<0$
,
![]() $x\rightarrow 0$
,
$x\rightarrow 0$
,
![]() $x>0$
) contains both a stable region (
$x>0$
) contains both a stable region (
![]() $\unicode[STIX]{x1D708}<2.51$
,
$\unicode[STIX]{x1D708}<2.51$
,
![]() $\unicode[STIX]{x1D6FF}<0$
) and an unstable region (
$\unicode[STIX]{x1D6FF}<0$
) and an unstable region (
![]() $\unicode[STIX]{x1D708}>2.51$
,
$\unicode[STIX]{x1D708}>2.51$
,
![]() $\unicode[STIX]{x1D6FF}>0$
), confirming our prediction that the breakup point (
$\unicode[STIX]{x1D6FF}>0$
), confirming our prediction that the breakup point (
![]() $\unicode[STIX]{x1D6FF}=0$
) is located at the bifurcation turning point at
$\unicode[STIX]{x1D6FF}=0$
) is located at the bifurcation turning point at
![]() $\unicode[STIX]{x1D708}=2.51$
. On the other hand, the dashed line (
$\unicode[STIX]{x1D708}=2.51$
. On the other hand, the dashed line (
![]() $\text{d}y_{0}/\text{d}x>0$
,
$\text{d}y_{0}/\text{d}x>0$
,
![]() $x\rightarrow 0$
,
$x\rightarrow 0$
,
![]() $x>0$
) represents an unstable physical situation (
$x>0$
) represents an unstable physical situation (
![]() $\unicode[STIX]{x1D6FF}>0$
) everywhere. It should be mentioned that
$\unicode[STIX]{x1D6FF}>0$
) everywhere. It should be mentioned that
![]() $\unicode[STIX]{x1D6FF}$
was found to be positive for all branches with
$\unicode[STIX]{x1D6FF}$
was found to be positive for all branches with
![]() $\unicode[STIX]{x1D708}>4$
, suggesting that no other steady stable shapes are expected.
$\unicode[STIX]{x1D708}>4$
, suggesting that no other steady stable shapes are expected.

Figure 5. The stability of the solution of an inviscid drop. Solid line:
![]() $\text{d}y_{0}/\text{d}x<0$
as
$\text{d}y_{0}/\text{d}x<0$
as
![]() $x\rightarrow 0$
(
$x\rightarrow 0$
(
![]() $x>0$
), with breakup point at
$x>0$
), with breakup point at
![]() $\unicode[STIX]{x1D708}=2.51$
; dashed line:
$\unicode[STIX]{x1D708}=2.51$
; dashed line:
![]() $\text{d}y_{0}/\text{d}x>0$
as
$\text{d}y_{0}/\text{d}x>0$
as
![]() $x\rightarrow 0$
(
$x\rightarrow 0$
(
![]() $x>0$
).
$x>0$
).
4.3 Time-dependent studies
In order to further confirm our stability analysis conclusions regarding the location of the stable and unstable steady shapes, here we shall perform a time-dependent study, which can also reveal the type of breakup mechanism. Following Sherwood (Reference Sherwood1984), we suggest a solution for the evolution of the inviscid drop in terms of a series expansion about the centre of the drop:
which, after substitution into the partial differential (2.11) (with
![]() $f=0$
), results in the following system of ordinary differential equations:
$f=0$
), results in the following system of ordinary differential equations:
Note that for an inviscid drop the internal pressure is uniform and can be obtained from (2.14), with
![]() $f=0$
. Clearly, the accuracy of the solution depends on the maximum value of
$f=0$
. Clearly, the accuracy of the solution depends on the maximum value of
![]() $k$
used in (4.18). We used
$k$
used in (4.18). We used
![]() $k=15$
(16 terms) for figures 6 and 7, and the accuracy of the solution can be verified by the conservation of the volume. In all of the following simulations, we choose a stationary shape (stable or unstable) for the initial conditions.
$k=15$
(16 terms) for figures 6 and 7, and the accuracy of the solution can be verified by the conservation of the volume. In all of the following simulations, we choose a stationary shape (stable or unstable) for the initial conditions.

Figure 6. The evolution of an inviscid drop originally located at the stable branch with a sudden change in
![]() $G$
. The drop is originally located at
$G$
. The drop is originally located at
![]() $\unicode[STIX]{x1D708}=1.5$
,
$\unicode[STIX]{x1D708}=1.5$
,
![]() $G=+0.00102$
and
$G=+0.00102$
and
![]() $x_{L}=12.7$
. At
$x_{L}=12.7$
. At
![]() $t=0$
$t=0$
![]() $G$
is changed to
$G$
is changed to
![]() $G=0$
before the breakup point. (a) The local radius of the drop; (b) the half-length of the drop; (c) the pressure inside the drop; (d) the volume of the drop.
$G=0$
before the breakup point. (a) The local radius of the drop; (b) the half-length of the drop; (c) the pressure inside the drop; (d) the volume of the drop.
In the first type of simulation experiments, we keep the nonlinear strength of the flow (
![]() $G$
positive or negative) constant. If the inviscid drop is located at the stable lower branch corresponding to
$G$
positive or negative) constant. If the inviscid drop is located at the stable lower branch corresponding to
![]() $\unicode[STIX]{x1D708}<2.51$
(
$\unicode[STIX]{x1D708}<2.51$
(
![]() $G$
positive or negative) and depicted in figure 2 by the solid line, no change in the drop is observed. On the other hand, if we place the drop at the unstable branch corresponding to
$G$
positive or negative) and depicted in figure 2 by the solid line, no change in the drop is observed. On the other hand, if we place the drop at the unstable branch corresponding to
![]() $2.51<\unicode[STIX]{x1D708}<4$
(
$2.51<\unicode[STIX]{x1D708}<4$
(
![]() $G$
negative, solid line in figure 2), changes in the drop will occur with time. An example of such a case at
$G$
negative, solid line in figure 2), changes in the drop will occur with time. An example of such a case at
![]() $\unicode[STIX]{x1D708}=3$
,
$\unicode[STIX]{x1D708}=3$
,
![]() $G=-7.54\times 10^{-5}$
and
$G=-7.54\times 10^{-5}$
and
![]() $x_{L}=38.3$
is presented in figure 12(d). Note that the steady inviscid drop is unstable and, after an incubation time, the drop breaks via a centre pinching mechanism. This mode of breakup mechanism has also been observed for the case of an inviscid drop under a small amount of external inertia (Favelukis et al.
Reference Favelukis, Lavrenteva and Nir2012). As we further increase the number of terms in (4.18), the initial steady shape is more accurate, and the evolution process takes longer. For this reason, in this type of simulation, no time is indicated.
$x_{L}=38.3$
is presented in figure 12(d). Note that the steady inviscid drop is unstable and, after an incubation time, the drop breaks via a centre pinching mechanism. This mode of breakup mechanism has also been observed for the case of an inviscid drop under a small amount of external inertia (Favelukis et al.
Reference Favelukis, Lavrenteva and Nir2012). As we further increase the number of terms in (4.18), the initial steady shape is more accurate, and the evolution process takes longer. For this reason, in this type of simulation, no time is indicated.

Figure 7. The evolution of an inviscid drop originally located at the stable branch with a sudden change in
![]() $G$
. The drop is originally located at
$G$
. The drop is originally located at
![]() $\unicode[STIX]{x1D708}=1.5$
,
$\unicode[STIX]{x1D708}=1.5$
,
![]() $G=+0.00102$
and
$G=+0.00102$
and
![]() $x_{L}=12.7$
. At
$x_{L}=12.7$
. At
![]() $t=0$
$t=0$
![]() $G$
is changed to
$G$
is changed to
![]() $G=-0.001$
beyond the breakup point. (a) The local radius of the drop; (b) the half-length of the drop; (c) the pressure inside the drop; (d) the volume of the drop.
$G=-0.001$
beyond the breakup point. (a) The local radius of the drop; (b) the half-length of the drop; (c) the pressure inside the drop; (d) the volume of the drop.
The next type of simulation is what we call the Sherwood (Reference Sherwood1984) experiment. Here we study the evolution of the drop when at
![]() $t=0$
a sudden change in the nonlinear strength of the flow is introduced. Figures 6 and 7 correspond to an inviscid drop originally located at the steady stable branch at
$t=0$
a sudden change in the nonlinear strength of the flow is introduced. Figures 6 and 7 correspond to an inviscid drop originally located at the steady stable branch at
![]() $\unicode[STIX]{x1D708}=1.5$
,
$\unicode[STIX]{x1D708}=1.5$
,
![]() $G=+0.00102$
and
$G=+0.00102$
and
![]() $x_{L}=12.7$
. In figure 6 we show the results of changing at
$x_{L}=12.7$
. In figure 6 we show the results of changing at
![]() $t=0$
the nonlinear strength of the flow from
$t=0$
the nonlinear strength of the flow from
![]() $G=+0.00102$
to
$G=+0.00102$
to
![]() $G=0$
. As expected, the original stable drop moves to another stable location at
$G=0$
. As expected, the original stable drop moves to another stable location at
![]() $\unicode[STIX]{x1D708}=2$
,
$\unicode[STIX]{x1D708}=2$
,
![]() $G=0$
and
$G=0$
and
![]() $x_{L}=20$
, corresponding to an inviscid drop in a linear extensional flow. Note that, contrary to the previous experiment depicted in figure 12(d), in this case we can indicate the times in our simulations. In figure 7, the change is made from
$x_{L}=20$
, corresponding to an inviscid drop in a linear extensional flow. Note that, contrary to the previous experiment depicted in figure 12(d), in this case we can indicate the times in our simulations. In figure 7, the change is made from
![]() $G=+0.00102$
to
$G=+0.00102$
to
![]() $G=-0.001$
, which is beyond the breakup point located at the bifurcation turning point at
$G=-0.001$
, which is beyond the breakup point located at the bifurcation turning point at
![]() $G=-9.62\times 10^{-5}$
. As expected, breakup takes place, once again via a centre pinching mechanism.
$G=-9.62\times 10^{-5}$
. As expected, breakup takes place, once again via a centre pinching mechanism.
5 Viscous drop
 $(\unicode[STIX]{x1D706}\neq 0)$
$(\unicode[STIX]{x1D706}\neq 0)$
We start this section by introducing a parameter characterizing the nonlinearity of the flow:
Here
![]() $-\infty <H<+\infty$
. When
$-\infty <H<+\infty$
. When
![]() $H=0$
the linear extensional flow (
$H=0$
the linear extensional flow (
![]() $G=0$
) is recovered, and
$G=0$
) is recovered, and
![]() $H\rightarrow \pm \infty$
corresponds to an inviscid drop (
$H\rightarrow \pm \infty$
corresponds to an inviscid drop (
![]() $f=0$
) under the influence of nonlinear (
$f=0$
) under the influence of nonlinear (
![]() $G\neq 0$
) extensional effects.
$G\neq 0$
) extensional effects.
Similar to our discussion in § 4.1, we define new variables
![]() $\unicode[STIX]{x1D719}=f^{6}x^{2}$
and
$\unicode[STIX]{x1D719}=f^{6}x^{2}$
and
![]() $\unicode[STIX]{x1D719}_{L}=f^{6}x_{L}^{2}$
, which avoids the need of a trial and error solution. The governing equation, equation (2.15), and the conservation of volume, equation (2.12), take now the form
$\unicode[STIX]{x1D719}_{L}=f^{6}x_{L}^{2}$
, which avoids the need of a trial and error solution. The governing equation, equation (2.15), and the conservation of volume, equation (2.12), take now the form
 $$\begin{eqnarray}\displaystyle & & \displaystyle 2\frac{\unicode[STIX]{x2202}^{2}y}{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}\unicode[STIX]{x2202}t}-\frac{2}{y}\frac{\unicode[STIX]{x2202}y}{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}}\frac{\unicode[STIX]{x2202}y}{\unicode[STIX]{x2202}t}+4(1+H\unicode[STIX]{x1D719})\unicode[STIX]{x1D719}\frac{\unicode[STIX]{x2202}^{2}y}{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}^{2}}-\frac{4(1+H\unicode[STIX]{x1D719})\unicode[STIX]{x1D719}}{y}\left(\frac{\unicode[STIX]{x2202}y}{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}}\right)^{2}\nonumber\\ \displaystyle & & \displaystyle \qquad +\left[4(1+2H\unicode[STIX]{x1D719})-\frac{1}{y}\right]\frac{\unicode[STIX]{x2202}y}{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}}+9Hy\nonumber\\ \displaystyle & & \displaystyle \quad =4\left[\frac{(1+H\unicode[STIX]{x1D719})}{y}+\frac{1}{2\unicode[STIX]{x1D719}^{1/2}y^{3}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\int _{0}^{\unicode[STIX]{x1D719}}y^{2}\unicode[STIX]{x1D719}^{-1/2}\,\text{d}\unicode[STIX]{x1D719}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle 2\frac{\unicode[STIX]{x2202}^{2}y}{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}\unicode[STIX]{x2202}t}-\frac{2}{y}\frac{\unicode[STIX]{x2202}y}{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}}\frac{\unicode[STIX]{x2202}y}{\unicode[STIX]{x2202}t}+4(1+H\unicode[STIX]{x1D719})\unicode[STIX]{x1D719}\frac{\unicode[STIX]{x2202}^{2}y}{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}^{2}}-\frac{4(1+H\unicode[STIX]{x1D719})\unicode[STIX]{x1D719}}{y}\left(\frac{\unicode[STIX]{x2202}y}{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}}\right)^{2}\nonumber\\ \displaystyle & & \displaystyle \qquad +\left[4(1+2H\unicode[STIX]{x1D719})-\frac{1}{y}\right]\frac{\unicode[STIX]{x2202}y}{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}}+9Hy\nonumber\\ \displaystyle & & \displaystyle \quad =4\left[\frac{(1+H\unicode[STIX]{x1D719})}{y}+\frac{1}{2\unicode[STIX]{x1D719}^{1/2}y^{3}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\int _{0}^{\unicode[STIX]{x1D719}}y^{2}\unicode[STIX]{x1D719}^{-1/2}\,\text{d}\unicode[STIX]{x1D719}\right],\end{eqnarray}$$
Note that, contrary to the inviscid case, where
![]() $\unicode[STIX]{x1D703}$
can be positive or negative, this time
$\unicode[STIX]{x1D703}$
can be positive or negative, this time
![]() $\unicode[STIX]{x1D719}\geqslant 0$
.
$\unicode[STIX]{x1D719}\geqslant 0$
.
5.1 Steady-state shapes
At steady state, the first two terms on the left-hand side and the last term on the right-hand side of (5.2) vanish. The solving procedure is identical to the one we applied for the inviscid drop. We first chose a value for the parameter
![]() $\unicode[STIX]{x1D708}$
, and the end of the drop
$\unicode[STIX]{x1D708}$
, and the end of the drop
![]() $\unicode[STIX]{x1D719}_{L}$
can be evaluated by solving the steady form of (5.2) from
$\unicode[STIX]{x1D719}_{L}$
can be evaluated by solving the steady form of (5.2) from
![]() $y(0)=1/(2\unicode[STIX]{x1D708})$
until
$y(0)=1/(2\unicode[STIX]{x1D708})$
until
![]() $y(\unicode[STIX]{x1D719}_{L})=0$
. Finally, the parameter
$y(\unicode[STIX]{x1D719}_{L})=0$
. Finally, the parameter
![]() $f$
is obtained from the conservation of volume given by (5.3).
$f$
is obtained from the conservation of volume given by (5.3).
As before, we are looking for a solution to the steady-state equation (5.2) in the form of a power series:
and the first few coefficients are
Once again,
![]() $\unicode[STIX]{x1D708}=0,2,4,6,\ldots$
are singular points, the solution has many branches; we shall focus our search of the stable solution in the region of
$\unicode[STIX]{x1D708}=0,2,4,6,\ldots$
are singular points, the solution has many branches; we shall focus our search of the stable solution in the region of
![]() $0<\unicode[STIX]{x1D708}<4$
.
$0<\unicode[STIX]{x1D708}<4$
.
Contrary to the inviscid case, for a viscous drop there are many possible solutions, depending on the combination of the parameters
![]() $\unicode[STIX]{x1D708}$
and
$\unicode[STIX]{x1D708}$
and
![]() $H$
. Therefore, and in order to facilitate the search, we will examine first the two-term approximate solution. Taking the first two terms of (5.4) and applying the boundary condition at the end of the drop
$H$
. Therefore, and in order to facilitate the search, we will examine first the two-term approximate solution. Taking the first two terms of (5.4) and applying the boundary condition at the end of the drop
![]() $y(x_{L})=y(\unicode[STIX]{x1D719}_{L})=0$
, and the conservation of volume, (2.12) or (5.3), we find
$y(x_{L})=y(\unicode[STIX]{x1D719}_{L})=0$
, and the conservation of volume, (2.12) or (5.3), we find
As before, the two-term approximation suggests a parabolic radius profile with
![]() $\text{d}y/\text{d}x<0$
as
$\text{d}y/\text{d}x<0$
as
![]() $x\rightarrow 0$
(
$x\rightarrow 0$
(
![]() $x>0$
), and cannot represent possible shapes with
$x>0$
), and cannot represent possible shapes with
![]() $\text{d}y/\text{d}x>0$
as
$\text{d}y/\text{d}x>0$
as
![]() $x\rightarrow 0$
, which, similar to the inviscid drop case, are probably unstable. Note that the two-term approximation equals the exact solution when the extensional flow is linear (
$x\rightarrow 0$
, which, similar to the inviscid drop case, are probably unstable. Note that the two-term approximation equals the exact solution when the extensional flow is linear (
![]() $H=0$
).
$H=0$
).
Figure 8 describes the deformation curve according to the approximate solution for different values of
![]() $H$
. The figure can be divided into two regions: a region to the left of the
$H$
. The figure can be divided into two regions: a region to the left of the
![]() $H=64/9=7.11$
line, having solutions for positive and negative values of
$H=64/9=7.11$
line, having solutions for positive and negative values of
![]() $H$
, and a region to the right of this curve, having solutions for positive values of
$H$
, and a region to the right of this curve, having solutions for positive values of
![]() $H$
only.
$H$
only.

Figure 8. The deformation curve of viscous drops, according to the approximate solution, for different values of
![]() $H$
. Solid circles are placed at bifurcation turning points. The solid square is placed at
$H$
. Solid circles are placed at bifurcation turning points. The solid square is placed at
![]() $\unicode[STIX]{x1D708}=2$
.
$\unicode[STIX]{x1D708}=2$
.
To the left of the
![]() $H=64/9=7.11$
curve, we can locate the linear extensional case (
$H=64/9=7.11$
curve, we can locate the linear extensional case (
![]() $H=0$
), where (5.6)–(5.7) also describes the exact solution, with
$H=0$
), where (5.6)–(5.7) also describes the exact solution, with
![]() $2\leqslant \unicode[STIX]{x1D708}<2.4$
being the steady stable branch and
$2\leqslant \unicode[STIX]{x1D708}<2.4$
being the steady stable branch and
![]() $\unicode[STIX]{x1D708}>2.4$
the steady unstable branch. The breakup point located at the bifurcation turning point at
$\unicode[STIX]{x1D708}>2.4$
the steady unstable branch. The breakup point located at the bifurcation turning point at
![]() $\unicode[STIX]{x1D708}=2.4$
is depicted by the solid circle. Other curves having
$\unicode[STIX]{x1D708}=2.4$
is depicted by the solid circle. Other curves having
![]() $H<64/9$
(positive or negative),
$H<64/9$
(positive or negative),
![]() $x_{L}>20$
and
$x_{L}>20$
and
![]() $\unicode[STIX]{x1D708}>2$
, behave in a similar manner. That is, two branches separated by a bifurcation turning point at the solid circle. We can predict that the lower branch represents the steady stable shape and the upper branch represents the unstable steady shape.
$\unicode[STIX]{x1D708}>2$
, behave in a similar manner. That is, two branches separated by a bifurcation turning point at the solid circle. We can predict that the lower branch represents the steady stable shape and the upper branch represents the unstable steady shape.
To the left of the
![]() $H=64/9=7.11$
line, there is another family of solutions, corresponding to
$H=64/9=7.11$
line, there is another family of solutions, corresponding to
![]() $H>64/9$
,
$H>64/9$
,
![]() $x_{L}<20$
and
$x_{L}<20$
and
![]() $\unicode[STIX]{x1D708}<2$
. These curves remind us of the lower solid branch in figure 2 (
$\unicode[STIX]{x1D708}<2$
. These curves remind us of the lower solid branch in figure 2 (
![]() $G>0$
,
$G>0$
,
![]() $\unicode[STIX]{x1D708}<2$
), which was found to be stable all along the curve; later we shall prove, via a stability analysis, that these curves are stable as well. Note that all lines to the left of the
$\unicode[STIX]{x1D708}<2$
), which was found to be stable all along the curve; later we shall prove, via a stability analysis, that these curves are stable as well. Note that all lines to the left of the
![]() $H=64/9=7.11$
line concentrate to a single point at
$H=64/9=7.11$
line concentrate to a single point at
![]() $f=0$
and
$f=0$
and
![]() $x_{L}=20$
, corresponding to an inviscid drop in linear extensional creeping flow (
$x_{L}=20$
, corresponding to an inviscid drop in linear extensional creeping flow (
![]() $\unicode[STIX]{x1D708}=2$
).
$\unicode[STIX]{x1D708}=2$
).
To the right of the
![]() $H=64/9=7.11$
line, there are some curves presenting solutions for positive values of
$H=64/9=7.11$
line, there are some curves presenting solutions for positive values of
![]() $H$
, where cases having very large values of
$H$
, where cases having very large values of
![]() $H$
exist, but cannot be shown as they are outside the range of the plot. These curves are located in a region in which the combination of the parameters
$H$
exist, but cannot be shown as they are outside the range of the plot. These curves are located in a region in which the combination of the parameters
![]() $H$
and
$H$
and
![]() $\unicode[STIX]{x1D708}$
predicts, according to the exact solution, given by (3.5), that
$\unicode[STIX]{x1D708}$
predicts, according to the exact solution, given by (3.5), that
![]() $\text{d}y/\text{d}x>0$
as
$\text{d}y/\text{d}x>0$
as
![]() $x\rightarrow 0$
(
$x\rightarrow 0$
(
![]() $x>0$
). Thus, all the curves to the right of the
$x>0$
). Thus, all the curves to the right of the
![]() $H=64/9=7.11$
line are expected to be unstable.
$H=64/9=7.11$
line are expected to be unstable.
Finally, the
![]() $H=64/9=7.11$
curve is actually composed of two branches. A lower branch (
$H=64/9=7.11$
curve is actually composed of two branches. A lower branch (
![]() $\unicode[STIX]{x1D708}<2$
,
$\unicode[STIX]{x1D708}<2$
,
![]() $x_{L}<20$
) and an upper branch (
$x_{L}<20$
) and an upper branch (
![]() $\unicode[STIX]{x1D708}>2$
,
$\unicode[STIX]{x1D708}>2$
,
![]() $x_{L}>20$
) merging at
$x_{L}>20$
) merging at
![]() $\unicode[STIX]{x1D708}=2$
,
$\unicode[STIX]{x1D708}=2$
,
![]() $f=0.207$
and
$f=0.207$
and
![]() $x_{L}=20$
, represented by the solid square. Clearly, this case cannot exist, since
$x_{L}=20$
, represented by the solid square. Clearly, this case cannot exist, since
![]() $\unicode[STIX]{x1D708}=2$
corresponds to an inviscid drop in linear extensional flow where
$\unicode[STIX]{x1D708}=2$
corresponds to an inviscid drop in linear extensional flow where
![]() $f=0$
and
$f=0$
and
![]() $x_{L}=20$
.
$x_{L}=20$
.
We now proceed to the exact solution represented by (5.4), calculated with
![]() $k=16$
and presented in figure 9. We start again with the family of curves corresponding to
$k=16$
and presented in figure 9. We start again with the family of curves corresponding to
![]() $H<64/9$
(positive or negative),
$H<64/9$
(positive or negative),
![]() $x_{L}>20$
,
$x_{L}>20$
,
![]() $\unicode[STIX]{x1D708}>2$
and, according to (3.5),
$\unicode[STIX]{x1D708}>2$
and, according to (3.5),
![]() $\text{d}y/\text{d}x<0$
as
$\text{d}y/\text{d}x<0$
as
![]() $x\rightarrow 0$
(
$x\rightarrow 0$
(
![]() $x>0$
). Here we easily locate the linear extensional case (
$x>0$
). Here we easily locate the linear extensional case (
![]() $H=0$
), where the approximate solution is also the exact solution given by (5.6)–(5.7). To the left of
$H=0$
), where the approximate solution is also the exact solution given by (5.6)–(5.7). To the left of
![]() $H=0$
, we find the solutions having
$H=0$
, we find the solutions having
![]() $H<0$
. These curves behave in a very similar manner to the approximate solution. That is, two branches separated by a bifurcation turning point (solid circle). However, contrary to the approximate solution, the upper unstable branch does not extend to infinity, but rather turns back and ends up at
$H<0$
. These curves behave in a very similar manner to the approximate solution. That is, two branches separated by a bifurcation turning point (solid circle). However, contrary to the approximate solution, the upper unstable branch does not extend to infinity, but rather turns back and ends up at
![]() $f=0$
and
$f=0$
and
![]() $x_{L}=60$
. To the right of the
$x_{L}=60$
. To the right of the
![]() $H=0$
case we find some curves with
$H=0$
case we find some curves with
![]() $H>0$
but still under the
$H>0$
but still under the
![]() $H<64/9$
condition. Some of these lines stop after the turning point (
$H<64/9$
condition. Some of these lines stop after the turning point (
![]() $H=1$
) and some stop before the turning point is achieved (
$H=1$
) and some stop before the turning point is achieved (
![]() $H=5$
). Later, our stability analysis will reveal that lines with bifurcation turning points are, as expected, stable at the lower branch and unstable at the upper branch, confirming that the turning point is the breakup point (see table 1). Lines without a bifurcation turning point, for example
$H=5$
). Later, our stability analysis will reveal that lines with bifurcation turning points are, as expected, stable at the lower branch and unstable at the upper branch, confirming that the turning point is the breakup point (see table 1). Lines without a bifurcation turning point, for example
![]() $H=5$
, are stable everywhere.
$H=5$
, are stable everywhere.
Table 1. Parameters at breakup point, according to the exact solution, for the family of solutions having:
![]() $H<64/9$
(positive or negative),
$H<64/9$
(positive or negative),
![]() $x_{L}>20$
,
$x_{L}>20$
,
![]() $\unicode[STIX]{x1D708}>2$
, with bifurcation turning points.
$\unicode[STIX]{x1D708}>2$
, with bifurcation turning points.

The next family of lines corresponds to
![]() $H>64/9$
,
$H>64/9$
,
![]() $x_{L}<20$
,
$x_{L}<20$
,
![]() $\unicode[STIX]{x1D708}<2$
and, according to (3.5),
$\unicode[STIX]{x1D708}<2$
and, according to (3.5),
![]() $\text{d}y/\text{d}x<0$
as
$\text{d}y/\text{d}x<0$
as
![]() $x\rightarrow 0$
(
$x\rightarrow 0$
(
![]() $x>0$
). These lines closely follow the approximate solution. However, it is difficult to determine the end point of these lines since, close to the end points, the slope of the radius at the end of the drop, according to the series solution, deviates from the asymptotic value given by (3.8). Thus, we cannot conclude if these lines extend to infinity or they just stop as a result of our numerical procedure. The stability analysis in the next section will confirm that this family of curves is stable everywhere.
$x>0$
). These lines closely follow the approximate solution. However, it is difficult to determine the end point of these lines since, close to the end points, the slope of the radius at the end of the drop, according to the series solution, deviates from the asymptotic value given by (3.8). Thus, we cannot conclude if these lines extend to infinity or they just stop as a result of our numerical procedure. The stability analysis in the next section will confirm that this family of curves is stable everywhere.
The third family of lines with
![]() $H>64/9$
,
$H>64/9$
,
![]() $\unicode[STIX]{x1D708}>2$
and
$\unicode[STIX]{x1D708}>2$
and
![]() $\text{d}y/\text{d}x>0$
as
$\text{d}y/\text{d}x>0$
as
![]() $x\rightarrow 0$
(
$x\rightarrow 0$
(
![]() $x>0$
) is not shown in the figure. Remember that in this family the local radius of the drop achieves a maximum, besides the one at the centre of the drop; similar to the inviscid case, we expect this family to be unstable. Their numerical solution results in non-smooth lines in the deformation curve, and the slope of the radius at the end of the drop deviates completely from the asymptotic value given by (3.8).
$x>0$
) is not shown in the figure. Remember that in this family the local radius of the drop achieves a maximum, besides the one at the centre of the drop; similar to the inviscid case, we expect this family to be unstable. Their numerical solution results in non-smooth lines in the deformation curve, and the slope of the radius at the end of the drop deviates completely from the asymptotic value given by (3.8).
Steady shapes (stable and unstable) for the two families of solutions with
![]() $\text{d}y/\text{d}x<0$
as
$\text{d}y/\text{d}x<0$
as
![]() $x\rightarrow 0$
(
$x\rightarrow 0$
(
![]() $x>0$
) are shown in figure 10. For comparison, the case of an inviscid drop in linear extensional flow (
$x>0$
) are shown in figure 10. For comparison, the case of an inviscid drop in linear extensional flow (
![]() $\unicode[STIX]{x1D708}=2$
,
$\unicode[STIX]{x1D708}=2$
,
![]() $G=0$
) is also plotted. Drops having
$G=0$
) is also plotted. Drops having
![]() $H=+100$
and
$H=+100$
and
![]() $\unicode[STIX]{x1D708}<2$
are shorter and fatter than the
$\unicode[STIX]{x1D708}<2$
are shorter and fatter than the
![]() $\unicode[STIX]{x1D708}=2$
case, and may have an inflection point, while for
$\unicode[STIX]{x1D708}=2$
case, and may have an inflection point, while for
![]() $H=-100$
and
$H=-100$
and
![]() $\unicode[STIX]{x1D708}>2$
they are longer and thinner than the
$\unicode[STIX]{x1D708}>2$
they are longer and thinner than the
![]() $\unicode[STIX]{x1D708}=2$
case. Note also that the approximate solution closely follows the exact one. The approximate solution (compared at the same
$\unicode[STIX]{x1D708}=2$
case. Note also that the approximate solution closely follows the exact one. The approximate solution (compared at the same
![]() $\unicode[STIX]{x1D708}$
) underestimates the half-length of the drop when
$\unicode[STIX]{x1D708}$
) underestimates the half-length of the drop when
![]() $\unicode[STIX]{x1D708}<2$
and overestimates the half-length at
$\unicode[STIX]{x1D708}<2$
and overestimates the half-length at
![]() $\unicode[STIX]{x1D708}>2$
. However, since the approximate solution is represented by a very simple mathematical expression, it can provide an excellent tool for fast and practical estimations.
$\unicode[STIX]{x1D708}>2$
. However, since the approximate solution is represented by a very simple mathematical expression, it can provide an excellent tool for fast and practical estimations.

Figure 9. The deformation curves of viscous drops with
![]() $\text{d}y/\text{d}x<0$
as
$\text{d}y/\text{d}x<0$
as
![]() $x\rightarrow 0$
(
$x\rightarrow 0$
(
![]() $x>0$
), according to the exact solution, for different values of
$x>0$
), according to the exact solution, for different values of
![]() $H$
. Solid circles are placed at bifurcation turning points.
$H$
. Solid circles are placed at bifurcation turning points.

Figure 10. Steady-state shapes of inviscid and viscous drops with
![]() $\text{d}y/\text{d}x<0$
as
$\text{d}y/\text{d}x<0$
as
![]() $x\rightarrow 0$
(
$x\rightarrow 0$
(
![]() $x>0$
), for different values of
$x>0$
), for different values of
![]() $\unicode[STIX]{x1D708}$
,
$\unicode[STIX]{x1D708}$
,
![]() $G$
and
$G$
and
![]() $H$
. Solid lines: exact solution; dotted lines: approximate solution.
$H$
. Solid lines: exact solution; dotted lines: approximate solution.
![]() $\unicode[STIX]{x1D708}=1.1$
and
$\unicode[STIX]{x1D708}=1.1$
and
![]() $H=100$
(stable),
$H=100$
(stable),
![]() $\unicode[STIX]{x1D708}=1.5$
and
$\unicode[STIX]{x1D708}=1.5$
and
![]() $H=100$
(stable),
$H=100$
(stable),
![]() $\unicode[STIX]{x1D708}=2$
and
$\unicode[STIX]{x1D708}=2$
and
![]() $G=0$
(stable),
$G=0$
(stable),
![]() $\unicode[STIX]{x1D708}=2.50$
and
$\unicode[STIX]{x1D708}=2.50$
and
![]() $H=-100$
(breakup point), and
$H=-100$
(breakup point), and
![]() $\unicode[STIX]{x1D708}=3$
and
$\unicode[STIX]{x1D708}=3$
and
![]() $H=-100$
(unstable).
$H=-100$
(unstable).
5.2 The stability of the solution
We repeat the procedure used in the case of an inviscid drop by defining the steady solution
![]() $y_{0}(\unicode[STIX]{x1D719})$
and a small axisymmetric disturbance
$y_{0}(\unicode[STIX]{x1D719})$
and a small axisymmetric disturbance
![]() $y_{1}(\unicode[STIX]{x1D719},t)$
, such that
$y_{1}(\unicode[STIX]{x1D719},t)$
, such that
which can be substituted into the governing (5.2) and by neglecting terms of
![]() $O(y_{1}^{2})$
or higher we obtain
$O(y_{1}^{2})$
or higher we obtain
 $$\begin{eqnarray}\displaystyle & \!\!\! & \displaystyle 2\frac{\unicode[STIX]{x2202}^{2}y_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}\unicode[STIX]{x2202}t}-\frac{2}{y_{0}}\frac{\text{d}y_{0}}{\text{d}\unicode[STIX]{x1D719}}\frac{\unicode[STIX]{x2202}y_{1}}{\unicode[STIX]{x2202}t}+4(1+H\unicode[STIX]{x1D719})\unicode[STIX]{x1D719}\frac{\unicode[STIX]{x2202}^{2}y_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}^{2}}+\left[4(1+2H\unicode[STIX]{x1D719})-\frac{8(1+H\unicode[STIX]{x1D719})\unicode[STIX]{x1D719}}{y_{0}}\frac{\text{d}y_{0}}{\text{d}\unicode[STIX]{x1D719}}-\frac{1}{y_{0}}\right]\frac{\unicode[STIX]{x2202}y_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}}\;\nonumber\\ \displaystyle & \!\!\! & \displaystyle \qquad +\left[\frac{4(1+H\unicode[STIX]{x1D719})\unicode[STIX]{x1D719}}{y_{0}^{2}}\left(\frac{\text{d}y_{0}}{\text{d}\unicode[STIX]{x1D719}}\right)^{2}+\frac{1}{y_{0}^{2}}\frac{\text{d}y_{0}}{\text{d}\unicode[STIX]{x1D719}}+9H+\frac{4(1+H\unicode[STIX]{x1D719})}{y_{0}^{2}}\right]y_{1}\nonumber\\ \displaystyle & \!\!\! & \displaystyle \quad =\frac{4}{\unicode[STIX]{x1D719}^{1/2}y_{0}^{3}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\int _{0}^{\unicode[STIX]{x1D719}}y_{0}y_{1}\unicode[STIX]{x1D719}^{-1/2}\,\text{d}\unicode[STIX]{x1D719}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \!\!\! & \displaystyle 2\frac{\unicode[STIX]{x2202}^{2}y_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}\unicode[STIX]{x2202}t}-\frac{2}{y_{0}}\frac{\text{d}y_{0}}{\text{d}\unicode[STIX]{x1D719}}\frac{\unicode[STIX]{x2202}y_{1}}{\unicode[STIX]{x2202}t}+4(1+H\unicode[STIX]{x1D719})\unicode[STIX]{x1D719}\frac{\unicode[STIX]{x2202}^{2}y_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}^{2}}+\left[4(1+2H\unicode[STIX]{x1D719})-\frac{8(1+H\unicode[STIX]{x1D719})\unicode[STIX]{x1D719}}{y_{0}}\frac{\text{d}y_{0}}{\text{d}\unicode[STIX]{x1D719}}-\frac{1}{y_{0}}\right]\frac{\unicode[STIX]{x2202}y_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}}\;\nonumber\\ \displaystyle & \!\!\! & \displaystyle \qquad +\left[\frac{4(1+H\unicode[STIX]{x1D719})\unicode[STIX]{x1D719}}{y_{0}^{2}}\left(\frac{\text{d}y_{0}}{\text{d}\unicode[STIX]{x1D719}}\right)^{2}+\frac{1}{y_{0}^{2}}\frac{\text{d}y_{0}}{\text{d}\unicode[STIX]{x1D719}}+9H+\frac{4(1+H\unicode[STIX]{x1D719})}{y_{0}^{2}}\right]y_{1}\nonumber\\ \displaystyle & \!\!\! & \displaystyle \quad =\frac{4}{\unicode[STIX]{x1D719}^{1/2}y_{0}^{3}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\int _{0}^{\unicode[STIX]{x1D719}}y_{0}y_{1}\unicode[STIX]{x1D719}^{-1/2}\,\text{d}\unicode[STIX]{x1D719}.\end{eqnarray}$$
Setting
![]() $y_{1}=g(\unicode[STIX]{x1D719})\exp (\unicode[STIX]{x1D6FF}t)$
into the last equation gives
$y_{1}=g(\unicode[STIX]{x1D719})\exp (\unicode[STIX]{x1D6FF}t)$
into the last equation gives
 $$\begin{eqnarray}\displaystyle & & \displaystyle 4(1+H\unicode[STIX]{x1D719})\unicode[STIX]{x1D719}\frac{\text{d}^{2}g}{\text{d}\unicode[STIX]{x1D719}^{2}}+\left[2\unicode[STIX]{x1D6FF}-\frac{8(1+H\unicode[STIX]{x1D719})\unicode[STIX]{x1D719}}{y_{0}}\frac{\text{d}y_{0}}{\text{d}\unicode[STIX]{x1D719}}+4(1+2H\unicode[STIX]{x1D719})-\frac{1}{y_{0}}\right]\frac{\text{d}g}{\text{d}\unicode[STIX]{x1D719}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\left[-\frac{2\unicode[STIX]{x1D6FF}}{y_{0}}\frac{\text{d}y_{0}}{\text{d}\unicode[STIX]{x1D719}}+\frac{4(1+H\unicode[STIX]{x1D719})\unicode[STIX]{x1D719}}{y_{0}^{2}}\left(\frac{\text{d}y_{0}}{\text{d}\unicode[STIX]{x1D719}}\right)^{2}+\frac{1}{y_{0}^{2}}\frac{\text{d}y_{0}}{\text{d}\unicode[STIX]{x1D719}}+9H+\frac{4(1+H\unicode[STIX]{x1D719})}{y_{0}^{2}}\right]g\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{4\unicode[STIX]{x1D6FF}}{\unicode[STIX]{x1D719}^{1/2}y_{0}^{3}}\int _{0}^{\unicode[STIX]{x1D719}}y_{0}g\unicode[STIX]{x1D719}^{-1/2}\,\text{d}\unicode[STIX]{x1D719}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle 4(1+H\unicode[STIX]{x1D719})\unicode[STIX]{x1D719}\frac{\text{d}^{2}g}{\text{d}\unicode[STIX]{x1D719}^{2}}+\left[2\unicode[STIX]{x1D6FF}-\frac{8(1+H\unicode[STIX]{x1D719})\unicode[STIX]{x1D719}}{y_{0}}\frac{\text{d}y_{0}}{\text{d}\unicode[STIX]{x1D719}}+4(1+2H\unicode[STIX]{x1D719})-\frac{1}{y_{0}}\right]\frac{\text{d}g}{\text{d}\unicode[STIX]{x1D719}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\left[-\frac{2\unicode[STIX]{x1D6FF}}{y_{0}}\frac{\text{d}y_{0}}{\text{d}\unicode[STIX]{x1D719}}+\frac{4(1+H\unicode[STIX]{x1D719})\unicode[STIX]{x1D719}}{y_{0}^{2}}\left(\frac{\text{d}y_{0}}{\text{d}\unicode[STIX]{x1D719}}\right)^{2}+\frac{1}{y_{0}^{2}}\frac{\text{d}y_{0}}{\text{d}\unicode[STIX]{x1D719}}+9H+\frac{4(1+H\unicode[STIX]{x1D719})}{y_{0}^{2}}\right]g\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{4\unicode[STIX]{x1D6FF}}{\unicode[STIX]{x1D719}^{1/2}y_{0}^{3}}\int _{0}^{\unicode[STIX]{x1D719}}y_{0}g\unicode[STIX]{x1D719}^{-1/2}\,\text{d}\unicode[STIX]{x1D719}.\end{eqnarray}$$
Let
where, once again,
![]() $d_{0}=1$
and the next coefficient is
$d_{0}=1$
and the next coefficient is
Already the expression for
![]() $d_{2}$
is so long that it is not presented here. The eigenvalues
$d_{2}$
is so long that it is not presented here. The eigenvalues
![]() $\unicode[STIX]{x1D6FF}$
are determined by solving the conservation of volume, given by (2.12), differentiated with respect to time:
$\unicode[STIX]{x1D6FF}$
are determined by solving the conservation of volume, given by (2.12), differentiated with respect to time:

Figure 11. The stability of the solution of viscous drops with
![]() $\text{d}y_{0}/\text{d}x<0$
as
$\text{d}y_{0}/\text{d}x<0$
as
![]() $x\rightarrow 0$
(
$x\rightarrow 0$
(
![]() $x>0$
), for different values of
$x>0$
), for different values of
![]() $H$
.
$H$
.
In figure 11 we show the highest real value of
![]() $\unicode[STIX]{x1D6FF}$
as a function of the parameter
$\unicode[STIX]{x1D6FF}$
as a function of the parameter
![]() $\unicode[STIX]{x1D708}$
, obtained with
$\unicode[STIX]{x1D708}$
, obtained with
![]() $k=9$
, for the two families of lines plotted in figure 10 having
$k=9$
, for the two families of lines plotted in figure 10 having
![]() $\text{d}y/\text{d}x<0$
as
$\text{d}y/\text{d}x<0$
as
![]() $x\rightarrow 0$
(
$x\rightarrow 0$
(
![]() $x>0$
), where we expect to find the stable steady shapes. We find that, for all cases, the largest
$x>0$
), where we expect to find the stable steady shapes. We find that, for all cases, the largest
![]() $\unicode[STIX]{x1D6FF}$
is real. As expected the stability analysis reveals that the family of curves corresponding to
$\unicode[STIX]{x1D6FF}$
is real. As expected the stability analysis reveals that the family of curves corresponding to
![]() $H<64/9$
(positive or negative),
$H<64/9$
(positive or negative),
![]() $x_{L}>20$
and
$x_{L}>20$
and
![]() $\unicode[STIX]{x1D708}>2$
is stable at the lower branch and unstable at the upper branch, with the turning point being the breakup point and located at
$\unicode[STIX]{x1D708}>2$
is stable at the lower branch and unstable at the upper branch, with the turning point being the breakup point and located at
![]() $\unicode[STIX]{x1D6FF}=0$
. Lines without a bifurcation turning point, such as
$\unicode[STIX]{x1D6FF}=0$
. Lines without a bifurcation turning point, such as
![]() $H=5$
, are stable everywhere. The other family of lines, having
$H=5$
, are stable everywhere. The other family of lines, having
![]() $H>64/9$
,
$H>64/9$
,
![]() $x_{L}<20$
,
$x_{L}<20$
,
![]() $\unicode[STIX]{x1D708}<2$
, is stable everywhere.
$\unicode[STIX]{x1D708}<2$
, is stable everywhere.
A few lines were omitted from figure 11 in order to make the figure more readable. Lines corresponding to
![]() $H=\pm 1000$
do not appear since they are almost identical to the
$H=\pm 1000$
do not appear since they are almost identical to the
![]() $H=\pm 100$
lines. Also, the linear extensional case
$H=\pm 100$
lines. Also, the linear extensional case
![]() $H=0$
is absent since, at this range of
$H=0$
is absent since, at this range of
![]() $\unicode[STIX]{x1D708}$
, it is almost identical to the
$\unicode[STIX]{x1D708}$
, it is almost identical to the
![]() $H=1$
line. Other cases with
$H=1$
line. Other cases with
![]() $\text{d}y/\text{d}x>0$
as
$\text{d}y/\text{d}x>0$
as
![]() $x\rightarrow 0$
(
$x\rightarrow 0$
(
![]() $x>0$
) that were not shown in figure 9 are also not shown here for the same reasons as discussed there. However, their non-smooth curves show positive values of
$x>0$
) that were not shown in figure 9 are also not shown here for the same reasons as discussed there. However, their non-smooth curves show positive values of
![]() $\unicode[STIX]{x1D6FF}$
, predicting unstable steady shapes.
$\unicode[STIX]{x1D6FF}$
, predicting unstable steady shapes.

Figure 12. The evolution of inviscid and viscous drops originally located at the unstable branch with
![]() $\text{d}y_{0}/\text{d}x<0$
as
$\text{d}y_{0}/\text{d}x<0$
as
![]() $x\rightarrow 0$
(
$x\rightarrow 0$
(
![]() $x>0$
), with no change in
$x>0$
), with no change in
![]() $G$
(inviscid drop) or
$G$
(inviscid drop) or
![]() $f$
(viscous drop). At
$f$
(viscous drop). At
![]() $t=0$
all drops are located at
$t=0$
all drops are located at
![]() $\unicode[STIX]{x1D708}=3$
: (a)
$\unicode[STIX]{x1D708}=3$
: (a)
![]() $H=+1$
; (b)
$H=+1$
; (b)
![]() $H=-1$
; (c)
$H=-1$
; (c)
![]() $H=-10$
; (d)
$H=-10$
; (d)
![]() $H=-\infty$
.
$H=-\infty$
.

Figure 13. The evolution of viscous drops originally located at the stable branch with a sudden change in
![]() $f$
beyond the breakup point. At
$f$
beyond the breakup point. At
![]() $t=0$
all drops are located at
$t=0$
all drops are located at
![]() $\unicode[STIX]{x1D708}=2.3$
: (a)
$\unicode[STIX]{x1D708}=2.3$
: (a)
![]() $H=+1$
,
$H=+1$
,
![]() $f$
changes from 0.150 to 0.155; (b)
$f$
changes from 0.150 to 0.155; (b)
![]() $H=0$
,
$H=0$
,
![]() $f$
changes from 0.147 to 0.155; (c)
$f$
changes from 0.147 to 0.155; (c)
![]() $H=-1$
,
$H=-1$
,
![]() $f$
changes from 0.144 to 0.150; (d)
$f$
changes from 0.144 to 0.150; (d)
![]() $H=-10$
,
$H=-10$
,
![]() $f$
changes from 0.129 to 0.135.
$f$
changes from 0.129 to 0.135.
5.3 Time-dependent studies
As before, we assume a solution to the evolution of the viscous drop in the form
But, contrary to the inviscid drop case, this time we find it more convenient to substitute the above equation into the differentiated governing equation, equation (2.15), to obtain
where already the case
![]() $k=2$
is so long that cannot be presented here. However, similar to (5.15), the
$k=2$
is so long that cannot be presented here. However, similar to (5.15), the
![]() $\text{d}y_{k}/\text{d}t$
equation involves
$\text{d}y_{k}/\text{d}t$
equation involves
![]() $y_{k+1}$
and
$y_{k+1}$
and
![]() $\text{d}y_{k+1}/\text{d}t$
terms. Thus, when choosing a maximum value of
$\text{d}y_{k+1}/\text{d}t$
terms. Thus, when choosing a maximum value of
![]() $k=n$
for the simulations, we need to assume that
$k=n$
for the simulations, we need to assume that
![]() $y_{n+1}=0$
. We used
$y_{n+1}=0$
. We used
![]() $n=6$
(7 terms) for the simulations, which were performed using Mathematica 9. Once again, stationary shapes (stable or unstable) were chosen for the initial conditions.
$n=6$
(7 terms) for the simulations, which were performed using Mathematica 9. Once again, stationary shapes (stable or unstable) were chosen for the initial conditions.
In figure 12(a–c), we explore viscous drops belonging to the family of solutions having
![]() $H<64/9$
(positive or negative),
$H<64/9$
(positive or negative),
![]() $x_{L}>20$
and
$x_{L}>20$
and
![]() $\text{d}y/\text{d}x<0$
as
$\text{d}y/\text{d}x<0$
as
![]() $x\rightarrow 0$
(
$x\rightarrow 0$
(
![]() $x>0$
). All cases in figure 12 are initially at
$x>0$
). All cases in figure 12 are initially at
![]() $\unicode[STIX]{x1D708}=3$
, which according to table 1 are beyond the bifurcation turning point and therefore represent steady unstable physical situations. In figure 12(a–c) (viscous drops) we keep the viscous strength of the flow (
$\unicode[STIX]{x1D708}=3$
, which according to table 1 are beyond the bifurcation turning point and therefore represent steady unstable physical situations. In figure 12(a–c) (viscous drops) we keep the viscous strength of the flow (
![]() $f$
) constant; for comparison in figure 12(d) (inviscid drop), a case previously discussed,
$f$
) constant; for comparison in figure 12(d) (inviscid drop), a case previously discussed,
![]() $G$
was kept constant. As explained in § 4.3, in this type of simulation, exact values of the time are not indicated, as they depend on the number of terms used in (5.14).
$G$
was kept constant. As explained in § 4.3, in this type of simulation, exact values of the time are not indicated, as they depend on the number of terms used in (5.14).
Figure 12(a), where
![]() $H=+1$
, is very surprising. Originally the drop is located at the unstable branch at
$H=+1$
, is very surprising. Originally the drop is located at the unstable branch at
![]() $f=0.141$
, beyond the breakup point, with a half-length slightly smaller than
$f=0.141$
, beyond the breakup point, with a half-length slightly smaller than
![]() $x_{L}=50$
(see figure 9). As time passes, the drop does not break, but jumps down to the stable branch at the same
$x_{L}=50$
(see figure 9). As time passes, the drop does not break, but jumps down to the stable branch at the same
![]() $f$
(since we kept it constant), but corresponding to a half-length slightly larger than
$f$
(since we kept it constant), but corresponding to a half-length slightly larger than
![]() $x_{L}=20$
. The next two figures, figure 12(b,c), corresponding to negative values of
$x_{L}=20$
. The next two figures, figure 12(b,c), corresponding to negative values of
![]() $H$
, are not so surprising, since we already mentioned below (2.15) that we anticipate some of the results of nonlinear extensional creeping flow, when
$H$
, are not so surprising, since we already mentioned below (2.15) that we anticipate some of the results of nonlinear extensional creeping flow, when
![]() $G<0$
(
$G<0$
(
![]() $H<0$
), to be similar to those of linear extensional flow under the influence of a small amount of external inertia (Favelukis et al.
Reference Favelukis, Lavrenteva and Nir2012). According to Favelukis et al. (Reference Favelukis, Lavrenteva and Nir2012), at low values of external inertia (including a viscous drop in creeping flow) the breakup mechanism is indefinite elongation, while at larger values of inertia (including an inviscid drop) the mode of breakup is centre pinching. A similar picture is discovered here. At low values of the nonlinearity of the flow (for example, figure 12(b), where
$H<0$
), to be similar to those of linear extensional flow under the influence of a small amount of external inertia (Favelukis et al.
Reference Favelukis, Lavrenteva and Nir2012). According to Favelukis et al. (Reference Favelukis, Lavrenteva and Nir2012), at low values of external inertia (including a viscous drop in creeping flow) the breakup mechanism is indefinite elongation, while at larger values of inertia (including an inviscid drop) the mode of breakup is centre pinching. A similar picture is discovered here. At low values of the nonlinearity of the flow (for example, figure 12(b), where
![]() $H=-1$
and
$H=-1$
and
![]() $f=0.136$
), the drop breaks via an indefinite elongation mechanism; but when the nonlinearity of the flow is significant (for example, figure 12(c), where
$f=0.136$
), the drop breaks via an indefinite elongation mechanism; but when the nonlinearity of the flow is significant (for example, figure 12(c), where
![]() $H=-10$
and
$H=-10$
and
![]() $f=0.123$
, or figure 12(d), with
$f=0.123$
, or figure 12(d), with
![]() $H=-\infty$
and
$H=-\infty$
and
![]() $f=0$
), a centre pinching breakup mode is observed.
$f=0$
), a centre pinching breakup mode is observed.
We continue with this family (
![]() $H<64/9$
positive or negative,
$H<64/9$
positive or negative,
![]() $x_{L}>20$
and
$x_{L}>20$
and
![]() $\text{d}y/\text{d}x<0$
as
$\text{d}y/\text{d}x<0$
as
![]() $x\rightarrow 0$
(
$x\rightarrow 0$
(
![]() $x>0$
), and at
$x>0$
), and at
![]() $t=0$
we introduce a sudden change in the viscous strength of the flow (
$t=0$
we introduce a sudden change in the viscous strength of the flow (
![]() $f$
). All cases in figure 13 start at
$f$
). All cases in figure 13 start at
![]() $\unicode[STIX]{x1D708}=2.3$
, representing steady stable drops (see table 1). Figure 13(a) corresponds to
$\unicode[STIX]{x1D708}=2.3$
, representing steady stable drops (see table 1). Figure 13(a) corresponds to
![]() $H=+1$
, where the bifurcation point is located at
$H=+1$
, where the bifurcation point is located at
![]() $\unicode[STIX]{x1D708}=2.39$
and
$\unicode[STIX]{x1D708}=2.39$
and
![]() $f=0.151$
. At
$f=0.151$
. At
![]() $t=0$
, the stable drop, located at
$t=0$
, the stable drop, located at
![]() $\unicode[STIX]{x1D708}=2.3$
and
$\unicode[STIX]{x1D708}=2.3$
and
![]() $f=0.150$
, is subjected to a sudden change to
$f=0.150$
, is subjected to a sudden change to
![]() $f=0.155$
beyond the breakup point. Note that the breakup mechanism reminds us of tip-streaming, where a cusp is developed at the end of the drop. This mode of breakup was also reported by Sherwood (Reference Sherwood1984). In figure 13(b) we have a drop in linear extensional flow with
$f=0.155$
beyond the breakup point. Note that the breakup mechanism reminds us of tip-streaming, where a cusp is developed at the end of the drop. This mode of breakup was also reported by Sherwood (Reference Sherwood1984). In figure 13(b) we have a drop in linear extensional flow with
![]() $H=0$
and the sudden change is from
$H=0$
and the sudden change is from
![]() $\unicode[STIX]{x1D708}=2.3$
and
$\unicode[STIX]{x1D708}=2.3$
and
![]() $f=0.147$
to
$f=0.147$
to
![]() $f=0.155$
. Here the breakup mode is by indefinite elongation, in accordance with previous studies (Sherwood Reference Sherwood1984; Favelukis et al.
Reference Favelukis, Lavrenteva and Nir2012). Note that a breakup mechanism by indefinite elongation with no tip-streaming was experimentally observed by Bentley & Leal (Reference Bentley and Leal1986) in a four-roll mill apparatus which produced a two-dimensional extensional flow. In their experiments the flow was near creeping, and the critical capillary number was less than one, while the condition for slender drops is
$f=0.155$
. Here the breakup mode is by indefinite elongation, in accordance with previous studies (Sherwood Reference Sherwood1984; Favelukis et al.
Reference Favelukis, Lavrenteva and Nir2012). Note that a breakup mechanism by indefinite elongation with no tip-streaming was experimentally observed by Bentley & Leal (Reference Bentley and Leal1986) in a four-roll mill apparatus which produced a two-dimensional extensional flow. In their experiments the flow was near creeping, and the critical capillary number was less than one, while the condition for slender drops is
![]() $\mathit{Ca}^{3}\gg 1$
. Figure 13(c) corresponds to a small negative nonlinear contribution of
$\mathit{Ca}^{3}\gg 1$
. Figure 13(c) corresponds to a small negative nonlinear contribution of
![]() $H=-1$
, and the sudden change is from
$H=-1$
, and the sudden change is from
![]() $\unicode[STIX]{x1D708}=2.3$
and
$\unicode[STIX]{x1D708}=2.3$
and
![]() $f=0.144$
until
$f=0.144$
until
![]() $f=0.150$
. As in figure 13(b), the breakup mechanism is by indefinite elongation, yet its shape, at long times, suggests a more uniform local radius than the linear case. Finally, in figure 13(d) a large negative nonlinear contribution of
$f=0.150$
. As in figure 13(b), the breakup mechanism is by indefinite elongation, yet its shape, at long times, suggests a more uniform local radius than the linear case. Finally, in figure 13(d) a large negative nonlinear contribution of
![]() $H=-10$
is studied. At
$H=-10$
is studied. At
![]() $t=0$
the change is from
$t=0$
the change is from
![]() $\unicode[STIX]{x1D708}=2.3$
and
$\unicode[STIX]{x1D708}=2.3$
and
![]() $f=0.129$
until
$f=0.129$
until
![]() $f=0.135$
, and breakup is by centre pinching.
$f=0.135$
, and breakup is by centre pinching.
6 Conclusions
The deformation and breakup of a slender drop in a nonlinear axisymmetric extensional and creeping flow has been the subject of this theoretical report. This interesting problem, which was first suggested by Sherwood (Reference Sherwood1984), is revisited, new results are presented, and a complete stability analysis is performed. The problem is governed by three dimensionless parameters: the capillary number (
![]() $\mathit{Ca}\gg 1$
), the viscosity ratio (
$\mathit{Ca}\gg 1$
), the viscosity ratio (
![]() $\unicode[STIX]{x1D706}\ll 1$
), and the nonlinear intensity of the flow (
$\unicode[STIX]{x1D706}\ll 1$
), and the nonlinear intensity of the flow (
![]() $E\ll 1$
), which contrary to the other two parameters can be positive or negative. A further exploration of the governing equation shows that the number of dimensionless parameters can be reduced from three to two, both having an order of magnitude of 1: the viscous strength of the flow
$E\ll 1$
), which contrary to the other two parameters can be positive or negative. A further exploration of the governing equation shows that the number of dimensionless parameters can be reduced from three to two, both having an order of magnitude of 1: the viscous strength of the flow
![]() $f=Ca\,\unicode[STIX]{x1D706}^{1/6}$
and the nonlinear strength of the flow
$f=Ca\,\unicode[STIX]{x1D706}^{1/6}$
and the nonlinear strength of the flow
![]() $G=Ca^{4}E$
.
$G=Ca^{4}E$
.
When the extensional flow is linear (
![]() $G=0$
), the literature suggests that the steady shape of the slender drop has a parabolic radius profile with pointed ends. As the capillary number increases, the drop becomes thinner and longer, and its surface area increases. Following Acrivos & Lo (Reference Acrivos and Lo1978), the radius at the centre of the drop is defined as
$G=0$
), the literature suggests that the steady shape of the slender drop has a parabolic radius profile with pointed ends. As the capillary number increases, the drop becomes thinner and longer, and its surface area increases. Following Acrivos & Lo (Reference Acrivos and Lo1978), the radius at the centre of the drop is defined as
![]() $1/(2\unicode[STIX]{x1D708})$
, where
$1/(2\unicode[STIX]{x1D708})$
, where
![]() $\unicode[STIX]{x1D708}$
is related to the steady pressure at the centre of the drop. The steady deformation curve is composed of a stable branch at
$\unicode[STIX]{x1D708}$
is related to the steady pressure at the centre of the drop. The steady deformation curve is composed of a stable branch at
![]() $2\leqslant \unicode[STIX]{x1D708}<2.4$
and an unstable branch at
$2\leqslant \unicode[STIX]{x1D708}<2.4$
and an unstable branch at
![]() $\unicode[STIX]{x1D708}>2.4$
, which are separated by a bifurcation turning (breakup) point. At this point
$\unicode[STIX]{x1D708}>2.4$
, which are separated by a bifurcation turning (breakup) point. At this point
![]() $\unicode[STIX]{x1D708}=2.4$
and
$\unicode[STIX]{x1D708}=2.4$
and
![]() $f=Ca\,\unicode[STIX]{x1D706}^{1/6}=0.148$
. Thus, it is not possible to break a bubble or an inviscid drop (
$f=Ca\,\unicode[STIX]{x1D706}^{1/6}=0.148$
. Thus, it is not possible to break a bubble or an inviscid drop (
![]() $\unicode[STIX]{x1D706}=0$
,
$\unicode[STIX]{x1D706}=0$
,
![]() $\unicode[STIX]{x1D708}=2$
) in linear extensional creeping flow.
$\unicode[STIX]{x1D708}=2$
) in linear extensional creeping flow.
The solution near the centre of the drop, together with a stability analysis, reveals that, contrary to the linear extensional flow case (
![]() $G=0$
), where the local radius of the drop decreases monotonically (at
$G=0$
), where the local radius of the drop decreases monotonically (at
![]() $z\geqslant 0$
), in a nonlinear extensional flow (
$z\geqslant 0$
), in a nonlinear extensional flow (
![]() $G\neq 0$
), two possible steady shapes exist. Steady shapes (stable or unstable) with the local radius decreasing monotonically, and steady shapes (unstable) where the local radius of the drop achieves a maximum, besides the one at the centre of the drop. On the other hand, the solution close to the end of the drop suggests that steady slender drops with or without nonlinear effects have pointed ends.
$G\neq 0$
), two possible steady shapes exist. Steady shapes (stable or unstable) with the local radius decreasing monotonically, and steady shapes (unstable) where the local radius of the drop achieves a maximum, besides the one at the centre of the drop. On the other hand, the solution close to the end of the drop suggests that steady slender drops with or without nonlinear effects have pointed ends.
Two types of solutions are presented for the case of an inviscid drop (
![]() $\unicode[STIX]{x1D706}=0$
) in a nonlinear (
$\unicode[STIX]{x1D706}=0$
) in a nonlinear (
![]() $G\neq 0$
) extensional creeping flow. A closed form involving the incomplete beta function and, as suggested by Sherwood (Reference Sherwood1984), a solution in the form of a power series, where here we suggest a simple and general expression for all the coefficients. The deformation curve and the stability analysis reveal that the solution, where the local radius decreases monotonically, has the form of a lobe, composed of two branches, and separated by a bifurcation turning (breakup) point at
$G\neq 0$
) extensional creeping flow. A closed form involving the incomplete beta function and, as suggested by Sherwood (Reference Sherwood1984), a solution in the form of a power series, where here we suggest a simple and general expression for all the coefficients. The deformation curve and the stability analysis reveal that the solution, where the local radius decreases monotonically, has the form of a lobe, composed of two branches, and separated by a bifurcation turning (breakup) point at
![]() $\unicode[STIX]{x1D708}=2.51$
and
$\unicode[STIX]{x1D708}=2.51$
and
![]() $G=-9.62\times 10^{-5}$
. In the first branch at
$G=-9.62\times 10^{-5}$
. In the first branch at
![]() $\unicode[STIX]{x1D708}<2$
and
$\unicode[STIX]{x1D708}<2$
and
![]() $G>0$
, and at
$G>0$
, and at
![]() $2<\unicode[STIX]{x1D708}<2.51$
and
$2<\unicode[STIX]{x1D708}<2.51$
and
![]() $G<0$
, the solution is stable. The second branch at
$G<0$
, the solution is stable. The second branch at
![]() $2.51<\unicode[STIX]{x1D708}<4$
and
$2.51<\unicode[STIX]{x1D708}<4$
and
![]() $G<0$
corresponds to unstable steady shapes. Steady shapes involving higher values of the parameter
$G<0$
corresponds to unstable steady shapes. Steady shapes involving higher values of the parameter
![]() $\unicode[STIX]{x1D708}$
are unstable. Thus, contrary to linear extensional flow, where an inviscid drop cannot be broken, the addition of nonlinear terms to the external flow can cause an inviscid drop to break.
$\unicode[STIX]{x1D708}$
are unstable. Thus, contrary to linear extensional flow, where an inviscid drop cannot be broken, the addition of nonlinear terms to the external flow can cause an inviscid drop to break.
Next, we considered the case of a viscous drop (
![]() $\unicode[STIX]{x1D706}\neq 0$
) in a nonlinear (
$\unicode[STIX]{x1D706}\neq 0$
) in a nonlinear (
![]() $G\neq 0$
) extensional creeping flow and find, as suggested by Sherwood (Reference Sherwood1984), that the solution is described as a power series. For simplicity we defined a parameter
$G\neq 0$
) extensional creeping flow and find, as suggested by Sherwood (Reference Sherwood1984), that the solution is described as a power series. For simplicity we defined a parameter
![]() $H=G/f^{6}$
, where
$H=G/f^{6}$
, where
![]() $H=0$
corresponds to linear extensional flow (
$H=0$
corresponds to linear extensional flow (
![]() $G=0$
), and
$G=0$
), and
![]() $H\rightarrow \pm \infty$
suggests a bubble or an inviscid drop (
$H\rightarrow \pm \infty$
suggests a bubble or an inviscid drop (
![]() $f=0$
) under the influence of nonlinear extensional effects. As before, we shall summarize our conclusions on steady shapes with the local radius decreasing monotonically, as there, according to the stability analysis, steady stable shapes were found. In the first family of solutions, corresponding to
$f=0$
) under the influence of nonlinear extensional effects. As before, we shall summarize our conclusions on steady shapes with the local radius decreasing monotonically, as there, according to the stability analysis, steady stable shapes were found. In the first family of solutions, corresponding to
![]() $\unicode[STIX]{x1D708}>2$
and
$\unicode[STIX]{x1D708}>2$
and
![]() $H<64/9$
(positive or negative), we find two types of deformation curves, with and without bifurcation turning points. As expected and validated by the stability analysis, lines with turning points are stable at the lower branch and unstable at the upper branch. Thus, the bifurcation turning point is the breakup point. Lines without a bifurcation turning point are always stable. The second family of lines, corresponding to
$H<64/9$
(positive or negative), we find two types of deformation curves, with and without bifurcation turning points. As expected and validated by the stability analysis, lines with turning points are stable at the lower branch and unstable at the upper branch. Thus, the bifurcation turning point is the breakup point. Lines without a bifurcation turning point are always stable. The second family of lines, corresponding to
![]() $\unicode[STIX]{x1D708}<2$
and
$\unicode[STIX]{x1D708}<2$
and
![]() $H>64/9$
, is stable everywhere.
$H>64/9$
, is stable everywhere.
For both inviscid and viscous drops, we suggest approximate solutions by taking the first two terms of the exact power series solution. These solutions, having a parabolic radius profile, are equivalent to the exact solution when nonlinear effects are absent. Fortunately, the approximate solution, having a monotonically decreasing local radius, can predict steady shapes curves where stable shapes can be located. These solutions are found to be in excellent agreement with the exact results at the steady stable branch. Also, since they are represented by simple mathematical expressions, without performing heavy numerical calculations, they can provide excellent, fast and practical estimations for steady stable drop deformations.
Finally, time-dependent studies were performed for both inviscid and viscous drops where the local radius decreases monotonically (
![]() $z>0$
). Two types of evolution simulations from originally steady (stable or unstable) drop shapes are presented: when the intensity of the flow was kept constant or was subjected to a sudden change. In agreement with Sherwood’s (Reference Sherwood1984) report, the results here reveal three types of breakup mechanism: (i) a centre pinching mode for inviscid drops or viscous drops, both with large negative nonlinear effects (
$z>0$
). Two types of evolution simulations from originally steady (stable or unstable) drop shapes are presented: when the intensity of the flow was kept constant or was subjected to a sudden change. In agreement with Sherwood’s (Reference Sherwood1984) report, the results here reveal three types of breakup mechanism: (i) a centre pinching mode for inviscid drops or viscous drops, both with large negative nonlinear effects (
![]() $H\rightarrow -\infty$
); (ii) indefinite elongation for viscous drops with zero or small negative nonlinear effects (
$H\rightarrow -\infty$
); (ii) indefinite elongation for viscous drops with zero or small negative nonlinear effects (
![]() $H\rightarrow -0$
); and (iii) a mechanism that remind us of tip-streaming, where a cusp is developed at the end of a viscous drop having relative small positive nonlinear effects (
$H\rightarrow -0$
); and (iii) a mechanism that remind us of tip-streaming, where a cusp is developed at the end of a viscous drop having relative small positive nonlinear effects (
![]() $0<H<64/9$
).
$0<H<64/9$
).
Acknowledgement
This research was supported by Shenkar – College of Engineering and Design.