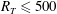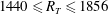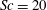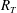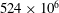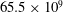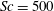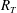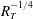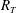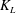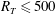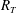1 Introduction
This paper considers the transport of low-solubility atmospheric gases, such as oxygen, across the air–water interface promoted by high-intensity isotropic turbulence diffusing from below. Because of the very low mass diffusivity of such gases in water, in combination with the high-intensity turbulence, the corresponding concentration boundary layer thickness at the surface is significantly smaller than the Kolmogorov length scale of the turbulent flow (e.g. Brumley & Jirka Reference Brumley and Jirka1988; Jähne & Haussecker Reference Jähne and Haussecker1998). Hence, an exceedingly fine resolution is needed to fully resolve the scalar transport dynamics. The latter is extremely challenging when performing both numerical simulations (see e.g. Rodi Reference Rodi2017) as well as laboratory experiments. Consequently, previously performed direct numerical simulations (DNS) and large-eddy simulations (LES) were limited to low turbulence intensities. The DNS were usually confined to relatively low Schmidt numbers,
![]() $Sc=\unicode[STIX]{x1D708}/D$
, where
$Sc=\unicode[STIX]{x1D708}/D$
, where
![]() $\unicode[STIX]{x1D708}$
is the kinematic viscosity and
$\unicode[STIX]{x1D708}$
is the kinematic viscosity and
![]() $D$
is the mass diffusivity (e.g. Handler et al.
Reference Handler, Saylor, Leighton and Rovelstad1999; Schwertfirm & Manhart Reference Schwertfirm and Manhart2007; Khakpour, Shen & Yue Reference Khakpour, Shen and Yue2011; Yang & Shen Reference Yang and Shen2017). High-Schmidt-number DNS were performed for buoyancy-induced mass transfer by Fredriksson et al. (Reference Fredriksson, Arneborg, Nilsson, Zhang and Handler2016) and Wissink & Herlina (Reference Wissink and Herlina2016) with surface heat fluxes of
$D$
is the mass diffusivity (e.g. Handler et al.
Reference Handler, Saylor, Leighton and Rovelstad1999; Schwertfirm & Manhart Reference Schwertfirm and Manhart2007; Khakpour, Shen & Yue Reference Khakpour, Shen and Yue2011; Yang & Shen Reference Yang and Shen2017). High-Schmidt-number DNS were performed for buoyancy-induced mass transfer by Fredriksson et al. (Reference Fredriksson, Arneborg, Nilsson, Zhang and Handler2016) and Wissink & Herlina (Reference Wissink and Herlina2016) with surface heat fluxes of
![]() $100~\text{W}~\text{m}^{-2}$
and up to
$100~\text{W}~\text{m}^{-2}$
and up to
![]() ${\sim}1600~\text{W}~\text{m}^{-2}$
, respectively, and for isotropic-turbulence-induced mass transfer by Herlina & Wissink (Reference Herlina and Wissink2014, Reference Herlina and Wissink2016). High-Schmidt-number LES was performed, for example, by Magnaudet & Calmet (Reference Magnaudet and Calmet2006) for open-channel flow, while Hasegawa & Kasagi (Reference Hasegawa and Kasagi2008) carried out a hybrid DNS–LES of surface-shear-driven mass transfer. Similarly, present experimental techniques still face difficulty in properly resolving the instantaneous scalar and flow properties within the concentration boundary layer (Chu & Jirka Reference Chu and Jirka1992; Atmane & George Reference Atmane and George2002; Variano & Cowen Reference Variano and Cowen2013). Hence, only in a limited number of experiments (e.g. Herlina & Jirka Reference Jirka2008; Janzen et al.
Reference Janzen, Herlina, Jirka, Schulz and Gulliver2010) were sufficiently detailed simultaneous measurements within the concentration boundary layer for varying grid-stirred turbulent intensities reported.
${\sim}1600~\text{W}~\text{m}^{-2}$
, respectively, and for isotropic-turbulence-induced mass transfer by Herlina & Wissink (Reference Herlina and Wissink2014, Reference Herlina and Wissink2016). High-Schmidt-number LES was performed, for example, by Magnaudet & Calmet (Reference Magnaudet and Calmet2006) for open-channel flow, while Hasegawa & Kasagi (Reference Hasegawa and Kasagi2008) carried out a hybrid DNS–LES of surface-shear-driven mass transfer. Similarly, present experimental techniques still face difficulty in properly resolving the instantaneous scalar and flow properties within the concentration boundary layer (Chu & Jirka Reference Chu and Jirka1992; Atmane & George Reference Atmane and George2002; Variano & Cowen Reference Variano and Cowen2013). Hence, only in a limited number of experiments (e.g. Herlina & Jirka Reference Jirka2008; Janzen et al.
Reference Janzen, Herlina, Jirka, Schulz and Gulliver2010) were sufficiently detailed simultaneous measurements within the concentration boundary layer for varying grid-stirred turbulent intensities reported.
The present DNS was motivated by the need for highly accurate unbiased data in the high-
![]() $R_{T}$
regime to further investigate the dynamics of mass transfer across a shear-free surface dominated by small-scale energy-dissipating turbulent motions (cf. Theofanous, Houze & Brumfield Reference Theofanous, Houze and Brumfield1976; Theofanous Reference Theofanous, Brutsaert and Jirka1984) that need to be fully resolved by the numerical mesh. These new results complement our previous DNS results obtained for low to moderate
$R_{T}$
regime to further investigate the dynamics of mass transfer across a shear-free surface dominated by small-scale energy-dissipating turbulent motions (cf. Theofanous, Houze & Brumfield Reference Theofanous, Houze and Brumfield1976; Theofanous Reference Theofanous, Brutsaert and Jirka1984) that need to be fully resolved by the numerical mesh. These new results complement our previous DNS results obtained for low to moderate
![]() $R_{T}$
, where mass transfer was driven by larger-scale energy-containing turbulent motions. Hence, both the large- and small-eddy-dominated regimes for isotropic-turbulence-driven mass transfer across a shear-free surface are covered. Note that for severely contaminated interfaces – modelled using a no-slip surface boundary condition – both regimes were already explored in Herlina & Wissink (Reference Herlina and Wissink2016, hereafter HW16).
$R_{T}$
, where mass transfer was driven by larger-scale energy-containing turbulent motions. Hence, both the large- and small-eddy-dominated regimes for isotropic-turbulence-driven mass transfer across a shear-free surface are covered. Note that for severely contaminated interfaces – modelled using a no-slip surface boundary condition – both regimes were already explored in Herlina & Wissink (Reference Herlina and Wissink2016, hereafter HW16).
The rate of mass transfer across the air–water interface is measured by the global transfer velocity
where
![]() $j$
is the interfacial mass flux, and
$j$
is the interfacial mass flux, and
![]() $c_{s}$
and
$c_{s}$
and
![]() $c_{b}$
are the average gas concentrations at the surface and in the bulk (well-mixed region), respectively. All conceptual models assume that the mass transfer is determined by no more than one length scale and one time scale (Brumley & Jirka Reference Brumley and Jirka1988). Many empirical relations between
$c_{b}$
are the average gas concentrations at the surface and in the bulk (well-mixed region), respectively. All conceptual models assume that the mass transfer is determined by no more than one length scale and one time scale (Brumley & Jirka Reference Brumley and Jirka1988). Many empirical relations between
![]() $K_{L}$
and measurable flow quantities have been suggested in the past, ranging from the film model of Lewis & Whitman (Reference Lewis and Whitman1924) to the surface renewal model of Danckwerts (Reference Danckwerts1951). Lewis & Whitman assumed the presence of stagnant films on both sides of the interface where molecular diffusion controls mass transfer, giving
$K_{L}$
and measurable flow quantities have been suggested in the past, ranging from the film model of Lewis & Whitman (Reference Lewis and Whitman1924) to the surface renewal model of Danckwerts (Reference Danckwerts1951). Lewis & Whitman assumed the presence of stagnant films on both sides of the interface where molecular diffusion controls mass transfer, giving
![]() $K_{L}=D/\unicode[STIX]{x1D6FF}_{\ast }$
, where
$K_{L}=D/\unicode[STIX]{x1D6FF}_{\ast }$
, where
![]() $\unicode[STIX]{x1D6FF}_{\ast }$
is the film thickness. The surface renewal model reads
$\unicode[STIX]{x1D6FF}_{\ast }$
is the film thickness. The surface renewal model reads
where
![]() $r$
is the surface renewal rate. The main problem for this model is the specification of the applicable renewal rate, which requires either direct determination or modelling. Fortescue & Pearson (Reference Fortescue and Pearson1967) suggested that
$r$
is the surface renewal rate. The main problem for this model is the specification of the applicable renewal rate, which requires either direct determination or modelling. Fortescue & Pearson (Reference Fortescue and Pearson1967) suggested that
![]() $r$
is determined by the time scale associated with the largest turbulent eddies, while Banerjee, Scott & Rhodes (Reference Banerjee, Scott and Rhodes1968) and Lamont & Scott (Reference Lamont and Scott1970) used the time scale of the small eddies.
$r$
is determined by the time scale associated with the largest turbulent eddies, while Banerjee, Scott & Rhodes (Reference Banerjee, Scott and Rhodes1968) and Lamont & Scott (Reference Lamont and Scott1970) used the time scale of the small eddies.
In the large-eddy model,
![]() $r$
is usually determined using characteristic turbulent velocity (
$r$
is usually determined using characteristic turbulent velocity (
![]() $u_{\infty }$
) and length (
$u_{\infty }$
) and length (
![]() $\unicode[STIX]{x1D6EC}$
) scales, resulting in
$\unicode[STIX]{x1D6EC}$
) scales, resulting in
On the other hand, in the small-eddy model,
![]() $r=\sqrt{\unicode[STIX]{x1D716}/\unicode[STIX]{x1D708}}$
is calculated using the Kolmogorov scales, where
$r=\sqrt{\unicode[STIX]{x1D716}/\unicode[STIX]{x1D708}}$
is calculated using the Kolmogorov scales, where
![]() $\unicode[STIX]{x1D716}$
is the turbulent dissipation rate, giving
$\unicode[STIX]{x1D716}$
is the turbulent dissipation rate, giving
Theofanous et al. (Reference Theofanous, Houze and Brumfield1976) performed a dimensional analysis and subsequently proposed to combine the large- and small-eddy models after concluding that the large eddies are most important for the smaller turbulent Reynolds numbers
![]() $R_{T}$
– defined in (4.4) below – while the small eddies become important for large
$R_{T}$
– defined in (4.4) below – while the small eddies become important for large
![]() $R_{T}$
. The critical turbulent Reynolds number dividing the two regimes was found to be
$R_{T}$
. The critical turbulent Reynolds number dividing the two regimes was found to be
![]() $R_{T}\approx 500$
.
$R_{T}\approx 500$
.
As mentioned above, because of limited computational resources, previous numerical work on interfacial gas transfer has been limited to relatively low turbulent Reynolds numbers and/or low Schmidt numbers. In this paper, we present the results of a DNS performed for a range of high turbulent Reynolds numbers (
![]() $1440\leqslant R_{T}\leqslant 1856$
) and Schmidt numbers of
$1440\leqslant R_{T}\leqslant 1856$
) and Schmidt numbers of
![]() $Sc=20$
and
$Sc=20$
and
![]() $500$
, where the latter is characteristic for the transport of atmospheric gases dissolved in water. The present
$500$
, where the latter is characteristic for the transport of atmospheric gases dissolved in water. The present
![]() $R_{T}$
is significantly larger than the critical
$R_{T}$
is significantly larger than the critical
![]() $R_{T}$
such that the Kolmogorov time scale will determine the interfacial mass transfer dynamics. The new high-
$R_{T}$
such that the Kolmogorov time scale will determine the interfacial mass transfer dynamics. The new high-
![]() $R_{T}$
results will be compared to our previous low- to moderate-
$R_{T}$
results will be compared to our previous low- to moderate-
![]() $R_{T}$
results from Herlina & Wissink (Reference Herlina and Wissink2014, hereafter HW14).
$R_{T}$
results from Herlina & Wissink (Reference Herlina and Wissink2014, hereafter HW14).
2 Numerical method
The fluid motion is determined by solving the non-dimensional incompressible Navier–Stokes equations, where the continuity equation reads
and the momentum equations are given by
where
![]() $j=1,2,3$
,
$j=1,2,3$
,
![]() $x_{1}=x$
,
$x_{1}=x$
,
![]() $x_{2}=y$
are the horizontal directions and
$x_{2}=y$
are the horizontal directions and
![]() $x_{3}=z$
is the vertical direction,
$x_{3}=z$
is the vertical direction,
![]() $u_{1}=u$
,
$u_{1}=u$
,
![]() $u_{2}=v$
and
$u_{2}=v$
and
![]() $u_{3}=w$
are the velocities in the
$u_{3}=w$
are the velocities in the
![]() $x$
,
$x$
,
![]() $y$
and
$y$
and
![]() $z$
directions,
$z$
directions,
![]() $p$
is the pressure and
$p$
is the pressure and
![]() $t$
denotes time. The Reynolds number is
$t$
denotes time. The Reynolds number is
![]() $Re=UL/\unicode[STIX]{x1D708}$
, where
$Re=UL/\unicode[STIX]{x1D708}$
, where
![]() $U$
and
$U$
and
![]() $L$
are reference velocity and length scales, respectively. Note that, in the absence of mean shear, to characterise the turbulent flow, it would be more appropriate to use a turbulent Reynolds number
$L$
are reference velocity and length scales, respectively. Note that, in the absence of mean shear, to characterise the turbulent flow, it would be more appropriate to use a turbulent Reynolds number
![]() $R_{T}$
(see (4.4)). However, the characteristic turbulent velocity and length scales used to calculate
$R_{T}$
(see (4.4)). However, the characteristic turbulent velocity and length scales used to calculate
![]() $R_{T}$
can only be determined after the computation and are basically time-dependent owing to the short simulation time. Hence,
$R_{T}$
can only be determined after the computation and are basically time-dependent owing to the short simulation time. Hence,
![]() $U$
and
$U$
and
![]() $L$
are used as place holders for the non-dimensionalisation. In our case, where
$L$
are used as place holders for the non-dimensionalisation. In our case, where
![]() $Re=1200$
(cf. § 3), a convenient choice would be
$Re=1200$
(cf. § 3), a convenient choice would be
![]() $U=12~\text{cm}~\text{s}^{-1}$
,
$U=12~\text{cm}~\text{s}^{-1}$
,
![]() $L=1$
cm and
$L=1$
cm and
![]() $\unicode[STIX]{x1D708}=10^{-6}~\text{m}^{2}~\text{s}^{-1}$
, which is relevant for the grid-stirred experiments of Herlina & Jirka (Reference Jirka2008), for example. In the subsequent analysis, most of the results are renormalised using the characteristic turbulent velocity and length scales.
$\unicode[STIX]{x1D708}=10^{-6}~\text{m}^{2}~\text{s}^{-1}$
, which is relevant for the grid-stirred experiments of Herlina & Jirka (Reference Jirka2008), for example. In the subsequent analysis, most of the results are renormalised using the characteristic turbulent velocity and length scales.
The non-dimensional convection–diffusion equation that governs the transport of the dimensionless passive scalar
![]() $c^{\ast }=c^{\ast }(x,y,z,t)$
reads
$c^{\ast }=c^{\ast }(x,y,z,t)$
reads
where
in which
![]() $c_{b,0}$
is the initial concentration in the bulk and
$c_{b,0}$
is the initial concentration in the bulk and
![]() $c_{s}$
is the concentration at the surface, which is assumed to be fully saturated at all times. Hereafter the dimensionless concentration
$c_{s}$
is the concentration at the surface, which is assumed to be fully saturated at all times. Hereafter the dimensionless concentration
![]() $c^{\ast }$
will be denoted by
$c^{\ast }$
will be denoted by
![]() $c$
. Note that the above implies that initially
$c$
. Note that the above implies that initially
![]() $c=1$
at the surface and
$c=1$
at the surface and
![]() $c=0$
in the bulk.
$c=0$
in the bulk.
The present DNS was performed using our solver that was specifically developed to accurately resolve low-diffusivity interfacial mass transfer. In the past, the code was extensively verified (e.g. Kubrak et al. Reference Kubrak, Herlina, Greve and Wissink2013; Herlina & Wissink Reference Herlina and Wissink2014) and was used to solve interfacial mass transfer problems driven by low to moderate levels of isotropic turbulence (Herlina & Wissink Reference Herlina and Wissink2014, Reference Herlina and Wissink2016; Wissink et al. Reference Wissink, Herlina, Akar and Uhlmann2017) and by buoyant convection (Wissink & Herlina Reference Wissink and Herlina2016). The three-dimensional incompressible Navier–Stokes equations were solved using a fourth-order-accurate kinetic-energy-conserving discretisation of the convective terms (Wissink Reference Wissink2004) combined with a fourth-order central discretisation of the diffusive terms. The pressure Poisson equation was solved using the conjugate gradient method with a simple diagonal preconditioning. The second-order-accurate Adams–Bashforth method was used for time integration.
Together with the flow, convection–diffusion equations for two scalars were solved simultaneously. The fifth-order-accurate weighted essentially non-oscillatory (WENO) scheme of Liu, Osher & Chan (Reference Liu, Osher and Chan1994) and the fourth-order-accurate central discretisation were used to discretise scalar convection and diffusion, respectively. A third-order Runge–Kutta method was used for the time integration. Because the scalar diffusivity can be more than two orders of magnitude smaller than the momentum diffusivity, a dual-meshing strategy was employed using a refined mesh for the scalar transport equations. The code was parallelised by dividing the mesh into a number of blocks of equal size. Communication between blocks was performed using the standard message passing interface (MPI) protocol. A more detailed description of the numerical method can be found in Kubrak et al. (Reference Kubrak, Herlina, Greve and Wissink2013).

Figure 1. Schematic illustration of the computational domain.
3 Computational set-up
A schematic of the computational domain is shown in figure 1. The interfacial mass transfer was calculated using a DNS. The size of the DNS domain (upper box in figure 1) was
![]() $20L\times 20L\times 5L$
in the
$20L\times 20L\times 5L$
in the
![]() $x$
,
$x$
,
![]() $y$
,
$y$
,
![]() $z$
directions, respectively (
$z$
directions, respectively (
![]() $L$
is the reference length scale, cf. § 2). To properly resolve the flow field and the scalar with
$L$
is the reference length scale, cf. § 2). To properly resolve the flow field and the scalar with
![]() $Sc=20$
, a
$Sc=20$
, a
![]() $1024\times 1024\times 500$
base mesh was used. For the scalar with
$1024\times 1024\times 500$
base mesh was used. For the scalar with
![]() $Sc=500$
, a refined mesh with
$Sc=500$
, a refined mesh with
![]() $5120\times 5120\times 2500$
was employed. In the
$5120\times 5120\times 2500$
was employed. In the
![]() $x$
and
$x$
and
![]() $y$
directions, a uniform mesh was used, while in the
$y$
directions, a uniform mesh was used, while in the
![]() $z$
direction the mesh was stretched according to
$z$
direction the mesh was stretched according to
for
![]() $k=1,\ldots ,n_{z}-1$
, with
$k=1,\ldots ,n_{z}-1$
, with
![]() $z_{1}=\unicode[STIX]{x1D703}/2$
and
$z_{1}=\unicode[STIX]{x1D703}/2$
and
![]() $z_{\unicode[STIX]{x1D719}}=kz_{1}/n_{z}$
, where
$z_{\unicode[STIX]{x1D719}}=kz_{1}/n_{z}$
, where
![]() $n_{z}$
is the number of nodes in the
$n_{z}$
is the number of nodes in the
![]() $z$
direction. The stretching is controlled by the parameter
$z$
direction. The stretching is controlled by the parameter
![]() $\unicode[STIX]{x1D703}$
, which is set to
$\unicode[STIX]{x1D703}$
, which is set to
![]() $\unicode[STIX]{x1D703}=4.7$
. The grid resolution near the interface is such that (i) the local vertical grid size
$\unicode[STIX]{x1D703}=4.7$
. The grid resolution near the interface is such that (i) the local vertical grid size
![]() $\unicode[STIX]{x0394}z$
is approximately 12 %
$\unicode[STIX]{x0394}z$
is approximately 12 %
![]() $L_{B}$
and (ii) the geometric mean of the grid cells is less than
$L_{B}$
and (ii) the geometric mean of the grid cells is less than
![]() $\unicode[STIX]{x03C0}L_{B}$
, where
$\unicode[STIX]{x03C0}L_{B}$
, where
![]() $L_{B}$
is the Batchelor scale. The two conditions indicate that the Grötzbach criterion is fulfilled and the scalar distribution is well resolved (Grötzbach Reference Grötzbach1983).
$L_{B}$
is the Batchelor scale. The two conditions indicate that the Grötzbach criterion is fulfilled and the scalar distribution is well resolved (Grötzbach Reference Grötzbach1983).
As in our previous simulations, the isotropic turbulence introduced at the bottom of the computational domain was generated in a separate LES that ran concurrently with the DNS. To achieve a high turbulent Reynolds number
![]() $R_{T}$
, a large
$R_{T}$
, a large
![]() $20L\times 20L\times 20L$
LES domain was combined with a relatively high Reynolds number of
$20L\times 20L\times 20L$
LES domain was combined with a relatively high Reynolds number of
![]() $Re=1200$
and a turbulent kinetic energy level of
$Re=1200$
and a turbulent kinetic energy level of
![]() $k=0.09375U^{2}$
(see also § 2). The LES box was discretised using a
$k=0.09375U^{2}$
(see also § 2). The LES box was discretised using a
![]() $256\times 256\times 256$
uniform mesh distributed over
$256\times 256\times 256$
uniform mesh distributed over
![]() $512$
processing cores. Periodic boundary conditions were employed for the velocities in all three directions. The subgrid-scale turbulence was modelled using the standard Smagorinsky method with constant
$512$
processing cores. Periodic boundary conditions were employed for the velocities in all three directions. The subgrid-scale turbulence was modelled using the standard Smagorinsky method with constant
![]() $C_{Smag}=0.22$
. At every time step the three components of the velocity field were rescaled so that the isotropy and the turbulence intensity were maintained.
$C_{Smag}=0.22$
. At every time step the three components of the velocity field were rescaled so that the isotropy and the turbulence intensity were maintained.
In the DNS, the surface was assumed to remain flat at all times. For the velocity field, free-slip boundary conditions were employed at the surface, while periodic boundary conditions were used in the horizontal directions. At the surface, the scalar concentration was assumed to be at saturation (
![]() $c=1$
) at all times, while the concentration was initialised by
$c=1$
) at all times, while the concentration was initialised by
where
![]() $\unicode[STIX]{x1D701}$
is the distance to the surface,
$\unicode[STIX]{x1D701}$
is the distance to the surface,
![]() $t^{\prime }=120L/U$
and
$t^{\prime }=120L/U$
and
![]() $Sc=20$
and
$Sc=20$
and
![]() $500$
. In the horizontal directions, periodic boundary conditions were employed; and at the bottom, symmetry boundary conditions
$500$
. In the horizontal directions, periodic boundary conditions were employed; and at the bottom, symmetry boundary conditions
![]() $(\unicode[STIX]{x2202}c/\unicode[STIX]{x2202}z=0)$
were used.
$(\unicode[STIX]{x2202}c/\unicode[STIX]{x2202}z=0)$
were used.
The interfacial mass transfer simulation was carried out on the SuperMUC cluster at LRZ in Munich using
![]() ${\approx}18\times 10^{6}$
CPU h and employing 20 992 cores.
${\approx}18\times 10^{6}$
CPU h and employing 20 992 cores.
4 Results
4.1 Characteristics of flow field
The interfacial mass transfer simulation was started using a fully developed turbulent flow field. This initial turbulent flow field was generated by running the simulation without calculating mass transfer. After a period of approximately
![]() $50L/U$
, the turbulence in the DNS domain (upper box in figure 1) was found to be fully developed, as verified by the statistically steady behaviour of the turbulent energy spectrum shown in figure 2. The mean energy spectrum, which was obtained by averaging the instantaneous energy spectrum at
$50L/U$
, the turbulence in the DNS domain (upper box in figure 1) was found to be fully developed, as verified by the statistically steady behaviour of the turbulent energy spectrum shown in figure 2. The mean energy spectrum, which was obtained by averaging the instantaneous energy spectrum at
![]() $z=2.75L$
over the interval
$z=2.75L$
over the interval
![]() $50L/U\leqslant t\leqslant 100L/U$
, clearly showed the existence of an inertial subrange with a
$50L/U\leqslant t\leqslant 100L/U$
, clearly showed the existence of an inertial subrange with a
![]() $\unicode[STIX]{x1D705}^{-5/3}$
behaviour, similar to Flores, Riley & Horner-Devine (Reference Flores, Riley and Horner-Devine2017), as well as a broad dissipative range where
$\unicode[STIX]{x1D705}^{-5/3}$
behaviour, similar to Flores, Riley & Horner-Devine (Reference Flores, Riley and Horner-Devine2017), as well as a broad dissipative range where
![]() $\unicode[STIX]{x1D705}>\unicode[STIX]{x1D702}$
. The same features were found in all spectra extracted at various other
$\unicode[STIX]{x1D705}>\unicode[STIX]{x1D702}$
. The same features were found in all spectra extracted at various other
![]() $z$
locations, indicating that the turbulent flow is very well resolved. Note that in the above
$z$
locations, indicating that the turbulent flow is very well resolved. Note that in the above
![]() $\unicode[STIX]{x1D705}$
is the wavenumber and
$\unicode[STIX]{x1D705}$
is the wavenumber and
![]() $\unicode[STIX]{x1D702}$
is the Kolmogorov length scale. Subsequently, at
$\unicode[STIX]{x1D702}$
is the Kolmogorov length scale. Subsequently, at
![]() $t=100L/U$
the full simulation was started by activating mass transfer.
$t=100L/U$
the full simulation was started by activating mass transfer.

Figure 2. The mean energy spectrum normalised by the Kolmogorov velocity
![]() $u_{\unicode[STIX]{x1D702}}$
and length
$u_{\unicode[STIX]{x1D702}}$
and length
![]() $\unicode[STIX]{x1D702}$
scales. The dashed line indicates the
$\unicode[STIX]{x1D702}$
scales. The dashed line indicates the
![]() $-5/3$
slope.
$-5/3$
slope.

Figure 3. Flow statistics, ensemble averaged over
![]() $103L/U$
: (a) turbulent integral length scale
$103L/U$
: (a) turbulent integral length scale
![]() $L_{11}$
; (b) root-mean-square (r.m.s.) of horizontal
$L_{11}$
; (b) root-mean-square (r.m.s.) of horizontal
![]() $u$
and vertical
$u$
and vertical
![]() $w$
velocity fluctuations; and (c) turbulent Reynolds number. The dotted lines in (a) and (c) correspond to
$w$
velocity fluctuations; and (c) turbulent Reynolds number. The dotted lines in (a) and (c) correspond to
![]() $\overline{L_{11}}(z/L)\pm \unicode[STIX]{x1D70E}_{L}$
and
$\overline{L_{11}}(z/L)\pm \unicode[STIX]{x1D70E}_{L}$
and
![]() $R_{T}(z/L)\pm \unicode[STIX]{x1D70E}_{R}$
, where
$R_{T}(z/L)\pm \unicode[STIX]{x1D70E}_{R}$
, where
![]() $\unicode[STIX]{x1D70E}_{L}$
and
$\unicode[STIX]{x1D70E}_{L}$
and
![]() $\unicode[STIX]{x1D70E}_{R}$
are the standard deviations of
$\unicode[STIX]{x1D70E}_{R}$
are the standard deviations of
![]() $L_{11}$
and
$L_{11}$
and
![]() $R_{T}$
, respectively.
$R_{T}$
, respectively.
The flow statistics shown in figure 3 were obtained by ensemble averaging the flow properties over the interval
![]() $50L/U\leqslant t\leqslant 153L/U$
. By combining time averaging with averaging in the large homogeneous horizontal directions, the size of this relatively short interval was deemed to be sufficient to obtain good-quality statistics. Figure 3(a) shows the variation in
$50L/U\leqslant t\leqslant 153L/U$
. By combining time averaging with averaging in the large homogeneous horizontal directions, the size of this relatively short interval was deemed to be sufficient to obtain good-quality statistics. Figure 3(a) shows the variation in
![]() $z$
of the time-averaged longitudinal integral length scale
$z$
of the time-averaged longitudinal integral length scale
![]() $\overline{L_{11}}$
(where
$\overline{L_{11}}$
(where
![]() $\overline{\,\cdot \,}$
denotes averaging over a period in time), with
$\overline{\,\cdot \,}$
denotes averaging over a period in time), with
where the longitudinal two-point correlation
![]() $R_{11}$
of the horizontal velocity
$R_{11}$
of the horizontal velocity
![]() $u$
is defined by
$u$
is defined by
 $$\begin{eqnarray}R_{11}(r,z)=\frac{\displaystyle \int _{x=0}^{L_{x}/2}\int _{y=0}^{L_{y}}u(x,y,z)u(x+r,y,z)\,\text{d}y\,\text{d}x}{\displaystyle \int _{x=0}^{L_{x}/2}\int _{y=0}^{L_{y}}u^{2}(x,y,z)\,\text{d}y\,\text{d}x},\end{eqnarray}$$
$$\begin{eqnarray}R_{11}(r,z)=\frac{\displaystyle \int _{x=0}^{L_{x}/2}\int _{y=0}^{L_{y}}u(x,y,z)u(x+r,y,z)\,\text{d}y\,\text{d}x}{\displaystyle \int _{x=0}^{L_{x}/2}\int _{y=0}^{L_{y}}u^{2}(x,y,z)\,\text{d}y\,\text{d}x},\end{eqnarray}$$
in which
![]() $L_{x}\times L_{y}$
is the size of the horizontal plane. As in the grid-stirred experiments of, for example, Hopfinger & Toly (Reference Hopfinger and Toly1976) and Herlina & Jirka (Reference Jirka2008), the integral length scale in most of the lower part of the computational domain was found to increase linearly with increasing distance from the turbulent source. Furthermore, it can be seen that the characteristic integral length scale
$L_{x}\times L_{y}$
is the size of the horizontal plane. As in the grid-stirred experiments of, for example, Hopfinger & Toly (Reference Hopfinger and Toly1976) and Herlina & Jirka (Reference Jirka2008), the integral length scale in most of the lower part of the computational domain was found to increase linearly with increasing distance from the turbulent source. Furthermore, it can be seen that the characteristic integral length scale
![]() $L_{\infty }$
, defined by
$L_{\infty }$
, defined by
in which
![]() $z_{\infty }$
is the location where
$z_{\infty }$
is the location where
![]() $\overline{L_{11}}$
is maximum, is approximately
$\overline{L_{11}}$
is maximum, is approximately
![]() $5.67L$
. The characteristic integral length scale
$5.67L$
. The characteristic integral length scale
![]() $L_{\infty }$
identifies the size of the largest eddies in the turbulent flow, which can only exist undisturbed at distances larger than
$L_{\infty }$
identifies the size of the largest eddies in the turbulent flow, which can only exist undisturbed at distances larger than
![]() $1L_{\infty }$
from the interface. Closer to the interface, inside the so-called surface-influenced layer, the turbulence starts to lose its isotropy (cf. e.g. Hunt & Graham Reference Hunt and Graham1978; Perot & Moin Reference Perot and Moin1995). Even though the depth of our DNS domain is somewhat smaller than
$1L_{\infty }$
from the interface. Closer to the interface, inside the so-called surface-influenced layer, the turbulence starts to lose its isotropy (cf. e.g. Hunt & Graham Reference Hunt and Graham1978; Perot & Moin Reference Perot and Moin1995). Even though the depth of our DNS domain is somewhat smaller than
![]() $5.67L$
, a reasonable isotropy (
$5.67L$
, a reasonable isotropy (
![]() $|1-w_{rms}/u_{rms}|<0.1$
) in most of the lower region (
$|1-w_{rms}/u_{rms}|<0.1$
) in most of the lower region (
![]() $z/L<2.5$
) is obtained (cf. figure 3
b). In agreement with Perot & Moin (Reference Perot and Moin1995) and Walker, Leighton & Garza-Rios (Reference Walker, Leighton and Garza-Rios1996), for example, figure 3(b) also shows an initial gradual decay in both horizontal and vertical fluctuations as the turbulence diffuses upwards. Close to the surface, a significant increase in decay rate of the vertical fluctuations
$z/L<2.5$
) is obtained (cf. figure 3
b). In agreement with Perot & Moin (Reference Perot and Moin1995) and Walker, Leighton & Garza-Rios (Reference Walker, Leighton and Garza-Rios1996), for example, figure 3(b) also shows an initial gradual decay in both horizontal and vertical fluctuations as the turbulence diffuses upwards. Close to the surface, a significant increase in decay rate of the vertical fluctuations
![]() $w_{rms}$
is observed, which in turn induces an increase in the horizontal fluctuations
$w_{rms}$
is observed, which in turn induces an increase in the horizontal fluctuations
![]() $u_{rms}$
due to the redistribution of the turbulent kinetic energy. More detailed discussions on this for free-slip and/or no-slip boundary conditions can be found elsewhere (e.g. Perot & Moin Reference Perot and Moin1995; Walker et al.
Reference Walker, Leighton and Garza-Rios1996; Magnaudet Reference Magnaudet2003; Bodart, Cazalbou & Joly Reference Bodart, Cazalbou and Joly2010; McCorquodale & Munro Reference McCorquodale and Munro2017).
$u_{rms}$
due to the redistribution of the turbulent kinetic energy. More detailed discussions on this for free-slip and/or no-slip boundary conditions can be found elsewhere (e.g. Perot & Moin Reference Perot and Moin1995; Walker et al.
Reference Walker, Leighton and Garza-Rios1996; Magnaudet Reference Magnaudet2003; Bodart, Cazalbou & Joly Reference Bodart, Cazalbou and Joly2010; McCorquodale & Munro Reference McCorquodale and Munro2017).
Typically, the turbulent Reynolds number for grid-stirred turbulence is defined by
where
![]() $\unicode[STIX]{x1D6EC}=2L_{\infty }$
(e.g. Hopfinger & Toly Reference Hopfinger and Toly1976; Brumley & Jirka Reference Brumley and Jirka1987). This definition is also adopted here, where we used
$\unicode[STIX]{x1D6EC}=2L_{\infty }$
(e.g. Hopfinger & Toly Reference Hopfinger and Toly1976; Brumley & Jirka Reference Brumley and Jirka1987). This definition is also adopted here, where we used
![]() $u_{\infty }=u_{rms}(z_{\infty })$
for the characteristic velocity scale. The time average of the corresponding local turbulent Reynolds number
$u_{\infty }=u_{rms}(z_{\infty })$
for the characteristic velocity scale. The time average of the corresponding local turbulent Reynolds number
shown in figure 3(c), was found to be approximately constant (
![]() $R_{T}(z)\approx 1856$
) in most of the lower DNS domain. In general, the turbulent flow statistics were similar to the far-field statistics in the experiments of Brumley & Jirka (Reference Brumley and Jirka1987) and Herlina & Jirka (Reference Jirka2008) and also to the statistics obtained at low to moderate
$R_{T}(z)\approx 1856$
) in most of the lower DNS domain. In general, the turbulent flow statistics were similar to the far-field statistics in the experiments of Brumley & Jirka (Reference Brumley and Jirka1987) and Herlina & Jirka (Reference Jirka2008) and also to the statistics obtained at low to moderate
![]() $R_{T}$
in HW14, where a more extended comparison with literature was presented.
$R_{T}$
in HW14, where a more extended comparison with literature was presented.
4.2 Statistics of turbulent scalar transport
As mentioned above, the scalar mass transfer calculations for
![]() $Sc=20$
and
$Sc=20$
and
![]() $500$
were activated at
$500$
were activated at
![]() $t=100L/U$
using the initial conditions given in (3.2). Owing to the high
$t=100L/U$
using the initial conditions given in (3.2). Owing to the high
![]() $R_{T}$
, the transfer of saturated fluid from the surface to the bulk was relatively fast. This, together with the large horizontal extent of the computational domain, resulted in a speedy convergence of the normalised horizontally averaged turbulent mass flux statistics. At
$R_{T}$
, the transfer of saturated fluid from the surface to the bulk was relatively fast. This, together with the large horizontal extent of the computational domain, resulted in a speedy convergence of the normalised horizontally averaged turbulent mass flux statistics. At
![]() $t=126L/U$
time units, the total mass flux near the interface (
$t=126L/U$
time units, the total mass flux near the interface (
![]() $0\leqslant \unicode[STIX]{x1D701}\leqslant 10\unicode[STIX]{x1D6FF}$
) was found to be independent of
$0\leqslant \unicode[STIX]{x1D701}\leqslant 10\unicode[STIX]{x1D6FF}$
) was found to be independent of
![]() $z$
. Scalar transport statistics were subsequently gathered in this quasi-steady regime from
$z$
. Scalar transport statistics were subsequently gathered in this quasi-steady regime from
![]() $t=126L/U$
until
$t=126L/U$
until
![]() $153L/U$
.
$153L/U$
.
As illustrated by the dotted lines in figure 3(a), the integral length scale of the turbulence
![]() $L_{11}$
varied significantly in time. Hence, it is expected that
$L_{11}$
varied significantly in time. Hence, it is expected that
![]() $L_{\infty }$
(and consequently
$L_{\infty }$
(and consequently
![]() $R_{T}$
) – when calculated using a moving average over a relatively small time window – will also become time-dependent. Using this we obtained a significant range of turbulent Reynolds numbers for the verification of the small-eddy model (cf. § 4.4). Note that for the smaller time windows
$R_{T}$
) – when calculated using a moving average over a relatively small time window – will also become time-dependent. Using this we obtained a significant range of turbulent Reynolds numbers for the verification of the small-eddy model (cf. § 4.4). Note that for the smaller time windows
![]() $L_{\infty }$
is the local maximum of
$L_{\infty }$
is the local maximum of
![]() $L_{11}$
nearest to the location where
$L_{11}$
nearest to the location where
![]() $L_{\infty }$
was obtained for the entire interval. The dependence of
$L_{\infty }$
was obtained for the entire interval. The dependence of
![]() $L_{\infty }$
and
$L_{\infty }$
and
![]() $R_{T}$
on the size of the time interval can also be seen in table 1, where, when averaging over the entire interval
$R_{T}$
on the size of the time interval can also be seen in table 1, where, when averaging over the entire interval
![]() $50L/U{-}153L/U$
, one has
$50L/U{-}153L/U$
, one has
![]() $L_{\infty }=5.67L$
and
$L_{\infty }=5.67L$
and
![]() $R_{T}=1856$
. On the other hand, by averaging over the smaller interval, values for
$R_{T}=1856$
. On the other hand, by averaging over the smaller interval, values for
![]() $L_{\infty }$
and
$L_{\infty }$
and
![]() $R_{T}$
of
$R_{T}$
of
![]() $4.54L$
and
$4.54L$
and
![]() $1440$
, respectively, were obtained.
$1440$
, respectively, were obtained.

Figure 4. Scalar statistics: (a) normalised mean concentration profiles, (b) normalised r.m.s. profiles, and (c) normalised diffusive and turbulent scalar fluxes.
Table 1. Mean flow parameters and the interval
![]() $\unicode[STIX]{x0394}t$
over which they are determined. Scalar statistics were only gathered over the smaller of the two intervals.
$\unicode[STIX]{x0394}t$
over which they are determined. Scalar statistics were only gathered over the smaller of the two intervals.

Figure 5. Influence of
![]() $Sc$
on the horizontally averaged boundary layer thickness at
$Sc$
on the horizontally averaged boundary layer thickness at
![]() $t=140L/U$
.
$t=140L/U$
.
The resulting scalar statistics can be seen in figure 4. The vertical axes show the distance to the surface
![]() $\unicode[STIX]{x1D701}$
normalised by the mean concentration boundary layer thickness
$\unicode[STIX]{x1D701}$
normalised by the mean concentration boundary layer thickness
![]() $\unicode[STIX]{x1D6FF}$
. The latter is defined by the distance to the surface where
$\unicode[STIX]{x1D6FF}$
. The latter is defined by the distance to the surface where
is maximum. Note that
![]() $\langle \,\cdot \,\rangle$
denotes averaging in the homogeneous (horizontal) directions. Similarly to the lower-
$\langle \,\cdot \,\rangle$
denotes averaging in the homogeneous (horizontal) directions. Similarly to the lower-
![]() $R_{T}$
cases in HW14, the horizontally averaged boundary layer thickness
$R_{T}$
cases in HW14, the horizontally averaged boundary layer thickness
![]() $\unicode[STIX]{x1D6FF}$
was found to scale with
$\unicode[STIX]{x1D6FF}$
was found to scale with
![]() $Sc^{-1/2}$
as illustrated for
$Sc^{-1/2}$
as illustrated for
![]() $t=140L/U$
in figure 5 (cf. further discussion in § 4.4).
$t=140L/U$
in figure 5 (cf. further discussion in § 4.4).
Figure 4(a) shows the mean concentration profiles near the surface, normalised by calculating
![]() $(\overline{\langle c\rangle }-\overline{\langle c_{b}\rangle })/(c_{s}-\overline{\langle c_{b}\rangle })$
. Immediately underneath the surface all profiles are approximately linear, which is a clear indication that molecular diffusion dominates gas transfer. It can also be seen that in that region the normalised profiles all collapse. For similar
$(\overline{\langle c\rangle }-\overline{\langle c_{b}\rangle })/(c_{s}-\overline{\langle c_{b}\rangle })$
. Immediately underneath the surface all profiles are approximately linear, which is a clear indication that molecular diffusion dominates gas transfer. It can also be seen that in that region the normalised profiles all collapse. For similar
![]() $Sc$
, deeper down in the bulk – due to the more effective vertical mixing – a slightly increased concentration at higher
$Sc$
, deeper down in the bulk – due to the more effective vertical mixing – a slightly increased concentration at higher
![]() $R_{T}$
is observed. This is in agreement with the trend found for lower
$R_{T}$
is observed. This is in agreement with the trend found for lower
![]() $R_{T}$
in HW14 and the experiments of Herlina & Jirka (Reference Jirka2008).
$R_{T}$
in HW14 and the experiments of Herlina & Jirka (Reference Jirka2008).
The normalised concentration fluctuations
![]() $c_{rms}/(c_{s}-\overline{\langle c_{b}\rangle })$
, shown in figure 4(b), can be seen to grow rapidly from zero at the surface to a local maximum, where approximately the horizontal turbulent exchange of saturated and unsaturated fluid is most intensive, before declining again to zero in the well-mixed region of the bulk. The peaks observed in the normalised
$c_{rms}/(c_{s}-\overline{\langle c_{b}\rangle })$
, shown in figure 4(b), can be seen to grow rapidly from zero at the surface to a local maximum, where approximately the horizontal turbulent exchange of saturated and unsaturated fluid is most intensive, before declining again to zero in the well-mixed region of the bulk. The peaks observed in the normalised
![]() $c_{rms}$
(figure 4
b) were found to be approximately 0.3 in all cases, which is typical for numerical simulations with free-slip surface boundary conditions (e.g. Magnaudet & Calmet Reference Magnaudet and Calmet2006) and is also found in some experiments (e.g. Atmane & George Reference Atmane and George2002). Some other experiments, however, show
$c_{rms}$
(figure 4
b) were found to be approximately 0.3 in all cases, which is typical for numerical simulations with free-slip surface boundary conditions (e.g. Magnaudet & Calmet Reference Magnaudet and Calmet2006) and is also found in some experiments (e.g. Atmane & George Reference Atmane and George2002). Some other experiments, however, show
![]() $c_{rms}$
peaks as low as 0.1–0.2 (e.g. Chu & Jirka Reference Chu and Jirka1992; Herlina & Jirka Reference Jirka2008). These relatively low peaks could be a consequence of a significant surface contamination as shown in the DNS studies of, for example, Khakpour et al. (Reference Khakpour, Shen and Yue2011) and Wissink et al. (Reference Wissink, Herlina, Akar and Uhlmann2017).
$c_{rms}$
peaks as low as 0.1–0.2 (e.g. Chu & Jirka Reference Chu and Jirka1992; Herlina & Jirka Reference Jirka2008). These relatively low peaks could be a consequence of a significant surface contamination as shown in the DNS studies of, for example, Khakpour et al. (Reference Khakpour, Shen and Yue2011) and Wissink et al. (Reference Wissink, Herlina, Akar and Uhlmann2017).
Figure 4(c) shows the mean diffusive
![]() $\overline{\langle -D\unicode[STIX]{x2202}c/\unicode[STIX]{x2202}z\rangle }$
and turbulent fluxes
$\overline{\langle -D\unicode[STIX]{x2202}c/\unicode[STIX]{x2202}z\rangle }$
and turbulent fluxes
![]() $\overline{\langle c^{\prime }w^{\prime }\rangle }$
normalised by the mean diffusive mass flux
$\overline{\langle c^{\prime }w^{\prime }\rangle }$
normalised by the mean diffusive mass flux
![]() $\overline{\langle \,j\rangle }$
at the interface, where
$\overline{\langle \,j\rangle }$
at the interface, where
The present results for
![]() $R_{T}\approx 1440$
with
$R_{T}\approx 1440$
with
![]() $Sc=20$
and
$Sc=20$
and
![]() $500$
are shown together with the GS500 results from HW14 with
$500$
are shown together with the GS500 results from HW14 with
![]() $R_{T}=507$
and
$R_{T}=507$
and
![]() $Sc=32$
. In agreement with the theory, the diffusive fluxes are maximum at the surface and rapidly decrease to zero in the bulk, while simultaneously the turbulent fluxes increase from zero at the surface such that the sum of the mean diffusive and turbulent fluxes remains constant at all
$Sc=32$
. In agreement with the theory, the diffusive fluxes are maximum at the surface and rapidly decrease to zero in the bulk, while simultaneously the turbulent fluxes increase from zero at the surface such that the sum of the mean diffusive and turbulent fluxes remains constant at all
![]() $z$
locations. The latter indicates that the simulation has run sufficiently long to achieve a quasi-steady state. For all cases, the depth at which the normalised fluxes are in equilibrium is approximately the same (
$z$
locations. The latter indicates that the simulation has run sufficiently long to achieve a quasi-steady state. For all cases, the depth at which the normalised fluxes are in equilibrium is approximately the same (
![]() $\unicode[STIX]{x1D701}\approx 0.65\unicode[STIX]{x1D6FF}$
).
$\unicode[STIX]{x1D701}\approx 0.65\unicode[STIX]{x1D6FF}$
).
Note that, even though the Schmidt numbers in the simulation differ significantly, all normalised scalar statistics shown in figure 4(b,c) nearly collapse. When applying the present normalisation to the lower-
![]() $R_{T}$
cases in HW14, a similar data collapse is observed. This is illustrated by including the
$R_{T}$
cases in HW14, a similar data collapse is observed. This is illustrated by including the
![]() $R_{T}=507$
results (which are typical for
$R_{T}=507$
results (which are typical for
![]() $84\leqslant R_{T}\leqslant 507$
) in figure 4. Based on this, we can conclude that the normalised results are almost invariant with respect to both
$84\leqslant R_{T}\leqslant 507$
) in figure 4. Based on this, we can conclude that the normalised results are almost invariant with respect to both
![]() $Sc$
and
$Sc$
and
![]() $R_{T}$
.
$R_{T}$
.
4.3 Role of large and small scales
4.3.1 Surface divergence
Figure 6 depicts a comparison between the surface divergence (
![]() $\unicode[STIX]{x1D6FD}=-\unicode[STIX]{x2202}w/\unicode[STIX]{x2202}z$
) and the instantaneous mass transfer velocity for
$\unicode[STIX]{x1D6FD}=-\unicode[STIX]{x2202}w/\unicode[STIX]{x2202}z$
) and the instantaneous mass transfer velocity for
![]() $Sc=20$
at an arbitrarily chosen time
$Sc=20$
at an arbitrarily chosen time
![]() $t=140L/U$
. The
$t=140L/U$
. The
![]() $\unicode[STIX]{x1D6FD}$
contours (figure 6
a) clearly show the presence of convection cells corresponding to large structures of size
$\unicode[STIX]{x1D6FD}$
contours (figure 6
a) clearly show the presence of convection cells corresponding to large structures of size
![]() ${\sim}L_{\infty }$
with positive surface divergence (upwelling of unsaturated fluid) separated by narrow regions of negative surface divergence (downwelling of saturated fluid). Compared to the surface divergence plot, the footprints of fine-scale turbulent structures can be more clearly identified in the corresponding instantaneous
${\sim}L_{\infty }$
with positive surface divergence (upwelling of unsaturated fluid) separated by narrow regions of negative surface divergence (downwelling of saturated fluid). Compared to the surface divergence plot, the footprints of fine-scale turbulent structures can be more clearly identified in the corresponding instantaneous
![]() $K_{L}$
contour plot (for a more detailed comparison see figure 11). An important reason for this discrepancy is the much higher diffusivity of the fluid (affecting
$K_{L}$
contour plot (for a more detailed comparison see figure 11). An important reason for this discrepancy is the much higher diffusivity of the fluid (affecting
![]() $\unicode[STIX]{x1D6FD}$
) compared to the scalar (affecting
$\unicode[STIX]{x1D6FD}$
) compared to the scalar (affecting
![]() $K_{L}$
). An increase in
$K_{L}$
). An increase in
![]() $R_{T}$
leads to an increase in fine-scale turbulent structures at the surface. Because of the aforementioned difference in diffusivities, these structures will remain clearly visible for much longer in the
$R_{T}$
leads to an increase in fine-scale turbulent structures at the surface. Because of the aforementioned difference in diffusivities, these structures will remain clearly visible for much longer in the
![]() $K_{L}$
contours than in the
$K_{L}$
contours than in the
![]() $\unicode[STIX]{x1D6FD}$
contours. This has a negative effect on the resulting time-averaged spatial correlation
$\unicode[STIX]{x1D6FD}$
contours. This has a negative effect on the resulting time-averaged spatial correlation
![]() $\unicode[STIX]{x1D70C}(K_{L},\unicode[STIX]{x1D6FD})$
at high
$\unicode[STIX]{x1D70C}(K_{L},\unicode[STIX]{x1D6FD})$
at high
![]() $R_{T}$
, as can be seen in figure 7, where in the present high-
$R_{T}$
, as can be seen in figure 7, where in the present high-
![]() $R_{T}$
simulation the value of
$R_{T}$
simulation the value of
![]() $\unicode[STIX]{x1D70C}(K_{L},\unicode[STIX]{x1D6FD})=0.78$
was lower than the values
$\unicode[STIX]{x1D70C}(K_{L},\unicode[STIX]{x1D6FD})=0.78$
was lower than the values
![]() $\unicode[STIX]{x1D70C}(K_{L},\unicode[STIX]{x1D6FD})=0.89$
, 0.81 and 0.81 obtained from HW14 for
$\unicode[STIX]{x1D70C}(K_{L},\unicode[STIX]{x1D6FD})=0.89$
, 0.81 and 0.81 obtained from HW14 for
![]() $R_{T}=84$
, 195 and 507, respectively. This reduction of
$R_{T}=84$
, 195 and 507, respectively. This reduction of
![]() $\unicode[STIX]{x1D70C}(K_{L},\unicode[STIX]{x1D6FD})$
with
$\unicode[STIX]{x1D70C}(K_{L},\unicode[STIX]{x1D6FD})$
with
![]() $R_{T}$
also impacts the applicability of the surface divergence model at high
$R_{T}$
also impacts the applicability of the surface divergence model at high
![]() $R_{T}$
. This is in agreement with the findings of Turney & Banerjee (Reference Turney and Banerjee2013), who observed a breakdown of the surface divergence model in the presence of small time scales. This will be further investigated below.
$R_{T}$
. This is in agreement with the findings of Turney & Banerjee (Reference Turney and Banerjee2013), who observed a breakdown of the surface divergence model in the presence of small time scales. This will be further investigated below.

Figure 6. Snapshots at
![]() $t=140L/U$
of (a) surface divergence
$t=140L/U$
of (a) surface divergence
![]() $\unicode[STIX]{x1D6FD}$
and (b)
$\unicode[STIX]{x1D6FD}$
and (b)
![]() $K_{L}$
for
$K_{L}$
for
![]() $Sc=20$
.
$Sc=20$
.

Figure 7. Time-averaged spatial correlation of the transfer velocity
![]() $K_{L}$
with the surface divergence
$K_{L}$
with the surface divergence
![]() $\unicode[STIX]{x1D6FD}$
for various
$\unicode[STIX]{x1D6FD}$
for various
![]() $R_{T}$
.
$R_{T}$
.
4.3.2 Vortical structures

Figure 8. Snapshots of vortical structures identified using
![]() $\unicode[STIX]{x1D706}_{2}=-200$
(upper panels) and
$\unicode[STIX]{x1D706}_{2}=-200$
(upper panels) and
![]() $\unicode[STIX]{x1D706}_{2}=-5$
(lower panels), normalised by
$\unicode[STIX]{x1D706}_{2}=-5$
(lower panels), normalised by
![]() $L_{\infty }$
and
$L_{\infty }$
and
![]() $u_{\infty }$
: (a,c) present DNS at
$u_{\infty }$
: (a,c) present DNS at
![]() $t=146.6L/U$
and (b,d) case GS500 from HW14 (
$t=146.6L/U$
and (b,d) case GS500 from HW14 (
![]() $R_{T}=507$
).
$R_{T}=507$
).
In figure 8, vortical structures in part of the computational domains are identified using the
![]() $\unicode[STIX]{x1D706}_{2}$
criterion of Jeong & Hussain (Reference Jeong and Hussain1995). To allow a direct comparison of the structures obtained in the present DNS and GS500 (HW14), the
$\unicode[STIX]{x1D706}_{2}$
criterion of Jeong & Hussain (Reference Jeong and Hussain1995). To allow a direct comparison of the structures obtained in the present DNS and GS500 (HW14), the
![]() $\unicode[STIX]{x1D706}_{2}$
eigenvalues were normalised using the relevant characteristic turbulent length (
$\unicode[STIX]{x1D706}_{2}$
eigenvalues were normalised using the relevant characteristic turbulent length (
![]() $L_{\infty }$
) and velocity (
$L_{\infty }$
) and velocity (
![]() $u_{\infty }$
) scales. Figure 8(a,b) shows that, because of the larger
$u_{\infty }$
) scales. Figure 8(a,b) shows that, because of the larger
![]() $R_{T}$
, significantly more vortical structures are found in the present simulation than in the GS500 simulation, while the thickness of the structures – which depends on the Kolmogorov length scale – is smaller. The lack of vortical structures, as observed in large areas of the GS500 simulation, indicates that the instantaneous turbulence is not uniformly distributed. Consequently, it is to be expected that the instantaneous mass transfer velocity will also not be uniformly distributed but will be elevated in regions with increased turbulence.
$R_{T}$
, significantly more vortical structures are found in the present simulation than in the GS500 simulation, while the thickness of the structures – which depends on the Kolmogorov length scale – is smaller. The lack of vortical structures, as observed in large areas of the GS500 simulation, indicates that the instantaneous turbulence is not uniformly distributed. Consequently, it is to be expected that the instantaneous mass transfer velocity will also not be uniformly distributed but will be elevated in regions with increased turbulence.

Figure 9. (a) Variation of the mean Kolmogorov length scale with depth. (b) Detailed view of (a) immediately beneath the surface.
To further explore what actually happens close to the surface, in figure 8(c,d) the vortical structures in the region
![]() $0\leqslant \unicode[STIX]{x1D701}/L_{\infty }\leqslant 0.04$
are visualised using
$0\leqslant \unicode[STIX]{x1D701}/L_{\infty }\leqslant 0.04$
are visualised using
![]() $\unicode[STIX]{x1D706}_{2}=-5$
. Again, the number and size of the vortical structures in the present simulation differ significantly from the ones in GS500. As explained below, because of the free-slip boundary condition at the top, the axes of the structures close to the surface are either parallel or orthogonal to the interface. Figure 9 shows the Kolmogorov length scale
$\unicode[STIX]{x1D706}_{2}=-5$
. Again, the number and size of the vortical structures in the present simulation differ significantly from the ones in GS500. As explained below, because of the free-slip boundary condition at the top, the axes of the structures close to the surface are either parallel or orthogonal to the interface. Figure 9 shows the Kolmogorov length scale
![]() $\unicode[STIX]{x1D702}$
for the present simulation as a function of the distance to the surface. Between
$\unicode[STIX]{x1D702}$
for the present simulation as a function of the distance to the surface. Between
![]() $\unicode[STIX]{x1D701}/L_{\infty }\approx 1$
(near the bottom) and
$\unicode[STIX]{x1D701}/L_{\infty }\approx 1$
(near the bottom) and
![]() $\unicode[STIX]{x1D701}/L_{\infty }\approx 0.05$
,
$\unicode[STIX]{x1D701}/L_{\infty }\approx 0.05$
,
![]() $\unicode[STIX]{x1D702}$
was found to increase as the turbulence diffusing from below dissipates. As seen in figures 8(a,c) and 3(b), when further approaching the surface, the flow rapidly becomes more and more two-dimensional. In upwelling regions, the increase in horizontal velocities towards the surface stretches initially ‘randomly’ oriented vortical structures and aligns them horizontally. Because of the large size of these upwelling regions (compared to the downwelling regions), this horizontal alignment is very common and causes vortical structures (on average) to become thinner towards the surface. As the diameter of the vortical structures scales with
$\unicode[STIX]{x1D702}$
was found to increase as the turbulence diffusing from below dissipates. As seen in figures 8(a,c) and 3(b), when further approaching the surface, the flow rapidly becomes more and more two-dimensional. In upwelling regions, the increase in horizontal velocities towards the surface stretches initially ‘randomly’ oriented vortical structures and aligns them horizontally. Because of the large size of these upwelling regions (compared to the downwelling regions), this horizontal alignment is very common and causes vortical structures (on average) to become thinner towards the surface. As the diameter of the vortical structures scales with
![]() $\unicode[STIX]{x1D702}$
(Jimenez et al.
Reference Jimenez, Wray, Saffman and Rogallo1993), the thinning mentioned above explains the decrease in
$\unicode[STIX]{x1D702}$
(Jimenez et al.
Reference Jimenez, Wray, Saffman and Rogallo1993), the thinning mentioned above explains the decrease in
![]() $\unicode[STIX]{x1D702}$
observed in figure 9 between
$\unicode[STIX]{x1D702}$
observed in figure 9 between
![]() $\unicode[STIX]{x1D701}/L_{\infty }\approx 0.05$
and
$\unicode[STIX]{x1D701}/L_{\infty }\approx 0.05$
and
![]() $0.008$
. Closer to the surface, the horizontal velocities become constant due to the free-slip boundary condition. As a result, the horizontal stretching no longer increases, which is an explanation of the slight increase in
$0.008$
. Closer to the surface, the horizontal velocities become constant due to the free-slip boundary condition. As a result, the horizontal stretching no longer increases, which is an explanation of the slight increase in
![]() $\unicode[STIX]{x1D702}$
observed between
$\unicode[STIX]{x1D702}$
observed between
![]() ${\approx}0.008$
and
${\approx}0.008$
and
![]() $0$
. In the relatively small downwelling-dominated regions, the downward velocity increases with distance from the surface, thereby stretching and strengthening the local surface-attached (surface-normal) vortical structures (SAVS). Note that the SAVS observed in the downwelling regions are seeded by relatively weak surface-normal vorticity transported upwards in the upwelling regions, where they attach to the surface and are subsequently moved towards the downwelling regions.
$0$
. In the relatively small downwelling-dominated regions, the downward velocity increases with distance from the surface, thereby stretching and strengthening the local surface-attached (surface-normal) vortical structures (SAVS). Note that the SAVS observed in the downwelling regions are seeded by relatively weak surface-normal vorticity transported upwards in the upwelling regions, where they attach to the surface and are subsequently moved towards the downwelling regions.
While the SAVS promote mixing in the horizontal direction, the structures with axes parallel to the interface promote the exchange of fluid between the upper bulk and the surface. Their relation with mass transfer is studied in figure 10(a), by combining contours of
![]() $K_{L}$
with a cross-section of the vortical structures from figure 8(c) at
$K_{L}$
with a cross-section of the vortical structures from figure 8(c) at
![]() $\unicode[STIX]{x1D701}/L_{\infty }=0.01$
. The horizontally aligned slender vortical structures can be found near the edges of areas with high
$\unicode[STIX]{x1D701}/L_{\infty }=0.01$
. The horizontally aligned slender vortical structures can be found near the edges of areas with high
![]() $K_{L}$
, adjacent to locations where saturated fluid is transported downwards. The SAVS, on the other hand, are generally located in areas with relatively low
$K_{L}$
, adjacent to locations where saturated fluid is transported downwards. The SAVS, on the other hand, are generally located in areas with relatively low
![]() $K_{L}$
. To distinguish the SAVS from the horizontally aligned vortical structures, in figure 10(b), the
$K_{L}$
. To distinguish the SAVS from the horizontally aligned vortical structures, in figure 10(b), the
![]() $\unicode[STIX]{x1D706}_{2}$
isolines are combined with contours of the surface-normal vorticity component
$\unicode[STIX]{x1D706}_{2}$
isolines are combined with contours of the surface-normal vorticity component
![]() $\unicode[STIX]{x1D714}_{z}$
. In contrast to the horizontally aligned vortices, SAVS are marked by elevated levels of
$\unicode[STIX]{x1D714}_{z}$
. In contrast to the horizontally aligned vortices, SAVS are marked by elevated levels of
![]() $\unicode[STIX]{x1D714}_{z}$
in their entire interior.
$\unicode[STIX]{x1D714}_{z}$
in their entire interior.

Figure 10. Isolines of
![]() $\unicode[STIX]{x1D706}_{2}=-5$
at
$\unicode[STIX]{x1D706}_{2}=-5$
at
![]() $\unicode[STIX]{x1D701}/L_{\infty }=0.01$
and
$\unicode[STIX]{x1D701}/L_{\infty }=0.01$
and
![]() $t=146.6L/U$
with (a) contours of
$t=146.6L/U$
with (a) contours of
![]() $K_{L}$
for
$K_{L}$
for
![]() $Sc=20$
and (b) contours of
$Sc=20$
and (b) contours of
![]() $|\unicode[STIX]{x1D714}_{z}|$
. Note that
$|\unicode[STIX]{x1D714}_{z}|$
. Note that
![]() $\unicode[STIX]{x1D706}_{2}$
,
$\unicode[STIX]{x1D706}_{2}$
,
![]() $K_{L}$
and
$K_{L}$
and
![]() $\unicode[STIX]{x1D714}_{z}$
were normalised using
$\unicode[STIX]{x1D714}_{z}$
were normalised using
![]() $L_{\infty }$
and
$L_{\infty }$
and
![]() $u_{\infty }$
.
$u_{\infty }$
.

Figure 11. Zoomed view of figure 6 combined with isolines of surface-normal vorticity magnitude at
![]() $|\unicode[STIX]{x1D714}_{z}|\,(L_{\infty }/u_{\infty })=14,~34,~51$
and
$|\unicode[STIX]{x1D714}_{z}|\,(L_{\infty }/u_{\infty })=14,~34,~51$
and
![]() $68$
. (a) Contours of
$68$
. (a) Contours of
![]() $\unicode[STIX]{x1D6FD}$
and (b) contours of
$\unicode[STIX]{x1D6FD}$
and (b) contours of
![]() $K_{L}$
.
$K_{L}$
.
Figure 11 shows a detailed view of the
![]() $\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FD}$
and
![]() $K_{L}$
contours from figure 6 combined with isolines of relatively high-intensity surface-normal vorticity
$K_{L}$
contours from figure 6 combined with isolines of relatively high-intensity surface-normal vorticity
![]() $|\unicode[STIX]{x1D714}_{z}|$
. As mentioned above, because of the stretching of SAVS, it is expected to see such isolines only in downwelling areas. When this downwelling is very strong, SAVS undergo significant stretching and quickly become exceedingly thin, leading to their dissipation within a relatively short time. SAVS in areas of very weak downwelling (as seen in figure 11
a) tend to survive for a long time in the absence of large-scale turbulent motion. Because of the extended exposure time at the surface, the fluid inside these structures has become highly saturated due to diffusive mass transfer, as indicated by the local low
$|\unicode[STIX]{x1D714}_{z}|$
. As mentioned above, because of the stretching of SAVS, it is expected to see such isolines only in downwelling areas. When this downwelling is very strong, SAVS undergo significant stretching and quickly become exceedingly thin, leading to their dissipation within a relatively short time. SAVS in areas of very weak downwelling (as seen in figure 11
a) tend to survive for a long time in the absence of large-scale turbulent motion. Because of the extended exposure time at the surface, the fluid inside these structures has become highly saturated due to diffusive mass transfer, as indicated by the local low
![]() $K_{L}$
values in figure 11(b). While the correlation of these SAVS with low
$K_{L}$
values in figure 11(b). While the correlation of these SAVS with low
![]() $K_{L}$
values is very good, the correlation with low
$K_{L}$
values is very good, the correlation with low
![]() $\unicode[STIX]{x1D6FD}$
values is rather poor. This indicates that the local correlation
$\unicode[STIX]{x1D6FD}$
values is rather poor. This indicates that the local correlation
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FD},K_{L})$
will be rather small. Note that the above observations are generally confirmed in all recorded snapshots.
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FD},K_{L})$
will be rather small. Note that the above observations are generally confirmed in all recorded snapshots.
The dynamics of vortical structures in open-channel flow and their influence on interfacial mass transfer has been discussed by, for example, Pan & Banerjee (Reference Pan and Banerjee1995), Nagaosa (Reference Nagaosa1999) and Nagaosa & Handler (Reference Nagaosa and Handler2003). Pan & Banerjee (Reference Pan and Banerjee1995) discovered the existence of relatively large ring-like vortices at the surface of open-channel flow that are associated with vertical mixing. In the interior of the ring, unsaturated fluid from the bulk is transported towards the surface (splat), while immediately outside of the ring, saturated fluid is transported down into the bulk (antisplat). Nagaosa & Handler (Reference Nagaosa and Handler2003) found that the ring-like vortical structures originate from near the bottom of the channel and start their life as hairpin vortices. In our case, in the absence of bottom shear and associated vortical structures like hairpin vortices, the vortical dynamics of the turbulent flow changes significantly. Individual upwellings are usually relatively small but tend to cluster together into larger areas separated by narrow regions with strong downwelling. The topology of the clusters is very complex and rapidly changes in time. As discussed above (see also figure 10), the vortices parallel to the surface, which are responsible for vertical mixing, tend to lie along the edges of upwelling regions and sometimes resemble parts of ring-like vortices, similar to the ones previously observed by, for example, Nagaosa & Handler (Reference Nagaosa and Handler2003). As mentioned earlier, the SAVS only promote horizontal mixing and hence do not directly contribute to the turbulent vertical mass transfer, which is in agreement with the findings of Nagaosa (Reference Nagaosa1999).
4.3.3 Spectra of turbulent mass flux

Figure 12. (a) Premultiplied cospectra of turbulent mass flux
![]() $c^{\prime }w^{\prime }$
at
$c^{\prime }w^{\prime }$
at
![]() $\unicode[STIX]{x1D701}=5\unicode[STIX]{x1D6FF}$
. Cumulative cospectra of
$\unicode[STIX]{x1D701}=5\unicode[STIX]{x1D6FF}$
. Cumulative cospectra of
![]() $c^{\prime }w^{\prime }$
at (b)
$c^{\prime }w^{\prime }$
at (b)
![]() $\unicode[STIX]{x1D701}=5\unicode[STIX]{x1D6FF}$
and (c)
$\unicode[STIX]{x1D701}=5\unicode[STIX]{x1D6FF}$
and (c)
![]() $\unicode[STIX]{x1D701}=\unicode[STIX]{x1D6FF}$
.
$\unicode[STIX]{x1D701}=\unicode[STIX]{x1D6FF}$
.
As illustrated above, the mass transfer is directly related to the presence of vortical structures immediately underneath the surface. With increasing
![]() $R_{T}$
, the quantity of vortical structures increases, while their diameter typically decreases. To further investigate the relative importance of large- and small-scale structures for vertical mass transfer, time-averaged spectra of the turbulent mass flux
$R_{T}$
, the quantity of vortical structures increases, while their diameter typically decreases. To further investigate the relative importance of large- and small-scale structures for vertical mass transfer, time-averaged spectra of the turbulent mass flux
![]() $c^{\prime }w^{\prime }$
are plotted as a function of the normalised wavenumber
$c^{\prime }w^{\prime }$
are plotted as a function of the normalised wavenumber
![]() $\unicode[STIX]{x1D705}L_{\infty }$
(cf. figure 12). The present results, obtained at
$\unicode[STIX]{x1D705}L_{\infty }$
(cf. figure 12). The present results, obtained at
![]() $R_{T}=1440$
, are compared to the results of GS500 at
$R_{T}=1440$
, are compared to the results of GS500 at
![]() $R_{T}=507$
and GS80 at
$R_{T}=507$
and GS80 at
![]() $R_{T}=84$
(see HW14).
$R_{T}=84$
(see HW14).
Figure 12(a) shows the cospectra premultiplied by the wavenumber
![]() $\unicode[STIX]{x1D705}$
. Compared to the present simulation at
$\unicode[STIX]{x1D705}$
. Compared to the present simulation at
![]() $R_{T}=1440$
, the energy-containing range at
$R_{T}=1440$
, the energy-containing range at
![]() $R_{T}=507$
moves to smaller values of
$R_{T}=507$
moves to smaller values of
![]() $\unicode[STIX]{x1D705}L_{\infty }$
. At
$\unicode[STIX]{x1D705}L_{\infty }$
. At
![]() $R_{T}=84$
, only a relatively narrow band of energy-containing scales was observed, which coincides with the largest energy-containing scales observed at
$R_{T}=84$
, only a relatively narrow band of energy-containing scales was observed, which coincides with the largest energy-containing scales observed at
![]() $R_{T}=507$
. Hence, it can be concluded that at low
$R_{T}=507$
. Hence, it can be concluded that at low
![]() $R_{T}$
large scales dominate the turbulent mass flux, while at high
$R_{T}$
large scales dominate the turbulent mass flux, while at high
![]() $R_{T}$
the contribution of the small scales becomes more important, supporting the two-regime mass transfer concept of Theofanous et al. (Reference Theofanous, Houze and Brumfield1976). Near the critical
$R_{T}$
the contribution of the small scales becomes more important, supporting the two-regime mass transfer concept of Theofanous et al. (Reference Theofanous, Houze and Brumfield1976). Near the critical
![]() $R_{T}$
, both small and large scales were found to contribute significantly to the overall turbulent mass transfer.
$R_{T}$
, both small and large scales were found to contribute significantly to the overall turbulent mass transfer.
To further illustrate the contribution of the different scales to the mass transfer, the cumulative cospectra of
![]() $c^{\prime }w^{\prime }$
are shown in figure 12(b,c) at
$c^{\prime }w^{\prime }$
are shown in figure 12(b,c) at
![]() $\unicode[STIX]{x1D701}=5\unicode[STIX]{x1D6FF}$
and
$\unicode[STIX]{x1D701}=5\unicode[STIX]{x1D6FF}$
and
![]() $\unicode[STIX]{x1D6FF}$
, respectively. It can be seen that with increasing
$\unicode[STIX]{x1D6FF}$
, respectively. It can be seen that with increasing
![]() $R_{T}$
the smaller scales become more and more important for the vertical turbulent mass transport. For instance, at
$R_{T}$
the smaller scales become more and more important for the vertical turbulent mass transport. For instance, at
![]() $\unicode[STIX]{x1D701}=5\unicode[STIX]{x1D6FF}$
, the contribution of relatively large scales with wavenumbers
$\unicode[STIX]{x1D701}=5\unicode[STIX]{x1D6FF}$
, the contribution of relatively large scales with wavenumbers
![]() $\unicode[STIX]{x1D705}L_{\infty }\leqslant 10$
to the total energy of the turbulent flux decreases from
$\unicode[STIX]{x1D705}L_{\infty }\leqslant 10$
to the total energy of the turbulent flux decreases from
![]() $70\,\%$
for
$70\,\%$
for
![]() $R_{T}=84$
to
$R_{T}=84$
to
![]() $55\,\%$
for
$55\,\%$
for
![]() $R_{T}=507$
and finally to
$R_{T}=507$
and finally to
![]() $34\,\%$
for
$34\,\%$
for
![]() $R_{T}=1440$
. Higher up in the boundary layer, at
$R_{T}=1440$
. Higher up in the boundary layer, at
![]() $\unicode[STIX]{x1D701}=\unicode[STIX]{x1D6FF}$
, the presence of the free-slip surface causes the flow to become increasingly two-dimensional. This is evidenced by the change in orientation of the vortical structures when approaching the surface as mentioned above (cf. figure 8
a,c). The inverse energy cascade, that is typical for two-dimensional turbulence, explains the increased importance of the larger scales to the vertical mass transfer when approaching the surface (cf. figure 12
c).
$\unicode[STIX]{x1D701}=\unicode[STIX]{x1D6FF}$
, the presence of the free-slip surface causes the flow to become increasingly two-dimensional. This is evidenced by the change in orientation of the vortical structures when approaching the surface as mentioned above (cf. figure 8
a,c). The inverse energy cascade, that is typical for two-dimensional turbulence, explains the increased importance of the larger scales to the vertical mass transfer when approaching the surface (cf. figure 12
c).
4.4 Scaling of transfer velocity with
 $Sc$
and
$Sc$
and
 $R_{T}$
$R_{T}$

Figure 13. Influence of
![]() $Sc$
on
$Sc$
on
![]() $K_{L}$
. Data shown are from the snapshot at
$K_{L}$
. Data shown are from the snapshot at
![]() $t=140L/U$
.
$t=140L/U$
.
In agreement with the experiments of Chu & Jirka (Reference Chu and Jirka1992), Atmane & George (Reference Atmane and George2002) and Herlina & Jirka (Reference Jirka2008), for example, in the HW14 simulations it was found that the concentration boundary layer thickness
![]() $\unicode[STIX]{x1D6FF}$
depends on the level of isotropic turbulence diffusing from below. This turbulence promotes the interchange of unsaturated fluid from the bulk with saturated fluid from the surface. For constant
$\unicode[STIX]{x1D6FF}$
depends on the level of isotropic turbulence diffusing from below. This turbulence promotes the interchange of unsaturated fluid from the bulk with saturated fluid from the surface. For constant
![]() $Sc$
, the boundary layer thickness (normalised by
$Sc$
, the boundary layer thickness (normalised by
![]() $L_{\infty }$
) decreases with increasing turbulence level, resulting in a steeper concentration gradient at the surface and therefore an increased normalised mass transfer velocity. On the other hand, for constant
$L_{\infty }$
) decreases with increasing turbulence level, resulting in a steeper concentration gradient at the surface and therefore an increased normalised mass transfer velocity. On the other hand, for constant
![]() $R_{T}$
, it was shown that
$R_{T}$
, it was shown that
![]() $\unicode[STIX]{x1D6FF}$
scales with
$\unicode[STIX]{x1D6FF}$
scales with
![]() $Sc^{-1/2}$
(cf. figure 5). The same scaling was found for
$Sc^{-1/2}$
(cf. figure 5). The same scaling was found for
![]() $K_{L}$
, as can be seen in figure 13. This implies that, for constant
$K_{L}$
, as can be seen in figure 13. This implies that, for constant
![]() $R_{T}$
and free-slip surface boundary conditions, the mass transfer velocity
$R_{T}$
and free-slip surface boundary conditions, the mass transfer velocity
![]() $K_{L}$
is proportional to
$K_{L}$
is proportional to
![]() $\unicode[STIX]{x1D6FF}$
. Note that the same instantaneous scaling behaviour
$\unicode[STIX]{x1D6FF}$
. Note that the same instantaneous scaling behaviour
![]() $K_{L}\propto Sc^{-1/2}$
was consistently found for all
$K_{L}\propto Sc^{-1/2}$
was consistently found for all
![]() $t\geqslant 126L/U$
. Also, this scaling is in agreement with the theoretical scaling found for free-slip surface conditions (e.g. Ledwell Reference Ledwell1984; Jähne & Haussecker Reference Jähne and Haussecker1998).
$t\geqslant 126L/U$
. Also, this scaling is in agreement with the theoretical scaling found for free-slip surface conditions (e.g. Ledwell Reference Ledwell1984; Jähne & Haussecker Reference Jähne and Haussecker1998).
Free-slip boundary conditions are applied to represent a clean (surfactant-free) surface. Contaminated surfaces, on the other hand, can be modelled, for example, by using a no-slip boundary condition to represent some of the physics pertinent to severe contamination (Herlina & Wissink Reference Herlina and Wissink2016) or by explicitly solving the surfactant transport at the surface and modelling the influence of surfactants on the near-surface velocity field (Shen, Yue & Triantafyllou Reference Shen, Yue and Triantafyllou2004; Khakpour et al.
Reference Khakpour, Shen and Yue2011; Wissink et al.
Reference Wissink, Herlina, Akar and Uhlmann2017). As seen in Wissink et al. (Reference Wissink, Herlina, Akar and Uhlmann2017), the scaling behaviour of the mass transfer velocity with the Schmidt number smoothly changes from
![]() $Sc^{-1/2}$
for clean surfaces to
$Sc^{-1/2}$
for clean surfaces to
![]() $Sc^{-2/3}$
for severely contaminated surfaces.
$Sc^{-2/3}$
for severely contaminated surfaces.

Figure 14. Variation of the normalised
![]() $K_{L}$
with
$K_{L}$
with
![]() $R_{T}$
. For the free-slip boundary condition, the present DNS results are combined with results from HW14 obtained at low to moderate
$R_{T}$
. For the free-slip boundary condition, the present DNS results are combined with results from HW14 obtained at low to moderate
![]() $R_{T}$
. In addition, results from HW16, using a no-slip boundary condition, are also shown. Note that the lines represent the fitted scaling laws.
$R_{T}$
. In addition, results from HW16, using a no-slip boundary condition, are also shown. Note that the lines represent the fitted scaling laws.
As mentioned above, the present high-
![]() $R_{T}$
, high-
$R_{T}$
, high-
![]() $Sc$
DNS study builds on our previous DNS of interfacial mass transfer driven by isotropic turbulence diffusing from below (see Herlina & Wissink Reference Herlina and Wissink2014, Reference Herlina and Wissink2016; Wissink et al.
Reference Wissink, Herlina, Akar and Uhlmann2017). Figure 14 shows the normalised mass transfer velocity as a function of the turbulent Reynolds number
$Sc$
DNS study builds on our previous DNS of interfacial mass transfer driven by isotropic turbulence diffusing from below (see Herlina & Wissink Reference Herlina and Wissink2014, Reference Herlina and Wissink2016; Wissink et al.
Reference Wissink, Herlina, Akar and Uhlmann2017). Figure 14 shows the normalised mass transfer velocity as a function of the turbulent Reynolds number
![]() $R_{T}$
,
$R_{T}$
,
where
![]() $n=1/2$
and
$n=1/2$
and
![]() $n=2/3$
for the free-slip and no-slip surface boundary conditions, respectively, while
$n=2/3$
for the free-slip and no-slip surface boundary conditions, respectively, while
![]() $q$
depends on the size of the dominating turbulent scales, as discussed below. Note that, after using
$q$
depends on the size of the dominating turbulent scales, as discussed below. Note that, after using
![]() $u_{\infty }$
and
$u_{\infty }$
and
![]() $\unicode[STIX]{x1D6EC}$
for non-dimensionalisation, it can be seen that for
$\unicode[STIX]{x1D6EC}$
for non-dimensionalisation, it can be seen that for
![]() $n=q=1/2$
equation (4.8) is equivalent to (1.3), while for
$n=q=1/2$
equation (4.8) is equivalent to (1.3), while for
![]() $n=1/2$
and
$n=1/2$
and
![]() $q=1/4$
it is equivalent to (1.4) (cf. Theofanous et al.
Reference Theofanous, Houze and Brumfield1976). The data shown in figure 14 originate from our previous (HW14) and present DNS of interfacial mass transfer driven by isotropic turbulence with free-slip surface boundary conditions. While HW14 only considered low to moderate
$q=1/4$
it is equivalent to (1.4) (cf. Theofanous et al.
Reference Theofanous, Houze and Brumfield1976). The data shown in figure 14 originate from our previous (HW14) and present DNS of interfacial mass transfer driven by isotropic turbulence with free-slip surface boundary conditions. While HW14 only considered low to moderate
![]() $R_{T}$
values, our present DNS for the first time combines high-
$R_{T}$
values, our present DNS for the first time combines high-
![]() $R_{T}$
turbulence (
$R_{T}$
turbulence (
![]() $R_{T}\approx 1440$
) with low-diffusivity mass transfer (
$R_{T}\approx 1440$
) with low-diffusivity mass transfer (
![]() $Sc$
up to
$Sc$
up to
![]() $500$
), which is typical for dissolved oxygen in water. In agreement with Theofanous (Reference Theofanous, Brutsaert and Jirka1984), two regimes can be identified in figure 14. For turbulent Reynolds numbers smaller than
$500$
), which is typical for dissolved oxygen in water. In agreement with Theofanous (Reference Theofanous, Brutsaert and Jirka1984), two regimes can be identified in figure 14. For turbulent Reynolds numbers smaller than
![]() $R_{T}\approx 500$
, the HW14 numerical results show a scaling of the normalised mass transfer velocity with
$R_{T}\approx 500$
, the HW14 numerical results show a scaling of the normalised mass transfer velocity with
![]() $R_{T}^{-1/2}$
, which supports the large-eddy model of Fortescue & Pearson (Reference Fortescue and Pearson1967). For larger
$R_{T}^{-1/2}$
, which supports the large-eddy model of Fortescue & Pearson (Reference Fortescue and Pearson1967). For larger
![]() $R_{T}$
, our present DNS results – obtained by combining horizontal averaging with ensemble averaging over time periods of
$R_{T}$
, our present DNS results – obtained by combining horizontal averaging with ensemble averaging over time periods of
![]() $30L/U$
– clearly show the presence of a different scaling law where
$30L/U$
– clearly show the presence of a different scaling law where
![]() $(K_{L}/u_{\infty }Sc^{-1/2})\propto R_{T}^{-1/4}$
, which is in agreement with the small-eddy model of Banerjee et al. (Reference Banerjee, Scott and Rhodes1968) and Lamont & Scott (Reference Lamont and Scott1970). The same
$(K_{L}/u_{\infty }Sc^{-1/2})\propto R_{T}^{-1/4}$
, which is in agreement with the small-eddy model of Banerjee et al. (Reference Banerjee, Scott and Rhodes1968) and Lamont & Scott (Reference Lamont and Scott1970). The same
![]() $K_{L}$
dependence on
$K_{L}$
dependence on
![]() $R_{T}^{-1/4}$
was reported in the experimental work of Herlina & Jirka (Reference Jirka2008). The data shown in figure 14 are complemented by results from our no-slip simulations (cf. HW16). As in the free-slip case, both the small- and large-eddy regimes can be clearly identified. It can be seen in Herlina & Wissink (Reference Herlina and Wissink2016) that the fitted line through the free-slip numerical results for high
$R_{T}^{-1/4}$
was reported in the experimental work of Herlina & Jirka (Reference Jirka2008). The data shown in figure 14 are complemented by results from our no-slip simulations (cf. HW16). As in the free-slip case, both the small- and large-eddy regimes can be clearly identified. It can be seen in Herlina & Wissink (Reference Herlina and Wissink2016) that the fitted line through the free-slip numerical results for high
![]() $R_{T}$
also agrees well with the upper bound of the experimental findings of McKenna & McGillis (Reference McKenna and McGillis2004) obtained using a clean surface. Note that, even though we expect a smooth transition between the two regimes, it was found that the line through the present free-slip DNS data also intersects the result obtained in HW14 at
$R_{T}$
also agrees well with the upper bound of the experimental findings of McKenna & McGillis (Reference McKenna and McGillis2004) obtained using a clean surface. Note that, even though we expect a smooth transition between the two regimes, it was found that the line through the present free-slip DNS data also intersects the result obtained in HW14 at
![]() $R_{T}=507$
. Further investigations would be needed to determine a detailed picture of the transitional regimes around
$R_{T}=507$
. Further investigations would be needed to determine a detailed picture of the transitional regimes around
![]() $R_{T}\approx 500$
for both the free-slip and the no-slip case.
$R_{T}\approx 500$
for both the free-slip and the no-slip case.
5 Conclusions
A large-scale DNS of interfacial mass transfer at moderate to high Schmidt numbers (up to
![]() $Sc=500$
) across a free-slip surface, driven by relatively high-intensity isotropic turbulence (
$Sc=500$
) across a free-slip surface, driven by relatively high-intensity isotropic turbulence (
![]() $R_{T}\approx 1440{-}1856$
), has been performed. The isotropic turbulence, generated in a concurrently running LES, was introduced at the bottom of the DNS domain. It was found that the missing subgrid scales in the LES energy spectrum established very rapidly as the turbulence diffused upwards in the DNS domain. Even though the depth of the computational domain was relatively small compared to the integral length scale, the statistics typical for shear-free turbulence near a free-slip surface were found to be consistent with previous data. For instance, the time-averaged turbulent Reynolds number was found to be approximately constant in most of the lower part of the DNS domain.
$R_{T}\approx 1440{-}1856$
), has been performed. The isotropic turbulence, generated in a concurrently running LES, was introduced at the bottom of the DNS domain. It was found that the missing subgrid scales in the LES energy spectrum established very rapidly as the turbulence diffused upwards in the DNS domain. Even though the depth of the computational domain was relatively small compared to the integral length scale, the statistics typical for shear-free turbulence near a free-slip surface were found to be consistent with previous data. For instance, the time-averaged turbulent Reynolds number was found to be approximately constant in most of the lower part of the DNS domain.
Previous numerical investigations of interfacial mass transfer driven by turbulence were mostly limited to low
![]() $R_{T}$
and/or low
$R_{T}$
and/or low
![]() $Sc$
. As far as the authors are aware, this is the first DNS in which both the Kolmogorov scale of the relatively highly turbulent flow (significantly higher than the critical
$Sc$
. As far as the authors are aware, this is the first DNS in which both the Kolmogorov scale of the relatively highly turbulent flow (significantly higher than the critical
![]() $R_{T}\approx 500$
, above which the small-eddy model is believed to be applicable for the estimation of the mass transfer velocity
$R_{T}\approx 500$
, above which the small-eddy model is believed to be applicable for the estimation of the mass transfer velocity
![]() $K_{L}$
) and the Batchelor scale, typical for the low-diffusivity mass transfer, are resolved. This was made possible by employing a dual-mesh approach in which the turbulent flow and the lower-Schmidt-number (
$K_{L}$
) and the Batchelor scale, typical for the low-diffusivity mass transfer, are resolved. This was made possible by employing a dual-mesh approach in which the turbulent flow and the lower-Schmidt-number (
![]() $Sc=20$
) scalar transport were resolved on the base mesh comprising
$Sc=20$
) scalar transport were resolved on the base mesh comprising
![]() $524\times 10^{6}$
grid points, while a refined mesh of
$524\times 10^{6}$
grid points, while a refined mesh of
![]() $65.5\times 10^{9}$
grid points was used for the higher-Schmidt-number (
$65.5\times 10^{9}$
grid points was used for the higher-Schmidt-number (
![]() $Sc=500$
) scalar transport, which is typical for oxygen in water. The presence of an inertial subrange with a
$Sc=500$
) scalar transport, which is typical for oxygen in water. The presence of an inertial subrange with a
![]() $\unicode[STIX]{x1D705}^{-5/3}$
behaviour and a broad dissipative range in the energy spectra, as found at various
$\unicode[STIX]{x1D705}^{-5/3}$
behaviour and a broad dissipative range in the energy spectra, as found at various
![]() $z$
locations, further confirms that the turbulent flow in the DNS is very well resolved.
$z$
locations, further confirms that the turbulent flow in the DNS is very well resolved.
Independent of
![]() $R_{T}$
and
$R_{T}$
and
![]() $Sc$
, the profiles of the mean concentration, the concentration fluctuation, the diffusive flux and the turbulent mass flux obtained in this simulation and our previous simulations (HW14) were found to nearly collapse when applying suitable normalisations. In agreement with the theory, the sum of the diffusive and turbulent fluxes in the upper bulk was observed to be equal to the diffusive flux at the surface.
$Sc$
, the profiles of the mean concentration, the concentration fluctuation, the diffusive flux and the turbulent mass flux obtained in this simulation and our previous simulations (HW14) were found to nearly collapse when applying suitable normalisations. In agreement with the theory, the sum of the diffusive and turbulent fluxes in the upper bulk was observed to be equal to the diffusive flux at the surface.
At constant
![]() $R_{T}$
, the scaling of both
$R_{T}$
, the scaling of both
![]() $\unicode[STIX]{x1D6FF}$
and
$\unicode[STIX]{x1D6FF}$
and
![]() $K_{L}$
with
$K_{L}$
with
![]() $Sc^{-1/2}$
was found to be accurately reproduced, indicating that
$Sc^{-1/2}$
was found to be accurately reproduced, indicating that
![]() $K_{L}$
varies linearly with
$K_{L}$
varies linearly with
![]() $\unicode[STIX]{x1D6FF}$
. At constant
$\unicode[STIX]{x1D6FF}$
. At constant
![]() $Sc$
, however, with increasing
$Sc$
, however, with increasing
![]() $R_{T}$
,
$R_{T}$
,
![]() $\unicode[STIX]{x1D6FF}/L_{\infty }$
is expected to become smaller, resulting in a steeper gradient of the vertical concentration profile near the surface giving rise to an increase in
$\unicode[STIX]{x1D6FF}/L_{\infty }$
is expected to become smaller, resulting in a steeper gradient of the vertical concentration profile near the surface giving rise to an increase in
![]() $K_{L}$
.
$K_{L}$
.
The instantaneous correlation of the surface divergence with the local
![]() $K_{L}$
at the surface was found to worsen with increasing
$K_{L}$
at the surface was found to worsen with increasing
![]() $R_{T}$
. As suggested by Turney & Banerjee (Reference Turney and Banerjee2013), this can be attributed to the presence of small time scales in the highly turbulent flow. Compared to our previous simulation at a lower
$R_{T}$
. As suggested by Turney & Banerjee (Reference Turney and Banerjee2013), this can be attributed to the presence of small time scales in the highly turbulent flow. Compared to our previous simulation at a lower
![]() $R_{T}=507$
, here the vortical structures were found to be smaller and far more numerous. As a result, the contribution of the smaller scales to the total turbulent mass flux was observed to be significantly larger than in the lower-
$R_{T}=507$
, here the vortical structures were found to be smaller and far more numerous. As a result, the contribution of the smaller scales to the total turbulent mass flux was observed to be significantly larger than in the lower-
![]() $R_{T}$
simulations. Also, close to the surface, the turbulent intensity in the present simulation remains highly significant, while the axes of the vortical structures in both simulations became either aligned with or orthogonal to the surface. The latter is a consequence of the flat, free-slip boundary condition at the top forcing the turbulent flow to become increasingly two-dimensional. The structures that aligned with the surface were located at the boundaries of upwelling and downwelling regions and contributed to the vertical mixing of saturated and unsaturated fluid, which at the surface is characterised by relatively high levels of
$R_{T}$
simulations. Also, close to the surface, the turbulent intensity in the present simulation remains highly significant, while the axes of the vortical structures in both simulations became either aligned with or orthogonal to the surface. The latter is a consequence of the flat, free-slip boundary condition at the top forcing the turbulent flow to become increasingly two-dimensional. The structures that aligned with the surface were located at the boundaries of upwelling and downwelling regions and contributed to the vertical mixing of saturated and unsaturated fluid, which at the surface is characterised by relatively high levels of
![]() $K_{L}$
. The orthogonal (surface-attached) structures, on the other hand, were mostly located in highly saturated areas and merely mixed already saturated fluid in the horizontal direction.
$K_{L}$
. The orthogonal (surface-attached) structures, on the other hand, were mostly located in highly saturated areas and merely mixed already saturated fluid in the horizontal direction.
Previously, the existence of the small- and large-eddy regimes in the presence of a no-slip surface boundary condition was confirmed numerically in Herlina & Wissink (Reference Herlina and Wissink2016). By ensemble averaging the data in the present simulation, we were able to obtain the mass transfer velocities for a range of
![]() $R_{T}$
values between approximately
$R_{T}$
values between approximately
![]() $1440$
and
$1440$
and
![]() $1856$
. In line with the observations above, the importance of small-scale turbulent structures was further confirmed by the scaling of the normalised mass transfer velocity
$1856$
. In line with the observations above, the importance of small-scale turbulent structures was further confirmed by the scaling of the normalised mass transfer velocity
![]() $K_{L}/(u_{\infty }Sc^{-1/2})$
with
$K_{L}/(u_{\infty }Sc^{-1/2})$
with
![]() $R_{T}^{-1/4}$
. The latter corresponds to the small-eddy model of Banerjee et al. (Reference Banerjee, Scott and Rhodes1968) and Lamont & Scott (Reference Lamont and Scott1970), which according to Theofanous (Reference Theofanous, Brutsaert and Jirka1984) is applicable for
$R_{T}^{-1/4}$
. The latter corresponds to the small-eddy model of Banerjee et al. (Reference Banerjee, Scott and Rhodes1968) and Lamont & Scott (Reference Lamont and Scott1970), which according to Theofanous (Reference Theofanous, Brutsaert and Jirka1984) is applicable for
![]() $R_{T}$
larger than
$R_{T}$
larger than
![]() ${\approx}500$
. Combining results from the present simulation with results from HW14 confirmed that, for interfacial mass transfer driven by isotropic turbulence diffusing from below, the critical
${\approx}500$
. Combining results from the present simulation with results from HW14 confirmed that, for interfacial mass transfer driven by isotropic turbulence diffusing from below, the critical
![]() $R_{T}$
is indeed approximately
$R_{T}$
is indeed approximately
![]() $500$
. It is likely, however, that there will be a smooth transition between the large-eddy and the small-eddy model, which needs further investigation.
$500$
. It is likely, however, that there will be a smooth transition between the large-eddy and the small-eddy model, which needs further investigation.
Acknowledgements
The authors would like to thank the German Research Foundation (DFG) for funding this project and the Gauss Centre for Supercomputing e.V. (www.gauss-centre.eu) for providing computing time on the GCS Supercomputer SuperMUC at Leibniz Supercomputing Centre (LRZ, www.lrz.de). Finally, the anonymous referees are acknowledged for their helpful comments. The data used in various plots can be found at http://www.ifh.kit.edu/dns_data/gas_transfer.