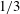1 Introduction
Suspended non-Brownian particles in a sheared emulsion or suspension experience shear-induced diffusion due to irreversible inter-particle hydrodynamic and other interactions (Eckstein, Bailey & Shapiro Reference Eckstein, Bailey and Shapiro1977; Davis Reference Davis1996). Shear-induced diffusion plays a critical role in chemical process engineering and microfluidic technologies by enhancing mixing (Lopez & Graham Reference Lopez and Graham2008) in low Reynolds number flows which is otherwise limited by slow molecular diffusion. In blood vessels, the radial concentration profile of blood cells is a result of the competition between shear-induced diffusion and wall-induced migration of cells towards the centre (Grandchamp et al. Reference Grandchamp, Coupier, Srivastav, Minetti and Podgorski2013). The mechanical properties of a blood cell, such as stiffness that influences shear-induced diffusivity, are a proxy for the health of the cells (Cooke, Mohandas & Coppel Reference Cooke, Mohandas and Coppel2001). More fundamentally, the spatial distribution of particles caused by the diffusion determines the local and global rheology of the flow. Here, we propose a direct numerical simulation technique and compute for the first time the collective diffusivity in a non-dilute emulsion of viscous drops.
In suspensions of rigid spheres, under the assumption of Stokes flow, hydrodynamic pair interaction is reversible. A symmetry breaking mechanism such as roughness is needed to give rise to diffusion from two-particle interactions (da Cunha & Hinch Reference da Cunha and Hinch1996). In case of drops or other deformable particles, pairwise hydrodynamic interaction is irreversible and nonlinear (Olapade, Singh & Sarkar Reference Olapade, Singh and Sarkar2009; Singh & Sarkar Reference Singh and Sarkar2009; Sarkar & Singh Reference Sarkar and Singh2013) leading to a diffusive behaviour (Loewenberg & Hinch Reference Loewenberg and Hinch1997). Shear-induced diffusion is generally separated into self-diffusion and collective or gradient diffusion (Rallison & Hinch Reference Rallison and Hinch1986; Rusconi & Stone Reference Rusconi and Stone2008). The first refers to the random walk-like motion exhibited by the particles and is present even in a uniformly mixed suspension or emulsion. It is characterized by the self-diffusion coefficient
![]() $D_{s}=\dot{\unicode[STIX]{x1D6FE}}a^{2}f_{s}(\unicode[STIX]{x1D719})$
with
$D_{s}=\dot{\unicode[STIX]{x1D6FE}}a^{2}f_{s}(\unicode[STIX]{x1D719})$
with
![]() $\dot{\unicode[STIX]{x1D6FE}}$
being the shear rate,
$\dot{\unicode[STIX]{x1D6FE}}$
being the shear rate,
![]() $a$
the particle radius and
$a$
the particle radius and
![]() $f_{s}(\unicode[STIX]{x1D719})$
the non-dimensional self-diffusivity, a function of the particle volume fraction
$f_{s}(\unicode[STIX]{x1D719})$
the non-dimensional self-diffusivity, a function of the particle volume fraction
![]() $\unicode[STIX]{x1D719}$
. The collective diffusion refers to a diffusive flux
$\unicode[STIX]{x1D719}$
. The collective diffusion refers to a diffusive flux
![]() $-D_{c}\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}$
in the presence of a particle concentration gradient and is similar to Fickian diffusion (Leshansky, Morris & Brady Reference Leshansky, Morris and Brady2008). The non-dimensional collective diffusivity
$-D_{c}\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}$
in the presence of a particle concentration gradient and is similar to Fickian diffusion (Leshansky, Morris & Brady Reference Leshansky, Morris and Brady2008). The non-dimensional collective diffusivity
![]() $f_{c}(\unicode[STIX]{x1D719})=D_{c}/\dot{\unicode[STIX]{x1D6FE}}a^{2}$
is usually higher in magnitude than
$f_{c}(\unicode[STIX]{x1D719})=D_{c}/\dot{\unicode[STIX]{x1D6FE}}a^{2}$
is usually higher in magnitude than
![]() $f_{s}(\unicode[STIX]{x1D719})$
. Both diffusion coefficients depend on the flow and are generally anisotropic.
$f_{s}(\unicode[STIX]{x1D719})$
. Both diffusion coefficients depend on the flow and are generally anisotropic.
Investigation into flow-induced diffusion was initiated by Eckstein et al. (Reference Eckstein, Bailey and Shapiro1977). They experimentally measured the lateral displacement of a tagged particle in a Couette flow to compute the self-diffusivity. Subsequently, numerous experimental, theoretical and computational studies explored various aspects of shear-induced diffusion. The collective diffusivity was for the first time indirectly inferred in the vorticity direction from the transient viscosity changes that were observed in a Couette flow viscometer (Leighton & Acrivos Reference Leighton and Acrivos1987). The changes were caused by the diffusion of particles from the high shear region (Couette gap) to the low shear region (fluid reservoir). A more robust procedure for computing self-diffusivity was developed using the time taken for a visually detectable particle to go around the Couette cell in successive revolutions (Leighton & Acrivos Reference Leighton and Acrivos1987). Instead of tracking a single particle that requires long temporal data to ensure ergodicity, positions of multiple tracer particles were recorded using a digital camera, reducing the time requirement by an order of magnitude and enabling the capture of the transient features of self-diffusion (Breedveld et al. Reference Breedveld, van den Ende, Tripathi and Acrivos1998; Breedveld Reference Breedveld2000). More recent experiments (Rusconi & Stone Reference Rusconi and Stone2008) have used microfluidic devices to measure the collective diffusivity in the vorticity direction of highly asymmetric plate-like particles. On the numerical side, pairwise interactions between two particles with surface roughness have been used to calculate the self- and collective diffusivities in the dilute regime (da Cunha & Hinch Reference da Cunha and Hinch1996). The diffusion was assumed to be exclusively due to two-particle interactions, and the diffusivities were calculated by integrating the displacement over all possible initial positions of the two particles. Stokesian dynamics (Brady & Bossis Reference Brady and Bossis1988) has been used to calculate the self-diffusivity for colloidal (Foss & Brady Reference Foss and Brady1999) and non-colloidal (Sierou & Brady Reference Sierou and Brady2004) suspensions directly from an ensemble averaged mean square displacement of the particles, and also by using the velocity autocorrelation function. The collective diffusivity was calculated from simulations of homogeneous suspensions (Marchioro & Acrivos Reference Marchioro and Acrivos2001), using the fact that the rate of relaxation of the microstructure on perturbation is proportional to the gradient diffusivity. A more robust method for calculating the all particle diffusivities from a single statistically homogeneous simulation using the dynamic structure factor of a sheared suspension has also been developed (Morris & Brady Reference Morris and Brady1996; Leshansky & Brady Reference Leshansky and Brady2005; Leshansky et al. Reference Leshansky, Morris and Brady2008).
In contrast to suspensions, there have been far fewer studies devoted to shear-induced diffusivity in emulsions. King & Leighton (Reference King and Leighton2001) did the first measurement of collective diffusivity, but the values they reported were lower than theoretical predictions, due to the presence of surfactants that were required to stabilize the droplets against coalescence. Hudson (Reference Hudson2003), using more viscous liquids that did not require surfactants, was the first to accurately measure the collective diffusivities of an emulsion. To our knowledge, there have been no experimental measurements of self-diffusivity in emulsions of drops. Self-diffusivities of red blood cells (Higgins et al. Reference Higgins, Eddington, Bhatia and Mahadevan2009), and red blood cell ghosts (Goldsmith & Marlow Reference Goldsmith and Marlow1979; Cha & Beissinger Reference Cha and Beissinger2001) have been measured experimentally. Grandchamp et al. (Reference Grandchamp, Coupier, Srivastav, Minetti and Podgorski2013) reported an experimental study of the collective diffusivity of red blood cells in a rectangular channel (also see Podgorski et al. Reference Podgorski, Callens, Minetti, Coupier, Dubois and Misbah2011; Bureau et al. Reference Bureau, Coupier, Dubois, Duperray, Farutin, Minetti, Misbah, Podgorski, Tsvirkun and Vysokikh2017). While we could not find any computation of the collective diffusivity in emulsions, computations of self-diffusivity have been attempted by computing two drop trajectories in shear and averaged mean square displacements by Loewenberg & Hinch (Reference Loewenberg and Hinch1997) using a boundary integral simulation of the Stokes flow. Tan, Le & Chiam (Reference Tan, Le and Chiam2012) simulated emulsions of capsules in a bounded shear flow to estimate the self-diffusivity in the vorticity direction. They showed that the emulsion can be sub-diffusive, diffusive or super-diffusive depending on the level of confinement. Pairwise simulations of vesicles have been used to calculate their self-diffusivity (Zhao & Shaqfeh Reference Zhao and Shaqfeh2013; Gires et al. Reference Gires, Srivastav, Misbah, Podgorski and Coupier2014). Calculating collective diffusivity with this method has not been possible for deformable particles, as the integral over all possible pair of drops is convergent only for zero capillary number, i.e. undeformed drops (King & Leighton Reference King and Leighton2001; Gires et al. Reference Gires, Srivastav, Misbah, Podgorski and Coupier2014). In the past, renormalization procedures have been applied to such divergent integrals; they use global constraints to obtain convergent expressions for effective stresses and sedimentation velocity (Batchelor Reference Batchelor1972; Batchelor & Green Reference Batchelor and Green1972) as well as shear-induced diffusion coefficients in a suspension (Wang, Mauri & Acrivos Reference Wang, Mauri and Acrivos1998). Such procedures have not been applied to the current problem.
We use a direct numerical simulation of a layer of randomly packed drops in a shear flow to compute the collective diffusivity varying the capillary number. In the following, we briefly describe the numerical method and our procedure to obtain the collective diffusivity from the simulation of a relatively small number of particles over a short time interval. We also provide a qualitative analysis of the shear induced diffusivity using the dynamic structure factor approach (Leshansky & Brady Reference Leshansky and Brady2005) that is based on the theory of dynamic light scattering. We discuss computed results, compare with previous experimental observations and offer a brief conclusion.
2 Simulation method
We solve the incompressible Navier–Stokes equations using a front-tracking method (Tryggvason et al. Reference Tryggvason, Bunner, Esmaeeli, Juric, Al-Rawahi, Tauber, Han, Nas and Jan2001):
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}=0,\\ {\displaystyle \frac{\unicode[STIX]{x2202}(\unicode[STIX]{x1D70C}\boldsymbol{u})}{\unicode[STIX]{x2202}t}}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\unicode[STIX]{x1D70C}\boldsymbol{u}\boldsymbol{u})=-\unicode[STIX]{x1D735}p+\unicode[STIX]{x1D735}\boldsymbol{\cdot }[\unicode[STIX]{x1D707}\{\unicode[STIX]{x1D735}\boldsymbol{u}+(\unicode[STIX]{x1D735}\boldsymbol{u})^{\text{T}}\}]-\displaystyle \int _{\unicode[STIX]{x2202}B}\unicode[STIX]{x1D705}\boldsymbol{n}\unicode[STIX]{x1D70E}\unicode[STIX]{x1D6FF}(\boldsymbol{x}-\boldsymbol{x}^{\prime })\,\text{d}S(\boldsymbol{x}^{\prime }).\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}=0,\\ {\displaystyle \frac{\unicode[STIX]{x2202}(\unicode[STIX]{x1D70C}\boldsymbol{u})}{\unicode[STIX]{x2202}t}}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\unicode[STIX]{x1D70C}\boldsymbol{u}\boldsymbol{u})=-\unicode[STIX]{x1D735}p+\unicode[STIX]{x1D735}\boldsymbol{\cdot }[\unicode[STIX]{x1D707}\{\unicode[STIX]{x1D735}\boldsymbol{u}+(\unicode[STIX]{x1D735}\boldsymbol{u})^{\text{T}}\}]-\displaystyle \int _{\unicode[STIX]{x2202}B}\unicode[STIX]{x1D705}\boldsymbol{n}\unicode[STIX]{x1D70E}\unicode[STIX]{x1D6FF}(\boldsymbol{x}-\boldsymbol{x}^{\prime })\,\text{d}S(\boldsymbol{x}^{\prime }).\end{array}\right\}\end{eqnarray}$$
Here
![]() $\boldsymbol{u}$
,
$\boldsymbol{u}$
,
![]() $p$
,
$p$
,
![]() $\unicode[STIX]{x1D70C}$
and
$\unicode[STIX]{x1D70C}$
and
![]() $\unicode[STIX]{x1D707}$
are the velocity, pressure, density and viscosity respectively.
$\unicode[STIX]{x1D707}$
are the velocity, pressure, density and viscosity respectively.
![]() $\unicode[STIX]{x1D705}$
is the local drop surface curvature,
$\unicode[STIX]{x1D705}$
is the local drop surface curvature,
![]() $\boldsymbol{n}$
is the unit outward normal to the surface
$\boldsymbol{n}$
is the unit outward normal to the surface
![]() $\unicode[STIX]{x2202}B$
of all drops and
$\unicode[STIX]{x2202}B$
of all drops and
![]() $\unicode[STIX]{x1D70E}$
is the interfacial tension. In this numerical method, all drops and their interactions are resolved. The method has been used by our group in many problems involving drops (Sarkar & Schowalter Reference Sarkar and Schowalter2001) and capsules (Li & Sarkar Reference Li and Sarkar2008) in viscous and viscoelastic fluids (Sarkar & Schowalter Reference Sarkar and Schowalter2000; Mukherjee & Sarkar Reference Mukherjee and Sarkar2009, Reference Mukherjee and Sarkar2013), including pairwise interactions (Singh & Sarkar Reference Singh and Sarkar2009, Reference Singh and Sarkar2015; Sarkar & Singh Reference Sarkar and Singh2013) and dense emulsions (Srivastava, Malipeddi & Sarkar Reference Srivastava, Malipeddi and Sarkar2016). The reader is referred to these earlier publications for the details of the algorithm and its verification and validation.
$\unicode[STIX]{x1D70E}$
is the interfacial tension. In this numerical method, all drops and their interactions are resolved. The method has been used by our group in many problems involving drops (Sarkar & Schowalter Reference Sarkar and Schowalter2001) and capsules (Li & Sarkar Reference Li and Sarkar2008) in viscous and viscoelastic fluids (Sarkar & Schowalter Reference Sarkar and Schowalter2000; Mukherjee & Sarkar Reference Mukherjee and Sarkar2009, Reference Mukherjee and Sarkar2013), including pairwise interactions (Singh & Sarkar Reference Singh and Sarkar2009, Reference Singh and Sarkar2015; Sarkar & Singh Reference Sarkar and Singh2013) and dense emulsions (Srivastava, Malipeddi & Sarkar Reference Srivastava, Malipeddi and Sarkar2016). The reader is referred to these earlier publications for the details of the algorithm and its verification and validation.

Figure 1. A sketch of the problem being simulated.
To compute the diffusion in a shear flow, we numerically simulate drops initially concentrated in a central layer subjected to a simple unbounded shear flow (figure 1). This is a departure from the experiments of King & Leighton (Reference King and Leighton2001) or Hudson (Reference Hudson2003), where drops were initially uniformly distributed between the walls and experience a bounded shear. The wall-induced lateral migration of drops away from the walls (Mukherjee & Sarkar Reference Mukherjee and Sarkar2013, Reference Mukherjee and Sarkar2014; Sarkar & Singh Reference Sarkar and Singh2013; Singh, Li & Sarkar Reference Singh, Li and Sarkar2013) competes with shear-induced collective diffusion to result in a concentration gradient towards the centre. In contrast, here the drops are not affected by walls. A uniform shear flow is generated in a computational domain, which is periodic in the
![]() $x$
and
$x$
and
![]() $z$
directions and has numerical walls in the
$z$
directions and has numerical walls in the
![]() $y$
direction moving with specified velocities. The distance between the walls is
$y$
direction moving with specified velocities. The distance between the walls is
![]() $L_{y}=28a$
(
$L_{y}=28a$
(
![]() $a$
is the drop radius), sufficiently large to simulate an unbounded shear (demonstrated below). The length of the domain in the
$a$
is the drop radius), sufficiently large to simulate an unbounded shear (demonstrated below). The length of the domain in the
![]() $x$
and
$x$
and
![]() $z$
directions is
$z$
directions is
![]() $L_{x}=L_{z}=14a$
. A
$L_{x}=L_{z}=14a$
. A
![]() $96\times 192\times 96$
uniform grid is used in the computational domain leading to 15 grid points per drop diameter, shown to be sufficient in our earlier studies. The drops are initially randomly close packed (Desmond & Weeks Reference Desmond and Weeks2009) in a thin (
$96\times 192\times 96$
uniform grid is used in the computational domain leading to 15 grid points per drop diameter, shown to be sufficient in our earlier studies. The drops are initially randomly close packed (Desmond & Weeks Reference Desmond and Weeks2009) in a thin (
![]() ${\sim}0.2L_{y}$
) layer parallel to the
${\sim}0.2L_{y}$
) layer parallel to the
![]() $xz$
-plane (figure 1) in the middle of the computational domain. In the
$xz$
-plane (figure 1) in the middle of the computational domain. In the
![]() $x$
and
$x$
and
![]() $z$
directions, the distribution of drops is homogeneous initially and remains so. The drops remain adequately separated from the
$z$
directions, the distribution of drops is homogeneous initially and remains so. The drops remain adequately separated from the
![]() $y$
-boundaries such that the wall effects are negligible on drops over the time scale necessary to characterize the diffusion (discussed further below). The front tracking finite difference code is used to solve the fluid dynamics equation for various capillary numbers, the ratio between the viscous and interfacial stresses
$y$
-boundaries such that the wall effects are negligible on drops over the time scale necessary to characterize the diffusion (discussed further below). The front tracking finite difference code is used to solve the fluid dynamics equation for various capillary numbers, the ratio between the viscous and interfacial stresses
![]() $Ca=\unicode[STIX]{x1D707}\dot{\unicode[STIX]{x1D6FE}}a/\unicode[STIX]{x1D70E}$
. The drops are viscosity matched. Note that the explicit nature of the code prevents us from simulating Stokes flow. The simulations are performed at small but finite Reynolds number of
$Ca=\unicode[STIX]{x1D707}\dot{\unicode[STIX]{x1D6FE}}a/\unicode[STIX]{x1D70E}$
. The drops are viscosity matched. Note that the explicit nature of the code prevents us from simulating Stokes flow. The simulations are performed at small but finite Reynolds number of
![]() $Re=\unicode[STIX]{x1D70C}\dot{\unicode[STIX]{x1D6FE}}a^{2}/\unicode[STIX]{x1D707}=0.1$
. Previously we have shown that results at this
$Re=\unicode[STIX]{x1D70C}\dot{\unicode[STIX]{x1D6FE}}a^{2}/\unicode[STIX]{x1D707}=0.1$
. Previously we have shown that results at this
![]() $Re$
matches sufficiently well with Stokes flow simulation of emulsions (Srivastava et al.
Reference Srivastava, Malipeddi and Sarkar2016).
$Re$
matches sufficiently well with Stokes flow simulation of emulsions (Srivastava et al.
Reference Srivastava, Malipeddi and Sarkar2016).
3 Collective/gradient diffusivity
Under the assumption of homogeneity in the
![]() $x$
and
$x$
and
![]() $z$
directions, the problem reduces to an unsteady, one-dimensional diffusion problem for the particle volume fraction
$z$
directions, the problem reduces to an unsteady, one-dimensional diffusion problem for the particle volume fraction
![]() $\unicode[STIX]{x1D719}=\unicode[STIX]{x1D719}(y,t)$
:
$\unicode[STIX]{x1D719}=\unicode[STIX]{x1D719}(y,t)$
:
Assuming that two-particle interaction dominates the dynamics, the collective diffusivity is proportional to the rate of two-particle interactions (collisions)
![]() $\dot{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D719}:\;D_{c}=\dot{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D719}a^{2}f_{2}$
, (i.e.
$\dot{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D719}:\;D_{c}=\dot{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D719}a^{2}f_{2}$
, (i.e.
![]() $f_{c,2}=f_{2}\unicode[STIX]{x1D719}$
) (da Cunha & Hinch Reference da Cunha and Hinch1996; Loewenberg & Hinch Reference Loewenberg and Hinch1997; Rusconi & Stone Reference Rusconi and Stone2008; Grandchamp et al.
Reference Grandchamp, Coupier, Srivastav, Minetti and Podgorski2013). Here
$f_{c,2}=f_{2}\unicode[STIX]{x1D719}$
) (da Cunha & Hinch Reference da Cunha and Hinch1996; Loewenberg & Hinch Reference Loewenberg and Hinch1997; Rusconi & Stone Reference Rusconi and Stone2008; Grandchamp et al.
Reference Grandchamp, Coupier, Srivastav, Minetti and Podgorski2013). Here
![]() $f_{2}$
is the non-dimensional collective diffusivity in the velocity-gradient direction, the focus of the present work. The assumption of linear dependence of
$f_{2}$
is the non-dimensional collective diffusivity in the velocity-gradient direction, the focus of the present work. The assumption of linear dependence of
![]() $D_{c}$
on volume fraction, or equivalently the dominance of pairwise interaction is a posteriori justified by the simulation results.
$D_{c}$
on volume fraction, or equivalently the dominance of pairwise interaction is a posteriori justified by the simulation results.

Figure 2. Snapshots from a simulation of 70 drops at
![]() $Ca=0.10$
showing a layer of drops spreading due to collective diffusion in shear.
$Ca=0.10$
showing a layer of drops spreading due to collective diffusion in shear.
The simulation shows that the drops spread in the gradient direction with time (figure 2; also see the movie in the supplemental material available online at https://doi.org/10.1017/jfm.2019.122). We non-dimensionalize time and length as
![]() $t=t^{\prime }/\dot{\unicode[STIX]{x1D6FE}},y=y^{\prime }a$
. It has been shown by a detailed analysis that when a fixed number of particles spread due to shear-induced diffusion, the transformed equation (3.1) admits a self-similar parabolic concentration (Grandchamp et al.
Reference Grandchamp, Coupier, Srivastav, Minetti and Podgorski2013)
$t=t^{\prime }/\dot{\unicode[STIX]{x1D6FE}},y=y^{\prime }a$
. It has been shown by a detailed analysis that when a fixed number of particles spread due to shear-induced diffusion, the transformed equation (3.1) admits a self-similar parabolic concentration (Grandchamp et al.
Reference Grandchamp, Coupier, Srivastav, Minetti and Podgorski2013)
in the similarity variable
![]() $\unicode[STIX]{x1D702}$
, where
$\unicode[STIX]{x1D702}$
, where
![]() $b$
is a free parameter. We see that the profile spreads with
$b$
is a free parameter. We see that the profile spreads with
![]() $t^{1/3}$
, which is slower than
$t^{1/3}$
, which is slower than
![]() $t^{1/2}$
growth known to occur in systems with a constant diffusivity (i.e. independent of concentration or volume fraction). Note that the characteristic scaling exponent depends on the details of the problem formulation. In case of particles spreading from one side in an initially Heaviside concentration profile (Rusconi & Stone Reference Rusconi and Stone2008), the characteristic exponent is
$t^{1/2}$
growth known to occur in systems with a constant diffusivity (i.e. independent of concentration or volume fraction). Note that the characteristic scaling exponent depends on the details of the problem formulation. In case of particles spreading from one side in an initially Heaviside concentration profile (Rusconi & Stone Reference Rusconi and Stone2008), the characteristic exponent is
![]() $1/2$
, even when
$1/2$
, even when
![]() $D_{c}=\dot{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D719}^{m}a^{2}f_{2}$
with
$D_{c}=\dot{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D719}^{m}a^{2}f_{2}$
with
![]() $m>1$
. In the experimental study of red blood cells (RBC) diffusing down a gradient (Grandchamp et al.
Reference Grandchamp, Coupier, Srivastav, Minetti and Podgorski2013), authors observed the RBC concentration to reach a self-similar parabolic concentration as predicted by the analytical solution (3.2) with its half-width at half-height,
$m>1$
. In the experimental study of red blood cells (RBC) diffusing down a gradient (Grandchamp et al.
Reference Grandchamp, Coupier, Srivastav, Minetti and Podgorski2013), authors observed the RBC concentration to reach a self-similar parabolic concentration as predicted by the analytical solution (3.2) with its half-width at half-height,
![]() $w$
, changing with time as
$w$
, changing with time as
Here
![]() $\text{}\underline{w}_{o}$
is the initial width and
$\text{}\underline{w}_{o}$
is the initial width and
![]() $N_{o}$
is a conserved quantity, related to the particular nature of the problem mentioned before – a fixed number of particles diffusing out. It was used to obtain the value of the collective diffusivity
$N_{o}$
is a conserved quantity, related to the particular nature of the problem mentioned before – a fixed number of particles diffusing out. It was used to obtain the value of the collective diffusivity
![]() $f_{2}$
.
$f_{2}$
.
We use two different methods to determine collective diffusivity
![]() $f_{2}$
from our simulation. The first one follows closely the approach mentioned above – determine width by fitting a parabolic profile to the concentration and use the width-versus-time data as per (3.3). For the simulation,
$f_{2}$
from our simulation. The first one follows closely the approach mentioned above – determine width by fitting a parabolic profile to the concentration and use the width-versus-time data as per (3.3). For the simulation,
![]() $N_{o}=NV/aL_{x}L_{z}$
, where
$N_{o}=NV/aL_{x}L_{z}$
, where
![]() $V$
is the drop volume and
$V$
is the drop volume and
![]() $N$
is the total number of drops in the domain. However, to obtain a robust parabolic approximation of the concentration for width estimation, one needs densely sampled data with a very large number of drops as, in fact, were obtained in past experiments (King & Leighton Reference King and Leighton2001; Hudson Reference Hudson2003; Grandchamp et al.
Reference Grandchamp, Coupier, Srivastav, Minetti and Podgorski2013). Obtaining similar quality data from a direct numerical solution of the Navier–Stokes equation requires expensive simulation with a large number of individually resolved drops in a large computational domain and a long simulation time. Figure 2 shows the time evolution of the drop layer over time from a typical simulation of 70 drops. As the layer of drops gets sparser, the quality of the concentration profile could become increasingly worse due to there not being enough drops in each bin, leading to problems with curve fitting. Instead of using drop centre positions to compute the profile, which would have restricted the resolution strictly to the drop size, we compute drop phase concentration over a far finer resolution (
$N$
is the total number of drops in the domain. However, to obtain a robust parabolic approximation of the concentration for width estimation, one needs densely sampled data with a very large number of drops as, in fact, were obtained in past experiments (King & Leighton Reference King and Leighton2001; Hudson Reference Hudson2003; Grandchamp et al.
Reference Grandchamp, Coupier, Srivastav, Minetti and Podgorski2013). Obtaining similar quality data from a direct numerical solution of the Navier–Stokes equation requires expensive simulation with a large number of individually resolved drops in a large computational domain and a long simulation time. Figure 2 shows the time evolution of the drop layer over time from a typical simulation of 70 drops. As the layer of drops gets sparser, the quality of the concentration profile could become increasingly worse due to there not being enough drops in each bin, leading to problems with curve fitting. Instead of using drop centre positions to compute the profile, which would have restricted the resolution strictly to the drop size, we compute drop phase concentration over a far finer resolution (
![]() $1/30$
$1/30$
![]() $a$
).
$a$
).
We also use a second method for calculating
![]() $f_{2}$
– instead of the half-width
$f_{2}$
– instead of the half-width
![]() $w$
of the concentration profile, we use the standard deviation
$w$
of the concentration profile, we use the standard deviation
![]() $w$
of the
$w$
of the
![]() $y$
-positions (
$y$
-positions (
![]() $y_{i}^{\prime }$
) of
$y_{i}^{\prime }$
) of
![]() $N$
drops (figure 2) as a representative of the width:
$N$
drops (figure 2) as a representative of the width:
 $$\begin{eqnarray}w=\sqrt{\frac{1}{N}\mathop{\sum }_{i=1}^{N}(y_{i}^{\prime }-\unicode[STIX]{x1D707})^{2}},\quad \unicode[STIX]{x1D707}=\frac{1}{N}\mathop{\sum }_{i=1}^{N}y_{i}^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}w=\sqrt{\frac{1}{N}\mathop{\sum }_{i=1}^{N}(y_{i}^{\prime }-\unicode[STIX]{x1D707})^{2}},\quad \unicode[STIX]{x1D707}=\frac{1}{N}\mathop{\sum }_{i=1}^{N}y_{i}^{\prime }.\end{eqnarray}$$
Theory predicts this ‘modified’ width relative to its initial value
![]() $w_{0}$
to also increase linearly with time with a slightly different constant than in (3.3)
$w_{0}$
to also increase linearly with time with a slightly different constant than in (3.3)
From the drop locations in a typical simulation (e.g. figure 2),
![]() $w$
is calculated and plotted on a log–log plot to show an eventual linear curve indicating the power-law dependence on time and
$w$
is calculated and plotted on a log–log plot to show an eventual linear curve indicating the power-law dependence on time and
![]() $f_{2}$
is computed. This way of computing
$f_{2}$
is computed. This way of computing
![]() $f_{2}$
avoids curve fitting at every time step and the associated errors. However, we will see that both methods lead to very similar values of
$f_{2}$
avoids curve fitting at every time step and the associated errors. However, we will see that both methods lead to very similar values of
![]() $f_{2}$
.
$f_{2}$
.

Figure 3. (a) The drop positions versus time at
![]() $Ca=0.05$
. A few drop tracks are coloured to highlight the random-walk-like movement. (b) Concentration profile at various times of drops spreading in shear at
$Ca=0.05$
. A few drop tracks are coloured to highlight the random-walk-like movement. (b) Concentration profile at various times of drops spreading in shear at
![]() $Ca=0.05$
. Solid lines are the best fit parabola. The inset shows the same scaled with
$Ca=0.05$
. Solid lines are the best fit parabola. The inset shows the same scaled with
![]() $t^{1/3}$
(as per (4.1)) collapse of different time curves due to the self-similar evolution. (c) Width at half-height of the concentration profile as a function of time on a log–log plot, showing the
$t^{1/3}$
(as per (4.1)) collapse of different time curves due to the self-similar evolution. (c) Width at half-height of the concentration profile as a function of time on a log–log plot, showing the
![]() $1/3$
exponent scaling. (d) Modified width based on the standard deviation of the drop position as a function of time showing the same scaling.
$1/3$
exponent scaling. (d) Modified width based on the standard deviation of the drop position as a function of time showing the same scaling.
4 Results and discussion
4.1 Collective diffusivity using two methods at
 $Ca=0.05$
$Ca=0.05$
Figure 2 shows a typical case of an initially concentrated layer of viscous drops experiencing shear-induced diffusion with time. Figure 3(a) plots individual drop positions with time for a low capillary number of
![]() $Ca=0.05$
. The drops exhibit a random-walk-like movement. The concentration profile for this case is plotted in figure 3(b), fitting a parabolic profile in successive time instants (also see the movie in the supplemental material). In the inset of figure 3(b), we plot the concentration profiles scaled by
$Ca=0.05$
. The drops exhibit a random-walk-like movement. The concentration profile for this case is plotted in figure 3(b), fitting a parabolic profile in successive time instants (also see the movie in the supplemental material). In the inset of figure 3(b), we plot the concentration profiles scaled by
![]() $t^{\prime -1/3}$
versus
$t^{\prime -1/3}$
versus
![]() $y^{\prime }/t^{\prime 1/3}$
to see that indeed they all collapse as they should according to the similarity profile
$y^{\prime }/t^{\prime 1/3}$
to see that indeed they all collapse as they should according to the similarity profile
![]() $\unicode[STIX]{x1D713}(\unicode[STIX]{x1D702})$
described in (3.2). Plotting the width
$\unicode[STIX]{x1D713}(\unicode[STIX]{x1D702})$
described in (3.2). Plotting the width
![]() $\text{}\underline{w}$
on a log–log plot in figure 3(c) shows an eventual linear curve indicating the
$\text{}\underline{w}$
on a log–log plot in figure 3(c) shows an eventual linear curve indicating the
![]() $1/3$
power-law dependence on time. The initial data (
$1/3$
power-law dependence on time. The initial data (
![]() $t^{\prime }<20$
) are discarded; starting from
$t^{\prime }<20$
) are discarded; starting from
![]() $t_{0}^{\prime }=20$
, the remaining portion is subdivided into smaller time intervals (15 inverse shear units). The slope of
$t_{0}^{\prime }=20$
, the remaining portion is subdivided into smaller time intervals (15 inverse shear units). The slope of
![]() $\text{}\underline{w}^{3}-\text{}\underline{w}_{o}^{3}$
in each subinterval and the corresponding value of
$\text{}\underline{w}^{3}-\text{}\underline{w}_{o}^{3}$
in each subinterval and the corresponding value of
![]() $f_{2}$
there according to (3.3) is computed. The dynamics over these different time intervals are approximately uncorrelated (Zinchenko & Davis Reference Zinchenko and Davis2002). The mean of this average is reported (under the assumption of ergodicity, it is equal to an ensemble average). The corresponding standard deviation of the values from different time intervals is reported as the uncertainty of the estimation. We obtain
$f_{2}$
there according to (3.3) is computed. The dynamics over these different time intervals are approximately uncorrelated (Zinchenko & Davis Reference Zinchenko and Davis2002). The mean of this average is reported (under the assumption of ergodicity, it is equal to an ensemble average). The corresponding standard deviation of the values from different time intervals is reported as the uncertainty of the estimation. We obtain
![]() $f_{2}=0.329\pm 0.02$
. In figure 3(d), the plot of the standard deviation
$f_{2}=0.329\pm 0.02$
. In figure 3(d), the plot of the standard deviation
![]() $w$
of the layer according to (3.4) against time also shows a similar
$w$
of the layer according to (3.4) against time also shows a similar
![]() $1/3$
slope with time. An identical analysis is executed on this data to obtain the average
$1/3$
slope with time. An identical analysis is executed on this data to obtain the average
![]() $f_{2}$
according to the second method to obtain
$f_{2}$
according to the second method to obtain
![]() $f_{2}=0.327\pm 0.021$
, very similar to the one obtained by the other method. Note that there is minimal ‘noise’ in both curves in figure 3(c,d), demonstrating the robust nature of the
$f_{2}=0.327\pm 0.021$
, very similar to the one obtained by the other method. Note that there is minimal ‘noise’ in both curves in figure 3(c,d), demonstrating the robust nature of the
![]() $1/3$
exponent. Presence of noise detracts from the confidence of the fitting; which is why ensemble averaging of mean square displacements in the computation of self-diffusivity requires a significantly larger number of particles (Marchioro & Acrivos Reference Marchioro and Acrivos2001).
$1/3$
exponent. Presence of noise detracts from the confidence of the fitting; which is why ensemble averaging of mean square displacements in the computation of self-diffusivity requires a significantly larger number of particles (Marchioro & Acrivos Reference Marchioro and Acrivos2001).

Figure 4. Effect of the computational domain: the width of drop layer as a function of time for different widths of the computational domain.
4.2 Effects of domain size
Although we are interested in computing the collective diffusivity in an emulsion in a free shear flow, i.e. without any boundary, our code requires walls to generate the shear flow. Therefore, it is important to show that the domain size chosen is sufficiently large and that the results are independent of the physical dimensions of the domain. The pairwise interaction between drops in a shear flow with walls was shown to be exactly the same as the free-shear interaction for
![]() $L_{y}\geqslant 25a$
when the drops are at the centre of the domain (Singh & Sarkar Reference Singh and Sarkar2015). However, unlike that case, the layer of drops considered here spreads its thickness with time and eventually would be affected by the walls. Figure 4 shows
$L_{y}\geqslant 25a$
when the drops are at the centre of the domain (Singh & Sarkar Reference Singh and Sarkar2015). However, unlike that case, the layer of drops considered here spreads its thickness with time and eventually would be affected by the walls. Figure 4 shows
![]() $w^{3}-w_{o}^{3}$
increasing with time for three different separations
$w^{3}-w_{o}^{3}$
increasing with time for three different separations
![]() $L_{y}$
between the walls. All three curves are linear for a substantial portion initially and all have the same slope. This shows that, in this linear region the walls do not affect the dynamics of the drops. For
$L_{y}$
between the walls. All three curves are linear for a substantial portion initially and all have the same slope. This shows that, in this linear region the walls do not affect the dynamics of the drops. For
![]() $L_{y}=21a$
, at approximately
$L_{y}=21a$
, at approximately
![]() $t^{\prime }-t_{0}^{\prime }=200$
, the linearity breaks down due to the wall effects. For
$t^{\prime }-t_{0}^{\prime }=200$
, the linearity breaks down due to the wall effects. For
![]() $L_{y}=28a$
, this happens at approximately
$L_{y}=28a$
, this happens at approximately
![]() $t^{\prime }-t_{0}^{\prime }=300$
and for
$t^{\prime }-t_{0}^{\prime }=300$
and for
![]() $L_{y}=42a$
there is no noticeable deviation in the curve until approximately
$L_{y}=42a$
there is no noticeable deviation in the curve until approximately
![]() $t^{\prime }-t_{0}^{\prime }=400$
. Table 1 shows the values of the diffusivity calculated in each of these cases from the linear portion. We obtain a similar value for all three cases with no particular trend. We choose
$t^{\prime }-t_{0}^{\prime }=400$
. Table 1 shows the values of the diffusivity calculated in each of these cases from the linear portion. We obtain a similar value for all three cases with no particular trend. We choose
![]() $L_{y}=28a$
for all subsequent simulations. For this wall separation, one can estimate the lateral velocity on a droplet induced by the bounding walls using a small deformation analysis (Chan & Leal Reference Chan and Leal1979):
$L_{y}=28a$
for all subsequent simulations. For this wall separation, one can estimate the lateral velocity on a droplet induced by the bounding walls using a small deformation analysis (Chan & Leal Reference Chan and Leal1979):
For a sample case of
![]() $Ca=0.1$
, the half-width of the spreading layer reaches
$Ca=0.1$
, the half-width of the spreading layer reaches
![]() $y\sim 4.5a$
. With a local volume fraction of
$y\sim 4.5a$
. With a local volume fraction of
![]() ${\sim}0.1$
, one obtains a Péclet number of
${\sim}0.1$
, one obtains a Péclet number of
![]() $Pe=V_{lat}/(f_{2}\dot{\unicode[STIX]{x1D6FE}}a\unicode[STIX]{x1D719})\sim 0.02$
, indicating negligible effects of the walls. We also study the effects of
$Pe=V_{lat}/(f_{2}\dot{\unicode[STIX]{x1D6FE}}a\unicode[STIX]{x1D719})\sim 0.02$
, indicating negligible effects of the walls. We also study the effects of
![]() $L_{x}$
, shown in table 2. In the interest of a reasonable computation time,
$L_{x}$
, shown in table 2. In the interest of a reasonable computation time,
![]() $L_{x}=14a$
is chosen which seems sufficient for our purpose.
$L_{x}=14a$
is chosen which seems sufficient for our purpose.
Table 1. Effect of domain length in the
![]() $y$
direction, i.e. the distance between the walls, on the diffusivity.
$y$
direction, i.e. the distance between the walls, on the diffusivity.

Table 2. Effect of domain length in the flow direction on the diffusivity.


Figure 5. Width of the drop layer as a function of time for
![]() $Ca=0.05$
in the power law regime for different values of
$Ca=0.05$
in the power law regime for different values of
![]() $N_{o}$
. Inset shows the same, scaled by
$N_{o}$
. Inset shows the same, scaled by
![]() $N_{o}$
, collapses onto a single curve.
$N_{o}$
, collapses onto a single curve.
4.3 Effects of
 $N_{o}$
(initial volume fraction in the layer) and initial configuration
$N_{o}$
(initial volume fraction in the layer) and initial configuration
In addition to the
![]() $t^{1/3}$
scaling of the width, the dependence of diffusivity on the quantity
$t^{1/3}$
scaling of the width, the dependence of diffusivity on the quantity
![]() $N_{o}$
that appears in (3.3) and (3.5) shows that the diffusion is mediated by inter-particle interactions. In experiments at high volume fractions (
$N_{o}$
that appears in (3.3) and (3.5) shows that the diffusion is mediated by inter-particle interactions. In experiments at high volume fractions (
![]() ${>}0.3$
), the effective coefficient of diffusion (
${>}0.3$
), the effective coefficient of diffusion (
![]() $K$
in (3.3)) increased quadratically with
$K$
in (3.3)) increased quadratically with
![]() $N_{o}$
, indicating a non-negligible contribution from three-particle interactions (Grandchamp et al.
Reference Grandchamp, Coupier, Srivastav, Minetti and Podgorski2013). It results in a linear increase of
$N_{o}$
, indicating a non-negligible contribution from three-particle interactions (Grandchamp et al.
Reference Grandchamp, Coupier, Srivastav, Minetti and Podgorski2013). It results in a linear increase of
![]() $f_{2}$
with
$f_{2}$
with
![]() $N_{o}$
. If only pairwise interactions dominate,
$N_{o}$
. If only pairwise interactions dominate,
![]() $f_{2}$
is expected to be independent of
$f_{2}$
is expected to be independent of
![]() $N_{o}$
. To verify this and to ensure that the size of the system is sufficient, we perform simulations with different initial configurations and different
$N_{o}$
. To verify this and to ensure that the size of the system is sufficient, we perform simulations with different initial configurations and different
![]() $N_{o}$
. Different
$N_{o}$
. Different
![]() $N_{o}$
values represent different volume fractions in the central layer at
$N_{o}$
values represent different volume fractions in the central layer at
![]() $t^{\prime }=t_{0}^{\prime }$
(after the power law sets in as seen in figure 3
c,d) – e.g. the curves for
$t^{\prime }=t_{0}^{\prime }$
(after the power law sets in as seen in figure 3
c,d) – e.g. the curves for
![]() $N_{o}=1.44$
and 3.28 correspond to 18 % and 31 % volume fraction. The curve for
$N_{o}=1.44$
and 3.28 correspond to 18 % and 31 % volume fraction. The curve for
![]() $N_{o}=2.44$
with an asterisk is for a volume fraction of 49 % obtained with an initial configuration with a smaller initial layer width. They also represent different layer widths from
$N_{o}=2.44$
with an asterisk is for a volume fraction of 49 % obtained with an initial configuration with a smaller initial layer width. They also represent different layer widths from
![]() ${\sim}6$
to
${\sim}6$
to
![]() ${\sim}8$
drop radii as well as different initial random configurations. Figure 5 shows
${\sim}8$
drop radii as well as different initial random configurations. Figure 5 shows
![]() $w^{3}-w_{o}^{3}$
versus time for these various cases. As expected from (3.5) the slope increases with
$w^{3}-w_{o}^{3}$
versus time for these various cases. As expected from (3.5) the slope increases with
![]() $N_{o}$
. The inset shows that upon scaling with
$N_{o}$
. The inset shows that upon scaling with
![]() $N_{o}$
all lines collapse onto a single line, indicating that the results are independent of
$N_{o}$
all lines collapse onto a single line, indicating that the results are independent of
![]() $N_{o}$
as well as initial configurations.
$N_{o}$
as well as initial configurations.
Note that the relation
![]() $w^{3}\propto t$
arising from (3.2) is contingent on the assumption of the dominance of pair interactions in determining the shear-induced diffusion, that gave rise to
$w^{3}\propto t$
arising from (3.2) is contingent on the assumption of the dominance of pair interactions in determining the shear-induced diffusion, that gave rise to
![]() $D_{c}\propto \unicode[STIX]{x1D719}$
. In contrast, if three-particle interactions were to dominate, the diffusivity would be proportional to
$D_{c}\propto \unicode[STIX]{x1D719}$
. In contrast, if three-particle interactions were to dominate, the diffusivity would be proportional to
![]() $\unicode[STIX]{x1D719}^{2}$
giving rise to
$\unicode[STIX]{x1D719}^{2}$
giving rise to
![]() $w^{4}\propto t$
(Grandchamp et al.
Reference Grandchamp, Coupier, Srivastav, Minetti and Podgorski2013). In general, at high enough concentrations, one would expect the higher-order interactions to be significant, and a clear scaling might not appear. In the initial part of the data in figure 3(c,d), when the local volume fraction is high in the closely packed layer, the deviation from the
$w^{4}\propto t$
(Grandchamp et al.
Reference Grandchamp, Coupier, Srivastav, Minetti and Podgorski2013). In general, at high enough concentrations, one would expect the higher-order interactions to be significant, and a clear scaling might not appear. In the initial part of the data in figure 3(c,d), when the local volume fraction is high in the closely packed layer, the deviation from the
![]() $1/3$
scaling – slopes are smaller – could be a signature of higher-order interactions in addition to the deviation from the parabolic profile. With time the local volume fraction continues to decrease and eventually higher than two-drop interactions become increasingly rare. Note that the time scale of drop deformation, the capillary time scale, is quite small – identical to
$1/3$
scaling – slopes are smaller – could be a signature of higher-order interactions in addition to the deviation from the parabolic profile. With time the local volume fraction continues to decrease and eventually higher than two-drop interactions become increasingly rare. Note that the time scale of drop deformation, the capillary time scale, is quite small – identical to
![]() $Ca$
in shear unit, i.e. 0.05–0.35 for the cases considered here. Therefore, the drops achieve their final deformed state long before the
$Ca$
in shear unit, i.e. 0.05–0.35 for the cases considered here. Therefore, the drops achieve their final deformed state long before the
![]() $1/3$
scaling behaviour sets in. Based on the scaling seen in figure 5 and the corresponding volume fractions (specifically the curve for
$1/3$
scaling behaviour sets in. Based on the scaling seen in figure 5 and the corresponding volume fractions (specifically the curve for
![]() $N_{o}=2.44$
), we conclude that the
$N_{o}=2.44$
), we conclude that the
![]() $1/3$
scaling (and the relationship
$1/3$
scaling (and the relationship
![]() $D_{c}\propto \unicode[STIX]{x1D719}$
) holds for
$D_{c}\propto \unicode[STIX]{x1D719}$
) holds for
![]() $\unicode[STIX]{x1D719}\leqslant \sim 0.5$
.
$\unicode[STIX]{x1D719}\leqslant \sim 0.5$
.

Figure 6. Snapshots of the drop layer at
![]() $t^{\prime }=\sim 17$
for three different
$t^{\prime }=\sim 17$
for three different
![]() $Ca$
.
$Ca$
.

Figure 7. (a) Width at half-height of the concentration profile as a function of time for different
![]() $Ca$
. (b) Modified width of the drop layer as a function of time for different
$Ca$
. (b) Modified width of the drop layer as a function of time for different
![]() $Ca$
. Cube of both quantities has been plotted to show their linear scaling.
$Ca$
. Cube of both quantities has been plotted to show their linear scaling.
4.4 Effects of capillary number
Figure 6 shows the drops at three different capillary numbers at approximately the same time when the drops achieve their deformed shapes. We compute the non-dimensional collective diffusivity
![]() $f_{2}$
using both methods at different capillary numbers. Figure 7(a,b) shows that
$f_{2}$
using both methods at different capillary numbers. Figure 7(a,b) shows that
![]() $\text{}\underline{w}^{3}-\text{}\underline{w}_{o}^{3}$
and
$\text{}\underline{w}^{3}-\text{}\underline{w}_{o}^{3}$
and
![]() $w^{3}-w_{o}^{3}$
both vary linearly and almost identically with
$w^{3}-w_{o}^{3}$
both vary linearly and almost identically with
![]() $t^{\prime }-t_{0}^{\prime }$
at different
$t^{\prime }-t_{0}^{\prime }$
at different
![]() $Ca$
values. Therefore,
$Ca$
values. Therefore,
![]() $f_{2}$
(the slopes) computed by the two methods are very similar at all values of
$f_{2}$
(the slopes) computed by the two methods are very similar at all values of
![]() $Ca$
, as has been tabulated in table 3. In figure 8, we plot
$Ca$
, as has been tabulated in table 3. In figure 8, we plot
![]() $f_{2}$
versus
$f_{2}$
versus
![]() $Ca$
using both methods. They resulted in very similar values. It shows a non-monotonic variation, as was also seen for the self-diffusivity (Loewenberg & Hinch Reference Loewenberg and Hinch1997; Tan et al.
Reference Tan, Le and Chiam2012). An intuitive explanation for the non-monotonic variation can be obtained as arising from a competition between the effects of increasing deformation and decreasing drop orientation angle with increasing
$Ca$
using both methods. They resulted in very similar values. It shows a non-monotonic variation, as was also seen for the self-diffusivity (Loewenberg & Hinch Reference Loewenberg and Hinch1997; Tan et al.
Reference Tan, Le and Chiam2012). An intuitive explanation for the non-monotonic variation can be obtained as arising from a competition between the effects of increasing deformation and decreasing drop orientation angle with increasing
![]() $Ca$
in pair interactions. The time variation of the average deformation and average inclination angle of the drops are plotted in figure 9. As noted before, the initially spherical drops quickly reach their equilibrium deformation over the capillary time scale
$Ca$
in pair interactions. The time variation of the average deformation and average inclination angle of the drops are plotted in figure 9. As noted before, the initially spherical drops quickly reach their equilibrium deformation over the capillary time scale
![]() $t_{capillary}^{\prime }=Ca$
. The inclination angle starts at the inclination of the extensional axis
$t_{capillary}^{\prime }=Ca$
. The inclination angle starts at the inclination of the extensional axis
![]() $45^{\circ }$
and decreases due to deformation (Taylor Reference Taylor1934). The fluctuations in their values are caused by the drop–drop interactions in the shear flow. Note that although the local volume fraction decreases due to diffusion of the drops, the average values of deformation and inclination angle do not change significantly over the time period considered.
$45^{\circ }$
and decreases due to deformation (Taylor Reference Taylor1934). The fluctuations in their values are caused by the drop–drop interactions in the shear flow. Note that although the local volume fraction decreases due to diffusion of the drops, the average values of deformation and inclination angle do not change significantly over the time period considered.

Figure 8. Dimensionless gradient diffusivity (
![]() $f_{2}$
), deformation parameter (
$f_{2}$
), deformation parameter (
![]() $D$
) and drop inclination angle (
$D$
) and drop inclination angle (
![]() $\unicode[STIX]{x1D703}$
) plotted as functions of
$\unicode[STIX]{x1D703}$
) plotted as functions of
![]() $Ca$
. Symbols are the results from the simulation. The solid and dash-dotted lines are predictions of small deformation perturbative analysis for
$Ca$
. Symbols are the results from the simulation. The solid and dash-dotted lines are predictions of small deformation perturbative analysis for
![]() $\unicode[STIX]{x1D703}$
and
$\unicode[STIX]{x1D703}$
and
![]() $D$
respectively. The dashed line is a quadratic fit of the simulated
$D$
respectively. The dashed line is a quadratic fit of the simulated
![]() $f_{2}$
values (solid triangles) obtained by standard deviation according to (4.2). The error bar corresponds to the
$f_{2}$
values (solid triangles) obtained by standard deviation according to (4.2). The error bar corresponds to the
![]() $f_{2}$
values.
$f_{2}$
values.

Figure 9. Average deformation (a) and average orientation angle (b) with time for a simulation at
![]() $Ca=0.05$
. The shading shows the standard deviation.
$Ca=0.05$
. The shading shows the standard deviation.
In figure 9, we plot the Taylor deformation parameter
![]() $D=(L-B)/(L+B)$
(
$D=(L-B)/(L+B)$
(
![]() $L$
and
$L$
and
![]() $B$
are the maximal and the minimal distances of the drop surface from the centroid) averaged over all drops and over the power-law regime shown in figure 3(c,d); it approximately matches with the small deformation perturbative result
$B$
are the maximal and the minimal distances of the drop surface from the centroid) averaged over all drops and over the power-law regime shown in figure 3(c,d); it approximately matches with the small deformation perturbative result
![]() $D=Ca(19\unicode[STIX]{x1D706}+16)/(16\unicode[STIX]{x1D706}+16)$
(
$D=Ca(19\unicode[STIX]{x1D706}+16)/(16\unicode[STIX]{x1D706}+16)$
(
![]() $\unicode[STIX]{x1D706}$
is the viscosity ratio) (Taylor Reference Taylor1934) for the entire range of the
$\unicode[STIX]{x1D706}$
is the viscosity ratio) (Taylor Reference Taylor1934) for the entire range of the
![]() $Ca$
considered here, the deviation also resulting from the interactions. The average drop inclination angle plotted in the same figure (figure 9) shows a decrease as also predicted by the small deformation perturbative analysis
$Ca$
considered here, the deviation also resulting from the interactions. The average drop inclination angle plotted in the same figure (figure 9) shows a decrease as also predicted by the small deformation perturbative analysis
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/4-Ca(2\unicode[STIX]{x1D706}+3)(19\unicode[STIX]{x1D706}+16)/(80\unicode[STIX]{x1D706}+80)$
(Chaffey & Brenner Reference Chaffey and Brenner1967).
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/4-Ca(2\unicode[STIX]{x1D706}+3)(19\unicode[STIX]{x1D706}+16)/(80\unicode[STIX]{x1D706}+80)$
(Chaffey & Brenner Reference Chaffey and Brenner1967).

Figure 10. Schematic showing two approaching drops in three different regimes of
![]() $Ca$
to explain the non-monotonic dependence of
$Ca$
to explain the non-monotonic dependence of
![]() $f_{2}$
on
$f_{2}$
on
![]() $Ca$
. The overlapping region increases initially and then decreases.
$Ca$
. The overlapping region increases initially and then decreases.
Table 3. Tabulated values of
![]() $f_{2}$
using two methods, (i) from standard deviation of the droplet position and (ii) width of the concentration profile.
$f_{2}$
using two methods, (i) from standard deviation of the droplet position and (ii) width of the concentration profile.

Figure 10 explains the effects of competition between increasing deformation and decreasing inclination with increasing
![]() $Ca$
. For small
$Ca$
. For small
![]() $Ca$
, increased deformation with increasing
$Ca$
, increased deformation with increasing
![]() $Ca$
enhances the irreversible relative displacement between droplets upon interactions increasing the diffusivity. However, with larger increase in
$Ca$
enhances the irreversible relative displacement between droplets upon interactions increasing the diffusivity. However, with larger increase in
![]() $Ca$
, as the angle of inclination decreases, the drops are more aligned, allowing sliding, and eventually this effect overcomes the other, decreasing the diffusivity above
$Ca$
, as the angle of inclination decreases, the drops are more aligned, allowing sliding, and eventually this effect overcomes the other, decreasing the diffusivity above
![]() $Ca\sim 0.2$
. The non-monotonic variation in relative displacement in the pair collisions between drops in shear has been investigated in detail in the past (Olapade et al.
Reference Olapade, Singh and Sarkar2009). Loewenberg & Hinch (Reference Loewenberg and Hinch1997) also found non-monotonicity in self-diffusivity versus
$Ca\sim 0.2$
. The non-monotonic variation in relative displacement in the pair collisions between drops in shear has been investigated in detail in the past (Olapade et al.
Reference Olapade, Singh and Sarkar2009). Loewenberg & Hinch (Reference Loewenberg and Hinch1997) also found non-monotonicity in self-diffusivity versus
![]() $Ca$
, and attributed it to the subtle difference in pairwise interactions between initially closely spaced drops at low and high
$Ca$
, and attributed it to the subtle difference in pairwise interactions between initially closely spaced drops at low and high
![]() $Ca$
numbers. At low
$Ca$
numbers. At low
![]() $Ca$
, initially closely spaced drops experience higher post-collision net displacements in their streamlines compared to drops which are initially far apart; the converse is true at higher
$Ca$
, initially closely spaced drops experience higher post-collision net displacements in their streamlines compared to drops which are initially far apart; the converse is true at higher
![]() $Ca$
. The authors argued that the balance between the decreasing near-field influence and the increasing far-field influence may have caused the non-monotonicity. Finally, we fitted the simulated values of
$Ca$
. The authors argued that the balance between the decreasing near-field influence and the increasing far-field influence may have caused the non-monotonicity. Finally, we fitted the simulated values of
![]() $f_{2}$
for different
$f_{2}$
for different
![]() $Ca$
by a quadratic curve and obtained a phenomenological relation
$Ca$
by a quadratic curve and obtained a phenomenological relation
The relation has been plotted in figure 8.
4.5 Comparison with past experiments and theory
The only experimental measurement of
![]() $f_{2}$
available in the literature is the one reported by Hudson (Reference Hudson2003), who used drops of poly(propylene glycol) or poly(ethylene-alt-propylene) dispersed in poly(ethylene glycol). We ran simulations with material properties and a capillary number corresponding to this experiment and computed the diffusivity. The comparison with the experiment, shown in table 4, is very good at
$f_{2}$
available in the literature is the one reported by Hudson (Reference Hudson2003), who used drops of poly(propylene glycol) or poly(ethylene-alt-propylene) dispersed in poly(ethylene glycol). We ran simulations with material properties and a capillary number corresponding to this experiment and computed the diffusivity. The comparison with the experiment, shown in table 4, is very good at
![]() $Ca=0.23$
but shows some departure at
$Ca=0.23$
but shows some departure at
![]() $Ca=0.05$
. At the large value of
$Ca=0.05$
. At the large value of
![]() $Ca=0.40$
, the simulation indicated drop break-up. In search of possible reasons for the difference between the computed results and measurements, one notes that the current simulation is for a purely monodisperse system and without any coalescence. However, Hudson noted that in their experiment the coalescence is rare and polydispersity is minor (the ratio between volume averaged and number averaged radii is
$Ca=0.40$
, the simulation indicated drop break-up. In search of possible reasons for the difference between the computed results and measurements, one notes that the current simulation is for a purely monodisperse system and without any coalescence. However, Hudson noted that in their experiment the coalescence is rare and polydispersity is minor (the ratio between volume averaged and number averaged radii is
![]() ${\sim}1.2$
).
${\sim}1.2$
).
Table 4. Comparison of the diffusivity calculated from the present simulations compared to the experimental values reported by Hudson (Reference Hudson2003).

In the limit of
![]() $Ca\rightarrow 0$
, the collective diffusivity for an emulsion of spherical drops was inferred from two drop interactions to be
$Ca\rightarrow 0$
, the collective diffusivity for an emulsion of spherical drops was inferred from two drop interactions to be
![]() ${\sim}0.20$
(Ramachandran, Loewenberg & Leighton Reference Ramachandran, Loewenberg and Leighton2010), which matches with the value obtained by extrapolating the present numerical result. There have been no other computations of
${\sim}0.20$
(Ramachandran, Loewenberg & Leighton Reference Ramachandran, Loewenberg and Leighton2010), which matches with the value obtained by extrapolating the present numerical result. There have been no other computations of
![]() $f_{2}$
in the literature. Grandchamp et al. (Reference Grandchamp, Coupier, Srivastav, Minetti and Podgorski2013) reported a value of
$f_{2}$
in the literature. Grandchamp et al. (Reference Grandchamp, Coupier, Srivastav, Minetti and Podgorski2013) reported a value of
![]() ${\sim}0.77$
(rescaled by particle volume) for red blood cells. Loewenberg & Hinch (Reference Loewenberg and Hinch1997) used boundary element simulation of pair collisions to obtain self-diffusivity 8–9 times smaller than the gradient diffusivity calculated here. As noted before, for emulsions, effort to compute the gradient diffusivity by integrating all possible pair collisions has been frustrated due to divergence of the integrals. However, for rough spheres pair collisions can be used to predict both diffusivities and the ratio of gradient to self-diffusivity has been found to be
${\sim}0.77$
(rescaled by particle volume) for red blood cells. Loewenberg & Hinch (Reference Loewenberg and Hinch1997) used boundary element simulation of pair collisions to obtain self-diffusivity 8–9 times smaller than the gradient diffusivity calculated here. As noted before, for emulsions, effort to compute the gradient diffusivity by integrating all possible pair collisions has been frustrated due to divergence of the integrals. However, for rough spheres pair collisions can be used to predict both diffusivities and the ratio of gradient to self-diffusivity has been found to be
![]() ${\sim}6$
(da Cunha & Hinch Reference da Cunha and Hinch1996), similar to what has been found here.
${\sim}6$
(da Cunha & Hinch Reference da Cunha and Hinch1996), similar to what has been found here.
4.6 Collective diffusivity computed using dynamic structure factor
As noted in the Introduction, Leshansky & Brady (Reference Leshansky and Brady2005) provided an elegant means of computing the collective diffusivity of a rigid sphere suspension from the simulation of a statistically homogeneous suspension in simple shear. It is based on the fact that even in a homogeneous system, stochastic fluctuations appear spontaneously and their decay can be used to compute self- as well as collective diffusivities (Morris & Brady Reference Morris and Brady1996). However, collective diffusivity intrinsically is a property of a non-homogeneous system with concentration gradients. Therefore, it will be of interest to apply any methodology for computing collective diffusivity to a non-homogeneous system. Here, we apply the method proposed by the above authors to our system, get an estimate of the collective diffusivity, qualitatively compare with the values obtained in the previous section and discuss the applicability of the results.
The dynamic structure factor approach to obtaining the collective diffusivity stemmed from the theory of dynamic light scattering, where the scattered response of a monochromatic beam of a laser from a scattering volume containing multiple scatterers (large macromolecules such as DNA, proteins, amino acids, viruses and bacteria) is measured. The scattered field fluctuates due to thermal fluctuations of the molecules and can provide structural and dynamic information about the system (Berne & Pecora Reference Berne and Pecora1976). For an infinitely dilute system of non-interacting scatterers, the autocorrelation of the fluctuation decays exponentially and the decay time is inversely proportional to the diffusivity. For concentrated systems, the fluctuating particle motions are however affected by their hydrodynamic interactions and the experimental observations require careful analysis (Altenberger & Deutch Reference Altenberger and Deutch1973; Altenberger Reference Altenberger1979; Russel & Glendinning Reference Russel and Glendinning1981) and proper interpretation, which then could furnish the collective or self-diffusivity (Rallison & Hinch Reference Rallison and Hinch1986) in appropriate limits. Leshansky & Brady (Reference Leshansky and Brady2005) carefully described the theory and applied it to shear-induced diffusion. Here, we briefly sketch the argument. Note that the analysis would lose its validity in the case of drop coalescence or break-up which are not considered here. In dynamic light scattering, the scattered light corresponding to the scattered wavenumber
![]() $\boldsymbol{k}$
(non-dimensionalized by
$\boldsymbol{k}$
(non-dimensionalized by
![]() $a$
) from
$a$
) from
![]() $N$
scatterers located at
$N$
scatterers located at
![]() $\boldsymbol{x}_{\unicode[STIX]{x1D6FC}}^{\prime }(t^{\prime })$
,
$\boldsymbol{x}_{\unicode[STIX]{x1D6FC}}^{\prime }(t^{\prime })$
,
![]() $\unicode[STIX]{x1D6FC}=1,2,\ldots ,N$
is proportional to the intermediate scattering function
$\unicode[STIX]{x1D6FC}=1,2,\ldots ,N$
is proportional to the intermediate scattering function
Note that by the property of the Dirac delta function, the number density of the scatterers (here droplets) and its spatial Fourier transform can be written as
Therefore,
![]() $F(\boldsymbol{k},t^{\prime })=1/N\langle \hat{n}(\boldsymbol{k},t^{\prime })\hat{n}^{\ast }(\boldsymbol{k},0)\rangle$
may be regarded as measuring the autocorrelation of the fluctuation
$F(\boldsymbol{k},t^{\prime })=1/N\langle \hat{n}(\boldsymbol{k},t^{\prime })\hat{n}^{\ast }(\boldsymbol{k},0)\rangle$
may be regarded as measuring the autocorrelation of the fluctuation
![]() $n^{\prime }(\boldsymbol{x}^{\prime },t^{\prime })$
(where
$n^{\prime }(\boldsymbol{x}^{\prime },t^{\prime })$
(where
![]() $n(\boldsymbol{x}^{\prime },t)=n_{o}+n^{\prime }(\boldsymbol{x}^{\prime },t^{\prime })$
) at wavenumber
$n(\boldsymbol{x}^{\prime },t)=n_{o}+n^{\prime }(\boldsymbol{x}^{\prime },t^{\prime })$
) at wavenumber
![]() $\boldsymbol{k}$
for a statistically homogeneous system, as the constant background
$\boldsymbol{k}$
for a statistically homogeneous system, as the constant background
![]() $n_{o}$
would not contribute to the autocorrelation. Our system is not homogeneous, but evolves from a non-homogeneous initial condition with a strong concentration gradient. However, one can note the following. Leshansky & Brady (Reference Leshansky and Brady2005) showed that the theory assumes a model of the number density satisfying an advection diffusion equation in a shear flow
$n_{o}$
would not contribute to the autocorrelation. Our system is not homogeneous, but evolves from a non-homogeneous initial condition with a strong concentration gradient. However, one can note the following. Leshansky & Brady (Reference Leshansky and Brady2005) showed that the theory assumes a model of the number density satisfying an advection diffusion equation in a shear flow
![]() $\boldsymbol{U}+\dot{\unicode[STIX]{x1D71E}}\boldsymbol{\cdot }\boldsymbol{x}$
(
$\boldsymbol{U}+\dot{\unicode[STIX]{x1D71E}}\boldsymbol{\cdot }\boldsymbol{x}$
(
![]() $\boldsymbol{U}$
is the average flow and
$\boldsymbol{U}$
is the average flow and
![]() $\dot{\unicode[STIX]{x1D71E}}$
is the velocity gradient tensor):
$\dot{\unicode[STIX]{x1D71E}}$
is the velocity gradient tensor):
One can use the same governing equation here, but unlike the homogeneous case considered by the previous authors, the initial condition for (4.5) here is different and represents the droplets concentrated in the central layer. Therefore, whereas the concentration variation in the previous case results from the fluctuations caused by the interactions of moving drops, here we introduce an initial inhomogeneous concentration variation. But (4.5) is linear and therefore, the different wavenumber components
![]() $\hat{n}(\boldsymbol{k},t^{\prime })$
are independent and the theory remains valid. One possible concern is the value of the diffusivity obtained being dependent on the strength of the variation and, in principle, one has to calculate for different strengths and the results extrapolated to zero as was also argued by Marchioro & Acrivos (Reference Marchioro and Acrivos2001) for one of their proposed methods for the computation of collective diffusivity. (Note that (4.5) is slightly different from the one in Leshansky & Brady (Reference Leshansky and Brady2005), where a non-local Fick’s law of diffusion was used to mathematically derive the expression governing the wavenumber dependent diffusivity in the Fourier domain. Alternatively one can postulate an independent linear Fick’s law in the Fourier domain (Russel & Glendinning Reference Russel and Glendinning1981).)
$\hat{n}(\boldsymbol{k},t^{\prime })$
are independent and the theory remains valid. One possible concern is the value of the diffusivity obtained being dependent on the strength of the variation and, in principle, one has to calculate for different strengths and the results extrapolated to zero as was also argued by Marchioro & Acrivos (Reference Marchioro and Acrivos2001) for one of their proposed methods for the computation of collective diffusivity. (Note that (4.5) is slightly different from the one in Leshansky & Brady (Reference Leshansky and Brady2005), where a non-local Fick’s law of diffusion was used to mathematically derive the expression governing the wavenumber dependent diffusivity in the Fourier domain. Alternatively one can postulate an independent linear Fick’s law in the Fourier domain (Russel & Glendinning Reference Russel and Glendinning1981).)
In spite of the advection terms in (4.5), in a simple shear due to the orthogonality of the
![]() $\boldsymbol{k}(=k\hat{\boldsymbol{y}})$
vector to the velocity field, one obtains a simple relation for the diffusivity in the gradient direction (Leshansky & Brady Reference Leshansky and Brady2005):
$\boldsymbol{k}(=k\hat{\boldsymbol{y}})$
vector to the velocity field, one obtains a simple relation for the diffusivity in the gradient direction (Leshansky & Brady Reference Leshansky and Brady2005):
Note that instead of
![]() $F$
, if one uses the self-intermediate scattering function
$F$
, if one uses the self-intermediate scattering function
![]() $F_{s}$
defined by
$F_{s}$
defined by
one obtains long-term self-diffusivity
![]() $D_{s,yy}^{\infty }$
from the same equation (4.6) (Morris & Brady Reference Morris and Brady1996). We compute
$D_{s,yy}^{\infty }$
from the same equation (4.6) (Morris & Brady Reference Morris and Brady1996). We compute
![]() $F(\boldsymbol{k},t^{\prime })$
according to (4.3) using the simulated drop evolution data positions after eliminating the initial part (
$F(\boldsymbol{k},t^{\prime })$
according to (4.3) using the simulated drop evolution data positions after eliminating the initial part (
![]() $t_{0}^{\prime }=20$
). The resulting intermediate scattering functions are averaged over overlapping intervals to obtain a smooth time evolution curve as was also executed by Leshansky & Brady (Reference Leshansky and Brady2005). In figure 11(a), we plot
$t_{0}^{\prime }=20$
). The resulting intermediate scattering functions are averaged over overlapping intervals to obtain a smooth time evolution curve as was also executed by Leshansky & Brady (Reference Leshansky and Brady2005). In figure 11(a), we plot
![]() $-\!\ln F(\boldsymbol{k}^{\prime },t)/k^{2}$
for
$-\!\ln F(\boldsymbol{k}^{\prime },t)/k^{2}$
for
![]() $Ca=0.05$
for different wavenumbers normalizing their initial values. They show a linear growth with time and the curves tend to converge to a single curve in the small
$Ca=0.05$
for different wavenumbers normalizing their initial values. They show a linear growth with time and the curves tend to converge to a single curve in the small
![]() $k$
limit. Accordingly, the slope of the curves asymptotes to a value as
$k$
limit. Accordingly, the slope of the curves asymptotes to a value as
![]() $k\rightarrow 0$
(large length scale limit), as shown in figure 11(c) for different
$k\rightarrow 0$
(large length scale limit), as shown in figure 11(c) for different
![]() $Ca$
values. Figure 11(d) plots this asymptotic value of the slope, i.e. the collective diffusivity
$Ca$
values. Figure 11(d) plots this asymptotic value of the slope, i.e. the collective diffusivity
![]() $D_{c,yy}$
(non-dimensionalized by
$D_{c,yy}$
(non-dimensionalized by
![]() $a$
and
$a$
and
![]() $\dot{\unicode[STIX]{x1D6FE}}$
) as a function of
$\dot{\unicode[STIX]{x1D6FE}}$
) as a function of
![]() $Ca$
. Similar to
$Ca$
. Similar to
![]() $f_{2}$
in figure 8,
$f_{2}$
in figure 8,
![]() $D_{c,yy}$
shows a non-monotonic behaviour with
$D_{c,yy}$
shows a non-monotonic behaviour with
![]() $Ca$
. Due to the spatial variation and continuous decrease in the local volume fraction
$Ca$
. Due to the spatial variation and continuous decrease in the local volume fraction
![]() $\unicode[STIX]{x1D711}(y^{\prime },t^{\prime })$
with time, one cannot directly compare the two values. However, the approximate ratio
$\unicode[STIX]{x1D711}(y^{\prime },t^{\prime })$
with time, one cannot directly compare the two values. However, the approximate ratio
![]() $D_{c,yy}/f_{2}\sim 0.1$
can be recognized as an average
$D_{c,yy}/f_{2}\sim 0.1$
can be recognized as an average
![]() $\unicode[STIX]{x1D711}\sim 0.1$
starting with a maximum local value of 0.25 (see figure 3
b).
$\unicode[STIX]{x1D711}\sim 0.1$
starting with a maximum local value of 0.25 (see figure 3
b).

Figure 11. (a) The dependence of
![]() $-\!\ln F(\boldsymbol{k},t^{\prime })/k^{2}$
on time for various wavenumbers obtained from individual particle positions. (b) The same computed using the autocorrelation function of the fitted parabolic concentration profile. (c) Slope of
$-\!\ln F(\boldsymbol{k},t^{\prime })/k^{2}$
on time for various wavenumbers obtained from individual particle positions. (b) The same computed using the autocorrelation function of the fitted parabolic concentration profile. (c) Slope of
![]() $-\!\ln F(\boldsymbol{k},t^{\prime })/k^{2}$
as a function of the wavenumber for both the previous calculations showing similar values. (d) Slope of
$-\!\ln F(\boldsymbol{k},t^{\prime })/k^{2}$
as a function of the wavenumber for both the previous calculations showing similar values. (d) Slope of
![]() $-\!\ln F(\boldsymbol{k},t^{\prime })/k^{2}$
at the lowest wavenumber obtained from both calculations. The dependence on
$-\!\ln F(\boldsymbol{k},t^{\prime })/k^{2}$
at the lowest wavenumber obtained from both calculations. The dependence on
![]() $Ca$
is similar to what was obtained for
$Ca$
is similar to what was obtained for
![]() $f_{2}$
versus
$f_{2}$
versus
![]() $Ca$
(figure 8).
$Ca$
(figure 8).
As noted before, unlike in Leshansky & Brady (Reference Leshansky and Brady2005), the results here are obtained from the evolution of an initially prescribed inhomogeneity instead of spontaneously occurring fluctuations. The scaled parabolic evolution (3.2) of the imposed initial condition also explains the increasing trend of the slope of
![]() $-\!\ln F(\boldsymbol{k},t^{\prime })/k^{2}$
with
$-\!\ln F(\boldsymbol{k},t^{\prime })/k^{2}$
with
![]() $k$
in figure 11(c). To further elucidate this fact, we interrogate the parabolic concentration profile
$k$
in figure 11(c). To further elucidate this fact, we interrogate the parabolic concentration profile
![]() $\bar{n}(y^{\prime },t^{\prime })=3\unicode[STIX]{x1D711}(y^{\prime },t^{\prime })/4\unicode[STIX]{x03C0}a^{3}$
fitted at successive time instants from the simulated droplet positions (as in figure 3
b). We compute fast Fourier transform (FFT) of the data
$\bar{n}(y^{\prime },t^{\prime })=3\unicode[STIX]{x1D711}(y^{\prime },t^{\prime })/4\unicode[STIX]{x03C0}a^{3}$
fitted at successive time instants from the simulated droplet positions (as in figure 3
b). We compute fast Fourier transform (FFT) of the data
![]() $\hat{\bar{n}}(k,t^{\prime })$
and find the corresponding autocorrelation
$\hat{\bar{n}}(k,t^{\prime })$
and find the corresponding autocorrelation
![]() $\bar{F}(k,t^{\prime })=1/N\langle \hat{\bar{n}}(k,t^{\prime })\hat{\bar{n}}^{\ast }(k,0)\rangle$
. The time evolution was averaged following a procedure identical to the one for
$\bar{F}(k,t^{\prime })=1/N\langle \hat{\bar{n}}(k,t^{\prime })\hat{\bar{n}}^{\ast }(k,0)\rangle$
. The time evolution was averaged following a procedure identical to the one for
![]() $F(\boldsymbol{k},t^{\prime })$
. For
$F(\boldsymbol{k},t^{\prime })$
. For
![]() $Ca=0.05$
in figure 11(b),
$Ca=0.05$
in figure 11(b),
![]() $-\!\ln \bar{F}(k,t^{\prime })/k^{2}$
shows behaviour very similar to that of
$-\!\ln \bar{F}(k,t^{\prime })/k^{2}$
shows behaviour very similar to that of
![]() $-\!\ln F(\boldsymbol{k},t^{\prime })/k^{2}$
shown in figure 11(a) derived directly from the discrete particle positions. The slopes at different
$-\!\ln F(\boldsymbol{k},t^{\prime })/k^{2}$
shown in figure 11(a) derived directly from the discrete particle positions. The slopes at different
![]() $k$
and
$k$
and
![]() $Ca$
from the fitted parabolic profiles plotted in figure 11(c) also follow the same curve. In figure 11(d), the dashed line from this procedure matches the one computed from discrete positions directly. Therefore, we emphasize that the increasing trend of the slope of
$Ca$
from the fitted parabolic profiles plotted in figure 11(c) also follow the same curve. In figure 11(d), the dashed line from this procedure matches the one computed from discrete positions directly. Therefore, we emphasize that the increasing trend of the slope of
![]() $-\!\ln F(\boldsymbol{k},t^{\prime })/k^{2}$
in figure 11(c) arises from the nonlinear diffusion of the imposed initial condition. For the same reason, interpretation of the values of
$-\!\ln F(\boldsymbol{k},t^{\prime })/k^{2}$
in figure 11(c) arises from the nonlinear diffusion of the imposed initial condition. For the same reason, interpretation of the values of
![]() $-\!\ln F(\boldsymbol{k},t^{\prime })/k^{2}$
for higher
$-\!\ln F(\boldsymbol{k},t^{\prime })/k^{2}$
for higher
![]() $k$
as wavenumber dependent diffusivity is not possible here. Note that in the limit of
$k$
as wavenumber dependent diffusivity is not possible here. Note that in the limit of
![]() $k\rightarrow \infty$
, in (4.3) due to the large variations in the phase factors for terms corresponding to
$k\rightarrow \infty$
, in (4.3) due to the large variations in the phase factors for terms corresponding to
![]() $\unicode[STIX]{x1D6FC}\neq \unicode[STIX]{x1D6FD}$
results in
$\unicode[STIX]{x1D6FC}\neq \unicode[STIX]{x1D6FD}$
results in
![]() $F(\boldsymbol{k},t^{\prime })\rightarrow F_{s}(\boldsymbol{k},t^{\prime })$
(Rallison & Hinch Reference Rallison and Hinch1986; Leshansky & Brady Reference Leshansky and Brady2005). Therefore, the slope of
$F(\boldsymbol{k},t^{\prime })\rightarrow F_{s}(\boldsymbol{k},t^{\prime })$
(Rallison & Hinch Reference Rallison and Hinch1986; Leshansky & Brady Reference Leshansky and Brady2005). Therefore, the slope of
![]() $-\!\ln F(\boldsymbol{k},t^{\prime })/k^{2}$
in this limit gives rise to self-diffusivity. However, with the small system size (which becomes more acute for the single summation in (4.7)), the values of self-diffusivity computed using (4.7) were too noisy to be quantitatively useful, although they were of the right magnitude (smaller by a factor of 5 compared to the gradient diffusivity). In any event, the above analysis demonstrates that the procedure for computation of dynamic structure factor and correspondingly the collective diffusivity can also be applied to inhomogeneous systems. We also note the following about our method vis-à-vis the dynamic structure factor method. In a statistically homogeneous or non-homogeneous (as in here) system, the accuracy of the results obtained from a particular analysis, to which one subjects the experimental or the simulated data (e.g. the droplet positions here) depends on the validity of the assumptions of the theory underlying the analysis. The dynamic structure factor theory assumes a linear governing equation (4.5), whereas the results obtained before based on the observed
$-\!\ln F(\boldsymbol{k},t^{\prime })/k^{2}$
in this limit gives rise to self-diffusivity. However, with the small system size (which becomes more acute for the single summation in (4.7)), the values of self-diffusivity computed using (4.7) were too noisy to be quantitatively useful, although they were of the right magnitude (smaller by a factor of 5 compared to the gradient diffusivity). In any event, the above analysis demonstrates that the procedure for computation of dynamic structure factor and correspondingly the collective diffusivity can also be applied to inhomogeneous systems. We also note the following about our method vis-à-vis the dynamic structure factor method. In a statistically homogeneous or non-homogeneous (as in here) system, the accuracy of the results obtained from a particular analysis, to which one subjects the experimental or the simulated data (e.g. the droplet positions here) depends on the validity of the assumptions of the theory underlying the analysis. The dynamic structure factor theory assumes a linear governing equation (4.5), whereas the results obtained before based on the observed
![]() ${\sim}t^{1/3}$
scaling indicates a nonlinear diffusion (3.2) with
${\sim}t^{1/3}$
scaling indicates a nonlinear diffusion (3.2) with
![]() $D_{c,yy}$
linear in
$D_{c,yy}$
linear in
![]() $\unicode[STIX]{x1D711}$
or
$\unicode[STIX]{x1D711}$
or
![]() $n$
. One can apply dynamic structure factor theory to simulations performed at different volume fractions, and obtain volume fraction dependence of diffusivity, as was executed by Leshansky & Brady (Reference Leshansky and Brady2005). However, the implicit assumption is that during the time of analysis the variation in the fluctuation remains sufficiently small so that the linear theory remains. Nonetheless, we argue that different analytical procedures can provide fruitful information about a system as long as their underlying assumptions are kept in mind.
$n$
. One can apply dynamic structure factor theory to simulations performed at different volume fractions, and obtain volume fraction dependence of diffusivity, as was executed by Leshansky & Brady (Reference Leshansky and Brady2005). However, the implicit assumption is that during the time of analysis the variation in the fluctuation remains sufficiently small so that the linear theory remains. Nonetheless, we argue that different analytical procedures can provide fruitful information about a system as long as their underlying assumptions are kept in mind.
5 Summary and concluding remarks
In summary, we have used fully resolved numerical simulations to compute the gradient or collective diffusivity of viscous drops in a sheared emulsion. We used two slightly different methods – the width of a fitted concentration profile, and the standard deviation of the droplet positions – using a relatively small number (70) of droplets. Both yielded very similar results and were roughly consistent with the single experimental observation available in the literature, as well as the limit value of a previous theoretical computation. The collective diffusivity was seen to vary non-monotonically with
![]() $Ca$
, due to the competition between the increasing deformation and decreasing inclination in the underlying drop dynamics, which in turn affects the drop–drop collision. An empirical correlation has been developed to describe the
$Ca$
, due to the competition between the increasing deformation and decreasing inclination in the underlying drop dynamics, which in turn affects the drop–drop collision. An empirical correlation has been developed to describe the
![]() $Ca$
dependence. We also applied an alternative method of computing collective diffusivity, using the dynamic structure factor, that was originally developed for statistically homogeneous suspensions. Although the results could not be directly compared, as the system is inhomogeneous, we show that the results from the alternative method when appropriately interpreted are in qualitative agreement with those from the other method including the prediction of the non-monotonic variation with capillary number. It indicates that the structure factor based method could provide valuable information even in a non-homogeneous system. In future, effects of viscosity ratio variation as well as more complex systems such as suspensions of capsules or vesicles will be investigated.
$Ca$
dependence. We also applied an alternative method of computing collective diffusivity, using the dynamic structure factor, that was originally developed for statistically homogeneous suspensions. Although the results could not be directly compared, as the system is inhomogeneous, we show that the results from the alternative method when appropriately interpreted are in qualitative agreement with those from the other method including the prediction of the non-monotonic variation with capillary number. It indicates that the structure factor based method could provide valuable information even in a non-homogeneous system. In future, effects of viscosity ratio variation as well as more complex systems such as suspensions of capsules or vesicles will be investigated.
Acknowledgements
K.S. acknowledges partial support from George Washington University. The authors acknowledge time on Colonial One cluster at GWU. The computation was also performed using the Comet cluster at the San Diego Supercomputer Center, through the Extreme Science and Engineering Discovery Environment (XSEDE) program (Towns et al. Reference Towns, Cockerill, Dahan, Foster, Gaither, Grimshaw, Hazlewood, Lathrop, Lifka, Peterson, Roskies, Scott and Wilkins-Diehr2014), which is supported by National Science Foundation grant no. ACI-1548562.
Supplementary movie
Supplementary movie is available at https://doi.org/10.1017/jfm.2019.122.