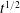1 Introduction
We previously reported (Walls et al.
Reference Walls, Haward, Shen and Fuller2016) on an experimental study of the spreading of sessile drops along with initial observations of the shape evolution of pendant drops when immersed within a second, miscible liquid. Through a series of experiments involving several pairs of miscible liquids and various imaging techniques, including particle tracking velocimetry (PTV) and confocal microscopy, we found that the shape evolution and power-law dynamics of sessile drops spreading in a miscible environment are distinctly different from those of sessile drops spreading in immiscible environments, which have been reported elsewhere (Huh & Scriven Reference Huh and Scriven1971; Voinov Reference Voinov1976; Tanner Reference Tanner1979; Didden & Maxworthy Reference Didden and Maxworthy1982; Huppert Reference Huppert1982; Cox Reference Cox1986a
,Reference Cox
b
; Cazabat Reference Cazabat1987; Joanny & Andelman Reference Joanny and Andelman1987; Pismen & Eggers Reference Pismen and Eggers2008; Eddi, Winkels & Snoeijer Reference Eddi, Winkels and Snoeijer2013). We found that two characteristic radii develop during the spreading of a sessile drop in a miscible environment: the radius of the three-phase contact line, and the radius of an elevated portion of the drop that leads its advancement across the surface. A diffusive flux arises across the miscible liquid–liquid interface due to the chemical potential difference between the two initially distinct, homogeneous liquids. This material flux imparts a time dependence to the properties of the liquids in the diffusive region – notably the interfacial tension, density and viscosity – that can influence the shape evolution. The diffuse layer drains downward along the liquid–liquid interface at the upper surface of the sessile drop and into an elevated leading edge of the drop, which grows radially as
![]() $t^{1/2}$
at long times. The contact line moves more slowly, never exceeding the
$t^{1/2}$
at long times. The contact line moves more slowly, never exceeding the
![]() $t^{1/8}$
power law that is found when a sessile drop spreads due to gravity in an immiscible environment across a solid substrate on which it has an equilibrium contact angle of zero. It was concluded that gravitational forces were the primary contributor to fluid motion. Capillary forces and Marangoni stresses were found to be of secondary importance due to the very small interfacial tensions that exist between miscible liquids (Smith, Van De Ven & Mason Reference Smith, Van De Ven and Mason1981; Kojima, Hinch & Acrivos Reference Kojima, Hinch and Acrivos1984; Joseph & Hu Reference Joseph and Hu1991; Pojman et al.
Reference Pojman, Whitmore, Liveri, Lombardo, Marszalek, Parker and Zoltowski2006; Zoltowski et al.
Reference Zoltowski, Chekanov, Masere, Pojman and Volpert2007; Lacaze et al.
Reference Lacaze, Guenoun, Beysens, Delsanti, Petitjeans and Kurowski2010). Measuring the interfacial tension between miscible liquids is inherently challenging due to the very small values and difficulty in establishing a distinct, stationary liquid–liquid interface in the absence of perturbations. Using sessile and pendant drops for measuring interfacial tension between immiscible liquids requires equilibrium or quasi-equilibrium shapes, which contrasts with the dynamic character of our experiments. Truzzolillo & Cipelletti (Reference Truzzolillo and Cipelletti2017) review a range of attempts to measure interfacial tension between miscible liquids, reviewing the limitations of traditional techniques developed for immiscible liquids. Although the interfacial tension between the two miscible liquids was found to be of lesser importance to the shape evolution of these droplets, the dynamics of the three-phase contact line of a sessile drop is influenced by the relative magnitudes of the two surface energies arising between (i) the solid substrate–spreading liquid and (ii) solid substrate–ambient liquid phases, as the two liquids compete to wet the solid surface in order to minimize the total energy of the system.
$t^{1/8}$
power law that is found when a sessile drop spreads due to gravity in an immiscible environment across a solid substrate on which it has an equilibrium contact angle of zero. It was concluded that gravitational forces were the primary contributor to fluid motion. Capillary forces and Marangoni stresses were found to be of secondary importance due to the very small interfacial tensions that exist between miscible liquids (Smith, Van De Ven & Mason Reference Smith, Van De Ven and Mason1981; Kojima, Hinch & Acrivos Reference Kojima, Hinch and Acrivos1984; Joseph & Hu Reference Joseph and Hu1991; Pojman et al.
Reference Pojman, Whitmore, Liveri, Lombardo, Marszalek, Parker and Zoltowski2006; Zoltowski et al.
Reference Zoltowski, Chekanov, Masere, Pojman and Volpert2007; Lacaze et al.
Reference Lacaze, Guenoun, Beysens, Delsanti, Petitjeans and Kurowski2010). Measuring the interfacial tension between miscible liquids is inherently challenging due to the very small values and difficulty in establishing a distinct, stationary liquid–liquid interface in the absence of perturbations. Using sessile and pendant drops for measuring interfacial tension between immiscible liquids requires equilibrium or quasi-equilibrium shapes, which contrasts with the dynamic character of our experiments. Truzzolillo & Cipelletti (Reference Truzzolillo and Cipelletti2017) review a range of attempts to measure interfacial tension between miscible liquids, reviewing the limitations of traditional techniques developed for immiscible liquids. Although the interfacial tension between the two miscible liquids was found to be of lesser importance to the shape evolution of these droplets, the dynamics of the three-phase contact line of a sessile drop is influenced by the relative magnitudes of the two surface energies arising between (i) the solid substrate–spreading liquid and (ii) solid substrate–ambient liquid phases, as the two liquids compete to wet the solid surface in order to minimize the total energy of the system.
This paper is concerned with extending our previous initial observations of pendant drops in miscible environments into a systematic experimental study. In addition, due to the complexity of the spatio-temporal variation in fluid composition and composition-dependent fluid properties, a complementary numerical approach for resolving the composition and velocity fields is undertaken. Matching numerical simulations to experimental observations ensures that the observed phenomena of the experiments are not due to any physical mechanisms excluded from the numerical simulations. Numerical techniques also allow for independent and systematic control of fluid properties such as density differences and the dependence of viscosity on concentration, which is limited in physical experiments due to inherent material properties. This independent control of material parameters can provide additional insights into the independent and collective influence of these parameters on the observed phenomena. We also revisit our study of sessile drops reported previously (Walls et al. Reference Walls, Haward, Shen and Fuller2016), reporting additional experiments and leveraging insights gained from numerical calculations. Further, through considering pendant and sessile configurations together, the adequacy of the numerical procedure can be evaluated for multiple configurations. Additionally, the effect of density differences and the direction of gravity relative to the drop and the diffuse layer can be clarified with regard to the shape evolution of miscible drops: gravity points away from the centre of mass of a pendant drop, pulling it away from the supporting needle, whereas gravity points towards the centre of mass of a sessile drop, pressing it against the solid substrate.
The gravitational, or buoyancy, forces that dominate the shape evolution of droplets in miscible environments arise through differences in density, and lead to so-called free convection. Variations in temperature, pressure and concentration can all influence the density of a fluid; here, concentration is the primary conduit in producing gradients in density, not only due to the different densities of the two homogeneous, miscible liquids, but the diffusion and mixing that occurs across the liquid–liquid interface over time as well. These buoyancy-driven flows are often modest, due to the small changes in density caused through variations in concentration, temperature and pressure. As a result, density is often adequately represented as a linear function of temperature or concentration using a Boussinesq approximation. However, even with such an approximation, the spatial variation of these properties, and possible time dependence, greatly complicates analytical treatments of the problem. Analytical solutions have been found for cases of simplified geometries and time-independent flows, such as Rayleigh–Taylor instabilities, Rayleigh–Bénard films and plate tectonics (Bejan Reference Bejan2013). In scenarios where other sources of convection are present, i.e. forced convection, free convection often can be ignored, depending on their relative magnitudes, which can make finding an analytical solution tractable, as in Whitehead’s paradox (Leal Reference Leal2007) and the work of Acrivos & Goddard (Reference Acrivos and Goddard1965). These studies of forced convection provide a reasonable basis for building intuition and scaling analyses of our experimental observations of free convection.
Two careful studies of miscible liquids by Chen & Meiburg (Reference Chen and Meiburg1996) and Petitjeans & Maxworthy (Reference Petitjeans and Maxworthy1996) examined the forced displacement of a viscous liquid from a capillary tube with a second, less viscous miscible liquid. Petitjeans & Maxworthy (Reference Petitjeans and Maxworthy1996) performed experiments, while Chen & Meiburg (Reference Chen and Meiburg1996) conducted numerical simulations to replicate the experimental observations in order to gain insight into the physical mechanisms present. These two studies provide a basis for the formulation of our numerical analysis and comparison to our experimental results. Petitjeans & Maxworthy (Reference Petitjeans and Maxworthy1996) found varying degrees of effectiveness of displacing the more viscous fluid depending on several dimensionless parameters, namely the Péclet number,
![]() $Pe$
, and a viscosity ratio in the form of an Atwood number,
$Pe$
, and a viscosity ratio in the form of an Atwood number,
![]() $At$
, which are defined as
$At$
, which are defined as
where
![]() $u_{c}$
and
$u_{c}$
and
![]() $l_{c}$
are the characteristic velocity and length, respectively;
$l_{c}$
are the characteristic velocity and length, respectively;
![]() ${\mathcal{D}}_{LA}$
is the diffusion coefficient between the two liquids; and
${\mathcal{D}}_{LA}$
is the diffusion coefficient between the two liquids; and
![]() $\unicode[STIX]{x1D707}_{L}$
and
$\unicode[STIX]{x1D707}_{L}$
and
![]() $\unicode[STIX]{x1D707}_{A}$
are the dynamic viscosities of the displaced and displacing liquids, respectively. For large
$\unicode[STIX]{x1D707}_{A}$
are the dynamic viscosities of the displaced and displacing liquids, respectively. For large
![]() $Pe$
and
$Pe$
and
![]() $At\rightarrow 1$
, a regime similar to that of the findings reported here, they observed a narrow diffuse layer between the two miscible fluids throughout the experiment. The complementary numerical study of Chen & Meiburg (Reference Chen and Meiburg1996) utilized a simplified set of governing equations, discarding terms related to interfacial tension, Korteweg stresses, and other stresses due to dissolution that can arise in a time-dependent fashion within a miscible system, as described by previous authors (Korteweg Reference Korteweg1901; Davis Reference Davis and Wheeler1988; Joseph Reference Joseph1990; Joseph & Hu Reference Joseph and Hu1991; Joseph, Huang & Hu Reference Joseph, Huang and Hu1996; Joseph & Renardy Reference Joseph and Renardy2013). Yet Chen & Meiburg (Reference Chen and Meiburg1996) justified their approximations with scaling analyses of these discarded stresses to viscous ones when
$At\rightarrow 1$
, a regime similar to that of the findings reported here, they observed a narrow diffuse layer between the two miscible fluids throughout the experiment. The complementary numerical study of Chen & Meiburg (Reference Chen and Meiburg1996) utilized a simplified set of governing equations, discarding terms related to interfacial tension, Korteweg stresses, and other stresses due to dissolution that can arise in a time-dependent fashion within a miscible system, as described by previous authors (Korteweg Reference Korteweg1901; Davis Reference Davis and Wheeler1988; Joseph Reference Joseph1990; Joseph & Hu Reference Joseph and Hu1991; Joseph, Huang & Hu Reference Joseph, Huang and Hu1996; Joseph & Renardy Reference Joseph and Renardy2013). Yet Chen & Meiburg (Reference Chen and Meiburg1996) justified their approximations with scaling analyses of these discarded stresses to viscous ones when
![]() $Pe$
is large and
$Pe$
is large and
![]() $At\rightarrow 1$
, showing close agreement between their simulations and the experiments of Petitjeans & Maxworthy (Reference Petitjeans and Maxworthy1996). This limit represents the experiments and pairs of miscible liquids of our study. However, the concerns outlined in Joseph & Hu (Reference Joseph and Hu1991) proved in certain parameter regimes explored by Petitjeans & Maxworthy (Reference Petitjeans and Maxworthy1996) and Chen & Meiburg (Reference Chen and Meiburg1996) to be consequential. Thus, subsequent studies by Chen & Meiburg (Reference Chen and Meiburg2002), Kuang, Maxworthy & Petitjeans (Reference Kuang, Maxworthy and Petitjeans2003), Kuang, Petitjeans & Maxworthy (Reference Kuang, Petitjeans and Maxworthy2004), Balasubramaniam et al. (Reference Balasubramaniam, Rashidnia, Maxworthy and Kuang2005) and Vanaparthy & Meiburg (Reference Vanaparthy and Meiburg2008) were conducted to expand the initial studies, exploring additional experimental materials and numerical details.
$At\rightarrow 1$
, showing close agreement between their simulations and the experiments of Petitjeans & Maxworthy (Reference Petitjeans and Maxworthy1996). This limit represents the experiments and pairs of miscible liquids of our study. However, the concerns outlined in Joseph & Hu (Reference Joseph and Hu1991) proved in certain parameter regimes explored by Petitjeans & Maxworthy (Reference Petitjeans and Maxworthy1996) and Chen & Meiburg (Reference Chen and Meiburg1996) to be consequential. Thus, subsequent studies by Chen & Meiburg (Reference Chen and Meiburg2002), Kuang, Maxworthy & Petitjeans (Reference Kuang, Maxworthy and Petitjeans2003), Kuang, Petitjeans & Maxworthy (Reference Kuang, Petitjeans and Maxworthy2004), Balasubramaniam et al. (Reference Balasubramaniam, Rashidnia, Maxworthy and Kuang2005) and Vanaparthy & Meiburg (Reference Vanaparthy and Meiburg2008) were conducted to expand the initial studies, exploring additional experimental materials and numerical details.
Another set of careful studies concerning miscible liquids were carried out by Didden & Maxworthy (Reference Didden and Maxworthy1982) and Huppert (Reference Huppert1982) in order to determine how a liquid spreads across a solid substrate when present in a miscible environment. Didden & Maxworthy (Reference Didden and Maxworthy1982) observed salt solutions spreading across a solid surface while submerged below a body of fresh water. These flows, known as viscous gravity currents, were fed at a constant rate and, in the case of axisymmetric spreading, the radius of the spreading liquid was observed to grow following a power law in time of
![]() $t^{1/2}$
. Huppert (Reference Huppert1982) uses a lubrication analysis balancing viscous and buoyancy forces to develop the theoretical spreading relationship
$t^{1/2}$
. Huppert (Reference Huppert1982) uses a lubrication analysis balancing viscous and buoyancy forces to develop the theoretical spreading relationship
where
![]() $r_{N}$
is the radius of the gravity current that spreads axisymmetrically from a central source at a constant volumetric flow rate,
$r_{N}$
is the radius of the gravity current that spreads axisymmetrically from a central source at a constant volumetric flow rate,
![]() $Q$
, and
$Q$
, and
![]() $\unicode[STIX]{x1D707}_{L}$
is the dynamic viscosity of the gravity current. These analyses form the basis of our scaling developments for sessile drops spreading in miscible environments. Notably, however, their analyses assume that mixing between the two liquids does not occur, as the time scales of their experiments were short, differing from the observations in our experiments with sessile drops.
$\unicode[STIX]{x1D707}_{L}$
is the dynamic viscosity of the gravity current. These analyses form the basis of our scaling developments for sessile drops spreading in miscible environments. Notably, however, their analyses assume that mixing between the two liquids does not occur, as the time scales of their experiments were short, differing from the observations in our experiments with sessile drops.
From this foundation of prior work and our experimental and numerical studies presented here, we hereafter aim to describe the fluid-mechanical mode of the shape evolution of pendant and sessile drops in miscible environments and its time dependence.
2 Experimental
The apparatus used to perform these experiments was developed and described previously (Walls et al. Reference Walls, Haward, Shen and Fuller2016). It allows for the observation of the evolution of both sessile and pendant drops in miscible environments with bright field and particle tracking velocimetry (PTV) imaging techniques.
Pendant drops were formed using liquids such as silicone oils (Clearco Products; 10 000, 60 000 and 100 000 cSt pure silicone fluids) and corn syrup (Karo; light corn syrup). Pendant drops of silicone oils were paired with an ambient liquid of a lower-viscosity silicone oil (1 cSt), and those of corn syrup were paired with deionized water (Milli-Q Academic A10). The density and viscosity of these liquids are displayed in table 1.
Table 1. Properties of the experimental pendant liquids.

The initial volume of pendant drops was varied between 1 nl and
![]() $1~\unicode[STIX]{x03BC}\text{l}$
. Stainless steel and polytetrafluoroethylene (PTFE)-coated stainless steel needles of the diameters 0.159, 0.362, 0.474 and 0.718 mm were used to suspend pendant drops of corn syrup. PTFE-coated stainless steel needles of the diameters 0.474 and 0.718 mm were used to suspend pendant drops of silicone oils.
$1~\unicode[STIX]{x03BC}\text{l}$
. Stainless steel and polytetrafluoroethylene (PTFE)-coated stainless steel needles of the diameters 0.159, 0.362, 0.474 and 0.718 mm were used to suspend pendant drops of corn syrup. PTFE-coated stainless steel needles of the diameters 0.474 and 0.718 mm were used to suspend pendant drops of silicone oils.
Liquids used as sessile drops were silicone oils (Clearco Products; 5, 10, 20, 50, 100, 200, 500, 1000, 5000 and 10 000 cSt pure silicone fluids), corn syrup (Karo; light corn syrup), glycerol (Alfa Aesar; ultrapure HPLC), and tricresyl phosphate (Aldrich; 90 % grade). Sessile drops of silicone oils were paired with ambient liquids of lower-viscosity silicone oils (1, 5, 10 cSt). Corn syrup and glycerol were paired with deionized water (Milli-Q Academic A10). Glycerol and tricresyl phosphate sessile drops were paired with ethanol (Fisher; anhydrous) and isopropanol (Fisher; HPLC). Experiments on hydrophilic and hydrophobic glass surfaces were performed previously (Walls et al. Reference Walls, Haward, Shen and Fuller2016), and we have expanded the study with the addition of two new surfaces, one an oleophobic film (Green Onions Supply; Oleophobic Screen Protector) and the other a Teflon surface. The density, viscosity, contact angles on hydrophilic, hydrophobic, oleophobic and Teflon surfaces in air and surface tension for these liquids are displayed in table 2.
The volumes of sessile drops were varied between 1 and
![]() $20~\unicode[STIX]{x03BC}\text{l}$
without observing a change in the spreading behaviour. Results presented here were gathered from experiments where the target volume of the sessile drops was
$20~\unicode[STIX]{x03BC}\text{l}$
without observing a change in the spreading behaviour. Results presented here were gathered from experiments where the target volume of the sessile drops was
![]() $5~\unicode[STIX]{x03BC}\text{l}$
.
$5~\unicode[STIX]{x03BC}\text{l}$
.
Volatility of the ambient liquids is not influential to the experiments, as the air–ambient liquid interface is sufficiently far from the spreading liquid–ambient liquid interface.
Table 2. Properties of the experimental sessile liquids.

3 Numerical
3.1 Governing equations
The problem to be analysed numerically is that of a liquid drop with a density of
![]() $\unicode[STIX]{x1D70C}_{L}$
and a dynamic viscosity of
$\unicode[STIX]{x1D70C}_{L}$
and a dynamic viscosity of
![]() $\unicode[STIX]{x1D707}_{L}$
immersed in a second, miscible fluid with a density of
$\unicode[STIX]{x1D707}_{L}$
immersed in a second, miscible fluid with a density of
![]() $\unicode[STIX]{x1D70C}_{A}$
and a viscosity of
$\unicode[STIX]{x1D70C}_{A}$
and a viscosity of
![]() $\unicode[STIX]{x1D707}_{A}$
. The liquid drop is either suspended within the ambient environment as a pendant drop, or rests atop a solid substrate, enveloped within the ambient environment as a sessile drop. The numerical simulations are a complement to, and will be discussed alongside, the experiments outlined in § 2. Throughout our derivation, dimensional variables are indicated with a prime,
$\unicode[STIX]{x1D707}_{A}$
. The liquid drop is either suspended within the ambient environment as a pendant drop, or rests atop a solid substrate, enveloped within the ambient environment as a sessile drop. The numerical simulations are a complement to, and will be discussed alongside, the experiments outlined in § 2. Throughout our derivation, dimensional variables are indicated with a prime,
![]() $^{\prime }$
, whereas the absence of a prime indicates a dimensionless variable.
$^{\prime }$
, whereas the absence of a prime indicates a dimensionless variable.
The Reynolds numbers,
![]() $Re$
, of the experiments are
$Re$
, of the experiments are
![]() $O(0.1)$
or less, so we neglect the nonlinear inertial terms within the conservation equations of momentum and start from the equations that govern incompressible Stokes flow. Since there are two liquids upon which to account, an additional equation is required for the conservation of the species mass, for which we use a convection–diffusion equation. This set of equations is commonly used to characterize incompressible, miscible two-component flows:
$O(0.1)$
or less, so we neglect the nonlinear inertial terms within the conservation equations of momentum and start from the equations that govern incompressible Stokes flow. Since there are two liquids upon which to account, an additional equation is required for the conservation of the species mass, for which we use a convection–diffusion equation. This set of equations is commonly used to characterize incompressible, miscible two-component flows:
Here
![]() $\boldsymbol{u}^{\prime }=(u_{1}^{\prime },u_{2}^{\prime },u_{3}^{\prime })$
denotes the fluid velocity vector,
$\boldsymbol{u}^{\prime }=(u_{1}^{\prime },u_{2}^{\prime },u_{3}^{\prime })$
denotes the fluid velocity vector,
![]() $p^{\prime }$
pressure,
$p^{\prime }$
pressure,
![]() $\unicode[STIX]{x1D749}^{\prime }$
the deviatoric stress tensor (which for an incompressible, Newtonian fluid is
$\unicode[STIX]{x1D749}^{\prime }$
the deviatoric stress tensor (which for an incompressible, Newtonian fluid is
![]() $\unicode[STIX]{x1D707}^{\prime }[\unicode[STIX]{x1D735}^{\prime }\boldsymbol{u}^{\prime }+\unicode[STIX]{x1D735}^{\prime }\boldsymbol{u}^{\prime \text{T}}]$
, with
$\unicode[STIX]{x1D707}^{\prime }[\unicode[STIX]{x1D735}^{\prime }\boldsymbol{u}^{\prime }+\unicode[STIX]{x1D735}^{\prime }\boldsymbol{u}^{\prime \text{T}}]$
, with
![]() $\unicode[STIX]{x1D707}^{\prime }$
the dynamic viscosity),
$\unicode[STIX]{x1D707}^{\prime }$
the dynamic viscosity),
![]() $\unicode[STIX]{x1D70C}^{\prime }$
density,
$\unicode[STIX]{x1D70C}^{\prime }$
density,
![]() $g$
the acceleration due to gravity pointing in the direction of the unit vector
$g$
the acceleration due to gravity pointing in the direction of the unit vector
![]() $\hat{\boldsymbol{e}}_{g}$
,
$\hat{\boldsymbol{e}}_{g}$
,
![]() $c$
the concentration of the liquid that forms the drop,
$c$
the concentration of the liquid that forms the drop,
![]() $t^{\prime }$
time and
$t^{\prime }$
time and
![]() ${\mathcal{D}}^{\prime }$
the diffusion coefficient. The concentration
${\mathcal{D}}^{\prime }$
the diffusion coefficient. The concentration
![]() $c$
is dimensionless and is defined relative to the densities of the pure liquids as
$c$
is dimensionless and is defined relative to the densities of the pure liquids as
![]() $(\unicode[STIX]{x1D70C}^{\prime }-\unicode[STIX]{x1D70C}_{A})/(\unicode[STIX]{x1D70C}_{L}-\unicode[STIX]{x1D70C}_{A})$
. Conversely, the concentration of the ambient liquid can be written as
$(\unicode[STIX]{x1D70C}^{\prime }-\unicode[STIX]{x1D70C}_{A})/(\unicode[STIX]{x1D70C}_{L}-\unicode[STIX]{x1D70C}_{A})$
. Conversely, the concentration of the ambient liquid can be written as
![]() $1-c$
. The axisymmetry of the problem allows us to adopt a cylindrical coordinate system, with the
$1-c$
. The axisymmetry of the problem allows us to adopt a cylindrical coordinate system, with the
![]() $z$
-axis either aligned with the central axis of the needle suspending a pendant drop, or orthogonal to the surface upon which a sessile drop rests. This selection simplifies the velocity vector to
$z$
-axis either aligned with the central axis of the needle suspending a pendant drop, or orthogonal to the surface upon which a sessile drop rests. This selection simplifies the velocity vector to
![]() $\boldsymbol{u}^{\prime }=(u_{r}^{\prime },u_{\unicode[STIX]{x1D703}}^{\prime },u_{z}^{\prime })=(u_{r}^{\prime },0,u_{z}^{\prime })$
, and thus we have a two-dimensional flow field. The density, viscosity and diffusion coefficient are assumed to be functions of concentration only,
$\boldsymbol{u}^{\prime }=(u_{r}^{\prime },u_{\unicode[STIX]{x1D703}}^{\prime },u_{z}^{\prime })=(u_{r}^{\prime },0,u_{z}^{\prime })$
, and thus we have a two-dimensional flow field. The density, viscosity and diffusion coefficient are assumed to be functions of concentration only,
and their specific forms are presented below.
As noted in Chen & Meiburg (Reference Chen and Meiburg1996), researchers such as Joseph and coworkers have raised concerns in using the approximate forms listed above for miscible flows. Joseph (Reference Joseph1990) calls out two potentially relevant effects, further elaborated within Joseph & Renardy (Reference Joseph and Renardy2013). The first point, that if the density of the mixture of miscible liquids is dependent on the concentration, indicates that the velocity field is not divergence-free, even for an incompressible fluid, which can be seen directly from the full continuity equation,
Spatial changes in the density of the fluid due to diffusion prevent the divergence of the velocity field from vanishing, which produces additional stresses within the conservation of momentum equations. As noted by Chen & Meiburg (Reference Chen and Meiburg2002), it is difficult to provide an exact value for these stresses, as they depend upon unknown material properties of the mixtures. Joseph & Hu (Reference Joseph and Hu1991), as well as Davis (Reference Davis and Wheeler1988), attend to a second set of additional stresses that can arise between miscible fluids due to differences in chemical potential, which would give rise to a pressure difference across the miscible liquid–liquid interface. Chen & Meiburg (Reference Chen and Meiburg2002) use scaling arguments to show that these two types of stresses are substantially smaller than viscous stresses when
![]() $Pe$
is large and
$Pe$
is large and
![]() $At$
approaches unity. This parameter space corresponds to our experimental regime of interest, and following the scaling approach of Chen & Meiburg (Reference Chen and Meiburg2002) leads us to proceed without including these stresses in the set of governing equations. Comparisons between our experimental and numerical results will provide an additional metric for the validity of the governing equations.
$At$
approaches unity. This parameter space corresponds to our experimental regime of interest, and following the scaling approach of Chen & Meiburg (Reference Chen and Meiburg2002) leads us to proceed without including these stresses in the set of governing equations. Comparisons between our experimental and numerical results will provide an additional metric for the validity of the governing equations.
To arrive at a dimensionless form for the governing equations, we choose a characteristic velocity,
![]() $u_{c}$
, and length,
$u_{c}$
, and length,
![]() $l_{c}$
. As the problem is one of free convection, no velocity is specified at the boundary of the domain and we calculate a characteristic velocity from a balance of viscous and buoyancy forces:
$l_{c}$
. As the problem is one of free convection, no velocity is specified at the boundary of the domain and we calculate a characteristic velocity from a balance of viscous and buoyancy forces:
The characteristic length is assigned as the diameter of the needle supporting a pendant drop,
![]() $d$
, or the initial radius of a sessile drop,
$d$
, or the initial radius of a sessile drop,
![]() $R_{o}$
. These selections are expected to be upper bounds in both cases, as density and viscosity vary across the domain, taking on intermediate values between those of the pure components. A characteristic pressure is constructed from
$R_{o}$
. These selections are expected to be upper bounds in both cases, as density and viscosity vary across the domain, taking on intermediate values between those of the pure components. A characteristic pressure is constructed from
![]() $\unicode[STIX]{x1D707}_{L}u_{c}/l_{c}$
; the density of the fluid is rendered dimensionless with the difference between the densities of the liquid constituting the drop and the ambient liquid,
$\unicode[STIX]{x1D707}_{L}u_{c}/l_{c}$
; the density of the fluid is rendered dimensionless with the difference between the densities of the liquid constituting the drop and the ambient liquid,
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{L}-\unicode[STIX]{x1D70C}_{A}$
; viscosity with respect to the viscosity of the liquid forming the drop,
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{L}-\unicode[STIX]{x1D70C}_{A}$
; viscosity with respect to the viscosity of the liquid forming the drop,
![]() $\unicode[STIX]{x1D707}_{L}$
; and the diffusion coefficient with respect to
$\unicode[STIX]{x1D707}_{L}$
; and the diffusion coefficient with respect to
![]() ${\mathcal{D}}_{max}$
, the maximum value of the diffusion coefficient, occurring when
${\mathcal{D}}_{max}$
, the maximum value of the diffusion coefficient, occurring when
![]() $c=0$
. This leads to the dimensionless forms of the governing equations:
$c=0$
. This leads to the dimensionless forms of the governing equations:
The governing dimensionless parameters are the Péclet number,
![]() $Pe$
, as before and a gravity number,
$Pe$
, as before and a gravity number,
![]() $F$
:
$F$
:
where
![]() $\unicode[STIX]{x1D708}_{L}$
is the kinematic viscosity of the liquid forming the drop. Values of
$\unicode[STIX]{x1D708}_{L}$
is the kinematic viscosity of the liquid forming the drop. Values of
![]() $Pe$
are between
$Pe$
are between
![]() $O(10^{3})$
and
$O(10^{3})$
and
![]() $O(10^{4})$
for our liquid pairings. Based on our choice of the characteristic velocity in (3.6), the gravity number,
$O(10^{4})$
for our liquid pairings. Based on our choice of the characteristic velocity in (3.6), the gravity number,
![]() $F$
, simplifies to the ratio between the dynamic viscosities of the ambient liquid and the liquid forming the drop, respectively. Thus, the gravity number is an alternate construction to the Atwood number,
$F$
, simplifies to the ratio between the dynamic viscosities of the ambient liquid and the liquid forming the drop, respectively. Thus, the gravity number is an alternate construction to the Atwood number,
![]() $At$
, for representing the viscosity ratio in the governing equations.
$At$
, for representing the viscosity ratio in the governing equations.
Within the problem, both momentum and mass diffuse. Their relative importance is captured in the Schmidt number,
which tends to be large for liquids. In the case of our study,
![]() $Sc$
is
$Sc$
is
![]() $O(10^{4})$
or larger, indicating that convective effects are influential in the species conservation of mass, but not in the conservation of momentum, as can be seen in the governing equations (3.7)–(3.9).
$O(10^{4})$
or larger, indicating that convective effects are influential in the species conservation of mass, but not in the conservation of momentum, as can be seen in the governing equations (3.7)–(3.9).
This leaves us with needing to specify the functional form of the density, viscosity and diffusion coefficient with respect to concentration. A linear relationship between density and concentration is a common and often reasonable approximation, and we write it in dimensionless form here:
The dependence of viscosity on concentration, however, often deviates appreciably from a linear relationship, particularly when the difference in viscosity between the two pure liquids is large. Previous researchers have used a number of mathematical relationships, including linear, exponential and polynomial (Manickam & Homsy Reference Manickam and Homsy1993; Chen & Meiburg Reference Chen and Meiburg1996; Petitjeans & Maxworthy Reference Petitjeans and Maxworthy1996; Yang & Yortsos Reference Yang and Yortsos1997; Vanaparthy & Meiburg Reference Vanaparthy and Meiburg2008), to represent viscosity as a function of concentration. In order to represent our experiments accurately, we measured the viscosity of blends of our liquid pairs to determine its behaviour with respect to concentration. The dependence of dimensionless viscosity on concentration varied amongst our liquid pairs, taking one of the following forms:
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}=\left\{\begin{array}{@{}ll@{}}\text{e}^{R(c-1)}\quad & \text{single exponential},\\ \text{e}^{R((\text{e}^{\text{e}^{c}}-\text{e}^{\text{e}})/(\text{e}^{\text{e}}-\text{e}))}\quad & \text{triple exponential},\\ \displaystyle \frac{1}{\unicode[STIX]{x1D707}_{L}}[\unicode[STIX]{x1D707}_{A}+(\unicode[STIX]{x1D707}_{L}-\unicode[STIX]{x1D707}_{A})c^{5}]\quad & \text{fifth-degree polynomial},\end{array}\right. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}=\left\{\begin{array}{@{}ll@{}}\text{e}^{R(c-1)}\quad & \text{single exponential},\\ \text{e}^{R((\text{e}^{\text{e}^{c}}-\text{e}^{\text{e}})/(\text{e}^{\text{e}}-\text{e}))}\quad & \text{triple exponential},\\ \displaystyle \frac{1}{\unicode[STIX]{x1D707}_{L}}[\unicode[STIX]{x1D707}_{A}+(\unicode[STIX]{x1D707}_{L}-\unicode[STIX]{x1D707}_{A})c^{5}]\quad & \text{fifth-degree polynomial},\end{array}\right. & & \displaystyle\end{eqnarray}$$
where
![]() $R=\ln (\unicode[STIX]{x1D707}_{L}/\unicode[STIX]{x1D707}_{A})$
. The experimental measurements along with the corresponding mathematical representations are displayed in figure 1.
$R=\ln (\unicode[STIX]{x1D707}_{L}/\unicode[STIX]{x1D707}_{A})$
. The experimental measurements along with the corresponding mathematical representations are displayed in figure 1.

Figure 1. Dimensionless viscosity,
![]() $\unicode[STIX]{x1D707}$
, as a function of concentration,
$\unicode[STIX]{x1D707}$
, as a function of concentration,
![]() $c$
, for several liquid pairs. Symbols signify experimental measurements and corresponding dashed lines fit the data. Symbol and line colours are coded by liquid pair. Colours black, light blue, dark blue, purple, pink and yellow indicate the liquid pair as corn syrup–water, glycerol–water, glycerol–ethanol, 10 000 cSt–1 cSt, 60 000 cSt–1 cSt and 100 000 cSt–1 cSt silicone oils, respectively. The pairs of silicone oils are fit as fifth-order polynomials; the pairing of glycerol–ethanol is fit as a single exponential; and glycerol–water and corn syrup–water are fit as triple exponentials. Glycerol data are taken from Glycerine Producers’ Association (1963).
$c$
, for several liquid pairs. Symbols signify experimental measurements and corresponding dashed lines fit the data. Symbol and line colours are coded by liquid pair. Colours black, light blue, dark blue, purple, pink and yellow indicate the liquid pair as corn syrup–water, glycerol–water, glycerol–ethanol, 10 000 cSt–1 cSt, 60 000 cSt–1 cSt and 100 000 cSt–1 cSt silicone oils, respectively. The pairs of silicone oils are fit as fifth-order polynomials; the pairing of glycerol–ethanol is fit as a single exponential; and glycerol–water and corn syrup–water are fit as triple exponentials. Glycerol data are taken from Glycerine Producers’ Association (1963).
Mass diffusion coefficients have been measured to vary with concentration (Petitjeans & Maxworthy Reference Petitjeans and Maxworthy1996; Rashidnia & Balasubramaniam Reference Rashidnia and Balasubramaniam2002, Reference Rashidnia and Balasubramaniam2004), and Vanaparthy & Meiburg (Reference Vanaparthy and Meiburg2008) used a generalized form of the Stokes–Einstein relation in their computations. For our numerical simulations, we adopt a similar form with the restriction that where the viscosity between our liquid pairs varies by as much as four orders of magnitude, the diffusion coefficient is specified to vary by one order of magnitude or less, following the results of Petitjeans & Maxworthy (Reference Petitjeans and Maxworthy1996) and Rashidnia & Balasubramaniam (Reference Rashidnia and Balasubramaniam2004). Thus, we define
 $$\begin{eqnarray}\displaystyle {\mathcal{D}}=\left\{\begin{array}{@{}ll@{}}\text{e}^{-{\mathcal{R}}c}\quad & \text{single exponential},\\ \text{e}^{-{\mathcal{R}}((\text{e}^{\text{e}^{c}}-\text{e})/(\text{e}^{\text{e}}-\text{e}))}\quad & \text{triple exponential},\\ \hspace{0.0pt}[1+(\text{e}^{{\mathcal{R}}}-1)c^{5}]^{-1}\quad & \text{fifth-degree polynomial},\end{array}\right. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{D}}=\left\{\begin{array}{@{}ll@{}}\text{e}^{-{\mathcal{R}}c}\quad & \text{single exponential},\\ \text{e}^{-{\mathcal{R}}((\text{e}^{\text{e}^{c}}-\text{e})/(\text{e}^{\text{e}}-\text{e}))}\quad & \text{triple exponential},\\ \hspace{0.0pt}[1+(\text{e}^{{\mathcal{R}}}-1)c^{5}]^{-1}\quad & \text{fifth-degree polynomial},\end{array}\right. & & \displaystyle\end{eqnarray}$$
and
![]() $0\leqslant {\mathcal{R}}\leqslant \ln (10)$
, depending on the liquid pair. This restriction is supported by the measurements of Petitjeans & Maxworthy (Reference Petitjeans and Maxworthy1996), who found the diffusion coefficient between water and glycerol to vary by an order of magnitude whereas the viscosity varies by three orders. We discuss the outcomes of this choice alongside the results.
$0\leqslant {\mathcal{R}}\leqslant \ln (10)$
, depending on the liquid pair. This restriction is supported by the measurements of Petitjeans & Maxworthy (Reference Petitjeans and Maxworthy1996), who found the diffusion coefficient between water and glycerol to vary by an order of magnitude whereas the viscosity varies by three orders. We discuss the outcomes of this choice alongside the results.

Figure 2. Schematics of the (a) pendant and (b) sessile drops. The coordinate system and characteristic length scale of each system are identified. At the solid surfaces (needle suspending the pendant drop, surface supporting the sessile drop), no-slip and no-penetration boundary conditions are imposed. At
![]() $t=0$
, the system is quiescent everywhere and the transition in concentration between the two liquids is represented as an error function with respect to
$t=0$
, the system is quiescent everywhere and the transition in concentration between the two liquids is represented as an error function with respect to
![]() $\sqrt{r^{2}+z^{2}}/\unicode[STIX]{x1D6FF}_{o}$
, where
$\sqrt{r^{2}+z^{2}}/\unicode[STIX]{x1D6FF}_{o}$
, where
![]() $\unicode[STIX]{x1D6FF}_{o}$
is a length scale to define the transition thickness, or initial thickness of the diffusive layer, which is set equal to the grid spacing.
$\unicode[STIX]{x1D6FF}_{o}$
is a length scale to define the transition thickness, or initial thickness of the diffusive layer, which is set equal to the grid spacing.
3.2 Boundary conditions
3.2.1 Miscible pendant drop
A pendant drop is suspended from above by a syringe needle, as can be seen in figure 2(a). We define
![]() $z=0$
at the bottom of the needle with diameter
$z=0$
at the bottom of the needle with diameter
![]() $d$
. Numerically, we represent this needle as a no-slip, no-penetration surface. At
$d$
. Numerically, we represent this needle as a no-slip, no-penetration surface. At
![]() $r=0$
, the axial velocity is at a maximum and the radial velocity is zero. Far from the drop and into the ambient liquid, the concentration
$r=0$
, the axial velocity is at a maximum and the radial velocity is zero. Far from the drop and into the ambient liquid, the concentration
![]() $c$
and velocities
$c$
and velocities
![]() $u_{r}$
and
$u_{r}$
and
![]() $u_{z}$
approach zero. We utilize the diameter of the needle,
$u_{z}$
approach zero. We utilize the diameter of the needle,
![]() $d$
, as the characteristic length scale to find the dimensionless boundary conditions:
$d$
, as the characteristic length scale to find the dimensionless boundary conditions:
3.2.2 Miscible sessile drop
A sessile drop is supported from below by a solid surface, as seen in figure 2(b). We define
![]() $z=0$
at the vertical position of the solid–liquid interface. At the solid surface, no-slip and no-penetration boundary conditions are applied. In our numerical description, the surface energies existing between each liquid and the solid surface are not explicitly considered. At
$z=0$
at the vertical position of the solid–liquid interface. At the solid surface, no-slip and no-penetration boundary conditions are applied. In our numerical description, the surface energies existing between each liquid and the solid surface are not explicitly considered. At
![]() $r=0$
, the axial velocity is at a maximum and the radial velocity is zero. Far from the drop and into the ambient liquid, the concentration
$r=0$
, the axial velocity is at a maximum and the radial velocity is zero. Far from the drop and into the ambient liquid, the concentration
![]() $c$
and velocities
$c$
and velocities
![]() $u_{r}$
and
$u_{r}$
and
![]() $u_{z}$
approach zero. Thus we have the following boundary conditions for a sessile drop:
$u_{z}$
approach zero. Thus we have the following boundary conditions for a sessile drop:
The size of the computational domain for both types of droplets was always at least five times the radius of the droplet in the direction of propagation: for the descending strand of a pendant drop, the
![]() $z$
-direction, and for the leading edge of a sessile drop, the
$z$
-direction, and for the leading edge of a sessile drop, the
![]() $r$
-direction. In the direction of the other coordinate, the size of the computational domain was at least three times the radius of the droplet. In this way, the boundaries of the domain were sufficiently far such that the dynamics of the droplet remained unaffected by the computational boundary conditions.
$r$
-direction. In the direction of the other coordinate, the size of the computational domain was at least three times the radius of the droplet. In this way, the boundaries of the domain were sufficiently far such that the dynamics of the droplet remained unaffected by the computational boundary conditions.
3.3 Computational approach
The symmetry of our problem allows us to construct a two-dimensional set of equations, which we solve using streamfunctions in a straightforward fashion. The set of partial differential equations (3.7)–(3.9), subject to the boundary conditions (3.15)–(3.20), or (3.21)–(3.24), depending on the type of drop, is recast in terms of streamfunctions and solved numerically with a finite central differencing scheme. An alternating direction implicit (ADI) scheme (Fletcher Reference Fletcher1988) is applied for solving the concentration equation. At time
![]() $t=0$
, the droplet is a spherical cap and the concentration profile between the drop and its ambient environment is defined in the form of an error function with respect to
$t=0$
, the droplet is a spherical cap and the concentration profile between the drop and its ambient environment is defined in the form of an error function with respect to
![]() $\sqrt{r^{2}+z^{2}}/\unicode[STIX]{x1D6FF}_{o}$
, where
$\sqrt{r^{2}+z^{2}}/\unicode[STIX]{x1D6FF}_{o}$
, where
![]() $\unicode[STIX]{x1D6FF}_{o}$
is a length scale to define the transition thickness, or initial thickness of the diffusive layer, which is set equal to the grid spacing. The fluid is initially quiescent at all points. The simulation is advanced in time by solving the concentration equation with an ADI scheme at discrete time steps. At each half and full time step in the ADI scheme, the streamfunction equation is solved to update the velocity field in the next iteration of solving for concentration.
$\unicode[STIX]{x1D6FF}_{o}$
is a length scale to define the transition thickness, or initial thickness of the diffusive layer, which is set equal to the grid spacing. The fluid is initially quiescent at all points. The simulation is advanced in time by solving the concentration equation with an ADI scheme at discrete time steps. At each half and full time step in the ADI scheme, the streamfunction equation is solved to update the velocity field in the next iteration of solving for concentration.
To incorporate the concentration-dependent, dimensionless diffusion coefficient,
![]() ${\mathcal{D}}$
, into this scheme, we construct it in two parts:
${\mathcal{D}}$
, into this scheme, we construct it in two parts:
The first term, 1, is a constant term and the second term,
![]() $(1-{\mathcal{D}})$
, is a variable term that corrects the value of the diffusion coefficient based on the local concentration
$(1-{\mathcal{D}})$
, is a variable term that corrects the value of the diffusion coefficient based on the local concentration
![]() $c$
. After separating the diffusion coefficient into constant and variable components, we treat constant diffusive terms implicitly and variable diffusive terms explicitly. Operating as such allows us to take significantly larger time steps without negatively influencing the stability of the numerical analysis.
$c$
. After separating the diffusion coefficient into constant and variable components, we treat constant diffusive terms implicitly and variable diffusive terms explicitly. Operating as such allows us to take significantly larger time steps without negatively influencing the stability of the numerical analysis.
A test case for the two-dimensional diffusion equation in the absence of convection was conducted and compared to the analytical solution provided by Crank (Reference Crank1975) for an isolated spherical droplet. Spatial discretization was selected based upon physical evidence from the experiments of the thickness of the diffusive draining layer. This grid spacing was varied over two orders of magnitude to ensure that its magnitude did not alter the thickness of the diffusive draining layer of the numerical calculations and that consistent results overall were achieved. The temporal discretization was selected with reference to the gravity number, which is indicative of the velocities that arise due to free convection. Identical physical scenarios were simulated using the various grid spacings, time steps and spatial domain sizes, obtaining consistent results. The comparison to experimental data serves as an additional check of the numerical results.
4 Results and discussion
4.1 Miscible pendant drop

Figure 3. (a) Image sequence taken in time of a pendant drop of corn syrup immersed in water. A strand emanates from the underside of the drop and continues to flow as the drop as a whole descends and elongates. (b) Image from a PTV experiment of a pendant drop of corn syrup immersed in water. The corn syrup contains
![]() $6~\unicode[STIX]{x03BC}\text{m}$
microspheres at a concentration of
$6~\unicode[STIX]{x03BC}\text{m}$
microspheres at a concentration of
![]() $10^{-3}~\text{g}~\text{ml}^{-1}$
, which scatter the incident laser light. The arrows indicate velocity vectors obtained from particle movement. Motion was found to be largely restricted to the corn syrup–water interface. Particles within the pendant drop and away from the liquid–liquid interface move with the drop as it descends and elongates; within the reference frame of the pendant drop, these interior particles do not move significantly. Refer to the supplemental material for full movies (Movie 1, Movie 2) available at https://doi.org/10.1017/jfm.2018.535 from which these frames were taken.
$10^{-3}~\text{g}~\text{ml}^{-1}$
, which scatter the incident laser light. The arrows indicate velocity vectors obtained from particle movement. Motion was found to be largely restricted to the corn syrup–water interface. Particles within the pendant drop and away from the liquid–liquid interface move with the drop as it descends and elongates; within the reference frame of the pendant drop, these interior particles do not move significantly. Refer to the supplemental material for full movies (Movie 1, Movie 2) available at https://doi.org/10.1017/jfm.2018.535 from which these frames were taken.
Figure 3 summarizes the initial observations that were made of pendant drops in miscible environments at the conclusion of our prior study (Walls et al. Reference Walls, Haward, Shen and Fuller2016); figure 3(a) shows a series of images taken of a pendant drop of corn syrup suspended in water, and figure 3(b) shows an image from a PTV experiment of the same liquids. From figure 3(a), one can see that at some time after immersion, a thin strand emanates from the underside of the drop and continues to flow downward. Concurrently, the drop as a whole descends and elongates, albeit more slowly. In figure 3(b), the arrows indicate velocity vectors obtained from individual particle movement. Motion was found to be largely restricted to the liquid–liquid interface on the main body of the drop and to a thin liquid jet descending from its underside. Particles within the main body of the drop move only due to the descent of the drop itself as it elongates. Particles descending along the liquid–liquid interface reach the bottom of the pendant drop and continue to flow downward in a thin strand.
Due to the high viscosity of the pendant liquid, it does not rapidly deform under the action of gravity as a body despite the difference in density between the pendant and ambient liquids. Instead, the pendant liquid at the surface of the drop is able to diffuse on a shorter time scale, creating a diffuse layer at the liquid–liquid interface of the pendant drop and ambient environment. Across this diffuse layer, the concentration transitions from the pure pendant liquid to the pure ambient liquid; thus, the density and viscosity correspondingly transition between the properties of the pure liquids across this layer. Whereas the densities of the pendant liquids diminish approximately linearly with dilution, the viscosities decrease much more sharply. As a result, the pendant liquid diffuses and forms a diffuse layer that subsequently drains, all more rapidly than the drop deforms as a single body. The boundary between the pendant drop and its ambient surroundings can be identified due to the sharp change in the concentration, and hence the refractive index of the fluid, as seen in figure 3(a). We define the volume of the pendant drop,
![]() $V$
, to be the liquid contained within its boundary, but excluding the thin draining strand. Throughout an experiment, we track the boundary of the body of the pendant drop to calculate its volume as a function of time.
$V$
, to be the liquid contained within its boundary, but excluding the thin draining strand. Throughout an experiment, we track the boundary of the body of the pendant drop to calculate its volume as a function of time.

Figure 4. Plots of volumetric measurements as functions of time for pendant drops of corn syrup immersed in water. Volume and time are plotted on logarithmic and linear scales, respectively. (a) Unscaled data. (b) The volumetric data are scaled by the maximum volume of each pendant drop,
![]() $V_{max}$
, and time is shifted by the time at which the maximum volume occurs,
$V_{max}$
, and time is shifted by the time at which the maximum volume occurs,
![]() $t_{max}$
, and scaled by a characteristic diffusion time,
$t_{max}$
, and scaled by a characteristic diffusion time,
![]() $t_{c,pendant}=(V_{max}/A_{max})^{2}/4{\mathcal{D}}_{LA}$
, where
$t_{c,pendant}=(V_{max}/A_{max})^{2}/4{\mathcal{D}}_{LA}$
, where
![]() $A_{max}$
is the surface area of the pendant drop at its maximum volume and
$A_{max}$
is the surface area of the pendant drop at its maximum volume and
![]() ${\mathcal{D}}_{LA}$
is the diffusion coefficient between the pendant and ambient liquids. A value of
${\mathcal{D}}_{LA}$
is the diffusion coefficient between the pendant and ambient liquids. A value of
![]() $1.30\times 10^{-4}~\text{mm}^{2}~\text{s}^{-1}$
was obtained from the literature for the mutual diffusion coefficient of corn syrup and water (Ray, Bunton & Pojman Reference Ray, Bunton and Pojman2007). Varying symbol shapes represent discrete experiments for a particular needle. Symbol colours purple, dark blue, green, red and black indicate the diameters of the supporting needle as 0.159, 0.362, 0.474*, 0.718* and 0.718 mm, respectively. Non-asterisked and asterisked values indicate that the needle is stainless steel and PTFE-coated stainless steel, respectively. The solid-black, dashed-white line in (b) represents an exponential decay,
$1.30\times 10^{-4}~\text{mm}^{2}~\text{s}^{-1}$
was obtained from the literature for the mutual diffusion coefficient of corn syrup and water (Ray, Bunton & Pojman Reference Ray, Bunton and Pojman2007). Varying symbol shapes represent discrete experiments for a particular needle. Symbol colours purple, dark blue, green, red and black indicate the diameters of the supporting needle as 0.159, 0.362, 0.474*, 0.718* and 0.718 mm, respectively. Non-asterisked and asterisked values indicate that the needle is stainless steel and PTFE-coated stainless steel, respectively. The solid-black, dashed-white line in (b) represents an exponential decay,
![]() $\exp (-\bar{t}/T)$
, with an exponential decay constant,
$\exp (-\bar{t}/T)$
, with an exponential decay constant,
![]() $T$
, of unity.
$T$
, of unity.
Figure 4(a) shows a plot of the volumetric measurements as a function of time for pendant drops of corn syrup suspended in water for a range of initial volumes supported by syringe needles of several diameters. Volume and time are plotted on logarithmic and linear scales, respectively. Initially, the volumes of the pendant drops increase to a maximum,
![]() $V_{max}$
, before ultimately diminishing in time. These increases correspond to the formation of the diffuse layer at the liquid–liquid interface between the pendant and ambient liquids; diffusion causes the initially distinct and infinitesimally thin interface to blur and grow in thickness, resulting in the swelling of the drop and the observation of its boundary moving radially outward. After reaching a maximum value, the volume of a pendant drop begins to diminish, corresponding to the draining of the diffuse layer. Additionally, the linear response of volume after attaining its maximum value when expressed in this semilogarithmic form reveals that the volume of the pendant drop diminishes exponentially in time as
$V_{max}$
, before ultimately diminishing in time. These increases correspond to the formation of the diffuse layer at the liquid–liquid interface between the pendant and ambient liquids; diffusion causes the initially distinct and infinitesimally thin interface to blur and grow in thickness, resulting in the swelling of the drop and the observation of its boundary moving radially outward. After reaching a maximum value, the volume of a pendant drop begins to diminish, corresponding to the draining of the diffuse layer. Additionally, the linear response of volume after attaining its maximum value when expressed in this semilogarithmic form reveals that the volume of the pendant drop diminishes exponentially in time as
![]() $\exp (-t/\unicode[STIX]{x1D70F}_{d})$
, where
$\exp (-t/\unicode[STIX]{x1D70F}_{d})$
, where
![]() $\unicode[STIX]{x1D70F}_{d}$
is the measured exponential decay time constant of a particular experiment.
$\unicode[STIX]{x1D70F}_{d}$
is the measured exponential decay time constant of a particular experiment.
If we scale the data of volume and time presented in figure 4(a) by the maximum volume,
![]() $V_{max}$
, and a characteristic diffusion time,
$V_{max}$
, and a characteristic diffusion time,
![]() $t_{c,pendant}$
, respectively, the plot shown in figure 4(b) is obtained. Scaling the volume by the maximum volume of each pendant drop collapses the vertical axis (
$t_{c,pendant}$
, respectively, the plot shown in figure 4(b) is obtained. Scaling the volume by the maximum volume of each pendant drop collapses the vertical axis (
![]() $\bar{V}=V/V_{max}$
). When the horizontal axis is scaled by a characteristic diffusion time and shifted by the time at which the maximum volume is reached (
$\bar{V}=V/V_{max}$
). When the horizontal axis is scaled by a characteristic diffusion time and shifted by the time at which the maximum volume is reached (
![]() $\bar{t}=(t-t_{max})/t_{c,pendant}$
), the data also largely collapse to reveal an exponential decay of the volume,
$\bar{t}=(t-t_{max})/t_{c,pendant}$
), the data also largely collapse to reveal an exponential decay of the volume,
![]() $\bar{V}\sim \exp (-\bar{t}/T)$
, with a dimensionless exponential decay time constant,
$\bar{V}\sim \exp (-\bar{t}/T)$
, with a dimensionless exponential decay time constant,
![]() $T$
, of unity. The shift in time accounts for the time necessary for the diffuse layer to form and the draining flow to establish itself through free convection. The characteristic diffusion time,
$T$
, of unity. The shift in time accounts for the time necessary for the diffuse layer to form and the draining flow to establish itself through free convection. The characteristic diffusion time,
![]() $t_{c,pendant}$
, is calculated as follows:
$t_{c,pendant}$
, is calculated as follows:
where
![]() $L$
is a characteristic length and
$L$
is a characteristic length and
![]() ${\mathcal{D}}_{LA}$
is the diffusion coefficient between the pendant and ambient liquids. We obtain
${\mathcal{D}}_{LA}$
is the diffusion coefficient between the pendant and ambient liquids. We obtain
![]() $L$
by taking the ratio of the maximum volume of the pendant drop,
$L$
by taking the ratio of the maximum volume of the pendant drop,
![]() $V_{max}$
, and the surface area of the pendant drop at its maximum volume,
$V_{max}$
, and the surface area of the pendant drop at its maximum volume,
![]() $A_{max}$
. A diffusion coefficient between corn syrup and water of
$A_{max}$
. A diffusion coefficient between corn syrup and water of
![]() $1.30\times 10^{-4}~\text{mm}^{2}~\text{s}^{-1}$
is used to scale the data in figure 4(b), which was obtained from the literature (Ray et al.
Reference Ray, Bunton and Pojman2007).
$1.30\times 10^{-4}~\text{mm}^{2}~\text{s}^{-1}$
is used to scale the data in figure 4(b), which was obtained from the literature (Ray et al.
Reference Ray, Bunton and Pojman2007).
This time scale emerges from the appropriate scaling of the convection–diffusion equation to describe the time-dependent, free-convection mass transfer of a pendant drop in a miscible environment. To obtain this time scale, we first begin from an analysis of time-independent, forced-convection heat transfer by Acrivos & Goddard (Reference Acrivos and Goddard1965) to identify an appropriate length scale for our analysis. Acrivos & Goddard (Reference Acrivos and Goddard1965) studied the time-independent case of the transfer of heat for a uniformly heated, solid sphere in a uniform flow in the limit in which
![]() $Re\ll 1$
and
$Re\ll 1$
and
![]() $Pe\gg 1$
, matching the limiting behaviour of the parameters in our study. They found that even as
$Pe\gg 1$
, matching the limiting behaviour of the parameters in our study. They found that even as
![]() $Pe\rightarrow \infty$
, there exists an inner region near the surface of the sphere where diffusion cannot be neglected at leading order. Acrivos & Goddard (Reference Acrivos and Goddard1965) determined that this inner region extended a distance
$Pe\rightarrow \infty$
, there exists an inner region near the surface of the sphere where diffusion cannot be neglected at leading order. Acrivos & Goddard (Reference Acrivos and Goddard1965) determined that this inner region extended a distance
![]() $O(aPe^{-1/3})$
from the surface of a sphere of radius
$O(aPe^{-1/3})$
from the surface of a sphere of radius
![]() $a$
. Since the pendant liquid in each of our experiments is several orders of magnitude more viscous than its ambient counterpart, the liquid–liquid interface can be treated as a no-slip boundary, with diffusion being non-negligible within a distance
$a$
. Since the pendant liquid in each of our experiments is several orders of magnitude more viscous than its ambient counterpart, the liquid–liquid interface can be treated as a no-slip boundary, with diffusion being non-negligible within a distance
![]() $O(aPe^{-1/3})$
from this interface. Second, considering Stokes’ law, the velocity within this inner region scales as
$O(aPe^{-1/3})$
from this interface. Second, considering Stokes’ law, the velocity within this inner region scales as
![]() $Pe^{-2/3}$
. Then, using these length and velocity scales in the time-dependent convection–diffusion equation retains both the convective and diffusive terms, while yielding the time scale
$Pe^{-2/3}$
. Then, using these length and velocity scales in the time-dependent convection–diffusion equation retains both the convective and diffusive terms, while yielding the time scale
![]() $(aPe^{-1/3})^{2}/{\mathcal{D}}_{max}$
, of the form of (4.1) with
$(aPe^{-1/3})^{2}/{\mathcal{D}}_{max}$
, of the form of (4.1) with
![]() $L\sim aPe^{-1/3}$
. Comparing
$L\sim aPe^{-1/3}$
. Comparing
![]() $aPe^{-1/3}$
to
$aPe^{-1/3}$
to
![]() $L$
, with
$L$
, with
![]() $a$
as
$a$
as
![]() $R_{max}$
, the radius of a pendant drop at its maximum volume, estimates
$R_{max}$
, the radius of a pendant drop at its maximum volume, estimates
![]() $aPe^{-1/3}\sim R_{max}/10$
, of a similar order to
$aPe^{-1/3}\sim R_{max}/10$
, of a similar order to
![]() $L=R_{max}/3$
. Additionally, for a given
$L=R_{max}/3$
. Additionally, for a given
![]() $Pe$
, one could expect the inner region of our experiments, a free-convection problem where the fluid motion arises from buoyancy effects near the surface and decays as
$Pe$
, one could expect the inner region of our experiments, a free-convection problem where the fluid motion arises from buoyancy effects near the surface and decays as
![]() $r\rightarrow \infty$
, to be thicker than that of a forced-convection problem, where the fluid motion is imposed from the far field and is only disturbed locally near the sphere.
$r\rightarrow \infty$
, to be thicker than that of a forced-convection problem, where the fluid motion is imposed from the far field and is only disturbed locally near the sphere.
We have not been able to rigorously develop an exponential relationship between pendant volume and time mathematically. However, two observations indicate its plausibility. First, the size of the pendant drop is linked to the total diffusive flux that arises across the pendant liquid–ambient liquid interface through its surface area,
![]() $A$
. As pendant liquid diffuses across the liquid–liquid interface and free convection carries it away, the volume of the pendant drop decreases as does its surface area. The draining flow from the diffuse layer acts to largely maintain the thickness of the diffuse layer throughout the experiment, indicating that the material flux per unit area, proportional to
$A$
. As pendant liquid diffuses across the liquid–liquid interface and free convection carries it away, the volume of the pendant drop decreases as does its surface area. The draining flow from the diffuse layer acts to largely maintain the thickness of the diffuse layer throughout the experiment, indicating that the material flux per unit area, proportional to
![]() ${\mathcal{D}}_{LA}\unicode[STIX]{x1D735}c$
, remains constant while the total diffusive flux, proportional to
${\mathcal{D}}_{LA}\unicode[STIX]{x1D735}c$
, remains constant while the total diffusive flux, proportional to
![]() $A\cdot {\mathcal{D}}_{LA}\unicode[STIX]{x1D735}c$
, diminishes solely due to diminishing surface area. This process fits the characteristics of an exponential decay, which arises when a decrease in a quantity is proportionate to its current value. Second, the scaled volumetric data for pendant drops of corn syrup in water in figure 4(b) fall along a single exponential curve,
$A\cdot {\mathcal{D}}_{LA}\unicode[STIX]{x1D735}c$
, diminishes solely due to diminishing surface area. This process fits the characteristics of an exponential decay, which arises when a decrease in a quantity is proportionate to its current value. Second, the scaled volumetric data for pendant drops of corn syrup in water in figure 4(b) fall along a single exponential curve,
![]() $\exp (-\bar{t}/T)$
, with a dimensionless decay time constant,
$\exp (-\bar{t}/T)$
, with a dimensionless decay time constant,
![]() $T$
, of unity.
$T$
, of unity.
Lastly, as expected for a pendant drop, the material of the suspending needle, either stainless steel or PTFE-coated stainless steel, was inconsequential to the behaviour of the experiment, as seen from the universal behaviour of the scaled data without accounting for this aspect.
Diffusion coefficients for the pairs of silicone oils listed in table 1 are not readily available in the literature to repeat the scaling analysis in figure 4 for these pairs directly. However, the scaling relationship of (4.1) suggests that diffusion coefficients for each liquid pair could be estimated from its corresponding set of experiments. For the set of experiments with pendant drops of corn syrup immersed in water, the overall dimensionless exponential decay time constant,
![]() $T$
, is unity, which indicates that the calculated characteristic diffusion time,
$T$
, is unity, which indicates that the calculated characteristic diffusion time,
![]() $t_{c,pendant}$
, and measured exponential decay time constant,
$t_{c,pendant}$
, and measured exponential decay time constant,
![]() $\unicode[STIX]{x1D70F}_{d}$
, are approximately equal for a given experiment. Thus, equation (4.1) can be rewritten as
$\unicode[STIX]{x1D70F}_{d}$
, are approximately equal for a given experiment. Thus, equation (4.1) can be rewritten as
![]() $L^{2}={\mathcal{D}}_{LA}\cdot 4\unicode[STIX]{x1D70F}_{d}$
, and plotting
$L^{2}={\mathcal{D}}_{LA}\cdot 4\unicode[STIX]{x1D70F}_{d}$
, and plotting
![]() $L^{2}$
against
$L^{2}$
against
![]() $4\unicode[STIX]{x1D70F}_{d}$
for each experiment within the corn syrup–water pairing should yield its diffusion coefficient as the slope of best fit. Indeed, when following this procedure for the set of experiments using corn syrup and water, the resultant slope is
$4\unicode[STIX]{x1D70F}_{d}$
for each experiment within the corn syrup–water pairing should yield its diffusion coefficient as the slope of best fit. Indeed, when following this procedure for the set of experiments using corn syrup and water, the resultant slope is
![]() $1.34\times 10^{-4}\pm 1.6\times 10^{-5}~\text{mm}^{2}~\text{s}^{-1}$
, comparing closely to the independently measured diffusion coefficient between corn syrup and water of
$1.34\times 10^{-4}\pm 1.6\times 10^{-5}~\text{mm}^{2}~\text{s}^{-1}$
, comparing closely to the independently measured diffusion coefficient between corn syrup and water of
![]() $1.30\times 10^{-4}~\text{mm}^{2}~\text{s}^{-1}$
by Ray et al. (Reference Ray, Bunton and Pojman2007), used above to scale the data presented in figure 4(b).
$1.30\times 10^{-4}~\text{mm}^{2}~\text{s}^{-1}$
by Ray et al. (Reference Ray, Bunton and Pojman2007), used above to scale the data presented in figure 4(b).
Using this method to estimate the diffusion coefficients of the pairs of silicone oils gives values of
![]() $9.9\times 10^{-5}\pm 2.5\times 10^{-5}$
,
$9.9\times 10^{-5}\pm 2.5\times 10^{-5}$
,
![]() $3.6\times 10^{-5}\pm 9.0\times 10^{-6}$
and
$3.6\times 10^{-5}\pm 9.0\times 10^{-6}$
and
![]() $4.7\times 10^{-5}\pm 1.2\times 10^{-5}~\text{mm}^{2}~\text{s}^{-1}$
as the diffusion coefficients between 1 cSt silicone oil and 10 000 cSt, 60 000 cSt and 100 000 cSt silicone oils, respectively. Further, the reliability of these estimates can be assessed. Prior researchers (Pollack & Enyeart Reference Pollack and Enyeart1985; Zwanzig & Harrison Reference Zwanzig and Harrison1985; Balasubramaniam et al.
Reference Balasubramaniam, Rashidnia, Maxworthy and Kuang2005) have developed empirical power-law relationships between diffusion coefficients and viscosity through the Stokes–Einstein relation, or modifications of it. They do so by keeping the viscosity of one of the liquids in the pair constant as the other is varied. Similarly, we construct such a relationship for pairs of silicone oils, where the viscosity of one silicone oil remains constant; by compiling a combined set of independent literature values (Rashidnia & Balasubramaniam Reference Rashidnia and Balasubramaniam2002; Balasubramaniam et al.
Reference Balasubramaniam, Rashidnia, Maxworthy and Kuang2005) (1 cSt–1000 cSt:
$4.7\times 10^{-5}\pm 1.2\times 10^{-5}~\text{mm}^{2}~\text{s}^{-1}$
as the diffusion coefficients between 1 cSt silicone oil and 10 000 cSt, 60 000 cSt and 100 000 cSt silicone oils, respectively. Further, the reliability of these estimates can be assessed. Prior researchers (Pollack & Enyeart Reference Pollack and Enyeart1985; Zwanzig & Harrison Reference Zwanzig and Harrison1985; Balasubramaniam et al.
Reference Balasubramaniam, Rashidnia, Maxworthy and Kuang2005) have developed empirical power-law relationships between diffusion coefficients and viscosity through the Stokes–Einstein relation, or modifications of it. They do so by keeping the viscosity of one of the liquids in the pair constant as the other is varied. Similarly, we construct such a relationship for pairs of silicone oils, where the viscosity of one silicone oil remains constant; by compiling a combined set of independent literature values (Rashidnia & Balasubramaniam Reference Rashidnia and Balasubramaniam2002; Balasubramaniam et al.
Reference Balasubramaniam, Rashidnia, Maxworthy and Kuang2005) (1 cSt–1000 cSt:
![]() $2.81\times 10^{-4}~\text{mm}^{2}~\text{s}^{-1}$
) and values determined from our experiments with pendant drops, we can verify whether a power law determined from our estimated values predicts the literature values. Figure 5 shows a plot of these values against the viscosity of the more viscous silicone oil. Indeed, the power-law relationship constructed from the three estimated diffusion coefficients predicts the independently measured quantity of Rashidnia & Balasubramaniam (Reference Rashidnia and Balasubramaniam2002), which further indicates their reliability for use in our scaling analyses of pendant drops of silicone oils immersed in silicone oils.
$2.81\times 10^{-4}~\text{mm}^{2}~\text{s}^{-1}$
) and values determined from our experiments with pendant drops, we can verify whether a power law determined from our estimated values predicts the literature values. Figure 5 shows a plot of these values against the viscosity of the more viscous silicone oil. Indeed, the power-law relationship constructed from the three estimated diffusion coefficients predicts the independently measured quantity of Rashidnia & Balasubramaniam (Reference Rashidnia and Balasubramaniam2002), which further indicates their reliability for use in our scaling analyses of pendant drops of silicone oils immersed in silicone oils.

Figure 5. Logarithmic plot of the diffusion coefficients between 1 cSt silicone oil and several silicone oils of higher viscosity versus the viscosity of the more viscous silicone oil. Filled and hollow symbols indicate values estimated from our experiments and those from literature, respectively. Error bars are indicated for estimates from our experiments. A best-fit power-law relationship constructed from the three estimated diffusion coefficients predicts the independently measured quantity of Rashidnia & Balasubramaniam (Reference Rashidnia and Balasubramaniam2002), which indicates their reliability.

Figure 6. Plots of volumetric measurements as functions of time for pendant drops. Volume and time are plotted on logarithmic and linear scales, respectively. (a) Unscaled data of silicone oils immersed in 1 cSt silicone oil. (b) The data of (a) are scaled in the same manner as, and presented alongside, the data from figure 4(b) for pendant drops of corn syrup immersed in water. Diffusion coefficients for the pairs of silicone oils were obtained from the method described in figure 5 (
![]() $9.9\times 10^{-5}$
,
$9.9\times 10^{-5}$
,
![]() $3.6\times 10^{-5}$
and
$3.6\times 10^{-5}$
and
![]() $4.7\times 10^{-5}~\text{mm}^{2}~\text{s}^{-1}$
for the diffusion coefficients between 1 cSt silicone oil and 10 000, 60 000 and 100 000 cSt silicone oils, respectively). Varying symbol shapes represent discrete experiments for a particular pendant liquid. Symbol colours purple, pink, yellow and black indicate the pendant liquid as 10 000 cSt, 60 000 cSt, 100 000 cSt silicone oils, and corn syrup, respectively. Pendant drops of silicone oils were supported by PTFE-coated stainless steel needles with diameters of 0.474 and 0.718 mm. The solid-black, dashed-white line in (b) represents an exponential decay,
$4.7\times 10^{-5}~\text{mm}^{2}~\text{s}^{-1}$
for the diffusion coefficients between 1 cSt silicone oil and 10 000, 60 000 and 100 000 cSt silicone oils, respectively). Varying symbol shapes represent discrete experiments for a particular pendant liquid. Symbol colours purple, pink, yellow and black indicate the pendant liquid as 10 000 cSt, 60 000 cSt, 100 000 cSt silicone oils, and corn syrup, respectively. Pendant drops of silicone oils were supported by PTFE-coated stainless steel needles with diameters of 0.474 and 0.718 mm. The solid-black, dashed-white line in (b) represents an exponential decay,
![]() $\exp (-\bar{t}/T)$
, with an exponential decay constant,
$\exp (-\bar{t}/T)$
, with an exponential decay constant,
![]() $T$
, of unity.
$T$
, of unity.
The estimated diffusion coefficients between silicone oils presented in figure 5 were obtained from the experimental data of the time-dependent, volumetric diminution of pendant drops of silicone oils shown in figure 6. Specifically, figure 6(a) shows the volume of pendant drops for experiments conducted with three viscous silicone oils (10 000 cSt, 60 000 cSt and 100 000 cSt) suspended in 1 cSt silicone oil. Volume and time are plotted on logarithmic and linear scales, respectively. Experiments with silicone oils were restricted to the use of PTFE-coated stainless steel needles to discourage silicone oils from wicking up the needle prior to initiating the experiments. However, in the course of an experiment, the coating does not influence the results, as seen earlier with the experiments using corn syrup and water. The volume behaves similarly in time to the data gathered for corn syrup and water, where an initial swelling is followed by an exponential decay. The data for volume and time in figure 6(a) can be scaled by the maximum volume and the characteristic diffusion time presented in (4.1), respectively, and combined with data from figure 4(b) to obtain the plot shown in figure 6(b). Again, values of the diffusion coefficients for pairs of silicone oils used in this scaling were obtained as described above in figure 5. The collapse of the draining behaviour is universal for the various liquid pairings studied, with all experimental volumes decreasing exponentially,
![]() $\bar{V}\sim \exp (-\bar{t}/T)$
, with a dimensionless decay constant,
$\bar{V}\sim \exp (-\bar{t}/T)$
, with a dimensionless decay constant,
![]() $T$
, of unity.
$T$
, of unity.

Figure 7. Sequences of images taken over time of a pendant drop of corn syrup suspended in water. The images in (a) were captured during an experiment and displayed in (b) with increased contrast to accentuate the diffuse regions near the body of the pendant drop. These experimental images are reproduced by a numerical simulation in (c). In the images of the numerical simulation, contour lines in concentration are plotted over top of a coarse grid of the velocity vectors in the fluid. Contours are marked at concentrations of the pendant liquid of 1, 5, 10, 20, 30, 40, 50, 60, 70, 80, 90, 95 and 99 %, and range from blue to red over this span. Thin strands emanate from the undersides of the drops and continue to flow as the drops descend and elongate as single bodies. Refer to the supplemental material for the full movies (Movie 3, Movie 4, Movie 5) from which these sets of frames were taken.
To complement our experiments and understand more fully these miscible pendant systems, we have performed a set of numerical simulations. In matching numerical simulations to the experimental observations, the negligible influence of the physical mechanisms excluded from the calculations on the observed phenomena can be confirmed. For example, surface tension and its associated effects were disregarded from our formulation of the governing equations. Figure 7(a) shows an image sequence taken during an experiment with a pendant drop of corn syrup suspended in water; in figure 7(b), the images are displayed with increased contrast to accentuate the diffuse regions near the body of the pendant drop. In figure 7(c), a reproduction of this experiment by a numerical simulation is depicted. In the images of the numerical simulation, contours in the concentration of the pendant liquid are plotted over top of a coarse grid of the velocity vectors in the fluid. Qualitatively, we see that the numerical simulation reproduces key features such as the initial swelling of the drop and the subsequent draining and emergence of a thin strand from the underside of the drop. Quantitatively, regarding the thicknesses of the diffuse layer along the pendant liquid–ambient liquid interface and the thin strand that emanates from the underside of the pendant drop, comparisons between the experimental images with increased contrast and those of the simulation indicate close agreement. Here, the thickness of the diffuse layer measures approximately
![]() $65~\unicode[STIX]{x03BC}\text{m}$
, draining into a thin strand approximately
$65~\unicode[STIX]{x03BC}\text{m}$
, draining into a thin strand approximately
![]() $110~\unicode[STIX]{x03BC}\text{m}$
in diameter. These thicknesses were consistently measured across all experiments with variously sized pendant drops of corn syrup immersed in water. Further, the simulated velocity field largely reproduces the experimental observations when compared to the PTV experiments, such as shown in figure 3(b). In both experiment and simulation, motion within the viscous pendant drop is effectively zero, with all motion generated at the pendant liquid–ambient liquid interface by buoyancy forces. For pendant drops of corn syrup immersed in water, the simulated velocities along the liquid–liquid interface compare closely with the observations of particle motion within PTV experiments of approximately
$110~\unicode[STIX]{x03BC}\text{m}$
in diameter. These thicknesses were consistently measured across all experiments with variously sized pendant drops of corn syrup immersed in water. Further, the simulated velocity field largely reproduces the experimental observations when compared to the PTV experiments, such as shown in figure 3(b). In both experiment and simulation, motion within the viscous pendant drop is effectively zero, with all motion generated at the pendant liquid–ambient liquid interface by buoyancy forces. For pendant drops of corn syrup immersed in water, the simulated velocities along the liquid–liquid interface compare closely with the observations of particle motion within PTV experiments of approximately
![]() $0.4~\text{mm}~\text{s}^{-1}$
. However, the body of the simulated pendant drop descends more slowly than its experimental counterpart. In the physical experiment, the syringe needle is hollow and filled with the pendant liquid, whereas the numerical representation is a no-slip, no-penetration boundary. Thus, the experimental pendant drop can deform and elongate more readily. Numerical simulations of the other liquid pairings were conducted across the range of experimental volumes, which showed similar qualitative and quantitative matching between experiment and simulation. Movies of the experimental and numerical pairs for pendant drops of corn syrup and silicone oils suspended in water and silicone oils, respectively, are included in the supplemental material (Movie 6, Movie 7).
$0.4~\text{mm}~\text{s}^{-1}$
. However, the body of the simulated pendant drop descends more slowly than its experimental counterpart. In the physical experiment, the syringe needle is hollow and filled with the pendant liquid, whereas the numerical representation is a no-slip, no-penetration boundary. Thus, the experimental pendant drop can deform and elongate more readily. Numerical simulations of the other liquid pairings were conducted across the range of experimental volumes, which showed similar qualitative and quantitative matching between experiment and simulation. Movies of the experimental and numerical pairs for pendant drops of corn syrup and silicone oils suspended in water and silicone oils, respectively, are included in the supplemental material (Movie 6, Movie 7).

Figure 8. Plots of volume as a function of time for simulated and experimental pendant drops. Volume and time are plotted on logarithmic and linear scales, respectively. (a) Unscaled data obtained from simulations of the physical experiments presented in figures 4 and 6. (b) The data of (a) are scaled in the same manner as, and presented alongside, the data from figure 6(b) for pendant drops of corn syrup and silicone oils immersed in water and 1 cSt silicone oil, respectively. The diffusion coefficients used in scaling the simulated data correspond to those used in scaling the experimental data in figures 4(b) and 6(b). Varying symbol shapes represent discrete experiments for a particular pendant liquid. Different lines represent discrete simulations for a particular pendant liquid. Symbol and line colours purple, pink, yellow and black indicate the pendant liquid as 10 000 cSt, 60 000 cSt, 100 000 cSt silicone oils and corn syrup, respectively. Simulated pendant drops were suspended by numerical representations of needles to match the diameters of the experiments. The solid-black, dashed-white line in (b) represents an exponential decay,
![]() $\exp (-\bar{t}/T)$
, with an exponential decay constant,
$\exp (-\bar{t}/T)$
, with an exponential decay constant,
![]() $T$
, of unity.
$T$
, of unity.
Additionally, we have calculated the volume of the simulated pendant drops in time. To do so, we have defined the boundary of the drop along a contour line of concentration at 1 % of the pendant liquid, while excluding the thin, draining strand. In figure 8(a), the volumes of pendant drops from simulations of corn syrup in water and silicone oil in silicone oil are plotted against time on a semilogarithmic scale. Volume and time are plotted on logarithmic and linear scales, respectively. The data obtained from the simulations show qualitatively similar behaviour to the experiments, where volume initially increases and passes through a maximum before beginning to diminish exponentially in time. Figure 8(b) shows the scaled experimental data of figure 6(b) along with the simulated data when the scalings of
![]() $V_{max}$
and (4.1) are applied to volume and time, respectively. The diffusion coefficients used in scaling the simulated data correspond to those used in scaling the experimental data in figures 4(b) and 6(b). Strong agreement in behaviour of the draining phenomena is seen between the experiments and simulations.
$V_{max}$
and (4.1) are applied to volume and time, respectively. The diffusion coefficients used in scaling the simulated data correspond to those used in scaling the experimental data in figures 4(b) and 6(b). Strong agreement in behaviour of the draining phenomena is seen between the experiments and simulations.
Varying the magnitude of the diffusion coefficient in the simulations does not alter their qualitative character; however, as expected, it does influence the time to reach the maximum volume and the rate of exponential decay. Varying the magnitude of the diffusion coefficient within its uncertainty has a marginal influence on the thicknesses of the diffuse layer and thin strand for given densities, viscosities and their dependence on concentration. This finding is supported by the characteristic length for the inner region near the pendant liquid–ambient liquid developed above, which scales with
![]() $Pe^{-1/3}\sim ({\mathcal{D}}_{max}\unicode[STIX]{x1D707}_{A}/\unicode[STIX]{x0394}\unicode[STIX]{x1D70C})^{1/3}$
. Varying the dependence of the diffusion coefficient on concentration through
$Pe^{-1/3}\sim ({\mathcal{D}}_{max}\unicode[STIX]{x1D707}_{A}/\unicode[STIX]{x0394}\unicode[STIX]{x1D70C})^{1/3}$
. Varying the dependence of the diffusion coefficient on concentration through
![]() ${\mathcal{R}}$
as described in (3.14) did not substantially alter the calculated volumes of the simulations, as the value of the diffusion coefficient at a concentration of 1 %, the numerical boundary of the pendant drop, is not substantially altered by changes in
${\mathcal{R}}$
as described in (3.14) did not substantially alter the calculated volumes of the simulations, as the value of the diffusion coefficient at a concentration of 1 %, the numerical boundary of the pendant drop, is not substantially altered by changes in
![]() ${\mathcal{R}}$
over the prescribed range. Small changes to the motion of the contour lines representing higher concentrations and the steepness of the concentration gradients were observed as expected, but the qualitative nature of the simulations was not altered.
${\mathcal{R}}$
over the prescribed range. Small changes to the motion of the contour lines representing higher concentrations and the steepness of the concentration gradients were observed as expected, but the qualitative nature of the simulations was not altered.
4.2 Miscible sessile drop
We previously observed (Walls et al. Reference Walls, Haward, Shen and Fuller2016) that a sessile drop spreading in a miscible environment progresses through distinctly different shape evolution and power-law dynamics as compared to those present in an immiscible environment, such as air. Here, we revisit these sessile drops in conjunction with the pendant drops discussed in the prior section. We do so in order to further demonstrate the capability of our numerical procedure and to provide additional insights to the experiments of Walls et al. (Reference Walls, Haward, Shen and Fuller2016) arising from this numerical analysis.

Figure 9. Snapshots of a sessile drop of corn syrup spreading across a hydrophobic glass surface while immersed in water. (a,b
) The drop captured with brightfield imaging from the bottom and the side, respectively. The black arrows indicate the most radially advanced portion of the drop, which is elevated above the solid surface, and we refer to it as the leading edge. The white arrows indicate the most radially advanced portion of the drop that remains in contact with the solid surface, and we refer to it as the contact line. (c) An image taken from a PTV experiment. The corn syrup contains
![]() $6~\unicode[STIX]{x03BC}\text{m}$
microspheres at a concentration of
$6~\unicode[STIX]{x03BC}\text{m}$
microspheres at a concentration of
![]() $10^{-3}~\text{g}~\text{ml}^{-1}$
, which scatter incident laser light. The arrows indicate velocity vectors obtained from individual particle movement. Motion was largely restricted to the corn syrup–water interface and particles within the drop and away from the liquid–liquid interface remain stationary. (d) A reconstructed side-view image from a confocal microscopy experiment. A frustum of the sessile drop, its base coinciding with the glass surface, was scanned along a radial slice, as indicated by the inset in (c). The corn syrup contains
$10^{-3}~\text{g}~\text{ml}^{-1}$
, which scatter incident laser light. The arrows indicate velocity vectors obtained from individual particle movement. Motion was largely restricted to the corn syrup–water interface and particles within the drop and away from the liquid–liquid interface remain stationary. (d) A reconstructed side-view image from a confocal microscopy experiment. A frustum of the sessile drop, its base coinciding with the glass surface, was scanned along a radial slice, as indicated by the inset in (c). The corn syrup contains
![]() $0.2~\unicode[STIX]{x03BC}\text{m}$
fluorescent polystyrene microspheres at a concentration of
$0.2~\unicode[STIX]{x03BC}\text{m}$
fluorescent polystyrene microspheres at a concentration of
![]() $10^{-3}~\text{g}~\text{ml}^{-1}$
, while the water contains no fluorescent material, revealing the elevated character of the leading edge. Refer to the supplemental material for the full movies (Movie 8, Movie 9, Movie 10, Movie 11) from which these frames were taken.
$10^{-3}~\text{g}~\text{ml}^{-1}$
, while the water contains no fluorescent material, revealing the elevated character of the leading edge. Refer to the supplemental material for the full movies (Movie 8, Movie 9, Movie 10, Movie 11) from which these frames were taken.
Figure 9 summarizes the primary observations of sessile drops in miscible environments through snapshots of a sessile drop of corn syrup spreading across a hydrophobic glass surface while immersed in water, captured using a variety of imaging techniques. Brightfield imaging was used to capture the spreading drop from below (figure 9 a) and the side (figure 9 b). From these two vantages, two radial features are readily apparent. First, the portion of the drop that leads its advancement is elevated above the liquid–solid interface, indicated by black arrows in both panels, and second, a trailing portion that is the three-phase contact line, indicated by white arrows in both panels. We refer to the most radially advanced and elevated portion of the drop as the leading edge, and the portion of the drop that remains in contact with the solid substrate as the contact line.
Figure 9(c) shows an image from a PTV experiment of a sessile drop of corn syrup containing
![]() $6~\unicode[STIX]{x03BC}\text{m}$
diameter polystyrene microspheres at a concentration of
$6~\unicode[STIX]{x03BC}\text{m}$
diameter polystyrene microspheres at a concentration of
![]() $10^{-3}~\text{g}~\text{ml}^{-1}$
in order to visualize the flow pattern that develops within the drop. The white arrows are velocity vectors obtained from the movement of particles, indicating that motion is largely restricted to the liquid–liquid interface and particles away from the interface do not move significantly. This draining phenomenon is similar to that of a pendant drop present in a miscible environment, except that the draining material flows into an elevated leading edge rather than a thin, descending strand. This behaviour was observed for other liquid pairs as well, however, it is most pronounced with viscous spreading liquids; drops formed from lower viscosity liquids are able to deform as a single body more readily, approaching a comparable time scale to that of a diffuse layer forming and draining.
$10^{-3}~\text{g}~\text{ml}^{-1}$
in order to visualize the flow pattern that develops within the drop. The white arrows are velocity vectors obtained from the movement of particles, indicating that motion is largely restricted to the liquid–liquid interface and particles away from the interface do not move significantly. This draining phenomenon is similar to that of a pendant drop present in a miscible environment, except that the draining material flows into an elevated leading edge rather than a thin, descending strand. This behaviour was observed for other liquid pairs as well, however, it is most pronounced with viscous spreading liquids; drops formed from lower viscosity liquids are able to deform as a single body more readily, approaching a comparable time scale to that of a diffuse layer forming and draining.
Figure 9(d) shows a reconstructed side-view image from a confocal microscopy experiment to observe the leading-edge radius more closely and confirm its elevated character. The drop of corn syrup contains
![]() $0.2~\unicode[STIX]{x03BC}\text{m}$
diameter fluorescent polystyrene microspheres at a concentration of
$0.2~\unicode[STIX]{x03BC}\text{m}$
diameter fluorescent polystyrene microspheres at a concentration of
![]() $10^{-3}~\text{g}~\text{ml}^{-1}$
, while the water contains no fluorescent material. A frustum of the sessile drop, its base coinciding with the glass surface, was scanned along a radial slice, as indicated by the inset into figure 9(c). The elevated character of the leading edge is clearly evident from the fluorescing microspheres, embedded in the corn syrup, propagating radially outward, and coasting above a thin film of water and the solid substrate. Confocal microscopy experiments using other liquid pairs showed similar behaviour in the development and propagation of an elevated leading edge.
$10^{-3}~\text{g}~\text{ml}^{-1}$
, while the water contains no fluorescent material. A frustum of the sessile drop, its base coinciding with the glass surface, was scanned along a radial slice, as indicated by the inset into figure 9(c). The elevated character of the leading edge is clearly evident from the fluorescing microspheres, embedded in the corn syrup, propagating radially outward, and coasting above a thin film of water and the solid substrate. Confocal microscopy experiments using other liquid pairs showed similar behaviour in the development and propagation of an elevated leading edge.
The leading-edge radius was previously found (Walls et al.
Reference Walls, Haward, Shen and Fuller2016) to follow a power law of
![]() $t^{1/2}$
at long times for all miscible liquid pairs studied, regardless of the initial volumes, viscosities or densities considered. We will show that a collective response can be obtained for these data of the leading-edge radius with a single scaling treatment and that the shape evolution of sessile drops in miscible environments can be reproduced numerically. After addressing the leading-edge radius, we will return to a discussion of the contact-line radius.
$t^{1/2}$
at long times for all miscible liquid pairs studied, regardless of the initial volumes, viscosities or densities considered. We will show that a collective response can be obtained for these data of the leading-edge radius with a single scaling treatment and that the shape evolution of sessile drops in miscible environments can be reproduced numerically. After addressing the leading-edge radius, we will return to a discussion of the contact-line radius.

Figure 10. Two sequences of images taken over time of a sessile drop of 10 000 cSt silicone oil immersed in 1 cSt silicone oil and spreading across a solid substrate. The images on the left were captured during an experiment and are reproduced by a numerical simulation on the right. In the experiment, the solid substrate is hydrophobic glass, and in each frame, the upper, light region is the ambient liquid and the lower, dark region is the substrate. In the images of the numerical simulation, contour lines in concentration are plotted over top of a coarse grid of the velocity vectors in the fluid. Contours are marked at concentrations of the spreading liquid of 1, 5, 10, 20, 30, 40, 50, 60, 70, 80, 90, 95 and 99 %, and range from blue to red over this span. The sessile drop begins to spread by developing an elevated leading edge that leads the advancement of the drop across the surface. Refer to the supplemental material for the full movies (Movie 12, Movie 13) from which these sets of frames were taken.
In figure 10, we show two sequences of images of a sessile drop of 10 000 cSt silicone oil immersed in 1 cSt silicone oil, viewed from the side while spreading across a solid substrate. The first set of images, presented on the left, was captured during an experiment, and the second, on the right, is a reproduction of that experiment by a numerical simulation. In the images of the numerical simulation, contours in the concentration of the spreading liquid are plotted over the top of a coarse grid of velocity vectors in the fluid. In the experimental sequence, the drop develops an elevated leading edge, which then leads the spreading process as it propagates radially outward. When looking at the numerical representation, one sees an elevated leading edge develop and propagate, but at later times, it does not appear as pronounced as in the experiment. The numerical boundary condition at the solid surface that prescribes a no-flux condition consequently imposes that all contours in concentration be orthogonal to the surface at the surface, which may contribute to this effect. To allow a more direct comparison with regard to the elevated leading edge, we performed numerical particle tracking in our simulations. In a flow-tracing experiment, the size of the particles is carefully chosen small enough to avoid disrupting the flow field, yet large enough to dampen Brownian motion. In our numerical calculations with particles, we likewise construct the particles to strictly follow the velocity field without undergoing Brownian motion. Figure 11 shows an image from such a simulation for a sessile drop of corn syrup immersed in water. The development of a prominent elevated leading edge is observed, similar to our present experimental observations and previous confocal studies (Walls et al.
Reference Walls, Haward, Shen and Fuller2016). This image is a numerical reproduction of the experimental confocal image presented in figure 9(d). The tips of the leading edges, both experimental and numerical, are elevated approximately
![]() $30~\unicode[STIX]{x03BC}\text{m}$
above the solid substrate. Performing numerical particle tracking with simulations for other pairs of liquids shows similar correspondence to their experimental counterparts.
$30~\unicode[STIX]{x03BC}\text{m}$
above the solid substrate. Performing numerical particle tracking with simulations for other pairs of liquids shows similar correspondence to their experimental counterparts.
Further, the numerical simulations enabled us to vary independently and systematically several parameters – viscosity, density, diffusion coefficient and their dependence on concentration as well as the initial macroscopic contact angle – which was limited in our physical experiments due to inherent material properties. First, we consider two spreading liquids, differing only in viscosity, immersed in the same ambient liquid. The calculated leading-edge radii for the spreading liquids asymptote to the same
![]() $t^{1/2}$
power law, at long times and at the same time. The two calculated leading-edge radii deviate only at short times, as the lower-viscosity spreading liquid deforms initially as a whole to increase its radius. However, at long times, the leading-edge radii overlap without any applied scaling. Second, we compare two calculations where only the initial macroscopic contact angle of the sessile drop differs. The drop with the relatively higher contact angle has a smaller initial radius, but in time its leading-edge radius grows to match the behaviour of the drop with a relatively lower contact angle without any need for additional scaling. Third, we take two sessile drops, differing only in their initial volume. Only the leading-edge radii, and not time, needs to be scaled; by using the cube root of each initial volume to scale the data, the leading-edge radii collapse onto one another. The relationship between viscosity and concentration also influences the growth of the leading-edge radius in time, notably in the transition to following a power law of
$t^{1/2}$
power law, at long times and at the same time. The two calculated leading-edge radii deviate only at short times, as the lower-viscosity spreading liquid deforms initially as a whole to increase its radius. However, at long times, the leading-edge radii overlap without any applied scaling. Second, we compare two calculations where only the initial macroscopic contact angle of the sessile drop differs. The drop with the relatively higher contact angle has a smaller initial radius, but in time its leading-edge radius grows to match the behaviour of the drop with a relatively lower contact angle without any need for additional scaling. Third, we take two sessile drops, differing only in their initial volume. Only the leading-edge radii, and not time, needs to be scaled; by using the cube root of each initial volume to scale the data, the leading-edge radii collapse onto one another. The relationship between viscosity and concentration also influences the growth of the leading-edge radius in time, notably in the transition to following a power law of
![]() $t^{1/2}$
. The leading-edge radius of a spreading fluid that more drastically reduces in viscosity upon dilution will asymptote to the power law of
$t^{1/2}$
. The leading-edge radius of a spreading fluid that more drastically reduces in viscosity upon dilution will asymptote to the power law of
![]() $t^{1/2}$
more rapidly, as a fluid of lower viscosity flows more readily than one of comparably higher viscosity. Each of these numerical outcomes is supported by our experimental findings.
$t^{1/2}$
more rapidly, as a fluid of lower viscosity flows more readily than one of comparably higher viscosity. Each of these numerical outcomes is supported by our experimental findings.

Figure 11. Numerical particle tracking of a sessile drop of corn syrup immersed in water spreading across a solid substrate. The black circles indicate particles that travel along fluid streamlines without diffusing. Blue arrows are aligned on a coarse grid that indicate the local velocity vectors. The grey line at the bottom of the image indicates the solid substrate. Comparison of the numerical result to that of the confocal experiment displayed in figure 9(d) shows agreement.

Figure 12. Plots of the leading-edge radius, determined both experimentally and numerically, as a function of time for a selection of the experimental liquid pairs on the four solid substrates. (a) Unscaled measurements and calculations. (b) The leading-edge radial data are scaled by the prefactor in (4.3),
![]() $(\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}gQ_{d}^{3}/3\unicode[STIX]{x1D707}_{A})^{1/8}$
, with time left unscaled, where
$(\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}gQ_{d}^{3}/3\unicode[STIX]{x1D707}_{A})^{1/8}$
, with time left unscaled, where
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}$
is the difference in density between the spreading and ambient liquids,
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}$
is the difference in density between the spreading and ambient liquids,
![]() $g$
is acceleration due to gravity,
$g$
is acceleration due to gravity,
![]() $Q_{d}$
is the constant flow rate generated by diffusion of the spreading liquid and
$Q_{d}$
is the constant flow rate generated by diffusion of the spreading liquid and
![]() $\unicode[STIX]{x1D707}_{A}$
is the viscosity of the ambient liquid. Individual symbols are experimental measurements; solid lines are numerical calculations; the dashed black line in each plot represents a square root power law, which is a time dependence indicative of a diffusive process. Symbol colour and shape are coded for the liquid pair and solid substrate, respectively. Symbol and dashed line colours light blue, black, light green, mid green, dark green, light purple, mid purple, dark purple indicate the liquid pairs are glycerol–water, corn syrup–water, and 1000–1 cSt, 1000–5 cSt, 1000–10 cSt, 10 000–1 cSt, 10 000–5 cSt and 10 000–10 cSt silicone oils, respectively. Symbol shapes ●, ♦, ▴ and ▪ indicate the surfaces are hydrophilic, hydrophobic, oleophobic and Teflon, respectively.
$\unicode[STIX]{x1D707}_{A}$
is the viscosity of the ambient liquid. Individual symbols are experimental measurements; solid lines are numerical calculations; the dashed black line in each plot represents a square root power law, which is a time dependence indicative of a diffusive process. Symbol colour and shape are coded for the liquid pair and solid substrate, respectively. Symbol and dashed line colours light blue, black, light green, mid green, dark green, light purple, mid purple, dark purple indicate the liquid pairs are glycerol–water, corn syrup–water, and 1000–1 cSt, 1000–5 cSt, 1000–10 cSt, 10 000–1 cSt, 10 000–5 cSt and 10 000–10 cSt silicone oils, respectively. Symbol shapes ●, ♦, ▴ and ▪ indicate the surfaces are hydrophilic, hydrophobic, oleophobic and Teflon, respectively.
Figure 12(a) shows a plot of the leading-edge radius,
![]() $r_{LE}$
, determined both experimentally and numerically, as a function of time for several liquid pairs on the four solid substrates. The experimental results are indicated with symbols and numerical results are indicated with solid lines. The variation in the initial radii of the sessile drops is largely dependent upon the contact angle that each spreading liquid forms on the substrates in air; a less significant influence on the initial radius is the slight variation in volume between experiments. As noted in our prior study, each liquid pairing approaches a similar power law in time at some point in the spreading process. A dashed black reference line is plotted alongside the data representing a power law of
$r_{LE}$
, determined both experimentally and numerically, as a function of time for several liquid pairs on the four solid substrates. The experimental results are indicated with symbols and numerical results are indicated with solid lines. The variation in the initial radii of the sessile drops is largely dependent upon the contact angle that each spreading liquid forms on the substrates in air; a less significant influence on the initial radius is the slight variation in volume between experiments. As noted in our prior study, each liquid pairing approaches a similar power law in time at some point in the spreading process. A dashed black reference line is plotted alongside the data representing a power law of
![]() $t^{1/2}$
, which is indicative of a diffusive process. Within a particular liquid pair, the modification of the substrate is inconsequential to the onset of the power-law growth of the leading-edge radius. Yet, across the different liquid pairs on the same substrate, the time to achieve this power-law growth varies significantly, even between liquid pairs that have ambient and spreading liquids of similar viscosity, and similar mutual diffusion coefficients, such as corn syrup in water and 10 000 cSt silicone oil in 1 cSt silicone oil. Here, the relationship between viscosity and concentration within the miscible pair is critical. The viscosity of glycerol and corn syrup diminishes exponentially when diluted with water, whereas the viscosities of silicone oils diluted in silicone oils of lower viscosity decrease more modestly, following a fifth-order polynomial, as shown in figure 1. A spreading silicone oil must dilute itself to a greater extent than glycerol or corn syrup within the diffuse layer in order to attain a viscosity conducive to flow due to the action of buoyancy forces. Thus, the thickness of the diffuse layer and the time required to reach it increase, which delays the development and propagation of the elevated leading edge for a spreading silicone oil. Examining the behaviour of the leading-edge radius of liquid pairs grouped by the functional form of viscosity, it is evident that increasing the viscosity of either the spreading or ambient liquid delays the onset of the power-law growth of the leading-edge radius. Numerical calculations closely follow the experimental behaviour for each liquid pair throughout the spreading process, from the time to develop the elevated leading edge to its propagation following a square root power law.
$t^{1/2}$
, which is indicative of a diffusive process. Within a particular liquid pair, the modification of the substrate is inconsequential to the onset of the power-law growth of the leading-edge radius. Yet, across the different liquid pairs on the same substrate, the time to achieve this power-law growth varies significantly, even between liquid pairs that have ambient and spreading liquids of similar viscosity, and similar mutual diffusion coefficients, such as corn syrup in water and 10 000 cSt silicone oil in 1 cSt silicone oil. Here, the relationship between viscosity and concentration within the miscible pair is critical. The viscosity of glycerol and corn syrup diminishes exponentially when diluted with water, whereas the viscosities of silicone oils diluted in silicone oils of lower viscosity decrease more modestly, following a fifth-order polynomial, as shown in figure 1. A spreading silicone oil must dilute itself to a greater extent than glycerol or corn syrup within the diffuse layer in order to attain a viscosity conducive to flow due to the action of buoyancy forces. Thus, the thickness of the diffuse layer and the time required to reach it increase, which delays the development and propagation of the elevated leading edge for a spreading silicone oil. Examining the behaviour of the leading-edge radius of liquid pairs grouped by the functional form of viscosity, it is evident that increasing the viscosity of either the spreading or ambient liquid delays the onset of the power-law growth of the leading-edge radius. Numerical calculations closely follow the experimental behaviour for each liquid pair throughout the spreading process, from the time to develop the elevated leading edge to its propagation following a square root power law.
If we scale the data for the leading-edge radii presented in figure 12(a) by a prefactor of the form of that developed by Huppert (Reference Huppert1982), shown in (1.2), the plot presented in figure 12(b) is obtained. When scaling the vertical axis accordingly, the experimental data and numerical calculations largely overlap to reveal a power-law response of the leading-edge radius at long times. This grouping indicates that the leading edge propagates by the diffusion of momentum radially outward from the draining boundary layer as it reaches the base of the drop. The deviation from a single response at shorter times is not unanticipated, as several factors collude to prevent universal behaviour across all time. At time zero, the radius of the leading edge is defined by the contact angle of the sessile droplet. As the drop proceeds to spread, it does so by deforming as a whole, or diffusing across the liquid–liquid interface to form a diffuse layer that can then drain. The leading edge grows as momentum from the draining of the materially diffuse layer along the liquid–liquid interface begins to diffuse radially outward; thus, the leading-edge radii grow following a square root power law in time. Through this progression, the leading-edge radius does not retain the memory of the droplet’s initial state, as evidenced by the grouping of measurements from experiments where the sole difference is initial contact angle without requiring any scaling operation. Additionally, this transition is influenced by the intrinsic difference in the functional form of viscosity with respect to concentration for the various liquid pairs. As seen in figure 1, these various forms cannot be grouped to a single response by a scaling analysis, which is evident at short times in figure 12(b).
The scaling used in figure 12(b) is of the same form as Huppert (Reference Huppert1982), however, the constant flux
![]() $Q$
is an independent parameter prescribed in the experiments of Huppert (Reference Huppert1982) as well as Didden & Maxworthy (Reference Didden and Maxworthy1982). The material flux into the elevated leading edge of our experiments arises from mass diffusion and subsequent drainage of material from the sessile drop, effectively producing a constant flux from a fixed volume. Thus, the elevated leading edge of our experiments is a gravity current by different means in the sense of Didden & Maxworthy (Reference Didden and Maxworthy1982) and Huppert (Reference Huppert1982). In the context of our experiments, the constant flux is determined by the interfacial area, mutual diffusivity and thickness of the diffuse layer between the two miscible liquids. This flow rate,
$Q$
is an independent parameter prescribed in the experiments of Huppert (Reference Huppert1982) as well as Didden & Maxworthy (Reference Didden and Maxworthy1982). The material flux into the elevated leading edge of our experiments arises from mass diffusion and subsequent drainage of material from the sessile drop, effectively producing a constant flux from a fixed volume. Thus, the elevated leading edge of our experiments is a gravity current by different means in the sense of Didden & Maxworthy (Reference Didden and Maxworthy1982) and Huppert (Reference Huppert1982). In the context of our experiments, the constant flux is determined by the interfacial area, mutual diffusivity and thickness of the diffuse layer between the two miscible liquids. This flow rate,
![]() $Q_{d}$
, can be determined through the diffusive flux that emerges between the sessile drop and its miscible surrounding like
$Q_{d}$
, can be determined through the diffusive flux that emerges between the sessile drop and its miscible surrounding like
where
![]() $A_{s}$
is the interfacial area between the sessile and ambient liquids,
$A_{s}$
is the interfacial area between the sessile and ambient liquids,
![]() $R_{o}$
is the initial radius of the sessile drop and
$R_{o}$
is the initial radius of the sessile drop and
![]() $h_{LE}$
is the thickness of the elevated leading edge. We approximate the interfacial area by squaring the initial radius of the sessile drop. The gradient in concentration is approximated with the inverse of the thickness of the leading edge, as the difference in concentration between the two pure liquids is unity and the thickness of the leading edge is indicative of the thickness of the diffuse layer, as this layer drains along the sessile liquid–ambient liquid interface to form the leading edge. Thus, combining the estimation of
$h_{LE}$
is the thickness of the elevated leading edge. We approximate the interfacial area by squaring the initial radius of the sessile drop. The gradient in concentration is approximated with the inverse of the thickness of the leading edge, as the difference in concentration between the two pure liquids is unity and the thickness of the leading edge is indicative of the thickness of the diffuse layer, as this layer drains along the sessile liquid–ambient liquid interface to form the leading edge. Thus, combining the estimation of
![]() $Q_{d}$
with the prior analysis of Huppert (Reference Huppert1982), the analogous relationship between the leading-edge radius of a sessile drop in a miscible environment and time is
$Q_{d}$
with the prior analysis of Huppert (Reference Huppert1982), the analogous relationship between the leading-edge radius of a sessile drop in a miscible environment and time is
This prefactor is used to scale the radial data in figure 12(b). Here, note that we use the viscosity of the ambient liquid to represent the viscosity of the material in the leading edge, as it contains liquid from the sessile drop that is significantly diluted in the ambient liquid.
The diffusion coefficients between glycerol and water, corn syrup and water, 1 cSt and 1000 cSt silicone oil, 5 cSt and 1000 cSt silicone oil and 10 cSt and 1000 cSt used to scale the respective data were taken from the literature (Glycerine Producers’ Association 1963; Rashidnia & Balasubramaniam Reference Rashidnia and Balasubramaniam2002; Ray et al. Reference Ray, Bunton and Pojman2007). The diffusion coefficient between 1 cSt and 10 000 cSt silicone oil employed was determined from our pendant drop experiments as previously described in § 4.1. Diffusion coefficients between 5 cSt and 10 000 cSt silicone oils, and 10 cSt and 10 000 cSt silicone oils were not immediately available in the literature. However, the measurements conducted by Rashidnia & Balasubramaniam (Reference Rashidnia and Balasubramaniam2002) for the series of silicone oil pairs of 1 cSt, 5 cSt or 10 cSt silicone oil with 1000 cSt silicone oil show a linear proportionality between the measured diffusion coefficient and the lesser viscosity in the pair. Using this proportionality along with the knowledge of the diffusion coefficient between 1 cSt and 10 000 cSt silicone oils provides an estimate for the two remaining silicone oil pairs. The observed collapse of the leading-edge radii between the different ambient silicone oils further supports the relationship.
We are restricted from carrying this scaling analysis further for the remaining experimental liquid pairs, as their mutual diffusion coefficients, or points of reference, are not reported in the literature. However, we expect the proposed scaling to hold for all of our experimental findings, as the trends described above were evident across all experiments.
The dynamics of the contact line is highly dependent on the relative values of the two surface energies existing between (i) the solid substrate–spreading liquid and (ii) solid substrate–ambient liquid phases, as the two liquids compete to wet the solid substrate in order to minimize the total energy of the system, as we stated in our prior work (Walls et al.
Reference Walls, Haward, Shen and Fuller2016). In that study, the contact line could not be located with sufficient precision after a short time for experiments with silicone oils due to very small differences in refractive indices of the liquid pairs. However, for other liquid pairs, the contact line never spread exceeding a power law of
![]() $t^{1/8}$
, which represents the growth in the radius of a sessile drop with a finite initial contact angle, spreading due to gravity in air across a surface on which it has an equilibrium contact angle of zero. Limited information regarding surface energies arising at liquid–solid interfaces is available in the literature for materials that are not in phase equilibrium, and our numerical calculations do not explicitly consider these surface energies. However, a comparison between the experimental observations and numerical calculations is possible for two of the liquid pairs (corn syrup in water and glycerol in water) on a hydrophobic substrate, which most closely resembles the condition of a sessile liquid immersed in water and spreading to an infinitesimally thin film. Figure 13 shows a plot of the contact-line radius,
$t^{1/8}$
, which represents the growth in the radius of a sessile drop with a finite initial contact angle, spreading due to gravity in air across a surface on which it has an equilibrium contact angle of zero. Limited information regarding surface energies arising at liquid–solid interfaces is available in the literature for materials that are not in phase equilibrium, and our numerical calculations do not explicitly consider these surface energies. However, a comparison between the experimental observations and numerical calculations is possible for two of the liquid pairs (corn syrup in water and glycerol in water) on a hydrophobic substrate, which most closely resembles the condition of a sessile liquid immersed in water and spreading to an infinitesimally thin film. Figure 13 shows a plot of the contact-line radius,
![]() $r_{CL}$
, determined both experimentally and numerically, as a function of time for these two liquid pairs. The experimental and numerical results are indicated with symbols and solid lines, respectively. The radial data are scaled by the initial radii of the sessile drops and time is left unscaled. A dashed black reference line is plotted alongside the data representing the power law of
$r_{CL}$
, determined both experimentally and numerically, as a function of time for these two liquid pairs. The experimental and numerical results are indicated with symbols and solid lines, respectively. The radial data are scaled by the initial radii of the sessile drops and time is left unscaled. A dashed black reference line is plotted alongside the data representing the power law of
![]() $t^{1/8}$
. The numerical contact-line radius is obtained by tracking the motion of the contour in concentration of the spreading liquid of 40 % at the solid surface. The close correspondence of the experimental data and numerical calculations for these liquid pairs indicates that our numerical description is also able to capture the dynamics of the contact line for certain surfaces.
$t^{1/8}$
. The numerical contact-line radius is obtained by tracking the motion of the contour in concentration of the spreading liquid of 40 % at the solid surface. The close correspondence of the experimental data and numerical calculations for these liquid pairs indicates that our numerical description is also able to capture the dynamics of the contact line for certain surfaces.

Figure 13. Plots of the contact-line radius, determined both experimentally and numerically, as a function of time for sessile droplets immersed in water and spreading across a hydrophobic glass surface. The contact-line radial data are scaled by the initial radius of the droplet and time is left unscaled. Individual symbols are experimental measurements; solid lines are numerical calculations; the dashed black line represents a power law of
![]() $t^{1/8}$
. The numerical results are obtained from the motion of a contour in concentration of the spreading liquid of 40 %. Colour indicates the spreading liquid, with light blue as glycerol and black as corn syrup.
$t^{1/8}$
. The numerical results are obtained from the motion of a contour in concentration of the spreading liquid of 40 %. Colour indicates the spreading liquid, with light blue as glycerol and black as corn syrup.
5 Conclusions
Pendant and sessile drops in miscible environments lead to distinctly different outcomes than those present in immiscible environments. The interfacial tension between the two initially distinct, miscible liquids is very small, and diminishes in time as the two liquids diffuse across their mutual boundary. Gravitational forces tend to be much larger, which then dominate the shape evolution of the droplets in conjunction with mass diffusion. As diffusion proceeds, a materially diffuse layer evolves at the liquid–liquid interface, across which the density and viscosity vary between those of the pure liquids. Whereas density responds approximately linearly with respect to concentration, the relationship between viscosity and concentration is typically nonlinear. As a result, the diffuse layer largely retains the density of the pendant or sessile liquid while greatly reducing in viscosity and, therefore, decreasing its resistance to flow. At some critical thickness of the diffuse layer, buoyancy forces lead to free convection that causes the diffuse layer to drain along the liquid–liquid interface, and into the thin strand of a pendant drop or elevated leading edge of a sessile drop. This draining flow along the liquid–liquid interface is clearly observed in the PTV experiments for both types of drops. As the viscosity of the liquid comprising the drop decreases, the resistance of the liquid to deforming as a single body decreases, with this deformation occurring on a time scale approaching that of the draining diffuse layer. However, it was found that within each type of drop, a single approach yields a universal response for our experimental measurements and numerical calculations irrespective of viscosity. The procedure for establishing the initial conditions and the liquids studied were chosen in order to establish an initial condition with as little induced convection and deformation of the drops as possible.
As the draining flow in the experiments with pendant drops proceeds, the body of the drop descends and elongates more slowly. The growth of the diffuse layer and its subsequent draining is seen in the measurements of volume of the pendant drops in time, as they initially swell to a maximum volume before decreasing. We found that the volume decays in time exponentially after reaching a maximum, following a single response obtained by scaling the volume by its maximum,
![]() $V_{max}$
, and time by the characteristic diffusion time
$V_{max}$
, and time by the characteristic diffusion time
![]() $t_{c,pendant}=(V_{max}/A_{max})^{2}/4{\mathcal{D}}_{LA}$
. Plotting measured exponential decay times,
$t_{c,pendant}=(V_{max}/A_{max})^{2}/4{\mathcal{D}}_{LA}$
. Plotting measured exponential decay times,
![]() $\unicode[STIX]{x1D70F}_{d}$
, against
$\unicode[STIX]{x1D70F}_{d}$
, against
![]() $(V_{max}/A_{max})^{2}$
of experiments within a particular liquid pair yields a straight line with the mutual diffusion coefficient
$(V_{max}/A_{max})^{2}$
of experiments within a particular liquid pair yields a straight line with the mutual diffusion coefficient
![]() ${\mathcal{D}}_{LA}$
as its slope, offering further support for the appropriateness of this scaling and the exponential character of the volume. Numerical simulations, based on a simplified set of governing equations that assumed a divergence-free velocity field, Stokes flow and captured the concentration field using a convection–diffusion equation, showed qualitative and quantitative agreement with our experiments. The assumptions in deriving the governing equations were utilized by previous researchers and were determined to be acceptable both by comparison to experiments, and in a scaling analysis between the magnitudes of viscous stresses present to other unaccounted stresses that could arise due to the non-zero divergence or differences in chemical potential.
${\mathcal{D}}_{LA}$
as its slope, offering further support for the appropriateness of this scaling and the exponential character of the volume. Numerical simulations, based on a simplified set of governing equations that assumed a divergence-free velocity field, Stokes flow and captured the concentration field using a convection–diffusion equation, showed qualitative and quantitative agreement with our experiments. The assumptions in deriving the governing equations were utilized by previous researchers and were determined to be acceptable both by comparison to experiments, and in a scaling analysis between the magnitudes of viscous stresses present to other unaccounted stresses that could arise due to the non-zero divergence or differences in chemical potential.
The range of viscosities studied was broader for sessile liquids, which allowed some spreading liquids to deform as a whole on time scales comparable to the draining of a diffuse boundary layer. However, as we found previously, the leading-edge radius grows following a power law of
![]() $t^{1/2}$
at long times, suggesting that a single effect dominates the propagation of the leading edge eventually, regardless of viscosity, density or initial volume. Adapting the numerical analysis developed for pendant drops to our continuing study of sessile drops in miscible environments allowed us to change several parameters of the miscible system independently and systematically, which was limited experimentally due to inherent material properties. Namely, by varying the initial contact angle and the viscosity, as well as its dependence on concentration, we gained insight into the physical mechanisms driving spreading, enabling us to interpret our experimental results more deftly. Scaling the data of the leading-edge radii by the prefactor in (4.3),
$t^{1/2}$
at long times, suggesting that a single effect dominates the propagation of the leading edge eventually, regardless of viscosity, density or initial volume. Adapting the numerical analysis developed for pendant drops to our continuing study of sessile drops in miscible environments allowed us to change several parameters of the miscible system independently and systematically, which was limited experimentally due to inherent material properties. Namely, by varying the initial contact angle and the viscosity, as well as its dependence on concentration, we gained insight into the physical mechanisms driving spreading, enabling us to interpret our experimental results more deftly. Scaling the data of the leading-edge radii by the prefactor in (4.3),
![]() $(\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}gQ_{d}^{3}/3\unicode[STIX]{x1D707}_{A})^{1/8}$
, and leaving time unscaled, following the treatment of Huppert (Reference Huppert1982), was effective in obtaining a single response at long times from the experimental results and numerical calculations for which diffusion coefficients are available in the literature or through this study. Further, the universal collapse of the data following this analysis indicates that the diffusive nature of the spreading of the elevated leading edge is due to the diffusion of momentum. At short times, the leading-edge radius deviates from a single response, as its growth transitions from its initial value, defined by the initial contact angle of the sessile drop, and progresses towards its growth as a diffusive power law. In the transition, the leading-edge radius does not retain the memory of the droplet’s initial state, as evidenced by the grouping of experimental measurements and numerical calculations without any scaling operation where the sole difference is the initial contact angle. This transition is influenced by the intrinsic difference in the functional form of viscosity with respect to concentration for the various liquid pairs as well. Additionally, the numerical model is able to capture the dynamics of the contact line for certain surfaces.
$(\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}gQ_{d}^{3}/3\unicode[STIX]{x1D707}_{A})^{1/8}$
, and leaving time unscaled, following the treatment of Huppert (Reference Huppert1982), was effective in obtaining a single response at long times from the experimental results and numerical calculations for which diffusion coefficients are available in the literature or through this study. Further, the universal collapse of the data following this analysis indicates that the diffusive nature of the spreading of the elevated leading edge is due to the diffusion of momentum. At short times, the leading-edge radius deviates from a single response, as its growth transitions from its initial value, defined by the initial contact angle of the sessile drop, and progresses towards its growth as a diffusive power law. In the transition, the leading-edge radius does not retain the memory of the droplet’s initial state, as evidenced by the grouping of experimental measurements and numerical calculations without any scaling operation where the sole difference is the initial contact angle. This transition is influenced by the intrinsic difference in the functional form of viscosity with respect to concentration for the various liquid pairs as well. Additionally, the numerical model is able to capture the dynamics of the contact line for certain surfaces.
Combining the experimental and numerical analyses with pendant and sessile drops present in miscible systems into a single study allowed for the inquiry into the effect of directionality of buoyancy forces relative to the drop on the behaviour of these two configurations. Additionally, the robustness of our numerical procedure could be tested on multiple configurations. We reiterate, however, that the formulation of the governing equations does not consider surface tension, Korteweg stresses and other stresses arising in miscible systems noted by Joseph (Reference Joseph1990) and Joseph & Renardy (Reference Joseph and Renardy2013). As reported by Chen & Meiburg (Reference Chen and Meiburg1996), when
![]() $Pe\gg 1$
and
$Pe\gg 1$
and
![]() $At\rightarrow 1$
, the viscous stresses dominate, which matches the regime of our experiments here. Although surface tension is not a dominant factor in the observations and calculations presented here for pendant and sessile drops in miscible liquids, we do not impugn its importance across all miscible configurations. Chen & Meiburg (Reference Chen and Meiburg1996) and Petitjeans & Maxworthy (Reference Petitjeans and Maxworthy1996) note that these other stresses become influential as
$At\rightarrow 1$
, the viscous stresses dominate, which matches the regime of our experiments here. Although surface tension is not a dominant factor in the observations and calculations presented here for pendant and sessile drops in miscible liquids, we do not impugn its importance across all miscible configurations. Chen & Meiburg (Reference Chen and Meiburg1996) and Petitjeans & Maxworthy (Reference Petitjeans and Maxworthy1996) note that these other stresses become influential as
![]() $Pe$
decreases and
$Pe$
decreases and
![]() $At$
increases. For example, Kojima et al. (Reference Kojima, Hinch and Acrivos1984) report in their experimental study with miscible liquids that a non-zero surface tension was necessary to match their analytical calculations and experimental observations.
$At$
increases. For example, Kojima et al. (Reference Kojima, Hinch and Acrivos1984) report in their experimental study with miscible liquids that a non-zero surface tension was necessary to match their analytical calculations and experimental observations.
Acknowledgements
The authors are grateful for funding from NSF CBET 1335632 (D.J.W., G.G.F.), the Stanford Graduate Fellowship in Science and Engineering (D.J.W.) and the Petroleum Research Fund, administered by the American Chemical Society, through grant number 54948-ND9 (E.M.). The authors would like to thank Professor A. Shen and Dr S. Haward for helpful discussions and support of experiments with sessile drops pertaining to confocal microscopy and particle tracking velocimetry, T. N. Rochinha and S. Dennler for their assistance in performing experiments with pendant drops, S. Singh for her assistance in performing experiments with sessile drops, and Professor J. Frostad for his assistance in developing the image processing techniques for experiments with pendant drops. The authors would also like to thank the referees for useful comments towards clarifying explanations of the findings.
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2018.535.